Mô hình hồi quy tuyến tính đơn | Bài giảng xác suất thống kê

Mô hình hồi quy tuyến tính đơn Nguyễn Hữu Toàn
Bộ môn Xác suất Thống kê Khoa Toán - Tin học
Trường ĐH Khoa học Tự nhiên, ĐHQG-HCM Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 1 / 35 Nội dung bài học 1
Giới thiệu và Đặt vấn đề 2
Mô hình và Ước lượng tham số 3
Đánh giá độ phù hợp của mô hình 4
Tính toán chi tiết các Hệ số Hồi quy 5
Đánh giá độ phù hợp mô hình 6
Lý thuyết phân phối của các hệ số 7
Tính toán Kiểm định và Khoảng tin cậy 8
Đối chiếu với phần mềm R 9 ANOVA và Dự báo 10 Bài tập thực hành Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 2 / 35
Giới thiệu và Đặt vấn đề Ví dụ mở đầu
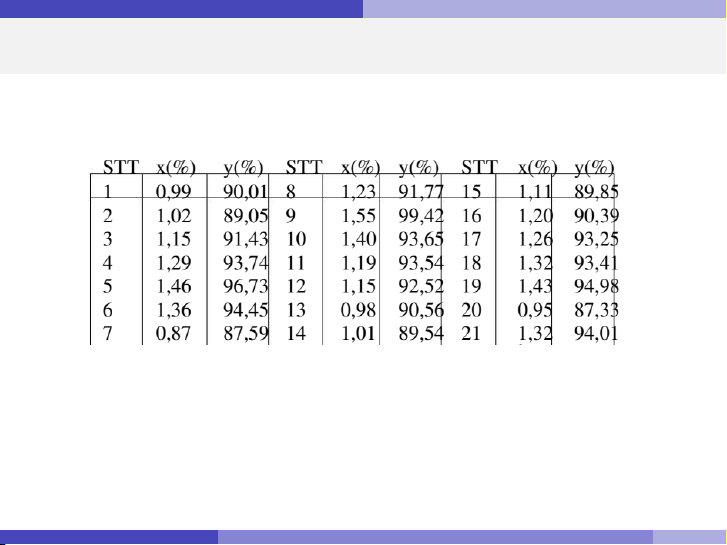
Xét bài toán về độ sạch của oxy và nồng độ hydrocarbon.
Hình: Bảng số liệu mẫu
Câu hỏi: Có mối liên hệ nào giữa nồng độ hydrocarbon (x ) và độ sạch của oxy (y )? Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 3 / 35
Giới thiệu và Đặt vấn đề
Biểu đồ phân tán (Scatter Plot)
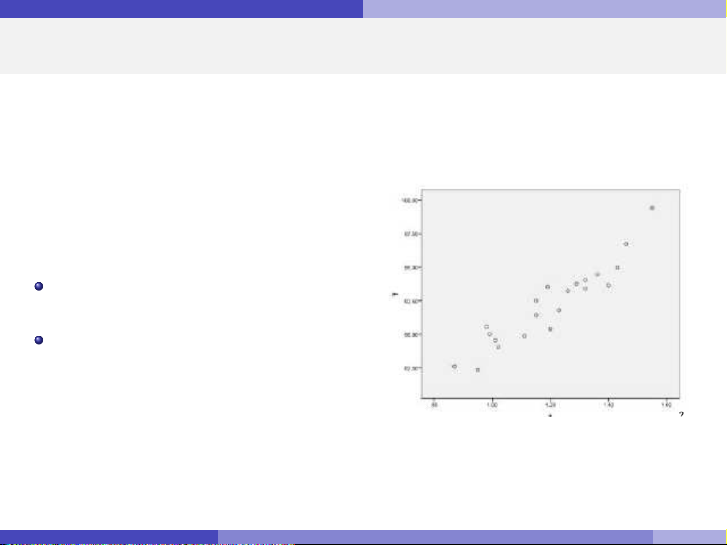
Khi thể hiện các điểm (xi , yi ) trên hệ
trục tọa độ, ta nhận được đồ thị phân tán.
Các điểm dường như phân tán quanh một đường thẳng.
Gợi ý mối quan hệ tuyến tính: y ≈ a + bx . Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 4 / 35
Giới thiệu và Đặt vấn đề
Khái niệm Mô hình Hồi quy Bản chất thống kê
Chúng ta giả định rằng giá trị trung bình của y tại một mức x cụ thể tuân theo hàm f (x ): E (y |x ) = f (x )
Vì dữ liệu thực tế luôn có sai số, mô hình xác suất đầy đủ là: y = f (x ) + ϵ
trong đó ϵ là sai số ngẫu nhiên (nhiễu). Hồi quy tuyến tính đơn
Nếu f (x ) là đường thẳng, ta có mô hình: y = β0 + β1x + ϵ Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 5 / 35
Mô hình và Ước lượng tham số
Các giả định của Mô hình (Assumptions)
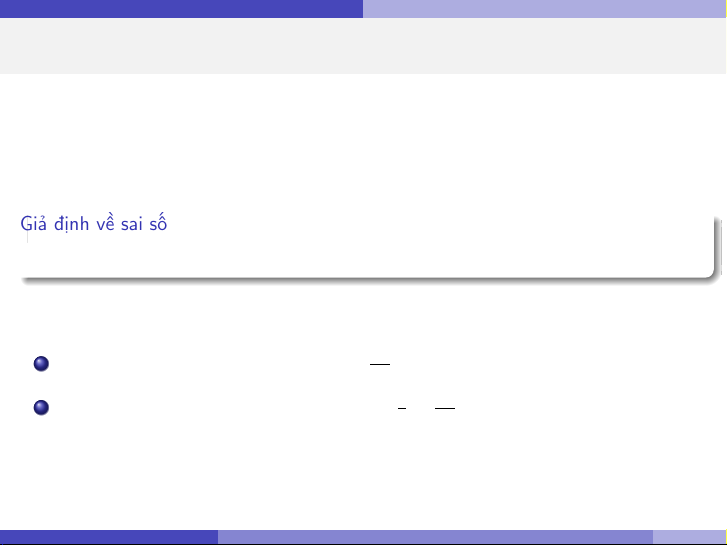
Để thực hiện suy diễn thống kê, ta cần các giả định về sai số ϵi : 1
Trung bình bằng 0: E (ϵi ) = 0. 2
Phương sai đồng nhất: Var (ϵi ) = σ2 (với mọi x). 3
Độc lập: Các ϵi và ϵj độc lập với nhau. 4
Phân phối chuẩn: ϵi ∼ N(0, σ2). Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 6 / 35
Mô hình và Ước lượng tham số
Phương trình hồi quy mẫu
Từ dữ liệu mẫu, ta tìm phương trình ước lượng: ˆ y = ˆ β0 + ˆ β1x ˆ β0, ˆ
β1: Các ước lượng của tham số tổng thể β0, β1. ˆ
y : Giá trị dự báo (hoặc giá trị khớp). ei = yi − ˆ
yi : Phần dư (Residuals) của mẫu. Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 7 / 35
Mô hình và Ước lượng tham số
Phương pháp Bình phương nhỏ nhất (OLS) Mục tiêu: Tìm ˆ β0, ˆ
β1 sao cho tổng bình phương sai số là nhỏ nhất. n n X X SSE = e2 = (y i i − ˆ β0 − ˆ β1xi )2 → min i =1 i =1
Giải hệ phương trình đạo hàm riêng bằng 0, ta có công thức: Công thức OLS (P x P i )(P yi ) P xi yi − ˆ Sxy (xi − ¯ x )(yi − ¯ y ) β n 1 = = = S P xx (xi − ¯ x )2 (P x P i )2 x 2 − i n ˆ β0 = ¯ y − ˆ β1 ¯ x Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 8 / 35
Đánh giá độ phù hợp của mô hình
Phân rã sự biến thiên (SST = SSR + SSE)
Ta có đẳng thức quan trọng: X X X (yi − ¯ y )2 = (ˆ yi − ¯ y )2 + (yi − ˆ yi )2 Hay: SST = SSR + SSE
SST (Total): Biến thiên toàn phần của y .
SSR (Regression): Biến thiên được giải thích bởi mô hình (x ).
SSE (Error): Biến thiên không giải thích được (do nhiễu). Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 9 / 35
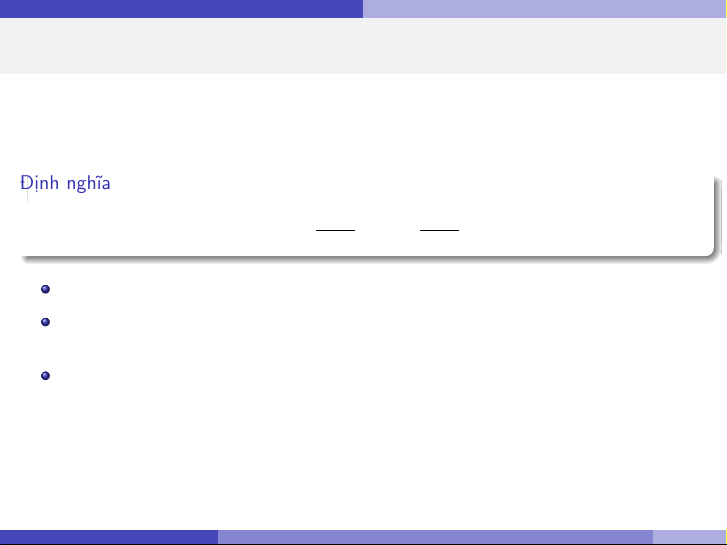
Đánh giá độ phù hợp của mô hình Hệ số xác định R2 Định nghĩa SSR SSE R2 = = 1 − SST SST 0 ≤ R2 ≤ 1.
Ý nghĩa: R2 cho biết bao nhiêu phần trăm sự biến thiên của y được giải thích bởi biến x .
Ví dụ: R2 = 0.85 nghĩa là 85% sự thay đổi của độ sạch oxy được giải thích
bởi nồng độ hydrocarbon. Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 10 / 35
Tính toán chi tiết các Hệ số Hồi quy
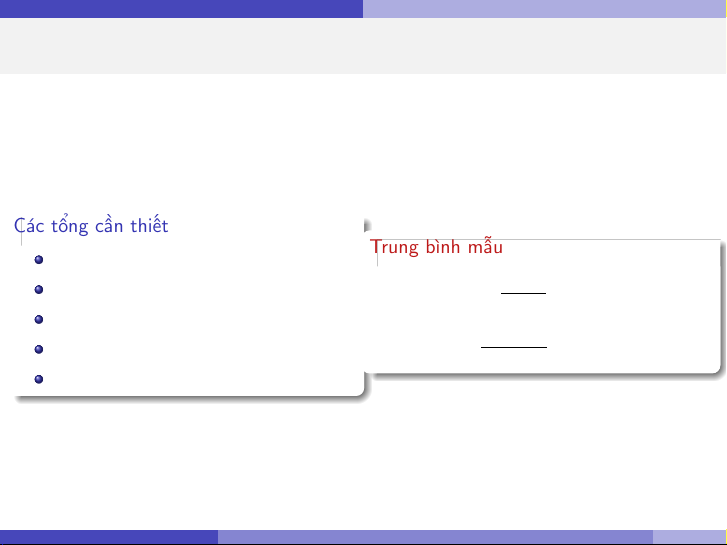
Bước 1: Tổng hợp dữ liệu (Summary Statistics)
Để bắt đầu tính toán, từ bảng số liệu thô (n = 20), ta tính được các tổng sau: Các tổng cần thiết Trung bình mẫu P xi = 23.92 P 23.92 yi = 1843.21 ¯ x = = 1.196 20 P x2 = 29.29 i 1843.21 P y 2 = 170044.53 ¯ y = = 92.1605 i 20 P xi yi = 2214.65 Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 11 / 35
Tính toán chi tiết các Hệ số Hồi quy
Bước 2: Tính các tổng độ lệch bình phương (Sxx, Sxy )
1. Tính Sxx (Tổng bình phương độ lệch của x): X (P xi )2 Sxx = x 2 − i n (23.92)2 = 29.29 − 20 = 29.29 − 28.60832 = 0.68168
2. Tính Sxy (Tổng tích độ lệch): X (P xi )(P yi ) Sxy = xi yi − n (23.92)(1843.21) = 2214.65 − 20
= 2214.65 − 2204.479 = 10.1708 Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 12 / 35
Tính toán chi tiết các Hệ số Hồi quy
Bước 3: Xác định các hệ số hồi quy ( ˆ β1, ˆ β0) Áp dụng công thức OLS: Hệ số góc ( ˆ β1): ˆ Sxy 10.1708 β1 = = ≈ 14.92 Sxx 0.68168 Hệ số chặn ( ˆ β0): ˆ β0 = ¯ y − ˆ β1 ¯ x = 92.1605 − (14.92 × 1.196) = 92.1605 − 17.844 = 74.32
Phương trình hồi quy mẫu: ˆ y = 74.32 + 14.92x Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 13 / 35
Đánh giá độ phù hợp mô hình
Bước 4: Tính các nguồn biến thiên (SST, SSR, SSE)
Ta cần tính Syy để có SST: X (P yi )2 SST = Syy = y 2 − i n (1843.21)2 = 170044.53 −
= 170044.53 − 169871.20 = 173.33 20
SSR (Biến thiên giải thích được): SSR = ˆ
β1 · Sxy = 14.92 × 10.1708 ≈ 151.75
SSE (Tổng bình phương sai số):
SSE = SST − SSR = 173.33 − 151.75 = 21.58 Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 14 / 35
Đánh giá độ phù hợp mô hình
Bước 5: Tính hệ số xác định R2 Kết quả tính toán SSR 151.75 R2 = = ≈ 0.8755 SST 173.33
Kết luận: Khoảng 87.55% sự biến thiên của độ sạch Oxy được giải thích bởi
nồng độ Hydrocarbon thông qua mô hình hồi quy tuyến tính. Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 15 / 35
Lý thuyết phân phối của các hệ số
Bản chất ngẫu nhiên của các hệ số Các ước lượng ˆ β0, ˆ
β1 được tính từ mẫu ngẫu nhiên Y1, ..., Yn. Do đó, chúng là các biến ngẫu nhiên. Giả định về sai số
Để tìm phân phối của ˆ
β, ta giả định sai số ϵi ∼ N(0, σ2) và độc lập nhau.
Dưới giả định này, ta có các kết quả lý thuyết quan trọng sau (Định lý Gauss-Markov mở rộng): 1 ˆ
β1 có phân phối chuẩn: ˆ β1 ∼ N β1, σ2 Sxx 2 ˆ
β0 có phân phối chuẩn: ˆ β0 ∼ N β0, σ2( 1 + ¯x2 ) n Sxx Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 16 / 35
Lý thuyết phân phối của các hệ số
Ước lượng phương sai sai số (σ2)
Vì σ2 của tổng thể thường chưa biết, ta phải ước lượng nó bằng Phương sai mẫu (s2): SSE s2 = MSE = n − 2 √ Đại lượng s =
MSE gọi là Sai số chuẩn của ước lượng (Residual Standard Error). Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 17 / 35
Lý thuyết phân phối của các hệ số
Từ Phân phối Chuẩn sang Phân phối Student
Khi thay thế σ (chưa biết) bằng s (ước lượng), biến chuẩn hóa của các hệ số sẽ
tuân theo phân phối Student (t) với bậc tự do df = n − 2.
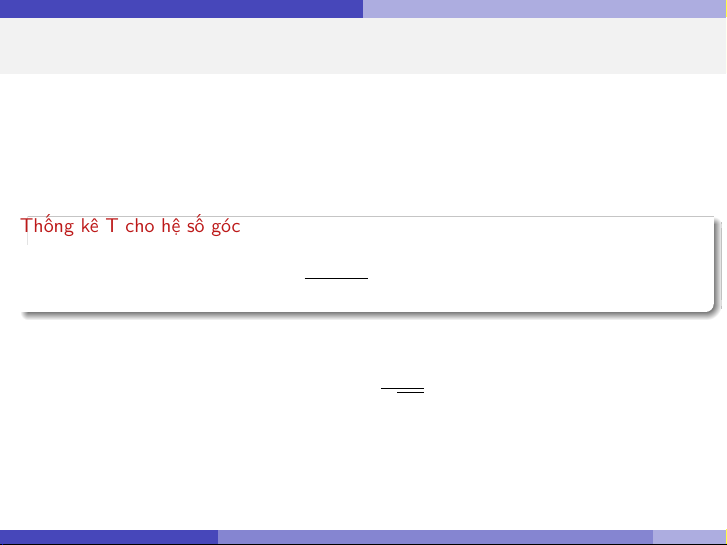
Thống kê T cho hệ số góc ˆ β1 − β1 T = ∼ t(n − 2) se( ˆ β1)
Trong đó Sai số chuẩn (Standard Error) của ˆ β1 là: s se( ˆ β1) = √Sxx Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 18 / 35
Tính toán Kiểm định và Khoảng tin cậy
Bước 6: Tính Sai số chuẩn (Standard Error)
1. Tính phương sai sai số (s2): SSE 21.58 21.58 s2 = = = ≈ 1.198 n − 2 20 − 2 18 √ ⇒ s = 1.198 ≈ 1.095
2. Tính sai số chuẩn của hệ số góc se( ˆ β1): s 1.095 1.095 se( ˆ β1) = √ = √ = ≈ 1.326 Sxx 0.68168 0.8256 Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 19 / 35
Tính toán Kiểm định và Khoảng tin cậy
Bước 7: Kiểm định giả thuyết cho hệ số góc
Xét cặp giả thuyết: H0 : β1 = 0 (Không liên hệ) vs H1 : β1 ̸= 0.
Tính Thống kê kiểm định t (t-statistic): ˆ β1 − 0 14.92 tobs = = ≈ 11.25 se( ˆ β 1.326 1)
So sánh với miền bác bỏ: Với α = 0.05, df = 18, tra bảng ta có t0.025,18 = 2.101.
Vì |tobs | = 11.25 > 2.101, ta bác bỏ H0.
Kết luận: Nồng độ Hydrocarbon có ảnh hưởng ý nghĩa thống kê tới độ sạch Oxy. Nguyễn Hữu Toàn Hồi quy tuyến tính đơn 20 / 35