lOMoAR cPSD| 36133485
1. Phân tích và gi愃ऀ i thích m quan hệ giữa mục tiêu, yêu cầu cần đạt với nội dung, PPDH trong
môn cụ thể. Cho ví dụ minh họa.
Quan hệ giữa yêu cầu cần đạt với nội dung dạy học, phương pháp và kĩ thuật dạy học trong môn Toán
Với CT GDPT 2018, GV sẽ xây dựng nội dung dạy học đáp ứng yêu cầu cần đạt của CT.
Yêu cầu cần đạt trong CT môn Toán gồm hai kiểu:
– Yêu cầu cần đạt về năng lực toán học được mô t愃ऀ theo từng cấp học với các biểu hiện cụ
thể theo từng năng lực thành phần: năng lực tư duy và lập luận toán học, năng lực mô hình hóa
toán học, năng lực gi愃ऀ i quyết vấn đề toán học, năng lực giao tiếp toán học và năng lực sử dụng
công cụ, phương tiện học toán. Ngoài ra, môn toán cũng góp phần phát triển các phẩm chất, năng
lực chung được quy định trong CT tổng thể.
– Yêu cầu cần đạt về mặt nội dung được mô t愃ऀ trong từng chủ đề của mạch kiến thức theo
từng cấp lớp (từ lớp 1 đến lớp 12).
Khi bàn về m quan hệ giữa ba yếu t cơ b愃ऀ n của quá trình dạy học toán (mục tiêu – nội
dung – phương pháp), Nguyễn Bá Kim và Bùi Huy Ngọc (2007) đ愃̀ khẳng định các yếu t này
“tác động lẫn nhau, quy định lẫn nhau, trong đó, mục tiêu giữ vai trò chủ đạo” (trang 20).
Với đặc thù của CT môn Toán “bao gồm hai nhánh liên kết chặt chẽ với nhau, một nhánh
mô tả sự phát triển của các mạch nội dung kiến thức cốt lõi và một nhánh mô tả sự phát
triển của năng lực, phẩm chất của HS” (CT GDPT Toán 2018, trang 4-5), chúng ta nên bắt
đầu từ yêu cầu cần đạt về mặt nội dung để xây dựng nội dung dạy học, rồi xem xét nó trong m
quan hệ biện chứng với PP, KTDH và đóng góp về sự phát triển năng lực, phẩm chất.
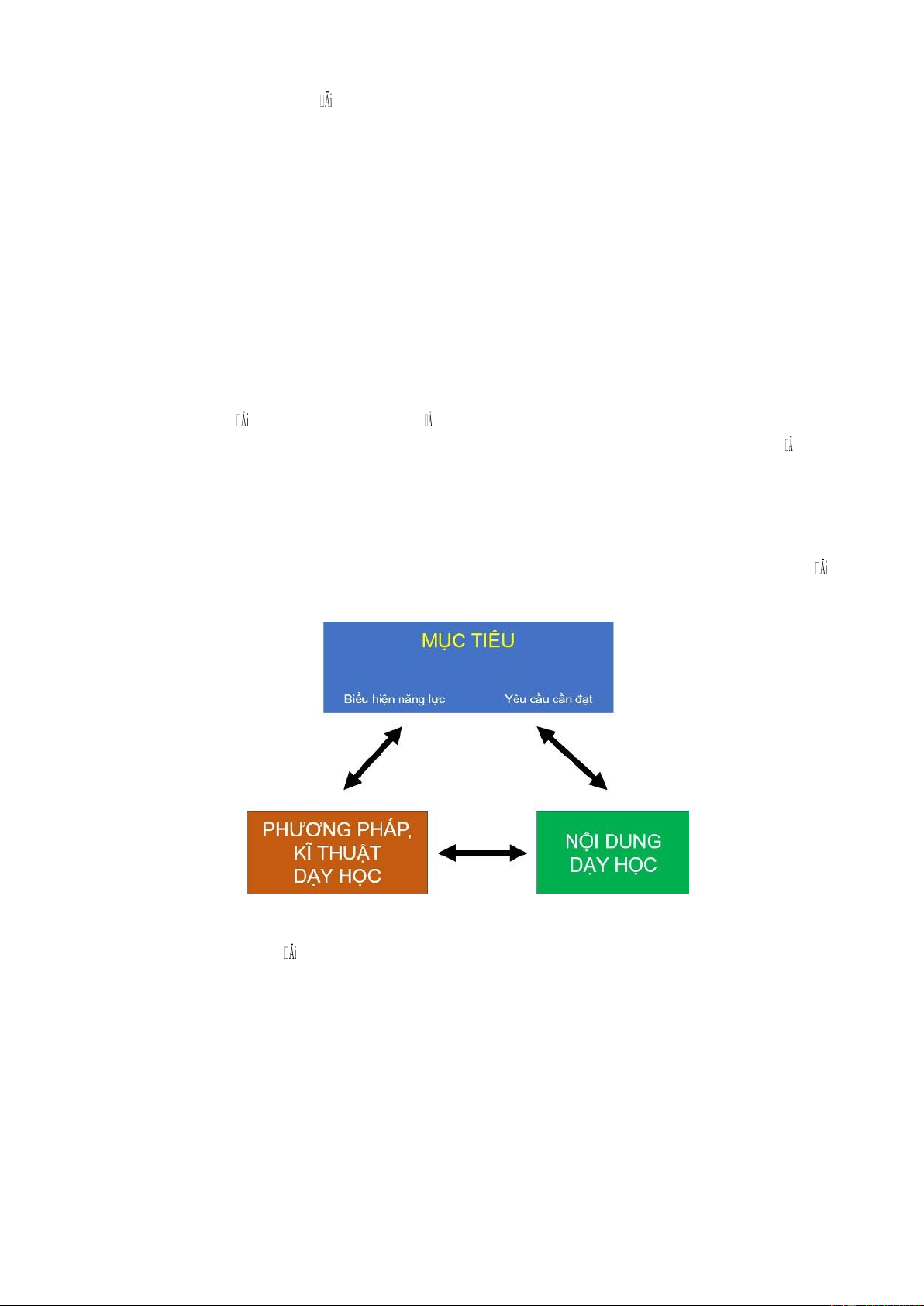
Sơ đồ 2.1. Mối quan hệ giữa mục tiêu, nội dung và PP, KTDH
Có thể hình dung m quan hệ giữa YCCĐ với nội dung dạy học, định hướng sử dụng PP,
KTDH trong một bài học/chủ đề qua ma trận như b愃ऀ ng 2.1 dưới đây. lOMoAR cPSD| 36133485 lOMoAR cPSD| 36133485
Bảng 2.1. Bảng ma trận kết nối giữa năng lực, YCCĐ với nội dung và PP, KTDH trong môn
Toán, lớp 10 Chủ đề: Một số khái niệm về xác suất cổ điển
Yêu cầu cần đạt Nội dung dạy học Phương pháp, kĩ
Năng lực, phẩm chất thuật dạy học
– Nhận biết được một - Thực hành một s Dạy học toán thông Năng lực mô hình hóa s khái niệm về xác thí nghiệm
ngẫu qua hoạt động tr愃ऀi toán học thể hiện qua
suất cổ điển: phép thử nhiên
nghiệm khi cho HS các biểu hiện:
ngẫu nhiên; không - Mô t愃ऀ kết qu愃ऀ có thể thực hành th愃ऀ một s - Mô t愃ऀ được không gian mẫu; biến c
x愃ऀ y ra (biến c sơ vật
(biến c là tập con cấp), tất c愃ऀ kết qu愃ऀ có
từ độ cao 30 cm gian mẫu, biến c sơ
của không gian mẫu); thể x愃ऀ y ra (không để thực hiện một phép cấp, biến c biến c biến c i. gian mẫu). thử ngẫu nhiên và ghi trong một s thí
– Mô t愃ऀ được không - Biểu diễn không nhận kết qu愃ऀ (bằng nghiệm đơn gi愃ऀ n bằng
gian mẫu, biến c gian mẫu bằng khái hình 愃ऀ nh, bằng một cách sử dụng các đ Āi
trong một s thí niệm tập hợp.
từ,..), HS tự làm một tượng toán học đ愃̀
nghiệm đơn gi愃ऀ n (ví - Mô t愃ऀ và nêu các vật dùng để tạo ra biết (khái niệm tập
dụ: tung đồng xu hai đặc trưng của phép phép thử ngẫu nhiên hợp, phần tử, tập hợp
lần, tung đồng xu ba thử ngẫu nhiên.
sao cho không gian con, phần bù của 1
lần, tung xúc xắc hai - Mô t愃ऀ , biểu diễn mẫu có k phần tử. tập hợp) Năng lực lần).
biến c (như là hợp Dạy học thông qua giao tiếp toán học thể
của nhiều biến c sơ mô hình hóa toán học hiện qua các biểu cấp), biến c i. khi yêu cầu HS sử hiện:
- Làm ra một vật dụng các tượng - Trình bày, diễn đạt,
dùng để tạo ra phép toán học để mô t愃ऀ nêu câu hỏi, th愃ऀ o
thử ngẫu nhiên sao không gian mẫu, biến luận, tranh luận (về
cho không gian mẫu c sơ cấp, biến c các đặc trưng của có k phần tử. biến c i. Kĩ thuật phép thử ngẫu nhiên,
khăn tr愃ऀ i bàn: tổ chức tính đồng khả cho HS trong nhóm
năng/không đồng khả
làm việc cá năng xuất hiện của nhân trên một nhiệm các biến c sơ cấp) vụ (nghiên cứu các đặc trưng của phép thử ngẫu nhiên) rồi cùng nhau xem xét và nhất để đưa ra
câu tr愃ऀ lời chung của nhóm.
2. Phân tích kh愃ऀ năng phát triển phẩm chất, năng lực cho HS trong môn cụ thể thông qua vận
dụng dạy học gi愃ऀ i quyết vấn đề trong môn cụ thể. Cho ví dụ minh họa.
– Nhận biết, phát hiện được vấn đề cần gi愃ऀ i quyết trong môn Toán.
– Lựa chọn, đề xuất được cách thức, gi愃ऀ i pháp gi愃ऀ i quyết vấn đề.
– Sử dụng được các kiến thức, kĩ năng toán học tương thích (bao gồm các công cụ và thuật
toán) để gi愃ऀ i quyết vấn đề đặt ra.
– Đánh giá được gi愃ऀ i pháp đề ra và khái quát hoá được cho vấn đề tương tự.
3. Phân tích kh愃ऀ năng phát triển phẩm chất, năng lực cho HS trong môn cụ thể thông qua vận
dụng các kỹ thuật dạy học. Cho ví dụ minh họa.
PP, KTDH phát triển phẩm chất, năng lực cho HS trong môn Toán cần đáp ứng các yêu cầu lOMoAR cPSD| 36133485 cơ b愃ऀ n sau:
– Phù hợp với tiến trình nhận thức của HS (đi từ cụ thể đến trừu tượng, từ dễ đến khó);
không chỉ coi trọng tính logic của khoa học toán học mà cần chú ý cách tiếp cận dựa trên
kinh nghiệm và sự tr愃ऀ i nghiệm của HS;
– Quán triệt tinh thần “lấy HS làm trung tâm”, phát huy tính tích cực, tự giác, chú ý nhu
cầu, năng lực nhận thức, cách thức học tập khác nhau của từng cá nhân HS; tổ chức quá trình dạy
học theo hướng kiến tạo, trong đó HS được tham gia tìm tòi, phát hiện, suy luận gi愃ऀ i quyết vấn đề;
– Linh hoạt trong việc vận dụng các PP, KTDH tích cực; kết hợp nhuần nhuyễn, sáng tạo
với việc vận dụng các PP, KTDH truyền
kết hợp các hoạt động dạy học trong lớp học với
hoạt động thực hành tr愃ऀ i nghiệm, vận dụng kiến thức toán học vào thực tiễn. Cấu trúc bài học b愃ऀ o
đ愃ऀ m tỉ lệ cân i, hài hoà giữa kiến thức c lõi, kiến thức vận dụng và các thành phần khác.
– Sử dụng đủ và hiệu qu愃ऀ các phương tiện, thiết bị dạy học t thiểu theo quy định với
môn Toán; có thể sử dụng các đồ dùng dạy học tự làm phù hợp với nội dung học và các tượng
HS; tăng cường sử dụng công nghệ thông tin và các phương tiện, thiết bị dạy học hiện đại một
cách phù hợp và hiệu qu愃ऀ .
4. Thiết kế một hoạt động học tập cho một nội dung môn Toán trong CT phổ thông 2018 có sử
dụng một trong các PPDH và KTDH phát triển phẩm chất, năng lực cho HS. Ví dụ minh hoạ
Trong nội dung “Hàm s liên tục” ở lớp 11 trong CT GDPT môn Toán 2018 (trang 93) với
yêu cầu cần đạt “Nhận dạng được tính liên tục của tổng, hiệu, tích, thương của hai hàm s liên
tục”, GV có thể tổ chức hoạt động sau:
Bước 1: Nhận biết vấn đề lOMoAR cPSD| 36133485
Trước đó, HS đ愃̀ được học về khái niệm hàm s liên tục tại một điểm. Vấn đề được nghiên
cứu trong buổi học là tổng, hiệu, tích, thương của hai hàm s liên tục tại một điểm có liên tục tại điểm đó hay không. GV nêu câu hỏi sau:
Gi愃ऀ sử y = f(x) và y = g(x) là hai hàm s liên tục tại điểm xo. Khi đó, các hàm s y
= f(x)+g(x), y = f(x)-g(x), y = f(x).g(x), y = f(x)/g(x) có liên tục tại xo không?
Lớp học được chia thành 4 nhóm. Mỗi nhóm xem xét một hàm s (trong hàm s được đề xuất).
Bước 2: Lập kế hoạch giải quyết vấn đề
GV tổ chức cho HS th愃ऀ o luận nhóm. Mục tiêu th愃ऀ o luận là đề xuất cách thức chứng minh nếu
như phán đoán tính liên tục được b愃ऀ o toàn, hoặc chỉ ra ph愃ऀ n ví dụ nếu như phán đoán tính liên tục
không được b愃ऀ o toàn.
Trong định hướng chứng minh, các nhóm cần làm rõ gi愃ऀ thiết và kết luận dựa trên định nghĩa
của khái niệm hàm s liên tục tại một điểm.
Bước 3: Thực hiện kế hoạch
Các nhóm thực hiện công việc theo định hướng đ愃̀ xác định trong bước 2. Sau thời gian quy
định, các nhóm cử đại diện trình bày kết qu愃ऀ trên b愃ऀ ng.
Bước 4: Kiểm tra, đánh giá và kết luận
Sau khi các nhóm đ愃̀ trình bày câu tr愃ऀ lời trên b愃ऀ ng, GV đề nghị các nhóm nhận xét chéo kết
qu愃ऀ làm việc của nhau. C
cùng GV đánh giá lời gi愃ऀ i từng nhóm và tổng kết kết qu愃ऀ làm việc của c愃ऀ
nhóm về tính liên tục của tổng, hiệu, tích, thương của hai hàm s liên tục. GV lưu ý
(đặt câu hỏi) trường hợp của hàm s y = f(x)/g(x) cần có thêm điều kiện g(xo) ≠ 0.
Hoạt động này hướng đến hình thành và phát triển cho HS các phẩm chất, năng lực được mô t愃ऀ trong b愃ऀ ng sau: Yêu cầu cần
Cơ hội phát triển đạt phẩm chất, Biểu hiện năng lực Trung thực
Khách quan, công bằng, đánh giá chính xác bài làm của Nhận dạng nhóm mình và nhóm bạn được tính liên Trách nhiệm
Hoàn thành công việc của nhóm và GV giao. tục của tổng,
- Nhận biết được vấn đề cần gi愃ऀ i quyết: chứng minh sự hiệu, tích, Năng lực gi愃ऀi
b愃ऀ o toàn tính chất liên tục (tại một điểm) của tổng, hiệu, thương của quyết vấn đề
tích, thương của hai hàm liên tục (tại một điểm); xác định hai hàm số toán học
được gi愃ऀ thiết và kết luận trong chứng minh. liên tục.
- Sử dụng được các phép toán (tổng, hiệu, tích, thương)
trên giới hạn hàm s trong chứng minh. lOMoAR cPSD| 36133485
- Sử dụng được phương pháp suy diễn để nêu ra một chứng Năng lực tư duy minh chặt chẽ. và lập luận
- Bổ sung được điều kiện g(xo) ≠ 0 trong trường hợp thương toán học
của hai hàm s liên tục (tại điểm xo) để có được lập luận chặt chẽ.
5. Thiết kế một hoạt động học tập cho một nội dung môn Ngữ văn/Toán trong CT phổ
thông 2018 có sử dụng một trong các KTDH phát triển phẩm chất, năng lực cho HS
Ví dụ sau đây minh họa cách tổ chức dạy học bài “Đồ thị hàm số bậc hai và ứng dụng” ở lớp 10 theo
2 bước của Dạy học mô hình hoá toán học nhằm đáp ứng các yêu cầu cần đạt sau: Mạch kiến thức
Yêu cầu cần đạt Đại s Nội
– Nhận biết được các tính chất cơ b愃ऀ n của Parabola như dung đỉnh, trục xứng.
– Hàm s bậc hai, đồ thị hàm s
– Vận dụng được kiến thức về hàm s bậc hai và đồ thị bậc hai và ứng dụng
vào gi愃ऀ i quyết bài toán thực tiễn (ví dụ: xác định độ cao
của cầu, cổng có hình dạng Parabola,...)
Học liệu: Hình cổng hầm.
Gợi ý các hoạt động dạy học:
Bước 1: Dạy học tri thức toán học
GV tổ chức hoạt động dạy học hàm s bậc hai và đồ thị của hàm s bậc hai.
Bước 2: Vận dụng tri thức vào việc giải quyết các bài toán ngoài toán học (thực tiễn)
mà ở đó cần đến mô hình hoá toán học Hoạt động của GV
Dự kiến hoạt động của HS
Thông báo bài toán thực tế:
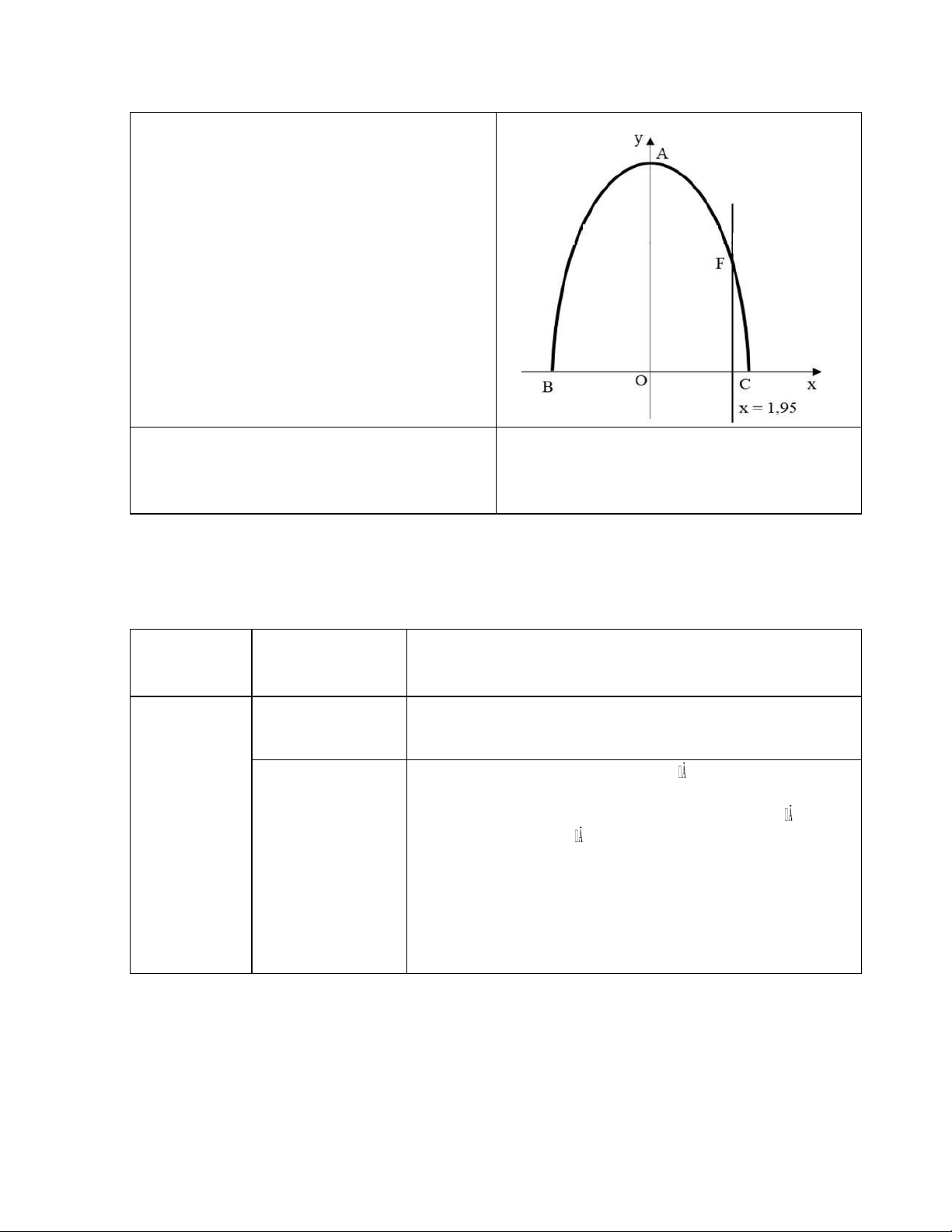
Một đường hầm nhân tạo có hình dáng và kích thước được cho biết như hình và chỉ cho phép
lưu thông một chiều. Một xe tải chở hàng với chiều cao được tính từ mặt đường đến nóc thùng
xe là 4,8m và bề ngang thùng xe là 3,9m.
Liệu xe tải có đi qua đường hầm được không? Giải thích vì sao? lOMoAR cPSD| 36133485
Giai đoạn 1: Xây dựng mô hình trung gian
- Đường hầm có hình dáng và kích thước của vấn đề
được cho biết như hình.
GV yêu cầu HS tóm tắt thông tin chính của
- Xe chỉ được phép lưu thông một chiều. vấn đề
- Xe t愃ऀ i có chiều cao từ mặt đường đến nóc
thùng xe là 4,8m và bề ngang thùng xe là 3,9m.
- Xe t愃ऀ i có qua được đường hầm không?
Giai đoạn 2: Xây dựng mô hình toán học
- Cổng hầm: đồ thị hàm s bậc 2
GV đặt câu hỏi cho HS chọn mô hình toán học - Xe: Hình chữ nhật kích thước 4,8m x 3,9m
phù hợp để biểu thị:
- Bài toán toán học: Hình chữ nhật có nằm lọt
- Cổng hầm có thể biểu thị bằng đường nào? trong Parabola không ?
- Biểu thị hình ảnh xe vào cổng hầm như thế nào?
GV yêu cầu HS phát biểu bài toán trong toán học:
- Bài toán cụ thể bây giờ là gì?
Giai đoạn 3: Giải quyết bài toán toán học
- Chọn hệ trục tọa độ thích hợp (trục hoành đi
GV đề nghị HS gi愃ऀ i quyết bài toán toán học và qua cạnh dưới đường hầm, trục tung đi qua
đưa ra câu tr愃ऀ trong toán học đỉnh vòm đường hầm) - Chọn hàm s bậc hai
- Xác định tọa độ 3 điểm thuộc Parabola
- Viết biểu thức hàm s bậc 2 qua 3 điểm tìm được
- Viết phương trình đường thẳng qua cạnh ph愃ऀ i của hình chữ nhật
- Tìm tung độ giao điểm của đường thẳng này và Parabola
- So sánh với chiều cao của hình chữ nhật lOMoAR cPSD| 36133485
Giai đoạn 4: Trả lời cho vấn đề thực tiễn
Tr愃ऀ lời cho thực tiễn:
GV đề nghị HS đưa ra câu tr愃ऀ lời cho vấn đề
- “Được”: nếu tung độ giao điểm lớn hơn 4,8 thực tế (m)
- “Không được”: trường hợp ngược lại.
Hoạt động này hướng đến hình thành và phát triển cho HS phẩm chất trách nhiệm và
các thành phần của năng lực toán học như: năng lực mô hình hóa toán học, năng lực gi愃ऀ i
quyết vấn đề toán học và năng lực giao tiếp toán học. B愃ऀ ng sau mô t愃ऀ biểu hiện cụ thể của
năng lực mô hình hóa toán học có thể hình thành cho HS: Yêu cầu
Cơ hội phát triển cần đạt phẩm chất, Biểu hiện năng lực Vận dụng Trách nhiệm
Có trách nhiệm với công việc được giao và có trách nhiệm được kiến
với kết qu愃ऀ hoạt động của nhóm. thức về hàm
- Sử dụng được đồ thị của hàm s bậc hai để biểu diễn số bậc hai và
hình dạng đường hầm, hình chữ nhật để biểu diễn xe t愃ऀ i. đồ thị vào
- Vận dụng được kiến thức liên quan đến hàm s bậc hai
giải quyết bài Năng lực mô hình và đồ thị của hàm s bậc hai để xác định xe t愃ऀ i có qua toán thực tiễn hóa toán học
được đường hầm hay không. (ví dụ: xác
- Chuyển câu tr愃ऀ lời toán học về câu tr愃ऀ lời cho bài toán định độ cao ban đầu. của cầu, cổng có hình dạng Parabola,...)