Ngân hàng đề thi môn Xử lý tín hiệu số | Học viện Công nghệ Bưu chính Viễn thông
Ngân hàng đề thi môn Xử lý tín hiệu số của Học viện Công nghệ Bưu chính Viễn thông với những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống. Mời bạn đọc đón xem!
Môn: Xử lý tín hiệu số (ELE1330)
Trường: Học viện Công Nghệ Bưu Chính Viễn Thông
Thông tin:
Tác giả:
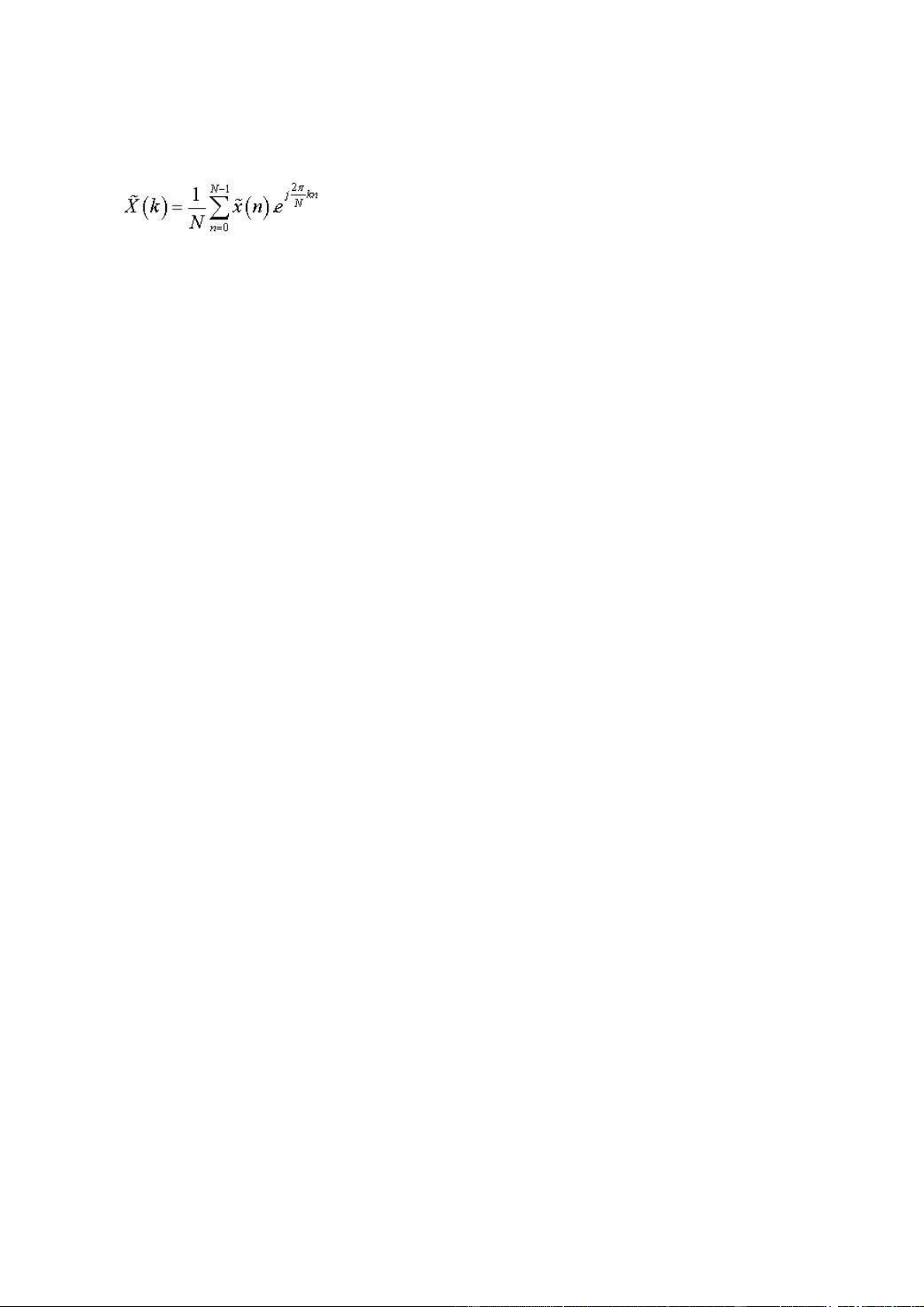
Preview text:
NGÂN HÀNG ĐỀ THI
XỬ LÝ TÍN HIỆU SỐ lOMoARcPSD| 36086670 NGÂN HÀNG ĐỀ THI
Môn: XỬ LÝ TÍN HIỆU SỐ
ĐTVT: 3 tín chỉ; CNTT: 4 tín chỉ 2 1
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a
Hệ thống bất biến. b Hệ thống phi tuyến c Hệ
thống tuyến tính bất biến. d Hệ thống tuyến tính.
4/ Phương trình sai phân tuyến tính mô tả hệ thống rời rạc nào sau ây: a Hệ thống tuyến tính. b Hệ thống phi tuyến c
Hệ thống bất biến. d Hệ
thống tuyến tính bất biến.
5/ Đối với một hệ thống, nếu ta có y(n) là áp ứng ứng với kích thích x(n) và y(n-k) là áp ứng ứng với
kích thích x(n-k) thì hệ thống ó ược gọi là: a Hệ thống nhân quả b Hệ thống tuyến tính c Hệ thống bất biến d Hệ thống ổn ịnh
6/ Một tín hiệu tương tự x ( ) ( ) a
t có tần số cao nhất là Fmax thì sau khi lấy mẫu, xa
t có thể ược phục
hồi một cách chính xác từ giá trị các mẫu của nó nếu tốc ộ lấy mẫu F thỏa mãn: s a
Fs ≤ 2Fmax b F ≥ s
2Fmax c Fs ≥ Fmax d Fs ≤ Fmax
7/ Hãy lựa chọn cách trả lời úng và ầy ủ nhất cho phát biểu " Về mặt biểu diễn toán học, tín hiệu số là
tín hiệu…" a Rời rạc theo biến số và rời rạc theo hàm số b Rời rạc theo biến số và liên tục theo hàm
số c Liên tục theo biến số và rời rạc theo hàm số d Liên tục theo biến số và liên tục theo hàm số
8/ Hãy lựa chọn cách trả lời úng và ầy ủ nhất cho phát biểu "Về mặt biểu diễn toán học, tín hiệu rời rạc
là tín hiệu…" a Liên tục theo biến số và rời rạc theo hàm số b Rời rạc theo biến số và rời rạc theo hàm
số c Rời rạc theo biến số và có thể liên tục hoặc rời rạc theo hàm số d Rời rạc theo biến số và liên tục theo hàm số
9/ Hệ thống tuyến tính là hệ thống thoả mãn nguyên lý xếp chồng T a x⎡⎣ . ( ) ( ) ( ) ( 1 n +b x. 2
n ⎤⎦= aT x. ⎣⎡ 1
n ⎦⎤+bT x. ⎡⎣ 2 n)⎤⎦ úng hay sai ? a Đúng b Sai
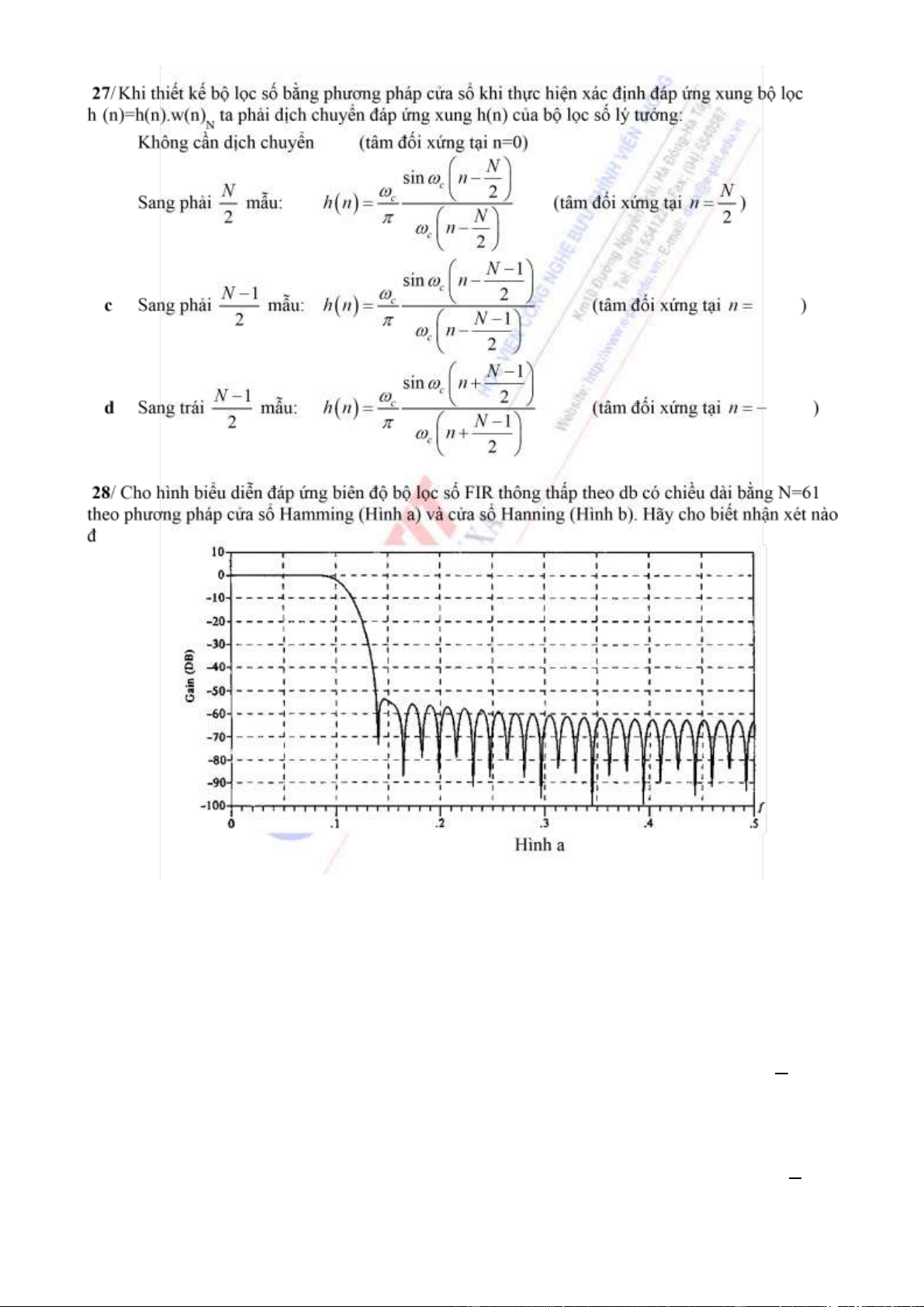
10/ Phép chập là phép toán chỉ thoả mãn tính chất hoán vị, không thoả mãn tính chất phân phối và kết
hợp úng hay sai? a Đúng b Sai
11/ Hãy cho biết cách nào sau ây biểu diễn tổng quát một tín hiệu rời rạc bất kỳ x(n)? a x( ) ( ) ( ) k=−∞ lOMoARcPSD| 36086670 b x( ) ( ) ( )
k=0 +∞ c x( )n =
∑ x n( ) (δk n− ) k=−∞ d x( ) ( ) ( ) k=−∞
12/ Đáp ứng xung h(n) của một hệ thống số ược cho bởi sơ ồ sau ây sẽ ược tính như thế nào ? a c 3
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670
13/ Ký hiệu x( )n a Đúng b Sai a lOMoARcPSD| 36086670 b a b c d dạng nào sau ây?
a b c d S = a ∞
S= ∑ h n( ) →∞ c n=−∞ ∞
S =∑ h n( ) →∞ d n=0 5
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b c d a b c lOMoARcPSD| 36086670
21/ Trong miền n, dãy dốc ơn vị ược ịnh nghĩa như sau a 0 n 0 n
r n( )=⎩⎧⎨n n ≤≠0 b
r n( )=⎨⎩⎧n n ≥≠0 n
c r n( )=⎧⎨⎩−0n n ≤≠0 d r n( )=⎧⎨⎩−0 n n n ≥≠0
22/ Trong miền n, dãy hàm mũ ược ịnh nghĩa như sau: 7
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b c d lOMoARcPSD| 36086670 d
x(n) nào sau ây tương ương với tín hiệu trên: ⎧ x(n)=⎪⎨ 4 −1 0≤ ≤n 4 ⎪⎩ 0 n ≠ b ⎧1− n0≤ ≤n 4 =⎪⎨ 4 x(n) c ⎩⎪ 0 n ≠ ⎪⎧ 1− 4 0≤ ≤n 4 x(n)=⎨ n ⎪⎩ 0 n ≠ d 9
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670
a b c d lOMoARcPSD| 36086670 a b c d a b c d a N > 0
29/ Hãy cho biết kết quả phép chập x (n) = x (n)*x (n) như biểu diễn ở ồ thị sau úng hay sai: 3 1 2 11
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b sai lOMoARcPSD| 36086670 a Sai b Đúng Rxy(n) = x(n).y(m− n) a m=−∞ Rxy( n) = x(m).y(m−n) b m=−∞ Rxy( n) = x(m).y(n
−m) c m=−∞ Rxy(n) = ∑+∞ x(
m).y(m− −n) d m=−∞
32/ Năng lượng của một tín hiệu x( )n ược ịnh nghĩa như sau: 13
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b
a x b x lOMoARcPSD| 36086670 a
y n( )= b x n ( )+ ( − + ( − ( − ( )+ ( − + 0 b x n1 1) b x n2 2)+b x n4
4) b y n( )= b x n0 b x n1 1) b x n ( − + + ( − ( )+ ( − + ( − + + ( 2 2) b3 b x n4
4) c y n( )= b x n0 b x n1 1) b x n2 2) 1 b x n4
− 4) d y n( )= b x n ( )− ( − − ( − − ( − 0 b x n1 1) b x n2 2) b x n4 4)
36/ Tín hiệu x(n) = u(n-2)-u(n-5) sẽ tương ương với tín hiệu: a rect (n-5) 3 b rect (n-5) 2 c rect (n-2) 3 d rect (n-2) 2 15
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 N N N
a A2 b 0 c A d ∞ lOMoARcPSD| 36086670 b 1 c 0 d ⎧ a ⎨ ⎩ ⎧ ⎪ b ⎨ ⎪ ⎪⎩ ⎧ 1−(b a. ) −1 n+1 d
y n( )=⎪⎪⎨ 1−(b a. ) −1 n ≥ 0 ⎪ ⎪⎩0 n < 0
CHƯƠNG II: BIỂU DIỄN TÍN HIỆU VÀ HỆ THỐNG RỜI RẠC TRONG MIỀN Z.
1/ Biến ổi z (2 phía) của một tín hiệu x(n) ược ịnh nghĩa như sau: X ( )
( ) n a n=−∞
X ( ) ( ) n b n=0
X ( ) ( ) n c
X ( )z =∑ x n z( )
−n d n=0
2/ Phần tử Z-1 trong hệ thống rời rạc là phần tử nào sau ây ? a Phần tử tích phân b Phần tử nghịch ảo c Phần tử vi phân d Phần tử trễ 17
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670
3/ Hệ thống số ặc trưng bởi hàm truyền ạt H(z) sẽ ổn ịnh nếu a Tất cả
các iểm không (Zero) z phân bố bên trong vòng tròn ơn vị. or b
Tất cả các iểm cực (Pole) z của hệ thống phân bố bên trong vòng tròn ơn vị. pk c
Tất cả các iểm không (Zero) z phân bố bên ngoài vòng tròn ơn vị. or d
Tất cả các iểm cực (Pole) z của hệ thống phân bố bên ngoài vòng tròn ơn vị. pk
4/ Trong miền z, áp ứng ra của hệ thống Y(z) sẽ ược xác ịnh bằng a Biến ổi
z của tín hiệu vào X(z) chập với hàm truyền ạt H(z) của hệ thống.
Y(z) = H(z).X(z). b Tỷ số giữa biến ổi z của tín hiệu vào trên hàm truyền ạt H(z) của hệ thống. Y(z) = H(z)*X(z). c
Tỷ số giữa biến ổi z của hàm truyền ạt H(z) của hệ thống trên biến ổi z của tín hiệu
vào.Y(z) = H(z)/X(z).. d
Biến ổi z của tín hiệu vào X(z) nhân với hàm truyền ạt H(z) của hệ thống. Y(z) = X(z)/H(z)
5/ Điểm cực z của hệ thống là iểm: pk a
Làm cho hàm truyền ạt H(z) không xác ịnh. H z( ) =∞ z z= b pk
Làm cho ầu vào hệ thống X(z) không xác ịnh. X z( ) =∞ z z= pk c
Làm cho hàm truyền ạt H(z) bằng không. H z( ) = z z= 0 d pk
Làm cho ầu vào hệ thống X(z) bằng không. X z( ) = z z= 0 pk
6/ Điểm không z của hệ thống là iểm: or a
Làm cho hàm truyền ạt H(z) bằng không. H z( ) = z z= 0 b 0r
Làm cho hàm truyền ạt H(z) không xác ịnh. H z( ) =∞ z z= 0r c
Làm cho ầu vào hệ thống X(z) bằng không. X z( ) = z z= 0 0r d
Làm cho ầu vào hệ thống X(z) không xác ịnh. X z( ) =∞ z z= 0r
7/ Nếu các hệ thống mắc song song với nhau thì hàm truyền ạt H(z) của hệ thống tổng quát sẽ bằng: N a
Tổng các hàm truyền ạt của các hệ thống thành phần H(z) = ∑H (z)i lOMoARcPSD| 36086670 c d a b c 19
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 d a Đúng b Sai b z = e c
z = re d hệ thống úng hay sai? a Sai b Đúng
12/ Tập hợp tất cả các giá trị của z mà tại ó chuỗi X ( )
( ) n hội tụ ược gọi là miền hội tụ n=−∞ của biến ổi z úng hay sai a Đúng b Sai
13/ Biến ổi z của tín hiệu xung ơn vị δ( )n sẽ là: a
ZT[ ( )]δ n = z−1 lOMoARcPSD| 36086670 c b 21
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 z
19/ Hệ thống có hàm truyền ạt H z( ) =
2 là hệ thống ổn ịnh úng hay sai ? z +3z + 2 a Đúng b Sai
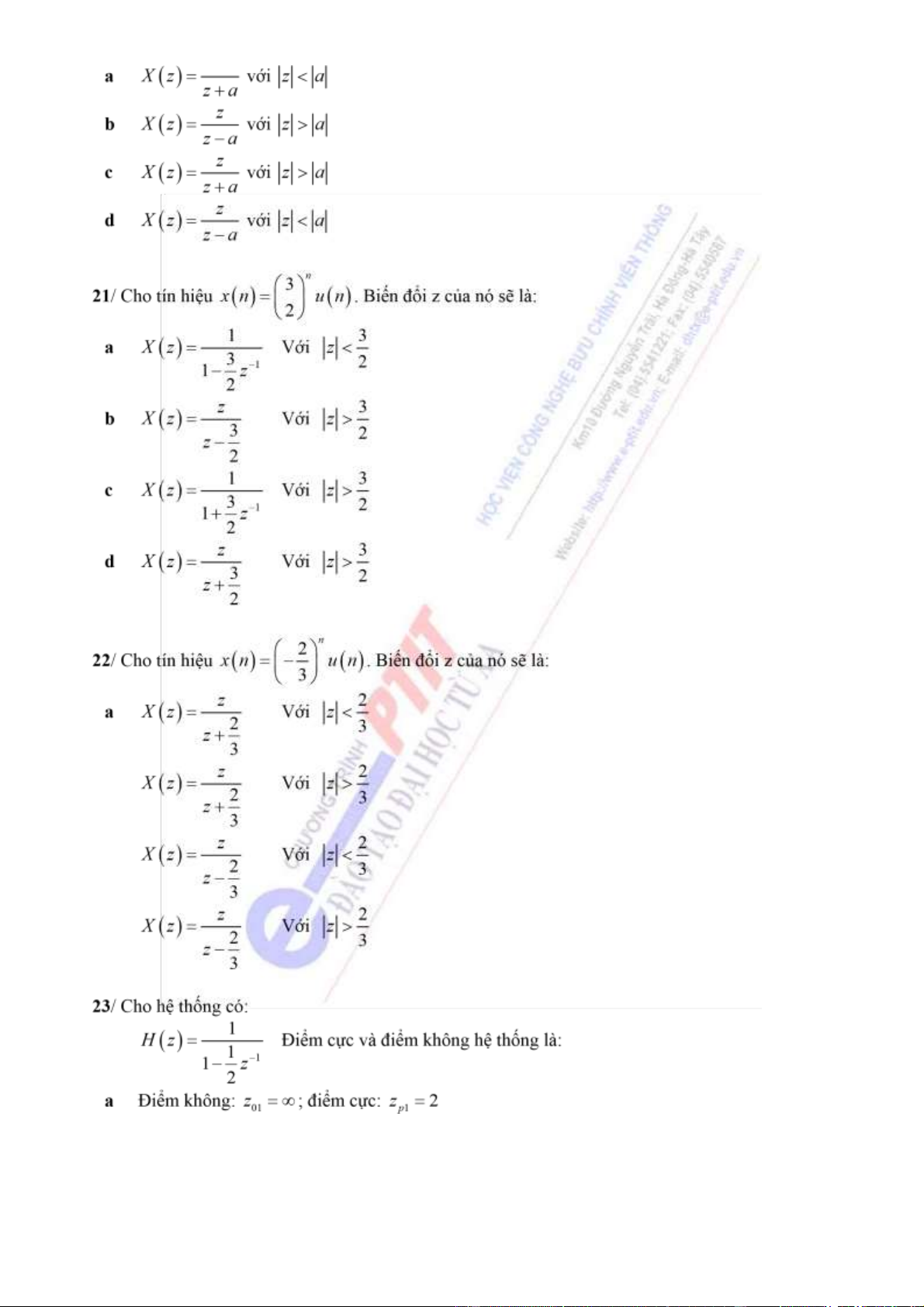
20/ Cho tín hiệu x( ) ( )n = a n u n( ). Biến ổi z của nó sẽ là: z lOMoARcPSD| 36086670 b c 23
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 d = 1 b
Điểm không: z = 0 ; iểm cực: 01 zp1 2 = 1 c
Điểm không: z =∞; iểm cực: 01 zp1 2 d
Điểm không: z = 0 ; iểm cực: = 01 zp1 2
24/ Miền hội tụ của biến ổi z của tín hiệu x(n)=(3)n u n( ) sẽ là: lOMoARcPSD| 36086670 d 0 25
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a Sai b Đúng c x(n) = (-A)n d x(n) = (-A)n. u(n)
28/ Cho X z( )= z với z A 0> > z A+ Hãy xác ịnh x(n) a x(n) = (-A)n b x(n) = (-A)n. u(n) c x(n) = (A)n d x(n) = (A)n. u(n) lOMoARcPSD| 36086670 k a Sai b Đúng a b 27
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670
a n b n0 c
z−n d z−n a b c d d X (az−1) > 1 34/ Cho X z( )= 1 với RC: z Hãy xác ịnh x(n). 1− z−1 2 a x(n) = (1/2)n. u(n) b x(n) = (1/2)n c x(n) = (-1/2)n. u(n) d x(n) = (-1/2)n lOMoARcPSD| 36086670 35/ Cho X z( )= a b c d 29
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b d a b c
38/ Cho tín hiệu x(n) = na u nn ( ) hãy cho biết trường hợp nào sau ây là biến ổi X(z) của nó: az a
1 )2 Với z > a (1−az− lOMoARcPSD| 36086670 c d 31
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 b c d a b
CHƯƠNG III: BIỂU DIỄN TÍN HIỆU VÀ HỆ THỐNG RỜI RẠC
TRONG MIỀN TẦN SỐ LIÊN TỤC
1/ Biến ổi Fourier FT của một tín hiệu x(n) ược ịnh nghĩa như sau: lOMoARcPSD| 36086670 a c 33
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 d a b d b c d b c 5/
Nếu bộ lọc số lý tưởng có pha bằng 0 thì quan hệ giữa áp ứng tần số
và áp ứng biên ộ tần số sẽ là: a b c d
6/ Thành phần tương ứng của x(n −k) khi chuyển sang miền tần số w sẽ là: lOMoARcPSD| 36086670 b c d
7/ Ký hiệu H e a b d 35
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670
8/ Ký hiệu X e a b d a b c d a b d a
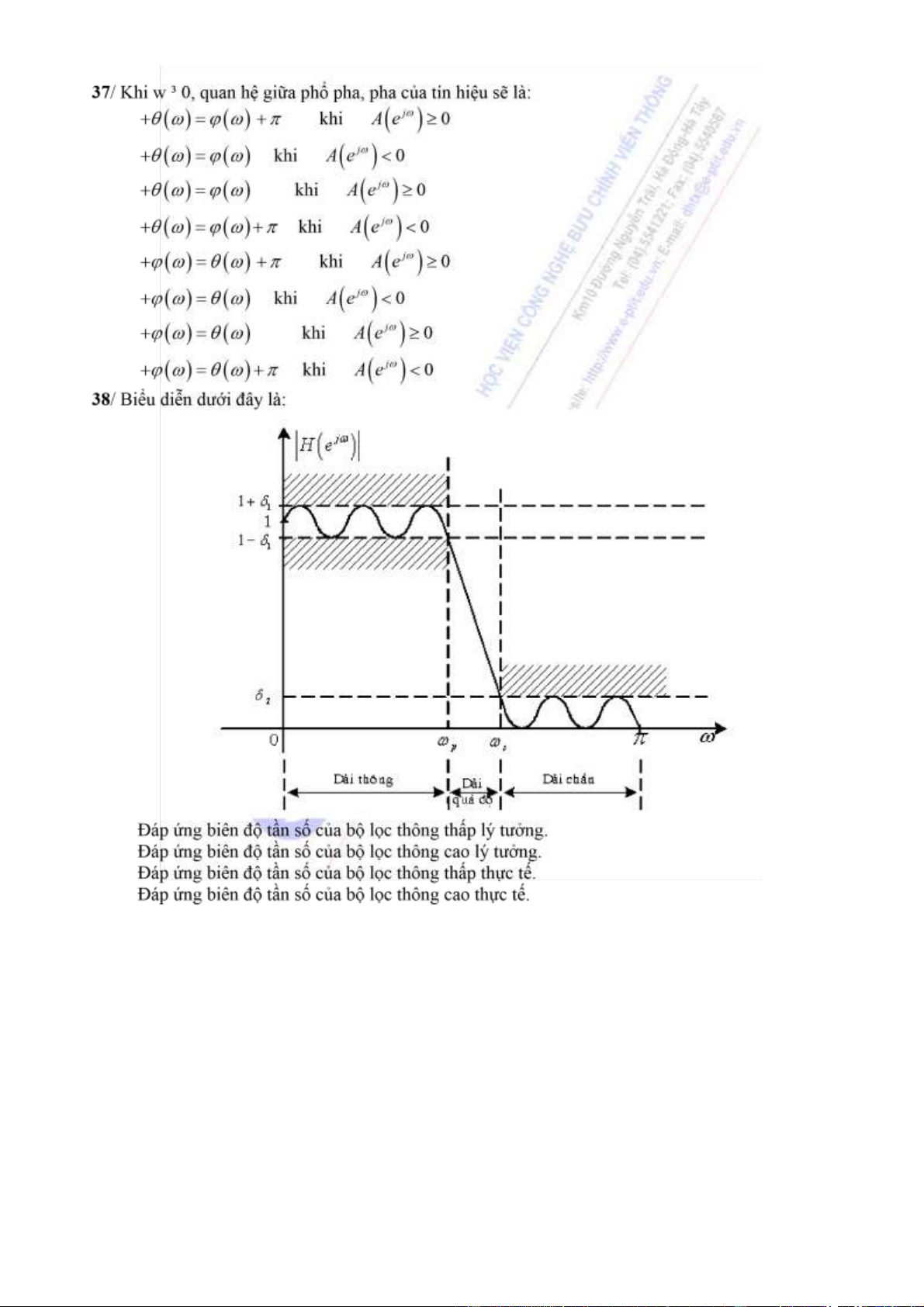
Biểu diễn phổ tín hiệu dưới
dạng ộ lớn và pha. b Biểu diễn phổ
tín hiệu dưới dạng modul và
argument. c Biểu diễn phổ tín hiệu
dưới dạng ộ lớn và phổ pha. d
Biểu diễn phổ tín hiệu dưới
dạng phổ biên ộ và pha. lOMoARcPSD| 36086670 ( ( ( b X e
= c X e = d X e = 37
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670
b X (e c X e a Đúng b Sai a Đúng b Sai úng hay sai ? b Sai b X e( 1+ e
( )n =⎛ ⎞⎜ ⎟⎝ ⎠43 n u n( ). Phổ của tín hiệu sẽ là áp án nào sau ây:
18/ Cho tín hiệu x ( a X e jω)= 1 1− e jω lOMoARcPSD| 36086670 c d X e a b 39
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 d a b c d a b c
22/ Đáp ứng xung h(n) của bộ lọc số chắn dải lý tưởng pha 0 với tần số cắt w < w ược biểu diễn c1 c2 ở dạng nào sau ây: a
h n( )=δ( )n +ωc2 sinωc2n−ωc1 sinωc1n π ω π ωc2n c1n b
h n( )=δ( )n −ωc2 sinωc2n−ωc1 sinωc1n lOMoARcPSD| 36086670
d h n( )=δ( )n −ωc1 sinωn ω sinω n π ω π ωn a b lớn). c d 41
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 lớn).
24/ Trong biểu diễn X e a Đúng b Sai a Đúng b Sai a Đúng b Sai a Sai
28/ Khi pha của bộ lọc bằng không θω( ) = 0, dẫn ến tâm ối xứng của bộ lọc nằm tại n = 0 (gốc tọa ộ) úng hay sai ? a Đúng b Sai
29/ Thành phần tương ứng của x( )n cosω0nkhi chuyển sang miền tần số w sẽ là: a X (ω+ω ) 0 b X (ω−ω ) 0 1 1 lOMoARcPSD| 36086670 b c d a b d 43
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b h n( )= a b b Đáp ứng xung h(n) phản
nhân quả c Đáp ứng xung h(n)
của bộ lọc số lý tưởng là không
nhân quả d Đáp ứng xung h(n) có tính chất ối xứng
35/ Biến ổi Fourier của tín hiệu x(n) = δ(n−1)+ δ(n+1) sẽ là: a
x(n) = 2sinω b x(n) = 2cosω c x(n) = cosω d x(n) = sinω
36/ Đáp ứng xung h(n) của bộ lọc số thông tất (All-pass filter) pha 0 chính là: a
Dãy nhảy ơn vị u(n) b
Dãy dốc ơn vi r n( ) c Dãy sinπn d Xung ơn vị δ( )n lOMoARcPSD| 36086670 a b c d 45
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b c d
39/ Quan hệ Parseval: thể hiện sự bảo toàn về mặt năng lượng khi chuyển từ miền thời gian sang
miền tần số ược thể hiện như sau: 1 ω a ∑∞ x( )n (Miền n) <=>
π∫ X (e jω) dω (Miền ) 2 n=−∞ −π lOMoARcPSD| 36086670 b ∑ n=−∞ ∞ c ∑ n=−∞ 47
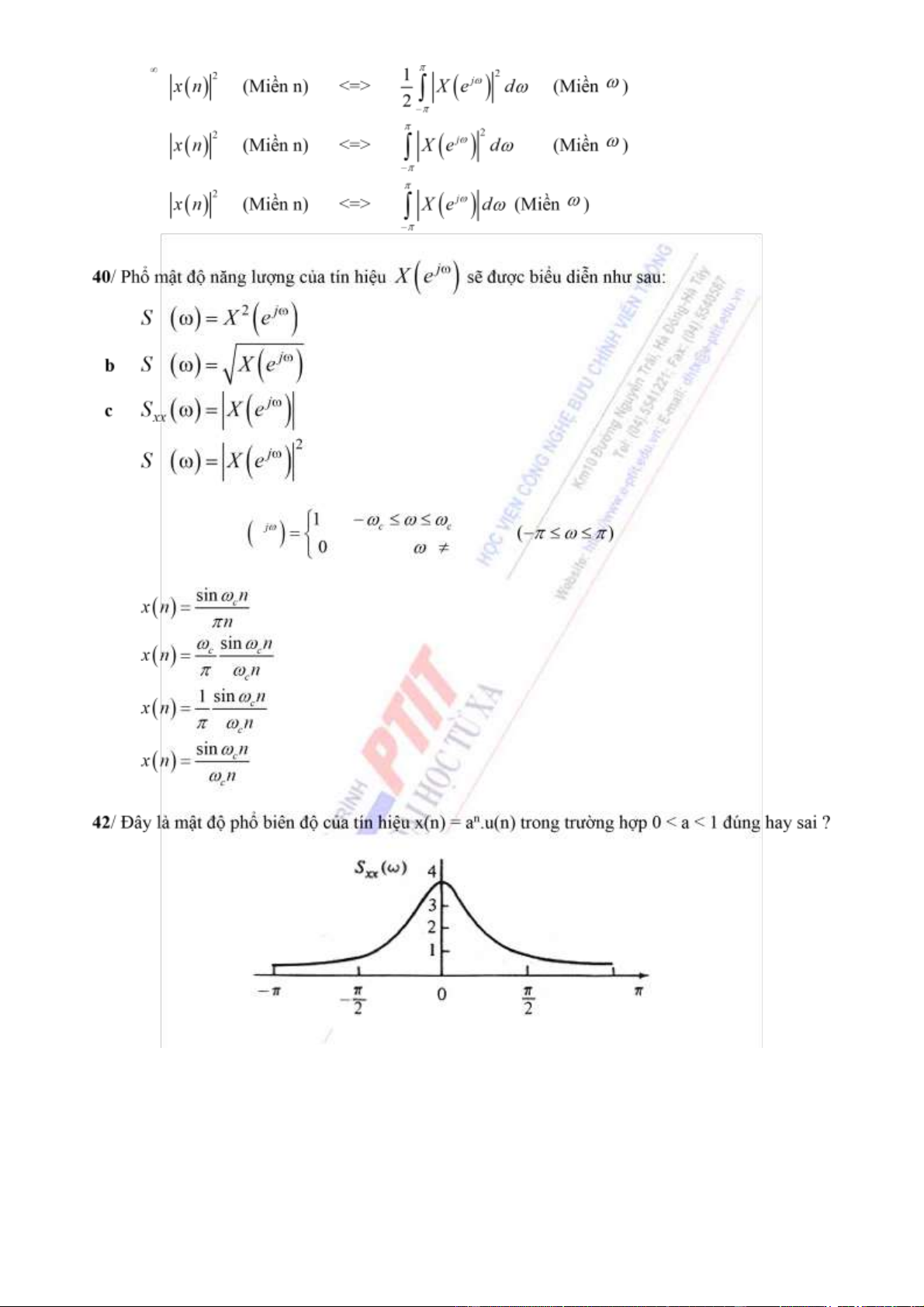
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 ∞ d ∑ n=−∞ a xx xx d xx
41/ Cho tín hiệu X e Hãy tìm x(n) ?
a b c d a Đúng b Sai
CHƯƠNG 4: BIỂU DIỄN TÍN HIỆU VÀ HỆ THỐNG RỜI RẠC
TRONG MIỀN TẦN SỐ RỜI RẠC k (HOẶC ωk )
1/ Biến ổi DFT có tính chất tuyến tính úng hay sai? a Đúng b Sai lOMoARcPSD| 36086670
2/ Biến ổi xuôi DFT và biến ổi ngược IDFT ược thực hiện theo hai thuật toán khác nhau úng hay 49
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a Sai b Đúng
8/ Biến ổi DFT của một tín hiệu tuần hoàn chu kỳ N x(n)N sẽ là: a lOMoARcPSD| 36086670 b d 51
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 b c d 0 ≤ ≤n N−1 n≠ 0 ≤ ≤n N−1 n≠ 0 ≤ ≤n N−1 d c N ≥ N + N -1 1 2 d N > N + N -1 1 2
12/ Ta có thể áp dụng ịnh nghĩa biến ổi Fourier rời rạc ối với dãy tuần hoàn x( )n M cho dãy có chiều
dài hữu hạn N x( )n N nếu ta coi: a x( )n : với M ≤
N là một dãy con bất kỳ có chiều dài N của dãy tuần hoàn có chu kỳ M x( )n M
N b x( )n : với M ≥
N là một dãy con bất kỳ có chiều dài N của dãy tuần hoàn có chu kỳ M x( )n M lOMoARcPSD| 36086670 x N c ( )n : với M ≤ N
N là một chu kỳ của dãy tuần hoàn có chu kỳ M x(n)M d x( )n N là
một chu kỳ của dãy tuần hoàn có chu kỳ M x(n) : với M ≥ N a b N c k Nπ 2kπ d 53
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 N a b c d sẽ có quan hệ như sau: a b c d
chu kỳ N x( )n
a x( )n = x n( ) rect ( )n b x( )n = = N
x n( )N .δ(n) c x( )n N x n( ) =
N .u n( ) d x( )n N x n( )N .r n( )
17/ Dãy x( )n =δ( ) N n là dãy có: a
Một mẫu bằng 1 tại n = 0 và N-1 mẫu bằng 0 b
Một mẫu bằng 0 c Một mẫu bằng 1 d Một mẫu bằng 0 và N-1 mẫu bằng 1
18/ Sơ ồ sau ể tính phép chập tuyến tính của 2 dãy x ( (
1 n)N1 và x2 n)N2 úng hay sai ? lOMoARcPSD| 36086670 b Sai a b c d 55
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b ∑ h n i ( ) i c d a X ( ) d X ( ) ( )N ( ) =
22/ Kết quả của phép chập tuần hoàn x ( ) ( ) ∑N−1 ( ) ( 1 n 8 * 8 x2 n 8 x1
m 8 x2 n −m)8 là: m=0 a
Một dãy tuần hoàn có chu kỳ là 8. b
Một dãy có chiều dài là 8. c Một
dãy có chiều dài là 16. d Một dãy
tuần hoàn có chu kỳ là 16. lOMoARcPSD| 36086670
23/ Biến ổi tương ương của dãy x(n −n ) sang miền tần số rời rạc ω sẽ là dãy: a WN b WN c WN d WN a b c d 57
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 biểu diễn sau: a x n ( ) i b x n ( ) i c x n ( ) i d x ni ( ) a b c d
27/ Phép trễ x(n-n ) chỉ ược xác ịnh trong khoảng: 0 N a Từ 0 ến N-1 b Từ n ến N -1 0 c Từ n ến N 0 d Từ 0 ến N
28/ Biến ổi DFT của dãy x( )n =δ( ) N n sẽ là:
a X k( )=⎧⎨⎩10 k0≠≤ ≤k N b X k(
)=⎧⎨⎩0 1 k0≠≤ ≤k N c
X k( )=⎧⎨1 0 ≤ ≤k N −1 lOMoARcPSD| 36086670 ⎩ d X k( )=⎨ ⎩ a b c d 59
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b c d
CHƯƠNG 5: TỔNG HỢP BỘ LỌC SỐ CÓ ĐÁP ỨNG XUNG CÓ
CHIỀU DÀI HỮU HẠN FIR
1/ Bộ lọc số FIR là bộ lọc: a
Có áp ứng tần số có chiều dài ⎡ ⎤
hữu hạn L H e ⎣ ( jω) ⎦= N b Có áp ứng xung có chiều dài vô hạn L h
n⎡⎣ ( )⎤⎦=∞ c
Có áp ứng xung có chiều dài hữu hạn L h n⎣⎡ ( )⎦⎤=[0,N − =1]
N d Có áp ứng tần số có chiều dài vô hạn L ⎡ ⎤
H e ⎣ ( jω) ⎦=∞
2/ Khi thiết kế bộ lọc số FIR pha tuyến tính thực chất là chúng ta xác ịnh: a Đặc tính pha của bộ
lọc b Các hệ số của bộ lọc c
Bậc của bộ lọc d Loại cấu trúc bộ lọc
3/ Khi thiết kế bộ lọc FIR bằng phương pháp cửa sổ, nếu bộ lọc chưa áp ứng ược các chỉ tiêu kỹ thuật thì ta phải: a
Thay ổi loại cửa sổ b Đồng thời tăng cả chiều dài của cửa sổ
và thay ổi loại cửa sổ. c
Thay dạng cấu trúc bộ lọc d Tăng chiều dài của cửa sổ
4/ Bộ lọc FIR loại I, loại II là bộ lọc có ặc iểm: α= N −1 lOMoARcPSD| 36086670 a
Tâm ối xứng của áp ứng xung h(n) tại : 2 và h(n) = h(N-n-1) α= N −1 b
Tâm ối xứng của áp ứng xung h(n) tại : 2 và h(n) = - h(N-n-1) α= N c
Tâm ối xứng của áp ứng xung h(n) tại : 2 và h(n) = h(N-n-1) α= N d
Tâm ối xứng của áp ứng xung h(n) tại : 2 và h(n) = - h(N-n-1)
5/ Bộ lọc FIR loại III, loại IV là bộ lọc có ặc iểm α= N −1 a
Tâm phản ối xứng của áp ứng xung h(n) tại : 2 và h(n) = - h(N-n-1) α= N b
Tâm phản ối xứng của áp ứng xung h(n) tại : 2 và h(n) = h(N-n-1) α= N −1 c
Tâm phản ối xứng của áp ứng xung h(n) tại : 2 và h(n) = h(N-n-1) α= N d
Tâm phản ối xứng của áp ứng xung h(n) tại : 2 và h(n) = -h(N-n-1)
6/ Việc thiết kế bộ lọc số FIR dùng phương pháp cửa sổ chính là: a
Dùng cửa sổ ể hạn chế chiều dài áp ứng xung h(n) của bộ lọc số lý tưởng thành hữu hạn. b
Dùng cửa sổ ể ưa áp ứng xung h(n) của bộ lọc số lý t ưởng trở thành nhân quả. c
Dùng cửa sổ ể hạn chế chiều dài áp ứng xung h(n) của bộ lọc số lý tưởng thành hữu hạn và ưa
áp ứng xung h(n) này trở thành nhân quả. d
Dùng cửa sổ ể áp ứng xung h(n) của bộ lọc số lý tưởng ối xứng qua trục tung.
7/ Khi thiết kế bộ lọc số FIR bằng các cửa sổ Tam giác, Hamming, Hanning ta thấy dải quá ộ của cả
3 phương pháp là như nhau úng hay sai? a Sai b Đúng
8/ Cửa sổ Tam giác sẽ cho ộ gợn sóng nhỏ hơn cửa sổ Hanning úng hay sai? a Sai b Đúng
9/ Cửa sổ chữ nhật w (n) là chính là một dãy chữ nhật rect (n) úng hay sai? R N N a Đúng b Sai
10/ Khi thiết kế, nếu ta tăng chiều dài N của cửa sổ, ta thấy: a Độ gợn ω
sóng ở cả dải thông và dải chắn tăng theo. ωp và tần số giới hạn chắn s xa
nhau hơn. b Tần số giới hạn dải thông c Độ gợn sóng ở cả dải thông và 61
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 ω
dải chắn giảm i. ωp và tần số giới hạn chắn s gần nhau hơn. d Tần số giới hạn dải thông
11/ Bộ lọc số FIR loại 3 là bộ lọc có bậc N thoả mãn a
Bậc N lẻ và pha tuyến tính có dạng θ(ω αω) = − . b
Bậc N lẻ và pha tuyến tính có dạng θ(ω βαω) = − . c
Bậc N chẵn và pha tuyến tính có dạng θ(ω βαω) = − . d
Bậc N chẵn và pha tuyến tính có dạng θ(ω αω) = −
12/ Bộ lọc số FIR loại 2 và loại 4 là bộ lọc có: a
Bậc N < 0 b Bậc N chẵn c Bậc N > 0 d Bậc N lẻ
13/ Bộ lọc số FIR loại 1 là bộ lọc có bậc N thoả mãn a
Bậc N lẻ và pha tuyến tính có dạng θ(ω αω) = − . b
Bậc N chẵn và pha tuyến tính có dạng θ(ω βαω) = − . c
Bậc N lẻ và pha tuyến tính có dạng θ(ω) =β−αω. d
Bậc N chẵn và pha tuyến tính có dạng θ(ω αω) = −
14/ Chất lượng cửa sổ sẽ tốt khi nào: a
Bề rộng ỉnh trung tâm Δω lớn và tỷ số giữa biên ộ ỉnh thứ cấp thứ nhất trên biên ộ ỉnh ( ) W e jωs λ= 20lg W (e ) j0 trung tâm: lớn. b
Bề rộng ỉnh trung tâm Δω
hẹp và tỷ số giữa biên ộ ỉnh thứ cấp thứ nhất trên biên ộ ỉnh lOMoARcPSD| 36086670 c d 63
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b c d a
Cửa sổ chữ nhật với chiều dài N = 6 b
Cửa sổ chữ nhật với chiều dài N = 7 c
Cửa sổ chữ nhật với chiều dài N = 3 d
Cửa sổ chữ nhật với chiều dài N = 4 ω
17/ Trong miền tần số , khi thiết kế bộ lọc FIR ta có: a
pha của cửa sổ và bộ lọc bằng không, tâm ối xứng của cửa sổ và bộ lọc trùng nhau. b
pha của cửa sổ và bộ lọc trùng nhau nhưng tâm ối xứng của cửa sổ và bộ lọc không trùng nhau. c
pha của cửa sổ và bộ lọc trùng nhau, tâm ối xứng của cửa sổ và bộ lọc cũng trùng nhau. d pha
của cửa sổ và bộ lọc bằng không, tâm ối xứng của cửa sổ và bộ lọc không trùng nhau.
18/ Tâm ối xứng của cửa sổ chữ nhật và cửa sổ tam giác sẽ là: lOMoARcPSD| 36086670 α= b α= c α=− d 65
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b c d a b c d a Đúng b Sai a
Dải quá ộ giữa dải thông và dải chắn của bộ lọc sẽ nhỏ, nghĩa là tần số w và w gần δ ,δ nhau. 1 2 p s b
Độ gợn sóng dải thông, dải chắn nhỏ. δ ,δ c
Độ gợn sóng dải thông, dải chắn 1 2 lớn. d
Dải quá ộ giữa dải thông và dải chắn của bộ lọc sẽ lớn, nghĩa là tần số w và w xa nhau. p s ω
23/ Khi giảm tham số bề rộng ỉnh trung tâm Δ ta sẽ có: lOMoARcPSD| 36086670 a b 67
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 ổi. d c d
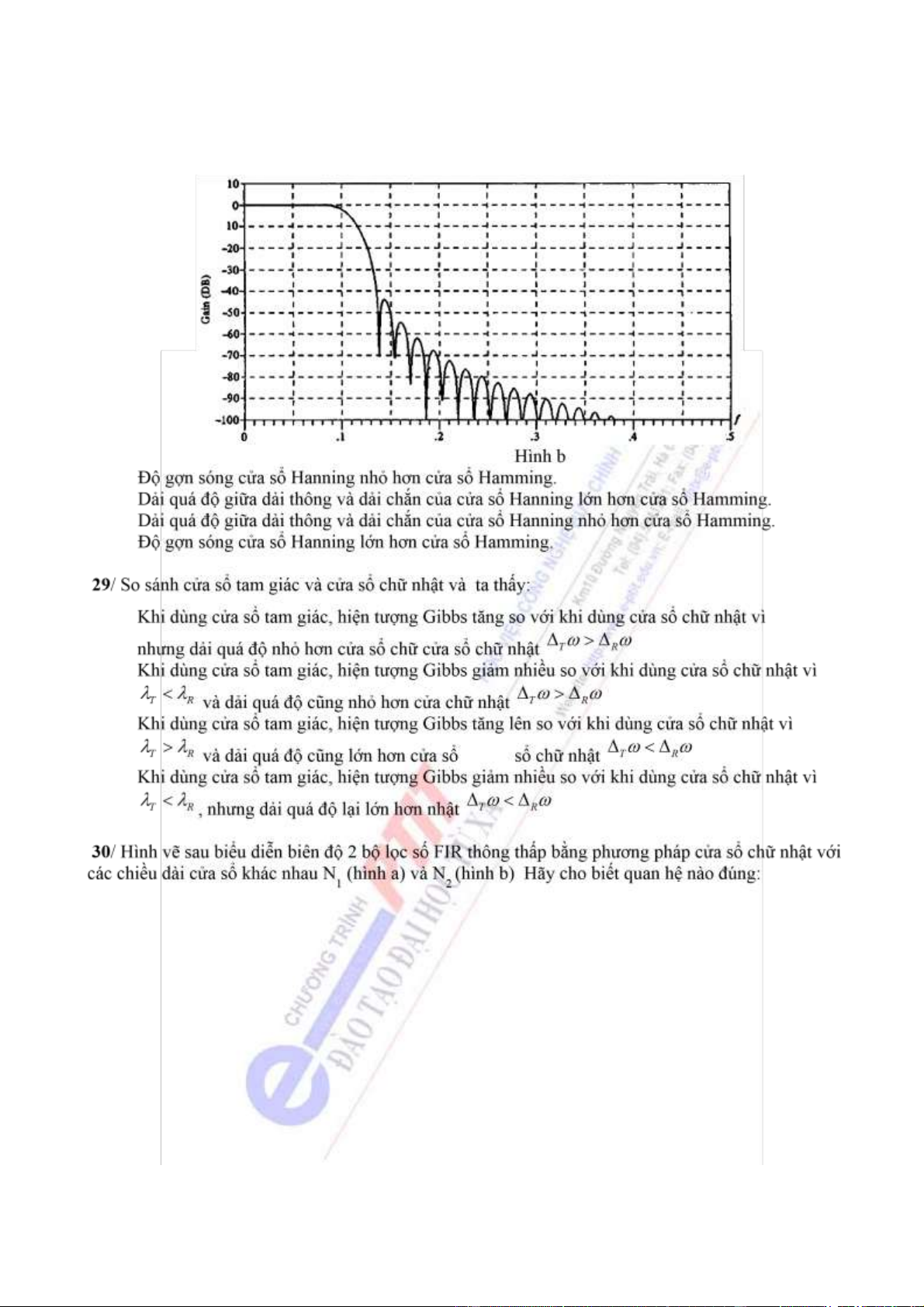
25/ Cửa sổ Hanning có chất lượng kém hơn cửa sổ Hamming vì: a
Bề rộng ỉnh trung tâm của cửa sổ Hanning lớn hơn cửa sổ Hamming b
Tỷ số giữa biên ộ ỉnh thứ cấp thứ nhất trên biên ộ ỉnh trung tâm của cửa sổ Hanning lớn hơn cửa
sổ Hamming. c Tỷ số giữa biên ộ ỉnh thứ cấp thứ nhất trên biên ộ ỉnh trung tâm của cửa sổ
Hanning nhỏ hơn cửa sổ Hamming. d
Bề rộng ỉnh trung tâm của cửa sổ Hanning nhỏ hơn cửa sổ Hamming
26/ Cửa sổ Blackman có ộ gợn sóng thấp nhất so với các cửa sổ Hanning, Hamming, tam giác và chữ nhật vì: a
Bề rộng ỉnh trung tâm của cửa sổ Blackman lớn nhất.
b Tỷ số giữa biên ộ ỉnh thứ cấp thứ nhất trên biên ộ ỉnh trung tâm của cửa sổ Blackman nhỏ nhất. c
Tỷ số giữa biên ộ ỉnh thứ cấp thứ nhất trên biên ộ ỉnh trung tâm của cửa sổ Blackman lớn nhất. d
Bề rộng ỉnh trung tâm của cửa sổ Blackman nhỏ nhất lOMoARcPSD| 36086670 d a b N −1 2 N −1 2 69
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 úng: a lOMoARcPSD| 36086670 b c d a λT >λR b T c T d T 71
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a 1 b c 1 d lOMoARcPSD| 36086670 a b c d a b c d
33/ Trong miền n, cửa sổ Hanning và Hamming ược ịnh nghĩa: w ( H ) 2π
n N =⎪⎨α α− −(1 )cos N
−1n 0 ≤ ≤n N −1 ⎧ ⎩⎪ 0 n ≠ Ta thấy: a
Khi α=1 ta có cửa sổ Hanning, khi α= 0.5 ta có cửa sổ Hamming. b
Khi α= 0.54 ta có cửa sổ Hanning, khi α= 0.5 ta có cửa sổ Hamming. c Khi α=
0.5 ta có cửa sổ Hanning, khi α=1 ta có cửa sổ Hamming. d Khi α= 0.5 ta có cửa
sổ Hanning, khi α= 0.54 ta có cửa sổ Hamming. 73
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670
34/ Khi dùng phương pháp cửa sổ thiết kế bộ lọc số FIR, ể kiểm tra bộ lọc vừa thiết kế có thỏa mãn
δ1,δωω2, p, s các chỉ tiêu kỹ thuật hay không ta sẽ căn cứ vào: a h (n) = w(n) .h(n) b c d a b c d lOMoARcPSD| 36086670
CHƯƠNG 6: THIẾT KẾ BỘ LỌC SỐ CÓ ĐÁP ỨNG XUNG
CÓ CHIỀU DÀI VÔ HẠN IIR.
1/ Đối với bộ lọc IIR, chiều dài áp ứng xung h(n) sẽ có tính chất: a
L h n⎣⎡ ( )⎤⎦=∞ 75
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 d
L h n⎡ ( )⎤= n a b c lOMoARcPSD| 36086670 d a b c d (ở ây a H z( )= z N
As Tkpk d 1 e (T: thời gian lấy mẫu)
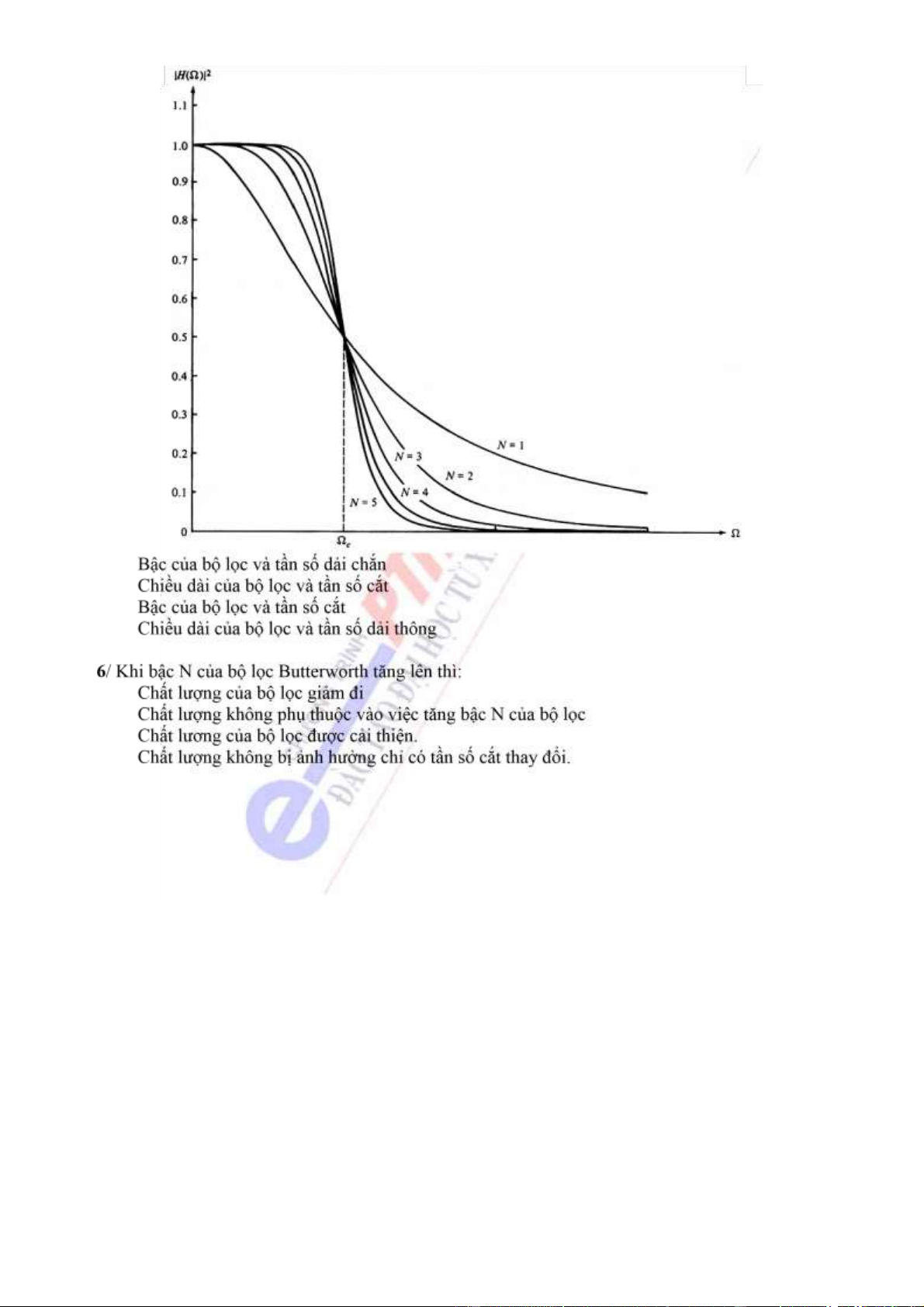
5/ Đáp ứng biên ộ tần số bộ lọc số IIR theo phương pháp Butterworth có dạng như hình sau. Hãy
cho biết tham số N và tham số Ωc như hình vẽ là: 77
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b c d a b c d
7/ 3 phương pháp tổng hợp - Butterworth lOMoARcPSD| 36086670
- Chebyshev - Elip hay Cauer ược dùng ể tổng hợp a Bộ
lọc số IIR b Bộ lọc số. c Bộ lọc số FIR d Bộ lọc tương tự. = s −1
8/ Bộ lọc tương tự có hàm truyền ạt H ( ) a s có: (s +1)(s −2) a
Có 2 iểm không là s = 1, s = - 2 và 1 iểm cực s = -1. 01 02 p1 b
Có 2 iểm không là s = -1, s = 2 và 1 iểm cực s = 1. 01 02 p1 c
Có 2 iểm cực là s = 1, s = - 2 và 1 iểm không s = -1. p1 p2 01 d
Có 2 iểm cực là s = -1, s = 2 và 1 iểm không s = 1. p1 p2 01 79
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 c d a b c d b c lOMoARcPSD| 36086670 d a b c d a b c d a b c
15/ Bình phương biên ộ của áp ứng tần số của bộ lọc Elip sẽ ược xác ịnh như sau (Với UN (x) là hàm
elíp Jacobian bậc N ).
H(Ω) 2 = 1 a 1+∈U (Ω Ω ) N / c 81
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 b c lOMoARcPSD| 36086670 d b c d a b c d H z( )= T /(1+T) a z −[1/(1+T)] (T: thời gian lấy mẫu) H z( )=
zT /(1+T) z b +[1/(1+T)] (T: thời gian lấy mẫu) z +[1/(1+T)] H z( )=
T /(1+T) c (T: thời gian lấy mẫu) 83
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 z −[1/(1+T)] H z( )=
zT /(1+T) d (T: thời gian lấy mẫu) c d lOMoARcPSD| 36086670 a b c d
CHƯƠNG 7: BIẾN ĐỔI FUORIER NHANH FFT
1/ Biến ổi Fourier nhanh FFT ược thực hiện trên tính toán một DFT N iểm, trong ó N có ặc iểm: a
Là số nguyên tố. b Có thể ược phân tích thành tổng của hai
số nguyên N = L + M c
Là phần nguyên của phép chia N L M= / d
Có thể ược phân tích thành tích của hai số nguyên N = LM
2/ Ta có thể tăng chiều dài của dãy (tín hiệu) trong biến ổi DFT bằng cách: a
Thực hiện phép cộng dãy ó với dãy u(n) b
Thực hiện phép nhân dãy ó với dãy u(n) c
Thêm một số các mẫu có giá trị bằng 0 d
Thêm một số các mẫu có giá trị bằng 1
3/ Khi tính toán DFT N iểm với N=L.M ta có thể phân tích thành:
a L biến ổi DFT, mỗi DFT ó có ộ lớn M iểm. b M biến ổi DFT, mỗi
DFT ó có ộ lớn N iểm. c N biến ổi DFT, mỗi DFT ó có ộ lớn M
iểm. d L biến ổi DFT, mỗi DFT ó có ộ lớn N iểm.
4/ Phép toán FFT cơ số 2 ược thực hiện ối với dãy có chiều dài N thoả mãn: a N = −2v 1 b N =ν2 c N = 2v d N = +2v 1 85
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670
5/ Phép toán FFT cơ số 2 ược thực hiện ối với dãy có chiều dài N thoả mãn: a N =ν4 b N = −4v 1 c N = +4v 1 d N = 4v
6/ Các thuật toán FFT phân tần số và FFT phân thời gian theo ồ hình cánh bướm có số các bước tính
giống hệt nhau, vì vậy số phép toán bao gồm phép nhân và cộng là như nhau dẫn ến hiệu quả của thuật toán là như nhau.
Nhận xét trên úng hay sai: a Đúng b Sai
7/ Khi thực hiện thuật toán FFT bằng phương pháp phân chia theo thời gian hay phân chia theo tần
số, các trật tự ầu ra không bị ảo lộn úng hay sai? a Sai b Đúng
8/ Các hệ số W k N hay còn ược gọi là các tính chất về pha trong biến ổi DFT ều có 2 tính chất:
Tính ối xứng : WNk+N2 =−WNk
Tính tuần hoàn : W k k
N +N =WN Đúng hay sai? a Đúng b Sai lOMoARcPSD| 36086670 b c d a b c d 87
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b c d
a A = +a W bNr , B = +a W bNr b
A = −a W bNr , B = −a W bNr c A
= +a W bNr , B = −a W bNr d A = −a W bNr , B = +a W bNr
13/ Phép tính cánh bướm cơ bản trong thuật toán FFT theo tần số như minh hoạ sau, hãy xác ịnh ầu ra A và B lOMoARcPSD| 36086670 a c a b 89
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670
so với tính toán DFT thông thường ta thấy: c
Số phép nhân giảm i và số phép cộng giữ nguyên. d
Số phép nhân, phép cộng cần thực hiện sẽ giảm i.
17/ Với ánh xạ theo hàng và cột, biến ổi DFT M −1 L−1 ∑∑ X p q( , )=
x l m W( ,) N(Mp q mL l+ )( + ) m=0 l=0 có thể ược biễu như sau:
X ( p q, )= ⎨⎧W ⎢⎡ − x l m W( , ) ⎤⎫ a ∑ ⎩ ⎣ ∑ ⎥⎦⎭⎬ l=L0 Nlq Mm =01 Mmq WLlp b X ( p q, )=∑ ⎨⎩⎧ ⎢⎡ ∑ l L0 WNlq m M0 x l m W( , ) ⎦⎥⎤⎭⎬⎫ Mmq WLlp = ⎣ = c
X ( p q, )=∑ = ⎨⎩⎧ ⎢⎣⎡ ∑ Ll −01 WNlq m M=0x l m W( , ) ⎦⎥⎤⎭⎬⎫ Mmq WLlp
X ( p q, )= − ⎨⎧W ⎢⎡ − x l m W( , ) ⎤⎫ d ∑ ⎩ ⎣ ∑ ⎦⎥⎭⎬ lL=01 Nlq Mm =01 Mmq WLlp
18/ Để thực hiện tính toán: X ( p q, )=∑ ⎨⎩⎧ ⎢⎣⎡ ∑ ⎥⎦⎤⎭⎬⎫ Ll=−01 WNlq Mm =−01x l m W( , ) Mmq WLlp
ta phải tính toán qua các bước:
a Bước 1. Đầu tiên, chúng ta tính các DFT M iểm. M −1 F l q x l m W q M m=0
với mỗi hàng l = 0,1, 2, , L −1. lOMoARcPSD| 36086670 ( ) ,
Bước 2. Tiếp ó, ta tính một mảng chữ nhật mới G l q ược xác ịnh như sau: ≤ ≤ M 1 G l q( ) ) 0 , =WNlqF l q( , 0
≤ ≤ql L −−1 Bước 3.
Cuối cùng, chúng ta tính toán các DFT L iểm. L−1 X p q( ,
)=∑G l q W( , ) Llp ( ) ,
l=0 với mỗi cột q = 0, 1, , M −1, của mảng G l q
. b Bước 1.Đầu tiên, ta tính ( )
một mảng chữ nhật mới G l q , ược xác ịnh như sau: M−1 F l q x l m W q M m=0
với mỗi hàng l = 0,1, 2, , L −1.
Bước 2. Tiếp ó, chúng ta tính toán các DFT L iểm.
L−1 X p q( , )
= ∑G l q W( , ) lp L ( ) , l=0
với mỗi cột q = 0, 1, , M −1, của mảng G l q . ( ) ,
Bước 3. Cuối cùng, ta tính một mảng chữ nhật mới G l q
ược xác ịnh như sau: G l
q( , )=WNlqF l q( , ) 00≤ ≤≤ ≤ql ML −−11 c Bước 1. Đầu tiên, chúng ta tính các DFT M iểm. ≤ ≤ M 1 G l q( ) ) 0 , =WNlqF l q( , 0
≤ ≤ql L −−1 Bước
2. Tiếp ó, chúng ta tính các DFT M iểm. M −1 F l q x l m W q M m=0
với mỗi hàng l = 0,1, 2, , L −1.
Bước 3. Cuối cùng, chúng ta tính toán các DFT L iểm. 91
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670
L−1 X p q( , )
= ∑G l q W( , ) lp L ( ) ,
l=0 với mỗi cột q = 0, 1, , M −1, của mảng G l q
. d Bước 1. Đầu tiên, chúng ta
tính toán các DFT L iểm.
L−1 X p q( , )
= ∑G l q W( , ) lp L ( ) , l=0
với mỗi cột q = 0, 1, , M −1, của mảng G l q .
Bước 2. Tiếp ó, chúng ta tính các DFT M iểm. M −1 F l q x l m W q M m=0
với mỗi hàng l = 0,1, 2, , L −1. ( ) ,
Bước 3. Cuối cùng, ta tính một mảng chữ nhật mới G l q
ược xác ịnh như sau: G l q(
, )=WNlqF l q( , ) 00≤ ≤≤ ≤ql ML −−11 x
19/ Khi chiều dài N = LM , dãy ( )n N có thể ược lưu trong một mảng hai chiều theo các cách khác ( )
nhau tuỳ theo việc ánh xạ của chỉ số n l m, cho các chỉ số với: a
l là chỉ số hàng 0 ≤ l ≤ L −1 m là chỉ số cột 0 ≤ m ≤ M −1 b
l là chỉ số hàng 0 ≤ l ≤ L −1 m là chỉ số cột 0 ≤ m ≤ M c l m
là chỉ số hàng 0 ≤ l ≤ L là chỉ số cột 0 ≤ m ≤ M −1 d l m
là chỉ số hàng 0 ≤ l ≤ L
là chỉ số cột 0 ≤ m ≤ M
20/ Nhờ tính thuận lợi của các tính chất ối xứng hình học và tính chất tuần hoàn của các hệ số mũ
WNkn trong các biểu diễn DFT N là số mũ cơ số 2, ta có thể: a
Tăng số lượng phép nhân cần thiết cho tính toán DFT từ N log2 N thành N 2 b
Giảm số lượng phép nhân cần thiết cho tính toán DFT từ N log2 N xuống N c N log
Tăng số lượng phép nhân cần thiết cho tính toán DFT từ N thành 2 N d
Giảm số lượng phép nhân cần thiết cho tính toán DFT từ N 2 xuống N log2 N lOMoARcPSD| 36086670
CHƯƠNG 8: CẤU TRÚC BỘ LỌC SỐ.
1/ Trong mô tả hàm truyền ạt H(z) của bộ lọc số: 93
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 Ta có a b c d lOMoARcPSD| 36086670 Ta có a b c d a b
Hàm truyền ạt mô tả hệ thống: b
Dựa trên phương trình sai phân mô tả hệ thống: y n( )=−∑N a y n ( − ( − k k)+∑M b x nr k) hoặc k 1= r 0= ∑ M b zr −r c
Chỉ dựa trên hàm truyền ạt mô tả hệ thống H(z) = r 0= N và không thể xây dựng theo 1 a zk −k phương trình sai phân. N M d Chỉ dựa trên
phương trình sai phân mô tả hệ thống y n( )=−∑a y n ( − ( − k k)+∑b x nr k) và 95
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 b c d lOMoARcPSD| 36086670 a b c d a
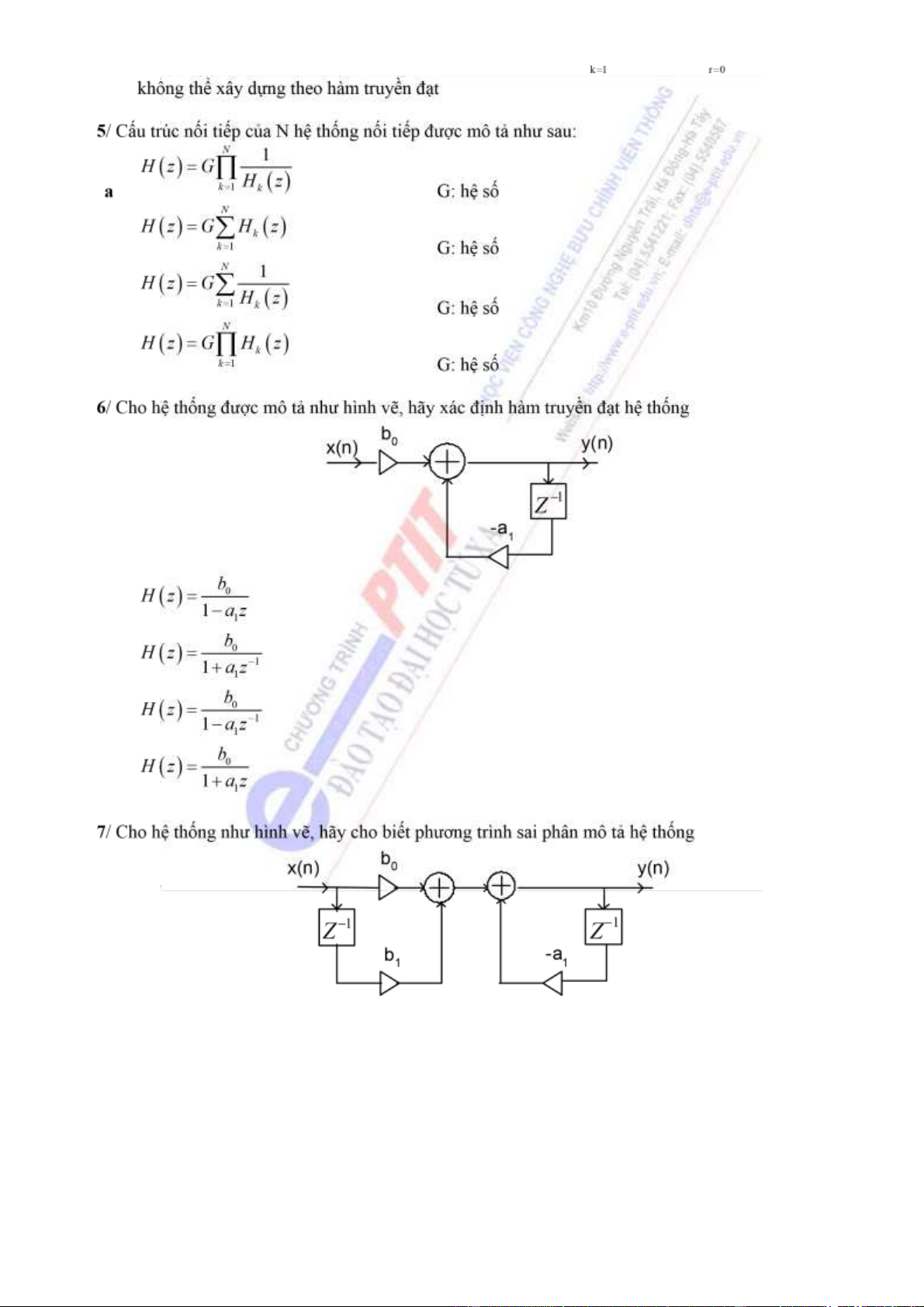
y(n) = -a y(n-1) - b x(n) - b x(n-1) 1 0 1 b
y(n) = a y(n-1) - b x(n) - b x(n-1) 1 0 1 c
y(n) = -a y(n-1) + b x(n) + b x(n-1) 1 0 1 d
y(n) = a y(n-1) + b x(n) + b x(n-1) 1 0 1
8/ Đáp ứng xung bộ lọc số FIR có tính chất: h n( ) = ±h N( − n) 97
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 d h n( ) = ±h N( b Đúng b Đúng lOMoARcPSD| 36086670 a b c d a Cấu trúc trực tiếp b Cấu trúc nối tiếp c Cấu trúc chuyển vị d
Cấu trúc trực tiếp chuẩn tắc II
13/ Cấu trúc nối tiếp của bô lọc số dựa trên biểu diễn hàm truyền ạt H z( )= G∏N H ( ) k z trong ó, k=1
hàm truyền ạt mỗi mắt lọc Hk ( )z có ặc iểm sau: a Hk ( )z là hàm bậc 1.
Hk ( )z = +1 b zk −1 b Hk ( )z là hàm có bậc bất
kỳ c Hk ( )z là hàm bậc 3 Hk ( )z = +1 b zk1 −1 +b zk2 −2 +b zk3 −3 H ( )z
H ( )z = +1 b z− + 1 b z−2 d k là hàm bậc 2 k k1 k2 99
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670
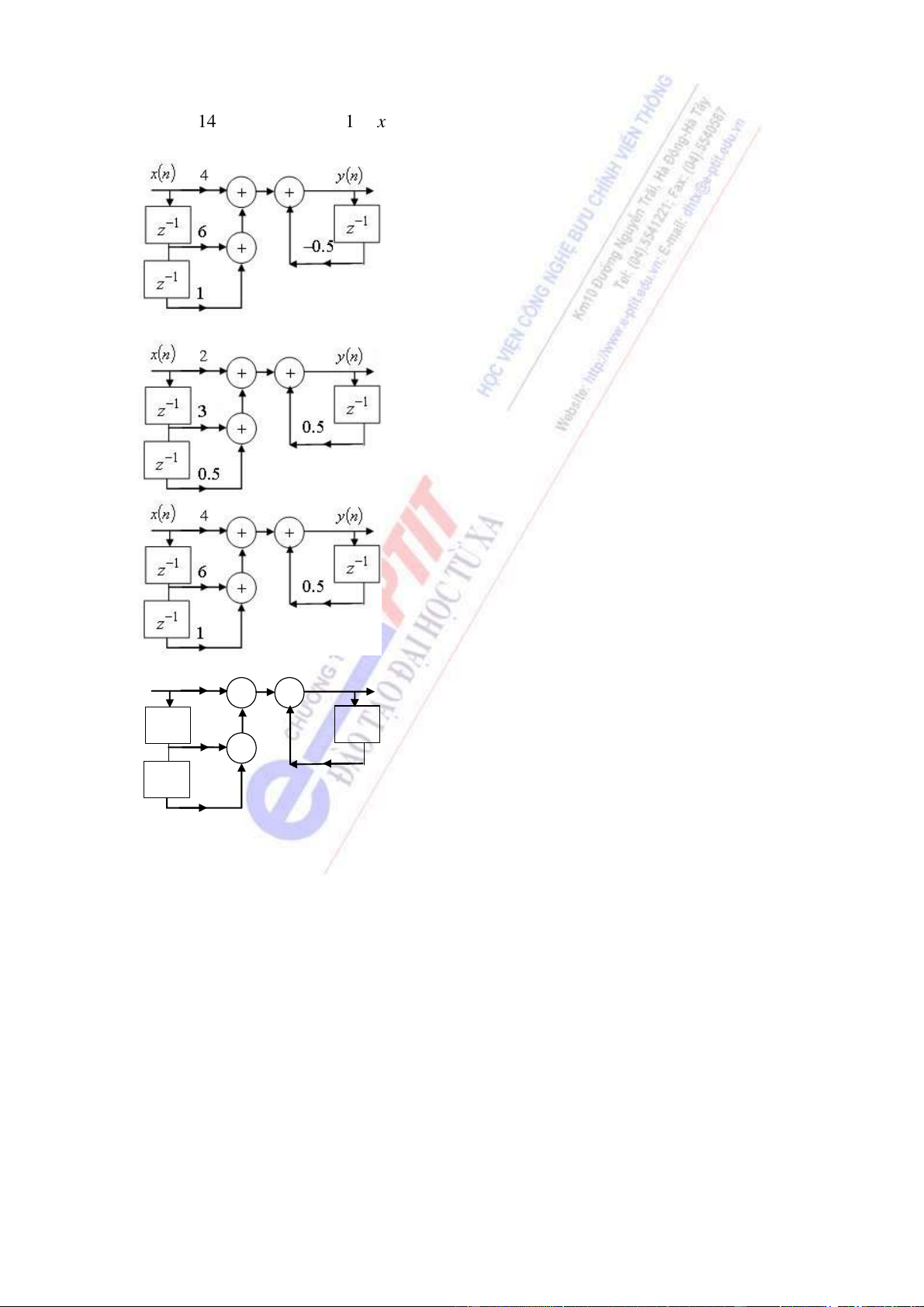
14 / Cho h ệ th ố ng ượ c mô t ả b ở i ph ươ ng trình sai phân sau: 2 () yn + ( yn − ) = 14 () xn +6 ( xn − ) 1 + ( xn −2 )
Hãy th ể hi ệ n h ệ th ố ng ở d ạ ng tr ự c ti ế p a () xn 2 () yn + + 1 − 1 − z 3 z + 0.5 − 1 − z 0.5
15 / Cho h ệ th ố ng có s ơ ồ nh ư sau, hãy xác ị nh b lOMoARcPSD| 36086670 c d a
2 y(n) + 3y(n-1) + 2y(n-2) = x(n) - 0.5x(n-1) - 2x(n-2)
y(n) + 0.5y(n-1) + 2y(n-2) = 2x(n) + 3x(n-1) + 2x(n-2)
2 y(n) + 3y(n-1) + 2y(n-2) = x(n) + 0.5x(n-1) + 2x(n-2)
y(n) - 0.5y(n-1) - 2y(n-2) = 2x(n) + 3x(n-1) + 2x(n-2)
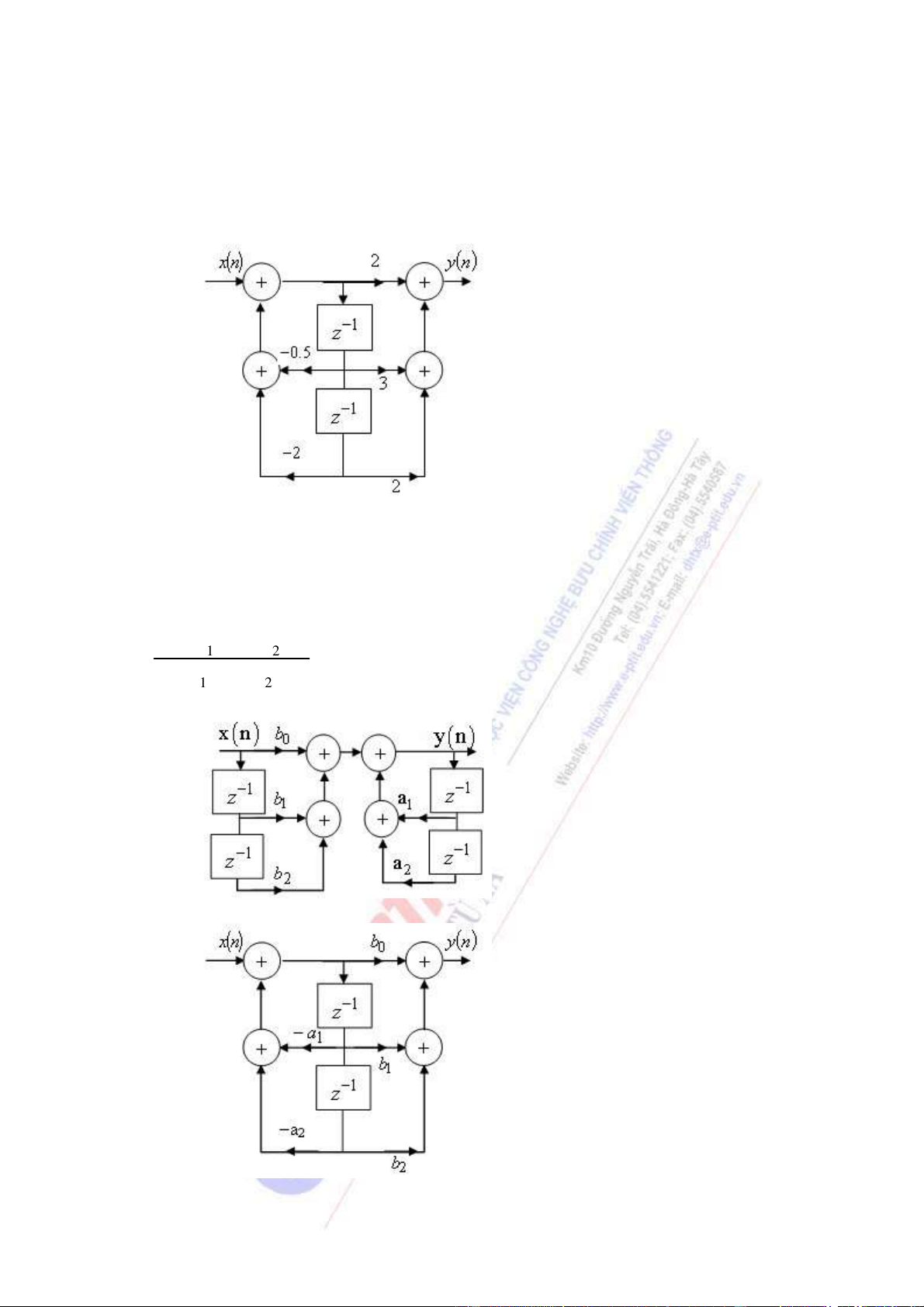
16 / Cho hàm truy ề n ạ t h ệ th ố ng có d ạ ng nh ư sau: 1 − 2 − b +bz + 0 1 bz 2 1 − 2 − 1 +az + 1 az 2
Hãy cho bi ế t c ấ u trúc d ạ ng tr ự c ti ế p chu ẩ n t ắ c II a 101
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 b c d H(z) = lOMoARcPSD| 36086670 b c 103
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 d 1 a 1 b 1 c 1 d
CHƯƠNG 9: LỌC SỐ NHIỀU NHỊP ′ F ′ < F
1/ Việc giảm tần số lấy mẫu từ một giá trị Fs _ về một giá trị Fs ( s s ) gọi là: a phép lấy mẫu. b phép phân chia. c phép nội suy. d phép giảm bậc. lOMoARcPSD| 36086670 a b c d a b c d 105
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b c d sau: a b c d a Sai b Đúng
7/ Bộ phân chia không gây ra hiện tượng chồng phổ, úng hay sai a Đúng b Sai
8/ Bộ nội suy không gây ra hiện tượng chồng phổ, úng hay sai a Đúng b Sai lOMoARcPSD| 36086670 a b c d 107
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b c d a Đúng b Sai a Đúng b Sai 13/ Phổ tín hiệu a Sai b Đúng 14/ Khi i qua bộ phân chia, tín hiệu sẽ có ặc iểm sau: a Trong miền n thì chiều dài tín hiệu giãn ra, trong miền ω tần số thì phổ tín hiệu bị dãn ra. b Trong miền lOMoARcPSD| 36086670 n thì chiều dài tín hiệu co lại, trong miền tần số ωthì phổ tín hiệu bị giãn ra c Trong miền n thì chiều dài tín hiệu giãn ra, trong miền ω tần số thì phổ tín hiệu cũng bị giãn ra d Trong miền n thì chiều dài tín hiệu co lại, trong miền tần số ωthì phổ tín hiệu cúng bị co lại 109
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 a b c d a lOMoARcPSD| 36086670 b c d ω ược a b c d
18/ Đối với bộ nội suy ta sẽ có quan hệ vào ra trong miền n như sau: ⎧ ⎛ ⎞ y ⎪ ⎜ ⎟L 2 x
n n = ±0, 1 ,L ±2 ,...L ( )n = ↑ ⎨ ⎝ ⎠ ⎪ a ⎩ 0 n ≠ b y↑ ( ) L
n = ⎧⎨⎩x L n0( . ) nn≠= 0, 1 ,± L ±2 ,...L 111
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 ⎧ ⎛ ⎞n
n = ±0, 1 ,L ±2 ,...L L lOMoARcPSD| 36086670 d ⎪⎩ a b c d Y ↓↑ a b ω b c d π ω = c M a
Đầu tiên tín hiệu x(n) i qua bộ lọc thông thấp với tần số cắt
, sau ó cho qua bộ phân chia hệ
số M ể tránh hiện tượng chồng phổ. π ωc = M b
Đầu tiên tín hiệu x(n) i qua bộ lọc thông cao với tần số cắt
, sau ó cho qua bộ phân chia hệ
số M ể tránh hiện tượng chồng phổ. π 113
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 ω= c M d lOMoARcPSD| 36086670 c d a b c d a c d 115
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670
26 / Quan h ệ vào ra c ủ a b ộ l ọ c phân chia ượ c bi ể u di ễ n trong mi ề n w nh ư sau:
27 / Quan h ệ vào ra c ủ a b ộ l ọ c n ộ i suy ượ c bi ể u di ễ n trong mi ề n n nh ư sau:
28 / Quan h ệ vào ra c ủ a b ộ l ọ c n ộ i suy ượ c bi ể u di ễ n trong mi ề n z nh ư sau: Y z = X z − Hz ↑ LH () L ( ) . () Y z = Xz − Hz ↑ LH () L ( ) . () Y z = Xz Hz ↑ LH () L ( ) . () Y z = X z − − Hz ↑ LH () L ( ) . () a b c d lOMoARcPSD| 36086670 a b c d a b c d
29/ Quan hệ vào ra của bộ lọc nội suy ược biểu diễn trong miền w như sau: a Y ( ) ) ) ↑ = LH e jω
X (−e jL.ω .H e( jω Y (e )= ) ) jω
X (−e− jL.ω .H e( jω b ↑LH Y ( ) ) ) ↑ = LH e jω
X e( − jL.ω .H e( jω c Y ( ) ) ) ↑ = LH e jω
X e( jL.ω .H e( jω d
30/ Quan hệ vào ra của hệ thống biến ổi nhịp lấy mẫu theo hệ số M/L trong miền z khi phân chia
trước và nội suy sau ược thể hiện theo quan hệ: 117
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670
31 / Quan h ệ vào ra c ủ a h ệ th ố ng bi ế n ổ i nh ị p l ấ y m ẫ u theo h ệ s ố M/L trong mi ề n z khi nôi suy tr ướ c và phân chia sau ượ c
th ể hi ệ n theo quan h ệ :
32 / Quan h ệ vào ra c ủ a h ệ th ố ng bi ế n ổ i nh ị p l ấ y m ẫ u theo h ệ s ố M/L trong mi ề n w khi phân chia
tr ướ c và n ộ i suy sau ượ c
th ể hi ệ n theo quan h ệ : a b lOMoARcPSD| 36086670 c d a b c d a b c d
33/ Quan hệ vào ra của hệ thống biến ổi nhịp lấy mẫu theo hệ số M/L trong miền w khi nôi suy trước và phân chia sau ược 119
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD| 36086670 b c d 34/ Cho tín hiệu: ⎧⎪1− x n( ) =⎨ lOMoARcPSD| 36086670 ⎪⎩0 a b c d
Khi X ( )z = z a ↓2 b ↓2 c 121
Downloaded by Dung Tran (tiendungtr12802@gmail.com)