Ôn tập Cấu trúc dữ liệu và giải thuật | Đại học Văn Lang

Ôn tập kết thúc môn học – CTDL&Giải thuật HK233 Giải: Lelt Mid Right 4 6 10 15 21 25 30 36 50 I = 0 I = 1 I = 2 I = 3 I = 4 I = 5 I = 6 I = 7 I = 8
B1: left = 0, Right = (n – 1) = (9 – 1)
B2: Mid = (left + right) / 2; Mid = (0 + 8) = 4(lấy nguyên)
Mid = 4  a[mid] = a[4] = 21 < x = 35
Left = mid + 1 = 4 + 1 = 5 (right = 8)
B3: Nếu left < right ; (5 < 8) Lelt Mid Right 4 6 10 15 21 25 30 36 50 I = 0 I = 1 I = 2 I = 3 I = 4 I = 5 I = 6 I = 7 I = 8 B2: Left = 5 , right = 8
Mid = (left + right) / 2; Mid = (5 + 8) / 2 = 6, 5(lấy nguyên) = 6
Mid = 6  a[mid] = a[6] = 30 < x = 35
Left = mid + 1= 5 + 1 = 6 (right = 8)
B3: Nếu left < right ; (6 < 8) Lelt Mid Right 4 6 10 15 21 25 30 36 50 I = 0 I = 1 I = 2 I = 3 I = 4 I = 5 I = 6 I = 7 I = 8 B2: Left = 6 , right = 8
Mid = (left + right) / 2; Mid = (6 + 8) / 2 = 7(lấy nguyên)
Mid = 7  a[mid] = a[7] = 36 > x = 35 Right = mid – 1 = 7 -1 = 6
B3: Nếu left < right) (6 <= 6) Left/Mid/ right 4 6 10 15 21 25 30 36 50 I = 0 I = 1 I = 2 I = 3 I = 4 I = 5 I = 6 I = 7 I = 8 B2: Left = 6 , right = 6
Mid = (left + right) / 2; Mid = (6 + 6) / 2 = 6(lấy nguyên)
Mid = 6  a[mid] = a[6] = 30 < x = 35
Right = Mid – 1 = 6 – 1 = 5
B3: Nếu left < right ; (6 < 5) Sai
 Kết luận x = 35 không có trong mảng a. Bài 2: Giải: Left Mid Right 1 2 4 5 6 8 12 15 I = 0 I = 1 I = 2 I = 3 I = 4 I = 5 I = 6 I = 7
B1: left = 0, Right = (n – 1) = (8 – 1) = 7
B2: Mid = (left + right) / 2; Mid = (0 + 7) = 3(lấy nguyên)
Mid = 3  a[mid] = a[3] = 5 < x = 12
Left = mid + 1; 3 + 1 = 4 (right = 7)
B3: Nếu left < right ; (4 < 7) Left Mid Right 1 2 4 5 6 8 12 15 I = 0 I = 1 I = 2 I = 3 I = 4 I = 5 I = 6 I = 7 B1: left = 4, Right = 7
B2: Mid = (left + right) / 2; Mid = (4 + 7) / 2 = 5 (lấy ngkuyên)
Mid = 5  a[mid] = a[5] = 8 < x = 12
Left = mid + 1 = 4 + 1 = 6 (right = 7)
B3: Nếu left < right ; (6 < 7) Left/mid Right 1 2 4 5 6 8 12 15 I = 0 I = 1 I = 2 I = 3 I = 4 I = 5 I = 6 I = 7 B1: left = 6, Right = 7
B2: Mid = (left + right) / 2; Mid = (6 + 7) = 6(lấy nguyên)
Mid = 6  a[mid] = a[6] = 12 = x = 12, End
Kết luận : Tìm được x ở vị trí i = 6 Bài 3: B1: i = 0 B2; j = 0
B3 Nếu A[0] > A[1]; 19 > 13, Hoán đổi vị trí 13 19 6 I = 0 I = 1 I = 2
B4: nếu j < n – i – 1; 0 < 2 – 0 – 1 , j = j + 1, j = 1 
B3 Nếu A[1] > A[2]; 19 > 6, Hoán đổi vị trí 13 6 19 I = 0 I = 1 I = 2
B4: nếu j < n – i – 1; 1 < 2 – 0 – 1 , False: Chuyển sang bước 5.
B5 : nếu i < n – 1, 0 < 2 – 1; i = i + 1, i = 1, j = 0.  B2: i = 1, j = 0
B3 Nếu A[0] > A[1]; 13 > 6, Hoán đổi vị trí 6 13 19 I = 0 I = 1 I = 2
B4: nếu j < n – i – 1; 0 < 2 – 1 – 1 , False: Chuyển sang bước 5.
B5 : nếu i < n – 1, 1 < 2 – 1 Fals  e = End Kết quả: A = [6, 13, 19] BAI 4: 40 15 75 30 I = 0 I = 1 I = 2 I = 3 B1: i = 0 B2; j = 0
B3 Nếu A[0] > A[1]; 40 > 15, Hoán đổi vị trí 15 40 75 30 I = 0 I = 1 I = 2 I = 3
B4: Nếu j < n – i – 1; 0 < 3 – 0 – 1; j = j + 1 j  = 1
B3 Nếu A[1] > A[2]; 40 > 75, Giữ nguyên.
B4: Nếu j < n – i – 1; 1 < 3 – 0 – 1; j = j + 1 j  = 2
B3 Nếu A[2] > A[3]; 75 > 30, Hoán đổi. 15 40 30 75 I = 0 I = 1 I = 2 I = 3
B4: Nếu j < n – i – 1; 2 < 3 – 1 – 1 Nêu sai chuyễn sang B5 
B5: i < n – 1; 0 < 3 – 1; i = i + 1 Quay lại B2  B2: i = 1, j = 0
B3 Nếu A[0] > A[1]; 15 > 40, Giữa nguyên.
B4: Nếu j < n – i – 1; 0 < 3 – 1 – 1; j = j + 1 j  = 1
B3 Nếu A[1] > A[2]; 40 > 30,Đúng thì Hoán đổi. 15 30 40 75 I = 0 I = 1 I = 2 I = 3
B4: Nếu j < n – i – 1; 1 < 3 – 1 – 1 Nếu sai qua B5 
B5: i < n – 1; 1 < 3 – 1; i = i + 1 ; i = 2 Qua  y lại B2 B2: i = 2 , j = 0
B3 Nếu A[0] > A[1]; 15 > 30, Nếu sai Giữa nguyên.
B4: Nếu j < n – i – 1; 0 < 3 – 2 – 1 Nếu sai qua B5 
B5: i < n – 1; 2 < 3 – 1; Nếu sai: END
Kết luận : a = [15, 30, 40, 75] Bài5:
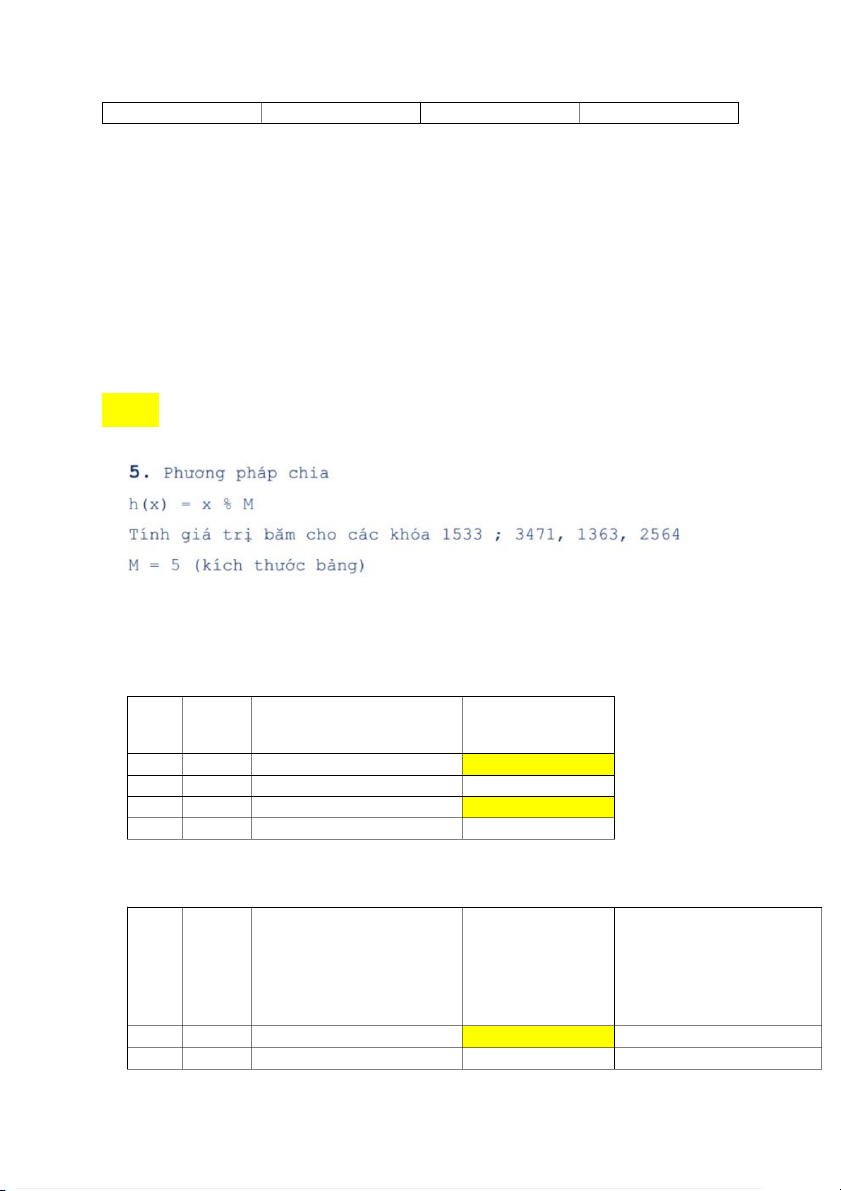
Ta có : x = 1533, 3471, 1363, 2564 M = 5 Sau khi Băm lần thứ 1: STT KEY Hash Chỉ mục mảng 1 1533 1533 % 5 = 3 3 2 3471 3471 % 5 = 1 1 3 1363 1363 % 5 = 3 3 4 2564 2564 % 5 = 4 4
Áp dụng tuyến tính sữ lý trùng lập (Tăng thêm đơn vị vào vị trí trống) STT KEY Hash Chỉ mục mảng
Sau kỹ thuật Linear Probing chỉ mục mảng 1 1533 1533 % 5 = 3 3 3 2 3471 3471 % 5 = 1 1 1 3 1363 1363 % 5 = 3 3 5 4 2564 2564 % 5 = 4 4 4 Bài 6: Bảng Băm 1: STT KEY Hash Chỉ mục mảng 1 1 1 % 20 = 1 1 2 2 2 % 20 = 2 2 3 42 42 % 20 = 2 2 4 4 4 % 20 = 4 4 5 12 12 % 20 = 12 12 6 14 14 % 20 = 14 14 7 17 17 % 20 = 17 17 8 13 13 % 20 = 13 13 9 37 37 % 20 = 17 17 Bảng tuyến tính: STT KEY Hash Chỉ mục mảng
Sau kỹ thuật Linear Probing chỉ mục mảng 1 1 1 % 20 = 1 1 1 2 2 2 % 20 = 2 2 2 3 42 42 % 20 = 2 2 3 4 4 4 % 20 = 4 4 4 5 12 12 % 20 = 12 12 12 6 14 14 % 20 = 14 14 14 7 17 17 % 20 = 17 17 17 8 13 13 % 20 = 13 13 13 9 37 37 % 20 = 17 17 18 Bài 7: A)
Bước 1: Bắt đầu, từ node góc có giá trị = 30, Do x = 30 > 22. Nên node cần tìm nằm phía bên trái,
B2: Node gốc của cây con bên trái = 20 , Do 20 < 22 , nên node cần tìm nằm ở bên phải cây con này ;
B3: Node tiếp theo nằm ở bên phải = 24, Do 24 > 22 , nên node cần tìm nằm bên trái cây con,
B4: Node có giá trị là 22 = x = 22, Ta thu được node cần tìm của cây nhị phân,
B) Mức (0) = 31 (Nút gốc), Mức (1) = 21, 41 , Mức (2) = 11, 25, 35, 47, Mức (3) = 7, 15, 23, 28 Bài 8: A)
B1: Bắt đầu, Từ node gốc là 71 , Do 71 < 75 , nên Node cần tìm nằm ở bên phải của cây.
B2: Node gốc bên phải là 79 , Do 79 > 75 , Nên node cần tìm nằm bên trái của cây,
B3: Node tiếp theo là 76 , Do 76 > 75 , Nên node cần tìm nằm bên trái của cây,
B4: Node có giá trị là 74 != x = 75 , Kết luân x không nằm trong cây.
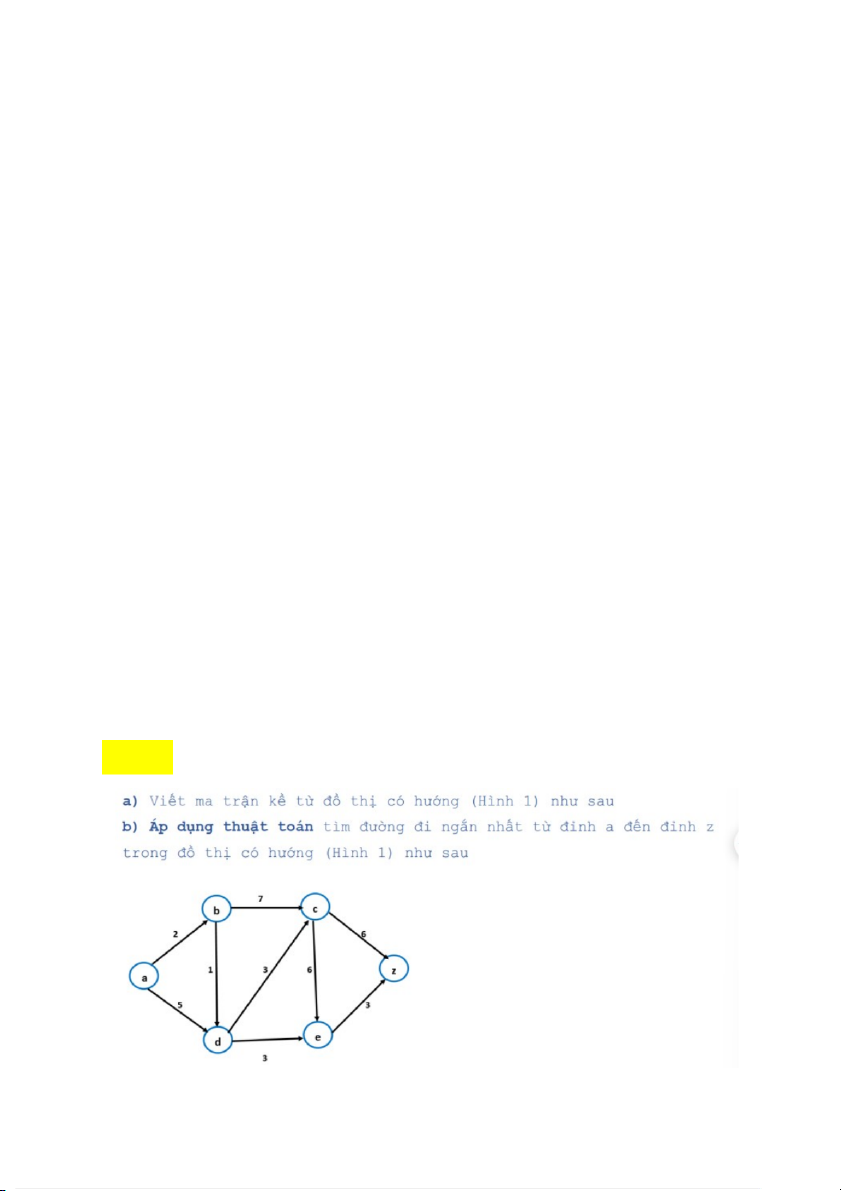
B) Mức (0) = 72 (node gốc), Mức (1) = 54, 80, Mức (2) = 43, 57, 78, 90, Mức (3) = 32, 46, 75, 79 Bài 9: A) Lập ma trận: A B C D E Z A 0 3 0 4 0 0 B 0 0 6 2 0 0 C 0 0 0 0 4 3 D 0 0 1 0 4 0 E 0 0 0 0 0 5 Z 0 0 0 0 0 0 B) Áp dụng thuật toán: Bước 1: T = {a, b, c, d, e, z}
L(a) = 0, L(b) = L(c) = L(d) = L(e) = L(z) := vô cùng Và
P(a) = P(b) = P(c) = P(d) = P(e) = P(z) := Ө Bước 2:
L(a) = min{L(x)| x thuột T} = 0
Suy ra: v = a và T := T – {a} = {b, c, d, e, z}
B3: Vì v != z , Sang bước 4
B4: Xét 2 đỉnh b , d kề đỉnh a.
L(b) := vô cùng > L(a) + w(a, b) = 0 + 3 = 3 L(b) := 3 , Gán P(b) := a(ghi nhớ đỉnh a  cạnh đỉnh b)
L(d) := vô cùng > L(a) + w(a, d) = 0 + 4 = 4 L(d) := 4 , Gán P(d) := a(ghi nhớ đỉnh a  cạnh đỉnh d) . B2
L(b) = min{L(x)| x thuột T} = 3
Suy ra: v = b và T := T – {b} = {c, d, e, z}
B3: Vì v != z , Sang bước 4
B4: Xét 2 đỉnh c, d kề đỉnh b.
L(‘c’) := vô cùng > L(b) + w(b, c) = 3 + 5 = 8 L(c) := 8 , Gán P(c) := b(ghi nhớ đỉnh b cạnh  đỉnh c) L(d) := 4 (không đổi) B2
L(d) = min{L(x)| x thuột T} = 4
Suy ra: v = d và T := T – {d} = {c, e, z}
B3: Vì v != z , Sang bước 4
B4: Xét 2 đỉnh c, e kề đỉnh d
L(‘c’) := 8 > L(d) + w(d, c) = 4 + 1= 5 L(c) := 5 , Gán P(c) := d(ghi nhớ đỉnh d cạnh đỉnh c) 
L(e) := vô cùng > L(d) + w(d, e) =4 + 4 = 8 L(e) := 8 , Gán P(e) := d(ghi nhớ đỉnh d cạnh  đỉnh e) B2
L(c) = min{L(x)| x thuột T} = 5
Suy ra: v = c và T := T – {c} = {e, z}
B3: Vì v != z , Sang bước 4
B4: Xét 2 đỉnh e, z kề đỉnh c
L(e) := 8 > L(c) + w(c, e) = 5 + 4 L(e) := 9 , Gán P(e) := c(ghi 
nhớ đỉnh c cạnh đỉnh e)
L(z) := vô cùng > L(c) + w(c, z) = 5 + 3 L(z) := 8 , Gán P(z) := c(ghi nhớ đỉnh c cạnh đỉnh z)  B2
L(z) = min{L(x)| x thuột T} = 8
Suy ra: v = z và T := T – {z} = {e} B3: Vì v = z , End  Kết quả: -
Đường đi ngắn nhất là: A D  C  Z  -
Tổng số đường đi được là = 8 Bai10: A) Viết ma trận: A B C D E Z A 0 2 0 5 0 0 B 0 0 7 1 0 0 C 0 0 0 0 6 6 D 0 0 3 0 3 0 E 0 0 0 0 0 3 Z 0 0 0 0 0 0 B) Thiết lập ma trận: Bước 1: T = {a, b, c, d, e, z}
L(a) = 0, L(b) = L(c) = L(d) = L(e) = L(z) := vô cùng Và
P(a) = P(b) = P(c) = P(d) = P(e) = P(z) := Ө Bước 2:
L(a) = min{L(x)| x thuột T} = 0
Suy ra: v = a, T = T - {a} = {b, c, d, e, z} B3: Vì v != z , Qua B4
B4: Có 2 đỉnh b, d kề a:
L(b) := vô cùng > L(a) + w(a, b) = 0 + 2 = 2, L(b) := 2, Gán P(b) := a(ghi nhớ đỉnh  a đến đỉnh b)
L(d) := vô cùng > L(a) + w(a, d) = 0 + 5 = 5, L(d) := 5, Gán P(d) := a(ghi nhớ đỉnh  a đến đỉnh d) Bước 2:
L(b) = min{L(x)| x thuột T} = 2
Suy ra: v = b, T = T - {b} = {c, d, e, z} B3: Vì v != z , Qua B4
B4: Có 2 đỉnh c, d kề b:
L(‘c’) := vô cùng > L(b) + w (b, c ) = 2 + 7 = 9, L(c) := 9 , Gán P(c) := b(ghi nhớ đỉnh b đến  đỉnh c)
L(d) := vô cùng > L(d) + w (b, d) = 2 + 1, L(d) := 3 , Gán P(c) := b(ghi nhớ đỉnh b đến đỉnh  d) Bước 2:
L(d) = min{L(x)| x thuột T} = 3
Suy ra: v = d, T = T - {d} = {c, e, z} B3: Vì v != z , Qua B4
B4: Có 2 đỉnh e, c kề d:
L(‘c’) := 9 > L(d) + w(d, c) = 3 + 3 = 6, L(c) := 6, Gán P(c) := d(ghi nhớ đỉnh d đến đỉnh e) 
L(e) := vô cùng > L(d) + w(d, e) = 3 + 3 = 6, L(e) := 6, Gán P(e) := d(ghi nhớ đỉnh d đến  đỉnh e) Bước 2:
L(e) = min{L(x)| x thuột T} = 6
Suy ra: v = e, T = T - {e} = {c, z} B3: Vì v != z , Qua B4 B4: Có 1 đỉnh z kề e:
L(z) := vô cùng > L(e) + w(e, z) = 6 + 3 = 9 L(z) := 9, Gán P(z) := e(ghi nhớ đỉnh e đến đỉnh z)  Bước 2:
L(z) = min{L(x)| x thuột T} = 9
Suy ra: v = z, T = T - {z} = {c} B3: Vì v = z , END Kết quả: A B  D  E
  Z và số đường là 9