



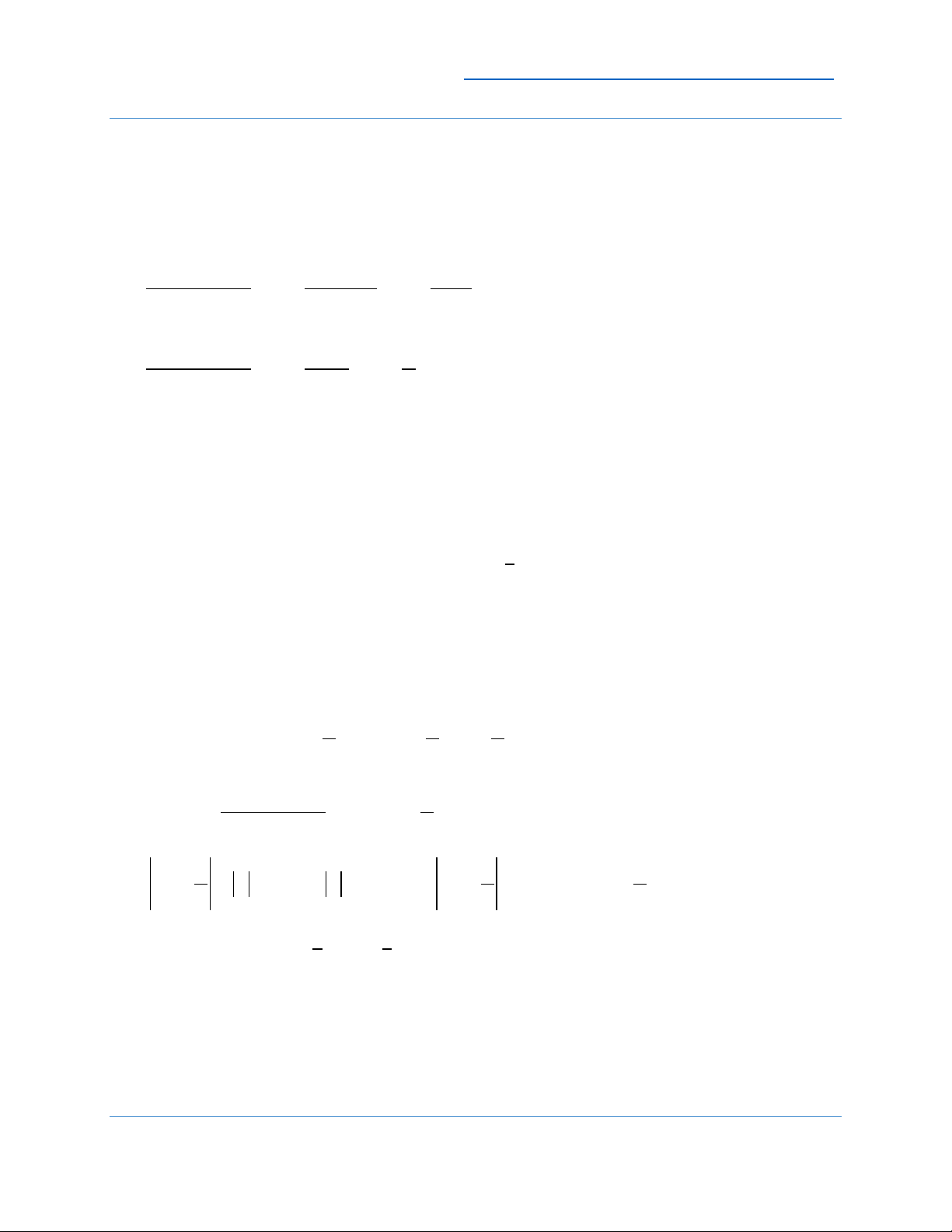







Preview text:
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179
ÔN TẬP GIẢI TÍCH 1 (PHẦN 3) Đạo hàm 1. Mở đầu:
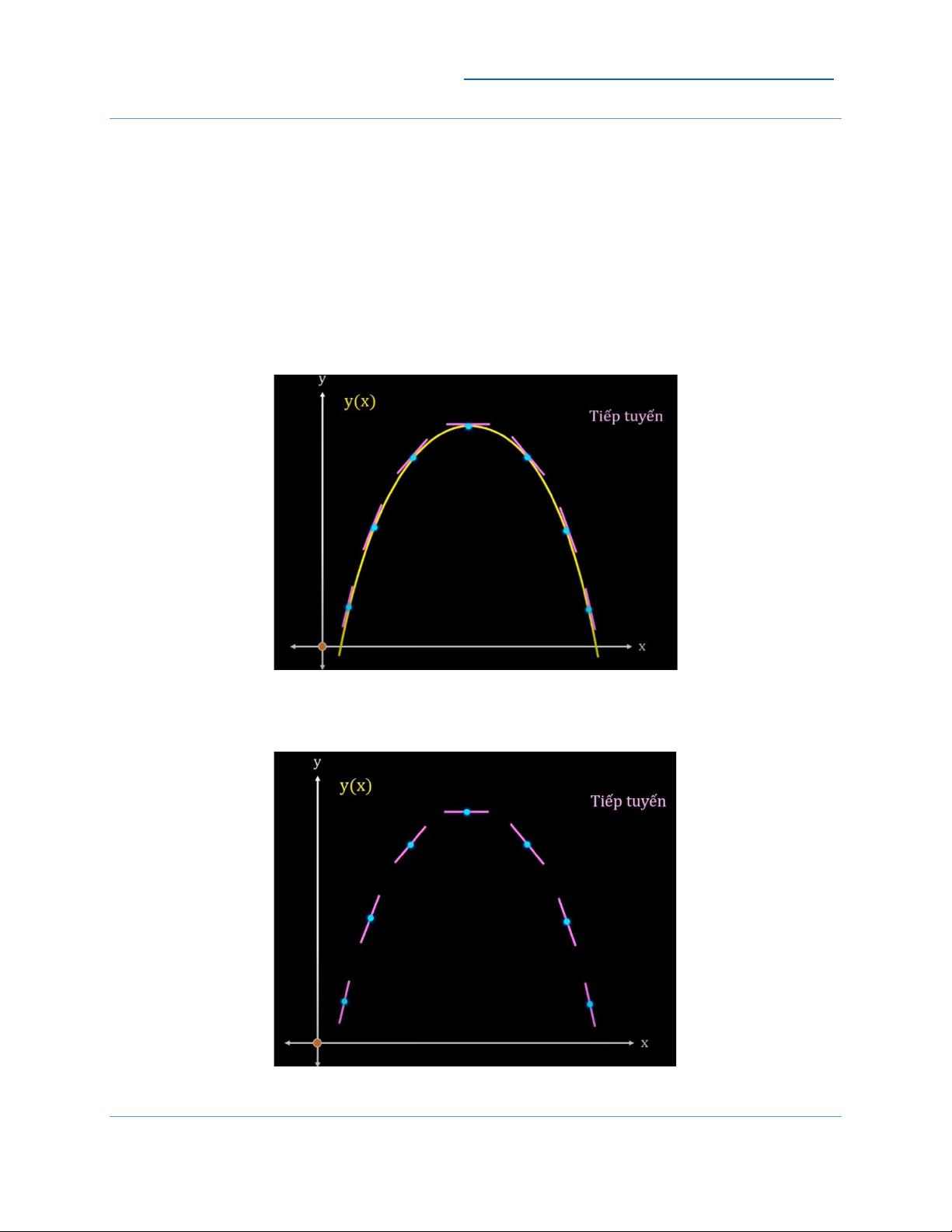
- Lấy một hàm số bất kì, dễ dàng thấy được đồ thị hàm số được cấu tạo bởi các
đoạn thẳng nhỏ, ở đó mỗi đoạn sẽ tiếp xúc với một điểm nằm trên đồ thị hàm số.
Các đoạn thẳng này còn được gọi là đường tiếp tuyến.
Nếu chúng ta không có đồ thị thì vẫn có thể hình dung được thông qua các đường tiếp tuyến. 1
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179
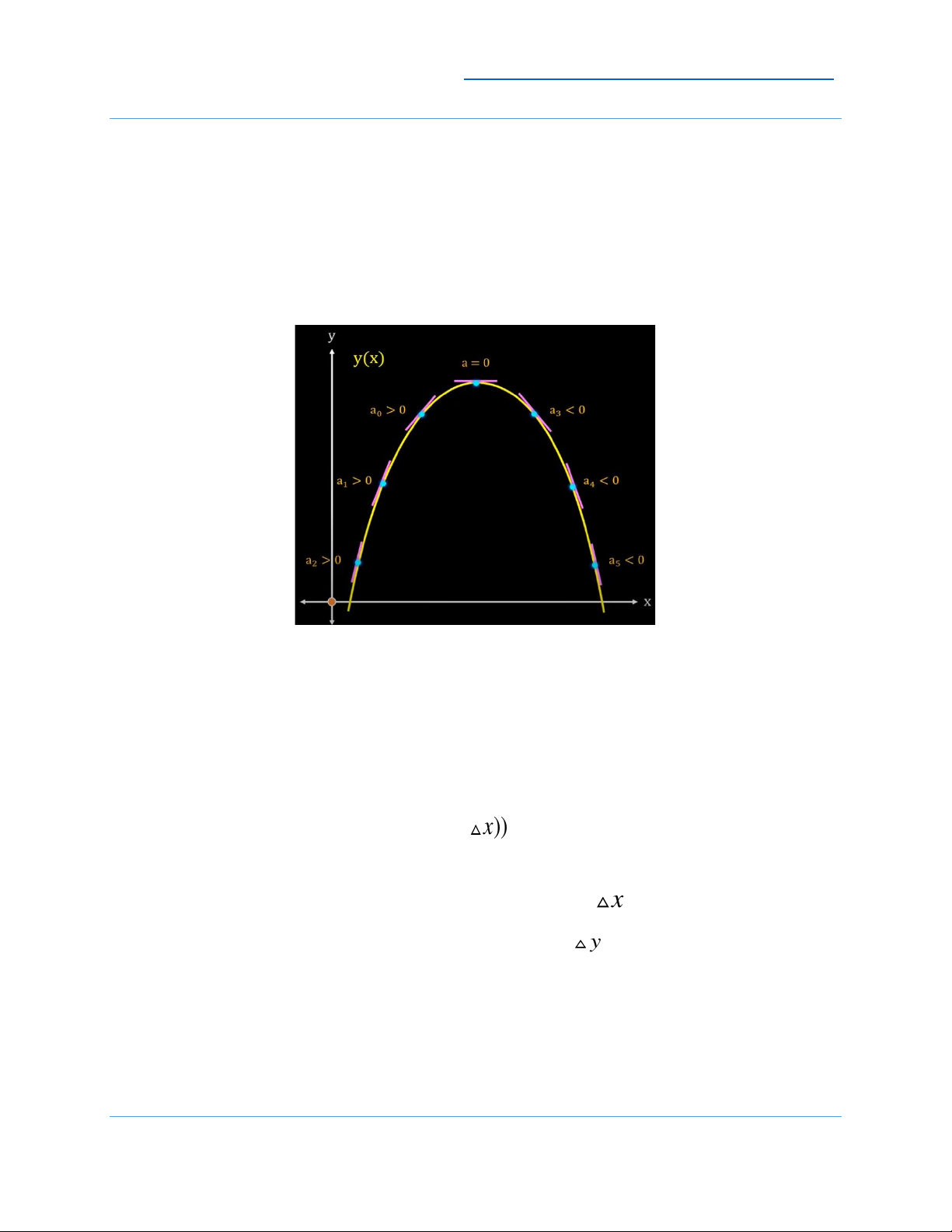
Bây giờ chúng ta sẽ khảo sát độ dốc của các đường tiếp tuyến. Độ dốc ở đây chính
là hệ số góc của các đường tiếp tuyến này. Dễ thấy rằng:
- Ba đường tiếp tuyến bên trái có độ dốc > 0.
- Đường tiếp tuyến ở giữa có độ dốc = 0 do nằm ngang.
- Ba đường tiếp tuyến bên phải có độ dốc < 0.
Vậy làm thế nào có thể tính được độ dốc chính xác?
Bài toán tìm hệ số góc của tiếp tuyến với một đường cong, bài toán tìm vận tốc của
một chất điểm,… dẫn đến khái niệm đạo hàm. Nhìn chung, muốn khảo sát một quá
trình diễn ra nhanh hay chậm, người ta dùng khái niệm đạo hàm.
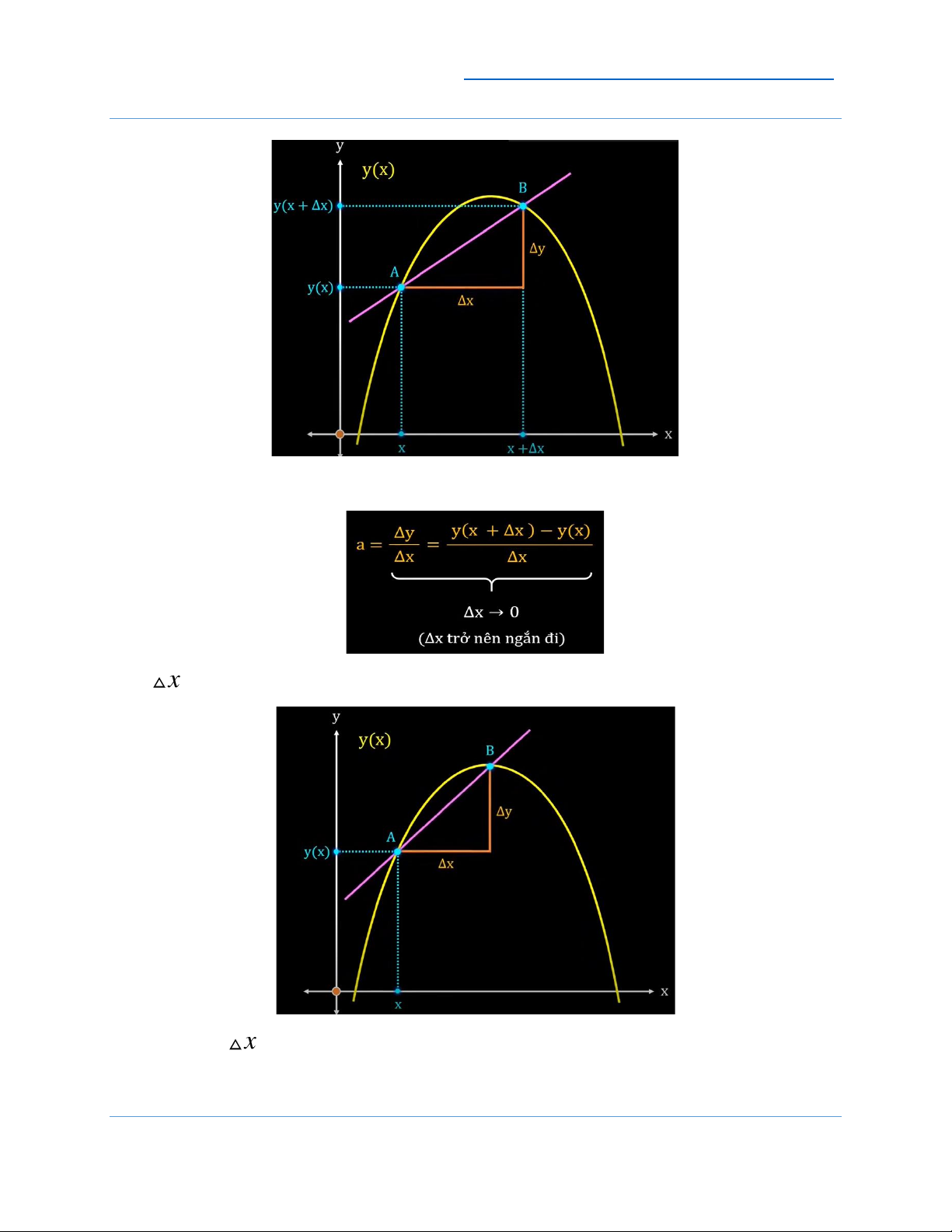
2. Xây dựng định nghĩa đạo hàm và hàm khả vi: - Xét hai điểm (
A x, y(x)), B(x + x
, y(x + x)) . Nối hai điểm này lại ta được đường cát tuyến AB.
Khoảng cách từ A đến B theo chiều ngang có độ dài là x .
Khoảng cách từ A đến B theo chiều dọc có độ dài là y . 2
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179
Khi đó hệ số góc của AB, hay độ dốc của AB được tính như sau:
Khi x trở nên nhỏ đi thì khi đó AB sẽ bị thu hẹp dần lại:
Tiếp tục cho x nhỏ đi thì AB càng bị thu hẹp tiếp: 3
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179
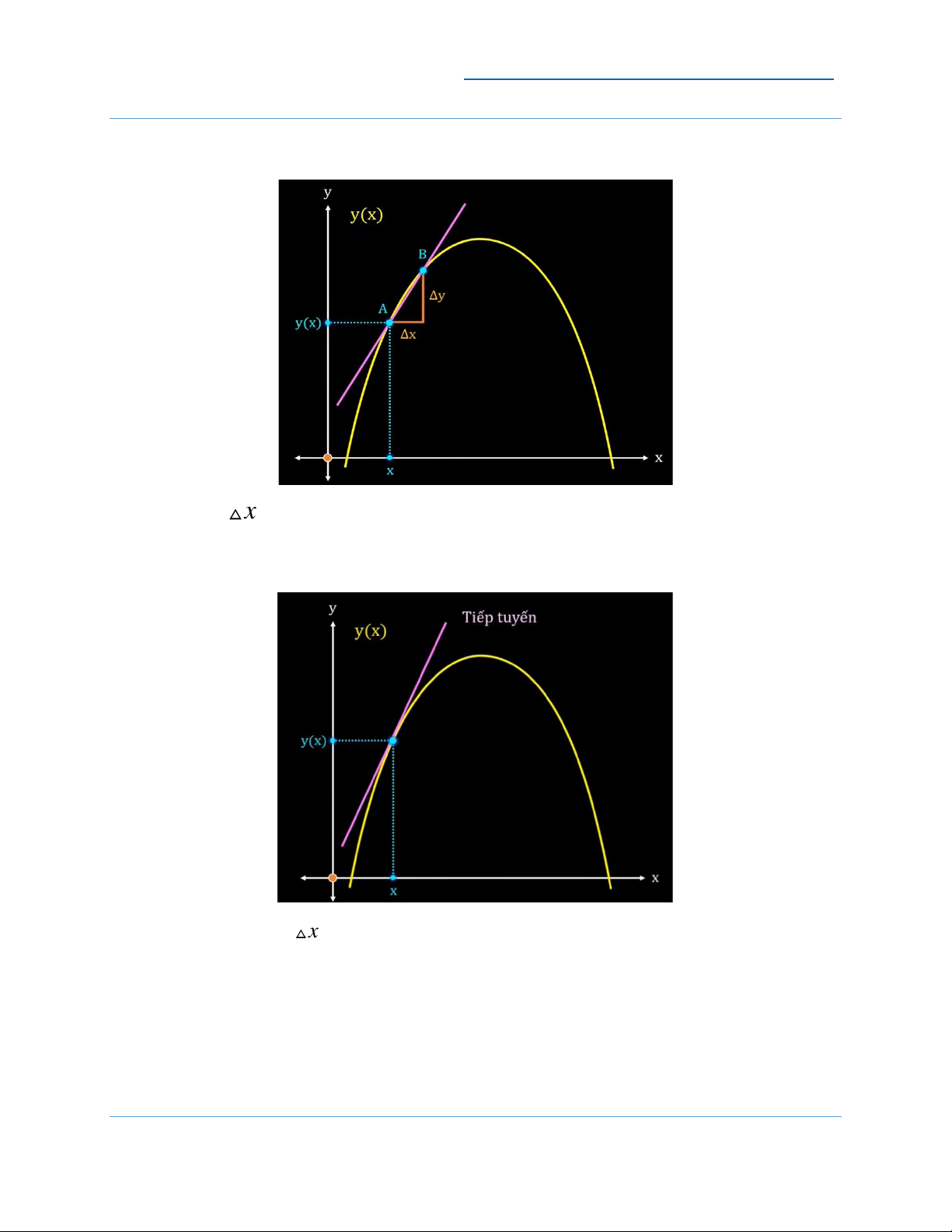
Tiếp tục cho x thật nhỏ và dần tới 0 (miễn là không bằng 0). Khi đó bằng mắt
thường ta thấy điểm B gần như trùng với điểm A (phải phóng thật to lên mới thấy chúng không chạm nhau).
Có thể thấy, khi cho x dần tới 0, ta đã biến cát tuyến AB thành đường tiếp tuyến
mà chúng ta đề cập ở phần đầu. Vậy ta có công thức để tính độ dốc của đường tiếp
tuyến tại tọa độ (x, y(x)) , đây chính là đạo hàm tại điểm x : 4
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179
Hay viết cách khác, đạo hàm của một hàm số tại điểm x , kí hiệu là f '(x ) hoặc o 0
y '(x ) , nghĩa là: 0
f (x) − f (x ) 0 f '(x ) = lim 0 x→ − 0 x x x0
f (x) − f (x )
Ta nói rằng hàm số f (x) khả vi tại điểm x nếu tồn tại giới hạn 0 lim 0 x→ − 0 x x x0
f (x) − f (x ) 0 lim . x→ − 0 x x x0
Nếu hàm số f (x) khả vi tại mọi điểm x (a,b) và xác định trong khoảng (a,b) thì
ta nói rằng: f (x) khả vi trong khoảng (a,b) .
Ví dụ 1: Xét tính khả vi của hàm số f (x) = 2x −1 tại x = 5 . 0
f (x) − f (5) 2x −1 − 3 2x −1 − 9 Giải: Xét lim = lim = lim x 5 → x 5 → x 5 x − 5 x − 5
→ (x − 5)( 2x −1 + 3) 2(x − 5) 2 1 = lim = lim = x 5 → x 5
(x − 5)( 2x −1 + 3) → 2x −1 + 3 3
f (x) − f (5) 1 Tức là lim
f (x) khả vi tại x = 5 và f '(5) = . 0 x 5 → x − 5 3
Ví dụ 2: Xét tính khả vi của hàm số 2
f (x) = x trên ℝ. 5
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179
Giải: Lấy x . Xét 0 2 2
f (x) − f (x ) x − x
(x − x )(x + x ) 0 0 0 0 lim = lim = lim
= lim(x + x ) = 2x 0 0 x→ → → → − − − 0 x x x x 0 x x x x 0 x x x x 0 x 0 0 0
f (x) − f (x ) 0 lim x
f (x) khả vi x . 0 0 x→ − 0 x x x0
3. Định nghĩa đạo hàm một phía:
- Như chúng ta đã biết một cách định nghĩa giới hạn khác đó là giới hạn một phía.
Đạo hàm cũng tương tự như vậy.
- Cần nằm rõ đạo hàm một phía bởi phần lớn các bài toán sẽ đề cập đến phần này. Định nghĩa 1:
f (x) − f (x )
Nếu tồn tại giới hạn (hữu hạn) bên phải 0 lim
, ta sẽ gọi giới hạn đó + x→ − 0 x x x0
là đạo hàm bên phải của hàm số y = f (x) tại x = x và kí hiệu là f '(x + ) . 0 0
f (x) − f (x )
Nếu tồn tại giới hạn (hữu hạn) bên trái 0 lim
, ta sẽ gọi giới hạn đó là − x→ − 0 x x x0
đạo hàm bên trái của hàm số y = f (x) tại x = x và kí hiệu là f '(x −) . 0 0
Định lí: Hàm số y = f (x) có đạo hàm tại + −
x = x khi và chỉ khi f '(x ), f (x ) tồn 0 0 0
tại và bằng nhau. Khi đó: f '(x + ) f (x − = ) = f '(x ) . 0 0 0
Ví dụ 3: Chứng minh rằng hàm số 𝑥2, 𝑥 ≥ 0 𝑓(𝑥) = { −𝑥, 𝑥 < 0
có các đạo hàm một bên, nhưng không có đạo hàm tại x = 0 . 0 Giải: Ta có: 6
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179 2 +
f (x) − f (0) x f '(0 ) = lim = lim = 0; + + x→0 − x→0 x 0 x −
f (x) − f (0) −x f '(0 ) = lim = lim = 1 − − − x→0 − x→0 x 0 x
Vậy tại x = 0 , hàm số này có đạo hàm bên phải bằng 0, đạo hàm bên trái bằng -1. 0
Vì các đạo hàm bên phải và bên trái khác nhau, nên hàm số không có đạo hàm tại x = 0 . 0 Lưu ý: 𝑢(𝑥), 𝑥 ≠ 𝑎 Nếu 𝑓(𝑥) = { 𝑚, 𝑥 = 𝑎
● x a : f '(x) = u '(x) ● x = a :
- Viết “ x = a : f '(a) = 0 ” là sai. f x − f a u x − m - Cách viết đúng là ( ) ( ) ( ) x = a : lim = lim . x→a x→a x − a x − a
(tức là tại một điểm phải viết đúng định nghĩa để tính đạo hàm)
4. Mối quan hệ giữa khả vi và liên tục:
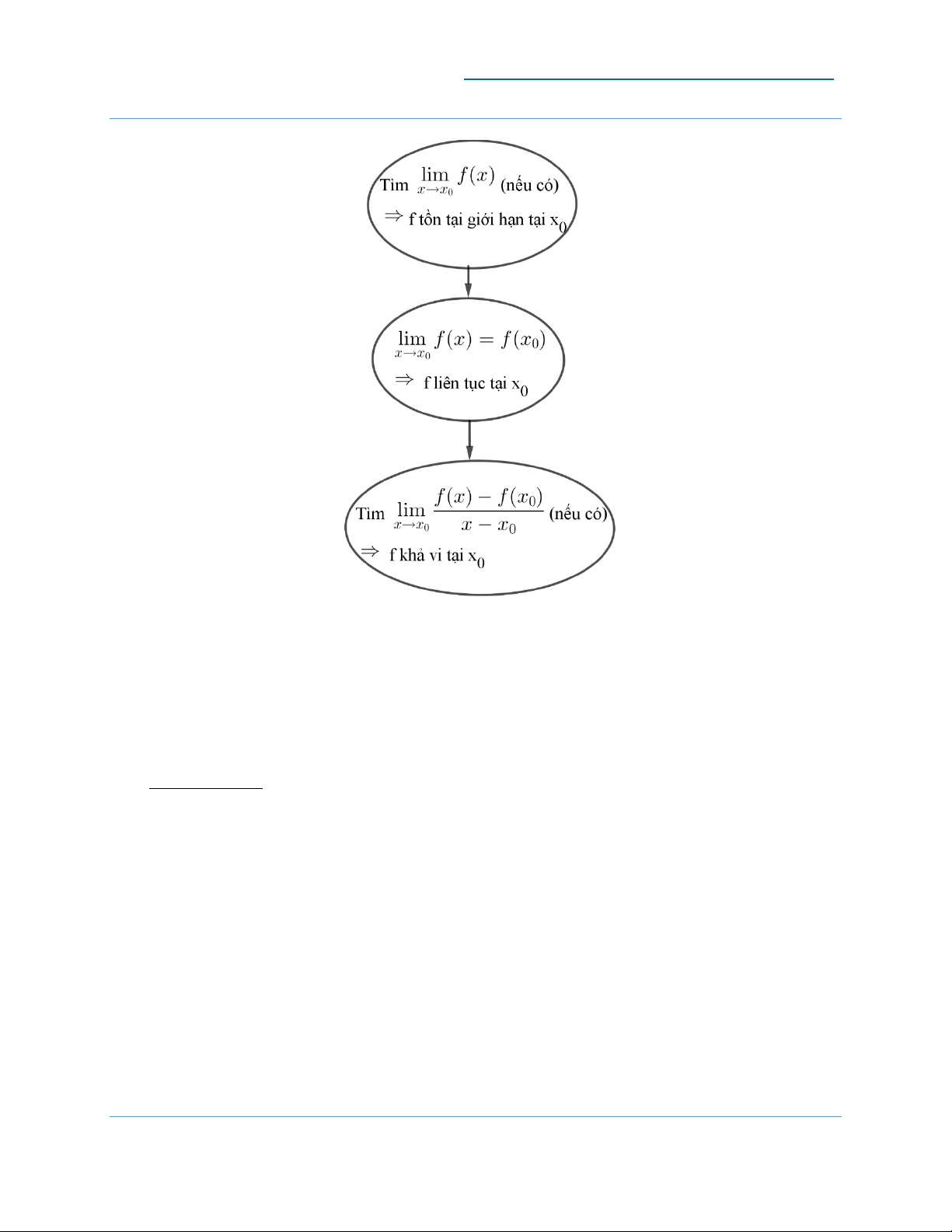
Ta có sơ đồ chứng minh hàm khả vi tại x sau đây: 0 7
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179 Nhận xét:
● Hàm số khả vi tại x liên tục tại x có giới hạn tại x (thừa nhận, không cần 0 0 0 chứng minh)
● Hàm số liên tục tại x chưa chắc khả vi tại x vì chưa chắc tồn tại 0 0
f (x) − f (x ) 0 lim . x→ − 0 x x x0
● Hàm số không liên tục tại x chắc chắn không khả vi tại x . 0 0
● Câu hỏi là tại những điểm nào thì hàm số không khả vi?
Ta đã biết bản chất khả vi tại 1 điểm x chính là sự tồn tại của 1 tiếp tuyến của 0
hàm số tại điểm x . Xét vài ví dụ sau: 0 ▲ Xét hàm số 2
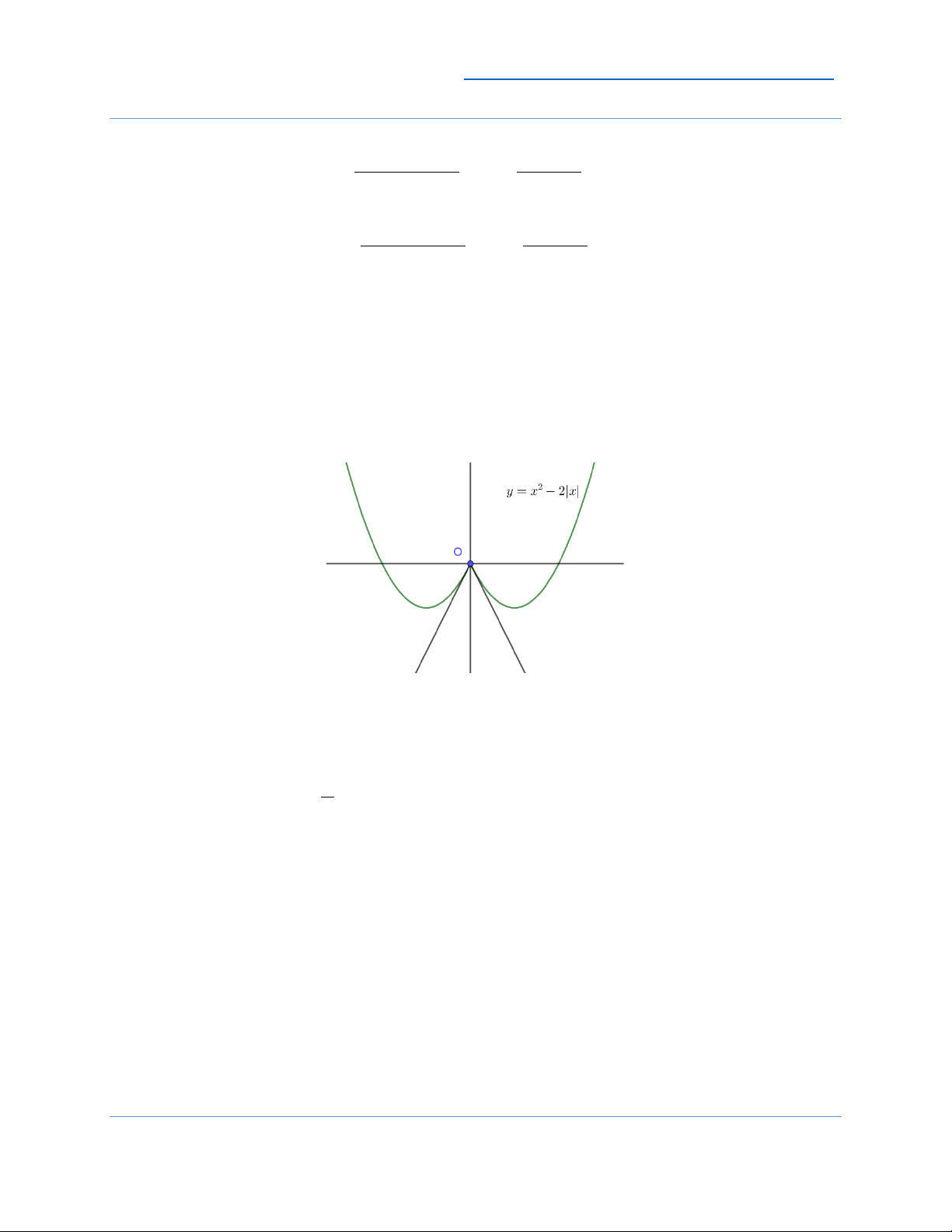
f (x) = x − 2 | x | . Ta có 8
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179 2
f (x) − f (0) x − 2x lim = lim = 2 − , + + x 0 → − x 0 x 0 → x 2
f (x) − f (0) x + 2x lim = lim = 2. − − x→0 − x→0 x 0 x
Do đó tại điểm x = 0, hàm số có đạo hàm bên phải f '(0+ ) = 2 − và đạo hàm bên
trái f '(0− ) = 2, nhưng không có đạo hàm tại điểm đó.
Có nghĩa là tại x = 0 thì tồn tại tận 2 tia tiếp tuyến với hệ số góc 2 và 2 − . Vì thế
hàm số không thể khả vi tại x = 0. Điểm x = 0 ở đây được gọi là điểm nơi hàm số bị gãy.
Dễ thấy tại điểm gãy thì hàm số vẫn liên tục, nhưng không khả vi. 1 , x 0
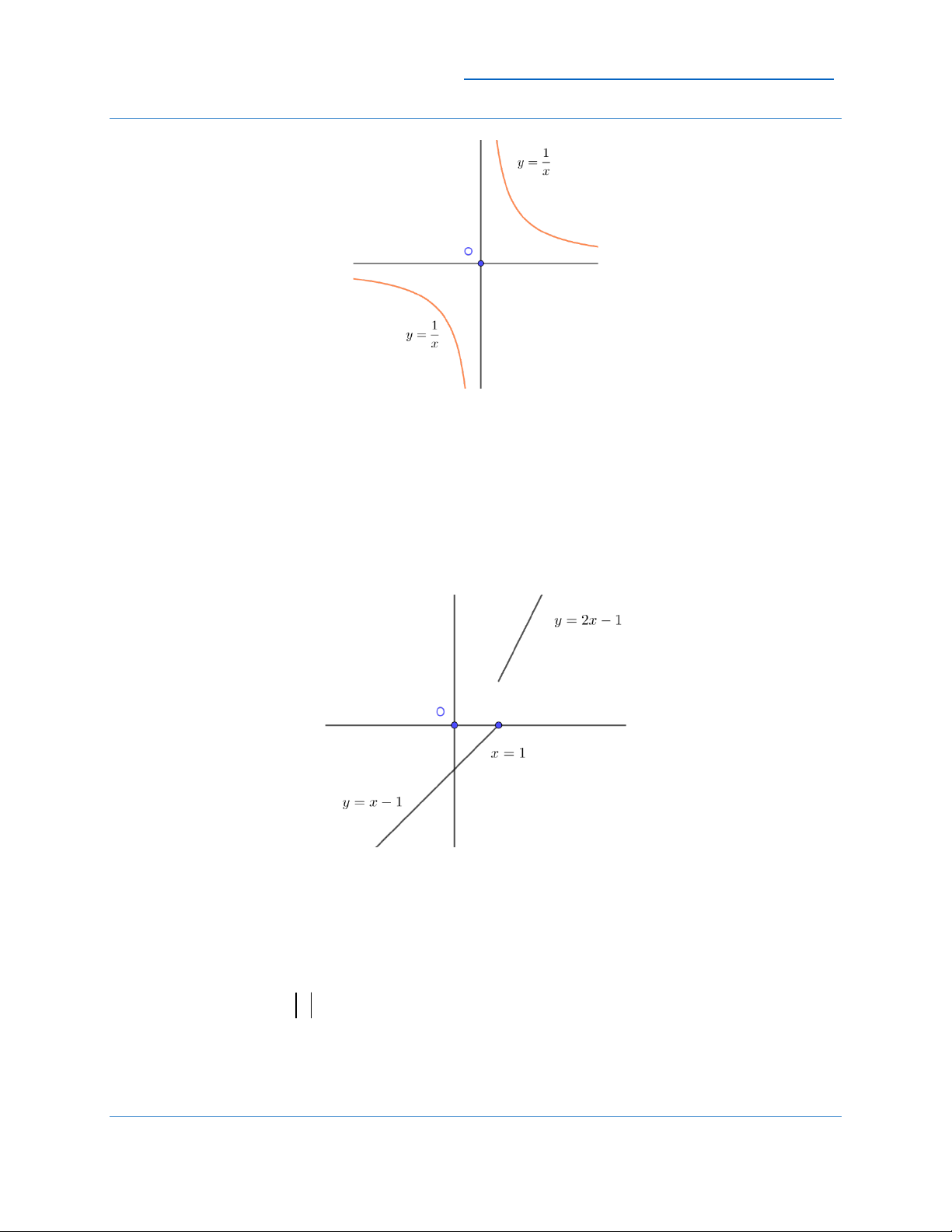
▲ Xét hàm số f (x) = x 0,x = 0
Nhận thấy x = 0 là điểm gián đoạn, ở đó hàm số bị đứt đoạn nên nó không liên tục.
Mà đã không liên tục thì chắc chắn không khả vi tại x = 0 . 9
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179
2x −1, x 1
▲ Xét hàm số f (x) =
x −1, x 1
Nhận thấy x = 1 là điểm gián đoạn, ở đó hàm số bị đứt đoạn nên nó không liên tục.
Mà đã không liên tục thì chắc chắn không khả vi tại x = 1.
Vậy kết luận, hàm số sẽ không khả vi tại điểm gãy và điểm đứt. 𝑥, 𝑥 ≥ 0
Ví dụ 4: Xét f (x) = x = { −𝑥, 𝑥 < 0 Ta thấy: 10
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179
lim f (x) = lim x = 0 + + x→0 x→0
lim f (x) = lim − x = 0 − − x→0 x→0
lim f (x) = 0 x→0
Tức hàm số có giới hạn tại x = 0 . Mà lim f (x) = f (0) = 0 hàm số liên tục tại x 0 → x = 0 .
Nhưng khi xét tính khả vi:
f (x) − f (0) x − 0 lim = lim =1 + + x 0 → − x 0 x 0 → x − 0
f (x) − f (0) −x − 0 lim = lim = 1 − − − x 0 → − x 0 x 0 → x − 0
f (x) − f (0)
f (x) − f (0) lim lim ∄ f '(0) . + − x 0 → − x 0 x 0 → x − 0
Ví dụ 5: Cho hàm số: sin 𝑥 , 𝑥 ∈ 𝑄 𝑓(𝑥) = { 𝑥, 𝑥 ∈ 𝐼
Xác định f '(x) . Giải:
Ta cần tìm x . Để khả vi tại x thì hàm số phải liên tục tại x . 0 0 0
Xét tính liên tục tại x : lim f (x) = lim f (x) = f (x ) sin x = x 0 0 0 0 x→ → 0 x x 0 x x Q x I
Ta thấy f (t) = t − sin t đồng biến trên
và f (0) = 0 t = sin t có nghiệm duy nhất t = 0 .
sin x = x x = 0 0 0 0 11
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179
+) x 0 sin x x hàm số không có giới hạn tại x = x hàm số không liên 0 0 0 0
tục tại x = x hàm số không có đạo hàm tại x = x . 0 0
+) x = 0 f (0) = 0 , khi đó: 0
f (x) − f (0) sin x − 0 sin x lim = lim = lim =1 x→0 x→0 x→0 x − 0 x − 0 x x Q x Q x Q
f (x) − f (0) x − 0 x lim = lim = lim =1 x→0 x→0 x→0 x − 0 x − 0 x x I x I x Q f '(0) =1.
Ví dụ 6: Cho hàm số 1 𝑥2 sin , 𝑥 ≠ 0 𝑓(𝑥) = { 𝑥 0, 𝑥 = 0
Chứng minh rằng: f (x) khả vi tại x = 0 nhưng f '(x) không liên tục tại x = 0 . Giải: ' 1 1 1 +) x 0 : 2
f '(x) = x sin = 2xsin − cos x x x
f (x) − f (0) 1 +) x = 0 : lim = lim xsin = 0 x 0 → x 0 x − 0 → x 1 1 1 (do x sin
x mà lim x = 0 lim xsin = 0 lim xsin = 0 ) x x→0 x→0 x→0 x x 1 1 2𝑥 sin − cos , 𝑥 ≠ 0 Ta có 𝑓′(𝑥) = { 𝑥 𝑥 0, 𝑥 = 0
Xét lim f '(x) : x→0 12
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179 1 +) lim 2x sin = 0 x→0 x +) Chọn hai dãy số: 1 1 x = → 0,limcos =1 n x 0 n2 → xn 1 1 y = → 0,limcos = 1 − n x 0 n2 + → yn 1
∄ limcos ∄ lim f '(x) . x→0 x x→0 Vi phân
1. Định nghĩa vi phân: f : A mở → , f khả vi / , x .
Vi phân của f tại x là 1 ánh xạ tuyến 0 0 tính: df (x ) : → 0
h → df (x )(h) = f '(x ).h 0 0
(ở đây h chính là x )
Áp dụng định nghĩa trên vào hàm số y = x , ta có
dx = d (x) = (x) ' x =1. x = x = . h
Do đó, với hàm số y = f (x) ta có
dy = df (x) = f '(x)d . x
Kết quả này sẽ được thường xuyên sử dụng để tính vi phân hàm số, và nó
cũng sẽ là cơ sở để chúng ta xây dựng công thức nguyên hàm, tích phân ở phần sau. 13
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179
Chú ý: Về bản chất, đạo hàm chính là vi phân.
Ví dụ 7: Tìm vi phân của các hàm số sau: a) 3
y = x − 5x + 1 b) 3 y = sin x Giải: a) 3 2
y = x − 5x + 1, y ' = 3x − 5. Vậy 3 2
dy = d (x − 5x + 1) = y 'dx = (3x − 5)d . x b) 3 2
y = sin x, y ' = 3sin x cos . x Vậy 3 2
dy = d (sin x) = y 'dx = (3sin x cos x)d . x
2. Các quy tắc tính vi phân (giống đạo hàm)
3. Ứng dụng của vi phân vào tính xấp xỉ:
Theo định nghĩa đạo hàm, ta đã xây dựng được y f '(x ) = lim . 0 x 0 → x Do đó với x
= h đủ nhỏ thì y
f '(x ) hay y
f '(x ) . x 0 x 0 Mà y
= f (x + x
) − f (x ) nên từ đó, ta có 0 0 f (x + x
) − f (x ) f '(x ) x 0 0 0
f (x + x
) f (x ) + f '(x ) x 0 0 0
Hay f (x + h) f (x ) + f '(x ).h 0 0 0
Đó là công thức tính gần đúng đơn giản nhất. 14
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179
Ví dụ 8: Tính giá trj gần đúng của 3,99. 1
Giải: Đặt f (x) =
x , ta có f '(x) = . 2 x
Theo công thức tính gần đúng, với x = 4, h = 0 − ,01 ta có 0
f (3,99) = f (4 − 0,01) f (4) + f '(4)( 0 − ,01) 1
Tức là 3,99 = 4 − 0,01 4 + .( 0 − ,01) =1,9975. 2 4
Ví dụ 9: Tính gần đúng arctan(1,01). 1
Giải: Đặt f (x) = arctan x , ta có f '(x) = . 2 1 + x
Theo công thức tính gần đúng, với x = 1, h = 0,01 ta có 0
f (1,01) = f (1 + 0,01) f (1) + f '(1)(0,01) 1
Tức là arctan(1,01) = arctan(1 + 0,01) arctan(1) + .0,01 = + 0,005. 2 1 + 1 4 Đạo hàm cấp cao 1. Định nghĩa:
Cho hàm số y = f (x) có đạo hàm cấp n − 1, kí hiệu là (n 1 − ) f
(x) (n , n 4) . Nếu (n 1 − ) f
(x) có đạo hàm (khả vi) thì đạo hàm của nó được gọi là đạo hàm cấp n của
f (x) , kí hiệu là (n) y hoặc (n) f (x). n ( n f x f − = x )' ( ) ( 1) ( ) ( ) 15
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179
Nói cách khác, ta hiểu đạo hàm cấp n của f (x) chính là đạo hàm hàm số f (x) liên tục n lần. Ví dụ 10: Với 5 y = x thì 4 3 2 (4) (5)
y ' = 5x , y" = 20x , y"' = 60x , y
=120x, y =120 và (n) y = 0 với n 5.
2. Các phép toán về đạo hàm:
Giả sử f , g có đạo hàm đến cấp n . Khi đó
( f + g)(n) (n) (n) = f + g
( f − g)(n) (n) (n) = f − g
Vậy còn đạo hàm cấp cao của 1 tích thì sao? Ta sẽ sử dụng công thức sau: ( fg) n (n) k (n−k ) (k ) = C .f .g (1) n k =0
Công thức trên được gọi là công thức Leibniz.
Chứng minh: Sử dụng nguyên lí quy nạp +) n = 1: (1) đúng.
+) Giả sử (1) đúng đến n . Ta có: ( fg)(n) 0 (n) 1 (n 1 − ) n (n)
= C . f .g + C . f
.g '+ ... + C . f .g n n n ( + fg )(n 1) 0 (n 1 + ) = C . f
.g + C + C f g + C + C f − g
+ + C − + C f − + g n+ ( 0 1 n n ) (n) . ' ( 1 2 n n ) (n 1) (2) . ... ( k 1 k n n ) (n k 1) (k ) . 1 n 1 + (n 1 + ) ...
+ + C . f .g n 1 + n 1 + ( + fg )(n 1) 0 (n 1 + ) k (n−k 1 + ) (k ) = C f g + ... + C f g
+ ... = Ck (n 1+−k) (k) f .g n 1 + n 1 + n 1 + k =0 Ví dụ 11: a) 3 2 = . x y x e . Tính (100) y . 16
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179 1 b) y = . Tính (n) y . 2 x − 4x + 3 Giải: a) 3 2 = . x y x e .
Áp dụng công thức Leibniz, ta có: − y = ( n n k k x . x e )(100) k
= C (x )( ).( x e n )( ) (100) 3 2 3 2 k =0 −
= C (x )(n) n n .( x e ) + ... n
+ C − (x )(4).( x e )( 4) + ... n + C x ( x e n n n )( ) 0 3 2 4 3 2 3 2 n−3 n−3 2 x n−2 n−2 2 x n 1 − 2 n 1 − 2 x n 3 n 2
= 0 + ... + 0 + C 6.2 .e + C 6 .2 x .e
+ C 3x .2 .e + C x .2 . x e n n n n n−3 2
= (n − 2)(n −1) .2 n . x e + (n −1) .3 n .2n x −2 2x 2 n 1 − 2 x 3 2 . + .3 .2 . + . x.2n e n x e x e 1 1 1 1 1 b) y = = = − 2 x − 4x + 3
(x −1)(x − 3) 2 x − 3 x −1 1 ( 1 − )n n! ( 1 − )n n n ! ( ) y = − n 1 + n 1 2 (x − 3) (x −1) +
Công thức Taylor và ứng dụng
1. Hai dạng khai triển của công thức Taylor:
● Công thức Taylor với số dư dạng Peano:
Nếu f khả vi đến cấp n trong (a,b) và f liên tục trong 1 lân cận của x thì ta có: 0 (k ) n f (x0) f (x) =
(x − x )k + 0 (x − x )n 0 ( 0 ) = k k ! 0 ở đây, 0(( − )n x x
là vô cùng bé bậc cao hơn ( − )n x x
, nghĩa là đa thức có lũy 0 ) 0
thừa của x − x từ n + 1 trở đi. 0 17
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179 Ví dụ 12:
a) Sử dụng khai triển Taylor, hãy khai triển f (x) = ln x tại x = 1. Giải: Ta có
f (x) = ln x f (1) = 0 1 f '(x) = f '(1) =1 x 1 f ' (x) = − f '(1) = −1 2 x 2 (3) (3) f (x) = f (1) = 2 3 x 6 (4) (4) f (x) = − f (1) = −6 4 x 24 (5) (5) f (x) = f (1) = 24 5 x ... n 1 + − n − n ( 1) ( 1)! ( ) (n) n 1 f (x) =
f (1) = (−1) + (n −1)! n x (1) (2) (3) (4) f (1) f (1) f (1) f (1) f (1) 0 2 3 4 ln x = (x −1) + (x −1) + (x −1) + (x −1) + (x −1) 0! 1! 2! 3! 4! (5) (n) f (1) f (1) 5 + (x −1) + .... +
(x −1)n + 0((x −1)n ) 5! n! 0 1 1 2 6 24 0 2 3 4 5
= (x −1) + (x −1) − (x −1) + (x −1) − (x −1) + (x −1) − .... 0! 1! 2! 3! 4! 5! n 1 ( 1 − ) + (n − +
1)!(x −1)n + 0((x −1)n) n! n 1 1 1 1 1 ( 1 − ) + 2 3 4 5
= (x −1) − (x −1) + (x −1) − (x −1) + (x −1) −... +
(x −1)n + 0 ((x −1)n ) 2 3 4 5 n b) Viết khai triển 3 f (x) =
x tại x = 1 đến bậc 3. Giải: Ta có 18
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179 3 f (x) = x f (1) = 1 2 1 − 1 3 f '(x) = x f '(1) = 3 3 5 2 − 2 3 f ' (x) = − x f '(1) = − 9 9 8 10 − 10 (3) (3) 3 f (x) = x f (1) = 27 27 (1) (2) (3) f (1) f (1) f (1) f (1) 3 0 2 3 x = (x −1) + (x −1) + (x −1) + (x −1) 0! 1! 2! 3! 1 1 5 2 3
=1+ (x −1) − (x −1) + (x −1) 3 9 81 1 1 1 2 1 5 5 5 5 2 3 2 3
=1+ x − − x + x − + x − x + x − + 0(x ) 3 3 9 9 9 81 27 27 81 40 20 8 5 2 3 3 = + x − x + x + 0(x ) 81 27 27 81
c) Viết khai triển đa thức 3 2
f (x) = x − 2x + 8x −1 theo lũy thừa nguyên dương của x + 1. Giải: (3) f ( 1 − ) f '( 1 − ) f ' ( 1 − ) f ( 1 − ) 0 2 3 f (x) = (x +1) + (x + 1) + (x + 1) + (x + 1) 0! 1! 2! 3!
(do f (x) là đa thức bậc 3 nên ta chỉ khai triển Taylor đến cấp 3) Ta có 3 2
f (x) = x − 2x + 8x −1 f ( 1 − ) = 12 − 2
f '(x) = 3x − 4x + 8 f '( 1 − ) =15
f ' (x) = 6x − 4 f ' ( 1 − ) = 10 − (3) f (x) = 6 19
Giải Tích Thực Một Biến https://www.facebook.com/vu.haison.733/
Vũ Hải Sơn – K68C HNUE 0904913179 (3) f ( 1 − ) f '( 1 − ) f ' ( 1 − ) f ( 1 − ) 2 3 f (x) = + (x + 1) + (x + 1) + (x + 1) 0! 1! 2! 3! 2 3 = 12
− +15(x +1) − 5(x +1) + (x +1)
● Công thức Taylor với số dư dạng Lagrange:
Nếu f khả vi đến cấp (n + 1) trong (a,b) thì x
(a,b) , ta có: n (k ) f (x ) + + f x = (x − x ) (n 1) k f (c) n ( ) + (x − x ) 1 0 0 0 = k n + k ! ( 1)! 0
c nằm giữa x và x . 0
Công thức này không được áp dụng rộng rãi như công thức Taylor số dư Peano, nó
chỉ được dùng để làm các bài tập chứng minh, tính gần đúng giá trị biểu thức với sai số cho trước.
Ví dụ 13: Chứng minh rằng: 2 x
a) ln(1 + x) x − , x 0. 2
Giải: Ta có x = 0 , từ đó 0 (3) f (0) f '(0) f ' (0) f (c) 0 2 3 f (x) = x + x + x + x 0! 1! 2! 3!
f (x) = ln(1 + x) f (0) = 0 1 f '(x) = f '(0) =1 1 + x 1 f ' (x) = − f '(0) = −1 2 (1 + x) 2 (3) f (x) = 0, x 0 3 (1 + x)
(ta chỉ cần khai triển đến bậc 2, theo đề bài yêu cầu chứng minh) 20