Ôn tập môn Tín hiệu hệ thống | Trường Đại học Bách Khoa Hà Nội

ÔN TẬP TÍN HIỆU HỆ THỐNG
• Tín hiệu tuần hoàn
- Tổng hai tín hiệu là tuần hoàn khi và chỉ khi tỷ số của hai chu kỳ có thể biểu
diễn dưới dạng số hữu tỷ: 𝑇1 = 𝑙1 𝑇2 𝑙2
• Tín hiệu năng lượng:
- Năng lượng của tín hiệu: 𝑬 |𝟐𝒅𝒕
Nếu 0 < 𝐸 < ∞ → 𝑥(𝑡) được gọi là tín hiệu năng lượng.
• Công suất trung bình của tín hiệu: 𝑷 = 𝐥𝐢𝐦 𝟐𝑻 𝟏 ∫−𝑻𝑻|𝒙(𝒕)|𝟐 𝑻→∞ - Nếu 0 <
𝑃 < ∞ → 𝑥(𝑡) được gọi là tín hiệu công suất.
NOTE: Một tín hiệu có thể là tín hiệu công suất hoặc tín hiệu năng lượng hoặc
không phải là một trong hai đó, nhưng không bao giờ là cả hai.
CÁC PHÉP BIẾN ĐỔI TÍN HIỆU CƠ BẢN:
- Phép dịch: 𝑦(𝑡) = 𝑥(𝑡 − 𝑡0): chỉ thay đổi về trục hoành, trục Oy không đổi.
+) Nếu 𝑡0 > 0 → dịch đồ thị về bên phải
+) Nếu 𝑡0 < 0 → dịch đồ thị về bên trái
- 𝑦(𝑡) = 𝑥(−𝑡 − 𝑡0)
+) Nếu 𝑡0 > 0 → dịch đồ thị về bên trái
+) Nếu 𝑡0 < 0 → dịch đồ thị về bên phải
- Phép lật 𝑦(𝑡) = 𝑥(−𝑡) → lấy đối xứng qua trục Oy
- Phép co dãn: 𝑥(𝑎𝑡) • Hàm u(t) 𝑢
• Xung Dirac: Chiều cao bằng và độ rộng , diện tích bằng 1 𝛿 𝛿 𝑡 - Mối quan hệ giữa 𝑢 và là: +) 𝑡 𝑑𝑢 𝑑𝑡 • Tính chất lấy mẫu: 𝑥 • 𝛿 |𝑎| 𝑎
CHƯƠNG 2: HỆ THỐNG Hệ tuyến tính.
Một hệ thống được coi là hệ tuyến tính nếu thỏa mãn xếp chồng.
+) Tính chất cộng: 𝑥1(𝑡) + 𝑥2(𝑡) → 𝐒 → 𝑦1(𝑡) + 𝑦2(𝑡)
+) Tính chất tỷ lệ: 𝑥1(𝑡) → 𝐒 → 𝑦1(𝑡)
𝑥2(𝑡) = 𝑐. 𝑥1(𝑡) → 𝐒 → 𝑦2(𝑡) = 𝑐. 𝑦1(𝑡) VD: 1. 𝑦(𝑡) = 𝑥(𝑡2)
+) Với tín hiệu đầu vào: 𝑥1(𝑡) = 𝑐. 𝑥(𝑡)
→ Tín hiệu đầu ra 𝑦1(𝑡) = 𝑥1(𝑡2) = 𝑐. 𝑥(𝑡2) = 𝑐. 𝑦(𝑡)
→ Thỏa mãn tính chất tỷ lệ
+) Với tín đầu vào 𝑥(𝑡) = 𝑥1(𝑡) + 𝑥2(𝑡)
→ Tín hiệu đầu ra 𝑦(𝑡) = 𝑥(𝑡2) = 𝑥1(𝑡2) + 𝑥2(𝑡2) = 𝑦1(𝑡) + 𝑦2(𝑡) →
Thỏa mãn tính chất cộng.
→ Thỏa mãn tính chất tuyến tính 2. 𝑦(𝑡) = 𝑥 (𝑡+4) 𝑥(𝑡−2)
+) Với tín hiệu đầu vào: 𝑥1(𝑡) = 𝑐. 𝑥(𝑡) → Tín hiệu đầu ra 𝑦 𝑥1(𝑡−2) 𝑐.𝑥(𝑡−2) 𝑥(𝑡−2)
→ Không thỏa mãn tính chất tỷ lệ
+) Với tín hiệu đầu vào: 𝑥(𝑡) = 𝑥1(𝑡) + 𝑥2(𝑡)
→ Tín hiệu đầu ra: 𝑦 𝑦2(𝑡)
→ Không thỏa mãn tính chất cộng
→ Không thỏa mãn tính chất tuyến tính
3. 𝑦(𝑡) = sin(𝑥(𝑡))
+) Với tín hiệu đầu vào: 𝑥1(𝑡) = 𝑐. 𝑥(𝑡)
→ Tín hiệu đầu ra 𝑦1(𝑡) = sin(𝑥1(𝑡)) = sin(𝑐. 𝑥(𝑡)) ≠ 𝑐. sin(𝑥(𝑡))
→ Không thỏa mãn tính chất tỷ lệ
+) Với tín hiệu đầu vào: 𝑥(𝑡) = 𝑥1(𝑡) + 𝑥2(𝑡) → Tín hiệu đầu ra
𝑦(𝑡) = sin(𝑥(𝑡)) = sin(𝑥1(𝑡) + 𝑥2(𝑡)) ≠ sin(𝑥1(𝑡)) + sin(𝑥2(𝑡)) = 𝑦1(𝑡) + 𝑦2(𝑡)
→ Không thỏa mãn tính chất cộng.
→ Không thỏa mãn tính chất tuyến tính
→ Thỏa mãn tính chất tuyến tính
4. 𝑦(𝑡) = 𝑥(𝑡) + 𝑎
+) Với tín hiệu đầu vào: 𝑥1(𝑡) = 𝑐. 𝑥(𝑡)
→ Tín hiệu đầu ra 𝑦1(𝑡) = 𝑥1(𝑡) + 𝑎 = 𝑐. 𝑥(𝑡) + 𝑎 ≠ 𝑐(𝑥(𝑡) + 𝑎) = 𝑐. 𝑦(𝑡) →
Không thỏa mãn tính chất tỷ lệ.
+) Với tín hiệu đầu vào: 𝑥(𝑡) = 𝑥1(𝑡) + 𝑥2(𝑡) → Tín hiệu đầu ra:
𝑦(𝑡) = 𝑥(𝑡) + 𝑎 = 𝑥1(𝑡) + 𝑥2(𝑡) + 𝑎 ≠ (𝑥1(𝑡) + 𝑎) + (𝑥2(𝑡) + 𝑎) = 𝑦1(𝑡) + 𝑦2(𝑡)
Hệ thống phụ thuộc vào thời gian – bất biến theo thời gian.
- Một hệ thống bất biến dịch chuyển đầu vào 𝑡0 → đầu ra dịch chuyển 𝑡0
𝑥(𝑡) → 𝐒 → 𝑦(𝑡)
𝑥(𝑡 − 𝑡0) → 𝐒 → 𝑦(𝑡 − 𝑡0) VD:
1. 𝑦(𝑡) = cos(𝑥(𝑡))
+) Ta có: 𝑦1(𝑡) = 𝑦(𝑡 − 𝑡0) = cos(𝑥(𝑡 − 𝑡0))
+) Với tín hiệu đầu vào: 𝑥2(𝑡) = 𝑥(𝑡 − 𝑡0)
Tín hiệu đầu ra: → 𝑦2(𝑡) = cos(𝑥2(𝑡)) = cos (𝑥(𝑡 − 𝑡0)) →
𝑦1(𝑡) = 𝑦2(𝑡) → Hệ thống bất biến theo thời gian.
2. 𝒚(𝒕) = ∫𝟎𝒕 𝒙(𝒗)𝒅𝒗 +) Ta có: 𝑦 𝑑𝑣
+ Với tín hiệu đầu vào: 𝑥2(𝑡) = 𝑥(𝑡 − 𝑡0)
Tín hiệu đầu ra: → 𝑦2(𝑡) = ∫0𝑡 𝑥2(𝑣)𝑑𝑣 = ∫0𝑡 𝑥(𝑣 − 𝑡0)𝑑(𝑣 − 𝑡0)
Đặt 𝑣 − 𝑡0 = 𝜆 → 𝑑𝑣 = 𝑑𝜆 → 𝑦 𝑑𝜆 3. 𝑦(𝑡) = 𝑥(𝑡2)
+) Ta có: 𝑦1(𝑡) = 𝑦(𝑡 − 𝑡0) = 𝑥((𝑡 − 𝑡0)2)
+) Với tín hiệu đầu vào: 𝑥2(𝑡) = 𝑥(𝑡 − 𝑡0)
Tín hiệu đầu ra: → 𝑦2(𝑡) = 𝑥2(𝑡2) = 𝑥(𝑡2 − 𝑡0) ≠ 𝑥((𝑡 − 𝑡0)2)
→ 𝑦1(𝑡) ≠ 𝑦2(𝑡) → Hệ thống không bất biến theo thời gian 4. 𝑦(𝑡) = 𝑥(𝑡−2)
+) Ta có: 𝑦1(𝑡) = 𝑦(𝑡 − 𝑡0) = 𝑥𝑥
((𝑡𝑡−−𝑡𝑡00+−24))
+) Với tín hiệu đầu vào: 𝑥2(𝑡) = 𝑥(𝑡 − 𝑡0)
Tín hiệu đầu ra: → 𝑦 𝑥2(𝑡−2) 𝑥(𝑡−2−𝑡0)
→ 𝑦1(𝑡) = 𝑦2(𝑡) → Hệ thống bất biến theo thời gian. 5. 𝑦(𝑡) = 𝑥(𝑡) 𝑅(𝑡)
+) Ta có: 𝑦1(𝑡) = 𝑦(𝑡 − 𝑡0) = 𝑅
𝑥((𝑡𝑡−−𝑡𝑡00))
+) Với tín hiệu đầu vào: 𝑥2(𝑡) = 𝑥(𝑡 − 𝑡0)
Tín hiệu đầu ra: → 𝑦 𝑅(𝑡) 𝑅(𝑡)
→ 𝑦1(𝑡) ≠ 𝑦2(𝑡) → Hệ thống không bất biến theo thời gian
Hệ không có nhớ (hệ động): Một hệ thống gọi là có nhớ, nếu hệ thống có giá trị
đầu ra ở hiện tại chỉ phụ thuộc vào giá trị đầu vào ở hiện tại: 𝑦(𝑡) = 𝑅𝑥(𝑡) VD:
𝑦(𝑡) = (𝑡 + 5)𝑥(𝑡)
Hệ thống có nhớ (hệ tĩnh): Một hệ thống được gọi là có nhớ nếu giá trị đầu ra ở
hiện tại không những phụ thuộc vào giá trị đầu vào ở hiện tại mà còn phụ thuộc vào
giá trị đầu vào ở quá khứ. 𝑦 𝑑𝜏
VD: 𝑦(𝑡) = 𝑥(5)
Hệ nhân quả: Nếu hệ đầu ra 𝑦(𝑡0) chỉ phụ thuộc vào giá trị đầu vào 𝑡 ≤ 0 (hiện tại và quá khứ)
Hệ thống tuyến tính bất biến là nhân quả: 𝒉(𝒕) = 𝟎 ∀ 𝒕 < 𝟎
Hệ phi nhân quả: Nếu giá trị đầu ra của hệ chỉ phụ thuộc vào giá trị đầu vào ở tương lai.
VD: 𝑦(𝑡) = 𝑥(−𝑡) → 𝑦(−1) = 𝑥(1) → Tại t=-1 giá trị 𝑦(−1) ở quá khứ phụ thuộc vào 𝑥(1) ở tương lai.
Hệ thống bị chặn:
|𝑥(𝑡)| < 𝐵1 < ∞, ∀𝑡 → |𝑦(𝑡)| < 𝐵2 < ∞ , ∀𝑡
 Hệ thống bị chặn theo tiêu chuẩn BIBO
Hệ thống ổn định: VD: 1.
Nếu |𝑥(𝑡)| < 𝐵1 < ∞, ∀𝑡 → |𝑦(𝑡)| < 𝐵2 < ∞ , ∀𝑡 𝑣ớ𝑖 𝐵2 = 2𝐵1
2. 𝑦(𝑡) = 𝛼1𝑥(𝑡 − 𝑇1) + 𝛼2𝑥(𝑡 − 𝑇2)
3. Giả sử: |𝑥(𝑡)| < 𝑀 < ∞
→ 𝑦(𝑡) ≤ |𝛼1|. |𝑥(𝑡 − 𝑇1)| + |𝛼2|. |𝑥(𝑡 − 𝑇2)| ≤ (|𝛼1| + |𝛼2|). 𝑀
Hệ thống tuyến tính - bất biến theo thời gian. (LTI)
Đáp ứng xung: 𝑥(𝑡) = 𝛿(𝑡) → 𝐒 → 𝑦(𝑡) = ℎ(𝑡) Tích chập:
𝑥(𝑡) → 𝑆𝑦𝑠𝑡𝑒𝑚 → 𝑦 𝑑𝜏 +)
Trong đó: ℎ(𝑡) là đáp ứng xung đơn vị 𝑦 𝑑𝜏
Tính chất của tích chập:
- Tính chất giao hoán: 𝑥(𝑡)⨂𝑦(𝑡) = 𝑦(𝑡)⨂𝑥(𝑡)
- Tính chất phân phối: 𝑥(𝑡)⨂[ℎ1(𝑡) + ℎ2(𝑡)] = 𝑥(𝑡)⨂ℎ1(𝑡) + 𝑥(𝑡)⨂ℎ2(𝑡) - Tính chất kết hợp:
𝑥(𝑡)⨂ℎ1(𝑡)⨂ℎ2(𝑡) = [𝑥(𝑡)⨂ℎ1(𝑡)]⨂ℎ2(𝑡) = 𝑥(𝑡)⨂[ℎ1(𝑡)⨂ℎ2(𝑡)]
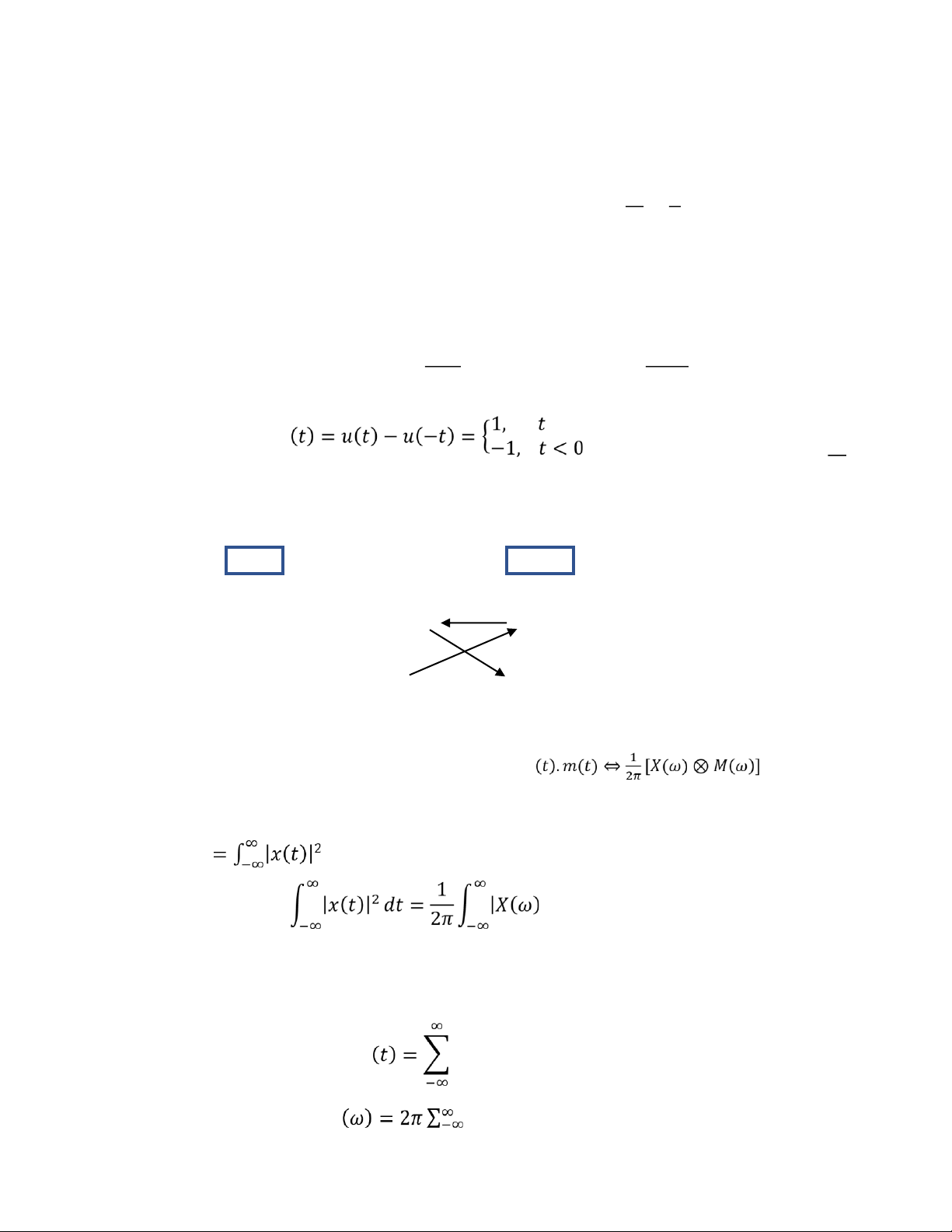
- Hệ thống mắc song song:
Ta có: 𝑦(𝑡) = 𝑦1(𝑡) + 𝑦2(𝑡) + ⋯ + 𝑦𝑁(𝑡)
= 𝑥(𝑡)⨂ℎ1(𝑡) + 𝑥(𝑡)⨂ℎ2(𝑡) + ⋯ + 𝑥(𝑡)⨂ℎ𝑁(𝑡)
= 𝑥(𝑡)⨂[ℎ1(𝑡) + ℎ2(𝑡) + ⋯ + ℎ𝑁(𝑡)]
→ 𝒉𝒕đ(𝒕) = 𝒉𝟏(𝒕) + 𝒉𝟐(𝒕) + ⋯ + 𝒉𝑵(𝒕) - Hệ thống mắc nối tiếp:
𝑥(𝑡) → ℎ 1 (𝑡) → 𝑧(𝑡) → ℎ 2 (𝑡) → 𝑦(𝑡)
+) Ta có: 𝑧(𝑡) = 𝑥(𝑡)⨂ℎ1(𝑡) ; 𝑦(𝑡) = 𝑧(𝑡)⨂ℎ2(𝑡) = [𝑥(𝑡)⨂ℎ1(𝑡)]⨂ℎ2(𝑡) =
𝑥(𝑡)⨂[ℎ1(𝑡)⨂ℎ2(𝑡)] = 𝑥(𝑡)⨂ℎ𝑡đ(𝑡) (ℎ𝑡đ(𝑡) = ℎ1(𝑡)⨂ℎ2(𝑡))
𝑥(𝑡) → ℎ 1 (𝑡)⨂ℎ 2 (𝑡) → 𝑦(𝑡)
CHƯƠNG 3: CHUỖI FOURIER
- Chuỗi Fourier làm việc với “tín hiệu tuần hoàn”. - Công thức: 𝑥
𝑐𝑛𝑒𝑗𝑛Ω0𝑡 ; Ω0 = 2 𝑇𝜋0 Với 𝑐𝑛
. 𝑒−𝑗𝑛Ω0𝑡 𝑑𝑡 𝑣ớ𝑖 𝑛 = 0; ±1; ±2; … * Tính chất:
- Tính chất tuyến tính: Cho hai tín hiệu tuần hoàn “cùng chu kỳ” 𝑇0 = Ω 2𝜋0 𝑥 𝛼𝑛𝑒 𝑡 ; 𝑦 𝛽𝑛𝑒
𝑡 → 𝑘1𝑥(𝑡) + 𝑘2𝑦(𝑡) 𝑛 𝑡 𝑛
- Tính chẵn, lẻ của tín hiệu:
Nếu 𝑥(𝑡) là hàm chẵn: 𝑥 𝑣ớ𝑖 𝑎𝑛 𝑑𝑡 𝑏𝑛 𝑑𝑡
Nếu 𝑥(𝑡) là hàm lẻ: 𝑣ớ𝑖
- Dịch theo thời gian: 𝑥
⇔ 𝑐𝑛 𝒕𝒉𝒆𝒏 𝑥
⇔ 𝑐𝑛𝑒−𝑗𝑛Ω0𝑡0
- Frequency-shifting: 𝑦 𝑡 → 𝑏𝑛 . 𝑒 𝑡𝑑𝑡
- Đạo hàm: 𝑦(𝑡) = 𝑑𝑥
𝑑𝑡(𝑡) ⇔ 𝑏𝑛 = 𝑗𝑛Ω0𝑐𝑛 với 𝑐𝑛, 𝑏𝑛 là hệ số Fourier của x(t) và y(t)
- Parseval’s theorem: Công suất của tín hiệu tuần hoàn: 𝑃 | 𝑑𝑡
-𝑁ếu: 𝑥(𝑡) ⇔ 𝛼𝑛 → |𝛼𝑚|2 - Hàm truyền:
+) Với 𝑥(𝑡) tuần hoàn: 𝑥 → 𝑦 → 𝑦 𝜏𝑑𝜏
▪ Hàm truyền đạt: 𝑡
Example: 𝑥(𝑡)=4cos(𝑡)−2cos(2𝑡)=2(𝑒𝑗𝑡 +𝑒−𝑗𝑡)−(𝑒2𝑗𝑡 +𝑒−2𝑗𝑡)=−𝑒−2𝑗𝑡 +2𝑒−𝑗𝑡 +2𝑒𝑗𝑡 −𝑒−2𝑗𝑡 → 𝑦
𝑐𝑛𝑒𝑗𝑛Ω0𝑡𝐻(𝑛Ω0) với: 𝑐𝑛 . 𝑒 𝑡 𝑑𝑡
→ 𝑏𝑛 = 𝑐𝑛𝐻(𝑛Ω0) : Hệ số của khi khai triển của:
CHƯƠNG 4: BIẾN ĐỔI FOURIER 𝑋
𝑗𝜔𝑡𝑑𝑡 → ℱ{𝑥(𝑡)} = 𝑋(𝜔) 𝑥
𝑒𝑗𝜔𝑡𝑑𝜔 → ℱ−1{𝑋(𝜔)} = 𝑥(𝑡) Ta có: 1 ∞ 1 = ∫ 𝛿 ( 𝜔 ) 𝑑𝜔 2 𝜋 − ∞ = 2 𝑒𝑗𝜔𝑡𝑑𝜔 𝜋
→ ℱ−1{2𝜋𝛿(𝜔)} = 1 → ℱ−1{𝐴. 2𝜋𝛿(𝜔)} = 𝐴
𝐴 ↔ 𝐴. 2𝜋𝛿(𝜔) → 𝑨𝒆𝒋𝝎𝟎𝒕 ⇔ 𝑨 𝟐𝝅𝜹(𝝎 − 𝝎𝟎) | 𝑥(𝑡) ⇔ 𝑋(𝜔) → 𝒙(𝒕)𝒆𝒋𝝎𝟎𝒕 ↔ 𝑿(𝝎 −
𝝎𝟎) - Hàm rect: 𝐴. 𝑟𝑒𝑐𝑡 (𝑡
−𝑇) 𝑣ớ𝑖 𝑇: 𝑙à 𝑡â𝑚 𝑥𝑢𝑛𝑔 ; 𝜏: 𝑙à độ 𝑟ộ𝑛𝑔 𝑐ủ𝑎 𝑥𝑢𝑛𝑔 𝜏
- Bảng biến đổi Fourier: 𝑓(𝑡) 𝐹(𝜔) 𝑓(𝑡) 𝐹(𝜔) 𝛿(𝑡) 1 sin (𝜔0𝑡) 𝜋 [𝛿(𝜔 − 𝜔 𝑗 0) − 𝛿((𝜔 + 𝜔0)] 𝛿(𝑡 − 𝑡0) 𝑒−𝑗𝜔𝑡0
𝑒−𝑎𝑡𝑢0(𝑡), 𝑎 > 0 1 , 𝑎 > 0 𝑗𝜔 + 𝑎 1 2𝜋𝛿(𝜔)
𝑡𝑒−𝑎𝑡𝑢0(𝑡), 𝑎 > 0 𝑎 > 0 𝑠𝑔𝑛(𝑡) 2
𝑒−𝑎𝑡 cos(𝜔0𝑡) 𝑢0(𝑡) 𝑗𝜔 + 𝑎 , 𝑎 > 0 𝑎 > 0 𝑗𝜔 (𝑗𝜔 + 𝑎)2 + 𝜔02 𝑢(𝑡) 1
𝑒−𝑎𝑡 sin(𝜔0𝑡)𝑢0(𝑡) 𝜔0 + 𝜋𝛿(𝜔) , 𝑎 > 0 𝑎 > 0 𝑗𝜔 (𝑗𝜔 + 𝑎)2 + 𝜔02 cos (𝜔0𝑡)
𝜋[𝛿(𝜔 − 𝜔0) + 𝛿((𝜔 + 𝜔0)]
𝐴[𝑢0(𝑡 +𝑇)−𝑢0(𝑡 −𝑇)] sin (𝜔𝑇) 𝑒𝑗𝜔0𝑡 2𝜋𝛿(𝜔 − 𝜔0) 2𝐴𝑇 𝜔𝑇 𝑒−𝑎|𝑡|,𝑎 > 0 2𝑎 sin(𝜔0𝑡)
𝑢(𝜔 + 𝜔0) − 𝑢(𝜔 − 𝜔0) 𝑎2 + 𝜔2 𝜋𝑡
- Điều kiện tồn tại biến đổi Fourier:
+) 𝑥(𝑡) là hàm khả tích tuyệt đối:
+) 𝑥(𝑡) số điểm kỳ dị (rời rạc (không liên tục), số điểm cực trị) trong một khoảng
thời gian là hữu hạn. ▪ Tính chất:
- Tuyến tính: 𝑰𝒇 𝑥1(𝑡) ⇔ 𝑋1(𝜔) ; 𝑥2(𝑡) ↔ 𝑋2(𝜔) 𝑡𝒉𝒆𝒏 𝑎𝑥1(𝑡) + 𝑏𝑥2(𝑡)𝑎𝑋1(𝜔) + 𝑏𝑋2(𝜔)
- Dịch thời gian: 𝑰𝒇 𝑥(𝑡) ⇔ 𝑋(𝜔) 𝒕𝒉𝒆𝒏 𝒙(𝒕 − 𝒕𝟎) ⇔ 𝑋(𝜔)𝑒−𝑗𝜔𝑡0 - Co dãn trong miền thời gian
: 𝑰𝒇 𝑥(𝑡) ⇔ 𝑋(𝜔) 𝒕𝒉𝒆𝒏 𝑥(𝑎𝑡) ⇔ 1 𝑋(𝜔) |𝑎| 𝑎
- Tính đối xứng (ít dùng): 𝐼𝑓 𝑥(𝑡) ⇔ 𝑋(𝜔) 𝑡ℎ𝑒𝑛 𝑿(−𝝎) = 𝑋∗(𝜔)
- Tính đạo hàm: 𝐼𝑓 𝑥(𝑡) ⇔ 𝑋(𝜔) 𝑡ℎ𝑒𝑛 𝑑𝑥
(𝑡) ⇔ 𝑗𝜔𝑋(𝜔) 𝑎𝑛𝑑 𝒅 𝒏𝒙 (𝒕) 𝒏 ⇔ (𝑗𝜔)𝑛𝑋(𝜔) 𝑑𝑡 𝒅𝒕
- Hàm dấu: 𝑥(𝑡) =
𝑠𝑖𝑔𝑛 > 0 → ℱ{𝒔𝒊𝒈𝒏(𝒕)} = 2 𝑗𝜔
- Convolution: 𝑰𝒇 𝑥(𝑡) ⇔ 𝑋(𝜔) , ℎ(𝑡) ⇔ 𝐻(𝜔) 𝒕𝒉𝒆𝒏 𝑥(𝑡) ⊗ ℎ(𝑡) ⇔ 𝑋(𝜔). 𝐻(𝜔)
𝑥(𝑡) → ℎ(𝑡) → 𝑥(𝑡) ⊗ ℎ(𝑡) | 𝑋(𝜔) → 𝐻(𝜔) → 𝑋(𝜔). 𝐻(𝜔) - Đối ngẫu:
𝐼𝑓: 𝑔(𝑡) 𝐺(𝜔)
𝑇ℎ𝑒𝑛: 𝑮(𝒕) 2𝜋𝑔(−𝜔)
- Multiplication: 𝐼𝑓 𝑥(𝑡) ⇔ 𝑋(𝜔) ; 𝑚(𝑡) ⇔ 𝑀(𝜔) 𝑡ℎ𝑒𝑛 𝑥
-Dịch tần số: 𝑥(𝑡) ⇔ 𝑋(𝜔) → 𝒙(𝒕)𝒆𝒋𝝎𝟎𝒕 ⇔ 𝑋(𝜔 − 𝜔0) - Parsaval’s: 𝐸 𝑑𝑡 |2𝑑𝜔
- Biến đổi Fourier đối với hàm tuần hoàn:
+) Nếu tín hiệu tuần hoàn có thể viết dưới dạng chuỗi Fourier: 𝑥 𝑐𝑛𝑒𝑗𝑛𝜔0𝑡
+) Biến đổi Fourier của nó là: 𝑋
𝑐𝑛𝛿(𝜔 − 𝑛𝜔0) Bộ lọc:
𝑥(𝑡) → ℎ(𝑡) → 𝑥(𝑡) ⊗ ℎ(𝑡) 𝑌(𝜔)
𝑋(𝜔) → 𝐻(ω) → 𝑋(𝜔). 𝐻(𝜔) = 𝑌(𝜔) ⇒ 𝐻(𝜔) = 𝑥 𝑥
∑ 𝑋(𝜔 − 𝑛𝜔𝑠) 𝑋(𝜔) 𝑇𝑠 𝑛=−∞
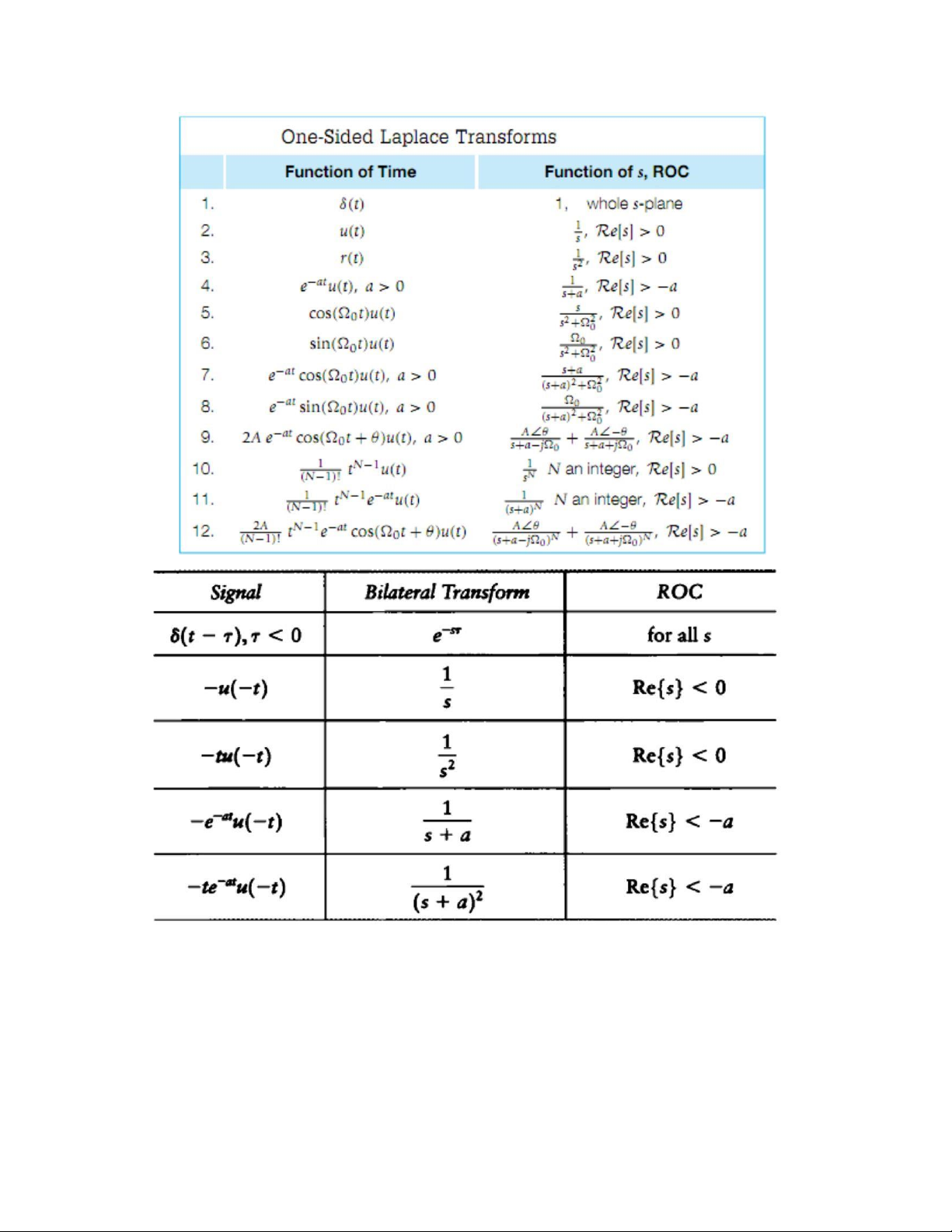
CHƯƠNG 5: LAPLACE TRANSFORM
Công thức tổng quát: 𝑋 𝑠𝑡𝑑𝑡 Hàm Gamma (hay sử dụng) 𝑑𝑥 • TÍNH CHẤT: - Tuyến tính:
𝑥1(𝑡) ⇔ 𝑋1(𝑠) 𝑥2(𝑡) ⇔ 𝑋2(𝑠) → 𝑎𝑥1 + 𝑏𝑥2 ⇔ 𝑎𝑋1(𝑠) + 𝑏𝑋2(𝑠)
- Dịch thời gian: 𝑥(𝑡) ⇔ 𝑋(𝑠) → 𝑥(𝑡 − 𝑡0)𝑢(𝑡 − 𝑡0) ⇔ 𝑋(𝑠)𝑒−𝑠𝑡0
- Dịch trên miền s:
𝑥(𝑡) ⇔ 𝑋(𝑠), 𝑅𝑒(𝑠) > 𝜎 → 𝑦(𝑡) = 𝑥(𝑡)𝑒𝑠0𝑡 ⇔ 𝑋(𝑠 − 𝑠0), 𝑅𝑒(𝑠) > 𝜎 + 𝑅𝑒(𝑠0)
- Co dãn: 𝑥(𝑡) ⇔ 𝑋(𝑠), 𝑅𝑒(𝑠) > 𝜎1 → 𝑥(𝑎𝑡) ⇔ 𝑎 1 𝑋 (𝑎𝑠) , 𝑅𝑒(𝑠) > 𝑎𝜎1 - Đạo hàm: If 𝑔(𝑡) ⇔ 𝐺(𝑠) Then: 𝑑𝑔
(𝑡) ⟷ 𝑠𝐺(𝑠) − 𝑔(0−) 𝑑𝑡 𝑑
2𝑔(𝑡) ⟷ 𝑠2𝐺(𝑠) − 𝑠𝑔(0−) − 𝑔′(0−) 𝑑𝑡 𝑑
𝑛𝑔(𝑡) ⟷ 𝑠𝑛𝐺(𝑠) − 𝑠𝑛−1𝐺𝑔(𝑠) − ⋯ − 𝑠𝑔(𝑛−2)(0−) − 𝑔(𝑛−1)(0−) 𝑑𝑡
- Tích phân: 𝑥(𝑡) ⟷ 𝑋(𝑠) → ∫0𝑡 𝑥(𝑡) ⟷ 1 𝑠 𝑋(𝑠) - Mô hình toán học của hệ thống:
𝑥(𝑡)−→ ℎ(𝑡) −→ 𝑦(𝑡) = 𝑥(𝑡) ⊗ ℎ(𝑡)
𝑋(𝑠)− → 𝐻(𝑠) −→ 𝑌(𝑠) = 𝑋(𝑠)𝐻(𝑠)
→ 𝐻(𝑠): Mô hình toán học của hệ thống.
- Với 𝑥(𝑡) = 𝛿(𝑡) −→ 𝑔(𝑡) −→ ℎ(𝑡) → 𝐺(𝑠). 1 = 𝐻(𝑠) Tổng quát: 𝐺(𝑠) =
𝑌(𝑠) → Mô hình toán học của hệ thống. 𝑋(𝑠)
- Đạo hàm trên miền s:
𝑥(𝑡) ⟷ 𝑋(𝑠) 𝑑𝑛𝑋(𝑠) (−𝑡)𝑛𝑥(𝑡) ⟷ 𝑑𝑠𝑛
- Tích chập: 𝑔(𝑡) ⟷ 𝐺(𝑠) , 𝑓(𝑡) ⟷ 𝐹(𝑠) −→ 𝑔(𝑡) ⊗ 𝑓(𝑡) ⟷
𝐺(𝑠). 𝐹(𝑠) → 𝐻(𝑠) =
𝐹(𝑠) : Gọi là hàm truyền đạt. 𝐺(𝑠)
- Modulation: 𝑥(𝑡) ⟷ 𝑋(𝑠)
𝑥(𝑡)cos (𝜔0𝑡) ⟷ [𝑋(𝑠 + 𝑗𝜔) + 𝑋(𝑠 − 𝑗𝜔)] 𝑗 𝑥
- Đinh lý giá trị đầu: 𝑥(0+) = lim 𝑠𝑋(𝑠) 𝑠→∞
- Định lý giá trị cuối: ∞