Ôn tập xác suất cổ điển. Xác suất có điều kiện môn Toán lớp 10

ÔN TẬP XÁC SUẤT CỔ ĐIỂN. XÁC SUẤT CÓ ĐIỀU KIỆN
I. ÔN TẬP XÁC SUẤT CỔ ĐIỂN
1. Quy tắc đếm. Hoán vị, tổ hợp, chỉnh hợp
Trường hợp sử dụng Quy tắc cộng
Khi công việc được thực hiện bởi nhiều trường hợp. Quy tắc nhân
Khi công việc được thực hiện bởi nhiều bước. Hoán vị
Dùng cho bài toán chỉ sắp xếp. P  n!  . n n  
1 .n  2.....2.1 n Tổ hợp
Dùng cho bài toán lấy ra và không sắp xếp (không quan trọng thứ tự). n k ! C  n k !.n  k ! Chỉnh hợp
Dùng cho bài toán lấy ra và có sắp xếp (quan trọng thứ tự). n k ! A  n n  k !
Câu 1. Anh Quân muốn du lịch vào Đà Nẵng chơi ít ngày để xả stress. Anh Quân đang
phân vân không biết chọn loại phương tiện gì để di chuyển. Dưới đây là một vài lựa chọn Hàng không: 3 hãng Tàu: 2 hãng
Ô tô đường dài: 5 hãng
Hỏi anh Quân có bao nhiêu cách chọn phương tiện để di chuyển vào Đà Nẵng? Đáp án:
Câu 2. Anh Quân cần ăn mặc thật bảnh để đi dự đám cưới người yêu cũ. Biết trong tủ đồ
của anh Quân có 5 cái áo, 3 cái quần và 3 đôi giày. Hỏi anh Quân có bao nhiêu cách phối đồ
(tức là chọn ra 1 bộ áo-quần-giày) để đi ăn đám cưới? Đáp án:
Câu 3. Có bao nhiêu cách xếp 7 bạn thành một hàng dọc? Đáp án:
Câu 4. Một nhóm học sinh gồm 5 bạn nam và 5 bạn nữ. Hỏi có bao nhiêu cách xếp 10 bạn
này thành một hàng ngang sao cho nam nữ đứng xen kẽ nhau? Đáp án: 1
Câu 5. Lớp 10QT có 25 bạn. Hỏi có bao nhiêu cách
a) Chọn ra 3 bạn để làm Lớp trưởng, Lớp phó, Bí thư của lớp.
b) Chọn ra 3 bạn để đi trực nhật.
2. Xác suất cổ điển P  A n  A 
là xác suất xảy ra biến cố A. n  Trong đó:
n A là số kết quả thuận lợi cho biến cố A.
n là số phần tử của không gian mẫu.
Câu 6. Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu
nhiên 3 quyển sách. Tính xác suất để 3 quyển được lấy ra thuộc 3 môn khác nhau. 2 5 1 37 A. . B. . C. . D. . 7 42 21 42
Câu 7. Một hộp chứa 3 quả cầu vàng, 5 cầu xanh và 6 cầu đỏ. Chọn ngẫu nhiên 2 quả cầu.
Tính xác suất chọn được 2 quả cầu khác màu. 47 63 9 15 A. . B. . C. . D. . 66 119 13 28
Câu 8. Một hộp chứa 10 bi trong đó: 4 bi đỏ, 3 bi xanh, 2 bi vàng, 1 bi trắng. Lấy ngẫu
nhiên một lúc 2 bi. Tính xác suất chọn được 2 khác màu 2 1 7 5 A. . B. . C. . D. . 9 9 9 9
Câu 9. (Mã 101 – 2020 – Lần 1) Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số đôi
một khác nhau và các chữ số thuộc tập 1;2;3;4;5;6;7;8; 
9 . Chọn ngẫu nhiên một số thuộc
S , xác suất để số đó không có hai chữ số liên tiếp nào cùng chẵn bằng 25 5 65 55 A. . B. . C. . D. . 42 21 126 126 2
3. Quy tắc tính xác suất
a) Quy tắc nhân xác suất cho biến cố độc lập
Hai biến cố A và B độc lập với nhau khi và chỉ khi
P AB  P A.PB
Công thức này gọi là công thức nhân xác suất cho hai biến cố độc lập.
b) Quy tắc cộng xác suất
 Nếu A và B xung khắc thì P A B  P 
A  PB .
 Trong trường hợp tổng quát, ta xét hai biến cố A và B. Khi đó, ta có:
P A B  P 
A  PB  P AB
Công thức này được gọi là công thức cộng xác suất.
Câu 10. Hai bạn Hạnh và Hà cùng chơi trò chơi bắn cung một cách độc lập. Mỗi bạn chỉ
bắn một lần. Xác suất để bạn Hạnh và bạn Hà bắn trung bia lần lượt là 0,6 và 0,7 trong lần
bắn của mình. Tính xác suất của biến cố:
a) C : “Bạn Hạnh và bạn Hà đều bắn trúng bia”.
b) D : “Bạn Hạnh và bạn Hà đều bắn trượt bia”.
c) E : “Có ít nhất một bạn bắn trúng bia”.
Câu 11. Hai cầu thủ đang sút penalty một cách độc lập. Xác suất để người thứ nhất đá vào
là 0,3; người thứ hai đá vào là 0,6 . Hãy tính xác suất để:
a) Cả hai người cùng đá vào A. 0,18 . B. 0,1. C. 0,2 . D. 0,8.
b) Cả hai người cùng không đá vào A. 0,2 . B. 0,18 . C. 0,28. D. 0,23.
c) Có ít nhất một người đá vào A. 0,24. B. 0,12 . C. 0,82 . D. 0,72. 3
Câu 12. Gieo một con súc sắc hai lần. Xác suất để ít nhất một lần xuất hiện mặt sáu chấm là? A. 12 11 6 8 . B. . C. . D. . 36 36 36 36
Câu 13. Phỏng vấn học sinh lớp 11A về môn thể thao yêu thích thu được kết quả có 70%
bạn thích môn Bóng đá, 20% bạn thích môn Bóng bàn và 10% bạn thích cả hai môn đó.
Chọn ngẫu nhiên một học sinh lớp 11A. Chọn ngẫu nhiên một bạn trong lớp. Gọi A là biến
cố học sinh được chọn thích bóng đá, B là biến cố học sinh được chọn thích bóng bàn.
Xét tính đúng sai của các khẳng định sau
a) P A  0,7 .
b) P A  B  0,1.
c) P A B  0,9.
d) Xác suất để chọn được bạn học sinh không thích chơi Bóng đá và Bóng bàn là P  A  B
và P  A B  0,2 .
II. XÁC SUẤT CÓ ĐIỀU KIỆN Định nghĩa
Cho A và B là hai biến cố, PB  0 . Xác suất để biến cố A xảy ra biết rằng biến cố B đã xảy ra là  P A  B P AB P A | B       P  B P  B
Xác suất này được gọi là xác suất của A với điều kiện B . Chú ý:   n A B
Cho hai biến cố A và B với PB  0 . Khi đó, ta có P  A | B    n  B
 Nếu A và B là hai biến cố bất kì thì:
P A B  P 
A .P A | B  PB.P A | B
Công thức trên được gọi là công thức nhân xác suất. 4
Câu 14. Cho hai biến cố ,
A B có P 
A  0, 4; PB  0,6; P AB  0,2 . Tính các xác suất
sau: P A | B, PB | A .
Câu 15. Trong kì kiểm tra môn Toán của một trường trung học phổ thông có 200 học sinh
tham gia, trong đó có 95 học sinh nam và 105 học sinh nữ. Khi công bố kết quả của kì
kiểm tra đó, có 50 học sinh đạt điểm giỏi, trong đó có 24 học sinh nam và 26 học sinh nữ.
Chọn ra ngẫu nhiên một học sinh trong số 200 học sinh đó. Tính xác suất để học sinh được
chọn ra đạt điểm giỏi, biết rằng học sinh đó là nữ? (làm tròn kết quả đến hàng phần trăm). Đáp án:
Câu 16. Trong hộp đựng 500 chiếc thẻ cùng loại có 200 chiếc thẻ màu vàng. Trên mỗi
chiếc thẻ màu vàng có ghi một trong năm số 1,2,3,4,5. Có 40 chiếc thẻ màu vàng ghi số 5 .
Chọn ra ngẫu nhiên một chiếc thẻ. Giả sử chiếc thẻ được chọn ra có màu vàng. Tính xác
suất để chiếc thẻ đó ghi số 5 . Đáp án:
Câu 17. Một công ty dược phẩm muốn so sánh tác dụng điều trị bệnh X của hai loại thuốc
M và N. Công ty đã tiến hành thử nghiệm với 4000 bệnh nhân mắc bệnh X trong đó 2400
bệnh nhân dùng thuốc M, 1600 bệnh nhân còn lại dùng thuốc N. Kết quả được cho trong
bảng dữ liệu thống kê như sau Uống thuốc Thuốc M Thuốc N Kết quả Khỏi bệnh 1600 1200 Không khỏi bệnh 800 400
Chọn ngẫu nhiên một bệnh nhân trong số 4000 bệnh nhân thử nghiệm sau khi uống thuốc.
Tính xác suất để bệnh nhân đó
a) Khỏi bệnh, biết rằng bệnh nhân đó uống thuốc M.
b) Không khỏi bệnh, biết rằng bệnh nhân đó uống thuốc N.
c) Uống thuốc M, biết rằng bệnh nhân đó khỏi bệnh.
d) Uống thuốc N, biết rằng bệnh nhân đó không khỏi bệnh. 5
Câu 18. Một hộp có 6 quả bóng màu xanh, 4 quả bóng màu đỏ; các quả bóng có kích thước
và khối lượng như nhau. Lấy ngẫu nhiên lần lượt hai quả bóng trong hộp, lấy không hoàn
lại. Tìm xác suất để lần thứ hai lấy được quả bóng màu đỏ, biết rằng lần thứ nhất đã lấy
được quả bóng màu xanh. Đáp án:
Câu 19. Theo một số liệu thống kê, năm 2004 ở Canada có 65% nam giới là thừa cân và
53, 4% nữ giới là thừa cân. Nam giới và nữ giới ở Canada đều chiếm 50% dân số cả nước.
Chọn ngẫu nhiên một người.
a) Tính xác suất để người được chọn bị thừa cân, biết rằng người đó là nữ.
b) Tính xác suất để người được chọn bị thừa cân. -----HẾT----- 6 BÀI TẬP VỀ NHÀ
Câu 1. Cho hai biến cố A và B , với P A  0,6 , PB  0,7 , P A B  0,3. Tính
P A | B . A 3 1 6 1 . . B. . C. . D. . 7 2 7 7
Câu 2. Cho hai biến cố A và B là hai biến cố độc lập, với P  A  0, 2024 ,
PB  0,2025. Tính P A | B . A. 0,7976. B. 0,7975. C. 0,2025. D. 0,2024.
Câu 3. Cho hai biến cố A và B, với P A  0,3, PB  0,6 , P A| B  0,4 . Tính
PB | A . A. 0,2 . B. 0,8. C. 0,12 . D. 0,38.
Câu 4. Trong hộp có 3 viên bi màu trắng và 7 viên bi màu đỏ. Lấy lần lượt mỗi lần một
viên theo cách lấy không trả lại.
a) Xác suất để viên bi lấy lần thứ hai là màu đỏ nếu biết rằng viên bi lấy lần thứ nhất cũng là màu đỏ là A 2 2 1 1 . . B. . C. . D. . 3 7 5 7
b) Xác suất để viên bi lấy lần thứ hai là màu đỏ nếu biết rằng viên bi lấy lần thứ nhất là màu trắng là: A 2 1 7 5 . . B. . C. . D. . 3 3 9 9
Câu 5. Một công ty xây dựng đấu thầu 2 dự án độc lập. Khả năng thắng thầu của các dự
án 1 là 0,6 và dự án 2 là 0,7.
a) Tìm xác suất công ty thắng thầu đúng 1 dự án. A. 0,28. B. 0,7 . C. 0,46. D. 0,18 .
b) Biết công ty thắng thầu dự án 1, tìm xác suất công ty thắng thầu dự án 2. 7 A. 0,6 . B. 0,7 . C. 0,46. D. 0,3.
c) Biết công ty không thắng thầu dự án 1, tìm xác suất công ty thắng thầu dự án 2. A. 0,4 . B. 0,7 . C. 0,28. D. 0,6 .
Câu 6. Cho một hộp kín có 6 thẻ ATM của BIDV và 4 thẻ ATM của Vietcombank. Lấy
ngẫu nhiên lần lượt 2 thẻ (lấy không hoàn lại). Tìm xác suất để lần thứ hai lấy được thẻ
ATM của Vietcombank nếu biết lần thứ nhất đã lấy được thẻ ATM của BIDV. A 5 2 7 4 . . B. . C. . D. . 9 3 9 9
Câu 7. Một bình đựng 9 viên bi xanh và 7 viên bi đỏ. Lần lượt lấy ngẫu nhiên ra 2 bi, mỗi
lần lấy 1 bi không hoàn lại. Tính xác suất để bi thứ 2 màu xanh nếu biết bi thứ nhất màu đỏ? A 3 9 9 21 . . B. . C. . D. . 5 16 17 80
Câu 8. Lớp Toán Sư Phạm có 95 Sinh viên, trong đó có 40 nam và 55 nữ. Trong kỳ thi
môn Xác suất thống kê có 23 sinh viên đạt điểm giỏi (trong đó có 12 nam và 11 nữ). Gọi tên
ngẫu nhiên một sinh viên trong danh sách lớp. Tìm xác suất gọi được sinh viên đạt điểm
giỏi môn Xác suất thống kê, biết rằng sinh viên đó là nữ? A 1 11 12 11 . . B. . C. . D. . 5 23 23 19
Câu 9. Lớp 12A có 30 học sinh, trong đó có 17 bạn nữ, còn lại là nam. Có 3 bạn tên Hiền,
trong đó có 1 bạn nữ và 2 bạn nam. Thầy giao gọi ngẫu nhiên 1 bạn lên bảng.
Xét tính đúng sai của các khẳng định sau 1
a) Xác suất để bạn lên bảng có tên Hiền là . 10 3
b) Xác suất để bạn lên bảng có tên Hiền, nhưng với điều kiện bạn đó là nữ là . 17
c) Xác suất để bạn lên bảng có tên Hiền, nhưng với điều kiện bạn đó là nam là 2 . 13 3
d) Nếu thầy giáo gọi 1 bạn có tên là Hiền lên bảng thì xác suất để bạn đó là bạn nữ là . 17 8
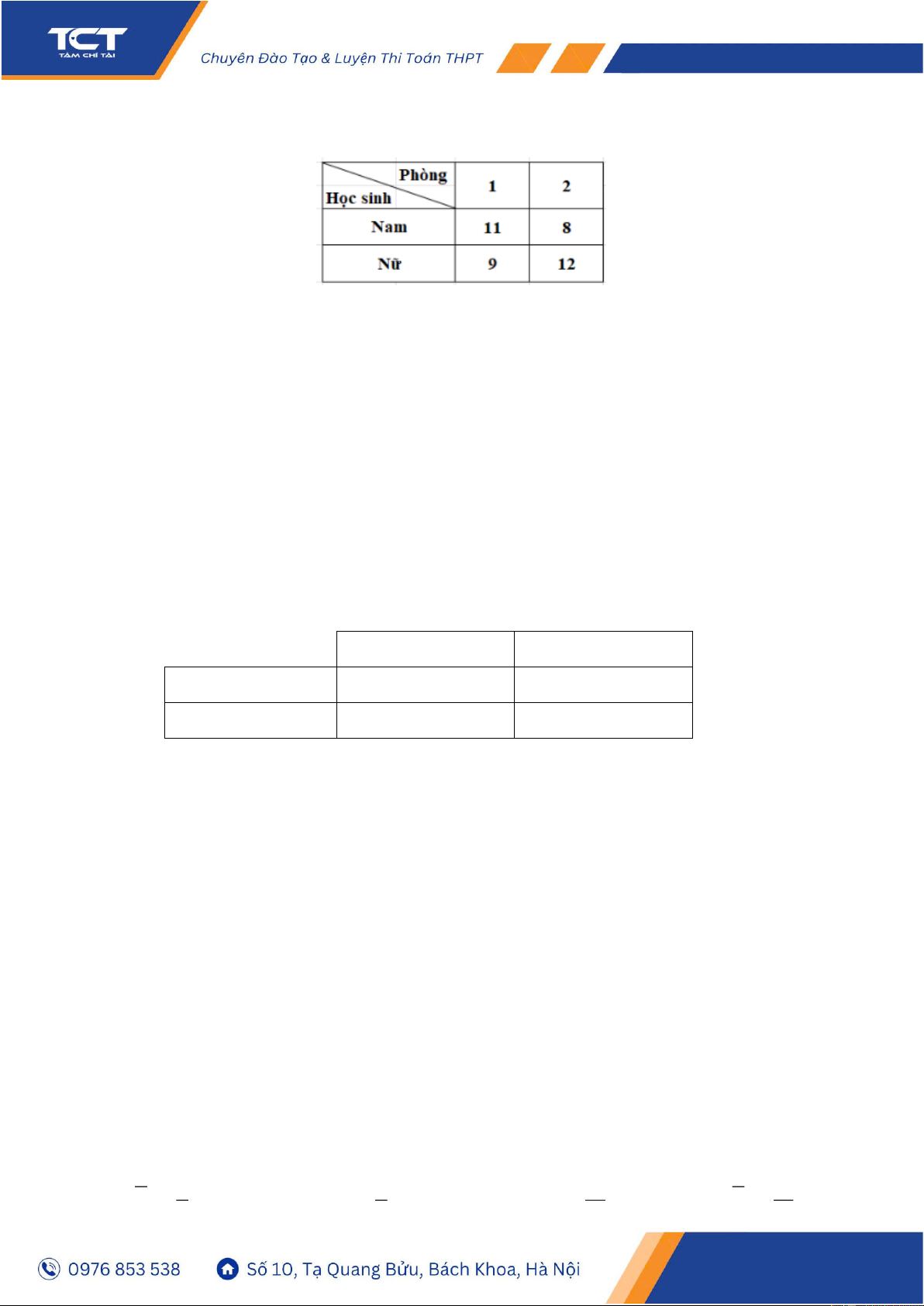
Câu 10. Lớp 12A có 40 học sinh. Trong một buổi kiểm tra định kì, số học sinh của lớp 12A
được chia thành hai phòng sau:
Chọn ngẫu nhiên một học sinh của lớp 12A. Tính xác suất để học sinh được chọn ở phòng
2, biết rằng học sinh được chọn là nữ (Kết quả làm tròn đến hàng phần chục) Đáp số:
Câu 11. Trước khi đưa ra thị trường một sản phẩm, công ty phỏng vấn 800 khách hàng và
được kết quả là 550 người nói sẽ mua, còn 250 người nói sẽ không mua. Theo kinh nghiệm
của nhà sản xuất thì trong những người nói mua sẽ có 60% số người chắc chắn mua, còn
trong những người nói sẽ không mua lại có 10% người chắc chắn mua. a) Hoàn thiện bảng sau Mua Không mua Nói sẽ mua Nói sẽ không mua
b) Chọn ngẫu nhiên một khách hàng. Xác suất chọn được khách hàng chắc chắn mua là bao nhiêu? Đáp số:
Câu 12. Một nhóm học sinh gồm 15 nam và 20 nữ đi tham quan Sunworld Hạ Long, tới lúc
tham gia trò chơi mỗi học sinh chọn một trong hai trò chơi là Phi long thần tốc hoặc Tê giác
cuồng nộ. Xác suất chọn trò chơi Phi long thần tốc của mỗi học sinh nam là 0,6 và của mỗi
học sinh nữ là 0,3. Chọn ngẫu nhiên một bạn của nhóm. Xét các biến cố sau
A là biến cố "Học sinh nam".
B là biến cố "Chọn trò chơi Phi long thần tốc".
Xét tính đúng sai của các khẳng định sau a) P A 4  b) P A 3  c) P AB 9  d) PB A 9 |  7 4 15 15 9
Câu 13. Một hộp có 12 quả bóng màu xanh, 7 quả bóng màu đỏ; các quả bóng có kích
thước và khối lượng như nhau. Lấy ngẫu nhiên lần lượt hai quả bóng trong hộp; lấy không
hoàn lại. Xét các biến cố:
A: "Lần thứ hai lấy được quả màu đỏ".
B : "Lần thứ nhất lấy được quả màu xanh".
Xét tính đúng sai của các khẳng định sau a) P  B 7  .
b) P  A  B 28  . c) P  A 12  . 19 57 19
Câu 14. Trong kỳ kiểm tra môn Toán của một trường THPT có 400 học sinh tham gia,
trong đó có 180 học sinh nam và 220 học sinh nữ. Khi công bố kết quả kỳ kiểm tra đó, tỉ lệ
học sinh đạt điểm giỏi tương ứng với nam và nữ lần lượt là 25% và 30%. Chọn ngẫu nhiên
một học sinh trong số 400 học sinh đó.
Gọi A là biến cố: "Học sinh được chọn ra đạt điểm giỏi".
Gọi B là biến cố: "Học sinh được chọn ra là học sinh nữ".
Xét tính đúng sai của các khẳng định sau a) PB 9  và PB 11  . 20 20
b) P  A | B  0,3.
c) P  A  0,7225 .
d) Trong số những bạn học sinh đạt diểm giỏi có 59% học sinh nữ đạt điểm giỏi trong kỳ
kiểm tra môn Toán (Kết quả tính theo phần trăm và được làm tròn đến hàng đơn vị).
Câu 15. Lớp 12A có 70% học sinh thích chơi thể thao. Biết rằng nếu một học sinh thích
chơi thể thao thì xác suất học sinh đó biết chơi cầu lông là 0,8; học sinh không thích chơi
thể thao thì xác suất học sinh đó biết chơi cầu lông là 0,1. Chọn ngẫu nhiên một học sinh.
Xét tính đúng sai của các khẳng định sau
a) Xác suất học sinh này không thích chơi thể thao là 0,3.
b) Xác suất học sinh này không biết chơi cầu lông với điều kiện không thích chơi thể thao là 0,41. -----HẾT----- 10