























































Preview text:
MỤC LỤC
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC MỤC LỤC
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ 1
Bài 20. TỈ LỆ THỨC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
A Trọng tâm kiến thức............................................................................................................1
1. Tỉ lệ thức ........................................................................................................................... 1
2. Tính chất của tỉ lệ thức ..................................................................................................... 1
B Các dạng bài tập..................................................................................................................1
Dạng 1. Nhận biết tỉ số - Tỉ lệ thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
Dạng 2. Tìm số chưa biết trong tỉ lệ thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Dạng 3. Lập tỉ lệ thức từ các số hoặc đẳng thức cho trước . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Dạng 4. Chứng minh tỉ lệ thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Dạng 5. Các bài toán thực tế sử dụng tỉ lệ thức. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7
C Bài tập vận dụng ................................................................................................................. 8
D Bài tập nâng cao ................................................................................................................ 13
Bài 21. TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
A Trọng tâm kiến thức .......................................................................................................... 17
1. Tính chất của dãy hai tỉ số bằng nhau.............................................................................17
2. Mở rộng tính chất cho dãy tỉ số bằng nhau.....................................................................17
B Các dạng bài tập ................................................................................................................ 17
Dạng 1. Sử dụng tính chất dãy tỉ số bằng nhau để tìm các đại lượng chưa biết . . . . . . . . . . . . . . . . . . . . . . . . . . 17
Dạng 2. Chứng minh tỉ lệ thức. Tính giá trị biểu thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21
Dạng 3. Áp dụng tính chất của dãy hai tỉ số bằng nhau để giải bài toán khác . . . . . . . . . . . . . . . . . . . . . . . . . . . .21
C Bài tập vận dụng................................................................................................................23
D Bài tập nâng cao ................................................................................................................ 27
Bài 22. ĐẠI LƯỢNG TỈ LỆ THUẬN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
A Trọng tâm kiến thức .......................................................................................................... 35
1. Đại lượng tỉ lệ thuận ........................................................................................................ 35
2. Tính chất:.........................................................................................................................35
3. Một số bài toán về đại lượng tỉ lệ thuận:.........................................................................35
B Các dạng bài tập ................................................................................................................ 35
Dạng 1. Nhận biết đại lượng tỉ lệ thuận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
Dạng 2. Tìm giá trị của một đại lượng tỉ lệ thuận khi biết giá trị của đại lượng kia . . . . . . . . . . . . . . . . . . . . 37
Dạng 3. Giải bài toán thực tế về hai đại lượng tỉ lệ thuận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .38
Dạng 4. Chia một số M thành những phần x, y, z tỉ lệ thuận với các số a, b, c cho trước . . . . . . . 40
C Bài tập vận dụng................................................................................................................41
D Bài tập nâng cao ................................................................................................................ 49 /82 /82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 i MỤC LỤC
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Bài 23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
A Trọng tâm kiến thức .......................................................................................................... 54
1. Đại lượng tỉ lệ nghịch ....................................................................................................... 54
2. Tính chất..........................................................................................................................54
3. Một số bài toán về đại lượng tỉ lệ nghịch.........................................................................54
B Các dạng bài tập ................................................................................................................ 54
Dạng 1. Nhận biết đại lượng tỉ lệ nghịch . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
Dạng 2. Tìm giá trị của một đại lượng tỉ lệ nghịch khi biết giá trị của đại lượng kia . . . . . . . . . . . . . . . . . . . 56
Dạng 3. Giải bài toán thực tế về hai đại lượng tỉ lệ nghịch . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
Dạng 4. Chia một số M thành những phần x, y, z tỉ lệ nghịch với các số a, b, c cho trước . . . . . . 62
C Bài tập vận dụng................................................................................................................63
D Bài tập nâng cao ................................................................................................................ 70
ÔN TẬP CHƯƠNG VI . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
A Bài tập rèn luyện ................................................................................................................ 74
B Bài tập bổ sung..................................................................................................................79 i/82 i/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 1
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Chûúng
TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ 6
TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ Baâi 20 TỈ LỆ THỨC A
TRỌNG TÂM KIẾN THỨC 1 Tỉ lệ thức a c
Tỉ lệ thức là đẳng thức của hai tỉ số = . b d a c Tỉ lệ thức =
còn được viết dưới dạng a : b = c : d. b d
2 Tính chất của tỉ lệ thức
Tính chất của tỉ lệ thức: a c ○ Nếu = thì ad = bc. b d
○ Nếu ad = bc (với a, b, c, d ̸= 0) thì ta có bốn tỉ lệ thức: a c a b d c d b = ; = ; = ; = . b d c d b a c a a c
Nhận xét. Từ tỉ lệ thức = (a, b, c, d ̸= 0) suy ra b d bc ad ad bc a = ; b = ; c = ; d = . d c b a A B CÁC DẠNG BÀI TẬP
Dạng 1. Nhận biết tỉ số - Tỉ lệ thức
c Ví dụ 1. Thay tỉ số sau đây bằng tỉ số giữa các số nguyên: 8 4 −5 3 9 a) : ; b) 0, 75 : 2, 5; c) : 1, 5; d) 0, 45 : 1, 35; e) : . 12 15 3 2 16 Lời giải. 8 4 8 15 5 a) : = · = . 12 15 12 4 2 75 25 75 10 3 b) 0, 75 : 2, 5 = : = · = . 100 10 100 25 10 −5 −5 15 −5 10 −10 c) : 1, 5 = : = · = . 3 3 10 3 15 9 1/82 1/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 2 20. TỈ LỆ THỨC
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC 45 135 1 d) 0, 45 : 1, 35 = : = . 100 100 3 3 9 3 16 8 e) : = · = . 2 16 2 9 3 □
c Ví dụ 2. Thay tỉ số sau đây bằng tỉ số giữa các số nguyên: 21 15 −11 1 5 9 a) : ; b) 2, 3 : 1, 65; c) : 2, 7; d) 5 : 5 ; e) 25, 5 : 1 . 16 20 9 4 6 42 Lời giải. 21 15 21 20 7 a) : = · = . 16 20 16 15 4 23 165 23 100 46 b) 2, 3 : 1, 65 = : = · = . 10 100 10 165 33 −11 −11 27 −11 10 −110 c) : 2, 7 = : = · = . 9 9 10 9 27 243 1 5 21 35 9 d) 5 : 5 = : = . 4 6 4 6 10 9 255 51 e) 25, 5 : 1 = : = 21 : 1. 42 10 42 □
c Ví dụ 3. Tìm các tỉ số bằng nhau trong các tỉ số sau rồi lập tỉ lệ thức: 8 2 a) 18 : 24 ; b) : ; c) 2, 7 : 3, 6. 15 3 Lời giải. 3 a) 18 : 24 = ; 4 8 2 8 3 4 b) : = · = ; 15 3 15 2 5 3 c) 2, 7 : 3, 6 = ; 4
Vậy ta lập được tỉ lệ thức 18 : 24 = 2, 7 : 3, 6. □
c Ví dụ 4. Tìm các tỉ số bằng nhau trong các tỉ số sau rồi lập tỉ lệ thức: 14 49 a) (−10) : (−35); b) : ; c) 1, 8 : (−6, 3). 11 11 Lời giải. −10 2 a) (−10) : (−35) = = ; −35 7 14 49 14 11 2 b) : = · = ; 11 11 11 49 7 −2 −4 c) 1, 8 : (−6, 3) = = ; 7 14 14 49
Vậy ta lập được tỉ lệ thức (−10) : (−35) = : . □ 11 11 2/82 2/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 3
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Dạng 2. Tìm số chưa biết trong tỉ lệ thức
c Ví dụ 5. Tìm x trong các tí lệ thức sau: x 15 12 3 x −11 a) = ; b) = ; c) = ; 6 8 x −8 16 12 11 −20 x 5 −6 9 d) = ; e) = ; f) = ; 10 x 0, 9 6 x −15 2x 5 x 5 x2 24 g) = ; h) = ; i) = . 6 3 8 4 6 25 Lời giải. x 15 6 · 15 45 a) = ⇒ x = = . 6 8 8 4 12 3 12 · (−8) b) = ⇒ x = = −32. x −8 3 x −11 16 · (−11) −44 c) = ⇒ x = = . 16 12 12 3 11 −20 10 · (−20) −200 d) = ⇒ x = = . 10 x 11 11 x 5 0, 9 · 5 e) = ⇒ x = = 0, 75. 0, 9 6 6 −6 9 (−6) · (−15) f) = ⇒ x = = 10. x −15 9 2x 5 g) =
⇒ (2x) · 3 = 6 · 5 ⇒ 6x = 6 · 5 ⇒ x = 5. 6 3 x 5 h) =
⇒ 4x = 8 · 5 ⇒ x = 2 · 5 = 10. 8 4 x2 24 6 · 24 144 12 i) = ⇒ x2 = ⇒ x2 = ⇒ x = ± . 6 25 25 25 5 □
c Ví dụ 6. Tìm x trong các tỉ lệ thức sau 14 9 3 3 x 8 3x − 7 5 a) : = x : ; b) 1 : 8 = 2, 5 : x; c) = ; d) = . 15 10 7 5 2 x 8 2 Lời giải. 14 9 3 14 3 9 4 a) : = x : ⇒ x = · : = . 15 10 7 15 7 10 9 3 8 b) 1
: 8 = 2, 5 : x ⇒ x = 8 · 2, 5 : = 12, 5. 5 5 x 8 c) = ⇒ x2 = 16 ⇒ x = ±4. 2 x 3x − 7 5 5 · 8 d) = ⇒ 3x − 7 =
= 20 ⇒ 3x = 27 ⇒ x = 27 : 3 = 9. 8 2 2 □ 3/82 3/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 4 20. TỈ LỆ THỨC
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC x x − y 3
c Ví dụ 7. Tìm tỉ số , biết = . y x + 2y 4 Lời giải. x − y 3 = ⇒ 4x − 4y = 3x + 6y x + 2y 4 ⇒ 4x − 3x = 6y + 4y ⇒ 4x − 3x = 6y + 4y x ⇒ x = 10y ⇒ = 10. y □
Dạng 3. Lập tỉ lệ thức từ các số hoặc đẳng thức cho trước
c Ví dụ 8. Lập một tỉ lệ thức từ các số sau 1 1 3 : 11; 0, 75 : 2 ; 4 : 14. 2 5 Lời giải. 3 1 3 5 3 1 21 3 3 : 11 = ; 0, 75 : 2 = : = ; 4 : 14 = : 14 = . 11 2 4 2 10 5 5 10 1 1
Do đó ta có tỉ lệ thức 0, 75 : 2 = 4 : 14. □ 2 5
c Ví dụ 9. Từ bốn số −2; 3; 4; −6 có thể lập được một tỉ lệ thức không? Nếu có, hãy lập tất cả các tỉ lệ thức từ bốn số đó. Lời giải. −2 4
Ta có (−2) · (−6) = 3 · 4. Do đó = . (1) 3 −6
Từ (1), hoán vị ta được ba tỉ lệ thức khác là −6 4 −2 3 −6 3 = (2); = (3); = . (4) 3 −2 4 −6 4 −2 □ 1
c Ví dụ 10. Cho năm số 3; 4; 4 ; 5; 6. Hãy chọn ra bốn số để lập thành tất cả các tỉ lệ thức. 2 Lời giải. Ta có 3 · 6 = 4 · 4, 5 (= 18).
Từ bốn số này ta có thể lập thành các tỉ lệ thức sau 3 4, 5 6 4, 5 3 4 6 4 = (1); = (2); = (3); = (4). 4 6 4 3 4, 5 6 4, 5 3 □
c Ví dụ 11. Lập tất cả các tỉ lệ thức có thể có được từ 4 số −25; −2; 4; 50. Lời giải. 4/82 4/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 5
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Ta có (−25) · 4 = (−2) · 50 = 100.
Từ đó ta có thể viết được các tỉ lệ thức sau −25 50 −25 −2 −2 4 50 4 = ; = ; = ; = . −2 4 50 4 −25 50 −25 −2 □ 1
c Ví dụ 12. Cho sáu số 1; 2; 3; 4; 4 ; 6. Hãy lập bộ bốn số trong sáu số đó sao cho mỗi bộ số này có thể 2
lập thành một tỉ lệ thức. Với mỗi bộ bốn số hãy lập thành một tỉ lệ thức. Lời giải.
Ta có thể lập được tất cả các bộ bốn số mà mỗi bộ bốn số này có thể lập thành một tỉ lệ thức. Đó là 1 3 (1) (1; 2; 3; 6) ⇒ = ; 2 6 2 4 (2) (2; 3; 4; 6) ⇒ = ; 3 6 Å 1 ã 3 4, 5 (3) 3; 4; 4 ; 6 ⇒ = . 2 4 6 □
c Ví dụ 13. Cho tập hợp các số A = {4; 8; 16; 32; 64}. Hãy liệt kê tất cả các tỉ lệ thức mà các số hạng của
nó là 4 số khác nhau trong các số đã cho. Lời giải.
Có 5 nhóm gồm 4 số thuộc A là {4; 8; 16; 32}, {8; 16; 32; 64}, {4; 8; 32; 64}, {4; 16; 32; 64}, {4; 8; 16; 64}.
○ Với bốn số {4; 8; 16; 32} ta có 8 · 16 = 4 · 32. Từ đó được 4 tỉ lệ thức 8 32 8 4 4 16 32 16 = ; = ; = ; = . 4 16 32 16 8 32 8 4
○ Với bốn số {8; 16; 32; 64} ta có 8 · 64 = 16 · 32. Từ đó được 4 tỉ lệ thức 8 32 8 16 16 64 32 64 = ; = ; = ; = . 16 64 32 64 8 32 8 16
○ Với bốn số {4; 8; 32; 64} ta có 4 · 64 = 8 · 32. Từ đó được 4 tỉ lệ thức 4 32 4 8 8 64 32 64 = ; = ; = ; = . 8 64 32 64 4 32 4 8
○ Với các nhóm 4 số {4; 16; 32; 64} và {4; 8; 16; 64} không thành lập được tỉ lệ thức nào. □
c Ví dụ 14. Lập tất cả các tỉ lệ thức có thể được từ đẳng thức 3 · 4 = 2 · 6. Lời giải. 3 6 3 2 2 4 6 4 Các tỉ lệ thức là = ; = ; = ; = . □ 2 4 6 4 3 6 3 2 −4 −5
c Ví dụ 15. Lập tất cả các tỉ lệ thức có thể được từ tỉ lệ thức = . 12 15 Lời giải. −4 12 12 15 −5 15 Các tỉ lệ thức = ; = ; = . □ −5 15 −4 −5 −4 12 5/82 5/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 6 20. TỈ LỆ THỨC
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Ví dụ 16. Lập tất cả các tỉ lệ thức có thể thu được từ đẳng thức: 18 · (−20) = (−8) · 45. Lời giải. 18 45
18 · (−20) = (−8) · 45 ⇒ = −8 −20 −8 −20 ⇒ = 18 45 −8 18 ⇒ = −20 45 −20 45 ⇒ = −8 18 □
c Ví dụ 17. Lập tất cả các tỉ lệ thức có thể thu được từ đẳng thức: (−10) · 20 = (−25) · 8. Lời giải. −10 8
(−10) · 20 = (−25) · 8 ⇒ = −25 20 −25 20 ⇒ = −10 8 −25 −10 ⇒ = 20 8 20 8 ⇒ = −25 −10 □
Dạng 4. Chứng minh tỉ lệ thức a c a c
c Ví dụ 18. Cho tỉ lệ thức = . Chứng minh rằng =
. (Giả thiết các tỉ số đều có nghĩa). a + b c + d b d Lời giải. Ta có a c =
⇒ a(c + d) = c(a + b) ⇒ ac + ad = ac + bc. a + b c + d a c Vậy ad = bc, suy ra = . □ b d a c a + b c + d
c Ví dụ 19. Cho tỉ lệ thức = . Chứng minh rằng =
. (Giả thiết các tỉ số đều có nghĩa). b d a − b c − d Lời giải. a c Ta đặt =
= k. Suy ra a = kb; c = kd. Khi đó b d a + b kb + b b(k + 1) k + 1 = = = . (1) a − b kb − b b(k − 1) k − 1 c + d kd + d d(k + 1) k + 1 = = = . (2) c − d kd − d d(k − 1) k − 1 a + b c + d Từ (1) và (2) suy ra = . □ a − b c − d 6/82 6/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 7
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Dạng 5. Các bài toán thực tế sử dụng tỉ lệ thức.
c Ví dụ 20. Phương cùng các bạn dự định làm các lá quốc kì Việt Nam bằng giấy đảm bảo tỉ lệ quy định,
chiều rộng 14 cm để tham gia Hội khoẻ Phù Đổng. Tính chiều dài của lá cờ. Lời giải.
Gọi x (cm) là chiều dài của lá cờ Phương và các bạn dự định làm. 14 2 14 · 3 Ta có tỉ lệ thức = . Suy ra x =
= 21 (cm). Vậy chiều dài của lá cờ là 21 cm. □ x 3 2
c Ví dụ 21. Để gói 10 chiếc bánh chưng, bà Nam cần 5 kg gạo nếp. Nếu bà muốn gói 45 chiếc bánh chưng
cùng loại gửi cho người dân vùng lũ thì bà cần bao nhiêu kilôgam gạo nếp? Lời giải.
Gọi x là số kg gạo nếp để làm 45 chiếc bánh chưng. x 5 5 · 45 Ta có tỉ lệ thức: = ⇒ x = = 22,5 (kg). 45 10 10
Vậy cần 22,5 kg gạo nếp để làm 45 chiếc bánh. □
c Ví dụ 22. Theo công thức làm một loại bánh, cứ 100 gam bột bánh thì cần 15 gam nho khô. Hỏi nếu có
36 gam nho khô thì cần bao nhiêu gam bột bánh để làm loại bánh đó? Lời giải.
Gọi x là số gam bột bánh cần dùng để làm với 35 gam nho khô. x 100 36 · 100 Ta có tỉ lệ thức: = ⇒ x = = 240 (g). 36 15 15
Vậy cần 240 gam bột bánh. □
c Ví dụ 23. Để làm 12 kg mứt tết, bác Nam cần dùng 2 kg đường. Hỏi nếu bác muốn làm 15 kg mứt tết
cùng loại thì cần bao nhiêu kg đường? Lời giải.
Gọi x là số kg đường cần dùng để làm 15 kg mứt tết. x 2 15 · 2 Ta có tỉ lệ thức: = ⇒ x = = 2,5 (kg). 15 12 12
Vậy cần 2,5 kg đường để làm 15 kg mứt tết. □
c Ví dụ 24. 15 người thợ may xong một đơn hàng trong 20 ngày. Hỏi nếu muốn hoàn thành đơn hàng đó
trong 12 ngày thì cần bao nhiêu người thợ (biết năng suất các người thợ là như nhau)? Lời giải.
Gọi x là số người thợ may cần có để hoàn thành đơn hàng trong 12 ngày. x 20 15 · 20 Ta có tỉ lệ thức: = ⇒ x = = 25 (người). 15 12 12
Vậy cần 25 người thợ may cần có để hoàn thành đơn hàng trong 12 ngày. □
c Ví dụ 25. Để sửa xong một đoạn đường cần 8 người công nhân làm trong 10 ngày. Hỏi nếu muốn sửa xong
đoạn đường đó trong 5 ngày thì cần bao nhiêu người công nhân (biết năng suất của các công nhân là như nhau)? Lời giải.
Gọi x là số người công nhân cần có để sửa xong đoạn đường đó trong 5 ngày. x 10 8 · 10 Ta có tỉ lệ thức: = ⇒ x = = 16 (người). 8 5 5
Vậy cần 16 người công nhân để sửa xong đoạn đường đó trong 5 ngày. □ 7/82 7/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 8 20. TỈ LỆ THỨC
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC A C BÀI TẬP VẬN DỤNG
c Bài 1. Thay tỉ số sau đây bằng tỉ số giữa các số nguyên: 9 27 −3 a) : b) 1, 25 : 0, 225 c) : 0,2 25 40 8 Lời giải. 9 27 8 50 −3 −15 a) : = b) 1, 25 : 0, 225 = c) : 0,2 = 25 40 15 9 8 8 □
c Bài 2. Thay tỉ số giữa các số hữu tỉ sau bằng tỉ số giữa các số nguyên: 3 1 2 a) 3, 75 : 18 . b) 2, 16 : 9, 3. c) 6 : 73 . 4 2 3 Lời giải. 3 15 75 Å 15 4 ã Å 75 4 ã a) Cách 1 : 3, 75 : 18 = : = · : · = 1 : 5. 4 4 4 4 15 4 15 3 15 75 15 4 1 Cách 2 : 3, 75 : 18 = : = · = = 1 : 5. 4 4 4 4 75 5 3 Cách 3 : 3, 75 : 18 = 3, 75 : 18, 75 = 1 : 5. 4
b) Tương tự: 2, 16 : 9, 3 = 36 : 155. 1 2 c) 6 : 73 = 3 : 34. 2 3 □
c Bài 3. Thay tỉ số giữa các số hữu tỉ sau bằng tỉ số giữa các số nguyên: 0, 1 : 0, 105; 1 : 0 · 0, 004; 18, 75 : 0, 0375; 46, 2 : 0, 1232 Lời giải. Ta có: 0, 1 : 0, 105 = 20 : 21 1 : 0, 004 = 250 : 1 18, 75 : 0, 0375 = 500 : 1 46, 2 : 0, 1232 = 375 : 1 □
c Bài 4. Tìm các tỉ số bằng nhau trong các tỉ số sau rồi lập tỉ lệ thức: (−21) : (−56) 6 −16 : 0, 375 : 1 15 15 Lời giải. 3 6 −16 −3 3 a) (−21) : (−56) = b) : = c) 0, 375 : 1 = 8 15 15 8 8 (−21) 0,375 Vậy tỉ lệ thức là = · □ (−56) 1 8/82 8/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 9
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Bài 5. Tìm x trong các tỉ lệ thức sau x 5 5 7 3 a) = ; b) : x = : . 1, 2 6 9 4 10 Lời giải. 2 a) x = 1. b) x = . 21 □
c Bài 6. Tìm x trong các tỉ lệ thức sau: x −9 27 −9 a) = · b) = · −16 12 x 3 Lời giải. x −9 27 −9 a) = b) = −16 12 x 3 (−16) · (−9) 3 · 27 ⇒ x = ⇒ x = 12 −9 ⇒ x = 12. ⇒ x = −9. □
c Bài 7. Tìm số hữu tỉ x trong các tỉ lệ thức sau: 1 1 1 1 1 a) x : 4 = 7 : 2 . b) 7, 5 : 3 = (48x) : 5 . 6 2 4 8 4 c) 16 : x2 = x : (−4). d) x : 0, 27 = 3 : x. x 16 e) 0, 81 : = : (−0 · 9). 2 x4 1
f) x : y = 3 : 2; y : z = 2 : 1 và z : 1 = 1 : 1 . 4
g) 7 : (8x) = 10 : y; 9 : (2y) = 5 : (3z); 10 : z = 9 : 4. Lời giải.
Áp dụng tính chất nhân chéo, ta có: Å 1 1 ã 1 125 8 a) x = 4 · 7 : 2 = = 13 . 6 2 4 9 9 Å 1 ã 1 63 21 b) 48x = 7, 5 · 5 : 3 = ⇒ x = . 4 8 5 80 c) x3 = −64 ⇒ x = −4. d) x2 = 0, 81 ⇒ x = ±0, 9. x 16 2 e) ·
= 0, 81 · (−0, 9)· ⇒ x = −2 . 2 x4 9
f) x = 0, 8 và y = 1, 6 ⇒ x = 2, 4. 4 g) z = 4 ⇒ y = 12 ⇒ x = 1, 05. 9 □ 9/82 9/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 10 20. TỈ LỆ THỨC
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Bài 8. Lập tất cả các tỉ lệ thức có thể thu được từ đẳng thức: a) (−3) · 12 = 4 · (−9); b) 5 · 125 = 252; c) 6 · 63 = 9 · 42. Lời giải. a) (−3) · 12 = 4 · (−9). 4 12 −3 −9 −3 4 −9 12 = = = = −3 −9 4 12 −9 12 −3 4 b) 5 · 125 = 252. 1 125 5 252 5 1 252 125 = = = = 5 252 1 125 252 125 5 1 c) 6 · 63 = 9 · 42 6 42 6 9 9 63 42 63 = = = = . 9 63 42 63 6 42 6 9 □ 8 12
c Bài 9. Cho tỉ lệ thức =
(1). Hãy hoán vị tỉ lệ thức này để được ba tỉ lệ thức khác. 3 4, 5 Lời giải. 4, 5 12 8 3 4, 5 3 = (2); = (3); = (4). 3 8 12 4, 5 12 8 □
c Bài 10. Lập tất cả các tỉ lệ thức có thể được
a) Từ bốn số 3; 4; 15; 20.
b) Từ bốn trong năm số 2; 3; 5; 6; 9. Lời giải.
a) Ta có 3 · 20 = 4 · 15, suy ra 3 15 20 15 3 4 20 4 = (1); = (2); = (3); = (4). 4 20 4 3 15 20 15 3
b) Ta có 2 · 9 = 3 · 6, suy ra 2 6 9 6 2 3 9 3 = (1); = (2); = (3); = (4). 3 9 3 2 6 9 6 2 □
c Bài 11. Tìm các tỉ số bằng nhau trong các tỉ số sau rồi lập thành một tỉ lệ thức: 15 2929 124 1515 124124 5 ; ; ; ; ; 26 37037 281 2626 281281 2 8 3 Lời giải. 15 1515 1515 5 5 15 124 124124 Ta có các tỉ lệ thức = ; = ; = ; = □ 26 2626 2626 2 2 26 281 281281 8 8 3 3 10/82 10/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 11
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Bài 12. Cho tập hợp các số A = {3; 9; 27; 81; 243}. Hãy liệt kê tất cả các tỉ lệ thức mà các số hạng của nó
là bốn số khác nhau trong tập hợp A. Lời giải.
Có tất cả 5 nhóm gồm 4 số thuộc tập hợp A
○ Với 4 số thuộc tập hợp {3; 9; 27; 81}, ta có đẳng thức 3 · 81 = 9 · 27. Từ đó ta được 4 tỉ lệ thức 3 27 3 9 9 81 27 81 = ; = ; = ; = . 9 81 27 81 3 27 3 9
○ Với 4 số thuộc tập hợp {3; 9; 81; 243}, ta có đẳng thức 3 · 243 = 9 · 81. Từ đó ta được 4 tỉ lệ thức 3 81 3 9 9 243 81 243 = ; = ; = ; = . 9 243 81 243 3 81 3 9
○ Với 4 số thuộc tập hợp {9; 27; 81; 243}, ta có đẳng thức 9 · 243 = 27 · 81. Từ đó ta được 4 tỉ lệ thức 9 81 9 27 27 243 81 243 = ; = ; = ; = . 27 243 81 243 9 81 9 27
○ Với 4 số thuộc tập hợp {3; 9; 27; 243} và {3; 27; 81; 243} thì không thiết lập được tỉ lệ thức nào. □
c Bài 13. Cách giải sau đúng hay sai? Giải thích/
a) Bốn số 1, 05 : 1, 47; 42; 30 lập thành một tỉ lệ thức vì nếu sắp xếp các số theo thứ tự tăng dần 1, 05 <
1 · 47 < 30 < 42, ta có 1, 05 · 42 = 1, 47 · 30(= 44, 1).
b) Bốn số −0, 2; 0, 1; −0, 1; 0, 2 không lập thành một tỉ lệ thức vì nếu sắp xếp theo thứ tự tăng dần −0, 2 <
−0, 1 < 0, 1 < 0, 2 ta có (−0, 2) · 0, 2 ̸= (−0, 1) · 0, 1 (vì −0, 04 ̸= −0, 01). Lời giải.
a) Đúng , vì đã chỉ ra được tích của hai cặp số bằng nhau, nhưng không cần sắp xếp theo thứ tự tăng dần.
b) Sai , vì (−0, 1) · 0, 2 = (−0, 2) · 0, 1(= −0, 02) nên ta có tỉ lệ thức: −0, 1 −0, 2 = 0, 1 0, 2 □
c Bài 14. Có thể lập được một tỉ lệ thức từ các nhóm bốn số sau không? 7 5 a) 4, 2; 77 ; 0, 03 và .
b) 15, 381125; 5, 35; 2, 3 và 0, 8. 9 9 c) 3, 4; 17; 0, 312 và 1, 56.
d) 32; 25; 1! + 2! + 3! và 2! + 3! + 4!. Lời giải. 7 7 5 7
a) Lập được một tỉ lệ thức vì 77 · 0, 03 = và 4, 2 · = . 9 3 9 3
b) Không lập được một tỉ lệ thức nào, vì:
15, 381125 · 5, 35 ̸= 2, 3 · 0, 8
15, 381125 · 2, 3 ̸= 5, 35 · 0, 8
15, 381125 · 0, 8 ̸= 2, 3 · 5, 35.
c) Lập được một tỉ lệ thức vì 3, 4 · 1, 56 = 5 · 304 và 17 · 0, 312 = 5, 304.
d) Lập được một tỉ lệ thức vì 32 · (2! + 3! + 4!) = 9 · 32 và 25 · (1! + 2! + 3!) = 32 · 9. □ 11/82 11/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 12 20. TỈ LỆ THỨC
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Bài 15. Có thể chọn ra bốn trong nhóm năm số (mỗi số chỉ chọn một lần) để lập thành một tỉ lệ thức được không? a) 1; 3; 9; 27; 81 b) 4; 5; 6; 7; 8 c) 21; 22; 23; 24; 25.
3−1; 3−3; 3−5; 3−7; 3−9 d) 31 181818 1818 3131 18 e) ; ; ; ; . 57 292929 2929 5757 29 Lời giải.
a) Có thể lập được một tỉ lệ thức vì chẳng hạn: 1 · 27 = 3 · 9.
b) Không lập được một tỉ lệ thức nào.
c) Có thể lập được một tỉ lệ thức vì chẳng hạn: 21 · 24 = 22 · 23.
d) Có thể lập được một tỉ lệ thức vì chẳng hạn: 3−1 · 3−7 = 3−3 · 3−5. 31 181818 1818 3131
e) Có thể lập được một tỉ lệ thức vì chẳng hạn: · = · . 57 292929 2929 5757 □
c Bài 16. Có thể lập được một tỉ lệ thức từ các số sau hay không, nếu được hãy viết tỉ lệ thức đó (chỉ viết
một tỉ lệ thức đại diện của nhóm)? a) 0, 7; 0, 3; 0, 9 và 2, 1.
b) 1, 1; 0, 22; 3, 3 và 0, 66. 2 1 1 1 1 5 3 1 c) ; ; ; . d) ; 1 ; 1 ; . 3 3 12 6 4 16 4 6
e) −6; 4, 15; 2, 075 và −0, 3.
f) a = (1 + 2 + 3)3; b = 33 + 43 + 53;
c = 13 + 23 + 33 + 43; d = (1 + 2 + 3 + 4)3 Lời giải. 0, 3 0, 9
a) Có 0, 3 · 2, 1 = 0, 63 và 0, 7 · 0, 9 = 0, 63. Ta có tỉ lệ thức = . 0, 7 2, 1 0, 22 1, 1
b) Có 0, 22 · 3, 3 = 0, 66 · 1, 1(= 0, 726). Ta có tỉ lệ thức = . 0, 66 3, 3 1 2 1 1 Å 1 ã 1 1 1 2 c) Có · = · = . Ta có tỉ lệ thức : = : . 12 3 6 3 18 12 3 6 3 d) Xét từng cặp tích: 1 3 7 1 5 21 ○ Có · 1 = khác với · 1 = . 6 4 24 4 16 64 1 5 7 1 3 7 ○ Có · 1 = khác với · 1 = . 6 16 32 4 4 16 1 1 1 3 5 147 ○ Có · = khác với 1 · 1 = . 6 4 24 4 16 64
Vậy bốn số đã cho không lập thành một tỉ lệ thức. e) Xét từng cặp tích:
○ Có (−6) · 4, 15 = −24, 9 khác với 2, 075 · (−0, 3) = −0, 6225.
○ Có (−6) · 2, 075 = −12, 45 khác với (−0, 3) · 4, 15 = −1, 245.
○ Có (−6) · (−0, 3) = 1, 8 khác với 4, 15 · 2, 075 = 8, 61125. 12/82 12/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 13
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Vậy bốn số đã cho không lập thành một tỉ lệ thức.
f) Có a = (1+2+3)3 = 63 = 216; b = 33+43+53 = 27+64+125 = 216; c = 13+23+33+43 = 1+8+27+64 = 100 (1 + 2 + 3)3 33 + 43 + 53
và d = (1 + 2 + 3 + 4)2 = 102 = 100. Có ac = bd. Vậy ta có tỉ lệ thức = . (1 + 2 + 3 + 4)2 13 + 23 + 33 + 43 □ 26 38
c Bài 17. Bớt ở số hạng trên và dưới của cả hai tỉ số và
cùng một số tự nhiên x vào để ta được hai 39 57
tỉ số mới lập thành một tỉ lệ thức? Lời giải. 26 2 · 13 2 38 2 · 19 2 Do = = và = =
nên ta không cần bớt số hạng nào cả. Do đó x = 0. □ 39 3 · 13 3 57 3 · 19 3
c Bài 18. Nhân dịp Tết Nguyên đán, một cửa hàng có chương trình khuyến mãi: mỗi khi khách hàng mua
5 hộp cam thì được tặng 2 hộp mứt. Hỏi nếu muốn được tặng 14 hộp mứt theo chương trình khuyến mãi đó
thì khách hàng cần mua bao nhiêu hộp cam? Lời giải.
Gọi x là số hộp cam cần phải mua để được tặng 14 hộp mứt (x ∈ N). x 5 14 · 5 Ta có : = ⇒ x = = 35. 14 2 2
Vậy cần phải mua 35 hộp cam để được tặng 14 hộp mứt. □
c Bài 19. Để chảy đầy một bể cạn, 3 máy bơm cần chảy trong 2 giờ. Hỏi nếu có 6 máy bơm cùng chảy vào
bể cạn đó thì sau bao lâu sẽ đầy bể? Lời giải.
Gọi x (giờ) là thời gian để 6 máy bơm cùng chảy vào bể cạn đầy bể.
Thời gian và số máy bơm tỷ lệ nghịch nên ta có 2 · 3 6 · x = 2 · 3 ⇒ x = = 1. 6
Vậy cần 1 giờ để 6 máy bơm chảy đầy bể. □ A D BÀI TẬP NÂNG CAO
c Bài 20. Tìm số hữu tỉ x, biết: 1 Å 1 ã Å 3 ã 7 a) (x − 2, 5) : 1 = x : 2. b) + x : x + = . 2 3 4 9 Lời giải. 1 3 1 a) (x − 2, 5) : 1 = x : 2 ⇔ 2(x − 2, 5) = x ⇔ x = 5 ⇔ x = 10. 2 2 2 Å 1 ã Å 3 ã 7 Å 1 ã Å 3 ã 9 9 b) + x : x + = ⇔ 9 + x = 7 x + ⇔ 2x = ⇔ x = . 3 4 9 3 4 4 8 □
c Bài 21. Tìm x, nếu:
a) y : 40 = 36 : 26; z : y = 25 : 20; x : z = 0, 65 : 1.
b) (x · y · z) : (y · z · 72) = 6300 : 7500.
c) (17 · 16 · 12) : (z · 12x · y) = (3 · 51 · 32) : (y · 6 · z). 13/82 13/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 14 20. TỈ LỆ THỨC
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
d) x : y = 3 : 2; y : z = 2 : 1 và z : 1 = 1 : 1, 25. Lời giải. 720 900
a) Vì y : 40 = 36 : 26 nên y = . Vì z : y = 25 : 20 nên z =
. Vì x : z = 0, 65 : 1 nên x = 45. 13 13 6300
b) Vì (x · y · z) : (y · z · 72) = 6300 : 7500 nên x = · 72 = 60, 48. 7500 17 · 16 · 12 3 · 51 · 32 z · 12x · y 17 · 16 · 12 1
c) Đẳng thức được viết lại là = ⇔ = ⇔ x = . z · 12x · y y · 6 · z y · 6 · z 3 · 51 · 32 3 4 8 12
d) Vì z : 1 = 1 : 1, 25 nên z = . Vì y : z = 2 : 1 nên y = . Vì x : y = 3 : 2 nên x = . 5 5 5 □
c Bài 22. Tìm x nếu x : y = 2 : 3 và xy = 54. Lời giải. x y Ta có x : y = 2 : 3 ⇔ = . 2 3 ® x y x = 2k Đặt = = k ⇒ 2 3 y = 3k.
Ta có: xy = 54 ⇔ 2k · 3k = 54 ⇔ 6k2 = 54 ⇔ k2 = 9 ⇔ k = ±3.
Với k = 3 ta có x = 6 và y = 9.
Với k = −3 ta có x = −6 và y = −9. □
c Bài 23. Tìm số hữu tỉ x mà: 26 6
a) Cùng thêm x vào số hạng trên và số hạng dưới của tỉ số
ta được một tỉ số có giá trị bằng . 39 7 26 5
b) Thêm x vào số hạng trên và bớt x ở số hạng dưới của tỉ số
ta được một tỉ số bằng . 39 8 Lời giải. 26 + x 6 a) Từ đề bài ta có = ⇔ x = 52. 39 + x 7 26 + x 5 b) Từ đề bài ta có = ⇔ x = −1. 39 − x 8 □ 5x − 2y 3
c Bài 24. Cho tỉ lệ thức = . Tính tỉ số x : y. 3x + 4y 4 Lời giải. x 5 − 2 5x − 2y y 3
Dễ thấy y ̸= 0 nên ta có thể chia cả hai số hạng của tỉ số cho y. Ta có: = . 3x + 4y x 3 + 4 4 y x
Áp dụng tính chất nhân chéo, ta có 4(5t − 2) = 3(3t + 4), với t = . y 20 x 20 Ta có t = , do đó = . □ 11 y 11
c Bài 25. Tìm số nguyên x mà: 14/82 14/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 15
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC 26 6
a) Cùng thêm vào tử và mẫu của phân số
ta được một phân số mới có giá trị bằng . 39 7 26 6
b) Thêm vào tử và bớt ở mẫu của phân số
ta được một phân số mới có giá trị bằng . 39 7 Lời giải. 26 + x 6 a) Có =
, suy ra 7 · (26 + x) = 6 · (39 + x). Suy ra x = 52. 39 + x 7 26 + x 6 b) Có =
, suy ra 7 · (26 + x) = 6 · (39 − x). Suy ra x = 4. 39 − x 7 □ a + b b + c
c Bài 26. Chứng minh rằng nếu =
, trong đó a + b + c + d ̸= 0 thì a = c. c + d d + a Lời giải. Ta có a + b b + c a + b b + c = ⇒ + 1 = + 1 c + d d + a c + d d + a a + b + c + d b + c + d + a ⇒ = . (1) c + d d + a
Vì a + b + c + d ̸= 0 nên từ (1) suy ra c + d = d + a ⇒ a = c. □ a c
c Bài 27. Chứng minh nếu các số a, b, c, d lập thành tỉ lệ thức =
thì ta cũng có các ti lệ thức sau: b d 2a + b 2c + d a2 + b2 c2 + d2 a) = b) = 3a − b 3c − d a2 − b2 c2 − d2 Lời giải. 2a + b 2c + d a) = 3a − b 3c − d a c Đặt = = k b d ⇒ a = b · k, c = d · k 2a + b 2bk + b b(2k + 1) 2k + 1 = = = · 3a − b 3bk − b b(3k − 1) 3k − 1 2c + d 2dk + d d(2k + 1) 2k + 1 = = = · 3c − d 3dk − d d(3k − 1) 3k − 1 2a + b 2c + d Vậy = · 3a − b 3c − d a2 + b2 c2 + d2 b) = a2 − b2 c2 − d2 a c Đặt = = k b d ⇒ a = b · k, c = d · k a2 + b2 (bk)2 + b2 b2(k2 + 1) k2 + 1 = = = · a2 − b2 (bk)2 − b2 b2(k2 − 1) k2 − 1 c2 + d2 (dk)2 + d2 d2(k2 + 1) k2 + 1 = = = · c2 − d2 (dk)2 − d2 d2(k2 − 1) k2 − 1 a2 + b2 c2 + d2 Vậy = a2 − b2 c2 − d2 □ 15/82 15/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 16 20. TỈ LỆ THỨC
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Bài 28. Tìm số hạng thứ tư lập thành một tỉ lệ thức với ba số hạng sau: −2 7 a) 36; 324; 9 b) ; 0, 03; 1 . c) (−2)5; (−2)3; (−2)7. d) 1!; 2!; 3! 3 9 Lời giải.
a) Gọi x là số hạng thứ tư của tỉ lệ thức, ta xét các trường hợp sau:
x = (36 · 324) : 9 = 1296. Ta có tỉ lệ thức 1296 : 324 = 36 : 9.
x = (324 · 9) : 36 = 81. Ta có tỉ lệ thức 81 : 9 = 324 : 36.
x = (9 · 36) : 324 = 1. Ta có tỉ lệ thức 1 : 36 = 9 : 324. Vậy x ∈ {1; 81; 1296}.
b) Gọi x là số hạng thứ tư của tỉ lệ thức, ta xét các trường hợp sau: Å −2 ã 7 −9 Å −9 ã Å −2 ã 7 x = · 0, 03 : 1 = . Ta có tỉ lệ thức : 0, 03 = : 1 . 3 9 800 800 3 9 Å 7 ã −2 −2 Å −2 ã 7 Å −2 ã x = 0, 03 · 1 : = . Ta có tỉ lệ thức : 1 = 0, 03 : . 9 3 25 25 9 3 Å 7 −2 ã 41 Å 41 ã 7 −2 x = 1 · : 0, 03 = −39 . Ta có tỉ lệ thức −39 : 1 = : 0, 03. 9 3 81 81 9 3 ß 41 2 9 ™ Vậy x ∈ −39 ; − ; − . 81 25 800
c) Tương tự, xét ba trường hợp ta có x ∈ (−2)9; (−2)5; −2 . ß 1 ™
d) Tương tự, xét ba trường hợp ta có x ∈ ; 3; 12 . 3 □ 16/82 16/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 17
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Baâi 21
TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU A
TRỌNG TÂM KIẾN THỨC
1 Tính chất của dãy hai tỉ số bằng nhau a c a c a + c a − c Từ tỉ lệ thức = suy ra = = = . b d b d b + d b − d
(Giả thiết các tỉ số đều có nghĩa).
2 Mở rộng tính chất cho dãy tỉ số bằng nhau a c e
Từ dãy tỉ số bằng nhau = = suy ra: b d f a c e a + c + e a − c + e = = = = . b d f b + d + f b − d + f
(Giả thiết các tỉ số đều có nghĩa). a c e Nếu = =
, ta còn nói các số a, c, e tỉ lệ với các số b, d, f . b d f
Khi đó ta cũng viết a : c : e = b : d : f . A B CÁC DẠNG BÀI TẬP
Dạng 1. Sử dụng tính chất dãy tỉ số bằng nhau để tìm các đại lượng chưa biết x y z
c Ví dụ 1. Tìm x, y, z biết = = và x − y + z = 70. 9 5 10 Lời giải. x y z x − y + z 70 Ta có = = = = = 5. 9 5 10 9 − 5 + 10 14 Do đó x = 5 ⇒ x = 45; 9 y = 5 ⇒ y = 25; 5z = 5 ⇒ z = 50. 10 □ x y z
c Ví dụ 2. Tìm x, y, z biết = = và − x + y − z = 60. 8 5 12 Lời giải. x y z −x + y − z 60 Ta có = = = = = −4. 8 5 12 −8 + 5 − 12 −15 Do đó x = −4 ⇒ x = −32; 8 17/82 17/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 18
21. TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC y = −4 ⇒ y = −20; 5z = −4 ⇒ z = −48. 12 □ x y z
c Ví dụ 3. Tìm x, y, z biết = = và x − 3z = 9. 7 4 2 Lời giải. x y z x y 3z x − 3z Ta có = = ⇒ = = = = 9. 7 4 2 7 4 6 7 − 6 Do đó x = 9 ⇒ x = 63; 7 y = 9 ⇒ y = 36; 4 z = 9 ⇒ z = 18. 2 □ x 7 y 10
c Ví dụ 4. Cho biết = ; = và x + y + z = 120. y 10 z 13 Tìm x, y, z. Lời giải. x 7 x y = ⇒ = . (1) y 10 7 10 y 10 y z = ⇒ = . (2) z 13 10 13 x y z x + y + z 120 Từ (1) và (2) suy ra = = = = = 4. 7 10 13 7 + 10 + 13 30 Do đó x = 4 ⇒ x = 28; 7y = 4 ⇒ y = 40; 10 z = 4 ⇒ z = 52. 13 □
c Ví dụ 5. Tìm x, y, z biết 3x = 4y = 5z và x − y − z = −42. Lời giải. Ta có 3x 4y 5z 3x = 4y = 5z ⇒ = = . 60 60 60 Do đó x y z x − y − z −42 = = = = = 6. 20 15 12 20 − 15 − 12 −7 Suy ra x = 6 ⇒ x = 120; 20 y = 6 ⇒ y = 90; 15 z = 6 ⇒ z = 72. 12 18/82 18/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 19
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Nhận xét. Từ đề bài, 3x = 4y = 5z, muốn biến đổi thành một dãy tỉ số bằng nhau ta đã chia 3x, 4y, 5z cho BCNN(3, 4, 5) = 60. □ c Ví dụ 6. x y
a) Tìm hai số x và y, biết: = và x + y = 60. 8 12 x y
b) Tìm hai số x và y, biết: = và x − y = 12. 6 10 y z
c) Tìm ba số x, y và z, biết: x = = và 2x − 4y + z = −6. 2 4 Lời giải. a) Ta có x y x + y = = = 3. 8 12 8 + 12 x y Suy ra = 3 ⇒ x = 24; = 3 ⇒ y = 36. 8 12 b) Ta có x y x − y = = = −3. 6 10 6 − 10 x y Suy ra = −3 ⇒ x = −18; = −3 ⇒ y = −30. 6 10 c) Ta có y z 2x 4y 2x − 4y + z x = = = = = = 3. 2 4 2 8 2 − 8 + 4 y z Suy ra x = 3; = 3 ⇒ y = 6; = 3 ⇒ z = 12. 2 4 □ c Ví dụ 7. a b
a) Tìm hai số a và b, biết: = và a + b = 38. 11 8 a b
b) Tìm hai số a và b, biết: = và b − a = 16. 15 7 a b c
c) Tìm ba số a, b và c, biết: = = và a − 5b + 4c = 23. 2 −4 6 Lời giải. a) Ta có a b a + b = = = 2. 11 8 11 + 8 a b Suy ra = 2 ⇒ a = 22; = 2 ⇒ b = 16. 11 8 b) Ta có a b b − a = = = −2. 15 7 7 − 15 a b Suy ra = −2 ⇒ a = −30; = −2 ⇒ b = −14. 15 7 19/82 19/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 20
21. TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC c) Ta có a b c 5b a − 5b + 4c 1 = = = = = . 2 −4 6 4c 2 + 20 + 24 2 −20 = 24 a 1 b 1 c 1 Suy ra = ⇒ a = 1; = ⇒ b = −2; = ⇒ c = 3. 2 2 −4 2 6 2 □ c Ví dụ 8. x y z
a) Tìm ba số x, y và z, biết: = = và xyz = 480. 3 4 5 x y z
b) Tìm ba số x, y và z, biết: = = và x2 + z2 = 80. 2 −3 −4 Lời giải. x y z x 3 y 3 z 3 xyz a) Ta có = = suy ra = = = = 8 = 23. 3 4 5 3 4 5 3 · 4 · 5 x y z Do đó = 2 ⇒ x = 6; = 2 ⇒ y = 8; = 2 ⇒ z = 10. 3 4 5 x y z Å ã2 Å ã2 x 2 y z x2 + z2 b) Ta có = = suy ra = = = = 4 = 22. 2 −3 −4 2 −3 −4 4 + 16 x Khi
= 2 suy ra x = 4; y = −6; z = −8. 2 x Khi
= −2 suy ra x = −4; y = 6; z = 8. 2 □ x y z
c Ví dụ 9. Tìm x, y, z biết = = và x · y · z = 288. 3 2 6 Lời giải. x y z Đặt = =
= k ⇒ x = 3k, y = 2k, z = 6k. 3 2 6 Khi đó
x · y · z = (3k) · (2k) · (6k) = 36k3 ⇒ 36k3 = 288 ⇒ k3 = 8 ⇒ k = 2.
Suy ra x = 3 · 2 = 6; y = 2 · 2 = 4; z = 6 · 2 = 12. □ c Ví dụ 10. a b c
a) Tìm ba số a, b và c, biết: = = và abc = −24. 8 6 4 a b c
b) Tìm ba số a, b và c, biết: = = và a2 − b2 = −60. 4 8 16 Lời giải. a b c Å ã3 a 3 b c 3 abc 1 a) Ta có = = suy ra = = = = − . 8 6 4 8 6 4 8 · 6 · 4 8 a b c 1 Suy ra = = = −
⇒ a = −4; b = −3; c = −2. 8 6 4 2 a b c Å ã2 a 2 b c 2 a2 − b2 5 b) Ta có = = suy ra = = = = . 4 8 16 4 8 16 16 − 64 4 √ a b c 5 √ √ √ Khi = = =
suy ra a = 2 5; b = 4 5; c = 8 5. 4 8 16 2√ a b c 5 √ √ √ Khi = = = −
suy ra a = −2 5; b = −4 5; c = −8 5. 4 8 16 2 □ 20/82 20/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 21
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Dạng 2. Chứng minh tỉ lệ thức. Tính giá trị biểu thức a c a2 − c2 ac
c Ví dụ 11. Cho tỉ lệ thức = . Chứng minh rằng =
(giả thiết các tỉ số đều có nghĩa). b d b2 − d2 bd Lời giải. a c a2 c2 ac Từ tỉ lệ thức = ⇒ = = . (1) b d b2 d2 bd a2 c2 a2 − c2
Áp dụng tính chất của dãy tỉ số bằng nhau ta có = = . (2) b2 d2 b2 − d2 a2 − c2 ac Từ (1) và (2) suy ra = . □ b2 − d2 bd a c a + 2c a − 3c
c Ví dụ 12. Cho tỉ lệ thức = . Chứng minh rằng =
(giả thiết các tỉ số đều có nghĩa). b d b + 2d b − 3d Lời giải. Ta có a c 2c a + 2c = = = . (1) b d 2d b + 2d a c 3c a − 3c = = = . (2) b d 3d b − 3d a + 2c a − 3c Từ (1) và (2) suy ra = . □ b + 2d b − 3d a + b − c a + c − b b + c − a
c Ví dụ 13. Cho các số a, b, c, d thỏa mãn a + b + c ̸= 0 và = = . Tính giá trị c b a biểu thức: (a + b)(b + c)(a + c) A = . abc Lời giải. Ta có a + b − c a + c − b b + c − a a + b + c = = = = 1. c b a a + b + c
Suy ra a + b = 2c; a + c = 2b và b + c = 2a. Suy ra (a + b)(b + c)(a + c) 2c · 2a · 2b A = = = 8. abc abc □ a + b a − b a c
c Ví dụ 14. Chứng minh rằng nếu = thì = . c + d c − d b d Lời giải. a + b a − b a + b + a − b 2a a Ta có = = = = . c + d c − d c + d + c − d 2c c a + b a − b a + b − a + b 2b b Ngoài ra ta có = = = = . c + d c − d c + d − c + d 2d d a b a c Do đó = ⇔ = . □ c d b d
Dạng 3. Áp dụng tính chất của dãy hai tỉ số bằng nhau để giải bài toán khác 21/82 21/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 22
21. TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC 1 2 3
c Ví dụ 15. Chia số 69 thành ba phần tỉ lệ với các số ; và . 2 3 4 Lời giải.
Gọi ba phần cần tìm lần lượt là x, y, z. Theo đề bài ta có x y z x + y + z 69 = = = = = 36. 1 2 3 1 2 3 23 + + 2 3 4 2 3 4 12 1 2 3 Suy ra x = · 36 = 18; y = · 36 = 24; z = · 36 = 27. □ 2 3 4
c Ví dụ 16. Chu vi của một tam giác là 81 cm. Các cạnh của nó tỉ lệ với 2, 3, 4. Tính độ dài mỗi cạnh. Lời giải.
Gọi độ dài ba cạnh của tam giác lần lượt là x, y, z. x y z Theo đề bài ta có = = và x + y + z = 81. 2 3 4 Ta có x y z x + y + z 81 = = = = = 9. 2 3 4 2 + 3 + 4 9
Suy ra x = 2 · 9 = 18; y = 3 · 9 = 27; z = 4 · 9 = 36.
Vậy độ dài ba cạnh của tam giác lần lượt là 18cm; 27cm; 36cm. □
c Ví dụ 17. Một khu vườn hình chữ nhật có diện tích là 960 m2. Chiều dài và chiều rộng tỉ lệ với 5 và 3.
Tính chiều dài và chiều rộng của khu vườn. Lời giải.
Gọi chiều dài của khu vườn là x (m).
Chiều rộng của khu vườn là y (m). x y Theo đề bài ta có = và xy = 960. 5 3 x y Đặt = = k > 0 ⇒ x = 5k; y = 3k. 5 3
Ta có x · y = (5k) · (3k) = 15k2 ⇒ 15k2 = 960 ⇒ k2 = 64 ⇒ k = 8 vì (k > 0). Suy ra x = 40; y = 24.
Vậy chiều dài khu vườn là 40m, chiều rộng khu vườn là 24m. □
c Ví dụ 18. Tỉ số số viên sỏi của Minh và Nam là 1,25. Hỏi mỗi bạn có bao nhiêu viên sỏi, biết rằng Minh
có nhiều hơn Nam là 10 viên sỏi? Lời giải.
Gọi x, y lần lượt là số viên sỏi của Minh và Nam trong đó x, y ∈ N. x 5 x y x − y Theo đề bài ta có = 1,25 = và x − y = 10 suy ra = = = 10. y 4 5 4 5 − 4 Suy ra x = 50; y = 40.
Vậy Minh có 50 viên sỏi và Nam có 40 viên sỏi. □
c Ví dụ 19. Tỉ số số học sinh nam và số học sinh nữ của lớp 7A là 0,75. Biết rằng số học sinh nam ít hơn
số học sinh nữ là 5 bạn. Hỏi lớp 7A có bao nhiêu học sinh nam và học sinh nữ? Lời giải.
Gọi x, y lần lượt là số học sinh nam và học sinh nữ của lớp 7A trong đó x, y ∈ N. x 3 x y y − x Theo đề bài ta có = 0,75 = và y − x = 5 suy ra = = = 5. y 4 3 4 4 − 3 Suy ra x = 15; y = 20.
Vậy lớp 7A có 15 học sinh nam và có 20 học sinh nữ. □ 22/82 22/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 23
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Ví dụ 20. Ba đội công nhân có tất cả 75 người và số công nhân của đội I, đội II và đội III tỉ lệ với 3; 5; 7.
Tính số công nhân của mỗi đội. Lời giải.
Gọi x, y, z lần lượt là số công nhân của đội I, đội II và đội III trong đó x, y, z ∈ N. x y z x y z x + y + z Theo đề bài ta có = = và x + y + z = 75 suy ra = = = = 5. 3 5 7 3 5 7 3 + 5 + 7 Suy ra x = 15; y = 25; z = 35.
Vậy đội I có 15 công nhân, đội II có 25 công nhân và đội III có 35 công nhân. □
c Ví dụ 21. Số bàn thắng ba đội bóng A, B, C ghi được tỉ lệ với 8, 10, 11. Hỏi mỗi đội ghi được bao nhiêu
bàn thắng biết cả ba đội ghi được 58 bàn thắng? Lời giải.
Gọi x, y, z lần lượt là số bàn thắng của đội A, đội B và đội C trong đó x, y, z ∈ N. x y z x y z x + y + z Theo đề bài ta có = = và x + y + z = 58 suy ra = = = = 2. 8 10 11 8 10 11 8 + 10 + 11 Suy ra x = 16; y = 20; z = 22.
Vậy đội A có 16 bàn thắng, đội B có 20 bàn thắng và đội C có 22 bàn thắng. □ A C BÀI TẬP VẬN DỤNG x 5
c Bài 1. Tính x và y, biết = và x + y = 70. y 9 Lời giải. Đáp số x = 25; y = 45. □ x y
c Bài 2. Tính x và y, biết = và x − 2y = 16. 15 7 Lời giải. Đáp số x = 240; y = 112. □ x y
c Bài 3. Tìm hai số x và y, biết: = và x + y = 80. 13 7 Lời giải. Ta có x y x + y = = = 4. 13 7 13 + 7 Suy ra x = 52; y = 28. □ a b
c Bài 4. Tìm hai số a và b, biết: = và a − b = 16. 3 7 Lời giải. Ta có a b a − b = = = −4. 3 7 3 − 7 Suy ra a = −12; b = −28. □ x y c Bài 5. Cho biết = và xy = 1000. Tìm x và y. 5 2 Lời giải. 23/82 23/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 24
21. TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC x y Đặt = = k. Tìm được k = ±10. 5 2
Suy ra x = 50; y = 20 hoặc x = −50; y = −20. □
c Bài 6. Tìm ba số m, n và p, biết: m : n : p = 6 : 8 : 9 và m − n + p = 21. Lời giải. Ta có m n p m − n + p = = = = 3. 6 8 9 6 − 8 + 9
Suy ra m = 18; n = 24 và p = 27. □ x y z
c Bài 7. Tìm x, y, z, biết = = và x − y − z = 6. 13 7 5 Lời giải.
Đáp số x = 79; y = 42; z = 30. □
c Bài 8. Tìm x, y, z, biết x 8 y 11 x y y z a) = ; = và x + y − z = 80. b) = ; = và x · y · z = −528. y 11 z 3 4 3 6 11 Lời giải. x y z a) Biến đổi thành dãy = = . 8 11 3
Đáp số x = 40; y = 55; z = 15. x y x y b) Ta có = ⇒ = . (1) 4 3 8 6 y z Mà = . (2) 6 11 x y z Từ (1) và (2) suy ra = = = k. 8 6 11
Ta tính được k = −1, suy ra x = −8; y = −6; z = −11. □ x − y 3y x
c Bài 9. Cho x, y, z là ba số dương phân biệt. Biết = = . z x − z y
Chứng minh rằng x = 2y và y = 2z. Lời giải. x − y 3y x x − y + 3y + x 2(x + y) = = = = = 2. z x − z y z + x − z + y x + y x Vậy
= 2 ⇒ x = 2y, từ đó tìm được y = 2z. □ y
c Bài 10. Cùng thêm một số khác 0 vào tử và mẫu của một phân số mà giá trị của phân số không đổi. Tìm phân số đã cho. Lời giải. a a a + c
Gọi phân số cần tìm là . Theo giả thiết, ta có =
. Do đó a = b, nghĩa là phân số cần tìm có tử số bằng b b b + c mẫu số. □ 2x + 1 3y − 2 2x + 3y − 1 c Bài 11. Cho = = . Tìm x và y. 5 7 6x Lời giải. 24/82 24/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 25
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC 2x + 1 3y − 2 2a + 3y − 1 2x + 3y − 1 2x + 3y − 1 Ta có = = = = . 5 7 5 + 7 12 6x
Trường hợp 1: 6x = 12 ⇒ x = 2 ⇒ y = 3. 2x + 1 3y − 2 1 2 Trường hợp 2: = = 0 ⇒ x = − ⇒ y = . □ 5 7 2 3
c Bài 12. Trong một thùng hoa quả, tỉ số số quả cam và số quả xoài là 2,5. Biết số quả cam nhiều hơn số
quả xoài là 15. Tính số quả cam và quả xoài trong thùng. Lời giải.
Gọi x, y lần lượt là số quả cam và số quả xoài trong đó x, y ∈ N. x 5 x y x − y Theo đề bài ta có = 2,5 = và x − y = 15 suy ra = = = 5. y 2 5 2 5 − 2 Suy ra x = 25; y = 10.
Vậy có 25 quả cam và 10 quả xoài. □
c Bài 13. Số quyển vở của ba bạn Ánh, Ngọc và Hằng tỉ lệ với 9; 5; 7. Hỏi mỗi bạn có bao nhiêu quyển vở
biết cả ba bạn có 63 quyển vở? Lời giải.
Gọi x, y, z lần lượt là số quyển vở của bạn Ánh, Ngọc và Hằng trong đó x, y, z ∈ N. x y z x y z x + y + z Theo đề bài ta có = = và x + y + z = 63 suy ra = = = = 3. 9 5 7 9 5 7 9 + 5 + 7 Suy ra x = 27; y = 15; z = 21.
Vậy Ánh có 27 quyển vở, Ngọc có 15 quyển vở và Hằng có 21 quyển vở. □
c Bài 14. Tìm hai số x và y, biết: x y x 2 x y a) = và 4x − y = 34; b) = và xy = 24; c) = và x2 − y2 = −45. 6 7 y 3 −2 3 Lời giải. x y 4x 4x − y a) Ta có = = = = 2. 6 7 24 24 − 7 Suy ra x = 12; y = 14. x 2 x y x 2 y 2 xy b) Ta có = suy ra = suy ra = = = 4. y 3 2 3 2 3 2 · 3 x y Khi = = 2 suy ra x = 4; y = 6. 2 3 x y Khi =
= −2 suy ra x = −4; y = −6. 2 3 x y Å x ã2 y 2 x2 − y2 c) Ta có = suy ra = = = 9. −2 3 −2 3 4 − 9 x y Khi = = 3 suy ra x = −6; y = 9. −2 3 x y Khi = = −3 suy ra x = 6; y = −9. −2 3 □
c Bài 15. Tìm các số a, b, c nếu: a b b c a + 3 b − 2 c − 1
a) 5a − 3b − 3c = −536 và = , = . b) 3a − 5b + 7c = 86 và = = . 4 6 5 8 5 3 7 a b b c c) a − 2b + c = 46 và = , = .
d) 5a = 8b = 3c và a − 2b + c = 34. 7 6 5 8
e) 3a = 7b và a2 − b2 = 160.
f) 15a = 10b = 6c và abc = −1920. 25/82 25/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 26
21. TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC a b c a b c
g) a2 + 3b2 − 2c2 = −16 và = = . h) a3 + b3 + c3 = 792 và = = . 2 3 4 2 3 4 Lời giải. a b a b a) Ta có = ⇒ = . 4 6 20 30 b c b c a b c 5a 3b 3c Ngoài ra = ⇒ = ⇒ = = ⇒ = = . 5 8 30 48 20 30 48 100 90 144
Áp dụng tính chất dãy tỉ số bằng nhau, ta có 5a 3b 3c 5a − 3b − 3c −536 = = = = = 4. 100 90 144 100 − 90 − 144 −134
Do đó a = 80, b = 120, c = 192. a + 3 b − 2 c − 1 3(a + 3) 5(b − 2) 7(c − 1) b) Ta có = = ⇒ = = . 5 3 7 15 15 49
Áp dụng tính chất dãy tỉ số bằng nhau, ta có 3(a + 3) 5(b − 2) 7(c − 1) 3a + 9 − 5b + 10 + 7c − 7 3a − 5b + 7c + 9 + 10 − 7 = = = = = 2. 15 15 49 15 − 15 + 49 49 Do đó a = 7, b = 8, c = 15. a b a b c) Ta có = ⇒ = . 7 6 35 30 b c b c a b c a 2b c Ngoài ra = ⇒ = ⇒ = = ⇒ = = . 5 8 30 48 35 30 48 35 60 48
Áp dụng tính chất dãy tỉ số bằng nhau, ta có a 2b c a − 2b + c 46 = = = = = 2. 35 60 48 35 − 60 + 48 23
Do đó a = 70, b = 60, c = 96. 5a 8b 3c a b c a 2b c d) Ta có 5a = 8b = 3c ⇒ = = ⇒ = = ⇒ = = . 120 120 120 24 15 40 24 30 40
Áp dụng tính chất dãy tỉ số bằng nhau, ta có a 2b c a − 2b + c 34 = = = = = 1. 24 30 40 24 − 30 + 40 34
Do đó a = 24, b = 15, c = 40. a b a2 b2 a2 − b2 160 e) Ta có 3a = 7b ⇒ = ⇒ = = = = 4. 7 3 72 32 72 − 32 40 Do đó a = ±14, b = ±6. 15a 10b 6c a b c f) Ta có 15a = 10b = 6c ⇒ = = ⇒ = = . 30 30 30 2 3 5 a = 2k a b c Đặt = = = k ⇒ b = 3k . 2 3 5 c = 5k
Ta có abc = −1920 ⇔ 2k · 3k · 5k = −1920 ⇔ k3 = −64 ⇔ k = −4.
Do đó a = −8, b = −12, c = −20. a b c a2 b2 c2 a2 3b2 2c2 a2 + 3b2 − 2c2 −16 g) Ta có = = ⇒ = = ⇒ = = = = = 16. 2 3 4 4 9 16 4 27 32 4 + 27 − 32 −1
Do đó a = ±8, b = ±12, c = ±16. a b c a3 b3 c3 a3 + b3 + c3 792 h) Ta có = = ⇒ = = = = = 8. 2 3 4 8 27 64 8 + 27 + 64 99
Do đó a = 4, b = 6, c = 8cxz. □ 26/82 26/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 27
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC a c
c Bài 16. Cho tỉ lệ thức =
. Chứng minh các tỉ lệ thức sau: b d a2 − b2 c2 − d2 (a + b)2 (c + d)2 = ; = . ab cd a2 + b2 c2 + d2 Lời giải. a2 − b2 a b c2 − d2 c d a c b d a2 − b2 c2 − d2 Ta có = − , và = − . Mà = và = nên ta có = . ab b a cd d c b d a c ab cd a c a b a2 b2 a2 + c2 Ta có = ⇔ = = = = . b d c d c2 d2 b2 + d2 a b a + c Å a + c ã2 Mặt khác, ta có = = = . c d c + d b + d Å a + b ã2 a2 + b2 (a + b)2 (c + d)2 Do đó = hay = . □ c + d c2 + d2 a2 + b2 c2 + d2 a c Å a + b ã3 a3 + b3
c Bài 17. Cho tỉ lệ thức = . Chứng minh rằng = . b d c + d c3 + d3 Lời giải. a c a b a3 b3 a3 + c3 Ta có = ⇔ = = = = . b d c d c3 d3 b3 + d3 a b a + c Å a + c ã3 Å a + b ã3 a3 + b3 Mặt khác, ta có = = = . Do đó = . □ c d c + d b + d c + d c3 + d3 a + b c + d
c Bài 18. Cho tỉ lệ thức =
, với a, b, c, d > 0. So sánh a và c. b + c d + a Lời giải.
Vì a, b, c, d > 0 nên a + b + c + d ̸= 0 a + b c + d a + b + c + d ⇒ = = = 1 ⇒ a = c. b + c d + a b + c + d + a □ a a a a c Bài 19. 1 2 3 n Chứng minh rằng nếu = = = . . . = thì a2 a3 a4 an+1 Å a ãn 1 + a2 + a3 + . . . + an a1 = . a2 + a3 + a4 + . . . + an+1 an+1 Lời giải. Ta có a1 a2 a3 an a1 + a2 + a3 + . . . + an = = = . . . = = a2 a3 a4 an+1 a2 + a3 + a4 + . . . + an+1 Å a ãn Å a ãn a a a a a ⇒ 1 + a2 + a3 + . . . + an 1 1 2 3 n 1 = = · · · · · · · = a2 + a3 + a4 + . . . + an+1 a2 a2 a3 a4 an+1 an+1 □ A D BÀI TẬP NÂNG CAO
c Câu 1. Tìm x, biết: a) (x + 15) : x = 4 : 3.
b) (7, 5 − x) : (3, 5 + x) = 5 : 6. 27/82 27/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 28
21. TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c) (x − 20) : (x − 10) = (x + 40) : (x + 70). Lời giải. x + 15 x (x + 15) − x a) Từ a), ta có: = = = 15, suy ra x = 45. 4 3 4 − 3 7, 5 − x 3, 5 + x (7, 5 − x) + (3, 5 + x) 11 b) Từ b), ta có: = = = = 1, suy ra x = 2, 5. 5 6 5 + 6 11
c) Theo tính chất dãy tỉ số bằng nhau, ta có x − 20 x + 40 (x + 40) − (x − 20) 3 = = = . x − 10 x + 70 (x + 70) − (x − 10) 4 x + 40 3 x + 40 x + 70 30 Tương tự = ⇒ = = = 30 ⇒ x = 50. x + 70 4 3 4 1 □
c Câu 2. Tìm các số x, y, z, biết rằng: x y z a) = = và x − 2y + 4z = 13.
b) 4x = 3y, 7y = 5z và x − y + z = −46. 20 9 6 x 2y 4z x 2y 3z c) = = và 3x + 5y + 7z = 123. d) = = và xyz = −108. 2 5 7 2 3 4 Lời giải.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có: x y z x − 2y + 4z 13 1 a) = = = = =
, suy ra x = 10; y = 4, 5 và z = 3. 20 9 6 20 − 2 · 9 + 4 · 6 26 2 x y y z x y z x − y + z −46 b) = và = ⇒ = = = = = −2. 3 4 5 7 15 20 28 15 − 20 + 28 23
Suy ra x = −30, y = −40 và z = −56. x 2y 4z x y z 1 c) = = ⇒ = = (nhân mỗi tỉ số với ). 2 5 7 8 10 7 4 x y z 3x + 5y + 7z 123 Suy ra = = = =
= 1. Vậy x = 8; y = 10 và z = 7. 8 10 7 3 · 8 + 5 · 10 + 7 · 7 123 x 2y 3z x 2y 3z xyz −108 d) Đặt = = = k thì k3 = · · = = = −27, suy ra k = −3. 2 3 4 2 3 4 4 4
Vậy x = −6; y = −4, 5 và z = −4. □
c Câu 3. Chứng minh rằng nếu có (a + b + c + d)(a − b − c + d) = (a − b + c − d)(a + b − c − d) thì bốn số
a, b, c và d lập thành một tỉ lệ thức. Lời giải. a + b + c + d a + b − c − d 2(a + b) a + b Ta có = = = . a − b + c − d a − b − c + d 2(a − b) a − b a + b + c + d a + b − c − d 2(c + d) c + d Mặt khác, ta có = = = . a − b + c − d a − b − c + d 2(c − d) c − d a + b c + d a + b a − b a b Do đó = ⇔ = = = . a − b c − d c + d c − d c d
Vậy a, b, c và d lập thành một tỉ lệ thức. □ 28/82 28/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 29
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC a + b − c b + c − a c + a − b Å b ã c a
c Câu 4. Cho abc ̸= 0 và = = . Tính P = 1 + 1 + 1 + . c a b a b c Lời giải. a + b − c b + c − a c + a − b 2b 2c 2a 2(a + b + c) Trường hợp 1: Ta có = = = = = = = 1. c a b a + c a + b b + c 2(a + b + c) a + c = 2b 8abc Do đó a + b = 2c ⇒ P = = 8. abc b + c = 2a a + b − c b + c − a c + a − b 2a − 2c Trường hợp 2: Ta có = = = = −2. c a b c − a a + b − c = −2 c a + b = −c b + c − a Do đó = −2 ⇔ b + c = −a a c + a = −b. c + a − b = −2 b −abc Vậy P = = −1. □ abc x y z
c Câu 5. Tìm x, y và z, nếu: x + y + z = = = . y + z − 2 z + x − 3 x + y + 5 Lời giải.
Dễ thấy nếu x = 0 thì y = z = 0, suy ra x = y = z = 0 là một bộ giá trị cần tìm.
Giả sử x, y và z khác 0 thì theo đề bài ra x + y + z ̸= 0. Sử dụng tính chất dãy tỉ số bằng nhau, ta có: x y z x + y + z 1 x + y + z = = = = = . y + z − 2 z + x − 3 x + y + 5 2(x + y + z) 2 1 5 11
Thay kết quả vào dãy tỉ số ban đầu, ta được: x = − ; y = − ; z = . 2 6 6 1 5 11
Vậy ta có: x = y = z = 0 hoặc x = − ; y = − ; z = . □ 2 6 6 x y z
c Câu 6. Cho dãy tỉ số bằng nhau = = . Chứng minh rằng a + 2b + c 2a + b − c 4a − 4b + c a b c = =
(giả thiết các tỉ số đều có nghĩa). x + 2y + z 2x + y − z 4x − 4y + z Lời giải.
Áp dụng tính chất dãy tỉ số bằng nhau (cộng các số hạng tương ứng), ta có: x y z = = a + 2b + c 2a + b − c 4a − 4b + c x + 2y + z x + 2y + z = = .
(a + 2b + c) + (4a + 2b − 2c) + (4a − 4b + c) 9a x + 2y + z 2x + y − z 4x − 4y + z a
Tương tự ta có kết quả = =
. Do các tỉ số đều có nghĩa ta suy ra = 9a 9b 9c x + 2y + z b c = . □ 2x + y − z 4x − 4y + z bz − cy cx − az ay − bx x y z c Câu 7. Cho = = . Chứng minh rằng: = = . a b c a b c Lời giải. 29/82 29/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 30
21. TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Từ giả thiết, ta có a, b và c đều khác 0 nên a2 + b2 + c2 ̸= 0.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có (do a, b, c ̸= 0): a(bz − cy) b(cx − az) c(ay − bx) 0 = = = = 0. a2 b2 c2 a2 + b2 + c2 y z z x
Do a, b và c đều khác 0 suy ra bz − cy = 0, nên = . Tương tự, ta có = . b c c a x y z Suy ra = = . □ a b c a b c ak2 + bk + c
c Câu 8. Chứng minh rằng nếu có dãy tỉ số = =
thì giá trị của tỉ số không phụ thuộc x y z xk2 + yk + z vào giá trị của k. Lời giải. ak2 + bk + c c
Nếu k = 0 thì hiển nhiên ta có: = . xk2 + yk + z z
Nếu k ̸= 0, áp dụng tính chất dãy tỉ số bằng nhau ta có: a b c ak2 bk ak2 + bk + c = = = = = . x y z xk2 yk xk2 + yk + z ak2 + bk + c a b c
Trong cả hai trường hợp thì giá trị của tỉ số
đều bằng giá trị của dãy tỉ số ban đầu = = , xk2 + yk + z x y z
nghĩa là không phụ thuộc vào giá trị của k. □ a b c
c Câu 9. Biết các số tự nhiên a, b, c, x, y, z khác 0 và lập thành một dãy tỉ số bằng nhau = = . Chứng x y z
minh rằng nếu c là số dư của phép chia số a cho số b thì z là số dư của phép chia số x cho số y. Lời giải.
Theo đều bài, c là số dư của phép chia số a cho số b nên theo định nghĩa phép chia có dư, tồn tại một số tự nhiên
q ̸= 0 mà a = bq + c với c < b. a b c bq + c
Áp dụng tính chất dãy tỉ số bằng nhau, ta có: = = = . x y z yq + z
Vì a = bq + c và c < b (q ∈ ∗ ∗
N ) nên x = yq + z và z < y (q ∈ N ), suy ra z là số dư của phép chia số x cho số y. □ a c a c
c Câu 10. Cho tỉ lệ thức =
, chứng minh tỉ lệ thức = . b d a + b c + d Lời giải.
Giả thiết tất cả các tỉ số đã cho đều có nghĩa.
Cách 1 : Phương pháp nhân chéo.
Xét các tích: a(c + d) = ac + ad và (a + b)c = ac + bc. a c a c Mà ad = bc do = , nên a(c + d) = (a + b)c hay = . b d a + b c + d
Cách 2 : Sử dụng tính chất dãy tỉ số bằng nhau. a c a b a + b
Hoán vị trung tỉ của tỉ lệ thức = ta được = = . b d c d c + d a a + b a c
Lại hoán vị trung tỉ của tỉ lệ thức = ta được = . c c + d a + b c + d
Cách 3 : Phương pháp định nghĩa. a c Đặt tỉ lệ thức = = k, suy ra a = bk và c = dk. b d a bk k c dk k Có = = và = = . a + b bk + b k + 1 c + d dk + d k + 1 a c Å k ã Suy ra = = . a + b c + d k + 1
Cách 4 : Phương pháp khác. 30/82 30/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 31
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC a c d b
Hoán vị cả trung tỉ và ngoại tỉ của tỉ lệ thức = ta được = . b d c a d b d + c b + a
Cộng vào hai vế của đẳng thức trên với 1 ta được + 1 = + 1 ⇒ = . c a c a d + c b + a c a
Lại hoán vị cả trung tỉ và ngoại tỉ của = ta được = . □ c a c + d a + b a3 + b3 + c3 a
c Câu 11. Cho abcd ̸= 0, b2 = ca và c2 = bd. Chứng minh tỉ lệ thức = . b3 + c3 + d3 d Lời giải. a b b c a b c Từ giả thiết suy ra = , = nên = = . (1) b c c d b c d a3 a b c a Từ (1) suy ra = · · = . (2) b3 b c d d a3 b3 c3 a3 + b3 + c3 Cũng từ (1) suy ra = = = . (3) b3 c3 d3 b3 + c3 + d3 a3 + b3 + c3 a Từ (2) và (3) suy ra = . □ b3 + c3 + d3 d ab b a2 + b2 a
c Câu 12. Cho tỉ lệ thức =
với c ̸= 0. Chứng minh tỉ lệ thức = . bc c b2 + c2 c Lời giải. ab b ab bc a b Từ = với c ̸= 0 ⇒ =
và a, b, c > 0, ta suy ra được = . bc c b c b c
Cách 1 : Phương pháp nhân chéo. a b Từ tỉ lệ thức =
hay ac = b2, ta có a2 + b2 c = a2 + ac c = a2c + ac2. b c
Tương tự có b2 + c2 a = a2c + ac2. a2 + b2 a
Suy ra a2 + b2 c = b2 + c2 a hay = . b2 + c2 c
Cách 2 : Sử dụng tính chất dãy tỉ số bằng nhau. a b a2 b2 a2 + b2 a b a2 a a a b a a2 + b2 a Có = ⇒ = = và = ⇒ = · = · = . Suy ra = . b c b2 c2 b2 + c2 b c b2 b b b c c b2 + c2 c
Cách 3 : Phương pháp định nghĩa. a b Đặt tỉ lệ thức = = k, suy ra a = bk và b = ck. b c a2 + b2 (bk)2 + b2 b2 k2 + 1 b2 (ck)2 a bk (ck)k a2 + b2 a Có = = = = = k2 và = = = k2, suy ra = . □ b2 + c2 (ck)2 + c2 c2 (k2 + 1) c2 c2 c c c b2 + c2 c ab bc ca
c Câu 13. Cho dãy tỉ số bằng nhau = =
. Chứng minh rằng a = b = c. b c a Lời giải. ab bc ca a b c Từ = = , ta suy ra được = =
với a, b, c > 0 và a + b + c ̸= 0. b c a b c a
Cách 1 : Sử dụng tính chất dãy tỉ số bằng nhau. a b c a + b + c Có = = =
= 1 do a + b + c ̸= 0, nên suy ra a = b = c. b c a b + c + a
Cách 2 : Phương pháp nhân chéo. a b c Từ giả thiết = =
, nhân chéo ta có b2 = ca, c2 = ab, a2 = bc. b c a
Do a, b và c khác 0 nên ta có b3 = b · ca; c3 = c · ab; a3 = a · bc.
Suy ra b3 = c3 = a3(= abc). Vậy a = b = c.
Cách 3 : Phương pháp định nghĩa. a b c Đặt dãy tỉ số đã cho = =
= k, suy ra a = bk, b = ck, c = ak. b c a 31/82 31/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 32
21. TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Do a, b, c > 0 nên ta sẽ chứng minh k = 1, từ đó suy ra a = b = c, bằng các cách sau:
○ Hoặc abc = abck3 ⇒ k3 = 1 ⇒ k = 1.
○ Hoặc a + b + c = (a + b + c)k ⇒ k = 1.
○ Hoặc a = bk = ck2 = ak3 ⇒ k3 = 1 ⇒ k = 1.
Cách 4 : Phương pháp so sánh. a b c
Có a, b, c > 0 nên nếu a < b ⇒ < 1 ⇒ < 1,
< 1 ⇒ a < b < c < a (vô lí). b c a
Tương tự, nếu a > b ta sẽ suy ra được a > b > c > a (vô lí). Vậy a = b, suy ra a = b = c. □ ab bc a b
c Câu 14. Cho tỉ lệ thức =
. Chứng minh tỉ lệ thức = với giả thiết c ̸= 0. a + b b + c b c Lời giải.
Từ giả thiết c ̸= 0 và ab, bc là các số có hai chữ số nên a, b, c > 0. Hoán vị các trung tỉ và áp dụng tính chất dãy tỉ số bằng nhau, ta có ab a + b ab − (a + b) 9a a (a + b) − a b ab bc a b = = = = = = ⇒ = ⇒ = . bc b + c bc − (b + c) 9b b (b + c) − b c b c b c □ a c c Câu 15. Cho =
, với a, b, c và d là các số tự nhiên khác 0. Kí hiệu (x; y) và [x; y] tương ứng là ước b d (a; d) [b; c]
chung lớn nhất và bội chung nhỏ nhất của hai số tự nhiên x và y. Chứng minh rằng = . (b; c) [a; d] Lời giải.
Sử dụng tính chất của hai số tự nhiên khác 0 là (x; y) · [x; y] = x · y, ta có: a c
(a; d) · [a; d] = ad và (b; c) · [b; c] = bc, mà ad = bc (vì = ). b d (a; d) [b; c]
⇒ (a; d) · [a; d] = (b; c) · [b; c] ⇒ = . □ (b; c) [a; d] ab b
c Câu 16. Cho a, b, c đôi một khác nhau và khác 0. Biết ab là số nguyên tố và = . Tìm số abc. bc c Lời giải. a b
Có a, b, c > 0, tương tự ví dụ 14, ta có = nên ac = b2. b c
Biết ab là một số nguyên tố có hai chữ số nên b ∈ {1; 3; 7; 9}.
Do ac = b2, ta xét từng trường hợp xảy ra:
○ b = 1 ⇒ a · c = 1 và a, c là các chữ số ⇒ a = c = 1 (loại, do a = c trái đề bài).
○ b = 3 ⇒ a · c = 9 = 1 · 9 (do a ̸= c) ⇒ ab = 13 do 93 không là số nguyên tố. ab 13 1 3 b Có = = = = (chọn). bc 39 3 9 c
○ b = 7 và b = 9 đều bị loại do dẫn đến a = c. Vậy abc = 139. □ abc bca a b
c Câu 17. Cho tỉ lệ thức =
, chứng minh tỉ lệ thức = . a + bc b + ca bc ca 32/82 32/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 33
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Lời giải. Ta có: abc bca = a + bc b + ca 100a + bc 100b + ca ⇔ = a + bc b + ca 99a + a + bc 99b + b + ca ⇔ = a + bc b + ca 99a 99b ⇔ = a + bc b + ca a b ⇔ = a + bc b + ca a a + bc a + bc − a bc ⇔ = = = b b + ca b + ca − b ca a b ⇔ = . bc ca □ ab + bc bc + ca ca + ab
c Câu 18. Cho dãy tỉ số = =
, chứng minh rằng a = b = c. a + b b + c c + a Lời giải. Ta có: ab + bc bc + ca ca + ab
10a + b + 10b + c + 10b + c + 10c + a + 10c + a + 10a + b = = = a + b b + c c + a a + b + b + c + a + b 22(a + b + c) = = 11. 2(a + b + c)
Do đó ab + bc = 11(a + b) ⇔ 10a + b + 10b + c = 11a + 11b ⇔ c = a.
Tương tự, bc + ca = 11(b + c) ⇔ 10b + c + 10c + a = 11b + 11c ⇔ b = a. Do đó a = b = c. □ a bbb . . . b ab a | {z } a
c Câu 19. Cho tỉ lệ thức = , chứng minh rằng n = với n là số tự nhiên. bc c bbb . . . b c c | {z } n Lời giải. ab a a 10a + b 9a + b 9ak + bk Từ = ⇒ = = = với k = 111 . . . 1. bc c c 10b + c 10b 10bk | {z } n a bbb . . . b a (10n − 1) a + bk 10na + bk | {z } Suy ra = = = n do 9k = 10n − 1. □ c 10bk 10bk + c bbb . . . b c | {z } n
c Câu 20. Tính giá trị của k, viết rằng: ab bc ca abc bca cab a) k = = = . b) k = = = . abc bca cab ab + c bc + a ca + b Lời giải.
Do ab, bc, ca và abc, bca, cab là các số có hai và ba chữ số nên a, b, c > 0, suy ra a + b + c ̸= 0.
Vì a + b + c ̸= 0 nên áp dụng tính chất dãy tỉ số bằng nhau, ta có: 33/82 33/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 34
21. TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC ab bc ca ab + bc + ca 11(a + b + c) 11 a) k = = = = = = . abc bca cab abc + bca + cab 111(a + b + c) 111 abc bca cab abc + bca + cab 111(a + b + c) 111 37 b) k = = = = = = = . ab + c bc + a ca + b ab + c + bc + a + ca + b 12(a + b + c) 12 4 □ 34/82 34/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 35
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Baâi 22
ĐẠI LƯỢNG TỈ LỆ THUẬN A
TRỌNG TÂM KIẾN THỨC
1 Đại lượng tỉ lệ thuận
Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ a (a là hằng số khác 0) nếu y = ax. Khi đó đại lượng x 1
cũng tỉ lệ thuận với đại lượng y (theo hệ số tỉ lệ
), vì vậy ta cũng nói x và y là hai đại lượng tỉ lệ thuận (với a nhau). 2 Tính chất:
Nếu đại lượng y tỉ lệ thuận với đại lượng x thì:
○ Tỉ số hai giá trị tương ứng của chúng luôn không đổi (và bằng hệ số tỉ lệ): y1 y2 y3 = = = . . . = a. x1 x2 x3
○ Tỉ số hai giá trị bất kì của đại lượng này bằng tỉ số hai giá trị tương ứng của đại lượng kia: y1 x1 y1 x1 y2 x2 = ; = ; = ; . . . y2 x2 y3 x3 y3 x3
3 Một số bài toán về đại lượng tỉ lệ thuận:
Để giải toán về đại lượng tỉ lệ thuận, ta cần nhận biết hai đại lượng tỉ lệ thuận trong bài toán. Từ đó ta có thể
lập các tỉ số bằng nhau và dựa vào tính chất của dãy tỉ số bằng nhau để tìm các yếu tố chưa biết. A B CÁC DẠNG BÀI TẬP
Dạng 1. Nhận biết đại lượng tỉ lệ thuận
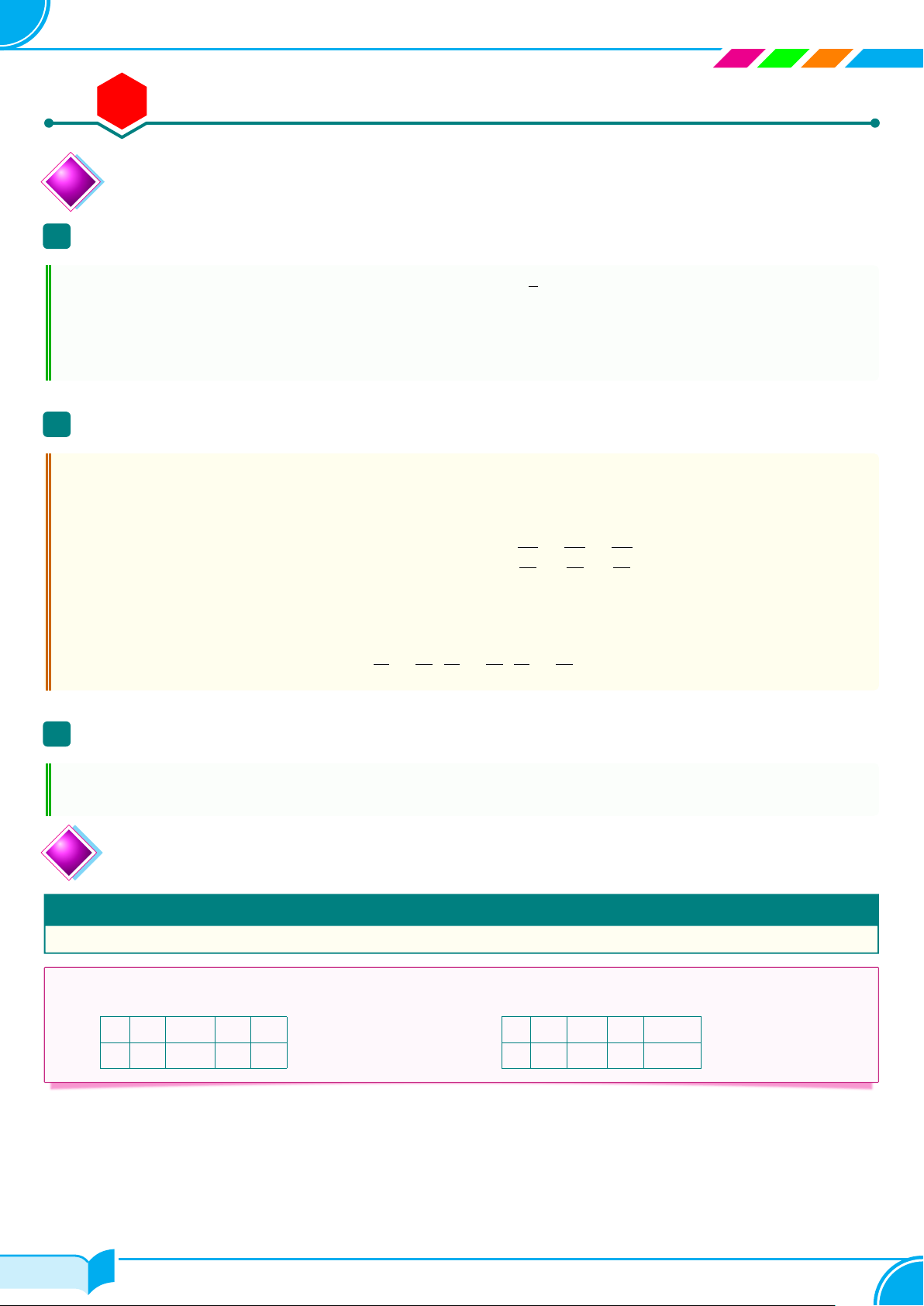
c Ví dụ 1. Theo bảng giá trị dưới đây, hai đại lượng x và y có phải là hai đại lượng tỉ lệ thuận không? x 3 −4 8 −7 x 2 −3 7 −7 a) b) y 15 −20 40 −35 y 6 9 21 −21 Lời giải.
a) x và y là hai đại lượng tỉ lệ thuận.
b) x và y không phải là hai đại lượng tỉ lệ thuận. □
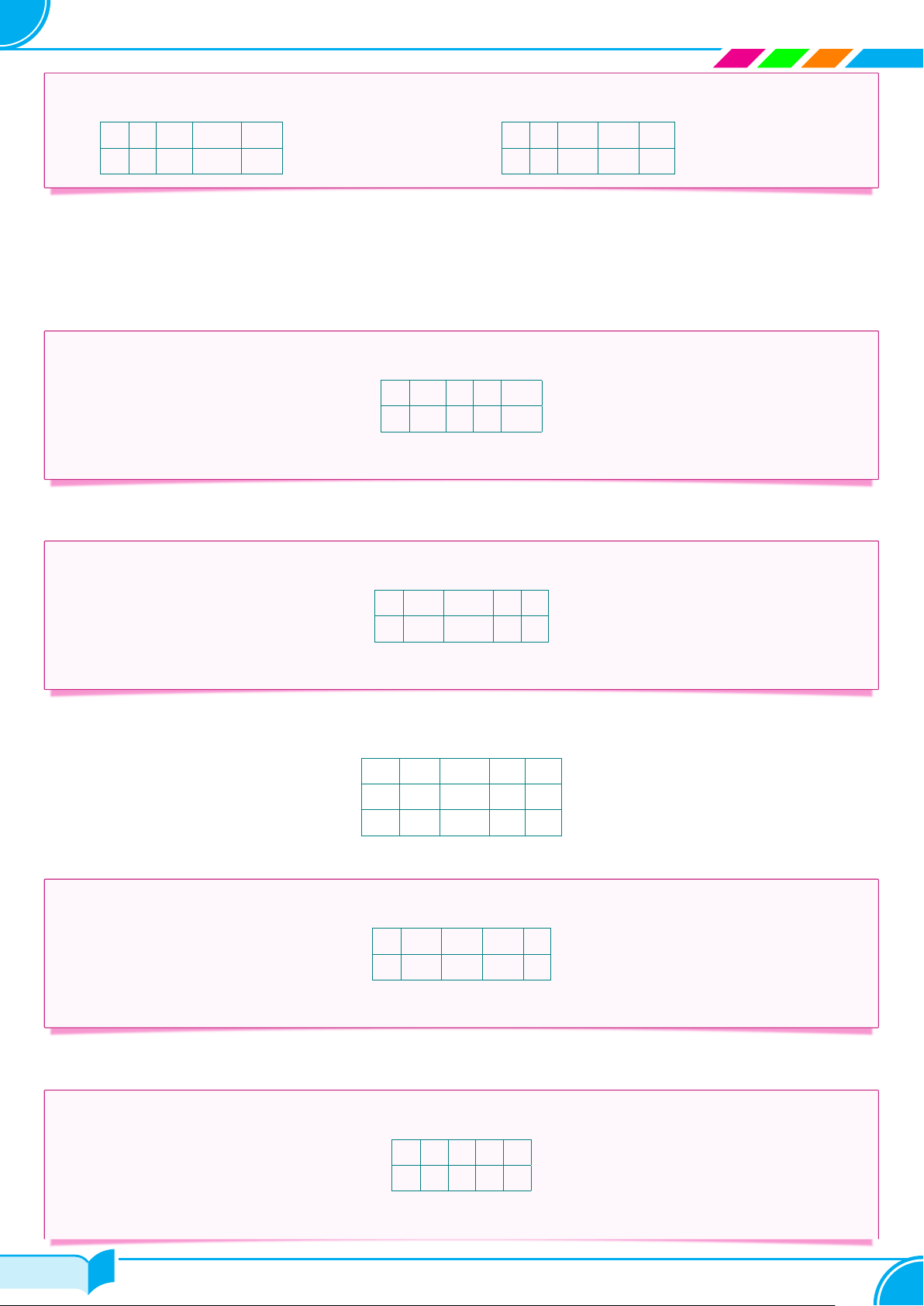
c Ví dụ 2. Theo bảng giá trị dưới đây, hai đại lượng a và b có phải là hai đại lượng tỉ lệ thuận không? a 10 −20 25 −30 a 8 −4 12 −14 a) b) b 2 −4 5 −5 b 4 −2 6 7 35/82 35/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 36
22. ĐẠI LƯỢNG TỈ LỆ THUẬN
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Lời giải.
a) a và b không phải là hai đại lượng tỉ lệ thuận.
b) a và b không phải là hai đại lượng tỉ lệ thuận. □
c Ví dụ 3. Các giá trị tương ứng của y và x được cho trong bảng sau: x 2 5 8 15 y 14 35 56 105
Hỏi hai đại lượng y và x có tỉ lệ thuận với nhau không? Lời giải. 14 35 56 105 Ta có = = =
= 7. Vậy hai đại lượng y và x tỉ lệ thuận với nhau. □ 2 5 8 15
c Ví dụ 4. Các giá trị tương ứng của y và x được cho trong bảng sau: x 3 4 5 6 y −12 −16 20 24
Hỏi hai đại lượng y và x có tỉ lệ thuận với nhau không? Lời giải. −16 20 Ta có ̸=
. Vậy hai đại lượng y và x không tỉ lệ thuận với nhau. □ 4 5
c Ví dụ 5. Các giá trị tương ứng của y và x được cho trong bảng sau: x 2 4 5 7 y −3 −6 −7,5 −10,5
Xét các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? 3
(A) Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ − . 2 2
(B) Đại lượng x tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ . 3 Lời giải. y −3 −6 −7,5 −10,5 3 ○ Ta có = = = =
= − . Vậy hai đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ x 2 4 5 7 2 3
lệ − . Do đó khẳng định (A) đúng. 2 3
○ Theo chứng minh trên, hai đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ − . Do đó đại lượng x tỉ 2 2
lệ thuận với đại lượng y theo hệ số tỉ lệ − . 3
Vậy khẳng định (B) sai về hệ số tỉ lệ. □
c Ví dụ 6. Cho biết x tỉ lệ thuận với y theo hệ số tỉ lệ 3, y tỉ lệ thuận với z theo hệ số tỉ lệ −4. Hỏi x tỉ lệ
thuận với z không? Nếu có thì hệ số tỉ lệ là bao nhiêu? 36/82 36/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 37
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Lời giải.
Ta có x tỉ lệ thuận với y theo hệ số tỉ lệ 3 nên x = 3y;
y tỉ lệ thuận với z theo hệ số tỉ lệ −4 nên y = −4z.
Suy ra x = −12z, hay x tỉ lệ thuận với z theo hệ số tỉ lệ là −12. □
c Ví dụ 7. Cho biết m tỉ lệ thuận với n theo hệ số tỉ lệ 5, n tỉ lệ thuận với p theo hệ số tỉ lệ 2. Hỏi m tỉ lệ
thuận với p không? Nếu có thì hệ số tỉ lệ là bao nhiêu? Lời giải.
m tỉ lệ thuận với p theo hệ số tỉ lệ là 10. □
Dạng 2. Tìm giá trị của một đại lượng tỉ lệ thuận khi biết giá trị của đại lượng kia
c Ví dụ 8. Cho biết y và x là hai đại lượng tỉ lệ thuận. Điền số thích hợp vào ô trống trong bảng sau: x x1 = −4 x2 = −1 x3 = 2 y y1 = 20 y4 = 2 Lời giải. y1 20
Vì x và y là hai đại lượng tỉ lệ thuận nên k = = = −5. x1 −4 Khi đó, ta có
○ y2 = k · x2 ⇒ y2 = (−5) · (−1) = 5;
○ y3 = k · x3 ⇒ y3 = (−5) · 2 = −10; y −15 ○ 4 x4 = ⇒ x4 = = 3 k −5
Vậy bảng được điền như sau x x1 = −4 x2 = −1 x3 = 2 x4 = 3 y y1 = 20 y2 = 5 y3 = −10 y4 = 2 □
c Ví dụ 9. Cho biết x và y là hai đại lượng tỉ lệ thuận. Điền số thích hợp vào bảng sau: x 2 3 7 y −4 −10 12 −2
Viết công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng x và y. Lời giải. x 2 3 7 5 −6 1 y −4 −6 −14 −10 12 −2
Công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng x và y là: y = −2x. □
c Ví dụ 10. Cho biết x và y là hai đại lượng tỉ lệ thuận. Điền số thích hợp vào bảng sau: x −3 −4 2 y −12 16 −20 24 37/82 37/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 38
22. ĐẠI LƯỢNG TỈ LỆ THUẬN
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Viết công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng x và y. Lời giải. x −3 −4 2 4 −5 6 y −12 −16 8 16 −20 24
Công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng x và y là: y = 4x. □ 2
c Ví dụ 11. Cho biết đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k = − . Cặp giá trị nào dưới 5
đây là cặp giá trị tương ứng của hai đại lượng nói trên: a) x = −4; y = 10; b) x = 10; y = −4; Lời giải. 2 2
Vì y tỉ lệ thuận với x theo hệ số tỉ lệ − nên y = − x. 5 5 2 a) Khi x = −4 thì y = −
· (−4) = 1,6 ̸= 10. Vậy cặp giá trị x = −4; y = 10 không phải là cặp giá trị tương 5
ứng của hai đại lượng nói trên. 2 b) Khi x = 10 thì y = −
· 10 = −4. Vậy cặp giá trị x = 10; y = −4 là cặp giá trị tương ứng của hai đại lượng 5 nói trên. □
c Ví dụ 12. Cho biết hai đại lượng y và x tỉ lệ thuận với nhau. Nếu x = 5 thì y = −4. Hai đại lượng y và x
liên hệ với nhau theo công thức nào? Lời giải. y −4
Vì y và x tỉ lệ thuận với nhau nên k = =
. Do đó hai đại lượng y và x liên hệ với nhau bởi công thức x 5 4 y = − x. □ 5
Dạng 3. Giải bài toán thực tế về hai đại lượng tỉ lệ thuận
c Ví dụ 13. Cứ xay xát 50 kg thóc thì được 36 kg gạo. Hỏi nếu xay xát 175 kg thóc thì được bao nhiêu ki-lô-gam gạo? Lời giải. Tóm tắt đề bài: Khối lượng thóc Khối lượng gạo 50 kg 36 kg 175 kg x kg
Khi xay xát thì khối lượng gạo tỉ lệ thuận với khối lượng xay xát. 50 36
Theo tính chất của hai đại lượng tỉ lệ thuận ta có = . 175 x 175 · 36 Suy ra x = = 126 (kg). 50
Vậy nếu xay xát 175 kg thóc thì được 126 kg. □ 38/82 38/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 39
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Ví dụ 14. Mua 6 gói kẹo thì hết 45000 đồng. Khi đó với 60000 đồng thì mua được mấy gói kẹo như thế? Lời giải. Tóm tắt đề bài: Số tiền Số gói kẹo 450000 đ 6 gói 600000 đ x gói
Số tiền và số gói kẹo mua được là hai đại lượng tỉ lệ thuận. 45000 6
Theo tính chất của hai đại lượng tỉ lệ thuận ta có = . 60000 x 60000 · 6 Suy ra x = = 8 gói. 45000
Vậy với 60000 đồng thì mua được 8 gói kẹo. □
c Ví dụ 15. Một ô tô chạy quãng đường 225 km trong 4,5 giờ. Với vận tốc đó xe chạy 150 km trong bao lâu? Lời giải. Tóm tắt đề bài: Quãng đường Thời gian 225 km 4,5 giờ 150 km x giờ
Với cùng một vận tốc thì quãng đường và thời gian xe chạy là hai đại lượng tỉ lệ thuận. 225 4,5
Theo tính chất của hai đại lượng tỉ lệ thuận ta có = . 150 x 150 · 4,5 Suy ra x = = 3 giờ. 225
Vậy xe chạy 150 km hết 3 giờ. □
c Ví dụ 16. Hai bình nước cùng có dạng hình trụ với đáy là những hình tròn bằng nhau. Chiều cao của cốc 2 nhỏ bằng
chiều cao của cốc to và dung tích cốc nhỏ bé hơn dung tích cốc lớn là 150 ml. Tính dung tích của 3 mỗi cốc. Lời giải. 2
Vì hai cốc nước cùng có dạng hình trụ với đáy là những hình tròn bằng nhau và chiều cao của cốc nhỏ bằng 3 2
chiều cao của cốc to nên dung tích cốc nhỏ bằng dung tích cốc lớn. 3
Suy ra dung tích của cốc nhỏ là 300 ml; của cốc to là 450 ml. □
c Ví dụ 17. Hai bức tranh hình chữ nhật có chiều rộng bằng nhau nhưng chiều dài bức tranh lớn gấp 3
chiều dài bức tranh nhỏ. Biết để sơn toàn bộ bề mặt của bức tranh nhỏ cần dùng 250 ml sơn, tính lượng sơn
cần dùng để sơn toàn bộ bề mặt của bức tranh lớn. Lời giải.
Lượng sơn cần để sơn toàn bộ bề mặt của bức tranh lớn là 750 ml. □
c Ví dụ 18. Một vị tỉ phú chia gia tài trị giá 10,5 tỉ đồng cho ba người con sao cho số tiền ba người con
nhận được tỉ lệ thuận với 6; 7; 8. Hỏi mỗi người con được chia bao nhiêu tiền? Lời giải.
Gọi x; y; z (tỉ đồng) lần lượt là số tiên mỗi người con được chia. x y z
Theo đề bài ta có x + y + z = 10,5 và = = . 6 7 8 39/82 39/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 40
22. ĐẠI LƯỢNG TỈ LỆ THUẬN
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Theo tính chất của dãy tỉ số bằng nhau ta có x y z x + y + z 10,5 1 = = = = = . 6 7 8 6 + 7 + 8 21 2 1 1 1 Suy ra x = · 6 = 3; y = · 7 = 3,5; z = · 8 = 4. 2 2 2
Vậy số tiền mỗi người con được chia lần lượt là 3 tỉ đồng; 3,5 tỉ đồng và 4 tỉ đồng. □
c Ví dụ 19. Bác An chia 84 chiếc bút chì vào ba hộp cỡ nhỏ, trung bình và lớn. Biết số bút chì trong ba
hộp nhỏ, trung bình và lớn tương ứng tỉ lệ thuận với 1; 2; 4; tính số bút chì có trong mỗi hộp. Lời giải.
Số bút chì có trong các hộp nhỏ, trung bình và lớn lần lượt là 12 bút, 24 bút và 48 bút. □
Dạng 4. Chia một số M thành những phần x, y, z tỉ lệ thuận với các số a, b, c cho trước
c Ví dụ 20. Chia số 850 thành ba phần tỉ lệ thuận với 3, 5, 9. Lời giải.
Gọi ba phần cần tìm lần lượt x, y và z. Do giả thiết ta có x + y + z = 850. (*) x y z Theo đề bài ta có = = . 3 5 9 x y z x + y + z
Áp dụng tính chất của dãy tỉ số bằng nhau ta suy ra = = = . 3 5 9 3 + 5 + 9 x y z 850 Do (*) nên = = = = 50. 3 5 9 17 x ○ Khi = 50 suy ra x = 150. 3 y ○ Khi = 50 suy ra y = 250. 5 z ○ Khi = 50 suy ra z = 450. 9
Vậy ba phần cần tìm là 150, 250 và 450. □
c Ví dụ 21. Số đo các góc b A, “ B, “
C của △ABC tỉ lệ thuận với 2, 3, 4. Hãy tính số đo mỗi góc của tam giác đó. Lời giải. Do b A + “ B + “ C = 180◦. (*) b A “ B “ C Theo đề bài ta có = = . 2 3 4 b A “ B “ C b A + “ B + “ C
Áp dụng tính chất của dãy tỉ số bằng nhau ta suy ra = = = . 2 3 4 2 + 3 + 4 b A “ B “ C 180◦ Do (*) nên = = = = 20◦. 2 3 4 9 ○ b A Khi = 20◦ suy ra b A = 40◦. 2 ○ “ B Khi = 20◦ suy ra “ B = 60◦. 3 ○ “ C Khi = 20◦ suy ra “ C = 80◦. 4
Vậy số đo các góc của tam giác △ABC là b A = 40◦, “ B = 60◦ và “ C = 80◦. □ 40/82 40/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 41
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Ví dụ 22. Độ dài ba cạnh của một tam giác tỉ lệ thuận với 4, 7, 9. Biết cạnh nhỏ nhất là 20 cm, tính độ
dài của cạnh lớn nhất. Lời giải.
Gọi độ dài các cạnh của tam giác lần lượt x (cm), y (cm), z (cm) với x < y < z. x y z Theo đề bài ta có = = . 4 7 9 x 20
Do giả thiết x = 20 (cm) nên = = 5. 4 4 y z z Ta suy ra = = 5. Khi = 5 suy ra z = 45 (cm). 7 9 9
Vậy độ dài cạnh lớn nhất là 45 cm. □
c Ví dụ 23. Chiều dài và chiều rộng của một hình chữ nhật tỉ lệ thuận với 5 và 3. Biết chu vi của hình chữ
nhật là 144 cm. Tính diện tích hình chữ nhật đó. Lời giải.
Gọi chiều dài, chiều rộng của hình chữ nhật lần lượt x (m), y (m), x ≥ y. x y Theo đề bài ta có =
và 2 (x + y) = 144 ⇒ x + y = 72 (m). (*) 5 3 x y x + y
Áp dụng tính chất của dãy tỉ số bằng nhau ta có = = . 5 3 5 + 3 x y 72 Do (*) nên = = = 9. 5 3 8 x ○ Khi = 9 suy ra x = 45 (m). 5 y ○ Khi = 9 suy ra y = 27 (m). 3
Vậy chiều dài là 45 m, chiều rộng là 27 m.
Do đó diện tích S của hình chữ nhật là S = 45 · 27 = 1215 m2. □ A C BÀI TẬP VẬN DỤNG
c Bài 1. Cho biết a và b là hai đại lượng tỉ lệ thuận. Điền số thích hợp vào bảng sau: a 9 12 −27 b −3 5 −6 −9
Viết công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng a và b. Lời giải. a 9 12 −27 −15 18 27 b −3 −4 9 5 −6 −9 Công thức: a = −3b. □
c Bài 2. Theo bảng giá trị dưới đây, hai đại lượng x và y có phải là hai đại lượng tỉ lệ thuận không? x 4 −6 8 −2 x 4 −8 −12 24 a) b) y 6 −9 12 −3 y 1 −2 3 6 Lời giải.
a) x và y là hai đại lượng tỉ lệ thuận. 41/82 41/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 42
22. ĐẠI LƯỢNG TỈ LỆ THUẬN
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
b) x và y không phải là hai đại lượng tỉ lệ thuận. □
c Bài 3. Cho biết y và x là hai đại lượng tỉ lệ thuận. Hãy điền số thích hợp vào ô trống trong bảng sau: x 3 6 9 y 2 8 Lời giải. y 2
Vì x và y là hai đại lượng tỉ lệ thuận nên k = = . x 3 Khi đó, ta có 2
○ Khi x = 6 suy ra y = k · x ⇒ y = · 6 = 4; 3 2
○ Khi x = 9 suy ra y = k · x ⇒ y = · 9 = 6; 3 y 3 ○ Khi y = 8 suy ra x = ⇒ x = 8 · = 12; k 2
Vậy bảng được điền như sau x 3 6 9 12 y 2 4 6 8 □
c Bài 4. Các giá trị tương ứng của hai đại lượng y và x được cho trong các bảng sau: x 1 2 3 4 x −2 −1 1 3 a) b) y 2,5 5 7,5 −10 y 8 4 −4 −12
Hỏi hai đại lượng y và x có tỉ lệ thuận không? Lời giải. y 2,5 5 7,5 −10 a) Ta có = = = = 2,5 ̸= = −2,5. x 1 2 3 4
Do đó hai đại lượng y và x không tỉ lệ thuận với nhau. y 8 4 −4 −12 b) Ta có = = = = = −4. x −2 −1 1 3
Do đó hai đại lượng y và x tỉ lệ thuận với nhau. □
c Bài 5. Cho các giá trị tương ứng của x và y trong bảng dưới. x 0,65 2,75 0,6 1,34 37 Bảng I y 5,2 22 4,8 10,72 296 x −25 −23 −21 22 24 Bảng II y 128 32 4 −16 −64
a) Trong mỗi bảng, các đại lượng x và y có tỉ lệ thuận với nhau không?
b) Nếu các đại lượng x và y tỉ lệ thuận với nhau, hãy chỉ ra hệ số tỉ lệ và viết công thức biểu thức biểu thị sự tương quan đó. 42/82 42/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 43
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Lời giải. Bảng I. a) Ta có 5,2 22 4,8 10,72 296 = = = = = 8. 0,65 2,75 0,6 1,34 37
Vậy các đại lượng y và x tỉ lệ thuận với nhau. y 5,2 b) ta có =
= 8 ⇒ y = 8x và hệ số tỉ lệ là 8. x 0,65
Nếu tất cả các tỉ số giá trị tương ứng của x và y đều bằng nhau thì hai đại lượng x và y tỉ lệ thuận với nhau. Bảng II. 4 128 128 32 −16 −64 Ta có ̸= (−2 ̸= −4) và = = = = −4. −21 −25 −25 −23 22 24
Vậy các đại lượng y và x không tỉ lệ thuận với nhau. □
c Bài 6. Biết x và y trong bảng sau là hai đại lượng tỉ lệ thuận, điền số thích hợp vào ô trống x 1 2 5 −2 2 y −2 −2 3 3
Tìm giá trị tương ứng của y với x, có thể dung 1 trong 2 tính chất của hai đại lượng tỉ lệ thuận. Lời giải.
Tìm giá trị của y tương ứng với x = 2. 2 − y −2 −4 ○ Cách 1. 3 = ⇒ y = 2 · = . 1 2 3 3 2 − 1 −2 −4 ○ Cách 2. 3 = ⇒ y = 2 · = . y 2 3 3
Tương tự với các ô trống còn lại, ta có bảng sau x 1 2 3 4 5 −2 1 2 1 y −1 −2 −2 −3 3 3 3 3 □
c Bài 7. Cho x và y là hai đại lượng tỉ lệ thuận. Kí hiệu x1 và x2 là hai giá trị của đại lượng x mà x1 = −1
và x2 = −3. Gọi y1 và y2 là hai giá trị tương ứng của đại lượng y mà y1 − y2 = −2.
a) Tìm các giá trị y1 và y2.
b) Đại lượng x và y liên hệ với nhau theo công thức nào? Lời giải.
a) Biết x và y là hai đại lượng tỉ lệ thuận, suy ra y = kx (k ̸= 0).
Theo tính chất của hai đại lượng tỉ lệ thuận,ta có y1 y2 y1 − y2 −2 = = = = −1 −1 −3 (−1) − (−3) 2
Suy ra y1 = (−1) · (−1) = 1 và y2 = (−1) · (−3) = 3. 43/82 43/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 44
22. ĐẠI LƯỢNG TỈ LỆ THUẬN
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
b) Vậy hai đại lượng x và y liên hệ với nhau theo công thức y = (−1) · x = −x. □
c Bài 8. Cứ 100 kg thóc cho 65 kg gạo. Chất bột chứa trong gạo là 80%.
a) Hỏi trong 30 kg thóc có bao nhiêu ki lô gam chất bột?
b) Từ 1 kg gạo người ta làm ra được 2,2 kg bún tươi. Hỏi để làm ra 14,3 kg bún tươi cần bao nhiêu ki-lô-gam thóc? Lời giải.
a) Vì 100 kg thóc được 65 kg gạo, suy ra tương quan giữa hai đại lượng thóc và gạo là tỉ lệ thuận. Ta có Tiêu chuẩn (kg) Hiện thực (kg) Khối lượng thóc 100 30 Khối lượng gạo 65 x 30 100 65 · 30
Theo tính chất đại lượng tỉ lệ thuận, ta có = ⇒ x = = 19, 5(kg gạo). x 65 100
Chất bột chứa trong gạo là 80%, suy ra tương quan giữa hai đại lượng gạo và chất bột là tương quan tỉ lệ thuận. Ta có Tiêu chuẩn (kg) Hiện thực (kg) Khối lượng thóc 100 19,5 Khối lượng gạo 80 y
Theo tính chất đại lượng tỉ lệ thuận, ta có 19, 5 100 19,5 · 80 = ⇒ y = = 15,6 (kg chất bột). y 80 100
Vậy trong 30 kg thóc có 15,6 kg chất bột.
b) Từ 1 kg gạo làm được 2,2 kg bún tươi, suy ra tương quan giữa gạo và bún tươi tỉ lệ thuận. x 1 1,4 · 3,1
Gọi khối lượng gạo cần là x, ta có = ⇒ x = = 6,5 (kg gạo). 14,3 2,2 2,2 y 100 100 · 6,5
Gọi khối lượng thóc phải có là y, ta có = ⇒ y = = 10 (kg thóc). 6,5 65 65
Vậy để sản xuất ra 14,3 kg bún tươi cần có 10 kg thóc. □
c Bài 9. Có hai đội công nhân. Đội một có 35 người, nếu mỗi người làm trong 16 ngày thì đào được 864 m3
đất. Hỏi 20 người của đội hai, mỗi người làm trong 14 ngày sẽ đào được bao nhiêu mét khối đất? (giả thiết
năng suất lao động của mỗi người là như nhau). Lời giải.
Một người đào đất trong một ngày được tính là 1 công lao động.
Vì số đất đào được : số công = năng suất lao động (hằng số) nên số đất đào được và số công là hai đại lượng tỉ
lệ thuận với nhau. Ta có 44/82 44/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 45
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Số đất đào được (m3) Số công lao động Đội một 864 560 = 35 · 16 Đội hai x 280 = 20 · 14
Theo tính chất của hai đại lượng tỉ lệ thuận, ta có 864 560 864 · 280 = ⇒ x = = 432. x 280 560
Vậy 20 người của đội hai mỗi người làm trong 14 ngày sẽ đào được 432 m3 đất. □
c Bài 10. Biết 78 người hoàn thành một công việc trong 65 ngày.
a) Nếu năng suất lao động của mỗi người như nhau thì cần thêm bao nhiêu người nữa để hoàn thành công việc đó trong 39 ngày?
b) Nếu cải tiến công cụ để năng suất lao động tăng thêm 20% thì cần giảm bao nhiêu người mà vẫn hoàn
thành công việc đó trong 65 ngày? Lời giải.
a) Cùng một công việc thì số người và số ngày làm việc là hai đại lượng tỉ lệ nghịch. Ta có Số người Số ngày làm việc Lúc trước 78 65 Lúc sau x 39
Theo tính chất của hai đại lượng tỉ lệ nghịch, ta có 78 39 78 · 65 = ⇒ x = = 130. x 65 39
Vậy để hoàn thành công việc đó trong 39 ngày thì cần có 130 người và số người cần thêm là 130 − 78 = 52 (người).
b) Cùng một công việc và số ngày làm việc như nhau thì năng suất lao động và số người là hai đại lượng tỉ lệ nghịch. Ta có Năng suất lao động (%) Số người Lúc trước 100 78 Lúc sau 120 x
Theo tính chất của hai đại lượng tỉ lệ nghịch, ta có 100 x 100 · 78 = ⇒ x = = 65. 120 78 120
Khi cải tiến công cụ để năng suất lao động tăng thêm 20% thì cần 65 người vẫn hoàn thành công việc mà
78 người làm trong 65 ngày. □
Trong bài toán này con số 65 ngày chỉ để minh họa cho số ngày là một số không đổi. 1
c Bài 11. Cà phê hạ giá 23 %. Với số tiền trước đây mua được 53, 8 kg cà phê thì nay mua được bao nhiêu 7 kg cà phê hạ giá? Lời giải.
Theo đề bài ta có số tiền không đổi.
Mà số hàng × giá hàng = số tiền (hằng số) nên số hàng và giá hàng là hai đại lượng tỉ lệ nghịch với nhau. Ta có 45/82 45/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 46
22. ĐẠI LƯỢNG TỈ LỆ THUẬN
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Số hàng (kg) Giá hàng (%) Lúc trước 53, 8 100 6 Lúc sau x 76 7
Theo tính chất của hai đại lượng tỉ lệ nghịch, ta có 6 53, 8 76 53, 8 · 100 = 7 ⇒ x = = 70. x 100 6 76 7
Vậy với số tiền trước đây mua được 53, 8 kg cà phê thì nay mua được 70 kg cà phê hạ giá. □
c Bài 12. Để truyền một chuyển động, người ta có thể dùng dây cu-roa, dùng xích hoặc dùng bánh xe có
răng. Ta xét một bộ máy truyền chuyển động có hai bánh răng được khớp vào nhau dưới đây:
a) Nếu bánh xe thứ nhất có 65 răng và quay 36 vòng/phút thì bánh xe thứ hai có 45 răng sẽ quay được bao nhiêu vòng/phút?
b) Muốn bánh xe thứ hai quay 78 vòng/phút thì bánh xe thứ nhất cần thiết kế có bao nhiêu răng? Lời giải.
Do hai bánh xe răng khớp vào nhau trong quá trình chuyển động nên số răng và số vòng quay của bánh xe là hai
đại lượng tỉ lệ nghịch. a) Ta có Số răng bánh xe Số vòng quay Bánh xe thứ nhất 65 36 Bánh xe thứ hai 45 x
Theo tính chất của hai đại lượng tỉ lệ nghịch, ta có 65 x 65 · 36 = ⇒ x = = 52. 45 36 45
Vậy số vòng quay của bánh xe thứ hai là 52 vòng/phút.
b) Tương tự ta có bánh xe thứ hai cần thiết kế có 30 răng. □
c Bài 13. Cho biết x tỉ lệ thuận với y theo hệ số tỉ lệ 6, y tỉ lệ thuận với z theo hệ số tỉ lệ 7. Hỏi x tỉ lệ
thuận với z không? Nếu có thì hệ số tỉ lệ là bao nhiêu? Lời giải.
x tỉ lệ thuận với z theo hệ số tỉ lệ là 42. □
c Bài 14. Hai bình đựng nước có dạng hình hộp chữ nhật có chiều dài và chiều rộng tương ứng bằng nhau.
Thể tích bình nhỏ và bình lớn lần lượt là 500 ml và 1 lít. Biết chiều cao của bình lớn là 40 cm, tính chiều cao của bình nhỏ. Lời giải.
Chiều cao của bình nhỏ là 20 cm. □
c Bài 15. Bạn Nhi chia 6,3 kg gạo vào ba túi sao cho lượng gạo trong ba túi tỉ lệ thuận với 2; 3; 4. Tính
khối lượng gạo có trong mỗi túi. Lời giải.
Khối lượng gạo có trong mỗi túi lần lượt là 1,4 kg; 2,1 kg và 2,8 kg. □ 46/82 46/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 47
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Bài 16. Bốn người thợ sửa 20 m đường trong 1,5 giờ. Hỏi trong 3 giờ, 8 người thợ sửa được bao nhiêu mét
đường (biết các người thợ có cùng năng suất)? Lời giải.
Vì các người thợ có cùng năng suất nên ta có các nhận xét:
+Với cùng thời gian, số người thợ và độ dài quãng đường sửa được là hai đại lượng tỉ lệ thuận.
+Với số người thợ không đổi, thời gian sửa và độ dài quãng đường sửa được là hai đại lượng tỉ lệ thuận.
Áp dụng các nhận xét trên, ta có:
Trong 1,5 giờ, 4 người thợ sửa được 20 m đường;
Suy ra trong 1,5 giờ, 8 người thợ sửa được 40 m đường;
Vậy trong 3 giờ, 8 người thợ sửa được 80 m đường. □
c Bài 17. Lúc 7 giờ, hai xe cùng xuất phát từ Hà Nội và đi trên cùng tuyến đường. Đến 9 giờ, khoảng cách
giữa hai xe là 20 km. Biết vận tốc xe thứ nhất gấp 1,5 lần vận tốc xe thứ hai, tính quãng đường mỗi xe đã đi. Lời giải.
Gọi vận tốc xe thứ nhất và xe thứ hai lần lượt là x (km/h) và y (km/h). ĐK: x > 0; y > 0.
Vì vận tốc xe thứ nhất gấp 1,5 lần vận tốc xe thứ hai nên ta có: 3 x y x = 1,5y ⇒ x = y ⇒ = . 2 3 2
Sau 2 giờ, khoảng cách giữa hai xe là 20 km nên ta có:
2x − 2y = 20 ⇒ x − y = 10.
Theo tính chất của dãy tỉ số bằng nhau ta có x y x − y 10 = = = = 10. 3 2 3 − 2 1
Suy ra: x = 3 · 10 = 30; y = 2 · 10 = 20.
Từ đó quãng đường xe thứ nhất đã đi là: 30 · 2 = 60 (km).
Quãng đường xe thứ hai đã đi là: 20 · 2 = 40 (km). □
c Bài 18. Hai đơn vị vận tải cùng chuyên chở đất đến công trường xây dựng. Đơn vị I có 12 xe, đơn vị II
có 15 xe, trọng tải các xe đều như nhau. Biết đơn vị I trở được 60 cm3 đất, hỏi đơn vị II trở được bao nhiêu mét khối đất? Lời giải.
Gọi x m3 là lượng đất của đơn vị II trở được. 60 12
Do các xe cùng trọng tải nên khối lượng đất trở được và số lượng xe là hai đại lượng tỉ lệ thuận ta có = . x 15 60 · 15 Suy ra x = = 75 m3. 12
Vậy khối lượng đất của đơn vị II trở được là 75 m3. □
c Bài 19. Chia số 455 thài ba phần tỉ lệ thuận với: 3 1 2 a) 3, 4, 6. b) , , . 5 4 3 Lời giải.
a) Gọi ba phần cần tìm lần lượt x, y và z. Do giả thiết ta có x + y + z = 455. (*) x y z Theo đề bài ta có = = . 3 4 6 x y z x + y + z
Áp dụng tính chất của dãy tỉ số bằng nhau ta suy ra = = = . 3 4 6 3 + 4 + 6 x y z 455 Do (*) nên = = = = 35. 3 4 6 13 47/82 47/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 48
22. ĐẠI LƯỢNG TỈ LỆ THUẬN
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC x ○ Khi = 35 suy ra x = 105. 3 y ○ Khi = 35 suy ra y = 140. 4 z ○ Khi = 35 suy ra z = 210. 6
Vậy ba phần cần tìm là 105, 140 và 210.
b) Gọi ba phần cần tìm lần lượt x, y và z. Do giả thiết ta có x + y + z = 455. (*) x y z Theo đề bài ta có = = . 3 1 2 5 4 3 x y z x + y + z
Áp dụng tính chất của dãy tỉ số bằng nhau ta suy ra = = = . 3 1 2 3 1 2 + + 5 4 3 5 4 3 x y z 455 455 60 Do (*) nên = = = = = 455 · = 300. 3 1 2 3 1 2 91 91 + + 5 4 3 5 4 3 60 x 3 ○ Khi = 300 suy ra x = 300 · ⇒ x = 180. 3 5 5 y 1 ○ Khi = 300 suy ra y = 300 · ⇒ y = 75 1 4 4 z 2 ○ Khi = 300 suy ra z = 300 · ⇒ z = 200 2 3 3
Vậy ba phần cần tìm là 180, 75 và 200. □
c Bài 20. Đoạn đường AB dài 275 km. Cùng một lúc, một ô tô chạy từ A và một xe máy chạy từ B, đi
ngược chiều để gặp nhau. Vận tốc ô tô là 60 km/h; vận tốc của xe máy là 50 km/h. Tính xem đến khi gặp
nhau thì mỗi xe đã đi được một quãng đường là bao nhiêu? Lời giải.
Gọi x (km), y (km) lần lượt là quãng đường ô tô, xe máy đã đi đến khi gặp nhau.
Do giả thiết ta có x + y = 275 (km). (*) x y
Vì trong cùng một thời gian thì quãng đường và vận tốc là hai đại lượng tỉ lệ thuận ta có = . 60 50 x y x + y
Áp dụng tính chất của dãy tỉ số bằng nhau ta suy ra = = . 60 50 60 + 50 x y 275 Do (*) nên = = = 2,5. 60 50 110 x ○ Khi
= 2,5 suy ra x = 60 · 2,5 ⇒ x = 150 (km). 60 y ○ Khi
= 2,5 suy ra y = 50 · 2,5 ⇒ y = 125 (km). 50
Vậy quãng đường ô tô đã đi là 150 km và quãng đường xe máy đã đi là 125 km. □
c Bài 21. Một xe đạp và một xa máy cùng đi một lúc từ thành phố A đến thành phố B. Vì vận tốc của xe
đạp nhỏ hơn vận tốc của xe máy là 18 km/h, nên khi xe máy tới B thì xe đạp mới tới C, cách B một quãng
đường bằn 0,6 quãng đường AB. Tìm vận tốc mỗi xe. Lời giải. CB 3 S1 AC 2
Kí hiệu các quãng đường AC là S1, và AB là S2 ta có = 0, 6 = , do đó = = . AB 5 S2 AB 5
Gọi vận tốc và thời gian người xe đạp từ A đến C là v1 và t1. 48/82 48/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 49
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Gọi vận tốc và thời gian người xe máy từ A đến B là v2 và t2.
Theo đề bài ta có v2 − v1 = 18 (km/h).
Hai xe đi cùng một lúc từ A, một xe tới C và một xe tới B, vì cùng thời gian nên quãng đường và vận tốc là hai
đại lượng tỉ lệ thuận. v1 S1 2 v1 v2 v2 − v1 18 Ta có = = , suy ra = = = = 6. v2 S2 5 2 5 5 − 2 3
Vậy vận tốc xe đạp là v1 = 6 · 3 = 12 (km/h) và vận tốc xe máy là v2 = 6 · 5 = 30 (km/h). □
c Bài 22. Chia số 38 thành ba số sao cho số thứ nhất và số thứ hai tỉ lệ theo 0,8 : 0,375, còn số thứ hai và
số thứ ba tỉ lệ theo 0,25 và 1,75. Lời giải.
Gọi số thứ nhất, thứ hai và thứ ba theo thứ tự là x, y, z.
Theo đề bài ta có x + y + z = 38. Biết x : y = 0,8 : 0,375 = 32 : 15. (1) và
y : z = 0,25 : 1,75 = 1 : 7 = 15 : 105. (2) Từ (1) và (2) suy ra x y z x + y + z 38 1 = = = = = = 0,25. 32 15 105 32 + 15 + 105 152 4
Vậy số thứ nhất bằng 8, số thứ hai bằng 3,75 và số thứ ba bằng 26,25. □ A D BÀI TẬP NÂNG CAO
c Câu 1. Một cửa hàng có ba súc vải cùng khổ và có tổng độ dài là 86,1 m. Khi bán 28% súc vải thứ nhất,
40% súc vài thứ hai và 64% súc vải thứ ba thì chiều dài bs súc vải còn lại đều bằng nhau. Hỏi chiều dài mỗi súc vải khi chưa bán? Lời giải.
Gọi chiều dài của ba súc vải khi chưa bán là x, y, z(m), với x, y, z > 0. ta có x + y + z = 86,1.
Sau khi bán, chiều dài các súc vải còn lại bằng nhau: 72% · x = 60% · y = 36% · z. Suy ra 1 1 1 x : y : z = : : = 5 : 6 : 10. 72% 60% 36%
Áp dụng tính chất của dãy tỉ số bằng nhau x y z x + y + z 86,1 = = = = = 4,1. 5 6 10 5 + 6 + 10 21
Chiều dài ba súc vải lần lượt là 20,5 m; 24,6 m; 41 m. □
c Câu 2. Một nông trường trồng rừng phòng hộ vào ba lô đất. Biết diện tích lô thứ nhất bằng 40% diện
tích cả ba lô. Còn diện thích lô thứ hai và thứ ba tỉ lệ theo 1,5 và 1,(3). Nếu diện tích lô thứ nhất lớn hơn
diện tích lô thứ ba lg 1,2 ha, thì diện tích của cả ba lô là bao nhiêu hecta? Lời giải.
Gọi diện tích ba lô đất lần lượt là x, y và z (ha). Điều kiện x, y, z > 0.
Theo đề bài ta có x = 40% (x + y − z); y : z = 1,5 : 1,(3) = 9 : 8 và x − z = 12 (ha). Suy ra 2 x x + y + z y + z x = . (x + y + z) ⇒ = = . (1) 5 2 5 3 y z y + z = = . (2) 9 8 17 49/82 49/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 50
22. ĐẠI LƯỢNG TỈ LỆ THUẬN
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Từ (1) và (2) suy ra x y + x y z = = = . 34 51 27 24 Ta có x y z x + y + z x − z 12 = = = = = = 1,2. 34 27 24 85 10 10
Vậy diện tích của cả ba lô đất bằng x + y + z = 1,2 · 85 = 102 (ha). □
c Câu 3. Một người thợ làm một chiếc hộp hình chữ nhật có dung tích 8900 cm3. Biết chiều dài và chiều
cao tỉ lệ theo 5 và 2, còn chiều rộng và chiều cao tỉ lệ theo 7 và 8. Tìm kích thước chiếc hộp. Lời giải.
Gọi chiều dài, chiều rộng, chiều cao của hình hộp lần lượt là x, y, z (cm). Có x, y, z > 0.
Ta có x : y = 5 : 2 và y : z = 7 : 8. x y z Suy ra = =
= k và x = 20k, y = 7k, z = 8k (k > 0). 20 7 8
Thể tích hình hộp V = (20k) · (7k) · (8k) = 1120k3 = 8960, do đó k = 2.
Vậy kích thước của hình hộp chữ nhật bằng 40 cm, 14 cm, 16 cm. □
c Câu 4. Chia số 38 thành ba số sao cho số thứ nhất và số thứ hai tỉ lệ theo 0, 8 và 0, 375; còn số thứ hai
và số thứ ba tỉ lệ theo 0, 25 và 1, 75. Lời giải.
Gọi số thứ nhất, số thứ hai và số thứ ba lần lượt là x, y, z. Điều kiện x, y, z ̸= 0.
Theo đề bài, ta có x : y = 0, 8 : 0, 375 = 32 : 15 và y : z = 0, 25 : 1, 75 = 15 : 105. x y z x + y + z 38 Suy ra = = = = = 0, 25. 32 15 105 152 152
Vậy số thứ nhất là 8, số thứ hai là 3, 75 và số thứ ba là 26, 25. □
c Câu 5. Nhà trường dự định chia vở viết cho ba lớp 7A, 7B và 7C tỉ lệ theo số học sinh là 7 : 6 : 5. Nhưng
sau đó vì có học sinh thuyên chuyển giữa ba lớp nên phải chia lại theo tỉ lệ 6 : 5 : 4. Như vậy có lớp đã nhận
được ít hơn theo dự định là 12 quyển vở. Tính số vở mỗi lớp nhận được. Lời giải.
Gọi số vở ba lớp 7A, 7B, 7C nhận được theo dự định tương ứng là x, y, z và số vở ba lớp nhận được trong thực
tế là a, b, c. Có x, y, z, a, b, c ∈ ∗ N . x y z x + y + z
Theo đề bài, ta có x : y : z = 7 : 6 : 5 hay = = = . 7 6 5 18 a b c a + b + c a : b : c = 6 : 5 : 4 hay = = = . 6 5 4 15 x y z x + y + z a b c a + b + c Suy ra = = = và = = = . 35 30 25 90 36 30 24 90
Do số học sinh chỉ thuyên chuyển giữa các lớp nên tổng số học sinh không đổi, kéo theo tổng số vở cũng không
đổi x + y + z = a + b + c và ta có x y z a b c = = = = = = k. 35 30 25 36 30 24 x a
Từ dãy tỉ số bằng nhau trên, ta nhận xét =
, do đó x < a nên số vở lớp 7A nhận được nhiều hơn so với dự 35 36
định. Tương tự, số vở lớp 7B nhận được không thay đổi và số vở lớp 7C nhận được ít hơn so với dự định. z − c Suy ra k = = 12. 25 − 24
Vậy lớp 7A nhận được 432 vở, lớp 7B nhận được 360 vở, lớp 7C nhận được 288 vở. □ 9
c Câu 6. Tìm ba phân số có tổng bằng 9
, biết các tử số tỉ lệ theo 3 : 4 : 5 và các mẫu số tương ứng tỉ lệ 70 theo 5 : 1 : 2. 50/82 50/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 51
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Lời giải. a b c
Gọi ba phân số phải tìm lần lượt là x = , y = và z = . Có a′, b′, c′ ̸= 0. a′ b′ c′ Ta có
a : b : c = 3 : 4 : 5 hay a = 3k, b = 4k và c = 5k (k ̸= 0).
a′ : b′ : c′ = 5 : 1 : 2 hay a′ = 5h, b′ = h và c′ = 2h (h ̸= 0). 3k 4k 5k 3 4 5 Suy ra x : y : z = : : = : : = 6 : 40 : 25. 5h h 2h 5 1 2 9 x y z x + y + z 9 9 Có = = = = 70 = . 6 40 25 71 71 70 27 1 3 Vậy x = , y = 5 , z = 3 . □ 35 7 14 5
c Câu 7. Hiện nay tuổi cha bằng 2, 2 lần tuổi con. Trước đây 25 năm tuổi con bằng tuổi cha. Hỏi khi 41
tuổi cha gấp 3 lần tuổi con thì con bao nhiêu tuổi? Lời giải.
Gọi tuổi cha và tuổi con hiện nay lần lượt là x và y. Điều kiện x, y ∈ Z và x, y > 0. x 11 x − 25 41
Ta có tỉ số giữa tuổi cha và con hiện nay = 2, 2 = và trước đây 25 năm là = . y 5 y − 25 5
Áp dụng tính chất dãy tỉ số bằng nhau, ta có x y x − y x − 25 y − 25 x − y = = và = = . 11 5 6 41 5 36 x y x − 25 y − 25 x − y Suy ra = = = = = k. 66 30 41 5 36 x − (x − 25) 25 Do đó k = = = 1. 66 − 41 25
Vậy hiện nay tuổi cha là 66, tuổi con là 30.
○ Cách thứ nhất: Giả sử trước (hoặc sau) t năm nữa thì tuổi cha gấp 3 lần tuổi con (t > 0 là sau t năm, còn x 66
t < 0 là trước t năm, do tỉ số giữa tuổi cha và con hiện nay là = ̸= 3). y 30 66 + t 30 + t 36 Có = =
= 18. Suy ra t = −12. Như vậy trước đây 12 năm tuổi cha gấp 3 lần tuổi con. khi 3 1 2 đó tuổi con là 18.
○ Cách thứ hai: Từ k = 1 ta có x − y = 36. Gọi tuổi cha và con khi tuổi cha gấp 3 lần tuổi con tương ứng là x′ y′ x′ − y′ 36
x′ và y′, ta có x′ − y′ = x − y (hiệu giữa tuổi cha và con không đổi). Có = = = = 18. Suy 3 1 3 − 1 2 ra khi đó con 18 tuổi.
Vậy khi tuổi cha gấp 3 lần tuổi con thì con 18 tuổi. □
c Câu 8. Anh hơn em 3 tuổi. Tìm tuổi anh và tuổi em, biết tuổi anh hiện nay bằng 2 lần tuổi em khi tuổi
anh bằng tuổi em hiện nay. Lời giải.
Gọi tuổi anh và em hiện nay là x và y.
Điều kiện và x > y, x, y ∈ ∗ N .
Anh hơn em 3 tuổi, nên ta có x = y + 3.
Khi tuổi anh bằng tuổi em hiện nay, thì tuổi anh là y và tuổi em là y − 3. Ta có bảng so sánh 51/82 51/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 52
22. ĐẠI LƯỢNG TỈ LỆ THUẬN
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Khi tuổi anh bằng tuổi Hiện nay em hiện nay Tuổi anh x y Tuổi em y y − 3
Biết tuổi anh hiện nay bằng 2 lần tuổi em khi tuổi anh bằng tuổi em hiện nay, ta có tỉ lệ x y − 3 = . 2 1 Mà y + 3 y − 3 x = y + 3 ⇒ = . 2 1
Áp dụng tính chất dãy tỉ số bằng nhau y + 3 y − 3 6 = = = 6 ⇒ y = 9, x = 12. 2 1 1
Vậy tuổi anh bằng 12 và tuổi em bằng 9. □
c Câu 9. Một người đi xe đạp và một người đi xe máy cùng đi một lúc từ A tới B. Vì vận tốc xe đạp nhỏ
hơn vận tốc của xe máy là 18 km/giờ nên khi xe đạp tới C thì xe máy đã tới D quá C một đoạn bằng 0, 6
quãng đường AD. Tính vận tốc của mỗi xe. Lời giải.
Kí hiệu quãng đường S1 = AC, S2 = AD. Ta có A C D B CD 3 S1 AC 2 = 0, 6 = , suy ra = = . AD 5 S2 AD 5
Gọi vận tốc và thời gian xe đạp đi từ A tới C là v1 và t1, vận tốc và thời gian xe máy đi từ A tới D là v2 và t2.
Theo đề bài ta có v2 − v1 = 18 (km/giờ).
Do hai xe cùng khởi hành một lúc từ A, xe đạp tới C và xe máy tới D nên cùng thời gian thì quãng đường đi
được và vận tốc là hai đại lượng tỉ lệ thuận. Do vậy v1 S1 2 v1 v2 v2 − v1 18 = = ⇒ = = = = 6. v2 S2 5 2 5 5 − 2 3
Vậy vận tốc xe đạp là v1 = 6 · 2 = 12 (km/giờ) và vận tốc xe máy là v1 = 6 · 5 = 30 (km/giờ). □
c Câu 10. Một chuyển động phải đi một quãng đường 900 km với vận tốc 10 km/giờ. Một chuyển động thứ
hai phải đi với quãng đường 400 km nhưng với vận tốc 20 km/giờ. Nếu cả hai cùng khởi hành một lúc thì sau
bao lâu quãng đường còn lại của chuyển động thứ nhất sẽ gấp 4 lần quãng đường còn lại của chuyển động thứ hai? Lời giải.
Giả sử chuyển động thứ nhất phải đi quãng A M B
đường AB = 900 km và chuyển động thứ hai
phải đi quãng đường AC = 400 km. Ta xét A N C
chuyển động thứ ba đi quãng đường AD =
1600 km với vận tốc 80 km/giờ. A H D
Nếu cả ba chuyển động đều cùng khởi hành một lúc từ A thì lần lượt sẽ đến các vị trí M , N , H (như hình vẽ
trên). Theo đề bài ta có M B = 4N C. (1)
Vì quãng đường và vận tốc của chuyển động thứ ba gấp 4 lần quãng đường và vận tốc của chuyển động thứ hai
nên quãng đường còn lại của chuyển động thứ ba sẽ gấp 4 lần quãng đường còn lại của chuyển động thứ hai, tức là HD = 4N C. (2)
Từ (1) và (2) ta suy ra HD = M B.
Ta xét bài toán giữa chuyển động thứ nhất và chuyển động thứ ba. Gọi quãng đường và vận tốc của chuyển động 52/82 52/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 53
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
thứ nhất và chuyển động thứ ba cùng đi trong thời gian t là S1, v1 và S3, v3. Do hai chuyển động cùng khởi hành
nên sau thời gian t, quãng đường và vận tốc là hai đại lượng tỉ lệ thuận với nhau, do đó S1 v1 10 1 = = = . S3 v2 80 8
Vì hai quãng đường còn lại bằng nhau nên S3 − S1 = 1600 − 900 = 700 km. Do vậy S1 S3 S3 − S1 700 = = = = 100. 1 8 8 − 1 7
Suy ra quãng đường chuyển động thứ nhất đi được trong thời gian t là S1 = 100 · 1 = 100 km.
Thời gian để quãng đường còn lại của chuyển động thứ nhất gấp 4 lần quãng đường còn lại của chuyển động thứ S1 100 hai là t = = = 10 giờ. v1 10
Thật vậy, sau 10 giờ kể từ lúc khởi hành thì quãng đường còn lại của
○ chuyển động thứ nhất là 900 − 100 = 800 km;
○ chuyển động thứ hai là 400 − 20 · 10 = 200 km.
Bài toán này còn có thể giải bằng nhiều cách khác, cách giải trên minh họa cho việc sử dụng đại lượng tỉ lệ thuận. □ 53/82 53/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 54
23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Baâi 23
ĐẠI LƯỢNG TỈ LỆ NGHỊCH A
TRỌNG TÂM KIẾN THỨC
1 Đại lượng tỉ lệ nghịch a
Nếu đại lượng y tỉ lệ nghịch với đại lượng x theo công thức y =
(a là hằng số khác 0) thì ta nói y tỉ lệ nghịch x
với x theo hệ số tỉ lệ a.
Nếu y tỉ lệ nghịch với x theo hệ số tỉ lệ a thì x cũng tỉ lệ nghịch với y theo hệ số tỉ lệ a. Khi đó ta nói
hai đại lượng x và y tỉ lệ nghịch với nhau. 2 Tính chất
Nếu hai đại lượng x và y tỉ lệ nghịch với nhau thì:
○ Tích hai giá trị tương ứng của chúng luôn không đổi (và bằng hệ số tỉ lệ): y1 y2 y3
x1y1 = x2y2 = x3y3 = . . . = a hay = = = . . . = a. 1 1 1 x1 x2 x3
○ Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tì số hai giá trị tương ứng của đại lượng kia: y1 x2 y1 x3 y2 x3 = ; = ; = ; . . . y2 x1 y3 x1 y3 x2
3 Một số bài toán về đại lượng tỉ lệ nghịch
Để giải toán về đại lượng tỉ lệ nghịch, ta cần nhận biết được hai đại lượng tỉ lệ nghịch trong bài toán. Từ đó
ta có thể lập các tỉ số bằng nhau và dựa vào tính chất của dãy tỉ số bằng nhau để tìm các yếu tố chưa biết. A B CÁC DẠNG BÀI TẬP
Dạng 1. Nhận biết đại lượng tỉ lệ nghịch
c Ví dụ 1. Theo bảng giá trị dưới đây, hai đại lượng x và y có phải là hai đại lượng tỉ lệ nghịch không? x 20 −10 4 2 x 10 −4 50 −100 a) b) y 3 −6 15 30 y 10 25 2 −1 Lời giải.
a) Đại lượng x và y là hai đại lượng tỉ lệ nghịch.
b) Đại lượng x và y không phải là hai đại lượng tỉ lệ nghịch. □ 54/82 54/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 55
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Ví dụ 2. Theo bảng giá trị dưới đây, hai đại lượng a và b có phải là hai đại lượng tỉ lệ nghịch không? a 9 2 −3 −6 a 8 −4 16 32 a) b) b 6 27 −18 −9 b 4 −8 −2 1 Lời giải.
a) Đại lượng a và b là hai đại lượng tỉ lệ nghịch.
b) Đại lượng a và b không phải hai đại lượng tỉ lệ nghịch. □
c Ví dụ 3. Các giá trị tương ứng của hai đại lượng y và x được cho trong bảng sau: x 2 3 4 5 y 12 8 6 4,8
Hỏi hai đại lượng y và x có tỉ lệ nghịch với nhau không? Lời giải.
Ta có 2 · 12 = 3 · 8 = 4 · 6 = 5 · 4,8 = 24. Vậy hai đại lượng y và x tỉ lệ nghịch với nhau theo hệ số tỉ lệ a = 24. □
c Ví dụ 4. Các giá trị tương ứng của x và y được cho trong bảng sau x −2 −1 4 8 y −8 −16 4 2
Hai đại lượng x và y có tỉ lệ nghịch với nhau hay không? Vì sao? Lời giải.
Thêm dòng xy vào bảng và điền các giá trị tương ứng cho nó ta được x −2 −1 4 8 y −8 −16 4 2 xy 16 16 16 16
Từ kết quả trong bảng trên, ta kết luận x và y tỉ lệ nghịch với nhau. □
c Ví dụ 5. Các giá trị tương ứng của hai đại lượng y và x được cho trong bảng sau: x −2 −3 6 9 y 27 18 −8 6
Hỏi hai đại lượng y và x có tỉ lệ nghịch với nhau không? Lời giải.
Ta có 6 · (−8) = −48 ̸= 9 · 6 = 54. Vậy hai đại lượng y và x không tỉ lệ nghịch với nhau. □
c Ví dụ 6. Bảng sau cho biết giá trị tương ứng của y và x: x 2 3 4 6 y 6 4 3 2
Khi đó thì trong các khẳng định sau, khẳng định nào là đúng, khẳng định nào sai? 55/82 55/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 56
23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC 1
a) Hai đại lượng y và x tỉ lệ nghịch với nhau theo hệ số tỉ lệ a = . 3
b) Hai đại lượng y và x tỉ lệ nghịch với nhau theo hệ số tỉ lệ a = 12. Lời giải.
○ Ta có x · y = 2 · 6 = 3 · 4 = 4 · 3 = 6 · 2 = 12. Vậy hai đại lượng y và x tỉ lệ nghịch với nhau theo hệ số tỉ lệ
a = 12. Do đó khẳng định a) sai về hệ số tỉ lệ.
○ Theo chứng minh trên, hai đại lượng y và x tỉ lệ nghịch với nhau theo hệ số tỉ lệ a = 12. Do đó khẳng định b) đúng. □
c Ví dụ 7. Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ 20, x tỉ lệ nghịch với z theo hệ số tỉ lệ 16. Hỏi y tỉ lệ
thuận hay tỉ lệ nghịch với z và hệ số tỉ lệ bằng bao nhiêu? Lời giải. 20
Ta có y tỉ lệ nghịch với x theo hệ số ti lệ 20 nên y = ; x 16
x tỉ lệ nghịch với z theo hệ số tỉ lệ 16 nên x = . z 20 5 5 Suy ra y = =
z, hay y tỉ lệ thuận với z theo hệ số tỉ lệ là . □ 16 4 4 z
c Ví dụ 8. Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ −10, x tỉ lệ nghịch với z theo hệ số tỉ lệ 15. Hỏi y tỉ
lệ thuận hay tỉ lệ nghịch với z và hệ số tỉ lệ bằng bao nhiêu? Lời giải. −10
Ta có y tỉ lệ nghịch với x theo hệ số tỉ lệ −10 nên y = ; x 15
x tỉ lệ nghịch với z theo hệ số tỉ lệ 15 nên x = . z −10 −2 −2 Suy ra y = =
z, hay y tỉ lệ thuận với z theo hệ số tỉ lệ là . □ 15 3 3 z
Dạng 2. Tìm giá trị của một đại lượng tỉ lệ nghịch khi biết giá trị của đại lượng kia
c Ví dụ 9. Cho biết x và y là hai đại lượng tỉ lệ nghịch. Điền số thích hợp vào bảng sau: x 3 1 −2 y −4 18 12 −1
Viết công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng x và y. Lời giải. x 3 1 −2 −2 −1 12 3 y −4 −12 6 18 12 −1 12
Công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng x và y là: y = − . □ x 56/82 56/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 57
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Ví dụ 10. Cho biết a và b là hai đại lượng tỉ lệ nghịch. Điền số thích hợp vào bảng sau: a 6 9 −4 b −6 3 −2 12
Viết công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng a và b. Lời giải. a 6 9 −4 −12 18 −3 b −6 −4 9 3 −2 12 36
Công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng a và b là b = − . □ a
c Ví dụ 11. Cho biết y và x là hai đại lượng tỉ lệ nghịch. Hãy điền số thích hợp vào ô trống trong bảng sau: x x1 = 8 x2 = 6 y y1 = −9 y3 = 18 Lời giải.
Vì x và y là hai đại lượng tỉ lệ nghịc nên a = x1 · y1 = 8 · (−9) = −72. Khi đó, ta có a −72 ○ y2 = ⇒ y2 = = −12; x2 6 a −72 ○ x3 = ⇒ x3 = = −4; y3 18
Vậy bảng được điền như sau x x1 = 8 x2 = 6 x3 = −4 y y1 = −9 y2 = −12 y3 = 18 □
c Ví dụ 12. Cho biết x và y là hai đại lượng tỉ lệ nghịch. Điền các số thích hợp vào ô trống trong bảng sau x 0,5 −1,2 4 6 y 3 −2 1,5 Lời giải.
Vì x và y tỉ lệ nghịch với nhau nên ta giả sử xy = k. 6
Dựa vào thông tin trong cột thứ 6 ta có k = 4 · 1,5 = 6. Vậy xy = 6 hay y = . x 6 Khi đó ta viết y =
vào dòng 2 cột 1 và từ đây ta sẽ điền được các thông tin tương ứng vào các ô trống, cụ thể x ta có bảng sau x 0,5 −1,2 2 −3 4 6 y = 6 12 −5 3 −2 1,5 1 x □ 1
c Ví dụ 13. Cho x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ k = . 2 57/82 57/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 58
23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC 1
a) Hãy biểu diễn y theo x.
b) Tính giá trị của y khi x = − . 16 Lời giải. 1 1 1
a) Vì x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ k = nên xy = hay y = . 2 2 2x 1 1 b) Với x = − thì y = = −8. 16 Å 1 ã 2 · − 16 □
c Ví dụ 14. Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau và khi x = 8 thì y = 15. a) Tìm hệ số tỉ lệ k.
b) Hãy biểu diễn y theo x.
c) Tính giá trị của y khi x = 6, x = 10. Lời giải.
a) Ta có xy = k nên k = 8 · 15 = 120. 120
b) Theo câu trên, ta có x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ k = 120 nên xy = 120 hay y = . x
c) Ta sử dụng bảng sau để tính giá trị của y theo x x 6 10 y = 120 20 12 x □
c Ví dụ 15. Cho biết hai đại lượng y và x là tỉ lệ nghịch với nhau theo hệ số tỉ lệ a = 6. Cặp giá trị nào
dưới đây là cặp giá trị tương ứng của hai đại lượng nói trên: 2 a) x = 12; y = 2; b) x = 9; y = ; 3 Lời giải. 6
Vì y tỉ lệ nghịch với x theo hệ số tỉ lệ a = 6 nên y = . x 6 1 a) Khi x = 12 thì y = =
̸= 2. Vậy cặp giá trị x = 12; y = 2 không phải là cặp giá trị tương ứng của hai 12 2 đại lượng nói trên. 6 2 2 b) Khi x = 9 thì y = =
. Vậy cặp giá trị x = 9; y =
là cặp giá trị tương ứng của hai đại lượng nói trên. 9 3 3 □
c Ví dụ 16. Cho biết hai đại lượng y và x tỉ lệ nghịch với nhau. Nếu x = −3 thì y = 8. Hỏi hai đại lượng y
và x liên hệ với nhau theo công thức nào? Lời giải.
Vì y và x tỉ lệ nghịch với nhau nên a = x · y = (−3) · 8 = −24. Do đó hai đại lượng y và x liên hệ với nhau bởi −24
công thức x · y = −24 hay y = . □ x 58/82 58/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 59
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Dạng 3. Giải bài toán thực tế về hai đại lượng tỉ lệ nghịch
c Ví dụ 17. Một ô tô chạy từ A đến B với vận tốc 60 km/h thì hết 2,5 giờ. Lúc từ B về A xe chạy với vận
tốc 50 km/h thì mất bao lâu? Lời giải. Tóm tắt đề bài: Vận tốc Thời gian 60 km/h 2,5 giờ 50 km/h x giờ
Trên cùng một quãng đường, vận tốc và thời gian là hai đại lượng tỉ lệ nghịch. 60 x
Theo tính chất của hai đại lượng tỉ lệ nghịch ta có = . 50 2,5 60 · 2,5 Suy ra x = = 3 giờ. 50
Vậy thời gian xe chạy từ B về A hết 3 giờ. □
c Ví dụ 18. Để hoàn thành một công việc cần 12 người làm trong 10 ngày. Nếu muốn làm xong sớm hơn 2
ngày thì cần điều động thêm bao nhiêu người (với năng suất như nhau)? Lời giải. Tóm tắt đề bài: Số ngày làm Số người làm 10 ngày 12 người 8 ngày x người
Với cùng một công việc thì số ngày làm và số người làm là hai đại lượng tỉ lệ nghịch. 10 x
Theo tính chất của hai đại lượng tỉ lệ nghịch ta có = . 8 12 10 · 12 Suy ra x = = 15 người. 8
Vậy số người cần điều động thêm là 15 − 12 = 3 người. □
c Ví dụ 19. Một ô tô chạy từ A đến B với vận tốc 50 km/h rồi chạy từ B về A xe chạy với vận tốc 40 km/h.
Cả đi lẫn về mất 4 giờ 30 phút. Tính thời gian đi và thời gian về. Lời giải. Tóm tắt đề bài: Vận tốc Thời gian 50 km/h x giờ 40 km/h y giờ
Trên cùng một quãng đường, vận tốc và thời gian là hai đại lượng tỉ lệ nghịch. 50 y x y
Theo tính chất của hai đại lượng tỉ lệ nghịch ta có = suy ra = . 40 x 40 50
Do giả thiết ta có x + y = 4,5 giờ. (*) x y x + y
Áp dụng tính chất của dãy tỉ số bằng nhau ta suy ra = = . 40 50 40 + 50 x y 4,5 1 Do (*) nên = = = . 40 50 90 20 x 1 1 ○ Khi = suy ra x = 40 · = 2 giờ. 40 20 20 59/82 59/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 60
23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC y 1 1 ○ Khi = suy ra y = 50 · = 2,5 giờ. 50 20 20
Vậy thời gian xe chạy từ A đến B hết 2 giờ và thời xe chạy từ B về B hết 2,5 giờ. □
c Ví dụ 20. Giá mỗi kg gạo loại II bằng 60% giá mỗi kg gạo loại I. Hỏi với cùng số tiền để mua 12 kg gạo
loại I có thể mua bao nhiêu kg gạo loại II? Lời giải.
Gọi a là giá tiền gạo loại I (a > 0).
Tổng số tiền để mua gạo 12a.
Vì giá gạo loại II bằng 60% loại I, nên số gạo loại II mua được với cùng số tiền là 12a 12a = = 18 (kg). 60%a 2a 3 □
c Ví dụ 21. Giá mỗi chai nước lớn bằng 125% giá mỗi chai nước nhỏ. Hỏi với cùng số tiền để mua 8 chai
nước lớn có thể mua bao nhiêu chai nước nhỏ? Lời giải.
Gọi a là giá tiền mỗi chai nước lớn (a > 0). a 4a
Giá tiền của mỗi chai nước nhỏ là = . 125% 5
Tổng số tiền để mua nước 8a.
Số chai nước loại nhỏ mua được với cùng số tiền là 8a = 10 (chai). 4a 5 □
c Ví dụ 22. Một ô tô đi từ A đến B với vận tốc 60 km/h và trở về A với vận tốc 48 km/h. Cả đi lẫn về
(không tính thời gian nghỉ) mất 13 giờ 30 phút. Tính độ dài quãng đường AB. Lời giải.
Giả sử ô tô đi từ A đến B với vận tốc 60 km/h với thời gian là t1 giờ và ô tô đi từ B về A với vận tốc 48 km/h
với thời gian là t2 giờ.
Vì vận tốc và thời gian của một chuyển động đều trên cùng một quãng đường là hai đại lượng tỉ lệ nghịch nên 60 t2 t2 5 t1 t2 = ⇔ = ⇔ = . (1) 48 t1 t1 4 4 5 1
Theo giả thiết ta có t1 + t2 = 13 giờ 30 phút = 13 giờ. 2
Khi đó, từ dãy tỉ số (1) ta được 1 t 13 1 t2 t1 + t2 3 = = = 2 = . 4 5 4 + 5 9 2 Suy ra t1 = 6 giờ.
Vậy độ dài quãng đường AB là 60 · 6 = 360 km. □
c Ví dụ 23. Ba nhóm học sinh cùng tham gia trồng cây (mỗi nhóm đều phải trồng n cây). Nhóm I trồng
xong trong 3 ngày, nhóm II trồng xong trong 5 ngày, nhóm III trồng xong trong 6 ngày. Hỏi mỗi nhóm có bao
nhiêu học sinh? Biết rằng nhóm II có nhiều hơn nhóm III 1 học sinh (năng suất trồng cây của mỗi học sinh 60/82 60/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 61
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC bằng nhau). Lời giải.
Giả sử số học sinh của nhóm I, nhóm II, nhóm III theo thứ tự là x, y, z.
○ Nhóm I với x học sinh hoàn thành công việc trong 3 ngày.
○ Nhóm II với y học sinh hoàn thành công việc trong 5 ngày.
○ Nhóm III với z học sinh hoàn thành công việc trong 6 ngày.
Theo giả thiết ta có y − z = 1. 1 1 1
Vì số học sinh và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch nên x, y, z tỉ lệ với , , , suy ra 3 5 6 x y z y − z 1 = = = = = 30. 1 1 1 1 1 1 − 3 5 6 5 6 30 1 1 1 Từ đó suy ra x = · 30 = 10, y = · 30 = 6, z = · 30 = 5. 3 5 6
Vậy nhóm I có 10 học sinh, nhóm II có 6 học sinh và nhóm III có 5 học sinh. □
c Ví dụ 24. Ba đội công nhân sửa ba đoạn đường có cùng chiều dài. Đội thứ nhất sửa xong trong 3 ngày,
đội thứ hai trong 4 ngày và đội thứ ba trong 9 ngày. Biết đội thứ hai có nhiều hơn đội thứ ba là 5 người, tính
số công nhân của mỗi đội (năng suất các công nhân như nhau). Lời giải.
Gọi x; y; z (công nhân) lần lượt là số người của mỗi đội công nhân.
Điều kiện: x; y; z nguyên dương.
Theo đề bài ta có y − z = 5.
Vì ba đội sửa ba đoạn đường có cùng chiêu dài nên: x y z 3x = 4y = 9z hay = = . 1 1 1 3 4 9
Theo tính chất của dãy tỉ số bằng nhau ta có x y z y − z 5 = = = = = 36. 1 1 1 1 1 5 − 3 4 9 4 9 36 1 1 1 Suy ra x = · 36 = 12; y = · 36 = 9; z = · 36 = 4. 3 4 9
Vậy số công nhân của mỗi đội lân lượt là 12 người; 9 người và 4 người. □
c Ví dụ 25. Ba xe khởi hành cùng một lúc để chở nguyên liệu từ kho đến phân xưởng. Thời gian ba xe di
chuyển lần lượt là 10 giờ, 15 giờ và 25 giờ. Biết vận tốc xe thứ nhất lớn hơn vận tốc xe thứ hai là 5 km/h,
tính vận tốc của mỗi xe. Lời giải.
Gọi x; y; z (km/h) lần lượt là vận tốc của mỗi xe.
Điều kiện: x; y; z là số dương.
Theo đề bài ta có x − y = 5.
Vì ba xe xuất phát cùng lúc và cùng tuyến đường nên: x y z 10x = 15y = 25z hay = = . 1 1 1 10 15 25 61/82 61/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 62
23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Theo tính chất của dãy tỉ số bằng nhau ta có x y z x − y 5 = = = = = 150. 1 1 1 1 1 1 − 10 15 25 10 15 30 1 1 1 Suy ra x = · 150 = 15; y = · 150 = 10; z = · 150 = 6. 10 15 25
Vận tốc của mỗi xe lần lượt là 15 km/h, 10 km/h và 6 km/h. □
Dạng 4. Chia một số M thành những phần x, y, z tỉ lệ nghịch với các số a, b, c cho trước
c Ví dụ 26. Chia số 200 thành ba phần tỉ lệ nghịch với 7, 4, 2. Lời giải.
Gọi ba phần cần tìm lần lượt x, y và z. Do giả thiết ta có x + y + z = 200. (*) x y z
Theo đề bài ta có 7 · x = 4 · y = 2 · z ⇒ = = . 1 1 1 7 4 2 x y z x + y + z
Áp dụng tính chất của dãy tỉ số bằng nhau ta suy ra = = = . 1 1 1 1 1 1 + + 7 4 2 7 4 2 x y z 200 200 28 Do (*) nên = = = = = 200 · = 224. 1 1 1 1 1 1 25 25 + + 7 4 2 7 4 2 28 x 1 ○ Khi = 224 suy ra x = 224 · = 32. 1 7 7 y 1 ○ Khi = 224 suy ra y = 224 · = 56. 1 4 4 z 1 ○ Khi = 224 suy ra z = 224 · = 112. 1 2 2
Vậy ba phần cần tìm là 32, 56 và 112.
Nhận xét. Bài toán trên ta có thể giải bằng cách khác như sau: 7 · x 4 · y 2 · z x y z
Theo đề bài ta có 7 · x = 4 · y = 2 · z ⇒ = = ⇒ = = . 28 28 28 4 7 14 x y z x + y + z 200
Áp dụng tính chất của dãy tỉ số bằng nhau ta suy ra = = = = = 8. 4 7 14 4 + 7 + 14 25
Do đó ta có x = 32, y = 56 và z = 112. □ 1 2
c Ví dụ 27. Chia số 116 thành ba phần tỉ lệ nghịch với , và 3. 2 5 Lời giải.
Gọi ba phần cần tìm lần lượt x, y và z. Do giả thiết ta có x + y + z = 116. (*) 1 2 x y z Theo đề bài ta có · x = · y = 3 · z ⇒ = = . 2 5 2 5 1 2 3 x y z x + y + z
Áp dụng tính chất của dãy tỉ số bằng nhau ta suy ra = = = . 2 5 1 5 1 2 + + 2 3 2 3 x y z 116 116 6 Do (*) nên = = = = = 116 · = 24. 2 5 1 5 1 29 29 2 + + 2 3 2 3 6 62/82 62/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 63
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC x ○ Khi = 24 suy ra x = 24 · 2 = 28. 2 y 5 ○ Khi = 24 suy ra y = 24 · = 60. 5 2 2 z 1 ○ Khi = 24 suy ra z = 24 · = 8. 1 3 3
Vậy ba phần cần tìm là 28, 24 và 8. □
c Ví dụ 28. Ba người A, B, C mua tất cả 5,75 m vải để may áo cỡ như nhau. Khổ vải mà A, B, C đã mua
lần lượt là 0,8 m, 0,9 m và 1,2 m. Hỏi mỗi người mua mấy mét vải? Lời giải.
Gọi số mét vải mỗi người A, B, C mua tương ứng là x (m), y (m), z (m).
Với cùng một cỡ áo như nhau thì chiều dài của mảnh vải tỉ lệ nghịch với khổ rộng của mảnh vải. 0,8 · x 0,9 · y 1,2 · z x y z
Theo đề bài ta có 0,8 · x = 0,9 · y = 1,2 · z ⇒ = = ⇒ = = . 7,2 7,2 7,2 9 8 6 x y z x + y + z
Áp dụng tính chất của dãy tỉ số bằng nhau ta suy ra = = = . 9 8 6 9 + 8 + 6 x y z 5,75 1
Do giả thiết x + y + z = 5,75 (m) nên = = = = . 9 8 6 23 4 x 1 1 ○ Khi = suy ra x = 9 · = 2,25 (m). 9 4 4 y 1 1 ○ Khi = suy ra y = 8 · = 2 (m) 8 4 4 z 1 1 ○ Khi = suy ra z = 6 · = 1,5 (m) 6 4 4
Vậy A mua 2,25 m vải, B mua 2 m vải, C mua 1,5 m vải. □ A C BÀI TẬP VẬN DỤNG
c Bài 1. Biết y và x là hai đại lượng tỉ lệ nghịch. Hãy điền số thích hợp vào ô trống trong bảng sau: x 2 3 4 y 18 −6 Lời giải.
Vì x và y là hai đại lượng tỉ lệ nghịch nên a = x · y nên a = 2 · 18 = 36. Khi đó, ta có a 36 ○ Khi x = 3 suy ra y = ⇒ y = = 12; x 3 a 36 ○ Khi x = 4 suy ra y = ⇒ y = = 9; x 4 a 36 ○ Khi y = −6 suy ra x = ⇒ x = = −6; y −6
Vậy bảng được điền như sau x 2 3 4 −6 y 18 12 9 −6 □ 63/82 63/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 64
23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Bài 2. Cho biết a và b là hai đại lượng tỉ lệ nghịch. Thay mỗi dấu “?” trong bảng sau bằng số thích hợp. a 15 10 −30 b −20 −6 60 −50
Viết công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng a và b. Lời giải. a 15 10 −30 50 −5 6 b −20 −30 10 −6 60 −50 300
Công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng a và b: b = − . □ a
c Bài 3. Theo bảng giá trị dưới đây, hai đại lượng x và y có phải là hai đại lượng tỉ lệ nghịch không? x −8 2 −4 1 x 4 −8 −12 24 a) b) y 8 −32 16 −64 y 30 −15 10 5 Lời giải.
a) x và y là hai đại lượng tỉ lệ nghịch.
b) x và y không phải là hai đại lượng tỉ lệ nghịch. □
c Bài 4. Các giá trị tương ứng của hai đại lượng y và x được cho trong các bảng sau. Hỏi hai đại lượng y và
x có tỉ lệ nghịch không? x 2 −3 4 24 x 1 2 4 −5 a) b) y −12 8 6 −1 y 10 5 2,5 −2 Lời giải.
a) Ta thấy x · y = 2 · (−12) = (−3) · 8 = 24 · (−1) = −24 ̸= 4 · 6 = 24.
Do đó hai đại lượng y và x không tỉ lệ nghịch với nhau.
b) Ta có x · y = 1 · 10 = 2 · 5 = 4 · 2,5 = (−5) · (−2) = 10 Do đó hai đại lượng y và x tỉ lệ nghịch với nhau. □
c Bài 5. Cho hai đại lượng x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ k = 16. 1
a) Hãy biểu diễn y theo x.
b) Tính giá trị của y khi x = − . 4 Lời giải. 16
a) Vì x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ k = 16 nên xy = 16 hay y = . x 1 16 b) Với x = − thì y = = −64. 4 1 − 4 □ 64/82 64/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 65
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Bài 6. Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau và khi x = 2 thì y = 9. a) Tìm hệ số tỉ lệ k.
b) Hãy biểu diễn y theo x.
c) Tính giá trị của y khi x = −2, x = 1, x = 3, x = 8. Lời giải.
a) Ta có xy = k nên k = 2 · 9 = 18. 18
b) Theo câu trên, ta có x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ k = 18 nên xy = 18 hay y = . x
c) Ta sử dụng bảng sau để tính giá trị của y theo x x −2 1 3 8 y = 18 −9 18 6 9 x 4 □
c Bài 7. Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau và khi x = 4 thì y = 9. a) Tìm hệ số tỉ lệ k.
b) Hãy biểu diễn y theo x.
c) Tính giá trị của y khi x = −9, x = −6, x = 3, x = 12, x = 36. Lời giải.
a) Ta có xy = k nên k = 4 · 9 = 36. 36
b) Theo câu trên, ta có x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ k = 36 nên xy = 36 hay y = . x
c) Ta sử dụng bảng sau để tính giá trị của y theo x x −9 −6 3 12 36 y = 36 −4 −6 12 3 1 x □
c Bài 8. Cho biết x và y là hai đại lượng tỉ lệ nghịch. Điền các số thích hợp vào ô trống trong bảng sau x −20 −12 2 3 4 5 y −5 10 Lời giải.
Vì x và y tỉ lệ nghịch với nhau nên ta giả sử xy = k. 60
Dựa vào thông tin trong cột thứ 3 ta có k = (−12) · (−5) = 60. Vậy xy = 60 hay y = . x 60 Khi đó ta viết y =
vào dòng 2 cột 1 và từ đây ta sẽ điền được các thông tin tương ứng vào các ô trống, cụ thể x ta có bảng sau x −20 −12 2 3 4 5 6 y = 60 −3 −5 30 20 15 12 10 x □ 65/82 65/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 66
23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Bài 9. Cho biết x và y là hai đại lượng tỉ lệ nghịch. Điền các số thích hợp vào ô trống trong bảng sau x −9 −1 3 y −27 27 Lời giải.
Vì x và y tỉ lệ nghịch với nhau nên ta giả sử xy = k. 27
Dựa vào thông tin trong cột thứ 3 ta có k = (−1) · (−27) = 27. Vậy xy = 27 hay y = . x 27 Khi đó ta viết y =
vào dòng 2 cột 1 và từ đây ta sẽ điền được các thông tin tương ứng vào các ô trống, cụ thể x ta có bảng sau x −9 −1 1 3 y = 27 −3 −27 27 9 x □
c Bài 10. Các giá trị tương ứng của x và y được cho trong bảng sau x 2 3 5 6 y 15 10 6 5
Hai đại lượng x và y có tỉ lệ nghịch với nhau hay không? Vì sao? Lời giải.
Thêm dòng xy vào bảng và điền các giá trị tương ứng cho nó ta được x 2 3 5 6 y 15 10 6 5 xy 30 30 30 30
Từ kết quả trong bảng trên, ta kết luận x và y tỉ lệ nghịch với nhau. □
c Bài 11. Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ 7, x tỉ lệ nghịch với z theo hệ số tỉ lệ −5. Hỏi y tỉ lệ
thuận hay tỉ lệ nghịch với z và hệ số tỉ lệ bằng bao nhiêu? Lời giải.
y tỉ lệ thuận với z theo hệ số ti lệ là −7 . □ 5
c Bài 12. Thể tích chai lớn bằng 140% thể tích chai nhỏ. Hỏi với cùng lượng nước để làm đầy 20 chai nước
lớn có thể làm đầy bao nhiêu chai nước nhỏ? Lời giải.
Với cùng lượng nước để làm đầy 20 chai nước lớn có thể làm đây 28 chai nước nhỏ. □
c Bài 13. Ba nhóm thợ cùng may một số lượng áo như nhau. Nhóm thứ nhất may xong trong 10 giờ, nhóm
thứ hai trong 12 giờ và nhóm thứ ba trong 20 giờ. Biết nhóm thứ ba có ít hơn nhóm thứ nhất là 3 người, tính
số thợ may của mỗi nhóm (năng suất các thợ may như nhau). Lời giải.
Số thợ may của mỗi nhóm lần lượt là 6 người; 5 người và 3 người. □
c Bài 14. Bốn hộp bánh có giá bằng nhau và chứa tổng cộng 34 gói bánh. Hỏi mỗi hộp chứa bao nhiêu gói
bánh biết giá mỗi gói bánh trong các hộp lần lượt là 3000 đồng, 6000 đồng, 8000 đồng và 12000 đồng? 66/82 66/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 67
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Lời giải.
Số gói bánh có trong mỗi hộp bánh lần lượt là 16 gói; 8 gói; 6 gói và 4 gói. □
c Bài 15. 20 công nhân cùng làm một công việc thì hết 6 giờ. Nếu có thêm 4 công nhân nữa cùng làm thì
sẽ xong sớm công việc được mấy giờ? Lời giải.
Gọi x giờ là thời gian là xong công việc khi thêm 4 công nhân. 20 x
Trong cùng một công việc nên số lượng công nhân và thời gian là hai đại lượng tỉ lệ nghịch ta có = . 24 6 6 · 20 Suy ra x = = 5 giờ. 24
Vậy thời gian sẽ làm xong sớm hơn là 6 − 5 = 1 giờ. □
c Bài 16. Chia số 7567 thài ba phần tỉ lệ nghịch với: 2 5 3 a) 4, 7, 6. b) , , . 3 6 8 Lời giải.
a) Gọi ba phần cần tìm lần lượt x, y và z. Do giả thiết ta có x + y + z = 7567 (∗). 4 · x 7 · y 6 · z x y z
Theo đề bài ta có 4 · x = 7 · y = 6 · z ⇒ = = ⇒ = = . 84 84 84 21 12 14 x y z x + y + z
Áp dụng tính chất của dãy tỉ số bằng nhau ta suy ra = = = . 21 12 14 21 + 12 + 14 x y z 7567 Do (∗) nên = = = = 161. 21 12 14 47 x ○ Khi
= 161 suy ra x = 161 · 21 = 3381. 21 y ○ Khi
= 161 suy ra y = 161 · 12 = 1932. 12 z ○ Khi
= 161 suy ra z = 161 · 14 = 2254. 14
Vậy ba phần cần tìm là 3381, 1932 và 2254.
b) Gọi ba phần cần tìm lần lượt x, y và z. Do giả thiết ta có x + y + z = 7567 (∗). 2 5 3 2 · x 5 · y 3 · z x y z Theo đề bài ta có · x = · y = · z ⇒ = = ⇒ = = . 3 6 8 90 180 240 45 36 80 x y z x + y + z
Áp dụng tính chất của dãy tỉ số bằng nhau ta suy ra = = = . 45 36 80 45 + 36 + 80 x y z 7567 Do (∗) nên = = = = 47. 45 36 80 161 x ○ Khi
= 47 suy ra x = 47 · 45 = 2115. 45 y ○ Khi
= 47 suy ra y = 47 · 36 = 1692. 36 z ○ Khi
= 47 suy ra z = 47 · 80 = 3760. 80
Vậy ba phần cần tìm là 2115, 1692 và 3760. □
c Bài 17. Một một ô tô đi từ A đến B với vận tốc ô tô là 50 km/h. Lúc đi từ B về A xe chạy với vận tốc là
60 km/h. Biết thời gian về ít hơn thời gian đi là 30 phút. Tính thời gian đi và thời gian về. Lời giải.
Gọi x giờ, y giờ lần lượt là thời gian ô tô đi từ A đến B và ngược lại.
Do giả thiết ta có x − y = 0,5 giờ (∗). 67/82 67/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 68
23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC 50 y x y
Vì trong cùng một quãng đường thời gian và vận tốc là hai đại lượng tỉ lệ nghịch ta có = ⇒ = . 60 x 60 50 x y x − y
Áp dụng tính chất của dãy tỉ số bằng nhau ta suy ra = = . 60 50 60 − 50 x y 0,5 1 Do (∗) nên = = = . 60 50 10 20 x 1 1 ○ Khi = suy ra x = 60 · ⇒ x = 3 giờ. 60 20 20 y 1 1 ○ Khi = suy ra y = 50 · ⇒ y = 2,5 giờ. 50 20 20
Vậy thời gian lúc đi của ô tô là 3 giờ và thời gian ô tô đi về là 2,5 giờ. □
c Bài 18. Một xe tải chạy từ thành phố A đến hải cảng B gồm ba chặng đường dài bằng nhau, nhưng chất
lượng mặt đường tốt xấu khác nhau nên vận tốc trên mỗi chặng đường lần lượt bằng 40, 24 và 60 (km/h).
Biết tổng thời gian đi từ A đến B là 5 giờ, tính độ dài quãng đường AB. Lời giải.
Gọi vận tốc và thời gian xe tải đi trên ba chặng đường lần lượt là v1, v2, v3, t1, t2, t3. Ta có t1 + t2 + t3 = 5.
Vì ba chặng đường dài bằng nhau nên cùng quãng đường, vận tốc thời gian là hai đại lượng tỉ lệ nghịch. Ta có 1 1 1 1 1 1 t1 : t2 : t3 = : : = : : = 3 : 5 : 2. v1 v2 v3 40 24 60
Áp dụng tính chất dãy tỉ số bằng nhau, ta có t1 t2 t3 t1 + t2 + t3 5 = = = = = 0, 5. 3 5 2 10 10
Suy ra t1 = 0, 5 · 3 = 1, 5 (h) và quãng đường AB = 3 · (40 · 1, 5) = 180 (km). □
c Bài 19. Một người mang một số tiền vào siêu thị hoa quả và nhẩm tính thấy với số tiền đó có thể mua
được 3 kg nho, hoặc 4 kg táo, hoặc 5 kg mận. Tính giá tiền mỗi loại, biết 3 kg táo đắt hơn 2 kg mận là 210000 đồng. Lời giải.
Gọi giá tiền nho, táo, mận là x, y, z (đồng/kg). Ta có 3y − 2z = 21000.
Vì cùng một số tiền có thể mua được 3 kg nho, hoặc 4 kg táo, hoặc 5 kg mận nên giá tiền và khối lượng là hai
đại lượng tỉ lệ nghịch. Ta có 3x = 4y = 5z. 1 1 1 Suy ra x : y : z = : : = 20 : 15 : 12 3 4 5 1 1 1 x y z
(hoặc có thể biến đổi như sau 3x · = 4y · = 5z · ⇒ = = ). 60 60 60 20 15 12
Áp dụng tính chất dãy tỉ số bằng nhau, ta có x y z 3y − 2z 210000 = = = = = 10000. 20 15 12 45 − 24 21
Suy ra giá nho, táo và mận tương ứng là 200000 (đồng/kg), 150000 (đồng/kg), 120000 (đồng/kg). □
c Bài 20. Một nhân viên văn phòng có thể đánh máy được 160 từ trong 2, 5 phút. Hỏi cần bao nhiêu phút
để người đó đánh được 800 từ? (giả thiết rằng thời gian để đánh được các từ là như nhau). Lời giải.
Gọi x (phút) là thời gian cần thiết để người đó đánh được 800 từ (x > 0).
Vì thời gian và số từ đánh được tỉ lệ nghịch với nhau nên ta có: x 800 800 · 2, 5 = ⇒ x = = 12, 5. 2, 5 160 160
Vậy người đó cần 12, 5 phút để đánh được 800 từ. □ 68/82 68/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 69
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Bài 21. Một ô tô đi từ A đến B hết 6 giờ. Hỏi khi từ B quay về A nó đi hết mấy giờ? Biết rằng vận tốc
lúc về bằng 1,5 lần vận tốc lúc đi. Lời giải.
Giả sử ô tô đi từ A đến B với vận tốc v1 km/h với thời gian là t1 = 6 giờ và ô tô đi từ B về A với vận tốc v2
km/h với thời gian là t2 giờ.
Vì vận tốc và thời gian của một chuyển động đều trên cùng một quãng đường là hai đại lượng tỉ lệ nghịch nên v1 t2 v1 t2 6v1 = ⇔ = ⇔ t2 = . (1) v2 t1 v2 6 v2 Theo giả thiết ta có v1 1 v2 = 1,5v1 ⇔ = . (2) v2 1,5 1
Thay (2) vào (1) ta được t2 = 6 · = 4 giờ. 1,5
Vậy với vận tốc khi quay về ô tô đi hết 4 giờ. □
c Bài 22. Biết 3 học sinh khi làm vệ sinh lớp học hết 3 phút. Hỏi 5 học sinh (cùng năng suất) sẽ làm vệ
sinh lớp học hết bao nhiêu phút? Lời giải.
Vì năng suất làm việc của mỗi học sinh là như nhau nên số học sinh và số phút làm vệ sinh xong lớp học là hai
đại lượng tỉ lệ nghịch.
Gọi x (x > 0) là số phút để 5 học sinh vệ sinh xong lớp học. Khi đó ta có 5 3 3 · 3 = ⇒ x =
= 1,8 phút = 1 phút 48 giây. 3 x 5
Vậy 5 học sinh sẽ làm vệ sinh lớp học hết 1 phút 48 giây. □
c Bài 23. 36 em học sinh chia làm bốn nhóm cùng tham gia trồng cây (mỗi nhóm đều phải trồng n cây).
Nhóm I trồng xong trong 4 ngày, nhóm II trồng xong trong 6 ngày, nhóm III trồng xong trong 10 ngày, nhóm
IV trồng xong trong 12 ngày. Hỏi mỗi nhóm có bao nhiêu học sinh? Biết rằng năng suất trồng cây của mỗi học sinh bằng nhau. Lời giải.
Giả sử số học sinh của nhóm I, nhóm II, nhóm III, nhóm IV theo thứ tự là x, y, z, t.
○ Nhóm I với x học sinh hoàn thành công việc trong 4 ngày.
○ Nhóm II với y học sinh hoàn thành công việc trong 6 ngày.
○ Nhóm III với z học sinh hoàn thành công việc trong 10 ngày.
○ Nhóm IV với t học sinh hoàn thành công việc trong 12 ngày.
Theo giả thiết ta có x + y + z + t = 36. 1 1 1 1
Vì số học sinh và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch nên x, y, z, t tỉ lệ với , , , , 4 6 10 12 suy ra x y z t x + y + z + t 36 = = = = = = 60. 1 1 1 1 1 1 1 1 36 + + + 4 6 10 12 4 6 10 12 60 1 1 1 1 Từ đó suy ra x = · 60 = 15, y = · 60 = 10, z = · 60 = 6, t = · 60 = 5. 4 6 10 12
Vậy nhóm I có 15 học sinh, nhóm II có 10 học sinh, nhóm III có 6 học sinh và nhóm IV có 5 học sinh. □ 69/82 69/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 70
23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Bài 24. Tìm độ dài ba cạnh của tam giác biết chu vi tam giác là 62 cm và độ dài ba cạnh tỉ lệ nghịch với 2; 3; 5. Lời giải.
Gọi x, y, z lần lượt là độ dài 3 cạnh của tam giác.
Vì x, y, z tỉ lệ nghịch với 2; 3; 5 nên 2x = 3y = 5z. x y z x + y + z 62 Ta có = = = = = 2. 15 10 6 15 + 10 + 6 31
Vậy độ dài 3 cạnh của tam giác là 30, 20, 12. □
c Bài 25. Ba đội máy cày, cài trên ba cánh đồng có cùng diện tích. Đội I cày xong cánh đồng trong 8 ngày;
đội II cày xong trong 9 ngày; đội III cày xong trong 12 ngày. Hỏi mỗi đội có bao nhiêu máy cày, biết rằng
cả ba đội có 69 máy cày (giả sử năng suất mỗi máy cày là như nhau). Lời giải.
Gọi x, y, z là số máy cày của mỗi đội.
Do số máy cày và thời gian cày xong cánh đồng là hai đại lượng tỉ lệ nghịch nên ta có x y z x + y + z 69 8x = 9y = 12z ⇔ = = = = = 3. 9 8 6 9 + 8 + 6 23 Vậy x = 27, y = 24, z = 18. □
c Bài 26. Để phục vụ cho việc in tài liệu học tập môn Toán cho học sinh khối 7, ba xưởng in dành ra tổng
cộng 12 máy in (cùng năng suất), và mỗi xưởng được giao in số lượng sách như nhau. Xưởng thứ nhất in xong
trong 4 ngày, xưởng thứ hai in xong trong 6 ngày, xưởng thứ ba in xong trong 12 ngày. Hỏi mỗi xưởng có bao
nhiêu máy in để phục vụ công tác này? Lời giải.
Gọi x, y, z là số máy in của mỗi xưởng.
Do số máy in tỉ lệ nghịch với số ngày để in xong. Ta có x y z x + y + z 12 4x = 6y = 12z ⇔ = = = = = 2. 3 2 1 3 + 2 + 1 6
Ta được x = 3 · 2 = 6; y = 2 · 2 = 4; z = 1 · 2 = 2.
Vậy số máy in của mỗi xưởng lần lượt là 6, 4, 2. □ A D BÀI TẬP NÂNG CAO
c Câu 1. Hai bà mua gạo hết cùng một số tiền. Bà thứ nhất mua loại 4000 đồng/kg, bà thứ hai mua loại
4800 đồng/kg. Biết bà thứ nhất mua nhiều hơn bà thứ hai là 2 kg. Hỏi mỗi bà đã mua bao nhiêu kg gạo? Lời giải.
Hai bà mùa hết gạo với cùng một số tiền nên số kg gạo tỉ lệ nghịch với số tiền mỗi kg gạo.
Gọi số gạo mỗi bà mua lần lượt là a, b. Khi đó a 4800 6 = = b 4000 5 a b a − b ⇔ = = = 2 (do a hơn b 2 kg) 6 5 6 − 5 ⇒ a = 12, b = 10.
Vậy số gạo bà thứ nhất mua là 12 kg; bà thứ hai mua là 10 kg. □ 70/82 70/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 71
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Câu 2. Hai cạnh của một tam giác dài 25 cm và 36 cm. Tổng độ dài hai đường cao tương ứng là 48, 8 cm.
Tính độ dài của mỗi đường cao nói trên. Lời giải. Cạnh Đường cao 25 cm x cm 36 cm y cm
Gọi x, y lần lượt là độ dài đường cao tương ứng với cạnh 25 cm và 36 cm. Ta có x + y = 48, 8.
Với diện tích của tam giác không đổi thì cạnh đáy tỉ lệ nghịch với chiều cao tương ứng. Do đó 25 y x y x + y 48, 8 = ⇒ = = = = 0, 8. 36 x 36 25 36 + 25 61
Vậy x = 0, 8 · 36 = 28, 8 cm; y = 0, 8 · 25 = 20 cm. □
c Câu 3. Để làm xong một công việc, một số công nhân cần làm trong một số ngày. Một bạn học sinh lập 1 1
luận rằng nếu tăng số công nhân thêm
thì thời gian sẽ giảm đi
. Lập luận của bạn học sinh đó đúng hay 3 3 sai? Lời giải. Số công nhân Số ngày làm a b 1 a + a · 3 x?
Với một công việc nhất định, số công nhân làm tỉ lệ nghịch với số ngày làm. a x 3 Do đó = ⇒ x = b. 4 b 4 a 3 3 1 1 1
Thời gian giảm được là b − b = b tức là giảm
số ngày cho trước, chứ không phải . 4 4 4 3
Vậy bạn đó đã lập luận sai. □
c Câu 4. Một xe chạy từ A đến B gồm ba chặng đường dài bằng nhau nhưng chất lượng mặt đường tốt xấu
khác nhau. Biết vận tốc trên mỗi chặn đường lần lượt là 72 km/giờ; 60 km/giờ; 40 km/giờ. Biết tổng thời
gian xe chạy từ A đến B là 4 giờ. Tính quãng đường AB. Lời giải.
Với quãng đường S như nhau thì vận tốc tỉ lệ nghịch với thời gian.
Gọi thời gian đi trên mỗi chặng đường lần lượt là x, y, z. Ta có 72x = 60y = 40z = S. 72x 60x 40z x y z x + y + z 4 1 Suy ra = = hay = = = = = . 360 360 360 5 6 9 5 + 6 + 9 20 5 1 Do đó x = · 5 = 1. 5
Mỗi chặng đường dài 72 · 1 = 72 km.
Vậy quãng đường AB = 72 · 3 = 216 km. □ 71/82 71/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 72
23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
c Câu 5. Hai ô tô cùng đi từ A đến B. Xe thứ nhất đi hết 1 giờ 20 phút, xe thứ hai đi hết 1 giờ 30 phút.
Tính vận tốc trung bình của mỗi xe, biết rằng trung bình 1 phút xe thứ nhất đi nhanh hơn xe thứ hai 100 m. Lời giải. 4 3 1 1 Ta có 1 giờ 20 phút = giờ; 1 giờ 30 phút = giờ; 1 phút = giờ và 1 m = km. 3 2 60 10
Gọi v1 km/h là vận tốc trung bình của xe thứ nhất và v2 km/h là vận tốc trung bình của xe thứ hai.
Trong 1 phút xe thứ nhất đi nhanh hơn xe thứ hai 100 m nên 1 1 1 v1 v2 1 v1 − v2 1 v1 · − v2 · = ⇔ − = ⇔ = ⇔ v1 − v2 = 6. 60 60 10 60 60 10 60 10
Vì vận tốc trung bình và thời gian của một chuyển động thẳng trên cùng một quãng đường là hai đại lượng tỉ lệ nghịch nên 3 v1 v1 v2 v1 − v2 6 = 2 ⇔ = = = = 36. v 4 3 4 3 4 1 2 − 3 2 3 2 3 6 3 4 Từ đó suy ra v1 = · 36 = 54 km/h, v2 = · 36 = 48 km/h. 2 3
Vậy vận tốc trung bình của xe thứ nhất bằng 54 km/h và vận tốc trung bình của xe thứ hai bằng 48 km/h. □
c Câu 6. Một ôtô chạy từ A đến B trong một thời gian nhất định. Nếu ôtô chạy với vận tốc 54 km/h thì
đến nơi sớm được 1 giờ. Nếu ôtô chạy với vận tốc 63 km/h thì đến nơi sớm được 2 giờ. Tính quãng đường AB
và thời gian dự định đi. Lời giải. Vận tốc Thời gian 54 km/h t1 giờ 63 km/h t2 giờ Trong đó, t1 − t2 = 1.
Với cùng quãng đường AB thì thời gian và vận tốc tỉ lệ nghịch với nhau. 54 t2 t1 t2 t1 − t2 1 Do đó = ⇒ = = = . 63 t1 63 54 63 − 54 9 1 Vậy t1 = · 63 = 7. 9
Quãng đường AB là 54 · 7 = 378 km.
Thời gian dự định đi là 7 + 1 = 8 giờ. □
c Câu 7. Để làm xong công việc thì 21 công nhân cần phải làm trong 15 ngày. Do cải tiến công cụ lao động
nên năng suất lao động của mỗi người tăng thêm 25%. Hỏi 18 công nhân phải làm bao lâu mới xong việc đó? Lời giải.
○ Nếu năng suất lao động vẫn như cũ thì ta có Số công nhân Số ngày làm 21 15 18 x? 72/82 72/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 73
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
Với một công việc nhất định, năng suất lao động không đổi, số công nhân làm tỉ lệ nghịch với số ngày làm, 21 x suy ra = ⇒ x = 17, 5 ngày. 18 15
○ Giữ nguyên số công nhân là 18, ta có Năng suất lao động Số ngày làm 100% 17, 5 125% y?
Với một công việc nhất định, số người làm không đổi thì số ngày làm tỉ lệ nghịch với năng suất lao động, 100% y suy ra = ⇒ y = 14. 125% 17, 5
Vậy 18 công nhân phải làm trong 14 ngày mới xong việc. □ 73/82 73/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 74
23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC ÔN TẬP CHƯƠNG VI A BÀI TẬP RÈN LUYỆN 1 −2 −8
c Bài 1. Lập tất cả các tỉ lệ thức có thể được từ bốn số sau: 0,2; ; ; . 60 9 3 Lời giải. −2 1 −8 Å −2 ã Ta có: 0,2 · = · = . 9 60 3 45
Suy ra các tỉ lệ thức lập được từ bốn số trên là −2 1 −8 1 −2 −8 0,2 0,2 ○ = 9 ; ○ = 60 ; ○ 3 = 60 ; ○ 9 = 3 . 1 −8 −2 −8 −2 0,2 0,2 1 60 3 9 3 9 60 □ 25 25
c Bài 2. Lập tất cả các tỉ lệ thức có thể được từ bốn số sau: 0,25; ; 1,5; . 18 3 Lời giải. 25 25 Å 25 ã Ta có: 0,25 · = · 1,5 = . 3 18 12
Suy ra các tỉ lệ thức lập được từ bốn số trên là 25 25 25 25 0,25 0,25 1,5 1,5 ○ = 3 ; ○ = 18 ; ○ = 18 ; ○ 3 = . 25 1,5 25 1,5 25 0,25 0,25 25 18 3 3 18 □
c Bài 3. Tìm thành phần chưa biết x trong các tỉ lệ thức sau: x 1,5 −9 x a) = . b) = . 20 6 x −4 Lời giải. x 1,5 −9 x a) Vì = b) Vì = 20 6 x −4 Nên Nên x · 6 = 1,5 · 20 x · x = (−9) · (−4) 6x = 30 x2 = 36 x = 30 : 6 x2 = 62 x = 5. x = 6 hoặc x = −6. □
c Bài 4. Tìm thành phần chưa biết x trong các tỉ lệ thức sau: x −8 25 x a) = b) = 2,6 3,9 x 4 74/82 74/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 75
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Lời giải. x −8 25 x a) Vì = b) Vì = Nên 2,6 3,9 x 4 Nên x · x = 25 · 4 x · 3,9 = 2,6 · (−8) x2 = 100 3,9x = 20,8 x2 = 102 x = 20,8 : 3,9 x = 10 hoặc x = −10. 16 x = . 3 □ a b
c Bài 5. Từ tỉ lệ thức =
(với a, b khác 0) có thể suy ra những tỉ lệ thức nào? 4 5 Lời giải. a b a 4 4 5 b 5 Từ tỉ lệ thức =
ta có thể suy ra các tỉ lệ thức = ; = ; = . □ 4 5 b 5 a b a 4 x 6
c Bài 6. Từ tỉ lệ thức =
(với x, y khác 0) có thể suy ra những tỉ lệ thức nào? 7 y Lời giải. x 6 x 7 6 y 7 y Từ tỉ lệ thức =
ta có thể suy ra các tỉ lệ thức = ; = ; = . □ 7 y 6 y x 7 x 6
c Bài 7. Các giá trị tương ứng của hai đại lượng x và y được cho trong bảng sau x 1 3 5 7 y 5 15 25 35
a) Đại lượng y có tỉ lệ thuận với đại lượng x không ?
b) Đại lượng y có phải là hàm số của đại lượng x không ?
Nếu y là hàm số của x, hãy viết công thức của hàm số đó. Lời giải. 5 15 25 35 a) Ta có = = = = 5. 1 3 5 7
Do đó đại lượng y tỉ lệ thuận với đại lượng x.
b) Mỗi giá trị của đại lượng x đều được tương ứng với một giá trị của đại lượng y nên đại lượng y là hàm số
của đại lượng x. Công thức y = 5x với x ∈ {1; 3; 5; 7}. □
c Bài 8. Cho biết đại lượng x tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ k. Đại lượng y tỉ lệ nghịch với đại
lượng z theo hệ số tỉ lệ k. Khi đó, xét các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?
a) Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k.
b) Đại lượng x tỉ lệ nghịch với đại lượng z theo hệ số tỉ lệ k.
c) Đại lượng x tỉ lệ nghịch với đại lượng z theo hệ số tỉ lệ 2k. 75/82 75/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 76
23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
d) Đại lượng x tỉ lệ nghịch với đại lượng z theo hệ số tỉ lệ k2. Lời giải.
○ Đại lượng x tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ k thì đại lượng y tỉ lệ thuận với đại lượng x theo hệ 1 số tỉ lệ . Vậy a) sai. k
○ Ta có x tỉ lệ thuận với y theo hệ số tỉ lệ k nên x = k · y (1)
Đại lượng y tỉ lệ nghịch với đại lượng z theo hệ số tỉ lệ k, nên k k y = ⇒ z = (2) z y k
Từ (1) và (2) ta có x.z = k · y · = k2. y
Do đó x và z tỉ lệ nghịch theo hệ số tỉ lệ k2. Vậy d) đúng; b) và c) sai. □
c Bài 9. Cứ xay xát 100 kg thóc thì được 74 kg gạo. Muốn được 185 kg gạo thì phải xay xát bao nhiêu ki-lô-gam thóc ? Lời giải. Tóm tắt đề bài Gạo Thóc 74 kg 100 kg 185 kg x kg ? 74 100
Vì khối lượng gạo tỉ lệ thuận với khối lượng thóc, nên theo tính chất của hai đại lượng tỉ lệ thuận, ta có = . 185 x 185.100 Suy ra x =
= 250. Vậy muốn được 185 kg gạo thì xay xát 250 kg thóc. □ 74
c Bài 10. 10 công nhân làm xong một công việc trong 18 ngày. Hỏi muốn làm xong công việc đó trong 12
ngày thì cần bao nhiêu công nhân ? Lời giải.
Với cùng một công việc thì thời gian và số người làm là hai đại lượng tỉ lệ nghịch. 18 x
Theo tính chất của hai đại lượng tỉ lệ nghịch, ta có = . 12 10 18.10 Suy ra x = = 15. 12
Vậy muốn hoàn thành công việc trong 12 ngày thì cần 15 công nhân. □
c Bài 11. Chia số 1316 thành ba phần 2 5 2 5 a) tỉ lệ thuận với ; và 2; b) tỉ lệ nghịch với ; và 2. 3 4 3 4 Lời giải.
a) Gọi ba phần cần tìm là x, y, z. 2 5
Vì x, y, z tỉ lệ thuận với ; và 2 nên ta có 3 4 x y z x + y + z 1316 = = = = = 336. 2 4 2 2 5 47 + + 2 3 3 4 12 2 5 Do đó x = · 336 = 224; y =
· 336 = 420; z = 2 · 336 = 672. 3 4 76/82 76/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 77
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC
b) Gọi ba phần cần tìm là x, y, z. 2 5 2 5
Vì x, y, z tỉ lệ nghịch với ; và 2 nên ta có x = · y = 2z. 3 4 3 4 x y x x + y + z 1316 Suy ra = = = = = 470. 3 5 2 3 4 1 14 + + 2 2 5 2 5 3 4 1 Do đó x = · 470 = 705; y = · 470 = 376; z = · 470 = 235. 2 5 2 □
c Bài 12. Trong một phân xưởng may, ba tổ nhận may một số hàng như sau. Tổ I có 10 người, tổ II có 12
người, tổ III có 15 người. Biết năng suất lao động của mỗi người là như nhau và số ngày làm của tổ I hơn số
ngày làm của tổ II là 3 ngày. Tính số ngày làm của mỗi tổ. Lời giải.
Gọi số ngày làm của ba tổ lần lượt là x, y, z.
Với cùng một công việc thì số người làm tỉ lệ nghịch với số ngày làm.
Do đó ta có 10x = 12y = 15z, trong đó x − y = 3. x y z x − y 3 Suy ra = = = = = 180. 10 1 1 1 1 1 − 12 15 10 12 60 1 1 1 Do đó x = · 180 = 18; y = · 180 = 15; z = · 180 = 12. 10 12 15
Vậy số ngày làm của ba tổ I, II, II lần lượt là: 18, 15, 12 (ngày). □
c Bài 13. Dặm là tên của một đơn vị chiều dài trong Hệ đo lường Anh. Biết rằng 1 dặm ≈ 1,6 km.
a) Hỏi một con đường dài 3 km sẽ có chiều dài là bao nhiêu dặm (làm tròn kết quả đến hàng phần trăm)?
b) Độ dài của một vật thể tính theo km có tỉ lệ thuận với độ dài của vật thể đó tính theo dặm không? Nếu
có thì hệ số tỉ lệ là bao nhiêu? Lời giải.
a) Độ dài (theo dặm) của một con đường dài 3 km là 3 : 1,6 = 1,875 ≈ 1,88 dặm.
b) Gọi x là độ dài của vật thể tính theo km. y là độ dài vật thể đó tính theo dặm.
Khi đó ta có x = 1,6y ⇒ x tỉ lệ thuận với y theo hệ số tỉ lệ là 1,6. □
c Bài 14. Pound (đọc là pao và viết tắt là lb) là tên một đơn vị khối lượng trong hệ đo lường Anh. Biết rằng 1 lb ≈ 0,4 kg.
a) Hỏi một người có khối lượng 60 kg sẽ có khối lượng là bao nhiêu pound (làm tròn kết quả đến hàng đơn vị)?
b) Khối lượng của một người tính theo kg có tỉ lệ thuận với khối lượng của người đó tính theo pound
không? Nếu có thì hệ số tỉ lệ là bao nhiêu? Lời giải.
a) Khối lượng của một người nặng 60 kg tính theo pound là 60 : 0,4 = 150 (pound).
b) Gọi x là khối lượng của người đó tính theo kg. y là khối lượng của của người đó tính theo pound.
Khi đó ta có x = 0,4 · y ⇒ x tỉ lệ thuận với y theo hệ số tỉ lệ là 0,4. □
c Bài 15. Số đo ba góc b A, “ B, “
C của tam giác ABC tỉ lệ với 2; 3; 4. Tính số đo ba góc của tam giác đó. 77/82 77/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 78
23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Lời giải. Ta có b A, “ B, “
C của tam giác ABC tỉ lệ với 2; 3; 4. b A “ B “ C Suy ra = = . 2 3 4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có b A “ B “ C b A + “ B + “ C 180◦ = = = = = 60◦. 2 3 4 2 + 3 + 4 9 ○ b A = 20◦ ⇒ b A = 20◦ · 2 = 40◦. 2 ○ “ B = 20◦ ⇒ “ B = 20◦ · 3 = 60◦. 3 ○ b A = 20◦ ⇒ “ C = 20◦ · 4 = 80◦. 4 Vậy b A = 40◦, “ B = 60◦, “ C = 80◦. □
c Bài 16. Số đo ba góc “ D, “ E, “
F của tam giác DEF tỉ lệ nghịch với 2; 3; 6. Tính số đo ba góc của tam giác đó. Lời giải. Ta có “ D, “ E, “
F của tam giác DEF tỉ lệ nghịch với 2; 3; 6. 2 3 6 ⇒ “ D “ E “ F “ E “ F 2 “ D = 3 “ E = 6“ F ⇒ = = ⇒ “ D = = . 6 6 6 3 2 1
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có “ D “ E “ F “ D + “ E + “ F 180◦ = = = = = 30◦. 3 2 1 3 + 2 + 1 6 ○ “ D = 30◦ ⇒ “ D = 30◦ · 3 = 90◦. 3 ○ “ E = 30◦ ⇒ “ E = 30◦ · 2 = 60◦. 2 ○ “ F = 30◦ ⇒ “ F = 30◦ · 1 = 30◦. 1 Vậy “ D = 90◦, “ E = 60◦, “ F = 30◦. □
c Bài 17. Ba đội xe tải cùng vận chuyển một lượng hàng hóa như nhau. Đội thứ nhất vận chuyển xong
trong 2 giờ, đội thứ hai trong 2,5 giờ và đội thứ ba trong 3 giờ. Biết đội thứ nhất nhiều hơn đội thứ ba là 10
xe, tính số xe của mỗi đội (lượng hàng hóa mỗi xe chở được là như nhau). Lời giải.
Gọi x, y, z lần lượt là số xe của mỗi đội (x, y, z ∈ N).
Đội thứ nhất nhiều hơn đội thứ ba 10 xe nên x − z = 10.
Vì với cùng một lượng hàng hóa như như nhau nên thời gian vận chuyển của mỗi đổi tỉ lệ nghịch với số xe của mỗi đội. x y z
Do đó 2 · x = 2,5 · y = 3 · z ⇒ = = . 15 12 10
Áp dụng tính chất dãy tỉ số bằng nhau, ta có x y z x − z 10 = = = = = 2. 15 12 10 15 − 10 5 x ○ = 2 ⇒ x = 2 · 15 = 30. 15 78/82 78/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 79
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC y ○ = 2 ⇒ y = 2 · 12 = 24. 12 z ○ = 2 ⇒ z = 2 · 10 = 20. 10
Vậy số xe của ba đội lần lượt là 30, 24, 20. □
c Bài 18. Ba nhóm thợ thực hiện xây các ngôi nhà giống nhau. Nhóm thứ nhất xây xong trong 40 ngày,
nhóm thứ hai trong 60 ngày và nhóm thứ ba trong 50 ngày. Biết nhóm thứ ba có ít hơn nhóm thứ nhất là 3
người thợ, tính số người thợ của mỗi nhóm (năng suất các người thợ là như nhau). Lời giải.
Gọi a, b, c lần lượt là số thợ của ba nhóm (a, b, c ∈ N).
Vì nhóm thứ ba có ít hơn nhóm thứ nhất 3 người thợ nên a − c = 3.
Vì ba nhóm thực hiện xây các ngôi nhà giống nhau nên số thợ của mỗi nhóm và số ngày để xây xong là hai đại lượng tỉ lệ nghịch. a b c
Do đó a · 40 = b · 60 = c · 50 ⇒ = = . 15 10 12
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có a b c a − c 3 = = = = = 1. 15 10 12 15 − 12 3 a ○ = 1 ⇒ a = 1 · 15 = 15. 15 b ○ = 1 ⇒ b = 1 · 10 = 10. 10 c ○ = 1 ⇒ c = 1 · 12 = 12. 12
Vậy số thợ của ba nhóm lần lượt là 15; 10; 12 □ A B BÀI TẬP BỔ SUNG −3
c Bài 19. Lập tất cả các tỉ lệ thức có thể được từ bốn số sau: 0,6; ; 16; −20. 4 Lời giải. −3 Ta có: 0,6 · (−20) = · 16 (= −12). 4
Suy ra các tỉ lệ thức lập được từ bốn số trên là 0,6 16 −3 ○ = ; −3 −20 −20 ○ = 4 ; 4 16 0,6 −3 16 −20 ○ = . 0,6 − ○ 3 = 4 ; 0,6 16 −20 4 □
c Bài 20. Tìm thành phần chưa biết x trong các tỉ lệ thức sau: 14 −21 x −16 a) = ; b) = . x 15 −4 x Lời giải. 79/82 79/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 80
23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC a) b) 14 −21 x −16 = = x 15 −4 x ⇒ x · (−21) = 14 · 15 ⇒ x · x = (−16) · (−4) −21x = 60 x2 = 64 60 −20 x = = . x2 = 82 −21 7 x = 8 hoặc x = −8. −20 Vậy x = . 7 Vậy x = 8 hoặc x = −8. □ x m
c Bài 21. Từ tỉ lệ thức =
(với x, y, m, n khác 0) có thể suy ra những tỉ lệ thức nào. y n Lời giải. x m x y y n m n Từ tỉ lệ thức =
ta có thể suy ra các tỉ lệ thức = , = , = . □ y n m n x m x y
c Bài 22. Cho y và x là hai đại lượng tỉ lệ thuận. Biết rằng khi x = 3 thì y = 5.
a) Hỏi y và x liên hệ với nhau theo công thức nào? b) Tìm x khi y = 7,5. Lời giải. 5 a) y = x; b) x = 4,5. 3 □
c Bài 23. Cho y và x là hai đại lượng tỉ lệ nghịch. Biết rằng x = −2 thì y = 3.
a) Hỏi y và x liên hệ với nhau theo công thức nào? b) Tìm y khi x = 5. Lời giải. −6 a) y = . b) y = −1,2. x □
c Bài 24. Chia số 351 thành ba phần
a) tỉ lệ thuận với 3; 4; 6; b) tỉ lệ nghịch 3; 4; 6. Lời giải. a) 81; 108; 162; b) 156; 117; 78. □
c Bài 25. Gallon (đọc là ga-lông và viết tắt là gal) là tên một đơn vị thể tích trong Hệ đo lường Anh. Biết rằng 1 gl ≈ 3,79 l.
a) Hỏi một can có dung tích 5 l sẽ có dung tích là bao nhiêu gallon (làm tròn kết quả đến hàng phần 80/82 80/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 81
Chương 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC nghìn)?
b) Dung tích của một vật tính theo l có tỉ lệ thuận với dung tích của vật đó tính theo gallon không? Nếu
có thì hệ số tỉ lệ là bao nhiêu? Lời giải. 500
a) Dung tích tính theo gallon của can 5 lít là 5 : 3,79 = ≈ 1,319 gallon. 319
b) Gọi x là dung tích vật đó tính theo lít, y là dung tích của vật đó tính theo gallon. Ta có x = y · 3,79.
Vậy x tỉ lệ thuận với y theo hệ số tỉ lệ là 3,79. □
c Bài 26. Số đo ba góc c M , “ N , “
P của tam giác M N P tỉ lệ với 5; 7; 8. Tính số đo ba góc của tam giác đó. Lời giải. Vì ba góc c M , “ N , “
P của tam giác M N P tỉ lệ với 5; 7; 8 c M “ N “ P Nên = = . 5 7 8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có c M “ N “ P c M + “ N + “ P 180◦ = = = = = 9◦. 5 7 8 5 + 7 + 8 20 ○ c M = 9◦ ⇒ c M = 9◦ · 5 = 45◦. 5 ○ “ N = 9◦ ⇒ “ N = 9◦ · 7 = 63◦. 7 ○ “ P = 9◦ ⇒ “ P = 9◦ · 8 = 72◦. 8 Vậy c M = 45◦, “ N = 63◦, “ P = 72◦. □
c Bài 27. Ba bạn Hoàng, Tuấn và Minh cùng đi một con đường từ sân bóng đá tới trường. Thời gian ba
bạn di chuyển lần lượt là 10 phút, 12 phút và 15 phút. Biết mỗi phút bạn Minh đi chậm hơn bạn Hoàng là 10
m, tính chiều dài quãng đường mỗi bạn đi. Lời giải.
Gọi x, y, z lần lượt là vận tốc của ba bạn Hoàng, Tuấn và Minh (x, y, z > 0).
Do mỗi phút bạn Minh đi chậm hơn bạn Hoàng 10 m nên x − z = 10.
Vì khi đi trên cùng một quãng đường, vận tốc và thời gian đi trên quãng đường đó là hai đại lượng tỉ lệ nghịch x y z
nên ta có 10 · x = 12 · y = 15 · z ⇒ = = . 6 5 4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có x y z x − z 10 = = = = = 5. 6 5 4 6 − 4 2 x = 5 ⇒ x = 5 · 6 = 30. 6
Vậy độ dãi quãng đường cả ba bạn đi là 30 · 10 = 300 m. □
c Bài 28 (*). Một tam giác có chu vi bằng 36 cm và độ dài ba đường cao tỉ lệ nghịch với 3; 4; 5. Tính diện tích tam giác đó. 81/82 81/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641 82
23. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
TÀI LIỆU TOÁN 7 KẾT NỐI TRI THỨC Lời giải.
Gọi độ dài cách cạnh của tam giác lần lượt là a, b, c (cm) (Điều kiện a, b, c > 0).
Kí hiệu các chiều cao tương ứng với các cạnh a, b, c lần lượt là ha, hb, hc (cm).
Kí hiệu diện tích tam giác là S (cm2). Theo đề bài ta có aha bhb chc
a + b + c = 36; 3 · ha = 4 · hb = 5 · hc và = = = S. 2 2 2 aha bhb chc 2S 2S 2S Ta có = = = S ⇒ ha = ; hb = ; hc = . 2 2 2 a b c 6S 8S 10S a b c
Mà 3 · ha = 4 · hb = 5 · hc ⇒ = = ⇒ = = . a b c 6 8 10
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có a b c a + b + c 36 3 = = = = = . 6 8 10 6 + 8 + 10 24 2 3 3 3 Suy ra a = · 6 = 9; b = · 8 = 12; c = · 10 = 15. 2 2 2
Độ dài các cạnh của tam giác lần lượt là 9 cm, 12 cm, 15 cm.
Diện tích của tam giác là 54 cm2. □
c Bài 29. Thời gian một người thợ làm 6 cái bánh bằng thời gian một máy tự động làm 15 cái bánh. Hỏi
mất bao lâu để người thợ đó làm được số bánh bằng số bánh máy tự động làm trong 24 giờ? Lời giải.
Vì thời gian một người thợ làm 6 cái bánh bằng thời gain một máy tự động làm 15 cái bánh nên trong cùng một 15 5
thời gian, số bánh máy tự động làm được gấp =
lần số bánh người thợ làm được. 6 2 5
Suy ra với cùng số lượng bánh, thời gian người thợ cần gấp
lần thời gain máy tự động cần. 2 5
Vậy để người thợ làm được số bánh bằng số bánh máy tự động làm trong 24 giờ thì người thợ cần 24 · = 60 2 (giờ). □ 82/82 82/82 GV. NGUYỄN BỈNH KHÔI – 0909 461 641
Document Outline
- TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
- TỈ LỆ THỨC
- Trọng tâm kiến thức
- Tỉ lệ thức
- Tính chất của tỉ lệ thức
- Các dạng bài tập
- blue!80124 Dạng 1. Nhận biết tỉ số - Tỉ lệ thức
- blue!80124 Dạng 2. Tìm số chưa biết trong tỉ lệ thức
- blue!80124 Dạng 3. Lập tỉ lệ thức từ các số hoặc đẳng thức cho trước
- blue!80124 Dạng 4. Chứng minh tỉ lệ thức
- blue!80124 Dạng 5. Các bài toán thực tế sử dụng tỉ lệ thức.
- Bài tập vận dụng
- Bài tập nâng cao
- Trọng tâm kiến thức
- TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU
- Trọng tâm kiến thức
- Tính chất của dãy hai tỉ số bằng nhau
- Mở rộng tính chất cho dãy tỉ số bằng nhau
- Các dạng bài tập
- blue!80124 Dạng 1. Sử dụng tính chất dãy tỉ số bằng nhau để tìm các đại lượng chưa biết
- blue!80124 Dạng 2. Chứng minh tỉ lệ thức. Tính giá trị biểu thức
- blue!80124 Dạng 3. Áp dụng tính chất của dãy hai tỉ số bằng nhau để giải bài toán khác
- Bài tập vận dụng
- Bài tập nâng cao
- Trọng tâm kiến thức
- ĐẠI LƯỢNG TỈ LỆ THUẬN
- Trọng tâm kiến thức
- Đại lượng tỉ lệ thuận
- Tính chất:
- Một số bài toán về đại lượng tỉ lệ thuận:
- Các dạng bài tập
- blue!80124 Dạng 1. Nhận biết đại lượng tỉ lệ thuận
- blue!80124 Dạng 2. Tìm giá trị của một đại lượng tỉ lệ thuận khi biết giá trị của đại lượng kia
- blue!80124 Dạng 3. Giải bài toán thực tế về hai đại lượng tỉ lệ thuận
- blue!80124 Dạng 4. Chia một số M thành những phần x, y, z tỉ lệ thuận với các số a, b, c cho trước
- Bài tập vận dụng
- Bài tập nâng cao
- Trọng tâm kiến thức
- ĐẠI LƯỢNG TỈ LỆ NGHỊCH
- Trọng tâm kiến thức
- Đại lượng tỉ lệ nghịch
- Tính chất
- Một số bài toán về đại lượng tỉ lệ nghịch
- Các dạng bài tập
- blue!80124 Dạng 1. Nhận biết đại lượng tỉ lệ nghịch
- blue!80124 Dạng 2. Tìm giá trị của một đại lượng tỉ lệ nghịch khi biết giá trị của đại lượng kia
- blue!80124 Dạng 3. Giải bài toán thực tế về hai đại lượng tỉ lệ nghịch
- blue!80124 Dạng 4. Chia một số M thành những phần x, y, z tỉ lệ nghịch với các số a, b, c cho trước
- Bài tập vận dụng
- Bài tập nâng cao
- Trọng tâm kiến thức
- magenta ÔN TẬP CHƯƠNG VI
- Bài tập rèn luyện
- Bài tập bổ sung
- Bài tập rèn luyện
- TỈ LỆ THỨC




