Phân tích, bình luận và phát triển đề thi thử Toán 2019 chuyên ĐH Vinh – Nghệ An lần 1

Đề thi thử Toán THPT Quốc gia 2019 lần 1 trường THPT chuyên Đại học Vinh – Nghệ An được đánh giá là có độ khó cao, chứa nhiều bài toán vận dụng hay độc đáo

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

97 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 1
“Chân thành cảm ơn tập thể thầy cô Tổ 4 – Strong Team .
Tâm huyết tạo lên sản phẩm vì thế hệ học sinh thân yêu của chúng ta.”
Admin Tổ 4 – Strong Team: Nguyễn Việt Hải – Hue Tran – Võ Minh Chung – Đỗ Thuận – Mê
Kiếm Hiệp
Thầy cô Tổ 4 – Strong Team
MÃ ĐỀ THI: 209
Câu 1. Số nghiệm âm của phương trình
2
log 3 0
x
là
A.
2
. B.
4
. C.
1
. D.
3
.
Câu 2. Cho hình chóp
.
S ABCD
có đáy
ABCD
hình chữ nhật với
3AB a
,
BC a
, cạnh bên
2SD a
và
SD
vuông góc với mặt phẳng đáy. Thể tích khối chóp
.
S ABCD
bằng
A.
3
3a
. B.
. C.
3
2a
. D.
3
6a
.
Câu 3. Trong không gian
Oxyz
, cho
3;4;0
a
,
5;0;12
b
. Côsin của góc giữa
a
và
b
bằng
A.
3
13
. B.
5
6
. C.
5
6
. D.
3
13
.
Câu 4. Giả sử
a
,
b
là các số thực dương bất kỳ. Biểu thức
2
ln
a
b
bằng
A.
1
ln ln
2
a b
. B.
1
ln ln
2
a b
. C.
ln 2lna b
. D.
ln 2lna b
.
Câu 5. Trong không gian
Oxyz
, cho
( 1;0;2)
E
và
(2;1; 5)
F
. Phương trình đường thẳng
EF
là
A.
1 2
3 1 7
x y z
. B.
1 2
3 1 7
x y z
.
C.
1 2
1 1 3
x y z
. D.
1 2
1 1 3
x y z
.
Câu 6. Cho cấp số nhân
n
u
, với
1 4
1
9,
3
u u
. Công bội của cấp số nhân đã cho bằng
A.
1
3
. B.
3
. C.
3
. D.
1
3
.
Câu 7. Đường cong ở hình vẽ bên là đồ thị của hàm số nào dưới đây
PHÂN TÍCH – BÌNH LUẬN – PHÁT TRIỂN
ĐỀ THI THỬ THPTQG LẦN 1 - 2018-2019
CHUYÊN ĐẠI HỌC VINH
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 2
A.
3
3 1y x x
. B.
1
1
x
y
x
. C.
1
1
x
y
x
. D.
3 2
3 1
y x x
.
Câu 8. Trong không gian
O
xyz
, mặt phẳng
P
đi qua điểm
3; 1; 4
M
, đồng thời vuông góc với
giá của vectơ
1; 1; 2
a
có phương trình là
A.
3 4 12 0
x y z
. B.
3 4 12 0
x y z
.
C.
2 12 0
x y z
. D.
2 12 0
x y z
.
Câu 9. Cho hàm số
y f x
liên tục trên
3;3
và có bảng xét dấu đạo hàm như hình bên.
Mệnh đề nào sau đây sai về hàm số đó?
A. Hàm số đạt cực tiểu tại
1x
. B. Hàm số đạt cực đại tại
1
x
.
C. Hàm số đạt cực đại tại
2
x
. D. Hàm số đạt cực tiểu tại
0
x
.
Câu 10. Giả sử
f x
là một hàm số bất kì liên tục trên khoảng
;
và
a
,
b
,
c
,
;
b c
. Mệnh
đề nào sau đây sai?
A.
d d d
b c b
a a c
f x x f x x f x x
. B.
d d d
b b c c
a a a
f x x f x x f x x
.
C.
d d d
b b c b
a a b c
f x x f x x f x x
. D.
d d d
b c c
a a b
f x x f x x f x x
.
Câu 11. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Mệnh đề nào
sau đây đúng về hàm số đó?
A. Nghịch biến trên khoảng
1;0 .
B. Đồng biến trên khoảng
3;1 .
C. Đồng biến trên khoảng
0;1 .
D. Nghịch biến trên khoảng
0;2 .
Câu 12. Tất cả các nguyên hàm của hàm số
( ) 3
x
f x
là
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 3
A.
3
ln3
x
C
. B.
3
x
C
. C.
3 ln 3
x
C
. D.
3
ln3
x
C
.
Câu 13. Phương trình
log 1 2
x
có nghiệm là
A.
11
. B.
9
. C.
101
. D.
99
.
Câu 14. Cho
k
,
n
k n
là các số nguyên dương bất kì. Mệnh đề nào sau đây đúng?
A.
!
!
k
n
n
A
k
. B.
!.
k k
n n
A k C
. C.
!
k! !
k
n
n
A
n k
. D.
!.
k k
n n
A n C
.
Câu 15. Cho các số phức
1 2 ,z i
w 2 .i
Điểm nào trong hình bên biểu diễn số phức
wz
?
A.
. B.
P
. C.
Q
. D.
M
.
Câu 16. Trong không gian với hệ tọa độ
Oxyz
, cho hai mặt phẳng
: 3 2 1 0,
P x y z
: 2 0
Q x z
. Mặt phẳng
vuông góc với cả
P
và
Q
đồng
thời cắt trục
Ox
tại điểm có hoành độ bằng 3. Phương trình của mp
là:
A.
3 0
x y z
. B.
3 0
x y z
. C.
2 6 0
x z
. D.
2 6 0
x z
.
Câu 17. Cho số phức
z
thỏa mãn
2
1 3 4 3i z i
. Môđun của
z
bằng
A.
5
4
. B.
5
2
. C.
2
5
. D.
4
5
.
Câu 18. Một hình trụ tròn xoay có độ dài đường sinh bằng đường kính đáy và thể tích của khối trụ bằng
16
. Diện tích toàn phần của khối trụ đã cho bằng
A.
16
. B.
12
. C.
8
. D.
24
.
Câu 19. Biết rằng phương trình
2
2 2
log 7 log 9 0
x x
có 2 nghiệm
1 2
,x x
. Giá trị
1 2
x x
bằng
A.
128
. B.
64
. C.
9
. D.
512
.
Câu 20. Đạo hàm của hàm số
3 1
( )
3 1
x
x
f x
là:
A.
2
2
( ) .3
3 1
x
x
f x
. B.
2
2
( ) .3
3 1
x
x
f x
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 4
C.
2
2
( ) .3 ln3
3 1
x
x
f x
. D.
2
2
( ) .3 ln3
3 1
x
x
f x
.
Câu 21. Cho
4 2
5 4
f x x x
. Gọi
S
là diện tích của hình phẳng giới hạn bởi đồ thị hàm số
y f x
và trục hoành. Mệnh đề nào sau đây sai ?
A.
2
2
dS f x x
. B.
1 2
0 1
2 d 2 dS f x x f x x
.
C.
2
0
2 dS f x x
. D.
2
0
2 dS f x x
.
Câu 22. Cho hàm số
y f x
có đạo hàm
2 2
1
f x x x
,
x
. Hàm số
2
y f x
đồng
biến trên khoảng
A.
2;

. B.
; 1
. C.
1;1
. D.
0;2
.
Câu 23. Đồ thị hàm số
3
3
4
3 2
x x
y
x x
có bao nhiêu đường tiệm cận?
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 24. Biết rằng
,
là các số thực thỏa mãn
2 2 2 8 2 2
. Giá trị của
2
bằng
A. 1. B. 2. C. 4. D. 3.
Câu 25. Cho hình lăng trụ tam giác đều
. ' ' 'ABC A B C
có
AB a
, góc giữa đường thẳng
'A C
và mặt
đáy bằng 45
0
. Tính thể tích khối lăng trụ
. ' ' 'ABC A B C
.
A.
3
3
4
a
. B.
3
3
2
a
. C.
3
3
12
a
. D.
3
3
6
a
.
Câu 26. Cho hàm số
y f x
có bảng biến thiên như hình vẽ bên dưới.
Hàm số
2y f x
đạt cực đại tại
A.
1
2
x
. B.
1
x
. C.
1x
. D.
2
x
.
Câu 27. Cho hình nón tròn xoay có bán kính bằng
3
và diện tích xung quanh bằng
6 3
. Góc ở đỉnh
của hình nón đã cho bằng
A.
60
. B.
150
. C.
90
. D.
120
.
Câu 28. Gọi
1 2
,z z
là các nghiệm phức của phương trình
2
4 7 0
z z
. Số phức
1 2 1 2
z z z z
bằng
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 5
A.
2
. B.
. C.
2i
. D.
10i
.
Câu 29. Gọi
m
,
M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
9
y x
x
trên đoạn
1;4
.
Giá trị của
m M
bằng
A.
65
4
. B.
. C.
49
4
. D.
.
Câu 30. Cho hình lập phương
.
ABCD A B C D
có
,I J
tương ứng là trung điểm của
BC
và
BB
. Góc
giữa hai đường thẳng
AC
và
IJ
bằng
A.
45
. B.
60
. C.
30
. D.
120
.
Câu 31. Giải bóng chuyền quốc tế VTV Cup có 8 đội tham gia, trong đó có hai đội Việt Nam. Ban tổ
chức bốc thăm ngẫu nhiên để chia thành hai bảng đấu, mỗi bảng 4 đội. Xác suất để hai đội của
Việt Nam nằm ở hai bảng khác nhau bằng
A.
2
7
. B.
5
7
. C.
3
7
. D.
4
7
.
Câu 32. Tất cả các nguyên hàm của hàm số
2
sin
x
f x
x
trên khoảng
0;
là
A.
cot ln sin
x x x C
. B.
cot ln sin
x x x C
.
C.
cot ln sin
x x x C
. D.
cot ln sin
x x x C
.
Câu 33. Cho hình lăng trụ đứng .
ABC A B C
có đáy
ABC
là tam giác vuông tại
A
. Gọi
E
là trung
điểm của
AB
. Cho biết
2AB a
,
13BC a
,
4CC a
. Khoảng cách giữa hai đường thẳng
A B
và
CE
bằng
A.
4
7
a
. B.
12
7
a
. C.
6
7
a
. D.
3
7
a
.
Câu 34. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên
m
để phương trình
3
3
f x x m
có 6 nghiệm phân biệt thuộc đoạn
1;2
?
A.
3
. B.
2
. C.
6
. D.
7
.
Câu 35. Có bao nhiêu số phức
z
thỏa mãn
2
2019
1 1
z z z i z z i
?
A. 4. B. 2. C. 1. D. 3.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 6
Câu 36. Cho
f x
mà hàm số
'y f x
có bảng biến thiên như hình vẽ bên. Tất cả các giá trị của
tham số
m
để bất phương trình
2 3
1
3
m x f x x
nghiệm đúng với mọi
0;3
x
là
A.
0
m f
. B.
0
m f
. C.
3
m f
. D.
2
1
3
m f
.
Câu 37. Trong không gian
Oxyz
, cho các điểm
(2;1;4)
M
,
(5;0;0)
N
,
(1; 3;1).
P
Gọi
( ; ; )I a b c
là tâm của
mặt cầu tiếp xúc với mặt phẳng
Oyz
đồng thời đi qua các điểm
M
,
,
P
. Tìm
c
biết rằng
5
a b c
.
A. 3. B. 2. C. 4. D. 1.
Câu 38. Biết rằng
1
0
d
ln 2 ln 3 ln5
3 5 3 1 7
x
a b c
x x
, với
, ,a b c
là các số hữu tỉ.
Giá trị của
a b c
bằng
A.
10
3
. B.
5
3
. C.
10
3
. D.
5
3
.
Câu 39. Trong không gian
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
và hai điểm
( 1;3;1)
A
và
0;2; 1
B
. Gọi
; ;C m n p
là điểm thuộc đường thẳng
d
sao cho diện tích tam giác
ABC
bằng
2 2
. Giá trị của tổng
m n p
bằng
A.
1
. B.
2
. C.
3
. D.
5
.
Câu 40. Bất phương trình
3
9 ln 5 0
x x x
có bao nhiêu nghiệm nguyên ?
A.
4
. B.
7
. C.
6
. D. Vô số.
Câu 41. Cho hàm số
( )f x
có đồ thị hàm
'( )y f x
như hình vẽ. Hàm số
2
(cos )
y f x x x
đồng
biến trên khoảng
A.
1;2
. B.
1;0
. C.
0;1
. D.
2; 1
.
Câu 42. Cho hàm số
( ) 2 2
x x
f x
. Gọi
0
m
là số lớn nhất trong các số nguyên
m
thỏa mãn
12
( ) (2 2 ) 0
f m f m
. Mệnh đề nào sau đây đúng?
A.
0
1513;2019
m
. B.
0
1009;1513
m
. C.
0
505;1009
m
. D.
0
1;505
m
.
Câu 43. Cho hàm số
f x
thỏa mãn
e ,
x
f x f x x
và
0 2
f
. Tất cả các nguyên hàm
của
2
e
x
f x
là
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 7
A.
2 e e
x x
x C
. B.
2
2 e e
x x
x C
. C.
1 e
x
x C
. D.
1 e
x
x C
.
Câu 44. Cho hàm số
f x
có đồ thị hàm số
y f x
được cho như hình vẽ bên.
Hàm số
2
1
0
2
y f x x f
có nhiều nhất bao nhiêu điểm cực trị trong khoảng
2;3
.
A.6. B.2. C.5. D.3
Câu 45. Cho hình chóp tứ giác đều
.
S ABCD
có
11
SA a
, cosin của góc hợp bởi hai mặt phẳng
SBC
và
SCD
bằng
1
10
. Thể tích của khối chóp
.
S ABCD
bằng
A.
3
3a
. B.
3
9a
. C.
3
4a
. D.
3
12a
.
Câu 46. Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách
điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ
bên dưới. Biết rằng
5
OO
cm
,
10
OA
cm
,
20
OB
cm
, đường cong
AB
là một phần của
parabol có đỉnh là điểm
A
. Thể tích của chiếc mũ bằng
A.
2750
3
3
cm
. B.
2500
3
3
cm
. C.
2050
3
3
cm
. D.
2250
3
3
cm
.
Câu 47. Giả sử
1 2
,z z
là hai trong các số phức thỏa mãn
6 8
z zi
là số thực. Biết rằng
1 2
4
z z
,
giá trị nhỏ nhất của
1 2
3z z
bằng
A.
5 21
. B.
20 4 21
. C.
20 4 22
. D.
5 22
.
Câu 48. Cho hàm số
y f x
có đồ thị như hình vẽ.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 8
Có bao nhiêu số nguyên
m
để phương trình
1
1
3 2
x
f x m
có nghiệm thuộc đoạn
2;2
?
A. 11. B. 9. C. 8. D. 10.
Câu 49. Trong không gian
Oxyz
cho ba đường thẳng
1
: ,
1 1 2
x y z
d
1
3 1
: ,
2 1 1
x y z
2
1 2
:
1 2 1
x y z
. Đường thẳng
vuông góc với
d
đồng thời cắt
1 2
,
tương ứng
tại
,H K
sao cho độ dài
HK
nhỏ nhất. Biết rằng
có một vectơ chỉ phương
; ;1 .
u h k
Giá trị
h k
bằng
A.
0.
B.
4.
C.
6.
D.
2.
Câu 50. Trong không gian
Oxyz
, cho
1; 1;0
a
và hai điểm
4;7;3
A
,
4;4;5
B
. Giả sử
M
,
là hai
điểm thay đổi trong mặt phẳng
Oxy
sao cho
MN

cùng hướng với
a
và
5 2
MN
. Giá trị lớn
nhất của
AM BN
bằng
A.
17
. B.
77
. C.
7 2 3
. D.
82 5
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 9
PHÂN TÍCH – BÌNH LUẬN – PHÁT TRIỂN ĐỀ THI THỬ ĐẠI HỌC VINH LẦN 1
NĂM 2018 -2019
Câu 1. Cho hình hộp chữ nhật
.
ABCD A B C D
có
AB a
,
2AD AA a
. Diện tích mặt cầu ngoại
tiếp hình hộp đã cho bằng
A.
2
9
a
. B.
2
3
4
a
. C.
2
9
4
a
. D.
2
3
a
.
Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hườ
ng
Chọn A
O
A
C
A'
C'
D'
B'
B
D
Mặt cầu ngoại tiếp hình hộp chữ nhật
.
ABCD A B C D
có tâm là
O
của hình hộp có bán kính
2 2
2 2 2 2
1 1 3
2 2
2 2 2
a
R AB AD AA a a a
.
Vậy diện tích mặt cầu ngoại tiếp hình hộp là
2
2
3
4 9
2
a
S a
.
Một số bài toán tương tự:
Câu 1.1. Cho hình hình lập phương cạnh
a
. Thể tích khối cầu nội tiếp hình lập phương là
A.
3
2
3
a
. B.
3
6
a
. C.
3
2
a
. D.
3
3
3
a
.
Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường
Chọn B
Khối cầu nội tiếp hình lập phương có bán kính
2
a
R
.
Vậy thể tích khối cầu nội tiếp hình lập phương là
3
3 3
4
4
2
3 3 6
a
R a
V
.
Câu 1.2. Cho hình hộp chữ nhật
.
ABCD A B C D
có
AB a
,
2AD a
,
3AA a
. Thể tích khối nón có
đỉnh trùng với tâm của hình chữ nhật
ABCD
, đường tròn đáy ngoại tiếp
A B C D
là
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 10
A.
3
15
4
a
. B.
3
5
4
a
. C.
3
15
a
. D.
3
5
a
.
Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường
Chọn B
O'
C
A
C'
A'
D
B'
D'
B
O
Gọi
,O O
lần lượt là tâm hình chữ nhật
ABCD
và hình chữ nhật
A B C D
.
Ta có đường cao khối nón
3h OO AA a
; bán kính
2
2
1 5
2
2 2
a
r A O a a
.
Vậy thể tích khối nón đã cho là
2
3
2
1 1 5 5
3
3 3 2 4
a a
V r h a
.
Một số bài toán tương tự trong các đề thi THPTQG:
Câu 1.3. (Mđ 104 –THPTQG 2017) Cho hình hộp chữ nhật
.
ABCD A B C D
có
8
AD
,
6
CD
,
12.
AC
Tính diện tích toàn phần
tp
S
của hình trụ có hai đường tròn đáy là hai đường tròn
ngoại tiếp hình chữ nhật
ABCD
và
.A B C D
A.
576
tp
S
. B.
10 2 11 5
tp
S
. C.
26
tp
S
. D.
5 4 11 5
tp
S
.
Câu 1.4. (Mđ 110 –THPTQG 2017) Cho mặt cầu bán kính
R
ngoại tiếp một hình lập phương
cạnh
a
. Mệnh đề nào dưới đây đúng?
A.
2 3
3
R
a
. B.
2a R
. C.
2 3a R
. D.
3
3
R
a
.
Câu 2. Cho hình chóp
.
S ABCD
có đáy
ABCD
hình chữ nhật với
3AB a
,
BC a
, cạnh bên
2SD a
và
SD
vuông góc với mặt phẳng đáy. Thể tích khối chóp
.
S ABCD
bằng
A.
3
3a
. B.
. C.
3
2a
. D.
3
6a
.
Lời giải
Tác giả: Nguyễn Thị Thơm; Fb: Thơm nguyễn
Chọn C
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 11
Chiều cao của khối chóp là
2SD a
và đáy là hình chữ nhật với
3AB a
,
BC a
nên ta có
3
1 1
. . . .2 .3 . 2
3 3
V SD AB BC a a a a
.
Câu 2.1 . Cho hình chóp
.
S ABCD
có đáy
ABCD
hình chữ nhật với
3AB a
,
2BC a
, cạnh bên
2SA a
và
SAB
và
SAD
cùng
vuông góc với mặt phẳng đáy. Thể tích khối chóp
.
S ABCD
bằng
A.
3
4a
. B.
. C.
3
12a
. D.
3
6a
.
Lời giải
Tácgiả: Nguyễn Thị Thơm; Fb: Thơm nguyễn
Chọn A
Vì
SAB
và
SAD
cùng
vuông góc với mặt phẳng đáy nên
SA ABCD
3
1 1
. . . .2 .3 .2 4
3 3
V SA AB BC a a a a
.
Câu 2.2 . Cho hình chóp
.
S ABCD
có đáy
ABCD
hình chữ nhật với
3AB a
,
4AD a
, cạnh bên
34
SC a
và
SAB
và
SAD
cùng
vuông góc với mặt phẳng đáy. Thể tích khối chóp
.
S ABCD
bằng
A.
3
4a
. B.
. C.
3
12a
. D.
3
6a
.
Lời giải
Tácgiả: Nguyễn Thị Thơm; Fb: Thơm nguyễn
Chọn D
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 12
Vì
SAB
và
SAD
cùng
vuông góc với mặt phẳng đáy nên
SA ABCD
Vì
ABCD
hình chữ nhật nên
2 2 2 2 2 2
9 16 25 5AC AB BC a a a AC a
SA ABCD SA AC
suy ra
SAC
vuông tại
A
.
2 2 2 2 2 2 2 2 2
34 25 9 3AC SA SC SA SC AC a a a SA a
3
1 1
. . . .3 .3 .4 12
3 3
V SA AB BC a a a a
.
Câu 3. Trong không gian
Oxyz
cho
3;4;0 ; 5;0;12
a b
. Cosin của góc giữa
a
và
b
bằng
A.
3
13
. B.
5
6
. C.
5
6
. D.
3
13
.
Lời giải
Tácgiả: Quỳnh Giao; Fb: QGiaoDo
Chọn D
15 3
cos ;
13
9 16. 25 144
a b
Câu 3.1. Trong không gian
Oxyz
cho
2;3; 1 ; 2; 1;3
a b
. Sin của góc giữa
a
và
b
bằng
A.
2
7
. B.
3 5
7
. C.
3 5
7
. D.
2
7
.
Lời giải
Tác giả: Quỳnh Giao; Fb: QGiaoDo
Chọn D
4 2
cos ;
7
4 9 1. 4 1 9
a b
2
3 5
sin ; 1 cos ;
7
a b a b
Câu 4. Giả sử
a
,
b
là các số thực dương bất kỳ. Biểu thức
2
ln
a
b
bằng
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 13
A.
1
ln ln
2
a b
. B.
1
ln ln
2
a b
. C.
ln 2lna b
. D.
ln 2lna b
.
Lời giải
Tác giả: Trần Thị Thơm; Fb: Tranthom
Chọn D
Với hai số thực dương
a
,
b
, ta có
2
2
ln ln ln ln 2 ln
a
a b a b
b
.
Phân tích:
*) Kiến thức trọng tâm liên quan đến bài toán: Sử dụng các tính chất của logarit, bao gồm:
1. Cho
, 0, 1
a b a
, ta có:
+)
log 1, log 1 0
a a
a
,
log
a
b
a b
.
+) Công thức bay (bay mũ) :
log log
a a
b b
;
1
log log
a
a
b b
;
2. Logarit của tích, thương :Cho 3 số dương
1 2
, ,a b b
với
1
a
, ta có:
1 2 1 2
log ( . ) log log
a a a
b b b b
1
1 2
2
log log log
a a a
b
b b
b
3. Công thức đổi cơ số:Với
, , 0
a b c
,
1, b 1, 1a c
ta có:
log
1
log
log log
c
a
c b
b
b
a a
;
*) Lỗi học sinh hay gặp:
+ Nhầm logarit của 1 tích bằng tích các logarit. Logarit của một thương bằng thương các
logarit. Ngược lại tổng hai logarit cùng cơ số bằng logarit của tổng các biểu thức logarit, hiệu
hai logarit cùng cơ số bằng logarit của một hiệu các biểu thức logarit…
+ Công thức bay mũ: Học sinh hay mắc sai lầm
Với
, 0
a b
,
1
a
thì
2
2
log log
a a
b b
.
Với
0
a
,
1
a
,
0
b
thì
l oog l g
a a
b b
(với số mũ
là số tự nhiên chẵn)
*) Các bài toán tương tự:
Mức độ nhận biết, thông hiểu
Câu 4.1 Với
a
là số thực dương tùy ý,
log 8 log 5a a
bằng
A.
log 8
log 5
a
a
. B.
log 3a
. C.
8
log
5
. D.
log8
log5
.
Lời giải
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 14
Tác giả: Trần Thị Thơm ; Fb: Tranthom
Chọn C
log 8 log 5a a
8
log
5
a
a
8
log
5
.
Câu 4.2 Với
a
là số thực dương tùy ý,
2
7
log
7
a
bằng
A.
7
2log 1a
. B.
2
ln 7
a
. C.
7
1 2log a
. D.
7
1
2log a
.
Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom
Chọn A
2
7
log
7
a
2
7 7
log log 7
a
7
2log 1a
.
Câu 4.3 Mệnh đề nào dưới đây đúng với mọi số dương
x
,
y
?
A.
2
2
2
2 log
4
log
log
x
x
y y
. B.
2 2
4
log log 4
x
x y
y
.
C.
2 2 2
4
log 2 log log
x
x y
y
.
D.
2 2 2
4
log 2 log log
x
x y
y
.
Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom
Chọn D
2
4
log
x
y
2 2
log 4 logx y
2 2
2 log logx y
.
Câu 4.4 Với
a
là số thực dương tùy ý,
4
log 16a
bằng
A.
4
2 log a
. B.
4
16log a
. C.
4
16 log a
. D.
4
2 log a
.
Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom
Chọn A
4
log 16a
4 4
log 16 log a
4
2 log a
.
Câu 4.5 Cho
log 4
a
b
và
log 5
a
c
. Tính
2 3 4
log
a
P a b c
.
A.
480
P
. B.
34
P
. C.
691
P
. D.
40000
P
.
Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom
Chọn B
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 15
Ta có:
2 3 4
log
a
P a b c
2 3 4
log log log
a a a
a b c
2log 3log 4log
a a a
a b c
2 3.4 4.5 34
.
Câu 4.6 Cho
a
là số thực dương tùy ý khác
1
. Mệnh đề nào dưới đây đúng?
A.
9
log 2log 3.
a
a
B.
9
3
2
log .
log
a
a
C.
9
1
log .
2log 3
a
a
D.
9
log 2log 3.
a
a
Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom
Chọn C
9
2
1
log
log 3
a
a
1
2log 3
a
.
Câu 4.7 Với
,a b
là các số thực dương tùy ý và
a
khác
1
, biết
log 2
a
b
. Tính
3
2 6
log log
a
a
P b b
.
Mệnh đề nào dưới đây đúng?
A.
6
P
. B.
2P
. C.
20
P
. D.
12P
.
Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom
Chọn D
3
2 6
log log
a
a
P b b
2
4log 2log
a a
b b
2
4 2 2 2 12
.
Câu 4.8 Cho hai số thực
,a b
, trong đó
0, 1, 0
a a b
. Khi đó
5
log
a
ab
bằng
A.
1 5log
a
b
. B.
6
. C.
1 5log
a
b
. D.
5
.
Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom
Chọn C
Ta có
5
log
a
ab
5
log log
a a
a b
1 5log
a
b
.
Câu 4.9 Cho
,a b
là các số thực dương tùy ý. Mệnh đề nào dưới đây là đúng?
A.
2
2
log 10 2 1 log 2logab a b
. B.
2
2
2
log 10 1 log 2log
ab a b
.
C.
2
2 2 4
log 10 100 log logab a b
. D.
2
2
log 10 1 log 2logab a b
.
Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom
Chọn A
Ta có
2
2
log 10
ab
2
2log 10
ab
2 1 log 2loga b
.
Câu 4.10 Cho các số thực
, 0
a b
với
1
a
. Trong các mệnh đề sau, mệnh đề nào đúng?
A.
2
1 1
log log .
2 2
a
a
ab b
B.
2
1
log log .
2
a
a
ab b
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 16
C.
2
log 2 2log .
a
a
ab b
D.
2 2 2
log log .log .
a a a
ab a b
Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom
Chọn A
Ta có:
2
1
log log
2
a
a
ab ab
1
log log
2
a a
a b
1 1
log
2 2
a
b
.
MỨC ĐỘ VẬN DỤNG
Câu 4.11 Cho
,x y
là các số thực dương thỏa mãn
2 2
ln 4ln 4ln .lnx y x y
.
Tính
2
1 log 2log
2 4log 9
x y
M
x y
.
A.
1
2
M
. B.
2M
. C.
1
4
M
. D.
1
2
M
Lời giải
Tác giả: Trần Thị Thơm ; Fb:Tranthom
Chọn D
Ta có
2 2
ln 4ln 4ln .lnx y x y
2 2
ln 2ln 4ln .ln 0
x y x y
2
ln 2ln 0
x y
ln 2lnx y
2
x y
.
Ta có:
2
1 log 2log
2 4log 9
x y
M
x y
2
1 log log
2 4log 9
x y
x x
1 2log
2 4log 10
x
x
1 2log
2 4 4log
x
x
1 2log 1
2 1 2log 2
x
x
.
Câu 5. Trong không gian
Oxyz
, cho
1;0;2
E
và
2;1; 5
F
. Phương trình đường thẳng
EF
là
A.
1 2
3 1 7
x y z
. B.
1 2
3 1 7
x y z
.
C.
1 2
1 1 3
x y z
. D.
1 2
1 1 3
x y z
.
Lời giải
Tác giả: Vũ Danh Được ; Fb: Danh Được Vũ
Chọn B
Đường thẳng
EF
có véc tơ chỉ phương là
3;1; 7
EF
.
Đường thẳng
EF
đi qua điểm
1;0;2
E
, có véc tơ chỉ phương
3;1; 7
nên phương trình
EF
là
1 2
3 1 7
x y z
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 17
Tổng quát: Trong không gian
Oxyz
, cho hai điểm
1 1 1
; ;A x y z
và
2 2 2
; ;B x y z
. Khi đó
đường thẳng
AB
có một phương trình dạng
1 1 1
2 1 2 1 2 1
x x y y z z
x x y y z z
.
Câu 6. Cho cấp số nhân
n
u
với
1 4
1
9;
3
u u
. Tìm công bội của cấp số nhân đã cho.
A.
B.
3.
C.
3.
D.
1
.
3
Lời giải
Tác giả: Văn Bùi Vũ; Fb: Van Tuan Vu
Chọn D
n
u
là cấp số nhân nên ta có:
3
4
3
3
4 1
1
1 1
. .
27 3
u
u u q q
u
Vậy công bội của cấp số nhân đã cho:
1
3
q
Phân tích và bình luận:
Bài toán khai thác kiến thức cơ bản công thức số hạng tổng quát của cấp số nhân học sinh cần
ghi nhớ:
1
1
. 2,
n
n
u u q n n
.
Câu hỏi tương tự:
Câu 6.1. Cho cấp số nhân
n
u
với
1 7
1
; 32
2
u u
. Tìm công bội của cấp số nhân đã cho.
A.
1
2
q
B.
2
q
C.
4
q
D.
1
q
Lời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu
Chọn B
n
u
là cấp số nhân nên ta có:
6 6
7
7 1
1
. 64
u
u u q q
u
2.
q
Vậy công bội của cấp số nhân đã cho:
2.
q
Câu 6.2. Cho cấp số nhân
n
u
với
1
3, 2
u q
. Số
192
là số hạng thứ mấy của cấp số nhân đã cho?
A. Số hạng thứ 5. B. Số hạng thứ 6.
C.Số hạng thứ 7. D. Không phải số hạng của
n
u
.
Lời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu
Chọn C
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 18
Giả sử
192
n
u
là số hạng thứ
n n
của cấp số nhân
n
u
.
Lúc đó:
1 1
192 3. 2 2 64 7.
n n
n
Vậy số
192
là số hạng thứ
7
của cấp số nhân đã cho.
Câu 7. Đường cong ở hình vẽ bên là đồ thị của hàm số nào dưới đây
A.
3
3 1y x x
. B.
1
1
x
y
x
. C.
1
1
x
y
x
. D.
3 2
3 1
y x x
.
Lời giải
Tác giả: Vũ Nga; Fb:
Nga Vu
Chọn B
Từ hình dáng đồ thị của hàm số ta có đồ thị hàm số có tiệm cận đứng là đường thẳng
1x
nên
loại phương án A, C, D.
Vậy chọn B.
BÀI TOÁN TỔNG QUÁT
Bài toán: Xác định hàm số
ax b
y
cx d
0
c
và
0
ad bc
khi biết đồ thị hàm số
hoặc bảng biến thiên của hàm số.
Kiến thức cần nhớ để vận dụng vào bài tập
Tập xác định:
\
d
D
c
.
Sự biến thiên:
2
ad bc
y
cx d
.
Bảng biến thiên
0
ad bc
0
ad bc
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 19
Đồ thị
- Đồ thị hàm số có tiệm cận đứng là đường thẳng
d
x
c
và tiệm cận ngang là
đường thẳng
a
y
c
.
- Đồ thị cắt trục
Ox
tại điểm
;0
b
a
( nếu
0
a
) và cắt trục
Oy
tại điểm
0;
b
d
( nếu
0
d
).
- Đồ thị
0
ad bc
0
ad bc
Phương pháp giải
- Nhận dạng đồ thị, từ đồ thị xác định được các yếu tố: đường tiệm cận đứng, đường
tiệm ngang của đồ thị, chiều biên thiên của hàm số, giao của đồ thị hàm số với các trục
tọa độ... từ đó sẽ xác định được hàm số tương ứng.
BÀI TOÁN TƯƠNG TỰ CÙNG MỨC ĐỘ
Xác định hàm số
ax b
y
cx d
0
c
và
0
ad bc
dựa vào hình dáng đồ thị hàm số và khai
thác thêm một trong các yếu tố đọc được từ đồ thị hoặc bảng biến thiên: tiệm cận, tính đơn
điệu, giao điểm với các trục tọa độ...
Câu 7.1 Bảng biến thiên ở hình dưới đây là bảng biến thiên của hàm số nào trong các hàm số sau ?
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 20
A.
4 2
2 1
y x x
. B.
4 2
2 1
y x x
. C.
3
2
x
y
x
. D.
3
2
x
y
x
.
Lời giải
Chọn C
Từ bảng biến thiên của hàm số ta thấy: đồ thị hàm số có tiệm cận ngang là đường thẳng
1y
nên loại các đáp án A, B, D, vậy chọn C.
BÀI TOÁN TƯƠNG TỰ MỨC ĐỘ CAO HƠN
Xác định hàm số
ax b
y
cx d
0
c
và
0
ad bc
dựa vào hình dáng đồ thị hàm số và khai
thác nhiều yếu tố đọc được từ đồ thị hoặc bảng biến thiên: tiệm cận, tính đơn điệu, giao điểm
với các trục tọa độ...
Câu 7.2 Bảng biến thiên ở hình dưới đây là bảng biến thiên của hàm số nào trong các hàm số sau ?
A.
2 7
2
x
y
x
. B.
2 3
2
x
y
x
. C.
3
2
x
y
x
. D.
3
2
x
y
x
.
Lời giải
Chọn C
Từ bảng biến thiên của hàm số ta thấy: đồ thị hàm số có tiệm cận ngang là đường thẳng
1y
nên loại đáp án A và B, hàm số ngịch biến trên mỗi khoảng
;2

và
2;
nên
0
y
với
\ 2
x
loại dáp án D, vậy chọn C.
Câu 7.3 Đường cong ở hình vẽ sau là đồ thị của hàm số nào dưới đây
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 21
A.
1x
y
x
. B.
1
1
x
y
x
. C.
2 2
x
y
x
. D.
1x
y
x
.
Chọn D
Từ bảng biến thiên của hàm số ta thấy:
- Đồ thị hàm số có tiệm cận cận đứng là trục
Oy
nên ta loại được đáp án B do đồ thị hàm số
1
1
x
y
x
có tiệm cận đứng là đường thẳng
1
x
.
- Đồ thị hàm số có tiệm cận ngang là đường thẳng
1y
nên ta loại được đáp án C do đồ thị
hàm số
2 2
x
y
x
có tiệm cận ngang là đường thẳng
2
y
.
- Đồ thị hàm số đi qua điểm
1;0
nên loại đáp án A.
Vậy chọn D.
Câu 7.4 Cho hàm số
ax b
y
cx d
với
0
a
có đồ thị như hình vẽ
Tìm khẳng định đúng trong các khẳng định sau
A.
0, 0, 0
b c d
. B.
0, 0, 0
b c d
. C.
0, 0, 0
b c d
. D.
0, 0, 0
b c d
.
Lời giải
Chọn B
Do đồ thị hàm số có tiệm cận đứng là đường thẳng
d
x
c
và tiệm cận ngang là đường thẳng
a
y
c
. Đồ thị cắt trục
Ox
tại điểm
;0
b
a
và cắt trục
Oy
tại điểm
0;
b
d
nên ta có:
0
0
0
0
d
c
a
c
b
a
b
d
. Mà
0
a
nên
0
0
0
c
b
d
. Vậy chọn B.
Câu 8 . Trong không gian
O
xyz
, mặt phẳng
P
đi qua điểm
3; 1; 4
M
, đồng thời vuông góc với
giá của vectơ
1; 1; 2
a
có phương trình là
A.
3 4 12 0
x y z
. B.
3 4 12 0
x y z
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 22
C.
2 12 0
x y z
. D.
2 12 0
x y z
.
Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạ
m
Chọn C
Do mặt phẳng
P
vuông góc với giá của vectơ
1; 1; 2
a
nên mặt phẳng
P
nhận vectơ
1; 1; 2
a
làm vectơ pháp tuyến và đi qua điểm
3; 1; 4
M
nên có phương trình:
1 3 1 1 2 4 0 2 12 0.
x y z x y z
Câu 8.1 . Trong không gian
O
xyz
, mặt phẳng
P
đi qua điểm
1; 1; 2
M
, đồng thời song song với
mặt phẳng
: 2 3 5 0
Q x y z
có phương trình là
A.
2 3 3 0
x y z
. B.
2 3 0
x y z
.
C.
2 3 3 0
x y z
. D.
2 3 0
x y z
.
Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạ
m
Chọn C
Do mặt phẳng
P
song song với mặt phẳng
: 2 3 5 0
Q x y z
nên mặt phẳng
P
nhận
vectơ pháp tuyến
2; 3; 1
Q
n
làm vectơ pháp tuyến và đi qua điểm
1; 1; 2
M
nên có
phương trình:
2 1 3 1 2 0 2 3 3 0.
x y z x y z
Nhận Xét: Đây là bài toán ở mức độ nhận biết của phần phương trình mặt phẳng. Giả thiết đã
cho 1 điểm thuộc mặt phẳng và VTPT của mặt phẳng. VTPT có thể cho trực tiếp, cho bằng
định nghĩa hoặc cho thông qua mặt phẳng song song với mặt phẳng đã cho.
Câu 9. Cho hàm số
y f x
liên tục trên
3;3
và có bảng xét dấu đạo hàm như hình bên.
Mệnh đề nào sau đây sai về hàm số đó?
A. Hàm số đạt cực tiểu tại
1x
. B. Hàm số đạt cực đại tại
1
x
.
C. Hàm số đạt cực đại tại
2
x
. D. Hàm số đạt cực tiểu tại
0
x
.
Lời giải
Tác giả: Lê Thị Phương Liên; Fb: Phuonglien Le
Chọn D
Dựa vào bảng xét dấu của đạo hàm đã cho ta thấy
' 0 0
f
và đạo hàm không đổi dấu khi
x
qua
0
0
x
nên hàm số đã cho không đạt cực tiểu tại
0
x
.
Bài toán tương tự
Câu 9.1 Cho hàm số
y f x
liên tục trên
2;4
và có bảng xét dấu đạo hàm như hình bên.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 23
Mệnh đề nào sau đây sai về hàm số đó?
A. Hàm số đạt cực tiểu tại
0
x
. B. Hàm số đạt cực đại tại
1
x
.
C. Hàm số đạt cực đại tại
2
x
. D. Hàm số đạt cực đại tại
1x
.
Lời giải
Chọn D
Dựa vào bảng xét dấu của đạo hàm đã cho ta thấy
' 1 0
f
và đạo hàm không đổi dấu khi
x
qua
0
1
x
nên hàm số đã cho không đạt cực đại tại
1x
.
Câu 10. Giả sử
f x
là hàm số bất kỳ liên tục trên khoảng
;
và
, , , ;
a b c b c
. Mệnh đề
nào sau đây sai ?
A.
d d d
b c b
a a c
f x x f x x f x x
. B.
d d d
b b c c
a a a
f x x f x x f x x
.
C.
d d d
b b c b
a a b c
f x x f x x f x x
. D.
d d d
b c c
a a b
f x x f x x f x x
.
Lời giải
Tác giả: Lê Hữu Đức ; Fb: Le Huu Duc
Chọn B
Đáp án A, C, D đúng vì theo tính chất tích phân.
Đáp án B sai vì
d d d d d
b c c b c a b c
a a a c c
f x x f x x f x x f x x f x x
.
Bài tương tự
Câu 10. Giả sử
f x
là hàm số bất kỳ liên tục trên khoảng
;
và
, , ;
a b c
. Mệnh đề nào
sau đây sai ?
A.
d d d
b b a
a c c
f x x f x x f x x
. B.
d d d
b c b
a a c
f x x f x x f x x
.
C.
d d d
b c b
a a c
f x x f x x f x x
. D.
d d d
b c a
a b c
f x x f x x f x x
.
Lời giải
Tác giả: Lê Hữu Đức ; Fb: Le Huu Duc
Chọn C
Đáp án A, B, D đúng vì theo tính chất tích phân.
Đáp án C sai.
Câu 11. Cho hàm số
( )y f x
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng về hàm số đó
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 24
-3
2
1
-1
O
1
x
y
A. Nghịch biến trên khoảng
1;0
. B. Đồng biến trên khoảng
3;1
.
C. Đồng biến trên khoảng
0;1
. D. Nghịch biến trên khoảng
0;2
.
Lời giải
Tác giả: Trần Mạnh Tường ; Fb: Trần Tuệ
Minh
Chọn C
Trên khoảng
0;1
đồ thị có hướng đi lên nên hàm số đồng biến ứng với khoảng này.
Bài tương tự
Câu 11.1 Cho hàm số
( )y f x
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng về hàm số đó
3
-1
-4
-1
2
O
1
x
y
A. Nghịch biến trên khoảng
1;0
. B. Đồng biến trên khoảng
4; 1
.
C. Đồng biến trên khoảng
1;0
. D. Nghịch biến trên khoảng
1;3
.
Lời giải
Tác giả: Trần Mạnh Tường ; Fb: Trần Tuệ
Minh
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 25
Chọn C
Trên khoảng
1;0
đồ thị có hướng đi lên nên hàm số đồng biến ứng với khoảng này.
Câu 12 . Tất cả các nguyên hàm của hàm số
3
x
f x
là
A.
3
ln3
x
C
. B.
3
x
C
. C.
3 ln3
x
C
. D.
3
ln3
x
C
.
Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn
Chọn A
Bài toán tương tự
Câu 12 .1 Tìm nguyên hàm
F x
của hàm số
x
f x e x
biết
0 2
F
A.
2
1
2
x
x
F x e
. B.
2
1
2
x
x
F x e
. C.
2
1
2
x
x
F x e
. D.
2
1
2
x
x
F x e
.
Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn
Chọn B
Ta có
2
d
2
x x
x
F x e x x e C
Theo bài ra
0 2
F
1 2
C
1
C
Vậy
2
1
2
x
x
F x e
.
Câu 13. Phương trình
log 1 2
x
có nghiệm là
A.
11
. B.
9
. C.
101
. D.
99
.
Lời giải
Tác giả: Nguyễn Mạnh Dũng ; Fb: Mạnh Dũng
Chọn D
Ta có :
log 1 2
x
2
1 10
1 0
x
x
99
1
x
x
99
x
.
Bài toán tương tự.
Câu 13.1. Phương trình
log 9 3
x
có nghiệm là
A.
91
. B.
9991
. C.
1009
. D.
991
.
Lời giải
Tác giả: Nguyễn Mạnh Dũng ; Fb: Mạnh Dũng
Chọn D
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 26
Ta có :
log 9 3
x
3
9 10
9 0
x
x
991
9
x
x
991
x
.
Câu14 . Cho
k
,
n
k n
là các số nguyên dương bất kì. Mệnh đề nào sau đây đúng?
A.
!
!
k
n
n
A
k
. B.
!.
k k
n n
A k C
. C.
!
k! !
k
n
n
A
n k
. D.
!.
k k
n n
A n C
.
Lời giải
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắ
t nâu
Chọn B
Ta có
! !
! !.
! ! !
k k
n n
n n
A k k C
n k k n k
nên B đúng.
* Phát triển câu mức độ tương tự
Câu 14.1. Tìm công thức tính số các tổ hợp chập
k
của một tập có
n
phần tử.
A.
!
!
k
n
n
C
n k
. B.
!
! !
k
n
n
C
n k k
. C.
!
!
k
n
n
A
n k
. D.
!
! !
k
n
n
A
n k k
.
Lời giải
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắ
t nâu
Chọn B
Số các tổ hợp chập
k
của một tập có
n
phần tử phần tử, kí hiệu là:
!
! !
k
n
n
C
n k k
.
Câu 14.2. Trong mệnh đề sau, mệnh để nào sai?
A.
3 11
14 14
C C
. B.
3 4 4
10 10 11
C C C
.
C.
0 1 2 3 4
4 4 4 4 4
16
C C C C C
. D.
4 4 5
10 11 11
C C C
.
Lời giải
Chọn D
Áp dụng công thức:
1 1
1
k k k
n n n
C C C
suy ra đáp án sai là
4 4 5
10 11 11
C C C
.
* Phát triển câu mức độ cao hơn
Câu 14.3. Cho số tự nhiên n thỏa mãn
2 2
9
n n
C A n
. Mệnh đề nào sau đây đúng?
A.
5n
. B.
3n
. C.
7n
. D.
2n
.
Lời giải
Chọn C
Phương pháp: Sử dụng các công thức
! !
;
! ! !
k k
n n
n n
C A
n k k n k
.
Giải: Điều kiện:
2
n
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 27
2 2
! ! 3
9 9 1 9 1 6 7
2 !2! 2 ! 2
n n
n n
C A n n n n n n n
n n
.
Câu 14.4. Có tất cả 120 cách chọn 3 học sinh từ nhóm
n
(chưa biết) học sinh. Số
n
là nghiệm của
phương trình nào sau đây?
A.
1 2 120
n n n
. B.
1 2 720
n n n
.
C.
1 2 120
n n n
. D.
1 2 720
n n n
.
Lời giải
Chọn D
Số cách chọn 3 trong
n
học sinh có
3
1 2
!
3 !3! 6
n
n n n
n
C
n
.
Khi đó
3
120 1 2 720
n
C n n n
.
Câu 15. Cho các số phức
1 2 ,z i
w 2 .i
Điểm nào trong hình bên biểu diễn số phức
wz
?
A.
. B.
P
. C.
Q
. D.
M
.
Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn
Chọn B
+ Tính
wz
1 2 2 1i i i
. Suy ra điểm biểu diễn là điểm có tọa độ
1;1
là điểm
P
.
Bài toán tương tự
Câu 15.1 Cho các số phức
,z a bi
w ,x yi
với
, , ,a b x y
. Điểm
M
biểu diễn số phức
wz
có
tọa độ là
A.
;
a x b y
. B.
;
a x b y
. C.
;
a b x y
. D.
;
a b x y
.
Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn
Chọn B
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 28
+ Theo quy tắc trừ số phức thì
wz
a bi x yi a x b y i
. Suy ra điểm biểu
diễn là điểm có tọa độ
;
a x b y
.
Câu 15.2 Gọi các số phức
1 2 3
; ;z z z
lần lượt có điểm biểu diễn trong hệ tọa độ
Oxy
là
, ,M N P
(như hình
vẽ bên dưới). Mệnh đề nào sau đây là đúng.
A.
1 2 3
z z z
. B.
2 1 3
z z z
. C.
3 2 1
z z z
. D.
1 2 3
z z z
.
Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễ
n
Chọn C
+ Dựa vào hình vẽ ta suy ra tọa độ
M 2;1 , N 1;2 ,P 1;3
nên
1 2 3
2 ; 1 2 ; 1 3z i z i z i
.
+ Theo quy tắc cộng số phức ta được
3 2 1
z z z
.
Câu 16. Trong không gian với hệ tọa độ
Oxyz
, cho hai mặt phẳng
( ) : 3 2 1 0
P x y z
,
( ) : 2 0
Q x z
.Mặt phẳng
vuông góc với cả
( )P
và
( )Q
đồng thời cắt trục
Ox
tại điểm
có hoành độ bằng 3. Phương trình của mp
là:
A.
3 0
x y z
. B.
3 0
x y z
. C.
2 6 0
x z
. D.
2 6 0
x z
.
Lời giải
Tác giả: Đổng Quang Phúc ; Fb: Đổ
ng Quang Phúc
Chọn A.
( )P
có vectơ pháp tuyến
1; 3;2
P
n
,
Q
có vectơ pháp tuyến
1;0; 1
Q
n
.
Vì mặt phẳng
vuông góc với cả
P
và
Q
nên
có một vectơ pháp tuyến là
; 3;3;3 3 1;1;1
P Q
n n
.
Vì mặt phẳng
cắt trục
Ox
tại điểm có hoành độ bằng 3 nên
đi qua điểm
3;0;0
M
.
Vậy
đi qua điểm
3;0;0
M
và có vectơ pháp tuyến
1;1;1
n
nên
có phương trình:
3 0
x y z
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 29
Câu 16.1 Trong không gian với hệ tọa độ
Oxyz
, cho hai mặt phẳng
( ) : 2 3 2 0
P x y z
,
( ) : 3 0
Q x y
.Mặt phẳng
vuông góc với cả
( )P
và
( )Q
đồng thời cắt trục
Ox
tại điểm
có hoành độ bằng 5. Phương trình của mp
là:
A.
3 3 15 0
x y z
. B.
3 0
x y z
. C.
2 6 0
x z
. D.
2 6 0
x z
.
Lời giải
Tác giả: Phạm Hoài Trung ; Fb: Phạ
m Hoài Trung
Chọn A.
( )P
có vectơ pháp tuyến
1; 2;3
P
n
,
Q
có vectơ pháp tuyến
1; 1;0
Q
n
.
Vì mặt phẳng
vuông góc với cả
P
và
Q
nên
có một vectơ pháp tuyến là
; 3;3;1
P Q
n n n

.
Vì mặt phẳng
cắt trục
Ox
tại điểm có hoành độ bằng 3 nên
đi qua điểm
5;0;0
M
.
Vậy
đi qua điểm
5;0;0
M
và có vectơ pháp tuyến
3;3;1
n
nên
có phương
trình:
3 3 15 0
x y z
.
Câu 17 . Cho số phức
z
thỏa mãn
2
1 3 3 4i z i
. Mô đun của
z
bằng
A.
5
4
B.
5
2
C.
2
5
D.
4
5
Lời giải
Tác giả: Phạm Ngọc Huệ; Fb: Phạm Ngọc Huệ
Chọn A
Phân tích: giả thiết là một phương trình bậc nhất với ẩn z, thực hiện phép toán thích hợp để tìm
z, nên sử dụng máy tính để tính cho nhanh và chính xác.
2
3 4 3 4 3 4 3 3
8 8
1 3
i
z i
i
2 2
3 4 3 4 3 3 5
8 8 4
z
Bài tập tương tự:
Câu 17.1 Cho số phức
z
thỏa mãn
2019
1
3 4
1
i
z i i
i
. Mô đun của
z
bằng
A. 5 B.
1
5
C.
2
5
D.
5
2
Lời giải
Tác giả: Phạm Ngọc Huệ; Fb: Phạm Ngọc Huệ
Chọn A
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 30
2019
1
3 4 . 3 4 3 4
1
i
z i i i z i i z i
i
. Vậy
5
z
Câu 18 . Cho hình trụ tròn xoay có độ dài đường sinh bằng đường kính đáy và thể tích khối trụ bằng
16
. Diện tích toàn phần của khối trụ đã cho bằng
A.
16
. B.
12
. C.
8
. D.
24
.
Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn
Chọn A
Theo bài ra ta có
r l h
2 3
16
V r h r
2
r
Diện tích toàn phần của khối trụ đã cho là :
2
2 4 16
tp
S r r l r
.
Câu 18.1 Một hình trụ có diện tích xung quanh bằng
8
và có chiều cao bằng đường kính đáy. Thể tích
khối trụ trương ứng bằng
A.
32
. B.
16
. C.
8
. D.
4
.
Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn
Chọn C
Theo bài ra ta có
r l h
2
2 2 8
xq
S rl r
2
r
Thể tích của khối trụ đã cho là :
2 3
8
V r h r
.
Câu 19 . Biết rằng phương trình
2
2 2
log 7log 9 0
x x
có hai nghiệm
1
x
,
2
x
. Giá trị của
1 2
x x
bằng
A.
128
. B.
64
. C.
9
. D.
512
.
Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn
Chọn A
Điều kiện
0
x
Với
1
x
,
2
x
là hai nghiệm của phương trình đã cho, áp dụng định lý Vi – ét, ta có
2 1 2 2
log log 7
x x
2 1 2
log 7
x x
7
1 2
2
x x
1 2
128
x x
.
Câu 19.1 Biết rằng phương trình
2
log 15log 2 2
x
x
có hai nghiệm
1
x
,
2
x
1 2
x x
. Giá trị của
1 2
16x x
bằng
A.
4095
8
. B.
30
. C.
34
. D.
4097
8
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 31
Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn
Chọn B
Điều kiện
0
1
x
x
2
log 15log 2 2
x
x
2
2
15
log 2
log
x
x
2
2 2
log 2log 15 0
x x
2
2
log 5
log 3
x
x
32
1
8
x
x
1
2
32
1
8
x
x
1 2
16 30
x x
.
Câu 20 . Đạo hàm của hàm số
3 1
( )
3 1
x
x
f x
là:
A.
2
2
'( ) .3
3 1
x
x
f x
. B.
2
2
'( ) .3
3 1
x
x
f x
C.
2
2
'( ) .3 ln3
3 1
x
x
f x
D.
2
2
'( ) .3 ln3
3 1
x
x
f x
Lời giải
Tác giả: Phạm Ngọc Huệ; Fb: Phạm Ngọc Huệ
Chọn C
Áp dụng công thức:
, ,
2
3 1 3 1 3 1 3 1
'( )
3 1
x x x x
x
f x
2 2
3 3 3 1 3 1 3 3
2
.3 ln3
3 1 3 1
x x x x
x
x x
ln ln
Câu tương tự.
Câu 20.1. Đạo hàm của hàm số
2 5
7
( ) 3
x
x
f x
là:
A.
2 5
'
7
2
19ln 3
( ) 3
7
x
x
f x
x
. B.
2 5
'
7
2
19
( ) 3
7
x
x
f x
x
C.
2 5
'
7
2
19
( ) 3
7
x
x
f x
x
D.
2 5
'
7
2
19ln 3
( ) 3
7
x
x
f x
x
Lời giải
Tác giả: Phạm Ngọc Huệ; Fb: Phạm Ngọc Huệ
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 32
Chọn A
Áp dụng công thức:
'
'
2 5 2 5 2 5
'
7 7 7
2 5
( ) 3 ( ) 3 3 ln 3.
7
x x x
x x x
x
f x f x
x
2 5
7
2
19ln 3
3
7
x
x
x
Chú ý áp dụng công thức tính nhanh
,
2
ax+b
cx+d
ad bc
cx d
Câu 21. Cho
4 2
5 4
f x x x
. Gọi
S
là diện tích của hình phẳng giới hạn bởi đồ thị hàm số
y f x
và trục hoành. Mệnh đề nào sau đây sai ?
A.
2
2
dS f x x
. B.
1 2
0 1
2 d 2 dS f x x f x x
.
C.
2
0
2 dS f x x
. D.
2
0
2 dS f x x
.
Lời giải
Tác giả: Nguyễn Ngọ
c Minh ; Fb: Minh Nguyen
Chọn D
Phương trình hoành độ giao điểm của đồ thị hàm số
4 2
5 4
f x x x
và trục hoành:
2
4 2
2
1 1
5 4 0
2
4
x x
x x
x
x
Diện tích hình phẳng cần tìm là:
2
2
d 1S f x x
2
0
2 d 2
f x x
(do
f x
là hàm số chẵn)
1 2
0 1
2 d 2 df x x f x x
1 2
0 1
2 d 2 d 3
f x x f x x
(do trong các khoảng
0;1 , 1;2
phương trình
0
f x
vô
nghiệm)
Từ
1
,
2
,
3
suy ra các đáp án A, B, C là đúng, đáp án D là sai.
Máy tính: Bấm máy tính kiểm tra, ba kết quả đầu bằng nhau nên đáp án sai là đáp án D.
Câu 21.1 Cho
4 2
6 8
f x x x
. Gọi
S
là diện tích của hình phẳng giới hạn bởi đồ thị hàm số
y f x
và trục hoành. Mệnh đề nào sau đây sai ?
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 33
A.
2
2
dS f x x
. B.
2 2
0
2
2 d 2 dS f x x f x x
.
C.
2
0
2 dS f x x
. D.
2
0
2 dS f x x
.
Lời giải
Tác giả:Phạm Hoài Trung; Fb: Phạ
m Hoài Trung
Chọn D
Phương trình hoành độ giao điểm của đồ thị hàm số
4 2
6 8
f x x x
và trục hoành:
2
4 2
2
2
2
6 8 0
2
4
x
x
x x
x
x
Diện tích hình phẳng cần tìm là:
2
2
d 1S f x x
2
0
2 d 2
f x x
(do
f x
là hàm số chẵn)
2 2
0
2
2 d 2 df x x f x x
2 2
0
2
2 d 2 d 3
f x x f x x
(do trong các khoảng
0; 2 , 2;2
phương trình
0
f x
vô nghiệm)
Từ
1
,
2
,
3
suy ra các đáp án A, B, C là đúng, đáp án D là sai.
Máy tính: Bấm máy tính kiểm tra, ba kết quả đầu bằng nhau nên đáp án sai là đáp án D.
Câu 22. Cho hàm số
y f x
có đạo hàm
2 2
1
f x x x
,
x
. Hàm số
2
y f x
đồng
biến trên khoảng
A.
2;

. B.
; 1

. C.
1;1
. D.
0;2
.
Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn
Chọn C
+ Ta có
2 2
1
f x x x
suy ra
5 3
2 2
1
5 3
x x
f x f x dx x x dx C
+ Suy ra
5 3
2 2
2 2
5 3
x x
y g x f x C
=
5 3
2 2
2
5 3
x x
C
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 34
+ Tính
' 2
g x f x
=
5 3
2 2
2
5 3
x x
C
=
4 2
2 2x x
2 2
2 1
x x
2
2
0 0
' 0
1
1 0
x x
g x
x
x
.
+ Bảng xét dấu
+ Hàm số
2
y g x f x
đồng biến trên
1;1
. Chọn C.
Bài toán tương tự
Câu 22.1 Cho hàm số
y f x
có đạo hàm
3 2
2f x x x
,
x
. Hàm số
2
y f x
đồng biến
trên khoảng
A.

2;
. B.
;2
. C.
4;2
. D.
.
Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn
Chọn A
+ Ta có
3 2
2f x x x
suy ra
4 3
3 2
2
2
4 3
x x
f x f x dx x x dx C
+ Suy ra
4 3
2 2 2
2
4 3
x x
y g x f x C
+ Tính
' 2
g x f x
=
4 3
2 2 2
4 3
x x
C
=
3 2
2 2 2
x x
2
2
x x
+ Hàm số đồng biến suy ra
' 0 0.
g x x
Chọn A..
Câu 22.2 Cho hàm số
y f x
nghịch biến
;x a b
. Hàm số
2
y f x
đồng biến trên khoảng
A.
2 ;2
b a
. B.
;2
a
. C.
;a b
. D.
2 ;b
.
Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn
Chọn A
+ Vì hàm số
y f x
nghịch biến
;x a b
nên
0; ;f x x a b
.
+ Xét
2
y g x f x
có
2
g x f x
+ Hàm số
2
y f x
đồng biến thì
0 2 0 2 0
g x f x f x
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 35
Suy ra
2 2 2
a x b b x a
. Chọn A.
Câu 23. Đồ thị hàm số
3
3
4
3 2
x x
y
x x
có bao nhiêu đường tiệm cận?
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắt nâu
Chọn D
TXĐ:
\ 1;2
D
.
Ta có:
3
3
4
lim lim 1
3 2
x x
x x
y
x x
 
. Suy ra, đồ thị hàm số đã cho có một tiệm cận ngang là
đường thẳng
1y
.
Lại có:
3
2 2
3
2 2 2 2
2 2 2
4 8
lim lim lim lim
3 2 9
1 2 1
x x x x
x x x x x
x x
y
x x
x x x
.
3
2 2
3
2 2 2 2
2 2 2
4 8
lim lim lim lim
3 2 9
1 2 1
x x x x
x x x x x
x x
y
x x
x x x
.
3
2 2
3
1 1 1 1
2 2 2
4
lim lim lim lim
3 2
1 2 1
x x x x
x x x x x
x x
y
x x
x x x

.
Suy ra, đồ thị hàm số đã cho có một tiệm cận đứng là đường thẳng
1
x
.
Vậy đồ thị hàm số có 2 đường tiệm cận.
ADMIN LƯU Ý NHẬN XÉT CHỈNH CON ĐƯỜNG GIẢI BÀI TOÁN NÀY
* Phát triển câu mức độ tương tự
Câu 23.1. Cho hàm số
2
3
9
x
y
x
. Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có tiệm cận ngang là
1y
.
B. Đồ thị hàm số chỉ có 1 tiệm cận đứng là
3
x
.
C. Đồ thị hàm số không có tiệm cận đứng.
D. Đồ thị hàm số có hai tiệm cận đứng là
3; 3
x x
.
Lời giải
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắ
t nâu
Chọn B
Điều kiện xác định:
2
3
9 0
3
x
x
x
.
A sai vì: Hàm phân thức, có bậc tử (bậc 1) nhỏ hơn bậc mẫu (bậc 2) nên đồ thị có 1 tiệm cận
ngang
0
y
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 36
Giải phương trình:
2
9 0 3
x x
.
(Học sinh dễ mắc sai lầm khi kết luận đồ thị hàm số có 2 tiệm cận đứng)
Kiểm tra giới hạn:
2 2
3 3
3 3 1
lim lim
9 9 6
x x
x x
x x
(học sinh có thể dùng máy tính kiểm tra), suy ra,
3
x
không là
tiệm cận đứng của đồ thị hàm số.
2
3
3
lim
9
x
x
x


(học sinh có thể dùng máy tính kiểm tra), suy ra
3
x
là tiệm cận đứng của
đồ thị hàm số.
Câu 23.2. Số đường tiệm cận của đồ thị hàm số
2
1
2
x
y
x
là:
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn A
Giải nhanh:
Điều kiện xác định:
2
1 1
1 0
1 1
2
2 0
x
x
x
x
x
.
Tập xác định của hàm số không chứa
suy ra đồ thị hàm số không có tiệm cận ngang.
2 0 2.
x x
Thay
2
x
lên tử số ta được:
2
1 2
không xác định, suy ra đồ thị hàm số không có tiệm
cận đứng.
Giải bản chất:
Điều kiện xác định:
2
1 1
1 0
1 1
2
2 0
x
x
x
x
x
.
Tập xác định của hàm số không chứa
, suy ra đồ thị hàm số không có tiệm cận ngang.
Xét tiệm cận đứng:
2
2
1
lim
2
x
x
x

;
2
2
1
lim
2
x
x
x

không có giới hạn, suy ra đồ thị hàm số không có tiệm cận.
* Phát triển câu mức độ cao hơn
Câu 23.3. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số
2
1
1
x
y
mx
có hai
tiệm cận ngang.
A.
0
m
. B.
0
m
.
C.
0
m
. D. Không có giá trị thực của m
Lời giải
Chọn C
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 37
Ta thấy khi
0
m
thì tập xác định của hàm số mới chứa
.
Nếu
0
m
thì hàm số
1y x
không có đường tiệm cận ngang.
Nếu
0
m
thì ta có
2
1
1
1
lim lim
1
x x
x
x
y
m
x m
x
 
, suy ra đồ thị hàm số có 2 tiệm cận ngang
là
1 1
,y y
m m
.
Câu 23.4. Có bao nhiêu giá trị
m
nguyên để đồ thị hàm số
2
2x
y
x mx m
có đúng một tiệm cận đứng.
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắ
t nâu
Chọn B
Dễ thấy tử số có một nghiệm
2
x
. Do đó để đồ thị hàm số
2
2x
y
x mx m
có đúng một tiệm
cận đứng thì cần xét hai trường hợp sau:
Trường hợp 1:
2
0
x mx m
có nghiệm kép
2
0
4 0
4
m
m m
m
.
Trường hợp 2:
2
0
x mx m
có 2 nghiệm phân biệt, trong đó có 1 nghiệm bằng 2.
2
4 0
4 2 0
m m
m
m m
.
Câu 23.5 (Nguyễn Việt Hải) Hỏi có bao nhiêu giá trị
m
nguyên thuộc đoạn
2019;2019
để đồ thị
hàm số
3
12
50 500
x m
y
x x
có đúng một đường tiệm cận.
Câu 24. Biết rằng
,
là các số thực thỏa mãn
2 2 2 8 2 2
. Giá trị của
2
bằng
A. 1. B. 2. C. 4. D. 3.
Lời giải
Tác giả: Nguyễn Mạnh Dũng ; Fb: Mạnh Dũng
Chọn D
Ta có:
2 2 2 8 2 2
1 1
2 2 2 8
2 2
.
2 2
2 2 2 8
2
8
2 2 2 0
2
.
8
2 0
2
(do
2 2 0
).
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 38
2
2 8
0
2
2
2 8 0
(do
2 0
).
2
2 8
2 3
2 2
2 3
.
Bài toán tổng quát
Câu 24.1. Biết rằng
, 0 1
a b a
,
, , , ,m n p
là các số thực thỏa mãn
p m n m n
a a a b a a
. Giá trị của
m n p
bằng
Lời giải
Tác giả: Nguyễn Mạnh Dũng ; Fb: Mạnh Dũng
Ta có:
p m n m n
a a a b a a
1 1
p m n
m n
a a a b
a a
.
m n
p m n
m n
a a
a a a b
a
0
m n p
m n
b
a a a
a
.
0
p
m n
b
a
a
(do
0
m n
a a
).
0
m n p
m n
a b
a
0
m n p
a b
(do
0
m n
a
).
m n p
a b
log
b
a
m n p
a a
log
b
a
m n p
.
Bài toán đặc biệt hóa.
Với
3, 81, 1, 4, 2
a b m n p
ta có bài toán sau:
Câu 24.2 Biết rằng
,
là các số thực thỏa mãn
2 4 4
3 3 3 81 3 3
. Giá trị của
6
bằng
A. 1. B. 2. C. 4. D. 3.
Lời giải
Tác giả: Nguyễn Mạnh Dũng ; Fb: Mạnh Dũng
Chọn C
Ta có:
2 4 4
3 3 3 81 3 3
2 4
4
1 1
3 3 3 81
3 3
.
4
2 4
4
3 3
3 3 3 81
3
4 2
4
81
3 3 3 0
3
.
2
4
81
3 0
3
(do
4
3 3 0
).
6
4
3 81
0
3
6
3 81 0
(do
4
3 0
).
6
3 81
6 4
3 3
6 4
.
Câu 25. Cho hình lăng trụ tam giác đều
.
ABC A B C
có
AB a
, góc giữa đường thẳng
A C
và mặt
phẳng
ABC
bằng
45
. Thể tích của khối lăng trụ
.
ABC A B C
bằng
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 39
A.
3
3
4
a
. B.
3
3
2
a
. C.
3
3
12
a
. D.
3
3
6
a
.
Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn
Chọn A
a
B'
C'
A
B
C
A'
Góc giữa đường thẳng
A C
và mặt phẳng
ABC
chính là góc giữa hai đường thẳng
A C
và
AC
suy ra
45
A CA
1
. .sin
2
ABC
S AB AC BAC
1
. .sin 60
2
a a
2
3
4
a
Tam giác vuông
A AC
cân suy ra
AA AC a
Thể tích khối chóp
.
ABC A B C
là :
3
.
3
. '
4
ABC A B C ABC
a
V S AA
.
Bài toán tương tự
Câu 25.1 Cho hình lăng trụ tam giác đều
.
ABC A B C
có
AB a
. Mặt phẳng
A BC
tạo với mặt phẳng
ABC
một góc
30
. Thể tích của khối lăng trụ
.
ABC A B C
bằng
A.
3
3
4
a
. B.
3
3
6
a
. C.
3
3
8
a
. D.
3
3
24
a
.
Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn
Chọn C
a
M
B'
C'
A
B
C
A'
Gọi
M
là trung điểm đoạn
BC
suy ra
AM BC
,
A M BC
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 40
Góc giữa mặt phẳng
A BC
và mặt phẳng
ABC
chính là góc giữa hai đường thẳng
A M
và
AM
suy ra
30
A MA
1
. .sin
2
ABC
S AB AC BAC
1
. .sin 60
2
a a
2
3
4
a
3
2
a
AM
Tam giác vuông
A AM
có
tan30
2
a
AA AM
Thể tích khối chóp
.
ABC A B C
là :
3
.
3
. '
8
ABC A B C ABC
a
V S AA
.
Câu 26. Cho hàm số
( )y f x
có bảng biến thiên như hình vẽ bên. Hàm số
(2 )y f x
đạt cực đại tại
1
-2
1
+∞
2
0-1-∞
f(x)
x
A.
1
2
x
. B.
1
x
. C.
1x
. D.
2
x
.
Lời giải
Tác giả: Trần Mạnh Tường ; Fb: Trần Tuệ Minh
Chọn C
Đặt
2
x t
.
Ta thấy
2 2 (2 ) 2 ( )f x f x f t
nên để hàm số
(2 )y f x
đạt cực đại thì hàm số
( )y f t
phải đạt cực đại
Theo bảng biến thiên thì hàm số
( )y f t
đạt cực đại tại
1
t
và
2t
Suy ra hàm số
(2 )y f x
đạt cực đại tại
2 1
x
và
2 2
x
hay
1
2
x
và
1x
Bài tương tự
Câu 26.1 Cho hàm số
( )y f x
có bảng biến thiên như hình vẽ bên. Hàm số
( 3)
y f x
đạt cực đại tại
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 41
1
-2
1
+∞
2
0-1-∞
f(x)
x
A.
1
x
B.
2
x
. C.
0
x
. D.
3
x
.
Lời giải
Tác giả: Trần Mạnh Tường ; Fb: Trần Tuệ Minh
Chọn D
Đặt
3x t
.
Ta thấy
3 ( 3) ( )f x f x f t
nên để hàm số
( 3)
y f x
đạt cực đại thì hàm
số
( )y f t
phải đạt cực tiểu
Theo bảng biến thiên thì hàm số
( )y f t
đạt cực tiểu tại
0t
Suy ra hàm số
( 3)
y f x
đạt cực đại tại
3 0
x
hay
3
x
Câu 27. Cho hình nón tròn xoay có bán kính đáy bằng
3
và diện tích xung quanh bằng
6 3
. Góc ở
đỉnh của hình nón đã cho bằng
A.
o
60
. B.
o
150
. C.
o
90
. D.
o
120
.
Lời giải
Tác giả: Lê Hữu Đức ; Fb: Le Huu Duc
Chọn D
R
l
h
Gọi góc ở đỉnh của hình nón bằng
2
.
Ta có:
6 3
xq
S
Rl 6 3
l 2 3
Nên
R 3
sin
l 2
o
60
Vậy góc ở đỉnh của hình nón bằng
o
120
.
Bài tương tự
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 42
Câu 27.1 Cho hình nón tròn xoay có bán kính đáy bằng
2
và diện tích xung quanh bằng
4 2
. Góc ở
đỉnh của hình nón đã cho bằng
A.
o
60
. B.
o
150
. C.
o
90
. D.
o
120
.
Lời giải
Tác giả: Lê Hữu Đức ; Fb: Le Huu Duc
Chọn C
R
l
h
Gọi góc ở đỉnh của hình nón bằng
2
.
Ta có:
4 2
xq
S
Rl 4 2
l 2 2
Nên
R 2
sin
l 2
o
45
Vậy góc ở đỉnh của hình nón bằng
o
90
.
Câu 28. Gọi
1 2
,z z
là các nghiệm phức của phương trình
2
4 7 0
z z
. Số phức
1 2 1 2
z z z z
bằng
A.
2
. B.
. C.
2i
. D.
10i
.
Lời giải
Tác giả: Lê Thị Phương Liên; Fb: Phuonglien Le
Chọn A
2
2 3
4 7 0
2 3
z i
z z
z i
1 2 1 2
2 3 2 3 2 3 2 3 2
z z z z i i i i
.
Vậy
1 2 1 2
2.
z z z z
Cách 2: Phương trình bậc hai
2
4 7 0
z z
có
'
3
là số nguyên âm nên phương trình có
hai nghiệm phức
1 2
,z z
và
1 2
z z
,
2 1
z z
.
Áp dụng định lý Viét, ta có:
1 2
1 2
4
. 7
z z
z z
Suy ra:
2
2 2
1 2 1 2 1 2 1 2 1 2
2 . 16 14 2.
z z z z z z z z z z
Bài toán tương tự
Câu 28.1 Gọi
1 2
,z z
là các nghiệm phức của phương trình
2
2 3 0
z z
. Số phức
1 2 1 2
z z z z
bằng
A.
2
. B.
5
. C.
2
. D.
5i
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 43
Lời giải
Chọn D
2
1 2
2 3 0
1 2
z i
z z
z i
1 2 1 2
1 2 1 2 1 2 1 2 2
z z z z i i i i
.
Vậy
1 2 1 2
2.
z z z z
Cách 2: Phương trình bậc hai
2
2 3 0
z z
có
'
2
là số nguyên âm nên phương trình
có hai nghiệm phức
1 2
,z z
và
1 2
z z
,
2 1
z z
.
Áp dụng định lý Viét, ta có:
1 2
1 2
2
. 3
z z
z z
Suy ra:
2
2 2
1 2 1 2 1 2 1 2 1 2
2 . 4 6 2.
z z z z z z z z z z
Câu 29. Gọi
m
,
M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
9
y x
x
trên đoạn
1;4
. Giá trị của
m M
bằng
A.
65
4
. B.
. C.
49
4
. D.
.
Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạ
m
Chọn B
Hàm số xác định và liên tục trên đoạn
1;4
. Đặt
y f x
Ta có:
2
9 9
1f x x
x x
.
2
9
0 1 0
f x
x
2
3 1;4
9 0
3 1;4
x
x
x
.
Có
25
1 10; 3 6; 4
4
f f f
1; 4
min 6
m y
và
1; 4
max 10
M y
.
Vậy
16
m M
.
Câu 29.1 Gọi
m
,
M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
2
2 5
f x x x
. Giá
trị của
2
m M
bằng
A.
5
. B.
25
. C.
5 2 5
. D.
45
.
Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạ
m
Chọn B
Hàm số xác định và liên tục trên đoạn
5; 5
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 44
Ta có
2
2 2
2 5
2
5 5
x x x
f x
x x
.
0
f x
2
2 5 0
x x
2
2 5
x x
.
2 2
0
4 5
x
x x
2
0
5 20 0
x
x
0
2 5; 5
2
2
x
x
x
x
.
Ta có:
5 2 5
f
;
2 5
f
;
5 2 5
f
.
Suy ra
5; 5
max 5
M f x
và
5; 5
min 2 5
m f x
.
Vậy
2
2
2 5 5 25
m M
.
Câu 30. Cho hình lập phương
.
ABCD A B C D
có
,I J
tương ứng là trung điểm của
BC
và
BB
. Góc
giữa hai đường thẳng
AC
và
IJ
bằng
A.
45
. B.
60
. C.
30
. D.
120
.
Lời giải
Tác giả: Phan Chí Dũng ; Fb: Phan Chí Dũng
Chọn B
Gọi
K
là trung điểm của
AB
vì
ABCD
là hình vuông nên
//KI AC
, suy ra góc giữa
AC
và
IJ
bằng góc giữa
KI
và
IJ
.
Ta có
1 1 1
; ;
2 2 2
IK AC IJ B C KJ AB
vì
.
ABCD A B C D
là hình lập phương nên
AC B C AB
suy ra
KI IJ JK
suy ra tam giác
IJK
là tam giác đều, suy ra
60
KIJ
.
Vậy góc giữa
AC
và
IJ
bằng
60
.
BÀI TOÁN TỔNG QUÁT
Bài toán: Xác định góc giữa hai đường thẳng trong không gian.
Kiến thức cần nhớ để vận dụng vào bài tập
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 45
Định nghĩa góc giữa hai đường thẳng
Góc giữa hai đường thẳng
a
và
b
là góc giữa hai đường thẳng
a
và
b
cùng đi qua một
điểm và lần lượt song song ( hoặc trùng ) với
a
và
b
.
a
a'
b'
b
O
Phương pháp giải
Cách 1: Sử dụng định nghĩa
Tìm hai đường thẳng
a
và
b
cùng đi qua một điểm
O
và lần lượt song song ( hoặc
trùng ) với
a
và
b
, thông thường ta chọn
O
thuận lợi thuộc đường thẳng
a
,
b
đi qua
O
và song song với
b
. Khi đó góc giữa
a
và
b
là góc giữa
a
và
b
.
a
b'
b
O
Cách 2: Sử dụng véc tơ
Gọi
là góc hai đường thẳng
a
và
b
.
1
u
và
2
u
lần lượt là các véc tơ chỉ phương của
a
và
b
.
- Nếu
0
1 2
; 90
u u
thì:
1 2
;u u
.
- Nếu
0
1 2
; 90
u u
thì:
0
1 2
180 ;u u
.
BÀI TOÁN TƯƠNG TỰ CÙNG MỨC ĐỘ
Tác giả: Vũ Nga; Fb: Nga Vu
Câu 30.1 Cho hình lập phương
.
ABCD A B C D
. Góc giữa hai đường thẳng
AC
và
A B
bằng
A.
45
. B.
60
. C.
30
. D.
120
.
Lời giải
Chọn B
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 46
Do
//
AC A C
nên góc giữa hai đường thẳng
AC
và
A B
là góc giữa hai đường thẳng
A C
và
A B
. Ta có
2A C A B BC a
( với
a
là độ dài cạnh của hình lập phương )
A BC
đều
0
60
BA C
góc giữa hai đường thẳng
AC
và
A B
là
60
.
Câu 30.2 Cho hình hộp chữ nhật
.
ABCD A B C D
có đáy là hình vuông cạnh
2a
, cạnh bên là
a
.
,I J
tương ứng là trung điểm của
BC
và
BB
. Góc giữa hai đường thẳng
AC
và
IJ
bằng
. Tính
osc
?
A.
10
os
5
c
. B.
5
os
5
c
. C.
1
os
2
c
. D.
3
os
2
c
.
Lời giải
Gọi
K
là trung điểm của
AB
vì
ABCD
là hình vuông nên
//KI AC
, suy ra góc giữa
AC
và
IJ
bằng góc giữa
KI
và
IJ
.
Ta có
2IK a
,
2
2
5
4 2
a a
JK JI a
os
2
KI
c JIK
IJ
10
5
10
os
5
c
.
Câu 31. Giải bóng chuyền quốc tế VTV Cup có 8 đội tham gia, trong đó có hai đội Việt Nam. Ban tổ
chức bốc thăm ngẫu nhiên để chia thành hai bảng đấu, mỗi bảng 4 đội. Xác suất để hai đội của
Việt Nam nằm ở hai bảng khác nhau bằng
A.
2
7
. B.
5
7
. C.
3
7
. D.
4
7
.
Lời giải
Tác giả: Phạm Văn Tuấn; Fb: Phạm Tuấn
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 47
Chọn D
Nhận định bài toán:
1) Đây là dạng bài toán phân chia một tập hợp ra thành các nhóm có số lượng bằng nhau.
2) Phương pháp:
Dạng bài toán này được phân chia làm 2 loại đó là:
- Các nhóm có thứ tự A, B, C, D…
- Các nhóm không phân biệt thứ tự.
Nếu không phân biệt rõ ràng 2 bài toán này thì rất dễ dẫn đến nhầm lẫn và sai kết quả.
Ví dụ: Có bao nhiêu cách chia 20 người thành 4 nhóm, mỗi nhóm có 5 người trong các trường
hợp sau:
a) Các nhóm được đánh tên theo thứ tự A, B, C, D.
b) Không phân biệt thứ tự nhóm.
Lời giải
a) Số cách chọn 5 người cho nhóm A là
5
20
C
. Ứng với mỗi cách chọn trên, ta có số cách chọn 5
người cho nhóm B là
5
15
C
, nhóm C là
5
10
C
và 5 người còn lại vào nhóm D.
Theo quy tắc nhân, ta được số cách chia nhóm là:
5 5 5
20 15 10
. . .1
C C C
(cách).
b) Vì các nhóm không phân biệt thứ tự nên khi ta hoán vị 4 nhóm trên sẽ cho cùng một kết quả.
Do đó số cách chia trong trường hợp này là
5 5 5
20 15 10
. . .1
4!
C C C
(cách)
3) Phân tích bài toán và lời giải.
Chia 8 đội thành hai bảng đấu, do đó hai bảng đấu này sẽ có thứ tự rõ ràng cho nên bài toán của
chúng ta thuộc loại chia nhóm có thứ tự.
Gọi hai bảng đấu là bảng A và bảng B.
Chọn 4 đội vào bảng A ta có
4
8
C
cách, bốn đội còn lại vào bảng B có 1 cách.
Theo quy tắc nhân, ta có số cách chia 8 đội vào hai bảng đấu là:
4
8
.1 70
n C
(cách)
Gọi A là biến cố “Hai đội Việt Nam nằm ở hai bảng khác nhau”.
Bảng A: Có 3 đội nước ngoài và 1 đội Việt Nam. Số cách chọn là
3 1
6 2
.C C
.
Bảng B: Chỉ còn 1 cách chọn duy nhất cho 3 đội nước ngoài và 1 đội Việt Nam còn lại vào
bảng B.
Do đó số cách chia 8 đội thành 2 bảng mỗi bảng có 1 đội Việt Nam là :
3 1
6 2
. .1 40
n A C C
(cách)
Vậy xác suất của biến cố A là:
40 4
70 7
n A
P A
n
.
Bài toán tương tự
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 48
Câu 31.1 Giải bóng chuyền quốc tế VTV Cup có 12 đội tham gia, trong đó có 3 đội Việt Nam. Ban tổ
chức bốc thăm ngẫu nhiên để chia thành 3 bảng đấu, mỗi bảng 4 đội. Tính xác suất để 3 đội của
Việt Nam cùng nằm ở một bảng đấu.
A.
3
55
. B.
1
330
. C.
1
110
. D.
6
55
.
Lời giải
Chọn A
Gọi ba bảng đấu có tên là A, B, C.
Chọn 4 đội cho bảng A có
4
12
C
cách, chọn 4 đội cho bảng B có
4
8
C
cách và 4 đội còn lại vào
bảng C có 1 cách.
Theo quy tắc nhân, số cách chia 12 đội thành 3 bảng đấu là:
4 4
12 8
. .1 34650
n C C
(cách)
Gọi A là biến cố “3 đội Việt Nam cùng nằm ở một bảng đấu.
Giả sử 3 đội Việt Nam cùng nằm ở bảng A.
Khi đó bảng A sẽ chọn 1 đội trong 9 đội nước ngoài và 3 đội Việt Nam, 8 đội còn lại chia vào
bảng B và C. Trong trường hợp này ta có số cách chọn là
1 4
9 8
.1. .1 630
C C
(cách)
Vì vai trò của các bảng là như nhau nên trường hợp 3 đội Việt Nam ở bảng B hay bảng C đều
cho kết quả như nhau.
Vậy số kết quả thuận lợi cho biến cố A là
1 4
9 8
. .3 1890
n A C C
(cách)
Xác suất của biến cố A là :
1890 3
34650 55
n A
P A
n
.
Câu 32. Tất cả các nguyên hàm của hàm số
2
sin
x
f x
x
trên khoảng
0;
là
A.
cot ln sin .x x x C
B.
cot ln sin .x x x C
C.
cot ln sin .x x x C
D.
cot ln sin .x x x C
Lời giải
Tác giả:Văn Bùi Vũ ; Fb: Van Tuan Vu
ChọnA
Gọi
2
d
sin
x
F x x
x
. Đặt
2
d d
1
cot
d d
sin
u x
u x
v x
v x
x
Khi đó:
2
cos
d cot d
sin sin
x x
F x x x x x
x x
d sin
cot cot ln sin .
sin
x
x x x x x C
x
Vì
0;
x
nên
sin 0
x
, suy ra
ln sin ln sinx x
.
Vậy:
cot ln sin .F x x x x C
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 49
Phân tích và bình luận:
Bài toán sử dụng nguyên hàm từng phần dạng đặc biệt kết hợp giữa đa thức và lượng
giác:
2 2
2 2
d ; d ; tan d ; cot d
sin cos
x x
x x x x x x x x
x x
và xét dấu hàm lượng giác.
Bài toán tương tự
Câu 32.1 Tất cả các nguyên hàm của hàm số
2
cos
x
f x
x
trên khoảng
0;
2
là
A.
tan ln cos .F x x x x C
B.
tan ln cos .F x x x x C
C.
tan ln cos .F x x x x C
D.
tan ln cos .F x x x x C
Lời giải
Tác giả:Văn Bùi Vũ ; Fb: Van Tuan Vu
Chọn A
Gọi
2
d
cos
x
F x x
x
. Đặt
2
d d
1
tan
d d
cos
u x
u x
v x
v x
x
Khi đó:
2
sin
d tan d
cos cos
x x
F x x x x x
x x
d cos
tan tan ln cos .
cos
x
x x x x x C
x
Vì
0;
2
x
nên
cos 0
x
, suy ra
ln cos ln cosx x
.
Vậy:
tan ln cos .F x x x x C
Câu 32.2 Tất cả các nguyên hàm của hàm số
2
tanf x x x
trên khoảng
;0
2
là
A.
2
tan ln cos .
2
x
F x x x x C
B.
2
tan ln cos .
2
x
F x x x x C
C.
2
tan ln cos .
2
x
F x x x x C
D.
2
tan ln cos .
2
x
F x x x x C
Lời giải
Tác giả:Văn Bùi Vũ ; Fb: Van Tuan Vu
Chọn A
Gọi
2 2 2
2
tan d tan 1 1 d tan 1 d d d d .
cos
x
F x x x x x x x x x x x x x x x
x
Đặt
2
d d
1
tan
d d
cos
u x
u x
v x
v x
x
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 50
Khi đó:
2
2
sin
d d tan d
cos cos 2
x x x
F x x x x x x x
x x
2 2
d cos
tan tan ln cos .
cos 2 2
x
x x
x x x x x C
x
Vì
;0
2
x
nên
cos 0
x
, suy ra
ln cos ln cosx x
.
Vậy:
2
tan ln cos .
2
x
F x x x x C
Câu 33. Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
A
. Gọi
E
là trung
điểm
AB
. Biết
2AB a
,
13
BC a
,
4CC a
. Khoảng cách giữa hai đường thẳng
A B
và
CE
bằng
A.
4
7
a
. B.
12
7
a
. C.
6
7
a
. D.
3
7
a
.
Lời giải
Tác giả: Nguyễn Bả
o Mai; Fb: Bao An
Chọn C
Phân tích:
* Kiến thức trọng tâm: Khoảng cách giữa hai đường thẳng chéo nhau.
* Hướng giải bài toán:
+ Dựng mặt phẳng đi qua một đường thẳng và song song với đường còn lại
+ Dùng tỉ số khoảng cách để đưa việc tính khoảng cách từ một điểm đến một mặt phẳng thành
tính khoảng cách từ một điểm khác đến mặt phẳng thuận lợi hơn.
+ Tính chiều cao của một tứ diện vuông
* Giải: Lấy trung điểm
F
của
AA
được
EF
song song với
CEF
đi qua
CE
và song
song với
A B
, , ,
d A B CE d B CEF d A CEF
.
Mặt khác
ACEF
là tứ diện vuông tại
A
nên
2 2 2
2
1 1 1 1
,
AF AE AC
d A CEF
.
Ta có
4AA CC a
2AF a
2AB a
AE a
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 51
2 2 2 2
13 4 3AC BC AB a a a
2 2 2 2
2
1 1 1 1 49
4 9 36
,
a a a a
d A CEF
6
,
7
a
d A CEF
6
,
7
a
d CE A B
.
Bài toán tươn tự
Câu 33.1 Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác đều cạnh
2a
. Gọi
E
là trung
điểm
AB
. Biết góc giữa
CB
và
BCC B
bằng
o
30
. Khoảng cách giữa hai đường thẳng
A B
và
CE
bằng
A.
6
3
a
. B.
2 6
3
a
. C.
6
6
a
. D.
2 6
6
a
.
Lời giải
Thấy
CE AB
,
CE AA
CE AA B B
hay
AA B B
chính là mặt phẳng qua
A B
,
vuông góc với
CE
. Gọi
là hình chiếu của
E
trên
A B
EH
chính là đoạn vuông góc
chung của
A B
và
CE
,
d CE A B EH
.
Mặt khác
CB
có hình chiếu là
EB
trên
BCC B
là
EB
, ,
CB BCC B CB EB CB E
o
30
CB E
2 2. 3CB CE a
2 2 2 2
12 4 2 2CC CB C B a a a
.
Gọi
K
là hình chiếu của
A
trên
A B
.
Ta có
1
2
EH AK
và
2 2 2 2 2 2
1 1 1 1 1 3
8 4 8AK AA AB a a a
2 2
3
a
AK
2 6
3
3
a a
EH
hay
6
,
3
a
d CE A B
.
Câu 34. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên
m
để phương trình
3
3
f x x m
có 6 nghiệm phân biệt thuộc đoạn
1;2
?
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 52
A.
3
. B.
2
. C.
6
. D.
7
.
Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được V
ũ
Chọn B
Đặt
3
3t x x
, xét hàm số
3
3t x x
trên đoạn
1;2
.
Ta có
2
1 2
3 3 0
1 2
x t
t x
x t
.
Ta có bảng biến thiên của hàm số
3
3t x x
trên đoạn
1;2
.
x
t'
t
-1
1
2
0
- +
-2
2
2
Từ đó bảng biến thiên trên ta thấy:
+) Nếu
2
t
thì
1 1;2
x
.
+) Nếu
2;2
t
thì có hai nghiệm phân biệt
1;2
x
.
Do đó phương trình
3
3
f x x m
có 6 nghiệm
x
phân biệt thuộc đoạn
1;2
khi phương
trình
f t m
có 3 nghiệm
t
phân biệt thuộc khoảng
2;2
*
.
Dựa vào đồ thị hàm số
y f x
đã cho và
m
là số nguyên ta thấy
0
m
hoặc
1
m
thỏa
mãn
*
.
Vậy có hai giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Bài toán tổng quát:
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 53
Cho hàm số
y f x
có đồ thị cho trước là
C
(hoặc cho trước bảng biến thiên). Biện luận
theo tham số
m
số nghiệm của phương trình
.
f n g x p h m
trên tập
D
cho trước
( D
); trong đó
,n p
là các số thực;
h m
là biểu thức với tham số
m
.
Cách giải:
Bước 1: Đặt
.
t n g x p
. Khi đó
.
f n g x p h m f t h m
.
Bước 2:
+) Tìm miền giá trị
D
của
t
ứng với
x D
.
+) Chỉ ra mối quan hệ giá trị tương ứng giữa
t D
và
x D
.
Bước 3: Dựa vào đồ thị
C
(hoặc bảng biến thiên của hàm số
y f x
), biện luận theo
m
số
nghiệm
t D
của phương trình
f t h m
.
Bước 4: Dựa vào mối quan hệ giữa
x
và
t
ở Bước 2 ta có biện luận số nghiệm
x D
của
phương trình
.
f n g x p h m
.
Bài toán tương tự
Câu 34.1. (Thi thử chuyên Sư Phạm HN lần 1 năm 2019) Cho hàm số
( )y f x
liên tục trên
và có
đồ thị như hình bên. Phương trình
(2sin )
f x m
có đúng ba nghiệm phân biệt thuộc đoạn
;
khi và chỉ khi
A.
3;1
m
. B.
3;1
m
. C.
3;1
m
. D.
3;1
m
.
Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được V
ũ
Chọn A
Đặt
2sin sin
2
t
t x x
.
Với
;
x
thì
1 sin 1 2;2
x t
.
+) Với
2t
thì có 1 nghiệm
x
thuộc
;
là
2
x
.
+) Với
2
t
thì có 1 nghiệm
x
thuộc
;
là
2
x
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 54
+) Với
0t
thì có 3 nghiệm
x
thuộc
;
là
0;x
.
+) Với
2;2 \ 0
t
thì có 2 nghiệm phân biệt
x
thuộc
;
.
Dựa vào đồ thị của hàm số
( )y f x
đã cho, để phương trình
(2sin )
f x m
có đúng ba
nghiệm phân biệt thuộc đoạn
;
thì phương trình
*
f t m
trên
2;2
xảy ra các
trường hợp sau:
TH1:
1
m
thì
*
có hai nghiệm là
1;2
t
nên thỏa mãn yêu cầu.
TH2:
3
m
thì
*
có hai nghiệm là
1; 2
t
nên thỏa mãn yêu cầu.
Vậy
3;1
m
thì thỏa mãn yêu cầu bài toán.
Câu 34.2. (Thi thử chuyên Lam Sơn lần 2 năm 2019) Cho hàm số
y f x
liên tục trên
có đồ thị
như hình vẽ bên. Phương trình
1 0
f f x
có tất cả bao nhiêu nghiệm thực phân biệt?
A.
6
. B.
5
. C.
7
. D.
4
.
Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ
Chọn C
Đặt
1 1t f x f x t
.
Từ đồ thị của hàm số đã cho, phương trình
0
f t
có ba nghiệm phân biệt:
1 2 3
2; 1 , 1;0 , 1;2
t t t
.
+) Với
1 1
2; 1 1 1 0
t t
, dựa vào đồ thị đã cho phương trình
1
1f x t
có 3
nghiệm thực
x
phân biệt.
+) Với
2 2
1;0 0 1 1
t t
, dựa vào đồ thị đã cho phương trình
2
1
f x t
có 3
nghiệm thực
x
phân biệt.
+) Với
3 3
1;2 2 1 3
t t
, dựa vào đồ thị đã cho phương trình
3
1
f x t
có 1 nghiệm
x
.
Vậy phương trình đã cho có 7 nghiệm thực phân biệt.
Câu 35. Có bao nhiêu số phức
z
thỏa mãn
2
2019
1 1
z z z i z z i
?
A. 4. B. 2. C. 1. D.3.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 55
Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom
Chọn D
Giả sử
z a bi
,
,a b
z a bi
.
Ta có:
1 1
z a bi
,
2z z bi
,
2z z a
.
1009
2019 2
i i i
1009
1
i i
.
Do đó
2
2019
1 1
z z z i z z i
2
2 2
2
1 2 . 2 1
a b b i a i
2
2
1 2 2 1a b b i ai
2
2
1 1
2 2 0
a b
b a
2 2
2 0
a a b
a b
2
2 2 0
b b
a b
0
1
b
b
a b
0
0
1
1
1
1
a
b
a
b
a
b
.
Vậy có 3 số phức
z
thỏa mãn yêu cầu bài toán.
Phân tích:
*) Kiến thức trọng tâm liên quan đến bài toán: Sử dụng các kiến thức về số phức liên hợp,
moddun của số phức, hai số phức bằng nhau, các phép toán trên số phức. Cụ thể:
1.1. Số phức liên hợp
Số phức liên hợp của
( , )
z a bi a b
là
z a bi
. ( Đổi dấu phần ảo của
z
).
1.2. Hai số phức bằng nhau:
'
( , , ', ' )
'
a a
a bi a b i a b a b
b b
.
1.3. Môđun của số phức:
2 2
z a bi a b
.
1.4. Tính
n
i
:
2 2
2 1 2
1
1
k
k
k
n
k
k
k
i i
i
i i i i
.
*) Lỗi học sinh hay gặp:
+ Khi lấy moddun:
2 2
z a b
+ Nhầm lẫn phần thực, phần ảo.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 56
*) Lưu ý với lớp bài toán tìm
z
: Khi tìm
z
mà trong giả thiết bài toán ngoài việc cho
z
, còn
có cả
z
,
z
,… thì ta thường sử dụng phép thay trực tiếp
( , )
z a bi a b
và các yếu tố liên
quan để tìm được mối liên hệ giữa phần thực, phần ảo của
z
.
*) Các bài toán tương tự:
Mức độ vận dụng
Câu 35.1 Cho các số phức
z
thỏa mãn
2020
2 1 2z i z i
. Tập hợp các điểm biểu diễn số phức
2 1 4w z i
trên mặt phẳng tọa độ là một đường thẳng. Khoảng cách từ
2; 3
I
đến đường
thẳng đó bằng
A.
18 5
5
. B.
18 13
13
. C.
10 3
3
. D.
10 5
5
.
Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom
Chọn D
Giả sử
z a bi
;a b
và
w x yi
;x y
.
Ta có
2020
2 1 2z i z i
1010
2
2 1 2a bi i a bi i
2 2 2
2
2 1 2
a b a b
2 4 1 0 1
a b
.
Theo giả thiết:
2 1 4w z i
2 1 4x yi a bi i
2 1 4 2x yi a b i
.
2 1
4 2
x a
y b
1
2
4
2
x
a
y
b
2
.
Thay
2
vào
1
ta được:
1 4
2. 4. 1 0
2 2
x y
2 6 0x y
.
Vậy:
10 5
,
5
d I
.
Câu 35.2 Cho các số phức
z
thỏa mãn
2021
2 2 3 1
iz i z
và
1
z
. Điểm biểu diễn cho số phức
z
có
hoành độ bằng
A.
4
. B.
4
. C.
1
. D.
1
.
Lời giải
Tác giả: Trần Thị Thơm ; Fb:Tranthom
Chọn C
Giả sử
z a bi
;a b
.
Ta có
2021
2 2 3 1
iz i z
1010
2
2 2 3 1
i a bi i i a bi
2 2 2 3 1 3a i b a bi
2 2
2 2
2 2 4 3 1 9a b a b
2 2
5 2 3 0 1
a b a
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 57
Mặt khác :
1
z
2 2
1 2
a b
.
Thay (2) vào (1) được
5.1 2 3 0 1
a a
.
Câu 36. Cho hàm số
y f x
có đạo hàm trên
. Bảng biến thiên của hàm số
'y f x
như hình
dưới
Tìm
m
để bất phương trình
2 3
1
3
m x f x x
nghiệm đúng với mọi
0;3
x
.
A.
(0)m f
. B.
(0)m f
. C.
(3)m f
. D.
2
(1)
3
m f
.
Lời giải
Tác giả : Võ Thị Ngọc Ánh ; Fb: Võ Ánh
Chọn B.
Ta có
2 3 3 2
1 1
3 3
m x f x x m f x x x
.
Đặt
3 2
1
3
g x f x x x
.
Ta có
2 2
2 2g x f x x x f x x x
.
2
0 2g x f x x x
.
Mà
1, 0;3
f x x
và
2
2
2 1 1 1, 0;3
x x x x
nên
0, 0;3
g x x
.
Từ đó ta có bảng biến thiên của
( )g x
:
Bất phương trình
3 2
1
3
m f x x x
nghiệm đúng với mọi
0;3
x
0 (0)m g m f
.
NHẬN XÉT: (Võ Thị Ngọc Ánh) Bài toán xây dựng dựa trên ý tưởng mối quan hệ giữa bảng
biến thiên của
'( )f x
hoặc đồ thị của
'( )f x
so sánh với
'( )h x
để suy ra sự biến thiên của hàm
số có dạng
( ) ( ) ( )g x f x h x
.
Bài toán tương tự
Câu 36.1. Cho hàm số
y f x
có đạo hàm trên
. Bảng biến thiên của hàm số
'y f x
như hình
dưới
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 58
Tìm
m
để bất phương trình
2sin
m x f x
nghiệm đúng với mọi
0;x

.
A.
(0)m f
. B.
(1) 2sin1
m f
. C.
(0)m f
. D.
(1) 2sin1
m f
.
Tác giả : Võ Thị Ngọc Ánh ; Fb: Võ Ánh
Lời giải
Chọn C.
Ta có
2sin 2sinm x f x m f x x
.
Đặt
2sing x f x x
.
Ta có
2cosg x f x x
.
0 2cosg x f x x
.
Mà
2, 0;f x x

và
2cosx 2, 0;x

nên
0, 0;g x x

.
'( ) 2
0 0
2cos 2
f x
g x x
x
.
Từ đó ta có bảng biến thiên của
( )g x
:
Bất phương trình
2 2 1 3
m f x x x
nghiệm đúng với mọi
3;x

0 (0)m g m f
.
Câu 36.2. (Phát triển từ câu 50 đề liên trường Nghệ An ) Cho hàm số
y f x
có đạo hàm trên
.
Đồ thị hàm số
'y f x
như hình vẽ bên dưới.
Tìm
m
để bất phương trình
2
2 2 4 3m x f x x
nghiệm đúng với mọi
3;x

.
A.
2 (0) 1
m f
. B.
2 (0) 1
m f
. C.
2 ( 1)
m f
. D.
2 ( 1)
m f
.
Lời giải
Tác giả : Võ Thị Ngọc Ánh ; Fb: Võ Ánh
Chọn B.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 59
Ta có
2 2
2 2 4 3 2 2 4 3m x f x x m f x x x
.
Đặt
2
2 2 4 3g x f x x x
. Ta có
2 2 2 4
g x f x x
.
0 2 2
g x f x x
.
Đặt
2t x
ta được
f t t
.
1
1
là phương trình hoành độ giao điểm của đồ thị
f t
và đường thẳng
d
:
y t
(hình vẽ)
Dựa vào đồ thị của
f t
và đường thẳng
y t
ta có
ta có
f t t
1
0
1
2
t
t
t
t
hay
3
2
1
0
x
x
x
x
.
Bảng biến thiên của hàm số
g x
.
Bất phương trình
2 2 1 3
m f x x x
nghiệm đúng với mọi
3;x

2 2 (0) 1
m g m f
.
Câu 36.3. (Phát triển từ đề thi đại học 2018) Cho hàm số
y f x
có đạo hàm trên
. Đồ thị của hàm
số
y f x
như hình dưới
Tìm
m
để bất phương trình
2
4 2 1 2m x f x x
nghiệm đúng với mọi
4;2
x
.
A.
2 (0) 1
m f
. B.
2 ( 3) 4
m f
. C.
2 (3) 16
m f
. D.
2 (1) 4
m f
.
Tác giả : Võ Thị Ngọc Ánh ; Fb: Võ Ánh
Lời giải
Chọn D.
2
2
4 2 1 2 2 1 2
m x f x x m f x x
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 60
Đặt
2
2 1 2
g x f x x
Ta có
2 1 2 2 2 1 2
g x f x x f x x
.
0 1 2
g x f x x
Đặt
1t x
ta được
1f t t
1
1
là phương trình hoành độ giao điểm của đồ thị
f t
và đường thẳng
d
:
1y t
(hình
vẽ)
Dựa vào đồ thị của
f t
và đường thẳng
1y t
ta có
ta có
1
3
1
3
t
t
t
hay
4
0
2
x
x
x
.
Xét hàm
( ) 1t t x x
đồng biến trên
suy ra bảng biến thiên của hàm số
g x
:
Bất phương trình
2
4 2 1 2m x f x x
nghiệm đúng với mọi
4;2
x
.
0 2 (1) 4
m g m f
.
Câu 37. Trong không gian
Oxyz
cho
2;1;4 ; 5;0;0 ; 1; 3;1
M N P
. Gọi
; ;I a b c
là tâm mặt cầu
tiếp xúc với mặt phẳng
Oyz
đồng thời đi qua các điểm
, , M N P
. Tìm
c
biết
5
a b c
A.
3
. B.
2
. C.
4
. D.
1
.
Lời giải
Tác giả:Quỳnh Giao; Fb: QGiaoDo
Chọn C
Mặt cầu tiếp xúc với mặt phẳng
Oyz
đồng thời đi qua các điểm
, , M N P
nên
;
d I Oyz IM IN IP
2 2 2
2
2 2 2 2
2 2
2 2 2 2
2 2
2 1 4
;
5 2 1 4
5 1 3 1
a a b c
d I Oyz IM
IN IM a b c a b c
IN IP
a b c a b c
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 61
2 2 2
2
2 1 4
3 4 2
4 3 7
a a b c
a b c
a b c
3
1
2
a
b
c
hoặc
5
3
4
a
b
c
So sánh với điều kiện
5
a b c
ta có
2
c
Bài toán tương tự
Câu 37.1. Trong không gian
Oxyz
cho
2;0;0 ; 0; 2;0 ; 0;0; 2
A B C
.
D
là điểm khác
O
sao cho
, , DA DB DC
đôi một vuông góc.
; ;I a b c
là tâm mặt cầu ngoại tiếp tứ diện
ABCD
. Tính
S a b c
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Tác giả:Quỳnh Giao; Fb: QGiaoDo
Chọn B
Gọi
; ;D x y z
= 2; ; ; = ; 2; ; = ; ; 2
DA x y z DB x y z DC x y z

Vì
, , DA DB DC
đôi một vuông góc nên
2
2
2
. 0
2 2 0
4
. 0 2 2 0
3
2 2 0
. 0
DA DB
x x y y z
DA DC x x y z z x y z
x y y z z
DB DC
; ;I a b c
là tâm mặt
Câu 38 . Biết rằng
1
0
d
ln 2 ln 3 ln5
3 5 3 1 7
x
a b c
x x
, với
, ,a b c
là các số hữu tỉ.
Giá trị của
a b c
bằng
A.
10
3
. B.
5
3
. C.
10
3
. D.
5
3
.
Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van
Chọn A
Đặt
3 1t x
2
3 1t x
2 d 3dt t x
Đổi cận:
0 1x t
;
1 2x t
.
Ta có:
1
0
d
3 5 3 1 7
x
x x
1
0
d
3 1 5 3 1 6
x
x x
2
2
1
2 d
3 5 6
t t
t t
2
1
2 3 2
d
3 3 2
t
t t
2 2
1 1
2
3ln 3 2ln 2
3
t t
2
3ln5 3ln 4 2ln 4 2ln 3
3
2
10ln 2 2ln 3 3ln 5
3
=
20 4
ln 2 ln3 2ln5
3 3
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 62
Suy ra:
20
3
a
,
4
3
b
,
2
c
.
Vậy
10
3
a b c
.
Bài toán tương tự
Câu 38.1 .Biết rằng
1
2
d
ln2 ln3 ln5
5 3 9
x
a b c
x x
, với
, ,a b c
là các số hữu tỉ.
Giá trị của
a b c
bằng
A.
10
. B.
5
. C.
10
. D.
5
.
Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van
Chọn A
Đặt
3
t x
2
3t x
2 d dt t x
Đổi cận:
2 1x t
;
1 2x t
.
Ta có:
1
2
d
5 3 9
x
x x
1
2
d
3 5 3 1 6
x
x x
2
2
1
d
2
5 6
t t
t t
2
1
3 2
2 d
3 2
t
t t
2 2
1 1
2 3ln 3 2ln 2
t t
2 5ln 4 2ln3 3ln5
=
20ln 2 4ln 3 6ln 5
Suy ra:
20
a
,
4
b
,
6
c
. Vậy
10
a b c
Câu 38.2 .Biết rằng
4
0
d
ln 3 ln 5 ln 7
4 1 5 2 1
x
a b c
x x
, với
, ,a b c
là các số hữu tỉ.
Giá trị của
a b c
bằng
A.
0
. B.
4
3
. C.
1
. D.
4
3
.
Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van
Chọn A
Đặt
2 1t x
2
2 1t x
d dt t x
Đổi cận:
0 1x t
;
4 3x t
.
Ta có:
4
0
d
4 1 5 2 1
x
x x
4
0
d
4 2 5 2 1 2
x
x x
3
2
1
d
2 5 2
t t
t t
3
1
2 2 1 2
1
d
3 2 1 2
t t
t
t t
3
1
1 2 1
d
3 2 2 1
t
t t
3
1
1 1
2ln 2 ln 2 1
3 2
t t
1 1 1
2ln5 2ln 3 ln 7 ln3
3 2 2
1 2 1
ln3 ln 5 ln 7
2 3 6
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 63
Suy ra:
1 2 1
, , 0
2 3 6
a b c a b c
.
Câu 39. Trong không gian
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
và hai điểm
( 1;3;1)
A
và
0;2; 1
B
. Gọi
; ;C m n p
là điểm thuộc đường thẳng
d
sao cho diện tích tam giác
ABC
bằng
2 2
. Giá trị của tổng
m n p
bằng
A.
1
. B.
2
. C.
3
. D.
5
.
Lời giải
Tácgiả: Nguyễn Thị Thơm; Fb: Thơm nguyễn
Chọn C
Phương trình tham số của đường thẳng
1 2
:
2
x t
d y t
z t
.
Vì
C
thuộc
d
nên tọa độ của
C
có dạng
1 2 ; ;2
C t t t
.
Ta có
1; 1; 2
AB

và
2 ; 3;1
AC t t t
.
Suy ra
, 3 7; 3 1;3 3
AB AC t t t
.
Diện tích tam giác
ABC
là
2 2 2
1 1
, (3 7) ( 3 1) (3 3)
2 2
ABC
S AB AC t t t
.
Theo bài ra ta có
2
1
2 2 27 54 59 2 2
2
ABC
S t t
.
2
27 54 59 32
t t
2
( 1) 0
t
1t
.
Với
1t
thì
1;1;1
C
nên
1; 1; 1m n p
.
Vậy giá trị của tổng
3
m n p
Bài toán tương tự
Câu 39.1 .Trong không gian
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
và hai điểm
( 1;3;1)
A
và
0;2; 1
B
. Gọi
; ;C m n p
là điểm thuộc đường thẳng
d
sao cho tam giác
ABC
vuông tại
A. Giá trị của tổng
2
m n p
bằng
A.
0
. B.
2
. C.
3
. D.
5
.
Lời giải
Tácgiả:Nguyễn Thị Thơm; Fb:Thơm nguyễn
Chọn A
Vì
C d
nên tọa độ của
C
có dạng
1 2 ; ;2
C t t t
Ta có
1; 1; 2
AB

và
2 ; 3;1
AC t t t
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 64
Vì
ABC
vuông tại A nên
1
. 0 2 3 2 2 0 3 1 0
3
AC AB t t t t t
.
5
3
5 1 4 1 5 2 7
; ; 2 0
3 3 3 3 3 3 3
7
3
m
C n m n p
p
.
Câu 39.2. Trong không gian
Oxyz
, cho đường thẳng
1 2
:
1 2 3
x y z
d
và mặt phẳng
: 2 2 3 0
P x y z
. Gọi
M
là điểm thuộc đường thẳng
d
sao cho khoảng cách từ
M
đến
mặt phẳng
P
bằng
2
. Nếu
M
có hoành độ âm thì tung độ của
M
bằng.
A.
3
. B.
21
. C.
3
. D.
1
.
Lời giải
Tácgiả:Nguyễn Thị Thơm; Fb:Thơm nguyễn
Chọn A
Phương trình tham số của đường thẳng
: 1 2
2 3
x t
d y t
z t
Vì
M d
nên tọa độ của
M
có dạng
; 1 2 ; 2 3M t t t
.
Vì khoảng cách từ
M
đến mặt phẳng
P
bằng
2
nên
2
2
2 1 2 2 2 3 3
2
1 2 2
t t t
2 4 4 6 3
2
1 4 4
t t t
1 1; 3; 5
5 6
5
2 5 6
5 6
3
11 11;21;31
t M
t
t
t
t
t M
Vì
M
có tung độ âm nên
1; 3; 5
M
Câu 40 . Bất phương trình
3
9 ln 5 0
x x x
có bao nhiêu nghiệm nguyên ?
A.
4
. B.
7
. C.
6
. D. Vô số.
Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường
Chọn C
Cách 1.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 65
Ta có:
3
9 ln 5 0
x x x
3
3
9 0
ln 5 0
9 0
ln 5 0
x x
x
x x
x
3
3 0
0 5 1
3
0 3
5 1
x
x
x
x
x
x
3
( )
3 0
5 4
3
0 3
4
x
vn
x
x
x
x
x
0 3
4 3
x
x
Vì
4; 3;0;1;2;3
x x
. Vậy có 6 nghiệm nguyên.
Cách 2.
Điều kiện:
5
x
(*).
Xét
3
3
0
9 0
3
9 ln 5 0
3
ln 5 0
4
x
x x
x
x x x
x
x
x
(thỏa mãn điều kiện (*)).
Bảng đan xen dấu của biểu thức
3
9 ln 5
f x x x x
trên khoảng
5;
.
Khi đó
4 3
0 .
0 3
x
f x
x
Vì
4; 3;0;1;2;3
x x
,Vậy có 6 nghiệm nguyên.
Bài toán tương tự:
Câu 40.1 . Bất phương trình
2
3 ln 2 0
x x x
có bao nhiêu nghiệm nguyên ?
A.
5
. B.
4
. C.
3
. D. Vô số.
Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường
Chọn A
Ta có:
2
3 ln 2 0
x x x
2
ln 2 0
3 0
ln 2 0
x
x x
x
2 1
0 3
2 1
x
x
x
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 66
1
0 3
1
x
x
x
1
0 3
x
x
.
Vì
1;0;1;2;3
x x
. Vậy có 5 nghiệm.
Câu 40.2. Bất phương trình
2 2
1
4 1 log 4 1 0
e
x x x x
có tổng tất cả các nghiệm nguyên là?
A.
6
. B.
8
. C.
4
. D.
10
.
Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường
Chọn C
Ta có:
2 2
1
4 1 log 4 1 0
e
x x x x
2
2
1
2 log 4 1 0
e
x x x
2
1
2 0
log 4 1 0
e
x
x x
2
2
4 1 1
x
x x
2
2
4 0
x
x x
2
0 4
x
x
.
Vì
1;3
x x
. Vậy tổng tất cả các nghiệm nguyên bằng
4
.
Câu 41. Cho hàm số
( )f x
có đồ thị hàm
'( )y f x
như hình vẽ. Hàm số
2
(cos )
y f x x x
đồng
biến trên khoảng
A.
1;2
. B.
1;0
. C.
0;1
. D.
2; 1
.
Lời giải
Tác giả: Nguyễn Việt Hải. FB: https://www.facebook.com/nvhaicqt
Chọn A
Phân tích:
Bản chất dạng toán này thường là đặc điểm: Tổng hai hàm dương (hàm đồng biến), tổng hai
hàm âm (hàm nghịch biến)
Tính chất:
Cho hàm số
y f x
tăng trên khoảng
1
D
, hàm số
y f x
tăng trên khoảng
2
D
. Khi đó ta
có hàm số
y f x g x
tăng trên khoảng
1 2
D D D
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 67
+ Quan sát bài toán:
2
1
' 2 1 0
2
y x x y x x
, nếu trắc nghiệm thấy ngay đáp án
A.
Hướng dẫn giải:
Ta có:
' sin . ' cos 2 1y x f x x
+ Vì
cos 1;1 sin . ' cos 1;1
x x f x
mà
2 1 1 1x x
+ Suy ra
' sin . ' cos 2 1 0, 1y x f x x x
hay hàm số tăng trên
[1; )
Câu 41.1 (Đề minh họa THPT QG 2018 – 2019) Cho hàm số
f x
có bảng xét dấu của đạo hàm như
sau:
Hàm số
3
3 2 3y f x x x
đồng biến trên khoảng nào dưới đây?
A.
1; .
B.
; 1 .
C.
1; 0 .
D.
0;2 .
Câu 41.2 (Nguyễn Việt Hải) Cho hàm số
( )f x
có đồ thị hàm
'( )y f x
như hình vẽ. Hàm số
4
3cos 4sin
3 2019
5
x x
y f x x
đồng biến trên khoảng
A.
1;2
. B.
1;0
. C.
0;1
. D.
2; 1
.
Câu 42. Cho hàm số
( ) 2 2
x x
f x
. Gọi
0
m
là số lớn nhất trong các số nguyên
m
thỏa mãn
12
( ) (2 2 ) 0
f m f m
. Mệnh đề nào sau đây đúng?
A.
0
1513;2019
m
. B.
0
1009;1513
m
. C.
0
505;1009
m
. D.
0
1;505
m
.
Lời giải
Tác giả: Nguyễn Việt Hải. FB: https://www.facebook.com/nvhaicqt
Chọn B
Phân tích:
+ Bài toán nếu thế vào:
12 12
2 2 2 2
( ) 2 2 2 2 0
m m m m
P m
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 68
+ Biểu thức
( )P m
khá phức tạp. Điều này chứng tỏ bài toán cho hàm số
( )y f x
chắc chắn
có tính chất đặc biệt.
+ Nhìn yếu tố xuất hiện hàm số
2 2
x x
y f x
. Ta có hàm số lẻ và tăng trên
. Đây
chính là chìa khóa ta giải quyết bài toán.
Hướng dẫn giải:
Ta có hàm số
( ) 2 2
x x
y f x
hàm số lẻ và tăng trên
Yêu cầu bài toán
12
12 12
2
2 2 2 2
3
f m f m f m m m m
m
nguyên lớn nhất là:
12
2
1365
3
m
Bài toán tổng quát:
Giải bất phương trình:
, , 0
f u x m f v x m
(*)
Với
( )f x
là hàm số lẻ và tăng (hoặc giảm) trên tập
f
D
Con đường sáng tạo bài toán: (VD: Một vài hàm đặc trưng f)
( ) ,0 1
x x
f x a a a
3
, 0
f x x ax a
f x a x a x
………………………
Ta có (*)
, ,u x m v x m
Đây là nguồn gốc chúng ta tạo lớp bài toán này.
Câu 42.1 (Nguyễn Việt Hải) Cho hàm số
2019 3
12f x x x x
. Hỏi có bao nhiêu giá trị nguyên
12;12
m
thỏa
3 2 2
2019 2019 70 300 0
f m m f m m
Câu 42.2 (Nguyễn Việt Hải) Cho hàm số
3 3
12 12
f x x x x
. Tìm giá trị
m
nguyên lớn nhất
thỏa
5
2 12
6
1
8 0
2
m
m
f f
Câu 42.3 (Nguyễn Việt Hải) Cho hàm số
12 12 2019
x x
f x x
.
S
là tập các phần tử
m
nguyên,
2019;2019
m
thỏa
3 2 2 2
2 4 0,f x mx x f m x x
. Hỏi tập S có bao nhiêu phần tử.
Nhận xét: Câu 42.3 tôi lấy thêm ý tưởng câu 49 đề minh họa THPT QG 2018 – 2019
Mỗi bài toán đều có nguồn gốc rõ ràng, xuất phát từ bài toán kiến thức cơ bản. Dạy toán:
Chúng ta không thể dạy học sinh đua cùng ngân hàng đề Toán, cũng không thể dạy học sinh đếm hết lá
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 69
cây trong một rừng cây, nhưng chúng ta dạy học sinh kiểm soát được bản chất nguồn gốc của lớp bài
toán cũng như đếm được gốc cây trong một rừng cây.
Câu 43. Cho hàm số
f x
thỏa mãn
e ,
x
f x f x x
và
0 2
f
. Tất cả các nguyên hàm
của
2
e
x
f x
là
A.
2 e e
x x
x C
. B.
2
2 e e
x x
x C
.
C.
1 e
x
x C
. D.
1 e
x
x C
.
Lời giải
Tác giả: Nguyễn Đình Hải ; Fb:Nguy
en Dinh Hai
Chọn D
Ta có
e
x
f x f x
e e 1
x x
f x f x
e 1
x
f x
e
x
f x x C
.
Vì
0 2
f
0
2.
e C
2
C
2
e 2 e
x x
f x x
.
Vậy
2
e d
x
f x x
2 e d
x
x x
2 d e
x
x
2 e e d 2
x x
x x
2 e e d
x x
x x
2 e e
x x
x C
1 e
x
x C
.
Phân tích: Bài toán cho hàm số
y f x
thỏa mãn điều kiện chứa tổng của
f x
và
f x
đưa ta tới công thức đạo hàm của tích
. . .u v u v u v
với
u f x
. Từ đó ta cần chọn hàm
v
cho phù hợp
Tổng quát: Cho hàm số
y f x
và
y g x
liên tục trên
K
, thỏa mãn
f x g x f x k x
(Chọn
G x
v e
).
Ta có
f x g x f x k x
G x G x G x
e f x g x e f x k x e
.
G x G x
e f x k x e
G x G x
e f x k x e dx
G x G x
f x e k x e dx
.
Với
G x
là một nguyên hàm của
g x
.
Admin tổ 4 – Strong team : Bản chất của bài toán là cho hàm số
y f x
thỏa mãn điều
kiện chứa tổng của
f x
và
f x
liên quan tới công thức đạo hàm của tích
. . .u v u v u v
với
u f x
. Khi đó ta cần chọn hàm
v
thích hợp. Cụ thể, với bài toán tổng
quát :
Cho hàm số
y f x
,
y g x
,
y h x
,
y k x
liên tục trên
K
,
0
g x
với
x K
và thỏa mãn
. .
g x f x h x f x k x
Ta sẽ đi tìm
v
như sau :
h x h x
v v
v g x v g
dx dx
x
Khi đó :
ln
x
h x
g x
d
dx e
h x
v v
g x
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 70
Câu tương tự:
Câu 43.1 Cho hàm số
f x
thỏa mãn
2
2 2 ,
x
f x xf x xe x
và
0 1
f
. Tất cả các nguyên
hàm của
2
. e
x
x f x
là
A.
2
2
1
x C
. B.
2
2
2
1
1
2
x
x e C
. C.
2
2
2
1
x
x e C
. D.
2
2
1
1
2
x C
.
Lời giải
Tác giả: Nguyễn Đình Hải ; Fb:Nguyen Dinh Hai
Chọn D
Ta có
2
2 2
x
f x xf x xe
2 2 2
2 .2
x x x
e f x xf x e xe
2
2
x
e f x x
2
2
2 d
x
e f x x x x C
.
Vì
(0) 1
f
1
C
2
2
1
x
f x x e
.
Vậy
2
d
x
xf x e x
2
1 dx x x
2 2
1
1 d 1
2
x x
2
2
1
1
2
x C
.
Câu 44. Cho hàm số
f x
có đồ thị hàm số
y f x
được cho như hình vẽ bên.
Hàm số
2
1
0
2
y f x x f
có nhiều nhất bao nhiêu cực trị trong khoảng
2;3
.
A.6. B.2. C.5. D.3
Lời giải
Tác giả: Nguyễn Huỳnh Tấn Trung ; Fb: Nguyễn Huỳnh Tấn Trung
Chọn D
Xét hàm số:
2
1
0
2
h x f x x f
.
Ta có
h x f x x
;
0
h x f x x
Nghiệm phương trình trên là hoành độ giao điểm của hai đồ thị
y x
và
y f x
Dựa vào đồ thị suy ra phương trình:
f x x
có ba nghiệm
2
0
2
x
x
x
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 71
Trên khoảng
2;3
, hàm số
h x
có một điểm cực trị là
2
x
, (do qua nghiệm
0
x
,
h x
không đổi dấu). Do đó đồ thị hàm số
y h x
cắt trục hoành tại tối đa 2 điểm.
Suy ra hàm số
y h x
có tối đa
2 1 3
điểm cực trị trong khoảng
2;3
.
PHÂN TÍCH VÀ PHÁT TRIỂN CÂU 44
Tác giả: Nguyễn Huỳnh Tấn Trung ; Fb: Nguyễn Huỳnh Tấn Trung
- Đây là bài toán hàm số có chứa dấu trị tuyệt đối.
- Đầu tiên, ta xét hàm số không chứa dấu trị tuyệt đối, và khảo sát hàm số đó.
- Sau đó, ta dựa vào sự tương giao với trục hoành, suy ra hàm số có chứa dấu trị
tuyệt đối có tối đa bao nhiêu cực trị.
Bài toán tương tự
Câu 44.1.Cho hàm số
f x
có đồ thị hàm số
y f x
được cho như hình vẽ bên.
Hàm số
2
0
y f x x f
có nhiều nhất bao nhiêu cực trị trong khoảng
3;3
.
A.6. B.2. C.5. D.3
Lời giải
Tác giả: Nguyễn Huỳnh Tấn Trung ; Fb: Nguyễn Huỳnh Tấn Trung
Chọn C
Xét hàm số:
2
0
g x f x x f
.
Ta có
/ /
2g x f x x
;
/ /
0 2g x f x x
Nghiệm phương trình trên là hoành độ giao điểm của hai đồ thị
2y x
và
/
y f x
Dựa vào đồ thị suy ra phương trình:
/
2f x x
có hai nghiệm
2
2
x
x
Trên khoảng
3;3
, hàm số
g x
có hai điểm cực trị là
2, 2
x x
. Do đó đồ thị hàm số
y g x
cắt trục hoành tại tối đa 3 điểm.
Suy ra hàm số
y g x
có tối đa
3 2 5
điểm cực trị trong khoảng
3;3
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 72
Câu 45 . Cho hình chóp tứ giác đều
.
S ABCD
có
11
SA a
, côsin góc hợp bởi hai mặt phẳng
SBC
và
SCD
bằng
1
10
. Thể tích của khối chóp
.
S ABCD
bằng
A.
3
3a
. B.
3
9a
. C.
3
4a
. D.
3
12a
.
Tác giả: Nguyễn Thị Thu Hằng ; Fb: Nguyễn Thu Hằng.
A. Phân tích bài toán:
1)Hình chóp
.
S ABCD
đều nên đáy
ABCD
là hình vuông và
SO ABCD
với
O AC BD
.Suy ra hình vẽ đã được xác định.
2)Theo tính chất hình chóp đều,các cạnh bên
11
SA SB SC SD a
. Từ đó các dữ kiện
tính toán có mối quan hệ với nhau.
3) Góc giữa hai mặt phẳng là góc không tù, cách xác định góc giữa hai mặt phẳng. Tận dụng
đặc điểm của hình chóp đều có
BD SAC
, kẻ hai đường thẳng lần lượt nằm trong 2 mặt
phẳng
SBC
và
SCD
và vuông góc với giao tuyến
SC
.Khi đó học sinh sẽ dễ ngộ nhận góc
giữa hai mặt phẳng là góc
BMD
, không phải góc
BMD
.Góc giữa hai mặt phẳng
SBC
và
SCD
là góc bù với góc
BMD
.Vì góc
BMD
là góc tù.
4) Định lí cosin trong tam giác
ABC
với
a BC
;
b AC
;
c AB
suy ra
2 2 2
2 cos
a b c bc BMD
.
Áp dụng định lí cosin trong tam giác
BMD
ta sẽ tìm được cạnh của hình vuông đáy. Dễ dàng
suy ra chiều cao
SO
của hình chóp. Thể tích đã được tính.
B. Lời giải
Chọn C
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 73
Có
BD AC
;
BD SO
BD SC
. Trong tam giác
SBC
kẻ đường cao
BM
DM SC
. Góc giữa hai mặt phẳng
SBC
và
SCD
chính là góc giữa hai đường
thẳng
MB
và
MD
.
Trong tam giác vuông
OMC
có
OM OC OB
2
OM BD
B D M
180
M M
90
M
. Hay góc
BMD
tù
1
cos
10
BMD
.
Đặt
AB x
,
SE
là đường cao trong tam giác
SBC
nên
. .SE BC BM SC
2
2
11 . . 11
4
x
a x BM a
2
2
. 11
4
11
x x
BM a
a
.
Áp dụng định lí cosin trong tam giác
BMD
có
2 2 2
2 . .cos
BD BM DM BM DM BMD
2 2 2
2 2 cos
BD BM BM BMD
2 2
2 1 cos
BD BM BMD
2
2
2
2
1
2 2 . 11 1
4 10
11
x x
x a
a
2 2
2 2
2
2 11
2 11
11 4 10
x x
x a
a
2
2
1
10 40
x
a
2x a
.
Thể tích của khối chóp
.
S ABCD
bằng
1
.
3
ABCD
V SO S
2
2 2
1
. 4
3
SC OC a
2 2
2 3
11 2
.4 4
3
a a
a a
.
Cách 2. (Nguyễn Việt Hải): Cách nhìn khác tìm yếu tố cạnh đáy.
Đặt
,2
x OB BMD
Ta có
2 2
2 2 2
2 2 2 2 2 2
1 9 9 11 1 1
cos2 2cos 1 cos
10 20 20 9 11
OM x
x
OM OB OM x a x
Hay
2
2 2
2
9 11
x
a x
đến đây OK.
C. Sai lầm học sinh hay mắc phải:
Xác định góc giữa hai mặt phẳng chính là góc
BMD
suy ra
1
cos
10
BMD
. Và bài toán sẽ
không giải được. Hoặc xét hai trường hợp sẽ mất thời gian cho bài toán:
1 1
cos cos
10 10
BMD BMD
D. Khai thác bài toán:
Từ hình chóp đều ta có tể sáng tạo ra các bài toán tương tự câu 45 khi ta biết hai dữ liệu:
Độ dài cạnh bên và 1 góc ( có thể là góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt
phẳng, góc giữa hai đường thẳng).
Độ dài cạnh bên và khoảng cách ( Đề thi học sinh giỏi tỉnh Đà Nẵng).
Và còn nhiều bài toán khác liên quan đến hình chóp đều khi các bạn biết hai dữ kiện.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 74
E. Sau đây là một vài bài tập tương tự.
Câu 45.1 . Cho hình chóp tứ giác đều
.
S ABCD
có
21
SA a
, côsin góc hợp bởi hai mặt phẳng
SAD
và
ABCD
bằng
1
10
. Thể tích của khối chóp
.
S ABCD
bằng
A.
3
19
3
a
. B.
3
2 19
3
a
. C.
3
4 19
3
a
. D.
3
4 19a
.
Lời giải
Chọn C
Gọi cạnh hình vuông đáy là
x
,góc hợp bởi hai mặt phẳng
SAD
và
ABCD
là góc nhọn
SMO
1
cos
10
SMO
1
10
OM
SM
2 2
1
10
1
2 21
4
x
a x
2 2
21
21
4
x a
2x a
.
Thể tích của khối chóp
.
S ABCD
bằng
1
.
3
ABCD
V SO S
2
2 2
1
. 4
3
SC OC a
2 2
2
21 2
.4
3
a a
a
3
4 19
3
a
.
Câu 45.2 . Cho hình chóp tứ giác đều
.
S ABCD
có
11
SA a
, côsin góc hợp bởi cạnh
SB
và
ABCD
bằng
1
10
. Thể tích của khối chóp
.
S ABCD
bằng
A.
3
121
150
a
. B.
3
121
50
a
. C.
3
121
500
a
. D.
3
11
500
a
.
Lời giải
Chọn C
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 75
Gọi cạnh hình vuông đáy là
x
,góc hợp bởi cạnh
SB
và
ABCD
là góc nhọn
SBO
1
cos
10
SMO
1
10
OB
SB
2 1
10
2. 11
x
a
11
5 2
x a
.
Thể tích của khối chóp
.
S ABCD
bằng
1
.
3
ABCD
V SO S
2
2 2
1 11
.
3 25.2
SC OC a
2 2
2
11
11
11
100
.
3 50
a a
a
3
121
500
a
.
Câu 45.3 . Cho hình chóp tứ giác đều
.
S ABCD
có
11
SA a
, côsin góc hợp bởi hai mặt phẳng
SAB
và
SCD
bằng
1
10
. Thể tích của khối chóp
.
S ABCD
bằng
A.
3
3a
. B.
3
9a
. C.
3
4a
. D.
3
12a
.
Gọi cạnh hình vuông đáy là
x
,góc hợp bởi hai mặt phẳng
SAB
và
SCD
là góc nhọn
ESM
1
cos
10
ESM
Áp dụng định lí cosin trong tam giác
BMD
có
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 76
2 2 2
2 . .cos
EM SE SM SE SM ESM
2 2
2 1 cos
x SE BMD
2
2
2 2
1
2 11 1
4 10
x
x a
2
2 2
9
11
4 5
x
x a
2
2
49 99
40 10
a
x
2 99
7
x a
.
Thể tích của khối chóp
.
S ABCD
bằng
1
.
3
ABCD
V SO S
2
2 2
1
. 4
3
SC OC a
.
Câu 45.4 . Cho hình chóp tam giác đều
.
S ABC
có
11
SA a
, côsin góc hợp bởi hai mặt phẳng
SBC
và
SAC
bằng
1
10
. Thể tích của khối chóp
.
S ABC
bằng
A.
3
3a
. B.
3
9a
. C.
3
4a
. D.
3
12a
.
Câu 45.5 . Cho hình chóp tam giác đều
.
S ABC
có
11
SA a
, côsin góc hợp bởi hai mặt phẳng
SBC
và
ABC
bằng
1
10
. Thể tích của khối chóp
.
S ABC
bằng
A.
3
3a
. B.
3
9a
. C.
3
4a
. D.
3
12a
.
Câu 45.6 . Cho hình chóp tam giác đều
.
S ABC
có
11
SA a
, côsin góc hợp bởi đường thẳng
SB
và
ABC
bằng
1
10
. Thể tích của khối chóp
.
S ABC
bằng
A.
3
3a
. B.
3
9a
. C.
3
4a
. D.
3
12a
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 77
Câu 45.7 .( Đề thi học sinh giỏi Đà Nẵng 2019). Cho hình chóp tam giác đều
.
S ABC
có góc giữa mặt
bên và mặt đáy
ABC
bằng
60
. Biết khoảng cách giữa hai đường thẳng
SA
và
BC
bằng
3 7
14
a
. Thể tích của khối chóp
.
S ABC
bằng
A.
3
3
12
a
. B.
3
3
16
a
. C.
3
3
18
a
. D.
3
3
24
a
.
Câu 46. Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách
điệu” cho Ông già Noel có hình dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như
hình vẽ bên. Biết rằng
'OO
=
5cm
,
OA
=
10cm
,
OB
=
20cm
, đường cong
AB
là một phần
của một parabol có đỉnh là điểm
A
. Thể tích của chiếc mũ bằng
B
O'
O
A
A.
3
2750
cm
3
. B.
3
2500
cm
3
. C.
3
2050
cm
3
. D.
3
2250
cm
3
.
Lời giải
Tác giả: Nguyễn Thị Nguyệt Cầ
m; Fb: Nguyet Cam Nguyen
Chọn B
Gọi
V
là thể tích của nón,
1
V
là thể tích khối trụ có chiều cao
'OO
, bán kính đáy
OA
, nên
2
1
5.10 . 500
V
.
Gọi
2
V
là thể tích phần còn lại của nón.
Cách 1: chọn hệ trục tọa độ như hình vẽ.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 78
x
y
B(0,20)
O'
O
A(10,0)
Khi đó,
2
V
là thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi nhánh parabol
AB
và hai trục tọa độ quanh trục
Oy
.
Phương trình parabol (P) chứa nhánh
AB
có dạng
2
10
y a x
.
Vì (P) đi qua điểm
(0;20)
B
nên
1
5
a
; do đó (P):
2
1
10
5
y x
.
Suy ra
5 10
x y
( do
10
x
). Vậy,
20
2
2
0
1000
5 10
3
V y dy
3
cm
Đáp số:
1 2
2500
3
V V V
3
cm
.
Cách 2: chọn hệ trục tọa độ như hình vẽ.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 79
x
y
O
A(0,10)
B(20,0)
Khi đó,
2
V
là thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi nhánh parabol
AB
và hai trục tọa độ quanh trục
Ox
.
Phương trình parabol (P) chứa nhánh
AB
có dạng
10
y a x
.
Vì (P) đi qua điểm
(20;0)
B
nên
5
a
; do đó (P):
5 10
y x
.
Vậy
20
2
2
0
1000
5 10
3
V x dx
3
cm
.
Đáp số:
1 2
2500
3
V V V
3
cm
.
Dạng toán: Tính thể tích khối tròn xoay.
Phương pháp: dùng ứng dụng của tích phân để tính khối tròn xoay, có thể dùng trực tiếp các
công thức tính thể tích chỏm cầu, chảo parabol, hình nêm, phiến trụ, nón cụt…
Bài toán tương tự
Câu 46.1 Cây dù ở khu vui chơi “công viên nước” của trẻ em có phần trên là một chỏm cầu, phần thân là
một khối nón cụt như hình vẽ. Biết
2ON OD m
;
40MN cm
;
40BC cm
;
20EF cm
.
Tính thể tích của cây dù
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 80
A D
M
F
E
B
O
C
N
A.
3
336000
cm
3
2750
cm
3
. B.
3
896000
3
cm
.
C.
3
112000
cm
3
2050
cm
3
. D.
3
896000
cm
3
2250
cm
3
.
Lời giải
Tác giả: Nguyễn Thị Nguyệt Cầm; Fb
: Nguyet Cam Nguyen
Chọn A
Thể tích phần trên của cây dù là thể tích của khối chỏm cầu:
2
1
3
h
V h R
2
. .
3
MN
MN ON
2
40
.40 200
3
3
896000
3
cm
.
Thể tích phần thân của cây dù là thể tích của khối nón cụt:
2 2
2 1 2 1 2
1
. . .
3
V h R R R R
2 2
1
. . .
3
OM MB OE MB OE
1
.160. 400 100 200
3
3
112000
3
cm
.
Vậy thể tích của cây dù:
1 2
V V V
896000 112000
3 3
3
336000
cm
.
Câu 47. Giả sử
1 2
,z z
là hai trong các số phức thỏa mãn
6 8
z zi
là số thực. Biết rằng
1 2
4
z z
,
giá trị nhỏ nhất của
1 2
3z z
bằng
A.
5 21
. B.
20 4 21
. C.
20 4 22
. D.
5 22
.
Lời giải
Chọn C
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 81
Giả sử
z x yi
,
,x y
.Gọi
,A B
lần lượt là điểm biểu diễn cho các số phức
1 2
,z z
. Suy ra
1 2
4
AB z z
.
* Ta có
6 8
z zi
6 . 8
x yi y xi
2 2
8 6 48 6 8
x y x y x y i
.
Theo giả thiết
6 8
z zi
là số thực nên ta suy ra
2 2
6 8 0
x y x y
. Tức là các điểm
,A B
thuộc đường tròn
C
tâm
3;4
I
, bán kính
5
R
.
* Xét điểm
M
thuộc đoạn
AB
thỏa
3 0 3 4
MA MB OA OB OM
    
.Gọi
là trung điểm
AB
. Ta tính được
2 2 2 2 2
21; 22
HI R HB IM HI HM
, suy ra điểm
M
thuộc
đường tròn
C
tâm
3;4
I
, bán kính
22
r
.
* Ta có
1 2
3 3 4 4
z z OA OB OM OM
, do đó
1 2
3z z
nhỏ nhất khi
OM
nhỏ nhất.
Ta có
0
min
5 22
OM OM OI r
.
Vậy
1 2 0
min
3 4 20 4 22
z z OM
.
Phân tích : Kiến thức cần nắm vững :
Quỹ tích điểm biểu diễn số phức.
Modun số phức
Bài toán liên quan tâm tỉ cự trong hình học.
Sai sót dễ gặp, không để ý đường tròn C đi qua gốc tọa độ.
Bài toán tương tự
Câu 47.1 Giả sử
1 2
,z z
là hai trong các số phức thỏa mãn
1 2z z i
là một số thuần ảo. Biết rằng
1 2
2
z z
, giá trị nhỏ nhất của
1 2
5z z
bằng
A.
13 5
. B.
3 5 13
. C.
3 5 2 13
. D.
5 22
.
Lời giải
Chọn B
Đặt
2 2
; 1 2 2 2 2 .z x yi x y z z i x y x y x y i
Theo giả thiết
1 2z z i
là số thuần ảo, suy ra
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 82
2
2
2 2 2 2
1 5 1 5
2 0 2 1 1 .
4 4 2 4
x y x y x x y y x y
tập hợp điểm biểu diễn số phức
z
là một đường tròn
1
C
tâm
1
; 1
2
I
,
5
2
R
Giả sử
z x yi
,
,x y
.Gọi
,A B
lần lượt là điểm biểu diễn cho các số phức
1 2
,z z
. Suy ra
1 2
2 2
z z AB
.
Gọi
M
là điểm thỏa mãn
5 0 5 6
MA MB OA OB OM
    
.
Gọi
là trung điểm
AB
ta có
2
2 2 2
2 2 2
2
1
4
13
36
IH
IH IA HA
IH IM HM
IM
.
Vậy tập hợp điểm
M
là đường tròn
2
C
tâm
1
; 1
2
I
,
13
6
r
.
Ta có
1 2
5 5 6 6
z z OA OB OM OM
.
Do
1
C
,
2
C
là hai đường tròn đồng tâm và
1
O C
Từ đó suy ra
1 2
5 13
5 6 6 6 3 5 13
2 6
Min
Min
z z OM R r
Câu 47.2 Giả sử
1 2
,z z
là hai trong số các số phức
z
thỏa mãn
2 1
iz i
và
1 2
2
z z
Giá trị lớn
nhất của
1 2
z z
bằng
A.
4
. B.
2 3
. C.
3 2
. D.
3.
.
Lời giải
Chọn A.
Ta có
2 1
iz i
2 1 1
i z i
1 2 1
z i
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 83
Điểm biểu diễn
z
thuộc đường tròn tâm
1; 2
I
,
1R
.
Gọi
M
,
là điểm biểu diễn
1
z
,
2
z
nên
2MN
là đường kính. Dựng hình bình hành
OMPN
ta có
1 2
2 3
z z OP
.
Ta có
2
2 2
1 2 1 2
2
z z z z
2 2
1 2 1 2
z z z z
16
1 2
4
z z
. Dấu bằng xảy ra
khi
1 2
z z
MN OI
(
OMPN
là hình thoi)
Câu 48. Cho hàm số
y f x
có đồ thị như hình vẽ.
Có bao nhiêu số nguyên
m
để phương trình
1
1
3 2
x
f x m
có nghiệm thuộc đoạn
2;2
?
A. 11. B. 9. C.8. D. 10.
Lời giải
Tác giả: Nguyễn Việt Hải; Fb: Nguyễn Việt Hả
i
Chọn C
Ta có
1 6 1 3 6
2
1
1
3 2 2
x xx
f x m f m
6 3 6
f t t m
Với
1
2
x
t
và
2;2
x
nên ta có
0;2
t
.
Xét hàm số
6y f t t
trên
0;2
.
Ta có
6 0
y f t
,
0;2
t
.
Phương trình có nghiệm
0;2
0;2
min 6 3 6 max 6f t t m f t t
0 3 6 2 12
f m f
4 3 6 6 12
m
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 84
10
4
3
m
.
Vì
m
nên
3; 2; 1;0;1;2;3;4
m
.
Phân tích:
Bản chất bài toán: Bài toán đã cho là giải phương trình hay bất phương trình bằng phương
pháp tương giao giữa hai đồ thị
y g x
và
y h m
- Đồ thị hàm số
y h m
bản chất là một đường thẳng song song hoặc trùng với trục
Ox
và
đi qua điểm có tung độ có giá trị là
h m
.
- Đồ thị hàm số
y g x
xác định được tính chất dựa vào các dữ kiện đã cho hàm số
y f x
ban đầu; hàm số
y f x
có thể cho bằng công thức, bằng đồ thị, bằng hàm đạo
hàm của nó, đồ thị của đạo hàm.
Vì đây là phần kiến thức tương đối rộng nên tôi xin chỉ khai thác ở một góc độ nào đó của
bài toán.
Khó khăn đối với học sinh:
- Từ đồ thị hàm số
y f x
suy ra đồ thị hàm số
y g x
.
- Trong trường hợp không thể dùng đồ thị hàm số thì học sinh khó khăn trong việc
kiểm soát đặc điểm của hàm số
y g x
do hàm số
y g x
có chứa biểu thức hàm hợp
phức tạp của hàm
y f x
.
- Phần lớn học sinh chưa phân biệt được kiến thức: “Số nghiệm của phương trình
chính là số giao điểm của đồ thị hai hàm số” và “Nghiệm của phương trình chính là hoành
độ của giao điểm”.
Giải pháp:
- Sử dụng một số phép biến đổi đồ thị cơ bản
- Sử dụng cách đặt ẩn phụ đưa về hàm số theo ẩn mới có chứa
y f t
.
Kiểu 1: Sử dụng một số phép biến đổi đồ thị cơ bản.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 85
Kiểu 2: Sử dụng cách đặt ẩn phụ đưa về hàm số theo ẩn mới có chứa
y f t
.
Sau đây tôi xin đưa ra lớp bài toán sưu tầm theo mức độ để giúp học sinh có cách nhìn dễ
dàng trong các bài thi trắc nghiệm:
Câu 48.1. Cho hàm số
y f x
có đồ thị như hình bên dưới
Số nghiệm của phương trình
2 3 0
f x
là
A.
4
. B.
2
. C.
0
. D.
3
.
O
x
y
2
2
2
2
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 86
Câu 48.2. Cho hàm số
y f x
có đồ thị là đường cong trong hình vẽ bên. Tìm số nghiệm của phương
trình
2019 1
f x
.
A.
2
. B.
1
. C.
3
. D.
4
.
Câu 48.3. Cho hàm số
y f x
có đồ thị như đường cong trong hình vẽ dưới đây. Tìm giá trị của tham
số
m
để phương trình
1
f x m
có
6
nghiệm phân biệt?
A.
4 3
m
. B.
4 5
m
. C.
5
m
. D.
0 4
m
.
Câu 48.4. Cho hàm số có bảng biến thiên như hình vẽ.
Số nghiệm của phương trình
1 2
f x
là
A.
5
. B.
4
. C.
2
. D.
3
.
Câu 48.5. Cho hàm số
y f x
có đồ thị như hình vẽ bên.
Phương trình
2 2f x
có bao nhiêu nghiệm thực phân biệt?
A.
4.
B.
2.
C.
6.
D.
3.
O
x
y
4
1
1
2
O
x
y
1
1
2
2
3
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 87
Câu 48.6. Cho hàm số
3 2
3f x x x
. Có bao nhiêu giá trị nguyên của
m
để đồ thị hàm số
g x f x m
cắt trục hoành tại
4
điểm phân biệt ?
A.
3
. B.
4
. C.
2
. D.
0
.
Câu 48.7. Cho hàm số
y f x
có bảng biến thiên dưới đây.
-2
-2
2
2
+∞
-∞
++
-
00
-1
3
20
-∞
+∞
f'(x)
f(x)
x
Tìm tất cả các giá trị thực của tham số
m
để phương trình
f x f m
có ba nghiệm phân
biệt.
A.
;
m
2 2
. B.
; \ ;
m
1 3 0 2
. C.
;
m
1 3
. D.
; \ ;
m
1 3 0 2
.
Câu 48.8. Hình vẽ bên là đồ thị của hàm số
y f x
.
Gọi
S
là tập hợp các giá trị nguyên dương của tham số
m
để hàm số
1
y f x m
có
5
điểm cực trị. Tổng giá trị tất cả các phần tử của
S
bằng
A.
12
. B.
15
. C.
18
. D.
9
.
Câu 48.9. Cho hàm số
4 2
y f x ax bx c
biết
0
a
,
2017
c
và
2017
a b c
. Số cực trị của
hàm số
2017
y f x
là:
A.
1
. B.
7
. C.
5
. D.
3
.
Câu 48.10. Cho hàm số
3 2
4 6 1
y x x
có đồ thị là đường cong trong hình dưới đây. Khi đó phương
trình
3 2
3 2 3 2
4 4 6 1 6 4 6 1 1 0
x x x x
có bao nhiêu nghiệm thực.
O
x
y
2
3
6
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 88
A.
3
. B.
6
. C.
7
. D.
9
.
Câu 48.11. Cho hàm số
y f x
có đồ thị như hình bên. Tồn tại bao nhiêu giá trị nguyên của tham số
m
để phương trình
sin
f x m
có đúng hai nghiệm thuộc đoạn
0;
?
A.
4
. B.
7
. C.
5
. D.
6
.
Câu 48.12. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Tìm số giá trị nguyên của
m
để phương
trình
2
2
f x x m
có đúng
4
nghiệm thực phân biệt thuộc đoạn
3 7
;
2 2
.
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 48.13. Cho hàm số
f x
xác định trên
\ 0
và có bảng biến thiên như hình vẽ.
x
O
y
1
1
1
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 89
Số nghiệm của phương trình
3 2 1 10 0
f x
là.
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 49. Trong không gian
Oxyz
cho ba đường thẳng
1
: ,
1 1 2
x y z
d
1
3 1
: ,
2 1 1
x y z
2
1 2
:
1 2 1
x y z
. Đường thẳng
vuông góc với
d
đồng thời cắt
1 2
,
tương ứng tại
,H K
sao cho độ dài
HK
nhỏ nhất. Biết rằng
có một vectơ chỉ phương
; ;1 .
u h k
Giá trị
h k
bằng
A.
0.
B.
4.
C.
6.
D.
2.
Lời giải
Tác giả: Nguyễn Việt Thảo ; FB:Việt Thảo
Chọn A
+ Gọi
1
3 2 ; ;1
H H t t t
.
+ Gọi
2
1 ;2 2 ;K K m m m
.
+ Tính được
2 2;2 2; 1
HK m t m t m t
.
+ Đường thẳng
d
có một VTCP là
1;1; 2
d
u
.
+ Vì
d
. 0
d
u HK
2 0 2 4; 2; 3 .
m t m t HK t t
+ Tính được
2 2 2 2
2
4 2 3 2 1 27 27,
HK t t t t
Suy ra
27,
minHK
đạt được khi
1
t
.
+ Khi đó ta có
3; 3; 3
HK
, suy ra
1;1;1 1 0.
u h k h k
BÀI PHÁT TRIỂN CÂU 49
Câu 49.1 Trong không gian
Oxyz
cho hai mặt phẳng
: 2 1 0,
P x y z
: 2 2 0,
P x y z
và
hai đường thẳng
1
1 1
: ,
2 1 2
x y z
2
2 1
:
1 1 2
x y z
. Đường thẳng
song song với hai
mặt phẳng
;P Q
và cắt
1 2
,
tương ứng tại
,H K
. Độ dài đoạn
HK
bằng
A.
8 11
7
. B.
5
C.
6.
D.
11
.
7
Lời giải
Tác giả: Nguyễn Việt Thảo ; FB:Việt Thảo
Chọn A
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 90
+ Tính
, 1; 1; 3
P Q
u n n
+ Gọi
2 ;1 ; 1 2 ; ;2 ;1 2H t t t K m m m
nên
2;1 ;2 2 2HK m m t m t
+ Vì song song với 2 mặt phẳng
;P Q
nên
.HK k u

suy ra
2 1 2 2 2
1 1 3
m t m t m t
tính ra được
2 3
;
7 7
m t
.
+ Suy ra
8 11
7
HK
.
Câu 50 . Trong không gian
Oxyz
, cho
1; 1;0
a
và hai điểm
4;7;3
A
,
4;4;5
B
. Giả sử
M
,
là hai điểm thay đổi trong mặt phẳng
Oxy
sao cho
MN

cùng hướng với
a
và
5 2
MN
.
Giá trị lớn nhất của
AM BN
bằng
A.
17
. B.
77
. C.
7 2 3
. D.
82 5
.
Lời giải
Tác giả: Nguyễ
n Trung Thành; Fb: Thanh Nguyen.
Chọn A
Vì
MN

cùng hướng với
a
nên
0 :
t MN ta

.
Hơn nữa,
5 2 . 5 2
MN t a
5t
. Suy ra
5; 5;0
MN
.
Gọi
; ;A x y z
là điểm sao cho
AA MN
 
4 5
7 5
3 0
x
y
z
1
2
3
x
y
z
1;2;3
A
.
Dễ thấy các điểm
,
B
đều nằm cùng phía so với mặt phẳng
Oxy
vì chúng đều có
cao độ
dương. Hơn nữa vì cao độ của chúng khác nhau nên đường thẳng
'A B
luôn cắt mặt
phẳng
Oxy
tại một điểm cố định.
Từ
AA MN
 
suy ra
AM A N
nên
' 'AM BN A N BN A B
dấu bằng xảy ra
khi
là giao điểm của đường thẳng
'A B
với mặt phẳng
Oxy
.
Do đó
2 2 2
max ' 4 1 4 2 5 3 17
AM BN A B
, đạt được khi
N A B Oxy
.
Nhận xét
Ý tưởng ra đề
Từ bất đẳng thức véc tơ
a)
| | | | .u v u v
Dấu “=” xảy ra khi và chỉ khi hai véc tơ
u
và
v
cùng chiều.
b)
| .u v u u
Dấu “=” xảy ra khi và chỉ khi hai véc tơ
u
và
v
cùng chiều.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 91
c)
| .u v u u
Dấu “=” xảy ra khi và chỉ khi hai véc tơ
u
và
v
ngược chiều.
Tác giả: Nguyễn Văn Hải, FB: https://www.facebook.com/nguyenvan.hai.96387
Bài trên xuất phát từ bất đẳng thức trên ta có bài toán gốc sau
Câu 50.1. Trong không gian
Oxyz
, cho hai điểm
1;2;3
A
,
4;4;5
B
. Giả sử
M
là điểm thay đổi trong
mặt phẳng
( ) : 2 2 2019 0.
P x y z
Tìm giá trị lớn nhất của biểu thức
.P AM BM
A.
17
. B.
77
. C.
7 2 3
. D.
82 5
.
Lời giải
Chọn A
Ta có:
2 2 2019 2 2 2019 0
A A A B B B
x y z x y z
nên các điểm
,A B
đều nằm cùng
phía so với mặt phẳng
( )P
và đường thẳng
AB
luôn cắt mặt phẳng
( )P
tại một điểm cố định.
Từ bất đẳng thức véc tơ
| | | | .u v u v
Ta có
.AM BM AB
Dấu bằng xảy ra khi
M
là
giao điểm của đường thẳng
AB
với mặt phẳng
( )P
.
Do đó
2 2 2
4 1 4 2 5 3 17
Max
AM BM AB
, đạt được khi
M AB P
.
Câu 50.2. Trong không gian
Oxyz
, cho
1;1;0 , 3; 1;4
A B
và mặt phẳng
: 1 0
x y z
. Tìm tọa
độ điểm
M
sao cho
MA MB
đạt giá trị lớn nhất.
A.
1;3; 1
M
. B.
3 5 1
; ;
4 4 2
M
. C.
1 2 2
; ;
3 3 3
M
. D.
0;2;1
M
.
Lời giải
Chọn B
Ta có:
1 1 1 1 0 1 3 1 4 1 0
A A A B B B
x y z x y z
nên hai điểm
A
và
B
cùng nằm về một phía của mặt phẳng
.
Ta có
2 6
MA MB AB
, nên
MA MB
lớn nhất khi và chỉ khi
M AB
.
Phương trình đường thẳng
AB
:
1 2
1 2
4
x t
y t
z t
, do đó tọa độ điểm
M
là nghiệm của hệ phương
trình
1 2
1 2
4
1 0
x t
y t
z t
x y z
1
8
3
4
5
4
1
2
t
x
y
z
. Do đó
3 5 1
; ;
4 4 2
M
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 92
Câu 50.3. Cho đường thẳng
1 1 2
:
1 1 2
x y z
và
(1;1;0),
A
(3; 1;4).
B
Tìm tọa độ điểm
M
thuộc
sao cho
MA MB
đạt giá trị nhỏ nhất.
A.
( 1;1; 2).
M
B.
1 1
; ;1 .
2 2
M
C.
3 3
; ; 3 .
2 2
M
D.
(1; 1;2).
M
Lời giải
Chọn D
Ta có:
2; 2;4
AB
cùng phương với
1; 1; 2
u
và
(1;1;0)A
(do
1 1 1 1
1 1
)
AB
//
AB
và
đồng phẳng.
* Xét mặt phẳng chứa
AB
và
:
Gọi
là điểm đối xứng của
A
qua
;
là mặt phẳng qua
A
, vuông góc với
Khi đó, giao điểm
của
với
là trung điểm của
AA
có phương trình:
2 0
x y z
Giả sử
1 ;1 ; 2 2H t t t
,
1 0;0;0
H t H
là trung điểm của
1; 1;0
AA A
Ta có:
min
MA MB MA MB A B MA MB A B
khi và chỉ khi
M
trùng với
0
M
là
giao điểm của
A B
và
Đường thẳng
A B
đi qua
1; 1;0
A
, có phương trình:
1
1
x t
y
z t
Mà
1
: 1
2 2
x t
y t
z t
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 93
Giải hệ phương trình:
1 1
2
1 1 2
2
2 2 2 2
t t t t
t
t t
t
t t t t
0
1; 1;2
M
Vậy, để
MA MB
đạt giá trị nhỏ nhất thì
1; 1;2
M
.
Câu 50.4. Cho đường thẳng
1 1 2
:
1 1 2
x y z
và hai điểm
(1;1;0),
A
( 1;0;1).
B
Biết điểm
( ; ; )M a b c
thuộc
sao cho biểu thức
T MA MB
đạt giá trị lớn nhất. Khi đó tổng
a b c
bằng:
A.
8
. B.
8 33
. C.
33
8
3
. D.
4 33
8
3
.
Lời giải
Chọn D
qua
C( 1;1; 2),
và có vectơ chỉ phương
(1; 1;2)
u
( 2; 1;1);
AB

( 2;0; 2)
AC
.
; 0
AB u AC
nên
;AB
không đồng phẳng
Vì điểm
M
thuộc
nên ta có
( 1 ;1 ; 2 2 ),M t t t
t
. Lúc đó
2 2 2 2 2
2
2 2 2 1 2 3
P MA MB t t t t t t
2 2
6 12 8 6 14 10 .
t t t t
2
2
1 7 11
6 1
3 6 6
P t t
Đặt
3
1; ,
3
u t
7 11
;
6 6
v t
. Ta có
| | | |
u v u v
.
Tức là
2
2
1 3 11
6.
6 3 6
P
.
Đẳng thức xảy ra khi và chỉ khi
3
1 33
3
3
7
3
11
6
6
t
t
t
.
Với
ta có
4 33
4 4 8
3
a b c t
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 94
Câu 50.5. Cho đường thẳng
1
:
1 1 1
x y z
và hai điểm
(0;1; 3),
A
( 1;0;2).
B
Biết điểm
M
thuộc
sao cho biểu thức
T MA MB
đạt giá trị lớn nhất là
max
.T
Khi đó,
max
T
bằng bao nhiêu?
A.
max
3
T
. B.
max
2 3
T
. C.
max
3 3
T
. D.
max
2
T
.
Lờigiải
Chọn C
Ta có
1; 1; 5
AB
, phương trình đường thẳng
AB
là
1 ( )
3 5
x t
y t t
z t
.
Xét vị trí tương đối giữa
AB
và
ta có
AB
cắt
tại
1 1 1
; ;
2 2 2
C
.
Suy ra
1 1 5 1
; ;
2 2 2 2
AC AC AB C
là trung điểm
AB
.
T MA MB AB
. Dấu “=” xảy ra khi
M A
hoặc
M B
.
Do đó
max
27 3 3
T AB
.
Câu 50.6. Cho mặt phẳng
: 2 1 0
x y z
và hai điểm
0; 1;1 , 1;1; 2
A B
. Biết
M
sao
cho
MA MB
đạt giá trị nhỏ nhất. Khi đó, hoành độ
M
x
của điểm
M
là
A.
1
3
M
x
. B.
1
M
x
. C.
2
M
x
. D.
2
7
M
x
.
Lời giải
Chọn D
Ta có:
2 1 2 1 0 1 2.1 1 1 1 4 1 0
A A A B B B
x y z x y z
nên hai điểm
A
và
B
nằm khác phía so với mặt phẳng
.
Nên
MA MB
đạt giá trị nhỏ nhất khi
M AB
.
Phương trình đường thẳng
AB
:
1 2
1 3
x t
y t
z t
, do đó tọa độ điểm
M
là nghiệm của hệ phương
trình
1 2
1 3
2 1 0
x t
y t
z t
x y z
2
7
2
7
3
7
1
7
t
x
y
z
. Do đó
2 3 1
; ;
7 7 7
M
,
2
7
M
x
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 95
Câu 50.7. Cho mặt phẳng
: 1 0
x y z
và hai điểm
1;1;0 , 3; 1;4
A B
. Gọi
M
là điểm thuộc
mặt phẳng
sao cho
P MA MB
đạt giá trị nhỏ nhất. Khi đó giá trị của
P
là:
A.
5
P
. B.
6
P
. C.
7
P
. D.
8
P
.
Lời giải
Chọn B
Ta có:
1 1 1 1 0 1 3 1 4 1 0
A A A B B B
x y z x y z
nên hai điểm
A
và
B
cùng nằm về một phía của mặt phẳng
.
Gọi
là hình chiếu vuông góc của
A
lên mặt phẳng
.
Phương trình đường thẳng
AH
:
1
1
x t
y t
z t
.
Do đó tọa độ điểm
là nghiệm của hệ phương trình
1
1
1 0
x t
y t
z t
x y z
1
3
2
3
4
3
1
3
t
x
y
z
.
Do đó
2 4 1
; ;
3 3 3
H
.
Gọi
đối xứng với
A
qua
, suy ra
1 5 2
; ;
3 3 3
A
.
Ta có
6
MA MB MA MB A B P A B
.
Câu 50.8. Cho mặt phẳng
: 3 5 0
x y z
và hai điểm
1; 1;2 , 5; 1;0
A B
. Biết
; ;M a b c
thuộc mặt phẳng
sao cho
MA MB
đạt giá trị nhỏ nhất. Khi đó, giá trị của biểu thức
2 3T a b c
bằng bao nhiêu?
A.
5
T
. B.
3
T
. C.
7
T
. D.
9
T
.
Lời giải
Chọn C
Ta có:
3 5 3 5 1 1 3.2 5 5 1 3.0 5 0
A A A B B B
x y z x y z
nên hai điểm
A
và
B
cùng nằm về một phía của mặt phẳng
.
Gọi
là hình chiếu vuông góc của
A
lên mặt phẳng
.
Phương trình đường thẳng
AH
:
1
1
2 3
x t
y t
z t
.
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 96
Do đó tọa độ điểm
là nghiệm của hệ phương trình
1
1
2 3
3 5 0
x t
y t
z t
x y z
1
2
0
1
t
x
y
z
.
Do đó
2;0; 1
H
.
Gọi
đối xứng với
A
qua
, suy ra
3;1; 4
A
.
Ta có
MA MB MA MB A B
nên
MA MB
nhỏ nhất khi
M A B
.
Phương trình đường thẳng
A B
:
3 4
1
4 3
x t
y t
z t
.
Do đó tọa độ điểm
M
là nghiệm của hệ phương trình
3 4
1
4 3
3 5 0
x t
y t
z t
x y z
12
11
15
11
1
11
20
11
t
x
y
z
.
Do đó
15 1 20
; ;
11 11 11
M
,
2 3 7
T a b c
.
Câu 50.9. Cho mặt cầu
2 2 2
( ) :( 1) ( 4) 8
S x y z
và hai điểm
(3;0;0), (4;2;1)
A B
. Gọi
M
là điểm
thuộc mặt mặt cầu
( ).S
Tính giá trị nhỏ nhất của biểu thức
2 .MA MB
A.
6.
B.
2 6.
C.
6 2.
D.
3 2.
Lời giải
Chọn C
Ý tưởng
Tìm điểm
'B
cố định sao cho
2 'MA MB
rồi áp dụng bất đẳng thức
| .u v u u
Cách 1: Gọi
( ; ; ) ( ),M a b c S
ta có
2 2 2 2 2 2
( 1) ( 4) 8 2 8 9a b c a b c a b
Do đó
2 2 2 2 2 2 2 2 2
( 3) 4( ) 3( ) 6 9
MA a b c a b c a b c a
2 2 2 2 2 2
2 6 9 2 ( 3) 2 'a b c b a b c MB
với
'(0;3;0).
B
Dễ thấy
'B
nằm trong mặt cầu,
B
nằm ngoài mặt cầu nên
2 2( ' )MA MB MB MB
nhỏ nhất
khi
', ,B M B
thẳng hàng.
Vậy, giá trị nhỏ nhất của biểu thức
2MA MB
là
2 ' 6 2.
BB
Cách 2:
GR FB: STRONG TEAM TOÁN VD-VDC ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc
Trang 97
M
0
E
I
A
B
B'
M
Ta có
4 2,
IA
với
I
là tâm mặt cầu.
Gọi
(1;2;0), '(0;3;0)
E B
lần lượt là trung điểm của
IA
và
.IE
+
M
là điểm nằm trên đường thẳng
IA
ta có
1
' .
2
MB MA
+
M
là điểm không nằm trên đường thẳng
IA
ta có
'IMB IAM
nên
' 1
2
MB IM
MA IA
,
ta có
1
' .
2
MB MA
Dễ thấy
'B
nằm trong mặt cầu,
B
nằm ngoài mặt cầu nên
2 2( ' )MA MB MB MB
nhỏ nhất
khi
', ,B M B
thẳng hàng.
0
M M
Vậy, giá trị nhỏ nhất của biểu thức
2MA MB
là
2 ' 6 2.
BB
| 1/97
| | Tải xuống

Có thể bạn quan tâm:

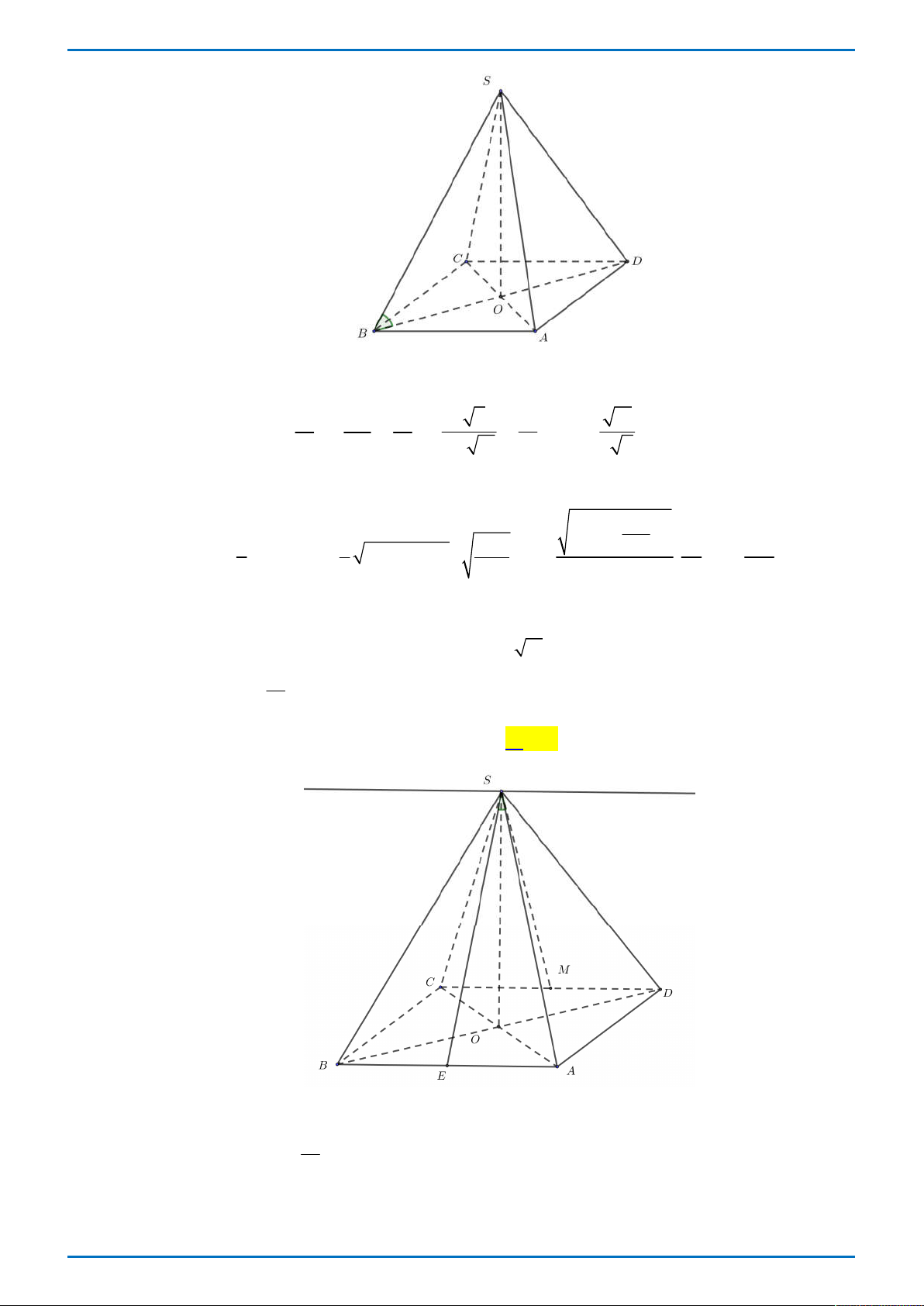
Preview text:

GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
PHÂN TÍCH – BÌNH LUẬN – PHÁT TRIỂN
ĐỀ THI THỬ THPTQG LẦN 1 - 2018-2019 CHUYÊN ĐẠI HỌC VINH
“Chân thành cảm ơn tập thể thầy cô Tổ 4 – Strong Team .
Tâm huyết tạo lên sản phẩm vì thế hệ học sinh thân yêu của chúng ta.”
Admin Tổ 4 – Strong Team: Nguyễn Việt Hải – Hue Tran – Võ Minh Chung – Đỗ Thuận – Mê Kiếm Hiệp
Thầy cô Tổ 4 – Strong Team MÃ ĐỀ THI: 209 Câu 1.
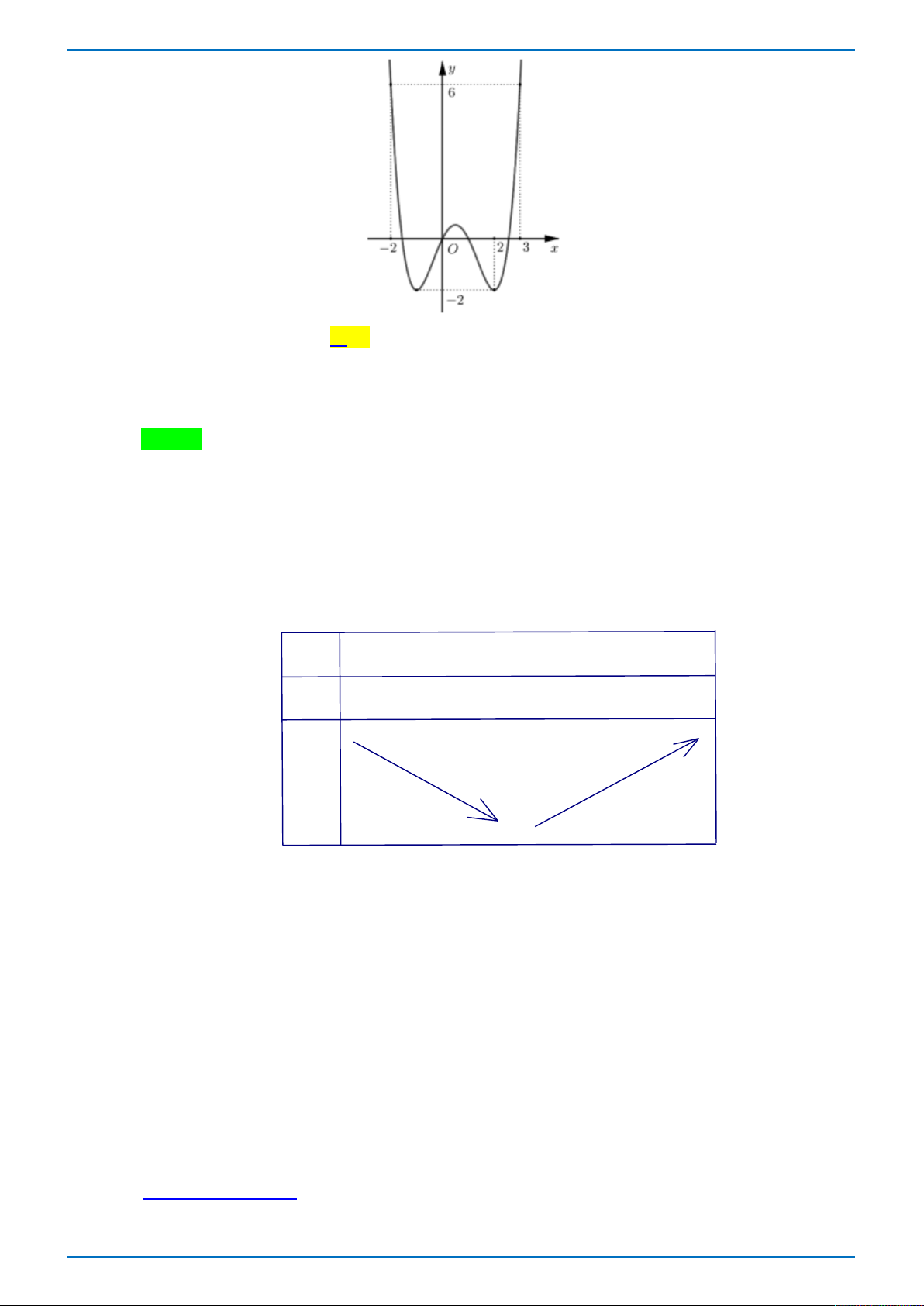
Số nghiệm âm của phương trình 2 log x  3  0 là A. 2 . B. 4 . C. 1. D. 3 . Câu 2.
Cho hình chóp S.ABCD có đáy ABCD hình chữ nhật với AB  3a , BC a , cạnh bên
SD  2a và SD vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng A. 3 3a . B. 3 a . C. 3 2a . D. 3 6a .     Câu 3.
Trong không gian Oxyz , cho a  3; 4;0 , b  5; 0;12 . Côsin của góc giữa a và b bằng 3 5 5 3 A. . B. . C.  . D.  . 13 6 6 13 a Câu 4.
Giả sử a , b là các số thực dương bất kỳ. Biểu thức ln bằng 2 b 1 1 A. ln a  ln b . B. ln a  ln b .
C. ln a  2 ln b .
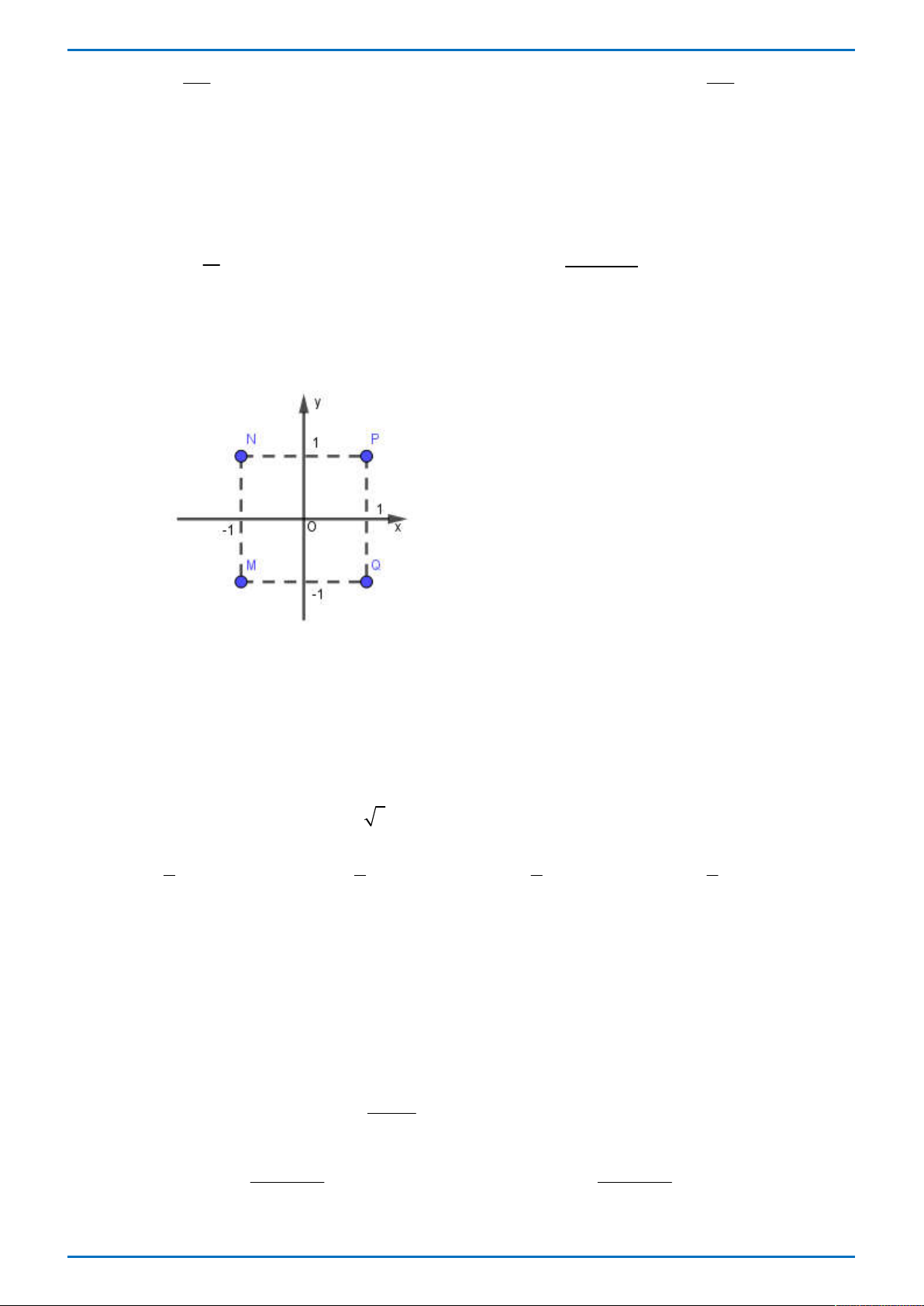
D. ln a  2 ln b . 2 2 Câu 5.
Trong không gian Oxyz , cho E(1; 0; 2) và F (2;1; 5
 ) . Phương trình đường thẳng EF là x 1 y z  2 x 1 y z  2 A.   . B.   . 3 1 7  3 1 7  x 1 y z  2 x 1 y z  2 C.   . D.   . 1 1 3  1 1 3 1 Câu 6.
Cho cấp số nhân u , với u  9  ,u
. Công bội của cấp số nhân đã cho bằng n  1 4 3 1 1 A. . B. 3 . C. 3 . D.  . 3 3 Câu 7.
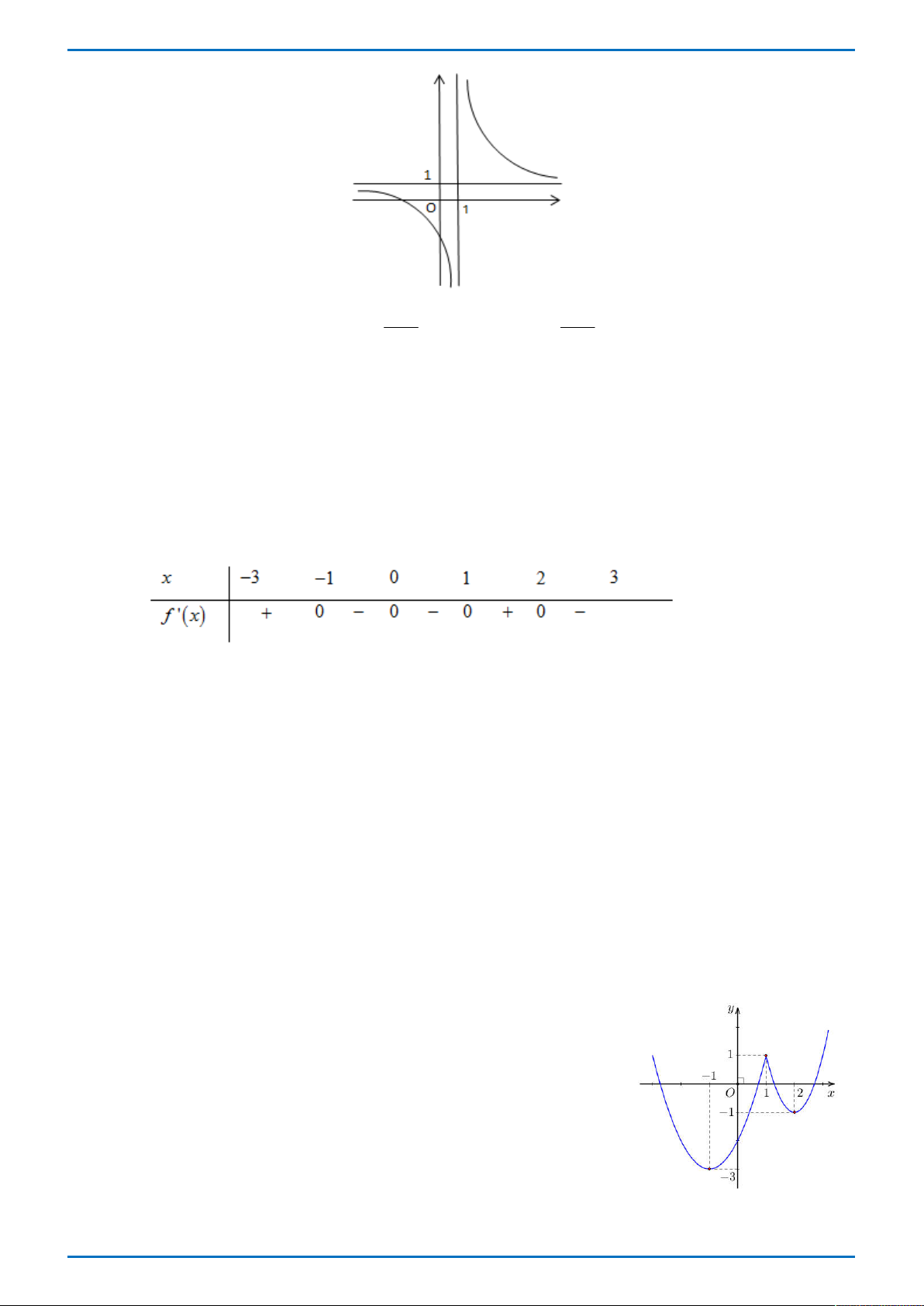
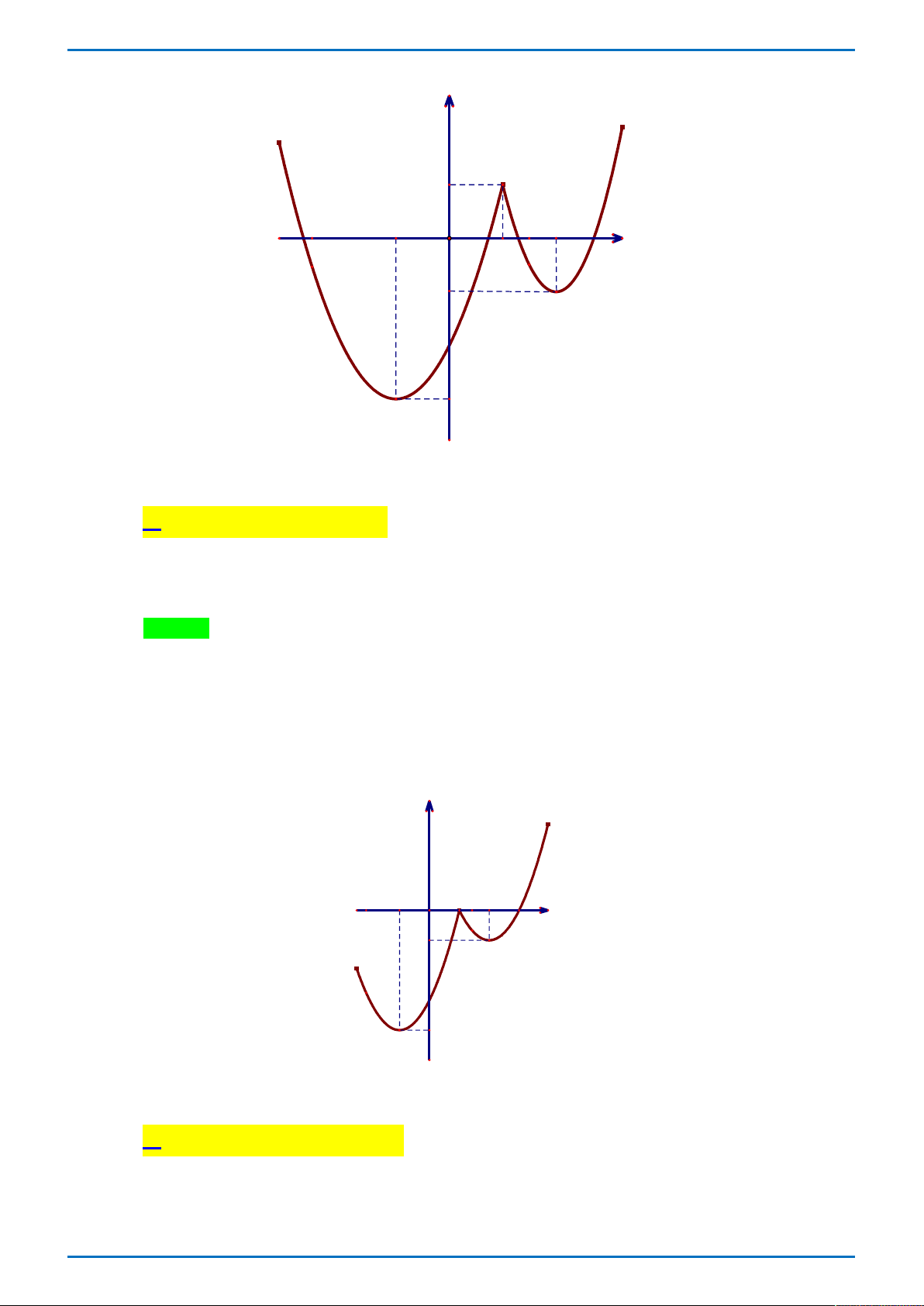
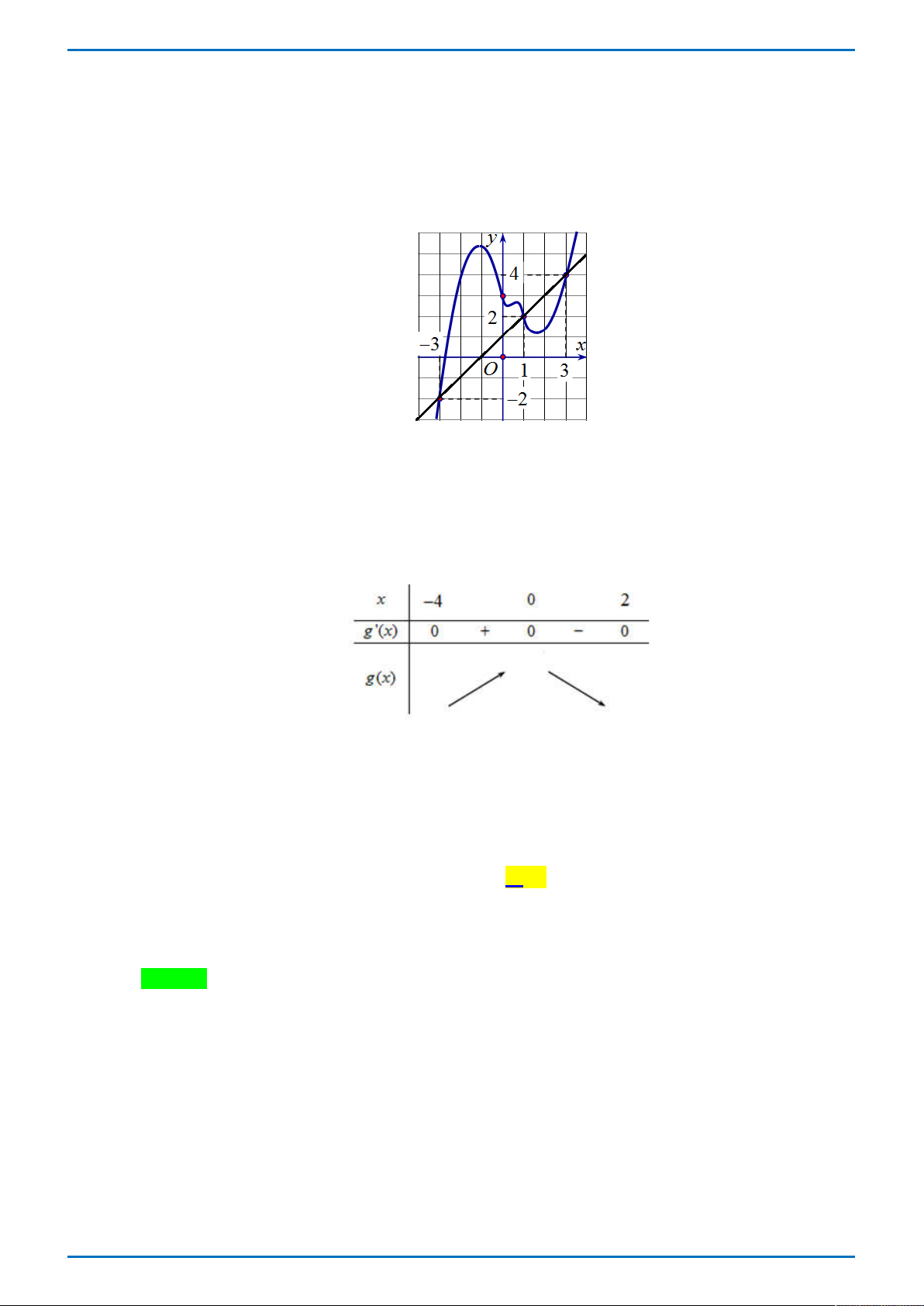
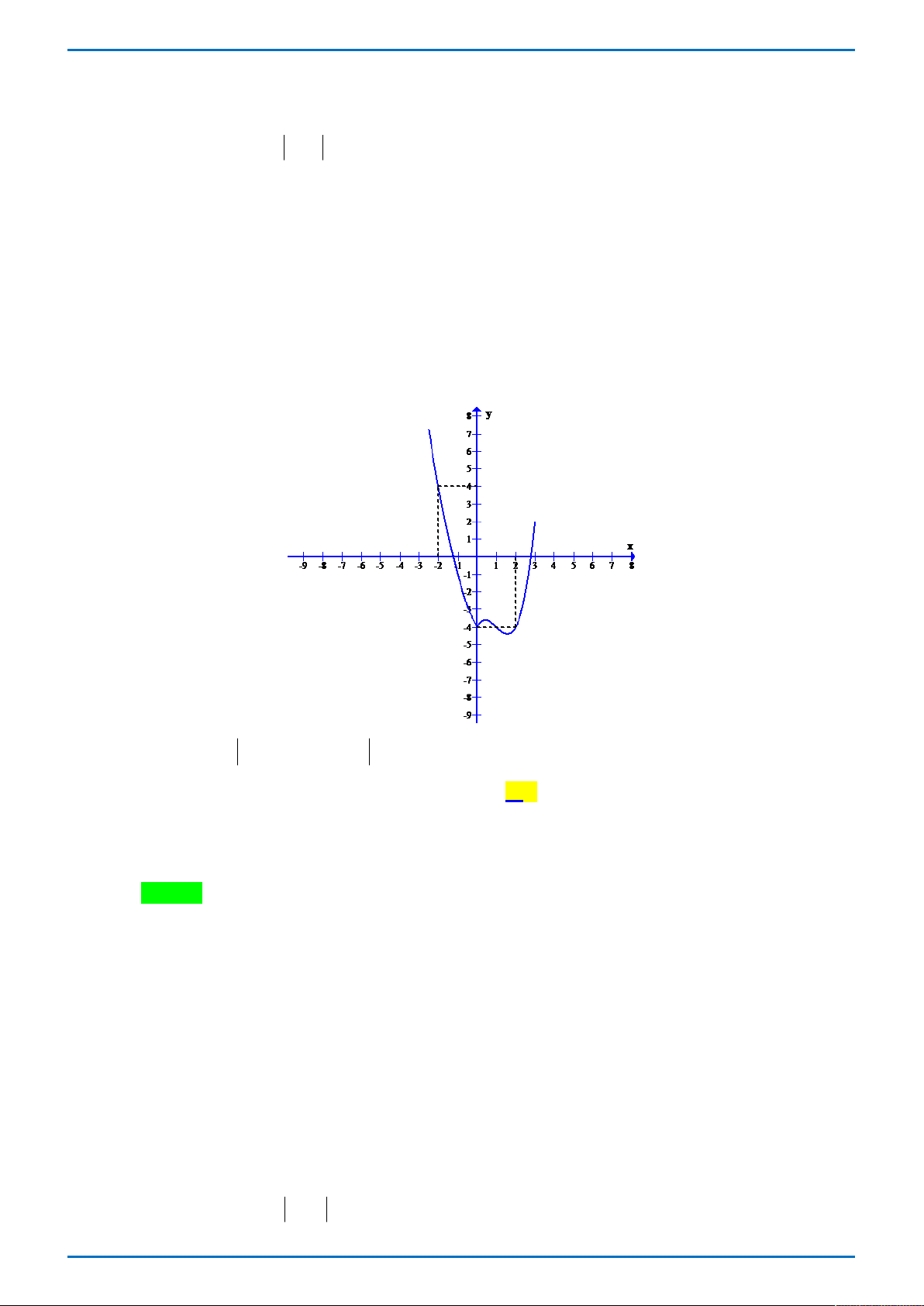
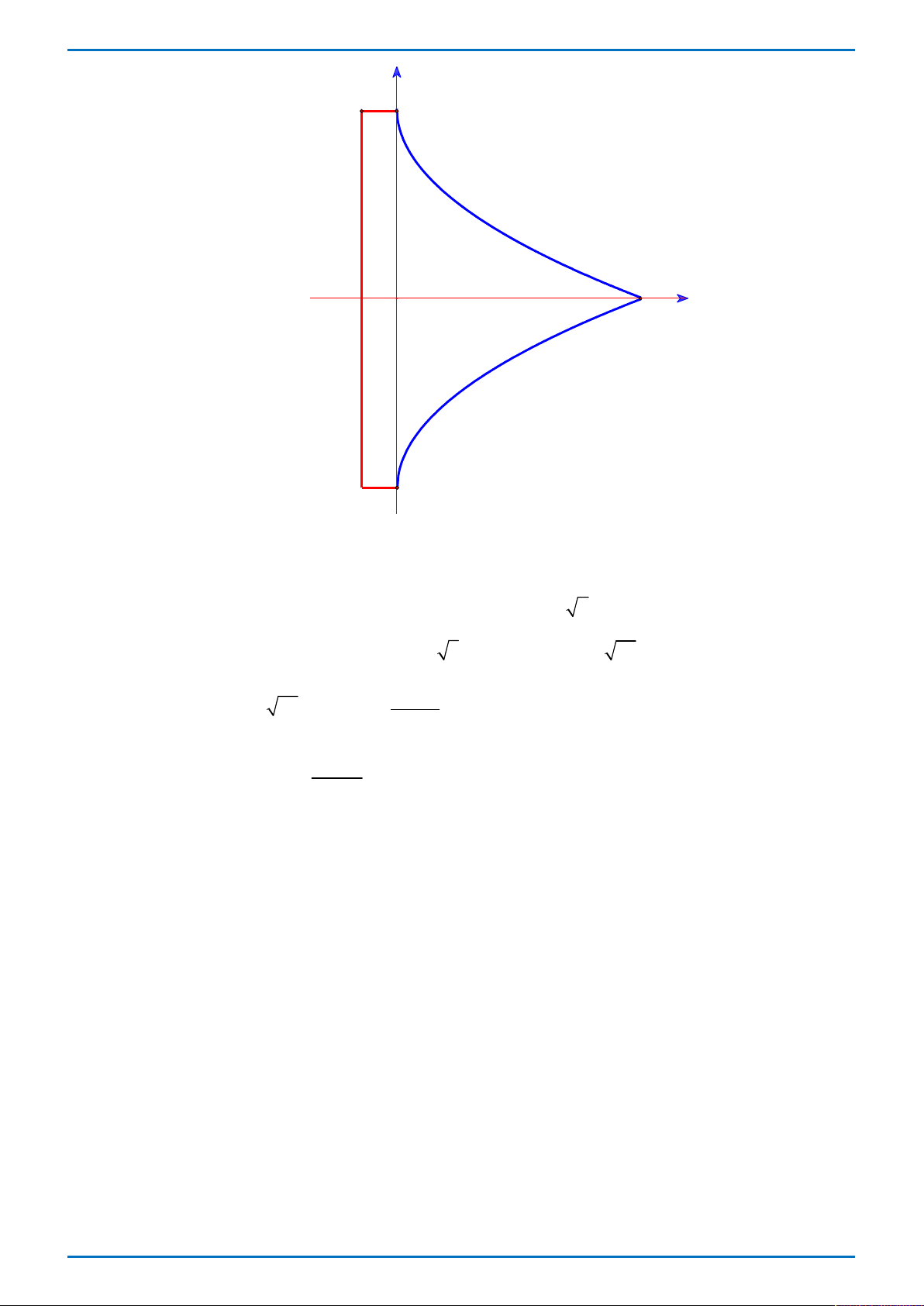
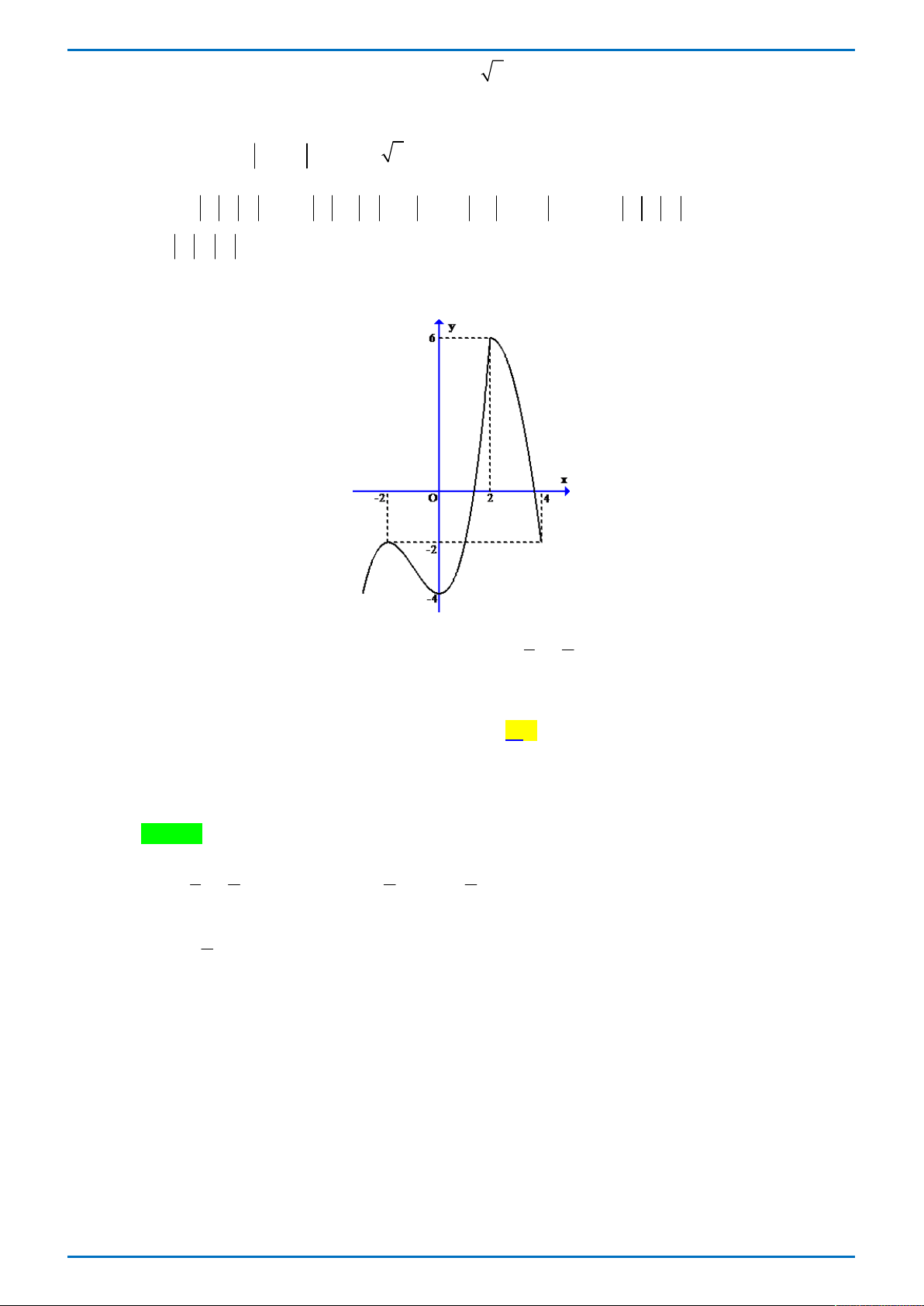
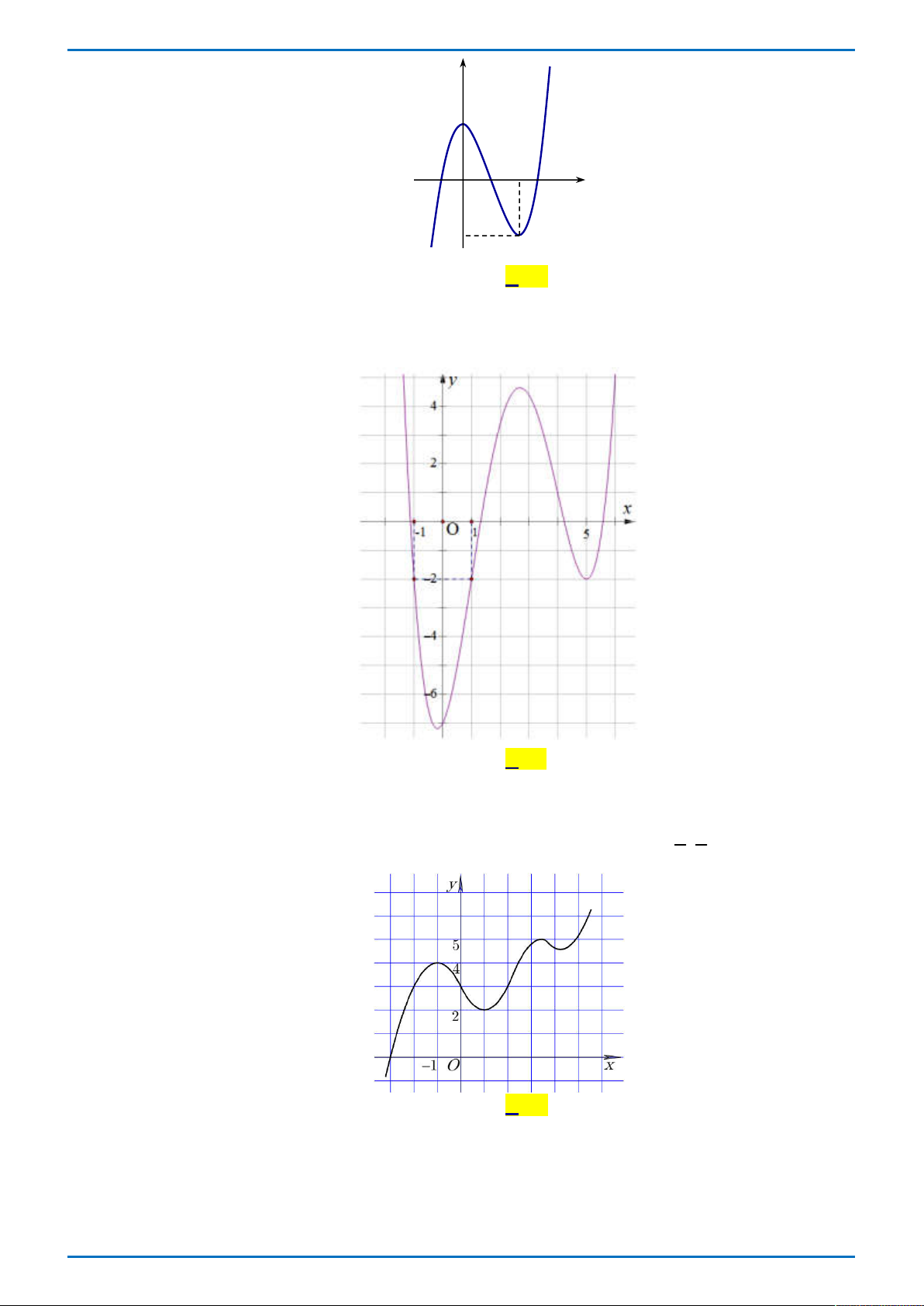
Đường cong ở hình vẽ bên là đồ thị của hàm số nào dưới đây
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 1
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 x 1 x 1 A. 3
y  x  3x 1 . B. y  . C. y  . D. 3 2
y x  3x 1. x 1 x 1 Câu 8.
Trong không gian Oxyz , mặt phẳng  P đi qua điểm M 3; 1; 4 , đồng thời vuông góc với 
giá của vectơ a 1; 1; 2 có phương trình là
A. 3x y  4z 12  0 .
B. 3x y  4z 12  0 .
C. x y  2z 12  0 .
D. x y  2z 12  0 . Câu 9.
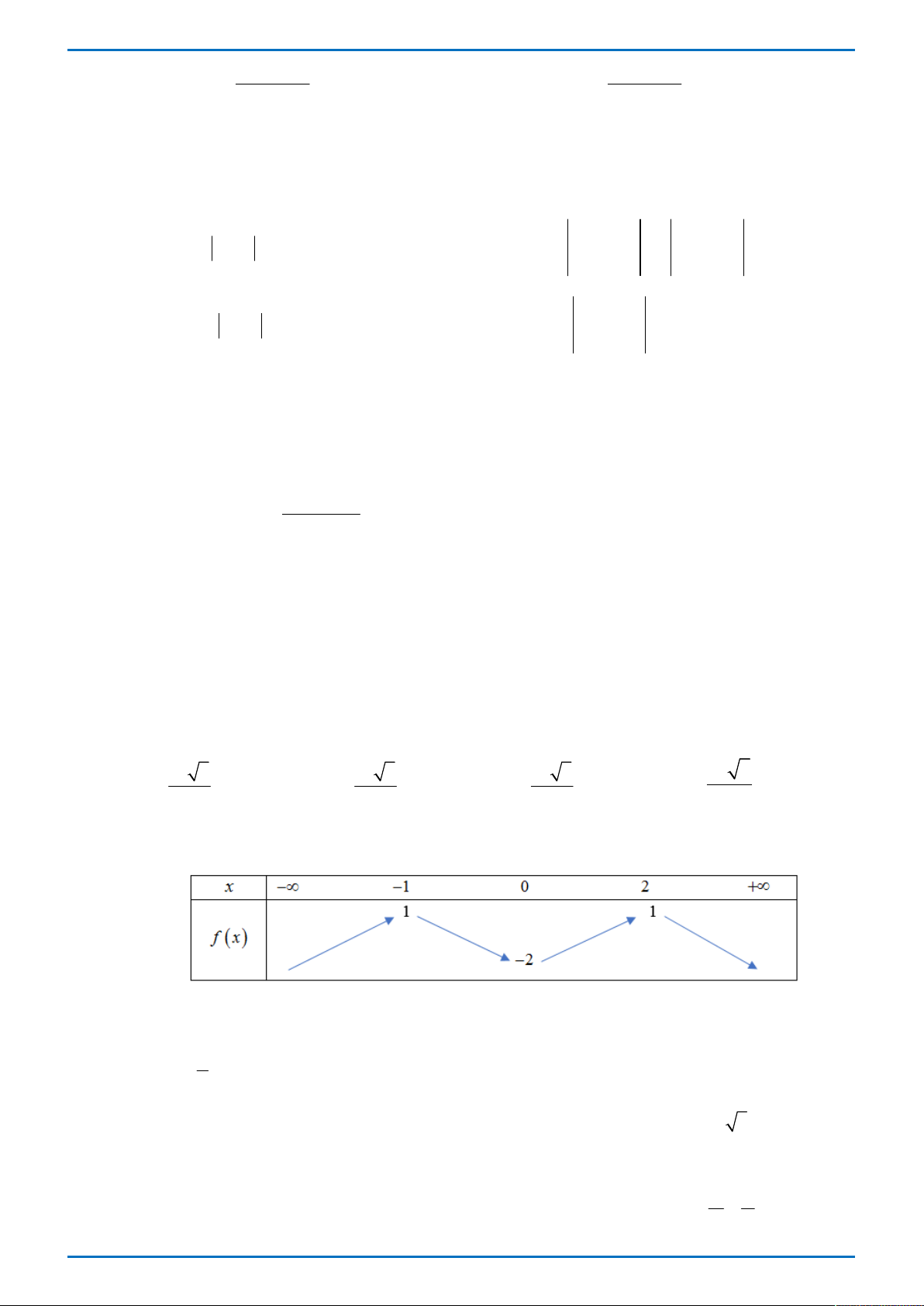
Cho hàm số y f x liên tục trên  3  ; 
3 và có bảng xét dấu đạo hàm như hình bên.
Mệnh đề nào sau đây sai về hàm số đó?
A. Hàm số đạt cực tiểu tại x  1 .
B. Hàm số đạt cực đại tại x  1  .
C. Hàm số đạt cực đại tại x  2 .
D. Hàm số đạt cực tiểu tại x  0 .
Câu 10. Giả sử f x là một hàm số bất kì liên tục trên khoảng ;   và a,b , c , b c ;   . Mệnh đề nào sau đây sai? b c b b bc c A.
f x dx f x dx f x dx    . B.
f x dx
f x dx f x dx    . a a c a a a b bc b b c c C.
f x dx
f x dx
f x dx    . D.
f x dx f x dx f x dx    . a a bc a a b
Câu 11. Cho hàm số y f x có đồ thị như hình vẽ bên. Mệnh đề nào
sau đây đúng về hàm số đó?
A. Nghịch biến trên khoảng  1  ;  0 .
B. Đồng biến trên khoảng  3   ;1 .
C. Đồng biến trên khoảng 0  ;1 .
D. Nghịch biến trên khoảng 0; 2.
Câu 12. Tất cả các nguyên hàm của hàm số ( ) 3 x f x   là
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 2
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 3x 3x A.   C .
B. 3 x C .
C. 3 x ln 3  C . D.  C . ln 3 ln 3
Câu 13. Phương trình log  x   1  2 có nghiệm là A. 11. B. 9 . C.101. D. 99 .
Câu 14. Cho k , n k n là các số nguyên dương bất kì. Mệnh đề nào sau đây đúng? n k ! n k ! A. A  . B. k
A k !. k C . C. A  . D. k
A n!. k C . n k ! n n n n n
k!n k !
Câu 15. Cho các số phức z  1
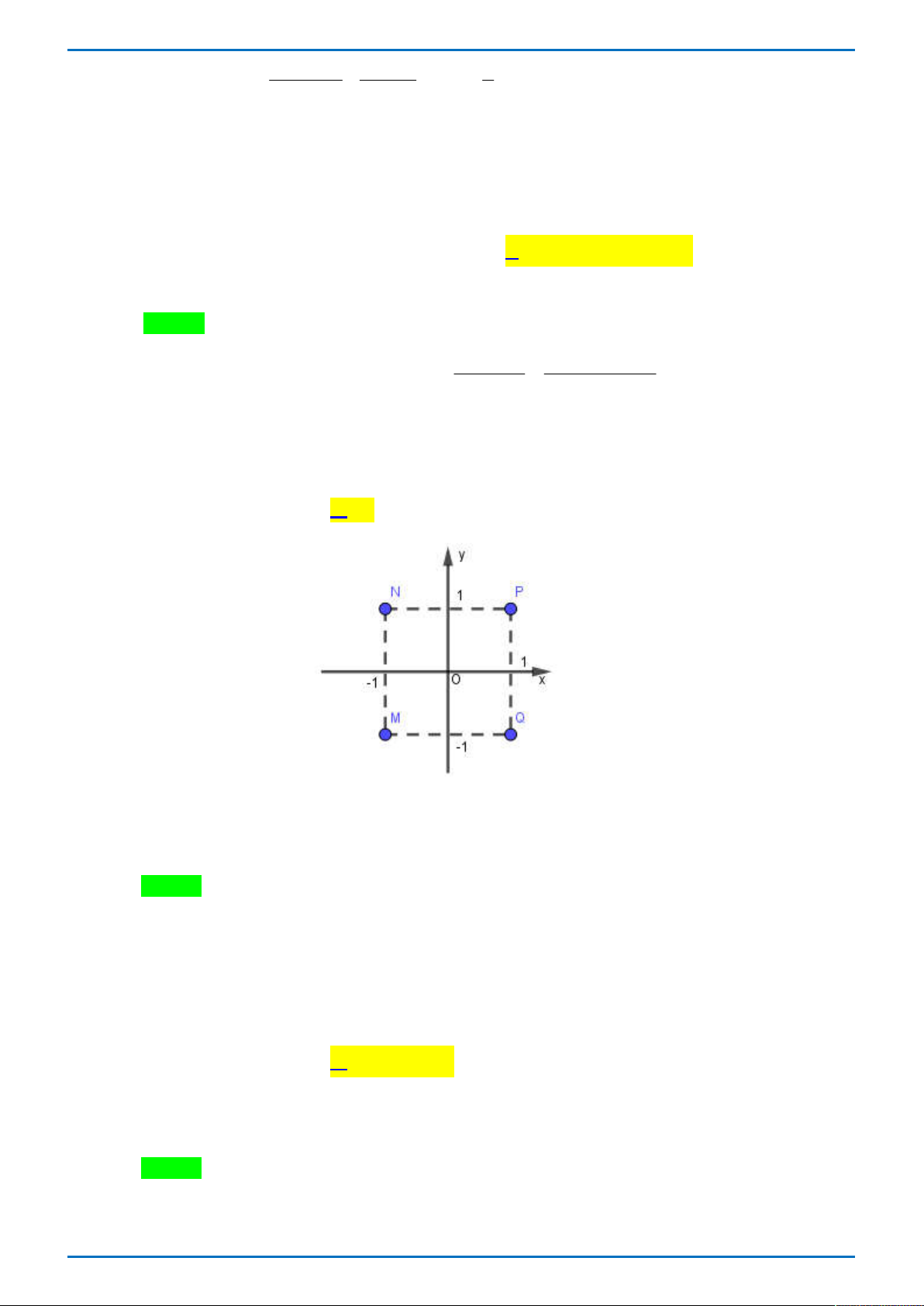
  2i, w  2  .
i Điểm nào trong hình bên biểu diễn số phức z  w ? A. N . B. P . C. Q . D. M . Câu 16. Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng
P : x  3y  2z 1  0, Q : x z  2  0 . Mặt phẳng   vuông góc với cả P và Q đồng
thời cắt trục Ox tại điểm có hoành độ bằng 3. Phương trình của mp   là:
A. x y z 3  0 .
B. x y z  3  0 . C.2x z  6  0 .
D.2x z  6  0 .
Câu 17. Cho số phức z thỏa mãn   i2 1 3
z  4  3i . Môđun của z bằng 5 5 2 4 A. . B. . C. . D. . 4 2 5 5
Câu 18. Một hình trụ tròn xoay có độ dài đường sinh bằng đường kính đáy và thể tích của khối trụ bằng
16 . Diện tích toàn phần của khối trụ đã cho bằng A. 16 . B. 12 . C. 8 . D. 24 .
Câu 19. Biết rằng phương trình 2
log x  7 log x  9  0 có 2 nghiệm x , x . Giá trị x x bằng 2 2 1 2 1 2 A.128 . B. 64 . C. 9. D. 512 . 3x 1
Câu 20. Đạo hàm của hàm số f (x)  là: 3x 1 2 2 x x A. f (  x)   .3 . B. f (  x)  .3 . 3x  2 1 3x  2 1
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 3
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 2 2 x x C. f (  x)  .3 ln 3 . D. f (  x)   .3 ln 3 . 3x  2 1 3x  2 1
Câu 21. Cho f x 4 2
x  5x  4 . Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị hàm số
y f x và trục hoành. Mệnh đề nào sau đây sai ? 2 1 2 A. S f   x dx . B. S  2 f
  xdx  2 f
  xdx . 2 0 1 2 2 C. S  2 f
  x dx . D. S  2 f
  xdx . 0 0
Câu 22. Cho hàm số y f x  có đạo hàm f  x 2  x  2 x  
1 , x   . Hàm số y  2 f x đồng biến trên khoảng A. 2;  . B.  ;    1 . C. 1;  1 . D. 0;2 . 3 x  4x
Câu 23. Đồ thị hàm số y
có bao nhiêu đường tiệm cận? 3 x  3x  2 A. 4 . B. 1. C. 3 . D. 2 .
Câu 24. Biết rằng ,  là các số thực thỏa mãn 2 2  2   82  2  . Giá trị của   2 bằng A. 1. B. 2. C. 4. D. 3.
Câu 25. Cho hình lăng trụ tam giác đều ABC.A ' B 'C ' có AB a , góc giữa đường thẳng A'C và mặt
đáy bằng 450. Tính thể tích khối lăng trụ ABC.A ' B 'C ' . 3 3 a 3 3 a 3 3 a 3 a 3 A. . B. . C. . D. . 4 2 12 6
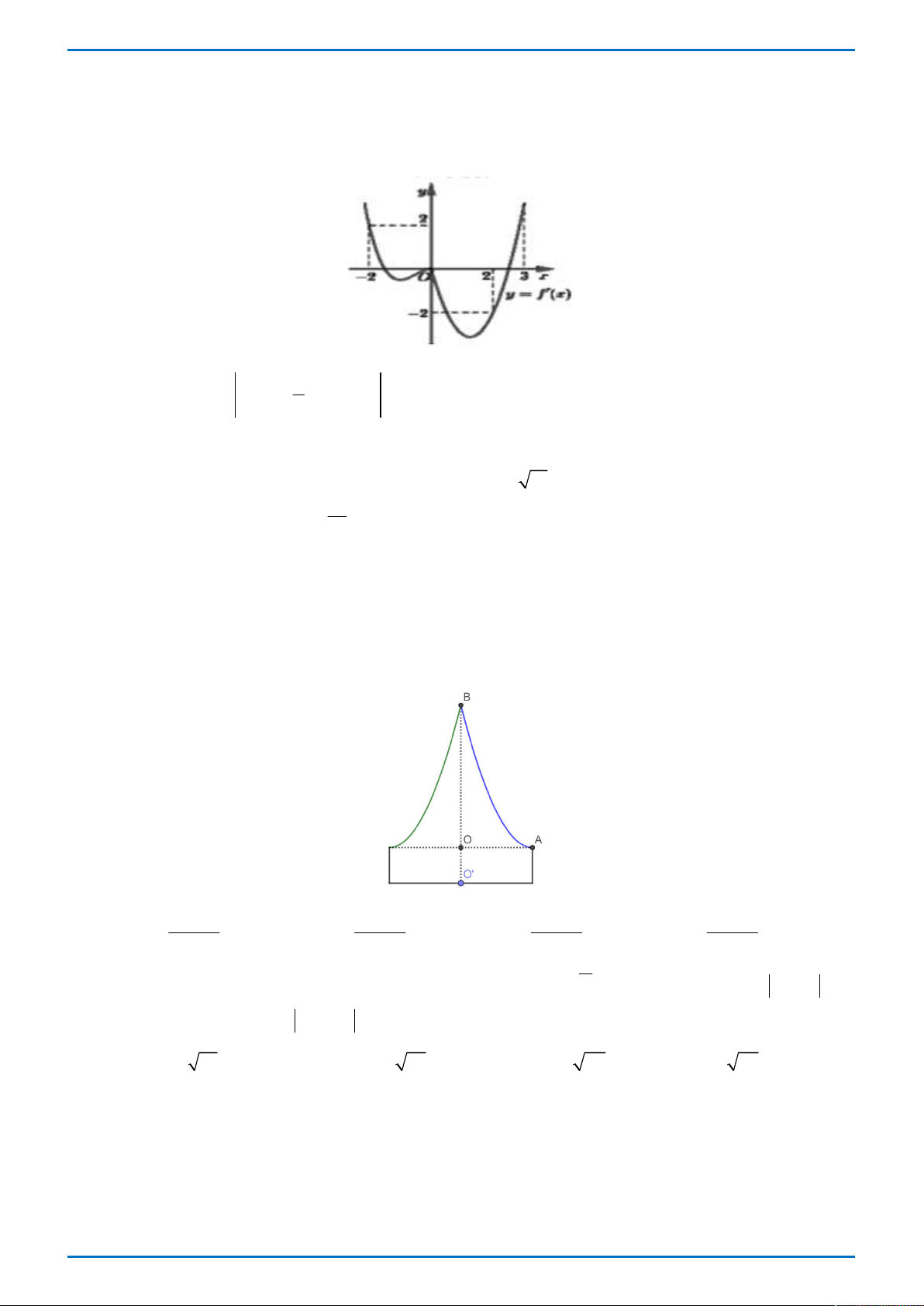
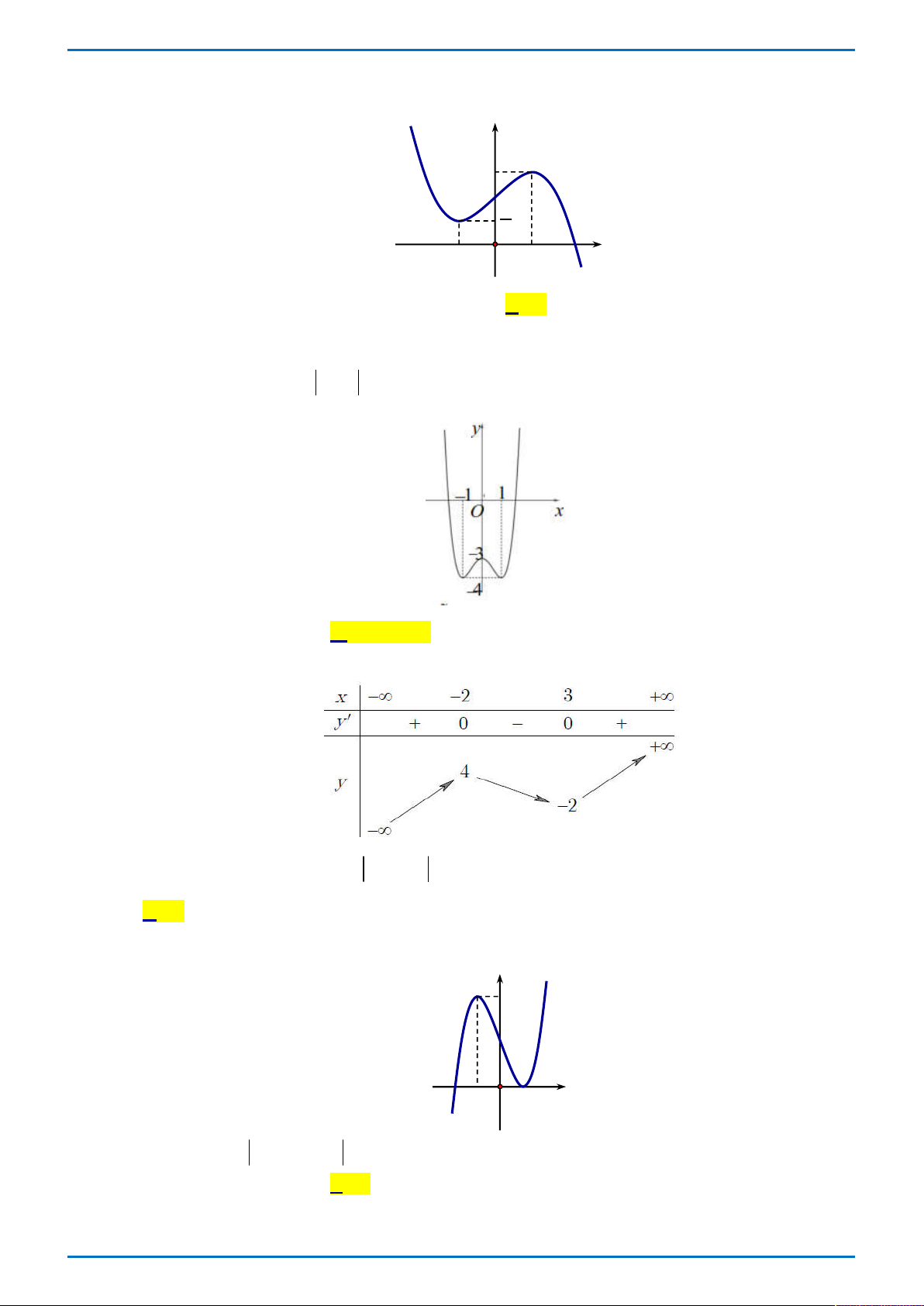
Câu 26. Cho hàm số y f x có bảng biến thiên như hình vẽ bên dưới.
Hàm số y f 2x đạt cực đại tại 1 A. x  . B. x  1  . C. x  1 . D. x  2  . 2
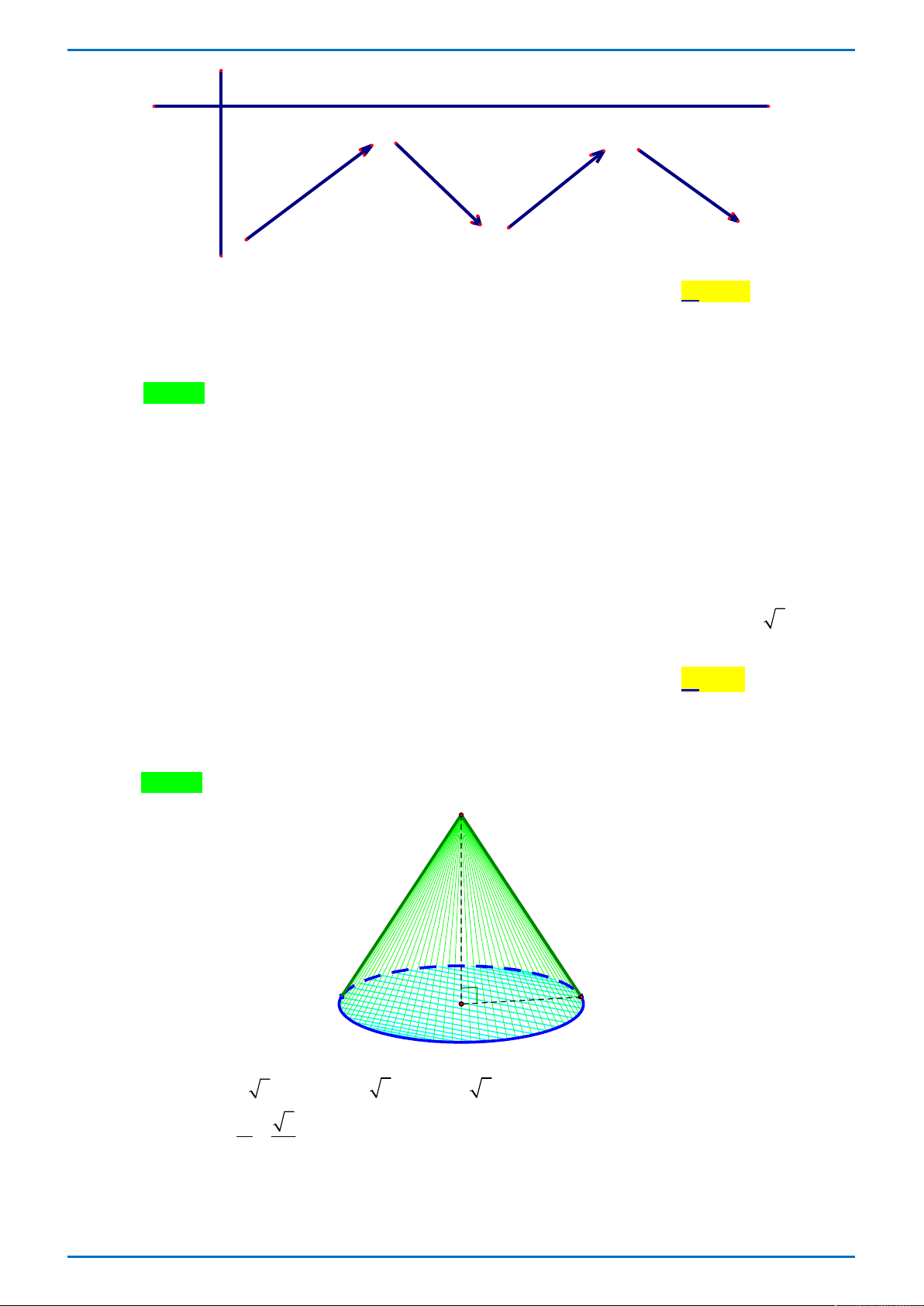
Câu 27. Cho hình nón tròn xoay có bán kính bằng 3 và diện tích xung quanh bằng 6 3 . Góc ở đỉnh
của hình nón đã cho bằng A. 60 . B. 150 . C. 90 . D. 120 .
Câu 28. Gọi z , z là các nghiệm phức của phương trình 2
z  4z  7  0 . Số phức z z z z bằng 1 2 1 2 1 2
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 4
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 A. 2 . B. 10 . C. 2i . D. 10i . 9
Câu 29. Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y x  trên đoạn 1; 4 . x
Giá trị của m M bằng 65 49 A. . B.16 . C. . D.10 . 4 4
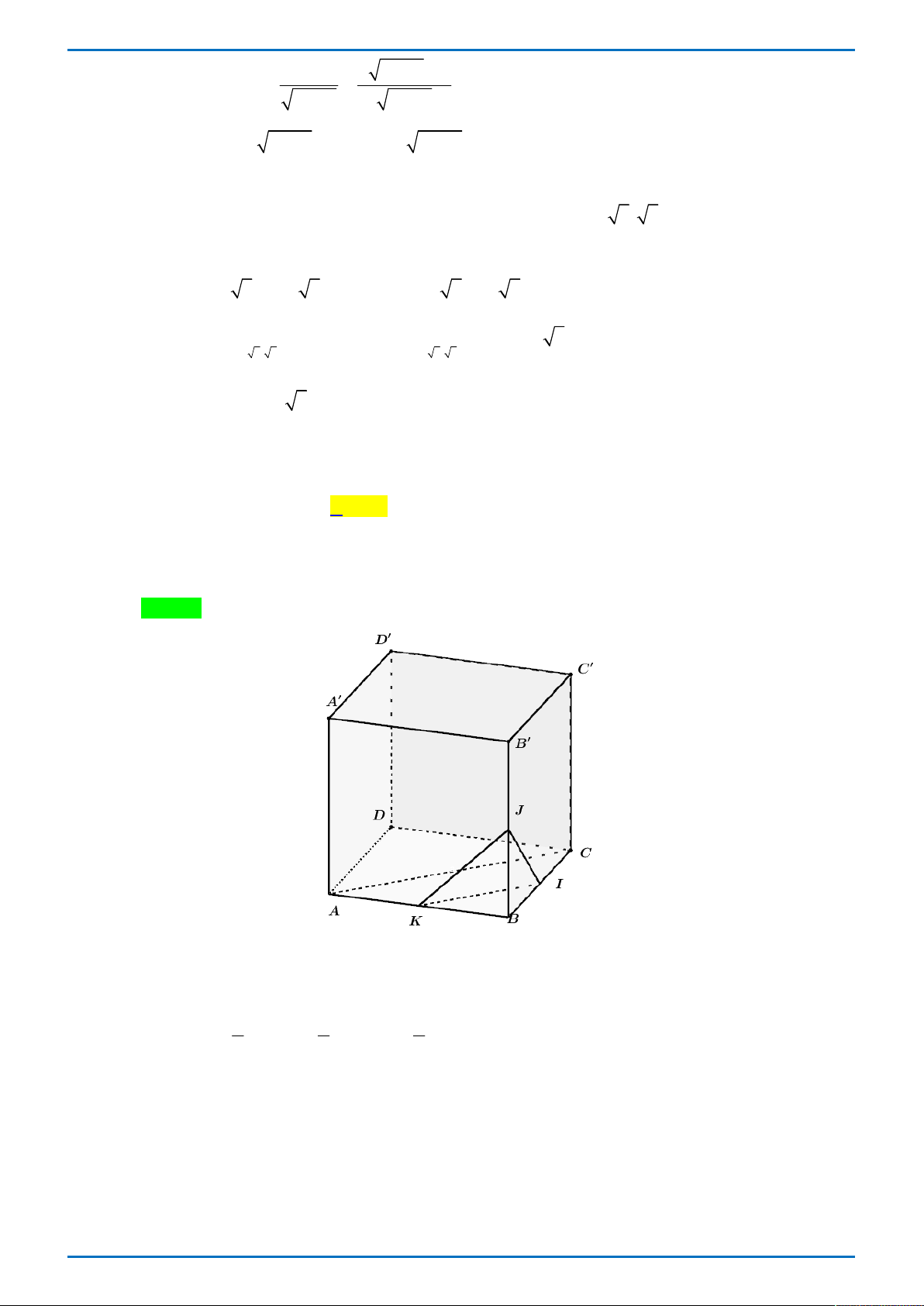
Câu 30. Cho hình lập phương ABC . D A BCD
  có I , J tương ứng là trung điểm của BC và BB . Góc
giữa hai đường thẳng AC và IJ bằng A. 45. B. 60 . C. 30 . D. 120 .
Câu 31. Giải bóng chuyền quốc tế VTV Cup có 8 đội tham gia, trong đó có hai đội Việt Nam. Ban tổ
chức bốc thăm ngẫu nhiên để chia thành hai bảng đấu, mỗi bảng 4 đội. Xác suất để hai đội của
Việt Nam nằm ở hai bảng khác nhau bằng 2 5 3 4 A. . B. . C. . D. . 7 7 7 7 x
Câu 32. Tất cả các nguyên hàm của hàm số f x 
trên khoảng 0;  là 2 sin x
A. x cot x  ln sinx  C .
B. x cot x  ln s inx C .
C. x cot x  ln s inx C . D. x cot x  ln s inx  C .
Câu 33. Cho hình lăng trụ đứng ABC. AB C
  có đáy ABC là tam giác vuông tại A. Gọi E là trung
điểm của AB . Cho biết AB  2a , BC  13 a , CC  4a . Khoảng cách giữa hai đường thẳng A B  và CE bằng 4a 12a 6a 3a A. . B. . C. . D. . 7 7 7 7
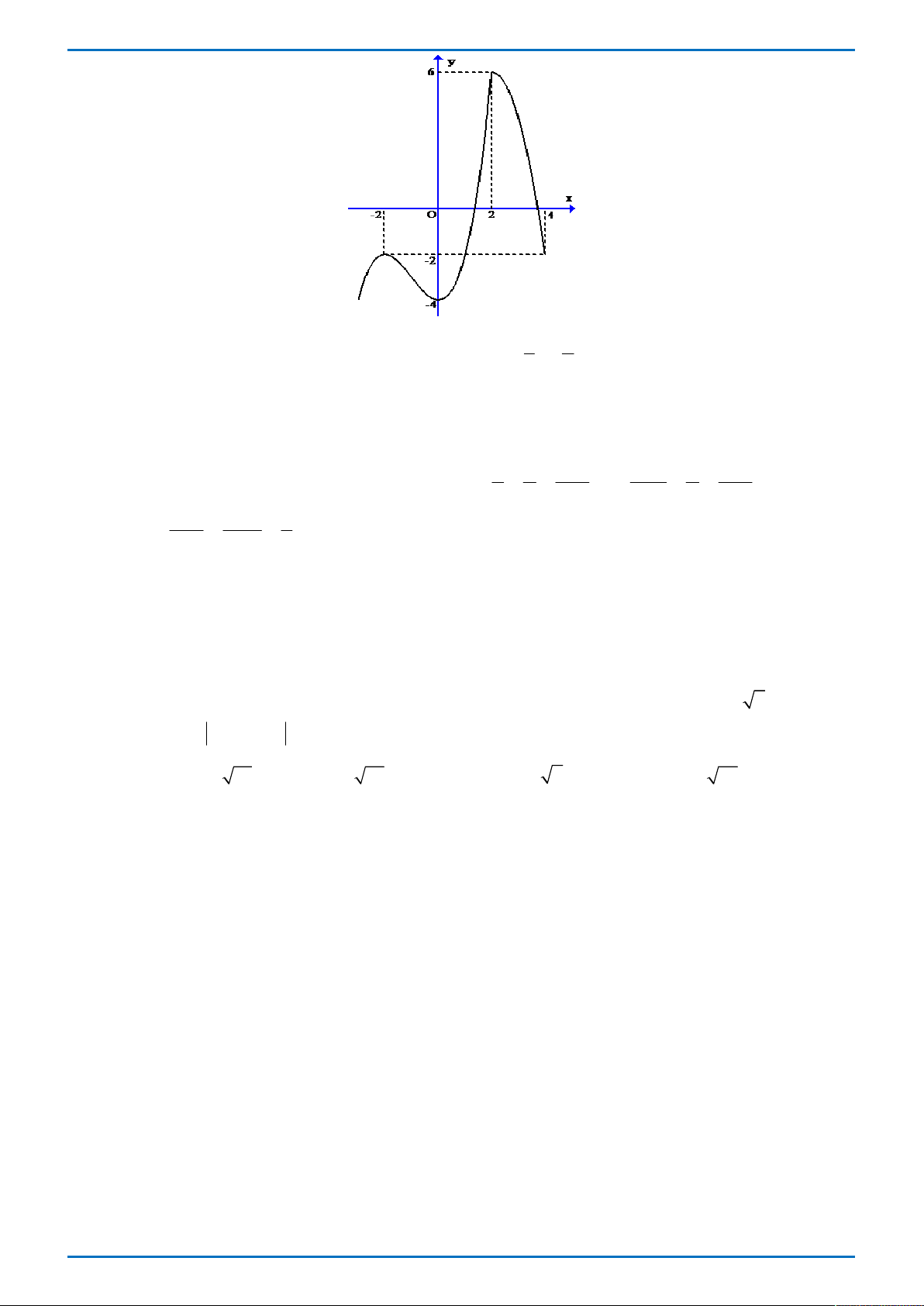
Câu 34. Cho hàm số y f x có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên m để phương trình f  3
x  3x  m có 6 nghiệm phân biệt thuộc đoạn  1  ; 2? A. 3 . B. 2 . C. 6 . D. 7 . 2
Câu 35. Có bao nhiêu số phức z thỏa mãn z
z z i   z z 2019 1 i  1 ? A. 4. B. 2. C. 1. D. 3.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 5
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
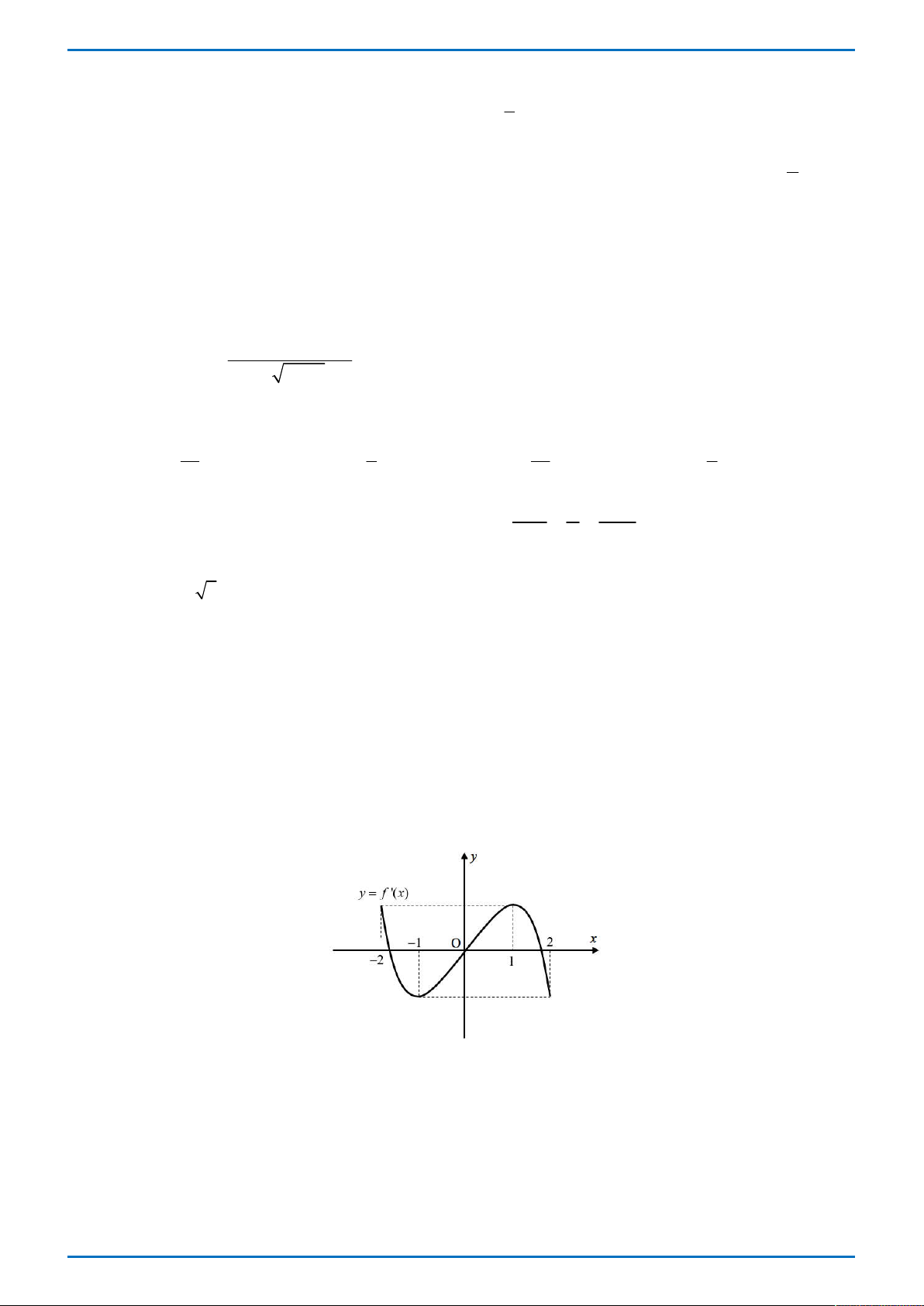
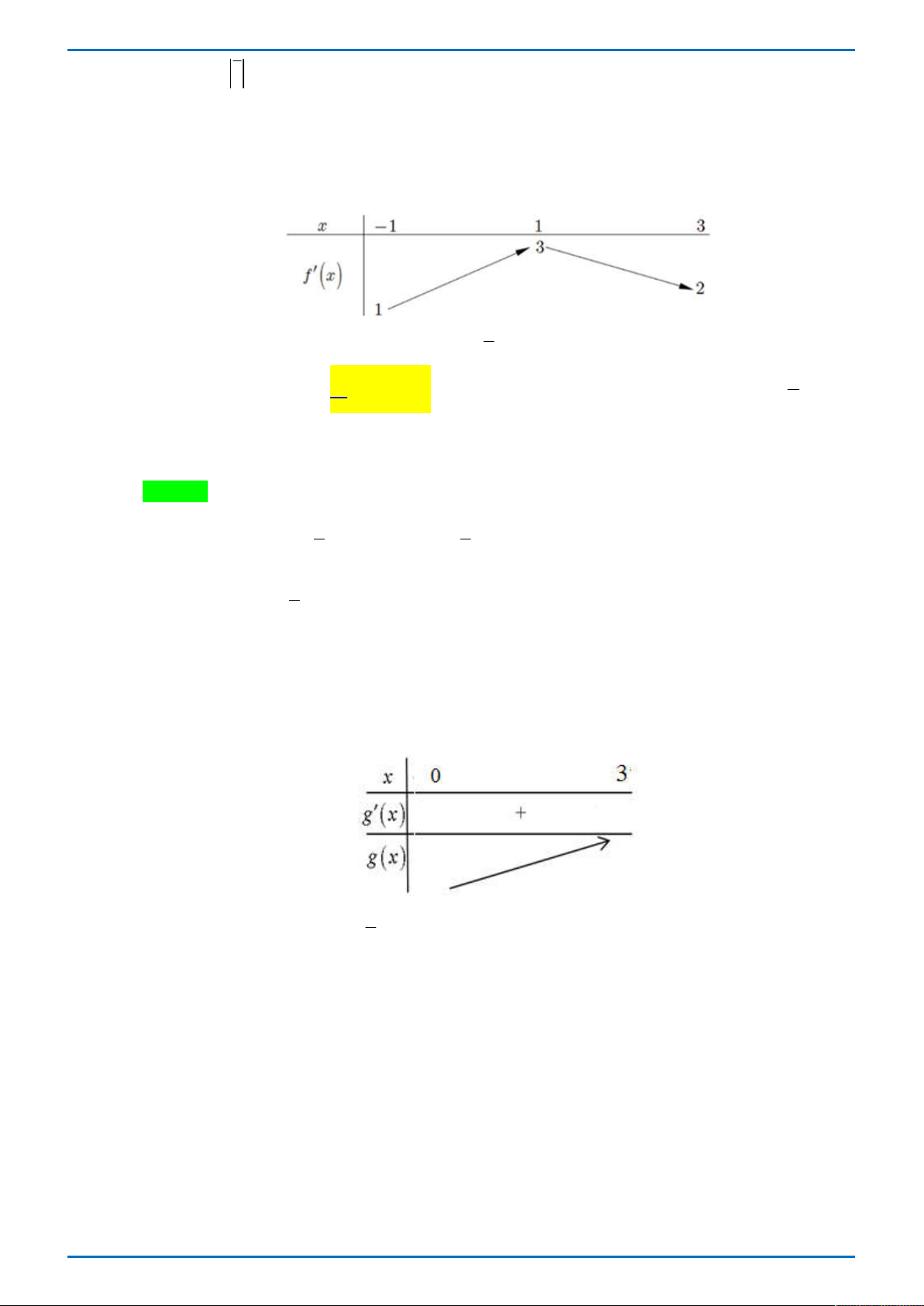
Câu 36. Cho f x mà hàm số y f ' x có bảng biến thiên như hình vẽ bên. Tất cả các giá trị của 1
tham số m để bất phương trình 2
m x f x 3 
x nghiệm đúng với mọi x 0;3 là 3 2
A. m f 0 .
B. m f 0 .
C. m f 3 .
D. m f   1  . 3
Câu 37. Trong không gian Oxyz , cho các điểm M (2;1; 4) , N (5; 0; 0) , P(1; 3
 ;1). Gọi I (a; ; b c) là tâm của
mặt cầu tiếp xúc với mặt phẳng Oyz đồng thời đi qua các điểm M , N , P . Tìm c biết rằng
a b c  5 . A. 3. B. 2. C. 4. D. 1. 1 dx Câu 38. Biết rằng
a ln 2  b ln 3  c ln 5  , với a, ,
b c là các số hữu tỉ.
3x  5 3x 1  7 0
Giá trị của a b c bằng 10 5 10 5 A.  . B.  . C. . D. . 3 3 3 3 x 1 y z  2
Câu 39. Trong không gian Oxyz , cho đường thẳng d :   và hai điểm ( A 1  ;3;1) và 2 1 1  B 0;2;  1 . Gọi C  ; m ;
n p là điểm thuộc đường thẳng d sao cho diện tích tam giác ABC
bằng 2 2 . Giá trị của tổng m n p bằng A. 1. B. 2 . C. 3 . D. 5 .
Câu 40. Bất phương trình  3
x  9xln  x  5  0 có bao nhiêu nghiệm nguyên ? A. 4 . B. 7 . C. 6 . D. Vô số.
Câu 41. Cho hàm số f (x) có đồ thị hàm y f '(x) như hình vẽ. Hàm số 2
y f (cos x)  x x đồng biến trên khoảng A. 1;2 . B.  1  ;0 . C. 0;  1 . D.  2  ;   1 . Câu 42. Cho hàm số ( ) 2x 2 x f x   
. Gọi m là số lớn nhất trong các số nguyên m thỏa mãn 0 12
f (m)  f (2m  2 )  0 . Mệnh đề nào sau đây đúng? A. m  1513; 2019 .
B. m  1009;1513 . C. m  505;1009 . D. m  1;505 . 0   0   0   0  
Câu 43. Cho hàm số f x thỏa mãn       ex f x f x , x
   và f 0  2 . Tất cả các nguyên hàm của   2 e x f x là
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 6
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
A.   2 ex  ex xC . B.    2 2 e x  ex xC . C.    1 ex xC . D.    1 ex xC .
Câu 44. Cho hàm số f x có đồ thị hàm số y f  x được cho như hình vẽ bên. 1
Hàm số y f x 2 
x f 0 có nhiều nhất bao nhiêu điểm cực trị trong khoảng  2  ;3 . 2 A.6. B.2. C.5. D.3
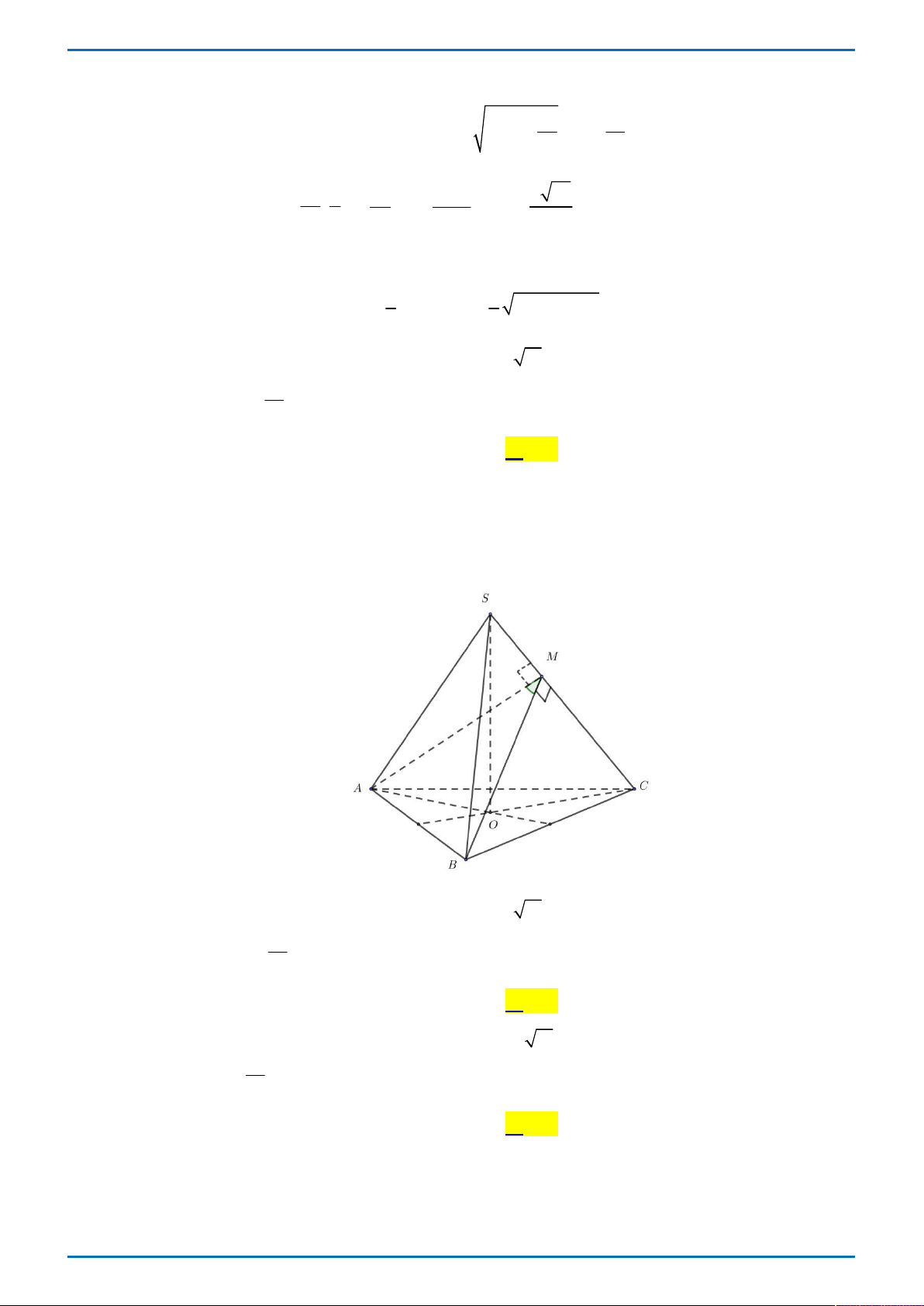
Câu 45. Cho hình chóp tứ giác đều S.ABCD có SA a 11 , cosin của góc hợp bởi hai mặt phẳng 1
SBC và SCD bằng
. Thể tích của khối chóp S.ABCD bằng 10 A. 3 3a . B. 3 9a . C. 3 4a . D. 3 12a .
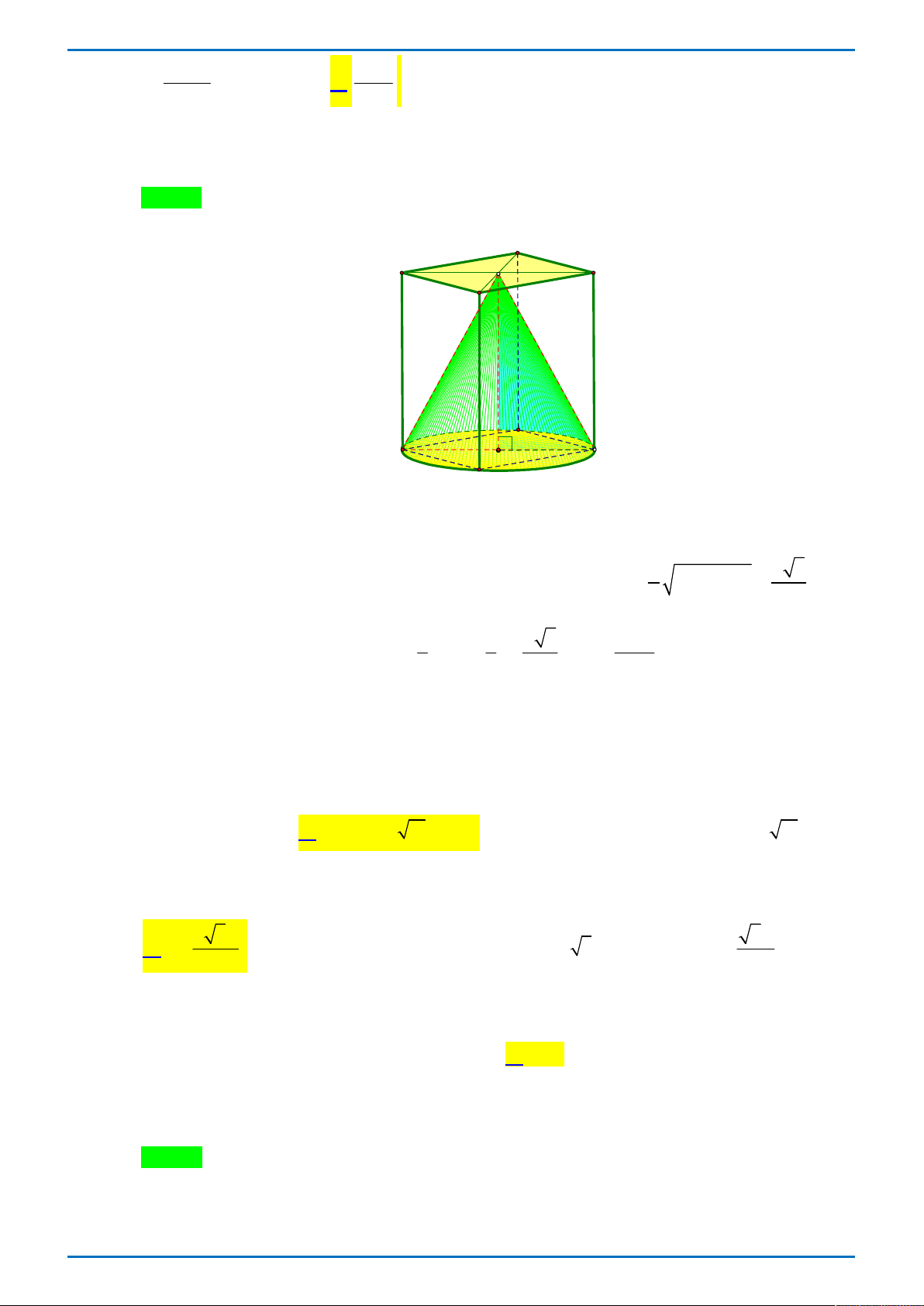
Câu 46. Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách
điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ
bên dưới. Biết rằng OO  5 cm , OA  10 cm , OB  20 cm , đường cong AB là một phần của
parabol có đỉnh là điểm A . Thể tích của chiếc mũ bằng 2750 2500 2050 2250 A.  3 cm  . B.  3 cm  . C.  3 cm  . D.  3 cm  . 3 3 3 3
Câu 47. Giả sử z , z là hai trong các số phức thỏa mãn  z  68  zi là số thực. Biết rằng z z  4 , 1 2 1 2
giá trị nhỏ nhất của z  3z bằng 1 2 A. 5  21 . B. 20  4 21 . C. 20  4 22 . D. 5  22 .
Câu 48. Cho hàm số y f x có đồ thị như hình vẽ.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 7
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 1  x
Có bao nhiêu số nguyên m để phương trình f 1  x m   có nghiệm thuộc đoạn 3  2   2  ; 2 ? A. 11. B. 9. C. 8. D. 10. x y z 1 x  3 y z 1
Câu 49. Trong không gian Oxyz cho ba đường thẳng d :   ,  :   , 1 1 2  1 2 1 1 x 1 y  2 z  :  
. Đường thẳng  vuông góc với d đồng thời cắt  ,  tương ứng 2 1 2 1 1 2 
tại H , K sao cho độ dài HK nhỏ nhất. Biết rằng  có một vectơ chỉ phương u  ; h k;  1 . Giá trị h k bằng A. 0. B. 4. C. 6. D. 2  . 
Câu 50. Trong không gian Oxyz , cho a 1;  1;0 và hai điểm A 4  ;7; 
3 , B 4;4;5 . Giả sử M , N là hai  
điểm thay đổi trong mặt phẳng Oxy sao cho MN cùng hướng với a và MN  5 2 . Giá trị lớn
nhất của AM BN bằng A. 17 . B. 77 . C. 7 2  3 . D. 82  5 .
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 8
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
PHÂN TÍCH – BÌNH LUẬN – PHÁT TRIỂN ĐỀ THI THỬ ĐẠI HỌC VINH LẦN 1 NĂM 2018 -2019 Câu 1.
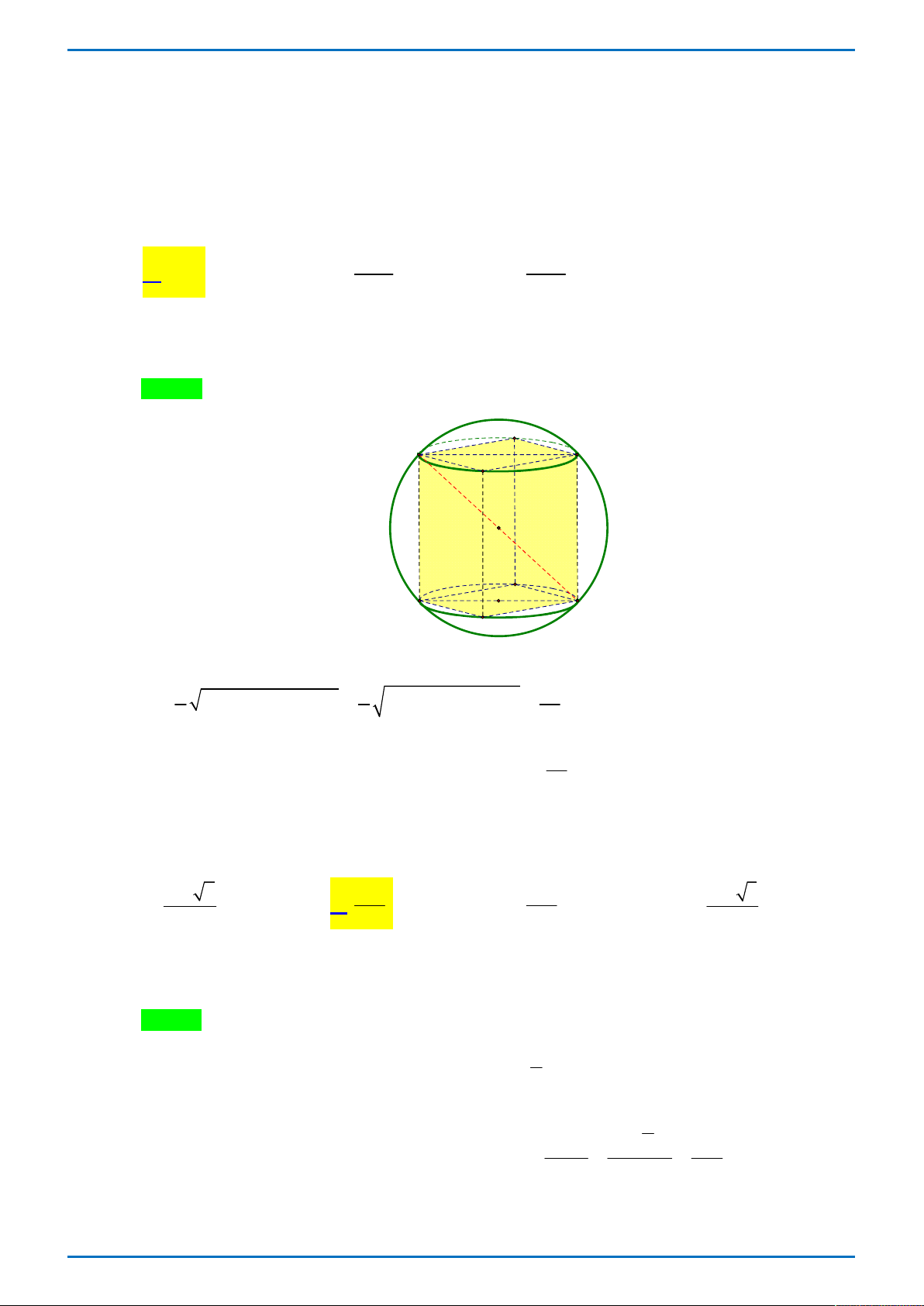
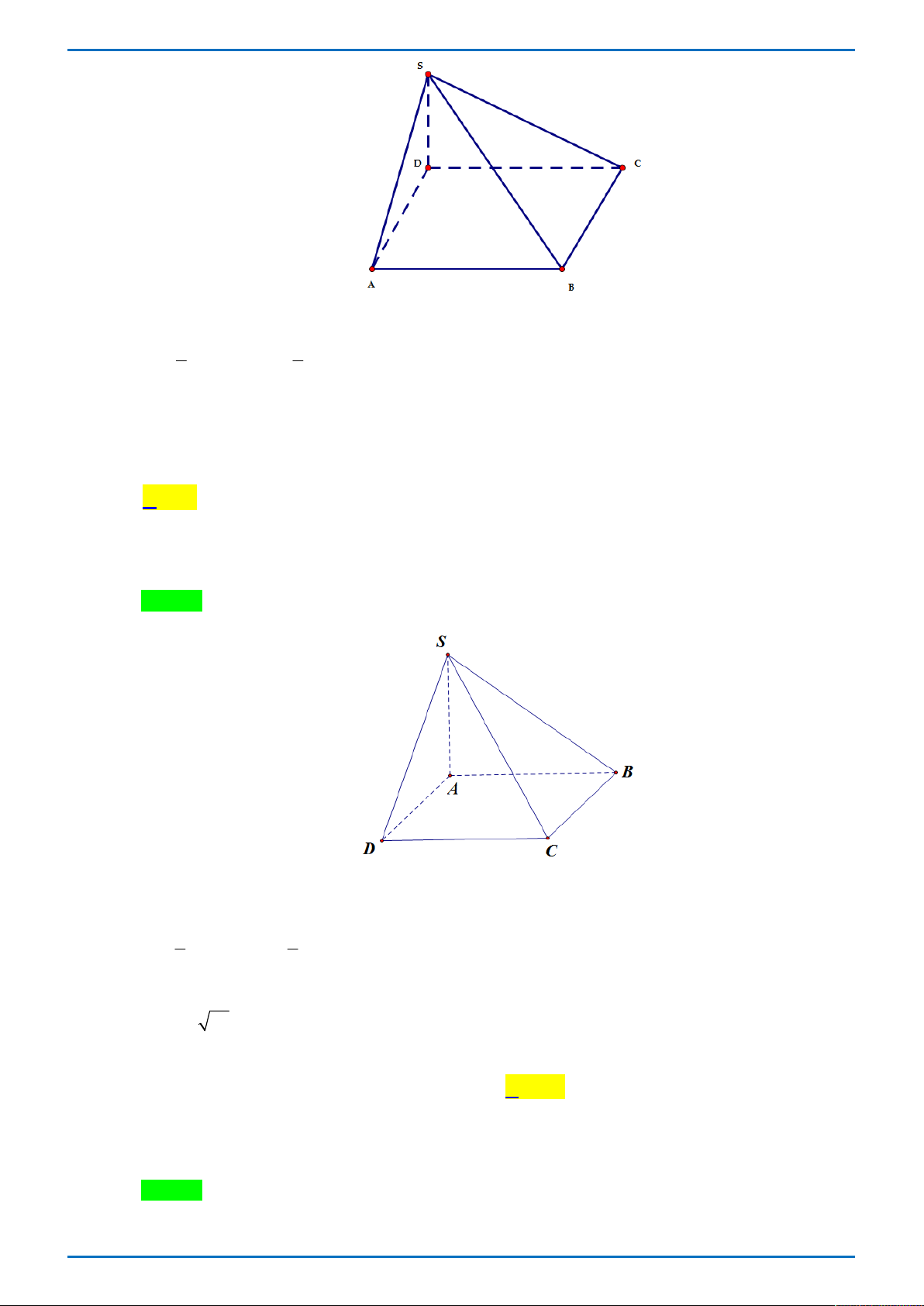
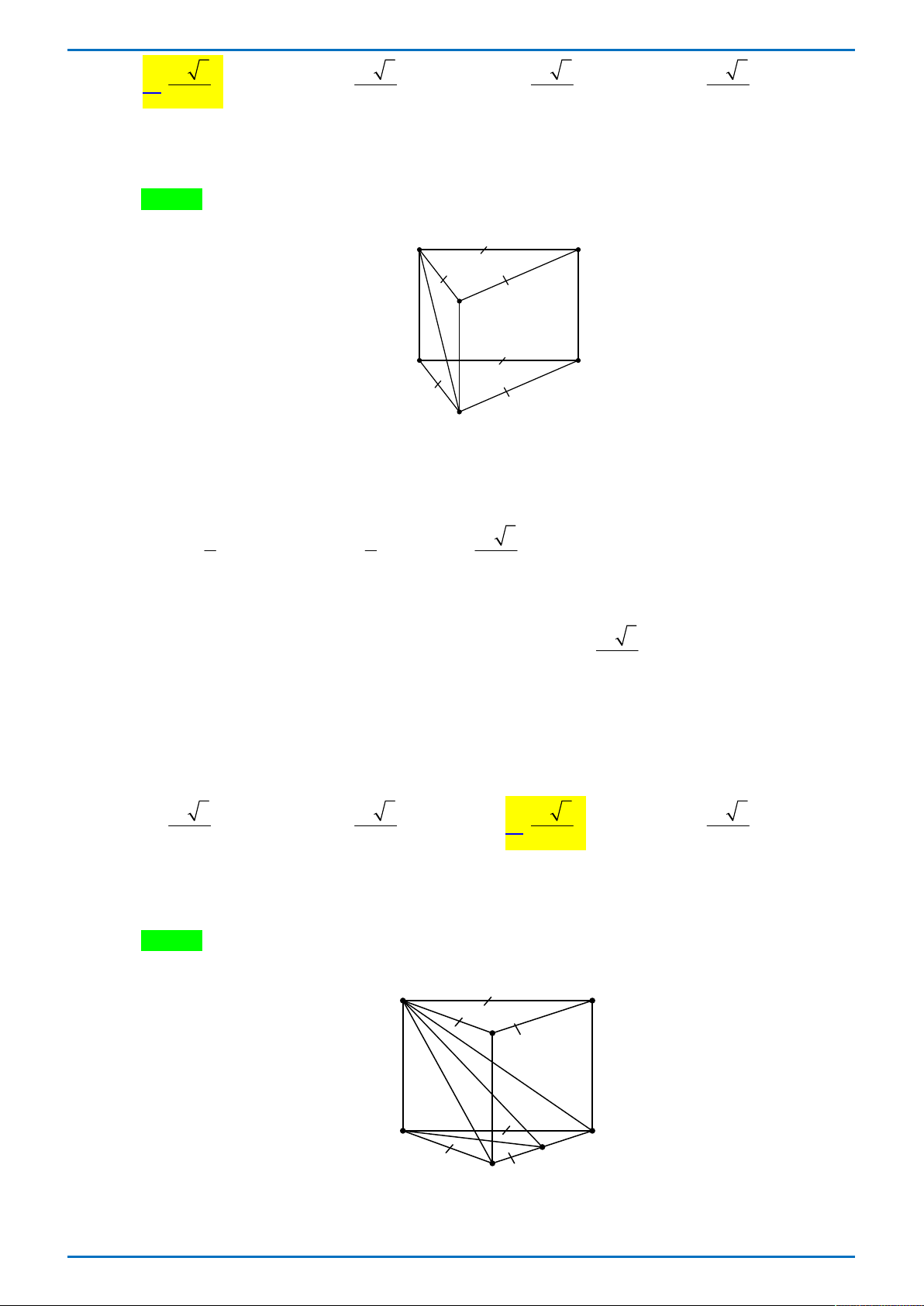
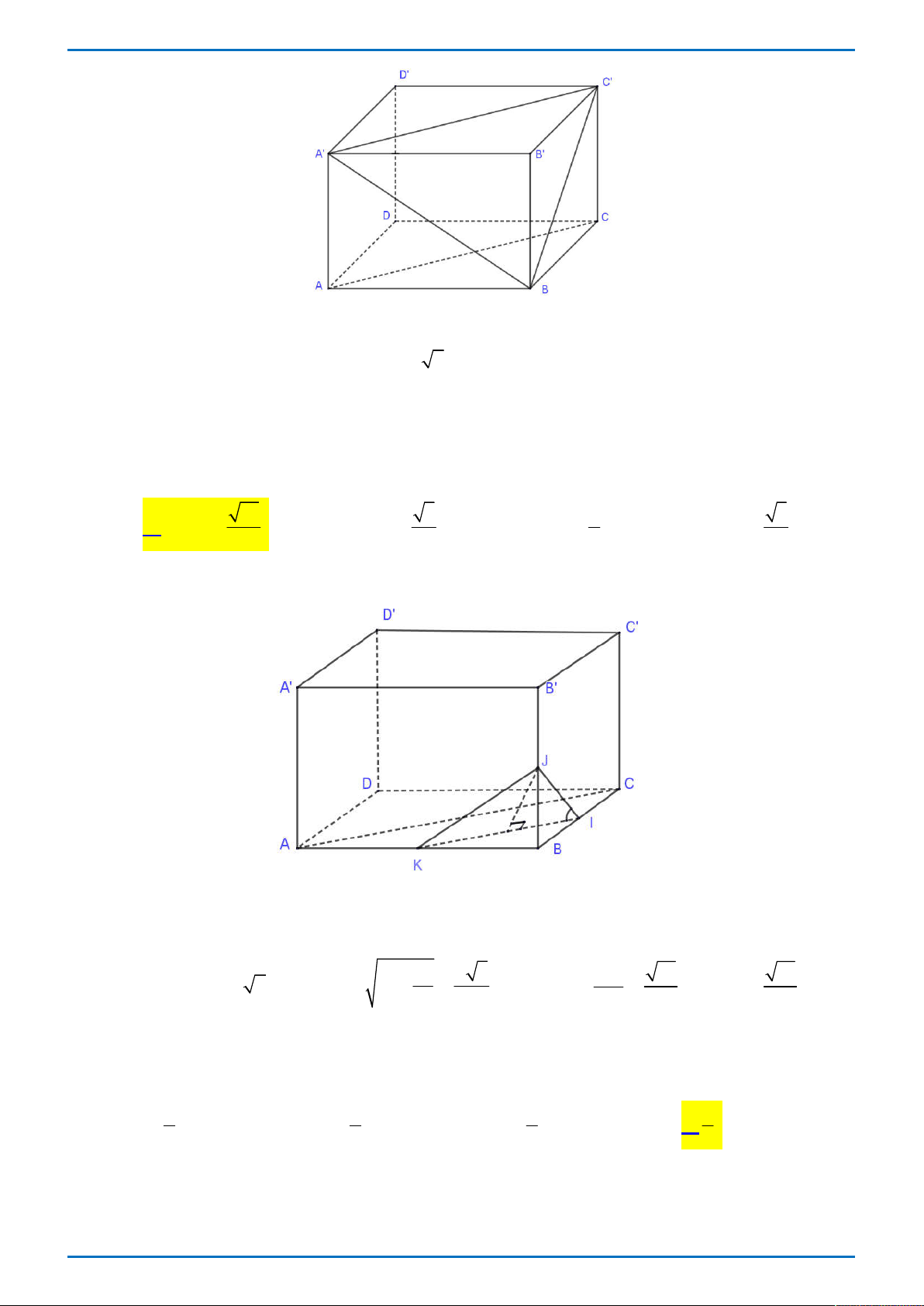
Cho hình hộp chữ nhật ABC . D A BCD
  có AB a , AD AA  2a . Diện tích mặt cầu ngoại
tiếp hình hộp đã cho bằng 2 3 a 2 9 a A. 2 9 a . B. . C. . D. 2 3 a . 4 4 Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường Chọn A D' A' C' B' O D A C B
Mặt cầu ngoại tiếp hình hộp chữ nhật ABC . D A BCD
  có tâm là O của hình hộp có bán kính 1 1 3a R
AB AD AA 
a  2a2  2a2 2 2 2 2  . 2 2 2 2  3a
Vậy diện tích mặt cầu ngoại tiếp hình hộp là 2 S  4  9 a   .  2 
Một số bài toán tương tự:
Câu 1.1. Cho hình hình lập phương cạnh a . Thể tích khối cầu nội tiếp hình lập phương là 3  a 2 3  a 3  a 3  a 3 A. . B. . C. . D. . 3 6 2 3 Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường Chọn B a
Khối cầu nội tiếp hình lập phương có bán kính R  . 2 3  a  4 3   3 4 R  2   a
Vậy thể tích khối cầu nội tiếp hình lập phương là V    . 3 3 6
Câu 1.2. Cho hình hộp chữ nhật ABC . D A BCD
  có AB a , AD  2a , AA  3a . Thể tích khối nón có
đỉnh trùng với tâm của hình chữ nhật ABCD , đường tròn đáy ngoại tiếp AB CD   là
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 9
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 3 15 a 3 5 a A. . B. . C. 3 15 a . D. 3 5 a . 4 4 Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường Chọn B D A C O B D' O' C' A' B'
Gọi O, O lần lượt là tâm hình chữ nhật ABCD và hình chữ nhật AB CD   . 1 a 5
Ta có đường cao khối nón h OO  AA  3a ; bán kính r A O    a  2a2 2  . 2 2 2 3 1 1  a 5  5 a
Vậy thể tích khối nón đã cho là 2
V   r h     3a  . 3 3  2  4  
Một số bài toán tương tự trong các đề thi THPTQG:
Câu 1.3. (Mđ 104 –THPTQG 2017) Cho hình hộp chữ nhật ABC . D A BCD
  có AD  8 , CD  6 ,
AC  12. Tính diện tích toàn phần S của hình trụ có hai đường tròn đáy là hai đường tròn tp
ngoại tiếp hình chữ nhật ABCD và A BCD  .
A. S  576 . B. S  10 2 11  5  . C. S  26 .
D. S  5 4 11  5  . tptptp tp
Câu 1.4. (Mđ 110 –THPTQG 2017) Cho mặt cầu bán kính R ngoại tiếp một hình lập phương
cạnh a . Mệnh đề nào dưới đây đúng? 2 3R 3R A. a
. B. a  2 R . C. a  2 3R . D. a  . 3 3 Câu 2.
Cho hình chóp S.ABCD có đáy ABCD hình chữ nhật với AB  3a , BC a , cạnh bên
SD  2a và SD vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng A. 3 3a . B. 3 a . C. 3 2a . D. 3 6a . Lời giải
Tác giả: Nguyễn Thị Thơm; Fb: Thơm nguyễn Chọn C
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 10
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Chiều cao của khối chóp là SD  2a và đáy là hình chữ nhật với AB  3a , BC a nên ta có 1 1 3 V  . . SD . AB BC  .2 .3 a . a a  2a . 3 3
Câu 2.1 . Cho hình chóp S.ABCD có đáy ABCD hình chữ nhật với AB  3a , BC  2a , cạnh bên
SA  2a và SAB và SAD cùng vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng A. 3 4a . B. 3 a . C. 3 12a . D. 3 6a . Lời giải
Tácgiả: Nguyễn Thị Thơm; Fb: Thơm nguyễn Chọn A
Vì  SAB và  SAD cùng vuông góc với mặt phẳng đáy nên SA   ABCD 1 1 3 V  . . SA . AB BC  .2 .3 a .2 a a  4a . 3 3
Câu 2.2 . Cho hình chóp S.ABCD có đáy ABCD hình chữ nhật với AB  3a , AD  4a , cạnh bên
SC a 34 và SAB và SAD cùng vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng A. 3 4a . B. 3 a . C. 3 12a . D. 3 6a . Lời giải
Tácgiả: Nguyễn Thị Thơm; Fb: Thơm nguyễn Chọn D
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 11
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Vì  SAB và  SAD cùng vuông góc với mặt phẳng đáy nên SA   ABCD
Vì ABCD hình chữ nhật nên 2 2 2 2 2 2
AC AB BC  9a 16a  25a AC  5a
SA   ABCD  SA AC suy ra SAC vuông tại A . 2 2 2 2 2 2 2 2 2
AC SA SC SA SC AC  34a  25a  9a SA  3a 1 1 3 V  . . SA . AB BC  .3 .3 a .4 a a  12a . 3 3     Câu 3.
Trong không gian Oxyz cho a 3; 4; 0; b 5; 0;12 . Cosin của góc giữa a và b bằng 3 5 5 3 A. . B. . C.  . D.  . 13 6 6 13 Lời giải
Tácgiả: Quỳnh Giao; Fb: QGiaoDo Chọn D     a b 15 3 cos ;    9 16. 25 144 13    
Câu 3.1. Trong không gian Oxyz cho a 2;3;  
1 ; b 2; 1;3 . Sin của góc giữa a và b bằng 2 3 5 3 5 2 A.  . B. . C.  . D. . 7 7 7 7 Lời giải
Tác giả: Quỳnh Giao; Fb: QGiaoDo Chọn D     a b 4 2 cos ;    4  9 1. 4 1 9 7     sin a;b 3 5 2
 1  cos a;b  7 a Câu 4.
Giả sử a, b là các số thực dương bất kỳ. Biểu thức ln bằng 2 b
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 12
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 1 1 A. ln a  ln b . B. ln a  ln b .
C. ln a  2 ln b .
D. ln a  2 ln b . 2 2 Lời giải
Tác giả: Trần Thị Thơm; Fb: Tranthom Chọn D a
Với hai số thực dương a, b , ta có 2 ln
 ln a  ln b  ln a  2 ln b . 2 b Phân tích:
*) Kiến thức trọng tâm liên quan đến bài toán: Sử dụng các tính chất của logarit, bao gồm:
1. Cho a, b  0, a  1 , ta có:
+) log a  1, log 1  0 , loga b ab . a a
+) Công thức bay (bay mũ) :
log b   log b ; a a 1 log  ;  b log b a a
2. Logarit của tích, thương :Cho 3 số dương a, b , b với a  1 , ta có: 1 2
log (b .b )  log b  log b a 1 2 a 1 a 2 b1 log
 log b  log b a a 1 a 2 b2
3. Công thức đổi cơ số:Với a, b, c  0 , a  1, b  1, c  1 ta có: log b 1 log c b   ; a log a log a c b
*) Lỗi học sinh hay gặp:
+ Nhầm logarit của 1 tích bằng tích các logarit. Logarit của một thương bằng thương các
logarit. Ngược lại tổng hai logarit cùng cơ số bằng logarit của tổng các biểu thức logarit, hiệu
hai logarit cùng cơ số bằng logarit của một hiệu các biểu thức logarit…
+ Công thức bay mũ: Học sinh hay mắc sai lầm
Với a, b  0 , a  1 thì  b 2 2 log   log b . a a
Với a  0 , a  1 , b  0 thì log b   o
l g b (với số mũ  là số tự nhiên chẵn) a a
*) Các bài toán tương tự:
Mức độ nhận biết, thông hiểu
Câu 4.1 Với a là số thực dương tùy ý, log 8a  log 5a bằng log 8a 8 log 8 A. . B. log 3a . C. log . D. . log 5a 5 log 5 Lời giải
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 13
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tác giả: Trần Thị Thơm ; Fb: Tranthom Chọn C 8a 8
log 8a  log 5a  log  log . 5a 5 2  a
Câu 4.2 Với a là số thực dương tùy ý, log bằng 7   7   1 A. 2 log a  1. B.  2 ln 7a  . C.1  2 log a . D. . 7 7 2 log a 7 Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom Chọn A 2  a  log 2
 log a  log 7  2 log a 1 . 7   7 7 7 7  
Câu 4.3 Mệnh đề nào dưới đây đúng với mọi số dương x, y ? 4x 2  log x 4x A. 2 log  . B. log  log 4x y . 2 2   2 y log y y 2 4x 4x C. log
 2  log x  log y . D. log
 2  log x  log y . 2 2 2 y 2 2 2 y Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom Chọn D 4x log  log
4x  log y  2  log x  log y . 2   2 y 2 2 2
Câu 4.4 Với a là số thực dương tùy ý, log 16a bằng 4   A. 2  log a . B.16 log a . C.16  log a . D. 2  log a . 4 4 4 4 Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom Chọn A
log 16a  log 16  log a  2  log a . 4   4 4 4
Câu 4.5 Cho log b  4 và log c  5 . Tính P   2 3 4 log a b c . aa a A. P  480 . B. P  34 . C. P  691. D. P  40000 . Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom Chọn B
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 14
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 Ta có: P   2 3 4 log a b c 2 3 4
 log a  log b  log c aa a a
 2 log a  3log b  4 log c  2  3.4  4.5  34 . a a a
Câu 4.6 Cho a là số thực dương tùy ý khác 1. Mệnh đề nào dưới đây đúng? 2 1 A. log a  2 log 3. B. log a  . C. log a  . D. log a  2  log 3. 9 a 9 log a 9 2 log 3 9 a 3 a Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom Chọn C 1 1 log a   . 9 2 log 3 2 log 3 a a
Câu 4.7 Với a, b là các số thực dương tùy ý và a 2 6
khác 1, biết log b  2  . Tính P  log b  log b . a 3 a a
Mệnh đề nào dưới đây đúng? A. P  6  . B. P  2  . C. P  20 . D. P  12 . Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom Chọn D 2 6 2 P  log b  log b 2
 4log b  2log b  4 2  2 2  12 . 3 a a a a
Câu 4.8 Cho hai số thực a, b , trong đó a  0, a  1,b  0 . Khi đó  5 log ab bằng a  A. 1  5 log b . B. 6 . C.1  5log b . D. 5 . a a Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom Chọn C Ta có  5 log ab 5
 log a  log b  1  5log b . aa a a
Câu 4.9 Cho a, b là các số thực dương tùy ý. Mệnh đề nào dưới đây là đúng? 2 2 2 A.  2
log 10ab   21  log a  2 log b . B.  2
log 10ab   1  log a  2 log b . C.  ab 2 2 2 4 log 10
 100  log a  log b . D.  ab 2 2 log 10
 1  log a  2 log b . Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom Chọn A Ta có  2 2 log 10ab   2
2 log 10ab   21 log a  2logb .
Câu 4.10 Cho các số thực a, b  0 với a  1 . Trong các mệnh đề sau, mệnh đề nào đúng? 1 1 1 A. log ab   log . b B. log ab  log . b 2   2   2 2 a a 2 a a
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 15
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 C. log ab  2  2 log . b D. log ab  log . a log . b 2   2   a a 2 2 a a a Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom Chọn A 1 1 1 1 Ta có: log ab  log ab
log a  log b   log b . 2     2 a a 2 a a 2 2 a MỨC ĐỘ VẬN DỤNG
Câu 4.11 Cho x, y là các số thực dương thỏa mãn 2 2
ln x  4 ln y  4 ln . x ln y .
1  log x  2 log y Tính M  . 2  4 log  2 x  9 y  1 1 1 A. M   . B. M  2 . C. M  . D. M  2 4 2 Lời giải
Tác giả: Trần Thị Thơm ; Fb:Tranthom Chọn D Ta có 2 2
ln x  4 ln y  4 ln . x ln y   x2   y 2 ln 2 ln  4 ln . x ln y  0   x y 2 ln 2 ln  0
 ln x  2ln y 2  x y .
1  log x  2 log y 2
1  log x  log y Ta có: M   2  4 log  2 x  9 y
2  4 log  x  9x 1  2 log x 1  2 log x 1  2 log x 1     . 2   4 log 10x 2   4  4 log x 2 1 2log x 2 Câu 5.
Trong không gian Oxyz , cho E  1
 ; 0; 2 và F 2;1; 5 . Phương trình đường thẳng EF là x 1 y z  2 x 1 y z  2 A.   . B.   . 3 1 7  3 1 7  x 1 y z  2 x 1 y z  2 C.   . D.   . 1 1 3  1 1 3 Lời giải
Tác giả: Vũ Danh Được ; Fb: Danh Được Vũ Chọn B 
Đường thẳng EF có véc tơ chỉ phương là EF  3;1; 7 .
Đường thẳng EF đi qua điểm E  1
 ; 0; 2 , có véc tơ chỉ phương 3;1; 7   nên phương trình x 1 y z  2 EF là   . 3 1 7 
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 16
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tổng quát: Trong không gian Oxyz , cho hai điểm Ax ; y ; z và B x ; y ; z . Khi đó 2 2 2  1 1 1  x x y y z z
đường thẳng AB có một phương trình dạng 1 1 1   . x x y y z z 2 1 2 1 2 1 1 Câu 6.
Cho cấp số nhân u  với u  9
 ;u  . Tìm công bội của cấp số nhân đã cho. n 1 4 3 1 1 A. . B. 3  . C. 3. D.  . 3 3 Lời giải
Tác giả: Văn Bùi Vũ; Fb: Van Tuan Vu Chọn D  u 1 1
u là cấp số nhân nên ta có: 3 4 3
u u .q q  3     . n 4 1 u 27 3 1 1
Vậy công bội của cấp số nhân đã cho: q   3 Phân tích và bình luận:
Bài toán khai thác kiến thức cơ bản công thức số hạng tổng quát của cấp số nhân học sinh cần ghi nhớ: n 1 u u .q    n
  2,n   . n 1 Câu hỏi tương tự: 1
Câu 6.1. Cho cấp số nhânu với u   ;u  32 . Tìm công bội của cấp số nhân đã cho. n  1 7 2 1 A. q   B. q  2  C. q  4  D. q  1 2 Lời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu Chọn B  u
u là cấp số nhân nên ta có: 6 6 7
u u .q q   64 n  7 1 u1  q  2. 
Vậy công bội của cấp số nhân đã cho: q  2. 
Câu 6.2. Cho cấp số nhânu với u  3, q  2
 . Số 192 là số hạng thứ mấy của cấp số nhân đã cho? n  1 A. Số hạng thứ 5. B. Số hạng thứ 6. C.Số hạng thứ 7.
D. Không phải số hạng củau . n  Lời giải
Tác giả: Văn Bùi Vũ ; Fb: Van Tuan Vu Chọn C
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 17
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Giả sử u  192 là số hạng thứ nn   của cấp số nhân u . n n n 1  n 1  Lúc đó: 192  3  . 2  2  64  n  7.
Vậy số 192 là số hạng thứ 7 của cấp số nhân đã cho. Câu 7.
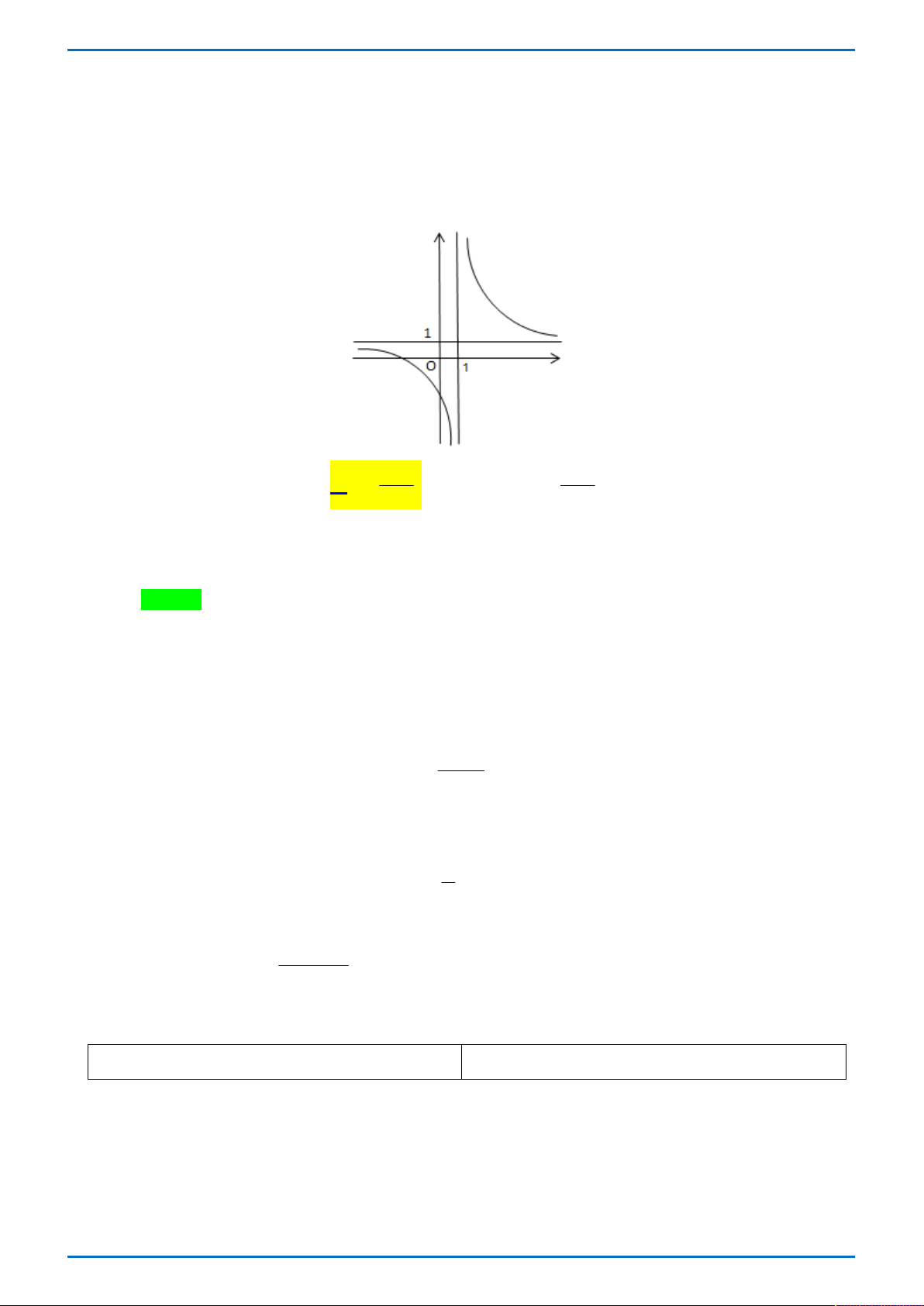
Đường cong ở hình vẽ bên là đồ thị của hàm số nào dưới đây x 1 x 1 A. 3
y  x  3x 1 . B. y  . C. y  . D. 3 2
y x  3x 1. x 1 x 1 Lời giải
Tác giả: Vũ Nga; Fb: Nga Vu Chọn B
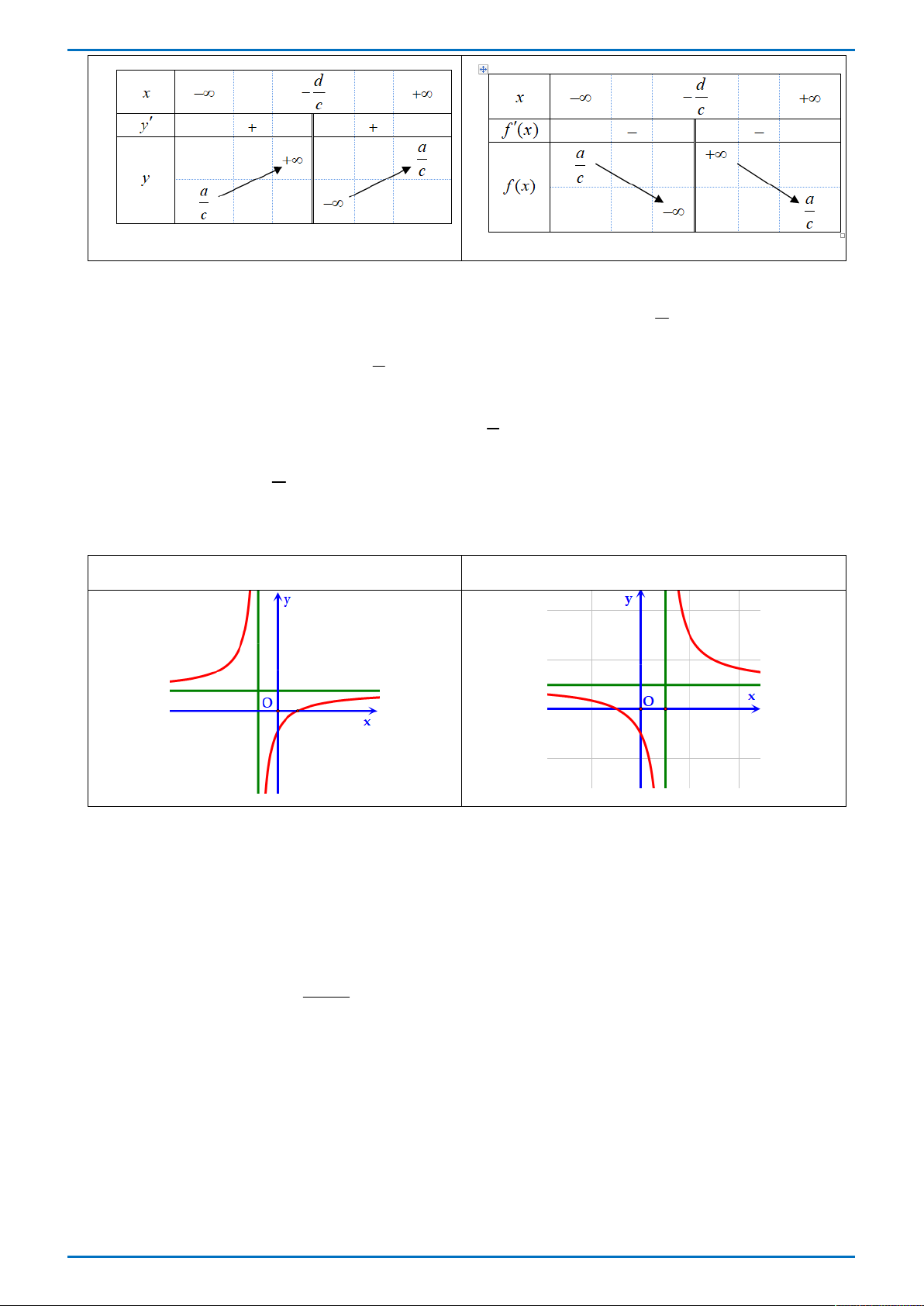
Từ hình dáng đồ thị của hàm số ta có đồ thị hàm số có tiệm cận đứng là đường thẳng x  1 nên loại phương án A, C, D. Vậy chọn B. BÀI TOÁN TỔNG QUÁT ax b
 Bài toán: Xác định hàm số y
c  0 và ad bc  0 khi biết đồ thị hàm số cx d
hoặc bảng biến thiên của hàm số.
 Kiến thức cần nhớ để vận dụng vào bài tập  d
 Tập xác định: D   \   .  c   Sự biến thiên: ad bc y  . cx d 2 Bảng biến thiên ad bc  0 ad bc  0
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 18
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019  Đồ thị d
- Đồ thị hàm số có tiệm cận đứng là đường thẳng x   và tiệm cận ngang là c a đường thẳng y  . cb
- Đồ thị cắt trục Ox tại điểm  ; 0 
 ( nếu a  0 ) và cắt trục Oy tại điểm  a   b  0;   ( nếu d  0 ).  d  - Đồ thị ad bc  0 ad bc  0  Phương pháp giải
- Nhận dạng đồ thị, từ đồ thị xác định được các yếu tố: đường tiệm cận đứng, đường
tiệm ngang của đồ thị, chiều biên thiên của hàm số, giao của đồ thị hàm số với các trục
tọa độ... từ đó sẽ xác định được hàm số tương ứng.
BÀI TOÁN TƯƠNG TỰ CÙNG MỨC ĐỘ ax b
Xác định hàm số y
c  0 và ad bc  0 dựa vào hình dáng đồ thị hàm số và khai cx d
thác thêm một trong các yếu tố đọc được từ đồ thị hoặc bảng biến thiên: tiệm cận, tính đơn
điệu, giao điểm với các trục tọa độ...
Câu 7.1 Bảng biến thiên ở hình dưới đây là bảng biến thiên của hàm số nào trong các hàm số sau ?
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 19
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 x  3 x  3 A. 4 2
y  x  2x 1. B. 4 2
y x  2x 1 . C. y  . D. y  . x  2 2  x Lời giải Chọn C
Từ bảng biến thiên của hàm số ta thấy: đồ thị hàm số có tiệm cận ngang là đường thẳng y  1
nên loại các đáp án A, B, D, vậy chọn C.
BÀI TOÁN TƯƠNG TỰ MỨC ĐỘ CAO HƠN ax b
Xác định hàm số y
c  0 và ad bc  0 dựa vào hình dáng đồ thị hàm số và khai cx d
thác nhiều yếu tố đọc được từ đồ thị hoặc bảng biến thiên: tiệm cận, tính đơn điệu, giao điểm
với các trục tọa độ...
Câu 7.2 Bảng biến thiên ở hình dưới đây là bảng biến thiên của hàm số nào trong các hàm số sau ? 2x  7 2x  3 x  3 x  3 A. y  . B. y  . C. y  . D. y  . x  2 x  2 x  2 x  2 Lời giải Chọn C
Từ bảng biến thiên của hàm số ta thấy: đồ thị hàm số có tiệm cận ngang là đường thẳng y  1
nên loại đáp án A và B, hàm số ngịch biến trên mỗi khoảng ; 2 và 2;   nên y  0 với x    \  
2  loại dáp án D, vậy chọn C.
Câu 7.3 Đường cong ở hình vẽ sau là đồ thị của hàm số nào dưới đây
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 20
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 x 1 x 1 2x  2 x 1 A. y  . B. y  . C. y  . D. y  . x x 1 x x Chọn D
Từ bảng biến thiên của hàm số ta thấy:
- Đồ thị hàm số có tiệm cận cận đứng là trục Oy nên ta loại được đáp án B do đồ thị hàm số x 1 y
có tiệm cận đứng là đường thẳng x  1 . x 1
- Đồ thị hàm số có tiệm cận ngang là đường thẳng y  1 nên ta loại được đáp án C do đồ thị 2x  2 hàm số y
có tiệm cận ngang là đường thẳng y  2 . x
- Đồ thị hàm số đi qua điểm 1;0 nên loại đáp án A. Vậy chọn D. ax b
Câu 7.4 Cho hàm số y
với a  0 có đồ thị như hình vẽ cx d
Tìm khẳng định đúng trong các khẳng định sau
A. b  0,c  0, d  0 .
B. b  0, c  0, d  0 . C. b  0, c  0, d  0 . D. b  0, c  0, d  0 . Lời giải Chọn B d
Do đồ thị hàm số có tiệm cận đứng là đường thẳng x  
và tiệm cận ngang là đường thẳng c ab   b y
. Đồ thị cắt trục Ox tại điểm  ; 0 
 và cắt trục Oy tại điểm 0;   nên ta có: ca   d   d   0  ca   0 c  0  c  
. Mà a  0 nên b  0 . Vậy chọn B. b   0 d  0  a   b   0  d
Câu 8 . Trong không gian Oxyz , mặt phẳng  P đi qua điểm M 3; 1; 4 , đồng thời vuông góc với 
giá của vectơ a 1; 1; 2 có phương trình là
A. 3x y  4z 12  0 .
B. 3x y  4z 12  0 .
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 21
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
C. x y  2z 12  0 .
D. x y  2z 12  0 . Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạm Chọn C 
Do mặt phẳng  P vuông góc với giá của vectơ a 1; 1; 2 nên mặt phẳng  P nhận vectơ
a1; 1; 2 làm vectơ pháp tuyến và đi qua điểm M 3; 1; 4 nên có phương trình:
1 x  3 1 y  
1  2 z  4  0  x y  2z 12  0.
Câu 8.1 . Trong không gian Oxyz , mặt phẳng  P đi qua điểm M 1; 1; 2 , đồng thời song song với
mặt phẳng Q : 2x  3y z  5  0 có phương trình là
A. 2x  3y z  3  0 . B. x y  2z  3  0 .
C. 2x  3y z  3  0 .
D. x y  2z  3  0 . Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạm Chọn C
Do mặt phẳng  P song song với mặt phẳng Q : 2x  3y z  5  0 nên mặt phẳng  P nhận  vectơ pháp tuyến n
làm vectơ pháp tuyến và đi qua điểm M 1; 1; 2 nên có Q  2 ; 3 ;  1  
phương trình: 2 x   1  3 y  
1   z  2  0  2x  3y z  3  0.
Nhận Xét: Đây là bài toán ở mức độ nhận biết của phần phương trình mặt phẳng. Giả thiết đã
cho 1 điểm thuộc mặt phẳng và VTPT của mặt phẳng. VTPT có thể cho trực tiếp, cho bằng
định nghĩa hoặc cho thông qua mặt phẳng song song với mặt phẳng đã cho. Câu 9.
Cho hàm số y f x liên tục trên  3  ; 
3 và có bảng xét dấu đạo hàm như hình bên.
Mệnh đề nào sau đây sai về hàm số đó?
A. Hàm số đạt cực tiểu tại x  1 .
B. Hàm số đạt cực đại tại x  1  .
C. Hàm số đạt cực đại tại x  2 .
D. Hàm số đạt cực tiểu tại x  0 . Lời giải
Tác giả: Lê Thị Phương Liên; Fb: Phuonglien Le Chọn D
Dựa vào bảng xét dấu của đạo hàm đã cho ta thấy f '0  0 và đạo hàm không đổi dấu khi x
qua x  0 nên hàm số đã cho không đạt cực tiểu tại x  0 . 0 Bài toán tương tự
Câu 9.1 Cho hàm số y f x liên tục trên  2
 ; 4 và có bảng xét dấu đạo hàm như hình bên.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 22
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Mệnh đề nào sau đây sai về hàm số đó?
A. Hàm số đạt cực tiểu tại x  0 .
B. Hàm số đạt cực đại tại x  1  .
C. Hàm số đạt cực đại tại x  2 .
D. Hàm số đạt cực đại tại x  1 . Lời giải Chọn D
Dựa vào bảng xét dấu của đạo hàm đã cho ta thấy f ' 
1  0 và đạo hàm không đổi dấu khi x
qua x  1 nên hàm số đã cho không đạt cực đại tại x  1 . 0
Câu 10. Giả sử f x là hàm số bất kỳ liên tục trên khoảng  ;   và a, ,
b c,b c  ;   . Mệnh đề nào sau đây sai ? b c b b bc c A.
f x dx f x dx f x dx    . B.
f x dx
f x dx f x dx    . a a c a a a b bc b b c c C.
f x dx
f x dx
f x dx    . D.
f x dx f x dx f x dx    . a a bc a a b Lời giải
Tác giả: Lê Hữu Đức ; Fb: Le Huu Duc Chọn B
Đáp án A, C, D đúng vì theo tính chất tích phân. bc c bc a bc Đáp án B sai vì
f x dx f x dx
f x dx f x dx
f x dx      . a a a c c Bài tương tự
Câu 10. Giả sử f x là hàm số bất kỳ liên tục trên khoảng  ;   và a, ,
b c  ;   . Mệnh đề nào sau đây sai ? b b a b c b A.
f x dx f x dx f x dx    . B.
f x dx f x dx f x dx    . a c c a a c b c b b c a C.
f x dx f x dx f x dx    . D.
f x dx   f x dx f x dx    . a a c a b c Lời giải
Tác giả: Lê Hữu Đức ; Fb: Le Huu Duc Chọn C
Đáp án A, B, D đúng vì theo tính chất tích phân. Đáp án C sai.
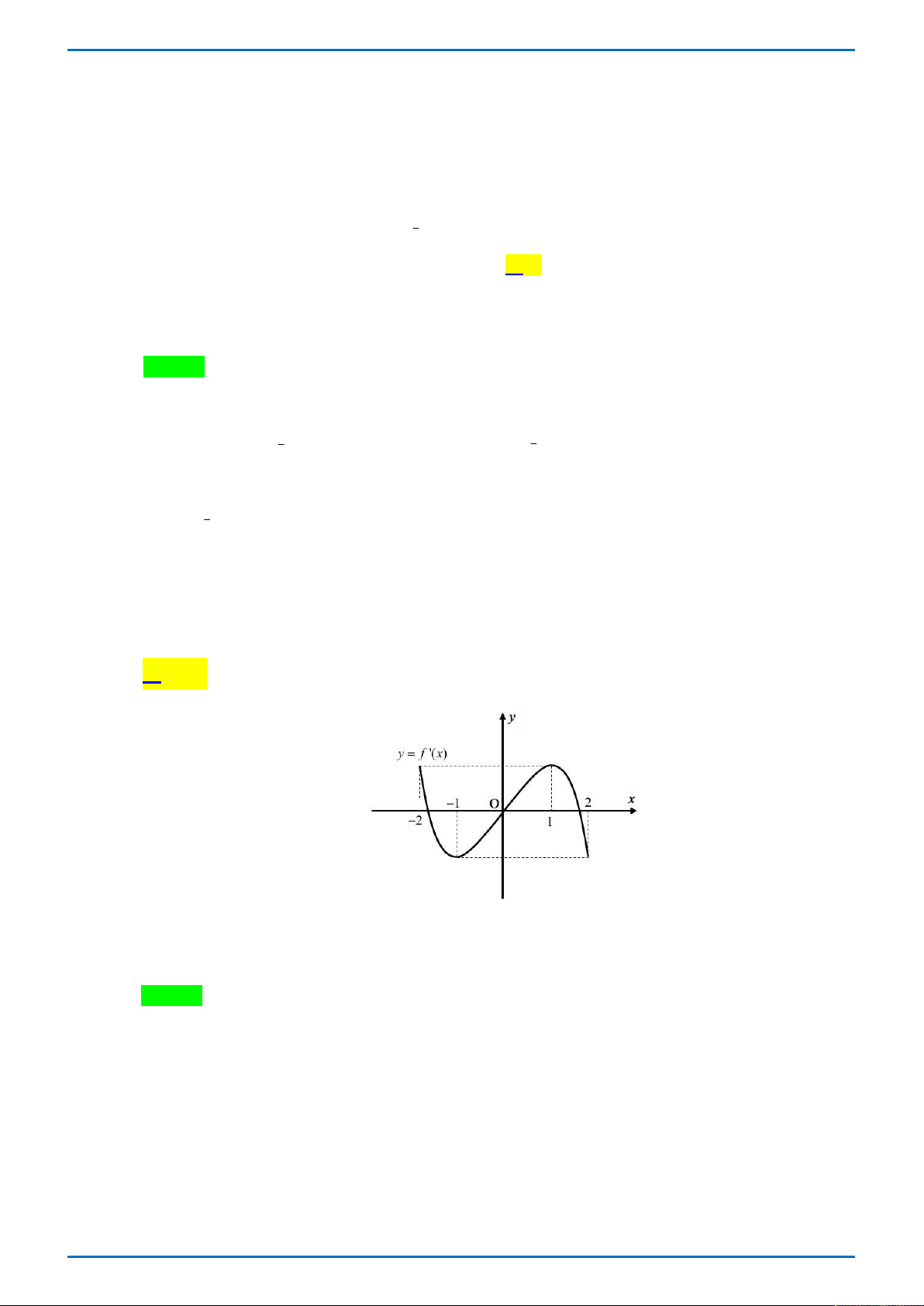
Câu 11. Cho hàm số y f (x) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng về hàm số đó
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 23
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 y 1 -1 2 x O 1 -3
A. Nghịch biến trên khoảng 1;0 .
B. Đồng biến trên khoảng  3  ;  1 .
C. Đồng biến trên khoảng 0;  1 .
D. Nghịch biến trên khoảng 0;2 . Lời giải
Tác giả: Trần Mạnh Tường ; Fb: Trần Tuệ Minh Chọn C Trên khoảng 0; 
1 đồ thị có hướng đi lên nên hàm số đồng biến ứng với khoảng này. Bài tương tự
Câu 11.1 Cho hàm số y f (x) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng về hàm số đó y -1 O 1 2 x 3 -1 -4
A. Nghịch biến trên khoảng 1;0 .
B. Đồng biến trên khoảng  4  ;  1 .
C. Đồng biến trên khoảng  1  ;0 .
D. Nghịch biến trên khoảng 1;3 . Lời giải
Tác giả: Trần Mạnh Tường ; Fb: Trần Tuệ Minh
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 24
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 Chọn C Trên khoảng  1
 ;0 đồ thị có hướng đi lên nên hàm số đồng biến ứng với khoảng này.
Câu 12 . Tất cả các nguyên hàm của hàm số   3 x f x   là 3x 3x A.   C . B. 3x   C .
C. 3x ln 3  C . D.  C . ln 3 ln 3 Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn Chọn A Bài toán tương tự
Câu 12 .1 Tìm nguyên hàm F x của hàm số   x
f x e x biết F 0  2 2 x 2 x 2 x 2 x A. F xxe
1 . B. F xxe
1 . C. F xxe
1 . D. F xxe  1 . 2 2 2 2 Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn Chọn B 2 x
Ta có F x   x e x d x x e   C 2
Theo bài ra F 0  2  1 C  2  C  1 2 x Vậy F xxe  1 . 2
Câu 13. Phương trình log  x   1  2 có nghiệm là A. 11. B. 9 . C. 101. D. 99 . Lời giải
Tác giả: Nguyễn Mạnh Dũng ; Fb: Mạnh Dũng Chọn D 2 x 1  10 x  99
Ta có : log  x   1  2      x  99 . x 1  0  x  1  Bài toán tương tự.
Câu 13.1. Phương trình log  x  9  3 có nghiệm là A. 91. B. 9991. C. 1009 . D. 991. Lời giải
Tác giả: Nguyễn Mạnh Dũng ; Fb: Mạnh Dũng Chọn D
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 25
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 3 x  9  10 x  991
Ta có : log  x  9  3      x  991 . x  9  0  x  9  
Câu14 . Cho k , n k n là các số nguyên dương bất kì. Mệnh đề nào sau đây đúng? n n k ! k ! A. A  . B. k
A k !. k C . C. A  . D. k
A n!. k C . n k ! n n n k  ! n k ! n n Lời giải
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắt nâu Chọn B n n k ! ! Ta có A   k !  k !. k C nên B đúng. nn k ! k  ! n k ! n
* Phát triển câu mức độ tương tự
Câu 14.1. Tìm công thức tính số các tổ hợp chập k của một tập có n phần tử. n n n n k ! k ! k ! k ! A. C  . B. C  . C. A  . D. A  . nn k ! n
n k !k! nn k ! n
n k !k ! Lời giải
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắt nâu Chọn B n k !
Số các tổ hợp chập k của một tập có n phần tử phần tử, kí hiệu là: C  . n
n k !k!
Câu 14.2. Trong mệnh đề sau, mệnh để nào sai? A. 3 11 C C . B. 3 4 4
C C C . 14 14 10 10 11 C. 0 1 2 3 4
C C C C C  16 . D. 4 4 5
C C C . 4 4 4 4 4 10 11 11 Lời giải Chọn D
Áp dụng công thức: k k 1  k 1 C C
C  suy ra đáp án sai là 4 4 5
C C C . n n n 1  10 11 11
* Phát triển câu mức độ cao hơn
Câu 14.3. Cho số tự nhiên n thỏa mãn 2 2
C A  9n . Mệnh đề nào sau đây đúng? n n A. n5 . B. n3 . C. n7 . D. n2 . Lời giải Chọn C n n k ! k !
Phương pháp: Sử dụng các công thức C  ; A  . n
n k !k ! nn k !
Giải: Điều kiện: n  2 .
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 26
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 n! n! 3 2 2
C A  9n    9n n n
n n    n n n   1 9 1 6 7 .
n  2!2! n  2! 2
Câu 14.4. Có tất cả 120 cách chọn 3 học sinh từ nhóm n (chưa biết) học sinh. Số n là nghiệm của
phương trình nào sau đây?
A. n n  
1 n  2  120 .
B. n n  
1 n  2  720 .
C. n n  
1 n  2  120 . D. nn  
1 n  2  720 . Lời giải Chọn D n! n n 1 n  2 3   
Số cách chọn 3 trong n học sinh có C   . nn  3!3! 6 Khi đó 3
C  120  n n  
1 n  2  720 . n
Câu 15. Cho các số phức z  1
  2i, w  2  .
i Điểm nào trong hình bên biểu diễn số phức z  w ? A. N . B. P . C. Q . D. M . Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn Chọn B + Tính z  w  1
  2i  2  i  1 i . Suy ra điểm biểu diễn là điểm có tọa độ 1;  1 là điểm P . Bài toán tương tự
Câu 15.1 Cho các số phức z a bi, w  x yi, với a, b, x, y   . Điểm M biểu diễn số phức z  w có tọa độ là A. a  ; x b y  .
B. a x;b y . C. a  ; b x y . D. a  ; b x y  . Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn Chọn B
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 27
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
+ Theo quy tắc trừ số phức thì z  w  a bi   x yi  a x  b yi . Suy ra điểm biểu
diễn là điểm có tọa độ a  ;
x b y .
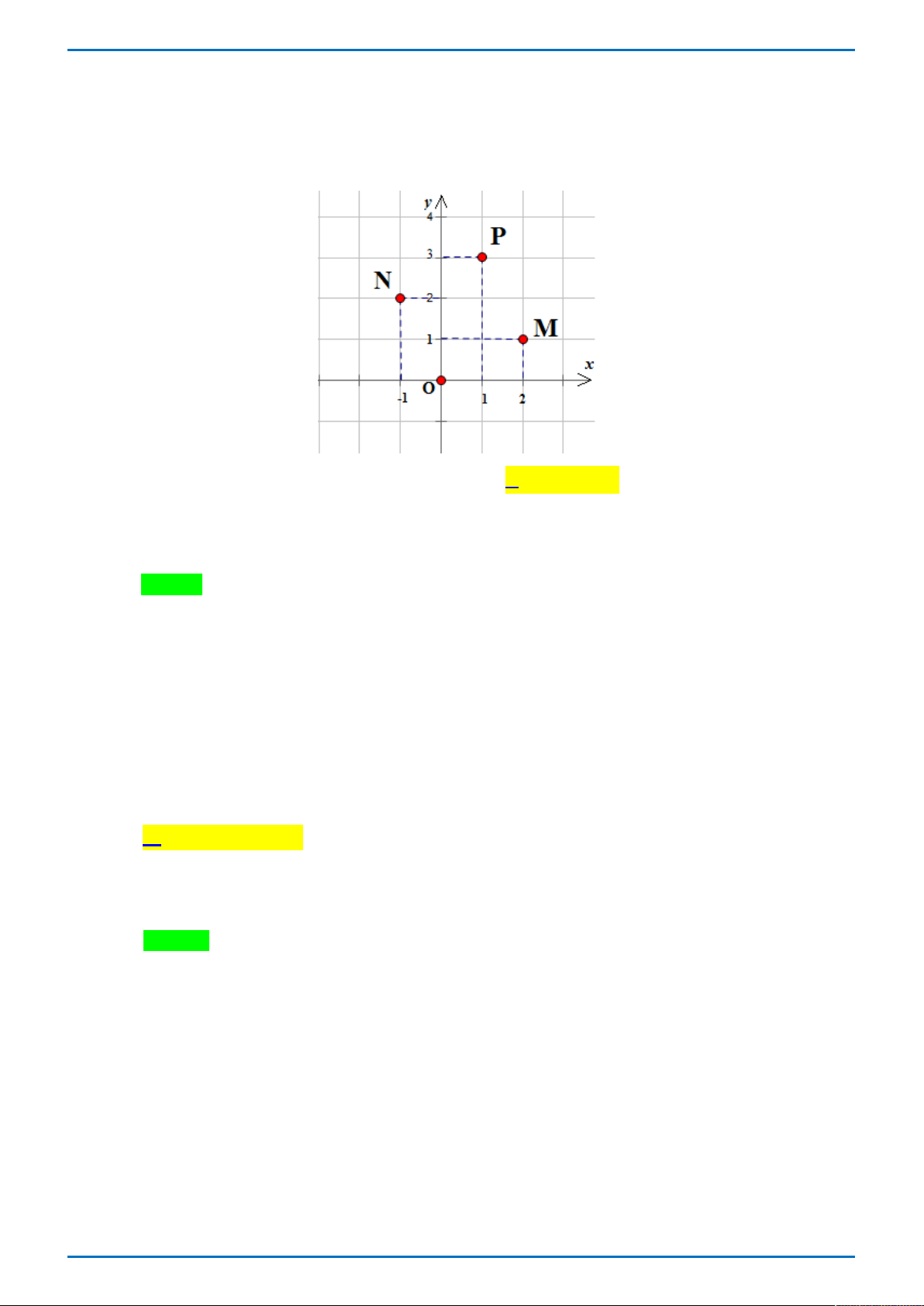
Câu 15.2 Gọi các số phức z ; z ; z lần lượt có điểm biểu diễn trong hệ tọa độ Oxy là M , N , P (như hình 1 2 3
vẽ bên dưới). Mệnh đề nào sau đây là đúng.
A. z z z .
B. z z z .
C. z z z .
D. z z z . 1 2 3 2 1 3 3 2 1 1 2 3 Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn Chọn C
+ Dựa vào hình vẽ ta suy ra tọa độ M 2  ;1 , N  1  ; 2, P1;3 nên z  2  ; i z  1   2 ;
i z  1 3i . 1 2 3
+ Theo quy tắc cộng số phức ta được z z z . 3 2 1
Câu 16. Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng (P) : x  3y  2z 1  0 ,
(Q) : x z  2  0 .Mặt phẳng   vuông góc với cả (P) và (Q) đồng thời cắt trục Ox tại điểm
có hoành độ bằng 3. Phương trình của mp   là: A.                 x y z 3 0 .
B. x y z 3 0 . C. 2x z 6 0 . D. 2x z 6 0 . Lời giải
Tác giả: Đổng Quang Phúc ; Fb: Đổng Quang Phúc Chọn A.  
(P) có vectơ pháp tuyến n  1; 3; 2 , Q có vectơ pháp tuyến n   . Q 1;0;  1 P
Vì mặt phẳng   vuông góc với cả P và Q nên   có một vectơ pháp tuyến là  
n ; n   3;3;3  31;1;  1 . P Q  
Vì mặt phẳng   cắt trục Ox tại điểm có hoành độ bằng 3 nên   đi qua điểm M 3;0;0 . 
Vậy   đi qua điểm M 3;0;0 và có vectơ pháp tuyến n
nên   có phương trình:  1;1;  1
x y z  3  0 .
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 28
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Câu 16.1 Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng (P) : x  2 y  3z  2  0 ,
(Q) : x y  3  0 .Mặt phẳng   vuông góc với cả (P) và (Q) đồng thời cắt trục Ox tại điểm
có hoành độ bằng 5. Phương trình của mp   là: A.                 3x 3y z 15
0 . B. x y z 3 0 . C. 2x z 6 0 . D. 2x z 6 0 . Lời giải
Tác giả: Phạm Hoài Trung ; Fb: Phạm Hoài Trung Chọn A.  
(P) có vectơ pháp tuyến n  1; 2;3 , Q có vectơ pháp tuyến n  1; 1;0 . QP
Vì mặt phẳng   vuông góc với cả P và Q nên   có một vectơ pháp tuyến là   
n  n ; n   .  3;3;  1 P Q  
Vì mặt phẳng   cắt trục Ox tại điểm có hoành độ bằng 3 nên   đi qua điểm M 5;0;0 . 
Vậy   đi qua điểm M 5;0;0 và có vectơ pháp tuyến n  nên   có phương  3;3;  1
trình: 3x  3y z 15  0 .
Câu 17 . Cho số phức z thỏa mãn   i 2 1 3
z  3  4i . Mô đun của z bằng 5 5 2 4 A. B. C. D. 4 2 5 5 Lời giải
Tác giả: Phạm Ngọc Huệ; Fb: Phạm Ngọc Huệ Chọn A
Phân tích: giả thiết là một phương trình bậc nhất với ẩn z, thực hiện phép toán thích hợp để tìm
z, nên sử dụng máy tính để tính cho nhanh và chính xác. 3  4i 3   4 3 4  3 3 z    i   i2 8 8 1 3 2 2  3   4 3   4  3 3  5 z         8   8  4    
Bài tập tương tự: 2019  1 i
Câu 17.1 Cho số phức z thỏa mãn z   
3  4ii . Mô đun của z bằng  1 i  1 2 5 A. 5 B. C. D. 5 5 2 Lời giải
Tác giả: Phạm Ngọc Huệ; Fb: Phạm Ngọc Huệ Chọn A
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 29
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 2019  1 i z   
3  4ii  .iz  3  4ii z  3  4i . Vậy z  5  1 i
Câu 18 . Cho hình trụ tròn xoay có độ dài đường sinh bằng đường kính đáy và thể tích khối trụ bằng
16 . Diện tích toàn phần của khối trụ đã cho bằng A. 16 . B. 12 . C. 8 . D. 24 . Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn Chọn A
Theo bài ra ta có r l h 2 3
V   r h   r  16  r  2
Diện tích toàn phần của khối trụ đã cho là :
S   r r l  2 2  4 r  16 . tp
Câu 18.1 Một hình trụ có diện tích xung quanh bằng 8 và có chiều cao bằng đường kính đáy. Thể tích
khối trụ trương ứng bằng A. 32 . B. 16 . C. 8 . D. 4 . Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn Chọn C
Theo bài ra ta có r l h 2  S
 2 rl  2 r  8  r  2 xq
Thể tích của khối trụ đã cho là : 2 3
V   r h   r  8 .
Câu 19 . Biết rằng phương trình 2
log x  7 log x  9  0 có hai nghiệm x , x . Giá trị của x x bằng 2 2 1 2 1 2 A. 128 . B. 64 . C. 9 . D. 512 . Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn Chọn A Điều kiện x  0
Với x , x là hai nghiệm của phương trình đã cho, áp dụng định lý Vi – ét, ta có 1 2
log x  log x  7  log x x  7 7
x x  2  x x  128 . 2  1 2  2 1 2 2 1 2 1 2
Câu 19.1 Biết rằng phương trình log x 15log 2  2 có hai nghiệm x , x x x . Giá trị của 1 2  2 x 1 2
x 16x bằng 1 2 4095 4097 A.  . B. 30 . C. 34 . D. . 8 8
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 30
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn Chọn B x  0 Điều kiện  x  1  15
log x 15log 2  2  log x   2 2
 log x  2 log x 15  0 2 x 2 log x 2 2 2  x  32  x  32 log x  5 1 2      1 
1  x 16x  30 . log x  3 1 2   x   x  2  8 2  8 3x 1
Câu 20 . Đạo hàm của hàm số f (x)  là: 3x 1 2 2
A. f '(x)   .3x . B. f '(x)  .3x 3x  2 1 3x  2 1 2 2 C. f '(x)  .3x ln 3
D. f '(x)   .3x ln 3 3x  2 1 3x  2 1 Lời giải
Tác giả: Phạm Ngọc Huệ; Fb: Phạm Ngọc Huệ Chọn C Áp dụng công thức: 3x  , 1 3x   1  3x   1 3x  , 1 f '(x)  3x  2 1 3x l 3 n 3x   1  3x   1 3x 3 ln 2   .3x ln 3 3x  2 1 3x  2 1 Câu tương tự. 2 x5
Câu 20.1. Đạo hàm của hàm số x7 f (x)  3 là: 2 x 5 19 ln 3 2 x 5 19 ' x 7 ' x 7 A. f ( x)  3 . B. f ( x)  3  2 x  72  x  7 2 x5 1  9 2 x 5 ' 19 ln 3 x7 ' x 7 C. f (x)  3 D. f ( x)  3  x  72  x  72 Lời giải
Tác giả: Phạm Ngọc Huệ; Fb: Phạm Ngọc Huệ
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 31
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 Chọn A Áp dụng công thức: ' ' 2 x5 2 x5 2 x5    2x  5 '  2 x5 x7 x7 x7 f (x)  3  f (x)  3  3 ln 3.   19 ln 3   x7  3    x  7   x  72 ,  ax+b  ad bc
Chú ý áp dụng công thức tính nhanh     cx+d  cx d 2
Câu 21. Cho f x 4 2
x  5x  4 . Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị hàm số
y f x và trục hoành. Mệnh đề nào sau đây sai ? 2 1 2 A. S f   x dx . B. S  2 f
  xdx  2 f
  xdx . 2 0 1 2 2 C. S  2 f
  x dx . D. S  2 f
  xdx . 0 0 Lời giải
Tác giả: Nguyễn Ngọc Minh ; Fb: Minh Nguyen Chọn D
Phương trình hoành độ giao điểm của đồ thị hàm số f x 4 2
x  5x  4 và trục hoành: 2  x  1 x  1 4 2
x  5x  4  0    2 x  2  x  4  
Diện tích hình phẳng cần tìm là: 2 S f
x dx   1 2 2  2 f
  x dx 2 (do f x là hàm số chẵn) 0 1 2  2 f
  x dx  2 f
  x dx 0 1 1 2  2 f
  xdx  2 f
  xdx 3 (do trong các khoảng 0 
;1 , 1; 2 phương trình f x  0 vô 0 1 nghiệm) Từ  
1 , 2 , 3 suy ra các đáp án A, B, C là đúng, đáp án D là sai.
Máy tính: Bấm máy tính kiểm tra, ba kết quả đầu bằng nhau nên đáp án sai là đáp án D.
Câu 21.1 Cho f x 4 2
x  6x  8 . Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị hàm số
y f x và trục hoành. Mệnh đề nào sau đây sai ?
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 32
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 2 2 2 A. S f   x dx . B. S  2 f
  xdx  2 f
  xdx . 2 0 2 2 2 C. S  2 f
  x dx . D. S  2 f
  xdx . 0 0 Lời giải
Tác giả:Phạm Hoài Trung; Fb: Phạm Hoài Trung Chọn D
Phương trình hoành độ giao điểm của đồ thị hàm số f x 4 2
x  6x  8 và trục hoành: 2 x  2  4 2 x   2
x  6x  8  0     2 x  4 x  2   
Diện tích hình phẳng cần tìm là: 2 S f
x dx   1 2 2  2 f
  x dx 2 (do f x là hàm số chẵn) 0 2 2  2 f
x dx  2 f   x dx 0 2 2 2  2 f
  xdx  2 f
  xdx 3 (do trong các khoảng 0; 2 , 2;2 phương trình 0 2
f x  0 vô nghiệm) Từ  
1 , 2 , 3 suy ra các đáp án A, B, C là đúng, đáp án D là sai.
Máy tính: Bấm máy tính kiểm tra, ba kết quả đầu bằng nhau nên đáp án sai là đáp án D.
Câu 22. Cho hàm số y f x  có đạo hàm f  x 2  x  2 x  
1 , x   . Hàm số y  2 f x đồng biến trên khoảng A. 2;  . B.  ;    1 . C. 1;  1 . D. 0;2 . Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn Chọn C 5 3 x x
+ Ta có f  x 2  x  2 x  
1 suy ra f x  f  xdx  2 x  2 x   1 dx      C 5 3  5 3 2 x  2 x 5 3 2x 2x
+ Suy ra y g x  2 f x    2C =    2C 5 3 5 3
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 33
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 5 3   2x 2x
+ Tính g ' x   2 f x = 2 2     2C  = 4 2
2x  2x  2x x   1  5 3   2 x 0 x 0 g ' x     0     . 2 x 1  0 x     1 + Bảng xét dấu
+ Hàm số y g x  2 f x đồng biến trên 1;  1 . Chọn C. Bài toán tương tự
Câu 22.1 Cho hàm số y f x  có đạo hàm f  x  3 x  2
2x , x   . Hàm số y f 2  x đồng biến trên khoảng A. 2;  . B. ;2 . C. 4;2 . D.  . Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn Chọn A 4 3 x 2x
+ Ta có f  x  3 x  2
2x suy ra f x  f  xdx   3 x  2 2x dx      C 4 3  4 3 2  x  2 2  x
+ Suy ra y g x  f 2  x    C 4 3 4 3 
 2 x 22 x    3 2
+ Tính g ' x  f 2  x =   
C =  2  x  22  x    2 2 x x  4 3   
+ Hàm số đồng biến suy ra g ' x  0  x  0.Chọn A..
Câu 22.2 Cho hàm số y f x  nghịch biến x  ;
a b . Hàm số y f 2  x đồng biến trên khoảng A. 2  ; b 2  a .
B. ;2  a . C.  ; a b . D. 2  ; b   . Lời giải
Tác giả: Nguyễn Văn Nghĩa ; Fb: Nghĩa Văn Nguyễn Chọn A
+ Vì hàm số y f x  nghịch biến x  ;
a b nên f x  0; x   ; a b .
+ Xét y g x  f 2  x có g x   f 2  x
+ Hàm số y f 2  x đồng biến thì g x   0   f 2  x  0  f 2  x  0
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 34
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Suy ra a  2  x b  2  b x  2  a . Chọn A. 3 x  4x
Câu 23. Đồ thị hàm số y
có bao nhiêu đường tiệm cận? 3 x  3x  2 A. 4 . B. 1. C. 3 . D. 2 . Lời giải
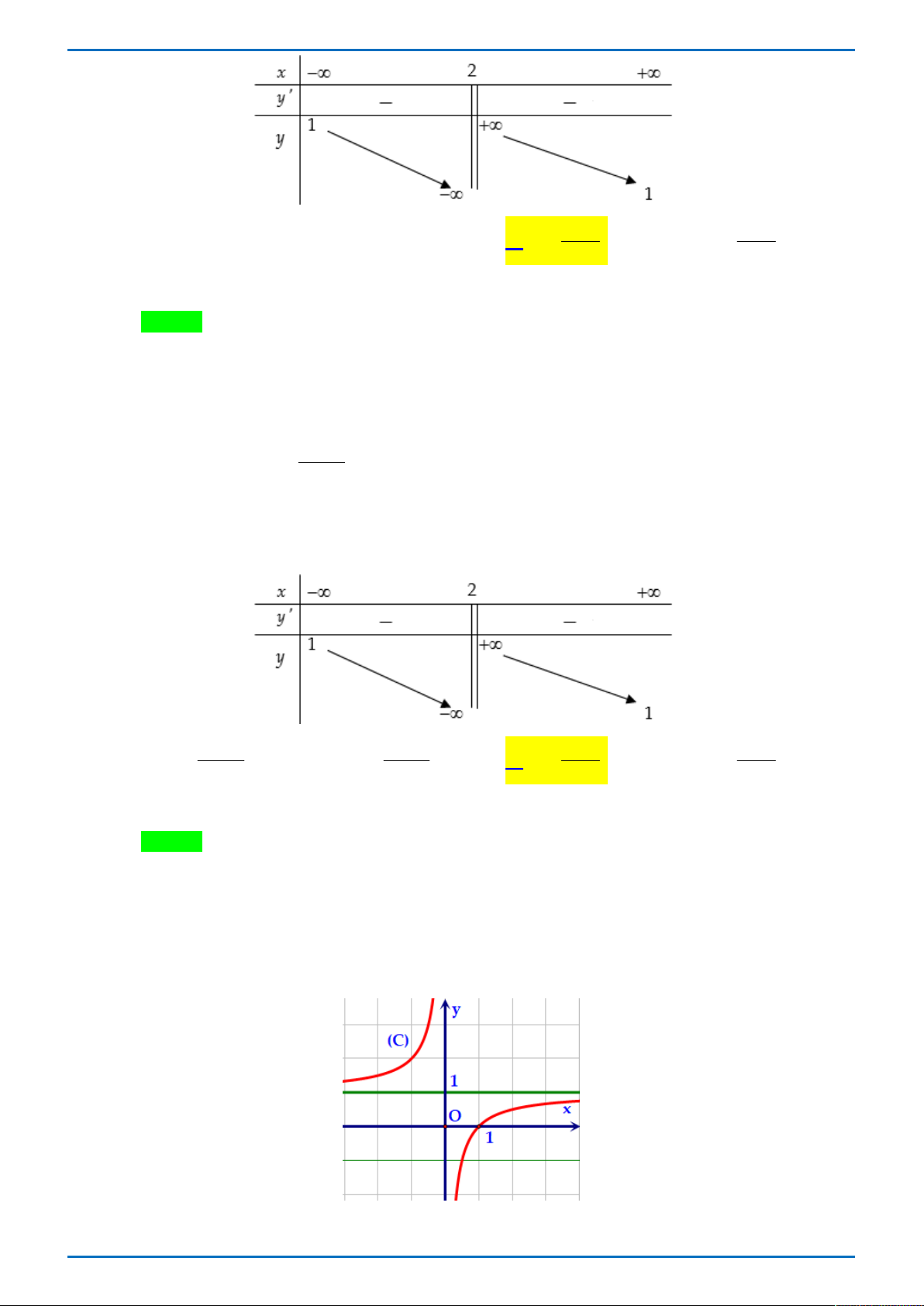
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắt nâu Chọn D TXĐ: D   \  1  ;  2 . 3 x  4x Ta có: lim y  lim
 1. Suy ra, đồ thị hàm số đã cho có một tiệm cận ngang là 3 x
x x  3x  2
đường thẳng y  1. Lại có: 3 x  4x
x x  2 x  2 x x  2 8 lim y  lim  lim  lim  .   3 x 2 x 2 x 2 x  3x  2   x  2 1  x  2 x 2      x  2 1 9 3 x  4x
x x  2 x  2 x x  2 8 lim y  lim  lim  lim  .   3 x 2 x 2 x 2 x  3x  2   x  2 1  x  2 x 2      x  2 1 9 3 x  4x
x x  2 x  2 x x  2 lim y  lim  lim  lim   .   3  2  2 x  1 x  1 x  3x  2 x  1  x   1  x  2 x  1  x   1
Suy ra, đồ thị hàm số đã cho có một tiệm cận đứng là đường thẳng x  1 .
Vậy đồ thị hàm số có 2 đường tiệm cận.
ADMIN LƯU Ý NHẬN XÉT CHỈNH CON ĐƯỜNG GIẢI BÀI TOÁN NÀY
* Phát triển câu mức độ tương tự x  3
Câu 23.1. Cho hàm số y
. Khẳng định nào sau đây đúng? 2 x  9
A. Đồ thị hàm số có tiệm cận ngang là y  1.
B. Đồ thị hàm số chỉ có 1 tiệm cận đứng là x  3 .
C. Đồ thị hàm số không có tiệm cận đứng.
D. Đồ thị hàm số có hai tiệm cận đứng là x  3; x  3 . Lời giải
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắt nâu Chọn B x  3 Điều kiện xác định: 2 x  9  0   . x  3  
A sai vì: Hàm phân thức, có bậc tử (bậc 1) nhỏ hơn bậc mẫu (bậc 2) nên đồ thị có 1 tiệm cận ngang y  0 .
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 35
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 Giải phương trình: 2
x  9  0  x  3  .
(Học sinh dễ mắc sai lầm khi kết luận đồ thị hàm số có 2 tiệm cận đứng) Kiểm tra giới hạn: x  3 x  3 1 lim  lim 
(học sinh có thể dùng máy tính kiểm tra), suy ra, x  3 không là  2  2 x3 x 3 x  9  x  9 6
tiệm cận đứng của đồ thị hàm số. x  3 lim
  (học sinh có thể dùng máy tính kiểm tra), suy ra x  3 là tiệm cận đứng của  2 x3 x  9 đồ thị hàm số. 2 1 x
Câu 23.2. Số đường tiệm cận của đồ thị hàm số y  là: x  2 A. 0. B. 1. C. 2. D. 3. Lời giải Chọn A Giải nhanh: 2 1   x  0  1   x  1
Điều kiện xác định:     1  x  1. x  2  0 x  2   
Tập xác định của hàm số không chứa  suy ra đồ thị hàm số không có tiệm cận ngang.
x  2  0  x  2. 
Thay x  2 lên tử số ta được:   2 1 2
không xác định, suy ra đồ thị hàm số không có tiệm cận đứng. Giải bản chất: 2 1   x  0  1   x  1
Điều kiện xác định:     1  x  1. x  2  0 x  2   
Tập xác định của hàm số không chứa  , suy ra đồ thị hàm số không có tiệm cận ngang. Xét tiệm cận đứng: 2 1 x 2 1 x lim ; lim
không có giới hạn, suy ra đồ thị hàm số không có tiệm cận. x 2  x  2 x 2  x  2
* Phát triển câu mức độ cao hơn x 1
Câu 23.3. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y  có hai 2 mx 1 tiệm cận ngang. A. m  0 . B. m  0 . C. m  0 .
D. Không có giá trị thực của m Lời giải Chọn C
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 36
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Ta thấy khi m  0 thì tập xác định của hàm số mới chứa  .
Nếu m  0 thì hàm số y x 1 không có đường tiệm cận ngang.  1  x 1    x  1
Nếu m  0 thì ta có lim y  lim  
, suy ra đồ thị hàm số có 2 tiệm cận ngang x x 1 m x m  2 x 1 1  là y  , y  . m m x  2
Câu 23.4. Có bao nhiêu giá trị m nguyên để đồ thị hàm số y
có đúng một tiệm cận đứng. 2
x mx m A. 1. B. 2. C. 3. D. 4. Lời giải
Tác giả: Trần Thị Thanh Thủy; Fb: Song tử mắt nâu Chọn B x  2
Dễ thấy tử số có một nghiệm x  2 . Do đó để đồ thị hàm số y  có đúng một tiệm 2
x mx m
cận đứng thì cần xét hai trường hợp sau: m  0 Trường hợp 1: 2
x mx m  0 có nghiệm kép 2
   m  4m  0   . m  4  Trường hợp 2: 2
x mx m  0 có 2 nghiệm phân biệt, trong đó có 1 nghiệm bằng 2. 2
  m  4m  0    m   .
4  2m m  0 
Câu 23.5 (Nguyễn Việt Hải) Hỏi có bao nhiêu giá trị m nguyên thuộc đoạn  20  19; 2019 để đồ thị x m 12 hàm số y
có đúng một đường tiệm cận. 3
x  50x  500
Câu 24. Biết rằng ,  là các số thực thỏa mãn 2 2  2   82  2  . Giá trị của   2 bằng A. 1. B. 2. C. 4. D. 3. Lời giải
Tác giả: Nguyễn Mạnh Dũng ; Fb: Mạnh Dũng Chọn D  
Ta có: 2 2  2   82  2         1 1 2 2 2  8    .  2 2                2 2 2 2 2  8          8 2 2 2   0   . 2      2   8  2   0 (do 2 2   0 ). 2 
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 37
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019  2 2   8   0  2  2
  8  0 (do 2  0 ). 2  2  2   8  2 3  2
 2    2  3 . Bài toán tổng quát Câu 24.1. Biết rằng
a,b  0a   1 , ,  , m, , n p là các số thực thỏa mãn p  mn     m n a a a b a
a   . Giá trị của m  n p  bằng Lời giải
Tác giả: Nguyễn Mạnh Dũng ; Fb: Mạnh Dũng  
Ta có: p  mn     m n a a a b aa   p
a   mn aa   1 1  b   . mn   a a   mn        b    a a p   am n aa   b m n p
 a a a   0 . m n    am n    a   b pa   0 (do mn a a    0 ). m n a
m npa   b   0
m np   a
  b  0 (do m n a    0 ). m n a
m np
m  np   a   b   logbaaa
m  n p   logb . a
Bài toán đặc biệt hóa.
Với a  3,b  81, m  1, n  4, p  2 ta có bài toán sau:
Câu 24.2 Biết rằng ,  là các số thực thỏa mãn 2   4      4 3 3 3 81 3
 3   . Giá trị của   6 bằng A. 1. B. 2. C. 4. D. 3. Lời giải
Tác giả: Nguyễn Mạnh Dũng ; Fb: Mạnh Dũng Chọn C     1 1  Ta có: 2   4      4 3 3 3 81 3  3   2  3  4 3  3   81   .  4   3 3    4        81    3 3  2   3  4 3  3   81 4 2   3  3  3   0 .  4    3   4    3   81 2  3   0 (do  4 3 3    0 ).  4 3   6 3   81   0  6  3   81  0 (do  4 3   0 ).  4 3   6  3   81  6 4  3
 3    6  4 .
Câu 25. Cho hình lăng trụ tam giác đều ABC.AB C
  có AB a , góc giữa đường thẳng AC và mặt
phẳng  ABC bằng 45 . Thể tích của khối lăng trụ ABC.AB C   bằng
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 38
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 4 2 12 6 Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn Chọn A B' A' C' A B a C
Góc giữa đường thẳng AC và mặt phẳng  ABC chính là góc giữa hai đường thẳng AC và  AC suy ra A CA 45   1  1 2 a 3 S  . AB AC.sin BAC . a . a sin 60   ABC 2 2 4
Tam giác vuông AAC cân suy ra AA  AC a 3 a 3
Thể tích khối chóp ABC.AB C   là : VS .AA'  .
ABC. AB C   ABC 4 Bài toán tương tự
Câu 25.1 Cho hình lăng trụ tam giác đều ABC.AB C
  có AB a . Mặt phẳng  ABC  tạo với mặt phẳng
ABC một góc 30 . Thể tích của khối lăng trụ ABC.AB C   bằng 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 4 6 8 24 Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Trang nguyễn Chọn C a B' A' C' A B M C
Gọi M là trung điểm đoạn BC suy ra AM BC , AM BC
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 39
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Góc giữa mặt phẳng  ABC  và mặt phẳng  ABC chính là góc giữa hai đường thẳng AM và  AM suy ra A MA 30   1  1 2 a 3 S  . AB AC.sin BAC . a . a sin 60   ABC 2 2 4 a 3 AM  2  a
Tam giác vuông AAM có AA  AM tan 30  2 3 a 3
Thể tích khối chóp ABC.AB C   là : VS .AA'  .
ABC. AB C   ABC 8
Câu 26. Cho hàm số y f (x) có bảng biến thiên như hình vẽ bên. Hàm số y f (2x) đạt cực đại tại x -∞ -1 0 2 +∞ 1 1 f(x) -2 1 A. x  . B. x  1. C. x 1. D. x  2 . 2 Lời giải
Tác giả: Trần Mạnh Tường ; Fb: Trần Tuệ Minh Chọn C
Đặt 2x t .
Ta thấy  f 2x    2 f (
 2x)  2 f (  t)  
nên để hàm số y f (2x) đạt cực đại thì hàm số y f (t) phải đạt cực đại
Theo bảng biến thiên thì hàm số y f (t) đạt cực đại tại t  1 và t  2 1
Suy ra hàm số y f (2x) đạt cực đại tại 2x  1 và 2x  2 hay x   và x 1 2 Bài tương tự
Câu 26.1 Cho hàm số y f (x) có bảng biến thiên như hình vẽ bên. Hàm số y f (x  3) đạt cực đại tại
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 40
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 x -∞ -1 0 2 +∞ 1 1 f(x) -2 A. x  1 B. x  2 . C. x  0 . D. x  3 . Lời giải
Tác giả: Trần Mạnh Tường ; Fb: Trần Tuệ Minh Chọn D
Đặt x  3  t .
Ta thấy  f x  3     f (
 x  3)   f (  t)  
nên để hàm số y f (x  3) đạt cực đại thì hàm
số y f (t) phải đạt cực tiểu
Theo bảng biến thiên thì hàm số y f (t) đạt cực tiểu tại t  0
Suy ra hàm số y f (x  3) đạt cực đại tại x  3  0 hay x  3
Câu 27. Cho hình nón tròn xoay có bán kính đáy bằng 3 và diện tích xung quanh bằng 6 3 . Góc ở
đỉnh của hình nón đã cho bằng A. o 60 . B. o 150 . C. o 90 . D. o 120 . Lời giải
Tác giả: Lê Hữu Đức ; Fb: Le Huu Duc Chọn D l h R
Gọi góc ở đỉnh của hình nón bằng 2 . Ta có: S
 6 3   Rl  6 3  l  2 3 xq R 3 Nên sin   o    60 l 2
Vậy góc ở đỉnh của hình nón bằng o 120 . Bài tương tự
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 41
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
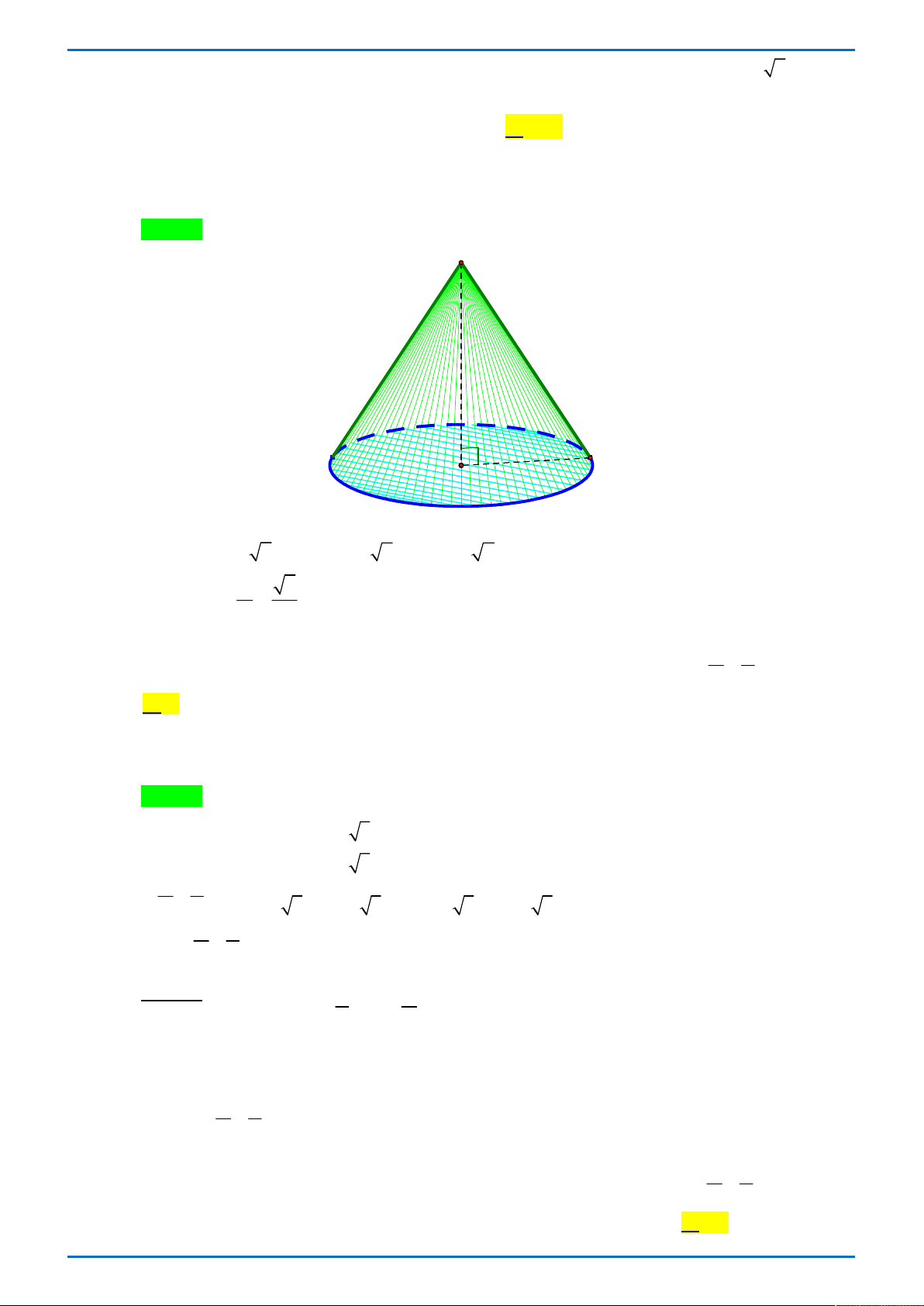
Câu 27.1 Cho hình nón tròn xoay có bán kính đáy bằng 2 và diện tích xung quanh bằng 4 2 . Góc ở
đỉnh của hình nón đã cho bằng A. o 60 . B. o 150 . C. o 90 . D. o 120 . Lời giải
Tác giả: Lê Hữu Đức ; Fb: Le Huu Duc Chọn C l h R
Gọi góc ở đỉnh của hình nón bằng 2 . Ta có: S
 4 2   Rl  4 2  l  2 2 xq R 2 Nên sin   o    45 l 2
Vậy góc ở đỉnh của hình nón bằng o 90 .
Câu 28. Gọi z , z là các nghiệm phức của phương trình 2
z  4z  7  0 . Số phức z z z z bằng 1 2 1 2 1 2 A. 2 . B. 10 . C. 2i . D. 10i . Lời giải
Tác giả: Lê Thị Phương Liên; Fb: Phuonglien Le Chọn A  z  2   3i 2
z  4z  7  0    z  2   3i
z z z z  2  3i 2  3i  2   3i 2  3i  2 . 1 2 1 2      
Vậy z z z z  2. 1 2 1 2
Cách 2: Phương trình bậc hai 2
z  4z  7  0 có '
  3 là số nguyên âm nên phương trình có
hai nghiệm phức z , z và z z , z z . 1 2 1 2 2 1
z z  4  
Áp dụng định lý Viét, ta có: 1 2  z .z  7  1 2
Suy ra: z z z z z z
  z z 2 2 2
 2z .z 16 14  2. 1 2 1 2 1 2 1 2 1 2 Bài toán tương tự
Câu 28.1 Gọi z , z là các nghiệm phức của phương trình 2
z  2z  3  0 . Số phức z z z z bằng 1 2 1 2 1 2 A. 2 . B. 5 . C. 2 . D. 5i .
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 42
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 Lời giải Chọn D
z  1 2i 2
z  2z  3  0  
z  1 2i
z z z z  1 2i 1   2i  1   2i 1 2i  2  . 1 2 1 2      
Vậy z z z z  2  . 1 2 1 2
Cách 2: Phương trình bậc hai 2
z  2z  3  0 có '   2 
là số nguyên âm nên phương trình
có hai nghiệm phức z , z và z z , z z . 1 2 1 2 2 1
z z  2  
Áp dụng định lý Viét, ta có: 1 2  z .z  3  1 2
Suy ra: z z z z z z
  z z 2 2 2
 2z .z  4  6  2. 1 2 1 2 1 2 1 2 1 2 9
Câu 29. Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y x  trên đoạn x
1;4 . Giá trị của m M bằng 65 49 A. . B.16 . C. . D.10 . 4 4 Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạm Chọn B
Hàm số xác định và liên tục trên đoạn 1; 4 . Đặt y f x 9    9
Ta có: f  x  x   1   . 2  x x 9  x  3 1; 4 2  
f  x  0  1
 0  x  9  0  . 2  x x  3  1; 4  25 Có f  
1  10; f 3  6; f 4 
m  min y  6 và M  max y  10 . 4 1; 4 1; 4
Vậy m M  16 .
Câu 29.1 Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số f x 2
 2x  5  x . Giá trị của 2 m M bằng A. 5 . B. 25 . C. 5  2 5 . D. 45 . Lời giải
Tác giả: Phạm Thị Thu Trang; Fb: Trang Phạm Chọn B
Hàm số xác định và liên tục trên đoạn  5; 5  .  
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 43
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 2 x 2 5  x x
Ta có f  x  2   . 2 2 5  x 5  x
f  x  0  2
2 5  x x  0 2
 2 5  x x . x  0 x  0  x  0     
 x  2  x  2 5; 5 . 4 2   2 5  x  2  x  5x  20  0  x  2 
Ta có: f  5  2 
5 ; f 2  5 ; f  5   2 5 .
Suy ra M  max f x  5 và m  min f x  2 5 .  5; 5  5; 5     
Vậy m M   2 2 2 5  5  25 .
Câu 30. Cho hình lập phương ABC . D A BCD
  có I , J tương ứng là trung điểm của BC và BB . Góc
giữa hai đường thẳng AC và IJ bằng A. 45. B. 60 . C. 30 . D. 120 . Lời giải
Tác giả: Phan Chí Dũng ; Fb: Phan Chí Dũng Chọn B
Gọi K là trung điểm của AB vì ABCD là hình vuông nên KI //AC , suy ra góc giữa AC và
IJ bằng góc giữa KI và IJ . 1 1 1 Ta có IK AC ; IJ B C  ; KJ AB vì ABC . D A BCD
  là hình lập phương nên 2 2 2 AC B C
  AB suy ra KI IJ JK suy ra tam giác IJK là tam giác đều, suy ra  KIJ  60 .
Vậy góc giữa AC và IJ bằng 60 . BÀI TOÁN TỔNG QUÁT
 Bài toán: Xác định góc giữa hai đường thẳng trong không gian.
 Kiến thức cần nhớ để vận dụng vào bài tập
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 44
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
 Định nghĩa góc giữa hai đường thẳng
Góc giữa hai đường thẳng a và b là góc giữa hai đường thẳng a và b cùng đi qua một
điểm và lần lượt song song ( hoặc trùng ) với a và b . a a' O b' b  Phương pháp giải
 Cách 1: Sử dụng định nghĩa
Tìm hai đường thẳng a và b cùng đi qua một điểm O và lần lượt song song ( hoặc
trùng ) với a và b , thông thường ta chọn O thuận lợi thuộc đường thẳng a , b đi qua O
và song song với b . Khi đó góc giữa a và b là góc giữa a và b . a O b' b
 Cách 2: Sử dụng véc tơ
Gọi  là góc hai đường thẳng a và b .  
u và u lần lượt là các véc tơ chỉ phương của a và b . 1 2    
- Nếu u ;u  0
 90 thì:   u ;u . 1 2  1 2    
- Nếu u ;u  0  90 thì: 0
  180  u ;u . 1 2  1 2
BÀI TOÁN TƯƠNG TỰ CÙNG MỨC ĐỘ
Tác giả: Vũ Nga; Fb: Nga Vu
Câu 30.1 Cho hình lập phương ABC . D A BCD
  . Góc giữa hai đường thẳng AC và A B  bằng A. 45. B. 60 . C. 30 . D. 120 . Lời giải Chọn B
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 45
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Do AC // AC nên góc giữa hai đường thẳng AC và A B
 là góc giữa hai đường thẳng AC và A B
 . Ta có AC  AB BC  a 2 ( với a là độ dài cạnh của hình lập phương ) 
  ABC đều 0
BAC  60  góc giữa hai đường thẳng AC và A B  là 60 .
Câu 30.2 Cho hình hộp chữ nhật ABC . D A BCD
  có đáy là hình vuông cạnh 2a , cạnh bên là a . I , J
tương ứng là trung điểm của BC và BB . Góc giữa hai đường thẳng AC và IJ bằng  . Tính o c s ? 10 5 1 3 A. os c   . B. o c s  . C. os c   . D. o c s  . 5 5 2 2 Lời giải
Gọi K là trung điểm của AB vì ABCD là hình vuông nên KI //AC , suy ra góc giữa AC và
IJ bằng góc giữa KI và IJ . 2 a a 5  KI 10 10
Ta có IK a 2 , 2
JK JI a    o c sJIK    o c s  . 4 2 2IJ 5 5
Câu 31. Giải bóng chuyền quốc tế VTV Cup có 8 đội tham gia, trong đó có hai đội Việt Nam. Ban tổ
chức bốc thăm ngẫu nhiên để chia thành hai bảng đấu, mỗi bảng 4 đội. Xác suất để hai đội của
Việt Nam nằm ở hai bảng khác nhau bằng 2 5 3 4 A. . B. . C. . D. . 7 7 7 7 Lời giải
Tác giả: Phạm Văn Tuấn; Fb: Phạm Tuấn
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 46
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 Chọn D
Nhận định bài toán:
1) Đây là dạng bài toán phân chia một tập hợp ra thành các nhóm có số lượng bằng nhau. 2) Phương pháp:
Dạng bài toán này được phân chia làm 2 loại đó là: -
Các nhóm có thứ tự A, B, C, D… -
Các nhóm không phân biệt thứ tự.
Nếu không phân biệt rõ ràng 2 bài toán này thì rất dễ dẫn đến nhầm lẫn và sai kết quả.
Ví dụ: Có bao nhiêu cách chia 20 người thành 4 nhóm, mỗi nhóm có 5 người trong các trường hợp sau:
a) Các nhóm được đánh tên theo thứ tự A, B, C, D.
b) Không phân biệt thứ tự nhóm. Lời giải
a) Số cách chọn 5 người cho nhóm A là 5
C . Ứng với mỗi cách chọn trên, ta có số cách chọn 5 20 người cho nhóm B là 5 C , nhóm C là 5
C và 5 người còn lại vào nhóm D. 15 10
Theo quy tắc nhân, ta được số cách chia nhóm là: 5 5 5
C .C .C .1 (cách). 20 15 10
b) Vì các nhóm không phân biệt thứ tự nên khi ta hoán vị 4 nhóm trên sẽ cho cùng một kết quả.
Do đó số cách chia trong trường hợp này là 5 5 5
C .C .C .1 20 15 10 (cách) 4!
3) Phân tích bài toán và lời giải.
Chia 8 đội thành hai bảng đấu, do đó hai bảng đấu này sẽ có thứ tự rõ ràng cho nên bài toán của
chúng ta thuộc loại chia nhóm có thứ tự.
Gọi hai bảng đấu là bảng A và bảng B.
Chọn 4 đội vào bảng A ta có 4
C cách, bốn đội còn lại vào bảng B có 1 cách. 8
Theo quy tắc nhân, ta có số cách chia 8 đội vào hai bảng đấu là: n  4
C .1  70 (cách) 8
Gọi A là biến cố “Hai đội Việt Nam nằm ở hai bảng khác nhau”.
Bảng A: Có 3 đội nước ngoài và 1 đội Việt Nam. Số cách chọn là 3 1 C .C . 6 2
Bảng B: Chỉ còn 1 cách chọn duy nhất cho 3 đội nước ngoài và 1 đội Việt Nam còn lại vào bảng B.
Do đó số cách chia 8 đội thành 2 bảng mỗi bảng có 1 đội Việt Nam là : n A 3 1
C .C .1  40 (cách) 6 2 n A 40 4
Vậy xác suất của biến cố A là: P A    . n  70 7 Bài toán tương tự
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 47
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Câu 31.1 Giải bóng chuyền quốc tế VTV Cup có 12 đội tham gia, trong đó có 3 đội Việt Nam. Ban tổ
chức bốc thăm ngẫu nhiên để chia thành 3 bảng đấu, mỗi bảng 4 đội. Tính xác suất để 3 đội của
Việt Nam cùng nằm ở một bảng đấu. 3 1 1 6 A. . B. . C. . D. . 55 330 110 55 Lời giải Chọn A
Gọi ba bảng đấu có tên là A, B, C.
Chọn 4 đội cho bảng A có 4
C cách, chọn 4 đội cho bảng B có 4
C cách và 4 đội còn lại vào 12 8 bảng C có 1 cách.
Theo quy tắc nhân, số cách chia 12 đội thành 3 bảng đấu là: n  4 4
C .C .1  34650 (cách) 12 8
Gọi A là biến cố “3 đội Việt Nam cùng nằm ở một bảng đấu.
Giả sử 3 đội Việt Nam cùng nằm ở bảng A.
Khi đó bảng A sẽ chọn 1 đội trong 9 đội nước ngoài và 3 đội Việt Nam, 8 đội còn lại chia vào
bảng B và C. Trong trường hợp này ta có số cách chọn là 1 4
C .1.C .1  630 (cách) 9 8
Vì vai trò của các bảng là như nhau nên trường hợp 3 đội Việt Nam ở bảng B hay bảng C đều cho kết quả như nhau.
Vậy số kết quả thuận lợi cho biến cố A là n A 1 4
C .C .3  1890 (cách) 9 8 n A 1890 3
Xác suất của biến cố A là : P A    . n  34650 55 x
Câu 32. Tất cả các nguyên hàm của hàm số f x 
trên khoảng 0; là 2 sin x
A. x cot x  ln sin x  C.
B. x cot x  ln sin x C.
C. x cot x  ln sin x C. D. x cot x  ln sin x  C. Lời giải
Tác giả:Văn Bùi Vũ ; Fb: Van Tuan Vu ChọnA u   x x  d  u  dx  
Gọi F x  dx  . Đặt    2 1 sin x d  v  dx v   cot x   2  sin x x cos x
Khi đó: F x 
dx  x cot x  dx   2 sin x sin x dsin x
 xcot x
 xcot x  ln sin x C.  sin x
Vì x  0; nên sin x  0 , suy ra ln sin x  lnsin x.
Vậy: F x  x cot x  lnsin x  C.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 48
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 Phân tích và bình luận:
Bài toán sử dụng nguyên hàm từng phần dạng đặc biệt kết hợp giữa đa thức và lượng x x giác: 2 2 d ; x d ; x x tan d x ; x x cot d x x    
và xét dấu hàm lượng giác. 2 2 sin x cos x Bài toán tương tự x
Câu 32.1 Tất cả các nguyên hàm của hàm số f x 
trên khoảng 0;  là 2 cos x    2 
A. F x  x tan x  lncos x C.
B. F x  x
 tan x  lncos x C.
C. F x  x tan x  lncos x . C
D. F x  x tan x  ln cos x C. Lời giải
Tác giả:Văn Bùi Vũ ; Fb: Van Tuan Vu Chọn A u   x x  d  u  dx  
Gọi F x  dx  . Đặt    2 1 cos x d  v  dx v   tan x   2  cos x x sin x
Khi đó: F x 
dx x tan x  dx   2 cos x cos x dcos x  x tan x
x tan x  ln cos x C.  cos x
Vì x  0;   
 nên cos x  0 , suy ra ln cos x lncos x .  2 
Vậy: F x  x tan x  lncos x C. 
Câu 32.2 Tất cả các nguyên hàm của hàm số f x 2
x tan x trên khoảng   ;0   là  2  2 x 2 x
A. F x  x tan x  lncos x  C.
B. F x  x tan x  lncos x  C. 2 2 2 x 2 x
C. F x  x tan x  lncos x  C.
D. F x  x tan x  ln cos x   C. 2 2 Lời giải
Tác giả:Văn Bùi Vũ ; Fb: Van Tuan Vu Chọn A Gọi F xx 2  x tan d x x x    2 tan x 1  1 dx x   2 tan x   1 dx  d x x  dx  d x . x    2 cos x u   x  d  u  dx   Đặt  1   d  v  dx v   tan x   2  cos x
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 49
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 2 x sin x x
Khi đó: F x  dx  d
x x x tan x  dx     2 cos x cos x 2  x 2 2 d cos x xx tan x  
x tan x  ln cos x   C.  cos x 2 2   Vì x    ;0  
 nên cos x  0 , suy ra ln cos x lncos x .  2  2 x
Vậy: F x  x tan x  lncos x  C. 2
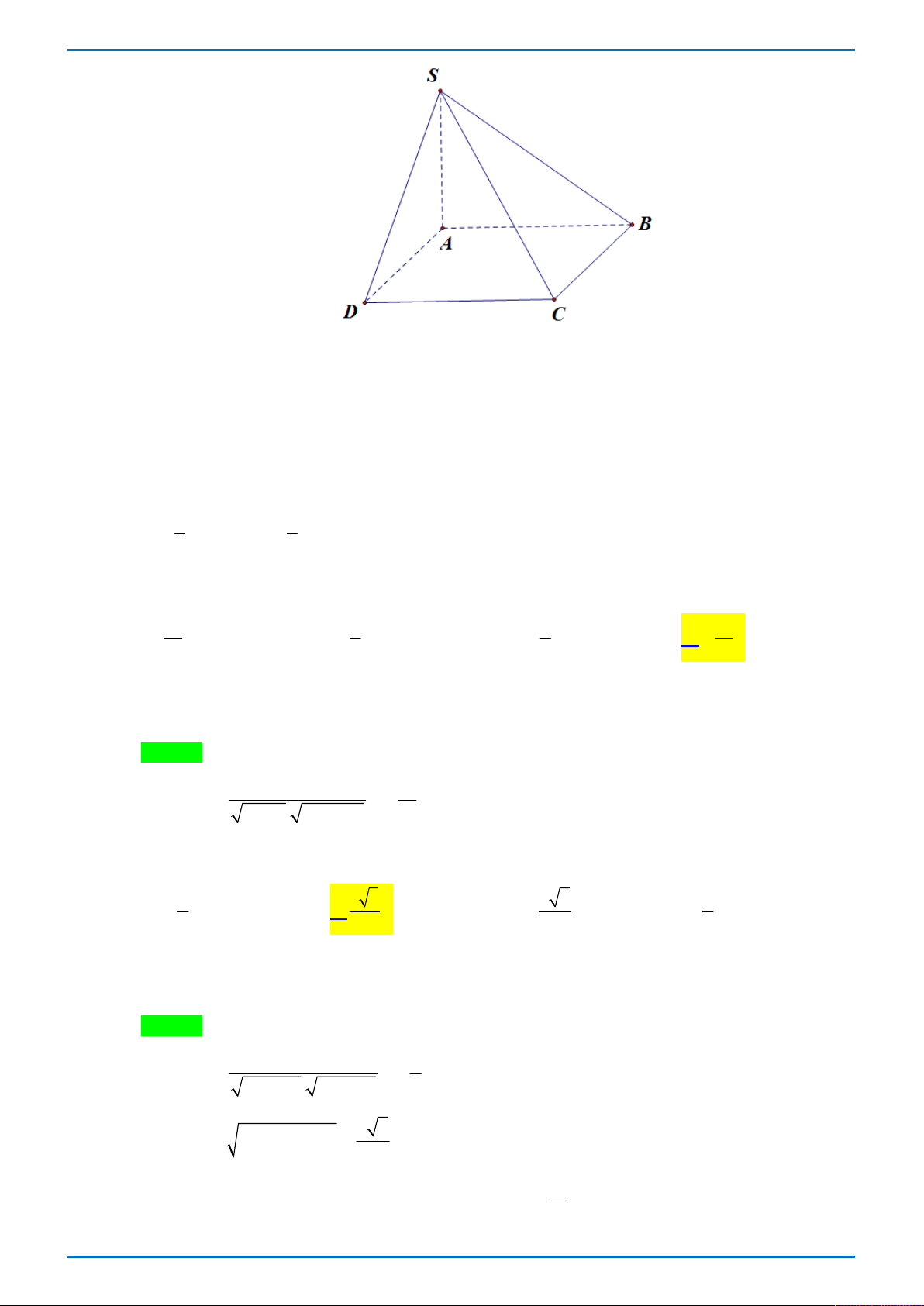
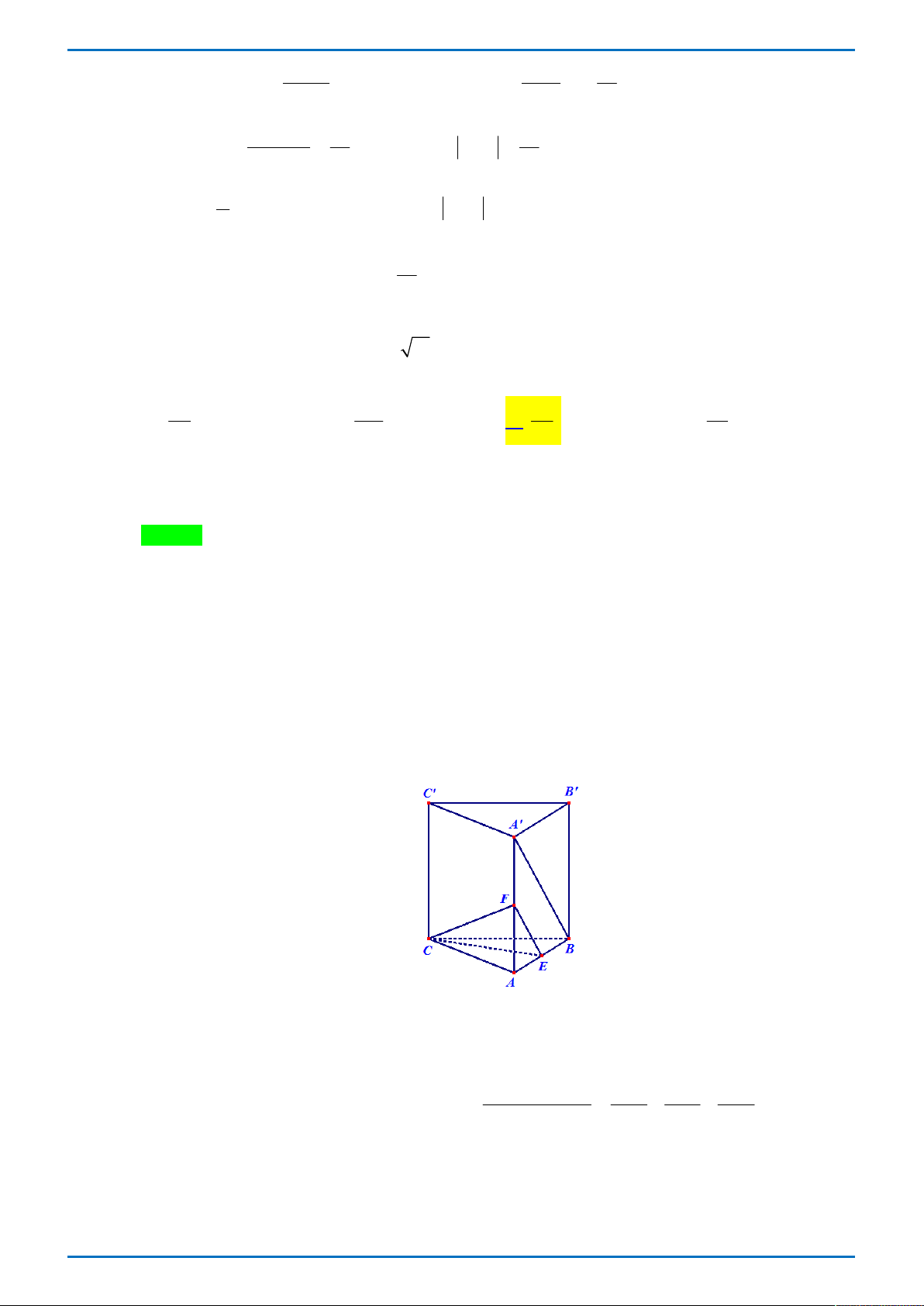
Câu 33. Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông tại A . Gọi E là trung
điểm AB . Biết AB  2a , BC a 13 , CC  4a . Khoảng cách giữa hai đường thẳng A B  và CE bằng 4a 12a 6a 3a A. . B. . C. . D. . 7 7 7 7 Lời giải
Tác giả: Nguyễn Bảo Mai; Fb: Bao An Chọn C Phân tích:
* Kiến thức trọng tâm: Khoảng cách giữa hai đường thẳng chéo nhau. * Hướng giải bài toán:
+ Dựng mặt phẳng đi qua một đường thẳng và song song với đường còn lại
+ Dùng tỉ số khoảng cách để đưa việc tính khoảng cách từ một điểm đến một mặt phẳng thành
tính khoảng cách từ một điểm khác đến mặt phẳng thuận lợi hơn.
+ Tính chiều cao của một tứ diện vuông
* Giải: Lấy trung điểm F của AA được EF song song với  CEF  đi qua CE và song song với A B
  d AB,CE   d B,CEF   d  ,
A CEF  . 1 1 1 1
Mặt khác ACEF là tứ diện vuông tại A nên    . 2 d  , A CEF  2 2 2 AF AE AC
Ta có AA  CC  4a AF  2a
AB  2a AE a
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 50
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 2 2 2 2 AC
BC AB  13a  4a  3a 1 1 1 1 49 a 6a     
d A CEF  6 , 
d CE, AB  . 2 d  , A CEF  2 2 2 2 4a a 9a 36a 7 7 Bài toán tươn tự
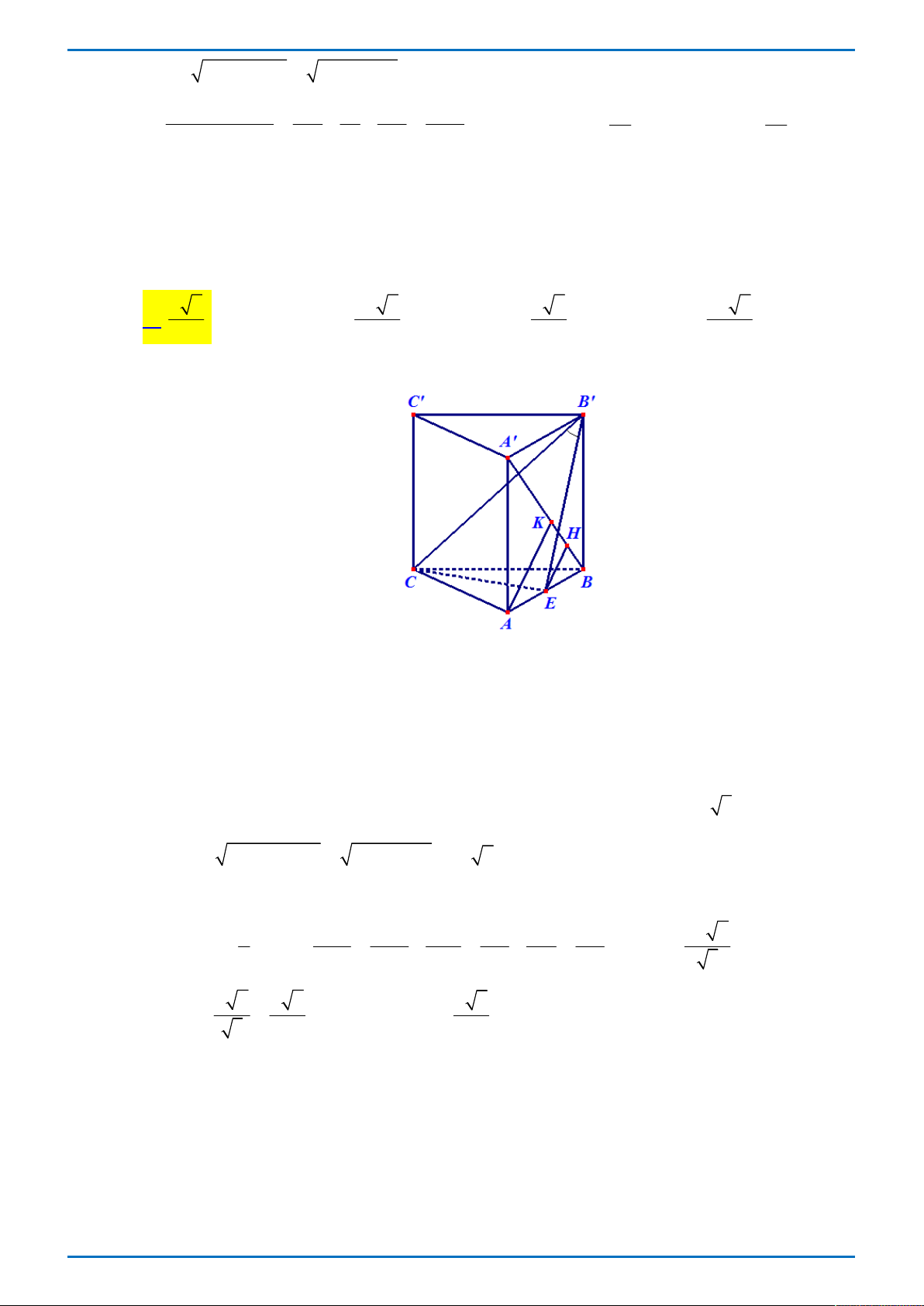
Câu 33.1 Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác đều cạnh 2a . Gọi E là trung
điểm AB . Biết góc giữa CB và  BCC B   bằng o
30 . Khoảng cách giữa hai đường thẳng A B  và CE bằng a 6 2a 6 a 6 2a 6 A. . B. . C. . D. . 3 3 6 6 Lời giải
Thấy CE AB , CE AA  CE   AA BB
  hay  AAB B
  chính là mặt phẳng qua A B  ,
vuông góc với CE . Gọi H là hình chiếu của E trên A B
  EH chính là đoạn vuông góc chung của A B
 và CE d CE, A B    EH .
Mặt khác CB có hình chiếu là EB trên  BCC B   là EB 
 CB BCC B
   CBEB  , ,  CB E  o  CB E
  30  CB  2CE  2.a 3 2 2 2 2
CC  CB  C B
   12a  4a  2a 2 .
Gọi K là hình chiếu của A trên A B  . 1 1 1 1 1 1 3 2a 2 Ta có EH AK và       AK  2 2 2 2 2 2 2 AK AAAB 8a 4a 8a 3 a 2 a 6 a 6  EH  
hay d CE, AB  . 3 3 3
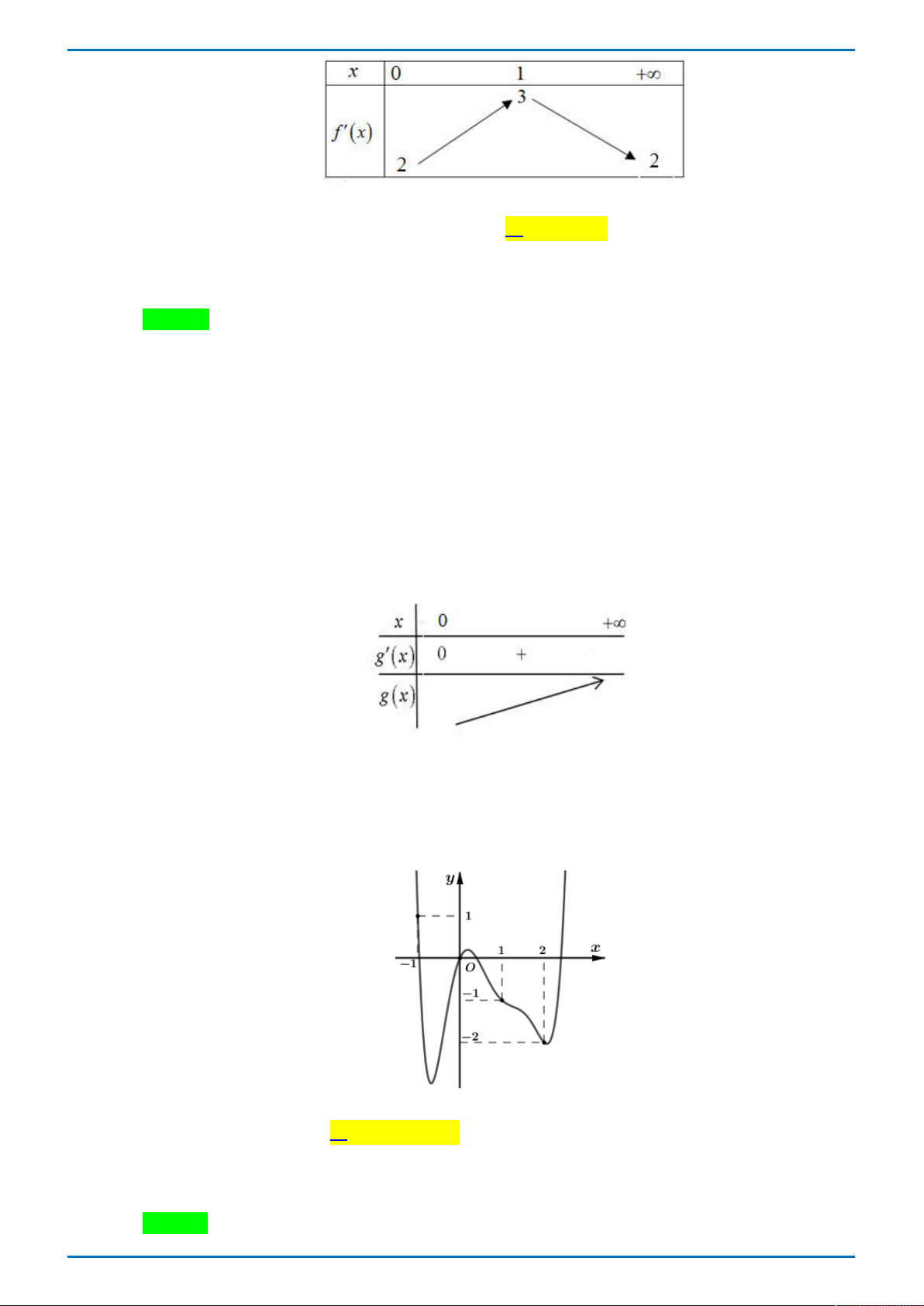
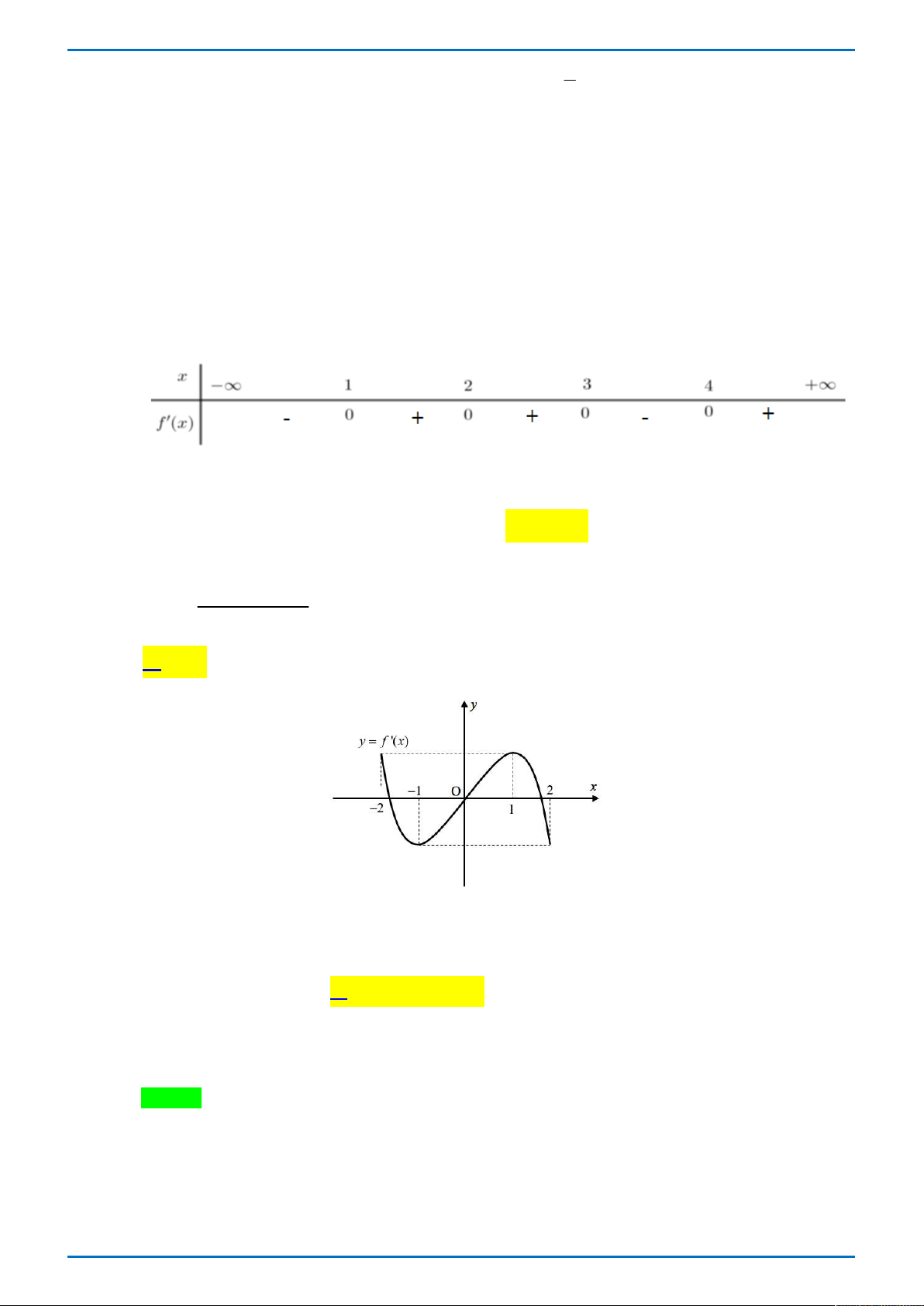
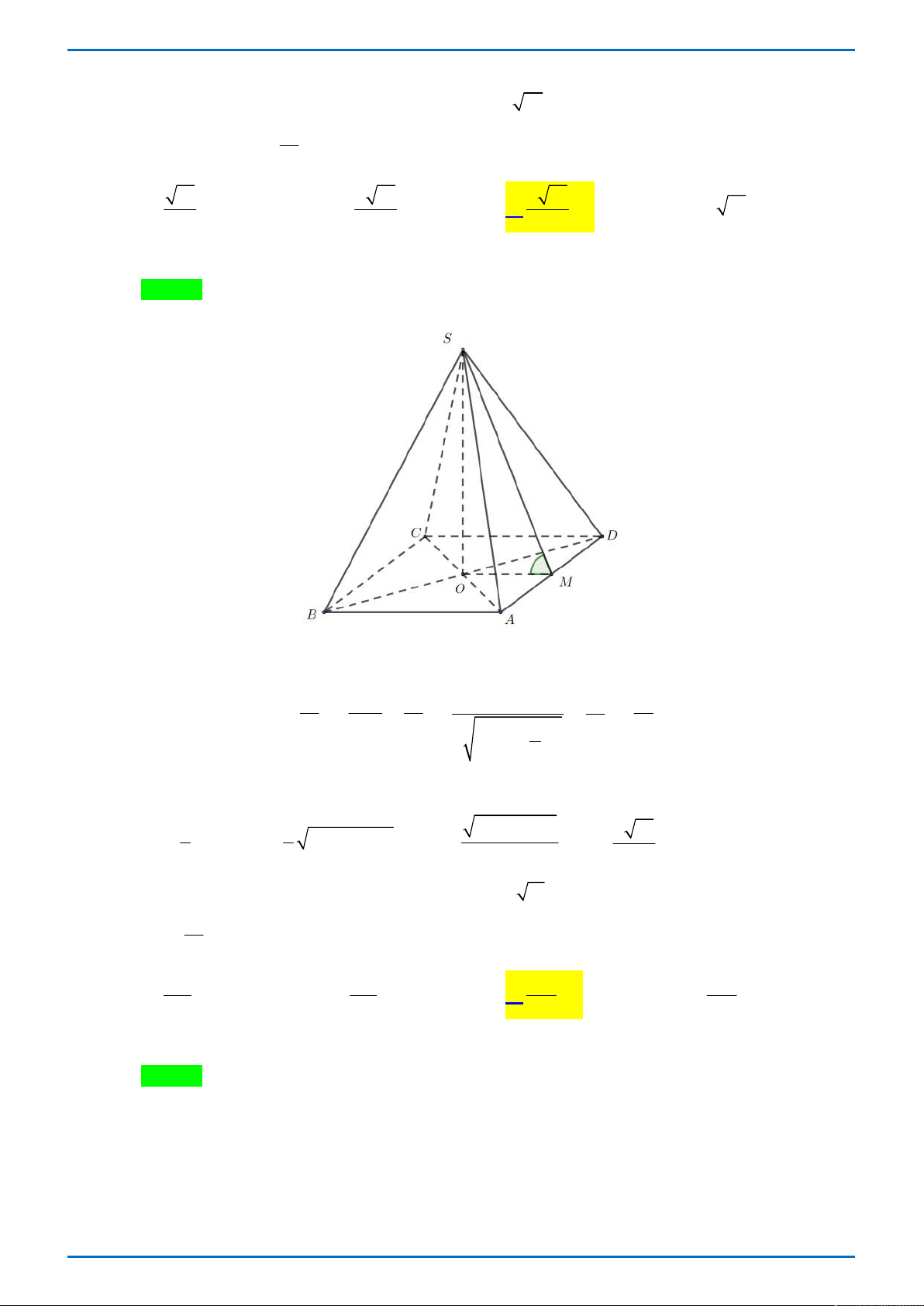
Câu 34. Cho hàm số y f x có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên m để phương trình f  3
x  3x  m có 6 nghiệm phân biệt thuộc đoạn  1  ; 2?
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 51
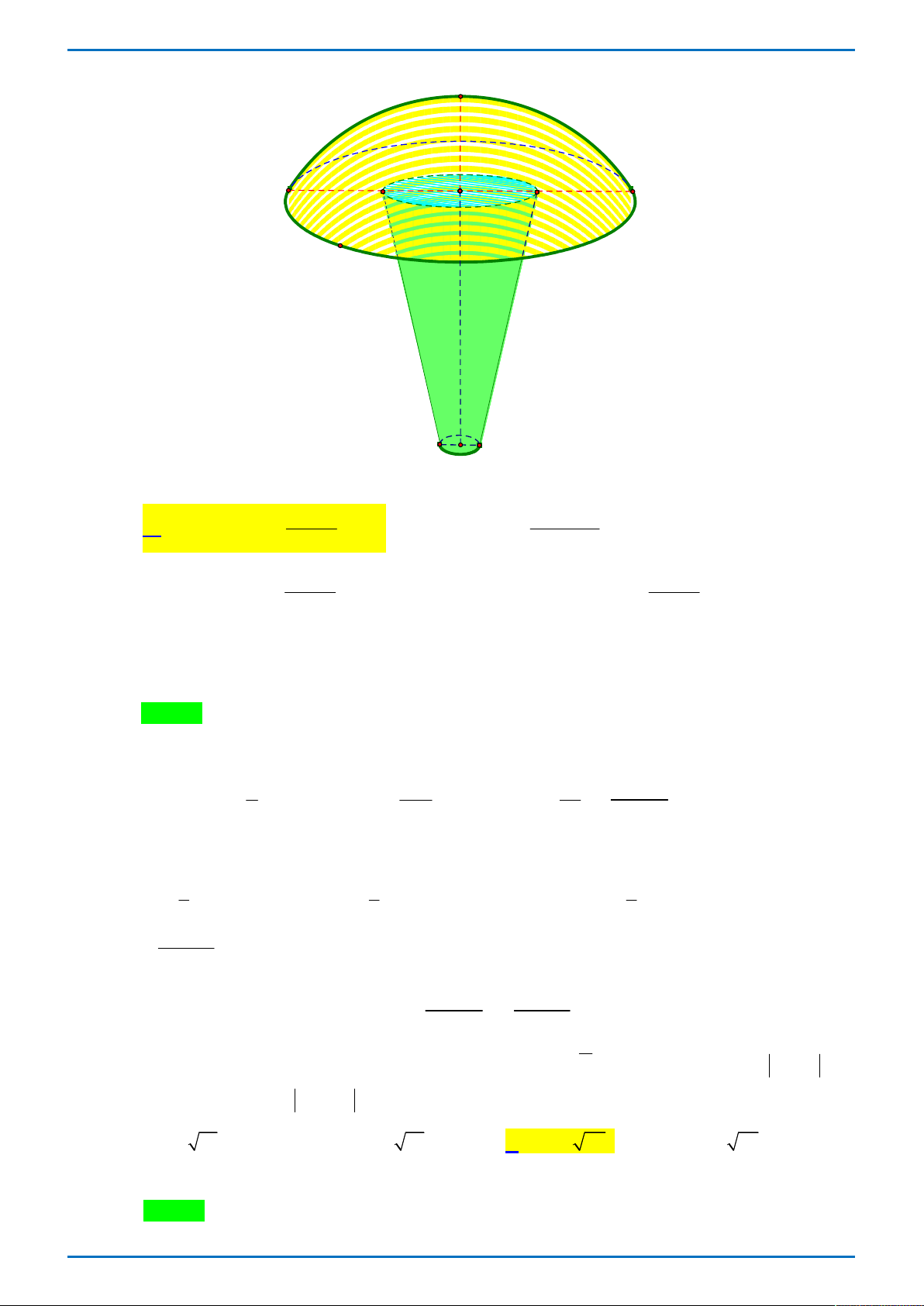
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 A. 3 . B. 2 . C. 6 . D. 7 . Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ Chọn B Đặt 3
t x  3x , xét hàm số 3
t x  3x trên đoạn  1  ; 2. x  1 t  2  Ta có 2
t  3x  3  0     . x  1  t  2  
Ta có bảng biến thiên của hàm số 3
t x  3x trên đoạn  1  ; 2. x -1 1 2 t' - 0 + 2 2 t -2
Từ đó bảng biến thiên trên ta thấy: +) Nếu t  2
 thì x  1 1  ; 2 . +) Nếu t   2
 ; 2 thì có hai nghiệm phân biệt x  1  ; 2 .
Do đó phương trình f  3
x  3x  m có 6 nghiệm x phân biệt thuộc đoạn  1  ; 2 khi phương
trình f t   m có 3 nghiệm t phân biệt thuộc khoảng  2  ; 2 * .
Dựa vào đồ thị hàm số y f x đã cho và m là số nguyên ta thấy m  0 hoặc m  1 thỏa mãn * .
Vậy có hai giá trị nguyên của m thỏa mãn yêu cầu bài toán. Bài toán tổng quát:
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 52
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Cho hàm số y f x có đồ thị cho trước là C (hoặc cho trước bảng biến thiên). Biện luận
theo tham số m số nghiệm của phương trình f  .
n g x  p  h m  
trên tập D cho trước
( D   ); trong đó ,
n p là các số thực; h m là biểu thức với tham số m . Cách giải:
Bước 1: Đặt t  .
n g x  p . Khi đó f  .
n g x  p  h m  f t   h m   . Bước 2:
+) Tìm miền giá trị D của t ứng với x D .
+) Chỉ ra mối quan hệ giá trị tương ứng giữa t D và x D .
Bước 3: Dựa vào đồ thị C (hoặc bảng biến thiên của hàm số y f x ), biện luận theo m số
nghiệm t D của phương trình f t   hm .
Bước 4: Dựa vào mối quan hệ giữa x và t ở Bước 2 ta có biện luận số nghiệm x D của phương trình f  .
n g x  p  h m   . Bài toán tương tự
Câu 34.1. (Thi thử chuyên Sư Phạm HN lần 1 năm 2019) Cho hàm số y f (x) liên tục trên  và có
đồ thị như hình bên. Phương trình f (2 sin x)  m có đúng ba nghiệm phân biệt thuộc đoạn  
 ;  khi và chỉ khi A. m 3;  1 . B. m  3   ;1 . C. m  3   ;1 . D. m  3   ;1 . Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ Chọn A t
Đặt t  2sin x  sin x  . 2 Với x    ;  thì 1
  sin x  1  t  2  ; 2 . 
+) Với t  2 thì có 1 nghiệm x thuộc    ;  là x  . 2  +) Với t  2
 thì có 1 nghiệm x thuộc  
 ;  là x   . 2
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 53
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
+) Với t  0 thì có 3 nghiệm x thuộc  
 ;  là x 0;    . +) Với t  2  ; 2 \ 
0 thì có 2 nghiệm phân biệt x thuộc    ;  .
Dựa vào đồ thị của hàm số y f (x) đã cho, để phương trình f (2 sin x)  m có đúng ba
nghiệm phân biệt thuộc đoạn  
 ;  thì phương trình f t  m   * trên  2  ; 2 xảy ra các trường hợp sau:
TH1: m  1 thì  
* có hai nghiệm là t  1  ; 
2 nên thỏa mãn yêu cầu. TH2: m  3
 thì * có hai nghiệm là t 1;  
2 nên thỏa mãn yêu cầu. Vậy m 3; 
1 thì thỏa mãn yêu cầu bài toán.
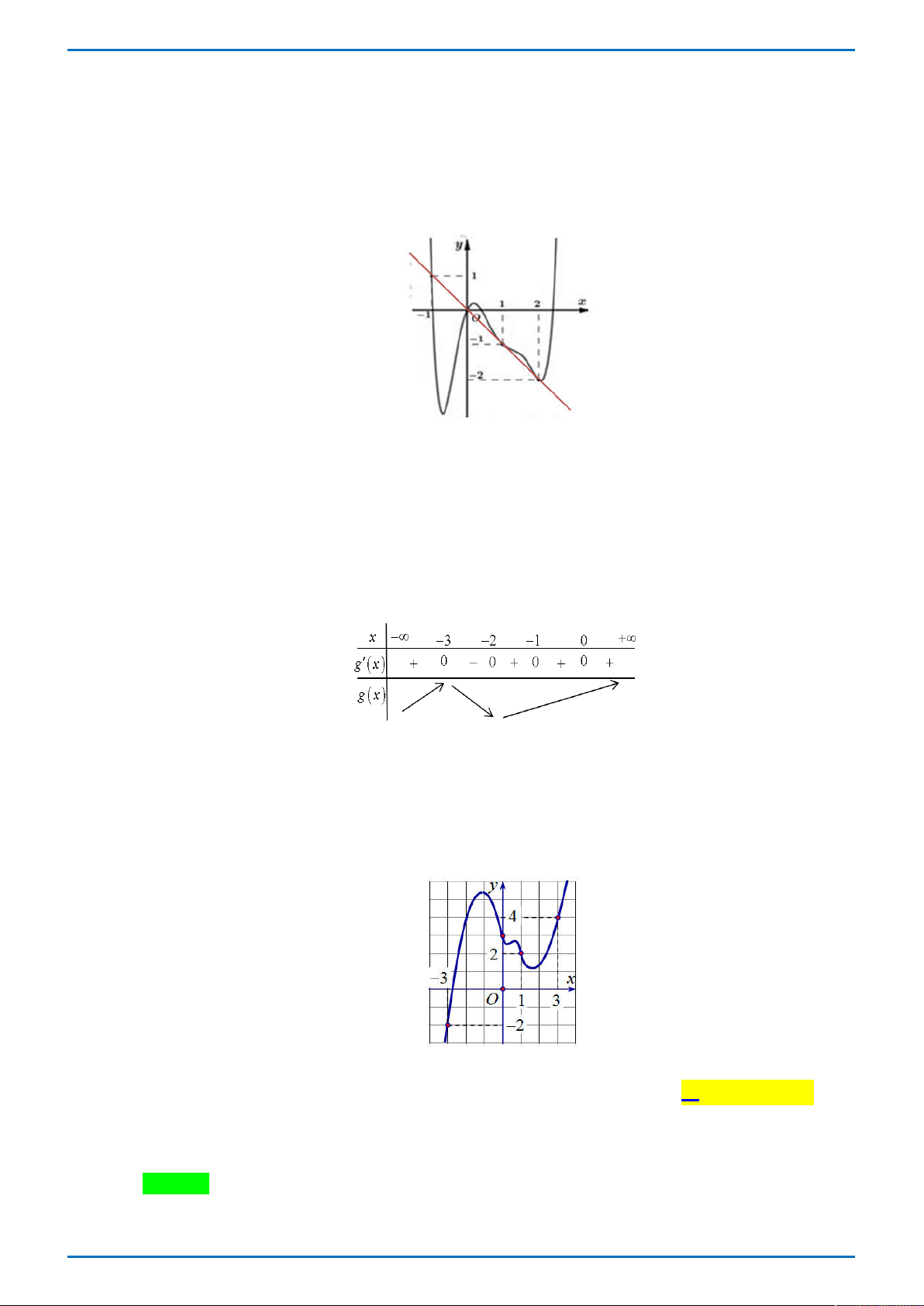
Câu 34.2. (Thi thử chuyên Lam Sơn lần 2 năm 2019) Cho hàm số y f x liên tục trên  có đồ thị
như hình vẽ bên. Phương trình f f x  
1  0 có tất cả bao nhiêu nghiệm thực phân biệt? A. 6 . B. 5 . C. 7 . D. 4 . Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ Chọn C
Đặt t f x 1  f x  t 1.
Từ đồ thị của hàm số đã cho, phương trình f t   0 có ba nghiệm phân biệt: t  2  ; 1  , t  1  ; 0 , t  1; 2 . 1   2   3   +) Với t  2  ; 1   1
  t 1  0 , dựa vào đồ thị đã cho phương trình f x  t 1 có 3 1   1 1
nghiệm thực x phân biệt. +) Với t  1
 ; 0  0  t 1  1 , dựa vào đồ thị đã cho phương trình f x  t 1 có 3 2   2 2
nghiệm thực x phân biệt.
+) Với t  1; 2  2  t 1  3 , dựa vào đồ thị đã cho phương trình f x  t 1 có 1 nghiệm 3   3 3 x .
Vậy phương trình đã cho có 7 nghiệm thực phân biệt. 2
Câu 35. Có bao nhiêu số phức z thỏa mãn z
z z i   z z 2019 1 i  1 ? A. 4. B. 2. C. 1. D.3.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 54
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom Chọn D
Giả sử z a bi , a,b    z a bi .
Ta có: z 1  a  1  bi , z z  2bi , z z  2a .   1009 2019 2 i i i   1009 1 i  i . 2 Do đó z
z z i   z z 2019 1 i  1 2  a   
2  b    b2 2 1 2
.i  2a i    1   2 2  a  2 2 1  b  1
a  2a b  0   a  2 2 1
b  2 b i  2ai  1     2 b  2a  0  a b     a  0  b  0    b  0  2 
2 b  2 b  0    a  1     b  1     . a b   b  1    a b    a 1   b  1  
Vậy có 3 số phức z thỏa mãn yêu cầu bài toán. Phân tích:
*) Kiến thức trọng tâm liên quan đến bài toán: Sử dụng các kiến thức về số phức liên hợp,
moddun của số phức, hai số phức bằng nhau, các phép toán trên số phức. Cụ thể: 1.1. Số phức liên hợp
Số phức liên hợp của z a bi (a, b  ) là z a bi . ( Đổi dấu phần ảo của z ). a a '
1.2. Hai số phức bằng nhau: a bi a  b i    (a, ,
b a ', b '  ) . b b ' 
1.3. Môđun của số phức: 2 2
z a bi a b . k 2 i  
 2i    k k 1 1.4. Tính n i : n i   . k 2 1 i    2
i i   k k 1 i
*) Lỗi học sinh hay gặp: + Khi lấy moddun: 2 2
z a b
+ Nhầm lẫn phần thực, phần ảo.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 55
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
*) Lưu ý với lớp bài toán tìm z : Khi tìm z mà trong giả thiết bài toán ngoài việc cho z , còn
có cả z , z ,… thì ta thường sử dụng phép thay trực tiếp z a bi (a, b  ) và các yếu tố liên
quan để tìm được mối liên hệ giữa phần thực, phần ảo của z .
*) Các bài toán tương tự: Mức độ vận dụng
Câu 35.1 Cho các số phức z thỏa mãn 2020 z  2i
z  1  2i . Tập hợp các điểm biểu diễn số phức
w  2 z  1  4i trên mặt phẳng tọa độ là một đường thẳng. Khoảng cách từ I 2;  3 đến đường thẳng đó bằng 18 5 18 13 10 3 10 5 A. . B. . C. . D. . 5 13 3 5 Lời giải
Tác giả: Trần Thị Thơm ; Fb: Tranthom Chọn D
Giả sử z a bi a;b   và w x yi  ; x y   . Ta có 2020 z  2i
z  1  2i a bi  i 1010 2 2
a bi  1  2i
 a  2  b  a  2    b2 2 2 1 2
 2a  4b 1  0  1 .
Theo giả thiết: w  2z  1  4i x yi  2a bi 1 4i x yi  2a 1 4  2bi .  x  1 a  x  2a 1   2     2 . y  4  2b  4  y b     2 x  1 4  y Thay 2 vào   1 ta được: 2.  4.
 1  0  x  2 y  6  0 . 2 2 10 5
Vậy: d I,   . 5
Câu 35.2 Cho các số phức z thỏa mãn 2021 2iz  2i
 3z  1 và z  1 . Điểm biểu diễn cho số phức z có hoành độ bằng A. 4 . B. 4 . C. 1. D. 1. Lời giải
Tác giả: Trần Thị Thơm ; Fb:Tranthom Chọn C
Giả sử z a bi a;b   . 1010 Ta có 2021 2iz  2i  3z  1 
i a bi   2 2 2 i
i  3a bi 1 2 2
 2a  2i  2b  3a   1  3bi   a   2
b   a   2 2 2 4 3 1  9b   2 2
5 a b   2a  3  0   1 .
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 56
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 Mặt khác : z  1 2 2
a b  12 .
Thay (2) vào (1) được 5.1  2a  3  0  a  1.
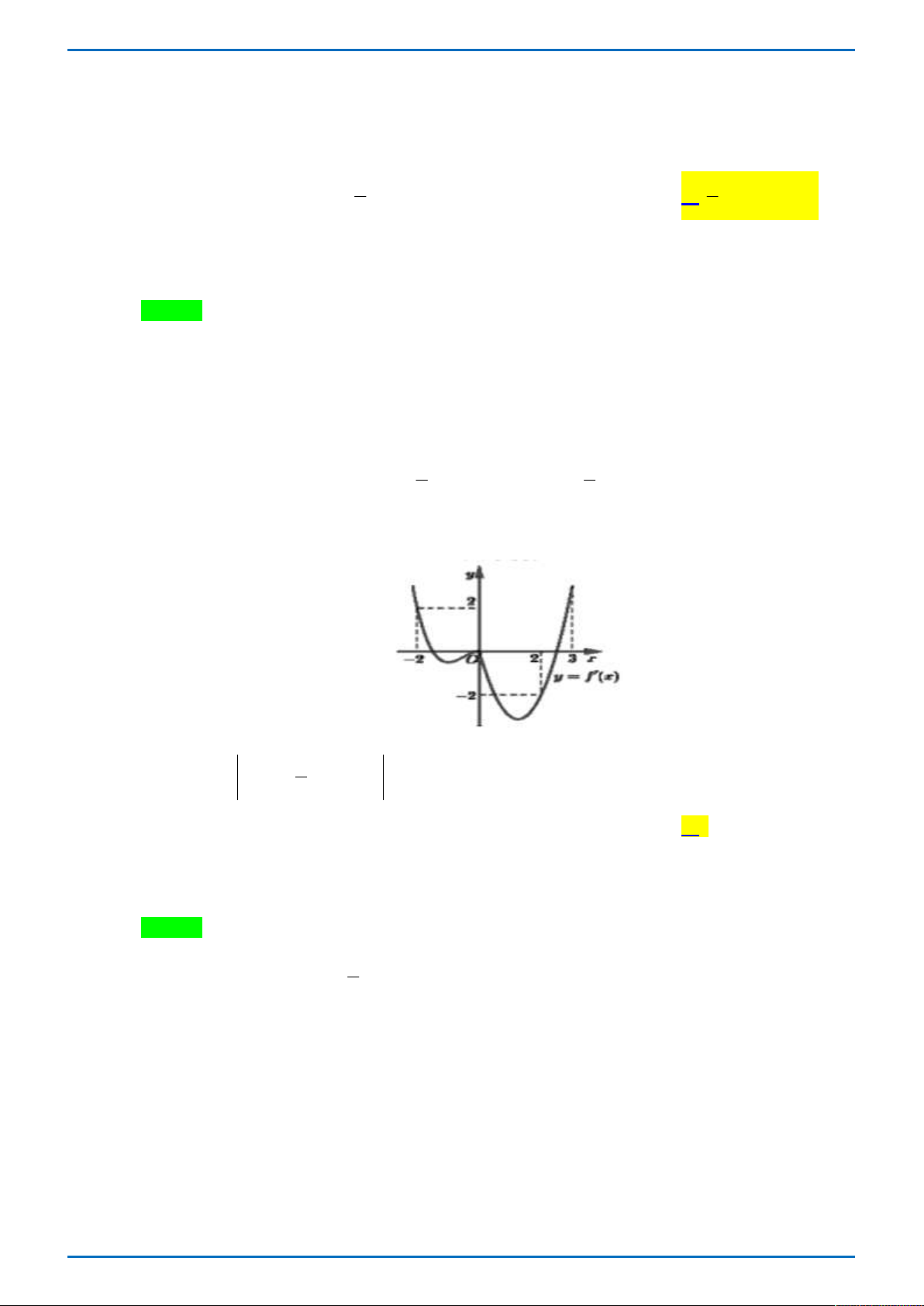
Câu 36. Cho hàm số y f x có đạo hàm trên  . Bảng biến thiên của hàm số y f ' x như hình dưới 1
Tìm m để bất phương trình 2
m x f x 3 
x nghiệm đúng với mọi x 0;3 . 3 2
A. m f (0) .
B. m f (0) .
C. m f (3) .
D. m f (1)  . 3 Lời giải
Tác giả : Võ Thị Ngọc Ánh ; Fb: Võ Ánh Chọn B. 1 1 Ta có 2
m x f x 3 
x m f x 3 2  x x . 3 3 1
Đặt g x  f x 3 2  x x . 3
Ta có g x  f  x 2
x x f  x   2 2
x  2x .
g x   f  x 2 0
 x  2x . 2
Mà f  x  1, x  0;3 và 2
x  2x  1   x   1
 1,x  0;3 nên g x  0, x  0;3 .
Từ đó ta có bảng biến thiên của g(x) : 1
Bất phương trình m f x 3 2 
x x nghiệm đúng với mọi x 0;3 3
m g 0  m f (0) .
NHẬN XÉT: (Võ Thị Ngọc Ánh) Bài toán xây dựng dựa trên ý tưởng mối quan hệ giữa bảng
biến thiên của f '(x) hoặc đồ thị của f '(x) so sánh với h '(x) để suy ra sự biến thiên của hàm
số có dạng g(x)  f (x)  h(x) . Bài toán tương tự
Câu 36.1. Cho hàm số y f x có đạo hàm trên  . Bảng biến thiên của hàm số y f ' x như hình dưới
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 57
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Tìm m để bất phương trình m  2sin x f x nghiệm đúng với mọi x 0;  .
A. m f (0) .
B. m f (1)  2sin1.
C. m f (0) .
D. m f (1)  2sin1.
Tác giả : Võ Thị Ngọc Ánh ; Fb: Võ Ánh Lời giải Chọn C.
Ta có m  2sin x f x  m f x  2sin x .
Đặt g x  f x  2sin x .
Ta có g x  f  x  2cos x .
g x  0  f  x  2 cos x .
Mà f  x  2, x
  0; và 2cosx  2, x
 0; nên g x  0, x  0; .  f '(x)  2
g x  0    x  0 . 2 cos x  2 
Từ đó ta có bảng biến thiên của g(x) :
Bất phương trình m  2 f x  2   x  
1  x  3 nghiệm đúng với mọi x  3  ; 
m g 0  m f (0) .
Câu 36.2. (Phát triển từ câu 50 đề liên trường Nghệ An ) Cho hàm số y f x có đạo hàm trên  .
Đồ thị hàm số y f ' x như hình vẽ bên dưới.
Tìm m để bất phương trình 2
m x  2 f x  2  4x  3 nghiệm đúng với mọi x  3  ;  .
A. m  2 f (0) 1.
B. m  2 f (0) 1. C. m  2 f ( 1  ) . D. m  2 f ( 1  ) . Lời giải
Tác giả : Võ Thị Ngọc Ánh ; Fb: Võ Ánh Chọn B.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 58
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 Ta có 2 m x
f x    x   m f x   2 2 2 4 3 2
2  x  4x  3 .
Đặt g x  f x   2 2
2  x  4x  3 . Ta có g x  2 f  x  2  2x  4 .
g x  0  f  x  2   x  2 .
Đặt t x  2 ta được f t   t  .   1  
1 là phương trình hoành độ giao điểm của đồ thị f t và đường thẳng d : y  t (hình vẽ)
Dựa vào đồ thị của f t và đường thẳng y  t ta có t  1   x  3   t  0 x  2
ta có f t   t    hay  . t  1  x  1   t  2  x  0 
Bảng biến thiên của hàm số g x .
Bất phương trình m  2 f x  2   x  
1  x  3 nghiệm đúng với mọi x  3  ; 
m g  2
   m  2 f (0) 1.
Câu 36.3. (Phát triển từ đề thi đại học 2018) Cho hàm số y f x có đạo hàm trên  . Đồ thị của hàm
số y f  x như hình dưới
Tìm m để bất phương trình 2
m x  4  2  f x  
1  2x  nghiệm đúng với mọi x  4  ; 2 .
A. m  2 f (0) 1. B. m  2 f ( 3  )  4 .
C. m  2 f (3) 16 .
D. m  2 f (1)  4 .
Tác giả : Võ Thị Ngọc Ánh ; Fb: Võ Ánh Lời giải Chọn D.
m x    f x    x  m f x     x  2 2 4 2 1 2 2 1 2
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 59
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Đặt g x  f x     x  2 2 1 2
Ta có g x  2 f  x  
1  2 x  2  2 f  x  
1   x  2 . g x  0  f  x   1  x  2
Đặt t x  1 ta được f t   t 1   1  
1 là phương trình hoành độ giao điểm của đồ thị f t và đường thẳng d : y t 1 (hình vẽ)
Dựa vào đồ thị của f t và đường thẳng y t 1 ta có t  3  x  4   ta có  
1  t  1 hay x  0 .   t  3   x  2 
Xét hàm t t(x)  x 1 đồng biến trên  suy ra bảng biến thiên của hàm số g x : Bất phương trình 2
m x  4  2  f x  
1  2x  nghiệm đúng với mọi x  4  ; 2 .
m g 0  m  2 f (1)  4 .
Câu 37. Trong không gian Oxyz cho M 2;1; 4; N 5;0;0; P 1; 3   ;1 . Gọi I  ; a ;
b c là tâm mặt cầu
tiếp xúc với mặt phẳng Oyz đồng thời đi qua các điểm M , N, P . Tìm c biết a b c  5 A. 3 . B. 2 . C. 4 . D. 1 . Lời giải
Tác giả:Quỳnh Giao; Fb: QGiaoDo Chọn C
Mặt cầu tiếp xúc với mặt phẳng Oyz đồng thời đi qua các điểm M , N, P nên
d I;Oyz  IM IN IP
d I;Oyz  IM
a  a  22  b  2 1  c  42 2       IN IM  
a  52  b c  a  22  b  2 1  c  42 2 2  IN IP    
  a  52  b c   a  2
1  b  32  c  2 2 2 1 
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 60
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
a  a  2  b  2  c  2 2 2 1 4  a  3  a  5     
3a b  4c  2
 b  1 hoặc b  3 
4a  3b c  7  c  2  c  4   
So sánh với điều kiện a b c  5 ta có c  2 Bài toán tương tự
Câu 37.1. Trong không gian Oxyz cho A 2  ; 0; 0; B0; 2  ;0; C 0;0; 2
  . D là điểm khác O sao cho D ,
A DB, DC đôi một vuông góc. I  ; a ;
b c là tâm mặt cầu ngoại tiếp tứ diện ABCD . Tính
S a b c A. 4 . B. 1 . C. 2 . D. 3 . Lời giải
Tác giả:Quỳnh Giao; Fb: QGiaoDo Chọn B    Gọi D  ;
x y; z  DA =  x  2; y; z ; DB =  x; y  2; z ; DC =  x; y; z  2 Vì D ,
A DB, DC đôi một vuông góc nên    D . A DB  0
x x  2  y y  2 2  z  0     4  D .
A DC  0   x x  2 2
y z z  2  0  x y z     3   2 x y DB DC
y  2  z z  2  0 . 0    I  ; a ; b c là tâm mặt 1 dx Câu 38 . Biết rằng
a ln 2  b ln 3  c ln 5  , với a, ,
b c là các số hữu tỉ.
3x  5 3x 1  7 0
Giá trị của a b c bằng 10 5 10 5 A.  . B.  . C. . D. . 3 3 3 3 Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van Chọn A
Đặt t  3x 1 2
t  3x 1  2tdt  3dx
Đổi cận: x  0  t  1; x  1  t  2 . 1 2 2 dx 1 dx 2 d t t 2  3 2  Ta có:        dt  
3x  5 3x 1  7
3x 1 5 3x 1  6 2 3 t  5t  6
3  t  3 t  2  0 0 1 1 2 2 2   2 2
3ln t  3  2 ln t  2 
3ln 5  3ln 4  2ln 4  2ln 3   1
 0 ln 2  2 ln 3  3ln 5 = 1 1  3 3 3 20  4  ln 2  ln 3  2 ln 5 3 3
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 61
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 20 4 Suy ra: a   , b  , c  2 . 3 3 10
Vậy a b c   . 3 Bài toán tương tự 1 dx Câu 38.1 .Biết rằng
a ln 2  b ln 3  c ln 5  , với a, ,
b c là các số hữu tỉ.
x  5 x  3  9 2 
Giá trị của a b c bằng A. 1  0 . B. 5 . C. 10. D. 5 . Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van Chọn A Đặt t x  3 2
t x  3  2tdt  dx Đổi cận: x  2
  t  1 ; x  1  t  2 . 1 dx 1 dx 2 d t t 2  3 2  Ta có:     2  2  dt  
x  5 x  3  9
x  3  5 3x 1  6 2 t  5t  6  t  3 t  2  2  2  1 1  2 2 2
3ln t  3  2 ln t  2  2 5
 ln 4  2 ln 3  3ln 5 =  20 ln 2  4 ln 3  6 ln 5 1 1 
Suy ra: a  20 , b  4 , c  6 . Vậy a b c  10  4 dx Câu 38.2 .Biết rằng
a ln 3  b ln 5  c ln 7  , với a, ,
b c là các số hữu tỉ.
4 x 1  5 2x 1 0  
Giá trị của a b c bằng 4 4 A. 0 . B.  . C. 1. D. . 3 3 Lời giải
Tác giả: Nguyễn Thị Thanh Vân; Fb: Thanh Van Chọn A Đặt t  2x 1 2
t  2x 1  tdt  dx
Đổi cận: x  0  t  1; x  4  t  3 . Ta có: 4 3 dx 4 dx d t t 3 1 2 2t   1  t  2       dt 2 
4 x 1  5 2x 1
4x  2  5 2x 1  2 2t  5t  2 3 2t 1 t  2 1    0   0 1 3 3 1  2 1  1  1  1  1 1    dt    2 ln t  2  ln 2t 1    2 ln 5  2 ln 3  ln 7  ln 3  
3  t  2 2t 1 3  2  3  2 2  1 1 1 2 1   ln 3  ln 5  ln 7 2 3 6
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 62
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 1 2 1
Suy ra: a   , b  , c  
a b c  0 . 2 3 6 x 1 y z  2
Câu 39. Trong không gian Oxyz , cho đường thẳng d :   và hai điểm ( A 1  ;3;1) và 2 1 1  B 0;2;  1 . Gọi C  ; m ;
n p là điểm thuộc đường thẳng d sao cho diện tích tam giác ABC
bằng 2 2 . Giá trị của tổng m n p bằng A. 1. B. 2 . C. 3 . D. 5 . Lời giải
Tácgiả: Nguyễn Thị Thơm; Fb: Thơm nguyễn Chọn C
x  1 2t
Phương trình tham số của đường thẳng d :  y t . z  2  t
Vì C thuộc d nên tọa độ của C có dạng C  1
  2t;t;2  t  .  
Ta có AB 1; 1; 2 và AC 2t;t  3;1 t  .  
Suy ra  AB, AC   3t  7;3t 1;3t  3 .   1   1
Diện tích tam giác ABC là 2 2 2 S
AB, AC  (3t  7)  ( 3
t 1)  (3t  3) . ABC 2   2 1 Theo bài ra ta có 2 S  2 2 
27t  54t  59  2 2  . ABC 2 2
 27t  54t  59  32 2
 (t 1)  0  t  1 .
Với t  1 thì C 1;1; 
1 nên m  1;n  1; p  1 .
Vậy giá trị của tổng m n p  3 Bài toán tương tự x 1 y z  2
Câu 39.1 .Trong không gian Oxyz , cho đường thẳng d :   và hai điểm ( A 1  ;3;1) và 2 1 1  B 0;2;  1 . Gọi C  ; m ;
n p là điểm thuộc đường thẳng d sao cho tam giác ABC vuông tại
A. Giá trị của tổng m  2n p bằng A. 0 . B. 2 . C. 3 . D. 5 . Lời giải
Tácgiả:Nguyễn Thị Thơm; Fb:Thơm nguyễn Chọn A
Vì C d nên tọa độ của C có dạng C  1
  2t;t; 2  t   
Ta có AB 1; 1; 2 và AC 2t;t  3;1 t
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 63
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019   1 
Vì ABC vuông tại A nên AC.AB  0  2t t  3  2  2t  0  3t 1  0  t  . 3  5 m   3   5 1 4   1 5 2 7 C ; ;    n
m  2n p     0 .  3 3 3  3 3 3 3   7 p    3 x y 1 z  2
Câu 39.2. Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 2 3
P : x  2y  2z  3  0 . Gọi M là điểm thuộc đường thẳng d sao cho khoảng cách từ M đến
mặt phẳng  P bằng 2. Nếu M có hoành độ âm thì tung độ của M bằng. A. 3 . B. 2  1. C. 3 . D. 1. Lời giải
Tácgiả:Nguyễn Thị Thơm; Fb:Thơm nguyễn Chọn A x t
Phương trình tham số của đường thẳng d :  y  1 2t
z  2  3t
Vì M d nên tọa độ của M có dạng M t; 1   2t; 2   3t  .
Vì khoảng cách từ M đến mặt phẳng  P bằng 2nên
t  21 2t   22  3t   3  2 1 2  22 2
t  2  4t  4  6t  3   2 1 4  4 5  t 5  t  6
t  1  M  1  ; 3; 5   
 2  5  t  6     3 5  t  6  
t  11  M 11; 21;  31 
Vì M có tung độ âm nên M  1  ; 3  ; 5  
Câu 40 . Bất phương trình  3
x  9xln  x  5  0 có bao nhiêu nghiệm nguyên ? A. 4 . B. 7 . C. 6 . D. Vô số. Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường Chọn C Cách 1.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 64
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019   x  3  3   
x  9x  0  3  x  0  ln    x  5  0  0  x  5  1  Ta có:  3
x  9x ln  x  5  0     3 
x  9x  0    x  3      ln   x  5  0   0  x  3     x  5  1     x  3  
 3  x  0 (vn)  5  x  4    0  x  3       x  3 4   x  3       0  x  3    x  4   
Vì x    x  4  ;  3;0;1; 2; 
3 . Vậy có 6 nghiệm nguyên. Cách 2. Điều kiện: x  5  (*).  x  0 3 x 9x 0     x  3 Xét  3 x
9x ln  x 5 0       
(thỏa mãn điều kiện (*)).
ln  x  5  0  x  3   x  4  
Bảng đan xen dấu của biểu thức f x   3
x  9xln  x  5 trên khoảng  5  ;   .  4   x  3 
Khi đó f x  0  . 0  x  3 
Vì x    x  4  ;  3;0;1; 2; 
3 ,Vậy có 6 nghiệm nguyên. Bài toán tương tự:
Câu 40.1 . Bất phương trình  2
x  3x ln  x  2  0 có bao nhiêu nghiệm nguyên ? A. 5 . B. 4 . C. 3 . D. Vô số. Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường Chọn A
 ln  x  2  0  x  2  1   Ta có:  2
x  3x ln  x  2  0 2  
 x  3x  0  0  x  3     ln   x  2  0  x  2  1  
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 65
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019  x  1    x  1 
 0  x  3    .  0  x  3   x  1 
Vì x    x  1  ; 0;1; 2;  3 . Vậy có 5 nghiệm.
Câu 40.2. Bất phương trình  2
x  4  x   1  log  2
x  4x  1  0 có tổng tất cả các nghiệm nguyên là? 1  e A. 6 . B. 8 . C. 4 . D. 10. Lời giải
Tác giả: Đoàn Thị Hường; Fb: Đoàn Thị Hường Chọn C Ta có:  2 2
x  4  x   1  log  2
x  4x  1  0   x  2 log  2
x  4x 1  0 1  1  e ex  2  0   x  2  x  2  x  2  log  2
x  4x 1  0     . 2  2  1  
x  4x 1  1 
x  4x  0  0  x  4   e
Vì x    x 1; 
3 . Vậy tổng tất cả các nghiệm nguyên bằng 4 .
Câu 41. Cho hàm số f (x) có đồ thị hàm y f '(x) như hình vẽ. Hàm số 2
y f (cos x)  x x đồng biến trên khoảng A. 1;2 . B.  1  ;0 . C. 0;  1 . D.  2  ;   1 . Lời giải
Tác giả: Nguyễn Việt Hải. FB: https://www.facebook.com/nvhaicqt Chọn A Phân tích:
Bản chất dạng toán này thường là đặc điểm: Tổng hai hàm dương (hàm đồng biến), tổng hai
hàm âm (hàm nghịch biến) Tính chất:
Cho hàm số y f x tăng trên khoảng D , hàm số y f x tăng trên khoảng D . Khi đó ta 1 2
có hàm số y f x  g x tăng trên khoảng D D D 1 2
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 66
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 1
+ Quan sát bài toán: 2
y x x y '  2x 1  0  x
, nếu trắc nghiệm thấy ngay đáp án 2 A. Hướng dẫn giải:
Ta có: y '   sin .
x f 'cos x  2x 1 + Vì cos x  1   ;1  sin .
x f 'cos x  1  
;1 mà 2x 1  1  x  1
+ Suy ra y '   sin .
x f 'cos x  2x 1  0, x
  1 hay hàm số tăng trên [1; )
Câu 41.1 (Đề minh họa THPT QG 2018 – 2019) Cho hàm số f x  có bảng xét dấu của đạo hàm như sau:
Hàm số y f x   3 3
2  x  3x đồng biến trên khoảng nào dưới đây? A. 1;. B.  ;    1 . C. 1; 0. D. 0;2.
Câu 41.2 (Nguyễn Việt Hải) Cho hàm số f (x) có đồ thị hàm y f '(x) như hình vẽ. Hàm số
 3cos x  4 sin x  4 y f
x  3x  2019  
đồng biến trên khoảng  5  A. 1;2 . B.  1  ;0 . C. 0;  1 . D.  2  ;   1 . Câu 42. Cho hàm số ( ) 2x 2 x f x   
. Gọi m là số lớn nhất trong các số nguyên m thỏa mãn 0 12
f (m)  f (2m  2 )  0 . Mệnh đề nào sau đây đúng? A. m  1513; 2019 .
B. m  1009;1513 . C. m  505;1009 . D. m  1;505 . 0   0   0   0   Lời giải
Tác giả: Nguyễn Việt Hải. FB: https://www.facebook.com/nvhaicqt Chọn B Phân tích: 12 12
+ Bài toán nếu thế vào: mm 2m2 2  m2 P( ) m  2  2  2  2  0
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 67
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
+ Biểu thức P(m) khá phức tạp. Điều này chứng tỏ bài toán cho hàm số y f (x) chắc chắn
có tính chất đặc biệt.
+ Nhìn yếu tố xuất hiện hàm số   2x 2 x y f x    
. Ta có hàm số lẻ và tăng trên . Đây
chính là chìa khóa ta giải quyết bài toán. Hướng dẫn giải: Ta có hàm số ( ) 2x 2 x y f x    
hàm số lẻ và tăng trên  12 2
Yêu cầu bài toán  f  12
2m  2    f m  f m 12
 2m  2  m m  3 12  2 
m nguyên lớn nhất là: m   1365   3   Bài toán tổng quát:
Giải bất phương trình: f u x, m  f v x, m  0 (*)
Với f (x) là hàm số lẻ và tăng (hoặc giảm) trên tập D f
Con đường sáng tạo bài toán: (VD: Một vài hàm đặc trưng f)  ( ) xx
f x a a , 0  a  1  f x 3
x ax , a  0 
f x  a x a x ……………………… Ta có (*)  u  ,
x m  v  , x m
Đây là nguồn gốc chúng ta tạo lớp bài toán này.
Câu 42.1 (Nguyễn Việt Hải) Cho hàm số f x 2019 3  x
x 12x . Hỏi có bao nhiêu giá trị nguyên m  1  2;12 thỏa f  3 2 m m   f  2 2019
2019m  70m  300  0
Câu 42.2 (Nguyễn Việt Hải) Cho hàm số f x 3 3
 12  x  12  x x . Tìm giá trị m nguyên lớn nhất thỏa    f  5 m 1 2 12 8  f  0  m6   2 
Câu 42.3 (Nguyễn Việt Hải) Cho hàm số
  12x 12x f x
 2019x . S là tập các phần tử m nguyên, m  2  019; 2019 thỏa f  3 2 2
x mx x   f  2 2
m  4 x  0, x
   . Hỏi tập S có bao nhiêu phần tử.
Nhận xét: Câu 42.3 tôi lấy thêm ý tưởng câu 49 đề minh họa THPT QG 2018 – 2019
Mỗi bài toán đều có nguồn gốc rõ ràng, xuất phát từ bài toán kiến thức cơ bản. Dạy toán:
Chúng ta không thể dạy học sinh đua cùng ngân hàng đề Toán, cũng không thể dạy học sinh đếm hết lá
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 68
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
cây trong một rừng cây, nhưng chúng ta dạy học sinh kiểm soát được bản chất nguồn gốc của lớp bài
toán cũng như đếm được gốc cây trong một rừng cây.
Câu 43. Cho hàm số f x thỏa mãn       ex f x f x , x
   và f 0  2 . Tất cả các nguyên hàm của   2 e x f x là
A.   2 ex  ex xC . B.    2 2 e x  ex xC . C.    1 ex xC . D.    1 ex xC . Lời giải
Tác giả: Nguyễn Đình Hải ; Fb:Nguyen Dinh Hai Chọn D  Ta có
      e x f x f x   
 ex   ex f x f x  1    ex f x  1   ex f xx C . Vì f 0  2 0
 2.e C C  2    2
e x    2 ex f x x . Vậy   2 e x f x dx     2 ex x dx     2 d  ex x
    2ex  ex x d  x  2 
   2 ex  ex x dx
   2 ex  ex xC     1 ex xC .
Phân tích: Bài toán cho hàm số y f x thỏa mãn điều kiện chứa tổng của f x và f  x
đưa ta tới công thức đạo hàm của tích u.v  u .v u.v với u f x . Từ đó ta cần chọn hàm v cho phù hợp
Tổng quát: Cho hàm số y f x và y g x liên tục trên K , thỏa mãn
f  x  g xf x  k x (Chọn G x v e ).
Ta có f  x  g xf x  k xG x  e
f   x  g xGxe
f x  k xGxe . Gx    e
f x  k xGxe Gx  e
f x  k xGxe dx   f x Gx  e
k xGxe dx  .
Với G x là một nguyên hàm của g x .
Admin tổ 4 – Strong team : Bản chất của bài toán là cho hàm số y f x thỏa mãn điều
kiện chứa tổng của f x và f  x liên quan tới công thức đạo hàm của tích
u.v  u .v u.vvới u f x . Khi đó ta cần chọn hàm v thích hợp. Cụ thể, với bài toán tổng quát :
Cho hàm số y f x , y g x , y hx , y k x liên tục trên K , g x  0 với x
  K và thỏa mãn g x. f  x  hx. f x  k xvh xvh x
Ta sẽ đi tìm v như sau :   dx dx   v g xv g xh x
hxx d  Khi đó : gx ln v
dx v eg x
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 69
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 Câu tương tự:
Câu 43.1 Cho hàm số f x thỏa mãn      2 2  2  x f x xf x xe , x
   và f 0  1. Tất cả các nguyên hàm của   2 . ex x f x là 2 1 2 1 A.  x  2 2 1  C . B.  2   2 1  x x e
C . C.  2   2 1  x x e
C . D.  x  2 2 1  C . 2 2 Lời giải
Tác giả: Nguyễn Đình Hải ; Fb:Nguyen Dinh Hai Chọn D 2 2 2 2  Ta có     2 2 2 x f x xf x xe    x      2   x  .2 x e f x xf x e xe    x
e f x  2x 2 xe f x 2  2 d
x x x C  .
Vì f (0)  1  C  1     2 2 1 x f x x e    . 1 1 Vậy   2x xf x e dx   x  2 x    1 dx   2 x   1 d  2 x    1  x  2 2 1  C . 2 2
Câu 44. Cho hàm số f x có đồ thị hàm số y f  x được cho như hình vẽ bên. 1
Hàm số y f x 2 
x f 0 có nhiều nhất bao nhiêu cực trị trong khoảng  2  ;3 . 2 A.6. B.2. C.5. D.3 Lời giải
Tác giả: Nguyễn Huỳnh Tấn Trung ; Fb: Nguyễn Huỳnh Tấn Trung Chọn D 1 2
Xét hàm số: hx  f x  x f 0 . 2
Ta có h x  f  x  x ; h x  0  f  x  x
Nghiệm phương trình trên là hoành độ giao điểm của hai đồ thị y  x và y f  x x  2  
Dựa vào đồ thị suy ra phương trình: f  x  x có ba nghiệm x  0  x  2 
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 70
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 Trên khoảng  2
 ;3 , hàm số hx có một điểm cực trị là x  2 , (do qua nghiệm x  0 , h x
không đổi dấu). Do đó đồ thị hàm số y hx cắt trục hoành tại tối đa 2 điểm.
Suy ra hàm số y h x có tối đa 2 1  3điểm cực trị trong khoảng  2  ;3 .
PHÂN TÍCH VÀ PHÁT TRIỂN CÂU 44
Tác giả: Nguyễn Huỳnh Tấn Trung ; Fb: Nguyễn Huỳnh Tấn Trung -
Đây là bài toán hàm số có chứa dấu trị tuyệt đối. -
Đầu tiên, ta xét hàm số không chứa dấu trị tuyệt đối, và khảo sát hàm số đó. -
Sau đó, ta dựa vào sự tương giao với trục hoành, suy ra hàm số có chứa dấu trị
tuyệt đối có tối đa bao nhiêu cực trị.
Bài toán tương tự
Câu 44.1.Cho hàm số f x có đồ thị hàm số y f  x được cho như hình vẽ bên.
Hàm số y f x 2
x f 0 có nhiều nhất bao nhiêu cực trị trong khoảng  3  ;3 . A.6. B.2. C.5. D.3 Lời giải
Tác giả: Nguyễn Huỳnh Tấn Trung ; Fb: Nguyễn Huỳnh Tấn Trung Chọn C
Xét hàm số: g x  f x 2
x f 0 . Ta có / g x /
f x  2x ; / g x /
 0  f x  2  x
Nghiệm phương trình trên là hoành độ giao điểm của hai đồ thị y  2  x và /
y f x x  2 
Dựa vào đồ thị suy ra phương trình: / f x  2
x có hai nghiệm x  2  Trên khoảng  3
 ;3 , hàm số g x có hai điểm cực trị là x  2, x  2
 . Do đó đồ thị hàm số
y g x cắt trục hoành tại tối đa 3 điểm.
Suy ra hàm số y g x có tối đa 3  2  5 điểm cực trị trong khoảng  3  ;3 .
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 71
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Câu 45 . Cho hình chóp tứ giác đều S .ABCD có SA a 11 , côsin góc hợp bởi hai mặt phẳng SBC 1 và SCD bằng
. Thể tích của khối chóp S .ABCD bằng 10 A. 3 3a . B. 3 9a . C. 3 4a . D. 3 12a .
Tác giả: Nguyễn Thị Thu Hằng ; Fb: Nguyễn Thu Hằng. A. Phân tích bài toán:
1)Hình chóp S.ABCD đều nên đáy ABCD là hình vuông và SO   ABCD với
O AC BD .Suy ra hình vẽ đã được xác định.
2)Theo tính chất hình chóp đều,các cạnh bên SA SB SC SD a 11 . Từ đó các dữ kiện
tính toán có mối quan hệ với nhau.
3) Góc giữa hai mặt phẳng là góc không tù, cách xác định góc giữa hai mặt phẳng. Tận dụng
đặc điểm của hình chóp đều có BD  SAC , kẻ hai đường thẳng lần lượt nằm trong 2 mặt
phẳng SBC và SCD và vuông góc với giao tuyến SC .Khi đó học sinh sẽ dễ ngộ nhận góc
giữa hai mặt phẳng là góc 
BMD , không phải góc 
BMD .Góc giữa hai mặt phẳng SBC và
SCDlà góc bù với góc  BMD .Vì góc  BMD là góc tù.
4) Định lí cosin trong tam giác ABC với a BC ; b AC ; c AB suy ra 2 2 2 
a b c  2bc cos BMD .
Áp dụng định lí cosin trong tam giác BMD ta sẽ tìm được cạnh của hình vuông đáy. Dễ dàng
suy ra chiều cao SO của hình chóp. Thể tích đã được tính. B. Lời giải Chọn C
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 72
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Có BD AC ; BD SO BD SC . Trong tam giác SBC kẻ đường cao
BM DM SC . Góc giữa hai mặt phẳng SBC và SCD chính là góc giữa hai đường
thẳng MB và MD .
Trong tam giác vuông OMC có
OM OC OB  2OM    
BD B D   
M 180 M  
M M  90 . Hay góc  BMD  1 tù  cos BMD   . 10
Đặt AB x , SE là đường cao trong tam giác SBC nên 2 x 2 2 x x
SE.BC BM .SC  11a
.x BM .a 11 2  BM  . 11a  . 4 a 11 4
Áp dụng định lí cosin trong tam giác BMD có 2 2 2 
BD BM DM  2 2 2 
2BM .DM .cos BMD BD  2BM  2BM cos BMD 2  2  2  x x   1  2 2 
BD  2BM 1cos BMD  x 2 2  2 . 11a     1          a 11 4   10  2 2 2x x 11   2 1 x 2 2  2x  1  1a      x  2a . 2   11a  4 10 2 10 40a
Thể tích của khối chóp S.ABCD bằng 1 1 2 2 11a  2a V S . O SSC OC  . 4a2 2 2 2 3  .4a  4a . 3 ABCD 3 3
Cách 2. (Nguyễn Việt Hải): Cách nhìn khác tìm yếu tố cạnh đáy. 
Đặt x OB, 2  BMD Ta có 2 2 1  9 OM 9 11 x  1 1 2 2 2 
 cos 2  2 cos  1  cos        x  2 2 2  2 2 2  10 20 OM OB 20 9 OMx 11a x  2 2 x Hay  đến đây OK. 2 2 9 11a x
C. Sai lầm học sinh hay mắc phải:  1
Xác định góc giữa hai mặt phẳng chính là góc 
BMD suy ra cos BMD  . Và bài toán sẽ 10
không giải được. Hoặc xét hai trường hợp sẽ mất thời gian cho bài toán:  1  1 cos BMD  cos BMD   10 10 D. Khai thác bài toán:
Từ hình chóp đều ta có tể sáng tạo ra các bài toán tương tự câu 45 khi ta biết hai dữ liệu:
Độ dài cạnh bên và 1 góc ( có thể là góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt
phẳng, góc giữa hai đường thẳng).
Độ dài cạnh bên và khoảng cách ( Đề thi học sinh giỏi tỉnh Đà Nẵng).
Và còn nhiều bài toán khác liên quan đến hình chóp đều khi các bạn biết hai dữ kiện.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 73
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
E. Sau đây là một vài bài tập tương tự.
Câu 45.1 . Cho hình chóp tứ giác đều S .ABCD có SA a 21 , côsin góc hợp bởi hai mặt phẳng SAD 1 và  ABCD bằng
. Thể tích của khối chóp S .ABCD bằng 10 19 2 19 4 19 A. 3 a . B. 3 a . C. 3 a . D. 3 4 19a . 3 3 3 Lời giải Chọn C
Gọi cạnh hình vuông đáy là x ,góc hợp bởi hai mặt phẳng SAD và  ABCD là góc nhọn  OM x 1 21 SMO  1  cos SMO  1     2 2 
x  21a x  2a . 10 SM 10 1 10 4 2 2 2 21a x 4
Thể tích của khối chóp S.ABCD bằng 1 1 2 2 21a  2a 4 19 V S . O SSC OC  . 4a2 2 2 2  .4a 3  a . 3 ABCD 3 3 3
Câu 45.2 . Cho hình chóp tứ giác đều S .ABCD có SA a 11 , côsin góc hợp bởi cạnh SB và  ABCD 1 bằng
. Thể tích của khối chóp S.ABCD bằng 10 121 121 121 11 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 150 50 500 500 Lời giải Chọn C
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 74
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Gọi cạnh hình vuông đáy là x ,góc hợp bởi cạnh SB và  ABCDlà góc nhọn  OB x SBO  1  cos SMO  1   2 1   11  x a . 10 SB 10 2.a 11 10 5 2
Thể tích của khối chóp S.ABCD bằng 11 2 2 2 11a a 1 1  11  100 11 121 V S . O S 2 2  SC OC . a 2 3    . a a . 3 ABCD 3  25.2  3 50 500
Câu 45.3 . Cho hình chóp tứ giác đều S .ABCD có SA a 11 , côsin góc hợp bởi hai mặt phẳng SAB 1 và SCD bằng
. Thể tích của khối chóp S .ABCD bằng 10 A. 3 3a . B. 3 9a . C. 3 4a . D. 3 12a .
Gọi cạnh hình vuông đáy là x ,góc hợp bởi hai mặt phẳng SAB và SCD là góc nhọn  ESM  1  cos ESM  10
Áp dụng định lí cosin trong tam giác BMD có
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 75
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 2 2 2 
EM SE SM  2SE.SM .cos ESM 2  2      2 2   x 1
x  2SE 1cos BMD 2 2
x  2 11a     1       4     10   2  x  9 2 2  2   49 99a x  1  1a   2     2 99    x x a .  4  5 40 10 7
Thể tích của khối chóp S.ABCD bằng 1 1 V S . O S
SC OC .4a2 2 2 . 3 ABCD 3
Câu 45.4 . Cho hình chóp tam giác đều S.ABC có SA a 11 , côsin góc hợp bởi hai mặt phẳng SBC 1 và SAC  bằng
. Thể tích của khối chóp S.ABC bằng 10 A. 3 3a . B. 3 9a . C. 3 4a . D. 3 12a .
Câu 45.5 . Cho hình chóp tam giác đều S.ABC có SA a 11 , côsin góc hợp bởi hai mặt phẳng SBC 1 và  ABC  bằng
. Thể tích của khối chóp S.ABC bằng 10 A. 3 3a . B. 3 9a . C. 3 4a . D. 3 12a .
Câu 45.6 . Cho hình chóp tam giác đều S.ABC có SA a 11 , côsin góc hợp bởi đường thẳng SB và  1 ABC  bằng
. Thể tích của khối chóp S.ABC bằng 10 A. 3 3a . B. 3 9a . C. 3 4a . D. 3 12a .
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 76
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Câu 45.7 .( Đề thi học sinh giỏi Đà Nẵng 2019). Cho hình chóp tam giác đều S.ABC có góc giữa mặt
bên và mặt đáy  ABC bằng 60 . Biết khoảng cách giữa hai đường thẳng SA và BC bằng
3a 7 . Thể tích của khối chóp S.ABC bằng 14 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 12 16 18 24
Câu 46. Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách
điệu” cho Ông già Noel có hình dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như
hình vẽ bên. Biết rằng OO ' = 5 cm , OA = 10 cm , OB = 20 cm , đường cong AB là một phần
của một parabol có đỉnh là điểm A . Thể tích của chiếc mũ bằng B A O O' 2750 2500 2050 2250 A.  3 cm  . B.  3 cm  . C.  3 cm  . D.  3 cm  . 3 3 3 3 Lời giải
Tác giả: Nguyễn Thị Nguyệt Cầm; Fb: Nguyet Cam Nguyen Chọn B
Gọi V là thể tích của nón, V là thể tích khối trụ có chiều cao OO ' , bán kính đáy OA , nên 1 2
V  5.10 . 500 . 1
Gọi V là thể tích phần còn lại của nón. 2
Cách 1: chọn hệ trục tọa độ như hình vẽ.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 77
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 y B(0,20) A(10,0) O x O'
Khi đó, V là thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi nhánh parabol AB 2
và hai trục tọa độ quanh trục Oy .
Phương trình parabol (P) chứa nhánh AB có dạng y ax  2 10 . 1 1
Vì (P) đi qua điểm B( 0; 20 ) nên a
; do đó (P): y  x 102 . 5 5 20 2 1000
Suy ra x   5y 10 ( do x 10 ). Vậy, V
 5y 10 dy    3 cm  2   3 0 2500
Đáp số: V V V   3 cm  . 1 2 3
Cách 2: chọn hệ trục tọa độ như hình vẽ.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 78
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 y A(0,10) O B(20,0) x
Khi đó, V là thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi nhánh parabol AB 2
và hai trục tọa độ quanh trục Ox .
Phương trình parabol (P) chứa nhánh AB có dạng y a x 10 .
Vì (P) đi qua điểm B( 20; 0 ) nên a   5 ; do đó (P): y   5x 10 . 20 2 1000 Vậy V
 5x 10 dx    3 cm  . 2   3 0 2500
Đáp số: V V V   3 cm  . 1 2 3
Dạng toán: Tính thể tích khối tròn xoay.
Phương pháp: dùng ứng dụng của tích phân để tính khối tròn xoay, có thể dùng trực tiếp các
công thức tính thể tích chỏm cầu, chảo parabol, hình nêm, phiến trụ, nón cụt… Bài toán tương tự
Câu 46.1 Cây dù ở khu vui chơi “công viên nước” của trẻ em có phần trên là một chỏm cầu, phần thân là
một khối nón cụt như hình vẽ. Biết ON OD  2m ; MN  40cm ; BC  40cm ; EF  20cm .
Tính thể tích của cây dù
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 79
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 N A B M C D E F O 2750 896000 A.   3 336000 cm   3 cm  . B.  3 cm  . 3 3 2050 2250 C.   3 112000 cm   3 cm  . D.   3 896000 cm   3 cm  . 3 3 Lời giải
Tác giả: Nguyễn Thị Nguyệt Cầm; Fb: Nguyet Cam Nguyen Chọn A
Thể tích phần trên của cây dù là thể tích của khối chỏm cầu:  hMN  40 896000 2    V   h R  2
  .MN . ON  2   .40 200     3 cm  . 1        3   3   3  3
Thể tích phần thân của cây dù là thể tích của khối nón cụt: 1 1 1 V   . . h  2 2
R R R .R   .OM . 2 2 MB OE  .
MB OE   .160.400 100  200 2 1 2 1 2  3 3 3 112000    3 cm  . 3 896000 112000
Vậy thể tích của cây dù: V V V        3 336000 cm  . 1 2 3 3
Câu 47. Giả sử z , z là hai trong các số phức thỏa mãn  z  68  zi là số thực. Biết rằng z z  4 , 1 2 1 2
giá trị nhỏ nhất của z  3z bằng 1 2 A. 5  21 . B. 20  4 21 . C. 20  4 22 . D. 5  22 . Lời giải Chọn C
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 80
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Giả sử z x yi , x, y   .Gọi ,
A B lần lượt là điểm biểu diễn cho các số phức z , z . Suy ra 1 2
AB z z  4 . 1 2
* Ta có  z  68  zi   x  6  yi.8  y  xi 2 2   
  8x  6 y  48   x y  6x  8 y i .
Theo giả thiết  z  68  zi là số thực nên ta suy ra 2 2
x y  6x  8y  0 . Tức là các điểm ,
A B thuộc đường tròn C tâm I 3; 4 , bán kính R  5 .      
* Xét điểm M thuộc đoạn AB thỏa MA  3MB  0  OA  3OB  4OM .Gọi H là trung điểm AB . Ta tính được 2 2 2 2 2
HI R HB  21; IM HI HM  22 , suy ra điểm M thuộc
đường tròn C tâm I 3; 4 , bán kính r  22 .   
* Ta có z  3z OA  3OB  4OM  4OM , do đó z  3z nhỏ nhất khi OM nhỏ nhất. 1 2 1 2 Ta có OM
OM OI r  5  22 . 0 min Vậy z  3z
 4OM  20  4 22 . 1 2 0 min
Phân tích : Kiến thức cần nắm vững :
 Quỹ tích điểm biểu diễn số phức.  Modun số phức
 Bài toán liên quan tâm tỉ cự trong hình học.
 Sai sót dễ gặp, không để ý đường tròn C đi qua gốc tọa độ. Bài toán tương tự
Câu 47.1 Giả sử z , z là hai trong các số phức thỏa mãn  z  
1  z  2i là một số thuần ảo. Biết rằng 1 2
z z  2 , giá trị nhỏ nhất của z  5z bằng 1 2 1 2 A. 13  5 . B. 3 5  13 . C. 3 5  2 13 . D. 5  22 . Lời giải Chọn B
Đặt z x yi x y     z   z i 2 2 ; 1
2  x y x  2 y  2x y  2 .i
Theo giả thiết  z  
1  z  2i là số thuần ảo, suy ra
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 81
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 2 1 5  1  5
x y x  2 y  0  x x
y  2 y 1   x      y  2 2 2 2 2 1  . 4 4  2  4  1  5
 tập hợp điểm biểu diễn số phức z là một đường tròn  1
C  tâm I  ; 1    , R   2  2
Giả sử z x yi , x, y   .Gọi ,
A B lần lượt là điểm biểu diễn cho các số phức z , z . Suy ra 1 2
z z  2  AB  2 . 1 2      
Gọi M là điểm thỏa mãn MA  5MB  0  OA  5OB  6OM .  2 1 2 2 2 IH  
IH IA HA   4
Gọi H là trung điểm AB ta có    . 2 2 2
IH IM HM 2 13  IM    36  1  13
Vậy tập hợp điểm M là đường tròn  2
C  tâm I  ; 1    , r  .  2  6    Ta có 1
z  5z2  OA  5OB  6 OM  6OM . Do  1 C  ,  2
C  là hai đường tròn đồng tâm và O  1 C   5 13  Từ đó suy ra 1 z  5z2  6OM
 6 R r  6    3 5  13 Min Min  2 6   
Câu 47.2 Giả sử z , z là hai trong số các số phức z thỏa mãn iz  2  i  1 và z z  2 Giá trị lớn 1 2 1 2
nhất của z z bằng 1 2 A. 4 . B. 2 3 . C. 3 2 . D. 3.. Lời giải Chọn A.
Ta có iz  2  i  1  i z i 2  1  1  z  1  i 2  1 .
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 82
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Điểm biểu diễn z thuộc đường tròn tâm I 1; 2  , R  1 .
Gọi M , N là điểm biểu diễn z , z nên MN  2 là đường kính. Dựng hình bình hành 1 2
OMPN ta có z z OP  2 3 . 1 2 2 2 2 2 2
Ta có  z z  2 zzz zz z
 16  z z  4 . Dấu bằng xảy ra 1 2   1 2  1 2 1 2 1 2
khi z z MN OI (OMPN là hình thoi) 1 2
Câu 48. Cho hàm số y f x có đồ thị như hình vẽ. 1  x
Có bao nhiêu số nguyên m để phương trình f 1  x m   có nghiệm thuộc đoạn 3  2   2  ; 2 ? A. 11. B. 9. C.8. D. 10. Lời giải
Tác giả: Nguyễn Việt Hải; Fb: Nguyễn Việt Hải Chọn C 1  x   x   x  Ta có f
1  x m f 1  6 1  3m  6      
f t   6t  3m  6 3  2   2   2  x Với t  1 và x  2
 ; 2 nên ta có t 0;2 . 2
Xét hàm số y f t   6t trên 0;2 .
Ta có y  f t   6  0 , t  0; 2 . Phương trình có nghiệm
 min  f t   6t   3m  6  max  f t   6t   f 0  3m  6  f 2 12 0;2 0;2  4
  3m  6  6 12
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 83
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 10    m  4 . 3
Vì m   nên m  3  ; 2  ; 1  ; 0;1; 2;3;  4 . Phân tích:
Bản chất bài toán: Bài toán đã cho là giải phương trình hay bất phương trình bằng phương
pháp tương giao giữa hai đồ thị y g x và y hm
- Đồ thị hàm số y h m bản chất là một đường thẳng song song hoặc trùng với trục Ox và
đi qua điểm có tung độ có giá trị là h m .
- Đồ thị hàm số y g x xác định được tính chất dựa vào các dữ kiện đã cho hàm số
y f x ban đầu; hàm số y f x có thể cho bằng công thức, bằng đồ thị, bằng hàm đạo
hàm của nó, đồ thị của đạo hàm.
Vì đây là phần kiến thức tương đối rộng nên tôi xin chỉ khai thác ở một góc độ nào đó của bài toán.
Khó khăn đối với học sinh: -
Từ đồ thị hàm số y f x suy ra đồ thị hàm số y g x . -
Trong trường hợp không thể dùng đồ thị hàm số thì học sinh khó khăn trong việc
kiểm soát đặc điểm của hàm số y g x do hàm số y g x có chứa biểu thức hàm hợp
phức tạp của hàm y f x . -
Phần lớn học sinh chưa phân biệt được kiến thức: “Số nghiệm của phương trình
chính là số giao điểm của đồ thị hai hàm số” và “Nghiệm của phương trình chính là hoành độ của giao điểm”. Giải pháp: -
Sử dụng một số phép biến đổi đồ thị cơ bản -
Sử dụng cách đặt ẩn phụ đưa về hàm số theo ẩn mới có chứa y f t  .
Kiểu 1: Sử dụng một số phép biến đổi đồ thị cơ bản.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 84
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Kiểu 2: Sử dụng cách đặt ẩn phụ đưa về hàm số theo ẩn mới có chứa y f t  .
Sau đây tôi xin đưa ra lớp bài toán sưu tầm theo mức độ để giúp học sinh có cách nhìn dễ
dàng trong các bài thi trắc nghiệm:
Câu 48.1. Cho hàm số y f x có đồ thị như hình bên dưới y 2  2 2 O x 2
Số nghiệm của phương trình 2 f x  3  0 là A. 4 . B. 2 . C. 0 . D. 3 .
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 85
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Câu 48.2. Cho hàm số y f x có đồ thị là đường cong trong hình vẽ bên. Tìm số nghiệm của phương
trình f x  2019  1. y 2 2 3 1 O 1 x A. 2 . B. 1. C. 3 . D. 4 .
Câu 48.3. Cho hàm số y f x có đồ thị như đường cong trong hình vẽ dưới đây. Tìm giá trị của tham
số m để phương trình f x 1  m có 6 nghiệm phân biệt? A. 4   m  3  . B. 4  m  5 . C. m  5 . D. 0  m  4 .
Câu 48.4. Cho hàm số có bảng biến thiên như hình vẽ.
Số nghiệm của phương trình f x   1  2 là A. 5 . B. 4 . C. 2 . D. 3 .
Câu 48.5. Cho hàm số y f x có đồ thị như hình vẽ bên. y 4 2 1 O 1 x
Phương trình f x  2  2   có bao nhiêu nghiệm thực phân biệt? A. 4. B. 2. C. 6. D. 3.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 86
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Câu 48.6. Cho hàm số f x 3 2
x  3x . Có bao nhiêu giá trị nguyên của m để đồ thị hàm số
g x  f x   m cắt trục hoành tại 4 điểm phân biệt ? A. 3 . B. 4 . C. 2 . D. 0 .
Câu 48.7. Cho hàm số y f x có bảng biến thiên dưới đây. x -1 -∞ 0 2 3 +∞ f'(x) + 0 - 0 + +∞ 2 2 f(x) -2 -2 -∞
Tìm tất cả các giá trị thực của tham số m để phương trình f x  f m có ba nghiệm phân biệt. A. m  ; 2 2 . B. m  ; 1 3 \  ; 0  2 . C. m  ; 1 3 . D. m  ; 1 3 \ ; 0  2 .
Câu 48.8. Hình vẽ bên là đồ thị của hàm số y f x . y 2 O x 3 6
Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số y f x   1  m có 5
điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng A. 12 . B. 15 . C. 18 . D. 9 . Câu 48.9. Cho hàm số    4 2 y
f x ax bx c biết a  0 , c  2017 và a b c  2017 . Số cực trị của
hàm số y f x  2017 là: A. 1. B. 7 . C. 5 . D. 3 . Câu 48.10. Cho hàm số 3 2
y  4x  6x 1 có đồ thị là đường cong trong hình dưới đây. Khi đó phương 3 2 trình  3 2
x x     3 2 4 4 6 1
6 4x  6x  
1 1  0 có bao nhiêu nghiệm thực.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 87
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 y 1 1 O x 1 A. 3. B. 6 . C. 7 . D. 9 .
Câu 48.11. Cho hàm số y f x có đồ thị như hình bên. Tồn tại bao nhiêu giá trị nguyên của tham số
m để phương trình f sin x  m có đúng hai nghiệm thuộc đoạn 0;  ? A. 4 . B. 7 . C. 5 . D. 6 .
Câu 48.12. Cho hàm số y f x có đồ thị như hình vẽ bên. Tìm số giá trị nguyên của m để phương  3 7  trình f  2
x  2x  m có đúng 4 nghiệm thực phân biệt thuộc đoạn  ;  . 2 2    A. 1. B. 4 . C. 2 . D. 3 .
Câu 48.13. Cho hàm số f x xác định trên  \  
0 và có bảng biến thiên như hình vẽ.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 88
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Số nghiệm của phương trình 3 f 2x   1 10  0 là. A. 2 . B. 1. C. 4 . D. 3 . x y z 1 x  3 y z 1
Câu 49. Trong không gian Oxyz cho ba đường thẳng d :   ,  :   , 1 1 2  1 2 1 1 x 1 y  2 z  :  
. Đường thẳng  vuông góc với d đồng thời cắt  ,  tương ứng tại 2 1 2 1 1 2 
H , K sao cho độ dài HK nhỏ nhất. Biết rằng  có một vectơ chỉ phương u  ; h k;  1 . Giá trị h k bằng A. 0. B. 4. C. 6. D. 2  . Lời giải
Tác giả: Nguyễn Việt Thảo ; FB:Việt Thảo Chọn A
+ Gọi H    H 3  2t;t;1 t . 1  
+ Gọi K    K 1 ; m 2  2 ; m m . 2   
+ Tính được HK  m  2t  2; 2m t  2; m t   1 . 
+ Đường thẳng d có một VTCP là u  1;1; 2  . d    
+ Vì   d u .HK  0  m t  2  0  m t  2  HK  t  4;t  2; 3. d 2 2 2 2 + Tính được 2
HK  t  4  t  2  3  2 t   1
 27  27, t   Suy ra minHK
27 , đạt được khi t  1.  
+ Khi đó ta có HK  3; 3; 3 , suy ra u 1;1; 
1  h k  1  h k  0. BÀI PHÁT TRIỂN CÂU 49
Câu 49.1 Trong không gian Oxyz cho hai mặt phẳng  P : x  2y z 1  0,  P : 2x y z  2  0, và x y 1 z 1 x y  2 z 1 hai đường thẳng  :   ,  :  
. Đường thẳng  song song với hai 1 2 1 2 2 1 1  2
mặt phẳng  P;Q và cắt  ,  tương ứng tại H , K . Độ dài đoạn HK bằng 1 2 8 11 11 A. . B. 5 C. 6. D. . 7 7 Lời giải
Tác giả: Nguyễn Việt Thảo ; FB:Việt Thảo Chọn A
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 89
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019   
+ Tính u  n , n    1  ; 1; 3  P Q    
+ Gọi H 2t;1 t; 1
  2t ; K  ; m 2  ;1
m  2m nên HK  m  2;1 m t; 2  2m  2t   
+ Vì song song với 2 mặt phẳng  P;Q nên HK k.u suy ra m  2t 1 m t 2  2m  2t 2 3   
tính ra được m  ;t  . 1 1 3 7 7 8 11 + Suy ra HK  . 7 
Câu 50 . Trong không gian Oxyz , cho a  1; 1;0 và hai điểm A 4  ;7; 
3 , B 4;4;5 . Giả sử M , N  
là hai điểm thay đổi trong mặt phẳng Oxy sao cho MN cùng hướng với a và MN  5 2 .
Giá trị lớn nhất của AM BN bằng A. 17 . B. 77 . C. 7 2  3 . D. 82  5 . Lời giải
Tác giả: Nguyễn Trung Thành; Fb: Thanh Nguyen. Chọn A    
Vì MN cùng hướng với a nên t  0 : MN ta .  
Hơn nữa, MN  5 2  t. a  5 2  t  5 . Suy ra MN  5;  5;0 . x  4  5 x  1    
Gọi A x ; y ; z là điểm sao cho AA  MN   y  7  5   y  2  A1;2;  3 . z  3  0   z  3 
Dễ thấy các điểm A , B đều nằm cùng phía so với mặt phẳng Oxy vì chúng đều có cao độ
dương. Hơn nữa vì cao độ của chúng khác nhau nên đường thẳng A' B luôn cắt mặt phẳng
Oxy tại một điểm cố định.  
Từ AA  MN suy ra AM AN nên AM BN A' N BN A' B dấu bằng xảy ra khi N
là giao điểm của đường thẳng A' B với mặt phẳng Oxy . Do đó
AM BN A B
  2    2    2 max ' 4 1 4 2 5 3  17 , đạt được khi N A B   Oxy . Nhận xét Ý tưởng ra đề
Từ bất đẳng thức véc tơ      
a) | u |  | v |  u v . Dấu “=” xảy ra khi và chỉ khi hai véc tơ u và v cùng chiều.      
b) | u v u u . Dấu “=” xảy ra khi và chỉ khi hai véc tơ u và v cùng chiều.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 90
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019      
c) | u v u u . Dấu “=” xảy ra khi và chỉ khi hai véc tơ u và v ngược chiều.
Tác giả: Nguyễn Văn Hải, FB: https://www.facebook.com/nguyenvan.hai.96387
Bài trên xuất phát từ bất đẳng thức trên ta có bài toán gốc sau
Câu 50.1. Trong không gian Oxyz , cho hai điểm A1; 2;3 , B 4;4; 
5 . Giả sử M là điểm thay đổi trong
mặt phẳng (P) : 2x  2 y z  2019  0. Tìm giá trị lớn nhất của biểu thức P AM BM . A. 17 . B. 77 . C. 7 2  3 . D. 82  5 . Lời giải Chọn A
Ta có: 2x  2y z  20192x  2y z  2019  0 nên các điểm ,
A B đều nằm cùng A A A B B B
phía so với mặt phẳng (P) và đường thẳng AB luôn cắt mặt phẳng (P) tại một điểm cố định.    
Từ bất đẳng thức véc tơ | u |  | v |  u v . Ta có AM BM A .
B Dấu bằng xảy ra khi M là
giao điểm của đường thẳng AB với mặt phẳng (P) . 2 2 2
Do đó AM BMAB  4  
1  4  2  5  3  17 , đạt được khi M AB  P . Max
Câu 50.2. Trong không gian Oxyz , cho A1;1;0, B 3; 1
 ; 4 và mặt phẳng   :x y z 1  0 . Tìm tọa
độ điểm M   sao cho MA MB đạt giá trị lớn nhất.  3 5 1   1 2 2  A. M 1;3;   1 . B. M ; ;    . C. M ; ;    . D. M 0; 2;  1 .  4 4 2   3 3 3  Lời giải Chọn B
Ta có:  x y z  
1  x y z   1  11 0   1 3 1 4  
1  0 nên hai điểm A và B A A A B B B
cùng nằm về một phía của mặt phẳng   .
Ta có MA MB AB  2 6 , nên MA MB lớn nhất khi và chỉ khi M AB    . x  1 2t
Phương trình đường thẳng AB :  y  1 2t , do đó tọa độ điểm M là nghiệm của hệ phương z  4t   1 t    8 x  1 2t  3  x
y  1 2t  4  3 5 1  trình    . Do đó M ; ;    . z  4t  5   4 4 2  y
x y z 1  0   4  1 z    2
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 91
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 x 1 y 1 z  2
Câu 50.3. Cho đường thẳng  :   và (
A 1;1; 0), B(3; 1
 ; 4). Tìm tọa độ điểm M thuộc 1 1  2
 sao cho MA MB đạt giá trị nhỏ nhất.  1 1   3 3  A. M ( 1  ;1; 2)  . B. M ;  ;1 .   C. M  ; ; 3 .   D. M (1; 1  ; 2).  2 2   2 2  Lời giải Chọn D   11 11
Ta có: AB 2; 2; 4 cùng phương với u 1; 1; 2 và ( A 1;1; 0)   (do  ) 1 1 
AB //   AB và  đồng phẳng.
* Xét mặt phẳng chứa AB và  :
Gọi A là điểm đối xứng của A qua  ;   là mặt phẳng qua A , vuông góc với 
Khi đó, giao điểm H của  với   là trung điểm của AA
  có phương trình: x y  2z  0 Giả sử H  1
  t;1 t; 2
  2t  , H    t  1  H 0;0;0
H là trung điểm của AA  A 1  ; 1  ;0
Ta có: MA MB MA  MB A B
  MA MB  A B
 khi và chỉ khi M trùng với M là min 0 giao điểm của A B  và  x  1   t  Đường thẳng A B  đi qua A 1  ; 1
 ;0 , có phương trình:  y  1 z t 
x  1 t
Mà  :  y  1 t
z  2  2t
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 92
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
1 t  1 tt   t   t    2 Giải hệ phương trình: 1   t  1  t   2   t  2   
2  2t t
2  2t t    M 1; 1  ; 2 0  
Vậy, để MA MB đạt giá trị nhỏ nhất thì M 1; 1  ; 2 . x 1 y 1 z  2
Câu 50.4. Cho đường thẳng  :   và hai điểm (
A 1;1; 0), B(1; 0;1). 1 1  2 Biết điểm M ( ; a ;
b c) thuộc  sao cho biểu thức T MA MB đạt giá trị lớn nhất. Khi đó tổng a b c bằng: 33 4 33 A. 8 . B. 8  33 . C. 8  . D. 8  . 3 3 Lời giải Chọn D   qua C( 1
 ;1;  2), và có vectơ chỉ phương u  (1; 1; 2)  
AB  (2 ; 1;1); AC  (2; 0;  2) .     ;
AB uAC  0 nên A ; B    không đồng phẳng
Vì điểm M thuộc  nên ta có M ( 1
  t ;1 t ;  2  2t), t . Lúc đó
P MA MB
t  2  t   t  2  t 2  t  2   t  2 2 2 2 2 1 2 3 2 2 
6t 12t  8  6t 14t 10 . 2   P  t  2 1 7 11 6 1   t     3  6  6   3    7 11     
Đặt u  t 1;
 , v   t  ;
. Ta có | u |  | v |  u v .   3      6 6   2 2 1  3 11    Tức là P  6.       . 6  3 6      3 t 1 33
Đẳng thức xảy ra khi và chỉ khi 3   t  3  . 7 11 3 t  6 6 4 33
Với ta có a b c  4t  4  8  . 3
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 93
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 x y 1 z
Câu 50.5. Cho đường thẳng  :   và hai điểm ( A 0;1; 3
 ), B(1; 0; 2). Biết điểm M thuộc 1 1 1
 sao cho biểu thức T MA MB đạt giá trị lớn nhất là T .Khi đó, T bằng bao nhiêu? max max A. T  3 . B. T  2 3 . C.T  3 3 . D. T  2 . max max max max Lờigiải Chọn C  x  t  
Ta có AB  1; 1; 5 , phương trình đường thẳng AB là  y  1 t (t  ) . z  3   5t   1 1 1 
Xét vị trí tương đối giữa AB và  ta có AB cắt  tại C  ; ;    .  2 2 2    1 1 5   1 
Suy ra AC   ;  ;  AC AB C   là trung điểm AB .  2 2 2  2
T MA MB AB . Dấu “=” xảy ra khi M A hoặc M B . Do đó TAB  27  3 3 . max
Câu 50.6. Cho mặt phẳng   : x y  2z 1  0 và hai điểm A0; 1   ;1 , B 1;1; 2
  . Biết M   sao
cho MA MB đạt giá trị nhỏ nhất. Khi đó, hoành độ x của điểm M là M 1 2 A. x  . B. x  1  . C. x  2  . D. x  . M 3 M M M 7 Lời giải Chọn D
Ta có:  x y  2z  
1  x y  2z   1  0 1 2.1  1 11 4  
1  0 nên hai điểm A A A A B B B
và B nằm khác phía so với mặt phẳng   .
Nên MA MB đạt giá trị nhỏ nhất khi M AB    . x t
Phương trình đường thẳng AB :  y  1 2t , do đó tọa độ điểm M là nghiệm của hệ phương z 1 3t   2 t   7  x t 2   x
y  1 2t  7  2 3 1  2 trình    . Do đó M ;  ;   , xz  1 3t M .  3   7 7 7  7 y  
x y  2z 1  0   7  1 z   7
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 94
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019
Câu 50.7. Cho mặt phẳng   : x y z 1  0 và hai điểm A1;1;0, B 3; 1
 ; 4 . Gọi M là điểm thuộc
mặt phẳng   sao cho P MA MB đạt giá trị nhỏ nhất. Khi đó giá trị của P là: A. P  5 . B. P  6 . C. P  7 . D. P  8 . Lời giải Chọn B
Ta có:  x y z  
1  x y z   1  11 0   1 3 1 4  
1  0 nên hai điểm A và A A A B B B
B cùng nằm về một phía của mặt phẳng   .
Gọi H là hình chiếu vuông góc của A lên mặt phẳng   . x  1  t
Phương trình đường thẳng AH :  y  1 t . z t   1 t    3  x  1 t 2   x   y  1 t  3
Do đó tọa độ điểm H là nghiệm của hệ phương trình    . z t  4  y
x y z 1  0   3  1 z    3  2 4 1  Do đó H ; ;    .  3 3 3   1 5 2 
Gọi A đối xứng với A qua   , suy ra A ; ;    .  3 3 3 
Ta có MA MB MA  MB AB P AB  6 .
Câu 50.8. Cho mặt phẳng   : x y  3z  5  0 và hai điểm A1; 1  ; 2, B  5  ; 1
 ;0 . Biết M  ; a ; b c
thuộc mặt phẳng   sao cho MA MB đạt giá trị nhỏ nhất. Khi đó, giá trị của biểu thức
T a  2b  3c bằng bao nhiêu? A.T  5 . B. T  3 . C.T  7 . D. T  9 . Lời giải Chọn C
Ta có:  x y  3z  5 x y  3z  5  11 3.2  5 5
 1 3.0  5  0 nên hai điểm A A A B B B
A và B cùng nằm về một phía của mặt phẳng   .
Gọi H là hình chiếu vuông góc của A lên mặt phẳng   . x  1  t
Phương trình đường thẳng AH :  y  1 t .
z  2  3t
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 95
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 x  1 tt  1    y  1   tx  2
Do đó tọa độ điểm H là nghiệm của hệ phương trình    . z  2  3ty  0 
x y  3z  5  0  z  1 
Do đó H 2;0;   1 .
Gọi A đối xứng với A qua   , suy ra A3;1;  4 .
Ta có MA MB MA  MB AB nên MA MB nhỏ nhất khi M A B    .
x  3  4t
Phương trình đường thẳng A B
 :  y  1 t . z  4   3t   12 t   11
x  3  4t  15  x    y  1 t  11
Do đó tọa độ điểm M là nghiệm của hệ phương trình    .
z  4  3t  1  y  
x y  3z  5  0   11  20 z    11  15 1 20  Do đó M  ;  ;  
 , T a  2b  3c  7  .  11 11 11  Câu 50.9. Cho mặt cầu 2 2 2
(S ) : (x 1)  ( y  4)  z  8 và hai điểm (
A 3;0;0), B(4; 2;1) . Gọi M là điểm
thuộc mặt mặt cầu (S). Tính giá trị nhỏ nhất của biểu thức MA  2 . MB A. 6. B. 2 6. C. 6 2. D. 3 2. Lời giải Chọn C Ý tưởng    
Tìm điểm B ' cố định sao cho MA  2MB ' rồi áp dụng bất đẳng thức | u v u u . Cách 1: Gọi M ( ; a ;
b c)  (S ), ta có 2 2 2 2 2 2
(a 1)  (b  4)  c  8  a b c  2
a  8b  9 Do đó 2 2 2 2 2 2 2 2 2 MA
(a  3)  b c
4(a b c )  3(a b c )  6a  9 2 2 2 2 2 2
2 a b c  6b  9  2 a  (b  3)  c  2MB ' với B '(0;3; 0).
Dễ thấy B ' nằm trong mặt cầu, B nằm ngoài mặt cầu nên MA  2MB  2(MB ' MB) nhỏ nhất
khi B ', M , B thẳng hàng.
Vậy, giá trị nhỏ nhất của biểu thức MA  2MB là 2BB '  6 2. Cách 2:
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 96
GR FB: STRONG TEAM TOÁN VD-VDC
ĐỀ THI THỬ ĐẠI HỌC VINH L1 – TỔ 4 – 2019 I B' E M A M0 B
Ta có IA  4 2, với I là tâm mặt cầu.
Gọi E(1; 2;0), B '(0;3;0) lần lượt là trung điểm của IA và IE. 1
+ M là điểm nằm trên đường thẳng IA ta có MB '  M . A 2 MB ' IM 1
+ M là điểm không nằm trên đường thẳng IA ta có IMB '  IAM nên   , MA IA 2 1 ta có MB '  M . A 2
Dễ thấy B ' nằm trong mặt cầu, B nằm ngoài mặt cầu nên MA  2MB  2(MB ' MB) nhỏ nhất
khi B ', M , B thẳng hàng. M M 0
Vậy, giá trị nhỏ nhất của biểu thức MA  2MB là 2BB '  6 2.
Tong Bien Tap: Thay NGUYEN VIET HAI-Admin STRONG- Chuyen Quang Trung- Binh Phuoc Trang 97