Phân Tích và Giải Thuật Các Thuật Toán Sắp Xếp | Môn Cấu trúc dữ liệu và thuật toán - Trường Đại học Khoa học, Đại học Huế

lOMoAR cPSD| 58702377 1.
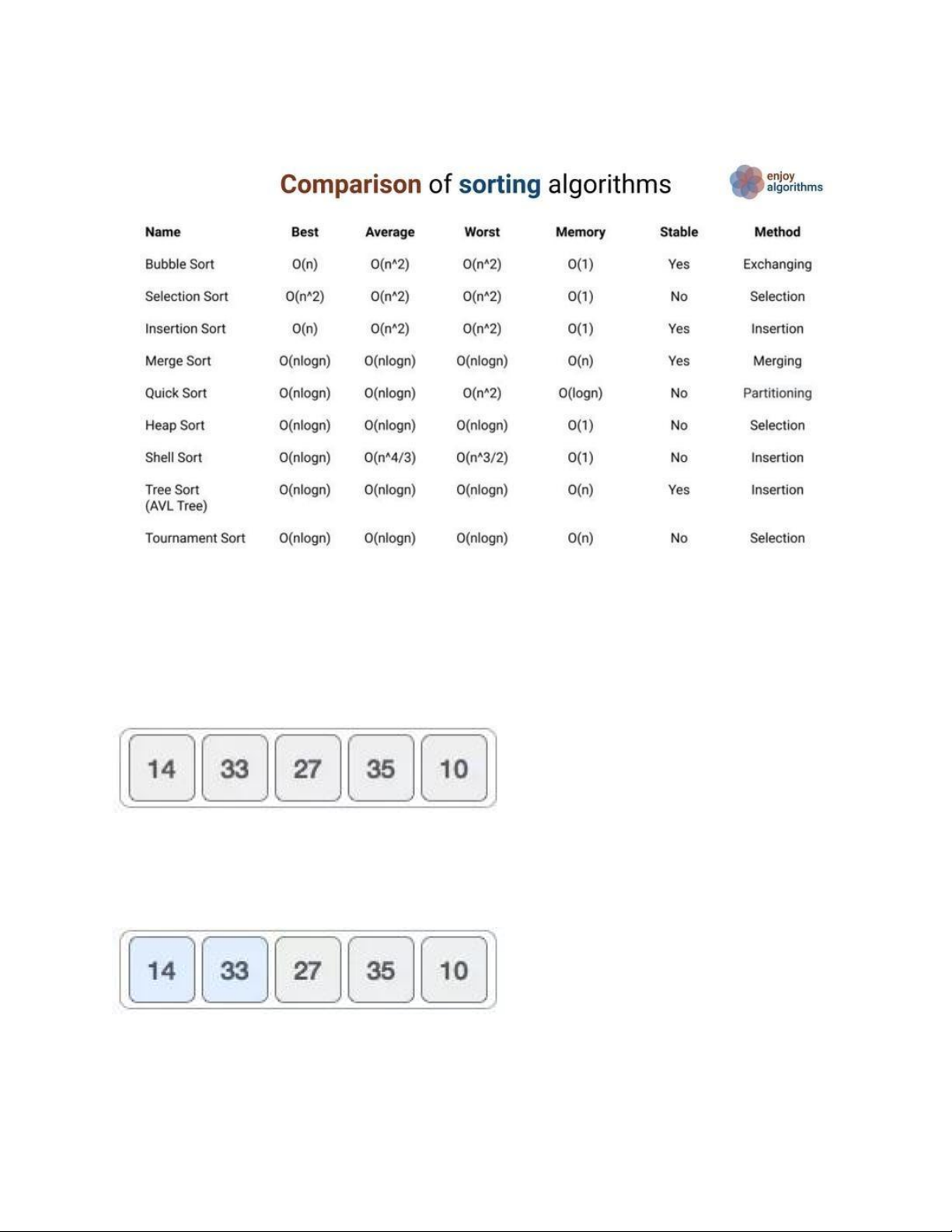
Độ phức tạp của các thuật toán sắp xếp – Tr2 2. Bubble sort – Tr2 3. Insertion sort – Tr5 4. Selection Sort – Tr8 5. Heap Sort – Tr12 6. Merge Sort – Tr26 7. Quick Sort – Tr29 8. Stack – Tr36 9. Queue – Tr41 10. Graph – Tr49 11. Hash table – Tr61 lOMoAR cPSD| 58702377
Độ phức tạp của thuật toán: Bubble Sort
2.1 Các bước thực hiện
Giả sử chúng ta có một mảng không có thứ tự gồm các phần tử như dưới đây. Bây
giờ chúng ta sử dụng giải thuật sắp xếp nổi bọt để sắp xếp mảng này.
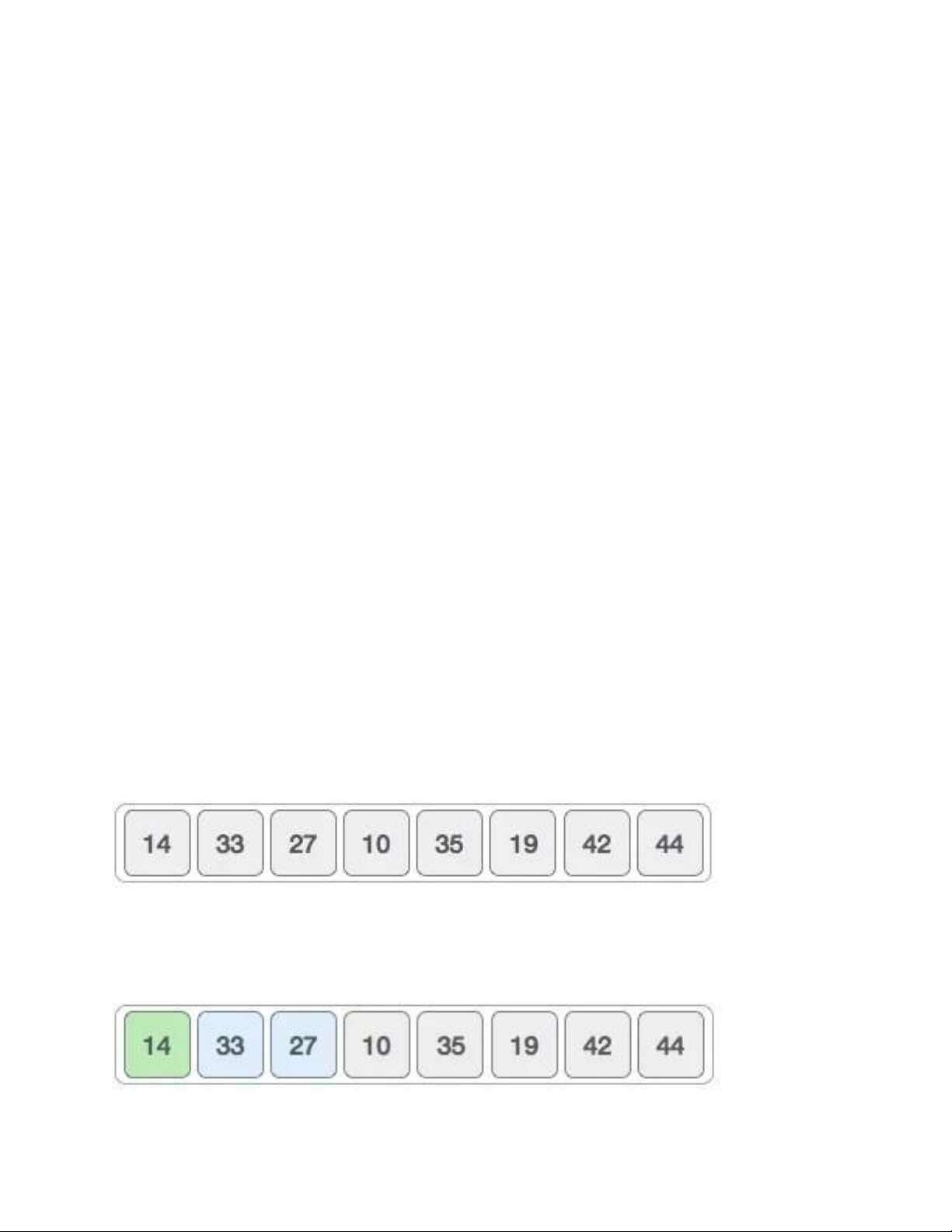
Giải thuật sắp xếp nổi bọt bắt đầu với hai phần tử đầu tiên, so sánh chúng để kiểm
tra xem phần tử nào lớn hơn. Trong trường hợp này, 33 lớn hơn 14, do đó hai phần
tử này đã theo thứ tự.
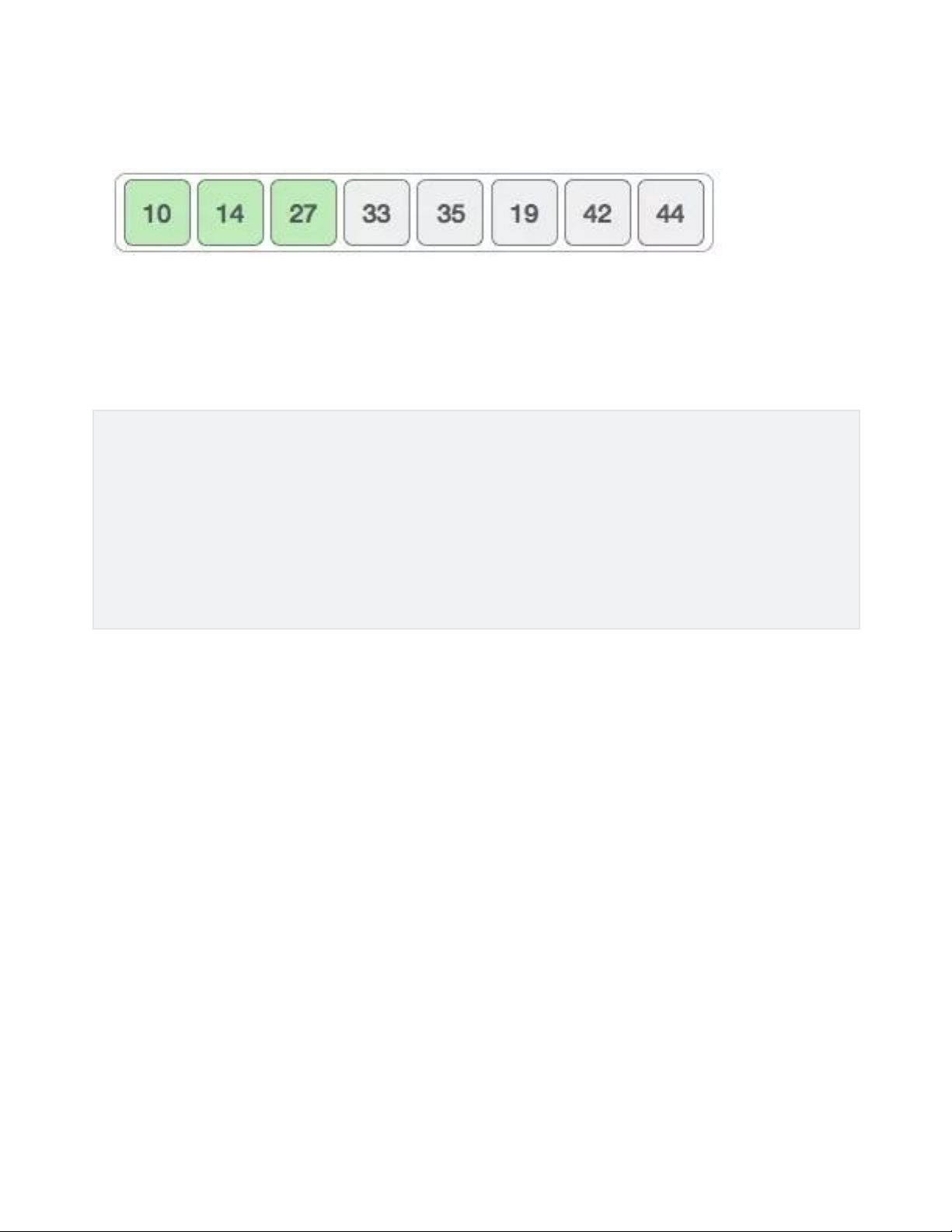
Tiếp đó chúng ta so sánh 33 và 27. lOMoAR cPSD| 58702377
Chúng ta thấy rằng 33 lớn hơn 27, do đó hai giá trị này cần được tráo đổi thứ tự.
Tiếp đó chúng ta so sánh 33 và 35. Hai giá trị này đã theo thứ tự.
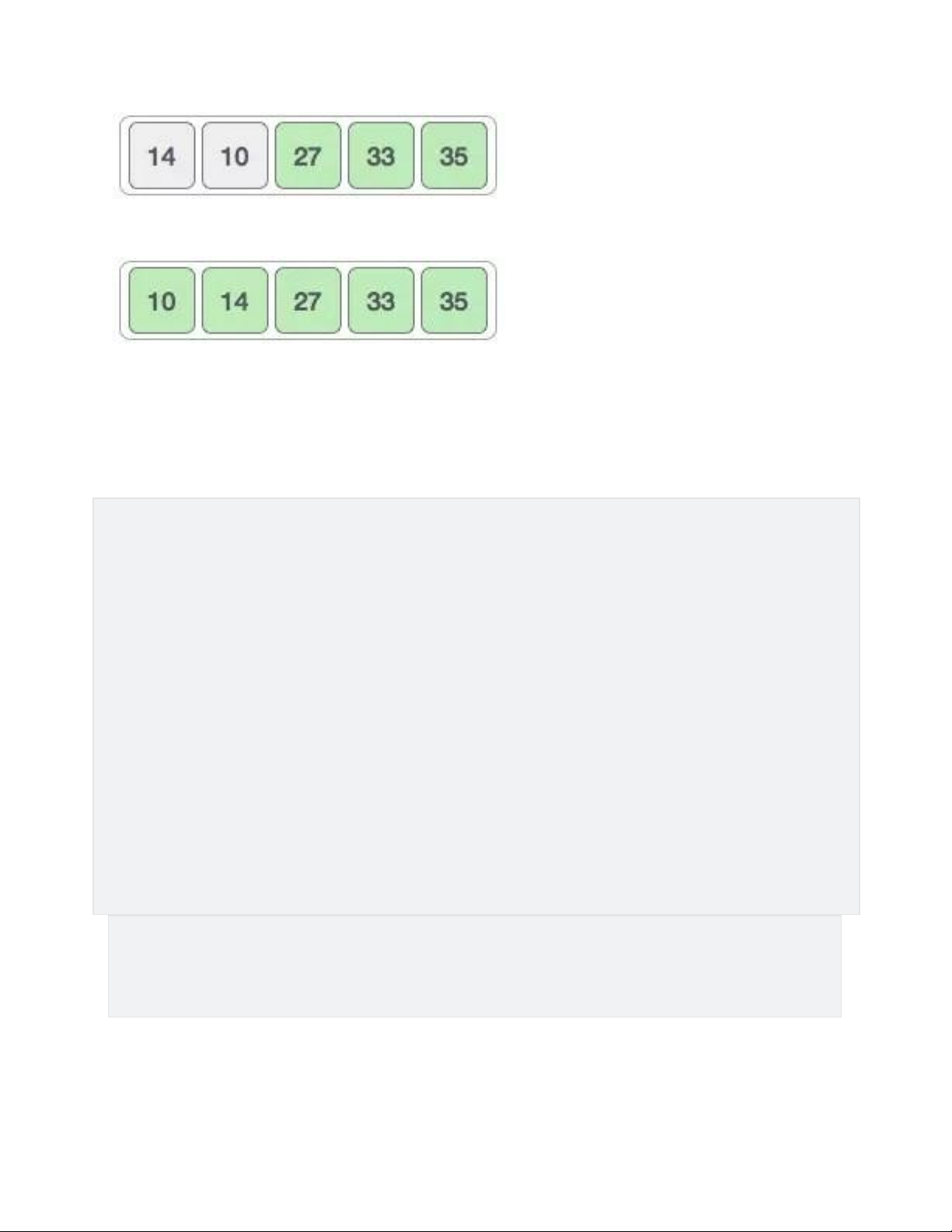
Sau đó chúng ta so sánh hai giá trị kế tiếp là 35 và 10, 10 nhỏ hơn
35 nên ta lại đổi vị trí 2 giá trị này cho nhau
Vậy là sau một vòng lặp, mảng sẽ trông như sau
Chúng ta lặp lại từ đầu quá trình so sánh như vậy, sau lần lặp thứ hai, mảng sẽ trông giống như Lần thứ 3 lOMoAR cPSD| 58702377 lần thứ 4
kết thúc lần thứ 4 chúng ta thấy dãy số đã được sắp xếp đúng thứ tự, thuật toán kết thúc. 2.2 Code
func sortWithhBubbleSort(_ array: [Int]) -> [Int]{
var insideArray = array for _ in
0.. for jIndex in 0..<(insideArray.count-1){
if insideArray[jIndex]>insideArray[jIndex+1]{
let value = insideArray[jIndex+1]
insideArray[jIndex+1] = insideArray[jIndex] insideArray[jIndex] = value } } } return insideArray } lOMoAR cPSD| 58702377 Insertion Sort
Sắp xếp chèn là một giải thuật sắp xếp dựa trên so sánh in-place.
*in-place ở đây nghĩa là không yêu cầu thêm bất kỳ bộ nhớ phụ và việc sắp xếp được
tiến hành trong chính phần bộ nhớ đã khai báo trước đó.
Một danh sách con luôn luôn được duy trì dưới dạng đã qua sắp xếp. Sắp xếp chèn là
chèn thêm một phần tử vào danh sách con đã qua sắp xếp.
Phần tử được chèn vào vị trí thích hợp sao cho vẫn đảm bảo rằng danh sách con đó vẫn sắp theo thứ tự.
Với cấu trúc dữ liệu mảng, chúng ta tưởng tượng là: mảng gồm hai phần: một danh
sách con đã được sắp xếp và phần khác là các phần tử không có thứ tự. Giải thuật
sắp xếp chèn sẽ thực hiện việc tìm kiếm liên tiếp qua mảng đó, và các phần tử không
có thứ tự sẽ được di chuyển và được chèn vào vị trí thích hợp trong danh sách con (của cùng mảng đó).
Giải thuật này không thích hợp sử dụng với các tập dữ liệu lớn khi độ phức tạp
trường hợp xấu nhất và trường hợp trung bình là Ο(n2) với n là số phần tử.
3.1 Các bước thực hiện
Chúng ta có 1 mảng các phần tử số như sau
Chúng ta sẽ so sánh 2 phần tử đầu tiên của mảng là 14 và 33, 2 phần tử này đã được
sắp xếp nên chúng ta đưa 14 vào mảng con đã qua sắp xếp, tiếp tục so sánh đến 2 phần tử 33 và 27 lOMoAR cPSD| 58702377
ở đây ta thấy 33 ko nằm đúng vị trí, chúng ta tiến hành tráo đổi vị trí 33 và 27
đồng thời thêm phần tử 27 vào danh sách con đã sắp xếp, trong danh sách con này
hiện có 2 phần tử 14, 27 2 phần tử này cũng đã nằm đúng vị trí nên không cần so
sánh tiếp Lại tiếp tục so sánh 33 và 10
2 phần tử này không đúng vị trí nên tiến hành tráo đổi chúng
Việc tráo đổi dẫn đến 27 và 10 không theo thứ tự.
Vì thế chúng ta cũng tráo đổi chúng.
Chúng ta lại thấy rằng 14 và 10 không theo thứ tự. lOMoAR cPSD| 58702377
Và chúng ta tiếp tục tráo đổi hai số này. Cuối cùng, sau vòng lặp thứ 3 chúng ta có 4 phần tử.
Cứ tiếp tục như vậy cho đến khi tất cả các phần từ trong mảng được sắp xếp thì thuật toán kết thúc. 3.2 Code
func sortWithhinsertionSort(_ array: [Int]) -> [Int] { var insideArray = array
for i in 0..let value = array[i] lOMoAR cPSD| 58702377 var j = i - 1 while j >= 0 { if array[j] > value{ insideArray[j+1] = array[j] } else { break } j -= 1 } insideArray[j+1] = value } return insideArray } Selection Sort
Giải thuật sắp xếp chọn (Selection Sort) là một giải thuật trong đó danh sách được
chia thành hai phần, phần được sắp xếp (sorted list) ở bên trái và phần chưa được
sắp xếp (unsorted list) ở bên phải. Ban đầu, phần được sắp xếp là trống và phần chưa
được sắp xếp là toàn bộ danh sách ban đầu.
Phần tử nhỏ nhất được lựa chọn từ mảng chưa được sắp xếp và được tráo đổi với
phần bên trái nhất và phần tử đó trở thành phần tử của mảng được sắp xếp. Tiến
trình này tiếp tục cho tới khi toàn bộ từng phần tử trong mảng chưa được sắp xếp
đều được di chuyển sang mảng đã được sắp xếp.
Giải thuật này không phù hợp với tập dữ liệu lớn khi mà độ phức tạp trường hợp xấu
nhất và trường hợp trung bình là O(n2) với n là số phần tử. lOMoAR cPSD| 58702377
4.1 Các bước thực hiện
Gỉa sử lúc đầu chúng ta có 1 mảng các phần tử số như sau
Vị trí đầu tiên có giá trị 14, chúng ta tìm toàn bộ danh sách và thấy rằng 10 là giá trị nhỏ nhất.
Do đó, chúng ta thay thế 14 với 10. Tại vị trí thứ hai, giá trị 33, chúng ta tiếp tục quét
phần còn lại của danh sách theo thứ tự từng phần tử.
Chúng ta thấy rằng 14 là giá trị nhỏ nhất thứ hai trong danh sách và nó nên xuất hiện
ở vị trí thứ hai. Chúng ta tráo đổi hai giá trị này.
Cứ thế áp dụng với phần còn lại của danh sách cho đến khi mảng
được sắp xếp đúng vị trí thì thuật toán kết thúc lOMoAR cPSD| 58702377 lOMoAR cPSD| 58702377 4.2 Code
func sortWithSelectionSort(_ array: [Int]) -> [Int] {
guard array.count > 1 else { return array } // 1 var a = array // 2
for x in 0 ..< a.count - 1 { // 3 var lowest = x
for y in x + 1 ..< a.count { // 4 if a[y] < a[lowest] { lowest = y } } if x != lowest { // 5 a.swapAt(x, lowest) } } return a } Heap sort
Heap là cấu trúc dữ liệu đặc biệt dựa trên cấu trúc của một cây nhị phân hoàn chỉnh
thỏa mãn thuộc tính heap, và có thể được biểu diễn dưới dạng một mảng. Một cây
nhị phân sẽ có các mục được lưu trữ theo một thứ tự đặc biệt. lOMoAR cPSD| 58702377
Thuật toán Heap sort sẽ được sử dụng để biểu diễn cho thuộc tính heap của một nút
trong cây nhị phân, bao gồm 2 loại: •
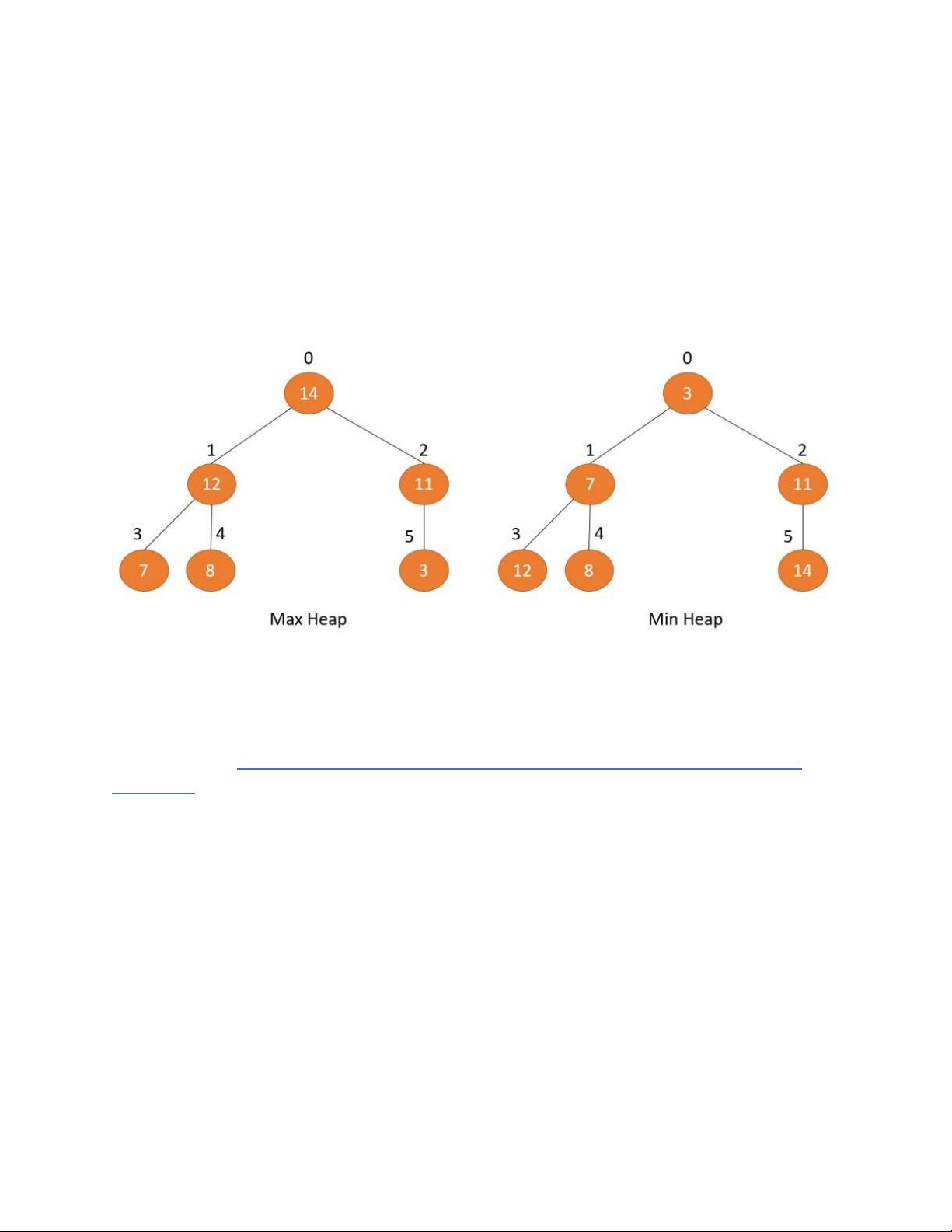
Max heap: Phần tử trong nút cha luôn có giá trị lớn hơn so với tất cả các phần
tử trong nút con. Và giá trị nút gốc là lớn nhất so với tất cả các nút khác. •
Min heap: Phần tử trong nút cha luôn có giá trị nhỏ hơn so với tất cả các phần
tử trong nút con. Và giá trị nút gốc là nhỏ nhất so với tất cả các nút khác.
Ví dụ về cấu trúc dữ liệu Min Heap và Max Heap:
Cấu trúc dữ liệu Max Heap và Min Heap.
Thuật toán heap sort có thể được biểu diễn qua một cây hoặc mảng nhị phân.
>>> Đọc ngay: FUNiX – Học lấy bằng đại học trực tuyến giá trị ngang bằng đại học chính quy
3. Làm thế nào để tạo cấu trúc dữ liệu Heap cho một cây nhị phân
Một số thuật toán Heap sort được sử dụng để thực hiện những thao tác quan trọng trong cấu trúc Heap.
Chúng ta có thể sửa đổi một cây nhị phân hoàn chỉnh trở thành Max Heap bằng cách
sử dụng hàm Heapify trên tất cả những phần tử không phải là nút lá của Heap. Ta sẽ
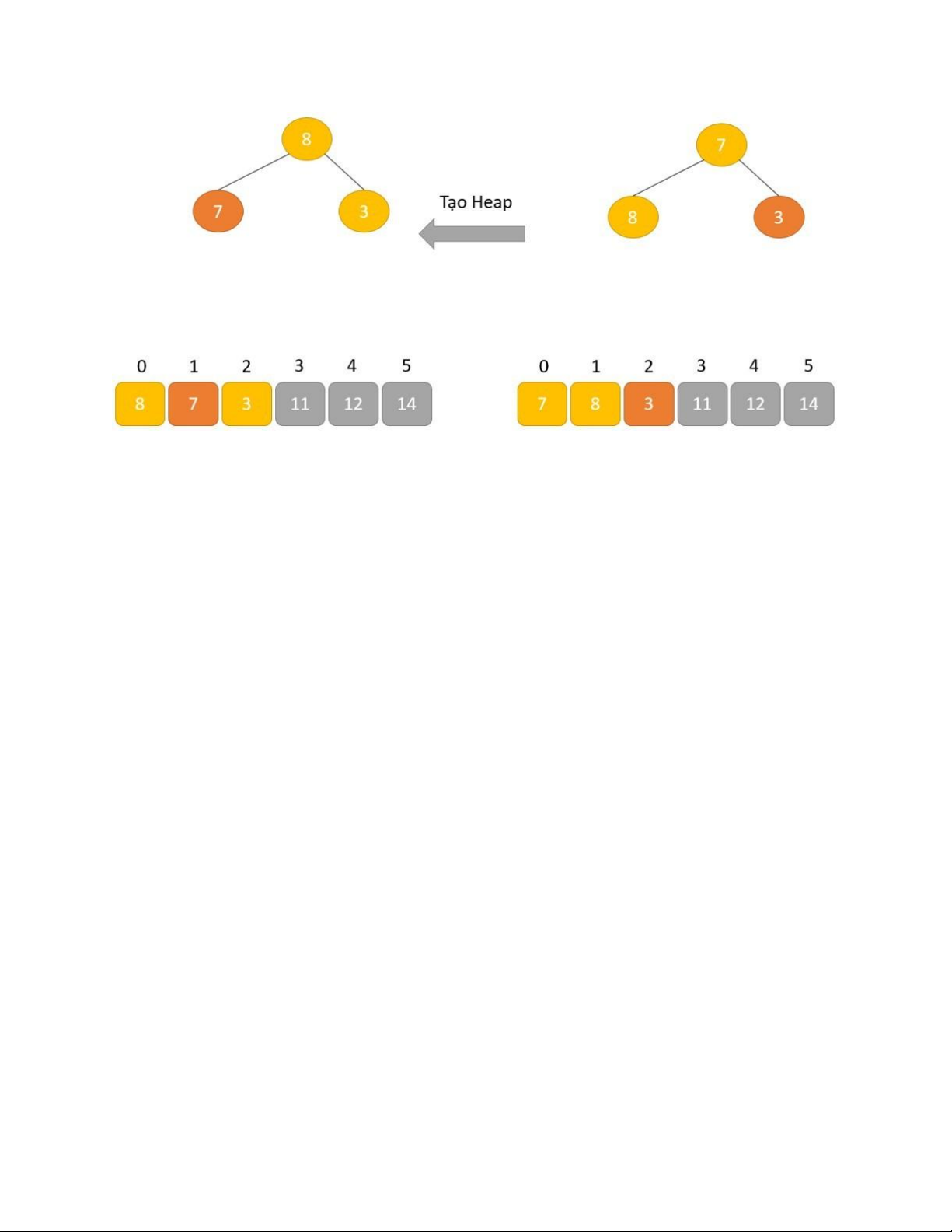
xem ví dụ về tạo cấu trúc dữ liệu Heap cho một cây nhị phân với 3 phần tử: heapify(array) Root = array[0] lOMoAR cPSD| 58702377
Largest = largest( array[0] , array [2*0 + 1]. array[2*0+2]) if(Root != Largest) Swap(Root, Largest)
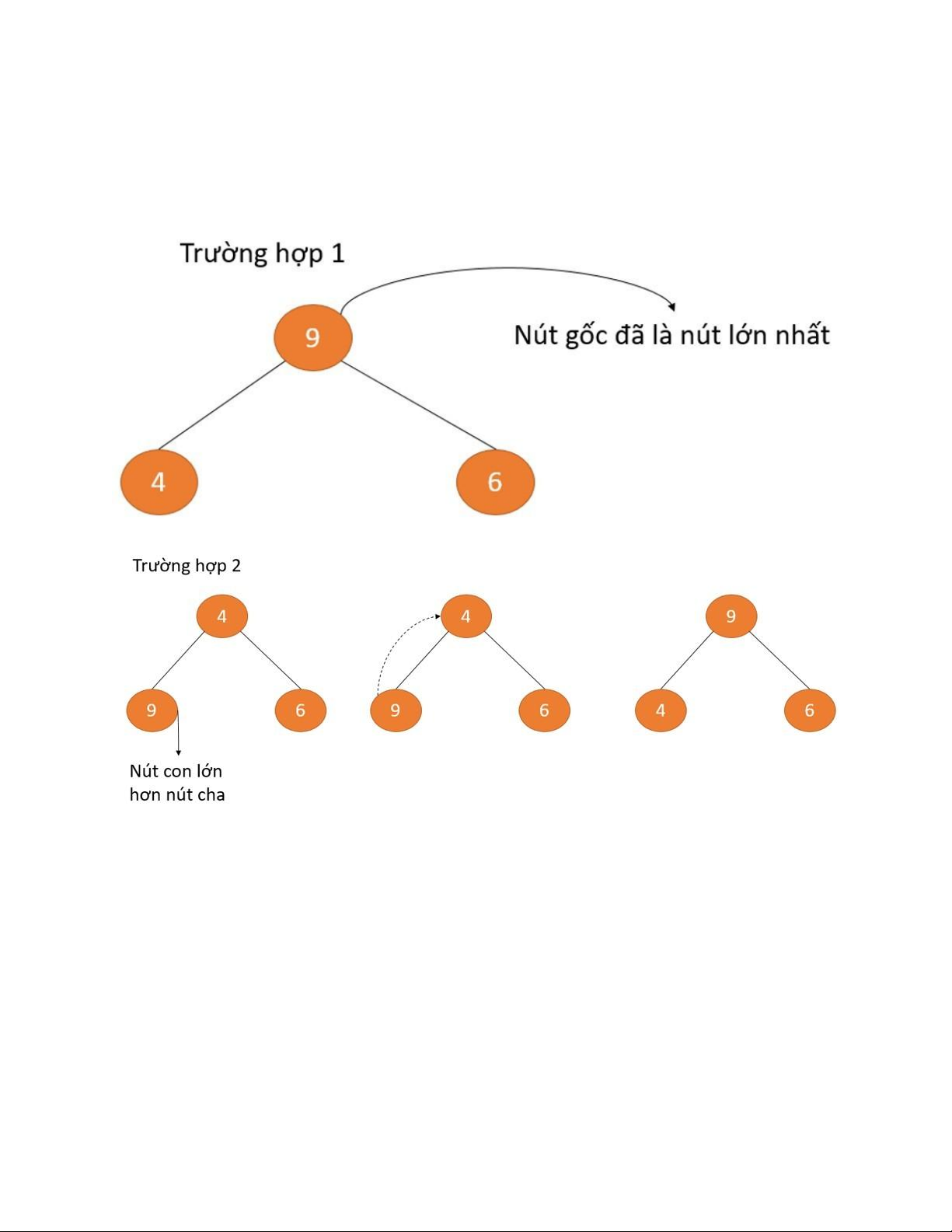
Trường hợp nút gốc lớn nhất
Trường hợp nút con lớn hơn nút cha.
Trong trường hợp 1, nút gốc của cây nhị phân là phần tử lớn nhất và chúng ta không
cần làm gì cả. Trường hợp 2, nút con chứa phần tử lớn hơn nút gốc, và ta cần hoán
đổi để duy trì thuộc tính Max Heap. Ví dụ 2: lOMoAR cPSD| 58702377
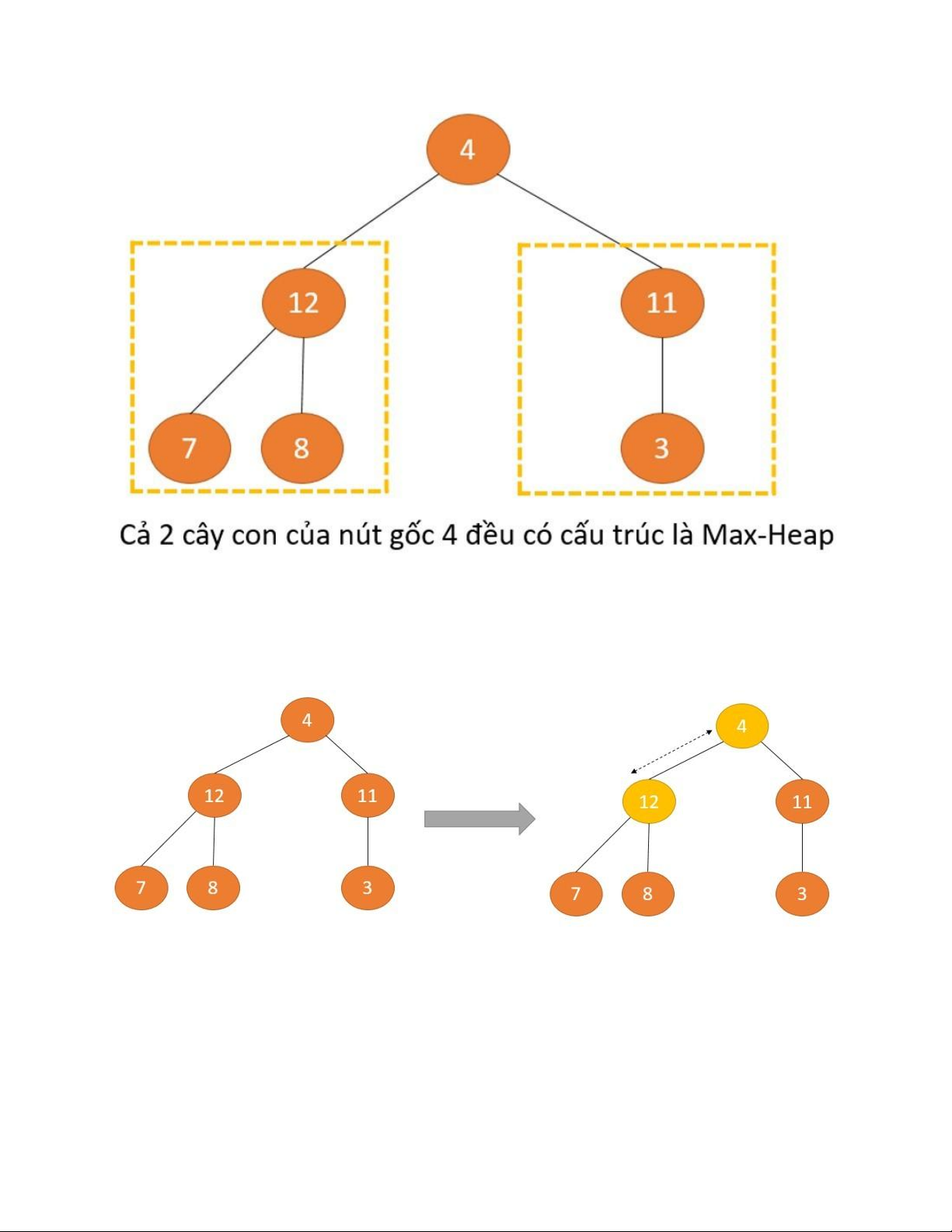
Hai cây con đều có cấu trúc Max-heap.
Trong ví dụ 2 này, cả 2 cây con đều có cấu trúc Max Heap, tuy nhiên nút gốc trên cùng
lại không phải là Max Heap. Nên để duy trì thuộc tính Max Heap cho toàn bộ cây,
chúng ta phải đẩy 2 cây xuống dưới cho đến khi đúng vị trí của nó.
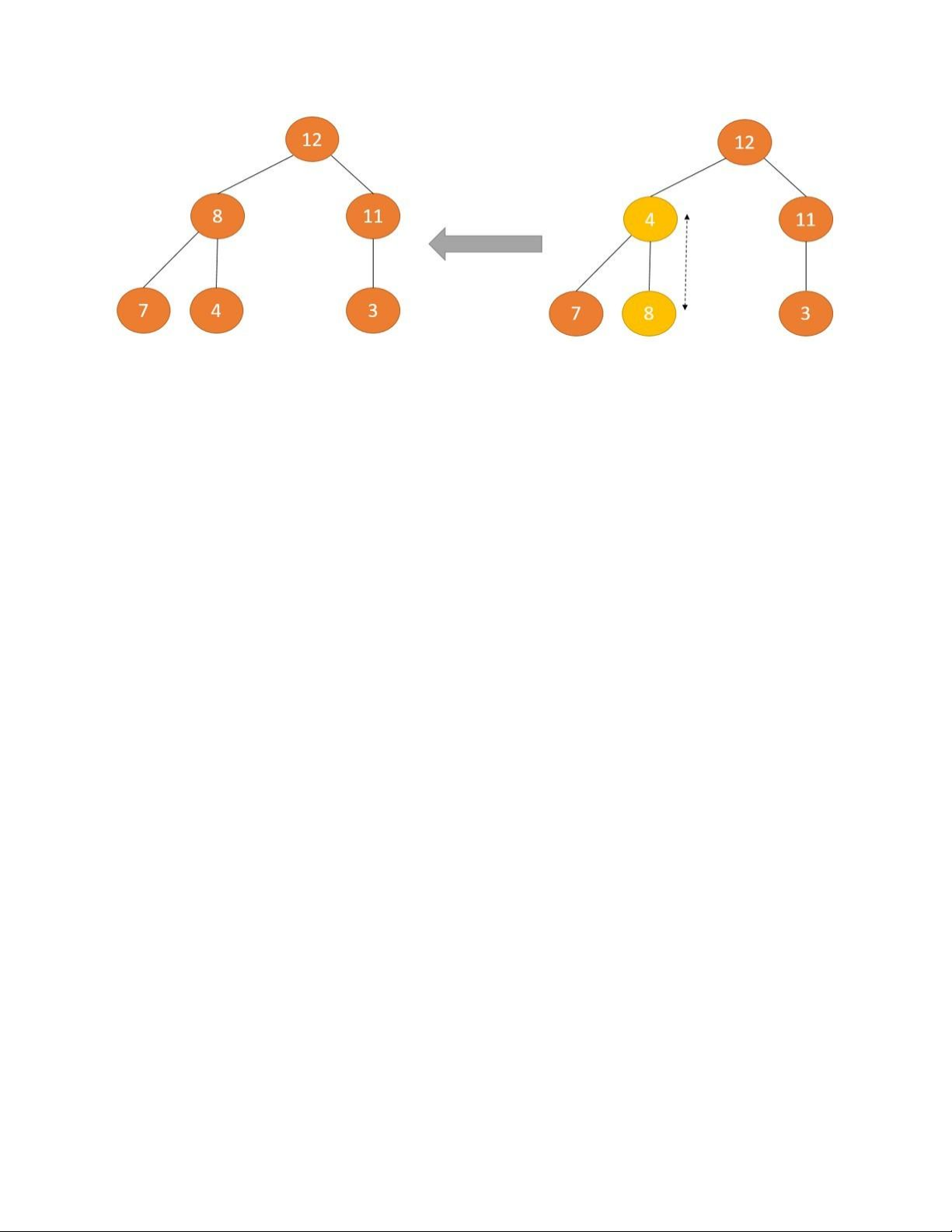
Đẩy 2 cây xuống đúng vị trí để duy trì thuộc tính Max Heap lOMoAR cPSD| 58702377
Tiếp tục đẩy xuống cho đến khi đúng vị trí.
Trong một cây nhị phân có cả hai cây con đều là Max Heap, muốn duy trì thuộc tính
Max Heap chúng ta cần phải thực hiện quá trình Heapify – tạo cấu trúc dữ liệu Heap
từ cây nhị phân Binary Heap trên nút gốc nhiều lần cho đến khi nó lớn hơn tất cả các nút con.
Chúng ta có thể kết hợp 2 điều kiện này trong một hàm Heapify như sau:
void heapify(int arr[], int n, int i) { int largest = i; int left = 2 * i + 1; int right = 2 * i + 2;
if (left < n && arr[left] > arr[largest]) largest = left;
if (right < n && arr[right] > arr[largest]) largest = right; if (largest != i) {
swap(&arr[i], &arr[largest]); heapify(arr, n, largest); } lOMoAR cPSD| 58702377 }
Chúng ta có thể di chuyển nút gốc đến vị trí chính xác để duy trì được thuộc tính Max
Heap cho bất kỳ cây nhị phân nào miễn là cây con có cấu trúc Max Heap.
>>> Đọc ngay: Hướng dẫn sử dụng cấu trúc cây, cây tìm kiếm nhị phân
4. Hoạt động của thuật toán Heap sort
Thuật toán Heap sort sẽ hoạt động dựa trên các nguyên tắc sau: •
Phần tử lớn nhất được đặt ở nút gốc theo thuộc tính Max Heap •
Loại bỏ phần tử gốc và đặt nó ở cuối mảng nhị phân. Đặt phần tử cuối cùng
của cây nhị phân vào chỗ trống. •
Giảm kích thước của Heap đi 1 đơn vị •
Tạo cấu trúc dữ liệu Heap cho phần tử gốc để nút gốc chứa phần tử có giá trị lớn nhất. •
Lặp lại quá trình này cho đến khi tất cả các phần tử của danh sách được sắp xếp đúng.
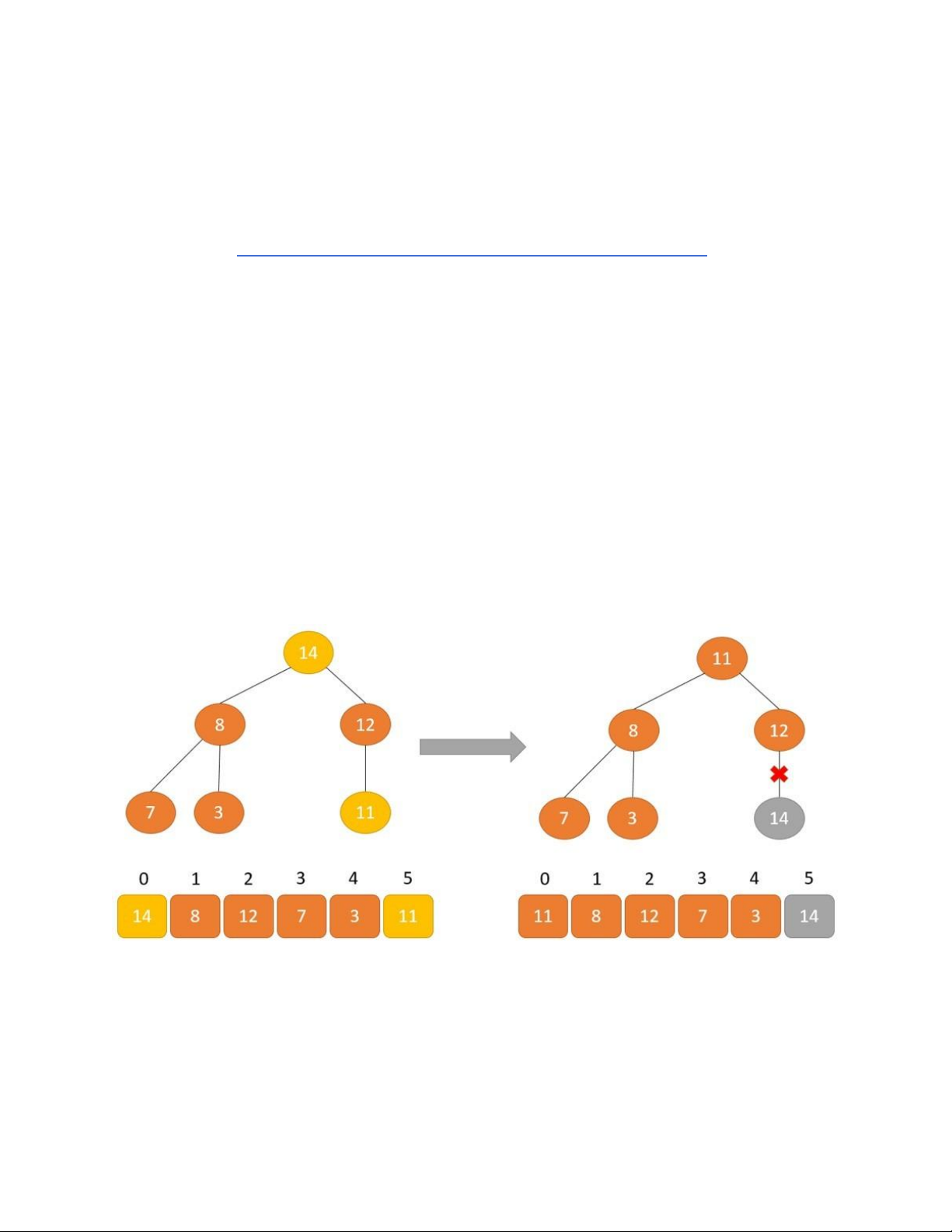
Loại bỏ phần tử gốc 14 và đặt ở cuối mảng nhị phân. lOMoAR cPSD| 58702377
Tạo cấu trúc dữ liệu Heap cho phần tử gốc 12.
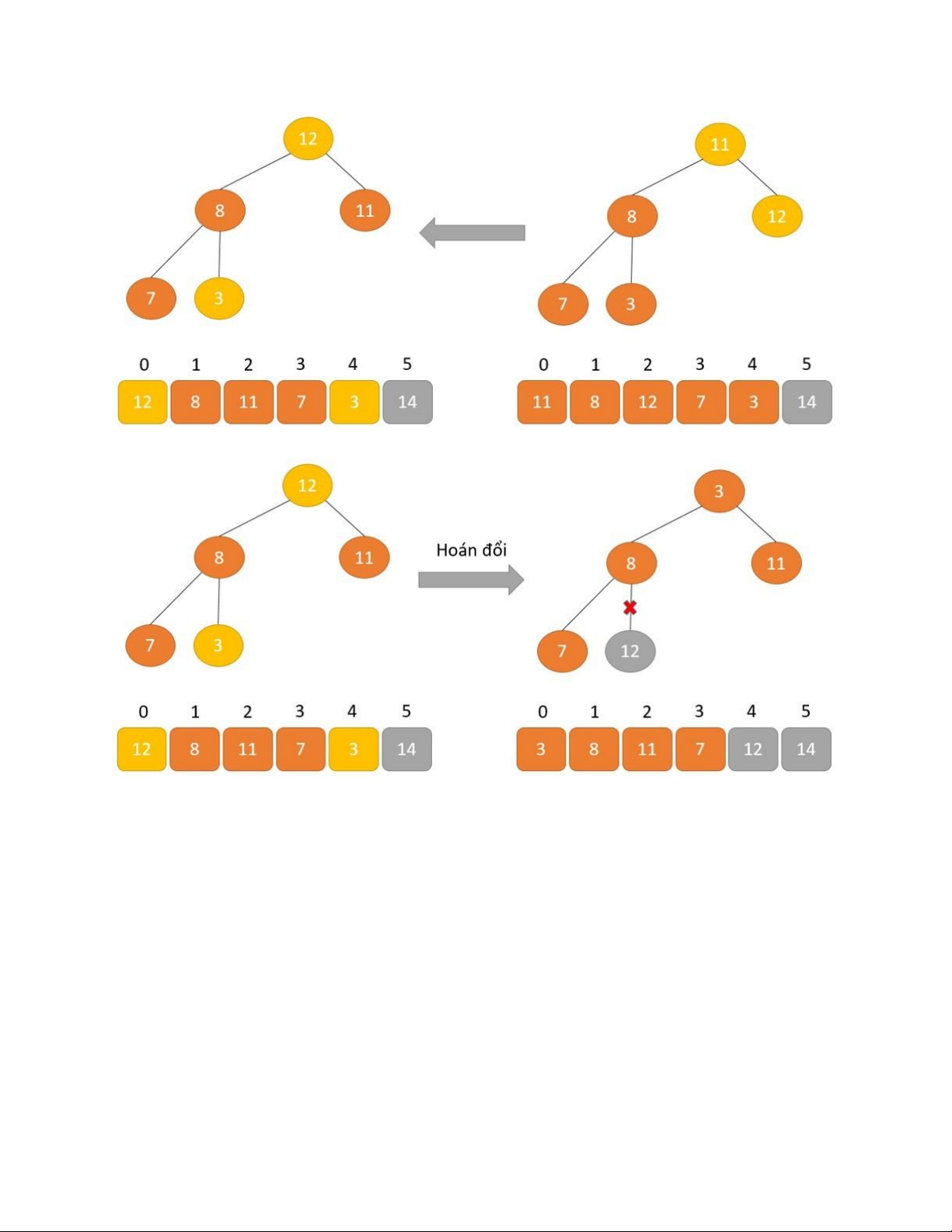
Hoán đổi để loại bỏ phần tử gốc 12. lOMoAR cPSD| 58702377
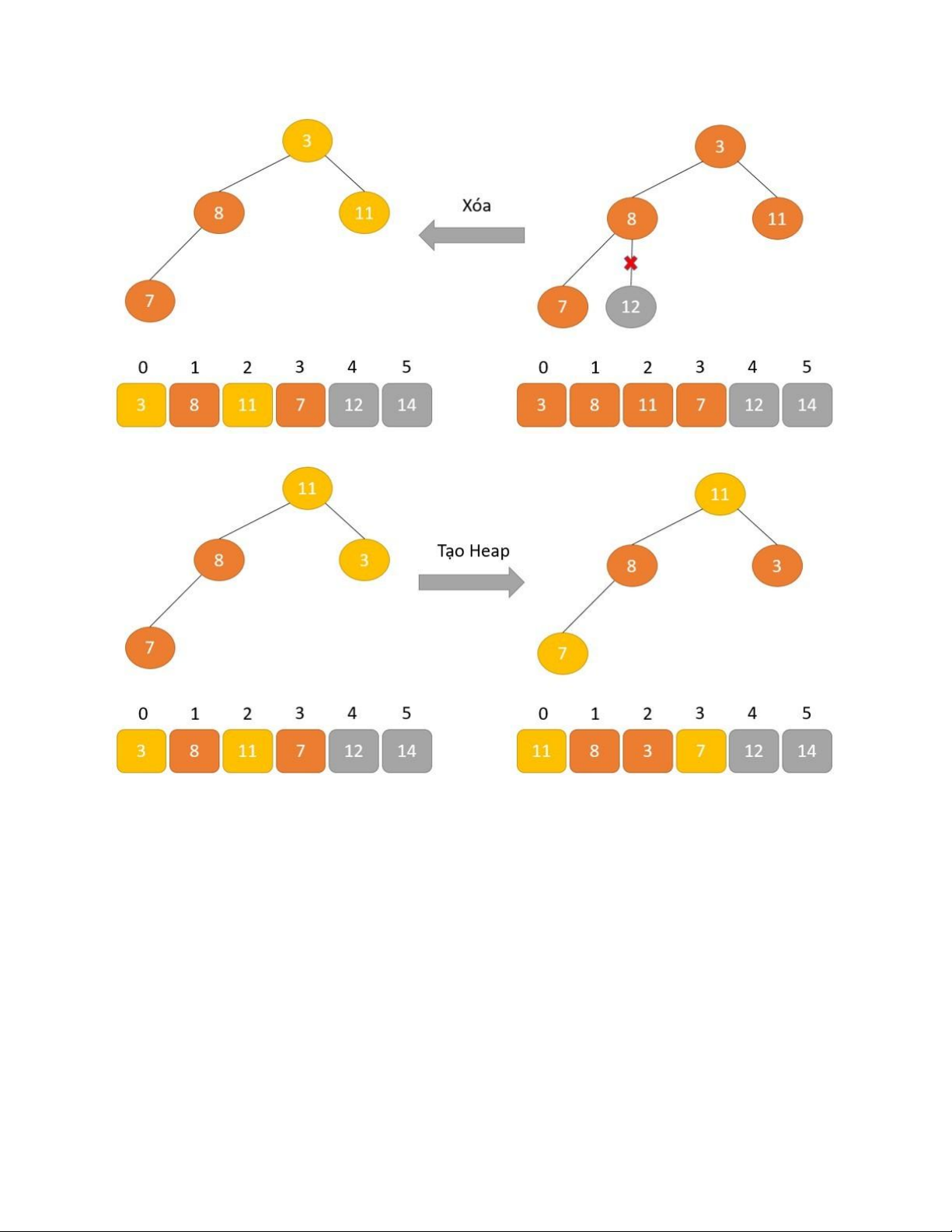
Xóa bỏ phần tử gốc 12.
Tiếp tục tạo cấu trúc dữ liệu Heap. lOMoAR cPSD| 58702377
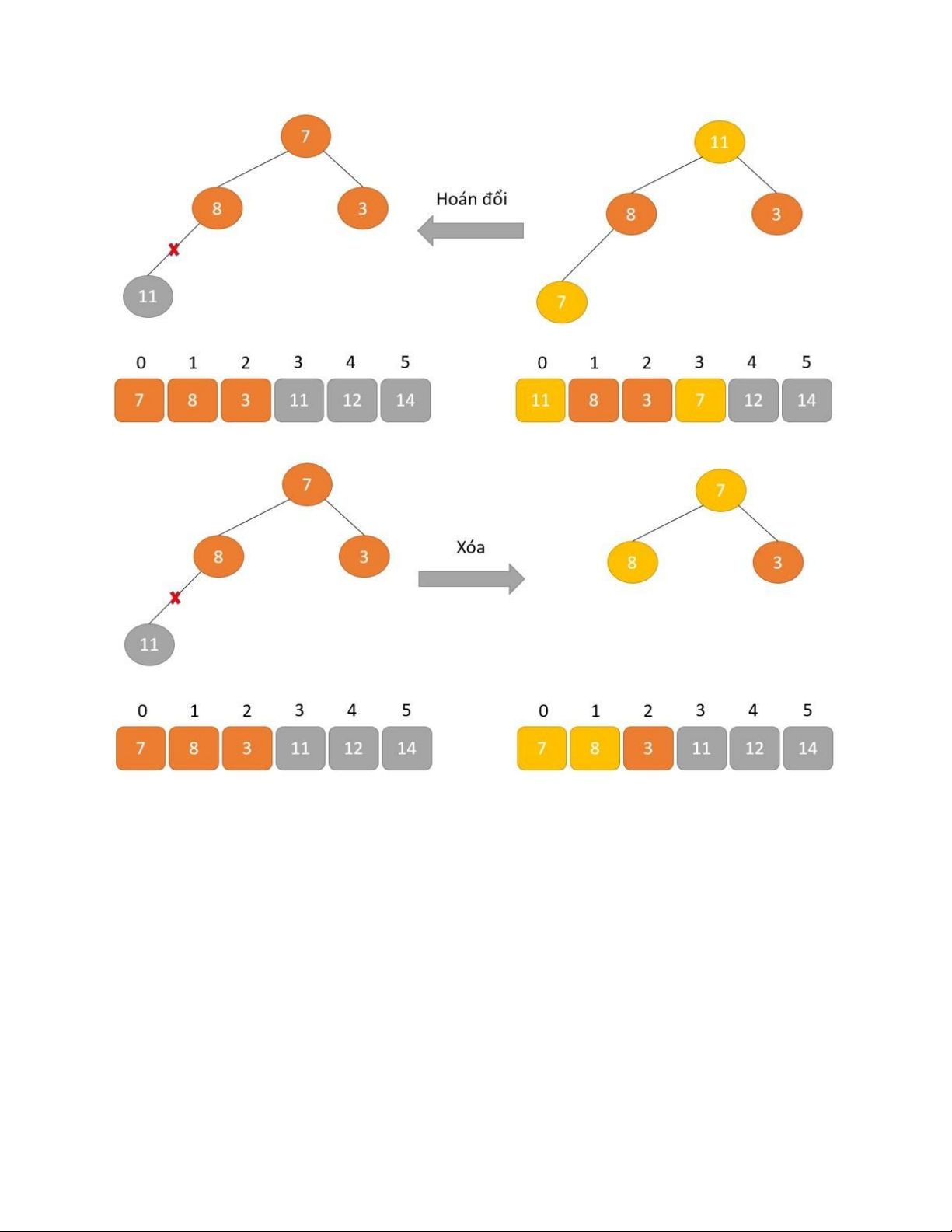
Lại hoán đổi để loại bỏ nút gốc 11. Xóa bỏ nút gốc 11. lOMoAR cPSD| 58702377