Phương Pháp Ghép Trục Hàm Số | Toán 12

PHƯƠNG PHÁP GHÉP BÀI 18 TRỤC HÀM SỐ P3 3 HÀM LỒNG HÀM
BÀI TOÁN 1 : Cho hàm số f (x ) . Tìm khoảng biến thiên, cực trị, tương giao của hàm số
y = a. f n (x ) + b. f n−1 (x ) + ... + c PHƯƠNG PHÁP
Bước 1. Tìm điểm cực trị của hàm số y = f (x ) ta được x1 ; x2
Bước 2. Đặt f ( x ) = u . Tìm điểm cực trị của hàm số g (u ) = a. u n + b. u n−1 + ... + c ta được a ; b Bước 3. Lập BBT
Bước 3.1. Lập BBT gồm 3 x hàng
u = f (x ) g (u )
Bước 3.2. Điền x 1 ; x2 vào x − x1 x2 + hàng 1
u = f (x ) g (u ) x x
Bước 3.3. Thay x 1 ; x2 vào x − 1 2 + u ( x )
u = f (x ) u (− ) u ( x1 ) u ( x2 ) u (+ ) g (u ) x x
Bước 3.4. Điền các các điểm cực x − 1 2 +
trị của y = g ( u) giữa 2
khoảng u ( xi ) (Theo thứ tự
u = f (x ) u (− ) a u ( x1 )b u ( x2 ) ab u (+ )
tăng dần của u ( xi ) ) g (u )
“Nếu hôm nay chưa học được gì thì đừng nên đi ngủ”
Bước 3.5. Giải các phương trình x − t1 x1 t3 x2 t2 t4 +
u (x ) = a ta được nghiệm
u = f (x ) u (− ) u ( x1 ) u ( x2 ) u (+ )
t1 ; t2 và u (x ) = b ta được a b a b
nghiệm t 3 ; t4 g (u )
Điền các nghiệm này vào hàng 1
trong BBT theo thứ tự tăng dần.
Bước 3.6. Nhìn giữa 2 khoảng x − x1 x2 +
u ( xi ) ; đối chiếu với đồ thị
(BBT) của hàm y = f (x ) vẽ
u = f (x ) u (− ) a u ( x1 ) b u ( x2 ) a b u (+ )
lại giá trị tương ứng. g (u )
BÀI TOÁN 2 : Cho hàm số f(x). Xét sự biến thiên, cực trị, tương giao của hàm lồng hàm y = f ( f (u )) PHƯƠNG PHÁP
Làm tương tự các bài ghép trục khác.
TÌM KHOẢNG BIẾN THIÊN, CỰC TRỊ, TƯƠNG GIAO
CỦA HÀM SỐ y = a. f n (x ) + b. f n−1 (x ) + ... + c
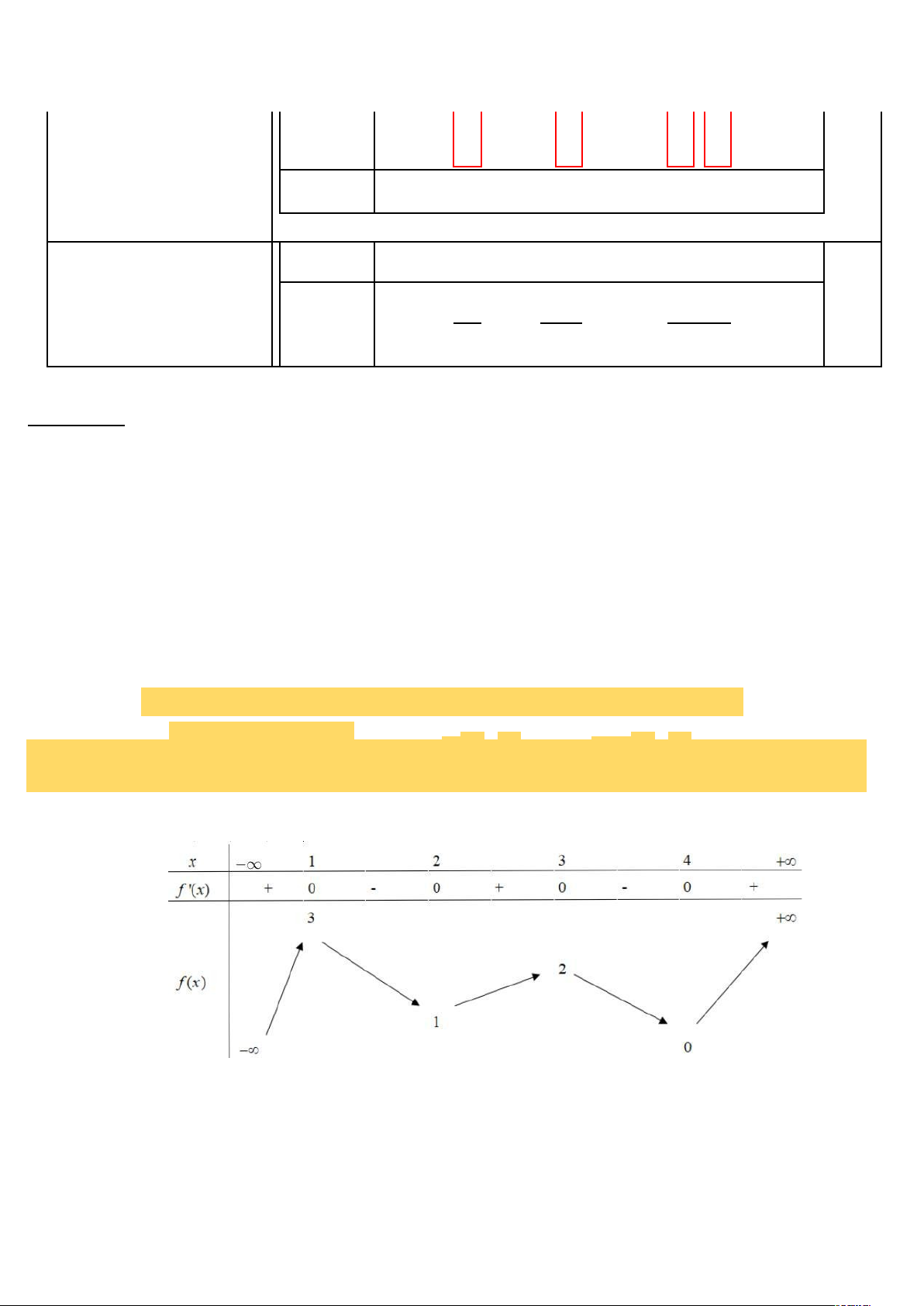
Ví dụ 1. Cho hàm số f (x ) có bảng biến thiên như sau:
Hàm số y = ( f (x ))3 − 3.( f (x))2 nghịch biến trên khoảng nào dưới đây? ( ) ( ) ( ) ( ) A. 1;2 . B. 3 ; 4 . C. − ;1 . D. 2 ; 3 .
“Nếu hôm nay chưa học được gì thì đừng nên đi ngủ”
Ví dụ 2. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hàm số
y = f (x ) có đồ thị như hình vẽ bên dưới:
Tìm tất cả các giá trị của tham số m để đồ thị hàm số
h (x ) = f 2 (x )+ f (x )+ m có đúng 3 cực trị. A. m 1 . B. m 1. 4 C. m 1. D. m 1 . 4
Xét sự biến thiên, cực trị, tương giao của hàm lồng hàm
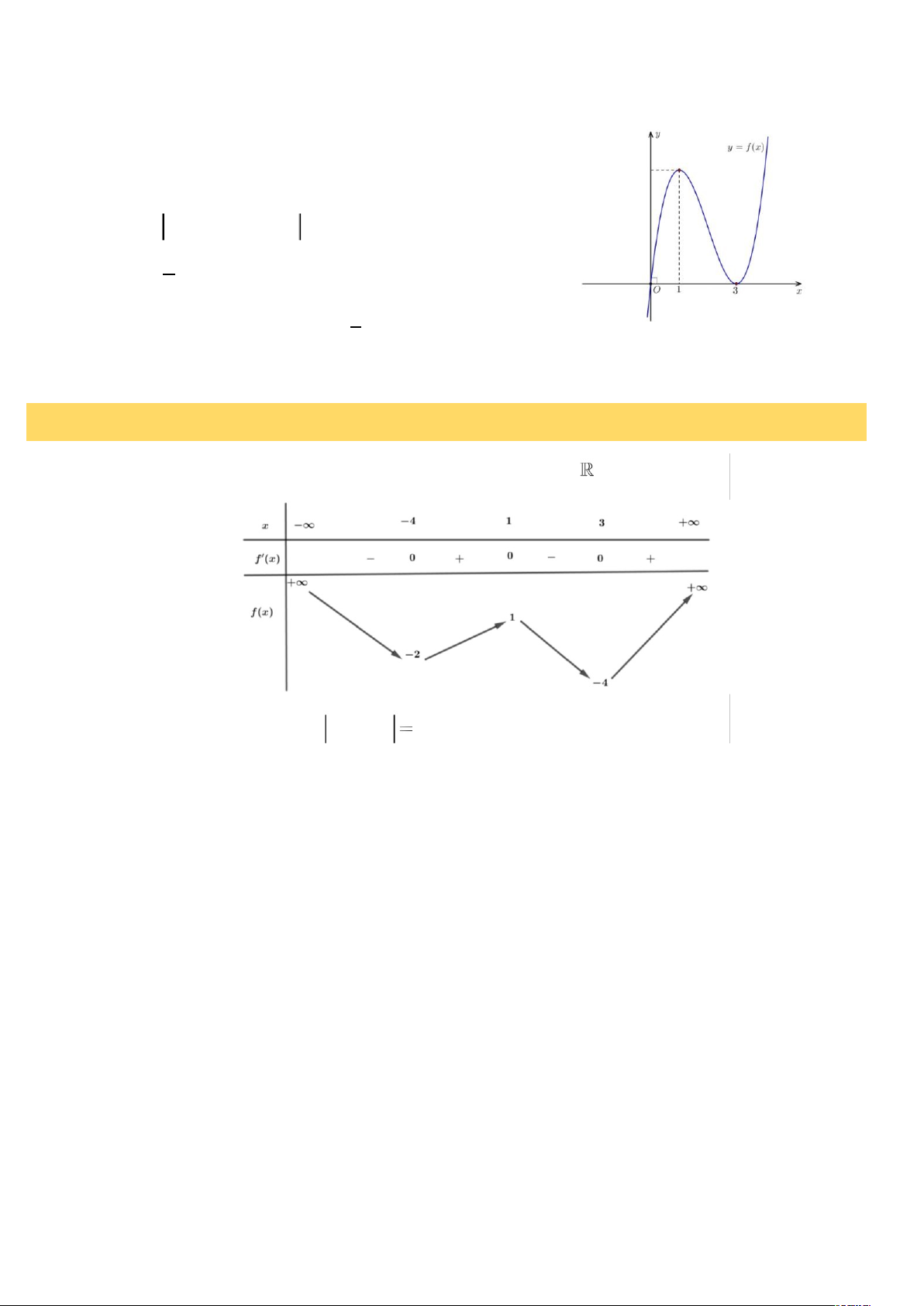
Ví dụ 3. (Sở Tuyên Quang - 2021) Cho hàm số y f x liên tục trên
và có bảng biến thiên như hình vẽ
Số nghiệm của phương trình f f x 2 là A. 4. B. 5. C. 9. D. 7.
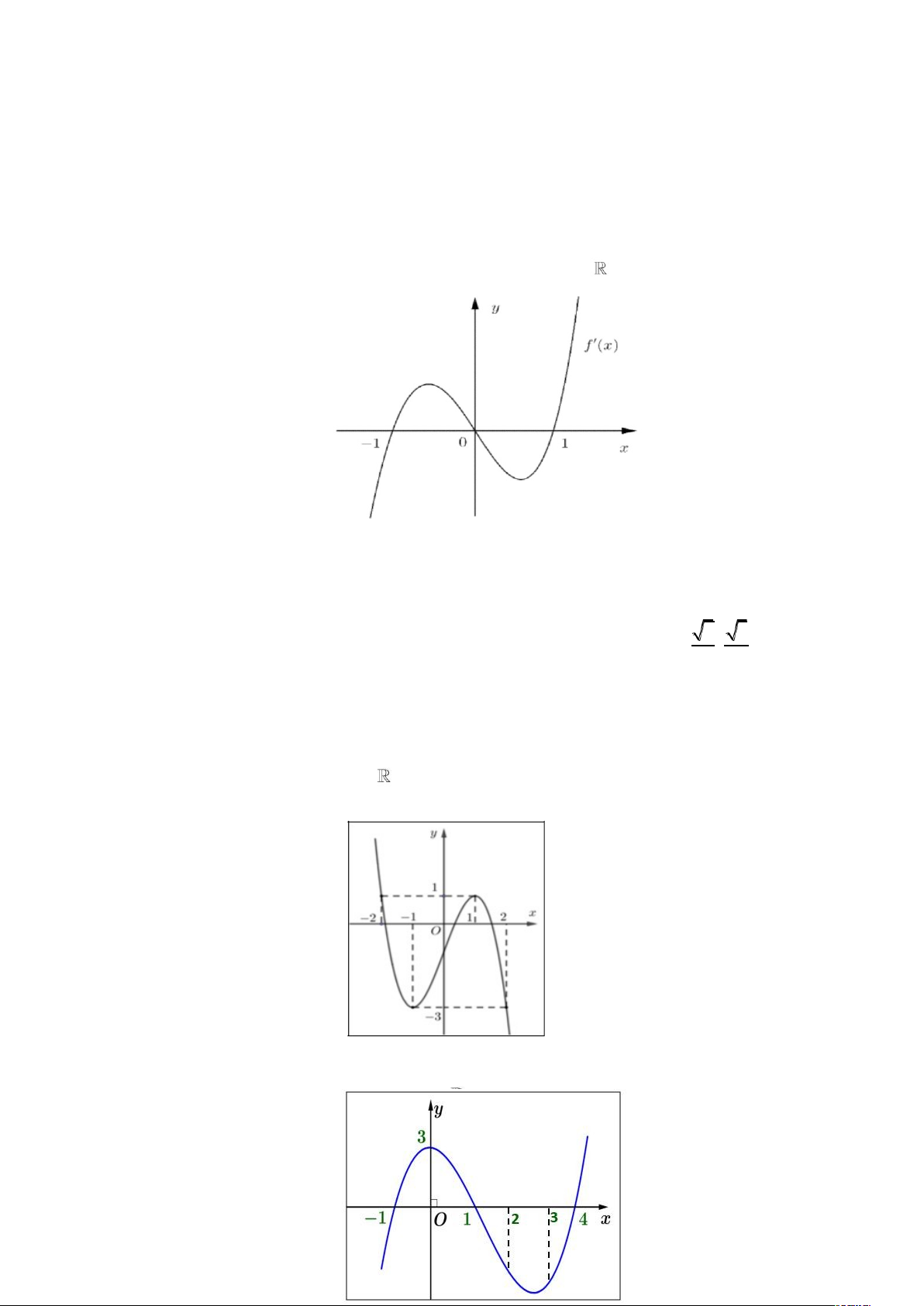
Ví dụ 4. Cho hàm số y = f (x ) có đạo hàm trên
và có đồ thị là đường cong như hình vẽ. y 3 −1 12 3 4 O x
Đặt g (x ) = 3 f ( f (x ))+ 4 . Số điểm cực trị của hàm số g (x ) là A. 2. B. 8. C. 10. D. 6.
“Nếu hôm nay chưa học được gì thì đừng nên đi ngủ”
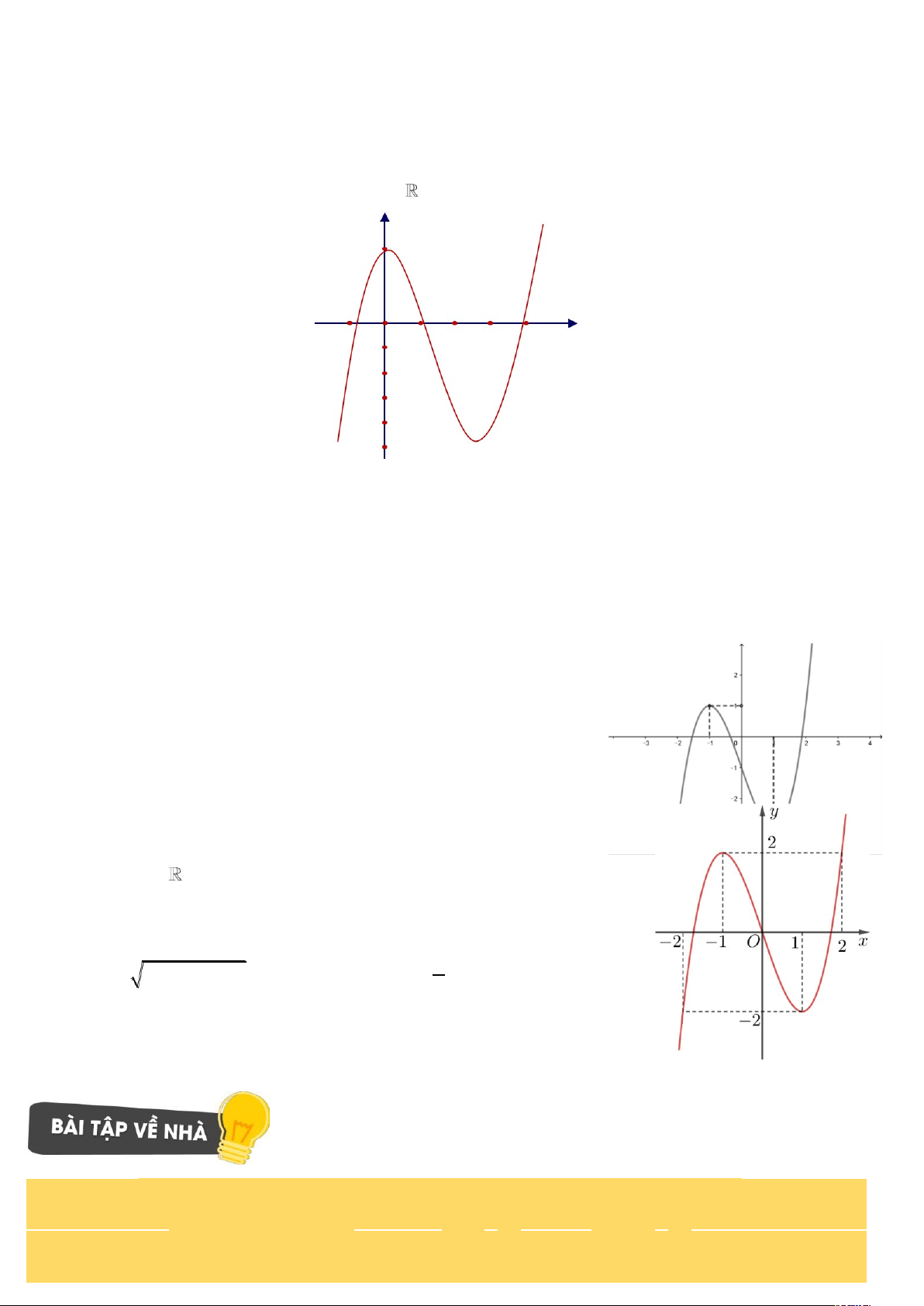
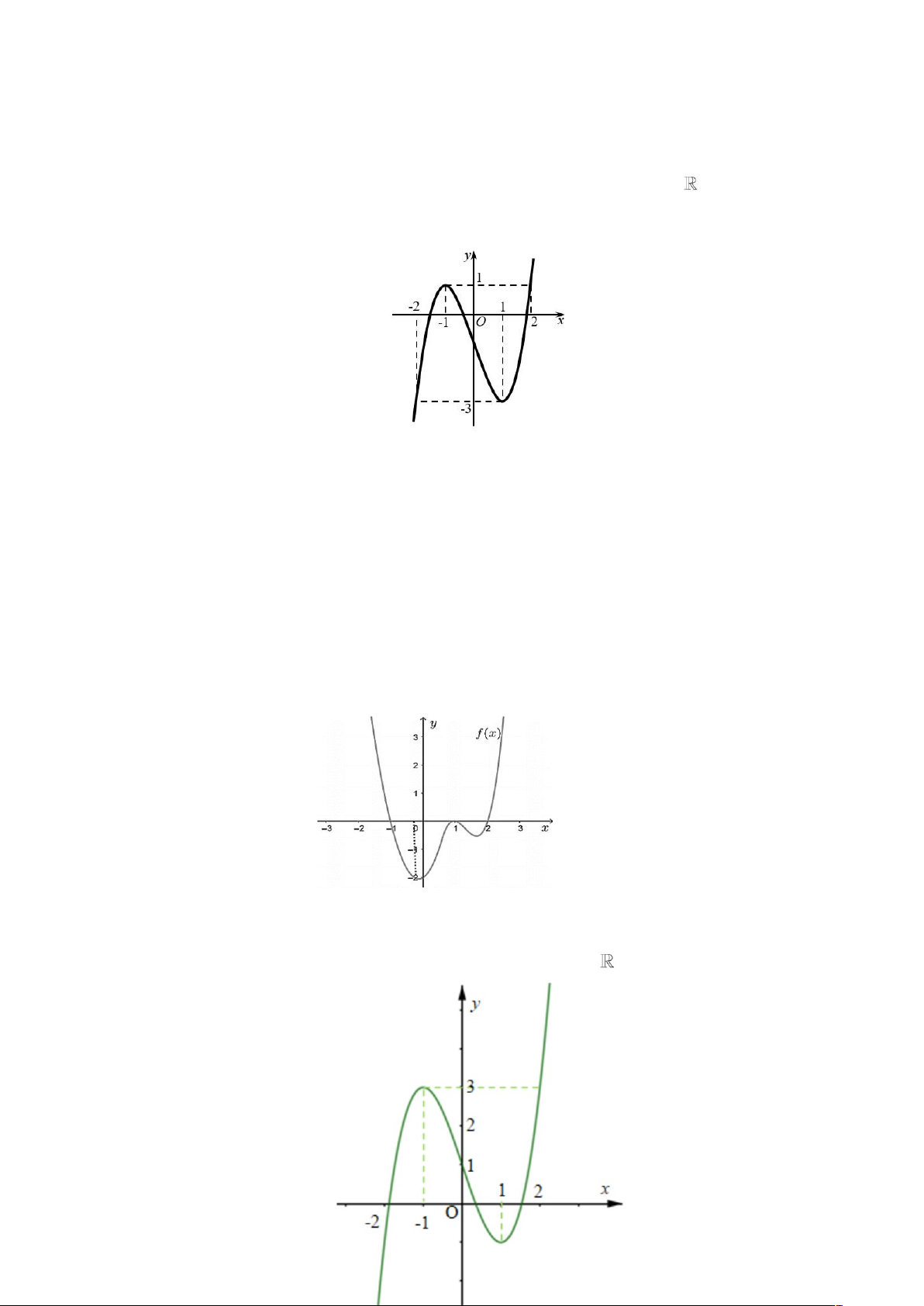
Ví dụ 5. (Chuyên Thái Bình - 2020) Cho y = f (x ) là hàm số đa thức
bậc 3 và có đồ thị như hình vẽ bên. Hỏi phương trình
f ( f (cos x) − 1) = 0 có bao nhiêu nghiệm thuộc đoạn 0; 3 ? A. 2 . B. 4. C. 5 . D. 6.
Ví dụ 6. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hàm số y = f (x ) liên tục trên có đồ thị hình vẽ.
Có bao nhiêu giá trị nguyên của tham số m để phương trình f ( 4 + 2 f cos x ) = m có nghiệm x 0; 2 A. 4. B. 5. C. 3. D. 2.
TÌM KHOẢNG BIẾN THIÊN, CỰC TRỊ, TƯƠNG GIAO
CỦA HÀM SỐ y = a. f n (x ) + b. f n−1 (x ) + ... + c
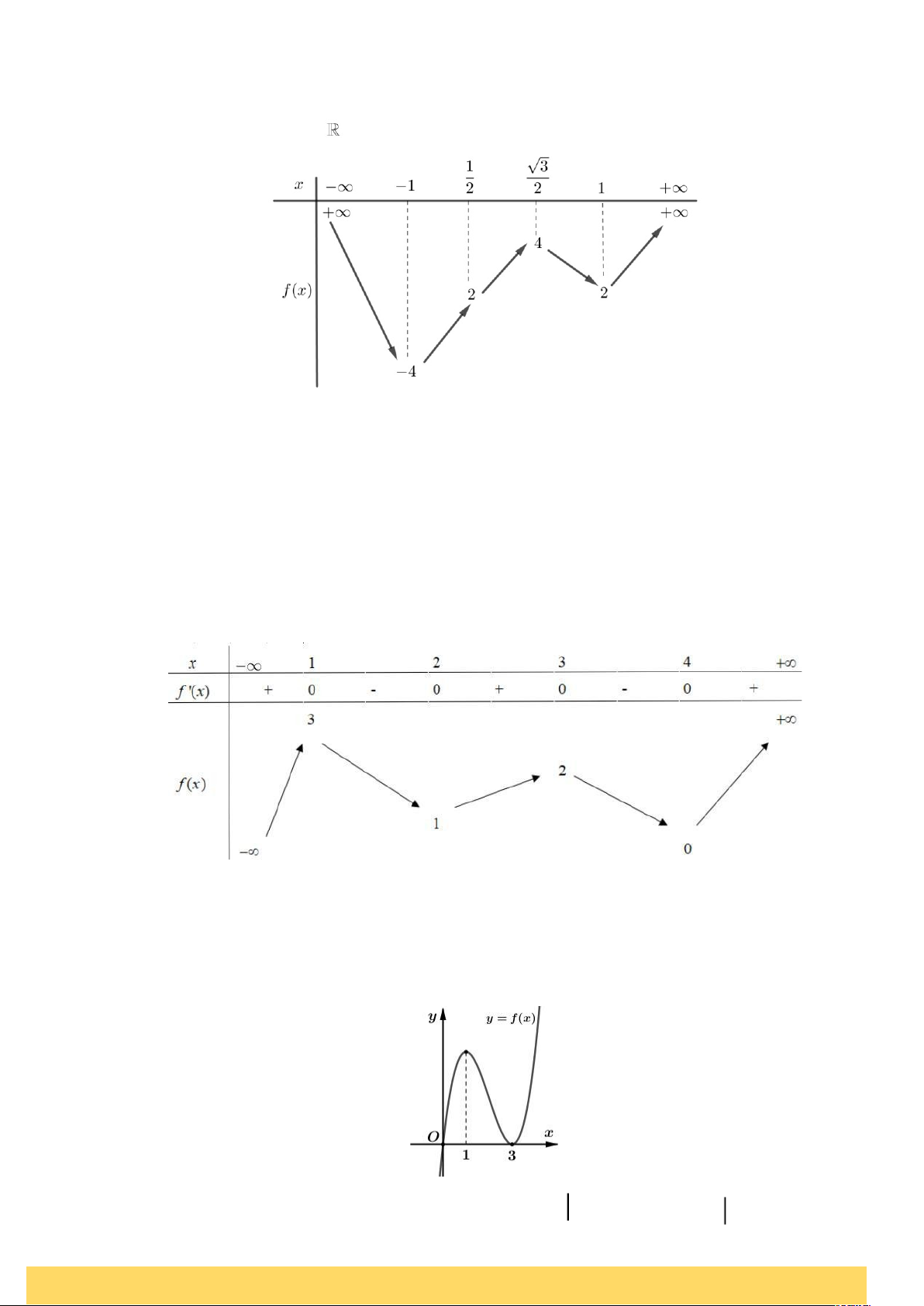
Câu 1. Cho hàm số f (x ) liên tục trên
và có bảng biến thiên như hình bên.
Số giá trị nguyên của tham số m để phương trình f 2 (cos x ) + ( 3 − m ) f (cos x ) + 2 m − 10 = 0 có đúng
4 nghiệm phân biệt thuộc đoạn − ;là 3 A. 5. B. 6. C. 7. D. 4.
“Nếu hôm nay chưa học được gì thì đừng nên đi ngủ”
Câu 2. Cho hàm số f (x ) có bảng biến thiên như sau:
Hàm số y = ( f (x ))3 − 3.( f (x))2 nghịch biến trên khoảng nào dưới đây? A. (1;2). B. (3;4). C. (− ; 1). D. (2; 3).
Câu 3. (THPT Thiệu Hóa – Thanh Hóa 2019) Cho hàm số y = f (x ) có đồ thị như hình vẽ bên dưới
Tìm tất cả các giá trị của tham số m để đồ thị hàm số h (x ) f 2 (x )+ 2 f (x )+ 2m có đúng 3 điểm = cực trị. A. m 1 B. m 1 C. m 2 D. m 2
Xét sự biến thiên, cực trị, tương giao của hàm lồng hàm
Câu 4: Cho hàm số y = f (x ), hàm số f (x ) = x 3 + ax 2 + bx + c (a , b , c ) có đồ thị như hình vẽ
“Nếu hôm nay chưa học được gì thì đừng nên đi ngủ”
Hàm số g (x ) = f ( f (x)) nghịch biến trên khoảng nào dưới đây? 3 3 A. (1;+ ). B. (− ; −2). C. (−1;0). D. − ; . 3 3
Câu 5: Cho hàm số y = f (x )= x − 2x . Số điểm cực trị của hàm số g ( x ) = f ( f (x ) −1 là 2 A. 8. ( ) B. 3 C. 4. D. 11. ( ( )) ( )
Câu 6: Cho hàm số y = f x
liên tục trêncó đồ thị như hình vẽ. Phương trình f 1− f x = 0 1 có tất
cả bao nhiêu nghiệm thực phân biệt? A. 5. B. 7. C. 4. D. 6.
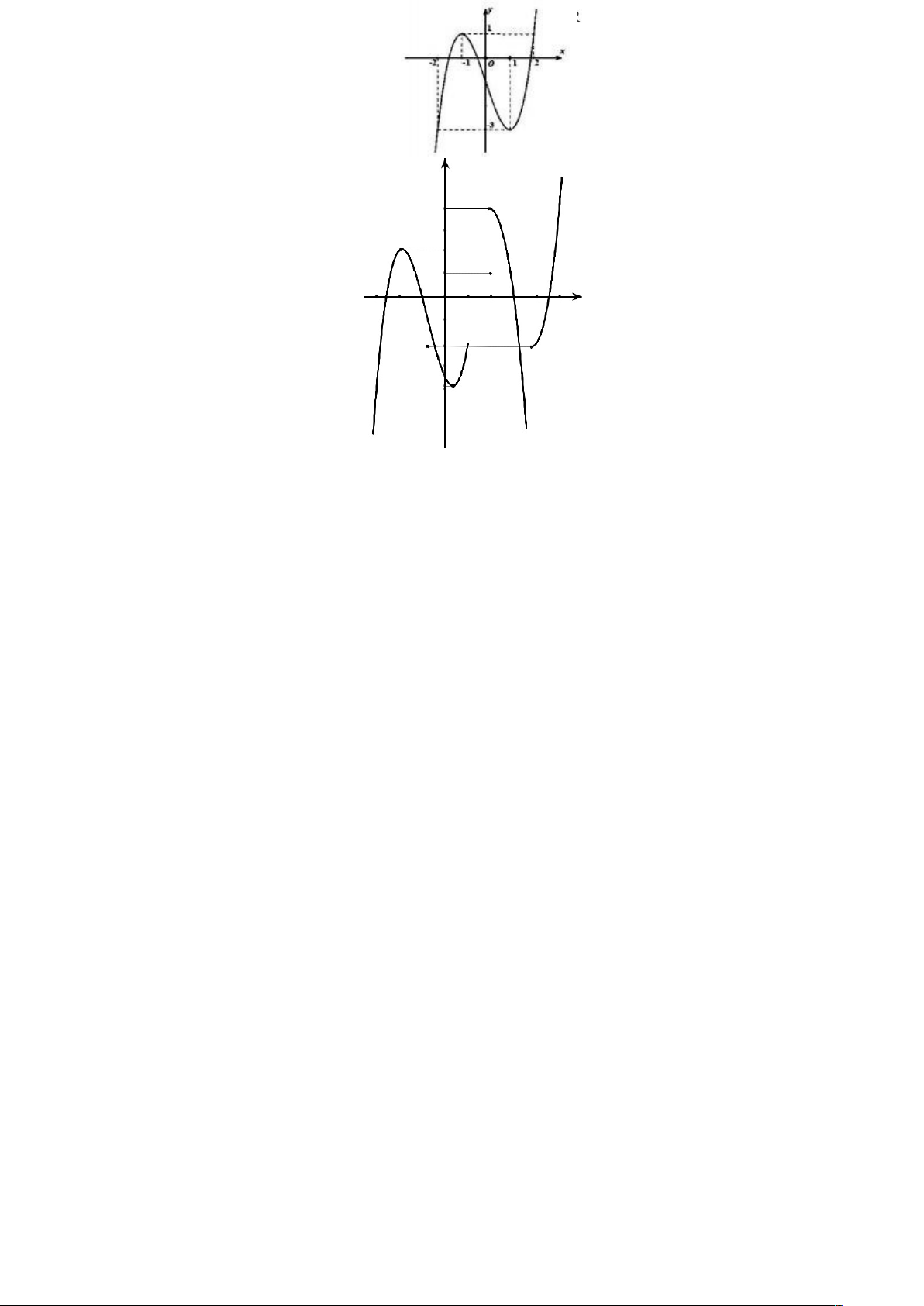
Câu 7: Cho hàm số y = f (x ) có đạo hàm trên
và có đồ thị là đường cong như hình vẽ. Đặt
g (x ) = 3 f ( f (x ))+ 4 . Số điểm cực trị của hàm số g (x ) là A. 2. B. 8. C. 10. D. 6.
Câu 8: (THPT Hoàng Hoa Thám - Hưng Yên 2019) Cho hàm số y = f ( x) có đạo hàm trên và có đồ thị là
đường cong như hình vẽ.
Đặt g (x ) = 3 f ( f (x)) + 4 . Tìm số cực trị của hàm số g ( x)
“Nếu hôm nay chưa học được gì thì đừng nên đi ngủ” A. 2. B. 8. C. 10. D. 6.
Câu 9: (Chuyên Lam Sơn 2019) Cho hàm số y = f (x )
liên tục trên và có đồ thị như hình vẽ bên. Phương
trình f f x − 1 = 0 có tất cả bao nhiêu nghiệm thực phân biệt? ( ( ) ) A. 6. B. 5. C. 7. D. 4.
Câu 10: (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Cho hai hàm số y = f (x ), y = g (x) có đồ thị như hình sau: y 4 y=f(x) 3 2 1 O 3 4 5 x -3 -2 -1 1 2 -1 -2 -3 -4 y=g(x)
Khi đó tổng số nghiệm của hai phương trình f (g (x )) = 0 và g ( f (x )) = 0 là A. 25. B. 22. C. 21. D. 26.
Câu 11: (Chuyên Lương Văn Chánh - Phú Yên - 2020) Cho hàm số
f (x ) có đồ thị như hình bên. Phương trình f f
cos x − 1 = 0 có bao nhiêu nghiệm thuộc đoạn 0; 2 ? ( )
“Nếu hôm nay chưa học được gì thì đừng nên đi ngủ” A. 2. B. 5. C. 4. D. 6.
Câu 12: (Bỉm Sơn - Thanh Hóa - 2020) Cho hàm số)
trong hình vẽ bên dưới. Đặt g (x ) = f f (x A. 8. B. 2. C. 4. D. 6.
Câu 13: (Lý Nhân Tông - Bắc Ninh - 2020) Cho hàm số y = f (x ) liên tục trên và có đồ thị như hình vẽ.
Phương trình f ( f (x ) − 1) = 0 có tất cả bao nhiêu nghiệm thực phân biệt? A. 6. B. 5. C. 7. D. 4.
“Nếu hôm nay chưa học được gì thì đừng nên đi ngủ”
Câu 14: (THPT Nguyễn Viết Xuân - 2020) Cho hàm số f (x ) có đồ thị như hình vẽ.
Đặt g (x ) = f ( f (x) −1).
Số nghiệm của phương trình g (x ) = 0 là A. 6. B. 10. C. 9. D. 8.
Câu 15: (Tiên Du - Bắc Ninh - 2020) Cho hàm số y = f ( x) liên tục trên và có đồ thị như hình vẽ bên
Số nghiệm thuộc đoạn 0; 7
của phương trình f ( f (cos x)) = 0 là 2 A. 7. B. 5. C. 8. D. 6.
“Nếu hôm nay chưa học được gì thì đừng nên đi ngủ”