





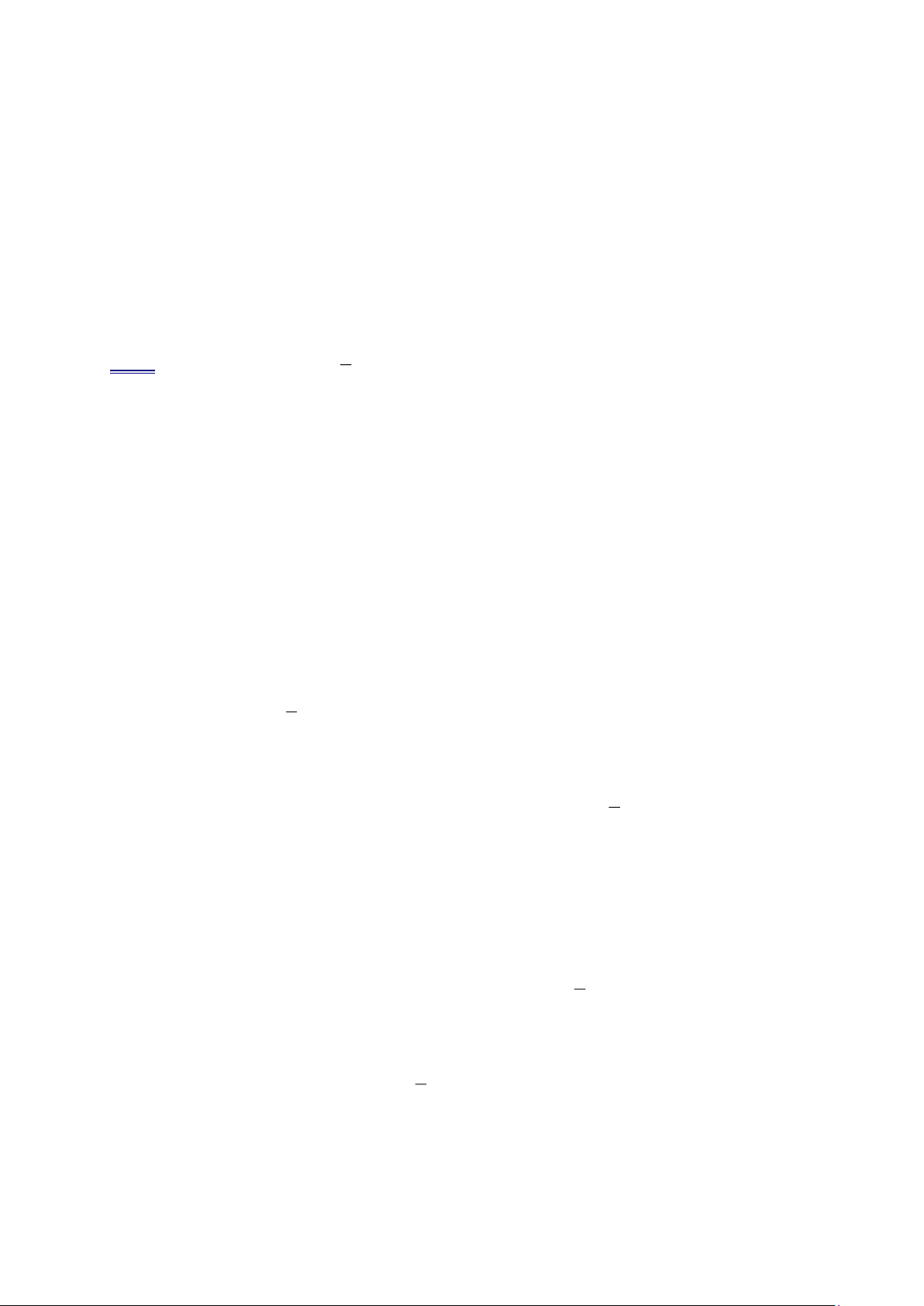
Preview text:
Bài 2. ĐỒ THỊ CỦA HÀM SỐ 2
y = ax (a 0)
A. KIẾN THỨC TRỌNG TÂM
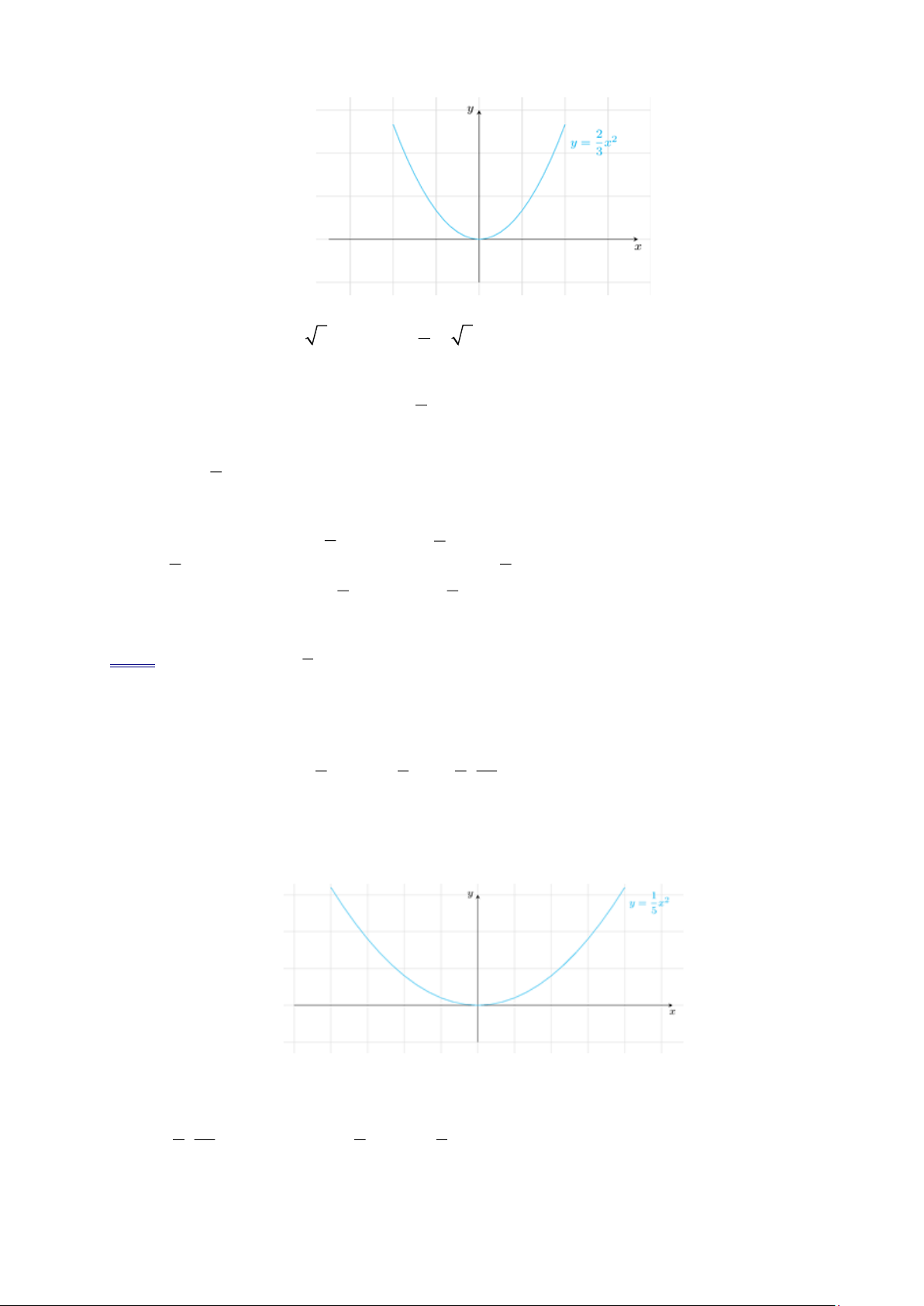
Đồ thị của hàm số 2
y = ax (a 0) là một parabol đi qua gốc tọa độ O , nhận Oy làm trục đối xứng
( O là đỉnh của parabol).
▪ Nếu a 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
▪ Nếu a 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Vẽ đồ thị hàm số
▪ Bước 1: Lập bảng các giá trị đặc biệt tương ứng giữa x và y của hàm số 2
y = ax (a ¹ 0) .
▪ Bước 2: Biểu diễn các điểm đặc biệt trên mặt phẳng tọa độ và vẽ đồ thị Parabol của hàm
số đi qua các điểm đó.
Ví dụ 1. Cho hàm số 2
y = f (x) = (m − 2)x ( m là tham số). Tìm m để: 1 3
a) Đồ thị hàm số đi qua điểm A ; . ĐS: m = 8 . 2 2 5 x + 2y = 5
b) Đồ thị hàm số đi qua điểm (x ; y ) với (x ; y ) là nghiệm của hệ phương trình . 0 0 0 0 3 x + y = 2 ĐS: m = 7 .
c) Vẽ đồ thị hàm số với các giá trị m tìm được trên cùng một mặt phẳng tọa độ.
Ví dụ 2. Cho hàm số 2
y = f (x) = (m +1)x ( m là tham số). Tìm m để: 5
a) Đồ thị hàm số đi qua điểm B (2;−6). ĐS: m = − . 2 x + 3y = 5
b) Đồ thị hàm số đi qua điểm (x ; y ) với (x ; y ) là nghiệm của hệ phương trình . 0 0 0 0 x + 2y = 3 ĐS: m = 1.
c) Vẽ đồ thị hàm số với các giá trị m tìm được trên cùng một mặt phẳng tọa độ. a
Ví dụ 3. Cho hàm số 2 y =
x (a 0) có đồ thị là parabol (P) . 2
a) Xác định a để (P) đi qua điểm ( A − 3;6) . ĐS: a = 4 .
b) Với giá trị a vừa tìm được ở trên, hãy:
i) Vẽ (P) trên mặt phẳng tọa độ. Trang 1
ii) Tìm các điểm trên (P) có hoành độ bằng 3 . 1 1 1 1
iii) Tìm các điểm trên (P) cách đều hai trục tọa độ. ĐS: B(3;18) ; ; ; − ; . 2 2 2 2
Ví dụ 4. Cho hàm số 2 2
y = (m − 2)x (m 2) có đồ thị là parabol (P) .
a) Xác định m để (P) đi qua điểm ( A − 2; 4) . ĐS: m = 2 .
b) Với giá trị m vừa tìm được ở trên, hãy:
i) Vẽ (P) trên mặt phẳng tọa độ.
ii) Tìm các điểm trên (P) có hoành độ bằng 3 . 1 1 1 1
iii) Tìm các điểm trên (P) cách đều hai trục tọa độ. ĐS: B(3;18) ; ; ; − ; . 2 2 2 2 1
Ví dụ 5. Cho hàm số 2
y = x có đồ thị là parabol (P) . 8
a) Vẽ (P) trên mặt phẳng tọa độ. 3 1
b) Trong các điểm A 2; ; B 2; −
; C(0;−2) , điểm nào thuộc P , điểm nào không thuộc (P) ? 8 2
Ví dụ 6. Cho hàm số 2
y = −7x có đồ thị là parabol (P) .
a) Vẽ (P) trên mặt phẳng tọa độ. b) Trong các điểm ( A 2; 28
− ) ; B(−1;7) ; C(0;−2) , điểm nào thuộc P , điểm nào không thuộc (P) ?
Dạng 2: Tọa độ giao điểm của Parabol và đường thẳng ▪ Cho Parabol 2
(P ) : y = ax (a ¹ 0) và đường thẳng d : y = mx + n . Để tìm tọa độ giao
điểm (nếu có) của (P) và d, ta làm như sau
▪ Bước 1: Xét phương trình hoành độ giao điểm của (P) và d: 2
ax = mx + n . (*)
▪ Bước 2: Giải phương trình (*) ta tìm được nghiệm (nếu có). Từ đó ta tìm được tọa độ giao điểm của (P) và d.
Chú ý: Số nghiệm của phương trình (*) đúng bằng số giao điểm của (P) và d, cụ thể
▪ Nếu (*) vô nghiệm thì d không cắt (P).
▪ Nếu (*) có nghiệm kép thì d tiếp xúc với (P).
▪ Nếu (*) có hai nghiệm phân biệt thì d cắt (P) tại hai điểm phân biệt.
Ví dụ 7. Cho parabol 2
(P) : y = 2x và đường thẳng d : y = −x + 3 .
a) Vẽ (P) và d trên cùng một mặt phẳng tọa độ. Trang 2 3 9
b) Xác định tọa độ giao điểm của (P) và d . ĐS: ( A 1;2); B − ; . 2 2 x 1
c) Dựa vào đồ thị, hãy giải bất phương trình 2
2x −x + 3 . ĐS: 3 . x − 2
Ví dụ 8. Cho parabol 2 (P) : y = 3
− x và đường thẳng d : y = 6x + 3 .
a) Vẽ (P) và d trên cùng một mặt phẳng tọa độ.
b) Xác định tọa độ giao điểm của (P) và d . ĐS: (−1; −3) .
c) Dựa vào đồ thị, hãy giải bất phương trình 2
3x + 6x + 3 0 .
ĐS: x −1.
Ví dụ 9. Cho hàm số 2
y = x có đồ thị là parabol (P) .
a) Vẽ (P) trên mặt phẳng tọa độ.
b) Dựa vào đồ thị, hãy biện luận số nghiệm của phương trình 2
x − m − 2 = 0 theo m .
Ví dụ 10. Cho hàm số 2
y = −2x có đồ thị là parabol (P) .
a) Vẽ (P) trên mặt phẳng tọa độ.
b) Dựa vào đồ thị, hãy biện luận số nghiệm của phương trình 2 2
− x + 2m −1 = 0 theo m . 1
Ví dụ 11. Cho parabol 2
(P) : y = x và đường thẳng d có phương trình y = x + m . Tìm m để: 4
a) d và (P) có điểm chung duy nhất. ĐS: m = 1.
b) d và (P) cắt nhau tại hai điểm phân biệt. ĐS: m 1.
c) d và (P) không có điểm chung. ĐS: m 1.
Ví dụ 12. Cho parabol 2
(P) : y = 2x và đường thẳng d có phương trình y = 3x + m . Tìm m để: 9
a) d và (P) có điểm chung duy nhất. ĐS: m = − . 16 9
b) d và (P) cắt nhau tại hai điểm phân biệt. ĐS: m − . 16 9
c) d và (P) không có điểm chung. ĐS: m − . 16 C. BÀI TẬP VẬN DỤNG Bài 1. Cho hàm số 2 2
y = f (x) = (m −1)x ( m là tham số). Tìm m để: Trang 3 1
a) Đồ thị hàm số đi qua điểm A ; 2 . ĐS: m = 3 . 2 3 x + 2y = 3
b) Đồ thị hàm số đi qua điểm (x ; y ) với (x ; y ) là nghiệm của hệ phương trình . 0 0 0 0 2x + y =1 ĐS: m = 2 .
c) Vẽ đồ thị hàm số với các giá trị m tìm được trên cùng một mặt phẳng tọa độ. a Bài 2. Cho hàm số 2
y = x (a 0) có đồ thị là parabol (P) . 3
a) Xác định a để (P) đi qua điểm ( A − 5;5) . ĐS: a = 2 .
b) Với giá trị vừa tìm được ở trên, hãy:
i) Vẽ (P) trên mặt phẳng tọa độ.
ii) Tìm các điểm trên (P) có hoành độ bằng 4 . 3 3 3 3
iii) Tìm các điểm trên (P) cách đều hai trục tọa độ. ĐS: B(4; 24) ; ; ; − ; . 2 2 2 2 1 Bài 3. Cho hàm số 2
y = x có đồ thị là parabol (P) . 5
a) Vẽ (P) trên mặt phẳng tọa độ. 2 6 3 9
b) Trong các điểm A 1; ; B 2; − ; C ;
, điểm nào thuộc (P) , điểm nào không thuộc 5 5 2 20 (P) ? 1 Bài 4. Cho parabol 2
(P) : y = − x và đường thẳng d : y = 2x + 2 . 2
a) Vẽ (P) và d trên cùng một mặt phẳng tọa độ.
b) Xác định tọa độ giao điểm của (P) và d . ĐS: (−2; −2) . Bài 5. Cho hàm số 2
y = 3x có đồ thị là parabol (P) .
a) Vẽ (P) lên mặt phẳng tọa độ.
b) Dựa vào đồ thị, hãy biện luận số nghiệm của phương trình 2
3x − m − 2 = 0 theo m . 1 Bài 6. Cho parabol 2
(P) : y = x và đường thẳng d có phương trình y = −x + m . Tìm m để: 2 1
a) d và (P) có điểm chung duy nhất. ĐS: m = − . 2 Trang 4 1
b) d và (P) cắt nhau tại hai điểm phân biệt.
ĐS: m − . 2 1
c) d và (P) không có điểm chung.
ĐS: m − . 2 Trang 5 HƯỚNG DẪN GIẢI
Ví dụ 1. Cho hàm số 2
y = f (x) = (m − 2)x ( m là tham số). Tìm m để: 1 3
a). Đồ thị hàm số đi qua điểm A ; . 2 2 5 x + 2y = 5
b). Đồ thị hàm số đi qua điểm (x ; y ) với (x ; y ) là nghiệm của hệ phương trình . 0 0 0 0 3 x + y = 2
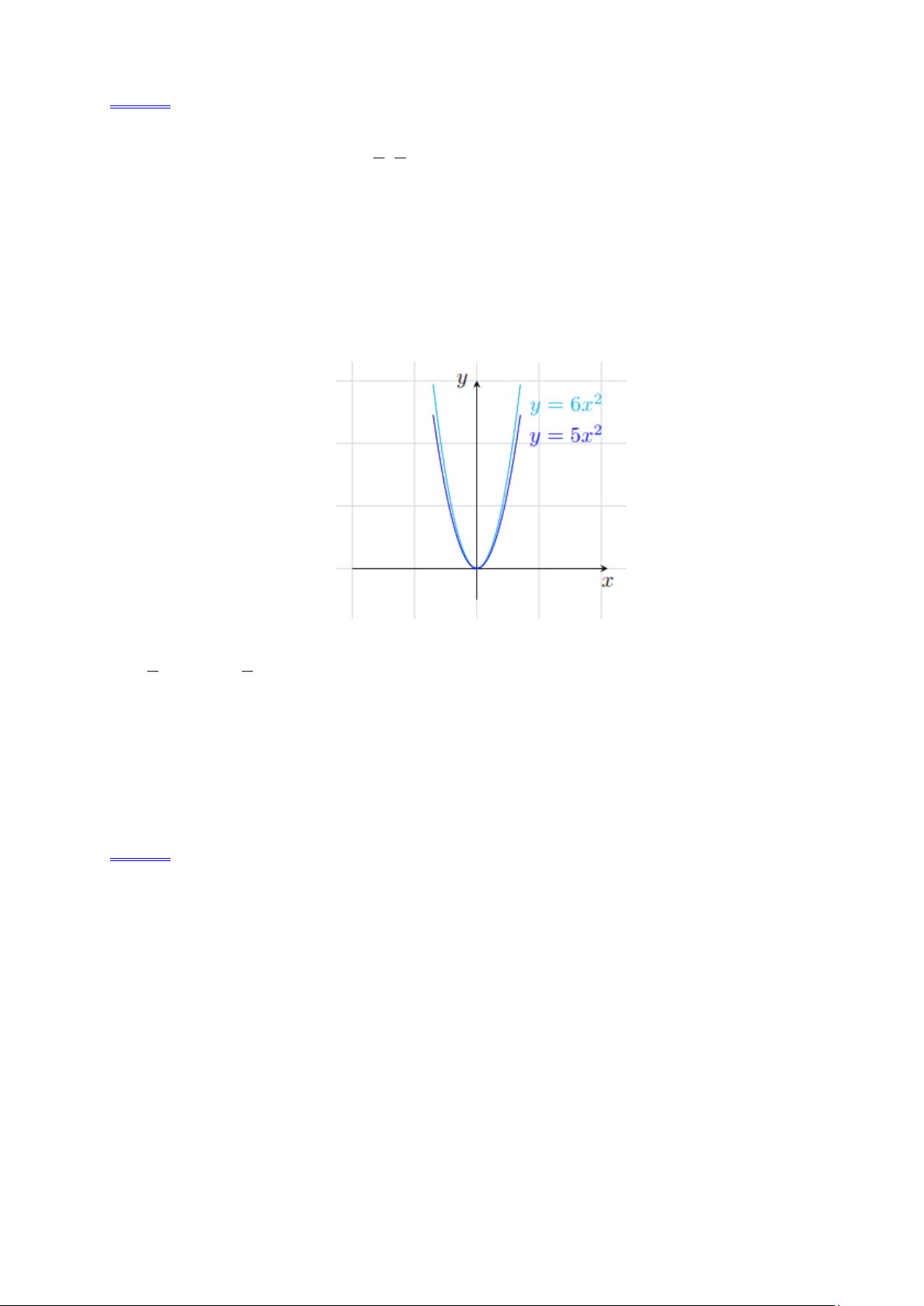
c). Vẽ đồ thị hàm số với các giá trị m tìm được trên cùng một mặt phẳng tọa độ. Lời giải. 2 3 1 a). = (m − 2)
m − 2 = 6 m = 8 . 2 2 5 x + 2y = 5 x = 1 − b). 2 5 = (m − 2)( 1 − ) m = 7 . 3 x + y = 2 y = 5
c). Với m = 8 và m = 7 thì 2
y = f (x) = 6x và 2
y = g(x) = 5x .
Ví dụ 2. Cho hàm số 2
y = f (x) = (m +1)x ( m là tham số). Tìm m để:
a). Đồ thị hàm số đi qua điểm B (2;−6). x + 3y = 5
b). Đồ thị hàm số đi qua điểm (x ; y ) với (x ; y ) là nghiệm của hệ phương trình . 0 0 0 0 x + 2y = 3
c). Vẽ đồ thị hàm số với các giá trị m tìm được trên cùng một mặt phẳng tọa độ. Lời giải. Trang 6 a). 2 3 5 6
− = (m +1)2 m +1 = − m = − . 2 2 x + 3y = 5 x = 1 − b). 2 2 = (m +1)( 1 − ) m =1. x + 2y = 3 y = 2 5 3
c). Với m − và m = 1 thì 2
y = f (x) = − x và 2
y = g(x) = 2x . 2 2 a
Ví dụ 3. Cho hàm số 2 y =
x (a 0) có đồ thị là parabol (P) . 2
a). Xác định a để (P) đi qua điểm ( A − 3;6) .
b). Với giá trị a vừa tìm được ở trên, hãy:
i) Vẽ (P) trên mặt phẳng tọa độ.
ii) Tìm các điểm trên (P) có hoành độ bằng 3 .
iii) Tìm các điểm trên (P) cách đều hai trục tọa độ. Lời giải. Trang 7 a
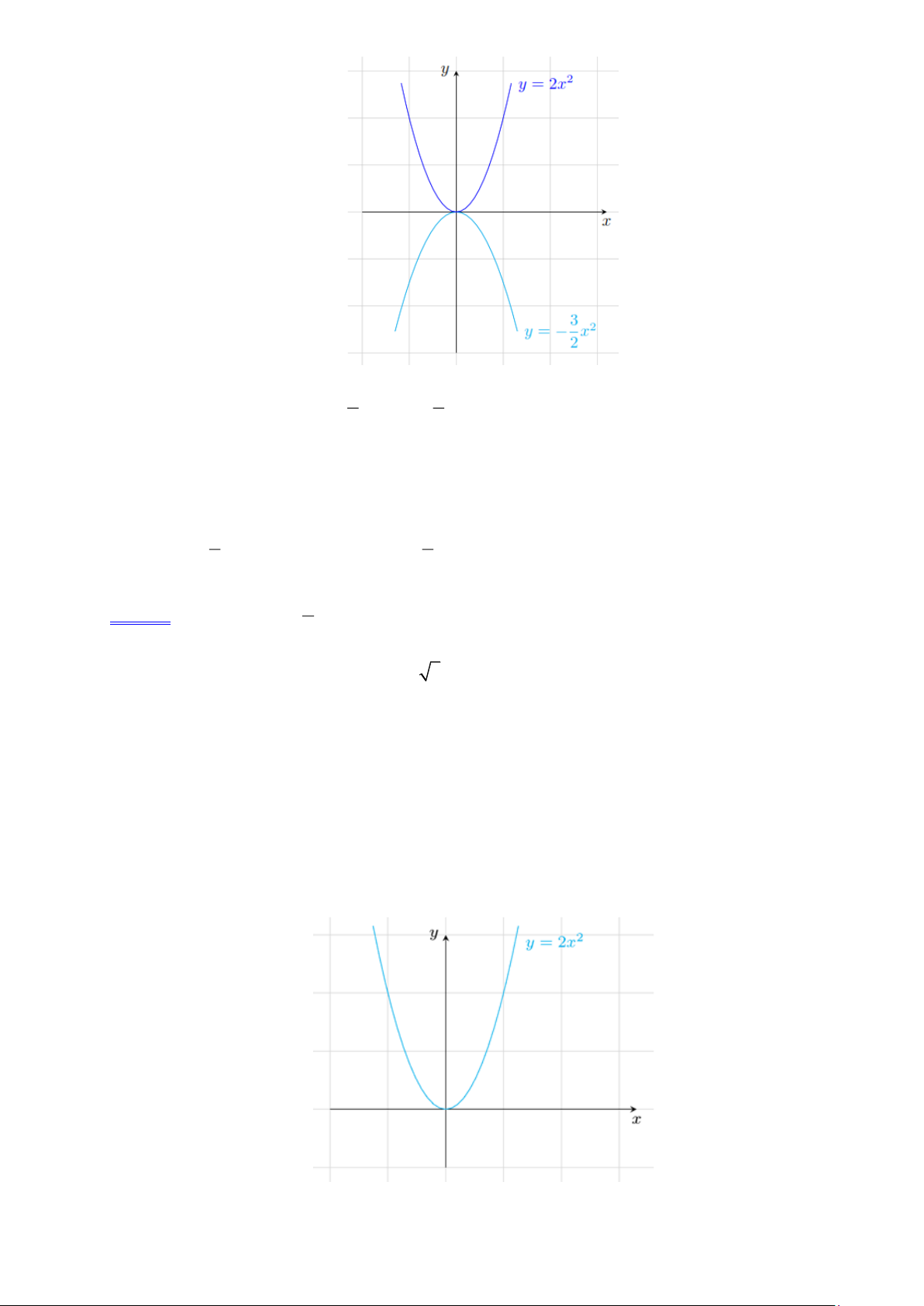
a). (P) đi qua điểm ( A 3;6) nên = (− )2 6 3 a = 4 . 2
b). i) Với a = 4 ta có hàm số 2 y = 2x . ii) Ta có 2
y = 2 3 = 18 suyra B(3;18) . 1 2 = = 2 x x x 1 iii) 2 y = 2x ; 2 | x | | = y | ; y = . 2 x = 2 − x 1 2 x = − 2
Ví dụ 4. Cho hàm số 2 2
y = (m − 2)x (m 2) có đồ thị là parabol (P) .
a). Xác định m để (P) đi qua điểm ( A − 2; 4) .
b). Với giá trị m vừa tìm được ở trên, hãy:
i) Vẽ (P) trên mặt phẳng tọa độ.
ii) Tìm các điểm trên (P) có hoành độ bằng 3 .
iii) Tìm các điểm trên (P) cách đều hai trục tọa độ. Lời giải.
a). (P) đi qua điểm ( A − 2; 4) nên 2 2
4 = (m − 2)(− 2) m = 2 .
b). i) Với m = 2 ta có hàm số 2 y = 2x . ii) Ta có 2
y = 2 3 = 18 suyra B(3;18) . 1 2 = = 2 x x x 1 iii) 2 y = 2x ; 2 | x | | = y | ; y = . 2 x = 2 − x 1 2 x = − 2 Trang 8 1
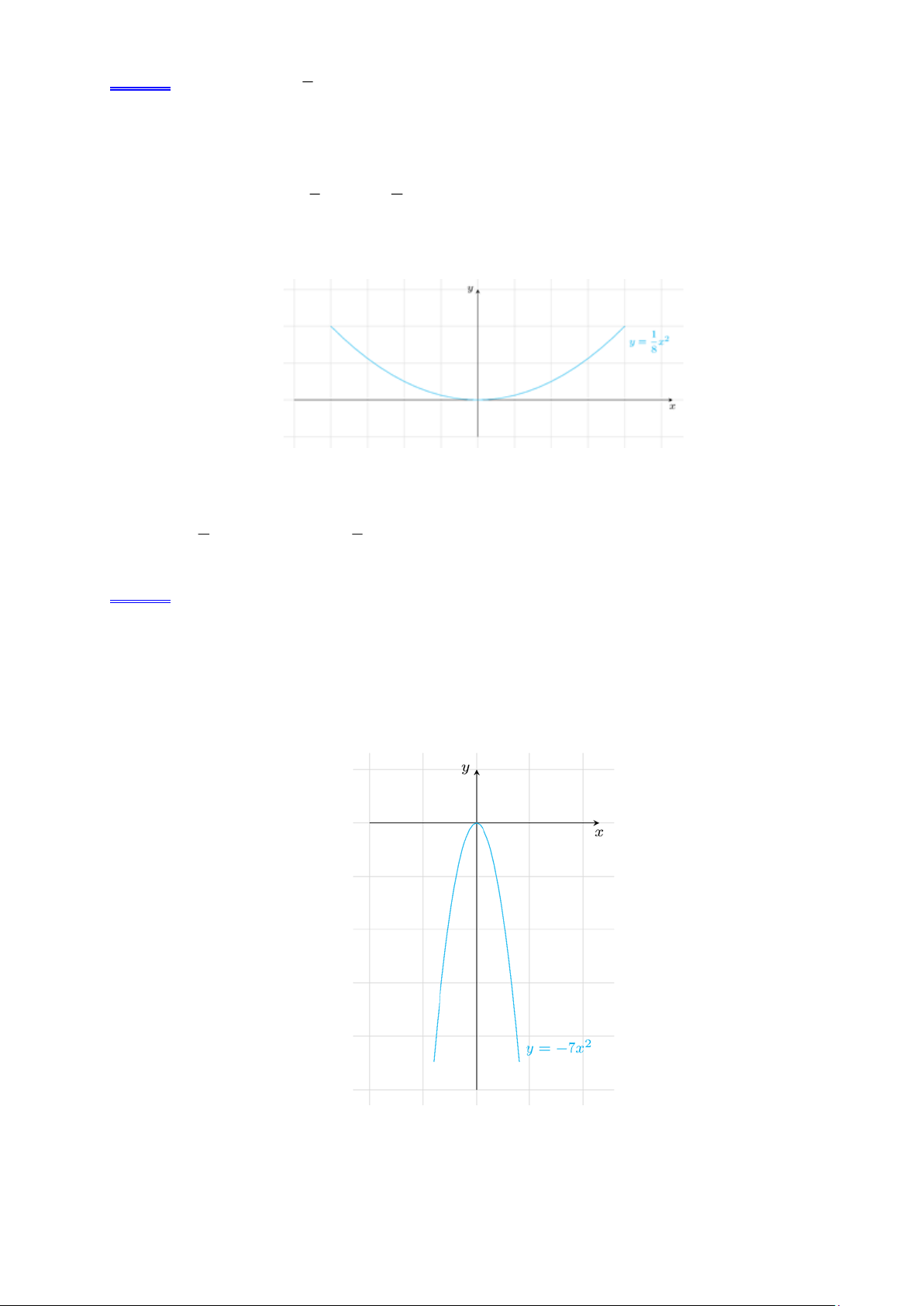
Ví dụ 5. Cho hàm số 2
y = x có đồ thị là parabol (P) . 8
a). Vẽ (P) trên mặt phẳng tọa độ. 3 1
b). Trong các điểm A 2; ; B 2; −
; C(0;−2) , điểm nào thuộc P , điểm nào không thuộc (P) ? 8 2 Lời giải. a). 1 3 b). B 2; −
thuộc (P) , A 2;
; C(0;−2) không thuộc (P) . 2 8
Ví dụ 6. Cho hàm số 2
y = −7x có đồ thị là parabol (P) .
a). Vẽ (P) trên mặt phẳng tọa độ.
b). Trong các điểm ( A 2; 28
− ) ; B(−1;7) ; C(0;−2) , điểm nào thuộc P , điểm nào không thuộc (P) ? Lời giải. a). b). ( A 2; 28
− ) thuộc (P) , B(−1;7) ; C(0;−2) không thuộc (P) . Trang 9
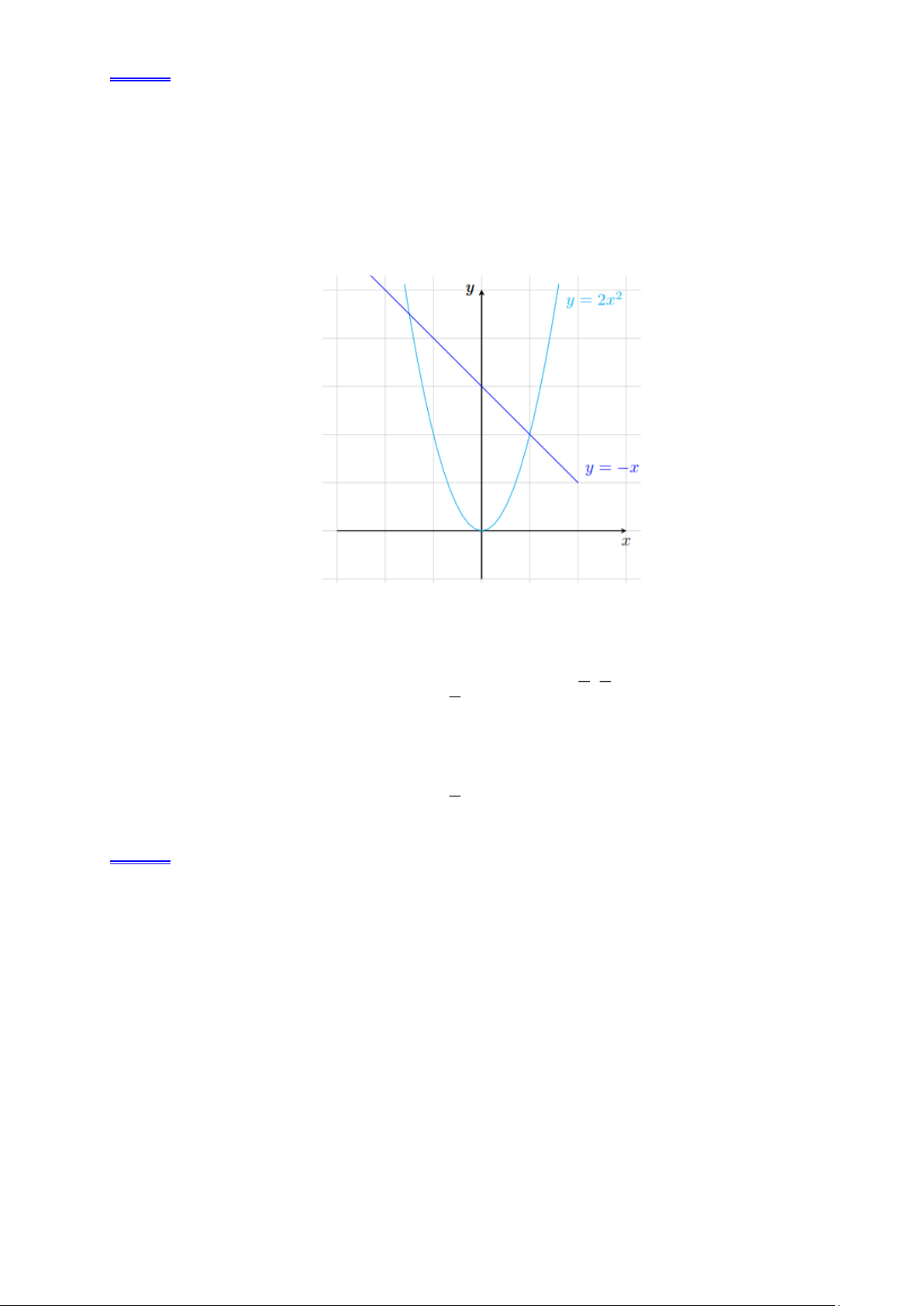
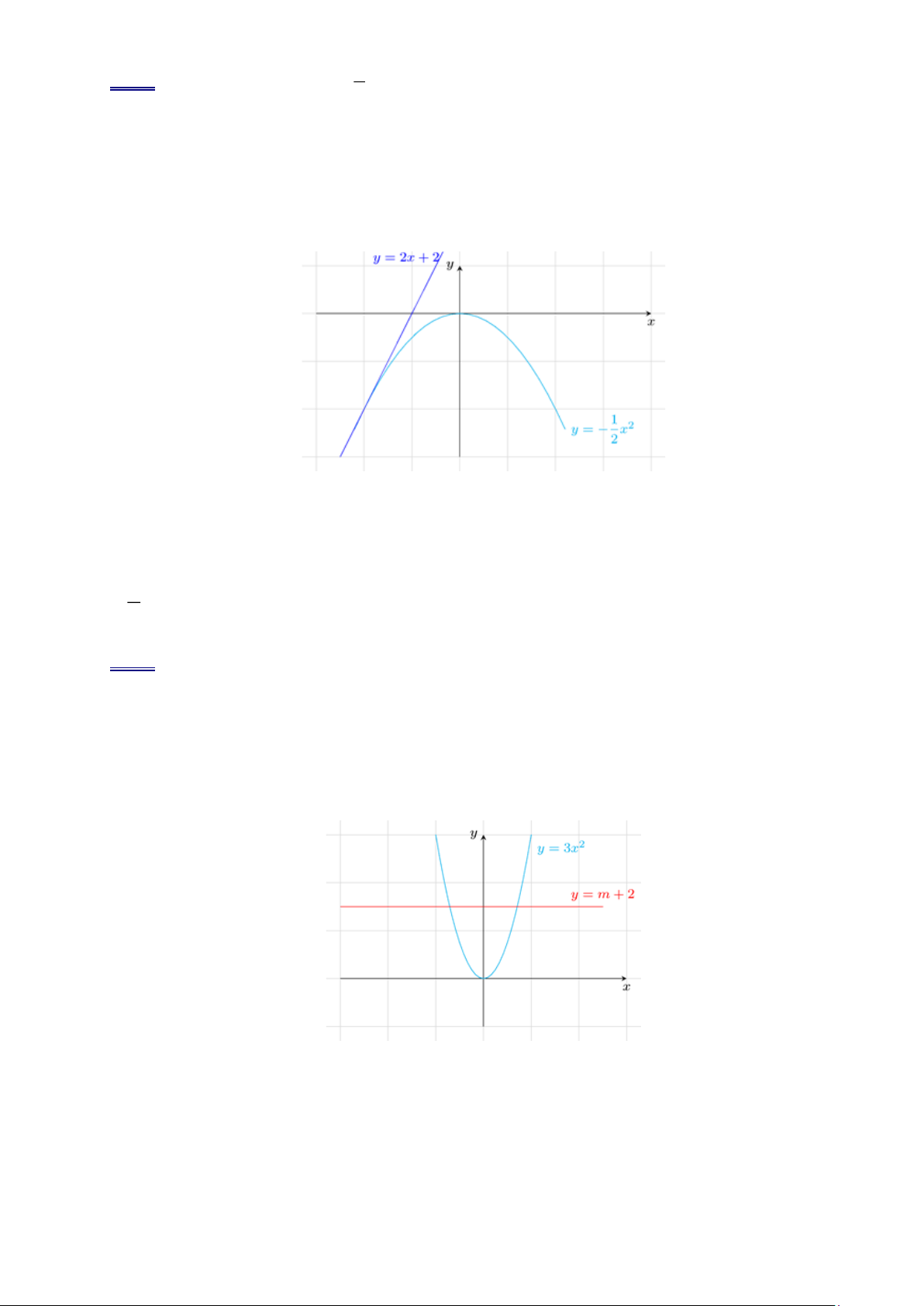
Ví dụ 7. Cho parabol 2
(P) : y = 2x và đường thẳng d : y = −x + 3 .
a). Vẽ (P) và d trên cùng một mặt phẳng tọa độ.
b). Xác định tọa độ giao điểm của (P) và d .
c). Dựa vào đồ thị, hãy giải bất phương trình 2
2x −x + 3 . Lời giải. a). x =1 3 9 b). 2 2 2x x 3 2x x 3 0 = − + + − = 3 ( A 1; 2); B − ; . x = − 2 2 2 x 1 c). 2 2
2x −x + 3 2x + x + 3 0 3 . x − 2
Ví dụ 8. Cho parabol 2 (P) : y = 3
− x và đường thẳng d : y = 6x + 3 .
a). Vẽ (P) và d trên cùng một mặt phẳng tọa độ.
b). Xác định tọa độ giao điểm của (P) và d .
c). Dựa vào đồ thị, hãy giải bất phương trình 2
3x + 6x + 3 0 . Lời giải. Trang 10 a). b). 2 2 3
− x = 6x + 3 3x + 6x + 3 = 0 x = 1 − y = −3 . c). 2 2
3x + 6x + 3 0 3(x +1) 0 x 1 − .
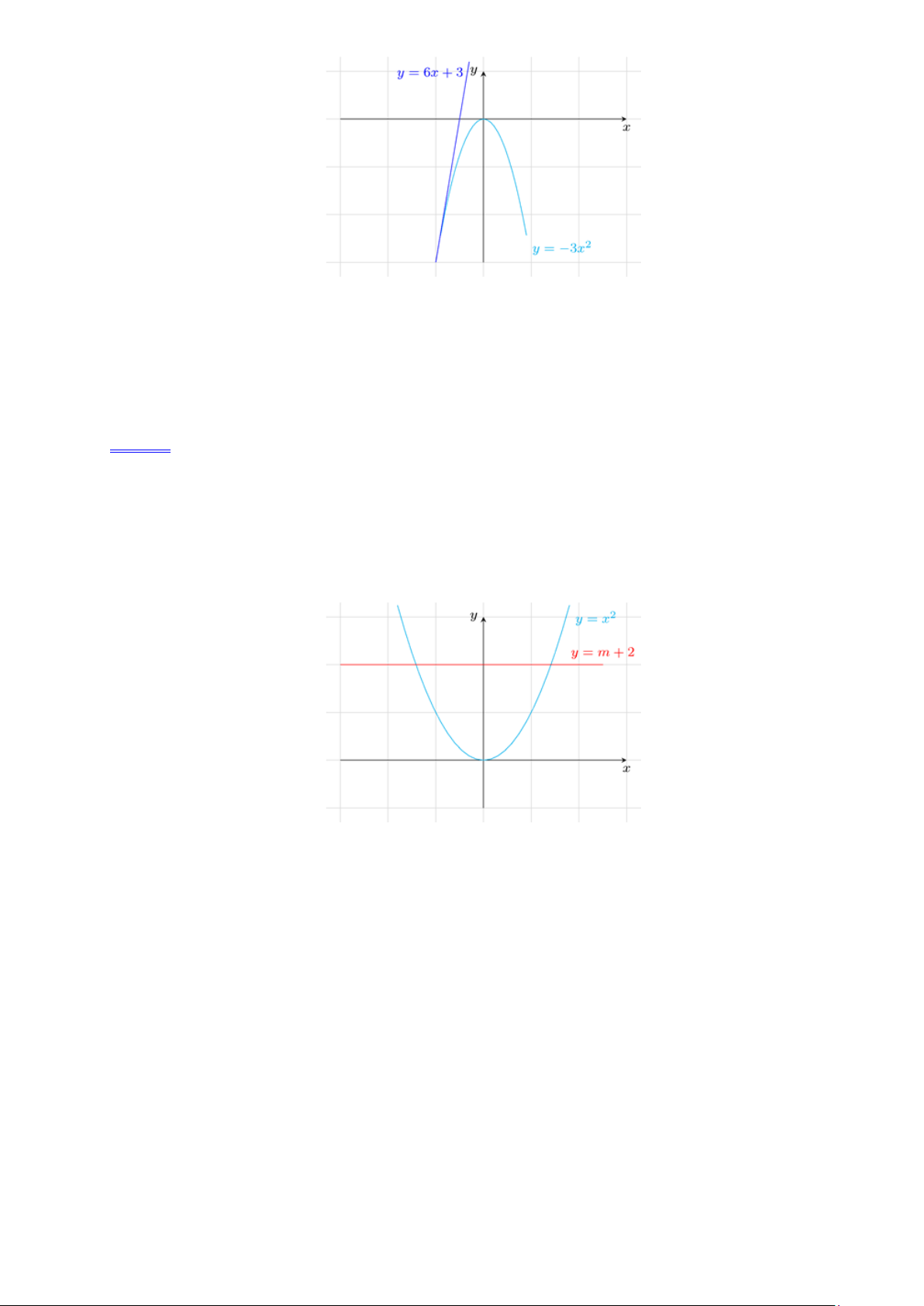
Ví dụ 9. Cho hàm số 2
y = x có đồ thị là parabol (P) .
a). Vẽ (P) trên mặt phẳng tọa độ.
b). Dựa vào đồ thị, hãy biện luận số nghiệm của phương trình 2
x − m − 2 = 0 theo m . Lời giải. a).
b). Xét đường thẳng d có phương trình y = m + 2 . Số nghiệm của phương trình 2
x − m − 2 = 0 (1)
là số giao điểm của đường thẳng d và (P) . Từ đồ thị ta thấy:
+ Với m + 2 0 hay m −2 , d không cắt (P) . Do đó phương trình (1) vô nghiệm.
+ Với m + 2 = 0 hay m = −2 , d tiếp xúc (P) . Do đó phương trình (1) có nghiệm kép.
+ Với m + 2 0 hay m −2 , d cắt (P) tại hai điểm phân biệt. Do đó phương trình (1) có hai nghiệm phân biệt. Vậy:
+ Với m −2 phương trình 2
x − m − 2 = 0 vô nghiệm. Trang 11
+ Với m = −2 phương trình 2
x − m − 2 = 0 có nghiệm kép.
+ Với m −2 phương trình 2
x − m − 2 = 0 có hai nghiệm phân biệt.
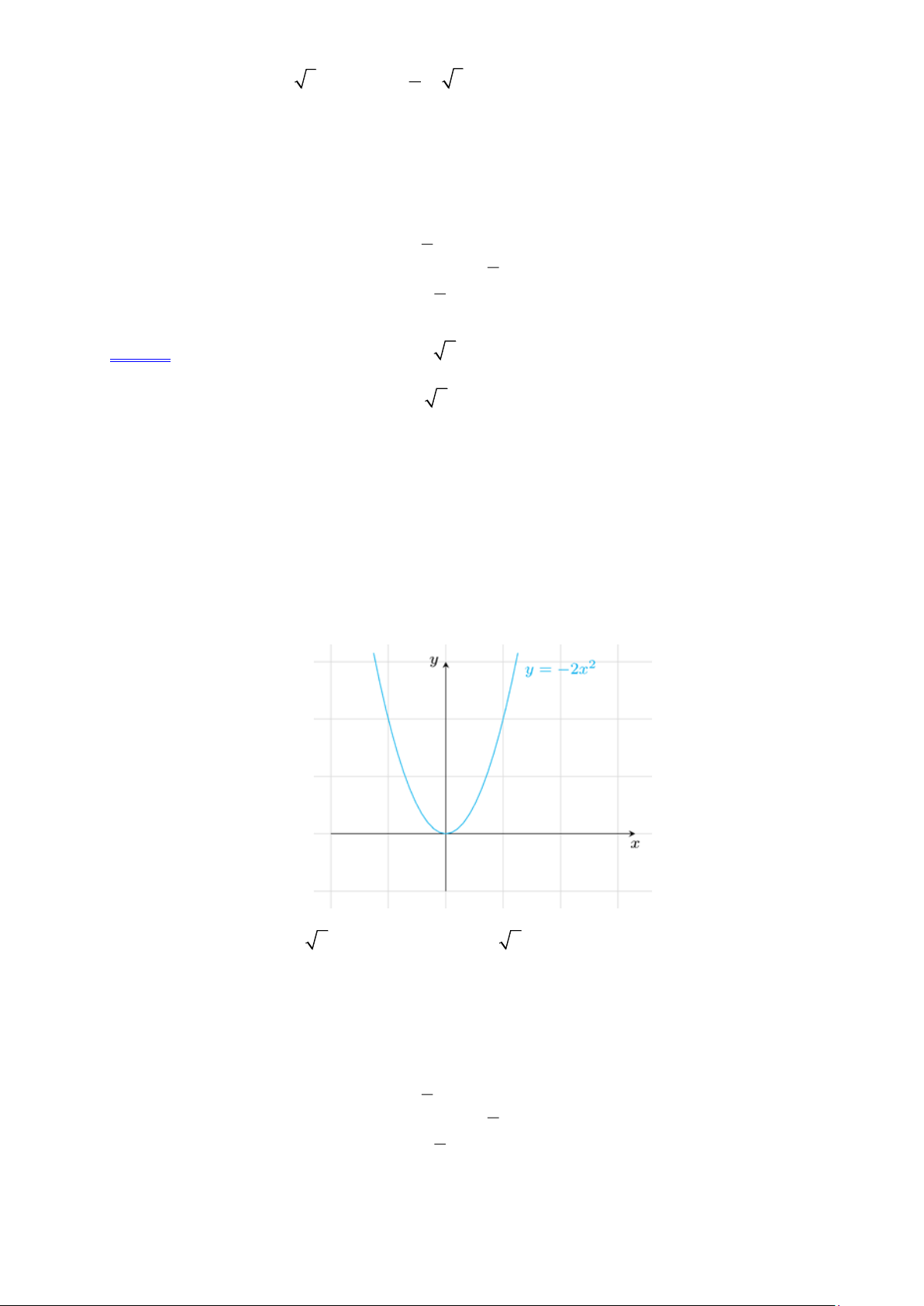
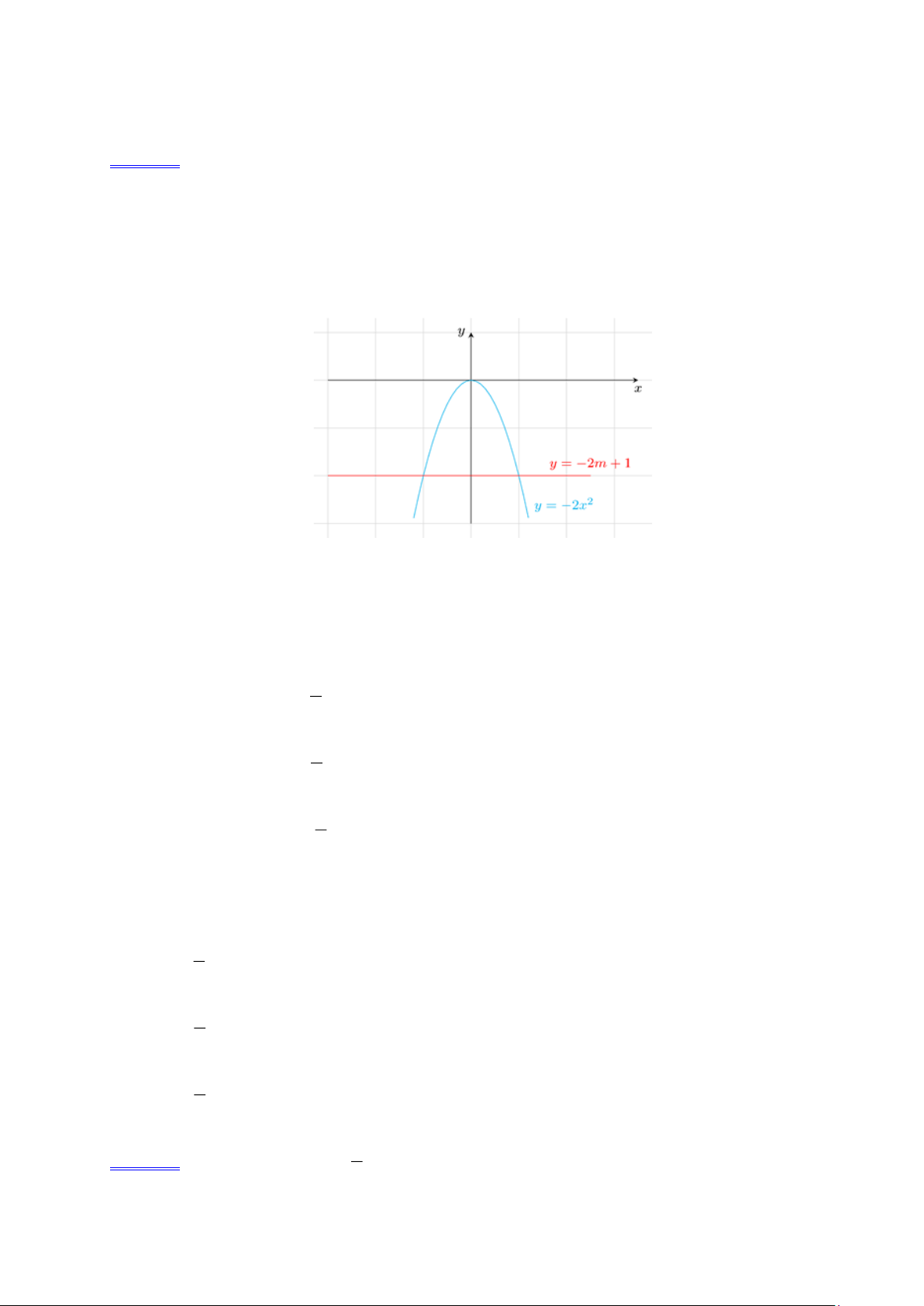
Ví dụ 10. Cho hàm số 2
y = −2x có đồ thị là parabol (P) .
a). Vẽ (P) trên mặt phẳng tọa độ.
b). Dựa vào đồ thị, hãy biện luận số nghiệm của phương trình 2 2
− x + 2m −1 = 0 theo m . Lời giải. a).
b). Xét đường thẳng d có phương trình y = −2m +1 . Số nghiệm của phương trình 2 2
− x + 2m −1 = 0 (1) là số giao điểm của đường thẳng d và (P) . Từ đồ thị ta thấy: 1
+ Với −2m +1 0 hay m , d không cắt (P) . Do đó phương trình (1) vô nghiệm. 2 1
+ Với −2m +1 = 0 hay m =
, d tiếp xúc (P) . Do đó phương trình (1) có nghiệm kép. 2 1
+ Với −2m +1 0 hay m
, d cắt (P) tại hai điểm phân biệt. Do đó phương trình (1) có hai 2 nghiệm phân biệt. Vậy: 1
+ Với m phương trình 2 2
− x + 2m −1 = 0 vô nghiệm. 2 1
+ Với m = phương trình 2 2
− x + 2m −1 = 0 có nghiệm kép. 2 1
+ Với m phương trình 2 2
− x + 2m −1 = 0 có hai nghiệm phân biệt. 2 1
Ví dụ 11. Cho parabol 2
(P) : y = x và đường thẳng d có phương trình y = x + m . Tìm m để: 4 Trang 12
a). d và (P) có điểm chung duy nhất.
b). d và (P) cắt nhau tại hai điểm phân biệt.
c). d và (P) không có điểm chung. Lời giải.
Cách 1: Vẽ đồ thị (P) và d trên cùng một mặt phẳng tọa độ. Chú ý hình dạng của d là một đường
thẳng song song với đường thẳng với trục Ox . Sử dụng thước di chuyển d trên đồ thị và nhận xét.
Cách 2: Xét phương trình hoành độ giao điểm 1 2 2 2
− x = x + m −x = 4x + 4m x + 4x + 4m = 0.1 4
a). Đường thẳng d và parabol (P) có điểm chung duy nhất khi và chỉ khi phương trình (1) có nghiệm kép 2
x + 4x + 4m = 0 có dạng hằng đẳng thức m = 1.
b). Đường thẳng d và parabol (P) cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình (1)
có hai nghiệm phân biệt. 2 2 2 2
x + 4x + 4m = 0 x + 4x + 4 + 4m − 4 = 0 x + 4x + 4 = 4 − 4m (x + 2) = 4 − 4 . m
Phương trình có hai nghiệm phân biệt khi 4 − 4m 0 m 1 .
c). Đường thẳng d và parabol (P) không có điểm chung khi và chỉ khi phương trình (1) vô nghiệm. 2
(x + 2) = 4 − 4m 0 m 1.
Ví dụ 12. Cho parabol 2
(P) : y = 2x và đường thẳng d có phương trình y = 3x + m . Tìm m để:
a). d và (P) có điểm chung duy nhất.
b). d và (P) cắt nhau tại hai điểm phân biệt.
c). d và (P) không có điểm chung. Lời giải.
Xét phương trình hoành độ giao điểm 2 2
2x = 3x + m 2x − 3x − m = 0.1
a). Đường thẳng d và parabol (P) có điểm chung duy nhất khi và chỉ khi phương trình (1) có 9 nghiệm kép 2
2x − 3x − m = 0 có dạng hằng đẳng thức m = − . 16
b). Đường thẳng d và parabol (P) cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình (1)
có hai nghiệm phân biệt. 2 2 3 9 9 2 9 3 2 9
2x − 3x − m = 0 x − x + − m −
= 0 x + 4x + 4 = m +
(x − ) = m + . 2 16 16 16 4 16 Trang 13 9 9
Phương trình có hai nghiệm phân biệt khi m + 0 m − . 16 16
c). Đường thẳng d và parabol (P) không có điểm chung khi và chỉ khi phương trình (1) vô 3 9 9 nghiệm. 2
(x − ) = m + 0 m − . 4 16 16
Bài 1. Cho hàm số 2 2
y = f (x) = (m −1)x ( m là tham số). Tìm m để: 1
a). Đồ thị hàm số đi qua điểm A ; 2 . 2 3 x + 2y = 3
b). Đồ thị hàm số đi qua điểm (x ; y ) với (x ; y ) là nghiệm của hệ phương trình . 0 0 0 0 2x + y =1
c). Vẽ đồ thị hàm số với các giá trị m tìm được trên cùng một mặt phẳng tọa độ. Lời giải. 2 1 a). 2 2 2 = (m −1)
m −1 = 8 m = 3 . 2 3 x + 2y = 3 x = 1 − b). 2 2 3 = (m −1)( 1 − ) m = 2 . 2x + y =1 y = 3
c). Với m = 2 và m = 3 thì 2
y = f (x) = 3x và 2
y = g(x) = 8x . a
Bài 2. Cho hàm số 2
y = x (a 0) có đồ thị là parabol (P) . 3
a). Xác định a để (P) đi qua điểm ( A − 5;5) .
b). Với giá trị vừa tìm được ở trên, hãy:
i) Vẽ (P) trên mặt phẳng tọa độ.
ii) Tìm các điểm trên (P) có hoành độ bằng 4 .
iii) Tìm các điểm trên (P) cách đều hai trục tọa độ. Trang 14 Lời giải. a
a). (P) đi qua điểm (
A − 5;5) nên = (− )2 5 5 a = 2 . 2 2
b). i) Với a = 2 ta có đồ thị hàm số 2 y = x . 3 2 ii) Ta có 2
y = 4 = 18 suyra B(4; 24) . 3 2 2 3 x = x x = 2 3 iii) 2 y = x ; 3 2 | x | | = y | ; y = . 3 2 3 2 2 x x = − x = − 3 2 1
Bài 3. Cho hàm số 2
y = x có đồ thị là parabol (P) . 5
a). Vẽ (P) trên mặt phẳng tọa độ. 2 6 3 9
b). Trong các điểm A 1; ; B 2; − ;C ;
, điểm nào thuộc (P) , điểm nào không thuộc 5 5 2 20 (P) ? Lời giải. a). 3 9 2 6 b). C ;
thuộc (P) , A 1; ; B 2; −
không thuộc (P) . 2 20 5 5 Trang 15 1
Bài 4. Cho parabol 2
(P) : y = − x và đường thẳng d : y = 2x + 2 . 2
a). Vẽ (P) và d trên cùng một mặt phẳng tọa độ.
b). Xác định tọa độ giao điểm của (P) và d . Lời giải. a).
b). Phương trình hoành độ giao điểm của d và (P) 1 2 2 2
− x = 2x + 2 −x = 4x + 4 = 0 x + 4x + 4 = 0 x = 2 − y = 2 − . 2
Bài 5. Cho hàm số 2
y = 3x có đồ thị là parabol (P) .
a). Vẽ (P) lên mặt phẳng tọa độ.
b). Dựa vào đồ thị, hãy biện luận số nghiệm của phương trình 2
3x − m − 2 = 0 theo m . Lời giải. a).
b). Xét đường thẳng d có phương trình y = m + 2 . Số nghiệm của phương trình 2
3x − m − 2 = 0
(1) là số giao điểm của đường thẳng d và (P) . Từ đồ thị ta thấy:
+ Với m + 2 0 hay m −2 , d không cắt (P) . Do đó phương trình (1) vô nghiệm. Trang 16
+ Với m + 2 = 0 hay m = −2 , d tiếp xúc (P) . Do đó phương trình (1) có nghiệm kép.
+ Với m + 2 0 hay m −2 , d cắt (P) tại hai điểm phân biệt. Do đó phương trình (1) có hai nghiệm phân biệt. Vậy:
+ Với m −2 phương trình 2
x − m − 2 = 0 vô nghiệm.
+ Với m = −2 phương trình 2
x − m − 2 = 0 có nghiệm kép.
+ Với m −2 phương trình 2
x − m − 2 = 0 có hai nghiệm phân biệt. 1
Bài 6. Cho parabol 2
(P) : y = x và đường thẳng d có phương trình y = −x + m . Tìm m để: 2
a). d và (P) có điểm chung duy nhất.
b). d và (P) cắt nhau tại hai điểm phân biệt.
c). d và (P) không có điểm chung. Lời giải.
Cách 1: Vẽ đồ thị (P) và d trên cùng một mặt phẳng tọa độ. Chú ý hình dạng của d là một đường
thẳng song song với đường thẳng với trục Ox . Sử dụng thước di chuyển d trên đồ thị và nhận xét.
Cách 2: Xét phương trình hoành độ giao điểm 1 2 2 2
x = −x + m x = 2
− x + 2m x + 2x − 2m = 0.1 2
a). Đường thẳng d và parabol (P) có điểm chung duy nhất khi và chỉ khi phương trình (1) có 1 nghiệm kép 2
x + 2x − 2m = 0 có dạng hằng đẳng thức m = − . 2
b). Đường thẳng d và parabol (P) cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình (1)
có hai nghiệm phân biệt. 2 2 2 2
x + 2x − 2m = 0 x + 2x +1− 2m −1 = 0 x + 2x +1 = 2m +1 (x +1) = 2m +1. 1
Phương trình có hai nghiệm phân biệt khi 2m +1 0 m − . 2
c). Đường thẳng d và parabol (P) không có điểm chung khi và chỉ khi phương trình (1) vô nghiệm. 2 1
(x +1) = 2m +1 0 m − . 2 --- HẾT --- Trang 17



