









Preview text:
PHƯƠNG TRÌNH VI PHÂN Bài giảng điện tử Ngày 6 tháng 12 năm 2016 PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 1 / 54 C H A P T E R 5 Initial-ValueProblems
for Ordinary Differential Equations Introduction
The motion of a swinging pendulum under certain simplifying assumptions is described by
the second-order differential equation d2θ g
Ta xét bài toán cơ bản về dao động+ sinθ = 0, dt2 củ L a con lắc đơn L θ
where L is the length of the pendulum, g ≈ 32.17 ft/s2 is the gravitational constant of the
earth, and θ is the angle the pendulum makes with the vertical. If, in addition, we specify
xác định bởi phương trình vi phân bậc hai
the position of the pendulum when the motion begins, θ(t0) = θ0, and its velocity at that
point, θ′(t0) = θ′, we have what is called an 0 initial-value problem.
For small values of θ, the approximation θ ≈ sin θ can be used to simplify this problem
to the linear initial-value problem d 2θ g d2θ g + sin θ = 0 + θ = 0, θ(t dt2 L 0) = θ0, θ ′(t0) = θ′0. dt2 L
This problem can be solved by a standard differential-equation technique. For larger values
of θ, the assumption that θ = sin θ is not reasonable so approximation methods must be
used. A problem of this type is considered in Exercise 8 of Section 5.9.
với L là chiều dài con lắc, g là hằng số hấp dẫn của trái đất, θ là góc tạo
Any textbook on ordinary differential equations details a number of methods for ex-
plicitly finding solutions to first-order initial-value problems. In practice, however, few of bởi con lắc và the trục problems originating thẳng from the
đứng. study of physical phenomena can be solved exactly. 259
Ta xét vị trí ban đầu của con lắc khi bắt đầu dao động là θ(t0) = θ0 và
Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.
vận tốc ban đầu tại điểm này là θ0(t0) = θ0 , ta có bài toán giá trị đầu. 0 PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 2 / 54
Với giá trị θ nhỏ, ta xấp xỉ θ ≈ sin θ, khi đó bài toán trở thành tuyến tính d 2θ g + θ = 0, θ(t0) = θ0, θ0(t0) = θ0 dt2 L 0
Bài toán này có thể giải bằng các phương pháp quen thuộc. Tuy nhiên với
giá trị θ lớn, ta không thể giả thiết θ = sin θ. Để tìm nghiệm cho bài toán
này, ta cần sử dụng các phương pháp xấp xỉ nghiệm. PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 3 / 54 Bài toán Cauchy Đặt vấn đề Bài toán Cauchy
Ta xét bài toán giá trị đầu bậc nhất, bài toán Cauchy, y 0(t) = f (t, y (t)), a 6 t 6 b, (1) y (a) = α
với y = y (t) là hàm cần tìm, khả vi trên đoạn [a, b], y0 là giá trị ban đầu
cho trước của y (t) tại t = a. PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 4 / 54 Bài toán Cauchy Đặt vấn đề
Đối với bài toán Cauchy (1) ta chỉ có thể tìm được nghiệm đúng của một
số phương trình đơn giản, còn đối với trường hợp f (x , y ) có dạng bất kỳ
thì nói chung không có phương pháp giải.
Ngoài ra, trong những trường hợp có thể tìm ra nghiệm đúng của bài toán
Cauchy (1) quá phức tạp thì người ta cũng ít dùng.
Vì vậy, việc tìm những phương pháp giải gần đúng bài toán Cauchy có vai
trò rất quan trọng trong thực tế. PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 5 / 54 Bài toán Cauchy Công thức Euler Công thức Euler
Để tìm nghiệm gần đúng của bài toán (1) ta chia đoạn [a, b] thành n đoạn nhỏ bằng nhau với b − a h = . n
Khi đó các điểm nút là t0 = a, tk = t0 + kh, k = 0, 1, 2, . . . , n, tn = b.
Giả sử y (t) là nghiệm duy nhất của bài toán (1), có đạo hàm đến cấp 2
liên tục trên đoạn [a, b].
Khi đó với mỗi k = 0, 1, 2, . . . , n − 1 theo công thức khai triển Taylor trên đoạn [tk , tk+1], ta có (tk+1 − tk )2
y (tk+1) = y (tk ) + y 0(tk )(tk+1 − tk ) + y 00(ξk ) , 2 với ξk ∈ (tk , tk+1). PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 6 / 54 Bài toán Cauchy Công thức Euler
Vì y = y (t) là nghiệm của phương trình (1) và h = tk+1 − tk nên ta có h2
y (tk+1) = y (tk ) + h.f (tk , yk ) + y 00(ξk ) 2
Bằng cách bỏ đi phần dư, ta xấp xỉ yk ≈ y (tk ) với k = 1, 2, . . . n, ta có công thức Euler y0 = α yk+1 ≈ yk + hf (tk , yk ),
với k = 0, 1, 2, . . . , n − 1. PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 7 / 54 268 C H A P T E 268 R 5 C H A P T Initial-V E R alue 5 Initial-V Problems for alue Problems Ordinary for
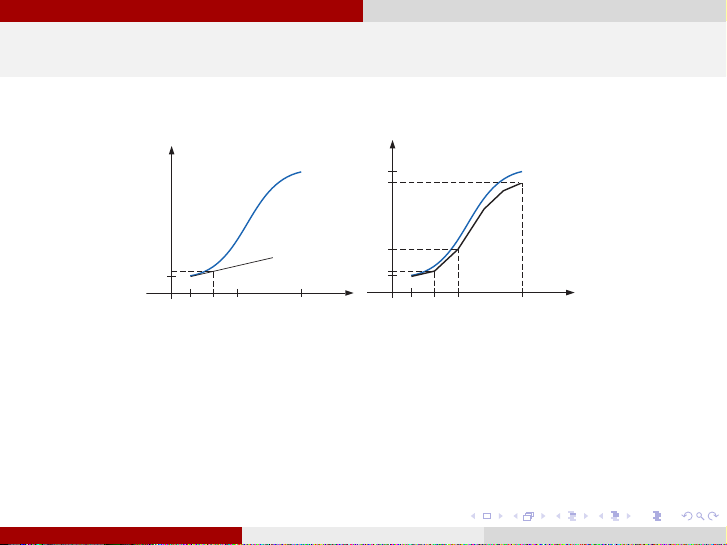
Differential Ordinary Differential Equations Equations The graph of the The graph function of the function
highlighting y(ti) highlighting is shown in y(t
Figure 5.2. One step in Euler’s
i) is shown in Figure 5.2. One step in Euler’s method appears in method Figure appears 5.3, and in a Figure series of5.3, and steps a series appears in of steps Figure appears 5.4. in Figure 5.4. Figure 5.2 Figure 5.2 y y y(t
y" ! f (t, y), N) ! y(b)
y(tN) ! y(b)
y" ! f (t, y), y(a) ! α y(a) ! α . . . . . . y(t2) y(t2) Bài toán Cauchy Công thức Euler y(t1) y(t1)
y(t0) ! α y(t
Ý nghĩa hình học của phương0) ! α t t . . . t b 0 ! a t1 2 pháp t N ! Euler tt . . . t t 0 ! a t1 2 N ! b Figure 5.3 y Figure 5.3 y Figure 5.4 y Figure 5.4 y
y" ! f (t, y),
y" ! f (t, y),
y" ! f (t, y),
y" ! f (t, y), y(b) y(ay( ) b) ! α y(a) ! α y(a) ! α y(a) ! α wN wN
Slope y"(a) ! f (a, αSlope )
y"(a) ! f (a, α) w2 w2 w1 w w 1 α α 1 w1 α α t t . . . t 0 ! a t1 2 t N ! b t t . . . t t t t . . . t t 0 ! a t1 2 N ! b 0 ! a t1 2 t N ! b t . . . t t 0 ! a t1 2 N ! b
Từ (t0, y0) = (a, α) thuộc đường cong y = y (t), kẻ tiếp tuyến với đường Example 1 Example Euler’s 1 method w Euler’ as s used method in the w first as used in the illustration first with h illustration = 0.5 to with h = 0.5 approximate to the approximate solution the solution cong to (có the hệinitial-v số alue
góc là y 0(a) = f (a, α)). Đường tiếp tuyến sẽ cắt t = t to the initial-v problem alue problem 1 tại
y1 chính là giá trị gần đúng của y (t1).
y′ = y − t2 + 1, y′0 = ≤ yt − ≤ t2 2, + 1, y(0) 0 = ≤ t 0.5.≤ 2, y(0) = 0.5.
Tại (t1, y1), ta kẻ đường thẳng với hệ số góc f (t1, y1) cắt t = t2 tại y2 là giá trị Use gần Algorithm đúng 5.1Use của yAlgorithm with N (t= 10 2). 5.1 to with N determine = 10 to determine
approximations, approximations, and compare theseand compare with the these with the exact values given exact by y( v t)alues = (t gi +ven 1)2 by − y(t 0.5 )et =
. (t + 1)2 − 0.5et.
Solution With N Solution = 10 we W havith e h N= = 10 0.2, t we i = hav 0.2 ei, hw= 0 0.2, = t 0.5, and
i = 0.2i, w0 = 0.5, and PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 8 / 54
wi+1 = wi + h(wi w − t2 − 0.04i2 + 1] = 1.2 0.008i2 + 0.2, i+i + 1 1 = w ) = i + h w(w i + 0.2[ i − t2w w i +
i 1) = wi + 0.2[wi − 0.04
i − i2 + 1] = 1.2wi − 0.008i2 + 0.2,
for i = 0, 1, . . . , 9. for
So i = 0, 1, . . . , 9. So w1 = 1.2(0.5) − w 0.008 0 + 0.2 = 0.8; = 1.2 0.8 0.008 1 + 0.2 = 1.152; 1 = ( 1.2 )2 (0.5) − 0.008(0)2 w2 + 0.2 = ( 0.8; ) − w2 =( 1.2
)2 (0.8) − 0.008(1)2 + 0.2 = 1.152; and so on. Table and 5.1 so sho on. ws T theable 5.1 shows comparison the comparison between the between approximate v the approximate alues at ti and v the alues at ti and the actual values. actual values.
Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it. Bài toán Cauchy Công thức Euler Ví dụ
Sử dụng phương pháp Euler để xấp xỉ nghiệm của bài toán Cauchy y 0(x ) = y − t2 + 1, 0 6 t 6 2, y (0) = 0.5
với n = 10. Tại những điểm nút chia so sánh giá trị gần đúng với giá trị
chính xác, biết nghiệm chính xác của bài toán là y (t) = (t + 1)2 − 0.5et . PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 9 / 54
Bấm máy. Y = Y + 0.2(Y − X 2 + 1) : X = X + 0.2 1 CALC Y = 0.5 =, X = 0 = 2 Y =, X = 0.2 = Bài toán Cauchy Công thức Euler Giải. 2 − 0 Với n = 10 thì h = = 0.2, tk = 0.2k, y0 = 0.5. 10
Công thức tính nghiệm gần đúng là yk+1 = yk + h(yk − t2k + 1) với k = 0, 1, . . . , 9. PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 10 / 54 Bài toán Cauchy Công thức Euler Giải. 2 − 0 Với n = 10 thì h = = 0.2, tk = 0.2k, y0 = 0.5. 10
Công thức tính nghiệm gần đúng là yk+1 = yk + h(yk − t2k + 1) với k = 0, 1, . . . , 9.
Bấm máy. Y = Y + 0.2(Y − X 2 + 1) : X = X + 0.2 1 CALC Y = 0.5 =, X = 0 = 2 Y =, X = 0.2 = PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 10 / 54 Bài toán Cauchy Công thức Euler k tk yk y (tk) |y (tk) − yk| 0 0.0 0.5000000 0.5000000 0.0000000 1 0.2 0.8000000 0.8292986 0.0292986 2 0.4 1.1520000 1.2140877 0.0620877 3 0.6 1.5504000 1.6489406 0.0985406 4 0.8 1.9884800 2.1272295 0.1387495 5 1.0 2.4581760 2.6408591 0.1826831 6 1.2 2.9498112 3.1799415 0.2301303 7 1.4 3.4517734 3.7324000 0.2806266 8 1.6 3.9501281 4.2834838 0.3333557 9 1.8 4.4281538 4.8151763 0.3870225 10 2.0 4.8657845 5.3054720 0.4396874 PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 11 / 54 Bài toán Cauchy Công thức Euler
Sai số của công thức Euler
Giả sử f là hàm liên tục và thỏa điều kiện
|f (t, y1) − f (t, y2)| ≤ L|y1 − y2|
với hằng số L > 0, và tồn tại M thỏa y 00(t) ≤ M với t ∈ [a, b].
Khi đó với y (t) là nghiệm chính xác của bài toán giá trị đầu y 0(t) = f (t, y ), a ≤ t ≤ b,
y (a) = α và y0, y1, . . . , yn là nghiệm
xấp xỉ của bài toán cho bởi công thức Euler, khi đó với mỗi k = 0, 1, . . . , n hM |y (tk ) − yk | ≤ [eL(tk −a) − 1] 2L PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 12 / 54 Bài toán Cauchy
Công thức Euler cải tiến
Công thức Euler cải tiến f (t Trong công thức Euler, thay k , yk ) + f (tk+1, yk+1) f (tk , yk ) bởi ta 2
được công thức Euler cải tiến f (tk , yk ) + f (tk+1, yk+1) y (tk+1) ≈ yk+1 = yk + h , 2
với k = 0, 1, 2, . . . , n − 1.
Việc tính toán theo công thức Euler cải tiến rất phức tạp vì cả 2 vế đều
chứa yk+1 là ẩn cần tìm. Để đơn giản ta thay yk+1 ở vế phải bởi yk + hf (tk , yk ). PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 13 / 54 Bài toán Cauchy
Công thức Euler cải tiến Lúc này ta có công thức
f (tk , yk ) + f (tk+1, yk + hf (tk , yk )) y (xk+1) ≈ yk+1 = yk + h , 2 k = 0, 1, 2, . . . , n − 1. PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 14 / 54 Bài toán Cauchy
Công thức Euler cải tiến Ví dụ
Sử dụng phương pháp Euler cải tiến để xấp xỉ nghiệm của bài toán Cauchy y 0(t) = y − t2 + 1, 0 6 t 6 2, y (0) = 0.5
với n = 10. Tại những điểm nút chia so sánh giá trị gần đúng với giá trị
chính xác, biết nghiệm chính xác của bài toán là y (t) = (t + 1)2 − 0.5et . PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 15 / 54 Bài toán Cauchy
Công thức Euler cải tiến 2 − 0 Với n = 10 thì h =
= 0.2, y0 = 0.5. Công thức tính nghiệm gần 10 đúng là
f (tk , yk ) + f (tk+1, yk + hf (tk , yk )) yk+1 = yk + h 2 với k = 0, 1, . . . , 9. Bấm máy.
Y = Y + 0.1 × (Y − X 2 + 1 + Y + 0.2(Y − X 2 + 1) − (X + 0.2)2 + 1) : X = X + 0.2 1 CALC Y = 0.5 = X = 0 = 2 Y =, X = 0.2 PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 16 / 54 Bài toán Cauchy
Công thức Euler cải tiến k tk yk y (tk) |y (tk) − yk| 0 0.0 0.5 0.5000000 0.0000000 1 0.2 0.826 0.8292986 0.0032986 2 0.4 1.20692 1.2140877 0.0071677 3 0.6 1.6372424 1.6489406 0.0116982 4 0.8 2.110235728 2.1272295 0.0169938 5 1.0 2.617687588 2.6408591 0.0231715 6 1.2 3.149578858 3.1799415 0.0303627 7 1.4 3.693686206 3.7324000 0.0387138 8 1.6 4.235097172 4.2834838 0.0483866 9 1.8 4.755618549 4.8151763 0.0595577 10 2.0 5.23305463 5.3054720 0.0724173 PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 17 / 54 Bài toán Cauchy
Công thức Euler cải tiến Bài tập
Sử dụng công thức Euler và công thức Euler cải tiến để xấp xỉ nghiệm của các bài toán sau 1
y 0 = te3t − 2y , 0 ≤ t ≤ 1, y (0) = 0 với h = 0.5. 2
y 0 = cos 2t + sin 3t, 0 ≤ t ≤ 1, y (0) = 1 với h = 0.25 3
y 0 = 1 + y /t, 1 ≤ t ≤ 2, y (1) = 2 với h = 0.25. 1 + t 4 y 0 =
, 1 ≤ t ≤ 2, y (1) = 2, với h = 0.25 1 + y PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 18 / 54 Bài toán Cauchy Công thức Runge-Kutta
Công thức Runge- Kutta bậc hai
Xét khai triển Taylor bậc hai của y (t), ta có h2 h3
y (tk+1) = y (tk ) + hy 0(tk ) + y 00(tk ) + y 000(ξ) 2 3! h2 h3
= y (tk ) + hf (tk , y (tk )) + f 0(tk , y (tk )) + y 000(ξ) 2 3! Ta lại có ∂f ∂f f 0(tk , y (tk ) = (tk , y (tk ) + (tk , y (tk )).y 0(tk ) ∂t ∂y
và y 0(tk ) = f (tk , y (tk )) h ∂f h ∂f
y (tk+1) ≈ y (tk )+h f (tk , y (tk )) + (tk , y (tk )) +
(tk , y (tk )).f (tk , y (tk )) 2 ∂t 2 ∂y PHƯƠNG TRÌNH VI PHÂN Ngày 6 tháng 12 năm 2016 19 / 54