Sách giáo khoa Vật Lí 11 - Chân trời sáng tạo

Xin gửi tới quý thày cô và bạn đọc file PDF cuốn sách giáo khoa VẬT LÍ 11 của bộ sách "Chân trời sáng tạo" theo chương trình giáo dục phổ thông mới. Cuốn sách gồm 127 trang giúp các bạn tra cứu nhanh lí thuyết, kiến thức và nội dung chương trình SGK. Mời bạn đọc đón xem!

110 55 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

HUÂN CHƯƠNG HỒ CHÍ MINH

VẬT LÍ

PHẠM NGUYỄN THÀNH VINH (Chủ biên)

TRẦN NGUYỄN NAM BÌNH – ĐOÀN HỒNG HÀ – BÙI QUANG HÂN – ĐỖ XUÂN HỘI

NGUYỄN NHƯ HUY – TRƯƠNG ĐẶNG HOÀI THU – TRẦN THỊ MỸ TRINH

VẬT LÍ 11

PHẠM NGUYỄN THÀNH VINH (Chủ biên)

NHÀ XUẤT BẢN GIÁO DỤC VIỆT NAM

 

*++</0

*++</0*++</0

,6%1

 

*++</0

*++</0*++</0

,6%1

 

*++</0

*++</0*++</0

,6%1

 

*++</0

*++</0*++</0

,6%1

 

*++</0

*++</0*++</0

,6%1

 

*++</0

*++</0*++</0

,6%1

 

*++</0

*++</0*++</0

,6%1

%QLQWK͵

6iFKNK{QJEiQ

Họ và tên Chức vụ Hội đồng

Bà ĐỖ HƯƠNG TRÀ

Chủ tịch

Ông NGUYỄN ANH THUẤN

Phó Chủ tịch

Ông NGUYỄN VĂN NGHIỆP

Uỷ viên,

Thư kí

Ông NGUYỄN QUANG LINH

Uỷ viên

Ông MAI HOÀNG PHƯƠNG

Uỷ viên

Ông PHÙNG VIỆT HẢI

Uỷ viên

Bà NGÔ THỊ QUYÊN

Uỷ viên

Ông PHẠM ĐÌNH MẪN

Uỷ viên

Bà NGUYỄN VŨ ÁNH TUYẾT

Uỷ viên

HỘI ĐỒNG QUỐC GIA

THẨM ĐỊNH SÁCH GIÁO KHOA

Môn: Vật lí – Lớp 11

VẬT LÍ 11



PHẠM NGUYỄN THÀNH VINH (Chủ biên)

TRẦN NGUYỄN NAM BÌNH – ĐOÀN HỒNG HÀ – BÙI QUANG HÂN – ĐỖ XUÂN HỘI

NGUYỄN NHƯ HUY – TRƯƠNG ĐẶNG HOÀI THU – TRẦN THỊ MỸ TRINH

VẬT LÍ

Hướng dẫn sử dụng sách

Trong mỗi bài học gồm các nội dung sau:

MỞ ĐẦU

Khởi động, đặt vấn đề, gợi mở và tạo hứng thú vào bài học

LUYỆN TẬP

VẬN DỤNG

MỞ RỘNG

HÌNH THÀNH KIẾN THỨC MỚI

cệiv auq iớm cứht nếik hnàht hnìh gnộđ tạoH

quan sát hình ảnh, thí nghiệm hoặc trải nghiệm thực tế

Tóm tắt kiến thức trọng tâm

Củng cố kiến thức và rèn luyện kĩ năng đã học

Vận dụng kiến thức và kĩ năng đã học vào thực tiễn

cuộc sống

Giới thiệu thêm kiến thức và ứng dụng liên quan đến

bài học, giúp các em tự học ở nhà

Các em hc sinh, quý thy, cô giáo và ph huynh thân mn!

Sách giáo khoa Vt lí 10 đã giúp các em trang b nhng kin thc nn tng v đng hc,

đng lc hc, năng lưng và công, đng lưng, chuyn đng tròn, s bin dng ca vt

rn, là nhng đi tưng chính ca Cơ hc – mt trong nhng nhánh nghiên cu đưc

xut hin sm nht trong lch s phát trin ca vt lí. Đng thi, các em cũng tìm hiu

v đi tưng, mc tiêu, phương pháp nghiên cu và nhng nh hưng sâu rng ca vt lí

đn mi lĩnh vc trong đi sng và kĩ thut.

Sách giáo khoa Vật lí 11 gm 4 chương mang đn cho các em nhng hiu bit v dao

đng, s lan truyn ca dao đng đ to ra sóng, đin tích – đin trưng và dòng đin

không đi.

Mi chương đưc chia thành mt s bài hc, mi bài hc gm mt chui các hot đng

nhm hình thành năng lc cho hc sinh bao gm: khi đng, khám phá, luyn tp, vn

dng, m rng và cui mi bài hc s có h thng bài tp giúp hc sinh rèn luyn và t

đánh giá kt qu hc tp ca mình. Hc sinh có th tra cu nhanh các thut ng khoa hc

liên quan đn bài hc da vào bng Gii thích thut ng cui sách.

Sách giáo khoa Vật lí 11 thuc b sách giáo khoa Chân trời sáng tạo ca Nhà xut bn

Giáo dc Vit Nam đưc biên son da trên đnh hưng phát trin phm cht và năng

lc ngưi hc và theo quan đim chú trng bn cht, ý nghĩa vt lí ca các đi tưng, đ

cao tính thc tin; to điu kin đ hc sinh phát trin tư duy khoa hc dưi góc đ vt lí,

khơi gi s ham thích trong hc tp b môn và tăng cưng kh năng vn dng kin thc,

kĩ năng vt lí trong thc tin dưi s giúp đ ca giáo viên.

Rt mong nhn đưc s góp ý ca quý thy, cô giáo, ph huynh và các em hc sinh đ

sách ngày càng hoàn thin hơn.

Các tác giả

/¢,1,ôp8

0&/&

Hưng dn s dng sách ................................................................................................. 2

Li nói đu ......................................................................................................................... 3

Mc lc ............................................................................................................................... 4

Chương 1: DAO ĐỘNG .................................................................................................. 5

Bài 1. Mô t dao đng ...................................................................................................... 5

Bài 2. Phương trình dao đng điu hoà ...................................................................... 14

Bài 3. Năng lưng trong dao đng điu hoà ............................................................... 22

Bài 4. Dao đng tt dn và hin tưng cng hưng .................................................. 26

Chương 2: SÓNG ................................................................................................34

Bài 5. Sóng và s truyn sóng ........................................................................................ 34

Bài 6. Các đc trưng vt lí ca sóng ............................................................................. 39

Bài 7. Sóng đin t .......................................................................................................... 46

Bài 8. Giao thoa sóng ..................................................................................................... 49

Bài 9. Sóng dng ............................................................................................................. 56

Bài 10. c hành đo tn s ca sóng âm và tc đ truyn âm ............................... 62

Chương 3: ĐIỆN TRƯỜNG .........................................................................................68

Bài 11. Đnh lut Coulomb v tương tác tĩnh đin .................................................... 68

Bài 12. Đin trưng ........................................................................................................ 73

Bài 13. Đin th và th năng đin ................................................................................. 80

Bài 14. T đin ................................................................................................................. 87

Bài 15. Năng lưng và ng dng ca t đin .............................................................. 93

Chương 4: DÒNG ĐIỆN KHÔNG ĐỔI ....................................................................98

Bài 16. Dòng đin. Cưng đ dòng đin ..................................................................... 98

Bài 17. Đin tr. Đnh lut Ohm ................................................................................ 103

Bài 18. Ngun đin .......................................................................................................108

Bài 19. Năng lưng đin. Công sut đin ..................................................................113

Bài 20. c hành xác đnh sut đin đng và đin tr trong ca pin .................117

Gii thích thut ng ..................................................................................................... 123

VẬT LÍ 11

'$2ïų1*

Chương 1

07l'$2ô1*

Bài

– Thí nghiệm đơn giản về dao động, một số ví dụ đơn giản về dao động tự do.

– Định nghĩa biên độ, chu kì, tần số, tần số góc, độ lệch pha.

– Mô tả dao động điều hoà.

S Hình 1.1. a) Đồng hồ quả lắc;

b) Chim ruồi đang hút mật

a) b)

Sự dao động của các vật diễn ra phổ biến trong cuộc

sống hằng ngày như: dao động của quả lắc đồng hồ

(Hình 1.1a), dao động của cánh chim ruồi

(*)

để giữ

cho cơ thể bay tại chỗ trong không trung khi hút mật

(Hình 1.1b). Vậy dao động có đặc điểm gì và được mô tả

như thế nào?

KHÁI NIỆM DAO ĐỘNG TỰ DO

Khái niệm dao động

Chuyển động của những vật trong Hình 1.1 (quả lắc,

cánh chim) có điểm chung là sự chuyển động có tính lặp lại

và có giới hạn trong không gian. Những chuyển động như vậy

được gọi là dao động cơ học. Một số vật thực hiện dao động

cơ học quanh một vị trí đặc biệt được gọi là vị trí cân bằng.

1. Từ một số dụng cụ đơn giản như:

lò xo nhẹ, dây nhẹ không dãn,

vật nặng và giá đỡ.

a) Em hãy thực hiện hai thí nghiệm sau:

– Cố định một đầu của lò xo, gắn

vật nặng vào đầu còn lại của lò

xo như Hình 1.2a. Kéo vật nặng

xuống một đoạn theo phương

thẳng đứng và buông nhẹ.

– Cố định một đầu của dây nhẹ

không dãn, gắn vật nặng vào

đầu còn lại của dây. Kéo vật

nặng để dây treo lệch một góc

xác định và buông nhẹ.

b) Quan sát và mô tả chuyển động

của các vật, nêu điểm giống

nhau về chuyển động của chúng.

Dao động cơ học là sự chuyển động có giới hạn trong

không gian của một vật quanh một vị trí xác định.

Vị trí đó gọi là vị trí cân bằng.

Dao động rất phổ biến trong tự nhiên và khoa học kĩ thuật.

Trong điện và từ học cũng có hiện tượng dao động. Dòng

điện được sử dụng trong sinh hoạt hằng ngày là dao động

điện từ.

(*)

Chim ruồi là loài chim có thân hình bé nhỏ, có khả năng bay cố định một chỗ trong không trung hoặc bay giật lùi.

VẬT LÍ 11

Dao đng mà trng thái chuyn đng ca vt (v trí và vn

tc) đưc lp li như cũ sau nhng khong thi gian bng

nhau đưc gi là dao động tuần hoàn, ví d: dao đng ca

qu lc đng h (Hình 1.1a).

Dao động tự do

Xét các h thc hin dao đng: con lc lò xo gm vt nng

đưc gn vào mt đu ca lò xo (Hình 1.2a), con lc đơn

gm vt nng đưc gn vào đu mt dây không dãn cùng vi

Trái Đt (Hình 1.2b). Lc đàn hi tác dng lên vt trong con

lc lò xo và trng lc tác dng lên vt trong con lc đơn gi là

ni lc ca h.

2. Nêu một số ví dụ về dao động

tuần hoàn.

3. Hãy nêu một ứng dụng của dao

động tuần hoàn trong cuộc sống.

Dao đng ca h xy ra dưi tác dng ch ca ni lc

đưc gi là dao động tự do (dao đng riêng).

Nêu một số ví dụ về các vật dao động tự do trong

thực tế.

Mục đích: Kho sát s ph thuc to đ ca vt dao đng theo thi gian.

Dụng cụ:

– H thng giá đ (1) và con lc lò xo (2).

– Cm bin khong cách (3).

– Dây cáp ni cm bin vi b ghi s liu (4).

– B ghi s liu (5).

– Dây cáp ni b ghi s liu và máy tính (6), máy tính (7).

DAO ĐNG ĐIU HOÀ

Giới thiệu thí nghiệm khảo sát sự phụ thuộc toạ độ của vật dao động theo thời gian

S Hình 1.3. Thí nghim kho sát s ph thuc to đ ca vt dao đng theo thi gian

(4)

(5)

(6)

(7)

(2)

(3)

(1)

S Hình 1.2. a) Con lắc lò xo;

b) Con lắc đơn

VẬT LÍ 11

4. Nhận xét về hình dạng đồ thị

toạ độ – thời gian của vật dao

động trong Hình 1.4.

t (s)

x (m) t (s) x (m)

t (s)

x (m)

t (s)

x (m) t (s) x (m)

0,00 –0,044 0,30 0,044 0,60 –0,038 0,90 0,031 1,20 –0,021

0,02 –0,043 0,32 0,045 0,62 –0,042 0,92 0,036 1,22 –0,028

0,06 –0,037 0,36 0,043 0,66 –0,043 0,96 0,043 1,26 –0,040

0,08 –0,032 0,38 0,040 0,68 –0,043 0,98 0,044 1,28 –0,042

0,12 –0,018 0,42 0,029 0,72 –0,036 1,02 0,042 1,32 –0,043

0,14 –0,010 0,44 0,022 0,74 –0,031 1,04 0,039

0,18 0,006 0,48 0,005 0,78 –0,017 1,08 0,028

0,20 0,016 0,50 –0,004 0,80 –0,009 1,10 0,021

0,24 0,031 0,54 –0,020 0,84 0,009 1,14 0,003

0,26 0,036 0,56 –0,027 0,86 0,017 1,16 –0,005

T Bảng 1.1. To đ ca vt nng ti nhng thi đim khác nhau

 Tiến hành thí nghiệm:

Tin hành b trí thí nghim như Hình 1.3. Khi đng các

thit b đ sn sàng ghi nhn tín hiu, sau đó kéo vt ra khi

v trí cân bng mt đon nh theo phương thng đng và

buông cho vt bt đu dao đng không vn tc ban đu.

To đ ca vt nng ti tng thi đim khác nhau đưc

hin th trên máy tính như trong Bng 1.1 và đ th to đ –

thi gian ca vt dao đng như trong Hình 1.4.

VẬT LÍ 11

Hình 1.5 cho bit v trí ca vt nng ti nhng thi đim khác nhau trên đưng đ th to đ –

thi gian khi tin hành thí nghim như b trí trong Hình 1.3.

Chn h trc to đ O[W như Hình 1.5, gc thi gian đưc chn vào lúc vt bt đu dao đng,

gc to đ đưc chn ti v trí cân bng ca vt, chiu dương ca trc to đ đưc chn theo

chiu thng đng hưng lên.

To đ ca vt tính t v trí cân bng ti mi thi đim đưc gi là li độ [ca vt dao đng.

Như vy, li đ có th có giá tr dương, âm hoc bng không.

5. Quan sát Hình 1.5 và chỉ ra

những điểm:

a) Có toạ độ dương, âm hoặc bằng

không.

b) Có khoảng cách đến vị trí cân

bằng cực đại.

c) Gần nhau nhất có cùng trạng thái

chuyển động.

S Hình 1.5. V trí ca vt nng trong h con lc lò xo

ti các thi đim khác nhau

x (m)

W (s)

N Q

Li độ, biên độ, chu kì dao động, tần số dao động

S Hình 1.4. Đ th to đ – thi gian ca vt dao đng trong thí nghim

VẬT LÍ 11

Li đ ca vt dao đng là to đ ca vt mà gc to

đ đưc chn trùng vi v trí cân bng.

Biên đ là đ ln cc đi ca li đ.

Dao đng điu hoà là dao đng tun hoàn mà li đ

ca vt dao đng là mt hàm cosin (hoc sin) theo

thi gian.

Trong Hình 1.5, ta thy ti các thi đim t

, t

và t

, vt nng

có cùng trng thái chuyn đng: đn biên âm và bt đu

chuyn đng đi lên. Khong thi gian ngn nht gia hai

ln vt có cùng trng thái chuyn đng đưc gi là chu kì

dao động T. Trong mt chu kì dao đng, vt hoàn thành

đưc mt dao đng hay mt chu trình dao đng.

Trên thc t, ngưi ta thưng s dng thut ng tần số

dao động như là mt đc trưng ca dao đng đ cho bit

s dao đng mà vt thc hin trong mt giây.

Khái niệm dao động điều hoà

Khi lc cn trong quá trình dao đng là không đáng k, đ

th to đ – thi gian, cũng chính là đ th li đ – thi gian,

có dng hình sin. Dao đng có tính cht này đưc gi là

dao động điều hoà.

Trong quá trình dao đng, vt nng s đn hai biên,

dng li và đi chiu chuyn đng. Biên ng vi to đ

dương đưc gi là biên dương, biên còn li là biên âm.

Khi  hai biên, li đ ca vt dao đng có đ ln cc đi.

Đ ln cc đi ca li đ đưc gi là biên độ A ca vt

dao đng. Biên đ dao đng luôn có giá tr dương.

Chu kì dao đng là khong thi gian đ vt

thc hin đưc mt dao đng. Tn s dao đng

đưc xác đnh bi s dao đng mà vt thc hin

đưc trong mt giây.

(1.1)

Trong h SI, chu kì dao đng có đơn v là giây (s) và

tn s dao đng có đơn v là héc (Hz).

S Hình 1.6. Ong mt bay ti ch

trong không trung

6. Một con ong mật đang bay tại chỗ

trong không trung (Hình 1.6),

đập cánh với tần số khoảng

300 Hz. Xác định số dao động mà

cánh ong mật thực hiện trong

1 s và chu kì dao động của

cánh ong.

VẬT LÍ 11

Pha dao đng là mt đi lưng đc trưng cho trng

thái ca vt trong quá trình dao đng. Đ lch pha

gia hai dao đng điu hoà cùng chu kì (cùng tn

s) đưc xác đnh theo công thc:





 2

(1.2)

Vt thc hin mt dao đng tương ng vi pha dao đng

thay đi mt lưng 2ʌ rad. Đi lưng đc trưng cho tc đ

bin thiên ca pha dao đng đưc gi là tần số góc Ȧ ca

dao đng.

Tn s góc ca dao đng là đi lưng đc trưng cho tc đ bin thiên ca pha dao

đng. Đi vi dao đng điu hoà, tn s góc có giá tr không đi và đưc xác đnh

theo công thc:











tt T



(1.3)

vi φ

và φ

ln lưt là pha dao đng ti thi đim t

và t

Trong h SI, tn s góc có đơn v là radian trên giây (rad/s).

Pha dao động, độ lệch pha, tần số góc

Ti mi thi đim, trng thái dao đng (li đ và vn tc) ca

vt đưc đc trưng bi mt đi lưng, gi là pha dao động φ.

Pha dao đng đưc đo bng đơn v ca góc, là đ hoc rad.

Vt thc hin mt dao đng tương ng vi pha dao đng

thay đi mt lưng 2ʌ rad.

Khi xét hai dao đng cùng chu kì (cùng tn s), ta thưng

quan tâm đn đi lưng độ lệch pha gia chúng.

Ví d: Hai vt đang dao đng có đ th li đ – thi gian đưc

biu din như Hình 1.7. Ti thi đim t = 0, vt 1 đi qua

v trí cân bng theo chiu dương ca trc to đ. Sau mt

khong thi gian ngn nht t, vt 2 mi đt đưc trng

thái tương t. Ta nói hai dao đng này lch pha nhau mt

lưng 'φ.

8. Dựa vào dữ kiện trong câu Thảo

luận 6, xác định tần số góc khi

ong đập cánh. Xem biên độ dao

động của cánh ong là không đổi.

Hình 1.7. Đ th li đ – thi gian

ca hai vt dao đng điu hoà

W(s)

x (cm)

¨W

1 2

7. Quan sát Hình 1.7, so sánh biên

độ và li độ của hai dao động 1

và 2 tại mỗi thời điểm.

S Hình 1.8. Đ th li đ – thi gian ca hai vt

dao đng điu hoà

1,0

W(s)

1,5 2,0

2,5

x (cm)

0,5

Quan sát đồ thị li độ – thời

gian của hai vật dao động

điều hoà được thể hiện trong

Hình 1.8. Hãy xác định biên

độ, chu kì, tần số, tần số góc

của mỗi vật dao động và độ

lệch pha giữa hai dao động.

–10

VẬT LÍ 11

9. Xác định độ lệch pha giữa hai

dao động trong Hình 1.9.

Ví dụ 1: Hình 1.9 th hin đ th li đ – thi gian ca mt

vt dao đng điu hoà đưc kích thích theo hai cách khác

nhau. Hãy xác đnh các đi lưng biên đ, chu kì, tn s và

tn s góc trong tng trưng hp.

Bài giải

 Trong trưng hp a), vt bt đu dao đng t v trí cân

bng theo chiu dương quy ưc. Trong trưng hp b), vt

bt đu dao đng t v trí biên dương, ngưc chiu dương

quy ưc.

 Trong hai trưng hp a) và b):

– Vt dao đng cùng biên đ A = 20 cm.

– Vt dao đng cùng chu kì T = 2 s.

– Tn s dao đng ca vt trong c hai trưng hp:

– Tn s góc ca vt trong c hai trưng hp:



 

2205

 f

., rad/s

Ví dụ 2: So sánh biên đ, chu kì, tn s, tn s góc và xác

đnh đ lch pha ca hai dao đng điu hoà trong ba trưng

hp đưc th hin  Hình 1.10.

Bài giải

 Trưng hp a):

– Biên đ dao đng ca vt 1 ln hơn biên đ dao đng ca

vt 2: A

> A

– Chu kì dao đng ca hai vt bng nhau: T

= T

– Tn s và tn s góc ca hai dao đng này cũng bng nhau:

= f

và Ȧ

= Ȧ

– Trong quá trình dao đng, hai vt luôn đn v trí cân bng

và hai biên cùng thi đim. Do đó, đi lưng ∆t trong công

thc (1.2) bng 0, dn đn 'φ = 0 rad. Ta nói hai vt dao

đng cùng pha vi nhau.

 Trưng hp b):

– Biên đ dao đng ca hai vt bng nhau: A

= A

= A.

– Chu kì dao đng ca vt 1 bng mt na chu kì dao đng

ca vt 2:

Vận dụng các đại lượng vật lí đặc trưng để mô tả dao động điều hoà

S Hình 1.9. Đ th li đ – thi gian

ca mt vt đưc kích thích dao

đng theo hai cách khác nhau

x (cm)

1,51

–20

–10

2,5 3,5

W (s)

0,5

–20

–10

x (cm)

1,51

2,5 3,5

W (s)

0,5

W (s)

x (cm)

W (s)

x (cm)

±$

S Hình 1.10. Đ th li đ – thi gian

ca hai vt dao đng trong các

trưng hp khác nhau

W (s)

±$

x (cm)

VẬT LÍ 11

Xét vật thứ nhất bắt đầu dao động điều hoà từ vị trí cân bằng, vật thứ hai dao động

điều hoà với biên độ lớn gấp hai lần, cùng chu kì và lệch pha









rad so với vật

thứ nhất. Vẽ phác đồ thị li độ – thời gian của hai vật trong hai chu kì dao động

đầu tiên.

Tìm hiểu và trình bày một số ứng dụng thực tiễn của hiện tượng dao động.

– Tn s và tn s góc dao đng ca vt 1 gp hai ln tn s

và tn s góc dao đng ca vt 2:

= 2f

và Ȧ

= 2Ȧ

– Do hai vt dao đng khác chu kì nên đ lch pha ca hai

dao đng thay đi theo thi gian.

 Trưng hp c):

– Biên đ dao đng ca hai vt bng nhau: A

= A

= A.

– Chu kì dao đng ca hai vt bng nhau: T

= T

= T.

– Tn s và tn s góc ca hai dao đng này cũng bng nhau:

= f

và Ȧ

= Ȧ

– Trong quá trình dao đng, vt th nht đi qua v trí cân

bng thì vt th hai đi qua v trí biên. Nghĩa là khong thi

gian ngn nht đ hai vt có cùng trng thái dao đng là

t



. eo công thc (1.2) ta suy ra:









rad. Ta nói

hai dao đng vuông pha vi nhau.

Mi liên h gia dao đng điu hoà và chuyn đng tròn đu

Xét một quả cầu được gắn cố định vào một

vành mảnh có thể chuyển động tròn đều trong

mặt phẳng thẳng đứng. Khi chiếu ánh sáng từ trên

xuống, ta thấy bóng của quả cầu dao động trên

một đoạn thẳng có phương song song với đường

thẳng đi qua tâm của chuyển động tròn. Quả cầu

xoay được một vòng tương ứng với bóng của nó

thực hiện được một dao động. Bằng một số tính

toán, ta rút ra được dao động điều hoà được xem

như là hình chiếu của một chuyển động tròn đều

lên một đường thẳng đi qua tâm và nằm trong

mặt phẳng quỹ đạo, biên độ của dao động bằng

bán kính quỹ đạo của chuyển động tròn đều.

4XҧFҫX

&KLӅX

FKX\ӇQ

ÿӝQJ

%yQJ

0jQ

ÈQKViQJ

9jQK[RD\

S Hình 1.11. Hình chiu ca mt

qu cu chuyn đng tròn đu lên

mt phng nm ngang

VẬT LÍ 11

1. Xác định biên độ, chu kì, tần số, tần số góc của mỗi dao động và độ lệch pha giữa hai dao động

có đồ thị li độ – thời gian như trong Hình 1P.1.

S Hình 1P.1. Đ th li đ – thi gian ca hai vt dao đng điu hoà

x (cm)

W (s)

–2

–4

–6

–8

0,060,03 0,120,09 0,180,15 0,240,21

2. Vẽ phác đồ thị li độ – thời gian của hai dao động điều hoà trong các trường hợp:

a) Cùng biên độ, chu kì của dao động thứ nhất bằng ba lần chu kì của dao động thứ hai.

b) Biên độ của dao động thứ nhất bằng hai lần biên độ của dao động thứ hai, cùng chu kì, cùng pha.

c) Cùng biên độ, cùng chu kì và có độ lệch pha

là ʌrad.

%j,7t3

Khi quả cầu trong Hình 1.11 quay được một vòng, vectơ bán kính nối tâm của quỹ đạo và vật

quét được một góc 2ʌ rad, tương ứng với bóng của vật thực hiện được một dao động.

Bảng 1.2 thể hiện sự tương tự trong dao động điều hoà và chuyển động tròn đều.

T Bảng 1.2. S tương t trong dao đng điu hoà và chuyn đng tròn đu

Kí hiu

Dao động điều hoà Chuyển động tròn đều

Li đ

To đ hình chiu ca vt trên trc to đ đi qua tâm và

nm trong mt phng ca qu đo tròn.

A Biên đ Bán kính

T Chu kì dao đng Chu kì quay

f Tn s dao đng Tn s quay

Tn s góc Tc đ góc

Ȧt +

Pha dao đng To đ góc

VẬT LÍ 11

3+¡1*751+

'$2ô1*ô,8+2j

Bài

– Độ dịch chuyển, vận tốc và gia tốc trong dao động điều hoà.

– Các phương trình về li độ, vận tốc và gia tốc của dao động điều hoà.

– Mối liên hệ giữa gia tốc và li độ trong dao động điều hoà.

Việc nghiên cứu các quá trình dao động điều hoà để ứng dụng vào thực tiễn như xây dựng mô hình dự báo

động đất yêu cầu ta phải mô tả chính xác trạng thái của vật dao động tại những thời điểm xác định. Ngoài ra, dao

động điều hoà có tính chất tuần hoàn theo thời gian và bị giới hạn trong không gian thì phương trình li độ, vận

tốc và gia tốc của vật dao động điều hoà có những khác biệt gì so với chuyển động thẳng đều và biến đổi đều mà

em đã học ở chương trình Vật lí 10?

LI Đ TRONG DAO ĐNG ĐIU HOÀ

Phương trình li độ của vật dao động

Phương trình li đ ca vt dao đng điu hoà có dng:

xA t





cos



(2.1)

Trong đó: x, A ln lưt là li đ và biên đ dao đng ca vt,

trong h SI có đơn v là m.

Ȧ là tn s góc ca dao đng, trong h SI có

đơn v là rad/s.

φ = Ȧt + φ

là pha ca dao đng ti thi đim t,

trong h SI có đơn v là rad.

là pha ban đu ca dao đng, trong h SI có

đơn v là rad.

1. Quan sát dao động của con lắc

lò xo và kết hợp với Hình 1.4,

hãy chỉ rõ sự khác nhau giữa

hình dạng quỹ đạo chuyển

động và đồ thị li độ của vật

dao động theo thời gian.

Trong Bài 1, ta đã bit mt vt đưc xem là đang thc hin

dao đng điu hoà khi đ th li đ – thi gian ca vt có

dng hình sin như Hình 1.4. Trong toán hc, ch có hàm

cosin (hoc sin) mi có đ th dng hình sin tương ng.

VẬT LÍ 11

VN TC TRONG DAO ĐNG ĐIU HOÀ

Phương trình vận tốc của vật dao động

Trong chương trình Vt lí 10, các em đã bit vn tc tc thi

ca vt đưc xác đnh bng thương s gia đ dch chuyn

d = x và thi gian t đ vt thc hin đ dch chuyn đó.

v 



(2.3)

vi điu kin t rt nh.

Đ th li đ – thi gian và vn tc – thi gian ca mt vt

dao đng điu hoà đưc xác đnh t thc nghim có dng

như Hình 2.3a và 2.3b. Quan sát Hình 2.3, ta thy:

Độ dịch chuyển của vật dao động

Trong chương trình Vt lí 10, các em đã bit đ dch chuyn

đưc xác đnh bng đ bin thiên to đ ca vt. Như vy,

ti mt thi đim bt kì, đ dch chuyn ca vt dao đng so

vi v trí ban đu đưc xác đnh bng công thc:

dxxx At A 

cos( )cos

 

(2.1)

Hình 2.1 minh ho đ th li đ – thi gian (đưng màu đ)

và đ dch chuyn – thi gian (đưng màu xanh dương)

đi vi mt vt dao đng điu hoà có A = 2 cm, T = 1 s và







Ta thy đ dch chuyn so vi v trí ban đu ca vt cũng

bin thiên điu hoà theo thi gian cùng biên đ, chu kì và

pha vi li đ ca vt dao đng. Ti tng thi đim, đ th

đ dch chuyn – thi gian dch xung mt đon

cos

trên trc tung so vi đ th li đ – thi gian như Hình 2.1.

T công thc (2.1), ta thy d trùng vi x khi gc thi gian

đưc chn lúc vt đi qua v trí cân bng (cosφ

= 0). Như vy,

li đ cũng chính là đ dch chuyn t v trí cân bng đn v

trí ca vt ti thi đim W.

2. Quan sát Hình 2.3a và 2.3b, hãy

xác định:

a) Hình dạng đồ thị vận tốc –

thời gian của vật.

b) Chu kì của vận tốc của vật.

c) Mối liên hệ giữa tốc độ cực đại và

biên độ của vật.

d) Độ lệch pha của vận tốc so với li

độ của vật.

Một vật dao động có đồ thị li độ – thời

gian được mô tả trong Hình 2.2. Hãy

xác định:

a) Biên độ dao động, chu kì, tần số, tần

số góc của dao động.

b) Li độ của vật dao động tại các thời

điểm t

, t

ứng với các điểm A, B, C

trên đường đồ thị li độ – thời gian.

c) Độ dịch chuyển so với vị trí ban đầu

tại thời điểm t

, t

trên đường đồ thị.

S Hình 2.2. Đ th li đ – thi gian

ca mt vt dao đng

x (cm)

W (s)

0,2

0,1

0,1 0,3 0,5 0,6

–0,1

–0,2

0,2 0,4

S Hình 2.1. Đ th li đ – thi gian

và đ dch chuyn – thi gian ca

mt vt dao đng điu hoà

W (s)

[G

(cm)

–3

–2

–1

0,2

0,4

0,8

0,6

VẬT LÍ 11

– Đ th vn tc – thi gian ca vt dao đng điu

hoà cũng có dng hình sin. Nghĩa là vn tc ca vt

dao đng điu hoà cũng bin đi điu hoà theo

thi gian.

– Vn tc và li đ ca vt dao đng điu hoà có

cùng chu kì T (cùng tn s f).

– T s ca tc đ cc đi và biên đ dao đng ca

vt bng Ȧ. Nghĩa là v

max

= ȦA.

– Sau mt khong thi gian

t



, li đ có cùng

trng thái dao đng vi vn tc. Nghĩa là vn tc

bin đi điu hoà theo thi gian lch pha

so vi

li đ.

T nhng nhn xét trên, kt hp vi vic s dng

công c toán hc phù hp, ta rút ra đưc:

Phương trình vn tc ca vt dao đng điu hoà có dng:

v 













 







cos



sin

(2.4)

Kết hợp các công thức (2.4) và (2.1), ta rút ra được công thức mô tả mối liên hệ giữa vận

tốc và li độ của vật dao động tại mỗi thời điểm:

max



(2.5)

Từ đồ thị trong Hình 2.3a và 2.3b, kết hợp với

phương trình (2.5), ta thấy:

– Khi vật đi qua vị trí cân bằng: x = 0,

PD[

. rvv

– Khi vật ở hai biên:

, rx A

v = 0.

Đồ thị mô tả mối liên hệ giữa vận tốc và li độ của vật dao động được thể hiện trong

Hình 2.4 là một đường ellipse có độ dài hai trục lần lượt là 2A và 2v

max

ȦA

–A

–ȦA

S Hình 2.4. Đ th mô t mi liên h

gia vn tc và li đ ca vt dao đng

Công thc mô t mi liên h gia vn tc và li đ ca vt dao đng

Một vật dao động điều hoà với biên độ 10 cm và chu kì 2 s. Chọn gốc thời gian là khi

vật qua vị trí cân bằng theo chiều dương. Xác định vận tốc của vật vào thời điểm đó.

S Hình 2.3. Đ th: a) li độ – thời gian; b) vận tốc – thời gian;

c) gia tốc – thời gian của một vật dao động điều hoà

x (cm)

W (s)

0,44

0,66

0,22

–0,22

–0,44

–0,66

0,33 0,66 0,99 1,32 1,65 1,98

1,98

–20

a (cm/s

)

W (s)

–40

0,33 0,66 0,99 1,32 1,65

1,98

W (s)

v (cm/s)

0,33 0,66 0,99 1,32 1,65

–2,10

–4,20

4,20

2,10

VẬT LÍ 11

3. Quan sát Hình 2.3a và 2.3c, hãy

xác định:

Hình dạng đồ thị gia tốc –

thời gian của vật.

b) Chu kì của gia tốc của vật.

c) Mối liên hệ giữa gia tốc cực đại

và biên độ của vật.

d) Độ lệch pha của gia tốc so với

li độ của vật.

4. Hãy vẽ phác đồ thị lực tác dụng –

thời gian của vật dao động điều

hoà có đồ thị li độ – thời gian

như Hình 2.2.

GIA TC TRONG DAO ĐNG ĐIU HOÀ

Phương trình gia tốc của vật dao động

Ta đã bit, gia tc tc thi đưc xác đnh bng thương s

gia bin thiên vn tc v và thi gian t đ vt thc hin

s bin thiên vn tc đó.





(2.6)

vi điu kin t rt nh.

Đ th gia tc – thi gian ca mt dao đng điu hoà đưc

xác đnh t thc nghim có dng như Hình 2.3c. Quan sát

Hình 2.3, ta thy:

– Đ th gia tc – thi gian ca vt dao đng điu hoà cũng

có dng hình sin. Nghĩa là gia tc ca vt dao đng điu hoà

cũng bin đi điu hoà theo thi gian.

– Gia tc và li đ ca vt dao đng điu hoà có cùng chu kì

T (cùng tn s f).

– T s ca đ ln cc đi ca gia tc và biên đ dao đng

ca vt bng Ȧ

. Nghĩa là a

max

= Ȧ

– Sau mt khong thi gian

t



, li đ có cùng trng thái

dao đng vi gia tc. Nghĩa là gia tc và li đ ca vt luôn

lch pha S so vi nhau (ngưc pha nhau).

T nhng nhn xét trên, kt hp vi vic s dng công c

toán hc phù hp, ta rút ra đưc:

Do ta có F = ma = –mȦ

x nên lc tác dng vào vt dao đng

điu hoà luôn hưng v v trí cân bng ca vt.

T đây, ta rút ra đưc điu kin đ mt vt thc hin dao

đng điu hoà là có lc tác dng vào vt đ luôn kéo vt v

v trí cân bng. Lc này có đ ln t l thun vi đ ln li đ

ca vt dao đng.

Phương trình gia tc ca vt dao đng điu hoà

có dng:

aA t

At x





 













cos



(2.7)

VẬT LÍ 11

Vận dụng phương trình gia tốc, mối liên hệ giữa gia tốc và li độ của vật dao động

Ví dụ: Mt vt dao đng điu hoà có phương trình gia tc

at













12 2





s.cm/s

(cm/s

)

a) Xác đnh biên đ, tn s góc, chu kì, tn s dao đng ca vt.

b) Vit phương trình li đ và phương trình vn tc ca vt.

%jLJLҧL

a) T công thc (2.7), ta có:

aAtAt 









 

os 

cm/s

(cm/s

)

So sánh vi phương trình gia tc ca vt, suy ra:

– Tn s góc: Ȧ = 2ʌ rad/s.

– Biên đ dao đng:

 

max

(







– Pha ban đu ca dao đng:







rad.

– Chu kì dao đng:









– Tn s dao đng:

1Hz.

Đồ thị mô tả mối liên hệ giữa gia tốc và li độ được thể

hiện trong Hình 2.5, là một đoạn thẳng đi qua gốc toạ độ

với hệ số góc có giá trị –Ȧ

. Gia tốc luôn có chiều hướng

về vị trí cân bằng của vật.

Dựa vào các đồ thị trong Hình 2.3:

a) Viết phương trình li độ, vận tốc và gia tốc của vật dao động điều hoà.

b) Mô tả định tính tính chất của li độ, vận tốc và gia tốc của vật tại các thời điểm:

0,5 s; 0,75 s và 1 s.

c) Dựa vào các phương trình được xây dựng ở câu a để kiểm chứng lại mô tả định tính

ở câu b.

–A

PD[

–a

PD[

S Hình 2.5. Đ th mô t mi liên h

gia gia tc – li đ ca vt dao đng

VẬT LÍ 11

5. Nhận xét về độ lệch pha giữa gia

tốc và vận tốc của vật dao động.

Một máy cơ khí khi hoạt động sẽ tạo ra những dao động được xem gần đúng là dao

động điều hoà với phương trình li độ có dạng:

x = 2cos(180SW) (mm)

a) Hãy xác định biên độ, chu kì, tần số và tần số góc của dao động.

b) Viết phương trình vận tốc và gia tốc của vật dao động.

Tìm hiểu và trình bày ngắn gọn nguyên tắc hoạt động của thiết bị đo khối lượng của các phi hành gia

trên tàu vũ trụ.



Xét một con lắc lò xo gồm một vật nặng

khối lượng m gắn vào đầu một lò xo nhẹ có

độ cứng k, đầu còn lại của lò xo được giữ cố

định. Vật có thể chuyển động trên mặt sàn

nằm ngang như Hình 2.6, ma sát giữa mặt

sàn và vật là không đáng kể. Kích thích cho

vật dao động.

Xét con lắc đơn gồm một vật nặng gắn vào

đầu một sợi dây nhẹ, không dãn, đầu còn lại

của sơi dây được giữ cố định như Hình 2.7.

Xem lực cản của không khí là không đáng kể.

Kích thích cho vật dao động.

Con lc lò xo

–A A

S Hình 2.6. Con lc lò xo



Con lc đơn

S Hình 2.7. Con lc đơn



– Phương trình li đ ca vt theo công thc (2.1):























(cm)

– Phương trình vn tc ca vt theo công thc (2.4):

 

cm/sFRV  FRV $W W

Z ZM

§·

 SS

¨¸

©¹

v

(cm/s)

VẬT LÍ 11

Ta có:

x

(2.10).

Kết hợp với phương trình (2.7) ta suy ra:





(2.11)

hay





chính là tần số góc của con lắc

lò xo dao động điều hoà.

Chọn hệ trục toạ độ OVnhư Hình 2.7.

Xét trên phương tiếp tuyến của quỹ đạo, ta có:

Fmgma 

sin



(2.12)

Khi vật dao động góc nhỏ (θ ≤ 10

), ta có:

sintan





(2.13)

Do đó:



smaa

(2.14)

Với s là độ dài cung

Kết hợp với phương trình (2.7) ta suy ra:





(2.15)

hay





chính là tần số góc của con lắc

đơn dao động điều hoà với biên độ góc

đủ nhỏ.

Lưu ý: Đối với một hệ dao động tự do, tần số góc có một giá trị xác định, phụ thuộc vào các

đặc tính của hệ.

Các lực tác dụng vào vật nặng gồm: trọng lực



, phản lực



và lực đàn hồi



Theo định luật II Newton, ta có:

GGG

PNFa m

(2.8)

Chọn hệ trục toạ độ Ox như Hình 2.6.

Chiếu lên phương chuyển động, ta có:

Fma

(2.9)

Lực đàn hồi



luôn hướng về vị trí cân bằng O

và có giá trị

Fkx

Các lực tác dụng vào vật nặng gồm: trọng lực



và lực căng dây



Trọng lực



được phân tích thành hai

thành phần: thành phần pháp tuyến



và

tiếp tuyến



Hợp lực của



và



hướng vào điểm cố

định của dây treo, đóng vai trò là lực hướng

tâm giúp vật chuyển động tròn.

Lực



luôn có tác dụng kéo vật về vị trí cân

bằng O.

VẬT LÍ 11

%j,7t3

1. Một vật dao động điều hoà có đồ thị li độ – thời gian và vận tốc – thời gian như Hình 2P.1.

Hãy viết phương trình li độ và phương trình vận tốc của dao động này. Từ đó suy ra phương

trình gia tốc của vật dao động.

2. Một chất điểm dao động điều hoà với biên độ 4 cm, tần số 1 Hz. Tại thời điểm ban đầu, vật

ở vị trí biên âm. Hãy xác định vận tốc và gia tốc của vật tại thời điểm t = 1 s.

3. Một vật dao động điều hoà có đồ thị gia tốc theo thời gian được thể hiện trong Hình 2P.2.

Xác định vị trí, vận tốc và gia tốc của vật tại các thời điểm W

, W

và W

tương ứng với các điểm

A, B và C trên đường đồ thị a(W).

D(cm/s

)

W(s)

S Hình 2P.2. Đ th gia tc – thi gian ca mt vt dao đng điu hoà

S Hình 2P.1. Đ th li đ – thi gian (a) và vn tc – thi gian (b) ca mt vt dao đng

x (cm)

1,5 2,5

–1

0,5

–0,5

W (s)

v (cm/s)

1,5 2,52 3

–2

–4

10,5

VẬT LÍ 11

1u1*/¦1*7521*

'$2ô1*ô,8+2j

Bài

Sự chuyển hoá động năng và thế năng trong dao động điều hoà.

Tiến hành thí nghiệm như mô tả trong Hình 3.1. Đặt một

tấm gỗ cố định lên tường, đưa vật nặng của con lắc đơn đến

vị trí tiếp xúc với tấm gỗ và thả nhẹ để vật nặng bắt đầu chuyển

động không vận tốc ban đầu. Khi dao động, vật nặng có va

chạm vào tấm gỗ hay không? Vì sao? Trong quá trình dao động,

vật nặng có những dạng năng lượng gì và sự chuyển hoá giữa chúng

như thế nào?

TH NĂNG TRONG DAO ĐNG ĐIU HOÀ

Biểu thức của thế năng trong dao động điều hoà

Xét h con lc lò xo dao đng điu hoà.  năng ca h

đưc tích lu trong lò xo và ph thuc vào mc đ lò xo

b kéo dãn hay nén li. Khi chn gc th năng ti v trí cân

bng, t mt s tính toán, ta rút ra đưc th năng trong dao

đng điu hoà:





(3.1)

Kt hp vi công thc (2.1) ta có:

S Hình 3.1. Thí nghim vi con lc đơn

7ҩPJӛ

 năng trong dao đng điu hoà đưc tính theo

công thc:





22 2





cos

(3.2)

1. Dựa vào công thức (3.2) và

Hình 3.2, mô tả sự thay đổi của

thế năng trong một chu kì dao

động của vật.

S Hình 3.2. Đ th th năng – thi gian

trong dao đng điu hoà

tmax

Do hàm cosin (hoc sin) bình phương có giá tr thay đi

t 0 đn 1 nên th năng trong dao đng điu hoà có giá tr

thay đi t 0 đn W

tmax

vi W

tmax

là giá tr cc

đi ca th năng.

VẬT LÍ 11

Sự biến đổi của thế năng theo thời gian

Kt hp công thc (3.2) và phép bin đi lưng giác

 FRV 

FRV



, ta có:

WmAm







22 22





cos

(3.3)

Như vy, th năng trong dao đng điu hoà bin đi tun

hoàn theo thi gian vi tn s góc bng hai ln tn s góc

ca li đ.

(3.4)

Một số toà nhà cao tầng sử dụng các con lắc nặng trong bộ giảm chấn khối lượng

(mass damper) để giảm thiểu sự rung động gây ra bởi gió hay những cơn địa chấn

nhỏ. Giả sử vật nặng của con lắc có khối lượng 3,0.10

kg, thực hiện dao động điều

hoà với với tần số 15 Hz với biên độ dao động là 15 cm. Hãy xác định thế năng cực

đại của hệ con lắc trong bộ giảm chấn khối lượng.

ĐNG NĂNG TRONG DAO ĐNG ĐIU HOÀ

Biểu thức của động năng trong dao động điều hoà

Đng năng ca mt vt đưc xác đnh bi công thc:

Kt hp vi công thc (2.4), ta có:

Tương t như th năng, đng năng ca vt dao đng điu hoà

có giá tr thay đi t 0 đn W

đmax

vi W

đmax

= W

tmax

PȦ

là giá tr cc đi ca đng năng.

Sự biến đổi của động năng theo thời gian

Kt hp công thc (3.5) và phép bin đi lưng giác

 RV a



, ta có:

Đng năng ca vt dao đng điu hoà đưc tính

theo công thc:

 

2 22 2

W mA

Z ZM



(3.5)

3. Dựa vào công thức (3.5) và

Hình 3.3, mô tả sự thay đổi của

động năng trong một chu kì

dao động của vật.

2. So sánh chu kì, tần số biến

thiên của thế năng với chu kì,

tần số dao động của vật.

S Hình 3.3. Đ th đng năng –

thi gian trong dao đng điu hoà

đmax

VẬT LÍ 11

Một vật có khối lượng 2 kg dao động điều hoà có đồ thị vận tốc – thời gian như

Hình 3.4. Xác định tốc độ cực đại và động năng cực đại của vật trong quá trình

dao động.

S Hình 3.4. Đ th vn tc – thi gian ca vt dao đng

v (m/s)

1,5

1,2

W (s)

0,6

0,3

0,4

0,3

0,2

0,1

–0,1

–0,2

–0,3

–0,4

0,9

5. Quan sát Hình 3.5 và mô tả sự

thay đổi của động năng và thế

năng khi vật dao động di chuyển

từ biên âm đến biên dương.

4. So sánh pha dao động của thế

năng và động năng khi vật dao

động điều hoà.

S Hình 3.5. S ph thuc ca th năng,

đng năng, cơ năng vào li đ ca vt

dao đng

–A A

1ăQJOѭӧQJ

/Lÿӝ

&ѫQăQJ

7KӃQăQJ

ĈӝQJQăQJ

S CHUYN HOÁ NĂNG LƯNG VÀ BO TOÀN CƠ NĂNG TRONG DAO ĐNG

ĐIU HOÀ

WmAm

–

 



22 22





cos

(3.6)

Như vy, đng năng ca vt dao đng điu hoà bin đi

tun hoàn theo thi gian vi tn s góc bng hai ln tn s

góc ca li đ theo công thc (3.4).

Sự chuyển hoá năng lượng trong dao động điều hoà

T các công thc (3.2) và (3.5), ta có th v đưc các đưng

đ th mô t s ph thuc ca th năng và đng năng vào

li đ ca h dao đng điu hoà như trong Hình 3.5.

Hình 3.5 th hin:

– Khi vt  biên, đ ln li đ cc đi và vn tc bng không,

th năng có giá tr cc đi còn đng năng bng không.

– Khi vt di chuyn t v trí biên v v trí cân bng, đ ln

li đ gim nên th năng gim và đ ln vn tc tăng nên

đng năng tăng.

– Khi vt  v trí cân bng, li đ bng không và đ ln vn

tc cc đi, th năng bng không và đng năng có giá tr

cc đi.

– Khi vt di chuyn t v trí cân bng ra biên, đ ln li đ

tăng nên th năng tăng và đ ln vn tc gim nên đng

năng gim.

Như vy, trong quá trình vt dao đng, đng năng và th

năng luôn thay đi và chuyn hoá qua li vi nhau.

VẬT LÍ 11

Sự bảo toàn cơ năng trong dao động điều hoà

Ta đã bit, cơ năng ca mt h bng tng đng năng và th

năng. Kt hp vi các công thc (3.2) và (3.5), ta rút ra đưc

công thc xác đnh cơ năng trong dao đng điu hoà:

= W

+ W

WWWm





t –



(3.7)

T biu thc (3.7), ta thy rng, xét vi mt dao đng điu

hoà, cơ năng t l thun vi bình phương biên đ dao đng

A ca vt và không thay đi theo thi gian. Như vy, trong

quá trình vt dao đng điu hoà, th năng W

và đng năng

bin đi liên tc theo thi gian nhưng cơ năng luôn

bo toàn.

6. Quan sát Hình 3.5 và 3.6, nhận

xét về độ lớn của động năng, thế

năng và cơ năng trong quá trình

dao động điều hoà của vật.

7. Dựa vào biểu thức (3.2) và (3.5),

hãy thiết lập biểu thức (3.7).

S Hình 3.6. Đ th biu din s ph

thuc ca th năng, đng năng và cơ

năng trong dao đng theo thi gian

1ăQJ

OѭӧQJ

ĈӝQJQăQJ 7KӃQăQJ &ѫQăQJ

7KӡLJLDQ

Biết phương trình li độ của một vật có khối lượng 0,2 kg dao động điều hoà là x = 5cos(20t) (cm).

a) Tính cơ năng trong quá trình dao động.

b) Viết biểu thức thế năng và động năng.

%j,7t3

1. Một hệ dao động điều hoà với chu kì 2 s. Chọn gốc thế năng tại vị trí cân bằng của vật. Thời điểm

hệ bắt đầu dao động thì động năng và thế năng bằng nhau lần thứ nhất. Hỏi sau bao lâu kể từ

khi hệ bắt đầu dao động, động năng và thế năng bằng nhau lần thứ hai?

2. Xét một vật bắt đầu dao động điều hoà từ vị trí cân bằng theo chiều âm của trục toạ độ. Chọn

gốc thế năng tại vị trí cân bằng của vật. Hãy vẽ phác đồ thị thể hiện sự phụ thuộc vào thời gian

của động năng và thế năng trong hai chu kì dao động trên cùng một hệ trục toạ độ. Chỉ ra trên

đồ thị những thời điểm mà động năng và thế năng có độ lớn bằng nhau.

Xét một vật bắt đầu dao động điều hoà từ vị trí cân bằng, hãy chỉ ra những khoảng

thời gian trong một chu kì dao động mà:

a) thế năng tăng dần trong khi động năng giảm dần.

b) thế năng giảm dần trong khi động năng tăng dần.

VẬT LÍ 11

'$2 ô1* 7w7 'p1 9j

+,17¦1*&1*+¤1*

Bài

– Dao động tắt dần, dao động cưỡng bức và hiện tượng cộng hưởng.

– Lợi ích và tác hại của hiện tượng cộng hưởng trong một số trường hợp cụ thể.

Bộ giảm chấn khối lượng (mass damper) (Hình 4.1) được sử dụng để

giảm thiểu sự rung lắc của các toà nhà cao tầng khi có gió mạnh hay địa chấn.

Toà nhà Taipei 101 tầng (cao 508 m) tại thành phố Đài Bắc, Đài Loan cũng

được trang bị bộ giảm chấn khối lượng, là một con lắc với vật nặng khoảng

728 tấn được treo tại trung tâm toà nhà từ tầng 92 xuống đến tầng 87.

Nhờ vậy, toà nhà có thể chịu được những cơn bão có sức gió lên tới 216 km/h

hay những cơn địa chấn lên đến 7 độ richter. Các kĩ sư xây dựng đã dựa trên

những hiện tượng vật lí nào?

S Hình 4.1. B gim chn khi lưng

DAO ĐNG TT DN

Quan sát hiện tượng dao động tắt dần

Khi kho sát hin tưng dao đng trong các bài trưc, ta

đã lí tưng hoá bài toán khi xem lc cn ca môi trưng là

không đáng k, có th b qua. Tuy nhiên, trên thc t, sau

khi ngng tác dng lc đ kích thích cho vt dao đng, biên

đ dao đng ca vt gim dn và vt s dng li sau mt

khong thi gian nht đnh.

Dao động tắt dần là dao đng có biên đ gim dn

theo thi gian.

1. Quan sát Hình 4.2 và mô tả chuyển

động của xích đu, ván nhảy cầu

sau khi ngừng tác dụng lực.

S Hình 4.2. Xích đu (a) và ván nhy cu (b)

a) b)

2. Nêu một số ví dụ thực tế khác về

hiện tượng dao động tắt dần.

VẬT LÍ 11

Giải thích hiện tượng dao động tắt dần

Ta đã bit, lc cn ca môi trưng tác dng lên vt luôn ngưc chiu chuyn đng ca vt.

Do đó, công ca lc cn tác dng lên vt luôn âm làm cho cơ năng gim. T đó biên đ dao

đng ca vt gim dn theo thi gian.

Tuỳ theo lực cản tác dụng lên vật mà dao động tắt dần có

thể chia thành các loại sau:

– Dao động tắt dần dưới hạn: Khi lực cản tác dụng lên vật

có độ lớn nhỏ, vật thực hiện dao động với biên độ giảm

dần theo thời gian và dừng lại sau một số chu kì dao động.

Đồ thị li độ – thời gian của dao động tắt dần dưới hạn

được thể hiện ở đường màu đỏ trong Hình 4.3.

Ví dụ: Con lắc lò xo dao động trên mặt phẳng ngang có

ma sát hoặc một số loại cửa có thể dao động khi được

đẩy ra hoặc kéo vào.

– Dao động tắt dần tới hạn: Khi lực cản tác dụng lên vật có độ lớn vừa đủ, vật không thể

thực hiện đủ một chu kì dao động mà trở về vị trí cân bằng sau một thời gian ngắn.

Đồ thị li độ – thời gian của dao động tắt dần tới hạn được thể hiện ở đường màu vàng trong

Hình 4.3.

Ví dụ: Một số loại cửa được lắp đặt hệ thống bản lề đặc biệt, để cửa không còn thực hiện được

dao động mà tự đóng lại sau một khoảng thời gian ngắn.

– Dao động tắt dần vượt hạn: Khi lực cản tác dụng lên vật có độ lớn tăng lên, vật không thể

thực hiện đủ một chu kì dao động mà trở về vị trí cân bằng sau một thời gian tương đối dài.

Đồ thị li độ – thời gian của dao động tắt dần vượt hạn được thể hiện ở đường màu xanh trong

Hình 4.3.

Ví dụ: Nếu lực cản trong hệ thống bản lề đóng cửa tự động tăng lên đáng kể, cửa vẫn không

thể thực hiện được dao động nhưng mất nhiều thời gian để tự đóng lại.

7ҳWGҫQWӟLKҥQ

7ҳWGҫQYѭӧWKҥQ

7ҳWGҫQGѭӟLKҥQ

S Hình 4.3. Đ th li đ – thi gian ca

các loi dao đng tt dn

Bố trí sơ đồ thí nghiệm như Hình 4.4. Kéo vật nặng của con lắc lò xo khỏi vị trí

cân bằng theo phương thẳng đứng một đoạn xác định và thả nhẹ để vật dao

động không vận tốc ban đầu. Dự đoán và thực hiện thí nghiệm kiểm chứng (nếu

có điều kiện) về dao động của con lắc trong các trường hợp vật nặng thực hiện

dao động trong: a) không khí; b) chất lỏng (nước/dầu); c) chất lỏng (nước/dầu)

khi có gắn thêm vật cản.

Hình 4.4. Vt nng ca con lc lò xo dao đng:

a) trong không khí; b) trong chất lỏng; c) trong chất lỏng khi có gắn thêm vật cản

/z[R

9ұWQһQJ

&KұXÿӵQJ

FKҩWOӓQJ

9ұWFҧQ

a) b) c)

VẬT LÍ 11

3. Trên thực tế, sau khi được kích

thích để dao động, xích đu

(Hình 4.2a) hoặc võng sẽ dao

động tắt dần. Làm cách nào để

chúng có thể dao động với biên

độ không đổi?

Đưa ra một số ví dụ về tác hại và lợi ích của dao động tắt dần. Từ đó tìm hiểu và sưu tầm hình ảnh về một số

ứng dụng của dao động tắt dần trong cuộc sống.

DAO ĐNG CƯNG BC VÀ HIN TƯNG CNG HƯNG

S Hình 4.5. Cơ ch b sung năng lưng

cho đng h qu lc

Dao động cưỡng bức

Trên thc t, đ mt vt dao đng không b tt, ta cn b

sung năng lưng đ bù li s tiêu hao năng lưng do lc cn

môi trưng.

ông thưng, ta có hai cách b sung năng lưng cho vt

dao đng:

– Truyn năng lưng b sung đúng bng phn năng lưng

tiêu hao  cui mi chu kì dao đng ca h bng mt lc

cùng chiu vi chuyn đng. Lc này không làm thay đi

chu kì dao đng riêng ca vt. Cơ ch này đưc gi là dao

đng duy trì. Ví d: h bù năng lưng cho con lc trong

đng h qu lc (Hình 4.5).

– S dng mt ngoi lc bin thiên điu hoà (ngoi lc điu

hoà) theo thi gian:

FF t





cos 



(4.1)

trong đó F

và  ln lưt là biên đ và tn s góc ca ngoi lc.

Đ th li đ – thi gian ca vt đưc th hin trong Hình 4.6

(trong trưng hp ngoi lc điu hoà cùng pha vi dao đng

cưng bc  giai đon n đnh) gm hai giai đon:

+ Giai đon chuyn tip, trong đó dao đng ca h chưa

n đnh, biên đ và chu kì dao đng bin thiên phc tp

theo thi gian.

+ Giai đon n đnh, trong đó biên đ và chu kì dao đng

ca vt không thay đi. Giai đon n đnh kéo dài cho đn

khi ngoi lc không còn tác dng.

01020304050607080

-0.3

-0.2

-0.1

0.1

0.2

0.3

-3

-2

-1

S Hình 4.6. Đ th: a) ngoại lực điều hoà – thời gian (đường màu đỏ);

b) li độ – thời gian của vật (đường màu xanh)

7KӡLJLDQV

/LÿӝP

1JRҥLOӵF1)

–0,3

–0,2

–0,1

0,1

0,2

0,3

7060 80

–3

–2

–1

VẬT LÍ 11

Mt trong nhng ví d ca dao đng cưng bc là h thng

võng máy t đng s dng đin như trong Hình 4.7.

Tính cht ca dao đng cưng bc:

– Dao đng cưng bc là dao đng điu hoà.

– Tn s góc ca dao đng cưng bc bng tn s góc  ca

lc cưng bc.

– Biên đ ca dao đng cưng bc ph thuc vào biên đ F

đ chênh lch gia tn s góc ca lc cưng bc và tn s

góc riêng ca h, lc cn ca môi trưng xung quanh.

Hiện tượng cộng hưởng

Khi gi biên đ F

không đi và thay đi tn s góc  ca

lc cưng bc, ta thy biên đ dao đng cưng bc A ca h

thay đi. Biên đ dao đng cưng bc đt giá tr cc đi A

max

khi tn s góc ca lc cưng bc tin đn bng tn s góc

riêng ca h dao đng  = Ȧnhư đ th trong Hình 4.8.

Khi tác dng vào vt, lc cưng bc đã thc hin công và b

sung năng lưng cho vt, giúp vt duy trì dao đng vi biên

đ không đi.

Dao đng ca vt dưi tác dng ca ngoi lc điu

hoà trong giai đon n đnh đưc gi là dao động

cưỡng bức. Ngoi lc điu hoà tác dng vào vt khi

này đưc gi là lực cưỡng bức.

Hiện tượng cộng hưởng xy ra khi tn s góc ca

lc cưng bc tin đn bng tn s góc riêng ca h

dao đng. Khi này, biên đ dao đng cưng bc ca

h đt giá tr cc đi A

max

Nêu một số ví dụ về dao động cưỡng bức trong thực tế.

S Hình 4.7. Võng máy t đng

s dng đin

9ұWGDRÿӝQJ

FѭӥQJEӭF

ĈӝQJFѫ

WҥRUDOӵF

FѭӥQJEӭF



S Hình 4.8. S ph thuc ca biên

đ dao đng cưng bc vào tn s

góc ca lc cưng bc

VẬT LÍ 11

Lợi ích và tác hại của hiện tượng cộng hưởng

Trong cuc sng, nhng hiu bit v hin tưng cng hưng

đưc ng dng trong lĩnh vc xây dng, âm nhc, y hc,

thông tin liên lc,...

– Khi thit k các công trình ln như nhà cao tng hoc

cu đưng, các kĩ sư cn có nhng phương án x lí kĩ thut

nhm tránh xy ra cng hưng trên h thng. Ví d: Cu

iên niên k ti London (Hình 4.11) đã phi tm đóng

sau ba ngày đón khách du lch vào năm 2000 vì hin tưng

cng hưng đã xy ra khi khách tham quan cùng đi trên cu,

vô tình to ra mt ngoi lc cưng bc có tn s dao đng

xp x tn s dao đng riêng ca cu, làm cho cu rung

Khi lc cn ca môi trưng thay đi, đ ln cc đi ca biên

đ dao đng cưng bc cũng thay đi. Hình 4.9 minh ho s

ph thuc ca biên đ dao đng cưng bc vào tn s góc

ca lc cưng bc ng vi các giá tr khác nhau ca lc cn

môi trưng. Kt qu cho thy khi đ ln ca lc cn môi

trưng tăng lên thì đnh ca đưng đ th loe ra và biên đ

dao đng cưng bc cc đi A

max

gim xung.

Bố trí thí nghiệm hệ con lắc Barton như Hình 4.10.

Mô hình gồm nhiều con lắc đơn có chiều dài dây treo

khác nhau được gắn trên cùng một dây treo đàn hồi.

Khi con lắc số 1 được kích thích để dao động, những

con lắc còn lại (từ số 2 đến 7) sẽ bắt đầu dao động.

Giải thích vì sao chúng dao động và dự đoán về biên

độ dao động của chúng.

Thực hiện thí nghiệm kiểm chứng.

S Hình 4.10. Con lc Barton

4. Trình bày một số lợi ích và tác

hại của hiện tượng cộng hưởng

trong thực tế mà em đã biết.

S Hình 4.11. Cu đi b Thiên niên k

ti London, Vương Quc Anh

/ӵFFҧQQKӓ



S Hình 4.9. S ph thuc ca biên đ dao đng cưng bc vào

tn s góc ca ngoi lc trong trưng hp lc cn ln và nh

/ӵFFҧQOӟQ

VẬT LÍ 11

Tìm hiểu và trình bày

hoạt động của bộ giảm

chấn khối lượng, là

một con lắc được treo

trên toà nhà Taipei 101

tại thành phố Đài Bắc,

Đài Loan (Hình 4.1).

%j,7t3

1. Cho ví dụ về một số ứng dụng của dao động tắt dần trong thực tiễn.

2. Hãy chỉ ra hai trường hợp cộng hưởng có lợi và hai trường hợp cộng hưởng có hại. Trong từng

trường hợp hãy chỉ rõ hệ dao động và nguồn gốc gây ra sự cộng hưởng.

3. Máy đo địa chấn được sử dụng để phát hiện và đo đạc những rung động địa chấn được tạo ra

bởi sự dịch chuyển của lớp vỏ Trái Đất. Năng lượng từ các cơn địa chấn có khả năng kích thích

con lắc lò xo bên trong máy đo làm đầu bút di chuyển để vẽ lên giấy (Hình 4P.1).

a) Dao động của con lắc lò xo trong máy đo địa chấn khi cơn

địa chấn xuất hiện là loại dao động gì? Giải thích.

b) Tần số của những cơn địa chấn thường nằm trong khoảng

30 Hz – 40 Hz. Để kết quả ghi nhận là tốt nhất, hệ con lắc lò

xo trong máy đo địa chấn cần được thiết kế để có tần số dao

động riêng trong khoảng nào? Giải thích.

S Hình 4P.1. Máy đo đa chn

lc rt mnh (Ngun: www.theguardian.com). Các kĩ sư đã

mt khong hai năm đ b sung b gim chn khi lưng

nhm to ra dao đng tt dn ti hn trên cu.

– Vào tháng 9/1985, mt trn đng đt ln (8,1 đ richter),

có tâm chn ti b bin phía tây ca nưc Mexico. Ti th đô

Mexico, cách tâm chn đn 400 km, sóng đa chn đã to ra

lc cưng bc lên các toà nhà, gây hin tưng cng hưng,

làm cho nhiu toà nhà có đ cao trung bình rung lc d di

và sp đ hoàn toàn, trong khi nhng toà nhà cao hơn hoc

thp hơn hn li đng vng. (Ngun: www.britannica.com)

– Trong lĩnh vc âm nhc: Mi nhc c phát ra nhng giai

điu âm thanh mang nét đc trưng riêng ca nhc c đó. Đ

khuch đi đ to ca âm thanh mà không làm mt đi nét

đc trưng riêng đó, ngưi ta s dng mt bung đc bit là

bung cng hưng như hp đàn guitar, hp vĩ cm.

Máy đo đa chn

Máy đo địa chấn là một thiết bị được dùng để ghi nhận những chuyển động bất thường của

mặt đất gây ra bởi sự lan truyền sóng chấn động từ tâm của những trận động đất. Đa phần

các máy đo địa chấn thường hoạt động như sau: Một giá treo được gắn chặt vào mặt đất,

một vật nặng được treo lơ lửng vào giá và có xu hướng đứng yên trong khi giá treo chuyển

động theo mặt đất. Chuyển động của lớp vỏ Trái Đất trong các trận động đất được đo tương

đối với bất kì vật thể nào, không phụ thuộc vào chuyển động của mặt đất. Khi mặt đất rung

chuyển, đầu bút trên quả nặng sẽ dao động và vạch lên bản ghi (một cuộn giấy được quay

đều). Việc phân tích tín hiệu thu được trên bản ghi cho ta biết thông tin của những sóng địa

chấn gây ra bởi những trận động đất.

Tìm hiểu và trình bày ngắn gọn

phương án kĩ thuật để hạn chế

thiệt hại cho các toà nhà, đặc

biệt là các toà nhà cao tầng, tại

những nơi thường xảy ra động

đất như Nhật Bản.

VẬT LÍ 11

71*.7&+¡1*

MÔ T DAO ĐNG

– Dao đng ca h xy ra dưi tác dng ch ca ni lc đưc gi là dao đng t do

(dao đng riêng).

– Li đ ca vt dao đng là to đ ca vt mà gc to đ đưc chn trùng vi v trí cân bng.

– Biên đ là đ ln cc đi ca li đ.

– Dao đng điu hoà là dao đng tun hoàn mà li đ ca vt dao đng là mt hàm cosin

(hoc sin) theo thi gian.

– Chu kì dao đng là khong thi gian đ vt thc hin đưc mt dao đng. Tn s dao

đng đưc xác đnh bi s dao đng mà vt thc hin đưc trong mt giây.

Trong h SI, chu kì dao đng có đơn v là giây (s) và tn s dao đng có đơn v là héc (Hz).

– Pha dao đng là mt đi lưng đc trưng cho trng thái ca vt trong quá trình dao

đng. Đ lch pha gia hai dao đng điu hoà cùng chu kì (cùng tn s) đưc xác đnh

theo công thc:





 2

– Tn s góc ca dao đng là đi lưng đc trưng cho tc đ bin thiên ca pha dao

đng. Đi vi dao đng điu hoà, tn s góc có giá tr không đi và đưc xác đnh theo

công thc:











tt T



vi φ

và φ

ln lưt là pha dao đng ti thi đim t

và t

Trong h SI, tn s góc có đơn v là radian trên giây (rad/s).

CÁC PHƯƠNG TRÌNH TRONG DAO ĐNG ĐIU HOÀ

– Phương trình li đ ca vt dao đng:

xA t





cos



– Phương trình vn tc ca vt dao đng:

v 













 







cos



sin

– Phương trình gia tc ca vt dao đng:

aAtx

 









cos

VẬT LÍ 11

NĂNG LƯNG TRONG DAO ĐNG ĐIU HOÀ

–  năng trong dao đng điu hoà đưc tính theo công thc:

 



22 22 2





cos

– Đng năng ca vt dao đng điu hoà đưc tính theo công thc:

mA t

–

 



2222





sin

– Cơ năng trong dao đng điu hoà:

= W

+ W

WWWm



t –



DAO ĐNG TT DN VÀ HIN TƯNG CNG HƯNG

– Dao đng tt dn là dao đng có biên đ gim dn theo thi gian.

– Dao đng ca vt dưi tác dng ca ngoi lc điu hoà trong giai đon n đnh đưc

gi là dao đng cưng bc. Ngoi lc điu hoà tác dng vào vt khi này đưc gi là lc

cưng bc.

– Hin tưng cng hưng xy ra khi tn s góc ca lc cưng bc tin đn bng tn s

góc riêng ca h dao đng. Khi này, biên đ dao đng cưng bc ca h đt giá tr cc

đi A

max

VẬT LÍ 11

6¶1*

Chương 2

61*9j6758<161*

Bài

– Quá trình truyền sóng.

– So sánh sóng dọc và sóng ngang.

– Một số tính chất đơn giản của âm thanh và ánh sáng.

Vào lúc 9 giờ 22 phút, sáng ngày 14/03/2022, một trận động đất xảy ra tại tỉnh Điện Biên (Theo Báo Tuổi trẻ).

Vì sao tại những nơi như một số huyện giáp ranh của tỉnh Sơn La cách tâm chấn khoảng 20 km, nhà cửa và các đồ đạc, vật

dụng của gia đình lại bị rung lắc? Động đất đã lan truyền như thế nào?

QUÁ TRÌNH TRUYN SÓNG

Khái niệm sóng

Mt bin đng đt ngt (hay còn gi là chn đng) đưc

lan truyn trong mt môi trưng gây ra hin tưng sóng

(Hình 5.1). Sóng t mt v trí xác đnh trong không gian

(ngun sóng) đưc phát ra và truyn đi thông qua môi

trưng vt cht (môi trưng rn, lng và khí) đưc gi

là sóng cơ. Ví d: Khi ngh sĩ kéo vĩ cm (Hình 5.2a),

sóng âm thanh t đàn truyn đn tai khán thính gi; sóng

nưc lan truyn trên mt h (Hình 5.2b),… Nu ngun

sóng thc hin dao đng tun hoàn, sóng phát ra cũng

có tính cht tun hoàn. Vy, sóng là dao đng lan truyn

trong không gian theo thi gian.

a) b)

S Hình 5.2. a) Nghệ sĩ kéo vĩ cầm; b) Sóng nước trên mặt hồ

Khi sóng truyn trong không gian, các phn t môi trưng

không truyn theo phương truyn sóng mà ch dao đng ti

ch. Ví d, xét mt qu bóng đưc th ni trên mt nưc

đang có sóng truyn qua như Hình 5.3. Gi s tri lng gió,

1. Dự đoán trạng thái của mặt nước

trong cốc nước khi ta gõ lên mặt

bàn một cách liên tục và đủ mạnh

tại một vị trí gần cốc nước. Giải

thích hiện tượng và tiến hành thí

nghiệm để kiểm chứng.

S Hình 5.1. Tay ngưi to ra

chn đng truyn đn cc nưc

VẬT LÍ 11

Năng lưng sóng đưc

truyn đi theo phương

truyn sóng. Do đó, quá

trình truyn sóng là quá

trình truyn năng lưng.

Quá trình truyền năng lượng của sóng

Tâm chấn

(nguồn sóng)

S Hình 5.4. Minh ho s lan truyn ca sóng đa chn (đng đt)

Sóng là dao đng lan truyn trong không gian theo

thi gian. Khi sóng truyn đi, phn t môi trưng

không truyn theo phương truyn sóng mà ch dao

đng ti ch.

Hình 5.4 cho thy khi sóng đa chn đưc phát ra t mt v

trí khi ngun ca đng đt (tâm chn), nhà ca, công trình

 nhng v trí cách xa tâm chn vn có th b nh hưng.

Điu này cho thy sóng đa chn mang năng lưng và năng

lưng này đã đưc truyn trong không gian dưi dng sóng.

Quá trình truyn sóng, dù là sóng cơ hay sóng đin t, đu

là quá trình truyền năng lượng. Khi sóng cơ truyn trong

mt môi trưng, năng lưng ca sóng là tng hp ca đng

năng và th năng ca phn t vt cht dao đng.

4. Quan sát Hình 5.5, hãy so sánh

phương truyền sóng và phương

dao động của từng điểm trên lò

xo trong hai trường hợp.

S Hình 5.5. Sóng truyn trên lò xo khi dùng tay to ra dao đng:

a) dọc theo trục lò xo; b) vuông góc với trục lò xo

SÓNG DC VÀ SÓNG NGANG

3. Em hãy cho biết những tác hại

của sóng địa chấn (động đất).

S Hình 5.3. Qu bóng

trên mt nưc có sóng

ta thy qu bóng không dch chuyn theo phương truyn

ca sóng trên mt nưc mà ch dao đng ti ch.

Ngoài sóng cơ, là sóng truyn trong môi trưng do các phn

t ca môi trưng thc hin dao đng thì còn có mt loi

sóng khác đó là sóng đin t. Sóng đin t có th lan truyn

qua c chân không. Đây là mt trong nhiu s khác bit

gia sóng đin t và sóng cơ. Ánh sáng hoc sóng vô tuyn

đin là sóng đin t.

2. Quan sát Hình 5.3 và dự đoán

phương chuyển động của quả

bóng khi có sóng trên mặt nước

trong điều kiện lặng gió.

VẬT LÍ 11

Xét mt lò xo có mt đu đưc gn c đnh vào vách, mt đu

t do như Hình 5.5. Khi dùng tay kích thích đ đu còn li

ca lò xo dao đng, ta thy dao đng này s đưc lan truyn

trên lò xo theo hai cách khác nhau.  c hai trưng hp

trong Hình 5.5, sóng đưc truyn trên lò xo theo phương

ngang t trái sang phi, trong khi tng phn t ca lò xo

dao đng theo phương truyn sóng (Hình 5.5a) hoc theo

phương vuông góc vi phương truyn sóng (Hình 5.5b),

tương ng vi hai loi sóng là sóng dc và sóng ngang.

Sóng dc là sóng mà phương dao đng ca mi phn

t môi trưng trùng vi phương truyn sóng.

Sóng ngang là sóng mà phương dao đng ca mi phn

t môi trưng vuông góc vi phương truyn sóng.

Sóng âm trong không khí là mt ví d ca sóng dc.

Xét màng loa khi hot đng, dao đng ca màng loa đưc

lan truyn làm các phn t ca không khí cũng dao đng.

Do đó, nhng vùng áp sut cao và thp liên tip nhau đưc

to thành và truyn đn tai ngưi nghe làm màng nhĩ dao

đng và to ra cm giác v âm thanh (Hình 5.6). Dao đng

ca các phn t không khí có phương trùng vi phương

truyn ca sóng âm. Sóng truyn  mt bàn trong thí nghim

 Hình 5.1 và sóng lan truyn trên mt nưc  Hình 5.3

là sóng ngang: các phn t trên mt bàn và trên mt nưc

dao đng theo phương thng đng, vuông góc vi phương

truyn sóng là phương ngang.

Sóng ngang có th truyn trong cht rn và b mt cht lng.

Sóng dc có th truyn trong các cht rn, lng và khí.

Lấy một số ví dụ về

sóng dọc và sóng

ngang trong thực tế.

S Hình 5.6. S lan truyn ca sóng âm

6yQJkPWUX\ӅQWӯORDÿӃQWDLQJѭӡL

/RD

7DL

Trong tự nhiên tồn tại

những loại sóng phức

tạp, là sự tổng hợp của

cả sóng dọc và sóng

ngang. Ví dụ như sóng

trên mặt nước: trong

thực tế, mỗi phần tử của

nước thực hiện chuyển

động tròn khi sóng

truyền qua. Chuyển

động này có thể phân

tích thành hai loại sóng

dọc và ngang đồng thời.

MT S TÍNH CHT CA SÓNG

Hiện tượng phản xạ

Khi sóng truyn t mt môi trưng đn mt phân cách vi

mt môi trưng khác, mt phn ca sóng ti đưc truyn

ngưc li vào môi trưng ban đu. Đây là hin tưng phn

x sóng.

Mt s ví d v hin tưng phn x ca sóng: âm thanh

khi gp vt cn (như bc tưng) s b phn x và to ra

ting vang như trong Hình 5.7, ta có th nhìn thy các vt

xung quanh (quyn sách, bàn) là do ánh sáng đưc truyn

t ngun sáng đn vt và phn x đ truyn t vt đn mt

ta (Hình 5.8).

5. Quan sát Hình 5.7, xét trên

phương vuông góc với bức

tường, nhận xét về chiều truyền

của sóng âm trước và sau khi

gặp bức tường.

VẬT LÍ 11

Hiện tượng khúc xạ

Hin tưng sóng đi phương truyn khi đi t mt môi

trưng này sang mt môi trưng khác đưc gi là hin

tưng khúc x. Hin tưng này có th d dàng quan sát đi

vi sóng ánh sáng như Hình 5.9. Các tia sáng khi truyn t

nưc ra không khí b đi phương truyn, do đó ta thy thìa

b gãy khúc ti mt tip xúc nưc – không khí. Ngoài ra,

hin tưng khúc x sóng cũng xy ra đi vi sóng bin và

sóng âm.

Giải thích vì sao vào những đêm mùa lạnh, ta có thể

nghe được âm thanh từ xa trong khi vào mùa nóng

ta lại không thể nghe được dù ở cùng khoảng cách.

S Hình 5.9. Chic thìa khi

đt vào cc nưc

Hiện tượng nhiễu xạ

Trên Hình 5.10, ta thy phương truyn ca sóng bin khi đi

qua khe đã thay đi và làm cho sóng lan rng  phía bên kia

khe. Đây là hin tưng nhiu x, là mt trong nhng đc

trưng ca sóng (ch có sóng mi có th gây ra hin tưng

này). Sóng âm cũng có th gây ra hin tưng nhiu x.

S Hình 5.10. Hin tưng nhiu x

ca sóng bin

Khi mở hé cánh cửa để ánh sáng đi qua khe hẹp

(Hình 5.11), ta quan sát thấy ánh sáng loang ra một

khoảng lớn hơn kích thước khe hẹp. Hãy giải thích

hiện tượng này.

Mt s hin tưng đc trưng cho sóng là phn x,

khúc x, nhiu x,...

6. Quan sát Hình 5.9, nhận xét về

hình dạng của chiếc thìa. Thực

hiện thí nghiệm kiểm chứng và

giải thích.

S Hình 5.11. Ánh sáng đi qua khe hp

khi m hé ca

S Hình 5.8. Sóng ánh sáng phn x khi gp mt bàn và quyn

sách nên mt ngưi có th nhìn thy hình nh ca các vt

S Hình 5.7. Sóng âm phn x khi gp bc

tưng nên tai ngưi nghe đưc âm thanh

vng li

SÓNG TỚI

SÓNG PHẢN XẠ

VẬT LÍ 11

Vận dụng những kiến thức về sóng để giải thích vì sao dơi (Hình 5.13)

có thể phát hiện ra chướng ngại vật bằng cơ chế phát sóng siêu âm (là

sóng âm có tần số lớn hơn 20 000 Hz).

S Hình 5.13. Dơi dang bay

2. Hình 5P.2 mô tả hai loại sóng địa chấn truyền trong môi

trường khi xảy ra động đất: sóng P (sóng sơ cấp) và sóng

S (sóng thứ cấp). Hãy phân biệt hai sóng địa chấn này

thuộc sóng dọc hay sóng ngang. Giải thích.

%j,7t3

1. Xét sóng nước truyền qua vị trí của phao câu cá đang nổi

trên mặt nước khi lặng gió như Hình 5P.1. Phao có trôi đi

theo phương truyền của sóng nước không? Vì sao?

S Hình 5P.1. Phao câu cá

S Hình 5P2. Hai loi sóng đa chn

6yQJ3VyQJVѫFҩS

6yQJ6VyQJWKӭFҩS

Trong một số điều kiện nhất định, ta có thể quan sát được hiện tượng nhiễu xạ của

sóng ánh sáng. Trong Hình 5.12a, khi kích thước của lỗ tròn đủ lớn, trên màn có một vệt

sáng đồng dạng với lỗ tròn theo đúng định luật truyền thẳng của ánh sáng. Tuy nhiên,

khi lỗ tròn có đường kính cỡ khoảng một phần mười milimét, ta không thấy một vệt

sáng mà lại thấy nhiều vệt sáng tối xen kẽ như ở Hình 5.12b. Điều này chỉ có thể được

giải thích dựa vào hiện tượng nhiễu xạ của sóng ánh sáng.

S Hình 5.12. Hin tưng quan sát đưc trên màn khi l tròn có kích thưc: a) lớn; b) đủ nhỏ

a) b)

0jQFKҳQFyOӛWUzQ

NtFKWKѭӟFOӟQ

0jQFKҳQFyOӛWUzQ

NtFKWKѭӟFÿӫQKӓ

0jQTXDQViW

1JXӗQViQJ

VẬT LÍ 11

&k&ôz&751*9t7/&$61*

Bài

Động đất cùng những dịch chuyển địa chất lớn ở mặt nước hoặc dưới

mặt nước sẽ sinh ra những đợt sóng lớn và đột ngột. Đó là hiện tượng sóng

thần (Hình 6.1). Sóng thần có thể gây ra những thiệt hại đáng kể về người

và vật chất. Để thực hiện những mô phỏng, dự báo chính xác nhất về sóng

thần, ta cần có những kiến thức vật lí nào liên quan đến hiện tượng sóng?

S Hình 6.1. Sóng thn ti Tohoku,

Nht Bn năm 2011

(Nguồn: https://www.ickr.com)

– Khái niệm bước sóng, biên độ, tần số, tốc độ và cường độ sóng.

– Vận dụng biểu thức mô tả mối liên hệ giữa tốc độ truyền sóng, tần số và bước sóng.

CÁC ĐI LƯNG ĐC TRƯNG CA SÓNG

Chu kì, tần số, biên độ sóng

Mt si dây đàn hi, không dãn, ban đu đưc gi nm

ngang, mt đu đưc gn c đnh vào tưng. Mt bn hc

sinh kích thích đ đu còn li ca dây dao đng (Hình 6.2a).

Ta thy có sóng lan truyn trên dây. Hin tưng này cũng có

th quan sát đưc trên thc t, trong mt s bài tp th dc

trong Hình 6.2b.

c nghim chng t, khi ngun sóng là đu O ca dây

đưc kích thích đ thc hin dao đng điu hoà theo

phương thng đng vi chu kì T (tn s f) thì mi đim trên

dây cũng thc hin dao đng vi cùng chu kì T và tn s f

vi đu O. Ta gi T và f ln lưt là chu kì và tần số của sóng.

Khi sóng truyn qua, mi đim trong không gian thc

hin dao đng ti ch. Vì ban đu tt c mi đim trên

phương truyn sóng đu đng yên nên đ dch chuyn

cũng chính là li đ dao đng ca chúng. Biên đ dao đng

ca các phn t môi trưng ti đim đó đưc gi là biên

độ sóng. Nhng đim trên phương truyn sóng có li đ

cc đi đưc gi là đỉnh sóng.

S Hình 6.2. a) Sóng trên một dây đàn hồi;

b) Sóng trên dây khi vận động viên

thực hiện bài tập thể dục

VẬT LÍ 11

Bước sóng và tốc độ truyền sóng

Xét si dây có mt đu đưc gn c đnh, mt đu đưc ni

vi ngun dao đng. Cho ngun dao đng điu hoà và ghi

nhn v trí ca tng đim trên dây ti nhng thi đim khác

nhau, ta có kt qu đưc minh ho như trong Hình 6.3.

1. Quan sát Hình 6.2, thực hiện các

yêu cầu sau:

a) Cho biết sóng truyền trên dây

là sóng dọc hay sóng ngang.

b) Mô tả chuyển động của từng

điểm trên dây.

Chu kì và tn s ca sóng ln lưt là chu kì và tn s

ca ngun sóng. Biên đ sóng ti mt đim là biên

đ dao đng ca phn t môi trưng ti đim đó.

Phân loi sóng âm theo tn s

– Sóng âm nghe đưc có tần số trong khoảng từ 16 Hz

đến 20 000 Hz.

– Sóng h âm có tần số nhỏ hơn 16 Hz. Sóng hạ âm có

thể được phát ra từ những hiện tượng như động đất, sấm,

núi lửa. Một số loài vật có thể sử dụng sóng hạ âm để giao

tiếp như voi, hà mã,…

– Sóng siêu âm có tần số lớn hơn 20 000 Hz. Một số loài

vật có thể cảm thụ được sóng siêu âm như chó, dơi,…

Quan sát Hình 6.3, hãy:

a) Chỉ ra những điểm trên dây

đang có trạng thái dao động giống

nhau tại thời điểm đang xét.

b) So sánh trạng thái dao động

của điểm D với trạng thái dao

động của nguồn O khi

W ≥ T.

9ӏWUt

O A B

t = 0

t = T

t = 2T

t =

C D

7KӡLÿLӇP

S Hình 6.3. Trng thái dao đng ca mt s v trí trên dây

ti nhng thi đim liên tip

E G H K

VẬT LÍ 11

T Hình 6.3, ta thy sau khong thi gian mt chu kì dao

đng T, sóng đưc truyn t ngun O đn đim D trên dây.

Sau đó, hai đim O và D luôn có cùng trng thái dao đng ti

tng thi đim, nghĩa là chúng dao đng cùng pha vi nhau.

Quãng đưng mà sóng truyn đi đưc trong mt chu kì dao

đng đưc gi là bước sóng, kí hiu là Ȝ. Bưc sóng cũng

chính là khong cách gia hai đim gn nhau nht trên

phương truyn sóng dao đng cùng pha vi nhau. Trong h

SI, bưc sóng có đơn v là mét (m).

Trong khong thi gian 'W, sóng truyn đi đưc quãng

đưng s. Vy tc đ truyn sóng đưc xác đnh bi:

v 

t

(6.1)

Trong h SI, tc đ truyn sóng có đơn v là m/s.

Khi 'W = T thì s = Ȝ, công thc (6.1) đưc vit li thành:

v 



(6.2)

Lưu ý:

– S truyn sóng là s truyền dao động gia các phn t

ca môi trưng truyn sóng. Trong quá trình sóng đưc

truyn đi, mi phn t thc hin dao đng quanh v trí cân

bng xác đnh ca nó.

– Cn phân bit hai khái nim tốc độ truyền sóng vi

tốc độ dao động. Tc đ truyn sóng trong mt môi trưng

xác đnh thưng là hng s. Trong khi đó, tc đ dao đng

là tc đ ca mt cht đim thc hin dao đng quanh v trí

cân bng, là đi lưng bin đi theo thi gian đã đưc kho

sát trong chương Dao đng.

– Sóng truyn trong không gian vi tc đ hu hn. Tc đ

truyn sóng ph thuc vào đc tính ca môi trưng truyn

như mt đ môi trưng, tính đàn hi, nhit đ, áp sut,…

– Tuy tc đ truyn sóng ph thuc tính cht ca môi

trưng truyn sóng, nhưng tn s sóng không ph thuc

vào môi trưng truyn sóng.

3. Tốc độ truyền sóng trong môi

trường nhanh hay chậm có phụ

thuộc tốc độ dao động tại chỗ của

các phần tử môi trường không?

Bưc sóng là quãng đưng sóng truyn đi đưc trong

mt chu kì dao đng.



 vT

Tc đ truyn sóng đưc xác đnh bng thương s gia

quãng đưng sóng truyn đi đưc và thi gian đ sóng

truyn đi quãng đưng đó.

v 

t

VẬT LÍ 11

Một bạn học sinh đang câu cá trên hồ nước. Khi có sóng đi qua, bạn quan sát thấy phao

câu cá nhô lên cao 6 lần trong 4 s. Biết tốc độ truyền sóng là 0,5 m/s. Tính khoảng cách

giữa hai đỉnh sóng liên tiếp.

 20

C và áp sut khí quyn (1 atm), sóng âm truyn trong

không khí vi tc đ là 343 m/s, trong nưc là 1 482 m/s,

trong nhôm là 6 420 m/s. Trong khi đó, tc đ ánh sáng có

giá tr khong 3.10

m/s trong chân không và thay đi tuỳ

vào môi trưng truyn ánh sáng.

Ví dụ: Sóng âm có tn s ln hơn 20 000 Hz (sóng siêu âm)

đưc s dng trong chn đoán hình nh y khoa (Hình 6.4).

Đ sóng siêu âm có tn s 1,5.10

Hz có th truyn xuyên qua

mô ca cơ th ngưi và cho hình nh rõ nét, bưc sóng ca

sóng siêu âm này không đưc ln hơn 1,0 mm. Xác đnh điu

kin v tc đ ca sóng siêu âm này.

Bài giải

T biu thc (6.2), ta có:





10,mm

Suy ra điu kin v tc đ ca sóng siêu âm này là:

v ≤ 1,5.10

m/s.

Hình 6.4. Chn đoán hình nh

bng siêu âm

Cường độ sóng

Ta đã bit quá trình truyn sóng là quá trình truyn năng

lưng. Ti mt v trí trên phương truyn sóng, đ mnh yu

ca sóng đưc đnh nghĩa bi đi lưng cường độ sóng.

Cưng đ sóng I là năng lưng sóng truyn qua mt

đơn v din tích vuông góc vi phương truyn sóng

trong mt đơn v thi gian.

St S





(6.3)

Trong h SI, cưng đ sóng có đơn v là W/m

Trong công thc (6.3),

P 

t

và S ln lưt là công sut ca

sóng (tính theo W) và din tích mà năng lưng sóng E (tính

theo J) truyn qua trong khong thi gian ∆t (tính theo s).

4. Từ ví dụ về tốc độ truyền sóng âm

trong các môi trường rắn, lỏng và

khí, hãy rút ra nhận xét và giải

thích sự khác nhau này.

VẬT LÍ 11

S Hình 6.5. Năng lưng sóng truyn

qua mt cu có bán kính khác nhau

0һWVyQJFҫX

1JXӗQVyQJ

Biết cường độ ánh sáng của Mặt Trời đo được tại Trái Đất là 1,37.10

W/m

và khoảng cách từ

Mặt Trời đến Trái Đất là 1,50.10

m. Hãy tính công suất bức xạ sóng ánh sáng của Mặt Trời.

PHƯƠNG TRÌNH SÓNG

Gi s ngun sóng O dao đng điu hoà theo phương vuông

góc vi trc Ox, có li đ đưc mô t bi phương trình:

uA t





cos



(6.4)

vi A là biên đ dao đng và Ȧlà tn s góc.

Xét mt đim M trên dây vi

OM x

, sóng cn mt thi

gian W

đ truyn t O đn M. Như vy li đ dao đng

ti

đim M vào thi đim t bng li đ dao đng ti đim O

vào thi đim



. Do đó, phương trình li đ ca đim M

đưc vit:

uA A

 











































2

(6.5)

X(cm)

W (s)

–A

S Hình 6.6.

a) Đồ thị li độ – khoảng cách của dây tại

một thời điểm sóng trên dây ổn định;

b) Đồ thị li độ – thời gian của điểm M trên

dây, cách nguồn sóng một đoạn x

[(cm)

(cm)

–A

Ví dụ: Mt còi báo đng có kích thưc nh phát sóng âm

trong môi trưng đng cht, đng hưng.  v trí cách còi

mt đon 15 m, cưng đ sóng âm là 0,25 W/m

. Xem gn

đúng sóng âm không b môi trưng hp th.  khong

cách nào t v trí ca còi thì sóng âm có cưng đ bng

0,010 W/m

Bài giải

Vì ngun âm đưc xem như là mt đim nên cưng đ sóng

âm trên mt mt cu có din tích S = 4Sr

(Hình 6.5) là

như nhau, vi r là bán kính mt cu (cũng là khong cách t

đim đang xét đn còi).

Ti v trí r

= 15 m và r

, ta có:





và





Suy ra:

025

0 010

75 ;

Vy  khong cách 75 m tính t v trí ca còi thì sóng âm có

cưng đ bng 0,010 W/m

VẬT LÍ 11

Trong phương trình (6.6), W và T ln lưt là thi đim đang

xét và chu kì sóng (tính theo s), x và Oln lưt là khong cách

t mt đim trên dây đn ngun và bưc sóng (tính theo m).

Ta có mt s nhn xét sau:

– Phương trình (6.6) có tính tun hoàn theo không gian vi

chu kì Ȝ (Hình 6.6a) và theo thi gian vi chu kì T (Hình 6.6b).

– Ti cùng mt thi đim, dao đng ti đim M tr pha hơn

dao đng ti ngun mt góc





(vi x là khong cách t

đim M đn ngun).

Ví dụ: Sóng truyn trên mt nưc  mt h nưc đưc mô

t bi phương trình u = 3,75cos(5,4t – 0,45x), trong đó u và x

đưc tính bng xentimét (cm) và t đưc tính bng giây (s).

Tính tc đ truyn sóng.

Bài giải

So sánh phương trình đã cho vi phương trình (6.6), ta có:







và

045









Tc đ truyn sóng là:

v  





0,45

5,4

cm/s.

Phương trình sóng truyn theo trc Ox là:

 













cos

22



(6.6)

5. Từ phương trình (6.6), xác định

khoảng cách giữa hai điểm gần

nhau nhất dao động cùng pha và

khoảng cách giữa hai điểm gần

nhau nhất dao động ngược pha

(theo bước sóng).

6. Quan sát Hình 6.3, xác định độ

lệch pha của hai điểm A và B

trên cùng phương truyền sóng

vào thời điểm

Giải thích vì sao ở Hình 6.6a, đường biểu diễn có một đoạn nằm ngang sau vị trí có toạ độ x

và ở Hình 6.6b, đường biểu diễn có một đoạn nằm ngang trước thời điểm t

Đề xuất phương án thí nghiệm và thực hiện thí nghiệm đơn giản để tạo ra sóng truyền trên một sợi dây và xác

định các đại lượng đặc trưng của sóng như chu kì, tần số.

Đ richter

Độ richter, được đề xuất khoảng năm 1935 bởi nhà vật lí Charles F. Richter (1900 – 1985),

là đơn vị được dùng để đánh giá độ lớn của cường độ (hay năng lượng phát ra) của các

trận động đất. Theo thang richter, biên độ sóng được tính theo thang logarithm, nghĩa

là biên độ sóng động đất ở độ 6 richter bằng 10 lần biên độ sóng động đất ở độ

5 richter.

– Độ richter nhỏ hơn 4,0: Động đất nhẹ, cảm nhận được nhưng ít gây thiệt hại.

– Độ richter từ 4,0 đến 6,0: Động đất trung bình, có thể gây thiệt hại cho các kiến trúc

không theo tiêu chuẩn phòng ngừa địa chấn.

VẬT LÍ 11

– Độ richter từ trên 6,0: Động đất mạnh và rất mạnh. Có thể có sức tàn phá nghiêm trọng.

Ở Việt Nam, hai trận động đất mạnh nhất ghi nhận được là trận động đất 6,8 độ richter tại

Điện Biên vào năm 1935 và trận động đất mạnh 6,7 độ richter tại Lai Châu vào năm 1983.

Trận động đất 9,5 độ richter xảy ra tại Chile vào năm 1960, được xem là trận động đất mạnh

nhất trên thế giới cho đến năm 2023.

Mc cưng đ âm

Trên thực tế, khi đề cập đến độ to của âm. Ta thường sử dụng khái niệm mc cưng đ âm.

Đối với cảm nhận của tai người, độ to của âm được đo bởi đại lượng mc cưng đ âm, tính

theo hàm logarithm cơ số 10 của tỉ số giữa cường độ âm I và cường độ âm chuẩn I

(6.7)

Mức cường độ âm có đơn vị là đêxiben (dB).

= 10

–12

W/m

là cường độ âm nhỏ nhất tai người có thể nghe được ở tần số 1

000 Hz.

Tai người có thể nghe được âm có cường độ từ 10

–12

W/m

đến 10

W/m

(ngưỡng đau).

Mức cường độ âm của cuộc nói chuyện bình thường khoảng 65 dB.

1. Khi đi biển, các thuỷ thủ trên thuyền có thể sử dụng kĩ thuật

sonar (một kĩ thuật phát ra sóng siêu âm) dùng để định vị

hay điều hướng thuyền nhằm tránh các tảng đá ngầm hoặc

phát hiện đàn cá (Hình 6P.1). Trong tự nhiên, nhiều loài động

vật như dơi, cá heo cũng có thể phát ra sóng siêu âm để di

chuyển và định vị con mồi. Kĩ thuật sonar sử dụng tính chất

nào của sóng? Theo em, sóng siêu âm do các tàu thuyền phát

ra có ảnh hưởng như thế nào đối với loài cá heo và cá voi?

S Hình 6P.1. S dng kĩ thut

sonar đ phát hin đàn cá

dưi bin

%j,7t3

2. Hai điểm gần nhất trên cùng phương truyền sóng dao động lệch pha nhau một góc

cách

nhau 60 cm. Biết tốc độ truyền sóng là 330 m/s. Tìm độ lệch pha:

a) giữa hai điểm trên cùng phương truyền sóng, cách nhau 360 cm tại cùng một thời điểm.

b) tại cùng một điểm trên phương truyền sóng sau một khoảng thời gian là 0,1 s.

3. Một sóng truyền trên một dây rất dài có phương trình:





10 2001co

s,

Trong đó u và x được tính bằng cm và t được tính bằng s. Hãy xác định:

a) Chu kì, tần số và biên độ sóng.

b) Bước sóng và tốc độ truyền sóng.

c) Giá trị của li độ u, tại điểm có x = 50 cm vào thời điểm t = 4s.

VẬT LÍ 11

ĐNH NGHĨA VÀ TÍNH CHT CA SÓNG ĐIN T

Định nghĩa sóng điện từ

Sóng đin t là s lan truyn ca đin trưng bin thiên và

t trưng bin thiên trong không gian. Trong quá trình lan

truyn, các thành phn vectơ đc trưng cho đin trưng và

t trưng dao đng cùng pha, vuông góc vi nhau và vuông

góc vi phương truyn sóng đin t như Hình 7.1. Do đó,

sóng đin t là sóng ngang.

%ѭӟFVyQJ

9HFWѫFѭӡQJÿӝÿLӋQWUѭӡQJ

9HFWѫFҧPӭQJWӯ

3KѭѫQJWUX\ӅQVyQJ

S Hình 7.1. S lan truyn ca sóng đin t

Sóng đin t là s lan truyn trong không gian ca

đin t trưng bin thiên. Ánh sáng có bn cht là

sóng đin t.

Tính chất của sóng điện từ

Sóng đin t có mt s tính cht sau:

– Tc đ truyn sóng ca sóng đin t trong chân không là

c = 3.10

m/s. Trong không khí, ta có th ly gn đúng tc

đ này bng 3.10

m/s.

Tại một số vùng xa xôi, đôi khi ta không thể sử dụng điện thoại để liên lạc bởi điện thoại đang nằm ngoài vùng

phủ sóng của đài phát sóng. Vậy sóng mà các đài phát sóng di động đang phát là sóng gì và có tính chất như thế nào?

1. So sánh sóng điện từ và sóng cơ

về: môi trường truyền, tốc độ

truyền, sóng ngang hay sóng dọc.

61*ô,177

Bài

Sóng điện từ và thang sóng điện từ.

VẬT LÍ 11

– Trong mi môi trưng vt cht, tc đ truyn ca sóng

đin t đu nh hơn c. Ví d: sóng đin t có tc đ truyn

xp x bng 2,25.10

m/s trong nưc và 1,24.10

m/s trong

kim cương.

– Mt s hin tưng đc trưng ca sóng đin t là: phn x,

khúc x, nhiu x,...

Lưu ý: Khi truyn qua các môi trưng khác nhau, tn s và

chu kì ca sóng đin t không thay đi.

Chit sut ca môi trưng

Tỉ số giữa tốc độ truyền sóng điện từ trong chân

không c và trong một môi trường xác định v được gọi là

chiết suất của môi trường đó:

(7.1)

Như vậy chiết suất của một môi trường luôn lớn hơn

hoặc bằng 1.

THANG SÓNG ĐIN T

Sóng đin t có th đưc phân loi da vào bưc sóng hoc

tn s (Hình 7.2).

3. Dựa vào Hình 7.2 và cho biết

bước sóng của vùng ánh sáng

nhìn thấy.

2. Khi sóng điện từ truyền qua

hai môi trường khác nhau,

bước sóng của nó có bị thay

đổi không? Giải thích.

 t ca các sóng đin t có bưc sóng t nh đn ln là:

Tia J(tia gamma), tia X hay tia Röntgen (Rơn-ghen), tia t

ngoi, ánh sáng nhìn thy tri dài t ánh sáng tím đn đ,

tia hng ngoi, các sóng vô tuyn (gm vi sóng – microwave,

các sóng FM, AM và các sóng có bưc sóng dài hơn).

4. Dựa vào số liệu trong Hình 7.2,

xác định tần số của ánh sáng

nhìn thấy.

Thang sóng đin t cho bit di bưc sóng và di tn s ng vi các loi bc x

khác nhau.

S Hình 7.2. Thang sóng đin t

Tia Jgamma) Tia X Hồng ngoại Sóng vô tuyến dàiVi sóngUV

–16

–14

–12

–11

–3

–10

–6

–8

–4

–2

Ȝ (m)

ÈQKViQJQKuQWKҩ\NKҧNLӃQ

7ҫQVӕWăQJGҫQ

%ѭӟFVyQJWăQJGҫQ

Tím – chàm

380

450

495

570

590

620

760

/DP /өF &DP Ĉӓ9jQJ

ȜQP

I (Hz)

Sóng vô tuyến

7ӱQJRҥL

VẬT LÍ 11

Các sóng đin t có bưc sóng càng nh thì mang năng lưng

càng ln. Đó là lí do tia X và tia J có kh năng đâm xuyên

mnh. Kh năng đâm xuyên này ph thuc vào khi lưng

nguyên t ca vt cht mà các tia này chiu đn. Khi lưng

nguyên t này càng ln thì kh năng đâm xuyên ca tia X và

tia J càng gim đi. Tính cht này đưc áp dng trong kĩ thut

chp nh bng tia X trong y khoa (Hình 7.3). Trong khi đó,

các sóng vô tuyn đưc s dng rng rãi trong quá trình thu

và phát sóng ca đin thoi di đng.

Vào thời điểm năm 2022, điện thoại di động ở Việt Nam sử dụng sóng điện từ có tần số

trong khoảng từ 850 MHz đến 2 600 MHz. Tính bước sóng của sóng điện từ tương ứng với

dải tần số này. Mắt chúng ta có thể thấy được các sóng này không? Vì sao?

Tìm hiểu và giải thích vì sao khi sử dụng tia X để chụp ảnh trong y khoa như Hình 7.3, ta có thể thấy được

xương của bàn tay.

Hình 7.3. Hình chp X-quang

bàn tay

1. Hình 7P.1 mô tả các hiện tượng xảy ra đối với sóng

vô tuyến có các tần số khác nhau do tác dụng của tầng

điện li ở khí quyển.

a) Gọi tên các hiện tượng liên quan đến sóng vô tuyến có

tần số 5 MHz và 100 MHz.

b) Giải thích vì sao các sóng vô tuyến ngắn được sử dụng để

truyền thông tin trên mặt đất.

2. Các tia UV-A (có bước sóng trong khoảng từ 320 nm đến 400 nm) trong ánh sáng mặt trời có

thể có tác dụng sinh học tốt như kích thích sự sản sinh vitamin D. Nhưng các tia UV-B có bước

sóng trong khoảng từ 280 nm đến 320 nm lại có thể nguy hiểm như gây ung thư da.

Bằng cách tra cứu sách, báo, hãy lập biểu đồ cho biết ở địa phương em, trong khoảng thời gian

nào của một năm và thời gian nào trong ngày ta cần phải phòng tránh tia UV-B.

3. Một vệ tinh nhân tạo chuyển động ở độ cao 575 km so với mặt đất phát sóng vô tuyến có tần số

92,4 MHz với công suất bằng 25,0 kW về phía mặt đất. Hãy tính cường độ sóng nhận được bởi

một máy thu vô tuyến ở mặt đất ngay phía dưới vệ tinh. Bỏ qua sự hấp thụ sóng của khí quyển.

%j,7t3

S Hình 7P.1. S lan truyn

sóng vô tuyn trong khí quyn

100 MHz

5 MHz

7ҫQJÿLӋQOL

VẬT LÍ 11

Hình 8.1 cho thấy hình ảnh sóng trên mặt nước là kết quả của sự

chồng chất sóng do hai con vịt tạo ra khi bơi. Trong một số trường hợp, sự

chồng chất sóng này dẫn đến một hiện tượng thú vị: có những điểm trên

mặt nước dao động mạnh và những điểm dao động yếu hoặc đứng yên.

Vậy hiện tượng đó là gì và điều kiện nào để hiện tượng này xảy ra?

GIAO THOA SÓNG CƠ

Thí nghiệm khảo sát hiện tượng giao thoa sóng

* Mục đích: Kho sát đnh tính hin tưng sóng trên mt

nưc khi có hai ngun dao đng cùng tn s và cùng pha

đt gn nhau.

* Dụng cụ:

– Khay nưc (1), đèn chiu (2), màn (3).

– Hai viên bi nh (4) gn vào cùng mt cn rung.

– Máy phát tn s (5).

– Gương phng (6).

* Tiến hành thí nghiệm:

Bước 1: B trí thí nghim như Hình 8.2.

Bước 2: Gn hai viên bi vào cn rung và ni cn rung vào

máy phát tn s.

Bước 3: Đt hai viên bi sao cho chúng kh chm vào mt nưc.

Bước 4: Bt đèn chiu. Bt máy phát tn s đ hai viên bi dao

đng theo phương thng đng là hai ngun to ra sóng lan

truyn trên mt nưc.

Bước 5: Điu chnh tn s đ quan sát rõ hin tưng.

* Báo cáo kết quả thí nghiệm: Quan sát hình nh sóng

nưc đưc chiu lên màn và rút ra kt lun.

1. Quan sát thí nghiệm và mô tả lại

hiện tượng quan sát được như

trong Hình 8.3.

*,$27+2$61*

Bài

– Giao thoa sóng cơ và giao thoa sóng ánh sáng.

– Công thức tính khoảng vân trong giao thoa ánh sáng qua hai khe hẹp.

S Hình 8.1. Sóng nưc do hai con vt to ra

S Hình 8.3. Hình nh giao thoa sóng

nưc thu đưc trên màn

S Hình 8.2. B trí thí nghim

kho sát hin tưng giao thoa sóng nưc

(5)

(2)

(1)

(6)

(3)

(4)

VẬT LÍ 11

Hiện tượng giao thoa sóng

Trong thí nghim giao thoa sóng (Hình 8.2), hai sóng trên

mt nưc đưc sinh ra t s dao đng ca hai viên bi có cùng

phương dao đng, cùng tn s và cùng pha vi nhau do đưc

ni vào cùng mt ngun dao đng. Hai viên bi đóng vai trò

như hai nguồn kết hợp. Hai sóng đưc to ra t hai ngun

kt hp đưc gi là hai sóng kt hp. Tng quát, hai sóng kt

hp là hai sóng có cùng phương dao đng, cùng tn s và đ

lch pha không đi theo thi gian.

Khi hai sóng kt hp gp nhau, trong môi trưng xut hin

nhng đim dao đng vi biên đ cc đi và nhng đim

dao đng vi biên đ cc tiu (có th bng không) ln lưt

tương ng vi trưng hp hai sóng tăng cưng (hai sóng

cùng pha ti nhng đim này) và làm suy gim nhau (hai

sóng ngưc pha ti nhng đim này). Đây chính là hin

tưng giao thoa sóng.

Hin tưng giao thoa sóng là hin tưng hai sóng kt

hp gp nhau, tăng cưng nhau hoc làm suy yu nhau

ti mt s v trí trong môi trưng. Điu kin đ có giao

thoa là phi có s kt hp t hai ngun sóng dao đng

cùng phương, cùng tn s và có đ lch pha không đi

theo thi gian.

2. Quan sát thí nghiệm được thực

hiện theo bố trí trong Hình 8.2

và nhận xét sóng tạo bởi hai

viên bi về: tần số, pha và

phương dao động.

Hin tưng giao thoa là hin tưng đc trưng ca sóng.

Nghĩa là ch có nhng đi tưng vt lí có bn cht sóng mi có

th sinh ra hin tưng này. Ngưc li, khi ta quan sát đưc hin

tưng giao thoa trong mt vùng không gian thì ta có th kt

lun trong vùng không gian đó có s tn ti ca sóng.

Trong môi trưng truyn sóng, khi hai ngun dao đng

cùng pha, nhng đim có khong cách đn hai ngun

ln lưt là d

và d

s dao đng vi biên đ cc đi khi:

– d

= NȜ(8.1)

và dao đng vi biên đ cc tiu khi:

dd k

 















(8.2)

vi k là mt s nguyên (k = 0, ±1, ±2,…).

Hình 8.4 minh ho tp hp nhng đim có biên đ sóng

tng hp đt cc đi (đưng màu đ) và cc tiu (đưng

màu xanh) ln lưt tương ng vi nhng v trí mà hai sóng

thành phn tăng cưng nhau hoc làm suy gim nhau.

VẬT LÍ 11

Trong thí nghiệm giao thoa sóng trên mặt nước

với hai nguồn kết hợp dao động cùng biên độ,

những điểm nằm trên đường trung trực của

đoạn thẳng nối hai nguồn sẽ dao động với biên

độ như thế nào nếu:

a) hai nguồn dao động cùng pha?

b) hai nguồn dao động ngược pha?

Giải thích vì sao trong tự nhiên, ta

thường không quan sát được hiện

tượng giao thoa của sóng như

trường hợp sóng nước tạo bởi hai

con vịt đang bơi (Hình 8.1).

Xác đnh v trí các vân giao thoa

Trong thí nghiệm giao thoa sóng (Hình 8.2), gọi S

và S

lần lượt là hai nguồn (hai viên bi)

dao động cùng biên độ A, cùng pha, cùng tần số f và có phương trình li độ:

uu AtA

 



















(8.3)

Xét một điểm M trên mặt nước cách S

một đoạn S

M = d

và cách S

một đoạn S

M = d

như Hình 8.5. Xem biên độ

dao động không thay đổi trong quá trình truyền sóng, theo

công thức (8.3), dao động u

và u

truyền đến M lần lượt có

phương trình:

và



























cos





(8.4)

S Hình 8.5. Đưng truyn

ca hai sóng t hai ngun

dao đng S

và S

đn M

W Hình 8.4. V trí ca các

đim cc đi, cc tiu

trong giao thoa sóng nưc

&ӵFÿҥL

WUXQJWkP

FӵFÿҥLEұF

&ӵFWLӇX

WKӭ

&ӵFÿҥL

EұF

&ӵFÿҥL

EұF

&ӵFÿҥL

EұF

&ӵFÿҥL

EұF

&ӵFÿҥL

EұF

&ӵFWLӇX

WKӭ

&ӵFWLӇX

WKӭ

&ӵFWLӇX

WKӭ

&ӵFWLӇX

WKӭ

&ӵFWLӇX

WKӭ

&ӵFÿҥL

EұF

VẬT LÍ 11

GIAO THOA SÓNG ÁNH SÁNG

Thí nghiệm Young về giao thoa ánh sáng

Ta đã bit, ánh sáng có bn cht sóng nên có th gây ra hin

tưng giao thoa. Có nhiu cách khác nhau đ to ra hin

tưng giao thoa ánh sáng, trong đó có phương án s dng

hai khe hp (đưc gi là khe Young) do omas Young

(o-mát Y-âng) (1773 – 1829) đ xut.

3. Quan sát Hình 8.6 và mô tả hình

ảnh nhận được trên màn M.

với





là bước sóng; v là tốc độ truyền sóng trên mặt nước.

Ta có phương trình li độ sóng tổng hợp tại điểm M có dạng:

uu u

MMM

































coscos









(8.5)

Độ lệch pha của hai dao động thành phần tại M:











( )

(8.6)

Biên độ sóng tổng hợp tại M:

















cos 



(8.7)

– A

đạt cực đại nếu hai dao động thành phần cùng pha:





 2k

, với k = 0, ±1, ±2,…

Do đó:

ddk





(8.8)

– A

đạt cực tiểu nếu hai dao động thành phần ngược pha:





()21k 

, với k = 0, ±1, ±2,…

Do đó:

 















(8.9)

S Hình 8.6. Thí nghim giao thoa khe Young s dng ngun laser đ

0jQ0

+DLNKH6

Yj6

VẬT LÍ 11

í nghim giao thoa ánh sáng đưc b trí như trong

Hình 8.6, trong đó ánh sáng t ngun laser đ s đn hai

khe rt nh S

và S

đưc đt rt gn nhau. Trên màn M

đt song song vi mt phng cha hai khe, ta quan sát thy

mt vùng sáng hp, trong đó xut hin nhng vch sáng

màu đ và các vch ti xen k, cách đu nhau và song song

vi hai khe (Hình 8.6).

Hin tưng quan sát đưc trong thí nghim minh ho trên

Hình 8.6 là hin tưng giao thoa ánh sáng. Các vch sáng,

vch ti đưc gi là vân giao thoa. Vch sáng ng vi biên

đ dao đng tng hp cc đi đưc gi là vân sáng, vch

ti ng vi biên đ dao đng tng hp cc tiu đưc gi là

vân tối.

Hin tưng giao thoa ánh sáng là hin tưng xut

hin các vch sáng xen k vi các vch ti khi hai

sóng ánh sáng kt hp gp nhau.

Khoảng vân và vị trí vân giao thoa trên màn

Trong sơ đ thí nghim Young v giao thoa ánh sáng (Hình 8.7),

xét đim A trên màn quan sát có to đ xác đnh bi

OA x

Đt S

= a, IO = D (khong cách t mt phng cha hai khe

hp đn màn quan sát M), S

A = d

và S

A = d

. Đ quan sát

rõ vân giao thoa trên màn, a phi rt nh so vi D (a khong

vài milimét, D khong vài chc hoc vài trăm xentimét).

Vi ánh sáng có bưc sóng Ȝ

– Đim A là vân sáng khi

ddk





, vi k là mt s

nguyên (k = 0, ±1, ±2,…). V trí các vân sáng trên màn đưc

xác đnh:





(8.10)

±ĈLӇPAOjYkQWӕLNKL

dd k

 















YӟLkOjPӝWVӕ

QJX\rQk «9ӏWUtFiFYkQWӕLWUrQPjQÿѭӧF

[iFÿӏQK

















(8.11)

4. Giải thích hiện tượng quan sát

được trong thí nghiệm Young về

giao thoa ánh sáng (Hình 8.6).

S Hình 8.7. V trí ca đim A trên

màn cách các ngun các khong

và d

0jQ0

VẬT LÍ 11

Khong cách gia hai vân sáng (hoc hai vân ti)

liên tip đưc gi là khoảng vân, kí hiu làL.





(8.12)

Trên màn giao thoa, vân sáng có v trí:

= NL (8.13)

và vân ti có v trí:

xk i















(8.14)

vi k là mt s nguyên (k = 0, ±1, ±2,…).

Vận dụng hiện tượng giao thoa ánh sáng

Ví dụ: Trong thí nghim Young v giao thoa ánh sáng,

khi ngun sáng là ánh sáng đơn sc có bưc sóng Ȝ,

ngưi ta đo khong cách gia 9 vân sáng liên tip là

25,3 mm. Cho bit khong cách gia hai khe là 0,200 mm và

khong cách t hai khe đn màn là 1 m.

a) Tính bưc sóng Ȝ.

b) Tính khong cách t vân sáng bc hai đn vân ti th tư

 cùng bên so vi vân sáng trung tâm (vân sáng cách đu

hai khe sáng).

Bài giải

a) Ta có: 8i = 25,3 mm, suy ra i = 3,16 mm.

T công thc (8.12), suy ra:



 





0 200 10 31610

0 632 10

,.., .

,. m

= 632 nm

b) Khong cách t vân sáng bc hai đn vân ti th tư  cùng

bên so vi vân sáng trung tâm là:

3,5i – 2i = 1,5i = 1,5.3,16 = 4,74 mm.

Tìm hiểu và mô tả sơ lược hình ảnh nhận được trên màn khi ta sử dụng nguồn sáng trắng (như ánh sáng mặt trời)

trong thí nghiệm Young về giao thoa ánh sáng.

Trong thí nghiệm Young về giao thoa ánh sáng, khoảng vân sẽ thay đổi thế nào

khi ta thay nguồn sáng đơn sắc có bước sóng Ȝ bằng ánh sáng đơn sắc có bước

sóng là 1,2Ȝ? Nếu khoảng cách từ hai khe đến màn quan sát giữ cố định, ta phải

thay đổi khoảng cách giữa hai khe như thế nào để khoảng vân lại có độ lớn như

ban đầu?

VẬT LÍ 11

1. Trong thí nghiệm giao thoa sóng trên mặt nước với hai nguồn kết hợp cùng pha, ta thấy tại một

điểm cách hai nguồn các khoảng lần lượt là 20 cm và 12 cm, sóng có biên độ cực đại, đồng thời

giữa điểm này và đường trung trực của hai nguồn có 4 dãy gồm những điểm dao động với biên

độ cực đại. Biết tốc độ truyền sóng là 40 cm/s. Tính tần số của sóng.

2. Thí nghiệm Young về giao thoa ánh sáng thường được sử dụng để đo bước sóng của ánh sáng

đơn sắc. Khi chiếu hai khe bằng một nguồn phát ánh sáng đơn sắc, ta thấy vân sáng thứ năm

cách vân trung tâm là 2,8 cm. Biết hai khe đặt cách nhau 0,2 mm và cách màn một khoảng

1,5 m. Xác định bước sóng của ánh sáng được dùng trong thí nghiệm.

3. Trong thí nghiệm Young về giao thoa ánh sáng, người ta sử dụng một nguồn sáng phát ra đồng

thời hai ánh sáng đơn sắc có bước sóng lần lượt là 400 nm và 600 nm. Biết khoảng cách giữa hai

khe là 0,2 mm và khoảng cách từ hai khe đến màn là 1,5 m.

a) Tính khoảng cách giữa hai vân sáng bậc ba cùng phía với vân trung tâm.

b) Vân trung tâm có màu gì? Tìm khoảng cách gần nhất của một vân cùng màu với vân trung tâm

cho đến vân trung tâm này.

%j,7t3

VẬT LÍ 11

61*'1*9

Bài

– Thí nghiệm tạo sóng dừng và giải thích sự hình thành sóng dừng.

– Xác định vị trí nút và bụng của sóng dừng.

Khi gảy đàn guitar, ta quan sát được dây đàn rung và tạo

thành các múi như Hình 9.1. Trong điều kiện nào thì ta có thể

quan sát được hiện tượng được gọi là sóng dừng này?

S PHN X SÓNG

Sự phản xạ sóng

Xét sóng truyn trên mt si dây có mt đu đưc

buc vào đim c đnh (Hình 9.2a) hoc đưc đ t do

(Hình 9.2b).

1. Quan sát Hình 9.2 và nhận xét

chiều biến dạng của dây khi có

sóng tới và sóng phản xạ trong

hai trường hợp: đầu dây cố định

và đầu dây tự do.

Khi gp vt cn, sóng s b phn x. Sóng đưc truyn t ngun phát đn vt cn đưc gi là

sóng tới, sóng đưc truyn ngưc li t vt cn đưc gi là sóng phản xạ.

c nghim chng t, sóng phn x có cùng tn s và bưc sóng vi sóng ti.

Trong trưng hp đu dây c đnh, ti đim phn x, sóng phn x ngưc pha vi sóng ti

(Hình 9.2a); trong trưng hp đu dây t do, sóng phn x cùng pha vi sóng ti (Hình 9.2b).

Hình 9.1. Hình nh dây đàn guitar khi đưc gy

S Hình 9.2. Quá trình phn x sóng trong trưng hp:

a) Đầu dây cố định; b) Đầu dây tự do

6yQJ

WӟL

6yQJ

WӟL

6yQJ

SKҧQ

[ҥ

6yQJ

SKҧQ

[ҥ

a) b)

ĈҫXGk\FӕÿӏQK ĈҫXGk\WӵGR

VẬT LÍ 11

HIN TƯNG SÓNG DNG

Thí nghiệm khảo sát hiện tượng sóng dừng

* Mục đích: Kho sát đnh tính hin tưng sóng dng.

* Dụng cụ:

– Si dây AB không dãn, đàn hi, có chiu dài khong 65 cm (1).

– H thng giá đ (2).

– ưc thng có đ chia nh nht là 1 mm (3).

– Máy phát tn s (4).

* Tiến hành thí nghiệm:

Bước 1: B trí thí nghim như Hình 9.3.

Bước 2: Ni đu dây A vào máy phát tn s, đu còn li ca

dây đưc gn c đnh vào giá đ.

Bước 3: Bt máy phát tn s, điu chnh tn s dao đng phù

hp đ xut hin hình nh sóng n đnh.

Bước 4: Điu chnh tn s máy phát; điu chnh chiu dài

ca dây đ thay đi hình dng sóng n đnh trên dây.

* Báo cáo kết quả thí nghiệm:

Quan sát hình nh sóng n đnh đưc hình thành trên dây.

Xác đnh s lưng và v trí ca nhng đim dao đng vi

biên đ cc đi và cc tiu trên dây tương ng vi các giá tr

tn s và chiu dài dây khác nhau.

Giải thích hiện tượng sóng dừng

Trong thí nghim trên, ta thy khi hình nh sóng đưc to

ra trên dây n đnh, trên dây xut hin nhng đim c đnh

dao đng vi biên đ ln nht (bng sóng) và xen k vi

nhng đim đng yên (nút sóng) (Hình 9.4).

Ti bng sóng, sóng ti và sóng phn x cùng pha; ti nút

sóng, sóng ti và sóng phn x ngưc pha. Sóng có các

nút sóng và bng sóng c đnh trong không gian gi là

sóng dừng.

Xét mt đim M trên mt dây đàn hi AB, đu A ca dây

gn vào nhánh ca mt ngun phát dao đng thng đng

vi biên đ nh đ to ra sóng ngang trên dây, đu B gn vào

mt đim c đnh (Hình 9.3). Ti mt đim M cách B mt

2. Nhận xét về sự phụ thuộc của

số lượng điểm cực đại, cực tiểu

trên dây với tần số của máy phát

tần số.

S Hình 9.3. B trí thí nghim

kho sát hin tưng sóng dng

(3)

(1)

(4)

(2)

S Hình 9.4. Hình dng n đnh ca

si dây khi có sóng dng

Nút

VyQJ

%өQJ

VyQJ

VẬT LÍ 11

3. Dựa vào sự hình thành của các

điểm dao động với biên độ cực đại

và cực tiểu trong hiện tượng giao

thoa, hãy dự đoán nguyên nhân

hình thành bụng sóng và nút sóng

trong hiện tượng sóng dừng.

đon MB = d, ta có s chng cht ca sóng ti t A và sóng

phn x t B. Khi sóng dng xut hin trên dây (Hình 9.4),

sóng tng hp ti đim M trên dây có cùng tn s vi sóng

ti và sóng phn x, có biên đ ph thuc vào khong cách

t đim M đn đu c đnh ca dây.















2

cos





(9.1).

trong đó O là bưc sóng ca sóng truyn trên dây.

Ta có:

* Vị trí bụng sóng: là nhng đim dao đng vi biên đ cc

đi A

= 2A tương ng vi:

dk















(k = 0, 1, 2,…) (9.2)

* Vị trí nút sóng: là nhng đim đng yên A

= 0 tương

ng vi:





(k = 0, 1, 2,…) (9.3)

Sóng dng là sóng có các nút sóng và bng sóng c đnh trong không gian.

Khi có hin tưng sóng dng, trên dây xut hin nhng đim dao đng vi biên đ

cc đi đưc gi là bụng sóng và nhng đim đng yên đưc gi là nút sóng.

V trí các bng sóng đưc xác đnh bng biu thc:

(k = 0, 1, 2,…)

dk















V trí các nút sóng đưc xác đnh bng biu thc:

(k = 0, 1, 2,…)





Trong đó, d là khong cách t mt đim trên dây đn mt đu dây.

Bng sóng và nút sóng xen k và cách đu nhau. Dc theo dây, hai nút sóng liên tip

hoc hai bng sóng liên tip cách nhau mt khong bng na bưc sóng.

Kho sát đnh lưng hin tưng sóng dng

Chọn gốc toạ độ O tại B, chiều dương của trục Ox từ B đến M. Gốc thời gian được chọn ngay

thời điểm sóng tới đến B và có phương trình:

uA tA ft



 



2

(9.4)

với f là tần số của nguồn phát sóng.

VẬT LÍ 11

ĐIU KIN Đ CÓ SÓNG DNG

Trường hợp sợi dây có hai đầu cố định

Đi vi si dây có hai đu c đnh hoc mt đu c đnh và

mt đu dao đng vi biên đ nh thì khi có sóng dng, hai

đu dây là hai nút sóng. Ta đã bit khong cách gia hai nút

sóng liên tip bng na bưc sóng. Do đó ta có điu kin

xut hin sóng dng trong trưng hp này là:

A  



(n = 1, 2, 3,…) (9.9)

vi v là tc đ truyn sóng trên dây.

Sóng tới truyền từ M đến B sớm pha hơn tại B và có phương trình:

uA t















cos





2

(9.5)

Do B là vật cản cố định, sóng phản xạ tại B có li độ ngược dấu với li độ của sóng tới và có

phương trình:

uAtA t

Bpx



 

coscos





(9.6)

Sóng phản xạ truyền từ B đến M trễ pha hơn tại B và có phương trình:

uA t

Mpx















cos







2

(9.7)

Khi sóng tới và sóng phản xạ cùng truyền qua M thì ở mỗi thời điểm, dao động tại M là kết

quả của sự chồng chất của sóng tới và sóng phản xạ nên phương trình li độ tổng hợp tại M

được xác định:

uuu

uA t

MM M

































tpx

coscos











Áp dụng công thức lượng giác, ta suy ra:





























coscos

 





(9.8)

Kết luận: Sóng tổng hợp tại điểm M trên dây có cùng tần số với sóng tới và sóng phản xạ, có

biên độ phụ thuộc vào khoảng cách từ điểm M đến đầu cố định của dây.















2

cos





Trên thực tế, sự phản xạ ở hai đầu A và B của dây xảy ra nhiều lần, khi sự cộng hưởng xuất

hiện trên dây, biên độ dao động tại bụng sóng lớn hơn 2A.

VẬT LÍ 11

S Hình 9.5. Đu ngón tay n lên

phím đàn

T công thc (9.9), ta thy vi v và A c đnh, tn s f ca

ngun dao đng phi tho mãn điu kin:

(9.10)

Xét sóng âm, ta có:

+ Khi n = 1:

đưc gi là ho âm bc 1 (âm cơ bn).

+ Tng quát:

fnf

đưc gi là ho âm bc n.

Trưng hp hai đu c đnh thưng gp  mt s nhc c

như đàn guitar, đàn tranh, đàn bu,… Chú ý là các nhc c

này đng thi phát ra âm cơ bn và các ho âm.

Một dây đàn guitar dài 64 cm phát ra âm cơ bản có

tần số Ikhi được gảy. Biết tốc độ truyền sóng trên

dây là 422 m/s.

a) Tính giá trị f.

b) Người chơi đàn ấn đầu ngón tay lên một phím

đàn để tạo thành một vật cản (cố định) làm cho

chiều dài của dây ngắn đi (Hình 9.5). Khoảng cách từ

phím đàn này đến đầu dây là 3,7 cm. Tính tần số âm

cơ bản phát ra bởi dây đàn trong trường hợp này.

Trường hợp sợi dây có một đầu cố định, một đầu tự do

Khi si dây có mt đu c đnh (đưc gn vào ngun phát

dao đng nh) và mt đu t do (vt cn t do), ta đã bit

sóng phn x khi gp vt cn t do cùng pha so vi sóng ti.

Khi xy ra hin tưng sóng dng, đu t do là mt bng

sóng như Hình 9.6. Khong cách gia mt bng sóng và

mt nút sóng lin k là

. Do đó ta có điu kin xut hin

sóng dng trong trưng hp này là:

A  ()21



(m = 1, 3, 5,…) (9.11)

T công thc (9.11), ta thy vi v và A c đnh, tn s f ca

ngun dao đng phi tho mãn điu kin:

(9.12)

Xét sóng âm, ta có:

+ Khi m = 1:

đưc gi là ho âm bc 1 (âm cơ bn).

+ Tng quát:

fmf

đưc gi là ho âm bc m.

%өQJ

VyQJ

Nút

VyQJ

0i\

UXQJ

S Hình 9.6. Mô hình hoá sóng

dng xut hin trên si dây có

mt đu c đnh, mt đu t do

VẬT LÍ 11

Trong thí nghiệm sóng dừng trên sợi dây AB dài 120 cm với đầu B tự do, đầu A được

kích thích để thực hiện dao động với biên độ nhỏ. Ngoài đầu A, trên dây xuất hiện

thêm một nút. Biết tần số sóng là 12,5 Hz.

a) Tính tốc độ truyền sóng.

b) Để có thêm một nút sóng trên dây thì tần số sóng khi này phải bằng bao nhiêu?

S Hình 9.7. Chnh dây đàn guitar

Giải thích vì sao khi vặn khoá để chỉnh dây đàn guitar (Hình 9.7),

ta có thể tạo ra hệ sóng dừng trên dây. Biết tốc độ truyền sóng

trên dây phụ thuộc lực căng dây.

Hiện tượng sóng dừng có thể xảy ra đối với sóng điện từ và

có nhiều ứng dụng trong cuộc sống. Ví dụ trong lò vi sóng

(Hình 9.8), sóng điện từ được phản xạ trên các thành lò

và tạo thành sóng dừng trong lò. Tại những bụng sóng,

năng lượng của sóng điện từ có giá trị lớn nhất và cung

cấp nhiệt cho thực phẩm (từ sự dao động của các phân

tử nước trong thực phẩm). Do đó, trong lò vi sóng còn có

đĩa quay để giúp thực phẩm nóng đều.

S Hình 9.8. Sóng dng hình thành

trong lò vi sóng

Điu kin đ có sóng dng:

– Dây có hai đu c đnh: chiu dài ca si dây phi bng mt s nguyên ln na

bưc sóng.

A  Q



(n = 1, 2, 3,…)

– Dây có mt đu c đnh, mt đu t do: chiu dài ca si dây phi bng mt s l

ln mt phn tư bưc sóng.

A  m



(m = 1, 3, 5,…)

1. Người ta thực hiện thí nghiệm sóng dừng trên một dây đàn hồi có hai đầu cố định dài

75,0 cm để đo tốc độ truyền sóng trên dây. Khi tần số sóng bằng 120 Hz thì trên dây xuất hiện

6 bụng sóng.

a) Tính tốc độ truyền sóng trên dây.

b) Tăng lực căng dây để tăng tốc độ truyền sóng gấp hai lần. Với những giá trị nào của tần số thì

sóng dừng có thể được hình thành trên dây?

2. Trong một thử nghiệm nướng bánh bằng lò vi sóng, người ta đo được khoảng cách giữa hai

phần nóng nhất và gần nhau nhất của bánh là khoảng 6,13 cm. Biết tần số sóng vi ba được sử

dụng trong lò là 2,45 GHz. Sử dụng các số liệu đã cho để ước lượng tốc độ của sóng điện từ.

%j,7t3

VẬT LÍ 11

Trong đời sống hằng ngày, chúng ta có thể nghe âm thanh từ mọi nơi. Ta đã biết âm thanh chính là sóng âm

được lan truyền trong môi trường vật chất. Âm thanh có thể có tần số xác định khi được phát ra từ một số nhạc cụ như

đàn guitar, đàn piano, sáo,… hoặc có tần số không xác định khi được phát ra từ động cơ xe, máy khoan,… Thời gian

âm thanh truyền từ nguồn phát đến tai ta phụ thuộc vào tốc độ truyền sóng âm. Vậy làm thế nào để đo được tần số của

sóng âm và tốc độ truyền âm?

Thí nghiệm đo tần số của sóng âm

* Mục đích: Đo đưc tn s ca sóng âm.

* Dụng cụ:

– Ngun âm (1):

+ Loa đin đng (Hình 10.1a) đưc kt ni vi máy phát

tns.

+ Âm thoa, búa và âm thoa gn trên hp cng hưng

(Hình 10.1b).

– Micro (2) đ chuyn dao đng âm thành dao đng đin.

– Dao đng kí đin t (3).

* Tiến hành thí nghiệm:

1. Dựa vào bộ dụng cụ thí nghiệm,

hãy thiết kế và thực hiện phương

án để đo tần số của sóng âm.

7+&+j1+ô27p16&$

61*o09j7&ô758<1o0

Bài

Thí nghiệm đo tần số của sóng âm và tốc độ truyền âm.

BӇớc 1: B trí thí nghim như Hình 10.2.

BӇớc 2: S dng ngun âm là loa đin đng, đt loa gn

micro (chú ý đm bo không có ngun âm khác  gn).

BӇớc 3: Bt micro và dao đng kí  ch đ làm vic.

(3)

(2)

(1)

S Hình 10.2. B trí thí nghim đo tn s ca sóng âm

a) b)

S Hình 10.1. a) Loa điện động;

b) Búa và âm thoa gắn trên hộp cộng hưởng

VẬT LÍ 11

Bước 4: Bt máy phát tn s.

Bước 5: Điu chnh dao đng kí đ ghi nhn đưc tín hiu.

Lp li bưc 2 đn bưc 5 khi s dng ngun âm là âm thoa.

Lưu ý: ng vi mi loi ngun âm, thc hin thí nghim ít

nht 3 ln.

* Báo cáo kết quả thí nghiệm:

– Da vào đ th dao đng trên màn hình dao đng kí,

ghi kt qu đo vào bng s liu như Bng 10.1.

– T s liu đo đưc, xác đnh tn s sóng âm.

Bảng 10.1. Bng s liu thí nghim đo tn s ca sóng âm

Ngun âm Ln

Chu kì

T (ms)

Tn

s f

(Hz)

Tn s

trung

bình

(Hz)

Sai s

tuyt đi

'f (Hz)

Loa đin

đng

1 – –

– –2 – –

3 – –

Âm thoa

1 – –

– –2 – –

– –

±.ӃWTXҧÿRWҫQVӕVyQJkPSKiWUDWӯ

ÆPWKRD



..................................................

/RDÿLӋQÿӝQJ



.........................................

Hiện nay, ứng dụng SmartScope Oscilloscope trên điện thoại thông minh có thể

được sử dụng để ghi nhận đồ thị dao động âm. Sử dụng ứng dụng này, kết hợp

với ứng dụng quay màn hình điện thoại, hãy tiến hành lại thí nghiệm đo tần số

của sóng âm và so sánh kết quả đo được với kết quả trong phương án thí nghiệm

(sử dụng dao động kí điện tử). Phân tích ưu, nhược điểm của hai phương án này.

Thí nghiệm đo tốc độ truyền âm

* Mục đích: Đo đưc tc đ truyn âm trong không khí.

* Dụng cụ:

– ng cng hưng (1) trong sut bng nha, dài 70 cm,

đưng kính 40 mm, có gn thưc thng.

3. So sánh kết quả tần số đo được

với giá trị tần số được ghi trên

âm thoa hoặc hiển thị trên màn

hình của máy phát tần số. Rút ra

kết luận.

2. Trình bày cách tính sai số tuyệt

đối của phép đo. Liệt kê một số

nguyên nhân gây ra sai số trong

phương án thí nghiệm và đề xuất

cách khắc phục.

VẬT LÍ 11

S Hình 10.3. B trí thí nghim

đo tc đ truyn âm trong

không khí

(3)

(1)

(2)

(5)

(6)

(7)

(4)

5. Liệt kê một số nguyên nhân gây ra

sai số trong phương án thí nghiệm

và đề xuất cách khắc phục.

– Pit-tông bng kim loi bc nha (2), đưng kính 38 mm,

có vch chun xác đnh v trí.

– Dây treo pit-tông (3) dài 1,5 m, mt đu có móc treo,

vt qua ròng rc có đưng kính 40 mm.

– H thng giá đ gm tr thép đc (4), dài 75 cm, đưng

kính 10 mm và đ ba chân bng thép.

– Loa đin đng (4  – 3 W) (5), lp trong hp bo v có

cán bng tr thép và l cm đin.

– Máy phát tn s (0,1 Hz – 1 kHz) (6), tín hiu hình sin,

đin áp ra cc đi 14 V.

– B hai dây ni mch đin (7), dài 50 cm, hai đu có

phích cm.

* Tiến hành thí nghiệm:

Bước 1: B trí thí nghim như Hình 10.3. Đt loa đin đng

gn sát đu h ca ng cng hưng.

Bước 2: Dùng hai dây dn đin cp đin cho loa t máy phát

tn s.

Bước 3: Điu chnh thang đo trên máy phát sang v trí

100 Hz – 1 kHz. Điu chnh tn s sóng âm cho phù hp.

Bước 4: Điu chnh biên đ đ nghe đưc âm phát ra t loa

va đ to.

Bước 5: Kéo dn pit-tông lên và lng nghe âm phát ra.

Xác đnh v trí th nht ca pit-tông khi âm nghe đưc to

nht và xác đnh chiu dài ct khí A

tương ng. Ghi s liu

vào Bng 10.2.

Bước 6: Tip tc kéo pit-tông lên và xác đnh v trí th hai

ca pit-tông khi âm nghe đưc li to nht và xác đnh chiu

dài ct khí A

tương ng. Ghi s liu vào Bng 10.2.

Bước 7: Cho pit-tông v li sát ming ng, lp li các bưc 5

và 6 thêm 4 ln na. Ghi s liu vào Bng 10.2.

* Báo cáo kết quả thí nghiệm:

Đo chiu dài ct khí A

, A

khi có âm to nht ln th nht và

ln th hai. Ghi vào bng s liu như Bng 10.2.

X lí s liu đ tính toán tc đ truyn sóng âm trong không

khí kèm theo sai s ca phép đo.

4. Dựa vào bộ dụng cụ thí nghiệm,

hãy thiết kế và thực hiện phương

án để đo tốc độ truyền âm trong

không khí.

VẬT LÍ 11

X lí s liu đ ghi nhn tc đ truyn âm:

– Tính giá tr trung bình:





()AA

và suy ra: v 



– Tính sai s 'Ȝ= 2('A

+ 'A

– Tính sai s ∆v t h thc:

v





và trình bày kt

qu:

vv v .

7ҫQVӕ+]

/ҫQ 1 2 3 4 5

7UXQJEuQK

(cm)

6DLVӕ

WX\ӋWÿӕL

(cm)

– – – – – – –

(cm)

– – – – – – –

Bảng 10.2. Bng s liu thí nghim đo tc đ truyn âm trong không khí

6. Giải thích vì sao ta có biểu thức:





Có thể xác định tốc độ truyền âm trong không khí thông qua việc đo khoảng thời

gian từ lúc bắt đầu thả một vật rơi tự do từ độ cao so với một bề mặt cứng đến khi

nghe được âm phát ra từ va chạm của vật với bề mặt. Thực hiện thí nghiệm này và

so sánh kết quả đo được với kết quả trong phương án thí nghiệm (sử dụng ống

cộng hưởng).

Cảm biến âm là cảm biến có nguyên tắc hoạt động tương tự micrô. Khi sóng âm được truyền tới cảm biến thì nó

sẽ chuyển tín hiệu âm thành tín hiệu điện có cùng tần số. Kết nối cảm biến âm với bộ xử lí số liệu sẽ thu được tín

hiệu điện này trên màn hình (Hình 10.4), dựa vào đồ thị và sự cài đặt tỉ lệ trục thời gian ban đầu ta có thể xác

định được chu kì của tín hiệu.

Nếu có hai sóng âm tới cảm biến cách nhau một khoảng thời gian nào đó thì bộ xử lí số liệu cũng sẽ hiển thị

đồng thời hai tín điện trên màn hình và cũng có thể xác định được hai thời điểm mà cảm biến bắt đầu ghi nhận

hai sóng âm.

Từ các thông tin trên, hãy đưa ra một phương án thí nghiệm xác định tần số của sóng âm và tốc độ truyền âm

với cảm biến âm và bộ xử lí số liệu.

Hình 10.4. a) Cảm biến âm; b) cảm biến âm kết nối bộ xử lí số liệu

a) b)

VẬT LÍ 11

71*.7&+¡1*

SÓNG VÀ S TRUYN SÓNG

±6yQJOjGDRÿӝQJODQWUX\ӅQWURQJNK{QJJLDQWKHRWKӡLJLDQ.KLVyQJWUX\ӅQÿLSKҫQ

WӱP{LWUѭӡQJNK{QJWUX\ӅQWKHRSKѭѫQJWUX\ӅQVyQJPjFKӍGDRÿӝQJWҥLFKӛ

±'ӵDWUrQPӕLOLrQKӋJLӳDSKѭѫQJWUX\ӅQVyQJYjSKѭѫQJGDRÿӝQJVyQJÿѭӧFSKkQ

WKjQKKDLORҥL6yQJGӑFOjVyQJPjSKѭѫQJGDRÿӝQJFӫDPӛLSKҫQWӱP{LWUѭӡQJWUQJ

YӟLSKѭѫQJWUX\ӅQVyQJ6yQJQJDQJOjVyQJPjSKѭѫQJGDRÿӝQJPӛLSKҫQWӱP{L

WUѭӡQJYX{QJJyFYӟLSKѭѫQJWUX\ӅQVyQJ

±&iFKLӋQWѭӧQJÿһFWUѭQJFӫDVyQJSKҧQ[ҥNK~F[ҥQKLӉX[ҥYjJLDRWKRD

CÁC ĐC TRƯNG VT LÍ CA SÓNG

±%ѭӟFVyQJOOjTXmQJÿѭӡQJVyQJWUX\ӅQÿLÿѭӧFWURQJPӝWFKXNuGDRÿӝQJT.



 vT

WURQJÿyvOjWӕFÿӝODQWUX\ӅQVyQJ7ӕFÿӝWUX\ӅQVyQJWURQJNK{QJJLDQOjKӳXKҥQ

YjSKөWKXӝFYjRWtQKFKҩWFӫDP{LWUѭӡQJWUX\ӅQVyQJQKѭPұWÿӝP{LWUѭӡQJWtQKÿjQ

KӗLQKLӋWÿӝiSVXҩW«

– Trên cùng mt phương truyn sóng, các đim dao đng cùng pha vi nhau cách nhau:

và các đim dao đng ngưc pha vi nhau cách nhau: k 















YӟLkOjPӝWVӕ

QJX\rQk = 0, ±1, ±2, ±3,…).

±&ѭӡQJÿӝVyQJIOjQăQJOѭӧQJVyQJWUX\ӅQTXDPӝWÿѫQYӏGLӋQWtFKYX{QJJyFYӟL

SKѭѫQJWUX\ӅQVyQJWURQJPӝWÿѫQYӏWKӡLJLDQ

St S





YӟLSOjGLӋQWtFKPjQăQJOѭӧQJVyQJEWUX\ӅQTXDWURQJPӝWNKRҧQJWKӡLJLDQ¨WKD\

F{QJVXҩWVyQJ

P 

t

7URQJKӋ6,FѭӡQJÿӝVyQJFyÿѫQYӏOj:P

– Phương trình truyn sóng theo trc Ox là:

 













cos

22



SÓNG ĐIN T

– 6yQJÿLӋQWӯOjÿLӋQWUѭӡQJYjWӯWUѭӡQJODQWUX\ӅQWURQJNK{QJJLDQGѭӟLGҥQJVyQJ

YӟLWӕFÿӝWURQJFKkQNK{QJEҵQJc = 3.10

m/s.

VẬT LÍ 11

– ÈQKViQJFyEҧQFKҩWOjVyQJÿLӋQWӯ%ѭӟFVyQJFӫDiQKViQJFyWҫQVӕfWURQJ

FKkQNK{QJ





±7KDQJVyQJÿLӋQWӯFKRELӃWGҧLEѭӟFVyQJYjGҧLWҫQVӕӭQJYӟLFiFORҥLEӭF[ҥ

NKiFQKDX

GIAO THOA SÓNG

±+LӋQWѭӧQJJLDRWKRDVyQJOjKLӋQWѭӧQJKDLVyQJNӃWKӧSJһSQKDXWăQJFѭӡQJQKDX

KRһFOjPVX\\ӃXQKDXWҥLPӝWVӕYӏWUtWURQJP{LWUѭӡQJĈLӅXNLӋQÿӇFyJLDRWKRDOj

SKҧLFyVӵNӃWKӧSWӯKDLQJXӗQVyQJGDRÿӝQJFQJSKѭѫQJFQJWҫQVӕYjFyÿӝOӋFK

SKDNK{QJÿәLWKHRWKӡLJLDQ

±7URQJP{LWUѭӡQJWUX\ӅQVyQJNKLKDLQJXӗQGDRÿӝQJFQJSKDQKӳQJÿLӇPFy

NKRҧQJFiFKÿӃQKDLQJXӗQOҫQOѭӧWOjd

Yjd

VӁGDRÿӝQJYӟLELrQÿӝFӵFÿҥLNKL

– d

= NȜYjGDRÿӝQJYӟLELrQÿӝFӵFWLӇXNKL

dd k

 















YӟLkOjPӝWVӕ

QJX\rQk = 0, ±1, ±2, ±3,…).

±+LӋQWѭӧQJJLDRWKRDiQKViQJOjKLӋQWѭӧQJ[XҩWKLӋQFiFYҥFKViQJELrQÿӝFӵF

ÿҥL[HQNӁYӟLFiFYҥFKWӕLELrQÿӝFӵFWLӇXNKLKDLVyQJiQKViQJNӃWKӧSJһSQKDX

±.KRҧQJFiFKJLӳDKDLYkQViQJKRһFKDLYkQWӕLOLrQWLӃSÿѭӧFJӑLOjNKRҧQJYkQ

NtKLӋXOjL.





YӟLȜOjEѭӟFVyQJiQKViQJaOjNKRҧQJFiFKJLӳDKDLNKHYjDOjNKRҧQJFiFKWӯKDL

NKHÿӃQPjQTXDQViW7UrQPjQTXDQViWYӏWUtYkQViQJOj

= NLYjYӏWUtYkQWӕLOj

xk i















YӟLkOjPӝWVӕQJX\rQk = 0, ±1, ±2, ±3,…).

SÓNG DNG

±6ӵJLDRWKRDFӫDKDLVyQJNӃWKӧSWUX\ӅQQJѭӧFFKLӅXQKDXWUrQFQJPӝWSKѭѫQJWҥR

WKjQKFiFEөQJVyQJFiFÿLӇPGDRÿӝQJYӟLELrQÿӝFӵFÿҥL[HQNӁYӟLFiFQ~WVyQJ

FiFÿLӇPÿӭQJ\rQ%өQJVyQJYjQ~WVyQJ[HQNӁYjFiFKÿӅXQKDX.KRҧQJFiFK

JLӳDKDLQ~WVyQJOLrQWLӃSOj

±9ӏWUtFiFEөQJVyQJÿӕLYӟLPӝWÿҫXFӕÿӏQKFӫDGk\ÿѭӧF[iFÿӏQKEҵQJELӇXWKӭF

dk















(k = 0, 1, 2,…)

±9ӏWUtFiFQ~WVyQJÿӕLYӟLPӝWÿҫXFӕÿӏQKFӫDGk\ÿѭӧF[iFÿӏQKEҵQJELӇXWKӭF

(k = 0, 1, 2,…)





VẬT LÍ 11

ô1+/8t7&28/20%

97¡1*7k&71+ô,1

Bài

Định luật Coulomb về lực tương tác giữa hai điện tích

điểm, đơn vị đo điện tích.

Vào những ngày thời tiết lạnh, đặc biệt là vào mùa đông, ta thường

hay gặp một số hiện tượng như: bị điện giật khi chạm tay vào tay nắm cửa

kim loại (Hình 11.1) hay nghe tiếng lách tách khi thay quần áo. Vậy nguyên

nhân của hiện tượng này là gì?

S TƯƠNG TÁC GIA CÁC ĐIN TÍCH

Hai loại điện tích

Mt vt b nhim đin có kh năng hút các vt nh khác thì

đưc gi là vt tích đin.

ï,ũ175óľ1*

Chương 3

Có 2 loi đin tích: đin tích dương và đin tích âm. Các đin tích cùng du thì đy

nhau, trái du thì hút nhau. Đơn v đo đin tích là culông (C).

Lưu ý: Vt tích đin có kích thưc rt nh so vi khong cách

ti v trí mà ta xét có th đưc xem là mt đin tích đim.

Trong mi vt luôn cha c hai loi đin tích dương và âm.

Mt vt nhim đin dương hoc âm khi vt cha lưng đin

tích dương nhiu hơn lưng đin tích âm hoc ngưc li. Khi

s đin tích dương bng s đin tích âm, hay tng đin tích

bng 0 thì vt trung hoà v đin.

Đin tích nguyên t có giá tr bng đ ln đin tích ca mt

ht mang đin tn ti đc lp trong t nhiên và có giá tr:

e = 1,6.10

–19

1. Xét quả cầu kim loại nhỏ có

điện tích –3,2.10

–7

C. Quả cầu

này thừa hay thiếu bao nhiêu

electron?

Electron là ht tích đin âm và có đ ln đin tích bng đin tích nguyên t.

Tt c các vt tích đin đu có đ ln đin tích q luôn là mt bi s ca đin tích nguyên t:

q = ne

vi n là s t nhiên.

Hình 11.1. Hin tưng b đin git khi

chm tay vào nm ca kim loi

VẬT LÍ 11

Nhim đin do c xát: là s nhim đin khi các vt khác bn

cht, trung hoà v đin đưc c xát vi nhau. Khi đó, hai vt

s nhim đin trái du. Ví d: Khi ta c xát lưc nha vi

tóc (đin môi hay cht cách đin), lưc nha s b nhim

đin âm và hút các mu giy vn (đin môi) (Hình 11.3a).

Nhim đin do tip xúc: là s nhim đin khi mt vt trung

hoà v đin đt tip xúc vi mt vt nhim đin. Khi đó, hai

vt s nhim đin cùng du. Ví d: Qu cu trung hoà đin

(vt dn đin), sau khi đt tip xúc vi thanh nhim đin

âm (vt dn đin) s tr nên nhim đin âm và hút đưc tóc

(Hình 11.3b).

Nhim đin do hưng ng: là s nhim đin khi mt vt A

(vt dn đin) trung hoà v đin đt gn (không tip xúc)

vi mt vt B nhim đin. Khi đó, hai đu vt A, gn và xa

vt B, ln lưt nhim đin trái du và cùng du vi vt B.

Khi đưa vt A ra xa vt B, vt A tr v trng thái trung hoà

như lúc đu (Hình 11.3c).

Một số hiện tượng nhiễm điện đã được biết đến từ thời cổ

đại. Khoảng thế kỉ VI trước Công nguyên, Thales (Ta-lét)

(khoảng 624 – 546 TCN) đã quan sát và mô tả hiện tượng

nhiễm điện thông qua khả năng hút các vật nhỏ, nhẹ của

các mẫu hổ phách khi được cọ xát (Hình 11.2) Vào thế kỉ

XVIII, các nhà vật lí đã nghiên cứu các hiện tượng điện một

cách có hệ thống và thu được một số kết quả như: vào

năm 1729, Stephen Gray (Xte-phần Gờ-ray) (1666 – 1736)

đã phát hiện ra tính dẫn điện của vật; vào năm 1733, Charles François de Cisternay du Fay

(Sác-lơ Phờ-răng-xoa đờ Xít-tờ-nay du Phay) (1698 – 1739) đã khám phá ra sự tồn tại của hai

loại điện tích: điện tích âm và điện tích dương; vào khoảng năm 1752, Benjamin Franklin

(Ben-gia-min Phờ-ranh-lin) (1706 – 1790) đã đề xuất cách thức chế tạo cột thu lôi.

S Hình 11.2. H phách nhim đin

hút các mu giy nh

Sự nhiễm điện của các vật

S Hình 11.3. Minh ho ba cách nhim đin cho vt: a) nhiễm điện do cọ xát;

b) nhiễm điện do tiếp xúc; c) nhiễm điện do hưởng ứng

a) c)

B A

2. Sử dụng một số dụng cụ đơn

giản như: vải khô, thước nhựa,

mảnh lụa, miếng thuỷ tinh, vụn

giấy nhỏ, lược nhựa, quả bóng

bay, vỏ lon,… em hãy thực

hiện thí nghiệm:

a) Làm nhiễm điện cho các vật.

b) Về tương tác giữa các vật

nhiễm điện.

VẬT LÍ 11

Thuyt electron

Thuyết electron được dùng để giải thích các hiện tượng về điện dựa trên sự cư trú và di chuyển

của các electron. Theo thuyết electron thì:

– Nguyên tử có cấu tạo gồm hạt nhân và các electron chuyển động xung quanh hạt nhân. Hạt

nhân nguyên tử mang điện tích dương và chiếm hầu hết khối lượng nguyên tử. Bình thường,

nguyên tử trung hoà về điện.

– Do khối lượng electron rất nhỏ so với khối lượng hạt nhân nguyên tử nên chúng rất linh

động. Dưới một tác nhân nào đó (ví dụ: cọ xát, tiếp xúc,…) electron có thể bứt ra khỏi nguyên

tử và di chuyển từ vật này sang vật khác.

Ngày nay, công nghệ sơn tĩnh điện

(Hình 11.4) được sử dụng rất phổ biến với

các ưu điểm vượt trội so với công nghệ sơn

thường. Từ các nguồn tư liệu sách, báo,

internet,... em hãy viết một bài giới thiệu

ngắn về công nghệ sơn tĩnh điện.

S Hình 11.4. Công nhân đang sơn vt bng

công ngh sơn tĩnh đin

ĐNH LUT COULOMB

Giải thích hiện tượng bị điện giật trong các trường hợp:

a) Khi chạm tay vào nắm cửa kim loại trong thời tiết hanh khô (Hình 11.1).

b) Khi chạm tay vào vỏ kim loại của máy tính đang hoạt động.

Đ kho sát đnh lưng tương tác gia các vt tích đin, t năm 1785 đn năm 1787,

Charles Augustin Coulomb (Sác-lơ Âu-gt-tin Cu-lông) (1736 – 1806) đã tin hành các đo

đc thc nghim v tương tác tĩnh đin gia hai qu cu tích đin có kích thưc rt nh

so vi khong cách gia chúng. Da vào kt qu tng hp t nhng thí nghim ca mình,

Coulomb đã nêu lên đnh lut mô t s tương tác gia hai đin tích đim như sau:

VẬT LÍ 11

Lưu ý: Khi đt hai đin tích vào mt môi trưng đin môi

đng cht, lc tương tác tĩnh đin s gim ε ln so vi khi

chúng đưc đt trong chân không:





(11.2)

vi ε là hng s đin môi, ch ph thuc vào bn cht ca

môi trưng. Bng 11.1 cho bit giá tr ca ε trong mt s cht.

Bảng 11.1. Hằng số điện môi của một số chất

Chất Hằng số điện môi

Chân không 1

Không khí 1,00059

Nylon 3,4

u tinh 3,7 – 10

Lc tương tác tĩnh đin gia hai đin tích đim đt

trong chân không có phương trùng vi đưng thng

ni hai đin tích đim đó (Hình 11.5), có đ ln t l

thun vi tích đ ln ca các đin tích và t l nghch

vi bình phương khong cách gia chúng.

(11.1)

Trong đó k là hng s ph thuc vào cách chn

đơn v ca các đi lưng; q

, q

là các giá tr

đi s ca hai đin tích. Trong h đơn v SI,

k 

910



, vi



88610



là hng s đin.

3. Các cặp lực

và

trong

Hình 11.5 có phải là các cặp lực

cân bằng không? Vì sao?

4. Một mẩu sắt nhỏ 6 g có thể chứa

khoảng 10

electron. Vậy vì sao

các electron này không bay

ra khỏi mẩu sắt, mặc dù giữa

chúng luôn tồn tại lực đẩy?

S Hình 11.5. Phương và chiu ca

lc tương tác tĩnh đin gia hai

đin tích đim



Ví dụ: Tính đ ln lc tương tác tĩnh đin gia electron và proton. Bit khong cách gia

electron – proton là r = 5,3.10

–11

m và môi trưng gia chúng là chân không. Electron và proton

ln lưt tích đin âm và dương vi cùng đ ln ca đin tích nguyên t.

Bài giải

Đin tích electron: q

= –1,6.10

–19

Đin tích ht nhân: q

= 1,6.10

–19

Lc tương tác tĩnh đin gia electron và proton là lc hút và có đ ln:

 





19 19

11 2

910

1610 1610

5310

8210.

(,.).( ,. )

(, .)

–

8

VẬT LÍ 11

Xét điện tích q chịu tác dụng bởi lực tĩnh điện của n điện

tích điểm, lực tổng hợp tác dụng lên điện tích q được

xác định:

 

…



=+++

(11.3)

5. Hai vật nhỏ tích điện cùng dấu,

ban đầu được giữ ở vị trí rất

gần nhau. Dựa vào công thức

(11.1), em hãy mô tả đặc điểm

chuyển động của hai vật ngay

thời điểm khi chúng được thả

tự do. Giả sử hai vật chỉ chịu

tác dụng của lực tương tác tĩnh

điện giữa chúng.

Theo mô hình nguyên tử của nhà vật lí

Ernest Rutherford (Ơ-nít Rơ-dơ-pho) (1871 –

1937), nguyên tử gồm hạt nhân (tập trung

hầu hết khối lượng của nguyên tử và có kích

thước rất nhỏ so với bán kính nguyên tử)

mang điện tích dương và các electron mang

điện tích âm chuyển động trên các quỹ đạo

tròn xung quanh hạt nhân.

Xét mô hình nguyên tử Rutherford cho

nguyên tử hydrogen (Hình 11.6), em hãy cho

biết lực giữ cho electron chuyển động tròn

quanh hạt nhân là lực gì? Xác định phương,

chiều của lực đó.

Tại 3 điểm A, B, C cố định trong chân không, đặt 3 điện tích điểm có giá trị lần lượt là q

= 6.10

–6

C, q

= –6.10

–6

C và

= 3.10

–6

C. Biết AB = 3 cm, AC = 4 cm và BC = 5 cm. Tính độ lớn lực tác dụng lên điện tích điểm đặt tại C.

1. Sau khi cọ xát thanh thuỷ tinh (trung hoà về điện) với mảnh lụa, thanh thuỷ tinh tích điện

dương và có giá trị 13 nC. Hãy giải thích quá trình tích điện cho thanh thuỷ tinh và xác định số

electron đã bị bứt ra khỏi thanh thuỷ tinh.

2. Một phân tử DNA bao gồm hai nhánh xoắn kép được liên kết với nhau có chiều dài

0,459.10

–6

m. Phần đuôi của phân tử có thể bị ion hoá mang điện tích âm q

= –1,6.10

–19

đầu còn lại mang điện tích dương q

= 1,6.10

–19

C. Phân tử xoắn ốc này hoạt động như một lò

xo và bị nén 1% sau khi bị tích điện. Xác định “độ cứng k” của phân tử. Biết phân tử DNA trong

nhân tế bào và môi trường xung quanh là nước; hằng số điện môi của nước là 81.

3. Hai quả cầu A, B có kích thước nhỏ được đặt cách nhau một khoảng 12 cm trong chân không.

Biết quả cầu A có điện tích –3,2.10

–7

C và quả cầu B có điện tích 2,4.10

–7

a) Tính lực tương tác giữa hai quả cầu.

b) Cho hai quả cầu tiếp xúc với nhau, sau đó đặt cách nhau một khoảng như lúc đầu. Biết rằng,

sau khi tiếp xúc, hai quả cầu có điện tích bằng nhau. Tính lực tương tác giữa hai quả cầu lúc này.

%j,7t3

S Hình 11.6. Mô hình nguyên t Rutherford

cho nguyên t hydrogen

3URWRQ

(OHFWURQ



VẬT LÍ 11

Khi một vật nhiễm điện được đặt gần một vật nhiễm điện khác, ta thấy hai vật có thể hút hoặc đẩy nhau, nghĩa

là giữa chúng có sự tương tác mặc dù không có sự tiếp xúc. Vậy, hai vật này tương tác với nhau bằng cách nào?

CƯNG Đ ĐIN TRƯNG

Khái niệm điện trường

Khi đt mt đin tích đim q

c đnh ti mt v trí xác đnh

trong không gian, sau đó đưa mt đin tích đim q

li gn,

ta thy hai đin tích đim này tương tác vi nhau. Ta đã bit

s tương tác này đưc mô t bi đnh lut Coulomb.

Dng vt cht bao quanh các đin tích đưc gi là điện trường.

Đin trưng tác dng lc đin lên các đin tích khác đt

trong nó. Tc đ lan truyn tương tác gia các đin tích

trong đin trưng có giá tr hu hn. Trong chân không,

tc đ này là 3.10

m/s, bng tc đ ánh sáng.

ô,175¢1*

Bài

– Khái niệm điện trường.

– Cường độ điện trường do điện tích điểm gây ra tại một điểm.

– Điện phổ.

Trong tự nhiên, một số loài vật như cá mập, ong vò vẽ (Hình 12.1) có

thể cảm nhận được điện trường. Điện trường do một số con mồi hoặc

kẻ địch tạo ra khi bơi qua được cá mập ghi nhận thông qua những tế

bào trên đầu, từ đó giúp nó phát hiện ra con mồi. Tính chất này dùng

để săn mồi và phát hiện nguy hiểm. Trong khi đó, sự chuyển động liên

tục của ong vò vẽ làm nó bị tích điện và tự tạo ra xung quanh mình

một điện trường. Khi đậu trên bông hoa, chúng truyền cho hoa một

phần điện tích. Từ đó, ong vò vẽ dùng râu của mình để nhận biết điện

trường do bông hoa gây ra. Tính chất đặc biệt đó giúp nó tìm được

mật hoa và phân biệt được hoa tươi với hoa đã hết mật.

S Hình 12.1. a) Cá mập; b) Ong vò vẽ

VẬT LÍ 11

Lưu ý: Trong chương này, ta ch xét đin trưng ca các

đin tích đng yên đi vi nhau, tc là điện trường tĩnh,

đưc gi tt là đin trưng.

Cường độ điện trường

Xét mt đin tích đim Q đt ti mt v trí xác đnh trong

không gian. Ln lưt đưa các đin tích th là nhng vt nh

tích đin dương, có đ ln khác nhau q

, q

…, q

vào

mt v trí xác đnh trong đin trưng do đin tích Q sinh ra

(Hình 12.2). c nghim cho thy, lc do đin tích Q tác

dng lên các đin tích q

, q

,…, q

có mt s đc đim:

+ Có cùng hưng.

+ Có đ ln khác nhau.

+ T s

Trong đó F

, F

,…, F

là lc do đin tích Q tác dng lên

các đin tích q

, q

,…, q

khi chúng đưc đt ti cùng

mt v trí.

Khi thay đi v trí đt các đin tích th thì t s

cũng thay

đi. Lúc này, ta thy rng t s

đc trưng cho đin

trưng

ti đim đang xét v mt tác dng lc và đưc gi là

cường độ điện trường.

1. Làm thế nào để biết trong một

vùng không gian nào đó có sự

xuất hiện của điện trường?

2. Làm thế nào để xác định được

độ mạnh yếu của điện trường tại

một điểm?

Đin trưng là dng vt cht bao quanh đin tích

và truyn tương tác gia các đin tích. Tính cht

cơ bn ca đin trưng là tác dng lc đin lên các

đin tích khác đt trong nó.

&ѭӡQJÿӝÿLӋQWUѭӡQJGRÿLӋQWtFKQVLQKUDWҥLPӝW

ÿLӇPOjÿҥLOѭӧQJÿһFWUѭQJFKRÿLӋQWUѭӡQJYӅPһW

WiFGөQJOӵFWҥLÿLӇPÿyĈk\OjPӝWÿҥLOѭӧQJYHFWѫ

YjÿѭӧF[iFÿӏQKEӣLELӇXWKӭF



(12.1)

Vi

là lc do đin tích Q tác dng lên mt đin

tích q đt ti đim đó. Trong h SI, cưng đ đin

trưng có đơn v là niutơn trên culông (N/C).

Ngoài ra, đơn v thưng dùng ca cưng đ đin

trưng là vôn trên mét (V/m).

Hình 12.2. Vectơ lc do đin tích

Q tác dng lên đin tích th q đưc

đt ti đim M và vectơ cưng đ

đin trưng do Q sinh ra ti đim M

trong trưng hp: a) Q > 0; b) Q < 0

Q !0

q !0



––

Q 0



VẬT LÍ 11

T (12.1), ta thy đ ln ca cưng đ đin trưng ti mt

đim bng t s gia đ ln lc tác dng lên mt đin tích

dương đt ti đim đó và đ ln ca đin tích đó:

(12.2)

Trong một vùng không gian có điện trường mà các

đường sức điện trường có phương nằm ngang, song

song với nhau và chiều như Hình 12.3. Hãy xác định

hướng của lực điện trường tác dụng lên điện tích q

trong các trường hợp:

a) q > 0.

b) q < 0.

Cường độ điện trường gây ra bởi điện tích điểm

Đt hai đin tích đim Q và q > 0 cách nhau mt đon r

trong chân không, lc tĩnh đin gia hai đin tích đưc xác

đnh bng đnh lut Coulomb theo công thc (11.1). Vì

đin tích th q > 0 nên cưng đ đin trưng ti v trí đt q

do đin tích đim Q gây ra cùng hưng vi lc tĩnh đin do

Q tác dng lên q.

Kt hp công thc (11.1) và (12.2), ta rút ra đưc công thc

xác đnh đ ln ca cưng đ đin trưng do đin tích đim

Q gây ra ti mt đim cách Q mt đon r.

CƯNG Đ ĐIN TRƯNG CA ĐIN TÍCH ĐIM

&ѭӡQJÿӝÿLӋQWUѭӡQJGRÿLӋQWtFKÿLӇPQJk\UDWҥL

PӝWÿLӇP0FiFKÿLӋQWtFKPӝWÿRҥQrWURQJFKkQ

NK{QJ Fy SKѭѫQJ QҵP WUrQ ÿѭӡQJ WKҷQJ QӕL ÿLӋQ

WtFKYjÿLӇP0,FyFKLӅXKѭӟQJUD[DÿLӋQWtFKQӃX

Q !  Yj KѭӟQJ OҥL JҫQ ÿLӋQ WtFK QӃX Q < 0

+uQKFyÿӝOӟQOj

(12.3)

YӟL

k  



910886 10





.,,. .



–



Hình 12.4. Cưng đ đim trưng

ca mt đim tích đim:

a) Q > 0; b) Q < 0



S Hình 12.3. Đin tích đim q

đt trong đin trưng

VẬT LÍ 11

Lưu ý: Cưng đ đin trưng do đin tích Q gây ra ti mt

đim trong môi trưng đin môi s gim ε ln so vi đim

trong chân không:





(12.4)

vi

là hng s đin môi.

Vận dụng biểu thức cường độ điện trường của điện tích điểm

Ví dụ: Đt hai qu cu nh có đin tích ln lưt là

= 3,210

–5

C và q

= –3,210

–6

C trong chân không ti

2 đim A, B cách nhau 9,0 cm. Xem hai qu cu là các đin

tích đim. Xác đnh t s đ ln ca hai vectơ cưng đ đin

trưng do hai qu cu gây ra ti đim M. Bit đim M cách A

3 cm, cách B 6 cm. Nhn xét phương, chiu ca hai vectơ này.

Bài giải

Đ ln cưng đ đin trưng do qu cu q

gây ra ti đim M:

910

3210

003

3210







,. V/m.

Đ ln cưng đ đin trưng do qu cu q

gây ra ti đim M:

910

3210

006

8010









,. V/m.

T s đ ln ca hai vectơ cưng đ đin trưng do hai qu

cu gây ra ti đim M:

3210

8010

Hai vectơ cưng đ đin trưng do hai qu cu gây ra ti

đim M có cùng phương và cùng chiu (Hình 12.5).

3. Tại hai điểm A và B trong chân

không, người ta đặt hai điện

tích trái dấu q

và q

. Tìm những

điểm sao cho hai vectơ cường độ

điện trường do hai điện tích q

và

gây ra tại đó có đặc điểm:

a) Cùng phương, cùng chiều.

b) Cùng phương, ngược chiều.

Điện trường của hệ điện tích

Xét hệ có n điện tích điểm Q

, Q

,…, Q

. Cường độ điện trường do mỗi

điện tích điểm gây ra tại điểm M là



…



,,,

Khi đó, cường độ

điện trường tổng hợp tại điểm M là:



…



E=E+EE



(12.5)

S Hình 12.5. Phương, chiu vectơ

cưng đ đin trưng tng hp ti M

A B

–

VẬT LÍ 11

ĐƯNG SC ĐIN

Điện phổ

Đt mt qu cu kim loi nh vào trong mt hp cha

du và bt mn cách đin. Tích đin cho qu cu. Dùng

tay gõ nh vào hp, ta thy các ht bt sp xp li thành

nhng hình dng đc bit. Đây là đin ph ca qu cu

tích đin (Hình 12.6).

4. Dựa vào hình ảnh điện phổ quan

sát được ở Hình 12.6, ta có thể

kết luận được dấu của mỗi điện

tích không? Vì sao?

5. Thiết kế phương án và thực hiện

thí nghiệm để quan sát hình ảnh

điện phổ của một vật tích điện.

a) c)b)

S Hình 12.6. Đin ph ca: a) điện tích điểm;

b) hai điện tích cùng dấu; c) hai điện tích trái dấu

Khái niệm đường sức điện

Ta đã bit, đin trưng không th quan sát đưc bng mt

thưng. Do đó, đ mô t đin trưng mt cách trc quan,

ta s dng khái nim đường sức điện. Đưng sc đin là

nhng đưng mô t “hình dng” ca đin trưng và cũng

là s mô hình hoá hình nh đin ph, sao cho tip tuyn

ti mt đim bt kì trên đưng trùng vi phương ca vectơ

cưng đ đin trưng ti đim đó, có chiu quy ưc trùng

vi chiu ca vectơ cưng đ đin trưng.

S Hình 12.7. Các đưng sc đin ca:

a) điện tích dương; b) điện tích âm; c) hai điện tích cùng độ lớn nhưng trái dấu; d) hai điện tích dương cùng độ lớn

b) c) d)a)

––

VẬT LÍ 11

6. Quan sát Hình 12.7, em hãy mô

tả hình dạng, điểm xuất phát,

điểm kết thúc của đường sức

điện và so sánh độ mạnh yếu của

điện trường tại hai vị trí A và B

cho mỗi trường hợp.

Đưng sc đin có các đc đim sau:

+ Ti mi đim trong đin trưng ch có mt đưng sc

đin đi qua. S lưng đưng sc đin qua mt đơn v din

tích vuông góc vi đưng sc ti mt đim trong không gian

đc trưng cho đ mnh yu ca đin trưng ti đim đó.

+ Các đưng sc đin là nhng đưng cong không kín.

Đưng sc đin phi bt đu t mt đin tích dương (hoc

 vô cc) và kt thúc  mt đin tích âm (hoc  vô cc).

Khái niệm điện trường đều

Đt hai tm kim loi phng, rng, song song vi nhau trong

đĩa cha du có bt mn cách đin. Tích đin trái du và

cùng đ ln cho hai tm kim loi và gõ nh vào đĩa du, ta

quan sát thy đin ph  gia hai tm kim loi có hình nh

như Hình 12.9.

 rìa hai tm kim loi, đin ph là nhng đưng cong. Trong

vùng không gian gia hai tm kim loi, đin ph là nhng

đưng thng gn như song song và cách đu nhau. Khi đó,

đin trưng gia hai tm kim loi gi là điện trường đều.

c nghim cho thy, ti mi đim trong đin trưng đu,

vectơ cưng đ đin trưng bng nhau.

7. Quan sát Hình 12.9, vẽ đường sức

điện trường trong vùng không

gian giữa hai tấm kim loại phẳng.

ĈLӋQWUѭӡQJÿӅXOjÿLӋQWUѭӡQJFyYHFWѫFѭӡQJÿӝ

ÿLӋQWUѭӡQJWҥLPӑLÿLӇPÿӅXEҵQJQKDXĈLӋQWUѭӡQJ

ÿӅXFyFiFÿѭӡQJVӭFÿLӋQVRQJVRQJFiFKÿӅXQKDX

Hình 12.9. Đin ph  hai tm kim

loi phng tích đin trái du,

cùng đ ln

+ –

ĈѭӡQJ VӭF ÿLӋQ Oj ÿѭӡQJ P{ Wҧ ÿLӋQ WUѭӡQJ VDR

FKRWLӃSWX\ӃQWҥLPӝWÿLӇPEҩWNuWUrQÿѭӡQJFǊQJ

WUQJYӟLSKѭѫQJFӫDYHFWѫFѭӡQJÿӝÿLӋQWUѭӡQJ

WҥLÿLӇPÿy+uQK

S Hình 12.8. Minh ho đưng sc

đin trưng và vectơ cưng đ

đin trưng ti đim M

VẬT LÍ 11

Từ các dụng cụ: pin, dây nối, 2 thanh kim loại, dầu cách điện (như dầu máy), thuốc tím (KMnO

), em hãy thiết kế

và thực hiện thí nghiệm để quan sát đường sức điện trường giữa hai thanh kim loại.

1. Trong điều kiện thời tiết bình thường, bên ngoài bề mặt Trái Đất được bao phủ bởi một

điện trường. Biết rằng điện trường này có các đường sức điện luôn hướng vào tâm Trái Đất.

Hãy xác định dấu của điện tích trên bề mặt Trái Đất trong tình huống này.

2. Đặt lần lượt một electron và một proton vào cùng một điện trường đều. Hạt nào sẽ chịu tác

dụng của lực tĩnh điện có độ lớn lớn hơn? Giả sử chỉ xét tương tác tĩnh điện, các tương tác

khác được bỏ qua. So sánh gia tốc hai hạt thu được.

3. Đặt hai quả cầu nhỏ có điện tích lần lượt là 3,0 µC và –3,5 µC tại 2 điểm A và B cách nhau một

khoảng 0,6 m. Xác định vị trí điểm C sao cho vectơ cường độ điện trường tại đó bằng không.

%j,7t3

Xét đường sức điện của hai điện tích điểm q

và q

như Hình 12.10.

Em hãy xác định dấu của hai điện tích q

, q

và so sánh độ lớn điện tích của chúng.

S Hình 12.10. Đưng sc đin

ca h hai đin tích q

và q

VẬT LÍ 11

Vào ngày 27/5/1994, đường dây cao thế 500 kV Bắc – Nam (Hình 13.1)

đã chính thức được đưa vào vận hành. Sự kiện này đánh dấu một cột mốc lịch

sử khi tạo ra sự liên kết lưới điện quốc gia. Vậy “thế” trong cụm từ “cao thế”

đặc trưng cho khả năng gì về điện?

TH NĂNG ĐIN. ĐIN TH

Công của lực điện

Xét đin tích đim q > 0 đưc bn vào mt vùng không

gian có đin trưng đu vi đ ln cưng đ đin trưng là

E. Đin tích q chuyn đng theo qu đo AB như Hình 13.2.

Đ xác đnh công ca lc đin tác dng lên q trong quá

trình chuyn đng t A đn B, ta chia đưng cong AB thành

các đon nh sao cho chúng có th xem là các đon thng.

Xét đon NP, công ca lc đin tác dng lên đin tích q là

AqE





NP , vi

là hình chiu ca NP lên phương

ca đưng sc đin trưng.

Vy, công ca lc đin tác dng lên đin tích q khi q chuyn

đng t A đn B là:

AqE





(13.1)

vi

là hình chiu ca AB lên phương ca đưng sc

đin trưng.

Lưu ý: Trong trưng hp q < 0, cách xác đnh công ca lc

đin là tương t như trưng hp q > 0.

1. Liệt kê một số lực thế đã được học.

Trình bày đặc điểm về công của

lực thế.

2. Quan sát Hình 13.2, xác định

công của lực điện tác dụng lên

điện tích q > 0 khi q di chuyển

từ A’ đến B’.

ô,17+9j7+1u1*ô,1

Bài

– Điện thế, thế năng điện.

– Mối liên hệ giữa cường độ điện trường và điện thế.

– Chuyển động của điện tích bay vào điện trường đều theo phương vuông góc với

đường sức và ứng dụng.

S Hình 13.2. Chuyn đng ca ht

mang đin q > 0 trong đin trưng đu

+ –

–

+ –

S Hình 13.1. Đưng dây 500 kV

Bc – Nam đi qua tnh Thanh Hoá

VẬT LÍ 11

Ta đã bit đ ln ca lc đin tác dng lên đin tích q đt

trong đin trưng t l thun vi đin tích q, do đó th năng

đin ti đim A cũng t l thun vi đin tích q. Chn gc

th năng  vô cùng, ta có:

= V

T(13.4)

Trong đó, h s t l V

là đi lưng không ph thuc vào

đin tích q mà ch ph thuc vào đin trưng ti v trí đim

A. Đi lưng V

đưc gi là đin th ti đim A, nó đc

trưng cho đin trưng v th năng ca đin tích q đt trong

đin trưng.

Kt hp (13.3) và (13.4), ta đưc:





(13.5)

Trong đó, A

A∞

là công ca lc đin đ dch chuyn mt đin

tích q dương t A ra vô cc. Ngoài ra, ta có A

A∞

vi

Công ca lc đin tác dng lên mt đin tích không

ph thuc vào dng đưng đi ca đin tích mà ch

ph thuc vào v trí đim đu và đim cui ca

đưng đi trong đin trưng.

Do đó, lc đin là lc th và đin trưng là mt

trưng th.

 năng đin ca mt đin tích q ti mt đim

trong đin trưng đc trưng cho kh năng sinh

công ca đin trưng đ dch chuyn đin tích q t

đim đó ra xa vô cùng.

Trong h SI, th năng đin có đơn v là jun (J).

Thế năng điện

Tương t như trưng hp ca trng lc, công ca lc đin

tác dng lên đin tích đim q đ dch chuyn q t đim A

đn đim B bng hiu thế năng điện gia hai đim này:

−W

(13.2)

ông thưng, gc th năng B đưc chn  vô cùng, khi đó

= 0 J, ta có:

= A

A∞

(13.3)

Điện thế

VẬT LÍ 11

Hiu đin th gia hai đim A và B trong đin trưng

là đi lưng đc trưng cho kh năng thc hin công

ca đin trưng đ dch chuyn mt đơn v đin tích

gia hai đim đó và đưc xác đnh bng biu thc:

(13.8)

Trong h SI, hiu đin th có đơn v là vôn (V).

3. Kết hợp công thức (13.5),

(13.6) và (13.7), em hãy rút ra

công thức (13.8).

là công mà ta cn thc hin đ đưa đin tích t vô cc

v đim A. Vy:

ĈLӋQWKӃWҥLPӝWÿLӇPWURQJÿLӋQWUѭӡQJOjÿҥLOѭӧQJ

ÿһFWUѭQJFKRWKӃQăQJÿLӋQWҥLYӏWUtÿyYjÿѭӧF[iF

ÿӏQKEҵQJF{QJPjWDFҫQWKӵFKLӋQÿӇGӏFKFKX\ӇQ

PӝWÿѫQYӏÿLӋQWtFKGѭѫQJWӯY{FӵFYӅÿLӇPÿy





(13.6)

Trong h SI, đin th có đơn v là vôn (V).

Hiệu điện thế

Ly hiu đin th gia đim A và đim B, ta đưc hiu đin

th gia hai đim A và B trong đin trưng:

= V

– V

(13.7)

Kt hp công thc (13.5), (13.6) và (13.7), ta đưc

Vy, ta rút ra đưc:

Công thc (13.8) cho ta thy: 1 V là hiu đin th gia

hai đim trong đin trưng mà công ca lc đin đ dch

chuyn mt đin tích dương 1 C gia hai đim đó bng 1 J.

Lưu ý: Đin th ti mt đim chính là giá tr hiu đin th

gia đim đó vi đim đưc chn làm gc đin th. Trong

mt s trưng hp, ta cũng có th chn gc đin th 

mt đt.

Ví dụ: Ta cn thc hin mt công 810

–5

J đ dch chuyn

mt đin tích 1,610

–4

C t vô cc đn đim M. Chn gc

đin th  vô cc, tính đin th ti M.

Bài giải

7DFy









J810

7KHRF{QJWKӭFWDFyÿLӋQWKӃWҥL0Oj

V.









810

1610

4. Xét hai điểm M và N trong điện

trường đều. Biết vectơ cường độ

điện trường hướng từ M đến N.

Hãy so sánh giá trị điện thế tại

điểm M và N.

VẬT LÍ 11

VN DNG CÔNG THC LIÊN H GIA CƯNG Đ ĐIN TRƯNG VÀ

HIU ĐIN TH

Ví dụ 1: Trong vùng không gian có đin trưng đu



, xét

ba đim A, B và C to thành mt tam giác vuông ti A, trong

đó cnh AB song song vi các đưng sc như Hình 13.3.

Cho BC = 10 cm và α = 60. Bit hiu đin th gia hai

đim B và C bng 100 V.

a) Tính đ ln cưng đ đin trưng E.

b) Tính hiu đin th gia hai đim A, C và gia hai đim A, B.

Bài giải

a) T công thc (13.10), ta có hiu đin th gia hai đim B, C

đưc xác đnh:

UEdE E

BC BC

BA BC....cos



Vi d

là hình chiu ca BC lên phương ca đưng sc đin.

Suy ra

 

BC.

V/m.

cos,cos



100

01 60

2000

b) Ta có:

+ Hiu đin th gia hai đim A, C:

= E.d

= 0 V.

+ Hiu đin th gia hai đim A, B:

= E.d

= –E.

UEdE E

BC BC

BC   cos



= –U

= –100 V.

Hình 13.3. Ba đim A, B, C

trong đin trưng đu

Mối liên hệ giữa cường độ điện trường với hiệu điện thế

T các công thc (13.1) và (13.8), ta rút ra:





(13.9)

Tng quát, ta có:

(13.10)

vi d là khong cách gia hai đim đang xét trên phương

ca vectơ cưng đ đin trưng.

Lưu ý: Cn xác đnh du ca

+ Nu



cùng chiu vi



dAB



 0

+ Nu



ngưc chiu vi



dAB







5. Giải thích vì sao cường độ điện

trường có thể được đo bằng đơn

vị vôn trên mét (V/m).



VẬT LÍ 11

Xét hai bản kim loại

song song, cách nhau

2,0 cm và có hiệu điện

thế 5,0 kV. Tính độ lớn

lực điện tác dụng lên

một hạt bụi nằm trong

khoảng giữa hai bản,

biết hạt bụi có điện tích

8,010

–19

Ví dụ 2: Xét hai bn kim loi hình vuông A và B đt song

song cách nhau 5 mm, tích đin bng nhau nhưng trái du.

Bit bn A tích đin dương và bn B tích đin âm. Hiu đin

th gia hai bn là U

= 25 V. Xem đin trưng gia hai bn

là đu, các đưng sc đin vuông góc vi các bn.

a) Xác đnh đ ln cưng đ đin trưng gia hai bn kim loi.

b) Xét mt ht electron bt đu chuyn đng t bn B.

Xác đnh đ ln lc đin tác dng lên electron và tc đ

ca electron khi nó đn bn A. Bit khi lưng electron





9110

,. kg.

Bài giải

a) Đ ln cưng đ đin trưng gia hai bn kim loi:

 



510

5000

V/m.

b) Đ ln lc đin tác dng lên electron:

F = |q

|(= 1,6.10

–19

. 5

000 = 8.10

–16

Đ bin thiên đng năng bng công ca lc đin trưng:

– W

đ0

= $

––











2161025

9110

29610

eBA

(,.)()

––

m/s.

Lưu ý: U

= V

– V

. Do đó, khi electron đi t bn âm sang

bn dương thì U

< 0.

Đo điện tim

Trong máy đo điện tim, các điện cực được sử dụng để đo hiệu

điện thế giữa các điểm khác nhau trên da của bệnh nhân,

thường không vượt quá 1 mV đối với người bình thường (Hình 13.4).

Đây là một phương pháp có độ nhạy cao để phát hiện sự bất thường

của chức năng tim. Dựa vào sách, báo, internet, các em hãy tìm hiểu

và trình bày ngắn gọn nguyên lí hoạt động của máy đo điện tim.

Hình 13.4. Bnh nhân

đang đưc đo đin tim

CHUYN ĐNG CA ĐIN TÍCH TRONG ĐIN TRƯNG ĐU

Điện tích chuyển động với vận tốc ban đầu song song với vectơ cường độ điện trường

Xét đin trưng đu đưc to bi 2 tm kim loi phng, đt

song song cách nhau mt khong d, tích đin trái du như

Hình 13.5. Ht electron chuyn đng vi vn tc ban đu

bng không t bn âm.

VẬT LÍ 11

Dưi tác dng ca lc đin

 q

, ht electron đưc gia

tc và chuyn đng theo phương song song nhưng ngưc

chiu vi đin trưng. eo đnh lí đng năng trong chương

trình Vt lí 10, ta có vn tc ca ht electron ti bn dương:

2qEd

(13.11)

Chuyn đng ca ht mang đin song song vi đin trưng

đưc ng dng trong máy gia tc tuyn tính. Máy gia tc

tuyn tính thưng đưc s dng trong quá trình x tr đ

điu tr bnh ung thư.

Nguyên tc hot đng ca máy gia tc tuyn tính: Các

electron vi năng lưng thp đưc sinh ra do bc x nhit t

súng đin t. Chúng đưc đưa vào bung gia tc (Hình 13.6).

Dưi tác dng ca lc đin, các electron đưc gia tc tr

thành electron năng lưng cao. Sau đó, chúng đưc lái ti

vùng cn x tr đ tiêu dit t bào ung thư.

6. Áp dụng định lí động năng, em

hãy rút ra công thức (13.11).

Súng đin t

Electron

năng lưng thp

Bung gia tc

Electron

năng lưng cao

S Hình 13.6. Sơ đ nguyên lí ca máy gia tc tuyn tính

dùng electron

Xét mt electron chuyn đng vi tc đ v

vào vùng đin

trưng đu đưc to bi 2 tm kim loi phng, đt song

song, tích đin trái du sao cho vn tc đu ca electron

song song vi 2 tm kim loi như Hình 13.7.

Điện tích chuyển động với vận tốc ban đầu vuông góc với vectơ cường độ điện trường

7. Xác định các lực tác dụng lên

electron trong Hình 13.7. Từ đó,

dự đoán chuyển động của electron.

8. Mô tả chuyển động của proton

chuyển động với vận tốc

vào vùng điện trường đều như

Hình 13.7.

–



S Hình 13.5. Chuyn đng ca electron song song vi

vectơ cưng đ đin trưng



–

S Hình 13.7. Chuyn đng ca electron trong đin trưng đu



VẬT LÍ 11

Khi trng lc ca electron có đ ln rt nh so vi lc đin

tác dng lên electron, mt cách gn đúng, electron ch chu

tác dng ca lc đin

 q

cùng chiu dương quy ưc.

Qu đo chuyn đng ca electron khi này ging vi qu

đo chuyn đng ca vt ném ngang đã đưc phân tích

trong chương trình Vt lí 10, gm 2 thành phn:

+ Trên phương Ox: Electron chuyn đng thng đu vi tc

đ v

+ Trên phương Oy: Lc đin

gây ra gia tc





Electron chuyn đng thng nhanh dn đu không vn tc đu.

Một electron chuyển động với vận tốc đầu 410

m/s vào vùng điện trường đều

theo phương vuông góc với các đường sức điện. Biết cường độ điện trường là

E = 10

V/m. Hãy xác định:

a) Gia tốc của electron.

b) Vận tốc của electron khi nó chuyển động được 210

–7

s trong điện trường.

Neutron là một hạt không mang điện, có khối lượng xấp xỉ proton. Một hạt neutron tự do có thể tồn tại khoảng

10 đến 15 phút, sau đó phân rã thành electron, proton và phản neutrino (là một hạt không mang điện, có khối

lượng rất bé, chuyển động với tốc độ gần bằng tốc độ ánh sáng trong chân không). Em hãy đề xuất phương án

để tách hai hạt electron và proton ngay sau khi neutron bị phân rã.

1. Độ chênh lệch điện thế giữa mặt trong và mặt ngoài của màng tế bào trong cơ thể người là

90 mV. Biết mặt trong và mặt ngoài của màng tế bào lần lượt mang điện âm và mang điện

dương. Xác định công mà tế bào cần thực hiện để đưa một ion Na

chuyển động từ bên trong

ra bên ngoài màng tế bào theo cơ chế chủ động qua kênh protein.

2. Một electron chuyển động với tốc độ ban đầu v

= 1,6

m/s

chuyển động vào vùng điện trường đều theo phương song

song với hai bản và ở chính giữa khoảng cách hai bản như

Hình 13P.1. Biết chiều dài mỗi bản là 3 cm và khoảng cách

giữa hai bản là 1 cm. Giữa hai bản có điện trường hướng

từ trên xuống, điện trường bên ngoài hai bản bằng 0. Biết

electron di chuyển đến vị trí mép ngoài của tấm bản phía

trên, tính độ lớn cường độ điện trường giữa hai bản.

%j,7t3

S Hình 13P.1.

–

VẬT LÍ 11

Màn hình cảm ứng (Hình 14.1) được sử dụng ngày càng phổ biến.

Trong đó, màn hình cảm ứng điện dung (sử dụng tụ điện) hoạt động dựa vào

khả năng nhường hoặc nhận điện tích của cơ thể con người khi có sự tiếp xúc

với các thiết bị điện. Vậy, tụ điện là thiết bị có những đặc tính gì?

S Hình 14.1. Màn hình cm ng

ĐIN MÔI TRONG ĐIN TRƯNG

7ô,1

Bài

– Điện dung, đơn vị đo điện dung.

– Ghép tụ điện nối tiếp, song song.

Nhng vt đưc cu to t các cht cha ít hoc không có

ht mang đin t do, không cho đin tích chy qua đưc gi

là điện môi. Ví d: nha, cao su, s, thu tinh,… Khi tích

đin cho khi đin môi, đin tích dư s nm ngay ti v trí

đưc đưa vào.

Khi đin môi đưc đt vào mt vùng không gian có đin

trưng, mi nguyên t ca đin môi b phân cực và làm cho

c khi đin môi b phân cc vi hai mt tích đin trái du

nhau như Hình 14.2. Điu này dn đn đin trưng tng

hp bên trong khi đin môi có đ ln nh hơn cưng đ

đin trưng ngoài.

Mi cht đin môi đưc đc trưng bi hng s đin môi, kí

hiu là ε. Hng s đin môi và đin trưng gii hn ca mt

s cht đin môi đưc cho trong Bng 14.1.

1. Liệt kê một số vật liệu có tính

cách điện trong đời sống.

ĈLӋQP{L

+ҵQJVӕ

ÿLӋQP{L

)

&ѭӡQJÿӝÿLӋQWUѭӡQJ

JLӟLKҥQ

9P

Không khí (khô) 1,00059 3

Cao su tng hp 6,7 12

Nylon 3,4 14

Giy 3,7 16

S 6 12

u tinh 3,7 – 10 9

S Bảng 14.1. Hng s đin môi và đin trưng gii hn ca mt s đin môi

a) b)

S Hình 14.2. Đin môi trưc và sau

khi đt vào trong mt đin trưng

–

(

VẬT LÍ 11

T ĐIN

Khái niệm tụ điện

T đin là mt linh kin đin t đưc s dng trong các

mch đin ca máy thu thanh, máy tính và các thit b đin

t khác. T đin có nhiu hình dng và kích thưc khác

nhau (Hình 14.3). Vai trò ca t đin là tích đin và phóng

đin trong mch.

7өÿLӋQOjPӝWKӋJӗPKDLYұWGүQÿһWJҫQQKDXYj

QJăQFiFKQKDXEҵQJPӝWOӟSFiFK ÿLӋQ0ӛLYұW

GүQÿѭӧFJӑLOjPӝWEҧQFӫDWөÿLӋQ+uQK

Da vào hình dng ca t đin, ngưi ta chia t đin thành

các loi: t đin phng, t đin tr và t đin cu.

Ngoài ra, t đin còn có th đưc phân loi da vào môi

trưng đin môi bên trong t: t không khí, t giy, t mica,...

Trong các sơ đ mch đin, t đin thưng đưc kí hiu

như Hình 14.5.

S Hình 14.5. Kí hiu t đin trong sơ đ mch đin

Khi ni hai bn ca t đin vào hai cc ca ngun đin như

Hình 14.4, hai bn này s tích đin bng nhau v đ ln

nhưng trái du. Đây là quá trình nạp điện (hay tích đin)

cho t.

Khi ni hai bn ca t đin đã đưc np đin vi mt đin

tr, mt dòng đin s xut hin và chy qua đin tr làm

đin tích ca t gim dn. Đây là quá trình phóng điện

(hay x đin) ca t.

Điện dung của tụ điện

Khi ni hai bn ca t đin vi hai cc ca ngun đin có

hiu đin th U, mt bn ca t s có đin tích Q, bn còn

li có đin tích –Q. Đ ln đin tích Q trên mi bn ca t

đin khi đã tích đin đưc gi là đin tích ca t đin. Khi

ni hai bn ca các t đin khác nhau vào cùng ngun

đin có hiu đin th U, đin tích ca các t khác nhau là

khác nhau.

2. Dựa vào cấu tạo của tụ điện ở

Hình 14.4, hãy cho biết tụ điện

có cho dòng điện một chiều đi

qua không.

S Hình 14.4. T đin

ni vào ngun đin

S Hình 14.3. Mt s loi t đin

7өJӕP

7өGiQ

7өKRi

7өPLFD 7өJLҩ\

VẬT LÍ 11

Đin dung ca t đin là đi lưng đc trưng cho

kh năng tích đin ca t, kí hiu là C và đưc xác

đnh bi:

(14.1)

Trong h SI, đin dung có đơn v là fara (F).

Các kho sát thc nghim chng t, đi vi mt t đin xác

đnh đưc ni vào ngun đin, khi thay đi hiu đin th

U thì đin tích Q ca t đin cũng thay đi. Tuy nhiên, t

s

là mt hng s. c hin kho sát tương t nhưng

cho các t đin khác nhau, t s

có giá tr không đi

tương ng vi tng t đin. Mt khác, t s

ÿӕLYӟLFiF

WөÿLӋQNKiFQKDXOjNKiFQKDX9ұ\WӍVӕ

ÿһFWUѭQJFKR

NKҧQăQJWtFKÿLӋQFӫDWө

T công thc (14.1), ta thy 1 F là đin dung ca mt t

đin mà khi đt vào gia hai bn t đin mt hiu đin th

1 V thì đin tích đưc tích trên t là 1 C.

ông thưng, các t đin có đin dung rt nh, c t

–12

F đn 10

–6

F. Vì vy, ta thưng dùng các ưc ca fara:

1 micrôfara (µF) = 10

–6

1 nanôfara

(nF) = 10

–9

1 picôfara (pF) = 10

–12

Mi t đin đu có mt giá tr hiu đin th gii hn. Đó là

hiu đin th ti đa mà t có th chu đưc. Nu vưt quá

giá tr này, t đin s b hng. ông thưng, trên v ca t

đin thưng ghi giá tr đin dung và hiu đin th gii hn

ca t.

Lưu ý: Đin dung ca mt t đin xác đnh ch ph thuc

vào cu to ca t đin (dng hình hc ca hai bn t, v trí

tương đi gia chúng và môi trưng đin môi bên trong t)

mà không ph thuc vào hiu đin th gia hai bn t.

VẬT LÍ 11

Tụ điện phẳng là một trường hợp riêng của tụ điện. Tụ điện

phẳng là hệ gồm hai bản kim loại có diện tích S bằng nhau,

được đặt cách nhau một khoảng d và tích điện trái dấu.

Các tính toán chứng tỏ điện dung của tụ điện phẳng được

xác định bằng công thức:







(14.2)

với ε là hằng số điện môi và

k 910

Trong kĩ thuật, một số tụ điện phẳng được chế tạo sao cho giá trị điện dung của tụ điện

có thể điều chỉnh được như tụ điện xoay. Tụ điện xoay có cấu tạo gồm hai hệ kim loại, một

hệ cố định và một hệ có thể xoay quanh một trục như Hình 14.6. Khi vặn nút điều khiển,

phần diện tích đối diện S giữa các bản tụ thay đổi, do đó điện dung của tụ cũng thay đổi.

Xét một tụ điện được tích điện. Khi thay đổi điện dung của tụ, hiệu điện thế và điện

tích của tụ có thay đổi không trong các trường hợp sau?

a) Tụ vẫn còn được mắc vào nguồn điện một chiều.

b) Tụ đã được tháo ra khỏi nguồn điện trước khi thay đổi điện dung.

Dựa vào sách, báo, internet, em hãy trình bày ngắn gọn vai trò của tụ điện trong màn hình cảm ứng

điện dung của thiết bị điện thoại.

GHÉP T ĐIN

Trong kĩ thut, đ to ra t đin vi đin dung thích hp,

ngưi ta thưng ghép các t đin thành b t. Có hai cách

ghép cơ bn: ghép ni tip và ghép song song.

Bộ tụ ghép nối tiếp

Hình 14.7 mô t sơ đ ghép ni tip t đin. Trong trưng

hp này, bn tích đin dương ca t đin này đưc ni vi

bn tích đin âm ca t đin sát bên. Bn th nht ca t

đin đu tiên đưc ni vi mt cc, bn th hai ca t đin

cui cùng đưc ni vi cc còn li ca ngun đin.

Gi U là hiu đin th đt vào hai đu ca b t đin;

, U

,…, U

ln lưt là hiu đin th gia hai đu t đin

, C

,…, C

Ta có:

UU UU



...

(14.3)

Gi C

là đin dung ca b t đin; Q, Q

, Q

,…, Q

ln lưt

là đ ln đin tích ca c b t đin và các t đin C

, C

,…, C

Kt hp hai công thc (14.3) và (14.1), ta có:

Hình 14.7. T đin ghép ni tip

S Hình 14.6. T đin xoay

Bản tụ

Nút vặn

VẬT LÍ 11



...

(14.4)

Nu các t đin lúc đu chưa đưc tích đin, thì đin tích các

bn t đin mc ni tip sau khi đưc ni vi ngun s bng

nhau và bng đin tích ca c b t đin Q = Q

= Q

= …= Q

ĈLӋQGXQJFӫDEӝWөÿLӋQJKpSQӕLWLӃSÿѭӧF[iFÿӏQK

...

(14.5)

Bộ tụ ghép song song

Hình 14.8 mô t sơ đ ghép t đin song song. Trong trưng

hp này, các t đin đưc mc vào cùng mt hiu đin th

U. Gi U

, U

,..., U

ln lưt là hiu đin th đt vào hai đu

các t đin C

, C

,..., C

. Ta có:

U = U

= U

= ...= U

(14.6)

Gi Q là đin tích ca b t đin; Q

, Q

,..., Q

ln lưt là đ

ln đin tích các t đin C

, C

,..., C

Do mt bn ca mi t

đin cùng đưc ghép vào cc dương ca ngun nên:

Q = Q

+ Q

+ ... + Q

(14.7)

3. Xét hai tụ điện có cùng điện

dung lần lượt được mắc nối tiếp

và song song để tạo ra hai bộ

tụ điện khác nhau. Hãy so sánh

điện dung của hai bộ tụ điện

trên với điện dung của mỗi tụ

điện thành phần.

ĈLӋQ GXQJ FӫD Eӝ Wө ÿLӋQ JKpS VRQJ VRQJ ÿѭӧF

[iFÿӏQK

= C

+ C

+ ... + C

(14.8)

Hình 14.8. T đin ghép

song song

A B

Xét mạch điện như Hình 14.9. Biết hiệu điện thế giữa hai điểm A, B bằng 6 V và điện

dung của hai tụ điện lần lượt là C

= 2 µF và C

= 4 µF. Xác định hiệu điện thế và điện

tích trên mỗi tụ điện. Giả sử ban đầu các tụ chưa tích điện.

S Hình 14.9. Hai t mc ni tip

A B

VẬT LÍ 11

Quan sát Hình 14.10 và cho biết:

a) giá trị điện dung của tụ điện.

b) ý nghĩa các thông số trên tụ điện.

Hình 14.10. T đin

1. Xét tụ điện như Hình 14.10.

a) Tính điện tích cực đại mà tụ có thể tích được.

b) Muốn tích cho tụ điện một điện tích là 4,8.10

–4

C thì cần phải đặt giữa hai bản tụ một hiệu điện

thế là bao nhiêu?

2. Hai tụ điện có điện dung lần lượt là C

= 0,5 µF và C

= 0,7 µF được ghép song song rồi mắc

vào nguồn điện có hiệu điện thế U < 60 V thì một trong hai tụ có điện tích 35 µC. Tính hiệu

điện thế U của nguồn và điện tích của tụ còn lại.

3. Cho các tụ điện C

= C

= 3,3 µF được mắc thành mạch như Hình 14P.1. Xác định điện

dung tương đương của bộ tụ.

%j,7t3

S Hình 14P.1. B t mc hn hp

VẬT LÍ 11

1u1*/¦1*9j1*'1*

&$7ô,1

Bài

– Năng lượng tụ điện.

– Ứng dụng của tụ điện trong cuộc sống.

Máy khử rung tim xách tay là thiết bị được các đội y tế thường dùng để

cấp cứu bệnh nhân bị rối loạn nhịp tim và tạo nhịp tim ổn định cho bệnh nhân.

Khi hoạt động, các điện cực của máy được đặt trên ngực của bệnh nhân để tạo

dòng điện đi qua tim bệnh nhân trong thời gian rất ngắn (Hình 15.1), tạo điều

kiện cho tim bệnh nhân hoạt động bình thường. Thiết bị này hoạt động dựa

vào khả năng tích trữ năng lượng điện của tụ điện bên trong thiết bị. Theo em,

tụ điện dự trữ được năng lượng dựa trên nguyên tắc nào?

NĂNG LƯNG T ĐIN

T đin là thit b đưc s dng đ tích đin và phóng đin

da vào năng lưng W mà t đin tích lũy đưc. Lưng

năng lưng này chính là công cn thit A đ di chuyn đin

tích đn các bn t đin.

Xét mt t đin ban đu chưa tích đin. Khi đó, trên mi

bn t đin có nhiu đin tích âm và dương vi s lưng

bng nhau, do đó gia hai bn không xut hin đin trưng.

Đ tích đin cho các bn t, cn mt công đ dch chuyn

mt lưng đin tích q t bn này sang bn kia ca t đin.

Khi đó, gia hai bn s xut hin mt hin đin th u vi

q = uC.

Đin tích q ca t đin và hiu đin th u gia hai bn t đin

t l thun vi nhau. Do đó, đ th hiu đin th – đin tích

ca t đin có dng đưng thng, đi qua gc to đ như

Hình 15.2 và có h s góc bng 1/C vi C là đin dung ca

t đin.

Hình 15.2. Đ th hiu đin th –

đin tích ca t đin

u (V)

q (C)

¨q

S Hình 15.1. Bnh nhân đang

đưc cp cu bng máy kh

rung tim xách tay

VẬT LÍ 11

Ta đã bit, công đ dch chuyn mt lưng đin tích 'q gia

hai đim có hiu đin th u

là 'A = 'q.u

chính là din

tích hình ch nht màu xanh trên đ th trong Hình 15.2.

Nu chia trc q thành nhng đon vô cùng bé, thì tng tt

c din tích các hình ch nht thành phn chính là din tích

ca hình tam giác OAH và chính là công tng cng đ tích

đin cho t đin t trng thái ban đu đn khi có đin tích Q.

Do đó, ta có:

(15.1)

Công này chính là năng lưng đưc d tr trong t đin

dưi dng năng lượng điện trường.

Năng lưng đin trưng đưc d tr bên trong t

đin:

WQUCU

(15.2)

Một tụ điện có điện dung

C = 2 pF được tích điện đến

điện tích 3,210

–8

C. Tính

năng lượng của tụ điện. Tụ

điện này có thể được dùng

để duy trì dòng điện trong

mạch hay không? Vì sao?

NG DNG CA T ĐIN

* Xây dựng ý tưởng dự án và quyết định chủ đề:

– Mục đích: Nghiên cu ng dng ca t đin trong cuc sng.

– Vấn đề thực tiễn:

Trong thi đi công ngh ngày nay, nhng thit b thông

minh đang ngày càng phát trin như máy tính xách tay,

đin thoi, máy chiu,… Trong s đó, phi k đn ô

tô đin (Hình 15.3). Ô tô đin có nhiu ưu đim như

chi phí bo dưng thp hơn xe s dng nhiên liu hoá

thch (xăng, du), kh năng vn hành n đnh, tit kim

nhiên liu và đc bit là gim thiu các vn đ ô nhim

môi trưng vì xe đin có th hn ch phát thi CO

. Tuy

nhiên, bên cnh các li ích ca xe đin thì vn tn ti

mt s hn ch như phm vi di chuyn, trm sc và đc

bit là chi phí thay pin. Vòng đi pin ca xe đin trung

bình khong 10 năm và chi phí đ thay mi lên đn hàng

nghìn USD. Do đó, đ khc phc vn đ này, các nhà

nghiên cu đang tin hành kho sát phương án thay th

2. Tìm hiểu và trình bày một số ứng

dụng của tụ điện trong cuộc sống.

Hình 15.3. Xe ô tô đang sc đin

1. Vận dụng kiến thức đã học và

công thức (15.1), em hãy rút ra

công thức (15.2).

VẬT LÍ 11

pin sc. Trong đó, thit b đang đưc quan tâm nhiu nht

là t đin. Các t đin có th sc, x hàng triu ln mà

không b chai, gim đin dung hoc b hng. Bên cnh

đó, tc đ sc, x ca t đin nhanh hơn pin và c quy.

Ngoài ra, h thng năng lưng kt hp song song gia

pin và t đin giúp h tr kéo dài tui th sc, x ca pin,

t đó nâng cao kh năng vn hành ca ô tô đin và tit

kim chi phí.

Ngoài ra, t đin cũng là mt linh kin đin t có vai trò

quan trng và đưc ng dng rng rãi trong kĩ thut.

Trong đó có th k đn bp t, micro vi đ nhy cao khi

có s dng t đin,…

* Lập kế hoạch thực hiện dự án:

– Tìm kim ngun tài liu đáng tin cy.

– Tin hành nghiên cu ng dng ca t đin trong cuc

sng v vai trò và nguyên lí hot đng (có th s dng các

ng dng đưc cho trong bài).

* Báo cáo kết quả: Công b sn phm và báo cáo kt qu

thc hin d án.

%j,7t3

1. Xét một đám mây tích điện –32 C. Xem đám mây và bề mặt Trái Đất như một tụ điện phẳng, biết

điện dung của tụ điện này khoảng 9,27 nF. Hãy tính:

a) Hiệu điện thế giữa hai bản của tụ điện.

b) Năng lượng của tụ điện này.

2. Xét một máy khử rung tim xách tay. Để cấp cứu cho bệnh nhân, nhân viên y tế đặt hai điện cực

của máy khử rung tim lên ngực bệnh nhân và truyền năng lượng dự trữ trong tụ điện cho bệnh

nhân. Giả sử tụ điện trong máy có điện dung 70 PF và hiệu điện thế giữa hai bản tụ là 5 000 V.

a) Xác định năng lượng của tụ.

b) Giả sử trung bình máy truyền một năng lượng khoảng 200 J qua bệnh nhân trong một xung

có thời gian khoảng 2 ms. Xác định công suất trung bình của xung.

VẬT LÍ 11

CÁC LOI ĐIN TÍCH

Đin tích đưc phân thành 2 loi: đin tích dương và đin tích âm. Các đin tích cùng

du thì đy nhau, trái du thì hút nhau. Đơn v đo đin tích là culông (C).

ĐNH LUT COULOMB

Lc tương tác tĩnh đin gia hai đin tích đim đt trong chân không có phương trùng

vi đưng thng ni hai đin tích đim đó, có đ ln t l thun vi tích đ ln ca các

đin tích và t l nghch vi bình phương khong cách gia chúng.

ĐIN TRƯNG  CƯNG Đ ĐIN TRƯNG

– Đin trưng là dng vt cht bao quanh đin tích và truyn tương tác gia các đin tích.

Tính cht cơ bn ca đin trưng là tác dng lc đin lên các đin tích khác đt trong nó.

– Cưng đ đin trưng do đin tích Q sinh ra ti mt đim là đi lưng đc trưng cho

đin trưng v mt tác dng lc ti đim đó. Đây là mt đi lưng vectơ và đưc xác đnh

bi biu thc:



– Đưng sc đin là đưng mô t đin trưng sao cho tip tuyn ti mt đim bt kì trên

đưng cũng trùng vi phương ca vectơ cưng đ đin trưng ti đim đó.

– Cưng đ đin trưng do đin tích đim Q gây ra ti mt đim M cách đin tích mt

đon r trong chân không có phương nm trên đưng thng ni đin tích và đim M, có

chiu hưng ra xa đin tích nu Q > 0 và hưng li gn đin tích nu Q < 0, có đ ln là:

TH NĂNG ĐIN  ĐIN TH

–  năng đin ca mt đin tích q ti mt đim trong đin trưng đc trưng cho kh

năng sinh công ca đin trưng đ dch chuyn đin tích q t đim đó ra xa vô cùng.

– Đin th ti mt đim trong đin trưng là đi lưng đc trưng cho th năng đin ti v

trí đó và đưc xác đnh bng công mà ta cn thc hin đ dch chuyn mt đơn v đin

tích dương t vô cc v đim đó:







– Mi liên h gia cưng đ đin trưng và hiu đin th:

71*.7&+¡1*

VẬT LÍ 11

T ĐIN  ĐIN DUNG

– T đin là mt h gm hai vt dn đt gn nhau và ngăn cách nhau bng mt lp cách

đin. Mi vt dn đưc gi là mt bn ca t đin.

– Đin dung ca t đin là đi lưng đc trưng cho kh năng tích đin ca t và đưc xác

đnh bi:

CÁC CÁCH GHÉP T ĐIN

– Ghép ni tip: Đin dung ca b t đin ghép ni tip đưc xác đnh:

...

– Ghép song song: Đin dung ca b t đin ghép song song đưc xác đnh:

= C

+ C

+ ... + C

NĂNG LƯNG T ĐIN

Năng lưng đin trưng đưc d tr bên trong t đin:

WQUCU

VẬT LÍ 11

'1*ô,1

&¢1*ô'1*ô,1

Bài

– Định nghĩa các khái niệm dòng điện, cường độ dòng điện, đơn vị điện lượng.

– Vận dụng được biểu thức: I = Snve.

KHÁI NIM DÒNG ĐIN

Khi bật công tắc, ta thấy bóng đèn sáng lên gần như ngay lập tức. Phải chăng các hạt tải điện trong dây dẫn

nối với bóng đèn đã di chuyển với vận tốc rất lớn? Có thể ước tính vận tốc này bằng cách nào? Ngoài ra, khi so sánh độ

sáng hai bóng đèn sợi đốt cùng loại nhưng được đặt vào hai hiệu điện thế khác nhau ta thấy có sự khác biệt (Hình 16.1).

Yếu tố nào của dòng điện đã tạo nên sự khác biệt này?

'µ1*ï,ũ1.+·1*ïű,

Chương 4

Trong môn Khoa hc t nhiên 8, các em đã bit dòng đin

là dòng dch chuyn có hưng ca các đin tích. Khi đưc

đt vào mt đin trưng ngoài, các đin tích dương và âm s

dch chuyn theo hai hưng ngưc nhau. Chiu dòng đin

đưc quy ưc là chiu dch chuyn có hưng ca các đin

tích dương (ngưc vi chiu dch chuyn có hưng ca các

đin tích âm).

Dòng đin là dòng dch chuyn có hưng ca các đin tích.

Chiu dòng đin đưc quy ưc là chiu dch chuyn có hưng ca các đin tích dương

(ngưc vi chiu dch chuyn có hưng ca các đin tích âm).

S Hình 16.1. Ánh sáng t hai bóng đèn si đt cùng loi nhưng có đ sáng khác nhau

VẬT LÍ 11

Thí nghiệm kiểm chứng

CƯNG Đ DÒNG ĐIN

* Mục đích:

Kim chng tác dng mnh hay yu ca dòng đin.

* Dụng cụ:

– Pin (1), các dây ni (2) và khoá K (3).

– Bin tr (là đin tr có giá tr có th thay đi đưc) (4).

– Ampe k (5).

– Bóng đèn si đt (6).

* Tiến hành thí nghiệm:

Bước 1: B trí thí nghim như sơ đ trong Hình 16.3.

Bước 2: Đóng khoá K, điu chnh bin tr. ng vi mi giá

tr ca bin tr, ghi nhn giá tr cưng đ dòng đin đưc

đo bi ampe k và nhn xét v đ sáng ca bóng đèn.

* Báo cáo kết quả thí nghiệm:

Nhn xét v mi liên h gia đ sáng ca đèn và s ch ca

ampe k khi thay đi giá tr ca bin tr.

Khái niệm cường độ dòng điện

Xét mt đon dây dn trong đó có dòng các đin tích dch

chuyn qua tit din thng S như Hình 16.4. Gi s trong

khong thi gian ∆t, lưng đin tích (đin lưng) dch

chuyn qua tit din thng S có đ ln ∆q.

1. Dựa vào bộ dụng cụ trong Hình

16.2, em hãy đề xuất phương án

thí nghiệm khác để kiểm chứng

tính mạnh yếu của dòng điện.

Tiến hành thí nghiệm (nếu có

điều kiện).

S Hình 16.2. B dng c thí nghim kim chng tác dng

mnh yu ca dòng đin

(1)

(4)

(5)

(6)

(3)

(2)

+ –

Hình 16.3. Sơ đ kim chng

tính cht ca cưng đ dòng đin

S Hình 16.4. Đin tích dch chuyn

qua tit din thng S

'A = v't

VẬT LÍ 11

100

Trong trưng hp tng quát, đin lưng dch chuyn qua

tit din thng S có th thay đi theo thi gian, nghĩa là

cưng đ dòng đin có th thay đi theo thi gian. Do đó,

công thc (16.1) chính là giá tr trung bình ca cưng đ

dòng đin trong khong thi gian 't.

Dòng đin có chiu và cưng đ không thay đi theo thi

gian đưc gi là dòng đin không đi. Cưng đ dòng đin

không đi I trong mt dây dn có th vit đơn gin:

(16.2)

2. Khi nói về dòng điện, chúng ta

thường nhắc tới chiều của nó.

Theo em, cường độ dòng điện I

là đại lượng vectơ hay vô hướng?

Đi lưng vt lí đc trưng cho tác dng mnh hay yu

ca dòng đin gi là cường độ dòng điện, đưc xác

đnh bng đin lưng dch chuyn qua tit din thng

S trong mt đơn v thi gian.





(16.1)

Trong h SI, cưng đ dòng đin có đơn v là ampe (A).

Định nghĩa đơn vị điện tích

T công thc (16.1), ta thy cưng đ dòng đin đưc đnh

nghĩa thông qua t s gia đin lưng dch chuyn qua tit

din thng và khong thi gian đ thc hin s dch chuyn

đó. Trong chương trình môn Khoa hc t nhiên 8, các em

đã đưc hc đơn v ca cưng đ dòng đin trong h SI (A)

đưc chn là đơn v cơ bn, do đó đơn v ca đin tích (C)

đưc đnh nghĩa li như sau:

3. Dựa vào công thức (16.1), hãy lập

luận để dẫn dắt ra định nghĩa

đơn vị đo điện lượng culông.

1 culông (1 C) là đin lưng chuyn qua tit din thng ca dây dn trong 1 s khi có

dòng đin không đi cưng đ 1 A chy qua.

1C = 1A.1s = 1A.s

Vận dụng

Ví dụ: Mt dây dn bng đng có dòng đin 5 A chy qua.

Bit rng các đin tích dch chuyn có hưng to nên dòng

đin này là các electron.

a) Hãy xác đnh đin lưng dch chuyn qua mt tit din

thng ca dây dn trong 4 phút.

b) Tính s electron đã chuyn qua tit din thng trong câu a.

VẬT LÍ 11

101

Mỗi khi trời mưa hay giông bão thường kèm theo các tia sét, đó là các dòng điện phóng từ đám mây xuống mặt

đất với cường độ trung bình cỡ 300 000 A. Tia sét kéo dài 1,5 s. Hãy tính điện lượng đã di chuyển giữa đám mây

và mặt đất trong mỗi tia sét.

Bài giải

a) T công thc đnh nghĩa:

qIt=⇒== =54601200.. .C

b) S electron:

== =

−

1200

1610

7510

ht.

Hãy so sánh cường độ của hai dòng điện không đổi sau:

Dòng điện 1: Cứ mỗi giây có 1,25.10

hạt electron chuyển qua tiết diện thẳng của

dây dẫn.

Dòng điện 2: Cứ mỗi phút có điện lượng 150 C chuyển qua tiết diện thẳng của dây dẫn.

VN TC TRÔI

Khái niệm vận tốc trôi

Khi chưa có đin trưng ngoài, các ht ti đin chuyn đng

nhit hn lon theo tt c các hưng, không có hưng nào

là ưu tiên, vì vy trong vt dn không có dòng đin.

Khi có đin trưng ngoài, các ht ti đin va chuyn đng

nhit, va chuyn đng có hưng to thành dòng đin.

Trong quá trình chuyn đng, các ht ti đin liên tc b va

đp vô s ln vi các ht khác ca vt dn. Do đó, các ht ti

đin chuyn đng hn lon nhưng có xu hưng theo mt

phương ưu tiên là phương ca đin trưng ngoài vi vn

tc trung bình không đi, gi là vn tc trôi ca ht ti đin.

Đ tìm h thc xác đnh đ ln vn tc trôi v, ta xét mt

dòng đin không đi, cưng đ I chy qua mt dây dn có

din tích tit din không đi S như Hình 16.4.

Gi n là mt đ ht ti đin trong dây dn, q là đin tích ca

mi ht ti đin.

Sau khong thi gian

A  v W

t, toàn b đin tích chuyn qua tit

din S ca dây dn cha trong mt hình tr đng có đáy S và

chiu dài

A  v W

. Đin lưng ca phn này là:

 

QnSqnS tq

A v

T đó:





nS qv

4. Vì sao khi chưa có điện trường

ngoài, các hạt tải điện trong dây

dẫn chuyển động nhiệt không

ngừng với tốc độ cỡ 10

m/s

mà không có dòng điện trong

dây dẫn?

VẬT LÍ 11

102

Vn tc trôi ca các ht ti đin t l vi cưng đ

dòng đin chy trong vt dn.

nS q

(16.3)

Lưu ý: ông thưng, vt dn hay đưc s dng là kim loi,

do đó ht ti đin là electron. Khi đó, công thc 16.3 đưc

vit li thành:

I nS ev

(16.4)

Vận dụng

Ví dụ: Dòng đin không đi I = 1,3 A chy trong mt dây dn

bng đng có đưng kính tit din d = 1,8 mm. Khi lưng

riêng và nguyên t lưng ca đng ln lưt là ρ = 9 tn/m

và

A = 64 g/mol. Gi s mi nguyên t đng có mt electron

t do. Tính đ ln vn tc trôi ca các electron t do to

nên dòng đin.

Bài giải

Vì đng là kim loi nên ht ti đin là electron.

T công thc (16.4), ta có:

v 

nSe

end

Trong đó, mt đ electron n đưc xác đnh bi:





n ρ

v=

nSe

deN 

ay s, ta đưc:

v 





41364

1810 1610 6 022 10 910

19 23 6

., .

,. ,. ., ...

≈ 0,04.10

–3

m/s = 0,04 mm/s.

5. Kết quả tính toán trong ví dụ

cho thấy độ lớn vận tốc trôi rất

nhỏ (cỡ 0,04 mm/s). Điều này có

mâu thuẫn gì với hiện tượng đèn

gần như sáng “tức thì” ngay khi

bật công tắc hay không?

1. Một ống chứa khí hydrogen bị ion hoá đặt trong điện trường mạnh giữa hai điện cực làm xuất

hiện dòng điện. Các electron chuyển động về cực dương, các proton chuyển động về cực âm.

Biết mỗi giây có 3,1.10

electron và 1,1.10

proton chuyển động qua một tiết diện của ống.

Hãy tính cường độ dòng điện và xác định chiều của nó.

2. Một quả cầu bằng đồng cô lập. Một dây dẫn kim loại mang dòng điện đi vào nó và một dây dẫn

kim loại khác mang dòng điện đi ra khỏi nó. Biết cường độ dòng điện đi vào lớn hơn cường độ

dòng điện đi ra khỏi quả cầu là 2 µA.

a) Hỏi số electron của quả cầu tăng hay giảm theo thời gian?

b) Tính thời gian để quả cầu tăng (hoặc giảm) một lượng 1 000 tỉ electron.

3. Cho dòng điện 4,2 A chạy qua một đoạn dây dẫn bằng kim loại dài 80 cm có đường kính tiết

diện 2,5 mm. Mật độ electron dẫn của kim loại này là 8,5.10

electron/m

. Hãy tính thời gian

trung bình mỗi electron dẫn di chuyển hết chiều dài đoạn dây.

%j,7t3

VẬT LÍ 11

103

ô,175¤ô1+/8t72+0

Bài

– Định nghĩa điện trở, đơn vị đo điện trở – Các nguyên nhân chính gây ra điện trở.

– Dạng đường đặc trưng I – U của vật dẫn kim loại ở nhiệt độ xác định.

– Định luật Ohm cho vật dẫn kim loại.

–

Sơ lược ảnh hưởng của nhiệt độ lên điện trở của đèn sợi đốt, điện trở nhiệt

(thermistor).

Khi vô tình chạm vào đoạn dây có điện bị hở lớp vỏ cách điện, một thợ sửa chữa bị điện giật nhẹ vì có một dòng

điện cỡ 10 mA chạy qua người. Nhưng một người khác cũng chạm vào đoạn dây trên thì có thể nguy hiểm đến tính mạng

do có dòng điện 90 mA chạy qua người. Điều gì tạo nên sự khác biệt này?

ĐIN TR

Khái niệm điện trở

Ta đã bit, khi đt mt hiu đin th vào hai đu ca vt dn,

các ht mang đin t do s dch chuyn có hưng dưi tác

dng ca đin trưng và to ra dòng đin. Quá trình dch

chuyn có hưng này luôn b cn tr bi s tương tác ca

chúng vi các ht cu thành vt dn và gia chúng vi nhau.

Các cu trúc, sp xp khác nhau ca các nguyên t cu

thành vt dn cũng như nhit đ và kích thưc ca vt cũng

nh hưng rõ rt lên chuyn đng có hưng ca các ht

mang đin. Đi lưng đc trưng cho kh năng cn tr dòng

đin ca mt vt dn đưc gi là đin tr.

1. Nêu nguyên nhân chính gây ra

điện trở của vật dẫn.

ĈLӋQWUӣFӫDPӝWYұWGүQOjÿҥLOѭӧQJÿһFWUѭQJFKR

NKҧQăQJFҧQWUӣGzQJÿLӋQFӫDYұWGүQ.KLKLӋX

ÿLӋQWKӃÿһWYjRKDLÿҫXYұWGүQFyJLiWUӏUGzQJ

ÿLӋQFKҥ\WURQJPҥFKFyFѭӡQJÿӝ,WKuÿLӋQWUӣÿѭӧF

[iFÿӏQKWKHRF{QJWKӭF

(17.1)

Trong h SI, đin tr có đơn v là ôm (). 1  là đin tr

ca mt vt dn mà khi đt mt hiu đin th 1 V vào hai

đu vt dn thì dòng đin chy qua vt dn có cưng đ 1 A.

Điện trở của một đoạn dây kim loại

 mt nhit đ xác đnh, đin tr ca mt đon dây kim

loi ph thuc vào hình dng, kích thưc và bn cht vt

liu ca nó.

S Hình 17.1. Mt đon dây dn kim loi

VẬT LÍ 11

104

ĈLӋQWUӣFӫDPӝWÿRҥQGk\NLPORҥLKuQKWUөFKLӅX

GjLAGLӋQWtFKWLӃWGLӋQS+uQKÿѭӧF[iFÿӏQK

WKHRF{QJWKӭF





(17.2)

trong đó ρ là mt h s t l, ph thuc vào bn cht vt liu

làm dây dn, đưc gi là điện trở suất.

Đin tr sut ca mt s kim loi  20

C đưc lit kê trong

Bng 17.1.

ĐNH LUT OHM

Định luật Ohm đối với đoạn mạch chỉ chứa điện trở

 mt nhit đ nht đnh, đin tr R ca mt đon dây kim loi có giá tr hu như không

ph thuc vào hiu đin th U gia hai đu đin tr hay cưng đ dòng đin I chy qua nó.

Georg Simon Ohm (1789 – 1854) là mt nhà vt lí ngưi Đc đã phát biu đnh lut mô t

liên h gia cưng đ dòng đin chy qua mt đin tr và hiu đin th gia hai đu ca nó

mang tên đnh lut Ohm.

2. Tìm hiểu và giải thích vì sao

người ta thường sử dụng đồng

để làm dây dẫn điện.

MÀU Vạch 1 Vạch 2 Vạch 3 Hệ số Dung sai

Đen 0 0 0 1 Ω

Nâu 1 1 1 10 Ω ± 1% (F)

Đỏ 2 2 2 100 Ω ± 2% (G)

Cam 3 3 3 1k Ω

Vàng 4 4 4 10k Ω

Xanh lá cây 5 5 5 100k Ω ± 0.5% (D)

Xanh da trời 6 6 6 1M Ω ± 0.25% (C)

Tím 7 7 7 10M Ω ± 0.10% (B)

Xám 8 8 8 ± 0.05%

Trắng 9 9 9

Hoàng kim 0.1 ± 5% (J)

Bạc 0.01 ± 10% (K)

4 vạch màu

560kΩ r 5%

237Ω r 1%

5 vạch màu

T Bảng 17.2. Bng quy ưc màu sc đ đc giá tr ca đin tr

Trong thực tế, điện trở có

hình dạng như Hình 17.2.

Trong đó, các vạch màu thể

hiện giá trị của điện trở với

quy ước màu được cho trong

Bảng 17.2.

S Hình 17.2. Hình nh đin tr

trong thc t

T Bảng 17.1. Giá tr đin tr sut ca mt s kim loi  20

.LPORҥL ĈLӋQWUӣVXҩWӣ

&P

Bc 1,62.10

–8

Đng 1,69.10

–8

Vàng 2,44.10

–8

Nhôm 2,75.10

–8

St 9,68.10

–8

VẬT LÍ 11

105

3. Các công thức (17.1) và (17.3)

có tương đương nhau không?

Giải thích.

&ѭӡQJÿӝGzQJÿLӋQ,FKҥ\TXDPӝWÿLӋQWUӣRWӍOӋ

WKXұQYӟLKLӋXÿLӋQWKӃUÿһWYjRKDLÿҫXÿLӋQWUӣ

(17.3)

Khi đó U = IR còn đưc gi là đ gim th trên R.

Đặt hiệu điện thế U = 1,5 V vào hai đầu một sợi dây dẫn bằng đồng có điện trở

R = 0,6 Ω. Tính cường độ dòng điện chạy qua sợi dây đồng.

Đường đặc trưng vôn – ampe

Đi vi nhiu loi vt dn, trong đó có kim loi, cưng đ

dòng đin I chy trong vt dn luôn t l thun vi hiu đin

th U đt vào hai đu vt dn đó  mt nhit đ xác đnh.

Nghĩa là đin tr ca vt dn không ph thuc vào U hay I.

Các vt liu to nên vt dn có tính cht này đưc gi là vt

liu thuần trở, các vt liu không có tính cht này đưc gi

là vt liu không thuần trở.

Trong chương trình môn Vt lí  cp Trung hc ph thông,

ta ch xét các vt liu thun tr. Khi đó, mt đon dây dn

thun tr đưc đc trưng bi mt giá tr đin tr duy nht 

mt nhit đ xác đnh.

Đưng biu din s ph thuc ca cưng đ dòng đin I chy

qua vt dn vào hiu đin th U đt vào hai đu vt dn đưc

gi là đường đặc trưng vôn – ampe ca vt dn đó.

Đi vi vt dn kim loi,  mt nhit đ xác đnh, đưng đc

trưng vôn – ampe là mt đon thng như Hình 17.3.

4. Xác định giá trị điện trở của đoạn

dây bằng đồng có đường đặc

trưng vôn – ampe như Hình 17.3.

Hình 17.3. Đưng đc trưng

vôn – ampe ca mt đon dây

kim loi  20 C

U (V)

I (A)

6,0

Đặt hiệu điện thế U (U có thể điều chỉnh được) vào hai đầu của một điện trở là

một đoạn dây bằng đồng dài 10 m, đường kính tiết diện 1 mm và điện trở suất

1,69.10

–8

Ωm ở 20

C. Dùng ampe kế đo cường độ dòng điện chạy qua đoạn dây

đồng. Điều chỉnh U, tương ứng với mỗi giá trị của U ta thu được một giá trị của I.

Kết quả thể hiện trong Bảng 17.3.

a) Dựa vào Bảng 17.3, em hãy vẽ đường đặc trưng vôn – ampe của điện trở trên.

b) Tính điện trở của đoạn dây dẫn. So sánh với giá trị thu được từ đường đặc trưng

vôn – ampe.

U (V)

0 0,2 0,4 0,6 0,8 1,0

I (A)

0 0,92 1,85 2,77 3,69 4,62

W Bảng 17.3.

VẬT LÍ 11

106

ĐÈN SI ĐT VÀ ĐIN TR NHIT

Đèn sợi đốt

Khi dòng đin chy qua mt đèn si đt làm bng dây dn

kim loi, các electron trong dòng đin thưng xuyên va đp,

đng thi truyn năng lưng cho các ion dương ti các nút

mng trong dây dn, làm cho các ion dương này dao đng

mnh hơn. Kt qu là nhit đ ca dây dn tăng theo, nói

cách khác, đèn si đt đã bin năng lưng ca dòng đin chy

qua nó thành nhit năng và mt phn năng lưng nhit này

đưc gii phóng dưi dng ánh sáng.

Mt khác, khi nhit đ đèn si đt càng tăng, dao đng ca

các ion dương ti các nút càng mnh và s hn lon đóng

góp vào chuyn đng ca các electron càng tăng. Kt qu là

s va đp gia các electron và các ion dương xy ra vi tn

s ln hơn, điu này có nghĩa chuyn đng có hưng to

nên dòng đin ca các electron b cn tr nhiu hơn. Nói

cách khác, đin tr kim loi ca đèn si đt tăng theo.

Đ th mô t s ph thuc ca đin tr mt đèn si đt vào

nhit đ đưc minh ho trong hình 17.4.

T đ th này, ta có nhn xét: Trong mt khong nhit đ

khá rng, đin tr tăng gn như tuyn tính theo nhit đ. 

vùng nhit đ cao, đưng biu din hơi cong lên, điu này

có nghĩa đin tr tăng theo nhit đ nhanh hơn so vi vùng

nhit đ thp.

ĈqQVӧLÿӕWOjÿqQFKLӃXViQJNKLEӏÿӕWQyQJQKӡ

WiFGөQJQKLӋWFӫDGzQJÿLӋQWURQJNLPORҥLĈLӋQWUӣ

FӫDÿqQVӧLÿӕWELӃQWKLrQFKұPWKHRQKLӋWÿӝ

Đưng đc trưng vôn – ampe ca mt đèn si đt đưc th

hin trong Hình 17.5.

Điện trở nhiệt

Khác vi đèn si đt, có mt s linh kin mà đin tr ca

chúng bin thiên rt nhanh theo nhit đ, đó là đin tr nhit

(thermistor). Chúng thưng đưc dùng làm các cm bin nhit.

ĈLӋQWUӣQKLӋW7KHUPLVWRUOjPӝWOLQKNLӋQÿLӋQWӱ

PjÿLӋQWUӣFӫDQyELӃQWKLrQQKDQKWKHRQKLӋWÿӝ

5. Thảo luận về ảnh hưởng của nhiệt

độ lên điện trở của đèn sợi đốt.

Có hai loi đin tr nhit chính:

– Đin tr nhit h s dương PTC (Positive Temperature

Coecient) hay còn gi là điện trở nhiệt thuận: có đin tr

tăng khi nhit đ tăng (Hình 17.6).

S Hình 17.4. S ph thuc ca đin

tr ca mt đèn si đt vào nhit đ

W (

R

S Hình 17.5. Đưng đc trưng

vôn – ampe ca mt đèn si đt

U (V)

I (A)

300

W (

R

100

200

S Hình 17.6. S ph thuc ca giá tr

đin tr đi vi đin tr nhit h s

dương (đưng màu đ) và h s âm

(đưng màu xanh dương) theo nhit đ

VẬT LÍ 11

107

Nêu một vài ứng dụng của điện trở nhiệt.

– Đin tr nhit h s âm NTC (Negative Temperature

Coecient) hay còn gi là điện trở nhiệt nghịch: có đin

tr gim khi nhit đ tăng (Hình 17.6).

1. Thông tin kĩ thuật của một loại cáp điện được in trên vỏ sản phẩm như sau: Diện tích tiết diện:

1,5 mm

, điện trở mỗi km chiều dài: 12,1 :. Hãy xác định điện trở suất của vật liệu làm cáp điện này.

2. Đường đặc trưng vôn – ampe của hai điện trở R

và R

được cho bởi Hình 17P.1.

a) Lập luận để xác định điện trở nào có giá trị lớn hơn.

b) Tính giá trị mỗi điện trở.

%j,7t3

1,25

I (A)

8(V)

S Hình 17P.1. Đưng đc trưng

vôn – ampe ca hai đin tr

Sơ lưc v s dn đin trong h thng thn kinh con ngưi

Dòng điện có ở khắp nơi và đem lại nhiều

lợi ích về mọi mặt của đời sống xã hội.

Điều thú vị là ngay trong thế giới sinh vật, trong

các cơ thể sống của động vật, dòng điện cũng

đóng một vai trò rất quan trọng: Dòng điện

trong hệ thống thần kinh giúp con người nhận

thức về thế giới, giao tiếp giữa các bộ phận bên

trong cơ thể và để kiểm soát các cơ,…

Thành phần cơ bản của hệ thần kinh là tế bào thần kinh (neuron) (Hình 17.7).

Khi chưa nhận được kích thích, tế bào ở trạng thái “nghỉ”, mặt trong của màng tế bào tích

điện âm và mặt ngoài của màng tế bào tích điện dương. Hiệu điện thế giữa mặt trong

và mặt ngoài, tuỳ theo loại tế bào, có giá trị trong khoảng từ –60 mV đến –90 mV. Hiệu

điện thế này có thể thay đổi do sự thẩm thấu qua màng tế bào của các ion, phổ biến là

, Na

, Cl

–

Khi gặp một kích thích như sơ ý chạm tay vào bình nước nóng, nhiệt độ cao làm xáo trộn

nồng độ các ion và làm thay đổi hiệu điện thế giữa mặt trong và ngoài của màng tế bào

của các đầu dây thần kinh dưới da bàn tay. Tuỳ theo kích thích mạnh hay yếu mà hiệu

điện thế này thay đổi từ khoảng –60 mV đến khoảng +40 mV, tạo thành một xung điện

kéo dài khoảng 1 ms và lan truyền dọc theo dây thần kinh dưới dạng dòng điện về não

với tốc độ từ 30 m/s đến 150 m/s. Não xử lí bằng cách tạo một xung điện khác truyền dọc

theo các dây thần kinh để điều khiển co bàn tay lại.

S Hình 17.7. Neuron thn kinh con ngưi

VẬT LÍ 11

108

Dòng điện đem lại rất nhiều lợi ích cho cuộc sống con người cũng như sự phát triển của xã hội. Ở chương trình

Trung học cơ sở, trong các thí nghiệm cần có dòng điện, các em đã được làm quen với một số nguồn điện (Hình 18.1) và

sử dụng chúng. Vì sao nguồn điện có thể tạo ra và duy trì dòng điện lâu dài? Những đại lượng vật lí nào đặc trưng cho

nguồn điện?

a) b) c)

S Hình 18.1. a) pin năng lượng mặt trời và điện gió; b) ắc quy; c) pin thông dụng

NGUN ĐIN

Khái niệm nguồn điện

Khi ni hai qu cu kim loi A và B có đin th khác nhau

(gi s V

> V

) bng mt dây dn kim loi, khi đó s có mt

dòng các electron dch chuyn t B đn A (Hình 18.2), đng

thi hiu đin th gia A và B cũng gim theo. Khi hiu đin

th gia A và B gim dn v không thì dòng đin cũng gim

dn v không.

Đ duy trì dòng đin, ta cn duy trì hiu đin th gia A và B

khác không. Điu này có nghĩa, trong khi dòng electron liên

tc di chuyn B đn A thì bng cách nào đó phi liên tc đưa

đưc các electron t A v B. it b to ra và duy trì hiu đin

th, t đó duy trì dòng đin trong mch gi là nguồn điện.

1*81ô,1

Bài

– Khái niệm nguồn điện.

– Định nghĩa suất điện động.

– Mô tả ảnh hưởng của điện trở trong của nguồn điện lên hiệu điện thế giữa hai cực

của nguồn điện.

– So sánh các khái niệm: suất điện động và hiệu điện thế.

S Hình 18.2. Ni hai qu cu kim

loi A và B có đin th khác nhau

bng dây dn kim loi

A B

1JXӗQÿLӋQOjWKLӃWEӏWҥRUDYjGX\WUuVӵFKrQKOӋFK

ÿLӋQWKӃQKҵPGX\WUuGzQJÿLӋQWURQJPҥFKNtQ

Lưu ý: Trong ngun đin, cc có đin th cao hơn là cc

dương, cc có đin th thp hơn là cc âm.

VẬT LÍ 11

109

Suất điện động của nguồn điện

Khi ni hai cc ca mt ngun đin bng dây dn kim

loi thì bên ngoài ngun, các electron di chuyn t cc

âm qua dây kim loi v cc dương ca ngun đin. Mt

khác, đ duy trì hiu đin th gia hai cc thì bên trong

ngun, các electron này phi tip tc đưc đy v cc

âm. Vì lc đin trưng có xu hưng gi cht các electron

 cc dương trong khi cc âm li đy chúng ra xa nó,

do đó, đ đy chúng v cc âm cn có mt ngun năng

lưng nào đó thc hin vic này. Ngun năng lưng đó

có th là hoá năng trong các pin hoá hc, c quy,… là cơ

năng trong các máy phát đin kiu cm ng, là quang

năng trong các pin mt tri,…

Lc tác dng lên các electron trong vic di chuyn chúng

v cc âm có bn cht không phi lc đin trưng và

đưc gi là lc l.

Đi vi các đin tích dương thì chiu di chuyn ngưc

vi chiu di chuyn ca các electron đã xét  trên.

Xét mt mch đin kín trong đó có dòng đin. Trong

khong thi gian W có lưng đin tích q > 0 di chuyn

trong toàn mch kín thì công ca lc l A t l bc nht

vi đin tích q:

A = E

mch kín

Trong đó, E

mch kín

là hng s và đưc gi là sut đin đng

trong toàn mch kín.

2. So sánh sự giống và khác nhau

của hai khái niệm: suất điện

động và hiệu điện thế.

1. Quan sát Hình 18.3, mô tả chiều

chuyển động của các hạt mang

điện trong dây dẫn và bên trong

nguồn điện.

6XҩWÿLӋQÿӝQJEFӫDQJXӗQÿLӋQOjÿҥLOѭӧQJYұWOt

ÿһFWUѭQJFKRNKҧQăQJVLQKF{QJFӫDQJXӗQÿLӋQ

QyÿѭӧFÿREҵQJWӍVӕJLӳDF{QJFӫDOӵFOҥAOjP

GLFKX\ӇQOѭӧQJÿLӋQWtFKq!WӯFӵFkPÿӃQFӵF

GѭѫQJErQWURQJQJXӗQÿLӋQYjÿLӋQWtFKq.

(

(18.1)

7URQJKӋ6,VXҩWÿLӋQÿӝQJE FyÿѫQYӏOjY{Q9

Nu mch cha ngun đin và mch ngoài là đin tr thì ngun đin là nguyên nhân duy

nht gây ra lc l tác dng lên các đin tích. Khi đó, công ca lc l A làm di chuyn đin

tích q trong toàn mch kín cũng chính bng công ca ngun đin làm di chuyn đin

tích q t cc âm đn cc dương trong ngun. Vì vy, E

mch kín

còn gi là sut đin đng

ca ngun đin và kí hiu là E.

Mi ngun đin có mt sut đin đng nht đnh. Giá tr ca đi lưng này đưc ghi trên v

ca ngun (pin, c quy,...) (Hình 18.4).

Hình 18.3. Dòng dch chuyn

ca các đin tích

(

–

và





lần lượt là lực điện và lực lạ)

–

1JXQÿLQ



–









+ –

VẬT LÍ 11

110

Xét một nguồn điện có suất điện động 12 V. Xác định công cần thiết của nguồn

điện để dịch chuyển một electron từ cực dương sang cực âm của nguồn.

Hình 18.4 thể hiện một số loại pin và ắc quy trên thị trường. Tìm hiểu và trình bày ngắn gọn thông số của các loại

pin và ắc quy này.

Điện trở trong của nguồn điện

Ngun đin lí tưng là ngun đin không có s cn tr đi

vi s dch chuyn ca các đin tích t cc này đn cc kia

bên trong ngun đin.

Trong thc t, khi các đin tích dch chuyn bên trong ngun

đin v các cc ca ngun dưi tác dng ca lc l, chúng

luôn va chm vi các ht vt cht cu to nên ngun. Do đó,

s dch chuyn ca các đin tích b cn tr. Đi lưng đc

trưng cho vic cn tr s dch chuyn ca các đin tích bên

trong ngun đin đưc gi là điện trở trong ca ngun,

thưng kí hiu là r (

Khi ngun đin không đưc ni vi mch ngoài, nghĩa là

không có dòng đin chy qua nó thì hiu đin th gia hai

cc ca ngun đin có giá tr bng sut đin đng ca ngun.

Khi ni ngun đin vi mch ngoài đ có dòng đin I như

Hình 18.5.  mch ngoài, dòng đin có chiu t cc dương

v cc âm, trong khi  bên trong ngun đin, dòng đin chy

t cc âm đn cc dương. Như vy, khi đi t cc âm đn

cc dương bên trong ngun đin, đin th tăng mt lưng

đúng bng sut đin đng E, đin tr trong ca ngun đin

li làm cho đin th b gim mt lưng Ir.

3. Khi di chuyển bên trong nguồn

từ một cực sang cực còn lại dưới

tác dụng của lực lạ, sự chuyển

động của các điện tích có bị cản

trở bởi yếu tố nào không?

S Hình 18.5. Ngun đin

phát dòng đin

EU

+ –

S Hình 18.4. Mt s loi pin và c quy thông dng

VẬT LÍ 11

111

Ghép ngun đin

* Ngun đin ghép ni tip:

Khi có Q nguồn điện được ghép nối tiếp với nhau như

Hình 18.7, cực âm của nguồn điện

nối với cực dương

của nguồn điện

, tương tự với các nguồn điện khác.

Khi đó, cực dương của nguồn đầu tiên và cực âm của

nguồn cuối cùng là hai cực của bộ nguồn điện.

Suất điện động của bộ nguồn điện được xác định theo

công thức:

= E

+ E

+ ... + E

(18.3)

Điện trở trong của bộ nguồn điện được xác định theo

công thức:

= r

+ r

+ ... + r

(18.4)

Lưu ý: Khi có hai nguồn điện ghép xung đối, tức là cực

âm (hoặc cực dương) của nguồn này được nối với cực âm

(hoặc cực dương) của nguồn kia như Hình 18.8, điện trở

trong của nguồn vẫn được xác định theo công thức (18.4).

Giả sử

!((

thì suất điện động của bộ nguồn điện được

xác định theo công thức:

= E

– E

(18.5)

Nguồn điện có suất điện động lớn hơn đóng vai trò là

nguồn phát, nguồn điện còn lại đóng vai trò là máy thu điện.

4. Mắc hai cực nguồn điện với một

điện trở qua một khoá K. Mắc

hai đầu một vôn kế vào hai cực

của nguồn (Hình 18.6). Bằng

lập luận, em hãy so sánh số chỉ

của vôn kế trong hai trường hợp

khoá K đóng và mở.

Em hãy giải thích vì sao lời khuyên khi cất giữ pin là cần để pin nơi khô

và thoáng mát.

Mắc hai cực của một pin có suất điện động 9 V vào

hai đầu của một mạch chứa điện trở. Cường độ

dòng điện trong mạch và hiệu điện thế giữa hai

đầu của mạch lần lượt có giá trị đo được là 0,1 A và

8,9 V. Xác định giá trị điện trở trong của pin.

+LӋXÿLӋQWKӃ8JLӳDKDLFӵFFӫDQJXӗQÿLӋQFyVXҩW

ÿLӋQÿӝQJEYjÿLӋQWUӣWURQJrNKLSKiWGzQJÿLӋQ

FѭӡQJÿӝIFKҥ\TXDQJXӗQÿѭӧF[iFÿӏQKEӣL

U = E – Ir (18.2)

Hình 18.6.

EU

S Hình 18.7. Ngun ghép ni tip

A B

U

+– – –

A B

U

+ +– –

S Hình 18.8. Ngun ghép xung đi

VẬT LÍ 11

112

* Ngun đin ghép song song:

Khi có Q nguồn điện giống nhau được ghép song song, các

cực cùng dấu được nối với nhau như Hình 18.9, suất điện

động của bộ nguồn điện được xác định theo công thức:

= E

= ... = E

(18.6)

Điện trở trong của bộ nguồn điện được xác định theo

công thức:

(18.7)

* Ngun đin ghép hn hp đi xng:

Khi có N nguồn điện giống nhau được ghép thành n dãy,

mỗi dãy gồm m nguồn điện ghép nối tiếp như Hình 18.10,

suất điện của bộ nguồn điện được xác định theo công thức:

= mE (18.8)

Điện trở trong của bộ nguồn điện được xác định theo

công thức:

(18.9)

S Hình 18.9. Ngun ghép song song

A B

EU

–

S Hình 18.10. Ngun ghép

hn hp đi xng

A B

–

1. Một nguồn điện có suất điện động 6 V và điện trở trong 0,5 Ω. Khi mắc hai cực của nguồn điện

với một vật dẫn thì trong mạch xuất hiện dòng điện 1,4 A. Bỏ qua điện trở các dây nối. Tính hiệu

điện thế giữa hai đầu vật dẫn.

2. Ghép nối tiếp một biến trở R với một điện trở R

thành bộ rồi nối hai đầu vào hai cực của một

nguồn điện không đổi. Điều chỉnh R, người ta thu được đồ thị đường biểu diễn sự phụ thuộc

của hiệu điện thế giữa hai đầu biến trở vào cường độ dòng điện như Hình 18P.1.

a) Xác định giá trị suất điện động của nguồn điện.

b) Xác định giá trị biến trở R ứng với điểm M trên đồ thị.

%j,7t3

4,8

S Hình 18P.1.

U (V)

I (A)

VẬT LÍ 11

113

Khi hoạt động, các thiết bị tiêu thụ điện biến đổi điện

năng thành các dạng năng lượng khác. Chẳng hạn, bóng đèn

(Hình 19.1a) biến đổi một phần điện năng thành quang năng,

quạt máy (Hình 19.1b) biến đổi một phần điện năng thành cơ

năng, bàn là (Hình 19.1c) biến đổi điện năng thành nhiệt năng,…

Năng lượng điện mà các thiết bị tiêu thụ phụ thuộc vào các

yếu tố nào?

Năng lượng tiêu thụ điện của một đoạn mạch

Khi đt hiu đin th U vào hai đu mt đon mch, lc

đin thc hin công làm cho các đin tích t do dch chuyn

có hưng to thành dòng đin. Gi s trong khong thi

gian t có lưng đin tích q chy qua đon mch. T công

thc (13.8), công ca dòng đin đã thc hin trong khong

thi gian t là:

A = Uq = 8,W

Tùy theo loi thit b tiêu th đin mà công ca dòng đin

thc hin s chuyn thành các dng năng lưng khác nhau.

Chng hn, vi đin tr thì công ca dòng đin thc hin

chuyn thành nhit to ra trên bin tr. Tng năng lưng

mà thit b tiêu th chính bng công ca dòng din đã thc

hin trên thit b đó.

Năng lưng tiêu th ca mt đon mch bng tích

ca hiu đin th gia hai đu đon mch vi cưng

đ dòng đin chy qua đon mch và vi thi gian

dòng đin chy qua.

AUIt

(19.1)

Trong h SI, năng lưng có đơn v là jun (J).

1u1*/¦1*ô,1 &1*68q7ô,1

Bài

– Khái niệm năng lượng tiêu thụ điện của đoạn mạch.

– Khái niệm công suất tiêu thụ điện của đoạn mạch.

– Tính năng lượng điện và công suất tiêu thụ điện của một đoạn mạch.

1. Dùng các dây dẫn (có điện trở

không đáng kể) nối hai đầu

một điện trở với hai cực của một

nguồn điện thành mạch kín. Khi

này, dòng điện có sinh công trên

các đoạn dây nối không? Vì sao?

S Hình 19.1. Mt s thit b đin gia dng:

a) đèn bàn; b) quạt máy; c) bàn là

NĂNG LƯNG VÀ CÔNG SUT TIÊU TH ĐIN CA ĐON MCH

a) b) c)

VẬT LÍ 11

114

Công suất tiêu thụ điện của một đoạn mạch

Khi so sánh năng lưng tiêu th đin ca hai thit b khác

nhau, chúng ta s không th xác đnh đưc thit b nào

“mnh” hơn nu ch da vào giá tr năng lưng tiêu th đin

ca chúng.

Đ so sánh, ta cn xét năng lưng tiêu th ca các thit b

trong cùng mt khong thi gian.

Công sut tiêu th ca mt đon mch là năng lưng

mà đon mch tiêu th trong mt đơn v thi gian.

= U I I+r I

  

(

(19.2)

Trong h SI, công sut có đơn v là oát (W).

Trường hợp đoạn mạch là điện trở

Khi dòng đin chy t đu này đn đu kia ca mt đin

tr, th năng ca các đin tích gim. Vic các ht ti đin

b mt năng lưng liên quan đn s va chm gia chúng

vi các ht cu thành đin tr, làm đin tr nóng lên và to

nhit ra môi trưng. Như vy, năng lưng dòng đin cung

cp đã chuyn thành nhit lưng to ra trên đin tr. Kt

lun này đã đưc Joule (James Prescott Joule) tìm ra ln đu

tiên vào năm 1840.

2. Xét hai điện trở R

và R

> R

)

được ghép song song thành bộ

và nối vào hai cực của một nguồn

điện. Hãy cho biết công suất tiêu

thụ điện của điện trở nào lớn hơn.

Giải thích.

Đặt một hiệu điện thế 12 V vào hai đầu một điện trở

8 Ω.

a) Tính công suất toả nhiệt trên điện trở.

b) Tính nhiệt lượng toả ra trên điện trở sau 1 phút.

Sự biến đổi năng lượng trong một nguồn đang phát điện

Xét mt ngun đin có sut đin đng E và đin tr trong r

ni vi mch ngoài thành mch kín. Trong mch, ngun

đang phát dòng đin I.

NĂNG LƯNG VÀ CÔNG SUT CA MT NGUN ĐIN

Nhit lưng to ra trên đin tr R đưc xác đnh bi:

QAUItRIt

(19.3)

Công sut to nhit đưc xác đnh bi:

= U I I+r I

  

(

P 

UI =RI

(19.4)

VẬT LÍ 11

115

3. Khi nguồn điện được nối với

mạch ngoài và phát ra dòng

điện, nhiệt độ của nguồn điện

có tăng lên không? Năng lượng

của nguồn điện có thể được

biến đổi thành những dạng

năng lượng nào?

0ӝWSKҫQQăQJOѭӧQJFӫDQJXӗQSKiWUDGzQJÿLӋQFXQJFҩSFKRPҥFKQJRjLSKҫQFzQ

OҥLFKX\ӇQWKjQKQKLӋWOѭӧQJWRҧUDErQWURQJQJXӗQ

Năng lượng và công suất điện

Trong công thc (19.6), s hng th nht là năng lưng

toàn phn do ngun đin sinh ra trên toàn mch:

= E,W (19.8)

Công sut ca ngun đin là đi lưng đc trưng cho tc

đ sn sinh năng lưng ca ngun đin và đưc tính theo

công thc:

= U I I+r I

  

(

I ( (19.9)

Công sut ca mt s ngun đin đưc cho trong Bng 19.1.

Như vy, công sut toàn phn ca ngun đin bng tng

công sut tiêu th  mch ngoài (có ích) và công sut to

nhit trên đin tr r bên trong ngun: rI

. Hiu sut ca

ngun đin đưc xác đnh bng t s:



(

= U I I+r I

  

(

= U I I+r I

  

(

(19.10)

Bên trong ngun, dòng đin chy t cc âm sang cc dương

vi hiu đin th gia hai cc ca ngun là U. Gi s trong

khong thi gian t, có mt lưng đin tích q > 0 đi t cc âm

sang cc dương ca ngun. Khi đó, th năng tĩnh đin ca

lưng đin tích này tăng thêm mt lưng:

W ==qU UIt

(19.5)

Phn năng lưng tăng thêm này bng vi phn năng lưng

mà ngun đin cung cp cho mch ngoài. Trong trưng

hp mch ngoài ch có đin tr thì chuyn hoá thành nhit

lưng to ra trên đin tr tương t như công thc (19.3).

Kt hp công thc (19.5) vi công thc (18.2) khi ngun

đang phát đin, ta suy ra năng lưng tiêu th đin trong

mch ngoài khi đưc ni vào mt ngun đang phát đin

đưc tính theo công thc:

A = W = E,W – rI

W (19.6)

Công sut tiêu th đin ca mch ngoài đưc tính theo

công thc:

= U I I+r I

  

(

P =

I(

(19.7)

Bảng 19.1. Công sut ca mt s

ngun đin

Nguồn điện

Công suất

(W)

Nhà máy thu

đin Sơn La

2,4.10

Nhà máy nhit

đin Ph Li 2

0,6.10

Máy phát đin

c nh

~ 2.10

B kích đin ô tô

s dng c quy

~ 10

Sc d phòng ~ 10

Pin AAA ~ 2,5

VẬT LÍ 11

116

Một nguồn điện có suất điện động 11,5 V và điện trở trong 0,8 Ω được nối với mạch

ngoài gồm các điện trở tạo thành một mạch kín. Nguồn phát dòng điện có cường

độ 1 A. Tính công suất điện mà nguồn cung cấp cho mạch ngoài.

Một pin hay ắc quy khi lưu hành trên thị trường sẽ có thêm thông số

cho biết về khả năng cung cấp điện của nó cho các thiết bị khác, đơn

vị Ah (ampe giờ). Ví dụ: Một ắc quy có thông số 10 Ah có nghĩa nó có

khả năng cung cấp dòng điện 1 A trong 10 giờ, hoặc cung cấp dòng

điện 5 A trong 2 giờ, hoặc cung cấp dòng điện 10 A trong 1 giờ,…

Hiện nay, pin sạc dự phòng (Hình 19.2) đang được sử dụng phổ biến

để nạp điện cho các thiết bị như điện thoại thông minh, máy tính

bảng. Xét một pin sạc dự phòng có thông số 15 000 mAh đã tích đầy

điện, khi được kết nối với một thiết bị di động sẽ hoạt động ở công

suất 10 W và hiệu điện thế giữa hai cực của pin bằng 5 V. Tính điện

lượng còn lại trong pin sạc dự phòng khi sử dụng nó để sạc thiết bị

trên trong 30 phút.

Hình 19.2. Pin sc d phòng

1. Mắc hai cực của một nguồn điện không đổi có suất điện động 6,0 V và điện trở trong 0,5 Ω vào

hai đầu một điện trở R = 3,5 Ω để tạo thành mạch kín. Bỏ qua điện trở các dây nối. Tính nhiệt

lượng toả ra trên điện trở R trong 1 phút.

2. Mắc hai cực của một nguồn điện không đổi vào hai đầu biến trở R. Điều chỉnh R người ta thu

được đồ thị biểu diễn sự phụ thuộc cường độ dòng điện chạy qua biến trở vào giá trị biến trở

(Hình 19.1P). Xác định suất điện động và điện trở trong của nguồn điện.

%j,7t3

3,0

I (A)

S Hình 19P.1. Đ th mô t s ph thuc ca

cưng đ dòng đin vào giá tr bin tr

R

VẬT LÍ 11

117

Ta đã biết, suất điện động và điện trở trong là hai đại lượng đặc trưng của một nguồn điện. Trong quá trình sử

dụng, suất điện động và điện trở trong của nguồn điện có thay đổi không? Làm thế nào để đo suất điện động và điện trở

trong của một nguồn điện?

* Mục đích:

Đo sut đin đng và đin tr trong ca pin chưa qua s

dng và pin đã qua s dng.

* Cơ sở lí thuyết:

Xét mch đin gm mt ngun đin có sut đin đng E và

đin tr trong r mc ni tip vi mch ngoài gm đin tr R

có giá tr đã bit và bin tr R mc ni tip như Hình 20.1.

Xem đin tr ca các dây dn không đáng k.

Khi đóng khoá K, trong mch xut hin dòng đin có cưng

đ là I đưc xác đnh theo công thc:

RR r





(

(20.1)

T (20.1), ta suy ra công thc xác đnh hiu đin th gia

hai đu đin tr R là:

U = IR = E– I(r + R

) (20.2)

T (20.1) và (20.2), ta thy khi thay đi R thì I và U cũng

thay đi. Theo (20.2), đ th mô t mi quan h gia I và

U là mt đon thng như Hình 20.2. Đon thng này có

đưng kéo dài ct trc tung OU (khi I = 0) ti đim có giá

tr U

= E và ct trc hoành OI (khi U = 0) ti đim có giá

tr





(

7+&+j1+;k&ô1+

68q7ô,1ô1*9j

ô,175¤7521*&$3,1

Bài

Đo suất điện động và điện trở trong của pin bằng dụng cụ thực hành.

S Hình 20.2. Đ th mô t mi

quan h gia cưng đ dòng đin I

chy trong mch và hiu đin th U

gia hai đu đin tr R

U (V)

I (A)

í nghiệm đo suất điện động và điện trở trong của nguồn điện

Hình 20.1. Sơ đ mch đin

EU

VẬT LÍ 11

118

Lưu ý: Khi mch h, hiu đin th gia hai cc ca ngun

đin có giá tr đúng bng sut đin đng E. Nu mc hai cc

ca ngun đin vi mt vôn k có đin tr rt ln (c M:)

thì s ch ca vôn k gn đúng bng E.

* Dụng cụ:

– 2 pin: 1 pin chưa s dng và 1 pin đã qua s dng, hp

đng pin (1).

– 1 bin tr R (2).

– 1 đin tr R

đã bit giá tr (3).

– 2 đng h đo đin đa năng hin s dùng làm ampe k mt

chiu và vôn k mt chiu (4).

– Khoá K (5).

– Bng đin (6) và dây ni (7).

1. Dựa vào cơ sở lí thuyết và dụng

cụ trong Hình 20.3, hãy thảo luận

nhóm để đưa ra một phương án

thí nghiệm xác định E và r của pin.

2. Tìm hiểu và thảo luận vai trò của

điện trở R

trong mạch điện.

* Tiến hành thí nghiệm:

Bước 1: Lp mch đin như Hình 20.1.

Lưu ý: Đng h đo th nht dùng làm ampe k đưc mc

ni tip vi bin tr và đin tr R

, đng h đo th hai dùng

làm vôn k đưc mc song song vi bin tr.

Bước 2: Chn pin cn đo đ lp vào hp đng pin.

Bước 3: Chn thang đo thích hp cho hai đng h đo đin

đa năng và đ bin tr  giá tr ln nht.

(4)(1)

(7)

(6)

(2)

(5)

(3)

S Hình 20.3. B dng c đo sut đin đng và đin tr

trong ca ngun đin

VẬT LÍ 11

119

Bước 4: Đóng khoá K. Đc giá tr ca cưng đ dòng đin I

chy trong mch và hiu đin th U gia hai đu bin tr,

ghi s liu vào Bng 20.1.

Bước 5: ay đi giá tr R ca bin tr, ng vi mi giá tr

ca bin tr, đc giá tr ca I và U tương ng, ghi s liu vào

Bng 20.1.

Lưu ý:

+ Cn ngt khoá K sau mi ln ly s liu.

+ ng vi mi pin, cn ly ít nht 5 cp s liu (I, U) đ gim

sai s trong quá trình x lí s liu.

* Báo cáo kết quả thí nghiệm:

– Da vào bng s liu, v đ th mô t mi quan h gia I

và U.

– Xác đnh sut đin đng E và đin tr trong r ca pin t

đ th.

Hãy nêu các nguyên nhân gây

ra sai số trong phương án thí

nghiệm lựa chọn và cách

khắc phục.

Lần 1 2 3 4 5

I (mA) – – – – –

U (V) – – – – –

TBảng 20.1. Bảng số liệu đo cường độ dòng điện trong mạch

và hiệu điện thế giữa hai đầu biến trở

Dựa vào phần lưu ý trong cơ sở lí thuyết, hãy đề xuất một phương án khác để đo suất điện động của nguồn điện.

Tiến hành thí nghiệm cho hai pin đã thực hiện đo và so sánh với kết quả đã nhận được.

Pin chưa sử dụng thường có điện trở trong nhỏ nên đồ thị thu được sẽ có độ dốc

nhỏ. Do đó, để xác định được giao điểm với trục hoành, ta cần phải lấy một dải số

liệu rộng hơn. Hãy đề xuất một cách xác định r mà không phải kéo dài đồ thị.

VẬT LÍ 11

120

Cách tính sai s ca đng h đo đin đa năng hin s

Việc xác định sai số của dụng cụ đo khi sử dụng đồng hồ đo điện đa năng hiện số được

trình bày trong Bảng 20.2 và 20.3 lần lượt cho phép đo hiệu điện thế một chiều và

cường độ dòng điện một chiều.

TBảng 20.2. Sai s ca dng c đo hiu đin th mt chiu

Giới hạn đo Độ chia nhỏ nhất (ĐCNN) Sai số

200 mV 100 PV ± (0,8% s đc + 10 u ĐCNN)

2 V 1 mV

± (0,5% s đc + 10 u ĐCNN)20 V 10 mV

200 V 100 mV

1000 V 1 V ± (1,0% s đc + 5 u ĐCNN)

TBảng 20.3. Sai s ca dng c đo cưng đ dòng đin mt chiu

Giới hạn đo Độ chia nhỏ nhất (ĐCNN) Sai số

20 PA 10 nA

± (2,0% s đc + 10 u ĐCNN)

200 PA 0,1 PA

2 mA 1 PA

± (1,2% s đc + 10 u ĐCNN)

20 mA 10 PA

200 mA 100 PA

± (1,5% s đc + 10 u ĐCNN)

2 A 1 mA

20 A 10 mA ± (3,5% s đc + 10 u ĐCNN)

Ví d:

– Khi dùng thang 20 V để đo hiệu điện thế một chiều, ta đọc được giá trị 12,36 V.

Sai số của phép đo này là: ± (0,5% × 12,36 + 10 × 0,01) = ± (0,06 + 0,1) = ± 0,16 V.

– Khi dùng thang 200 mA để đo cường độ dòng điện một chiều, ta đọc được giá trị

15,7 mA.

Sai số của phép đo này là: ± (1,5% × 15,7 + 10 × 0,1) = ± (0,235 + 1,0) = ± 1,2 mA.

VẬT LÍ 11

121

71*.7&+¡1*

DÒNG ĐIN. CƯNG Đ DÒNG ĐIN

±'zQJÿLӋQOjGzQJFKX\ӇQGӡLFyKѭӟQJFӫDFiFÿLӋQWtFK&KLӅXGzQJÿLӋQÿѭӧF

TX\ѭӟFOjFKLӅXGӏFKFKX\ӇQFyKѭӟQJFӫDFiFÿLӋQWtFKGѭѫQJQJѭӧFYӟLFKLӅXGӏFK

FKX\ӇQFyKѭӟQJFӫDFiFÿLӋQWtFKkP

±ĈҥLOѭӧQJYұWOtÿһFWUѭQJFKRWiFGөQJPҥQKKD\\ӃXFӫDGzQJÿLӋQJӑLOjFѭӡQJÿӝ

GzQJÿLӋQÿѭӧF[iFÿӏQKEҵQJÿLӋQOѭӧQJGӏFKFKX\ӇQTXDWLӃWGLӋQWKҷQJSWURQJPӝW

ÿѫQYӏWKӡLJLDQ

∆

7URQJKӋ6,FѭӡQJÿӝGzQJÿLӋQFyÿѫQYӏOjDPSH$

7URQJKӋ6,ÿLӋQWtFKFyÿѫQYӏOjFXO{QJ&& $V

S PH THUC CƯNG Đ DÒNG ĐIN VÀO VN TC TRÔI

9ұQWӕFWU{LFӫDFiFKҥWWҧLÿLӋQWӍOӋYӟLFѭӡQJÿӝGzQJÿLӋQFKҥ\WURQJYұWGүQ

nS q

ĐIN TR  ĐÈN SI ĐT VÀ ĐIN TR NHIT

±ĈLӋQWUӣFӫDPӝWYұWGүQOjÿҥLOѭӧQJÿһFWUѭQJFKRNKҧQăQJFҧQWUӣGzQJÿLӋQFӫDYұW

GүQ.KLKLӋXÿLӋQWKӃÿһWYjRKDLÿҫXYұWGүQFyJLiWUӏUGzQJÿLӋQFKҥ\WURQJPҥFKFy

FѭӡQJÿӝIWKuÿLӋQWUӣÿѭӧF[iFÿӏQKWKHRF{QJWKӭF



7URQJKӋ6,ÿLӋQWUӣFyÿѫQYӏOj{Pȍȍ 9$

±ĈqQVӧLÿӕWOjÿqQFKLӃXViQJNKLEӏÿӕWQyQJQKӡWiFGөQJQKLӋWFӫDGzQJÿLӋQOrQGk\

GүQNLPORҥLĈLӋQWUӣFӫDÿqQVӧLÿӕWWăQJJҫQQKѭWX\ӃQWtQKYӟLQKLӋWÿӝ

±ĈLӋQWUӣQKLӋWOjOLQKNLӋQÿLӋQWӱPjJLiWUӏÿLӋQWUӣFӫDQyELӃQWKLrQUҩWQKҥ\WKHR

QKLӋWÿӝ

SUT ĐIN ĐNG  ĐNH LUT OHM CHO CÁC ĐON MCH

±6XҩWÿLӋQÿӝQJFӫDQJXӗQÿLӋQÿһFWUѭQJFKRNKҧQăQJVLQKF{QJFӫDQJXӗQ

( =

VẬT LÍ 11

122

±ĈRҥQPҥFKFKӭDÿLӋQWUӣR+LӋXÿLӋQWKӃUYjFѭӡQJÿӝGzQJÿLӋQIWKRҧ

±ĈRҥQPҥFKFKӭDQJXӗQÿDQJSKiWGzQJÿLӋQI+LӋXÿLӋQWKӃYjFѭӡQJÿӝGzQJ

ÿLӋQIWKRҧ

U = E – rI

NĂNG LƯNG TIÊU TH VÀ CÔNG SUT TIÊU TH CA MT MCH ĐIN

±1ăQJOѭӧQJWLrXWKөFӫDPӝWÿRҥQPҥFKEҵQJWtFKFӫDKLӋXÿLӋQWKӃJLӳDKDLÿҫXÿRҥQ

PҥFKYӟLFѭӡQJÿӝGzQJÿLӋQFKҥ\TXDÿRҥQPҥFKYjYӟLWKӡLJLDQGzQJÿLӋQFKҥ\TXD

A = UIt

7URQJKӋ6,QăQJOѭӧQJFyÿѫQYӏOjMXQ-

±&{QJVXҩWFӫDGzQJÿLӋQÿһFWUѭQJFKRWӕFÿӝVLQKF{QJFӫDGzQJÿLӋQ

= U I I+r I

  

(

P 

7URQJKӋ6,F{QJVXҩWFyÿѫQYӏOjRiW:.

ĐNH LUT JOULE  LENZ

±1KLӋWOѭӧQJWRҧUDWUrQÿLӋQWUӣR:

QUIt RI t=

t

– &{QJVXҩWWRҧQKLӋWWUrQÿLӋQWUӣR:

= U I I+r I

  

(



UI RI

NĂNG LƯNG VÀ CÔNG SUT CA NGUN ĐIN

±1ăQJOѭӧQJWRjQSKҫQFӫDQJXӗQÿLӋQ

AItUIt rI t



(

±&{QJVXҩWWRjQSKҫQFӫDQJXӗQÿLӋQ

±+LӋXVXҩWFӫDQJXӗQÿLӋQ



(

= U I I+r I

  

(

VẬT LÍ 11

123

CHƯƠNG THUẬT NGỮ GIẢI THÍCH THUẬT NGỮ TRANG

2 Cm ng t

Cm ng t ti mt đim trong t trưng là đi lưng đc trưng cho

đ mnh yu ca t trưng ti đim đó.

4 Chuyn đng nhit Chuyn đng hn lon không ngng v mi phía. 101

4 Công sut to nhit Nhit lưng to ra môi trưng trong mt đơn v thi gian. 114

3 Đin cc

Đin cc là phn t dn đin đưc s dng đ to ra kt ni đin

gia mch đin và môi trưng, có th trao đi electron vi môi

trưng đó.

4 Đin tích t do

Đin tích không liên kt vi phân t, nguyên t hay ion và có th

chuyn đng t do.

113

Đng h đo đin

đa năng

it b đo đin dùng đ đo hiu đin th, cưng đ dòng đin, đin

tr, đin dung, kim tra điôt, kim tra thông mch,…

118

2 Ho âm Nhng âm có tn s là bi s ca tn s âm cơ bn. 60

3 Ion hóa

Quá trình mt nguyên t hay phân t nhn thêm hay mt đi electron đ

to thành các ion âm hay dương.

3 Lc đin Lc do đin trưng tác dng lên các ht đin tích đt trong nó. 73

3 Lc tĩnh đin Lc gia hai vt mang đin tích đng yên. 72

2 Mt đ môi trưng Lưng vt cht trong mt đơn v th tích môi trưng (rn, lng, khí). 41

4 Máy thu đin

Chuyn hoá mt phn đin năng tiêu th thành các dng năng lưng

khác, ngoài nhit năng.

111

3 Năng lưng đin

Năng lưng đưc sinh ra bi s chuyn đng có hưng ca dòng

đin tích.

4 Nguyên t lưng Khi lưng ca mt nguyên t tính bng đơn v carbon (đvC). 102

3 Nhim đin

S tích t ca các đin tích trên b mt ca mt vt. Vt nhim đin có

th hút, hoc đy hoc phóng tia la đin qua các vt khác.

4 Nhit lưng

Nhit lưng là phn nhit năng mà vt nhn đưc hay mt đi trong

quá trình truyn nhit.

114

3 Phân rã S bin đi t phát ca mt ht không bn thành các ht khác. 86

2 Sóng âm

Sóng cơ truyn trong các môi trưng vt cht (rn, lng, khí), khi đn

tai ngưi, sóng âm s làm cho màng nhĩ dao đng to nên cm giác âm.

*,l,7+&+7+8t71*

VẬT LÍ 11

124

Nhà xuất bản Giáo dục Việt Nam xin trân trọng cảm ơn

các tác giả có tác phẩm, tư liệu được sử dụng, trích dẫn

trong cuốn sách này

Chu trách nhim xut bn:

Tổng Giám đốc HOÀNG LÊ BÁCH

Chu trách nhim ni dung:

Tổng biên tập PHẠM VĨNH THÁI

Biên tập nội dung:

Biên tập kĩ – mĩ thuật:

Thiết kế sách:

Trình bày bìa:

Minh hoạ:

Sửa bản in:

Chế bản tại:

NGUYỄN BÔNG – PHẠM TRƯỜNG THỊNH

PHẠM THỊ HẠ LIÊN

TỐNG THANH THẢO – ĐẶNG NGỌC HÀ

ANH NHÂN – TRÚC LINH

NGUYỄN BÔNG – PHẠM TRƯỜNG THỊNH

CÔNG TY CỔ PHẦN DỊCH VỤ XUẤT BẢN GIÁO DỤC GIA ĐỊNH

9t7/&K±QWUäLVQJW°R

Mã s: G2HHYL002M23

In………bản, (QĐ in số…) Khổ 19x26,5 cm.

Đơn vị in:………………………

Cơ sở in:………………………

Số ĐKXB: 9-2023/CXBIPH/43-2142/GD

Số QĐXB: … ngày … tháng … năm 20 …

In xong và nộp lưu chiểu tháng … năm 20…

Mã số ISBN: 978-604-0-35188-3

%ҧQTX\ӅQWKXӝF1Kj[XҩWEҧQ*LiRGөF9LӋW1DP

yƵҤƚďңŶƉŚҦŵĜĆĜĉŶŐŬşƋƵǇҲŶƚĄĐŐŝңdҤƚĐңĐĄĐƉŚҥŶĐӆĂŶҾŝĚƵŶŐĐƵҺŶƐĄĐŚŶăǇĜҲƵŬŚƀŶŐ

ĜӇӄĐƐĂŽĐŚĠƉůӇƵƚƌӋĐŚƵǇҳŶƚŚҳĚӇӀŝďҤƚŬŞŚŞŶŚƚŚӈĐŶăŽŬŚŝĐŚӇĂĐſƐӌĐŚŽƉŚĠƉďҪŶŐǀĉŶďңŶ

ĐӆĂEŚăǆƵҤƚďңŶ'ŝĄŽĚӅĐsŝҵƚEĂŵ

HUÂN CHƯƠNG HỒ CHÍ MINH

VẬT LÍ

PHẠM NGUYỄN THÀNH VINH (Chủ biên)

TRẦN NGUYỄN NAM BÌNH – ĐOÀN HỒNG HÀ – BÙI QUANG HÂN – ĐỖ XUÂN HỘI

NGUYỄN NHƯ HUY – TRƯƠNG ĐẶNG HOÀI THU – TRẦN THỊ MỸ TRINH

VẬT LÍ 11

PHẠM NGUYỄN THÀNH VINH (Chủ biên)

NHÀ XUẤT BẢN GIÁO DỤC VIỆT NAM

 

*++</0

,6%1

 

*++</0

,6%1

 

*++</0

,6%1

 

*++</0

,6%1

 

*++</0

,6%1

 

*++</0

,6%1

 

*++</0

,6%1

%QLQWK͵

6iFKNK{QJEiQ

Bấm Tải xuống để xem toàn bộ.

| 1/127

| | Tải xuống

Preview text:

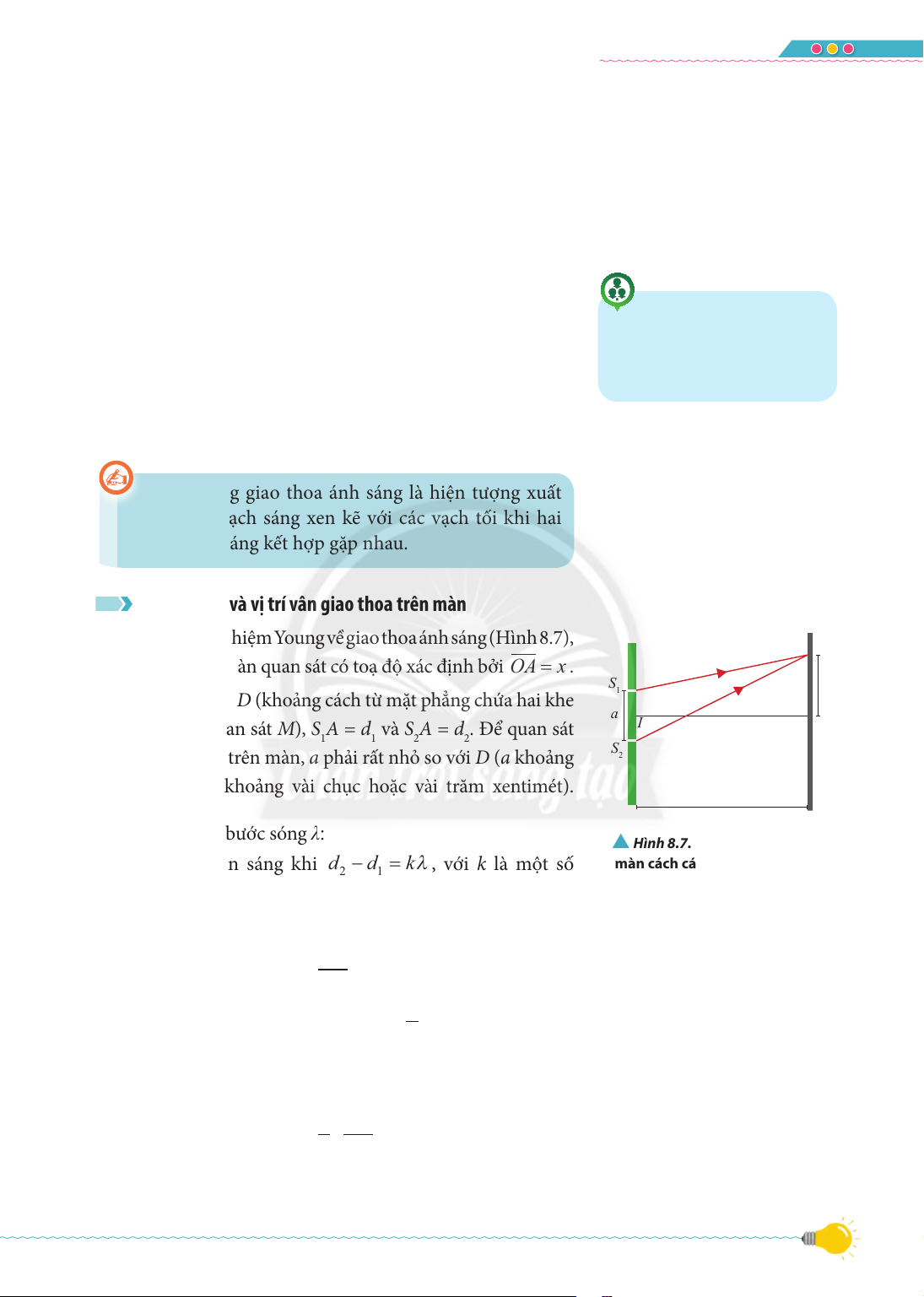
PHẠM NGUYỄN THÀNH VINH (Chủ biên) PHẠ
TRẦN NGUYỄN NAM BÌNH – ĐOÀN HỒNG HÀ – BÙI QUANG HÂN – ĐỖ XUÂN HỘI M NGUY
NGUYỄN NHƯ HUY – TRƯƠNG ĐẶNG HOÀI THU – TRẦN THỊ MỸ TRINH ỄN THÀNH
HUÂN CHƯƠNG HỒ CHÍ MINH VINH ( Chủ biên) VẬT LÍ 11 VẬT LÍ 11 ,6%1 ,6%1 ,6%1 ,6%1 *++0 *++0 *++0 *++0 %̫QLQWK͵
NHÀ XUẤT BẢN GIÁO DỤC VIỆT NAM 6iFKNK{QJEiQ ,6%1 ,6%1 ,6%1 ,6%1 *++0 *++0 *++0 *++0 ,6%1 ,6%1 ,6%1 ,6%1 *++0 *++0 *++0 *++0 ,6%1 ,6%1 ,6%1 ,6%1 *++0 *++0 *++0 *++0 ,6%1 ,6%1 ,6%1 ,6%1 *++0 *++0 *++0 *++0 ,6%1 ,6%1 ,6%1 ,6%1 *++0 *++0 *++0 *++0 ,6%1 ,6%1 ,6%1 ,6%1 *++0 *++0 *++0 *++0 HỘI ĐỒNG QUỐC GIA
THẨM ĐỊNH SÁCH GIÁO KHOA
Môn: Vật lí – Lớp 11 Họ và tên Chức vụ Hội đồng Bà ĐỖ HƯƠNG TRÀ Chủ tịch
Ông NGUYỄN ANH THUẤN Phó Chủ tịch
Ông NGUYỄN VĂN NGHIỆP Uỷ viên, Thư kí
Ông NGUYỄN QUANG LINH Uỷ viên
Ông MAI HOÀNG PHƯƠNG Uỷ viên
Ông PHÙNG VIỆT HẢI Uỷ viên Bà NGÔ THỊ QUYÊN Uỷ viên
Ông PHẠM ĐÌNH MẪN Uỷ viên
Bà NGUYỄN VŨ ÁNH TUYẾT Uỷ viên VẬT LÍ 11
PHẠM NGUYỄN THÀNH VINH (Chủ biên)
TRẦN NGUYỄN NAM BÌNH – ĐOÀN HỒNG HÀ – BÙI QUANG HÂN – ĐỖ XUÂN HỘI
NGUYỄN NHƯ HUY – TRƯƠNG ĐẶNG HOÀI THU – TRẦN THỊ MỸ TRINH VẬT LÍ11 1
Hướng dẫn sử dụng sách
Trong mỗi bài học gồm các nội dung sau: MỞ ĐẦU
Khởi động, đặt vấn đề, gợi mở và tạo hứng thú vào bài học
HÌNH THÀNH KIẾN THỨC MỚI o H t ạ đ g n ộ hì h n t n à h h kiến th c ứ ớ m i u q a việ c
quan sát hình ảnh, thí nghiệm hoặc trải nghiệm thực tế
Tóm tắt kiến thức trọng tâm LUYỆN TẬP
Củng cố kiến thức và rèn luyện kĩ năng đã học VẬN DỤNG
Vận dụng kiến thức và kĩ năng đã học vào thực tiễn cuộc sống MỞ RỘNG
Giới thiệu thêm kiến thức và ứng dụng liên quan đến
bài học, giúp các em tự học ở nhà 2 /¢,1,ôp8
Các em học sinh, quý thầy, cô giáo và phụ huynh thân mến!
Sách giáo khoa Vật lí 10 đã giúp các em trang bị những kiến thức nền tảng về động học,
động lực học, năng lượng và công, động lượng, chuyển động tròn, sự biến dạng của vật
rắn, là những đối tượng chính của Cơ học – một trong những nhánh nghiên cứu được
xuất hiện sớm nhất trong lịch sử phát triển của vật lí. Đồng thời, các em cũng tìm hiểu
về đối tượng, mục tiêu, phương pháp nghiên cứu và những ảnh hưởng sâu rộng của vật lí
đến mọi lĩnh vực trong đời sống và kĩ thuật.
Sách giáo khoa Vật lí 11 gồm 4 chương mang đến cho các em những hiểu biết về dao
động, sự lan truyền của dao động để tạo ra sóng, điện tích – điện trường và dòng điện không đổi.
Mỗi chương được chia thành một số bài học, mỗi bài học gồm một chuỗi các hoạt động
nhằm hình thành năng lực cho học sinh bao gồm: khởi động, khám phá, luyện tập, vận
dụng, mở rộng và cuối mỗi bài học sẽ có hệ thống bài tập giúp học sinh rèn luyện và tự
đánh giá kết quả học tập của mình. Học sinh có thể tra cứu nhanh các thuật ngữ khoa học
liên quan đến bài học dựa vào bảng Giải thích thuật ngữ cuối sách.
Sách giáo khoa Vật lí 11 thuộc bộ sách giáo khoa Chân trời sáng tạo của Nhà xuất bản
Giáo dục Việt Nam được biên soạn dựa trên định hướng phát triển phẩm chất và năng
lực người học và theo quan điểm chú trọng bản chất, ý nghĩa vật lí của các đối tượng, đề
cao tính thực tiễn; tạo điều kiện để học sinh phát triển tư duy khoa học dưới góc độ vật lí,
khơi gợi sự ham thích trong học tập bộ môn và tăng cường khả năng vận dụng kiến thức,
kĩ năng vật lí trong thực tiễn dưới sự giúp đỡ của giáo viên.
Rất mong nhận được sự góp ý của quý thầy, cô giáo, phụ huynh và các em học sinh để
sách ngày càng hoàn thiện hơn. Các tác giả 0&/&
Hướng dẫn sử dụng sách ................................................................................................. 2
Lời nói đầu ......................................................................................................................... 3
Mục lục ............................................................................................................................... 4
Chương 1: DAO ĐỘNG .................................................................................................. 5
Bài 1. Mô tả dao động ...................................................................................................... 5
Bài 2. Phương trình dao động điều hoà ...................................................................... 14
Bài 3. Năng lượng trong dao động điều hoà ............................................................... 22
Bài 4. Dao động tắt dần và hiện tượng cộng hưởng .................................................. 26
Chương 2: SÓNG ................................................................................................34
Bài 5. Sóng và sự truyền sóng ........................................................................................ 34
Bài 6. Các đặc trưng vật lí của sóng ............................................................................. 39
Bài 7. Sóng điện từ .......................................................................................................... 46
Bài 8. Giao thoa sóng ..................................................................................................... 49
Bài 9. Sóng dừng ............................................................................................................. 56
Bài 10. Thực hành đo tần số của sóng âm và tốc độ truyền âm ............................... 62
Chương 3: ĐIỆN TRƯỜNG .........................................................................................68
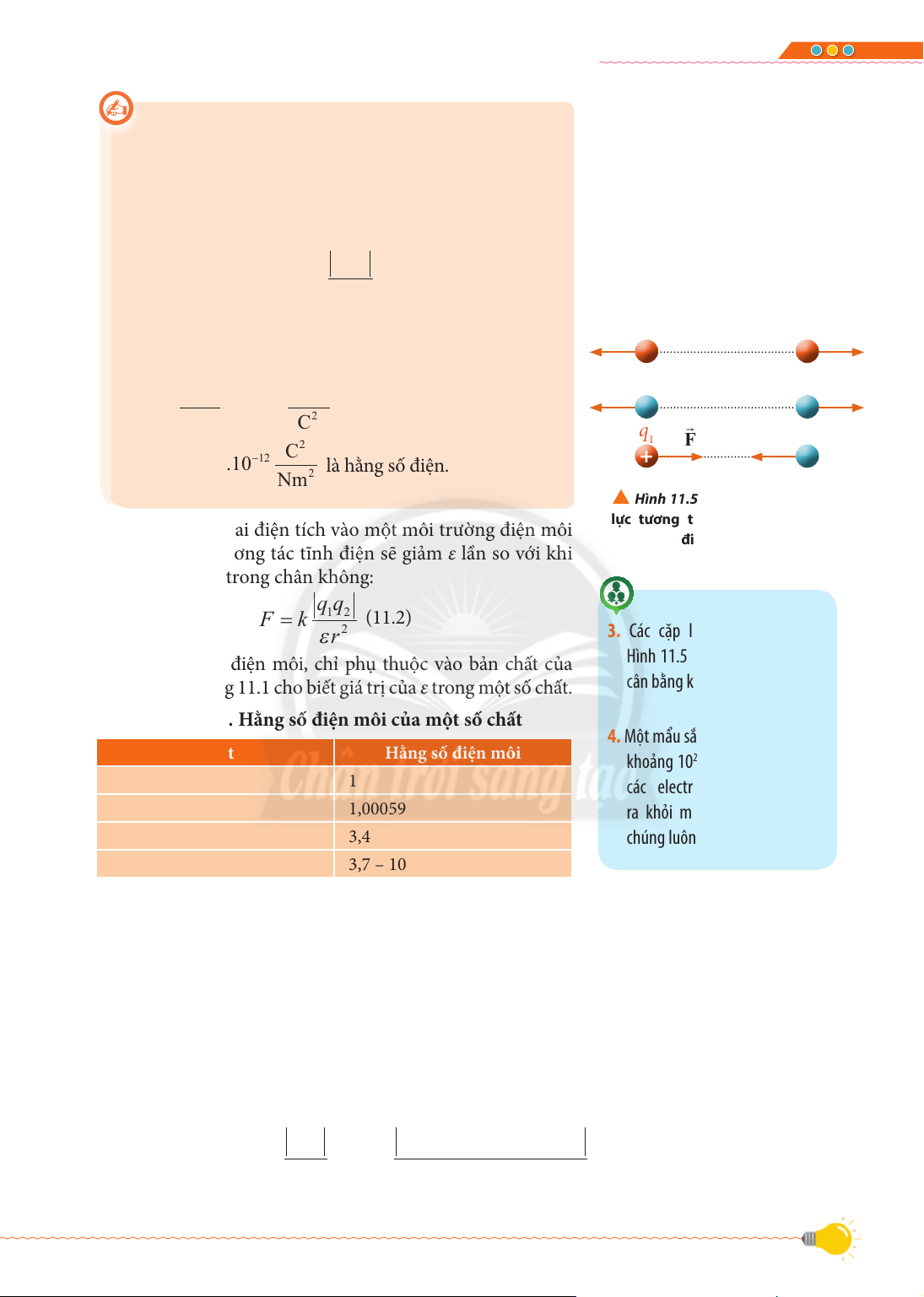
Bài 11. Định luật Coulomb về tương tác tĩnh điện .................................................... 68
Bài 12. Điện trường ........................................................................................................ 73
Bài 13. Điện thế và thế năng điện ................................................................................. 80
Bài 14. Tụ điện ................................................................................................................. 87
Bài 15. Năng lượng và ứng dụng của tụ điện .............................................................. 93
Chương 4: DÒNG ĐIỆN KHÔNG ĐỔI ....................................................................98
Bài 16. Dòng điện. Cường độ dòng điện ..................................................................... 98
Bài 17. Điện trở. Định luật Ohm ................................................................................ 103
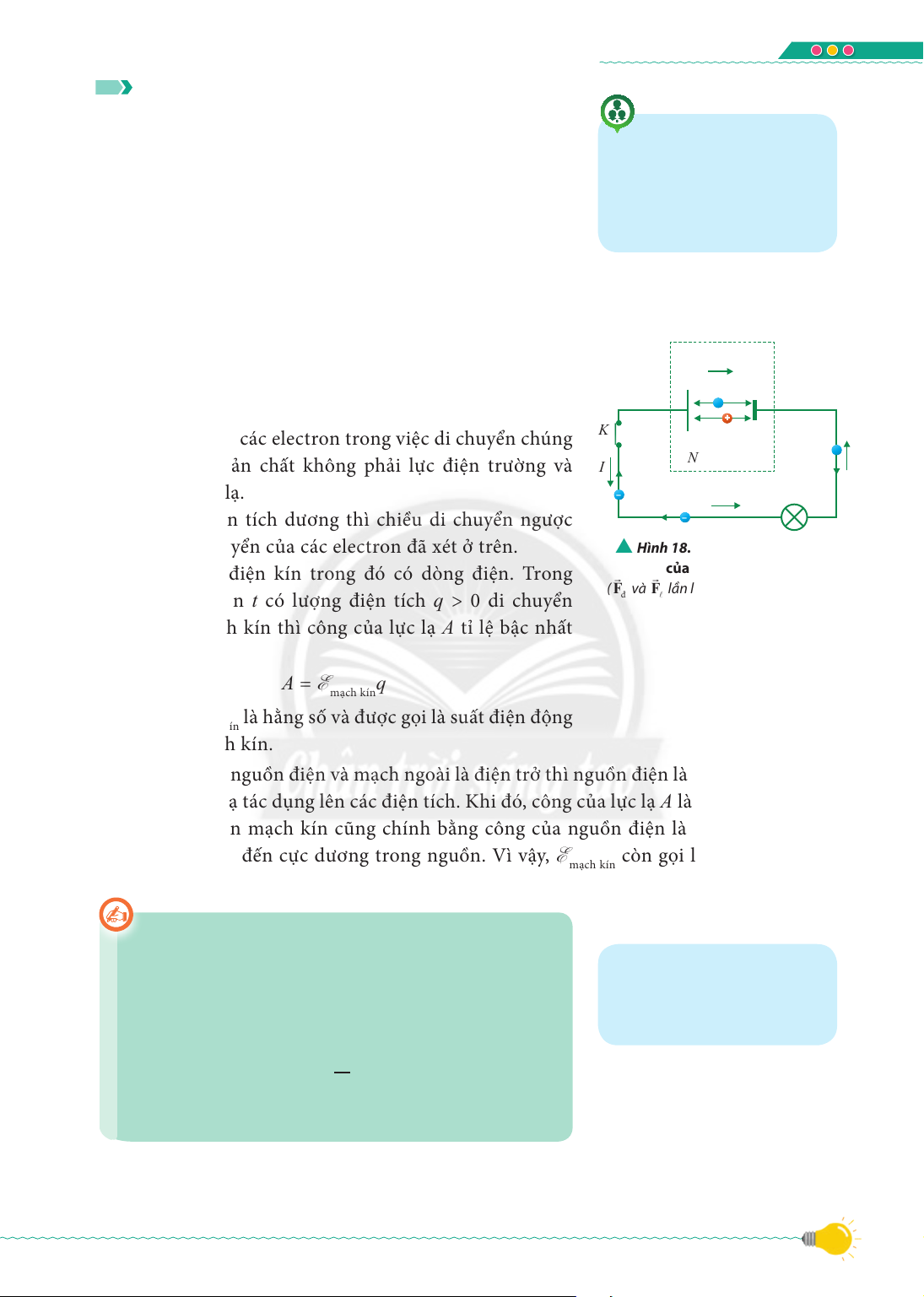
Bài 18. Nguồn điện ....................................................................................................... 108
Bài 19. Năng lượng điện. Công suất điện .................................................................. 113
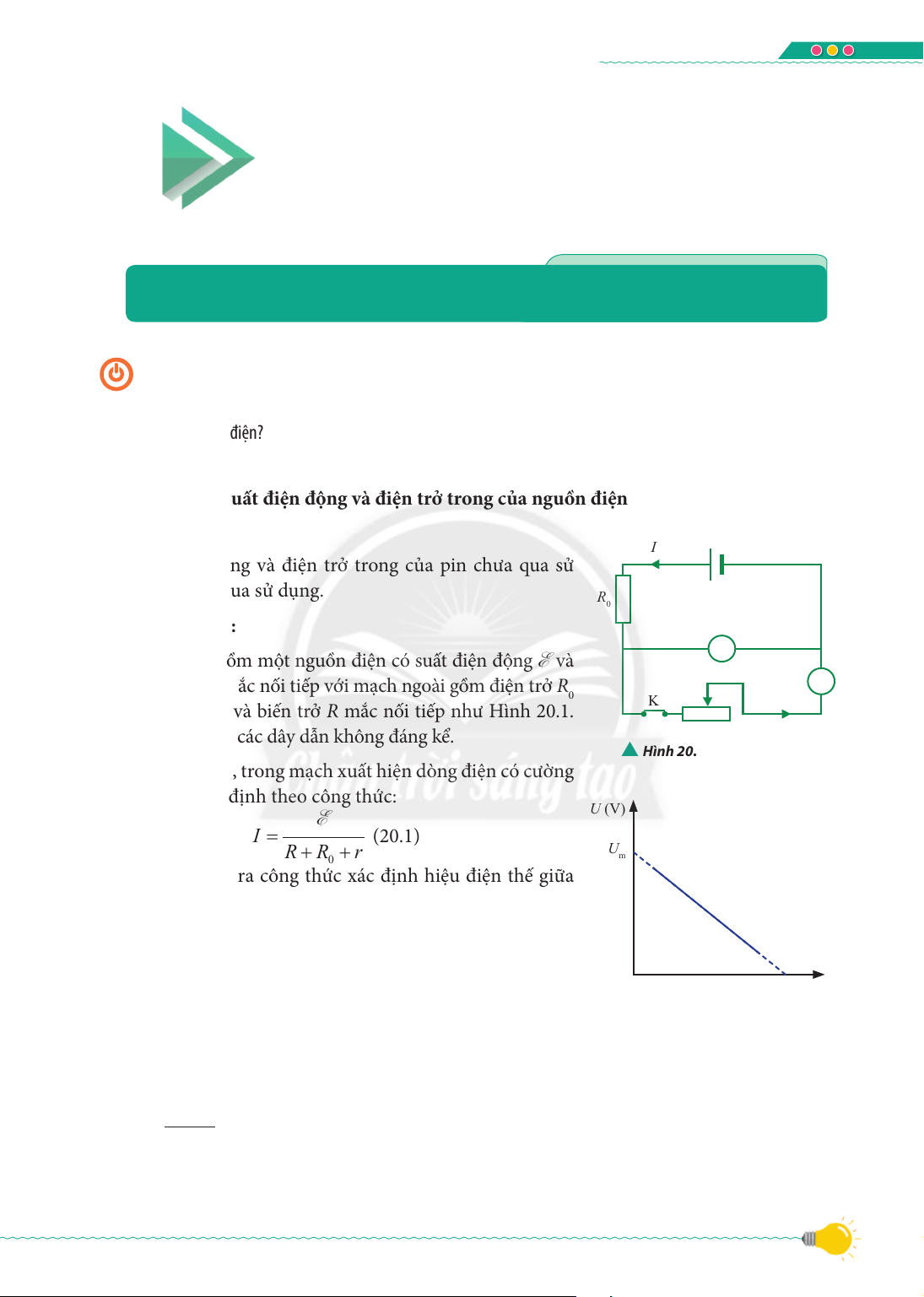
Bài 20. Thực hành xác định suất điện động và điện trở trong của pin ................. 117
Giải thích thuật ngữ ..................................................................................................... 123 4 VẬT LÍ 11 '$2ïų1* Chương 1 Bài 1 07l'$2ô1*
– Thí nghiệm đơn giản về dao động, một số ví dụ đơn giản về dao động tự do.
– Định nghĩa biên độ, chu kì, tần số, tần số góc, độ lệch pha.
– Mô tả dao động điều hoà.
Sự dao động của các vật diễn ra phổ biến trong cuộc
sống hằng ngày như: dao động của quả lắc đồng hồ
(Hình 1.1a), dao động của cánh chim ruồi(*) để giữ
cho cơ thể bay tại chỗ trong không trung khi hút mật
(Hình 1.1b). Vậy dao động có đặc điểm gì và được mô tả như thế nào? a) b)
S Hình 1.1. a) Đồng hồ quả lắc;
b) Chim ruồi đang hút mật
1 KHÁI NIỆM DAO ĐỘNG TỰ DO
Khái niệm dao động
1. Từ một số dụng cụ đơn giản như:
Chuyển động của những vật trong Hình 1.1 (quả lắc,
lò xo nhẹ, dây nhẹ không dãn,
cánh chim) có điểm chung là sự chuyển động có tính lặp lại vật nặng và giá đỡ.
và có giới hạn trong không gian. Những chuyển động như vậy
a) Em hãy thực hiện hai thí nghiệm sau:
được gọi là dao động cơ học. Một số vật thực hiện dao động
– Cố định một đầu của lò xo, gắn
vật nặng vào đầu còn lại của lò
cơ học quanh một vị trí đặc biệt được gọi là vị trí cân bằng.
xo như Hình 1.2a. Kéo vật nặng
xuống một đoạn theo phương
Dao động cơ học là sự chuyển động có giới hạn trong
thẳng đứng và buông nhẹ.
không gian của một vật quanh một vị trí xác định.
– Cố định một đầu của dây nhẹ
không dãn, gắn vật nặng vào
Vị trí đó gọi là vị trí cân bằng.
đầu còn lại của dây. Kéo vật
nặng để dây treo lệch một góc
Dao động rất phổ biến trong tự nhiên và khoa học kĩ thuật. xác định và buông nhẹ.
Trong điện và từ học cũng có hiện tượng dao động. Dòng
b) Quan sát và mô tả chuyển động
điện được sử dụng trong sinh hoạt hằng ngày là dao động
của các vật, nêu điểm giống điện từ.
nhau về chuyển động của chúng.
(*) Chim ruồi là loài chim có thân hình bé nhỏ, có khả năng bay cố định một chỗ trong không trung hoặc bay giật lùi. 5 VẬT LÍ 11
Dao động mà trạng thái chuyển động của vật (vị trí và vận
tốc) được lặp lại như cũ sau những khoảng thời gian bằng
2. Nêu một số ví dụ về dao động
nhau được gọi là dao động tuần hoàn, ví dụ: dao động của tuần hoàn.
quả lắc đồng hồ (Hình 1.1a).
3. Hãy nêu một ứng dụng của dao Dao động tự do
động tuần hoàn trong cuộc sống.
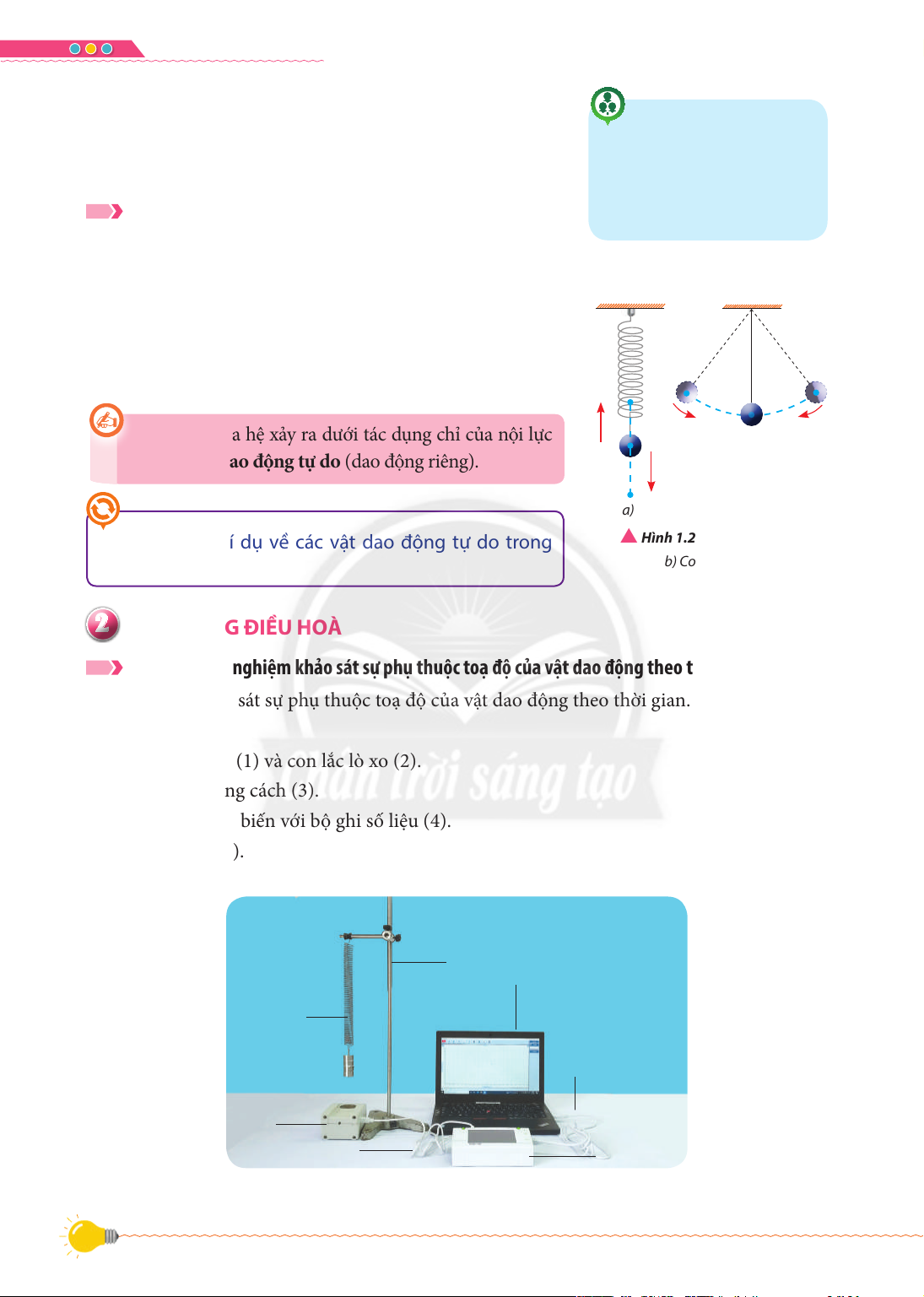
Xét các hệ thực hiện dao động: con lắc lò xo gồm vật nặng
được gắn vào một đầu của lò xo (Hình 1.2a), con lắc đơn
gồm vật nặng được gắn vào đầu một dây không dãn cùng với
Trái Đất (Hình 1.2b). Lực đàn hồi tác dụng lên vật trong con
lắc lò xo và trọng lực tác dụng lên vật trong con lắc đơn gọi là nội lực của hệ.
Dao động của hệ xảy ra dưới tác dụng chỉ của nội lực
được gọi là dao động tự do (dao động riêng). a) b)
Nêu một số ví dụ về các vật dao động tự do trong
S Hình 1.2. a) Con lắc lò xo; thực tế. b) Con lắc đơn
2 DAO ĐỘNG ĐIỀU HOÀ
Giới thiệu thí nghiệm khảo sát sự phụ thuộc toạ độ của vật dao động theo thời gian
Mục đích: Khảo sát sự phụ thuộc toạ độ của vật dao động theo thời gian. Dụng cụ:
– Hệ thống giá đỡ (1) và con lắc lò xo (2).
– Cảm biến khoảng cách (3).
– Dây cáp nối cảm biến với bộ ghi số liệu (4). – Bộ ghi số liệu (5).
– Dây cáp nối bộ ghi số liệu và máy tính (6), máy tính (7). (1) (7) (2) (6) (3) (4) (5)
S Hình 1.3. Thí nghiệm khảo sát sự phụ thuộc toạ độ của vật dao động theo thời gian 6 VẬT LÍ 11
Tiến hành thí nghiệm:
Tiến hành bố trí thí nghiệm như Hình 1.3. Khởi động các
thiết bị để sẵn sàng ghi nhận tín hiệu, sau đó kéo vật ra khỏi
4. Nhận xét về hình dạng đồ thị
vị trí cân bằng một đoạn nhỏ theo phương thẳng đứng và
toạ độ – thời gian của vật dao
buông cho vật bắt đầu dao động không vận tốc ban đầu. động trong Hình 1.4.
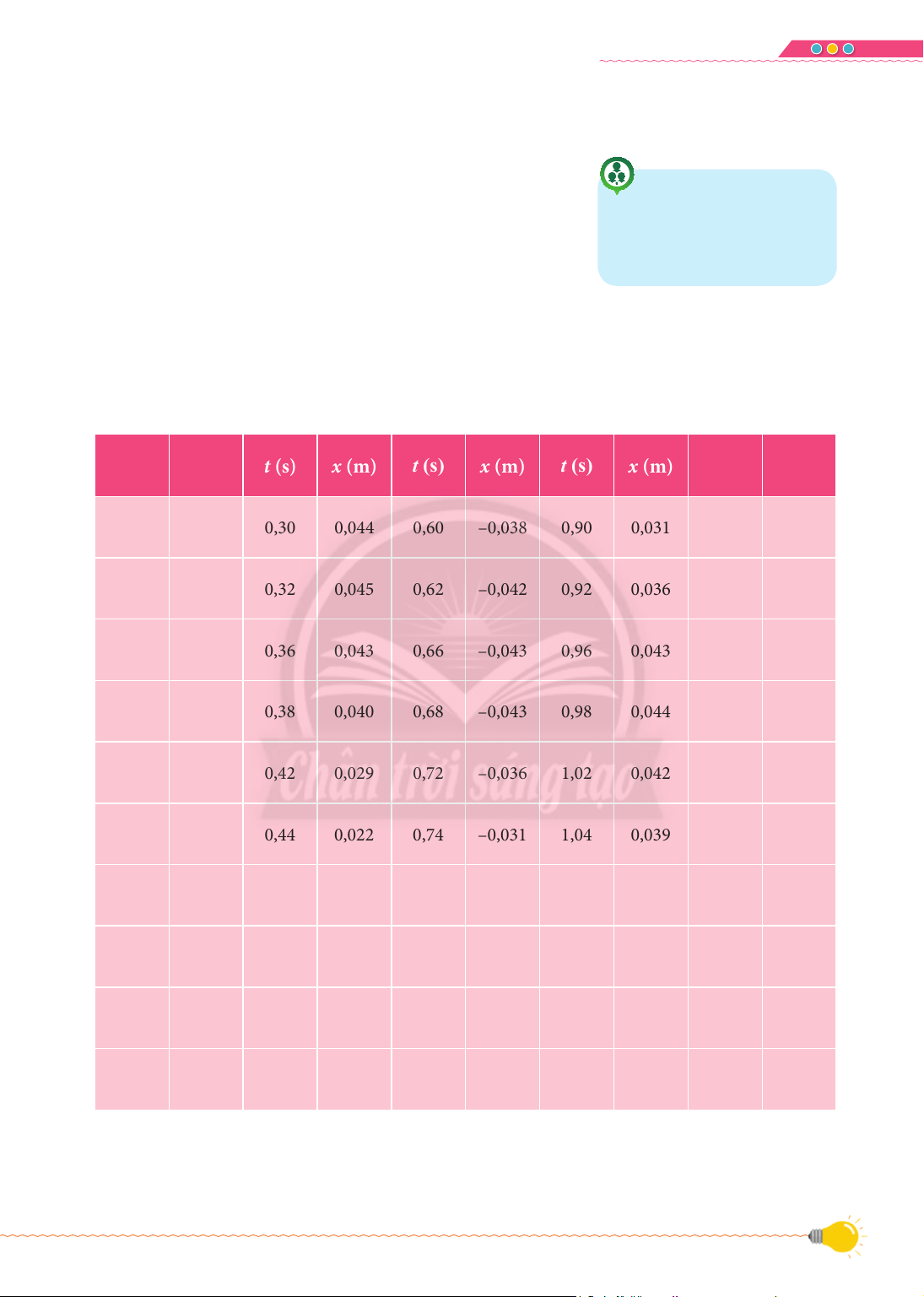
Toạ độ của vật nặng tại từng thời điểm khác nhau được
hiển thị trên máy tính như trong Bảng 1.1 và đồ thị toạ độ –
thời gian của vật dao động như trong Hình 1.4.
T Bảng 1.1. Toạ độ của vật nặng tại những thời điểm khác nhau t (s) x (m) t (s) x (m) t (s) x (m) t (s) x (m) t (s) x (m) 0,00 –0,044 0,30 0,044 0,60 –0,038 0,90 0,031 1,20 –0,021 0,02 –0,043 0,32 0,045 0,62 –0,042 0,92 0,036 1,22 –0,028 0,06 –0,037 0,36 0,043 0,66 –0,043 0,96 0,043 1,26 –0,040 0,08 –0,032 0,38 0,040 0,68 –0,043 0,98 0,044 1,28 –0,042 0,12 –0,018 0,42 0,029 0,72 –0,036 1,02 0,042 1,32 –0,043 0,14 –0,010 0,44 0,022 0,74 –0,031 1,04 0,039 0,18 0,006 0,48 0,005 0,78 –0,017 1,08 0,028 0,20 0,016 0,50 –0,004 0,80 –0,009 1,10 0,021 0,24 0,031 0,54 –0,020 0,84 0,009 1,14 0,003 0,26 0,036 0,56 –0,027 0,86 0,017 1,16 –0,005 7 VẬT LÍ 11
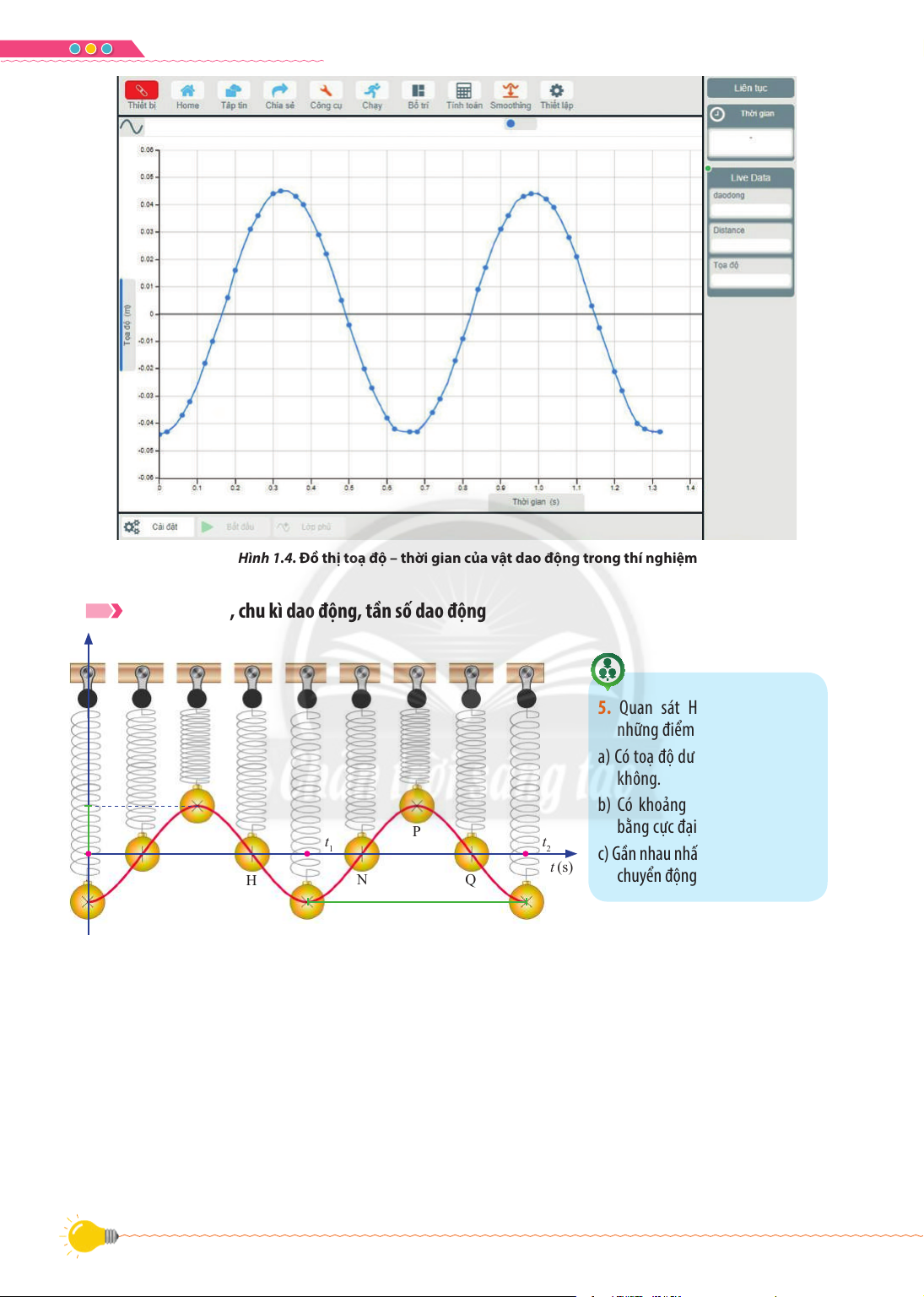
S Hình 1.4. Đồ thị toạ độ – thời gian của vật dao động trong thí nghiệm
Li độ, biên độ, chu kì dao động, tần số dao động x (m)
5. Quan sát Hình 1.5 và chỉ ra những điểm:
a) Có toạ độ dương, âm hoặc bằng không.
b) Có khoảng cách đến vị trí cân A G P bằng cực đại. W W W O 0 1 2
c) Gần nhau nhất có cùng trạng thái W (s) F H N Q chuyển động. T E M R
S Hình 1.5. Vị trí của vật nặng trong hệ con lắc lò xo
tại các thời điểm khác nhau
Hình 1.5 cho biết vị trí của vật nặng tại những thời điểm khác nhau trên đường đồ thị toạ độ –
thời gian khi tiến hành thí nghiệm như bố trí trong Hình 1.3.
Chọn hệ trục toạ độ O[W như Hình 1.5, gốc thời gian được chọn vào lúc vật bắt đầu dao động,
gốc toạ độ được chọn tại vị trí cân bằng của vật, chiều dương của trục toạ độ được chọn theo
chiều thẳng đứng hướng lên.
Toạ độ của vật tính từ vị trí cân bằng tại mỗi thời điểm được gọi là li độ [của vật dao động.
Như vậy, li độ có thể có giá trị dương, âm hoặc bằng không. 8 VẬT LÍ 11
Trong quá trình dao động, vật nặng sẽ đến hai biên,
dừng lại và đổi chiều chuyển động. Biên ứng với toạ độ
dương được gọi là biên dương, biên còn lại là biên âm.
Khi ở hai biên, li độ của vật dao động có độ lớn cực đại.
Độ lớn cực đại của li độ được gọi là biên độ A của vật
dao động. Biên độ dao động luôn có giá trị dương.
Li độ của vật dao động là toạ độ của vật mà gốc toạ
độ được chọn trùng với vị trí cân bằng.
Biên độ là độ lớn cực đại của li độ.
Trong Hình 1.5, ta thấy tại các thời điểm t , t và t , vật nặng 0 1 2
có cùng trạng thái chuyển động: đến biên âm và bắt đầu
chuyển động đi lên. Khoảng thời gian ngắn nhất giữa hai
lần vật có cùng trạng thái chuyển động được gọi là chu kì
dao động T. Trong một chu kì dao động, vật hoàn thành 6. Một con ong mật đang bay tại chỗ
được một dao động hay một chu trình dao động.
trong không trung (Hình 1.6),
đập cánh với tần số khoảng
Trên thực tế, người ta thường sử dụng thuật ngữ tần số
300 Hz. Xác định số dao động mà
dao động như là một đặc trưng của dao động để cho biết
cánh ong mật thực hiện trong
1 s và chu kì dao động của
số dao động mà vật thực hiện trong một giây. cánh ong.
Chu kì dao động là khoảng thời gian để vật
thực hiện được một dao động. Tần số dao động
được xác định bởi số dao động mà vật thực hiện được trong một giây. f 1 (1.1) T
Trong hệ SI, chu kì dao động có đơn vị là giây (s) và
S Hình 1.6. Ong mật bay tại chỗ trong không trung
tần số dao động có đơn vị là héc (Hz).
Khái niệm dao động điều hoà
Khi lực cản trong quá trình dao động là không đáng kể, đồ
thị toạ độ – thời gian, cũng chính là đồ thị li độ – thời gian,
có dạng hình sin. Dao động có tính chất này được gọi là
dao động điều hoà.
Dao động điều hoà là dao động tuần hoàn mà li độ
của vật dao động là một hàm cosin (hoặc sin) theo thời gian. 9 VẬT LÍ 11
Pha dao động, độ lệch pha, tần số góc
Tại mỗi thời điểm, trạng thái dao động (li độ và vận tốc) của
vật được đặc trưng bởi một đại lượng, gọi là pha dao động φ.
Pha dao động được đo bằng đơn vị của góc, là độ hoặc rad.
7. Quan sát Hình 1.7, so sánh biên
Vật thực hiện một dao động tương ứng với pha dao động
độ và li độ của hai dao động 1
và 2 tại mỗi thời điểm.
thay đổi một lượng 2ʌ rad.
Khi xét hai dao động cùng chu kì (cùng tần số), ta thường x (cm)
quan tâm đến đại lượng độ lệch pha giữa chúng. 1 2 ¨W
Ví dụ: Hai vật đang dao động có đồ thị li độ – thời gian được O T W(s)
biểu diễn như Hình 1.7. Tại thời điểm t = 0, vật 1 đi qua
vị trí cân bằng theo chiều dương của trục toạ độ. Sau một
S Hình 1.7. Đồ thị li độ – thời gian
khoảng thời gian ngắn nhất Δt, vật 2 mới đạt được trạng
của hai vật dao động điều hoà
thái tương tự. Ta nói hai dao động này lệch pha nhau một lượng 'φ.
Pha dao động là một đại lượng đặc trưng cho trạng
thái của vật trong quá trình dao động. Độ lệch pha
giữa hai dao động điều hoà cùng chu kì (cùng tần
số) được xác định theo công thức: 2 t (1.2) T
Vật thực hiện một dao động tương ứng với pha dao động
8. Dựa vào dữ kiện trong câu Thảo
thay đổi một lượng 2ʌ rad. Đại lượng đặc trưng cho tốc độ
luận 6, xác định tần số góc khi
biến thiên của pha dao động được gọi là tần số góc Ȧ của
ong đập cánh. Xem biên độ dao dao động.
động của cánh ong là không đổi.
Tần số góc của dao động là đại lượng đặc trưng cho tốc độ biến thiên của pha dao
động. Đối với dao động điều hoà, tần số góc có giá trị không đổi và được xác định theo công thức: 2 2 1 (1.3) t t T 2 1
với φ và φ lần lượt là pha dao động tại thời điểm t và t . 1 2 1 2
Trong hệ SI, tần số góc có đơn vị là radian trên giây (rad/s).
Quan sát đồ thị li độ – thời x (cm)
gian của hai vật dao động 2 10
điều hoà được thể hiện trong
Hình 1.8. Hãy xác định biên O W(s)
độ, chu kì, tần số, tần số góc 0,5 1,0 1,5 2,0 2,5 –10 1
của mỗi vật dao động và độ
S Hình 1.8. Đồ thị li độ – thời gian của hai vật
lệch pha giữa hai dao động.
dao động điều hoà 10 VẬT LÍ 11
Vận dụng các đại lượng vật lí đặc trưng để mô tả dao động điều hoà
Ví dụ 1: Hình 1.9 thể hiện đồ thị li độ – thời gian của một
vật dao động điều hoà được kích thích theo hai cách khác
9. Xác định độ lệch pha giữa hai
nhau. Hãy xác định các đại lượng biên độ, chu kì, tần số và dao động trong Hình 1.9.
tần số góc trong từng trường hợp. Bài giải x (cm) 20
Trong trường hợp a), vật bắt đầu dao động từ vị trí cân 10
bằng theo chiều dương quy ước. Trong trường hợp b), vật O 0,5
bắt đầu dao động từ vị trí biên dương, ngược chiều dương
1 1,5 2 2,5 3 3,5 W (s) –10 quy ước. –20 a)
Trong hai trường hợp a) và b): x (cm)
– Vật dao động cùng biên độ A = 20 cm. 20
– Vật dao động cùng chu kì T = 2 s. 10
– Tần số dao động của vật trong cả hai trường hợp:
O 0,5 1 1,5 2 2,5 3 3,5 W (s) –10 f 1 1 –20 0,5 Hz T 2 b)
– Tần số góc của vật trong cả hai trường hợp:
S Hình 1.9. Đồ thị li độ – thời gian
của một vật được kích thích dao 2f 2 0 . ,5 rad/s
động theo hai cách khác nhau
Ví dụ 2: So sánh biên độ, chu kì, tần số, tần số góc và xác
định độ lệch pha của hai dao động điều hoà trong ba trường
hợp được thể hiện ở Hình 1.10. x (cm) 1 Bài giải A1 A2 2 Trường hợp a): O
– Biên độ dao động của vật 1 lớn hơn biên độ dao động của W (s)
vật 2: A > A . 1 2
– Chu kì dao động của hai vật bằng nhau: T = T . a) 1 2 x (cm)
– Tần số và tần số góc của hai dao động này cũng bằng nhau: A 2
f = f và Ȧ = Ȧ . 1 1 2 1 2 O
– Trong quá trình dao động, hai vật luôn đến vị trí cân bằng W (s) ±$
và hai biên cùng thời điểm. Do đó, đại lượng ∆t trong công b)
thức (1.2) bằng 0, dẫn đến 'φ = 0 rad. Ta nói hai vật dao x (cm) động cùng pha với nhau. A 2 Trường hợp b): O 1 W (s)
– Biên độ dao động của hai vật bằng nhau: A = A = A. ±$ 1 2
– Chu kì dao động của vật 1 bằng một nửa chu kì dao động c)
S Hình 1.10. Đồ thị li độ – thời gian của vật 2: T T2 .
của hai vật dao động trong các 1 2
trường hợp khác nhau 11 VẬT LÍ 11
– Tần số và tần số góc dao động của vật 1 gấp hai lần tần số
và tần số góc dao động của vật 2:
f = 2f và Ȧ = 2Ȧ . 1 2 1 2
– Do hai vật dao động khác chu kì nên độ lệch pha của hai
dao động thay đổi theo thời gian. Trường hợp c):
– Biên độ dao động của hai vật bằng nhau: A = A = A. 1 2
– Chu kì dao động của hai vật bằng nhau: T = T = T. 1 2
– Tần số và tần số góc của hai dao động này cũng bằng nhau:
f = f và Ȧ = Ȧ . 1 2 1 2
– Trong quá trình dao động, vật thứ nhất đi qua vị trí cân
bằng thì vật thứ hai đi qua vị trí biên. Nghĩa là khoảng thời
gian ngắn nhất để hai vật có cùng trạng thái dao động là t T
. Theo công thức (1.2) ta suy ra: rad. Ta nói 4 2
hai dao động vuông pha với nhau.
Xét vật thứ nhất bắt đầu dao động điều hoà từ vị trí cân bằng, vật thứ hai dao động
điều hoà với biên độ lớn gấp hai lần, cùng chu kì và lệch pha rad so với vật 4
thứ nhất. Vẽ phác đồ thị li độ – thời gian của hai vật trong hai chu kì dao động đầu tiên.
Tìm hiểu và trình bày một số ứng dụng thực tiễn của hiện tượng dao động.
Mối liên hệ giữa dao động điều hoà và chuyển động tròn đều
Xét một quả cầu được gắn cố định vào một ÈQKViQJ
vành mảnh có thể chuyển động tròn đều trong
mặt phẳng thẳng đứng. Khi chiếu ánh sáng từ trên
xuống, ta thấy bóng của quả cầu dao động trên 9jQK[RD\
một đoạn thẳng có phương song song với đường &KLӅX
thẳng đi qua tâm của chuyển động tròn. Quả cầu FKX\ӇQ ÿӝQJ
xoay được một vòng tương ứng với bóng của nó
thực hiện được một dao động. Bằng một số tính 4XҧFҫX %yQJ 0jQ
toán, ta rút ra được dao động điều hoà được xem
như là hình chiếu của một chuyển động tròn đều
lên một đường thẳng đi qua tâm và nằm trong S
mặt phẳng quỹ đạo, biên độ của dao động bằng
Hình 1.11. Hình chiếu của một
quả cầu chuyển động tròn đều lên
bán kính quỹ đạo của chuyển động tròn đều.
mặt phẳng nằm ngang 12 VẬT LÍ 11
Khi quả cầu trong Hình 1.11 quay được một vòng, vectơ bán kính nối tâm của quỹ đạo và vật
quét được một góc 2ʌ rad, tương ứng với bóng của vật thực hiện được một dao động.
Bảng 1.2 thể hiện sự tương tự trong dao động điều hoà và chuyển động tròn đều.
T Bảng 1.2. Sự tương tự trong dao động điều hoà và chuyển động tròn đều Kí hiệu
Dao động điều hoà
Chuyển động tròn đều x Li độ
Toạ độ hình chiếu của vật trên trục toạ độ đi qua tâm và
nằm trong mặt phẳng của quỹ đạo tròn. A Biên độ Bán kính T Chu kì dao động Chu kì quay f Tần số dao động Tần số quay Ȧ Tần số góc Tốc độ góc Ȧt + φ Pha dao động Toạ độ góc 0 %j,7t3
1. Xác định biên độ, chu kì, tần số, tần số góc của mỗi dao động và độ lệch pha giữa hai dao động
có đồ thị li độ – thời gian như trong Hình 1P.1. x (cm) 8 6 4 2 O W (s) –2 –4 –6 –8 0,03 0,06 0,09 0,12 0,15 0,18 0,21 0,24
S Hình 1P.1. Đồ thị li độ – thời gian của hai vật dao động điều hoà
2. Vẽ phác đồ thị li độ – thời gian của hai dao động điều hoà trong các trường hợp:
a) Cùng biên độ, chu kì của dao động thứ nhất bằng ba lần chu kì của dao động thứ hai.
b) Biên độ của dao động thứ nhất bằng hai lần biên độ của dao động thứ hai, cùng chu kì, cùng pha.
c) Cùng biên độ, cùng chu kì và có độ lệch pha là ʌrad. 13 VẬT LÍ 11 3+¡1*751+ Bài 2 '$2ô1*ô,8+2j
– Độ dịch chuyển, vận tốc và gia tốc trong dao động điều hoà.
– Các phương trình về li độ, vận tốc và gia tốc của dao động điều hoà.
– Mối liên hệ giữa gia tốc và li độ trong dao động điều hoà.
Việc nghiên cứu các quá trình dao động điều hoà để ứng dụng vào thực tiễn như xây dựng mô hình dự báo
động đất yêu cầu ta phải mô tả chính xác trạng thái của vật dao động tại những thời điểm xác định. Ngoài ra, dao
động điều hoà có tính chất tuần hoàn theo thời gian và bị giới hạn trong không gian thì phương trình li độ, vận
tốc và gia tốc của vật dao động điều hoà có những khác biệt gì so với chuyển động thẳng đều và biến đổi đều mà
em đã học ở chương trình Vật lí 10?
1 LI ĐỘ TRONG DAO ĐỘNG ĐIỀU HOÀ
Phương trình li độ của vật dao động
Trong Bài 1, ta đã biết một vật được xem là đang thực hiện
dao động điều hoà khi đồ thị li độ – thời gian của vật có 1. Quan sát dao động của con lắc
dạng hình sin như Hình 1.4. Trong toán học, chỉ có hàm
lò xo và kết hợp với Hình 1.4,
hãy chỉ rõ sự khác nhau giữa
cosin (hoặc sin) mới có đồ thị dạng hình sin tương ứng.
hình dạng quỹ đạo chuyển
động và đồ thị li độ của vật
Phương trình li độ của vật dao động điều hoà có dạng: dao động theo thời gian.
x Acost (2.1) 0
Trong đó: x, A lần lượt là li độ và biên độ dao động của vật,
trong hệ SI có đơn vị là m.
Ȧ là tần số góc của dao động, trong hệ SI có đơn vị là rad/s.
φ = Ȧt + φ là pha của dao động tại thời điểm t, 0
trong hệ SI có đơn vị là rad.
φ là pha ban đầu của dao động, trong hệ SI có 0 đơn vị là rad. 14 VẬT LÍ 11
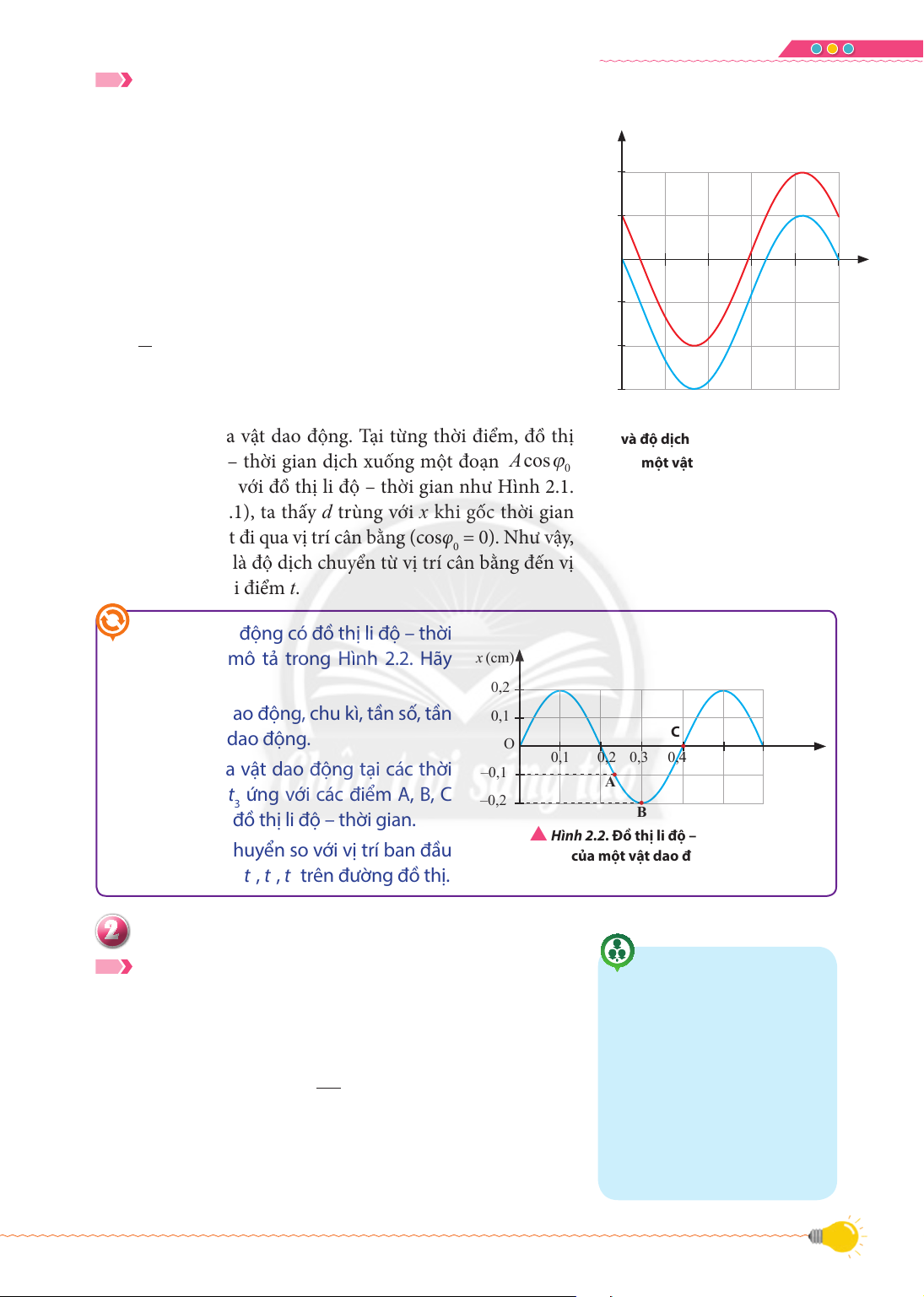
Độ dịch chuyển của vật dao động
Trong chương trình Vật lí 10, các em đã biết độ dịch chuyển
được xác định bằng độ biến thiên toạ độ của vật. Như vậy, [G
tại một thời điểm bất kì, độ dịch chuyển của vật dao động so (cm)
với vị trí ban đầu được xác định bằng công thức: 2 d x x x A x
cos(t ) Acos (2.1) 1 0 0 0 d
Hình 2.1 minh hoạ đồ thị li độ – thời gian (đường màu đỏ) O
và độ dịch chuyển – thời gian (đường màu xanh dương) 0,2 0,4 0,6 0,8 1 W (s)
đối với một vật dao động điều hoà có A = 2 cm, T = 1 s và –1 . –2 0 3
Ta thấy độ dịch chuyển so với vị trí ban đầu của vật cũng –3
biến thiên điều hoà theo thời gian cùng biên độ, chu kì và
S Hình 2.1. Đồ thị li độ – thời gian
pha với li độ của vật dao động. Tại từng thời điểm, đồ thị
và độ dịch chuyển – thời gian của
độ dịch chuyển – thời gian dịch xuống một đoạn AcosM
một vật dao động điều hoà 0
trên trục tung so với đồ thị li độ – thời gian như Hình 2.1.
Từ công thức (2.1), ta thấy d trùng với x khi gốc thời gian
được chọn lúc vật đi qua vị trí cân bằng (cosφ = 0). Như vậy, 0
li độ cũng chính là độ dịch chuyển từ vị trí cân bằng đến vị
trí của vật tại thời điểm W.
Một vật dao động có đồ thị li độ – thời
gian được mô tả trong Hình 2.2. Hãy x (cm) xác định: 0,2
a) Biên độ dao động, chu kì, tần số, tần 0,1 số góc của dao động. C O
b) Li độ của vật dao động tại các thời 0,1 0,2 0,3 0,4 0,5 0,6 W (s) –0,1 A
điểm t , t , t ứng với các điểm A, B, C 1 2 3 –0,2
trên đường đồ thị li độ – thời gian. B
S Hình 2.2. Đồ thị li độ – thời gian
c) Độ dịch chuyển so với vị trí ban đầu
của một vật dao động
tại thời điểm t , t , t trên đường đồ thị. 1 2 3
2 VẬN TỐC TRONG DAO ĐỘNG ĐIỀU HOÀ
Phương trình vận tốc của vật dao động
Trong chương trình Vật lí 10, các em đã biết vận tốc tức thời
2. Quan sát Hình 2.3a và 2.3b, hãy xác định:
của vật được xác định bằng thương số giữa độ dịch chuyển
a) Hình dạng đồ thị vận tốc –
d = Δx và thời gian Δt để vật thực hiện độ dịch chuyển đó. thời gian của vật. x v (2.3)
b) Chu kì của vận tốc của vật. t
c) Mối liên hệ giữa tốc độ cực đại và
với điều kiện Δt rất nhỏ. biên độ của vật.
Đồ thị li độ – thời gian và vận tốc – thời gian của một vật
d) Độ lệch pha của vận tốc so với li
dao động điều hoà được xác định từ thực nghiệm có dạng độ của vật.
như Hình 2.3a và 2.3b. Quan sát Hình 2.3, ta thấy: 15 VẬT LÍ 11 x (cm)
– Đồ thị vận tốc – thời gian của vật dao động điều 0,66 0,44
hoà cũng có dạng hình sin. Nghĩa là vận tốc của vật 0,22 O –0,22 W (s)
dao động điều hoà cũng biến đổi điều hoà theo –0,44 –0,66 thời gian. 0,33 0,66 0,99 1,32 1,65 1,98 a)
– Vận tốc và li độ của vật dao động điều hoà có v (cm/s) 4,20
cùng chu kì T (cùng tần số f). 2,10
– Tỉ số của tốc độ cực đại và biên độ dao động của O W (s) –2,10
vật bằng Ȧ. Nghĩa là v = ȦA. max –4,20 0,33 0,66 0,99 1,32 1,65 1,98
– Sau một khoảng thời gian t T , li độ có cùng b) 4 a (cm/s2)
trạng thái dao động với vận tốc. Nghĩa là vận tốc 40
biến đổi điều hoà theo thời gian lệch pha S so với 20 2 li độ. O W (s) –20
Từ những nhận xét trên, kết hợp với việc sử dụng –40 0,33 0,66 0,99 1,32 1,65 1,98
công cụ toán học phù hợp, ta rút ra được: c)
S Hình 2.3. Đồ thị: a) li độ – thời gian; b) vận tốc – thời gian;
c) gia tốc – thời gian của một vật dao động điều hoà
Phương trình vận tốc của vật dao động điều hoà có dạng: v Acos t sin (2.4) 0 A t 0 2
Một vật dao động điều hoà với biên độ 10 cm và chu kì 2 s. Chọn gốc thời gian là khi
vật qua vị trí cân bằng theo chiều dương. Xác định vận tốc của vật vào thời điểm đó.
Công thức mô tả mối liên hệ giữa vận tốc và li độ của vật dao động
Kết hợp các công thức (2.4) và (2.1), ta rút ra được công thức mô tả mối liên hệ giữa vận
tốc và li độ của vật dao động tại mỗi thời điểm: v ȦA v2 2 x (2.5) v 1 2 2 A –A A max O x
Từ đồ thị trong Hình 2.3a và 2.3b, kết hợp với
phương trình (2.5), ta thấy: –ȦA
– Khi vật đi qua vị trí cân bằng: x = 0, v rv . PD[
S Hình 2.4. Đồ thị mô tả mối liên hệ
– Khi vật ở hai biên: x r , A v = 0.
giữa vận tốc và li độ của vật dao động
Đồ thị mô tả mối liên hệ giữa vận tốc và li độ của vật dao động được thể hiện trong
Hình 2.4 là một đường ellipse có độ dài hai trục lần lượt là 2A và 2v . max 16 VẬT LÍ 11
3 GIA TỐC TRONG DAO ĐỘNG ĐIỀU HOÀ
Phương trình gia tốc của vật dao động
Ta đã biết, gia tốc tức thời được xác định bằng thương số 3. Quan sát Hình 2.3a và 2.3c, hãy
giữa biến thiên vận tốc Δv và thời gian Δt để vật thực hiện xác định:
sự biến thiên vận tốc đó.
a) Hình dạng đồ thị gia tốc – v thời gian của vật. a (2.6) t
b) Chu kì của gia tốc của vật.
với điều kiện Δt rất nhỏ.
c) Mối liên hệ giữa gia tốc cực đại và biên độ của vật.
Đồ thị gia tốc – thời gian của một dao động điều hoà được
d) Độ lệch pha của gia tốc so với
xác định từ thực nghiệm có dạng như Hình 2.3c. Quan sát li độ của vật. Hình 2.3, ta thấy:
– Đồ thị gia tốc – thời gian của vật dao động điều hoà cũng
có dạng hình sin. Nghĩa là gia tốc của vật dao động điều hoà
cũng biến đổi điều hoà theo thời gian.
– Gia tốc và li độ của vật dao động điều hoà có cùng chu kì
T (cùng tần số f).
– Tỉ số của độ lớn cực đại của gia tốc và biên độ dao động
của vật bằng Ȧ2. Nghĩa là a = Ȧ2A. max
– Sau một khoảng thời gian t T
, li độ có cùng trạng thái 2
dao động với gia tốc. Nghĩa là gia tốc và li độ của vật luôn
lệch pha S so với nhau (ngược pha nhau).
Từ những nhận xét trên, kết hợp với việc sử dụng công cụ
toán học phù hợp, ta rút ra được:
Phương trình gia tốc của vật dao động điều hoà
có dạng:a2Acost 0 2 Acost 2 (2.7) 0 x
Do ta có F = ma = –mȦ2x nên lực tác dụng vào vật dao động
4. Hãy vẽ phác đồ thị lực tác dụng –
điều hoà luôn hướng về vị trí cân bằng của vật.
thời gian của vật dao động điều
Từ đây, ta rút ra được điều kiện để một vật thực hiện dao
hoà có đồ thị li độ – thời gian như Hình 2.2.
động điều hoà là có lực tác dụng vào vật để luôn kéo vật về
vị trí cân bằng. Lực này có độ lớn tỉ lệ thuận với độ lớn li độ của vật dao động. 17 VẬT LÍ 11
Dựa vào các đồ thị trong Hình 2.3:
a) Viết phương trình li độ, vận tốc và gia tốc của vật dao động điều hoà.
b) Mô tả định tính tính chất của li độ, vận tốc và gia tốc của vật tại các thời điểm: 0,5 s; 0,75 s và 1 s.
c) Dựa vào các phương trình được xây dựng ở câu a để kiểm chứng lại mô tả định tính ở câu b.
Đồ thị mô tả mối liên hệ giữa gia tốc và li độ được thể a
hiện trong Hình 2.5, là một đoạn thẳng đi qua gốc toạ độ aPD[
với hệ số góc có giá trị –Ȧ2. Gia tốc luôn có chiều hướng A
về vị trí cân bằng của vật. –A O x –aPD[
S Hình 2.5. Đồ thị mô tả mối liên hệ
giữa gia tốc – li độ của vật dao động
Vận dụng phương trình gia tốc, mối liên hệ giữa gia tốc và li độ của vật dao động
Ví dụ: Một vật dao động điều hoà có phương trình gia tốc a 2 12 cos 2 t 2 cm/s (cm/s.2) 2
a) Xác định biên độ, tần số góc, chu kì, tần số dao động của vật.
b) Viết phương trình li độ và phương trình vận tốc của vật. %jLJLҧL
a) Từ công thức (2.7), ta có: a 2A t 2 2 cos cos cm/s (cm/s2) 0 A t 0
So sánh với phương trình gia tốc của vật, suy ra:
– Tần số góc: Ȧ = 2ʌ rad/s. 2
– Biên độ dao động: A a 12 max 3 2 ( 2 2 cm.
– Pha ban đầu của dao động: rad. 0 2 2
– Chu kì dao động: T 2 2 1 s. 2
– Tần số dao động: f 1 1 T 1 Hz. 1 18 VẬT LÍ 11 b)
– Phương trình li độ của vật theo công thức (2.1): x Acost 3 2 cm (cm) 0 cos t
5. Nhận xét về độ lệch pha giữa gia 2
tốc và vận tốc của vật dao động.
– Phương trình vận tốc của vật theo công thức (2.4):
v Z$FRV§ZW M S · SFRV W S ¨ ¸ cm/s 0 (cm/s) © 2 ¹
Một máy cơ khí khi hoạt động sẽ tạo ra những dao động được xem gần đúng là dao
động điều hoà với phương trình li độ có dạng:
x = 2cos(180SW) (mm)
a) Hãy xác định biên độ, chu kì, tần số và tần số góc của dao động.
b) Viết phương trình vận tốc và gia tốc của vật dao động.
Tìm hiểu và trình bày ngắn gọn nguyên tắc hoạt động của thiết bị đo khối lượng của các phi hành gia trên tàu vũ trụ. F Con lắc lò xo Con lắc đơn ș N T A m F m s M x O Pt ș –A O A PQ P P
S Hình 2.6. Con lắc lò xo
S Hình 2.7. Con lắc đơn
Xét một con lắc lò xo gồm một vật nặng
Xét con lắc đơn gồm một vật nặng gắn vào
khối lượng m gắn vào đầu một lò xo nhẹ có đầu một sợi dây nhẹ, không dãn, đầu còn lại
độ cứng k, đầu còn lại của lò xo được giữ cố của sơi dây được giữ cố định như Hình 2.7.
định. Vật có thể chuyển động trên mặt sàn Xem lực cản của không khí là không đáng kể.
nằm ngang như Hình 2.6, ma sát giữa mặt Kích thích cho vật dao động.
sàn và vật là không đáng kể. Kích thích cho vật dao động. 19 VẬT LÍ 11
Các lực tác dụng vào vật nặng gồm: trọng lực
Các lực tác dụng vào vật nặng gồm: trọng lực
P , phản lực N và lực đàn hồi F.
P và lực căng dây T.
Theo định luật II Newton, ta có:
Trọng lực P được phân tích thành hai G G G G
P N F a m (2.8)
thành phần: thành phần pháp tuyến PQ và
Chọn hệ trục toạ độ Ox như Hình 2.6. tiếp tuyến Pt.
Chiếu lên phương chuyển động, ta có:
Hợp lực của T và PQ hướng vào điểm cố F ma (2.9)
định của dây treo, đóng vai trò là lực hướng
Lực đàn hồi F luôn hướng về vị trí cân bằng O tâm giúp vật chuyển động tròn.
và có giá trị F kx.
Lực Pt luôn có tác dụng kéo vật về vị trí cân k bằng O.
Ta có: a x (2.10). m
Chọn hệ trục toạ độ OVnhư Hình 2.7.
Kết hợp với phương trình (2.7) ta suy ra:
Xét trên phương tiếp tuyến của quỹ đạo, ta có: k sin 2 F mg ma (2.11) (2.12) m
Khi vật dao động góc nhỏ (θ ≤ 10o), ta có: k s hay
chính là tần số góc của con lắc sin tan (2.13) m A mg g
lò xo dao động điều hoà. Do đó:
s ma a s (2.14) A A
Với s là độ dài cung OM q .
Kết hợp với phương trình (2.7) ta suy ra: g 2 (2.15) A g hay
chính là tần số góc của con lắc A
đơn dao động điều hoà với biên độ góc đủ nhỏ.
Lưu ý: Đối với một hệ dao động tự do, tần số góc có một giá trị xác định, phụ thuộc vào các đặc tính của hệ. 20 VẬT LÍ 11 %j,7t3
1. Một vật dao động điều hoà có đồ thị li độ – thời gian và vận tốc – thời gian như Hình 2P.1.
Hãy viết phương trình li độ và phương trình vận tốc của dao động này. Từ đó suy ra phương
trình gia tốc của vật dao động. v (cm/s) x (cm) 4 1 2 0,5 O O W (s) W (s) –0,5 –2 –1 0,5 1 1,5 2 2,5 3 –4 0,5 1 1,5 2 2,5 3 a) b)
S Hình 2P.1. Đồ thị li độ – thời gian (a) và vận tốc – thời gian (b) của một vật dao động
2. Một chất điểm dao động điều hoà với biên độ 4 cm, tần số 1 Hz. Tại thời điểm ban đầu, vật
ở vị trí biên âm. Hãy xác định vận tốc và gia tốc của vật tại thời điểm t = 1 s.
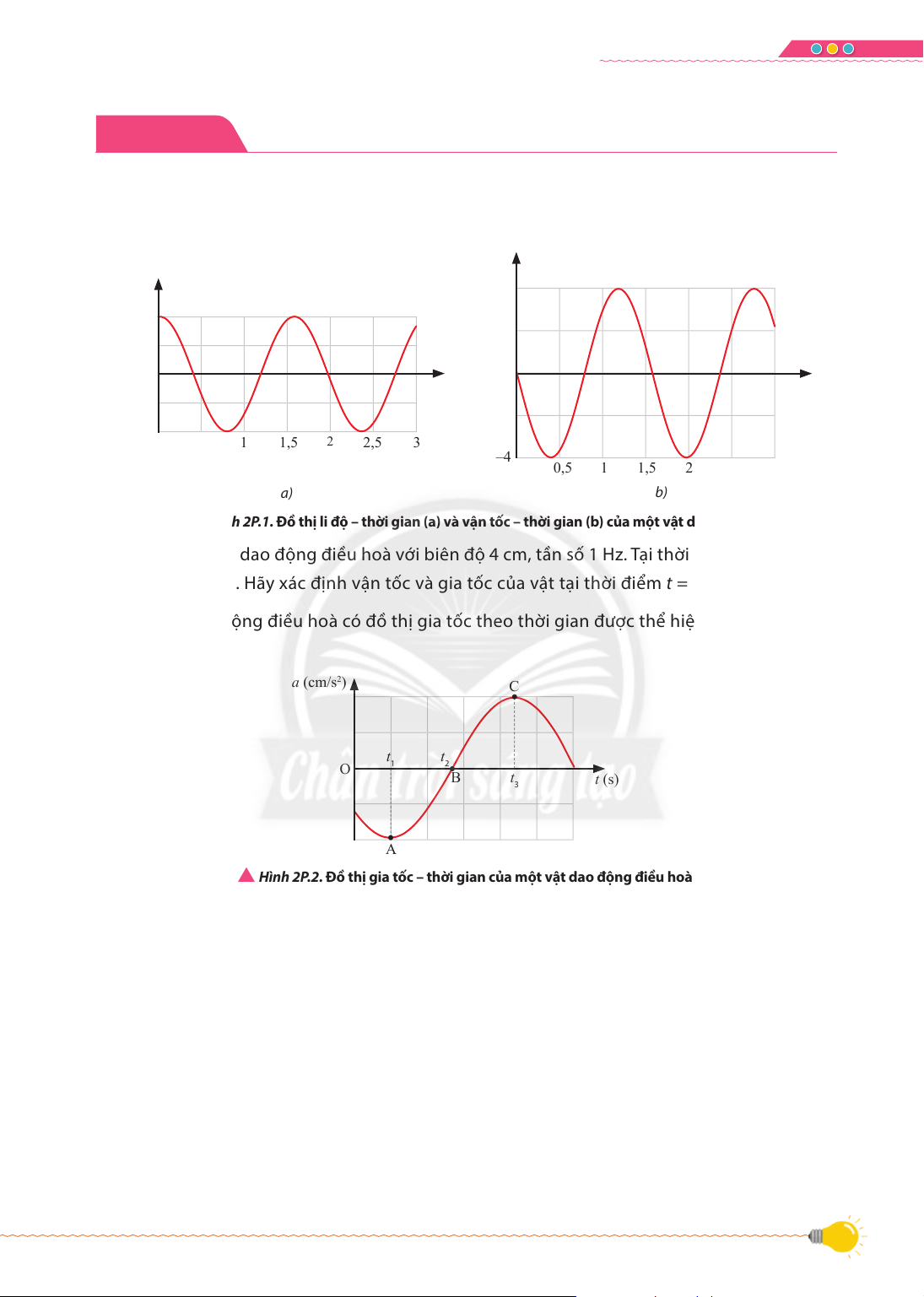
3. Một vật dao động điều hoà có đồ thị gia tốc theo thời gian được thể hiện trong Hình 2P.2. D(cm/s2) C W W O 1 2 B W W(s) 3 A
S Hình 2P.2. Đồ thị gia tốc – thời gian của một vật dao động điều hoà
Xác định vị trí, vận tốc và gia tốc của vật tại các thời điểm W , W và W tương ứng với các điểm 1 2 3
A, B và C trên đường đồ thị a(W). 21 VẬT LÍ 11 1u1*/¦1*7521* Bài 3 '$2ô1*ô,8+2j
Sự chuyển hoá động năng và thế năng trong dao động điều hoà. 7ҩPJӛ
Tiến hành thí nghiệm như mô tả trong Hình 3.1. Đặt một
tấm gỗ cố định lên tường, đưa vật nặng của con lắc đơn đến
vị trí tiếp xúc với tấm gỗ và thả nhẹ để vật nặng bắt đầu chuyển
động không vận tốc ban đầu. Khi dao động, vật nặng có va
chạm vào tấm gỗ hay không? Vì sao? Trong quá trình dao động,
vật nặng có những dạng năng lượng gì và sự chuyển hoá giữa chúng như thế nào?
S Hình 3.1. Thí nghiệm với con lắc đơn
1 THẾ NĂNG TRONG DAO ĐỘNG ĐIỀU HOÀ
Biểu thức của thế năng trong dao động điều hoà
Xét hệ con lắc lò xo dao động điều hoà. Thế năng của hệ
được tích luỹ trong lò xo và phụ thuộc vào mức độ lò xo 1. Dựa vào công thức (3.2) và
bị kéo dãn hay nén lại. Khi chọn gốc thế năng tại vị trí cân
Hình 3.2, mô tả sự thay đổi của
bằng, từ một số tính toán, ta rút ra được thế năng trong dao
thế năng trong một chu kì dao động điều hoà: động của vật.
W 1 m 2x2 (3.1) t 2
Kết hợp với công thức (2.1) ta có: Wt Wtmax
Thế năng trong dao động điều hoà được tính theo công thức: W 1 m 2 A2 2 cos t (3.2) 0 t O T T 3T 5T 3T W 2 T 4 2 4 4 2
S Hình 3.2. Đồ thị thế năng – thời gian
trong dao động điều hoà
Do hàm cosin (hoặc sin) bình phương có giá trị thay đổi
từ 0 đến 1 nên thế năng trong dao động điều hoà có giá trị
thay đổi từ 0 đến W với W = 1 2 2 là giá trị cực tmax tmax mZ A 2 đại của thế năng. 22 VẬT LÍ 11
Sự biến đổi của thế năng theo thời gian
Kết hợp công thức (3.2) và phép biến đổi lượng giác 2 FRV FRV a a , ta có: 2 W 1 m 2 A2 1 m 2
A2 cos 2t (3.3)
2. So sánh chu kì, tần số biến 0 t 4 4
thiên của thế năng với chu kì,
Như vậy, thế năng trong dao động điều hoà biến đổi tuần
tần số dao động của vật.
hoàn theo thời gian với tần số góc bằng hai lần tần số góc của li độ. Z ' 2Z (3.4)
Một số toà nhà cao tầng sử dụng các con lắc nặng trong bộ giảm chấn khối lượng
(mass damper) để giảm thiểu sự rung động gây ra bởi gió hay những cơn địa chấn
nhỏ. Giả sử vật nặng của con lắc có khối lượng 3,0.105 kg, thực hiện dao động điều
hoà với với tần số 15 Hz với biên độ dao động là 15 cm. Hãy xác định thế năng cực
đại của hệ con lắc trong bộ giảm chấn khối lượng.
2 ĐỘNG NĂNG TRONG DAO ĐỘNG ĐIỀU HOÀ
Biểu thức của động năng trong dao động điều hoà
Động năng của một vật được xác định bởi công thức:
3. Dựa vào công thức (3.5) và 1
Hình 3.3, mô tả sự thay đổi của 2 W ñ mv 2
động năng trong một chu kì dao động của vật.
Kết hợp với công thức (2.4), ta có: Wđ
Động năng của vật dao động điều hoà được tính Wđmax theo công thức: 1 2 1 2 2 2 W ñ
Pv mZ A ViQ ZW M0 (3.5) 2 2 O T T 3T 5T 3T W T 4 2 4 4 2
Tương tự như thế năng, động năng của vật dao động điều hoà
S Hình 3.3. Đồ thị động năng –
có giá trị thay đổi từ 0 đến W với W = W = 1 PȦ
thời gian trong dao động điều hoà 2A2 đmax đmax tmax 2
là giá trị cực đại của động năng.
Sự biến đổi của động năng theo thời gian
Kết hợp công thức (3.5) và phép biến đổi lượng giác 2 s c LQ RV a a , ta có: 2 23 VẬT LÍ 11 W 1 2 2 1 2 2 cos 2 (3.6) 0 – m A m A t 4 4
4. So sánh pha dao động của thế
Như vậy, động năng của vật dao động điều hoà biến đổi
năng và động năng khi vật dao
tuần hoàn theo thời gian với tần số góc bằng hai lần tần số động điều hoà.
góc của li độ theo công thức (3.4).
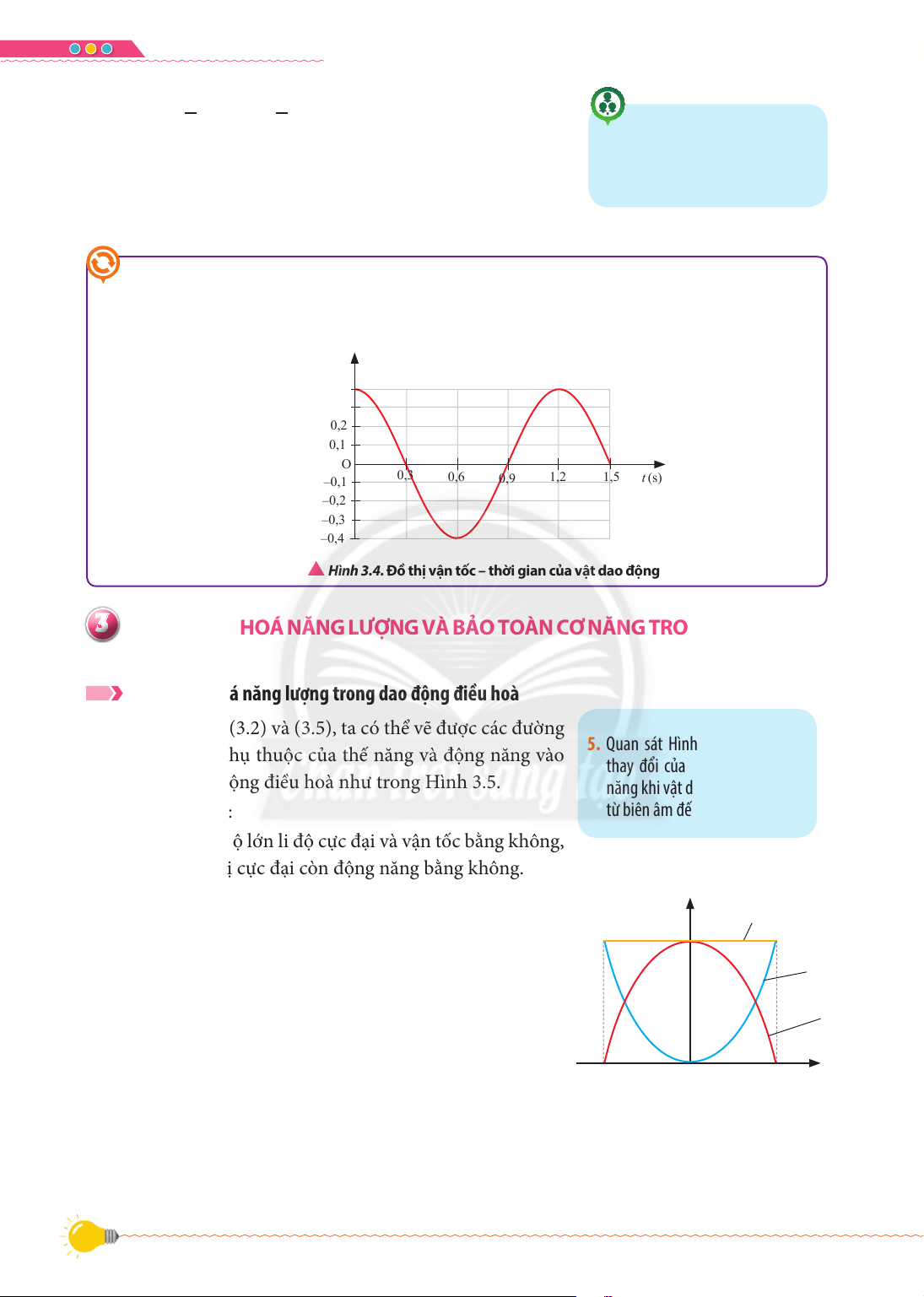
Một vật có khối lượng 2 kg dao động điều hoà có đồ thị vận tốc – thời gian như
Hình 3.4. Xác định tốc độ cực đại và động năng cực đại của vật trong quá trình dao động. v (m/s) 0,4 0,3 0,2 0,1 O 0,3 0,6 0,9 1,2 1,5 W (s) –0,1 –0,2 –0,3 –0,4
S Hình 3.4. Đồ thị vận tốc – thời gian của vật dao động
3 SỰ CHUYỂN HOÁ NĂNG LƯỢNG VÀ BẢO TOÀN CƠ NĂNG TRONG DAO ĐỘNG ĐIỀU HOÀ
Sự chuyển hoá năng lượng trong dao động điều hoà
Từ các công thức (3.2) và (3.5), ta có thể vẽ được các đường 5. Quan sát Hình 3.5 và mô tả sự
đồ thị mô tả sự phụ thuộc của thế năng và động năng vào
thay đổi của động năng và thế
li độ của hệ dao động điều hoà như trong Hình 3.5.
năng khi vật dao động di chuyển Hình 3.5 thể hiện:
từ biên âm đến biên dương.
– Khi vật ở biên, độ lớn li độ cực đại và vận tốc bằng không,
thế năng có giá trị cực đại còn động năng bằng không.
– Khi vật di chuyển từ vị trí biên về vị trí cân bằng, độ lớn 1ăQJOѭӧQJ &ѫQăQJ
li độ giảm nên thế năng giảm và độ lớn vận tốc tăng nên động năng tăng. 7KӃQăQJ
– Khi vật ở vị trí cân bằng, li độ bằng không và độ lớn vận
tốc cực đại, thế năng bằng không và động năng có giá trị ĈӝQJQăQJ cực đại.
– Khi vật di chuyển từ vị trí cân bằng ra biên, độ lớn li độ –A O A /Lÿӝ
tăng nên thế năng tăng và độ lớn vận tốc giảm nên động S Hình 3.5. Sự phụ thuộc của thế năng, năng giảm.
động năng, cơ năng vào li độ của vật
Như vậy, trong quá trình vật dao động, động năng và thế dao động
năng luôn thay đổi và chuyển hoá qua lại với nhau. 24 VẬT LÍ 11
Sự bảo toàn cơ năng trong dao động điều hoà 1ăQJ OѭӧQJ ĈӝQJQăQJ 7KӃQăQJ &ѫQăQJ
Ta đã biết, cơ năng của một hệ bằng tổng động năng và thế
năng. Kết hợp với các công thức (3.2) và (3.5), ta rút ra được
công thức xác định cơ năng trong dao động điều hoà: W= W + W 1 O 2 2 (3.7) T 7KӡLJLDQ – m A t t đ 2
S Hình 3.6. Đồ thị biểu diễn sự phụ
Từ biểu thức (3.7), ta thấy rằng, xét với một dao động điều
thuộc của thế năng, động năng và cơ
năng trong dao động theo thời gian
hoà, cơ năng tỉ lệ thuận với bình phương biên độ dao động
A của vật và không thay đổi theo thời gian. Như vậy, trong
quá trình vật dao động điều hoà, thế năng W và động năng
6. Quan sát Hình 3.5 và 3.6, nhận t
W biến đổi liên tục theo thời gian nhưng cơ năng luôn
xét về độ lớn của động năng, thế đ
năng và cơ năng trong quá trình bảo toàn.
dao động điều hoà của vật.
7. Dựa vào biểu thức (3.2) và (3.5),
hãy thiết lập biểu thức (3.7).
Xét một vật bắt đầu dao động điều hoà từ vị trí cân bằng, hãy chỉ ra những khoảng
thời gian trong một chu kì dao động mà:
a) thế năng tăng dần trong khi động năng giảm dần.
b) thế năng giảm dần trong khi động năng tăng dần.
Biết phương trình li độ của một vật có khối lượng 0,2 kg dao động điều hoà là x = 5cos(20t) (cm).
a) Tính cơ năng trong quá trình dao động.
b) Viết biểu thức thế năng và động năng. %j,7t3
1. Một hệ dao động điều hoà với chu kì 2 s. Chọn gốc thế năng tại vị trí cân bằng của vật. Thời điểm
hệ bắt đầu dao động thì động năng và thế năng bằng nhau lần thứ nhất. Hỏi sau bao lâu kể từ
khi hệ bắt đầu dao động, động năng và thế năng bằng nhau lần thứ hai?
2. Xét một vật bắt đầu dao động điều hoà từ vị trí cân bằng theo chiều âm của trục toạ độ. Chọn
gốc thế năng tại vị trí cân bằng của vật. Hãy vẽ phác đồ thị thể hiện sự phụ thuộc vào thời gian
của động năng và thế năng trong hai chu kì dao động trên cùng một hệ trục toạ độ. Chỉ ra trên
đồ thị những thời điểm mà động năng và thế năng có độ lớn bằng nhau. 25 VẬT LÍ 11 '$2 ô1* 7w7 'p1 9j Bài 4 +,17¦1*&1*+¤1*
– Dao động tắt dần, dao động cưỡng bức và hiện tượng cộng hưởng.
– Lợi ích và tác hại của hiện tượng cộng hưởng trong một số trường hợp cụ thể.
Bộ giảm chấn khối lượng (mass damper) (Hình 4.1) được sử dụng để
giảm thiểu sự rung lắc của các toà nhà cao tầng khi có gió mạnh hay địa chấn.
Toà nhà Taipei 101 tầng (cao 508 m) tại thành phố Đài Bắc, Đài Loan cũng
được trang bị bộ giảm chấn khối lượng, là một con lắc với vật nặng khoảng
728 tấn được treo tại trung tâm toà nhà từ tầng 92 xuống đến tầng 87.
Nhờ vậy, toà nhà có thể chịu được những cơn bão có sức gió lên tới 216 km/h
hay những cơn địa chấn lên đến 7 độ richter. Các kĩ sư xây dựng đã dựa trên
những hiện tượng vật lí nào?
S Hình 4.1. Bộ giảm chấn khối lượng
1 DAO ĐỘNG TẮT DẦN
Quan sát hiện tượng dao động tắt dần
1. Quan sát Hình 4.2 và mô tả chuyển
động của xích đu, ván nhảy cầu
sau khi ngừng tác dụng lực. a) b)
S Hình 4.2. Xích đu (a) và ván nhảy cầu (b)
Khi khảo sát hiện tượng dao động trong các bài trước, ta
đã lí tưởng hoá bài toán khi xem lực cản của môi trường là
không đáng kể, có thể bỏ qua. Tuy nhiên, trên thực tế, sau
khi ngừng tác dụng lực để kích thích cho vật dao động, biên
2. Nêu một số ví dụ thực tế khác về
độ dao động của vật giảm dần và vật sẽ dừng lại sau một
hiện tượng dao động tắt dần.
khoảng thời gian nhất định.
Dao động tắt dần là dao động có biên độ giảm dần theo thời gian. 26 VẬT LÍ 11
Tuỳ theo lực cản tác dụng lên vật mà dao động tắt dần có x 7ҳWGҫQWӟLKҥQ
thể chia thành các loại sau:
– Dao động tắt dần dưới hạn: Khi lực cản tác dụng lên vật 7ҳWGҫQYѭӧWKҥQ
có độ lớn nhỏ, vật thực hiện dao động với biên độ giảm
dần theo thời gian và dừng lại sau một số chu kì dao động. O W
Đồ thị li độ – thời gian của dao động tắt dần dưới hạn
được thể hiện ở đường màu đỏ trong Hình 4.3. 7ҳWGҫQGѭӟLKҥQ
Ví dụ: Con lắc lò xo dao động trên mặt phẳng ngang có S Hình 4.3. Đồ thị li độ – thời gian của
ma sát hoặc một số loại cửa có thể dao động khi được
các loại dao động tắt dần đẩy ra hoặc kéo vào.
– Dao động tắt dần tới hạn: Khi lực cản tác dụng lên vật có độ lớn vừa đủ, vật không thể
thực hiện đủ một chu kì dao động mà trở về vị trí cân bằng sau một thời gian ngắn.
Đồ thị li độ – thời gian của dao động tắt dần tới hạn được thể hiện ở đường màu vàng trong Hình 4.3.
Ví dụ: Một số loại cửa được lắp đặt hệ thống bản lề đặc biệt, để cửa không còn thực hiện được
dao động mà tự đóng lại sau một khoảng thời gian ngắn.
– Dao động tắt dần vượt hạn: Khi lực cản tác dụng lên vật có độ lớn tăng lên, vật không thể
thực hiện đủ một chu kì dao động mà trở về vị trí cân bằng sau một thời gian tương đối dài.
Đồ thị li độ – thời gian của dao động tắt dần vượt hạn được thể hiện ở đường màu xanh trong Hình 4.3.
Ví dụ: Nếu lực cản trong hệ thống bản lề đóng cửa tự động tăng lên đáng kể, cửa vẫn không
thể thực hiện được dao động nhưng mất nhiều thời gian để tự đóng lại.
Giải thích hiện tượng dao động tắt dần
Ta đã biết, lực cản của môi trường tác dụng lên vật luôn ngược chiều chuyển động của vật.
Do đó, công của lực cản tác dụng lên vật luôn âm làm cho cơ năng giảm. Từ đó biên độ dao
động của vật giảm dần theo thời gian.
Bố trí sơ đồ thí nghiệm như Hình 4.4. Kéo vật nặng của con lắc lò xo khỏi vị trí
cân bằng theo phương thẳng đứng một đoạn xác định và thả nhẹ để vật dao
động không vận tốc ban đầu. Dự đoán và thực hiện thí nghiệm kiểm chứng (nếu
có điều kiện) về dao động của con lắc trong các trường hợp vật nặng thực hiện
dao động trong: a) không khí; b) chất lỏng (nước/dầu); c) chất lỏng (nước/dầu)
khi có gắn thêm vật cản. /z[R 9ұWQһQJ 9ұWFҧQ &KұXÿӵQJ FKҩWOӓQJ a) b) c)
S Hình 4.4. Vật nặng của con lắc lò xo dao động:
a) trong không khí; b) trong chất lỏng; c) trong chất lỏng khi có gắn thêm vật cản 27 VẬT LÍ 11
Đưa ra một số ví dụ về tác hại và lợi ích của dao động tắt dần. Từ đó tìm hiểu và sưu tầm hình ảnh về một số
ứng dụng của dao động tắt dần trong cuộc sống.
2 DAO ĐỘNG CƯỠNG BỨC VÀ HIỆN TƯỢNG CỘNG HƯỞNG
Dao động cưỡng bức
Trên thực tế, để một vật dao động không bị tắt, ta cần bổ
sung năng lượng để bù lại sự tiêu hao năng lượng do lực cản môi trường.
3. Trên thực tế, sau khi được kích
thích để dao động, xích đu
Thông thường, ta có hai cách bổ sung năng lượng cho vật
(Hình 4.2a) hoặc võng sẽ dao dao động:
động tắt dần. Làm cách nào để
– Truyền năng lượng bổ sung đúng bằng phần năng lượng
chúng có thể dao động với biên
tiêu hao ở cuối mỗi chu kì dao động của hệ bằng một lực độ không đổi?
cùng chiều với chuyển động. Lực này không làm thay đổi
chu kì dao động riêng của vật. Cơ chế này được gọi là dao
động duy trì. Ví dụ: hệ bù năng lượng cho con lắc trong
đồng hồ quả lắc (Hình 4.5).
– Sử dụng một ngoại lực biến thiên điều hoà (ngoại lực điều hoà) theo thời gian: F F cos (4.1) 0 t 0
trong đó F và lần lượt là biên độ và tần số góc của ngoại lực. 0
Đồ thị li độ – thời gian của vật được thể hiện trong Hình 4.6
(trong trường hợp ngoại lực điều hoà cùng pha với dao động
cưỡng bức ở giai đoạn ổn định) gồm hai giai đoạn:
+ Giai đoạn chuyển tiếp, trong đó dao động của hệ chưa
ổn định, biên độ và chu kì dao động biến thiên phức tạ S
p Hình 4.5. Cơ chế bổ sung năng lượng theo thời gian.
cho đồng hồ quả lắc
+ Giai đoạn ổn định, trong đó biên độ và chu kì dao động
của vật không thay đổi. Giai đoạn ổn định kéo dài cho đến
khi ngoại lực không còn tác dụng. 0.3 3 0,3 3 D 0.2 2 0,2 2 b ) 0.1 1 0,1 1 30 50 0 0 0 0 /LÿӝP 10 20 40 60 70 80 -0.1 -1 –0,1 –1 1JRҥLOӵF1 -0.2 -2 –0,2 –2 -0.3 -3 –0,3 –3 0 10 20 30 40 50 60 70 80 7KӡLJLDQV
S Hình 4.6. Đồ thị: a) ngoại lực điều hoà – thời gian (đường màu đỏ);
b) li độ – thời gian của vật (đường màu xanh) 28 VẬT LÍ 11
Một trong những ví dụ của dao động cưỡng bức là hệ thống
võng máy tự động sử dụng điện như trong Hình 4.7. 9ұWGDRÿӝQJ FѭӥQJEӭF
Dao động của vật dưới tác dụng của ngoại lực điều
hoà trong giai đoạn ổn định được gọi là dao động ĈӝQJFѫ
cưỡng bức. Ngoại lực điều hoà tác dụng vào vật khi WҥRUDOӵF FѭӥQJEӭF
này được gọi là lực cưỡng bức.
S Hình 4.7. Võng máy tự động sử dụng điện
Tính chất của dao động cưỡng bức:
– Dao động cưỡng bức là dao động điều hoà.
– Tần số góc của dao động cưỡng bức bằng tần số góc của lực cưỡng bức.
– Biên độ của dao động cưỡng bức phụ thuộc vào biên độ F , 0
độ chênh lệch giữa tần số góc của lực cưỡng bức và tần số
góc riêng của hệ, lực cản của môi trường xung quanh.
Nêu một số ví dụ về dao động cưỡng bức trong thực tế.
Hiện tượng cộng hưởng
Khi giữ biên độ F không đổi và thay đổi tần số góc của A 0
lực cưỡng bức, ta thấy biên độ dao động cưỡng bức A của hệ
thay đổi. Biên độ dao động cưỡng bức đạt giá trị cực đại A max
khi tần số góc của lực cưỡng bức tiến đến bằng tần số góc
riêng của hệ dao động = Ȧnhư đồ thị trong Hình 4.8. O Ȧ
Khi tác dụng vào vật, lực cưỡng bức đã thực hiện công và bổ
S Hình 4.8. Sự phụ thuộc của biên
sung năng lượng cho vật, giúp vật duy trì dao động với biên độ dao động cưỡng bức vào tần số độ không đổi.
góc của lực cưỡng bức
Hiện tượng cộng hưởng xảy ra khi tần số góc của
lực cưỡng bức tiến đến bằng tần số góc riêng của hệ
dao động. Khi này, biên độ dao động cưỡng bức của
hệ đạt giá trị cực đại A . max 29 VẬT LÍ 11 /ӵFFҧQQKӓ A /ӵFFҧQOӟQ O Ȧ
S Hình 4.9. Sự phụ thuộc của biên độ dao động cưỡng bức vào
tần số góc của ngoại lực trong trường hợp lực cản lớn và nhỏ
Khi lực cản của môi trường thay đổi, độ lớn cực đại của biên
độ dao động cưỡng bức cũng thay đổi. Hình 4.9 minh hoạ sự
phụ thuộc của biên độ dao động cưỡng bức vào tần số góc
của lực cưỡng bức ứng với các giá trị khác nhau của lực cản
môi trường. Kết quả cho thấy khi độ lớn của lực cản môi
trường tăng lên thì đỉnh của đường đồ thị loe ra và biên độ
dao động cưỡng bức cực đại A giảm xuống. max
Bố trí thí nghiệm hệ con lắc Barton như Hình 4.10.
Mô hình gồm nhiều con lắc đơn có chiều dài dây treo
khác nhau được gắn trên cùng một dây treo đàn hồi.
Khi con lắc số 1 được kích thích để dao động, những 2 3
con lắc còn lại (từ số 2 đến 7) sẽ bắt đầu dao động. 4 1 5 6 7
Giải thích vì sao chúng dao động và dự đoán về biên
độ dao động của chúng.
Thực hiện thí nghiệm kiểm chứng.
S Hình 4.10. Con lắc Barton
Lợi ích và tác hại của hiện tượng cộng hưởng
Trong cuộc sống, những hiểu biết về hiện tượng cộng hưởng
4. Trình bày một số lợi ích và tác
được ứng dụng trong lĩnh vực xây dựng, âm nhạc, y học,
hại của hiện tượng cộng hưởng thông tin liên lạc,...
trong thực tế mà em đã biết.
– Khi thiết kế các công trình lớn như nhà cao tầng hoặc
cầu đường, các kĩ sư cần có những phương án xử lí kĩ thuật
nhằm tránh xảy ra cộng hưởng trên hệ thống. Ví dụ: Cầu
Thiên niên kỉ tại London (Hình 4.11) đã phải tạm đóng
sau ba ngày đón khách du lịch vào năm 2000 vì hiện tượng
cộng hưởng đã xảy ra khi khách tham quan cùng đi trên cầu,
vô tình tạo ra một ngoại lực cưỡng bức có tần số dao động S Hình 4.11. Cầu đi bộ Thiên niên kỉ
xấp xỉ tần số dao động riêng của cầu, làm cho cầu rung
tại London, Vương Quốc Anh 30 VẬT LÍ 11
lắc rất mạnh (Nguồn: www.theguardian.com). Các kĩ sư đã Tìm hiểu và trình bày
mất khoảng hai năm để bổ sung bộ giảm chấn khối lượng
hoạt động của bộ giảm
nhằm tạo ra dao động tắt dần tới hạn trên cầu. chấn khối lượng, là
– Vào tháng 9/1985, một trận động đất lớn (8,1 độ richter), một con lắc được treo
có tâm chấn tại bờ biển phía tây của nước Mexico. Tại thủ đô trên toà nhà Taipei 101
Mexico, cách tâm chấn đến 400 km, sóng địa chấn đã tạo ra
tại thành phố Đài Bắc,
lực cưỡng bức lên các toà nhà, gây hiện tượng cộng hưởng, Đài Loan (Hình 4.1).
làm cho nhiều toà nhà có độ cao trung bình rung lắc dữ dội
và sụp đổ hoàn toàn, trong khi những toà nhà cao hơn hoặc
thấp hơn hẳn lại đứng vững. (Nguồn: www.britannica.com)
Tìm hiểu và trình bày ngắn gọn
– Trong lĩnh vực âm nhạc: Mỗi nhạc cụ phát ra những giai
phương án kĩ thuật để hạn chế
điệu âm thanh mang nét đặc trưng riêng của nhạc cụ đó. Để
thiệt hại cho các toà nhà, đặc
khuếch đại độ to của âm thanh mà không làm mất đi nét
biệt là các toà nhà cao tầng, tại
đặc trưng riêng đó, người ta sử dụng một buồng đặc biệt là
những nơi thường xảy ra động
buồng cộng hưởng như hộp đàn guitar, hộp vĩ cầm. đất như Nhật Bản. Máy đo địa chấn
Máy đo địa chấn là một thiết bị được dùng để ghi nhận những chuyển động bất thường của
mặt đất gây ra bởi sự lan truyền sóng chấn động từ tâm của những trận động đất. Đa phần
các máy đo địa chấn thường hoạt động như sau: Một giá treo được gắn chặt vào mặt đất,
một vật nặng được treo lơ lửng vào giá và có xu hướng đứng yên trong khi giá treo chuyển
động theo mặt đất. Chuyển động của lớp vỏ Trái Đất trong các trận động đất được đo tương
đối với bất kì vật thể nào, không phụ thuộc vào chuyển động của mặt đất. Khi mặt đất rung
chuyển, đầu bút trên quả nặng sẽ dao động và vạch lên bản ghi (một cuộn giấy được quay
đều). Việc phân tích tín hiệu thu được trên bản ghi cho ta biết thông tin của những sóng địa
chấn gây ra bởi những trận động đất. %j,7t3
1. Cho ví dụ về một số ứng dụng của dao động tắt dần trong thực tiễn.
2. Hãy chỉ ra hai trường hợp cộng hưởng có lợi và hai trường hợp cộng hưởng có hại. Trong từng
trường hợp hãy chỉ rõ hệ dao động và nguồn gốc gây ra sự cộng hưởng.
3. Máy đo địa chấn được sử dụng để phát hiện và đo đạc những rung động địa chấn được tạo ra
bởi sự dịch chuyển của lớp vỏ Trái Đất. Năng lượng từ các cơn địa chấn có khả năng kích thích
con lắc lò xo bên trong máy đo làm đầu bút di chuyển để vẽ lên giấy (Hình 4P.1).
a) Dao động của con lắc lò xo trong máy đo địa chấn khi cơn
địa chấn xuất hiện là loại dao động gì? Giải thích.
b) Tần số của những cơn địa chấn thường nằm trong khoảng
30 Hz – 40 Hz. Để kết quả ghi nhận là tốt nhất, hệ con lắc lò
xo trong máy đo địa chấn cần được thiết kế để có tần số dao
động riêng trong khoảng nào? Giải thích.
S Hình 4P.1. Máy đo địa chấn 31 VẬT LÍ 11 X 71*.7&+¡1* X 1 MÔ TẢ DAO ĐỘNG
– Dao động của hệ xảy ra dưới tác dụng chỉ của nội lực được gọi là dao động tự do (dao động riêng).
– Li độ của vật dao động là toạ độ của vật mà gốc toạ độ được chọn trùng với vị trí cân bằng.
– Biên độ là độ lớn cực đại của li độ.
– Dao động điều hoà là dao động tuần hoàn mà li độ của vật dao động là một hàm cosin (hoặc sin) theo thời gian.
– Chu kì dao động là khoảng thời gian để vật thực hiện được một dao động. Tần số dao
động được xác định bởi số dao động mà vật thực hiện được trong một giây. f 1T
Trong hệ SI, chu kì dao động có đơn vị là giây (s) và tần số dao động có đơn vị là héc (Hz).
– Pha dao động là một đại lượng đặc trưng cho trạng thái của vật trong quá trình dao
động. Độ lệch pha giữa hai dao động điều hoà cùng chu kì (cùng tần số) được xác định theo công thức: 2 t T
– Tần số góc của dao động là đại lượng đặc trưng cho tốc độ biến thiên của pha dao
động. Đối với dao động điều hoà, tần số góc có giá trị không đổi và được xác định theo công thức: 2 2 1 t t T 2 1
với φ và φ lần lượt là pha dao động tại thời điểm t và t . 1 2 1 2
Trong hệ SI, tần số góc có đơn vị là radian trên giây (rad/s).
2 CÁC PHƯƠNG TRÌNH TRONG DAO ĐỘNG ĐIỀU HOÀ
– Phương trình li độ của vật dao động:
x Acost 0
– Phương trình vận tốc của vật dao động: v Acos t sin 0 A t 0 2
– Phương trình gia tốc của vật dao động: a 2A t 2 cos 0 x 32 VẬT LÍ 11
3 NĂNG LƯỢNG TRONG DAO ĐỘNG ĐIỀU HOÀ
– Thế năng trong dao động điều hoà được tính theo công thức: W 1 m 2 x2 1 m 2 A2 2 cos t 0 t t 2 2
– Động năng của vật dao động điều hoà được tính theo công thức: W 1 2 v 1 2 2 2 sin 0 – m m A t đ 2 2
– Cơ năng trong dao động điều hoà: W= W + W 1 2 2 – m A t t đ 2
4 DAO ĐỘNG TẮT DẦN VÀ HIỆN TƯỢNG CỘNG HƯỞNG
– Dao động tắt dần là dao động có biên độ giảm dần theo thời gian.
– Dao động của vật dưới tác dụng của ngoại lực điều hoà trong giai đoạn ổn định được
gọi là dao động cưỡng bức. Ngoại lực điều hoà tác dụng vào vật khi này được gọi là lực cưỡng bức.
– Hiện tượng cộng hưởng xảy ra khi tần số góc của lực cưỡng bức tiến đến bằng tần số
góc riêng của hệ dao động. Khi này, biên độ dao động cưỡng bức của hệ đạt giá trị cực đại A . max 33 VẬT LÍ 11 6¶1* Chương 2 Bài 5 61*9j6 758<161*
– Quá trình truyền sóng.
– So sánh sóng dọc và sóng ngang.
– Một số tính chất đơn giản của âm thanh và ánh sáng.
Vào lúc 9 giờ 22 phút, sáng ngày 14/03/2022, một trận động đất xảy ra tại tỉnh Điện Biên (Theo Báo Tuổi trẻ).
Vì sao tại những nơi như một số huyện giáp ranh của tỉnh Sơn La cách tâm chấn khoảng 20 km, nhà cửa và các đồ đạc, vật
dụng của gia đình lại bị rung lắc? Động đất đã lan truyền như thế nào?
1 QUÁ TRÌNH TRUYỀN SÓNG Khái niệm sóng
Một biến động đột ngột (hay còn gọi là chấn động) được
lan truyền trong một môi trường gây ra hiện tượng sóng
1. Dự đoán trạng thái của mặt nước
(Hình 5.1). Sóng từ một vị trí xác định trong không gian
trong cốc nước khi ta gõ lên mặt
(nguồn sóng) được phát ra và truyền đi thông qua môi
bàn một cách liên tục và đủ mạnh
trường vật chất (môi trường rắn, lỏng và khí) được gọi
tại một vị trí gần cốc nước. Giải
là sóng cơ. Ví dụ: Khi nghệ sĩ kéo vĩ cầm (Hình 5.2a),
thích hiện tượng và tiến hành thí
sóng âm thanh từ đàn truyền đến tai khán thính giả; sóng nghiệm để kiểm chứng.
nước lan truyền trên mặt hồ (Hình 5.2b),… Nếu nguồn
sóng thực hiện dao động tuần hoàn, sóng phát ra cũng
có tính chất tuần hoàn. Vậy, sóng là dao động lan truyền
trong không gian theo thời gian.
S Hình 5.1. Tay người tạo ra
chấn động truyền đến cốc nước a) b)
S Hình 5.2. a) Nghệ sĩ kéo vĩ cầm; b) Sóng nước trên mặt hồ
Khi sóng truyền trong không gian, các phần tử môi trường
không truyền theo phương truyền sóng mà chỉ dao động tại
chỗ. Ví dụ, xét một quả bóng được thả nổi trên mặt nước
đang có sóng truyền qua như Hình 5.3. Giả sử trời lặng gió, 34 VẬT LÍ 11
ta thấy quả bóng không dịch chuyển theo phương truyền
của sóng trên mặt nước mà chỉ dao động tại chỗ.
2. Quan sát Hình 5.3 và dự đoán
Ngoài sóng cơ, là sóng truyền trong môi trường do các phần
phương chuyển động của quả
tử của môi trường thực hiện dao động thì còn có một loại
bóng khi có sóng trên mặt nước
sóng khác đó là sóng điện từ. Sóng điện từ có thể lan truyền
trong điều kiện lặng gió.
qua cả chân không. Đây là một trong nhiều sự khác biệt
giữa sóng điện từ và sóng cơ. Ánh sáng hoặc sóng vô tuyến
điện là sóng điện từ.
Sóng là dao động lan truyền trong không gian theo
thời gian. Khi sóng truyền đi, phần tử môi trường
không truyền theo phương truyền sóng mà chỉ dao
S Hình 5.3. Quả bóng động tại chỗ.
trên mặt nước có sóng
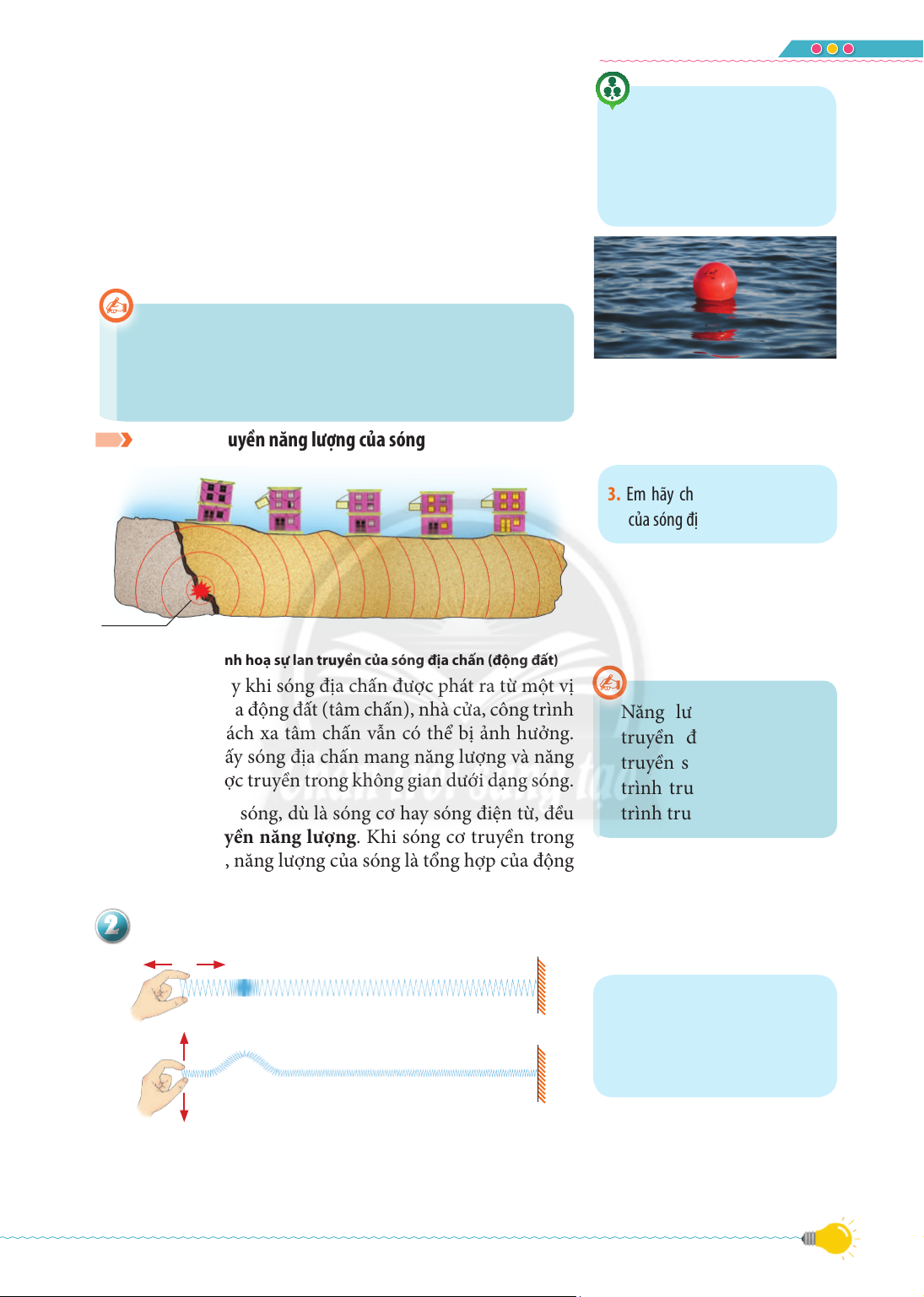
Quá trình truyền năng lượng của sóng
3. Em hãy cho biết những tác hại
của sóng địa chấn (động đất). Tâm chấn (nguồn sóng)
S Hình 5.4. Minh hoạ sự lan truyền của sóng địa chấn (động đất)
Hình 5.4 cho thấy khi sóng địa chấn được phát ra từ một vị
trí khởi nguồn của động đất (tâm chấn), nhà cửa, công trình Năng lượng sóng được
ở những vị trí cách xa tâm chấn vẫn có thể bị ảnh hưởng. truyền đi theo phương
Điều này cho thấy sóng địa chấn mang năng lượng và năng truyền sóng. Do đó, quá
lượng này đã được truyền trong không gian dưới dạng sóng.
trình truyền sóng là quá
Quá trình truyền sóng, dù là sóng cơ hay sóng điện từ, đều
trình truyền năng lượng.
là quá trình truyền năng lượng. Khi sóng cơ truyền trong
một môi trường, năng lượng của sóng là tổng hợp của động
năng và thế năng của phần tử vật chất dao động.
2 SÓNG DỌC VÀ SÓNG NGANG a)
4. Quan sát Hình 5.5, hãy so sánh
phương truyền sóng và phương
dao động của từng điểm trên lò xo trong hai trường hợp. b)
S Hình 5.5. Sóng truyền trên lò xo khi dùng tay tạo ra dao động:
a) dọc theo trục lò xo; b) vuông góc với trục lò xo 35 VẬT LÍ 11
Xét một lò xo có một đầu được gắn cố định vào vách, một đầu
tự do như Hình 5.5. Khi dùng tay kích thích để đầu còn lại Trong tự nhiên tồn tại
của lò xo dao động, ta thấy dao động này sẽ được lan truyền những loại sóng phức
trên lò xo theo hai cách khác nhau. Ở cả hai trường hợp
tạp, là sự tổng hợp của
trong Hình 5.5, sóng được truyền trên lò xo theo phương cả sóng dọc và sóng
ngang từ trái sang phải, trong khi từng phần tử của lò xo ngang. Ví dụ như sóng
dao động theo phương truyền sóng (Hình 5.5a) hoặc theo trên mặt nước: trong
phương vuông góc với phương truyền sóng (Hình 5.5b),
thực tế, mỗi phần tử của
tương ứng với hai loại sóng là sóng dọc và sóng ngang.
nước thực hiện chuyển động tròn khi sóng
Sóng dọc là sóng mà phương dao động của mỗi phần
tử môi trường trùng với phương truyền sóng. truyền qua. Chuyển động này có thể phân
Sóng ngang là sóng mà phương dao động của mỗi phần tích thành hai loại sóng
tử môi trường vuông góc với phương truyền sóng.
dọc và ngang đồng thời.
Sóng âm trong không khí là một ví dụ của sóng dọc.
Xét màng loa khi hoạt động, dao động của màng loa được
lan truyền làm các phần tử của không khí cũng dao động. /RD 7DL
Do đó, những vùng áp suất cao và thấp liên tiếp nhau được
tạo thành và truyền đến tai người nghe làm màng nhĩ dao
động và tạo ra cảm giác về âm thanh (Hình 5.6). Dao động
6yQJkPWUX\ӅQWӯORDÿӃQWDLQJѭӡL
của các phần tử không khí có phương trùng với phương S Hình 5.6. Sự lan truyền của sóng âm
truyền của sóng âm. Sóng truyền ở mặt bàn trong thí nghiệm
ở Hình 5.1 và sóng lan truyền trên mặt nước ở Hình 5.3
là sóng ngang: các phần tử trên mặt bàn và trên mặt nước
dao động theo phương thẳng đứng, vuông góc với phương
truyền sóng là phương ngang.
Lấy một số ví dụ về
Sóng ngang có thể truyền trong chất rắn và bề mặt chất lỏng. sóng dọc và sóng
Sóng dọc có thể truyền trong các chất rắn, lỏng và khí. ngang trong thực tế.
3 MỘT SỐ TÍNH CHẤT CỦA SÓNG
Hiện tượng phản xạ
Khi sóng truyền từ một môi trường đến mặt phân cách với
một môi trường khác, một phần của sóng tới được truyền
ngược lại vào môi trường ban đầu. Đây là hiện tượng phản xạ sóng.
5. Quan sát Hình 5.7, xét trên
Một số ví dụ về hiện tượng phản xạ của sóng: âm thanh
phương vuông góc với bức
khi gặp vật cản (như bức tường) sẽ bị phản xạ và tạo ra
tường, nhận xét về chiều truyền
tiếng vang như trong Hình 5.7, ta có thể nhìn thấy các vật
của sóng âm trước và sau khi
xung quanh (quyển sách, bàn) là do ánh sáng được truyền gặp bức tường.
từ nguồn sáng đến vật và phản xạ để truyền từ vật đến mắt ta (Hình 5.8). 36 VẬT LÍ 11 SÓNG TỚI SÓNG PHẢN XẠ
S Hình 5.7. Sóng âm phản xạ khi gặp bức
S Hình 5.8. Sóng ánh sáng phản xạ khi gặp mặt bàn và quyển
tường nên tai người nghe được âm thanh
sách nên mắt người có thế nhìn thấy hình ảnh của các vật vọng lại
Hiện tượng khúc xạ
Hiện tượng sóng đổi phương truyền khi đi từ một môi 6. Quan sát Hình 5.9, nhận xét về
trường này sang một môi trường khác được gọi là hiện
hình dạng của chiếc thìa. Thực
tượng khúc xạ. Hiện tượng này có thể dễ dàng quan sát đối
hiện thí nghiệm kiểm chứng và
với sóng ánh sáng như Hình 5.9. Các tia sáng khi truyền từ giải thích.
nước ra không khí bị đổi phương truyền, do đó ta thấy thìa
bị gãy khúc tại mặt tiếp xúc nước – không khí. Ngoài ra,
hiện tượng khúc xạ sóng cũng xảy ra đối với sóng biển và sóng âm.
Giải thích vì sao vào những đêm mùa lạnh, ta có thể
nghe được âm thanh từ xa trong khi vào mùa nóng
ta lại không thể nghe được dù ở cùng khoảng cách.
S Hình 5.9. Chiếc thìa khi
đặt vào cốc nước
Hiện tượng nhiễu xạ
Trên Hình 5.10, ta thấy phương truyền của sóng biển khi đi
qua khe đã thay đổi và làm cho sóng lan rộng ở phía bên kia
khe. Đây là hiện tượng nhiễu xạ, là một trong những đặc
trưng của sóng (chỉ có sóng mới có thể gây ra hiện tượng
này). Sóng âm cũng có thể gây ra hiện tượng nhiễu xạ.
S Hình 5.10. Hiện tượng nhiễu xạ của sóng biển
Một số hiện tượng đặc trưng cho sóng là phản xạ, khúc xạ, nhiễu xạ,...
Khi mở hé cánh cửa để ánh sáng đi qua khe hẹp
(Hình 5.11), ta quan sát thấy ánh sáng loang ra một
khoảng lớn hơn kích thước khe hẹp. Hãy giải thích S hiện tượng này.
Hình 5.11. Ánh sáng đi qua khe hẹp khi mở hé cửa 37 VẬT LÍ 11
Trong một số điều kiện nhất định, ta có thể quan sát được hiện tượng nhiễu xạ của
sóng ánh sáng. Trong Hình 5.12a, khi kích thước của lỗ tròn đủ lớn, trên màn có một vệt
sáng đồng dạng với lỗ tròn theo đúng định luật truyền thẳng của ánh sáng. Tuy nhiên,
khi lỗ tròn có đường kính cỡ khoảng một phần mười milimét, ta không thấy một vệt
sáng mà lại thấy nhiều vệt sáng tối xen kẽ như ở Hình 5.12b. Điều này chỉ có thể được
giải thích dựa vào hiện tượng nhiễu xạ của sóng ánh sáng. 0jQFKҳQFyOӛWUzQ 0jQTXDQViW 0jQFKҳQFyOӛWUzQ 0jQTXDQViW NtFKWKѭӟFOӟQ NtFKWKѭӟFÿӫQKӓ 1JXӗQViQJ 1JXӗQViQJ a) b)
S Hình 5.12. Hiện tượng quan sát được trên màn khi lỗ tròn có kích thước: a) lớn; b) đủ nhỏ
Vận dụng những kiến thức về sóng để giải thích vì sao dơi (Hình 5.13)
có thể phát hiện ra chướng ngại vật bằng cơ chế phát sóng siêu âm (là
sóng âm có tần số lớn hơn 20 000 Hz).
S Hình 5.13. Dơi dang bay %j,7t3
1. Xét sóng nước truyền qua vị trí của phao câu cá đang nổi
trên mặt nước khi lặng gió như Hình 5P.1. Phao có trôi đi
theo phương truyền của sóng nước không? Vì sao?
S Hình 5P.1. Phao câu cá 6yQJ3VyQJVѫFҩS
2. Hình 5P.2 mô tả hai loại sóng địa chấn truyền trong môi
trường khi xảy ra động đất: sóng P (sóng sơ cấp) và sóng
S (sóng thứ cấp). Hãy phân biệt hai sóng địa chấn này
thuộc sóng dọc hay sóng ngang. Giải thích. 6yQJ6VyQJWKӭFҩS
S Hình 5P2. Hai loại sóng địa chấn 38 VẬT LÍ 11 Bài 6
&k&ôz&751*9t7/&$61*
– Khái niệm bước sóng, biên độ, tần số, tốc độ và cường độ sóng.
– Vận dụng biểu thức mô tả mối liên hệ giữa tốc độ truyền sóng, tần số và bước sóng.
Động đất cùng những dịch chuyển địa chất lớn ở mặt nước hoặc dưới
mặt nước sẽ sinh ra những đợt sóng lớn và đột ngột. Đó là hiện tượng sóng
thần (Hình 6.1). Sóng thần có thể gây ra những thiệt hại đáng kể về người
và vật chất. Để thực hiện những mô phỏng, dự báo chính xác nhất về sóng
thần, ta cần có những kiến thức vật lí nào liên quan đến hiện tượng sóng?
S Hình 6.1. Sóng thần tại Tohoku, Nhật Bản năm 2011
(Nguồn: https://www.flickr.com)
1 CÁC ĐẠI LƯỢNG ĐẶC TRƯNG CỦA SÓNG
Chu kì, tần số, biên độ sóng
Một sợi dây đàn hồi, không dãn, ban đầu được giữ nằm
ngang, một đầu được gắn cố định vào tường. Một bạn học vG
sinh kích thích để đầu còn lại của dây dao động (Hình 6.2a).
Ta thấy có sóng lan truyền trên dây. Hiện tượng này cũng có
thể quan sát được trên thực tế, trong một số bài tập thể dục trong Hình 6.2b. a)
Thực nghiệm chứng tỏ, khi nguồn sóng là đầu O của dây
được kích thích để thực hiện dao động điều hoà theo
phương thẳng đứng với chu kì T (tần số f) thì mỗi điểm trên
dây cũng thực hiện dao động với cùng chu kì T và tần số f
với đầu O. Ta gọi T và f lần lượt là chu kì và tần số của sóng.
Khi sóng truyền qua, mỗi điểm trong không gian thực b)
hiện dao động tại chỗ. Vì ban đầu tất cả mọi điểm trên S Hình 6.2. a) Sóng trên một dây đàn hồi;
b) Sóng trên dây khi vận động viên
phương truyền sóng đều đứng yên nên độ dịch chuyển
thực hiện bài tập thể dục
cũng chính là li độ dao động của chúng. Biên độ dao động
của các phần tử môi trường tại điểm đó được gọi là biên
độ sóng. Những điểm trên phương truyền sóng có li độ
cực đại được gọi là đỉnh sóng. 39 VẬT LÍ 11
Chu kì và tần số của sóng lần lượt là chu kì và tần số
1. Quan sát Hình 6.2, thực hiện các
của nguồn sóng. Biên độ sóng tại một điểm là biên yêu cầu sau:
độ dao động của phần tử môi trường tại điểm đó.
a) Cho biết sóng truyền trên dây
là sóng dọc hay sóng ngang.
b) Mô tả chuyển động của từng
Phân loại sóng âm theo tần số điểm trên dây.
– Sóng âm nghe được có tần số trong khoảng từ 16 Hz đến 20 000 Hz.
– Sóng hạ âm có tần số nhỏ hơn 16 Hz. Sóng hạ âm có
thể được phát ra từ những hiện tượng như động đất, sấm,
núi lửa. Một số loài vật có thể sử dụng sóng hạ âm để giao tiếp như voi, hà mã,…
– Sóng siêu âm có tần số lớn hơn 20 000 Hz. Một số loài
vật có thể cảm thụ được sóng siêu âm như chó, dơi,…
Bước sóng và tốc độ truyền sóng
Xét sợi dây có một đầu được gắn cố định, một đầu được nối
với nguồn dao động. Cho nguồn dao động điều hoà và ghi
nhận vị trí của từng điểm trên dây tại những thời điểm khác
nhau, ta có kết quả được minh hoạ như trong Hình 6.3. 9ӏWUt 7KӡLÿLӇP O A B C D E G H K t = 0 t = T4 t = T2
2. Quan sát Hình 6.3, hãy:
a) Chỉ ra những điểm trên dây t = 3T 4 O
đang có trạng thái dao động giống t = T
nhau tại thời điểm đang xét.
b) So sánh trạng thái dao động t = 5T 4
của điểm D với trạng thái dao t = 6T 4
động của nguồn O khi W ≥ T. t = 7T 4 t = 2T
S Hình 6.3. Trạng thái dao động của một số vị trí trên dây
tại những thời điểm liên tiếp 40 VẬT LÍ 11
Từ Hình 6.3, ta thấy sau khoảng thời gian một chu kì dao
động T, sóng được truyền từ nguồn O đến điểm D trên dây.
Sau đó, hai điểm O và D luôn có cùng trạng thái dao động tại
từng thời điểm, nghĩa là chúng dao động cùng pha với nhau.
Quãng đường mà sóng truyền đi được trong một chu kì dao
động được gọi là bước sóng, kí hiệu là Ȝ. Bước sóng cũng
chính là khoảng cách giữa hai điểm gần nhau nhất trên
phương truyền sóng dao động cùng pha với nhau. Trong hệ
SI, bước sóng có đơn vị là mét (m).
Trong khoảng thời gian 'W, sóng truyền đi được quãng
đường s. Vậy tốc độ truyền sóng được xác định bởi: v s (6.1) t
Trong hệ SI, tốc độ truyền sóng có đơn vị là m/s.
Khi 'W = T thì s = Ȝ, công thức (6.1) được viết lại thành: v f (6.2) T
Bước sóng là quãng đường sóng truyền đi được trong
một chu kì dao động. vT
Tốc độ truyền sóng được xác định bằng thương số giữa
quãng đường sóng truyền đi được và thời gian để sóng
truyền đi quãng đường đó. v st Lưu ý:
– Sự truyền sóng là sự truyền dao động giữa các phần tử
của môi trường truyền sóng. Trong quá trình sóng được
truyền đi, mỗi phần tử thực hiện dao động quanh vị trí cân bằng xác định của nó.
– Cần phân biệt hai khái niệm tốc độ truyền sóng với
tốc độ dao động. Tốc độ truyền sóng trong một môi trường
xác định thường là hằng số. Trong khi đó, tốc độ dao động
là tốc độ của một chất điểm thực hiện dao động quanh vị trí
cân bằng, là đại lượng biến đổi theo thời gian đã được khảo
sát trong chương Dao động.
3. Tốc độ truyền sóng trong môi
– Sóng truyền trong không gian với tốc độ hữu hạn. Tốc độ
trường nhanh hay chậm có phụ
truyền sóng phụ thuộc vào đặc tính của môi trường truyền
thuộc tốc độ dao động tại chỗ của
như mật độ môi trường, tính đàn hồi, nhiệt độ, áp suất,…
các phần tử môi trường không?
– Tuy tốc độ truyền sóng phụ thuộc tính chất của môi
trường truyền sóng, nhưng tần số sóng không phụ thuộc
vào môi trường truyền sóng. 41 VẬT LÍ 11
Ở 20 oC và áp suất khí quyển (1 atm), sóng âm truyền trong
không khí với tốc độ là 343 m/s, trong nước là 1 482 m/s,
trong nhôm là 6 420 m/s. Trong khi đó, tốc độ ánh sáng có 4. Từ ví dụ về tốc độ truyền sóng âm
giá trị khoảng 3.108 m/s trong chân không và thay đổi tuỳ
trong các môi trường rắn, lỏng và
khí, hãy rút ra nhận xét và giải
vào môi trường truyền ánh sáng. thích sự khác nhau này.
Ví dụ: Sóng âm có tần số lớn hơn 20 000 Hz (sóng siêu âm)
được sử dụng trong chẩn đoán hình ảnh y khoa (Hình 6.4).
Để sóng siêu âm có tần số 1,5.106 Hz có thể truyền xuyên qua
mô của cơ thể người và cho hình ảnh rõ nét, bước sóng của
sóng siêu âm này không được lớn hơn 1,0 mm. Xác định điều
kiện về tốc độ của sóng siêu âm này. Bài giải
Từ biểu thức (6.2), ta có: v f 1,0 mm
S Hình 6.4. Chẩn đoán hình ảnh
Suy ra điều kiện về tốc độ của sóng siêu âm này là: bằng siêu âm v ≤ 1,5.103 m/s.
Một bạn học sinh đang câu cá trên hồ nước. Khi có sóng đi qua, bạn quan sát thấy phao
câu cá nhô lên cao 6 lần trong 4 s. Biết tốc độ truyền sóng là 0,5 m/s. Tính khoảng cách
giữa hai đỉnh sóng liên tiếp. Cường độ sóng
Ta đã biết quá trình truyền sóng là quá trình truyền năng
lượng. Tại một vị trí trên phương truyền sóng, độ mạnh yếu
của sóng được định nghĩa bởi đại lượng cường độ sóng.
Cường độ sóng I là năng lượng sóng truyền qua một
đơn vị diện tích vuông góc với phương truyền sóng
trong một đơn vị thời gian. I E P (6.3) S t S
Trong hệ SI, cường độ sóng có đơn vị là W/m2.
Trong công thức (6.3), P E và S lần lượt là công suất của t
sóng (tính theo W) và diện tích mà năng lượng sóng E (tính
theo J) truyền qua trong khoảng thời gian ∆t (tính theo s). 42 VẬT LÍ 11
Ví dụ: Một còi báo động có kích thước nhỏ phát sóng âm vG
trong môi trường đồng chất, đẳng hướng. Ở vị trí cách còi
một đoạn 15 m, cường độ sóng âm là 0,25 W/m2. Xem gần
đúng sóng âm không bị môi trường hấp thụ. Ở khoảng vG
cách nào từ vị trí của còi thì sóng âm có cường độ bằng 0,010 W/m2? vG 0һWVyQJFҫX Bài giải
Vì nguồn âm được xem như là một điểm nên cường độ sóng 1JXӗQVyQJ
âm trên một mặt cầu có diện tích S = 4Sr2 (Hình 6.5) là S Hình 6.5. Năng lượng sóng truyền
như nhau, với r là bán kính mặt cầu (cũng là khoảng cách từ
qua mặt cầu có bán kính khác nhau
điểm đang xét đến còi).
Tại vị trí r = 15 m và r , ta có: I P và I P . 1 2 1 r2 4 2 r2 4 1 2 2 Suy ra: I r 0, 25 1 2 ; r r I1 I r 15 75 m. 2 2 1 I 0, 010 2 1 2
Vậy ở khoảng cách 75 m tính từ vị trí của còi thì sóng âm có
cường độ bằng 0,010 W/m2.
Biết cường độ ánh sáng của Mặt Trời đo được tại Trái Đất là 1,37.103 W/m2 và khoảng cách từ
Mặt Trời đến Trái Đất là 1,50.1011 m. Hãy tính công suất bức xạ sóng ánh sáng của Mặt Trời. 2 PHƯƠNG TRÌNH SÓNG
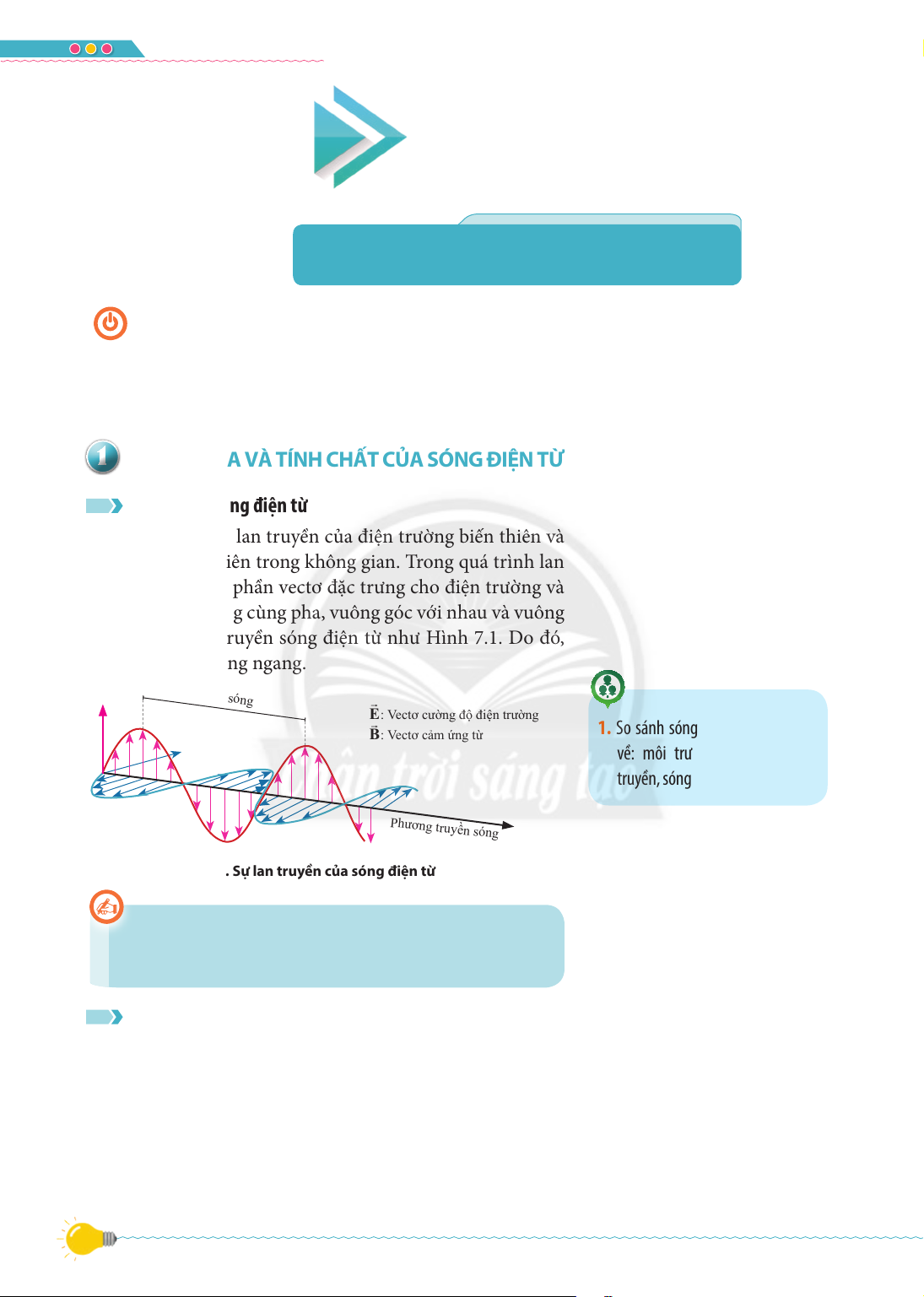
Giả sử nguồn sóng O dao động điều hoà theo phương vuông u
góc với trục Ox, có li độ được mô tả bởi phương trình: (cm) x λ A M u Acost O O (6.4) x1 [(cm) –A
với A là biên độ dao động và Ȧlà tần số góc. a)
Xét một điểm M trên dây với OM x , sóng cần một thời X(cm) T x A
gian W = để truyền từ O đến M. Như vậy li độ dao động 1 v O W1 W (s)
tại điểm M vào thời điểm t bằng li độ dao động tại điểm O –A b) vào thời điểm t x
. Do đó, phương trình li độ của điểm M S Hình 6.6. v
a) Đồ thị li độ – khoảng cách của dây tại được viết:
một thời điểm sóng trên dây ổn định; u 2
b) Đồ thị li độ – thời gian của điểm M trên cos t x cost x M A A (6.5) v T v
dây, cách nguồn sóng một đoạn x 43 VẬT LÍ 11
Phương trình sóng truyền theo trục Ox là:
5. Từ phương trình (6.6), xác định u 2 2 Acos t x (6.6) T
khoảng cách giữa hai điểm gần
nhau nhất dao động cùng pha và
Trong phương trình (6.6), W và T lần lượt là thời điểm đang
khoảng cách giữa hai điểm gần
xét và chu kì sóng (tính theo s), x và Olần lượt là khoảng cách
nhau nhất dao động ngược pha
từ một điểm trên dây đến nguồn và bước sóng (tính theo m). (theo bước sóng).
Ta có một số nhận xét sau:
6. Quan sát Hình 6.3, xác định độ
– Phương trình (6.6) có tính tuần hoàn theo không gian với
lệch pha của hai điểm A và B
chu kì Ȝ (Hình 6.6a) và theo thời gian với chu kì T (Hình 6.6b).
trên cùng phương truyền sóng
– Tại cùng một thời điểm, dao động tại điểm M trễ pha hơn vào thời điểm t T 7 .
dao động tại nguồn một góc 2x (với x là khoảng cách từ 4
điểm M đến nguồn).
Ví dụ: Sóng truyền trên mặt nước ở một hồ nước được mô
tả bởi phương trình u = 3,75cos(5,4t – 0,45x), trong đó u và x
được tính bằng xentimét (cm) và t được tính bằng giây (s).
Tính tốc độ truyền sóng. Bài giải
So sánh phương trình đã cho với phương trình (6.6), ta có: 2 5, 4 1 T s và 2 0, 45 1 cm .
Tốc độ truyền sóng là: v 2 5,4 T 12 cm/s. 0,45 2
Giải thích vì sao ở Hình 6.6a, đường biểu diễn có một đoạn nằm ngang sau vị trí có toạ độ x 1
và ở Hình 6.6b, đường biểu diễn có một đoạn nằm ngang trước thời điểm t .1
Đề xuất phương án thí nghiệm và thực hiện thí nghiệm đơn giản để tạo ra sóng truyền trên một sợi dây và xác
định các đại lượng đặc trưng của sóng như chu kì, tần số. Độ richter
Độ richter, được đề xuất khoảng năm 1935 bởi nhà vật lí Charles F. Richter (1900 – 1985),
là đơn vị được dùng để đánh giá độ lớn của cường độ (hay năng lượng phát ra) của các
trận động đất. Theo thang richter, biên độ sóng được tính theo thang logarithm, nghĩa
là biên độ sóng động đất ở độ 6 richter bằng 10 lần biên độ sóng động đất ở độ 5 richter.
– Độ richter nhỏ hơn 4,0: Động đất nhẹ, cảm nhận được nhưng ít gây thiệt hại.
– Độ richter từ 4,0 đến 6,0: Động đất trung bình, có thể gây thiệt hại cho các kiến trúc
không theo tiêu chuẩn phòng ngừa địa chấn. 44 VẬT LÍ 11
– Độ richter từ trên 6,0: Động đất mạnh và rất mạnh. Có thể có sức tàn phá nghiêm trọng.
Ở Việt Nam, hai trận động đất mạnh nhất ghi nhận được là trận động đất 6,8 độ richter tại
Điện Biên vào năm 1935 và trận động đất mạnh 6,7 độ richter tại Lai Châu vào năm 1983.
Trận động đất 9,5 độ richter xảy ra tại Chile vào năm 1960, được xem là trận động đất mạnh
nhất trên thế giới cho đến năm 2023. Mức cường độ âm
Trên thực tế, khi đề cập đến độ to của âm. Ta thường sử dụng khái niệm mức cường độ âm.
Đối với cảm nhận của tai người, độ to của âm được đo bởi đại lượng mức cường độ âm, tính
theo hàm logarithm cơ số 10 của tỉ số giữa cường độ âm I và cường độ âm chuẩn I :0 I L 10lg (6.7) I0
Mức cường độ âm có đơn vị là đêxiben (dB).
I = 10–12 W/m2 là cường độ âm nhỏ nhất tai người có thể nghe được ở tần số 1 000 Hz. 0
Tai người có thể nghe được âm có cường độ từ 10–12 W/m2 đến 103 W/m2 (ngưỡng đau).
Mức cường độ âm của cuộc nói chuyện bình thường khoảng 65 dB. %j,7t3
1. Khi đi biển, các thuỷ thủ trên thuyền có thể sử dụng kĩ thuật
sonar (một kĩ thuật phát ra sóng siêu âm) dùng để định vị
hay điều hướng thuyền nhằm tránh các tảng đá ngầm hoặc
phát hiện đàn cá (Hình 6P.1). Trong tự nhiên, nhiều loài động
vật như dơi, cá heo cũng có thể phát ra sóng siêu âm để di
chuyển và định vị con mồi. Kĩ thuật sonar sử dụng tính chất
nào của sóng? Theo em, sóng siêu âm do các tàu thuyền phát
ra có ảnh hưởng như thế nào đối với loài cá heo và cá voi?
S Hình 6P.1. Sử dụng kĩ thuật
sonar để phát hiện đàn cá dưới biển S
2. Hai điểm gần nhất trên cùng phương truyền sóng dao động lệch pha nhau một góc cách 2
nhau 60 cm. Biết tốc độ truyền sóng là 330 m/s. Tìm độ lệch pha:
a) giữa hai điểm trên cùng phương truyền sóng, cách nhau 360 cm tại cùng một thời điểm.
b) tại cùng một điểm trên phương truyền sóng sau một khoảng thời gian là 0,1 s.
3. Một sóng truyền trên một dây rất dài có phương trình: u 10cos2 t 0,01 x
Trong đó u và x được tính bằng cm và t được tính bằng s. Hãy xác định:
a) Chu kì, tần số và biên độ sóng.
b) Bước sóng và tốc độ truyền sóng.
c) Giá trị của li độ u, tại điểm có x = 50 cm vào thời điểm t = 4s. 45 VẬT LÍ 11 Bài 7 61*ô,17
Sóng điện từ và thang sóng điện từ.
Tại một số vùng xa xôi, đôi khi ta không thể sử dụng điện thoại để liên lạc bởi điện thoại đang nằm ngoài vùng
phủ sóng của đài phát sóng. Vậy sóng mà các đài phát sóng di động đang phát là sóng gì và có tính chất như thế nào?
1 ĐỊNH NGHĨA VÀ TÍNH CHẤT CỦA SÓNG ĐIỆN TỪ
Định nghĩa sóng điện từ
Sóng điện từ là sự lan truyền của điện trường biến thiên và
từ trường biến thiên trong không gian. Trong quá trình lan
truyền, các thành phần vectơ đặc trưng cho điện trường và
từ trường dao động cùng pha, vuông góc với nhau và vuông
góc với phương truyền sóng điện từ như Hình 7.1. Do đó,
sóng điện từ là sóng ngang. G %ѭӟFVyQJ G E
E9HFWѫFѭӡQJÿӝÿLӋQWUѭӡQJ G G B9HFWѫFҧPӭQJWӯ
1. So sánh sóng điện từ và sóng cơ B
về: môi trường truyền, tốc độ O
truyền, sóng ngang hay sóng dọc. 3KѭѫQJWUX\ӅQVyQJ
S Hình 7.1. Sự lan truyền của sóng điện từ
Sóng điện từ là sự lan truyền trong không gian của
điện từ trường biến thiên. Ánh sáng có bản chất là sóng điện từ.
Tính chất của sóng điện từ
Sóng điện từ có một số tính chất sau:
– Tốc độ truyền sóng của sóng điện từ trong chân không là
c = 3.108 m/s. Trong không khí, ta có thể lấy gần đúng tốc độ này bằng 3.108 m/s. 46 VẬT LÍ 11
– Trong mọi môi trường vật chất, tốc độ truyền của sóng
điện từ đều nhỏ hơn c. Ví dụ: sóng điện từ có tốc độ truyền
xấp xỉ bằng 2,25.108 m/s trong nước và 1,24.108 m/s trong
2. Khi sóng điện từ truyền qua kim cương.
hai môi trường khác nhau,
– Một số hiện tượng đặc trưng của sóng điện từ là: phản xạ,
bước sóng của nó có bị thay khúc xạ, nhiễu xạ,... đổi không? Giải thích.
Lưu ý: Khi truyền qua các môi trường khác nhau, tần số và
chu kì của sóng điện từ không thay đổi.
Chiết suất của môi trường
Tỉ số giữa tốc độ truyền sóng điện từ trong chân
3. Dựa vào Hình 7.2 và cho biết
không c và trong một môi trường xác định v được gọi là
bước sóng của vùng ánh sáng
chiết suất của môi trường đó: nhìn thấy. n c (7.1) v
Như vậy chiết suất của một môi trường luôn lớn hơn hoặc bằng 1.
2 THANG SÓNG ĐIỆN TỪ
Sóng điện từ có thể được phân loại dựa vào bước sóng hoặc tần số (Hình 7.2). 7ӱQJRҥL 7ҫQVӕWăQJGҫQ 1024 1022 1020 1018 1016 1014 1012 1010 108 106 104 102 100 I (Hz) Tia Jgamma) Tia X UV Hồng ngoại Vi sóng Sóng vô tuyến dài Sóng vô tuyến 10–16 10–14 10–12 10–11 10–10 10–8 10–6 10–4 10–3 10–2 100 102 104 106 108 Ȝ (m) %ѭӟFVyQJWăQJGҫQ ÈQKViQJQKuQWKҩ\NKҧNLӃQ 380 450 495 570 590 620 760 Tím – chàm /DP /өF 9jQJ &DP Ĉӓ ȜQP
S Hình 7.2. Thang sóng điện từ
Thang sóng điện từ cho biết dải bước sóng và dải tần số ứng với các loại bức xạ khác nhau.
Thứ tự của các sóng điện từ có bước sóng từ nhỏ đến lớn là:
Tia J(tia gamma), tia X hay tia Röntgen (Rơn-ghen), tia tử
4. Dựa vào số liệu trong Hình 7.2,
ngoại, ánh sáng nhìn thấy trải dài từ ánh sáng tím đến đỏ,
xác định tần số của ánh sáng
tia hồng ngoại, các sóng vô tuyến (gồm vi sóng – microwave, nhìn thấy.
các sóng FM, AM và các sóng có bước sóng dài hơn). 47 VẬT LÍ 11
Các sóng điện từ có bước sóng càng nhỏ thì mang năng lượng
càng lớn. Đó là lí do tia X và tia J có khả năng đâm xuyên
mạnh. Khả năng đâm xuyên này phụ thuộc vào khối lượng
nguyên tử của vật chất mà các tia này chiếu đến. Khối lượng
nguyên tử này càng lớn thì khả năng đâm xuyên của tia X và
tia J càng giảm đi. Tính chất này được áp dụng trong kĩ thuật
chụp ảnh bằng tia X trong y khoa (Hình 7.3). Trong khi đó,
các sóng vô tuyến được sử dụng rộng rãi trong quá trình thu
S Hình 7.3. Hình chụp X-quang
và phát sóng của điện thoại di động. bàn tay
Vào thời điểm năm 2022, điện thoại di động ở Việt Nam sử dụng sóng điện từ có tần số
trong khoảng từ 850 MHz đến 2 600 MHz. Tính bước sóng của sóng điện từ tương ứng với
dải tần số này. Mắt chúng ta có thể thấy được các sóng này không? Vì sao?
Tìm hiểu và giải thích vì sao khi sử dụng tia X để chụp ảnh trong y khoa như Hình 7.3, ta có thể thấy được xương của bàn tay. %j,7t3
1. Hình 7P.1 mô tả các hiện tượng xảy ra đối với sóng
vô tuyến có các tần số khác nhau do tác dụng của tầng 100 MHz điện li ở khí quyển. 7ҫQJÿLӋQOL
a) Gọi tên các hiện tượng liên quan đến sóng vô tuyến có 5 MHz tần số 5 MHz và 100 MHz.
b) Giải thích vì sao các sóng vô tuyến ngắn được sử dụng để
truyền thông tin trên mặt đất.
S Hình 7P.1. Sự lan truyền
sóng vô tuyến trong khí quyển
2. Các tia UV-A (có bước sóng trong khoảng từ 320 nm đến 400 nm) trong ánh sáng mặt trời có
thể có tác dụng sinh học tốt như kích thích sự sản sinh vitamin D. Nhưng các tia UV-B có bước
sóng trong khoảng từ 280 nm đến 320 nm lại có thể nguy hiểm như gây ung thư da.
Bằng cách tra cứu sách, báo, hãy lập biểu đồ cho biết ở địa phương em, trong khoảng thời gian
nào của một năm và thời gian nào trong ngày ta cần phải phòng tránh tia UV-B.
3. Một vệ tinh nhân tạo chuyển động ở độ cao 575 km so với mặt đất phát sóng vô tuyến có tần số
92,4 MHz với công suất bằng 25,0 kW về phía mặt đất. Hãy tính cường độ sóng nhận được bởi
một máy thu vô tuyến ở mặt đất ngay phía dưới vệ tinh. Bỏ qua sự hấp thụ sóng của khí quyển. 48 VẬT LÍ 11 Bài 8 *,$27+2$61*
– Giao thoa sóng cơ và giao thoa sóng ánh sáng.
– Công thức tính khoảng vân trong giao thoa ánh sáng qua hai khe hẹp.
Hình 8.1 cho thấy hình ảnh sóng trên mặt nước là kết quả của sự
chồng chất sóng do hai con vịt tạo ra khi bơi. Trong một số trường hợp, sự
chồng chất sóng này dẫn đến một hiện tượng thú vị: có những điểm trên
mặt nước dao động mạnh và những điểm dao động yếu hoặc đứng yên.
Vậy hiện tượng đó là gì và điều kiện nào để hiện tượng này xảy ra?
S Hình 8.1. Sóng nước do hai con vịt tạo ra 1 GIAO THOA SÓNG CƠ (6) (4)
Thí nghiệm khảo sát hiện tượng giao thoa sóng (3)
* Mục đích: Khảo sát định tính hiện tượng sóng trên mặt
nước khi có hai nguồn dao động cùng tần số và cùng pha đặt gần nhau. (1) (2) * Dụng cụ: (5)
– Khay nước (1), đèn chiếu (2), màn (3).
– Hai viên bi nhỏ (4) gắn vào cùng một cần rung. – Máy phát tần số (5).
S Hình 8.2. Bố trí thí nghiệm – Gương phẳng (6).
khảo sát hiện tượng giao thoa sóng nước
* Tiến hành thí nghiệm:
Bước 1: Bố trí thí nghiệm như Hình 8.2.
1. Quan sát thí nghiệm và mô tả lại
Bước 2: Gắn hai viên bi vào cần rung và nối cần rung vào
hiện tượng quan sát được như máy phát tần số. trong Hình 8.3.
Bước 3: Đặt hai viên bi sao cho chúng khẽ chạm vào mặt nước.
Bước 4: Bật đèn chiếu. Bật máy phát tần số để hai viên bi dao
động theo phương thẳng đứng là hai nguồn tạo ra sóng lan truyền trên mặt nước.
Bước 5: Điều chỉnh tần số để quan sát rõ hiện tượng.
* Báo cáo kết quả thí nghiệm: Quan sát hình ảnh sóng
nước được chiếu lên màn và rút ra kết luận.
S Hình 8.3. Hình ảnh giao thoa sóng
nước thu được trên màn 49 VẬT LÍ 11
Hiện tượng giao thoa sóng
Trong thí nghiệm giao thoa sóng (Hình 8.2), hai sóng trên
mặt nước được sinh ra từ sự dao động của hai viên bi có cùng
phương dao động, cùng tần số và cùng pha với nhau do được
2. Quan sát thí nghiệm được thực
nối vào cùng một nguồn dao động. Hai viên bi đóng vai trò
hiện theo bố trí trong Hình 8.2
như hai nguồn kết hợp. Hai sóng được tạo ra từ hai nguồn
và nhận xét sóng tạo bởi hai
kết hợp được gọi là hai sóng kết hợp. Tổng quát, hai sóng kết
viên bi về: tần số, pha và
hợp là hai sóng có cùng phương dao động, cùng tần số và độ phương dao động.
lệch pha không đổi theo thời gian.
Khi hai sóng kết hợp gặp nhau, trong môi trường xuất hiện
những điểm dao động với biên độ cực đại và những điểm
dao động với biên độ cực tiểu (có thể bằng không) lần lượt
tương ứng với trường hợp hai sóng tăng cường (hai sóng
cùng pha tại những điểm này) và làm suy giảm nhau (hai
sóng ngược pha tại những điểm này). Đây chính là hiện
tượng giao thoa sóng.
Hiện tượng giao thoa sóng là hiện tượng hai sóng kết
hợp gặp nhau, tăng cường nhau hoặc làm suy yếu nhau
tại một số vị trí trong môi trường. Điều kiện để có giao
thoa là phải có sự kết hợp từ hai nguồn sóng dao động
cùng phương, cùng tần số và có độ lệch pha không đổi theo thời gian.
Hiện tượng giao thoa là hiện tượng đặc trưng của sóng.
Nghĩa là chỉ có những đối tượng vật lí có bản chất sóng mới có
thể sinh ra hiện tượng này. Ngược lại, khi ta quan sát được hiện
tượng giao thoa trong một vùng không gian thì ta có thể kết
luận trong vùng không gian đó có sự tồn tại của sóng.
Trong môi trường truyền sóng, khi hai nguồn dao động
cùng pha, những điểm có khoảng cách đến hai nguồn
lần lượt là d và d sẽ dao động với biên độ cực đại khi: 1 2
d – d = NȜ(8.1) 2 1
và dao động với biên độ cực tiểu khi: d d k 1 2 1 (8.2) 2
với k là một số nguyên (k = 0, ±1, ±2,…).
Hình 8.4 minh hoạ tập hợp những điểm có biên độ sóng
tổng hợp đạt cực đại (đường màu đỏ) và cực tiểu (đường
màu xanh) lần lượt tương ứng với những vị trí mà hai sóng
thành phần tăng cường nhau hoặc làm suy giảm nhau. 50 VẬT LÍ 11 &ӵFÿҥL &ӵFÿҥL WUXQJWkP &ӵFÿҥL EұF FӵFÿҥLEұF EұF &ӵFWLӇX &ӵFWLӇX &ӵFWLӇX &ӵFWLӇX &ӵFÿҥL WKӭ WKӭ WKӭ WKӭ &ӵFÿҥL EұF EұF &ӵFWLӇX &ӵFWLӇX WKӭ WKӭ &ӵFÿҥL &ӵFÿҥL EұF EұF
W Hình 8.4. Vị trí của các S S 1 2
điểm cực đại, cực tiểu
trong giao thoa sóng nước
Trong thí nghiệm giao thoa sóng trên mặt nước
với hai nguồn kết hợp dao động cùng biên độ,
Giải thích vì sao trong tự nhiên, ta
những điểm nằm trên đường trung trực của
thường không quan sát được hiện
đoạn thẳng nối hai nguồn sẽ dao động với biên
tượng giao thoa của sóng như độ như thế nào nếu:
trường hợp sóng nước tạo bởi hai
a) hai nguồn dao động cùng pha?
con vịt đang bơi (Hình 8.1).
b) hai nguồn dao động ngược pha?
Xác định vị trí các vân giao thoa
Trong thí nghiệm giao thoa sóng (Hình 8.2), gọi S và S lần lượt là hai nguồn (hai viên bi) 1 2
dao động cùng biên độ A, cùng pha, cùng tần số f và có phương trình li độ: 2 t u u Acost Acos (8.3) 1 2 T M
Xét một điểm M trên mặt nước cách S một đoạn S M = d 1 1 1
và cách S một đoạn S M = d như Hình 8.5. Xem biên độ 2 2 2 d2
dao động không thay đổi trong quá trình truyền sóng, theo d1
công thức (8.3), dao động u và u truyền đến M lần lượt có 1 2 phương trình: S2 2 t 2 d u 1 cos 1M A T và (8.4)
S1 S Hình 8.5. Đường truyền 2 t 2 d u A 2
của hai sóng từ hai nguồn cos 2M T
dao động S và S đến M 1 2 51 VẬT LÍ 11 v với vT
là bước sóng; v là tốc độ truyền sóng trên mặt nước. f
Ta có phương trình li độ sóng tổng hợp tại điểm M có dạng: u M u1M u2M d d d d 2 cos 2 1 cos t 2 1 A (8.5)
Độ lệch pha của hai dao động thành phần tại M: 2 (d d (8.6) ) 2 1
Biên độ sóng tổng hợp tại M: d d A 2 1 M 2A cos (8.7)
– A đạt cực đại nếu hai dao động thành phần cùng pha: 2k, với k = 0, ±1, ±2,… M
Do đó: d d k (8.8) 2 1
– A đạt cực tiểu nếu hai dao động thành phần ngược pha: (2k , với k = 0, ±1, ±2,… M ) 1 Do đó: d d 1 k (8.9) 2 1 2
2 GIAO THOA SÓNG ÁNH SÁNG
Thí nghiệm Young về giao thoa ánh sáng
Ta đã biết, ánh sáng có bản chất sóng nên có thể gây ra hiện
tượng giao thoa. Có nhiều cách khác nhau để tạo ra hiện 3. Quan sát Hình 8.6 và mô tả hình
tượng giao thoa ánh sáng, trong đó có phương án sử dụng
ảnh nhận được trên màn M.
hai khe hẹp (được gọi là khe Young) do Thomas Young
(Tho-mát Y-âng) (1773 – 1829) đề xuất. 0jQ0 +DLNKH6 Yj6 1 2
S Hình 8.6. Thí nghiệm giao thoa khe Young sử dụng nguồn laser đỏ 52 VẬT LÍ 11
Thí nghiệm giao thoa ánh sáng được bố trí như trong
Hình 8.6, trong đó ánh sáng từ nguồn laser đỏ sẽ đến hai
khe rất nhỏ S và S được đặt rất gần nhau. Trên màn M 1 2
đặt song song với mặt phẳng chứa hai khe, ta quan sát thấy
một vùng sáng hẹp, trong đó xuất hiện những vạch sáng
màu đỏ và các vạch tối xen kẽ, cách đều nhau và song song với hai khe (Hình 8.6).
Hiện tượng quan sát được trong thí nghiệm minh hoạ trên
Hình 8.6 là hiện tượng giao thoa ánh sáng. Các vạch sáng,
4. Giải thích hiện tượng quan sát
vạch tối được gọi là vân giao thoa. Vạch sáng ứng với biên
được trong thí nghiệm Young về
độ dao động tổng hợp cực đại được gọi là vân sáng, vạch
giao thoa ánh sáng (Hình 8.6).
tối ứng với biên độ dao động tổng hợp cực tiểu được gọi là vân tối.
Hiện tượng giao thoa ánh sáng là hiện tượng xuất
hiện các vạch sáng xen kẽ với các vạch tối khi hai
sóng ánh sáng kết hợp gặp nhau.
Khoảng vân và vị trí vân giao thoa trên màn
Trong sơ đồ thí nghiệm Young về giao thoa ánh sáng (Hình 8.7), A
xét điểm A trên màn quan sát có toạ độ xác định bởi OA x . d1 S x
Đặt S S = a, IO = D (khoảng cách từ mặt phẳng chứa hai khe 1 d 1 2 2 a
hẹp đến màn quan sát M), S A = d và S A = d . Để quan sát I O 1 1 2 2
rõ vân giao thoa trên màn, a phải rất nhỏ so với D (a khoảng S2
vài milimét, D khoảng vài chục hoặc vài trăm xentimét). D 0jQ0
Với ánh sáng có bước sóng Ȝ
S Hình 8.7. Vị trí của điểm A trên
– Điểm A là vân sáng khi d d k , với k là một số
màn cách các nguồn các khoảng 2 1
nguyên (k = 0, ±1, ±2,…). Vị trí các vân sáng trên màn được
d và d 1 2 xác định: x (8.10) s k D a
±ĈLӇPAOjYkQWӕLNKLd d k 1 2 1 YӟLkOjPӝWVӕ 2
QJX\rQk «9ӏWUtFiFYkQWӕLWUrQPjQÿѭӧF [iFÿӏQK x 1 k D (8.11) t 2 a 53 VẬT LÍ 11
Khoảng cách giữa hai vân sáng (hoặc hai vân tối)
liên tiếp được gọi là khoảng vân, kí hiệu làL. i D (8.12) a
Trên màn giao thoa, vân sáng có vị trí: x = NL (8.13) s và vân tối có vị trí: x 1 k i (8.14) t 2
với k là một số nguyên (k = 0, ±1, ±2,…).
Vận dụng hiện tượng giao thoa ánh sáng
Ví dụ: Trong thí nghiệm Young về giao thoa ánh sáng,
khi nguồn sáng là ánh sáng đơn sắc có bước sóng Ȝ,
người ta đo khoảng cách giữa 9 vân sáng liên tiếp là
25,3 mm. Cho biết khoảng cách giữa hai khe là 0,200 mm và
khoảng cách từ hai khe đến màn là 1 m.
a) Tính bước sóng Ȝ.
b) Tính khoảng cách từ vân sáng bậc hai đến vân tối thứ tư
ở cùng bên so với vân sáng trung tâm (vân sáng cách đều hai khe sáng). Bài giải
a) Ta có: 8i = 25,3 mm, suy ra i = 3,16 mm.
Từ công thức (8.12), suy ra: 3 3 ai 0,200 10 . 3 . ,16 1 . 0 6 D 0, 632.10 m = 632 nm 1
b) Khoảng cách từ vân sáng bậc hai đến vân tối thứ tư ở cùng
bên so với vân sáng trung tâm là:
3,5i – 2i = 1,5i = 1,5.3,16 = 4,74 mm.
Trong thí nghiệm Young về giao thoa ánh sáng, khoảng vân sẽ thay đổi thế nào
khi ta thay nguồn sáng đơn sắc có bước sóng Ȝ bằng ánh sáng đơn sắc có bước
sóng là 1,2Ȝ? Nếu khoảng cách từ hai khe đến màn quan sát giữ cố định, ta phải
thay đổi khoảng cách giữa hai khe như thế nào để khoảng vân lại có độ lớn như ban đầu?
Tìm hiểu và mô tả sơ lược hình ảnh nhận được trên màn khi ta sử dụng nguồn sáng trắng (như ánh sáng mặt trời)
trong thí nghiệm Young về giao thoa ánh sáng. 54 VẬT LÍ 11 %j,7t3
1. Trong thí nghiệm giao thoa sóng trên mặt nước với hai nguồn kết hợp cùng pha, ta thấy tại một
điểm cách hai nguồn các khoảng lần lượt là 20 cm và 12 cm, sóng có biên độ cực đại, đồng thời
giữa điểm này và đường trung trực của hai nguồn có 4 dãy gồm những điểm dao động với biên
độ cực đại. Biết tốc độ truyền sóng là 40 cm/s. Tính tần số của sóng.
2. Thí nghiệm Young về giao thoa ánh sáng thường được sử dụng để đo bước sóng của ánh sáng
đơn sắc. Khi chiếu hai khe bằng một nguồn phát ánh sáng đơn sắc, ta thấy vân sáng thứ năm
cách vân trung tâm là 2,8 cm. Biết hai khe đặt cách nhau 0,2 mm và cách màn một khoảng
1,5 m. Xác định bước sóng của ánh sáng được dùng trong thí nghiệm.
3. Trong thí nghiệm Young về giao thoa ánh sáng, người ta sử dụng một nguồn sáng phát ra đồng
thời hai ánh sáng đơn sắc có bước sóng lần lượt là 400 nm và 600 nm. Biết khoảng cách giữa hai
khe là 0,2 mm và khoảng cách từ hai khe đến màn là 1,5 m.
a) Tính khoảng cách giữa hai vân sáng bậc ba cùng phía với vân trung tâm.
b) Vân trung tâm có màu gì? Tìm khoảng cách gần nhất của một vân cùng màu với vân trung tâm
cho đến vân trung tâm này. 55 VẬT LÍ 11 Bài 9 61*'1*
– Thí nghiệm tạo sóng dừng và giải thích sự hình thành sóng dừng.
– Xác định vị trí nút và bụng của sóng dừng.
Khi gảy đàn guitar, ta quan sát được dây đàn rung và tạo
thành các múi như Hình 9.1. Trong điều kiện nào thì ta có thể
quan sát được hiện tượng được gọi là sóng dừng này?
S Hình 9.1. Hình ảnh dây đàn guitar khi được gảy
1 SỰ PHẢN XẠ SÓNG Sự phản xạ sóng
Xét sóng truyền trên một sợi dây có một đầu được
buộc vào điểm cố định (Hình 9.2a) hoặc được để tự do (Hình 9.2b).
1. Quan sát Hình 9.2 và nhận xét
chiều biến dạng của dây khi có 6yQJ WӟL 6yQJ
sóng tới và sóng phản xạ trong WӟL
hai trường hợp: đầu dây cố định 6yQJ SKҧQ 6yQJ và đầu dây tự do. [ҥ SKҧQ [ҥ ĈҫXGk\FӕÿӏQK ĈҫXGk\WӵGR a) b)
S Hình 9.2. Quá trình phản xạ sóng trong trường hợp:
a) Đầu dây cố định; b) Đầu dây tự do
Khi gặp vật cản, sóng sẽ bị phản xạ. Sóng được truyền từ nguồn phát đến vật cản được gọi là
sóng tới, sóng được truyền ngược lại từ vật cản được gọi là sóng phản xạ.
Thực nghiệm chứng tỏ, sóng phản xạ có cùng tần số và bước sóng với sóng tới. 1 1 Trong trườn
1g hợp đầu dây cố định, tại điểm phản xạ, sóng phản xạ ngược pha với sóng tới
(Hình 9.2a); trong trường hợp đầu dây tự do, sóng phản xạ cùng pha với sóng tới (Hình 9.2b). 56 VẬT LÍ 11
2 HIỆN TƯỢNG SÓNG DỪNG
Thí nghiệm khảo sát hiện tượng sóng dừng
* Mục đích: Khảo sát định tính hiện tượng sóng dừng. B * Dụng cụ:
– Sợi dây AB không dãn, đàn hồi, có chiều dài khoảng 65 cm (1). d (1)
– Hệ thống giá đỡ (2). (3)
– Thước thẳng có độ chia nhỏ nhất là 1 mm (3). M
– Máy phát tần số (4). (2)
* Tiến hành thí nghiệm:
Bước 1: Bố trí thí nghiệm như Hình 9.3. A (4)
Bước 2: Nối đầu dây A vào máy phát tần số, đầu còn lại của
dây được gắn cố định vào giá đỡ.
Bước 3: Bật máy phát tần số, điều chỉnh tần số dao động phù
S Hình 9.3. Bố trí thí nghiệm
hợp để xuất hiện hình ảnh sóng ổn định.
khảo sát hiện tượng sóng dừng
Bước 4: Điều chỉnh tần số máy phát; điều chỉnh chiều dài
của dây để thay đổi hình dạng sóng ổn định trên dây.
* Báo cáo kết quả thí nghiệm:
2. Nhận xét về sự phụ thuộc của
Quan sát hình ảnh sóng ổn định được hình thành trên dây.
số lượng điểm cực đại, cực tiểu
Xác định số lượng và vị trí của những điểm dao động với
trên dây với tần số của máy phát
biên độ cực đại và cực tiểu trên dây tương ứng với các giá trị tần số.
tần số và chiều dài dây khác nhau. B
Giải thích hiện tượng sóng dừng
Trong thí nghiệm trên, ta thấy khi hình ảnh sóng được tạo O 2
ra trên dây ổn định, trên dây xuất hiện những điểm cố định
dao động với biên độ lớn nhất (bụng sóng) và xen kẽ với O
những điểm đứng yên (nút sóng) (Hình 9.4). Nút 4 VyQJ %өQJ VyQJ
Tại bụng sóng, sóng tới và sóng phản xạ cùng pha; tại nút
sóng, sóng tới và sóng phản xạ ngược pha. Sóng có các
nút sóng và bụng sóng cố định trong không gian gọi là sóng dừng.
Xét một điểm M trên một dây đàn hồi AB, đầu A của dây A
gắn vào nhánh của một nguồn phát dao động thẳng đứng
với biên độ nhỏ để tạo ra sóng ngang trên dây, đầu B gắn vào
một điểm cố định (Hình 9.3). Tại một điểm M cách B một
S Hình 9.4. Hình dạng ổn định của
sợi dây khi có sóng dừng 57 VẬT LÍ 11
đoạn MB = d, ta có sự chồng chất của sóng tới từ A và sóng
phản xạ từ B. Khi sóng dừng xuất hiện trên dây (Hình 9.4),
sóng tổng hợp tại điểm M trên dây có cùng tần số với sóng
3. Dựa vào sự hình thành của các
tới và sóng phản xạ, có biên độ phụ thuộc vào khoảng cách
điểm dao động với biên độ cực đại
và cực tiểu trong hiện tượng giao
từ điểm M đến đầu cố định của dây.
thoa, hãy dự đoán nguyên nhân 2 d A 2 cos M A (9.1).
hình thành bụng sóng và nút sóng 2
trong hiện tượng sóng dừng.
trong đó O là bước sóng của sóng truyền trên dây. Ta có:
* Vị trí bụng sóng: là những điểm dao động với biên độ cực
đại A = 2A tương ứng với: M d 1
k (k = 0, 1, 2,…) (9.2) 2 2
* Vị trí nút sóng: là những điểm đứng yên A = 0 tương M ứng với:
d k (k = 0, 1, 2,…) (9.3) 2
Sóng dừng là sóng có các nút sóng và bụng sóng cố định trong không gian.
Khi có hiện tượng sóng dừng, trên dây xuất hiện những điểm dao động với biên độ
cực đại được gọi là bụng sóng và những điểm đứng yên được gọi là nút sóng.
Vị trí các bụng sóng được xác định bằng biểu thức: d 1 k (k = 0, 1, 2,…) 2 2
Vị trí các nút sóng được xác định bằng biểu thức: d k (k = 0, 1, 2,…) 2
Trong đó, d là khoảng cách từ một điểm trên dây đến một đầu dây.
Bụng sóng và nút sóng xen kẽ và cách đều nhau. Dọc theo dây, hai nút sóng liên tiếp
hoặc hai bụng sóng liên tiếp cách nhau một khoảng bằng nửa bước sóng.
Khảo sát định lượng hiện tượng sóng dừng
Chọn gốc toạ độ O tại B, chiều dương của trục Ox từ B đến M. Gốc thời gian được chọn ngay
thời điểm sóng tới đến B và có phương trình: u cos cos2 B A t A ft (9.4) t
với f là tần số của nguồn phát sóng. 58 VẬT LÍ 11
Sóng tới truyền từ M đến B sớm pha hơn tại B và có phương trình: 2 d u cos (9.5) tM A t
Do B là vật cản cố định, sóng phản xạ tại B có li độ ngược dấu với li độ của sóng tới và có phương trình: u cos cos B A t A t (9.6) px
Sóng phản xạ truyền từ B đến M trễ pha hơn tại B và có phương trình: 2 d u cos (9.7) M A t px
Khi sóng tới và sóng phản xạ cùng truyền qua M thì ở mỗi thời điểm, dao động tại M là kết
quả của sự chồng chất của sóng tới và sóng phản xạ nên phương trình li độ tổng hợp tại M được xác định: u M u M u t p M x 2 d 2 d u A cos t Acost M
Áp dụng công thức lượng giác, ta suy ra: 2 d u 2 cos cos M A t (9.8) 2 2
Kết luận: Sóng tổng hợp tại điểm M trên dây có cùng tần số với sóng tới và sóng phản xạ, có
biên độ phụ thuộc vào khoảng cách từ điểm M đến đầu cố định của dây. 2 d A 2 cos M A 2
Trên thực tế, sự phản xạ ở hai đầu A và B của dây xảy ra nhiều lần, khi sự cộng hưởng xuất
hiện trên dây, biên độ dao động tại bụng sóng lớn hơn 2A.
3 ĐIỀU KIỆN ĐỂ CÓ SÓNG DỪNG
Trường hợp sợi dây có hai đầu cố định
Đối với sợi dây có hai đầu cố định hoặc một đầu cố định và
một đầu dao động với biên độ nhỏ thì khi có sóng dừng, hai
đầu dây là hai nút sóng. Ta đã biết khoảng cách giữa hai nút
sóng liên tiếp bằng nửa bước sóng. Do đó ta có điều kiện
xuất hiện sóng dừng trong trường hợp này là: v A n n
(n = 1, 2, 3,…) (9.9) 2 2 f
với v là tốc độ truyền sóng trên dây. 59 VẬT LÍ 11
Từ công thức (9.9), ta thấy với v và A cố định, tần số f của
nguồn dao động phải thoả mãn điều kiện: f v n (9.10) 2A
Xét sóng âm, ta có:v + Khi n = 1: f
được gọi là hoạ âm bậc 1 (âm cơ bản). 1 2A + Tổng quát: f n
nf1 được gọi là hoạ âm bậc n.
Trường hợp hai đầu cố định thường gặp ở một số nhạc cụ
như đàn guitar, đàn tranh, đàn bầu,… Chú ý là các nhạc cụ
này đồng thời phát ra âm cơ bản và các hoạ âm.
Một dây đàn guitar dài 64 cm phát ra âm cơ bản có
tần số Ikhi được gảy. Biết tốc độ truyền sóng trên dây là 422 m/s. a) Tính giá trị f.
b) Người chơi đàn ấn đầu ngón tay lên một phím
đàn để tạo thành một vật cản (cố định) làm cho
chiều dài của dây ngắn đi (Hình 9.5). Khoảng cách từ
S Hình 9.5. Đầu ngón tay ấn lên
phím đàn này đến đầu dây là 3,7 cm. Tính tần số âm phím đàn
cơ bản phát ra bởi dây đàn trong trường hợp này.
Trường hợp sợi dây có một đầu cố định, một đầu tự do 0i\
Khi sợi dây có một đầu cố định (được gắn vào nguồn phát UXQJ
dao động nhỏ) và một đầu tự do (vật cản tự do), ta đã biết O
sóng phản xạ khi gặp vật cản tự do cùng pha so với sóng tới. 2
Khi xảy ra hiện tượng sóng dừng, đầu tự do là một bụng O %өQJ 4
sóng như Hình 9.6. Khoảng cách giữa một bụng sóng và VyQJ Nút VyQJ
một nút sóng liền kề là O . Do đó ta có điều kiện xuất hiện 4
sóng dừng trong trường hợp này là: v A
S Hình 9.6. Mô hình hoá sóng (2n ) 1 m
(m = 1, 3, 5,…) (9.11)
dừng xuất hiện trên sợi dây có 4 4 f
một đầu cố định, một đầu tự do
Từ công thức (9.11), ta thấy với v và A cố định, tần số f của
nguồn dao động phải thoả mãn điều kiện: f v m (9.12) 4A Xét sóng âm, ta có: + Khi m = 1: f v
được gọi là hoạ âm bậc 1 (âm cơ bản). 1 4A + Tổng quát: f m
mf1 được gọi là hoạ âm bậc m. 60 VẬT LÍ 11
Điều kiện để có sóng dừng:
– Dây có hai đầu cố định: chiều dài của sợi dây phải bằng một số nguyên lần nửa bước sóng.
A Q (n = 1, 2, 3,…) 2
– Dây có một đầu cố định, một đầu tự do: chiều dài của sợi dây phải bằng một số lẻ
lần một phần tư bước sóng.
A m (m = 1, 3, 5,…) 4
Trong thí nghiệm sóng dừng trên sợi dây AB dài 120 cm với đầu B tự do, đầu A được
kích thích để thực hiện dao động với biên độ nhỏ. Ngoài đầu A, trên dây xuất hiện
thêm một nút. Biết tần số sóng là 12,5 Hz.
a) Tính tốc độ truyền sóng.
b) Để có thêm một nút sóng trên dây thì tần số sóng khi này phải bằng bao nhiêu?
Giải thích vì sao khi vặn khoá để chỉnh dây đàn guitar (Hình 9.7),
ta có thể tạo ra hệ sóng dừng trên dây. Biết tốc độ truyền sóng
trên dây phụ thuộc lực căng dây.
S Hình 9.7. Chỉnh dây đàn guitar
Hiện tượng sóng dừng có thể xảy ra đối với sóng điện từ và
có nhiều ứng dụng trong cuộc sống. Ví dụ trong lò vi sóng O
(Hình 9.8), sóng điện từ được phản xạ trên các thành lò 2
và tạo thành sóng dừng trong lò. Tại những bụng sóng,
năng lượng của sóng điện từ có giá trị lớn nhất và cung
cấp nhiệt cho thực phẩm (từ sự dao động của các phân
tử nước trong thực phẩm). Do đó, trong lò vi sóng còn có
đĩa quay để giúp thực phẩm nóng đều.
S Hình 9.8. Sóng dừng hình thành trong lò vi sóng %j,7t3
1. Người ta thực hiện thí nghiệm sóng dừng trên một dây đàn hồi có hai đầu cố định dài
75,0 cm để đo tốc độ truyền sóng trên dây. Khi tần số sóng bằng 120 Hz thì trên dây xuất hiện 6 bụng sóng.
a) Tính tốc độ truyền sóng trên dây.
b) Tăng lực căng dây để tăng tốc độ truyền sóng gấp hai lần. Với những giá trị nào của tần số thì
sóng dừng có thể được hình thành trên dây?
2. Trong một thử nghiệm nướng bánh bằng lò vi sóng, người ta đo được khoảng cách giữa hai
phần nóng nhất và gần nhau nhất của bánh là khoảng 6,13 cm. Biết tần số sóng vi ba được sử
dụng trong lò là 2,45 GHz. Sử dụng các số liệu đã cho để ước lượng tốc độ của sóng điện từ. 61 VẬT LÍ 11 7+ &+j1+ô27p16&$ Bài 10 61*o09j7&ô758<1o0
Thí nghiệm đo tần số của sóng âm và tốc độ truyền âm.
Trong đời sống hằng ngày, chúng ta có thể nghe âm thanh từ mọi nơi. Ta đã biết âm thanh chính là sóng âm
được lan truyền trong môi trường vật chất. Âm thanh có thể có tần số xác định khi được phát ra từ một số nhạc cụ như
đàn guitar, đàn piano, sáo,… hoặc có tần số không xác định khi được phát ra từ động cơ xe, máy khoan,… Thời gian
âm thanh truyền từ nguồn phát đến tai ta phụ thuộc vào tốc độ truyền sóng âm. Vậy làm thế nào để đo được tần số của
sóng âm và tốc độ truyền âm?
Thí nghiệm đo tần số của sóng âm
* Mục đích: Đo được tần số của sóng âm. * Dụng cụ: – Nguồn âm (1):
1. Dựa vào bộ dụng cụ thí nghiệm,
+ Loa điện động (Hình 10.1a) được kết nối với máy phát
hãy thiết kế và thực hiện phương tần số.
án để đo tần số của sóng âm.
+ Âm thoa, búa và âm thoa gắn trên hộp cộng hưởng (Hình 10.1b).
– Micro (2) để chuyển dao động âm thành dao động điện.
– Dao động kí điện tử (3).
* Tiến hành thí nghiệm: (3) (2) (1) a) b)
S Hình 10.1. a) Loa điện động;
S Hình 10.2. Bố trí thí nghiệm đo tần số của sóng âm
b) Búa và âm thoa gắn trên hộp cộng hưởng
BӇớc 1: Bố trí thí nghiệm như Hình 10.2.
BӇớc 2: Sử dụng nguồn âm là loa điện động, đặt loa gần
micro (chú ý đảm bảo không có nguồn âm khác ở gần).
BӇớc 3: Bật micro và dao động kí ở chế độ làm việc. 62 VẬT LÍ 11
Bước 4: Bật máy phát tần số.
Bước 5: Điều chỉnh dao động kí để ghi nhận được tín hiệu.
2. Trình bày cách tính sai số tuyệt
Lặp lại bước 2 đến bước 5 khi sử dụng nguồn âm là âm thoa.
đối của phép đo. Liệt kê một số
nguyên nhân gây ra sai số trong
Lưu ý: Ứng với mỗi loại nguồn âm, thực hiện thí nghiệm ít
phương án thí nghiệm và đề xuất nhất 3 lần. cách khắc phục.
* Báo cáo kết quả thí nghiệm:
– Dựa vào đồ thị dao động trên màn hình dao động kí,
ghi kết quả đo vào bảng số liệu như Bảng 10.1.
– Từ số liệu đo được, xác định tần số sóng âm.
3. So sánh kết quả tần số đo được
TBảng 10.1. Bảng số liệu thí nghiệm đo tần số của sóng âm
với giá trị tần số được ghi trên Tần Tần số Sai số
âm thoa hoặc hiển thị trên màn Nguồn âm Lần Chu kì trung
hình của máy phát tần số. Rút ra T (ms) số f tuyệt đối (Hz) bình f ' kết luận. (Hz) f (Hz) 1 – – Loa điện động 2 – – – – 3 – – 1 – – Âm thoa 2 – – – – 3 – –
±.ӃWTXҧÿRWҫQVӕVyQJkPSKiWUDWӯ
ÆPWKRD f f f
= ..................................................
/RDÿLӋQÿӝQJ f f f
= .........................................
Hiện nay, ứng dụng SmartScope Oscilloscope trên điện thoại thông minh có thể
được sử dụng để ghi nhận đồ thị dao động âm. Sử dụng ứng dụng này, kết hợp
với ứng dụng quay màn hình điện thoại, hãy tiến hành lại thí nghiệm đo tần số
của sóng âm và so sánh kết quả đo được với kết quả trong phương án thí nghiệm
(sử dụng dao động kí điện tử). Phân tích ưu, nhược điểm của hai phương án này.
Thí nghiệm đo tốc độ truyền âm
* Mục đích: Đo được tốc độ truyền âm trong không khí. * Dụng cụ:
– Ống cộng hưởng (1) trong suốt bằng nhựa, dài 70 cm,
đường kính 40 mm, có gắn thước thẳng. 63 VẬT LÍ 11
– Pit-tông bằng kim loại bọc nhựa (2), đường kính 38 mm,
có vạch chuẩn xác định vị trí.
– Dây treo pit-tông (3) dài 1,5 m, một đầu có móc treo,
vắt qua ròng rọc có đường kính 40 mm.
4. Dựa vào bộ dụng cụ thí nghiệm,
– Hệ thống giá đỡ gồm trụ thép đặc (4), dài 75 cm, đường
hãy thiết kế và thực hiện phương
kính 10 mm và đế ba chân bằng thép.
án để đo tốc độ truyền âm trong không khí.
– Loa điện động (4 Ω – 3 W) (5), lắp trong hộp bảo vệ có
cán bằng trụ thép và lỗ cắm điện.
– Máy phát tần số (0,1 Hz – 1 kHz) (6), tín hiệu hình sin,
điện áp ra cực đại 14 V.
– Bộ hai dây nối mạch điện (7), dài 50 cm, hai đầu có phích cắm.
* Tiến hành thí nghiệm:
Bước 1: Bố trí thí nghiệm như Hình 10.3. Đặt loa điện động
gần sát đầu hở của ống cộng hưởng. (3)
Bước 2: Dùng hai dây dẫn điện cấp điện cho loa từ máy phát (1) tần số.
Bước 3: Điều chỉnh thang đo trên máy phát sang vị trí (4)
100 Hz – 1 kHz. Điều chỉnh tần số sóng âm cho phù hợp. (2) (7)
Bước 4: Điều chỉnh biên độ để nghe được âm phát ra từ loa (5) (6) vừa đủ to.
Bước 5: Kéo dần pit-tông lên và lắng nghe âm phát ra.
Xác định vị trí thứ nhất của pit-tông khi âm nghe được to
nhất và xác định chiều dài cột khí A tương ứng. Ghi số liệu 1
S Hình 10.3. Bố trí thí nghiệm vào Bảng 10.2.
đo tốc độ truyền âm trong
Bước 6: Tiếp tục kéo pit-tông lên và xác định vị trí thứ hai không khí
của pit-tông khi âm nghe được lại to nhất và xác định chiều
dài cột khí A tương ứng. Ghi số liệu vào Bảng 10.2. 2
Bước 7: Cho pit-tông về lại sát miệng ống, lặp lại các bước 5
và 6 thêm 4 lần nữa. Ghi số liệu vào Bảng 10.2.
* Báo cáo kết quả thí nghiệm:
5. Liệt kê một số nguyên nhân gây ra
Đo chiều dài cột khí A , A khi có âm to nhất lần thứ nhất và 1 2
sai số trong phương án thí nghiệm
lần thứ hai. Ghi vào bảng số liệu như Bảng 10.2.
và đề xuất cách khắc phục.
Xử lí số liệu để tính toán tốc độ truyền sóng âm trong không
khí kèm theo sai số của phép đo. 64 VẬT LÍ 11
T Bảng 10.2. Bảng số liệu thí nghiệm đo tốc độ truyền âm trong không khí 7ҫQVӕ +] 7UXQJEuQK 6DLVӕ /ҫQ 1 2 3 4 5 WX\ӋWÿӕL A (cm) A ' (cm) A (cm) – – – – – – – 1 A (cm) – – – – – – – 2
Xử lí số liệu để ghi nhận tốc độ truyền âm:
– Tính giá trị trung bình: 2(A2 1
A ) và suy ra: v f .
6. Giải thích vì sao ta có biểu thức:
– Tính sai số 'Ȝ= 2('A + 'A ). 1 2 A . 2 A v 1 2
– Tính sai số ∆v từ hệ thức:
f và trình bày kết v f
quả: v v v .
Có thể xác định tốc độ truyền âm trong không khí thông qua việc đo khoảng thời
gian từ lúc bắt đầu thả một vật rơi tự do từ độ cao so với một bề mặt cứng đến khi
nghe được âm phát ra từ va chạm của vật với bề mặt. Thực hiện thí nghiệm này và
so sánh kết quả đo được với kết quả trong phương án thí nghiệm (sử dụng ống cộng hưởng).
Cảm biến âm là cảm biến có nguyên tắc hoạt động tương tự micrô. Khi sóng âm được truyền tới cảm biến thì nó
sẽ chuyển tín hiệu âm thành tín hiệu điện có cùng tần số. Kết nối cảm biến âm với bộ xử lí số liệu sẽ thu được tín
hiệu điện này trên màn hình (Hình 10.4), dựa vào đồ thị và sự cài đặt tỉ lệ trục thời gian ban đầu ta có thể xác
định được chu kì của tín hiệu.
Nếu có hai sóng âm tới cảm biến cách nhau một khoảng thời gian nào đó thì bộ xử lí số liệu cũng sẽ hiển thị
đồng thời hai tín điện trên màn hình và cũng có thể xác định được hai thời điểm mà cảm biến bắt đầu ghi nhận hai sóng âm.
Từ các thông tin trên, hãy đưa ra một phương án thí nghiệm xác định tần số của sóng âm và tốc độ truyền âm
với cảm biến âm và bộ xử lí số liệu. a) b)
S Hình 10.4. a) Cảm biến âm; b) cảm biến âm kết nối bộ xử lí số liệu 65 VẬT LÍ 11 X 71*.7&+¡1* X
1 SÓNG VÀ SỰ TRUYỀN SÓNG
±6yQJOjGDRÿӝQJODQWUX\ӅQWURQJNK{QJJLDQWKHRWKӡLJLDQ.KLVyQJWUX\ӅQÿLSKҫQ
WӱP{LWUѭӡQJNK{QJWUX\ӅQWKHRSKѭѫQJWUX\ӅQVyQJPjFKӍGDRÿӝQJWҥLFKӛ
±'ӵDWUrQPӕLOLrQKӋJLӳDSKѭѫQJWUX\ӅQVyQJYjSKѭѫQJGDRÿӝQJVyQJÿѭӧFSKkQ
WKjQKKDLORҥL6yQJGӑFOjVyQJPjSKѭѫQJGDRÿӝQJFӫDPӛLSKҫQWӱP{LWUѭӡQJWUQJ
YӟLSKѭѫQJWUX\ӅQVyQJ6yQJQJDQJOjVyQJPjSKѭѫQJGDRÿӝQJPӛLSKҫQWӱP{L
WUѭӡQJYX{QJJyFYӟLSKѭѫQJWUX\ӅQVyQJ
±&iFKLӋQWѭӧQJÿһFWUѭQJFӫDVyQJSKҧQ[ҥNK~F[ҥQKLӉX[ҥYjJLDRWKRD
2 CÁC ĐẶC TRƯNG VẬT LÍ CỦA SÓNG
±%ѭӟFVyQJOOjTXmQJÿѭӡQJVyQJWUX\ӅQÿLÿѭӧFWURQJPӝWFKXNuGDRÿӝQJT. vT
WURQJÿyvOjWӕFÿӝODQWUX\ӅQVyQJ7ӕFÿӝWUX\ӅQVyQJWURQJNK{QJJLDQOjKӳXKҥQ
YjSKөWKXӝFYjRWtQKFKҩWFӫDP{LWUѭӡQJWUX\ӅQVyQJQKѭPұWÿӝP{LWUѭӡQJWtQKÿjQ KӗLQKLӋWÿӝiSVXҩW«
– Trên cùng một phương truyền sóng, các điểm dao động cùng pha với nhau cách nhau:
kO và các điểm dao động ngược pha với nhau cách nhau: 1
k YӟLkOjPӝWVӕ 2
QJX\rQk = 0, ±1, ±2, ±3,…).
±&ѭӡQJÿӝVyQJIOjQăQJOѭӧQJVyQJWUX\ӅQTXDPӝWÿѫQYӏGLӋQWtFKYX{QJJyFYӟL
SKѭѫQJWUX\ӅQVyQJWURQJPӝWÿѫQYӏWKӡLJLDQ I E P S t S
YӟLSOjGLӋQWtFKPjQăQJOѭӧQJVyQJEWUX\ӅQTXDWURQJPӝWNKRҧQJWKӡLJLDQ¨WKD\
F{QJVXҩWVyQJ P E 7URQJKӋ6,FѭӡQJÿӝVyQJFyÿѫQYӏOj:P2. t
– Phương trình truyền sóng theo trục Ox là: u 2 2 Acos t x T 3 SÓNG ĐIỆN TỪ
– 6yQJÿLӋQWӯOjÿLӋQWUѭӡQJYjWӯWUѭӡQJODQWUX\ӅQWURQJNK{QJJLDQGѭӟLGҥQJVyQJ
YӟLWӕFÿӝWURQJFKkQNK{QJEҵQJc = 3.108 m/s. 66 VẬT LÍ 11
– ÈQKViQJFyEҧQFKҩWOjVyQJÿLӋQWӯ%ѭӟFVyQJFӫDiQKViQJFyWҫQVӕfWURQJ FKkQNK{QJ c . f
±7KDQJVyQJÿLӋQWӯFKRELӃWGҧLEѭӟFVyQJYjGҧLWҫQVӕӭQJYӟLFiFORҥLEӭF[ҥ NKiFQKDX 4 GIAO THOA SÓNG
±+LӋQWѭӧQJJLDRWKRDVyQJOjKLӋQWѭӧQJKDLVyQJNӃWKӧSJһSQKDXWăQJFѭӡQJQKDX
KRһFOjPVX\\ӃXQKDXWҥLPӝWVӕYӏWUtWURQJP{LWUѭӡQJĈLӅXNLӋQÿӇFyJLDRWKRDOj
SKҧLFyVӵNӃWKӧSWӯKDLQJXӗQVyQJGDRÿӝQJFQJSKѭѫQJFQJWҫQVӕYjFyÿӝOӋFK SKDNK{QJÿәLWKHRWKӡLJLDQ
±7URQJP{LWUѭӡQJWUX\ӅQVyQJNKLKDLQJXӗQGDRÿӝQJFQJSKDQKӳQJÿLӇPFy
NKRҧQJFiFKÿӃQKDLQJXӗQOҫQOѭӧWOjd Yjd VӁGDRÿӝQJYӟLELrQÿӝFӵFÿҥLNKL 1 2
d – d = NȜYjGDRÿӝQJYӟLELrQÿӝFӵFWLӇXNKL d d k 1 2 1 2 1 YӟLkOjPӝWVӕ 2
QJX\rQk = 0, ±1, ±2, ±3,…).
±+LӋQWѭӧQJJLDRWKRDiQKViQJOjKLӋQWѭӧQJ[XҩWKLӋQFiFYҥFKViQJELrQÿӝFӵF
ÿҥL[HQNӁYӟLFiFYҥFKWӕLELrQÿӝFӵFWLӇXNKLKDLVyQJiQKViQJNӃWKӧSJһSQKDX
±.KRҧQJFiFKJLӳDKDLYkQViQJKRһFKDLYkQWӕLOLrQWLӃSÿѭӧFJӑLOjNKRҧQJYkQ NtKLӋXOjL. i D a
YӟLȜOjEѭӟFVyQJiQKViQJaOjNKRҧQJFiFKJLӳDKDLNKHYjDOjNKRҧQJFiFKWӯKDL
NKHÿӃQPjQTXDQViW7UrQPjQTXDQViWYӏWUtYkQViQJOj x = NLYjYӏWUtYkQWӕLOj s x 1
k i YӟLkOjPӝWVӕQJX\rQk = 0, ±1, ±2, ±3,…). t 2 5 SÓNG DỪNG
±6ӵJLDRWKRDFӫDKDLVyQJNӃWKӧSWUX\ӅQQJѭӧFFKLӅXQKDXWUrQFQJPӝWSKѭѫQJWҥR
WKjQKFiFEөQJVyQJFiFÿLӇPGDRÿӝQJYӟLELrQÿӝFӵFÿҥL[HQNӁYӟLFiFQ~WVyQJ
FiFÿLӇPÿӭQJ\rQ%өQJVyQJYjQ~WVyQJ[HQNӁYjFiFKÿӅXQKDX.KRҧQJFiFK O JLӳDKDLQ~WVyQJOLrQWLӃSOj . 2
±9ӏWUtFiFEөQJVyQJÿӕLYӟLPӝWÿҫXFӕÿӏQKFӫDGk\ÿѭӧF[iFÿӏQKEҵQJELӇXWKӭF d 1 k (k = 0, 1, 2,…) 2 2
±9ӏWUtFiFQ~WVyQJÿӕLYӟLPӝWÿҫXFӕÿӏQKFӫDGk\ÿѭӧF[iFÿӏQKEҵQJELӇXWKӭF d k (k = 0, 1, 2,…) 2 67 VẬT LÍ 11 ï,ũ175óľ1* Chương 3 ô1+/8t7&28/20% Bài 11 97¡1*7k&71+ô,1
Định luật Coulomb về lực tương tác giữa hai điện tích
điểm, đơn vị đo điện tích.
Vào những ngày thời tiết lạnh, đặc biệt là vào mùa đông, ta thường
hay gặp một số hiện tượng như: bị điện giật khi chạm tay vào tay nắm cửa
kim loại (Hình 11.1) hay nghe tiếng lách tách khi thay quần áo. Vậy nguyên
nhân của hiện tượng này là gì?
S Hình 11.1. Hiện tượng bị điện giật khi
chạm tay vào nắm cửa kim loại
1 SỰ TƯƠNG TÁC GIỮA CÁC ĐIỆN TÍCH
Hai loại điện tích
Một vật bị nhiễm điện có khả năng hút các vật nhẹ khác thì
được gọi là vật tích điện.
Có 2 loại điện tích: điện tích dương và điện tích âm. Các điện tích cùng dấu thì đẩy
nhau, trái dấu thì hút nhau. Đơn vị đo điện tích là culông (C).
Lưu ý: Vật tích điện có kích thước rất nhỏ so với khoảng cách
tới vị trí mà ta xét có thể được xem là một điện tích điểm.
Trong mỗi vật luôn chứa cả hai loại điện tích dương và âm.
Một vật nhiễm điện dương hoặc âm khi vật chứa lượng điện
tích dương nhiều hơn lượng điện tích âm hoặc ngược lại. Khi
số điện tích dương bằng số điện tích âm, hay tổng điện tích
1. Xét quả cầu kim loại nhỏ có
bằng 0 thì vật trung hoà về điện.
điện tích –3,2.10–7 C. Quả cầu
này thừa hay thiếu bao nhiêu
Điện tích nguyên tố có giá trị bằng độ lớn điện tích của một electron?
hạt mang điện tồn tại độc lập trong tự nhiên và có giá trị: e = 1,6.10–19 C
Electron là hạt tích điện âm và có độ lớn điện tích bằng điện tích nguyên tố.
Tất cả các vật tích điện đều có độ lớn điện tích q luôn là một bội số của điện tích nguyên tố: q = ne
với n là số tự nhiên. 68 VẬT LÍ 11
Một số hiện tượng nhiễm điện đã được biết đến từ thời cổ
đại. Khoảng thế kỉ VI trước Công nguyên, Thales (Ta-lét)
(khoảng 624 – 546 TCN) đã quan sát và mô tả hiện tượng
nhiễm điện thông qua khả năng hút các vật nhỏ, nhẹ của
các mẫu hổ phách khi được cọ xát (Hình 11.2) Vào thế kỉ
XVIII, các nhà vật lí đã nghiên cứu các hiện tượng điện một
cách có hệ thống và thu được một số kết quả như: vào S Hình 11.2. Hổ phách nhiễm điện
năm 1729, Stephen Gray (Xte-phần Gờ-ray) (1666 – 1736)
hút các mẩu giấy nhỏ
đã phát hiện ra tính dẫn điện của vật; vào năm 1733, Charles François de Cisternay du Fay
(Sác-lơ Phờ-răng-xoa đờ Xít-tờ-nay du Phay) (1698 – 1739) đã khám phá ra sự tồn tại của hai
loại điện tích: điện tích âm và điện tích dương; vào khoảng năm 1752, Benjamin Franklin
(Ben-gia-min Phờ-ranh-lin) (1706 – 1790) đã đề xuất cách thức chế tạo cột thu lôi.
Sự nhiễm điện của các vật B A a) b) c)
S Hình 11.3. Minh hoạ ba cách nhiễm điện cho vật: a) nhiễm điện do cọ xát;
b) nhiễm điện do tiếp xúc; c) nhiễm điện do hưởng ứng
Nhiễm điện do cọ xát: là sự nhiễm điện khi các vật khác bản
chất, trung hoà về điện được cọ xát với nhau. Khi đó, hai vật
sẽ nhiễm điện trái dấu. Ví dụ: Khi ta cọ xát lược nhựa với
2. Sử dụng một số dụng cụ đơn
tóc (điện môi hay chất cách điện), lược nhựa sẽ bị nhiễm
giản như: vải khô, thước nhựa,
mảnh lụa, miếng thuỷ tinh, vụn
điện âm và hút các mẩu giấy vụn (điện môi) (Hình 11.3a).
giấy nhỏ, lược nhựa, quả bóng
Nhiễm điện do tiếp xúc: là sự nhiễm điện khi một vật trung
bay, vỏ lon,… em hãy thực
hoà về điện đặt tiếp xúc với một vật nhiễm điện. Khi đó, hai hiện thí nghiệm:
vật sẽ nhiễm điện cùng dấu. Ví dụ: Quả cầu trung hoà điện
a) Làm nhiễm điện cho các vật.
(vật dẫn điện), sau khi đặt tiếp xúc với thanh nhiễm điện
b) Về tương tác giữa các vật
âm (vật dẫn điện) sẽ trở nên nhiễm điện âm và hút được tóc nhiễm điện. (Hình 11.3b).
Nhiễm điện do hưởng ứng: là sự nhiễm điện khi một vật A
(vật dẫn điện) trung hoà về điện đặt gần (không tiếp xúc)
với một vật B nhiễm điện. Khi đó, hai đầu vật A, gần và xa
vật B, lần lượt nhiễm điện trái dấu và cùng dấu với vật B.
Khi đưa vật A ra xa vật B, vật A trở về trạng thái trung hoà
như lúc đầu (Hình 11.3c). 69 VẬT LÍ 11 Thuyết electron
Thuyết electron được dùng để giải thích các hiện tượng về điện dựa trên sự cư trú và di chuyển
của các electron. Theo thuyết electron thì:
– Nguyên tử có cấu tạo gồm hạt nhân và các electron chuyển động xung quanh hạt nhân. Hạt
nhân nguyên tử mang điện tích dương và chiếm hầu hết khối lượng nguyên tử. Bình thường,
nguyên tử trung hoà về điện.
– Do khối lượng electron rất nhỏ so với khối lượng hạt nhân nguyên tử nên chúng rất linh
động. Dưới một tác nhân nào đó (ví dụ: cọ xát, tiếp xúc,…) electron có thể bứt ra khỏi nguyên
tử và di chuyển từ vật này sang vật khác.
Giải thích hiện tượng bị điện giật trong các trường hợp:
a) Khi chạm tay vào nắm cửa kim loại trong thời tiết hanh khô (Hình 11.1).
b) Khi chạm tay vào vỏ kim loại của máy tính đang hoạt động.
Ngày nay, công nghệ sơn tĩnh điện
(Hình 11.4) được sử dụng rất phổ biến với
các ưu điểm vượt trội so với công nghệ sơn
thường. Từ các nguồn tư liệu sách, báo,
internet,... em hãy viết một bài giới thiệu
ngắn về công nghệ sơn tĩnh điện.
S Hình 11.4. Công nhân đang sơn vật bằng
công nghệ sơn tĩnh điện
2 ĐỊNH LUẬT COULOMB
Để khảo sát định lượng tương tác giữa các vật tích điện, từ năm 1785 đến năm 1787,
Charles Augustin Coulomb (Sác-lơ Âu-gớt-tin Cu-lông) (1736 – 1806) đã tiến hành các đo
đạc thực nghiệm về tương tác tĩnh điện giữa hai quả cầu tích điện có kích thước rất nhỏ
so với khoảng cách giữa chúng. Dựa vào kết quả tổng hợp từ những thí nghiệm của mình,
Coulomb đã nêu lên định luật mô tả sự tương tác giữa hai điện tích điểm như sau: 70 VẬT LÍ 11
Lực tương tác tĩnh điện giữa hai điện tích điểm đặt
trong chân không có phương trùng với đường thẳng
nối hai điện tích điểm đó (Hình 11.5), có độ lớn tỉ lệ
thuận với tích độ lớn của các điện tích và tỉ lệ nghịch
với bình phương khoảng cách giữa chúng. q q F k 1 2 (11.1) r2
Trong đó k là hằng số phụ thuộc vào cách chọn G q q G
đơn vị của các đại lượng; q , q là các giá trị F 1 2 F 21 12 1 2 + +
đại số của hai điện tích. Trong hệ đơn vị SI, G q q G 2 1 2 F F k 1 Nm 9 109 , với 21 – – 12 4 2 . C G G 0 q q 1 F 2 F 2 21 12 12 C + – 8 86 10 , . là hằng số điện. 0 Nm2
S Hình 11.5. Phương và chiều của
Lưu ý: Khi đặt hai điện tích vào một môi trường điện môi
lực tương tác tĩnh điện giữa hai điện tích điểm
đồng chất, lực tương tác tĩnh điện sẽ giảm ε lần so với khi
chúng được đặt trong chân không: q q F k 1 2 (11.2) G G r2
3. Các cặp lực F và F trong 12 21
với ε là hằng số điện môi, chỉ phụ thuộc vào bản chất của
Hình 11.5 có phải là các cặp lực
môi trường. Bảng 11.1 cho biết giá trị của ε trong một số chất. cân bằng không? Vì sao?
Bảng 11.1. Hằng số điện môi của một số chất
4. Một mẩu sắt nhỏ 6 g có thể chứa Chất
Hằng số điện môi
khoảng 1024 electron. Vậy vì sao Chân không 1 các electron này không bay Không khí 1,00059
ra khỏi mẩu sắt, mặc dù giữa Nylon 3,4
chúng luôn tồn tại lực đẩy? Thuỷ tinh 3,7 – 10
Ví dụ: Tính độ lớn lực tương tác tĩnh điện giữa electron và proton. Biết khoảng cách giữa
electron – proton là r = 5,3.10–11 m và môi trường giữa chúng là chân không. Electron và proton
lần lượt tích điện âm và dương với cùng độ lớn của điện tích nguyên tố. Bài giải
Điện tích electron: q = –1,6.10–19 C. e
Điện tích hạt nhân: q = 1,6.10–19 C. p
Lực tương tác tĩnh điện giữa electron và proton là lực hút và có độ lớn: q q 19 19 – F ( 1, 6 10 . ) 1 .( , 6.10 ) k e p 9 9 1 . 0 8 r 8, 2 10 . N. 2 11 2 5 ( ,3 10 . ) 71 VẬT LÍ 11
Xét điện tích q chịu tác dụng bởi lực tĩnh điện của n điện
5. Hai vật nhỏ tích điện cùng dấu,
tích điểm, lực tổng hợp tác dụng lên điện tích q được xác định:
ban đầu được giữ ở vị trí rất
F = F +F +…+F (11.3)
gần nhau. Dựa vào công thức q q 1 2q nq
(11.1), em hãy mô tả đặc điểm
chuyển động của hai vật ngay
thời điểm khi chúng được thả
Theo mô hình nguyên tử của nhà vật lí
tự do. Giả sử hai vật chỉ chịu
Ernest Rutherford (Ơ-nít Rơ-dơ-pho) (1871 –
tác dụng của lực tương tác tĩnh
1937), nguyên tử gồm hạt nhân (tập trung điện giữa chúng.
hầu hết khối lượng của nguyên tử và có kích
thước rất nhỏ so với bán kính nguyên tử)
mang điện tích dương và các electron mang
điện tích âm chuyển động trên các quỹ đạo tròn xung quanh hạt nhân. 3URWRQ +
Xét mô hình nguyên tử Rutherford cho
nguyên tử hydrogen (Hình 11.6), em hãy cho –
biết lực giữ cho electron chuyển động tròn (OHFWURQ
quanh hạt nhân là lực gì? Xác định phương,
S Hình 11.6. Mô hình nguyên tử Rutherford chiều của lực đó.
cho nguyên tử hydrogen
Tại 3 điểm A, B, C cố định trong chân không, đặt 3 điện tích điểm có giá trị lần lượt là q = 6.10–6 C, q = –6.10–6 C và 1 2
q = 3.10–6 C. Biết AB = 3 cm, AC = 4 cm và BC = 5 cm. Tính độ lớn lực tác dụng lên điện tích điểm đặt tại C. 3 %j,7t3
1. Sau khi cọ xát thanh thuỷ tinh (trung hoà về điện) với mảnh lụa, thanh thuỷ tinh tích điện
dương và có giá trị 13 nC. Hãy giải thích quá trình tích điện cho thanh thuỷ tinh và xác định số
electron đã bị bứt ra khỏi thanh thuỷ tinh.
2. Một phân tử DNA bao gồm hai nhánh xoắn kép được liên kết với nhau có chiều dài
0,459.10–6 m. Phần đuôi của phân tử có thể bị ion hoá mang điện tích âm q = –1,6.10–19 C, 1
đầu còn lại mang điện tích dương q = 1,6.10–19 C. Phân tử xoắn ốc này hoạt động như một lò 2
xo và bị nén 1% sau khi bị tích điện. Xác định “độ cứng k” của phân tử. Biết phân tử DNA trong
nhân tế bào và môi trường xung quanh là nước; hằng số điện môi của nước là 81.
3. Hai quả cầu A, B có kích thước nhỏ được đặt cách nhau một khoảng 12 cm trong chân không.
Biết quả cầu A có điện tích –3,2.10–7 C và quả cầu B có điện tích 2,4.10–7 C.
a) Tính lực tương tác giữa hai quả cầu.
b) Cho hai quả cầu tiếp xúc với nhau, sau đó đặt cách nhau một khoảng như lúc đầu. Biết rằng,
sau khi tiếp xúc, hai quả cầu có điện tích bằng nhau. Tính lực tương tác giữa hai quả cầu lúc này. 72 VẬT LÍ 11 Bài 12 ô,175¢1*
– Khái niệm điện trường.
– Cường độ điện trường do điện tích điểm gây ra tại một điểm. – Điện phổ.
Khi một vật nhiễm điện được đặt gần một vật nhiễm điện khác, ta thấy hai vật có thể hút hoặc đẩy nhau, nghĩa
là giữa chúng có sự tương tác mặc dù không có sự tiếp xúc. Vậy, hai vật này tương tác với nhau bằng cách nào?
1 CƯỜNG ĐỘ ĐIỆN TRƯỜNG
Khái niệm điện trường
Khi đặt một điện tích điểm q cố định tại một vị trí xác định 1
trong không gian, sau đó đưa một điện tích điểm q lại gần, 2
ta thấy hai điện tích điểm này tương tác với nhau. Ta đã biết
sự tương tác này được mô tả bởi định luật Coulomb.
Dạng vật chất bao quanh các điện tích được gọi là điện trường.
Điện trường tác dụng lực điện lên các điện tích khác đặt
trong nó. Tốc độ lan truyền tương tác giữa các điện tích
trong điện trường có giá trị hữu hạn. Trong chân không,
tốc độ này là 3.108 m/s, bằng tốc độ ánh sáng.
Trong tự nhiên, một số loài vật như cá mập, ong vò vẽ (Hình 12.1) có
thể cảm nhận được điện trường. Điện trường do một số con mồi hoặc
kẻ địch tạo ra khi bơi qua được cá mập ghi nhận thông qua những tế
bào trên đầu, từ đó giúp nó phát hiện ra con mồi. Tính chất này dùng
để săn mồi và phát hiện nguy hiểm. Trong khi đó, sự chuyển động liên a)
tục của ong vò vẽ làm nó bị tích điện và tự tạo ra xung quanh mình
một điện trường. Khi đậu trên bông hoa, chúng truyền cho hoa một
phần điện tích. Từ đó, ong vò vẽ dùng râu của mình để nhận biết điện
trường do bông hoa gây ra. Tính chất đặc biệt đó giúp nó tìm được
mật hoa và phân biệt được hoa tươi với hoa đã hết mật. b)
S Hình 12.1. a) Cá mập; b) Ong vò vẽ 73 VẬT LÍ 11
Điện trường là dạng vật chất bao quanh điện tích
và truyền tương tác giữa các điện tích. Tính chất
1. Làm thế nào để biết trong một
cơ bản của điện trường là tác dụng lực điện lên các
vùng không gian nào đó có sự
điện tích khác đặt trong nó.
xuất hiện của điện trường?
Lưu ý: Trong chương này, ta chỉ xét điện trường của các
điện tích đứng yên đối với nhau, tức là điện trường tĩnh,
được gọi tắt là điện trường.
Cường độ điện trường
Xét một điện tích điểm Q đặt tại một vị trí xác định trong
không gian. Lần lượt đưa các điện tích thử là những vật nhỏ
2. Làm thế nào để xác định được
tích điện dương, có độ lớn khác nhau q , q , q …, q vào 1 2 3 n
độ mạnh yếu của điện trường tại
một vị trí xác định trong điện trường do điện tích Q sinh ra một điểm?
(Hình 12.2). Thực nghiệm cho thấy, lực do điện tích Q tác
dụng lên các điện tích q , q , q ,…, q có một số đặc điểm: 1 2 3 n + Có cùng hướng. G + Có độ lớn khác nhau. Q !0 q !0 F E + + + Tỉ số F F F F 1 2 3 ! n O a) M q q q q . 1 2 3 n Q 0 G q !0
Trong đó F , F , F ,…, F là lực do điện tích Q tác dụng lên E F 1 2 3 n – +
các điện tích q , q , q ,…, q khi chúng được đặt tại cùng O 1 2 3 n b) M một vị trí.
S Hình 12.2. Vectơ lực do điện tích
Khi thay đổi vị trí đặt các điện tích thử thì tỉ số F cũng thay Q tác dụng lên điện tích thử q được q
đặt tại điểm M và vectơ cường độ
đổi. Lúc này, ta thấy rằng tỉ số F đặc trưng cho điện
điện trường do Q sinh ra tại điểm M q
trường trong trường hợp: a) Q > 0; b) Q < 0
tại điểm đang xét về mặt tác dụng lực và được gọi là
cường độ điện trường.
&ѭӡQJÿӝÿLӋQWUѭӡQJGRÿLӋQWtFKQVLQKUDWҥLPӝW
ÿLӇPOjÿҥLOѭӧQJÿһFWUѭQJFKRÿLӋQWUѭӡQJYӅPһW
WiFGөQJOӵFWҥLÿLӇPÿyĈk\OjPӝWÿҥLOѭӧQJYHFWѫ
YjÿѭӧF[iFÿӏQKEӣLELӇXWKӭF E F (12.1) q G
Với F là lực do điện tích Q tác dụng lên một điện
tích q đặt tại điểm đó. Trong hệ SI, cường độ điện
trường có đơn vị là niutơn trên culông (N/C).
Ngoài ra, đơn vị thường dùng của cường độ điện
trường là vôn trên mét (V/m). 74 VẬT LÍ 11
Từ (12.1), ta thấy độ lớn của cường độ điện trường tại một
điểm bằng tỉ số giữa độ lớn lực tác dụng lên một điện tích
dương đặt tại điểm đó và độ lớn của điện tích đó: E F (12.2) q
Trong một vùng không gian có điện trường mà các E
đường sức điện trường có phương nằm ngang, song q
song với nhau và chiều như Hình 12.3. Hãy xác định
hướng của lực điện trường tác dụng lên điện tích q trong các trường hợp:
S Hình 12.3. Điện tích điểm q a) q > 0.
đặt trong điện trường b) q < 0.
2 CƯỜNG ĐỘ ĐIỆN TRƯỜNG CỦA ĐIỆN TÍCH ĐIỂM
Cường độ điện trường gây ra bởi điện tích điểm
Đặt hai điện tích điểm Q và q > 0 cách nhau một đoạn r
trong chân không, lực tĩnh điện giữa hai điện tích được xác
định bằng định luật Coulomb theo công thức (11.1). Vì
điện tích thử q > 0 nên cường độ điện trường tại vị trí đặt q
do điện tích điểm Q gây ra cùng hướng với lực tĩnh điện do
Q tác dụng lên q. E +
Kết hợp công thức (11.1) và (12.2), ta rút ra được công thức
xác định độ lớn của cường độ điện trường do điện tích điểm
Q gây ra tại một điểm cách Q một đoạn r. a)
&ѭӡQJÿӝÿLӋQWUѭӡQJGRÿLӋQWtFKÿLӇPQJk\UDWҥL
PӝWÿLӇP0FiFKÿLӋQWtFKPӝWÿRҥQrWURQJFKkQ
NK{QJ Fy SKѭѫQJ QҵP WUrQ ÿѭӡQJ WKҷQJ QӕL ÿLӋQ
WtFKYjÿLӇP0,FyFKLӅXKѭӟQJUD[DÿLӋQWtFKQӃX E –
Q ! Yj KѭӟQJ OҥL JҫQ ÿLӋQ WtFK QӃX Q < 0 +uQKFyÿӝOӟQOjQ E k (12.3) r2 YӟL b) 2 2 k 1 Nm C
Hình 12.4. Cường độ điểm trường 9 1 . 09 , 8,86 10 12 . . 4 2 0 C Nm2
của một điểm tích điểm: 0
a) Q > 0; b) Q < 0 75 VẬT LÍ 11
Lưu ý: Cường độ điện trường do điện tích Q gây ra tại một
điểm trong môi trường điện môi sẽ giảm ε lần so với điểm trong chân không: Q E k (12.4) r2
với H là hằng số điện môi.
Điện trường của hệ điện tích
3. Tại hai điểm A và B trong chân
Xét hệ có n điện tích điểm Q , Q ,…, Q . Cường độ điện trường do mỗi
không, người ta đặt hai điện 1 2 n
điện tích điểm gây ra tại điểm M là E ,E , , . Khi đó, cường độ 1 2 … E
tích trái dấu q và q . Tìm những n 1 2
điểm sao cho hai vectơ cường độ
điện trường tổng hợp tại điểm M là:
điện trường do hai điện tích q và 1 E = E + E (12.5) 1 2 … E M n
q gây ra tại đó có đặc điểm: 2
a) Cùng phương, cùng chiều.
Vận dụng biểu thức cường độ điện trường của điện tích điểm
b) Cùng phương, ngược chiều.
Ví dụ: Đặt hai quả cầu nhỏ có điện tích lần lượt là
q = 3,210–5 C và q = –3,210–6 C trong chân không tại 1 2
2 điểm A, B cách nhau 9,0 cm. Xem hai quả cầu là các điện
tích điểm. Xác định tỉ số độ lớn của hai vectơ cường độ điện
trường do hai quả cầu gây ra tại điểm M. Biết điểm M cách A
3 cm, cách B 6 cm. Nhận xét phương, chiều của hai vectơ này. Bài giải
Độ lớn cường độ điện trường do quả cầu q gây ra tại điểm M: 1 q 5 , . E k 3 2 10 1 9 8 9 10 3,2 10 . V/m. 1 2 2 AM . 0, 03
Độ lớn cường độ điện trường do quả cầu q gây ra tại điểm M: 2 q 6 3 ,2.10 E k 2 9 6 9 10 8,0.10 V/m. 2 2 2 BM . 0, 06
Tỉ số độ lớn của hai vectơ cường độ điện trường do hai quả q >0 q <0 1 M 2 cầu gây ra tại điểm M: + JG JG – A 1 E 1 E B E 2 1 8 3, 2 10 . 1 40
S Hình 12.5. Phương, chiều vectơ 6 E 8, 0.10
cường độ điện trường tổng hợp tại M 2
Hai vectơ cường độ điện trường do hai quả cầu gây ra tại
điểm M có cùng phương và cùng chiều (Hình 12.5). 76 VẬT LÍ 11
3 ĐƯỜNG SỨC ĐIỆN Điện phổ
Đặt một quả cầu kim loại nhỏ vào trong một hộp chứa
dầu và bột mịn cách điện. Tích điện cho quả cầu. Dùng
tay gõ nhẹ vào hộp, ta thấy các hạt bột sắp xếp lại thành
4. Dựa vào hình ảnh điện phổ quan
những hình dạng đặc biệt. Đây là điện phổ của quả cầu
sát được ở Hình 12.6, ta có thể tích điện (Hình 12.6).
kết luận được dấu của mỗi điện tích không? Vì sao?
5. Thiết kế phương án và thực hiện
thí nghiệm để quan sát hình ảnh
điện phổ của một vật tích điện. a) b) c)
S Hình 12.6. Điện phổ của: a) điện tích điểm;
b) hai điện tích cùng dấu; c) hai điện tích trái dấu
Khái niệm đường sức điện
Ta đã biết, điện trường không thể quan sát được bằng mắt
thường. Do đó, để mô tả điện trường một cách trực quan,
ta sử dụng khái niệm đường sức điện. Đường sức điện là
những đường mô tả “hình dạng” của điện trường và cũng
là sự mô hình hoá hình ảnh điện phổ, sao cho tiếp tuyến
tại một điểm bất kì trên đường trùng với phương của vectơ
cường độ điện trường tại điểm đó, có chiều quy ước trùng
với chiều của vectơ cường độ điện trường. A A B B + – – + + + A B A B a) b) c) d)
S Hình 12.7. Các đường sức điện của:
a) điện tích dương; b) điện tích âm; c) hai điện tích cùng độ lớn nhưng trái dấu; d) hai điện tích dương cùng độ lớn 77 VẬT LÍ 11 GE1 M
ĈѭӡQJ VӭF ÿLӋQ Oj ÿѭӡQJ P{ Wҧ ÿLӋQ WUѭӡQJ VDR
FKRWLӃSWX\ӃQWҥLPӝWÿLӇPEҩWNuWUrQÿѭӡQJFǊQJ
S Hình 12.8. Minh hoạ đường sức
WUQJYӟLSKѭѫQJFӫDYHFWѫFѭӡQJÿӝÿLӋQWUѭӡQJ
điện trường và vectơ cường độ WҥLÿLӇPÿy+uQK
điện trường tại điểm M
Đường sức điện có các đặc điểm sau:
+ Tại mỗi điểm trong điện trường chỉ có một đường sức
điện đi qua. Số lượng đường sức điện qua một đơn vị diện 6. Quan sát Hình 12.7, em hãy mô
tích vuông góc với đường sức tại một điểm trong không gian
tả hình dạng, điểm xuất phát,
đặc trưng cho độ mạnh yếu của điện trường tại điểm đó.
điểm kết thúc của đường sức
điện và so sánh độ mạnh yếu của
+ Các đường sức điện là những đường cong không kín.
điện trường tại hai vị trí A và B
Đường sức điện phải bắt đầu từ một điện tích dương (hoặc cho mỗi trường hợp.
ở vô cực) và kết thúc ở một điện tích âm (hoặc ở vô cực).
Khái niệm điện trường đều
Đặt hai tấm kim loại phẳng, rộng, song song với nhau trong
đĩa chứa dầu có bột mịn cách điện. Tích điện trái dấu và
cùng độ lớn cho hai tấm kim loại và gõ nhẹ vào đĩa dầu, ta
quan sát thấy điện phổ ở giữa hai tấm kim loại có hình ảnh như Hình 12.9. + –
Ở rìa hai tấm kim loại, điện phổ là những đường cong. Trong
vùng không gian giữa hai tấm kim loại, điện phổ là những
đường thẳng gần như song song và cách đều nhau. Khi đó,
điện trường giữa hai tấm kim loại gọi là điện trường đều.
Thực nghiệm cho thấy, tại mọi điểm trong điện trường đều, S Hình 12.9. Điện phổ ở hai tấm kim
vectơ cường độ điện trường bằng nhau.
loại phẳng tích điện trái dấu, cùng độ lớn
7. Quan sát Hình 12.9, vẽ đường sức
ĈLӋQWUѭӡQJÿӅXOjÿLӋQWUѭӡQJFyYHFWѫFѭӡQJÿӝ
điện trường trong vùng không
ÿLӋQWUѭӡQJWҥLPӑLÿLӇPÿӅXEҵQJQKDXĈLӋQWUѭӡQJ
gian giữa hai tấm kim loại phẳng.
ÿӅXFyFiFÿѭӡQJVӭFÿLӋQVRQJVRQJFiFKÿӅXQKDX 78 VẬT LÍ 11
Xét đường sức điện của hai điện tích điểm q và q như Hình 12.10. 1 2
Em hãy xác định dấu của hai điện tích q , q và so sánh độ lớn điện tích của chúng. 1 2 q q 1 2
S Hình 12.10. Đường sức điện
của hệ hai điện tích q và q 1 2
Từ các dụng cụ: pin, dây nối, 2 thanh kim loại, dầu cách điện (như dầu máy), thuốc tím (KMnO ), em hãy thiết kế 4
và thực hiện thí nghiệm để quan sát đường sức điện trường giữa hai thanh kim loại. %j,7t3
1. Trong điều kiện thời tiết bình thường, bên ngoài bề mặt Trái Đất được bao phủ bởi một
điện trường. Biết rằng điện trường này có các đường sức điện luôn hướng vào tâm Trái Đất.
Hãy xác định dấu của điện tích trên bề mặt Trái Đất trong tình huống này.
2. Đặt lần lượt một electron và một proton vào cùng một điện trường đều. Hạt nào sẽ chịu tác
dụng của lực tĩnh điện có độ lớn lớn hơn? Giả sử chỉ xét tương tác tĩnh điện, các tương tác
khác được bỏ qua. So sánh gia tốc hai hạt thu được.
3. Đặt hai quả cầu nhỏ có điện tích lần lượt là 3,0 µC và –3,5 µC tại 2 điểm A và B cách nhau một
khoảng 0,6 m. Xác định vị trí điểm C sao cho vectơ cường độ điện trường tại đó bằng không. 79 VẬT LÍ 11 Bài 13 ô,17+9j7+1u1*ô,1
– Điện thế, thế năng điện.
– Mối liên hệ giữa cường độ điện trường và điện thế.
– Chuyển động của điện tích bay vào điện trường đều theo phương vuông góc với
đường sức và ứng dụng.
Vào ngày 27/5/1994, đường dây cao thế 500 kV Bắc – Nam (Hình 13.1)
đã chính thức được đưa vào vận hành. Sự kiện này đánh dấu một cột mốc lịch
sử khi tạo ra sự liên kết lưới điện quốc gia. Vậy “thế” trong cụm từ “cao thế”
đặc trưng cho khả năng gì về điện?
S Hình 13.1. Đường dây 500 kV
Bắc – Nam đi qua tỉnh Thanh Hoá
1 THẾ NĂNG ĐIỆN. ĐIỆN THẾ
Công của lực điện
1. Liệt kê một số lực thế đã được học.
Xét điện tích điểm q > 0 được bắn vào một vùng không
Trình bày đặc điểm về công của
gian có điện trường đều với độ lớn cường độ điện trường là lực thế.
E. Điện tích q chuyển động theo quỹ đạo AB như Hình 13.2.
2. Quan sát Hình 13.2, xác định
Để xác định công của lực điện tác dụng lên q trong quá
công của lực điện tác dụng lên
điện tích q > 0 khi q di chuyển
trình chuyển động từ A đến B, ta chia đường cong AB thành từ A’ đến B’.
các đoạn nhỏ sao cho chúng có thể xem là các đoạn thẳng. y
Xét đoạn NP, công của lực điện tác dụng lên điện tích q là + JG1E –
A qENP, với N P
c c là hình chiếu của NP lên phương + B – NP
của đường sức điện trường. + –
Vậy, công của lực điện tác dụng lên điện tích q khi q chuyển + P – động từ A đến B là: + N JG – F A qEA B (13.1) + q – AB với A B c c + –
là hình chiếu của AB lên phương của đường sức điện trường. + A – O A' N' P' B' x
Lưu ý: Trong trường hợp q < 0, cách xác định công của lực S Hình 13.2. Chuyển động của hạt
điện là tương tự như trường hợp q > 0.
mang điện q > 0 trong điện trường đều 80 VẬT LÍ 11
Công của lực điện tác dụng lên một điện tích không
phụ thuộc vào dạng đường đi của điện tích mà chỉ
phụ thuộc vào vị trí điểm đầu và điểm cuối của
đường đi trong điện trường.
Do đó, lực điện là lực thế và điện trường là một trường thế. Thế năng điện
Tương tự như trường hợp của trọng lực, công của lực điện
tác dụng lên điện tích điểm q để dịch chuyển q từ điểm A
đến điểm B bằng hiệu thế năng điện giữa hai điểm này:
A =W −W (13.2) AB A B
Thông thường, gốc thế năng B được chọn ở vô cùng, khi đó W = 0 J, ta có: B W = A (13.3) A A∞
Thế năng điện của một điện tích q tại một điểm
trong điện trường đặc trưng cho khả năng sinh
công của điện trường để dịch chuyển điện tích q từ điểm đó ra xa vô cùng.
Trong hệ SI, thế năng điện có đơn vị là jun (J). Điện thế
Ta đã biết độ lớn của lực điện tác dụng lên điện tích q đặt
trong điện trường tỉ lệ thuận với điện tích q, do đó thế năng
điện tại điểm A cũng tỉ lệ thuận với điện tích q. Chọn gốc
thế năng ở vô cùng, ta có: W = V T(13.4) A A
Trong đó, hệ số tỉ lệ V là đại lượng không phụ thuộc vào A
điện tích q mà chỉ phụ thuộc vào điện trường tại vị trí điểm
A. Đại lượng V được gọi là điện thế tại điểm A, nó đặc A
trưng cho điện trường về thế năng của điện tích q đặt trong điện trường.
Kết hợp (13.3) và (13.4), ta được: V AA A (13.5) q
Trong đó, A là công của lực điện để dịch chuyển một điện A∞
tích q dương từ A ra vô cực. Ngoài ra, ta có A = A với A∞ 'fA 81 VẬT LÍ 11
A'f là công mà ta cần thực hiện để đưa điện tích từ vô cực A về điểm A. Vậy:
ĈLӋQWKӃWҥLPӝWÿLӇPWURQJÿLӋQWUѭӡQJOjÿҥLOѭӧQJ
ÿһFWUѭQJFKRWKӃQăQJÿLӋQWҥLYӏWUtÿyYjÿѭӧF[iF
ÿӏQKEҵQJF{QJPjWDFҫQWKӵFKLӋQÿӇGӏFKFKX\ӇQ
PӝWÿѫQYӏÿLӋQWtFKGѭѫQJWӯY{FӵFYӅÿLӇPÿy V A ' A (13.6) A q
Trong hệ SI, điện thế có đơn vị là vôn (V). Hiệu điện thế
Lấy hiệu điện thế giữa điểm A và điểm B, ta được hiệu điện
thế giữa hai điểm A và B trong điện trường:
U = V – V (13.7) AB A B
Kết hợp công thức (13.5), (13.6) và (13.7), ta được U AAB . AB
3. Kết hợp công thức (13.5), q Vậy, ta rút ra được:
(13.6) và (13.7), em hãy rút ra công thức (13.8).
Hiệu điện thế giữa hai điểm A và B trong điện trường
là đại lượng đặc trưng cho khả năng thực hiện công
của điện trường để dịch chuyển một đơn vị điện tích
giữa hai điểm đó và được xác định bằng biểu thức: U AAB (13.8) AB q
Trong hệ SI, hiệu điện thế có đơn vị là vôn (V).
Công thức (13.8) cho ta thấy: 1 V là hiệu điện thế giữa
hai điểm trong điện trường mà công của lực điện để dịch 4. Xét hai điểm M và N trong điện
chuyển một điện tích dương 1 C giữa hai điểm đó bằng 1 J.
trường đều. Biết vectơ cường độ
điện trường hướng từ M đến N.
Lưu ý: Điện thế tại một điểm chính là giá trị hiệu điện thế
Hãy so sánh giá trị điện thế tại
giữa điểm đó với điểm được chọn làm gốc điện thế. Trong điểm M và N.
một số trường hợp, ta cũng có thể chọn gốc điện thế ở mặt đất.
Ví dụ: Ta cần thực hiện một công 810–5 J để dịch chuyển
một điện tích 1,610–4 C từ vô cực đến điểm M. Chọn gốc
điện thế ở vô cực, tính điện thế tại M. Bài giải 7DFy A . 8 10 5 . J M
7KHRF{QJWKӭFWDFyÿLӋQWKӃWҥL0Oj 5 V A 8 1 . 0 M 0,5 V. M q 1, 6.10 4 82 VẬT LÍ 11
Mối liên hệ giữa cường độ điện trường với hiệu điện thế
Từ các công thức (13.1) và (13.8), ta rút ra: E U AB (13.9) AB Tổng quát, ta có: E U (13.10) d
với d là khoảng cách giữa hai điểm đang xét trên phương
của vectơ cường độ điện trường. Lưu ý:
5. Giải thích vì sao cường độ điện
Cần xác định dấu của c A Bc:
trường có thể được đo bằng đơn
+ Nếu AcBc cùng chiều với E : d AB 0 . vị vôn trên mét (V/m).
+ Nếu AcBc ngược chiều với E : d AB 0 .
2 VẬN DỤNG CÔNG THỨC LIÊN HỆ GIỮA CƯỜNG ĐỘ ĐIỆN TRƯỜNG VÀ HIỆU ĐIỆN THẾ
Ví dụ 1: Trong vùng không gian có điện trường đều E , xét
ba điểm A, B và C tạo thành một tam giác vuông tại A, trong C
đó cạnh AB song song với các đường sức như Hình 13.3. E
Cho BC = 10 cm và α = 60o. Biết hiệu điện thế giữa hai Į điểm B và C bằng 100 V. B A
a) Tính độ lớn cường độ điện trường E.
S Hình 13.3. Ba điểm A, B, C
trong điện trường đều
b) Tính hiệu điện thế giữa hai điểm A, C và giữa hai điểm A, B. Bài giải
a) Từ công thức (13.10), ta có hiệu điện thế giữa hai điểm B, C được xác định: U E d . E BA . E BC . .cos BC BC
Với d là hình chiếu của BC lên phương của đường sức điện. BC Suy ra E U 100 BC 2000V/m. o BC.cos , 0 1cos 60 b) Ta có:
+ Hiệu điện thế giữa hai điểm A, C:
U = E.d = 0 V. AC AC
+ Hiệu điện thế giữa hai điểm A, B: UU BA = – BC U cos = –100 V. BC = E
E .dBC= –E. E E AB AB BC 83 VẬT LÍ 11
Ví dụ 2: Xét hai bản kim loại hình vuông A và B đặt song
song cách nhau 5 mm, tích điện bằng nhau nhưng trái dấu.
Biết bản A tích điện dương và bản B tích điện âm. Hiệu điện
thế giữa hai bản là U = 25 V. Xem điện trường giữa hai bản AB
là đều, các đường sức điện vuông góc với các bản.
a) Xác định độ lớn cường độ điện trường giữa hai bản kim loại.
b) Xét một hạt electron bắt đầu chuyển động từ bản B.
Xác định độ lớn lực điện tác dụng lên electron và tốc độ
của electron khi nó đến bản A. Biết khối lượng electron m 9 1 10 31 , . kg. e Bài giải
a) Độ lớn cường độ điện trường giữa hai bản kim loại: E U 25 AB d 5000 V/m. 5 10 3 . Xét hai bản kim loại
b) Độ lớn lực điện tác dụng lên electron: song song, cách nhau
F = |q |(= 1,6.10–19. 5 000 = 8.10–16 N. e 2,0 cm và có hiệu điện
thế 5,0 kV. Tính độ lớn
Độ biến thiên động năng bằng công của lực điện trường:
lực điện tác dụng lên 1 2 một hạt bụi nằm trong W W A m v e 0 q U – – W W–0 = $ đ đ0 2 e BA khoảng giữa hai bản, 19
biết hạt bụi có điện tích q U – – v 2 ( , . ) ( ) e BA 2 1 6 10 25 6 2,96 1 . 0 m/s. 31 8,010–19 C. m , . e 9 1 10
Lưu ý: U = V – V . Do đó, khi electron đi từ bản âm sang BA B A
bản dương thì U < 0. BA Đo điện tim
Trong máy đo điện tim, các điện cực được sử dụng để đo hiệu
điện thế giữa các điểm khác nhau trên da của bệnh nhân,
thường không vượt quá 1 mV đối với người bình thường (Hình 13.4).
Đây là một phương pháp có độ nhạy cao để phát hiện sự bất thường
của chức năng tim. Dựa vào sách, báo, internet, các em hãy tìm hiểu
S Hình 13.4. Bệnh nhân
và trình bày ngắn gọn nguyên lí hoạt động của máy đo điện tim.
đang được đo điện tim
3 CHUYỂN ĐỘNG CỦA ĐIỆN TÍCH TRONG ĐIỆN TRƯỜNG ĐỀU
Điện tích chuyển động với vận tốc ban đầu song song với vectơ cường độ điện trường
Xét điện trường đều được tạo bởi 2 tấm kim loại phẳng, đặt
song song cách nhau một khoảng d, tích điện trái dấu như
Hình 13.5. Hạt electron chuyển động với vận tốc ban đầu bằng không từ bản âm. 84 VẬT LÍ 11 – – – – – – – – F E + + + + + + +
S Hình 13.5. Chuyển động của electron song song với
vectơ cường độ điện trường G G
Dưới tác dụng của lực điện F qeE, hạt electron được gia
tốc và chuyển động theo phương song song nhưng ngược
chiều với điện trường. Theo định lí động năng trong chương
trình Vật lí 10, ta có vận tốc của hạt electron tại bản dương: v 2q Ed e m (13.11)
6. Áp dụng định lí động năng, em
hãy rút ra công thức (13.11).
Chuyển động của hạt mang điện song song với điện trường
được ứng dụng trong máy gia tốc tuyến tính. Máy gia tốc
tuyến tính thường được sử dụng trong quá trình xạ trị để điều trị bệnh ung thư.
Nguyên tắc hoạt động của máy gia tốc tuyến tính: Các
electron với năng lượng thấp được sinh ra do bức xạ nhiệt từ
súng điện tử. Chúng được đưa vào buồng gia tốc (Hình 13.6).
Dưới tác dụng của lực điện, các electron được gia tốc trở
thành electron năng lượng cao. Sau đó, chúng được lái tới
vùng cần xạ trị để tiêu diệt tế bào ung thư. Electron Electron
Súng điện tử năng lượng thấp Buồng gia tốc năng lượng cao
S Hình 13.6. Sơ đồ nguyên lí của máy gia tốc tuyến tính dùng electron
Điện tích chuyển động với vận tốc ban đầu vuông góc với vectơ cường độ điện trường
Xét một electron chuyển động với tốc độ v vào vùng điện 0
trường đều được tạo bởi 2 tấm kim loại phẳng, đặt song
song, tích điện trái dấu sao cho vận tốc đầu của electron
7. Xác định các lực tác dụng lên
song song với 2 tấm kim loại như Hình 13.7.
electron trong Hình 13.7. Từ đó, – – – – – – –
dự đoán chuyển động của electron. O x Gv – 0 F
8. Mô tả chuyển động của proton E G
chuyển động với vận tốc v0 y
vào vùng điện trường đều như + + + + + + + Hình 13.7.
S Hình 13.7. Chuyển động của electron trong điện trường đều 85 VẬT LÍ 11
Khi trọng lực của electron có độ lớn rất nhỏ so với lực điện
tác dụng lên electron, một cách gần đúng, electron chỉ chịu G G
tác dụng của lực điện F qeE cùng chiều dương quy ước.
Quỹ đạo chuyển động của electron khi này giống với quỹ
đạo chuyển động của vật ném ngang đã được phân tích
trong chương trình Vật lí 10, gồm 2 thành phần:
+ Trên phương Ox: Electron chuyển động thẳng đều với tốc độ v . 0 G E
+ Trên phương Oy: Lực điện F gây ra gia tốc a qe . m
Electron chuyển động thẳng nhanh dần đều không vận tốc đầu.
Một electron chuyển động với vận tốc đầu 4107 m/s vào vùng điện trường đều
theo phương vuông góc với các đường sức điện. Biết cường độ điện trường là
E = 103 V/m. Hãy xác định: a) Gia tốc của electron.
b) Vận tốc của electron khi nó chuyển động được 210–7 s trong điện trường.
Neutron là một hạt không mang điện, có khối lượng xấp xỉ proton. Một hạt neutron tự do có thể tồn tại khoảng
10 đến 15 phút, sau đó phân rã thành electron, proton và phản neutrino (là một hạt không mang điện, có khối
lượng rất bé, chuyển động với tốc độ gần bằng tốc độ ánh sáng trong chân không). Em hãy đề xuất phương án
để tách hai hạt electron và proton ngay sau khi neutron bị phân rã. %j,7t3
1. Độ chênh lệch điện thế giữa mặt trong và mặt ngoài của màng tế bào trong cơ thể người là
90 mV. Biết mặt trong và mặt ngoài của màng tế bào lần lượt mang điện âm và mang điện
dương. Xác định công mà tế bào cần thực hiện để đưa một ion Na+ chuyển động từ bên trong
ra bên ngoài màng tế bào theo cơ chế chủ động qua kênh protein.
2. Một electron chuyển động với tốc độ ban đầu v = 1,6.106 m/s 0
chuyển động vào vùng điện trường đều theo phương song
song với hai bản và ở chính giữa khoảng cách hai bản như + + + + + + G
Hình 13P.1. Biết chiều dài mỗi bản là 3 cm và khoảng cách v0 –
giữa hai bản là 1 cm. Giữa hai bản có điện trường hướng JG,E
từ trên xuống, điện trường bên ngoài hai bản bằng 0. Biết – – – – – –
electron di chuyển đến vị trí mép ngoài của tấm bản phía
S Hình 13P.1.
trên, tính độ lớn cường độ điện trường giữa hai bản. 86 VẬT LÍ 11 Bài 14 7ô,1
– Điện dung, đơn vị đo điện dung.
– Ghép tụ điện nối tiếp, song song.
Màn hình cảm ứng (Hình 14.1) được sử dụng ngày càng phổ biến.
Trong đó, màn hình cảm ứng điện dung (sử dụng tụ điện) hoạt động dựa vào
khả năng nhường hoặc nhận điện tích của cơ thể con người khi có sự tiếp xúc
với các thiết bị điện. Vậy, tụ điện là thiết bị có những đặc tính gì?
S Hình 14.1. Màn hình cảm ứng
1 ĐIỆN MÔI TRONG ĐIỆN TRƯỜNG
Những vật được cấu tạo từ các chất chứa ít hoặc không có
hạt mang điện tự do, không cho điện tích chạy qua được gọi
1. Liệt kê một số vật liệu có tính
là điện môi. Ví dụ: nhựa, cao su, sứ, thuỷ tinh,… Khi tích
cách điện trong đời sống.
điện cho khối điện môi, điện tích dư sẽ nằm ngay tại vị trí được đưa vào.
Khi điện môi được đặt vào một vùng không gian có điện – + – + – + – +
trường, mỗi nguyên tử của điện môi bị phân cực và làm cho – + – + – + – +
cả khối điện môi bị phân cực với hai mặt tích điện trái dấu – + – + – + – +
nhau như Hình 14.2. Điều này dẫn đến điện trường tổng G G G ( 0 E
hợp bên trong khối điện môi có độ lớn nhỏ hơn cường độ 0 a) b) điện trường ngoài.
S Hình 14.2. Điện môi trước và sau
khi đặt vào trong một điện trường
Mỗi chất điện môi được đặc trưng bởi hằng số điện môi, kí
hiệu là ε. Hằng số điện môi và điện trường giới hạn của một
số chất điện môi được cho trong Bảng 14.1. +ҵQJVӕ ĈLӋQP{L
&ѭӡQJÿӝÿLӋQWUѭӡQJ ÿLӋQP{LH ) JLӟLKҥQ69P Không khí (khô) 1,00059 3 Cao su tổng hợp 6,7 12 Nylon 3,4 14 Giấy 3,7 16 Sứ 6 12 Thuỷ tinh 3,7 – 10 9
S Bảng 14.1. Hằng số điện môi và điện trường giới hạn của một số điện môi 87 VẬT LÍ 11 2 TỤ ĐIỆN
Khái niệm tụ điện
Tụ điện là một linh kiện điện tử được sử dụng trong các
mạch điện của máy thu thanh, máy tính và các thiết bị điện 7өJӕP 7өKRi
tử khác. Tụ điện có nhiều hình dạng và kích thước khác
nhau (Hình 14.3). Vai trò của tụ điện là tích điện và phóng điện trong mạch. 7өPLFD 7өJLҩ\
7өÿLӋQOjPӝWKӋJӗPKDLYұWGүQÿһWJҫQQKDXYj
QJăQFiFKQKDXEҵQJPӝWOӟSFiFKÿLӋQ0ӛLYұW
GүQÿѭӧFJӑLOjPӝWEҧQFӫDWөÿLӋQ+uQK 7өGiQ S
Dựa vào hình dạng của tụ điện, người ta chia tụ điện thành
Hình 14.3. Một số loại tụ điện
các loại: tụ điện phẳng, tụ điện trụ và tụ điện cầu.
Ngoài ra, tụ điện còn có thể được phân loại dựa vào môi
trường điện môi bên trong tụ: tụ không khí, tụ giấy, tụ mica,...
Trong các sơ đồ mạch điện, tụ điện thường được kí hiệu như Hình 14.5. C
S Hình 14.4. Tụ điện
S Hình 14.5. Kí hiệu tụ điện trong sơ đồ mạch điện
nối vào nguồn điện
Khi nối hai bản của tụ điện vào hai cực của nguồn điện như
Hình 14.4, hai bản này sẽ tích điện bằng nhau về độ lớn
nhưng trái dấu. Đây là quá trình nạp điện (hay tích điện)
2. Dựa vào cấu tạo của tụ điện ở cho tụ.
Hình 14.4, hãy cho biết tụ điện
Khi nối hai bản của tụ điện đã được nạp điện với một điện
có cho dòng điện một chiều đi
trở, một dòng điện sẽ xuất hiện và chạy qua điện trở làm qua không.
điện tích của tụ giảm dần. Đây là quá trình phóng điện
(hay xả điện) của tụ.
Điện dung của tụ điện
Khi nối hai bản của tụ điện với hai cực của nguồn điện có
hiệu điện thế U, một bản của tụ sẽ có điện tích Q, bản còn
lại có điện tích –Q. Độ lớn điện tích Q trên mỗi bản của tụ
điện khi đã tích điện được gọi là điện tích của tụ điện. Khi
nối hai bản của các tụ điện khác nhau vào cùng nguồn
điện có hiệu điện thế U, điện tích của các tụ khác nhau là khác nhau. 88 VẬT LÍ 11
Các khảo sát thực nghiệm chứng tỏ, đối với một tụ điện xác
định được nối vào nguồn điện, khi thay đổi hiệu điện thế
U thì điện tích Q của tụ điện cũng thay đổi. Tuy nhiên, tỉ Q
số U là một hằng số. Thực hiện khảo sát tương tự nhưng Q
cho các tụ điện khác nhau, tỉ số U có giá trị không đổi
tương ứng với từng tụ điện. Mặt khác, tỉ số Q ÿӕLYӟLFiF U Q
WөÿLӋQNKiFQKDXOjNKiFQKDX9ұ\WӍVӕ ÿһFWUѭQJFKR U NKҧQăQJWtFKÿLӋQFӫDWө
Điện dung của tụ điện là đại lượng đặc trưng cho
khả năng tích điện của tụ, kí hiệu là C và được xác định bởi: C Q (14.1) U
Trong hệ SI, điện dung có đơn vị là fara (F).
Từ công thức (14.1), ta thấy 1 F là điện dung của một tụ
điện mà khi đặt vào giữa hai bản tụ điện một hiệu điện thế
1 V thì điện tích được tích trên tụ là 1 C.
Thông thường, các tụ điện có điện dung rất nhỏ, cỡ từ
10–12 F đến 10–6 F. Vì vậy, ta thường dùng các ước của fara: 1 micrôfara (µF) = 10–6 F 1 nanôfara (nF) = 10–9 F 1 picôfara (pF) = 10–12 F
Mỗi tụ điện đều có một giá trị hiệu điện thế giới hạn. Đó là
hiệu điện thế tối đa mà tụ có thể chịu được. Nếu vượt quá
giá trị này, tụ điện sẽ bị hỏng. Thông thường, trên vỏ của tụ
điện thường ghi giá trị điện dung và hiệu điện thế giới hạn của tụ.
Lưu ý: Điện dung của một tụ điện xác định chỉ phụ thuộc
vào cấu tạo của tụ điện (dạng hình học của hai bản tụ, vị trí
tương đối giữa chúng và môi trường điện môi bên trong tụ)
mà không phụ thuộc vào hiệu điện thế giữa hai bản tụ. 89 VẬT LÍ 11
Tụ điện phẳng là một trường hợp riêng của tụ điện. Tụ điện
phẳng là hệ gồm hai bản kim loại có diện tích S bằng nhau, Nút vặn Bản tụ
được đặt cách nhau một khoảng d và tích điện trái dấu.
Các tính toán chứng tỏ điện dung của tụ điện phẳng được
xác định bằng công thức: C S (14.2) 4 kd 2
với ε là hằng số điện môi và k Nm 9 1 . 09 . 2
S Hình 14.6. Tụ điện xoay C
Trong kĩ thuật, một số tụ điện phẳng được chế tạo sao cho giá trị điện dung của tụ điện
có thể điều chỉnh được như tụ điện xoay. Tụ điện xoay có cấu tạo gồm hai hệ kim loại, một
hệ cố định và một hệ có thể xoay quanh một trục như Hình 14.6. Khi vặn nút điều khiển,
phần diện tích đối diện S giữa các bản tụ thay đổi, do đó điện dung của tụ cũng thay đổi.
Xét một tụ điện được tích điện. Khi thay đổi điện dung của tụ, hiệu điện thế và điện
tích của tụ có thay đổi không trong các trường hợp sau?
a) Tụ vẫn còn được mắc vào nguồn điện một chiều.
b) Tụ đã được tháo ra khỏi nguồn điện trước khi thay đổi điện dung.
Dựa vào sách, báo, internet, em hãy trình bày ngắn gọn vai trò của tụ điện trong màn hình cảm ứng
điện dung của thiết bị điện thoại. 3 GHÉP TỤ ĐIỆN
Trong kĩ thuật, để tạo ra tụ điện với điện dung thích hợp,
người ta thường ghép các tụ điện thành bộ tụ. Có hai cách
ghép cơ bản: ghép nối tiếp và ghép song song.
Bộ tụ ghép nối tiếp
Hình 14.7 mô tả sơ đồ ghép nối tiếp tụ điện. Trong trường A B
hợp này, bản tích điện dương của tụ điện này được nối với
bản tích điện âm của tụ điện sát bên. Bản thứ nhất của tụ C C C 1 2 Q
điện đầu tiên được nối với một cực, bản thứ hai của tụ điện S Hình 14.7. Tụ điện ghép nối tiếp
cuối cùng được nối với cực còn lại của nguồn điện.
Gọi U là hiệu điện thế đặt vào hai đầu của bộ tụ điện;
U , U ,…, U lần lượt là hiệu điện thế giữa hai đầu tụ điện 1 2 n
C , C ,…, C Ta có: 1 2 n
U U U ...U (14.3) 1 2 n
Gọi C là điện dung của bộ tụ điện; Q, Q , Q ,…, Q lần lượt b 1 2 n
là độ lớn điện tích của cả bộ tụ điện và các tụ điện C , C ,…, C 1 2 n
Kết hợp hai công thức (14.3) và (14.1), ta có: 90 VẬT LÍ 11 Q Q Q Q 1 2 n ... (14.4) C C C C b 1 2 n
Nếu các tụ điện lúc đầu chưa được tích điện, thì điện tích các
bản tụ điện mắc nối tiếp sau khi được nối với nguồn sẽ bằng
nhau và bằng điện tích của cả bộ tụ điện Q = Q = Q = …= Q 1 2 n
ĈLӋQGXQJFӫDEӝWөÿLӋQJKpSQӕLWLӃSÿѭӧF[iFÿӏQK 1 1 1 1 ... C C C C (14.5) b 1 2 n
Bộ tụ ghép song song C1
Hình 14.8 mô tả sơ đồ ghép tụ điện song song. Trong trường
hợp này, các tụ điện được mắc vào cùng một hiệu điện thế C2
U. Gọi U , U ,..., U lần lượt là hiệu điện thế đặt vào hai đầu 1 2 n
các tụ điện C , C ,..., C . Ta có: 1 2 n A B
U = U = U = ...= U (14.6) Cn 1 2 n
Gọi Q là điện tích của bộ tụ điện; Q , Q ,..., Q lần lượt là độ 1 2 n
S Hình 14.8. Tụ điện ghép
lớn điện tích các tụ điện C , C ,..., C Do một bản của mỗi tụ song song 1 2 n
điện cùng được ghép vào cực dương của nguồn nên:
Q = Q + Q + ... + Q (14.7) 1 2 n
3. Xét hai tụ điện có cùng điện
dung lần lượt được mắc nối tiếp
và song song để tạo ra hai bộ
ĈLӋQ GXQJ FӫD Eӝ Wө ÿLӋQ JKpS VRQJ VRQJ ÿѭӧF
tụ điện khác nhau. Hãy so sánh [iFÿӏQK
điện dung của hai bộ tụ điện
C = C + C + ... + C (14.8)
trên với điện dung của mỗi tụ b 1 2 n điện thành phần.
Xét mạch điện như Hình 14.9. Biết hiệu điện thế giữa hai điểm A, B bằng 6 V và điện
dung của hai tụ điện lần lượt là C = 2 µF và C = 4 µF. Xác định hiệu điện thế và điện 1 2
tích trên mỗi tụ điện. Giả sử ban đầu các tụ chưa tích điện. A B C C 1 2
S Hình 14.9. Hai tụ mắc nối tiếp 91 VẬT LÍ 11
Quan sát Hình 14.10 và cho biết:
a) giá trị điện dung của tụ điện.
b) ý nghĩa các thông số trên tụ điện.
S Hình 14.10. Tụ điện %j,7t3
1. Xét tụ điện như Hình 14.10.
a) Tính điện tích cực đại mà tụ có thể tích được.
b) Muốn tích cho tụ điện một điện tích là 4,8.10–4 C thì cần phải đặt giữa hai bản tụ một hiệu điện thế là bao nhiêu?
2. Hai tụ điện có điện dung lần lượt là C = 0,5 µF và C = 0,7 µF được ghép song song rồi mắc 1 2
vào nguồn điện có hiệu điện thế U < 60 V thì một trong hai tụ có điện tích 35 µC. Tính hiệu
điện thế U của nguồn và điện tích của tụ còn lại.
3. Cho các tụ điện C = C = C = C = 3,3 µF được mắc thành mạch như Hình 14P.1. Xác định điện 1 2 3 4
dung tương đương của bộ tụ. C C 1 2 M A B N C C 3 4
S Hình 14P.1. Bộ tụ mắc hỗn hợp 92 VẬT LÍ 11 1u1*/¦1*9j1*'1* Bài 15 &$7ô,1
– Năng lượng tụ điện.
– Ứng dụng của tụ điện trong cuộc sống.
Máy khử rung tim xách tay là thiết bị được các đội y tế thường dùng để
cấp cứu bệnh nhân bị rối loạn nhịp tim và tạo nhịp tim ổn định cho bệnh nhân.
Khi hoạt động, các điện cực của máy được đặt trên ngực của bệnh nhân để tạo
dòng điện đi qua tim bệnh nhân trong thời gian rất ngắn (Hình 15.1), tạo điều
kiện cho tim bệnh nhân hoạt động bình thường. Thiết bị này hoạt động dựa
vào khả năng tích trữ năng lượng điện của tụ điện bên trong thiết bị. Theo em,
S Hình 15.1. Bệnh nhân đang
tụ điện dự trữ được năng lượng dựa trên nguyên tắc nào?
được cấp cứu bằng máy khử rung tim xách tay
1 NĂNG LƯỢNG TỤ ĐIỆN
Tụ điện là thiết bị được sử dụng để tích điện và phóng điện u (V)
dựa vào năng lượng W mà tụ điện tích lũy được. Lượng A
năng lượng này chính là công cần thiết A để di chuyển điện
tích đến các bản tụ điện. uQ
Xét một tụ điện ban đầu chưa tích điện. Khi đó, trên mỗi
bản tụ điện có nhiều điện tích âm và dương với số lượng
bằng nhau, do đó giữa hai bản không xuất hiện điện trường. O H q (C)
Để tích điện cho các bản tụ, cần một công để dịch chuyển ¨q
một lượng điện tích q từ bản này sang bản kia của tụ điện. S
Khi đó, giữa hai bản sẽ xuất hiện một hiện điện thế u với
Hình 15.2. Đồ thị hiệu điện thế –
điện tích của tụ điện q = uC.
Điện tích q của tụ điện và hiệu điện thế u giữa hai bản tụ điện
tỉ lệ thuận với nhau. Do đó, đồ thị hiệu điện thế – điện tích
của tụ điện có dạng đường thẳng, đi qua gốc toạ độ như
Hình 15.2 và có hệ số góc bằng 1/C với C là điện dung của tụ điện. 93 VẬT LÍ 11
Ta đã biết, công để dịch chuyển một lượng điện tích 'q giữa
hai điểm có hiệu điện thế u là 'A = 'q.u , chính là diện n n
tích hình chữ nhật màu xanh trên đồ thị trong Hình 15.2.
1. Vận dụng kiến thức đã học và
Nếu chia trục q thành những đoạn vô cùng bé, thì tổng tất
công thức (15.1), em hãy rút ra công thức (15.2).
cả diện tích các hình chữ nhật thành phần chính là diện tích
của hình tam giác OAH và chính là công tổng cộng để tích
điện cho tụ điện từ trạng thái ban đầu đến khi có điện tích Q. Do đó, ta có: A 1 QU (15.1) 2
Công này chính là năng lượng được dự trữ trong tụ điện
dưới dạng năng lượng điện trường.
Một tụ điện có điện dung
C = 2 pF được tích điện đến
Năng lượng điện trường được dự trữ bên trong tụ
điện tích 3,210–8 C. Tính điện:
năng lượng của tụ điện. Tụ 2
W 1 QU 1 CU 2 Q (15.2)
điện này có thể được dùng 2 2 C 2
để duy trì dòng điện trong mạch hay không? Vì sao?
2 ỨNG DỤNG CỦA TỤ ĐIỆN
* Xây dựng ý tưởng dự án và quyết định chủ đề:
– Mục đích: Nghiên cứu ứng dụng của tụ điện trong cuộc sống.
– Vấn đề thực tiễn:
Trong thời đại công nghệ ngày nay, những thiết bị thông
2. Tìm hiểu và trình bày một số ứng
minh đang ngày càng phát triển như máy tính xách tay,
dụng của tụ điện trong cuộc sống.
điện thoại, máy chiếu,… Trong số đó, phải kể đến ô
tô điện (Hình 15.3). Ô tô điện có nhiều ưu điểm như
chi phí bảo dưỡng thấp hơn xe sử dụng nhiên liệu hoá
thạch (xăng, dầu), khả năng vận hành ổn định, tiết kiệm
nhiên liệu và đặc biệt là giảm thiểu các vấn đề ô nhiễm
môi trường vì xe điện có thể hạn chế phát thải CO . Tuy 2
nhiên, bên cạnh các lợi ích của xe điện thì vẫn tồn tại
một số hạn chế như phạm vi di chuyển, trạm sạc và đặc S Hình 15.3. Xe ô tô đang sạc điện
biệt là chi phí thay pin. Vòng đời pin của xe điện trung
bình khoảng 10 năm và chi phí để thay mới lên đến hàng
nghìn USD. Do đó, để khắc phục vấn đề này, các nhà
nghiên cứu đang tiến hành khảo sát phương án thay thế 94 VẬT LÍ 11
pin sạc. Trong đó, thiết bị đang được quan tâm nhiều nhất
là tụ điện. Các tụ điện có thể sạc, xả hàng triệu lần mà
không bị chai, giảm điện dung hoặc bị hỏng. Bên cạnh
đó, tốc độ sạc, xả của tụ điện nhanh hơn pin và ắc quy.
Ngoài ra, hệ thống năng lượng kết hợp song song giữa
pin và tụ điện giúp hỗ trợ kéo dài tuổi thọ sạc, xả của pin,
từ đó nâng cao khả năng vận hành của ô tô điện và tiết kiệm chi phí.
Ngoài ra, tụ điện cũng là một linh kiện điện tử có vai trò
quan trọng và được ứng dụng rộng rãi trong kĩ thuật.
Trong đó có thể kể đến bếp từ, micro với độ nhạy cao khi
có sử dụng tụ điện,…
* Lập kế hoạch thực hiện dự án:
– Tìm kiếm nguồn tài liệu đáng tin cậy.
– Tiến hành nghiên cứu ứng dụng của tụ điện trong cuộc
sống về vai trò và nguyên lí hoạt động (có thể sử dụng các
ứng dụng được cho trong bài).
* Báo cáo kết quả: Công bố sản phẩm và báo cáo kết quả thực hiện dự án. %j,7t3
1. Xét một đám mây tích điện –32 C. Xem đám mây và bề mặt Trái Đất như một tụ điện phẳng, biết
điện dung của tụ điện này khoảng 9,27 nF. Hãy tính:
a) Hiệu điện thế giữa hai bản của tụ điện.
b) Năng lượng của tụ điện này.
2. Xét một máy khử rung tim xách tay. Để cấp cứu cho bệnh nhân, nhân viên y tế đặt hai điện cực
của máy khử rung tim lên ngực bệnh nhân và truyền năng lượng dự trữ trong tụ điện cho bệnh
nhân. Giả sử tụ điện trong máy có điện dung 70 PF và hiệu điện thế giữa hai bản tụ là 5 000 V.
a) Xác định năng lượng của tụ.
b) Giả sử trung bình máy truyền một năng lượng khoảng 200 J qua bệnh nhân trong một xung
có thời gian khoảng 2 ms. Xác định công suất trung bình của xung. 95 VẬT LÍ 11 X 71*.7&+¡1* X
1 CÁC LOẠI ĐIỆN TÍCH
Điện tích được phân thành 2 loại: điện tích dương và điện tích âm. Các điện tích cùng
dấu thì đẩy nhau, trái dấu thì hút nhau. Đơn vị đo điện tích là culông (C).
2 ĐỊNH LUẬT COULOMB
Lực tương tác tĩnh điện giữa hai điện tích điểm đặt trong chân không có phương trùng
với đường thẳng nối hai điện tích điểm đó, có độ lớn tỉ lệ thuận với tích độ lớn của các
điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa chúng. q q F k 1 2 r2
3 ĐIỆN TRƯỜNG – CƯỜNG ĐỘ ĐIỆN TRƯỜNG
– Điện trường là dạng vật chất bao quanh điện tích và truyền tương tác giữa các điện tích.
Tính chất cơ bản của điện trường là tác dụng lực điện lên các điện tích khác đặt trong nó.
– Cường độ điện trường do điện tích Q sinh ra tại một điểm là đại lượng đặc trưng cho
điện trường về mặt tác dụng lực tại điểm đó. Đây là một đại lượng vectơ và được xác định bởi biểu thức: E F q
– Đường sức điện là đường mô tả điện trường sao cho tiếp tuyến tại một điểm bất kì trên
đường cũng trùng với phương của vectơ cường độ điện trường tại điểm đó.
– Cường độ điện trường do điện tích điểm Q gây ra tại một điểm M cách điện tích một
đoạn r trong chân không có phương nằm trên đường thẳng nối điện tích và điểm M, có
chiều hướng ra xa điện tích nếu Q > 0 và hướng lại gần điện tích nếu Q < 0, có độ lớn là: Q E k r2
4 THẾ NĂNG ĐIỆN – ĐIỆN THẾ
– Thế năng điện của một điện tích q tại một điểm trong điện trường đặc trưng cho khả
năng sinh công của điện trường để dịch chuyển điện tích q từ điểm đó ra xa vô cùng.
– Điện thế tại một điểm trong điện trường là đại lượng đặc trưng cho thế năng điện tại vị
trí đó và được xác định bằng công mà ta cần thực hiện để dịch chuyển một đơn vị điện
tích dương từ vô cực về điểm đó: V AA A . q
– Mối liên hệ giữa cường độ điện trường và hiệu điện thế: E U . d 96 VẬT LÍ 11
5 TỤ ĐIỆN – ĐIỆN DUNG
– Tụ điện là một hệ gồm hai vật dẫn đặt gần nhau và ngăn cách nhau bằng một lớp cách
điện. Mỗi vật dẫn được gọi là một bản của tụ điện.
– Điện dung của tụ điện là đại lượng đặc trưng cho khả năng tích điện của tụ và được xác định bởi: C Q . U
6 CÁC CÁCH GHÉP TỤ ĐIỆN
– Ghép nối tiếp: Điện dung của bộ tụ điện ghép nối tiếp được xác định: 1 1 1 1 ... C C C C b 1 2 n
– Ghép song song: Điện dung của bộ tụ điện ghép song song được xác định:
C = C + C + ... + C b 1 2 n
7 NĂNG LƯỢNG TỤ ĐIỆN
Năng lượng điện trường được dự trữ bên trong tụ điện: 2
W 1 QU 1 CU 2 Q 2 2 C 2 97 VẬT LÍ 11
'µ1*ï,ũ1.+·1*ïű, Chương 4 '1*ô,1 Bài 16 &¢1*ô'1*ô,1
– Định nghĩa các khái niệm dòng điện, cường độ dòng điện, đơn vị điện lượng.
– Vận dụng được biểu thức: I = Snve.
S Hình 16.1. Ánh sáng từ hai bóng đèn sợi đốt cùng loại nhưng có độ sáng khác nhau
Khi bật công tắc, ta thấy bóng đèn sáng lên gần như ngay lập tức. Phải chăng các hạt tải điện trong dây dẫn
nối với bóng đèn đã di chuyển với vận tốc rất lớn? Có thể ước tính vận tốc này bằng cách nào? Ngoài ra, khi so sánh độ
sáng hai bóng đèn sợi đốt cùng loại nhưng được đặt vào hai hiệu điện thế khác nhau ta thấy có sự khác biệt (Hình 16.1).
Yếu tố nào của dòng điện đã tạo nên sự khác biệt này?
1 KHÁI NIỆM DÒNG ĐIỆN
Trong môn Khoa học tự nhiên 8, các em đã biết dòng điện
là dòng dịch chuyển có hướng của các điện tích. Khi được
đặt vào một điện trường ngoài, các điện tích dương và âm sẽ
dịch chuyển theo hai hướng ngược nhau. Chiều dòng điện
được quy ước là chiều dịch chuyển có hướng của các điện
tích dương (ngược với chiều dịch chuyển có hướng của các điện tích âm).
Dòng điện là dòng dịch chuyển có hướng của các điện tích.
Chiều dòng điện được quy ước là chiều dịch chuyển có hướng của các điện tích dương
(ngược với chiều dịch chuyển có hướng của các điện tích âm). 98 VẬT LÍ 11
2 CƯỜNG ĐỘ DÒNG ĐIỆN
Thí nghiệm kiểm chứng * Mục đích:
Kiểm chứng tác dụng mạnh hay yếu của dòng điện. * Dụng cụ:
– Pin (1), các dây nối (2) và khoá K (3).
– Biến trở (là điện trở có giá trị có thể thay đổi được) (4). – Ampe kế (5).
– Bóng đèn sợi đốt (6). (5) (4)
1. Dựa vào bộ dụng cụ trong Hình (1)
16.2, em hãy đề xuất phương án
thí nghiệm khác để kiểm chứng
tính mạnh yếu của dòng điện. (6) (3)
Tiến hành thí nghiệm (nếu có điều kiện). (2)
S Hình 16.2. Bộ dụng cụ thí nghiệm kiểm chứng tác dụng
mạnh yếu của dòng điện + –
* Tiến hành thí nghiệm: K
Bước 1: Bố trí thí nghiệm như sơ đồ trong Hình 16.3.
Bước 2: Đóng khoá K, điều chỉnh biến trở. Ứng với mỗi giá
trị của biến trở, ghi nhận giá trị cường độ dòng điện được A R
đo bởi ampe kế và nhận xét về độ sáng của bóng đèn. Ĉ S
* Báo cáo kết quả thí nghiệm:
Hình 16.3. Sơ đồ kiểm chứng
tính chất của cường độ dòng điện
Nhận xét về mối liên hệ giữa độ sáng của đèn và số chỉ của
ampe kế khi thay đổi giá trị của biến trở. 'A = v't S
Khái niệm cường độ dòng điện
Xét một đoạn dây dẫn trong đó có dòng các điện tích dịch
chuyển qua tiết diện thẳng S như Hình 16.4. Giả sử trong
khoảng thời gian ∆t, lượng điện tích (điện lượng) dịch
chuyển qua tiết diện thẳng S có độ lớn ∆q.
S Hình 16.4. Điện tích dịch chuyển
qua tiết diện thẳng S 99 VẬT LÍ 11
Đại lượng vật lí đặc trưng cho tác dụng mạnh hay yếu
2. Khi nói về dòng điện, chúng ta
của dòng điện gọi là cường độ dòng điện, được xác
thường nhắc tới chiều của nó.
định bằng điện lượng dịch chuyển qua tiết diện thẳng
Theo em, cường độ dòng điện I
S trong một đơn vị thời gian.
là đại lượng vectơ hay vô hướng? I q (16.1) t
Trong hệ SI, cường độ dòng điện có đơn vị là ampe (A).
Trong trường hợp tổng quát, điện lượng dịch chuyển qua
tiết diện thẳng S có thể thay đổi theo thời gian, nghĩa là
cường độ dòng điện có thể thay đổi theo thời gian. Do đó,
công thức (16.1) chính là giá trị trung bình của cường độ
dòng điện trong khoảng thời gian 't.
Dòng điện có chiều và cường độ không thay đổi theo thời
gian được gọi là dòng điện không đổi. Cường độ dòng điện
không đổi I trong một dây dẫn có thể viết đơn giản: I q (16.2) t
Định nghĩa đơn vị điện tích
Từ công thức (16.1), ta thấy cường độ dòng điện được định
nghĩa thông qua tỉ số giữa điện lượng dịch chuyển qua tiết
diện thẳng và khoảng thời gian để thực hiện sự dịch chuyển
3. Dựa vào công thức (16.1), hãy lập
đó. Trong chương trình môn Khoa học tự nhiên 8, các em
luận để dẫn dắt ra định nghĩa
đã được học đơn vị của cường độ dòng điện trong hệ SI (A)
đơn vị đo điện lượng culông.
được chọn là đơn vị cơ bản, do đó đơn vị của điện tích (C)
được định nghĩa lại như sau:
1 culông (1 C) là điện lượng chuyển qua tiết diện thẳng của dây dẫn trong 1 s khi có
dòng điện không đổi cường độ 1 A chạy qua. 1C = 1A.1s = 1A.s Vận dụng
Ví dụ: Một dây dẫn bằng đồng có dòng điện 5 A chạy qua.
Biết rằng các điện tích dịch chuyển có hướng tạo nên dòng
điện này là các electron.
a) Hãy xác định điện lượng dịch chuyển qua một tiết diện
thẳng của dây dẫn trong 4 phút.
b) Tính số electron đã chuyển qua tiết diện thẳng trong câu a. 100 VẬT LÍ 11 Bài giải
a) Từ công thức định nghĩa: I q
= ⇒ q = It = 5 4 . 6 . 0 = t 1200 . C b) Số electron: n q = = 1200 = 21 e − 7,5 10 . hạt. 1, 6.10 19
Hãy so sánh cường độ của hai dòng điện không đổi sau:
Dòng điện 1: Cứ mỗi giây có 1,25.1019 hạt electron chuyển qua tiết diện thẳng của dây dẫn.
Dòng điện 2: Cứ mỗi phút có điện lượng 150 C chuyển qua tiết diện thẳng của dây dẫn.
Mỗi khi trời mưa hay giông bão thường kèm theo các tia sét, đó là các dòng điện phóng từ đám mây xuống mặt
đất với cường độ trung bình cỡ 300 000 A. Tia sét kéo dài 1,5 s. Hãy tính điện lượng đã di chuyển giữa đám mây
và mặt đất trong mỗi tia sét. 3 VẬN TỐC TRÔI
Khái niệm vận tốc trôi
Khi chưa có điện trường ngoài, các hạt tải điện chuyển động
nhiệt hỗn loạn theo tất cả các hướng, không có hướng nào
là ưu tiên, vì vậy trong vật dẫn không có dòng điện.
4. Vì sao khi chưa có điện trường
ngoài, các hạt tải điện trong dây
Khi có điện trường ngoài, các hạt tải điện vừa chuyển động
dẫn chuyển động nhiệt không
nhiệt, vừa chuyển động có hướng tạo thành dòng điện.
ngừng với tốc độ cỡ 106 m/s
Trong quá trình chuyển động, các hạt tải điện liên tục bị va
mà không có dòng điện trong
đập vô số lần với các hạt khác của vật dẫn. Do đó, các hạt tải dây dẫn?
điện chuyển động hỗn loạn nhưng có xu hướng theo một
phương ưu tiên là phương của điện trường ngoài với vận
tốc trung bình không đổi, gọi là vận tốc trôi của hạt tải điện.
Để tìm hệ thức xác định độ lớn vận tốc trôi v, ta xét một
dòng điện không đổi, cường độ I chạy qua một dây dẫn có
diện tích tiết diện không đổi S như Hình 16.4.
Gọi n là mật độ hạt tải điện trong dây dẫn, q là điện tích của mỗi hạt tải điện. Sau khoảng thời g Aian
v Wt, toàn bộ điện tích chuyển qua tiết
diện S của dây dẫn chứa trong một hình trụ đứng có đáy S và chiều dài A
v W . Điện lượng của phần này là:
Q nSA q nS v t q Từ đó: I Q nSv q . t 101 VẬT LÍ 11
Vận tốc trôi của các hạt tải điện tỉ lệ với cường độ
dòng điện chạy trong vật dẫn. v I nS q (16.3)
Lưu ý: Thông thường, vật dẫn hay được sử dụng là kim loại,
do đó hạt tải điện là electron. Khi đó, công thức 16.3 được viết lại thành: I nS e v (16.4) Vận dụng
Ví dụ: Dòng điện không đổi I = 1,3 A chạy trong một dây dẫn
bằng đồng có đường kính tiết diện d = 1,8 mm. Khối lượng
riêng và nguyên tử lượng của đồng lần lượt là ρ = 9 tấn/m3 và
A = 64 g/mol. Giả sử mỗi nguyên tử đồng có một electron
tự do. Tính độ lớn vận tốc trôi của các electron tự do tạo nên dòng điện. Bài giải
Vì đồng là kim loại nên hạt tải điện là electron.
Từ công thức (16.4), ta có:I 4I v
5. Kết quả tính toán trong ví dụ nSe n d 2e
cho thấy độ lớn vận tốc trôi rất
Trong đó, mật độ electron n được xác định bởi:
nhỏ (cỡ 0,04 mm/s). Điều này có
mâu thuẫn gì với hiện tượng đèn N N I 4IA Am NA n ρ v =
gần như sáng “tức thì” ngay khi V AV A nSe 2 d eN ρ bật công tắc hay không? A Thay số, ta được: v 4 1 . ,3 6 . 4 2 1,8.10 3 1, 6.10 19.6, 022.1023 .9.106
≈ 0,04.10–3 m/s = 0,04 mm/s. %j,7t3
1. Một ống chứa khí hydrogen bị ion hoá đặt trong điện trường mạnh giữa hai điện cực làm xuất
hiện dòng điện. Các electron chuyển động về cực dương, các proton chuyển động về cực âm.
Biết mỗi giây có 3,1.1018 electron và 1,1.1018 proton chuyển động qua một tiết diện của ống.
Hãy tính cường độ dòng điện và xác định chiều của nó.
2. Một quả cầu bằng đồng cô lập. Một dây dẫn kim loại mang dòng điện đi vào nó và một dây dẫn
kim loại khác mang dòng điện đi ra khỏi nó. Biết cường độ dòng điện đi vào lớn hơn cường độ
dòng điện đi ra khỏi quả cầu là 2 µA.
a) Hỏi số electron của quả cầu tăng hay giảm theo thời gian?
b) Tính thời gian để quả cầu tăng (hoặc giảm) một lượng 1 000 tỉ electron.
3. Cho dòng điện 4,2 A chạy qua một đoạn dây dẫn bằng kim loại dài 80 cm có đường kính tiết
diện 2,5 mm. Mật độ electron dẫn của kim loại này là 8,5.1028 electron/m3. Hãy tính thời gian
trung bình mỗi electron dẫn di chuyển hết chiều dài đoạn dây. 102 VẬT LÍ 11 Bài 17 ô,175¤ô1+/8t72+0
– Định nghĩa điện trở, đơn vị đo điện trở – Các nguyên nhân chính gây ra điện trở.
– Dạng đường đặc trưng I – U của vật dẫn kim loại ở nhiệt độ xác định.
– Định luật Ohm cho vật dẫn kim loại.
– Sơ lược ảnh hưởng của nhiệt độ lên điện trở của đèn sợi đốt, điện trở nhiệt (thermistor).
Khi vô tình chạm vào đoạn dây có điện bị hở lớp vỏ cách điện, một thợ sửa chữa bị điện giật nhẹ vì có một dòng
điện cỡ 10 mA chạy qua người. Nhưng một người khác cũng chạm vào đoạn dây trên thì có thể nguy hiểm đến tính mạng
do có dòng điện 90 mA chạy qua người. Điều gì tạo nên sự khác biệt này? 1 ĐIỆN TRỞ
Khái niệm điện trở
Ta đã biết, khi đặt một hiệu điện thế vào hai đầu của vật dẫn,
các hạt mang điện tự do sẽ dịch chuyển có hướng dưới tác
dụng của điện trường và tạo ra dòng điện. Quá trình dịch
chuyển có hướng này luôn bị cản trở bởi sự tương tác của
chúng với các hạt cấu thành vật dẫn và giữa chúng với nhau.
Các cấu trúc, sắp xếp khác nhau của các nguyên tử cấu
thành vật dẫn cũng như nhiệt độ và kích thước của vật cũng
ảnh hưởng rõ rệt lên chuyển động có hướng của các hạt
mang điện. Đại lượng đặc trưng cho khả năng cản trở dòng
điện của một vật dẫn được gọi là điện trở.
ĈLӋQWUӣFӫDPӝWYұWGүQOjÿҥLOѭӧQJÿһFWUѭQJFKR
NKҧQăQJFҧQWUӣGzQJÿLӋQFӫDYұWGүQ.KLKLӋX
ÿLӋQWKӃÿһWYjRKDLÿҫXYұWGүQFyJLiWUӏUGzQJ
ÿLӋQFKҥ\WURQJPҥFKFyFѭӡQJÿӝ,WKuÿLӋQWUӣÿѭӧF
1. Nêu nguyên nhân chính gây ra [iFÿӏQKWKHRF{QJWKӭF
điện trở của vật dẫn. R U (17.1) I
Trong hệ SI, điện trở có đơn vị là ôm (Ω). 1 Ω là điện trở
của một vật dẫn mà khi đặt một hiệu điện thế 1 V vào hai
đầu vật dẫn thì dòng điện chạy qua vật dẫn có cường độ 1 A. A
Điện trở của một đoạn dây kim loại S R U S
Ở một nhiệt độ xác định, điện trở của một đoạn dây kim
loại phụ thuộc vào hình dạng, kích thước và bản chất vật R A U liệu của nó. S S
Hình 17.1. Một đoạn dây dẫn kim loại 103 VẬT LÍ 11
ĈLӋQWUӣFӫDPӝWÿRҥQGk\NLPORҥLKuQKWUөFKLӅX
GjLAGLӋQWtFKWLӃWGLӋQS+uQKÿѭӧF[iFÿӏQK WKHRF{QJWKӭF
2. Tìm hiểu và giải thích vì sao R A (17.2)
người ta thường sử dụng đồng S để làm dây dẫn điện.
trong đó ρ là một hệ số tỉ lệ, phụ thuộc vào bản chất vật liệu
làm dây dẫn, được gọi là điện trở suất.
Điện trở suất của một số kim loại ở 20 oC được liệt kê trong Bảng 17.1.
T Bảng 17.1. Giá trị điện trở suất của một số kim loại ở 20 oC .LPORҥL ĈLӋQWUӣVXҩWӣR&P Bạc 1,62.10–8 Đồng 1,69.10–8 Vàng 2,44.10–8 Nhôm 2,75.10–8 Sắt 9,68.10–8
T Bảng 17.2. Bảng quy ước màu sắc để đọc giá trị của điện trở 4 vạch màu
Trong thực tế, điện trở có 560kΩ r 5% hình dạng như Hình 17.2.
Trong đó, các vạch màu thể MÀU Vạch 1 Vạch 2 Vạch 3 Hệ số Dung sai
hiện giá trị của điện trở với Đen 0 0 0 1 Ω
quy ước màu được cho trong Nâu 1 1 1 10 Ω ± 1% (F) Bảng 17.2. Đỏ 2 2 2 100 Ω ± 2% (G) Cam 3 3 3 1k Ω Vàng 4 4 4 10k Ω Xanh lá cây 5 5 5 100k Ω ± 0.5% (D) Xanh da trời 6 6 6 1M Ω ± 0.25% (C) Tím 7 7 7 10M Ω ± 0.10% (B) Xám 8 8 8 ± 0.05% Trắng 9 9 9 Hoàng kim 0.1 ± 5% (J) Bạc 0.01 ± 10% (K)
S Hình 17.2. Hình ảnh điện trở trong thực tế 237Ω r 1% 5 vạch màu 2 ĐỊNH LUẬT OHM
Định luật Ohm đối với đoạn mạch chỉ chứa điện trở
Ở một nhiệt độ nhất định, điện trở R của một đoạn dây kim loại có giá trị hầu như không
phụ thuộc vào hiệu điện thế U giữa hai đầu điện trở hay cường độ dòng điện I chạy qua nó.
Georg Simon Ohm (1789 – 1854) là một nhà vật lí người Đức đã phát biểu định luật mô tả
liên hệ giữa cường độ dòng điện chạy qua một điện trở và hiệu điện thế giữa hai đầu của nó mang tên định luật Ohm. 104 VẬT LÍ 11
&ѭӡQJÿӝGzQJÿLӋQ,FKҥ\TXDPӝWÿLӋQWUӣRWӍOӋ
3. Các công thức (17.1) và (17.3)
WKXұQYӟLKLӋXÿLӋQWKӃUÿһWYjRKDLÿҫXÿLӋQWUӣ
có tương đương nhau không? I U (17.3) Giải thích. R
Khi đó U = IR còn được gọi là độ giảm thế trên R.
Đặt hiệu điện thế U = 1,5 V vào hai đầu một sợi dây dẫn bằng đồng có điện trở
R = 0,6 Ω. Tính cường độ dòng điện chạy qua sợi dây đồng.
Đường đặc trưng vôn – ampe
Đối với nhiều loại vật dẫn, trong đó có kim loại, cường độ
dòng điện I chạy trong vật dẫn luôn tỉ lệ thuận với hiệu điện I (A)
thế U đặt vào hai đầu vật dẫn đó ở một nhiệt độ xác định. 6,0
Nghĩa là điện trở của vật dẫn không phụ thuộc vào U hay I.
Các vật liệu tạo nên vật dẫn có tính chất này được gọi là vật
liệu thuần trở, các vật liệu không có tính chất này được gọi
là vật liệu không thuần trở.
Trong chương trình môn Vật lí ở cấp Trung học phổ thông, O 25 U (V)
ta chỉ xét các vật liệu thuần trở. Khi đó, một đoạn dây dẫn
S Hình 17.3. Đường đặc trưng
thuần trở được đặc trưng bởi một giá trị điện trở duy nhất ở
vôn – ampe của một đoạn dây kim loại ở 20 oC
một nhiệt độ xác định.
Đường biểu diễn sự phụ thuộc của cường độ dòng điện I chạy
qua vật dẫn vào hiệu điện thế U đặt vào hai đầu vật dẫn được
4. Xác định giá trị điện trở của đoạn
gọi là đường đặc trưng vôn – ampe của vật dẫn đó.
dây bằng đồng có đường đặc
Đối với vật dẫn kim loại, ở một nhiệt độ xác định, đường đặc
trưng vôn – ampe như Hình 17.3.
trưng vôn – ampe là một đoạn thẳng như Hình 17.3.
Đặt hiệu điện thế U (U có thể điều chỉnh được) vào hai đầu của một điện trở là
một đoạn dây bằng đồng dài 10 m, đường kính tiết diện 1 mm và điện trở suất
1,69.10–8 Ωm ở 20 oC. Dùng ampe kế đo cường độ dòng điện chạy qua đoạn dây
đồng. Điều chỉnh U, tương ứng với mỗi giá trị của U ta thu được một giá trị của I.
Kết quả thể hiện trong Bảng 17.3. U (V) 0 0,2 0,4 0,6 0,8 1,0 W Bảng 17.3. I (A) 0 0,92 1,85 2,77 3,69 4,62
a) Dựa vào Bảng 17.3, em hãy vẽ đường đặc trưng vôn – ampe của điện trở trên.
b) Tính điện trở của đoạn dây dẫn. So sánh với giá trị thu được từ đường đặc trưng vôn – ampe. 105 VẬT LÍ 11
3 ĐÈN SỢI ĐỐT VÀ ĐIỆN TRỞ NHIỆT Đèn sợi đốt
Khi dòng điện chạy qua một đèn sợi đốt làm bằng dây dẫn
5. Thảo luận về ảnh hưởng của nhiệt
kim loại, các electron trong dòng điện thường xuyên va đập,
đồng thời truyền năng lượng cho các ion dương tại các nút
độ lên điện trở của đèn sợi đốt.
mạng trong dây dẫn, làm cho các ion dương này dao động
mạnh hơn. Kết quả là nhiệt độ của dây dẫn tăng theo, nói
cách khác, đèn sợi đốt đã biến năng lượng của dòng điện chạy R
qua nó thành nhiệt năng và một phần năng lượng nhiệt này
được giải phóng dưới dạng ánh sáng.
Mặt khác, khi nhiệt độ đèn sợi đốt càng tăng, dao động của
các ion dương tại các nút càng mạnh và sự hỗn loạn đóng
góp vào chuyển động của các electron càng tăng. Kết quả là
sự va đập giữa các electron và các ion dương xảy ra với tần
số lớn hơn, điều này có nghĩa chuyển động có hướng tạo 0 W (RC)
nên dòng điện của các electron bị cản trở nhiều hơn. Nói S Hình 17.4. Sự phụ thuộc của điện
cách khác, điện trở kim loại của đèn sợi đốt tăng theo.
trở của một đèn sợi đốt vào nhiệt độ
Đồ thị mô tả sự phụ thuộc của điện trở một đèn sợi đốt vào
nhiệt độ được minh hoạ trong hình 17.4. I (A)
Từ đồ thị này, ta có nhận xét: Trong một khoảng nhiệt độ
khá rộng, điện trở tăng gần như tuyến tính theo nhiệt độ. Ở
vùng nhiệt độ cao, đường biểu diễn hơi cong lên, điều này
có nghĩa điện trở tăng theo nhiệt độ nhanh hơn so với vùng nhiệt độ thấp.
ĈqQVӧLÿӕWOjÿqQFKLӃXViQJNKLEӏÿӕWQyQJQKӡ 0
WiFGөQJQKLӋWFӫDGzQJÿLӋQWURQJNLPORҥLĈLӋQWUӣ U (V)
S Hình 17.5. Đường đặc trưng
FӫDÿqQVӧLÿӕWELӃQWKLrQFKұPWKHRQKLӋWÿӝ
vôn – ampe của một đèn sợi đốt
Đường đặc trưng vôn – ampe của một đèn sợi đốt được thể hiện trong Hình 17.5. Điện trở nhiệt R
Khác với đèn sợi đốt, có một số linh kiện mà điện trở của 104
chúng biến thiên rất nhanh theo nhiệt độ, đó là điện trở nhiệt
(thermistor). Chúng thường được dùng làm các cảm biến nhiệt. 103
ĈLӋQWUӣQKLӋW7KHUPLVWRUOjPӝWOLQKNLӋQÿLӋQWӱ 102
PjÿLӋQWUӣFӫDQyELӃQWKLrQQKDQKWKHRQKLӋWÿӝ 100 100 200 300 W (RC)
Có hai loại điện trở nhiệt chính:
S Hình 17.6. Sự phụ thuộc của giá trị
– Điện trở nhiệt hệ số dương PTC (Positive Temperature
điện trở đối với điện trở nhiệt hệ số
Coefficient) hay còn gọi là điện trở nhiệt thuận: có điện trở
dương (đường màu đỏ) và hệ số âm
(đường màu xanh dương) theo nhiệt độ
tăng khi nhiệt độ tăng (Hình 17.6). 106 VẬT LÍ 11
– Điện trở nhiệt hệ số âm NTC (Negative Temperature
Coefficient) hay còn gọi là điện trở nhiệt nghịch: có điện
trở giảm khi nhiệt độ tăng (Hình 17.6).
Nêu một vài ứng dụng của điện trở nhiệt.
Sơ lược về sự dẫn điện trong hệ thống thần kinh con người
Dòng điện có ở khắp nơi và đem lại nhiều
lợi ích về mọi mặt của đời sống xã hội.
Điều thú vị là ngay trong thế giới sinh vật, trong
các cơ thể sống của động vật, dòng điện cũng
đóng một vai trò rất quan trọng: Dòng điện
trong hệ thống thần kinh giúp con người nhận
thức về thế giới, giao tiếp giữa các bộ phận bên
trong cơ thể và để kiểm soát các cơ,…
S Hình 17.7. Neuron thần kinh con người
Thành phần cơ bản của hệ thần kinh là tế bào thần kinh (neuron) (Hình 17.7).
Khi chưa nhận được kích thích, tế bào ở trạng thái “nghỉ”, mặt trong của màng tế bào tích
điện âm và mặt ngoài của màng tế bào tích điện dương. Hiệu điện thế giữa mặt trong
và mặt ngoài, tuỳ theo loại tế bào, có giá trị trong khoảng từ –60 mV đến –90 mV. Hiệu
điện thế này có thể thay đổi do sự thẩm thấu qua màng tế bào của các ion, phổ biến là K+, Na+, Cl–.
Khi gặp một kích thích như sơ ý chạm tay vào bình nước nóng, nhiệt độ cao làm xáo trộn
nồng độ các ion và làm thay đổi hiệu điện thế giữa mặt trong và ngoài của màng tế bào
của các đầu dây thần kinh dưới da bàn tay. Tuỳ theo kích thích mạnh hay yếu mà hiệu
điện thế này thay đổi từ khoảng –60 mV đến khoảng +40 mV, tạo thành một xung điện
kéo dài khoảng 1 ms và lan truyền dọc theo dây thần kinh dưới dạng dòng điện về não
với tốc độ từ 30 m/s đến 150 m/s. Não xử lí bằng cách tạo một xung điện khác truyền dọc
theo các dây thần kinh để điều khiển co bàn tay lại. %j,7t3
1. Thông tin kĩ thuật của một loại cáp điện được in trên vỏ sản phẩm như sau: Diện tích tiết diện:
1,5 mm2, điện trở mỗi km chiều dài: 12,1 :. Hãy xác định điện trở suất của vật liệu làm cáp điện này. I (A) 1,25 R1
2. Đường đặc trưng vôn – ampe của hai điện trở R và R 1 2
được cho bởi Hình 17P.1.
a) Lập luận để xác định điện trở nào có giá trị lớn hơn. R2
b) Tính giá trị mỗi điện trở. 0 10 8(V)
S Hình 17P.1. Đường đặc trưng
vôn – ampe của hai điện trở 107 VẬT LÍ 11 Bài 18 1*81ô,1
– Khái niệm nguồn điện.
– Định nghĩa suất điện động.
– Mô tả ảnh hưởng của điện trở trong của nguồn điện lên hiệu điện thế giữa hai cực của nguồn điện.
– So sánh các khái niệm: suất điện động và hiệu điện thế. a) b) c)
S Hình 18.1. a) pin năng lượng mặt trời và điện gió; b) ắc quy; c) pin thông dụng
Dòng điện đem lại rất nhiều lợi ích cho cuộc sống con người cũng như sự phát triển của xã hội. Ở chương trình
Trung học cơ sở, trong các thí nghiệm cần có dòng điện, các em đã được làm quen với một số nguồn điện (Hình 18.1) và
sử dụng chúng. Vì sao nguồn điện có thể tạo ra và duy trì dòng điện lâu dài? Những đại lượng vật lí nào đặc trưng cho nguồn điện? NGUỒN ĐIỆN
Khái niệm nguồn điện
Khi nối hai quả cầu kim loại A và B có điện thế khác nhau
(giả sử V > V ) bằng một dây dẫn kim loại, khi đó sẽ có một A B
dòng các electron dịch chuyển từ B đến A (Hình 18.2), đồng
thời hiệu điện thế giữa A và B cũng giảm theo. Khi hiệu điện VA VB
thế giữa A và B giảm dần về không thì dòng điện cũng giảm dần về không. A B
Để duy trì dòng điện, ta cần duy trì hiệu điện thế giữa A và B S Hình 18.2. Nối hai quả cầu kim
khác không. Điều này có nghĩa, trong khi dòng electron liên
loại A và B có điện thế khác nhau
tục di chuyển B đến A thì bằng cách nào đó phải liên tục đưa
bằng dây dẫn kim loại
được các electron từ A về B. Thiết bị tạo ra và duy trì hiệu điện
thế, từ đó duy trì dòng điện trong mạch gọi là nguồn điện.
1JXӗQÿLӋQOjWKLӃWEӏWҥRUDYjGX\WUuVӵFKrQKOӋFK
ÿLӋQWKӃQKҵPGX\WUuGzQJÿLӋQWURQJPҥFKNtQ
Lưu ý: Trong nguồn điện, cực có điện thế cao hơn là cực
dương, cực có điện thế thấp hơn là cực âm. 108 VẬT LÍ 11
Suất điện động của nguồn điện
Khi nối hai cực của một nguồn điện bằng dây dẫn kim
loại thì bên ngoài nguồn, các electron di chuyển từ cực
1. Quan sát Hình 18.3, mô tả chiều
âm qua dây kim loại về cực dương của nguồn điện. Mặt
chuyển động của các hạt mang
khác, để duy trì hiệu điện thế giữa hai cực thì bên trong
điện trong dây dẫn và bên trong
nguồn, các electron này phải tiếp tục được đẩy về cực nguồn điện.
âm. Vì lực điện trường có xu hướng giữ chặt các electron
ở cực dương trong khi cực âm lại đẩy chúng ra xa nó,
do đó, để đẩy chúng về cực âm cần có một nguồn năng
lượng nào đó thực hiện việc này. Nguồn năng lượng đó
có thể là hoá năng trong các pin hoá học, ắc quy,… là cơ E
năng trong các máy phát điện kiểu cảm ứng, là quang G Fđ F – + –
năng trong các pin mặt trời,… – +
Lực tác dụng lên các electron trong việc di chuyển chúng K F – I
về cực âm có bản chất không phải lực điện trường và 1JX͛QÿL͏Q I được gọi là lực lạ. – I
Đối với các điện tích dương thì chiều di chuyển ngược –
với chiều di chuyển của các electron đã xét ở trên.
S Hình 18.3. Dòng dịch chuyển
Xét một mạch điện kín trong đó có dòng điện. Trong
của các điện tích G
khoảng thời gian W có lượng điện tích q > 0 di chuyển (F F – và
lần lượt là lực điện và lực lạ) đ
trong toàn mạch kín thì công của lực lạ A tỉ lệ bậc nhất với điện tích q: A = E q mạch kín Trong đó, E
là hằng số và được gọi là suất điện động mạch kín trong toàn mạch kín.
Nếu mạch chứa nguồn điện và mạch ngoài là điện trở thì nguồn điện là nguyên nhân duy
nhất gây ra lực lạ tác dụng lên các điện tích. Khi đó, công của lực lạ A làm di chuyển điện
tích q trong toàn mạch kín cũng chính bằng công của nguồn điện làm di chuyển điện
tích q từ cực âm đến cực dương trong nguồn. Vì vậy, E
còn gọi là suất điện động mạch kín
của nguồn điện và kí hiệu là E.
6XҩWÿLӋQÿӝQJEFӫDQJXӗQÿLӋQOjÿҥLOѭӧQJYұWOt
ÿһFWUѭQJFKRNKҧQăQJVLQKF{QJFӫDQJXӗQÿLӋQ
2. So sánh sự giống và khác nhau
QyÿѭӧFÿREҵQJWӍVӕJLӳDF{QJFӫDOӵFOҥAOjP
của hai khái niệm: suất điện
GLFKX\ӇQOѭӧQJÿLӋQWtFKq!WӯFӵFkPÿӃQFӵF
động và hiệu điện thế.
GѭѫQJErQWURQJQJXӗQÿLӋQYjÿLӋQWtFKq. E ( A (18.1) q
7URQJKӋ6,VXҩWÿLӋQÿӝQJE FyÿѫQYӏOjY{Q9
Mỗi nguồn điện có một suất điện động nhất định. Giá trị của đại lượng này được ghi trên vỏ
của nguồn (pin, ắc quy,...) (Hình 18.4). 109 VẬT LÍ 11
Xét một nguồn điện có suất điện động 12 V. Xác định công cần thiết của nguồn
điện để dịch chuyển một electron từ cực dương sang cực âm của nguồn.
Hình 18.4 thể hiện một số loại pin và ắc quy trên thị trường. Tìm hiểu và trình bày ngắn gọn thông số của các loại pin và ắc quy này.
S Hình 18.4. Một số loại pin và ắc quy thông dụng
Điện trở trong của nguồn điện
Nguồn điện lí tưởng là nguồn điện không có sự cản trở đối
với sự dịch chuyển của các điện tích từ cực này đến cực kia bên trong nguồn điện.
Trong thực tế, khi các điện tích dịch chuyển bên trong nguồn
điện về các cực của nguồn dưới tác dụng của lực lạ, chúng
luôn va chạm với các hạt vật chất cấu tạo nên nguồn. Do đó,
3. Khi di chuyển bên trong nguồn
sự dịch chuyển của các điện tích bị cản trở. Đại lượng đặc
từ một cực sang cực còn lại dưới
trưng cho việc cản trở sự dịch chuyển của các điện tích bên
tác dụng của lực lạ, sự chuyển
trong nguồn điện được gọi là điện trở trong của nguồn,
động của các điện tích có bị cản
thường kí hiệu là r ( : ).
trở bởi yếu tố nào không?
Khi nguồn điện không được nối với mạch ngoài, nghĩa là
không có dòng điện chạy qua nó thì hiệu điện thế giữa hai EU
cực của nguồn điện có giá trị bằng suất điện động của nguồn. + –
Khi nối nguồn điện với mạch ngoài để có dòng điện I như I K
Hình 18.5. Ở mạch ngoài, dòng điện có chiều từ cực dương
về cực âm, trong khi ở bên trong nguồn điện, dòng điện chạy R
từ cực âm đến cực dương. Như vậy, khi đi từ cực âm đến
S Hình 18.5. Nguồn điện
cực dương bên trong nguồn điện, điện thế tăng một lượng phát dòng điện
đúng bằng suất điện động E, điện trở trong của nguồn điện
lại làm cho điện thế bị giảm một lượng Ir. 110 VẬT LÍ 11
+LӋXÿLӋQWKӃ8JLӳDKDLFӵFFӫDQJXӗQÿLӋQFyVXҩW
4. Mắc hai cực nguồn điện với một
ÿLӋQÿӝQJEYjÿLӋQWUӣWURQJrNKLSKiWGzQJÿLӋQ
điện trở qua một khoá K. Mắc
FѭӡQJÿӝIFKҥ\TXDQJXӗQÿѭӧF[iFÿӏQKEӣL
hai đầu một vôn kế vào hai cực
U = E – Ir (18.2)
của nguồn (Hình 18.6). Bằng
lập luận, em hãy so sánh số chỉ
của vôn kế trong hai trường hợp
Mắc hai cực của một pin có suất điện động 9 V vào khoá K đóng và mở.
hai đầu của một mạch chứa điện trở. Cường độ
dòng điện trong mạch và hiệu điện thế giữa hai
đầu của mạch lần lượt có giá trị đo được là 0,1 A và EU
8,9 V. Xác định giá trị điện trở trong của pin. V
Em hãy giải thích vì sao lời khuyên khi cất giữ pin là cần để pin nơi khô và thoáng mát. R K S Hình 18.6. Ghép nguồn điện
* Nguồn điện ghép nối tiếp:
Khi có Q nguồn điện được ghép nối tiếp với nhau như E U E U E U 1 1 Q Q
Hình 18.7, cực âm của nguồn điện E nối với cực dương 2 2 1 + – + – + –
của nguồn điện E , tương tự với các nguồn điện khác. 2 A B
Khi đó, cực dương của nguồn đầu tiên và cực âm của
S Hình 18.7. Nguồn ghép nối tiếp
nguồn cuối cùng là hai cực của bộ nguồn điện.
Suất điện động của bộ nguồn điện được xác định theo công thức: E = E + E + ... + E (18.3) b 1 2 Q
Điện trở trong của bộ nguồn điện được xác định theo công thức:
r = r + r + ... + r (18.4) b 1 2 Q E U E U 1 1 2 2
Lưu ý: Khi có hai nguồn điện ghép xung đối, tức là cực + – – +
âm (hoặc cực dương) của nguồn này được nối với cực âm A B
(hoặc cực dương) của nguồn kia như Hình 18.8, điện trở
S Hình 18.8. Nguồn ghép xung đối
trong của nguồn vẫn được xác định theo công thức (18.4). Giả sử ( ! ( 1
2 thì suất điện động của bộ nguồn điện được
xác định theo công thức: E = E – E (18.5) b 1 2
Nguồn điện có suất điện động lớn hơn đóng vai trò là
nguồn phát, nguồn điện còn lại đóng vai trò là máy thu điện. 111 VẬT LÍ 11 + –
* Nguồn điện ghép song song: EU
Khi có Q nguồn điện giống nhau được ghép song song, các + –
cực cùng dấu được nối với nhau như Hình 18.9, suất điện Q
động của bộ nguồn điện được xác định theo công thức: A EU B E = E = E = ... = E (18.6) b 1 2 n + –
Điện trở trong của bộ nguồn điện được xác định theo EU công thức: r r
S Hình 18.9. Nguồn ghép song song b (18.7) n
* Nguồn điện ghép hỗn hợp đối xứng: m
Khi có N nguồn điện giống nhau được ghép thành n dãy, + – + – + –
mỗi dãy gồm m nguồn điện ghép nối tiếp như Hình 18.10,
suất điện của bộ nguồn điện được xác định theo công thức: + – + – + – E = mE (18.8) b Q
Điện trở trong của bộ nguồn điện được xác định theo A B công thức: + – + – + – r mr b (18.9) n
S Hình 18.10. Nguồn ghép
hỗn hợp đối xứng %j,7t3
1. Một nguồn điện có suất điện động 6 V và điện trở trong 0,5 Ω. Khi mắc hai cực của nguồn điện
với một vật dẫn thì trong mạch xuất hiện dòng điện 1,4 A. Bỏ qua điện trở các dây nối. Tính hiệu
điện thế giữa hai đầu vật dẫn.
2. Ghép nối tiếp một biến trở R với một điện trở R thành bộ rồi nối hai đầu vào hai cực của một 0
nguồn điện không đổi. Điều chỉnh R, người ta thu được đồ thị đường biểu diễn sự phụ thuộc
của hiệu điện thế giữa hai đầu biến trở vào cường độ dòng điện như Hình 18P.1.
a) Xác định giá trị suất điện động của nguồn điện.
b) Xác định giá trị biến trở R ứng với điểm M trên đồ thị. U (V) 12 M 0 4,8 I (A)
S Hình 18P.1. 112 VẬT LÍ 11 Bài 19 1u1*/¦1*ô,1 &1*68q7ô,1
– Khái niệm năng lượng tiêu thụ điện của đoạn mạch.
– Khái niệm công suất tiêu thụ điện của đoạn mạch.
– Tính năng lượng điện và công suất tiêu thụ điện của một đoạn mạch.
Khi hoạt động, các thiết bị tiêu thụ điện biến đổi điện
năng thành các dạng năng lượng khác. Chẳng hạn, bóng đèn
(Hình 19.1a) biến đổi một phần điện năng thành quang năng,
quạt máy (Hình 19.1b) biến đổi một phần điện năng thành cơ
năng, bàn là (Hình 19.1c) biến đổi điện năng thành nhiệt năng,…
Năng lượng điện mà các thiết bị tiêu thụ phụ thuộc vào các a) b) c)
S Hình 19.1. Một số thiết bị điện gia dụng: yếu tố nào?
a) đèn bàn; b) quạt máy; c) bàn là
1 NĂNG LƯỢNG VÀ CÔNG SUẤT TIÊU THỤ ĐIỆN CỦA ĐOẠN MẠCH
Năng lượng tiêu thụ điện của một đoạn mạch
Khi đặt hiệu điện thế U vào hai đầu một đoạn mạch, lực
1. Dùng các dây dẫn (có điện trở
điện thực hiện công làm cho các điện tích tự do dịch chuyển
không đáng kể) nối hai đầu
có hướng tạo thành dòng điện. Giả sử trong khoảng thời
một điện trở với hai cực của một
gian t có lượng điện tích q chạy qua đoạn mạch. Từ công
nguồn điện thành mạch kín. Khi
thức (13.8), công của dòng điện đã thực hiện trong khoảng
này, dòng điện có sinh công trên thời gian t là:
các đoạn dây nối không? Vì sao?
A = Uq = 8,W
Tùy theo loại thiết bị tiêu thụ điện mà công của dòng điện
thực hiện sẽ chuyển thành các dạng năng lượng khác nhau.
Chẳng hạn, với điện trở thì công của dòng điện thực hiện
chuyển thành nhiệt toả ra trên biến trở. Tổng năng lượng
mà thiết bị tiêu thụ chính bằng công của dòng diện đã thực
hiện trên thiết bị đó.
Năng lượng tiêu thụ của một đoạn mạch bằng tích
của hiệu điện thế giữa hai đầu đoạn mạch với cường
độ dòng điện chạy qua đoạn mạch và với thời gian
dòng điện chạy qua.AUIt (19.1)
Trong hệ SI, năng lượng có đơn vị là jun (J). 113 VẬT LÍ 11
Công suất tiêu thụ điện của một đoạn mạch
Khi so sánh năng lượng tiêu thụ điện của hai thiết bị khác
nhau, chúng ta sẽ không thể xác định được thiết bị nào
“mạnh” hơn nếu chỉ dựa vào giá trị năng lượng tiêu thụ điện của chúng.
Để so sánh, ta cần xét năng lượng tiêu thụ của các thiết bị
trong cùng một khoảng thời gian.
Công suất tiêu thụ của một đoạn mạch là năng lượng
mà đoạn mạch tiêu thụ trong một đơn vị thời gian. A A 2 P = U UI I ( (19.2) I +r I t W '
Trong hệ SI, công suất có đơn vị là oát (W).
Trường hợp đoạn mạch là điện trở
Khi dòng điện chạy từ đầu này đến đầu kia của một điện
trở, thế năng của các điện tích giảm. Việc các hạt tải điện
bị mất năng lượng liên quan đến sự va chạm giữa chúng
2. Xét hai điện trở R và R (R > R ) 1 2 2 1
với các hạt cấu thành điện trở, làm điện trở nóng lên và toả
được ghép song song thành bộ
nhiệt ra môi trường. Như vậy, năng lượng dòng điện cung
và nối vào hai cực của một nguồn
cấp đã chuyển thành nhiệt lượng toả ra trên điện trở. Kết
điện. Hãy cho biết công suất tiêu
luận này đã được Joule (James Prescott Joule) tìm ra lần đầu
thụ điện của điện trở nào lớn hơn. tiên vào năm 1840. Giải thích.
Nhiệt lượng toả ra trên điện trở R được xác định bởi: 2
Q A UIt RI 2t U t (19.3) R
Công suất toả nhiệt được xác định bởi: A 2 2 U 2 P =UI U = RI I ( I +r I (19.4) W ' R
Đặt một hiệu điện thế 12 V vào hai đầu một điện trở 8 Ω.
a) Tính công suất toả nhiệt trên điện trở.
b) Tính nhiệt lượng toả ra trên điện trở sau 1 phút.
2 NĂNG LƯỢNG VÀ CÔNG SUẤT CỦA MỘT NGUỒN ĐIỆN
Sự biến đổi năng lượng trong một nguồn đang phát điện
Xét một nguồn điện có suất điện động E và điện trở trong r
nối với mạch ngoài thành mạch kín. Trong mạch, nguồn
đang phát dòng điện I. 114 VẬT LÍ 11
Bên trong nguồn, dòng điện chạy từ cực âm sang cực dương
với hiệu điện thế giữa hai cực của nguồn là U. Giả sử trong
khoảng thời gian t, có một lượng điện tích q > 0 đi từ cực âm
sang cực dương của nguồn. Khi đó, thế năng tĩnh điện của
lượng điện tích này tăng thêm một lượng:
W = qU = UIt (19.5)
Phần năng lượng tăng thêm này bằng với phần năng lượng
mà nguồn điện cung cấp cho mạch ngoài. Trong trường
hợp mạch ngoài chỉ có điện trở thì chuyển hoá thành nhiệt
3. Khi nguồn điện được nối với
lượng toả ra trên điện trở tương tự như công thức (19.3).
mạch ngoài và phát ra dòng
điện, nhiệt độ của nguồn điện
Kết hợp công thức (19.5) với công thức (18.2) khi nguồn
đang phát điện, ta suy ra năng lượng tiêu thụ điện trong
có tăng lên không? Năng lượng
mạch ngoài khi được nối vào một nguồn đang phát điện
của nguồn điện có thể được
được tính theo công thức:
biến đổi thành những dạng năng lượng nào?
A = W = E,W – rI 2W (19.6)
Công suất tiêu thụ điện của mạch ngoài được tính theo công thức: A 2 2 P = = A UI ( I rI ( I +r (19.7) I t W '
0ӝWSKҫQQăQJOѭӧQJFӫDQJXӗQSKiWUDGzQJÿLӋQFXQJFҩSFKRPҥFKQJRjLSKҫQFzQ
OҥLFKX\ӇQWKjQKQKLӋWOѭӧQJWRҧUDErQWURQJQJXӗQ
Năng lượng và công suất điện
Trong công thức (19.6), số hạng thứ nhất là năng lượng
toàn phần do nguồn điện sinh ra trên toàn mạch: A = E,W (19.8) T 0
Bảng 19.1. Công suất của một số
Công suất của nguồn điện là đại lượng đặc trưng cho tốc nguồn điện
độ sản sinh năng lượng của nguồn điện và được tính theo Nguồn điện Công suất (W) công thức: Nhà máy thuỷ P A0 2 P = A ( I 0 ( (19.9) 0= U I I +r I W 't điện Sơn La 2,4.109
Công suất của một số nguồn điện được cho trong Bảng 19.1. Nhà máy nhiệt điện Phả Lại 2 0,6.109
Như vậy, công suất toàn phần của nguồn điện bằng tổng Máy phát điện
công suất tiêu thụ ở mạch ngoài (có ích) và công suất toả cỡ nhỏ ~ 2.103
nhiệt trên điện trở r bên trong nguồn: rI 2. Hiệu suất của Bộ kích điện ô tô
nguồn điện được xác định bằng tỉ số: sử dụng ắc quy ~ 103 A 2 P ( Sạc dự phòng ~ 10 H P = U U I I +r I AW ' (19.10) P 2 P ( Pin AAA ~ 2,5 0= ( 0 U I I +r I W ' 115 VẬT LÍ 11
Một nguồn điện có suất điện động 11,5 V và điện trở trong 0,8 Ω được nối với mạch
ngoài gồm các điện trở tạo thành một mạch kín. Nguồn phát dòng điện có cường
độ 1 A. Tính công suất điện mà nguồn cung cấp cho mạch ngoài.
Một pin hay ắc quy khi lưu hành trên thị trường sẽ có thêm thông số
cho biết về khả năng cung cấp điện của nó cho các thiết bị khác, đơn
vị Ah (ampe giờ). Ví dụ: Một ắc quy có thông số 10 Ah có nghĩa nó có
khả năng cung cấp dòng điện 1 A trong 10 giờ, hoặc cung cấp dòng
điện 5 A trong 2 giờ, hoặc cung cấp dòng điện 10 A trong 1 giờ,…
Hiện nay, pin sạc dự phòng (Hình 19.2) đang được sử dụng phổ biến
để nạp điện cho các thiết bị như điện thoại thông minh, máy tính
bảng. Xét một pin sạc dự phòng có thông số 15 000 mAh đã tích đầy
điện, khi được kết nối với một thiết bị di động sẽ hoạt động ở công
suất 10 W và hiệu điện thế giữa hai cực của pin bằng 5 V. Tính điện
lượng còn lại trong pin sạc dự phòng khi sử dụng nó để sạc thiết bị
S Hình 19.2. Pin sạc dự phòng trên trong 30 phút. %j,7t3
1. Mắc hai cực của một nguồn điện không đổi có suất điện động 6,0 V và điện trở trong 0,5 Ω vào
hai đầu một điện trở R = 3,5 Ω để tạo thành mạch kín. Bỏ qua điện trở các dây nối. Tính nhiệt
lượng toả ra trên điện trở R trong 1 phút.
2. Mắc hai cực của một nguồn điện không đổi vào hai đầu biến trở R. Điều chỉnh R người ta thu
được đồ thị biểu diễn sự phụ thuộc cường độ dòng điện chạy qua biến trở vào giá trị biến trở
(Hình 19.1P). Xác định suất điện động và điện trở trong của nguồn điện. I (A) 3,0 0 12 R
S Hình 19P.1. Đồ thị mô tả sự phụ thuộc của
cường độ dòng điện vào giá trị biến trở 116 VẬT LÍ 11 7+ &+j1+;k&ô1+ Bài 20 68q7ô,1ô1*9j ô,175¤7521*&$3,1
Đo suất điện động và điện trở trong của pin bằng dụng cụ thực hành.
Ta đã biết, suất điện động và điện trở trong là hai đại lượng đặc trưng của một nguồn điện. Trong quá trình sử
dụng, suất điện động và điện trở trong của nguồn điện có thay đổi không? Làm thế nào để đo suất điện động và điện trở
trong của một nguồn điện?
Thí nghiệm đo suất điện động và điện trở trong của nguồn điện * Mục đích: EU I
Đo suất điện động và điện trở trong của pin chưa qua sử
dụng và pin đã qua sử dụng. R0 * Cơ sở lí thuyết:
Xét mạch điện gồm một nguồn điện có suất điện động E và V
điện trở trong r mắc nối tiếp với mạch ngoài gồm điện trở R A 0
có giá trị đã biết và biến trở R mắc nối tiếp như Hình 20.1. K I
Xem điện trở của các dây dẫn không đáng kể. R
S Hình 20.1. Sơ đồ mạch điện
Khi đóng khoá K, trong mạch xuất hiện dòng điện có cường
độ là I được xác định theo công thức: E U (V) I ( (20.1) R R U 0 r m
Từ (20.1), ta suy ra công thức xác định hiệu điện thế giữa
hai đầu điện trở R là:
U = IR = E– I(r + R ) (20.2) 0
Từ (20.1) và (20.2), ta thấy khi thay đổi R thì I và U cũng O
thay đổi. Theo (20.2), đồ thị mô tả mối quan hệ giữa I và I I (A) m
U là một đoạn thẳng như Hình 20.2. Đoạn thẳng này có
S Hình 20.2. Đồ thị mô tả mối
quan hệ giữa cường độ dòng điện I
đường kéo dài cắt trục tung OU (khi I = 0) tại điểm có giá chạy trong mạch và hiệu điện thế U
trị U = E và cắt trục hoành OI (khi U = 0) tại điểm có giá
giữa hai đầu điện trở R m (E trị I . m r R0 117 VẬT LÍ 11
Lưu ý: Khi mạch hở, hiệu điện thế giữa hai cực của nguồn
điện có giá trị đúng bằng suất điện động E. Nếu mắc hai cực
của nguồn điện với một vôn kế có điện trở rất lớn (cỡ M:)
thì số chỉ của vôn kế gần đúng bằng E. * Dụng cụ:
– 2 pin: 1 pin chưa sử dụng và 1 pin đã qua sử dụng, hộp
1. Dựa vào cơ sở lí thuyết và dụng đựng pin (1).
cụ trong Hình 20.3, hãy thảo luận
nhóm để đưa ra một phương án
– 1 biến trở R (2).
thí nghiệm xác định E và r của pin.
– 1 điện trở R đã biết giá trị (3). 0
2. Tìm hiểu và thảo luận vai trò của
– 2 đồng hồ đo điện đa năng hiện số dùng làm ampe kế một
điện trở R trong mạch điện. 0
chiều và vôn kế một chiều (4). – Khoá K (5).
– Bảng điện (6) và dây nối (7). (1) (4) (5) (3) (7) (6) (2)
S Hình 20.3. Bộ dụng cụ đo suất điện động và điện trở
trong của nguồn điện
* Tiến hành thí nghiệm:
Bước 1: Lắp mạch điện như Hình 20.1.
Lưu ý: Đồng hồ đo thứ nhất dùng làm ampe kế được mắc
nối tiếp với biến trở và điện trở R , đồng hồ đo thứ hai dùng 0
làm vôn kế được mắc song song với biến trở.
Bước 2: Chọn pin cần đo để lắp vào hộp đựng pin.
Bước 3: Chọn thang đo thích hợp cho hai đồng hồ đo điện
đa năng và để biến trở ở giá trị lớn nhất. 118 VẬT LÍ 11
Bước 4: Đóng khoá K. Đọc giá trị của cường độ dòng điện I
chạy trong mạch và hiệu điện thế U giữa hai đầu biến trở,
ghi số liệu vào Bảng 20.1.
Bước 5: Thay đổi giá trị R của biến trở, ứng với mỗi giá trị
của biến trở, đọc giá trị của I và U tương ứng, ghi số liệu vào
3. Hãy nêu các nguyên nhân gây Bảng 20.1.
ra sai số trong phương án thí
nghiệm lựa chọn và cách Lưu ý: khắc phục.
+ Cần ngắt khoá K sau mỗi lần lấy số liệu.
+ Ứng với mỗi pin, cần lấy ít nhất 5 cặp số liệu (I, U) để giảm
sai số trong quá trình xử lí số liệu.
* Báo cáo kết quả thí nghiệm:
– Dựa vào bảng số liệu, vẽ đồ thị mô tả mối quan hệ giữa I và U.
– Xác định suất điện động E và điện trở trong r của pin từ đồ thị.
TBảng 20.1. Bảng số liệu đo cường độ dòng điện trong mạch
và hiệu điện thế giữa hai đầu biến trở Lần 1 2 3 4 5 I (mA) – – – – – U (V) – – – – –
Pin chưa sử dụng thường có điện trở trong nhỏ nên đồ thị thu được sẽ có độ dốc
nhỏ. Do đó, để xác định được giao điểm với trục hoành, ta cần phải lấy một dải số
liệu rộng hơn. Hãy đề xuất một cách xác định r mà không phải kéo dài đồ thị.
Dựa vào phần lưu ý trong cơ sở lí thuyết, hãy đề xuất một phương án khác để đo suất điện động của nguồn điện.
Tiến hành thí nghiệm cho hai pin đã thực hiện đo và so sánh với kết quả đã nhận được. 119 VẬT LÍ 11
Cách tính sai số của đồng hồ đo điện đa năng hiện số
Việc xác định sai số của dụng cụ đo khi sử dụng đồng hồ đo điện đa năng hiện số được
trình bày trong Bảng 20.2 và 20.3 lần lượt cho phép đo hiệu điện thế một chiều và
cường độ dòng điện một chiều.
TBảng 20.2. Sai số của dụng cụ đo hiệu điện thế một chiều Giới hạn đo
Độ chia nhỏ nhất (ĐCNN) Sai số 200 mV 100 PV
± (0,8% số đọc + 10 u ĐCNN) 2 V 1 mV 20 V 10 mV
± (0,5% số đọc + 10 u ĐCNN) 200 V 100 mV 1000 V 1 V
± (1,0% số đọc + 5 u ĐCNN)
TBảng 20.3. Sai số của dụng cụ đo cường độ dòng điện một chiều Giới hạn đo
Độ chia nhỏ nhất (ĐCNN) Sai số 20 PA 10 nA
± (2,0% số đọc + 10 u ĐCNN) 200 PA 0,1 PA 2 mA 1 PA
± (1,2% số đọc + 10 u ĐCNN) 20 mA 10 PA 200 mA 100 PA
± (1,5% số đọc + 10 u ĐCNN) 2 A 1 mA 20 A 10 mA
± (3,5% số đọc + 10 u ĐCNN) Ví dụ:
– Khi dùng thang 20 V để đo hiệu điện thế một chiều, ta đọc được giá trị 12,36 V.
Sai số của phép đo này là: ± (0,5% × 12,36 + 10 × 0,01) = ± (0,06 + 0,1) = ± 0,16 V.
– Khi dùng thang 200 mA để đo cường độ dòng điện một chiều, ta đọc được giá trị 15,7 mA.
Sai số của phép đo này là: ± (1,5% × 15,7 + 10 × 0,1) = ± (0,235 + 1,0) = ± 1,2 mA. 120 VẬT LÍ 11 X 71*.7&+¡1* X
1 DÒNG ĐIỆN. CƯỜNG ĐỘ DÒNG ĐIỆN
±'zQJÿLӋQOjGzQJFKX\ӇQGӡLFyKѭӟQJFӫDFiFÿLӋQWtFK&KLӅXGzQJÿLӋQÿѭӧF
TX\ѭӟFOjFKLӅXGӏFKFKX\ӇQFyKѭӟQJFӫDFiFÿLӋQWtFKGѭѫQJQJѭӧFYӟLFKLӅXGӏFK
FKX\ӇQFyKѭӟQJFӫDFiFÿLӋQWtFKkP
±ĈҥLOѭӧQJYұWOtÿһFWUѭQJFKRWiFGөQJPҥQKKD\\ӃXFӫDGzQJÿLӋQJӑLOjFѭӡQJÿӝ
GzQJÿLӋQÿѭӧF[iFÿӏQKEҵQJÿLӋQOѭӧQJGӏFKFKX\ӇQTXDWLӃWGLӋQWKҷQJSWURQJPӝW ÿѫQYӏWKӡLJLDQ I q ∆ = t ∆
7URQJKӋ6,FѭӡQJÿӝGzQJÿLӋQFyÿѫQYӏOjDPSH$
7URQJKӋ6,ÿLӋQWtFKFyÿѫQYӏOjFXO{QJ&& $V
2 SỰ PHỤ THUỘC CƯỜNG ĐỘ DÒNG ĐIỆN VÀO VẬN TỐC TRÔI
9ұQWӕFWU{LFӫDFiFKҥWWҧLÿLӋQWӍOӋYӟLFѭӡQJÿӝGzQJÿLӋQFKҥ\WURQJYұWGүQ v I nS q
3 ĐIỆN TRỞ – ĐÈN SỢI ĐỐT VÀ ĐIỆN TRỞ NHIỆT
±ĈLӋQWUӣFӫDPӝWYұWGүQOjÿҥLOѭӧQJÿһFWUѭQJFKRNKҧQăQJFҧQWUӣGzQJÿLӋQFӫDYұW
GүQ.KLKLӋXÿLӋQWKӃÿһWYjRKDLÿҫXYұWGүQFyJLiWUӏUGzQJÿLӋQFKҥ\WURQJPҥFKFy
FѭӡQJÿӝIWKuÿLӋQWUӣÿѭӧF[iFÿӏQKWKHRF{QJWKӭF R U I
7URQJKӋ6,ÿLӋQWUӣFyÿѫQYӏOj{Pȍȍ 9$
±ĈqQVӧLÿӕWOjÿqQFKLӃXViQJNKLEӏÿӕWQyQJQKӡWiFGөQJQKLӋWFӫDGzQJÿLӋQOrQGk\
GүQNLPORҥLĈLӋQWUӣFӫDÿqQVӧLÿӕWWăQJJҫQQKѭWX\ӃQWtQKYӟLQKLӋWÿӝ
±ĈLӋQWUӣQKLӋWOjOLQKNLӋQÿLӋQWӱPjJLiWUӏÿLӋQWUӣFӫDQyELӃQWKLrQUҩWQKҥ\WKHR QKLӋWÿӝ
4 SUẤT ĐIỆN ĐỘNG – ĐỊNH LUẬT OHM CHO CÁC ĐOẠN MẠCH
±6XҩWÿLӋQÿӝQJFӫDQJXӗQÿLӋQÿһFWUѭQJFKRNKҧQăQJVLQKF{QJFӫDQJXӗQ E ( = Aq 121 VẬT LÍ 11
±ĈRҥQPҥFKFKӭDÿLӋQWUӣR+LӋXÿLӋQWKӃUYjFѭӡQJÿӝGzQJÿLӋQIWKRҧ I = UR
±ĈRҥQPҥFKFKӭDQJXӗQÿDQJSKiWGzQJÿLӋQI+LӋXÿLӋQWKӃYjFѭӡQJÿӝGzQJ ÿLӋQIWKRҧ U = E – rI
5 NĂNG LƯỢNG TIÊU THỤ VÀ CÔNG SUẤT TIÊU THỤ CỦA MỘT MẠCH ĐIỆN
±1ăQJOѭӧQJWLrXWKөFӫDPӝWÿRҥQPҥFKEҵQJWtFKFӫDKLӋXÿLӋQWKӃJLӳDKDLÿҫXÿRҥQ
PҥFKYӟLFѭӡQJÿӝGzQJÿLӋQFKҥ\TXDÿRҥQPҥFKYjYӟLWKӡLJLDQGzQJÿLӋQFKҥ\TXD A = UIt
7URQJKӋ6,QăQJOѭӧQJFyÿѫQYӏOjMXQ-
±&{QJVXҩWFӫDGzQJÿLӋQÿһFWUѭQJFKRWӕFÿӝVLQKF{QJFӫDGzQJÿLӋQ A 2 P = U
UI I ( I +r I t W '
7URQJKӋ6,F{QJVXҩWFyÿѫQYӏOjRiW:.
6 ĐỊNH LUẬT JOULE – LENZ
±1KLӋWOѭӧQJWRҧUDWUrQÿLӋQWUӣR: 2
Q UIt RI 2t = U t R
– &{QJVXҩWWRҧQKLӋWWUrQÿLӋQWUӣR: A Q 2 2 U 2 P = U UI I ( RI I +r I t W ' R
7 NĂNG LƯỢNG VÀ CÔNG SUẤT CỦA NGUỒN ĐIỆN
±1ăQJOѭӧQJWRjQSKҫQFӫDQJXӗQÿLӋQ A I ( t UIt rI 2 t 0
±&{QJVXҩWWRjQSKҫQFӫDQJXӗQÿLӋQ A0 0 P I ( 0 t ±+LӋXVXҩWFӫDQJXӗQÿLӋQ A 2 P =
U I ( I +r I H P U W ' P0 P ( 0 122 VẬT LÍ 11 *,l,7+&+7+8t71* CHƯƠNG THUẬT NGỮ
GIẢI THÍCH THUẬT NGỮ TRANG 2 Cảm ứng từ
Cảm ứng từ tại một điểm trong từ trường là đại lượng đặc trưng cho
độ mạnh yếu của từ trường tại điểm đó. 46 4
Chuyển động nhiệt Chuyển động hỗn loạn không ngừng về mọi phía. 101 4
Công suất toả nhiệt Nhiệt lượng toả ra môi trường trong một đơn vị thời gian. 114
Điện cực là phần tử dẫn điện được sử dụng để tạo ra kết nối điện 3 Điện cực
giữa mạch điện và môi trường, có thể trao đổi electron với môi 84 trường đó. 4 Điện tích tự do
Điện tích không liên kết với phân tử, nguyên tử hay ion và có thể chuyển động tự do. 113 4
Đồng hồ đo điện Thiết bị đo điện dùng để đo hiệu điện thế, cường độ dòng điện, điện đa năng
trở, điện dung, kiểm tra điôt, kiểm tra thông mạch,… 118 2 Hoạ âm
Những âm có tần số là bội số của tần số âm cơ bản. 60 3 Ion hóa
Quá trình một nguyên tử hay phân tử nhận thêm hay mất đi electron để
tạo thành các ion âm hay dương. 72 3 Lực điện
Lực do điện trường tác dụng lên các hạt điện tích đặt trong nó. 73 3 Lực tĩnh điện
Lực giữa hai vật mang điện tích đứng yên. 72 2
Mật độ môi trường Lượng vật chất trong một đơn vị thể tích môi trường (rắn, lỏng, khí). 41 4 Máy thu điện
Chuyển hoá một phần điện năng tiêu thụ thành các dạng năng lượng khác, ngoài nhiệt năng. 111 3 Năng lượng điện
Năng lượng được sinh ra bởi sự chuyển động có hướng của dòng điện tích. 93 4 Nguyên tử lượng
Khối lượng của một nguyên tử tính bằng đơn vị carbon (đvC). 102 3 Nhiễm điện
Sự tích tụ của các điện tích trên bề mặt của một vật. Vật nhiễm điện có
thể hút, hoặc đẩy hoặc phóng tia lửa điện qua các vật khác. 68 4 Nhiệt lượng
Nhiệt lượng là phần nhiệt năng mà vật nhận được hay mất đi trong quá trình truyền nhiệt. 114 3 Phân rã
Sự biến đổi tự phát của một hạt không bền thành các hạt khác. 86 2 Sóng âm
Sóng cơ truyền trong các môi trường vật chất (rắn, lỏng, khí), khi đến
tai người, sóng âm sẽ làm cho màng nhĩ dao động tạo nên cảm giác âm. 34 123 VẬT LÍ 11
Nhà xuất bản Giáo dục Việt Nam xin trân trọng cảm ơn
các tác giả có tác phẩm, tư liệu được sử dụng, trích dẫn
trong cuốn sách này
Chịu trách nhiệm xuất bản:
Tổng Giám đốc HOÀNG LÊ BÁCH
Chịu trách nhiệm nội dung:
Tổng biên tập PHẠM VĨNH THÁI Biên tập nội dung:
NGUYỄN BÔNG – PHẠM TRƯỜNG THỊNH
Biên tập kĩ – mĩ thuật: PHẠM THỊ HẠ LIÊN Thiết kế sách: PHẠM THỊ HẠ LIÊN Trình bày bìa:
TỐNG THANH THẢO – ĐẶNG NGỌC HÀ Minh hoạ: ANH NHÂN – TRÚC LINH Sửa bản in:
NGUYỄN BÔNG – PHẠM TRƯỜNG THỊNH Chế bản tại:
CÔNG TY CỔ PHẦN DỊCH VỤ XUẤT BẢN GIÁO DỤC GIA ĐỊNH
%ҧQTX\ӅQWKXӝF1Kj[XҩWEҧQ*LiRGөF9LӋW1DP
yƵҤƚďңŶƉŚҦŵĜĆĜĉŶŐŬşƋƵǇҲŶƚĄĐŐŝң͘dҤƚĐңĐĄĐƉŚҥŶĐӆĂŶҾŝĚƵŶŐĐƵҺŶƐĄĐŚŶăǇĜҲƵŬŚƀŶŐ
ĜӇӄĐƐĂŽĐŚĠƉ͕ůӇƵƚƌӋ͕ĐŚƵǇҳŶƚŚҳĚӇӀŝďҤƚŬŞŚŞŶŚƚŚӈĐŶăŽŬŚŝĐŚӇĂĐſƐӌĐŚŽƉŚĠƉďҪŶŐǀĉŶďңŶ
ĐӆĂEŚăǆƵҤƚďңŶ'ŝĄŽĚӅĐsŝҵƚEĂŵ͘ 9t7/&K±QWUäLVQJW°R Mã số: G2HHYL002M23
In………bản, (QĐ in số…) Khổ 19x26,5 cm.
Đơn vị in:………………………
Cơ sở in:………………………
Số ĐKXB: 9-2023/CXBIPH/43-2142/GD
Số QĐXB: … ngày … tháng … năm 20 …
In xong và nộp lưu chiểu tháng … năm 20…
Mã số ISBN: 978-604-0-35188-3 124
PHẠM NGUYỄN THÀNH VINH (Chủ biên) PHẠ
TRẦN NGUYỄN NAM BÌNH – ĐOÀN HỒNG HÀ – BÙI QUANG HÂN – ĐỖ XUÂN HỘI M NGUY
NGUYỄN NHƯ HUY – TRƯƠNG ĐẶNG HOÀI THU – TRẦN THỊ MỸ TRINH ỄN THÀNH
HUÂN CHƯƠNG HỒ CHÍ MINH VINH ( Chủ biên) VẬT LÍ 11 VẬT LÍ 11 ,6%1 ,6%1 ,6%1 ,6%1 *++0 *++0 *++0 *++0 %̫QLQWK͵
NHÀ XUẤT BẢN GIÁO DỤC VIỆT NAM 6iFKNK{QJEiQ ,6%1 ,6%1 ,6%1 ,6%1 *++0 *++0 *++0 *++0 ,6%1 ,6%1 ,6%1 ,6%1 *++0 *++0 *++0 *++0 ,6%1 ,6%1 ,6%1 ,6%1 *++0 *++0 *++0 *++0 ,6%1 ,6%1 ,6%1 ,6%1 *++0 *++0 *++0 *++0 ,6%1 ,6%1 ,6%1 ,6%1 *++0 *++0 *++0 *++0 ,6%1 ,6%1 ,6%1 ,6%1 *++0 *++0 *++0 *++0

Sách giáo khoa Vật Lí 11 - Chân trời sáng tạo

Thông tin :

Tài liệu liên quan:

Sách giáo khoa Vật Lí 11 - Cánh diều

Sách giáo khoa Vật Lí 11 - Kết nối tri thức