Sai số của phép đo các đại lượng vật lý - Thí nghiệm vật lí | Trường Đại học Bách khoa Thành phố Hồ Chí Minh
Khi nghiên cứu các hiện tượng tự nhiên, trong Vật lý học người ta thường dùng phương pháp thực nghiệm: tiến hành các phép đo các đại lượng vật lý đặc trưng cho hiện tượng, xác định mối liên hệ giữa chúng, từ đó rút ra quy luật vật lý. Để thực hiện các phép đo, ta phải có các dụng cụ đo. Tuy nhiên trong thực tế, hầu như không một dụng cụ đo nào, không một phép đo nào có thể cho ta giá trị thực của đại lượng cần đo. Các kết quả thu được chỉ là gần đúng. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !
Môn: Vật lý
Trường: Đại học Bách khoa Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
lOMoAR cPSD| 46958826 lOMoAR cPSD| 46958826 Trang+8 BÀI MỞ ĐẦU
SAI SỐ CỦA PHÉP ĐO CÁC ĐẠI LƯỢNG VẬT LÝ
Khi nghiên cứu các hiện tượng tự nhiên, trong Vật lý học người ta thường dùng phương
pháp thực nghiệm: tiến hành các phép đo các đại lượng vật lý đặc trưng cho hiện tượng, xác
định mối liên hệ giữa chúng, từ đó rút ra quy luật vật lý.
Để thực hiện các phép đo, ta phải có các dụng cụ đo. Tuy nhiên trong thực tế, hầu như
không một dụng cụ đo nào, không một phép đo nào có thể cho ta giá trị thực của đại lượng cần
đo. Các kết quả thu được chỉ là gần đúng. Vì sao vậy? Điều này có mâu thuẫn hay không với quan
niệm cho rằng Vật lý là một môn khoa học chính xác? Để trả lời câu hỏi này, trước hết ta cần làm
rõ khái niệm: phép đo các đại lượng vật lý là gì? Vì sao có sự sai lệch giữa giá trị thực của đại
lượng cần đo và kết quả đo? Từ đó xác định kết quả và đánh giá được độ chính xác của phép đo.
I PHÉP ĐO CÁC ĐẠI LƯỢNG VẬT LÝ. HỆ ĐƠN VỊ SI.
Phép đo các đại lượng vật lý
Ta dùng một cái cân để đo khối lượng một vật. Cái cân là một dụng cụ đo, và phép đo
khối lượng của vật thực chất là phép so sánh khối lượng của nó với khối lượng của các quả
cân, là những mẫu vật được quy ước có khối lượng bằng một đơn vị (1 gam, 1 kilôgam...)
hoặc bằng bội số nguyên lần đơn vị khối lượng. Vậy:
Phép đo một đại lượng vật lý là phép so sánh nó với đại lượng cùng loại được quy ước
làm đơn vị để có kết quả bằng số so với đơn vị đo.
Phép đo trực tiếp : Công cụ để thực hiện việc so sánh nói trên gọi là dụng cụ đo, phép
so sánh trực tiếp thông qua dụng cụ đo gọi là phép đo trực tiếp.
Ví dụ : Đo điện trở R bằng Ohm kế.
Phép đo gián tiếp: Trong nhiều trường hợp giá trị của đại lượng cần đo được suy ta từ giá
trị của các đại lượng đo trực tiếp thông qua một biểu thức toán học. Nhiều đại lượng vật lý có thể
đo trực tiếp như chiều dài, khối lượng, thời gian,... trong khi những đại lượng vật lý khác như gia
tốc, khối lượng riêng, thể tích,... không có sẵn dụng cụ đo để đo trực tiếp, nhưng có thể xác định
thông qua một công thức liên hệ với các đại lượng đo trực tiếp. Ví dụ, gia tốc rơi tự do g có
thể xác định theo công thức g = 2s , thông qua hai phép đo trực tiếp là phép đo độ dài quãng t 2
đường s và thời gian rơi t. Phép đo như thế gọi là phép đo gián tiếp.
Hệ đơn vị đo
Đơn vị đo là giá trị đơn vị tiêu chuẩn về một đại lượng đo nào đó được quốc tế quy định
mà mỗi quốc gia đều lựa chọn và cam kết tuân thủ. Trên thế giới người ta đã chế tạo ra những
đơn vị tiêu chuẩn được gọi là các chuẩn. Việc chế tạo, thống nhất và lựa chọn các chuẩn ngày
càng hoàn thiện cùng với sự tiến bộ của khoa học kỹ thuật. lOMoAR cPSD| 46958826
Lịch sử phát triển và hoàn thiện các chuẩn quốc tế bắt đầu từ năm 1881 tại Hội nghị
Quốc tế ở Pari. Lần đầu tiên một ủy ban quốc tế quản lý việc thiết lập các đơn vị chuẩn được
thành lập. Trải qua nhiều năm các chuẩn quốc tế dần được thống nhất và ấn định. Bắt đầu từ
năm 1960, một hệ thống các đơn vị đo các đại lượng vật lý đã được quy định thống nhất áp
dụng tại nhiều nước trên thế giới, trong đó có Việt Nam, gọi là hệ SI (System International;
tiếng Pháp: Système International d'unités).
Hệ SI quy định 7 đơn vị cơ bản, đó là: - Đơn vị độ dài : mét (m)
- Đơn vị thời gian : giây (s)
- Đơn vị khối lượng : kilôgam (kg) -
Đơn vị nhiệt độ : kenvin (K)
Đơn vị cường độ dòng điện : ampe (A)
- Đơn vị cường độ sáng : canđela (Cd)
- Đơn vị lượng chất : mol (mol).
Ngoài 7 đơn vị cơ bản, các đơn vị khác là những đơn vị dẫn xuất, được suy ra từ các đơn vị cơ kg .m
bản theo một công thức, ví dụ: đơn vị lực F là niutơn (N), được định nghĩa: 1N = 1 . Ngoài s 2
ra có một số đại lượng không thứ nguyên (dimensionless quantity) là đại lượng mà không có
thứ nguyên vật lý nào gán với nó, thu được như là kết quả của việc chia hai đại lượng cùng
thứ nguyên (ví dụ : chiết suất).
Các bội, ước thập phân của đơn vị đo lường chính thức thuộc hệ đơn vị SI
Bội, ước thập phân của một đơn vị đo lường chính thức thuộc hệ đơn vị SI
được thiết lập bằng cách ghép tên, ký hiệu của một tiền tố SI liền vào phía trước tên, ký
hiệu đơn vị đo lường này;
Tên, ký hiệu của tiền tố SI và thừa số quy đổi quy định trong Bảng 1. Bảng 1 Tên Ký hiệu Thừa số Quốc tế Việt Nam Bội yotta yôtta Y
1 000 000 000 000 000 000 000 000 = 1024 zetta zetta Z
1 000 000 000 000 000 000 000 = 1021 exa exa E
1 000 000 000 000 000 000 = 1018 peta peta P 1 000 000 000 000 000 = 1015 tera tera T 1 000 000 000 000 = 1012 giga giga G 1 000 000 000 = 109 lOMoAR cPSD| 46958826 Tên Ký hiệu Thừa số Quốc tế Việt Nam mega mega M 1 000 000 = 106 kilo kilô k 1 000 = 103 hecto hectô h 100 = 102 deca deca da 10 = 101 Ước deci deci d 0,1 = 10-1 centi centi c 0,01 = 10-2 mili mili m 0,001 = 10-3 0,000 001 = 10-6 micro micrô m nano nanô n 0,000 000 001 = 10-9 pico picô p 0,000 000 000 001 = 10-12 femto femtô f 0,000 000 000 000 001 = 10-15 atto attô a
0,000 000 000 000 000 001 = 10-18 zepto zeptô z
0,000 000 000 000 000 000 001 = 10-21 yocto yoctô y
0,000 000 000 000 000 000 000 001 = 10-24
Để thiết lập một (01) bội hoặc ước thập phân của đơn vị đo lường chính thức thuộc
hệ đơn vị SI, chỉ được sử dụng một tiền tố SI đơn nhất để kết hợp với đơn vị đo lường này.
Ví dụ: nanômét: 1 nm hoặc 10-9 m (không được viết: milimicrômét: mmm).
Trong đó: nanô là tên gọi; n là ký hiệu và 10-9 là thừa số của tiền tố này.
Ghi chú: Quy định này không áp dụng khi kết hợp với đơn vị cơ bản kilôgam. Vì
lý do lịch sử, kilôgam đã chứa một tiền tố là kilô của gam. Các ước hoặc bội thập phân
của kilôgam được hình thành trên cơ sở kết hợp với tiền tố SI của gam. lOMoAR cPSD| 46958826 II SAI SỐ PHÉP ĐO
Khi đo một đại lượng vật lý, dù là đo trực tiếp hay gián tiếp, bao giờ ta cũng mắc phải
những sai số. Các dụng cụ đo không thể nào giúp chúng ta thu nhận được k ết quả đo chính xác
tuyệt đối, kể cả được chế tạo tỉ mỉ đến mức nào. Do đó mọi dụng cụ đo có một giới hạn là cấp
chính xác của nó. Ví dụ đối với thước mm có cấp chính xác là 0.5mm, khi tiến hành đo khoảng
cách hay chiều dài, chúng ta phải thực hiện so sánh ở hai vị trí khác nhau (ứng với hai vạch
khác nhau trên thước mm). Do đó, sai số dụng cụ trong trường hợp đo khoảng cách là đúng
bằng 1 độ chia nhỏ nhất trên thước mm, bằng 1mm. Sai số tuyệt đối cho bất kỳ một dụng cụ
đo nào chính là độ chia nhỏ nhất của nó. Tất cả các phép đo thực hiện 01 lần thì sai số tuyệt
đối cũng chính là độ chia nhỏ nhất của dụng cụ được sử dụng.
Do không thể tránh khỏi có sai số trong kết quả đo, trong giới hạn môn học này
chúng được tạm phân thành hai loại:
Sai số hệ thống
Giả sử một vật có độ dài thực là l = 32,7mm. Dùng một thước có độ chia nhỏ nhất 1mm để đo l,
ta chỉ có thể xác định được l có giá trị nằm trong khoảng giữa 32 và 33mm, còn phần lẻ không thể
đọc trên thước đo. Sự sai lệch này, do chính đặc điểm cấu tạo của dụng cụ đo gây ra, gọi là
sai số dụng cụ.
Sai số d ụng cụ là không thể tránh khỏi, thậm chí nó còn tăng lên khi điểm 0 ban đầu bị
lệch đi, mà ta sơ suất trước khi đo không hiệu chỉnh lại. Kết quả là giá trị đại lượng đo thu
được luôn lớn hơn, hoặc nhỏ hơn giá trị thực. Sai lệch do những nguyên nhân trên gây ra gọi
là sai số hệ thống. Sai số hệ thống xuất hiện do sai sót của dụng cụ đo hoặc do lý thuyết
phương pháp đo chưa hoàn chỉnh, chưa tính đến hết các yếu tố ảnh hưởng đến kết quả đo.
Sai số hệ thống có thể lo ại trừ được bằng cách kiểm tra, điều chỉnh lại các dụng cụ, bằng cách
hoàn thiện lý thuyết phương pháp đo hoặc đưa vào các số hiệu chỉnh.
a) Sai số hệ thống dụng cụ đo chia vạch
Cấp chính xác (CCX) của dụng cụ đo chia vạch bằng 1/2 độ chia nhỏ nhất (ĐCNN) của dụng ệ ố ụ ụ đo ệ ố ∆ = ố
cụ chia vạch. ℎ
1 độ chia nhỏ nhất. × + .
- cấp chính xác của dụng cụ đo∆ hiệ= %ố b) Sai s h th ng do d ng c hi n s ℎ % ị đo hiệ ố ự ế ể ị ụ ụ đo) n s - giá tr
n s (th c t hi n th trên d ng c
- số tự nhiên (1, 2, 3, …)
- độ phân giải.
c) Sai số hệ thống do dụng cụ đo điện bằng kim ∆ ℎ = %× lOMoAR cPSD| 46958826 % ấ ủ ụ
- giá trị cực đại hay thang đo
- c p chính xác c a d ng cụ đo hiện số ả %,
- những thông số thiết bị thường được ghi nhận trong bảng thông số kỹ thuật của nhà s n xuất. Sai số ngẫu nhiên
Lặp lại phép đo thời gian rơi tự do của cùng một vật giữa hai điểm A, B, ta nhận được các
giá trị khác nhau. Sự sai lệch này không có nguyên nhân rõ ràng, có thể do hạn chế về khả năng
giác quan của con người dẫn đến thao tác đo không chuẩn, hoặc do điều kiện làm thí nghiệm
không ổn định, chịu tác động của các yếu tố ngẫu nhiên bên ngoài ... Sai số gây ra trong trường
hợp này gọi là sai số ngẫu nhiên. Sai số ngẫu nhiên làm cho kết quả do lệch cả về hai phía (khi lớn
hơn, khi nhỏ hơn) so với giá tr ị thực của đại lượng cần đo. Sai số ngẫu nhiên không thể loại trừ
hẳn được. Trong các phép đo ta cần phải đánh giá được sai số ngẫu nhiên.
Trong các phép đo ta cũng có thể mắc phải sai lầm. Sai lầm khác với các sai số nói trên,
sinh ra chủ yếu do sự cẩu thả, thiếu cẩn thận của người làm thực nghiệm, làm cho kết quả
đo lệch quá xa giá trị thực của đại lượng cần đo. Sai lầm được loại bỏ bằng cách lặp lại phép
đo và loại bỏ kết quả khỏi tập hợp kết quả đo.
Giá trị trung bình (Khi các đại lượng trên lý thuyết là hằng số)
Sai số ngẫu nhiên làm cho kết quả phép đo trở nên kém tin cậy. Để khắc phục người ta lặp
lại phép đo nhiều lần. Khi đo n lần cùng một đại lượng A, ta nhận được các giá trị khác nhau:
A1, A2, …An. Giá trị trung bình của chúng:
A = A +A +...+A 1 2 n (1) n
sẽ là giá trị gần đúng nhất với giá trị thực của đại lượng A.
Cách xác định sai số của phép đo
Trị tuyệt đối của hiệu số giữa trị trung bình và giá trị của mỗi lần đo gọi là
sai số tuyệt đối ứng với lần đo đó: ố ệt đố
ủa phép đo là độ ệ ủa phép đo khỏ ị ự Sai s tuy i c l ch∆ c = | − | i giá tr th c : trong đó:
A- là giá trị thực chính xác;
a - là giá trị đo được.
Sai số tỉ đối A của phép đo là tỉ số giữa sai số tuyệt đối và giá trị A (hoặc giá trị trung
bình) của đại lượng đo, tính bằng phần trăm:
A = A.100% A lOMoAR cPSD| 46958826
Sai số tỉ đối càng nhỏ thì phép đo càng chính xác.
Độ lệch của từng lần đo so với giá trị trung bình: A = = = (2) 1
A− A1 ;A2
A− A2 ;A3 A− A3 ;...
Nếu hầu hết độ lệch của từng lần đo so với giá trị trung bình là rất nhỏ, các giá trị đo được
của từng lần đo gần nhau và gần giá trị chính xác. Môt số độ lệch là số dương, một số độ lệch là số
âm. N ếu sai số tuân theo phân phối ngẫu nhiên, số độ lệch có trị số âm và số độ lệch có trị số
dương là ngang bằng nhau. Trong trường hợp môn học này, chúng ta sẽ lấy giá trị tuyệt đối tất
cả các độ lệch như ở (2). Sai số tuyệt đối trung bình của n lần đo được tính theo công thức:
A = A + A +...+ A (3) 1 2 n n
Giá trị A xác định theo (3) là sai số ngẫu nhiên. Như vậy, để xác định sai số ngẫu nhiên ta
phải đo nhiều lần. Trong trường hợp không cho phép thực hiện phép đo nhiều lần (n < 5), người
ta không tính sai số ngẫu nhiên bằng cách lấy trung bình theo công thức (3), mà chọn giá trị cực
đại Amax , trong số các giá trị sai số tuyệt đối thu được từ (2). Sai số trung bình là chỉ số đánh
giá thô độ chính xác của phép đo. Ưu điểm cơ bản là đơn giản, giúp phát hiện nhanh chóng
những sai sót trong quá trình thí nghiệm.
Sai số toàn phương trung bình
Sai số toàn phương trung bình của một phép đo riêng biệt được tính theo công thức: = √∑ (∆ )2 =1− 1
Khi số lần đo đủ lớn (n > 10), có thể biểu diễn kết quả của một lần đo riêng biệt với sai số phép đo lặ ạ ần đượ ứ − ; +
toàn phương trung bình:
. Như thế có nghĩa là xác suất khoảng 2/3 kết quả đo nhận được ±
các giá trị trong khoảng .
Sai số toàn phương[
trung bình ]của p l i n l c tính theo công th c: ∑ =1 (∆ )2 ̅ = √ √ ( −1)
đo Sai số toàn phương trung bình của giá trị trung bình tỉ lệ nghịch với căn bậc hai của số lần
( ). Rõ ràng có thể tăng độ chính xác của các kết quả đo bằng cách tăng số lần đo n. ̅ ể →∞, ̅ →0 ̅ → √ Khi nghĩa là
. Kết luận này chỉ đúng v ới sai s ố ngẫu nhiên. Nếu b iết
, ta có th biết với xác suất bao nhiêu, giá trị trung bình rơi vào trong một khoảng cho trước
đối với giá trị thực X. lOMoAR cPSD| 46958826
Bảng 2 cho biết khoảng tin cậy, xác suất tin cậy % tương ứng số lần đo. Số lần đo
Khoảng tin cậy của ̅ ̅ = (± ) ̅ = 3 (±3 ) ̅ = 2 (±2 ) 2 60 78 83
Xác suất tin cậy 3 76 92 96 (%) 4 85 96 99,10 5 91 98,5 99,40 6 93 99,4 99,92 7 95 99,7 99,96 chính xác ̅
Cần phân biệt rõ việc sử dụng sai số toàn phương trung bình của một lần thực hiện phép
đo riêng biệt và sai số toàn phương trung bình của giá trị
. Cần tính khi muốn chú ý độ
bình s ố học tất cả các kết quả đo đ ã th ực hiện, ta tính ̅ .
(hay độ tản mạn) của một phương pháp đo. Còn khi muốn đánh giá sai số của một trung
Ví dụ: Đo đường kính d của hình trụ kim loại bằng thước kẹp có độ chia nhỏ nhất 0,1mm. ∆ (∆ ) 2 Lần đo d (mm) 1 12,5 0,16 0,0256 2 12,3 0,04 0,0016 3 12,3 0,04 0,0016 4 12,2 0,14 0,0196 5 12,4 0,06 0,0036 6 12,3 0,04 0,0016 7 12,4 0,06 0,0036 n = 7 7 ̅ ̅ ∑(∆ )2 = 0,0572 = 12,34 ∆ = 0,07714 =1 0,0572 = √ = 0,098 ≈ 0,1 6 ∆ = ̅ = 0,098
= 0,037 ≈ 0,04 ( á ấ ậ 95%) √7 ∆ ℎ = 0,1 ∆ = 0,04 + 0,1 = 0,14 0,14 Kết quả: = . 100 = 1,13% 12, 34 = 12,34 ± 0,14 lOMoAR cPSD| 46958826
Để đơn giản hóa việc tính toán, trong phạm vi điều kiện thí nghiệm của môn học này,
chúng ta sẽ áp dụng chung phần tính toán như sau:
Sai số toàn phần c∆ ủa =phép̅̅∆ đo+ là∆ tổng=sai0,077sống+ẫu0,1nhiên=0,177 vàsaisốdụng cụ (hoặc hệ thống) Kết quả: = 12,34 ± 0,18 ℎ
Sai số toàn phần của phép đo là tổng sai số ngẫu nhiên và sai số dụng
cụ (hoặc hệ thống):
A = A+A' (4)
Trong đó A’ là sai số hệ thống gây bởi dụng cụ, thông thường có thể lấy một độ chia
nhất trên dụng cụ. Trong một số nhỏ dụng cụ đo có cấu tạo phức tạp, ví dụ đồng hồ đo điện
hiện số, sai số dụng cụ được tính đa năng theo một công thức do nhà sản xuất quy định. Lưu ý:
Sai số hệ thống do lệch điểm 0 ban đầu là loại sai số cần phải loại trừ, bằng cách chú ý
hiệu chỉnh chính xác điểm 0 ban đầu của dụng cụ đo trước khi tiến hành đo.
Sai sót: Trong khi đo, còn có thể mắc phải sai sót. Do lỗi sai sót, kết quả nhận được
khác xa giá trị thực. Trong trường hợp nghi ngờ có sai sót, cần phải đo lại và loại bỏ giá trị sai sót.
Cách viết kết quả đo
Kết quả đo đại lượng A không cho dưới dạng một con số, mà cho dưới dạng một khoảng
giá trị trong đó chắc chắn có chứa giá trị thực của đại lượng A:
(A−A) A (A+ A) hay A= AA (5)
Tất cả các chữ số trong hệ số thập phân, trừ các số không đứng đầu con số (phía bên trái),
đều được gọi là các chữ số có nghĩa. Trong kết quả cuối cùng c ủa phép đo, bao giờ cũng có
hai phần: giá trị trung bình và sai số (kể cả sai số tương đối). Thông thường, sai số được làm
tròn còn một hoạc hai chữ số khác không. Số chữ số có nghĩa của giá trị trung bình được xác
định sao cho bậc của chữ số có nghĩa cuối cùng của giá trị trung bình phải bằng bậc của sai số.
Đối với những con số quá nhỏ hoặc quá lớn, người ta biễu diễn chúng dưới dạng lũy thừa của
10. Trong trường= h216 ợpsai số của đại lượng vật lý không được chỉ rõ, và người ta chỉ đưa ra mộ=t
216,0consố,±ví0,5 dụ
, thì có thể coi rằng sai số bằng nửa đơn vị của chữ số cuối cùng:
. Điều này thường gặp với các đại lượng vật lý cho sẵn như : = , và ∆ = , ;
= , / và ∆ = , / .
Lưu ý: Sai số tuyệt đối của phép đo A thu được từ phép tính sai số thường chỉ được viết đến
một hoặc tối đa là hai chữ số có nghĩa, còn giá trị trung bình A được viết đến bậc thập phân lOMoAR cPSD| 46958826
tương ứng. Các chữ số có nghĩa là tất cả các chữ số có trong con số, tính từ trái sang phải, kể
từ chữ số khác 0 đầu tiên. ̅ = 1,36832 ̅ = 1,368 ± ế
ả đo đượ ế ớ ∆ = 0, 0031.
Ví dụ: Phép đo độ dài s cho giá trị trung bình
, với sai số phép đo tính được là ắ ố 0, 003 , thì k t qu
c vi t, v i s lấy một chữ số có nghĩa, như sau: Quy t c là tròn s
Trong con số kết quả, chỉ giữ lại những chữ số có nghĩa, còn những chữ số khác được làm tròn theo quy tắc :
Chữ số giữ lại cuối cùng là không đổi nếu chữ số lớn nhất bỏ đi nhỏ hơn 5.
Chữ số giữ lại cuối cùng tăng lên một đơn vị nếu chữ số lớn nhất bỏ đi lớn hơn 5.
Nếu phần bỏ đi chỉ có một chữ số 5 duy nhất thì chữ số giữ lại cuối cùng giữ nguyên
khi nó là số chẵn và tăng lên 1 đơn vị nếu nó là số lẻ.
Ví dụ : làm tròn đến hai số lẻ các con số
sau 275,163; 3,037; 6,1351; 0,485; 61,035
Sau khi làm tròn ta có : 275,16; 3,04; 6,14; 0,48; 61,04
Cách xác định sai số phép đo gián tiếp
Để xác định sai số của phép đo gián tiếp, ta có thể vận dụng quy tắc sau đây:
Sai số tuyệt đối của một tổng hay hiệu thì bằng tổng các sai số tuyệt đối của các số hạng. F 2 2 F 2 2 F 2 2 F = (X ) + (Y ) + (Z ) X Y Z
Khi không cần độ chính xác cao người ta lấy giới hạn trên (sai số cực đại) dùng : F F F F = X + Y + Z X Y Z
Sai số tỉ đối của một tích hay thương thì bằng tổng các sai số tỉ đối của các thừa số. F ln F 2 2 ln F 2 2 ln F 2 2 = (X ) + (Y ) + (Z ) F X Y Z
Khi không cần độ chính xác cao người ta lấy giới hạn trên (sai số cực đại) dùng: F ln F ln F ln F = X + Y + Z F X Y Z
Ví dụ: Giả sử F=f(X, Y, Z) là đại lượng đo gián tiếp, còn X, Y, Z là những đại lượng đo trực tiếp.
Nếu: F = X + 2Y − 3Z , thì: F = X + 2Y − 3Z lOMoARcPSD|469 588 26 1 F X Y 1 Z
- Nếu: F = XY −2 Z 3 , thì: = + 2 + F X Y 3 Z
Nếu trong công thức vật lý xác định đại lượng đo gián tiếp có chứa các hằng số (ví dụ: ,
e,…) thì hằng số phải được lấy gần đúng đến số lẻ thập phân sao cho sai số tỉ đối do phép lấy gần
đúng gây ra có thể bỏ qua, nghĩa là nó phải nhỏ hơn 1/10 tổng các sai số tỉ đối có mặt trong
cùng công thức tính.
Ví dụ: Xác định diện tích vòng tròn thông qua phép đo trực tiếp đường kính d của nó. Biết d=50,6 0,1 mm. d 2 Ta có S =
, do đó sai số tỉ đối của phép đo S: 4 S = d 2 + = 0,4% + S d Trong trườ
ng hợp này, phải lấy = 3,142 để cho 0,04%. = , ∆
Để= ,giúp ; = , / và ∆ = , / .
đơn giản hơn trong các thí nghiệm sau, sinh viên có thể lấy giá trị và
Nếu công thức xác định đại lượng đo gián tiếp tương đối phức tạp, các dụng cụ đo trực
tiếp có độ chính xác tương đối cao, sai số phép đo chủ yếu gây bởi các yếu tố ngẫu nhiên, thì
người ta thường bỏ qua sai số dụng cụ. Đại lượng đo gián tiếp được tính cho mỗi lần đo, sau
đó lấy trung bình và tính sai số ngẫu nhiên trung bình như trong các công thức (1), (2), (3).
SAI SỐ PHÉP ĐO TRONG BIỂU DIỄN ĐỒ THỊ VẬT LÝ
Biểu diễn kết quả phép đo bằng đồ thị có các ưu điểm sau :
Thể hiện trực quan sự phụ thuộc của đại lượng vật lý này vào một đại lượng vật lý khác.
Có thể xác định quy luật biến đổi vật lý thông qua các phương pháp dữ liệu tương
quan hoặc hồi quy.
Có thể xác định giá trị của biến số bất kỳ dựa vào các giá trị đo được một cách rời rạc,
dựa vào phép biến đổi nội suy hoặc ngoại suy.
Thông thường, đối với các phép đo phụ thuộc vào một biến, các đại lượng biến đổi độc lập
được biểu diễn trên trục hoành của hệ tọa độ vuông góc, còn đại lượng phụn thuộc thể hiện
trên trục tung. Đồ thị phải có tiêu đề, các trục phải có ký hiệu các đại lượng và đơn vị.
Một số nguyên tắc cơ bản để thể hiện sai số phép đo trong biễu diễn đồ thị vật lý như sau :
Phải chọn tỉ lệ xích sao cho đồ thị chiếm toàn bộ diện tích dành cho đồ thị nhằm quan
sát tốt quy luật biến đổi của đồ thị. Độ lớn đơn vị các đại lượng trên các trục nên được
chọn một các phù hợp nhằm có thể quan sát được sai số các điểm đo.
Thể hiện đầy đủ giá trị trung bình và các sai số tương ứng tại các vị trí đo. lOMoAR cPSD| 46958826
Trước khi v(ẽ, trình,) bày số liệu dưới dạng bảng. Mỗi điểm∆ trên,∆ đồ thị tương ứng với một
(cặp, giá) trịđo được (với các( , sai) số tương ứng). 2∆ Ứng àvớ i2∆ mỗi điểm
ta vẽ hình chữ nhật tâm làvà các cạnh tương2∆ ứng àlà 2∆ . Hình
chữ nhật này gọi là ô sai số có độ dài các cạnh tương ứng là.
Khi vẽ đường liên tục biểu diễn hàm phụ thuộc, trước nhất lưu ý đến những dạng hàm
phụ thuộc đơn giản có thể xảy ra theo lý thuyết (tuyến tính, đa thức, hàm mũ, hàm log
… ) và cố gắng vẽ đồ thị các hàm đó sao cho tiếp cận một cách tốt nhất các điểm thực
nghiệm (nhất thiết phải đi qua các ô sai số của các điểm đo). Trong trường hợp chưa
biết quy luật quan hệ, cố gắng vẽ một đường trơn tru ít uốn khúc nhất. Tránh nối điểm
bằng những đoạn thẳng gấp khúc. lOMoAR cPSD| 46958826 TÓM TẮT
❖ Phép đo một đại lượng vật lý là phép so sánh nó với đại lượng cùng loại được quy ước
làm đơn vị.
Phép so sánh trực tiếp thông qua dụng cụ đo gọi là phép đo trực tiếp.
Phép xác định một đại lượng vật lý qua một công thức liên hệ với các đại lượng đo
trực tiếp, gọi là phép đo gián tiếp.
❖ Giá trị trung bình khi đo nhiều lần một đại lượng A:
A = A +A +...+A , là giá trị gần nhất với giá trị thực của đại lượng A. 1 2 n n
❖ Sai số tuyệt đối ứng với mỗi lần đo: A = = = 1
A− A1 ;A2 A− A2 ;A3 A− A3 ;...
Sai số ngẫu nhiên là sai số tuyệt đối trung bình của n lần đo:
A = A + A +...+ A 1 2 n n
Sai số dụng cụ A' có thể lấy bằng nửa hoặc một độ chia nhỏ nhất trên dụng cụ.
❖ Kết quả đo đại lượng A được cho dưới dạng: A = A A , trong đó A là tổng sai số
ngẫu nhiên và sai số dụng cụ: A = A + A' , được lấy tối đa đến hai chữ số có nghĩa,
còn A được viết đến bậc thập phân tương ứng.
Sai số tỉ đối A của phép đo là tỉ số giữa sai số tuyệt đối và giá trị trung bình của đại A
lượng đo, tính bằng phần trăm: A = .100% . A
Sai số của phép đo gián tiếp, được xác định theo các quy tắc:
Sai số tuyệt đối của một tổng hay hiệu, thì bằng tổng các sai số tuyệt đối của các số hạng.
Sai số tỉ đối của một tích hay thương, thì bằng tổng các sai số tỉ đối của các thừa số. lOMoAR cPSD| 46958826 BÀI TẬP
Bài tập mẫu
Dùng thước kẹp có ĐCNN 0,1 mm để đo 5 lần đường kính d và chiều cao h của một trụ
thép, cho kết quả như trong bảng sau: Lần đo d (mm) h (mm) 1 30,0 19,9 2 30,1 19,8 3 30,0 20,0 4 30,1 19,7 5 30.1 19,9
Hãy cho biết kết quả phép đo d, h và tính thể tích của trụ thép. Giải :
Phép đo d, h là phép đo trực tiếp, giá trị trung bình và sai số ngẫu nhiên tính trong bảng sau: Lần đo d (mm) d h (mm) h 30,0 0,06 19,9 0,04 30,1 0,04 19,8 0,06 30,0 0,06 20,0 0,14 30,1 0,04 19,7 0,16 30,1 0,06 19,9 0,04 TB30,06 0,05 19,86 0,09
Sai số dụng cụ bằng 0,1 mm. Vậy:
Sai số phép đo đường kính trụ là: d = 0,05 + 0,1 = 0,15 mm.
Sai số phép đo chiều cao trụ là: h = 0,09 + 0,1 = 0,19 mm. Kết quả:
d = 30,06 0,15 (mm).
h = 19,86 0,19 (mm).
Thể tích trung bình của trụ: 2 d h V = = 3,142.30,062.19,86 = 14100 (mm3). + 19,86 = 0,02 4 = + 2 + ℎ = 3, 14 + 2 30,06 4 ∆ ∆ ∆ ∆ℎ 0,005 0,15 0,19
Sai số tỉ đối:
Sai số tuyệt đối: V = V. = 0,02.14100 = 282 (mm ) V 3
Kết quả: V = 14100 282 (mm3) lOMoAR cPSD| 46958826
Bài tập vận dụng
Dùng một đồng hồ đo thời gian có ĐCNN 0,001 s để đo n lần thời gian rơi tự do không vận
tốc đầu của một vật, bắt đầu từ điểm A (VA = 0) đến điểm B, kết quả cho trong bảng dưới đây: n T t t ' i 1 0,399 2 0,408 3 0,406 4 0,405 5 0,402 TB
Hãy tính thời gian rơi trung bình, sai số ngẫu nhiên, sai số dụng cụ, và sai số phép đo
thời gian. Phép đo này là trực tiếp hay gián tiếp? Nếu chỉ đo 3 lần (n=1, 2, 3) thì kết quả đo bằng bao nhiêu?
Dùng một thước mm đo 5 lần khoảng cách s giữa hai điểm A, B đều cho một giá trị
như nhau bằng 798 mm. Tính sai số phép đo này và viết kết quả đo. 2s
c) Cho công thức tính vận tốc tại B: v = 2s
và gia tốc rơi tự do g = . Dựa vào các kết quả t t 2
đo ở trên và các quy tắc tính sai số đại lượng đo gián tiếp đã học, tính v, g, v , g và viết các
hãy kết quả cuối cùng? lOMoAR cPSD| 46958826 Bài 1
ĐO KHỐI LƯỢNG RIÊNG CỦA VẬT RẮN ĐỒNG NHẤT
DỤNG CỤ THÍ NGHIỆM
1 thước kẹp 0 150mm, chính xác 0,02mm;
1 cân kỹ thuật 0 200g, chính xác 0,02g;
1 hộp quả cân 0 200g;
3 mẫu vật cần đo (khối lập phương, vòng đồng, viên bi thép).
I CƠ SỞ LÝ THUYẾT
Khối lượng riêng của một vật là đại lượng vật lý biểu thị phân bố khối lượng tại từng vị trí
trên vật, có trị số bằng khối lượng của một đơn vị thể tích. Đối với một vật đồng nhất có khối lượ
ng M và thể tích V, khối lượng riêng được tính bằng: M V
Trong hệ SI, khối lượng riêng có đơn vị kg/m3. Vậy để xác định khối lượng riêng của
một vật đồng nhất, ta cần phải xác định khối lượng M và thể tích V của vật. Đó là nội dung
của hai phần thí nghiệm được trình bày trong phần trình tự thí nghiệm dưới đây.
II TRÌNH TỰ THÍ NGHIỆM
ĐO KÍCH THƯỚC VÀ XÁC ĐỊNH THỂ TÍCH CỦA CÁC VẬT RẮN CÓ
HÌNH DẠNG ĐỐI XỨNG
1. ĐO KÍCH THƯỚC DỂ XÁC ĐỊNH THỂ TÍCH CỦA MỘT CHIẾC VÒNG ĐỒNG BẰNG THƯỚC KẸP Thước kẹp
Thước kẹp (Vernier Caliper) là loại dụng cụ dùng đo độ dài chính xác hơn thước thẳng
milimét. Độ chia nhỏ nhất của thước kẹp, tuỳ loại, có thể đạt tới 0,1mm, 0,05mm hoặc
0,02mm. Trên Hình 1 giới thiệu một thước kẹp thông dụng có thể đo độ dài từ 0 đến 150mm
với độ chia nhỏ nhất 0,1mm.
Cấu tạo của thước kẹp gồm một thân thước chính dạng chữ T, trên thân thước khắc vạch từ 0
đến 150, mỗi vạch cách nhau 1mm. Một thước T’ nhỏ hơn ôm lấy thân thước chính T và có thể
trượt dọc theo thân thước chính, gọi là du xích. Thước nhỏ trên du xích được chia đều ra N vạch,
sao cho độ dài của N vạch của thước này đúng bằng độ dài của (kN - 1) vạch trên thước chính (k =
1, 2). Gọi a là độ dài vạch chia trên thước chính, b là độ dài vạch chia trên du xích, ta có: N.b = (kN - 1).a Suy ra: (ka-b) = a/N. lOMoARcPSD|469 588 26 2 2' 3 T 0 10 20 30 40 50 60 0 5 10 T/ 1 1'
Hình1 . Cấu tạo thước kẹp loại N=10, k=1
Các thước kẹp thông dụng a=1mm, nên độ chia nhỏ nhất của của thước kẹp tính theo công thức:
= a = 1 mm N N
Ví dụ: - Nếu N = 1, thì = 0,1mm
Nếu N = 20, thì = 0,05mm
Nếu N = 50, thì = 0,02mm
Đầu đo của thước chính T có hai hàm kẹp 1, 2 cố định (Hình 1). Hai hàm kẹp di động 1’,
2’ gắn với đầu của du xích. Hai đầu 1-1’ dùng đo kích thước ngoài, còn hai đầu 2-2’ dùng
đo kích thước trong của các vật.
Ví dụ: Khi cần đo đường kính D của một vòng kim loại, ta nới nhẹ vít 3 để có thể kéo du
xích trượt trên thân thước T, rồi kẹp vòng vào giữa hai hàm kẹp 1-1’ (Hình 2). Xiết nhẹ vít
3 để cố định vị trí của du xích.
Cách đọc giá trị độ dài của đường kính D như sau:
Ban đầu khi chưa có vòng, hàm kẹp di động 1’ nằm sát với hàm kẹp cố định 1,
thì vạch số 0 trên thước chính ’
T trùng với vạch số 0 của du xích T .
Sau khi kẹp vòng, vạch 0 của du xích trượt sang phải, vượt qua vạch thứ n trên thước
chính. Như vậy, ta xác định được phần nguyên của độ dài đường kính D bằng n milimét.
Cách đọc phần lẻ của D: Quan sát hai dãy vạch đối diện nhau trên du xích T’ và
trên thước chính T, tìm xem có cặp vạch nào trùng nhau hoặc nằm đối diện sát nhau
nhất, giả sử là vạch thứ m trên du xích. Phần lẻ của độ dài đường kính D tính bằng m
milimét, với là giá trị của độ chia nhỏ nhất của thước kẹp, được ghi ngay trên thước
kẹp. Đường kính D sẽ là: D = n + m (mm). lOMoAR cPSD| 46958826 Hình 2
Đo kích thước của vòng kim loại và xác định thể tích V của nó
Thể tích của khối trụ rỗng tính theo công thức:
( D − d ) h V = 2 2 (1) 4
Ta dùng thước kẹp đo đường kính ngoài D, đường kính trong d và độ cao h của khối trụ rỗng.
Từ đó xác định thể tích V theo công thức (1).
Đo đường kính ngoài D, đường kính trong d và độ cao h của chiếc vòng đồng
Thực hiện 3 lần đối với mỗi phép đo của D, d và h tại các vị trí khác nhau của chiếc
vòng đồng. Đọc và ghi các giá trị của D, d và h trong mỗi lần đo vào bảng 1 để tính thể tích
V của chiếc vòng đồng.
A.2. XÁC ĐỊNH THỂ TÍCH CỦA KHỐI HÌNH HỘP BẰNG THÉP ĐẶC BIỆT
Đo chiều dài a, chiều rộng b và chiều cao c bằng thước kẹp
Đặt các chiều a, b và c của vật vào đầu 1 và 1’ của thước kẹp đo tương tự như trên.
Thực hiện 3 lần phép đo các chiều a, b và c của vật tại các vị trí khác nhau. Đọc và ghi
giá trị của a, b, c trong mỗi lần đo vào bảng 2 để tính thể tích V của khối thép đặc biệt.
Thể tích của khối thép đặc biệt tính theo công thức V=a.b.c (2)
A.3. XÁC ĐỊNH THỂ TÍCH CỦA VIÊN BI THÉP (KHỐI CẦU)
Đo đường kính của viên bi bằng thước kẹp
Đặt viên bi tựa vào đầu 1 và 1’ của thước kẹp đo đường kính D đọc tương tự như trên.
Thực hiện 3 lần phép đo đường kính D của viên bi tại các vị trí khác nhau của viên bi.
Đọc và ghi giá trị của D trong mỗi lần đo vào bảng 3 để tính thể tích V của viên bi.
Thể tích của viên bi thép hình cầu tính theo công thức V = 1 .D3 (3) 6
Đối với viên bi nhỏ có đường kính D vào cỡ vài milimét, ta phải dùng thước kẹp để đo
đường kính của nó. Từ đó có thể xác định chính xác thể tích V của nó theo công thức (3). lOMoAR cPSD| 46958826
CÂN KHỐI LƯỢNG CỦA MỘT VẬT TRÊN CÂN KỸ THUẬT
B.1. NGUYÊN TẮC CHUNG
Cân khối lượng của một vật là so sánh khối lượng của vật đó với khối lượng của những
quả cân (tức là những vật mẫu được qui ước chọn làm đơn vị đo để so sánh).
Giả sử có một đòn cân O1O2, tức là một thanh thẳng nhẹ và cứng, đặt tựa trên một
điểm O. Treo vật có trọng lượng P vào đầu O1 và treo các quả cân có tổng trọng lượng Po vào
đầu O2 sao cho đòn cân O1O2 nằm thẳng ngang (Hình 3). Hình 3
Khi đó mômen của các trọng lực P và Po đối với điểm tựa O bằng nhau: P.L = 1 P0 .L2 (4) với L
và L = OO là các cánh tay của đòn cân. Nếu
, thì ta có : P=P (5) 1 OO1 2 2 L L 0 1 2 hay m = m (6) 0
Như vậy, đối với các loại cân có cánh tay đòn bằng nhau, trọng lượng P hoặc khối
lượng m của vật treo ở một đầu đòn cân sẽ đúng bằng tổng trọng lượng P0 hoặc khối lượng
m0 của các quả cân treo ở đầu kia của đòn cân khi đòn cân cân bằng (bỏ qua lực đẩy Acsimét
của không khí). B.2. CÂN KỸ THUẬT
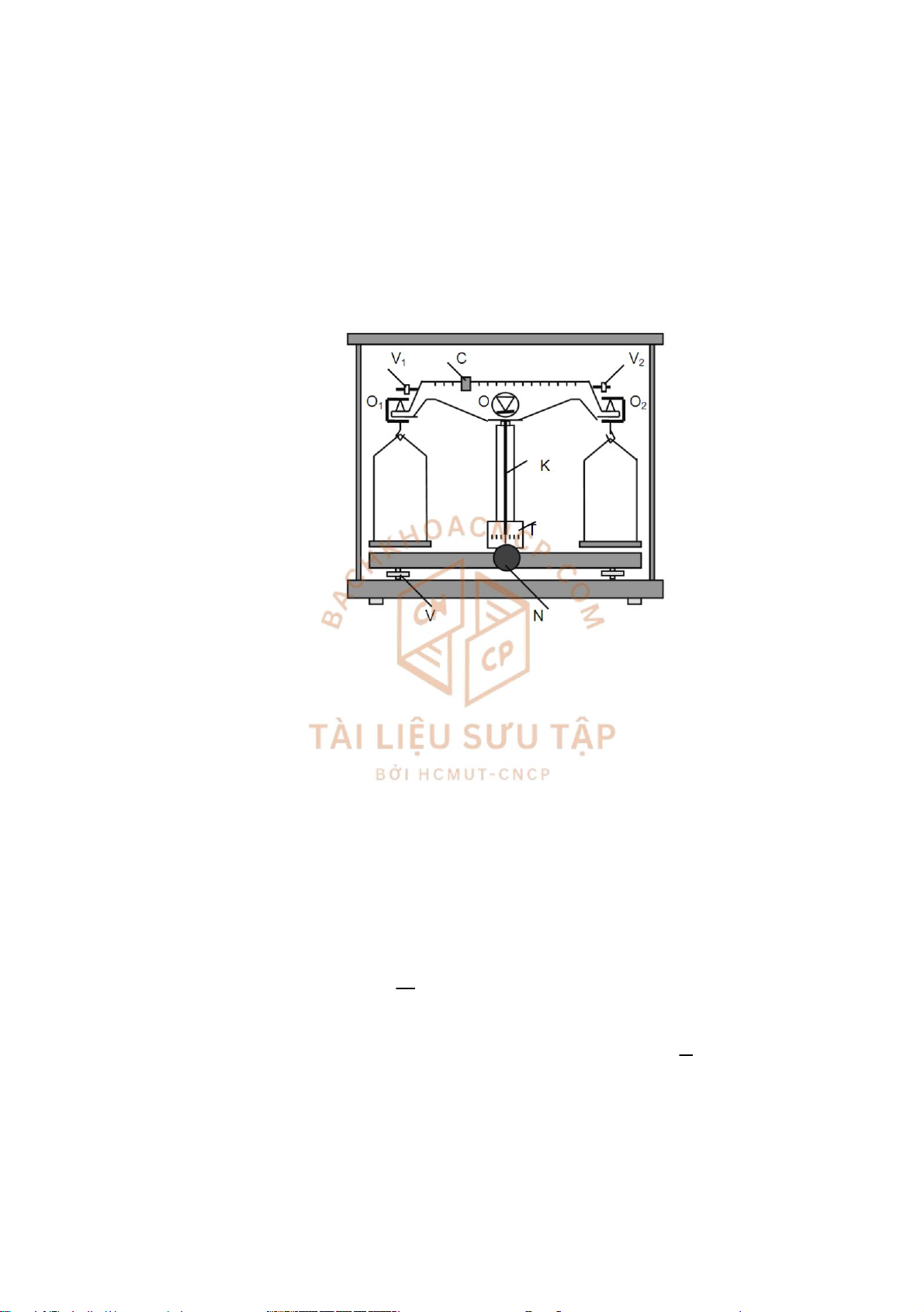
Cân kỹ thuật (Hình 4) là dụng cụ dùng đo khối lượng của các vật trong giới hạn 0 200g,
chính xác tới 0,02g. Cấu tạo của nó gồm phần chính là một đòn cân làm bằng hợp kim nhẹ, trên
đòn cân có các độ chia từ 0 đến 50. Ở chính giữa thân của đòn cân có gắn một con dao
hình lăng trụ tam giác bằng thép cứng, cạnh của dao O quay xuống phía dưới và tựa trên một
gối đỡ phẳng ngang (bằng đá mã não) đặt ở đỉnh của trụ cân. Ở hai đầu đòn cân có hai con dao
O1 và O2 giống như con dao O. Các cạnh của hai con dao này quay lên phía trên, đặt song song
và cách đều cạnh của con dao O, nên các cánh tay của đòn cân OO1 = L1 và OO2 = L2 có độ dài
bằng nhau. Hai chiếc móc mang hai đĩa cân giống nhau được đặt tựa trên cạnh của hai dao O1 và
O2. Mặt dưới của đế cân có hai vít xoay V dùng điều chỉnh cho trụ cân thẳng đứng.
Đòn cân được nâng lên hoặc hạ xuống nhờ một núm xoay N ở phía chân của trụ cân. Khi
hạ đòn cân xuồng, cạnh của con dao O không tựa vào mặt gối đỡ trên trụ cân: cân ở trạng thái
"nghỉ". Khi nâng đòn cân lên, cạnh của dao O tựa trên mặt gối đỡ, đòn cân có thể dao động nhẹ
quanh cạnh của con dao O: cân ở trạng thái "hoạt động". Nhờ một kim chỉ thị K gắn thẳng đứng
chính giữa đòn cân (phía dưới con dao O) và một thước nhỏ T gắn ở chân trụ cân, ta có thể xác lOMoAR cPSD| 46958826
định được vị trí cân bằng của đòn cân hay còn gọi là vị trí số 0 của cân khi nó "hoạt động".
Trong trường hợp này, đầu dưới của kim K đứng yên hoặc dao động đều về hai phía số 0 của thước T.
Có thể điều chỉnh vị trí số 0 của cân cân nhờ văn nhẹ hai vít nhỏ V1 và V2 ở hai đầu đòn
cân. Toàn bộ cân được đặt trong một tủ kính bảo vệ tránh ảnh hưởng của gió khi cân "hoạt động".
Các quả cân từ 1g đến 100g và chiếc kẹp dùng để lấy các quả cân này đựng trong một hộp gỗ nhỏ.
Ngoài ra, còn có một quả cân nhỏ C - gọi là con mã, có thể dịch chuyển trên đòn cân dùng để thêm
(hoặc bớt) những khối lượng nhỏ từ 20mg đến 1000mg trên đĩa cân bên phải. Hình 4
B.3. CÂN KHỐI LƯỢNG m CỦA MỘT VẬT
a) Xác định độ nhạy S và chính xác α của cân
- Chưa đặt vật hoặc quả cân lên các đĩa cân. Gạt con mã về vị trí số 0 của nó trên đòn cân.
Vặn núm xoay N (thuận chiều kim đồng hồ) để cân "hoạt động" trong điều kiện
không tải. Nếu kim chỉ thị K không chỉ đúng số 0 hoặc dao động không đều về hai phía số 0
trên thước T thì phải điều chỉnh cân để đạt được vị trí số 0.
Vặn núm xoay N (ngược chiều kim đồng hồ) để cân ở trạng thái “nghỉ”. Đặt quả cân
10mg lên đĩa cân bên trái, sau đó lại vặn núm xoay N để cân “hoạt động”. Đọc số độ chia n trên
thước T ứng với độ dời của kim chỉ thị K so với vị trí số 0 trên thước T. Khi đó độ nhạy S của
cân được xác đị
nh bởi công thức: S = n (độ chia/mg) 10
Đại lượng nghịch đảo của độ nhạy S gọi là độ chính xác của cân: α = 1 (mg/độ chia) S
Chú ý : Mỗi lần điều chỉnh cân hoặc thêm bớt khối lượng trên các đĩa cân, nhất thiết
phải vặn núm xoay N (ngược chiều kim đồng hồ) để đặt cân ở trạng thái "nghỉ".
Phương pháp cân đơn lOMoAR cPSD| 46958826
Đặt vật cần cân lên đĩa cân bên trái. Chọn các quả cân (theo thứ tự từ lớn đến nhỏ
dần, kể cả con mã) và lần lượt đặt chúng lên đĩa cân bên phải cho tới khi vặn núm xoay N để
cân ở trạng thái "hoạt động" có tải thì đòn cân vẫn ở vị trí cân bằng.
Thực hiện 3 lần phép cân khối lượng của vật. Đọc và ghi giá trị tổng khối m của các 0
quả lượng cân (kể cả con mã) đặt trên đĩa cân bên phải trong mỗi lần đo vào bảng 4.
KẾT QUẢ THÍ NGHIỆM
Viết kết quả đo của mỗi đại lượng trong các bảng 1, 2, 3 và 4.
Điền đầy các kết quả tính toán vào các ô trống trong các bảng 1, 2, 3 và 4.
Xác định thể tích của chiếc vòng đồng (trụ rỗng), của khối thép đặc biệt (khối hộp) và
của viên bi thép (khối cầu). Tính sai số tương đối, sai số tuyệt đối và viết kết quả của
mỗi phép đo thể tích này.
Xác định khối lượng m của vật bằng phương pháp cân đơn trên cân kỹ thuật và độ
chính xác của phép cân này.
5. Xác định khối lượng riêng của các mẫu vật trên, tính sai số tương đối, sai số tuyệt đối
và viết kết quả phép đo.