lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
TR ƯỜ NG ĐẠ I H Ọ C NGÂN HÀNG TPHCM
KHOA H Ệ TH Ố NG THÔNG TIN QU Ả N LÝ Chương 5 ĐỒ THỊ -GRAPH 1 lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý Nộidung
Định nghĩa và các khái niệm Biểu diễn đồ thị Duyệt đồ thị 2 lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý Định nghĩa Vinh
Đ à N ẵ ng
C ầ n Th ơ
Hà N ộ i
TP. H ồ Chí Minh
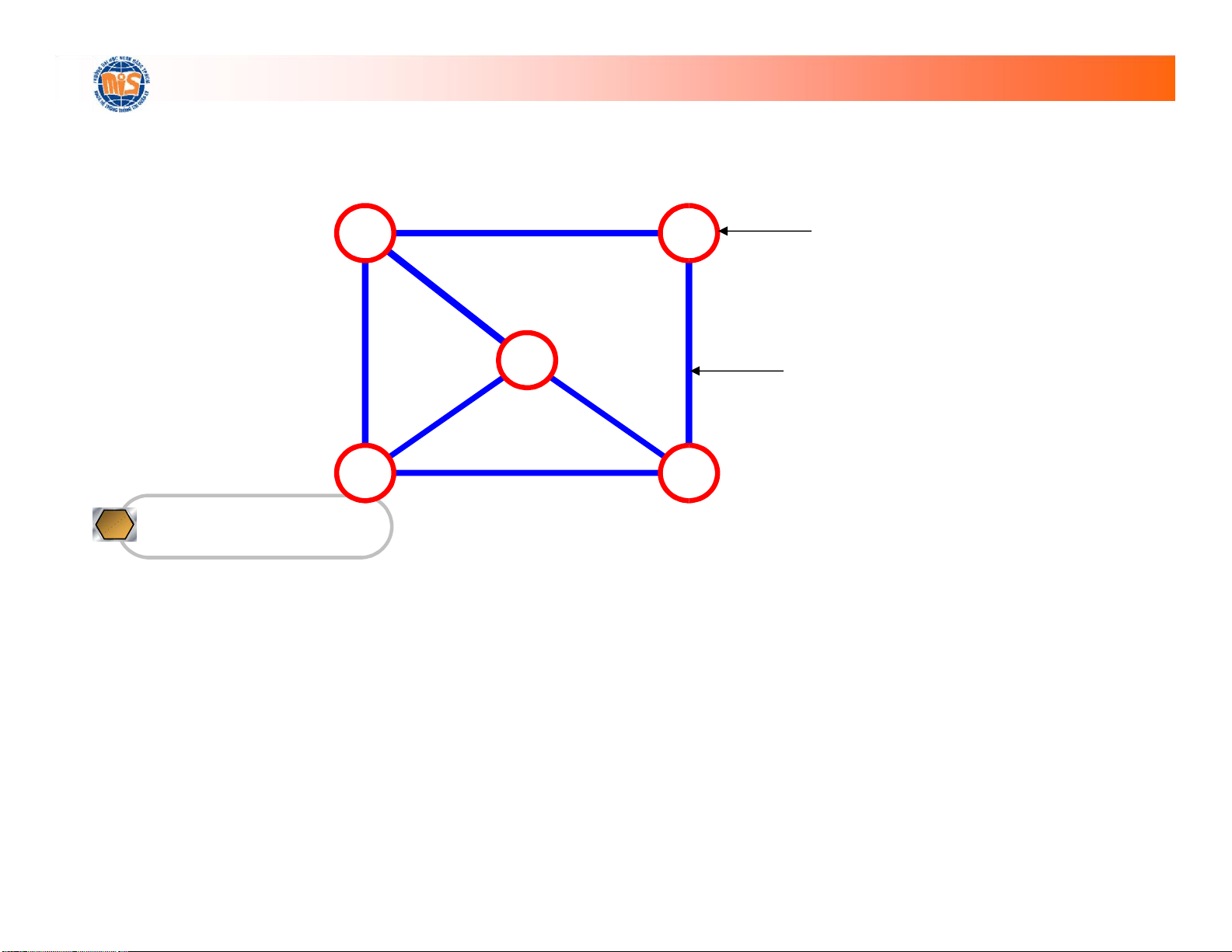
H ả i Phòng Hu ế Nha Trang Định nghĩa • Đồ thị G = (V,E)
– V = tập hợp hữu hạn các phần tử (đỉnh hay nút) lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
– E ⊆ V × V, tập hữu hạn các cạnh (cung) a b Đỉnh c Cung d e Định nghĩa lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
• BIỂU DIỄN MẠCH ĐIỆN Định nghĩa lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý • YÊU CẦU TRÌNH TỰ Định nghĩa
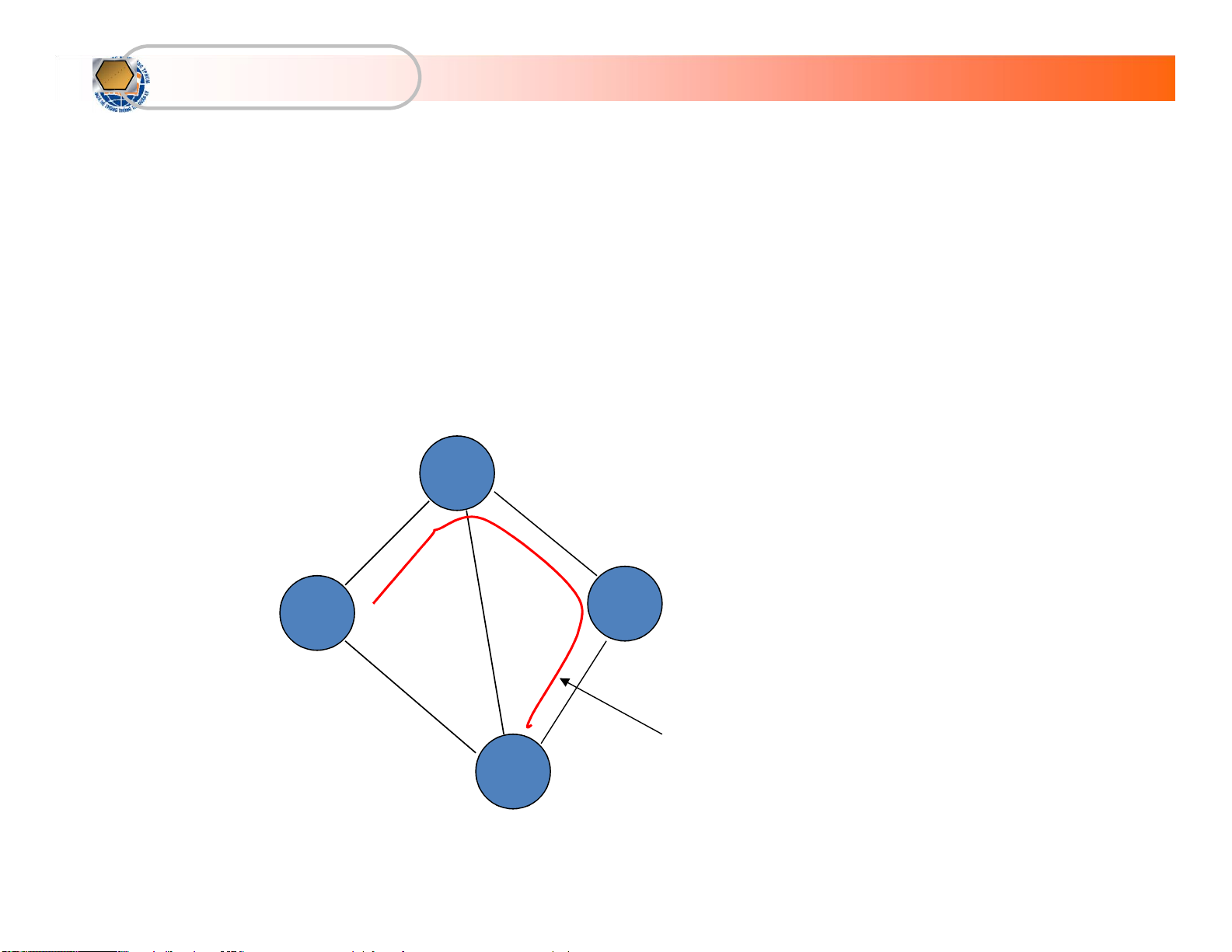
• TRUYỀN THÔNG MẠNG MÁY TÍNH lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý Định nghĩa lOMoARcPSD| 36667950
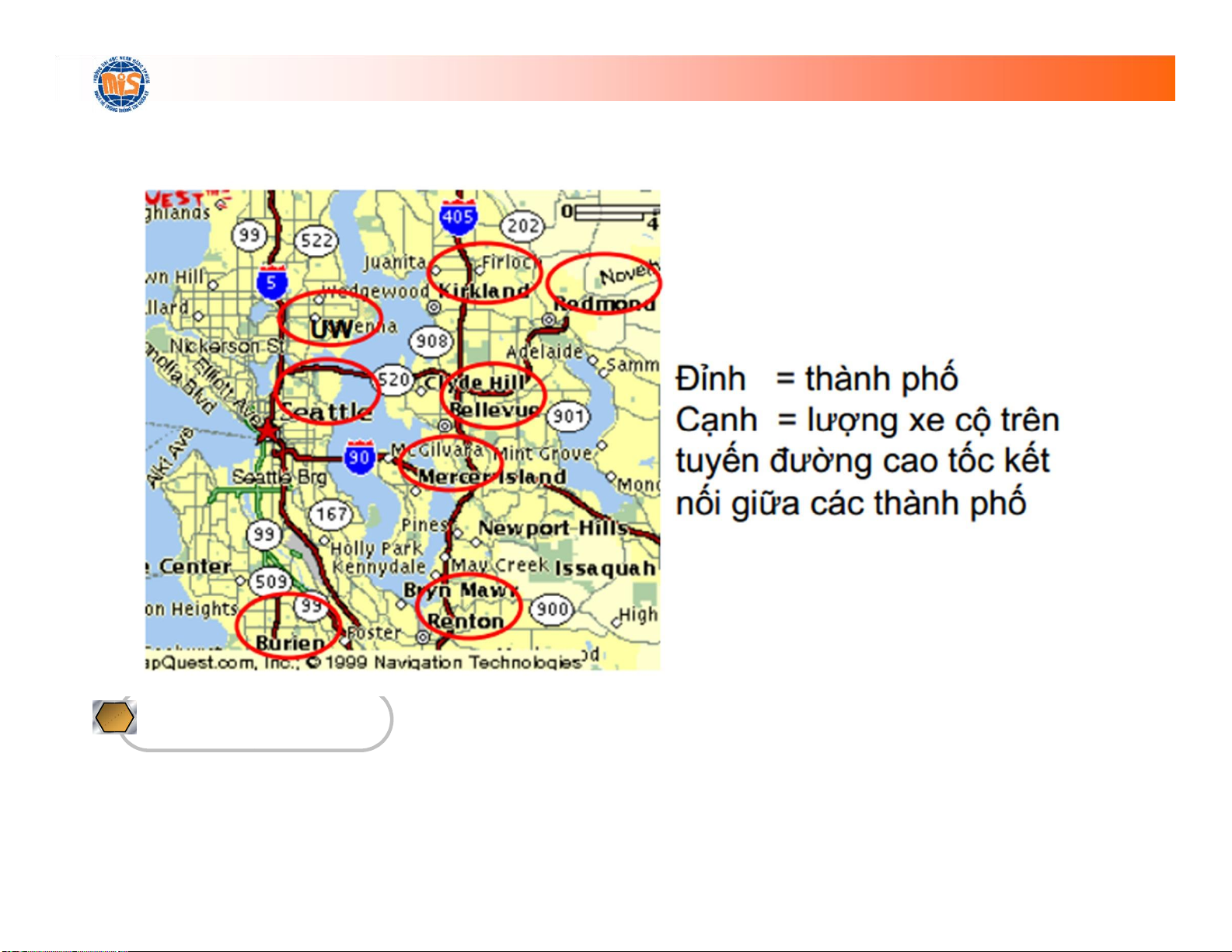
KhoaHệThốngThôngTin Quảnlý • LUỒNG GIAO THÔNG Định nghĩa lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý • SƠ ĐỒ ĐƯỜNG PHỐ lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý Các khái niệm
• Cho đồ thị G = (V, E). V gọi là tập các đỉnh (vertex )
và E gọi là tập các cạnh (Edges)
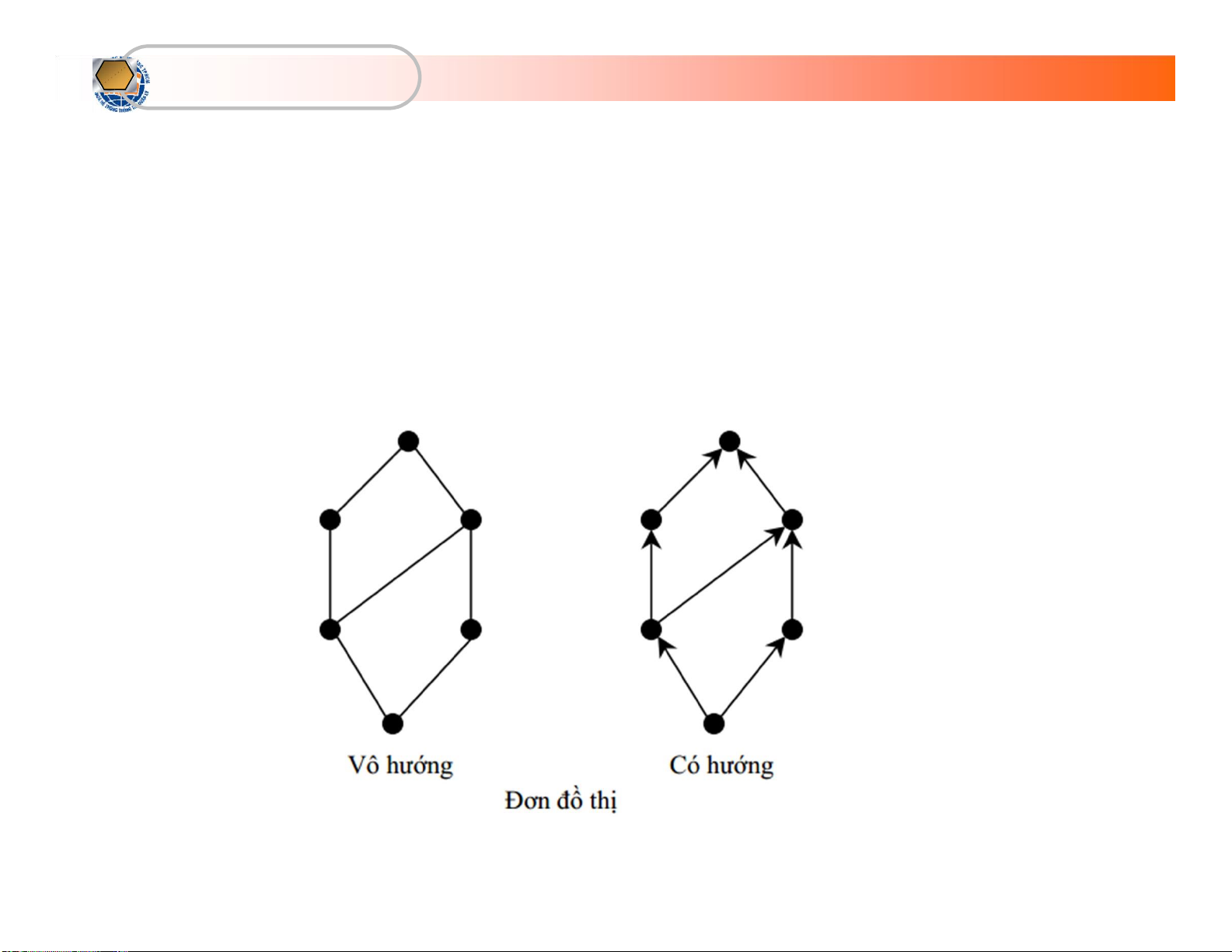
G được gọi là đơn đồ thị nếu giữa hai đỉnh u, v của
V có nhiều nhất là 1 cạnh trong E nối từ u tới v lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý Các khái niệm
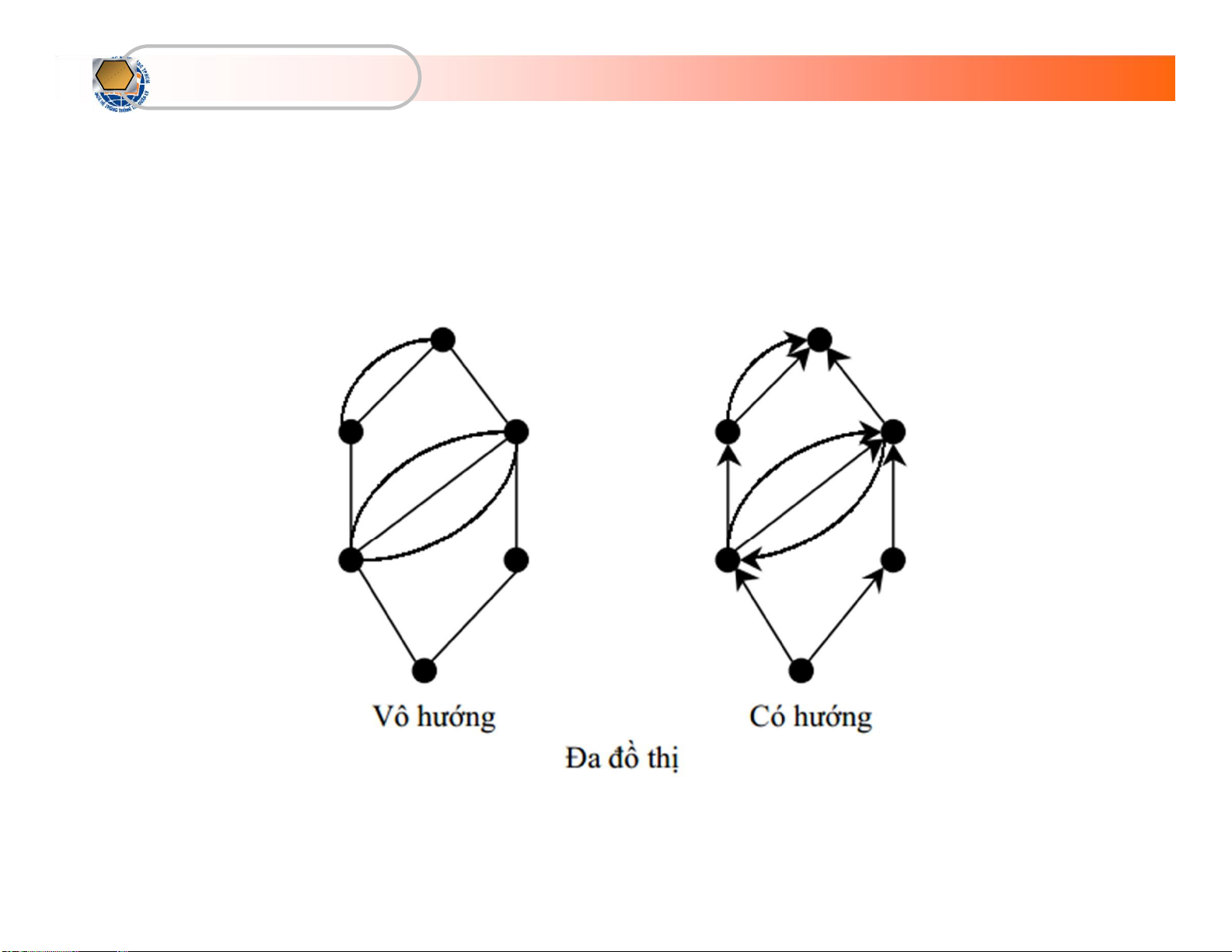
• G được gọi là đa đồ thị nếu giữa hai đỉnh x, y của V
có thể có nhiều hơn 1 cạnh trong E nối từ x tới y lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý Các khái niệm • Nếu (x,y) ∈ E
• x gọi là đỉnh gốc, y là ngọn
• Nếu x ≡ y, (x,y) gọi là khuyên
• Đường đi: Một dãy u1,u2,…,un, ∀ui ∈ V (i=1,n)
gọi là một đường, nếu (ui-1,ui) ∈ E
(1, 2, 3, 4) là đường đi đơn độ dài bằng 3, đi từ đỉnh 1 tới đỉnh 4. Bởi (1, 2) (2, 3) và (3,
4) đều là các cạnh (hay cung) lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý Các khái niệm
• Độ dài đường: length(u1,u2,…,un)=n
• Đường đi đơn: (u1,u2,…,un) là đường đi đơn, nếu
ui≠uj, 1<∀i≠jbiệt, ngoại trừ đỉnh đầu và đỉnh cuối) B C A Đườ ng đ đơ i n D lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý Các khái niệm (tt)
• Đồ thị có hướng (directed graph): G được gọi là đồ thị có
hướng nếu các cạnh trong E là có định hướng, có thể có
cạnh nối từ đỉnh x tới đỉnh y nhưng chưa chắc đã có cạnh
nối từ đỉnh y tới đỉnh x. Cách khác:
– ∀(x,y) ∈ E : (x,y) ≠ (y,x)
• Đồ thị vô hướng: G được gọi là đồ thị vô hướng nếu các
cạnh trong E là không định hướng, tức là cạnh nối hai đỉnh
x, y bất kỳ cũng là cạnh nối hai đỉnh y, x. Cách khác:
– ∀(x,y) ∈ E : (y,x) ∈ E – (x,y) ≡ (y,x) lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý Các khái niệm (tt)
Đồ thị vô hướng Đồ thị có hướng Các khái niệm (tt)
• Chu trình (cycle) : Là đường đi khép kín, tức là có
đỉnh đầu trùng với đỉnh cuối: lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
– (cycle) = (u1,u2,…,un), u1≡ un B C A D Chu trì nh lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý Các khái niệm (tt) Các khái niệm (tt) lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý Bậc của đỉnh
Giả sử G là đồ thị vô hướng, v∈V là một đỉnh nào đó
• Bậc của đỉnh v, deg(v), là số cạnh kề với nó.
• Đỉnh bậc 0 được gọi là đỉnh cô lập (isolated).
• Đỉnh bậc 1 được gọi là đỉnh treo (pendant). Các khái niệm (tt) lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
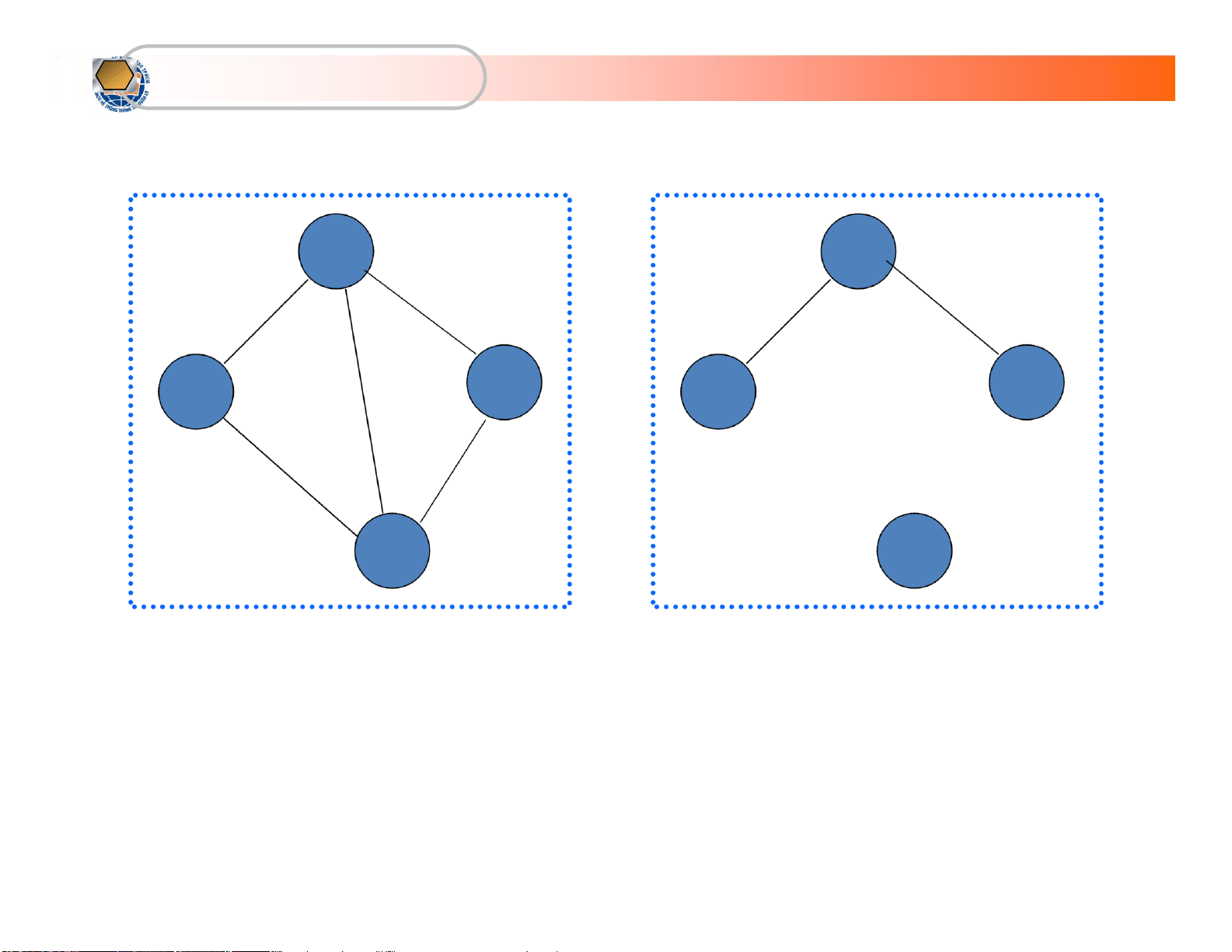
• Tính liên thông (connectivity)
– Trong đồ thị G, hai đỉnh x, y gọi là liên thông
(connected), nếu có một đường từ x đến y
– Đồ thị vô hướng được gọi là liên thông nếu luôn
tìm được đường đi giữa hai đỉnh bất kỳ của nó.
G liên thông, nếu ∀x, y ∈ V, ∃ đường đi từ x đến y lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý Các khái niệm (tt) Đồ thị liên thông
Đồ thị không liên thông lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý Các khái niệm (tt)
• Đồ thị có trọng số: Đồ thị G gọi là có trọng số,
nếu mỗi cung được gán một giá trị số đặc trưng 0 10 20 1 1 2 4 5 3 lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
Biểu diễn đồ thị
• Biểu diễn bằng ma trận kề – Adjacency matrice
• Biểu diễn bằng danh sách kề – Adjacency list
Biểu diễn bằng ma trận kề
• Xét G=(V,E) với V={x1,…,xn}
• Biểu diễn G bằng ma trận A=(aij), i,j=1..n
– aij=1, nếu Ǝ (xi,xj) ∈ E
– aij=0, nếu !Ǝ (xi,xj) ∈ E lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
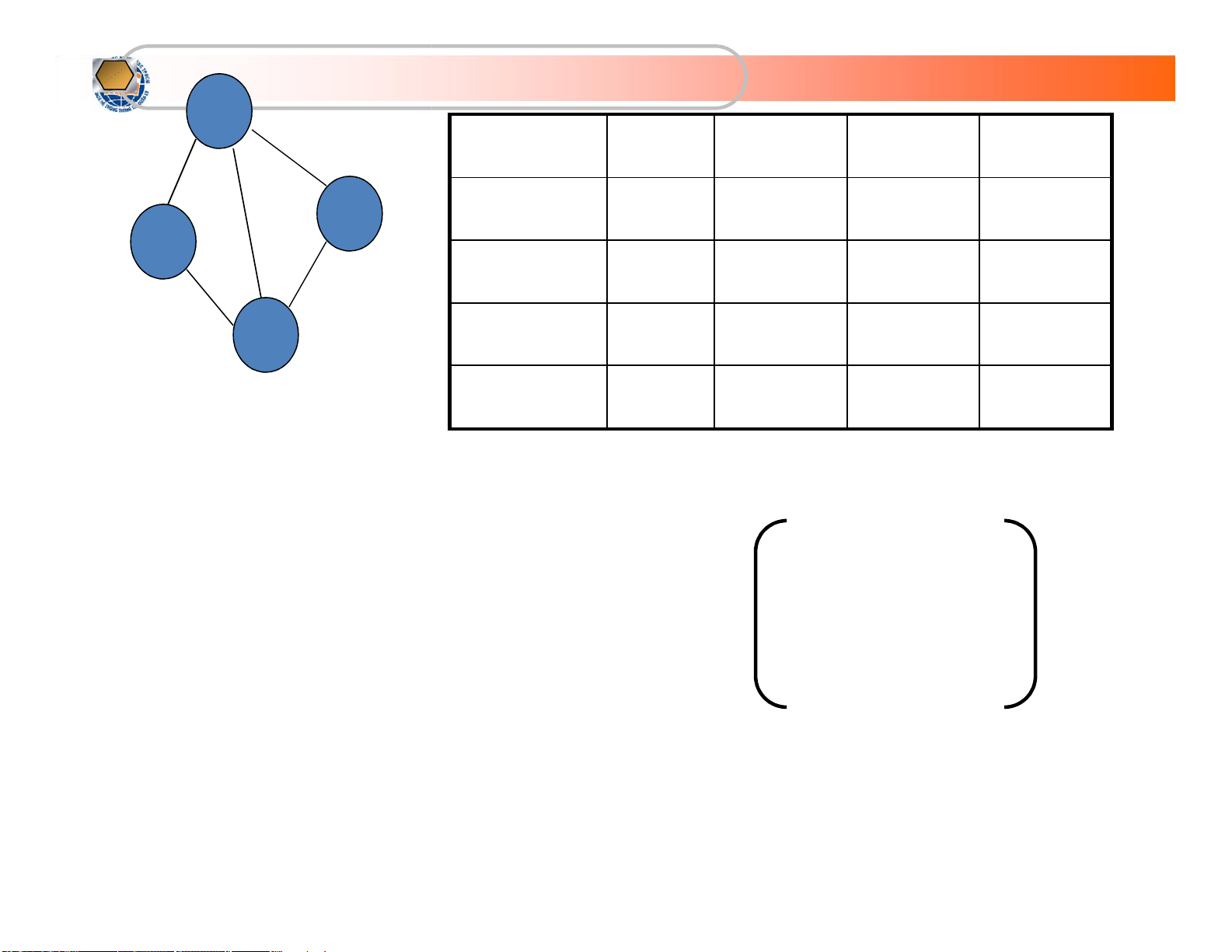
Biểu diễn bằng ma trận kề (tt) 0 1 2 3 A[i][j] 0 1 2 3 0 1 0 1 0 0 0 1 1 1 0 1 1 1 2 1 1 0 1 2 2 3 0 1 1 0 3 3 0 1 1 0 1 0 1 1 A = 1 1 0 1 0 1 1 0 lOMoARcPSD| 36667950
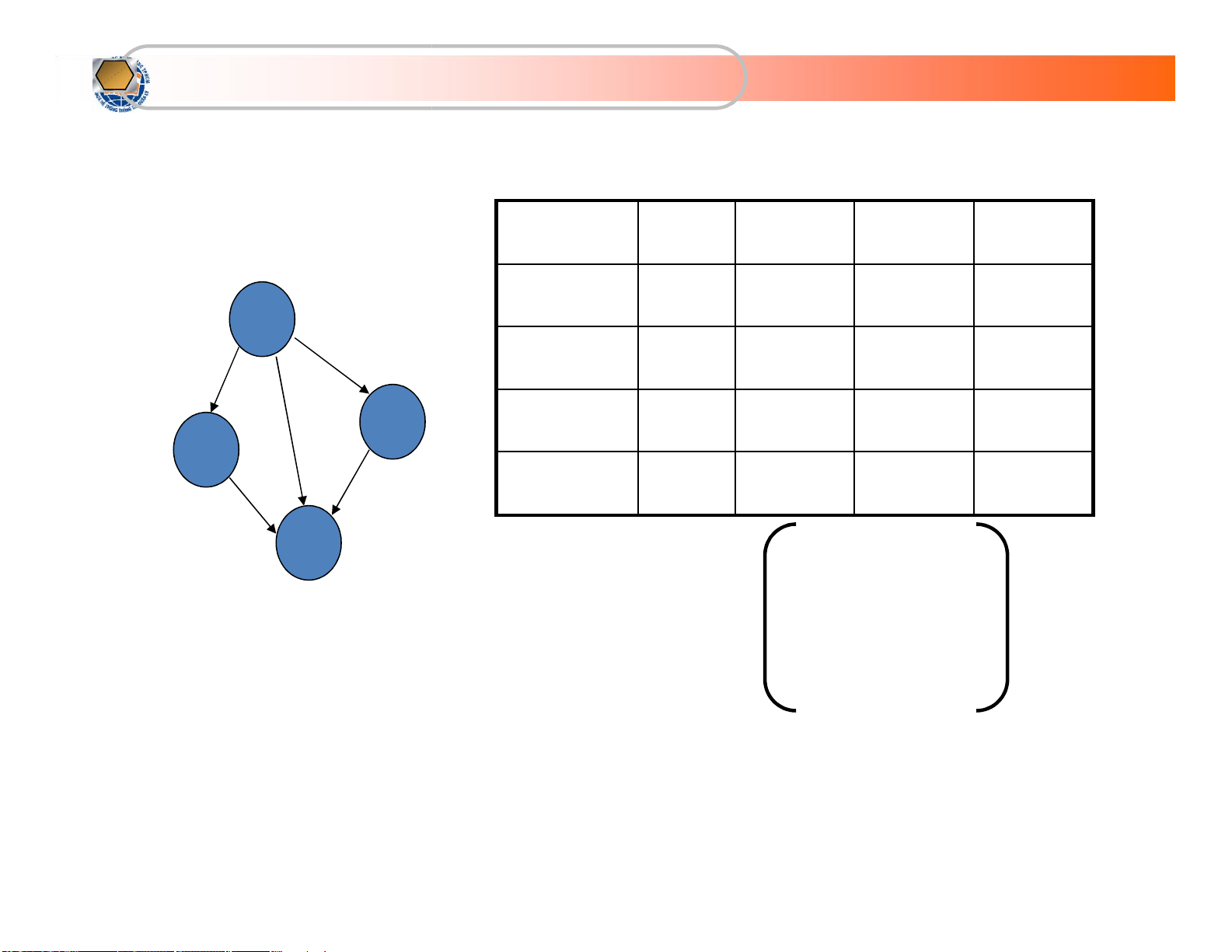
KhoaHệThốngThôngTin Quảnlý
Biểu diễn bằng ma trận kề (tt) A[i][j] 0 1 2 3 0 0 1 1 1 0 1 0 0 0 1 2 0 0 0 1 1 2 3 0 0 0 0 3 0 1 1 1 A = 0 0 0 1 0 0 0 1 0 0 0 0 lOMoARcPSD| 36667950
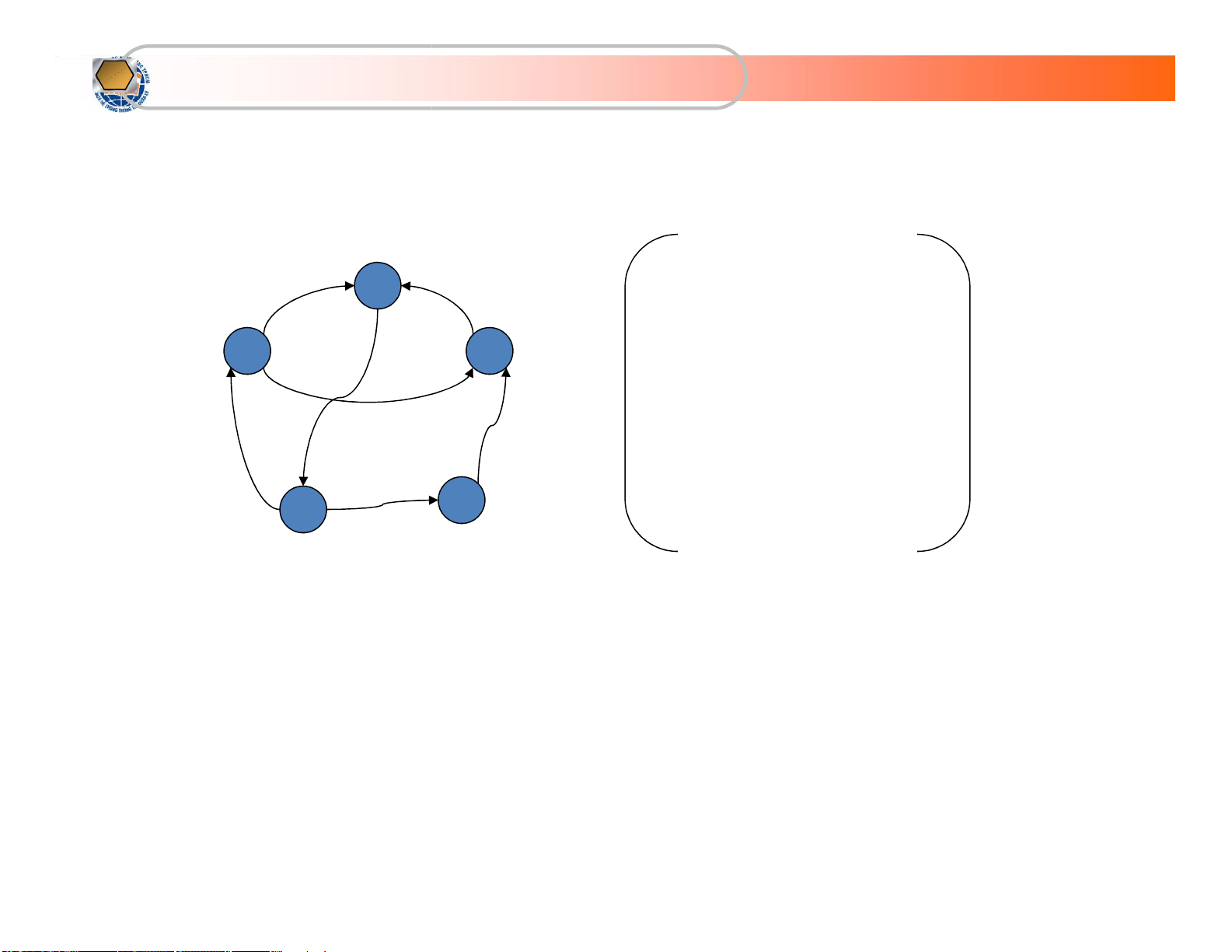
KhoaHệThốngThôngTin Quảnlý
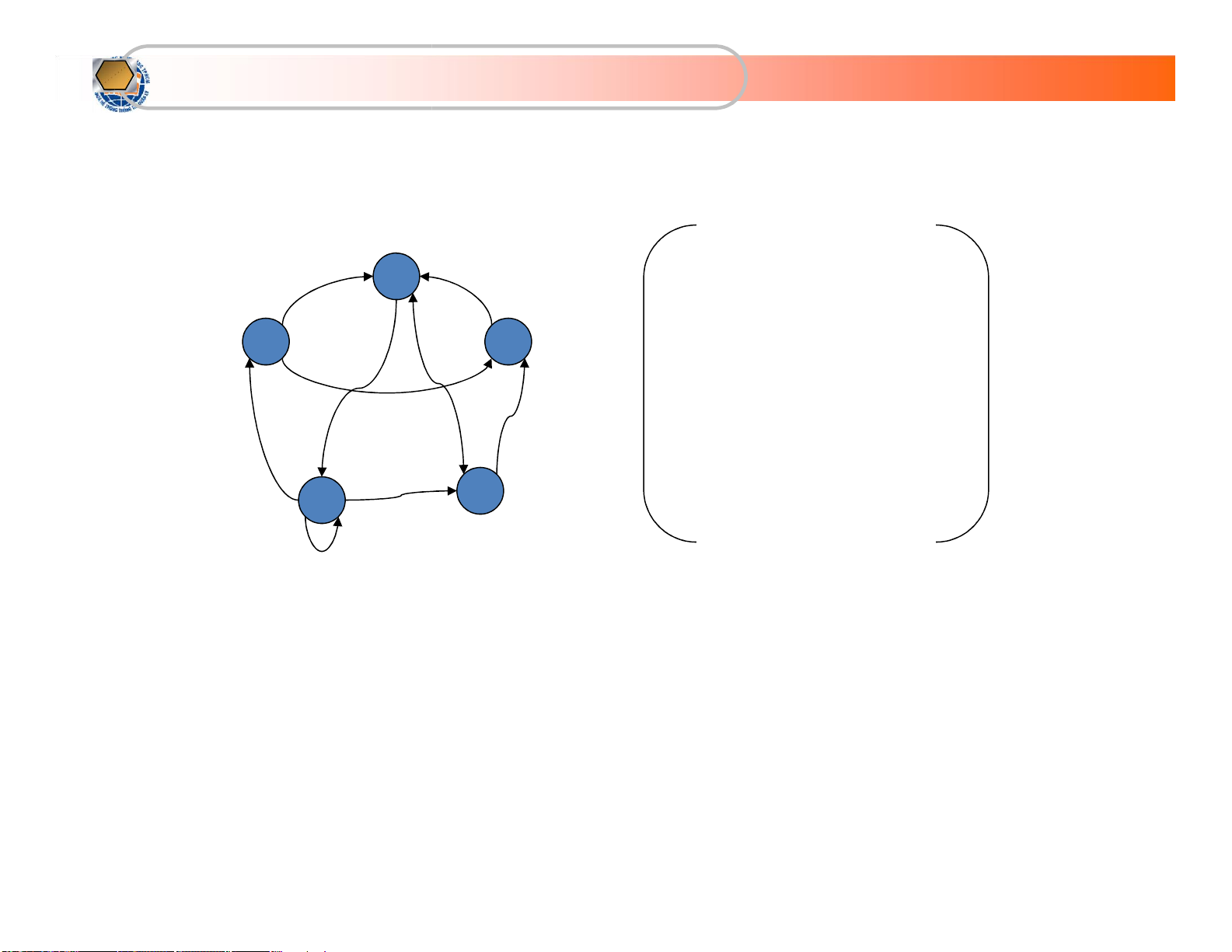
Biểu diễn bằng ma trận kề (tt) x 2 0 1 1 0 0 x x 1 3 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 x x 4 5 1 0 0 1 0 lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
Biểu diễn bằng ma trận kề (tt) x 2 0 1 1 0 0 x x 1 3 0 0 0 1 1 0 1 0 0 0 0 1 1 0 0 x x 4 5 1 0 0 1 1 lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý 0 20 A[i][j] 0 1 2 3 10 0 0 20 10 1 1 1 2 1 20 0 0 5 5 4 2 10 0 0 4 3 Biểu diễn bằng 3 1 5 4 0 ma trận kề (tt) 0 20 10 1 20 0 0 5 A = 10 0 0 4 1 5 4 0 lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
Biểu diễn bằng ma trận kề (tt) • Chú ý
– Đối với đồ thị không định hướng, ma trận kề là ma trận đối xứng
– Đối với đồ thị định hướng, số lượng phần tử 0 khá lớn
– Đối với đồ thị có trọng số, thay thế giá trị 1 bằng giá trị trọng số
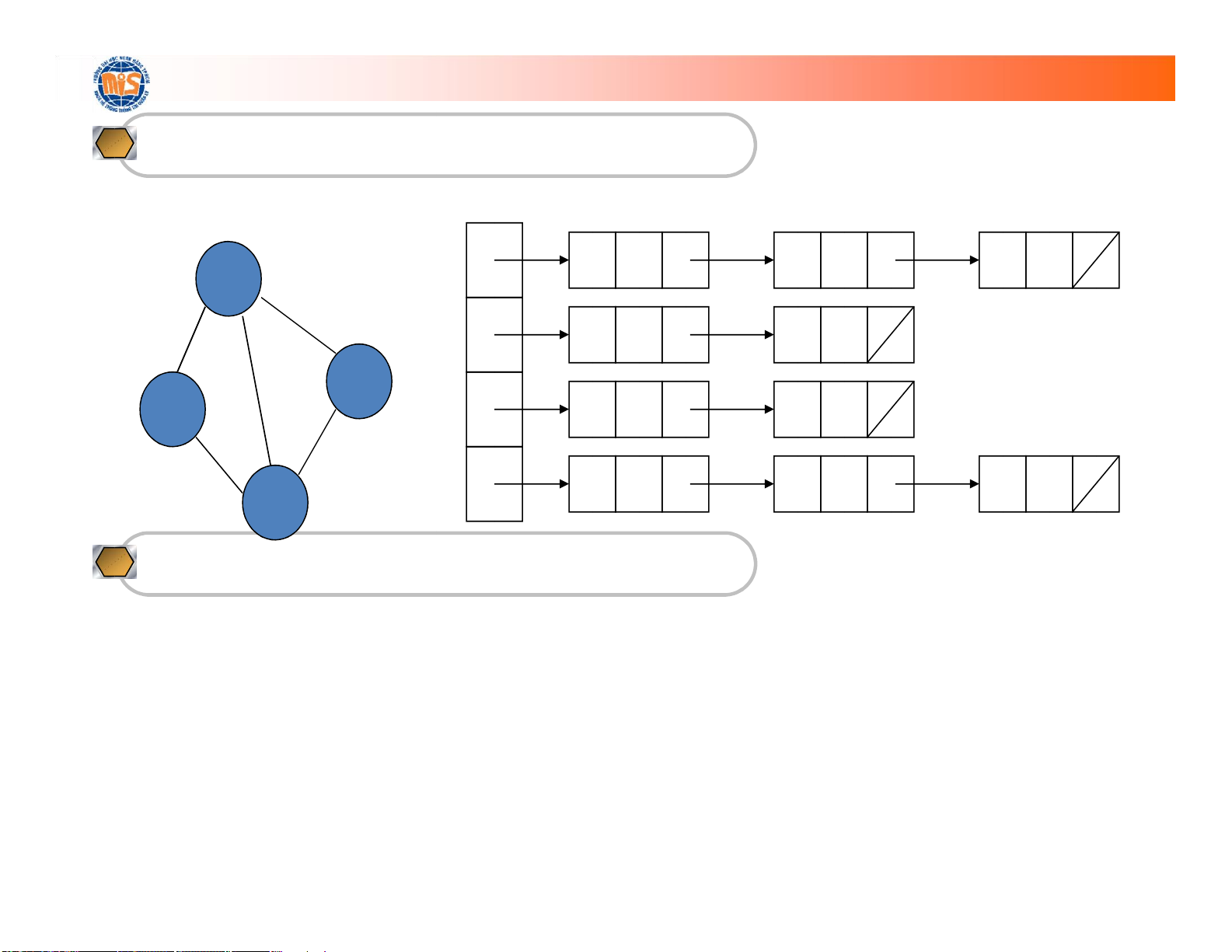
Biểu diễn bằng danh sách kề
• Là một mảng các danh sách
• Ở đây, n hàng của ma trận kề thay thế bằng
n danh sách liên kết động lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
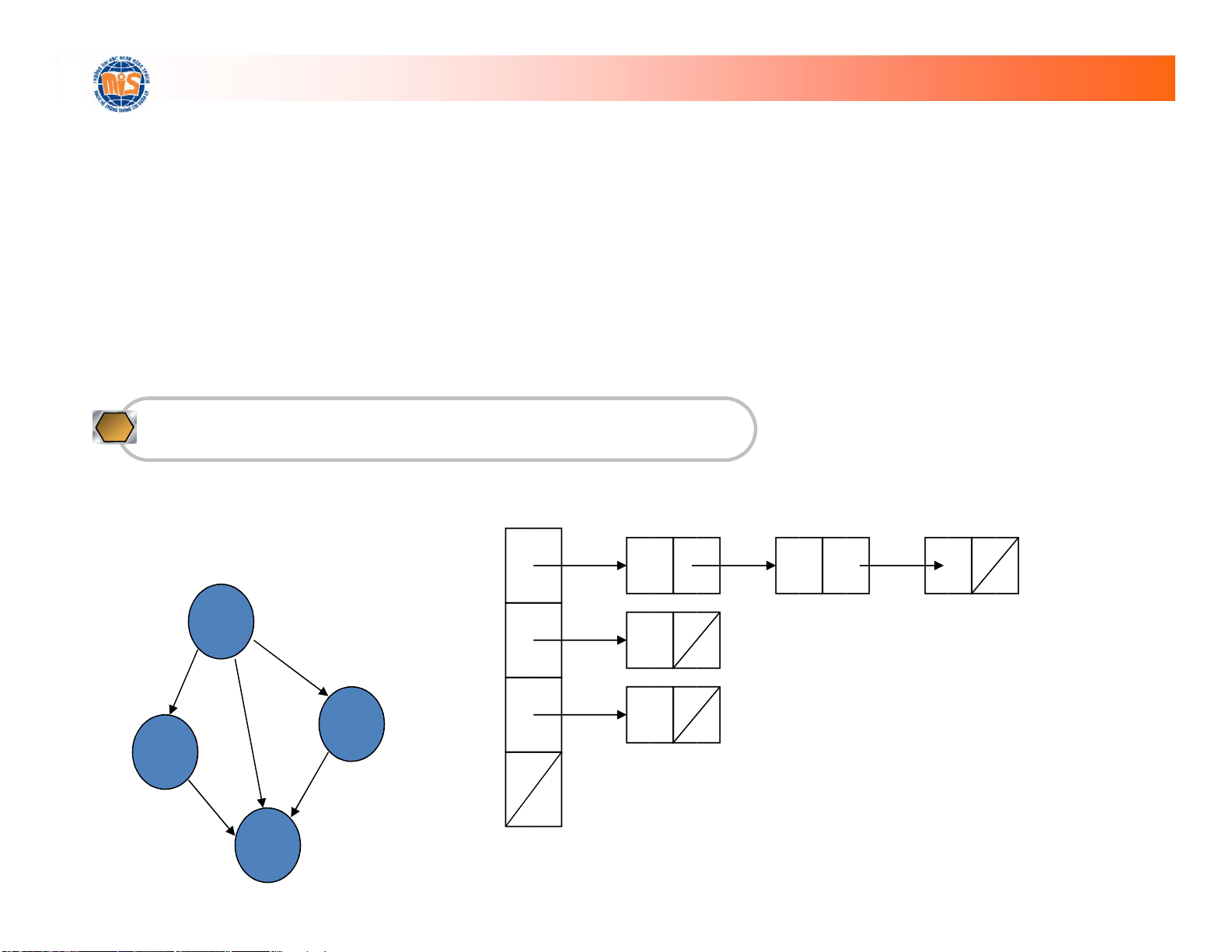
• Mỗi đỉnh của G có một danh sách, mỗi nút
trong danh sách thể hiện các đỉnh lân cận
của nút này – Cấu trúc mỗi nút
• id: tên đỉnh (chỉ số, danh hiệu)
• next: con trỏ đến nút kế tiếp
Biểu diễn bằng danh sách kề (tt) 0 1 2 3 0 1 3 1 2 3 2 3 3 lOMoARcPSD| 36667950
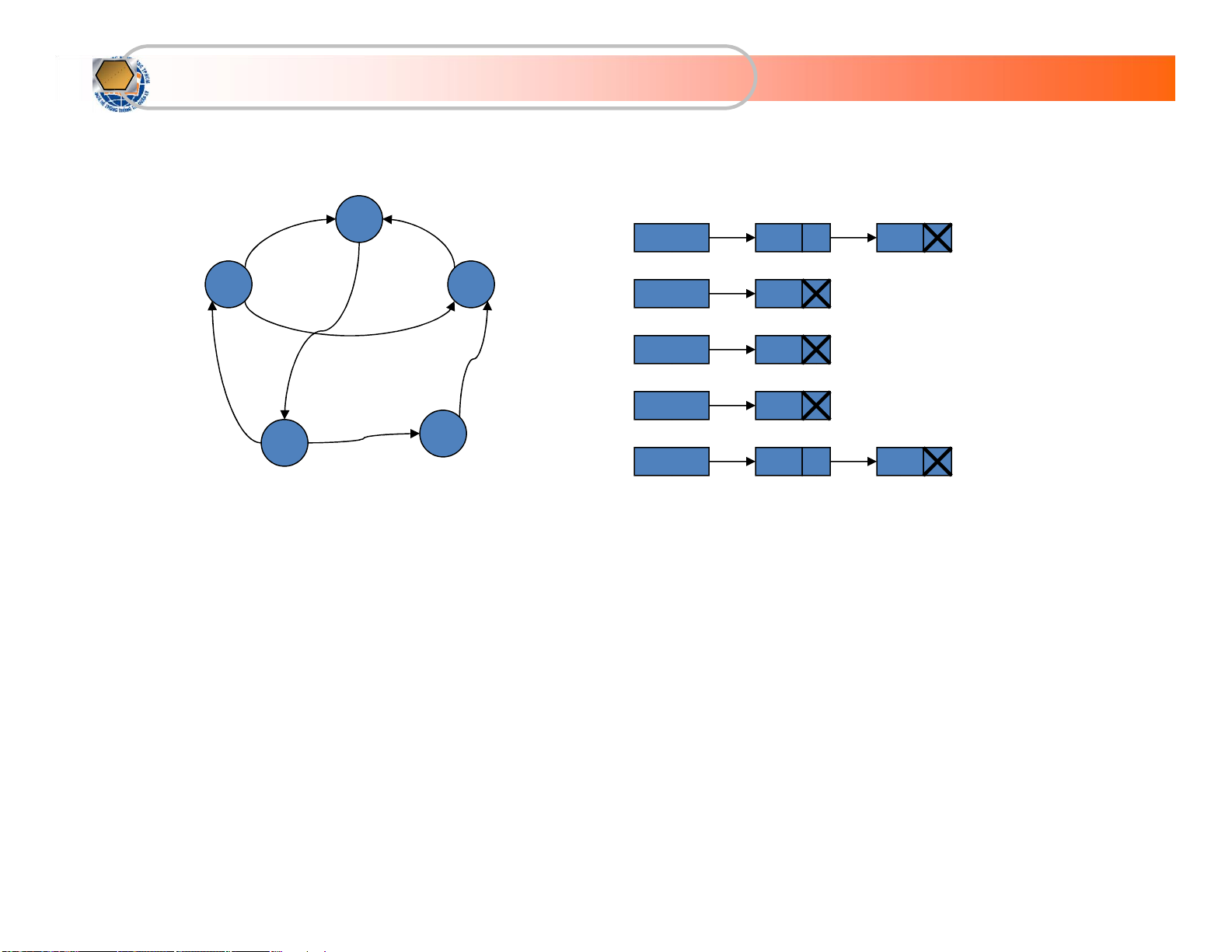
KhoaHệThốngThôngTin Quảnlý
Biểu diễn bằng danh sách kề (tt) x 2 x[1] 2 3 x x 1 3 x[2] 5 x[3] 2 x[4] 3 x x 4 5 x[5] 1 4 lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
Biểu diễn bằng danh sách kề (tt) 0 1 0 10 2 20 3 1 10 20 1 0 10 3 4 1 1 2 2 0 20 3 5 4 5 3 0 3 1 1 4 2 5
Biểu diễn bằng danh sách kề (tt) • Chú ý
– Các nút đầu danh sách được lưu vào một mảng (truy cập nhanh) lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
– Với đồ thị không định hướng có n đỉnh và e
cạnh, thì cần n nút đầu và 2e nút ‘trong’ danh sách
– Với đồ thị định hướng có n đỉnh và e cạnh, thì
chỉ cần e nút ‘trong’ danh sách
– Thứ tự các nút không quan trọng
Phép duyệt đồ thị
• Từ một đỉnh, liệt kê tất cả các đỉnh của đồ thị
– Phép tìm kiếm theo chiều sâu
• Depth First Search - DFS
– Phép tìm kiếm theo chiều rộng lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
• Breadth First Search - BFS
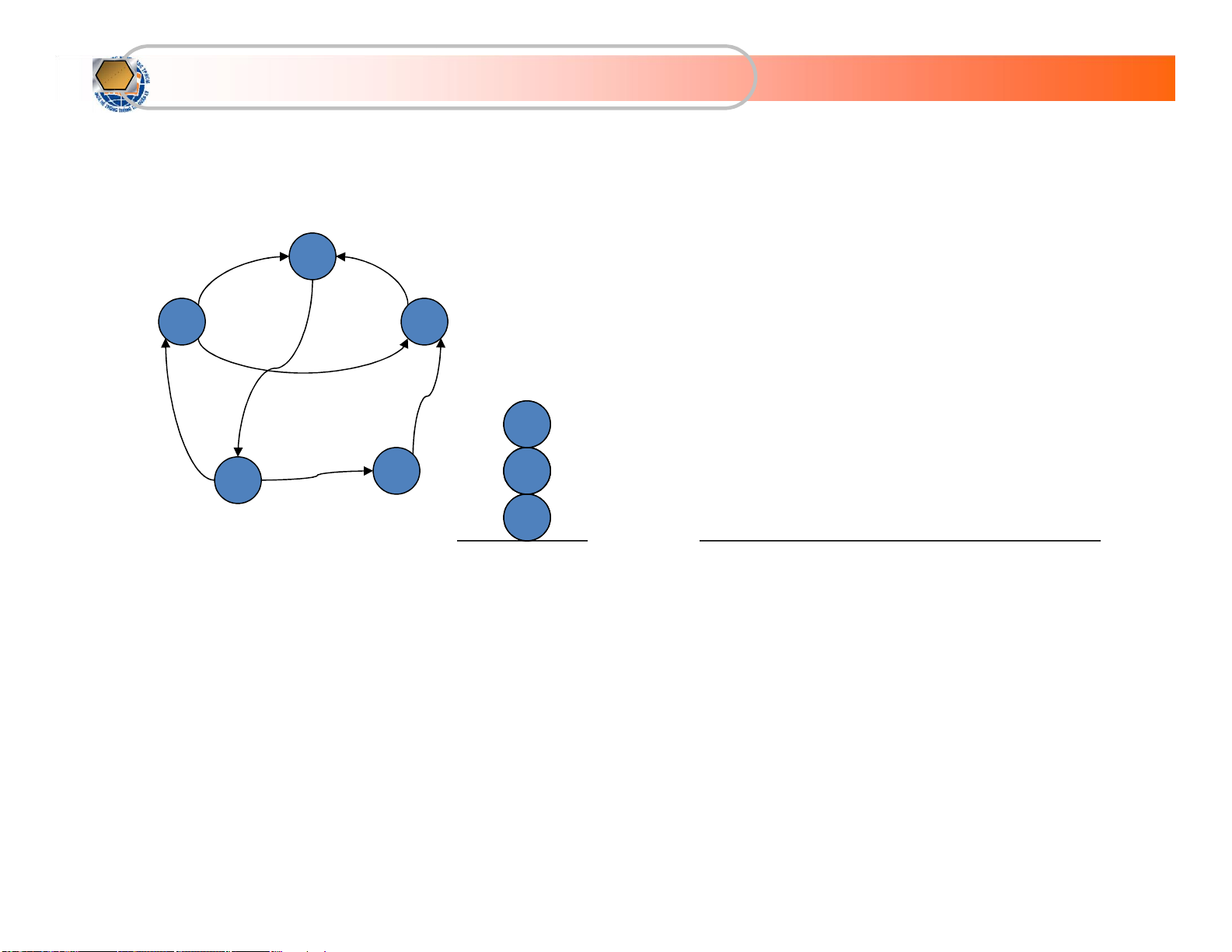
Phép tìm kiếm theo chiều sâu - DFS • Ý tưởng
– Tư tưởng cơ bản của thuật toán tìm kiếm
theo chiều sâu là bắt đầu tại một đỉnh v0 nào
đó, chọn một đỉnh u bất kỳ kề với v0 và lấy
nó làm đỉnh duyệt tiếp theo.
– Cách duyệt tiếp theo được thực hiện tương
tự như đối với đỉnh v0 với đỉnh bắt đầu là u lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
Phép tìm kiếm theo chiều sâu (tt) x 2 x x 1 3 x4 3 x x x 4 3 2 5 1 5 x1 2 lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
Phép tìm kiếm theo chiều sâu (tt) lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
Phép tìm kiếm theo chiều sâu (tt) lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
Phép tìm kiếm theo chiều sâu (tt) • Nhậnxét
– Thời gian thực hiện giải thuật ~ (n+e), nếu G
được biểu diễn bằng danh sách kề
– Thời gian thực hiện giải thuật ~ n2, nếu G
được biểu diễn bằng ma trận kề
– Giải thuật này sử dụng để chứng minh một đồ
thị có liên thông hay không
– Với thuật toán tìm kiếm theo chiều sâu, đỉnh
thăm càng muộn sẽ trở thành đỉnh sớm được
duyệt xong. Đó là kết quả tất yếu vì các đỉnh
thăm được nạp vào stack trong thủ tục đệ quy. lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
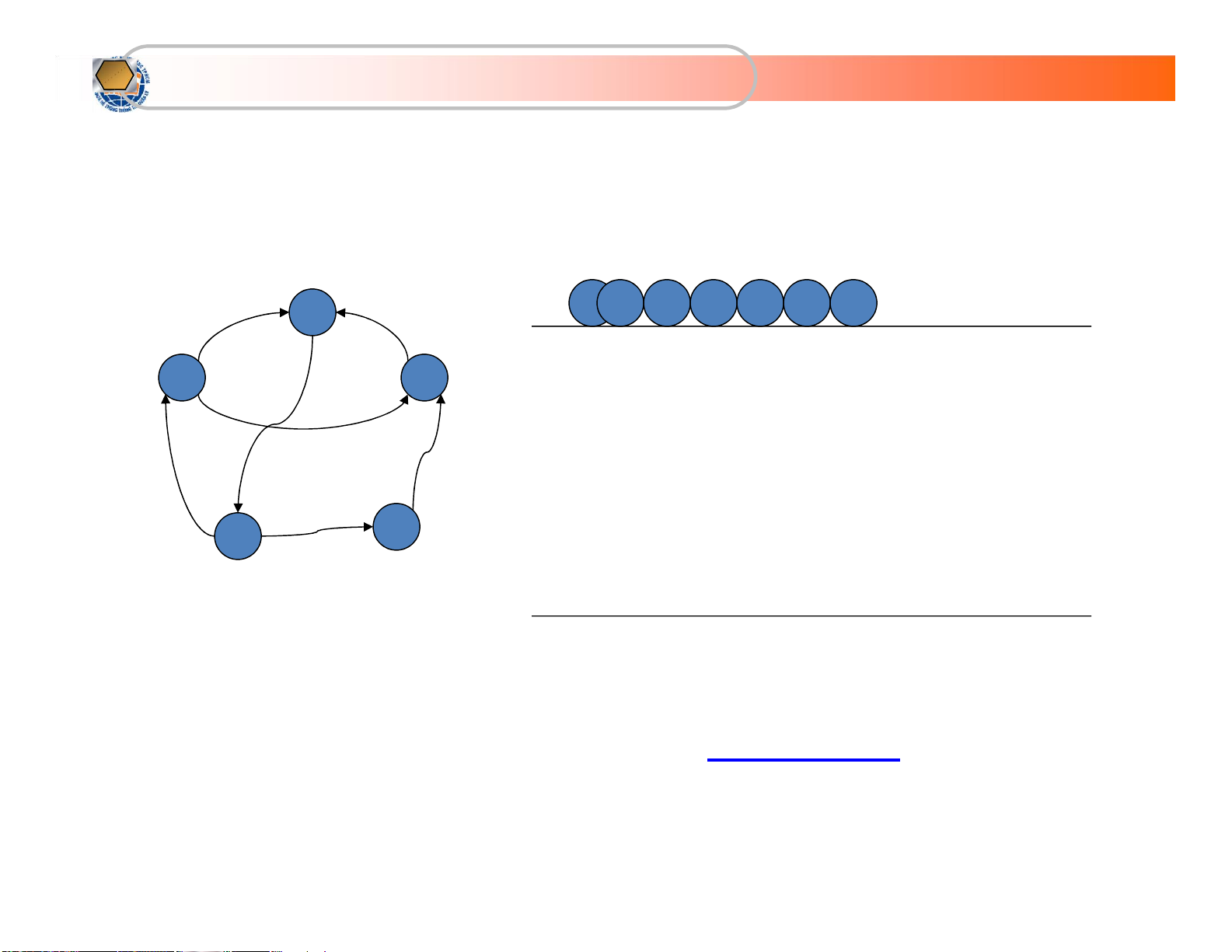
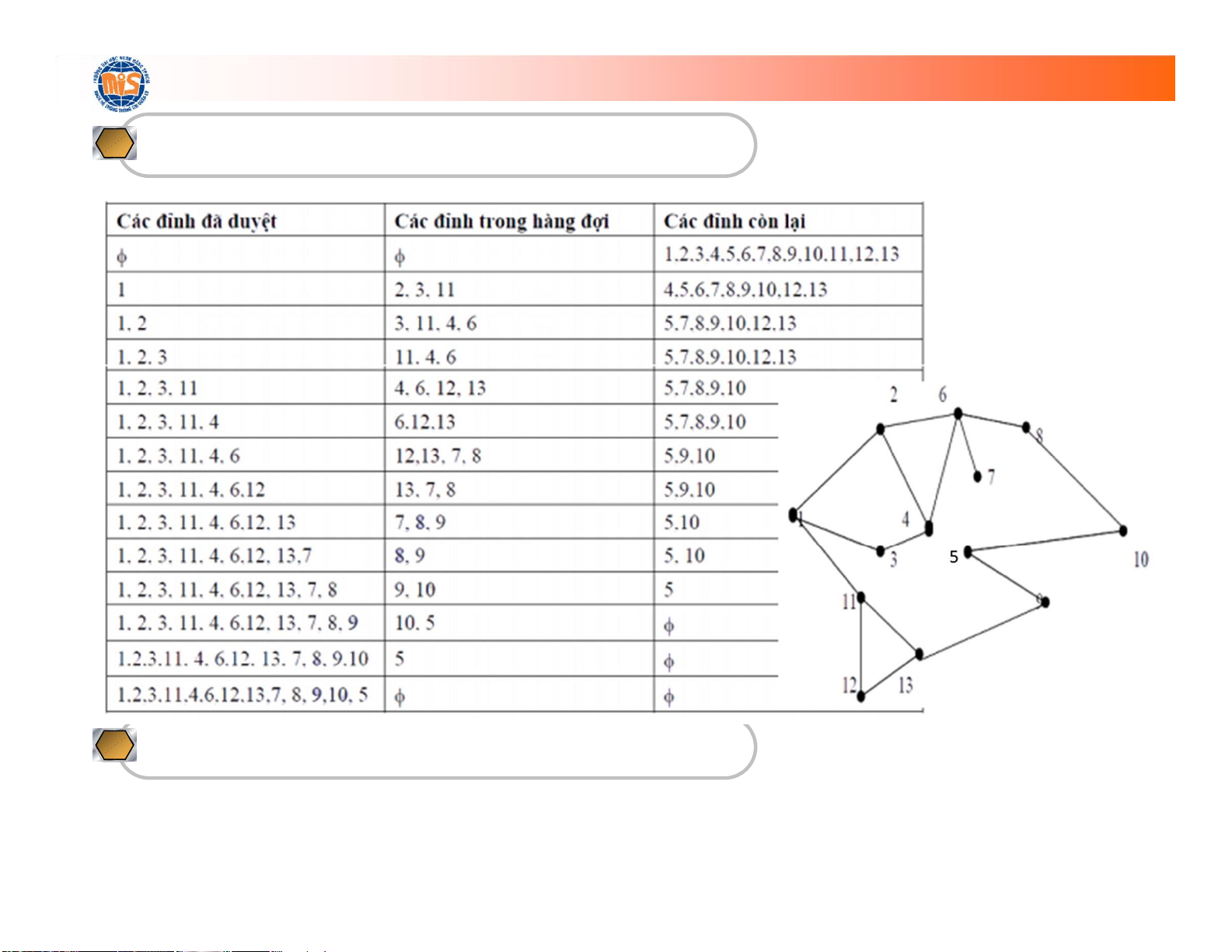
Phép tìm kiếm theo chiều rộng - BFS
• Tại điểm v bất kỳ, duyệt đỉnh v, thu được tập hợp
W gồm các đỉnh w xuất phát từ v
• Lặp lại thao tác trên đối với tất cả các đỉnh w
trong W, thu được tập hợp đỉnh Z
• Lặp lại thao tác trên đối với tất cả các đỉnh z trong Z
• Lặp lại cho đến khi tất cả mọi đỉnh đều được
duyệt qua ít nhất một lần lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
Phép tìm kiếm theo chiều rộng (tt) x x x x x x x x 1 2 3 5 2 1 4 2 x x 1 3 x x 4 5
Tại điểm v bất kỳ, duyệt đỉnh v, thu được tập hợp
W gồm các đỉnh w xuất phát từ v
Lặp lại thao tác trên đối với tất cả các đỉnh w trong
W, thu được tập hợp đỉnh Z
Lặp lại thao tác trên đối với tất cả các đỉnh z trong Z Tham khảo
Lặp lại cho đến khi tất cả mọi đỉnh đều được duyệt qua ít nhất một lần lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
Phép tìm kiếm theo chiều rộng (tt)
Phép tìm kiếm theo chiều rộng (tt) • Nhận xét lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
– Thời gian thực hiện giải thuật ~ (n+e), nếu G
được biểu diễn bằng danh sách kề
– Thời gian thực hiện giải thuật ~ n2, nếu G
được biểu diễn bằng ma trận kề
Cây khung (Spanning tree)
• T=(V,E’) ⊆ G=(V,E), với E ⊇ E’ bao gồm
các cung thuộc một phép duyệt từ một
đỉnh đến các đỉnh còn lại trong V
• Giá của cây khung T = tổng trọng số của các cung thuộc E’ lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý Cây khung T
Đồ thị Gcủa đồ thị G Cây khung (Spanning tree) • Chú ý
– Một đồ thị G có thể có nhiều cây khung
– Cây khung theo chiều rộng, theo chiều sâu
– Các cung trong cây khung không tạo nên chu trình
• Giữa hai đỉnh trong một cây khung chỉ tồn tại duy
nhất một đường đi từ đỉnh này đến đỉnh kia lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý
– Nếu đồ thị có n đỉnh, thì cây khung có n-1 cạnh
Cây khung cực tiểu
• Là cây khung với tổng các trọng số là cực tiểu 6 10 6 10 1 1 7 20 5 5 lOMoARcPSD| 36667950
KhoaHệThốngThôngTin Quảnlý Q&A