Sự tương giao và tiếp xúc của mặt cầu với mặt phẳng, đường thẳng | Chuyên đề Toán 12

Chuyên đề Toán 12 sự tương giao, tiếp xúc của mặt cầu với mặt
phẳng, đường thẳng
A. Các kiến thức cần nhớ về sự tương giao, sự tiếp xúc mặt cầu
Các điều kiện tiếp xúc:
+ Đường thẳng  là tiếp tuyến của (S)  d I;  . R
+ Mặt phẳng() là tiếp diện của (S)  d I;   . R
Lưu ý các dạng toán liên quan như tìm tiếp điểm, tương giao.
B. Bài tập tương giao, tiếp xúc của mặt cầu với mặt phẳng, đường thẳng tong không gian
Bài tập 1: Cho đường thẳng  x y 1 z  2 :  
và và mặt cầu S  : 2 1 1 2 2 2
x  y  z  2x  4z 1 0 . Tìm số điểm chung của  và S  ? Hướng dẫn giải 
Đường thẳng đi qua M 0;1;2 và có một vectơ chỉ phương là u  2;1;  1
Mặt cầu S  có tâm I 1;0; 2 và bán kính R  2.    Ta có MI  1; 1  ; 4
  và u,MI    5  ;7; 3       u,MI 
 d I    498 ,    u 6
Vì d I,  R nên  không cắt mặt cầu S .
Bài tập 2: Cho điểm I 1; 2
 ;3. Phương trình mặt cầu tâm I và tiếp xúc với trục Oy là:
A. x  2   y  2 z  2 1 2 3  10.
B. x  2  y  2 z  2 1 2 3 10.
C. x  2   y  2 z  2 1 2 3 10.
D.x  2   y  2 z  2 1 2 3  9. Hướng dẫn giải
Gọi M là hình chiếu của I 1; 2
 ;3 lên Oy, ta có: M 0;2;0 .  IM   1  ;0; 3
   R  d I,Oy  IM  10 là bán kính mặt cầu cần tìm.
Phương trình mặt cầu là: x  2  y  2 z  2 1 2 3 10.
Bài tập 3: Cho điểm I 1; 2
 ;3và đường thẳng d có phương trình
x 1 y  2 z  3  
. Viết phương trình mặt cầu tâm I, tiếp xúc với d ? 2 1 1 Hướng dẫn giải
Đường thẳng d  đi qua I 1;2;3 và có VTCP    u, AM  u  2;1;  1 d  , A d        5 2 u
Phương trình mặt cầu là: x  2   y  2 z  2 1 2 3  50.
Bài tập 4: Xác định phương trình mặt cầu S  tâm I(2;3;- ) 1 cắt đường thẳng
x 11 y z  25 d :  
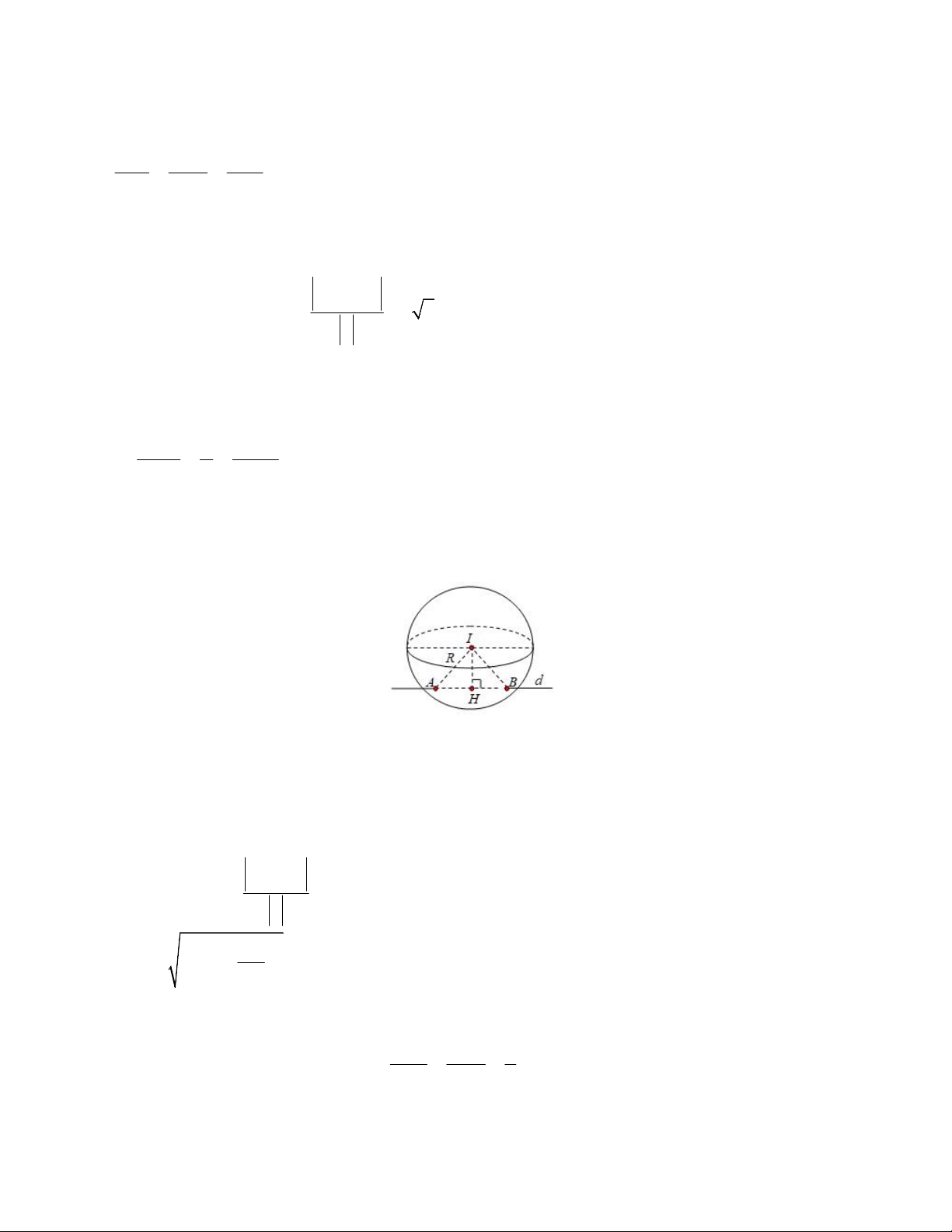
tại 2 điểm A, B sao cho AB 16 2 1 2 ? Hướng dẫn giải Hình vẽ minh họa
Đường thẳng d  đi qua M 11; 0;25 và có vectơ 
chỉ phương u  2;1; 2.
Gọi H là hình chiếu của I trên (d). Ta có:   u,MI 
IH d I, AB       15 u 2 2  AB   R  IH     17 .  2 
Vậy S  : x  2   y  2  z  2 2 3 1  289.
Bài tập 5: Cho đường thẳng x  5 y  7 :   z d
và điểm I(4;1;6) . Đường thẳng d 2 2 1
cắt mặt cầu S  có tâm I, tại hai điểm A, B sao cho AB  6. Phương trình của mặt cầu S  là:
A. x  2  y  2  z  2 4 1 6 18.
B.x  2  y  2  z  2 4 1 6 18.
C. x  2   y  2  z  2 4 1 6  9.
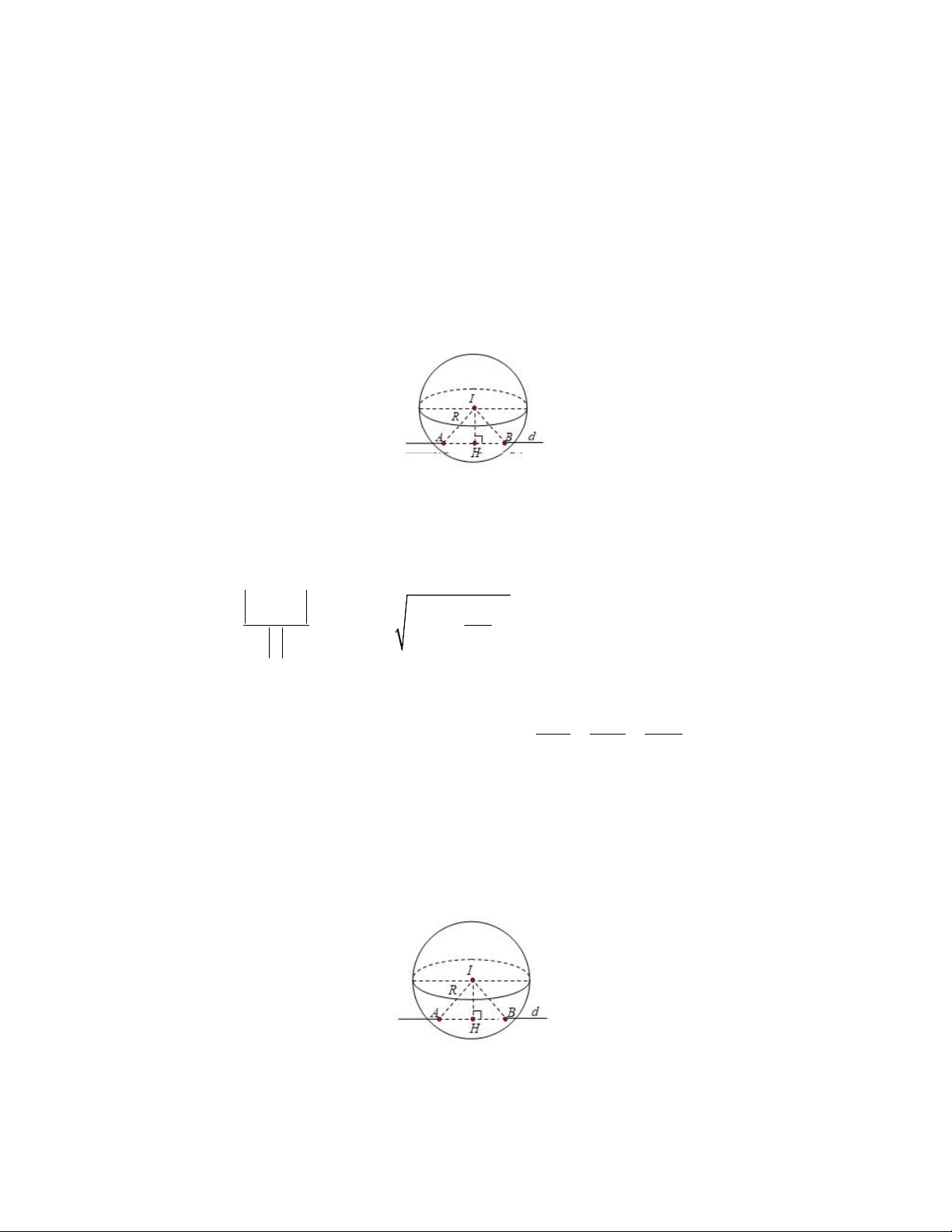
D.x  2  y  2  z  2 4 1 6 16. Hướng dẫn giải Hình vẽ minh họa
Đường thẳng d đi qua M (5;7;0) và có vectơ chỉ
phương u  (2;2;1) . Gọi H là hình chiếu của I trên (d). Ta có :   u,MI  2
IH d I, AB      AB    3 2  R  IH     18 u  2 
Vậy S : x  2  y  2  z  2 4 1 6 18.
Bài tập 8: Cho điểm I 1;0;0và đường thẳng
x 1 y 1 z  2 d :   . Tìm phương 1 2 1
trình mặt cầu S có tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB đều ? Hướng dẫn giải Hình vẽ minh họa
Đường thẳng đi qua M  1;1; 2 và có vectơ chỉ 
phương u  1;2;  1    Ta có MI  0; 1
 ;2và u,MI   5; 2  ; 1    
Gọi H là hình chiếu của I trên (d). Ta có :   u,MI 
IH d I, AB       5 . u Xét tam giác IAB, có 3 2IH 2 15 IH  . R  R   2 3 3
Vậy phương trình mặt cầu là: x  2 2 2 20
1  y  z  . 3
Bài tập 9: Cho mặt cầu 2 2 2
(S) : x  y  z  4x  2y 6z 5  0 . Viết phương trình tiếp
tuyến của mặt cầu (S) qua A0;0;5 biết:
a) Tiếp tuyến có một vectơ chỉ phương u  1;2;2 .
b) Vuông góc với mặt phẳng (P) : 3x  2y  2z 3  0. Hướng dẫn giải
a) Đường thẳng d qua A0;0;5 và có một vectơ chỉ phương u  1;2;2 , có phương x  t
trình d: y  2t . z  5  2t
b) Mặt phẳng (P) có một vectơ pháp tuyến là n  . P 3;2;2
Đường thẳng d qua A0;0;5 và vuông góc với mặt phẳng (P) nên có một vectơ x  3t chỉ phương n 
, có phương trình d: y  2t . P 3;2;2 z  2t   5 Bài tập 10: Cho 2 2 2
(S) : x  y  z  6x  6y  2z  3  0 và hai đường thẳng
x 1 y 1 z 1  :   ; 1 3 2 2 x y 1 z  2  :   . 2 2 2 1
Viết phương trình mặt phẳng (P) song song với  và  đồng thời tiếp xúc với 1 2 (S). Hướng dẫn giải
Mặt cầu (S) có tâm I 3;3;  1 , R  4 .
Ta có:  có một vectơ chỉ phương là u  3;2;2 . 1   1
 có một vectơ chỉ phương là u  2;2;1 . 2   2
Gọi n là một vectơ pháp của mặt phẳng (P).  P   n   Do: ( ) / / u 1 1    
     chọn n  u ,u  2;1;2 1 2    (P) / / n   u 2  2
Lúc đó, mặt phẳng (P) có dạng : 2x  y  2z  m  0 . 
Để mặt phẳng (P) tiếp xúc với (S) m  d I P  5 ;( )  R   4 3 m  7
 5 m  12   . m  17
Kết luận: Vậy tồn tại 2 mặt phẳng là : 2x  y  2z  7  0,2x  y  2z 17  0 .
Bài tập 11: Viết phương trình tiếp diện của mặt cầu S 2 2 2
: x  y  z  2x  4y  6z  5  0 , biết tiếp diện: a) qua M 1;1;  1 .
b) song song với mặt phẳng (P) : x  2y  2z 1 0 .
b) vuông góc với đường thẳng
x  3 y 1 z  2 d :   . 2 1 2 Hướng dẫn giải
Mặt cầu (S) có tâm I 1;2;3 , bán kính R  3. 
a) Để ý rằng, M S  . Tiếp diện tại M có một vectơ pháp tuyến là IM  2; 1  ; 2   , có phương trình :
 : 2x 1y 12 z 1 0  2x  y 2z 1 0.
b) Do mặt phẳng   / / P nên   có dạng: x  2y  2z  m  0 .
Do   tiếp xúc với (S) dI,   R m  3 m  6 
 3  m 3  9  . 3  m  12 * Với m  6
 suy ra mặt phẳng có phương trình: x  2y  2z  6  0.
* Với m 12 suy ra mặt phẳng có phương trình: x  2y  2z 12  0.
c) Đường thẳng d có một vectơ chỉ phương là u  . d 2;1; 2  
Do mặt phẳng    d nên   nhận u 
làm một vectơ pháp tuyến. d 2;1; 2  
Suy ra mặt phẳng   có dạng: 2x  y  2z  m  0 . Do  m  6 m  
  tiếp xúc với (S)  d I,  3  R 
 3  m  6  9  . 3  m  15 * Với m  3
 suy ra mặt phẳng có phương trình: x  2y  2z  3  0.
* Với m 15 suy ra mặt phẳng có phương trình: x  2y  2z 15  0.