











Preview text:
lOMoARcPSD|50202050
TRƯỜNG ĐẠI HỌC HẢI PHÒNG KHOA CÔNG NGHỆ THÔNG TIN ------------- -------------- BÁO CÁO BÀI TẬP LỚN Học phần: Lập trình python Đề tài: Mã hoá và giải mã Rabin ***
HỌ VÀ TÊN SINH VIÊN: Phạm Tiến Huy
Đinh Thị Hồng Nhung
Phạm Thị Thanh Huyền
Lớp: Công nghệ thông tin 1.K22
GIẢNG VIÊN HƯỚNG DẪN: PGS.TS.LÊ ĐẮC NHƯỜNG Hải Phòng 2023 MỤC LỤC 1 lOMoARcPSD|50202050
I.GIỚI THIỆU HỆ MÃ HOÁ RABIN ............................................................. 3
1.Michael O.Rabin.................................................................................. 3
2.Giới thiệu hệ mã hoá Rabin .................................................................. 3
3.Giới thiệu PIP ...................................................................................... 4
II.KHẢO SÁT VÀ PHÂN TÍCH HỆ MÃ HOÁ RABIN .................................. 4
Phần I.Sơ đồ hệ mã hoá rabin ...................................................................... 4
1.Giải thuật tạo khoá cho hệ mã Rabin ..................................................... 6
2. Giải thuật mã hoá công khai Rabin ...................................................... 6
3. Giải thuật giải mã cho hệ mã hoá Rabin ............................................... 7
4. Ví dụ .................................................................................................. 8
Phần 2: Các đặc trưng của hệ mã Rabin ....................................................... 9
1.Tính an toàn của hệ mã ........................................................................ 9
2. Sử dụng dư thừa dữ liệu .................................................................... 10
3. Tính hiệu quả .................................................................................... 10
4. Ưu và nhược điểm của hệ mã Rabin................................................... 11
III.GIỚI THIỆU CODE ................................................................................ 11
IV.ỨNG DỤNG CỦA HỆ MÃ RABIN ......................................................... 14 LỜI NÓI ĐẦU
Hệ thống mã hóa Rabin là một trong những phương pháp mã hóa khóa công
khai phức tạp và mạnh mẽ, dựa trên tính toán toán học phức tạp.
Khi chúng ta bắt đầu thảo luận về mã hóa và giải mã Rabin, thường sẽ bắt
đầu bằng việc tạo ra một cặp khóa, bao gồm khóa công khai (public key) và khóa
bí mật (private key). Khóa công khai có thể được chia sẻ với mọi người, trong khi
khóa bí mật được giữ bí mật.
Lý do tại sao hệ thống mã hóa Rabin được sử dụng để bảo vệ thông tin là
do tính toán các giá trị nguyên tố lớn và các phép toán toán học phức tạp liên quan
đến các số nguyên tố. Nó có tính khả thi cho việc giải mã mà không có khóa bí
mật phù hợp. Thành công trong việc giải mã Rabin yêu cầu việc tìm ra các ước số
của một số nguyên tử lớn, điều này được coi là một vấn đề tính toán rất khó.
Lưu ý rằng mã hóa và giải mã Rabin thường sử dụng trong các ứng dụng
bảo mật thông tin và giao tiếp an toàn. Nó không chỉ đơn giản là một cách để bảo
vệ dữ liệu mà còn đóng vai trò quan trọng trong việc đảm bảo tính toàn vẹn và
bảo mật của thông tin quan trọng. 2 lOMoARcPSD|50202050
I.GIỚI THIỆU HỆ MÃ HOÁ RABIN 1. Michael O.Rabin
Michael Oser Rabin là một nhà toán học người Israel sinh ngày 1 tháng 9
năm 1931 tại Bessarabia (nay là Moldova). Ông là giáo sư tại Trường Đại học
Harvard và Trường Đại học Hebrew Jerusalem, và đã đóng góp đáng kể cho lĩnh vực khoa học máy tính.
Michael O. Rabin đã đạt được nhiều thành tựu trong nghiên cứu toán học
và khoa học máy tính. Ông đã đưa ra các ý tưởng quan trọng về lý thuyết tính
toán, bao gồm bài toán chấp nhận ngôn ngữ (acceptance of languages) và thuật toán Monte Carlo.
Ngoài ra, Michael O. Rabin cũng là một trong những nhà toán học đầu tiên
đóng góp cho lĩnh vực mật mã học, với việc phát triển hệ mã hóa Rabin, một thuật
toán mã hóa khóa công khai. Hệ mã hóa Rabin được coi là một trong những thuật
toán mã hóa khóa công khai đầu tiên được phát triển sau thuật toán RSA.
Vì những đóng góp của mình trong lĩnh vực khoa học máy tính và toán học,
Michael O. Rabin đã được trao nhiều giải thưởng danh giá, bao gồm giải thưởng
Turing năm 1976 và giải thưởng Israel trong lĩnh vực khoa học máy tính và toán học vào năm 2002.
2. Giới thiệu hệ mã hoá Rabin
Một đặc điểm quan trọng đáng mong muốn của bất kì lược đồ mã hóa nào
là nó phải chứng minh được là việc phá khóa tương đương với việc giải một bài
toán nào đó đã biết, mà người ta tin tưởng là rất khó, giống như việc phân tích ra
thừa số hay giải bài logarit rời rạc.
Chẳng bao lâu sau sự công bố hệ thống RSA, năm 1979 Michael O.Rabin
đã cho ra đời hệ thống mã hóa công khai của riêng mình. Đó là sự phá vỡ của cái
khó khăn mà sự phân tích thành nhân tử của hệ mã hóa RSA đã gặp phải.
Hệ mã hóa công khai Rabin là một ví dụ đầu tiên về một lược đồ khóa công
khai đã được chứng minh về tính an toàn. Khó khăn mà một người tấn công thụ
động gặp phải khi giải mã đó là độ khó tương đương về mặt tính toán với việc phân tích ra thừa số.
Nghĩa là với một số bất kỳ(n công khai) thì sự giải mã sẽ khó tương đương
với giải bài toán phân tích ra thừa số nguyên tố.
Hệ mã hóa Rabin sử dụng phương pháp mã hóa và giải mã khóa công khai,
tức là sử dụng hai khóa khác nhau để mã hóa và giải mã thông tin. Khóa công khai
được công khai cho tất cả mọi người, trong khi khóa riêng (private key) được giữ
bí mật bởi người nhận thông tin. 3 lOMoARcPSD|50202050
Thuật toán mã hóa Rabin sử dụng một hàm băm (hash function) để chuyển
đổi thông tin cần mã hóa thành một số nguyên. Sau đó, thuật toán sử dụng khóa
công khai để mã hóa số này. Người nhận sẽ sử dụng khóa riêng để giải mã số này
và chuyển đổi trở lại thành thông tin gốc ban đầu. 3. Giới thiệu PIP
PIP (Package Installer for Python) là một trình quản lý gói mở rộng và phổ
biến được sử dụng trong Python để cài đặt và quản lý các thư viện và gói mô-đun
từ Python Package Index (PyPI) và từ các kho lưu trữ khác. PIP giúp người dùng
dễ dàng cài đặt và quản lý các thư viện và gói mô-đun Python một cách hiệu quả.
Dưới đây là một số tính năng chính của PIP: -
Cài đặt Gói: PIP cho phép người dùng cài đặt các gói mô-đun Python từ
PyPIhoặc từ các kho lưu trữ khác bằng cách sử dụng lệnh đơn giản pip install . -
Quản lý Gói: PIP cũng cung cấp các chức năng quản lý gói như cập nhật,
gỡcài đặt hoặc xem thông tin về gói mô-đun cụ thể. -
Tải và Cập nhật Gói: PIP cho phép người dùng tải và cập nhật các phiên
bảnmới của gói mô-đun từ PyPI hoặc từ các kho lưu trữ khác. -
Xử lý Phụ thuộc: PIP tự động xử lý các phụ thuộc và cài đặt các gói phụ
thuộccần thiết cho một gói cụ thể. -
Tạo Môi trường ảo: PIP cung cấp tính năng tạo môi trường ảo để cách ly
vàquản lý các phụ thuộc của dự án một cách độc lập. -
Sử dụng PIP, người dùng có thể dễ dàng quản lý và cài đặt các gói mô -
đunPython từ một nguồn tài nguyên phong phú như PyPI, giúp việc phát triển và
quản lý dự án Python trở nên hiệu quả và thuận tiện hơn.
II.KHẢO SÁT VÀ PHÂN TÍCH HỆ MÃ HOÁ RABIN
Phần I. Sơ đồ hệ mã hoá rabin
Sơ đồ hệ mật mã khóa công khai Rabin được cho bởi: S=(P, C, K, E, D) Trong đó:
P=C=Z , trong đó n là một số nguyên Blum, n
n=p×q, với p và q là 2 số nguyên
tố có tính chất p≡3mod4 ,q≡3mod 4.
K={¿ (khóa công khai) ¿(n,B),K “ (khóa bí mật) ¿ ( p,q) ,0≤B≤n−1} 4 lOMoARcPSD|50202050
Các thuật toán E và D được xác định bởi:
E (K' ,x)=y=x (x B ) modn, D¿
Trong một mạng truyền tin bảo mật với sơ đồ mật mã Rabin, mỗi người tham
gia chọn cho mình các yếu tố n, B, p, q để lập nên khóa công khai và khóa bí mật của mình.
Thuật toán giải mã dK =D left ({K} ^ {¿, y¿¿: 2 Đặt B
C= , ta có dK (y)= left (sqrt {C} - {B} over {2} right ) mod , do đó để có 4 dK”(y) ta
cần tính √ Cmodn, tức cần giải phương trình Z2≡C modn.
• Theo định lý số dư Trung Quốc, phương trình đó tương đương với hệ thống
gồm 2 phương trình sau đây: (¿) Z2≡C mod p Z2 ≡C modq
Định lý Fermat: nếu p là số nguyên tố thì: Cp−1≡1mod p
• Theo tiêu chuẩn Euler: khi p là số nguyên tố thì số a là thặng dư bậc 2
mod p nếu và chỉ nếu a(p−1)/2≡1modp
Vì p là số nguyên tố và C là thặng dư bậc 2 mod p nên ta có:
C(p−1)/2≡1modp
Tương tự, vì q là số nguyên tố và C là thặng dư bậc 2 mod q nên ta có:
C(q−1)/2≡1modq
• Theo giả thuyết, p≡3mod4 ,q≡3mod 4 nên (p+1)/4 và(q+1)/4 là các số nguyên và ta có:
(±C(p+1)/4)2≡Cmod p 5 lOMoARcPSD|50202050
(±C(p+1)/4)2≡Cmod q
Do đó, phương trình Z2≡C modn hay hệ phương trình (¿) có 4 nghiệm theo mod
n tương ứng với 4 hệ phương trình sau đây: (1)
Z ≡C( p+1)/4 mod p
(3) Z ≡−C(p+1)/4 mod p
Z≡C ( p+1) / 4 modq
Z≡C ( p+1) / 4 modq (2)
Z ≡C( p+1)/4 mod p
(4 ) Z ≡−C( p+1)/4 mod p
Z≡−C(p+1)/4modq
Z≡−C(p+1)/4modq
Cả 4 nghiệm của 4 hệ phương trình đó theo mod n đều được viết chung dưới một
ký hiệu là C mod n, vì vậy thuật toán giải mã dK”(y) sẽ cho ta 4 giá trị khác nhau
theo mod n mà bản rõ là 1 trong 4 giá trị đó. Việc chọn giá trị nào trong 4 giá trị
tìm được làm bản rõ tùy thuộc vào những đặc trưng khác của bản rõ mà người giải
mã nhận biết ( ví dụ: bản rõ dưới dạng số phải có biểu diễn nhị phân là mã của
một văn bản tiếng anh thông thường).
1. Giải thuật tạo khoá cho hệ mã Rabin
Mỗi bên tạo 1 khóa công khai và một khóa bí mật tương ứng. Bên A phải làm các việc sau:
a. Tạo 2 số ngẫu nhiên lớn và khác nhau p và q, p gần bằng q. b. Tính n = pq.
c. Khóa công khai của a là n, khóa bí mật của A là (p, q).
2. Giải thuật mã hoá công khai Rabin
Sau khi A đã tạo và công khai khóa mã hóa công khai. Lúc đó B muốn gửi
thông điệp cho A thì B sẽ dùng khóa công khai của A để mã hóa và sau đó A sẽ
giải mã thông điệp bằng khóa bí mật tương ứng của mình.
-> Khi đó B cần làm các việc sau:
Nhận khóa công khai được xác thực của A là n.
Giả sử thông điệp là một số nguyên m trong khoảng [0,1,...,n-1] Tính c = m^2 mod n Gửi bản mã hóa c cho A. 6 lOMoARcPSD|50202050
*Chú ý: Vấn đề chọn p và q thì ta có thể chọn p và q là một só nguyên tố bất kỳ.
Nhưng chúng ta có thể chọn p ≡ q ≡ mod 4 để việc giải mã được đơn giản.
-> Khi đó chúng ta có hai cách để giải mã:
i.Giải mã khi chọn p và q bất kỳ ii.Giải mã khi p ≡ q ≡ 3 mod 4
Cách mã hóa thì ta vẫn làm như nhau.
3. Giải thuật giải mã cho hệ mã hoá Rabin
Sau khi A nhận được thông điệp đã được mã hóa từ B. A đã có khóa bí mật
là p và q với n = pq, để nhận được bản rõ m từ c, A phải làm các việc sau:
a.Giải mã theo cách chọn p và q bất kỳ:
• Chọn ngẫu nhiên b ϵ Z cho đến khi p
b2−4 a là một só không dư bậc 4 b2−4a mod p, nghĩa là =1 p
• Gọi f là một đa thức f=x2−bx+a trong Zp [ x ]
• Tính r=C( p+1)/4mod f ( r sẽ là một số nguyên) • Trả lại(r, -r)
• Thực hiện tương tự để tìm 2 căn bậc 2 của a theo mod q. Kết quả sẽ được (s, -s)
• Sử dụng giải thuật Euclidean mở rộng để tìm các số nguyên c và d thỏa mãn: cp + dp = 1
• Đặt x = (rdq + scp) mod n và y = (rdq – scp) mod n
• Kết quả trả về sẽ là (±x mod n, ±y mod n)
b. Giải mã theo cách chọn p ≡ q ≡ 3 mod 4
Nếu p và q được chọn để cả p ≡ q ≡ 3 mod 4 thì thuật toán để tìm 4 căn bậc 2
của c mod n có thể đơn giảm như sau:
• Dùng thuật toán Euclide mở rộng để tìm 2 số nguyên a và b thỏa mãn: ap + bq = 1 7 lOMoARcPSD|50202050
• Tính r=c( p+1)/4mod p
• Tính s=c(q+1) /4mod q
• Tính x = (aps + bqr) mod n
• Tính y = (aps – bqr) mod n
• Bốn căn bậc hai của c mod n là x, -x mod n, y và -y mod n 4. Ví dụ a. Tạo khóa
A chọn số nguyên tố p = 311, q = 311, có p ≡ q ≡ 3 mod 4 và tính n = pq = 102941.
Khóa công khai của A là n = 102941.
Khóa bí mật của A là (p = 311, q = 311). b. Mã hóa
Giả sử 6 bit cuối cùng của thông điệp ban đầu cần phải được lặp lại trước khi mã hóa.
Để mã hóa thông điệp 10 bit m =633_((10) )= 1001111001111001_((2) )
Theo hệ 10 thì m = 40569 Sau đó B tính:
c=m2 modn=405692 mod102941=23053 và gửi cho A c. Giải mã
Dùng thuật toán Euclide mở rộng tìm 2 số nguyên và b thỏa mãn: ap + bq = 1
Tìm được a = 140, b = -149
Tính r = c^((p+1)/4)mod p = 23053^((331+1)/4)mod 331 = 144
Tính s = c^((p+1)/4)mod q = 23053^((311+1)/4)mod 311 = 139
Tính x = (aps + bqr) mod n = (6052060 – 6672816) mod 102941 = -25674
Tính x = (aps - bqr) mod n = (6052060 + 6672816) mod 102941 = 40569
Bốn căn bậc 2 của c mod n là x, -x mod n, y và -y mod n. 8 lOMoARcPSD|50202050
m1 = 25674(10) = 644 A (H ) = 0110010001001010(2 )
m2 = 77265(10 ) = 2DD3( H) = 0010110111010011(2 )
m3 = 40569 (10) = 9E79( H ) = 1001111001111001(2)
m4 = 62372(10 ) = F3A4( H ) = 1111001110100100(2 )
Vì chỉ có m3 có dư thừa dữ liệu yêu cầu, A giải mã c thành m3 (bỏ 6 bit lặp cuối
cùng) và phục hồi ban đầu là m =1001111001_((2) )=633_((10) ) Ví dụ:
Ví dụ 1: Cho n = 77, thông điệp c = 56. Giải mã thông điệp trên.
Dựa vào thuật toán Euclide mở rộng tìm được
a = -8, b = 3 p = 7, q = 19 Tính: r
= c(p+1)/4mod p = 4(7+1)/4mod 7 = 2 s
= c(q+1)/4mod q = 4(19+1)/4mod 19 = 17 x = (aps + bqr) mod
n = (-952 + 114) mod 133 = 93 y = (aps – bqr) mod n = ( -952 –
114) mod 133 = 131 m1 = x = 93 m2 = -x mod n = -93 mod 133 = 40 m3 = y = 131 m4 = -y mod n = -131 mod 133 = 2.
Phần 2: Các đặc trưng của hệ mã Rabin
1.Tính an toàn của hệ mã
a.Một người tấn công bị động cần phục hồi bản rõ m từ bản mã c. Đây chính
là giải toán căn bậc 2 ở trên. Vấn đề phân tích ra thừa số n và tính căn bặc 2 theo
module n là tương đương về mặt tính toán. Vì vậy giải sử việc phân tích ra thừa
số số n là khó về mặt tính toán thì lược đồ mã hóa công khai Rabin được chứng
minh là an toàn đối với một người tấn công bị động.
b.Trong khi được chứng minh là an toàn đối với một người tấn công bị động,
lược đồ mã hóa công khai Rabin lại không chống nổi một cuộc tấn công bản mã
lựa chọn. Một cuộc tấn công như vậy có thể mô tả như sau: 9 lOMoARcPSD|50202050
Người tấn công chọn 1 số nguyên mEZ*n và tính c=m^2 mod n. Người tấn công
sau đó đưa c đến máy giải mã của A, giải mã c và trả lại một bản rõ y nào đó. Vì
A không biết m, và m được chọn ngẫu nhiên, bản rõ y không nhất thiết phải giống
hệt m. Với khả năng 1⁄2, y≢± m mod n, khi đó gcd(m-y, n) là một trong các thừa
số của n. Nếu y ≢± m mod n, người tấn công lại lặp lại với một số m mới.
c.Lược đồ mã hóa công khai Rabin dễ bị thương tổn bởi những cuộc tấn
công tương tự như với các trường hợp của hệ mã hóa RSA. Giống hệt như RSA,
các cuộc tấn công (a) và (b) có thể bị thất bại bằng cách biến đổi bản rõ, trong khi
các cuộc tấn công đó có thể tránh được bằng cách thêm dư thừa dữ liệu trước khi mã hóa.
2. Sử dụng dư thừa dữ liệu
a.Một nhược điểm của hệ mã hóa công khai Rabin là người nhận phải có
nhiệm vụ chọn bản rõ đúng từ 4 khả năng. Sự nhầm lẫn trong việc giải mã có thể
vượt qua một cách dễ dàng bằng cách thêm dư thừa dữ liệu vào bản rõ gốc một
cách xác định trước khi mã hóa. (ví dụ; 64 bit cuói cùng của thông điệp có thể được lặp lại).
Với khả năng cao, chỉ 1 trong 4 căn bậc 2 của bản mã c là m1, m2, m3, m4
có được dư thừa đó. Người giải mã sẽ chọn bản này làm bản rõ. Nếu không có căn
bậc 2 nào của c có dư thừa này, người nhận sẽ từ chối c, vì nó là giả mạo.
b.Nếu sử dụng dư thừa dữ liệu như trên, lược đồ Rabin sẽ không còn dễ bị
thương tổn bởi các cuộc tấn công bản mã lựa chọn như nói trên. Nếu người tấn
công chọn một thông điệp m có dư thừa dữ liệu như yêu cầu và đưa c = m^2mod
n vào máy giải mã của A, khả năng rất cao là máy sẽ trả lại bản rõ m cho người
tấn công (vì 3 căn bậc 2 của c kia sẽ có khả năng rất cao là không chứa dư thừa
dữ liệu như yêu cầu), không đưa ra thông tin mới nào. Mặt khác, nếu người tấn
công chọn một thông điệp m mà không có dư thừa dữ liệu cần thiết, khả năng cao
là cả 4 căn bậc 2 của c mod n đều không có dư thừa dữ liệu cần thiết.
Trường hợp này máy giải mã sẽ thất bại trong việc giải mã c và không trả lời
người tấn công. Chú ý rằng chứng minnh tính tương đương của việc phá khóa
lược đồ cải tiến này bởi một người tấn công thụ động với việc phân tích ra thừa
số không còn giá trị nữa. Tuy nhiên, nếu giả sử rằng việc giải mã Rabin gồm 2
giai đoạn: giai đoạn thứ nhất là tìm 4 căn bậc 2 của c mod n và giai đoạn thứ 2 là
lữa chọn căn bậc 2 làm bản rõ thì vẫn chứng minh được tính tương đương.
Vì vậy lược đồ mã hóa công khai Rabin, được sửa đổi một cách thích hợp bằng
cách thêm dư thừa dữ liệu là rất được quan tâm ứng dụng. 3. Tính hiệu quả
Việc mã hóa Rabin cực kỳ nhanh vì nó chỉ liên quan dến việc tính một bình
phương theo module duy nhất. Để so sánh mã hóa của hệ RSA với e = 3 cần một 10 lOMoARcPSD|50202050
phép nhân module và một phép bình phương module. Giải mã Rabin chậm hơn
mã hóa nhưng có thể sánh được tốc độ giải mã của hệ RSA.
4. Ưu và nhược điểm của hệ mã Rabin a.Ưu điểm: •
Độ an toàn cao: Hệ mã hóa Rabin dựa trên tính khó giải của bài toánphân
tích số nguyên tố, giúp nó có độ an toàn cao. •
Không yêu cầu tính toán phức tạp: So với các hệ mã hóa khác, hệ mãhóa
Rabin không yêu cầu tính toán phức tạp, đặc biệt là ở bước giải mã. •
Khả năng chống lại tấn công đưa vào: Hệ mã hóa Rabin có khả năngchống
lại tấn công đưa vào, chẳng hạn như tấn công theo ký tự hay tấn công đặt lại khóa. b.Nhược điểm: •
Tốc độ mã hóa chậm: Hệ mã hóa Rabin có tốc độ mã hóa chậm hơnso với
một số hệ mã hóa khác, chẳng hạn như hệ mã hóa RSA. •
Sử dụng hàm băm: Hệ mã hóa Rabin sử dụng hàm băm để chuyển đổithông
tin thành một số nguyên, vì vậy nếu hàm băm không được chọn cẩn thận, nó có
thể gây ra lỗ hổng an ninh. •
Sử dụng hai số nguyên tố lớn: Hệ mã hóa Rabin yêu cầu sử dụng haisố
nguyên tố lớn để tạo khóa, điều này đôi khi gây khó khăn trong việc triển khai hệ mã hóa này.
III.GIỚI THIỆU CODE
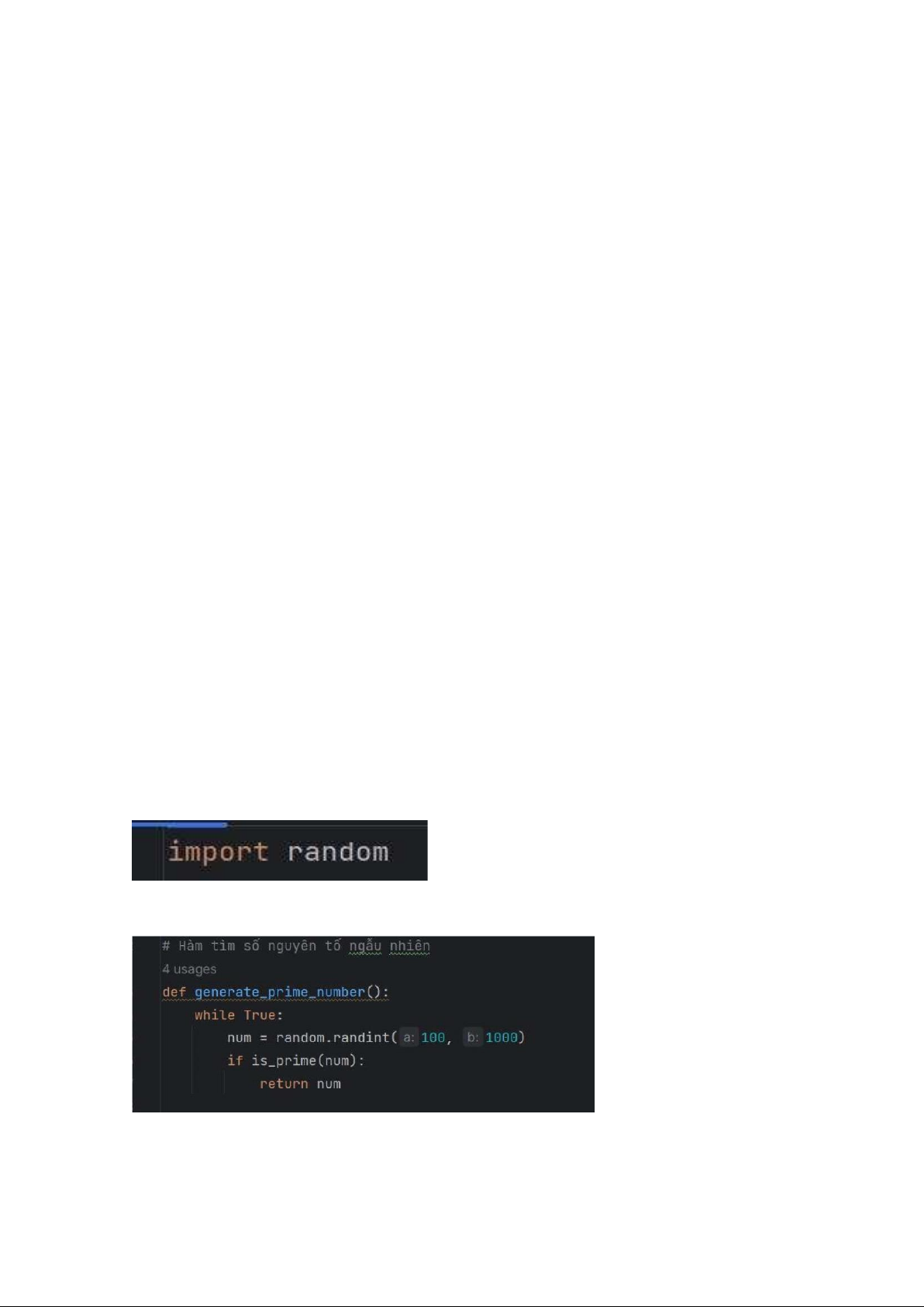
1. Mã nguồn bắt đầu bằng việc nhập thư viện .
2. generate_prime_number(): Hàm này được sử dụng để tạo một số nguyên tố
ngẫu nhiên trong khoảng từ 100 đến 1000.
3. is_prime(num): Hàm kiểm tra xem một số có phải là số nguyên tố hay không.
Nó kiểm tra từ 2 đến căn bậc hai của số đó. 11 lOMoARcPSD|50202050
4. find_n_m(): Hàm này tạo khóa bằng cách tạo hai số nguyên tố ngẫu nhiên p
và q. Sau đó, nó tính toán n bằng tích của p và q và tạo m bằng một số nguyên
tố khác. Nó đảm bảo rằng p và q là khác nhau.
5. encrypt(message, n): Hàm này mã hóa một thông điệp bằng cách chuyển đổi
mỗi ký tự trong thông điệp thành một số và sau đó tính bình phương của số đó và lấy modulo n. 12 lOMoARcPSD|50202050
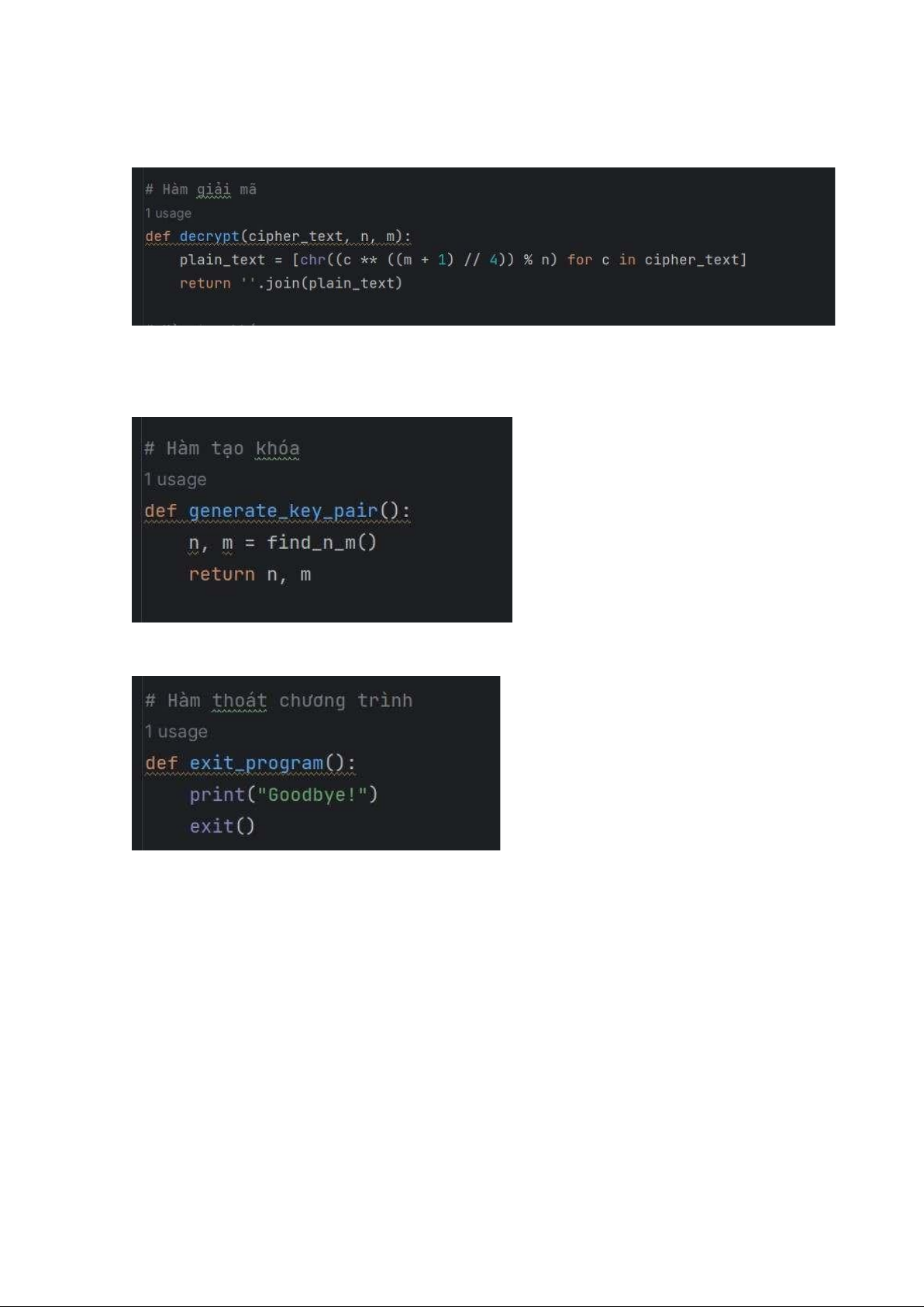
6. decrypt(cipher_text, n, m): Hàm này giải mã một bản mã đã được tạo bằng
cách tính căn bậc hai bình phương của mỗi số trong bản mã và sau đó lấy
modulo n để lấy lại ký tự ban đầu.
7. generate_key_pair(): Hàm này tạo khóa bằng cách gọi find_n_m() và trả về cặp giá trị n và m.
8. exit_program(): Hàm này đơn giản là thoát chương trình.
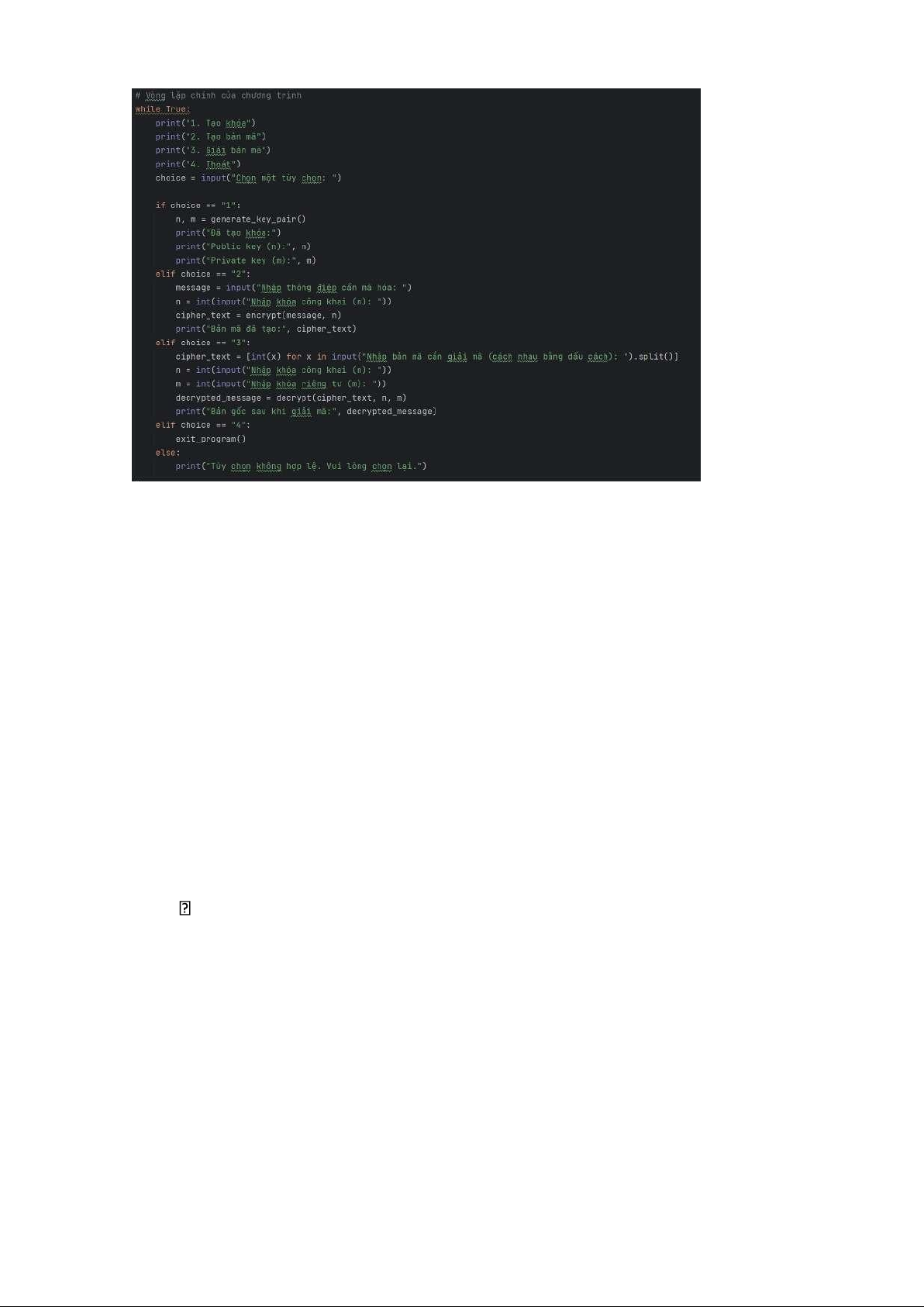
9. Trong vòng lặp chính, chương trình cho phép bạn chọn một trong các tùy chọn sau: •
"1": Tạo khóa và in ra khóa công khai (n) và khóa riêng tư (m). •
"2": Nhập một thông điệp và mã hóa nó bằng cách sử dụng khóa công khai (n). •
"3": Nhập một bản mã và giải mã nó bằng cách sử dụng khóa công
khai (n) và khóa riêng tư (m). •
"4": Thoát khỏi chương trình. 13 lOMoARcPSD|50202050
IV.ỨNG DỤNG CỦA HỆ MÃ RABIN 1.
Một trong những ứng dụng của hệ mã hóa Rabin là trong việc bảo
vệthông tin truyền tải qua mạng internet. Cụ thể, hệ mã hóa Rabin có thể được sử
dụng để bảo vệ dữ liệu quan trọng trước khi truyền tải qua mạng internet. 2.
Hệ mã hóa Rabin cũng được sử dụng trong các ứng dụng khác
nhưchứng thực người dùng (user authentication) và ký số điện tử (digital
signature). Khi sử dụng để ký số điện tử, hệ mã hóa Rabin cho phép một bên tạo
ra một chữ ký số từ thông tin nhất định và cho phép người nhận xác thực rằng
thông tin này chưa bị thay đổi từ khi chữ ký số được tạo ra. 3.
Ngoài ra, hệ mã hóa Rabin còn được sử dụng trong các ứng dụng y
tếđể bảo vệ thông tin bệnh nhân. Ví dụ, hệ mã hóa Rabin có thể được sử dụng để
mã hóa các thông tin bệnh nhân như kết quả xét nghiệm và lịch sử bệnh án để
đảm bảo rằng thông tin này chỉ có thể được truy cập bởi những người được ủy quyền.
Mặc dù hệ mã hóa Rabin đã tồn tại trong nhiều năm và được sử dụng rộng
rãi trong lĩnh vực bảo mật thông tin, nhưng vẫn có một số đề xuất để cải tiến và
tăng cường tính bảo mật của hệ mã hóa này trong tương lai. Sau đây là một số đề xuất đó: a.
Sử dụng hệ số trường hợp đặc biệt để tăng tốc độ mã hóa và giải
mã:Hiện tại, tốc độ mã hóa và giải mã của hệ mã hóa Rabin chậm hơn so với nhiều
hệ mã hóa khác. Có thể sử dụng hệ số trường hợp đặc biệt để tăng tốc độ mã hóa và giải mã. b.
Sử dụng các thuật toán tìm kiếm số nguyên tố mới để tăng tính bảo 14 lOMoARcPSD|50202050
mật: Các thuật toán tìm kiếm số nguyên tố mới như thuật toán tìm kiếm số nguyên
tố ngẫu nhiên Miller-Rabin có thể được sử dụng để tăng tính bảo mật của hệ mã hóa Rabin. c.
Tối ưu hóa phương pháp lựa chọn khóa: Phương pháp lựa chọn
khóahiện tại của hệ mã hóa Rabin có thể được tối ưu hóa để tăng tính bảo mật của hệ mã hóa. d.
Nghiên cứu và phát triển các biến thể của hệ mã hóa Rabin: Có
thểnghiên cứu và phát triển các biến thể của hệ mã hóa Rabin để tăng cường tính
bảo mật và hiệu quả của hệ mã hóa này. Ví dụ như hệ mã hóa Rabin gốc hay Rabin-Williams.
Tóm lại, hệ mã hóa Rabin là một trong những hệ mã hóa khóa
côngkhai nổi tiếng và được sử dụng phổ biến trong lĩnh vực bảo mật thông tin.
Nó được thiết kế dựa trên tính khó giải của bài toán phân tích số nguyên tố và bài
toán căn bậc hai trong trường hợp đặc biệt, giúp nó có độ an toàn cao.
Hệ mã hóa Rabin có thể chống lại nhiều tấn công thông thường như tấn công theo
ký tự hay tấn công đặt lại khóa, tuy nhiên tốc độ mã hóa của nó chậm hơn so với
một số hệ mã hóa khác. Nó có thể được sử dụng để mã hóa và giải mã các thông
điệp nhỏ hoặc tệp tin với độ dài ngắn.
Tuy nhiên, để sử dụng hệ mã hóa Rabin hiệu quả, cần phải chú ý đến việc lựa
chọn khóa và phải sử dụng nó cẩn thận để đảm bảo tính bảo mật của thông tin
được mã hóa và giải mã. Tài liệu tham khảo:
http://123tailieu.net/trinh-bay-ve-he-ma-hoa-rabin.html.
http://123tailieu.net/ma-khoa-cong-khai-ma-khoa-cong-khai-he-ma-rsa-
varabin.html. https://en.wikipedia.org/wiki/Rabin cryptosystem.
https://www.math.aucklan.ac.nz/~sgal018/crypto-book/ch24.pdf
http://soict.hust.edu.vn/~vannk/AntoanThongtin/GTATTT/GTATTT Chuong3.pdf 15
![[ TỔNG HỢP ] Review for students. British culture | Trường Đại học Hải Phòng](https://docx.com.vn/storage/uploads/images/documents/banner/f820cc6278be6a11785c1351b50204b4.jpg)
![[ TỔNG HỢP ] Đề Thi Chuyên Anh Hà Nội | Trường Đại học Hải Phòng](https://docx.com.vn/storage/uploads/images/documents/banner/a78a3f856dd440591a99ce2a24c4b801.jpg)
![[ TỔNG HỢP ] KEY TEST - ENGLISH | Trường Đại học Hải Phòng](https://docx.com.vn/storage/uploads/images/documents/banner/b70b13ffdb12c0da572f41d0832df332.jpg)
![[ TỔNG HỢP ] QUY CHE KIEN TAP SV | Trường Đại học Hải Phòng](https://docx.com.vn/storage/uploads/images/documents/banner/4bfbd7ddc5f2c2262a133f1fa04410d4.jpg)