Tài liệu học tập ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số Toán 12

TÀI LIỆU HỌC TẬP TOÁN 12
Biên soạn theo chương trình GDPT 2018 Dùng chung cho 4 bộ sách CHƯƠNG 1: HÀM SỐ
Trong chương này, chúng ta ứng dụng đạo hàm để khảo sát
một số tính chất quan trọng của hàm số (như tính đơn điệu, NĂM HỌC
cực trị, giá trị lớn nhất, giá trị nhỏ nhất) và tìm các đường tiệm 2024 - 2025
cận, từ đó vẽ đồ thị hàm số hoặc giải quyết những vấn đề thực tiễn liên quan. THS. LA HỒ TUẤN DUY ĐT: 0817 68.22.68 Tài liệu Toán 12
CÔNG THỨC ĐẠI SỐ VÀ GIẢI TÍCH
1. Các phép tính toán học a c ad  bc
ab  c  ab  ac   b d bd a a  c a c   a d ad b    b b b c b c bc d
2. Phép toán lũy thừa và căn m x m . n m n x x x   mn  x n x  n n 1 m m.n x  x x  n x n n    n x x n    . n xy x y      n  y y 1 m m n n x  x n m n x 
x  n x n x x n n  .n xy x y n  n y y
3. Hằng đẳng thức đáng nhớ x  y2 2 2
 x  2xy  y x y2 2 2
 x  2xy  y 2 2
x  y  x  yx  y x  y3 3 2 2 3
 x  3x y  3xy  y x y3 3 2 2 3
 x 3x y  3xy  y 3 3      2 2 x y x
y x  xy  y  3 3      2 2 x y x
y x  xy  y 
x  y  z2 2 2 2
 x  y  z  2xy  2yz  2xz
4. Phương trình bậc hai 2
ax  bx  c  0 b Biệt thức 2
  b 4ac (hoặc 2
  b ac với b  ) 2 Ths: La Hồ Tuấn Duy 0817 682268 Tài liệu Toán 12
   0 : Phương trình vô nghiệm   b b
  0 : Phương trình có nghiệm kép x   (hoặc x   ) 2a a         b b
  0 : Phương trình có 2 nghiệm phân biệt x  (hoặc x  ) 2a a Định lý vi-ét b c
Tổng: S  x  x  
Tích: P  x x  1 2 a 1 2 a
5. Phương trình chứa căn B  0 B  0    A  B       A B  A  B  2 A  B 
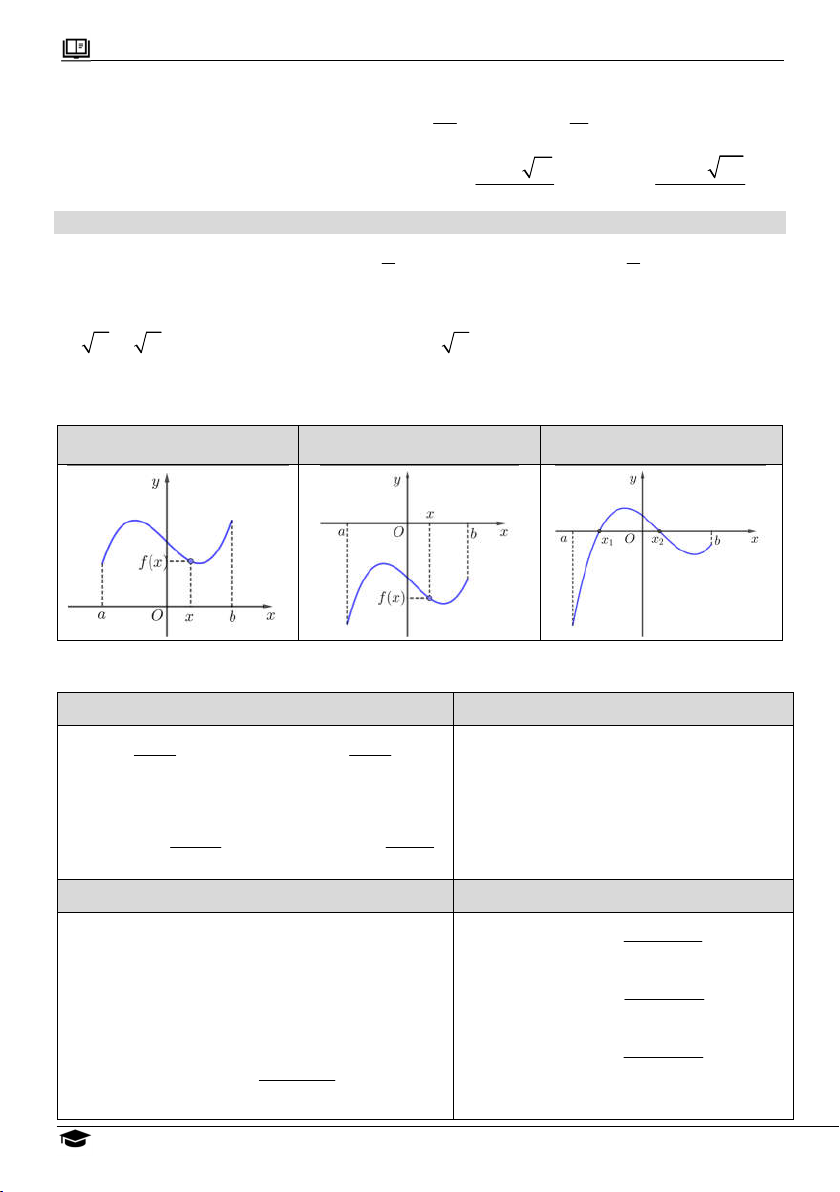
6. Dấu của hàm số dựa vào đồ thị
f x  0, x  a;b
f x  0, x  a;b
f x  f x  0 1   2
7. Công thức lượng giác Hệ thức cơ bản Công thức cộng sin x x
sin x  y  sin .
x cos y  cos . x sin y tan x  cos cot x  cos x sin x
sin x  y  sin .
x cos y  cos . x sin y 2 2
sin x  cos x  1 tan .
x cot x  1
cosx  y  cos .
x cos y  sin . x sin y 1 1 2 1 tan x  2 1 cot x  2 cosx  y cos x 2 sin x  cos .
x cos y  sin . x sin y
Công thức nhân đôi
Công thức hạ bậc  sin 2x  2sin . x cos x 1 cos 2x 2 sin x  2 2 2 cos 2x
 cos x sin x 1 cos 2x 2  2 2 cos x 1 cos x  2 2 1 2sin x 1 cos 2x 2 tan x  2 tan x  tan 2x  1 cos 2x 2 1 tan x Ths: La Hồ Tuấn Duy 0817 682268 Tài liệu Toán 12
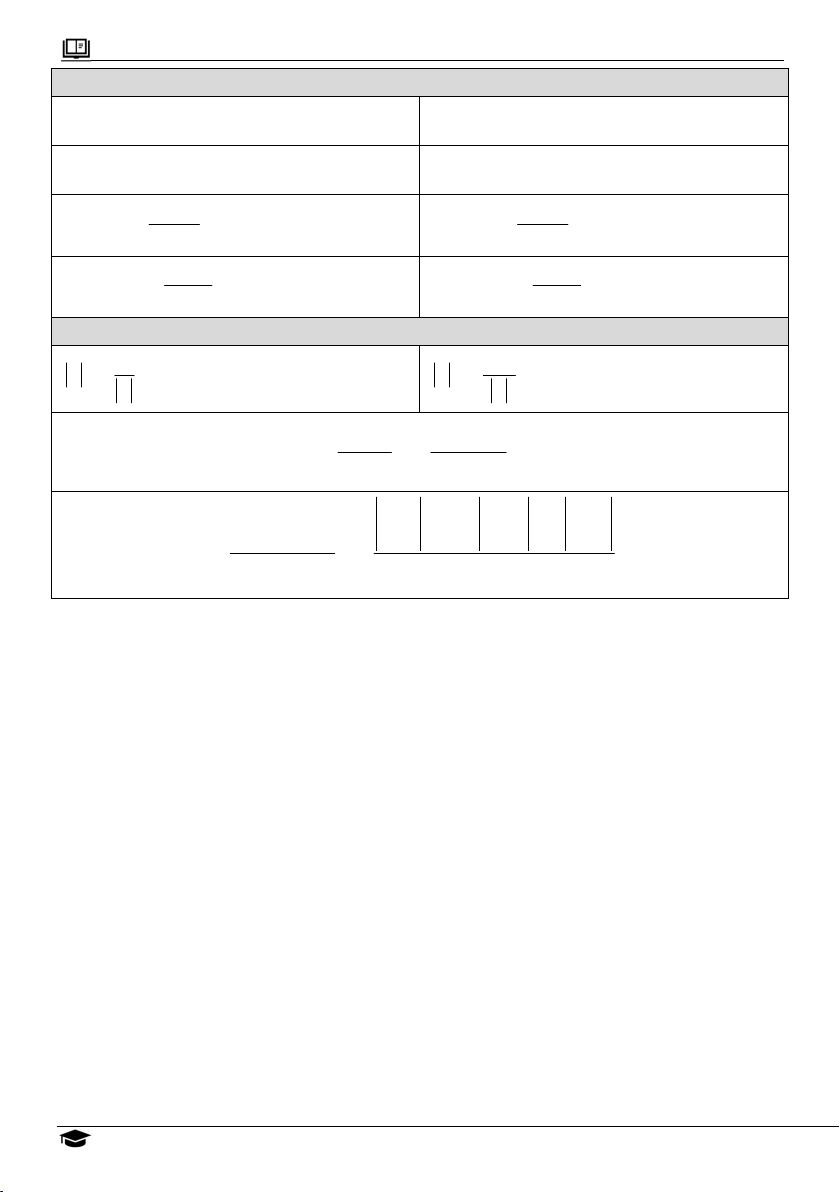
8. Phương trình lượng giác cơ bản
x    k2
 sin x  sin    k   
x     k 2 
x    k2
 cos x  cos   k    x     k2 
9. Quy tắc đạo hàm
u v  u v
u v  uv  .
u v  u .v  v .u u  u v  v u         2  v  v
10. Công thức đạo hàm ĐẠO HÀM CƠ BẢN ĐẠO HÀM HÀM HỢP  
k   0 ( k là hằng số)   x  1
kx  k
ku  k.u    n x  n 1  nx   n u  n 1
 nu  .u    1  1   1 u             2    x  x 2 u u    u x 1   u  2 x 2 u  x x  a  a .ln a  u u a  a .ln . a u  x x  e  e  u  u e  e .u    u  x  log u  a  a  1 log x ln a u ln a    1  u  ln x  ln u  x u Ths: La Hồ Tuấn Duy 0817 682268 Tài liệu Toán 12
ĐẠO HÀM LƯỢNG GIÁC   
sin x  cos x
sin u  ucosu   
cos x  sin x cosu  u  sin u     u tan x 1 2  1 tan x tan u   u 2 1 tan u 2  2 cos x cos u     u x 1 cot     2  1 cot x cot u    u   2 1 cot u 2  2  sin x sin u
ĐẠO HÀM ĐẶC BIỆT x  u.u  x  u  x u   ax b ad bc        cx  d  cx  d2 a b a c b c 2 x  2 x   2
 ax bx c  d e d f e f        2
dx  ex  f 
dx ex f 2 2
Công thức đạo hàm hàm hợp: y  y.u x u x Ths: La Hồ Tuấn Duy 0817 682268 Tài liệu Toán 12 Trang 1 CHUẨN KIẾN THỨC
I. Các phương trình cơ bản
1. Phương trình bậc hai 2
Ax  Bx  C  0 2  B Biệt thức 2
  B  4AC hoặc       AC   .  2 
   0 : Phương trình vô nghiệm.  B
  0 : Phương trình có nghiệm kép x   . 0 2 A     B
  0 : Phương trình có 2 nghiệm phân biệt x  . 2 A
2. Phương trình chứa căn B  0   A  B   . 2 A  B  B  0  
A  B   . A  B 
II. Xét dấu biểu thức f x
Xét dấu biểu thức y  f x.gx; y  gx
Bước 1: Giải f x  0; g x  0 tìm các nghiệm x , x , x ,... 1 2 3
Bước 2: Sắp xếp các nghiệm từ nhỏ đến lớn và lập bảng xét dấu theo quy tắc:
 Xác định dấu tại một ô trong bảng (thường là ô ngoài cùng bên phải)
 Qua nghiệm đơn đổi dấu.
 Qua nghiệm kép không đổi dấu.
Ví dụ 1: Lập bảng xét dấu của các biểu thức sau: a. 2
y  2x 3x 1 b. y   2
x  4x32x Ths: La Hồ Tuấn Duy 0817 682268 Tài liệu Toán 12 Trang 2 2 2x  5x  2 c. y  2 x  4
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
Ví dụ 2: Lập bảng xét dấu của đạo hàm f x , biết: 1 a. f x 3 2
 x 3x  5x 1 3 b. f x 4 2
 x  4x  3 x  c. f x 3 1  x  2 2 x  3x  3 d. f x  x  2
________________________________________________________________ Ths: La Hồ Tuấn Duy 0817 682268 Tài liệu Toán 12 Trang 3
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________ Ths: La Hồ Tuấn Duy 0817 682268 Tài liệu Toán 12 Trang 4
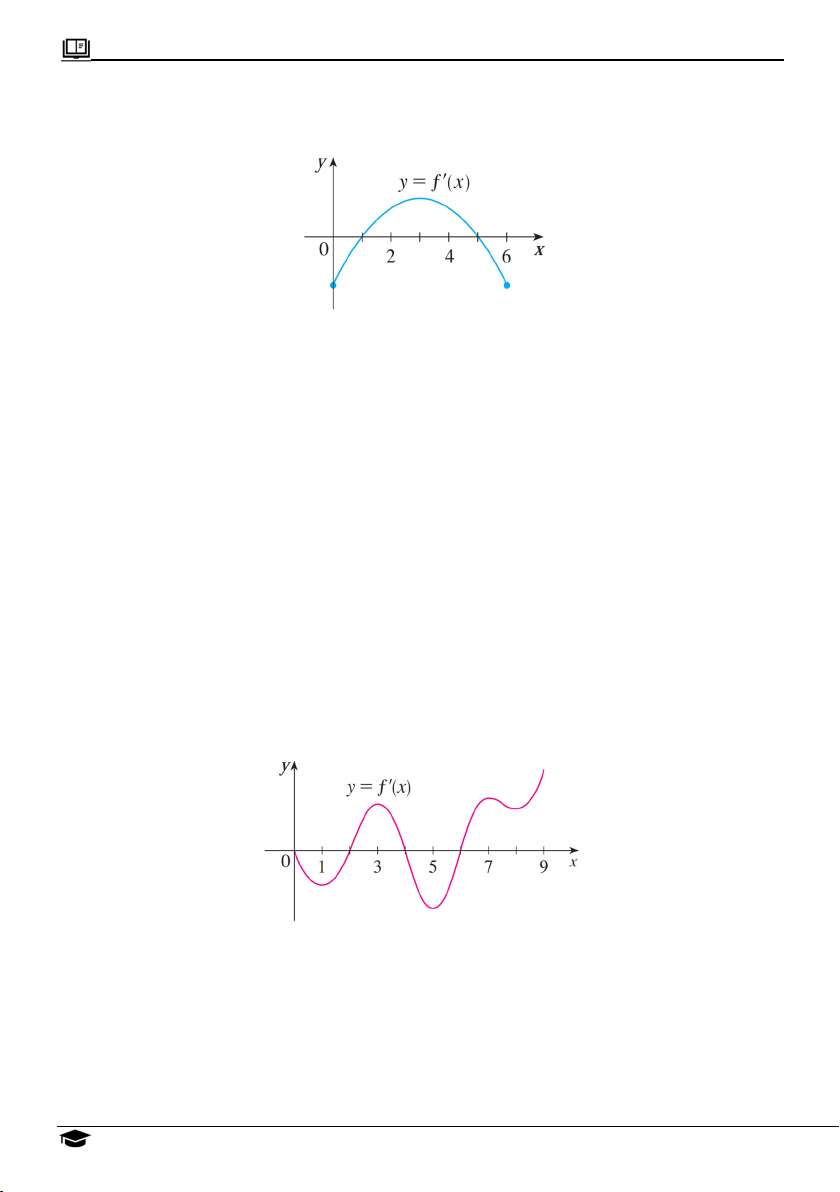
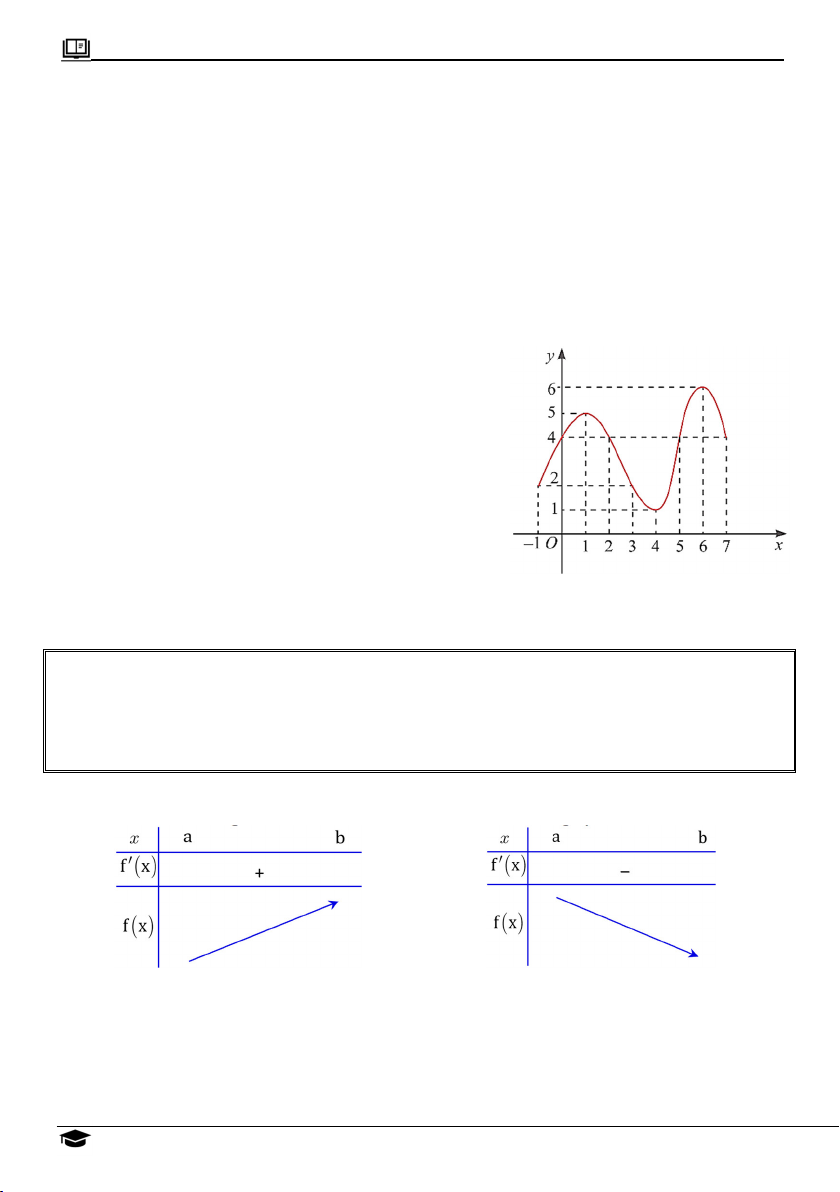
Ví dụ 3: Cho hàm số f x có đạo hàm trên đoạn 0;6, đồ thị f x trên đoạn
0;6 được cho bởi hình vẽ sau
Lập bảng xét dấu của f x trên đoạn 0;6.
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
Ví dụ 4: Cho hàm số f x có đạo hàm trên khoảng 0;, đồ thị f x trên
khoảng 0; được cho bởi hình vẽ sau
Lập bảng xét dấu của f x trên khoảng 0;.
________________________________________________________________
________________________________________________________________
________________________________________________________________ Ths: La Hồ Tuấn Duy 0817 682268 Tài liệu Toán 12 Trang 5
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
III. Tính giới hạn hàm số
1. Các giới hạn cơ bản
Giới hạn tại x
Giới hạn tại vô cực Giới hạn vô cực 0
lim C  C lim n x   1 x lim   0 x x  x0 x
lim x  x  nếu n chẵn 0  xx lim n x 1 0 x  nếu n lẻ lim    x0 1 x lim  0 n 1 x x lim    xa x  a 1 lim    xa x  a Lưu ý:
1. Quy tắc tính giới hạn tại    Đặt n
x làm nhân tử chung ( n là số mũ lớn nhất)
⎧ lim f x  a  0 x 0 x 2.
 lim f x.gx 
⎨ lim gx  x 0 x ⎩ x 0 x
⎧ lim f x  a  0 x 0 x 3.
 lim f x.gx 
⎨ lim gx  x 0 x ⎩ x 0 x Ths: La Hồ Tuấn Duy 0817 682268 Tài liệu Toán 12 Trang 6
⎧ lim f x  a  0 x f x 0 x 4.  lim   ⎨
lim g x  0
x x0 g x ⎩ x 0 x
Ví dụ 1: Tính giới hạn a.  3
lim 2x  3x   1 3x  2 x c. lim
x 2x 1 b.  4 2
lim x  4x  2 2 x x  2x 1 d. lim x 2x 1
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________ Ths: La Hồ Tuấn Duy 0817 682268 Tài liệu Toán 12 Trang 7
Ví dụ 2: Tính giới hạn x 1 2 x 1 a. lim c. lim  x0 x  x2 2  x 3x 1 b. lim  x 1  x 1
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
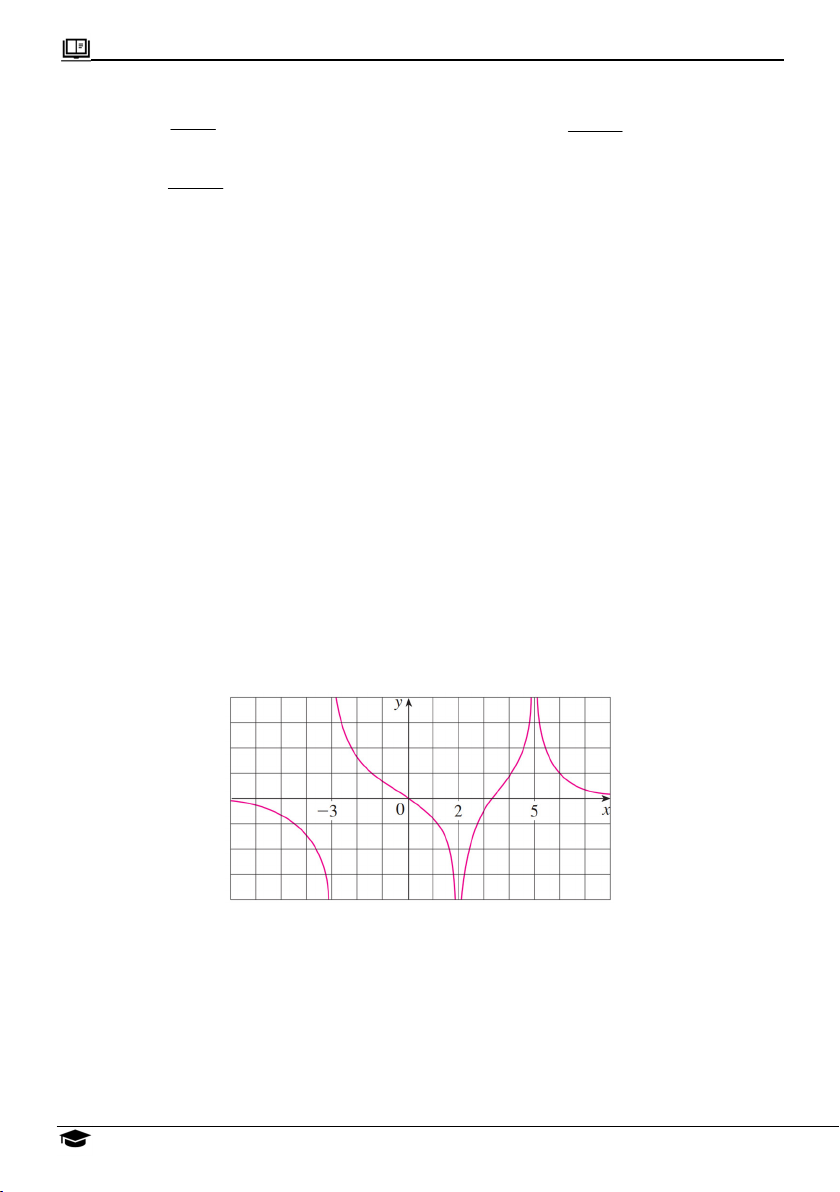
Ví dụ 3: Cho hàm số y  f x có đồ thị như hình vẽ sau
Dựa vào đồ thị, tính các giới hạn sau
a. lim f x. x0
b. lim f x; lim f x và lim f x (nếu có).   x2 x2 x2 c.
lim f x; lim f x và lim f x (nếu có).   x 3  x 3  x 3  d.
lim f x; lim f x . x x Ths: La Hồ Tuấn Duy 0817 682268 Tài liệu Toán 12 Trang 8
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
2. Bấm giới hạn bằng MTCT 2 3x  2x 1
Ví dụ 4: Cho hàm số f x  . x  2
Tính các giới hạn lim f x; lim f x; lim f x; lim f x. x x     x2 x2 Hướng dẫn
Nhập vào máy tính hàm f x Ths: La Hồ Tuấn Duy 0817 682268 Tài liệu Toán 12 Trang 9
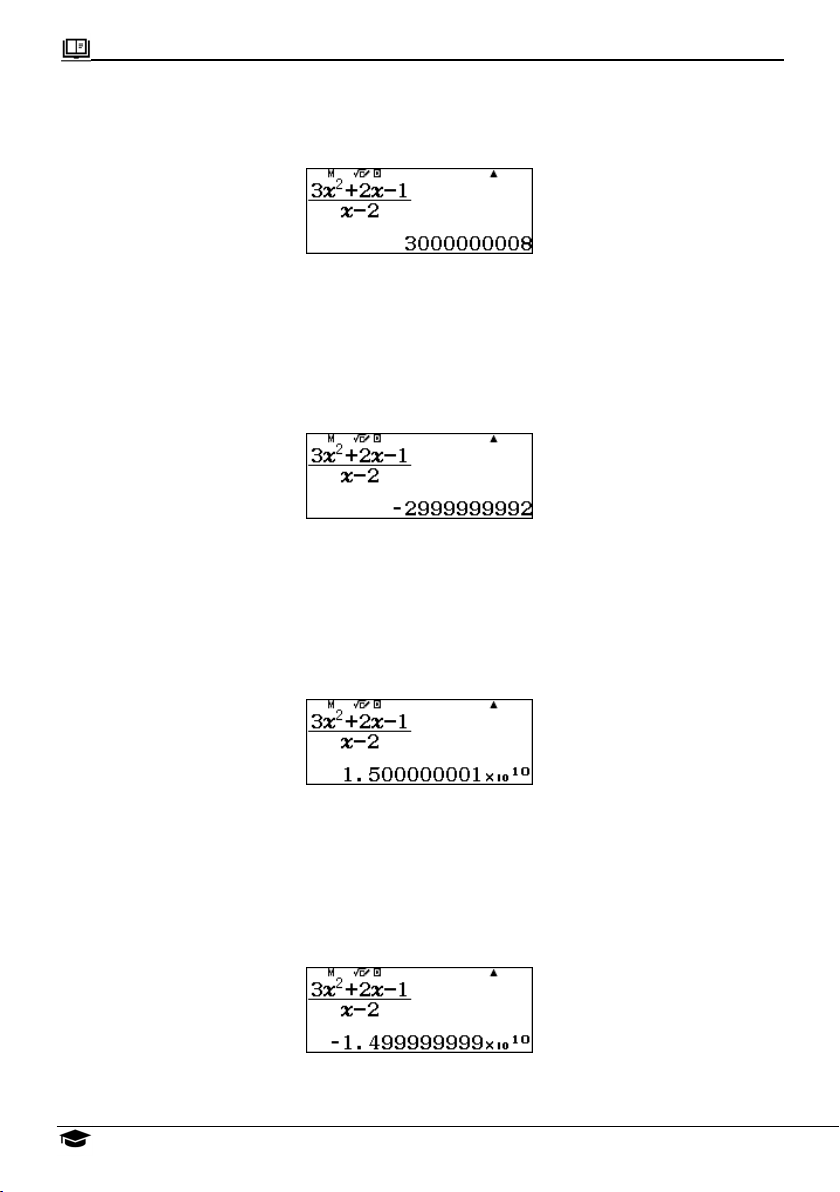
 Tính lim f x x Ấn phím r , nhập 9 x  10 :
Đọc kết quả: lim f x  . x
 Tính lim f x x Ấn phím r , nhập 9 x  10 :
Đọc kết quả: lim f x  . x
 Tính lim f x  x2 Ấn phím r , nhập 9 x  2 10 :
Đọc kết quả: lim f x  .  x2
 Tính lim f x  x2 Ấn phím r , nhập 9 x  2 10 :
Đọc kết quả: lim f x  .  x2 Ths: La Hồ Tuấn Duy 0817 682268 Tài liệu Toán 12 Trang 10 CHƯƠNG I: HÀM SỐ
Bài 1: TÍNH ĐƠN ĐIỆU VÀ CỰC TRỊ CỦA HÀM SỐ
I. Tính đơn điệu của hàm số
Cho K là một khoảng, đoạn hoặc nửa khoảng. Xét hàm số f x xác định trên
K và x , x  K 1 2 ĐỒNG BIẾN (Tăng)
NGHỊCH BIẾN (Giảm) Định nghĩa
x  x  f x  f x
x  x  f x  f x 1 2  1  2 1 2  1  2 Minh họa
Đồ thị đi lên từ trái sang
Đồ thị đi xuống từ trái sang Tính chất phải. phải.
Hàm số đồng biến hoặc nghịch biến trên K gọi chung là đơn điệu trên K. Lưu ý:
+ Xét tính đơn điệu của hàm số y  f x là tìm tất cả các khoảng đồng biến và
nghịch biến của hàm số f x .
Ví dụ 1: Tìm các khoảng đơn điệu của hàm số
y  f x có đồ thị như hình bên.
_____________________________________
_____________________________________
_____________________________________
Ths: La Hồ Tuấn Duy – THPT Gia Định 0817 682268 Tài liệu Toán 12 Trang 11
II. Cực trị của hàm số
Cho hàm số f x xác đinh và liên tục trên tập hợp D , khoảng a;b chứa điểm
x và a;b D . 0
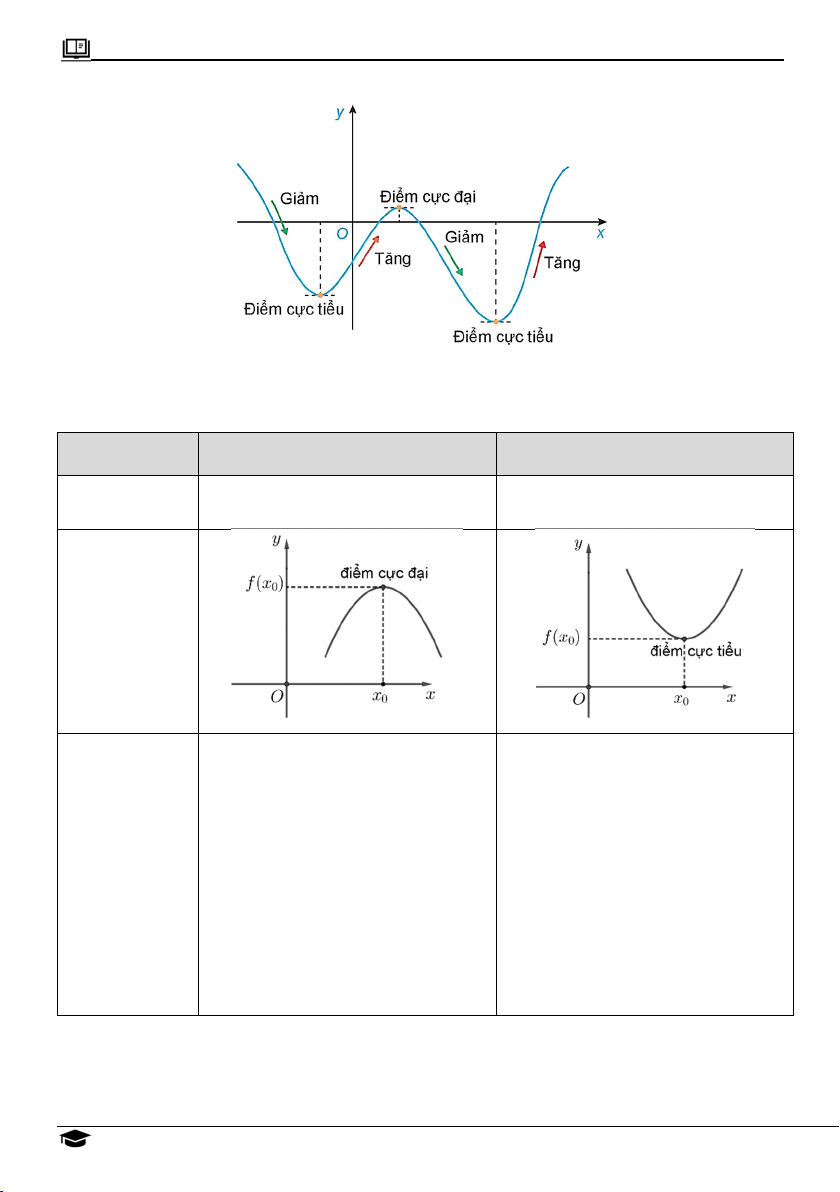
ĐIỂM CỰC ĐẠI (Đỉnh)
ĐIỂM CỰC TIỂU (Đáy) Định nghĩa
f x  f x , x  a;b \ x
f x  f x , x  ; a b \ x 0       0 0       0 Minh họa
+ x là điểm cực đại của hàm
+ x là điểm cực tiểu của hàm 0 0 số. Kí hiệu xCĐ số. Kí hiệu xCT
+ f x là giá trị cực đại
+ f x là giá trị cực tiểu 0  0  Tính chất
(hay cực đại) của hàm số. Kí
(hay cực tiểu) của hàm số. Kí hiệu yCĐ hiệu yCT
+ M x ; f x gọi là điểm
+ M x ; f x gọi là điểm 0  0 0  0
cực đại của đồ thị hàm số .
cực tiểu của đồ thị hàm số . Lưu ý:
+ Các điểm cực đại, điểm cực tiểu gọi chung là điểm cực trị của hàm số.
Ths: La Hồ Tuấn Duy – THPT Gia Định 0817 682268 Tài liệu Toán 12 Trang 12
+ Giá trị cực đại (giá trị cực tiểu) gọi chung là giá trị cực trị (hay cực trị) của hàm số.
+ Nếu x là một điểm cực trị (điểm cực đại, điểm cực tiểu) của hàm số y  f x 0
thì ta nói hàm số y  f x đạt cực trị (cực đại, cực tiểu) tại x 0
+ Một hàm số có thể đạt cực trị tại nhiều điểm, cũng có thể không có cực trị.
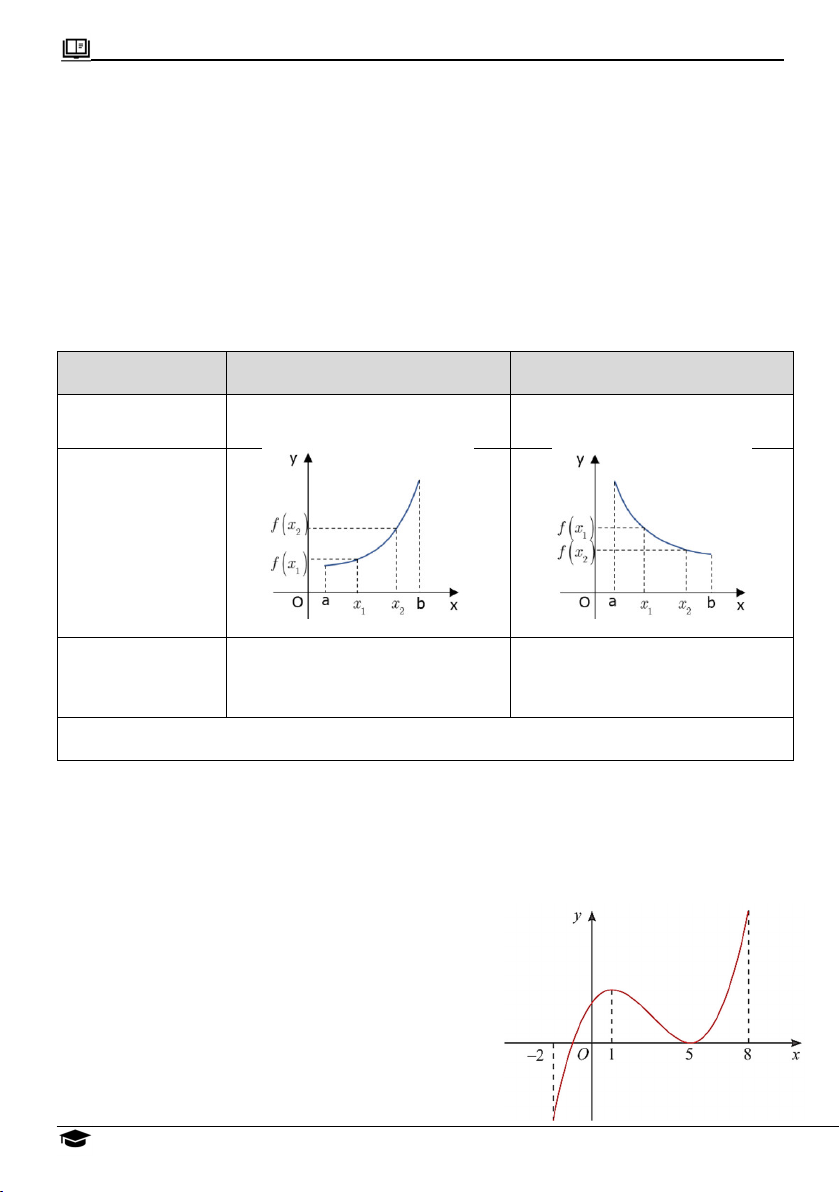
Ví dụ 2: Tìm các điểm cực trị và giá trị cực trị của hàm số y  f x có đồ thị được cho bởi hình sau.
_____________________________________
_____________________________________
_____________________________________
_____________________________________
_____________________________________
_____________________________________
III. Liên hệ giữa đạo hàm và tính đơn điệu của hàm số
ĐỊNH LÍ 1: Cho hàm số y  f x có đạo hàm trên khoảng K.
+ Nếu f x 0, x  K thì hàm số f x đồng biến trên K.
+ Nếu f x 0, x  K thì hàm số f x nghịch biến trên K. Bảng biến thiên Đồng biến Nghịch biến Lưu ý:
+ Định lí trên vẫn đúng trong trường hợp f x  0 tại một số điểm hữu hạn trong khoảng K.
+ Nếu f x  0, x  K thì f x là hàm hằng trên K.
Ths: La Hồ Tuấn Duy – THPT Gia Định 0817 682268 Tài liệu Toán 12 Trang 13
Các bước xét tính đơn điệu của hàm số y  f x
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
Ví dụ 3: Xét tính đơn điệu của các hàm số sau a. f x 2
 x  4x  3 b. f x 3 2
 x  3x c.   1 f x  x  x
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
Ths: La Hồ Tuấn Duy – THPT Gia Định 0817 682268 Tài liệu Toán 12 Trang 14
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
Ví dụ 4: Chứng minh rằng
a. Hàm số f x  sin x  3x nghịch biến trên  . x 
b. Hàm số f x 3 1 
đồng biến trên mỗi khoảng  ;  0 và 0;. x
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
Ths: La Hồ Tuấn Duy – THPT Gia Định 0817 682268 Tài liệu Toán 12 Trang 15
IV. Liên hệ giữa đạo hàm và cực trị của hàm số
ĐỊNH LÍ 2: Cho hàm số y  f x liên tục trên khoảng  ;
a b chứa điểm x và 0
có đạo hàm trên khoảng  ; a b hoặc  ; a b \ x . 0 
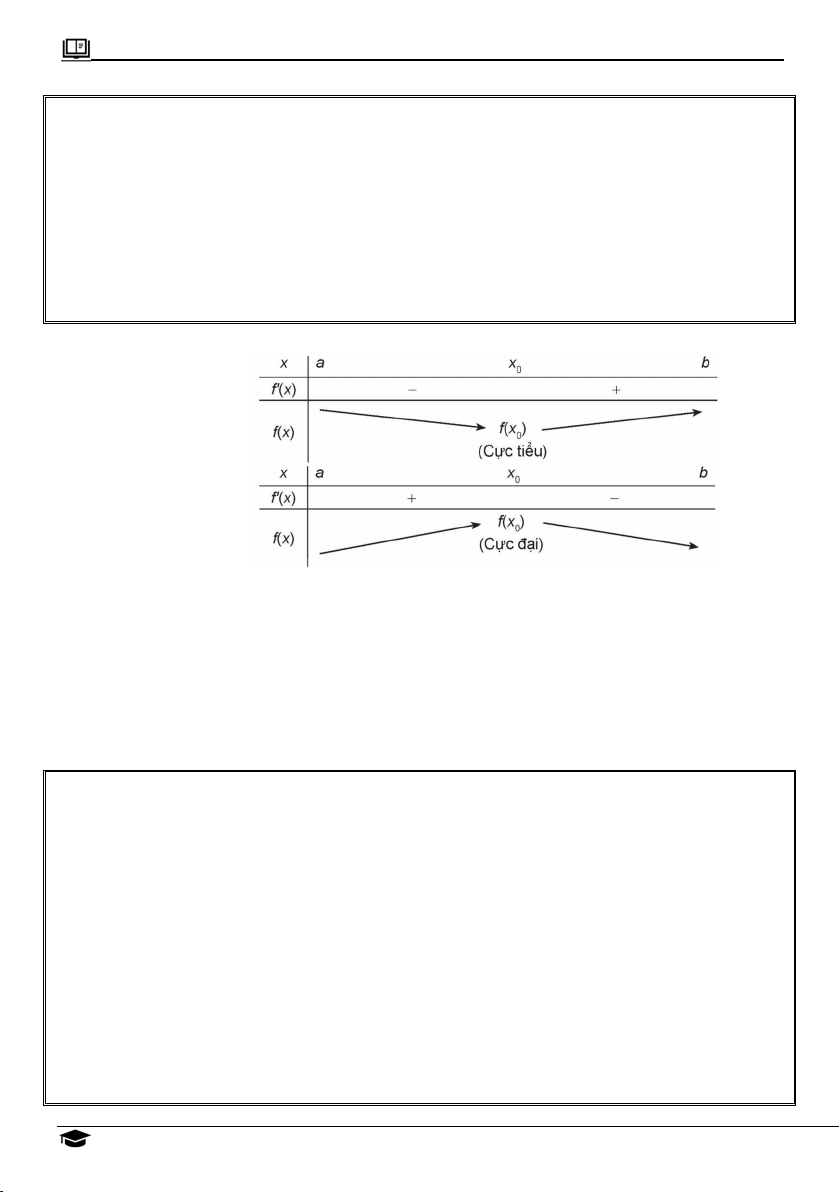
+ Nếu f x đổi dấu từ âm sang dương khi qua x thì thì hàm số f x đạt cực 0
tiểu tại điểm x . 0
+ Nếu f x đổi dấu từ dương sang âm khi qua x thì thì hàm số f x đạt cực 0
đại tại điểm x . 0 Bảng biến thiên Cực tiểu Cực đại Lưu ý:
+ Nếu hàm số có đạo hàm và đạt cực trị tại x thì f x  0 . 0  0
+ Nếu f x  0 nhưng f  không đổi dấu khi qua x thì hàm số không có cực 0  0 trị tại x . 0
+ Nếu f x không đổi dấu trên khoảng K thì hàm số không có cực trị trên K.
Các bước tìm cực trị của hàm số y  f x
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
Ths: La Hồ Tuấn Duy – THPT Gia Định 0817 682268