HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG
CƠ SỞ THÀNH PHỐ HỒ CHÍ MINH KHOA VIỄN THÔNG 2 BỘ MÔN VÔ TUYẾN
TÀI LIỆU HƯỚNG DẪN THÍ NGHIỆM
Môn học: Mô phỏng hệ thống truyền thông Phòng thí Online nghiệm: GV: KVT2
Họ và Tên sinh viên: Kiều Văn Sơn – N21DCVT087 Nhóm: 2 Tổ: Lớp: D21CQVT01-N Điểm Nhận xét
Mục tiêu của môn học: Giúp sinh viên hiểu được những khái niệm cơ bản về ngôn ngữ
Matlab, hiểu được cách thức mô phỏng các mô hình kênh thông tin cở bản trong viễn thông.
Kiểm chứng lại các mô hình toán học của các kênh thông tin cơ bản.
Yêu cầu: Cài đặt và sử dụng phần mềm Matlab phiên bản 2019a trở lên hoặc dùng hỗ trợ
phần mềm Matlab online tại https://www.mathworks.com/products/matlab-online.html PHẦN L
Ý THUYẾT LIÊN QUAN CẦN CHUẨN BỊ
a) Lý thuyết về xác suất f
Cho biến ngẫu nhiên X có hàm mật độ phân phối xác suất là X x
+ X là biến ngẫu nhiên liên tục x F f X x X x dx Kỳ vọng E X : E X xf X x dx Phương sai V X E X 2 E X 2
+ X là biến ngẫu nhiên rời rạc FX x Kỳ vọng pi E X Phương sai xi pi V X E X 2 E X 2
b) Lý thuyết về kênh thông tin cơ bản
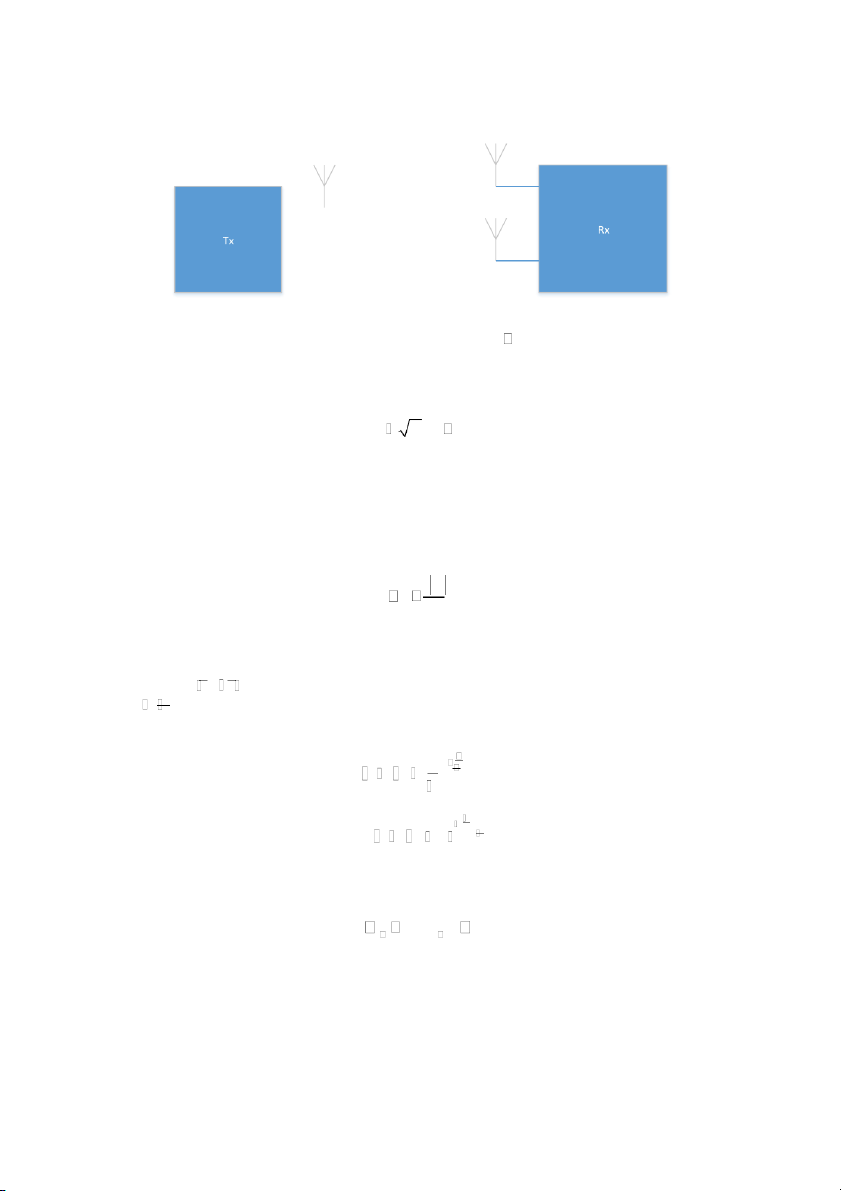
Xét mô hình kênh thông tin đơn giản phân tập thu như hình vẽ
Phía máy phát Tx trang bị 1 ăng ten phát, máy thu Rx trang bị 2 ăng ten thu. Giả sử công suất phát tín hiệu
tại máy phát Tx là P , khi đó tín hiệu nhận được tại ăng ten thứ i(i 1, của máy thu Rx được kí hiệu 2) là r Ph x n i i i với h
truyền từ anten phát đến anten thứ i của máy thu, n nhiễu trắng lạ i i là hệ số kênh i là
anten máy thu có công suất là
N0 . Tỷ số tín hiệu trên nhiễu tại anten thứi có dạng như sau P h 2 i i N 0
Giả sử kênh truyền đang xét là kênh Rayleigh fading, và các kênh truyền từ máy phát đến máy thu l
à như nhau nên tỷ số tín hiệu trên nhiễu trung bình tại các nhánh là như nhau có
nghĩa là 1 2 ta có hàm PDF và CDF của các kênh truyền có dạng: f 1 e  i F 1 e  i
Trong mô hình trên, giả sử phía máy thu sử dụng kỹ thuật SC(select combining), khi đó tỷ số tí
n hiệu tương đương phía máy thu ký hiệu là max i 1,2 i
Giả sử khoảng cách giữa các ăng ten phía máy thu đủ lớn, do đó cács ẽ độc lập với nhau, i
hàm phân bố tích lũy xác suất của như sau: 2 F F i i 1 2 1 e
Xác suất dừng của hệ thống OP F th  2 th 1 e
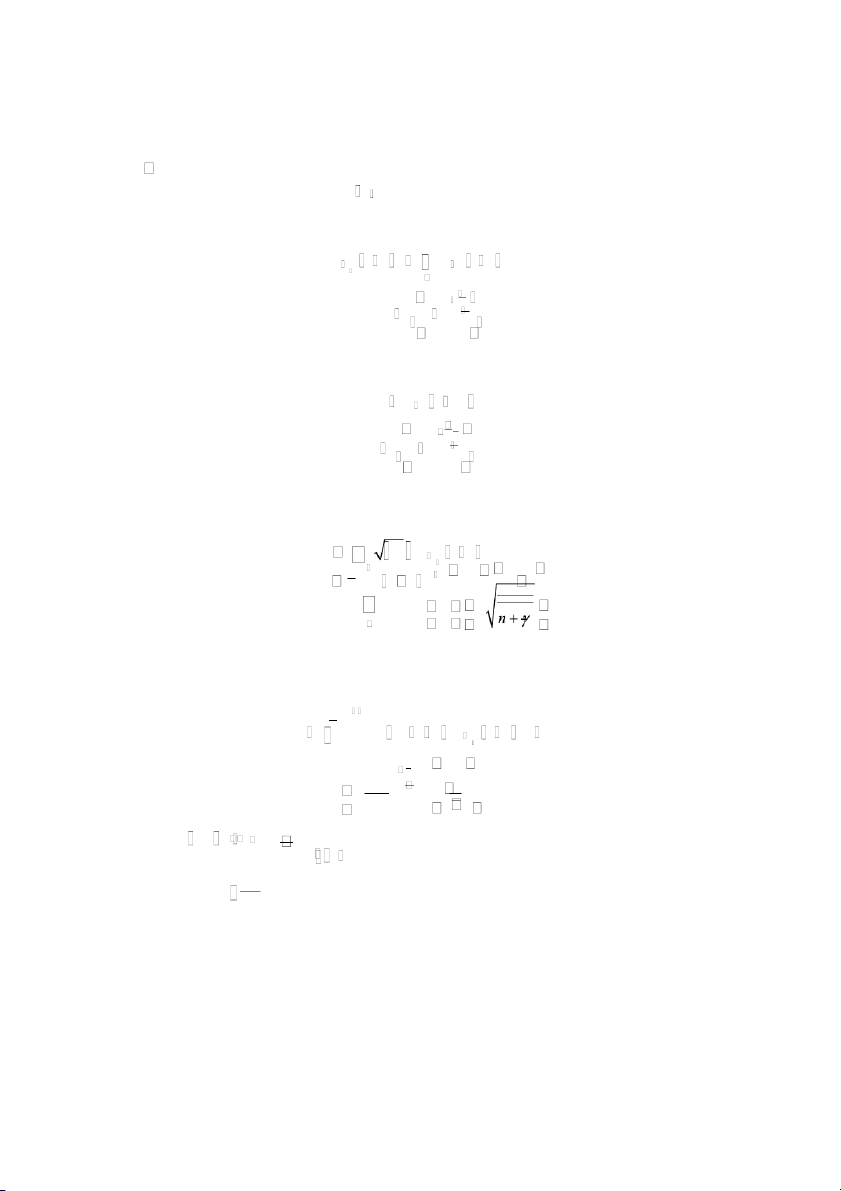
Tỷ lệ lỗi bit trung bình:  BER Q2  f 0 1 N 2 1 n 1 N 1  2 n n  1
Dung lượng Shannon của hệ thống C B log 2 1 f d 0 B 1 1 e Ei  ln 2 Với Ei x e t dt và E t  x
PHẦN THỰC HÀNH BUỔI 1
CÂU HỎI CHUẨN B Ị Ở NHÀ
Tìm hiểu và điền vào bảng chức năng các hàm matlab dưới đây TT Hàm Chức năng
Hàm này được sử dụng để tạo ra các ma 1 rand
trận hoặc vectơ ngẫu nhiên có các giá trị
trong khoảng từ 0 đến 1.
Hàm này được sử dụng để vẽ đồ thị của các 2 plot
điểm dữ liệu. Nó có thể vẽ đồ thị đường
(line plot), đồ thị chấm (scatter plot), đồ thị thanh (bar plot), vv.
Hàm này được sử dụng để tạo ra một lưới 3 suplot
đồ thị và chọn một phần tử cụ thể trong lưới đó để vẽ đồ thị.
Hàm này được sử dụng để thêm nhãn cho 4 xlabel
trục hoành trên đồ thị.
Hàm này được sử dụng để thêm nhãn cho 5 ylabel
trục tung trên đồ thị.
Hàm này được sử dụng để thêm chú thích 6 legend
cho đồ thị, giải thích ý nghĩa của các dòng
hoặc điểm trên đồ thị.
Hàm này được sử dụng để thêm tiêu đề cho 7 title đồ thị.
Hàm này trả về số phần tử trong một vectơ 8 length
hoặc kích thước của một chiều trong một ma trận.
Hàm này được sử dụng để tạo ra một ma 9 zeros
trận hoặc vectơ với tất cả các phần tử là số 0.
Hàm này trả về kích thước của một ma trận, 10 demention
tức là số hàng và số cột.
Trả về giá trị lớn nhất trong một mảng hoặc 11 max
tìm giá trị lớn nhất trong các chiều của mảng
Hàm này được sử dụng để sắp xếp các phần 12 sort
tử của một vectơ hoặc ma trận theo thứ tự
tăng dần hoặc giảm dần.
PHẦN CÁC KIẾN THỨC LỆNH LẬP TRÌNH CƠ BẢN
Bài 1: Viết chương trình nhập một số v
à trả về số bằng chữ. Ví dụ nhập N 111 trả về một trăm mười một. N = 111; result = so_bang_chu(N); disp(result);
Bài 2: Viết chương trình nhập vào số bằng chữ và trả về số bằng số.
chu = 'một trăm hai mươi ba'; result = chu_bang_so(chu); disp(result);
Bài 3: Cho một cell array lưu trữ họ và tên các sinh viên, ví dụ fullname={‘Nguyen Van
Tí’, ‘Tran Van Tho’, ‘Nguyen Canh Chan’, ‘ Tran Luu Nam’, ‘ Tan Hiep Phap’}. Hãy lập
trình trả về danh sách xếp theo thứ tự abc theo tên .
ful name = {'Nguyen Van Ti', 'Tran Van Tho', 'Nguyen Canh Chan', 'Tran Luu Nam', 'Tan Hiep Phap'};
sorted_ful name = sort(ful name);
disp('Danh sách sau khi sắp xếp theo tên:'); disp(sorted_ful name);
Bài 4: Hãy khai báo một cấu trú
c thông tin của sinh viên gồm 3 thành phần gồm họ và tên,
năm sinh, giới tính. Kiểm tra có phải là cấu trúc không?
a. Liệt kê ra các trường của cấu trúc
b. Kiểm tra ‘Gioi_Tinh’ có phải là 1 trường trong cấu trúc sinh viên không?
c. Xếp thứ tự các trường
d. Thêm một trường ‘Noi_Sinh’ e. Kiểm tr
a tên trường “Ho_va_Ten” có hợp lệ không?
f. Tạo ra một mảng cấu trúc với sinh viên thứ 2. i. Lấy năm sinh của hai
% a. Liệt kê ra các trường của cấu trúc
student = struct('Ho_va_ten', ' , 'Nam_sinh', ' , 'Gioi_tinh', ' );
% b. Kiểm tra .Gioi_Tinh có phải là 1 trường trong cấu trúc sinh viên không?
isFieldExist = isfield(student, 'Gioi_tinh');
% c. Xếp thứ tự các trường
fieldNames = fieldnames(student);
% d. Thêm một trường 'Noi_sinh' student.Noi_sinh = ' ;
% e. Kiểm tra tên trường "Ho_va_ten” có hợp lệ không?
isValidFieldName = isfield(student, 'Ho_va_ten');
% f. Tạo ra một mảng cấu trúc với sinh viên thứ 2 student2 = student;
% i. Lấy năm sinh của hai
Nam_Sinh_sv1 = student.Nam_sinh;
PHẦN THỰC HÀN
H VỀ MẢNG CHUỖI
Bài 5: Cho vector chứa một chuỗi số, hãy trả về một chuỗi số khác đếm các phần tử có
trong chuỗi số. Ví dụ x 5, 5, 2,1,1,1,1, 3 tr ả y 2, 5,1, 2, 4,1,1, 3 . về x = [5, 5, 2, 1, 1, 1, 1, 3]; unique_elements = unique(x);
y = histcounts(x, [unique_elements, max(unique_elements)+1]); disp(y);
Bài 6: Cho ma trận n hàng và 2 cột, chứa tọa độ xOy của n điểm. Hãy tìm hai điểm có
khoảng cách xa nhất và trả về chỉ số hàng của hai điểm đó.
matrix = [1, 2; 3, 4; 5, 6; 7, 8];
[idx1, idx2] = farthestPoints(matrix); disp(idx1); disp(idx2);
function [idx1, idx2] = farthestPoints(matrix)
distances = pdist2(matrix, matrix); [~, idx] = max(distances(:));
[idx1, idx2] = ind2sub(size(distances), idx); end x 1 1 2 3 trả
Bài 7: Cho một chuỗi số, trả về chuỗi các số không trùng lặp .Ví dụ 3 về y 1 2 3 . x = [1, 1, 2, 3, 3]; y = unique(x); disp(y);
Bài 8: Tạo một ma trận ngẫu nhiên A có kích thước m,n nhập t
ừ bàn phím. Ma trận B có
kích thước n,k với k nhập từ bàn phím a) Thực hiện tha
o tác xóa hàng i và cột j của ma trận ngẫu nhiên vừa tạo. Với i = (n+m)mod n và j=(n+m) mod m
b) Thêm hàng i+1 và cột j+1 vào ma trận A. c) Xóa phần tử A[i,j]
d) Đưa ra các phần tử đường chéo của ma trận A
e) Đưa ra ma trận chuyển vị và ma trận nghịch đảo của ma trận A f) Tính ma trận A*B. Code:
% Nhập kích thước của ma trận A và B từ bàn phím
m = input('Nhập số hàng của ma trận A: ');
n = input('Nhập số cột của ma trận A: ');
k = input('Nhập số cột của ma trận B: ');
% Tạo ma trận ngẫu nhiên A và B A = randn(m, n); B = randn(n, k);
% a) Xóa hàng i và cột j của ma trận A
i = mod(n + m, n) + 1; % Vị trí hàng cần xóa
j = mod(n + m, m) + 1; % Vị trí cột cần xóa A(i, :) = []; A(:, j) = [];
% b) Thêm hàng i+1 và cột j+1 vào ma trận A
i = i + 1; % Vị trí hàng cần thêm
j = j + 1; % Vị trí cột cần thêm
new_row = randn(1, size(A, 2)); % Tạo hàng mới
new_column = randn(size(A, 1), 1); % Tạo cột mới A = [A; new_row]; A = [A, new_column]; % c) Xóa phần tử A[i, j] A(i, j) = [];
% d) Đưa ra các phần tử đường chéo của ma trận A diagonal_elements = diag(A);
disp('Các phần tử đường chéo của ma trận A:'); disp(diagonal_elements);
% e) Đưa ra ma trận chuyển vị và ma trận nghịch đảo của ma trận A transpose_A = A'; inverse_A = inv(A);
disp('Ma trận chuyển vị của ma trận A:'); disp(transpose_A);
disp('Ma trận nghịch đảo của ma trận A:'); disp(inverse_A); % f) Tính ma trận A*B matrix_product = A * B;
disp('Kết quả của A*B:'); disp(matrix_product);