Tài liệu ôn tập 57 câu Hệ phương trình tuyến tính môn Đại số tuyến tính | Đại học Thủy Lợi
Tài liệu ôn tập 57 câu Hệ phương trình tuyến tính môn Đại số tuyến tính. Tài liệu được sưu tầm gồm 4 trang, giúp các bạn ôn luyện và phục vụ cho việc học tập, đạt kết quả tốt. Mời các bạn đón xem!
Môn: Đại số tuyến tính (DSTT 01) 10 tài liệu
Trường: Đại học Thủy Lợi 466 tài liệu
Tác giả:
Preview text:
lOMoAR cPSD| 58647650
Hệ phương trình tuyến tính (57 câu)
Câu 1. Cho hệ phương trình tuyến tính
Ma trận hệ số của hệ là D. A. B. C. 0 bằng cách dùng
Câu 2. Khi giải hệ phương trình tuyến tính AX = B với det(A)
ma trận nghịch đảo. Công thức nghiệm của hệ là A. X= B.A-1 B. X = -1 C. X= A -1 B D. X = A.B
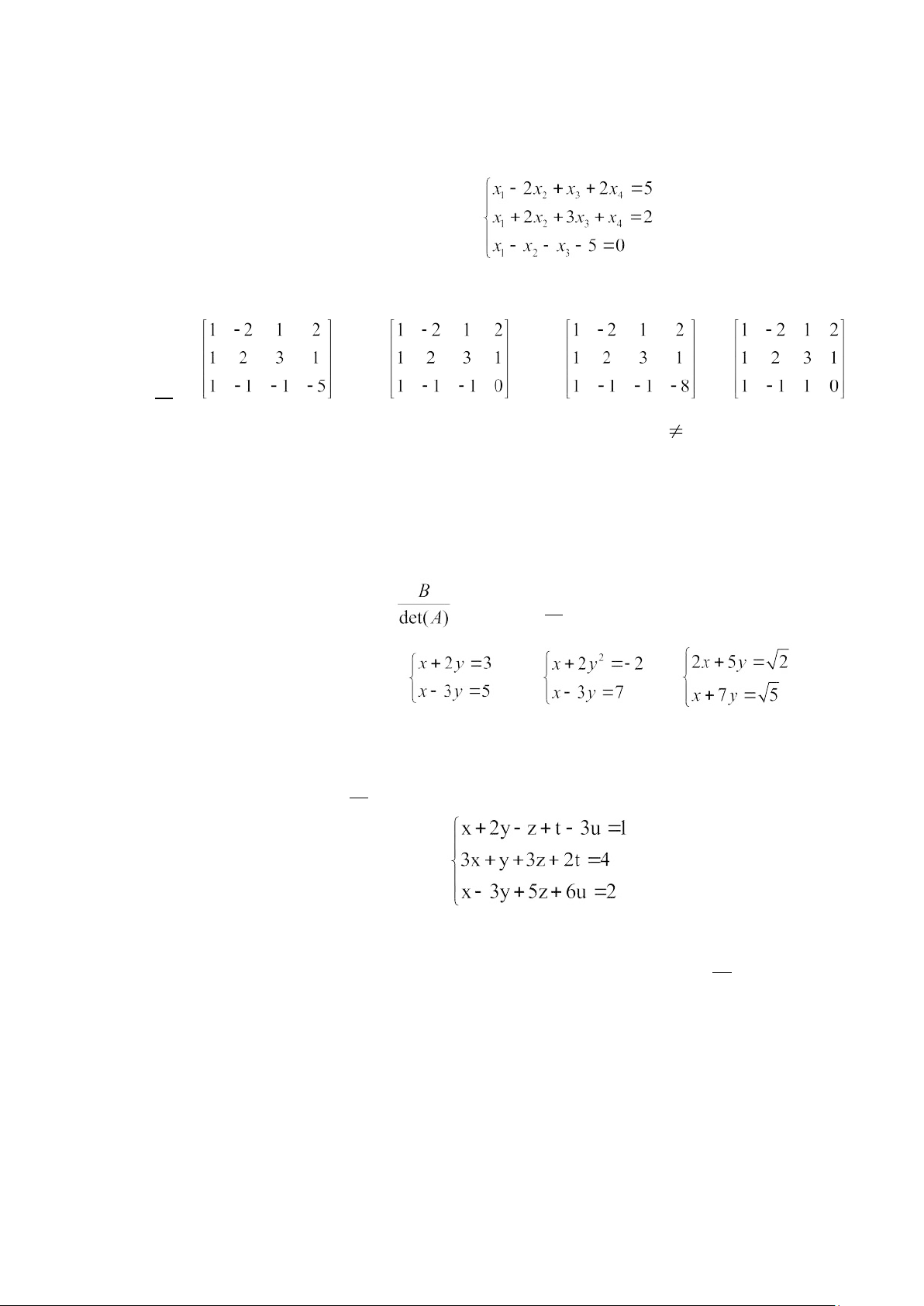
Câu 3. Hệ nào trong các II) III) hệ: I) là hệ tuyến tính? A. Chỉ có I B. I và III C. I, II và III D. I và II
Câu 4. Nghiệm của hệ phương trình
phụ thuộc vào bao nhiêu tham số? A. 0 B. 1 C. 2 D. 3
I.1. Giải hệ phương trình tuyến tính (12 câu) lOMoAR cPSD| 58647650 là
Câu 1. Nghiệm của hệ phương trình tuyến tính A. x1 = 3+ , x 2 = , x 3 = B. x1 = 3+ , x 2 = , x 3 = C. x1 = 1+ , x 2 = , x 3 = D. x1 = 8- , x 2 = , x 3 = là
Câu 2. Nghiệm của hệ phương trình tuyến tính A. x1 = 1-3 , x 2 = , x 3 = B. x1 = 1+ , x2 =1, x3= C. x1 = , x 2 = , x 3 = 1- D. x1 = 2, x2 =1, x3=1 Câu 3. Hệ phương trình có nghiệm với là A. 15 B. 1 C. 2 D. 0
Câu 4. Hệ phương trình có nghiệm với là A. 0 B. 1 C. 2 D. 3
Câu 5. Xét hệ phương trình
Nghiệm của hệ phương trình trên là
A. (a, b, –2a, –2b + 1, a)
B. (2 + 3a – 5b – 6c, a, b, 6b – 5a + 9c – 1, c)
C. (a , –5a+ b +4, b, –2b, a – 2b) D. (a, 4 – 3a – 3b – 2c, b, c, a – 2b + 1 )
(Với a, b, c là các tham số thực)
Câu 6. Hệ nghiệm cơ bản của hệ phương trình là A. (–5, 2, 1)
B. (5, –2, –1) và (–15, 6, 3) lOMoAR cPSD| 58647650 C. (0, 0, 0)
D. (5, –2, –1) và (1, 0, 5)
Câu 7. Nghiệm của hệ phương trìnhlà A. (0, 1, 1, 0) B. C. ( ) D. Vô nghiệm
Câu 8. Nghiệm tổng quát của hệ phương trình là A. (0, 0, 0) B. (1, 3, 1) C. (a, 3a, 0) ( ) D. (a, 3a, a) ( )
Câu 9. Tìm tất cả nghiệm của hệ phương trình B. (a, b, a, – 2b) với A. Vô nghiệm C. D. (2, 1, 3, – 1) Câu
10. Khi hệ có vô số nghiệm, nghiệm tổng quát là A. (a, 1, – a) ( ) B.
Không xảy ra trường hợp hệ vô số nghiệm. lOMoAR cPSD| 58647650 C. (a, a, 1 – 2a) ( ) ) D. (a, b, 1 – a – b) (
Câu 11. Nghiệm của hệ phương là trình A. Vô nghiệm B. (– 1, 2, 2, 0) C. (0, 1, 1, 0) D. ( )
Câu 12. Một nghiệm riêng của hệ phương trình là A. (0, 2, 1, –1) B. (2, 0, –1, –1) C. (1, 1, 0, – 1) D. (1, 0, 1, 0)