lOMoAR cPSD| 47708777
BÀI TẬP THAM KHẢO HỌC PHẦN TOÁN GIẢI TÍCH 12-2020
Chương 1: Hàm một biến
Dạng 1: Tính gần úng có áp dụng vi phân.
Dạng 2: Tìm a thức Tay-lor, a thức Mac-lau-ranh (Maclaurin).
Chương 2: Các phép tính tích phân hàm một biến
Dạng 3: Tính nguyên hàm, tích phân xác ịnh bằng phương pháp ổi biến số.
Dạng 4: Tính nguyên hàm, tích phân xác ịnh bằng phương pháp TP từng phần.
Dạng 5: Tính ộ dài ường cong 𝐴𝐵̂ .
Dạng 6. Xét sự hội tụ và tính tích phân suy rộng. Chương 3: Chuỗi số
Dạng 7: Xét sự hội tụ và tính tổng của chuỗi số
Dạng 8: Tìm miền hội tụ của chuỗi hàm (ĐỌC THÊM)
Chương 4: Hàm nhiều biến
Dạng 9: Tính các ạo hàm riêng cấp 1, cấp 2 (của hàm 2 biến, 3 biến)
Dạng 10: Tính vi phân toàn phần (cấp 1) và ứng dụng ể tính gần úng
Dạng 11: Tìm cực trị của hàm hai biến (không yêu cầu tính cực trị có iều kiện) Chương 5: Tích phân bội
Dạng 12: Tính tích phân kép trên miền hình chữ nhật vuông (các cận là hằng số) + miền hình chữ nhật cong (một
cận xác ịnh và một cận phụ thuộc biến (bậc nhất))
Dạng 13: Tính tích phân kép có ổi biến số (Đổi biến trong hệ tọa ộ De-các ể ưa miền hình bình hành về
hình chữ nhật + Đổi biến trong hệ tọa ộ cực ể ưa miền hình tròn hoặc elip, về h.c.n cong) Chương 6:
Phương trình vi phân
Dạng 14: Phương trình vi phân cấp 1, (PTVP có biến số phân ly + PTVP tuyến tính cấp 1)
Dạng 15: Phương trình vi phân cấp 2 tuyến tính với hệ số hằng (Hàm mũ, không chồng chất nghiệm, vế phải có
dạng 𝑒𝛼𝑥. 𝑃𝑛(𝑥)) Chương 1: Hàm một biến
Bài 0: Tính các giới hạn sau:
Bài 1: Tính gần úng các biểu thức sau (áp dụng vi phân). 2. 3. 4. 5. 6. 1. 𝐴 = 3√
0.97 𝐵̂ = cos 310 𝐶 = arctan 0.02
𝐷 = sin 580 𝐸 = 𝑒0.03. 𝐹 = ln 1.01
Bài 2: Tìm a thức Tay-lor, a thức Mac-lau-ranh (Maclaurin).
1. Tìm a thức Taylor bậc 3 của hàm số .
BỘ MÔN TOÁN-KHOA CÔNG NGHỆ THÔNG TIN-HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 1 lOMoAR cPSD| 47708777
BÀI TẬP THAM KHẢO HỌC PHẦN TOÁN GIẢI TÍCH 12-2020
2. Tìm a thức Maclaurin bậc 4 của hàm 𝑝(𝑥) = (𝑥 + 1). ln(𝑥 + 1) 3. Tìm a
thức Taylor bậc 4 của hàm 𝑔(𝑥) = (𝑥2 + 2). 𝑒𝑥−2 tại iểm 𝑥 = 2.
4. Tìm a thức Taylor bậc 3 của hàm số ℎ(𝑥) = 𝑥2 sin(𝑥 + 2) tại 𝑥 = −2. Chương 2:
Các phép tính tích phân hàm một biến
Bài 3: Tính nguyên hàm, tích phân xác ịnh bằng phương pháp ổi biến số.
Bài 4: Tính nguyên hàm, tích phân xác ịnh bằng phương pháp TP từng phần.
Bài 5: Tính ộ dài ường cong 𝐴𝐵̂ (ĐỌC THÊM). 1.
𝑦 = ln 𝑥 từ iểm 𝑥 = 1 ến iểm 2.
từ iểm (0,0) ến iểm có hoành ộ 𝑥 = 2 . 3. 4. .
Bài 6A: Tính các tích phân suy rộng sau. 1. 3. 5. 4. 2. 6.
Bài 6B: Xét sự hội tụ của các tích phân suy rộng sau.
BỘ MÔN TOÁN-KHOA CÔNG NGHỆ THÔNG TIN-HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 2 lOMoAR cPSD| 47708777
BÀI TẬP THAM KHẢO HỌC PHẦN TOÁN GIẢI TÍCH 12-2020
Chương 3: Chuỗi số và chuỗi hàm
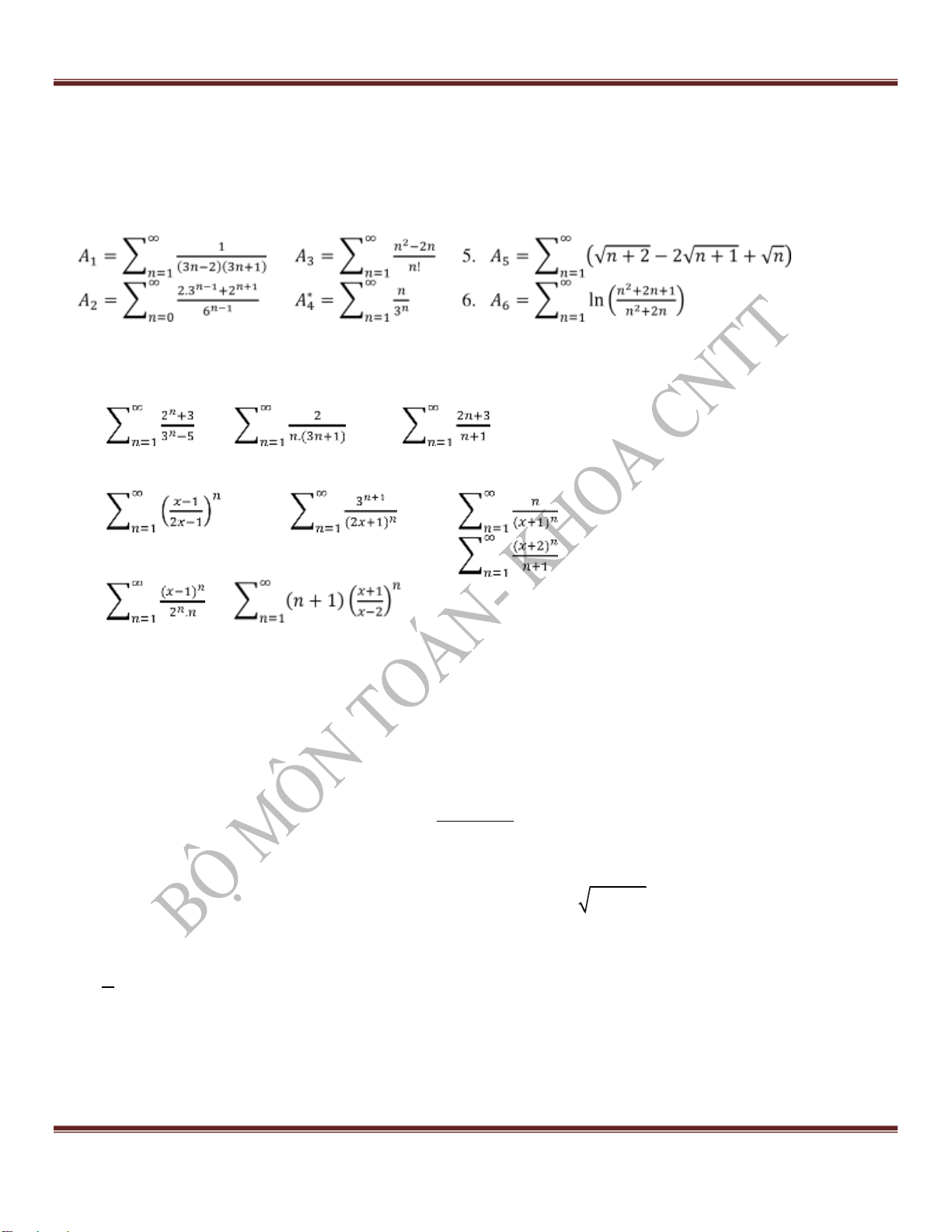
Bài 7A: Tính tổng của các chuỗi số sau. 1. 3. 2.4.
Bài 7B: Xét sự hội tụ của các chuỗi số sau 1. 2. 3.
Bài 8: Tìm miền hội tụ của các chuỗi hàm sau (ĐỌC THÊM). 1. . 3. . 5. 2. 4. 6.
Chương 4: Hàm nhiều biến
Bài 9: Tính các ạo hàm riêng cấp 1, cấp 2 (của hàm 2 biến, 3 biến) = = x x5 + 5xy3 − 4 2 −
x.y + x − 2 b/ z xy+1 a/ z y−2 c/ z=ln(x2 +y2 −1)
d/ z = sinxc. osy +ex −e2y e/ u(x, y,z) = arcsin(x+2y−3z) f/
u(x, y,z) = x2 +2y.ln z g/ f (x, y) =(x−2y)3 h/ g(x, y) = xe. y + y.ex −
x3 + 2y i/ z = y +sin xy k/ u(x, y,z) = x.sin y+ y.sinz+ z.sinx x
Bài 10A: Tìm vi phân toàn phần của hàm số:
BỘ MÔN TOÁN-KHOA CÔNG NGHỆ THÔNG TIN-HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 3 lOMoAR cPSD| 47708777
BÀI TẬP THAM KHẢO HỌC PHẦN TOÁN GIẢI TÍCH 12-2020
a/ z =sin(x2 + y2) b/ z =ln(x2 −xy+2y3) c/ f =
ex.(xsin y +cos y) d/ u=x y+y z+z x
Bài 10B: Cho hàm số f (x, y) =ex x2 + y2
a/. Tìm vi phân toàn phần của hàm số trên. b/. Tính gần úng giá trị biểu thức P=e0,02 0,022 +1,012
Bài 10C: Cho hàm số f (x, y) = 3 x2 + y2
a/. Tìm vi phân toàn phần của hàm số trên.
b/. Tính gần úng giá trị biểu thức P= 3 1,022 +0,052
Bài 10D: Áp dụng vi phân toàn phần, tính gần úng: a/ A= 4,052 + 2,932 b/ B= 0,093 +0,993 1 , 05 c/ C = arctan
d/ D= 0,99.sin32o (gợi ý: ổi 32o = + (radian) ) 0,92 6 90
Bài 11: Tìm các iểm cực trị và giá trị cực trị nếu có của các hàm số sau:
a/ z = x2 + xy + y2 + x − y +1. b/ z = x3 + 6xy + 2y2 + 6x. c/ f (x, y) = x + y − xe. y d/ f
(x, y) = 2x4 + y4 − x2 −2y2 . e/ f (x, y) = x2 −12xy + xy3 f/ f (x, y) = 4(x − y)− x2 − y2 Chương 5: Tích phân bội
Bài 12: Tính tích phân kép trên miền hình chữ nhật vuông (các cận là hằng số) + miền hình chữ nhật cong (một
cận xác ịnh và một cận phụ thuộc biến (bậc nhất)) ( x 2 + D
3xy+4y2 −x+ y)dxdy trên miền D : 0 1 y 2 1 . = a/ I x = b/ J
exy dxdy với 𝐷 = {(𝑥; 𝑦) ∈ ℝ2||𝑥| ≤ 1; |𝑦| ≤ 1 }.
BỘ MÔN TOÁN-KHOA CÔNG NGHỆ THÔNG TIN-HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 4 lOMoAR cPSD| 47708777
BÀI TẬP THAM KHẢO HỌC PHẦN TOÁN GIẢI TÍCH 12-2020 = ( D c/ K
sin x+cosy)dxdy trên miền giới hạn bởi các ường thẳng x = 0, x = , y = 0, y = . = D 4 4 d/ A
(x+2y)dxdy với miền D: 1 x 5, x −1 y x + 2. = D e/ B
y2dxdy trên miền D giới hạn bởi 3 ường thẳng: y = 0, x = 2, x = y. D x− y f/ C =
D ex+ydxdy, với D là miền giới hạn bởi x x 0y; y1 0 = g/ E
ydxdy với D là miền giới hạn bởi các ường y =1, y = x, y = 4− x. D
Bài 13: Tính tích phân kép có ổi biến số (Đổi biến trong hệ tọa ộ De-các ể ưa miền hình bình hành về hình chữ
nhật + Đổi biến trong hệ tọa ộ cực ể ưa miền hình tròn về h.c.n cong) = a/ A
(x+ y)3.(x− y)2dxdy với D là miền giới hạn bởi các ường: x+y=1, x− y = −1, x+ y =3, x−y=1 D b/ = B
(x− y) dxdy với D là miền giới hạn bởi các ường thẳng: y=x+1, y = x−2, y = 2x−1, y = 2x−4 D
y=x+1;y=x−3 = c/ C
(y − x)dxdy , với D là miền giới hạn bởi x 7 x = D
y=− 3 + 3;y=− 3 + 5 d/ I
(x− y)dxdy với D: x2 + y2 4, x 0, y 0. D = e/ J ex + 2
y2dxdy trên nửa hình tròn D : x2 + y2 9, y 0. D
BỘ MÔN TOÁN-KHOA CÔNG NGHỆ THÔNG TIN-HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 5 lOMoAR cPSD| 47708777
BÀI TẬP THAM KHẢO HỌC PHẦN TOÁN GIẢI TÍCH 12-2020 = f/ K
dxdy trên miền D : x2 + y2 1, y 0, x 0. ) D g/ L=
( x2 +y2 −1 dxdy trên miền giới hạn bởi ường tròn: x2 + y2 = 4 D = h/ G
dxdyvới miền D: x2 + y2 −2x 0, y 0 D
Chương 6: Phương trình vi phân
Bài 14A: Giải các phương trình vi phân cấp 1 sau (PTVP có biến số phân ly): +
a/ x(1− y).y
2y b/ x3.(y+1)dx (x4 −1)dy =0 c/ = 1+ y y 2 d/ )
dx = cos2 x.(sin y −cos y dy 2 1 −x ) 1 2 e/ (y3 + 1 −x 1 y ' =
f) x(1+ y2)dx+ y(1+x2)dy =0 = 1− 2x
g) (1+e2x)y2dy =exdx h) yy ' y
Bài 14B: Giải các phương trình vi phân cấp 1 sau (PTVP tuyến tính cấp 1): a/ y
y = ex/2 , y(0) = −1 b/ y 2xy = − 2y
xe. −x2 , y(0) = c/ y = x3 x − 2y = 1 d/ − y xy = sin xe. x22 e) y' = (x+1)3 , y(0)
x+1 i) y'+ x 22+x 1 y= x21+1 2
BỘ MÔN TOÁN-KHOA CÔNG NGHỆ THÔNG TIN-HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 6 lOMoAR cPSD| 47708777
BÀI TẬP THAM KHẢO HỌC PHẦN TOÁN GIẢI TÍCH 12-2020 y
f) xy '+ 2 = x2 g) y'+2y = 4x
h) xy '− y = x2 arctan x
Bài 15: Giải các phương trình vi phân cấp 2 tuyến tính với hệ số hằng (vế phải có dạng mũ 𝑒𝛼𝑥. 𝑃𝑛(𝑥)) a/ y 3y
2y = ex b/ y 3y 2−6x
c/ 𝑦′′ −𝑦=𝑒2𝑥 d/ y 5y
6y = xe. x, y(0) = − , y (0) = 0. e/ y 2y y = 4e2x
BỘ MÔN TOÁN-KHOA CÔNG NGHỆ THÔNG TIN-HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 7