TÓM T T LÝ THUY T V T LÝ Đ I C ƠNG 2 BÀI 1: ĐI N TR NG TŬNH
1. Định lu t b o ỗoỪn đi n tích:
- Định luật b o toàn điện tích: Tổng đại số các điện tích trong một hệ cô lập là không đổi.
- Mật độ điện tích phân bố trong thể tích hay mật độ điện khối, kí hiệu là , được định nghĩa là: dq   (C/m3) dV
trong đó dq là điện tích chứa trong yếu tố thể tích dV của vật mang điện.
- Mật độ điện tích mặt phân bố trên bề mặt hay mật độ điện mặt, kí hiệu là , được định nghĩa là: dq   (C/m2) dS
đó dq là điện tích chứa trong yếu tố diện tích bề mặt dS của vật mang điện.
- Mật độ điện tích phân bố dọc theo chiều dài hay mật độ điện dài, kí hiệu là , được định nghĩa là: dq   (C/m) d
trong đó dq là điện tích chứa trong yếu tố chiều dài d của vật mang điện.
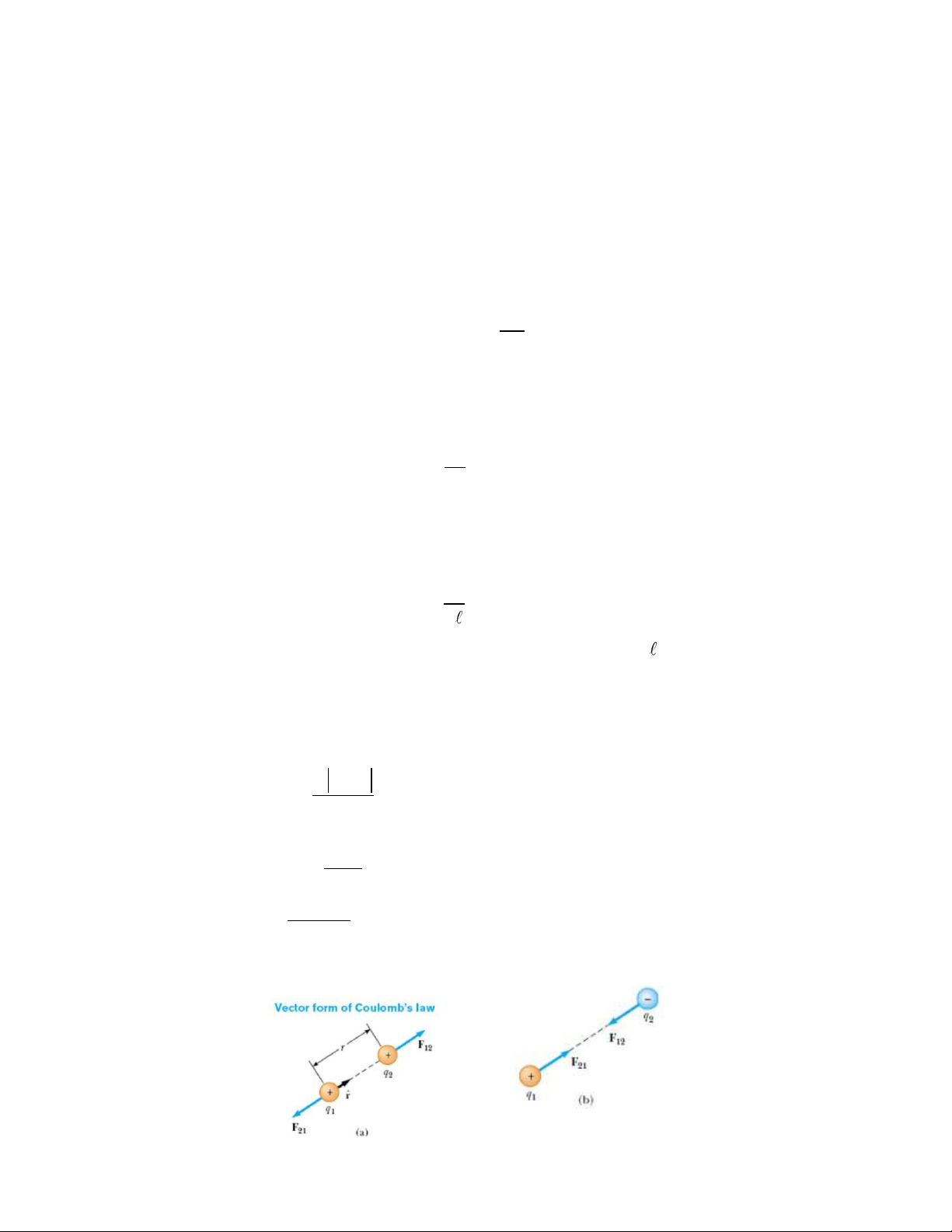
2. Định lu t Coulomb: Lực tương tác giữa hai điện tích điểm q1, q2 đứng yên
cách nhau kho ng cách r, chịu tác dụng của lực tĩnh điện: k q .q 1 2 F  2 .r (N) 1 Với: k =
= 9.10 9 (Nm2/C2): là hệ số tỉ lệ; 4o 1 o =
= 8,85.10 – 12 (F/m): là hằng số điện. 9 36 10 .
: là hằng số điện môi của môi trường. BÀI 2: ĐI N TR NG TŬNH 1. Đi n ỗr
ng: là vùng môi trường xung quanh các điện tích Q và tác dụng lực lên các
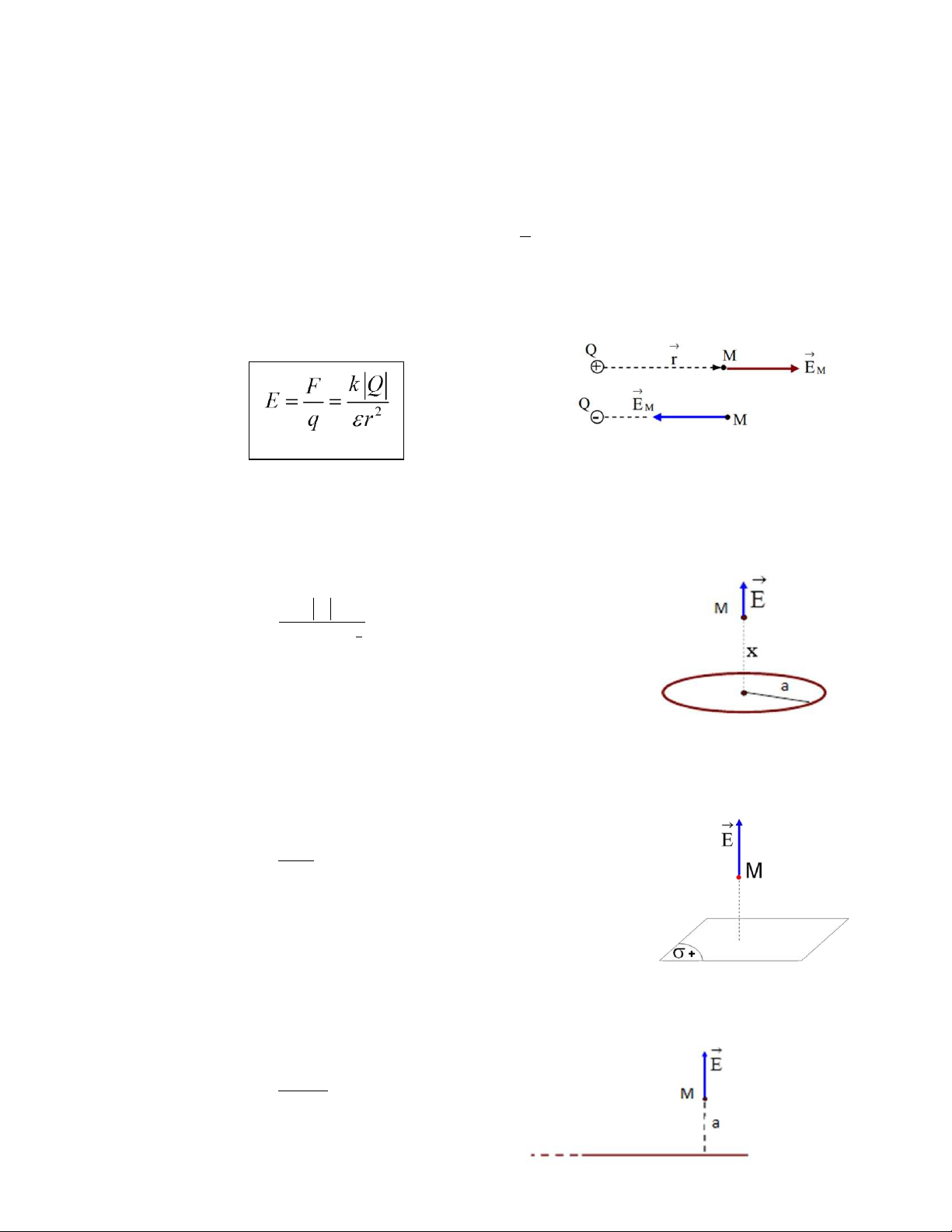
điện tích q khác đặt trong nó:   F E  (V/m) q Đi n ỗr ng: Gây ra bởi:
a. Một điện tích điểm: (V/m) Q>0: E hướng ra xa Q
Q<0; E hướng l i gần Q b.
Vòng dây tròn, bán kính a, tích điện đều Q: Điện trường t i M cách tâm O một kho ng cách x: k Q x E  3 2 2 2 (a  x )
=> T i tâm O: x= 0  E=0 c.
Mặt rộng vô hạn, ỗích đi n đ u v i m ỗ đ đi n tích mặt σ> 0: Điện trường t i
điểm M trên trục, cách tâm một đo n x: |  | E  2o (với 12  8.85.10  F/m) 0
Chứng tỏ điện trường của mặt rộng vô h n này không
phụ thuộc vào kho ng cách từ điểm kh o sát M đến mặt phẳng.
d. Thanh dài (dây dài) vô hạn, tích điện đều với mật độ dài λ> 0: Điện trường t i
điểm M cách thanh một đo n a: 2k |  | E  a 
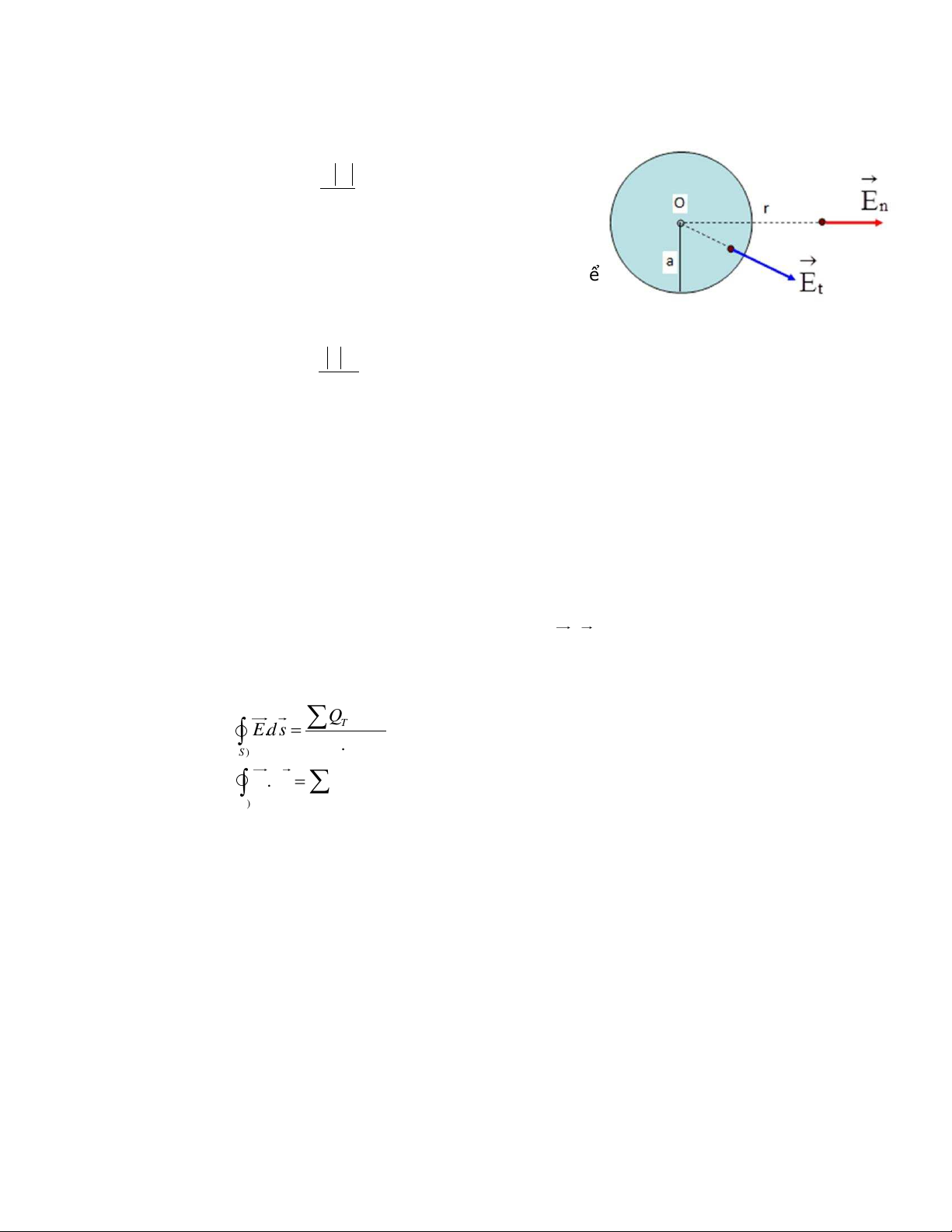
e. Khối cầu tâm O, bán kính a, tích điện đều với mật độ khối ρ > 0:
- Điện trường tại điểm M nằm ngoài khối cầu: k Q Engoài  2 r 
(Nhận thấy công thức tính điện trường t i điểm
nằm ngoài khối cầu giống như một điện tích điểm đặt t i tâm gây ra.)
- Điện trường tại điểm M nằm trong khối cầu:  r Etrong  3 0 2.
Đi n thông- ỗhẾng l ợng đi n c m:  
- Điện thông:
  d  E.d S  EdScos  (V.m) E E    (S) (S) (S)
Nếu E là điện trường đều và S là mặt phẳng:   . E S.cos E   -
Đi n c m: D   E (C/m2) 0 -
Thông lượng điện cảm :   d  Dd S  . D dS.cos D D    (S ) (S ) (S ) (C) 3. Định lý Gauss: QTrong(S)
  E.ds   E  . (S ) 0  D d s Q D  .    Trong(S) (S )
BÀI 3: ĐI N TH - HI U ĐI N TH
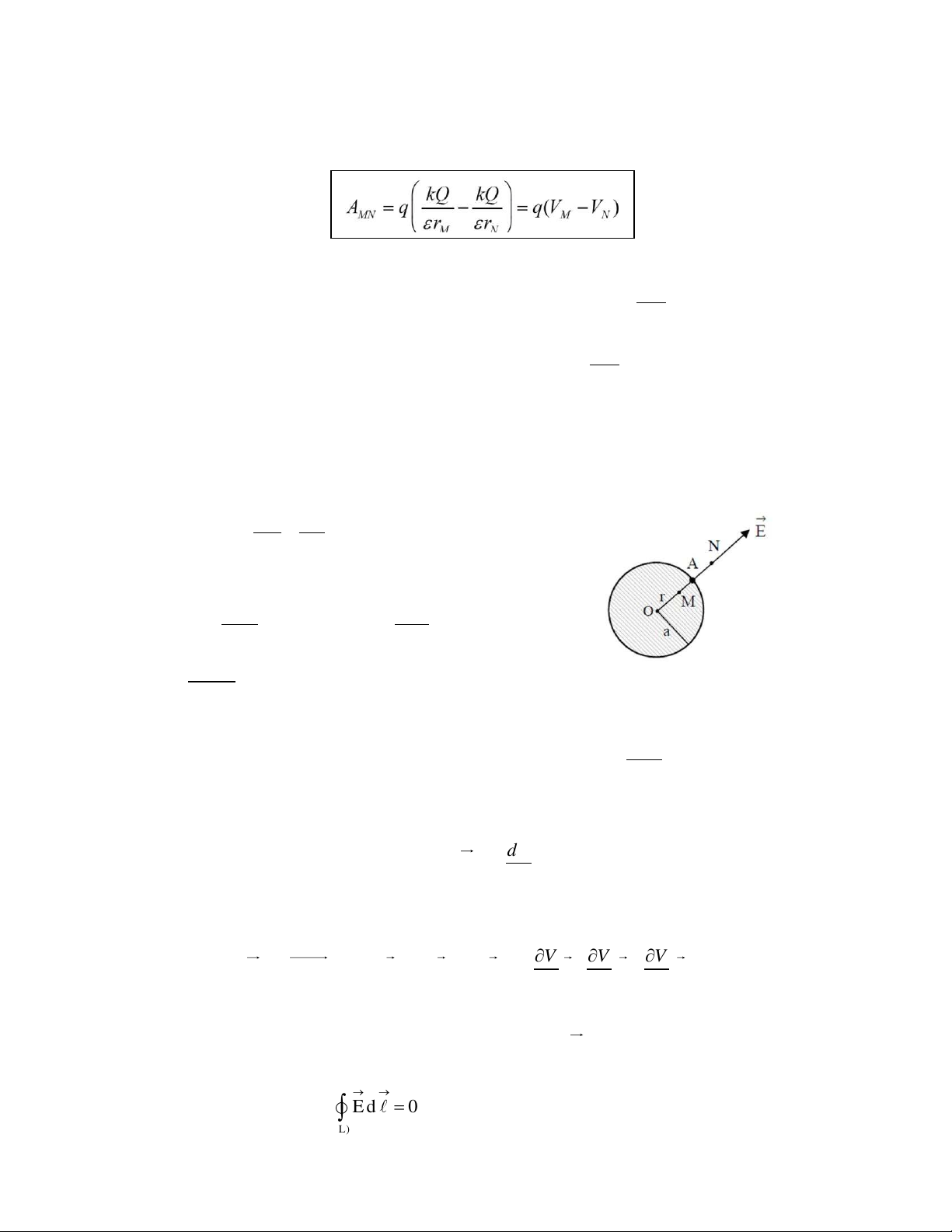
1. Công lực đi n ỗr
ng: Công của lực điện trường để di chuyển điện tích q từ điểm M đến N : (J) 2. Đi n th : kQ
a. Điện thế tại điểm M do điện tích Q gây ra: V   C M rM kQ
- Nếu gốc điện thế ở vô cùng  C  0=>V  M rM
- Hiệu điện thế : V
V V  A  . q V V MN M N MN  M N 
b. Khối cầu tâm O, bán kính a, tích điện đều với mật độ khối �:
- Điện thế tại điểm N ngoài khối cầu: kQ kQ V V   N A r r N A
- Điện thế tại điểm M trong khối cầu: 2 .r 2 .r M V V   ; A V V   M 0 6 A 0 6 0 0
Lưu ý: Gốc điện thế t i A => VA= 0.
c. Mặt rộng vô hạn, tích điện đều với mật độ mặt � >0 : Điệ  x
n thế t i M cách mặt phẳng kho ng cách x: V   20
3. Mối liên h giữa E và V :
Độ lớn của vectơ cường độ điện trường, bằng độ gi m của điện thế trên một đơn vị chiều dV
dài dọc theo đường sức điện trường : E   dn
Trong hệ tọa độ Descartes: V  V  V 
E  grad.V  E .i  E . j  E .k  (  .i  . j  .k) x y z x  y  z  -
Điện trường đều :U V V  .
E d (d là kho ng cách 2 mặt điện thế) 12 1 2 -
Lưu thông cuả vecto cường độ điện trường: . E dl V  V V M N MN   
Đường cong kín : E d  0  (L) BÀI 4: V T D N
1. V t d n là những v t bằng kim lo i
2. Tính chất c a v t d n:
- Trong lòng vật dẫn không có điện trường Etrong=0.
- Toàn bộ vật dẫn là khối đẳng thế. 
- Vecto cường độ điện trường E vuông góc với bề mặt vật dẫn, và có độ lớn E  0
- Điện tích chỉ phân bố bề mặt ngoài vật dẫn.
3. Hiện tượng mũi nhọn bị mất dần điện tích và t o thành gió điện được gọi là hi u ng mũi nhọn.
4. Hiện tượng xuất hiện các điện tích c m ứng trên bề mặt vật dẫn khi đặt vật dẫn trong
điện trường ngoài gọi là hi n ỗ ợng đi n h ởng.
5. Khi nối hai qu cầu l i thì chúng trở thành vật dẫn duy nhất ,V  V vật dẫn là một 1 2 mặt đẳng thế. Q
6. Đi n dung c a v t d n cô l p: C  V
Điện dung của vật dẫn cô lập phụ thuộc vào hình d ng, kích thước vật dẫn. a. T phẳng: . .S 0 C  d (F) 6 9 12
1F 10 F 10 nF 10 pF
Với S: diện tích hai b n cực (m2)
d :kho ng cách hai b n cực (m) 12  8,85.10  F / m 0 C: điện dung (F) b. Tụ cầu: R .R 1 2 C  4..0  R R 2 1
R1: bán kính trong; R2: bán kính ngoài. l
c. Tụ trụ: C  2.. ( : là chiều cao trụ) 0  R  2 ln   R  1  7. Ghép t : a. Ghép nối ti p:
Q  Q  Q  Q  ...  Q 1 2 3 n
U  U U U  ...U 1 2 3 n 1 1 1 1 1    ..... C C C C C d t 1 2 3 n C
Nếu các tụ giống nhau thì C  td n b. Ghép song song:
Q  Q  Q  Q  ... Q 1 2 3 n
U  U  U  U  ...  U 1 2 3 n
C  C  C  C  ... C td 1 2 3 n
Nếu các tụ giống nhau: C  nC td 1
8. Năng l ợng c a t đi n: 2 W  .CU 2
9. Năng l ợng đi n ỗr ng:
Nơi nào có điện trường thì nơi đó có năng lượng. 1 1 2 W   dV   E dV  EDdV E 0    2 2 (V) (V) (V)  1 1
là mật độ năng lượng điện trường: 2    E  ED E E 0 2 2 BÀI 5: T TR NG TŬNH
0. T thông cho biết số lượng đường sức từ gởi qua mặt (S).  
  d  BdScosα  B.d S m m    (S) (S) (S)
Trong hệ SI, đơn vị đo từ thông là vêbe (Wb).   1. So sứnh Đi n ỗr ng E và T ỗr ng H . Đi n ỗr ng T ỗr ng
- Xung quanh điện tích có điện trường.
- Xung quanh dòng điện có từ trường.
- Đặc trưng cho điện trường t i mỗi điểm là - Đặc trưng cho từ trường t i mỗi điểm là  
vectơ cường độ điện trường E . vectơ c m ứng từ B .
- Vectơ cường độ điện trường gây bởi một - Vectơ c m ứng từ gây bởi một yếu tố   điện tích điể Q  m: E  k dòng điện: 0 d B  Id ,r 2 r  3 4 r   
- Hằng số điện: 0 = 8,85.10 – 12 F/m
- Hằng số từ: 0 = 4.10 – 7 H/m - Hệ số điện môi:  - Hệ số từ môi:     
- Vectơ c m ứng điện: D   E
- Vectơ c m ứng từ: B   H 0 0 - Đường sức điện - Đường sức từ
- Điện thông E: cho biết số lượng đường - Từ thông m: cho biết số lượng đường sức
sức điện trường E gửi qua mặt S: từ B gửi qua mặt S:   E.dS  E.dS.cos   B.dS  B.dS.cos  E  m  (S) (S)      
- Lực điện trường: F  q E - Lực từ: d F  Id , B     q  - Định lý Gauss: trong(S) E.dS    - Định lý Gauss: B.dS  0  (s) 0 (s)
- Lưu thông của vectơ cđđt: E.d  U  AB 
- Lưu thông của vectơ cđtt: Hd I   k (AB) k (C)
2. Xức định c m ng t c a dòng đi n:
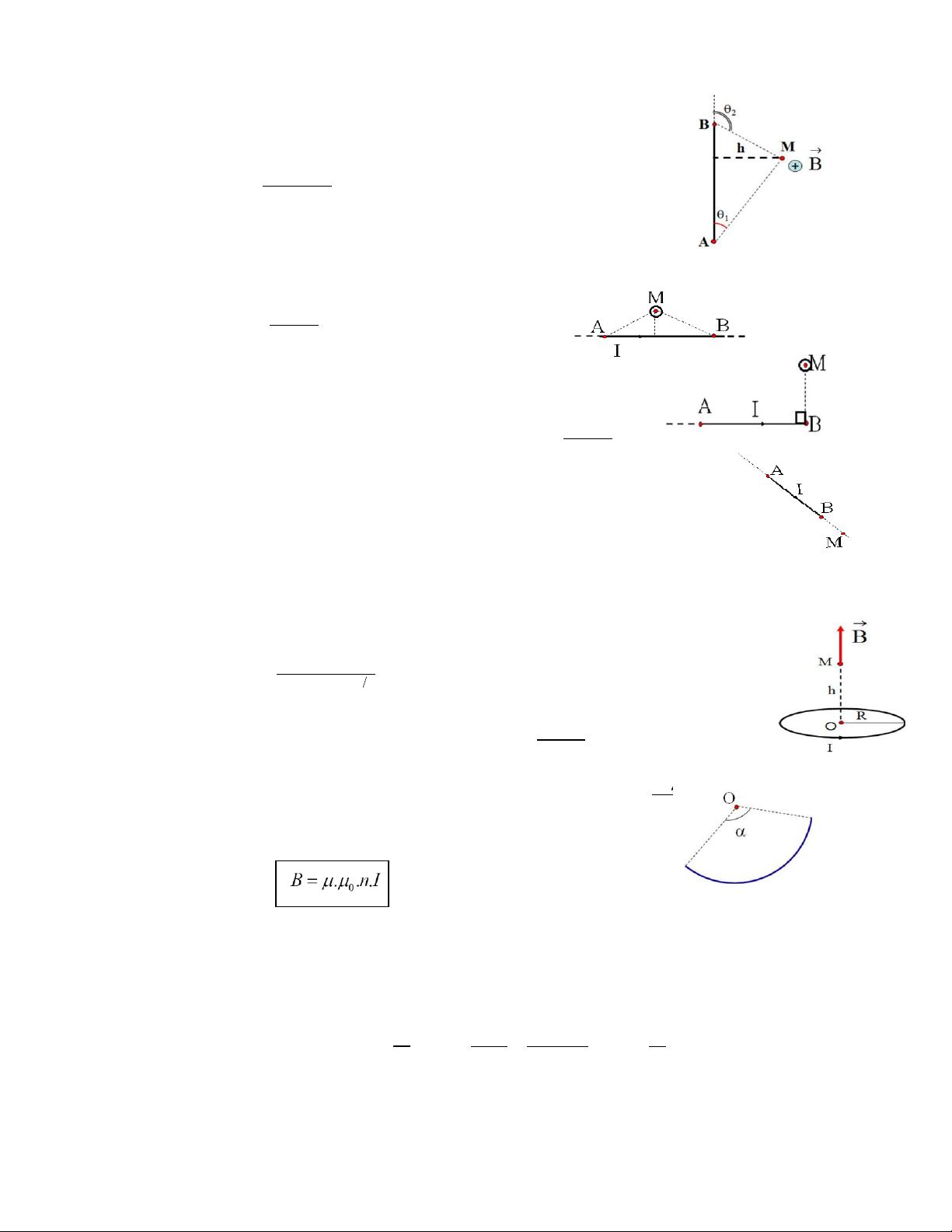
a. Cảm ứng từ của dòng điện thẳng: . .I 0 B  . cos  cos  1 2  4 .h
+ Dòng điện rất dài, hay điểm kh o sát nằm gần dòng điện: . .I 0 B  M 2.h
+ Dòng điện rất dài, điểm kh o sát nằm trên đường . .I
vuông góc với dòng điện tai một đầu: 0 B  M 4.h
+ Điểm kh o sát nằm trên đường thẳng chứa dòng điện: B  0 M
b. Cảm ứng từ tại điểm M cách tâm O của trục vòng điện tròn bán kính R,
một khoảng h: 2 . .I.R 0 B  M
2R  h 3 2 2 2 . .I
+ C m ứng từ t i tâm O (h=0) : 0 B  0 2R . .I
+ Nếu cung tròn chắn một góc α ở tâm thì : 0 B  . 0( ) 4.R
c. Cảm ứng từ trong lòng ống dây:
với: n: mật độ dòng (vòng/m)
L : chiều dài ống dây (m)
N : số vòng dây quấn trên ống (vòng) N B . . .nI N
+ Dây Soneloid: n   0 H    . n I  .I L . . L 0 0
Vậy: Từ trường trong lòng ống dây Soneloid là từ trường đều. N B . . .nI N + Dây Torid: 0 n   H    . n I  .I 2 r . . 2 r 0 0
Vậy: Từ trường trong lòng ống dây Teroid là từ trường không đều. 3. Tác d ng c a t ỗr ng lên dòng đi n:
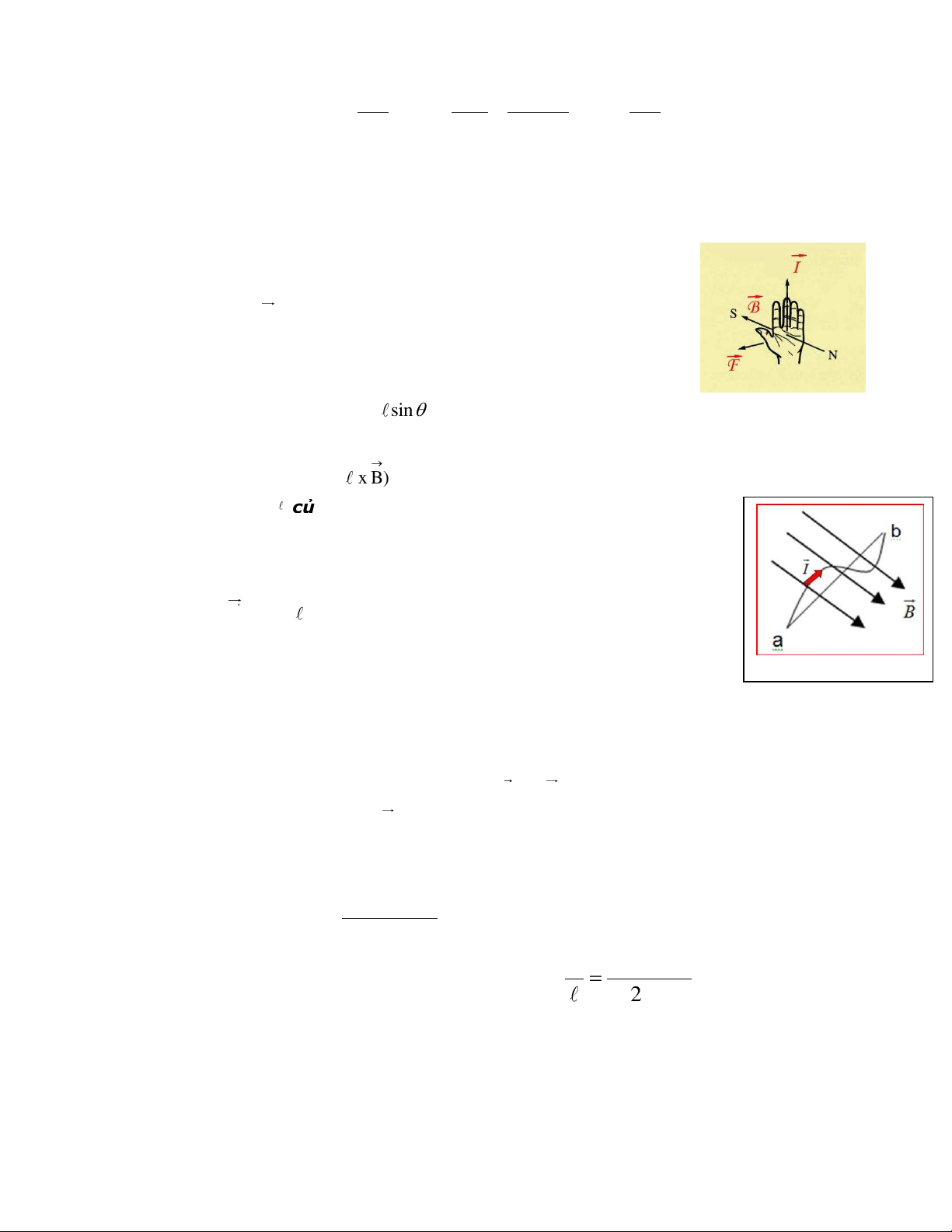
 Tác dụng của từ trường đều lên đoạn dòng điện thẳng: Lực từ F có:
+ Phương vuông góc với mặt phẳng chứa dòng I và B
+ Chiều theo quy tắc tay trái.
+ Độ lớn F  BI sin
+ Điểm đặt t i trung điểm của đo n dòng điện I.     F  d F  I( x B) 
 Tác dụng của từ trường đều lên đoạn dòng điện cong bất kỳ.    F  I L'  B  với ' L  d
 là tổng các vectơ độ dời từ điểm a đến điểm b (ab)
Nếu đường cong kín thì F=0.
 Tác dụng của từ trường đều lên khung dây :
Mômen lực từ tác dụng khung lên khung dây: M  N. . B I.S.sin
trong đó: α là góc giữa 2 vevtơ n và B .
N số vòng dây, B c m ứng từ (T)
I cường độ dòng điện (A), S diện tích khung dây (m2)
 Lực tương tác giữa 2 dòng điện thẳng dài vô hạn:
. .I .I .l 0 1 2 F  2 d F . .I .I 0 1 2
Lực tương tác trên mỗi đơn vị chiều dài: f   2 d
+ Hai dòng điện song song cùng chiều: hút nhau.
+ Hai dòng điện song song ngược chiều: đẩy nhau.
 Công của lực từ:
A  I    I.   12  2 1 m
M ch tịnh tiến trong từ trường đều A=0.
BÀI 6: CHUY N Đ NG C A H T ĐI N TRONG T TR NG 1. Tác d ng c a t ỗr
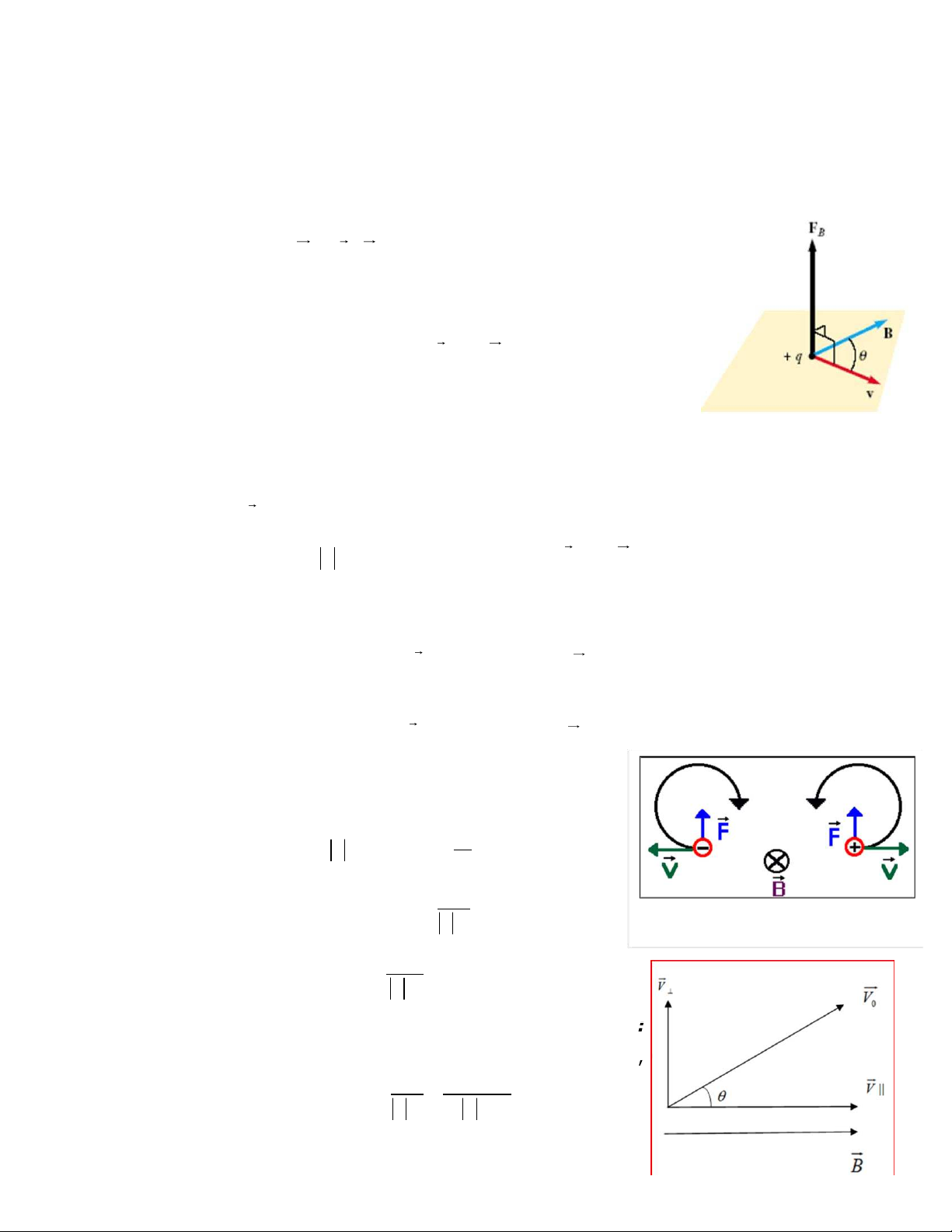
ng lên đi n tích chuy n đ ng- Lực Lorentz:
 H t mang điện chuyển động trong từ trường chịu tác dụng của lực từ, lực này gọi là lực Lotentz:
F  qv B
Các đặc điểm của lực Lorentz:
 Có phương vuông góc với v và . B
 Có chiều theo quy tắc bàn tay trái đối với điện tích
dương, quy tắc bàn tay ph i đối với điện tích âm: Đặt
bàn tay trái (hoặc ph i) sao cho các đường c m ứng
từ hướng xuyên qua lòng bàn tay, chiều đi từ cổ tay đến bốn ngón tay là chiều
của v , thì ngón tay cái choãi ra 900 sẽ chỉ chiều của lực Lorentz.
 Độ lớn: F  q vBsin , với  là góc giữa v và . B
 Điểm đặt t i điện tích q.
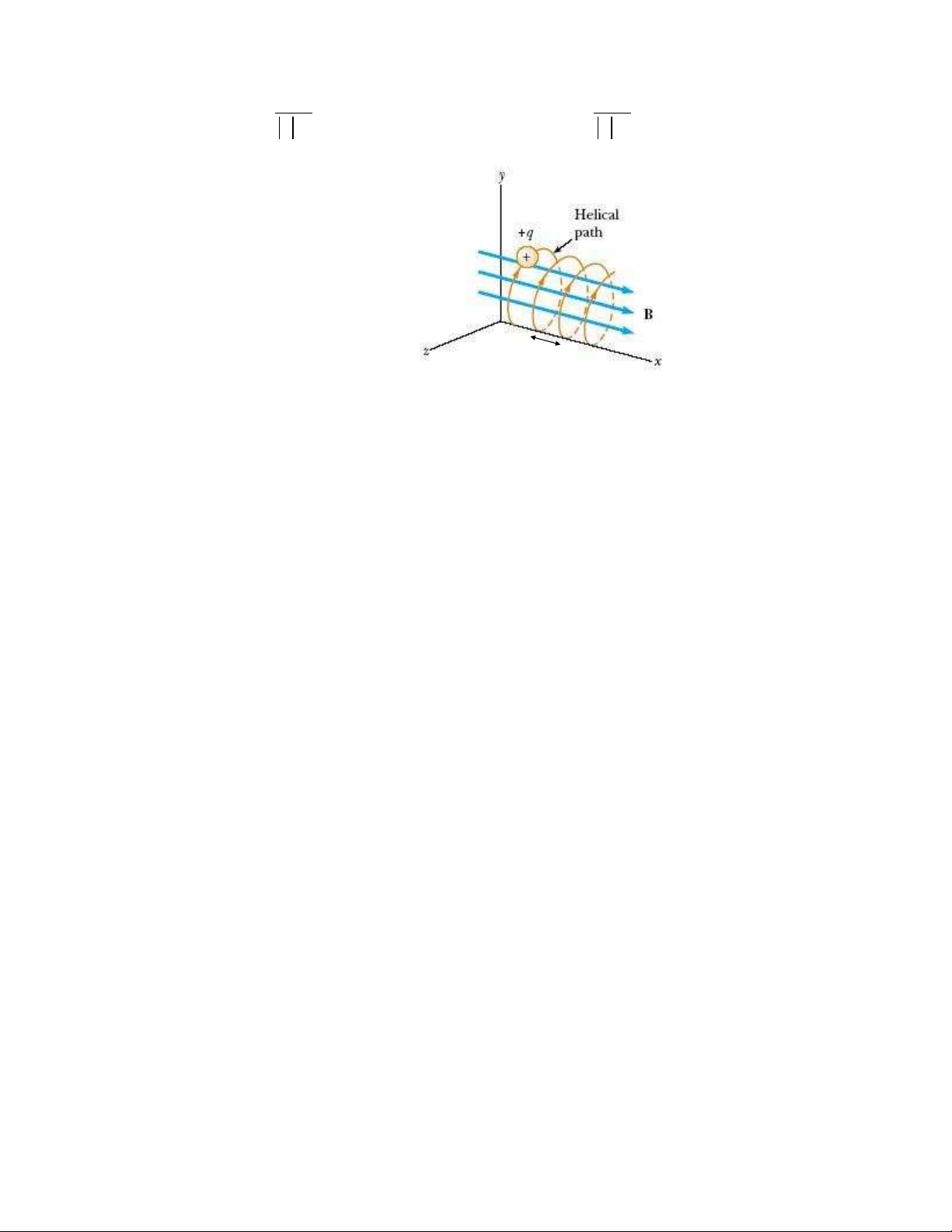
2. Chuy n đ ng c a h ỗ đi n tích trong t ỗr ng đ u:
a. Nếu vecto vận tốc đầu v song song với B :
 F =0 điện tích chuyển động thẳng đều theo hướng cũ.
b. Nếu vecto vận tốc đầu v vuông góc với B :
 Điện tích chuyển động tròn đều với lực
Lorents hướng vào tâm, có: 2 v
- Độ lớn: F  q Bv  ma  m n r mv
- Bán kính quỹ đ o: r  q B 2 m  - Chu kỳ quay: T q B
c. Nếu vecto vận tốc ban đầu tạo với B một góc �:
Quỹ đ o của điện trường là những đường xoắn lò xo, với mv mv sin   - Bán kính xoắn lò xo: 0 r   q B q B 2 m 2 m - Chu kỳ T 
Bước xoắn h  v .T  v o c s q B / / 0 q B 3. Hi u ng Hall:
Khi một vật dẫn có dòng điện ch y qua được đặt trong từ trường thì do tác dụng của lực
từ đã làm xuất hiện chuyển động phụ của các h t t i điện. Do chuyển động phụ này mà
các h t t i điện bị dịch chuyển về hai bề mặt vật dẫn t o nên một hiệu điện thế. Hiện
tượng này gọi là hi u ng Hall, hiệu điện thế xuất hiện giữa hai bề mặt vật dẫn trong
trường hợp này gọi là hi u đi n th Hall. BÀI 7: C M NG ĐI N T 1. Định lu t Lenz:
Định luật khẳng định: “Dòng điện cảm ứng trong một mạch kín phải có chiều sao cho từ
trường mà nó sinh ra chống lại nguyên sinh ra nó.”
2. Định lu t Faraday v suấỗ đi n đ ng c m ng:
Suất điện động cảm ứng bằng về trị số và trái dấu với tốc độ biến thiên của từ thông qua d mạch: m    dt   Trong đó,   Bd S m  là từ thông qua m ch. (S)
a) Khung dây quay đều trong từ trường đều:
Nếu m ch điện có N vòng dây quấn trên một khung cứng thì: d m   N dt
Nếu vòng dây thẳng và từ trường đều thì   BScos , ta có: m   d d ( . B S.cos ) m   N  N dt dt
Suất điện động cực đ i:   NBS 0
b) Đoạn dây dẫn chuyển động trong từ trường đều: | d | m    Bv sin dt
Nếu m ch hở thì hai đầu đo n MN có hiệu điện thế: U  
3. H số tự c m:   LI m
trong đó, L là hệ số tỉ lệ, được gọi là hệ số tự cảm hay độ tự cảm của m ch điện. 2  . .N S
- Hệ số từ c m của ống dây Soneloid: m 0 L   I 1
- Năng lượng từ trường: 2 W  LI 2
BÀI 8-9: SÓNG ĐI N T VÀ GIAO THOA ÁNH SÁNG
- Sóng điện từ truyền trong chân không, với vận tốc c= 3.108m/s c
- Sóng điện từ truyền trong môi trường chiết suất n, với vận tốc: v  n
- Bước sóng của sóng điện từ trong chân không là:  
- Bước sóng truyền trong môi trường chiết suất n là: 0   n
 Khi truyền từ môi trường này sang môi trường khác: Chỉ vận tốc v và bước sóng λ
thay đổi, chu kỳ T và tần số f không đổi. 1. Quang l :
Quang lộ của ánh sáng trong thời gian t là quãng đường mà ánh sáng truyền được s
trong chân không trong khoảng thời gian đó: L  ct  c  ns v
Trong hệ SI, đơn vị đo quang lộ là mét (m). 2. Giao thoa:
Hiện tượng hai hay nhiều sóng ánh sáng gặp nhau, t o nên trong không gian
những d i sáng, tối xen kẽ nhau gọi là sự giao thoa ánh sáng.
Những d i sáng và tối đó được gọi là những cực đại và cực tiểu giao thoa, hay các
vân giao thoa; chúng tương ứng với những giá trị cực đ i và cực tiểu của cường độ ánh sáng.
a. Đi u ki n đ có có giao thoa: hai sóng ph i là hai sóng kết hợp và có cùng phương truyền sóng.
Sóng kết hợp: là những sóng ánh sáng có cùng tần số và độ lệch pha không đổi
theo thời gian.
b. Giao thoa bởi hai nguồn đi m:
- Đi u ki n đ có cực đ i giao thoa:
Tại những điểm mà hiệu quang lộ của hai sóng tới bằng số nguyên lần bước sóng
sẽ cho cực đại giao thoa: L2 – L1 = k
với k = 0, 1, 2, …, gọi là bậc giao thoa.
- Đi u ki n đ có cực ti u giao thoa:
Tại những điểm mà hiệu quang lộ của hai sóng tới bằng số bán nguyên lần bước
sóng sẽ cho cực tiểu giao thoa L2 – L1 = (k + 0,5) 3. Giao thoa Young:
Gọi khoảng cách giữa hai vân sáng liên tiếp hoặc giữa hai vân tối liên tiếp là D
khoảng vân i, thì: i  a
Với:  là bước sóng, D: kho ng cách từ khe tới màn, a: kho ng cách giữa hai khe.
Khi đó, vị trí của vân sáng ph i thỏa công thức: xs = ki
và vị trí của vân tối ph i thỏa công thức: xt = (k + 0,5)i 4. Giao thoa do ph n x :
Sóng điện từ bị đ o pha 1800 khi ph n x từ bề mặt môi trường có chiết suất lớn
hơn môi trường tới. Nếu ph n x từ bề mặt môi trường có chiết suất nhỏ hơn chiết
suất của môi trường tới thì tia ph n x không bị đ o pha. 5.
Giao thoa bởi hai b n mỏng:
Hiệu ứng giao thoa thường quan sát trên các lớp màn mỏng như: ván dầu trên mặt
nước, bong bóng xà phòng, hơi nước trên tấm kính,…là kết qu sự giao thoa của
hai chùm tia ph n x trên hai bề mặt b n mỏng.
- Nêm không khí: vân giao thoa trên mặt nêm là những đo n thẳng song song 
nằm trên mặt nêm, cách đều nhau một kho ng vân i: i  (α: góc nghiêng 2 
của nêm). To độ vân sáng bậc k: x  (k  0,5) s 2 
To độ vân tối bậc k: x  k t 2
- Vân tròn Newton: Vân giao thoa là những vòng sáng tối xen kẽ, do Newton
khám phá nên gọi là vân tròn Newton. 
Vị trí của vân sáng thoã điều kiện: d  (k  0,5) 2 
Vị trí của vân tối thoã điều kiện: d  k 2
Bán kính vân sáng thứ k: r  2Rd  (k  0,5)R s
Bán kính vân tối thứ k: r  2Rd  kR t
BÀI 10: NHI U X ÁNH SÁNG
1. Hiện tượng nhiễu xạ ánh sáng: là hiện tượng ánh sáng bị lệch khỏi phương truyền
thẳng trong môi trường đồng tính khi đi gần các vật c n.
2. Nguyên lý Fresnel: Biên độ và pha của nguồn thứ cấp là biên độ và pha do nguồn
thực gây ra t i vị trí của nguồn thứ cấp.
Để tính biên độ sóng tổng hợp do nguồn sáng điểm S0 gây ra t i điểm quan sát M, ta
dùng phương pháp đới cầu Fresnel.
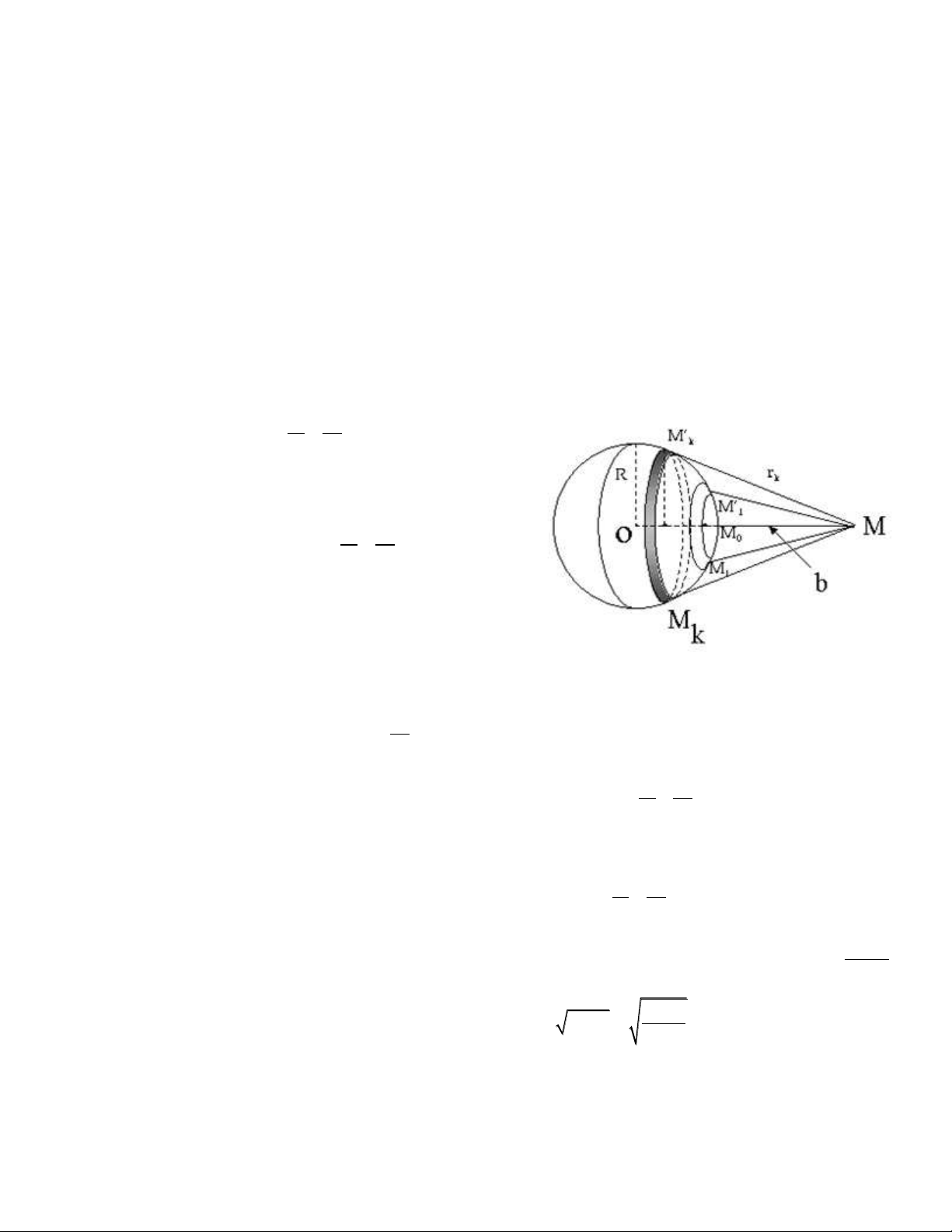
3. Nhi u x FRESNEL qua l tròn:
Gi sử lỗ tròn chứa được n đới cầu Fresnel thì biên độ sóng tổng hợp t i điểm M là: a a 1 n a   M 2 2
và cường độ sáng t i điểm M là: 2  a a  2 1 n I  (a )    M  2 2  
Lấy dấu “+” khi số đới cầu chứa trong lỗ tròn
là số lẻ và lấy dấu “–“ khi số đới cầu chứa
trong lỗ tròn là số chẵn. 2 a
- Nếu lỗ tròn quá lớn thì: 1 I   I 0 4 2  a a 
- Nếu lỗ tròn chứa số lẻ đới cầu Fresnel thì 2 1 n I  (a )   
  I : Điểm M là điểm M 0 2 2   sáng. 2  a a 
- Nếu lỗ tròn chứa số lẻ đới cầu Fresnel thì 2 1 n I  (a )   
  I : Điểm M là tối. M 0 2 2   Rb
- Các đới cầu Fresnel có diện tích như nhau và diện tích của mỗi đới cầu là: S   R  b kRb
- Bán kính của các đới cầu Fresnel thứ k là: r  2Rh  k k R  b
Với: k: đới cầu thứ k;
R: bán kính của mặt cầu.
: bước sóng ánh sáng của nguồn S0 phát ra;
b: kho ng cách từ điểm kháo sát M đến mặt đới.
4. Nhi u x FRESNEL qỘa đŭa ỗròn ch n sáng:
Các vân nhiễu x là những vòng tròn, tâm của nh nhiễu x luôn là điểm sáng ứng với
mọi vị trí của đĩa tròn và màn (E). Biên độ sóng tổng hợp t i điểm M là: a a a m 1   m 1 a     M 2 2 2 2 Cường độ  a  sáng t i M: 2 m 1 I  (a )   
  0 : M luôn là điểm sáng. M 2  
5. Nhi u x FRAUNHOFER qua n khe hẹp:
nh nhiễu x có các cực đ i chính, cực đ i phụ, cực tiểu chính (hay cực tiểu nhiễu xạ), cực tiểu phụ. 
- Các cực tiểu này ứng với góc nhiễu x  thỏa công thức: sin   k b
Trong đó:  là bước sóng ánh sáng; b là độ rộng của khe hẹp; k = 1, 2, 3, … 
- Vị trí các cực đ i chính thỏa công thức: sin   k d
với k = 0, 1, 2, 3, …, gọi là bậc của cực đ i chính. Cực đ i chính bậc không, ứng với k
= 0 và  = 0, sẽ nằm trùng với tiêu điểm F của thấu kính L2, ta gọi đó là cực đại trung tâm.
- Giữa hai cực đ i chính có (n-2) cực đ i phụ và (n-1) cực tiểu phụ.
Để quan sát được các cực đ i chính thì  < d. Cường độ ảnh nhiễu xạ qua 1 Cực đại chính Cực tiểu chính (cực tiểu nhiễu ạ Cực đại phụ sin Cực tiểu phụ
Hình 10.13: Phân bố cường độ ảnh nhiễu xạ qua 3 khe hẹp.