Đỗ Thành Nam – robotden@gmail.com
Thiết kế bộ lọc FIR sử dụng chương trình Matlab
Đỗ Thành Nam – Lớp TKCTHTĐKTL – K41
Học Viện Kỹ Thuật Quân Sự
Email: robotden@gmail.com
Hiện nay, có một vài công cụ dùng để thiết kế các bộ lọc, nhưng phổ biến
nhất là phần mềm Matlab. Trong Matlab, ta có thể sử dụng cả: SPTool,
FDATool, hoặc là các hàm của Matlab để thiết kế bộ lọc.
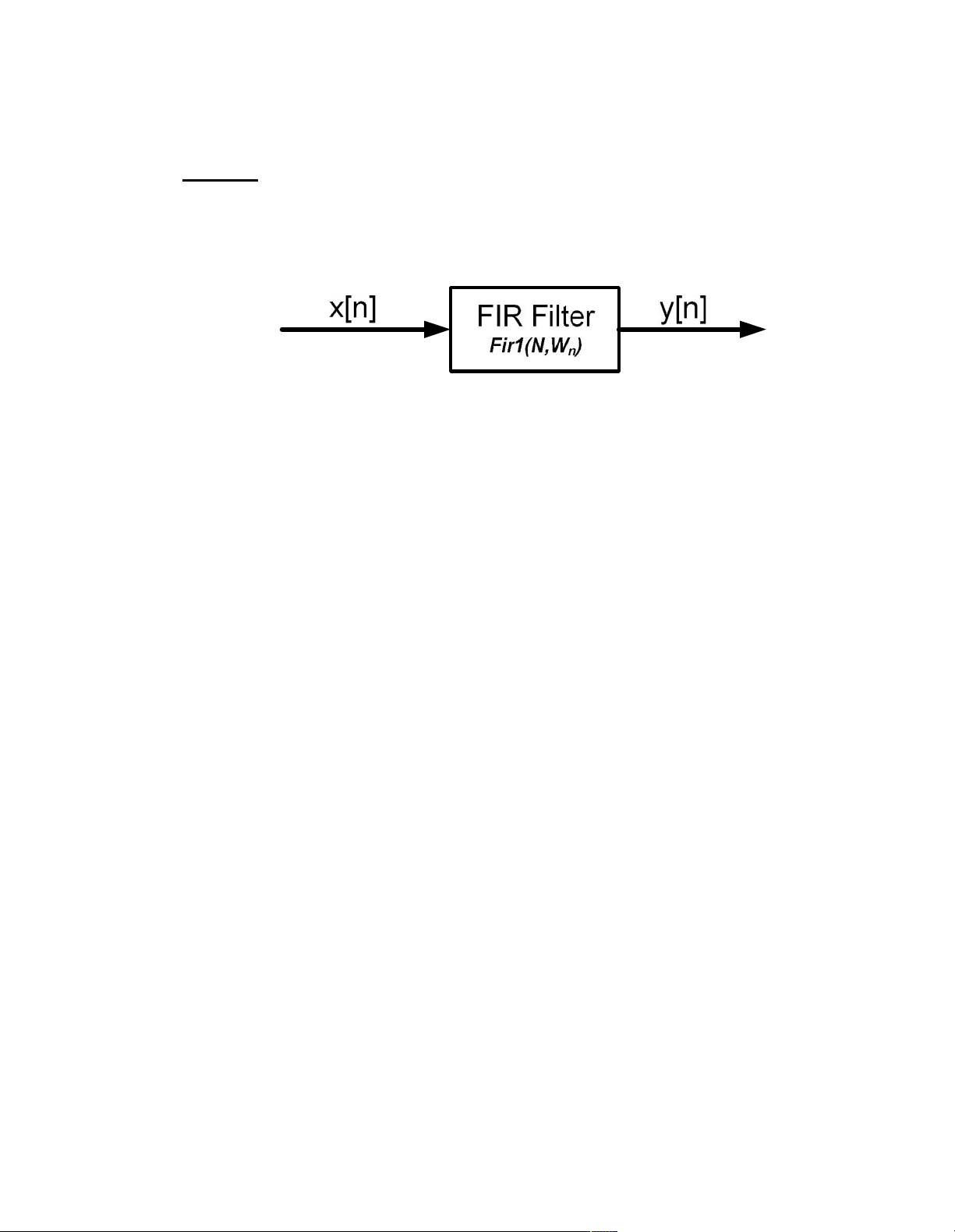
Cách 1: Sử dụng hàm trong Matlab để thiết kế bộ lọc FIR
 Hàm fir1(N,Wn,window)
>> b = fir1(N,Wn,window);
 b - là véctơ dòng, nó chứa (N+1) hệ số của bộ lọc FIR thông thấp
pha tuyến tính bậc N với tần số cắt Wn, hệ số của bộ lọc được sắp xếp
theo thứ tự như trong phương trình dưới đây:
yn b0. 
x n b1.  x n   1  ...  bM .  x n  M 
 Wn - là tần số cắt chuẩn hóa (chuẩn hoá với π) và là một số nằm
trong khoảng (0,1). Nếu tần số cắt Wn, là một véctơ 2 thành phần
Wn=[w1 w2], thì trở thành một bộ lọc với băng thông: w1 < w < w2.
 N - là bậc của bộ lọc
 Window - là một véctơ cột chứa (N+1) thành phần đã được chỉ rõ
bởi hàm cửa sổ w(n). Nếu không có cửa sổ nào được chỉ ra, fir1 dùng cửa sổ Hamming.
 Các bộ lọc thông cao, băng thông và băng chặn được thiết kế bằng
việc thêm chuỗi “high” và “stop” vào trong lệnh như sau:
>> b = fir1(N,Wn,’high’,window);
>> b = fir1(N,Wn,’stop’,window);
 Tương tự, ta có một số hàm: fir2(N,f,H,window), freqz(B,A,. ),
filter(B,A,X), firpm(N,F,A),… Để biết them thông tin về các hàm này,
trong cửa sổ lệnh của Matlab, ví dụ, ta gõ lệnh sau: >> help firpm
FIRPM Parks-McClellan optimal equiripple FIR filter design.
B=FIRPM(N,F,A) returns a length N+1 linear phase (real, symmetric
coefficients) FIR filter which has the best approximation to the desired
frequency response described by F and A in the minimax sense. F is a
vector of frequency band edges in pairs, in ascending order between 0 and 1.
1 corresponds to the Nyquist frequency or half the sampling frequency. A is 1
Đỗ Thành Nam – robotden@gmail.com
a real vector the same size as F which specifies the desired amplitude of the
frequency response of the resultant filter B. ………  Ví dụ 1:
Thiết kế bộ lọc FIR sử dụng hàm: fir1(N,Wn,window)
Thiết kế bộ lọc FIR băng thông giữa tần số 1.6 (= 0.4*(Fs/2)) KHz
và 2.4 (= 0.6*(Fs/2)) KHz, tại tần số lấy mẫu Fs = 8 KHz, sử dụng để lọc tín hiệu. % tạo tín hiệu tổ hợp
>> Fs=8e3; tần số lấy mẫu Fs=8000 (Hz)
>> Ts=1/Fs; chu kỳ lấy mẫu
>> Ns=512; số mẫu được biểu diễn trên đồ thị
>> t=[0:Ts:Ts*(Ns-1)]; tạo một mảng thời gian chứa Ns thành phần >> f1=500; >> f2=1800; >> f3=2000; >> f4=3200; >> x1=sin(2*pi*f1*t); >> x2=sin(2*pi*f2*t); >> x3=sin(2*pi*f3*t); >> x4=sin(2*pi*f4*t);
>> x=x1+x2+x3+x4; tạo tín hiệu hỗn hợp
% thiết kế bộ lọc và vẽ đáp ứng biên độ và
đáp ứng pha của bộ lọc
>> N=16; bậc của bộ lọc
>> wn=[0.4 0.6]; bộ lọc băng thông giữa: 0.4*(Fs/2) và 0.6*(Fs/2) >> b=fir1(N,wn); >> b b = Columns 1 through 7
0.0051 -0.0000 -0.0294 0.0000 0.1107 -0.0000 -0.2193 Columns 8 through 14 2
Đỗ Thành Nam – robotden@gmail.com
-0.0000 0.2710 -0.0000 -0.2193 -0.0000 0.1107 0.0000 Columns 15 through 17 -0.0294 -0.0000 0.0051
>> a=1; bộ lọc không có cực, chỉ có không điểm
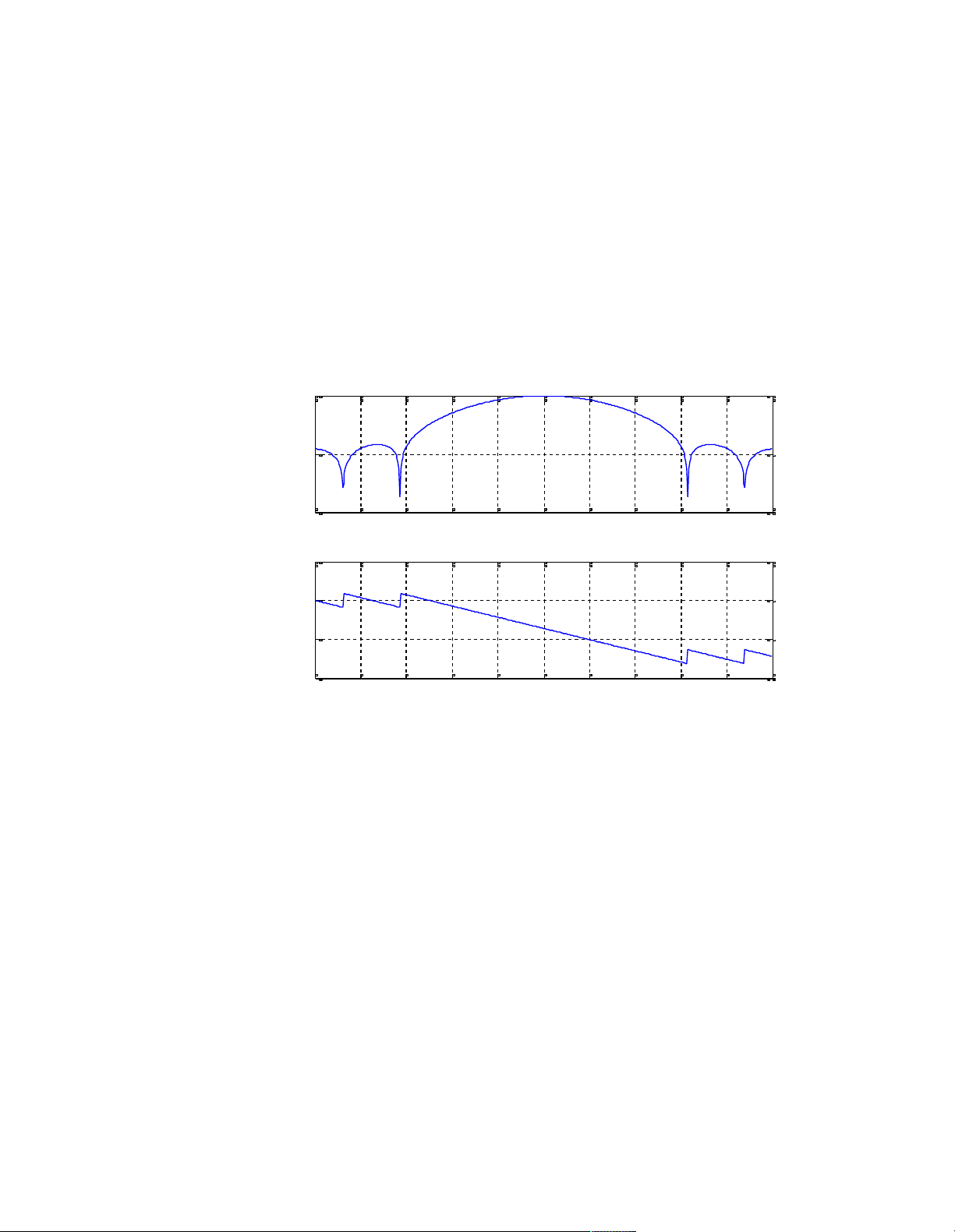
>> freqz(b,a); đáp ứng biên độ và đáp ứng pha >> pause; >> figure; ) 0 B (d e d itu n -50 g a M -100 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
N orm aliz ed F requenc y (  rad/s am ple) 500 ra 0 u a d o h -500 p -1000 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 tan s o (H z )
Hình 3.1 Đáp ứng biên độ và đáp ứng pha của bộ lọc
% vẽ biểu đồ mô tả tín hiệu vào và tín hiệu ra sau khi qua bộ lọc
>> subplot(2,1,1); >> Npts=200;
>> plot(t(1:Npts),x(1:Npts));
>> title('Bieu do thoi gian dau vao va dau ra');
>> xlabel('time (s)');
>> ylabel('Dau vao');
>> y=filter(b,a,x); lọc, thu tín hiệu đầu ra sau bộ lọc
>> subplot(2,1,2);
>> plot(t(1:Npts),y(1:Npts));
>> xlabel('time (s)');
>> ylabel('Dau ra'); 3
Đỗ Thành Nam – robotden@gmail.com >> pause; >> figure;
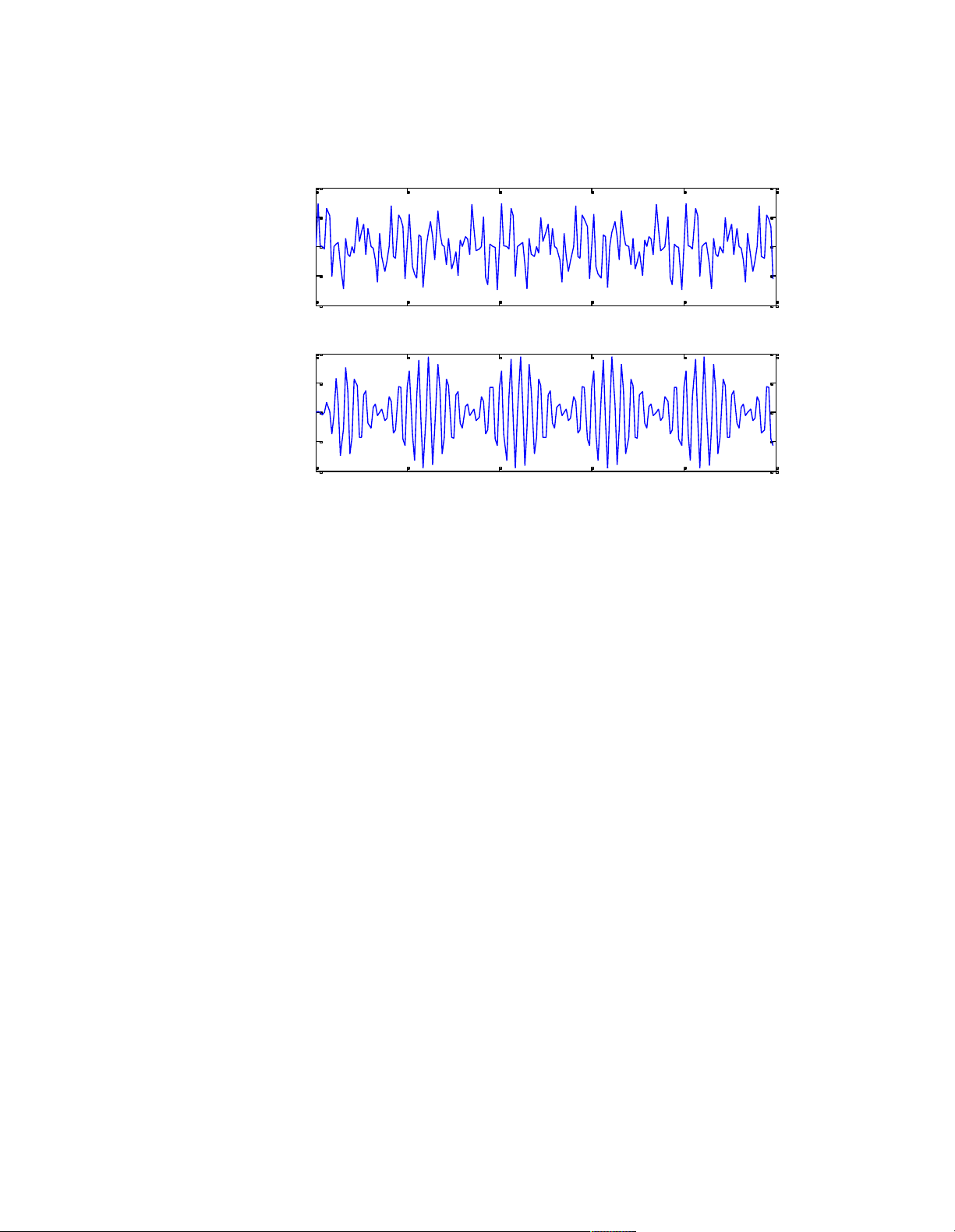
B ieu do thoi gian dau vao va dau ra 4 o a 2 v u a 0 D -2 -4 0 0.005 0.01 0.015 0.02 0.025 tim e (s ) 2 1 ra u a 0 D -1 -2 0 0.005 0.01 0.015 0.02 0.025 tim e (s )
Hình 3.2 Tín hiệu đầu vào và đầu ra sau khi qua bộ lọc
% vẽ và tính toán phổ của tín hiệu đầu vào và tín hiệu đầu ra
>> subplot(2,1,1);
>> xfftmag=(abs(fft(x,Ns)));
>> xfftmagh=xfftmag(1:length(xfftmag)/2);
>> f=[1:1:length(xfftmagh)]*Fs/Ns;
>> plot(f,xfftmagh);
>> title('Pho dau vao va dau ra');
>> xlabel('tan so (Hz)');
>> ylabel('pho dau vao')
>> subplot(2,1,2);
>> yfftmag=(abs(fft(y,Ns)));
>> yfftmagh=yfftmag(1:length(yfftmag)/2);
>> plot(f,yfftmagh);
>> xlabel('tan so (Hz)');
>> ylabel('pho dau ra'); 4
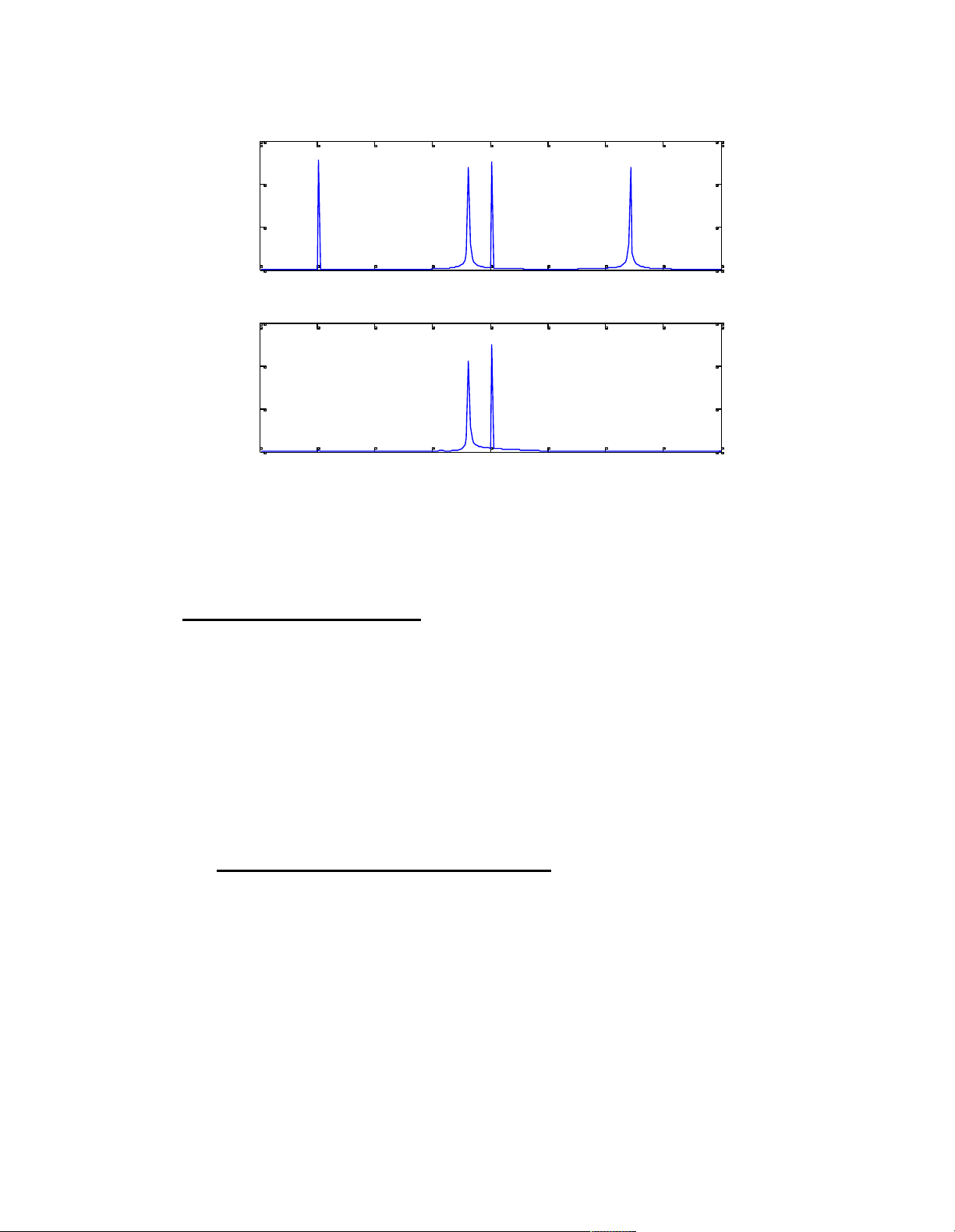
Đỗ Thành Nam – robotden@gmail.com P ho dau vao va dau ra 300 200 pho dau vao 100 0 0 500 1000 1500 2000 2500 3000 3500 4000 tan so (Hz) 300 200 pho dau ra 100 0 0 500 1000 1500 2000 2500 3000 3500 4000 tan so (Hz)
Hình 3.3 Phổ của tín hiệu đầu vào và tín hiệu đầu ra sau bộ lọc
Thiết kế với cửa sổ Keisel fsamp = 8000;
fcuts = [1000 1500]; mags = [1 0];
devs = [0.05 0.01];
[n,Wn,beta,ftype] = kaiserord(fcuts,mags,devs,fsamp);
hh = fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale'); freqz(hh)
Cách 2: Sử dụng FDATool để thiết kế bộ lọc
FDATool là một công cụ hết sức hữu dụng và chúng được sử dụng
rộng rãi để thiết kế bộ lọc hiện nay. Để kích hoạt công cụ thiết kế này, trong
cửa sổ lệnh của Matlab, ta thực hiện nhập lệnh sau: >> fdatool
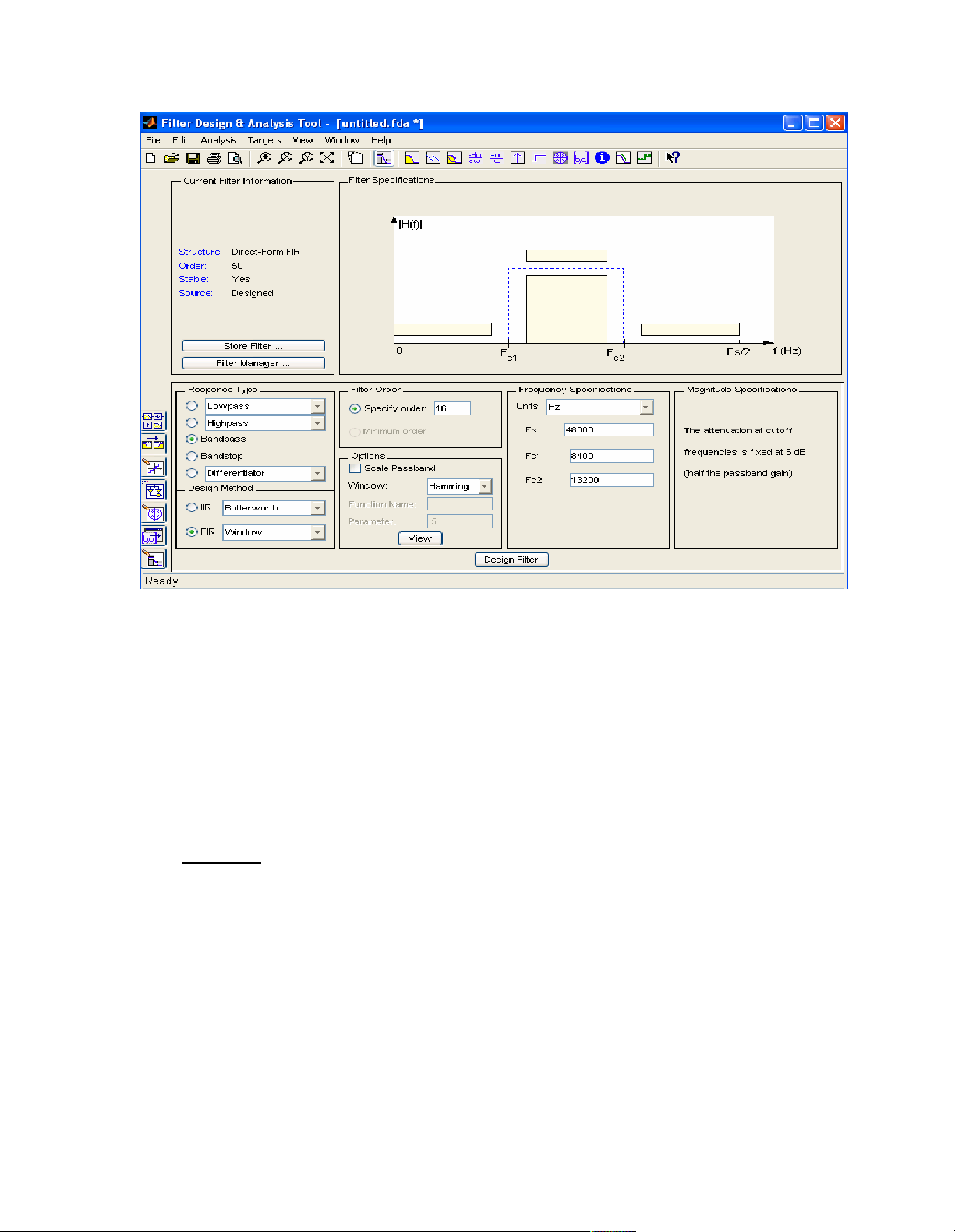
Và cửa sổ FDATool được gọi ra như sau: 5
Đỗ Thành Nam – robotden@gmail.com
Hình 3.4 Cửa sổ FDATool
Từ đây, ta có thể chọn một vài loại đáp ứng (của các bộ lọc): Thông
thấp (Lowpass), Thông cao (Highpass), Dải thông (Bandpass), Dải chặn
(Bandstop) và Bộ vi phân (Differentiator). Các đặc điểm kỹ thuật của bộ lọc
thay đổi theo loại đáp ứng và phương pháp thiết kế.
Như hình 3.4, chúng ta có thể nhập: Bậc của bộ lọc (Filter Order), Các tùy
chọn (Options), Đặc tính tần số (Frequency Specifications), Đặc tính biên
độ ( Magnitude Specifications).
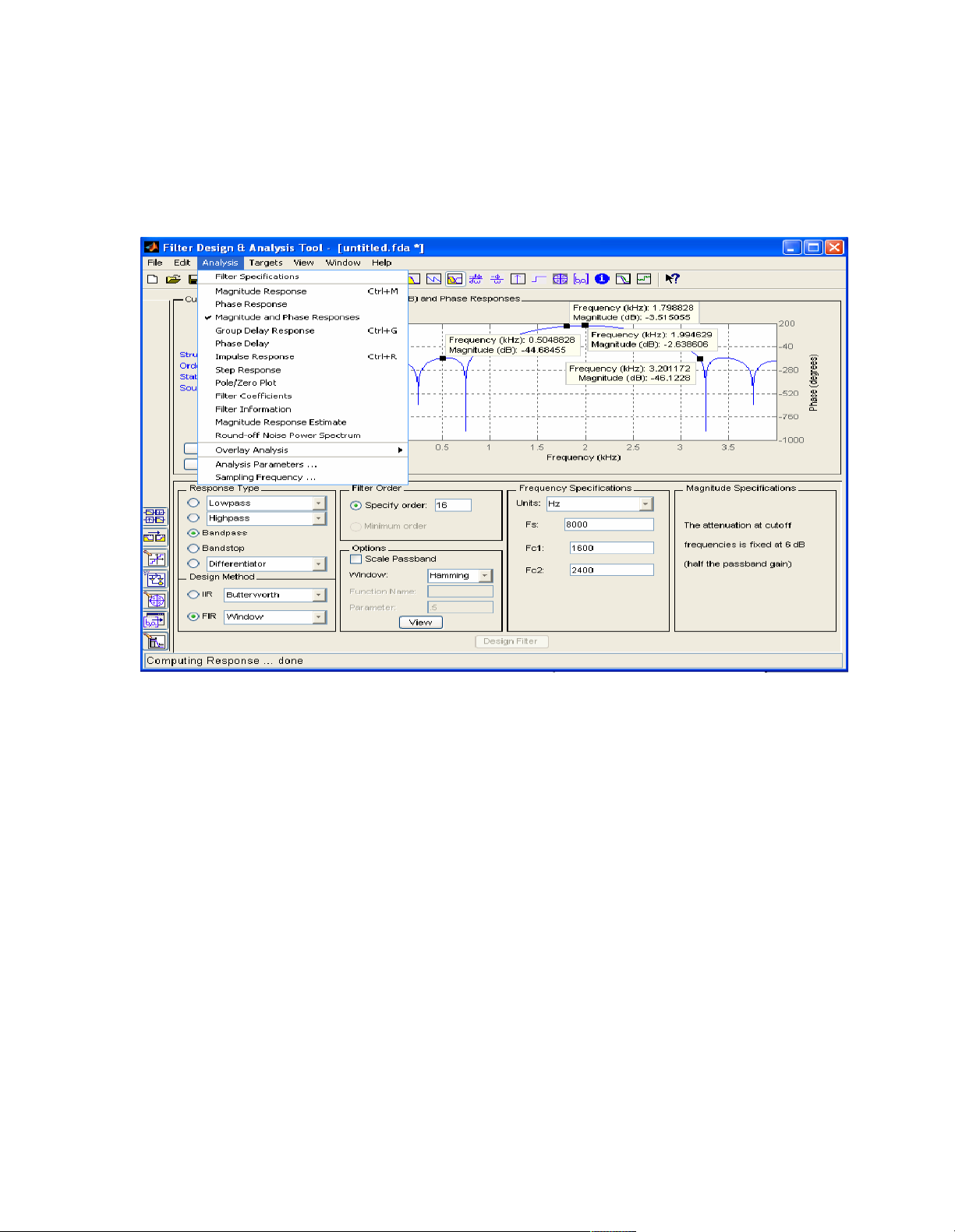
Ví dụ 2: Thiết kế bộ lọc dải thông có đặc tính kỹ thuật như bộ lọc dải
thông được thiết kế trong ví dụ 1.
Trong cửa sổ FDATool,
 Ta chọn Bandpass, trong miền Response Type.
 Trong miền Design Method, ta chọn FIR và thẻ Window.
 Trong miền Filter Order, ta chọn Specify Order và nhập số 16.
 Trong miền Options, chọn thẻ Hamming tại tùy chọn Window.
 Trong miền Frequency Specifications, ở tùy chọn units ta chọn
Hz, nhập 8000 trong Fs, 1600 trong Fc1 và 2400 trong Fc2. 6
Đỗ Thành Nam – robotden@gmail.com
 Thêm vào đó, từ manu Analysis kéo xuống, chúng ta có thể phân
tích đáp ứng biên độ (Magnitude Response), đáp ứng pha
(Phase Response), hệ số bộ lọc (Filter Ceofficients),…
 Click vào Design Filter, ta thu được kết quả cần thiết kế.
Các tùy chọn này được thực hiện như hình 3.5 dưới đây:
Hình 3.5 Chọn tham số và đặc tính kỹ thuật của bộ lọc
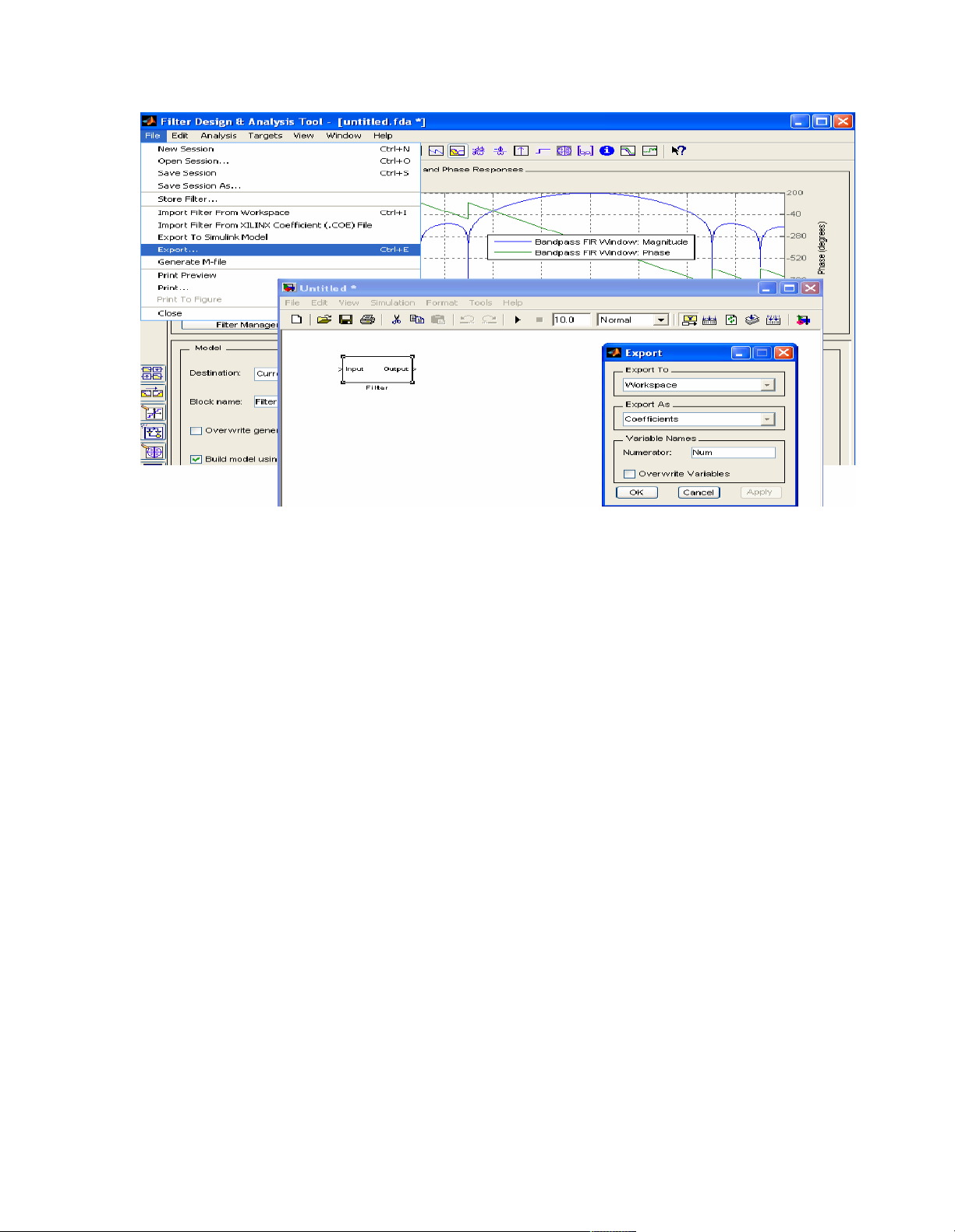
Hơn nữa, chúng ta có thể export các hệ số của bộ bằng việc sử dụng
tùy chọn Export trong manu File. Từ Export to ta có thể chọn Workspace,
Coefficient File (ASCII), MAT-File và SPTool. Từ Export As ta cũng có
thể chọn Coefficients và Objects. Chúng ta cũng có thể nhập tên biến trong
trường Variable Names. Sau đó Click lần lượt Apply, OK, ta thu được kết
quả như hình 3.6 dưới đây: 7
Đỗ Thành Nam – robotden@gmail.com
Hình 3.6 Cửa sổ Export các hệ số bộ lọc
Để thêm thông tin chi tiết, có thể tham khảo Signal Processing Toolbox
User’s, và tìm hiểu cách thức thiết kế bộ lọc sử dụng công cụ SPTool. 8