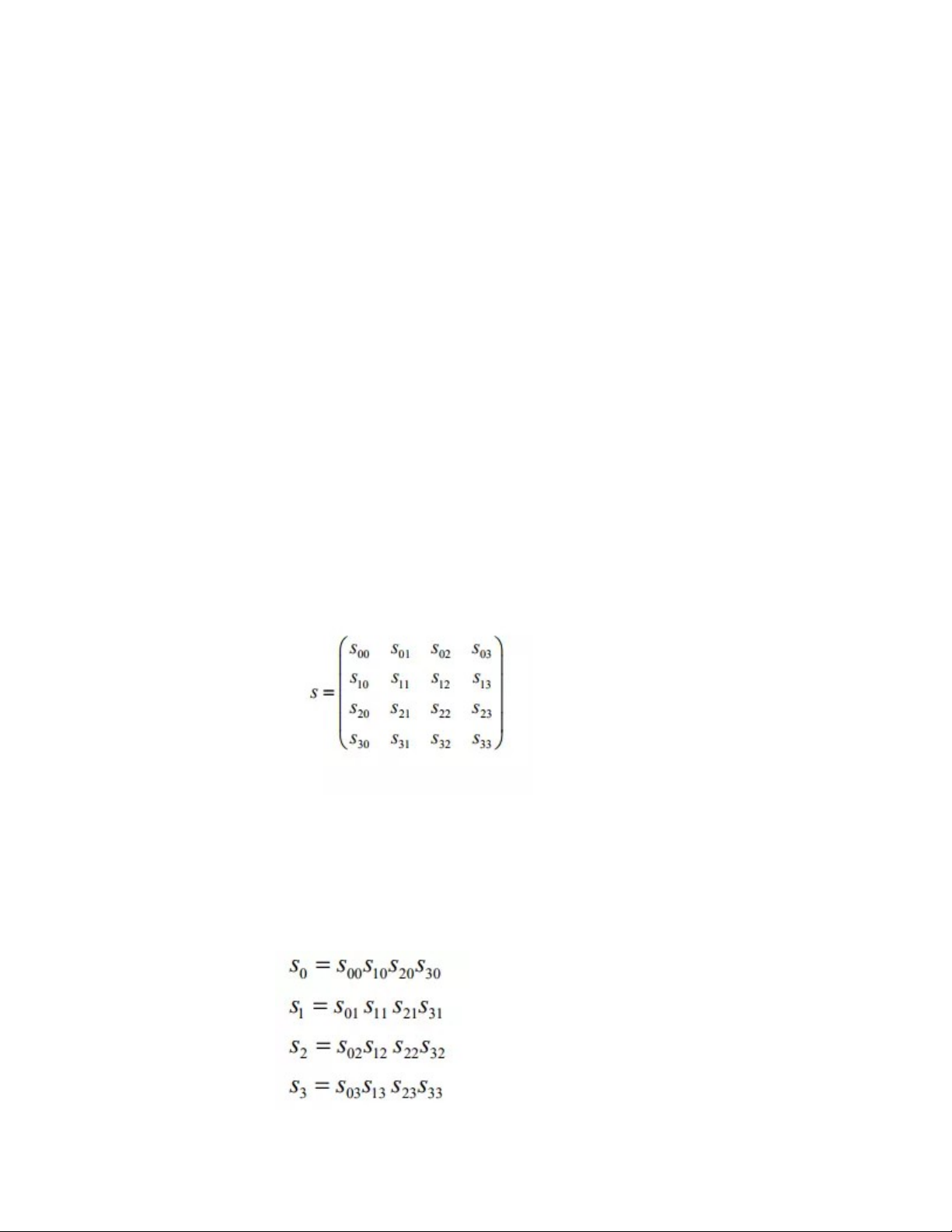











Preview text:
THUẬT TOÁN AES
1. Định nghĩa
AES là một mã khối, nhưng khác với các mã khối khác được biết đến trước đây (DES, IDEA,…), dữ liệu trong AES không được biểu diễn dưới dạng một mảng các byte hay các bit mà được biểu diễn dưới dạng một ma trận 4xNb và được gọi là mảng trạng thái (state). Trong đó, đối với AES, Nb luôn có giá trị bằng 4. Trong khi thuật toán Rijndael hỗ trợ ba giá trị của Nb là 4, 6, 8 tương ứng với kích thước khối 128, 192 và 256 bit. Dữ liệu đầu vào được đọc vào ma trận state theo từng cột, theo thứ tự từ trên xuống dưới, từ trái qua phải. Dữ liệu đầu ra được đọc từ ma trận cũng theo quy tắc trên. AES (Advanced Encryption Standard) là thuật toán mã hóa đối xứng mạnh nhất thế giới hiện nay. Nó giống như một "tiêu chuẩn vàng" để bảo vệ dữ liệu từ tin nhắn, mật khẩu ngân hàng,… đến bí mật quốc gia. Đây là mã hóa đối xứng. Nghĩa là dùng một chìa khóa để khóa cửa (mã hóa) và cũng chính chìa khóa đó để mở cửa (giải mã). Nếu mất chìa, dữ liệu coi như mất trắng.
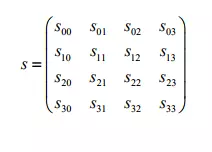
Khái niệm từ (Word) trong AES: Bốn byte trên mỗi cột trong mảng trạng thái state tạo thành 1 từ 32 bit, trong đó số thứ tự của hàng r (0≤r<4) cho biết chỉ số của bốn byte trong mỗi từ. Từ định nghĩa state ở trên có thể coi state là mảng một chiều chứa các từ 32 bit
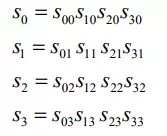
Tương tự như đối với mảng khóa cũng có thể biểu diễn thành mảng một chiều chứa các từ 32 bit như công thức dưới đây với số lượng từ khóa phụ thuộc vào Nk (Nk=4, 6, 8).
2. Thuật toán AES được mô tả khái quát gồm 3 bước như sau:
- 1 Vòng khởi tạo chỉ gồm phép AddRoundKey
- Nr -1 Vòng lặp gồm 4 phép biển đổi lần lượt: SubBytes, ShiftRows, MixColumns, AddRoundKey.
- 1 Vòng cuối gồm các phép biến đổi giống vòng lặp và không có phép MixColumns.

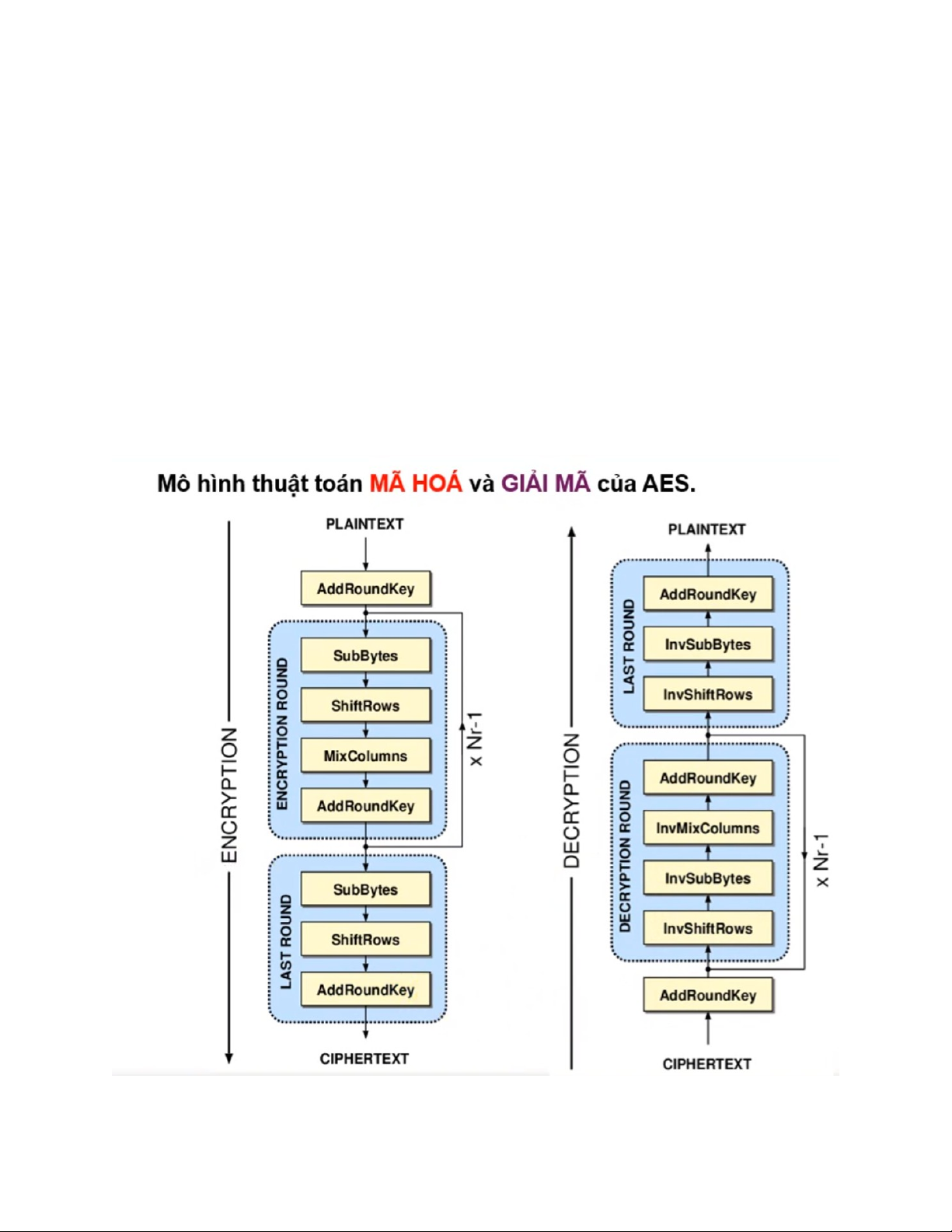
3. Cấu trúc tổng thể
Cả hai quá trình đều được chia thành 3 giai đoạn chính:
- Khởi đầu: Một phép toán AddRoundKey.
- Các vòng lặp chính (Encryption/Decryption Round): Lặp lại Nr - 1 lần
- Vòng cuối (Last Round): Thực hiện một quy trình rút gọn (không có bước trộn cột).
4. Quá trình Mã hóa (Encryption)
AddRoundKey khởi đầu: Dữ liệu bản rõ được XOR với khóa vòng đầu tiên (K0).
Ở bước này, thuật toán thực hiện phép toán XOR (Exclusive OR) bitwise giữa từng byte của Ma trận Trạng thái (State) với từng byte tương ứng của Khóa vòng (Round Key).
- Ma trận State: Chứa dữ liệu bản rõ (Plaintext) được chia thành khối 16 byte (4 x 4).
- Ma trận Khóa vòng K0: Chính là 16 byte của khóa chính ban đầu (Cipher Key).
- Công thức toán học:
Statei,j = Statei,j Keyi,j
(Trong đó i là hàng, j là cột từ 0 đến 3).
Việc thực hiện XOR với khóa trước khi đi vào các vòng lặp chính giúp "khóa" dữ liệu ngay lập tức. Điều này đảm bảo rằng mọi biến đổi tiếp theo đều phụ thuộc vào giá trị của khóa bí mật. Ngay cả khi kẻ tấn công biết thuật toán xử lý dữ liệu như thế nào, họ cũng không biết giá trị thực tế đang được xử lý là gì vì nó đã bị làm nhiễu bởi khóa bí mật.
Ví dụ minh họa cụ thể:
Giả sử chúng ta xét byte đầu tiên của bản rõ và byte đầu tiên của khóa.
- Byte bản rõ (s0,0): 0x41 (Ký tự 'A' trong mã ASCII).
- Dạng nhị phân: 0100 0001
- Byte khóa vòng (k0,0): 0x1F.
- Dạng nhị phân: 0001 1111
Thực hiện phép XOR bitwise:
Thành phần | Bit 7 | Bit 6 | Bit 5 | Bit 4 | Bit 3 | Bit 2 | Bit 1 | Bit 0 |
Bản rõ (0x41) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
Khóa (0x1F) | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
Kết quả XOR | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
- Kết quả nhị phân: 0101 1110
- Giá trị Hex: 0x5E -> kí tự ‘^’
Giải thích kết quả:
Sau bước này, byte 0x41 ban đầu đã biến thành 0x5E. Ma trận State mới này sẽ tiếp tục được đưa vào vòng lặp thứ nhất để thực hiện bước SubBytes (tra bảng S-box). Quá trình này lặp lại cho toàn bộ 16 byte của khối dữ liệu.
Đặc điểm quan trọng của phép XOR trong AES
Tính tự nghịch đảo: Nếu lấy kết quả (0x5E) XOR lại với chính khóa đó (0x1F), bạn sẽ thu được đúng bản rõ ban đầu (0x41). Đây là lý do AES dùng chung bước AddRoundKey cho cả mã hóa và giải mã.
Tốc độ cực nhanh: Phép XOR là phép toán cơ bản nhất của CPU, giúp AES đạt hiệu suất cực cao trên cả phần cứng và phần mềm.
Vòng lặp chính:
- SubBytes: Thay thế từng byte dữ liệu qua bảng S-box (tạo tính phi tuyến).
Tại sao SubBytes lại quan trọng? (Tính phi tuyến)
Nếu một thuật toán mã hóa chỉ toàn các phép toán tuyến tính (như cộng, nhân, dịch bit), kẻ tấn công có thể dùng các hệ phương trình toán học để giải ngược ra khóa rất nhanh.
- Vai trò: SubBytes là bước duy nhất trong AES có tính phi tuyến tính.
- Tác dụng: Nó phá vỡ mối liên hệ đơn giản giữa đầu vào và đầu ra. Một thay đổi nhỏ ở đầu vào sẽ tạo ra sự thay đổi phức tạp ở đầu ra, giúp chống lại các kỹ thuật thám mã tuyến tính và thám mã sai biệt.
Cấu tạo toán học của SubBytes
không chỉ là tra bảng, mà nó được tạo ra từ hai bước toán học trong Trường hữu hạn GF(2^8):
Nghịch đảo nhân (Multiplicative Inverse): Mỗi byte a trong ma trận trạng thái được thay thế bằng nghịch đảo của nó a^-1 sao cho a.a^-1 1 (modP(x)). Riêng số 00 được quy định biến thành chính nó.
Biến đổi Affine (Affine Transformation): Kết quả trên được nhân với một ma trận cố định và cộng với một hằng số (thường là 0x63). Bước này giúp "làm rối" thêm cấu trúc của S-box để không còn quy luật toán học đơn giản nào sót lại.
Ví dụ cụ thể: Tính SubBytes cho giá trị 0x01
Bước 1: Tìm nghịch đảo nhân
Trong trường hữu hạn, nghịch đảo nhân của x là số sao cho x.a 1 (mod P(x)).
- Với x = 0x01, ta có 0x0.0x01 = 0x01.
- Vậy Inv(0x01) = 0x01.
- Biểu diễn dưới dạng vector bit (b0 đến b7): [1, 0, 0, 0, 0, 0, 0, 0]^T.
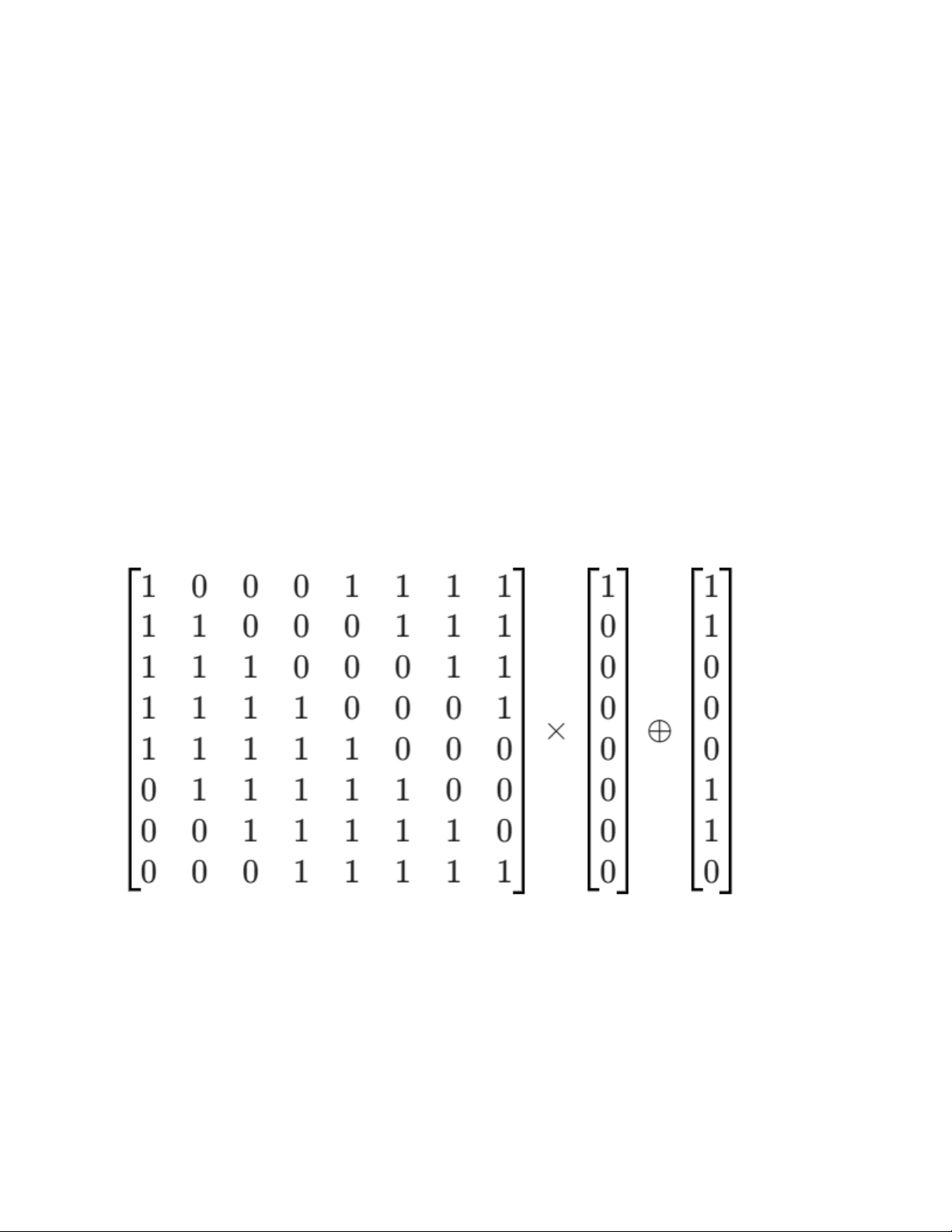
Bước 2: Biến đổi Affine
Ta sử dụng ma trận M cố định và vector hằng số C = 0x63(nhị phân là 01100011).
Phép toán là: B' = (M . B) C
Trong đó ma trận M của AES là:

Thực hiện tính toán:
- Nhân ma trận (M . B): Vì vector B chỉ có bit đầu tiên là 1, kết quả phép nhân chính là cột đầu tiên của ma trận M:
- Kết quả tạm thời: [1, 1, 1, 1, 1, 0, 0, 0]^T(tương ứng số Hex là 0x1F).
- Cộng vector hằng số (C): Ta lấy kết quả trên XOR với C (0x63):
- Nhị phân kết quả tạm: 0001 1111 (0x1F)
- Nhị phân hằng số C: 0110 0011 (0x63)
Phép XOR:
0001 1111
XOR
0110 0011
-----------
0111 1100
- Kết quả cuối cùng: 0111 1100 nhị phân tương ứng với giá trị Hex là 0x7C
- ShiftRows: Dịch chuyển các hàng của ma trận dữ liệu (khuếch tán ngang).
Quy tắc dịch chuyển
Trong ma trận trạng thái 4 x 4, các hàng được đánh số từ 0 đến 3. Phép dịch chuyển được thực hiện xoay vòng sang trái theo quy tắc tăng dần:
- Hàng 0: Không dịch chuyển. Hàng này giữ nguyên vị trí ban đầu.
- Hàng 1: Dịch trái xoay vòng 1 byte. Byte đầu tiên của hàng sẽ chuyển xuống cuối hàng.
- Hàng 2: Dịch trái xoay vòng 2 byte.
- Hàng 3: Dịch trái xoay vòng 3 byte (tương đương với việc dịch phải 1 byte).
Tại sao phải ShiftRows?
- Khuếch tán ngang: ShiftRows đảm bảo rằng 4 byte ban đầu của một cột sẽ được phân tán ra 4 cột khác nhau sau khi dịch chuyển.
- Chuẩn bị cho MixColumns: Khi bước vào bước tiếp theo là MixColumns (trộn cột), các byte từ các cột ban đầu khác nhau sẽ được kết hợp lại với nhau.
- Hiệu ứng thác đổ: Chỉ sau vài vòng lặp, một sự thay đổi nhỏ của 1 byte ở đầu vào sẽ lan tỏa ra toàn bộ 16 byte của bản mã. Đây là yếu tố then chốt giúp AES chống lại các cuộc tấn công thám mã sai biệt.
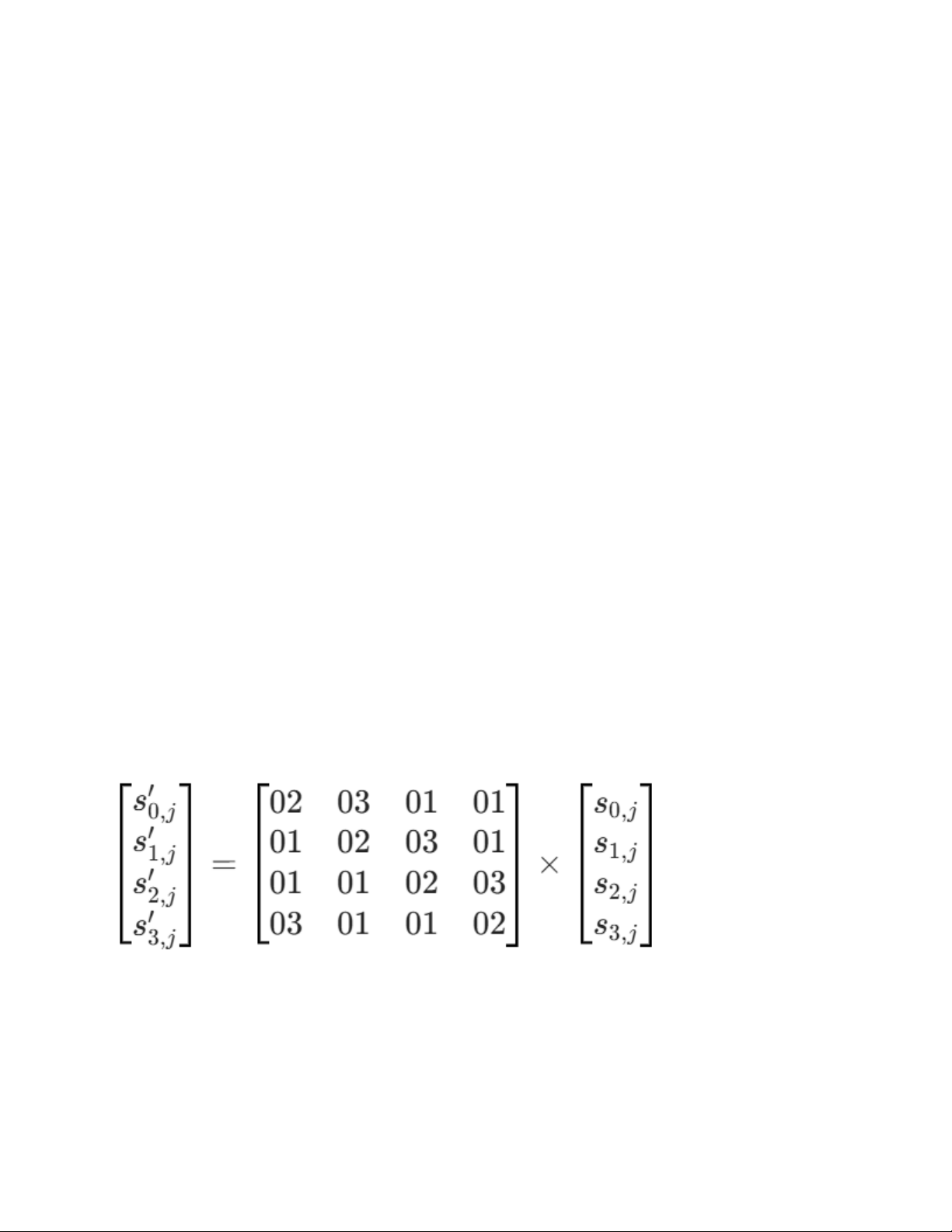
- MixColumns: Trộn các cột bằng toán học trường hữu hạn (khuếch tán dọc).
Nguyên lý hoạt động
Trong bước này, mỗi cột của ma trận State được coi là một đa thức bậc 3 trên trường hữu hạn GF(2^8). Thuật toán thực hiện nhân từng cột này với một ma trận hằng số cố định.
Phép toán này được thực hiện như sau:
- Lấy một cột của ma trận State (gồm 4 byte).
- Nhân cột đó với một ma trận đặc biệt (ma trận MDS - Maximum Distance Separable).
- Kết quả thu được là một cột hoàn toàn mới, trong đó mỗi byte mới là sự kết hợp của cả 4 byte cũ trong cột đó.
2. Công thức toán học
Ma trận hằng số dùng để nhân trong AES là:

Tại sao phải MixColumns?
- Khuếch tán dọc: Nó đảm bảo rằng nếu bạn thay đổi chỉ 1 byte ở đầu vào, thì sau bước này, cả 4 byte trong cột đó đều bị thay đổi.
- Hiệu ứng thác đổ mạnh mẽ: Khi kết hợp với ShiftRows, sự thay đổi của 1 byte ban đầu sẽ lan rộng ra toàn bộ ma trận chỉ sau 2 vòng lặp. Đây là lý do AES cực kỳ an toàn trước các kỹ thuật thám mã thống kê.
- Tính không thể đảo ngược (nếu không có khóa): Phép trộn này làm mất đi hoàn toàn cấu trúc ban đầu của dữ liệu.
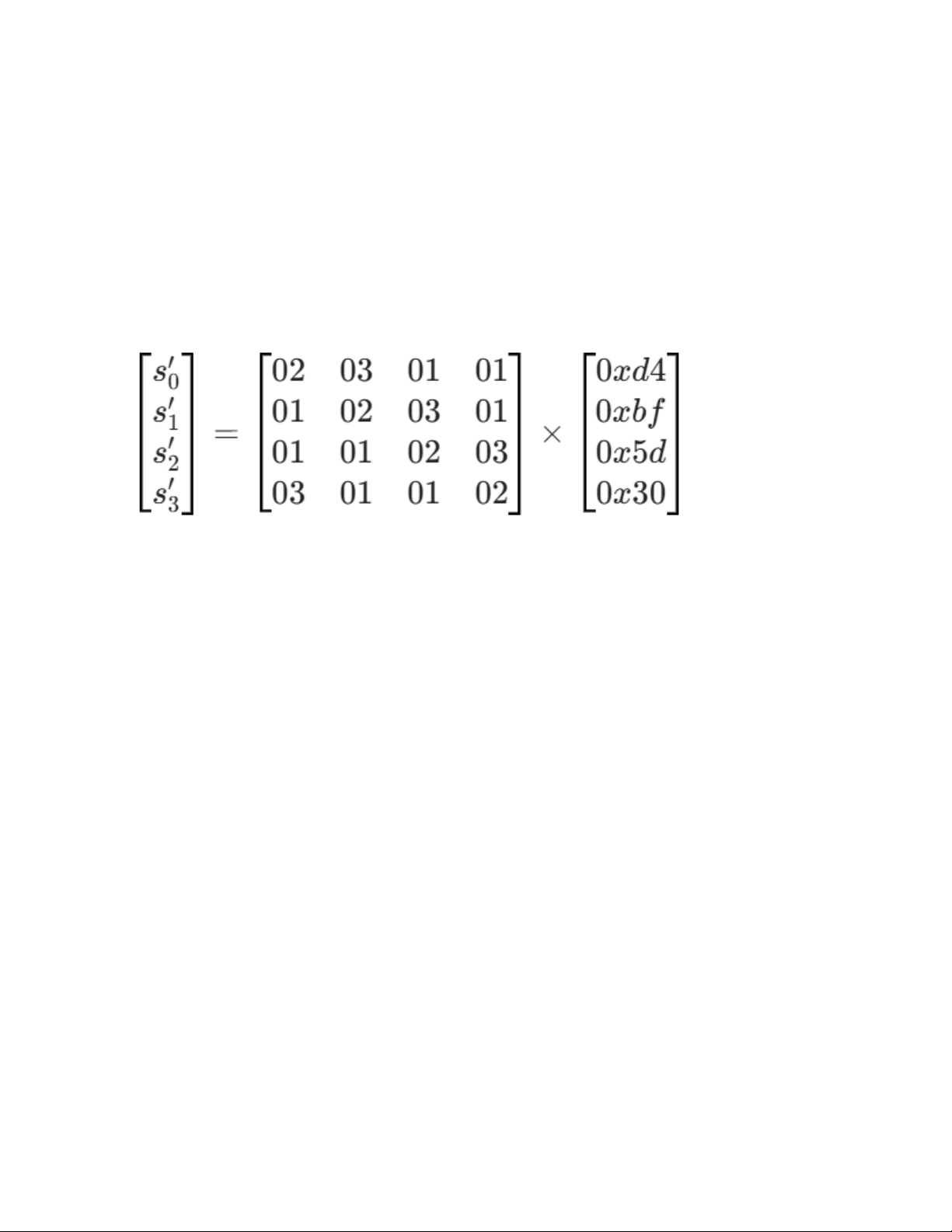
Ví dụ:

Tính toán chi tiết cho byte đầu tiên (s'0)
Công thức tính là:
s'0 = (02 . 0xd4) (03 . 0xbf) (01 . 0x5d) (01 . 0x30)
Bước A: Tính 02 . 0xd4
- 0xd4 nhị phân là 1101 0100.
- Dịch trái 1 bit: 1010 1000 (bit 1 ở đầu bị tràn).
- Vì có tràn bit, ta XOR với 0x1B (0001 1011):
1010 1000 0001 1011 = 1011 0011 -> 0xb3.
Bước B: Tính03 . 0xbf
- Ta biết 03 . x = (02 . x) x.
- Tính 02 . 0xbf:
- 0xbf nhị phân là 1011 1111.
- Dịch trái 1 bit: 0111 1110 (có tràn bit 1).
- XOR với 0x1B: 0111 1110 0001 1011 = 0110 0101 (0x65).
- Lấy kết quả XOR với số gốc: 0x65 0xbf = 0xda.
Bước C: Tính các phần còn lại
- 01 . 0x5d = 0x5d (giữ nguyên).
- 01 . 0x30 = 0x30 (giữ nguyên).
Bước D: Tổng hợp bằng phép XOR
s'0 = 0xb3 0xda 0x5d 0x30
- 0xb3 0xda = 0x69
- 0x69 0x5d = 0x34
- 0x34 0x30 = 0x04.
Vậy byte đầu tiên của cột mới là 0x04.
- AddRoundKey: XOR với khóa của vòng đó (K1 đến K9).
- Vòng cuối (Last Round): Thực hiện SubBytes, ShiftRows và kết thúc bằng AddRoundKey.
- Kết quả: Tạo ra CIPHERTEXT (Bản mã).
5. Quá trình Giải mã (Decryption)
- AddRoundKey khởi đầu: Lấy bản mã XOR với khóa vòng cuối cùng (K10 với AES-128).
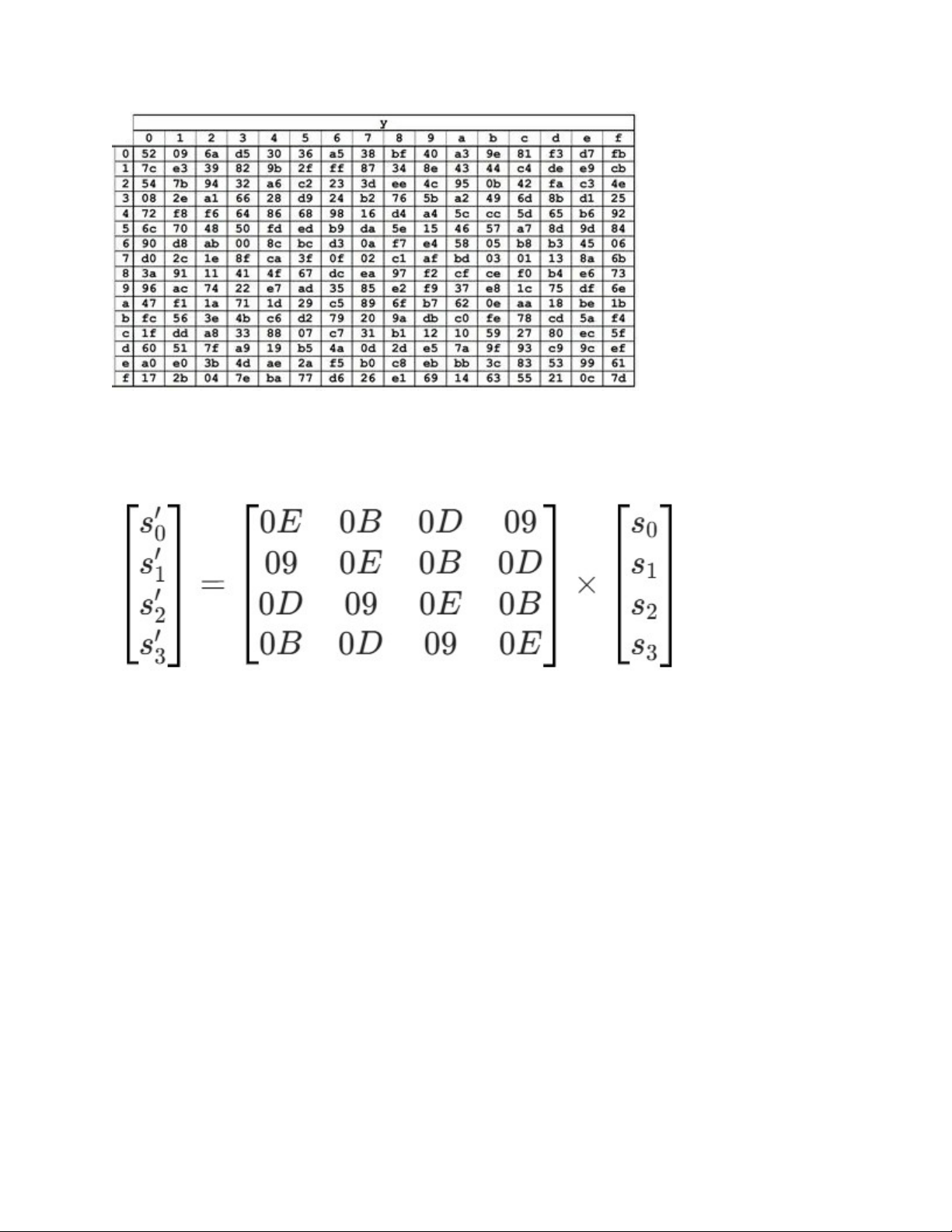
- Vòng lặp giải mã: Sử dụng các hàm nghịch đảo (Inverse):
- InvShiftRows: Dịch hàng ngược lại về vị trí cũ (dịch phải thay vì dịch trái).
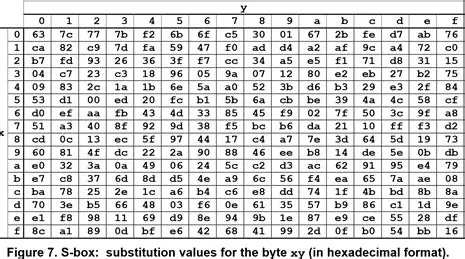
- InvSubBytes: Tra bảng S-box ngược để tìm lại byte ban đầu.
- InvMixColumns: Sử dụng ma trận nghịch đảo để "tháo" các cột đã bị trộn.

- AddRoundKey: XOR với khóa vòng tương ứng.
- Vòng cuối (Last Round): Thực hiện InvShiftRows, InvSubBytes và AddRoundKey (với khóa gốc K0).
- Kết quả: Trả về PLAINTEXT (Bản rõ ban đầu).
Việc vỏ MixColumns ở vòng cuối tạo sự đối xứng cho quá trình Giải mã
Lý do quan trọng nhất là để làm cho cấu trúc của quá trình Mã hóa và Giải mã trở nên tương đồng (đối xứng) nhất có thể.
- Vấn đề: Trong mã hóa, bước cuối cùng thường là AddRoundKey. Nếu vòng cuối cùng có MixColumns, thì khi giải mã, chúng ta sẽ phải thực hiện InvMixColumns ngay lập tức trước khi thực hiện các bước khác.
- Giải pháp: Bằng cách bỏ MixColumns ở vòng cuối, các nhà thiết kế giúp cho cấu trúc của bộ giải mã có thể sử dụng lại gần như y hệt sơ đồ của bộ mã hóa, chỉ thay thế các hàm bằng hàm nghịch đảo.
- Lợi ích: Điều này cực kỳ quan trọng khi sản xuất chip hoặc phần cứng bảo mật. Nó giúp giảm diện tích mạch điện, tiết kiệm chi phí và năng lượng vì không cần thiết kế hai quy trình quá khác biệt cho mã hóa và giải mã.
MixColumns ở vòng cuối không làm tăng tính bảo mật: mục đích của MixColumns: Khuếch tán dữ liệu cho vòng lặp kế tiếp.
- Mục tiêu của MixColumns: Trộn các byte trong một cột để sự thay đổi của một byte sẽ ảnh hưởng đến cả 4 byte ở vòng sau.
- Tại vòng cuối cùng: Vì sau đó không còn vòng lặp nào nữa, việc trộn các cột ở bước này không tạo thêm sự khuếch tán nào cho các bước tiếp theo. Bản mã (Ciphertext) thu được sau bước AddRoundKey cuối cùng đã đủ độ hỗn loạn cần thiết từ các vòng trước đó.
- Kết luận: Thêm MixColumns vào vòng cuối chỉ làm tốn thêm tài nguyên tính toán (CPU, RAM) mà không thực sự giúp bản mã khó bị bẻ hơn đối với các thám mã.
Hiệu ứng "Wide Trail" và sự tối ưu
AES được thiết kế theo chiến lược Wide Trail Strategy, đảm bảo rằng chỉ sau 2-4 vòng lặp, mọi bit của bản rõ đã ảnh hưởng đến mọi bit của bản mã.
- Với 10-14 vòng lặp, thuật toán đã đạt đến trạng thái bão hòa về độ khuếch tán.
- Việc bỏ qua một phép tính ma trận phức tạp như MixColumns ở vòng cuối giúp tăng tốc độ xử lý tổng thể của thuật toán, đặc biệt là trên các thiết bị di động hoặc thẻ thông minh (Smart card).
6 . Giải thuật sinh khóa
Giải thuật Sinh khóa phụ (Key Expansion) là một thành phần quan trọng trong AES, có nhiệm vụ biến đổi khóa chính (Cipher Key) ban đầu thành một dãy các khóa vòng (Round Keys) để sử dụng cho từng vòng lặp mã hóa và giải mã.
Dưới đây là chi tiết cách giải thuật này vận hành:
AES xử lý khóa theo đơn vị Word.
- 1 Word = 4 Byte = 32 bit.
- Khóa AES-128 (128 bit) tương đương với 4 Word.
- Mục tiêu của giải thuật là tạo ra tổng cộng 4 x (Nr + 1) Word (Ví dụ: AES-128 cần 44 Word cho 11 lần AddRoundKey).
Quy trình thực hiện tổng quát
Khóa chính ban đầu được nạp vào các Word đầu tiên (W0, W1, W2, W3). Các Word tiếp theo (Wi được tính toán dựa trên các Word đứng trước nó theo quy tắc:
- Nếu i không phải bội số của 4: Word mới đơn giản là kết quả của phép XOR:
Wi = Wi-4 Wi-1
- Nếu i là bội số của 4 (vị trí bắt đầu khóa vòng mới): Trước khi XOR, Word Wi-1 phải đi qua một hàm biến đổi phức tạp gọi là Hàm g để phá vỡ tính quy luật.
Chi tiết hàm biến đổi g
Hàm g thực hiện 3 bước trên Word Wi-1:
- RotWord (Dịch byte): Hoán vị vòng tròn các byte trong Word [b0, b1, b2, b3] -> [b1, b2, b3, b0].
- SubWord (Thay thế byte): Từng byte trong Word được thay thế qua bảng S-box (giống bước SubBytes trong mã hóa).
- XOR với Rcon (Round Constant): Kết quả được XOR với một hằng số vòng cố định. Việc này giúp mỗi khóa vòng trở nên độc nhất và chống lại các cuộc tấn công đối xứng.
Ví dụ minh họa cụ thể
Giả sử ta đang tính khóa vòng 1 cho AES-128 (tức là tìm W4). Ta cần dựa vào W3 để qua hàm g.
Giả sử W3 = [09, cf, 4f, 3c] (dạng Hex):
- Thực hiện RotWord:
[09, cf, 4f, 3c] -> [cf, 4f, 3c, 09]
- Thực hiện SubWord (Tra bảng S-box):
- cf: Hàng c, Cột f -> 8a
- 4f: Hàng 4, Cột f -> 84
- 3c: Hàng 3, Cột c -> eb
- 09: Hàng 0, Cột 9 -> 01
- Kết quả tạm thời: [8a, 84, eb, 01]
- XOR với Rcon (Vòng 1, Rcon = [01, 00, 00, 00]):
[8a 01, 84 00, eb 00, 01 00] = [8b, 84, eb, 01]
- Kết quả cuối cùng của g(W3) = [8b, 84, eb, 01].
Tính W4:
Nếu W0 = [2b, 7e, 15, 16], thì:
W4 = W0 g(W3) = [2b 8b, 7e 84, 15 eb, 16 01] = [a0, fa, fe, 17]
Sự khác biệt giữa các phiên bản AES
Số lượng Word cần sinh ra phụ thuộc vào độ dài khóa:
- AES-128: Sinh ra 44 Word (11 khóa vòng).
- AES-192: Sinh ra 52 Word (13 khóa vòng).
- AES-256: Sinh ra 60 Word (15 khóa vòng). Đặc biệt, AES-256 có thêm một bước SubWord bổ sung ở giữa chu kỳ để tăng cường độ an toàn do khóa quá dài.
Tại sao giải thuật này quan trọng?
- Hiệu ứng thác đổ trên khóa: Một thay đổi nhỏ ở khóa chính sẽ làm thay đổi hoàn toàn tất cả các khóa vòng sau đó.
- Loại bỏ khóa yếu: AES không có "khóa yếu" (weak keys) như các thuật toán cũ, vì giải thuật sinh khóa phụ đảm bảo tính hỗn loạn rất tốt.
- Hỗ trợ giải mã: Sơ đồ bạn cung cấp cho thấy quá trình giải mã sử dụng các khóa vòng này theo thứ tự ngược lại (từ K1 về K0).
Giải thuật này đảm bảo rằng dù kẻ tấn công có biết một phần của một khóa vòng, họ cũng cực kỳ khó khăn để suy ngược lại khóa chính hoặc các khóa vòng khác.
7 . 1 số loại tấn công
A. Tấn công Kênh kề (Side-Channel Attacks - SCA)
Đây là nhóm tấn công nguy hiểm nhất trong thực tế. Kẻ tấn công không giải toán mà quan sát các biểu hiện vật lý của phần cứng khi đang mã hóa.
- Timing Attack (Tấn công thời gian): Đo thời gian xử lý dữ liệu. Nếu việc tra bảng S-box hoặc nhân ma trận mất thời gian khác nhau cho các byte khác nhau, kẻ tấn công có thể suy luận ra khóa.
- Power Analysis (Phân tích điện năng): Theo dõi mức tiêu thụ điện của CPU/Chip. Các phép toán XOR hoặc dịch bit tiêu tốn năng lượng đặc trưng, làm lộ bit của khóa.
- Electromagnetic Analysis (EM): Đo sóng điện từ phát ra từ thiết bị.
B. Tấn công Thám mã (Cryptanalytic Attacks)
Đánh vào cấu trúc toán học của AES.
- Brute-force (Duyệt toàn bộ): Thử mọi khả năng của khóa. Với AES-128, con số này là 2^128, hiện tại là không thể phá vỡ.
- Related-Key Attack: Tấn công dựa trên mối liên hệ giữa các khóa (ví dụ khóa sau bằng khóa trước cộng 1). AES-256 dễ bị tổn thương bởi dạng này hơn AES-128 do cấu trúc sinh khóa phụ.
- Biclique Attack: Giúp tìm khóa nhanh hơn brute-force khoảng 4 lần (vẫn rất chậm, chỉ mang tính lý thuyết).
C. Tấn công vào Chế độ hoạt động (Operational Attacks)
Đây là lỗi do người lập trình chọn sai cách "lắp ghép" các khối AES.
- ECB Mode Attack: Ở chế độ ECB, các khối dữ liệu giống nhau cho ra bản mã giống nhau, làm lộ cấu trúc (ví dụ: hình ảnh vẫn hiện rõ hình dạng sau mã hóa).
- Padding Oracle Attack: Tấn công vào phần dữ liệu đệm (Padding) ở chế độ CBC để giải mã từng byte mà không cần khóa.
8. Cách phòng chống (Countermeasures)
Về mặt lập trình (Implementation)
- Constant-time Programming: Viết code sao cho mọi phép toán đều mất thời gian bằng nhau, không phụ thuộc vào giá trị của khóa (chống Timing Attack).
- Sử dụng thư viện chuẩn: Tuyệt đối không tự viết lại AES. Hãy dùng các thư viện đã được kiểm chứng như OpenSSL, Libsodium hoặc tập lệnh AES-NI tích hợp sẵn trong CPU.
Về mặt thiết kế hệ thống
- Sử dụng Chế độ xác thực (Authenticated Encryption): Thay vì dùng CBC, hãy dùng AES-GCM. Chế độ này không chỉ mã hóa mà còn tạo ra một "Tag" xác thực, giúp phát hiện ngay nếu bản mã bị kẻ tấn công thay đổi dù chỉ 1 bit.
- Sử dụng IV (Vector khởi tạo) ngẫu nhiên: Luôn dùng một số IV mới cho mỗi lần mã hóa để đảm bảo cùng một nội dung sẽ cho ra các bản mã khác nhau.
Quản lý khóa (Key Management)
- Sử dụng KDF (Key Derivation Function): Không dùng mật khẩu trực tiếp làm khóa. Hãy dùng các hàm như Argon2 hoặc PBKDF2 để sinh khóa có độ hỗn loạn (entropy) cao.
- Lưu trữ an toàn: Sử dụng HSM (Hardware Security Module) hoặc các dịch vụ quản lý khóa (KMS) để khóa không bao giờ xuất hiện dưới dạng văn bản rõ trong bộ nhớ máy tính.
9.Tấn công Lượng tử và Tương lai
Máy tính lượng tử trong tương lai có thể sử dụng Thuật toán Grover để giảm độ an toàn của AES xuống còn một nửa:
- AES-128 chỉ còn tương đương 64-bit (Yếu).
- Giải pháp: Chuyển sang AES-256. Với máy tính lượng tử, AES-256 vẫn giữ được độ an toàn 128-bit, đủ để bảo vệ dữ liệu trong nhiều thập kỷ tới.