Tích phân hàm lượng giác: Phương pháp giải nhanh và ví dụ minh họa dễ hiểu | Chuyên đề Toán 12

Tích phân hàm lượng giác
A. MỘT SỐ CÔNG THỨC VÀ KĨ NĂNG BIẾN ĐỔI
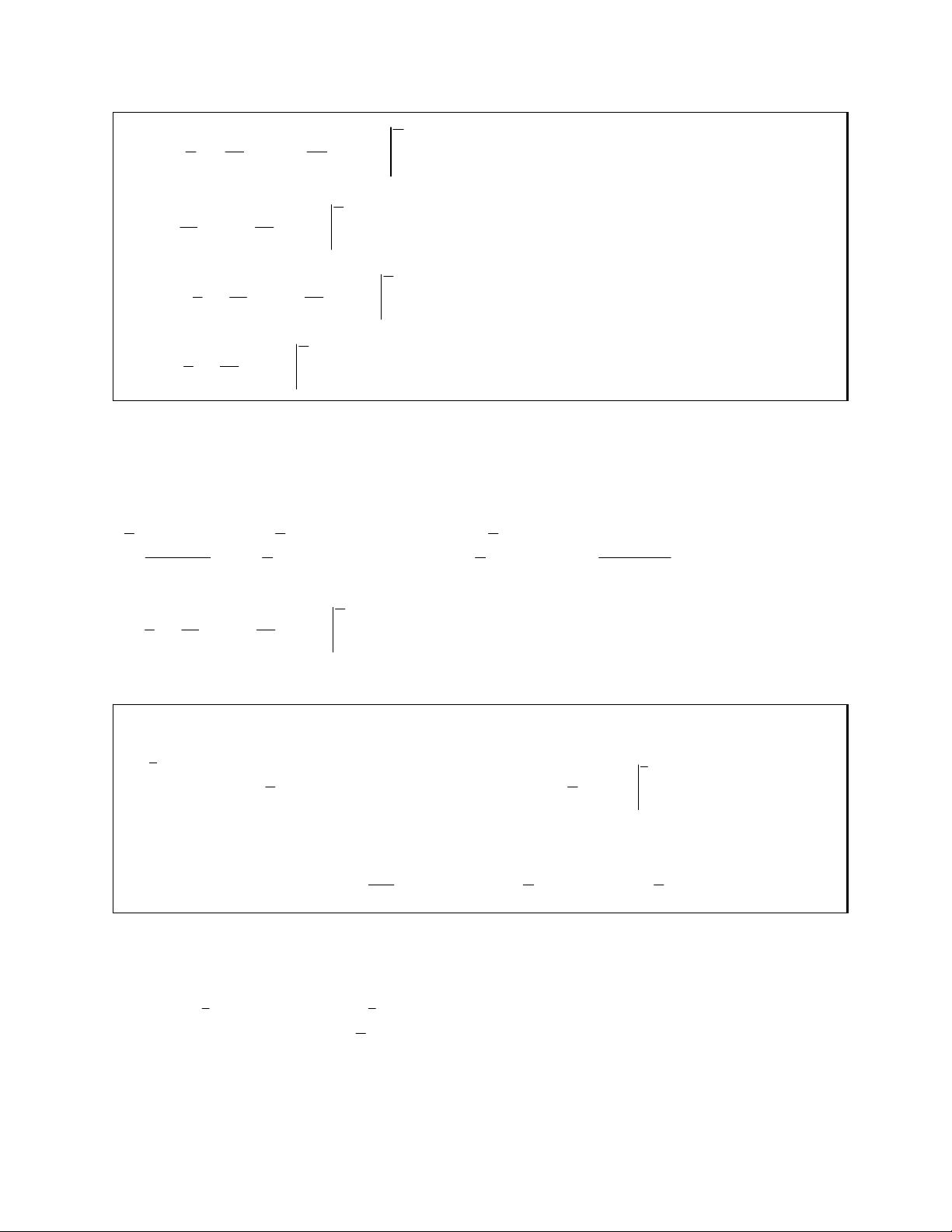
Các công thức nguyên hàm của hàm lượng giác
 ax b 1 cos
dx  sin ax  b  C a
 ax b 1 sin
dx   cosax  b  C a dx 1 
ax  b  C
 cos xaxb tan  2 a dx 1  
ax  b  C
 sin axb cot   2 a
B. CÁC DẠNG TOÁN TÍNH TÍCH PHÂN HÀM LƯỢNG GIÁC b b
Dạng 1: Tính tích phân: 1 I  sin n x d ; x I  cos n x dx 1   2 2    1 a 2 a
1. Nếu n chẵn thì ta sử dụng công thức hạ bậc.
2. Nếu n  3 thì ta sử dụng công thức hạ bậc hoặc biến đổi theo trường hợp 3.
3. Nếu n  3 và n lẻ n  2p  
1 thì ta thực hiện biến đổi. 1 b b b b I sin x 1
n dx sin x 1 2 p 1   
dx  sin x 1
2 p .sin xdx   2 1 cos p x d cos x 1    1 a 1 a 1 a 1 a
Sử dụng công thức khai triển nhị thức Newton để khai triển  2 1 cos p x .
Từ đây ta giải quyết dc bài toán. 2 b b b b I  cosx 2
ndx cosx 2 2 p 1   
dx   cos x 2
2 p .cos .xdx   2 1 sin p x d sin x 2    2 a 2 a 2 a 2 a
Sử dụng công thức khai triển nhị thức Newton để khai triển  2 1 sin p x .
Từ đây ta giải quyết dc bài toán.  10 Ví dụ 1: Cho 4 I  cos 3xdx 
. Đẳng thức nào sau đây đúng? 0  A. 10 3 1 1 I x sin 6x sin12x    8 12 96    0  B. 10  1 1 I sin 6x sin12x   12 96    0  C. 10  3 1 1 I x sin 6x sin12x      8 12 96    0  D. 10 3 1 I x sin12x   8 96    0 Đáp án A. Lời giải Ta có    2 10 10 1 cos6x  1     10 2 1  1 cos12 1 2cos6 cos 6 1 2cos6 x dx x x dx x             dx  2  4 4  2 0 0 0   10 3 1 1 x sin 6x sin12x     . 8 12 96    0
Từ đây ta giải quyết được bài toán. Ví dụ 2: Cho:   3 I sin5x 3 9 1  3 5 7 1 9 dx
cos5x a cos 5x b cos 5x c cos 5x cos 5x         . 5  9  0  0
Đặt S  a b  c . Giá trị của S bằng A. S  3 B. 74 S   C. 5 S   D. 1 S  105 4 9 Đáp án B. Lời giải   3 3
Ta có I   x8 1
sin5 sin5xdx    2
1 cos 5x4 d cos5x 5 0 0  3 1 2 4 6 8   1
  4cos 5x  6cos 5x  4cos 5x  cos 5x d  cos5x 5   0  3 1  4 3 6 5 4 7 1 9  cos5x cos 5x cos 5x cos 5x cos 5x       5 3 5 7 9    0 4 6 4 74
 a   ;b  ;c    S   . 3 5 7 105 b
Dạng 2*: Tính tích phân I  sinm .xcosn xdx  . a Phương pháp chung
a. Trường hợp 1: m; n là các số nguyên
1. Nếu m chẵn, n chẵn thì sử dụng công thức hạ bậc, biến đổi tích thành tổng.
2. Nếu m chẵn, n lẻ n  2p   1 thì biến đổi b b I
 xm  x2p 1  dx  
 xm  x2 sin cos sin cos p cos xdx a a b
  xm   x2 2 sin 1 sin d sin x  . a
Sử dụng công thức khai triển nhị thức Newton để khai triển và giải quyết bài toán.
3. Nếu m lẻ m  2p  
1 , n chẵn thì ta biến đổi b b I  x2p 1 
 x n dx     x 2 sin . cos sin
p . cosx n.sin xdx a a b   2
1 cos xp.cos xn d cos x . a
Sử dụng công thức khai triển nhị thức Newton để khai triển và giải quyết bài toán.
4. Nếu m lẻ, n lẻ thì sử dụng biến đổi 2 hoặc 3 cho số mũ lẻ bé hơn.
b. Trường hợp 2: m; n là các số hữu tỉ b b n 1  sinb n 1  I  sinm . x cosn xdx  
sin xm. 2 cos x cos m xdx  u   2 2
1 u  2 du  * a a sin a  3
Ví dụ 1: Cho I  sin2x7.cos2x100 dx. Đẳng thức nào sau đây là đúng? 0  101 103 105 107 3   A. cos2x 3cos2x 3cos2x cos2x I       .  10 103 105 107    0  101 103 105 107 3   B. cos2x 3cos2x 3cos2x cos2x I  2      10 103 105 107    0  101 103 105 107 3   C. 1 cos2x 3cos2x 3cos2x  cos2x  I        2  10 103 105 107    0  101 103 105 107 3   D. 1 cos2x 3cos2x 3cos2x cos2x I       2  101 103 105 107    0 Đáp án C. Lời giải
Nhận xét: Trong bài toán này, ta thấy m lẻ, n chẵn nên ta áp dụng phương pháp
3 trong bài toán tổng quát phía trên. Ta có:   3 3 I   x100  x 6 1 cos2 . sin 2
.sin 2xdx    cos2x 100  2
1 cos 2x 3d cos2x  2 0 0  3 1
  cos2x100. 2 4 6
1 3cos 2x  3cos 2x  cos 2xd cos2x 2 0 
1 cos2x101 3cos2x103 3cos2x105 cos2x107 3         . 2  101 103 105 107    0 b b
Dạng 3: Tính tích phân 1
I  tan x 2
n d ;xI   cot xn dx  * n . 1 2  1 a a2 Phương pháp chung
Sử dụng các công thức sau:  2 1 tan  dx x dx   d 
 tan x  tan x C 2 cos x  2 1 cot  dx x dx    d 
 cot x  cot x C 2 sin x sin x d cos x tan xdx  dx  
 ln cos x  C   cosx  cosx cos x d sin x cot xdx  dx 
 ln sin x  C   sinx  sinx
Dạng 4*: Tích phân liên kết. Phương pháp chung b
Bài toán 1: Tính tích phân cos xdx
I   sinxcosx a b b * cos xdx I  sin xdx I  1  . Xét tích phân liên kết sin x   cos x 2 sin x  cos x a a b  b
I  I  dx  x 1 1  a Ta có  a  b  cos x  sin b x
d sin x  cos x I  I  dx 
 ln sin x  cos b x 1 2   sinx   cos x sin x   cos a x a a  1 b I
x ln sin x cosx     1   
Giải hệ phương trình ta được   2  a   1 b I
x ln sin x cosx      2     2    a 
Bài toán 2: Tính tích phân sin xdx I  1    a cos x bsin x Phương pháp chung 
Xét tính phân liên kết với I là cos xdx  1 I2    a cos x bsin x   Ta có
acos x  bsin x bI  aI 
dx  dx  x  1 2  acosx   bsin x   
 bcos x  asin x
 d acos x  bsin x bI  aI  dx 
 ln acos x bsin x  2 1     
acos x bsin x   a cos x bsin x
Giải hệ phương trình ta được I ;I . 1 2 Chú ý:
Các trường hợp thường gặp:
* I  I khi đó tính I  I      . 1 2 1 2 I I 1 2 2
* I là một tích phân đơn giản, thường thì các hàm số dưới dấu tích phân f x ; 2
g x (của hai tích phân liên kết) thường có tính cân xứng hoặc bổ sung cho nhau
như ở bài toán 1 và bài toán 2.
Việc tìm được tích phân liên kết phụ thuộc vào kinh nghiệm giải toán của người đọc. Mở rộng kiến thức
Từ hai bài toán trên ta đưa ra kết luận về tích phân liên kết như sau: b
Trong một số bài toán tính tích phân I  f x dx , ta sẽ sử dụng tích phân 1    a b
I  g x dx là tích phân liên kết của I sao cho ta có thể xác lập được mối quan 2    1 a
hệ ràng buộc giữa I và I thành hệ phương trình như sau: 1 2
mI  nI   1 2
 pI  qI    1 2
Giải hệ phương trình ta dễ dàng tìm được I ;I . 1 2