Tích phân hàm phân thức hữu tỉ: Phương pháp giải và ví dụ chi tiết | Chuyên đề Toán 12

Tích phân hàm phân thức hữu tỉ
Trong bài toán này, ta sẽ tham khảo lại phần “Nguyên hàm phân thức hữu tỉ” phía
trên để hiểu được các định nghĩa phân thức hữu tỉ, phân thức hữu tỉ thực sự và
phân thức đơn giản, cùng các định lý đã được nêu ở phần nguyên hàm ở phần trước.
Dưới đây là một số bài toán thường gặp về dạng này.
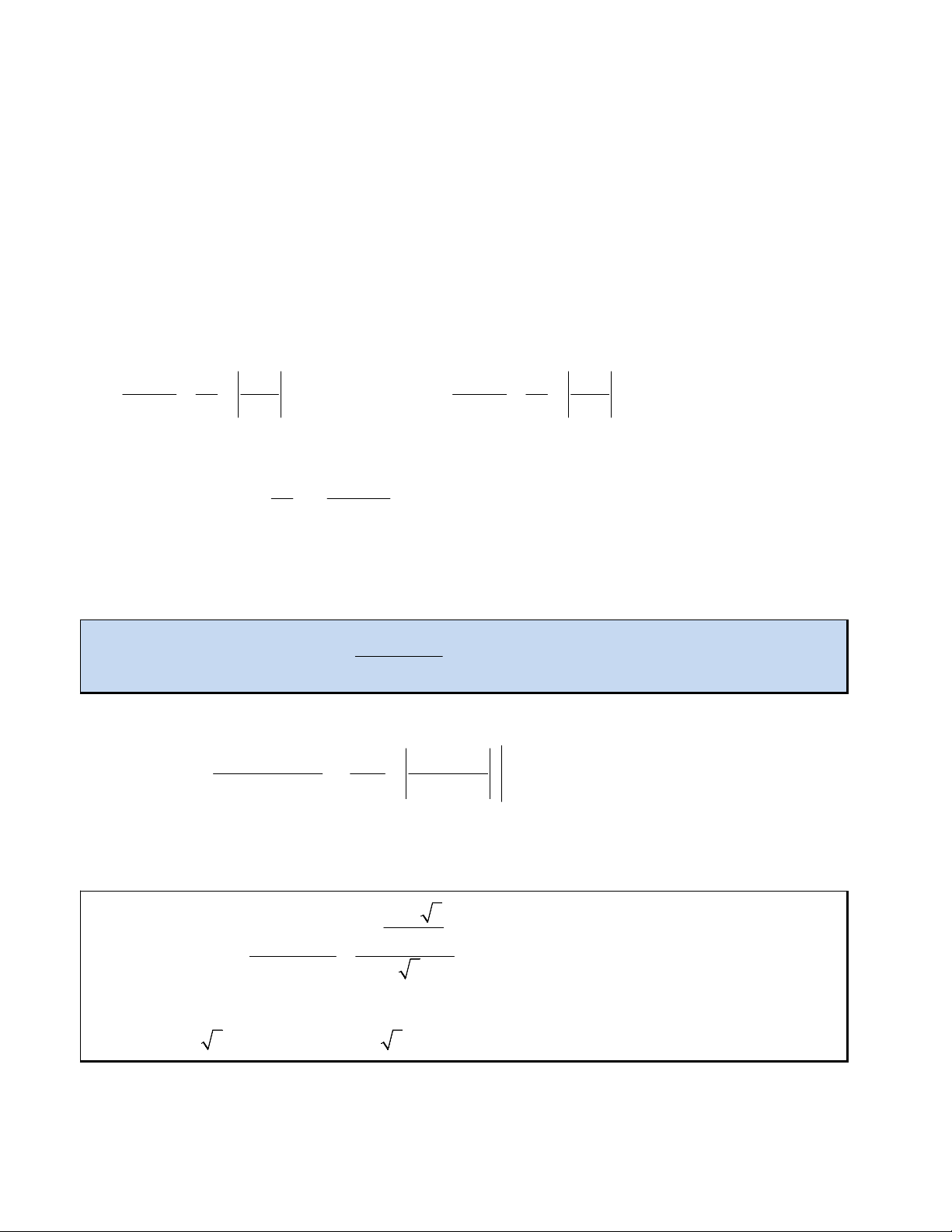
A. MỘT SỐ CÔNG THỨC VÀ KĨ NĂNG BIẾN ĐỔI 1. du 1  
ln u a  C  2. du 1  ln a u  C 2 2 u  .  a 2a u 1 2 2 a u 2a a u
Kỹ năng biến đổi tam thức bậc hai 2 2     1. 2 b b 4ac
ax  bx  c  a  x    2   2a  4a  
2. 2      2 2 ax bx c mx n  p
B. CÁC DẠNG TOÁN TÍCH PHÂN HÀM PHÂN THỨC HỮU TỈ 
Dạng 1: Tích phân dạng dx I  1  . 2    ax bx c Phương pháp chung       Biến đổi dx 1     ln mx n p I1       mx n2 2 p 2mp mx n p  
Chú ý: Khi mẫu thức có dạng tam thức bậc hai thì thường đưa về dạng 2      2 2 ax bx c mx n  p
 a  b 3  ln   1 dx 13
Ví dụ 1: Cho I      , với a, ,
b c ;c  0 . Đặt S  a b  c , lúc 2 4x  8x 1 0 c 3
này S có giá trị bằng
A. S  20  37 3
B. S  37  24 3 C. S  57 D. S  61 Đáp án D. b b Gợi ý: dx  1        ln mx n p I1 
mx  n  p  mp
mx  n  p a  2 2 2 a Lời giải
Áp dụng bài toán tổng quát trên ta có 1 1 dx  1 2x  2  3  I     ln   2x  22     0 3 4 3 2x 2 3  0  37  20 3  ln   1  2.1 2  3 2.0  2  3  13  ln ln       4 3  2.1 2 3 2.0 2 3      4 3  
 S  a b  c  37  37  20 4  61. 0 Ví dụ 2: Cho dx 1 b  53 I   .ln  với ;
a b ;a  0. Tích ab có giá trị 2     7 10x 4x 1 a 53 b 53 bằng A. ‒24 B. 24 C. ‒48 D. 48 Đáp án A. Lời giải
Áp dụng bài toán tổng quát trên ta có 0 0 dx dx I     2  2 2 2 1  53   5  1  5   53      2x    2x   2    2   2    2    0  1 4x  5 53  1  4.0  5 53 4.  1  5 53    .ln    .ln  ln   2 53 4x  5 53  2 53  4.0  5 53 4.  1  5 53  1    1 12  53   .ln 2 53 12  53  a  2
 ;b 12  ab  2  4. 
Dạng 2: Tính tích phân mx  n I  dx 2  2    ax bx c Phương pháp chung Cách 1: m    2   mb
ax b  n  2a 
2a  m  2ax  bdx  mb   dx I       n  2 2 2   2          ax bx c 2a  ax bx c 2a  ax bx c m  d  2
ax bx  c  mb   m  2 ln   mb n I ax bx c n                 I 2 1 1 2a    ax bx c  2a   2a    2a 
Cách 2: Phương pháp hệ số bất định (Sử dụng khi mẫu có nghiệm)
* Nếu mẫu số có nghiệm kép x  x tức là 2
ax  bx  c  a  x  x ta giả sử 0 2 0 mx  n A B   2
ax  bx  c x  x0 x  x0 2
Quy đồng vế phải và đồng nhất hệ số hai vế để tìm A; B. 
Sau khi tìm được A; B thì ta có     .ln B I A x  x  . 2 0 x x    0  
* Nếu mẫu số có 2 nghiệm phân biệt x ; x : 2
ax  bx  c  a  x  x x  x thì ta giả sử: 1   2  1 2 mx  n A B   2
ax  bx  c x  x x  x 1 2
Quy đồng và đồng nhất hệ số để tìm A; B.
Sau khi tìm được A; B ta có I  Aln x  x  B ln x  x   2  1 2  .  0 Ví dụ 1: Cho 2x 9 I 
dx  a ln 3 b ln 2  , ;
a b thì a  2b có giá trị bằng 2    x 3x 2 2 A. ‒35 B. ‒2 C. 2 D. 3 Đáp án D. Lời giải 0 2x  3 0 0 Cách 1: Ta có  6 2x 3 6dx I  dx  dx   2  2  2        x 3x 2  x 3x 2  x 3x 2 2 2 2 0  3 1  0  2 3 2 0 x dx x x dx       2 2 2   6  l  
 n x  3 x 2  6ln 2 2 2     x 3x 2 3 1 2 2  3   1     x  x        2 2 2 2      2 0     
x  x   x 2 ln 1 2  6ln
 7ln x 1  5ln x    2  02  x 1  2
 7 ln1 5ln 2  7 ln 3  5ln 4  7 ln 3 10ln 2  5ln 2  7 ln 3  5ln 2 .
 a  2b  3. Cách 2: Ta thấy x  1 2
x  3x  2  0   . x  2 2x 9 A B 2x 9
A B x 2A B Giả sử     2 2 2
x 3x  2 x 1 x  2 x 3x  2 x 3x  2
Đồng nhất hệ số ta có A  B  2 A  7   2A B 9    B  5  Áp dụng công thức ta có 0
I  7ln x 1  5ln x  2   7ln 3 5ln 2   . 2
Cách 3: Sử dụng máy tính cầm tay.
Trong bài toán này ta có thể sử dụng chức năng TABLE để giải quyết, tuy nhiên cách làm
này chỉ mang tính chất “mò” (tức dự đoán khoảng của a; b).
Giải thích cách sử dụng máy tính cầm tay:
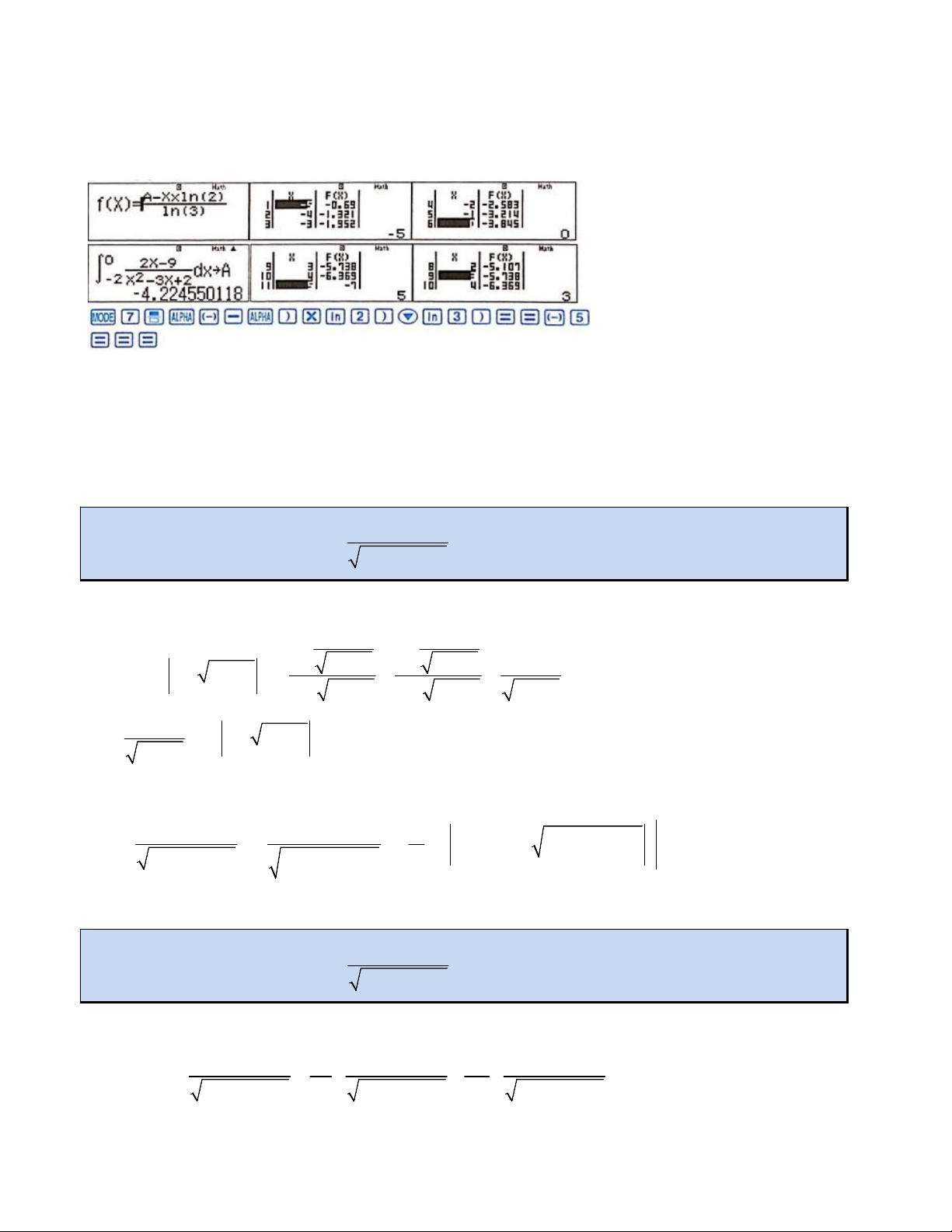
Ta thấy khi nhập vào màn hình 
f  X  A X.ln 2 
thì ta đã coi b (biến X) chạy trong khoảng từ ln 3
5;5 và step là 1. Ở đây ta chọn STEP 1 vì đề cho a; b nguyên. Lúc này màn hình sẽ hiện giá trị
của b (chính là X) và giá trị tương ứng của a (chính là cột f  X  ). Do a; b nguyên nên ta sẽ chọn
a;b  7;5 . Ta thấy I  . b ln 2 I  . a ln 3 . b ln 2  a  . ln 3
1. Lúc này ta nhập biểu thức tích phân vào máy tính và gán giá trị này cho biến A.
2. Tiếp tục sử dụng MODE 7 TABLE để chạy biến giá trị của b từ đó tìm ra bảng giá
trị tương ứng của a.
Ta thấy chỉ có trường hợp X  5; F  X   7 là thỏa mãn 2 số nguyên, do đó ta kết luận a  7
 ;b  5  a  2b  3 .
D. CÁC DẠNG TOÁN TÍCH PHÂN HÀM PHÂN THỨC CHỨA CĂN Ở MẪU THỨC 
Dạng 1: Tính tích phân dx I  3  2 
ax  bx  c Phương pháp chung 1 u  1 u 
Ta có  u u k  2 2 2 u  k u  k 1 ln '    2 2 2
u  u  k u  u  k u  k du 2 
 ln u  u  k  C  2u k
Áp dụng bài toán vừa chứng minh ở trên ta áp dụng vào bài toán biến đổi sau:  dx  dx  1  I .ln  
mx n mx n2 k         3 2   
ax  bx  c  mx  n2  m k  
Chú ý: Phương pháp này chỉ áp dụng được khi hệ số a  0.
 mx  n
Dạng 2: Tính tích phân dx I  4  . 2 
ax  bx  c Phương pháp chung
 mx  ndx
m  2ax  b   Ta có dx mb dx I    4    2 2 2 
ax  bx  c 2a  ax  bx  c 2a  ax  bx  c m  d  2
ax bx  c mb   .I  3 2
2a  ax bx  c 2a 
Dạng 3: Tính tích phân dx I  5
pxq 2
ax  bx  c Phương pháp chung Đặt 1 dt 1 1 px q pdx ;x  q         . Khi đó 2 t t p t    1  p q dx d  t I   5  
  px  q  2 2
ax  bx  c 1 2 1 a 1  b 1  p q pt . q  q      c 2 t p  t  p  t  1 p q dt   
(quay trở về bài toán dạng 1). 2 1
At  Bt   p q