UBND TỈNH QUẢNG BÌNH
TRƯỜNG ĐẠI HỌC QUẢNG BÌNH ------------ TIỂU LUẬN
HỌC PHẦN: LỊCH SỬ TOÁN
HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
LỊCH SỬ HÌNH THÀNH VÀ SỰ THỂ HIỆN
TRONG CHƯƠNG TRÌNH TOÁN THPT
Họ và tên sinh viên: Hoàng Ánh Nguyệt
Lớp: Đại Học Sư Phạm Toán K65 Quảng Bình, 01/2024 2 MỤC LỤC
I. PHẦN MỞ ĐẦU:..............................................................................................3
1. Lý do chọn đề tài:..........................................................................................3
2. Mục đích nghiên cứu:....................................................................................4
3. Phương pháp nghiên cứu:.............................................................................4
4. Nội dung nghiên cứu:....................................................................................4
II. PHẦN NỘI DUNG:..........................................................................................5
1. Lịch sử hình thành và phát triển của khái niệm hàm số:...........................5
1.1. Thời Cổ Đại:............................................................................................5
1.2. Thời Trung Đại:.......................................................................................6
1.3. Thời Cận Đại:..........................................................................................6
1.4. Thời Hiện Đại:.........................................................................................8
2. Ý nghĩa của Hệ bất phương trình bậc nhất hai ẩn:..................................10
2.1. Mô Hình Hóa Thực Tế:.........................................................................10
2.2. Lý Thuyết Đại Số Tuyến Tính:..............................................................10
2.3. Cơ Sở Cho Hệ Thống Phương Trình Tuyến Tính:...............................10
2.4. Ứng Dụng Trong Vật Lý và Kỹ Thuật:.................................................10
2.5. Làm Nền Tảng Cho Các Nghiên Cứu Toán Học Tiên Tiến:...............10
2.6. Áp Dụng Trong Xử Lý Tín Hiệu và Thống Kê:....................................10
3. Hệ bất phương trình bậc nhất hai ẩn và sự thể hiện trong THPT:.........11
3.1. Sự thể hiện ngầm ẩn:............................................................................11
3.2. Sự tường minh:......................................................................................12 III.
PHẦN KẾT LUẬN:.....................................................................................17
1. So sánh và nhận xét.....................................................................................17
1.1. Về tiến trình xuất hiện:..........................................................................17
1.2. Về định nghĩa khái niệm hệ phương trình bậc nhất hai ẩn:....................17
2. Về phương tiện biểu diễn của hệ phương trình bậc nhất hai ẩn:............18
2.1. Trong lịch sử:.........................................................................................18
2.2. Trong sách giáo khoa phổ thông:..........................................................19
3. Kết luận:.......................................................................................................19 3 I. PHẦN MỞ ĐẦU:
1. Lý do chọn đề tài:
Hiện nay, quan điểm khoa học luận và sư phạm về dạy học toán đang phổ
biến trong nhiều nước là : “Thực hiện việc dạy học thỏa mãn hơn khoa học lí
luận và tôn trọng hơn quá trình nhận thức của học sinh”. Điều đó đòi hỏi
trong dạy học phải đồng thời tính đến những kết quả nghiên cứu về khoa học
lí luận lịch sử toán học và về khả năng nhận thức của học sinh. Tuy nhiên, ở
Việt Nam, các đối tượng toán học thường được đưa vào chương trình và
SGK giáo khoa theo truyền thống và kinh nghiệm chủ quan, tách rời khỏi
lịch sử phát triển của đối tượng và ít quan tâm đến nhận thức của học sinh.
Điều này có ảnh hưởng như thế nào đến việc học tập của học sinh? Việc tìm
lời đáp cho câu hỏi này thực sự rất cần thiết và cấp bách cho việc cải tiến
phương pháp dạy học toán ở trường phổ thông.
Phương trình là một trong những chủ đề quan trọng và lâu đời nhất trong
lịch sử toán học. Nó mang trong mình sự đa dạng để ứng dụng vào nhiều
ngành lĩnh vực như Toán học, Vật lý, Kinh tế,... Do đó, việc giảng dạy
phương trình luôn có tầm quan trọng đặc biệt trong dạy học toán ở bất cứ nền
giáo dục nào. Dù thể hiện dưới dạng ngầm ẩn hay tường minh, thì phương
trình cũng đã được đưa vào chương trình toán từ rất sớm – từ những năm đầu
tiên của chương trình toán tiểu học, và tiến triển liên tục, ở những mức độ
khác nhau, lần lượt qua các chương trình toán trung học cơ sở, rồi đến những
năm đầu của chương trình toán phổ thông trung học. Do đó, phương trình –
trong đó có biến thể của nó, hệ bất phương trình bậc nhất hai ẩn – đã trải qua
nhiều dạng khác nhau, tương ứng với nó là nhiều cách giải khác nhau.
Hệ bất phương trình bậc nhất hai ẩn xuất phát từ lĩnh vực của đại số tuyến
tính và toán học. Phát triển của nó được liên quan đến nhu cầu giải quyết các
vấn đề thực tế trong đời sống và các lĩnh vực ứng dụng khác nhau. Bởi vậy,
cá nhân chuyên đề lịch sử hình thành của hệ bất phương trình bậc nhất hai ẩn
có sự liên kết chặt chẽ với sự hình thành và phát triển qua từng giai đoạn của
lĩnh vực của đại số tuyến tính nói riêng và toán học nói chung.
Việc thực hiện việc nghiên cứu đề tài này sẽ giúp chúng ta hiểu rõ về các
đặc trưng khoa học luận của khái niệm hệ bất phương trình bậc nhất hai ẩn
qua các thời kỳ lịch sử phát triển của nó, các khái niệm đó được đưa vào
chương trình trung học phổ thông như nào, học sinh quan niệm như thế nào
về đối tượng này. Qua đó, không chỉ hiểu rõ hơn những đặc trưng khoa học 4
luận của khái niệm hệ bất phương trình bậc nhất hai ẩn, nắm vững hơn
chương trình SGK giáo khoa phổ thông mà nó còn cho phép hiểu rõ hơn
những ảnh hưởng tích cực cũng như tiêu cực của việc lựa chọn quan điểm
trình bày khái niệm hệ bất phương trình bậc nhất hai ẩn và đưa vào chương
trình SGK giáo khoa phổ thông hiện hành đối với việc học tập của học sinh.
Điều này thuận lợi cho việc thiết lập, tổ chức những tình huống dạy học khái
niệm của hệ bất phương trình bậc nhất hai ẩn một cách phù hợp hiệu quả góp
phần vào việc đổi mới phương pháp dạy học nhằm nâng cao chất lượng dạy và học.
2. Mục đích nghiên cứu:
- Làm rõ những đặc trưng khoa học luận của khái niệm hệ bất phương trình
bậc nhất hai ẩn cũng như sự phát triển của chúng qua các thời kỳ khác nhau
trong lịch sử hình thành và phát triển khái niệm này.
- Làm rõ tiến trình cách tổ chức đưa vào khái niệm hệ bất phương trình trong
chương trình và SGK giáo khoa phổ thông. Đặc biệt là sự triển khai các đặc
trưng khoa học luận của khái niệm này và tầm quan trọng của nó qua các cấp
độ lớp ở trường phổ thông.
Để từ đó tìm ra phương pháp dạy học hợp lý phần hệ bất phương trình bậc
nhất hai ẩn ở chương trình phổ thông.
3. Phương pháp nghiên cứu:
Để đạt được những mục tiêu đã đề ra ở trên, tôi sử dụng phương pháp phân
tích - tổng hợp để nghiên cứu lí luận: sử dụng SGK các cấp học, các tài liệu
tham khảo, các bài nghiên cứu trong và ngoài nước để tìm hiểu về lịch sử
hình thành cũng như sự phát triển của khái niệm hệ bất phương trình bậc
nhất hai ẩn. Qua đó thực hiện mục đích nghiên cứu của bài luận.
4. Nội dung nghiên cứu:
Nội dung nghiên cứu gồm có:
- Lịch sử hình thành và phát triển của khái niệm hệ bất phương trình bậc
nhất hai ẩn: Thông qua tìm hiểu và phân tích lịch sử phát triển của khái
niệm để làm rõ những yếu tố khoa học luận của khái niệm này. Qua đó
xác định những đặc trưng chủ yếu qua từng thời kì phát triển của khái
niệm hệ bất phương trình bậc nhất hai ẩn.
- Ý nghĩa của hệ bất phương trình bậc nhất hai ẩn: Thông qua việc nêu ví
dụ toán học và ví dụ thực tế, qua đó cho ta cái nhìn rõ ràng về ý nghĩa của
hệ bất phương trình bậc nhất hai ẩn trong Toán học nói riêng và mọi lịch
vực khác trong đời sống cũng như nghiên cứu nói chung. 5
- Hệ bất phương trình bậc nhất hai ẩn trong chương trình trung học phổ
thông: Thông qua việc phân tích chương trình và SGK trung học phổ
thông làm rõ sự hiện diện và tiến triển của các đặc trưng khoa học luận
của khái niệm hệ phương trình bậc nhất hai ẩn, tầm quan trọng của mỗi
đặc trưng đó qua các cấp độ lớp. II. PHẦN NỘI DUNG:
1. Lịch sử hình thành và phát triển của khái niệm hàm số: 1.1.
Thời Cổ Đại:
Trong thời cổ đại, chúng ta có thể thấy các dấu hiệu của giải quyết các
vấn đề tương đối phức tạp dựa trên bất phương trình và hệ bất phương
trình bậc nhất hai ẩn trong các nền văn minh cổ đại như Babylon, Ai Cập, và Hy Lạp.
1.1.1. Nền Văn Minh Babylon:
Người Babylon đã có đóng góp đáng kể vào lịch sử toán học.
Trong các văn bản cổ đại của họ, có những ghi chú về cách giải
quyết các vấn đề thực tế, bao gồm cả việc sử dụng bất phương
trình và hệ bất phương trình. Một trong những ví dụ nổi tiếng
là Bảng Xem của Babylon, trong đó có nhiều ví dụ về việc giải
các vấn đề liên quan đến lãi suất, phân phối tài nguyên, và thương mại.
1.1.2. Hy Lạp và Lưu Danh Euclid:
Trong thời kỳ cổ đại Hy Lạp, Euclid, nhà toán học nổi tiếng
nhất của thời đại, đã viết tác phẩm "Elements" (Thành phần),
nơi ông giới thiệu nhiều định lý và bổ đề liên quan đến hệ bất
phương trình. Mặc dù công trình của Euclid tập trung chủ yếu
vào phương trình tuyến tính và giải tích hình học, nhưng những
ý tưởng về hệ bất phương trình đã được đề cập đến.
1.1.3. Trí Tuệ Trung Đông:
Trong thời kỳ này, các triết gia và nhà toán học ở Trung Đông,
như Al-Khwarizmi, cũng đóng góp vào lịch sử toán học. Al-
Khwarizmi được biết đến với công trình "Al-Kitab al-
Mukhtasar fi Hisab al-Jabr wal-Muqabala" (Cuốn sách về đại
số và lượng giác), nơi ông trình bày các phương pháp giải
phương trình và bất phương trình.
1.1.4. Văn Minh Ấn Độ: 6
Trong Ấn Độ cổ đại, cũng có sự phát triển về toán học và giải
các vấn đề sử dụng hệ bất phương trình. Những nhà toán học
như Brahmagupta đã viết về cách giải bất phương trình bậc nhất và bậc hai. 1.2. Thời Trung Đại:
Trong thời Trung Cổ, lịch sử hệ bất phương trình bậc nhất hai ẩn
tiếp tục phát triển qua sự đóng góp của các nhà toán học và nhà
triết học của thời kỳ. Dưới đây là một số diễn biến quan trọng
trong lịch sử của hệ bất phương trình bậc nhất hai ẩn trong thời Trung Cổ:
1.2.1. Al-Khwarizmi và Đại Số:
Al-Khwarizmi, một nhà toán học và nhà triết học ảnh hưởng
đến thời Trung Cổ, có đóng góp đáng kể vào lịch sử của hệ bất
phương trình bậc nhất hai ẩn. Công trình "Al-Kitab al-
Mukhtasar fi Hisab al-Jabr wal-Muqabala" của ông (cuốn sách
về đại số và lượng giác) bao gồm cả các phương trình và bất
phương trình bậc nhất và bậc hai.
1.2.2. Omar Khayyam với The Treatise on Demonstration of Problems of Algebra:
Được biết đến với việc giải một số trường hợp của phương
trình bậc hai trong tác phẩm của ông, và ông đã có đóng góp
đáng kể trong việc phát triển phương pháp giải phương trình
bậc ba. Tác phẩm lớn của ông như "The Treatise on
Demonstration of Problems of Algebra" đã cung cấp thêm
thông tin về cách ông tiếp cận các vấn đề liên quan đến đại số
và phương trình trong thời kỳ Trung đại. 1.3. Thời Cận Đại:
Trong giai đoạn thế kỷ XV tới XVIII, toán học đang trải qua
những thay đổi quan trọng và lịch sử hệ bất phương trình bậc nhất
hai ẩn cũng phản ánh sự phát triển trong lĩnh vực này. Dưới đây là
một số điểm chính về lịch sử của hệ bất phương trình bậc nhất hai ẩn trong giai đoạn này:
1.3.1. Leonhard Euler và Phương Trình Bậc Nhất:
Trong thế kỷ 18, nhà toán học Leonhard Euler đã làm việc với
nhiều dạng phương trình và bất phương trình, bao gồm cả
những loại liên quan đến đại số tuyến tính. Euler đã đóng góp 7
vào sự hiểu biết của chúng ta về cách giải quyết và áp dụng các
bài toán thực tế thông qua các biểu diễn toán học.
1.3.2. François Viète (1540 - 1603):
François Viète, một nhà toán học người Pháp, được biết đến
với đóng góp của mình vào lịch sử của đại số tuyến tính và hệ
bất phương trình. Trong tác phẩm của ông, "In Artem
Analyticam Isagoge," Viète đã giới thiệu khái niệm về biến và
hệ số, đặt ra nền tảng cho việc giải quyết các phương trình và
bất phương trình bậc nhất.
1.3.3. Thomas Harriot (1560 - 1621):
Thomas Harriot, một nhà toán học và nhà thiên văn học Anh,
cũng là một trong những người đầu tiên đặt vấn đề về giải các
hệ bất phương trình bậc nhất. Công trình của ông thường được
xem xét trong ngữ cảnh của việc nghiên cứu về đại số tuyến
tính và quy hoạch tuyến tính.
1.3.4. John Wallis (1616 - 1703):
John Wallis, một nhà toán học Anh, là người tiếp tục phát triển
lý thuyết và phương pháp giải của hệ bất phương trình. Trong
tác phẩm "Arithmetica Infinitorum," ông giới thiệu một số khái
niệm mới về vô hạn và liên quan đến lượng giác.
1.3.5. Pierre de Fermat (1607 - 1665):
Pierre de Fermat, một nhà toán học người Pháp nổi tiếng với
Định lý Fermat, đã có những đóng góp quan trọng vào lý
thuyết số và đại số. Mặc dù ông không viết nhiều về hệ bất
phương trình, nhưng những ý tưởng của ông đã góp phần vào
sự phát triển của toán học đại số tuyến tính.
1.3.6. Joseph Fourier (1768 - 1830):
Joseph Fourier, một nhà toán học và nhà vật lý người Pháp,
đóng góp đáng kể vào lĩnh vực đại số tuyến tính và hệ bất
phương trình. Ông nổi tiếng với việc phát triển chuỗi Fourier
và phương trình nhiệt độ Fourier, một dạng của hệ phương trình vi phân tuyến tính.
1.3.7. Daniel Bernoulli (1700 - 1782):
Daniel Bernoulli, một nhà toán học và nhà vật lý Thụy Sĩ, là
người nghiên cứu về nhiều lĩnh vực toán học và vật lý. Ông đã
đóng góp vào lý thuyết xác suất và là một trong những người 8
đầu tiên áp dụng đại số tuyến tính để giải các vấn đề trong vật lý.
1.3.8. Pierre-Simon Laplace (1749 - 1827):
Pierre-Simon Laplace, nhà toán học và nhà vật lý người Pháp,
nổi tiếng với công trình của mình về thống kê và cơ học thiên
thạch. Ông đã sử dụng phương trình và bất phương trình tuyến
tính để mô tả các hệ thống động lực trong vật lý. 1.4. Thời Hiện Đại:
Trong nửa đầu thế kỷ XIX, lĩnh vực toán học tiếp tục phát triển
với nhiều đóng góp quan trọng từ nhiều nhà toán học nổi tiếng.
Dưới đây là một số điểm chính về lịch sử của hệ bất phương trình
bậc nhất hai ẩn trong giai đoạn này:
1.4.1. Augustin-Louis Cauchy (1789 - 1857):
Augustin-Louis Cauchy, một nhà toán học người Pháp, là
người đã đóng góp vào lĩnh vực phân tích thực và lý thuyết
đồng dạng. Công trình của ông trong việc giải các hệ phương
trình và bất phương trình tuyến tính có ảnh hưởng sâu rộng trong toán học.
1.4.2. Niels Henrik Abel (1802 - 1829):
Niels Henrik Abel, một nhà toán học người Na Uy, nổi tiếng
với công trình về đại số và lý thuyết số. Mặc dù ông qua đời
khi còn rất trẻ, nhưng những ý tưởng của Abel đã góp phần vào
phát triển của hệ bất phương trình và đại số tuyến tính.
1.4.3. Siméon Denis Poisson (1781 - 1840):
Siméon Denis Poisson, một nhà toán học và nhà vật lý người
Pháp, là người đưa ra các phương pháp giải quyết hệ bất
phương trình tuyến tính trong ngữ cảnh của vật lý toán học, đặc
biệt là trong cơ học và nhiệt độ.
1.4.4. Carl Friedrich Gauss (1777 - 1855):
Carl Friedrich Gauss, một trong những nhà toán học vĩ đại nhất
trong lịch sử, tiếp tục công trình của mình từ thế kỷ trước. Ông
đã đóng góp vào lý thuyết đồng dạng và phương trình tuyến
tính, mở ra những hướng nghiên cứu mới về hệ bất phương trình.
1.4.5. Lý Thuyết Toán Học Nghiên Cứu Số (Mathematical Analysis of Research Number): 9
Trong giai đoạn này, lý thuyết về các hệ số đồng dạng và các
đại số liên quan đến lý thuyết số bắt đầu trở nên phổ biến. Các
nhà toán học đang tìm kiếm phương pháp giải quyết hệ bất
phương trình bậc nhất hai ẩn thông qua việc nghiên cứu sâu
rộng về đại số và phân tích thực.
1.4.6. David Hilbert (1862 - 1943):
David Hilbert, một nhà toán học Đức, đóng góp vào lĩnh vực
đại số và lý thuyết số. Ông đã đề xuất một loạt các vấn đề mở
trong toán học, trong đó có một số liên quan đến hệ bất phương
trình và bài toán tuyến tính.
1.4.7. Phương Pháp Đại Số Tuyến Tính:
Phương pháp đại số tuyến tính tiếp tục phát triển mạnh mẽ
trong giai đoạn này, đặc biệt là sau khi các khái niệm như
không gian vector và ma trận trở nên quan trọng. Những
phương pháp này đã mở ra cánh cửa cho giải quyết hệ bất
phương trình bậc nhất hai ẩn thông qua các phương pháp đại số hiện đại.
1.4.8. Lý Thuyết Đồng Dạng và Khối Ký Hiệu:
Lý thuyết đồng dạng và sự phát triển của các khối ký hiệu đã
cung cấp một cách tiếp cận mạnh mẽ cho việc giải các hệ bất
phương trình bậc nhất hai ẩn. Các nhà toán học như Élie Cartan
và Hermann Weyl đã đóng góp vào việc phát triển lý thuyết này.
1.4.9. Khám Phá Của Max Planck (1858 - 1947) và Albert Einstein (1879 - 1955):
Các nhà vật lý Max Planck và Albert Einstein đã đưa ra các
định luật về bức xạ và hiệu ứng Compton, mà trong đó giải
quyết các hệ phương trình và bất phương trình tuyến tính đóng một vai trò quan trọng.
Giai đoạn này đã chứng kiến sự phát triển đáng kể trong cả lý
thuyết và ứng dụng của hệ bất phương trình bậc nhất hai ẩn, đặt
nền móng cho nhiều khám phá và tiến bộ trong lĩnh vực này trong tương lai.
2. Ý nghĩa của Hệ bất phương trình bậc nhất hai ẩn: 10
Hệ bất phương trình bậc nhất hai ẩn đóng vai trò quan trọng trong nhiều
lĩnh vực toán học và ứng dụng. Dưới đây là một số ý nghĩa chính của hệ
bất phương trình bậc nhất hai ẩn: 2.1.
Mô Hình Hóa Thực Tế:
Hệ bất phương trình bậc nhất hai ẩn được sử dụng để mô hình hóa
nhiều vấn đề thực tế và tự nhiên. Các biến trong hệ có thể đại diện
cho các yếu tố khác nhau, và giải phương trình hoặc bất phương
trình trong hệ giúp dự đoán và giải quyết các vấn đề trong thực tế. 2.2.
Lý Thuyết Đại Số Tuyến Tính:
Hệ bất phương trình bậc nhất hai ẩn là một phần của lý thuyết đại
số tuyến tính, mà là một lĩnh vực toán học quan trọng trong nghiên
cứu và ứng dụng. Việc hiểu và giải quyết các hệ bất phương trình
này giúp phát triển lý thuyết và phương pháp toán học. 2.3.
Cơ Sở Cho Hệ Thống Phương Trình Tuyến Tính:
Hệ bất phương trình bậc nhất hai ẩn là một trường hợp đơn giản
trong lý thuyết hệ thống phương trình tuyến tính nhiều biến. Việc
giải quyết hệ này giúp xây dựng cơ sở cho việc hiểu và giải quyết
các hệ phức tạp hơn với nhiều biến và điều kiện hơn. 2.4.
Ứng Dụng Trong Vật Lý và Kỹ Thuật:
Trong nhiều lĩnh vực như vật lý, kỹ thuật, và công nghệ, hệ bất
phương trình bậc nhất hai ẩn được sử dụng để mô hình hóa và giải
quyết các vấn đề có ảnh hưởng đến thế giới thực. Điều này bao
gồm cả việc điều khiển hệ thống, tối ưu hóa tài nguyên, và dự đoán các sự kiện. 2.5.
Làm Nền Tảng Cho Các Nghiên Cứu Toán Học Tiên Tiến:
Các hệ bất phương trình bậc nhất hai ẩn thường làm nền tảng cho
các nghiên cứu toán học tiên tiến hơn, đặc biệt là trong lĩnh vực
đại số tuyến tính và lý thuyết đồng dạng. Nó cung cấp những
trường hợp cơ bản và kỹ thuật giải quyết cho các vấn đề phức tạp hơn. 2.6.
Áp Dụng Trong Xử Lý Tín Hiệu và Thống Kê:
Trong xử lý tín hiệu và thống kê, hệ bất phương trình bậc nhất hai
ẩn được sử dụng để phân tích và xử lý dữ liệu. Việc giải quyết các
hệ này có thể cung cấp thông tin về mối quan hệ và ảnh hưởng giữa các biến. 11
Tổng cộng, hệ bất phương trình bậc nhất hai ẩn không chỉ có ý nghĩa
trong việc giải quyết các vấn đề cụ thể mà còn đóng vai trò quan trọng
trong việc phát triển lý thuyết toán học và ứng dụng trong nhiều lĩnh vực khác nhau.
3. Hệ bất phương trình bậc nhất hai ẩn và sự thể hiện trong chương trình THPT:
Hệ bất phương trình bậc nhất hai ẩn nói riêng và hệ phương trình nói
chung thường được thể hiện và giảng dạy trong sách giáo trình và chương
trình trung học phổ thông (THPT) với một cách tiếp cận hệ thống và lý
thuyết. Dưới đây là một sự thể hiện phổ biến của hệ bất phương trình bậc
nhất hai ẩn trong sách giáo trình và chương trình THPT: 3.1.
Sự thể hiện ngầm ẩn:
Trong chương trình toán học ở Việt Nam, sự thể hiện ngầm ẩn hệ
phương trình thường được thực hiện thông qua các bài toán và tình
huống thực tế. Hệ phương trình là một công cụ mạnh mẽ để mô
hình hóa và giải quyết các vấn đề thực tế, và việc giải các bài toán
thường đòi hỏi việc thiết lập và giải hệ phương trình.
Dưới đây là một số cách mà hệ phương trình có thể được thể hiện
ngầm trong chương trình toán học ở Việt Nam:
3.1.1. Bài toán Thực Tế: Các bài toán thực tế thường đưa ra tình
huống phức tạp và đòi hỏi việc sử dụng hệ phương trình để giải
quyết. Ví dụ các bài toán về tỷ lệ pha trộn của các hạt chất
trong hóa học có thể dẫn đến hệ phương trình tuyến tính.
3.1.2. Kết Hợp Với Hình Học: Việc sử dụng hình học để giải các vấn
đề và vẽ đồ thị của hệ phương trình giúp học sinh hiểu rõ hơn
về cách các đại lượng tương tác và làm thế nào hệ phương trình
mô tả mối quan hệ giữa chúng.
3.1.3. Bài Toán Gia Đình và Xã Hội: Các bài toán về phân phối tài
sản, thu nhập, hay tình hình lao động trong gia đình và xã hội
có thể dẫn đến hệ phương trình. Việc giải các bài toán như vậy
giúp học sinh thấy rõ ứng dụng của toán học trong cuộc sống hàng ngày.
3.1.4. Tính Toán Số Liệu: Trong bài toán tính toán số liệu, việc giải
hệ phương trình giúp tìm ra giải pháp cho các vấn đề có tính 12
chất phức tạp, ví dụ như dự báo tình hình tài chính hay thống kê y tế.
3.1.5. Bài Toán Tối Ưu Hóa: Các bài toán về tối ưu hóa thường dẫn
đến việc giải hệ phương trình, ví dụ như tối ưu hóa chi phí sản xuất hay lợi nhuận. 3.2.
Sự tường minh: Sự thể hiện rõ ràng của hệ phương trình trong
chương trình toán ở Việt Nam thường được thực hiện qua các bộ
SGK Toán cũng như các phần học và bài tập.
3.2.1. Các bộ SGK Toán:
Trong chương trình THPT, hệ bất phương trình bậc nhất hai ẩn
thường được giảng dạy như một phần của đại số tuyến tính. Nó
được kết nối với kiến thức về ma trận, đại số vectơ, và lý thuyết đồng dạng. 3.2.1.1.
Khái niệm: Hệ bất phương trình bậc nhất hai ẩn là một
hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn.
Cặp số (x0;y ) là nghiệm của một hệ bất phương trình 0
bậc nhất hai ẩn khi (x0;y ) đồng thời là nghiệm của tất cả 0
các bất phương trình trong hệ đó. STT
Các bất phương trình bậc nhất hai ẩn 1 ax+by2 ax+by>c 3 ax+by≤c 4 ax+by≥c
Hình 1. Bảng các bất phương trình bậc nhất hai ẩn 3.2.1.2.
Biểu diễn: miền nghiệm của hệ bất phương trình bậc
nhất hai ẩn trên mặt phẳng tọa độ:
3.2.1.2.1. Biểu diễn miền nghiệm: Trong mặt phẳng tọa độ, tập
hợp các điểm có tọa độ là nghiệm của hệ bất phương 13
trình bậc nhất hai ẩn là miền nghiệm của hệ bất
phương trình đó. Miền nghiệm của hệ là giao các
miền nghiệm của các bất phương trình trong hệ.
3.2.1.2.2. Cách xác định miền nghiệm: Trên cùng một mặt
phẳng tọa độ, xác định miền nghiệm của mỗi bất
phương trình bậc nhất hai ẩn trong hệ và gạch bỏ
miền còn lại. Miền không bị gạch là miền nghiệm
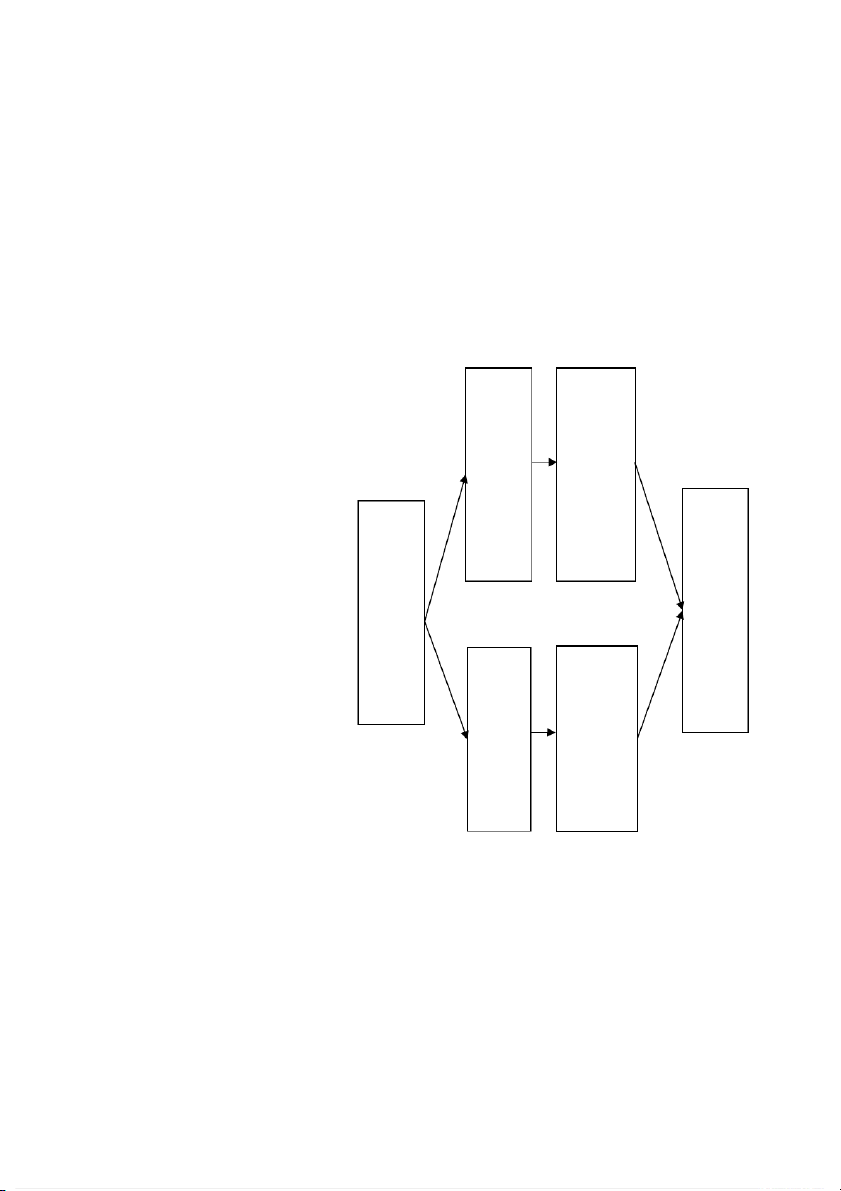
của hệ bất phương trình đã cho. Nghiệ Gạch m của bỏ phần phươ không ng phải trình nghiệm phương Giải trình Đồ thị hệ biểu phươ diễn ng miền trình nghiệ m của phươ Khôn Giữ ng g nguyên trình phải phần nghiệ nghiệm m của của phương phươ trình ng trình
Hình 1. Sơ đồ xác định miền nghiệm
của hệ bất phương trình 3.2.1.3.
Cách giải: Để giải hệ bất phương trình này, ta có thể
thực hiện các bước sau đây:
- Bước 1 : Xác định số lượng biến trong hệ bất phương
trình. Trong trường hợp này, số lượng biến là 2. 14
- Bước 2 : Xác định số lượng và dạng của các phương
trình trong hệ bất phương trình. Ví dụ: hệ bất phương
trình bậc nhất 2 ẩn có thể bao gồm các phương trình
dạng ax + by ≤ c hoặc ax + by ≥ c.
- Bước 3 : Tùy thuộc vào yêu cầu của bài toán cụ thể, ta
có thể giải hệ bất phương trình này bằng các phương
pháp như đồ thị hóa, phương pháp thử và sai, hoặc phương pháp đại số. 3.2.1.4.
Ví dụ bài toán về hệ bất phương trình bậc nhất hai ẩn:
VD1: Trong tình huống mở đầu, gọi x và y lần lượt là số
máy điều hòa hai chiều và một chiều mà cửa hàng cần
nhập. Tính số tiền vốn cửa hàng phải bỏ ra để nhập hai
loại máy điều hòa theo x và y.
a) Do nhu cầu của thị trường không quá 100 máy nên x
và y cần thỏa mãn điều kiện gì?
b) Vì số vốn mà chủ cửa hàng có thể đầu tư không vượt
quá 1,2 tỉ đồng nên x và y phải thỏa mãn điều kiện gì?
c) Tính số tiền lãi mà chủ cửa hàng dự kiến thu được theo x và y. ĐH hai chiều ĐH 1 chiều 10 triệu đồng/ 1 Giá mua vào 20 triệu đồng/ 1 máy máy Lợi nhuận dự 2 triệu đồng/ 1 3,5 triệu đồng/1 máy kiến máy
Bảng 1.1. Bảng giá mua và lợi nhuận dự kiến của cửa hàng Lời giải:
Do x và y là số máy điều hòa mà cửa hàng cần nhập nên x ≥ 0, y ≥ 0. 15
Số tiền vốn mà chủ cửa hàng phải bỏ ra để nhập hai loại
máy điều hòa theo x và y là:20x + 10y (triệu đồng)
a) Do nhu cầu của thị trường không quá 100 máy nên x + y ≤ 100.
b) Vì số vốn mà chủ cửa hàng có thể đầu tư không vượt
quá 1,2 tỉ đồng nên 20x + 10y ≤ 1 200 .
c) Số tiền lãi mà cửa hàng dự kiến thu được là: 3,5x + 2y (triệu đồng).
VD2: Xác định miền nghiệm của hệ bất phương trình
bậc nhất hai ẩn sau: { x+y−2≥0
x−3 y+ 3≤ 0 Lời giải:
Vẽ các đường thẳng (d):x+y−2=0, (d′):x−3y+3=0 trên mặt phẳng tọa độ Oxy.
Xét điểm O(0;0), thấy (0;0) không phải là nghiệm của
bất phương trình x+y−2≥0 và x−3y+3≤0.
Do đó miền nghiệm cần tìm là phần mặt phẳng không
được tô màu trên hình vẽ kể cả hai đường thẳng (d) và (d′). y 2 (d’) 1 x 3 O 2 (d)
3.2.2. Các phần học và bài tập: Hình 1. 16
Phần học và bài tập ở chương trình Toán THPT cho giáo viên
và học sinh cái nhìn bao quát nhưng cũng rõ ràng tường tận
nhất về Phương trình nói chung và Hệ bất phương trình bậc
nhất hai ẩn nói riêng. Trong đó, bao gồm: 3.2.2.1.
Hiểu Rõ Cơ Bản về Phương Trình và Hệ Phương Trình:
- Học sinh thường bắt đầu với việc hiểu rõ về phương trình và hệ phương
trình bậc nhất, bậc hai.
- Họ được giảng dạy cách giải phương trình và hệ phương trình đơn lẻ, sau
đó mở rộng sang việc giải hệ phương trình. 3.2.2.2.
Làm Việc Với Các Loại Hệ Phương Trình:
- Hệ phương trình tuyến tính và phi tuyến, hệ phương trình vô số nghiệm,
hay hệ phương trình không có nghiệm thường được xem xét và giảng dạy.
- Học sinh học cách xác định số nghiệm của hệ phương trình thông qua
phương pháp đồ thị hay phương pháp đại số tuyến tính. 3.2.2.3.
Mô Hình Hóa Tình Huống Thực Tế:
- Hệ phương trình thường được sử dụng để mô hình hóa tình huống thực tế
như phân phối nguồn lực, dự báo kinh doanh, hay mô phỏng các hiện tượng tự nhiên.
- Học sinh cần có khả năng thiết lập và giải quyết hệ phương trình dựa trên bối cảnh cụ thể. 3.2.2.4.
Tích Hợp Toán Học và Tin Học:
- Các phần mềm và công cụ tính toán có thể được sử dụng để giải hệ
phương trình và học sinh thường được khuyến khích tích hợp kỹ năng
toán học với công nghệ. 3.2.2.5.
Thực Hành Bài Toán Hệ Phương Trình:
- Bài toán thực hành đòi hỏi học sinh áp dụng kiến thức đã học để giải
quyết các vấn đề cụ thể.
- Các bài toán đa dạng giúp họ phát triển kỹ năng giải quyết vấn đề và ứng
dụng toán học vào thực tế. 3.2.2.6. Ôn Tập và Nâng Cao:
- Học sinh được khuyến khích ôn tập và nâng cao kỹ năng giải hệ phương
trình qua việc giải các bài toán có độ khó tăng dần và đòi hỏi sự sáng tạo. 17
Sự thể hiện rõ ràng của hệ phương trình thường được đo lường qua khả năng của
học sinh trong việc áp dụng kiến thức đã học vào các bài toán và tình huống thực tế,
cũng như khả năng giải quyết vấn đề và mô hình hóa. III. PHẦN KẾT LUẬN:
1. So sánh và nhận xét
Qua việc phân tích ở phần I và phần II, ta có thể so sánh tiến trình xuất hiện khái
niệm hệ bất phương trình bậc nhất hai ẩn nói riêng hay phương trình nói chung và
các phương tiện biểu diễn của nó trong sách giáo khoa phổ thông với trong lịch sử
hình thành và phát triển của khái niệm này như sau: 1.1.
Về tiến trình xuất hiện:
1.1.1. Trong lịch sử: Khái niệm hệ bất phương trình bậc nhất
hai ẩn xuất hiện theo bốn giai đoạn: - Thời Kỳ Cổ Đại - Thời Kỳ Trung Đại - Thời Kỳ Cận Đại - Thời Kỳ Hiện Đại
1.1.2. Trong sách giáo khoa phổ thông: Khái niệm hệ bất
phương trình bậc nhất hai ẩn được đưa vào theo hai giai đoạn: - Giai đoạn ngầm ẩn. - Giai đoạn tường minh. 1.2.
Về định nghĩa khái niệm hệ phương trình bậc nhất hai ẩn:
1.2.1. Trong lịch sử: Khái niệm đầu tiên về hệ bất phương
trình bậc nhất hai ẩn xuất hiện trong quá trình phát triển
của đại số và toán học lý thuyết. Tuy không có thông tin
cụ thể về người sáng tạo hay lịch sử cụ thể, tuy nhiên
các nhà khoa học để tìm thấy một định nghĩa được coi là
định nghĩa thô sơ nhất về hệ bất phương trình bậc nhất
hai ẩn. Đó là: Một hệ bất phương trình bậc nhất hai ẩn
đơn giản có thể được biểu diễn bởi các biểu thức như
sau: {ax+by≤c . dx+ ey ≥ f
Trong đó, a,b,c,d,e,f≤ là các hằng số và x,y là các biến. 18
1.2.2. Trong sách giáo khoa phổ thông: Ở sách giáo khoa
Toán 10 trong bộ sách Kết nối tri thức, khái niệm về hệ
bất phương trình bậc nhất hai ẩn được trình bày như sau:
Hệ bất phương trình bậc nhất hai ẩn là một hệ gồm hai
hay nhiều bất phương trình bậc nhất hai ẩn. Cặp số
(x0;y0) là nghiệm của một hệ bất phương trình bậc nhất hai ẩn khi (x0;y )
0 đồng thời là nghiệm của tất cả các bất
phương trình trong hệ đó. Giai đoạn sau này, đặc trưng
biến thiên của hệ phương trình được trình bày một cách
tường minh và trở thành một trong những phép toán đại
số tuyến tính được quan tâm nghiên cứu.
2. Về phương tiện biểu diễn của hệ phương trình bậc nhất hai ẩn: 2.1.
Trong lịch sử:
2.1.1. Phương trình Tổ hợp: Trong thời kỳ cổ đại, các nhà
toán học thường sử dụng phương trình tổ hợp để biểu
diễn hệ phương trình. Chẳng hạn, Euclid, một nhà toán
học Hy Lạp, đã sử dụng phương trình tổ hợp để giải một số bài toán hình học.
2.1.2. Biểu đồ Đồ thị: Khi đồ thị được sử dụng trong toán học,
biểu đồ đồ thị trở thành một công cụ quan trọng để hiểu
và giải hệ phương trình. Các hệ phương trình hai ẩn có
thể được biểu diễn trên mặt phẳng Cartesius, và giải
bằng cách xác định điểm giao của đồ thị.
2.1.3. Phương trình Ma trận: Trong thế kỷ 20, sự phát triển
của đại số tuyến tính đã mở ra khả năng sử dụng ma trận
để biểu diễn và giải hệ phương trình. Công cụ này làm
cho việc xử lý các hệ phương trình trở nên hiệu quả và thuận tiện.
2.1.4. Phương pháp Elimination và Substitution: Trong quá
trình phát triển, các phương pháp như phương pháp loại
bỏ và thế đã được sử dụng để biểu diễn và giải hệ
phương trình. Các phương pháp này thường liên quan
đến việc thực hiện các phép biến đổi đại số trên các
phương trình để giảm số lượng ẩn và tìm nghiệm. 19
2.1.5. Phương pháp đồng dư: Phương pháp đồng dư cũng đã
được áp dụng để giải hệ phương trình bậc nhất hai ẩn.
Các nhà toán học sử dụng các phương trình đồng dư để
xác định điều kiện cho sự tồn tại và duy nhất của nghiệm. 2.2.
Trong sách giáo khoa phổ thông:
Phương trình tương đương là biểu diễn khác của hệ phương
trình, thường được thu được bằng cách thực hiện các phép biến
đổi đại số trên các phương trình ban đầu
Qua sự so sánh ở trên ta thấy tiến trình triển khai khái niệm hệ bất phương trình bậc
nhất hai ẩn trong sách giáo khoa phổ thông cũng bắt đầu từ hình thức ngầm ẩn như
trong lịch sử. Nghĩa là hệ bất phương trình bậc nhất hai ẩn xuất hiện trước hết trong
vai trò công cụ ngầm ẩn trước khi nó được định nghĩa và nghiên cứu tường minh.
Cách triển khai này là phù hợp vì nó giúp cho học sinh được tiếp xúc, làm quen một
cách ngầm ẩn với một số đặc trưng và cách biểu diễn của hệ bất phương trình bậc
nhất hai ẩn trước khi được học định nghĩa và nghiên cứu về nó. Từ đó học sinh hiểu
rõ thêm về phương trình, phương trình bậc nhất hai ẩn, bất phương trình bậc nhất
hai ẩn, hệ bất phương trình bậc nhất hai ẩn, từ đó ứng dụng giải các bài toán thực tế. 3. Kết luận:
Bằng cách sử dụng phương pháp phân tích - tổng hợp để nghiên cứu lí luận, sử
dụng SGK các cấp học, các tài liệu tham khảo, các bài nghiên cứu trong và ngoài
nước để tìm hiểu về lịch sử hình thành cũng như sự phát triển của khái niệm hệ bất
phương trình bậc nhất hai ẩn, tôi đã có thể àm rõ những đặc trưng khoa học luận của
khái niệm hệ bất phương trình bậc nhất hai ẩn cũng như sự phát triển của chúng qua
các thời kỳ khác nhau trong lịch sử hình thành và phát triển khái niệm này. Ngoài ra
thì tôi cũng làm rõ tiến trình cách tổ chức đưa vào khái niệm hệ bất phương trình
trong chương trình và SGK giáo khoa phổ thông. Đặc biệt là sự triển khai các đặc
trưng khoa học luận của khái niệm này và tầm quan trọng của nó qua các cấp độ lớp
ở trường phổ thông. Bên cạnh đó, tôi cũng đã đem ra ứng dụng của hệ bất phương
trình bậc nhất hai ẩn trong nghiên cứu cũng như trong đời sống. Tài liệu tham khảo
Harold R. Jacobs (1979). Elementary Algebra.
Richard G. Brown, Mary P. Do (1991). Algebra: Structure and Method, Book 1.
Marvin L. Bittinger (1994). Intermediate Algebra. 20
Michael Sullivan (1993). College Algebra: Concepts Through Functions.
Robert F. Blitzer (2007). Algebra and Trigonometry.
Đoàn Quỳnh, Khu Quốc Anh, Nguyễn Anh Kiệt, Tạ Mân, Nguyễn Doãn Tuấn
(2009). Giáo Trình Đại Số Tuyến Tính Và Hình Học Giải Tích.
Đỗ Trung Hiệu, Nguyễn Hùng Quang, Kiều Đức Thành (2000). Phương pháp dạy
học Toán. NXB Giáo dục Việt Nam.
Nguyễn Ngọc Thắng, Nguyễn Đình Hóa (2006). Quy hoạch tuyến tính. NXB Đại học Quốc gia Hà Nội.
Phạm Thị Thu Hà (2018). Xây dựng hệ thống bài toán thực tiễn trong dạy học chủ
đề phương trình, hệ phương trình, hệ bất phương trình cho học sinh lớp 10. Khóa
luận tốt nghiệp Đại học - Trường Đại học Sư phạm Hà Nội 2.
Polya, G. (1975). Sáng tạo toán học. NXB Giáo dục.
Trần Việt Cường, Nguyễn Ngọc Trang, Nguyễn Phúc Binh (2014). Tổ chức dạy học
theo dự án trong dạy học môn Toán cho học sinh trung học phổ thông. Tạp chí Giáo dục, 325, 44-46; 53.
Trần Nam Dũng, Trần Đức Huyên, Nguyễn Thành Anh, Vũ Như Thu Hương, Ngô
Hoàng Long, Phạm Hoàng Quân, Phạm Thị Thu Thủy (2021). Toán 10 (tập 1)
(Chân trời sáng tạo). NXB Giáo dục Việt Nam.
Đỗ Đức Thái, Phạm Xuân Chung, Nguyễn Sơn Hà, Nguyễn Thị Phương Loan,
Phạm Sỹ Nam, Phạm Minh Phương, Phạm Hoàng Quân (2021). Toán 10 (tập 1)
(Cánh diều). NXB Đại học Sư phạm.
Hà Huy Khoái, Cung Thế Anh, Trần Văn Tấn, Đặng Hùng Thắng, Hạ Vũ Anh,
Trần Mạnh Cường, Phan Thị Hà Dương, Nguyễn Đạt Đăng, Phạm Hoàng Hà, Đặng
Đình Hanh, Phan Thanh Hồng, Nguyễn Thị Kim Sơn, Dương Anh Tuấn, Nguyễn
Chu Gia Vượng (2021). Đại số 10 (tập 1) (Kết nối tri thức với cuộc sống). NXB Giáo dục Việt Nam. 21