Tiểu luận môn Lập trình Windows | Trường Đại học Sư phạm Thành phố Hồ Chí Minh

lOMoAR cPSD| 22014077
BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC SƯ PHẠM TP. HỒ CHÍ MINH
KHOA CÔNG NGHỆ THÔNG TIN TIỂU LUẬN Học phần:
Thành phố Hồ Chí Minh, ngày 15 tháng 12 năm 2021 lOMoAR cPSD| 22014077
BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC SƯ PHẠM TP. HỒ CHÍ MINH
KHOA CÔNG NGHỆ THÔNG TIN TIỂU LUẬN
< MÔ PHỎNG THUẬT TOÁN CỦA LÝ THUYẾT ĐỒ THỊ >
Học phần: < COMP101904 – Lập Trình trên Window > Nhóm : Windows Progamming - Nguyễn Phước Thịnh - Lâm Chấn Huy - Nguyễn Đạt Minh - Lê Đình Anh Tuấn
Giảng viên hướng dẫn: Th.S Võ Tiến An
Thành phố Hồ Chí Minh, ngày 15 tháng 12 năm 2021 lOMoAR cPSD| 22014077 LỜI CAM ĐOAN
Nhóm Windows Progamming chúng em xin giới thiệu với thầy và mọi người
đề tài ”Mô phỏng thuật toán của Lý Thuyết Đồ Thị”. Chúng em chọn đề tài này
vì nó thiết thực và bổ ích cho các bạn sinh viên trong học tập cũng như trong môi
trường làm việc với máy tính trở nên thông dụng như hiện nay.
Trong quá trình thực hiện đề tài này còn có nhiều thiếu sót do kiến thức còn
sơ sài nhưng những nội dung trình bày trong quyển báo cáo này là những biểu
hiện kết quả của chúng em đạt được dưới sự hướng dẫn của Thạc sĩ Võ Tiến An
Chúng em xin cam đoan rằng: Những nội dung trình bày trong quyển báo
cáo đồ án môn Lập Trình trên Window là do chúng em viết dựa trên tài liệu và
hướng dẫn của thầy. Nếu không đúng sự thật, chúng em xin chịu mọi trách nhiệm trước thầy. lOMoAR cPSD| 22014077
MỤC LỤC NHIỆM VỤ THÀNH VIÊN
NHÓM.................................................4 MỞ
ĐẦU..............................................................................................6 NỘI
DUNG..........................................................................................1 1
GIỚI THIỆU THUẬT TOÁN.....................................................1 1.1
THUẬT TOÁN XÉT LIÊN THÔNG...........................................................1 1.2
THUẬT TOÁN BFS – DFS.....................................................................1
1.2.1 Thuật toán BFS................................................................................1 1.2.2
Thuật toán DFS...............................................................................2 1.3
THUẬT TOÁN PRIM...............................................................................2 1.4
THUẬT TOÁN KRUSKAL.......................................................................3 1.5
THUẬT TOÁN DIJKSTRA......................................................................3 2
GIỚI THIỆU VỀ CHƯƠNG TRÌNH........................................5 2.1 TỔNG QUAN VỀ GIAO
DIỆN...................................................................5
CODE Giao Diện Chính.................................................................5 2.2 CÁC FILE XỬ LÍ THUẬT TOÁN TRONG CHƯƠNG
TRÌNH......................8 2.3
FORMGRAPH.CS................................................................................. ..9
2.3.1 Vẽ Đồ Thị.........................................................................................9
2.3.2 Các thuật toán chương trình hỗ trợ:.............................................15 3
HƯỚNG DẪN SỬ DỤNG.........................................................19 3.1 DOWNLOAD SOURCE
CODE...............................................................19 3.2 CHẠY CHƯƠNG
TRÌNH........................................................................19 KẾT
LUẬN........................................................................................20
TÀI LIỆU THAM KHẢO................................................................21 lOMoAR cPSD| 22014077
NHIỆM VỤ THÀNH VIÊN NHÓM
- Thành viên 1: 46.01.104.176 – Nguyễn Phước Thịnh – COMP101904
(CODE BFS-DFS,GIAO DIỆN,EVENT XỬ LÝ HIỂN THỊ ,CLICK)
- Thành viên 2: 46.01.104.069 – Lâm Chấn Huy – COMP101904
(CODE PRIM,WORD,GIAO DIỆN)
- Thành viên 3: 46.01.104.100 – Nguyễn Đạt Minh – COMP101904
(CODE KRUSKAL,WORD,GIAO DIỆN)
- Thành viên 4: 46.01.104.209 – Lê Đình Anh Tuấn – COMP101904
(CODE DIJKSTRA,VIDEO DEMO) lOMoAR cPSD| 22014077
DANH MỤC CÁC HÌNH VẼ
Hình 2.3.2.a Các chức năng trong chương trình ................................................. 13
Hình 2.3.2.b Mô phỏng thuật toán Xét liên thông .............................................. 14
Hình 2.3.2.c Mô phỏng thuật toán DFS .............................................................. 14
Hình 2.3.2.d Mô Phỏng thuật toán BFS .............................................................. 14
Hình 2.3.2.e Mô phỏng thuật toán Kruskal ......................................................... 15
Hình 2.3.2.f Mô Phỏng thuật toán Prim .............................................................. 15
Hình 2.3.2.g Mô phỏng thuật toán Dịkstra ......................................................... 16 lOMoAR cPSD| 22014077 MỞ ĐẦU 1. Lý do chọn đề tài
Lý thuyết đồ thị là một ngành khoa học được phát triển từ lâu nhưng lại có
nhiều ứng dụng hiện đại. Những tư tưởng cơ bản của lý thuyết đồ thị được đề
xuất vào những năm đầu của thế kỷ 18 bởi nhà toán học lỗi lạc người Thụy Sỹ
Lenhard Euler. Đồ thị được sử dụng để giải các bài toán trong nhiều lĩnh lực
khác nhau . Chẳng hạn , đồ thị có thể sử để xác định mạch vòng trong vấn đề
giải tích mạch điện. Đồ thị có trọng số trên các cạnh có thể sử dụng để giải các
bài toán như: Tìm đường đi ngắn nhất giữa hai thành phố trong mạnh giao
thông. Chúng ta cũng có thể sử dụng đồ thị để giải các bài toán về lập lịch ,
thời khoa biểu… Đặc biệt trong khoảng vài mươi năm trở lại đây, cùng với sự
ra đời của máy tính điện tử và sự phát triển nhanh chóng của tin học, lí thuyến
đồ thị càng được quan tâm đến nhiều hơn. Các thuật toán trên đồ thị đã có
nhiều ứng dụng trong nhiều lĩnh vực khác nhau như:
Mạng máy tính, Lí thuyết mã, Tối ưu hoá,…
Chính vì thế nhóm em đã lựa chọn đề tài “ Minh họa trực quan bằng giao diện
đồ họa các thuật toán tìm thành phần liên thông của đồ thị, duyệt đồ thị theo
chiều rộng và theo chiều sâu, thuật toán Prim, thuật toán Kruskal, thuật toán
Dijsktra” để nghiên cứu, tìm hiểu tạo ra một giao diện trực quan giúp cho
người dùng dễ tiếp cận và sử dụng , hiểu hơn về các thuật toán tìm đường đi
duyệt theo chiều sâu (DFS) hay duyệt theo chiều rộng (BFS), tìm thành phần
liên thông của của đồ thị, thuật toán Prim, thuật toán Kruskal, thuật toán Dijkstra. 2. Mục tiêu nghiên cứu
Mục tiêu của đồ án này nhằm giúp chúng em có được sự hiểu biết sâu hơn về các
thuật toán tìm đường đi duyệt theo chiều sâu (DFS) hay duyệt theo chiều rộng
(BFS), tìm thành phần liên thông của của đồ thị, tìm cây khung ngắn nhất bằng
hai thuật toán Kruskal và Prim và tìm đường đi ngắn nhất bằng thuật toán Dijkstra.
Đồng thời cũng tạo ra một giao diện trực quan để giúp cho người dùng có hướng
tiếp cận dễ dàng hơn cũng như có cách nhìn trực quan hơn về các thuật toán này. lOMoAR cPSD| 22014077 1 NỘI DUNG
1 GIỚI THIỆU THUẬT TOÁN.
1.1 Thuật toán xét liên thông.
Định nghĩa: là đồ thị chỉ có 01 thành phần liên thông, hay nói cách khác
giữa 2 đỉnh bất kỷ trong đồ thị luôn có đường đi từ đỉnh này tới đỉnh kia (trực tiếp
hay gián tiếp qua các đỉnh trung gian).
Một đồ thị không liên thông sẽ bao gồm nhiều đồ thị con liên thông, các đồ
thị con này được gọi là các thành phần liên thông (connected component).
Các thành phần liên thông: Một đồ thị không liên thông sẽ bao gồm nhiều
đồ thị con liên thông, các đồ thị con này được gọi là các thành phần liên thông.
Đồ thị liên thông khi và chỉ khi có một thành phần liên thông.
1.2 Thuật toán BFS – DFS.
1.2.1 Thuật toán BFS
Định nghĩa: Trong lý thuyết đồ thị, tìm kiếm theo chiều rộng (BFS) là một
thuật toán tìm kiếm trong đồ thị trong đó việc tìm kiếm chỉ bao gồm 2 thao tác:
(a) cho trước một đỉnh của đồ thị; (b) thêm các đỉnh kề với đỉnh vừa cho vào danh
sách có thể hướng tới tiếp theo. Có thể sử dụng thuật toán tìm kiếm theo chiều
rộng cho hai mục đích: tìm kiếm đường đi từ một đỉnh gốc cho trước tới một đỉnh
đích, và tìm kiếm đường đi từ đỉnh gốc tới tất cả các đỉnh khác.
Các bước duyệt đồ thị như sau:
Cho G là đồ thị liên thông với tập đỉnh {v1, v2, ..., vn} Bước
1. Xuất phát từ 1 đỉnh cho trước nào đó.
Bước 2. Xử lý đỉnh này và đánh dấu để không xử lý lần sau.
Bước 3. Đưa tất cả các đỉnh kề với nó vào danh sách xử lý và lần lượt xử lý
các đỉnh kề với đỉnh đang xét
Bước 4. Quay lại Bước 2 cho đến khi không còn đỉnh trong danh sách.
Cây T thu được là cây khung của đồ thị. lOMoAR cPSD| 22014077 2
1.2.2 Thuật toán DFS
Định nghĩa: Tìm kiếm ưu tiên chiều sâu hay tìm kiếm theo chiều sâu ( Depth-
first search - DFS) là một thuật toán duyệt hoặc tìm kiếm trên một cây hoặc một
đồ thị. Thuật toán khởi đầu tại gốc (hoặc chọn một đỉnh nào đó coi như gốc) và
phát triển xa nhất có thể theo mỗi nhánh.
Thông thường, DFS là một dạng tìm kiếm thông tin không đầy đủ mà quá
trình tìm kiếm được phát triển tới đỉnh con đầu tiên của nút đang tìm kiếm cho tới
khi gặp được đỉnh cần tìm hoặc tới một nút không có con. Khi đó giải thuật quay
lui về đỉnh vừa mới tìm kiếm ở bước trước. Trong dạng không đệ quy, tất cả các
đỉnh chờ được phát triển được bổ sung vào một ngăn xếp.
Các bước duyệt đồ thị như sau:
Cho G là đồ thị liên thông với tập đỉnh {v1, v2, ..., vn} Bước
1: Xuất phát từ 1 đỉnh cho trước nào đó.
Bước 2: Xử lý đỉnh này và đánh dấu đã duyệt để không xử lý lần sau.
Bước 3: Đưa tất cả các đỉnh kề với nó vào danh sách xử lý và chọn 1 đỉnh để xử lý tiếp theo.
Bước 4: Quay lại Bước 2 cho đến khi không còn đỉnh trong danh sách.
Cây T thu được là cây khung của đồ thị. 1.3 Thuật toán Prim
Định Nghĩa:Thuật toán Prim là một thuật toán tham lam để tìm cây bao trùm
nhỏ nhất của một đồ thị vô hướng có trọng số liên thông. Nghĩa là nó tìm một tập
hợp các cạnh của đồ thị tạo thành một cây chứa tất cả các đỉnh, sao cho tổng trọng
số các cạnh của cây là nhỏ nhất.
Cho G = (V, E) là một đồ thị liên thông có trọng số gồm n đỉnh.
Bước 1: Chọn tùy ý một đỉnh bất kỳ v ∈ V và khởi tạo: Y = {v} và T = ∅.
Bước 2: Trong số những cạnh e = (v, w), trong đó v ∈ Y và w ∈ V\Y, ta
chọn cạnh có độ dài nhỏ nhất.
Bước 3: Gán Y = Y ∪ {w} và T = T ∪ {e}
Bước 4: Nếu T đủ n – 1 phần tử thì dừng, ngược lại làm tiếp bước 2.
T chính là cây khung nhỏ nhất. lOMoAR cPSD| 22014077 3
1.4 Thuật Toán Kruskal.
Định nghĩa: Thuật toán Kruskal là một thuật toán trong lý thuyết đồ thị để
tìm cây bao trùm nhỏ nhất của một đồ thị liên thông có trọng số. Nói cách khác,
nó tìm một tập hợp các cạnh tạo thành một cây chứa tất cả các đỉnh của đồ thị và
có tổng trọng số các cạnh là nhỏ nhất.
Cho G = (V, E) là một đồ thị liên thông có trọng số gồm n đỉnh.
Bước 1. Sắp xếp các cạnh theo thứ tự độ dài tăng dần và khởi tạo: T = ∅
Bước 2. Lần lượt lấy từng cạnh e trong danh sách đã sắp xếp. Nếu T + {e}
không tạo thành chu trình thì gán T = T + {e}
Bước 3. Nếu T đủ n – 1 phần tử thì dừng, ngược lại làm tiếp bước 2.
T chính là cây khung nhỏ nhất.
1.5 Thuật Toán Dijkstra.
Định nghĩa: Thuật toán Dijkstra là là một thuật toán giải quyết bài toán
đường đi ngắn nhất từ một đỉnh đến các đỉnh còn lại của đồ thị có hướng
không có cạnh mang trọng số không âm. Thuật toán thường được sử dụng
trong định tuyến với một chương trình con trong các thuật toán đồ thị hay
trong công nghệ Hệ thống định vị toàn cầu. Bước 1: Gán T = X
Length[x]=0; Length[k]=+, kX\{x} LastV[k]=-1, ∀k∈X.
Bước 2: Nếu yT thì dừng.
Bước 3: Chọn đỉnh vT sao cho Length[v] nhỏ nhất và loại v khỏi T: T =T\{v}.
Bước 4: ∀k∈T và có cạnh nối từ v đến k,
Nếu Length[k]>Length[v]+L thì vk Length[k]=Length[v]+ Lvk LastV[k]=v Cuối nếu Cuối
Bước 5: Tiếp tục với Bước 2. lOMoAR cPSD| 22014077 4
2 GIỚI THIỆU VỀ CHƯƠNG TRÌNH.
2.1 Tổng quan về giao diện.
Hình 2. 1 Giao diện chương trình • Đồ Thị
- Chức năng đồ thị dùng để vẽ đồ thị và mô phỏng các thuật toán.
• Thông Tin Sản Phầm
- Giới thiệu sơ về chương trình của nhóm
- Cho biết các thông tin của từng thành viên trong nhóm
- Cho thông tin liên hệ của nhóm trưởng (nếu cần )
CODE Giao Diện Chính
public partial class Form1 : Form { //
private IconButton currentBtn; private Panel leftBorderBtn;
private Form currentChildForm; //constructor // public Form1() { InitializeComponent(); leftBorderBtn = new Panel();
leftBorderBtn.Size = new Size(7, 69);
panelMenu.Controls.Add(leftBorderBtn); this.Text = string.Empty; this.ControlBox = false; this.DoubleBuffered = true; this.MaximizedBounds =
Screen.FromHandle(this.Handle).WorkingArea; lOMoAR cPSD| 22014077 5 }
// Hàm RGBcolor để lưu màu của giao diện. private struct RGBcolors {
public static Color color1 = Color.FromArgb(172, 126, 241);
public static Color color2 = Color.FromArgb(249, 118, 176);
public static Color color3 = Color.FromArgb(253, 138, 114);
public static Color color4 = Color.FromArgb(95, 77, 221);
public static Color color5 = Color.FromArgb(249, 88, 115);
public static Color color6 = Color.FromArgb(24, 161, 251); } //methods
// thay đổi hoạt ảnh button khi chọn button “Đồ Thị” hoặc “Thông tin sản phảm”
private void ActivateButton(object senderBtn, Color color) { if (senderBtn != null) { DisableButton(); //button
currentBtn = (IconButton)senderBtn;
currentBtn.BackColor = Color.FromArgb(37, 36, 81);
currentBtn.ForeColor = color; currentBtn.TextAlign =
ContentAlignment.MiddleCenter;
currentBtn.IconColor = color;
currentBtn.TextImageRelation =
TextImageRelation.TextBeforeImage; currentBtn.ImageAlign = ContentAlignment.MiddleRight; //left border button
leftBorderBtn.BackColor = color;
leftBorderBtn.Location = new Point(0, currentBtn.Location.Y);
leftBorderBtn.Visible = true; leftBorderBtn.BringToFront(); //iconTittle
iconcurrentChildform.IconChar = currentBtn.IconChar;
iconcurrentChildform.IconColor = currentBtn.IconColor;
lblTittleChildForm.Text = currentBtn.Text; } }
// hàm giao diện con để chuyển giao diện thành xem thông tin hay đồ
thị. private void openChildForm(Form childForm) { lOMoAR cPSD| 22014077 6
if (currentChildForm != null) { currentChildForm.Close(); }
currentChildForm = childForm; childForm.TopLevel = false;
childForm.FormBorderStyle = FormBorderStyle.None;
childForm.Dock = DockStyle.Fill;
pnlDesktop.Controls.Add(childForm); pnlDesktop.Tag = childForm; childForm.BringToFront(); childForm.Show(); } //Trả về lại ban đầu private void DisableButton() { if (currentBtn != null) {
currentBtn.BackColor = Color.FromArgb(31, 30, 68);
currentBtn.ForeColor = Color.Gainsboro; currentBtn.TextAlign =
ContentAlignment.MiddleCenter;
currentBtn.IconColor = Color.Gainsboro;
currentBtn.TextImageRelation =
TextImageRelation.ImageBeforeText;
currentBtn.ImageAlign = ContentAlignment.MiddleLeft;
leftBorderBtn.Visible = false;
iconcurrentChildform.IconChar = IconChar.Home;
lblTittleChildForm.Text = "Home";
iconcurrentChildform.IconColor = Color.MediumPurple; } }
//mở ra giao diện đồ thị private void
btnGraph_Click(object sender, EventArgs e) {
ActivateButton(sender, RGBcolors.color1);
openChildForm(new FormGraph());
panelMenu.BorderStyle = BorderStyle.FixedSingle; }
[DllImport("user32.DLL", EntryPoint = "ReleaseCapture")]
private extern static void ReleaseCapture();
[DllImport("user32.DLL", EntryPoint = "SendMessage")]
private extern static void SendMessage(System.IntPtr hWnd,
int wMsg, int wParam, int lParam);
private void pnlTittle_MouseDown(object sender, MouseEventArgs e) { ReleaseCapture();
SendMessage(this.Handle, 0x112, 0xf012, 0); }
//reset lại trang giao diện private void
logoHCMUE_Click(object sender, EventArgs e) lOMoAR cPSD| 22014077 7 { if(currentChildForm != null) { currentChildForm.Close(); } DisableButton(); }
//thoát khoi chương trình private void
btnClose_Click(object sender, EventArgs e) { Application.Exit(); }
//mở rộng hoặc thu nhỏ của sổ chương trình
private void btnZoom_Click(object sender, EventArgs e) {
if (WindowState == FormWindowState.Normal) {
btnZoom.IconChar = IconChar.WindowRestore;
WindowState = FormWindowState.Maximized; } else {
btnZoom.IconChar = IconChar.WindowMaximize;
WindowState = FormWindowState.Normal; }
} //ẩn chương trình private void
btnhide_Click(object sender, EventArgs e) {
WindowState = FormWindowState.Minimized; }
// Mở giao diện Thông Tin Sản Phẩm
private void btnThongTin_Click(object sender, EventArgs e) {
ActivateButton(sender, RGBcolors.color1);
openChildForm(new ThongTinSanPham());
panelMenu.BorderStyle = BorderStyle.FixedSingle; }
2.2 Các file xử lí thuật toán trong chương trình.
Chúng ta sẽ giới thiệu những file, hàm sự kiện còn lại trong chương trình.
Egde.cs: Định nghĩa cạnh của đồ thị và các hàm bổ trợ có liên quan
FS-Graph.cs: Xử lí thuật toán trong chương trình
NodeGraphs.cs: Định nghĩa đỉnh và các hàm bổ trợ của liên quan 2.3 FormGraph.cs 2.3.1 Vẽ Đồ Thị a) Vẽ Đỉnh lOMoAR cPSD| 22014077 8
Hình 2.3.1.a Vẽ Đỉnh
Dùng sự kiện Mouseclick panel để tạo ra một button đại diện cho đỉnh Code :
private void pnlVeDoThi_MouseClick(object sender, MouseEventArgs e) { if (Checkiconbtn == true) { Button btn = new Button(); btn.Width = 30; btn.Height = 30;
btn.Location = new Point(e.X, e.Y);
btn.Name = string.Format("{0},{1}", e.X, e.Y);
btn.Text = string.Format("{0}", sodinh++);
btn.Click += new EventHandler(getToaDo);
pnlVeDoThi.Controls.Add(btn); Nod.x = e.X; Nod.y = e.Y; ListarrNod.Add(Nod);
Nod = new Class_FS_Graph.NodeGraph(); } b) Vẽ Cạnh
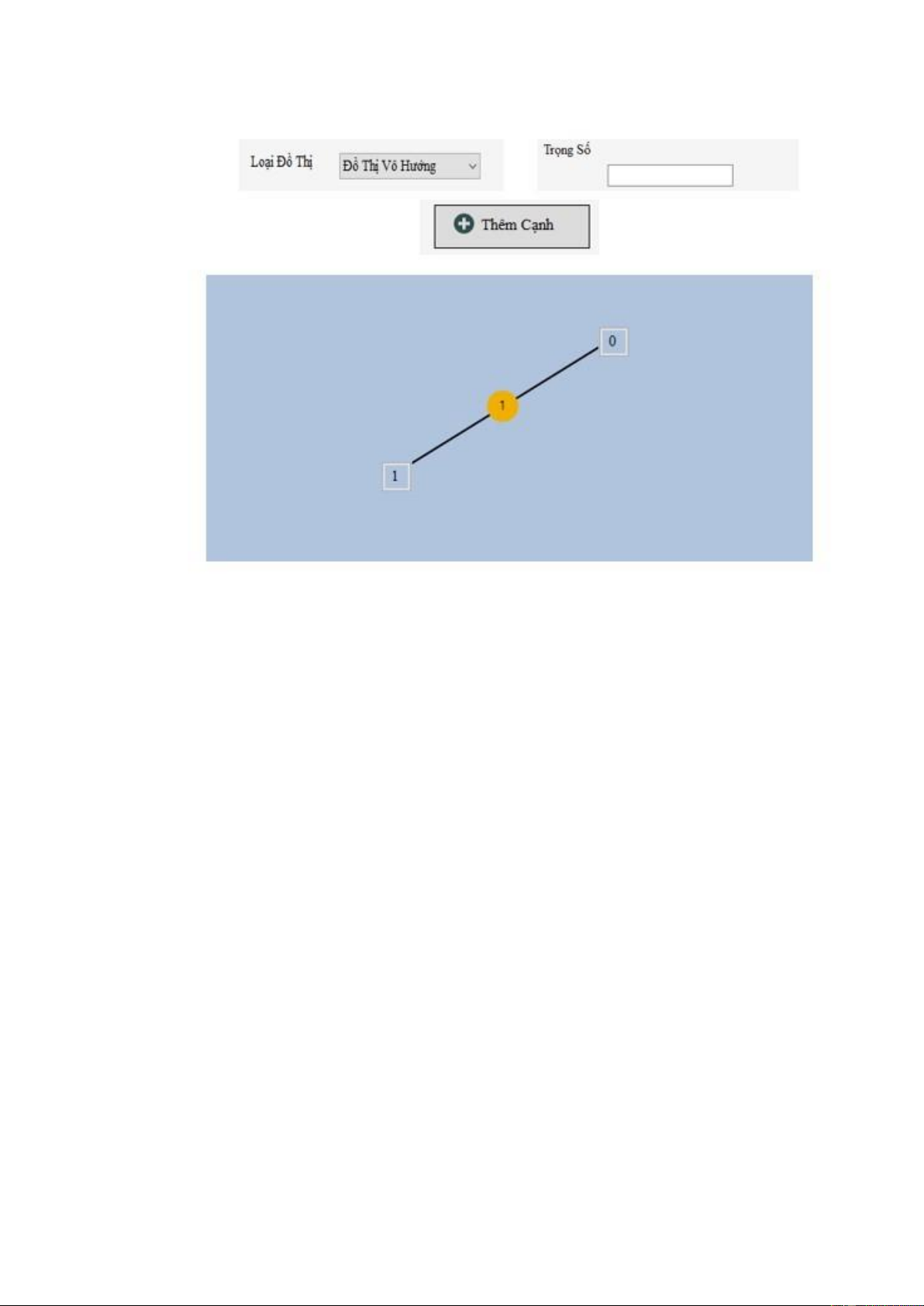
Thông qua một button “Thêm Cạnh” để tạo liên kết giữa 2 đỉnh mà người
dùng chọn, với 2 lựa chọn là cạnh vô hướng hoặc cạnh có hướng với trọng
số được nhập từ người dùng hoặc chương trình mặt định là 1 lOMoAR cPSD| 22014077 9
Hình 2.3.1.b Vẽ Cạnh
private void btnThemCanh_Click(object sender, EventArgs e) {
if(txtTrongSo.Text == "0" && cbxChucNang.Text != "Dijkstra") {
MessageBox.Show("Trọng số bằng 0 không thể vẽ cạnh",
"Thông Báo", MessageBoxButtons.OK, MessageBoxIcon.Warning);
Egdes = new Class_FS_Graph.Egde();
Nod = new Class_FS_Graph.NodeGraph(); btncreate = null; dx = dy = dx1 = dy1 = 0; d1 = d2 = -1; Dinh1 = Dinh2 = -1;
labTrongSo.Text = "Trọng Số";
txtTrongSo.Text = String.Empty;
txtKetqua.Text = "Kết Quả"; return; } VeDoThi(Egdes);
Egdes = new Class_FS_Graph.Egde();
Nod = new Class_FS_Graph.NodeGraph(); btncreate = null; dx = dy = dx1 = dy1 = 0; d1 = d2 = -1; lOMoAR cPSD| 22014077 10 Dinh1 = Dinh2 = -1;
labTrongSo.Text = "Trọng Số";
txtKetqua.Text = "Kết Quả";
txtTrongSo.Text =String.Empty; } c) Xóa cạnh.
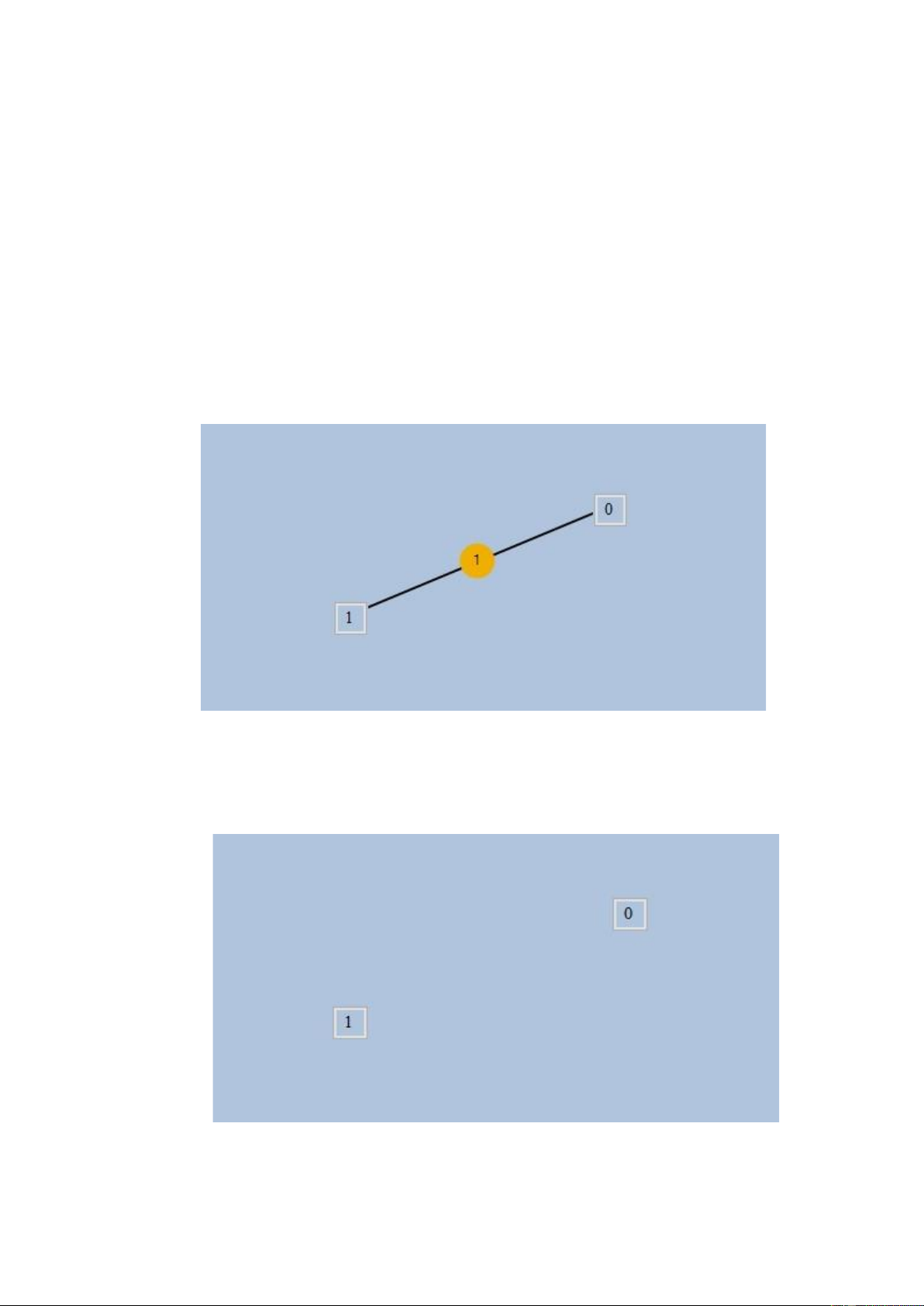
Người dùng lựa chọn cạnh mà mình muốn xóa và sau đó click vào button “Xóa Cạnh” Cạnh trước khi xóa:
Hình 2.3.1.c Trước khi xóa Cạnh Cạnh sau khi xóa:
Hình 2.3.1.d Sau khi xóa Cạnh Code: pnlVeDoThi.Invalidate(); pnlVeDoThi.Refresh(); int n = ListarrEgde.Count; lOMoAR cPSD| 22014077 11
for (int i = 0; i < ListarrEgde.Count; i++) {
if (cbxLoaiDoThi.Text == "Đồ Thị Vô Hướng") {
if (!ListarrEgde[i].SoSanhEgdeVH(Egdes)) { VeDoThi1(ListarrEgde[i]); } else { ListarrEgde.RemoveAt(i); i = i - 1; Matrix[d1, d2] = 0; Matrix[d2, d1] = 0; } }
if (cbxLoaiDoThi.Text == "Đồ Thị Có Hướng") {
if (!ListarrEgde[i].SoSanhEgdeCH(Egdes)) { VeDoThi1(ListarrEgde[i]); } else { ListarrEgde.RemoveAt(i); i = i - 1; Matrix[d1, d2] = 0; }
if (!CheckHuong && ListarrEgde.Count >= 0) { CheckHuong =
ListarrEgde[i].CheckHuong(Egdes); } } } d) Chức năng Xóa Đỉnh
Người dùng có thể xóa đỉnh tại các đỉnh mình muốn xóa và sau đó click vào button “Xóa Đỉnh” Đỉnh trước khi xóa: lOMoAR cPSD| 22014077 12
Hình 2.3.1.e Trước khi xóa Đỉnh Đính sau khi xóa:
Hình 2.3.1.f Sau khi xóa Đỉnh
Sau khi xóa một đỉnh, các cạnh nối của đỉnh đó sẽ tự động xóa đi và các đỉnh còn
lại sẽ tự động thay đổi số sao cho phù hợp với đồ thị.
for (int i = 0; i < ListarrNod.Count; i++) {
if (!Nod.SoSanhNode(ListarrNod[i])) { Button btn = new Button(); btn.Width = 30; btn.Height = 30; btn.Location = new Point(ListarrNod[i].x, ListarrNod[i].y);