Tìm giá trị lớn nhất nhỏ nhất của hàm số trên khoảng | Chuyên đề Toán 12

Chuyên đề Toán 12: Tìm giá trị lớn nhất nhỏ nhất của hàm số trên khoảng
A. Giá trị lớn nhất, nhỏ nhất của hàm số
Cho hàm số y  f x xác định trên tập D .
Số M được gọi là giá trị lớn nhất (GTLN) của hàm số y  f x trên tập D
x D : f x  M nếu  D
x  D : f x  M  0  0 
Kí hiệu M  max f x D
Số m được gọi là giá trị nhỏ nhất (GTNN) của hàm số y  f x trên tập nếu:
x D : f x  m 
x  D : f x  m  0  0 
Kí hiệu m  min f x D
B. Cách tìm GTLN, GTNN của hàm số trên tập xác định
Để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  f x trên tập xác định ta làm như sau:
Bước 1. Tìm tập xác định D
Bước 2. Tìm f 'x
Bước 3. Tại các điểm x mà tại đó f 'x  hoặc các điểm x mà tại đó f 'xi  i  0 i i
không xác định nhưng hàm số vẫn xác định tại điểm đó.
Bước 4. Lập bảng biến thiên (Hoặc một biểu đồ có cơ chế giống bảng biến thiên).
Bước 5. Kết luận.
C. Cách tìm GTLN, GTNN của hàm số trên khoảng Phương pháp giải
Để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  f x trên đoạn a;b ta làm như sau.
Bước 1. Tìm đạo hàm f 'x
Bước 2. Xác định tất cả các nghiệm x ; x ;. .; x trên  ;
a b mà tại đó f 'x  0 và tất 1 2 n
cả các điểm   a b làm cho f 'x không xác định. i  ; 
Bước 3. Tính A  lim f x;B  lim f x; f x f  .   i  ;  i  xa xb
Bước 4. So sánh các giá trị tính được và kết luận M  max f x;m  min f x  a;b a;b
Nếu giá trị lớn nhất (nhỏ nhất) là A hoặc B thì kết luận không có giá trị lớn nhất (nhỏ nhất) Chú ý:
Hàm số liên tục trên một khoảng có thể không có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng đó.
D. Cách tìm giá trị lớn nhất nhỏ nhất của hàm số trên tập A bất kì Phương pháp giải
Để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  f x trên tập A ta làm như sau.
Bước 1. Tìm các điểm hàm số không xác định trên tập A.
Bước 2. Tính f 'x. Tìm các điểm x  A mà tại đó f 'x  0 hoặc các điểm mà tại i
đó f 'x không xác định nhưng hàm số vẫn xác định tại điểm đó.
Bước 3. Tính f x với x là các điểm thuộc bước 2 hoặc các điểm ở đầu mút i  i
ngoạc vuông và giới hạn của hàm số tại các điểm hàm số không xác định (giới
hạn 1 bên hoặc giới hạn cả 2 bên, tùy thuộc vào tập A) hoặc giới hạn tại các điểm
dạng ngoặc tròn của tập A (kể cả  ).
Bước 4. So sánh các giá trị tìm được và kết luận giá trị lớn nhất và nhỏ nhất với
các lưu ý quan trọng như sau:
Giá trị lớn nhất của hàm số y  f x khi x A phải thỏa mãn tất cả các điều kiện sau:
 Là giá trị y lớn nhất khi x A
 Giá trị y lớn nhất đó phải là 1 số cụ thể (không được phép là  ).
 Tồn tại giá trị x cụ thể (không được phép là vô cực hoặc giới hạn) để đạt 0 được GTLN đó.
Giá trị nhỏ nhất của hàm số y  f x khi x A phải thỏa mãn tất cả các điều kiện sau:
 Là giá trị y nhỏ nhất khi x A
 Giá trị y nhỏ nhất đó phải là 1 số cụ thể (không được phép là  ).
 Tồn tại giá trị x cụ thể (không được phép là vô cực hoặc giới hạn) để đạt 0 được GTNN đó.
Ví dụ. Tìm giá trị lớn nhất của hàm số 3   
y  3sin x  4sin x trên khoảng ;    ? 2 2    Hướng dẫn giải
Đặt sin x  t  t 1;  1 . Khi đó: f t 2 '  1  2t  3 f t 1 '  0  t   2 So sánh 1 f    và 1 f    ta thấy GTLN là 1 f      1. 2       2   2 
Ví dụ: Giá trị lớn nhất của hàm số 2
y  x  4x trên khoảng (0; 3) Hướng dẫn giải
Tập xác định D  0;4 Xét hàm số 2
y  x  4x trên khoảng (0;3) Ta có: x  2 y '  2 x  4x
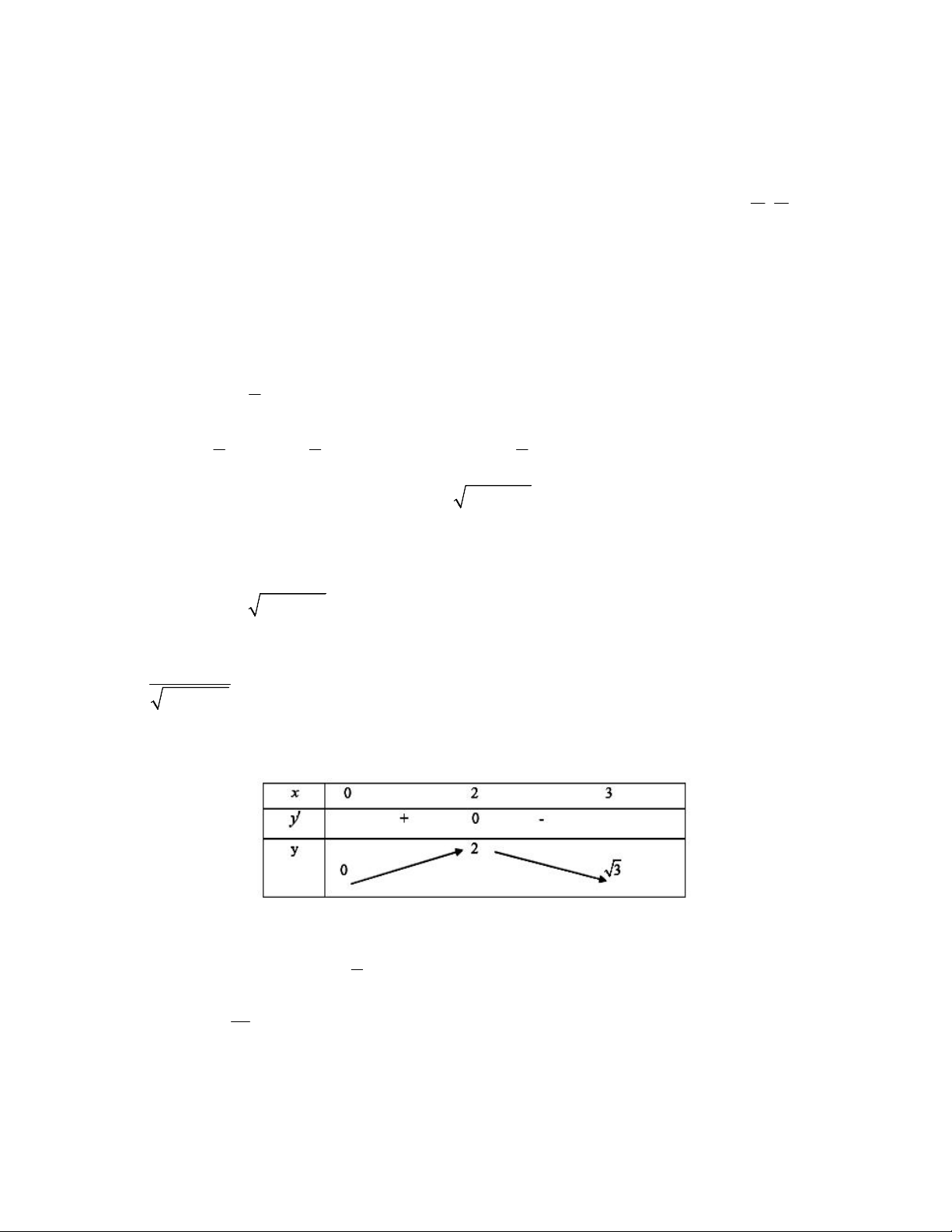
y '  0  x  2 Ta có bảng biến thiên:
Trên khoảng (0; 3) giá trị lớn nhất của hàm số y = 2 Ví dụ: Cho hàm số 3 3 2
y  x  x 1. Gọi M là giá trị lớn nhất của hàm số trên 2 khoảng  11 25;    . Tìm M. 10    Hướng dẫn giải Ta có: 2
y '  3x  3x  x  1
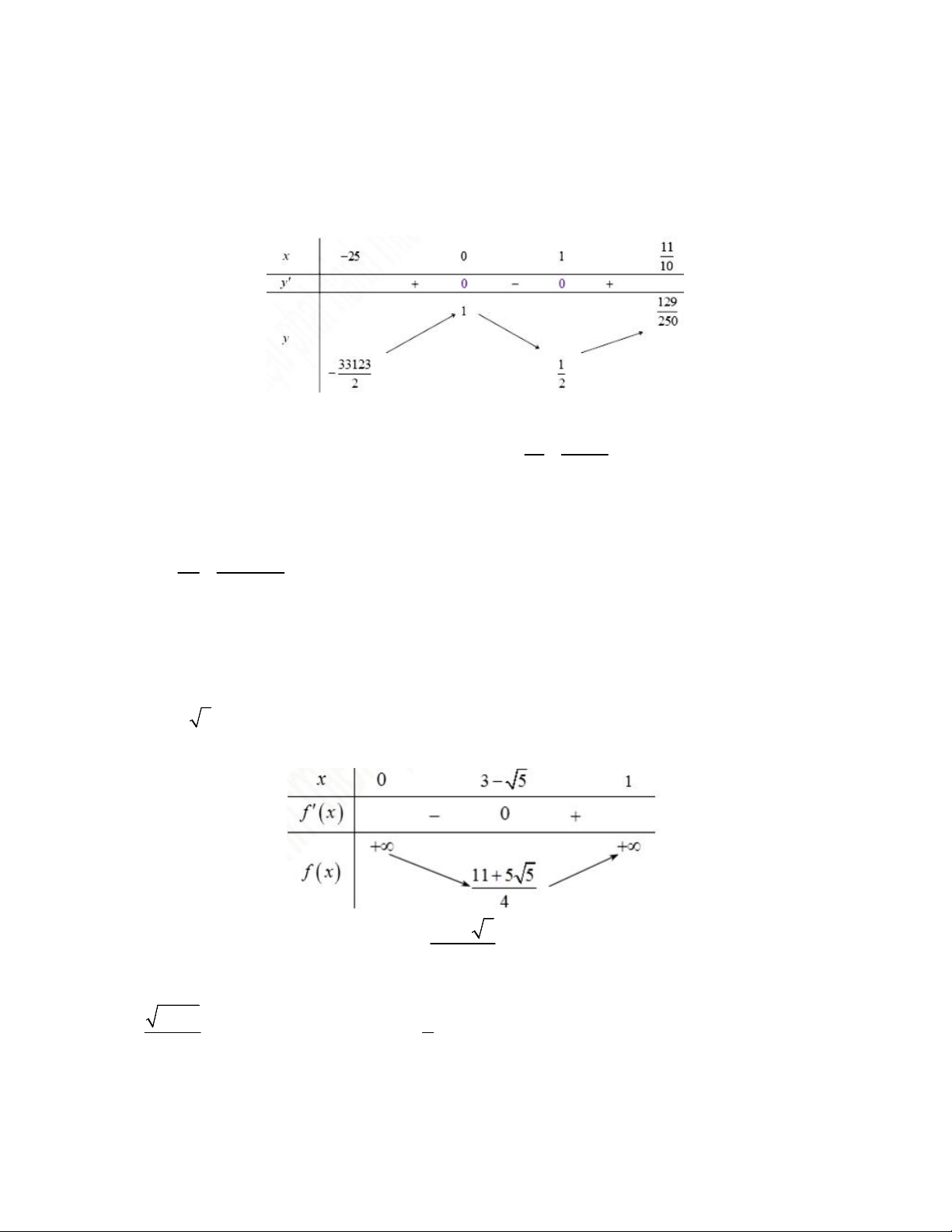
y '  0  x  0 Ta có bảng biến thiên
Từ bảng biến thiên ta có M = 1
Ví dụ: Tìm giá trị nhỏ nhất của hàm số f x 2 1   trên khoảng (0; 1)? 2 x 2x  2 Hướng dẫn giải
Hàm số xác định và liên tục trên (0; 1) ta có:  f  x 4 1 '   3 x 2 x  2 1
f ' x  0 3 2
 x 8x 16x 8  0   x  2 2
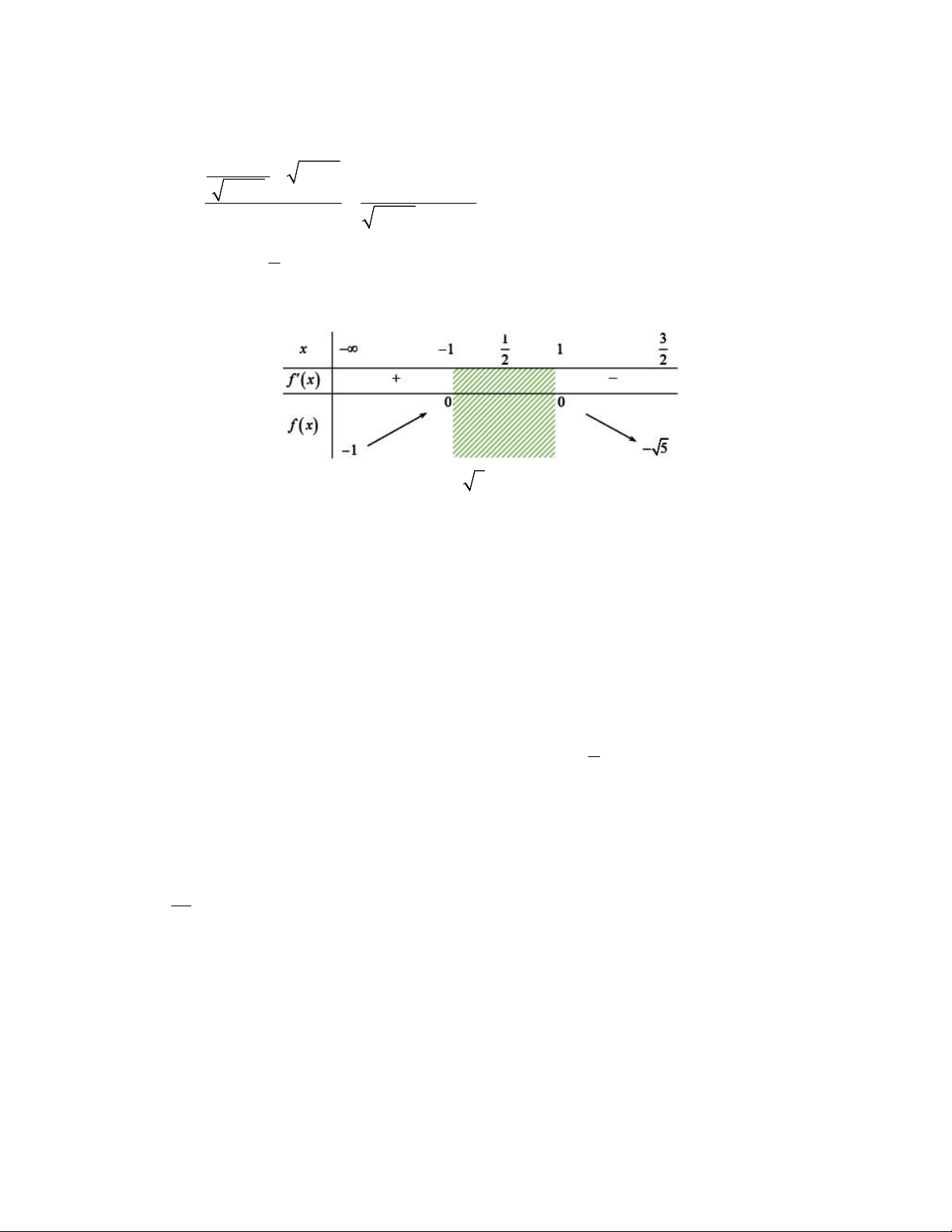
x  6x  4  0  x  3 5 Lập bảng biến thiên:
Từ bảng biến thiên ta có:  f x 11 5 5 min  0; 1 4
Ví dụ: Gọi M và m lần lượt là giá trị lớn nhất và giá tị nhỏ nhát của hàm số 2 x 1 y  trên tập D    3 ; 1 1;     
. Tính giá trị H của m.M. x  2  2   Hướng dẫn giải
Tập xác định của hàm số y là:  ;    1 1; \  2 xx  2 2  x 1 2 x 1 2x 1   Ta có: y ' x  22 2
x 1x  22 1
y '  0  x  2
Ta có bảng biến thiên như sau:
Từ bảng biến thiên ta được: M  0,m   5  H  . m M  0
Ví dụ. Giá trị lớn nhất của hàm số 3
y  x  3x 1trên khoảng 0; Hướng dẫn giải Ta có: 2 y '  3  x  3
 x 1tm
y '  0  x  1  L
=> Giá trị lớn nhất của hàm số trên khoảng đã cho bằng 3 khi x = 1
Ví dụ: Giả sử m là giá trị nhỏ nhất của hàm số 4
y  x  trên khoảng 0;. Tính x giá trị của m. Hướng dẫn giải Ta có: 4 y ' 1 2 x
 x  2tm
y '  0  x  2  L
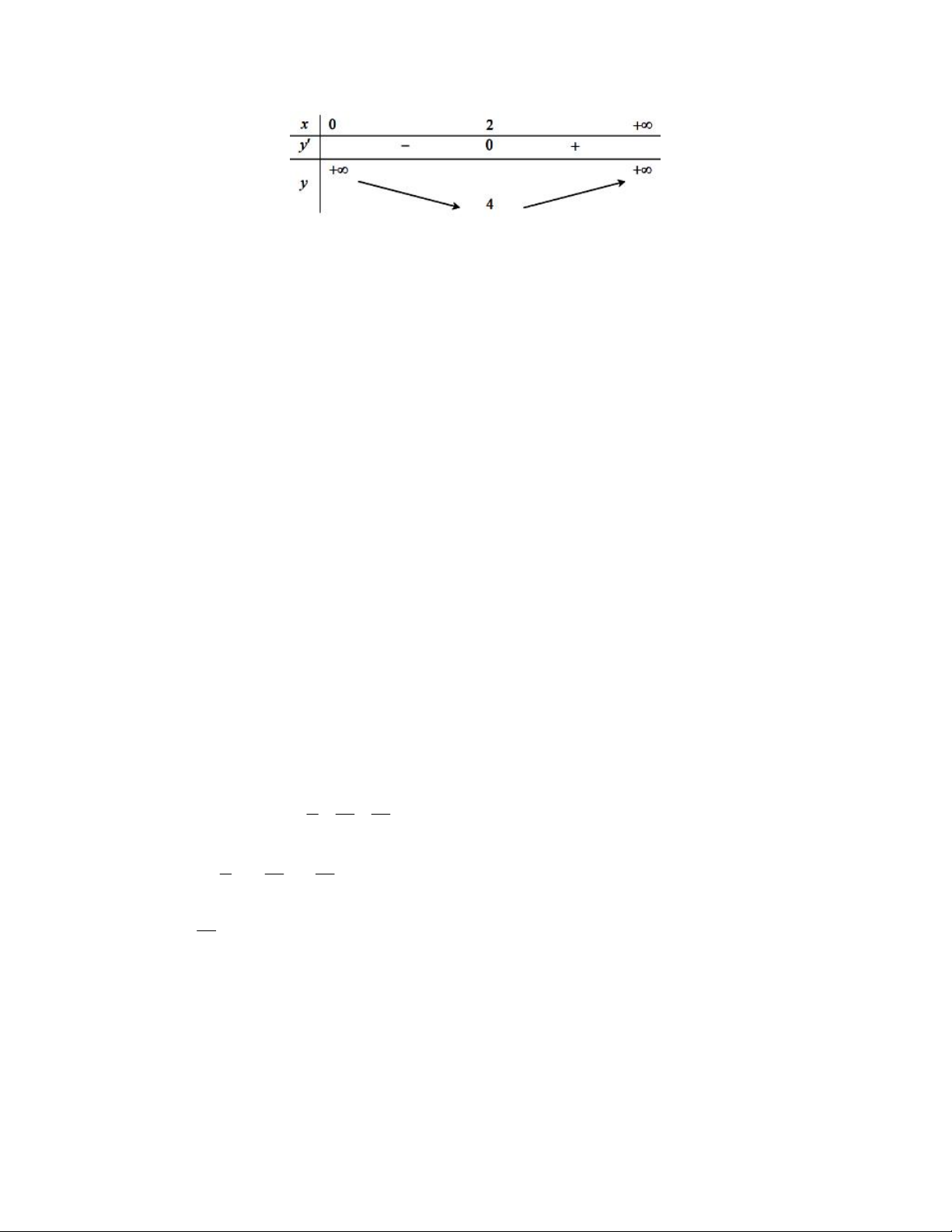
Ta có bảng biến thiên như sau:
=> Giá trị nhỏ nhất của hàm số bằng 4 => y(2) = 4 => m = 4
Ví dụ: Xác định giá trị nhỏ nhất của biểu thức P   2 2
4 m  n  m n, biết
   3    3 3 y x m
x n  x với ,
m n là tham số và hàm số đồng biến trên  ;   . Hướng dẫn giải Ta có:
y '  3 x  m2  3 x  n2 2  3x 2
 3x  2m  n 2 2
x  m  n   
Hàm số đã cho đồng biến trên  y '  0; x  
   m  n2 2 2 '
 m  n  0  mn  0 Ta lại có: P   2 2
4 m  n  m  n
 m  n2 4
 8mn  m  n    2
4 m n  m  n
 m  n2 
m n 1 1 1 4 2.2 .   4 16 16 2  
m n 1 1 1 2      4   16 16 1  P   min 16