Tìm tiệm cận của đồ thị hàm số Toán 12 | Chuyên đề Toán 12

Tiệm cận của đồ thị hàm số
A. Đường tiệm cận ngang
Cho đồ thị hàm số y  f x có tập xác định D.
Nếu lim f x  y hoặc lim f x  y thì đường thẳng y  y được gọi là tiệm cận 0 x 0 x 0
ngang của đồ thị hàm số.
Chú ý. Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ
thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
lim f x  y ; lim f x  y 0   0 x x
Cách tìm tiệm cận ngang của đồ thị hàm số Phương pháp giải
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính các giới hạn của hàm số đó tại vô cực (nếu có). Từ đó xác định đường tιệm cận ngang.
Công thức tính tiệm cận ngang của hàm phân thức hữu tỉ: Hàm số Tiệm cận ngang m m 1
a x  a x   . . a m = n a 0 1 m y  0 y  n n 1
b x  b x   . . b b 0 1 m 0
a  0,b  0;m 1;n 1;m,n  m > n Không có tiệm cận 0 0 ngang m < n y = 0
Công thức tính tiệm cận ngang của hàm phân thức vô tỷ Hàm số Tiệm cận ngang ax  b y  c < 0 Không có tiệm cận 2
cx  dx  e ngang a,c  0 c > 0 a y   c
B. Đường tiệm cận đứng
Cho đồ thị hàm số y  f x có tập xác định D.
Nếu lim f x   hoặc lim f x   thì đường thẳng x  x là đường tiệm cận     x 0  0 x x 0 x
đứng của đồ thị hàm số.
Chú ý. Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ
thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
lim f  x   ;
 lim f  x   x    0 x x 0 x
C. Đường tiệm cận xiên
- Điều kiện tìm đường tiệm cận xiên: lim f x   hoặc lim f x   x x
Tìm tiệm cận xiên có 2 cách:
Cách 1: Phân tích y  f x thành dạng y  ax  b  gx với lim gx  0 thì x
y  ax  b,a  0 là đường tiệm cận xiên của đồ thị hàm số y  f x .
Cách 2: Giả sử tiệm cận xiên của đồ thị hàm số là y  ax  b , ta sẽ tìm a, b theo  f x  a  lim công thức: x  x
b  lim  f 
 x  ax x 
Khi đó đường thẳng y  ax  b,a  0 là phương trình đường tiệm cận xiên của đồ thị hàm số.
E. Đường tiệm cận của các hàm thông dụng  : d TCÐ x   a. Hàm số ax  b y 
,ad  bc  0có  c cx  d   : a TCN y   c  p 2  TCÐ: x  b. Hàm số
ax  bx  c r y   Ax  B  ,ap  0 có  c  q px  q px  q T
 CN : y  Ax   B Px
c. Hàm số hữu tỉ: y 
không chia hết có đường tiệm cận xiên khi bậc của tử Qx
lớn hơn bậc của mẫu một bậc.
F. Bài tập đường tiệm cận của hàm số 2 Ví dụ. Cho hàm số x  4 y 
. Xác định các đường tiệm cận của đồ thị hàm số? x 1 Hướng dẫn giải
Tập xác định: D  ;22;
Ta thấy rằng x = 1 không thuộc D => Đồ thị hàm số không có tiệm cận đứng. 4 2 x 1 2 x  4 x x lim y  lim  lim  lim x x x 1 x  1 1 x  x x   x     lim y 1  x   lim y  1 x
=> y = 1 và y = -1 là hai tiệm cận ngang của đồ thị hàm số.
Ví dụ. Xác định các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số 2 x 1  x y  ? 2 x 9  4 Hướng dẫn giải 2  x  9   0 Tập xác định: 
 x; 
3  3; \   5 2  x  9  4
Khi đó lim f x  0; lim f x  2 x x
=> Đồ thị hàm số có hai tiệm cận ngang
Mặt khác lim f x   ;
 lim f x   x 5 x 5  
=> Đồ thị hàm số có hai tiệm cận đứng
Vậy đồ thị hàm số đã cho có 4 đường tiệm cận.  2 x 1  khi x  1
Ví dụ. Cho hàm số     x y f x  
. Xác định số đường tiệm cận của  2x khi x < 1  x 1
đồ thị hàm số y = f(x)? Hướng dẫn giải Ta có:   2 lim  lim x f x   x 1 x 1   x 1
=> Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số. 2x 2 lim  lim
 2 => y = 2 là tiệm cận ngang của đồ thị hàm số
x x 1 x 1 1 x 2 x 1 1 lim  lim 2 
1 => đường thẳng y = 1 là tiệm cận ngang của đồ thị 2 x x x  x hàm số. 2 Ví dụ. Cho hàm số
x  x  3  2x 1 y 
. Trong các khẳng định sau, khẳng định 3 2
x  2x  x  2
nào là khẳng định đúng?
A. Đồ thị hàm số không có tiệm cận đứng, không có tiệm cận ngang.
B. Đồ thị hàm số không có tiệm cận đứng và có đúng một tiệm cận ngang.
C. Đồ thị hàm số có đúng ba tiệm cận đứng và hai tiệm cận ngang.
D. Đồ thị hàm số có đúng hai tiệm cận đứng và một tiệm cận ngang. Hướng dẫn giải  1  1 2    3  0 x  x x x   2  2 Điều kiện     2x 1 0
 x  2   x  2  3 2 x 2x x 2 0  x 1        x  1      Từ điều kiện ta có:
 2x  x32x1
y   2x 3x2x1 2xx3 2x1 2 x  3x  2
y   2x 3x2x1 2xx3 2x1 1
y  x 1 2xx3 2x1
Đồ thị hàm số không có tiệm cận đứng Mặt khác f x 1 lim  lim  0 x x     2 1 1 3 2 1
x .1  1    2 2  x  x x x x   
=> y = 0 là tiệm cận ngang của đồ thị hàm số
Không tồn tại lim f x x
Vậy đồ thị hàm số không có tiệm cận đứng và có đúng một tiệm cận ngang.
Ví dụ. Cho hàm số y  f x có bảng biến thiên như hình vẽ dưới đây.
Xác sịnh số đường tiệm cận của đồ thị hàm số 2 y  ?
f x  2018 Hướng dẫn giải
Phương trình f x  2018 có 2 nghiệm phân biệt => Đồ thị hàm số 2 y 
có 2 đường tiệm cận đứng.
f x  2018 Khi 2 2
x   thì y  5  y  
f x  2018 2  013 Khi x 2 2
  thì y  5  y  
f x  2018 2  013 Vậy đồ thị hàm số 2 y  có 1 tiệm cận ngang.
f x  2018
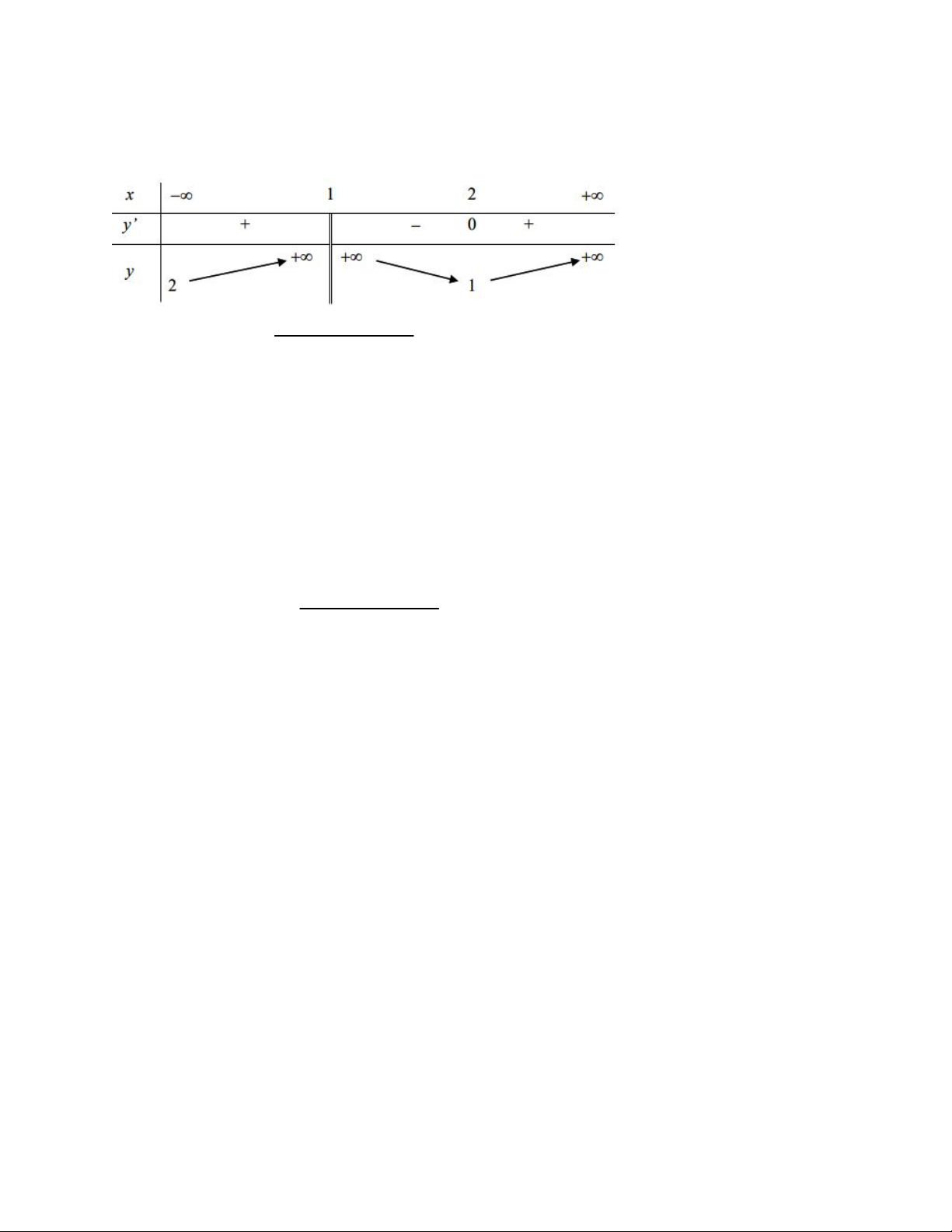
Ví dụ. Cho hàm số y  f x xác định trên \ 
1 và có bảng biến thiên như hình vẽ: Đồ thị hàm số x  2 y 
có bao nhiêu tiệm cận đứng? 2
f x 5 f x  4 Hướng dẫn giải  f x  4 Ta có: 2
f x 5 f x  
 4  0   f x1
Phương trình f x  4 có 3 nghiệm phân biệt khác 2.
Phương trình f x 1 có một nghiệm kép là x  2 (do vậy mẫu số có dạng x  2
2 nên x  2 vẫn là TCĐ của đồ thị hàm số => Đồ thị hàm số x  2 y 
có 4 đường tiệm cận đứng. 2
f x 5 f x  4