Tóm tắt bài giảng môn Giải tích 2 | Trường Đại học Thủy Lợi

lOMoAR cPSD| 58448089 NHTHO WORDPRESS COM
Bài giảng môn Giải tích 2 TS. Nguy
Đây là bài giảng môn Giải tích 2 dành cho sinh viên năm thứ nhất của Khoa Cơ khí và Khoa Điện –
Điện tử của Trường đại học thủy lợi. Giáo trình chính
Giải tích hàm nhiều biến (Lưu hành nội bộ) Sách dịch, do Bộ Môn Toán Trường Đại học Thủy Lợi biên dịch 1. 2. 3. Bài số 1
HỆ TỌA ĐỘ TRONG KHÔNG ℝ3 . MỘT SỐ MẶT CONG TRONG ℝ3
I. Nhắc lại những vấn đề cơ bản về hệ tọa độ trong không gian
1. Nhắc lại hệ tọa độ Đề các trong ℝ3 . Đường thẳng và mặt phẳng. chuẩn.
Kết luận Bất cứ một phương trình trong hệ toạ độ Oxy khuyết một biến đều biểu diễn một mặt trụ với các
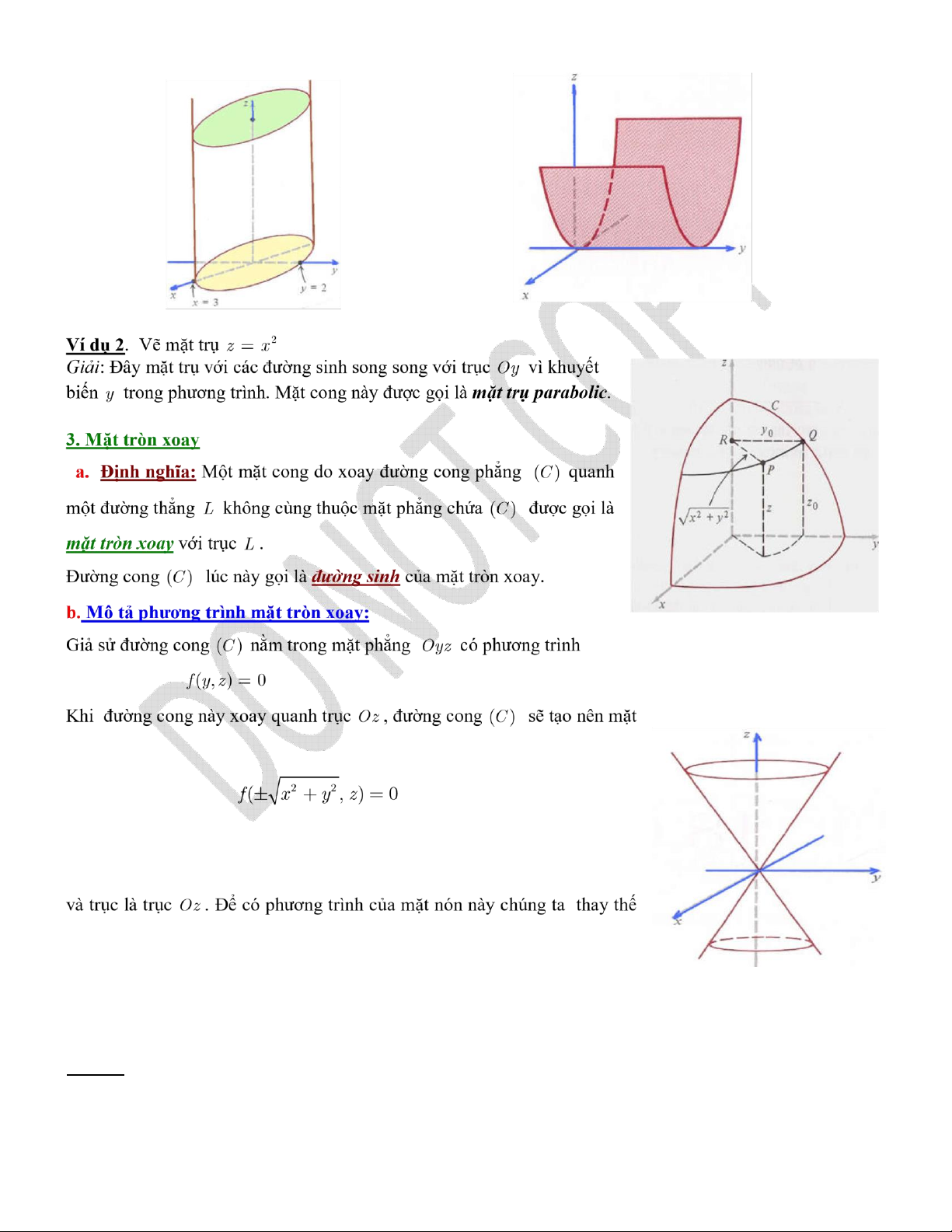
đường sinh song song với trục toạ độ tương ứng với biến bị khuyết. x2 y2 Ví dụ 1. Vẽ mặt trụ: + = 1 . 9 4
Giải + Đây là phương trình của mặt trụ vì khuyết z trong Oxyz với các đường sinh song song với trục Oz . Mặt
cong này được gọi là mặt trụ elliptic. tròn xoay có p/t: f(± +x
Ví dụ 3. Nếu đuờng thẳng z = 3y trong mặt phẳng Oyz xoay tròn quanh trục Oz
thì mặt tròn xoay là một mặt nón hai tầng với đỉnh tại gốc toạ độ
y trong phương trình z = 3y bởi ± x2 + y2 và sau đó hữu tỷ hoá bằng bình phương:
z = ±3 x2 + y2 ⇔ z2 = 9(x2 + y2). 2. Mặt bậc hai
a. Phương trình tổng quát của mặt bậc hai
Trong không gian ba chiều, dạng tổng quát của phương trình bậc hai có dạng:
Ax2 + By2 +Cz2 + Dxy + Exz + Fyz +Gx + Hy + Iz + J = 0
giả thiết rằng tất cả các hệ số A B, ,...,F không đồng thời bằng không nên bậc của phương trình thực sự là bậc
2. Đồ thị của các phương trình này được gọi là mặt bậc hai. 1. 2. 3. 4. 5. 6. c. Một số ví dụ:
+ Bậc của x y z, , độ.
là một hyperboloid một tầng. x2 y2 z2 a
thì chúng ta nhận thấy lát cắt ngang trong mặt phẳng z = k là các ellip, và các elip này
lớn dần khi dịch chuyển xa mặt phẳng Oxy . y2 z2
+ Lát cắt của mặt cong trong mặt phẳng Oyz là hyperbol : b2 − c2 = 1 rỗng. z =± x, + Khi a b= các parabol: z = ax ,
là các elip nếu k > 0,
Ví dụ 6. Mặt paraboloid hyperbolic (với a b, cùng dấu): z = by2 − ax2
+ Lát cắt với mặt phẳng yz là parabol z = by2 mở quay lên và trong mặt phẳng Oxz là parabol z = −ax2 mở quay xuống.
+ Trong tất cả các mặt phẳng y = k song song với mặt phẳng Oxz , các lát cắt là các parabol mở quay xuống
và có các đỉnh chạy dọc theo parabol z = by2 .
+ Càng gần gốc toạ độ, mặt cong tăng theo y và giảm theox nên nó có hình dạng của yên ngựa hoăc khe núi,
vì vậy, mặt cong này thường đuợc gọi là mặt yên ngựa với gốc toạ độ là tâm yên ngựa. Bài số 2
HÀM NHIỀU BIẾN. ĐẠO HÀM RIÊNG.
MẶT PHẲNG TIẾP XÚC VỚI MẶT CONG. Ví dụ: 2. Miền xác định
Xét hàm số z = g x y( , ) = MXĐ: D = (x y, ) 9− −x 3. Giới hạn .
Định nghĩa Cho hàm số z = f x y( , ) xác định trong lân cận của điểm M x y0( 0, 0). Ta nói rằng lim f x y( , ) = L (x y, )→(x y0 0, )
nếu với mọi điểm ε> 0 nhỏ tuy ý luôn tồn tại số δ = >δ ε( )
0 sao cho với mọi điểm M x y( , ) sao cho d M M( , 0) = (x −x0)2 + −(y y0)2 <ε
thì ta luôn có f x( )− L < ε.
Chú ý: Ta cũng có định nghĩa tương tự đối với hàm 3 biến, hàm n biến (n>3 ), các định nghĩa khác về giới hạn
của hàm nhiều biến cũng được định nghĩa tương tự như đối với các hàm một biến.
4. Tính liên tục: Hàm số f x y( , ) được nói là liên tục tại một điểm (x y, ) trong miền xác định của nó nếu
f(x,y)− f x y( , o) bé tuỳ ý khi x −x m ≠ 0 thì 5. Đường mức
Định nghĩa: Xét hàm số z = f x y( , ). Một đường cong
được gọi là một đường mức nếu nó nằm trong miền xác định
của hàm số, và trên đó z = f x y( , ) có giá trị không đổi c . Ứng
dụng: + Mô tả bản chất hình học của một hàm số
+ Trong vẽ bản đồ địa hình với thung lũng, đồi và núi: nhận được một hình ảnh rõ ràng về các sự thể trên
mặt đất trong không gian ba chiều từ sự mô tả trong không gian hai chiều.
Tập hợp các đường mức được gọi là bản đồ trắc địa.
Tương tự, nếu x cố định và y thay đổi thì đạo hàm riêng của z theo y là :
Bài giảng môn Giải tích 2 TS. Nguy ¶z f x y( ; +Dy) - f x y( ; ) = lim ¶y D ®y 0 Dy ¶z ¶f
kí hiệu trong truờng hợp này là : ¶y ; zy; fy; ¶y ; f x yy( ; ).
Tương tự ta cũng có định nghĩa đạo hàm riêng cho hàm nhiều hơn hai biến.
Quy tắc: lấy đạo hàm riêng của hàm nhiều biến số theo một biến chúng ta coi tất cả các biến độc lập khác
là hằng số và khi đó ta thực hiện các phép toán đạo hàm riêng (theo một biến đó) như các phép toán lấy
đạo hàm của hàm một biến.
Ví dụ 4. Xét hàm số : f x y( , ) = −x3 3x y2 3 +y2 . Tính các ĐHR Ví dụ 5
(a) Nếu f x y( , ) = xy2 + x3 thì fx = ???;fy = ????……
(b) Nếu g x y( , ) = xexy2 thì gx = ???;gy = ????……. .
(c) Nếu h x y( , ) = sinx2 cos3y thì hx = ???;hy = ????
Ví dụ 6: Nếu w = f x y z u v( , , ,
, ) = xy2 + 2x 3 + xyz + zu + tanuv thì ……
Chú ý: + Trong trường hợp một biến, chúng ta biết đạo hàm có thể coi là phân số: thương của các vi phân dy và dx .
+ Đối với hàm nhiều biến: đạo hàm riêng không được hiểu theo cách như vậy.
Ví dụ 7. Định luật khí lí tưởng nói rằng số lượng khí đã có, áp suất p, thể tích V, nhiệt độ tuyệt đối T được
liên hệ với nhau bởi phương trình pV = nRT
trong đó n là số lượng phân tử gam khí ở điều kiện lí tưởng và R là hằng số. Ta có nRT nRT pV p = , V = , T = V p nR ∂p nRT ∂V nR ∂T V nên : ∂ V = − V 2 , ∂ T = p , ∂ p = nR suy ra : ∂∂Vp∂∂VT∂∂Tp = −nRTV 2 nRp nRV = − nRTpV = −1.
Kết quả bằng -1 : không thể coi các đạo hàm riêng ở vế trái như là các phân số.
2. Ý nghĩa hình học của đạo hàm riêng cấp một cong. 0 Số tan α = tan β =
Ÿ Các đạo hàm riêng cấp hai thuần tuý: ∂ 2f ∂ 2f = = fxx ∂ x 2 và fyy ∂ y2
Ý nghĩa: biểu thị tốc độ biến thiên của tốc độ biến thiên của f .
Bài giảng môn Giải tích 2 TS. Nguyễn Hữu Thọ 2019 -2 020 ∂2f ∂2f
Ÿ Các đạo hàm riêng cấp hai hỗn hợp: và . ∂x y∂ ∂ ∂y x Ý nghĩa: ∂2f