Tóm tắt công thức Nhiệt động lực học - Chương 1 đến 5

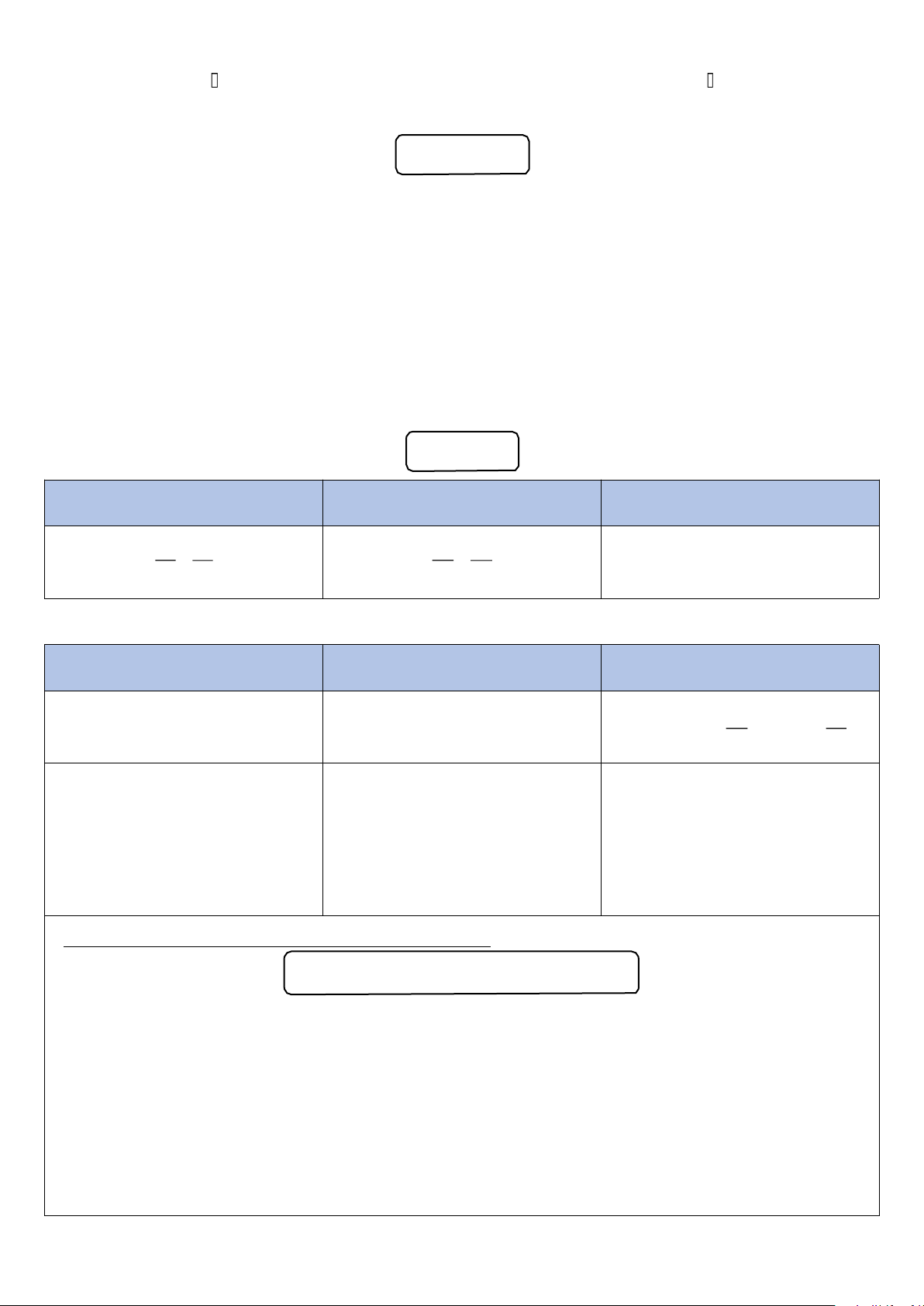
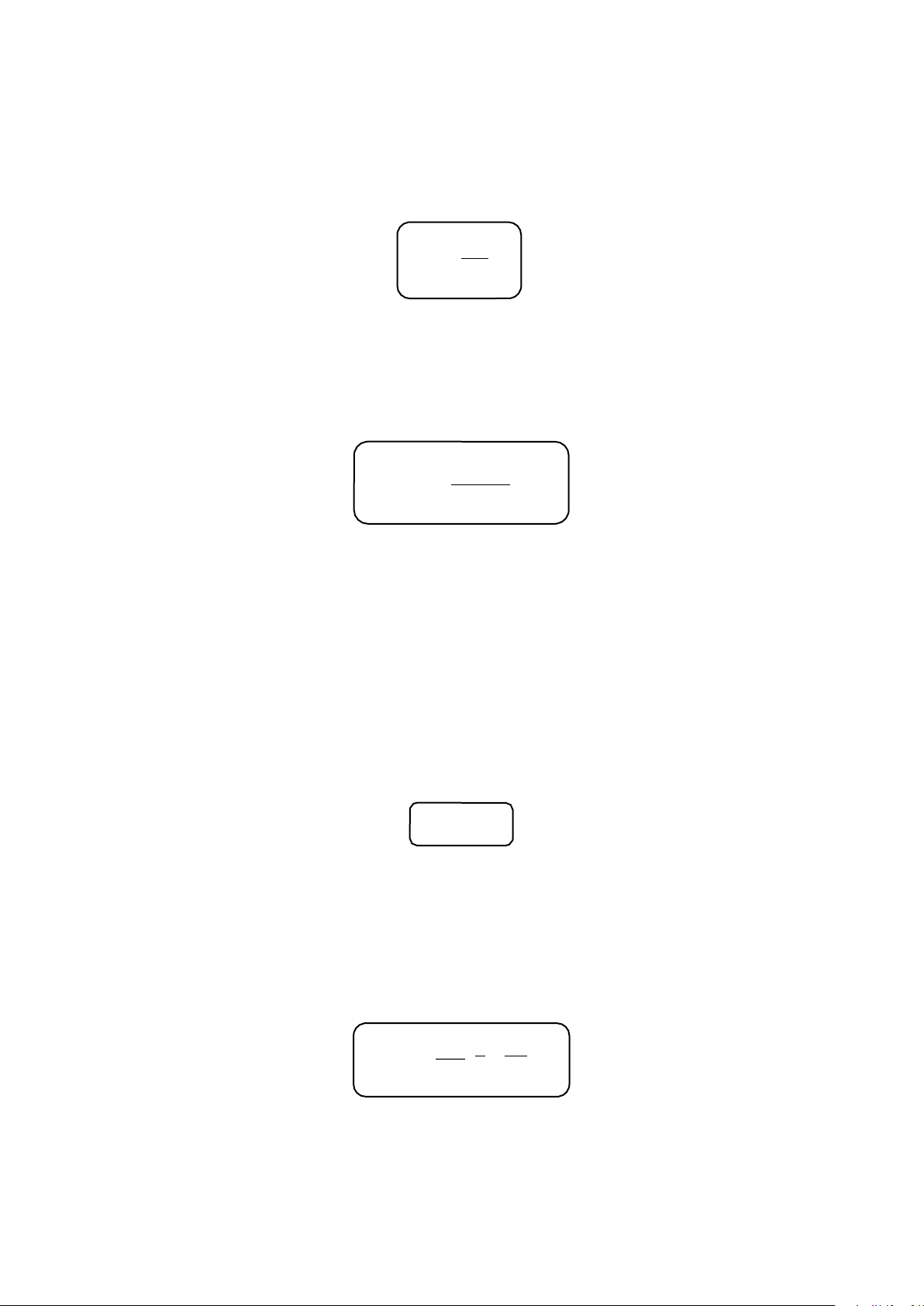
- - - CHƯƠNG 1. NGUYÊN LÍ I NHIỆT ĐỘNG LỰC HỌC - - - 1.1. NGUYÊN LÝ I ∆U = A + Q Trong đó
- A và Q lần lượt là công và nhiệt
• Tỏa nhiệt (giải phóng nhiệt): Q < 0.
• Thực hiện công (sinh công): A < 0.
• Thu nhiệt (nhận nhiệt): Q > 0. • Nhận công: A > 0.
- ∆U là biến thiên nội năng của hệ
• Nội năng của hệ tăng: ∆U > 0.
• Nội năng của hệ giảm: ∆U < 0.
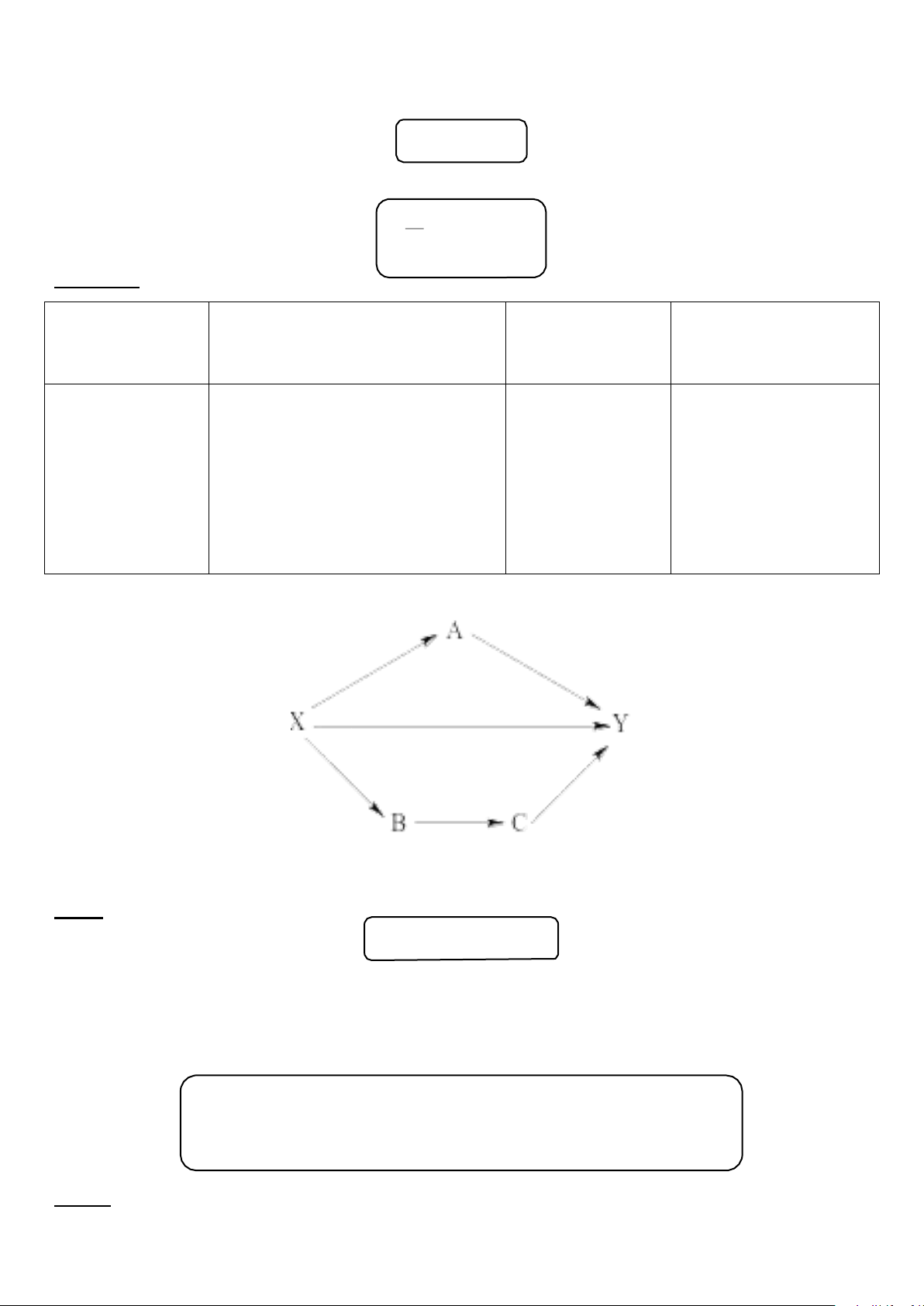
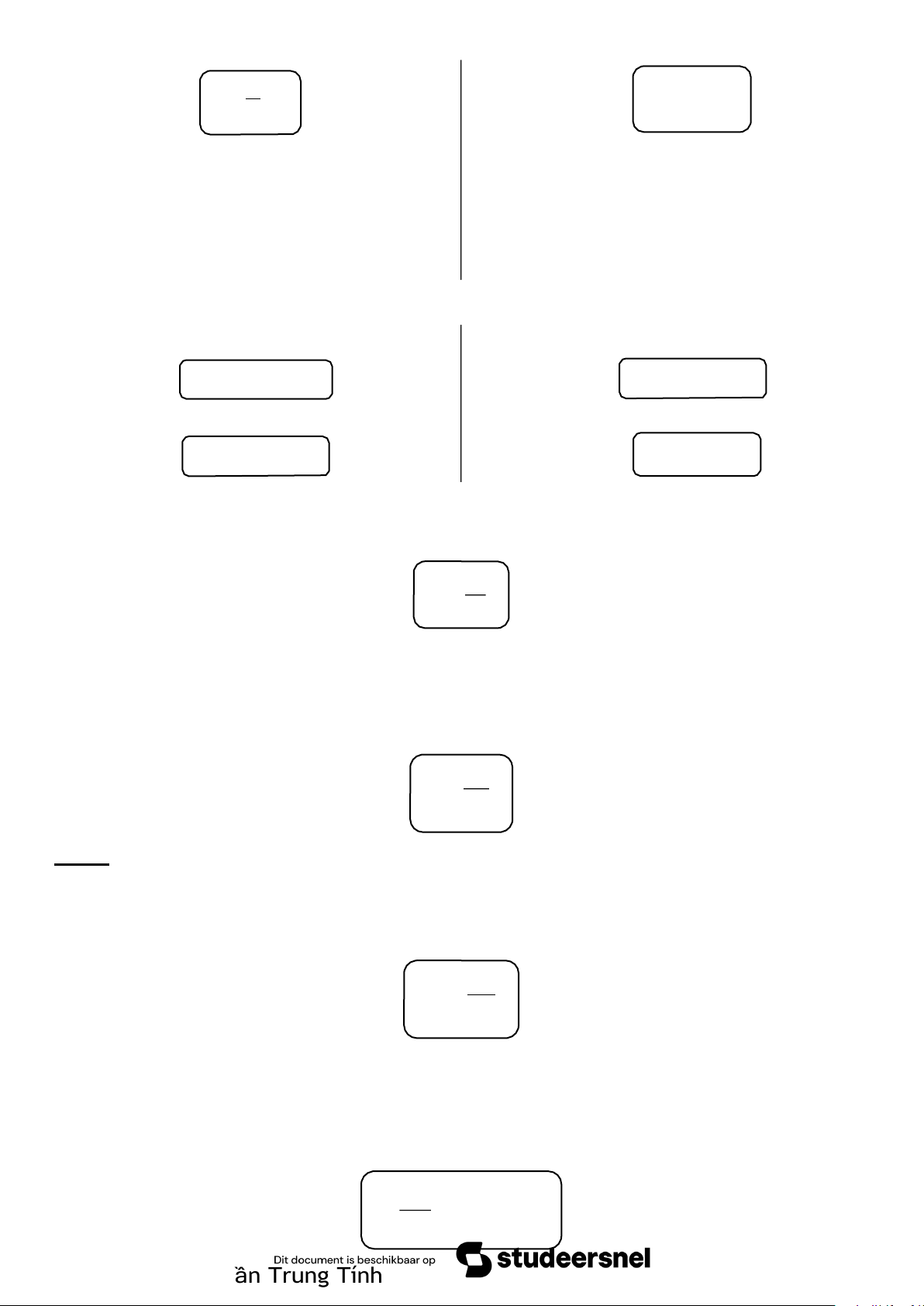
1.2. PHƯƠNG TRÌNH TRẠNG THÁI KHÍ LÍ TƯỞNG pV = nRT Đẳng tích Đẳng áp Đẳng nhiệt P1 P2 = V 1 V2 = T T T T P1V1 = P2V2 1 2 1 2
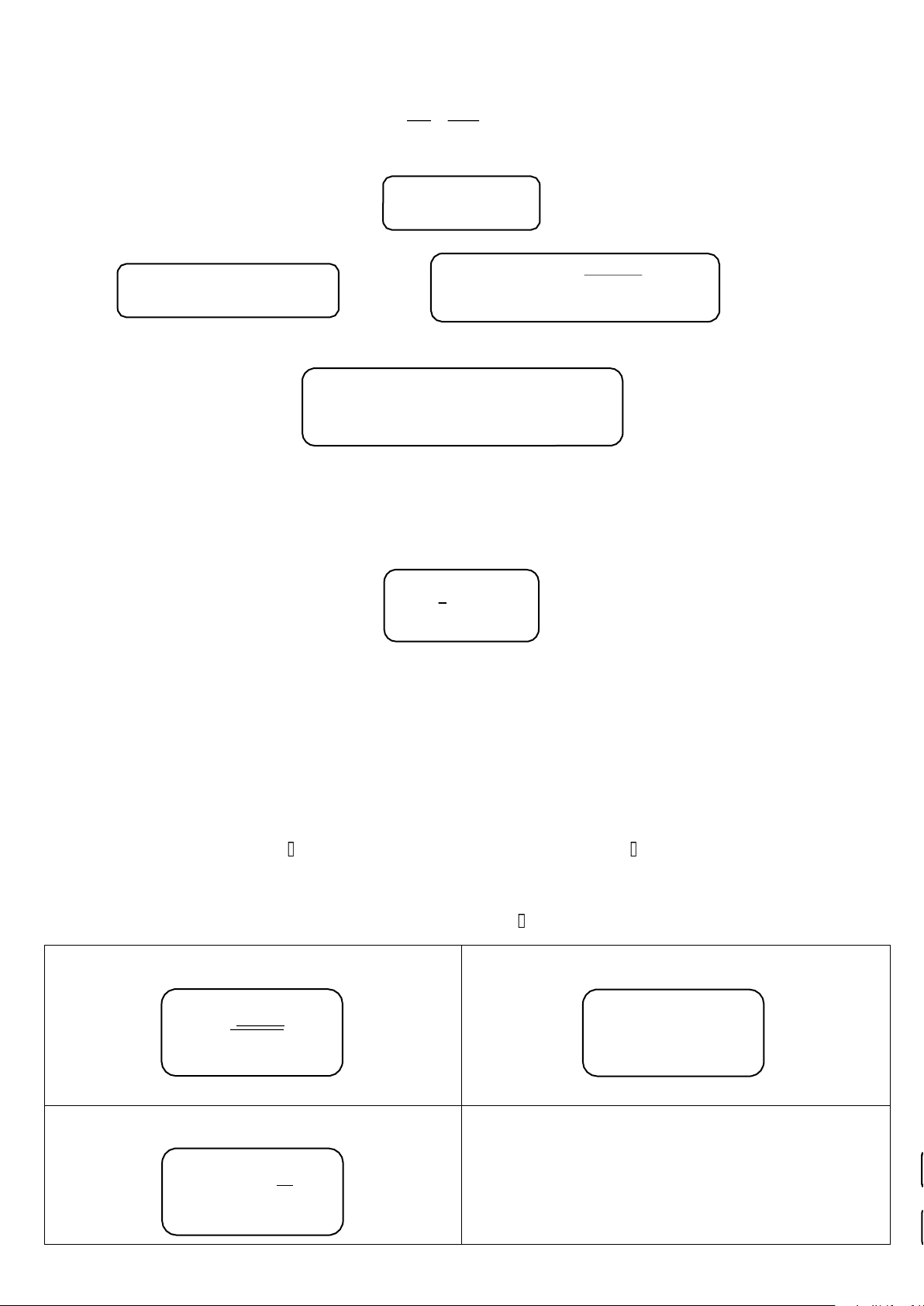
1.3. TÍNH CÔNG VÀ NHIỆT CHO MỘT SỐ QUÁ TRÌNH Đẳng tích Đẳng áp Đẳng nhiệt V A = 0
A = – P∆V = – P (V 2 P1 2 – V1) A=−nRTln =−nRTln V P 1 2 T 2 T 2
Qv=n∫Cv dT
Qp=n∫C pdT T 1 T 1 Q *Nếu C T = – A (∆U = 0) v = const *Nếu Cp = const
Qv=∆U =nCv ∆T
Qp=∆ H=n C p ∆T
*Mối liên hệ giữa hiệu ứng nhiệt đẳng áp và đẳng tích
Qp = Qv + ∆nRT hay ∆H = ∆U + ∆nRT Trong đó:
- R là hằng số khí lý tưởng:
R = 8,314 J.K-1.mol-1 = 0,082 L.atm.K-1.mol-1 = 1,987 cal.K-1.mol-1
- Qp = ∆H là nhiệt đẳng áp
- Qv = ∆U là nhiệt đẳng tích
- ∆n là biến thiên số mol khí của quá trình. DHSHOA22A Trần Trung Tính 1.4. NHIỆT DUNG
Mối liên hệ giữa nhiệt dung đẳng áp và đẳng tích Cp = Cv + R
Mối liên hệ giữa nhiệt dung trung bình và nhiệt dung thực T2 C .∆T =∫CdT T1
*Đổi đơn vị 1 atm = 1,013.105 Pa (N/m2) 1 dm3 = 1 L Áp suất Thể tích 1 atm = 760 mmHg 1 cm3 = 1 mL 1 cal = 4,184 J 1 eV = 1,602.10-19 J Năng lượng 1 Wh = 3600 J 1 atm.L = 101,3 J = 24,2 cal 1 cal = 41,3 mL.atm
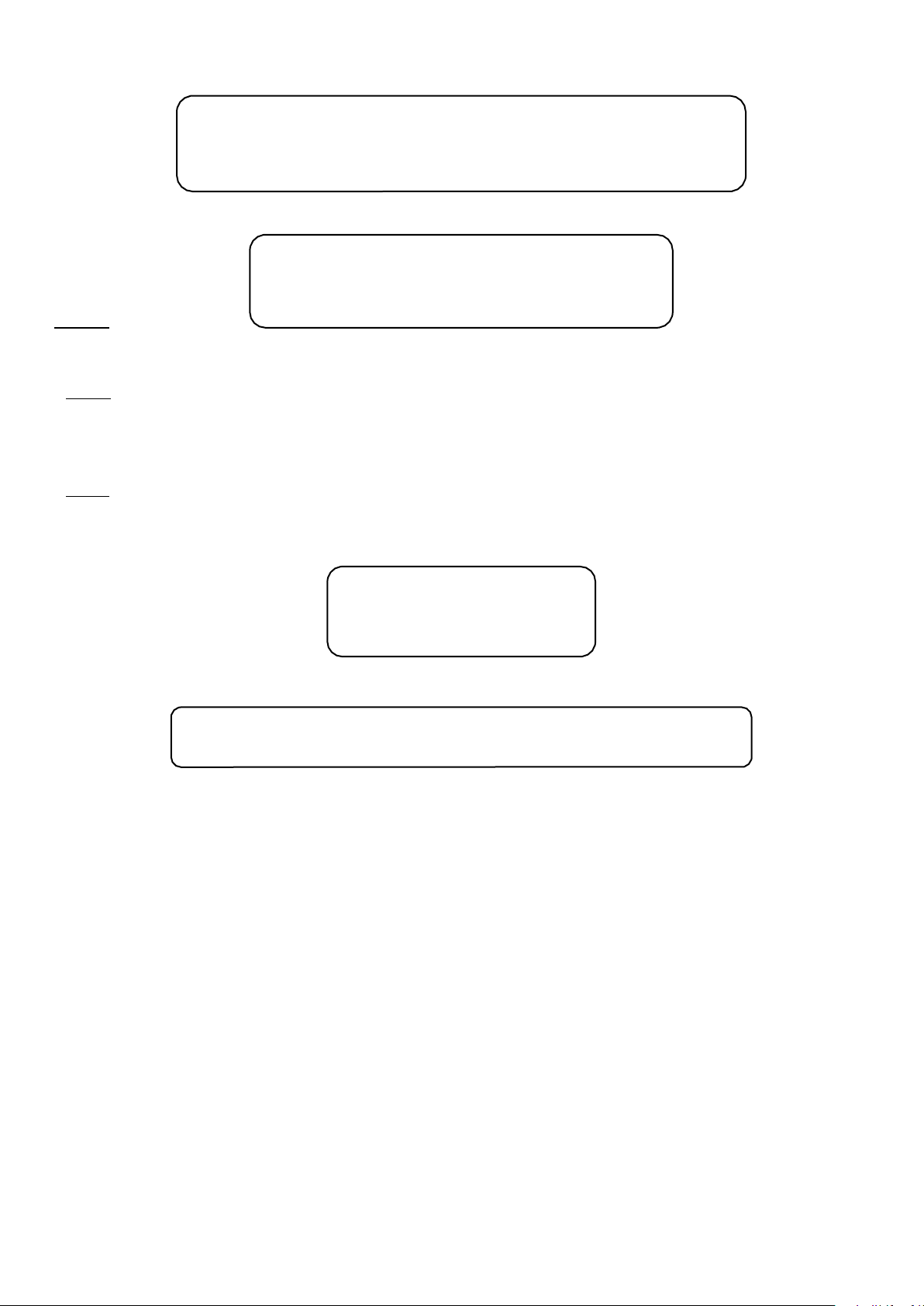
1.5. ĐỊNH LUẬT HESS ∆H1 ∆H2 ∆H ∆H3 ∆H5 ∆H4
=> Áp dụng định luật Hess: ∆H = ∆H1 + ∆H2 = ∆H3 + ∆H4 + ∆H5 *Lưu ý
∆H thuận = – ∆H nghịch
1.6. TÍNH BIẾN THIÊN ENTHALPY TRONG PHẢN ỨNG HÓA HỌC
Xét phản ứng: aA + bB → cC + dD
Dựa vào biến thiên enthalpy tạo thành tiêu chuẩn (nhiệt tạo thành, sinh nhiệt) ∆ H0 r 298 = ∑ ∆ H0 f 298 (sp) – ∑ ∆ H0 f 298 (cđ)
= c∆f H0298 (C) + d∆f H0298 (D) – a∆f H0298 (A) – b∆f H0298 (B) 0
*Lưu ý: Biến thiên enthalpy tạo thành tiêu chuẩn của đơn chất bền bằng 0. Ví dụ: ∆f H 298 (O2, g) = 0 DHSHOA22A Trần Trung Tính
Dựa vào nhiệt đốt cháy (thiêu nhiệt) ∆ H0 r 298 = ∑ ∆ H 0 c
298 (cđ) – ∑ ∆ H 0 c 298 (sp)
= a∆c H0298 (A) + b∆c H0298 (B) – c∆cH0298 (C) – d∆c H0298 (D)
➂ Dựa vào năng lượng liên kết
∆r H0298 = ∑ Eb (cđ) – ∑ E b (sp) *Lưu ý:
= aEb (A) + bEb (B) – cEb(C) – dEb (D)
• Nếu ∆H > 0 → phản ứng thu nhiệt.
Ví dụ: phản ứng cháy, phản ứng tạo gỉ sắt, phản ứng oxi hóa glucose trong cơ thể, phản ứng giữa
nước và acid mạnh, phản ứng giữa CaO và nước,…
• Nếu ∆H < 0 →phản ứng tỏa nhiệt.
Ví dụ: phản ứng trong lò nung vôi, nung clinker xi măng, phá vỡ các phân tử khí, hòa tan C sủi vào trong nước,…
1.7. PHƯƠNG TRINH KIRCHOFF T 2 ∆ HT ∫ 2 =∆ H T + ∆C pdT 1 T 1 Trong đó
∆Cp = ∑Cp(sp) – ∑Cp(cđ) = cCp(C) + dCp (D) – aCp (A) – bCp (B) DHSHOA22A Trần Trung Tính
- - - CHƯƠNG 2. NGUYÊN LÍ II NHIỆT ĐỘNG LỰC HỌC - - -
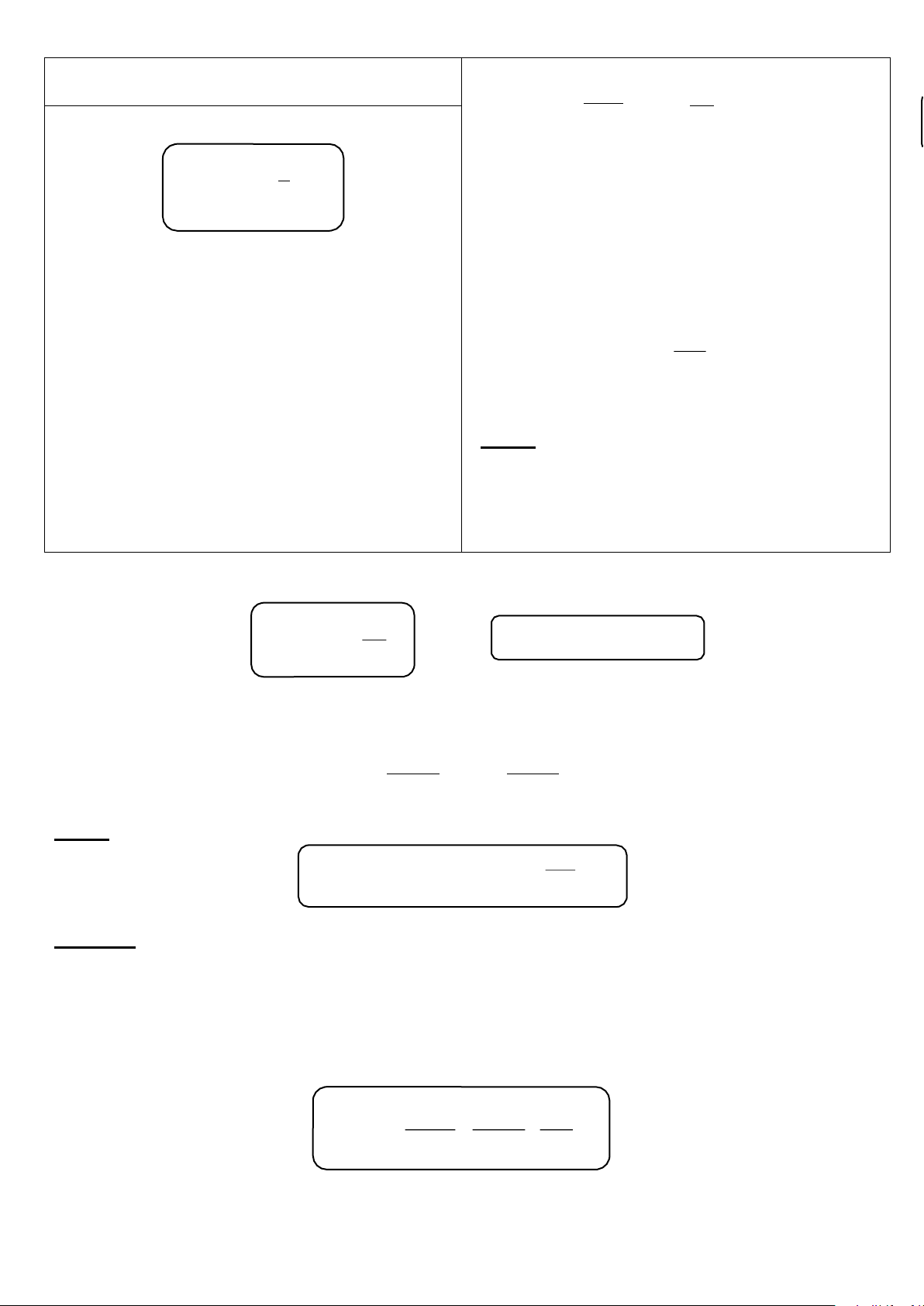
2.1. TÍNH BIẾN THIÊN ENTROPY TRONG MỘT SỐ QUÁ TRÌNH THUẬN NGHỊCH Đẳng tích Đẳng áp Đẳng nhiệt Q T T 2 dT T2 dT ∆ S=
∆ S=n∫ C T v ∆ S T =n∫Cp T T1 T1
*Đối với các quá trình chuyển *Nếu Cv = const *Nếu Cp = const
pha: nóng chảy, bay hơi, thăng T T hoa, kết tinh,…. 2 2
∆ S=n Cv ln T
∆ S=n Cp ln T ∆ HT λ 1 1
∆ S= T = T
*Quá trình dãn nở đẳng nhiệt khí lí tưởng V2 P1
∆ S=nRln V =nRln P 1 2
2.2. TÍNH BIẾN THIÊN ENTROPY TRONG PHẢN ỨNG HÓA HỌC
Xét phản ứng: aA + bB → dD + eE ∆ S0
r 298 = ∑ S0298 (sp) - ∑ S0298 (cđ)
= dS0298(D) + eS0298 (E) – aS0298(A) – bS0298 (B)
2.3. ENTROPY TUYỆT ĐỐI
Biến thiên entropy của một chất ở nhiệt độ T T dT
∆ S=ST −S0=∫C p T 0
Định đề của Planck “Entropy của những tinh thể lý tưởng ở nhiệt độ 0K bằng không” → S0 = 0. T dT
∆ S=ST=∫ Cp T 0
ST được gọi là entropy tuyệt đối.
*Tính ST của 1 mol khí ở nhiệt độ T, biết 0K đến T (K) khí đó trải qua 3 trạng thái rắn, lỏng, khí. 0 Tnc Tbh T Rắn Lỏng Khí
Entropy của 1 mol khí ở nhiệt độ T Tnc dT ∆ H T bh dT ∆H T dT
ST=∫Cp(s) T + nc T
p ( l) T + bh T p ( g) T bh +∫ C nc +∫ C 0 T T nc bh DHSHOA22A Trần Trung Tính
2.4. THẾ NHIỆT ĐỘNG – ĐIỀU KIỆN TỰ DIỄN BIẾN TRONG PHẢN ỨNG HÓA HỌC
Thế đẳng nhiệt – đẳng tích (Thế đẳng tích)
Thế đẳng nhiệt – đẳng áp (Thế đẳng áp) Hàm năng lượng Hemholtz
Hàm năng lượng tự do Gibbs
∆F = ∆U – T∆S
∆ G = ∆ H – T∆S
- Tự phát (tự diễn ra) ∆ F < 0
- Tự phát (tự diễn ra) ∆G < 0
- Không tự phát (không tự diễn ra) ∆F > 0
- Không tự phát (không tự diễn ra) ∆G > 0 - Cân bằng ∆ F = 0 - Cân bằng ∆G = 0
2.5. TÍNH BIẾN THIÊN THẾ ĐẲNG ÁP TRONG PHẢN ỨNG HÓA HỌC
Thông qua biến thiên enthalpy và entronpy của phản ứng ở điều kiện chuẩn ∆ G0 r
298 = ∆ r H 0298– T∆ S0 r 298
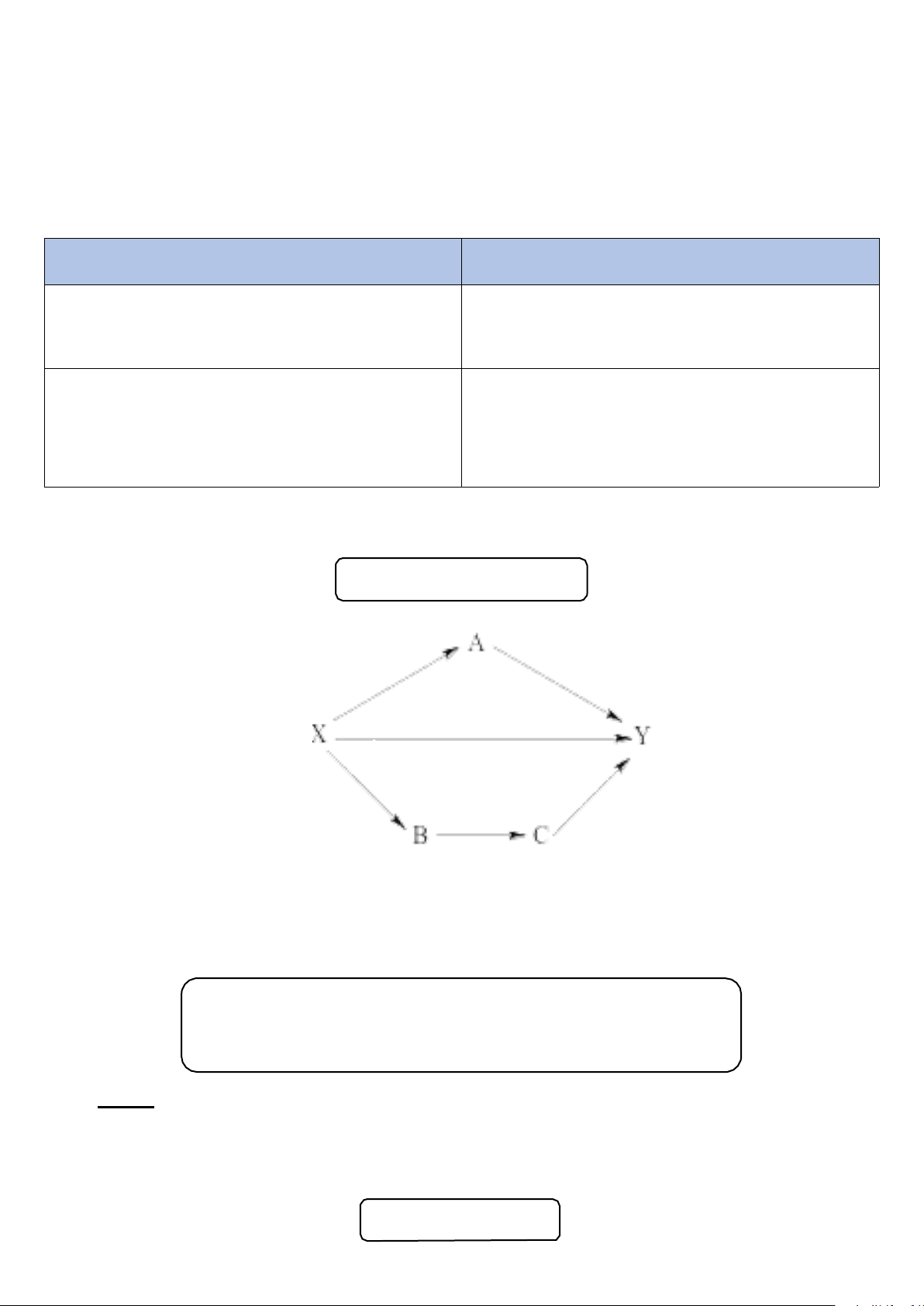
Thông qua chu trình nhiệt động lực học ∆G ∆G 1 2 ∆G3 ∆G5 ∆G4
∆G = ∆G1 + ∆G2 = ∆G3 + ∆G4 + ∆G5
➂ Thông qua biến thiên thế đẳng áp tạo thành chuẩn của các chất
Xét phản ứng: aA + bB → cC + dD ∆ G0 r 298 = ∆ G ∑ 0 f 298 (sp) – ∆ G ∑ 0 f 298 (cđ)
= c∆f G0298 (C) + d∆f G0298 (D) – a∆f G0298 (A) – b∆f G0298 (B)
*Lưu ý: Biến thiên thế đẳng áp tạo thành tiêu chuẩn của các đơn chất bền bằng 0. 0
Ví dụ: ∆f G298 (O2, g) = 0.
➃ Thông qua hằng số cân bằng ∆G0298 = – RTlnKcb DHSHOA22A Trần Trung Tính
Thông thế điện cực tiêu chuẩn ∆G0298 = – nE0F
2.5. CÁC YẾU TỐ ẢNH HƯỞNG ĐẾN THẾ ĐẲNG ÁP
Sự phụ thuộc của thế đẳng áp vào nhiệt độ
∆GT =T 2{∆GT1 (1 1 )} 2 T + ∆ H − T2 T 1 1
Sự phụ thuộc của thế đẳng áp vào áp suất ∆G =nRTln P2 P1 DHSHOA22A Trần Trung Tính
- - - CHƯƠNG 3. CÂN BẰNG PHA - - -
3.1. QUY TẮC PHA GIBBS c = k – f + n Trong đó - c là số bậc tự do. - f là số pha.
- n là thông số bên ngoài tác động lên hệ.
- k là số cấu tử độc lập.
Số cấu tử độc lập = Tổng số cấu tử - Số hệ thức liên hệ giữa các nồng độ.
*Nếu yếu tố bên ngoài tác dụng lên hệ chỉ có P và T thì c = k – f + 2
3.2. ẢNH HƯỞNG CỦA ÁP SUẤT ĐẾN NHIỆT ĐỘ CHUYỂN PHA
Phương trình Clausius – Claypeyron I dP = ∆H dT T ∆V Trong đó:
- T: nhiệt độ chuyển pha.
- ∆ H: nhiệt chuyển pha.
- ∆V = V2 – V1: biến thiên thể tích.
3.3. ẢNH HƯỞNG CỦA NHIỆT ĐỘ ĐẾN ÁP SUẤT HƠI BÃO HÒA
Phương trình Clausius – Claypeyron II dlnP= ∆ H dlgP= ∆H dT RT2 dT 2,303 RT2
*Nếu lấy tích phân 2 vế ta được biểu thức: ln P2=−∆H hh P (1 1− ) 1 R T2 T1 Trong đó: - T: nhiệt độ (K). - P: áp suất (atm). - ∆ Hhh: nhiệt hóa
- R: là hằng số khí lí tưởng. DHSHOA22A Trần Trung Tính
- - - CHƯƠNG 4. DUNG DỊCH - - -
4.1. CÁCH BIỂU DIỄN THÀNH PHẦN CỦA DUNG DỊCH
Nồng độ phần trăm khối lượng Nồng độ mol n C =C mct 00% % M = V.1 mdd Trong đó: Trong đó:
- C%: nồng độ phần trăm khối lượng (%).
- CM: nồng độ mol (M hay mol/L).
- mct: khối lượng chất tan (g).
- n: số mol của chất tan (mol).
- mdd: khối lượng dung dịch (g).
- V: thể tích của dung dịch (L). ➂ Nồng độ molan
➃ Nồng độ phần mol n N = C A n A m= mn ∑ Adm Trong đó: Trong đó:
- Cm: nồng độ molan (m hay mol/kg).
- NA: nồng độ phần mol.
- n: số mol của chất tan (mol)
- nA: số mol của chất A.
- mdm: khối lượng dung môi (kg).
- ∑ nA: tổng mol các chất trong dung dịch. DHSHOA22A Trần Trung Tính
Nồng độ đương lượng gam
Một số công thức khác m *Khối lượng riêng C ct N = Dm.V d= dd Trong đó: V
- CN: nồng độ đương lượng gam (N).
*Công thức liên hệ giữa CM và CN
- mct: khối lượng chất tan (g). C =n' .C
- V: thể tích dungNdịch (LM). - D: đương lượng gam
*Công thức liên hệ giữa CM và C%
C D=10M.d . C% M= n 'M
• Nếu là acid, n’ bằng số H+.
*Liên hệ giữa dung môi và dung dịch
• Nếu là base, n’ bằng số OH–.
• Nếu là muối,mnd’db=ằmngdmtổ+nmgchtóa trị kim loại.
• Nếu là chất oxi hóa/khử, n’ bằng số
electron nhận/nhường của chất đó.
4.2. DUNG DỊCH VÔ CÙNG LOÃNG – DUNG DỊCH LÝ TƯỞNG
Độ giảm áp suất hơi bão hòa của dung dịch
∆P = P0A . xB Trong đó: - ∆P = P0 - x
A – PA: độ giảm áp suất bão hòa. A: phần mol của dung môi. - P0 - x
Alà áp suất bão hòa dung môi nguyên chất.
B: phần mol chất tan trong dung dịch.
- Áp suất hơi bão hòa dung dịch P = P0A . xA
- Chất tan tuân theo định luật Henry PB = KH . xB
Giản đồ “áp suất – thành phần” (P – x)
Áp dụng định luật Raoult cho dung dịch lý tưởng của hai cấu tử (A - B):
PA = P0 . xl = P0 . (1 - xl ) (1) A A A B PB = P0 . xl (2) B B Áp suất tổng của hệ: DHSHOA22A Trần Trung Tính
Pt = PA + PB = P0 . (1 - xl ) + P0 . xl = P0 + xl (P0 - P0 ) (3) A B B B A B B A
Biểu diễn các phương trình (1), (2) và (3) lên đồ thị “áp suất - thành phần” (P - x)
Giản đồ áp suất hơi (P - x) của dung dịch 2 cấu tử lý tưởng
➂ Thành phần pha hơi – Định luật Konovalap I
Xét hệ dung dịch lý tưởng của hai cấu tử A và B nằm cân bằng với pha hơi của chúng. xh P0 xl xl
B = B . B =α . B xh P0 xl xl A A A A Trong đó P0
α= B: hệ số tách (hệ số chưng cất) hoặc tỷ số áp suất hơi P0A
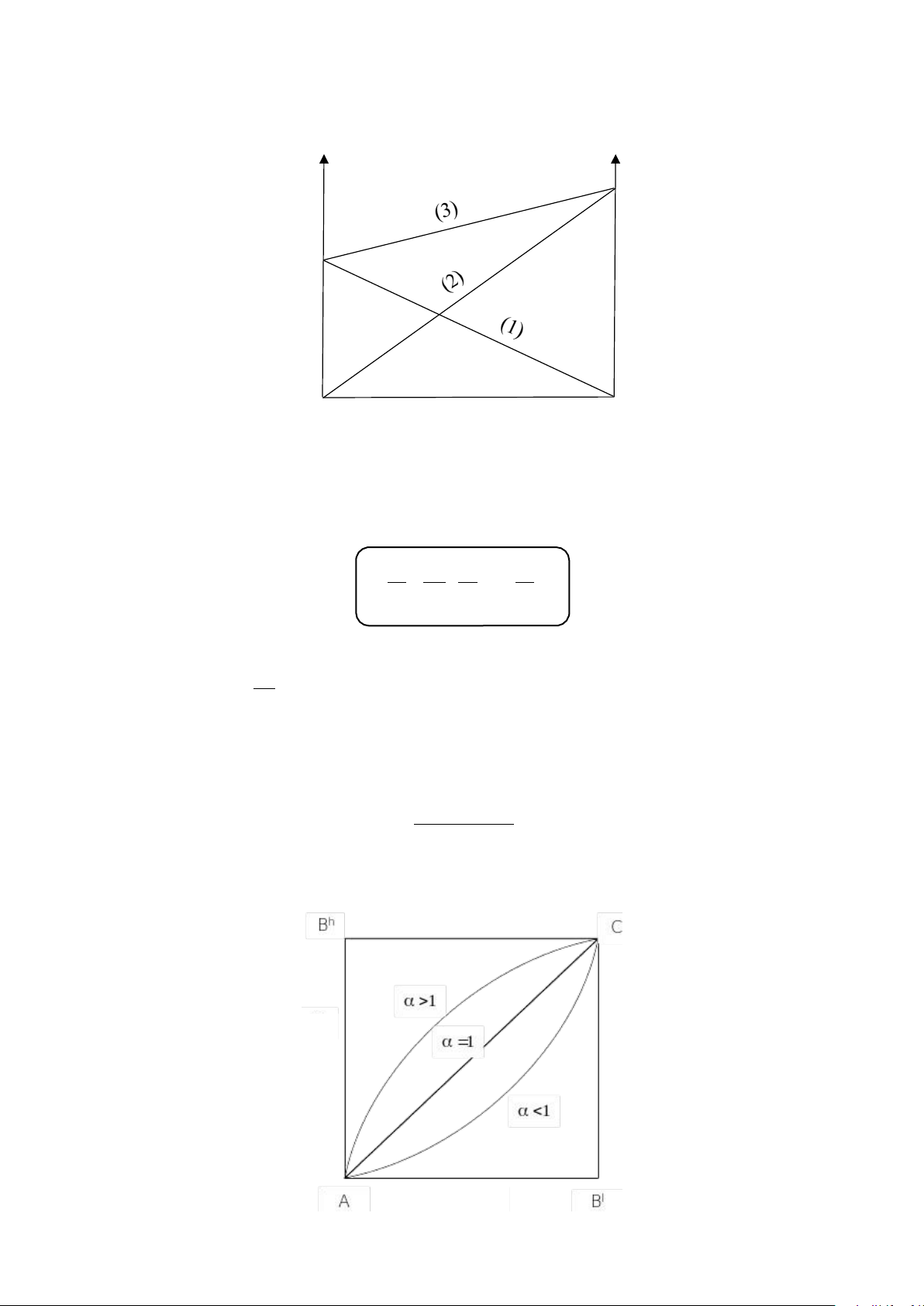
➃ Giản đồ “thành phần hơi – thành phần lỏng”
Từ định luật Konovalap I, ta được α.xl xh = B (4) B
1+( α−1) . xlB
Biểu diễn (4) lên đồ thị “thành phần khí – thành phần lỏng” (xh – xl) xhB xlB DHSHOA22A Trần Trung Tính
Độ tăng nhiệt độ sôi và độ giảm nhiệt độ đông đặc của dung dịch
*Độ tăng nhiệt độ sôi của dung dịch
∆Ts = T0s(dung dịch) – T0s(dung môi) = Ks.Cm Trong đó:
- ∆Ts: độ tăng nhiệt độ sôi.
- Cm: nồng độ molan của chất tan trong dung dịch (m).
- Ks: hằng số nghiệm sôi của dung môi. R(T0)2 s M K = A s 1000 ∆H bh, A
*Độ giảm nhiệt độ đông đặc của dung dịch
∆Tđ = T0đ(dung môi) – T0(đdung dịch) = Kđ.Cm Trong đó:
- ∆Tđ: độ giảm nhiệt đông đặc.
- Cm: nồng độ molan của chất tan trong dung dịch.
- Kđ: hằng số nghiệm đông của dung môi. R (T0)2 đ M K = A đ 1000∆ Hnc,A
*Ứng dụng tính khối lượng nguyên tử/khối lượng phân tử 1000.K 1000. K M s . mct M đ . mct ct = m ct = dm . ∆T s mdm .∆T đ
*Bảng hằng số nghiệm sôi và hằng số nghiệm đông của một số dung môi
T0 (℃) K K đ đ
T0(℃) s s Nước 0 1,86 100 0,52 Benzen 5,5 5,12 80,1 2,53 Rượu etylic -117,3 1,99 78,4 1,22 Axit axetic 66,6 3,9 117,9 2,93 Xiclohexan 6,6 20 80,7 2,79
Áp suất thẩm thấu – Định luật Van’t Hoff π = CMRT DHSHOA22A Trần Trung Tính Trong đó
- π là áp suất thẩm thấu (atm). - R = 0,082 atm.L.K-1.mol-1 - CM là nồng độ mol (M).
- T là nhiệt độ tuyệt đối (K).
Định luật phân bố Nernst
*Sự phân bố của một cấu tử i trong 2 dung môi ít tan vào nhau C A K= i CBi Trong đó
- C A và CBlà nồng độ của cấu tử I tan trong dung A và B. i i - K là hệ số phân bố
*Ứng dụng định luật phân bố trong phép chiết K V gn=g 0( 0 K V )n 0 +V Trong đó
- g0 là khối lượng (g) ban đầu của chất cần chiết.
- gn là khối lượng còn lại sau lần thứ n với thể tích V (mL).
- V0 là thể tích ban đầu chứa g0 chất cần tách.
4.3. SỰ HÒA TAN CỦA KHÍ TRONG CHẤT LỎNG
Ảnh hưởng của áp suất xi = kH.Pi Trong đó: - kH là hằng số Henry.
- Pi là áp suất hơi của pha khí trên pha lỏng.
Ảnh hưởng của nhiệt độ
Xét cân bằng: i (khí) = i (dung dịch có nồng độ xi) + ∆Hhòa tan −λ ln x = i i R (1− 1 T T0 )
4.4. DUNG DỊCH CHẤT ĐIỆN LI
Độ điện li (α) DHSHOA22A Trần Trung Tính α=α n i−1 = υ−1 n0 Trong đó Trong đó
- n là số mol bị phân li.
- i: hệ số đẳng trương (hệ số Van’t Hoff, i > - n 1).
0 là tổng số mol hòa tan.
- υ là số ion mà 1 phân tử điện li ra.
Tính chất của dung dịch
*Độ giảm áp suất hơi bão hòa
*Độ giảm nhiệt độ đông đặc
∆P∆T=đi=.Pi0.K Nđ2.Cm
*Độ tăng nhiệt độ sôi
*Áp suất thẩu thấu
∆Ts =π =i.KiCs.C MR mT
4.5. HOẠT ĐỘ DUNG DỊCH Hệ số hoạt độ a γ i i= Ni
Nếu dung dịch là lí tưởng thì γi = 1.
Nếu dung dịch không lí tưởng thì γi ≠ 1.
Phương pháp xác định hoạt độ
*Đo áp suất hơi P a i i= Pchi *Lưu ý:
• Đối với dung dịch khí hòa tan có hạn lỏng thì trạng thái chuẩn của dung môi lỏng vẫn chọn là chất nguyên chất.
• Đối với chất tan ta chọn trạng thái chuẩn như sau: Pch= 1 i K H
*Xác độ hoạt độ theo định luật phân bố
Muốn xác định hoạt độ của cấu tử trong dung môi A, ai (A). Ta chọn một dung môi B hoàn toàn không
tan lẫn với A và là dung dịch vô cùng loãng.
Theo định luật phân bố Nernst ai(A)
a =Kn=const i(B ) DHSHOA22A Trần Trung Tính
Khi nồng độ trong còn nhỏ thì C a A i( A ) = C =K n B ai(B) Hoạt độ của A a .C i( A)=Kn B
➃ Hoạt độ đối với chất điện li AnBm a γ
A B =γ A B . C A B A ¿ n m n m n m
n Bm=n+m√γA¿+γ ¿B¿
*Phương trình Debye và Huckel
log γ An Bm =−A ¿¿ Trong đó
- A: hằng số (đối với dung dịch nước ở 25℃, A = 0,5). - Z: điện tích ion.
- I: lực ion của dung dịch I=1 C z2 2 ∑ i i
- - - CHƯƠNG 5. CÂN BẰNG HÓA HỌC - - -
5.1. HẰNG SỐ CÂN BẰNG
Xét phản ứng: aA (g) + bB (g) cC (g) + dD (g)
Hằng số cân bằng theo áp suất
➃ Hằng số cân bằng theo phần mol KK=(PC. PD) xcc.xdd p x Pxaa. Pxbb AA BB ccbb
Hằng số cân bằng theo nồng độ
Mối quan hệ giữa các hằng số cân bằng
K =( C D) Cc .Cd
Kpp= KxCP(∆RnT )∆n C Ca .Cb A B cb KC = KnV−∆n DHSHOA22A Trần Trung Tính P ∆n RT ∆n
➂ Hằng số cân bằng theo số mol
Kp = Kn(∑n) =Kn( V )
K =( C D) nc .nd n na .nb Trong đó A B cb
- P: áp suất chung của hệ.
- ∆n: biến thiên số mol khí của khí.
∆n = c + d – a – b ni
- Phần mol chất i: xi=∑ i
- Áp suất riêng phần chất i: Pi = xiP *Lưu ý:
• Chất rắn không có mặt trong biểu thức cân bằng.
• Nếu ∆n = 0 thì KC = Kp = Kx = Kn.
5.2. PHƯƠNG TRÌNH ĐẲNG NHIỆT VAN’T HOFF Q ∆G =RTln p ∆G K =∆G0+ RTln Q p p Trong đó Pc . Pd Pc .Pd Q C D p=( K = C D A B )bđ ( A B) Pa . Pb p Pa .Pb cb *Lưu ý: −∆G0
∆G0=−RTln K → K =e RT p p *Nhận xét:
• Nếu Qp > Kp: phản ứng xảy ra theo chiều nghịch.
• Nếu Qp < Kp: phản ứng xảy ra theo chiều thuận.
• Nếu Qp = Kp: phản ứng đạt trạng thái cân bằng.
5.3. HẰNG SỐ CÂN BẰNG VÀ ĐẠI LƯỢNG NHIỆT ĐỘNG LỰC HỌC
ln K p= −∆G0 −∆ H0 ∆ S0
RT = RT + R
5.4. CÁC YẾU TỐ ẢNH HƯỞNG ĐẾN HẰNG SỐ CÂN BẰNG
Ảnh hưởng của nhiệt độ DHSHOA22A Trần Trung Tính
Phương trình đẳng áp Van’t Hoff dln K p= ∆H dT RT2
Trong khoảng nhiệt độ T1 đến T2 và ∆H không đổi, lấy tích phân 2 vế ta được K
ln p(T ) −∆ H 1 1 K 2 = ( − ) p(T ) R T 1 2 T 1 *Nhận xét:
• Nếu phản ứng thu nhiệt ∆H > 0 thì dln Kp > 0 dT
⮱ Khi nhiệt độ tăng, giá trị Kp cũng tăng, phản ứng chuyển dịch theo chiều thuận.
• Nếu phản ứng tỏa nhiệt ∆H < 0 thì dln Kp < 0 dT
⮱ Khi nhiệt độ tăng, giá trị Kp sẽ giảm, phản ứng chuyển dịch theo chiều nghịch.
Ảnh hưởng của áp suất Kp = KxP∆n = const. *Nhận xét:
• Nếu ∆n > 0: Khi tăng áp suất P, giá trị P∆n cũng tăng, do đó Kx giảm
⮱ Cân bằng sẽ dịch chuyển theo chiều nghịch.
• Nếu ∆n < 0: Khi tăng áp suất P, giá trị P∆ngiảm, do đó Kx tăng
⮱ Cân bằng dịch chuyển theo chiều thuận.
• Nếu ∆n = 0: Kp = Kx = const.
⮱ Áp suất chung P không ảnh hưởng đến cân bằng phản ứng.
➂ Ảnh hưởng của các khí trơ (không tham gia phản ứng)
a) Phản ứng trong dung dịch KC = KnV−∆n
• Khi thêm khí trơ hay dung môi thì thể tích V của hệ tăng
⮱ Cân bằng chuyển dịch theo chiều tăng số mol của hệ.
b) Phản ứng trong hệ khí ( P ∆n
K p=Kn ∑ ¿K n
n ( RT )∆n=const i) V
• Nếu thêm khí trơ không làm thể tích V của hệ thay đổi
⮱ Không ảnh hưởng đến cân bằng.
• Nếu thêm khí trơ trong điều kiện áp suất P không đổi thì thể tích V của hệ tăng lên
⮱ Cân bằng chuyển dịch theo chiều tăng số mol của hệ.
5.5. ĐỊNH LÍ NHIỆT NERNST
ln K p=∫ ∆H dT+∆ j RT 2 DHSHOA22A Trần Trung Tính Trong đó
- j là hằng số hóa học thực và j của các chất rắn bằng 0.
∆j = ∑ jcuối - ∑ jđầu
*Công thức gần đúng Nernst
lg K = −∆ H +1,75.∆n.lgT +∆i p 4,575 T Trong đó
- i là hằng số hóa học quy ước
∆i = ∑ icuối - ∑ iđầu
- ∆n là biến thiên số mol chất khí.
5.6. CÂN BẰNG TRONG DUNG DỊCH CHẤT ĐIỆN LI AB A+ + B– Ban đầu: C0 Phản ứng: C0α C0α C0α
Cân bằng: C0(1 – α) C0α C0α
Theo định luật tác dụng khối lượng: K=¿¿ *Lưu ý:
• Nếu α ≪ 1 thì K = C0α2.
• Dung dịch càng loãng thì độ điện li càng tăng. DHSHOA22A Trần Trung Tính
Document Outline

• - - - CHƯƠNG 1. NGUYÊN LÍ I NHIỆT ĐỘNG LỰC HỌC
• 1.2.PHƯƠNG TRÌNH TRẠNG THÁI KHÍ LÍ TƯỞNG
• 1.3.TÍNH CÔNG VÀ NHIỆT CHO MỘT SỐ QUÁ TRÌNH
  •  Mối liên hệ giữa nhiệt dung đẳng áp và đẳng tíc
• 1.5.ĐỊNH LUẬT HESS
• 1.6.TÍNH BIẾN THIÊN ENTHALPY TRONG PHẢN ỨNG HÓA HỌC
  •  Dựa vào biến thiên enthalpy tạo thành tiêu chuẩ
  •  Dựa vào nhiệt đốt cháy (thiêu nhiệt)
• 1.7.PHƯƠNG TRINH KIRCHOFF
• 2.3.ENTROPY TUYỆT ĐỐI
  • *Tính ST của 1 mol khí ở nhiệt độ T, biết 0K đến T
• 2.4.THẾ NHIỆT ĐỘNG – ĐIỀU KIỆN TỰ DIỄN BIẾN TRONG PHẢN
  •  Thông qua biến thiên enthalpy và entronpy của p
  • ➂ Thông qua biến thiên thế đẳng áp tạo thành chuẩn
• 2.5. CÁC YẾU TỐ ẢNH HƯỞNG ĐẾN THẾ ĐẲNG ÁP
• - - - CHƯƠNG 3. CÂN BẰNG PHA - - -
• 3.2.ẢNH HƯỞNG CỦA ÁP SUẤT ĐẾN NHIỆT ĐỘ CHUYỂN PHA
• 3.3.ẢNH HƯỞNG CỦA NHIỆT ĐỘ ĐẾN ÁP SUẤT HƠI BÃO HÒA
  •  Độ giảm áp suất hơi bão hòa của dung dịch
  •  Giản đồ “áp suất – thành phần” (P – x)
  • ➂ Thành phần pha hơi – Định luật Konovalap I
  • ➃ Giản đồ “thành phần hơi – thành phần lỏng”
  •  Độ tăng nhiệt độ sôi và độ giảm nhiệt độ đông đ
    • *Độ tăng nhiệt độ sôi của dung dịch
    • *Độ giảm nhiệt độ đông đặc của dung dịch
  •  Áp suất thẩm thấu – Định luật Van’t Hoff
  •  Định luật phân bố Nernst
    • *Sự phân bố của một cấu tử i trong 2 dung môi ít t
    • *Ứng dụng định luật phân bố trong phép chiết
• 4.3.SỰ HÒA TAN CỦA KHÍ TRONG CHẤT LỎNG
  •  Ảnh hưởng của áp suất
  •  Ảnh hưởng của nhiệt độ
• 4.4.DUNG DỊCH CHẤT ĐIỆN LI
  •  Tính chất của dung dịch
• 4.5.HOẠT ĐỘ DUNG DỊCH
  •  Hệ số hoạt độ
  •  Phương pháp xác định hoạt độ
    • *Đo áp suất hơi
    • *Xác độ hoạt độ theo định luật phân bố
  • ➃ Hoạt độ đối với chất điện li AnBm
    • *Phương trình Debye và Huckel
• - - - CHƯƠNG 5. CÂN BẰNG HÓA HỌC - - -
• 5.2.PHƯƠNG TRÌNH ĐẲNG NHIỆT VAN’T HOFF
• 5.3.HẰNG SỐ CÂN BẰNG VÀ ĐẠI LƯỢNG NHIỆT ĐỘNG LỰC HỌC
  •  Ảnh hưởng của nh
  •  Ảnh hưởng của áp suất
  • ➂ Ảnh hưởng của các khí trơ (không tham gia phản ứ
    • a)Phản ứng trong dung dịch
    • b)Phản ứng trong hệ khí
• 5.5.ĐỊNH LÍ NHIỆT NERNST
  • *Công thức gần đúng Nernst
• 5.6.CÂN BẰNG TRONG DUNG DỊCH CHẤT ĐIỆN LI