Tóm tắt lý thuyết cần nhớ môn học Xử lý tín hiệu số về "Tín hiệu và hệ thống rời rạc"

lOMoARcPSD| 36086670
TÍN HIỆU VÀ HỆ THỐNG RỜI RẠC
1. Định lý lấy mẫu (Định lý Nyquist)
Ta chú ý rằng một tín hiệu sẽ ược khôi phục khi tần số lấy mẫu phải lớn hơn hoặc bằng hai lần bề rộng
phổ của tín hiệu. Fs 2B (B=Fmax)
2. Phân loại tín hiệu, hệ thống xử lý tín hiệu.
Theo ịnh nghĩa về mặt toán học, tín hiệu bao gồm tín hiệu liên tục (biến liên tục) và tín hiệu rời rạc (biến rời rạc).
Tín hiệu liên tục (biến liên tục) bao gồm tín hiệu tương tự (biên ộ liên tục) và tín hiệu lượng tử hoá (biên ộ rời rạc).
Tín hiệu rời rạc (biến rời rạc) bao gồm tín hiệu lấy mẫu (biên ộ liên tục) và tín hiệu số (biên ộ rời rạc).
Các hệ thống xử lý tín hiệu ược phân loại theo tín hiệu xuất hiện trong hệ:
- Hệ thống xử lý tín hiệu tương tự: ầu vào và ầu ra của hệ thống ều là tín hiệu tương tự; phần lõi bên trong
hệ thống ều là các hệ xử lý tương tự.
- Hệ thống xử lý tín hiệu số: ầu vào và ầu ra của hệ thống ều là tín hiệu số.
- Hệ thống xử lý số tín hiệu: ầu vào và ầu ra của hệ thống ều là tín hiệu tương tự; phần lõi bên trong hệ
thống ều là các hệ xử lý tín hiệu số.
3. Cách biểu diễn tín hiệu rời rạc.
Lưu ý khi biểu diễn tín hiệu người ta thường chuẩn hoá chu kỳ lấy mẫu Ts = 1. Tức là x(nTs) = x(n). Có
3 cách biểu diễn tín hiệu:
- Biểu diễn bằng biểu thức toán học.
- Biểu diễn bằng ồ thị.
- Biểu diễn bằng dãy số.
Còn một cách biểu diễn nữa rất quan trọng chúng ta cần phải nhớ ó là một tín hiệu bất kỳ x(n) ều ược biểu
diễn thông qua áp ứng xung dạng tổng quát như sau: x n( )=
x k( ) (. n−k) k=−
4. Các tín hiệu (dãy) cơ bản
Các dãy cơ bản cần nhớ bao gồm: = 1 n
- Dãy xung ơn vị ( )n : ( )n 0 n= 0 n 0
- Dãy nhảy ơn vị u(n): u n( )= 10 n - Dãy chữ nhật rect ( )
N(n): w( )n = rectN n = 1 0 n N −1 0 n còn lai
- Dãy dốc ơn vị r(n): r n( )= n n 0 0 n còn lai lOMoARcPSD| 36086670 ( ) an n 0
- Dãy hàm mũ e(n): e n = 0 n còn lai
5. Các phép toán cơ bản
Các phép toán cơ bản cần nhớ bao gồm:
- Phép cộng, phép nhân hai tín hiệu.
- Phép nhân một tín hiệu với hằng số. - Phép trễ tín hiệu.
6. Các khái niệm cơ bản
Một số khái niệm cơ bản bao gồm:
- Dãy tuần hoàn x n( )N : x(n) = x (n + N)= x (n + lN) l: số nguyên; N: chu kỳ
- Dãy có chiều dài hữu hạn N. L[x(n)] = N =
- Năng lượng của dãy: E ( ) 2 x x n n=−
+ Dãy có năng lượng hữu hạn
+ Dãy có năng lượng vô hạn N 1
- Công suất của dãy: P = lim x n( )2 N→ 2N +1 n N=− + Tín hiệu công suất
+ Tín hiệu không công suất
7. Hệ thống tuyến tính bất biến. Đáp ứng xung h(n)
- Hệ thống tuyến tính thoả mãn nguyên lý xếp chồng: T[a.x1(n) + b.x2(n)] = a.T[x1(n)] + b.T[x2(n)].
- Hệ thống tuyến tính bất biến: ứng với kích thích ầu vào x(n) ta có áp ứng ra là y(n) thì tương tự
ứng với kích thích ầu vào x(n-k) ta có áp ứng ra là y(n-k).
- Khi ta có ầu vào hệ thống tuyến tính bất biến là xung ơn vị ( )n thì ầu ra là áp ứng xung h(n). Đáp
ứng xung h(n) là ặc trưng hoàn toàn
h n( )= y n( x n( )= (
cho hệ thống tuyến tính bất biến: ) )n 8. Phép chập
Đây là phép toán quan trọng nhất trong xử lý tín hiệu ể xác ịnh ầu ra y(n) hệ thống khi biết ầu vào x(n) và áp ứng xung h(n).
y n( )= x n( )*h n( )= x k h n( ) (. −k) lOMoARcPSD| 36086670 k=−
Phép chập có tính chất: giao hoán, phân phối, kết hợp.
9. Hệ thống TTBB nhân quả, tín hiệu nhân quả.
Hệ thống TTBB ược gọi là hệ thống nhân quả khi áp ứng xung h(n) của nó thoả mãn h(n) = 0 với n<0. Tín hiệu x(n) ược gọi
+ Tín hiệu nhân quả khi x(n) = 0 với n < 0.
+ Tín hiệu phản nhân quả khi x(n) = 0 với n > 0.
+ Tín hiệu không nhân quả khi không thỏa mãn 2 tính chất trên
Lưu ý: Các hệ thống nhân quả và tín hiệu nhân quả mới tồn tại trong thực tế.
Hệ thống TTBB ổn ịnh (BIBO)
Hệ thống ổn ịnh là hệ thống BIBO, áp ứng xung h(n) của nó phải thoả mãn iều kiện sau: = S h n( ) n=−
10. Phương trình sai phân tuyến tính hệ số hằng.
Hệ thống tuyến tính mô tả bởi phương trình sai phân tuyến tính
Hệ thống tuyến tính bất biến mô tả bởi phương trình sai phân tuyến tính hệ số hằng: ( ) ( ( ) ( − N ak n y n−k)= M b n x nr r) k=0 r=0
Các hệ số ak, br ặc trưng hoàn toàn cho hệ thống có vai trò tương tự như áp ứng xung h(n).
Giải phương trình sai phân tuyến tính hệ số hằng: y(n) = y0(n) + yp(n)
Bước 1. Giải phương trình ặc trưng ể tìm nghiệm tổng quát: y0(n) Bước 2. Tìm nghiệm riêng yp(n):
+ Kích thích ầu vào khác nghiệm pt ặc trưng: y0(n) = Bx(n)
+ Kích thích ầu vào trùng với nghiệm pt ặc trưng: y0(n) = Bnx(n) Bước 3. Dựa
vào giả thuyết ể tìm nghiệm của phương trình sai phân
Từ PTSPTTHSH trên ta sẽ có một số khái niệm về: N a ( ) ( ( ) ( − k n y n−k)= M b n x nr r) k=0 r=0
- Hệ thống không ệ quy khi N = 0. Bản chất của hệ thống này là không có thành phần hồi tiếp.
- Hệ thống ệ quy khi N 0. Bản chất của hệ thống này là có thành phần hồi tiếp.
- Hệ thống ệ quy thuần tuý khi N 0. M = 0. Hệ thống này chỉ gồm duy nhất các thành phần ệ quy.
Lưu ý: Như vậy ến ây ta có hai cách thể hiện quan hệ vào ra hệ thống rời rạc.
- Thể hiện theo phép chập: y(n) = x(n)*h(n)
- Thể hiện theo PT SPTTHSH: y n( )= M b x n ( − − ( − r r) N a y nk
k) thường phải chuẩn hoá a0 = 1 r=0 k=1 lOMoARcPSD| 36086670
11. Thực hiện hệ thống
Các phần tử thực hiện hệ thống bao gồm: phần tử cộng, phần tử nhân, nhân với hằng số, phần tử trễ D.
Khi thực hiện hệ thống phải dựa vào phương trình SPTT-HSH, luôn nhớ phải chuẩn hoá hệ số a0 =1 ể có y n( )= M b x n ( − − ( − r r) N a y nk
k) rồi mới vẽ sơ ồ hệ thống. Trên thực tế người ta sẽ dùng các bộ xử lý toán r=0
k=1 học ALU, các thanh ghi dịch... ể thực hiện hệ thống xử lý tín hiệu số theo sơ ồ.
12. Tương quan tín hiệu
Phép tương quan thường dùng ể nhận biết các tín hiệu, phân biệt tín hiệu với nhiễu, phát hiện vật thể... có hai loại tương quan: + =
Tự tương quan: Tương quan tín hiệu x(n) với chính nó:R xx (n) x(m).x(m−n) m=− + =
Tương quan chéo: Tương quan tín hiệu x(n) với y(n):R xy(n) x(m).y(m−n) m=−
Nhắc lại kiến thức toán học Tổng cấp số nhân. an = 1 Nếu a 1 n 0= 1 −a 1−a N n 1−aN 1+ a = n 0=
BIỂU DIỄN TÍN HIỆU VÀ HỆ THỐNG TRONG MIỀN Z 1. Biến ổi z
Định nghĩa biến ổi z : X z( )= x n z( ) −n n=− Nếu thay ổi cận: X z( )= x n z( ) −n n=0
Ta có biến ổi Z một phía.
Nhớ rằng Z là một biến số phức nên có thể ược biểu diễn theo 2 cách. 2.
Miền hội tụ của biến ổi Z
Tập hợp tất cả các giá trị của Z mà tại ó chuỗi X z( )= x n z( ) −n hội tụ ược gọi là miền hội tụ của biến ổi lOMoARcPSD| 36086670 n=− Z.
Ký hiệu miền hội tụ là RoC. Ta phải chú ý ến miền hội tụ khi thực hiện biến ổi z.
+ Dãy nhân quả: Miền ngoài vòng tròn bán kính R ( ) x− Z Rx−
+ Dãy phản nhân quả: Miền trong vòng tròn bán kính R ( ) x+ Z Rx+ + Dãy không nhân quả:
• Chiều dài vô hạn: Miền vành khăn bán kính trong R ( )
x− , bán kính ngoài R + Rx− Z Rx+ x
3. Điểm cực iểm không
Nếu tín hiệu X(z) có dạng phân thức X z( )= N zD z( )( ) thì: - Điểm cực z =
pk của tín hiệu X(z) là tập các iểm làm cho X(z) không xác ịnh: X z( ) . Nghĩa là z z z= pk pk là nghiệm của D(z) - Điểm không z =
0r của tín hiệu X(z) là tập các iểm làm cho X(z) triệt tiêu: X z( ) z z= 0. or
Nghĩa là z0r là nghiệm của N(z)
Lưu ý rằng iểm cực iểm không của hệ thống ược xác ịnh theo hàm truyền ạt H(z).
- Điểm cực của hệ thống là tập các iểm z =
pk làm cho H(z) không xác ịnh H z( ) z z= pk
- Điểm không của hệ thống là tập các iểm z =
0r làm cho H(z) triệt tiêuH z( ) z z=
0 Do vậy hàm truyền ạt H(z) 0r
còn ược biểu diễn theo dạng iểm cực và iểm không: rN=1 hay:
H z( )= N zD z( )( ) = baMN (z − z ) pk M k=1 ( ) bM
M z − z0r
G= là hệ số truyền aN
(z − z0r ) =
H z( )= G. r 1 N Trong ó (z − z ) pk k=1 lOMoARcPSD| 36086670
4. Biến ổi Z ngược
Định nghĩa biến ổi Z ngược: x n( )= 1 j C X z z( ). n−1dz 2 Trong ó
- Đường cong kín i qua gốc tọa ộ i ngược chiều kim ồng hồ. C
Chúng ta phải nhớ 3 phương pháp ể tìm tích phân ường này:
1. Phương pháp thặng dư ể tìm trực tiếp tích phân.
2. Khai triển thành chuỗi lũy thừa, tìm biến ổi z ngược cơ bản.
3. Khai triển thành các phân thức tối giản.
Trong ó các bài tập sẽ tập trung ở phương pháp thứ ba. Khi làm bài tập về biến ổi Z ngược chúng ta phải nhớ
các biến ổi tương ương hay gặp:
Nếu ta ưa X(z) về dạng phân thức tối giản X z( Miền Z RoC[X(Z)] Miền n 1 −z z ) pk −1 z zpk (zpk n u n( ) 1 1
−(z )n u n(− − pk z zpk −1 z zpk 1 −1) z−1 ( z 1 − nu n( ) z ) −1 2 1
)= Nk=1 z −Akzpk Các biến ổi tương ương thường gặp: Tính chất Miền n Miền z Miền hội tụ lOMoARcPSD| 36086670 Định nghĩa R − Z R + n( )= 1
X z z dz( ) −1 2 j xx z( )= x n z( ) −n C n=− Tuyến tính ax n ( )+ ( ) ( )+ ( ) ( ) 1 bx n2 aX z1 bX z2 RoC X z 1 RoC X z ( ) 2 Trễ thời gian − n n( − ) R − Z R + 0 n z X zn ( ) 0 x x Thay ổi tỷ lệ a x nn ( ) a R − Z a R + trong miền Z a z( −1 ) x x
5. Các tính chất biến ổi z
6. Biểu diễn hệ thống trong miền z.
Ta phải nhớ rằng ặc trưng cho hệ thống trong miền z là hàm truyền ạt H(z). Hàm truyền ạt có vai trò như áp ứng
xung h(n) của hệ thống trong miền thời gian rời rạc.
Hàm truyền ạt H(z) ược hiểu theo hai khái niệm:
- Hàm truyền ạt H(z) là tỷ số của biến ổi z tín hiệu ra trên biến ổi z tín hiệu vào. ( )= Y zX z( )( ) H z
- Hàm truyền ạt H(z) là biến ổi z của áp ứng xung h(n).
7. Liên hệ giữa biến ổi z và phương trình sai phân.
Biến ổi z hai vế của phương trình sai phân tuyến tính hệ số hằng: N a y n ( − ( − k k)= M b x nr r) lOMoARcPSD| 36086670 Vi phân trong nx n( ) −zdX z( ) R − Z R + miền Z xx dz Dãy liên hợp x*(n) X*(z*) phức Đảo biến x n(− ) 1 X z Tích chập x n x n ( )* ( ) X z X z ( ). ( ) trong miền n 1 2 1 2 Tích chập x n x n ( ). ( ) 1 ( ) z trong miền Z 1 2 1 2 −1 j C X v X v v dv 2 Tương quan 1
x n x ( )* (−n) tín hiệu 1 2 X z X ( ) 1 . 2 z k=0 r=0 ta thu ược:
( ) rM0b zr −r H z( )= Y z( ) = N k
nên nhớ luôn chuẩn hoá a0 = 1 ể
dễ vẽ sơ ồ thực hiện. = + X z 1 a z−k k=1
Các phần tử thực hiện hệ thống trong miền z cũng giống như trong miền thời gian rời rạc n: phần tử cộng, nhân,
nhân với hằng số. Phần tử trễ D trong miền n khi sang miền z trở thành phần tử z-1.
Có 3 dạng cấu trúc thông thường của hệ thống: song song, nối tiếp, hồi tiếp. Cách xác inh hàm truyền ạt hệ
thống tổng quát tương ứng như sau:
- Nếu có N hệ thống mắc song song với nhau thì: H z( )= N H (z)i i 1=
- Nếu có N hệ thống mắc nối tiếp với nhau thì:H z( )= N H (z)i i 1= lOMoARcPSD| 36086670
- Nếu H2(z) mắc hồi tiếp với H1(z) thì hàm truyền ạt của hệ thống tổng quát sẽ bằng: H( )z = H z1( )
1+ H z H1( ).2( )z
8. Sự ổn ịnh của hệ thống trong miền z.
Một hệ thống TTBB nhân quả trong miền z muốn ổn ịnh phải thoả mãn: Tất cả các iểm cực zpk của hàm
truyền ạt H(z) phải nằm bên trong vòng tròn ơn vị tức là: 1 . zpk
Ta có: H z( )= N zD z( )( ) . Khi bậc N của hệ thống tức bậc của a thức ặc trưng D(z) lớn hơn 2 thì ta phải dùng
tiêu chuẩn Jury ể xét tính ổn ịnh. lOMoARcPSD| 36086670
BIỂU DIỄN TÍN HIỆU VÀ HỆ THỐNG TRONG MIỀN TẦN SỐ LIÊN TỤC
1. Biến ổi Fourier – FT Định nghĩa: ( ) X e = j x n e(
) − j n n=−
Các cách thể hiện của X e( j ): ( ) ( ) +) X e = + j Re X e j jIm X ( ) ) ) e = j +) X e( j
X e( j .e j ( ) : •
X e( j ): Phổ của tín hiệu x(n) ) •
X e( j ) : Phổ biên ộ của tín hiệu x(n) X e( j ) = Re2 X e( j +Im2 X e( j ) ( Im X e ) • ) ( ) = j ( )= arg X e( j
: Phổ pha của tín hiệu x(n) arg X e j ( ) arctan Re X e j +) X e( )= ) j
A e( j .e j ( ) : = •
A e( j ) : Độ lớn của tín hiệu x(n) (có thể dương (>0) âm (<0) hoặc bằng X e( A e( 0) • j ) j ) ( ) ( (
: Pha của tín hiệu x(n):
( ) = arg X e j ) −arg A e j ) = ( )− ( arg A e j ) ( ) • arg A e = j 0 (( A eA e 2. Điều
kiện ể tồn tại biến ổi Fourier )) j j 00 lOMoARcPSD| 36086670
Một dãy x(n) thực hiện ược biến ổi Fourier nếu và chỉ nếu: x n( ) n=−
3. Quan hệ giữa biến ổi Fourier và biến ổi z
- Biến ổi Fourier chính là biến ổi z ược thực hiện trên vòng tròn ơn vị:
X e( j )= X z( ) z e= j
- Như vậy, biến ổi Fourier chỉ là trường hợp riêng của biến ổi z.
4. Biến ổi Fourier ngược - IFT Định nghĩa: x n( )= 1 X e( ) j e dj n 2 −
5. Tính chất của biến ổi Fourier Tính chất Miền n Miền Ký hiệu x n( )
X e( j ) ( Định nghĩa ( ) x n( ) = 1 X e j )e j X e = j
x n e( ) − j n n=− nd 2 − Tuyến tính ax n ( )+ ( ) ( j )+ ( j ) 1 bx2 n aX e1 bX e2 Trễ trong miền ) e )
j n0 X e( j − thời gian n x n( −n0 X ( )= ) * e j X e( − j ( ) ( ) Re X e = j Re X e − j x(n) là thực Tính ối xứng
+) Re, Im, module là các hàm chẵn ( ) ( ) Im X e = j Im X e − j +) argument là hàm lẻ ( ( X e
j ) = X e − j ) ( ) ( ) arg X e = − j arg X e − j Liên hợp phức x*(n) X ( ) * e− j Biến số ảo x(-n) X e( ) − j lOMoARcPSD| 36086670 Tích chập trong ( ) ( ) ( ) ( ) miền n x n1 *x2 n
X1 e j .X2 e j Tích chập trong ( ) ( ) 1 ( ) ) j ( ) 1 ( − 2 j miền tần số x n x1 . 2 n X e .X e d 2 − dX e( j ) Vi phân trong j miền tần số nx(n) d Trễ tần số e ) j 0nx n( ) X e j( − 0 Tính chất iều chế 1 j( + ) + ) 0 1 X e j( − 0 x n( )cos 0n X e 2 2 Định lý Weiner ( ) ( ) ( ) 1 1 j 2* j Khinchine x n x * ( ) 1 . 2 n X e .X e d n=− 2 − ) Quan hệ Parseval 1 ( j 2 x n( ) 2 X ed n=− 2 −
6. Đáp ứng tần số
Đáp ứng tần số H(e j ) của hệ thống trong miền tần số liên tục ược xây dựng theo hai cách:
- Đáp ứng tần số H(e j ) của hệ thống là tỷ số giữa biến ổi Fourier của tín hiệu ra trên biến ổi Fourier của tín hiệu vào.
- Đáp ứng tần số H(e j ) là biến ổi Fourier của áp ứng xung h(n).
Đáp ứng tần số của hệ thống ược thể hiện như sau: H(e )= ) j H(e j e j ( ) trong ó:
H(e j ) : Đáp ứng tần số của biên ộ (áp ứng biên ộ). lOMoARcPSD| 36086670
( )= arg H (e j ) : Đáp ứng tần số của pha (áp ứng pha). hay ộ lớn và pha: H(e )= ) j A(e j e j ( )
Một số kiến thức toán học cần thiết ể nghiên cứu học tập trong chương này.
+ Tích phân thông dụng ể tính IFT: e dt = t 1 e t + Tổng cấp số nhân: an = 1 Nếu a 1 n 0= 1−a N n 1−aN 1+ a = n 0= 1−a + Công thức Euler:
e j = cos + sinj
e− j = cos − sinj
+ Một số khai triển thông thường:
e j +e− j cos = e 2 − j e− j sin = 2 j
BIỂU DIỄN TÍN HIỆU VÀ HỆ THỐNG TRONG MIỀN TẦN SỐ RỜI RẠC
1. Cặp biến ổi Fourier rời rạc ối với dãy tuần hoàn có chu kỳ N. Biến ổi DFT N−1 − j2 kn lOMoARcPSD| 36086670 X k( )= x n e( ). N n=0 2 − j kn W = Nkn e N
Biến ổi ngược IDFT x n( )= 1
N−1X k e( ). j2N kn N k=0 Lưu ý:
- X k( ) cũng tuần hoàn với chu kỳ N.
- Đặc iểm nổi bật của DFT là biến ổi xuôi và ngược tương ương như nhau, chỉ khác nhau về hệ số 1/N và dấu ở
số mũ, hay nói cách khác biến ổi xuôi và ngược là cùng thuật toán. Tính chất: Miền n Miền k x n( ) X k( ) 1 − − 1 x n( )= X k( )=
N X k W( ) N−kn
N 1 x n W( ) Nkn N k=0 k=0 ax n ( ) + ( ) ( ) + ( ) 1 N bx2 n N aX1 k N bX2 k N x n( −n ) 0 N WNkn0 X k( ) W x n ln ( ) N X k( +l) − X ( ) ( ) 1 k N X2 k N ( ) x n ( ) ( ) = N 1 ( ) 1 N * N x2 n N x m x1 2 (n−m) m=0 x n ( ) ( ) ( ) ( ) 1 N x2 n N 1 N−1 N
X1 m N X1 k −m N m=0 ( ) X ( ) ( ) 1 k N * X2 k N * X*(−k) x n( ) lOMoARcPSD| 36086670 x*(−n) X k( ) * x n( ) thực
X k( )= X*(−k) Re X k( ) = Re X (−k) Im X k( ) = Im X (−k)
X k( ) = X (−k) arg X k( ) =−arg X (−k)
2. Cặp biến ổi Fourier rời rạc ối với dãy có chiều dài hữu hạn N.
Đối với các dãy có chiều dài hữu hạn N ( ký hiệu là x(n)N) , ể biến ổi ược DFT người coi nó là 1 chu kỳ của 1
dãy tuần hoàn, do vậy thực hiện ược biến ổi DFT và sau ó lấy kết quả trong một chu kỳ. Cụ thể biến ổi DFT ối
với dãy có chu kỳ N ược ịnh nghĩa như sau: Biến ổi DFT ( ) ( ) N−1 N x n W kn 0 −k X k = n=0 N 1 k 0 Biến ổi IDFT N − 1 ( ) 1 ( ) k 0 −kn = N = X k WN 0 −n x n N 1 0 n Tính chất Miền n
Miền tần số rời rạc k ( )N 1 ( ) − N−1 N N−kn n N 1 x n ( ) N−1 ( ) N kn
x n W 0 −k N 1 = X k = k=0 N N N k=0 X k W 0 0 k 0 n ax n( ) + = = ( ) + ( ) = ( ) N
bx n( )N x n( )N , N3 max N aX k1 N3 bX k2 N3 X k3 N3 N1, 2 1 2 3 x n( −n ) 0 N
WNkn0 X k( )N W ) N k n0 x n( )
X k( −k0 N − lOMoARcPSD| 36086670 N−1 X ( ) ( ) 1 k N X2 k N x m ( ) ( = ( ) ( ) ( ) 1
N x2 n−m)N x n1 N * N x2 n N m=0 x n ( ) ( ) ( ) () 1 N x2 n N 1 N−1 N 2 N X1 l X k −l N l=0 x*( )n N
X*(−k)N
x*(−n)N X*( )k N () Re x n( )N 1 ( )N 1 * N X k + X −k 2 2 () jRe x n( ) N N 1 ( )N 1 * X k − X −k 2 2 Với x n( ) = N thực X k( )N
X*(−k)N X*( )k = N
X (−k)N Re X k( ) = N Re
X (−k)N Im X k( ) =− N Im
X (−k)N X k( ) = N
X (−k)N arg X k( ) =− N arg
X (−k)N N−1 ( ) 2 1 N−1 2 x n( ) X k n=0 N h=0 N
3. Các tính chất của biến ổi Fourier rời rạc DFT
Trong phần này chúng ta nên lưu ý ể phân biệt một số khái niệm: Các ký hiệu:
- x(n)N: tín hiệu x(n) có chiều dài hữu hạn N.
- x n( ) : tín hiệu tuần hoàn có chu kỳ N N .
- Phân biệt rõ x(n)N x(n). lOMoARcPSD| 36086670 Các tính chất:
Phân biệt rõ các khái niệm trễ tuyến tính, trễ tuần hoàn, trễ vòng ặc biệt là phân biệt 3 khái niệm: -
Phép chập tuyến tính x1(n)*x2(n)
- Phép chập tuần hoàn x n ( ) ( ) 1 N ( ) N x2 n N
- Phép chập vòng x1(n)N (*)N x2(n)N
Từ ây ta thấy, kết quả của phép chập tuyến tính giữa hai tín hiệu có chiều dài hữu hạn x1(n) có chiều dài N1,
x2(n) có chiều dài N2 ã học trong chương 1 có thể tính ược thông qua biến ổi DFT nếu chiều dài thực hiện DFT
N N1 + N2-1. Như vậy việc thực hiện phép chập sẽ dễ dàng hơn vì biến ổi DFT và IDFT ược thực hiện cùng một thuật toán. BỘ LỌC SỐ
Trong chương này chúng ta tìm hiểu về bộ lọc số. Các nội dung kiến thức cần nhớ trong chương này sẽ ược ề cập sau ây:
1. Các bộ lọc số lý tưởng
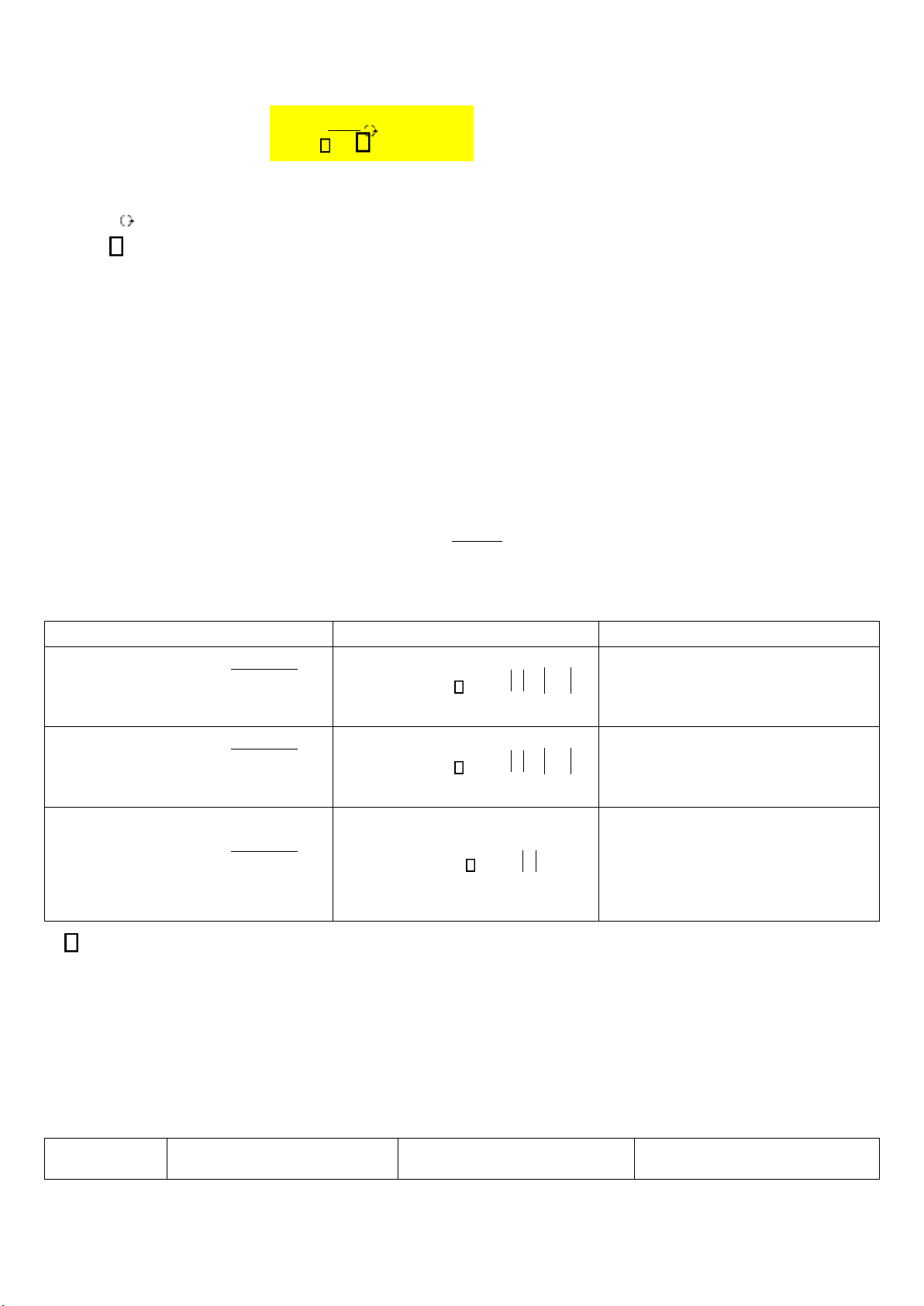
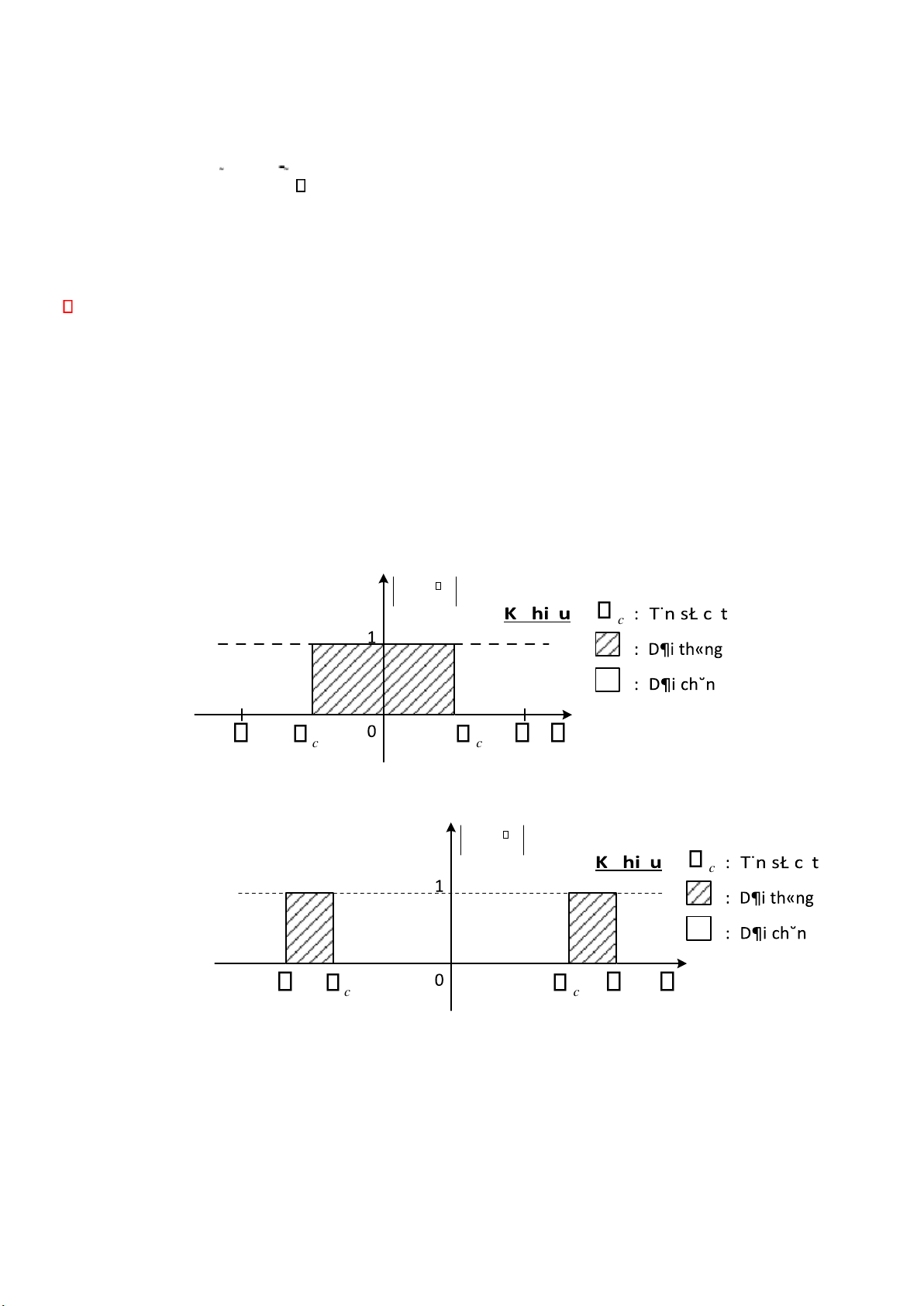
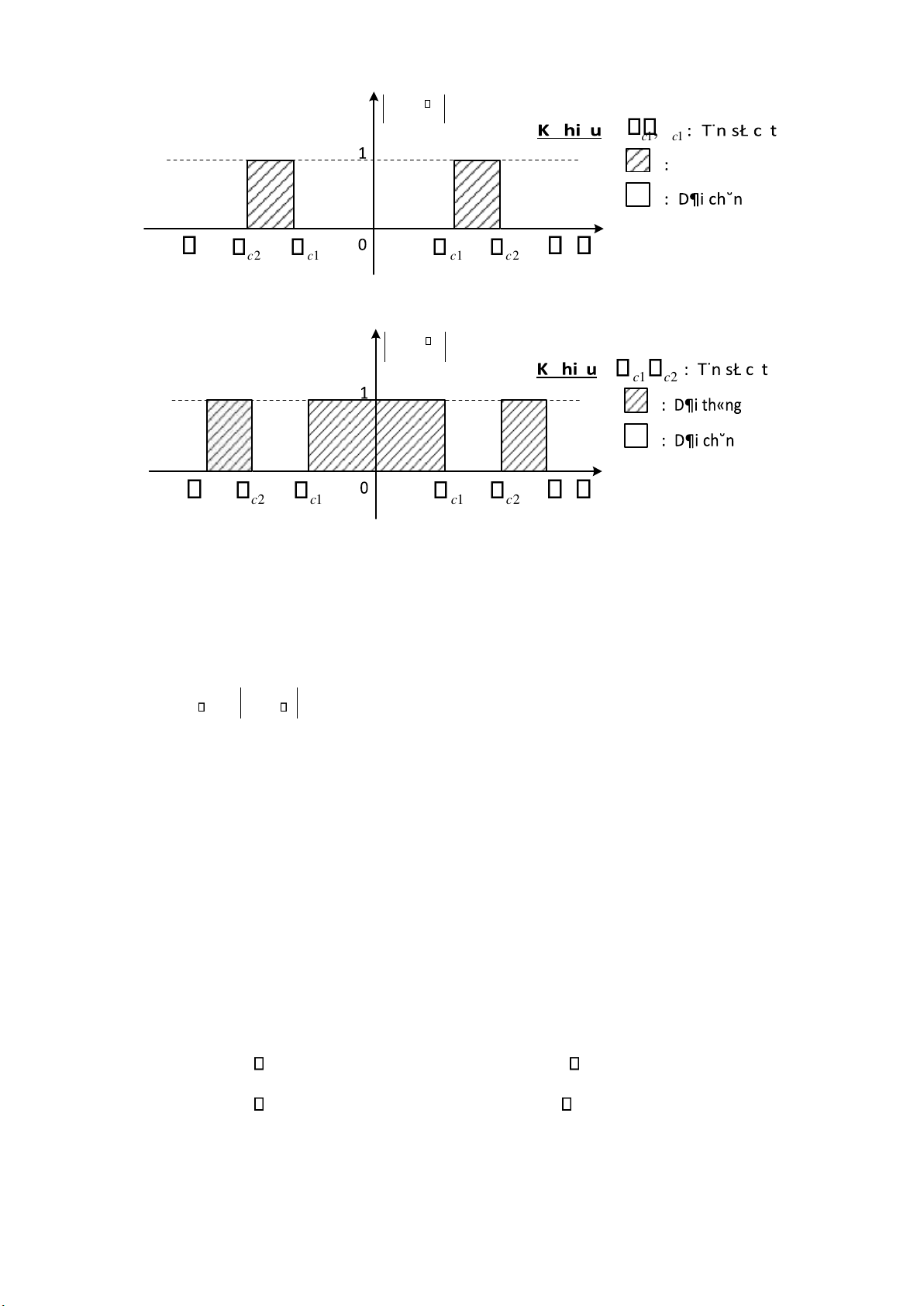
Trong phần này, chúng ta phải nắm ược bốn bộ lọc số lý tưởng thông qua các áp ứng biên ộ của chúng. Bộ lọc thông thấp: j H ( e ) c − − c c Bộ lọc thông cao: j H ( e ) c − − c c lOMoARcPSD| 36086670 Bộ lọc thông dải: H ( j e ) , 1 c 1 c D¶i th«ng − − − c2 1 c c1 c2 Bộ lọc chắn dải: H ( j e ) 1 c c2 − − − c2 1 c 1 c c2
Một số vấn ề của bộ lọc số lý tưởng cần lưu ý:
- Đáp ứng xung h(n) của bộ lọc số lý tưởng có chiều dài vô hạn, và áp ứng xung này là không nhân quả. Do vậy
các bộ lọc số lý tưởng này không thực hiện ược trong thực tế.
- Đối với bộ lọc số lý tưởng pha 0 ta có áp ứng biên ộ trùng với áp ứng tần số: ( (
H e j ) = H e j )
- Đáp ứng xung h(n) của bộ lọc số lý tưởng pha 0 ối xứng qua trục tung, ối xứng Helmitte.
- Các áp ứng xung h(n) của các bộ lọc số lý tưởng pha 0 có quan hệ như sau: + h ( ) ( ) ( ) HP n = hAP n −hLP n + h ( ) BP
n = hAP ( )n −hLP ( )n −hHP ( )n + h ( ) BS
n = hLP ( )n +hHP ( )n
2. Các chỉ tiêu kỹ thuật của bộ lọc số
Chúng ta phải nắm vững các thông số chỉ tiêu của bộ lọc số số thực tế:
+ Tần số giới hạn dải thông P
+ Độ gợn sóng dải thông 1
+ Tần số giới hạn dải thông S
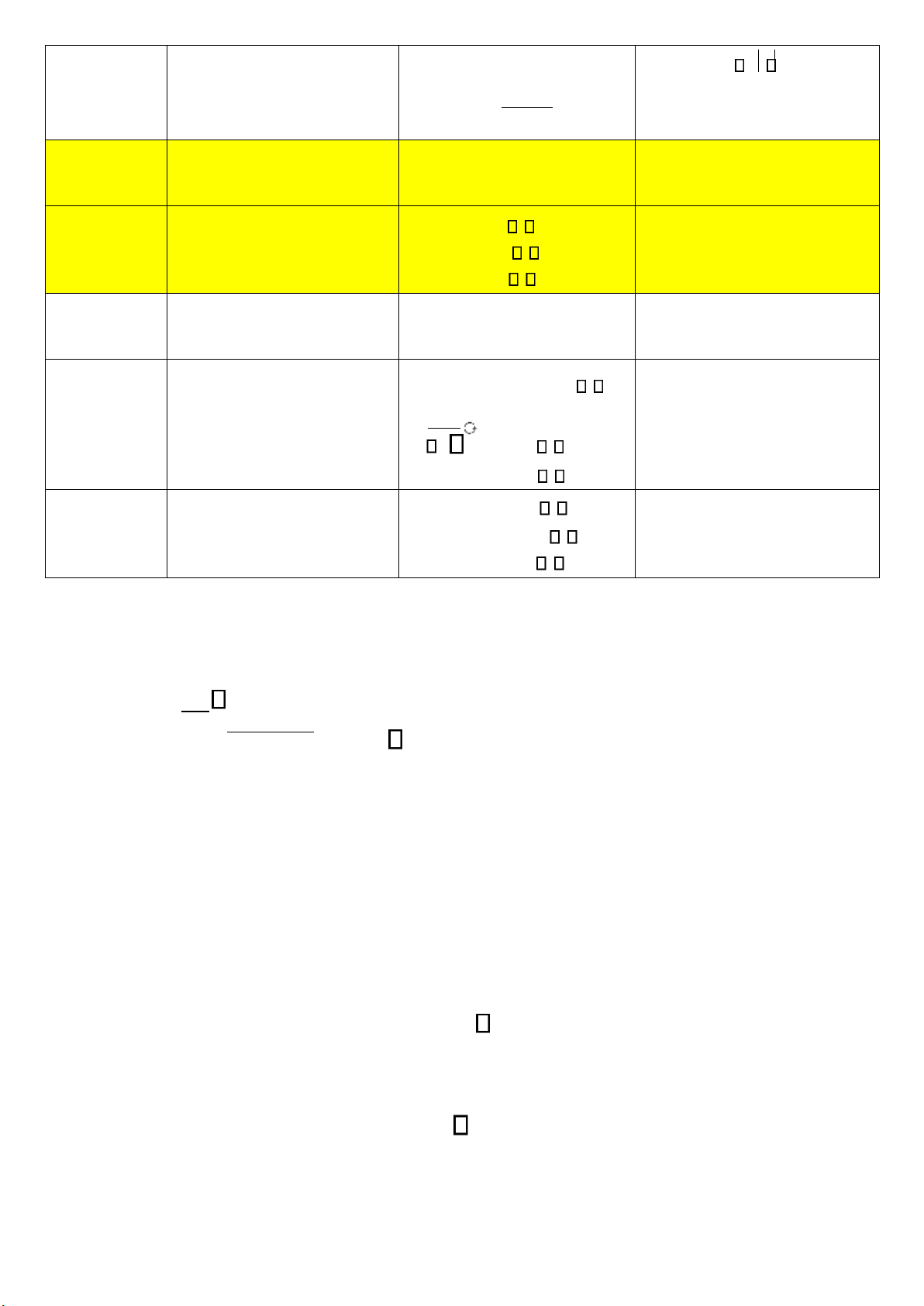
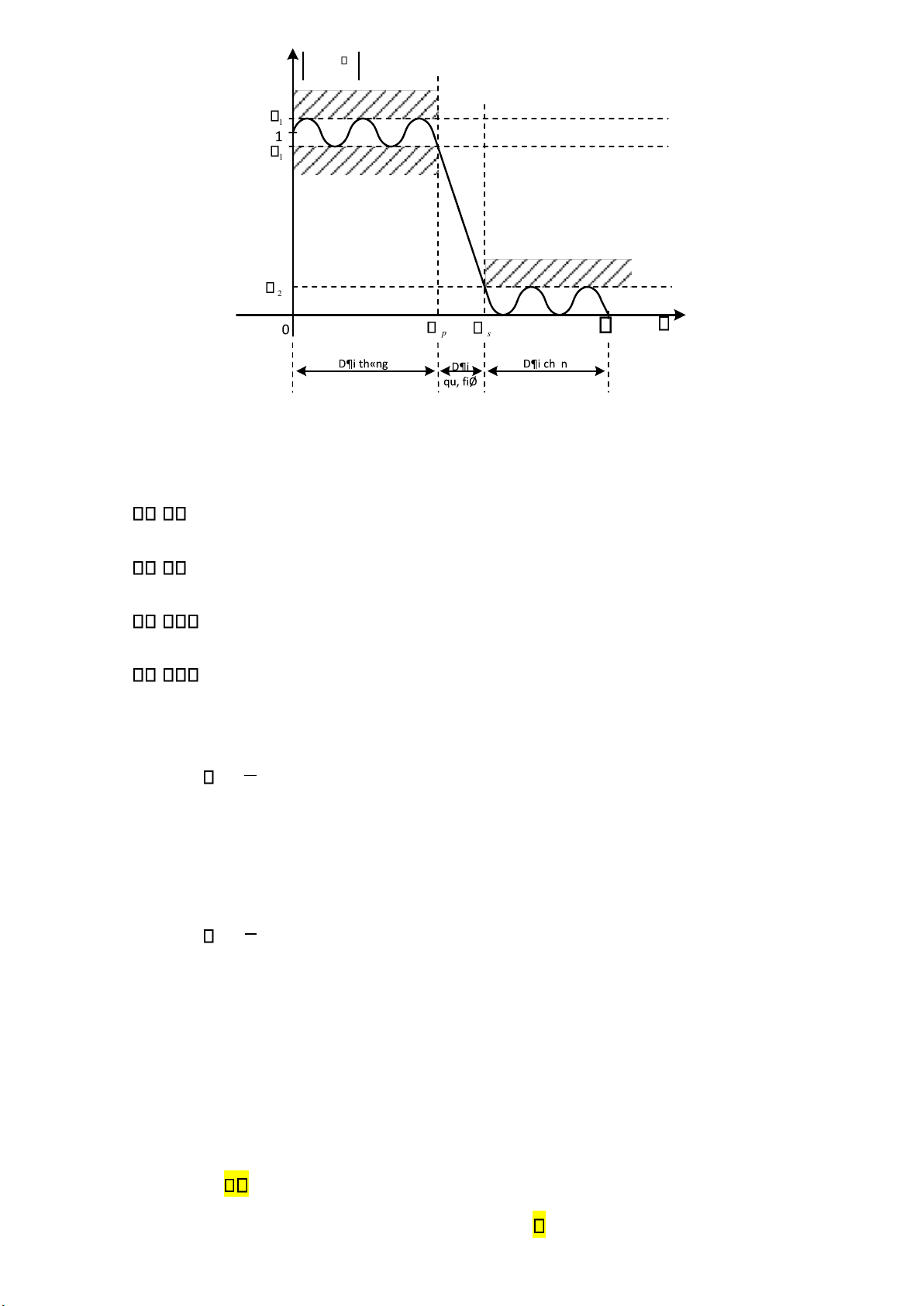
+ Độ gợn sóng dải chắn 2 lOMoARcPSD| 36086670 ( j He ) 1 + 1 1 − 1 2 p s
3. Đặc iểm bộ lọc số FIR
Ta chỉ xét bộ lọc số pha tuyến tính, cho nên các bộ lọc số FIR ược chia ra làm 4 loại: - Khi
( )=− và N lẻ, ta có bộ lọc số FIR loại I, h(n) ối xứng. - Khi
( )=− và N chẵn, ta có bộ lọc số FIR loại II, h(n) ối xứng. - Khi
( )= − và N lẻ, ta có bộ lọc số FIR loại III, h(n) phản ối xứng - Khi
( )= − và N chẵn, ta có bộ lọc số FIR loại IV, h(n) phản ối xứng.
Bộ lọc FIR loại I, loại II ta có: - Tâm ối xứng của áp ứng
xung h(n) tại : = N−1 2 - h(n) = h(N-1-n)
Bộ lọc FIR loại III, loại IV ta có: - Tâm phản ối xứng của áp ứng
xung h(n) tại : = N−1 2 - h(n) = -h(N-1-n)
4. Phương pháp cửa sổ ể thiết kế bộ lọc FIR
Nội dung của phương pháp này là dùng cửa sổ ể biến áp ứng xung h(n) của bộ lọc số lý tưởng thành nhân quả
và có chiều dài hữu hạn.
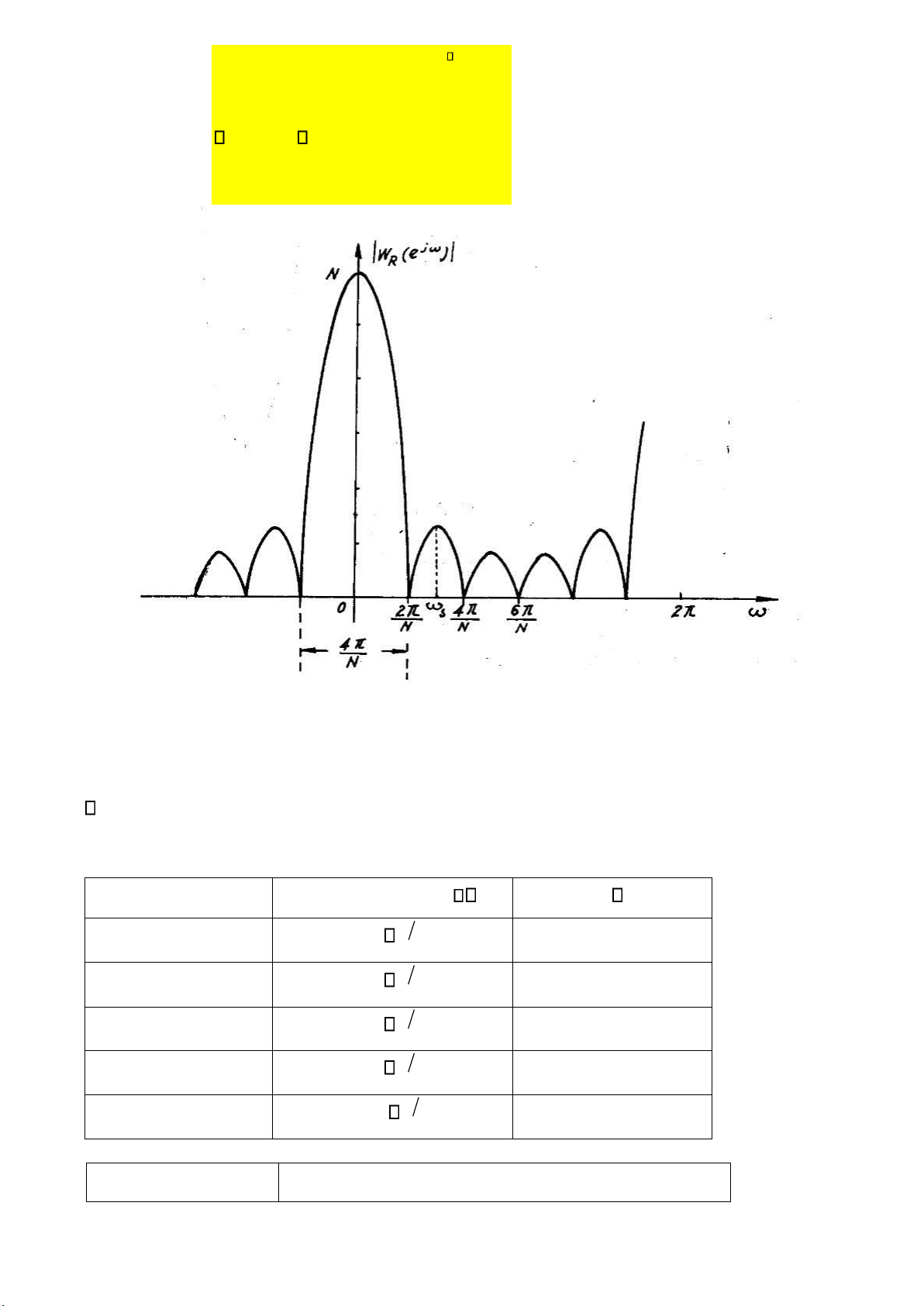
Trong thực tế, ặc trưng cho các cửa sổ ta dùng hai tham số:
- Bề rộng ỉnh trung tâm .
- Tỷ số giữa biên ộ ỉnh thứ cấp thứ nhất trên biên ộ ỉnh trung tâm : lOMoARcPSD| 36086670 j ( ) W e s = ) 20log −1 = 10 20log10 j0 (dB) ( W e
Đây là hai chỉ tiêu ánh giá chất lượng của cửa sổ.
Sau ây ta phải lưu ý bảng tổng kết các tham số và các hàm cửa sổ:
Hiện tượng Gibbs là hiện tượng các dao ộng ở dải thông và dải chắn xung quanh trục chuyển biến ột
ngột c do việc hạn chế chiều dài của áp ứng xung h n( ) của bộ lọc số lý tưởng bằng cửa sổ.
Bảng 0.1 Các tham số quan trọng của một số hàm cửa sổ Loại cửa sổ Bề rộng ỉnh trung tâm . Tỷ số (dB) Chữ nhật 4 N -13 Tam giác (Bartlett) 8 N -27 Hanning 8 N -32 Hamming 8 N -43 Blackman 12 N -58
Bảng 0.2 Một số hàm cửa sổ ể tổng hợp bộ lọc FIR Tên cửa sổ Định nghĩa lOMoARcPSD| 36086670 Chữ nhật
1 0 n N −1 w ( R )n = N 0 n 2n n N −1 Bartlett (Tam N −1 0 2 giác) N w ( ) = T n N 2− 2−n1 2−1 n N −1 N 0 n Hanning − 2 n 0 −n N 1 w ( ) = Han n N 0,5 0,5cos N −1 0 n Hamming 2 −0,46cos n 0 −n N 1 ( ) = Han n N 0,54 1 w N − 0 n Blackman
0.42−0.5cos 2 n +0,08cos 4 n N−1 N−1 0
N −1 2 − n− N −1 2 I 2 2 Kaiser I − 0 N2−1
5. Bộ lọc số IIR Ta nhớ rằng bộ lọc này ược xây dựng từ bộ lọc tương tự, tức là ta phải xác ịnh ược hàm truyền ạt tương tự H ( ) ( ) a
s , người ta có 3 phương pháp tổng hợp ể xác ịnhHa s : - Butterworth - Chebyshev - Elip hay Cauer Khi có ược H ( ) a
s ta sẽ ánh xạ tương ương sang miền số ể có ược bộ lọc số IIR bằng 3 phương pháp sau:
- Phương pháp bất biến xung
- Phương pháp biến ổi song tuyến tính lOMoARcPSD| 36086670
- Phương pháp tương ương vi phân
Các nội dung chính chúng ta cần nhớ trong chương này là:
Nếu cho sơ ồ bộ lọc tương tự thì: H ( ) a s = ura uvao
Phương pháp bất biến xung
Khi ta xác ịnh ược hàm truyền ạt tương tự của bộ lọcH ( ) a
s , ta sẽ ưa về dạng: H s ( ) = a N Ak k 1= s s− pk
Sau ó hàm truyền ạt H(z) bộ lọc số IIR sẽ ược xác ịnh theo phương pháp bất biến xung như sau: H z( )= − k 1N e zAs Tpkk −1 = 1
Phương pháp biến ổi song tuyến tính
Hàm truyền ạt H(z) bộ lọc số IIR sẽ ược xác ịnh theo phương pháp biến ổi song tuyến tính từ H ( ) a s theo ánh xạ sau: ( ) H z( ) = H sa
s=T211+−zz−−11
Phương pháp tương ương vi phân
Hàm truyền ạt H(z) bộ lọc số IIR sẽ ược xác ịnh theo phương pháp biến ổi tương ương vi phân từ H ( ) a s theo ánh xạ sau: H z( ) = H s ( ) a s=1−z−1 T