

Preview text:
Lý thuyết HKG 11-12 1
A – KIẾN THỨC CƠ BẢN
1 . Chứng minh đường thẳng d song song mp() (d ( ))
Cách 1. Chứng minh d //d ' và d ' ( )
Cách 2. Chứng minh d ( ) và ( ) / /( )
Cách 3. Chứng minh d và () cùng vuông góc với 1 đường thẳng hoặc
cùng vuông góc với 1 mặt phẳng
2 . Chứng minh mp() song song với mp()
Cách 1. Chứng minh mp () chứa hai đường thẳng cắt nhau cùng song
song với () (Nghĩa là 2 đường thẳng cắt nhau trong mặt này
song song với 2 đường thẳng trong mặt phẳng kia)
Cách 2. Chứng minh () và () cùng song song với 1 mặt phẳng hoặc
cùng vuông góc với 1 đường thẳng.
3 . Chứng minh hai đường thẳng song song:
Cách 1. Hai mặt phẳng (), () có điểm chung S lần lượt chứa hai
đường thẳng song song a và b thì () () = Sx // a // b.
Cách 2. () // a, a () () () = b // a
Cách 3. Hai mặt phẳng cắt nhau cùng song song với một đường thẳng
thì giao tuyến của chúng song song với đường thẳng đó.
Cách 4. Một mặt phẳng cắt hai mặt phẳng song song cho 2 giao tuyến song song.
Cách 5. Một mặt phẳng song song với giao tuyến của 2 mặt phẳng cắt
nhau, ta được 3 giao tuyến song song.
Cách 6. Hai đường thẳng cùng song song với đường thẳng thứ 3 hoặc
cùng vuông góc với một mặt phẳng thì song song với nhau.
Cách 7. Sử dụng phương pháp hình học phẳng: đường trung bình,
định lí Thales đảo, cạnh đối tứ giác đặc biệt, … Lý thuyết HKG 11-12 2
4 . Chứng minh đường thẳng d vuông góc với mặt phẳng ()
Cách 1. Chứng minh đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong ().
Cách 2. Chứng minh d nằm trong một trong hai mặt phẳng vuông góc
và d vuông góc với giao tuyến d vuông góc với mp còn lại.
Cách 3. Chứng minh d là giao tuyến của hai mặt phẳng cùng vuông góc với mặt thứ 3.
Cách 4. Chứng minh đường thẳng d song song với a mà a ().
Cách 5. Đường thẳng nào vuông góc với một trong hai mặt phẳng
song song thì cũng vuông góc với mặt phẳng còn lại.
Cách 6. Chứng minh d là trục của tam giác ABC nằm trong ()
5 . Chứng minh hai đường thẳng d và d vuông góc:
Cách 1. Chứng minh d () và () d.
Cách 2. Sử dụng định lí 3 đường vuông góc.
Cách 3. Chứng tỏ góc giữa d, d bằng 900.
6 . Chứng minh hai mặt phẳng () và () vuông góc:
Cách 1. Chứng minh () d và d ().
Cách 2. Chứng tỏ góc giữa hai mặt phẳng () và () bằng 900.
Cách 3. Chứng minh a // () mà () a
Cách 4. Chứng minh () // (P) mà () (P) Lý thuyết HKG 11-12 3 B – CÔNG THỨC CƠ BẢN I. TAM GIÁC 1 . Tam giác thường: 1 1 abc
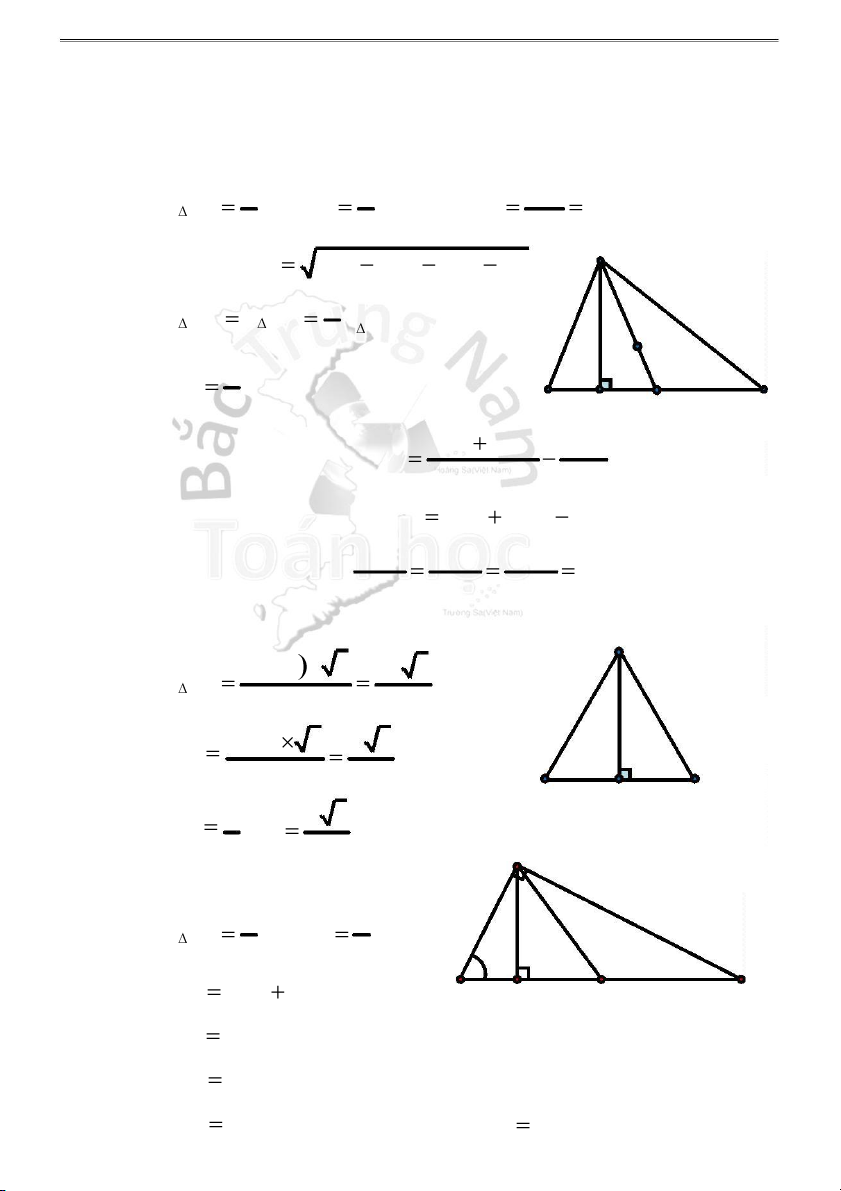
① SABC BC.AH AB.AC.sin A pr 2 2 4R A
p( p a)(p b)(p c) 1
② SABM SACM S ABC 2 G 2
③ AG AM (G là trọng tâm) 3 B H M C 2 AB2 AC BC2
④ Độ dài trung tuyến: AM 2 2 4
⑤ Định lí hàm số cosin: BC 2 AB2 AC 2 2 AB.AC.cos A a b c
⑥ Định lí hàm số sin: 2R
sin A sin B sinC
2 . Tam giác đều ABC cạnh a, G là trọng tâm: A
(cạnh2 3 a 2 3
① SABC 4 4 a
cạnh 3 a 3 ② AH 2 2 B H C 2 a 3
③ AG AH 3 3 A
3. Tam giác ABC vuông tại A: 1 1
① SABC AB.AC AH.BC 2 2
② BC2 AB2 AC 2 B H M C
③ BA2 BH.BC
④ CA2 CH.CB
⑤ HA2 HB.HC
⑥ AH.BC AB.AC Lý thuyết HKG 11-12 4 1 1 1 HB AB2 1 ⑦ ⑧
⑨ AM BC AH 2 AB2 AC2 HC AC2 2 AC AB AC AB ⑩ sin B ⑪ cos B ⑫ tan B ⑬ cot B BC BC AB AC C
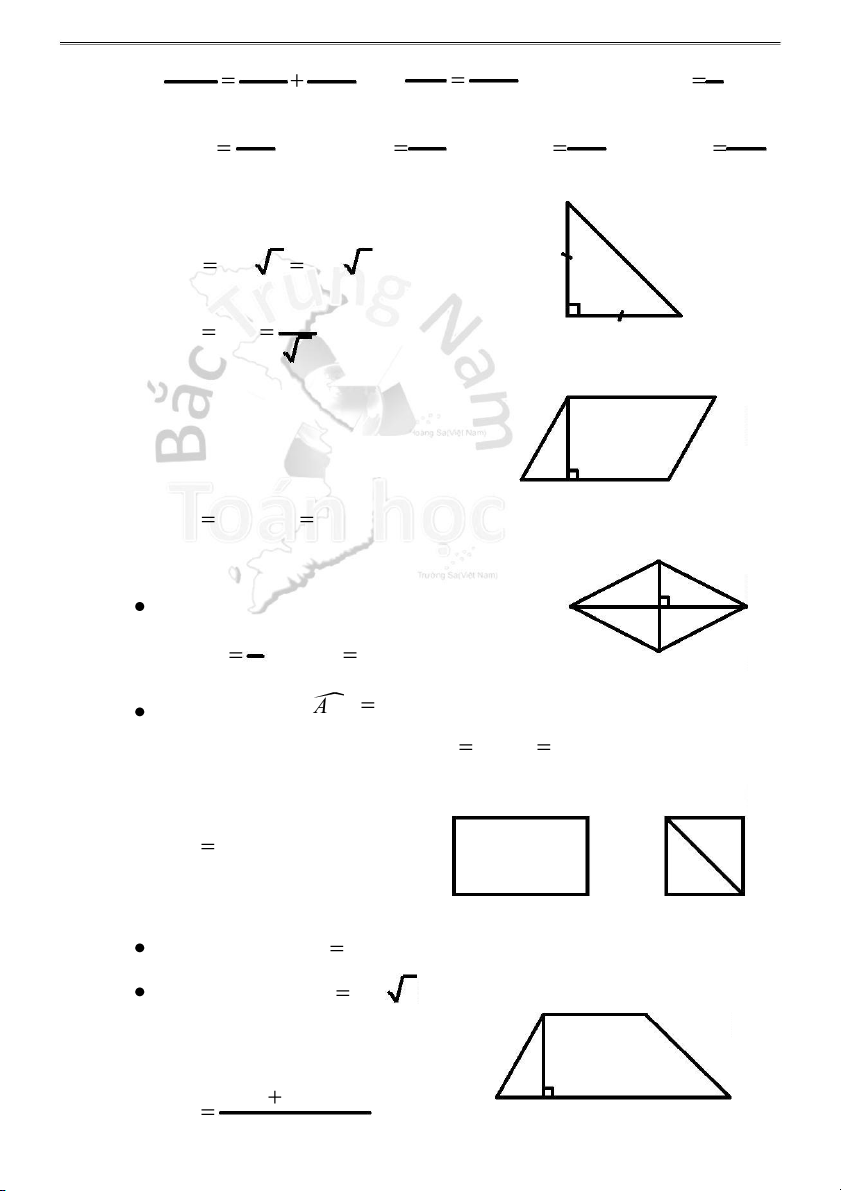
4 . Tam giác ABC vuông cân tại A
① BC AB 2 AC 2 BC
② AB AC A B 2 A D II. TỨ GIÁC 1 . Hình bình hành: Diện tích: B H C S
BC.AH AB.AD.sin A ABCD A 2 . Hình thoi: Diện tích: B D 1 S
AC.BD AB.AD.sin A ABCD C 2
Đặc biệt: khi A
BC 60o hoặc 𝐵𝐴𝐶
̂ = 120o thì các tam giác
ABC, ACD đều. Khi đó S
2SABC 2SADC ABCD A 3 . Hình chữ nhật: D A D S AB.AD ABCD 4 . Hình vuông: B C B C Diện tích: S AB2 ABCD
Đường chéo: AC AB 2 A D 5 . Hình thang:
(AD BC).AH S B H C ABCD 2 Lý thuyết HKG 11-12 5
III.CÁC HÌNH TRONG KHÔNG GIAN 1 . Hình lăng trụ:
① Thể tích khối lăng trụ: V = Sđáy.Chiều cao
② Diện tích xung quanh: Sxq = Tổng diện tích các mặt bên
③ Diện tích toàn phần: S tp = S xq + S2đáy 2 . Hình chóp: 1
① Thể tích khối chóp: V = Sđáy.Chiều cao 3
② Diện tích xung quanh: Sxq = Tổng diện tích các mặt bên
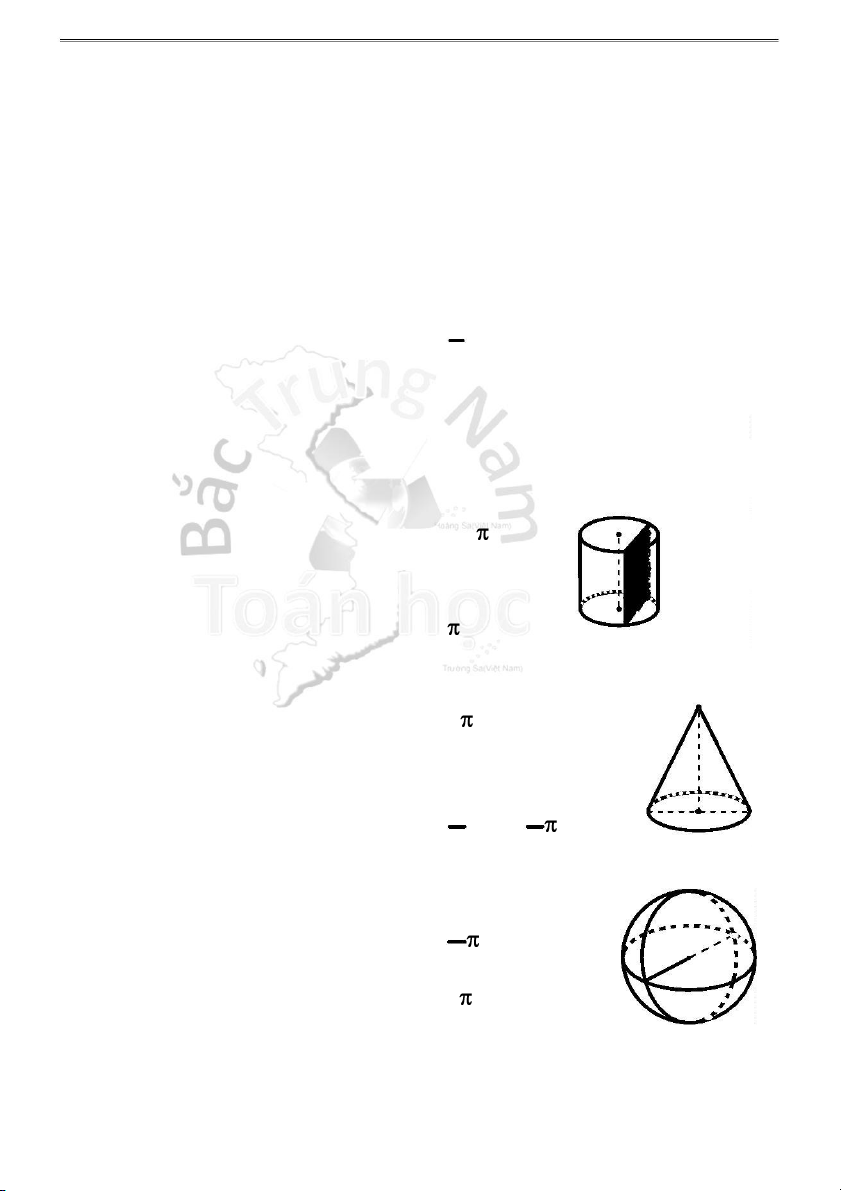
③ Diện tích toàn phần: S tp = S xq + S đá y 3. Hình trụ:
① Diện tích xung quanh:
S = 2 R.h O xq
② Diện tích toàn phần: S = S + 2S tp xq ñaùy O'
③ Thể tích của khối trụ :
V = R2 .h 4 . Hình nón: O
① Diện tích xung quanh:
Sxq = R.l
② Diện tích toàn phần: S = S + S l tp xq ñaùy 1 1 R I
③ Thể tích của khối nón: V = S.h = R2 .h 3 3 5 . Hình cầu: 4 B
① Thể tích khối cầu:
V = R3 3 O Diện tích mặt cầu: A ②
S = 4 R2 Lý thuyết HKG 11-12 6
C - VÀI HÌNH THƯỜNG GẶP HÌNH 1
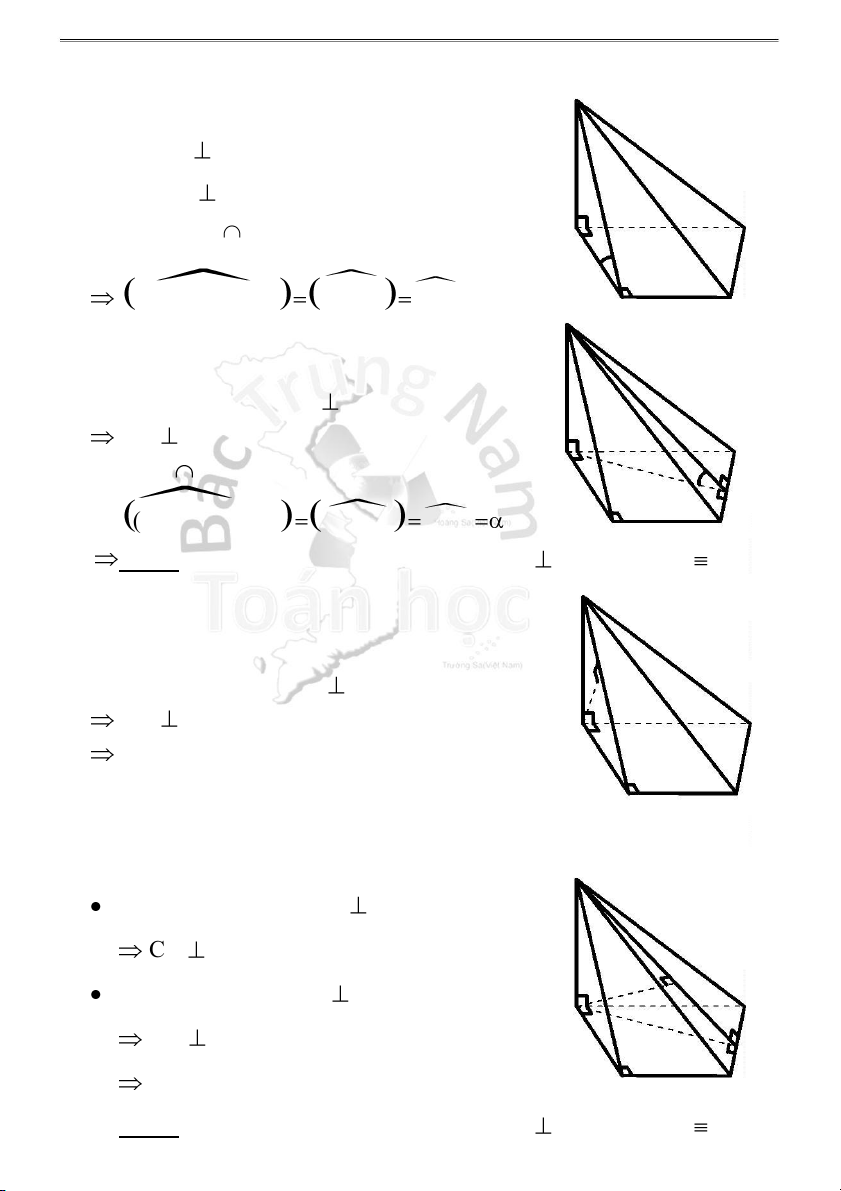
Hình chóp S.ABCD, có đáy ABCD là hình chữ nhật
(hoặc hình vuông) và SA vuông góc với đáy
H1.1 - Đáy, đường cao, cạnh đáy, cạnh bên, mặt bên của hình chóp
1 . Đáy: ABCD là hình vuông hoặc hình chữ nhật S 2 . Đường cao: SA
3 . Cạnh bên: SA, SB, SC, SD
4 . Cạnh đáy: AB, BC, CD, DA
5. Mặt bên: SAB là tam giác vuông tại A. D
SBC là tam giác vuông tại B. A
SCD là tam giác vuông tại D.
SAD là tam giác vuông tại A. B C
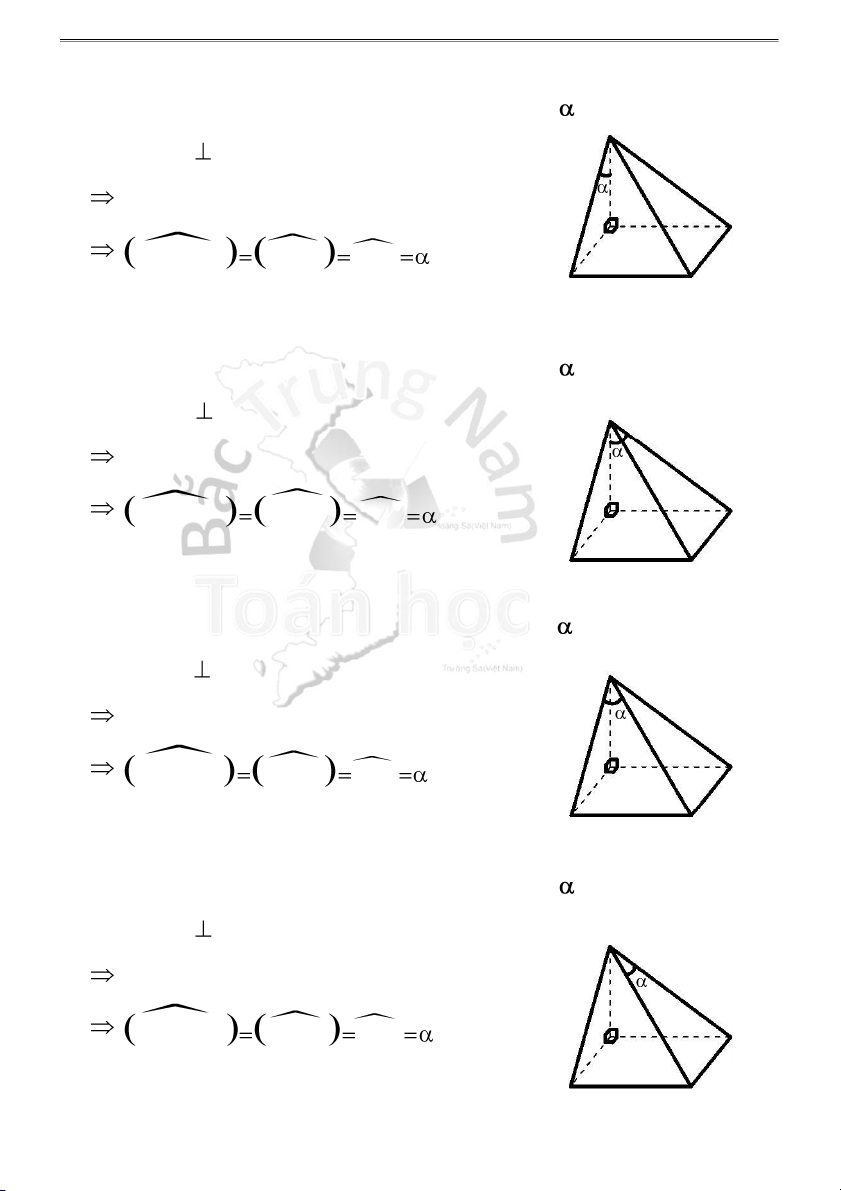
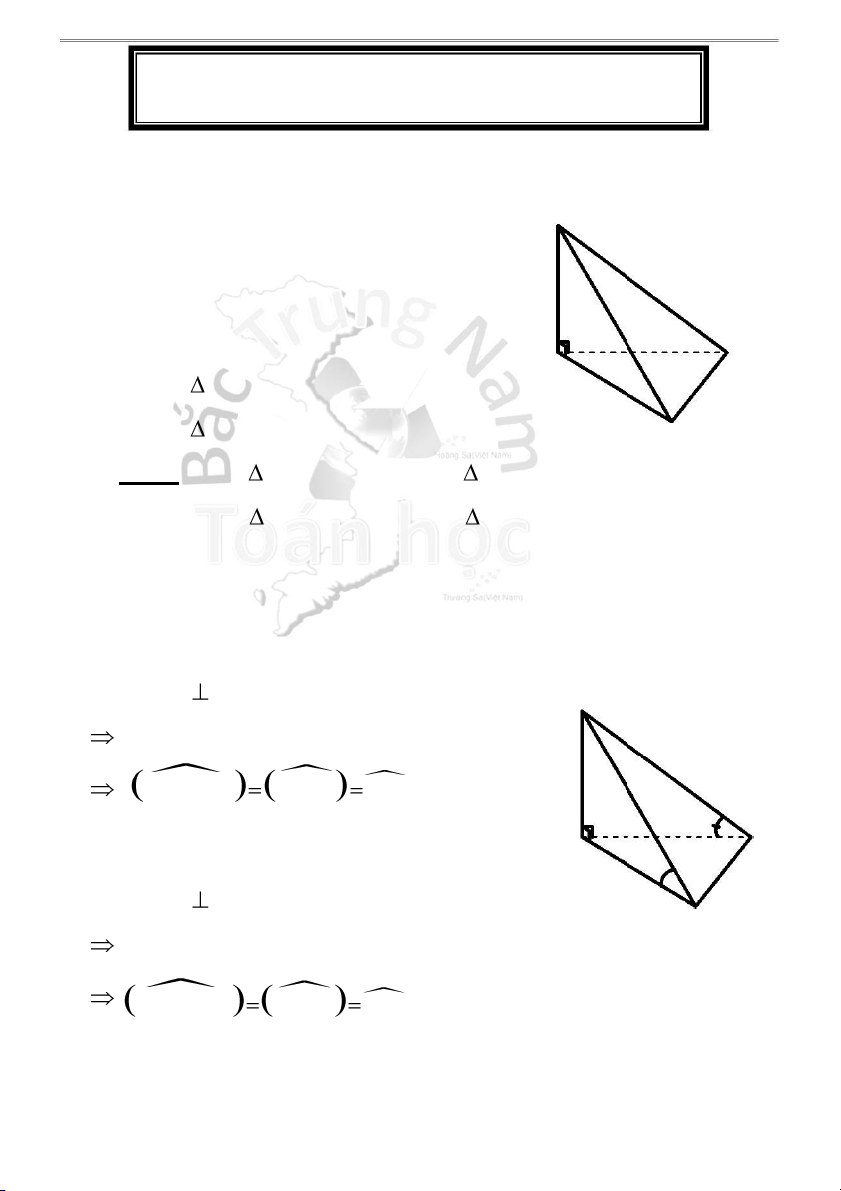
H1.2 - Góc giữa cạnh bên và đáy S
1 . Góc giữa cạnh bên SB và mặt đáy (ABCD) bằng : Ta có: SA (ABCD) (gt) D A
Hình chiếu của SB lên (ABCD) là AB SB, (A BCD) SB, AB SB A B C S
2 . Góc giữa cạnh bên SD và mặt đáy (ABCD) bằng : Ta có: SA (ABCD) (gt) D
Hình chiếu của SD lên (ABCD) là AD SD,(AB A CD) SD, AD SDA B C S
3 . Góc giữa cạnh bên SC và mặt đáy (ABCD) bằng : Ta có: SA (ABCD) (gt)
Hình chiếu của SC lên (ABCD) là AC D SC,(AB CD) A SC, AC SCA B C Lý thuyết HKG 11-12 7
H1.3 - Góc giữa cạnh bên và mặt bên:
1 . Góc giữa cạnh bên SB và mặt bên (SAD) bằng : S Ta có: AB (SAD)
Hình chiếu của SB lên (SAD) là SA D SB, (SA D)
SB, SA BSA A B C
2 . Góc giữa cạnh bên SD và mặt bên (SAB) bằng : Ta có: AD (SAB) S
Hình chiếu của SD lên (SAB) là SA
SD, (SAB) SD,SA DSA D A B C
3 . Góc giữa cạnh bên SC và mặt bên (SAB) bằng : S Ta có: BC (SAB)
Hình chiếu của SC lên (SAB) là SB
SC, (SAB) SC,SB BSC D A B C
4 . Góc giữa cạnh bên SC và mặt bên (SAD) bằng : Ta có: DC (SAD) S
Hình chiếu của SC lên (SAD) là SD
SC, (SAD) SC,SD DSC D A B C Lý thuyết HKG 11-12 8
H1.4 - Góc giữa mặt bên và mặt đáy:
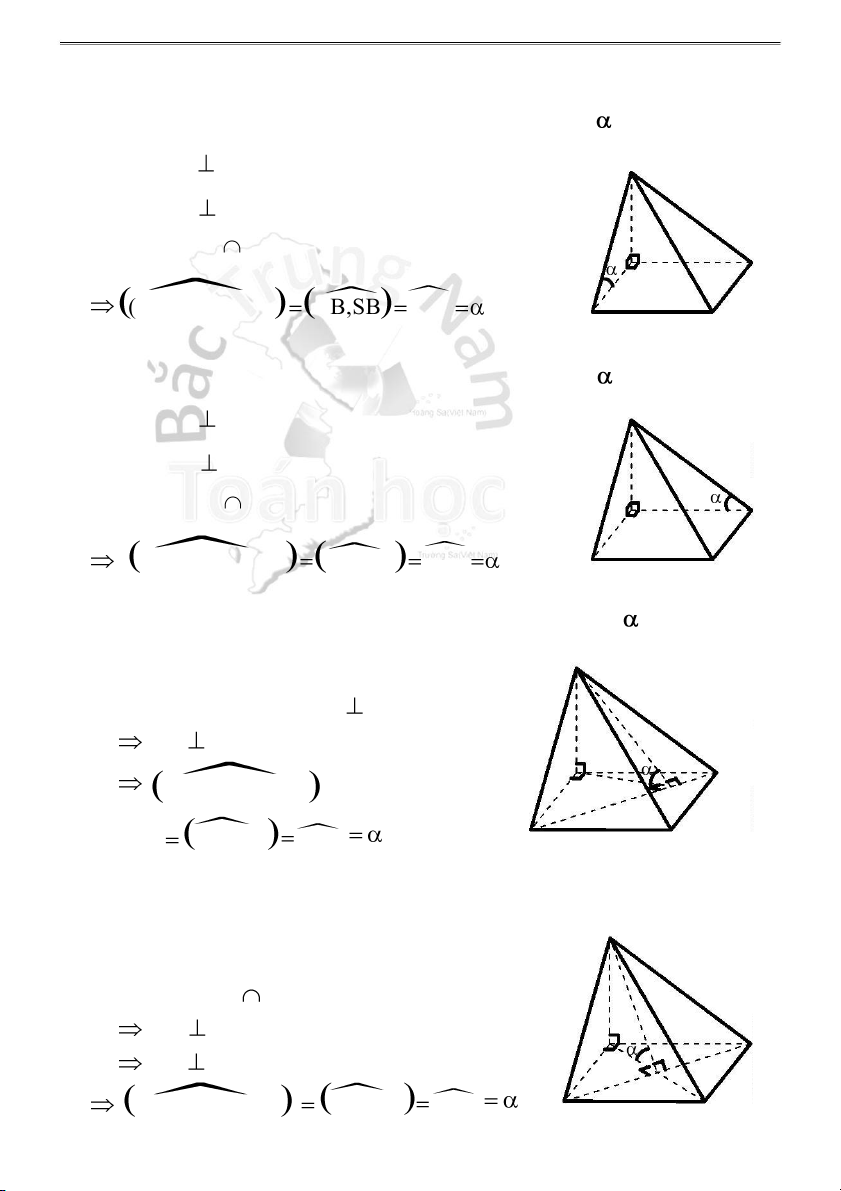
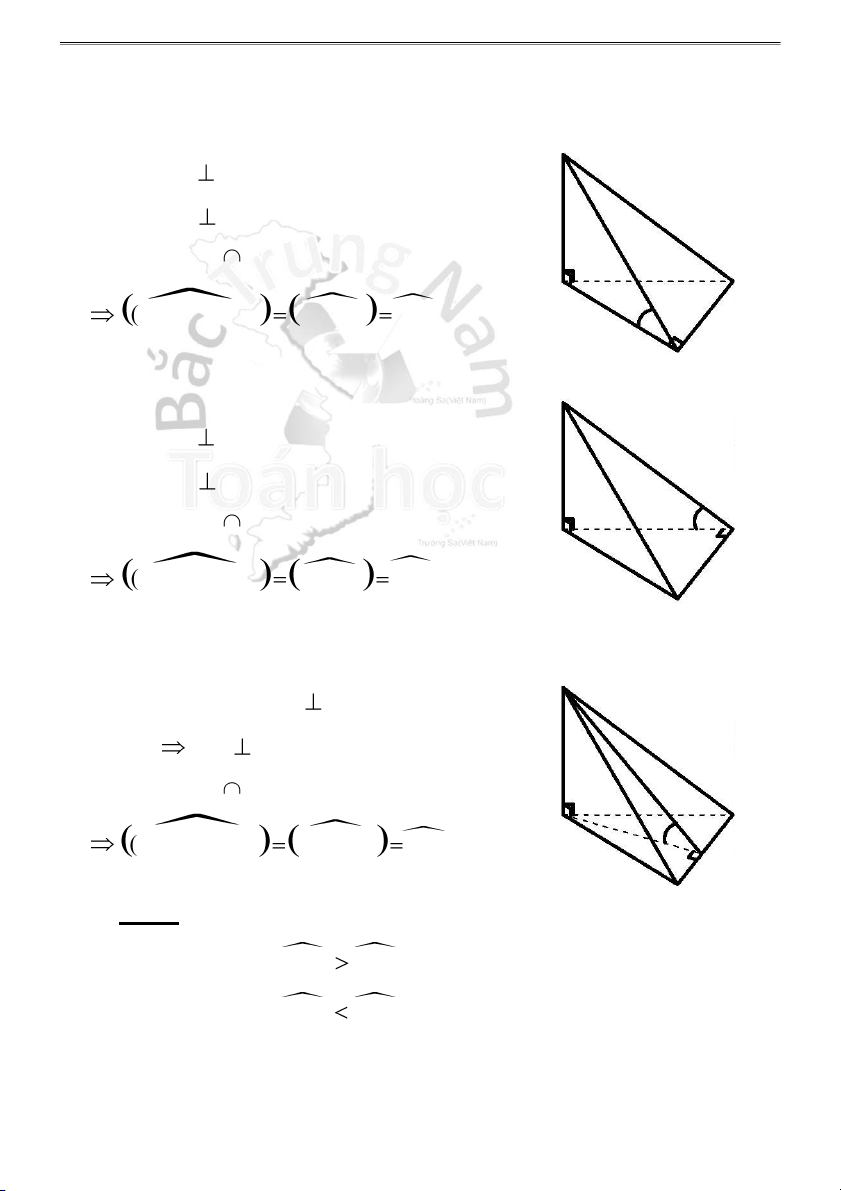
1 . Góc giữa mặt bên (SBC) và mặt đáy (ABCD) bằng : Ta có: BC AB tại B S BC SB tại B (SBC) (ABCD) = BC D A (SBC),(ABCD) AB ,SB SBA B C
2 . Góc giữa mặt bên (SCD) và mặt đáy (ABCD) bằng : S Ta có: CD AD tại D CD SD tại D (SCD) (ABCD) = CD D A ( SCD),(AB CD) AD,S D SDA B C
3 . Góc giữa mặt phẳng (SBD) và mặt đáy (ABCD) bằng : S
❖ Đáy ABCD là hình chữ nhật:
Trong (ABCD), vẽ AH BD tại H BD SH (S BD),(AB A D CD) H AH,SH SHA B C
Chú ý: Nếu AB < AD thì điểm H ở gần B hơn
Nếu AB > AD thì điểm H ở gần D hơn S
❖ Đáy ABCD là hình vuông: Gọi O = AC BD AO BD A D BD SO SO, AO O (SBD),(ABCD) S OA B C Lý thuyết HKG 11-12 9
H1.5 – Khoảng cách “điểm – mặt” S
1 . Khoảng cách từ A đến mặt phẳng (SCD)
Trong mp(SAD), vẽ AH SD tại H H D AH (SCD) A d[A,(SCD)] = AH B C
2 . Khoảng cách từ B đến mặt phẳng (SCD)
Vì AB // (SCD) nên d[B,(SCD)] = d[A,(SCD)] (xem dạng 1) 3 S
. Khoảng cách từ A đến mặt phẳng (SBC)
Trong mp(SAB), vẽ AH SB tại H AH (SBC) H D d[A,(SBC)] = AH A
4 . Khoảng cách từ D đến mặt phẳng (SBC) B C
Vì AD // (SBC) nên d[D,(SBC)] = d[A,(SBC)] (xem dạng 3)
5 . Khoảng cách từ A đến mặt phẳng (SBD) S
❖ Đáy ABCD là hình chữ nhật:
Trong (ABCD), vẽ AI BD tại I BD H (SAI) A D
Trong (SAI), vẽ AH SI tại H I AH (SBD) B C d[A, (SBD)] = AH
Chú ý: Nếu AB < AD thì điểm I ở gần B hơn
Nếu AB > AD thì điểm I ở gần D hơn
❖ Đáy ABCD là hình vuông: S Gọi O = AC BD AO BD BD (SAO) H
Trong (SAO), vẽ AH SO tại H A D AH (SBD) O d[A, (SBD)] = AH B C
6 . Khoảng cách từ C đến mặt phẳng (SBD)
Vì O là trung điểm của AC nên d[C,(SBD)] = d[A,(SBD)] Lý thuyết HKG 11-12 10 HÌNH 2
Hình chóp S.ABCD, có đáy ABCD là hình thang
vuông tại A và B và SA vuông góc với đáy
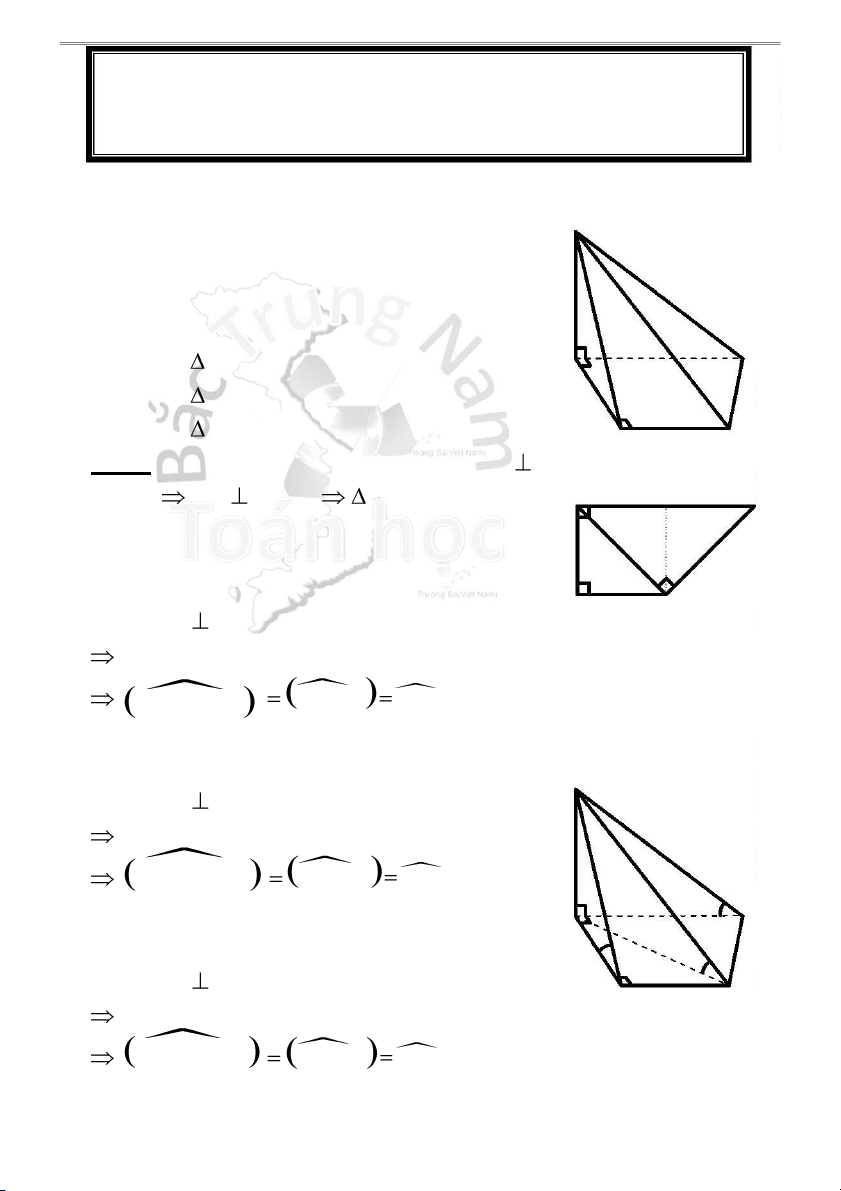
H2.1 - Đáy, đường cao, cạnh đáy, cạnh bên, mặt bên của hình chóp S
1 . Đáy: Hình thang ABCD vuông tại A và B 2 . Đường cao: SA
3 . Cạnh bên: SA, SB, SC, SD
4 . Cạnh đáy: AB, BC, CD, DA
5. Mặt bên: SAB là tam giác vuông tại A. A D
SBC là tam giác vuông tại B.
SAD là tam giác vuông tại A. B C
Chú ý: Nếu AB = BC và AD = 2BC thì AC CD
CD (SAC) SCD vuông tại C A D
H2.2 - Góc giữa cạnh bên SB và đáy
1 . Góc giữa cạnh bên SB và mặt đáy (ABCD): B C Ta có: SA ABCD (gt)
Hình chiếu của SB lên (ABCD) là AB S B, (AB CD) SB, AB SB A
2 . Góc giữa cạnh bên SD và mặt đáy (ABCD): S Ta có: SA ABCD (gt)
Hình chiếu của SD lên (ABCD) là AD S D,(AB CD) SD, AD SDA A D
3 . Góc giữa cạnh bên SC và mặt đáy (ABCD): Ta có: SA ABCD (gt) B C
Hình chiếu của SC lên (ABCD) là AC SC,(AB CD) SC, AC SC A Lý thuyết HKG 11-12 11
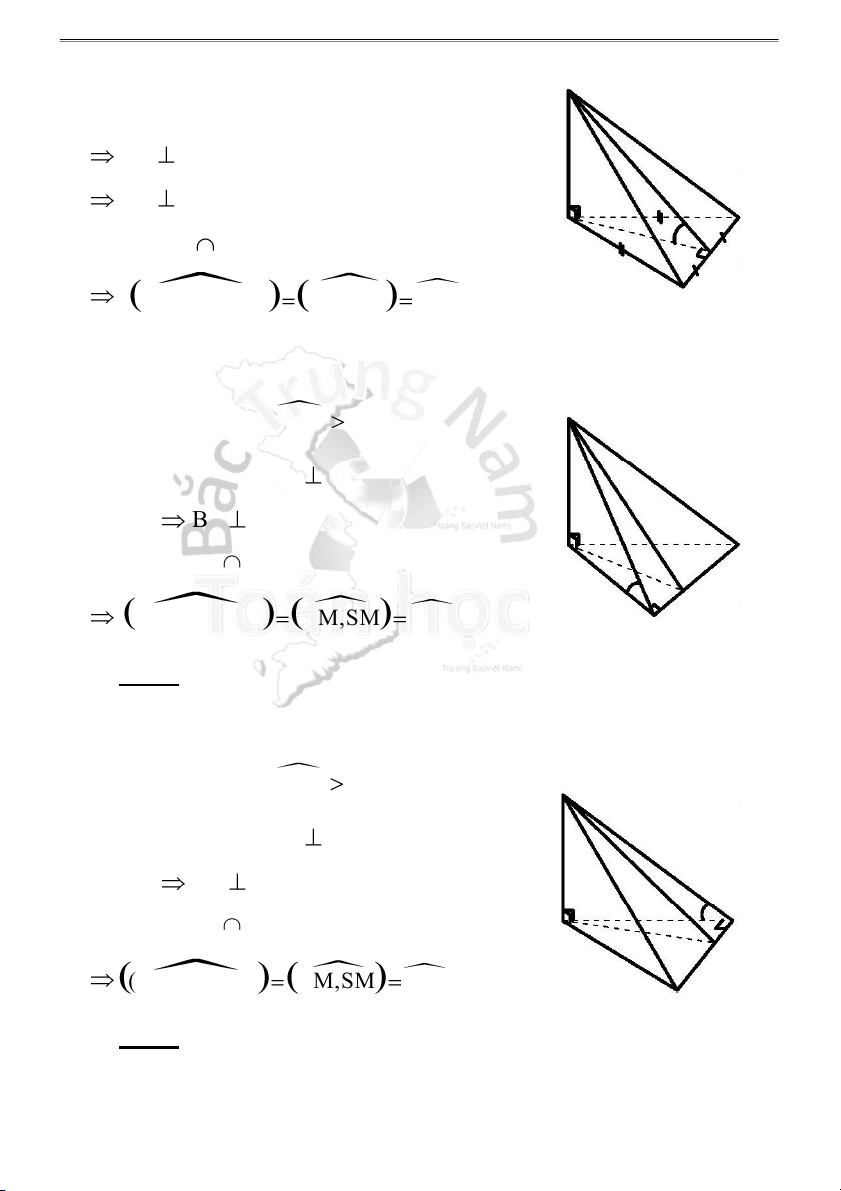
H2.3 - Góc giữa mặt bên và mặt đáy: S
1 . Góc giữa mặt bên (SBC) và mặt đáy (ABCD): Ta có: BC AB tại B BC SB tại B A D (SBC) (ABCD) = BC
(SBC),(ABCD) AB,SB SBA S B C
2 . Góc giữa mặt bên (SCD) và mặt đáy (ABCD):
Trong (ABCD), vẽ AM CD tại M SM CD tại M A D SCD) (ABCD) = CD Mà ( M
(SCD),(ABCD) AM, SM SMA B C
Chú ý: Nếu AB = BC và AD = 2BC thì AC CD. Do đó M C. S
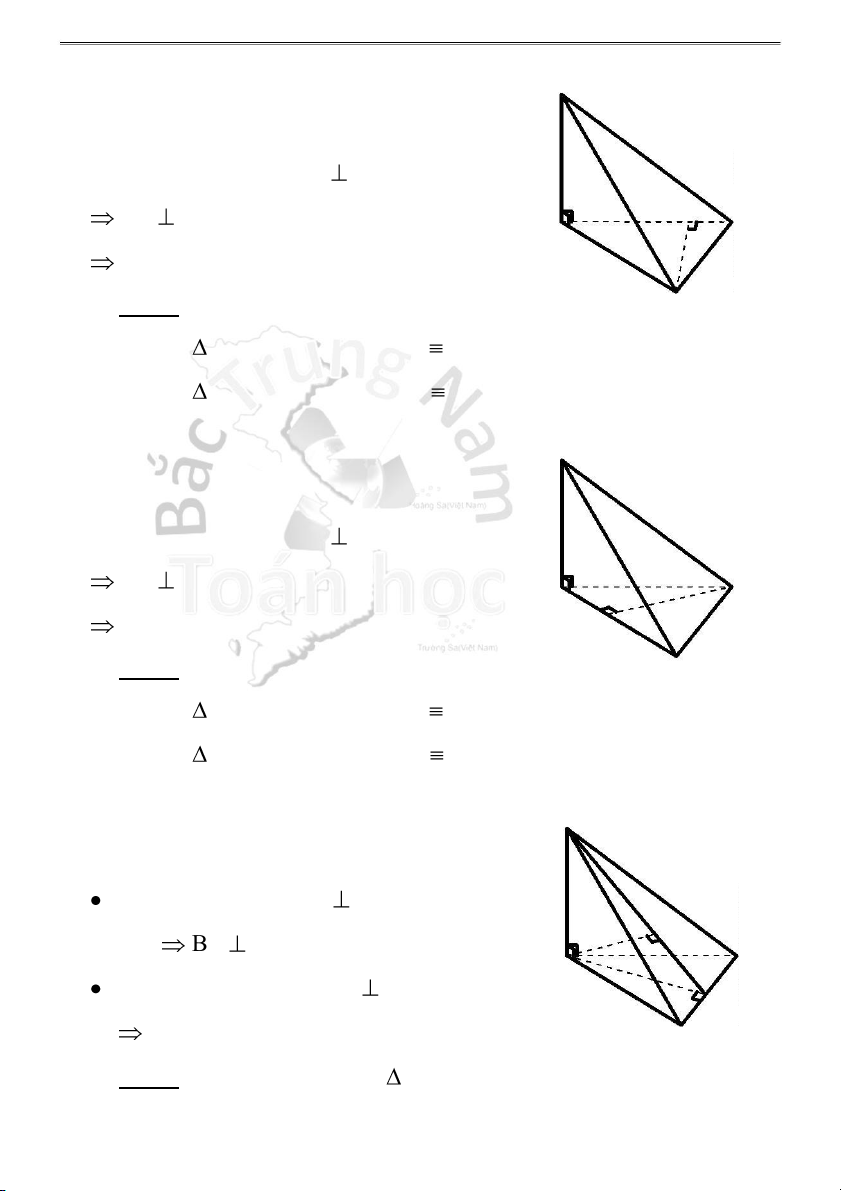
H2.4 – Khoảng cách “điểm – mặt”
1 . Khoảng cách từ A đến mặt phẳng (SBC) H
Trong mp(SAB), vẽ AH SB tại H AH (SBC) A D d[A,(SBC)] = AH
2 . Khoảng cách từ D đến mặt phẳng (SBC) B C
Vì AD // (SBC) nên d[D,(SBC)] = d[A,(SBC)] (xem dạng 3) 3 S
. Khoảng cách từ A đến mặt phẳng (SCD)
Trong (ABCD), vẽ AM CD tại M CD (SAM) H
Trong (SAM), vẽ AH SM tại H A D AH (SCD) M D[A,(SCD)] = AH B C
Chú ý: Nếu AB = BC và AD = 2BC thì AC CD. Do đó M C. Lý thuyết HKG 11-12 12 HÌNH 3
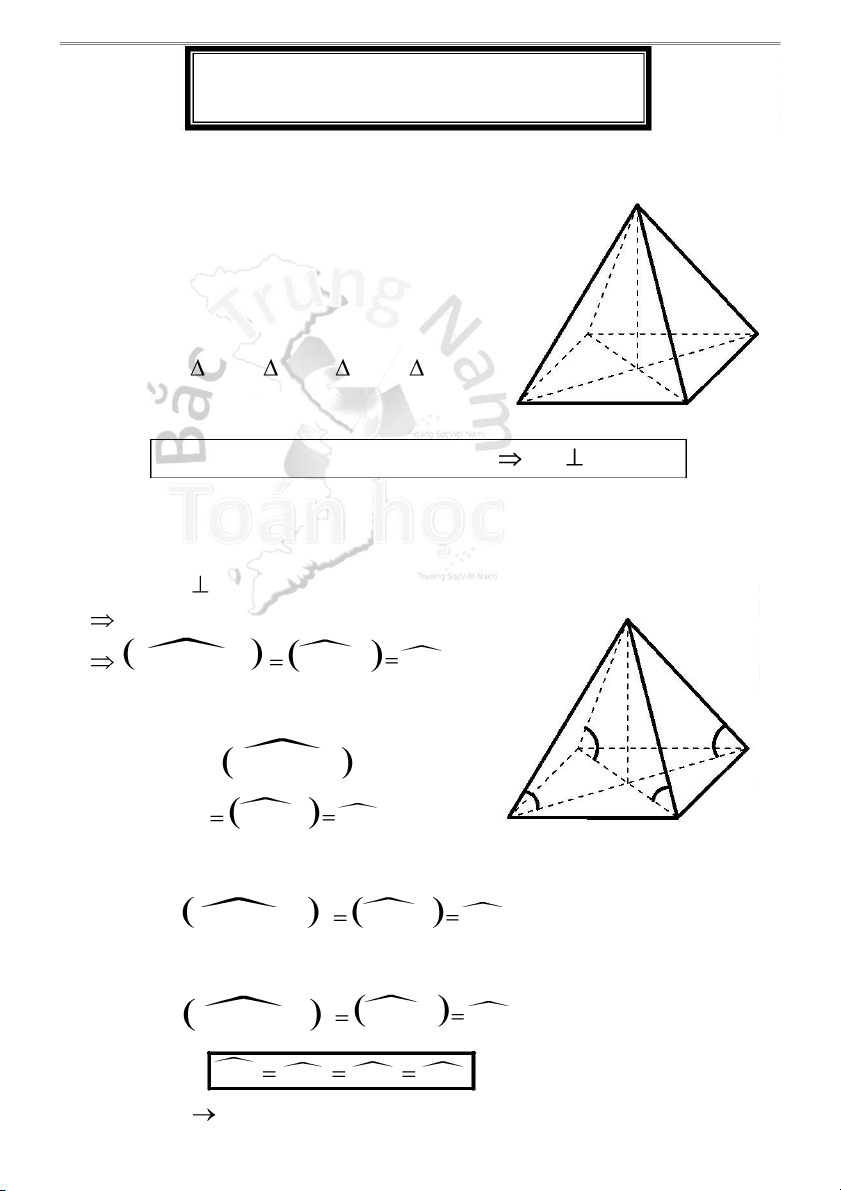
Hình chóp tứ giác đều S.ABCD
H3.1 - Đáy, đường cao, cạnh đáy, cạnh bên, mặt bên của hình chóp S
1 . Đáy: ABCD là hình vuông 2 . Đường cao: SO
3 . Cạnh bên: SA = SB = SC = SD
4 . Cạnh đáy: AB = BC = CD = DA A D
5. Mặt bên: SAB, SBC, SCD, SAD O
là các tam giác cân tại S và bằng nhau. B C
Gọi O là tâm hình vuông ABCD SO (ABCD)
H3.2 - Góc giữa cạnh bên và đáy
1 . Góc giữa cạnh bên SA và mặt đáy (ABCD): Ta có: SO (ABCD) S
Hình chiếu của SA lên (ABCD) là AO S
A,(ABC D) SA, AO SAO
2 . Góc giữa cạ nh bên SB và mặt đáy (ABCD): A D Tương tự SB, (ABCD) O SB, BO SBO B C
3 . Góc giữa c ạnh bên SC và mặt đáy (ABCD): Tương tự SC,(AB CD) SC, CO SC O
4 . Góc giữa cạ nh bên SD và mặt đáy (ABCD): Tương tự SD,(AB CD) SD, DO SDO
Chú ý: SAO S BO SC O SDO
“Góc giữa các cạnh bên với mặt đáy bằng nhau” Lý thuyết HKG 11-12 13
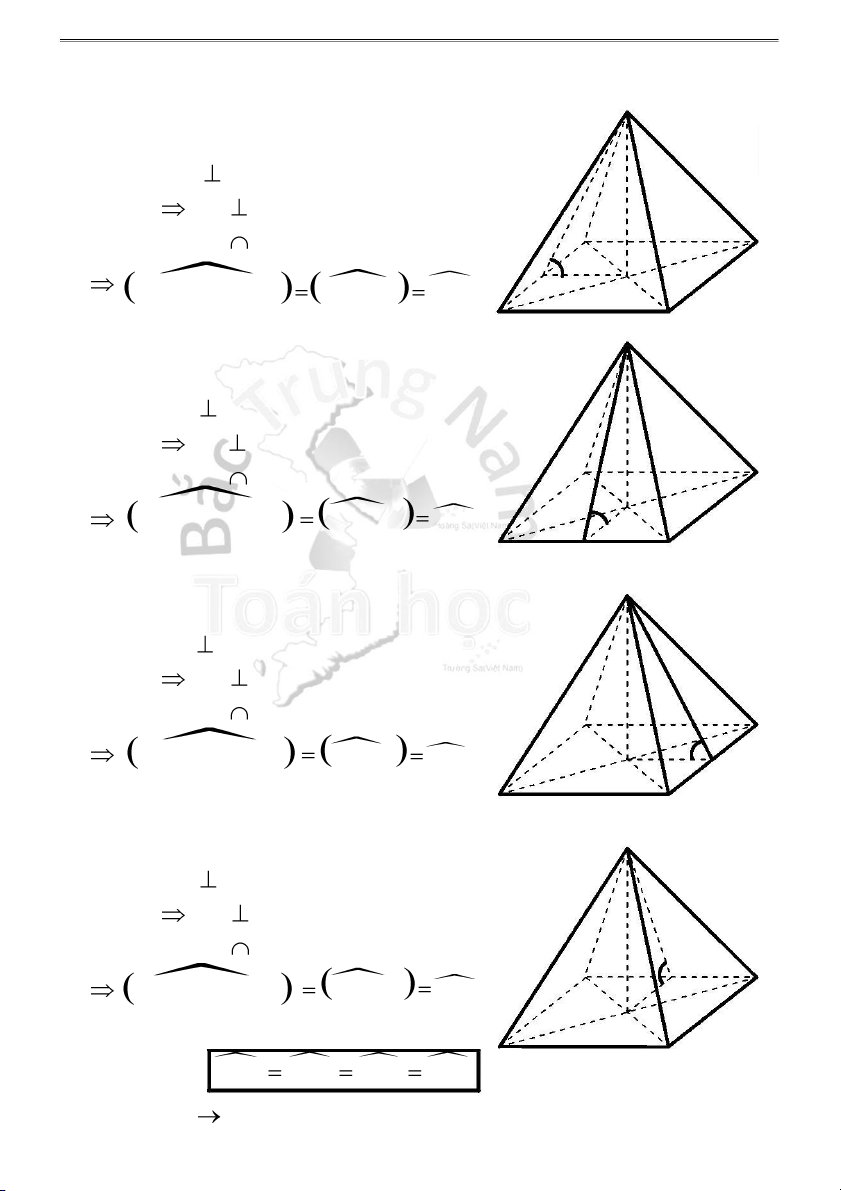
H3.3 - Góc giữa mặt bên và mặt đáy: S
1 . Góc giữa mặt bên (SAB) và mặt đáy (ABCD): Ta có: OM AB tại M AB SM tại M A Mà (SAB) (ABCD) = AB D M
(SAB),(ABCD) OM,SM SMO O B C S
2 . Góc giữa mặt bên (SBC) và mặt đáy (ABCD): Ta có: ON BC tại N BC SN tại N A Mà (SBC) (ABCD) = BC D (S BC),(AB CD) ON,SN SNO O B N C S
3 . Góc giữa mặt bên (SCD) và mặt đáy (ABCD): Ta có: OP CD tại P CD SP tại P Mà (SCD) (ABCD) = CD A D (S CD),(AB CD) OP,S P SPO O P B C
4 . Góc giữa mặt bên (SAD) và mặt đáy (ABCD): S Ta có: OQ AD tại Q AD SQ tại Q Mà (SAD) (ABCD) = AD Q D OQ, SQ S A (SAD),(ABCD) QO O B C
Chú ý: SMO SNO SPO SQO
“Góc giữa các mặt bên với mặt đáy bằng nhau” Lý thuyết HKG 11-12 14
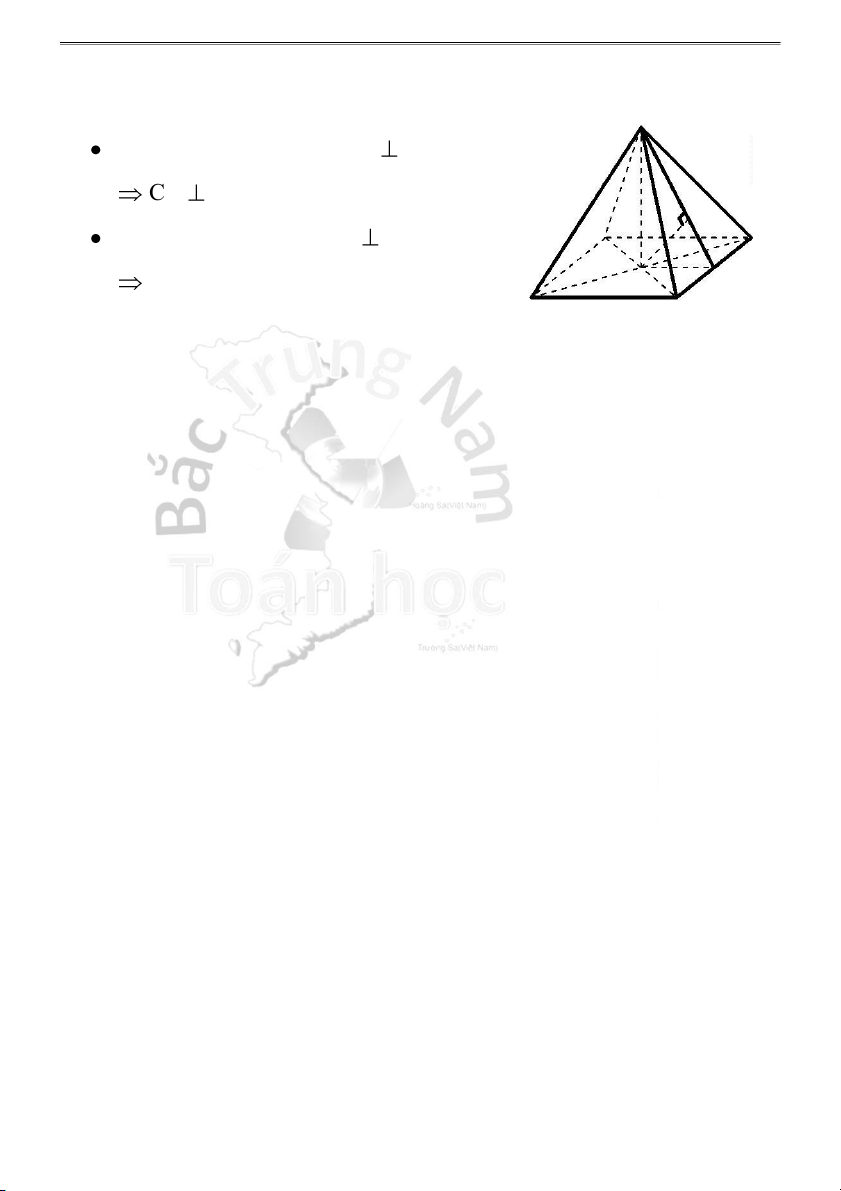
H3.4 – Khoảng cách “điểm – mặt”
1 . Khoảng cách từ O đến mặt phẳng (SCD) S
Trong mp(ABCD), vẽ OM CD tại M CD (SOM) H
Trong mp(SOM), vẽ OH SM tại H A D d[O,(SCD)] = OH O M B C
2 . Khoảng cách từ A đến mặt phẳng (SCD)
Vì O là trung điểm của AC nên d[A,(SCD)] = 2d[O,(SCD)]
3 . Khoảng cách từ B đến mặt phẳng (SCD)
Vì O là trung điểm của BD nên d[B,(SCD)] = 2d[O,(SCD)] Lý thuyết HKG 11-12 15 HÌNH 4
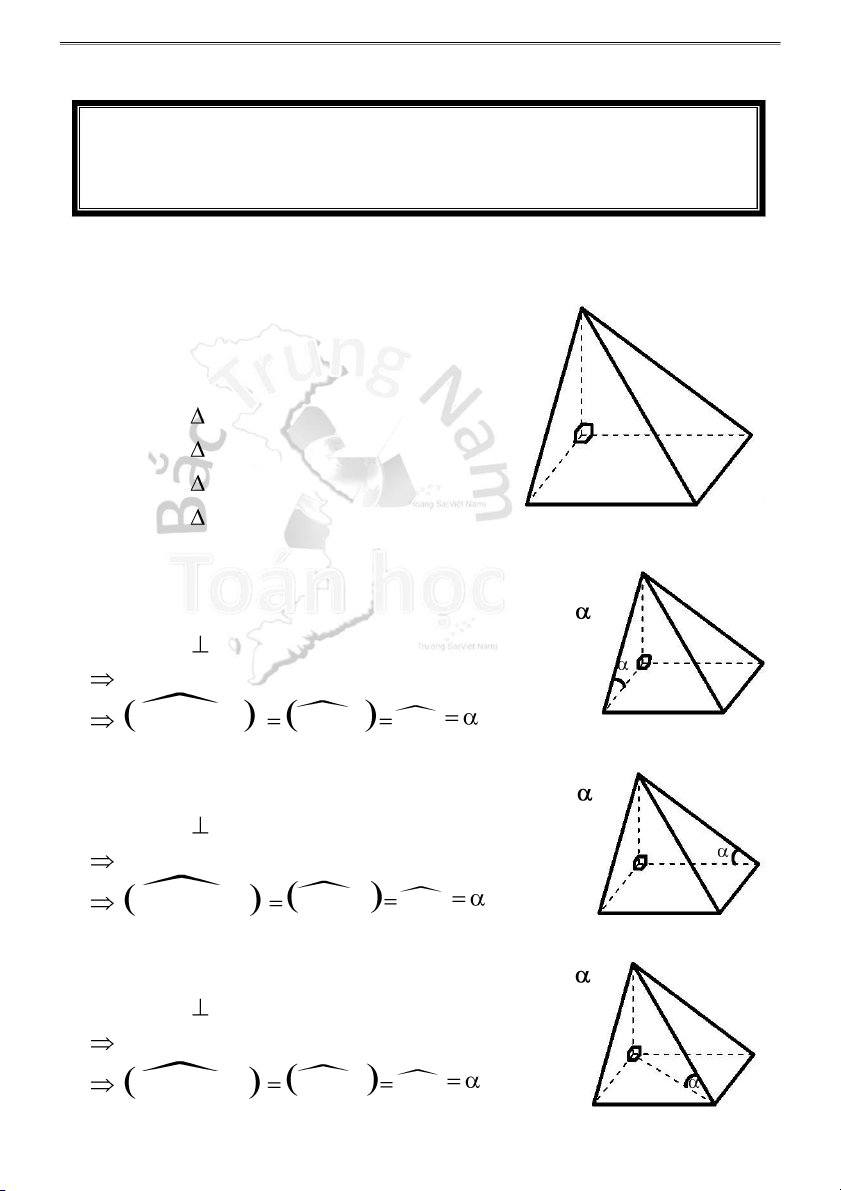
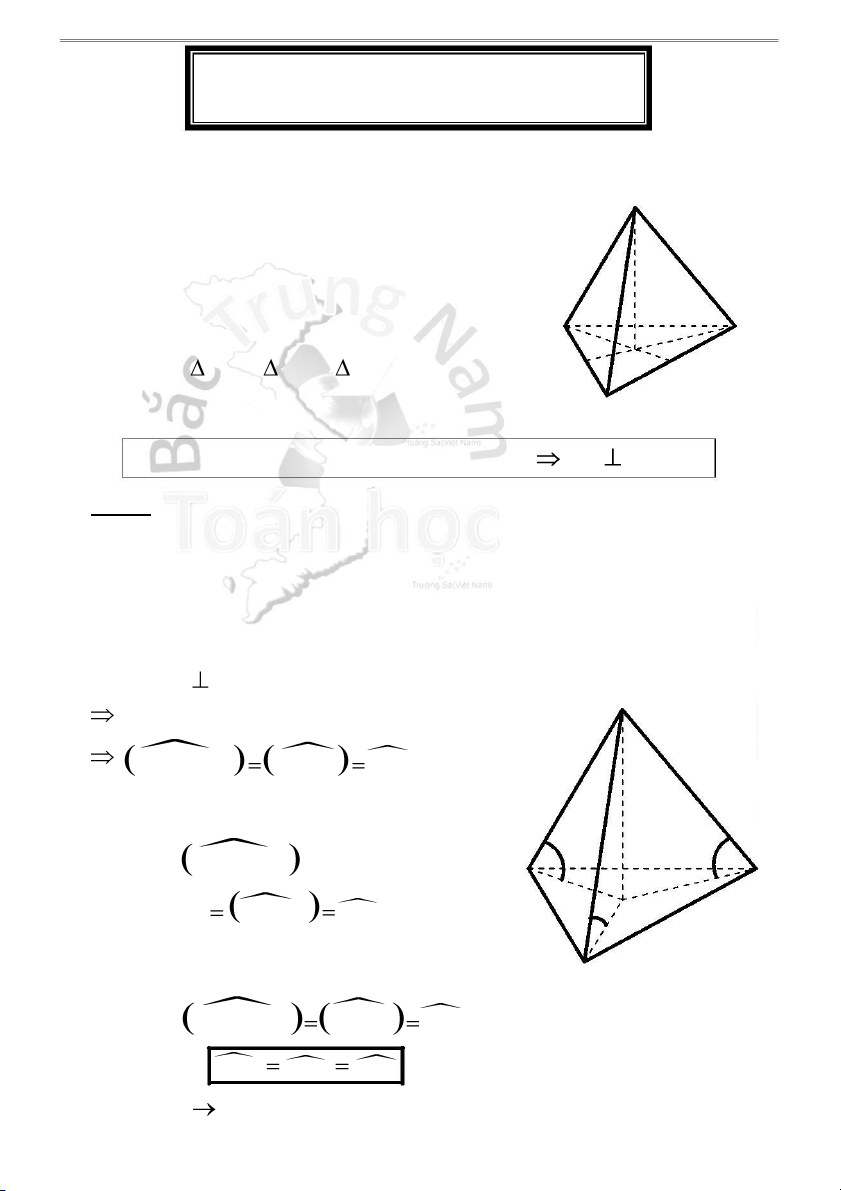
Hình chóp S.ABC, SA vuông góc với đáy
H4.1 - Đáy, đường cao, cạnh đáy, cạnh bên, mặt bên của hình chóp
1 . Đáy: tam giác ABC S 2 . Đường cao: SA
3 . Cạnh bên: SA, SB, SC
4 . Cạnh đáy: AB, BC, CA C A
5. Mặt bên: SAB là tam giác vuông tại A.
SAC là tam giác vuông tại A. B
Chú ý: Nếu ABC vuông tại B thì SBC vuông tại B
Nếu ABC vuông tại C thì SBC vuông tại C
H4.2 - Góc giữa cạnh bên và đáy
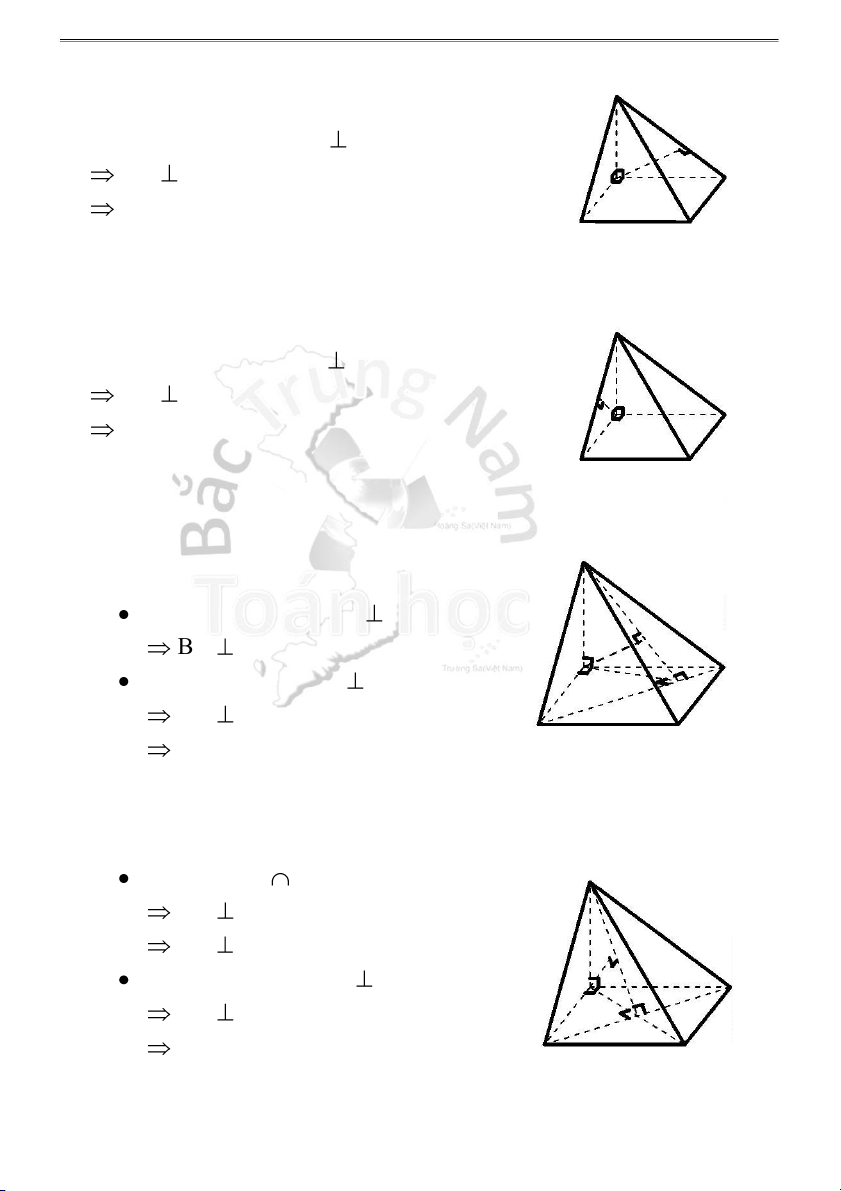
1 . Góc giữa cạnh bên SB và mặt đáy (ABC): Ta có: SA (ABC) (gt) S
Hình chiếu của SB lên (ABC) là AB
SB, (ABC) SB, AB SBA C A
2 . Góc giữa cạnh bên SC và mặt đáy (ABC): Ta có: SA (ABC) (gt) B
Hình chiếu của SC lên (ABC) là AC S C,(AB C) SC, AC SCA Lý thuyết HKG 11-12 16
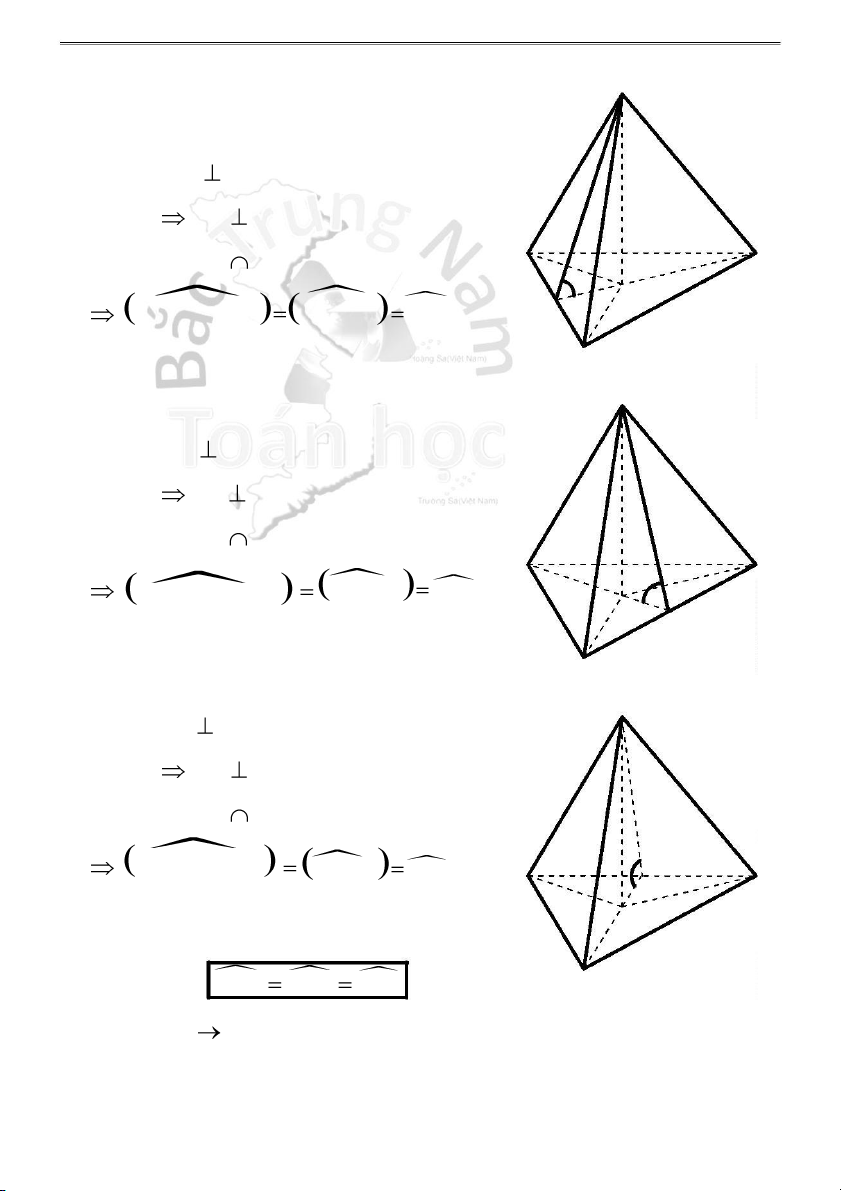
H4.3 - Góc giữa mặt bên (SBC) và mặt đáy (ABC):
1 . Tam giác ABC vuông tại B S Ta có: BC AB tại B BC SB tại B (SBC) (ABC) = BC C A ( SBC),(A BC) AB,S B SBA B
2 . Tam giác ABC vuông tại C S Ta có: BC AC tại C BC SC tại C (SBC) (ABC) = BC C A (S BC),(AB C) AC, SC SCA B
3 . Tam giác ABC vuông tại A S
Trong (ABC), vẽ AM BC tại M BC SM tại M (SBC) (ABC) = BC C A (S BC),(AB C) AM,SM SMA M B
Chú ý: M không là trung điểm BC
Nếu ABC ACB thì M ở trên đoạn BC và gần B hơn
Nếu ABC ACB thì M ở trên đoạn BC và gần C hơn
Nếu AB > AC thì M ở trên đoạn BC và gần C hơn
Nếu AB < AC thì M ở trên đoạn BC và gần B hơn Lý thuyết HKG 11-12 17
4 . Tam giác ABC cân tại A (hoặc đều) S Gọi M là trung điểm BC BC AM tại M BC SM tại M C A Mà ( SBC) (ABC) = SM M ( SBC),(A BC) AM,S M SMA B S
5 . Tam giác ABC có ABC 900
Trong (ABC), vẽ AM BC tại M BC SM tại M C A (SBC) (ABC) = BC B
(SBC),(ABC) AM,SM SMA M
Chú ý: M nằm ngoài đoạn BC và ở về phía B S
6 . Tam giác ABC có ACB 900
Trong (ABC), vẽ AM BC tại M BC SM tại M (SBC) M (ABC) = BC A C
(SBC),(ABC) AM,SM SMA B
Chú ý: M nằm ngoài đoạn BC và ở về phía C Lý thuyết HKG 11-12 18
H4.4 – Khoảng cách “điểm – mặt” S
1 . Khoảng cách từ B đến mặt phẳng (SAC)
Trong mp(ABC), vẽ BH AC tại H H BH (SAC) C A d[B,(SAC)] = BH Chú ý: B
Nếu ABC vuông tại A thì H A và khi đó AB = d[B,(SAC)]
Nếu ABC vuông tại C thì H C và khi đó BC = d[B,(SAC)] S
2 . Khoảng cách từ C đến mặt phẳng (SAB)
Trong mp(ABC), vẽ CH AB tại H CH (SAB) C A d[C,(SAB)] = CH H Chú ý: B
Nếu ABC vuông tại A thì H A và khi đó CA = d[C,(SAB)]
Nếu ABC vuông tại B thì H C và khi đó CB = d[B,(SAB)] S
3 . Khoảng cách từ A đến mặt phẳng (SBC)
Trong (ABC), vẽ AM BC tại M H BC SM tại M C A
Trong mp(SAM), vẽ AH SM tại H M d[A,(SBC)] = AH B
Chú ý: Tùy đặc điểm của ABC để các định đúng vị trí của điểm
M trên đường thẳng BC. Lý thuyết HKG 11-12 19 HÌNH 5
Hình chóp tam giác đều S.ABC
H5.1 - Đáy, đường cao, cạnh đáy, cạnh bên, mặt bên của hình chóp S
1 . Đáy: Tam giác ABC đều 2 . Đường cao: SO
3 . Cạnh bên: SA = SB = SC = SD
4 . Cạnh đáy: AB = BC = CA A C
5. Mặt bên: SAB, SBC, SCA O
là các tam giác cân tại S và bằng nhau. B
Gọi O là trọng tâm của tam giác ABC SO (ABC) Chú ý:
Tứ diện đều S.ABC là hình chóp có đáy và các mặt bên là
những tam giác đều bằng nhau.
H5.2 - Góc giữa cạnh bên và đáy
1 . Góc giữa cạnh bên SA và mặt đáy (ABC): Ta có: SO (ABC) S
Hình chiếu của SA lên (ABC) là AO
SA,(ABC) SA, AO SAO
2 . Góc giữa cạnh bên SB và mặt đáy (ABC): Tương tự SB,(AB C) C A SB, BO SB O O
3 . Góc giữa cạnh bên SC và mặt đáy (ABC): B
Tương tự SC,(ABC) SC, CO SCO
Chú ý: SAO S BO SCO
“Góc giữa các cạnh bên với mặt đáy bằng nhau” Lý thuyết HKG 11-12 20
H5.3 - Góc giữa mặt bên và mặt đáy: S
1 . Góc giữa mặt bên (SAB) và mặt đáy (ABC): Ta có: OM AB tại M AB SM tại M C A Mà (SAB) (ABC) = AB O
(SAB), (ABC) OM,SM SMO M B S
2 . Góc giữa mặt bên (SBC) và mặt đáy (ABC): Ta có: ON BC tại N BC SN tại N Mà (SBC) (ABC) = BC C A (
SBC),(AB CD) ON,SN SNO O N 3 B
. Góc giữa mặt bên (SAC) và mặt đáy (ABC): S Ta có: OP AC tại P AC SP tại P Mà (SAC) (ABC) = AC ( SAC),(A BC) P OP,SP SPO C A O
Chú ý: SMO SNO SPO B
“Góc giữa các mặt bên với mặt đáy bằng nhau”



