Tổng hợp 250 câu hỏi trắc nghiệm vận dụng cao – Nhóm Toán

Tổng hợp 250 câu hỏi trắc nghiệm vận dụng cao – Nhóm Toán được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

215 108 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

199 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
1
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
PHẦN 1 : ĐỀ BÀI
Câu 1.1. Đường thẳng đi qua 2 đim cc tr của đồ th hm s
2
23
1
xx
y
x

hợp
với 2 trục tọa độ 1 tam giác có diện tích S bằng :
A. S=1,5 B. S=2 C.S=3 D.S=1
Câu 1.2. Khi cầu nội tiếp hình tứ diện đều có cạnh bằng a thì th tích khi cầu là :
A.
3
6
216
a
B.
3
6
124
a
C.
3
3
96
a
D.
3
3
144
a
Câu 1.3. Tìm m đ phương trình
2
30
xx
e me m
có nghiệm
A.
2m
B.
C.m<3 D.m>0
Câu 1.4. Giá tr của tham s m đ diện tích hình phẳng giới hạn bởi đồ th hàm s
22
3 2 1y x mx m
, trục hoành, trục tung v đường thẳng x = 2 đạt giá tr nhỏ nhất
là:
A. m = 2 B. m = 1 C. m = -1 D. m = - 2
Câu 1.5. Phương trình no sau đây không phải l phương trình hình chiếu vuông
góc của đường thẳng d:
12
2 3 ,
3
xt
y t t R
zt


trên mặt phẳng (Oxy) :
A.
3 2 '
1 3 ' , '
0
xt
y t t R
z

B.
1 4 '
2 6 ', '
0
xt
y t t R
z

C.
1 2 '
2 3 ', '
0
xt
y t t R
z

D.
5 2 '
4 3 ', '
0
xt
y t t R
z

Câu 1.6. Gọi A, B, C lần lượt l các đim biu diễn của 3 s phức :
26
1 2i; (1 )(1 2 );
3
i
ii
i
.Diện tích của tam giác ABC bằng :
A.
1
4
B.
1
2
C.
5
5
D.
5
2
Câu 2.1. Cho hàm s
32
21y x x m x m
có đồ th
C
. Giá tr của
m
thì
C
cắt trục hoành tại 3 đim phân biệt
1 2 3
,,x x x
sao cho
222
1 2 3
4xxx
là
2
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
1m
B.
1
1
4
0
m
m
C.
1
1
4
m
D.

1
1
4
m
Câu 2.2. Cho lăng trụ
ABC.A'B'C'
có đáy l tam giác đều cạnh a. Hình chiếu vuông
góc của đim
A'
lên mặt phẳng
(ABC)
trùng với trọng tâm tam giá
ABC
. Biết
khoảng cách giữa hai đường thẳng
AA'
và
BC
bằng
a3
4
. Khi đó th tích của khi
lăng trụ là
A.
3
3
12
a
B.
3
3
6
a
C.
3
3
3
a
D.
3
3
24
a
Câu 2.3. Phương trình
2 3 2 3
xx
m
(1) có nghiệm khi:
A.
;5m 
B.
;5m 
C.
2;m
D.
2;m 
Câu 2.4. Tính
2
3
0
.sin
x
I e xdx
A.
3
2
11
22
Ie

B.
3
2
11
22
Ie

C.
3
2
1Ie

D.
3
2
1Ie

Câu 2.5. Trong không gian tọa độ Oxyz , cho đim
A B C
(0;1;1), (1;0; 3), ( 1; 2; 3)
và mặt
cầu (S) có phương trình:
x y z x z
2 2 2
2 2 2 0
. Tìm tọa độ đim D trên mặt cầu (S)
sao cho tứ diện ABCD có th tích lớn nhất.
A.
D
1;0;1
B.
D
7 4 1
;;
3 3 3




C.




D
1 4 5
;;
3 3 3
D. D(1; - 1; 0)
Câu 2.6. Tính tổng mô-đun tất cả các nghiệm của phương trình:
23
10z i z z i
A. 3 B. 4 C.6 D. 8
Câu 3.1. Cho hàm s
3
2
31y x m x m
. Gọi M l đim cc đại của đồ th hàm
s
1
ứng với một giá tr m thích hợp đồng thời l đim cc tiu của đồ th hàm s
1
ứng với một giá tr khác của m. S đim M thỏa mãn yêu cầu đề bài là:
3
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.1 B. 2 C.3 D.0
Câu 3.2. Cho tứ diện
ABCD
với
BC a
,các cạnh còn lại đều bằng
3
2
a
và
là góc
tạo bởi hai mặt phẳng
ABC
và
BCD
. Gọi I,J lần lượt l trung đim các cạnh
,BC AD
. Giả sử hình cầu đường IJ kính tiếp xúc với CD. Giá tr
cos
là:
A.
3 2 3
B.
2 3 3
C.
23
3
D.
23
3
Câu 3.3. Cho
,,x y z
là các s thc thỏa mãn
2 3 6
x y z

. Giá tr biu thức
M xy yz xz
là:
A.0 B.1 C.6 D.3
Câu 3.4. Gọi
a
S
là diện tích hình phẳng giới hạn bởi đồ th hàm s
2
2
xx
y e e
, trục
Ox v đường thẳng
xa
với
ln2a
. Kết quả giới hạn
lim
a
a
S

là:
A.1 B.2 C.3 D.4
Câu 3.5. Trong không gian Oxyz, cho đim
1,0, 1A
và mặt phẳng
: 3 0P x y z
. Mặt cầu S có tâm I nằm trên mặt phẳng
P
, đi qua đim A và
gc tọa độ O sao cho chu vi tam giác OIA bằng
62
. Phương trình mặt cầu S là:
A.
2 2 2
2 2 1 9x y z
hoặc
2 2 2
2 2 1 9.x y z
B.
2 2 2
2 2 1 9x y z
hoặc
2 2 2
1 2 2 9x y z
C.
2 2 2
2 2 1 9x y z
hoặc
2 2 2
2 2 1 9x y z
D.
2 2 2
2 2 1 9x y z
hoặc
2 2 2
1 2 2 9x y z
Câu 3.6. Cho
z
là s phức có mô đun bằng 2017 và
w
là s phức thỏa mãn
1 1 1
wwzz

. Mô đun của s phức
w
là
A.2015 B.1 C.2017 D.0
Câu 4.1. Một công ty mun làm một đường ng dẫn từ một đim
A trên bờ đến một đim B trên một hòn đảo. Hòn đảo cách bờ bin
6km. Giá đ xây đường ng trên bờ là 50.000USD mỗi km, và
130.000USD mỗi km đ xây dưới nước. B’ l đim trên bờ bin sao
cho BB’ vuông góc với bờ bin. Khoảng cách từ A đến B’ là 9km. V
9km
6km
đảo
bờ biển
biển
A
B
B'
4
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
3
2
60
0
S
A
C
B
H
K
trí C trên đoạn AB’ sao cho khi ni ng theo ACB thì s tiền ít nhất. Khi đó C cách
A một đoạn bằng:
A. 6.5km B. 6km
C. 0km D.9km
Câu 4.2.
Cho hình chóp SABC với SA vuông góc với mặt phẳng (ABC) và
BC=
3
a,
60
o
BAC
. Gọi H, K lần lượt là hình chiếu của A lên SB
và SC. Mặt cầu qua các đim A, B, C, H, K có bán kính bằng:
A.1 B.2
C.
3
D. Không đủ dữ kiện đ tính
Câu 4.3. Cho
55log2log3log
666
cba
, với
ba,
và
c
là các s
hữu tỷ. Các khẳng đnh sau đây, khẳng đnh no đúng?
A.
ba
B.
ba
C.
ab
D.
bac
Câu 4.4.
Một khi cầu có bán kính 5dm, người ta cắt bỏ 2 phần bằng 2 mặt phẳng vuông
góc bán kính v cách tâm 3dm đ lm một chiếc lu đng. Tính th tích m chiếc lu
chứa được.
A.
132
(dm
3
) B.
41
(dm
3
)
C.
100
3
(dm
3
) D.
43
(dm
3
)
Câu 4.5. Trong không gian với hệ trục tọa độ Oxyz, cho hai
đim
(0; 1;2)M
và
( 1;1;3)N
. Mặt phẳng (P) đi qua M, N sao
cho khoảng cách từ
0; 0;2K
đến (P) đạt giá tr lớn nhất. (P) có vectơ pháp tuyến là:
A.
(1;1; 1)
B.
(1; 1;1)
C.
(1; 2;1)
D.
(2; 1;1)
Câu 4.6. Cho s phức z thoả mãn điều kiện
2 3 3zi
. Tìm giá tr nhỏ nhất của
z
A.
13 3
B. 2 C.
13 2
D. 2
5dm
3dm
3dm
5
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 5.1. Cho hm s
32
3 3 1y x mx m
. Với giá tr no của m thì đồ th hm s
đã cho có cc đại v cc tiu đi xứng nhau qua đường thẳng
: 8 74 0d x y
A.
1m
B.
2m 
C.
2m
D.
1m 
Câu 5.2. Cho hình chóp S.ABC có đáy l tam giác đều cạnh a, góc giữa SC và
mp(ABC) là 45
. Hình chiếu của S lên mp(ABC) l đim H thuộc AB sao cho HA =
2HB.Biết
7
3
a
CH
. Tính khoảng cách giữa 2 đường thẳng SA và BC:
A.
210
30
a
B.
210
20
a
C.
210
45
a
D.
210
15
a
Câu 5.3. Cho phương trình
22
2 2 2 4 2 2
5 5 2 0
x mx x mx
x mx m
. Tìm m đ phương
trình vô nghiệm?
A.
0m
B.
1m
C.
01m
D.
1
0
m
m

Câu 5.4. Diện tích hình phẳng giới hạn bởi
2
xln(x 2)
y
4x
và trục hoành là:
A.
ln2 2 3
3
B.
2ln2 2
4

C.
23
3

D.
2ln2 2 3
3
Câu 5.5. Trong không gian với hệ trục tọa độ Oxyz, cho hai đim A(1;2;2), B(5;4;4)
và mặt phẳng (P): 2x + y – z + 6 =0. Tọa độ đim M nằm trên (P) saocho MA
2
+ MB
2
nhỏ nhất là:
A. (-1;3;2) B. (2;1;-11) C.(-1;1;5) D(1;-1;7)
Câu 5.6. S phức z có mô đun lớn nhất và thỏa mãn điều kiện
là:
13
1 3 2
2
Z i i
6
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
13zi
B.
21
22
zi
C.
31
22
zi
D.
Câu 6.1. Trong không gian với hệ toạ độ Oxyz cho A(2;
1;6), B(
1;2;4) v I(
1;
3;2).
Phương trình mặt phẳng (P) đi qua A, B sao cho khoảng cách từ I đến (P) lớn nhất
là
A.
3x 7y 6z 35 0
B.
3x 7y 6z 35 0
C.
3x 7y 6z 35 0
D.
3x 7y 6z 35 0
Câu 6.2. Tìm m đ đồ th hàm s
32
y x 3mx 1
có hai đim cc tr A, B sao cho
tam giác OAB có diện tích bằng 1 (O là gc tọa độ).
A.
m2
B.
m1
C.
m5
D.
m3
Câu 6.3. Cho s phức z thoả mãn
5
2
1
zi
i
z

. Tìm phần thc và phần ảo của s
phức
2
w1zz
lần lượt là
A. 2 và 3 B. 3 và 2 C. 1 và 3 D. 3 và 1
Câu 6.4. Cho hình chóp S.ABC có đường thẳng SA vuông góc với mặt phẳng
(ABC), tam giác ABC l tam giác đều cạnh bằng a, SB=2a. Khoảng cách từ trọng
tâm G của tam giác ABC đến mặt phẳng (SBC) l
A.
15
( ;( ))
16
a
d G SBC
B.
15
( ;( ))
15
a
d G SBC
C.
5
( ;( ))
15
a
d G SBC
D.
( ;( ))
15
a
d G SBC
Câu 6.5. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA=AC=5a,
AB=a,
0
120BAC
. Khoảng cách từ A đến mặt phẳng (SBC) là
A.
5 381
.
127
a
B.
381
127
a
3 15
44
zi
7
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
C.
5 381
27
a
D.
74a
Câu 6.6. Cho hình chóp tam giác S.ABC có đường thẳng SA vuông góc với mặt
phẳng (ABC), AB=2a, AC=3a, BC=4a. Góc giữa mặt phẳng (SBC) và mặt phẳng
(ABC) bằng 60
0
. Th tích của khi chóp S.ABC là
A.
3
53
32
a
V
B.
3
43
32
a
V
C.
3
45 3
2
a
V
D.
3
45 3
32
a
V
Câu 7.1. Một người thợ xây, mun xây dng một bồn
chứa nước hình trụ tròn với th tích là
3
150m
(như hình
vẽ bên). Đáy lm bằng bê tông , thành làm bằng tôn và
bề làm bằng bằng nhôm. Tính chi phí thấp nhất đ bồn
chứa nước (lm tròn đến hàng nghìn). Biết giá thành các
vật liệu như sau: bê tông
100
nghìn đồng một
2
m
, tôn
90
một
2
m
và nhôm
120
nghìn đồng một
2
m
.
A.
15037000
đồng. B.
15038000
đồng. C.
15039000
đồng. D.
15040000
đồng.
Câu 7.2. Tìm tất cả các giá tr của tham s
m
sao cho bất phương trình sau có tập
nghiệm là
;0
:
1
2 2 1 3 5 3 5 0
xx
x
mm
.
A.
1
2
m 
. B.
1
2
m
. C.
1
2
m
. D.
1
2
m 
.
Câu 7.3. Một vật di chuyn với gia tc
2
20 1 2a t t
2
/ms
. Khi
0t
thì vận
tc của vật là
30 /ms
. Tính quảng đường vật đó di chuyn sau 2 giây (làm tròn kết
quả đến chữ s hng đơn v).
A.
106Sm
. B.
107Sm
. C.
108Sm
. D.
109Sm
.
Câu 7.4. Cho s phức
0z
thỏa mãn
2z
. Tìm tổng giá tr lớn nhất và giá tr nhỏ
nhất của biu thức
zi
P
z
.
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 7.5. Cho hình chóp
.S ABC
, có đáy
ABC
l tam giác đều cạnh
a
. Các mặt bên
SAB
,
SAC
,
SBC
lần lượt tạo với đáy các góc lần lượt là
000
30 ,45 ,60
. Tính th
8
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
tích
V
của khi chóp
.S ABC
. Biết rằng hình chiếu vuông góc của
S
trên mặt
phẳng
ABC
nằm bên trong tam giác
ABC
.
A.
3
3
43
a
V
. B.
3
3
2 4 3
a
V
. C.
3
3
4 4 3
a
V
. D.
3
3
8 4 3
a
V
.
Câu 7.6. Trong không gian tọa độ
Oxyz
, cho tám đim
2; 2;0A 
,
3; 2;0B
,
3;3;0C
,
2;3;0D
,
2; 2;5M 
,
2; 2;5N 
,
3; 2;5P
,
2;3;5Q
. Hỏi hình đa
diện tạo bởi tám đim đã cho có bao nhiêu mặt đi xứng.
A. 3. B. 6. C. 8. D.9
Câu 8.1 Đ phương trình:
x x m
42
8cos 9cos 0
với
x
[0; ]
có 2 nghiệm thì giá
tr của m là
A.
m
81
1
32

B.
m
01
C.
m
81
32
D.
m
0
Câu 8.2. S nghiệm phương trình:
22
22
9 3 3 2 2 0
xx
xx
là
A. 0 B.1 C.2 D.3
Câu 8.3. Cho
2
x
0
sinxI e dx
. Giá tr của I là
A.
2
2
ee
I
B.
2
2
ee
I
C.
2
2
e
I
D.
2
I e e

Câu 8.4. Cho s phức
0z
thỏa mãn . Đ
zi
P
z
đạt giá tr nhỏ nhất thì z là
A. z=i B.
2zi
C.
2
12
zi
D.
2z
Câu 8.5. Người ta cắt một tờ giấy hình vuông cạnh bằng 1 đ gấp thành một hình
chóp tứ giác đều sao cho bn đỉnh của hình vuông dán lại thnh đỉnh của hình
chóp. Đ th tích khi chóp lớn nhất thì cạnh đáy hình chóp l
9
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
2
x
5
B.
22
x
5
C.
x 2 2
D.
2
x
5
Câu 8.6. Trong không gian với hệ tọa độ Oxyz, cho hai đim A(-3; 5; -5), B(5; -3; 7)
và mặt phẳng (P): x + y + z - 6 = 0.Đim M(x; y; z) trên mặt phẳng (P) sao cho
MA
2
+ MB
2
đạt giá tr nhỏ nhất. Tổng (x+y+z) có giá tr là
A. 6 B. 5 C. 4 D.3
Câu 9.1. Cho một tam giác đều ABC cạnh a. Người ta dng một hình chữ nhật
MNPQ có cạnh MN nằm trên cạnh BC, hai đỉnh P và Q theo thứ t nằm trên hai
cạnh AC và AB của tam giác. Xác đnh giá tr lớn nhất của hình chữ nhật đó?
A.
2
3
a
8
B.
2
3
a
4
C.
0
D.
2
3
a
2
Câu 9.2. Cho hình chóp tứ giác đều
.S ABCD
có đáy l hình vuông ABCD cạnh a,
góc giữa mặt bên và mặt phẳng đáy l
thoả mãn
cos =
1
3
. Mặt phẳng
P
qua
AC và vuông góc với mặt phẳng
SAD
chia khi chóp
.S ABCD
thành hai khi đa
diện. Tỉ lệ th tích hai khi đa diện là gần nhất với giá tr nào trong các giá tr sau
A. 0,11 B. 0,13 C. 0,7 D. 0,9
Câu 9.3. Cho biết chu kì bán hủy của chất phóng xạ Plutôni Pu
239
l 24360 năm (tức
là một lượng Pu
239
sau 24360 năm phân hủy thì chỉ còn lại một nửa). S phân hủy
được tính theo công thức S = Ae
rt
, trong đó A l lượng chất phóng xạ ban đầu, r là
tỉ lệ phân hủy hng năm (r<0), t lthời gian phân hủy, S l lượng còn lại sau thời
gian phân hủy t. Hỏi sau bao nhiêu năm thì 10 gam Pu
239
sẽ phân hủy còn 1 gam
có giá tr gần nhất với giá tr nào sau?
A. 82135 B. 82335 C. 82235 D. 82435
Câu 9.4. Tìm giá tr của tham s m sao cho:
3
y x 3x 2
và y = m(x+2) giới hạn
bởi hai hình phẳng có cùng diện tích
A. 0 < m < 1 B. m = 1 C.
1 m 9
D. m = 9
Câu 9.5. Cho đường thẳng d là giao tuyến của hai mặt phẳng
( ):x 2y 2z 4 0
( ):2x 2y z 1 0,
và mặt cầu S có phương trình
2 2 2
x y z 4x 6y m 0
.
10
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Tìm m đ đường thẳng d cắt mặt cầu (S) tại hai đim phân biệt A, B sao cho AB =
8.
A. 9 B. 12 C. 5 D. 2
Câu 9.6. Tìm phần thc của s phức
n
z (1 i) , n
thỏa mãn phương trình
44
log (n 3) log (n 9) 3
A.
5 B. 6 C. 7 D. 8
Câu 10.1. Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng : Nếu
trên mỗi đơn v diện tích của mặt hồ có
n
con cá thì trung bình mỗi con cá sau một
vụ cân nặng
( ) 480 20 ( )P n n gam
. Hỏi phải thả bao nhiêu con cá trên một đơn v diện
tích của mặt hồ đ sau một vụ thu hoạch được nhiều cá nhất ?
A.
10
B.
12
C.
16
D.
24
Câu 10.2. Một cửa hàng bán lẻ bán 2500 cái ti vi mỗi năm. Chi phí gởi trong kho là
10$ một cái mỗi năm. Đ đặt hàng chi phí c đnh cho mỗi lần đặt là 20$ cộng
thêm 9$ mỗi cái. Cửa hng nên đặt hàng bao nhiêu lần trong mỗi năm v mỗi lần
bao nhiêu cái đ chi phí hàng tồn kho là nhỏ nhất?
Câu 10.3. Một đại lý xăng dầu cần làm một cái bồn chứa dầu hình trụ bằng tôn có
th tích
3
16 m
. Tìm bán kính đáy r của hình trụ sao cho hình trụ được làm ra ít tn
nguyên vật liệu nhất.
A.
0,8m
B.
1,2m
C.
2m
D.
2,4m
Câu 10.4. Một xưởng cơ khí nhận làm những chiếc thùng phi với th tích theo yêu
cầu là
lít mỗi chiếc. Hỏi bán kính đáy v chiều cao của thùng lần lượt bằng
bao nhiêu đ tiết kiệm vật liệu nhất?
A.
1m
và
2m
B.
1dm
và
2dm
C.
2m
và
1m
D.
2dm
và
1dm
Câu 10.5. Người ta mun mạ vàng bên ngoài cho một cái hộp có đáy hình vuông,
không nắp, th tích hộp là
4
lít. Giả sử đồ dày của lớp mạ tại một đim trên hộp là
như nhau. Gọi chiều cao và cạnh đáy lần lượt là
x
và
h
. Giá tr của
x
và
h
đ
lượng vàng cần dùng nhỏ nhất là:
A.
3
3
4
4;
16
xh
B.
3
3
12
12;
144
xh
C.
2; 1xh
D.
1; 2xh
11
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 10.6. Có một tấm nhôm hình chữ nhật có chiều dài bằng
24( )cm
, chiều rộng
bằng
18( )cm
. Người ta cắt ở bn góc của tấm nhôm đó bn hình vuông bằng nhau,
mỗi hình vuông có cạnh bằng
()x cm
rồi gấp tấm nhôm lại như hình vẽ dưới đây đ
được một cái hộp không nắp. Hỏi th tích lớn nhất của cái hộp là bao nhiêu?
A.
3
640
max
V cm
B.
3
617,5
max
V cm
C.
3
845
max
V cm
D.
3
645
max
V cm
Câu 10.7. Người ta mun rào quanh một khu đất với một s vật liệu cho trước là
180
mét thẳng hàng rào. Ở đó người ta tận dụng một bờ giậu có sẵn đ làm một
cạnh của hàng rào và rào thành mảnh đất hình chữ nhật. Hỏi mảnh đất hình chữ
nhật được rào có diện tích lớn nhất bằng bao nhiêu?
A.
2
3600
max
Sm
B.
2
4000
max
Sm
C.
2
8100
max
Sm
D.
2
4050
max
Sm
Câu 10.8. Một lão nông chia đất cho con trai đ người con canh tác riêng, biết
người con sẽ được chọn miếng đất hình chữ nhật có chu vi bằng
800( )m
. Hỏi anh ta
chọn mỗi kích thước của nó bằng bao nhiêu đ diện tích canh tác lớn nhất?
A.
200 200mm
B.
300 100mm
C.
250 150mm
D.Đáp án
khác
Câu 11.1. Hai đim M, N thuộc hai nhánh của đồ th
31
3
x
y
x
. Khi đó độ di đoạn
thẳng MN ngắn nhất bằng?
A. 8 B. 4 C.
3
M
x
D.
82
.
Câu 11.2. Tính th tích hình cầu ngoại tiếp tứ diện ABCD, có cạnh AB =
2
3a
và
các cạnh còn lại đều bằng a.
A.
3
13 13
162
a
B.
3
13 13
216
a
C.
3
13 13
648
a
D.
3
13
162
a
.
Câu 11.3. S giá tr nguyên của tham s m sao cho bất phương trình:
22
log5 log(x 1) log( 4 )mx x m
nghiệm đúng với mọi x thuộc R?
A. 0 B.
mZ
v
3m
C. 1 D. 2.
12
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 11.4. Cho hm s
3
( ) .
(x 1)
x
a
f x b xe
. Biết rằng
'(0) 22f 
v
1
0
( ) 5f x dx
. Khi
đó tổng
ab
bằng?
A.
146
13
B.
26
11
C.
26
11
D.
146
13
.
Câu 11.5. Trong không gian với hệ trục toạ độ Oxyz, cho đim
2;5;3A
v đường
thẳng
12
:
2 1 2
x y z
d


. Gọi
(
𝑃
)
là mặt phẳng chứa đường thẳng 𝑑 sao cho
khoảng cách từ 𝐴 đến
(
𝑃
)
lớn nhất. Tính khoảng cách từ đim
1;2; 1M
đến mặt
phẳng
(
𝑃
)
?
A.
11 18
18
B.
32
C.
11
18
D.
4
3
Câu 11.6. Trong các s phức thỏa điền kiện
4 2 2z i i z
, modun nhỏ nhất của
s phức z bằng?
A.
22
B. 2 C. 1 D.
32
.
Câu 12.1. Trong vật lí, sphân rã của các chất phóng xạ được biu diễn bởi công
thức:
0
1
2
t
T
m t m
, trong đó
0
m
l khi lượng ban đầu của chất phóng xạ (tại thời
điểm t = 0); T là chu kì bán rã (tức là khoảng thời gian để một nửa khối lượng chất phóng
xạ bị biến thành chất khác). Chu kì bán rã của Cabon
14
C
l khoảng 5730 năm. Cho
trước mẫu Cabon có khi lượng 100g. Hỏi sau khoảng thời gian t thì khi lượng
còn bao nhiêu?
A.
ln2
5730
100.
t
m t e
B.
5730
1
100.
2
mt
C.
100
5730
1
100
2
t
mt
D.
100
5730
100.
t
m t e
Câu 12.2. Trong vật lí, sphân rã của các chất phóng xạ được biu diễn bởi công
thức:
0
1
2
t
T
m t m
, trong đó
0
m
l khi lượng ban đầu của chất phóng xạ (tại thời
điểm t = 0); T là chu kì bán rã (tức là khoảng thời gian để một nửa khối lượng chất phóng
xạ bị biến thành chất khác). Chu kì bán rã của Cabon
14
C
l khoảng 5730 năm. Người
13
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
ta tìm được trong một mẫu đồ cổ một lượng Cabon v xác đnh được nó đã mất
khoảng 25% lượng Cabon ban đầu của nó. Hỏi mẫu đồ cổ đó có tuổi l bao nhiêu?
A. 2378 năm B. 2300 năm C. 2387 năm D. 2400 năm
Câu 12.3. Một nghiên cứu cho thấy một nhóm học sinh được cho xem cùng một
danh sách các loi động vật v được kim tra lại xem họ nhớ bao nhiêu % mỗi
tháng. Sau t tháng, khả năng nhớ trung bình của nhóm học sinh được cho bởi công
thức
75 20ln 1 , 0M t t t
(đơn v %). Hỏi sau khoảng bao lâu thì nhóm học
sinh nhớ được danh sách đó dưới 10%?
A. 24.79 tháng B. 23 tháng C. 24 tháng D. 22 tháng
Câu 12.4. Một công ty vừa tung ra th trường sản phẩm mới vhọ tổ chức quảng
cáo trên truyền hình mỗi ngy. Một nghiên cứu th trường cho thấy, nếu sau x
quảng cáo được phát thì s % người xem mua sản phẩm l
0.015
100
( ) , 0
1 49
x
P x x
e
. Hãy tính s quảng cáo được phát ti thiu đ s người
mua đạt hơn 75%.
A. 333 B. 343 C. 330 D. 323
Câu 12.5. Ông Năm gửi
320
triệu đồng ở hai ngân hng X v Y theo phương thức
lãi kép. S tiền thứ nhất gửi ở ngân hng X với lãi suất
2,1
một quý trong thời
gian
15
tháng. S tiền còn lại gửi ở ngân hng Y với lãi suất
0,73
một tháng
trong thời gian
9
tháng. Tổng lợi tức đạt được ở hai ngân hng l
27507 768,13
(chưa lm tròn). Hỏi s tiền ông Năm lần lượt gửi ở ngân hng X v Y l bao
nhiêu?
A.
140
triệu v
180
triệu. B.
180
triệu v
140
triệu.
C.
200
triệu v
120
triệu. D.
120
triệu v
200
triệu.
Câu 13.1. Cho hàm s y = - x
3
+ 3mx
2
-3m – 1. Tìm các giá tr của m đ hàm s có
cc đại, cc tiu. Với giá tr nào của m thì đồ th hàm s có đim cc đại, đim cc
tiu đi xứng với nhau qua đường thẳng d: x + 8y – 74 = 0.
Đáp án: m=2
Câu 13.2. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC l tam giác đều cạnh a, th
tích khi lăng trụ bằng
3
3
4
a
. Tính khoảng cách giữa hai đường thẳng AA’ v
BC’.
Đáp án:
21
7
a
Câu 13.3. Tìm m đ phương trình
16 3.4 2 1 0
xx
m
(1) có hai nghiệm phân biệt
14
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Đáp án:
51
82
m

Câu 13.4. Tính diện tích hình phẳng giới hạn bởi hai đường cong
1 ; 1
x
y e x y e x
Câu 13.5. Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình:
2 2 2
2 6 4 2 0x y z x y z
. Viết phương trình mặt phẳng (P) song song với
giá của véc tơ
(1;6;2)v
, vuông góc với mặt phẳng
( ): 4 11 0x y z
và tiếp
xúc với (S).
Đáp án: (P):
2 2 3 0x y z
hoặc (P):
2 2 21 0x y z
Câu 13.6. Phương trình
4
1
1
1
z
z



có bao nhiêu nghiệm.
Đáp án: 3 nghiệm
Câu 14.1. Đ hàm s
2
y x m x m
đồng biến trên khoảng (1;2) thì giá tr của m
phải là
A.
2.m
B.
3.m
C.
2 3.m
D. Với mọi
m.
Câu 14.2. Cho hình chóp
.S ABCD
có đáy
ABCD
l hình vuông cạnh
a
. Mặt bên
SAB
l tam giác đều v vuông góc với đáy. Gọi
M
l đim thuộc cạnh
SC
sao
cho
2.SM MC
Tính th tích hình chóp
.M ABC
.
A.
3
a3
6
B.
3
a3
36
C.
3
a3
18
D.
3
3
24
a
Câu 14.3. Hàm s
2
21y x x m
có tập xác đnh là khi:
A.
1m 
hoặc
0m
B.
0m
C.
0m
D.
03m
Câu 14.5. Cho biết tích phân
42
2
1
..
2 ln
4
e
a e b e c
I x x x dx

với
,,abc
l các ước
nguyên của 4. Tổng
?abc
A. 2 B. 4 C. 3 D. 1
15
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 14.5. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba đim
0;2;0 , 1;1;4AB
và
3; 2;1C
. Mặt cầu
S
tâm
I
đi qua
,,A B C
v độ dài
5OI
(biết tâm
I
có
honh độ nguyên,
O
là gc tọa độ). Bán kính mặt cầu
S
là
A.
1R
B.
3R
C.
4R
D.
5R
Câu 14.6. S phức
, ( , )z a bi a b
thỏa
2
(2 3 ) 5 2i z i z i
. Tính
ab
?
A.
5
3
B.
7
4
C.
3
4
D.
11
12
Câu 15.1. Cho hàm số:
2
1
x
yC
x
. Tìm
a
sao cho từ A(0,
a
) kẻ được hai tiếp
tuyến đến (C) nằm ở hai phía trục Ox.
A.
2
;
3




B.
2; \ 1 
C.
2; 
D.
2
; \ 1
3




Câu 15.2. Cho hình chóp S.ABCD có đáy ABCD l hình vuông cạnh a, cạnh bên SA
= a, hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) l đim H thuộc
đoạn AC,
4
AC
AH
. Gọi CM l đường cao của tam giác SAC. Tính th tích khi tứ
diện SMBC theo a.
3
14
48
a
3
14
24
a
3
14
16
a
3
14
8
a
Câu 15.3. Tìm s nghiệm của phương trình:
2
2
2 1 1
log 2 1 log 2 1 4 1
xx
x x x

.
A. 0
B. 1
C. 2
D. 3
Câu 15. 4. Tính tích phân:
2
4
2
2
1 tan tan
n
x
n
I e x x dx
A.
2
2
4
n
n
I e e

B.
2
4
n
Ie
C.
2n
Ie
D.
21
2
4
n
n
I e e

Câu 15.5. Cho hai đim A(-1, 3, -2); B(-9, 4, 9) và mặt phẳng (P): 2x-y+z+1=0. Đim
M thuộc (P). Tính GTNN của AM + BM.
16
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
6 204
B.
7274 31434
6
C.
2004 726
3
D.
3 26
Câu 15.6. Cho s phức
8
1
n
zi
A.
4
2
n
B.
0
C.
8
2
n
D.
4
2
n
Câu 16.1. Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta mun cắt một hình
thang như hình vẽ. Tìm tổng x + y đ diện tích hình thang EFGH đạt giá tr nhỏ
nhất.
y cm
x cm
3cm
2 cm
A
D
C
B
E
F
H
G
A. 7 B. 5 C.
72
2
D.
42
.
Câu 16.2. Người ta thả một lá bèo vào một hồ nước. Kinh nghiệm cho thấy sau 9
giờ bèo sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, lượng lá bèo tăng gấp 10
lần lượng lá bèo trước đó v tc độ tăng không đổi. Hỏi sau mấy giờ thì s lá bèo
phủ kín
1
3
cái hồ ?
A. 3 B.
9
10
3
C. 9 – log3 D.
9
log3
.
Câu 16.3. Một vật chuyn động với vận tc v(t) (m/s) có gia tc
2
( ) 3a t t t
(m/s
2
). Vận tc ban đầu của vật là 2 (m/s). Hỏi vận tc của vật sau 2s .
A. 10 m/s B. 12 m/s C. 16 m/s D. 8 m/s.
Câu 16.4.
Cho tứ diện
, , ,ABCD M N P
lần lượt thuộc
,,BC BD AC
sao cho
4 , 2 ,BC BM BD BN
3AC AP
, mặt phẳng (MNP) cắt AD tại Q. Tính tỷ s th
tích hai phần khi tứ diện ABCD b chia bởi mặt phẳng (MNP).
17
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
2
3
B.
7
13
C.
5
13
D.
1
3
.
Câu 16.5. Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương
trình 2x – y + z + 1 = 0 v hai đim M(3; 1; 0), N(- 9; 4; 9). Tìm đim I(a; b; c) thuộc
mặt phẳng (P) sao cho
IM IN
đạt giá tr lớn nhất. Biết a, b, c thỏa mãn điều kiện:
A.
21abc
B.
14abc
C.
5abc
D.
19.abc
Câu 16.6 Tìm s phức Z có mô đun lớn nhất và thỏa mãn điều kiện
13
1 3 2
2
Z i i
.
A.
3 15
44
zi
B.
15
44
zi
C.
3 15
44
zi
D.
15
44
zi
Câu 16.7. Một đại lý xăng dầu cần làm một cái bồn chứa dầu hình trụ bằng tôn có
th tích
3
16 m
. Tìm bán kính đáy r của hình trụ sao cho hình trụ được làm ra ít tn
nguyên vật liệu nhất.
A.
0,8m
B.
1,2m
C.
2m
D.
2,4m
Câu 17.1. Trên sân bay một máy bay cất cánh trên đường băng d (từ trái sang phải)
và bắt đầu rời mặt đất tại đim O. Gọi (P) là mặt phẳng vuông góc với mặt đất và
cắt mặt đất theo giao tuyến l đường băng d của máy bay. Dọc theo đường băng d
cách v trí máy bay cất cánh O một khoảng 300(m) về phía bên phải có 1 người
quan sát A. Biết máy bay chuyền động trong mặt phẳng (P) vđộ cao y của máy
bay xác đnh bởi phương trình
2
yx
(với x l độ dời của máy bay dọc theo đường
thẳng d và tính từ O). Khoảng cách ngắn nhất từ người A (đứng c đnh) đến máy
bay là:
A.
300( )m
B.
100. 5( )m
C.
200( )m
D.
100 3( )m
Câu 17.2.
Cho hình chóp S.ABCD có SA vuông góc với đáy,
6SA a
. Đáy ABCD l hình
thang vuông tại A và B,
1
.
2
AB BC AD a
Gọi E ltrung đim của AD. Tính bán
kính mặt cầu ngoại tiếp hình chóp S.ECD.
18
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
2
.
2
a
R
B.
6.Ra
C.
30
.
3
a
R
D.
26
.
2
a
R
Câu 17.3. Một bà mẹ Việt Nam anh hùng được hưởng s tiền là 4 triệu đồng trên
một tháng (chuyn vào tại khoản của mẹ ở ngân hng vo đầu tháng). Từ tháng 1
năm 2016 mẹ không đi rút tiền m đ lại ngân hng v được tính lãi suất 1% trên
một tháng. Đến đầu tháng 12 năm 2016 mẹ rút toàn bộ s tiền (gồm s tiền của
tháng 12 và s tiền đã gửi từ tháng 1). Hỏi khi đó mẹ lĩnh về bao nhiêu tiền? (Kết
quả lm tròn theo đơn v nghìn đồng).
A. 50 triệu 730 nghìn đồng B. 48 triệu 480 nghìn đồng
C. 53 triệu 760 nghìn đồng D. 50 triệu 640 nghìn đồng
Câu 17.4.
Cho một vật th bằng gỗ có dạng khi trụ với bán kính đáy bằng R. Cắt khi trụ
bởi một mặt phẳng có giao tuyến với đáy l một đường kính của đáy v tạo với
đáy góc
0
45
. Th tích của khi gỗ bé là:
A.
3
2
.
3
R
V
B.
3
.
6
R
V
C.
3
.
3
R
V
D.
3
.
3
R
V
Câu 17.5.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
( ): 1 0P x y z
và hai
đim
(1; 3;0), 5; 1; 2AB
. M là một đim trên mặt phẳng
()P
. Giá tr lớn nhất của
T MA MB
là:
A.
2 5.T
B.
2 6.T
C.
46
.
2
T
D.
23
.
3
T
Câu 17.6.
S nghiệm phức của phương trình :
25
86zi
z
là?
A. 0 B. 1 C. 2 D. 4
Câu 18.1. Một ngọn hải đăng đặt tại v trí
A
có khoảng cách đến bờ bin
5
AB km
.Trên bờ bin có một cái kho ở v trí
C
cách
B
một khoảng
7
km
.Người canh hải
đăng có th
chèo đò từ
A
đến
M
trên bờ binvới vận tc
4/
km h
rồi đi bộ
19
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
đến
C
với vận tc
6/
km h
.V trí của đim
M
cách B một
khoảng bao nhiêu đ người đó đi đến kho nhanh nhất?
A.
0km
B.
7km
C.
25km
D.
14 5 5
km
12
Câu 18.2.
Một cửa hàng nhận làm những chiếc xô bằng nhôm hình trụ không nắp chứa 10 lít
nước. Hỏi bán kính đáy (đơn v cm, lm tròn đến hàng phần chục) của chiếc xô
bằng bao nhiêu đ cửa hàng tn ít vật liệu nhất.
A. 14,7cm. B. 15cm.
C. 15,2cm. D. 14cm.
Câu 18.3. Huyện A có 100 000 người. Với mức tăng dân s bình quân 1,5% năm thì
sau n năm dân s sẽ vượt lên 130 000 người. Hỏi n nhỏ nhất là bao nhiêu?
A. 18 năm B. 17 năm C. 19 năm D. 16
năm
Câu 18.4. Cho đường cong
:C y x
. Gọi (H) là hình phẳng giới hạn bởi (C), trục
tung v đường thẳng
y = m (m > 0). Cho (H) quay xung quanh trục tung ta được một vật th tròn xoay
có th tích
32
5
V
(đvtt). Khi đó giá tr của m là:
A. m = 1 B. m = 2 C. m = 3 D. m = 4
Câu 18.5.
Trong không gian với hệ toạ độ
Oxyz
, gọi
là mặt phẳng qua hai đim
2;0;1A
và
2;0;5B
đồng thời hợp với mặt phẳng
Oxz
một góc
0
45
. Khoảng cách từ
O
tới
là:
A.
.
3
2
B.
3
.
2
C.
1
.
2
D.
2
.
2
Câu 18.6. S phức có đim biu diễn ở phần tô đậm trong hình vẽ sau là:
20
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
12z
và phần ảo lớn hơn
1
.
2
B.
12z
và phần ảo lớn hơn
1
.
2
C.
12z
và phần ảo nhỏ hơn
1
.
2
D.
12z
và phần ảo nhỏ hơn
1
.
2
Câu 19.1. Cho hàm s
24
1
x
y
x
có đồ thi
C
đim
( 5;5)A
. Tìm
m
đ đường thẳng
y x m
cắt đồ th
C
tại hai đim phân biệt
M
và
N
sao cho tứ giác
OAMN
là
hình bình hành (
O
là gc toạ độ).
A.
0m
B.
0; 2mm
C.
2m
D.
2m
Câu 19.2.
Làm 1 m
2
mặt nón cần : 120 lá nón ( Đã qua sơ chế) .Giá 100 lá nón l 25.000 đồng
. Vậy đ làm 100 cái nón có chu vi vành nón là 120 cm, và khoảng từ đỉnh nón tới 1
đim trên vành nón là 25 cm thì cần bao nhiêu tiền mua lá nón?
A. 400.000đ B. 450.000đ C.500.000đ D. 550.000đ
Câu 19.3.
Hệ phương trình
2
2
2007
1
2007
1
x
y
y
e
y
x
e
x


có bao nhiêu nghiệm thỏa mãn x > 0, y > 0.
A. 0 B. 1 C.2 D.3
21
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 19.4. Một ô tô chạy với vận tc 20m/s thì người lái xe đạp phanh còn được gọi
l “thắng”. Sau khi đạp phanh, ô tô chuyn động chậm dần đều với vận tc
( ) 40 20( / ).v t t m s
Trong đó t l khoảng thời gian tính bằng giây k từ lúc bắt đầu
đạp phanh . Quãng đường ô tô di chuyn từ lúc đạp phanh đến khi dừng hẳn là
bao nhiêu?
A. 2m B.3m C.4m D. 5m
Câu 19.5.
Trong không gian với hệ tọa độ Oxyz, cho hai đim A(1;5;0), B(3;3;6) v đường
thẳng
có phương trình tham s
1 2 ; 1 ; 2 x t y t z t
. Một đim M thay đổi
trên đường thẳng
, xác đnh v trí của đim M đ chu vi tam giác MAB đạt giá tr
nhỏ nhất.
A. M(1 ;0 ;2) B. M(-1 ;0 ; 2) C. M (1 ;0 ; -2) D. M (-1 ; 0 ; -
2)
Câu 19.6.
Tìm s phức z biết z thỏa mãn phương trình
z
z2
z

A. 1 B. 1+i C.1-i D. i
Câu 20.1 . Một máy tính được lập trình đ vẽ một chuỗi các hình chữ nhật ở góc
phần tư thứ nhất của trục tọa độ Oxy , nội tiếp dưới đường cong y=e
-x
. Hỏi diện
tích lớn nhất của hình chữ nhật có th được vẽ bằng cách lập trình trên
A. 0,3679 ( đvdt) B. 0,3976 (đvdt)
C. 0,1353
( đvdt) D 0,5313
( đvdt)
Câu 20.2. Cho hình trụ nội tiếp trong hình cầu bán kính R. Xác đnh chiều cao và
bán kính đáy đ hình trụ có th tích lớn nhất.
A. B. C. D.
Câu 20.3. Cho biết chu kỳ bán rã của chất phóng xạ Plutoni Pu
239
l 24360 năm . S
phân hủy được tính theo công thức
.
rt
S Ae
. Trong đó A l s lượng chất phóng
xạ ban đầu, r là tỷ lệ phân hủy hằng năm (r<0) ,t l thời gian phân hủy, S l lượng
còn lại sau thời gian phân hủy t. Hỏi 10 gam Pu
239
sau bao nhiêu năm phân hủy sẽ
còn 1 gam
22
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A. 80922 năm B. 24360 năm C.35144 năm D. 48720 năm
Câu 20.4. Cho Elip (E) có phương trình
2
2
1
4
x
y
Hãy tính diện tích hình phẳng
giới hạn bởi (E) đã cho
A. π B. 2π C.
4
D.
2
Câu 20.5. Cho hình chóp O.ABC có OA=a , OB=b, OC=c đôi một vuông góc với
nhau . Đim M c đnh thuộc tam giác ABC có khoảng các lần lượt đến các mặt
phẳng (OBC) , (OCA), (OAB) là 1,2,3 . Khi tồn tại a,b,c thỏa th tích khi chóp
O.ABC nhỏ nhất, giá tr nhỏ nhất của th tích khi chóp O.ABC là
A. 18 B. 27
C. 6 D. Không tồn tại a,b,c thỏa yêu cầu bài toán
Câu 20.6. Một hình vuông tâm là gc tọa độ O, các cạnh song song với các trục tọa
độ v có độ dài bằng 4. Hãy xác đnh điều kiện của a v b đ đim biu diễn s
phức z=a+bi nằm trên đường chéo của hình vuông
A.
2ab
B.
2ab
C.
2ab
D.
2ab
Câu 21.1. Có một tấm gỗ hình vuông cạnh 200 cm. Cắt một tấm gỗ có hình tam
giác vuông, có tổng của một cạnh góc vuông và cạnh huyền bằng hằng s
120cm
từ
tấm gỗ trên sao cho tấm gỗ hình tam giác vuông có diện tích lớn nhất. Hỏi cạnh
huyền của tấm gỗ này là bao nhiêu?
A.
40cm
. B.
40 3cm
. C.
80cm
. D.
40 2cm
.
Câu 21.2.
Một hình trụ có bán kính đáy l R v chiều cao
3R
. Hai đim A và B lần lượt nằm
trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng
0
30
.
Tính
khoảng cách giữa AB và trục của hình trụ.
A.
3
3
R
. B.
3
2
R
. C.
33
4
R
. D.
23
3
R
.
Câu 21.3. Gọi
1
S
là tập nghiệm của bất phương trình
2.2 3.3 6 1 0
x x x
.
Gọi
2
S
là tập nghiệm của bất phương trình
24
x
.
23
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Gọi
3
S
là tập nghiệm của bất phương trình
1
2
log 1 0x
.
Trong các khẳng đnh sau, khẳng đnh no đúng khi nói về mi quan hệ giữa các
tập nghiệm
1 2 3
,,S S S
?
A.
1 3 2
S S S
.
B.
3 2 1
S S S
.
C.
3 1 2
S S S
.
D.
1 2 3
S S S
.
Câu 21.4.
Cho tích phân
3
b
x
x
a
e
C dx
e
trong đó a l nghiệm của phương trình
2
1
22
x
, b là
một s dương v
ba
. Gọi
2
2
1
A x dx
. Tìm chữ s hng đơn v của b sao cho
3CA
.
A. 3 B. 2 C.4 D. 5
Câu 21.5. Trong không gian Oxyz, cho 2 đường thẳng d :
3
2
2

xt
yt
zt
v d’ :
'
5'
2 ' 3 2 5

xt
yt
zt
Viết phương trình mặt phẳng () chứa (d) v tạo với mặt phẳng Oyz một góc
nhỏ nhất.
A.
3 2 7 0 x y z
. B.
3 2 7 0 x y z
.
C.
3 2 7 0 x y z
. D.
3 2 7 0 x y z
.
Câu 21.6.
Trên tập hợp s phức cho phương trình
2
3 1 0 zz
(*). Gọi
1, 2
zz
là nghiệm của
phương trình (*). Tìm môđun của s phức
12
4 2 4
,
nn
zz
w n N
ii
A. 1. B. 2. C.4. D. 6.
24
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 22.1. Bạn An là một học sinh lớp 12, b bạn là một thợ hàn. B bạn đnh làm
một chiếc thùng hình trụ từ một mảnh tôn có chu vi 120 cm theo cách dưới đây:
Bằng kiến thức đã học em giúp b bạn chọn mảnh tôn đ lm được chiếc thùng có
th tích lớn nhất, khi đó chiều dài, rộng của mảnh tôn lần lượt là:
A.
35 ;25cm cm
B.
40 ;20cm cm
C.
50 ;10cm cm
D.
30 ;30cm cm
Câu 22.2. Cho bát diện đều; tính tỷ s giữa th tích khi cầu nội tiếp và th tích
khi cầu ngoại tiếp hình bát diện đều đó.
A.
1
2
B.
1
22
C.
1
3
D.
1
33
Câu 22.3. Bác B gửi tiết kiệm s tiền ban đầu là 20 triệu đồng theo kỳ hạn 3 tháng
với lãi suất 0,72%/tháng. Sau một năm, bác B rút cả vn lẫn lãi và gửi lại theo kỳ
hạn 6 tháng với lãi suất 0,78%/tháng. Sau khi gửi được đúng một kỳ hạn 6 tháng
do gia đình có việc nên bác gửi thêm một s tháng nữa thì phải rút tiền trước kỳ
hạn cả gc lẫn lãi được s tiền l 23263844,9 đồng (chưa lm tròn). Biết rằng khi
rút tiền trước thời hạn lãi suất được tính theo lãi suất không kỳ hạn, tức tính theo
hàng tháng. Trong một s tháng bác gửi thêm lãi suất là:
A. 0,4% B. 0,3% C. 0,5% D. 0,6%
Câu 22.4. Một ô tô xuất phát với vận tc
1
2 10 /v t t m s
sau khi đi được một
khoảng thời gian t1 thì bất ngờ gặp chướng ngại vật nên tài xế phanh gấp với vận
tc
2
20 4 /v t t m s
v đi thêm một khoảng thời gian t2 nữa thì dừng lại. Biết tổng
thời gian từ lúc xuất phát đến lúc dừng lại là 4 (s). Hỏi xe đã đi được quãng đường
bao nhiêu mét.
A. 57 m B. 64 m C. 50 m D. 47 m
Câu 22.5. Trong không gian với hệ trục toạ độ Oxyz cho đim
1;1; 2M
và hai
đường thẳng
1
2 1 6
1: ; 2 :
1 1 1 2 1 1
yy
x z x z
. Lấy trên
1
đim N và trên
2
đim P sao cho M,N,P thẳng hàng. Toạ độ trung đim của NP là:
A.
1;1; 3I
B.
1;1; 2I
C.
0;2;3I
D.
2;0; 7I
25
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 22.6. Gọi
1 2 3 4
; ; ;z z z z
là 4 nghiệm phức của phương trình
42
4 4 0z m z m
.
Tìm tất cả các giá tr m đ
1 2 3 4
6z z z z
.
A.
1m
B.
2m
C.
3m
D.
1m
Câu 23.1. Đường dây điện 110KV kéo từ trạm phát (đim A) trong đất liền ra Côn
Đảo (đim C). biết khoảng cách ngắn nhất từ C đến B là 60km, khoảng cách từ A
đến B là 100km, mỗi km dây điện dưới nước chi phí là 5000 USD, chi phí cho mỗi
km dây điện trên bờ là 3000 USD. Hỏi đim G cách A bao nhiêu đ mắc dây điện
từ A đến G rồi từ G đến C chi phí ít nhất.
A: 40km B: 45km C: 55km D: 60km
Câu 23.2. Công ty chuyên sản xuất bao bì đng sản phẩm sữa nhận đơn đặt hàng
sản xuất hộp đng sữa có th tích
3
1dm
. Các nhân viên thiết kế phân vân giữa làm
hộp đng dạng hình trụ hay hình hộp chữ nhật đáy hình vuông. Hỏi công ty sẽ
làm hộp hình gì đ chi phí nguyên liệu nhỏ nhất.
A: Hình trụ B: Hình hộp chữ nhật đáy hình vuông
C: Cả hai như nhau D: Hình lập phương
Câu 23.3. Cô giáo Thảo ra trường xa quê lập nghiệp, đến năm 2014 sau gần 5 năm
làm việc tiết kiệm được x(triệu đồng) v đnh dùng s tiền đó đ mua nh nhưng
trên thc tế cô giáo phải cần 1,55x( triệu đồng). Cô quyết đnh gửi tiết kiệm vào
ngân hàng với lãi suất l 6,9% /năm với lãi hàng tháng nhập gc và cô không rút
trước kì hạn. Hỏi năm bao nhiêu cô mua được căn nh đó, biết rằng chủ nh đó
vẫn bán giá như cũ.
A: Năm 2019 B: Năm 2020 C: Năm 2021 D: Năm 2022
Câu 23.4. Thành ph đnh xây cây cầu bắc ngang con sông dài 500m, biết rằng
người ta đnh xây cầu có 10 nhp cầu hình dạng parabol,mỗi nhp cách nhau
40m,biết 2 bên đầu cầu và giữa mi nhp ni người ta xây 1 chân trụ rộng 5m. Bề
dày nhp cầu không đổi là 20cm. Biết 1 nhp cầu như hình vẽ. Hỏi lượng bê tông
đ xây các nhp cầu là bao nhiêu (bỏ qua diện tích ct sắt trong mỗi nhp cầu)
A:
3
20m
B:
3
50m
C:
3
40m
D:
3
100m
26
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 23.5. Trong không gian với hệ tọa độ Oxyz cho đim A(1 ;2 ;2) ; B(-1 ;2 ;-1) ;
C(1 ;6 ;-1) ; D(-1 ;6 ;2). ABCD là tứ diện gì ?
A : Tứ diện đều B : Tứ diện vuông C: Tứ diện gần đều D : Tứ diện
thường
Câu 23.6. Cho s phức
1 2 3
4 2 6
; (1 )(1 2 );
13
ii
z z i i z
ii

có đim biu diễn trong
mặt phẳng phức lần lượt là H;I;V. Tìm tọa độ E sao cho HIVE là hình vuông.
A: Đim E(-1;-1) B: Đim E(-1; 1) C: Đim E(1;-1) D: Đim E(1;1)
Câu 24.1. Một công ti bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê
mỗi căn hộ với giá 2 000 000 đồng một tháng thì mọi căn hộ đều có người thuê và
cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm 100 000 đồng một tháng thì có thêm
hai căn hộ b bỏ trng. Hỏi mun có thu nhập cao nhất, công ti đó phải cho thuê
mỗi căn hộ với giá tr bao nhiêu một tháng? (đồng/tháng)
A. 2 250 000 B. 2 450 000 C. 2 300 000 D. 2 225 000
Câu 24.2. Cho hình lăng trụ tam giác đều ABC.A’B’C’, có cạnh đáy bằng
a
và cạnh
bên bằng
2a
. Lấy M, N lần lượt trên cạnh AB’, A’C sao cho
'1
' ' 3
AM A N
AB A C
. Tính
th tích V của khi BMNC’C.
A.
3
6
108
a
B.
3
26
27
a
C.
3
36
108
a
D.
3
6
27
a
Câu 24.3. Cho ba s dương a, b, c đôi một khác nhau và khác 1. Xét các khẳng đnh
sau:
27
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
(I)
22
log log
aa
bc
cb
;
(II)
22
2
1
log log
log
ab
c
bc
a
;
(III) Trong ba s
2 2 2
log ; log ; log
a b c
b c a
c a b
b c a
luôn có ít nhất một s lớn hơn 1.
Khẳng đnh no đúng?
A. Chỉ (I) và (II) B. Chỉ (I) và (III) C. Chỉ (I) D. Cả (I), (II) và (III)
Câu 24.4. Cho
2
0
cos
n
n
I xdx
,
n
,
2n
. Khẳng đnh no sau đây đúng?
A.
1
1
nn
n
II
n
B.
2
2
nn
n
II
n
C.
2
1
nn
n
II
n
D.
2
2
nn
II
Câu 24.5. Trong không gian tọa độ Oxyz, cho các phương trình mặt phẳng
2
: 3 5 1 4 20 0, 1;1
m
mx m y mz m
.
Xét các mệnh đề sau:
(I) Với mọi
1;1m
thì các mặt phẳng
m
luôn tiếp xúc với một mặt cầu không
đổi.
(II) Với mọi
0m
thì các mặt phẳng
m
luôn cắt mặt phẳng (Oxz).
(III)
; 5, 1;1
m
d O m
.
Khẳng đnh no sau đây đúng?
28
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A. Chỉ (I) và (II) B. Chỉ (I) và (III) C. Chỉ (II) và (III) D. Cả 3 đều
đúng.
Câu 24.6. Cho hai s phức phân biệt
12
;zz
thỏa điều kiện
12
12
zz
zz
là s ảo. Khẳng
đnh no sau đây l đúng?
A.
12
1; 1zz
B.
12
zz
C.
12
zz
D.
12
zz
Câu 25.1. Cho hàm s
32
1
y = x x
2
có đồ th là (C).
Tìm tất cả những đim trên đồ th (C) sao cho hệ s góc của tiếp tuyến với
đồ th (C) tại những đim đó l giá tr lớn nhất của hàm s:
2
4
4x +3
g(x) =
x +1
.
A.
1
;0
2



B.
3
1;
2




;
4 40
;
3 27



C.
2 1 2
;
24





;
2 1 2
;
24





D.
1
;0
2



;
2; 10
Câu 25.2. Cho hình chóp S.ABC có đáy ABC l tam giác đều cạnh a, hình chiếu
vuông góc của đỉnh S trên mặt phẳng (ABC) l trung đim cạnh BC. Góc giữa
đường thẳng SA và mặt phẳng (ABC) bằng 60
0
. Gọi G là trọng tâm tam giác SAC.
Bán kính mặt cầu tâm G và tiếp xúc với mặt phẳng (SAB) là:
A.
13
13
a
B.
13
39
a
C.
3 13
26
a
D.
13
26
a
Câu 25.3. Với
0, 1aa
, cho biết :
11
1 log 1 log
;
aa
ut
t a v a


. Chọn khẳng đnh đúng :
A.
1
1 log
a
v
ua
B.
1
1 log
a
t
ua
C.
1
1 log
a
v
ua
D.
1
1 log
a
v
ua
Câu 25.4. Th tích khi tròn xoay khi cho hình phẳng giới hạn bởi đồ th hàm s
5
1 3 2
x
y
x

, trục honh v hai đường thẳng
1; 3xx
quay quanh trục hoành
là:
29
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
5ln2 1
B.
5ln2 1
C.
5ln2 1
D.
5ln2 1
Câu 25.5. Trong không gian với hệ toạ độ Oxyz, cho 2 đường thẳng:
1
2 1 1
:
1 2 3
x y z
,
2
:2
12
xt
yt
zt

và mặt cầu
2 2 2
( ): 2 2 6 5 0S x y z x y z
Viết phương trình mặt phẳng
()
song song với hai đường thẳng
12
,
và cắt mặt
cầu (S) theo giao tuyến l đường tròn (C) có chu vi bằng
2 365
5
.
A.
5 3 4 0; 5 3 10 0x y z x y z
B.
5 3 10 0x y z
C.
5 3 3 511 0; 5 3 3 511 0x y z x y z
D.
5 3 4 0x y z
Câu 25.6. Cho s phức z thỏa điều kiện
1z z i
. S phức
23zi
có
môđun nhỏ nhất là:
A.
13
22
i

B.
11
22
i
C.
11
22
i

D.
13
22
i
Câu 26.1 Tìm diện tích lớn nhất của hình chữ nhật nội tiếp trong nửa đường tròn
bán kính
10cm
, biết một cạnh của hình chữ nhật nằm dọc trên đường kính của
đường tròn.
A.
2
80cm
B.
2
100cm
C.
2
160cm
D.
2
200cm
Câu 26.2.
Cho hình chóp
.S ABC
có chân đường cao nằm trong tam giác
ABC
; các mặt phẳng
()SAB
,
()SAC
và
()SBC
cùng tạo với mặt phẳng
()ABC
một góc bằng nhau. Biết
25AB
,
17BC
,
26AC
; đường thẳng
SB
tạo với mặt đáy một góc bằng
45
.
Tính th tích
V
của khi chóp
.S ABC
.
A.
680V
B.
408V
C.
578V
D.
600V
Câu 26.3.
30
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Tìm tất cả các giá tr thc của tham s
m
đ phương trình
2 2 2
2 1 4
2
log log 3 log 3x x m x
có nghiệm thuộc
32;
?
A.
1; 3m
. B.
1; 3m
. C.
1; 3m
. D.
3;1m
.
Câu 26.4.
Cho hàm s
32
11
22
33
y x mx x m
có đồ th (C). Tìm
5
0;
6
m
sao cho hình
phẳng giới hạn bởi đồ th (C) v các đường thẳng
0, 2, 0xxy
và có diện tích
bằng 4.
A.
1
4
m
B.
1
3
m
C.
1
2
m
D.
1m
Câu 26.5.
Trong không gian tọa độ Oxyz cho đường thẳng
: 1 2
2
xt
d y t
zt
và mp
: 2 2 2 0P x y z
. Viết phương trình mặt phẳng
R
qua d và tạo với
P
một
góc nhỏ nhất .
A.
30x y z
B.
30x y z
C.
30x y z
D.
30x y z
Câu 26.6.
Cho
12
1 ; 1z i z i
. Tìm
3
z
sao cho các đim biu diễn của
1 2 3
,,z z z
tạo
thnh tam giác đều.
A.
33
2 1 2 1z i và z i
B.
33
3 1 3 1z i và z i
C.
33
2 1 2 1z i và z i
D.
33
3 1 3 1z i và z i
Câu 27.1 . Cho hàm s
42
y x 2mx 1 m
. Đnh m đ đồ th hàm s trên có ba
đim cc tr nhận gc tọa độ làm trc tâm.
A.
1
B. 0 C. 1 D. 2
Câu 27.2. Có một miếng nhôm hình vuông, cạnh là 3dm, một người d tính tạo
thành các hình trụ (không đáy ) theo hai cách sau:
31
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Cách 1: gò hai mép hình vuông đ thành mặt xung quanh của một hình trụ, gọi
th tích là của khi trụ đó l V1
Cách 2: cắt hình vuông ra làm ba, và gò thành mặt xung quanh của ba hình trụ, gọi
tổng th tích của chúng là V2.
Khi đó, tỉ s
1
2
V
V
là:
A. 3 B. 2 C.
1
2
D.
1
3
Câu 27.3. Một người nọ đem gửi tiết kiệm ở một ngân hàng với lãi suất là 12%
năm. Biết rằng cứ sau mỗi một quý ( 3 tháng ) thì lãi sẽ được cộng dồn vào vn
gc. Hỏi sau ti thiu bao nhiêu năm thì người đó nhận lại được s tiền ( bao gồm
cả vn lẫn lãi ) gấp ba lần s tiền ban đầu.
A. 8 B. 9 C. 10 D. 11
Câu 27.4. Có một người cần làm một cái của cổng c xưa, có hình dạng một
parabol bậc hai như hình vẽ. Giả sử đặt cánh cổng vào một hệ trục tọa độ như
hình vẽ ( mặt đất là trục Ox). Hãy tính diện tích của cánh cửa cổng.
32
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
16
3
B.
32
3
C. 16 D.
28
3
Câu 27.5. Trong không gian với hệ trục tọa độ Oxyz, cho bn đim
A 1,2,0
,
B 3, 1,2
,
C 2, 1,1
,
D 0,2, 1
. Có bao nhiêu mặt phẳng cách đều năm đim O, A,
B, C, D.
A. 4 B. 5 C. 6 D. 7
Câu 27.6. Có bao nhiêu đim có tọa độ là s nguyên biu diễn cho s phức z có
phần ảo dương v đông thời thỏa mãn
z z 4
,
z z 6
A. 20 B. 15 C. 6 D. 10
Câu 28.1 Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu
trên mỗi đơn v diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một
vụ cân nặng
480 20 .P n n gam
Hỏi phải thả bao nhiêu con cá trên một đơn
v diện tích của mặt hồ đ sau một vụ thu hoạch được nhiều cá nhất ?
A.
10
B.
12
C.
16
D.
24
Câu 28.2.
Một hình hộp có 6 mặt đều là các hình thoi có góc bằng 60
0
và cạnh bằng a. Tính
th tích của hình hộp đó.
A.
3
2
a
B.
3
2
2
a
C.
3
2
3
a
D.
3
22
3
a
Câu 28.3.
33
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Có bao nhiêu giá tr của tham s m đ phương trình
22
5 6 1 6 5
.2 2 2.2
x x x x
mm
có 3 nghiệm phân biệt.
A. 1 B. 2 C. 3 D. 4
Câu 28.4.
Trong hệ trục Oxy, cho tam giác OAB vuông ở A, đim B nằm trong góc phn tư
thứ nhất. A nằm trên trục hoành, OB = 2017. Góc
, 0 .
3
AOB




Khi quay
tam giác đó quanh trục Ox ta được khi nón tròn xoay. Th tích của khi nón lớn
nhất khi :
A.
6
sin
3
B.
3
cos
2
C.
1
cos
2
D.
2
sin
3
Câu 28.5.
Cho hai đim
1;2;3 , 2;4;4MA
và hai mặt phẳng
: 2 1 0,P x y z
: 2 4 0Q x y z
. Viết phương trình đường thẳng
qua
M
cắt
,P
Q
lần lượt
tại
,BC
sao cho tam giác
ABC
cân tại
A
và nhận
AM
l đường trung tuyến.
A.
1 2 3
:
1 1 1
x y z

B.
1 2 3
:
2 1 1
x y z
C.
1 2 3
:
1 1 1
x y z
D.
1 2 3
:
1 1 1
x y z
Câu 28.6.
Cho s phức
z
thỏa mãn
1z
và s phức
21
2
z
iz
w
. Khi đó mô đun của s phức
w
là:
A.
w2
B.
1 w 2.
C.
w1
D.
w2
Câu 29.1. Một Bác nông dân cần xây dng một h ga
không có nắp dạng hình hộp chữ nhật có th tích
3
3200cm
,
tỉ s giữa chiều cao của h và chiều rộng của đáy bằng
2
.
Hãy xác đnh diện tích của đáy h ga đ khi xây tiết kiệm
nguyên vật liệu nhất?
A.
2
1200cm
B.
2
160cm
C.
2
1600cm
D.
2
120cm
34
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 29.2.
Cho hình chóp
.S ABCD
có đáy l hình bình hnh v có th tích l V . Đim P là
trung đim của
SC
, một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M
và N .Gọi
1
V
là th tích của khi chóp
.S AMPN
. Tìm giá tr nhỏ nhất của
1
V
V
?
A.
3
8
B.
1
3
C.
2
3
D.
1
8
Câu 29.3. Một Bác nông dân vừa bán một con trâu được s tiền là 20.000.000
(đồng) .Do chưa cần dùng đến s tiền nên Bác nông dân mang toàn bộ s tiền đó
đi gửi tiết kiệm loại kỳ hạn 6 tháng vào ngân hàng với lãi suất 8.5% một năm thì
sau 5 năm 8 tháng Bác nông dân nhận được bao nhiêu tiền cả vn lẫn lãi .Biết rằng
Bác nông dân đó không rút cả vn lẫn lãi tất cả các đnh kì trước và nếu rút trước
thời hạn thì ngân hàng trả lãi suất theo loại không kì hạn 0.01% một ngày (1 tháng
tính 30 ngày)
A.
31802750 09, ®ång
B.
30802750 09, ®ång
C.
32802750 09, ®ång
D.
33802750 09, ®ång
35
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 29.4.
Từ một khúc gõ hình trụ có đường kính 30cm , người ta cắt khúc gỗ bởi một mặt
phẳng đi qua đường kính đáy v nghiêng với đáy một góc
0
45
đ lấy một hình
nêm (xem hình minh họa dưới đây)
Hình 1 Hình 2
Kí hiệu
V
l th tích của hình nêm (Hình 2). Tính
V
.
A.
V cm
3
2250
B.
V cm
3
225
4
C.
V cm
3
1250
D.
V cm
3
1350
Câu 29.5.
Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
xt
y t t
zt
2
: 1 2
3

hai
đim
A 2;0;3
và
B 2; 2; 3
. Biết đim
M x y z
0 0 0
;;
thuộc
thì
MA MB
44
nhỏ nhất
.Tìm
x
0
A.
x
0
0
B.
x
0
1
C.
x
0
2
D.
x
0
3
Câu 29.6.
Cho các s phức
z
thỏa mãn
z 12
. Biết rằng tập hợp các đim biu diễn các s
phức
w i z1 3 2
l một đường tròn . Tính bán kính
r
của đường tròn đó?
A.
4r
B.
r 2
C.
r 16
D.
r 25
36
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 30.1. Nh Nam có một chiếc bn tròn có bán kính bằng
2
m. Nam mun
mắc một bóng điện ở phía trên v chính giữa chiếc bn sao cho mép bn nhận
được nhiều ánh sáng nhất. Biết rằng cường độ sáng C của bóng điện được biu
th bởi công thức
2
sin
Cc
l
(
l góc tạo bởi tia sáng tới mép bn v mặt bn, c -
hằng s tỷ lệ chỉ phụ thuộc vo nguồn sáng, l khoảng cách từ mép bn tới bóng
điện) . Khoảng cách nam cần treo bóng điện tính từ mặt bn l
A. 1m B. 1,2m C. 1.5 m D. 2m
Câu 30.2. Với một miếng tôn hình tròn có bán kính bằng R = 6cm. Người ta mun
lm một cái phễu bằng cách cắt đi một hình quạt của hình tròn ny v gấp phần
còn lại thnh hình nón ( Như hình vẽ). Hình nón có th tích lớn nhất khi người ta
cắt cung tròn của hình quạt bằng
A.
6
cm B.
66
cm C.
26
cm D.
86
cm
Câu 30.3. Tập các giá tr của m đ baapts phương trình
2
2
2
2
log
log 1
x
m
x
nghiệm đúng
với mọi x > 0 bằng
A.
( ;1]
B.
[1; )
C.
5;2
D.
[0;3)
Câu 30.4. Cho hình phẳng giới hạn bởi hai đường
2 2 2 2
: 4; ' : 2 0C x y C x y x
. Diện tích hình phẳng đó bằng
A.
B.
2
C.
3
D.
4
37
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 30.5. Cho parabol (P)
2
yx
v hai đim A, B thuộc (P) sao cho AB = 2. Tìm A,
B sao cho diện tích hình phẳng giới hạn bởi (P) v đường thẳng AB đạt giá tr lớn
nhất
A.
4
3
B.
3
4
C.
2
3
D.
3
2
Câu 30.6. Trong hệ trục tọa độ Oxyz cho 3 đim
;0;0 , 0; ;0 , 0;0;A a B b C c
với
, , 0abc
.Giả sử
,,abc
thay đổi nhưng thỏa mãn
2 2 2 2
a b c k
không đổi. Diện
tích tam giác ABC đạt giá tr lớn nhất bằng
A.
2
3
2
k
B.
2
3
6
k
C.
2
3k
D.
2
k
Câu 30.7. Trong không gian với hệ toạ độ Oxyz, phương trình mặt phẳng (P) đi
qua đim
M
(9;1;1)
, cắt các tia Ox, Oy, Oz tại A, B, C sao cho th tích tứ diện OABC
có giá tr nhỏ nhất là
A.
1
7 3 3
x y z
B.
1
27 3 3
x y z
C.

1
27 3 3
x y z
D.
1
27 3 3
x y z
Câu 30.8. Trong mặt phẳng phức cho 3 đim A,B,C theo thứ t biu diễn các s
4 2 6
, 1 1 2 ,
13
ii
ii
ii


. S phức biu diễn bởi đim D sao cho tứ giác ABCD là
hình vuông là
A.
1 i
B.
15i
C.
1 i
D.
15i
Câu 31.1. Cho x và y là hai s thc dương thay đổi sao cho:
22
2 4 0x x y
. Giá tr
lớn nhất của tích xy gần nhất với s nào?
A. 0,5 B. 0,6 C. 0,7 D. 0,8
Câu 31.2. Nếu một tứ diện chỉ có đúng một cạnh có độ dài lớn hơn 1 thì th tích tứ
diện đó lớn nhất là bao nhiêu?
A.
1
4
B.
3
4
C.
1
8
D.
5
8
38
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 31.3. Giả sử p và q là các s thc dương sao cho:
9 12 16
log log logp q p q
.
Tìm giá tr của
p
q
A.
4
3
B.
8
5
C.
1
13
2
D.
1
15
2
Câu 31.4. Cho tích phân
2
2017
32
0
32K x x dx
. Giá tr của K bằng bao nhiêu?
A. 0 B. 1 C. 2 D. 1
Câu 31.5. Trong không gian Oxyz cho 4 đim
2;3;2A
,
6; 1; 2B 
,
1; 4;3C 
,
1;6; 5D
. Gọi M là một đim nằm trên đường thẳng CD sao cho tam giác MAB có
chu vi bé nhất. Khi đó toạ độ đim M là:
A.
0;1; 1M
B.
2;11; 9M
C.
3;16; 13M
D.
1; 4;3M 
Câu 31.6. Cho
2
1i 
, có bao nhiêu s nguyên n sao cho
4
ni
là một s nguyên?
A. 1 B. 2 C. 3 D. 4
Câu 32.1. Đường cong hình dưới l đồ th của một trong bn hàm s được cho
trong bn phương án A,B,C v D dưới đây. Hỏi hàm s đó l hm s nào ?
A.
y = x
3
- 3 x
2
+1
. B.
y = -x
4
- x
2
+1
. C.
y = x
3
- 3x
2
+1
. D.
y = x
4
-8x
2
+1
.
Câu 32.2. Cho hình chóp S.ABCD có ABCD là hình vuông cạnh 2a, tam giác SAB
đều và nằm trong mặt phẳng vuông góc với (ABCD). Tính bán kính của mặt cầu
ngoại tiếp hình chóp trên.
39
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
7
2
a
. B.
a 21
6
. C.
7
4
a
. D.
21
3
a
.
Câu 32.3. Tập nghiệm của bất phương trình:
22
1 1 1
3 3 3 3
x x x x
.
A.
7
2
a
. B.
a 21
6
. C.
7
4
a
. D.
21
3
a
.
Câu 32.4. Với giá tr nào của
m
thì diện tích hình phẳng giới hạn bởi parabol
P : y x x
2
2
và
d : y mx m0
bằng 27 đơn v diện tích.
A.
m = -1
. B.
m = -2
. C.
m = Æ
. D.
m Î
.
Câu 32.5. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng
: 1 0P x y z
v hai đim
1; 3;0A
,
5; 1; 2B 
. Tìm tọa độ đim M trên mặt phẳng
P
sao
cho
MA MB
đạt giá tr lớn nhất.
A.
M(-2;-3;3)
. B.
M(-2;-3;2)
. C.
M(-2;-3;6)
. D.
M(-2;-3;0)
.
Câu 32.6. Cho các s phức
z ,z ,z ,z ,z
1 2 3 4 5
có đim biu diễn lần lượt là A, B, C, D, E
trong mặt phẳng phức tạo thành một ngũ giác lồi. Gọi M, N, P, Q lần lượt là trung
đim các cạnh AB, BC, CD, DE. Gọi I, J lần lượt l trung đim các đoạn MP và NQ.
Biết I, J l đim biu diễn hai s phức
I
z i;1
J
zi 2
và
E
zi45
là s phức có
đim biu diễn là E. Tìm s phức
z
1
?
A.
z
1
= 2-3i
. B.
z
1
= 4-7i
. C.
z
1
= 8-7i
. D.
z
1
= 8- 2i
.
Câu 33.1. Cho hàm s:
4 2 2
2( 2) 5 5y x m x m m
. Với giá tr nào của m thì đồ
th hám s có cc đại và cc tiu, đồng thời các đim này tạo thành một tam giác
đều
A.
3
23m 
B.
23
C.
32
D.
3
32
Câu 33.2.
Cho hình lăng trụ
. ' ' 'ABC A B C
có đáy
ABC
l tam giác đều cạnh
a
, hình chiếu
vuông góc của
'A
lên măt phẳng
ABC
trùng với tâm
G
của tam giác
ABC
.
Biết khoảng cách giữa
'AA
và
BC
là
3
4
a
. Tính th tích
V
của khi lăng trụ
. ' ' 'ABC A B C
.
40
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
3
3
3
a
V
B.
3
3
6
a
V
C.
3
3
12
a
V
D.
3
3
36
a
V
Câu 33. 3.
Tìm các giá tr của m đ phương trình:
3 3 5 3
xx
m
có 2 nghiệm phân biệt:
A.
3 5 4m
B.
2 2 4m
C.
2 2 3 5m
22m
Câu 33.4.
Tính tích phân:
2
2
1
1 2 1
3
dx
x x x




ta thu được kết quả là:
ln2ab
với
,ab
.
Chọn khẳng đnh đúng trong các khẳng đnh:
A.
1ab
B.
0a
C.
22
10ab
D.
20ba
Câu 33.5.
Trong không gian với hệ tọa độ
Oxyz
, cho hai đim
1;5;0A
,
3;3;6B
v đường
thẳng
có phương trình tham s
12
1
2
xt
y t t
zt
. Một đim
M
thay đổi trên
đường thẳng
, xác đnh v trí của đim
M
đ chu vi tam giác
MAB
đạt giá tr nhỏ
nhất. Khi đó toạ độ của đim M là:
A.
1;0;2M
B.
2;4;3M
C.
3;2; 2M 
D.
1;4;3M
Câu 33.6.
Trong mặt phẳng tọa độ, tập hợp đim biu din các s phức
z
thỏa mãn
1z i i z
l:
A. Đường tròn có phương trình
22
4 2 1 0x y x y
B. Đường tròn có phương trình
22
2 3 0x y y
C. Đường tròn có phương trình
22
2 1 0x y x
41
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
D. Đường tròn có phương trình
22
2 1 0x y y
Câu 34.1. Cho hàm s
y x mx
3
2
có đồ th (Cm) . Tìm m đ đồ th (Cm) cắt trục
hoành tại một đim duy nhất.
A.
3m
B.
3m
C.
3m
D.
3m
Câu 34.2.
Cho hình chóp đều
.S ABCD
, M l trung đim SA, N, K lần lượt thuộc SB, SC sao
cho SB=3SN, SC=4SK. Hãy chọn đáp án đúng
A.
..
1
8
S MNK S ABC
VV
B.
..
23
48
MNK CBA S ABCD
VV
C.
..
1
12
S MNK S ABD
VV
D. Cả 3 đáp án A, B, C đều sai
Câu 34.3. Cho
12
1 1 1
...
log log log
n
b b b
a a a
A
. Biu thức rút gọn của A là:
A.
2 ( 1)
3.log
b
a
nn
B.
2 (2 1)
log
b
a
nn
C.
( 1)
2.log
b
a
nn
D.
( 2)
3log
b
a
nn
Câu 35.4.
Nếu hàm s f(x) liên tục và là hàm s chẵn trên [-a; a] thì
()
a
a
I f x dx
bằng
A. 0 B.
0
2 ( )
a
f x dx
C.
0
2 ( )
a
f x dx
D.
2 ( )
a
a
f x dx
Câu 35. 5. Trong hệ trục tọa độ Oxyz cho A(1;2;3).Tìm cặp vecto chỉ phương của
mặt (P) đi qua A v khoảng cách từ O đến (P) là lớn nhất.
A.
1
2
( 3;0;1)
(1;1; 1)
u
u


B.
1
2
( 3;0;1)
(0; 1; 2)
u
u

C.
1
2
( 3;0;1)
(1;0; 1)
u
u


D.
1
2
( 3;0;1)
(2;1;0)
u
u

Câu 35.6.
42
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Kết quả rút gọn của biu thức
4 2017
2016
11ii
P
ii


là:
A. 0 B. i C.1-i D. -1-i
Câu 36. 1.
Nhà của 3 bạn A, B, C nằm ở 3 v trí tạo thành một tam giác vuông tại B (
như hình vẽ), AB = 10 km; BC = 25 km và 3 bạn tổ chức họp mặt ở nhà bạn C. Bạn
B hẹn chở bạn A tại v trí M trên đoạn đường BC. Từ nhà, bạn A đi xe buýt đến
đim hẹn M với tc độ 30km/h và từ M hai bạn A, B di chuyn đến nhà bạn C
bằng xe máy với tc độ 50km/h. Hỏi đim hẹn M cách nhà bạn B bao nhiêu km đ
bạn A đến nhà bạn C nhanh nhất ?
A. 5 km B. 7,5 km C.10 km D. 12,5 km
Câu 36. 2.
Cho hình chóp S.ABC có đáy ABC l tam giác đều cạnh bằng a, đường
thẳng SA vuông góc với mặt đáy v SA = 2a. Gọi (P) là mặt phẳng đi qua B v
vuông góc với SC.
Khi đó diện tích của thiết diện của hình chóp S.ABC khi cắt bởi mặt phẳng
(P) là ?
A.
2
15
10
a
B.
2
15
5
a
C.
2
15
15
a
D.
2
15
20
a
Câu 36.3.
C
M
B
A
C
N
B
A
S
M
43
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Ông A gửi tiết kiệm 100 triệu đồng gửi vào ngân hàng với lãi suất 5% một năm.
Ông B cũng đem 100 triệu đồng gửi vào ngân hàng với lãi suất
5
12
% một tháng.
Sau 10 năm, hai ông A v B cùng đến ngân hàng rút tiền ra. Khẳng đnh nào sau
đây l đúng ? ( Lưu ý: tiền lãi được tính theo công thức lãi kép v được làm tròn
đến hàng hàng triệu)
A. S tiền của hai ông A, B khi rút ra l như nhau.
B. Ông B có s tiền nhiều hơn ông A l 1 triệu.
C. Ông B có s tiền nhiều hơn ông A là 2 triệu.
D. Ông B có s tiền nhiều hơn ông A l 3 triệu.
Câu 36.4.
Hình phẳng (H) giới hạn bởi các đường (P):
2
45y x x
và hai tiếp tuyến của (P)
tại đim A(1;2); B(4;5). Diện tích của (H) là ?
A.
27
4
B.
9
4
C.
15
4
D.
5
2
Câu 36.5.
Trong không gian với hệ tọa độ Oxyz, cho đim A(1;2;3) v đường thẳng d:
31
2 1 1


x y z
.
Mặt phằng (P) chứa đường thẳng d và có khoảng cách từ A đến (P) là lớn nhất.
Khi đó (P) có một véctơ pháp tuyến là
A.
4 5 13( ; ; )n
B.
4 5 13( ; ; )n 
C.
4 5 13( ; ; )n 
D.
4 5 13( ; ; )n 
Câu 36.6.
Cho hình vuông ABCD có tâm H và A,B,C,D,H lần lượt l đim biu diễn cho các
s phức a,b,c,d,h. Biết
;a i h i 2 1 3
và s phức b có phần ảo dương. Khi đó
môđun của s phức b là
A.
26
B.
13
C.
42
D.
10
44
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 37.1. Trên : có hai đim phân biệt và
sao cho tiếp tuyến tại mỗi đim đó vuông góc với đường thẳng
và . Khi đó tất cả các giá tr của m thỏa mãn các điều kiện
trên là ?
A. B. C. D.
Câu 37.2 . Cho phương trình có nghiệm là thì bằng giá tr
của biu thức nào trong các biu thức dưới đây , biết rằng các hàm s dưới đây
luôn tồn tại.
A. B. C.
D.
Câu 37.3. Nhân ngày phụ nữ Việt Nam 20 -10 năm 2017 , ông A quyết đnh mua
tặng vợ một món qu v đặt nó vào trong một chiếc hộp có th tích l 32 ( đvtt )
có đáy hình vuông v không có nắp . Đ món quà trở nên thật đặc biệt và xứng
đáng với giá tr của nó ông quyết đnh mạ vàng cho chiếc hộp , biết rằng độ dạy
lớp mạ tại mọi đim trên hộp l như nhau . Gọi chiều cao và cạnh đáy của chiếc
hộp lần lượt là . Đ lượng vàng trên hộp là nhỏ nhất thì giá tr của phải là
?
A. B. C. D.
Câu 37.4. Giá tr lớn nhất của hàm s
2
44
2sin
sin cos
22
x
fx
xx
là
A. 0 B. 4 C.8 D. 2
Câu 37.5.
m
C
32
12
61
33
y x mx m x
11
;M x y
22
;N x y
3 6 0xy
12
23xx
3
3
2
m
mm
3
3
2
m
3
3
2

m
3
2
xx12
5 5 124
x
0
x
0
log log
aa
a
ba
b
3
3
2
log log
aa
a
ab a
b
3
3
2
log log
aa
a
a
b
3
3
2
log log
aa
a
ba
b
3
3
h;x
h;x
x 2;h 4
x 4;h 2
3
4;
2
xh
1; 2xh
45
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
2BC a
. Tam giác SAB
có góc
60 ,
o
ASB SB a
và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng
cách từ đim B đến mặt phẳng (SAC).
A.
a
B.
3
2
19
a
C.
3
19
a
D.
3
2
16
a
Câu 37.6.
Tập nghiệm của bất phương trình:
2 2 1
2
81.9 3 .3 0
3
x x x x
là
A.
1; 0 .S
B.
1; .S 
C.
0; .S
D.
2; 0 .S 
Câu 37.7.
Tìm tham s
m
đ đồ th hàm s
42
22y x mx m C
cắt trục
ox
tại bn đim
phân biệt và thỏa mãn hình phẳng giới hạn bởi đồ th (C) và trục
ox
của phần nằm
phía trên trục
ox
có diện tích bằng diện tích hình phẳng giới hạn bởi đồ th (C) và
trục
ox
của phần nằm phía dưới trục
ox
.
A. 3 B. -3 C.2 D. 4
Câu 37.8.
Trong không gian tọa độ Oxyz cho đim
(0;1;1), (1;0; 3), ( 1; 2; 3)A B C
và mặt cầu (S) có
phương trình :
2 2 2
2 2 2 0x y z x z
.Tìm tọa độ đim D trên mặt cầu (S) sao cho tứ
diện ABCD có th tích lớn nhất.
A.
7 4 1
;;
3 3 3
D




B.
1 4 5
;;
3 3 3
D




C.
7 4 1
;;
3 3 3
D



D.
7 4 1
;;
3 3 3
D



Câu 37.9.
Tìm phần ảo của s phức
z
, biết s phức z thỏa mãn
2 2017
. 2 1 ... 1 .i z i i i
A.
1
B.
1009
2
C.
1009
2
D.
1009
2 i
Câu 38.1. Cho hm s
32
69y x x x m
có đồ th (C), với m l tham s. Giả sử
đồ th (C) cắt trục honh tại ba đim phân biệt có honh độ thỏa mãn
1 2 3
.x x x
Khẳng đnh no sau đây l đúng?
A.
1 2 3
1 3 4x x x
B.
1 2 3
0 1 3 4x x x
C.
1 2 3
0 1 3 4x x x
D.
1 2 3
1 3 4x x x
46
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 38.2. Cho tứ diện ABCD có tam giác ABD vuông cân tại D,
AD a
, tam giác
ABC cân tại C,
22
AC a x
. Biết
22
2CD a x
, (x>0) hãy tính góc giữa
hai đường thẳng AB, CD bằng bao nhiêu?
A.
0
45
B.
0
90
C.
0
60
D.
0
30
Câu 38.3. Cho
n
u
l cấp s nhân với s hạng tổng quát
0; 1
nn
uu
. Khi đó
khẳng đnh no sau đây l đúng?
A.
11
11
log 2017 log 2017 log 2017
log 2017 log 2017 log 2017
k k k
k k k
u u u
u u u


B.
11
11
log 2017 log 2017 log 2017
log 2017 log 2017 log 2017
k k k
k k k
u u u
u u u


C.
11
11
log 2017 log 2017 log 2017
log 2017 log 2017 log 2017
k k k
k k k
u u u
u u u


D.
11
11
log 2017 log 2017 log 2017
log 2017 log 2017 log 2017
k k k
k k k
u u u
u u u


Câu 38.4. Cho hm s
42
4y x x m
có đồ th l (C). Gọi S l diện tích hình
phẳng giới hạn bởi đồ th (C) với y<0 v trục honh, S’ l diện tích hình phẳng
giới hạn bởi đồ th (C) với y>0 v trục honh. Với giá tr no của m thì
'SS
?
A.
2m
B.
2
9
m
C.
20
9
m
D.
1m
Câu 38.5. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (Q):
x y z
2 5 0
v đường thẳng
x y z
d
1 1 3
:
2 1 1

. Phương trình mặt phẳng (P) chứa đường
thẳng d và tạo với mặt phẳng (Q) một góc nhỏ nhất l
A.
: 4 0
P y z
B.
: x 4 0
Pz
C.
: x 4 0
P y z
D.
: 4 0
P y z
Câu 38.6. Gieo một con súc sắc cân đi đồng chất hai lần. Ký hiệu
;ab
l kết quả
xảy ra sau khi gieo, trong đó a, b lần lượt l s chấm xuất hiện lần thứ nhất, thứ
hai. Gọi A l biến c s chấm xuất hiện trên hai lần gieo như nhau. Tập hợp các kết
quả thuận lợi cho biến c A l tập hợp con của tập hợp các đim biu diễn của s
phức z thỏa mãn điều kiện no sau đây?
A.
2 3 12zi
B.
2 3 10zi
C.
2 3 13zi
D.
2 3 11zi
47
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 39. Một người có một dải ruy băng di 130cm, người đó cần bọc dải ruy băng đó
quanh một hộp quà hình trụ. Khi bọc qu, người này dùng 10cm của dải ruy băng đ thắt
nơ ở trên nắp hộp (như hình vẽ minh họa). Hỏi dải dây duy băng có th bọc được hộp
quà có th tích lớn nhất là là nhiêu ?
A.
3
4000 cm
B.
3
1000 cm
C.
3
2000 cm
D.
3
1600 cm
Câu 39.2. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
,a
SA
vuông góc
với mặt phẳng đáy v góc giữa
SC
với mặt phẳng
()SAB
bằng
0
30 .
Gọi
M
l đim di
động trên cạnh
CD
và
H
là hình chiếu vuông góc của
S
trên đường thẳng
.BM
Khi
đim
M
di động trên cạnh
CD
thì th tích của khi chóp
.S ABH
đạt giá tr lớn nhất
bằng?
A.
3
2
3
a
B.
3
2
2
a
C.
3
2
6
a
D.
3
2
12
a
Câu 39.3. Trong một bản hợp ca, coi mọi ca sĩ đều hát với cường độ âm và coi cùng tần
s. Khi một ca sĩ hát thì cường độ âm là 68dB. Khi cả ban hợp ca cùng hát thì đo được
mức cường độ âm là 80dB. Tính s ca sĩ có trong ban hợp ca đó, biết mức cường độ âm L
được tính theo công thức
0
10
I
L log
I
trong đó I l cường độ âm và
0
I
l cường độ âm
chuẩn
A. 16 người B. 12 người C. 10 người D. 18 người
Câu 39.4. Một ô tô đang chạy đều với vận tc
(m/ s)a
thì người lái đạp phanh. Từ thời
đim đó, ô tô chuyn động chậm dần đều với vận tc
(t) 5 t ( m/ s)va
, trong đó t l
thời gian tính bằng giây k từ lúc đạp phanh. Hỏi từ vận tc ban đầu a của ô tô là bao
nhiêu, biết từ lúc đạp phanh đến khi dừng hẳn ô tô di chuyn được 40 mét.
A.
20a
B.
10a
C.
40a
D.
25a
Câu 39.5. Trong không gian với hệ trục Oxyz, cho đường thẳng d có phương trình
12
:
1 1 2
x y z
d
v đim A(1 ;4 ;2). Gọi (P) là mặt phẳng chứa d . Khoảng cách lớn
nhất
max
d
từ A đến (P) là :
48
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
max
5d
B.
max
210
3
d
C.
max
65d
D.
max
25d
Câu 39.6. Cho s phức z có phần thc dương thỏa mãn
5z
và
2 3 4zi
. Tính
13 1
2
z
A
z
A.
898A
B.
98A
C.
890A
D.
198A
Câu 40.1. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
tan 2
tan
x
y
xm
đồng biến trên
khoảng
0; .
4



A. m 0 hoặc 1 m 2. B. m 0. C. 1 m 2. D. m 2.
Câu 40.2. Sự tăng trưởng của một loài vi khuẩn được tính theo công thức
rx
f x Ae()
, trong đó .
A
là số lượng vi khuẩn ban đầu,
r
là tỷ lệ tăng trưởng
r 0
,
x
(tính theo giờ) là thời gian tăng
trưởng. Biết số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Hỏi sao bao lâu thì số
lượng vi khuẩn tăng gấp 10 lần
A.
5ln20
(giờ) B.
5ln10
(giờ) C.
5
10log 10
(giờ) D.
5
10log 20
(giờ)
Câu 40.3. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
2( 1) ,
x
y x e
trục tung và trục
hoành. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A.
4 2 .Ve
B.
(4 2 ) .Ve

C.
2
5.Ve
D.
2
( 5) .Ve

Câu 40.4. Cho các số phức
z
thỏa mãn
4z
. Biết rằng tập hợp các điểm biểu diễn các số phức
(3 4 )w i z i
là một đường tròn. Tính bán kính r của đường tròn đó.
A. r 4. B. r 5. C. r 20. D. r 22.
Câu 40.5. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam
giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại
tiếp hình chóp đã cho.
A. V =
5 15
18
B. V =
5 15
54
C. V =
43
27
D. V =
5
.
3
Câu 40.6. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; –2; 0), B(0; –1; 1), C(2; 1; –1)
và D(3; 1; 4). Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó ?
A. 1 mặt phẳng. B. 4 mặt phẳng. C. 7 mặt phẳng. D. Có vô số mặt phẳng.
1
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
PHẦN 2 : HƯỚNG DẪN GIẢI
Câu 1.1. Đường thẳng đi qua 2 đim cc tr của đồ th hm s
2
23
1
xx
y
x

hợp với 2 trục tọa độ 1
tam giác có diện tích S bằng :
A. S=1,5 B. S=2 C.S=3 D.S=1
Ta có kết quả : Nếu đồ th hàm s
()
()
ux
y
vx
có đim cc tr
( ; )
oo
xy
thì
/
/
()
()
o
o
o
ux
y
vx
Suy ra phương trình đường thẳng đi qua 2 đim cc tr là y=2x-2 (d)
(d) cắt 2 trục tọa độ tại 2 đim A(0;-2) ,B(1;0) nên diện tích tam giác OAB bằng 1( Đáp án D)
Câu 1.2. Khi cầu nội tiếp hình tứ diện đều có cạnh bằng a thì th tích khi cầu là :
A.
3
6
216
a
B.
3
6
124
a
C.
3
3
96
a
D.
3
3
144
a
Hướng dẫn giải :
Sử dụng kết quả :
Bán kính mặt cầu nội tiếp tứ diện đều cạnh a có bán kính
6
12
a
R
,
3
3
4 6 6
3 12 216
aa
V





Câu 1.3. Tìm m đ phương trình
2
30
xx
e me m
có nghiệm
A.
2m
B.
2m
C.m<3 D.m>0
Hướng dẫn giải :
Đặt t=
x
e
, t >0. Biến đổi phương trình về dạng :
2
3
1
t
m
t
Khảo sát hàm f(t) =
2
3
1
t
t
, t >0 ta có
( ) 2ft
.Suy ra
2m
Đáp án A (dùng casio đ tìm nhanh hơn )
Câu 1.4. Giá tr của tham s m đ diện tích hình phẳng giới hạn bởi đồ th hàm s
22
3 2 1y x mx m
, trục hoành, trục tung v đường thẳng x = 2 đạt giá tr nhỏ nhất là:
2
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A. m = 2 B. m = 1 C. m = -1 D. m = - 2
Hướng dẫn giải :
Vì với m tùy ý ta luôn có
22
3 2 1 0x mx m x
nên diện tích hình phẳng cần tìm l
2
2
2
2 2 3 2 2 2
0
0
3 2 1 1 2 4 10 2 1 8S x mx m dx x mx m x m m m


S đạt giá tr nhỏ nhất bằng 8 khi m = - 1
( dùng casio thử nhanh hơn )
Câu 1.5. Phương trình no sau đây không phải l phương trình hình chiếu vuông góc của đường
thẳng d:
12
2 3 ,
3
xt
y t t R
zt


trên mặt phẳng (Oxy) :
A.
3 2 '
1 3 ' , '
0
xt
y t t R
z

B.
1 4 '
2 6 ', '
0
xt
y t t R
z

C.
1 2 '
2 3 ', '
0
xt
y t t R
z

D.
5 2 '
4 3 ', '
0
xt
y t t R
z

Hướng dẫn giải :
A(1;-2;3) , B(3;1;4) thuộc d. Hình chiếu của A ,B trên mặt phẳng (Oxy) l A
/
(1;-2;0) , B
/
(3;1;0)
Phương trình hình chiếu đi qua
/
A
hoặc
/
B
v nhận véc tơ cùng phương với
//
2;3;0AB
lm véc tơ chỉ phương .
Đáp án C
Câu 1.6. Gọi A, B, C lần lượt l các đim biu diễn của 3 s phức :
26
1 2i; (1 )(1 2 );
3
i
ii
i
.Diện
tích của tam giác ABC bằng :
A.
1
4
B.
1
2
C.
5
5
D.
5
2
Hướng dẫn giải :
Dùng máy tính casio ta có A(1;2) , B(3;1) ,C(0;2)
Dùng công thức
1
,
2
S AB AC


Với
2; 1;0 , 1;0;0AB AC
Dùng máy tính ta có kết quả B : S=1/2
(Có th dùng công thức tính diện tích phần Oxy tính nhanh hơn )
3
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 2.1. Cho hàm s
32
21y x x m x m
có đồ th
C
. Giá tr của
m
thì
C
cắt trục hoành
tại 3 đim phân biệt
1 2 3
,,x x x
sao cho
222
1 2 3
4xxx
là
A.
1m
B.
1
1
4
0
m
m
C.
1
1
4
m
D.

1
1
4
m
Hướng dẫn giải:
Phương trình honh độ giao đim của (C) và trục hoành là
32
2 1 0x x m x m
2
1
0
x
x x m
(C) và trục hoành cắt nhau tại 3 đim pb
0
1
4
m
m

Xét
2
222
1 2 3 1 2 1 2
4 2 1 4 1 2 1 4 1x x x x x x x m m
Chọn B.
Câu 2.2. Cho lăng trụ
ABC.A'B'C'
có đáy l tam giác đều cạnh a. Hình chiếu vuông góc của đim
A'
lên mặt phẳng
(ABC)
trùng với trọng tâm tam giá
ABC
. Biết khoảng cách giữa hai đường thẳng
AA'
và
BC
bằng
a3
4
. Khi đó th tích của khi lăng trụ là
A.
3
3
12
a
B.
3
3
6
a
C.
3
3
3
a
D.
3
3
24
a
Hướng dẫn giải:
B’
A’
C’
A
B
C
M
H
G
4
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Gọi
M
l trung đim BC, dng MH vuông góc với A’A. suy ra
3
,'
4
a
MH d BC A A
Đặt AH=x, ta có
2
2
'
3
a
A A x
Từ A’A.MH=A’G.AM, suy ra
3
a
x
.
Vậy
23
33
.
3 4 12
a a a
V 
.
Chọn A.
Câu 2.3. Phương trình
2 3 2 3
xx
m
(1) có nghiệm khi:
A.
;5m 
B.
;5m 
C.
2;m 
D.
2;m 
Hướng dẫn giải:
Đặt
2 3 , 0
x
tt
, phương trình đã cho thnh:
2
10t mt
(2)
(1) có nghiệm khi (2) có nghiệm dương.
Do tích 2 nghiệm =1 nên suy ra (2) có 2 nghiệm dương.
2
40
2
0
m
m
m

.
Chọn D.
Câu 2.4. Tính
2
3
0
.sin
x
I e xdx
A.
3
2
11
22
Ie

B.
3
2
11
22
Ie

C.
3
2
1Ie

D.
3
2
1Ie

Hướng dẫn giải :
5
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
2 2 2
3 3 3 3
2
0
0 0 0
3
22
3 3 3
2
2
0
00
.sin cos .cos .cos
1 . sin 1 .sin .sin 1
x x x x
x x x
I e xdx e d x e x e xdx
e d x e x e xdx e I


Do đó
3
2
11
22
Ie

.
Chọn B
Câu 2.5. Trong không gian tọa độ Oxyz , cho đim
A B C
(0;1;1), (1;0; 3), ( 1; 2; 3)
và mặt cầu (S) có phương
trình:
x y z x z
2 2 2
2 2 2 0
. Tìm tọa độ đim D trên mặt cầu (S) sao cho tứ diện ABCD có th tích lớn
nhất.
A.
D
1;0;1
B.
D
7 4 1
;;
3 3 3




C.




D
1 4 5
;;
3 3 3
D. D(1; - 1; 0)
Hướng dẫn giải :
Ta thấy câu C v D có đim D không thuộc (S). Loại C,D.
Ta tính th tích cho đim D ở câu A v câu B. Đim B ở câu B có th tích lớn hơn.
Chọn B.
Câu 2.6. Tính tổng mô-đun tất cả các nghiệm của phương trình:
23
10z i z z i
A. 3 B. 4 C.6 D. 8
Hướng dẫn giải :
23
33
2
1
1
1 0 1
0
5
10
2
zi
zi
zi
z
z
z i z z i z
zi
zi
zi
i
z iz
z







Suy ra tổng mô-đun các nghiệm bằng 6.
6
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 3.1 (Kshs). Cho hàm s
3
2
31y x m x m
. Gọi M l đim cc đại của đồ th hàm s
1
ứng với một giá tr m thích hợp đồng thời l đim cc tiu của đồ th hàm s
1
ứng với một giá tr
khác của m. S đim M thỏa mãn yêu cầu đề bài là:
A.1 B. 2 C.3 D.0
Hướng dẫn giải :
Ta có
2
3 3, 6y x m y x m
Suy ra
1
0
1
xm
y
xm



.
Vì
1
1, 1 0x x m y m

nên hàm s đạt cc đại
1
1x x m
tại và giá tr cc đại là
2
1
32y m m
.
Tương t, ta có hàm s đạt cc tiu tại
2
1x x m
và giá tr cc tiu là
2
2
32y m m
.
Ta giả sử đim M l đim cc đạ của đồ th hàm s ứng với giá tr
1
m
v l đim cc tiu ứng của
đồ th hàm s ứng với với giá tr
2
m
.
Từ YCBT suy ra hệ phương trình
12
22
1 1 2 2
11
3 2 3 2
mm
m m m m
Giải hệ ta tìm được nghiệm
12
31
,
22
mm
và suy ra tồn tại duy nhât một điêm
11
,
24
M



thỏa
bài toán.
Chọn đáp án A.
Câu 3.2 (Thể tích- mặt cầu- mặt nón- mặt trụ). Cho tứ diện
ABCD
với
BC a
,các cạnh còn lại đều
bằng
3
2
a
và
là góc tạo bởi hai mặt phẳng
ABC
và
BCD
. Gọi I,J lần lượt l trung đim các
cạnh
,BC AD
. Giả sử hình cầu đường IJ kính tiếp xúc với CD. Giá tr
cos
là:
A.
3 2 3
B.
2 3 3
C.
23
3
D.
23
3
Hướng dẫn giải:
7
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Gọi O l trung đim IJ và F l đim tiếp xúc giữa hình cầu đường kính IJ v đường thẳng CD. Hình
cầu đường kính IJ tiếp xúc với CD khi và chỉ khi khoảng cách từ O đến CD bằng nữa độ dài IJ.
Ta có
2
2
a
AI DI
.
Vì FC và CI là hai tiếp tuyến xuất phát từ một đim nên
2
a
FC CI
Tương t ta có
3
22
aa
DJ DF
Tam giác ADI cân có IJ l đường trung tuyến nên tam giác IDJ vuông tại J.
Suy ra
31
62
2
sin sin
22
2
2
a
JD
JID
DI
a
Do vậy
cos 2 3 3

nên chọn đáp án B.
Câu 3.3 (Mũ- logarit). Cho
,,x y z
là các s thc thỏa mãn
2 3 6
x y z

. Giá tr biu thức
M xy yz xz
là:
A.0 B.1 C.6 D.3
Hướng dẫn giải:
Khi một trong ba s
,,x y z
bằng 0 thì các s còn lại bằng 0. Khi đó M=0
Khi
, , 0x y z
ta đặt
2 3 6
x y z
k
suy ra
1
1
1
2 ,3 ,6
y
x
z
k k k
.
Do 2.3=6 nên
1
1
1
.
y
x
z
k k k
hay
1 1 1
x y z
Từ đó suy ra M=0
Vậy cần chọn đáp án A.
Câu 3.4 (Tích phân- Ứng dụng). Gọi
a
S
là diện tích hình phẳng giới hạn bởi đồ th hàm s
2
2
xx
y e e
, trục Ox v đường thẳng
xa
với
ln2a
. Kết quả giới hạn
lim
a
a
S

là:
A.1 B.2 C.3 D.4
8
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Hướng dẫn giải:
Ta có
ln2
22
1
2 2 2
2
x x a a
a
a
S e e dx e e
Suy ra
lim 2
a
a
S

, chọn đáp án B.
Câu 3.5 (Oxyz). Trong không gian Oxyz, cho đim
1,0, 1A
và mặt phẳng
: 3 0P x y z
.
Mặt cầu S có tâm I nằm trên mặt phẳng
P
, đi qua đim A và gc tọa độ O sao cho chu vi tam giác
OIA bằng
62
. Phương trình mặt cầu S là:
A.
2 2 2
2 2 1 9x y z
hoặc
2 2 2
2 2 1 9.x y z
B.
2 2 2
2 2 1 9x y z
hoặc
2 2 2
1 2 2 9x y z
C.
2 2 2
2 2 1 9x y z
hoặc
2 2 2
2 2 1 9x y z
D.
2 2 2
2 2 1 9x y z
hoặc
2 2 2
1 2 2 9x y z
Hướng dẫn giải:
Gọi
,,I x y z
là tâm của S.
Khi đó
, , 6 2I P IO IA IO IA AO
nên ta suy ra hệ
22
2 2 2 2
2 2 2 2 2 2
11
10
2 2 6 2 9
30
30
x y z x y z
xz
x y z x y z
x y z
x y z


Giải hệ ta tìm được
2,2,1I
hoặc
1,2, 2I 
Suy ra phương trình mặt cầu v đáp án cần chọn là D.
Câu 3.6 (Số phức). Cho
z
là s phức có mô đun bằng 2017 và
w
là s phức thỏa mãn
1 1 1
wwzz

. Mô đun của s phức
w
là
A.2015 B.1 C.2017 D.0
Hướng dẫn giải:
9
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Từ
1 1 1
wwzz

ta suy ra
22
w w 0zz
2
2
w 3w 1 3
w
2 2 2 2
ii
zz



Lấy mô đun hai vế ta có
w 2017z 
.
Vậy đáp án đúng l C.
Câu 4.1 (Kshs). Một công ty mun làm một đường ng dẫn từ một đim A trên bờ đến một đim B
trên một hòn đảo. Hòn đảo cách bờ bin 6km. Giá đ xây đường ng trên bờ là 50.000USD mỗi km,
và 130.000USD mỗi km đ xây dưới nước. B’ l đim trên bờ bin sao cho BB’ vuông góc với bờ
bin. Khoảng cách từ A đến B’ là 9km. V trí C trên đoạn AB’ sao cho khi ni ng theo ACB thì s
tiền ít nhất. Khi đó C cách A một đoạn bằng:
A. 6.5km B. 6km
C. 0km D.9km
Đáp án:
Lời giải.
Đặt
' ( ) , [0;9]x B C km x
2
36; 9 BC x AC x
Chi phí xây dng đường ng là
2
( ) 130.000 36 50.000(9 ) ( ) C x x x USD
Hàm
()Cx
, xác đnh, liên tục trên
[0;9]
và
2
13
'( ) 10000. 5
36




x
Cx
x
2
'( ) 0 13 5 36 C x x x
2 2 2
25 5
169 25( 36)
42
x x x x
(0) 1.230.000C
;
5
1.170.000
2



C
;
(9) 1.406.165C
Vậy chi phí thấp nhất khi
2,5x
. Vậy C cần cách A một khoảng 6,5km.
Câu 4.2. (Thể tích – mặt cầu-mặt nón – mặt trụ).
x km
(9 - x)km
6km
đảo
bờ biển
biển
A
B
B'
C
10
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
3
2
60
0
S
A
C
B
H
K
Cho hình chóp SABC với SA vuông góc với mặt phẳng (ABC) và BC=
3
a,
60
o
BAC
. Gọi H, K lần lượt là hình chiếu của A lên SB và SC. Mặt
cầu qua các đim A, B, C, H, K có bán kính bằng:
A.1 B.2
C.
3
D. Không đủ dữ kiện đ tính
Đáp án:
Lời giải.
Gọi AD l đường kính của đường tròn (ABC)
Suy ra,
AC DC
, suy ra
()CD SAC
hay
AE DE
Tương t,
AH HD
. Suy ra mặt cầu qua các đim A, B, C, H, K có đường
kính AD
0
2
sin60
BC

.
Câu 4.3: Cho
55log2log3log
666
cba
, với
ba,
và
c
là các s hữu tỷ. Các khẳng đnh sau đây,
khẳng đnh no đúng?
A.
ba
B.
ba
C.
ab
D.
bac
Hướng dẫn giải :
6
log 3 2 5 5
a b c

5 5 5 0
3 .2 .5 6 3 .2 .5
a b c
Do a, b, c là các số hữu tỷ nên
5
0
ab
c

Câu 4.4. (Tích phân - Ứng dụng )
Một khi cầu có bán kính 5dm, người ta cắt bỏ 2 phần bằng 2 mặt phẳng vuông góc bán kính v
cách tâm 3dm đ lm một chiếc lu đng. Tính th tích m chiếc lu chứa được.
A.
132
(dm
3
) B.
41
(dm
3
)
C.
100
3
(dm
3
) D.
43
(dm
3
)
60
0
S
A
C
B
D
H
K
5dm
3dm
3dm
11
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
P
M
N
K
H'
H
Hướng dẫn: Đặt hệ trục với tâm O, l tâm của mặt cầu; đường thẳng đứng l Ox, đường ngang l
Oy; đường tròn lớn có phương trình
22
25xy
.
Th tích l do hình giới hạn bởi Ox, đường cong
2
25yx
,
3, 3xx
quay quanh Ox.
3
2
3
(25 )V x dx

=
132
(bấm máy)
Câu 4.5: Trong không gian với hệ trục tọa độ Oxyz, cho hai đim
(0; 1;2)M
và
( 1;1;3)N
. Mặt phẳng
(P) đi qua M, N sao cho khoảng cách từ
0; 0;2K
đến (P) đạt giá tr lớn nhất. (P) có vectơ pháp tuyến
là:
A.
(1;1; 1)
B.
(1; 1;1)
C.
(1; 2;1)
D.
(2; 1;1)
Hướng dẫn giải :
- Khoảng cách từ K đến (P) lớn nhất bằng KH, khi H’ trùng
H
- Vậy mặt phẳng (P) qua MN và vuông góc với KH.
- Tìm H và viết (P) hoặc:
- (P) chứa MN và vuông góc với (MNP).
Gọi H, H’ là hình chiếu của K lên MN và (P).
Ta có:
( ,( )) '
d k P KH KH
không đổi.
Vậy
( ,( ))
d K P
lớn nhất khi và chỉ khi H’ trùng H hay (P) vuông góc với KH.
(0;1;0); (1; 1; 1)
MK NK
;
( 1;2;1)
MN
(MNK) có vtpt là


, ( 1;0; 1)
n MK NK
Do
()
HK MNK
HK MN
nên HK có vtcp là



, (2;2; 2)
MN n
.
Câu 4.6: Cho s phức z thoả mãn điều kiện
2 3 3zi
. Tìm giá tr nhỏ nhất của
z
A.
13 3
B. 2 C.
13 2
D. 2
Hướng dẫn giải :
12
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
y
x
z
C
O
I
M
Các đim M biu diễn s phức z thoả mãn
2 3 3zi
nằm trên đường tròn (C) tâm I(2; −3) v
bán kính R =
3
.
(Ý nghĩa hình học của
z
: độ dài OM)
Ta có |z| đạt giá tr nhỏ nhất đim M(C) và OM nhỏ nhất .
(Bài toán hình học giải tích quen thuộc)
Ta có : OM
OI – IM = OI – R =
13 3
.
Dấu « = » xảy ra khi M l giao đim của (C) v đoạn thẳng OI.
Vậy GTNN của
z
là :
13 3
.
Câu 5.1. Cho hm s
32
3 3 1y x mx m
. Với giá tr no của m thì đồ th hm s đã cho có cc
đại v cc tiu đi xứng nhau qua đường thẳng
: 8 74 0d x y
A.
1m
B.
2m 
C.
2m
D.
1m 
Đáp án: C
Hướng dẫn:
+
2
y' 0 3x 6mx 0
. Đồ th có 2 đim cc tr khi:
m0
+ Phương trình đường thẳng đi qua 2 đim cc tr là: y = 2m
2
.x - 3m - 3
+ Trung đim 2 đim cc tr là
3
( ;2 3 1)I m m m
+ Điều kiện đ 2 đim cc tr đi xứng qua
: 8 74 0d x y
2
3
1
2 .( ) 1
8
8(2 3 1) 74 0
m
m m m
+ Từ đó thấy m = 2 thỏa mãn hệ trên. Vậy chọn C.
13
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 5.2. Cho hình chóp S.ABC có đáy l tam giác đều cạnh a, góc giữa SC và mp(ABC) là 45
. Hình
chiếu của S lên mp(ABC) l đim H thuộc AB sao cho HA = 2HB.Biết
7
3
a
CH
. Tính khoảng cách
giữa 2 đường thẳng SA và BC:
A.
210
30
a
B.
210
20
a
C.
210
45
a
D.
210
15
a
Đâp án: B
Hướng dẫn:
+ D l đỉnh của hình bình hành ABCD thì d(SA;BC)=d(B;(SAD))=1,5.d(H;(SAD))
+ Kẻ HE vuông AD, E thuộc AD. Kẻ HI vuông SE, I thuộc AE thì d(H;(SAD))=HI
+ Tính
210
30
a
HI
Suy ra chọn B.
Câu 5.3. Cho phương trình
22
2 2 2 4 2 2
5 5 2 0
x mx x mx
x mx m
. Tìm m đ phương trình vô
nghiệm?
A.
0m
B.
1m
C.
01m
D.
1
0
m
m

Đâp án: C
Hướng dẫn:
+Phương trình tương đương:
22
2 2 2 2 4 2 2
5 ( 2 2) 5 (2 4 2)
x mx x mx
x mx x mx
+ Do hàm f(t)=5
t
+ t đồng biến trên R nên ta có:
22
( 2 2) (2 4 2)x mx x mx
14
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
+ Từ đó điều kiện đ pt vô nghiệm là C.
Câu 5.4. Diện tích hình phẳng giới hạn bởi
2
xln(x 2)
y
4x
và trục hoành là:
A.
ln2 2 3
3
B.
2ln2 2
4

C.
23
3

D.
2ln2 2 3
3
Đáp án: D
Hướng dẫn:
+ Phương trình y = 0 có nghiệm: x=-1;x=0. Từ đó
0
2
1
xln(x 2)
S dx
4x
+ Sử dụng máy Casio, suy ra D.
Câu 5.5. Trong không gian với hệ trục tọa độ Oxyz, cho hai đim A(1;2;2), B(5;4;4) và mặt phẳng (P):
2x + y – z + 6 =0. Tọa độ đim M nằm trên (P) saocho MA
2
+ MB
2
nhỏ nhất là:
A. (-1;3;2) B. (2;1;-11) C.(-1;1;5) D(1;-1;7)
Đâp án: C
Hướng dẫn:
+ Kim tra phương án A không thuộc (P).
+ Tính trc tiếp MA
2
+ MB
2
trong 3 phương án B,C,D v so sánh. Chọn C.
Câu 5.6. S phức z có mô đun lớn nhất và thỏa mãn điều kiện là:
A.
13zi
B.
21
22
zi
C.
31
22
zi
D.
13
1 3 2
2
Z i i
3 15
44
zi
15
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Đáp án: D
Hướng dẫn:
+ Gọi z=x+yi. Từ giả thiết ta có:
22
13
( 3) ( 2)
4
x y x y
+ Đồng thời
22
z x y
lớn nhất. Kim tra các đáp án v so sánh ta chọn D.
CÂU 6.1: Trong không gian với hệ toạ độ Oxyz cho A(2;
1;6), B(
1;2;4) v I(
1;
3;2).
Viết phương trình mặt phẳng (P) đi qua A, B sao cho khoảng cách từ I đến (P) lớn nhất.
HƯỚNG DẪN GIẢI
Ta có
222
IA 3 2 4 29
v
2 2 2
IB 0 5 2 29
. Gọi M l trung đim của đoạn
thẳng AB, vì IA=IB nên IM
AB, ta có
11
M ; ;5 ;
22



94
IM
2
.
Gọi H l hình chiếu vuông góc của I lên mặt phẳng (P):
Nếu H, M l hai đim phân biệt thì tam giác IHM vuông tại H, IH<IM hay
94
IH
2
.
Nếu H trùng với M thì
94
IH IM
2

. Vậy ta có
94
IH
2
, IH lớn nhất khi H
M.
16
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Khi đó (P) có vectơ pháp tuyến l
P
37
n IH IM ; ;3
22


. Vậy phương trình mặt phẳng (P) l
37
x 2 y 1 3 z 6 0
22
hay
3x 7y 6z 35 0
CÂU 6.2: Tìm m đ đồ th hàm s
32
y x 3mx 1
có hai đim cc tr A, B sao cho tam giác OAB
có diện tích bằng 1 (O là gc tọa độ).
HƯỚNG DẪN GIẢI
Ta có
2
y' 3x 6mx 3x x 2m
. Đ đồ th hàm s có hai đim cc tr thì
m0
.
Khi đó hai đim cc tr của đồ th hàm s là
A(0;1)
và
3
B(2m; 4m 1)
. Gọi H là hình chiếu
vuông góc của đim B lên trục tung, ta có
BH 2m
. Diện tích của tam giác OAB là
11
S BH.OA . 2m
22

Theo đề bài S=1 nên ta có
1
. 2m 1
2
suy ra
m1
. Vậy m=±1 là giá tr cần tìm.
CÂU 6.3: Cho s phức z thoả mãn
5
2
1
zi
i
z

. Tìm phần thc và phần ảo của s phức
2
w1zz
HƯỚNG DẪN GIẢI
Đặt z=a+bi (a,b
R), ta có
z a bi
5
2 5 2 1
1
a bi i
i a bi i i a bi
a bi


5 2( 1) 3 2 1
5 5 2 ( 1) 7 6 1
a a b a b a
b b a a b b
Vậy ta có z=1+i
2
2 w 1 (1 ) (2 ) 2 3z i i i i
. Vậy phần thc của s phức là 2, phần ảo là 3.
CÂU 6.4: Cho hình chóp S.ABC có đường thẳng SA vuông góc với mặt phẳng (ABC), tam giác ABC
l tam giác đều cạnh bằng a, SB=2a. Tính theo a khoảng cách từ trọng tâm G của tam giác ABC đến
mặt phẳng (SBC).
17
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
HƯỚNG DẪN GIẢI
Gọi M l trung đim của BC, ta có
;BC AM BC SA
()BC SAM
. Kẻ đường cao AN của
tam giác SAM, vì
;AN BC AN SM
nên
()AN SBC
Khoảng cách từ A đến (SBC) l
( ;( ))d A SBC AN
Ta có
2 2 2 2 2 2
1 1 1 1 4 5
3 3 3AN AS AM a a a
Suy ra
15
5
a
AN
Kẻ GH//AN; H
SM; vì
()AN SBC
nên
()GH SBC
Khoảng cách từ G đến (SBC) l
( ;( ))d G SBC GH
Ta có
1 1 15
3 3 15
GH MG a
GH AN
AN AM
Vậy khoảng cách từ G đến (SBC) l
15
( ;( ))
15
a
d G SBC
CÂU 6.5: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA=AC=5a, AB=a,
0
120BAC
. Tính theo a khoảng cách từ A đến mặt phẳng (SBC).
HƯỚNG DẪN GIẢI
18
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Kẻ AMBC, AHSM (MBC, HSM). Ta có BCAM, BCSA nên BC(SAM), suy ra AH BC.
Vậy ta có AH(SBC), khoảng cách từ A đến mặt phẳng (SBC) là d(A,(SBC))=AH.
Áp dụng đnh lí côsin trong tam giác ABC ta có
2 2 2 0 2
2 . .cos120 31
BC AB AC AB AC a
31
BC a
.
Diện tích của tam giác ABC là

2
0
1 5 3
. .sin120
24
ABC
a
S AB AC
.
Mặt khác
2
1 5 93
..
2 62
ABC
ABC
S
S AM BC AM a
BC
Ta có
2 2 2 2
1 1 1 127 5 381
127
75
AH a
AH AM AS a
. Khoảng cách từ A đến mặt phẳng (SBC) là
d(A,(SBC))=
5 381
127
a
.
CÂU 6.6: Cho hình chóp tam giác S.ABC có đường thẳng SA vuông góc với mặt phẳng (ABC),
AB=2a, AC=3a, BC=4a. Góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng 60
0
. Tính theo a th
tích của khi chóp S.ABC.
HƯỚNG DẪN GIẢI
19
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Xét tam giác ABC ta có
2 2 2 2 2 2
16 4 9 11
cosB=
2 . 2.4 .2 16
BC AB AC a a a
BC AB a a

(áp dụng đnh lý
côsin)
với 0
0
<B<180
0
, suy ra
2
2
11 3 15
sinB= 1 cos 1
16 16
B



Ta kẻ đường cao AH của tam giác ABC, ta có
3 15 3 15
sinB= .sin 2 .
16 8
AH a
AH AB B a
AB
Do đó diện tích tam giác ABC là
2
1 1 3 15 3 15
. .4
2 2 8 4
ABC
aa
S AH BC a
Vì
, ( ),BC AH BC SA BC SAH BC SH
nên góc SHA là góc giữa hai mặt phẳng
(SBC) và (ABC), bằng 60
0
.
Xét tam giác SAH ta có
00
3 15 9 5
tan60 tan60 . 3
88
SA a a
SA AH
AH
20
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Vậy th tích khi chóp S.ABC là
23
1 1 3 15 9 5 45 3
. . .
3 3 4 8 32
ABC
a a a
V S SA
Câu 7.1: Một người thợ xây, mun xây dng một bồn chứa
nước hình trụ tròn với th tích là
3
150m
(như hình vẽ bên).
Đáy lm bằng bê tông , thành làm bằng tôn và bề làm bằng
bằng nhôm. Tính chi phí thấp nhất đ bồn chứa nước (làm
tròn đến hàng nghìn). Biết giá thành các vật liệu như sau: bê
tông
100
nghìn đồng một
2
m
, tôn
90
một
2
m
và nhôm
120
nghìn đồng một
2
m
.
A.
15037000
đồng. B.
15038000
đồng. C.
15039000
đồng. D.
15040000
đồng.
Đáp án: C.
Hướng dẫn giải: Gọi
,rh
2
m
0, 0rh
lần lượt l bán kính đường tròn đáy v đường cao của
hình trụ. theo đề ta có
2
2
150
150r h h
r
. Khi đó chi phí lm nên bồn chứa nước được xác đnh
theo hàm s
22
2
150 27000
220 90.2 220f r r r r
rr
(nghìn đồng).
2
27000
' 440f r r
r

,
3
675
'0
11
f r r a
.
BBT:
Da vào BBT ta suy ra chi phí thấp nhất là
3
675
15038,38797
11
f a f





nghìn đồng.
Lưu ý: Khi làm tròn các bạn nhớ số tiền tối thiểu phải lớn hơn hoạc bằng số tiền hoàn thành sản phẩm, nên
dù cho trong bài toán này kết quả gần với số
15038
hơn, nhưng đáp án ta phải chọn
15039
. Vì nếu chọn
15038
thì chi phí thấp nhất nhỏ hơn chi phí hoàn thành sản phẩm nên không thể làm được sản phẩm.
Câu 7.2: Tìm tất cả các giá tr của tham s
m
sao cho bất phương trình sau có tập nghiệm là
;0
:
1
2 2 1 3 5 3 5 0
xx
x
mm
.
A.
1
2
m 
. B.
1
2
m
. C.
1
2
m
. D.
1
2
m 
.
21
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Đáp án: D.
Hướng dẫn giải: Phương trình đã cho tương đương
3 5 3 5
2 2 1 0 1
22
xx
mm

. Đặt
35
0
2
x
t





ta được:
2
1
2 2 1 0 2 2 1 0 2m m t f t t mt m
t
. Bất phương trình
1
nghiệm đúng
0x
nên
bất phương trình
2
có nghiệm
01t
, suy ra phương trình
0ft
có 2 nghiệm
12
,tt
thỏa
12
01tt
00
2 1 0
4 2 0
10
f
m
m
f




0,5
0,5
m
m


. Vậy
1
2
m 
thỏa.
Câu 7.3: Một vật di chuyn với gia tc
2
20 1 2a t t
2
/ms
. Khi
0t
thì vận tc của vật là
30 /ms
. Tính quảng đường vật đó di chuyn sau 2 giây (làm tròn kết quả đến chữ s hng đơn v).
A.
106Sm
. B.
107Sm
. C.
108Sm
. D.
109Sm
.
Đáp án: C.
Hướng dẫn giải: Ta có
2
10
20 1 2
12
v t a t dt t dt C
t

. Theo đề ta có
0 30 10 30 20v C C
. Vậy quãng đường vật đó đi được sau 2 giây là:
2
2
0
0
10
20 5ln 1 2 20 5ln5 100 108
12
S dt t t m
t



.
Câu 7.4: Cho s phức
0z
thỏa mãn
2z
. Tìm tổng giá tr lớn nhất và giá tr nhỏ nhất của biu
thức
zi
P
z
.
A.
1
. B.
2
. C.
3
. D.
4
.
Đáp án: B.
Hướng dẫn giải: Ta có
11
1 1 1 1 1 1
i i i i
z z z z z z
. Mặt khác
11
2
2
z
z
suy ra
13
22
P
. Suy ra giá tr lớn nhất và giá tr nhỏ nhất là
31
,
22
. Vậy tổng tổng giá tr lớn nhất và giá tr
nhỏ nhất của biu thức
P
là
2
.
22
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 7.5: Cho hình chóp
.S ABC
, có đáy
ABC
l tam giác đều cạnh
a
. Các mặt bên
SAB
,
SAC
,
SBC
lần lượt tạo với đáy các góc lần lượt là
000
30 ,45 ,60
. Tính th tích
V
của khi chóp
.S ABC
.
Biết rằng hình chiếu vuông góc của
S
trên mặt phẳng
ABC
nằm bên trong tam giác
ABC
.
A.
3
3
43
a
V
. B.
3
3
2 4 3
a
V
. C.
3
3
4 4 3
a
V
. D.
3
3
8 4 3
a
V
.
Đáp án: D.
Hướng dẫn giải: Gọi
H
là hình chiếu vuông góc
của
S
trên mặt phẳng
ABC
. Kẻ
HD AB D AB
,
HE AC E AC
,
HF BC E BC
. Khi đó ta có
0
3
tan30
SH
HD SH
,
0
tan45
SH
HE SH
,
0
tan60
3
SH SH
HF 
. Ta có
2
3
4
ABC
a
S
suy ra
2
1 1 3 3
13
24
3
2 4 3
aa
SH a SH



.
Vậy
23
1 3 3 3
..
34
2 4 3 8 4 3
a a a
V 

.
Câu 7.6: Trong không gian tọa độ
Oxyz
, cho tám đim
2; 2;0A 
,
3; 2;0B
,
3;3;0C
,
2;3;0D
,
2; 2;5M 
,
2; 2;5N 
,
3; 2;5P
,
2;3;5Q
. Hỏi hình đa diện tạo bởi tám đim đã cho có bao
nhiêu mặt đi xứng.
A. 3. B. 6. C. 8. D.9
Đáp án: D.
Hướng dẫn giải: Vì tám đim đã chõ tạo nên một hình lập phương, nên hình đa diện tạo bởi tám
đim này có 9 mặt đi xứng.
Câu 8.1.
Xét phương trình:
x x m
42
8cos 9cos 0
với
x
[0; ]
(1)
Đặt
tx
cos
, phương trình (1) trở thành:
t t m
42
8 9 0
(2)
Vì
x
[0; ]
nên
t
[ 1;1]
, giữa x và t có sự tương ứng một đối một, do đó số nghiệm của phương trình
23
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
(1) và (2) bằng nhau.
Ta có:
t t m
42
(2) 8 9 1 1
(3)
Gọi (C1):
y t t
42
8 9 1
với
t
[ 1;1]
và (d):
ym
1
.
Dựa vào đồ thị(BBT) ta có kết luận sau:
m
01
Câu 8.2. Giải: Đặt
2
3
x
t
điều kiện
1t
vì
20
2
0 3 3 1
x
x
Khi đó phương trình trở thành:
2 2 2
3 2 2 0t x t x
22
2 2 2
2
2
3 4 2 2 1
1
t
x x x
tx
Khi đó:
+ Với
2
33
2
2 3 2 log 2 log 2
x
t x x
+ Với
22
2
1 3 1
x
t x x
ta có nhận xét:
2
2
11
31
0
11
11
x
VT VT
x
VP VP
x
Vậy phương trình có 3 nghiệm
3
log 2; 0xx
.
Câu 8.3.
2 2 2
x
0 0 0
sinx osx osx osxdx
2
0
x x x
e dx e d c e c e c e J





22
22
00
sinx sinx sinxdx=e
2
0
x x x
J e d e e I I J e



24
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Vậy ta có hệ :
2
2
2
ee
I J e
I
I J e



Câu 8.4. Bi giải.
Đặt
zi
w
z
. Ta có
,1
1
z i i
w z w
zw
Do
1
2 2 1
12
i
zw
w
. Như vậy tập hợp s phức w l hình tròn tâm I(1; 0 ), bán
kính
1
2
R
, (Bỏ đim I) giá tr
Pw
l khoảng cách từ gc O đến đim M(x; y) thuộc hình
tròn tương ứng với s phức z.
P nhỏ nhất l
1
2
tại
1
;0
2
A
,
2
12
zi
.
Câu 8.5. ĐÁP ÁN B
* Gọi cạnh đáy hình chóp l x,
2
x (0; )
2
.
Chiều cao của hình chóp là :
2
2
2 x x 1 x 2
h
2 2 2 2






Th tích của khi chóp :
45
2
1 1 x 2 1 x x 2
Vx
3 2 3 2


1
2
A
B
I( 0; 1 )
O( 0; 0 )
25
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
* Xét hàm s :
45
y x x 2
trên
2
(0; )
2
34
x 0 (l)
y' 4x 5x 2 ; y' 0
22
x (n)
5
BBT :
X
0
22
5
2
2
y’
║ + 0 - ║
Y
║ ║
║ ║
Vậy khi
22
x
5
thì khi chóp đạt GTLN
Câu 8.6. Gọi I l trung đim của AB I ( 1; 1; 1)
+) MA
2
+ MB
2
= 2MI
2
+ IA
2
+ IB
2
Do IA
2
+ IB
2
không đổi nên MA
2
+ MB
2
nhỏ nhất khi MI
nhỏ nhất
M là hình chiếu của I lên mặt phẳng (P)
+) Phương trình đường thẳng MI :
x-1 y-1 z-1
==
1 1 1
.
M l giao đim của MI và mặt phẳng (P).
Từ đó tìm được M(2; 2; 2).
Câu 9.1. Cho một tam giác đều ABC cạnh a. Người ta dng một hình chữ nhật MNPQ có cạnh MN
nằm trên cạnh BC, hai đỉnh P và Q theo thứ t nằm trên hai cạnh AC và AB của tam giác. Xác đnh
giá tr lớn nhất của hình chữ nhật đó?
A.
2
3
a
8
B.
2
3
a
4
C.
0
D.
2
3
a
2
26
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A
B
C
Q
P
M
H
N
Hướng dẫn giải:
Gọi H l trung đim của BC BH = CH =
a
2
Đặt BM = x
a
§iÒu kiÖn 0 x
2




, ta có:
a
MN 2MH 2(BH BM) 2 x a 2x
2



Tam giác MBQ vuông ở M,
0
B 60
và BM = x
QM x 3
Hình chữ nhật MNPQ có diện tích:
S(x) = MN.QM =
2
(a 2x)x 3 3(ax 2x )
aa
S'(x) 3(a 4x); S'(x) 0 x 0;
42



x
0
a
4
a
2
S’
+ 0
S
2
3
a
8
Vậy
2
a
x 0;
2
3
maxS(x) a
8



khi x =
a
4
Câu 9.2. Cho hình chóp tứ giác đều
.S ABCD
có đáy l hình vuông ABCD cạnh a, góc giữa mặt bên
và mặt phẳng đáy l
thoả mãn
cos =
1
3
. Mặt phẳng
P
qua AC và vuông góc với mặt phẳng
27
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
SAD
chia khi chóp
.S ABCD
thành hai khi đa diện. Tỉ lệ th tích hai khi đa diện là gần nhất với
giá tr nào trong các giá tr sau
A. 0,11 B. 0,13 C. 0,7 D. 0,9
Hướng dẫn giải :
.S ABCD
là hình chóp tứ giác đều
SO ABCD
. Gọi N l trung đim CD
,

CD SN CD ON
SCD ABCD CD
,SCD ABCD SNO
Kẻ
CM SD
. Ta có

AC BD
AC SBD AC SD
AC SO
SD ACM ACM SAD
nên mặt phẳng
P
là
ACM
+ Xét tam giác SON vuông tại N có :
3
2
1
2
cos
3
a
ON a
SN
SNO
22
22
3
2
22
aa
SO SN ON a
+ Xét tam giác SOD vuông tại O có :
2
2
22
2 10
2
22




aa
SD SO OD a
Ta có
11
..
22

SCD
S CM SD SN CD
3
.
. 3 10
2
10
10
2
a
a
SN CD a
CM
SD
a
O
B
D
A
S
C
N
M
28
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
- Xét tam giác MCD vuông tại M có :
2
2 2 2
3 10 10
10 10




aa
DM CD CM a
Ta có :
10
1 1 1 1
10
. . . . .
2. 2 2 2 10
10
2
MACD MACD
SABCD SACD
a
VV
DM DA DC DM
V V DS DA DA DS
a
1
10

MACD SABCD
VV
. Mặt phẳng
P
chia khi chóp S.ABCD thành 2 khi
MACD
và
SABCM
SABCD MACD SABCM
V V V
9
10

SABCM SABCD
VV
Do đó :
1
0,11
9

MACD
SABCM
V
V
Câu 9.3. Cho biết chu kì bán hủy của chất phóng xạ Plutôni Pu
239
l 24360 năm (tức là một lượng
Pu
239
sau 24360 năm phân hủy thì chỉ còn lại một nửa). S phân hủy được tính theo công thức S =
Ae
rt
, trong đó A l lượng chất phóng xạ ban đầu, r là tỉ lệ phân hủy hng năm (r<0), t l thời gian
phân hủy, S l lượng còn lại sau thời gian phân hủy t. Hỏi sau bao nhiêu năm thì 10 gam Pu
239
sẽ
phân hủy còn 1 gam có giá tr gần nhất với giá tr nào sau?
A. 82135 B. 82335 C. 82235 D. 82435
Hướng dẫn giải:
Vì Pu
239
có chu kì bán hủy l 24360 năm nên e
r24360
=
S1
A2
r 0,000028
Công thức phân hủy của Pu
239
là S = A.e
0,000028t
Theo giả thiết: 1 = 10. e
0,000028t
t 82235,18 năm
Câu 9.4. Tìm giá tr của tham s m sao cho:
3
y x 3x 2
và y = m(x+2) giới hạn bởi hai hình
phẳng có cùng diện tích
A. 0 < m < 1 B. m = 1 C.
1 m 9
D. m = 9
29
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Hướng dẫn giải:
Phương trình honh độ giao đim :
3
x 3x 2 m(x 2)
x 2 hoÆc x 1 m , m 0.
Điều kiện d: y = m(x+2) và (C):
3
y x 3x 2
giới hạn 2 hình phẳng:
0 m 9.
Gọi S1, S2 lần lượt là diện tích các hình phẳng nhận được theo thứ t từ trái sang phải.
Nếu m = 1: d đi qua đim un (0;2) của (C). Khi đó S1 = S2 =
0
3
2
(x 4x)dx 4

Nếu 0 < m < 1: S1 > 4 > S2
Nếu 1 < m < 9: S1 < 4 < S2
Nếu m > 9
1 m 2; 1 m 4.
Khi đó:
2 1 m
33
12
2
1m
S x 3x 2 m(x 2) dx; S x 3x 2 m(x 2) dx


S2 S1 = 2m
m0
Vậy m = 1 thỏa yêu cầu bài toán
Câu 9.5. Cho đường thẳng d là giao tuyến của hai mặt phẳng
( ): x 2y 2z 4 0
( ):2x 2y z 1 0,
và mặt cầu S có phương trình
2 2 2
x y z 4x 6y m 0
. Tìm m đ
đường thẳng d cắt mặt cầu (S) tại hai đim phân biệt A, B sao cho AB = 8.
A. 9 B. 12 C. 5 D. 2
Hướng dẫn giải:
Ta có
12
n (2; 2; 1), n (1;2; 2)
lần lượt là VTPT của (α) v (β)
Suy ra VTCP của đường thẳng d là
12
1
u n ;n (2;1;2),
3



30
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Ta có A(6;4;5) l đim chung của hai mặt phẳng (α) v (β) nên Ad.
Mặt cầu (S) có tâm I(-2;3;0), bán kính
R 13 m
với m < 13.
IA (8;1;5) IA,u ( 3; 6;6) d(I,d) 3


Gọi H l trung đim của AB
AB
AH 4 vµ IH 3
2
.
Trong tam giác vuông IHA ta có:
2 2 2 2
IA IH AH R 9 16
13 m 25 m 12
Vậy m = 12 là giá tr cần tìm.
Câu 9.6. Tìm phần thc của s phức
n
z (1 i) , n
thỏa mãn phương trình
44
log (n 3) log (n 9) 3
A.
5 B. 6 C. 7 D. 8
Hướng dẫn giải:
Điều kiện n > 3,
n
Phương trình
4 4 4
log (n 3) log (n 9) 3 log (n 3)(n 9) 3 n 7
(so đk)
3
2
73
z (1 i) (1 i). 1 i (1 i)(2i) 8 8i


Vậy phần thc của s phức z là 8.
1. Cho s phức
z
thỏa mãn:
3 4 4zi
. Tìm giá tr nhỏ nhất của
z
.
Lời giải
Giả sử
z a bi

, ta có:
22
3 4 4 3 4 16a bi i a b
31
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Đặt
3 4sin 3 4sin
4 4cos 4cos 4
aa
bb





2
2 2 2 2
9 16sin 24sin 16cos 16 32cos
41 24sin 32cos
34
41 40( sin cos )
55
z a b


Đặt
34
cos ,sin
55


2
22
41 40sin( ) 1z a b

.
Dấu “=” xảy ra khi
22
22
kk

.
Vậy
1Min z
.
2. Tính tích phân :
22
3
3
4
1
2016
x x x
I dx
x

Lời giải :
Ta có :
3
2 2 2 2
2
33
11
1
1
2016
x
I dx I dx M N
xx

3
22
2
3
1
1
1
x
M dx
x
. Đặt
3
7
3
2
3
3
2
0
1 3 21 7
1
2 128
t M t dt
x
2 2 2 2
3
32
11
2016 2016
2016 882
2
N dx x dx
xx




Vậy
3
21 7
882
128
I

32
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
3. Cho hàm s
1
x
y
x
()
C
. Tìm
m
đ đường thẳng
:1
d y mx m
cắt
()
C
tại hai đim
phân biệt
,
MN
sao cho
22
AM AN
đạt giá tr nhỏ nhất với
( 1;1)
A
.
Lời giải :
Phương trình honh độ giao đim của
()
C
và
d
:
2
1
1
1
2 1 0(1)
x
x
mx m
x
mx mx m
d
cắt
()
C
tại hai đim phân biệt
(1)
có 2 nghiệm phân biệt khác 1
0
m

Gọi
I
l trung đim của
MN
(1; 1)
I

c đnh .
Ta có :
2
2 2 2
2
2
MN
AM AN AI
Do
22
AM AN
nhỏ nhất
MN
nhỏ nhất
2 2 2
21
4
( ) (1 ) 4 8
MN x x m m
m
. Dấu “=” xảy ra
1
m
Vậy
22
min( ) 20
AM AN

khi
1
m

4. Trong không gian với hệ tọa độ
Oxyz
, cho hai đường thẳng
1
12
:
1 2 1
x y z
d


và
2
21
:
2 1 2
x y z
d


. Viết phương trình mặt phẳng
()
P
chứa
1
d
sao cho góc giữa mặt phẳng
()
P
v đường thẳng
2
d
là lớn nhất .
Lời giải :
Ta có :
1
d
đi qua
(1; 2;0)
M
và có
(1;2; 1)
VTCPu

.
Phương trình mặt phẳng
()
P
có dạng :
2 2 2
( 1) ( 2) 0,( 0)
A x B y Cz A B C
.
Ta có :
( ) . 0 2
d P u n C A B
Gọi
2
2
22
22
43
1 (4 3 )
(( ), ) sin .
3
2 4 5
3 2 4 5
AB
AB
Pd
A AB B
A AB B



33
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Với
0
B
22
sin
3

Với
0
B
. Đặt
A
t
B
, ta được
2
2
1 (4 3)
sin .
3
2 4 5
t
tt

Xét hàm s
2
2
(4 3)
()
2 4 5
t
ft
tt

. Ta có :
2
22
16 124 84
'( )
(2 4 5)
tt
ft
tt


3
'( ) 0
4
7
t
ft
t



BBT :
t

-7
3
4

'( )
ft
+ 0 - 0 +
()
ft
25
3
Da vào BBT ta có :
25
max ( )
3
ft
khi
7
t

7
A
B
Khi đó :
53
sin ( 7)
9
f
Vậy
53
sin
9
khi
7
A
B

Phương trình mặt phẳng
( ) : 7 5 9 0
P x y z
5. Cho phương trình :
22
5 6 1 6 5
.2 2 2.2 (1)
x x x x
mm
. Tìm
m
đ PT có 4 nghiệm phân biệt .
Lời giải :
Viết lại PT
(1)
dưới dạng :
22
5 6 1 6 5
.2 2 2.2
x x x x
mm
2 2 2 2
5 6 1 ( 5 6) (1 )
.2 2 2
x x x x x x
mm
2 2 2 2
5 6 1 5 6 1
.2 2 2 .2
x x x x x x
mm
34
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Đặt :
2
2
56
1
2
, , 0
2
xx
x
u
uv
v

. Khi đó PT tương đương với :
2
2
2
56
1
1
3
1 2 1
( 1)( ) 0 2
2
2 (*)
xx
x
x
x
u
mu v uv m u v m x
vm
m
m


Đ
(1)
có 4 nghiệm phân biệt
(*)
có 2 nghiệm phân biệt khác 2 và 3 .
(*)
22
22
00
1 log 1 log
mm
x m x m







. Khi đó điều kiện là :
2
2
2
0
0
2
1 log 0
11
1
(0;2) \ ;
1 log 4
8 256
8
1
1 log 9
256
m
m
m
m
m
m
m
m
m








Vậy với
11
(0;2) \ ;
8 256
m



thỏa điều kiện đề bài .
6. Cho hình chóp
.
S ABC
có
ABC
l tam giác đều cạnh
2,
a SAB
cân tại
S
và
( ) ( )
SAB ABC
.
Xác đnh tâm và bán kính mặt cầu ngoại tiếp khi chop biết
3
SA a
.
Lời giải :
Gọi
H
l trung đim
AB SH AB

.
S
B
C
A
H
G
I
O
35
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
( ) ( )
( ) ( )
SAB ABC
SAB ABC AB
SH AC
()
SH ABC

.
Gọi
O
l tâm đường tròn ngoại tiếp
SAB
bán kính
.
r
22
22
SH SA AH a
,
2
1
. 2 2
2
ABC
S SH AB a

,
..
2
4
SAB
SASB AB
ra
S

2 2 2 2
OH OA AH r AH a
Gọi
G
l tâm đường tròn ngoại tiếp
ABC
Do
ABC
đều
3
HC a

,
13
33
a
GH HC

Dng
d
qua
O
và vuông góc
()
SAB
Dng
qua
G
và song song
()
SH ABC
Gọi
Id
.
Do đó
I d IS IA IB
(1) ,
I IA IB IC
(2)
Từ (1),(2)
IA IB IC IS
I
là tâm mặt cầu ngoại tiếp khi chop có bán kính
R IA
2
2 2 2
2 21
33
a
R IA AG IG HC OH



.
1. S giá tr nguyên âm của m đ
.9 2 1 .6 .4 0
x x x
m m m
với
0;1x
là
A. 6 B. 4 C. 5 D. 3
2. Cho hàm s
32
y x 3mx m 1
. Giá tr của m đ đồ th hàm s có hai đim cc tr A, B sao
cho trọng tâm tam giác OAB thuộc đường thẳng
2
yx
3
là
36
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A. m = 0 hoặc
m1
B. m = 2 hoặc
m1
C. m = 1 hoặc
m2
D. m = 1 hoặc
m3
3. Cho phương trình
32
3 37 0z az az
có ba nghiệm là – 1 và 2 nghiệm còn lại
12
;zz
. Gọi A,
M, N l các đim biu diễn s phức
z –1
và
12
;zz
. Khi đó tam giác AMN l tam giác gì?
A.
9a
v ∆AMN vuông.
B.
9a 
v ∆AMN cân.
C.
9a 
v ∆AMN vuông.
D.
9a
v ∆AMN cân.
4. Cho hình vẽ sau. Công thức tích phân no dưới đây ứng với phần diện tích phần gạch chéo
trong hình vẽ trên. Biết
A 4;1
;
B 2;1
;
C 0;3
;
5
D 0;
2




;
5
F 0;
2




.
6
4
2
2
4
6
8
15
10
5
5
10
15
F
C
B
A
D
O
37
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
5
1
53


S x x dx
B.
2
2
1
53


S y y dy
C.
5
2
1
2
S y y dy
D.
2
1
53


S y y dy
5. Khi sản xuất cái phễu hình nón (không có nắp) bằng nhôm, các nhà thiết kế luôn đặt mục
tiêu sao cho chi phí nguyên liệu làm phễu là ít nhất, tức là diện tích xung quanh của hình nón là
nhỏ nhất. Giá tr gần đúng diện tích xung quanh của phễu khi ta mun có th tích của phễu là 1dm
3
là ?
(Làm tròn đến chữ số thập phân thứ hai)
A. 4.18 dm
2
B. 4.17 dm
2
C. 4.19 dm
2
D. 4.1 dm
2
6. Cho hình chóp S.ABCD có đáy l tứ giác ABCD có
0
90ABC ADC
,
AB AD a
và
2CD CB a
. Cạnh SA vuông góc mp(ABCD) và mp(SBC) hợp với đáy một góc
0
45
. Gọi (S) là
mặt cầu ngoại tiếp hình chóp S.ABCD. Th tích của khi cầu tạo nên bởi mặt cầu (S) bằng?
A.
3
2
3
a
B.
3
4
3
a
C.
3
8
3
a
D.
3
10
3
a
7. Trong không gian với hệ tọa độ Oxyz, cho các đim
2;1;1 , 1;0;0 , 0;3; 2A B M
. Gọi (P)
là mặt phẳng đi qua A, B sao cho khoảng cách từ đim M đến mp(P) lớn nhất. Khoảng cách từ đim
1;0;0N
đến mp(P) bằng :
38
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
1
14
B.
4
14
C.
2
14
D.
3
14
Câu 10.1. Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng : Nếu trên mỗi đơn v diện tích của
mặt hồ có
n
con cá thì trung bình mỗi con cá sau một vụ cân nặng
( ) 480 20 ( )P n n gam
. Hỏi phải thả bao
nhiêu con cá trên một đơn v diện tích của mặt hồ đ sau một vụ thu hoạch được nhiều cá nhất ?
A.
10
B.
12
C.
16
D.
24
Giải:Gọi
n
là s con cá trên một đơn v diện tích hồ
( 0)n
. Khi đó :
Cân nặng của một con cá là :
( ) 480 20 ( )P n n gam
Cân nặng của
n
con cá là :
2
. ( ) 480 20 ( )n P n n n gam
Xét hàm s :
2
( ) 480 20 , (0; )f n n n n
. Ta có :
'( ) 480 40f n n
, cho
'( ) 0 12f n n
Lập bảng biến thiên ta thấy s cá phải thả trên một đơn v diện tích hồ đ có thu hoạch nhiều nhất là
12
con.
Câu 10.2. Một cửa hàng bán lẻ bán 2500 cái ti vi mỗi năm. Chi phí gởi trong kho là 10$ một cái mỗi năm. Đ
đặt hàng chi phí c đnh cho mỗi lần đặt là 20$ cộng thêm 9$ mỗi cái. Cửa hng nên đặt hàng bao nhiêu lần
trong mỗi năm v mỗi lần bao nhiêu cái đ chi phí hàng tồn kho là nhỏ nhất?
Gọi x là s ti vi mà cửa hng đặt mỗi lần (
1;2500x
, đơn v: cái )
S lượng ti vi trung bình gởi trong kho là
2
x
nên chi phí lưu kho tương ứng là
10 5
2
x
x
S lần đặt hàng mỗi năm l
2500
x
v chi phí đặt hàng là :
2500
(20 9 )x
x
Khi đó chi phí m cửa hàng phải trả là:
2500 50000
( ) (20 9 ) 5 5 22500C x x x x
xx
Lập bảng biến thiên ta được :
min
(100) 23500CC
Kết kết luận: đặt hàng 25 lần, mỗi lần 100 cái ti vi.
Câu 10.3. Một đại lý xăng dầu cần làm một cái bồn chứa dầu hình trụ bằng tôn có th tích
3
16 m
. Tìm bán
kính đáy r của hình trụ sao cho hình trụ được làm ra ít tn nguyên vật liệu nhất.
A.
0,8m
B.
1,2m
C.
2m
D.
2,4m
Gọi
()xm
l bán kính đáy của hình trụ
( 0)x
. Ta có:
2
2
16
.V x h h
r
Diện tích toàn phần của hình trụ là: S(x) =
22
32
( ) 2 2 . 2 ,( 0)S x x x h x x
x
39
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Khi đó: S’(x) =
2
32
'( ) 4S x x
x
, cho
'( ) 0 2S x x
Lập bảng biến thiên, ta thấy diện tích đạt giá tr nhỏ nhất khi
2( )xm
nghĩa l bán kính l
2( ).m
Câu 10.4. Một xưởng cơ khí nhận làm những chiếc thùng phi với th tích theo yêu cầu là
2000
lít mỗi chiếc.
Hỏi bán kính đáy v chiều cao của thùng lần lượt bằng bao nhiêu đ tiết kiệm vật liệu nhất?
A.
1m
và
2m
B.
1dm
và
2dm
C.
2m
và
1m
D.
2dm
và
1dm
Đổi
3
2000 ( ) 2 ( )lit m
. Gọi bán kính đáy v chiều cao lần lượt là
()xm
và
()hm
.
Ta có th tích thùng phi
2
.2V x h
2
2
h
x
Vật liệu tỉ lệ thuận với diện tích toàn phần nên ta chỉ cần tìm
x
đ diện tích toàn phần bé nhất.
22
2
22
2 2 . 2 ( ) 2 ( )
tp
S x x h x x x
x
x
Đạo hàm lập BBT ta tìm đc
()fx
GTNN tại
1x
, khi đó
2.h
Câu 10.5. Người ta mun mạ vàng bên ngoài cho một cái hộp có đáy hình vuông, không nắp, th tích hộp là
4
lít. Giả sử đồ dày của lớp mạ tại một đim trên hộp l như nhau. Gọi chiều cao và cạnh đáy lần lượt là
x
và
h
. Giá tr của
x
và
h
đ lượng vàng cần dùng nhỏ nhất là:
A.
3
3
4
4;
16
xh
B.
3
3
12
12;
144
xh
C.
2; 1xh
D.
1; 2xh
Gọi
()x dm
là cạnh đáy của hình hộp,
h
là chiều cao của hộp,
()Sx
là diện tích cần mạ vàng.
Vì khi lượng vàng tỉ lệ thuận với diện tích nên ta đưa về bài toán tìm
x
đ
()Sx
nhỏ nhất.
Ta có :
2
2
2
2
( ) 4
16
()
S x xh x
V
h S x x
x
x
V x h
Đạo hàm, lập BBT ta tìm được
()Sx
đạt GTNN tại
2x
, khi đó
1h
Câu 10.6. Có một tấm nhôm hình chữ nhật có chiều dài bằng
24( )cm
, chiều rộng bằng
18( )cm
. Người ta cắt ở
bn góc của tấm nhôm đó bn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng
()x cm
rồi gấp tấm nhôm
lại như hình vẽ dưới đây đ được một cái hộp không nắp. Hỏi th tích lớn nhất của cái hộp là bao nhiêu?
A.
3
640
max
V cm
B.
3
617,5
max
V cm
C.
3
845
max
V cm
D.
3
645
max
V cm
Chiều dài, chiều rộng đáy của cái hộp lần lượt là:
24 2x
và
18 2 .x
Diện tích đáy của cái hộp:
(24 2 )(18 2 )xx
.
Th tích cái hộp là:
32
(24 2 )(18 2 ) 4( 21 108 )V x x x x x x
với
09x
Ta có:
2
'( ) 4(3 42 108).V x x x
Cho
'( ) 0Vx
, giải ta nhận nghiệm
7 13 3,4x
40
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Lập bảng biến thiên ta thấy
(7 13) 645
max
VV
khi
7 13 3,4x
Câu 10.7. Người ta mun rào quanh một khu đất với một s vật liệu cho trước là
180
mét thẳng hàng rào. Ở
đó người ta tận dụng một bờ giậu có sẵn đ làm một cạnh của hàng rào và rào thành mảnh đất hình chữ
nhật. Hỏi mảnh đất hình chữ nhật được rào có diện tích lớn nhất bằng bao nhiêu?
A.
2
3600
max
Sm
B.
2
4000
max
Sm
C.
2
8100
max
Sm
D.
2
4050
max
Sm
Gọi
x
là chiều dài cạnh song song với bờ giậu và
y
là chiều dài cạnh vuông góc với bờ giậu, theo
bài ra ta có
2 180xy
. Diện tích của miếng đất là
(180 2 )S y y
.
Ta có:
2
2
(2 180 2 )
1 1 180
(180 2 ) 2 (180 2 ) 4050
2 2 4 8
yy
y y y y
Dấu
'' ''
xảy ra
2 180 2 45y y y m
.
Vậy
2
4050
max
Sm
khi
90 , 45x m y m
.
Câu 10.8. Một lão nông chia đất cho con trai đ người con canh tác riêng, biết người con sẽ được chọn miếng
đất hình chữ nhật có chu vi bằng
800( )m
. Hỏi anh ta chọn mỗi kích thước của nó bằng bao nhiêu đ diện tích
canh tác lớn nhất?
A.
200 200mm
B.
300 100mm
C.
250 150mm
D.Đáp án khác
Gọi chiều dài và chiều rộng của miếng đất lần lượt là:
()xm
và
( ) ( , 0).y m x y
Diện tích miếng đất:
S xy
Theo đề bài thì:
2( ) 800xy
hay
400yx
. Do đó:
2
(400 ) 400S x x x x
với
0x
Đạo hàm:
'( ) 2 400S x x
. Cho
' 0 200yx
.
Lập bảng biến thiên ta được:
max
40000S
khi
200 200xy
.
Kết luận: Kích thước của miếng đất hình chữ nhật là
200 200
(là hình vuông).
Lưu ý: Có th đánh giá bằng BĐT Cô-Sy.
Câu 11.1 (Kshs). Hai đim M, N thuộc hai nhánh của đồ th
31
3
x
y
x
. Khi đó độ di đoạn thẳng
MN ngắn nhất bằng?
A. 8 B. 4 C.
3
M
x
D.
82
.
Hướng dẫn giải:
Giả sử
3
M
x
,
3
N
x
, khi đó M
8
3 ;3m
m




, N
8
3 ;3n
n




với
,0mn
41
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
M
C
2
2
2 2 2
8 8 1 1 64
( ) (2 ) 64 2 . 4 64MN m n mn mn
m n m n mn




8MN
. Kết luận MN ngắn nhất bằng 8
Câu 11.2 ( Thể tch – mặt cầu – mặt nn – mặt trụ). Tính th tích hình cầu ngoại tiếp tứ diện ABCD,
có cạnh AB =
2
3a
và các cạnh còn lại đều bằng a.
A.
3
13 13
162
a
B.
3
13 13
216
a
C.
3
13 13
648
a
D.
3
13
162
a
.
Hướng dẫn giải:
Gọi
I
l trung đm cạnh
CD
.
Theo đề ta có
AI CD
BI CD
AB
a
BIAI
2
3
,
(1)
A
D
I
ABI
là mp trung trc cạnh
CD
.
Gọi
M
l giao đim của
BI
với mặt cầu
S
ngoại tiếp tứ diện
ABCD
.
Đường tròn lớn của
S
l đường tròn
ABM
. Mặt phẳng
BCD
cắt
S
theo
đường tròn
BCD
qua M, hơn nữa BM là
đường kính.
3
2
60sin
0
aa
BM
Từ (1)
ABI
đều
ABM = 60
0
12
13
60cos.2
022
aBMABBMABAM
B
42
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
6
13
60sin2
0
aAM
R
33
162
1313
3
4
aRV
Câu 11.3 (Mũ – Logarit). S giá tr nguyên của tham s m sao cho bất phương trình:
22
log5 log(x 1) log( 4 )mx x m
nghiệm đúng với mọi x thuộc R?
A. 0 B.
mZ
v
3m
C. 1 D. 2.
Hướng dẫn giải:
Bất phương trình xác đnh với mọi x thuộc R khi
2
40mx x m x R
2
0
0
2
0
40
m
m
m
m



(1)
Bất phương trình nghiệm đúng với mọi x thuộc R khi
22
5 5 4 ,x mx x m x R
2
(5 ) 4 5 0m x x m x R
2
5
50
3
0
10 21 0
m
m
m
mm



(2)
Từ (1) v (2) ta được
23m
,
3m Z m
. Vậy có 1 giá tr m.
Câu 11.4 (Tch phân – ứng dụng). Cho hm s
3
( ) .
(x 1)
x
a
f x b xe
. Biết rằng
'(0) 22f 
v
1
0
( ) 5f x dx
. Khi đó tổng
ab
bằng?
A.
146
13
B.
26
11
C.
26
11
D.
146
13
.
Hướng dẫn giải:
43
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
4
3
'(x) (1 )
(x 1)
'(0) 22 3a b 22 (1)
x
a
f be x
f
1 1 1
3
0 0 0
1
( ) 5 5
(x 1)
5 (2)
4
x
f x dx a dx b xe dx
a
b
Giải hệ (1) v (2) ta được:
108 38
,
13 13
ab
. Vậy chọn đáp án D.
Câu 11.5 (Oxyz). Trong không gian với hệ trục toạ độ Oxyz, cho đim
2;5;3A
v đường thẳng
12
:
2 1 2
x y z
d


. Gọi
󰇛
󰇜
là mặt phẳng chứa đường thẳng sao cho khoảng cách từ đến
󰇛
󰇜
lớn
nhất. Tính khoảng cách từ đim
1;2; 1M
đến mặt phẳng
󰇛
󰇜
?
A.
11 18
18
B.
32
C.
11
18
D.
4
3
Hướng dẫn giải:
Gọi là hình chiếu của trên ; là hình chiếu
của trên
󰇛
󰇜
.
Ta có 
󰇛
󰇜
 󰇛󰉱󰇜
󰉻
󰇛
󰇜


󰇛
󰇜
lớn nhất khi .
Ta có
󰇛
 
󰇜
,
󰇛
󰇜
qua và 
: 4 3 0P x y z
Vậy
11 18
,
18
d M P
.
Câu 11.6 (Số phức). Trong các s phức thỏa điền kiện
4 2 2z i i z
, modun nhỏ nhất của s
phức z bằng?
P
d'
A
K
H
44
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
22
B. 2 C. 1 D.
32
.
Hướng dẫn giải:
Giả sử s phức
,z x yi x y R
Theo đề
4 2 2z i i z
2 2 2 2
(x 2) (y 4) (y 2)
40
4 (1)
x
xy
yx
M
2 2 2 2
(4 x)z x y x
(thay (1) vo)
2
2( 2) 8 2 2x
.
Vậy chọn đáp án A.
Câu 12.1. Trong vật lí, s phân rã của các chất phóng xạ được biu diễn bởi công thức:
0
1
2
t
T
m t m
, trong đó
0
m
là khi lượng ban đầu của chất phóng xạ (tại thời điểm t = 0); T
là chu kì bán rã (tức là khoảng thời gian để một nửa khối lượng chất phóng xạ bị biến thành chất
khác). Chu kì bán rã của Cabon
14
C
l khoảng 5730 năm. Cho trước mẫu Cabon có khi
lượng 100g. Hỏi sau khoảng thời gian t thì khi lượng còn bao nhiêu?
A.
ln2
5730
100.
t
m t e
B.
5730
1
100.
2
mt
C.
100
5730
1
100
2
t
mt
D.
100
5730
100.
t
m t e
Hướng dẫn giải
Theo công thức
0
kt
m t m e
ta có:
.5730
100 ln2
5730 50 100.
2 5730
k
m e k
suy ra
ln2
5730
100
t
m t e
Đáp án: A.
Câu 12.2. Trong vật lí, s phân rã của các chất phóng xạ được biu diễn bởi công thức:
0
1
2
t
T
m t m
, trong đó
0
m
l khi lượng ban đầu của chất phóng xạ (tại thời điểm t = 0); T là chu
45
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
kì bán rã (tức là khoảng thời gian để một nửa khối lượng chất phóng xạ bị biến thành chất khác). Chu kì
bán rã của Cabon
14
C
l khoảng 5730 năm. Người ta tìm được trong một mẫu đồ cổ một lượng
Cabon v xác đnh được nó đã mất khoảng 25% lượng Cabon ban đầu của nó. Hỏi mẫu đồ cổ đó có
tuổi l bao nhiêu?
A. 2378 năm B. 2300 năm C. 2387 năm D. 2400 năm
Hướng dẫn giải
Giả sử khi lượng ban đầu của mẫu đồ cổ chứa Cabon l
0
m
, tại thời đim t tính từ thời
đim ban đầu ta có:
ln2 ln 2
0
5730 5730
00
3
5730 ln
3
4
2378
4 ln2
tt
m
m t m e m e t
(năm)
Đáp án: A.
Câu 12.3. Một nghiên cứu cho thấy một nhóm học sinh được cho xem cùng một danh sách các loi
động vật v được kim tra lại xem họ nhớ bao nhiêu % mỗi tháng. Sau t tháng, khả năng nhớ trung
bình của nhóm học sinh được cho bởi công thức
75 20ln 1 , 0M t t t
(đơn v %). Hỏi sau
khoảng bao lâu thì nhóm học sinh nhớ được danh sách đó dưới 10%?
A. 24.79 tháng B. 23 tháng C. 24 tháng D. 22 tháng
Hướng dẫn giải
Theo công thức tính tỉ lệ % thì cần tìm t thỏa mãn:
75 20ln 1 10 ln 1 3.25 24.79t t t
Đáp án: A.
Câu 12.4. Một công ty vừa tung ra th trường sản phẩm mới vhọ tổ chức quảng cáo trên truyền
hình mỗi ngy. Một nghiên cứu th trường cho thấy, nếu sau x quảng cáo được phát thì s % người
xem mua sản phẩm l
0.015
100
( ) , 0
1 49
x
P x x
e
. Hãy tính s quảng cáo được phát ti thiu đ s
người mua đạt hơn 75%.
A. 333 B. 343 C. 330 D. 323
Hướng dẫn giải
Khi có 100 quảng cáo phát ra thì tỉ lệ người xem mua sản phẩm l:
1.5
100
100 9.3799%
1 49
P
e
Khi có 200 quảng cáo phát ra thì tỉ lệ người xem mua sản phẩm l:
3
100
200 29.0734%
1 49
P
e
Khi có 500 quảng cáo phát ra thì tỉ lệ người xem mua sản phẩm l:
46
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
7.5
100
500 97.3614%
1 49
P
e
Đáp án: A.
Câu 12.5. Ông Năm gửi
320
triệu đồng ở hai ngân hng X v Y theo phương thức lãi kép. S tiền
thứ nhất gửi ở ngân hng X với lãi suất
2,1
một quý trong thời gian
15
tháng. Stiền còn lại gửi
ở ngân hng Y với lãi suất
0,73
một tháng trong thời gian
9
tháng. Tổng lợi tức đạt được ở hai
ngân hàng là
27507 768,13
(chưa lm tròn). Hỏi s tiền ông Năm lần lượt gửi ở ngân hng X v Y l
bao nhiêu?
A.
140
triệu v
180
triệu. B.
180
triệu v
140
triệu.
C.
200
triệu v
120
triệu. D.
120
triệu v
200
triệu.
Hướng dẫn giải
Tổng s tiền cả vn v lãi (lãi chính l lợi tức) ông Năm nhận được từ cả hai ngân hng l
347,507 76813
triệu đồng.
Gọi
x
(triệu đồng) l s tiền gửi ở ngân hng X, khi đó
320 x
(triệu đồng) l s tiền gửi
ở ngân hng Y. Theo giả thiết ta có:
59
(1 0,021) (320 )(1 0,0073) 347,507 76813xx
Ta được
140x
. Vậy ông Năm gửi
140
triệu ở ngân hng X v
180
triệu ở ngân hng Y.
Đáp án: A.
Câu 13.1. Cho hàm s y = - x
3
+ 3mx
2
-3m – 1. Tìm các giá tr của m đ hàm s có cc đại, cc tiu.
Với giá tr nào của m thì đồ th hàm s có đim cc đại, đim cc tiu đi xứng với nhau qua đường
thẳng d: x + 8y – 74 = 0.
Đáp án: m=2
Bài giải:
+ D=R
+ y’ = - 3x
2
+ 6mx ; y’ = 0 x = 0 v x = 2m.
Hàm s có cc đại, cc tiu y’ = 0 có hai nghiệm phân biệt m 0.
Hai đim cc tr là A(0; - 3m - 1) ; B(2m; 4m
3
– 3m – 1)
Trung đim I của đoạn thẳng AB là: I(m ; 2m
3
– 3m – 1)
Vectơ
3
(2 ;4 )AB m m
; Một vectơ chỉ phương của đường thẳng d là
(8; 1)u 
.
47
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Hai đim cc đại , cc tiu A v B đi xứng với nhau qua đường thẳng d
Id
AB d
3
8(2 3 1) 74 0
.0
m m m
ABu
m = 2
Câu 13.2. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC l tam giác đều cạnh a, th tích khi lăng trụ
bằng
3
3
4
a
. Tính khoảng cách giữa hai đường thẳng AA’ v BC’.
Đáp án:
21
7
a
Bài giải:
3
. ' ' '
. ' ' '
2
3
4
'. '
3
4
ABC A B C
ABC A B C ABC
ABC
a
V
V AA S AA a
S
a
Do AA’ // BB’ nên AA’ // (BB’C’C)
Suy ra: d(AA’,BC’)=d(AA’,(BB’C’C))=d(A,(BB’C’C))
Hạ
AM BC
và
'BC AA
. Suy ra:
' ' ' ' 'BC BCC B A AM BCC B
Hạ
' ' 'AH A M AH BCC B
Do đó, d(A,(BB’C’C))=AH
Ta có:
2 2 2 2 2 2
1 1 1 1 4 7 21
' 3 3 7
a
AH
AH AM A A a a a
Câu 13.3. Tìm m đ phương trình
16 3.4 2 1 0
xx
m
(1) có hai nghiệm phân biệt
Đáp án:
51
82
m

Bài giải:
Đặt:
4 , 0
x
tt
, phương trình trở thành:
2
3 2 1 0t t m
(2)
Phương trình (1) có hai nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm dương
phân biệt
5
0 9 4( 2 1) 0
5 8 0
8
0 3 0
1
1
0 1 2 0
2
2
m
m
m
S
m
m
Pm



48
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 13.4. Tính diện tích hình phẳng giới hạn bởi hai đường cong
1 ; 1
x
y e x y e x
Xét phương trình:
0
1 1 0
1
xx
x
e x e x x e e
x
Vậy diện tích cần tìm là:
1
0
1
2
x
e
S x e e dx
Câu 13.5. Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình:
2 2 2
2 6 4 2 0x y z x y z
. Viết phương trình mặt phẳng (P) song song với giá của véc tơ
(1;6;2)v
, vuông góc với mặt phẳng
( ): 4 11 0x y z
và tiếp xúc với (S).
Đáp án: Vậy: (P):
2 2 3 0x y z
hoặc (P):
2 2 21 0x y z
Bài giải:
(S) có tâm I(1; –3; 2) và bán kính R = 4. VTPT của
()
là
(1;4;1)n
.
VTPT của (P) là:
, (2; 1;2)
P
n n v
PT của (P) có dạng:
2 2 0x y z m
.
Vì (P) tiếp xúc với (S) nên
( ,( )) 4d I P
21
3
m
m

.
Vậy: (P):
2 2 3 0x y z
hoặc (P):
2 2 21 0x y z
.
Câu 13.6. Phương trình
4
1
1
1
z
z



có bao nhiêu nghiệm.
Đáp án: 3 nghiệm
Bài giải:
2
4
2
1,(1)
1
1,(2)
zi
zi
zi
zi
zi
zi











1
10
0
1
zi
z i z i i i
zi
z
z i z i z i z
zi




(loại)
49
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
(2)
11
11
zi
i
z i iz z
zi
z i z i iz z
i
zi




Vậy nghiệm phương trình l: z=0, z=1, z=-1.
Câu 14.1. Đ hàm s
2
y x m x m
đồng biến trên khoảng (1;2) thì giá tr của m phải là
A.
2.m
B.
3.m
C.
2 3.m
D. Với mọi m.
Hướng dẫn giải :
Vì
2
12
' 3 2 3 ; ' 0 0
3
m
y x mx x x m y x x
Vì hệ s a < 0 nên
12
2
0 1 2 3
3
m
x x m
nên chọn B
Câu 14.2. Cho hình chóp
.S ABCD
có đáy
ABCD
l hình vuông cạnh
a
. Mặt bên
SAB
l tam giác đều
v vuông góc với đáy. Gọi
M
là đim thuộc cạnh
SC
sao cho
2.SM MC
Tính th tích hình chóp
.M ABC
.
A.
3
a3
6
B.
3
a3
36
C.
3
a3
18
D.
3
3
24
a
Hướng dẫn giải :
Ta có: (SAB)
(ABCD)
(SAB)
(ABCD) = AB
SH
(SAB)
SH
AB ( l đường cao của
SAB đều)
Suy ra: SH
(ABCD)
Tính: SH =
a3
2
(vì
SAB đều cạnh a)
50
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
SABCD = a
2
Tính: VS.ABCD =
1
3
Bh =
1
3
SABCD.SH=
3
a3
6
. . .
1 1 3
3 6 36
M ABC S ABC S ABCD
a
V V V
Câu 14.3. Hàm s
2
21y x x m
có tập xác đnh là khi:
A.
1m 
hoặc
0m
B.
0m
C.
0m
D.
03m
Hướng dẫn giải :
Điều kiện:
2
2 1 0 ' 0 1 ( 1) 0 0x x m x R m m
Câu 14.4. Cho biết tích phân
42
2
1
..
2 ln
4
e
a e be c
I x x x dx

với
,,abc
l các ước nguyên của 4. Tổng
?abc
A. 2 B. 4 C. 3 D. 1
Hướng dẫn giải :
23
1 1 1
2 ln 2 ln
e e e
I x x x dx x dx x xdx
.
3 4 4
1
1
11
21
22
e
e
x dx x e
Ta có
2
2 2 2 2
11
1 1 1 1 1
ln ln
11
2 2 2 4
ee
ee
e
x xdx x x x dx e x
x








2 4 2
24
1
1 1 2e 1
2 ln 1
2 4 4
e
ee
I x x x dx e
Câu 14.5. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba đim
0;2;0 , 1;1;4AB
và
3; 2;1C
. Mặt
cầu
S
tâm
I
đi qua
,,A B C
v độ dài
5OI
(biết tâm
I
có honh độ nguyên,
O
là gc tọa độ). Bán
kính mặt cầu
S
là
51
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
1R
B.
3R
C.
4R
D.
5R
Hướng dẫn giải :
Phương trình mặt cầu (S) có dạng:
2 2 2
2 2 2 0x y z ax by cz d
Vì
4
đim
,,,O A B C
thuộc mặt cầu (S) nên ta có hệ:
( ) 4 4 0
( ) 2 2 8 18 0
( ) 6 4 2 14 0
A S b d
B S a b c d
C S a b c d





2 2 2 2
5 5 5OI OI a b c
Suy ra
1; 0; 2; 4 3a b c d R
Nên chọn đáp án B
Câu 14.6. S phức
, ( , )z a bi a b
thỏa
2
(2 3 ) 5 2i z i z i
. Tính
ab
?
A.
5
3
B.
7
4
C.
3
4
D.
11
12
Hướng dẫn giải :
, ( , )z a bi a b
2
(2 3 ) 5 2
2 2 3 3 5 2
3 2 (3 3 5) 0
i a bi i a bi i
a bi ai b i a bi
a b b a i
3
3 2 0
4
3 3 5 0 11
12
a
ab
ba
b


Vậy phần thc của z là
3
4
a
và phần ảo là
11
.
12
b
Chọn đáp án A.
Câu 15.1 (Kshs). Cho hàm số:
2
1
x
yC
x
. Tìm
a
sao cho từ A(0,
a
) kẻ được hai tiếp tuyến đến
(C) nằm ở hai phía trục Ox.
52
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
2
;
3




B.
2; \ 1 
C.
2; 
D.
2
; \ 1
3




Hướng dẫn giải :
Đường thẳng qua A(0,
a
) có hệ s góc k có phương trình
y kx a
tiếp xúc (C)
<=>
2
1
x
kx a
x

có nghiệm kép <=>
12kx a x x
có nghiệm kép
<=>
2
1 2 0kx k a x a
có nghiệm kép
2
0
1 4 2 0
k
k a k a

2
2
0
( ) 2 5 1 0
k
h k k a k a

có 2 nghiệm
k
phân biệt
2
12 2 0
2; \ 1 1
(0) 1 0
a
a
ha
 
Khi đó
11
11
1
22
22
2
11
22
11
22
k a k a
xy
k
k a k a
xy
k


Mà
1 2 1 2
2
1 2 1 2
0 1 1 0
1 1 4 3 2 0
2
2
3
y y k a k a
k k a k k a a
a



Từ (1) và (2)
2
; \ 1
3
a

 


Đáp án: D
Câu 15.2.
Cho hình chóp S.ABCD có đáy ABCD l hình vuông cạnh a, cạnh bên SA = a, hình chiếu vuông góc
của đỉnh S trên mặt phẳng (ABCD) l đim H thuộc đoạn AC,
4
AC
AH
. Gọi CM l đường cao của
tam giác SAC. Tính th tích khi tứ diện SMBC theo a.
3
14
48
a
3
14
24
a
3
14
16
a
3
14
8
a
53
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Hướng dẫn giải :
Gọi O là tâm của hình vuông ABCD.
Ta có:
2
.2
.
4
2
a
a
AM AH AH AC a
AM
AC SA SA a

2
2
22
7
2
22
aa
MC AC AM a




2
1 1 7 7
.
2 2 2 2 8
SMC
a a a
S SM MC
23
1 1 2 7 14
.
3 3 2 8 48
SMAC SMC
a a a
V BO S
Đáp án: A.
H
O
D
C
B
A
S
M
Câu 15.3.
Tìm s nghiệm của phương trình:
2
2
2 1 1
log 2 1 log 2 1 4 1
xx
x x x

.
A. 0
B. 1
C. 2
D. 3
Hướng dẫn giải :
Điều kiện:
1
2
1
x
x
2
1
1
1
log 2 1
1 2log 2 1 4
log 2 1
x
x
x
xx
x
x


11
1
1
log 2 1 log 1
2log 2 1 4
log 2 1
xx
x
x
xx
x
x


1
1
1
1 2log 2 1 4 3
log 2 1
x
x
x
x

Đặt
1
log 2 1
x
tx

, khi đó (3)
2
1
1
2 3 0 2 3 1 0
1
2
t
t t t
t
t
  
1
1
log 2 1 1
2
1 2 1
5
1
1 2 1
log 2 1
4
2
x
x
x
x
xx
x
xx
x

 

Đáp án: C
54
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 15.4. Tính tích phân:
2
4
2
2
1 tan tan
n
x
n
I e x x dx
A.
2
2
4
n
n
I e e

B.
2
4
n
Ie
C.
2n
Ie
D.
21
2
4
n
n
I e e

Hướng dẫn giải :
2 2 2
4 4 4
22
2 2 2
11
tan tan
cos cos
n n n
x x x
n n n
I e x dx e dx e xdx
xx



22
44
22
tan tan
nn
xx
nn
I e d x e xdx






22
44
2
4
2
22
.tan .tan tan
nn
n
x x x
n
nn
I e x e xdx e xdx





22
44
2
.tan
nn
x
n
I e x e




Đáp án: B
Câu 15.5. Cho hai đim A(-1, 3, -2); B(-9, 4, 9) và mặt phẳng (P): 2x-y+z+1=0. Đim M thuộc (P). Tính
GTNN của AM + BM.
A.
6 204
B.
7274 31434
6
C.
2004 726
3
D.
3 26
Hướng dẫn giải :
Ta có: (2.(-1)-3+(-2)+1)(2.(-9)-4+9+1)=72 > 0 => A,B nằm cùng phía so với mặt phẳng (P).
Gọi A’ l đim đi xứng của A qua (P). Mặt phẳng (P) có vtpt
2, 1,1n
Đường thẳng AA’ đi qua A(-1, 3, -2) có vtcp
2, 1,1n
có pt:
12
3
2
xt
yt
zt

Gọi H là giao của AA’ v (P) ta có: 2(-1+2t) - (3-t) + (-2 + t) + 1 =0 => t=1 => H(1, 2, -1).
Ta có H l trung đim của AA’ => A’(3, 1, 0).
55
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Đường A’B đi qua A’(3, 1, 0) có vtcp
' 12,3,9AB
có pt:
34
1
3
xt
yt
zt


Gọi N là giao đim của A’B v mặt phẳng (P) ta có :
2.(3-4t) – (1+t) + 3t +1 =0 => t=1 => N(-1, 2, 3).
Đ MA+MB nhỏ nhất thì
MN
khi đó MA+MB = A’B =
2
22
12 3 9 234 3 26
Đáp án D.
Câu 15.6. Cho s phức
8
1
n
zi
A.
4
2
n
B.
0
C.
8
2
n
D.
4
2
n
Hướng dẫn giải :
Ta có
1 2 cos sin
44
ii




8
4
2 cos sin 2 . cos2 sin2
44
n
n
z i n i n









4
2
n
Đáp án A.
Câu 16.1. Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta mun cắt một hình thang như hình
vẽ. Tìm tổng x + y đ diện tích hình thang EFGH đạt giá tr nhỏ nhất.
y cm
x cm
3cm
2 cm
A
D
C
B
E
F
H
G
A. 7 B. 5 C.
72
2
D.
42
.
Hướng dẫn giải: Ta có
EFGH
S
nhỏ nhất
AEH CGF DGH
S S S S
lớn nhất.
Tính được
2 2 3 (6 )(6 y) xy 4x 3y 36S x y x
(1)
56
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Mặt khác
AEH
đồng dạng
CGF
nên
6
AE AH
xy
CG CF
(2)
Từ (1) và (2) suy ra
18
2 42 (4x )S
x
. Ta có 2S lớn nhất khi và chỉ khi
18
4x
x
nhỏ nhất.
Biu thức
18
4x
x
nhỏ nhất
18 3 2
4 2 2
2
x x y
x
. Vậy đáp án cần chọn là C.
Câu 16.2. (Mũ v lôgarit) Người ta thả một lá bèo vào một hồ nước. Kinh nghiệm cho thấy sau 9 giờ
bèo sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, lượng lá bèo tăng gấp 10 lần lượng lá bèo trước
đó v tc độ tăng không đổi. Hỏi sau mấy giờ thì s lá bèo phủ kín
1
3
cái hồ ?
A. 3 B.
9
10
3
C. 9 – log3 D.
9
log3
.
Hướng dẫn giải: Gọi t là thời gian các lá bèo phủ kín
1
3
cái hồ. Vì tc độ tăng không đổi nên, 1 giờ
tăng gấp 10 lần nên ta có
9
1
10 10 9 log3
3
t
t
. Đáp án cần chọn là C.
Câu 16.3. (Tích phân và ứng dụng) Một vật chuyn động với vận tc v(t) (m/s) có gia tc
2
( ) 3a t t t
(m/s
2
). Vận tc ban đầu của vật là 2 (m/s). Hỏi vận tc của vật sau 2s .
A. 10 m/s B. 12 m/s C. 16 m/s D. 8 m/s.
Hướng dẫn giải: Ta có
2
23
(t) ( )dt (3t t)dt
2
t
v a t t C

(m/s).
Vận tc ban đầu của vật là 2 (m/s)
(0) 2 C 2v
.
Vậy vận tc của vật sau 2s là:
2
3
2
(2) 2 2 12
2
V
(m/s).
Đáp án B.
Câu 16.4. (Hình học không gian) Cho tứ diện
, , ,ABCD M N P
lần lượt thuộc
,,BC BD AC
sao cho
4 , 2 ,BC BM BD BN
3AC AP
, mặt phẳng (MNP) cắt AD tại Q. Tính tỷ s th tích hai phần
khi tứ diện ABCD b chia bởi mặt phẳng (MNP).
57
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
K
Q
H
I
B
C
D
A
M
N
P
A.
2
3
B.
7
13
C.
5
13
D.
1
3
.
Hướng dẫn giải: Gọi
,I MN CD Q PI AD
, kẻ
/ / , / /DH BC H IM DK AC K IP
1
3
ID DH BM
NMB NDH
IC CM CM
1 1 2
3 2 3 3
IK DK ID DK DK
IP CP IC AP AP
APQ
đồng dạng
DKQ
33
25
AQ AP AQ
DQ DK AD
Đặt
ABCD
VV
Ta có:
1 1 1
.,
5 2 10
ANPQ
ANCD DACN
ANPQ
ANCD ABCD DABC
V
VV
AP AQ DN
VV
V AC AD V V DB
.
1 1 1 1 1
.
2 2 2 2 4
CDMP
CDMP N ABMP DABMP CDMP
CDBA
V
CM CP
V V V V V V V
V CB CA
.
77
20 13
ABMNQP
ABMNQP ANPQ N ABMP
CDMNQP
V
V V V V
V
Vậy mặt phẳng
MNP
chia khi chóp thành hai phần với tỉ lệ th tích
7
13
. Đáp án B.
Câu 16.5. (Hình giải tích 12) Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) có
phương trình 2x – y + z + 1 = 0 v hai đim M(3; 1; 0), N(- 9; 4; 9). Tìm đim I(a; b; c) thuộc mặt
phẳng (P) sao cho
IM IN
đạt giá tr lớn nhất. Biết a, b, c thỏa mãn điều kiện:
A.
21abc
B.
14abc
C.
5abc
D.
19.abc
Hướng dẫn giải: Nhận thấy 2 đim M, N nằm về hai phía của mặt phẳng (P).
Gọi R là đim đi xứng của M qua mặt phẳng (P), khi đó đường thẳng MR đi qua đim M(3; 1; 0) và
vuông góc với mặt phẳng (P) có phương trình:
31
2 1 1
x y z

. Gọi
(P) (1;2; 1) ( 1;3; 2)H MR H R
.
58
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Ta có
IM IN IR IN RN
. Đẳng thức xảy ra khi I, N, R thẳng hng. Do đó tọa độ đim I là giao
đim của đường thẳng NR:
18
3
2 11
xt
yt
zt

(t là tham s ) và mặt phẳng (P). Dễ dng tìm được I(7; 2;
13). Vậy đáp án cần tìm là A.
Câu 16.6. (S phức). Tìm s phức Z có mô đun lớn nhất và thỏa mãn điều kiện
13
1 3 2
2
Z i i
.
A.
3 15
44
zi
B.
15
44
zi
C.
3 15
44
zi
D.
15
44
zi
Hướng dẫn giải: Gọi
( , )z x yi x y R z x yi
22
13 39
(1 ) 3 2 5 0
28
z i i x y x y
Gọi M (x;y) l đim biu diễn của z trong mặt phẳng tọa độ Oxy
()MC
l đường tròn có tâm
15
( ; )
22
I
và bán kính
26
4
R
Gọi d l đường thẳng đi qua O v I
:5d y x
. M1, M2 l hai giao đim của d và (C)
1
3 15
( ; )
44
M
và
2
15
( ; )
44
M
Ta thấy
12
1
( ( ))
OM OM
OM OI R OM M C
s phức cần tìm ứng với đim biu diễn M1 hay
3 15
44
zi
. Đáp án cần chọn là A.
Câu 16.7 . Một đại lý xăng dầu cần làm một cái bồn chứa dầu hình trụ bằng tôn có th tích
3
16 m
.
Tìm bán kính đáy r của hình trụ sao cho hình trụ được làm ra ít tn nguyên vật liệu nhất.
A.
0,8m
B.
1,2m
C.
2m
D.
2,4m
Hướng dẫn giải :
Gọi
()xm
l bán kính đáy của hình trụ
( 0)x
. Ta có:
2
2
16
.V x h h
r
59
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Diện tích toàn phần của hình trụ là: S(x) =
22
32
( ) 2 2 . 2 ,( 0)S x x x h x x
x
Khi đó: S’(x) =
2
32
'( ) 4S x x
x
, cho
'( ) 0 2S x x
Lập bảng biến thiên, ta thấy diện tích đạt giá tr nhỏ nhất khi
2( )xm
nghĩa l bán kính l
2( ).m
Câu 17.1 (Kshs). Trên sân bay một máy bay cất cánh trên đường băng d (từ trái sang phải) và bắt
đầu rời mặt đất tại đim O. Gọi (P) là mặt phẳng vuông góc với mặt đất và cắt mặt đất theo giao
tuyến l đường băng d của máy bay. Dọc theo đường băng d cách v trí máy bay cất cánh O một
khoảng 300(m) về phía bên phải có 1 người quan sát A. Biết máy bay chuyền động trong mặt phẳng
(P) v độ cao y của máy bay xác đnh bởi phương trình
2
yx
(với x l độ dời của máy bay dọc theo
đường thẳng d và tính từ O). Khoảng cách ngắn nhất từ người A (đứng c đnh) đến máy bay là:
A.
300( )m
B.
100. 5( )m
C.
200( )m
D.
100 3( )m
Hướng dẫn giải :
Xét hệ trục Oxy với gc tọa độ O là v trí máy bay rời mặt đất, trục Ox trùng với đường thẳng d và
chiều dương hướng sang phải, trục Oy vuông góc với mặt đất.
Gọi
2
( ; ) ( 0)B t t t
là tọa độ của máy bay trong hệ Oxy. Tọa độ của người A là
(3;0)A
.
Khoảng cách từ người A đến máy bay B bằng
24
(3 ) d t t
. Suy ra
2 4 2
6 9 . d t t t f t
3
'( ) 4 2 6.
'( ) 0 1.
f t t t
f t t
Lập bảng biến thiên, ta thấy
2
()d f t
đạt giá tr nhỏ nhất bằng 5 khi
1t
. Vậy khoảng cách nhỏ
nhất là
100 5( )m
Câu 17.2. (Thể tích – mặt cầu-mặt nón – mặt trụ
60
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Cho hình chóp S.ABCD có SA vuông góc với đáy,
6SA a
. Đáy ABCD l hình thang vuông tại A
và B,
1
.
2
AB BC AD a
Gọi E l trung đim của AD. Tính bán kính mặt cầu ngoại tiếp hình chóp
S.ECD.
A.
2
.
2
a
R
B.
6.Ra
C.
30
.
3
a
R
D.
26
.
2
a
R
Hướng dẫn giải:
.
a
a
R
R
x
K
H
E
A
D
B
C
S
I
Gọi H l trung đim của CD v d l đường thẳng qua H và vuông góc với đáy. Gọi I và R là tâm và
bán kính mặt cầu ngoại tiếp S.CDE. Suy ra I thuộc d. Đặt
.IH x
Trong mp(ASIH) kẻ đường thẳng qua I và song song với AH cắt AS tại K.
Ta có:
2
2 2 2 2
.
2
a
ID IH HD x
2
2 2 2 2 2 2 2 2 2 2
IS 2 ( 6 )
2
a
IK KS AH KS AC CH KS a a x
Suy ra:
22
2 2 2
26
2 ( 6 ) .
2 2 3
a a a
x a a x x
Vậy bán kính mặt cầu bằng
30
.
3
a
R
Câu 17.3. (Mũ – Logarit)
61
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Một bà mẹ Việt Nam anh hùng được hưởng s tiền là 4 triệu đồng trên một tháng (chuyn vào tại
khoản của mẹ ở ngân hng vo đầu tháng). Từ tháng 1 năm 2016 mẹ không đi rút tiền m đ lại
ngân hng v được tính lãi suất 1% trên một tháng. Đến đầu tháng 12 năm 2016 mẹ rút toàn bộ s
tiền (gồm s tiền của tháng 12 và s tiền đã gửi từ tháng 1). Hỏi khi đó mẹ lĩnh về bao nhiêu tiền?
(Kết quả lm tròn theo đơn v nghìn đồng).
A. 50 triệu 730 nghìn đồng B. 48 triệu 480 nghìn đồng
C. 53 triệu 760 nghìn đồng D. 50 triệu 640 nghìn đồng
Hướng dẫn giải :
S tiền tháng 1 mẹ được nhận là 4 triệu, gửi đến đầu tháng 12 (được 11 kỳ hạn), vậy cả vn lẫn lãi
do s tiền tháng 1 nhận sinh ra là:
11 11
1
4.(1 ) 4 1,01
100
(triệu đồng).
Tương t s tiền tháng 2 nhận sẽ sinh ra:
10
4 1,01
(triệu đồng)
......................................................
S tiền tháng 12 mẹ lĩnh luôn nên l: 4 (triệu đồng).
Vậy tổng s tiền mẹ lĩnh l:
12
11 10
1 1,01
4 1,01 4 1,01 ... 4 1,01 4 4 50,730
1 1,01
(50 triệu 730
nghìn đồng). Đáp án A.
Câu 17.4. (Tích phân - Ứng dụng)
Cho một vật th bằng gỗ có dạng khi trụ với bán kính đáy bằng R. Cắt khi trụ bởi một mặt phẳng
có giao tuyến với đáy l một đường kính của đáy v tạo với đáy góc
0
45
. Th tích của khi gỗ bé là:
A.
3
2
.
3
R
V
B.
3
.
6
R
V
C.
3
.
3
R
V
D.
3
.
3
R
V
Hướng dẫn giải
62
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Chọn hệ trục Oxy như hình vẽ. Cắt khi gỗ bé bởi các mặt phẳng vuông góc với Ox tại đim có
honh độ x ta được thiết diện l tam giác vuông có diện tích bằng
22
1
()
2
A x R x
. Vậy th tích
khi gỗ bé bằng:
3
22
12
.
23
R
R
R
V R x
Đáp án A.
Câu 17.5. (Oxyz)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
( ): 1 0P x y z
v hai đim
(1; 3;0), 5; 1; 2AB
. M là một đim trên mặt phẳng
()P
. Giá tr lớn nhất của
T MA MB
là:
A.
2 5.T
B.
2 6.T
C.
46
.
2
T
D.
23
.
3
T
Hướng dẫn giải :
Ta có: A, B nằm khác phía so với (P). Gọi B’ l đim đi xứng với B qua (P). Suy ra
'( 1; 3;4)B 
.
' ' 2 5.T MA MB MA MB AB
Đẳng thức xảy ra khi M, A, B’ thẳng hàng.
Đáp án A.
Câu 17.6. (Số phức)
S nghiệm phức của phương trình :
25
86zi
z
là?
A. 0 B. 1 C. 2 D. 4
Hướng dẫn giải :
Giả sử z = a +bi với ; a,b R v a,b không đồng thời bằng 0.
y
x
O
22
Rx
22
Rx
63
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Khi đó
22
11
;
a bi
z a bi
z a bi a b

Khi đó phương trình
22
25 25( )
8 6 8 6
a bi
z i a bi i
z a b
2 2 2 2
2 2 2 2
( 25) 8( ) (1)
(2)
( 25) 6( )
a a b a b
b a b a b
. Lấy (1) chia (2) theo vế ta có
3
4
ba
thế vào (1)
Ta có a = 0 v a = 4
Với a = 0 b = 0 ( Loại)
Với a = 4 b = 3 . Ta có s phức z = 4 + 3i.
Đáp án B.
Câu 18.1. Một ngọn hải đăng đặt tại v trí
A
có khoảng cách đến bờ bin
5
AB km
.Trên bờ bin có
một cái kho ở v trí
C
cách
B
một khoảng
7
km
.Người canh hải đăng có th
chèo đò từ
A
đến
M
trên bờ binvới vận tc
4/
km h
rồi đi bộ
đến
C
với vận tc
6/
km h
.V trí của đim
M
cách B một
khoảng bao nhiêu đ người đó đi đến kho nhanh nhất?
A.
0km
B.
7km
C.
25km
D.
14 5 5
km
12
Hướng dẫn giải :
Đặt
( ) 7 ( )BM x km MC x km
,(0 7)x
.
Ta có:
Thời gian chèo đò từ
A
đến
M
là:
2
25
( ).
4
AM
x
th
Thời gian đi bộ đi bộ đến
C
là:
7
()
6
MC
x
th
Thời gian từ
A
đến kho
2
25 7
46
xx
t


Khi đó:
2
1
6
4 25
x
t
x

, cho
0 2 5tx
Lập bảng biến thiên, ta thấy thời gian đến kho nhanh nhất khi
2 5( ).x km
64
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 18.2.
Một cửa hàng nhận làm những chiếc xô bằng nhôm hình trụ không nắp chứa 10 lít nước. Hỏi bán
kính đáy (đơn v cm, lm tròn đến hàng phần chục) của chiếc xô bằng bao nhiêu đ cửa hàng tn ít
vật liệu nhất.
A. 14,7cm. B. 15cm.
C. 15,2cm. D. 14cm.
Hướng dẫn giải :
. Gọi x(cm) l bán kính đáy của chiếc xô. x > 0
. khi đó
2
2
V
V x h h
x
. Đ tiết kiện vật liệu thì diện tích toàn phần của chiếc xô bé nhất
. Ta có: 1lít = 1dm
3
= 1000cm
3
.
. Diện tích toàn phần của chiếc xô là
2
20000
Sx
x

.
3
22
20000 2 20000
2.
x
Sx
xx
.
3
10
0 10 14,2 .S x cm
. Lập bảng biến thiên, ta thấy diện tích toàn phần của chiếc xô bé nhất khi
14,2x cm
Câu 18.3. Huyện A có 100 000 người. Với mức tăng dân s bình quân 1,5% năm thì sau n năm dân
s sẽ vượt lên 130 000 người. Hỏi n nhỏ nhất là bao nhiêu?
A. 18 năm B. 17 năm C. 19 năm D. 16 năm
Hướng dẫn giải :
. áp dụng công thức
1
100
1 log
100
n
n
n
r
S
r
S A n
A









. trong đó A = 100 000; r = 1,5; Sn = 130 000
.
17,6218n
65
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 18.4. Cho đường cong
:C y x
. Gọi (H) là hình phẳng giới hạn bởi (C), trục tung v đường
thẳng
y = m (m > 0). Cho (H) quay xung quanh trục tung ta được một vật th tròn xoay có th tích
32
5
V
(đvtt). Khi đó giá tr của m là:
A. m = 1 B. m = 2 C. m = 3 D. m = 4
Hướng dẫn giải :
.
55
24
00
0
.
55
m
mm
ym
V x dy y dy

. Kết hợp giả thiết ta được
2.m
Câu 18.5.
Trong không gian với hệ toạ độ
Oxyz
, gọi
là mặt phẳng qua hai đim
2;0;1A
và
2;0;5B
đồng thời hợp với mặt phẳng
Oxz
một góc
0
45
. Khoảng cách từ
O
tới
là:
A.
.
3
2
B.
3
.
2
C.
1
.
2
D.
2
.
2
Hướng dẫn giải :
45
0
H
K
O
Gọi
;KH
lần lượt là hình chiếu vuông góc đim
O
lên đường thẳng
AB
và mặt phẳng
.
Ta có:
,A B Oxz
Oxz AB
66
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
OH
HK AB
OK AB
OK AB

,,Oxz KH OK OKH
Suy ra tam giác
OHK
vuông cân tại
H
Khi đó:
,.
2
OK
d O OH

Mặt khác:
3
,.
2
OA AB
OK d O AB
AB
Khi đó:
3
,.
2
2
OK
d O OH
Câu 18.6. S phức có đim biu diễn ở phần tô đậm trong hình vẽ sau là:
A.
12z
và phần ảo lớn hơn
1
.
2
B.
12z
và phần ảo lớn hơn
1
.
2
C.
12z
và phần ảo nhỏ hơn
1
.
2
D.
12z
và phần ảo nhỏ hơn
1
.
2
Hướng dẫn giải :
. phần ảo của z nhỏ hơn hoặc bằng
1
2
,
12z
67
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 19.1 (Kshs). Cho hàm s
24
1
x
y
x
có đồ thi
C
đim
( 5;5)A
. Tìm
m
đ đường thẳng
y x m
cắt đồ th
C
tại hai đim phân biệt
M
và
N
sao cho tứ giác
OAMN
là hình bình hành
(
O
là gc toạ độ).
A.
0m
B.
0; 2mm
C.
2m
D.
2m
Hướng dẫn giải :
Do các đim
O
và
A
thuộc đường thẳng
: yx
nên đ
OAMN
là hình bình hành thì
52MN OA
Honh độ của
M
và
N
là nghiệm của pt:
2
24
(3 ) ( 4) 0 ( 1) (1)
1
x
x m x m x m x
x
Vì
2
2 25 0,m m m
,nên
1
luôn có hai nghiệm phân biệt ,
d
luôn cắt
C
tại hai đim phân
biệt
Giả sử
12
,xx
là nghiệm của
1
ta có:
12
12
3
( 4)
x x m
x x m
Gọi
2 2 2 2
1 1 2 2 1 2 1 2 1 2
( ; ), ( ; ) 2( ) 2 ( ) 4 2 4 50M x x m N x x m MN x x x x x x m m


2
2
5 2 2 4 50 50
0
m
MN m m
m
+
0m
thì
, , ,O A M N
thẳng hàng nên không thoã mãn.
+
2m
thoã mãn.
Câu 19.2. (Thể tích – mặt cầu-mặt nón – mặt trụ).....
Làm 1 m
2
mặt nón cần : 120 lá nón ( Đã qua sơ chế) .Giá 100 lá nón l 25.000 đồng . Vậy đ làm 100
cái nón có chu vi vành nón là 120 cm, và khoảng từ đỉnh nón tới 1 đim trên vành nón là 25 cm thì
cần bao nhiêu tiền mua lá nón?
A. 400.000đ B. 450.000đ C.500.000đ D. 550.000đ
Hướng dẫn giải :
Làm 100 cái nón hết 450.000 đ tiền để mua lá nón.
68
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 19.3. (Mũ - Logarit)
Hệ phương trình
2
2
2007
1
2007
1
x
y
y
e
y
x
e
x


có bao nhiêu nghiệm thỏa mãn x > 0, y > 0.
A. 0 B. 1 C.2 D.3
Hướng dẫn giải :
Dùng tính hàm s đ chỉ ra x = y khi đó xét hm s
2
2007
1
x
x
f x e
x
.
Nếu x < 1 thì
02007
1
exf
suy ra hệ phương trình vô nghiệm.
Nếu x > 1 dùng đnh lý Rôn và chỉ ra với x0 = 2 thì f(2) < 0 đ suy ra phương trình có 2 nghiệm thỏa
mãn
Câu 19.4. (Tích phân - Ứng dụng )
Một ô tô chạy với vận tc 20m/s thì người lái xe đạp phanh còn được gọi l “thắng”. Sau khi đạp
phanh, ô tô chuyn động chậm dần đều với vận tc
( ) 40 20( / ).v t t m s
Trong đó t l khoảng thời
gian tính bằng giây k từ lúc bắt đầu đạp phanh . Quãng đường ô tô di chuyn từ lúc đạp phanh
đến khi dừng hẳn là bao nhiêu?
A. 2m B.3m C.4m D. 5m
Hướng dẫn giải :
Lấy mc thời gian là lúc ô tô bắt đầu phanh (t = 0)
Gọi T là thời đim ô tô dừng lại. Khi đó vận tc lúc dừng là v(T) = 0
Vậy thời gian từ lúc đạp phanh đến lúc dừng là
1
( ) 0 40 20 0
2
v T T T
Gọi s(t) l quãng đường ô tô đi được trong khoảng thời gian T.
Ta có
( ) '( )v t s t
suy ra s(t) là nguyên hàm của v(t)
Vây trong ½ (s) ô tô đi được quãng đường là :
1/2
1
2
2
0
0
( ) ( 40 20) ( 20 20 ) 5( )
T
t
v t dt t dt t t m

69
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 19.5. (Oxyz)
Trong không gian với hệ tọa độ Oxyz, cho hai đim A(1;5;0), B(3;3;6) v đường thẳng
có phương
trình tham s
1 2 ; 1 ; 2 x t y t z t
. Một đim M thay đổi trên đường thẳng
, xác đnh v trí
của đim M đ chu vi tam giác MAB đạt giá tr nhỏ nhất.
A. M(1 ;0 ;2) B. M(-1 ;0 ; 2) C. M (1 ;0 ; -2) D. M (-1 ; 0 ; -2)
Hướng dẫn giải :
Gọi P là chu vi của tam giác MAB thì P = AB + AM + BM.
Vì AB không đổi nên P nhỏ nhất khi và chỉ khi AM + BM nhỏ nhất.
Đim
M
nên
1 2 ;1 ;2 M t t t
.
2 2 2 2
(3 ) (2 5) (3 6) (2 5) AM BM t t
Trong mặt phẳng tọa độ Oxy, ta xét hai vectơ
3 ;2 5ut
và
3 6;2 5 vt
.
Ta có
2
2
2
2
| | 3 2 5
| | 3 6 2 5

ut
vt
| | | | AM BM u v
và
6;4 5 | | 2 29 u v u v
Mặt khác, ta luôn có
| | | | | | u v u v
Như vậy
2 29AM BM
Đẳng thức xảy ra khi và chỉ khi
,uv
cùng hướng
3 2 5
1
36
25

t
t
t
1;0;2 M
và
min 2 29AM BM
. Vậy khi M(1;0;2) thì minP =
2 11 29
Câu 19.6. (Số phức)..................................................................
Tìm s phức z biết z thỏa mãn phương trình
z
z2
z

A. 1 B. 1+i C.1-i D. i
Hướng dẫn giải :
22
22
2 2 2
z
z 2 z z.z 2z
z
a bi a b 2(a bi)
(a a b ) bi 2a 2bi
a1
z1
b0
a a b 2a a a 0
b 2b b 0
a0
z 0(loai)
b0







.
70
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
.
Câu 20.1 (Kshs). Một máy tính được lập trình đ vẽ một chuỗi các hình chữ nhật ở góc phần tư thứ
nhất của trục tọa độ Oxy , nội tiếp dưới đường cong y=e
-x
. Hỏi diện tích lớn nhất của hình chữ nhật
có th được vẽ bằng cách lập trình trên
A. 0,3679 ( đvdt) B. 0,3976 (đvdt)
C. 0,1353
( đvdt) D 0,5313
( đvdt)
Hướng dẫn giải :
Diện tích hình chữ nhật tại đim x là
S=xe
-x
'( ) (1 )
x
S x e x

'( ) 0 1S x x
Da vào bảng biến thiên ta có Smax =
1
0,3679e
khi x=1
Đáp án A
Câu 20.2. (Thể tích – mặt cầu-mặt nón – mặt trụ)
71
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Cho hình trụ nội tiếp trong hình cầu bán kính R. Xác đnh chiều cao v bán kính đáy đ hình trụ có
th tích lớn nhất.
A. B. C. D.
Hướng dẫn giải :
.Gọi h là chiều cao của hình trụ , r l bán kính đáy của hình trụ . Ta có
2 2 2
()
2
h
rR
.Th tích của hình trụ là
3
22
..
4
h
V r h R h
.Xét hàm
3
22
( ) . .
4
h
V h r h R h
2
3
'( )
4
V h R h

'( ) 0Vh
khi
23
3
R
h
Từ bảng biến thiên ta có tại
23
3
R
h
thì V(h) đạt giá tr lớn nhất .Suy ra
6
3
rR
Câu 20.3. (Mũ - Logarit)
Cho biết chu kỳ bán rã của chất phóng xạ Plutoni Pu
239
l 24360 năm . S phân hủy được tính theo
công thức
.
rt
S Ae
. Trong đó A l s lượng chất phóng xạ ban đầu, r là tỷ lệ phân hủy hằng năm
(r<0) ,t là thời gian phân hủy, S l lượng còn lại sau thời gian phân hủy t. Hỏi 10 gam Pu
239
sau bao
nhiêu năm phân hủy sẽ còn 1 gam
A. 80922 năm B. 24360 năm C.35144 năm D. 48720 năm
Hướng dẫn giải :
. Theo giả thiết ta có
24360. 24360.
1
22
rr
A
Ae e
Với A=10 gam, gọi t là thời gian phân hủy đ còn lại S=1gam ta có phương trình
72
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
24360. .
24360
1 10 0,1
t
r
rt
ee
80922t
( năm).
.
Câu 20.4. (Tích phân - Ứng dụng )
Cho Elip (E) có phương trình
2
2
1
4
x
y
Hãy tính diện tích hình phẳng giới hạn bởi (E) đã cho
A. π B. 2π C.
4
D.
2
Hướng dẫn giải :
.Diện tích hình phẳng H là
22
2
2
11
4 1 2 4
4
x
S dx x dx

Đặt :
2sin
2cos
00
2
2
xt
dx tdt
xt
xt
.Vậy:
2 2 2
22
0 0 0
2
2
0
0
2 4 sin 2cos 8 cos cos 8 cos
sin2
4 (1 cos2 ) 4( ) 2
2
S t tdt t tdt tdt
t
t dt t
.Chọn đáp án B
Câu 20.5. (Oxyz)
73
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Cho hình chóp O.ABC có OA=a , OB=b, OC=c đôi một vuông góc với nhau . Đim M c đnh thuộc
tam giác ABC có khoảng các lần lượt đến các mặt phẳng (OBC) , (OCA), (OAB) là 1,2,3 . Khi tồn tại
a,b,c thỏa th tích khi chóp O.ABC nhỏ nhất, giá tr nhỏ nhất của th tích khi chóp O.ABC là
A. 18 B. 27
C. 6 D. Không tồn tại a,b,c thỏa yêu cầu bài toán
Hướng dẫn giải :
.Chọn hệ trục tọa độ thỏa
O(0,0,0) , A(a,0,0), B(0,b,0) , C(0,0,c)
Đim M c đnh thuộc tam giác ABC có khoảng các lần lượt đến các mặt phẳng (OBC) , (OCA),
(OAB) là 1,2,3 nên tọa độ đim M là (1,2,3)
.Phương trình mặt phẳng (ABC) là
1
x y z
a b c
Vì M thuộc mặt phẳng (ABC) nên
1 2 3
1
abc
.VOABC=
1
6
abc
Áp dụng bất đẳng thức Cauchy ta có
3
1 2 3 1 1 1 1
1 3 . . 27
6
abc
a b c a b c
Chọn đáp án B
Câu 20.6. (Số phức)
Một hình vuông tâm là gc tọa độ O, các cạnh song song với các trục tọa độ v có độ dài bằng 4.
Hãy xác đnh điều kiện của a v b đ đim biu diễn s phức z=a+bi nằm trên đường chéo của hình
vuông
A.
2ab
B.
2ab
C.
2ab
D.
2ab
Hướng dẫn giải :
Vì đim biu diễn s phức z nằm trên đường chéo của hình vuông nên
74
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
22a
;
22b
và
ab
ab

Vậy điều kiện là
2ab
Chọn đáp án C.
Câu 21.1 (Kshs). Có một tấm gỗ hình vuông cạnh 200 cm. Cắt một tấm gỗ có hình tam giác vuông,
có tổng của một cạnh góc vuông và cạnh huyền bằng hằng s
120cm
từ tấm gỗ trên sao cho tấm gỗ
hình tam giác vuông có diện tích lớn nhất. Hỏi cạnh huyền của tấm gỗ này là bao nhiêu?
A.
40cm
. B.
40 3cm
. C.
80cm
. D.
40 2cm
.
Hướng dẫn giải :
Kí hiệu cạnh góc vuông
,0 60 AB x x
Khi đó cạnh huyền
120BC x
, cạnh góc vuông kia là
2 2 2
120 240 AC BC AB x
Diện tích tam giác ABC là:
2
1
. 120 240
2
S x x x
. Ta tìm giá trị lớn nhất của hàm số này trên khoảng
0;60
Ta có
2
22
1 1 240 14400 360
, 120 240 . ' 0 40
22
2 120 240 2 120 240


x
S x x x S x x
xx
Lập bảng biến thiên :
Lập bảng biến thiên ta có:
x
0
40
60
S' x
0
Sx
40S
Tam giác ABC có diện tích lớn nhất khi
80BC
Từ đó chọn đáp án C
75
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 21.2. (Thể tích – mặt cầu-mặt nón – mặt trụ)
Một hình trụ có bán kính đáy l R và chiều cao
3R
. Hai đim A và B lần lượt nằm trên hai đường
tròn đáy sao cho góc giữa AB và trục của hình trụ bằng
0
30
.
Tính khoảng cách giữa AB và trục của
hình trụ.
A.
3
3
R
. B.
3
2
R
. C.
33
4
R
. D.
23
3
R
.
Hướng dẫn giải :
Kẻ BB’ // OO’ cắt đường tròn ( O) tại B’
Góc giữa AB và OO’ là góc ABB’
0
30
Hạ OH vuông góc AB’.
Khoảng cách giữa AB và OO’ bằng khoảng cách giữa OO’ và (ABB’) vì OO’//(ABB’)
Khi đó
'; '; 'd OO AB d OO ABB OH
22
3
'
2
R
AB R OH OA AH
Chọn đáp án B
Câu 21.3. (Mũ - Logarit) Gọi
1
S
là tập nghiệm của bất phương trình
2.2 3.3 6 1 0
x x x
.
Gọi
2
S
là tập nghiệm của bất phương trình
24
x
.
Gọi
3
S
là tập nghiệm của bất phương trình
1
2
log 1 0x
.
Trong các khẳng đnh sau, khẳng đnh no đúng khi nói về mi quan hệ giữa các tập nghiệm
1 2 3
,,S S S
?
76
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
1 3 2
S S S
.
B.
3 2 1
S S S
.
C.
3 1 2
S S S
.
D.
1 2 3
S S S
.
Hướng dẫn giải :
1 1 1
2.2 3.3 6 1 0 2.2 3.3 1 6 2. 3. 1
3 2 6
x x x
x x x x x x
Dùng tính đơn điệu của hàm số suy ra
1
2; S
2
2 4 2 2 2;

x
x x S
13
2
log 1 0 1 1 2 2; x x x S
1 3 2
S S S
Chọn đáp án A.
Câu 21.4. (Tích phân - Ứng dụng )..................................................................
Cho tích phân
3
b
x
x
a
e
C dx
e
trong đó a l nghiệm của phương trình
2
1
22
x
, b là một s dương v
ba
. Gọi
2
2
1
A x dx
. Tìm chữ s hng đơn v của b sao cho
3CA
.
A. 3 B. 2 C.4 D. 5
Hướng dẫn giải :
Giải phương trình
2
1
2 2 0 0
x
xa
Tính tích phân C. Đặt:
2
33
xx
t e t e
2
x
tdt e dx
3
2
2
b
e
t
C dt
t
3
3
2
2
= 2 2 2 3 4
b
b
e
e
b
dt t e
Tính tích phân A ta có
7
3
A
Theo giả thiết
7 11 109 109
3 2 3 4 3. 3 ln 3,305053521
3 2 4 4
b b b
C A e e e b
Chọn đáp án A.
77
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 21.5: ( Oxyz) Trong không gian Oxyz, cho 2 đường thẳng d :
3
2
2

xt
yt
zt
v d’ :
'
5'
2 ' 3 2 5

xt
yt
zt
Viết phương trình mặt phẳng () chứa (d) v tạo với mặt phẳng Oyz một góc nhỏ nhất.
A.
3 2 7 0 x y z
. B.
3 2 7 0 x y z
.
C.
3 2 7 0 x y z
. D.
3 2 7 0 x y z
.
Hướng dẫn giải :
Giả sử (β) :
0 Ax By Cz D
(đk :
2 2 2
0 A B C
), (β) có vtpt là
( ; ; )
n A B C
d
(β)
()
.0

A
na
3 2 0
20
A B D
A B C
22
2

D A C
B A C
cos(( ),( )) cos( , )

Oyz n i
=
2 2 2
( 2)
A
A A C C
TH 1 : A = 0 (không thoả đb hoặc
( ),( )Oyz
không nhỏ nhất)
TH 2 : A ≠ 0 , ta có :
cos(( ),( ))Oyz
=
22
1
1 (1 2) ( )
CC
AA
=
22
1
6 12
( 3) 2. 2 ( )
39
CC
AA
=
2
1
6 12
( 3 )
39

C
A
( ),( )Oyz
nhỏ nhất
cos(( ),( ))Oyz
lớn nhất
2
6
( 3 )
3
C
A
nhỏ nhất
6
30
3

C
A
1 (choïn)
2
3

A
C
nên
1
3
7
3

B
D
78
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Vậy : (β) :
3 2 7 0 x y z
Chọn đáp án D
Câu 21.6. (Số phức)
Trên tập hợp s phức cho phương trình
2
3 1 0 zz
(*). Gọi
1, 2
zz
là nghiệm của phương trình (*).
Tìm môđun của s phức
12
4 2 4
,
nn
zz
w n N
ii
A. 1. B. 2. C.4. D. 6.
Hướng dẫn giải :
.Giải phương trình ta được :
31
22
z = i
hay
31
22
z = i
.Ta có
4 2 4
1; 1
nn
ii
. Khi đó
12
4 2 4
1
nn
zz
wi
ii
, chọn đáp án A
Câu 22.1. (Kshs). Bạn An là một học sinh lớp 12, b bạn là một thợ hàn. B bạn đnh làm một chiếc
thùng hình trụ từ một mảnh tôn có chu vi 120 cm theo cách dưới đây:
Bằng kiến thức đã học em giúp b bạn chọn mảnh tôn đ lm được chiếc thùng có th tích lớn nhất,
khi đó chiều dài, rộng của mảnh tôn lần lượt là:
A.
35 ;25cm cm
B.
40 ;20cm cm
C.
50 ;10cm cm
D.
30 ;30cm cm
Hướng dẫn giải :
Gọi một chiều dài là
x cm
(0 60)x
, khi đó chiều còn lại là
60 x cm
, giả sử quấn cạnh có chiều
dài là x lại thì bán kính đáy l
; 60 .
2
x
r h x
Ta có:
32
2
60
..
4
xx
V r h
Xét hàm s:
32
( ) 60 , 0;60f x x x x
2
0
'( ) 3 120 ; '( ) 0
40
x
f x x x f x
x
79
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Lập bảng biến thiên, ta thấy
32
( ) 60 , 0;60f x x x x
lớn nhất khi x=40. 60-x=20. Khi đó chiều dài là
40 cm; chiều rộng là 20 cm. Chọn đáp án B
Câu 22.2. (Thể tích, tròn xoay) Cho bát diện đều; tính tỷ s giữa th tích khi cầu nội tiếp và th
tích khi cầu ngoại tiếp hình bát diện đều đó.
A.
1
2
B.
1
22
C.
1
3
D.
1
33
Hướng dẫn giải :
.
B
C
D
A
O
S
S'
M
H
Gọi cạnh bát diện đều là a; bát diện đều có các mặt chéo là hình vuông; khi đó độ di các đường
chéo AC=BD=SS’=
2a
. Mặt cầu nội tiếp và ngoại tiếp đều có tâm O, khi đó bán kính mặt cầu ngoại tiếp là
2
22
AC a
R OA
. Bán kính mặt cầu nội tiếp là khoảng cách từ O đến các mặt bên. Hình trên có
22
.SO OM
r OH
SO OM
2
2
2
.
6
22
6
2
22
aa
a
aa
+) Có
1
3
r
R
khi đó tỷ s th tích khi cầu nội tiếp cho khi cầu ngoại tiếp là:
3
3
11
3 3 3
r
R
chọn D
80
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 22.3. (Mũ v lôgarit) Bác B gửi tiết kiệm s tiền ban đầu là 20 triệu đồng theo kỳ hạn 3 tháng
với lãi suất 0,72%/tháng. Sau một năm, bác B rút cả vn lẫn lãi và gửi lại theo kỳ hạn 6 tháng với lãi
suất 0,78%/tháng. Sau khi gửi được đúng một kỳ hạn 6 tháng do gia đình có việc nên bác gửi thêm
một s tháng nữa thì phải rút tiền trước kỳ hạn cả gc lẫn lãi được s tiền l 23263844,9 đồng (chưa
làm tròn). Biết rằng khi rút tiền trước thời hạn lãi suất được tính theo lãi suất không kỳ hạn, tức tính
theo hàng tháng. Trong một s tháng bác gửi thêm lãi suất là:
A. 0,4% B. 0,3% C. 0,5% D. 0,6%
Hướng dẫn giải :
. Gửi được 1 năm coi như gửi được 4 kỳ hạn 3 tháng; thêm một kỳ hạn 6 tháng s tiền khi đó l:
4
20000000. 1 0,72.3 :100 1 0,78.6 : 100
. Giả sử lãi suất không kỳ hạn là A%; gửi thêm B tháng khi đó s tiền là:
4
20000000. 1 0,72.3 :100 1 0,78.6 :100 1 : 10 23263844,90
B
A
. Lưu ý:
15B
v B nguyên dương, nhập máy tính:
4
20000000. 1 0,72.3 :100 1 0,78.6 :100 1 : 10 23263844,90
B
A
thử với
0,3A
rồi thử B từ 1 đến 5,
sau đó lại thử
0,5A
rồi thử B từ 1 đến 5, ... cứ như vậy đến bao giờ kết quả đúng bằng 0 hoặc xấp
xỉ bằng 0 thì chọn.
Kết quả:
0,5; 4AB
chọn C
Câu 22.4. (Tích phân - Ứng dụng ) Một ô tô xuất phát với vận tc
1
2 10 /v t t m s
sau khi đi
được một khoảng thời gian t1 thì bất ngờ gặp chướng ngại vật nên tài xế phanh gấp với vận tc
2
20 4 /v t t m s
v đi thêm một khoảng thời gian t2 nữa thì dừng lại. Biết tổng thời gian từ lúc
xuất phát đến lúc dừng lại là 4 (s). Hỏi xe đã đi được quãng đường bao nhiêu mét.
A. 57 m B. 64 m C. 50 m D. 47 m
Hướng dẫn giải :
. Đến lúc phanh vận tc của xe là: 2t1+10 đó cũng l vận tc khởi đim cho quãng đường đạp phanh;
sau khi đi thêm t2 thì vận tc là 0 nên
1 2 1 2
2 10 20 4 2 5t t t t
. Lại có
12
4tt
lập hệ được t1=3 s; t2=1 s.
. Tổng quãng đường đi được là:
31
00
2 10 20 4 57S x dx x dx m
chọn A
81
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 22.5. (Oxyz) Trong không gian với hệ trục toạ độ Oxyz cho đim
1;1; 2M
v hai đường thẳng
1
2 1 6
1: ; 2 :
1 1 1 2 1 1
yy
x z x z
. Lấy trên
1
đim N và trên
2
đim P sao cho M,N,P thẳng
hàng. Toạ độ trung đim của NP là:
A.
1;1; 3I
B.
1;1; 2I
C.
0;2;3I
D.
2;0; 7I
Hướng dẫn giải :
. Lập phương trình mặt phẳng
; 1 : 2 0M x y
từ đó
2
;1PM
tìm được
2;0; 7P
. Lập phương trình mặt phẳng
; 2 :2 3 3 0M x y z
từ đó
12
;NM
tìm được
0;2;3N
Tìm được
1;1; 2I
chọn đáp án B
Câu 22.6. (Số phức) Gọi
1 2 3 4
; ; ;z z z z
là 4 nghiệm phức của phương trình
42
4 4 0z m z m
. Tìm
tất cả các giá tr m đ
1 2 3 4
6z z z z
.
A.
1m
B.
2m
C.
3m
D.
1m
Hướng dẫn giải :
.
1;2
4 2 2 2
3;4
2
4 4 0 4 0
zi
z m z m z z m
zm
nếu
0m
hoặc
1;2
3;4
2zi
z i m
nếu
0m
. Khi đó
1 2 3 4
6 4 2
1
0
z z z z m
m
m
. hoặc
1 2 3 4
6 4 2
1
0
z z z z m
m
m
Kết hợp lại thì
1m
thoả mãn bài toán. Chọn D
Câu 23.1: Đường dây điện 110KV kéo từ trạm phát (đim A) trong đất liền ra Côn Đảo (đim C).
biết khoảng cách ngắn nhất từ C đến B là 60km, khoảng cách từ A đến B là 100km, mỗi km dây điện
dưới nước chi phí là 5000 USD, chi phí cho mỗi km dây điện trên bờ là 3000 USD. Hỏi đim G cách
A bao nhiêu đ mắc dây điện từ A đến G rồi từ G đến C chi phí ít nhất.
A: 40km B: 45km C: 55km D: 60km
Giải: Gọi BG = x (0<x<100)
100AG x
Ta có
2 2 2
3600GC BC GC x
82
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Chi phi mắc dây điện theo giải thiết là:
2
( ) 3000.(100 ) 5000. 3600f x x x
Khảo sát hm ta được
45x
chọn phương án B
83
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 23.2: Công ty chuyên sản xuất bao bì đng sản phẩm sữa nhận đơn đặt hàng sản xuất hộp
đng sữa có th tích
3
1dm
. Các nhân viên thiết kế phân vân giữa làm hộp đng dạng hình trụ hay
hình hộp chữ nhật đáy hình vuông. Hỏi công ty sẽ làm hộp hình gì đ chi phí nguyên liệu nhỏ nhất.
A: Hình trụ B: Hình hộp chữ nhật đáy hình vuông C: Cả hai
như nhau D: Hình lập phương
Giải:
TH1: Nếu làm hình trụ có bán kính đáy l
()x dm
và chiều cao là
()h dm
Ta có
2
2
1
1V x h h
x
22
3
2
2 2 2 3 2
AM GM
tp
S xh x x
x
5,5
2
()dm
TH2: Nếu làm hình hộp chữ nhật có đáy hình vuông cạnh
()x dm
và cao
()h dm
2
2
1
.1V x h h
x
22
4
4 2 2 6
AM GM
tp
S xh x x
x
Kết luận: Chọn đáp án A
Lời bình: Thc tế các loại thc phẩm, nước ung có loại dùng hình trụ (các loại nước giải khát như
coca, pepsi…) có loại hình hộp (như sữa…). Nếu tính toán chi tiết ta thấy cùng 1 đơn v th tích,
nếu làm hình hộp thì đó sẽ là hình lập phương,nhưng đa s chúng ta thấy các hộp đng sữa là
dạng hình hộp thường (là do đặc tính riêng về chi tiết quảng cáo trên sản phẩm,do cách bảo quản
sữa trong tủ lạnh v đôi khi do tính tiện dụng cầm nắm) vì thế các bài toán về chi phí sản xuất vật
liệu cần phải đi sâu sát hơn vo đời sng, tìm hiu kĩ nhu cầu tiêu dùng,s hài lòng khách hàng. Do
đó nhiều khi cần phải “tn tiền cho vật liệu”.
Câu 23.3: Cô giáo Thảo ra trường xa quê lập nghiệp, đến năm 2014 sau gần 5 năm lm việc tiết kiệm
được x(triệu đồng) v đnh dùng s tiền đó đ mua nh nhưng trên thc tế cô giáo phải cần 1,55x(
triệu đồng). Cô quyết đnh gửi tiết kiệm vào ngân hàng với lãi suất l 6,9% /năm với lãi hàng tháng
nhập gc v cô không rút trước kì hạn. Hỏi năm bao nhiêu cô mua được căn nh đó, biết rằng chủ
nh đó vẫn bán giá như cũ.
A: Năm 2019 B: Năm 2020 C: Năm 2021 D: Năm 2022
Giải: Tiền lãi sau n (năm) tiết kiệm là
.(1 0,069) (1,069) .
nn
n
x x x
Theo giả thiết ta có
1,069
1,55 (1,069) 1,55 log 1,55 6,56
n
n
x x n
Vì
n
do đó sau 7 năm cô giáo Thảo mua được nh,năm đó l 2021, đáp án C
Câu 23.4: Thành ph đnh xây cây cầu bắc ngang con sông dài 500m, biết rằng người ta đnh xây
cầu có 10 nhp cầu hình dạng parabol,mỗi nhp cách nhau 40m,biết 2 bên đầu cầu và giữa mi nhp
84
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
ni người ta xây 1 chân trụ rộng 5m. Bề dày nhp cầu không đổi là 20cm. Biết 1 nhp cầu như hình
vẽ. Hỏi lượng bê tông đ xây các nhp cầu là bao nhiêu (bỏ qua diện tích ct sắt trong mỗi nhp cầu)
A:
3
20m
B:
3
50m
C:
3
40m
D:
3
100m
Giải: Chọn hệ trục tọa độ như hình vẽ với gc O(0;0) là chân cầu (đim tiếp xúc Parabol trên), đỉnh
I(25; 2), đim A(50;0) (đim tiếp xúc Parabol trên với chân đế)
Gọi Parabol trên có phương trình (
1
P
):
22
1
y ax bx c ax bx
(do (P) đi qua O)
22
2
20 1
100 5
y ax bx ax bx
l phương trình parabol dưới
Ta có
1
(P
) đi qua I v A
22
1 1 2
2 4 2 4 1
( ):
625 25 625 25 5
P y x x y x x
Khi đó diện tích mỗi nhp cầu là
1
2SS
với
1
S
là phần giới hạn bởi
12
;yy
trong khoảng
(0;25)
0,2
25
2
0 0,2
2 4 1
2 ( )
625 25 5
()S x x dx dx

2
9,9m
Vì bề dày nhp cầu không đổi nên coi th tích là tích diện tích và bề dày
85
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
3
.0,2 9,9.0,2 1,98V S m
s lượng bê tông cần cho mỗi nhip cầu
3
2m
Vậy 10 nhp cầu 2 bên cần
3
40m
bê tông. Chọn đáp án C
Câu 23.5: Trong không gian với hệ tọa độ Oxyz cho đim A(1 ;2 ;2) ; B(-1 ;2 ;-1) ; C(1 ;6 ;-1) ; D(-
1 ;6 ;2). ABCD là tứ diện gì ?
A : Tứ diện đều B : Tứ diện vuông C: Tứ diện gần đều D : Tứ diện thường
Giải : Ta có
13; 5; 5 13 2AB CD AC BD AD BC ABCD
là tứ diện gần đều. Chọn
C
Câu 23.6 : Cho s phức
1 2 3
4 2 6
; (1 )(1 2 );
13
ii
z z i i z
ii

có đim biu diễn trong mặt phẳng phức
lần lượt là H;I;V. Tìm tọa độ E sao cho HIVE là hình vuông.
A: Đim E(-1;-1) B: Đim E(-1; 1) C: Đim E(1;-1) D: Đim E(1;1)
Giải: Dễ dàng có H(2;-2); I(3;1); V(0;2),
HIV
vuông cân tại I. Đ HIVE là hình vuông thì
( 1; 1)VE IH E
Chọn A
Câu 24.1 (Kshs). Một công ti bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ
với giá 2 000 000 đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê
mỗi căn hộ thêm 100 000 đồng một tháng thì có thêm hai căn hộ b bỏ trng.
Hỏi mun có thu nhập cao nhất, công ti đó phải cho thuê mỗi căn hộ với giá tr bao nhiêu một
tháng? (đồng/tháng)
A. 2 250 000 B. 2 450 000 C. 2 300 000 D. 2 225 000
Hướng dẫn giải:
Gọi
x
(đồng/tháng) là s tiền tăng thêm của giá cho thuê mỗi căn hộ. (
0x
)
Khi đó s căn hộ b bỏ trng là:
2
100 000
x
(căn hộ).
Khi đó, s tiền công ti thu được là:
2
2 000000 50
100000
x
T x x
2
2
100000 000 10
100000
x
x
(đồng/tháng).
Khảo sát hàm s
Tx
trên
0;
.
86
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
'Tx
4
10
100000
x
.
' 0 1000 000 4 0 250000T x x x
.
Bảng biến thiên
x
0 250 000
T’
0
T
Do đó
0
max 250000
x
T x T
.
Vậy đ có thu nhập cao nhất thì s tiền cho thuê một căn hộ mỗi tháng l 2 250 000 đồng.
Đáp án A.
Câu 24.2 (Thể tích – mặt cầu – mặt nón – mặt trụ). Cho hình lăng trụ tam giác đều ABC.A’B’C’, có
cạnh đáy bằng
a
và cạnh bên bằng
2a
. Lấy M, N lần lượt trên cạnh AB’, A’C sao cho
'1
' ' 3
AM A N
AB A C
. Tính th tích V của khi BMNC’C.
A.
3
6
108
a
B.
3
26
27
a
C.
3
36
108
a
D.
3
6
27
a
Hướng dẫn giải:
Gọi G, K lần lượt là tâm các hình chữ nhật ABB’A’ v AA’C’C.
H
K
G
M
N
I
B'
C'
A
C
B
A'
87
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Ta có:
12
' 3 3
AM AM
AB AG
(Do G trung đim AB’).
Xét tam giác ABA’ có AG l trung tuyến và
2
3
AM
AG
. Suy ra
M
là trọng tâm tam giác ABA’. Do đó
BM đi qua trung đim I của AA’.
Ta có:
' 1 ' 2
' 3 ' 3
A N A N
A C A K
(Do K l trung đim A’C).
Xét tam giác AA’C’ có A’K l trung tuyến và
'2
'3
AN
AK
. Suy ra N là trọng tâm của tam giác AA’C’.
Do đó C’N đi qua trung đim I của AA’.
Từ
M
là trọng tâm tam giác ABA’ v N l trọng tâm của tam giác AA’C’. Suy ra:
1
'3
IM IN
IB IC
.
Gọi
12
;VV
lần lượt là th tích các khi chóp IMNC; IBCC’. Ta có:
1
2
1
..
'9
V
IM IN IC
V IB IC IC
Mà
12
V V V
. Suy ra
2
8
9
VV
.
Hạ AH vuông góc với BC tại H thuộc BC. Ta được AH vuông góc với mặt phẳng (BB’C’C). AA’
song song với mặt phẳng
''BB C C
nên khoẳng cách từ I đến mặt phẳng (BB’C’C) bằng khoẳng
cách từ A đến (BB’C’C) v bằng AH.
Ta có:
3
2
a
AH
.
88
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
23
2'
1 1 3 2 6
. ; ' ' . . .
3 3 2 2 12
BCC
a a a
V d I BB C C S
.
Suy ra
3
2
8 2 6
9 27
a
VV
.
Đáp án B.
Câu 24.3 (Mũ - Logarit). Cho ba s dương a, b, c đôi một khác nhau và khác 1. Xét các khẳng đnh
sau:
(I)
22
log log
aa
bc
cb
;
(II)
22
2
1
log log
log
ab
c
bc
a
;
(III) Trong ba s
2 2 2
log ; log ; log
a b c
b c a
c a b
b c a
luôn có ít nhất một s lớn hơn 1.
Khẳng đnh no đúng?
A. Chỉ (I) và (II) B. Chỉ (I) và (III) C. Chỉ (I) D. Cả (I), (II) và (III)
Hướng dẫn giải:
+
22
22
log log log log log log
a a a a a a
bc
b c c b
cb
. Khẳng đnh (I) đúng.
+
22
2
1
log log
log
ab
c
bc
a
2 2 2
log log log 1
a b c
bca
2
log log log 1
a b c
b c a
89
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
2
log 1
a
a
. Khẳng đnh (II) đúng.
+ Theo khẳng đnh (I) ta có:
22
log log
aa
bb
cb
bc
;
22
log log
bb
cc
ac
ca
;
22
log log
cc
aa
ba
ab
.
Suy ra
2 2 2 2 2 2
log .log .log log .log .log 1
a b c a b c
b c a b c a
c a b b c a
b c a c a b
(theo câu b).
Do a, b, c đôi một khác nhau nên các s
;;
a c b a b c
b b c c a a
. Suy ra các s
log ;log ;
ab
bc
ca
bc
log
c
a
b
a
đều khác 1.
Ta cũng có
2 2 2
0a b a c b c
2 2 2
0a bc b ac c ab
.
Suy ra ít nhất một trong ba s
2 2 2
;;a bc b ac c ab
khác 0. Do đó ít nhất một trong ba s
log ;log ; log
a b c
b c a
c a b
b c a
khác
1
.
Khi đó, trong ba s
log ;log ;
ab
bc
ca
bc
log
c
a
b
a
luôn có ít nhất một s khác 1.
Mà
2 2 2
log .log .log 1
a b c
b c a
c a b
b c a
. Do đó khẳng đnh (III) đúng.
Đáp án D.
Câu 24.4 (Tích phân - Ứng dụng). Cho
2
0
cos
n
n
I xdx
,
n
,
2n
. Khẳng đnh no sau đây
đúng?
A.
1
1
nn
n
II
n
B.
2
2
nn
n
II
n
C.
2
1
nn
n
II
n
D.
2
2
nn
II
90
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Hướng dẫn giải:
Với
2
01
0
; cos 1
2
I I xdx
.
Đặt
12
cos 1 cos .sin
nn
u x du n x xdx
.
cosdv xdx
chọn
sinvx
.
Suy ra
22
1 2 2
2
0
00
cos cos .sin 1 cos .sin
n n n
xdx x x n x xdx
2
22
0
1 cos . 1 cos
n
n x x dx
.
22
2
00
1 cos . 1 cos .
nn
n x dx n x dx
.
Do đó
22
2
00
1
cos . cos .
nn
n
x dx x dx
n
.
Đáp án C.
Câu 24.5 (Oxyz). Trong không gian tọa độ Oxyz, cho các phương trình mặt phẳng
2
: 3 5 1 4 20 0, 1;1
m
mx m y mz m
.
Xét các mệnh đề sau:
(I) Với mọi
1;1m
thì các mặt phẳng
m
luôn tiếp xúc với một mặt cầu không đổi.
91
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
(II) Với mọi
0m
thì các mặt phẳng
m
luôn cắt mặt phẳng (Oxz).
(III)
; 5, 1;1
m
d O m
.
Khẳng đnh no sau đây đúng?
A. Chỉ (I) và (II) B. Chỉ (I) và (III) C. Chỉ (II) và (III) D. Cả 3 đều đúng.
Hướng dẫn giải:
+ Ta có
2 2 2
20
20
;4
25
9 25 1 16
m
dO
m m m
, với mọi
1;1m
.
Do đó với mọi m thay đổi trên
1;1
thì các mặt phẳng
m
luôn tiếp xúc với mặt cầu tâm O, bán
kính
4R
. Khẳng đinh (I) đúng.
+ Vectơ pháp tuyến của mặt phẳng
m
là
2
3 ;5 1 ;4n m m m
v vectơ pháp tuyến của mặt
phẳng (Oxz) là
0;1;0j
.
m
cắt (Oxz) khi và chỉ khi
; 0 0n j m
. Khẳng đinh (II) đúng.
+ Khẳng đinh (III) sai.
Đáp án A.
Câu 24.6 (Số phức). Cho hai s phức phân biệt
12
;zz
thỏa điều kiện
12
12
zz
zz
là s ảo. Khẳng đnh
no sau đây l đúng?
A.
12
1; 1zz
B.
12
zz
C.
12
zz
D.
12
zz
92
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Hướng dẫn giải:
1
z
2 1 2
0z z z
.
Thì
12
12
zz
zz
là s ảo
1 2 1 2
1 2 1 2
0
z z z z
z z z z
.
1 2 1 2
12
12
0
z z z z
zz
zz
1 2 1 2 1 2 1
0z z z z z z z z
.
1 1 2 2
20z z z z
1 1 2 2
0z z z z
.
12
0zz
.
Đáp án C.
Câu 25.1. Cho hàm s
32
1
y = x x
2
có đồ th là (C).
Tìm tất cả những đim trên đồ th (C) sao cho hệ s góc của tiếp tuyến với đồ th (C) tại
những đim đó l giá tr lớn nhất của hàm s:
2
4
4x +3
g(x) =
x +1
.
A.
1
;0
2



B.
3
1;
2




;
4 40
;
3 27



C.
2 1 2
;
24





;
2 1 2
;
24





D.
1
;0
2



;
2; 10
Đáp án: B
93
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Hướng dẫn giải:
* Tìm giá tr lớn nhất của hàm s:
2
4
4x +3
g(x) =
x +1
- Đặt t = x
2
, với
t0
ta có hàm s
2
t4 +3
g(t) =
t +1
;
-
22
2
4t 6t +4
g'(t) =
(t +1)

; g’(t) = 0
1
t = 2;t =
2
;
- Ta lại có:
lim ( ) 0
t
gt

;
lim ( ) 0
t
gt

, bảng biến thiên của hàm s:
t

–2
0
1
2

g’(t)
–
0 +
+
0 –
g(t)
0
–1
3
4
0
- Vậy giá tr lớn nhất của hàm s là
(x)g
= 4, đạt được khi
2
2
x 
* Tìm các đim thuộc đồ th (C)
- Ta có: y’ = 3x
2
– x , giả sử đim M0(x0, f(x0))
(C), thì hệ s góc tiếp tuyến của (C) tại M0 l f’(x0)=
2
00
3x x
- Vậy:
2
00
3x x = 4
suy ra x0 = –1; x0 =
4
3
, tung độ tương ứng f(–1) = –
3
2
; f(
4
3
) =
40
27
+ Có hai đim thỏa mãn giải thiết
3
1;
2




;
4 40
;
3 27



.
Câu 25.2. Cho hình chóp S.ABC có đáy ABC l tam giác đều cạnh a, hình chiếu vuông góc của đỉnh
S trên mặt phẳng (ABC) l trung đim cạnh BC. Góc giữa đường thẳng SA và mặt phẳng (ABC)
94
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
bằng 60
0
. Gọi G là trọng tâm tam giác SAC. Bán kính mặt cầu tâm G và tiếp xúc với mặt phẳng
(SAB) là:
A.
13
13
a
B.
13
39
a
C.
3 13
26
a
D.
13
26
a
Đáp án: A
Hướng dẫn giải:
+ Gọi H l trung đim BC
+
( ,( )) 60
o
SA ABC SAH
+
0
33
, tan60
22
aa
AH SH AH
+ Bán kính mặt cầu là:
12
( ,( )) ( ,( )) ( ,( ))
33
R d G SAB d C SAB d H SAB
+ Gọi E là hình chiếu của H trên AB và K là hình chiếu của H trên SE.
Chứng minh: HK (SAB)
+ Tính được:
33
;
4
2 13
aa
HE HK
+
2
3
13
a
R HK
Câu 25.3. Với
0, 1aa
, cho biết :
11
1 log 1 log
;
aa
ut
t a v a


. Chọn khẳng đnh đúng :
A.
1
1 log
a
v
ua
B.
1
1 log
a
t
ua
C.
1
1 log
a
v
ua
D.
1
1 log
a
v
ua
Đáp án: D
G
M
E
H
C
B
A
S
K
95
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Hướng dẫn giải:
Từ giả thiết suy ra:
11
log .log
1 log 1 log
aa
aa
ta
uu


1 log
1 1 1
log .log
1
1 log 1 log log
1
1 log
a
aa
a a a
a
u
va
t t u
u
1
1 log
1
log log 1 log log (1 log ) 1 log
1 log
a
v
a a a a a a
a
v u u u v u u a
v
Câu 25.4. Th tích khi tròn xoay khi cho hình phẳng giới hạn bởi đồ th hàm s
5
1 3 2
x
y
x

, trục
honh v hai đường thẳng
1; 3xx
quay quanh trục hoành là:
A.
5ln2 1
B.
5ln2 1
C.
5ln2 1
D.
5ln2 1
Đáp án: C
Hướng dẫn giải:
+ Th tích khi tròn xoay tạo ra là V =
3
2
1
5
(1 3 2 )
x
dx
x

(1)
+ Đặt t = 1 +
32x
32x
= t – 1
3 + 2x = (t – 1)
2
dx = (t – 1)dt
x = – 1
t = 2 ; x = 3
t = 4
+ V =
4
2
2
2
1 2 8
( 1)
2
tt
t dt
t

=
4
2
2
1 10 8
3
2
t dt
tt



=
4
2
2
18
3 10ln
22
t
tt
t



=
5ln2 1
Chú ý: Học sinh có th sử dụng máy tính đ thử kết quả sau khi xác đnh được (1).
96
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 25.5. Trong không gian với hệ toạ độ Oxyz, cho 2 đường thẳng:
1
2 1 1
:
1 2 3
x y z
,
2
:2
12
xt
yt
zt

và mặt cầu
2 2 2
( ): 2 2 6 5 0S x y z x y z
Viết phương trình mặt phẳng
()
song song với hai đường thẳng
12
,
và cắt mặt cầu (S) theo giao
tuyến l đường tròn (C) có chu vi bằng
2 365
5
.
A.
5 3 4 0; 5 3 10 0x y z x y z
B.
5 3 10 0x y z
C.
5 3 3 511 0; 5 3 3 511 0x y z x y z
D.
5 3 4 0x y z
Đáp án: B
Hướng dẫn giải:
+
1
qua
1
(2; 1;1)M
v có vectơ chỉ phương
1
(1;2; 3)u 
.
2
qua
2
(0;2;1)M
v có vectơ chỉ phương
2
(1; 1;2)u 
.
+ Mặt phẳng () song song với
12
,
nên có vectơ pháp tuyến:
12
, (1; 5; 3)uu


Phương trình mặt phẳng () có dạng:
5 3 0x y z D
+ Mặt cầu (S) có tâm
I(1; 1;3)
và bán kính
4R
.
Gọi r l bán kính đường tròn (C), ta có:
2 365 365
2
55
rr
Khi đó:
22
35
,( )
5
d I R r
4
3
35
10
5
35
D
D
D

+ Phương trình mặt phẳng
( ): 5 3 4 0 (1) hay 5 3 10 0 (2)x y z x y z
.
Vì
12
/ /( ), / /( )


nên M1 và M2 không thuộc
()
loại (1).
97
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Vậy phương trình mặt phẳng () cần tìm là:
5 3 10 0x y z
.
Câu 25.6. Cho s phức z thỏa điều kiện
1z z i
. S phức
23zi
có môđun nhỏ nhất là:
A.
13
22
i

B.
11
22
i
C.
11
22
i

D.
13
22
i
Đáp án:B
Hướng dẫn giải:
+Đặt :
( , )a bi a b R
( 3) ( 2)z a b i
+ Từ
1z z i
1ba
+
2 2 2
2 2 1a b a a
.
+
nhỏ nhất khi
11
22
ab
+ Vậy
11
22
i
.
Câu 26.1 (Kshs).
Tìm diện tích lớn nhất của hình chữ nhật nội tiếp trong nửa đường tròn bán kính
10cm
, biết một
cạnh của hình chữ nhật nằm dọc trên đường kính của đường tròn.
A.
2
80cm
B.
2
100cm
C.
2
160cm
D.
2
200cm
Hướng dẫn giải:
Gọi
()x cm
l độ dài cạnh hình chữ nhật không nằm dọc theo đường kính đường tròn
0 10x
.
Khi đó độ dài cạnh hình chữ nhật nằm dọc trên đường tròn là:
22
2 10 .x cm
Diện tích hình chữ nhật:
22
2 10S x x
Ta có
2
2 2 2 2
22
2
2 10 2.10 4
10
x
S x x
x
98
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
z=17
z=17
y=9
y=9
x=8
x=8
A
B
C
S
J
H
L
K
10 2
thoûa
2
0
10 2
khoâng thoûa
2
x
S
x
10 2
8 40 2 0
2
S x S
. Suy ra
10 2
2
x
l đim cc đại của hàm
Sx
.
Vậy diện tích lớn nhất của hình chữ nhật là:
2
22
10
S 10 2. 10 100
2
cm
Câu 26.2. (Thể tích – mặt cầu-mặt nón – mặt trụ)
Cho hình chóp
.S ABC
có chân đường cao nằm trong tam giác
ABC
; các mặt phẳng
()SAB
,
()SAC
và
()SBC
cùng tạo với mặt phẳng
()ABC
một góc bằng nhau. Biết
25AB
,
17BC
,
26AC
;
đường thẳng
SB
tạo với mặt đáy một góc bằng
45
. Tính th tích
V
của khi chóp
.S ABC
.
A.
680V
B.
408V
C.
578V
D.
600V
Hướng dẫn giải:
Gọi J l chân đường cao của hình chóp S.ABC; H, K và L
lần lượt là hình chiếu của J trên các cạnh AB, BC và CA.
Suy ra,
SHJ
,
SLJ
và
SKJ
lần lượt là góc tạo bởi
mặt phẳng
()ABC
với các mặt phẳng
(S )AB
,
()SBC
và
()SAC
.
Theo giả thiết, ta có
SHJ SLJ SKJ
,
suy ra các tam giác vuông
,SJH SJL
và
SJK
bằng nhau.
Từ đó,
JH JL JK
. Mà J nằm trong tam giác ABC nên J là tâm đường tròn nội tiếp tam giác
ABC.
Áp dụng công thức Hê-rông, ta tính được diện tích của tam giác ABC là
204S
. Kí hiệu
p
là
nửa chu vi tam giác ABC,
r
l bán kính đường tròn nội tiếp của ABC. Ta có
204
6
34
S
r
p
. Đặt
x BH BL
,
y CL CK
,
z AH AK
.
99
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
z
z
y
y
x
x
L
K
H
J
A
B
C
Ta có hệ phương trình
17
25
26
xy
xz
yz
.
Giải ra được
( ; ; ) (8;9;17)x y z
2 2 2 2
6 8 10JB JH BH
.
Ta có
( ,( )) 45SBJ SB ABC
, suy ra SJB là tam giác vuông cân tại J.
10SJ JB
.
Th tích V của khi chóp S.ABC là
1
. 680
3
ABC
V SJ S
Câu 26.3. (Mũ – Logarit)
Tìm tất cả các giá tr thc của tham s
m
đ phương trình
2 2 2
2 1 4
2
log log 3 log 3x x m x
có
nghiệm thuộc
32;
?
A.
1; 3m
. B.
1; 3m
. C.
1; 3m
. D.
3;1m
.
Hướng dẫn giải:
Điều kiện:
0.x
Khi đó phương trình tương đương:
2
2 2 2
log 2 log 3 log 3x x m x
.
Đặt
2
logtx
với
22
32 log log 32 5xx
hay
5.t
Phương trình có dạng
2
2 3 3 *t t m t
.
Khi đó bi toán được phát biu lại l: “Tìm
m
đ phương trình (*) có nghiệm
5t
”
Với
5t
thì
(*) 3 . 1 3 3. 1 3 0t t m t t t m t
1
1 3 0
3
t
t m t m
t
Ta có
14
1.
33
t
tt
Với
44
5 1 1 1 3
3 5 3
t
t
hay
11
1 3 1 3
33
tt
tt
suy ra
1 3.m
Vậy phương trình có nghiệm với
1 3.m
Câu 26.4. (Tích phân - Ứng dụng )
Cho hàm s
32
11
22
33
y x mx x m
có đồ th (C). Tìm
5
0;
6
m
sao cho hình phẳng giới hạn
bởi đồ th (C) v các đường thẳng
0, 2, 0xxy
và có diện tích bằng 4.
100
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
1
4
m
B.
1
3
m
C.
1
2
m
D.
1m
Hướng dẫn giải:
Xét hàm s
32
11
22
33
y x mx x m
trên
0;2
. Ta có
2
22y x mx
,
2
2
2
0
2
x m m
y
x m m
. Do
5
0;
6
m
nên
22
2 0, 0 2 2m m m m
và
15
0 2 0, 2 2 0.
33
y m y m
Ta có bảng biến thiên trong
0;2
x
0
2
2mm
2
y
0
y
0y
2y
Da vào BBT suy ra
0, 0;2yx
Gọi S là diện tích hình phẳng cần tìm. Ta có:
2
32
0
2
32
0
11
4 2 2 4
33
1 1 4 10 1
2 2 4 4
3 3 3 2
S x mx x m dx
m
x mx x m dx m
Câu 26.5. (Oxyz)
Trong không gian tọa độ Oxyz cho đường thẳng
: 1 2
2
xt
d y t
zt
và mp
: 2 2 2 0P x y z
.
Viết phương trình mặt phẳng
R
qua d và tạo với
P
một góc nhỏ nhất .
A.
30x y z
B.
30x y z
C.
30x y z
D.
30x y z
Hướng dẫn giải:
101
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Đường thẳng d là giao tuyến của hai mặt phẳng :
1
2 1 0
12
2 2 0
11
xy
xy
x z x z
.
Do vậy mặt phẳng
R
qua d thì
R
thuộc chùm mặt phẳng:
2 1 2 0x y m x z
.
Hay mp
R
:
2 1 2 0m x y mz m
(*). Mp
R
có
1
2;1; ; 2; 1; 2
P
n m m n
.
Vậy :
1
2 2 2
2
1
2 2 1 2
.
5 5 1 5
cos
3
33
3 2 4 5
2 1 4 1 4 2 1 3
P
P
mm
nn
mm
nn
m m m
Do nhỏ nhất cho nên
cos
lớn nhất khi
1m
.
Vậy thay vào (*) ta có mp
: 3 0R x y z
.
Câu 26.6. (Số phức)
Cho
12
1 ; 1z i z i
. Tìm
3
z
sao cho các đim biu diễn của
1 2 3
,,z z z
tạo thành tam giác
đều.
A.
33
2 1 2 1z i và z i
B.
33
3 1 3 1z i và z i
C.
33
2 1 2 1z i và z i
D.
33
3 1 3 1z i và z i
Hướng dẫn giải:
Đ giải bài toán này ta cần chú ý đến kiến thức sau:
Giả sử
1 1 1
;M x y
biu diễn s phức
1 1 1
z x y i
Giả sử
2 2 2
;M x y
biu diễn s phức
2 2 2
z x y i
Khi đó khoảng cách giữa hai đim
12
MM
bằng môđun của s phức
12
zz
.
Vậy
22
1 2 1 2 1 2 1 2
M M z z x x y y
Áp dụng vào bài toán: Giả sử
3
z x yi
102
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Đ các đim biu diễn của
1 2 3
,,z z z
tạo thành một tam giác đều thì
1 2 1 3
1 2 2 3
z z z z
z z z z
22
22
22
4 4 1 1
1 1 8
0
4 4 1 1
xy
xy
xy
xy
2
2 6 3 3y y x
Vậy có hai s phức thoả mãn là:
33
3 1 3 1z i và z i
.
Câu 27.1 (Kshs) Cho hàm s
42
y x 2mx 1 m
. Đnh m đ đồ th hàm s trên có ba đim cc tr
nhận gc tọa độ làm trc tâm.
A.
1
B. 0 C. 1 D. 2
Hướng dẫn giải :
.
3
y' 4x 4mx
, với
m0
thì đồ th hàm s có ba cc tr là:
A 0,1 m
,
2
B m,1 m m
,
2
C m,1 m m
.
. ycbt
32
OB.AC 0 m m m m 1 0 m 0 m 0 m 1
. Vậy đáp án l C.
Câu 27.2. (Th tích – mặt cầu-mặt nón – mặt trụ) Có một miếng nhôm hình vuông, cạnh là 3dm,
một người d tính tạo thành các hình trụ (không đáy ) theo hai cách sau:
Cách 1: gò hai mép hình vuông đ thành mặt xung quanh của một hình trụ, gọi th tích là của khi
trụ đó l V1
Cách 2: cắt hình vuông ra làm ba, và gò thành mặt xung quanh của ba hình trụ, gọi tổng th tích của
chúng là V2.
103
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Khi đó, tỉ s
1
2
V
V
là:
A. 3 B. 2 C.
1
2
D.
1
3
Hướng dẫn giải :
.Gọi R1 l bán kính đáy của khi trụ thứ nhất, có
11
3
2 R 3 R
2
2
11
27
V R h
4
. Gọi R1 l bán kính đáy của khi trụ thứ nhất, có
21
1
2 R 1 R
2
2
21
9
V 3 R h
4
Vậy đáp án l A.
Câu 27.3. (Mũ - Logarit) Một người nọ đem gửi tiết kiệm ở một ngân hàng với lãi suất l 12% năm.
Biết rằng cứ sau mỗi một quý ( 3 tháng ) thì lãi sẽ được cộng dồn vào vn gc. Hỏi sau ti thiu bao
nhiêu năm thì người đó nhận lại được s tiền ( bao gồm cả vn lẫn lãi ) gấp ba lần s tiền ban đầu.
A. 8 B. 9 C. 10 D. 11
Hướng dẫn giải : Gọi s tiền người đó gửi là A, lãi suất mỗi quý là 0,03
.Sau n quý, tiền m người đó nhận được là:
n
A 1 0,03
.
.
n
1,03
ycbt A 1 0,03 3A n log 3 37,16
Vậy s năm ti thiu là xấp xỉ 9,29 năm. Vậy đáp án l C.
Câu 27.4. (Tích phân - Ứng dụng ) Có một người cần làm một cái của cổng c xưa, có hình dạng
một parabol bậc hai như hình vẽ. Giả sử đặt cánh cổng vào một hệ trục tọa độ như hình vẽ ( mặt
đất là trục Ox). Hãy tính diện tích của cánh cửa cổng.
104
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
16
3
B.
32
3
C. 16 D.
28
3
Hướng dẫn giải :
.Da vo đồ th , ta xây dng được công thức của hàm s là
2
y 4 x
.
.Diện tích là:
2
2
2
32
S 4 x dx
3
. Vậy đáp án l B.
Câu 27.5. (Oxyz) Trong không gian với hệ trục tọa độ Oxyz, cho bn đim
A 1,2,0
,
B 3, 1,2
,
C 2, 1,1
,
D 0,2, 1
. Có bao nhiêu mặt phẳng cách đều năm đim O, A, B, C, D.
A. 4 B. 5 C. 6 D. 7
Hướng dẫn giải :
.Chứng minh được ABCD là hình bình hành và OABCD là hình chóp tứ giác.
.Vậy có 5 mặt phẳng thỏa bi toán. Đáp án l B.
Câu 27.6. (S phức) Có bao nhiêu đim có tọa độ là s nguyên biu diễn cho s phức z có phần ảo
dương v đông thời thỏa mãn
z z 4
,
z z 6
A. 20 B. 15 C. 6 D. 10
Hướng dẫn giải :
.Gọi
z a bi
,
gt 2a 4 2 a 2
và
2bi 6 3 b 3
. Mà z có phần ảo dương, nên
b0
0 b 3
.
Vậy có 10 đim thỏa mãn. Nên đáp án l D.
Câu 28.1 (Kshs).
Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn v diện tích của
mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng
480 20 .P n n gam
Hỏi
105
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
phải thả bao nhiêu con cá trên một đơn v diện tích của mặt hồ đ sau một vụ thu hoạch được nhiều
cá nhất ?
A.
10
B.
12
C.
16
D.
24
Hướng dẫn giải:
Gọi n là s con cá trên một đơn v diện tích hồ (n>0). Khi đó:
Trên một đơn v diện tích thu được
. 480 20 .n P n n n gam
Xét hàm s
2
480 20 , 0; .f n n n n 
Ta tìm được n = 12 thì lượng cá lớn nhất.
Đáp án B.
Câu 28.2. (Thể tích – mặt cầu-mặt nón – mặt trụ)
Một hình hộp có 6 mặt đều là các hình thoi có góc bằng 60
0
và cạnh bằng a. Tính th tích của hình
hộp đó.
A.
3
2
a
B.
3
2
2
a
C.
3
2
3
a
D.
3
22
3
a
Hướng dẫn giải :
Ta có: AB = AD = BD = a; AA’ = A’B = A’D = a
A’ABCD l tứ diện đều
Chân đường cao A’H trùng với tâm của
ABD
HA = HB = HD =
2
3
AO =
2
3
33
23
aa
A’H2 = AA’2 – AH2 = a
2
-
2
3
9
a
=
2
6
9
a
A’H =
6
3
a
Từ đó tìm được
3
2
2
a
V
Đáp án B.
60
0
60
0
60
0
a
C
O
A'
B'
D'
D
B
A
C'
H
106
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 28.3. (Mũ - Logarit)
Có bao nhiêu giá tr của tham s m đ phương trình
22
5 6 1 6 5
.2 2 2.2
x x x x
mm
có 3
nghiệm phân biệt.
A. 1 B. 2 C. 3 D. 4
Hướng dẫn giải :
2 2 2 2 2
5 6 1 5 6 5 6 1
2 1 2 1 2 2 1 2 0
x x x x x x x x
Pt m m
2
2
2
56
1
1
2
2 2 0
3
2
2 *
xx
x
x
x
x
m
m


TH1: (*) có nghiệm duy nhất ( nghiệm x =0)
2.m
TH2: (*) Có 2 nghiệm phân biệt trong đó có một nghiệm là 2 và nghiệm còn lại khác 3
3
2.m

TH3: (*) Có 2 nghiệm phân biệt trong đó có một nghiệm là 3 và nghiệm còn lại khác 2
8
2.m

Vậy, có 3 giá tr của m thỏa mãn.
Đáp án C.
Câu 28.4. (Tích phân - Ứng dụng )
Trong hệ trục Oxy, cho tam giác OAB vuông ở A, đim B nằm trong góc phn tư thứ nhất. A nằm
trên trục hoành, OB = 2017. Góc
, 0 .
3
AOB




Khi quay tam giác đó quanh trục Ox ta được
khi nón tròn xoay. Th tích của khi nón lớn nhất khi :
A.
6
sin
3
B.
3
cos
2
C.
1
cos
2
D.
2
sin
3
Hướng dẫn giải :
Phương trình đường thẳng
: .tan ; 2017cos .OB y x OA


107
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Khi đó th tích nón tròn xoay là:
2017.cos
33
2 2 2 2
0
2017 . 2017 .
tan . .cos .sin .cos 1 cos .
33
V x dx

Đặt
1
cos 0; .
2
tt



Xét hàm s
2
1
1 , 0;
2
f t t t t



.
Ta tìm được
ft
lớn nhất khi
3 3 6
cos sin .
3 3 3
t

Đáp án A.
Câu 28.5. (Oxyz).
Cho hai đim
1;2;3 , 2;4;4MA
và hai mặt phẳng
: 2 1 0,P x y z
: 2 4 0Q x y z
. Viết phương trình đường thẳng
qua
M
cắt
,P
Q
lần lượt tại
,BC
sao
cho tam giác
ABC
cân tại
A
và nhận
AM
l đường trung tuyến.
A.
1 2 3
:
1 1 1
x y z

B.
1 2 3
:
2 1 1
x y z
C.
1 2 3
:
1 1 1
x y z
D.
1 2 3
:
1 1 1
x y z
Hướng dẫn giải :
Gọi
;;B a b c
, từ giả thiết suy ra
M
l trung đim của
BC
, suy ra
2 ;4 ;6C a b c
.
,B P C Q
nên có hai pt:
2 1 0 1 2 8 0 2 .a b c a b c ;
1; 2; 1 , 2 2 ;4 2 ;6 2 .AM BC a b c
Tam giác
ABC
cân tại
A
nên:
. 0 2 8 0 3 .AM BC a b c
Từ
1 , 2
và
3
có hệ:
2 1 0 0
2 8 0 3 0;3;2 , 2;1;4 .
2 8 0 2
a b c a
a b c b B C
a b c c





Đường thẳng
qua
B
và
C
có pt
1 2 3
:
1 1 1
x y z
.
108
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Đáp án D.
Câu 28.6. (Số phức).
Cho s phức
z
thỏa mãn
1z
và s phức
21
2
z
iz
w
. Khi đó mô đun của s phức
w
là:
A.
w2
B.
1 w 2.
C.
w1
D.
w2
Hướng dẫn giải :
Giả sử
,.z a bi a b
22
1 1.z a b
2
2
2
2
4 2 1
21
.
2
2
ab
z
iz
ba


Xét
2
2
22
2
2
4 2 1
21
1 1 ... 1.
2
2
ab
z
ab
iz
ba


(vô lí)
Nên
1.w
Đáp án C.
Câu 29.1 (Kshs). Một Bác nông dân cần xây dng một h ga không có nắp dạng hình hộp chữ nhật
có th tích
3
3200cm
, tỉ s giữa chiều cao của h và chiều rộng của đáy bằng
2
. Hãy xác đnh diện
tích của đáy h ga đ khi xây tiết kiệm nguyên vật liệu nhất?
A.
2
1200cm
B.
2
160cm
C.
2
1600cm
D.
2
120cm
Hướng dẫn giải :
Gọi
, ( , 0)x y x y
lần lượt l chiều rộng, chiều di của đáy h ga.
Gọi
h
l chiều cao của h ga (
0h
). Ta có
2 2 1
h
hx
x
suy ra th tích của h ga l :
2
3200 1600
3200 2V xyh y
xh
x
Diện tích ton phần của h ga l:
22
6400 1600 8000
2 2 4 4 ( )S xh yh xy x x f x
x x x
109
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Khảo sát hm s
( ), 0y f x x
suy ra diện tích ton phần của h ga nhỏ nhất bằng
2
1200cm
khi
10 16x cm y cm
Suy ra diện tích đáy của h ga l
2
10.16 160cm
Câu 29.2. (Thể tích – mặt cầu-mặt nón – mặt trụ)..................................................................
Cho hình chóp
.S ABCD
có đáy l hình bình hành và có th tích l V . Đim P l trung đim của
SC
, một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N .Gọi
1
V
là th tích của khi chóp
.S AMPN
. Tìm giá tr nhỏ nhất của
1
V
V
?
A.
3
8
B.
1
3
C.
2
3
D.
1
8
Hướng dẫn giải :
Đặt
; ,(0 , 1)
SM SN
x y x y
SD SB
khi đó ta có :
2
SABC SADC SABD SBCD
V
V V V V
Ta có :
1
11
.1
2 2 2 4
SAMPN SAMP SANP SAMP SANP
SADC SABC
V V V V V V
SM SP SN SP
xy
V V V V V SD SC SB SC
Lại có :
1
1 1 3
2
2 2 2 2 4
SAMPN SAMN SMNP
SABD SBCD
V V V V
xy xy xy
V V V V
110
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Từ (1) và (2) suy ra :
13
4 4 3 1
x
x y xy y
x
do
1
0 1 1
3 1 2
x
yx
x
Từ (2) suy ra
2
1
3 3 3 3 1
. . ( ), 1
4 4 3 1 4 2
4 3 1
V
xx
xy x f x x
Vx
x
Khảo sát hm s
1
1
1
2
1 2 4 1
( ), 1 min ( )
2 3 9 3
xx
V
y f x x f x f
V
Câu 29.3. (Mũ - Logarit)..................................................................
Một Bác nông dân vừa bán một con trâu được s tiền l 20.000.000 (đồng) .Do chưa cần dùng đến
s tiền nên Bác nông dân mang toàn bộ s tiền đó đi gửi tiết kiệm loại kỳ hạn 6 tháng vào ngân
hàng với lãi suất 8.5% một năm thì sau 5 năm 8 tháng Bác nông dân nhận được bao nhiêu tiền cả
vn lẫn lãi .Biết rằng Bác nông dân đó không rút cả vn lẫn lãi tất cả các đnh kì trước và nếu rút
trước thời hạn thì ngân hàng trả lãi suất theo loại không kì hạn 0.01% một ngày (1 tháng tính 30
ngày)
A.
31802750 09, ®ång
B.
30802750 09, ®ång
C.
32802750 09, ®ång
D.
33802750 09, ®ång
Hướng dẫn giải :
Một kì hạn 6 tháng có lãi suất là
8.5% 4.25
.6
12 100
. Sau 5 năm 6 tháng (có nghĩa l 66 tháng tức là 11
kỳ hạn) , s tiền cả vn lẫn lãi Bác nôn dân nhận được là :
11
4 25
20000000 1
100
A
.
. (®ång)
.Vì 5 năm
8 tháng thì có 11 kỳ hạn v dư 2 tháng hay dư 60 ngy nên s tiền A được tính lãi suất không kỳ
hạn trong 60 ngày là :
11
0 01 4 25
60 120000 1
100 100
BA
..
. . . (®ång)
. Suy ra sau 5 năm 8 tháng s tiền bác nông dân nhận
được là
11 11
4 25 4 25
20000000 1 120000 1 31802750 09
100 100
C A B
..
. . , ®ång
111
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 29.4. (Tích phân - Ứng dụng )..................................................................
Từ một khúc gõ hình trụ có đường kính 30cm , người ta cắt khúc gỗ bởi một mặt phẳng đi qua
đường kính đáy v nghiêng với đáy một góc
0
45
đ lấy một hình nêm (xem hình minh họa dưới
đây)
Hình 1 Hình 2
Kí hiệu
V
l th tích của hình nêm (Hình 2). Tính
V
.
A.
V cm
3
2250
B.
V cm
3
225
4
C.
V cm
3
1250
D.
V cm
3
1350
Hướng dẫn giải :
Chọn hệ trục tọa độ như hình vẽ .Khi đó hình nêm có đáy
là nửa hình tròn có phương trình :
y x x
2
225 , 15;15


Một một mặt phẳng cắt vuông góc với trục Ox tại đim có honh độ
x
,
x 15;15



cắt hình nêm theo thiết diện có diện tích là
Sx
(xem hình).
Dễ thấy
NP y
và
02
tan 45 15MN NP y x
khi đó
2
11
. . 225
22
S x MN NP x
suy ra
th tích hình nêm là :
15
15
V S x dx
x dx cm
15
23
15
1
. 225 2250
2
Câu 29.5. (Oxyz)..................................................................
112
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
xt
y t t
zt
2
: 1 2
3

hai đim
A 2;0;3
và
B 2; 2; 3
. Biết đim
M x y z
0 0 0
;;
thuộc
thì
MA MB
44
nhỏ nhất .Tìm
x
0
A.
x
0
0
B.
x
0
1
C.
x
0
2
D.
x
0
3
Hướng dẫn giải :
Phương trình đường thẳng AB là :
x
y t t
zt
11
1
2
33


. Dễ thấy đường thẳng
và AB cắt nhau tại
đim
I 2; 1;0
suy ra AB và
đồng phẳng . Lại có
IA IB IA IB IA IB AB0;1;3 , 0; 1; 3
.
Ta có :
MA MB MA MB MA MB AB IA IB
2
2
24
4 4 2 2 4
1 1 1 1 1
2 2 2 8 8



.
Do đó
MA MB
44
nhỏ nhất khi
M
trùng với đim
I 2; 1;0
Câu 29.6. (Số phức)..................................................................
Cho các s phức
z
thỏa mãn
z 12
. Biết rằng tập hợp các đim biu diễn các s phức
w i z1 3 2
l một đường tròn . Tính bán kính
r
của đường tròn đó?
A.
4r
B.
r 2
C.
r 16
D.
r 25
Hướng dẫn giải :
Giả sử
z a bi w x yi a b x y a b
2
2
; ; , , , 1 4
Theo đề
x a b x a b
w i z x yi i z
y b a y b a
2 3 3 1 3
1 3 2 1 3 2
3 3 3 1





113
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
x y a b b a a b
2 2 2
22
2
3 3 1 3 1 3 4 1 16




xy
2
2
3 3 16
suy ra bán kính đường tròn l
r 16 4
.
Cách 2 : Ta có :
w i z w i i z i1 3 2 2 1 3 1 3 1 3
w i z w i i z1 3 2 2 1 3 1 3 1
w i i z3 3 1 3 1 4
.
Câu 30.1: (kshs) Nh Nam có một chiếc bn tròn có bán kính bằng
2
m. Nam mun mắc một
bóng điện ở phía trên vchính giữa chiếc bn sao cho mép bn nhận được nhiều ánh sáng nhất.
Biết rằng cường độ sáng C của bóng điện được biu th bởi công thức
2
sin
Cc
l
(
l góc tạo bởi
tia sáng tới mép bn v mặt bn, c - hằng s tỷ lệ chỉ phụ thuộc vo nguồn sáng, l khoảng cách từ
mép bn tới bóng điện) . Khoảng cách nam cần treo bóng điện tính từ mặt bn l
A. 1m B. 1,2m C. 1.5 m D. 2m
Hướng dẫn giải :
h
l
α
2
M
N
I
Đ
114
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Gọi h l độ cao của bóng điện so với mặt bn (h > 0); Đ l bóng điện; I l hình chiếu của Đ lên mặt
bn. MN l đường kính của mặt bn.( như hình vẽ)
Ta có
sin
h
l
và
22
2hl
, suy ra cường độ sáng l:
2
3
2
( ) ( 2)
l
C l c l
l

.
2
42
6
' . 0 2
.2
l
C l c l
ll
' 0 6 2C l l l
Lập bảng biến thiên ta thu được kết quả C lớn nhất khi
6l
, khi đó
2h
Câu 30.2: (Th tích – mặt cầu-mặt nón – mặt trụ)
Với một miếng tôn hình tròn có bán kính bằng R = 6cm. Người ta mun lm một cái phễu bằng
cách cắt đi một hình quạt của hình tròn ny v gấp phần còn lại thnh hình nón ( Như hình vẽ).
Hình nón có th tích lớn nhất khi người ta cắt cung tròn của hình quạt bằng
A.
6
cm B.
66
cm C.
26
cm D.
86
cm
Hướng dẫn giải :
115
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Gọi x (x>0) l chiều di cung tròn của phần được xếp lm hình nón.
Như vậy, bán kính R của hình tròn sẽ l đường sinh của hình nón v đường tròn đáy của hình nón
sẽ có độ di l x.
Bán kính r của đáy được xác đnh bởi đẳng thức
2
2
x
r x r
.
Chiều cao của hình nón tính theo Đnh lý Pitago l: h =
2
2 2 2
2
4
x
R r R
.
Th tích của khi nón:
2
2
22
2
1
.
3 3 2 4
xx
V r H R




.
Áp dụng Bất đẳng thức Côsi ta có:
3
2 2 2
2
2 2 2 2 2 2 6
2 2 2
22
2 2 2
4 4 4
8 8 4
. . ( ) .
9 8 8 4 9 3 9 27
x x x
R
x x x R
VR






Do đó V lớn nhất khi v chỉ khi
22
2
2
84
xx
R


2
6 6 6
3
x R x
(Lưu ý bi toán có th sử dụng đạo hm đ tìm giá tr lớn nhất, tuy nhiên lời giải bi toán sẽ di
hơn)
Câu 30.3. ( mũ logarit)
r
R
h
M
N
I
S
116
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Tập các giá tr của m đ baapts phương trình
2
2
2
2
log
log 1
x
m
x
nghiệm đúng với mọi x > 0 bằng
A.
( ;1]
B.
[1; )
C.
5;2
D.
[0;3)
Hướng dẫn giải :
Đặt
2
2
t log 1xt
Khi đó ta có
*
1
t
m
t
Bất phương trình ban đầu có nghiệm với mọi x > 0
*
nghiệm đúng với mọi t > 1
Xét hàm s
1
t
ft
t
trên
1; 
3
2
'
1
t
ft
t
' 0 2f t t
lim
t
ft


1
lim
t
ft

BBT
Từ BBT ta có kết luận bất phương trình có nghiệm với mọi t > 1
1m
Câu 30.4. ( tích phân)
Cho hình phẳng giới hạn bởi hai đường
2 2 2 2
: 4; ' : 2 0C x y C x y x
. Diện tích hình phẳng
đó bằng
1
0
+
∞
+
∞
f(t)
f'(t)
t
+
∞
2
1
117
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
B.
2
C.
3
D.
4
Hướng dẫn giải :
Ta có
C
có tâm I (0;0) bán kính R = 2;
'C
có tâm I' (- 1; 0) bán kính R' = 1.
Sử dụng hệ trục tọa độ vẽ 2 đường tròn (C), (C') ta thấy diện tích hình phẳng cần tìm bằng
22
2 1 3S
Lưu ý: có th sử dụng tích phân đ tính nhưng cách lm sẽ dài dòng phức tạp hơn
Câu30. 5. ( tích phân)
Cho parabol (P)
2
yx
v hai đim A, B thuộc (P) sao cho AB = 2. Tìm A, B sao cho diện tích hình
phẳng giới hạn bởi (P) v đường thẳng AB đạt giá tr lớn nhất
A.
4
3
B.
3
4
C.
2
3
D.
3
2
Hướng dẫn giải :
Giả sử
22
; , ,A a a B b b P b a
sao cho AB = 2
Phương trình đường thẳng AB:
y b a x ab
Gọi S là diện tích hình phẳng cần tìm, ta có
3
22
1
| | [ ]
6
bb
aa
S b a x ab x dx b a x ab x dx b a

Vì AB = 2 nên
| b a | b a 2
x
y
1
A
B
118
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
4
3
S
Câu 30.6. (Oxyz) Trong hệ trục tọa độ Oxyz cho 3 đim
;0;0 , 0; ;0 , 0;0;A a B b C c
với
, , 0abc
.Giả sử
,,abc
thay đổi nhưng thỏa mãn
2 2 2 2
a b c k
không đổi. Diện tích tam giác ABC đạt giá
tr lớn nhất bằng
A.
2
3
2
k
B.
2
3
6
k
C.
2
3k
D.
2
k
Hướng dẫn giải :
Phương trình (ABC):
1
x y z
a b c
Gọi
;;H x y z
là hình chiếu vuông góc của O lên
ABC
Khi đó
22
2 2 2
22
2 2 2
22
2 2 2
0
0
ab c
x
ab bc ca
H ABC
bcx cay abz abc
a bc
OH AB ax by y
ab bc ca
OH AC ax cz
abc
z
ab bc ca




2 2 2
abc
OH
ab bc ca


Ta có
11
..
66
OABC
V OAOBOC abc
2 2 2
3
1
2
ABCD
ABC
V
S ab bc ca
OH
Áp dụng bất đẳng thức Cosi ta có
4 4 4 4 4 4
2 2 2 2 2 2 4 4 4
2 2 2
a b b c c a
a b b c c a a b c
Dấu “=” xảy ra khi và chỉ khi
abc
119
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Vậy
42
13
max
2 3 6
kk
S 
Câu 30.7. ( Oxyz)
Trong không gian với hệ toạ độ Oxyz, phương trình mặt phẳng (P) đi qua đim
M
(9;1;1)
, cắt các tia
Ox, Oy, Oz tại A, B, C sao cho th tích tứ diện OABC có giá tr nhỏ nhất là
A.
1
7 3 3
x y z
B.
1
27 3 3
x y z
C.

1
27 3 3
x y z
D.
1
27 3 3
x y z
Giá sử
A a Ox B b Oy C c Oz
( ;0;0) , (0; ;0) , (0;0; )
a b c
( , , 0)
.
Khi đó PT mặt phẳng (P) có dạng:
x y z
a b c
1
.
Ta có:
MP
(9;1;1) ( )
a b c
9 1 1
1
(1);
OABC
V abc
1
6
(2)
(1)
abc bc ac ab
9
≥
abc
2
3
3 9( )
abc abc abc
32
( ) 27.9( ) 243
Dấu "=" xảy ra
a
bc ac ab
b
c
a b c
27
9
3
9 1 1
1
3


(P):
x y z
1
27 3 3
.
Câu 30.8. (s phức)
Trong mặt phẳng phức cho 3 đim A,B,C theo thứ t biu diễn các s
4 2 6
, 1 1 2 ,
13
ii
ii
ii


. S
phức biu diễn bởi đim D sao cho tứ giác ABCD là hình vuông là
A.
1 i
B.
15i
C.
1 i
D.
15i
Hướng dẫn giải :
Ta có
4
2 2 2; 2
1
i
iA
i
1 1 2 3 3;1i i i B
26
2 0;2
3
i
iC
i

120
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Vẽ hệ trục tọa độ biu diễn các đim A, B, C và tọa độ đim D trong các đáp án, dễ dàng kim tra
được tam giác ABC vuông cân tại B và
1; 1D 
thì ABCD là hình vuông.
(có thể ktra bằng phép toán
222
10; 10; 20BC BA CA
2 2 2
BA BC
AC AB BC

ABCD là hình vuông
1; 1 1AB DC D z i
)
Câu 31.1: Cho x và y là hai s thc dương thay đổi sao cho:
22
2 4 0x x y
. Giá tr lớn nhất của
tích xy gần nhất với s nào?
A. 0,5 B. 0,6 C. 0,7 D. 0,8
Giải: Ta có
22
2 4 0x x y
2
1
2
2
y x x
(do
0y
), suy ra
2
1
2
2
xy x x x
Xét hàm s
2
1
( ) 2
2
g x x x x
xác đnh trên
0;2
;
2
2
32
'( )
2
xx
gx
xx
,
'( ) 0gx
3
2
x
Vậy
()gx
cũng l xy đạt giá tr lớn nhất khi
3
2
x
và GTLN của xy là:
2
1 3 3 3 3 3
. 2. 0.64
2 2 2 2 8



Chọn đáp án B.
Câu 31.2: Nếu một tứ diện chỉ có đúng một cạnh có độ dài lớn hơn 1 thì th tích tứ diện đó lớn nhất
là bao nhiêu?
A.
1
4
B.
3
4
C.
1
8
D.
5
8
Giải: Giả sử tứ diện ABCD có cạnh lớn nhất là AB, suy ra các tam giác ACD và BCD có tất cả các
cạnh đều không lớn hơn 1. Các chiều cao AF và BE của chúng không lớn hơn
2
1
4
a
, trong đó
1CD a
.
Chiều cao của hình tứ diện
2
1
4
a
AH AF
121
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
(do tam giác AHF vuông tại H có AF là cạnh huyền)
Th tích của khi tứ diện là:
2
2
D
1 1 1 1 1 1
. . . . . . . . 1 4
3 3 2 3 2 4 24
BC
a
V S AH BE CD AH a a a



Đ tìm giá tr lớn nhất của V ta xét biu thức
2
4aa
.
Vì
01a
nên
2
43aa
và
2
11
4
24 8
V a a
. Chọn đáp án C.
Câu 31.3: Giả sử p và q là các s thc dương sao cho:
9 12 16
log log logp q p q
. Tìm giá tr của
p
q
A.
4
3
B.
8
5
C.
1
13
2
D.
1
15
2
Giải: Đặt:
9 12 16
log log logt p q p q
thì:
9
t
p
,
12
t
q
,
16 9 12
t t t
pq
(1)
Chia hai vế của (1) cho
9
t
ta được:
2
44
1
33
tt

, đặt
4
0
3
t
q
x
p



đưa về phương trình:
2
10xx
1
15
2
x 
do
0x
, suy ra
1
15
2
q
p

. Chọn đáp án D.
Câu 31.4: Cho tích phân
2
2017
32
0
32K x x dx
. Giá tr của K bằng bao nhiêu?
A. 0 B. 1 C. 2 D. 1
Giải: Ta có
3
32
3 2 1 3 1x x x x
Đặt
1tx
dt dx
. Khi
0x
1t 
; Khi
2x
1t
Khi đó
1
2017
3
1
30K t t dt
(do hàm s
2017
3
( ) 3f t t t
là hàm s lẻ trên đoạn
1;1
. Chọn đáp
án A.
122
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 31.5: Trong không gian Oxyz cho 4 đim
2;3;2A
,
6; 1; 2B 
,
1; 4;3C 
,
1;6; 5D
. Gọi M
là một đim nằm trên đường thẳng CD sao cho tam giác MAB có chu vi bé nhất. Khi đó toạ độ đim
M là:
A.
0;1; 1M
B.
2;11; 9M
C.
3;16; 13M
D.
1; 4;3M 
Giải: Tam giác MAB có độ dài cạnh
43AB
không đổi, do đó chu vi bé nhất khi và chỉ khi
MA MB
bé nhất.
4; 4; 4AB
;
2;10; 8CD 
. Vì
.0ABCD
nên
AB CD
, suy ra đim M cần tìm là hình chiếu
vuông góc của A, cũng l hình chiếu vuông góc của B lên đường thẳng CD. Từ đó tìm ra đim
0;1; 1M
. Chọn đáp án A.
Câu 31.6: Cho
2
1i 
, có bao nhiêu s nguyên n sao cho
4
ni
là một s nguyên?
A. 1 B. 2 C. 3 D. 4
Giải: Vì
2
1i 
nên
4
4 2 3
6 1 4 4n i n n n n i
. S này là s thc khi và chỉ khi:
3
4 4 0nn
0n
hoặc
1n 
. Chọn đáp án C.
Câu 32.1.(Kshs) Đường cong hình dưới l đồ th của một trong bn hàm s được cho trong bn
phương án A,B,C v D dưới đây. Hỏi hàm s đó l hm s nào ?
A.
y = x
3
- 3 x
2
+1
. B.
y = -x
4
- x
2
+1
. C.
y = x
3
- 3x
2
+1
. D.
y = x
4
-8x
2
+1
.
Hướng dẫn giải:
123
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
+) Đồ th đi xứng qua trục tung nên loại A.
+) Đồ th đi qua đim (1;-1) loại D.
+) B chỉ có 1 đim cc tr nên loại.
+) Chọn đáp án C.
Câu 32.2.(Hhkg) Cho hình chóp S.ABCD có ABCD là hình vuông cạnh 2a, tam giác SAB đều và nằm
trong mặt phẳng vuông góc với (ABCD). Tính bán kính của mặt cầu ngoại tiếp hình chóp trên.
A.
7
2
a
. B.
a 21
6
. C.
7
4
a
. D.
21
3
a
.
Hướng dẫn giải:
R
(S )
= R
ntSAB
( )
2
+ R
ntABCD
( )
2
-
AB
2
æ
è
ç
ö
ø
÷
2
=
a 21
3
. Chọn đáp án D.
Trong đó:
+)
R
ntSAB
l bán kính đường tròn ngoại tiếp tam giác SAB
+)
R
ntABCD
l bán kính đường tròn ngoại tiếp hình vuông ABCD
+)
(SAB)Ç(ABCD)= AB
Câu 32.3. (Mũ-Logarit).Tập nghiệm của bất phương trình:
22
1 1 1
3 3 3 3
x x x x
.
A.
7
2
a
. B.
a 21
6
. C.
7
4
a
. D.
21
3
a
.
Hướng dẫn giải:
Điều kiện:
1x
.
Ta có:
2 2 2 2
1 1 1 1 1 1
3 3 3 3 3 3.3 3.3 9 0
x x x x x x x x
Û 3
x
2
-3
( )
3
x-1
-3
( )
£ 0
+ Với
1x
: thoả mãn;
+ Với
1x
:
Û 3
x-1
£ 3Û x -1 £ 1Û1£ x £ 2
.
124
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Vậy nghiệm của bất phương trình l:
12x
Chọn đáp án A
Câu 32.4 (Tích Phân) Với giá tr nào của
m
thì diện tích hình phẳng giới hạn bởi parabol
P : y x x
2
2
và
d : y mx m0
bằng 27 đơn v diện tích.
A.
m = -1
. B.
m = -2
. C.
m = Æ
. D.
m Î
.
Hướng dẫn giải:
Phương trình honh độ giao đim
x
x x mx x m x
xm
22
0
2 2 0
20
m
mm
x mx
S x x mx dx x x mx dx x
m m m





2
22
32
2 2 2
00
0
32
22
32
6 12 8 27
Do đó
m 1
. Chọn đáp A.
Câu 32.5.(Oxyz) Trong không gian với hệ tọa độ Oxyz cho mặt phẳng
: 1 0P x y z
và hai
đim
1; 3;0A
,
5; 1; 2B 
. Tìm tọa độ đim M trên mặt phẳng
P
sao cho
MA MB
đạt giá
tr lớn nhất.
A.
M(-2;-3;3)
. B.
M(-2;-3;2)
. C.
M(-2;-3;6)
. D.
M(-2;-3;0)
.
Hướng dẫn giải:
Kim tra thấy
A
và
B
nằm khác phía so với mặt phẳng
P
.
Gọi
' ; ;B x y z
l đim đi xứng với
5; 1; 2B 
Suy ra
' 1; 3;4B 
Lại có
' ' constMA MB MA MB AB
Vậy
MA MB
đạt giá tr lớn nhất khi
, , 'M A B
thẳng hàng hay
M
l giao đim của đường
thẳng
'AB
với mặt phẳng
P
125
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
'AB
có phương trình
1
3
2
xt
y
zt



Tọa độ
;;M x y z
là nghiệm của hệ
13
32
23
1 0 6
x t t
yx
z t y
x y z z







Vậy đim
2; 3;6M 
Chọn đáp án C
Câu 32.6. (Số Phức) Cho các s phức
z ,z ,z ,z ,z
1 2 3 4 5
có đim biu diễn lần lượt là A, B, C, D, E trong
mặt phẳng phức tạo thành một ngũ giác lồi. Gọi M, N, P, Q lần lượt l trung đim các cạnh AB, BC,
CD, DE. Gọi I, J lần lượt l trung đim các đoạn MP và NQ. Biết I, J l đim biu diễn hai s phức
I
z i;1
J
zi 2
và
E
zi45
là s phức có đim biu diễn là E. Tìm s phức
z
1
?
A.
z
1
= 2-3i
. B.
z
1
= 4-7i
. C.
z
1
= 8-7i
. D.
z
1
= 8- 2i
.
Ta có
IJ IQ IN42
Mà
IM IP0
do đó
IQ IN IM MQ IP PN MQ PN
AE BD DB AE
1 1 1
2 2 2
Suy ra
A
A
A
A
x
x
4IJ=AE
y
y



4 0 1 4
8
7
4 2 1 5
.
Chọn đáp án C
Câu 33.1 (Kshs).
Cho hàm s:
4 2 2
2( 2) 5 5y x m x m m
. Với giá tr nào của m thì đồ th hám s có cc đại và
cc tiu, đồng thời các đim này tạo thành một tam giác đều
A.
3
23m 
B.
23
C.
32
D.
3
32
126
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Hướng dẫn giải:
Ta có:
3
' 4 4( 2)y x m x
2
0
'0
2
x
y
xm


Hàm s có CĐ, CT PT
'0fx
có 3 nghiệm phân biệt
2m
(*)
Khi đó toạ độ các đim cc tr là:
2
0, 5 5A m m
,
2 ;1B m m
,
2 ;1C m m
22
2 ; 4 4 ; 2 ; 4 4AB m m m AC m m m
Do ABC luôn cân tại A, nên bài
toán thoả mãn khi
0
1
60 cos
2
AA
3
.
0 2 3
AB AC
m
AB AC
Câu 33.2. (Thể tích cầu-nón-trụ)
Cho hình lăng trụ
. ' ' 'ABC A B C
có đáy
ABC
l tam giác đều cạnh
a
, hình chiếu vuông góc của
'A
lên măt phẳng
ABC
trùng với tâm
G
của tam giác
ABC
. Biết khoảng cách giữa
'AA
và
BC
là
3
4
a
. Tính th tích
V
của khi lăng trụ
. ' ' 'ABC A B C
.
A.
3
3
3
a
V
B.
3
3
6
a
V
C.
3
3
12
a
V
D.
3
3
36
a
V
Hướng dẫn giải:
M
A
B
C
A'
B'
C'
G
K
H
127
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Gọi M l trung đim B
( ' )BC A AM
Gọi H,K lần lượt là hình chiếu vuông góc của G,M trên AA’
Vậy KM l đọan vuông góc chung củaAA’v BC, do đó
3
( A',BC)
4
a
d A KM
.
3
2
KM
AGH AMH
GH
23
36
a
GH KH
AA’G vuông tại G,HG l đường cao,
'
3
a
AG
3
. ' ' '
3
.'
12
ABC A B C ABC
a
V S A G
Câu 33.3. (Mũ - Logarit)
Tìm các giá tr của m đ phương trình:
3 3 5 3
xx
m
có 2 nghiệm phân biệt:
A.
3 5 4m
B.
2 2 4m
C.
2 2 3 5m
22m
Hướng dẫn giải :
ĐK:
3
log 5x
Đặt
( ) 3 3 5 3
xx
fx
với
3
log 5x
3 ln3 5 3 3 3
3 ln3 3 ln3
'( )
2 3 3 2 5 3
2 3 3 5 3
x x x
xx
xx
xx
fx



'( ) 0 5 3 3 3 1
xx
f x x
lim ( ) 3 5
x
fx


Bảng biến thiên:
128
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
x
-∞ 1
3
log 5
f’(x)
+ 0 −
f(x)
4
35
22
Da vo BBT ta có: Đáp án A
Câu 33.4. (Tích phân - Ứng dụng )
Tính tích phân:
2
2
1
1 2 1
3
dx
x x x




ta thu được kết quả là:
ln2ab
với
,ab
. Chọn khẳng
đnh đúng trong các khẳng đnh:
A.
1ab
B.
0a
C.
22
10ab
D.
20ba
Hướng dẫn giải:
Ta có:
2
2
1
1 2 1
3
dx
x x x




=
11
ln 3 2ln 3ln2
2
xx
x



Suy ra:
1
;3
2
ab
chọn đáp án A
Câu 33.5. (Oxyz)
129
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Trong không gian với hệ tọa độ
Oxyz
, cho hai đim
1;5;0A
,
3;3;6B
v đường thẳng
có
phương trình tham s
12
1
2
xt
y t t
zt
. Một đim
M
thay đổi trên đường thẳng
, xác đnh v trí
của đim
M
đ chu vi tam giác
MAB
đạt giá tr nhỏ nhất. Khi đó toạ độ của đim M là:
A.
1;0;2M
B.
2;4;3M
C.
3;2; 2M 
D.
1;4;3M
Hướng dẫn giải:
Gọi
P
là chu vi của tam giác
MAB
thì
P AB AM BM
Vì
AB
không đổi nên
P
nhỏ nhất khi và chỉ khi
AM BM
nhỏ nhất.
Đim
M
nên
1 2 ;1 ;2 M t t t
;
2 2 2 2
(3 ) (2 5) (3 6) (2 5) AM BM t t
Trong mặt phẳng tọa độ
Oxy
, ta xét hai vectơ
3 ;2 5ut
và
3 6;2 5 vt
.
Ta có
2
2
2
2
| | 3 2 5
| | 3 6 2 5

ut
vt
| | | | AM BM u v
và
6;4 5 | | 2 29 u v u v
Mặt khác, ta luôn có
| | | | | | u v u v
Như vậy
2 29AM BM
Đẳng thức xảy ra khi và chỉ khi
,uv
cùng hướng
3 2 5
1
36
25

t
t
t
1;0;2 M
và
min 2 29AM BM
. Vậy khi
1;0;2M
thì
min 2 11 29P 
Câu 33.6. (Số phức)
Trong mặt phẳng tọa độ, tập hợp đim biu din các s phức
z
thỏa mãn
1z i i z
l:
A. Đường tròn có phương trình
22
4 2 1 0x y x y
B. Đường tròn có phương trình
22
2 3 0x y y
C. Đường tròn có phương trình
22
2 1 0x y x
130
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
D. Đường tròn có phương trình
22
2 1 0x y y
Hướng dẫn giải:
Đặt
z x yi
,xy
và
;M x y
l đim biu diễn của
z
trên mặt phẳng
Oxy
ta có:
11z i i z x yi i i x iy
1x y i x y x y i
2 2 2
2
1x y x y x y
2 2 2 2 2 2
2 1 2 2x y y x xy y x xy y
22
2 1 0x y y
Tập hợp đim
M
biu din của s phức
z
l đường tròn có phương trình
22
2 1 0x y y
Vậy chọn D
Câu 34.1 (Kshs). Cho hàm s
y x mx
3
2
có đồ th (Cm) . Tìm m đ đồ th (Cm) cắt trục hoành
tại một đim duy nhất.
A.
3m
B.
3m
C.
3m
D.
3m
Hướng dẫn giải :
S giao đim của đồ th (Cm) với Ox là s nghiệm của phương trình
3
20
x mx
Với m=0 vô nghiệm nên không có giao đim
Với
0m
ta có

m x f x
x
x
f x x x
xx
2
3
22
2
( );(*)
2 2( 1)
'( ) 2 0 1
131
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
M
A
B
C
D
S
N
K
Ta có bảng biến thiên của f(x) như sau:
x

0 1

'( )fx
+ + 0 -
()fx

-3



S nghiệm phương trình (*) l s giao đim của đồ th hm f(x) v đường thẳng y=m.
Da vào bảng biến thiên ta thấy
3m
thì phương trình (*) có 1 nghiệm duy nhất.
Vậy chọn A.
Câu 34.2. (Thể tích – mặt cầu-mặt nón – mặt trụ)
Cho hình chóp đều
.S ABCD
, M l trung đim SA, N, K lần lượt thuộc SB, SC sao cho SB=3SN,
SC=4SK. Hãy chọn đáp án đúng
A.
..
1
8
S MNK S ABC
VV
B.
..
23
48
MNK CBA S ABCD
VV
C.
..
1
12
S MNK S ABD
VV
D. Cả 3 đáp án A, B, C đều sai
Hướng dẫn giải:
Câu 34.3. (Mũ - Logarit) Cho
12
1 1 1
...
log log log
n
b b b
a a a
A
. Biu thức rút gọn của A là:
Áp dụng đnh lý tỷ s th tích ta có

.
.
1
..
24
S MNK
S ABC
V
SM SN SK
V SA SB SC


.
.
.
.
23
24
23
48
MNK ABC
S ABC
MNK ABC
S ABCD
V
V
V
V
Vậy chọn B
132
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A.
2 ( 1)
3.log
b
a
nn
B.
2 (2 1)
log
b
a
nn
C.
( 1)
2.log
b
a
nn
D.
( 2)
3log
b
a
nn
Hướng dẫn giải :
Ta có
12
1 1 1 1
... (1 2 ... )
log log log log
( 1)
2.log
n
b b b b
a a a a
b
a
An
nn
Vậy chọn C
Câu 34.4. (Tích phân - Ứng dụng )
Nếu hàm s f(x) liên tục và là hàm s chẵn trên [-a; a] thì
()
a
a
I f x dx
bằng
A. 0 B.
0
2 ( )
a
f x dx
C.
0
2 ( )
a
f x dx
D.
2 ( )
a
a
f x dx
Hướng dẫn giải :
Ta có
0
1
00
( ) ( ) ( ) ( )
a a a
aa
I f x dx f x dx f x dx I f x dx

Đặt
00
1
0
00
( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( )
aa
aa
a
x t I f x dx f t d t
f t d t f t d t f x d x


0
2 ( ) ( )
a
I f x d x
Vậy chọn B.
Câu 34.5. (Oxyz) Trong hệ trục tọa độ Oxyz cho A(1;2;3).Tìm cặp vecto chỉ phương của mặt (P) đi
qua A và khoảng cách từ O đến (P) là lớn nhất.
A.
1
2
( 3;0;1)
(1;1; 1)
u
u


B.
1
2
( 3;0;1)
(0; 1; 2)
u
u

C.
1
2
( 3;0;1)
(1;0; 1)
u
u


D.
1
2
( 3;0;1)
(2;1;0)
u
u

Hướng dẫn giải :
133
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Khoảng cách từ O đến mặt phẳng (P) lớn nhất khi OA vuông góc với mp(P). Khi đó
(1;2;3)OA
là
vecto pháp tuyến của mp(P).
Ta thấy
( 3;0;1),(1;1; 1) ( 1; 2; 3)
cùng phương với
(1;2;3)OA
nên
( 1; 2; 3)n
cũng l vecto
pháp tuyến của mp(P).
Vậy chọn A.
Câu 34.6. (Số phức)
Kết quả rút gọn của biu thức
4 2017
2016
11ii
P
ii


là:
A. 0 B. i C.1-i D. -1-i
Hướng dẫn giải :
Ta có
4
2017 4 504
11
.( )
i i
i i i i
2
2
2
1 ( 1)
1
i i i
P i i i
ii

. Vậy chọn D
Câu 36.1. Nhà của 3 bạn A, B, C nằm ở 3 v trí tạo thành một tam giác vuông tại B ( như hình vẽ),
AB = 10 km; BC = 25 km và 3 bạn tổ chức họp mặt ở nhà bạn C. Bạn B hẹn chở bạn A tại v trí M trên
đoạn đường BC. Từ nhà, bạn A đi xe buýt đến đim hẹn M với tc độ 30km/h và từ M hai bạn A, B
di chuyn đến nhà bạn C bằng xe máy với tc độ 50km/h. Hỏi đim hẹn M cách nhà bạn B bao
nhiêu km đ bạn A đến nhà bạn C nhanh nhất ?
A. 5 km B. 7,5 km C.10 km D. 12,5 km
Hướng dẫn giải :
C
M
B
A
134
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Đặt BM = x (km),
0x
Thời gian đ bạn A di chuyn từ A đến M rồi đến nhà C là:
2
100 25
30 50
()
xx
tx


(h)
Lập bảng biến thiên, ta tìm được giá tr nhỏ nhất của
()tx
là
23
30
khi
15
2
x
Chọn đáp án B
Câu 36.2.
Cho hình chóp S.ABC có đáy ABC l tam giác đều cạnh bằng a, đường thẳng SA vuông góc
với mặt đáy v SA = 2a. Gọi (P) là mặt phẳng đi qua B v vuông góc với SC.
Khi đó diện tích của thiết diện của hình chóp S.ABC khi cắt bởi mặt phẳng (P) là ?
A.
2
15
10
a
B.
2
15
5
a
C.
2
15
15
a
D.
2
15
20
a
Hướng dẫn giải :
Gọi M l trung đim của AC ; Kẻ BN vuông góc SC tại N
Khi đó: thiết diện cần tìm là tam giác BMN vuông tại M
Ta có:
5
5
MN CM a
CMN CSA MN
SA CS
Vậy: diện tích tam giác BMN bằng
2
15
20
a
Chọn đáp án D
Câu 36.3. Ông A gửi tiết kiệm 100 triệu đồng gửi vào ngân hàng với lãi suất 5% một năm. Ông B
cũng đem 100 triệu đồng gửi vào ngân hàng với lãi suất
5
12
% một tháng. Sau 10 năm, hai ông A v
C
N
B
A
S
M
135
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
B cùng đến ngân hàng rút tiền ra. Khẳng đnh no sau đây l đúng ? ( Lưu ý: tiền lãi được tính theo
công thức lãi kép v được lm tròn đến hàng hàng triệu)
A. S tiền của hai ông A, B khi rút ra l như nhau.
B. Ông B có s tiền nhiều hơn ông A l 1 triệu.
C. Ông B có s tiền nhiều hơn ông A l 2 triệu.
D. Ông B có s tiền nhiều hơn ông A l 3 triệu.
Hướng dẫn giải :
Sau 10 năm:
- S tiền của ông A có được: 100.000.000(1+5%)
10
163.000.000.( lm tròn đến hàng triệu)
- S tiền của ông B có được: 100.000.000(1+5/12%)
120
165.000.000.(lm tròn đến hàng triệu)
Chọn đáp án C
Câu 36.4. Hình phẳng (H) giới hạn bởi các đường (P):
2
45y x x
và hai tiếp tuyến của (P) tại
đim A(1;2); B(4;5). Diện tích của (H) là ?
A.
27
4
B.
9
4
C.
15
4
D.
5
2
Hướng dẫn giải :
Phương trình tiếp tuyến của (P) tại A, B lần lượt là
2 4 4 11( ) : ;( ):a y x b y x
Ta có:
5
2 4 4 11
2
x x x
Khi đó diện tích của (H) là:
5
4
2
22
5
1
2
9
4 5 2 4 4 5 4 11
4
( ) ( )S x x x dx x x x dx

Chọn đáp án B
Câu 36.5. Trong không gian với hệ tọa độ Oxyz, cho đim A(1;2;3) v đường thẳng d:
31
2 1 1


x y z
.
136
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Mặt phằng (P) chứa đường thẳng d và có khoảng cách từ A đến (P) là lớn nhất. Khi đó (P) có một
véctơ pháp tuyến là
A.
4 5 13( ; ; )n
B.
4 5 13( ; ; )n 
C.
4 5 13( ; ; )n 
D.
4 5 13( ; ; )n 
Hướng dẫn giải :
Gọi H,K lần lươt l hình chiếu vuông góc của A lên d và (P)
Khi đó: d(A,(P)) = AK
AH hay d(A,(P)) lớn nhất khi và chỉ khi
HK
Ta có:
3 2 1 2 1 1( ; ; ); ( ; ; )H t t t a
và
4
0
3
.AH a t
Suy ra:
4 5 13
3 3 3
( ; ; )AH
Hay một véctơ pháp tuyến của (P) là
4 5 13( ; ; )n
Chọn đáp án A.
Câu 36.6.
Cho hình vuông ABCD có tâm H và A,B,C,D,H lần lượt l đim biu diễn cho các s phức
a,b,c,d,h. Biết
;a i h i 2 1 3
và s phức b có phần ảo dương. Khi đó môđun của s phức b
là
A.
26
B.
13
C.
42
D.
10
Hướng dẫn giải :
Ta có:
2 1 1 3 4 5( ; ); ( ; ) ( ; )A H C
Tam giác ABC vuông cân tại B nên :
0.
AB BC
AB BC
Giải hệ tìm được
44( ; );B
( Loại
02( ; )B
)
Chọn đáp án C.
Câu 37.1.Đường thẳng
3 6 0xy
có hệ s góc
1
3
k 
.
Tiếp tuyến tại
M
và
N
lần lượt có hệ s góc
11
'k y x
,
22
'k y x
, từ giả thiết
12
kk
=3
137
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
2
11
2 6 1 3x mx m
và
2
22
2 6 1 3x mx m
, trong đó
12
;xx
là nghiệm phương trình
2
2 6 9 0x mx m
(1)
Phương trình (1) có
2
nghiệm
23xm
và
3x
Phương trình (1) có hai nghiệm phân biệt
12
;xx
thỏa mãn
12
23xx
2 3 3
2 3 0
2 3 3 2 3
m
m
m

3
3
2
m
. Vậy
3
3
2
m
thỏa mãn. Chọn đáp án A
Câu 37.2.
.
x x x
x
12
25
5 5 124 5 5 124 0
5
Đặt
pt
x2
t 25(tm)
25
t 5 ;t 0 5t 124 0 5t 124t 25 0
1
t
t (l)
5
Khi đó
x
5 25 x 2
Biến đổi thì thấy
log log
aa
a
ab a
b
3
3
2
, thật vậy
log log log log log . log log
a a a a a a a
a
ab a a b a a b a
b
2
3
3
22
3
3
2
Vậy chọn đáp án B
Câu 37.3.Ta có
S xh x
S x. x x
V
x
V x h h
x
xx
2
22
2
2
22
4
32 128
4
32
, đ lượng vàng cần dùng là nhỏ
nhất thì Diện tích S phải nhỏ nhất ta có
S x f x f' x x x
x
x
2
2
128 128
2 0 4
,
h 2
Chọn đáp án B
Câu 37.4. (Kshs). Giá tr lớn nhất của hàm s
2
44
2sin
sin cos
22
x
fx
xx
là
138
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
A. 0 B. 4 C.8 D. 2
Hướng dẫn giải :
TXĐ:
D
, ta có
2 2 2
2
4 4 2
2sin 2sin 4sin
1
2 sin
sin cos 1 sin
2 2 2
x x x
fx
xx
x
x
.
Đặt
2
sin 0;1x t t
, hàm s trở thành
4
2
t
gt
t
với
0;1t
, ta có
2
8
' 0 0;1
2
g t t
t
, suy ra hàm s đồng biến trên
0;1
, vậy
0;1
max ax 1 4
xt
f x m g t g
, xảy ra khi
1
2
t x k k
Câu 37.5. (Thể tích – mặt cầu-mặt nón – mặt trụ)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
2BC a
. Tam giác SAB có góc
60 ,
o
ASB SB a
và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ đim B đến
mặt phẳng (SAC).
A.
a
B.
3
2
19
a
C.
3
19
a
D.
3
2
16
a
Hướng dẫn giải :
S
K
H
A
B
C
SAB ABC SAB ABC AB BC AB BC SAB
,;
Trong mp (SAB) kẻ
BH SA
. Trong tam giác BCH kẻ
BK CH
.Ta có
BK SAC
.
Vậy khoảng cách từ B đến (SAC) là BK.
139
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
3
60
2
o
a
BH SB
.sin
; Xét tam giác vuông CBH , ta có
2 2 2
1 1 1 3
2
19
BK a
BK BH BC
. Vậy
3
2
19
d B SAC a
,
.
Câu 37.6. (Mũ – Logarit)
Tập nghiệm của bất phương trình:
2 2 1
2
81.9 3 .3 0
3
x x x x
là
A.
1; 0 .S 
B.
1; .S
C.
0; .S
D.
2; 0 .S 
Hướng dẫn giải :
ĐKXĐ:
0.x
BPT đã cho
2
92
81. 3 .3 .3.3 0
81 3
x
x x x
22
3 3 .3 2.3 0
x x x x
3 3 3 2.3 0
x x x x
3 3 0
xx
(vì
3 2.3 0, 0.
xx
x
)
11
33
0
0
xx
xx
xx
x
x

Vậy tập nghiệm của BPT đã cho l
1; 0 .S 
Câu 37.7. (Tích phân - Ứng dụng )
Tìm tham s
m
đ đồ th hàm s
42
22y x mx m C
cắt trục
ox
tại bn đim phân biệt và thỏa
mãn hình phẳng giới hạn bởi đồ th (C) và trục
ox
của phần nằm phía trên trục
ox
có diện tích
bằng diện tích hình phẳng giới hạn bởi đồ th (C) và trục
ox
của phần nằm phía dưới trục
ox
.
A. 3 B. -3 C.2 D. 4
Hướng dẫn giải :
Điều kiện đ (C) cắt trục ox tại 4 đim phân biệt là
2m
140
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Do tính đi xứng của đồ th qua trục tung nên bài toán xảy ra khi
3
4
3
4 2 4 2
0
2 2 2 2
x
x
x
x mx m dx x mx m dx

4
4 2 4 2
44
0
2 2 0 3 10 15 2 0
x
x mx m dx x mx m
Suy ra
4
x
là nghiệm của hệ
42
44
2
4
42
44
2 2 0
36
3
3 10 15 2 0
x mx m
m
xm
m
x mx m
Câu37.8. (Oxyz)
Trong không gian tọa độ Oxyz cho đim
(0;1;1), (1;0; 3), ( 1; 2; 3)A B C
và mặt cầu (S) có phương trình :
2 2 2
2 2 2 0x y z x z
.Tìm tọa độ đim D trên mặt cầu (S) sao cho tứ diện ABCD có th tích lớn nhất.
A.
7 4 1
;;
3 3 3
D




B.
1 4 5
;;
3 3 3
D




C.
7 4 1
;;
3 3 3
D



D.
7 4 1
;;
3 3 3
D



Hướng dẫn giải :
Ta có (S)
2 2 2
:( 1) ( 1) 4 x y z
suy ra (S) có tâm I(1;0;-1), bán kính
R2
Và
(1; 1; 4); ( 1; 3; 4)AB AC
Mặt phẳng (ABC) có một vectơ pháp tuyến là
, ( 8;8; 4)n AB AC


Suy ra mp(ABC) có phương trình:
8x 8(y 1) 4(z 1) 0 2x 2y z 1 0
Ta có
1
( ;( )).
3
ABCD ABC
V d D ABC S
nên
ABCD
V
lớn nhất khi và chỉ khi
( ;( ))d D ABC
lớn nhất . Gọi
12
DD
là đường kính của mặt cầu (S) vuông góc với mp(ABC). Ta thấy với D l 1 đim bất kỳ thuộc (S) thì
12
( ;( )) max ( ;( )); ( ;( ))d D ABC d D ABC d D ABC
.
Dấu “=” xảy ra khi D trùng với D1 hoặc D2
Đường thẳng
12
DD
đi qua I(1;0;-1), và có VTCP là
(2; 2;1)
ABC
n 
141
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Do đó (D1D2) có phương trình:
12
2
1


xt
yt
zt
.
Tọa độ đim D1 và D2 thỏa mãn hệ:
2 2 2
12
2
2
3
12
3
( 1) ( 1) 4
xt
t
yt
zt
t
x y z


12
7 4 1 1 4 5
; ; & ; ;
3 3 3 3 3 3
DD
Ta thấy:
12
( ;( )) ( ;( ))d D ABC d D ABC
. Vậy đim
7 4 1
;;
3 3 3
D




l đim cần tìm
Câu 37.9. (Số phức)
Tìm phần ảo của s phức
z
, biết s phức z thỏa mãn
2 2017
. 2 1 ... 1 .i z i i i
A.
1
B.
1009
2
C.
1009
2
D.
1009
2 i
Hướng dẫn giải :
Ta thấy
2 2017
1; 1 ; 1 ; ........; 1i i i
lập thành một cấp s nhân gồm 2018 s hạng với
1
1u
công bội
1qi
.
Suy ra
2018
2018
2018
2018 1
11
1
.1
1
i
q
i z S u i i i
qi

1009
2018 2 1009
1009
1009
1 1 1 1 1 2 1 2
12
z i i i i
zi


Vậy phần ảo của z là
1009
2
.
Câu 38.1 (kshs).
Cho hm s
32
69y x x x m
có đồ th (C), với m l tham s. Giả sử đồ th (C) cắt trục honh
tại ba đim phân biệt có honh độ thỏa mãn
1 2 3
.x x x
Khẳng đnh no sau đây l đúng?
A.
1 2 3
1 3 4x x x
B.
1 2 3
0 1 3 4x x x
142
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
C.
1 2 3
0 1 3 4x x x
D.
1 2 3
1 3 4x x x
Hướng dẫn giải:
Khảo sát v vẽ đồ th hm s
32
69y x x x
. Da vo đồ th ta tìm được
40m
thì đồ
th hm s
32
69y x x x m
cắt Ox tại 3 đim phân biệt.
Ta có
0 . 1 0; 1 . 3 0; 3 . 4 0y y y y y y
do đó
1 2 3
0 1 3 4x x x
Câu 38.2 (Thể tch – mặt cầu – mặt nn – mặt trụ).
Cho tứ diện ABCD có tam giác ABD vuông cân tại D,
AD a
, tam giác ABC cân tại C,
22
AC a x
. Biết
22
2CD a x
, (x>0) hãy tính góc giữa hai đường thẳng AB, CD bằng
bao nhiêu?
A.
0
45
B.
0
90
C.
0
60
D.
0
30
Hướng dẫn giải:
Gọi H l hình chiếu của C lên mặt phẳng (ABD)
Đặt
CH b
. Khi đó ta chứng minh được
bx
Khi đó AHBD l hình vuông.
Suy ra AB vuông góc với CD. Vậy góc giữa AB, CD bằng
0
90
Câu 38.3 (Mũ – Lôgarit).
Cho
n
u
l cấp s nhân với s hạng tổng quát
0; 1
nn
uu
. Khi đó khẳng đnh no sau đây l
đúng?
A.
11
11
log 2017 log 2017 log 2017
log 2017 log 2017 log 2017
k k k
k k k
u u u
u u u


B.
11
11
log 2017 log 2017 log 2017
log 2017 log 2017 log 2017
k k k
k k k
u u u
u u u


C.
11
11
log 2017 log 2017 log 2017
log 2017 log 2017 log 2017
k k k
k k k
u u u
u u u


D.
11
11
log 2017 log 2017 log 2017
log 2017 log 2017 log 2017
k k k
k k k
u u u
u u u


Hướng dẫn giải:
Vì
n
u
l cấp s nhân nên
2
11
.
k k k
u u u

2017 2017 1 2017 1
2log log log
k k k
u u u

143
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
11
11
11
1 1 1 1
log 2017 log 2017 log 2017 log 2017
log 2017 log 2017 log 2017
log 2017 log 2017 log 2017
k k k k
k k k
k k k
u u u u
u u u
u u u




Câu 38.4 (Tch phân – Ứng dụng).
Cho hm s
42
4y x x m
có đồ th l (C). Gọi S l diện tích hình phẳng giới hạn bởi đồ th (C)
với y<0 v trục honh, S’ l diện tích hình phẳng giới hạn bởi đồ th (C) với y>0 v trục honh. Với
giá tr no của m thì
'SS
?
A.
2m
B.
2
9
m
C.
20
9
m
D.
1m
Hướng dẫn giải:
Phương trình honh độ giao đim
42
40x x m
(*)
Đặt
2
;0x t t
, phương trình trở thnh:
2
40t t m
(**)
Đ S>0, S’>0 thì 0<m<4. Khi đó (*) có 4 nghiệm phân biệt
2 1 1 2
; ; ;t t t t
với
1 2 1 2
;,t t t t
l hai nghiệm dương phân biệt của (**)
Do ĐTHS hm bậc 4 nhận Oy lm trục đi xứng nên
11
2
2
4 2 4 2
0
2
42
22
0
' 4 4
4
4 0 0
53
tt
t
t
S S x x m dx x x m dx
tt
x x m dx m

Kết hợp với (**) ta được
20
9
m
.
Câu 38.5 (Hnh Oxyz).
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (Q):
x y z
2 5 0
v đường thẳng
x y z
d
1 1 3
:
2 1 1

. Phương trình mặt phẳng (P) chứa đường thẳng d và tạo với mặt phẳng (Q)
một góc nhỏ nhất l
A.
: 4 0
P y z
B.
: x 4 0
Pz
C.
: x 4 0
P y z
D.
: 4 0
P y z
Hướng dẫn giải:
PT mặt phẳng (P) có dạng:
ax by cz d a b c
2 2 2
0 ( 0)
. Gọi
PQ
(( ),( ))a
.
Chọn hai đim
M N d
( 1; 1;3), (1;0;4)
. Ta có:
M P c a b
N P d a b
()
( ) 7 4



144
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
(P):
ax by a b z a b
( 2 ) 7 4 0
ab
a ab b
22
3
cos .
6
5 4 2

TH1: Nếu a = 0 thì
b
b
2
33
cos .
2
6
2

0
30a
.
TH2: Nếu a 0 thì
b
a
bb
aa
2
1
3
cos .
6
5 4 2




. Đặt
b
x
a
và
fx
2
( ) cos
Xét hàm s
xx
fx
xx
2
2
9 2 1
( ) .
6
5 4 2


.
Da vào BBT, ta thấy
fx
00
min ( ) 0 cos 0 90 30
a
Do đó chỉ có trường hợp 1 thoả mãn, tức a = 0. Khi đó chọn
b c d
1, 1, 4
.
Vậy: (P):
yz
40
.
Câu 38.6 (Số phức).
Gieo một con súc sắc cân đi đồng chất hai lần. Ký hiệu
;ab
l kết quả xảy ra sau khi gieo, trong
đó a, b lần lượt l s chấm xuất hiện lần thứ nhất, thứ hai. Gọi A l biến c s chấm xuất hiện trên
hai lần gieo như nhau. Tập hợp các kết quả thuận lợi cho biến c A l tập hợp con của tập hợp các
đim biu diễn của s phức z thỏa mãn điều kiện no sau đây?
A.
2 3 12zi
B.
2 3 10zi
C.
2 3 13zi
D.
2 3 11zi
Hướng dẫn giải:
Ta có
1;1 , 2;2 , 3;3 , 4;4 , 5;5 , 6;6A
Gọi
;,z x yi x y R
khi đó
22
2 3 2 3z i x y
Giả sử
22
2 3 2 3z i R x y R
22
2
23x y R
. Khi đó tập hợp các đim biu diễn s phức z l những đim thuộc
miền trong v trên đường tròn tâm
2; 3I 
v bán kính R.
Đ tập hợp các kết quả thuận lợi cho biến c A l tập hợp con của tập hợp các đim biu diễn của s
phức z thì
;IM R M A
Khi đó ta được R=13
Câu 39.1 (Kshs). Một người có một dải ruy băng di 130cm, người đó cần bọc dải ruy băng đó
quanh một hộp quà hình trụ. Khi bọc qu, người này dùng 10cm của dải ruy băng đ thắt nơ ở trên
145
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
nắp hộp (như hình vẽ minh họa). Hỏi dải dây duy băng có th bọc được hộp quà có th tích lớn
nhất là là nhiêu ?
A.
3
4000 cm
B.
3
1000 cm
C.
3
2000 cm
D.
3
1600 cm
Hướng dẫn giải :
Gọi
(c ) ;y ( c )x m m
lần lượt l bán kính đáy v chiều của hình trụ
( , 0; 30)x y x
.
Dải dây duy băng còn lại khi đã thắt nơ là:
120cm
Ta có
(2 ).4 120 30 2x y y x
Th tích khi hộp quà là:
22
. (30 2 )V x y x x
Th tích V lớn nhất khi hàm s
2
( ) (30 2 )f x x x
với
0 30x
đạt giá tr lớn nhất.
2
'( ) 6 60f x x x
, cho
2
'( ) 6 60 0 10f x x x x
Lập bảng biến thiên, ta thấy th tích đạt giá tr lớn nhất là
3
1000 (cm )V
.
Câu 39.2. (Thể tích – mặt cầu-mặt nón – mặt trụ). Cho hình chóp
.S ABCD
có đáy
ABCD
là hình
vuông cạnh
,a
SA
vuông góc với mặt phẳng đáy v góc giữa
SC
với mặt phẳng
()SAB
bằng
0
30 .
Gọi
M
l đim di động trên cạnh
CD
và
H
là hình chiếu vuông góc của
S
trên đường thẳng
.BM
Khi đim
M
di động trên cạnh
CD
thì th tích của khi chóp
.S ABH
đạt giá tr lớn nhất bằng?
A.
3
2
3
a
B.
3
2
2
a
C.
3
2
6
a
D.
3
2
12
a
Hướng dẫn giải :
Ta có góc giữa SC và mặt phẳng (SAB) là
0
30CSB
Trong tam giác SBC có
0
. 30 3SB BC cot a
146
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Trong tam giác SAB có
22
2SA SB AB a
Th tích khi chóp S.ABH là:
.
1 1 1 2
. . . . 2 .
3 3 2 6
S ABH ABH
a
V S SA HAHB a HAHB
Ta có
2 2 2 2
HA HB AB a
và theo bất đẳng thức AM-GM ta có
2
2 2 2
2. . .
2
a
a HA HB HAHB HAHB
Đẳng thức xảy ra khi
0
45HA HB ABM M D
Khi đó
23
.
2 2 2
..
6 6 2 12
S ABH
a a a a
V HAHB
Câu 39.3. (Mũ - Logarit). Trong một bản hợp ca, coi mọi ca sĩ đều hát với cường độ âm và coi cùng
tần s. Khi một ca sĩ hát thì cường độ âm là 68dB. Khi cả ban hợp ca cùng hát thì đo được mức
cường độ âm là 80dB. Tính s ca sĩ có trong ban hợp ca đó, biết mức cường độ âm L được tính theo
công thức
0
10
I
L log
I
trong đó I l cường độ âm và
0
I
l cường độ âm chuẩn
A. 16 người B. 12 người C. 10 người D. 18 người
Hướng dẫn giải :
Gọi
1
;
n
II
lần lượt l cường độ âm của một người và của n người.
Ta có
1
1
n
n
I
I nI n
I
Ta có
1
1
0
10 68
I
L log
I
;
0
10 80
n
n
I
L log
I
Khi đó
1
1
0 0 1
10 10 10
nn
n
I I I
L L log log log
I I I
1
6
10 5
1
10 10 15, 89
n
LL
n
I
n
I
Vậy có 16 ca sĩ.
147
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 39.4. (Tích phân - Ứng dụng ). Một ô tô đang chạy đều với vận tc
(m/ s)a
thì người lái đạp
phanh. Từ thời đim đó, ô tô chuyn động chậm dần đều với vận tc
(t) 5 t ( m/ s)va
, trong
đó t l thời gian tính bằng giây k từ lúc đạp phanh. Hỏi từ vận tc ban đầu a của ô tô là bao nhiêu,
biết từ lúc đạp phanh đến khi dừng hẳn ô tô di chuyn được 40 mét.
A.
20a
B.
10a
C.
40a
D.
25a
Hướng dẫn giải :
Khi xe dừng hẳn thì vận tc bằng 0 nên
5 t 0
5
a
at
Ta có
55
2
00
1
(t) ( 5 t )
10
aa
S v dt a dt a
2
1
40 40 20
10
S a a
Câu 39.5. (Oxyz). Trong không gian với hệ trục Oxyz, cho đường thẳng d có phương trình
12
:
1 1 2
x y z
d
v đim A(1 ;4 ;2). Gọi (P) là mặt phẳng chứa d . Khoảng cách lớn nhất
max
d
từ
A đến (P) là :
A.
max
5d
B.
max
210
3
d
C.
max
65d
D.
max
25d
Hướng dẫn giải :
Từ A kẻ một đường thẳng vuông góc với đường thẳng d và cắt đường thẳng d tại H nên
(A;d)d AH
Từ A kẻ một đường thẳng vuông góc với mặt phẳng (P) tại K nên
(A;(P))d AK
.
Trong tam giác AKH vuông tại K thì
AH AK
Do đó đ khoảng cách từ A đến (P) lớn nhất khi
(A;(P)) (A;d)d d AH
.
Ta có
(1; 2;0)Md
,
(0; 6; 2)AM
, vectơ chỉ phương của d là
( 1;1;2)u
.
max
,
210
(A;d)
3
AM u
dd
u
.
148
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 39.6. (Số phức). Cho s phức z có phần thc dương thỏa mãn
5z
và
2 3 4zi
.
Tính
13 1
2
z
A
z
A.
898A
B.
98A
C.
890A
D.
198A
Hướng dẫn giải :
Gọi
z a bi
với a và b là các s thc và
0a
.
Theo giả thiết ta có
22
22
5
( 2) ( 3) 16
ab
ab
Giải hệ trên ta được
2; 1ab
.
Với
2 13 27 89 8z i A i
.
Câu 40.1. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
tan 2
tan
x
y
xm
đồng biến trên khoảng
0; .
4



A. m 0 hoặc 1 m 2. B. m 0. C. 1 m 2. D. m 2.
HƯỚNG DẪN GIẢI
22
2 2 2
11
(tan ) (tan 2)
2
cos cos
'
(tan ) cos (tan )
x m x
m
xx
y
x m x x m


Hàm số đồng biến trên
0;
4



khi và chỉ khi hàm số xác định trên
0;
4



và y’ ≥ 0 x
0;
4



tan , 0;
0
4
12
20
xx
m
m
m






Chọn A
149
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 40.2. Sự tăng trưởng của một loài vi khuẩn được tính theo công thức
rx
f x Ae()
, trong đó
A
là số
lượng vi khuẩn ban đầu,
r
là tỷ lệ tăng trưởng
r 0
,
x
(tính theo giờ) là thời gian tăng trưởng. Biết số vi
khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Hỏi sao bao lâu thì số lượng vi khuẩn tăng gấp 10 lần
A.
5ln20
(giờ) B.
5ln10
(giờ) C.
5
10log 10
(giờ) D.
5
10log 20
(giờ)
HƯỚNG DẪN GIẢI
Gọi thời gian cần tìm là t. Ta có: 5000 = 1000. e
10r
nên r =
ln5
10
.
Do đó, 10000 = 1000. e
rt
suy ra t =
5
ln10 10ln10
10log 10
ln5r

giờ nên chọn câu C.
Câu 40.3. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
2( 1) ,
x
y x e
trục tung và trục hoành. Tính
thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A.
4 2 .Ve
B.
(4 2 ) .Ve

C.
2
5.Ve
D.
2
( 5) .Ve

HƯỚNG DẪN GIẢI
Ta có
11
2
22
1
00
2( 1) 4 ( 2 1) 4
xx
V x e dx x x e dx I



Đặt
2
1
2
22
2
2
2
0
22
2 1 1
1
( 2 1) ( 1)
0
22
2
x
x
x
x
du x
u x x
e
I x x x e dx I
e
v
dv e dv



Đặt
1
1
2 2 2
1
2
2
1
2
0
1
1
1
11
1 1 3
( 1)
00
2 2 2 4 4 4
2
xx
x
x
x
du dx
ux
e e e
I x e dx
e
dv e dx
v


Do vậy
2
1
5
4
e
I
suy ra
2
5Ve

Nên chọn D.
Câu 40.4. Cho các số phức
z
thỏa mãn
4z
. Biết rằng tập hợp các điểm biểu diễn các số phức
(3 4 )w i z i
là một đường tròn. Tính bán kính r của đường tròn đó.
A. r 4. B. r 5. C. r 20. D. r 22.
150
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
HƯỚNG DẪN GIẢI
Gọi
w a bi
, ta có
2
( 1) (3 4 )
( 1)
(3 4 )
3 4 9 16
a b i i
a b i
w a bi i z i z
ii


22
(3 4 4) (3 4 3)
3 4 4 (3 4 3)
.
25 25 25
a b b a
a b b a
iz
Mà
z
= 4 nên
2 2 2 2 2
(3 4 4) (3 4 3) 100 2 399a b b a a b b
Theo giả thiết, tập hợp các điểm biểu diễn các số phức
(3 4 )w i z i
là một đường tròn nên ta có
2 2 2 2
2 399 ( 1) 400 400 20a b b a b r
Nên chọn C.
Câu 40.5. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.
A. V =
5 15
18
B. V =
5 15
54
C. V =
43
27
D. V =
5
.
3
HƯỚNG DẪN GIẢI
Đặt R là bán kính mặt cầu ngoại tiếp khối chóp
Dựng hình như hình bên với IG là trục đường tròn ngoại tiếp tam giác
ABC và IG’ là trục đường tròn ngoại tiếp tam giác SAB
Ta có:
3 3 6
';
6 6 6
G H GH IH
Do vậy
2 2 3
15 4 5 15
6 3 54
R IH HA V R
Nên chọn B
Câu 40.6. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; –2; 0), B(0; –1; 1), C(2; 1; –1) và D(3; 1;
4). Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó ?
A. 1 mặt phẳng. B. 4 mặt phẳng. C. 7 mặt phẳng. D. Có vô số mặt phẳng.
HƯỚNG DẪN GIẢI
151
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Ta có:
( 1;1;1); (1;3; 1); (2;3;4)AB AC AD
Khi đó:
; . 24 0AB AC AD


do vậy A,B,C,D không đồng phẳng
Do đó có 7 mặt phẳng cách đều 4 điểm đã cho bao gồm.
+) Mặt phẳng qua trung điểm của AD và song song với mặt phẳng (ABC)
+) Mặt phẳng qua trung điểm của AB và song song với mặt phẳng (ACD)
+) Mặt phẳng đi qua trung điểm của AC và song song với mặt phẳng (ABD)
+) Mặt phẳng đi qua trung điểm của AB và song song với mặt phẳng (BCD)
+) Mặt phẳng qua trung điểm của AB và CD đồng thời song song với BC và AD
+) Mặt phẳng qua trung điểm của AD và BC đồng thời song song với AB và CD
+) Mặt phẳng qua trung điểm của AC và BD đồng thời song song với BC và AD
Nên chọn C.
| 1/199
| | Tải xuống

Có thể bạn quan tâm:

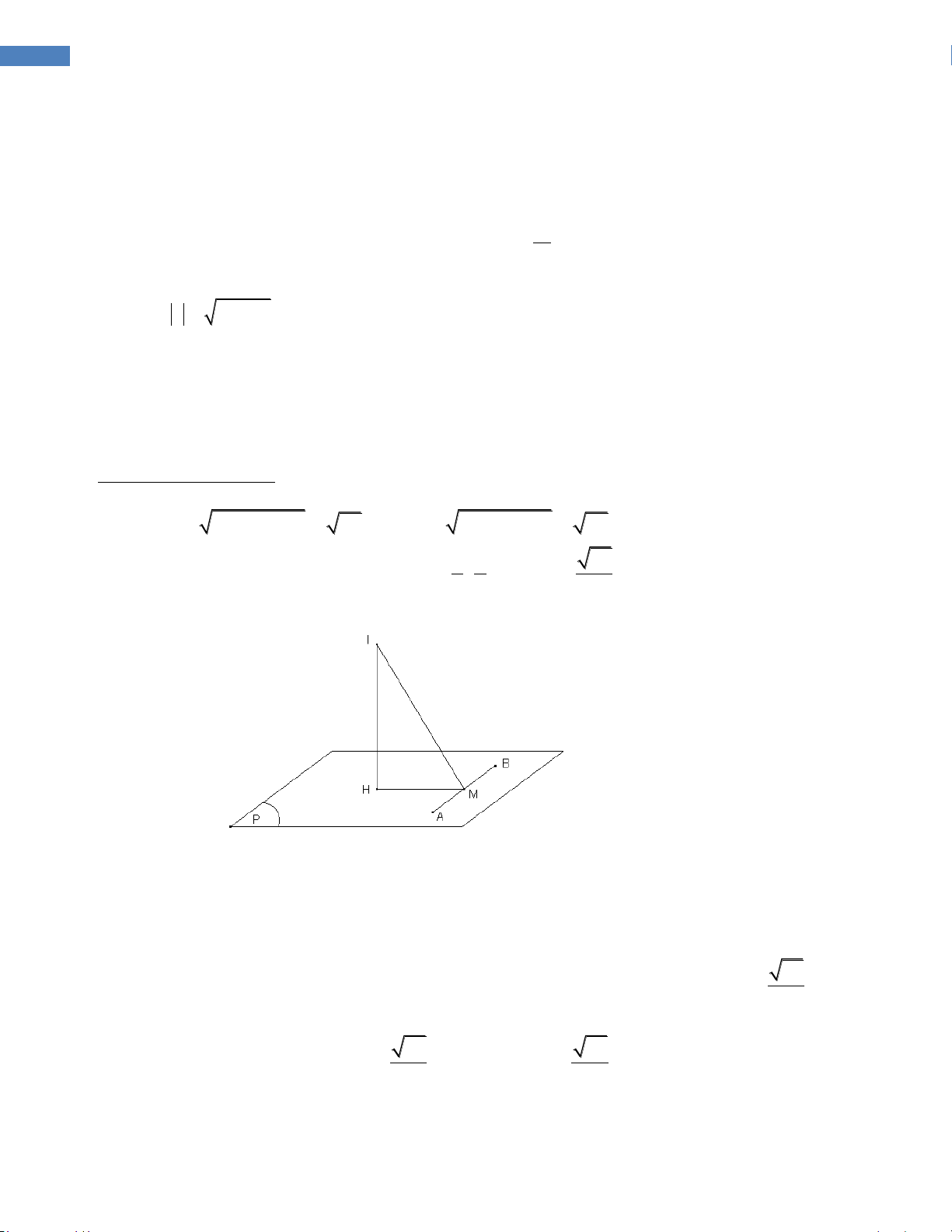
Preview text:

1
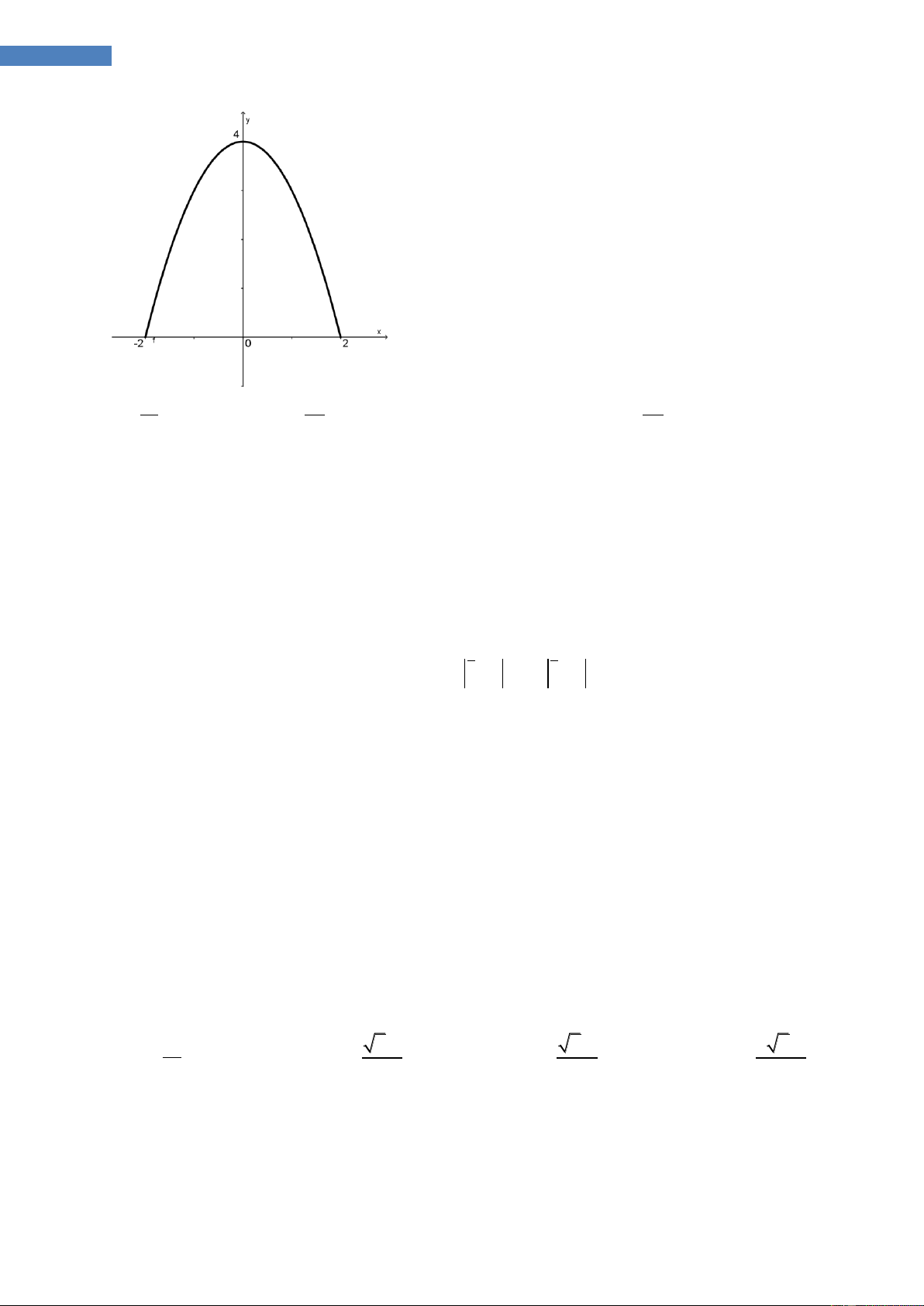
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 PHẦN 1 : ĐỀ BÀI 2 x  2x  3
Câu 1.1. Đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số y  hợp x 1
với 2 trục tọa độ 1 tam giác có diện tích S bằng : A. S=1,5 B. S=2 C.S=3 D.S=1
Câu 1.2. Khối cầu nội tiếp hình tứ diện đều có cạnh bằng a thì thể tích khối cầu là : 3 a  6 3 a  6 3 a  3 3 a  3 A. B. C. D. 216 124 96 144
Câu 1.3. Tìm m để phương trình 2x x e
me  3 m  0 có nghiệm
A. m  2 B. m  2 C.m<3 D.m>0
Câu 1.4. Giá trị của tham số m để diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 2
y  3x  2mx m 1 , trục hoành, trục tung và đường thẳng x = 2 đạt giá trị nhỏ nhất là: A. m = 2 B. m = 1 C. m = -1 D. m = - 2
Câu 1.5. Phương trình nào sau đây không phải là phương trình hình chiếu vuông x 1 2t
góc của đường thẳng d: y  2
  3t ,t R trên mặt phẳng (Oxy) : z  3t
x  3 2t '
x 1 4t '
x 1 2t '   
A. y  1 3t ' ,t ' R B. y  2
  6t ',t ' R C. y  2  3t ',t ' R D.    z  0  z  0  z  0 
x  5  2t ' 
y  4  3t ',t ' R z  0 
Câu 1.6. Gọi A, B, C lần lượt là các điểm biểu diễn của 3 số phức : 2  i  i  6
1 2i; (1 )(1 2i); 3i .Diện tích của tam giác ABC bằng : 1 1 5 5 A. B. C. D. 4 2 5 2
Câu 2.1. Cho hàm số 3 2
y x  2x  1 mx m có đồ thị C . Giá trị của m thì C
cắt trục hoành tại 3 điểm phân biệt x , x , x sao cho 2 2 2
x x x  4 là 1 2 3 1 2 3 2
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017  1   m  1 1 1 A. m  1 B.  4 C.   m 1 D.  m  1  4 4 m  0
Câu 2.2. Cho lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông
góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm tam giá ABC . Biết
khoảng cách giữa hai đường thẳng AA' và BC bằng a 3 . Khi đó thể tích của khối 4 lăng trụ là 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 12 6 3 24 x x
Câu 2.3. Phương trình 2 3 2 3
m (1) có nghiệm khi: A. m  ;5   B. m   ;5 C. m 2; D. m 2;  2 Câu 2.4. Tính 3x
I e .sin xdx 0 3    1 1 3 1 1 3 3 A. 2 I   e B. 2 I   e C. 2 I  1 e D. 2 I  1 e 2 2 2 2
Câu 2.5. Trong không gian tọa độ Oxyz , cho điểm A(0;1;1), B(1;0; 3)
 , C( 1; 2; 3) và mặt
cầu (S) có phương trình: x2  y2  z2  2x  2z  2  0 . Tìm tọa độ điểm D trên mặt cầu (S)
sao cho tứ diện ABCD có thể tích lớn nhất.       A. D 1;0;  1 B. D 7 4 1 ; ;  D 1 4 5 ; ; 3 3 3  C.      3 3 3 D. D(1; - 1; 0) 
Câu 2.6. Tính tổng mô-đun tất cả các nghiệm của phương trình:
z i 2z   3
1 z i  0 A. 3 B. 4 C.6 D. 8
Câu 3.1. Cho hàm số y   x m3 2
3x m  
1 . Gọi M là điểm cực đại của đồ thị hàm số  
1 ứng với một giá trị m thích hợp đồng thời là điểm cực tiểu của đồ thị hàm số  
1 ứng với một giá trị khác của m. Số điểm M thỏa mãn yêu cầu đề bài là: 3
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 A.1 B. 2 C.3 D.0 a 3
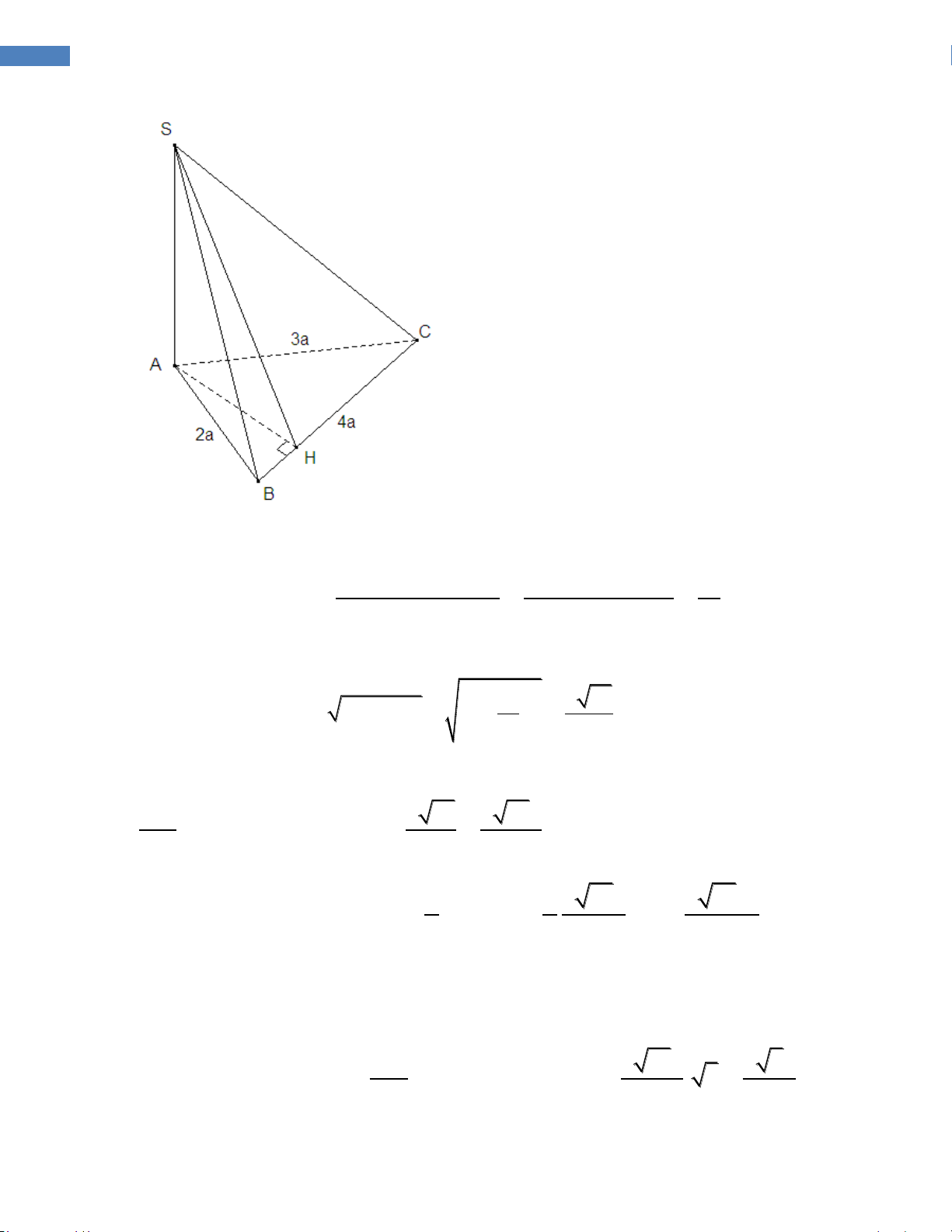
Câu 3.2. Cho tứ diện ABCD với BC a ,các cạnh còn lại đều bằng và  là góc 2
tạo bởi hai mặt phẳng  ABC và BCD . Gọi I,J lần lượt là trung điểm các cạnh
BC, AD . Giả sử hình cầu đường IJ kính tiếp xúc với CD. Giá trị cos là: 2 3 2  3 A. 3  2 3 B. 2 3  3 C. D. 3 3 Câu 3.3. Cho  ,
x y, z là các số thực thỏa mãn 2x  3y  6 z . Giá trị biểu thức
M xy yz xz là: A.0 B.1 C.6 D.3
Câu 3.4. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 x   2 x y e e , trục a
Ox và đường thẳng x a với a  ln 2 . Kết quả giới hạn lim S là: a a A.1 B.2 C.3 D.4
Câu 3.5. Trong không gian Oxyz, cho điểm A1,0,   1 và mặt phẳng
P: xy z 3  0 . Mặt cầu S có tâm I nằm trên mặt phẳng P , đi qua điểm A và
gốc tọa độ O sao cho chu vi tam giác OIA bằng 6  2 . Phương trình mặt cầu S là: A.  2 2 2
x  2   y  2   z  2 2 2 1
 9 hoặc x  2  y  2 z   1  9. B.  2 2 2
x  2   y  2   z  2 2 2 1
 9 hoặc x  
1   y  2   z  2  9 C.  2 2 2
x  2   y  2   z  2 2 2 1
 9 hoặcx  2  y  2  z   1  9 D.  2 2 2
x  2   y  2   z  2 2 2 1
 9 hoặc x  
1   y  2   z  2  9
Câu 3.6. Cho z là số phức có mô đun bằng 2017 và w là số phức thỏa mãn 1 1 1  
. Mô đun của số phức w là z w z  w A.2015 B.1 C.2017 D.0
Câu 4.1. Một công ty muốn làm một đường ống dẫn từ một điểm đảo
A trên bờ đến một điểm B trên một hòn đảo. Hòn đảo cách bờ biển B
6km. Giá để xây đường ống trên bờ là 50.000USD mỗi km, và biển 6km
130.000USD mỗi km để xây dưới nước. B’ là điểm trên bờ biển sao
cho BB’ vuông góc với bờ biển. Khoảng cách từ A đến B’ là 9km. Vị B' 9km bờ biển A 4
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
trí C trên đoạn AB’ sao cho khi nối ống theo ACB thì số tiền ít nhất. Khi đó C cách
A một đoạn bằng: A. 6.5km B. 6km C. 0km D.9km Câu 4.2.
Cho hình chóp SABC với SA vuông góc với mặt phẳng (ABC) và S BC= 3 a,  60o BAC
. Gọi H, K lần lượt là hình chiếu của A lên SB K
và SC. Mặt cầu qua các điểm A, B, C, H, K có bán kính bằng: A.1 B.2 H 3 A C 600 C. 3
D. Không đủ dữ kiện để tính 2
Câu 4.3. Cho a log 3  blog 2  c log 5  5 , với a, b và c là các số 6 6 6 B
hữu tỷ. Các khẳng định sau đây, khẳng định nào đúng? A.  
a b B. a b C. b a D. c a b Câu 4.4.
Một khối cầu có bán kính 5dm, người ta cắt bỏ 2 phần bằng 2 mặt phẳng vuông
góc bán kính và cách tâm 3dm để làm một chiếc lu đựng. Tính thể tích mà chiếc lu chứa được. A. 132 (dm3) B. 41 (dm3) 100 C.  (dm3) D. 43 (dm3) 3 3dm 5dm 3dm
Câu 4.5. Trong không gian với hệ trục tọa độ Oxyz, cho hai
điểm M(0; 1;2) và N( 1;1;3). Mặt phẳng (P) đi qua M, N sao
cho khoảng cách từ K 0;0;2 đến (P) đạt giá trị lớn nhất. (P) có vectơ pháp tuyến là: A. (1;1; 1  ) B. (1; 1  ;1) C. (1; 2  ;1) D. (2; 1  ;1)
Câu 4.6. Cho số phức z thoả mãn điều kiện z  2  3i  3 . Tìm giá trị nhỏ nhất của z A. 13  3 B. 2 C. 13  2 D. 2 5
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 5.1. Cho hàm số 3 2
y  x  3mx  3m 1. Với giá trị nào của m thì đồ thị hàm số
đã cho có cực đại và cực tiểu đối xứng nhau qua đường thẳng d : x 8y  74  0 A. m 1 B. m  2  C. m  2 D. m  1 
Câu 5.2. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, góc giữa SC và
mp(ABC) là 45  . Hình chiếu của S lên mp(ABC) là điểm H thuộc AB sao cho HA = a 7 2HB.Biết CH
. Tính khoảng cách giữa 2 đường thẳng SA và BC: 3 a 210 a 210 a 210 a 210 A. B. C. D. 30 20 45 15 2 2
Câu 5.3. Cho phương trình x 2mx2 2x 4mx2 2 5  5
x  2mx m  0. Tìm m để phương trình vô nghiệm? m  1 A. m  0 B. m  1 C. 0  m  1 D.  m   0 x ln(x  2)
Câu 5.4. Diện tích hình phẳng giới hạn bởi y  và trục hoành là: 2 4  x     A. ln 2  2   3 B. 2ln 2  2 
C. 2   3 D. 2ln 2  2   3 3 4 3 3
Câu 5.5. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;2;2), B(5;4;4)
và mặt phẳng (P): 2x + y – z + 6 =0. Tọa độ điểm M nằm trên (P) saocho MA2 + MB2 nhỏ nhất là: A. (-1;3;2) B. (2;1;-11) C.(-1;1;5) D(1;-1;7)
Câu 5.6. Số phức z có mô đun lớn nhất và thỏa mãn điều kiện Z   i 13 1  3  2i  là: 2 6
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2 1 3 1 3 15 A. z 13i B. z   i C. z   i D. z   i 2 2 2 2 4 4
Câu 6.1. Trong không gian với hệ toạ độ Oxyz cho A(2;  1;6), B(  1;2;4) và I(  1;  3;2).
Phương trình mặt phẳng (P) đi qua A, B sao cho khoảng cách từ I đến (P) lớn nhất là
A. 3x  7y  6z  35  0
B. 3x  7y  6z  35  0
C. 3x  7y  6z  35  0
D. 3x  7y  6z  35  0
Câu 6.2. Tìm m để đồ thị hàm số 3 2
y  x  3mx 1 có hai điểm cực trị A, B sao cho
tam giác OAB có diện tích bằng 1 (O là gốc tọa độ). A. m  2  B. m  1  C. m  5  D. m  3  5 z i
Câu 6.3. Cho số phức z thoả mãn
 2  i . Tìm phần thực và phần ảo của số z 1 phức 2
w  1 z z lần lượt là A. 2 và 3 B. 3 và 2 C. 1 và 3 D. 3 và 1
Câu 6.4. Cho hình chóp S.ABC có đường thẳng SA vuông góc với mặt phẳng
(ABC), tam giác ABC là tam giác đều cạnh bằng a, SB=2a. Khoảng cách từ trọng
tâm G của tam giác ABC đến mặt phẳng (SBC) là a 15 a 15 A. d( ; G (SBC))  B. d( ; G (SBC))  16 15 a 5 a C. d ( ; G (SBC))  D. d( ; G (SBC))  15 15
Câu 6.5. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA=AC=5a, AB=a, 0
BAC  120 . Khoảng cách từ A đến mặt phẳng (SBC) là 5 381 381 A. . a B. a 127 127 7
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 5 381 C. a D. a 74 27
Câu 6.6. Cho hình chóp tam giác S.ABC có đường thẳng SA vuông góc với mặt
phẳng (ABC), AB=2a, AC=3a, BC=4a. Góc giữa mặt phẳng (SBC) và mặt phẳng
(ABC) bằng 600. Thể tích của khối chóp S.ABC là 3 5 3a 3 4 3a A. V  B. V 32 32 3 45 3a 3 45 3a C. V  D. V 2 32
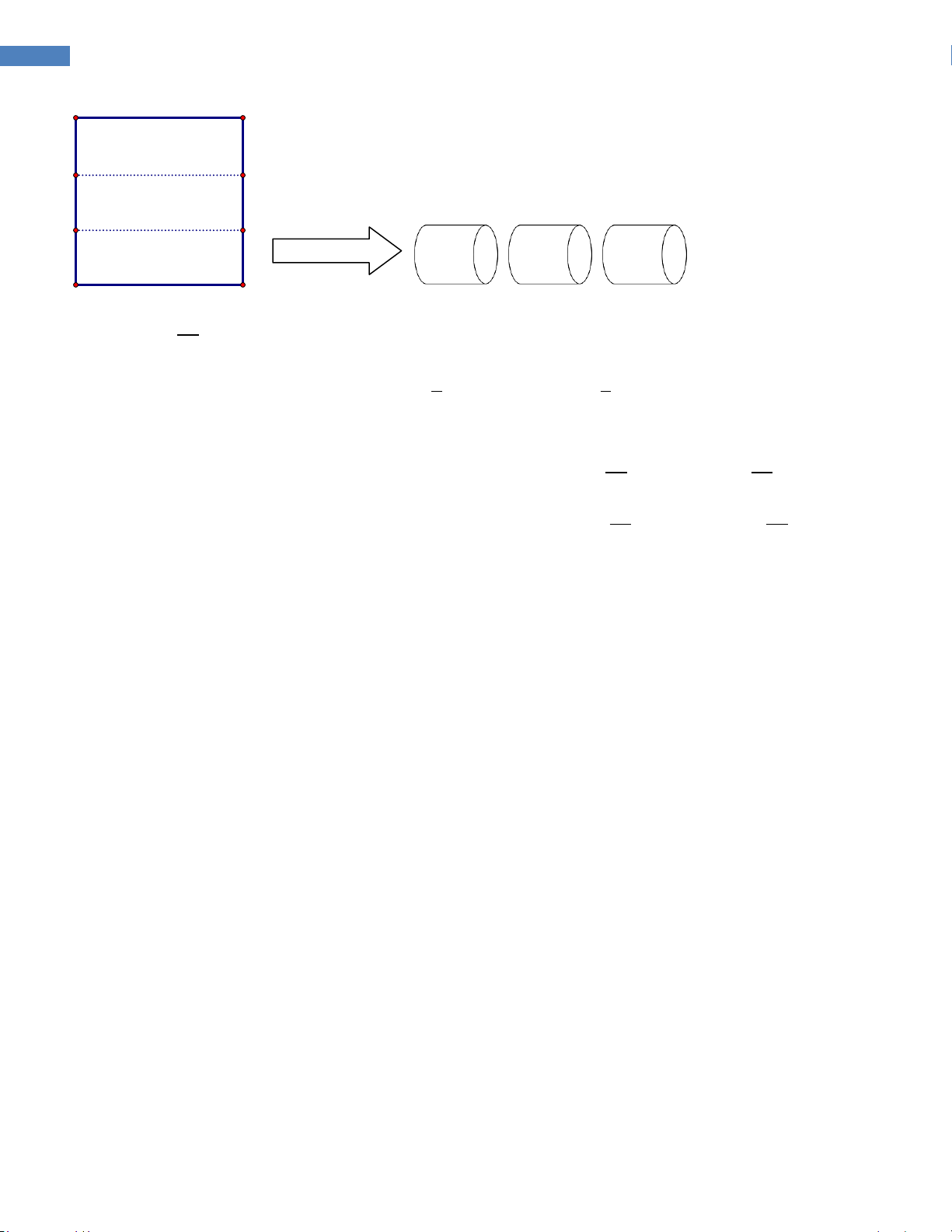
Câu 7.1. Một người thợ xây, muốn xây dựng một bồn
chứa nước hình trụ tròn với thể tích là 3 150m (như hình
vẽ bên). Đáy làm bằng bê tông , thành làm bằng tôn và
bề làm bằng bằng nhôm. Tính chi phí thấp nhất để bồn
chứa nước (làm tròn đến hàng nghìn). Biết giá thành các
vật liệu như sau: bê tông 100nghìn đồng một 2 m , tôn 90 một 2
m và nhôm 120 nghìn đồng một 2 m . A. 15037000đồng.
B. 15038000đồng. C. 15039000đồng. D. 15040000đồng.
Câu 7.2. Tìm tất cả các giá trị của tham số m sao cho bất phương trình sau có tập x x nghiệm là  ;0   : x 1
m2   2m  
1 3 5  3 5  0 . 1 1 1 1 A. m   . B. m  . C. m  . D. m   . 2 2 2 2 
Câu 7.3. Một vật di chuyển với gia tốc at     t 2 20 1 2  2
m / s  . Khi t  0 thì vận
tốc của vật là 30m / s . Tính quảng đường vật đó di chuyển sau 2 giây (làm tròn kết
quả đến chữ số hàng đơn vị).
A. S 106m .
B. S 107m .
C. S 108m .
D. S 109m .
Câu 7.4. Cho số phức z  0 thỏa mãn z  2 . Tìm tổng giá trị lớn nhất và giá trị nhỏ z i
nhất của biểu thức P  . z A. 1. B. 2 . C. 3 . D. 4 .
Câu 7.5. Cho hình chóp S.ABC , có đáy ABC là tam giác đều cạnh a . Các mặt bên
SAB, SAC, SBC lần lượt tạo với đáy các góc lần lượt là 0 0 0 30 , 45 , 60 . Tính thể 8
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
tích V của khối chóp S.ABC . Biết rằng hình chiếu vuông góc của S trên mặt
phẳng  ABC nằm bên trong tam giác ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. V   . B. V  . C. V  . D. V  . 4  3  24  3 44  3 84  3
Câu 7.6. Trong không gian tọa độ Oxyz , cho tám điểm A 2  ; 2  ;0 , B3; 2  ;0 ,
C 3;3;0 , D 2  ;3;0 , M  2  ; 2  ;5 , N  2  ; 2  ;5 , P3; 2  ;5, Q 2  ;3;5 . Hỏi hình đa
diện tạo bởi tám điểm đã cho có bao nhiêu mặt đối xứng. A. 3. B. 6. C. 8. D.9
Câu 8.1 Để phương trình: 4 x 2 8cos
 9cos x  m  0 với x[0;] có 2 nghiệm thì giá trị của m là A.  m 81 1  0  1   32 B. m C. m 81 32 D. m 0 2 2
Câu 8.2. Số nghiệm phương trình: x 2 x 2 9 x 3 3 2x 2 0 là A. 0 B.1 C.2 D.3  2 Câu 8.3. Cho x
I e s inxdx  . Giá trị của I là 0     2 e e 2 e e 2 e A. I  B. I  C. I  D. 2
I e e 2 2 2 z i
Câu 8.4. Cho số phức z
0 thỏa mãn . Để P
đạt giá trị nhỏ nhất thì z là z 2 A. z=i B. z 2i C. z
i D. z  2 1 2
Câu 8.5. Người ta cắt một tờ giấy hình vuông cạnh bằng 1 để gấp thành một hình
chóp tứ giác đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình
chóp. Để thể tích khối chóp lớn nhất thì cạnh đáy hình chóp là 9
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2 2 2 2 A. x  B. x  C. x  2 2 D. x  5 5 5
Câu 8.6. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-3; 5; -5), B(5; -3; 7)
và mặt phẳng (P): x + y + z - 6 = 0.Điểm M(x; y; z) trên mặt phẳng (P) sao cho
MA2 + MB2 đạt giá trị nhỏ nhất. Tổng (x+y+z) có giá trị là A. 6 B. 5 C. 4 D.3
Câu 9.1. Cho một tam giác đều ABC cạnh a. Người ta dựng một hình chữ nhật
MNPQ có cạnh MN nằm trên cạnh BC, hai đỉnh P và Q theo thứ tự nằm trên hai
cạnh AC và AB của tam giác. Xác định giá trị lớn nhất của hình chữ nhật đó? 3 3 3 A. 2 a B. 2 a C. 0 D. 2 a 8 4 2
Câu 9.2. Cho hình chóp tứ giác đều .
S ABCDcó đáy là hình vuông ABCD cạnh a, 1
góc giữa mặt bên và mặt phẳng đáy là  thoả mãn cos = . Mặt phẳng P qua 3
AC và vuông góc với mặt phẳng SAD chia khối chóp .
S ABCD thành hai khối đa
diện. Tỉ lệ thể tích hai khối đa diện là gần nhất với giá trị nào trong các giá trị sau A. 0,11 B. 0,13 C. 0,7 D. 0,9
Câu 9.3. Cho biết chu kì bán hủy của chất phóng xạ Plutôni Pu239 là 24360 năm (tức
là một lượng Pu239 sau 24360 năm phân hủy thì chỉ còn lại một nửa). Sự phân hủy
được tính theo công thức S = Aert, trong đó A là lượng chất phóng xạ ban đầu, r là
tỉ lệ phân hủy hàng năm (r<0), t là thời gian phân hủy, S là lượng còn lại sau thời
gian phân hủy t. Hỏi sau bao nhiêu năm thì 10 gam Pu239 sẽ phân hủy còn 1 gam
có giá trị gần nhất với giá trị nào sau? A. 82135 B. 82335 C. 82235 D. 82435
Câu 9.4. Tìm giá trị của tham số m sao cho: 3
y  x  3x  2 và y = m(x+2) giới hạn
bởi hai hình phẳng có cùng diện tích A. 0 < m < 1 B. m = 1 C. 1  m  9 D. m = 9
Câu 9.5. Cho đường thẳng d là giao tuyến của hai mặt phẳng ( )
 : x  2y  2z  4  0 ( )
 : 2x  2y  z 1  0, và mặt cầu S có phương trình 2 2 2
x  y  z  4x  6y  m  0 . 10
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Tìm m để đường thẳng d cắt mặt cầu (S) tại hai điểm phân biệt A, B sao cho AB = 8. A. 9 B. 12 C. 5 D. 2
Câu 9.6. Tìm phần thực của số phức n z  (1 i) , n  thỏa mãn phương trình
log (n  3)  log (n  9)  3 4 4 A. 5 B. 6 C. 7 D. 8
Câu 10.1. Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng : Nếu
trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng ( P ) n 480 20 ( n ga )
m . Hỏi phải thả bao nhiêu con cá trên một đơn vị diện
tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất ? A. 10 B. 12 C.16 D. 24
Câu 10.2. Một cửa hàng bán lẻ bán 2500 cái ti vi mỗi năm. Chi phí gởi trong kho là
10$ một cái mỗi năm. Để đặt hàng chi phí cố định cho mỗi lần đặt là 20$ cộng
thêm 9$ mỗi cái. Cửa hàng nên đặt hàng bao nhiêu lần trong mỗi năm và mỗi lần
bao nhiêu cái để chi phí hàng tồn kho là nhỏ nhất?
Câu 10.3. Một đại lý xăng dầu cần làm một cái bồn chứa dầu hình trụ bằng tôn có thể tích 3
16 m . Tìm bán kính đáy r của hình trụ sao cho hình trụ được làm ra ít tốn nguyên vật liệu nhất. A. 0,8m B. 1,2m C. 2m D. 2,4m
Câu 10.4. Một xưởng cơ khí nhận làm những chiếc thùng phi với thể tích theo yêu
cầu là 2000 lít mỗi chiếc. Hỏi bán kính đáy và chiều cao của thùng lần lượt bằng
bao nhiêu để tiết kiệm vật liệu nhất? A. 1m và 2m
B. 1dm và 2dm C. 2m và 1m D. 2dm và 1dm
Câu 10.5. Người ta muốn mạ vàng bên ngoài cho một cái hộp có đáy hình vuông,
không nắp, thể tích hộp là 4 lít. Giả sử đồ dày của lớp mạ tại một điểm trên hộp là
như nhau. Gọi chiều cao và cạnh đáy lần lượt là x và h . Giá trị của x và h để
lượng vàng cần dùng nhỏ nhất là: A. 3 4 12 x 4; h B. 3 x 12; h C. x 2;h 1 D. x 1;h 2 3 16 3 144 11
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 10.6. Có một tấm nhôm hình chữ nhật có chiều dài bằng 24( ) cm , chiều rộng bằng 18( )
cm . Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau,
mỗi hình vuông có cạnh bằng ( x c )
m rồi gấp tấm nhôm lại như hình vẽ dưới đây để
được một cái hộp không nắp. Hỏi thể tích lớn nhất của cái hộp là bao nhiêu? A. 3 V 640cm B. 3 V 617,5cm C. 3 V 845cm D. max max max 3 V 645cm max
Câu 10.7. Người ta muốn rào quanh một khu đất với một số vật liệu cho trước là
180 mét thẳng hàng rào. Ở đó người ta tận dụng một bờ giậu có sẵn để làm một
cạnh của hàng rào và rào thành mảnh đất hình chữ nhật. Hỏi mảnh đất hình chữ
nhật được rào có diện tích lớn nhất bằng bao nhiêu? A. 2 S 3600m B. 2 S 4000m max max C. 2 S 8100m D. 2 S 4050m max max
Câu 10.8. Một lão nông chia đất cho con trai để người con canh tác riêng, biết
người con sẽ được chọn miếng đất hình chữ nhật có chu vi bằng 800( ) m . Hỏi anh ta
chọn mỗi kích thước của nó bằng bao nhiêu để diện tích canh tác lớn nhất?
A. 200m 200m
B. 300m 100m
C. 250m 150m D.Đáp án khác 3x 1
Câu 11.1. Hai điểm M, N thuộc hai nhánh của đồ thị y
. Khi đó độ dài đoạn x  3
thẳng MN ngắn nhất bằng? A. 8 B. 4 C. x  3 D. 8 2 . M a 3
Câu 11.2. Tính thể tích hình cầu ngoại tiếp tứ diện ABCD, có cạnh AB = và 2
các cạnh còn lại đều bằng a. 13 13 13 13 13 13 13 A. 3  a B. 3  a C. 3  a D. 3  a . 162 216 648 162
Câu 11.3. Số giá trị nguyên của tham số m sao cho bất phương trình: 2 2
log 5  log(x 1)  log(mx  4x  )
m nghiệm đúng với mọi x thuộc R? A. 0 B. m
 Z và m  3 C. 1 D. 2. 12
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 a 1
Câu 11.4. Cho hàm số f (x)   . x
b xe . Biết rằng f '(0)  2
 2 và f (x)dx  5  . Khi 3 (x1) 0
đó tổng a b bằng? 146  26 26 146 A. B. C. D. . 13 11 11 13
Câu 11.5. Trong không gian với hệ trục toạ độ Oxyz, cho điểm A2;5;3 và đường x 1 y z  2 thẳng d :  
. Gọi (𝑃) là mặt phẳng chứa đường thẳng 𝑑 sao cho 2 1 2
khoảng cách từ 𝐴 đến (𝑃) lớn nhất. Tính khoảng cách từ điểm M 1;2;  1 đến mặt phẳng (𝑃)? 11 18 11 4 A. B. 3 2 C. D. 18 18 3
Câu 11.6. Trong các số phức thỏa điền kiện z  4i  2  2i z , modun nhỏ nhất của số phức z bằng? A. 2 2 B. 2 C. 1 D. 3 2 .
Câu 12.1. Trong vật lí, sự phân rã của các chất phóng xạ được biểu diễn bởi công t 1 T thức: m t m
, trong đó m là khối lượng ban đầu của chất phóng xạ (tại thời 0 2 0
điểm t = 0); T là chu kì bán rã (tức là khoảng thời gian để một nửa khối lượng chất phóng
xạ bị biến thành chất khác). Chu kì bán rã của Cabon 14C là khoảng 5730 năm. Cho
trước mẫu Cabon có khối lượng 100g. Hỏi sau khoảng thời gian t thì khối lượng còn bao nhiêu? 100t t ln 2 5730 1 5730 1 A. 5730 m t 100.e B. m t 100. C. m t 100 D. 2 2 100t 5730 m t 100.e
Câu 12.2. Trong vật lí, sự phân rã của các chất phóng xạ được biểu diễn bởi công t 1 T thức: m t m
, trong đó m là khối lượng ban đầu của chất phóng xạ (tại thời 0 2 0
điểm t = 0); T là chu kì bán rã (tức là khoảng thời gian để một nửa khối lượng chất phóng
xạ bị biến thành chất khác). Chu kì bán rã của Cabon 14C là khoảng 5730 năm. Người 13
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
ta tìm được trong một mẫu đồ cổ một lượng Cabon và xác định được nó đã mất
khoảng 25% lượng Cabon ban đầu của nó. Hỏi mẫu đồ cổ đó có tuổi là bao nhiêu? A. 2378 năm B. 2300 năm C. 2387 năm D. 2400 năm
Câu 12.3. Một nghiên cứu cho thấy một nhóm học sinh được cho xem cùng một
danh sách các loài động vật và được kiểm tra lại xem họ nhớ bao nhiêu % mỗi
tháng. Sau t tháng, khả năng nhớ trung bình của nhóm học sinh được cho bởi công thức M t 75 20 ln t 1 ,t
0 (đơn vị %). Hỏi sau khoảng bao lâu thì nhóm học
sinh nhớ được danh sách đó dưới 10%? A. 24.79 tháng B. 23 tháng C. 24 tháng D. 22 tháng
Câu 12.4. Một công ty vừa tung ra thị trường sản phẩm mới và họ tổ chức quảng
cáo trên truyền hình mỗi ngày. Một nghiên cứu thị trường cho thấy, nếu sau x
quảng cáo được phát thì số % người xem mua sản phẩm là 100 P(x) ,x
0 . Hãy tính số quảng cáo được phát tối thiểu để số người 0.015 1 49 x e mua đạt hơn 75%. A. 333 B. 343 C. 330 D. 323
Câu 12.5. Ông Năm gửi 320 triệu đồng ở hai ngân hàng X và Y theo phương thức
lãi kép. Số tiền thứ nhất gửi ở ngân hàng X với lãi suất 2,  1 một quý trong thời
gian 15 tháng. Số tiền còn lại gửi ở ngân hàng Y với lãi suất 0,7  3 một tháng
trong thời gian 9 tháng. Tổng lợi tức đạt được ở hai ngân hàng là 27 507 768,13
(chưa làm tròn). Hỏi số tiền ông Năm lần lượt gửi ở ngân hàng X và Y là bao nhiêu?
A.140 triệu và 180 triệu.
B.180 triệu và 140 triệu.
C. 200 triệu và 120 triệu.
D. 120 triệu và 200 triệu.
Câu 13.1. Cho hàm số y = - x3 + 3mx2 -3m – 1. Tìm các giá trị của m để hàm số có
cực đại, cực tiểu. Với giá trị nào của m thì đồ thị hàm số có điểm cực đại, điểm cực
tiểu đối xứng với nhau qua đường thẳng d: x + 8y – 74 = 0. Đáp án: m=2
Câu 13.2. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, thể 3 a 3
tích khối lăng trụ bằng
. Tính khoảng cách giữa hai đường thẳng AA’ và 4 BC’. a 21 Đáp án: 7
Câu 13.3. Tìm m để phương trình 16x  3.4x  2m 1  0 (1) có hai nghiệm phân biệt 14
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 5  1 Đáp án: m  8 2
Câu 13.4. Tính diện tích hình phẳng giới hạn bởi hai đường cong     1 ;  1 x y e x ye x
Câu 13.5. Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình: 2 2 2
x y z  2x  6y  4z  2  0 . Viết phương trình mặt phẳng (P) song song với
giá của véc tơ v  (1;6;2) , vuông góc với mặt phẳng () : x  4y z 11  0 và tiếp xúc với (S).
Đáp án: (P): 2x y  2z  3  0 hoặc (P): 2x y  2z  21  0 4  z 1
Câu 13.6. Phương trình  1   có bao nhiêu nghiệm.  z 1 Đáp án: 3 nghiệm
Câu 14.1. Để hàm số 2
y x m x  m đồng biến trên khoảng (1;2) thì giá trị của m phải là A. m  2. B. m  3.
C. 2  m  3. D. Với mọi m.
Câu 14.2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Mặt bên
SAB là tam giác đều và vuông góc với đáy. Gọi M là điểm thuộc cạnh SC sao cho SM  2M .
C Tính thể tích hình chóp M.ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 6 36 18 24 
Câu 14.3. Hàm số y   2
x  2x m   1 có tập xác định là khi: A. m  1
 hoặc m  0 B. m  0 C. m  0 D. 0  m  3 e . a e  . b e c
Câu 14.5. Cho biết tích phân I x2x  ln x 4 2 2 dx   với a, , b c là các ước 4 1
nguyên của 4. Tổng a b c  ? A. 2 B. 4 C. 3 D. 1 15
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 14.5. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A0;2;0, B 1  ;1;4 và C 3; 2  ; 
1 . Mặt cầu S  tâm I đi qua , A ,
B C và độ dài OI  5 (biết tâm I có
hoành độ nguyên, O là gốc tọa độ). Bán kính mặt cầu S  là A. R 1 B. R  3 C. R  4 D. R  5
Câu 14.6. Số phức z a bi, ( , a b  ) thỏa 2
(2  3i)z  5i z  2i . Tính a b ? 5 7 3 11 A.  B.  C.  D.  3 4 4 12 x  2
Câu 15.1. Cho hàm số: y
C . Tìm a sao cho từ A(0, a ) kẻ được hai tiếp x 1
tuyến đến (C) nằm ở hai phía trục Ox.  2      2   A. 2; \ 1 C.  2;   ;    B.     D. ;  \     1  3   3 
Câu 15.2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA
= a, hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là điểm H thuộc AC đoạn AC, AH
. Gọi CM là đường cao của tam giác SAC. Tính thể tích khối tứ 4 diện SMBC theo a. 3 a 14 3 a 14 3 a 14 3 a 14 48 24 16 8
Câu 15.3. Tìm số nghiệm của phương trình: log x x   x   . x  2 1 logx 2 2 2 1 4 1 2 1 1   A. 0 B. 1 C. 2 D. 3  2n  4 x I e   2
1 tan x  tan x
Câu 15. 4. Tính tích phân: dx 2n     2n  2n  C. 2n I e 2n 2n 1   A. 2 4 nI ee B. 4 I e D.   I  e e  4
Câu 15.5. Cho hai điểm A(-1, 3, -2); B(-9, 4, 9) và mặt phẳng (P): 2x-y+z+1=0. Điểm
M thuộc (P). Tính GTNN của AM + BM. 16
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 A.   6 204 7274 31434 2004 726 D. 3 26 B. 6 C. 3   n z 1 i8
Câu 15.6. Cho số phức A. 4 2 n B. 0 C. 8 2 n D. 4 2 n
Câu 16.1. Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình
thang như hình vẽ. Tìm tổng x + y để diện tích hình thang EFGH đạt giá trị nhỏ nhất. A E 2 cm B x cm 3cm H F D C G y cm 7 2 A. 7 B. 5 C. D. 4 2 . 2
Câu 16.2. Người ta thả một lá bèo vào một hồ nước. Kinh nghiệm cho thấy sau 9
giờ bèo sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, lượng lá bèo tăng gấp 10
lần lượng lá bèo trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì số lá bèo 1 phủ kín cái hồ ? 3 9 10 9 A. 3 B. C. 9 – log3 D. . 3 log 3
Câu 16.3. Một vật chuyển động với vận tốc v(t) (m/s) có gia tốc 2
a(t)  3t t
(m/s2). Vận tốc ban đầu của vật là 2 (m/s). Hỏi vận tốc của vật sau 2s .
A. 10 m/s B. 12 m/s C. 16 m/s D. 8 m/s. Câu 16.4. Cho tứ diện ABC ,
D M , N, P lần lượt thuộc BC, B , D AC sao cho
BC  4BM , BD  2BN, AC  3AP , mặt phẳng (MNP) cắt AD tại Q. Tính tỷ số thể
tích hai phần khối tứ diện ABCD bị chia bởi mặt phẳng (MNP). 17
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2 7 5 1 A. B. C. D. . 3 13 13 3
Câu 16.5. Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương
trình 2x – y + z + 1 = 0 và hai điểm M(3; 1; 0), N(- 9; 4; 9). Tìm điểm I(a; b; c) thuộc
mặt phẳng (P) sao cho IM IN đạt giá trị lớn nhất. Biết a, b, c thỏa mãn điều kiện:
A. a b c  21 B. a b c 14 C. a b c  5 D.
a b c  19.
Câu 16.6 Tìm số phức Z có mô đun lớn nhất và thỏa mãn điều kiện Z   i 13 1  3 2i  . 2 3 15 1 5 3 15 A. z   i B. z
i C. z    i D. 4 4 4 4 4 4 1 5 z   i 4 4
Câu 16.7. Một đại lý xăng dầu cần làm một cái bồn chứa dầu hình trụ bằng tôn có thể tích 3
16 m . Tìm bán kính đáy r của hình trụ sao cho hình trụ được làm ra ít tốn nguyên vật liệu nhất. A. 0,8m B. 1,2m C. 2m D. 2,4m
Câu 17.1. Trên sân bay một máy bay cất cánh trên đường băng d (từ trái sang phải)
và bắt đầu rời mặt đất tại điểm O. Gọi (P) là mặt phẳng vuông góc với mặt đất và
cắt mặt đất theo giao tuyến là đường băng d của máy bay. Dọc theo đường băng d
cách vị trí máy bay cất cánh O một khoảng 300(m) về phía bên phải có 1 người
quan sát A. Biết máy bay chuyền động trong mặt phẳng (P) và độ cao y của máy
bay xác định bởi phương trình 2
y x (với x là độ dời của máy bay dọc theo đường
thẳng d và tính từ O). Khoảng cách ngắn nhất từ người A (đứng cố định) đến máy bay là: A. 300( ) m B. 100. 5( ) m C. 200( ) m D. 100 3( ) m Câu 17.2.
Cho hình chóp S.ABCD có SA vuông góc với đáy, SA a 6 . Đáy ABCD là hình 1
thang vuông tại A và B, AB BC AD  .
a Gọi E là trung điểm của AD. Tính bán 2
kính mặt cầu ngoại tiếp hình chóp S.ECD. 18
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2 30 26 A.  a R . B. R a 6. C.  a R . D.  a R . 2 3 2
Câu 17.3. Một bà mẹ Việt Nam anh hùng được hưởng số tiền là 4 triệu đồng trên
một tháng (chuyển vào tại khoản của mẹ ở ngân hàng vào đầu tháng). Từ tháng 1
năm 2016 mẹ không đi rút tiền mà để lại ngân hàng và được tính lãi suất 1% trên
một tháng. Đến đầu tháng 12 năm 2016 mẹ rút toàn bộ số tiền (gồm số tiền của
tháng 12 và số tiền đã gửi từ tháng 1). Hỏi khi đó mẹ lĩnh về bao nhiêu tiền? (Kết
quả làm tròn theo đơn vị nghìn đồng).
A. 50 triệu 730 nghìn đồng
B. 48 triệu 480 nghìn đồng
C. 53 triệu 760 nghìn đồng
D. 50 triệu 640 nghìn đồng Câu 17.4.
Cho một vật thể bằng gỗ có dạng khối trụ với bán kính đáy bằng R. Cắt khối trụ
bởi một mặt phẳng có giao tuyến với đáy là một đường kính của đáy và tạo với đáy góc 0
45 . Thể tích của khối gỗ bé là: 3 2R 3  R 3 R 3  R A. V  . B. V  . C. V  . D. V  . 3 6 3 3 Câu 17.5.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( )
P : x y z 1  0 và hai điểm ( A 1; 3
 ;0), B5;1; 
2 . M là một điểm trên mặt phẳng (P) . Giá trị lớn nhất của
T MA MB là: 4 6 2 3 A. T  2 5. B. T  2 6. C. T  . D. T  . 2 3 Câu 17.6. 25
Số nghiệm phức của phương trình : z   8  6i là? z A. 0 B. 1 C. 2 D. 4
Câu 18.1. Một ngọn hải đăng đặt tại vị trí A có khoảng cách đến bờ biển AB  5km
.Trên bờ biển có một cái kho ở vị trí C cách B một khoảng 7km.Người canh hải đăng có thể
chèo đò từ A đến M trên bờ biểnvới vận tốc 4km/ h rồi đi bộ 19
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
đến C với vận tốc 6km/ h .Vị trí của điểm M cách B một
khoảng bao nhiêu để người đó đi đến kho nhanh nhất? A. 0 km B. 7 km C. 2 5 km D. 14  5 5 km 12 Câu 18.2.
Một cửa hàng nhận làm những chiếc xô bằng nhôm hình trụ không nắp chứa 10 lít
nước. Hỏi bán kính đáy (đơn vị cm, làm tròn đến hàng phần chục) của chiếc xô
bằng bao nhiêu để cửa hàng tốn ít vật liệu nhất. A. 14,7cm. B. 15cm. C. 15,2cm. D. 14cm.
Câu 18.3. Huyện A có 100 000 người. Với mức tăng dân số bình quân 1,5% năm thì
sau n năm dân số sẽ vượt lên 130 000 người. Hỏi n nhỏ nhất là bao nhiêu? A. 18 năm B. 17 năm C. 19 năm D. 16 năm C 
Câu 18.4. Cho đường cong : y
x . Gọi (H) là hình phẳng giới hạn bởi (C), trục tung và đường thẳng
y = m (m > 0). Cho (H) quay xung quanh trục tung ta được một vật thể tròn xoay 32  có thể tích V
5 (đvtt). Khi đó giá trị của m là: A. m = 1 B. m = 2 C. m = 3 D. m = 4 Câu 18.5.
Trong không gian với hệ toạ độ Oxyz , gọi   là mặt phẳng qua hai điểm A 2;0;1 và B
2;0;5 đồng thời hợp với mặt phẳng Oxz một góc 0
45 . Khoảng cách từ O tới   là: 3 1 2 A. 3 . B. . C. . D. . 2 2 2 2
Câu 18.6. Số phức có điểm biểu diễn ở phần tô đậm trong hình vẽ sau là: 20
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 1 1
A. 1  z  2 và phần ảo lớn hơn  .
B. 1  z  2 và phần ảo lớn hơn  . 2 2 1
C. 1  z  2 và phần ảo nhỏ hơn  .
D. 1  z  2 và phần ảo nhỏ hơn 2 1  . 2 
Câu 19.1. Cho hàm số 2x 4 y
có đồ thi C điểm ( A 5
 ;5) . Tìm m để đường thẳng x  1
y  xm cắt đồ thị C tại hai điểm phân biệt M và N sao cho tứ giác OAMN là
hình bình hành (O là gốc toạ độ). A. m 0 B. m 0;m 2 C. m 2 D. m 2 Câu 19.2.
Làm 1 m2 mặt nón cần : 120 lá nón ( Đã qua sơ chế) .Giá 100 lá nón là 25.000 đồng
. Vậy để làm 100 cái nón có chu vi vành nón là 120 cm, và khoảng từ đỉnh nón tới 1
điểm trên vành nón là 25 cm thì cần bao nhiêu tiền mua lá nón? A. 400.000đ B. 450.000đ C.500.000đ D. 550.000đ Câu 19.3. y x e  2007   2 Hệ phương trình  y  1 
có bao nhiêu nghiệm thỏa mãn x > 0, y > 0. xy e  2007   2  x  1 A. 0 B. 1 C.2 D.3 21
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 19.4. Một ô tô chạy với vận tốc 20m/s thì người lái xe đạp phanh còn được gọi
là “thắng”. Sau khi đạp phanh, ô tô chuyển động chậm dần đều với vận tốc v(t)  4
 0t  20(m/ )
s . Trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu
đạp phanh . Quãng đường ô tô di chuyển từ lúc đạp phanh đến khi dừng hẳn là bao nhiêu? A. 2m B.3m C.4m D. 5m Câu 19.5.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;5;0), B(3;3;6) và đường
thẳng  có phương trình tham số x  1
  2t; y 1t; z  2t . Một điểm M thay đổi
trên đường thẳng  , xác định vị trí của điểm M để chu vi tam giác MAB đạt giá trị nhỏ nhất. A. M(1 ;0 ;2) B. M(-1 ;0 ; 2) C. M (1 ;0 ; -2) D. M (-1 ; 0 ; - 2) Câu 19.6. z
Tìm số phức z biết z thỏa mãn phương trình  z  2 z A. 1 B. 1+i C.1-i D. i
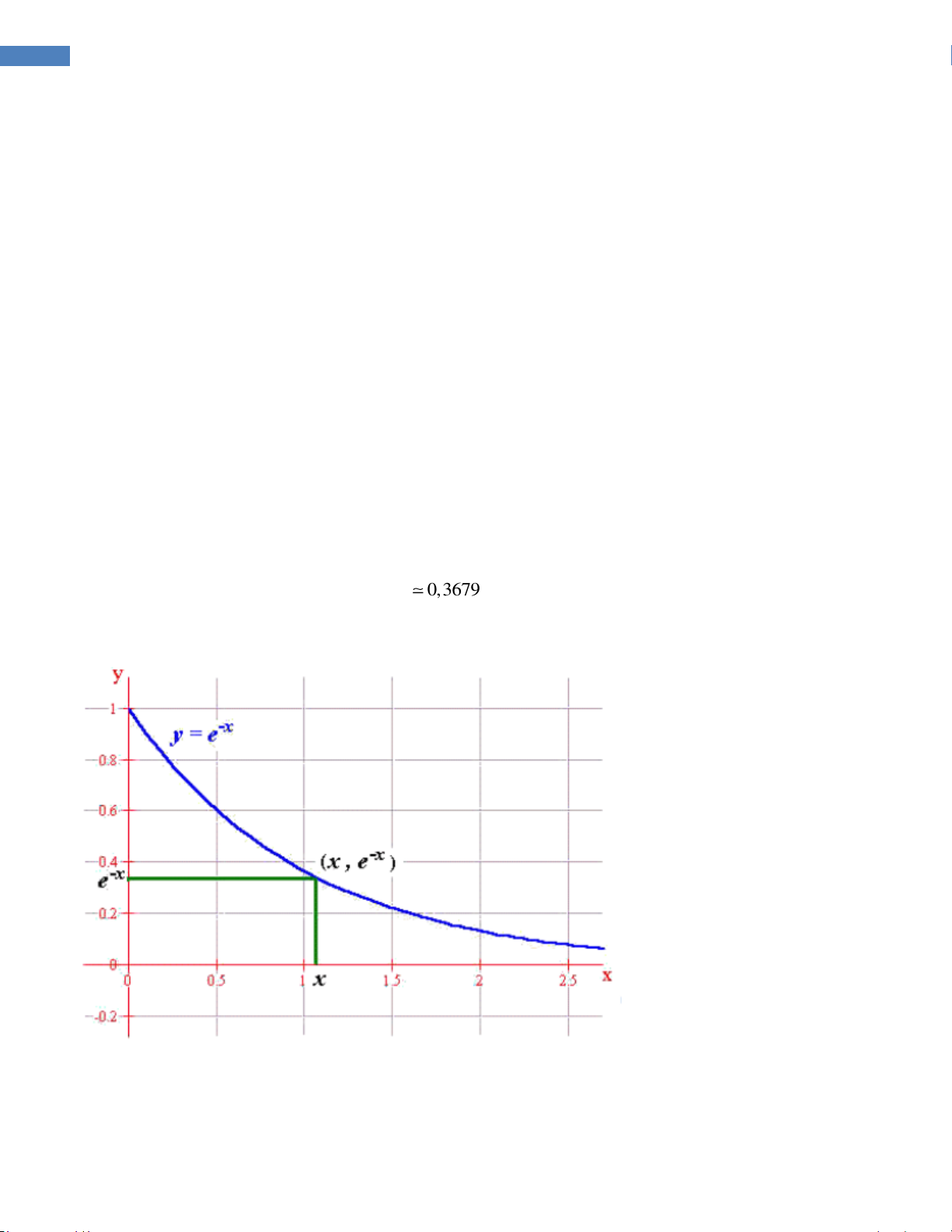
Câu 20.1 . Một máy tính được lập trình để vẽ một chuỗi các hình chữ nhật ở góc
phần tư thứ nhất của trục tọa độ Oxy , nội tiếp dưới đường cong y=e-x. Hỏi diện
tích lớn nhất của hình chữ nhật có thể được vẽ bằng cách lập trình trên
A. 0,3679 ( đvdt) B. 0,3976 (đvdt) C. 0,1353 ( đvdt) D 0,5313 ( đvdt)
Câu 20.2. Cho hình trụ nội tiếp trong hình cầu bán kính R. Xác định chiều cao và
bán kính đáy để hình trụ có thể tích lớn nhất. A. B. C. D.
Câu 20.3. Cho biết chu kỳ bán rã của chất phóng xạ Plutoni Pu239 là 24360 năm . Sự 
phân hủy được tính theo công thức . rt S
A e . Trong đó A là số lượng chất phóng
xạ ban đầu, r là tỷ lệ phân hủy hằng năm (r<0) ,t là thời gian phân hủy, S là lượng
còn lại sau thời gian phân hủy t. Hỏi 10 gam Pu239 sau bao nhiêu năm phân hủy sẽ còn 1 gam 22
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 A. 80922 năm B. 24360 năm C.35144 năm D. 48720 năm 2 x 2  
Câu 20.4. Cho Elip (E) có phương trình y 1 4
Hãy tính diện tích hình phẳng
giới hạn bởi (E) đã cho   A. π B. 2π C. D. 4 2
Câu 20.5. Cho hình chóp O.ABC có OA=a , OB=b, OC=c đôi một vuông góc với
nhau . Điểm M cố định thuộc tam giác ABC có khoảng các lần lượt đến các mặt
phẳng (OBC) , (OCA), (OAB) là 1,2,3 . Khi tồn tại a,b,c thỏa thể tích khối chóp
O.ABC nhỏ nhất, giá trị nhỏ nhất của thể tích khối chóp O.ABC là A. 18 B. 27 C. 6
D. Không tồn tại a,b,c thỏa yêu cầu bài toán
Câu 20.6. Một hình vuông tâm là gốc tọa độ O, các cạnh song song với các trục tọa
độ và có độ dài bằng 4. Hãy xác định điều kiện của a và b để điểm biểu diễn số
phức z=a+bi nằm trên đường chéo của hình vuông
A. a b  2
B. a b  2
C. a b  2
D. a b  2
Câu 21.1. Có một tấm gỗ hình vuông cạnh 200 cm. Cắt một tấm gỗ có hình tam
giác vuông, có tổng của một cạnh góc vuông và cạnh huyền bằng hằng số 120cmtừ
tấm gỗ trên sao cho tấm gỗ hình tam giác vuông có diện tích lớn nhất. Hỏi cạnh
huyền của tấm gỗ này là bao nhiêu?
A. 40cm .
B. 40 3cm .
C. 80cm .
D. 40 2cm . Câu 21.2.
Một hình trụ có bán kính đáy là R và chiều cao R 3 . Hai điểm A và B lần lượt nằm
trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng 0 30 .Tính
khoảng cách giữa AB và trục của hình trụ. R 3 R 3 3R 3 2R 3 A. . B. . C. . D. . 3 2 4 3 x x x  
Câu 21.3. Gọi S1 là tập nghiệm của bất phương trình 2.2 3.3 6 1 0 .  x
Gọi S2 là tập nghiệm của bất phương trình 2 4 . 23
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 log x 1  0 1  
Gọi S3 là tập nghiệm của bất phương trình . 2
Trong các khẳng định sau, khẳng định nào đúng khi nói về mối quan hệ giữa các
tập nghiệm S , S , S 1 2 3 ? S S S S S S A. S . S . S . 1 3 2 B. 3 2 1 C. 3 1 2 D.
S S S . 1 2 3 Câu 21.4. b x e
Cho tích phân C  
dx trong đó a là nghiệm của phương trình 2 x 1 2   2 , b là x a e  3 2
một số dương và b a . Gọi 2
A   x dx . Tìm chữ số hàng đơn vị của b sao cho C  3A 1 . A. 3 B. 2 C.4 D. 5 x  3 t
Câu 21.5. Trong không gian Oxyz, cho 2 đường thẳng d :  y  2  t và d’ :  z  2tx t ' 
y  5  t ' 
z  2t ' 3 2  5
Viết phương trình mặt phẳng () chứa (d) và tạo với mặt phẳng Oyz một góc nhỏ nhất.
A. 3x y  2z  7  0 .
B. 3x y  2z  7  0 . C. 3
x y  2z  7  0 .
D. 3x y  2z  7  0 . Câu 21.6.
Trên tập hợp số phức cho phương trình 2
z  3z 1  0 (*). Gọi z z là nghiệm của 1, 2 z z
phương trình (*). Tìm môđun của số phức 1 2 w   , n N 4n2 4n i i A. 1. B. 2. C.4. D. 6. 24
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 22.1. Bạn An là một học sinh lớp 12, bố bạn là một thợ hàn. Bố bạn định làm
một chiếc thùng hình trụ từ một mảnh tôn có chu vi 120 cm theo cách dưới đây:
Bằng kiến thức đã học em giúp bố bạn chọn mảnh tôn để làm được chiếc thùng có
thể tích lớn nhất, khi đó chiều dài, rộng của mảnh tôn lần lượt là: A. 35c ; m 25cm B. 40c ; m 20cm C. 50c ; m 10cm D. 30c ; m 30cm
Câu 22.2. Cho bát diện đều; tính tỷ số giữa thể tích khối cầu nội tiếp và thể tích
khối cầu ngoại tiếp hình bát diện đều đó. A. 1 B. 1 C. 1 D. 1 2 2 2 3 3 3
Câu 22.3. Bác B gửi tiết kiệm số tiền ban đầu là 20 triệu đồng theo kỳ hạn 3 tháng
với lãi suất 0,72%/tháng. Sau một năm, bác B rút cả vốn lẫn lãi và gửi lại theo kỳ
hạn 6 tháng với lãi suất 0,78%/tháng. Sau khi gửi được đúng một kỳ hạn 6 tháng
do gia đình có việc nên bác gửi thêm một số tháng nữa thì phải rút tiền trước kỳ
hạn cả gốc lẫn lãi được số tiền là 23263844,9 đồng (chưa làm tròn). Biết rằng khi
rút tiền trước thời hạn lãi suất được tính theo lãi suất không kỳ hạn, tức tính theo
hàng tháng. Trong một số tháng bác gửi thêm lãi suất là: A. 0,4% B. 0,3% C. 0,5% D. 0,6%
Câu 22.4. Một ô tô xuất phát với vận tốc v t 2t 10 m / s 1 sau khi đi được một
khoảng thời gian t1 thì bất ngờ gặp chướng ngại vật nên tài xế phanh gấp với vận tốc v t 20 4t m / s 2
và đi thêm một khoảng thời gian t2 nữa thì dừng lại. Biết tổng
thời gian từ lúc xuất phát đến lúc dừng lại là 4 (s). Hỏi xe đã đi được quãng đường bao nhiêu mét. A. 57 m B. 64 m C. 50 m D. 47 m
Câu 22.5. Trong không gian với hệ trục toạ độ Oxyz cho điểm M 1;1; 2 và hai x 2 y z 1 x y 1 đường thẳng z 6 1 : ; 2 :
. Lấy trên 1 điểm N và trên 2 1 1 1 2 1 1
điểm P sao cho M,N,P thẳng hàng. Toạ độ trung điểm của NP là: A. I 1;1; 3 B. I 1;1; 2 C. I 0;2;3 D. I 2;0; 7 25
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 22.6. Gọi z ; z ; z ; z là 4 nghiệm phức của phương trình 4 2 z 4 m z 4m 0 . 1 2 3 4
Tìm tất cả các giá trị m để z z z z 6 . 1 2 3 4 A. m 1 B. m 2 C. m 3 D. m 1
Câu 23.1. Đường dây điện 110KV kéo từ trạm phát (điểm A) trong đất liền ra Côn
Đảo (điểm C). biết khoảng cách ngắn nhất từ C đến B là 60km, khoảng cách từ A
đến B là 100km, mỗi km dây điện dưới nước chi phí là 5000 USD, chi phí cho mỗi
km dây điện trên bờ là 3000 USD. Hỏi điểm G cách A bao nhiêu để mắc dây điện
từ A đến G rồi từ G đến C chi phí ít nhất.
A: 40km B: 45km C: 55km D: 60km
Câu 23.2. Công ty chuyên sản xuất bao bì đựng sản phẩm sữa nhận đơn đặt hàng
sản xuất hộp đựng sữa có thể tích 3
1dm . Các nhân viên thiết kế phân vân giữa làm
hộp đựng dạng hình trụ hay hình hộp chữ nhật đáy hình vuông. Hỏi công ty sẽ
làm hộp hình gì để chi phí nguyên liệu nhỏ nhất.
A: Hình trụ B: Hình hộp chữ nhật đáy hình vuông
C: Cả hai như nhau D: Hình lập phương
Câu 23.3. Cô giáo Thảo ra trường xa quê lập nghiệp, đến năm 2014 sau gần 5 năm
làm việc tiết kiệm được x(triệu đồng) và định dùng số tiền đó để mua nhà nhưng
trên thực tế cô giáo phải cần 1,55x( triệu đồng). Cô quyết định gửi tiết kiệm vào
ngân hàng với lãi suất là 6,9% /năm với lãi hàng tháng nhập gốc và cô không rút
trước kì hạn. Hỏi năm bao nhiêu cô mua được căn nhà đó, biết rằng chủ nhà đó vẫn bán giá như cũ.
A: Năm 2019 B: Năm 2020 C: Năm 2021 D: Năm 2022
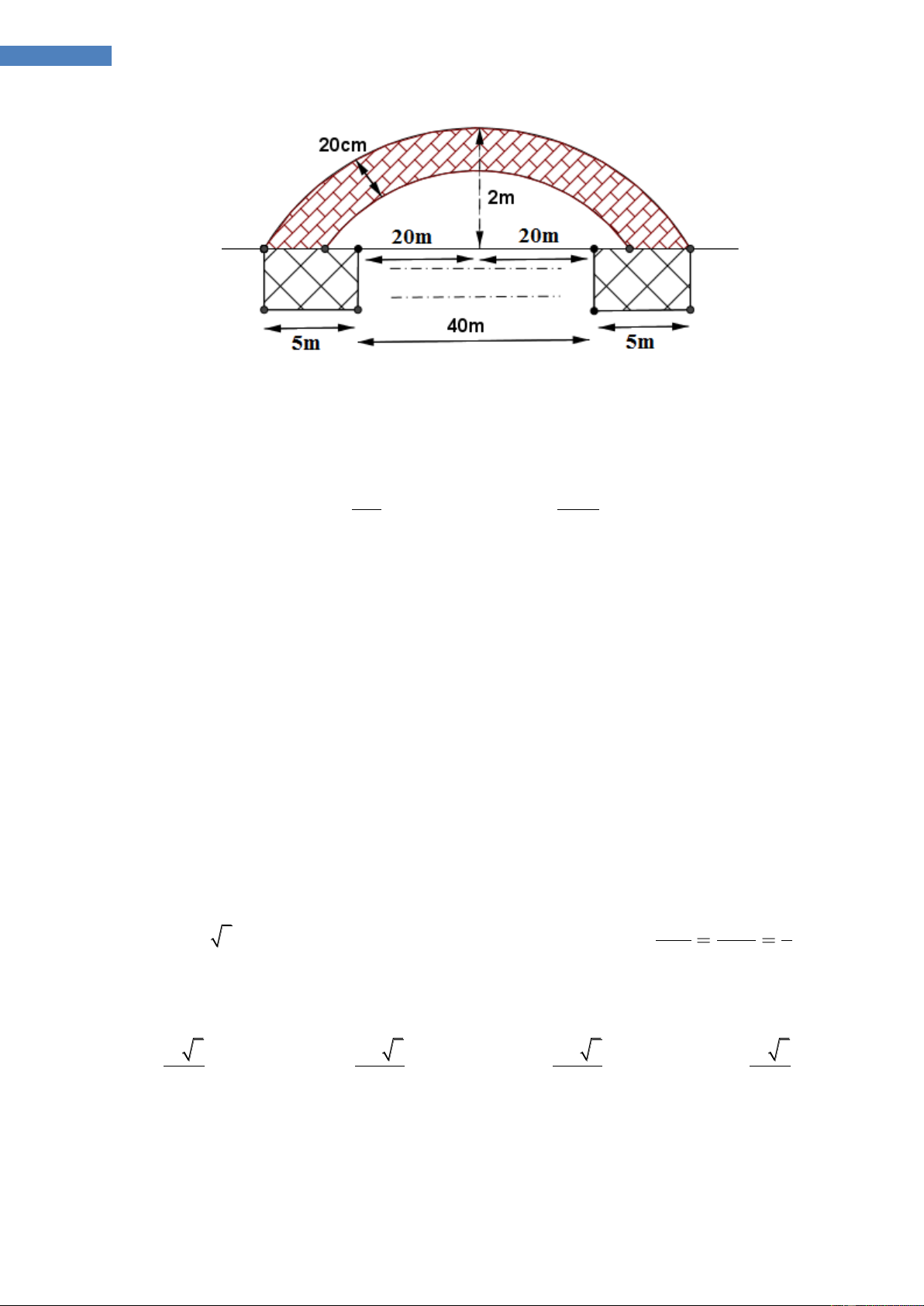
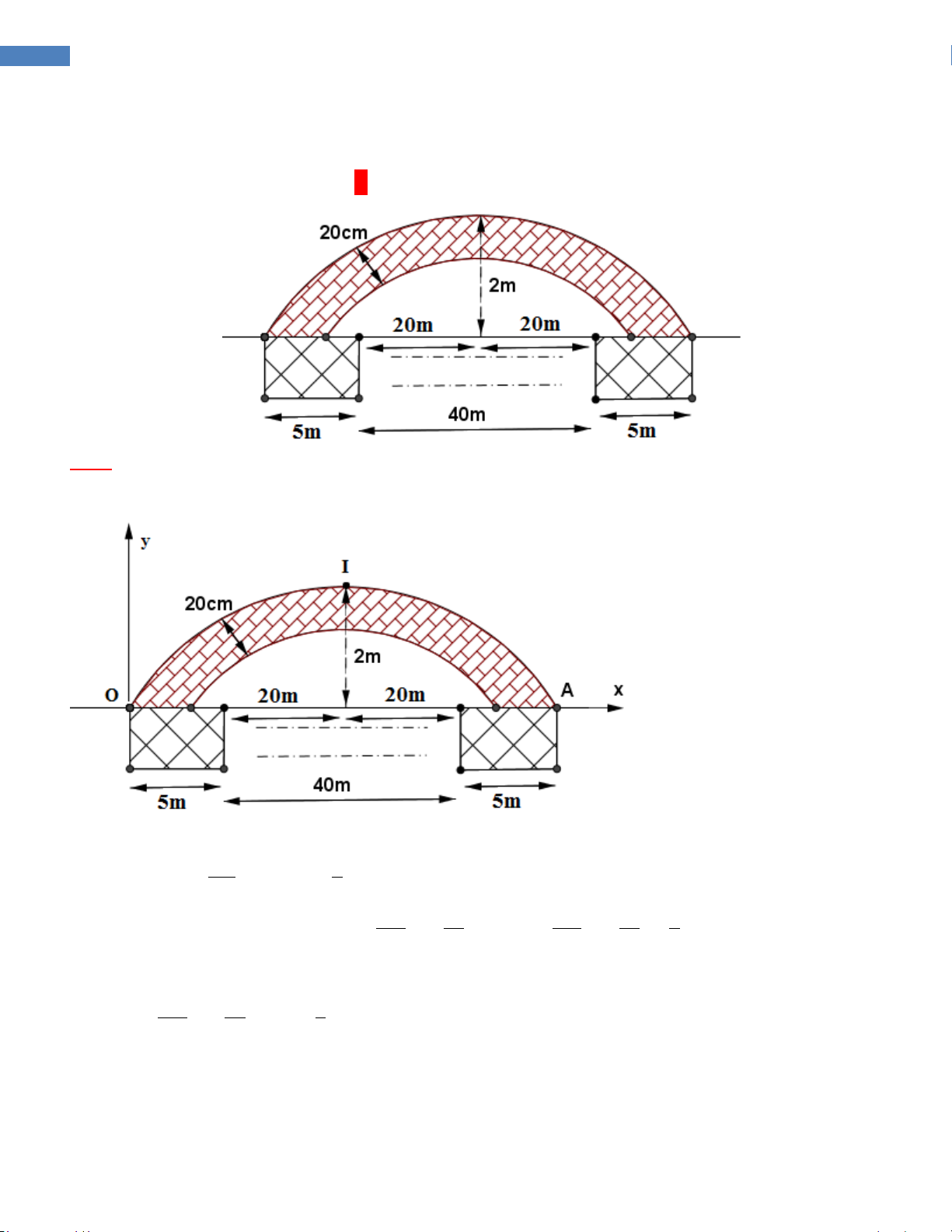
Câu 23.4. Thành phố định xây cây cầu bắc ngang con sông dài 500m, biết rằng
người ta định xây cầu có 10 nhịp cầu hình dạng parabol,mỗi nhịp cách nhau
40m,biết 2 bên đầu cầu và giữa mối nhịp nối người ta xây 1 chân trụ rộng 5m. Bề
dày nhịp cầu không đổi là 20cm. Biết 1 nhịp cầu như hình vẽ. Hỏi lượng bê tông
để xây các nhịp cầu là bao nhiêu (bỏ qua diện tích cốt sắt trong mỗi nhịp cầu) A: 3 20m B: 3 50m C: 3 40m D: 3 100m 26
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 23.5. Trong không gian với hệ tọa độ Oxyz cho điểm A(1 ;2 ;2) ; B(-1 ;2 ;-1) ;
C(1 ;6 ;-1) ; D(-1 ;6 ;2). ABCD là tứ diện gì ?
A : Tứ diện đều B : Tứ diện vuông C: Tứ diện gần đều D : Tứ diện thường 4i 2  6i
Câu 23.6. Cho số phức z
; z  (1 i)(1 2i); z
có điểm biểu diễn trong 1 2 3 i 1 3  i
mặt phẳng phức lần lượt là H;I;V. Tìm tọa độ E sao cho HIVE là hình vuông.
A: Điểm E(-1;-1) B: Điểm E(-1; 1) C: Điểm E(1;-1) D: Điểm E(1;1)
Câu 24.1. Một công ti bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê
mỗi căn hộ với giá 2 000 000 đồng một tháng thì mọi căn hộ đều có người thuê và
cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm 100 000 đồng một tháng thì có thêm
hai căn hộ bị bỏ trống. Hỏi muốn có thu nhập cao nhất, công ti đó phải cho thuê
mỗi căn hộ với giá trị bao nhiêu một tháng? (đồng/tháng) A. 2 250 000 B. 2 450 000 C. 2 300 000 D. 2 225 000
Câu 24.2. Cho hình lăng trụ tam giác đều ABC.A’B’C’, có cạnh đáy bằng a và cạnh AM A'N 1
bên bằng a 2 . Lấy M, N lần lượt trên cạnh AB’, A’C sao cho . Tính AB ' A'C 3
thể tích V của khối BMNC’C. 3 a 6 3 2a 6 3 3a 6 3 a 6 A. B. C. D. 108 27 108 27
Câu 24.3. Cho ba số dương a, b, c đôi một khác nhau và khác 1. Xét các khẳng định sau: 27
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 b c (I) 2 2 log log ; a a c b 1 (II) 2 2 log b log c ; a b 2 log a c c a b (III) Trong ba số 2 2 2 log ; log ; log
luôn có ít nhất một số lớn hơn 1. a b c b c a b c a Khẳng định nào đúng? A. Chỉ (I) và (II) B. Chỉ (I) và (III) C. Chỉ (I) D. Cả (I), (II) và (III) 2 Câu 24.4. Cho I cosn xdx , n , n
2 . Khẳng định nào sau đây đúng? n 0 n 1 n 2 n 1 A. I I B. I I C. I I D.I 2I n n 1 n n n 2 n n n 2 n n n 2
Câu 24.5. Trong không gian tọa độ Oxyz, cho các phương trình mặt phẳng 2 : 3mx 5 1 m y 4mz 20 0, m 1;1 . m Xét các mệnh đề sau: (I) Với mọi m 1;1 thì các mặt phẳng
luôn tiếp xúc với một mặt cầu không m đổi. (II) Với mọi m 0 thì các mặt phẳng
luôn cắt mặt phẳng (Oxz). m (III) d ; O 5, m 1;1 . m
Khẳng định nào sau đây đúng? 28
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 A. Chỉ (I) và (II) B. Chỉ (I) và (III) C. Chỉ (II) và (III) D. Cả 3 đều đúng. z z
Câu 24.6. Cho hai số phức phân biệt z ; z thỏa điều kiện 1 2 là số ảo. Khẳng 1 2 z z 1 2
định nào sau đây là đúng? A. z 1; z 1 B. z z C. z z D. z z 1 2 1 2 1 2 1 2 1
Câu 25.1. Cho hàm số 3 2
y = x  x có đồ thị là (C). 2
Tìm tất cả những điểm trên đồ thị (C) sao cho hệ số góc của tiếp tuyến với 2 4x + 3
đồ thị (C) tại những điểm đó là giá trị lớn nhất của hàm số: g(x) = . 4 x +1  1   3   4 40  A. ; 0   B. 1  ;   ; ;    2   2   3 27   2 1 2   2 1   2   1  C.   ;     ;  ;    D. ; 0   ;  2  ; 1  0 2 4   2 4    2 
Câu 25.2. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu
vuông góc của đỉnh S trên mặt phẳng (ABC) là trung điểm cạnh BC. Góc giữa
đường thẳng SA và mặt phẳng (ABC) bằng 600. Gọi G là trọng tâm tam giác SAC.
Bán kính mặt cầu tâm G và tiếp xúc với mặt phẳng (SAB) là: 13a 13a 3 13a 13a A. B. C. D. 13 39 26 26 1 1 Câu 25.3. Với  
a  0, a  1 , cho biết : 1 log u 1 log a  ; a t t a v a
. Chọn khẳng định đúng : 1  1 1 1 A. 1log    a v u a B. 1 loga t u a C. 1 loga v u a D. 1 loga v u a
Câu 25.4. Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số x  5 y
, trục hoành và hai đường thẳng x  1
 ; x  3 quay quanh trục hoành 1 3  2x là: 29
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 A.  5ln 2   1 B. 5ln 2 1 C.  5ln 2   1 D. 5ln 2 1
Câu 25.5. Trong không gian với hệ toạ độ Oxyz, cho 2 đường thẳng: x t x  2 y 1 z 1   :  
,  :  y  2  t và mặt cầu 2 2 2
(S) : x y z  2x  2y  6z  5  0 1 1 2 3  2 z 1 2t
Viết phương trình mặt phẳng ( ) song song với hai đường thẳng  ,  và cắt mặt 1 2 2 365
cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng . 5
A. x 5y 3z  4  0; x 5y 3z 10  0
B. x 5y 3z 10  0
C. x 5y 3z  3 511  0; x  5y  3z  3 511  0
D. x 5y 3z  4  0
Câu 25.6. Cho số phức z thỏa điều kiện z 1  z i . Số phức   z  2i 3 có môđun nhỏ nhất là: 1 3 1 1 1 1
A.    i B.     i C.    i D. 2 2 2 2 2 2 1 3     i 2 2
Câu 26.1 Tìm diện tích lớn nhất của hình chữ nhật nội tiếp trong nửa đường tròn
bán kính 10cm , biết một cạnh của hình chữ nhật nằm dọc trên đường kính của đường tròn. A. 2 80cm B. 2 100cm C. 2 160cm D. 2 200cm Câu 26.2.
Cho hình chóp S.ABC có chân đường cao nằm trong tam giác ABC ; các mặt phẳng
(SAB) , (SAC) và (SBC) cùng tạo với mặt phẳng (ABC) một góc bằng nhau. Biết AB
25, BC 17 , AC 26 ; đường thẳng SB tạo với mặt đáy một góc bằng 45 .
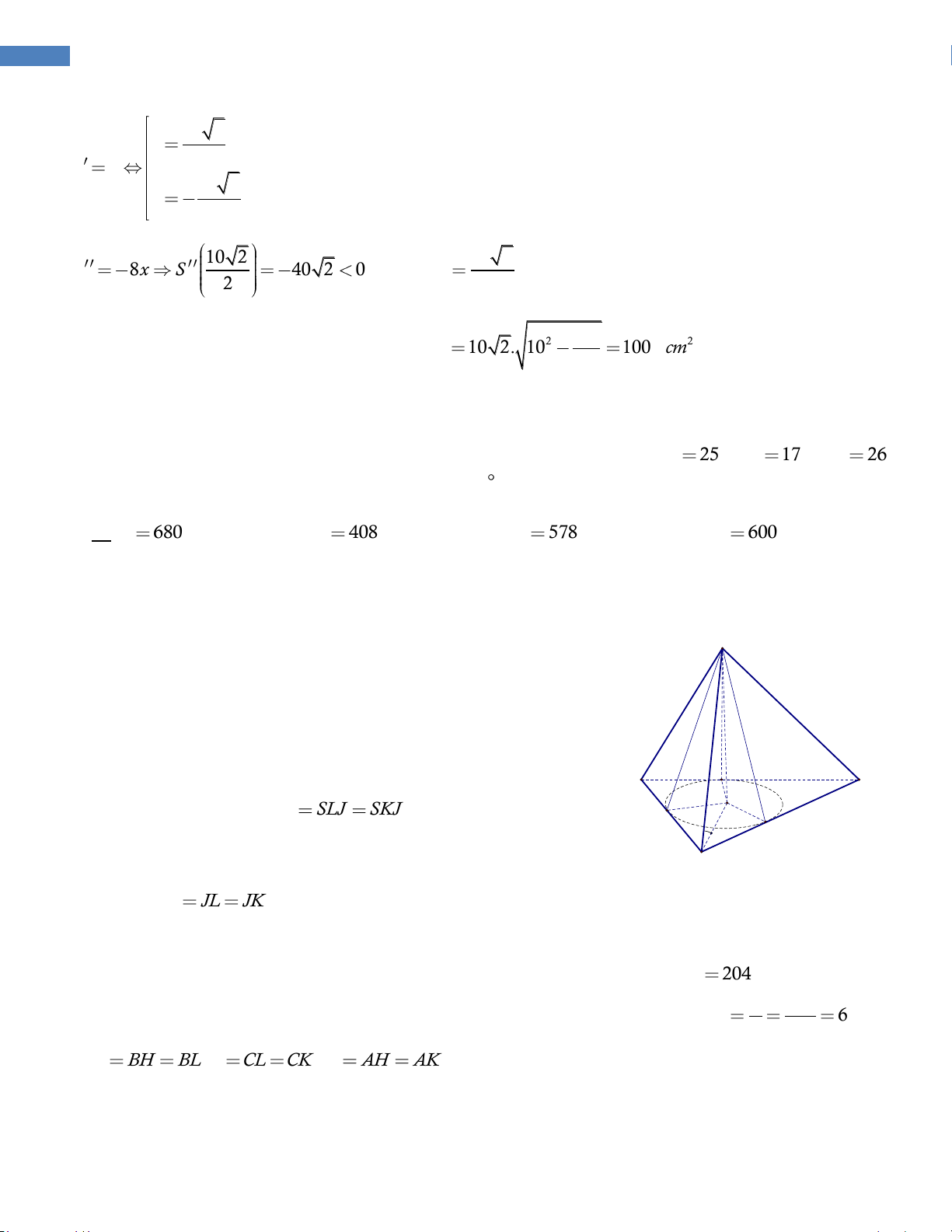
Tính thể tích V của khối chóp S.ABC . A. V 680 B. V 408 C. V 578 D. V 600 Câu 26.3. 30
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Tìm tất cả các giá trị thực của tham số m để phương trình 2 2 2 log x log x 3 m log x 3 2 1 4 có nghiệm thuộc 32; ? 2 A. m 1; 3 . B. m 1; 3 . C. m 1; 3 . D. m 3;1 . Câu 26.4. 1 1 5 Cho hàm số 3 2 y x mx 2x 2m
có đồ thị (C). Tìm m 0; sao cho hình 3 3 6
phẳng giới hạn bởi đồ thị (C) và các đường thẳng x 0, x 2, y 0 và có diện tích bằng 4. 1 1 1 A. m B. m C. m D. m 1 4 3 2 Câu 26.5. x t
Trong không gian tọa độ Oxyz cho đường thẳng d : y 1 2t và mp z 2 t P : 2x y 2z 2
0 . Viết phương trình mặt phẳng R qua d và tạo với P một góc nhỏ nhất . A. x y z 3 0 B. x y z
3 0 C. x y z 3 0 D. x y z 3 0 Câu 26.6. Cho z 1 i; z 1 i z z , z , z 1 2 . Tìm 3
sao cho các điểm biểu diễn của 1 2 3 tạo thành tam giác đều. A. z
2 1 i và z 2 1 i z
3 1 i và z 3 1 i 3 3 B. 3 3 C. z
2 1 i và z 2 1 i z
3 1 i và z 3 1 i 3 3 D. 3 3
Câu 27.1 . Cho hàm số 4 2
y  x  2mx 1 m . Định m để đồ thị hàm số trên có ba
điểm cực trị nhận gốc tọa độ làm trực tâm. A. 1  B. 0 C. 1 D. 2
Câu 27.2. Có một miếng nhôm hình vuông, cạnh là 3dm, một người dự tính tạo
thành các hình trụ (không đáy ) theo hai cách sau: 31
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Cách 1: gò hai mép hình vuông để thành mặt xung quanh của một hình trụ, gọi
thể tích là của khối trụ đó là V1
Cách 2: cắt hình vuông ra làm ba, và gò thành mặt xung quanh của ba hình trụ, gọi
tổng thể tích của chúng là V2. V Khi đó, tỉ số 1 là: V2 1 1 A. 3 B. 2 C. D. 2 3
Câu 27.3. Một người nọ đem gửi tiết kiệm ở một ngân hàng với lãi suất là 12%
năm. Biết rằng cứ sau mỗi một quý ( 3 tháng ) thì lãi sẽ được cộng dồn vào vốn
gốc. Hỏi sau tối thiểu bao nhiêu năm thì người đó nhận lại được số tiền ( bao gồm
cả vốn lẫn lãi ) gấp ba lần số tiền ban đầu. A. 8 B. 9 C. 10 D. 11
Câu 27.4. Có một người cần làm một cái của cổng cố xưa, có hình dạng một
parabol bậc hai như hình vẽ. Giả sử đặt cánh cổng vào một hệ trục tọa độ như
hình vẽ ( mặt đất là trục Ox). Hãy tính diện tích của cánh cửa cổng. 32
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 16 32 28 A. B. C. 16 D. 3 3 3
Câu 27.5. Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A1,2,0 , B3, 1  ,2 , C2, 1  ,  1 , D0, 2, 1
 . Có bao nhiêu mặt phẳng cách đều năm điểm O, A, B, C, D. A. 4 B. 5 C. 6 D. 7
Câu 27.6. Có bao nhiêu điểm có tọa độ là số nguyên biểu diễn cho số phức z có
phần ảo dương và đông thời thỏa mãn z  z  4 , z  z  6 A. 20 B. 15 C. 6 D. 10
Câu 28.1 Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu
trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một
vụ cân nặng Pn  480  20ngam. Hỏi phải thả bao nhiêu con cá trên một đơn
vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất ? A. 10 B. 12 C. 16 D. 24 Câu 28.2.
Một hình hộp có 6 mặt đều là các hình thoi có góc bằng 600 và cạnh bằng a. Tính
thể tích của hình hộp đó. 3 a 3 2a 3 2a 3 2 2a A. B. C. D. 2 2 3 3 Câu 28.3. 33
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Có bao nhiêu giá trị của tham số m để phương trình 2 2 x 5x6 1x 65 .2  2  2.2 x m
m có 3 nghiệm phân biệt. A. 1 B. 2 C. 3 D. 4 Câu 28.4.
Trong hệ trục Oxy, cho tam giác OAB vuông ở A, điểm B nằm trong góc phàn tư   
thứ nhất. A nằm trên trục hoành, OB = 2017. Góc AOB  , 0    .   Khi quay  3 
tam giác đó quanh trục Ox ta được khối nón tròn xoay. Thể tích của khối nón lớn nhất khi : 6 3 1 2 A. sin  B. cos  C. cos  D. sin  3 2 2 3 Câu 28.5.
Cho hai điểm M 1;2;3, A
2;4;4 và hai mặt phẳng P: x y  2z 1 0,
Q: x2y z 4  0. Viết phương trình đường thẳng  qua M cắt P, Q lần lượt tại , B C
sao cho tam giác ABC cân tại A và nhận AM là đường trung tuyến. x 1 y  2 z  3 x 1 y  2 z  3 A.  :   B.  :   1  1  1 2 1  1 x 1 y  2 z  3 x 1 y  2 z  3 C.  :   D.  :   1 1 1 1 1  1 Câu 28.6. 2z 1
Cho số phức z thỏa mãn z  1 và số phức w 
. Khi đó mô đun của số phức 2  iz w là:
A. w  2 B. 1  w  2. C. w  1 D. w  2
Câu 29.1. Một Bác nông dân cần xây dựng một hố ga
không có nắp dạng hình hộp chữ nhật có thể tích 3 3200cm ,
tỉ số giữa chiều cao của hố và chiều rộng của đáy bằng 2 .
Hãy xác định diện tích của đáy hố ga để khi xây tiết kiệm nguyên vật liệu nhất? A. 2 1200cm B. 2 160cm C. 2 1600cm D. 2 120cm 34
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Câu 29.2.
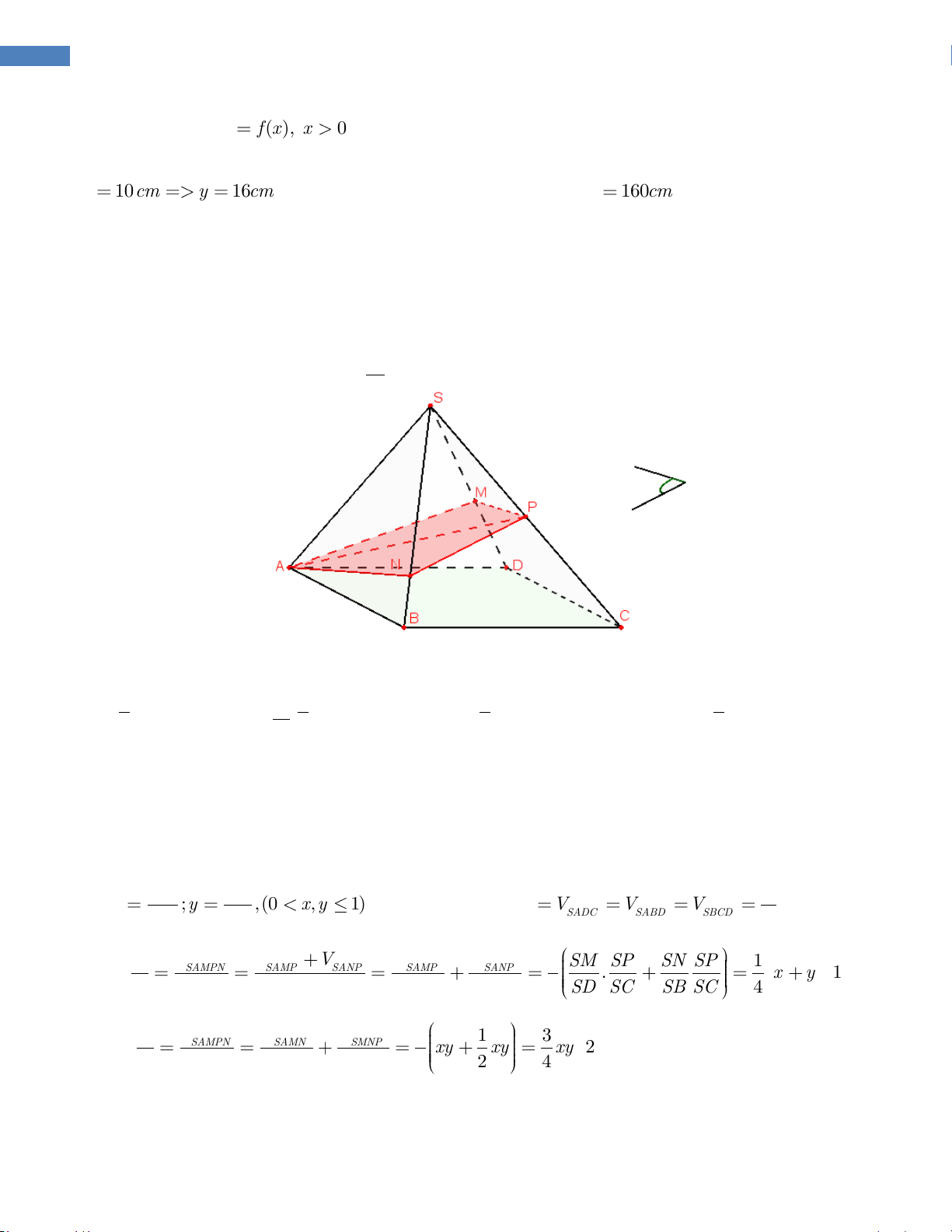
Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là V . Điểm P là
trung điểm của SC , một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M V
và N .Gọi V là thể tích của khối chóp S.AMPN . Tìm giá trị nhỏ nhất của 1 ? 1 V 3 1 2 1 A. B. C. D. 8 3 3 8
Câu 29.3. Một Bác nông dân vừa bán một con trâu được số tiền là 20.000.000
(đồng) .Do chưa cần dùng đến số tiền nên Bác nông dân mang toàn bộ số tiền đó
đi gửi tiết kiệm loại kỳ hạn 6 tháng vào ngân hàng với lãi suất 8.5% một năm thì
sau 5 năm 8 tháng Bác nông dân nhận được bao nhiêu tiền cả vốn lẫn lãi .Biết rằng
Bác nông dân đó không rút cả vốn lẫn lãi tất cả các định kì trước và nếu rút trước
thời hạn thì ngân hàng trả lãi suất theo loại không kì hạn 0.01% một ngày (1 tháng tính 30 ngày)
A. 31802750,09 ®ång B. 30802750,09 ®ång C. 32802750,09 ®ång D. 33802750,09 ®ång 35
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Câu 29.4.
Từ một khúc gõ hình trụ có đường kính 30cm , người ta cắt khúc gỗ bởi một mặt
phẳng đi qua đường kính đáy và nghiêng với đáy một góc 0 45 để lấy một hình
nêm (xem hình minh họa dưới đây) Hình 1 Hình 2
Kí hiệuV là thể tích của hình nêm (Hình 2). Tính V . 225 A. V  cm3 2250  B. V
cm3 C. V  cm3 1250  D. 4 V  cm3 1350  Câu 29.5. x   2  t
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng  : y   1   t 2 t   hai z   t3 
điểm A2;0;3 và B 2; 2  ; 3
 . Biết điểmM x ;y ;z thuộc  thì MA4 MB4  nhỏ nhất 0 0 0  .Tìm x 0 A. x  0 B. x  1 C. x  2 D. x  3 0 0 0 0 Câu 29.6.
Cho các số phức z thỏa mãn z  1  2 . Biết rằng tập hợp các điểm biểu diễn các số
phức w  1  i 3z  2 là một đường tròn . Tính bán kính r của đường tròn đó? A. r  4 B. r  2 C. r  16 D. r  25 36
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
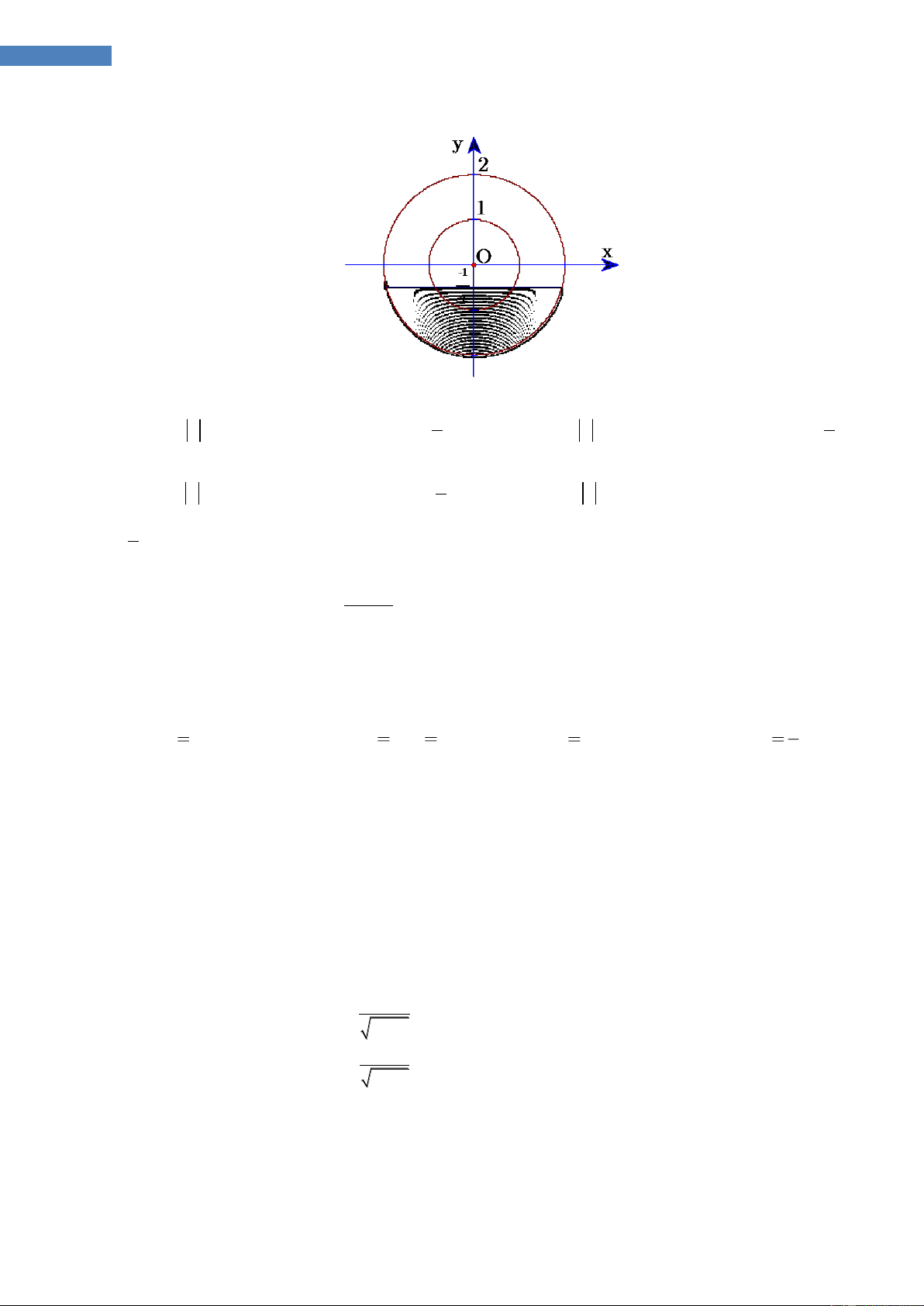
Câu 30.1. Nhà Nam có một chiếc bàn tròn có bán kính bằng 2 m. Nam muốn
mắc một bóng điện ở phía trên và chính giữa chiếc bàn sao cho mép bàn nhận
được nhiều ánh sáng nhất. Biết rằng cường độ sáng C của bóng điện được biểu sin
thị bởi công thức C c
(  là góc tạo bởi tia sáng tới mép bàn và mặt bàn, c - 2 l
hằng số tỷ lệ chỉ phụ thuộc vào nguồn sáng, l khoảng cách từ mép bàn tới bóng
điện) . Khoảng cách nam cần treo bóng điện tính từ mặt bàn là A. 1m B. 1,2m C. 1.5 m D. 2m
Câu 30.2. Với một miếng tôn hình tròn có bán kính bằng R = 6cm. Người ta muốn
làm một cái phễu bằng cách cắt đi một hình quạt của hình tròn này và gấp phần
còn lại thành hình nón ( Như hình vẽ). Hình nón có thể tích lớn nhất khi người ta
cắt cung tròn của hình quạt bằng A.  6 cm B. 6 6 cm C. 2 6 cm D. 8 6 cm 2 log x
Câu 30.3. Tập các giá trị của m để baapts phương trình 2  m nghiệm đúng 2 log x 1 2
với mọi x > 0 bằng A. ( ;  1] B. [1; )  C.  5  ;2 D. [0;3)
Câu 30.4. Cho hình phẳng giới hạn bởi hai đường C 2 2 x y  C  2 2 : 4;
' : x y  2x  0
. Diện tích hình phẳng đó bằng A.  B. 2 C. 3 D. 4 37
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 30.5. Cho parabol (P) 2
y x và hai điểm A, B thuộc (P) sao cho AB = 2. Tìm A,
B sao cho diện tích hình phẳng giới hạn bởi (P) và đường thẳng AB đạt giá trị lớn nhất 4 3 2 3 A. B. C. D. 3 4 3 2
Câu 30.6. Trong hệ trục tọa độ Oxyz cho 3 điểm A ;
a 0;0, B0; ;
b 0,C 0;0; c với , a ,
b c  0 .Giả sử a, ,
b c thay đổi nhưng thỏa mãn 2 2 2 2
a b c k không đổi. Diện
tích tam giác ABC đạt giá trị lớn nhất bằng 2 k 3 2 k 3 A. B. C. 2 k 3 D. 2 k 2 6
Câu 30.7. Trong không gian với hệ toạ độ Oxyz, phương trình mặt phẳng (P) đi
qua điểm M(9;1;1) , cắt các tia Ox, Oy, Oz tại A, B, C sao cho thể tích tứ diện OABC
có giá trị nhỏ nhất là x y z x y z x y z x y z A.    1 1 7 3 3 B.    1 27 3 3 C.    D.    1 27 3 3 27 3 3
Câu 30.8. Trong mặt phẳng phức cho 3 điểm A,B,C theo thứ tự biểu diễn các số 4i  
i  i 2 6i , 1 1 2 ,
. Số phức biểu diễn bởi điểm D sao cho tứ giác ABCD là i 1 3  i hình vuông là A. 1  i B. 1 5i C. 1 i D. 1 5i
Câu 31.1. Cho x và y là hai số thực dương thay đổi sao cho: 2 2
x  2x  4y  0 . Giá trị
lớn nhất của tích xy gần nhất với số nào? A. 0,5 B. 0,6 C. 0,7 D. 0,8
Câu 31.2. Nếu một tứ diện chỉ có đúng một cạnh có độ dài lớn hơn 1 thì thể tích tứ
diện đó lớn nhất là bao nhiêu? 1 3 1 5 A. B. C. D. 4 4 8 8 38
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 31.3. Giả sử p và q là các số thực dương sao cho: log p  log q  log p q . 9 12 16   p Tìm giá trị của q 4 8 1 1 A. B. C. 1 3 D. 1 5 3 5 2 2 2 2017
Câu 31.4. Cho tích phân K   3 2
x  3x  2
dx . Giá trị của K bằng bao nhiêu? 0 A. 0 B. 1 C. 2 D. 1
Câu 31.5. Trong không gian Oxyz cho 4 điểm A2;3;2 , B6; 1  ; 2   , C 1  ; 4  ;3 , D 1;6; 5
 . Gọi M là một điểm nằm trên đường thẳng CD sao cho tam giác MAB có
chu vi bé nhất. Khi đó toạ độ điểm M là:
A. M 0;1;  1 B. M 2;11; 9   C. M 3;16; 1  3 D. M  1  ; 4  ;3 Câu 31.6. Cho 2 i  1
 , có bao nhiêu số nguyên n sao cho   4
n i là một số nguyên? A. 1 B. 2 C. 3 D. 4
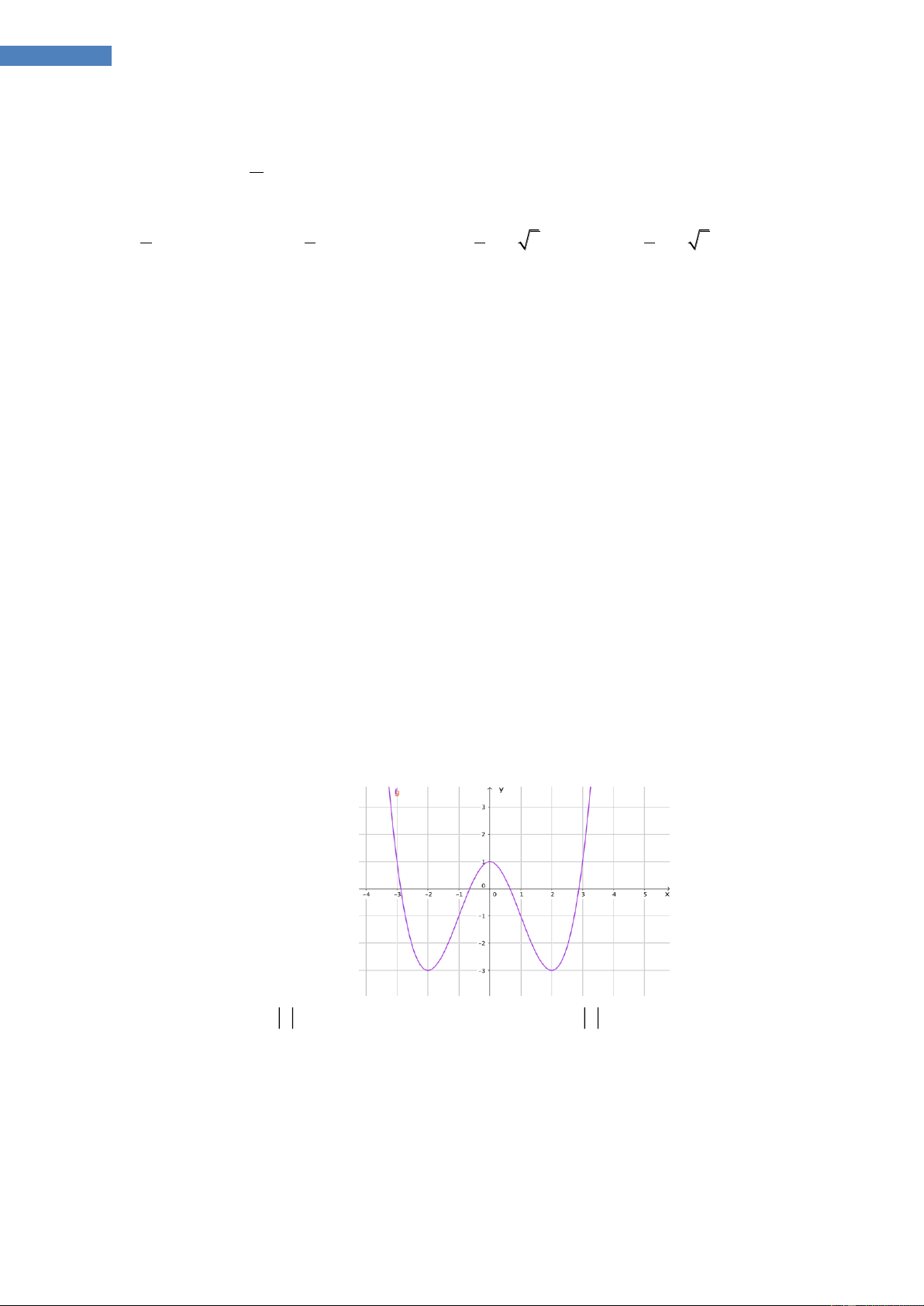
Câu 32.1. Đường cong hình dưới là đồ thị của một trong bốn hàm số được cho
trong bốn phương án A,B,C và D dưới đây. Hỏi hàm số đó là hàm số nào ?
A. y = x3 - 3 x 2 +1. B. y = -x4 - x2 +1.
C. y = x 3 - 3x2 +1. D.
y = x4 - 8x2 +1.
Câu 32.2. Cho hình chóp S.ABCD có ABCD là hình vuông cạnh 2a, tam giác SAB
đều và nằm trong mặt phẳng vuông góc với (ABCD). Tính bán kính của mặt cầu
ngoại tiếp hình chóp trên. 39
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 a 7 a 21 a 7 a 21 A. . B. . C. . D. . 2 6 4 3 2 2
Câu 32.3. Tập nghiệm của bất phương trình: x x 1  1  x x 1 3 3 3 3     . a 7 a 21 a 7 a 21 A. . B. . C. . D. . 2 6 4 3
Câu 32.4. Với giá trị nào của m thì diện tích hình phẳng giới hạn bởi parabol
P: y  x2 2x và d: y mxm  0 bằng 27 đơn vị diện tích. A. m = -1. B. m = -2. C. m = Æ. D. m Î .
Câu 32.5. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng P : x y z 1  0
và hai điểm A1; 3  ;0, B5; 1  ; 2
 . Tìm tọa độ điểm M trên mặt phẳng P sao
cho MA MB đạt giá trị lớn nhất.
A. M(-2;-3;3).
B. M(-2;-3;2).
C. M(-2;-3;6).
D. M(-2;-3;0).
Câu 32.6. Cho các số phức z ,z ,z ,z ,z có điểm biểu diễn lần lượt là A, B, C, D, E 1 2 3 4 5
trong mặt phẳng phức tạo thành một ngũ giác lồi. Gọi M, N, P, Q lần lượt là trung
điểm các cạnh AB, BC, CD, DE. Gọi I, J lần lượt là trung điểm các đoạn MP và NQ.
Biết I, J là điểm biểu diễn hai số phức z  1 i; z  2i và z  4  i 5 là số phức có I J E
điểm biểu diễn là E. Tìm số phức z ? 1 A. = 2 - 3i. B. = 4 - 7i. C. = 8- 7i. D. = 8- 2i. z1 z1 z1 z1
Câu 33.1. Cho hàm số: 4 2 2
y x  2(m  2)x m  5m  5 . Với giá trị nào của m thì đồ
thị hám số có cực đại và cực tiểu, đồng thời các điểm này tạo thành một tam giác đều A. 3 m  2  3 B. 2  3 C. 3  2 D. 3 3  2 Câu 33.2.
Cho hình lăng trụ ABC.A' B 'C ' có đáy ABC là tam giác đều cạnh a , hình chiếu
vuông góc của A ' lên măt phẳng ABC trùng với tâm G của tam giác ABC . a 3
Biết khoảng cách giữa AA' và BC là
. Tính thể tích V của khối lăng trụ 4
ABC.A' B 'C ' . 40
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 3 a 3 3 a 3 3 a 3 A. V B. V C. V D. 3 6 12 3 a 3 V 36 Câu 33. 3.
Tìm các giá trị của m để phương trình: 3x  3  5  3x m có 2 nghiệm phân biệt: A. 3  5  m  4 B. 2 2  m  4
C. 2 2  m  3  5 m  2 2 Câu 33.4. 2  1 2 1  Tính tích phân:   dx 
 ta thu được kết quả là: a bln 2 với , a b  . 2
x  3 x x  1
Chọn khẳng định đúng trong các khẳng định:
A. a b  1 B. a  0 C. 2 2 a b  10
D. b  2a  0 Câu 33.5.
Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1;5;0 , B3;3;6 và đường x  1   2t
thẳng  có phương trình tham số y  1 t
t  . Một điểm M thay đổi trên z  2t
đường thẳng  , xác định vị trí của điểm M để chu vi tam giác MAB đạt giá trị nhỏ
nhất. Khi đó toạ độ của điểm M là: A. M 1;0;2 B. M 2;4;3 C. M  3  ;2; 2   D. M 1;4;3 Câu 33.6.
Trong mặt phẳng tọa độ, tập hợp điểm biểu diển các số phức z thỏa mãn z i 1 i z là:
A. Đường tròn có phương trình 2 2 x y 4x 2y 1 0
B. Đường tròn có phương trình 2 2 x y 2y 3 0
C. Đường tròn có phương trình 2 2 x y 2x 1 0 41
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
D. Đường tròn có phương trình 2 2 x y 2y 1 0
Câu 34.1. Cho hàm số y  x3  mx  2 có đồ thị (Cm) . Tìm m để đồ thị (Cm) cắt trục
hoành tại một điểm duy nhất. A. m 3 B. m 3 C. m 3 D. m 3 Câu 34.2.
Cho hình chóp đềuS.ABCD , M là trung điểm SA, N, K lần lượt thuộc SB, SC sao
cho SB=3SN, SC=4SK. Hãy chọn đáp án đúng 1 23 A. V  V V V . S MNK S.ABC B.  MNK.CBA S.ABCD 8 48 1 C. V  V . S MNK S.ABD
D. Cả 3 đáp án A, B, C đều sai 12 1 1 1 
Câu 34.3. Cho A   ... logb logb
logb . Biểu thức rút gọn của A là: 1 2 n a a a 2n(n 1) 2n(2n 1) n(n 1) n(n  2) A. B. C. D. 3.logb logb 2.logb 3logb a a a a Câu 35.4. a
Nếu hàm số f(x) liên tục và là hàm số chẵn trên [-a; a] thì I f (x)dx  bằng a a a a A. 0
B. 2 f (x)dx  C. 2  f (x)dx
D. 2 f (x)dx  0 0 a
Câu 35. 5. Trong hệ trục tọa độ Oxyz cho A(1;2;3).Tìm cặp vecto chỉ phương của
mặt (P) đi qua A và khoảng cách từ O đến (P) là lớn nhất. u   ( 3  ;0;1) u   ( 3  ;0;1) u   ( 3  ;0;1) A. 1  B. 1  C. 1  D. u   (1;1; 1  )  u   (0; 1  ; 2  ) u   (1;0;1) 2  2  2 u   ( 3  ;0;1) 1  u   (2;1;0)  2 Câu 35.6. 42
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 4 2017 i 1 i 1
Kết quả rút gọn của biểu thức P   là: 2016 i i A. 0 B. i C.1-i D. -1-i Câu 36. 1.
Nhà của 3 bạn A, B, C nằm ở 3 vị trí tạo thành một tam giác vuông tại B (
như hình vẽ), AB = 10 km; BC = 25 km và 3 bạn tổ chức họp mặt ở nhà bạn C. Bạn
B hẹn chở bạn A tại vị trí M trên đoạn đường BC. Từ nhà, bạn A đi xe buýt đến
điểm hẹn M với tốc độ 30km/h và từ M hai bạn A, B di chuyển đến nhà bạn C
bằng xe máy với tốc độ 50km/h. Hỏi điểm hẹn M cách nhà bạn B bao nhiêu km để
bạn A đến nhà bạn C nhanh nhất ? A B C M A. 5 km B. 7,5 km C.10 km D. 12,5 km Câu 36. 2.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a, đường
thẳng SA vuông góc với mặt đáy và SA = 2a. Gọi (P) là mặt phẳng đi qua B và vuông góc với SC.
Khi đó diện tích của thiết diện của hình chóp S.ABC khi cắt bởi mặt phẳng (P) là ? S N M A C B 2 a 15 2 a 15 2 a 15 2 a 15 A. B. C. D. 10 5 15 20 Câu 36.3. 43
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Ông A gửi tiết kiệm 100 triệu đồng gửi vào ngân hàng với lãi suất 5% một năm. 5
Ông B cũng đem 100 triệu đồng gửi vào ngân hàng với lãi suất % một tháng. 12
Sau 10 năm, hai ông A và B cùng đến ngân hàng rút tiền ra. Khẳng định nào sau
đây là đúng ? ( Lưu ý: tiền lãi được tính theo công thức lãi kép và được làm tròn đến hàng hàng triệu)
A. Số tiền của hai ông A, B khi rút ra là như nhau.
B. Ông B có số tiền nhiều hơn ông A là 1 triệu.
C. Ông B có số tiền nhiều hơn ông A là 2 triệu.
D. Ông B có số tiền nhiều hơn ông A là 3 triệu. Câu 36.4. 2   
Hình phẳng (H) giới hạn bởi các đường (P): y x
4x 5 và hai tiếp tuyến của (P)
tại điểm A(1;2); B(4;5). Diện tích của (H) là ? 27 9 15 5 A. B. C. D. 4 4 4 2 Câu 36.5.
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và đường thẳng d: x  3 y 1   z . 2 1 1 
Mặt phằng (P) chứa đường thẳng d và có khoảng cách từ A đến (P) là lớn nhất.
Khi đó (P) có một véctơ pháp tuyến là A. n  (4;5;13) B. n  (4;5; 1  3) C. n  (4; 5  ;13) D. n  ( 4  ;5;13) Câu 36.6.
Cho hình vuông ABCD có tâm H và A,B,C,D,H lần lượt là điểm biểu diễn cho các
số phức a,b,c,d,h. Biết a  2  ; i h  1 i
3 và số phức b có phần ảo dương. Khi đó
môđun của số phức b là A. 26 B. 13 C. 4 2 D. 10 44
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 1 2
Câu 37.1. Trên C 3 2
y x mx  6m   1 x M  1 x ; 1 y m  :
có hai điểm phân biệt và 3 3 N  2
x ; y2  sao cho tiếp tuyến tại mỗi điểm đó vuông góc với đường thẳng
x  3y  6  0 và x x
. Khi đó tất cả các giá trị của m thỏa mãn các điều kiện 1 2 2 3 trên là ? 3 3 3 3 A.  m  3
B. m   m  3
C. m  3
D. m 2 2 2 2
Câu 37.2 . Cho phương trình x 1 2 x 5 5 124 có nghiệm là x x 0 thì 0 bằng giá trị
của biểu thức nào trong các biểu thức dưới đây , biết rằng các hàm số dưới đây luôn tồn tại. 3 a 3 a 3 a A. log log b3 a2 log log ab3 a2 log log 3 a2 a a B. a a C. a a b b b 3 a D. log log b3 a a a b
Câu 37.3. Nhân ngày phụ nữ Việt Nam 20 -10 năm 2017 , ông A quyết định mua
tặng vợ một món quà và đặt nó vào trong một chiếc hộp có thể tích là 32 ( đvtt )
có đáy hình vuông và không có nắp . Để món quà trở nên thật đặc biệt và xứng
đáng với giá trị của nó ông quyết định mạ vàng cho chiếc hộp , biết rằng độ dạy
lớp mạ tại mọi điểm trên hộp là như nhau . Gọi chiều cao và cạnh đáy của chiếc
hộp lần lượt là h;x . Để lượng vàng trên hộp là nhỏ nhất thì giá trị của h;x phải là ? A. 3 x 2; h
4 B. x 4;h 2 C. x 4;h D. x 1;h 2 2 2 2sin x
Câu 37.4. Giá trị lớn nhất của hàm số f x là x x 4 4 sin cos 2 2 A. 0 B. 4 C.8 D. 2 Câu 37.5. 45
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC
2a . Tam giác SAB có góc 60o ASB , SB
a và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng
cách từ điểm B đến mặt phẳng (SAC). 3 3 3 A. a B. 2a C. a D. 2a 19 19 16 Câu 37.6. xxx 2
Tập nghiệm của bất phương trình: 2 2 x 1 81.9 3 .3     0 là 3
A. S  1;   0 .
B. S  1;.
C. S  0;. D.
S  2;   0 . Câu 37.7.
Tìm tham số m để đồ thị hàm số 4 2
y x  2mx m  2C cắt trục ox tại bốn điểm
phân biệt và thỏa mãn hình phẳng giới hạn bởi đồ thị (C) và trục ox của phần nằm
phía trên trục ox có diện tích bằng diện tích hình phẳng giới hạn bởi đồ thị (C) và
trục ox của phần nằm phía dưới trục ox . A. 3 B. -3 C.2 D. 4 Câu 37.8.
Trong không gian tọa độ Oxyz cho điểm ( A 0;1;1), (1 B ;0; 3)  , ( C 1;  2;  3)  và mặt cầu (S) có phương trình : 2 2 2
x y z  2x  2z  2  0 .Tìm tọa độ điểm D trên mặt cầu (S) sao cho tứ
diện ABCD có thể tích lớn nhất.  7 4 1   1  4 5    7 4 1   7 4 1  A. D ;  ;    B. D ; ;   C. D ; ;   D. D ;  ;    3 3 3   3 3 3   3 3 3   3 3 3  Câu 37.9.
Tìm phần ảo của số phức 2 2017
z , biết số phức z thỏa mãn .
i z  2  i  1 i ... 1 i . A. 1 B. 1009 2 C. 1009 2  D. 1009 2 i
Câu 38.1. Cho hàm số 3 2
y x  6x  9x m có đồ thị (C), với m là tham số. Giả sử
đồ thị (C) cắt trục hoành tại ba điểm phân biệt có hoành độ thỏa mãn x x x . 1 2 3
Khẳng định nào sau đây là đúng?
A. 1  x x  3  x  4
B. 0  x  1  x  3  x  4 1 2 3 1 2 3
C. x  0  1  x  3  x  4
D. 1  x  3  x  4  x 1 2 3 1 2 3 46
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 38.2. Cho tứ diện ABCD có tam giác ABD vuông cân tại D, AD a , tam giác ABC cân tại C, 2 2
AC a x . Biết 2 2
CD  2a x , (x>0) hãy tính góc giữa
hai đường thẳng AB, CD bằng bao nhiêu? A. 0 45 B. 0 90 C. 0 60 D. 0 30
Câu 38.3. Cho u là cấp số nhân với số hạng tổng quát u  0; u  1. Khi đó n n n
khẳng định nào sau đây là đúng? log 2017 log 2017  log 2017 A. u u u k 1  k 1  k  log 2017 log 2017  log 2017 u u u k 1  k k 1  log 2017 log 2017  log 2017 B. u u u k 1  k 1  k  log 2017 log 2017  log 2017 u u u k 1  k k 1  log 2017 log 2017  log 2017 C. u u u k 1  k 1  k  log 2017 log 2017  log 2017 u u u k 1  k k 1  log 2017 log 2017  log 2017 D. u u u k 1  k k 1   log 2017 log 2017  log 2017 u u u k 1  k k 1 
Câu 38.4. Cho hàm số 4 2
y x  4x m có đồ thị là (C). Gọi S là diện tích hình
phẳng giới hạn bởi đồ thị (C) với y<0 và trục hoành, S’ là diện tích hình phẳng
giới hạn bởi đồ thị (C) với y>0 và trục hoành. Với giá trị nào của m thì S S ' ? 2 20 A. m  2 B. m  C. m  D. m  1 9 9
Câu 38.5. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (Q): x  2y  z 5  0 x  y z và đường thẳng d 1 1 3 :   2 1
1 . Phương trình mặt phẳng (P) chứa đường
thẳng d và tạo với mặt phẳng (Q) một góc nhỏ nhất là
A. P  : y z 4  0
B. P  : x z 4  0
C. P  : x y z 4  0
D. P  : y z 4  0
Câu 38.6. Gieo một con súc sắc cân đối đồng chất hai lần. Ký hiệu  ;
a b là kết quả
xảy ra sau khi gieo, trong đó a, b lần lượt là số chấm xuất hiện lần thứ nhất, thứ
hai. Gọi A là biến cố số chấm xuất hiện trên hai lần gieo như nhau. Tập hợp các kết
quả thuận lợi cho biến cố A là tập hợp con của tập hợp các điểm biểu diễn của số
phức z thỏa mãn điều kiện nào sau đây?
A. z  2  3i  12
B. z  2  3i  10
C. z  2  3i  13
D. z  2  3i  11 47
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 39. Một người có một dải ruy băng dài 130cm, người đó cần bọc dải ruy băng đó
quanh một hộp quà hình trụ. Khi bọc quà, người này dùng 10cm của dải ruy băng để thắt
nơ ở trên nắp hộp (như hình vẽ minh họa). Hỏi dải dây duy băng có thể bọc được hộp
quà có thể tích lớn nhất là là nhiêu ? A. 3 4000 cm B. 3 1000 cm C. 3 2000 cm D. 3 1600 cm
Câu 39.2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc
với mặt phẳng đáy và góc giữa SC với mặt phẳng (SAB) bằng 0
30 . Gọi M là điểm di
động trên cạnh CD và H là hình chiếu vuông góc của S trên đường thẳng BM. Khi
điểm M di động trên cạnh CD thì thể tích của khối chóp S.ABH đạt giá trị lớn nhất bằng? 3 a 2 3 a 2 3 a 2 3 a 2 A. B. C. D. 3 2 6 12
Câu 39.3. Trong một bản hợp ca, coi mọi ca sĩ đều hát với cường độ âm và coi cùng tần
số. Khi một ca sĩ hát thì cường độ âm là 68dB. Khi cả ban hợp ca cùng hát thì đo được
mức cường độ âm là 80dB. Tính số ca sĩ có trong ban hợp ca đó, biết mức cường độ âm L I L 10log I
được tính theo công thức
I trong đó I là cường độ âm và 0 là cường độ âm 0 chuẩn A. 16 người B. 12 người C. 10 người D. 18 người a(m/ s)
Câu 39.4. Một ô tô đang chạy đều với vận tốc
thì người lái đạp phanh. Từ thời ( v t) 5 t ( a m/ s)
điểm đó, ô tô chuyển động chậm dần đều với vận tốc , trong đó t là
thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi từ vận tốc ban đầu a của ô tô là bao
nhiêu, biết từ lúc đạp phanh đến khi dừng hẳn ô tô di chuyển được 40 mét. A. a 20 B. a 10 C.a 40 D. a 25
Câu 39.5. Trong không gian với hệ trục Oxyz, cho đường thẳng d có phương trình x 1 y 2 z d :
và điểm A(1 ;4 ;2). Gọi (P) là mặt phẳng chứa d . Khoảng cách lớn 1 1 2 nhất d
từ A đến (P) là : max 48
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 210 A. d 5 B. d C. d 6 5 D. d 2 5 max max 3 max max z 5 z 2 3i 4
Câu 39.6. Cho số phức z có phần thực dương thỏa mãn và . Tính 13z 1 A z 2 A. A 898 B. A 98 C. A 890 D. A 198 tan x  2
Câu 40.1. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y  đồng biến trên tan x m    khoảng 0; .    4 
A. m  0 hoặc 1  m  2. B. m  0.
C. 1  m  2. D. m  2.
Câu 40.2. Sự tăng trưởng của một loài vi khuẩn được tính theo công thức rx f x
( )  Ae , trong đó .
A là số lượng vi khuẩn ban đầu, r là tỷ lệ tăng trưởng r  0 , x (tính theo giờ) là thời gian tăng
trưởng. Biết số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Hỏi sao bao lâu thì số
lượng vi khuẩn tăng gấp 10 lần
A. 5 ln 20 (giờ) B. 5 ln10 (giờ) C. 10 log 10 (giờ) D. 10 log 20 (giờ) 5 5
Câu 40.3. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số  2( 1) x y x
e , trục tung và trục
hoành. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A. V  4  2 . e
B. V  (4  2 ) e . C. 2
V e  5. D. 2
V  (e  5).
Câu 40.4. Cho các số phức z thỏa mãn z  4 . Biết rằng tập hợp các điểm biểu diễn các số phức
w  (3  4i)z i là một đường tròn. Tính bán kính r của đường tròn đó. A. r  4. B. r  5. C. r  20. D. r  22.
Câu 40.5. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam
giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho. 5 15 5 15 4 3 5 A. V = B. V = C. V = D. V = . 18 54 27 3
Câu 40.6. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; –2; 0), B(0; –1; 1), C(2; 1; –1)
và D(3; 1; 4). Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó ? A. 1 mặt phẳng. B. 4 mặt phẳng. C. 7 mặt phẳng.
D. Có vô số mặt phẳng. 1
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
PHẦN 2 : HƯỚNG DẪN GIẢI 2 x  2x  3
Câu 1.1. Đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số y
hợp với 2 trục tọa độ 1 x 1
tam giác có diện tích S bằng : A. S=1,5 B. S=2 C.S=3 D.S=1 /  u(x) u (x )
Ta có kết quả : Nếu đồ thị hàm số y
có điểm cực trị (x ; y ) thì o y v(x) o o o / v (x ) o
 Suy ra phương trình đường thẳng đi qua 2 điểm cực trị là y=2x-2 (d)
 (d) cắt 2 trục tọa độ tại 2 điểm A(0;-2) ,B(1;0) nên diện tích tam giác OAB bằng 1( Đáp án D)
Câu 1.2. Khối cầu nội tiếp hình tứ diện đều có cạnh bằng a thì thể tích khối cầu là : 3 a  6 3 a  6 3 a  3 3 a  3 A. B. C. D. 216 124 96 144 Hướng dẫn giải : Sử dụng kết quả :  a 6
Bán kính mặt cầu nội tiếp tứ diện đều cạnh a có bán kính R  , 12 3 3     4 a 6 a 6 V        3 12 216  
Câu 1.3. Tìm m để phương trình 2x x e
me  3 m  0 có nghiệm
A. m  2 B. m  2 C.m<3 D.m>0 Hướng dẫn giải : 2   t 3 Đặt t= x
e , t >0. Biến đổi phương trình về dạng :  m t 1 2   t 3 Khảo sát hàm f(t) =
, t >0 ta có f (t)  2 .Suy ra m  2 t 1
 Đáp án A (dùng casio để tìm nhanh hơn )
Câu 1.4. Giá trị của tham số m để diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 2
y  3x  2mx m 1 , trục hoành, trục tung và đường thẳng x = 2 đạt giá trị nhỏ nhất là: 2
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 A. m = 2 B. m = 1 C. m = -1 D. m = - 2 Hướng dẫn giải :
 Vì với m tùy ý ta luôn có 2 2
3x  2mx m 1  0 x
 nên diện tích hình phẳng cần tìm là 2
S  3x  2mx m  
1 dx  x mx   m   2
1 x  2m  4m 10  2m  2 2 2 3 2 2 2 1  8   0 0
 S đạt giá trị nhỏ nhất bằng 8 khi m = - 1
 ( dùng casio thử nhanh hơn )
Câu 1.5. Phương trình nào sau đây không phải là phương trình hình chiếu vuông góc của đường x 1 2t  thẳng d:  y  2
  3t ,t R trên mặt phẳng (Oxy) : z  3t
x  3 2t '
x 1 4t '
x 1 2t '
x  5  2t '    
A.  y  1 3t ' ,t ' R B.  y  2
  6t ',t ' R C. y  2  3t ',t ' R D. y  4 3t ',t ' R     z  0  z  0  z  0  z  0  Hướng dẫn giải :
 A(1;-2;3) , B(3;1;4) thuộc d. Hình chiếu của A ,B trên mặt phẳng (Oxy) là A/(1;-2;0) , B/(3;1;0)
 Phương trình hình chiếu đi qua / A hoặc /
B và nhận véc tơ cùng phương với / / A B  2;3;0
làm véc tơ chỉ phương .  Đáp án C 2  6i
Câu 1.6. Gọi A, B, C lần lượt là các điểm biểu diễn của 3 số phức :1 2 i; (1 i)(1 2i); 3i .Diện
tích của tam giác ABC bằng : 1 1 5 5 A. B. C. D. 4 2 5 2 Hướng dẫn giải :
 Dùng máy tính casio ta có A(1;2) , B(3;1) ,C(0;2)  1
Dùng công thức S  AB, AC 
 Với AB  2; 1  ;0, AC   1  ;0;0 2 
Dùng máy tính ta có kết quả B : S=1/2 
(Có thể dùng công thức tính diện tích phần Oxy tính nhanh hơn ) 3
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 2.1. Cho hàm số 3 2
y x  2x  1 mx m có đồ thị C . Giá trị của m thì C  cắt trục hoành
tại 3 điểm phân biệt x , x , x sao cho 2 2 2
x x x  4 là 1 2 3 1 2 3  1   m  1 1 1 A. m  1 B.  4 C.   m  1 D.  m  1  4 4 m  0 Hướng dẫn giải:
Phương trình hoành độ giao điểm của (C) và trục hoành là x 1 3 2
x  2x  1 mx m  0   2
x x m  0 m  0  
(C) và trục hoành cắt nhau tại 3 điểm pb  1 m     4
x x x  4  x x
 2x x 1 4 1 2m 1 4  m 1 1 2 3  1 22 2 2 2 Xét 1 2 Chọn B.
Câu 2.2. Cho lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm
A ' lên mặt phẳng (ABC) trùng với trọng tâm tam giá ABC . Biết khoảng cách giữa hai đường thẳng
AA' và BC bằng a 3 . Khi đó thể tích của khối lăng trụ là 4 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 12 6 3 24 Hướng dẫn giải: C’ B’ A’ H M C B G A 4
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 a
Gọi M là trung điểm BC, dựng MH vuông góc với A’A. suy ra MH d BC A A 3 , '  4 2 a Đặt AH=x, ta có 2 A' A x  3 a
Từ A’A.MH=A’G.AM, suy ra x  . 3 2 3 a a 3 a 3 Vậy V  .  . 3 4 12 Chọn A. x x
Câu 2.3. Phương trình 2 3 2 3
m (1) có nghiệm khi: A. m  ;5   B. m   ;5 C. m 2; D. m 2; Hướng dẫn giải: x
Đặt t  2  3 ,t  0 , phương trình đã cho thành: 2
t mt 1  0 (2)
(1) có nghiệm khi (2) có nghiệm dương. 2 m  4  0
Do tích 2 nghiệm =1 nên suy ra (2) có 2 nghiệm dương.    m  2 . m  0 Chọn D.  2 Câu 2.4. Tính 3x
I e .sin xdx 0 3    1 1 3 1 1 3 3 A. 2 I   e B. 2 I   e C. 2 I  1 e D. 2 I  1 e 2 2 2 2
Hướng dẫn giải : 5
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017    2 2  x I e .sin x xdx   e d   cos x 2 3 3 3x 3 2  e .cos x xe .cos xdx  0 0 0 0   2  2 3 3 1 xe .d  sin x 3x 3 2 x 2
1 e .sin x e .sin xdx 1 e I  0 0 0 3 1 1 2 I   e 2 2 Do đó . Chọn B
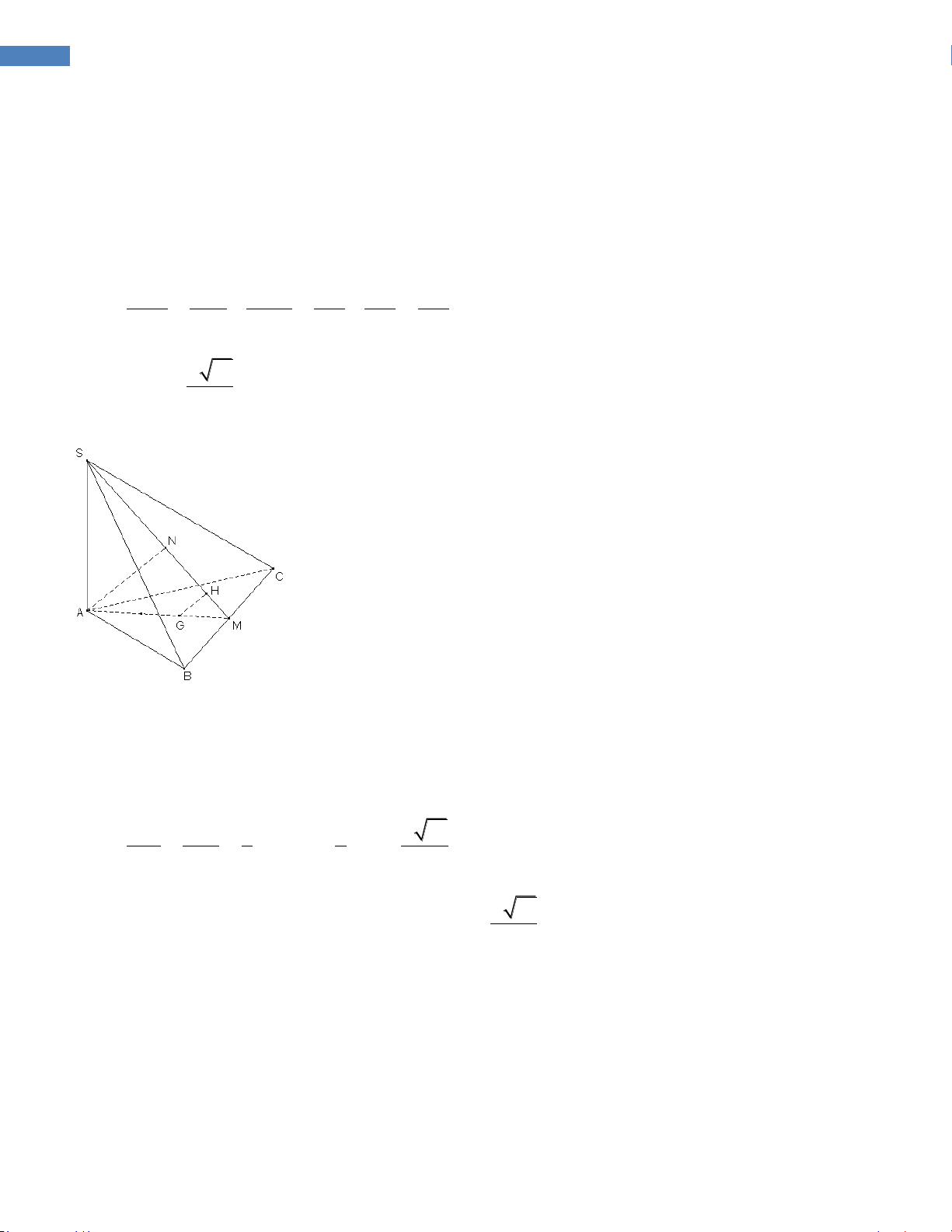
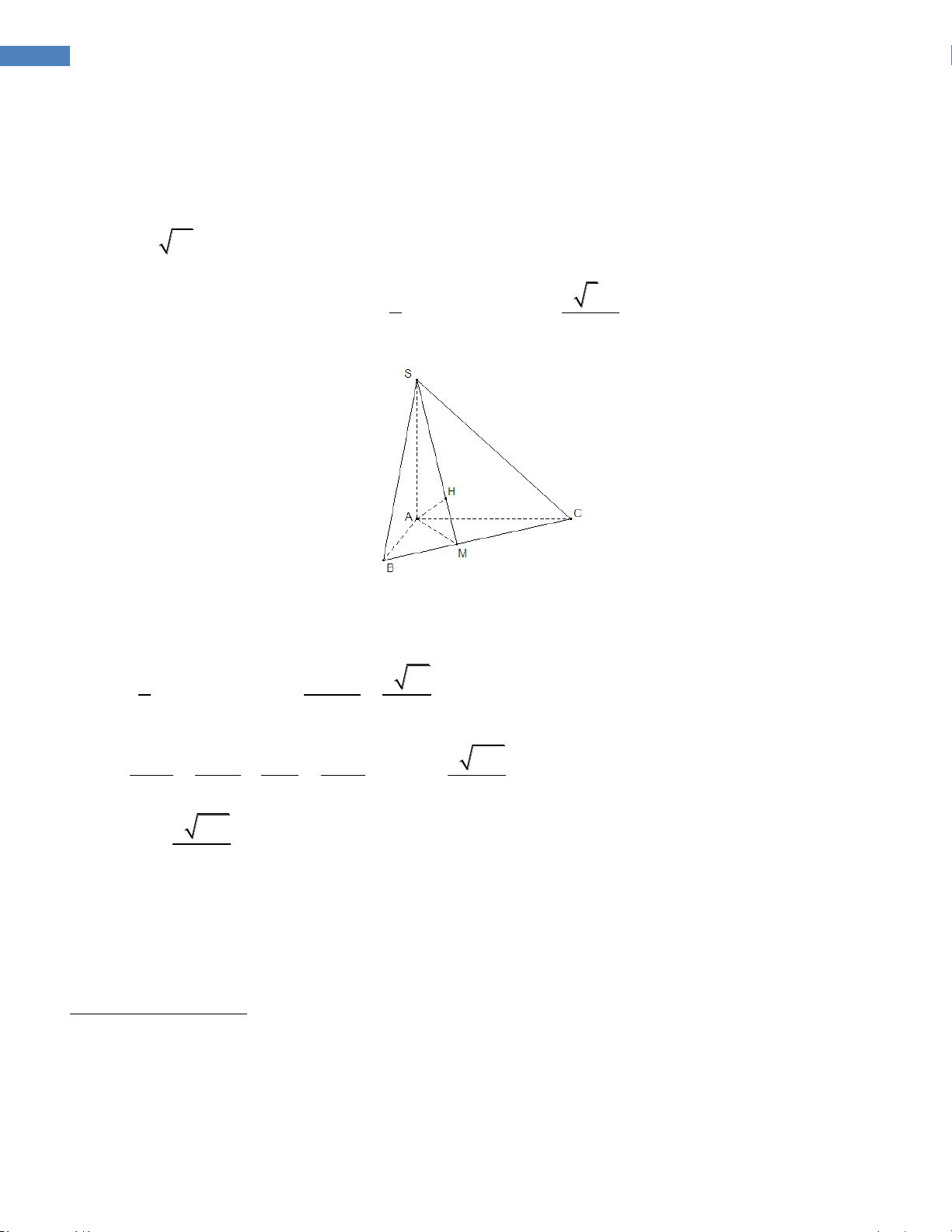
Câu 2.5. Trong không gian tọa độ Oxyz , cho điểm A(0;1;1), B(1;0; 3)
 , C( 1; 2; 3) và mặt cầu (S) có phương 2 2 2
trình: x  y  z  2x  2z  2  0 . Tìm tọa độ điểm D trên mặt cầu (S) sao cho tứ diện ABCD có thể tích lớn nhất.       A. D 1;0;  1 B. D 7 4 1 ; ;  D 1 4 5 ; ; 3 3 3  C.      3 3 3 D. D(1; - 1; 0) 
Hướng dẫn giải :
Ta thấy câu C và D có điểm D không thuộc (S). Loại C,D.
Ta tính thể tích cho điểm D ở câu A và câu B. Điểm B ở câu B có thể tích lớn hơn. Chọn B.
Câu 2.6. Tính tổng mô-đun tất cả các nghiệm của phương trình:  z i 2 z   3 1 z i  0 A. 3 B. 4 C.6 D. 8
Hướng dẫn giải : z i  z i   z i   z  1        z i z 1 2 z   1  3
z i  0  z  1    z i  z i  3 3
z i  0     2 i 5
z iz 1  0 z   2
Suy ra tổng mô-đun các nghiệm bằng 6. 6
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 3.1 (Kshs). Cho hàm số y   x m3 2
3x m  
1 . Gọi M là điểm cực đại của đồ thị hàm số   1
ứng với một giá trị m thích hợp đồng thời là điểm cực tiểu của đồ thị hàm số  
1 ứng với một giá trị
khác của m. Số điểm M thỏa mãn yêu cầu đề bài là: A.1 B. 2 C.3 D.0
Hướng dẫn giải :
Ta có y   x m2 3
3, y  6x m x m 1
Suy ra y  0   . x m 1
Vì x x m 1, ym 1  0 nên hàm số đạt cực đại x x m 1 tại và giá trị cực đại là 1   1 2
y m  3m  2 . 1
Tương tự, ta có hàm số đạt cực tiểu tại x x m 1 và giá trị cực tiểu là 2
y m  3m  2 . 2 2
Ta giả sử điểm M là điểm cực đạ của đồ thị hàm số ứng với giá trị m và là điểm cực tiểu ứng của 1
đồ thị hàm số ứng với với giá trị m . 2
m 1  m 1
Từ YCBT suy ra hệ phương trình 1 2  2 2
m  3m  2  m  3m  2  1 1 2 2 3 1  1 1 
Giải hệ ta tìm được nghiệm m  , m   và suy ra tồn tại duy nhât một điêm M ,  thỏa 1 2   2 2  2 4  bài toán. Chọn đáp án A.
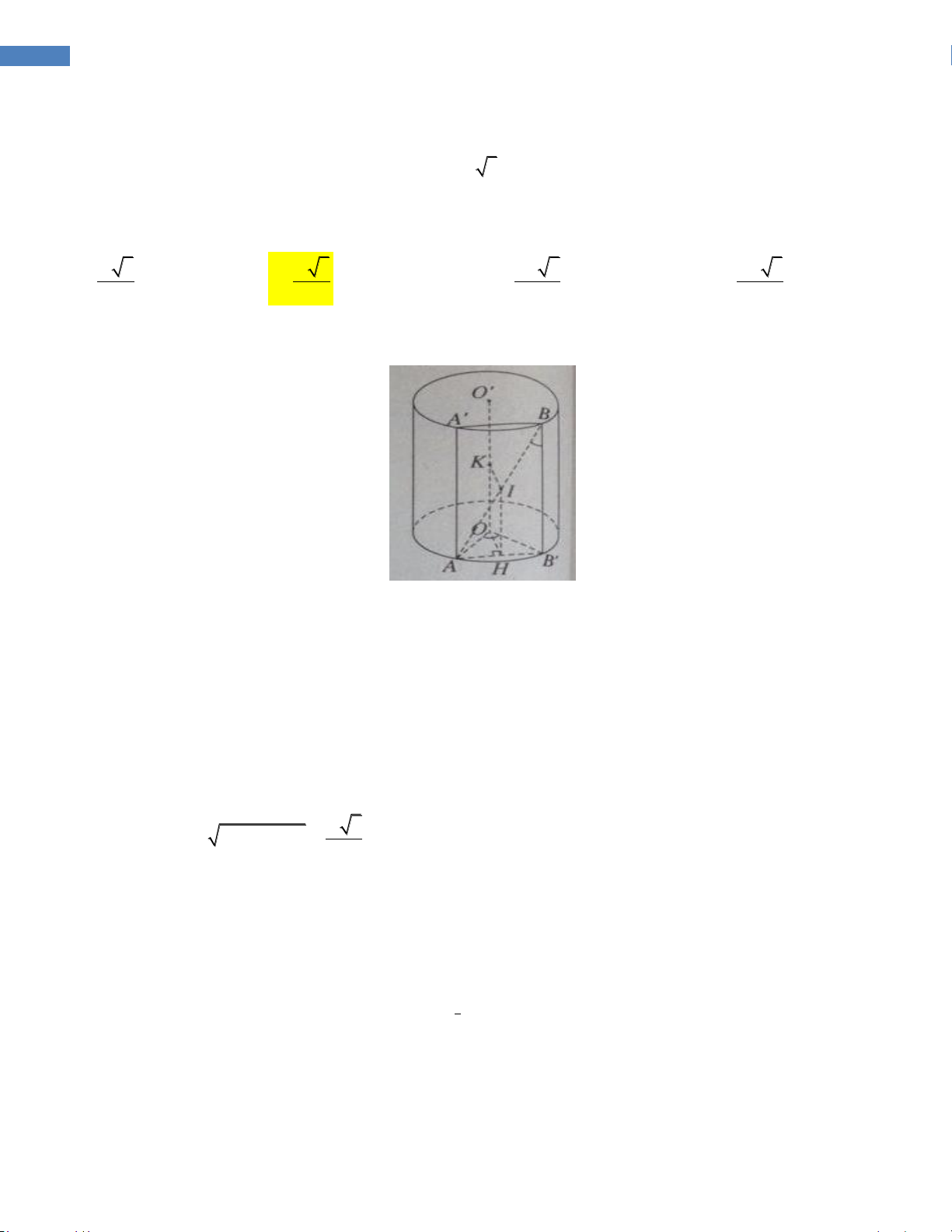
Câu 3.2 (Thể tích- mặt cầu- mặt nón- mặt trụ). Cho tứ diện ABCD với BC a ,các cạnh còn lại đều a 3 bằng
và  là góc tạo bởi hai mặt phẳng  ABC và  BCD . Gọi I,J lần lượt là trung điểm các 2
cạnh BC, AD . Giả sử hình cầu đường IJ kính tiếp xúc với CD. Giá trị cos là: 2 3 2  3 A. 3  2 3 B. 2 3  3 C. D. 3 3 Hướng dẫn giải: 7
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
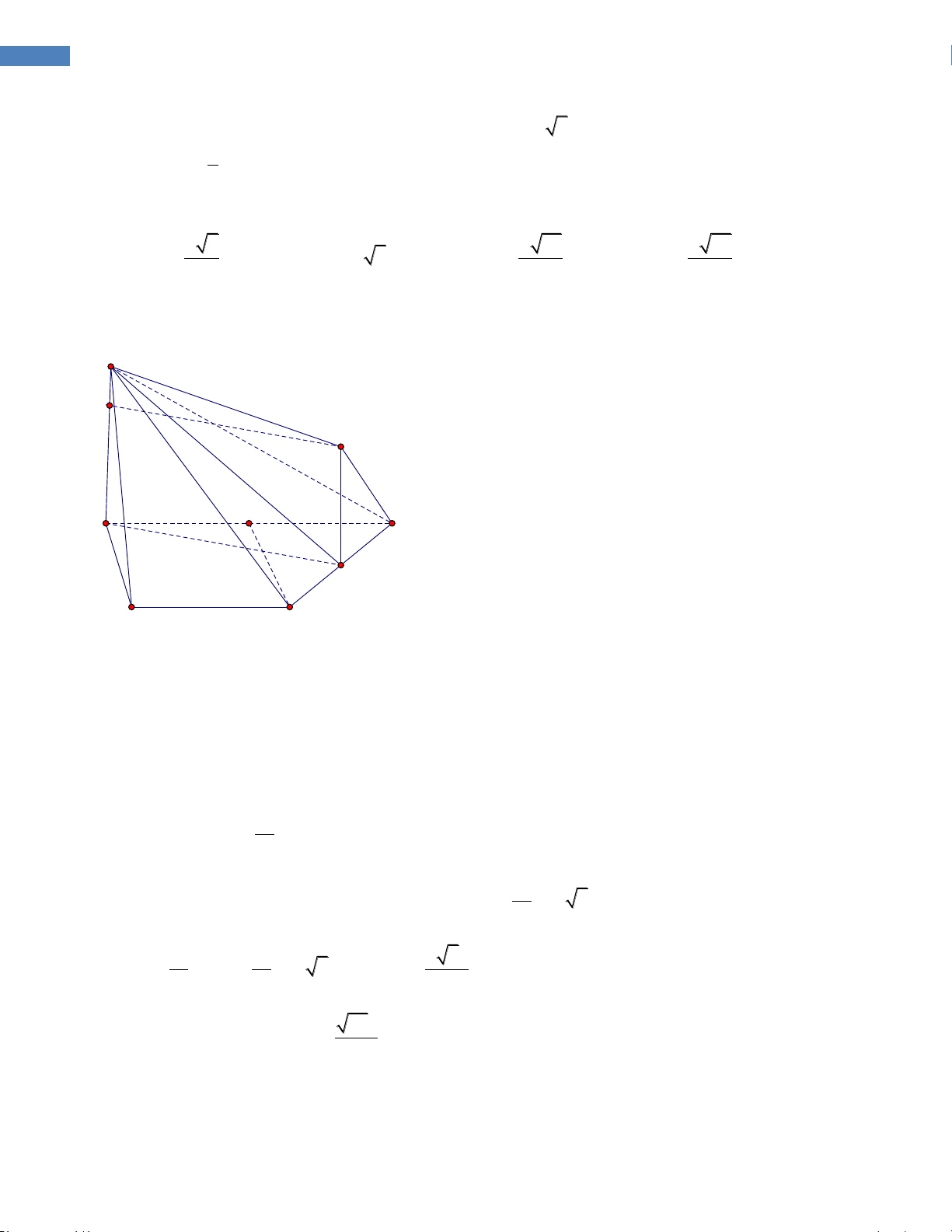
Gọi O là trung điểm IJ và F là điểm tiếp xúc giữa hình cầu đường kính IJ và đường thẳng CD. Hình
cầu đường kính IJ tiếp xúc với CD khi và chỉ khi khoảng cách từ O đến CD bằng nữa độ dài IJ. a 2
Ta có AI DI  . 2 a
Vì FC và CI là hai tiếp tuyến xuất phát từ một điểm nên FC CI  2 a 3 a
Tương tự ta có DJ DF   2 2
Tam giác ADI cân có IJ là đường trung tuyến nên tam giác IDJ vuông tại J. a   JD  3 1 6 2 Suy ra 2 sin  sin JID    2 DI a 2 2 2
Do vậy cos  2 3  3 nên chọn đáp án B.
Câu 3.3 (Mũ- logarit). Cho  ,
x y, z là các số thực thỏa mãn 2x  3y  6 z . Giá trị biểu thức
M xy yz xz là: A.0 B.1 C.6 D.3 Hướng dẫn giải: Khi một trong ba số ,
x y, z bằng 0 thì các số còn lại bằng 0. Khi đó M=0 1 1 1  Khi ,
x y, z  0 ta đặt 2x  3y  6z k suy ra 2  ,3 y x  , 6 z k kk . 1 1 1  1 1 1 Do 2.3=6 nên . y x z k k k hay    x y z Từ đó suy ra M=0
Vậy cần chọn đáp án A.
Câu 3.4 (Tích phân- Ứng dụng). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số a 2 x   2 x y e
e , trục Ox và đường thẳng x a với a  ln 2 . Kết quả giới hạn lim S là: a a A.1 B.2 C.3 D.4 8
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Hướng dẫn giải: ln 2 x x 1 Ta có S e
e dx e e   a  2 2  2a 2 a 2 2 a
Suy ra lim S  2 , chọn đáp án B. a a
Câu 3.5 (Oxyz). Trong không gian Oxyz, cho điểm A1,0,  
1 và mặt phẳng P : x y z  3  0 .
Mặt cầu S có tâm I nằm trên mặt phẳng  P , đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác
OIA bằng 6  2 . Phương trình mặt cầu S là: A.  2 2 2
x  2   y  2   z  2 2 2 1
 9 hoặc x  2   y  2  z   1  9. B.  2 2 2
x  2   y  2   z  2 2 2 1
 9 hoặc x  
1   y  2   z  2  9 C.  2 2 2
x  2   y  2   z  2 2 2 1
 9 hoặcx  2  y  2  z   1  9 D.  2 2 2
x  2   y  2   z  2 2 2 1
 9 hoặc x  
1   y  2   z  2  9 Hướng dẫn giải: Gọi I  ,
x y, z là tâm của S.
Khi đó I P, IO I ,
A IO IA AO  6  2 nên ta suy ra hệ  x 2
1  y   z  2 2 2 2 2 1
x y z
x z 1  0   2 2 2 2 2 2
2 x y z  2  6  2
 x y z  9  
x y z  3  0
x y z  3  0   
Giải hệ ta tìm được I 2, 2,  1 hoặc I  1  ,2, 2  
Suy ra phương trình mặt cầu và đáp án cần chọn là D. 1 1 1
Câu 3.6 (Số phức). Cho z là số phức có mô đun bằng 2017 và w là số phức thỏa mãn   z w z  w
. Mô đun của số phức w là A.2015 B.1 C.2017 D.0 Hướng dẫn giải: 9
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 1 1 1 Từ   ta suy ra 2 2 z  w  w z  0 z w z  w 2 2  w   i 3w   1 i 3   z     
  z      w      2  2 2 2    
Lấy mô đun hai vế ta có z  w  2017 .
Vậy đáp án đúng là C.
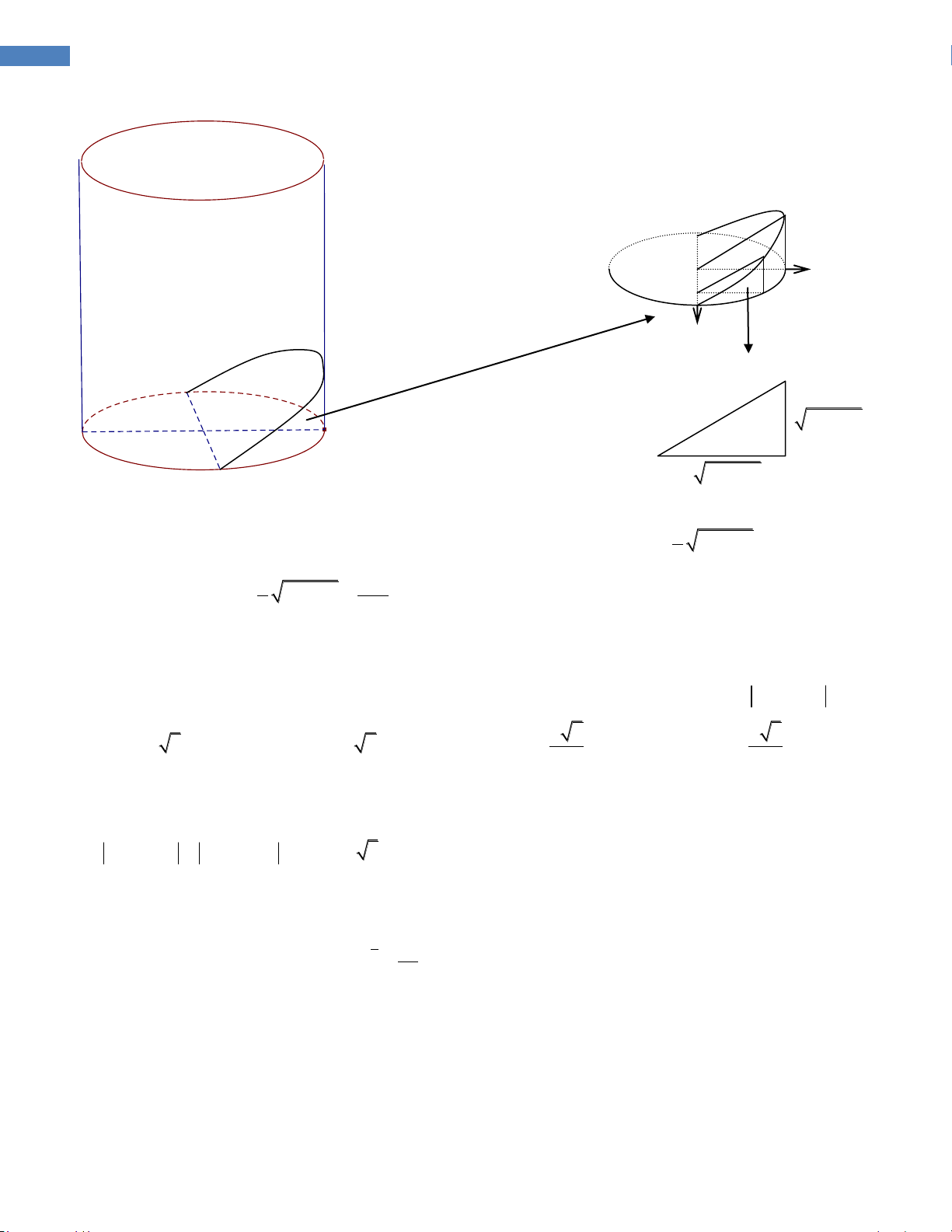
Câu 4.1 (Kshs). Một công ty muốn làm một đường ống dẫn từ một điểm A trên bờ đến một điểm B
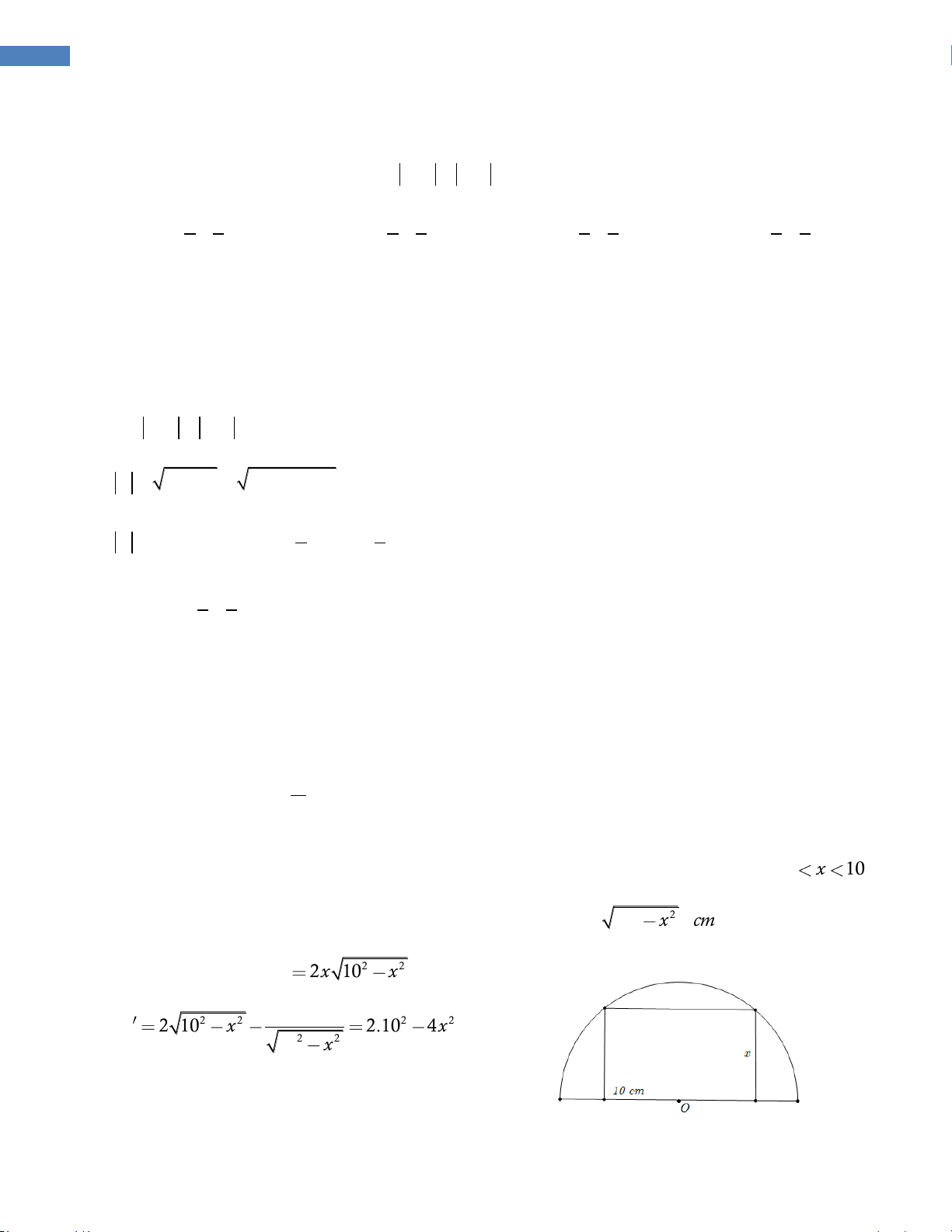
trên một hòn đảo. Hòn đảo cách bờ biển 6km. Giá để xây đường ống trên bờ là 50.000USD mỗi km,
và 130.000USD mỗi km để xây dưới nước. B’ là điểm trên bờ biển sao cho BB’ vuông góc với bờ
biển. Khoảng cách từ A đến B’ là 9km. Vị trí C trên đoạn AB’ sao cho khi nối ống theo ACB thì số
tiền ít nhất. Khi đó C cách A một đoạn bằng: A. 6.5km B. 6km đảo C. 0km D.9km B Đáp án: biển 6km Lời giải. C
Đặt x B 'C (km) , x [0;9] B' x km (9 - x)km A bờ biển 2 BC
x  36; AC  9  x
Chi phí xây dựng đường ống là 2
C(x)  130.000 x  36  50.000(9  x) (USD)  13x
Hàm C(x) , xác định, liên tục trên [0;9] và C '(x)  10000.  5 2  x  36  25 5 2
C '(x)  0  13x  5 x  36 2 2 2
169x  25(x  36)  x   x  4 2  5 
C(0)  1.230.000 ; C  1.170.000   ; C(9)  1.406.165  2 
Vậy chi phí thấp nhất khi x  2,5 . Vậy C cần cách A một khoảng 6,5km.
Câu 4.2. (Thể tích – mặt cầu-mặt nón – mặt trụ). 10
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Cho hình chóp SABC với SA vuông góc với mặt phẳng (ABC) và BC= 3 S a,  60o BAC
. Gọi H, K lần lượt là hình chiếu của A lên SB và SC. Mặt K
cầu qua các điểm A, B, C, H, K có bán kính bằng: A.1 B.2 H 3 A C 600 C. 3
D. Không đủ dữ kiện để tính 2 Đáp án: B Lời giải. S
Gọi AD là đường kính của đường tròn (ABC) K
Suy ra, AC DC , suy ra CD  (SAC) hay AE DE H
Tương tự, AH HD . Suy ra mặt cầu qua các điểm A, B, C, H, K có đường A C 600 BC kính AD   2 . D 0 sin 60 B
Câu 4.3: Cho a log 3  b log 2  c log 5  5 , với a, b và c là các số hữu tỷ. Các khẳng định sau đây, 6 6 6 khẳng định nào đúng? A.  
a b B. a b C. b a D. c a b
Hướng dẫn giải :
log 3a2b5c   5 6 a b c 5 5 5 0
 3 .2 .5  6  3 .2 .5 a b  5
Do a, b, c là các số hữu tỷ nên c  0
Câu 4.4. (Tích phân - Ứng dụng )
Một khối cầu có bán kính 5dm, người ta cắt bỏ 2 phần bằng 2 mặt phẳng vuông góc bán kính và
cách tâm 3dm để làm một chiếc lu đựng. Tính thể tích mà chiếc lu chứa được. A. 132 (dm3) B. 41 (dm3) 100 C.  (dm3) D. 43 (dm3) 3 3dm 5dm 3dm 11
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Hướng dẫn: Đặt hệ trục với tâm O, là tâm của mặt cầu; đường thẳng đứng là Ox, đường ngang là
Oy; đường tròn lớn có phương trình 2 2
x y  25 .
Thể tích là do hình giới hạn bởi Ox, đường cong 2
y  25  x , x  3, x  3  quay quanh Ox. 3 2
V   (25  x )dx  =132 (bấm máy) 3 
Câu 4.5: Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M(0; 1;2) và N( 1;1;3) . Mặt phẳng
(P) đi qua M, N sao cho khoảng cách từ K 0;0;2 đến (P) đạt giá trị lớn nhất. (P) có vectơ pháp tuyến là: A. (1;1; 1  ) B. (1; 1  ;1) C. (1; 2  ;1) D. (2; 1  ;1)
Hướng dẫn giải : K
- Khoảng cách từ K đến (P) lớn nhất bằng KH, khi H’ trùng H
- Vậy mặt phẳng (P) qua MN và vuông góc với KH.
- Tìm H và viết (P) hoặc: H'
- (P) chứa MN và vuông góc với (MNP). M N P H
Gọi H, H’ là hình chiếu của K lên MN và (P). Ta có: d( ,
k (P))  KH  KH ' không đổi. Vậy d( ,
K (P)) lớn nhất khi và chỉ khi H’ trùng H hay (P) vuông góc với KH.
MK  (0;1;0); NK  (1;1;1) ; MN  (1;2;1)
(MNK) có vtpt là n  MK, NK  (1;0;   1) HK  (MNK) Do  MN,n (2;2; 2) . HK  MN
nên HK có vtcp là      
Câu 4.6: Cho số phức z thoả mãn điều kiện z  2  3i  3 . Tìm giá trị nhỏ nhất của z A. 13  3 B. 2 C. 13  2 D. 2
Hướng dẫn giải : 12
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Các điểm M biểu diễn số phức z thoả mãn z  2  3i  3 nằm trên đường tròn (C) tâm I(2; −3) và bán kính R = 3 . y
(Ý nghĩa hình học của z : độ dài OM) x O z
Ta có |z| đạt giá trị nhỏ nhất  điểm M(C) và OM nhỏ nhất . M C
(Bài toán hình học giải tích quen thuộc) I
Ta có : OM OI – IM = OI – R = 13  3 .
Dấu « = » xảy ra khi M là giao điểm của (C) và đoạn thẳng OI.
Vậy GTNN của z là : 13  3 .
Câu 5.1. Cho hàm số 3 2
y  x  3mx  3m 1. Với giá trị nào của m thì đồ thị hàm số đã cho có cực
đại và cực tiểu đối xứng nhau qua đường thẳng d : x  8y  74  0 A. m 1 B. m  2  C. m  2 D. m  1  Đáp án: C Hướng dẫn: + 2 y '  0  3
 x  6mx  0 . Đồ thị có 2 điểm cực trị khi: m  0
+ Phương trình đường thẳng đi qua 2 điểm cực trị là: y = 2m2.x - 3m - 3
+ Trung điểm 2 điểm cực trị là 3 I ( ;
m 2m  3m 1)
+ Điều kiện để 2 điểm cực trị đối xứng qua d : x  8y  74  0  1 2 2m .( )  1   8 3
m8(2m 3m1)74  0
+ Từ đó thấy m = 2 thỏa mãn hệ trên. Vậy chọn C. 13
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 5.2. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, góc giữa SC và mp(ABC) là 45  . Hình a 7
chiếu của S lên mp(ABC) là điểm H thuộc AB sao cho HA = 2HB.Biết CH  . Tính khoảng cách 3
giữa 2 đường thẳng SA và BC: a 210 a 210 a 210 a 210 A. B. C. D. 30 20 45 15 Đâp án: B Hướng dẫn:
+ D là đỉnh của hình bình hành ABCD thì d(SA;BC)=d(B;(SAD))=1,5.d(H;(SAD))
+ Kẻ HE vuông AD, E thuộc AD. Kẻ HI vuông SE, I thuộc AE thì d(H;(SAD))=HI 210 + Tính  a HI 30 Suy ra chọn B. 2 2
Câu 5.3. Cho phương trình x 2mx2 2x 4mx2 2 5  5
x  2mx m  0. Tìm m để phương trình vô nghiệm? m  1 A. m  0 B. m  1 C. 0  m  1 D.  m   0 Đâp án: C Hướng dẫn: 2 2
+Phương trình tương đương: x 2mx2 2 2x 4mx
x mx   2  2 5 ( 2 2) 5
(2x  4mx  2) 2 2
+ Do hàm f(t)=5t + t đồng biến trên R nên ta có: (x  2mx  2)  (2x  4mx  2) 14
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
+ Từ đó điều kiện để pt vô nghiệm là C. x ln(x  2)
Câu 5.4. Diện tích hình phẳng giới hạn bởi y  và trục hoành là: 2 4  x     A. ln 2  2   3 B. 2ln 2  2 
C. 2   3 D. 2ln 2  2   3 3 4 3 3 Đáp án: D Hướng dẫn: 0 x ln(x  2)
+ Phương trình y = 0 có nghiệm: x=-1;x=0. Từ đó S  dx  2  1  4 x
+ Sử dụng máy Casio, suy ra D.
Câu 5.5. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;2;2), B(5;4;4) và mặt phẳng (P):
2x + y – z + 6 =0. Tọa độ điểm M nằm trên (P) saocho MA2 + MB2 nhỏ nhất là: A. (-1;3;2) B. (2;1;-11) C.(-1;1;5) D(1;-1;7) Đâp án: C Hướng dẫn:
+ Kiểm tra phương án A không thuộc (P).
+ Tính trực tiếp MA2 + MB2 trong 3 phương án B,C,D và so sánh. Chọn C.
Câu 5.6. Số phức z có mô đun lớn nhất và thỏa mãn điều kiện Z   i 13 1  3  2i  là: 2 2 1 3 1 3 15 A.   z 1 3i B. z   i C. z   i D. z i 2 2 2 2 4 4 15
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Đáp án: D Hướng dẫn: 13 2 2
+ Gọi z=x+yi. Từ giả thiết ta có: (x y  3)  (x y  2)  4 2 2 z x y + Đồng thời
lớn nhất. Kiểm tra các đáp án và so sánh ta chọn D.
CÂU 6.1: Trong không gian với hệ toạ độ Oxyz cho A(2;  1;6), B(  1;2;4) và I(  1;  3;2).
Viết phương trình mặt phẳng (P) đi qua A, B sao cho khoảng cách từ I đến (P) lớn nhất. HƯỚNG DẪN GIẢI Ta có 2 2 2
IA  3  2  4  29 và 2 2 2
IB  0  5  2  29 . Gọi M là trung điểm của đoạn  1 1  94
thẳng AB, vì IA=IB nên IM  AB, ta có M ; ;5 ;   IM  .  2 2  2
Gọi H là hình chiếu vuông góc của I lên mặt phẳng (P): 94
Nếu H, M là hai điểm phân biệt thì tam giác IHM vuông tại H, IH. 2 94 94
Nếu H trùng với M thì IH  IM  . Vậy ta có IH 
, IH lớn nhất khi H  M. 2 2 16
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017  3 7 
Khi đó (P) có vectơ pháp tuyến là n  IH  IM  ; ;3 P 
. Vậy phương trình mặt phẳng (P) là  2 2  3    7 x 2  y 
1  3z  6  0 hay 3x  7y  6z  35  0 2 2
CÂU 6.2: Tìm m để đồ thị hàm số 3 2
y  x  3mx 1 có hai điểm cực trị A, B sao cho tam giác OAB
có diện tích bằng 1 (O là gốc tọa độ). HƯỚNG DẪN GIẢI Ta có 2
y '  3x  6mx  3x x  2m . Để đồ thị hàm số có hai điểm cực trị thì m  0 .
Khi đó hai điểm cực trị của đồ thị hàm số là A(0;1) và 3 B(2m; 4
 m 1) . Gọi H là hình chiếu
vuông góc của điểm B lên trục tung, ta có BH  2m . Diện tích của tam giác OAB là 1 1 S  BH.OA  . 2m 2 2 1
Theo đề bài S=1 nên ta có . 2m  1 suy ra m  1
 . Vậy m=±1 là giá trị cần tìm. 2 5 z i
CÂU 6.3: Cho số phức z thoả mãn
 2  i . Tìm phần thực và phần ảo của số phức z 1 2
w  1 z z HƯỚNG DẪN GIẢI
Đặt z=a+bi (a,b R), ta có z a bi
5a bi i 
 2  i  5a bi i  2 ia bi   1 a bi 1 5
a  2(a 1)  b 3
a b  2 a 1        5
b  5  2b  (a 1)
a  7b  6  b  1 Vậy ta có z=1+i 2
z  2i  w 1 (1 i)  (2i)  2  3i . Vậy phần thực của số phức là 2, phần ảo là 3.
CÂU 6.4: Cho hình chóp S.ABC có đường thẳng SA vuông góc với mặt phẳng (ABC), tam giác ABC
là tam giác đều cạnh bằng a, SB=2a. Tính theo a khoảng cách từ trọng tâm G của tam giác ABC đến mặt phẳng (SBC). 17
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 HƯỚNG DẪN GIẢI
Gọi M là trung điểm của BC, ta có BC AM; BC SA BC  (SAM ) . Kẻ đường cao AN của
tam giác SAM, vì AN B ;
C AN SM nên AN  (SBC)
Khoảng cách từ A đến (SBC) là d( ;
A (SBC))  AN 1 1 1 1 4 5 Ta có      2 2 2 2 2 2 AN AS AM 3a 3a 3a a 15 Suy ra AN  5
Kẻ GH//AN; HSM; vì AN  (SBC) nên GH  (SBC)
Khoảng cách từ G đến (SBC) là d( ;
G (SBC))  GH GH MG 1 1 a 15 Ta có 
  GH AN AN AM 3 3 15 a 15
Vậy khoảng cách từ G đến (SBC) là d ( ; G (SBC))  15
CÂU 6.5: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA=AC=5a, AB=a, 0
BAC  120 . Tính theo a khoảng cách từ A đến mặt phẳng (SBC). HƯỚNG DẪN GIẢI 18
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Kẻ AMBC, AHSM (MBC, HSM). Ta có BCAM, BCSA nên BC(SAM), suy ra AH  BC.
Vậy ta có AH(SBC), khoảng cách từ A đến mặt phẳng (SBC) là d(A,(SBC))=AH. 2 2 2 0 2
Áp dụng định lí côsin trong tam giác ABC ta có BC  AB  AC  2A . B AC.cos120  31a  BC  a 31 . 2 1 0 5 3a
Diện tích của tam giác ABC là S  A . B AC.sin120  ABC 2 4 . Mặt khác 1 2S 5 93 S  A . M BC  AM  ABC  . ABC a 2 BC 62 1 1 1 127 5 381 Ta có     AH  a 2 2 2 2 AH AM AS
. Khoảng cách từ A đến mặt phẳng (SBC) là 75a 127 5 381 d(A,(SBC))= a 127 .
CÂU 6.6: Cho hình chóp tam giác S.ABC có đường thẳng SA vuông góc với mặt phẳng (ABC),
AB=2a, AC=3a, BC=4a. Góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng 600. Tính theo a thể
tích của khối chóp S.ABC. HƯỚNG DẪN GIẢI 19
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2 2 2 2 2 2
BC AB AC
16a  4a  9a 11
Xét tam giác ABC ta có cosB=   (áp dụng định lý 2BC.AB 2.4 . a 2a 16 côsin) 2  11  3 15 2 với 00B  1    16  16
Ta kẻ đường cao AH của tam giác ABC, ta có AH 3 15 3 15a sinB=  AH A . B sin B  2 . aAB 16 8 2 1 1 3 15a 3 15a   
Do đó diện tích tam giác ABC là S AH.BC .4a ABC 2 2 8 4
Vì BC AH, BC SA BC  (SAH ), BC SH nên góc SHA là góc giữa hai mặt phẳng (SBC) và (ABC), bằng 600. SA 3 15a 9 5a 0 0
Xét tam giác SAH ta có tan 60 
SA AH tan 60  . 3  AH 8 8 20
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Vậy thể tích khối chóp S.ABC là 2 3 1 1 3 15a 9 5a 45 3a V S .SA  . .  3 ABC 3 4 8 32
Câu 7.1: Một người thợ xây, muốn xây dựng một bồn chứa
nước hình trụ tròn với thể tích là 3
150m (như hình vẽ bên).
Đáy làm bằng bê tông , thành làm bằng tôn và bề làm bằng
bằng nhôm. Tính chi phí thấp nhất để bồn chứa nước (làm
tròn đến hàng nghìn). Biết giá thành các vật liệu như sau: bê
tông 100 nghìn đồng một 2 m , tôn 90 một 2 m và nhôm 120 nghìn đồng một 2 m . A. 15037000đồng.
B. 15038000đồng. C. 15039000đồng. D. 15040000đồng. Đáp án: C.
Hướng dẫn giải: Gọi r, h  2
m  r  0, h  0 lần lượt là bán kính đường tròn đáy và đường cao của 150
hình trụ. theo đề ta có 2
r h 150  h
. Khi đó chi phí làm nên bồn chứa nước được xác định 2 r 150 27000 27000
theo hàm số f r 2 2
 220r  90.2r  220r
(nghìn đồng). f 'r  440 r  , 2 r r 2 r f 'r  675 3  0  r   a . 11 BBT:
Dựa vào BBT ta suy ra chi phí thấp nhất là   f a 675 3  f   15038,38797   nghìn đồng. 11  
Lưu ý: Khi làm tròn các bạn nhớ số tiền tối thiểu phải lớn hơn hoạc bằng số tiền hoàn thành sản phẩm, nên
dù cho trong bài toán này kết quả gần với số 15038 hơn, nhưng đáp án ta phải chọn 15039 . Vì nếu chọn
15038 thì chi phí thấp nhất nhỏ hơn chi phí hoàn thành sản phẩm nên không thể làm được sản phẩm.
Câu 7.2: Tìm tất cả các giá trị của tham số m sao cho bất phương trình sau có tập nghiệm là  ;0   : x x x 1
m2   2m  
1 3 5  3 5  0 . 1 1 1 1 A. m   . B. m  . C. m  . D. m   . 2 2 2 2 21
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Đáp án: D.
Hướng dẫn giải: Phương trình đã cho tương đương x x       x  3 5 
m   m   3 5 3 5 2 2 1       0  1     . Đặt t     0   ta được: 2 2     2  
m   m  1 2 2 1
t  0  f t 2
t  2mt  2m 1 02. Bất phương trình   1 nghiệm đúng x   0 nên t
bất phương trình 2 có nghiệm 0  t 1, suy ra phương trình f t   0 có 2 nghiệm t ,t thỏa 1 2  f  0  0 2m 1 0 m  0  ,5 1
t  0  1  t       . Vậy m   thỏa. 1 2  f    1  0 4m  2  0 m  0  ,5 2 
Câu 7.3: Một vật di chuyển với gia tốc a t      t  2 20 1 2  2
m / s  . Khi t  0 thì vận tốc của vật là
30m / s . Tính quảng đường vật đó di chuyển sau 2 giây (làm tròn kết quả đến chữ số hàng đơn vị).
A. S 106m .
B. S 107m .
C. S 108m .
D. S 109m . Đáp án: C.
Hướng dẫn giải: Ta có
v t   a
 tdt      t 2 10 20 1 2 dt
C . Theo đề ta có 1 2t
v 0  30  C 10  30  C  20 . Vậy quãng đường vật đó đi được sau 2 giây là: 2  10  S   20 dt   
5ln12t20t2  5ln5100 108m. 0 1 2t  0
Câu 7.4: Cho số phức z  0 thỏa mãn z  2 . Tìm tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu z i thức P  . z A. 1. B. 2 . C. 3 . D. 4 . Đáp án: B. i i i 1 i 1 1 1
Hướng dẫn giải: Ta có 1  1 1 1  1 1
. Mặt khác z  2   suy ra z z z z z z z 2 1 3  3 1 P
. Suy ra giá trị lớn nhất và giá trị nhỏ nhất là , . Vậy tổng tổng giá trị lớn nhất và giá trị 2 2 2 2
nhỏ nhất của biểu thức P là 2 . 22
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 7.5: Cho hình chóp S.ABC , có đáy ABC là tam giác đều cạnh a . Các mặt bên SAB , SAC ,
SBC lần lượt tạo với đáy các góc lần lượt là 0 0 0
30 , 45 , 60 . Tính thể tích V của khối chóp S.ABC .
Biết rằng hình chiếu vuông góc của S trên mặt phẳng  ABC nằm bên trong tam giác ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. V   . B. V  . C. V  . D. V  . 4  3  24  3 44  3 84  3 Đáp án: D.
Hướng dẫn giải: Gọi H là hình chiếu vuông góc của S trên mặt phẳng  ABC. Kẻ
HD AB D AB ,
HE AC E AC ,
HF BC E BC . Khi đó ta có SH SH HD   SH 3 , HE   SH , 0 tan 30 0 tan 45 SH SH 2 a 3 HF   . Ta có S  suy ra 0  tan 60 ABC 3 4 2 1  1  a 3 3a SH 1 3  a   SH    . 2  3  4 24  3 2 3 1 3a a 3 a 3 Vậy V  .  . 24  3 . 3 4 84  3
Câu 7.6: Trong không gian tọa độ Oxyz , cho tám điểm A 2  ; 2  ;0 , B3; 2
 ;0 , C 3;3;0 , D 2  ;3;0 , M  2  ; 2  ;5 , N  2  ; 2  ;5 , P3; 2  ;5, Q 2
 ;3;5 . Hỏi hình đa diện tạo bởi tám điểm đã cho có bao nhiêu mặt đối xứng. A. 3. B. 6. C. 8. D.9 Đáp án: D.
Hướng dẫn giải: Vì tám điểm đã chõ tạo nên một hình lập phương, nên hình đa diện tạo bởi tám
điểm này có 9 mặt đối xứng. 4 2
Câu 8.1. Xét phương trình: 8cos x  9cos x  m  0 với x[0; ] (1) 4 2
Đặt t  cos x , phương trình (1) trở thành: t 8  t 9  m  0 (2)
Vì x[0; ] nên t [ 1
 ;1], giữa x và t có sự tương ứng một đối một, do đó số nghiệm của phương trình 23
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
(1) và (2) bằng nhau. 4 2 Ta có: (2)  t 8  t 9 1 1 m (3) 4 2 Gọi (C1): y  t 8  t 9 1 với t [ 1
 ;1] và (d): y 1 m .
Dựa vào đồ thị(BBT) ta có kết luận sau: 0  m  1 2 2 2 x 0
Câu 8.2. Giải: Đặt 3x t điều kiện t 1 vì x 0 3 3 1 2 2 2
Khi đó phương trình trở thành: t x 3 t 2x 2 0 2 2 t 2 2 2 2 x 3 4 2x 2 x 1 2 t 1 x Khi đó: 2 x 2 + Với t 2 3 2 x log 2 x log 2 3 3 2 2 x 2 + Với t 1 x 3
1 x ta có nhận xét: 2 1 1 3x VT VT 1 x 0 VP 1 VP 1 2 1 x 1
Vậy phương trình có 3 nghiệm x log 2;x 0 3 .       2 2 2   Câu 8.3. x sinx x      osx x   osx  2 x e dx e d c e ce o
c sxdx  e J   0 0 0  0       2   x J e d  sinx 2 x x 2 2
e sinx 2  e sinxdx=e  I I J e  0 0 0 24
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017    2    2 e e   Vậy ta có hệ : I J e   I  2
I J e
Câu 8.4. Bài giải. z i z i i Đặt w . Ta có w z , w 1 z z w 1 i 1 Do z 2 2 w 1
. Như vậy tập hợp số phức w là hình tròn tâm I(1; 0 ), bán w 1 2 1 kính R
, (Bỏ điểm I) giá trị P
w là khoảng cách từ gốc O đến điểm M(x; y) thuộc hình 2
tròn tương ứng với số phức z. 1 2 O( 0; 0 ) A I( 0; 1 ) B 1 1 2 P nhỏ nhất là tại A ;0 , z i . 2 2 1 2 Câu 8.5. ĐÁP ÁN B 2
* Gọi cạnh đáy hình chóp là x, x  (0; ) . 2
Chiều cao của hình chóp là : 2 2  2 x   x  1 x 2 h         2 2    2  2 4 5 1 1 x 2 1 x  x 2
Thể tích của khối chóp : 2 V  x  3 2 3 2 25
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2 * Xét hàm số : 4 5 y  x  x 2 trên (0; ) 2 x  0 (l) 3 4  y '  4x  5x 2 ; y '  0  2 2  x  (n)  5 BBT : X 2 2 2 0 5 2 y’ ║ + 0 - ║ Y ║ ║ ║ ║ 2 2 Vậy khi x 
thì khối chóp đạt GTLN 5
Câu 8.6. Gọi I là trung điểm của AB  I ( 1; 1; 1)
+) MA2 + MB2 = 2MI2 + IA2 + IB2
Do IA2 + IB2 không đổi nên MA2 + MB2 nhỏ nhất khi MI nhỏ nhất
 M là hình chiếu của I lên mặt phẳng (P) x-1 y-1 z-1
+) Phương trình đường thẳng MI : = = . 1 1 1
M là giao điểm của MI và mặt phẳng (P).
Từ đó tìm được M(2; 2; 2).
Câu 9.1. Cho một tam giác đều ABC cạnh a. Người ta dựng một hình chữ nhật MNPQ có cạnh MN
nằm trên cạnh BC, hai đỉnh P và Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định
giá trị lớn nhất của hình chữ nhật đó? 3 3 3 A. 2 a B. 2 a C. 0 D. 2 a 8 4 2 26
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Hướng dẫn giải: a A
Gọi H là trung điểm của BC  BH = CH = 2  a    Q P Đặt BM = x § iÒu kiÖn 0 x  , ta có:  2   a  B
MN  2MH  2(BH  BM)  2  x  a  2x    2  M H N C Tam giác MBQ vuông ở M, 0
B  60 và BM = x  QM  x 3
Hình chữ nhật MNPQ có diện tích: S(x) = MN.QM = 2
 (a  2x)x 3  3(ax  2x ) a  a 
S'(x)  3(a  4x); S'(x)  0  x   0;   4  2  x a a 0 4 2 S’ + 0  3 2 a S 8 3 a Vậy 2 max S(x)  a khi x =  a  8 4 x 0;    2 
Câu 9.2. Cho hình chóp tứ giác đều .
S ABCD có đáy là hình vuông ABCD cạnh a, góc giữa mặt bên 1
và mặt phẳng đáy là  thoả mãn cos = . Mặt phẳng P qua AC và vuông góc với mặt phẳng 3 27
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
SADchia khối chóp .SABCD thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là gần nhất với
giá trị nào trong các giá trị sau A. 0,11 B. 0,13 C. 0,7 D. 0,9
Hướng dẫn giải : .
S ABCD là hình chóp tứ giác đều SO  ABCD . Gọi N là trung điểm CD
CD SN,CD   ON  
 SCD,ABCD  SNO
SCD  ABCD   CD
Kẻ CM SD . Ta có AC BD S
AC  SBD  AC AC SDSO
SD  ACM  ACM  SAD nên mặt phẳng P là  M ACMA D + Xét tam giác SON vuông tại N có : a O N ON 3 2    a SN B C 1 2 cos SNO 3 2 2
a   a 2 2 3
SO SN ON        a 2  2   2    a a
+ Xét tam giác SOD vuông tại O có : SD SO OD  a  2 2 2 2 2 10 2      2  2   3a .a 1 1 SN.CD 3a 10 Ta có S
CM.SD SN. 2  CM     CD SCD 2 2 SD a 10 10 2 28
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2   a a
- Xét tam giác MCD vuông tại M có : 2 2 2 3 10 10
DM CD CM a      10  10   a 10 V V 1 DM DA DC 1 DM 1 1 Ta có : MACD MACD 10   . . .  .  .  V 2.V 2 DS DA DA 2 DS 2 SABCD SACD a 10 10 2 1  VV
. Mặt phẳng P chia khối chóp S.ABCD thành 2 khối MACD và SABCM MACD 10 SABCD  9 VVVVV SABCD MACD SABCM SABCM 10 SABCD V 1 Do đó : MACD   0,11 V 9 SABCM
Câu 9.3. Cho biết chu kì bán hủy của chất phóng xạ Plutôni Pu239 là 24360 năm (tức là một lượng
Pu239 sau 24360 năm phân hủy thì chỉ còn lại một nửa). Sự phân hủy được tính theo công thức S =
Aert, trong đó A là lượng chất phóng xạ ban đầu, r là tỉ lệ phân hủy hàng năm (r<0), t là thời gian
phân hủy, S là lượng còn lại sau thời gian phân hủy t. Hỏi sau bao nhiêu năm thì 10 gam Pu239 sẽ
phân hủy còn 1 gam có giá trị gần nhất với giá trị nào sau? A. 82135 B. 82335 C. 82235 D. 82435 Hướng dẫn giải: S 1
Vì Pu239 có chu kì bán hủy là 24360 năm nên er24360 =   r  0,000028 A 2
 Công thức phân hủy của Pu239 là S = A.e0,000028t
Theo giả thiết: 1 = 10. e0,000028t  t  82235,18 năm
Câu 9.4. Tìm giá trị của tham số m sao cho: 3
y  x  3x  2 và y = m(x+2) giới hạn bởi hai hình
phẳng có cùng diện tích A. 0 < m < 1 B. m = 1 C. 1  m  9 D. m = 9 29
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Hướng dẫn giải:
Phương trình hoành độ giao điểm : 3 x  3x  2  m(x  2)  x  2
 hoÆc x 1 m , m  0.
Điều kiện d: y = m(x+2) và (C): 3
y  x  3x  2 giới hạn 2 hình phẳng: 0  m  9.
Gọi S1, S2 lần lượt là diện tích các hình phẳng nhận được theo thứ tự từ trái sang phải. 0
Nếu m = 1: d đi qua điểm uốn (0;2) của (C). Khi đó S 3 1 = S2 = (x  4x)dx  4  2 
Nếu 0 < m < 1: S1 > 4 > S2
Nếu 1 < m < 9: S1 < 4 < S2
Nếu m > 9  1 m  2  ; 1 m  4. Khi đó: 2  1 m 3 3 S 
x  3x  2  m(x  2) dx; S 
x  3x  2  m(x  2) dx   1 2 1 m 2  S  2  S1 = 2m m 0
Vậy m = 1 thỏa yêu cầu bài toán
Câu 9.5. Cho đường thẳng d là giao tuyến của hai mặt phẳng ( )
 : x  2y  2z  4  0 ( )
 : 2x  2y  z 1  0, và mặt cầu S có phương trình 2 2 2
x  y  z  4x  6y  m  0 . Tìm m để
đường thẳng d cắt mặt cầu (S) tại hai điểm phân biệt A, B sao cho AB = 8. A. 9 B. 12 C. 5 D. 2 Hướng dẫn giải: Ta có n  (2; 2  ; 1  ), n  (1;2; 2
 ) lần lượt là VTPT của (α) và (β) 1 2 1
Suy ra VTCP của đường thẳng d là u  n ;n   (2;1;2), 1 2   3 30
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Ta có A(6;4;5) là điểm chung của hai mặt phẳng (α) và (β) nên Ad.
Mặt cầu (S) có tâm I(-2;3;0), bán kính R  13  m với m < 13.
IA  (8;1;5)  IA, u  ( 3  ; 6  ;6)  d(I,d)  3   AB
Gọi H là trung điểm của AB  AH   4 vµ IH  3. 2
Trong tam giác vuông IHA ta có: 2 2 2 2
IA  IH  AH  R  9 16 13 m  25  m  1  2
Vậy m = 12 là giá trị cần tìm.
Câu 9.6. Tìm phần thực của số phức n z  (1 i) , n  thỏa mãn phương trình
log (n  3)  log (n  9)  3 4 4 A. 5 B. 6 C. 7 D. 8 Hướng dẫn giải: Điều kiện n > 3, n 
Phương trình log (n  3)  log (n  9)  3  log (n  3)(n  9)  3  n  7 (so đk) 4 4 4        3 2 7 3 z (1 i)
(1 i). 1 i   (1  i)(2i)  8  8i  
Vậy phần thực của số phức z là 8.
1. Cho số phức z thỏa mãn: z  3  4i  4 . Tìm giá trị nhỏ nhất của z . Lời giải 2 2
Giả sử z  a  bi , ta có: a bi  3  4i  4  a  3  b  4 16 31
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017a  3  4sin a  3 4sin Đặt    b   4  4cos b   4cos  4 2 2 2 2 2
z a b  9 16sin   24sin 16cos  16  32cos
 41 24sin  32cos 3 4
 41 40( sin  cos) 5 5 3 4 Đặt cos  ,sin  5 5 2 2 2
z a b  41 40sin( ) 1.  
Dấu “=” xảy ra khi    
k2      k2 . 2 2 Vậy Min z  1 . 2 2 3 3 x  x  2016x
2. Tính tích phân : I  dx  4 x 1 Lời giải : 1 3 2 2 1 2 2 2 x 2016 Ta có : I  dx  I  dx  M  N   3 3 x x 1 1 1 3 3 7 2 2 1 2 x 2 3 1 3 21 7 M  dx  3 3 t  1  M   t dt   3 x . Đặt  2 x 2 128 1 0 2 2 2 2 2016   3  2016 N  dx  2016x dx    882   3  2 x  2x  1 1  3 21 7 Vậy I  882  128 32
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 x 3. Cho hàm số y  (C) d y  mx  m C 1
. Tìm m để đường thẳng :
1 cắt ( ) tại hai điểm  x phân biệt , M N sao cho 2 2
AM  AN đạt giá trị nhỏ nhất với ( A 1  ;1) . Lời giải : x x  1
Phương trình hoành độ giao điểm của (C) và d :  mx  m  1   2 1 x
mx  2mx  m1  0(1)
d cắt (C) tại hai điểm phân biệt  (1) có 2 nghiệm phân biệt khác 1  m 0
Gọi I là trung điểm của MN  I(1; 1  ) cố định . 2 MN Ta có : 2 2 2 AM  AN  2AI  2 Do 2 2
AM  AN nhỏ nhất  MN nhỏ nhất 2 2 2 4 MN  (x  x ) (1 ) m  4  m  8  m   2 1 m . Dấu “=” xảy ra 1 Vậy 2 2
min(AM  AN )  20 khi m  1  x 1 y 2 z
4. Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng d :   1 1 2 1 và  x  2 y1 z d :   P d 2 2 1
. Viết phương trình mặt phẳng ( ) chứa
sao cho góc giữa mặt phẳng  2 1
(P) và đường thẳng d2 là lớn nhất . Lời giải : Ta có : d M  VTCPu   1 đi qua (1; 2;0) và có (1;2; 1) .
Phương trình mặt phẳng (P) có dạng : 2 2 2 ( A x1)  (
B y 2) Cz  0,(A  B C  0) . Ta có : d  (P)  . u n  0  C  A 2B 2 4A 3B 1 (4A 3 ) B
Gọi   ((P), d )  sin   . 2 2 2 2 2 3 3 2A  4AB 5B 2A  4AB 5B 33
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2 2 
Với B  0  sin  3 A 2 1 (4t  3)
 Với B  0 . Đặt t  sin  . B , ta được 2 3 2t  4t  5 2 (4t  3) 2 16t 124t  84 Xét hàm số f (t)  f '(t)  2 . Ta có : 2t  4t  5 2 2 (2t  4t  5)  3 t f '(t) 0      4  t  7  3 BBT : t  -7  4  f '(t) + 0 - 0 + 25 f(t) 3 25 A
Dựa vào BBT ta có : max f (t)  t      3 khi 7 7 B 5 3 Khi đó : sin  f ( 7  )  9 5 3 A Vậy sin    P x y z  9 khi 7 B
 Phương trình mặt phẳng ( ) : 7 5 9 0 2 2
5. Cho phương trình : x 5x6 1x 65 .2  2  2.2 x m  (
m 1) . Tìm m để PT có 4 nghiệm phân biệt . Lời giải :
Viết lại PT (1) dưới dạng : 2 2 x 5x6 1x 65 .2  2  2.2 x m  m 2 2 2 2 x 5x6 1x (x 5x6)(1x )  .2 m  2  2  m 2 2 2 2 x 5x6 1x x 5x6 1  .2  2  2 .2 x m  m 34
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2 x 5x6 u  2 Đặt :  , ,
u v  0 . Khi đó PT tương đương với : 2 1 v  2 x x  3 2 x 5x6 u  1 2  1 mu v uv m (u 1)(v ) m 0              x  2 2  1 v  m 2 x  m 2  1 2 x  ( m *)
Để (1) có 4 nghiệm phân biệt  (*) có 2 nghiệm phân biệt khác 2 và 3 . m  0 m  0 (*)   
. Khi đó điều kiện là : 2  2 1   x  log m  x  1 log m 2  2 m  0 m  0 m 2   1   log m  0 2  1 1 1    m  m(0;2) \   ; 1  log m  4   8 256  2 8  1  log m 9    1  2 m   256 1 1 Vậy với m   (0;2) \  ;
8 256  thỏa điều kiện đề bài .   6. Cho hình chóp . S ABC có A
 BC là tam giác đều cạnh 2 , a S  AB cân tại S và (SA ) B  (ABC) .
Xác định tâm và bán kính mặt cầu ngoại tiếp khối chop biết SA 3a . Lời giải : S I O A G C H
Gọi H là trung điểm AB  SH  AB . B 35
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 (  SA ) B  (ABC) (   SA )
B (ABC)  AB  SH  (ABC) . SH  AC 
Gọi O là tâm đường tròn ngoại tiếp S  AB bán kính r. 2 2 SH 1 S . AS . B AB  SA  AH  2a 2 , 2 S  SH.AB  2a 2 r   a 2 ABC 2 , 4S SAB 2 2 2 2
OH  OA  AH  r  AH  a
Gọi G là tâm đường tròn ngoại tiếp A  BC 1 a 3 Do A
 BC đều  HC  a 3 , GH  HC  3 3
Dựng d qua O và vuông góc (SA ) B
Dựng  qua G và song song SH    (ABC) Gọi I  d  .
Do đó I d  IS  IA IB (1) , I   IA IB  IC (2)
Từ (1),(2)  IA IB  IC  IS
 I là tâm mặt cầu ngoại tiếp khối chop có bán kính R  IA 2   a 2 2 2 2 21 R  IA AG  IG  HC   OH   .  3  3 1.
Số giá trị nguyên âm của m để .9x  2   1 .6x  .4x m m m  0 với x  0;  1 là A. 6 B. 4 C. 5 D. 3 2. Cho hàm số 3 2
y  x  3mx  m 1. Giá trị của m để đồ thị hàm số có hai điểm cực trị A, B sao 2
cho trọng tâm tam giác OAB thuộc đường thẳng y  x  là 3 36
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 A. m = 0 hoặc m  1  B. m = 2 hoặc m  1  C. m = 1 hoặc m  2  D. m = 1 hoặc m  3  3. Cho phương trình 3 2
z az  3az  37  0 có ba nghiệm là – 1 và 2 nghiệm còn lại z ; z . Gọi A, 1 2
M, N là các điểm biểu diễn số phức z  –1 và z ; z . Khi đó tam giác AMN là tam giác gì? 1 2 A.
a  9 và ∆AMN vuông. B. a  9  và ∆AMN cân. C. a  9  và ∆AMN vuông. D.
a  9 và ∆AMN cân. 4.
Cho hình vẽ sau. Công thức tích phân nào dưới đây ứng với phần diện tích phần gạch chéo  5    5 
trong hình vẽ trên. Biết A4;  1 ; B2;  1 ; C0;3 ; D 0;    ; F0;    . 2   2   6 4 C D 2 B 15 10 5 5 10 15 O A 2 F 4 6 8 37
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 5 A.
S   5  x   3 x   dx 1 2 B. S     2
5  y   3 ydy 1  5 C. S   2
y y  2dy 1 2 D. S   5 y   3 y   dy 1  5.
Khi sản xuất cái phễu hình nón (không có nắp) bằng nhôm, các nhà thiết kế luôn đặt mục
tiêu sao cho chi phí nguyên liệu làm phễu là ít nhất, tức là diện tích xung quanh của hình nón là
nhỏ nhất. Giá trị gần đúng diện tích xung quanh của phễu khi ta muốn có thể tích của phễu là 1dm3 là ?
(Làm tròn đến chữ số thập phân thứ hai) A. 4.18 dm2 B. 4.17 dm2 C. 4.19 dm2 D. 4.1 dm2 6.
Cho hình chóp S.ABCD có đáy là tứ giác ABCD có 0
ABC ADC  90 , AB AD a và
CD CB a 2 . Cạnh SA vuông góc mp(ABCD) và mp(SBC) hợp với đáy một góc 0 45 . Gọi (S) là
mặt cầu ngoại tiếp hình chóp S.ABCD. Thể tích của khối cầu tạo nên bởi mặt cầu (S) bằng? 3 2 a 3 4 a 3 8 a 3 10 a A. B. C. D. 3 3 3 3 7.
Trong không gian với hệ tọa độ Oxyz, cho các điểm A 2  ;1;  1 , B 1
 ;0;0, M 0;3; 2   . Gọi (P)
là mặt phẳng đi qua A, B sao cho khoảng cách từ điểm M đến mp(P) lớn nhất. Khoảng cách từ điểm
N 1;0;0 đến mp(P) bằng : 38
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 1 4 2 3 A. B. C. D. 14 14 14 14
Câu 10.1. Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng : Nếu trên mỗi đơn vị diện tích của
mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng ( P ) n 480 20 ( n ga )
m . Hỏi phải thả bao
nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất ? A. 10 B. 12 C. 16 D. 24
Giải:Gọi n là số con cá trên một đơn vị diện tích hồ (n 0) . Khi đó :
Cân nặng của một con cá là : ( P ) n 480 20 ( n ga ) m
Cân nặng của n con cá là : 2 . n ( P ) n
480n 20n (ga ) m Xét hàm số : 2 f ( ) n
480n 20n , n (0; ) . Ta có : f '( ) n
480 40n , cho f '( ) n 0 n 12
Lập bảng biến thiên ta thấy số cá phải thả trên một đơn vị diện tích hồ để có thu hoạch nhiều nhất là 12 con.
Câu 10.2. Một cửa hàng bán lẻ bán 2500 cái ti vi mỗi năm. Chi phí gởi trong kho là 10$ một cái mỗi năm. Để
đặt hàng chi phí cố định cho mỗi lần đặt là 20$ cộng thêm 9$ mỗi cái. Cửa hàng nên đặt hàng bao nhiêu lần
trong mỗi năm và mỗi lần bao nhiêu cái để chi phí hàng tồn kho là nhỏ nhất?
Gọi x là số ti vi mà cửa hàng đặt mỗi lần ( x 1; 2500 , đơn vị: cái ) x x
Số lượng ti vi trung bình gởi trong kho là nên chi phí lưu kho tương ứng là 10 5x 2 2 2500 2500
Số lần đặt hàng mỗi năm là
và chi phí đặt hàng là : (20 9x) x x 2500 50000
Khi đó chi phí mà cửa hàng phải trả là: ( C ) x (20 9 ) x 5x 5x 22500 x x
Lập bảng biến thiên ta được : C ( C 100) 23500 min
Kết kết luận: đặt hàng 25 lần, mỗi lần 100 cái ti vi.
Câu 10.3. Một đại lý xăng dầu cần làm một cái bồn chứa dầu hình trụ bằng tôn có thể tích 3 16 m . Tìm bán
kính đáy r của hình trụ sao cho hình trụ được làm ra ít tốn nguyên vật liệu nhất. A. 0,8m B. 1,2m C. 2m D. 2,4m 16 Gọi ( x )
m là bán kính đáy của hình trụ (x 0) . Ta có: 2 V x .h h 2 r
Diện tích toàn phần của hình trụ là: S(x) = 2 2 32 ( S x) 2 x 2 . x h 2 x ,(x 0) x 39
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 32
Khi đó: S’(x) = S'(x) 4 x , cho S'( ) x 0 x 2 2 x
Lập bảng biến thiên, ta thấy diện tích đạt giá trị nhỏ nhất khi x 2( )
m nghĩa là bán kính là 2( ) m .
Câu 10.4. Một xưởng cơ khí nhận làm những chiếc thùng phi với thể tích theo yêu cầu là 2000 lít mỗi chiếc.
Hỏi bán kính đáy và chiều cao của thùng lần lượt bằng bao nhiêu để tiết kiệm vật liệu nhất? A. 1m và 2m
B. 1dm và 2dm C. 2m và 1m
D. 2dm và 1dm Đổi 3 2000 (li ) t
2 (m ) . Gọi bán kính đáy và chiều cao lần lượt là ( x ) m và ( h ) m . 2
Ta có thể tích thùng phi 2 V x .h 2 h 2 x
Vật liệu tỉ lệ thuận với diện tích toàn phần nên ta chỉ cần tìm x để diện tích toàn phần bé nhất. 2 2 2 2 S 2 x 2 . x h 2 ( x x ) 2 (x ) tp 2 x x
Đạo hàm lập BBT ta tìm đc f (x) GTNN tại x 1 , khi đó h 2.
Câu 10.5. Người ta muốn mạ vàng bên ngoài cho một cái hộp có đáy hình vuông, không nắp, thể tích hộp là
4 lít. Giả sử đồ dày của lớp mạ tại một điểm trên hộp là như nhau. Gọi chiều cao và cạnh đáy lần lượt là x
và h . Giá trị của x và h để lượng vàng cần dùng nhỏ nhất là: 4 12 A. 3 x 4; h B. 3 x 12; h C. x 2;h 1 D. x 1; h 2 3 16 3 144 Gọi ( x d )
m là cạnh đáy của hình hộp, h là chiều cao của hộp, (
S x) là diện tích cần mạ vàng.
Vì khối lượng vàng tỉ lệ thuận với diện tích nên ta đưa về bài toán tìm x để ( S x) nhỏ nhất. 2 ( S x) 4xh x V 16 Ta có : 2 h ( S x) x 2 2 V x h x x
Đạo hàm, lập BBT ta tìm được (
S x) đạt GTNN tại x 2 , khi đó h 1
Câu 10.6. Có một tấm nhôm hình chữ nhật có chiều dài bằng 24( )
cm , chiều rộng bằng 18( )
cm . Người ta cắt ở
bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng ( x c )
m rồi gấp tấm nhôm
lại như hình vẽ dưới đây để được một cái hộp không nắp. Hỏi thể tích lớn nhất của cái hộp là bao nhiêu? A. 3 V 640cm B. 3 V 617,5cm C. 3 V 845cm D. 3 V 645cm max max max max
Chiều dài, chiều rộng đáy của cái hộp lần lượt là: 24 2x và 18 2 . x
Diện tích đáy của cái hộp: (24 2 ) x (18 2 ) x . Thể tích cái hộp là: 3 2 V (24 2 ) x (18 2 ) x x 4(x 21x 108 ) x với 0 x 9 Ta có: 2 V '( ) x 4(3x 42x 108). Cho V '( ) x
0 , giải ta nhận nghiệm x 7 13 3,4 40
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Lập bảng biến thiên ta thấy V V(7 13) 645 khi x 7 13 3,4 max
Câu 10.7. Người ta muốn rào quanh một khu đất với một số vật liệu cho trước là 180 mét thẳng hàng rào. Ở
đó người ta tận dụng một bờ giậu có sẵn để làm một cạnh của hàng rào và rào thành mảnh đất hình chữ
nhật. Hỏi mảnh đất hình chữ nhật được rào có diện tích lớn nhất bằng bao nhiêu? A. 2 S 3600m B. 2 S 4000m max max C. 2 S 8100m D. 2 S 4050m max max
Gọi x là chiều dài cạnh song song với bờ giậu và y là chiều dài cạnh vuông góc với bờ giậu, theo bài ra ta có x 2y
180 . Diện tích của miếng đất là S ( y 180 2y) . 2 2 1 1 (2y 180 2y) 180 Ta có: ( y 180 2y) 2 ( y 180 2y) 4050 2 2 4 8 Dấu ' ' xảy ra 2y 180 2y y 45m . Vậy 2 S 4050m khi x 90 , m y 45m. max
Câu 10.8. Một lão nông chia đất cho con trai để người con canh tác riêng, biết người con sẽ được chọn miếng
đất hình chữ nhật có chu vi bằng 800( )
m . Hỏi anh ta chọn mỗi kích thước của nó bằng bao nhiêu để diện tích canh tác lớn nhất?
A. 200m 200m
B. 300m 100m
C. 250m 150m D.Đáp án khác
Gọi chiều dài và chiều rộng của miếng đất lần lượt là: ( x ) m và ( y ) m (x, y 0).
Diện tích miếng đất: S xy
Theo đề bài thì: 2(x y) 800 hay y 400 x . Do đó: 2 S ( x 400 ) x x 400x với x 0 Đạo hàm: S'( ) x 2x 400 . Cho y' 0 x 200 .
Lập bảng biến thiên ta được: S 40000 khi x 200 y 200 . max
Kết luận: Kích thước của miếng đất hình chữ nhật là 200 200 (là hình vuông).
Lưu ý: Có thể đánh giá bằng BĐT Cô-Sy. 3x 1
Câu 11.1 (Kshs). Hai điểm M, N thuộc hai nhánh của đồ thị y
. Khi đó độ dài đoạn thẳng x  3 MN ngắn nhất bằng? A. 8 B. 4 C. x  3 D. 8 2 . M Hướng dẫn giải:  8   8 
Giả sử x  3 , x  3 , khi đó M 3  ; m 3  , N 3  ; n 3  với , m n  0 M N      m   n  41
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2 2  8 8   1 1   64  2 2 2
MN  (m n)    (2 mn)  64    2 .   4 mn   64      m n m n    mn
MN  8 . Kết luận MN ngắn nhất bằng 8
Câu 11.2 ( Thể tích – mặt cầu – mặt nón – mặt trụ). Tính thể tích hình cầu ngoại tiếp tứ diện ABCD, a 3 có cạnh AB =
và các cạnh còn lại đều bằng a. 2 13 13 13 13 13 13 13 A. 3  a B. 3  a C. 3  a D. 3  a . 162 216 648 162 Hướng dẫn giải:
Gọi I là trung đểm cạnh CD . AI CD Theo đề ta có  (1)  a 3 BI CD , AI BI   AB 2 A
 ABI  là mp trung trực cạnh CD .
Gọi M là giao điểm của BI với mặt cầu
S ngoại tiếp tứ diện ABCD . D
 Đường tròn lớn của S là đường tròn I M
ABM . Mặt phẳng BCD cắt S theo B
đường tròn BCD qua M, hơn nữa BM là C đường kính. a 2aBM   sin 600 3 Từ (1)  ABI  đều  ABM = 600 2 2 0 13 AM AB BM  2 .
AB BM cos 60  a 12 42
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 AM a 13  R   2sin 600 6 4 13 13 3 3 V R   a  3 162
Câu 11.3 (Mũ – Logarit). Số giá trị nguyên của tham số m sao cho bất phương trình: 2 2
log 5  log(x 1)  log(mx  4x  )
m nghiệm đúng với mọi x thuộc R? A. 0 B. m
 Z và m  3 C. 1 D. 2. Hướng dẫn giải:
Bất phương trình xác định với mọi x thuộc R khi 2
mx  4x m  0 x  R m  0 m  0      m  2 (1) 2   0 4  m  0
Bất phương trình nghiệm đúng với mọi x thuộc R khi 2 2
5x  5  mx  4x  , m x   R 2  (5 )
m x  4x  5  m  0 x   R 5   m  0 m  5      m  3 (2) 2   0
m 10m  21 0
Từ (1) và (2) ta được 2  m  3 , mZ m  3 . Vậy có 1 giá trị m. a
Câu 11.4 (Tích phân – ứng dụng). Cho hàm số f (x)   . x
b xe . Biết rằng f '(0)  2  2 và 3 (x1) 1
f (x)dx  5 
. Khi đó tổng a b bằng? 0 146  26 26 146 A. B. C. D. . 13 11 11 13 Hướng dẫn giải: 43
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 3  a f '(x) x   be (1 x) 4 (x1) f '(0)  2  2  3  a b  2  2 (1) 1 1 1 1 ( )  5 x f x dxa
dx b xe dx  5    3 (x1) 0 0 0 a   b  5 (2) 4 108 38
Giải hệ (1) và (2) ta được: a  , b  . Vậy chọn đáp án D. 13 13
Câu 11.5 (Oxyz). Trong không gian với hệ trục toạ độ Oxyz, cho điểm A2;5;3 và đường thẳng x 1 y z  2 d :  
. Gọi (𝑃) là mặt phẳng chứa đường thẳng 𝑑 sao cho khoảng cách từ 𝐴 đến (𝑃) lớn 2 1 2
nhất. Tính khoảng cách từ điểm M 1;2;  
1 đến mặt phẳng (𝑃)? 11 18 11 4 A. B. 3 2 C. D. 18 18 3 Hướng dẫn giải:
Gọi 𝐻 là hình chiếu của 𝐴 trên 𝑑; 𝐾 là hình chiếu A của 𝐴 trên (𝑃).
Ta có 𝑑(𝐴, (𝑃)) = 𝐴𝐾 ≤ 𝐴𝐻 ( 𝑘ℎô𝑛𝑔 đổ𝑖)
⟹ 𝐺𝑇𝐿𝑁 𝑐ủ𝑎 𝑑(𝐴, (𝑃)) 𝑙à 𝐴𝐻 d' K
⟹ 𝑑(𝐴, (𝑃)) lớn nhất khi 𝐾 ≡ 𝐻. H
Ta có 𝐻(3; 1; 4), (𝑃) qua 𝐻 và ⊥ 𝐴𝐻 P
P:x  4y z 3  0
Vậy d M P 11 18 ,  . 18
Câu 11.6 (Số phức). Trong các số phức thỏa điền kiện z  4i  2  2i z , modun nhỏ nhất của số phức z bằng? 44
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 A. 2 2 B. 2 C. 1 D. 3 2 . Hướng dẫn giải:
Giả sử số phức z x yi , x y R
Theo đề z  4i  2  2i z 2 2 2 2
 (x 2)  (y 4)  x  (y 2)
x y  4  0
y  4  x (1) Mà 2 2 2 2 z x y
x  (4  x) (thay (1) vào) 2
 2(x  2) 8  2 2 . Vậy chọn đáp án A.
Câu 12.1. Trong vật lí, sự phân rã của các chất phóng xạ được biểu diễn bởi công thức: t 1 T m t m
, trong đó m là khối lượng ban đầu của chất phóng xạ (tại thời điểm t = 0); T 0 2 0
là chu kì bán rã (tức là khoảng thời gian để một nửa khối lượng chất phóng xạ bị biến thành chất
khác). Chu kì bán rã của Cabon 14C là khoảng 5730 năm. Cho trước mẫu Cabon có khối
lượng 100g. Hỏi sau khoảng thời gian t thì khối lượng còn bao nhiêu? 100t t ln 2 5730 1 5730 1 100t A. 5730 m t 100.e B. m t 100. C. m t 100 D. 5730 m t 100.e 2 2 Hướng dẫn giải Theo công thức kt m t m e ta có: 0 100 ln 2 t k ln 2 .5730 m 5730 50 100.e k suy ra 5730 m t 100e 2 5730 Đáp án: A.
Câu 12.2. Trong vật lí, sự phân rã của các chất phóng xạ được biểu diễn bởi công thức: t 1 T m t m
, trong đó m là khối lượng ban đầu của chất phóng xạ (tại thời điểm t = 0); T là chu 0 2 0 45
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
kì bán rã (tức là khoảng thời gian để một nửa khối lượng chất phóng xạ bị biến thành chất khác). Chu kì
bán rã của Cabon 14C là khoảng 5730 năm. Người ta tìm được trong một mẫu đồ cổ một lượng
Cabon và xác định được nó đã mất khoảng 25% lượng Cabon ban đầu của nó. Hỏi mẫu đồ cổ đó có tuổi là bao nhiêu? A. 2378 năm B. 2300 năm C. 2387 năm D. 2400 năm Hướng dẫn giải
Giả sử khối lượng ban đầu của mẫu đồ cổ chứa Cabon là m , tại thời điểm t tính từ thời 0 điểm ban đầu ta có: 3 5730 ln ln 2 ln 2 t 3m t 4 5730 0 5730 m t m e m e t 2378 (năm) 0 0 4 ln 2 Đáp án: A.
Câu 12.3. Một nghiên cứu cho thấy một nhóm học sinh được cho xem cùng một danh sách các loài
động vật và được kiểm tra lại xem họ nhớ bao nhiêu % mỗi tháng. Sau t tháng, khả năng nhớ trung
bình của nhóm học sinh được cho bởi công thức M t 75 20 ln t 1 ,t 0 (đơn vị %). Hỏi sau
khoảng bao lâu thì nhóm học sinh nhớ được danh sách đó dưới 10%? A. 24.79 tháng B. 23 tháng C. 24 tháng D. 22 tháng Hướng dẫn giải
Theo công thức tính tỉ lệ % thì cần tìm t thỏa mãn: 75 20 ln 1 t 10 ln t 1 3.25 t 24.79 Đáp án: A.
Câu 12.4. Một công ty vừa tung ra thị trường sản phẩm mới và họ tổ chức quảng cáo trên truyền
hình mỗi ngày. Một nghiên cứu thị trường cho thấy, nếu sau x quảng cáo được phát thì số % người 100
xem mua sản phẩm là P(x) ,x
0 . Hãy tính số quảng cáo được phát tối thiểu để số 0.015 1 49 x e người mua đạt hơn 75%. A. 333 B. 343 C. 330 D. 323 Hướng dẫn giải
Khi có 100 quảng cáo phát ra thì tỉ lệ người xem mua sản phẩm là: 100 P 100 9.3799% 1.5 1 49e
Khi có 200 quảng cáo phát ra thì tỉ lệ người xem mua sản phẩm là: 100 P 200 29.0734% 3 1 49e
Khi có 500 quảng cáo phát ra thì tỉ lệ người xem mua sản phẩm là: 46
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 100 P 500 97.3614% 7.5 1 49e Đáp án: A.
Câu 12.5. Ông Năm gửi 320 triệu đồng ở hai ngân hàng X và Y theo phương thức lãi kép. Số tiền
thứ nhất gửi ở ngân hàng X với lãi suất 2, 
1 một quý trong thời gian 15 tháng. Số tiền còn lại gửi
ở ngân hàng Y với lãi suất 0, 7 
3 một tháng trong thời gian 9 tháng. Tổng lợi tức đạt được ở hai
ngân hàng là 27 507 768,13 (chưa làm tròn). Hỏi số tiền ông Năm lần lượt gửi ở ngân hàng X và Y là bao nhiêu?
A.140 triệu và 180 triệu.
B.180 triệu và 140 triệu.
C. 200 triệu và 120 triệu.
D. 120 triệu và 200 triệu. Hướng dẫn giải
Tổng số tiền cả vốn và lãi (lãi chính là lợi tức) ông Năm nhận được từ cả hai ngân hàng là
347,507 76813 triệu đồng.
Gọi x (triệu đồng) là số tiền gửi ở ngân hàng X, khi đó 320
x (triệu đồng) là số tiền gửi
ở ngân hàng Y. Theo giả thiết ta có: 5 9 x(1 0, 021) (320 x)(1 0, 0073) 347,507 76813 Ta được x
140. Vậy ông Năm gửi 140 triệu ở ngân hàng X và 180 triệu ở ngân hàng Y. Đáp án: A.
Câu 13.1. Cho hàm số y = - x3 + 3mx2 -3m – 1. Tìm các giá trị của m để hàm số có cực đại, cực tiểu.
Với giá trị nào của m thì đồ thị hàm số có điểm cực đại, điểm cực tiểu đối xứng với nhau qua đường thẳng d: x + 8y – 74 = 0. Đáp án: m=2 Bài giải: + D=R
+ y’ = - 3x2 + 6mx ; y’ = 0  x = 0 v x = 2m.
Hàm số có cực đại, cực tiểu  y’ = 0 có hai nghiệm phân biệt  m  0.
Hai điểm cực trị là A(0; - 3m - 1) ; B(2m; 4m3 – 3m – 1)
Trung điểm I của đoạn thẳng AB là: I(m ; 2m3 – 3m – 1) Vectơ 3 AB  (2 ;
m 4m ) ; Một vectơ chỉ phương của đường thẳng d là u  (8; 1  ) . 47
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017I d
Hai điểm cực đại , cực tiểu A và B đối xứng với nhau qua đường thẳng d    AB d 3
m 8(2m 3m 1)  74  0   m = 2 A . B u  0
Câu 13.2. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, thể tích khối lăng trụ 3 a 3 bằng
. Tính khoảng cách giữa hai đường thẳng AA’ và BC’. 4 a 21 Đáp án: 7 Bài giải: 3 3 a
VABC.A'B'C' 4 VAA'.SAA'    a
ABC. A' B 'C ' ABC SABC 3 2 a 4
Do AA’ // BB’ nên AA’ // (BB’C’C)
Suy ra: d(AA’,BC’)=d(AA’,(BB’C’C))=d(A,(BB’C’C))
Hạ AM BC và BC AA' . Suy ra: BC  BCC ' B'   A' AM   BCC ' B'
Hạ AH A'M AH  BCC 'B'
Do đó, d(A,(BB’C’C))=AH 1 1 1 1 4 7 a 21 Ta có:       AH  2 2 2 2 2 2 AH AM A' A a 3a 3a 7
Câu 13.3. Tìm m để phương trình 16x  3.4x  2m 1  0 (1) có hai nghiệm phân biệt 5  1 Đáp án: m  8 2 Bài giải: Đặt:  4x t
,t  0 , phương trình trở thành: 2
t  3t  2m 1  0 (2)
Phương trình (1) có hai nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm dương  5    0 9
  4(2m 1)  0 5   8m  0 m       8
phân biệt  S  0  3   0   1   m  1     P  0 1 2m  0    2 m   2 48
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 13.4. Tính diện tích hình phẳng giới hạn bởi hai đường cong     1 ;  1 x y e x ye xx
Xét phương trình: e   x   x
e x xx e e 0 1 1  0   x 1 1 e
Vậy diện tích cần tìm là: S x
  xe edx  1 2 0
Câu 13.5. Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình: 2 2 2
x y z  2x  6y  4z  2  0 . Viết phương trình mặt phẳng (P) song song với giá của véc tơ
v  (1;6;2) , vuông góc với mặt phẳng () : x  4y z 11  0 và tiếp xúc với (S).
Đáp án: Vậy: (P): 2x y  2z  3  0 hoặc (P): 2x y  2z  21  0 Bài giải:
(S) có tâm I(1; –3; 2) và bán kính R = 4. VTPT của ( ) là n  (1;4;1) .
 VTPT của (P) là: n  n,v  (2; 1
 ;2)  PT của (P) có dạng: 2x y  2z m  0. Pm  
Vì (P) tiếp xúc với (S) nên d(I,(P))  21 4   . m  3
Vậy: (P): 2x y  2z  3  0 hoặc (P): 2x y  2z  21  0. 4  z 1
Câu 13.6. Phương trình  1   có bao nhiêu nghiệm.  z 1 Đáp án: 3 nghiệm Bài giải: 2
 z i    1,(1) 4    z i
 z i   1    2  z i    z i    1  ,(2)  
 z i z i 1    
z i z ii i z i  1      z  0   (loại) z i
z i  z iz  0  1   z i 49
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
z i i  
z i iz 1 z  1 z i (2)       z i
z i iz  1 z  1   i   z i
Vậy nghiệm phương trình là: z=0, z=1, z=-1.
Câu 14.1. Để hàm số 2
y x m x  m đồng biến trên khoảng (1;2) thì giá trị của m phải là A. m  2. B. m  3.
C. 2  m  3. D. Với mọi m.
Hướng dẫn giải : m Vì 2 y '  3
x  2mx  x3x m; y'  0  x  0 x  1 2 3 2m
Vì hệ số a < 0 nên x  0  1  2 
x m  3nên chọn B 1 2 3
Câu 14.2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Mặt bên SAB là tam giác đều
và vuông góc với đáy. Gọi M là điểm thuộc cạnh SC sao cho SM  2M .
C Tính thể tích hình chóp M.ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 6 36 18 24
Hướng dẫn giải : Ta có: (SAB)  (ABCD) (SAB)  (ABCD) = AB SH  (SAB)
SH  AB ( là đường cao của  SAB đều) Suy ra: SH  (ABCD) a 3 Tính: SH =
(vì  SAB đều cạnh a) 2 50
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 SABCD = a2 1 1 3 a 3
Tính: VS.ABCD = Bh = SABCD.SH= 3 3 6 1 1 a 3 VVVM .ABC S .ABC S . 3 6 ABCD 36 
Câu 14.3. Hàm số y   2
x  2x m   1 có tập xác định là khi: A. m  1
 hoặc m  0 B. m  0 C. m  0 D. 0  m  3
Hướng dẫn giải : Điều kiện: 2
x  2x m 1  0 x
  R  '  0 1 (m 1)  0  m  0 e . a e  . b e c
Câu 14.4. Cho biết tích phân I x 2x  ln x 4 2 2 dx   với a, ,
b c là các ước nguyên của 4. Tổng 4 1
a b c  ? A. 2 B. 4 C. 3 D. 1
Hướng dẫn giải : e I x   e e 2 2x  ln x 3
dx  2 x dx x ln xdx   . 1 1 1 e e 1 1 3 4 2 x dx x   4 e   1 2 2 1 1 e e 2 1  e 1  1  1 ee 1 Ta có 2 2 2 2 x ln xdx  
x ln x x dx
  e x   2  1 x   2 2 1 4 1 1    e   e   e I
x 2x  ln x 1 dx  e   2 4 2 1 2e 1 2 4 1    2 4 4 1
Câu 14.5. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A0;2;0, B 1
 ;1;4 và C3; 2  ;  1 . Mặt
cầu S  tâm I đi qua , A ,
B C và độ dài OI  5 (biết tâm I có hoành độ nguyên, O là gốc tọa độ). Bán
kính mặt cầu S  là 51
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 A. R 1 B. R  3 C. R  4 D. R  5
Hướng dẫn giải :
Phương trình mặt cầu (S) có dạng: 2 2 2
x y z  2ax  2by  2cz d  0 Vì 4 điểm , O , A ,
B C thuộc mặt cầu (S) nên ta có hệ: A(S)
4b d  4  0  
B (S)   2
a  2b  8c d 18  0   C  (S)
6a  4b  2c d 14  0   2 2 2 2
OI  5  OI  5  a b c  5 Suy ra a  1
 ;b  0;c  2  ;d  4   R  3
Nên chọn đáp án B
Câu 14.6. Số phức z a b , i ( , a b  ) thỏa 2
(2  3i)z  5i z  2i . Tính a b ? 5 7 3 11 A.  B.  C.  D.  3 4 4 12
Hướng dẫn giải :
z a bi, ( , a b  )
  i a bi 2 (2 3 )
 5i a bi  2i
 2a  2bi  3ai  3b  5i a bi  2
a  3b  2  (3b  3a  5)i  0  3  a
a  3b  2  0  4     3
b  3a  5  0 1  1 b    12 3  11 
Vậy phần thực của z là   a b . 4 và phần ảo là 12
Chọn đáp án A. x  2
Câu 15.1 (Kshs). Cho hàm số: y
C . Tìm a sao cho từ A(0, a ) kẻ được hai tiếp tuyến đến x 1
(C) nằm ở hai phía trục Ox. 52
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017  2   B.  2  ; \  1 C.  2;    2   A. ;    D. ;  \     1  3   3 
Hướng dẫn giải :
Đường thẳng qua A(0, a ) có hệ số góc k có phương trình y kx a tiếp xúc (C) x  2
<=> kx a
có nghiệm kép <=> kx a x  
1  x  2 có nghiệm kép x 1 <=> 2
kx  k a  
1 x  a  2  0 có nghiệm kép k  0  k  0     
có 2 nghiệm k phân biệt   
k a  2
1  4k a  2  0
h(k)  k  2 
a 5k a  2 2 1  0  12  a  2  0    a  2  ; \  1   h(0)   a   1 2 1  0  k a 1 k a 1 1   1   x   y   1 1  2k 2 Khi đó 1  k a 1 k a 1  2   2   x   y  2 2  2k 2  2 Mà
y y  0  k a 1  k a 1   0 1 2  1   2  
 k k  a  
1 k k   a  2 1  4  3a  2  0 1 2 1 2   2   a  2 3  2  
Từ (1) và (2)  a  ;  \     1  3  Đáp án: D Câu 15.2.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = a, hình chiếu vuông góc AC
của đỉnh S trên mặt phẳng (ABCD) là điểm H thuộc đoạn AC, AH
. Gọi CM là đường cao của 4
tam giác SAC. Tính thể tích khối tứ diện SMBC theo a. 3 a 14 3 a 14 3 a 14 3 a 14 48 24 16 8 53
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Hướng dẫn giải : S
Gọi O là tâm của hình vuông ABCD. M A a 2 .a 2 D AM AH AH.AC a H Ta có: 4   AM    AC SA SA a 2 O C       a a B MC AC AM a 2  2 2 7 2 2      2  2 2 1 1 a a 7 a 7  SSM.MC   SMC 2 2 2 2 8 2 3 1 1 a 2 a 7 a 14  VB . O S   SMAC 3 SMC 3 2 8 48 Đáp án: A. Câu 15.3. 2 2     
Tìm số nghiệm của phương trình: log 2x x 1 log 2x 1 4 1 . 2 x 1    x 1      A. 0 B. 1 C. 2 D. 3
Hướng dẫn giải :  1 x  Điều kiện:  2 x 1 log x x x  2 2 1 1    1   2log 2x 1  4  log 2x 1 x x 1    1   log 2x 1  log x 1 x 1    x 1      2log 2x 1  4  log 2x 1 x x 1    1   1 1  2log 2x 1  4 3  log 2x  1 x x 1    1     t 1 1 Đặt t  log 2x 1 , khi đó (3) 2 2t 3 0 2t 3t 1 0 
         x 1    1 tt   2 log 2x 1  1 x  2 x 1   
x 1  2x 1   1    5  log 2x 1 
x 1  2x 1 x x 1     2  4 Đáp án: C 54
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017  2n  4 x I e   2
1 tan x  tan x
Câu 15.4. Tính tích phân: dx 2n     2n  2n  C. 2n I e 2n 2n  1  A. 2 4 nI  e eI ee B. 4 I e D. 4
Hướng dẫn giải :    2n  2n  2n  4 4 4   x 1 x 1 I e  tan x x dx e dx e tan xdx      2 2  cos x  cos x 2n 2n 2n   2n  2n  4 x I e d  tan x 4 xe tan xdx  2n 2n   2n  2n   4 4 2n  x 4 I e .tan x xe .tan x xdx e tan xdx   2n 2n 2n   2n  2n  x 4 4
I e .tan xe 2nĐáp án: B
Câu 15.5. Cho hai điểm A(-1, 3, -2); B(-9, 4, 9) và mặt phẳng (P): 2x-y+z+1=0. Điểm M thuộc (P). Tính GTNN của AM + BM.    A. 6 204 7274 31434 2004 726 D. 3 26 B. 6 C. 3
Hướng dẫn giải :
Ta có: (2.(-1)-3+(-2)+1)(2.(-9)-4+9+1)=72 > 0 => A,B nằm cùng phía so với mặt phẳng (P).
Gọi A’ là điểm đối xứng của A qua (P). Mặt phẳng (P) có vtpt n2, 1  ,  1 x  1   2t
Đường thẳng AA’ đi qua A(-1, 3, -2) có vtcp n2, 1  , 
1 có pt:  y  3  tz  2   t
Gọi H là giao của AA’ và (P) ta có: 2(-1+2t) - (3-t) + (-2 + t) + 1 =0 => t=1 => H(1, 2, -1).
Ta có H là trung điểm của AA’ => A’(3, 1, 0). 55
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
x  3  4t
Đường A’B đi qua A’(3, 1, 0) có vtcp A' B  1
 2,3,9 có pt: y 1 t z  3t
Gọi N là giao điểm của A’B và mặt phẳng (P) ta có :
2.(3-4t) – (1+t) + 3t +1 =0 => t=1 => N(-1, 2, 3).
Để MA+MB nhỏ nhất thì M N khi đó MA+MB = A’B =  2 2 2 12  3  9  234  3 26 Đáp án D.   n z 1 i8
Câu 15.6. Cho số phức 4 A. 2 n B. 0 C. 8 2 n D. 4 2 n
Hướng dẫn giải :     8n     
Ta có 1 i  2 cos  isin   4   2 cos  sin  2 .n z i   
cos2n isin2n  4 2 n   4 4    4 4  Đáp án A.
Câu 16.1. Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình
vẽ. Tìm tổng x + y để diện tích hình thang EFGH đạt giá trị nhỏ nhất. A E 2 cm B x cm 3cm H F D C G y cm 7 2 A. 7 B. 5 C. D. 4 2 . 2
Hướng dẫn giải: Ta có SS SSS EFGH nhỏ nhất AEH CGF DGH lớn nhất.
Tính được 2S  2x  3y  (6  )
x (6  y)  xy 4 x3y36 (1) 56
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 AE AH Mặt khác AEH  đồng dạng CGF nên   xy  6 (2) CG CF 18 18
Từ (1) và (2) suy ra 2S  42  (4 x
) . Ta có 2S lớn nhất khi và chỉ khi 4 x nhỏ nhất. x x 18 18 3 2 Biểu thức 4 x
nhỏ nhất  4x   x
y  2 2 . Vậy đáp án cần chọn là C. x x 2
Câu 16.2. (Mũ và lôgarit) Người ta thả một lá bèo vào một hồ nước. Kinh nghiệm cho thấy sau 9 giờ
bèo sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, lượng lá bèo tăng gấp 10 lần lượng lá bèo trước 1
đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì số lá bèo phủ kín cái hồ ? 3 9 10 9 A. 3 B. C. 9 – log3 D. . 3 log 3 1
Hướng dẫn giải: Gọi t là thời gian các lá bèo phủ kín cái hồ. Vì tốc độ tăng không đổi nên, 1 giờ 3 t 1
tăng gấp 10 lần nên ta có 9
10  10  t  9  log 3 . Đáp án cần chọn là C. 3
Câu 16.3. (Tích phân và ứng dụng) Một vật chuyển động với vận tốc v(t) (m/s) có gia tốc 2
a(t)  3t t (m/s2). Vận tốc ban đầu của vật là 2 (m/s). Hỏi vận tốc của vật sau 2s .
A. 10 m/s B. 12 m/s C. 16 m/s D. 8 m/s. 2 t Hướng dẫn giải: Ta có 2 3
v(t)  a(t) dt  (3 t  t) dt  t   C   (m/s). 2
Vận tốc ban đầu của vật là 2 (m/s)  v(0)  2  C  2. 2 2
Vậy vận tốc của vật sau 2s là: 3 V (2)  2   2 12 (m/s). 2 Đáp án B.
Câu 16.4. (Hình học không gian) Cho tứ diện ABC ,
D M , N, P lần lượt thuộc BC, B , D AC sao cho
BC  4BM , BD  2BN, AC  3AP , mặt phẳng (MNP) cắt AD tại Q. Tính tỷ số thể tích hai phần
khối tứ diện ABCD bị chia bởi mặt phẳng (MNP). 57
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2 7 5 1 A. B. C. D. . 3 13 13 3
Hướng dẫn giải: Gọi I MN CD,Q PI AD , kẻ DH / /BC H IM , DK / / AC K IPA ID DH BM 1 NMB NDH     IC CM CM 3 P Q IK DK ID 1 DK 1 DK 2 K        I IP CP IC 3 2AP 3 AP 3 H B N D APQ  đồng dạng DKQ M AQ AP 3 AQ 3      DQ DK 2 AD 5 C Đặt V V Ta có: ABCD VANPQ AP AQ 1 V V DN 1 1  .  , ANCD DACN     VV V AC AD 5 V V DB 2 ANPQ 10 ANCD ABCD DABC V CM CP 1 1 1 1 1 CDMP  .  VV VVV VV CDMP N . ABMP DABMPCDMP V CB CA 2 2 2 2 4 CDBA 7 VABMNQP 7  VVVV   ABMNQP ANPQ N . ABMP 20 V 13 CDMNQP 7
Vậy mặt phẳng MNP chia khối chóp thành hai phần với tỉ lệ thể tích . Đáp án B. 13
Câu 16.5. (Hình giải tích 12) Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) có
phương trình 2x – y + z + 1 = 0 và hai điểm M(3; 1; 0), N(- 9; 4; 9). Tìm điểm I(a; b; c) thuộc mặt
phẳng (P) sao cho IM IN đạt giá trị lớn nhất. Biết a, b, c thỏa mãn điều kiện:
A. a b c  21 B. a b c 14 C. a b c  5 D. a b c  19.
Hướng dẫn giải: Nhận thấy 2 điểm M, N nằm về hai phía của mặt phẳng (P).
Gọi R là điểm đối xứng của M qua mặt phẳng (P), khi đó đường thẳng MR đi qua điểm M(3; 1; 0) và x  3 y 1 z vuông góc với mặt phẳng (P) có phương trình:   . Gọi 2 1  1
H MR  (P)  H (1;2; 1  )  ( R 1  ;3; 2  ) . 58
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Ta có IM IN IR IN RN . Đẳng thức xảy ra khi I, N, R thẳng hàng. Do đó tọa độ điểm I là giao x  1  8t
điểm của đường thẳng NR:  y  3  t
(t là tham số ) và mặt phẳng (P). Dễ dàng tìm được I(7; 2; z  2  11t
13). Vậy đáp án cần tìm là A.
Câu 16.6. (Số phức). Tìm số phức Z có mô đun lớn nhất và thỏa mãn điều kiện Z   i 13 1  3  2i  . 2 3 15 1 5 3 15 1 5 A. z   i B. z
i C. z    i D. z   i 4 4 4 4 4 4 4 4
Hướng dẫn giải: Gọi z x yi(x, y R)  z x yi 13 39 2 2
z (1 i)  3  2i
x y x  5y   0 2 8
Gọi M (x;y) là điểm biểu diễn của z trong mặt phẳng tọa độ Oxy  M (C) là đường tròn có tâm 1 5 26
I ( ; ) và bán kính R  2 2 4 3 15
Gọi d là đường thẳng đi qua O và I  d : y  5x . M 
1, M2 là hai giao điểm của d và (C) M ( ; ) 1 4 4 1 5 và M ( ; ) 2 4 4 OM OM Ta thấy 1 2 
số phức cần tìm ứng với điểm biểu diễn M1 hay
OM OI R OM (M  (C))  1 3 15 z  
i . Đáp án cần chọn là A. 4 4
Câu 16.7 . Một đại lý xăng dầu cần làm một cái bồn chứa dầu hình trụ bằng tôn có thể tích 3 16 m .
Tìm bán kính đáy r của hình trụ sao cho hình trụ được làm ra ít tốn nguyên vật liệu nhất. A. 0,8m B. 1,2m C. 2m D. 2,4m
Hướng dẫn giải : 16 Gọi ( x )
m là bán kính đáy của hình trụ (x 0) . Ta có: 2 V x .h h 2 r 59
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Diện tích toàn phần của hình trụ là: S(x) = 2 2 32 ( S x) 2 x 2 . x h 2 x ,(x 0) x 32
Khi đó: S’(x) = S'(x) 4 x , cho S'( ) x 0 x 2 2 x
Lập bảng biến thiên, ta thấy diện tích đạt giá trị nhỏ nhất khi x 2( )
m nghĩa là bán kính là 2( ) m .
Câu 17.1 (Kshs). Trên sân bay một máy bay cất cánh trên đường băng d (từ trái sang phải) và bắt
đầu rời mặt đất tại điểm O. Gọi (P) là mặt phẳng vuông góc với mặt đất và cắt mặt đất theo giao
tuyến là đường băng d của máy bay. Dọc theo đường băng d cách vị trí máy bay cất cánh O một
khoảng 300(m) về phía bên phải có 1 người quan sát A. Biết máy bay chuyền động trong mặt phẳng
(P) và độ cao y của máy bay xác định bởi phương trình 2
y x (với x là độ dời của máy bay dọc theo
đường thẳng d và tính từ O). Khoảng cách ngắn nhất từ người A (đứng cố định) đến máy bay là: A. 300( ) m B. 100. 5( ) m C. 200( ) m D. 100 3( ) m
Hướng dẫn giải :
Xét hệ trục Oxy với gốc tọa độ O là vị trí máy bay rời mặt đất, trục Ox trùng với đường thẳng d và
chiều dương hướng sang phải, trục Oy vuông góc với mặt đất. Gọi 2
B(t;t ) (t  0) là tọa độ của máy bay trong hệ Oxy. Tọa độ của người A là ( A 3;0) .
Khoảng cách từ người A đến máy bay B bằng 2 4
d  (3  t)  t . Suy ra 2 4 2
d t t  6t  9  f t . 3 f '(t) 4t 2t 6. f '(t) 0 t 1.
Lập bảng biến thiên, ta thấy 2
d f (t) đạt giá trị nhỏ nhất bằng 5 khi t
1 . Vậy khoảng cách nhỏ nhất là 100 5( ) m
Câu 17.2. (Thể tích – mặt cầu-mặt nón – mặt trụ 60
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Cho hình chóp S.ABCD có SA vuông góc với đáy, SA a 6 . Đáy ABCD là hình thang vuông tại A 1
và B, AB BC AD  .
a Gọi E là trung điểm của AD. Tính bán kính mặt cầu ngoại tiếp hình chóp 2 S.ECD. 2 30 26 A.  a R . B. R a 6. C.  a R . D.  a R . 2 3 2 Hướng dẫn giải: S R K I R x E A D a H B a C .
Gọi H là trung điểm của CD và d là đường thẳng qua H và vuông góc với đáy. Gọi I và R là tâm và
bán kính mặt cầu ngoại tiếp S.CDE. Suy ra I thuộc d. Đặt IH  . x
Trong mp(ASIH) kẻ đường thẳng qua I và song song với AH cắt AS tại K. Ta có: 2 2 2 2 2     a ID IH HD x . 2 2 a 2 2 2 2 2 2 2 2 2 2
IS  IK KS AH KS AC CH KS  2a
 (a 6  x) 2 2 2 a a 2 6a Suy ra: 2 2 2 x   2a
 (a 6  x)  x  . 2 2 3 30
Vậy bán kính mặt cầu bằng  a R . 3
Câu 17.3. (Mũ – Logarit) 61
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Một bà mẹ Việt Nam anh hùng được hưởng số tiền là 4 triệu đồng trên một tháng (chuyển vào tại
khoản của mẹ ở ngân hàng vào đầu tháng). Từ tháng 1 năm 2016 mẹ không đi rút tiền mà để lại
ngân hàng và được tính lãi suất 1% trên một tháng. Đến đầu tháng 12 năm 2016 mẹ rút toàn bộ số
tiền (gồm số tiền của tháng 12 và số tiền đã gửi từ tháng 1). Hỏi khi đó mẹ lĩnh về bao nhiêu tiền?
(Kết quả làm tròn theo đơn vị nghìn đồng).
A. 50 triệu 730 nghìn đồng
B. 48 triệu 480 nghìn đồng
C. 53 triệu 760 nghìn đồng
D. 50 triệu 640 nghìn đồng
Hướng dẫn giải :
Số tiền tháng 1 mẹ được nhận là 4 triệu, gửi đến đầu tháng 12 (được 11 kỳ hạn), vậy cả vốn lẫn lãi 1
do số tiền tháng 1 nhận sinh ra là: 11 11 4.(1
)  41,01 (triệu đồng). 100
Tương tự số tiền tháng 2 nhận sẽ sinh ra: 10 41,01 (triệu đồng)
......................................................
Số tiền tháng 12 mẹ lĩnh luôn nên là: 4 (triệu đồng). 12 11,01
Vậy tổng số tiền mẹ lĩnh là: 11 10
41,01  41,01  ...  41,01 4  4  50,730 (50 triệu 730 11,01 nghìn đồng). Đáp án A.
Câu 17.4. (Tích phân - Ứng dụng)
Cho một vật thể bằng gỗ có dạng khối trụ với bán kính đáy bằng R. Cắt khối trụ bởi một mặt phẳng
có giao tuyến với đáy là một đường kính của đáy và tạo với đáy góc 0
45 . Thể tích của khối gỗ bé là: 3 2R 3  R 3 R 3  R A. V  . B. V  . C. V  . D. V  . 3 6 3 3 Hướng dẫn giải 62
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 O y x 2 2 R x 2 2 R x
Chọn hệ trục Oxy như hình vẽ. Cắt khối gỗ bé bởi các mặt phẳng vuông góc với Ox tại điểm có 1
hoành độ x ta được thiết diện là tam giác vuông có diện tích bằng 2 2 ( A x) 
R x . Vậy thể tích 2 R 3 1 2R khối gỗ bé bằng: 2 2 V R x  .  Đáp án A. 2 3 R Câu 17.5. (Oxyz)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( )
P : x y z 1  0 và hai điểm ( A 1; 3  ;0), B5; 1  ; 2
  . M là một điểm trên mặt phẳng (P) . Giá trị lớn nhất của T MAMB là: 4 6 2 3 A. T  2 5. B. T  2 6. C. T  . D. T  . 2 3
Hướng dẫn giải :
Ta có: A, B nằm khác phía so với (P). Gọi B’ là điểm đối xứng với B qua (P). Suy ra B'( 1  ; 3  ;4) .
T MA MB MA MB '  AB '  2 5. Đẳng thức xảy ra khi M, A, B’ thẳng hàng. Đáp án A.
Câu 17.6. (Số phức) 25
Số nghiệm phức của phương trình : z   8  6i là? z A. 0 B. 1 C. 2 D. 4
Hướng dẫn giải :
Giả sử z = a +bi với ; a,b  R và a,b không đồng thời bằng 0. 63
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 1 1 a bi
Khi đó z a bi ;   2 2 z a bi a b 25 25(a bi)
Khi đó phương trình z
 8  6i a bi   8  6i 2 2 z a b 2 2 2 2       a(a b 25) 8(a b ) (1) 3 
. Lấy (1) chia (2) theo vế ta có b a thế vào (1) 2 2 2 2  (
b a b  25)  6(a b ) (2) 4 Ta có a = 0 v a = 4
Với a = 0  b = 0 ( Loại)
Với a = 4  b = 3 . Ta có số phức z = 4 + 3i. Đáp án B.
Câu 18.1. Một ngọn hải đăng đặt tại vị trí A có khoảng cách đến bờ biển AB  5km .Trên bờ biển có
một cái kho ở vị trí C cách B một khoảng 7km.Người canh hải đăng có thể
chèo đò từ A đến M trên bờ biểnvới vận tốc 4km/ h rồi đi bộ
đến C với vận tốc 6km/ h .Vị trí của điểm M cách B một
khoảng bao nhiêu để người đó đi đến kho nhanh nhất? 14  5 5 A. 0 km B. 7 km C. 2 5 km D. km 12
Hướng dẫn giải : Đặt BM ( x k ) m MC 7 ( x k ) m ,(0 x 7) . Ta có: 2 x  25
Thời gian chèo đò từ A đến M là: t  (h). AM 4 7  x
Thời gian đi bộ đi bộ đến C là: t  (h) MC 6 2 x  25 7  x
Thời gian từ A đến kho t   4 6 x 1 Khi đó: t 
 , cho t  0  x  2 5 2  6 4 x 25
Lập bảng biến thiên, ta thấy thời gian đến kho nhanh nhất khi x 2 5(k ) m . 64
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Câu 18.2.
Một cửa hàng nhận làm những chiếc xô bằng nhôm hình trụ không nắp chứa 10 lít nước. Hỏi bán
kính đáy (đơn vị cm, làm tròn đến hàng phần chục) của chiếc xô bằng bao nhiêu để cửa hàng tốn ít vật liệu nhất. A. 14,7cm. B. 15cm. C. 15,2cm. D. 14cm.
Hướng dẫn giải :
. Gọi x(cm) là bán kính đáy của chiếc xô. x > 0 V . khi đó 2
V   x h h  2  x
. Để tiết kiện vật liệu thì diện tích toàn phần của chiếc xô bé nhất
. Ta có: 1lít = 1dm3 = 1000cm3. 20000
. Diện tích toàn phần của chiếc xô là 2 S   x x 3 20000 2 x 20000 . S 2    x   . 2 2 x x 10 .  3
S  0  x  10 14,2c . m
. Lập bảng biến thiên, ta thấy diện tích toàn phần của chiếc xô bé nhất khi x 14, 2cm
Câu 18.3. Huyện A có 100 000 người. Với mức tăng dân số bình quân 1,5% năm thì sau n năm dân
số sẽ vượt lên 130 000 người. Hỏi n nhỏ nhất là bao nhiêu? A. 18 năm B. 17 năm C. 19 năm D. 16 năm
Hướng dẫn giải : nr   S
. áp dụng công thức S A 1  n  log n n      r  1  100      A   100 
. trong đó A = 100 000; r = 1,5; Sn = 130 000 . n 17,6218 65
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017C 
Câu 18.4. Cho đường cong : y
x . Gọi (H) là hình phẳng giới hạn bởi (C), trục tung và đường thẳng
y = m (m > 0). Cho (H) quay xung quanh trục tung ta được một vật thể tròn xoay có thể tích 32
V  5 (đvtt). Khi đó giá trị của m là: A. m = 1 B. m = 2 C. m = 3 D. m = 4
Hướng dẫn giải : m m m 5 5 ym . 2 4
V   x dy   y dy    .   5 5 0 0 0
. Kết hợp giả thiết ta được m  2. Câu 18.5.
Trong không gian với hệ toạ độ Oxyz , gọi   là mặt phẳng qua hai điểm A 2;0;1 và B 2;0;5
đồng thời hợp với mặt phẳng Oxz một góc 0
45 . Khoảng cách từ O tới   là: 3 3 1 2 A. . B. . C. . D. . 2 2 2 2
Hướng dẫn giải : O K 450 H 
Gọi K; H lần lượt là hình chiếu vuông góc điểm O lên đường thẳng AB và mặt phẳng . Ta có: ,
A B Oxz
  Oxz  AB 66
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 OH     HK AB    O  K AB OK AB
 Oxz,  KH,OK  OKH
Suy ra tam giác OHK vuông cân tại H OK Khi đó: d  ,
O    OH  . 2 OA AB
Mặt khác: OK d O AB 3 ,   . AB 2 OK
Khi đó: d O   3 ,  OH   . 2 2
Câu 18.6. Số phức có điểm biểu diễn ở phần tô đậm trong hình vẽ sau là: 1 1
A. 1  z  2 và phần ảo lớn hơn  .
B. 1  z  2 và phần ảo lớn hơn  . 2 2 1 1
C. 1  z  2 và phần ảo nhỏ hơn  .
D. 1  z  2 và phần ảo nhỏ hơn  . 2 2
Hướng dẫn giải : 1
. phần ảo của z nhỏ hơn hoặc bằng  , 1  z  2 2 67
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2x  4
Câu 19.1 (Kshs). Cho hàm số y
có đồ thi C điểm ( A 5
 ;5). Tìm m để đường thẳng x  1
y  xm cắt đồ thị C tại hai điểm phân biệt M và N sao cho tứ giác OAMN là hình bình hành
(O là gốc toạ độ). A. m 0 B. m 0; m 2 C. m 2 D. m 2
Hướng dẫn giải :
Do các điểm O và Athuộc đường thẳng  : y  x nên để OAMN là hình bình hành thì
MN OA  5 2 
Hoành độ của M và N là nghiệm của pt: 2x 4 2
 x m x  (3  )
m x  (m  4)  0 (x  1  ) (1) x  1 Vì 2
  m  2m  25  0, m
 ,nên 1 luôn có hai nghiệm phân biệt , d luôn cắt C tại hai điểm phân biệt
x x m  3
Giả sử x , x là nghiệm của 1 ta có: 1 2  1 2
x x  (m  4)  1 2 Gọi 2 2 2 2
M (x ; x  )
m , N(x ; x   )
m MN  2(x x )  2 (
x x ) 4x x  2m 4  m 5  0 1 1 2 2 1 2  1 2 1 2  m  2 2
MN  5 2  2m  4m  50  50   m  0 + m 0thì , O ,
A M,N thẳng hàng nên không thoã mãn. + m 2 thoã mãn.
Câu 19.2. (Thể tích – mặt cầu-mặt nón – mặt trụ).....
Làm 1 m2 mặt nón cần : 120 lá nón ( Đã qua sơ chế) .Giá 100 lá nón là 25.000 đồng . Vậy để làm 100
cái nón có chu vi vành nón là 120 cm, và khoảng từ đỉnh nón tới 1 điểm trên vành nón là 25 cm thì
cần bao nhiêu tiền mua lá nón? A. 400.000đ B. 450.000đ C.500.000đ D. 550.000đ
Hướng dẫn giải :
Làm 100 cái nón hết 450.000 đ tiền để mua lá nón. 68
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 19.3. (Mũ - Logarit) y x e  2007   2 Hệ phương trình  y  1 
có bao nhiêu nghiệm thỏa mãn x > 0, y > 0. xy e  2007   2  x  1 A. 0 B. 1 C.2 D.3
Hướng dẫn giải : x
Dùng tính hàm số để chỉ ra x = y khi đó xét hàm số f xxe   2007 . 2 x  1
Nếu x < 1 thì f x 1   e
 2007  0 suy ra hệ phương trình vô nghiệm.
Nếu x > 1 dùng định lý Rôn và chỉ ra với x0 = 2 thì f(2) < 0 để suy ra phương trình có 2 nghiệm thỏa mãn
Câu 19.4. (Tích phân - Ứng dụng )
Một ô tô chạy với vận tốc 20m/s thì người lái xe đạp phanh còn được gọi là “thắng”. Sau khi đạp   
phanh, ô tô chuyển động chậm dần đều với vận tốc v(t) 40t 20(m / )
s . Trong đó t là khoảng thời
gian tính bằng giây kể từ lúc bắt đầu đạp phanh . Quãng đường ô tô di chuyển từ lúc đạp phanh
đến khi dừng hẳn là bao nhiêu? A. 2m B.3m C.4m D. 5m
Hướng dẫn giải :
Lấy mốc thời gian là lúc ô tô bắt đầu phanh (t = 0)
Gọi T là thời điểm ô tô dừng lại. Khi đó vận tốc lúc dừng là v(T) = 0 1
Vậy thời gian từ lúc đạp phanh đến lúc dừng là v(T )  0  4
 0T  20  0  T  2
Gọi s(t) là quãng đường ô tô đi được trong khoảng thời gian T.
Ta có v(t)  s '(t) suy ra s(t) là nguyên hàm của v(t) 1/ 2 1 T 2
Vây trong ½ (s) ô tô đi được quãng đường là : 2
v(t)dt  ( 4
 0t  20)dt  ( 2  0t  20t)  5( ) m   t 0 0 69
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Câu 19.5. (Oxyz)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;5;0), B(3;3;6) và đường thẳng  có phương
trình tham số x  1
  2t; y 1t; z  2t . Một điểm M thay đổi trên đường thẳng  , xác định vị trí
của điểm M để chu vi tam giác MAB đạt giá trị nhỏ nhất. A. M(1 ;0 ;2) B. M(-1 ;0 ; 2) C. M (1 ;0 ; -2) D. M (-1 ; 0 ; -2)
Hướng dẫn giải :
Gọi P là chu vi của tam giác MAB thì P = AB + AM + BM.
Vì AB không đổi nên P nhỏ nhất khi và chỉ khi AM + BM nhỏ nhất.
Điểm M  nên M  1
  2t;1 t;2t . 2 2 2 2
AM BM  (3t)  (2 5)  (3t  6)  (2 5)
Trong mặt phẳng tọa độ Oxy, ta xét hai vectơ u  3t;2 5 và v   3  t  6;2 5.
|u | 3t   2 52 2 Ta có   AM BM |
u |  | v | và u v  6;4 5 |
u v | 2 29
| v | 3t 6   2 52 2 
Mặt khác, ta luôn có | u |  | v | |
u v | Như vậy AM BM  2 29 3t 2 5
Đẳng thức xảy ra khi và chỉ khi u, v cùng hướng    t 1 3  t  6 2 5
M 1;0;2 và min AM BM   2 29 . Vậy khi M(1;0;2) thì minP = 2 11  29
Câu 19.6. (Số phức).................................................................. z
Tìm số phức z biết z thỏa mãn phương trình  z  2 z A. 1 B. 1+i C.1-i D. i
Hướng dẫn giải :
z  z  2  z  z.z  2z z 2 2
 a  bi  a  b  2(a  bi) 2 2
 (a  a  b )  bi  2a  2bi  . a  1   z 1 2 2 2 a  a  b  2a a  a  0 b  0     b 2b b 0     a  0   z  0(loai) b  0 70
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 .
Câu 20.1 (Kshs). Một máy tính được lập trình để vẽ một chuỗi các hình chữ nhật ở góc phần tư thứ
nhất của trục tọa độ Oxy , nội tiếp dưới đường cong y=e-x. Hỏi diện tích lớn nhất của hình chữ nhật
có thể được vẽ bằng cách lập trình trên
A. 0,3679 ( đvdt) B. 0,3976 (đvdt) C. 0,1353 ( đvdt) D 0,5313 ( đvdt)
Hướng dẫn giải :
Diện tích hình chữ nhật tại điểm x là S=xe-x '( ) x
S x e (1 x)
S '(x)  0  x  1
Dựa vào bảng biến thiên ta có Smax = 1 e 0,3679 khi x=1 Đáp án A
Câu 20.2. (Thể tích – mặt cầu-mặt nón – mặt trụ) 71
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Cho hình trụ nội tiếp trong hình cầu bán kính R. Xác định chiều cao và bán kính đáy để hình trụ có thể tích lớn nhất. A. B. C. D.
Hướng dẫn giải :
.Gọi h là chiều cao của hình trụ , r là bán kính đáy của hình trụ . Ta có h 2 2 2
( )  r R 2
.Thể tích của hình trụ là 3 h 2 2
V   .r .h   R h   4 3 h .Xét hàm 2 2
V (h)   .r .h   R h   4 3 2
V '(h)   R h 4 2 3R V '( )
h  0 khi h 3 2 3R 6
Từ bảng biến thiên ta có tại h
thì V(h) đạt giá trị lớn nhất .Suy ra r R 3 3
Câu 20.3. (Mũ - Logarit)
Cho biết chu kỳ bán rã của chất phóng xạ Plutoni Pu239 là 24360 năm . Sự phân hủy được tính theo  công thức . rt S
A e . Trong đó A là số lượng chất phóng xạ ban đầu, r là tỷ lệ phân hủy hằng năm
(r<0) ,t là thời gian phân hủy, S là lượng còn lại sau thời gian phân hủy t. Hỏi 10 gam Pu239 sau bao
nhiêu năm phân hủy sẽ còn 1 gam A. 80922 năm B. 24360 năm C.35144 năm D. 48720 năm
Hướng dẫn giải : . Theo giả thiết ta có A r r 1 24360. 24360.  Aee  2 2
Với A=10 gam, gọi t là thời gian phân hủy để còn lại S=1gam ta có phương trình 72
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 t 24360.r. rt 24360
1  10e  0,1  e
t 80922 ( năm). .
Câu 20.4. (Tích phân - Ứng dụng ) 2 x 2  
Cho Elip (E) có phương trình y 1 4
Hãy tính diện tích hình phẳng giới hạn bởi (E) đã cho   A. π B. 2π C. D. 4 2
Hướng dẫn giải :
.Diện tích hình phẳng H là 2 2 2 x 2 S  4 1 dx  2 4  x dx   4 1 1 Đặt : x  2 sin t dx  2 cos tdt
x  0  t  0
x  2  t  2 .Vậy:    2 2 2 2 2 S  2
4  sin t 2 cos tdt  8 cos t cos tdt  8 cos tdt    0 0 0   2 2 sin 2t
 4 (1 cos 2t)dt  4(t  )  2  2 0 0 .Chọn đáp án B Câu 20.5. (Oxyz) 73
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Cho hình chóp O.ABC có OA=a , OB=b, OC=c đôi một vuông góc với nhau . Điểm M cố định thuộc
tam giác ABC có khoảng các lần lượt đến các mặt phẳng (OBC) , (OCA), (OAB) là 1,2,3 . Khi tồn tại
a,b,c thỏa thể tích khối chóp O.ABC nhỏ nhất, giá trị nhỏ nhất của thể tích khối chóp O.ABC là A. 18 B. 27 C. 6
D. Không tồn tại a,b,c thỏa yêu cầu bài toán
Hướng dẫn giải :
.Chọn hệ trục tọa độ thỏa
O(0,0,0) , A(a,0,0), B(0,b,0) , C(0,0,c)
Điểm M cố định thuộc tam giác ABC có khoảng các lần lượt đến các mặt phẳng (OBC) , (OCA),
(OAB) là 1,2,3 nên tọa độ điểm M là (1,2,3) x y z
.Phương trình mặt phẳng (ABC) là   1 a b c 1 2 3
Vì M thuộc mặt phẳng (ABC) nên    1 a b c 1 .VOABC= abc 6 1 2 3 1 1 1 1
Áp dụng bất đẳng thức Cauchy ta có 3 1     3 . .  abc  27 a b c a b c 6 Chọn đáp án B
Câu 20.6. (Số phức)
Một hình vuông tâm là gốc tọa độ O, các cạnh song song với các trục tọa độ và có độ dài bằng 4.
Hãy xác định điều kiện của a và b để điểm biểu diễn số phức z=a+bi nằm trên đường chéo của hình vuông
A. a b  2
B. a b  2
C. a b  2
D. a b  2
Hướng dẫn giải :
Vì điểm biểu diễn số phức z nằm trên đường chéo của hình vuông nên 74
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017a b 2   a  2; 2   b  2 và  a b
Vậy điều kiện là a b  2 Chọn đáp án C.
Câu 21.1 (Kshs). Có một tấm gỗ hình vuông cạnh 200 cm. Cắt một tấm gỗ có hình tam giác vuông,
có tổng của một cạnh góc vuông và cạnh huyền bằng hằng số 120cm từ tấm gỗ trên sao cho tấm gỗ
hình tam giác vuông có diện tích lớn nhất. Hỏi cạnh huyền của tấm gỗ này là bao nhiêu?
A. 40cm .
B. 40 3cm .
C. 80cm .
D. 40 2cm . Hướng dẫn giải :
Kí hiệu cạnh góc vuông AB  ,
x 0  x  60
Khi đó cạnh huyền BC  120  x , cạnh góc vuông kia là 2 2 2 AC
BC AB  120  240x 1
Diện tích tam giác ABC là: S x 2  .
x 120  240x . Ta tìm giá trị lớn nhất của hàm số này trên khoảng 2 0;60 1 1 2  40 14400  360x
Ta có S, x 2  120  240x  . x
S 'x  0  x  40 2 2 2 2 2 120  240x 2 120  240x
Lập bảng biến thiên :
Lập bảng biến thiên ta có: x 0 40 60
S' x 0 S 40
S x
Tam giác ABC có diện tích lớn nhất khi BC  80 Từ đó chọn đáp án C 75
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 21.2. (Thể tích – mặt cầu-mặt nón – mặt trụ)
Một hình trụ có bán kính đáy là R và chiều cao R 3 . Hai điểm A và B lần lượt nằm trên hai đường
tròn đáy sao cho góc giữa AB và trục của hình trụ bằng 0
30 .Tính khoảng cách giữa AB và trục của hình trụ. R 3 R 3 3R 3 2R 3 A. . B. . C. . D. . 3 2 4 3
Hướng dẫn giải :
Kẻ BB’ // OO’ cắt đường tròn ( O) tại B’
Góc giữa AB và OO’ là góc ABB’ 0  30
Hạ OH vuông góc AB’.
Khoảng cách giữa AB và OO’ bằng khoảng cách giữa OO’ và (ABB’) vì OO’//(ABB’)
Khi đó d OO'; AB  d OO'; ABB'  OH 3 2 2 '      R AB R OH OA AH
Chọn đáp án B 2 x x x  
Câu 21.3. (Mũ - Logarit) Gọi S1 là tập nghiệm của bất phương trình 2.2 3.3 6 1 0 . x
Gọi S2 là tập nghiệm của bất phương trình 2 4 . log x 1  0 1  
Gọi S3 là tập nghiệm của bất phương trình . 2
Trong các khẳng định sau, khẳng định nào đúng khi nói về mối quan hệ giữa các tập nghiệm S , S , S 1 2 3 ? 76
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 S S S S S S S S A. S . S . S . S . 1 3 2 B. 3 2 1 C. 3 1 2 D. 1 2 3
Hướng dẫn giải : x x x x x x x x x 1   1   1 
2.2  3.3  6 1  0  2.2  3.3 1  6  2.  3.  1        3  2   6  S  2; 1  
Dùng tính đơn điệu của hàm số suy ra
2x  4  x  2  2
  x S  2  ; 2   log
x 1  0  x 1  1  x  2  S  2; 1     3   2
S S S 1 3 2 Chọn đáp án A.
Câu 21.4. (Tích phân - Ứng dụng ).................................................................. b x e 2
Cho tích phân C  
dx trong đó a là nghiệm của phương trình x 1
2   2 , b là một số dương và x a e  3 2 b a . Gọi 2
A   x dx . Tìm chữ số hàng đơn vị của b sao cho C  3A. 1 A. 3 B. 2 C.4 D. 5
Hướng dẫn giải :  2
Giải phương trình x 1
2   2  x  0  a  0
Tính tích phân C. Đặt: x 2   3   x t e t e  3  2  x tdt e dx b e 3 b e 3  2t b e 3 C   dt = 2  2  2 b dt t e  3  4  t 2 2 2  7
Tính tích phân A ta có A 3  b 7 b 11 b 109 109
Theo giả thiết C  3A  2 e  3  4  3.  e  3   e   b  ln  3,305053521 3 2 4 4
Chọn đáp án A. 77
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017x  3 t
Câu 21.5: ( Oxyz) Trong không gian Oxyz, cho 2 đường thẳng d :  y  2  t và d’ :  z  2tx t ' 
y  5  t ' 
z  2t ' 3 2  5
Viết phương trình mặt phẳng () chứa (d) và tạo với mặt phẳng Oyz một góc nhỏ nhất.
A. 3x y  2z  7  0 .
B. 3x y  2z  7  0 . C. 3
x y  2z  7  0 .
D. 3x y  2z  7  0 .
Hướng dẫn giải :
Giả sử (β) : Ax By Cz D  0 (đk : 2 2 2
A B C  0 ), (β) có vtpt là n  ( ; A ; B C) A( ) 
3A  2B D  0 
D  A 2C 2
d (β)   n.a  0
AB C 2  0
B AC 2   A
cos(( ),(Oyz))  cos(n, i ) = 2 2 2
A  ( A C 2)  C
TH 1 : A = 0 (không thoả đb hoặc ( ),(Oyz) không nhỏ nhất)
TH 2 : A ≠ 0 , ta có : 1 1 1
cos(( ),(Oyz)) = = = C C 2 2 1 (1  2)  ( ) C C 6 12 C 6 12 2 2 ( 3)  2. 2  ( )  2 ( 3  )  A A A A 3 9 A 3 9 C 6 C 6
( ),(Oyz) nhỏ nhất cos(( ),(Oyz)) lớn nhất 2 ( 3 
) nhỏ nhất 3   0 A 3 A 3   1 A  1 (choïn) B      3  2 nên C   7  D   3  3 78
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Vậy : (β) : 3x y  2z  7  0 Chọn đáp án D
Câu 21.6. (Số phức)
Trên tập hợp số phức cho phương trình 2
z  3z 1  0 (*). Gọi z z là nghiệm của phương trình (*). 1, 2 z z
Tìm môđun của số phức 1 2 w   , n N 4n2 4n i i A. 1. B. 2. C.4. D. 6.
Hướng dẫn giải : 3 1 3 1
.Giải phương trình ta được : z =i hay z =i 2 2 2 2 z z .Ta có 4n2 4  1  ; n i i 1. Khi đó 1 2 w  
i  1, chọn đáp án A 4n2 4n i i
Câu 22.1. (Kshs). Bạn An là một học sinh lớp 12, bố bạn là một thợ hàn. Bố bạn định làm một chiếc
thùng hình trụ từ một mảnh tôn có chu vi 120 cm theo cách dưới đây:
Bằng kiến thức đã học em giúp bố bạn chọn mảnh tôn để làm được chiếc thùng có thể tích lớn nhất,
khi đó chiều dài, rộng của mảnh tôn lần lượt là: A. 35c ; m 25cm B. 40c ; m 20cm C. 50c ; m 10cm D. 30c ; m 30cm
Hướng dẫn giải :
Gọi một chiều dài là x cm (0 x 60) , khi đó chiều còn lại là 60 x cm , giả sử quấn cạnh có chiều x 3 2 x x
dài là x lại thì bán kính đáy là r ; h 60 . x Ta có: 2 60 V r .h . 2 4 Xét hàm số: 3 2 f ( ) x x 60x ,x 0; 60 x 0 2 f '(x) 3x
120x; f '(x) 0 x 40 79
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Lập bảng biến thiên, ta thấy 3 2 f ( ) x x 60x ,x
0; 60 lớn nhất khi x=40. 60-x=20. Khi đó chiều dài là
40 cm; chiều rộng là 20 cm. Chọn đáp án B
Câu 22.2. (Thể tích, tròn xoay) Cho bát diện đều; tính tỷ số giữa thể tích khối cầu nội tiếp và thể
tích khối cầu ngoại tiếp hình bát diện đều đó. 1 1 1 1 A. B. C. D. 2 2 2 3 3 3
Hướng dẫn giải : S H A D O M B C . S'
Gọi cạnh bát diện đều là a; bát diện đều có các mặt chéo là hình vuông; khi đó độ dài các đường
chéo AC=BD=SS’= a 2
. Mặt cầu nội tiếp và ngoại tiếp đều có tâm O, khi đó bán kính mặt cầu ngoại tiếp là AC a 2 R OA 2 2 S . O OM
. Bán kính mặt cầu nội tiếp là khoảng cách từ O đến các mặt bên. Hình trên có r OH 2 2 SO OM a 2 a . a 6 2 2 2 2 6 a 2 a 2 2 3 3 r 1 r 1 1 +) Có
khi đó tỷ số thể tích khối cầu nội tiếp cho khối cầu ngoại tiếp là: R 3 R 3 3 3 chọn D 80
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 22.3. (Mũ và lôgarit) Bác B gửi tiết kiệm số tiền ban đầu là 20 triệu đồng theo kỳ hạn 3 tháng
với lãi suất 0,72%/tháng. Sau một năm, bác B rút cả vốn lẫn lãi và gửi lại theo kỳ hạn 6 tháng với lãi
suất 0,78%/tháng. Sau khi gửi được đúng một kỳ hạn 6 tháng do gia đình có việc nên bác gửi thêm
một số tháng nữa thì phải rút tiền trước kỳ hạn cả gốc lẫn lãi được số tiền là 23263844,9 đồng (chưa
làm tròn). Biết rằng khi rút tiền trước thời hạn lãi suất được tính theo lãi suất không kỳ hạn, tức tính
theo hàng tháng. Trong một số tháng bác gửi thêm lãi suất là: A. 0,4% B. 0,3% C. 0,5% D. 0,6%
Hướng dẫn giải :
. Gửi được 1 năm coi như gửi được 4 kỳ hạn 3 tháng; thêm một kỳ hạn 6 tháng số tiền khi đó là: 4 20000000. 1 0,72.3 : 100 1 0,78.6 : 100
. Giả sử lãi suất không kỳ hạn là A%; gửi thêm B tháng khi đó số tiền là: 4 B 20000000. 1 0,72.3 : 100 1 0,78.6 : 100 1 A : 100 23263844,9 . Lưu ý: 1 B 5 và B nguyên dương, nhập máy tính: 4 B 20000000. 1 0,72.3 : 100 1 0,78.6 : 100 1 A : 100
23263844,9 thử với A
0,3 rồi thử B từ 1 đến 5,
sau đó lại thử A 0,5 rồi thử B từ 1 đến 5, ... cứ như vậy đến bao giờ kết quả đúng bằng 0 hoặc xấp xỉ bằng 0 thì chọn.
Kết quả: A 0,5; B 4 chọn C
Câu 22.4. (Tích phân - Ứng dụng ) Một ô tô xuất phát với vận tốc v t 2t 10 m / s 1 sau khi đi
được một khoảng thời gian t1 thì bất ngờ gặp chướng ngại vật nên tài xế phanh gấp với vận tốc v t 20 4t m / s 2
và đi thêm một khoảng thời gian t2 nữa thì dừng lại. Biết tổng thời gian từ lúc
xuất phát đến lúc dừng lại là 4 (s). Hỏi xe đã đi được quãng đường bao nhiêu mét. A. 57 m B. 64 m C. 50 m D. 47 m
Hướng dẫn giải :
. Đến lúc phanh vận tốc của xe là: 2t1+10 đó cũng là vận tốc khởi điểm cho quãng đường đạp phanh;
sau khi đi thêm t2 thì vận tốc là 0 nên 2t 10 20 4t t 2t 5 1 2 1 2 . Lại có t t
4 lập hệ được t1=3 s; t2=1 s. 1 2 3 1
. Tổng quãng đường đi được là: S 2x 10 dx 20 4x dx 57 m chọn A 0 0 81
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 22.5. (Oxyz) Trong không gian với hệ trục toạ độ Oxyz cho điểm M 1;1; 2 và hai đường thẳng x 2 y z 1 x y 1 z 6 1 : ; 2 :
. Lấy trên 1 điểm N và trên 2 điểm P sao cho M,N,P thẳng 1 1 1 2 1 1
hàng. Toạ độ trung điểm của NP là: A. I 1;1; 3 B. I 1;1; 2 C. I 0; 2; 3 D. I 2;0; 7
Hướng dẫn giải :
. Lập phương trình mặt phẳng M; 1 :x y 2 0 từ đó P
M; 1 tìm được P 2;0; 7 2
. Lập phương trình mặt phẳng M; 2 :2x 3y z 3 0 từ đó N M;
tìm được N 0; 2; 3 1 2
Tìm được I 1;1; 2 chọn đáp án B
Câu 22.6. (Số phức) Gọi z ; z ; z ; z là 4 nghiệm phức của phương trình 4 2 z 4 m z 4m 0 . Tìm 1 2 3 4
tất cả các giá trị m để z z z z 6 . 1 2 3 4 A. m 1 B. m 2 C. m 3 D. m 1
Hướng dẫn giải : z 2i z 2i . 1;2 4 2 2 2 z 4 m z 4m 0 z 4 z m 0
nếu m 0 hoặc 1;2
nếu m 0 z m z i m 3;4 3;4 6 z z z z 4 2 m . Khi đó 1 2 3 4 m 1 m 0 6 z z z z 4 2 m . hoặc 1 2 3 4 m 1 m 0
Kết hợp lại thì m
1 thoả mãn bài toán. Chọn D
Câu 23.1: Đường dây điện 110KV kéo từ trạm phát (điểm A) trong đất liền ra Côn Đảo (điểm C).
biết khoảng cách ngắn nhất từ C đến B là 60km, khoảng cách từ A đến B là 100km, mỗi km dây điện
dưới nước chi phí là 5000 USD, chi phí cho mỗi km dây điện trên bờ là 3000 USD. Hỏi điểm G cách
A bao nhiêu để mắc dây điện từ A đến G rồi từ G đến C chi phí ít nhất.
A: 40km B: 45km C: 55km D: 60km
Giải: Gọi BG = x (0AG 100  x Ta có 2 2 2
GC BC GC x  3600 82
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Chi phi mắc dây điện theo giải thiết là: 2
f (x)  3000.(100  x)  5000. x  3600
Khảo sát hàm ta được x  45 chọn phương án B 83
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 23.2: Công ty chuyên sản xuất bao bì đựng sản phẩm sữa nhận đơn đặt hàng sản xuất hộp
đựng sữa có thể tích 3
1dm . Các nhân viên thiết kế phân vân giữa làm hộp đựng dạng hình trụ hay
hình hộp chữ nhật đáy hình vuông. Hỏi công ty sẽ làm hộp hình gì để chi phí nguyên liệu nhỏ nhất.
A: Hình trụ B: Hình hộp chữ nhật đáy hình vuông C: Cả hai
như nhau D: Hình lập phương Giải:
TH1: Nếu làm hình trụ có bán kính đáy là x(d )
m và chiều cao là ( h d ) m 1 2 AM GM Ta có 2
V   x h  1  h  2 2 3
S  2 xh  2 x   2 x  3 2  5,5 2 (dm ) 2  x tp x
TH2: Nếu làm hình hộp chữ nhật có đáy hình vuông cạnh x(d ) m và cao ( h d ) m 1 4 AM GM 2
V x .h  1  h  2 2
S  4xh  2x   2x  6 2 x tp x
Kết luận: Chọn đáp án A
Lời bình: Thực tế các loại thực phẩm, nước uống có loại dùng hình trụ (các loại nước giải khát như
coca, pepsi…) có loại hình hộp (như sữa…). Nếu tính toán chi tiết ta thấy cùng 1 đơn vị thể tích,
nếu làm hình hộp thì đó sẽ là hình lập phương,nhưng đa số chúng ta thấy các hộp đựng sữa là
dạng hình hộp thường (là do đặc tính riêng về chi tiết quảng cáo trên sản phẩm,do cách bảo quản
sữa trong tủ lạnh và đôi khi do tính tiện dụng cầm nắm) vì thế các bài toán về chi phí sản xuất vật
liệu cần phải đi sâu sát hơn vào đời sống, tìm hiểu kĩ nhu cầu tiêu dùng,sự hài lòng khách hàng. Do
đó nhiều khi cần phải “tốn tiền cho vật liệu”.
Câu 23.3: Cô giáo Thảo ra trường xa quê lập nghiệp, đến năm 2014 sau gần 5 năm làm việc tiết kiệm
được x(triệu đồng) và định dùng số tiền đó để mua nhà nhưng trên thực tế cô giáo phải cần 1,55x(
triệu đồng). Cô quyết định gửi tiết kiệm vào ngân hàng với lãi suất là 6,9% /năm với lãi hàng tháng
nhập gốc và cô không rút trước kì hạn. Hỏi năm bao nhiêu cô mua được căn nhà đó, biết rằng chủ
nhà đó vẫn bán giá như cũ.
A: Năm 2019 B: Năm 2020 C: Năm 2021 D: Năm 2022
Giải: Tiền lãi sau n (năm) tiết kiệm là x  .
x (1 0, 069)n  (1, 069)n.x n
Theo giả thiết ta có x 1,55x  (1,069)n 1,55  n  log 1,55  6,56 n 1,069
Vì n  do đó sau 7 năm cô giáo Thảo mua được nhà,năm đó là 2021, đáp án C
Câu 23.4: Thành phố định xây cây cầu bắc ngang con sông dài 500m, biết rằng người ta định xây
cầu có 10 nhịp cầu hình dạng parabol,mỗi nhịp cách nhau 40m,biết 2 bên đầu cầu và giữa mối nhịp 84
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
nối người ta xây 1 chân trụ rộng 5m. Bề dày nhịp cầu không đổi là 20cm. Biết 1 nhịp cầu như hình
vẽ. Hỏi lượng bê tông để xây các nhịp cầu là bao nhiêu (bỏ qua diện tích cốt sắt trong mỗi nhịp cầu) A: 3 20m B: 3 50m C: 3 40m D: 3 100m
Giải: Chọn hệ trục tọa độ như hình vẽ với gốc O(0;0) là chân cầu (điểm tiếp xúc Parabol trên), đỉnh
I(25; 2), điểm A(50;0) (điểm tiếp xúc Parabol trên với chân đế)
Gọi Parabol trên có phương trình ( P ): 2 2
y ax bx c ax bx (do (P) đi qua O) 1 1 20 1 2 2
y ax bx
ax bx  là phương trình parabol dưới 2 100 5 2 4 2 4 1
Ta có (P ) đi qua I và A 2 2
 (P) : y   x x y   x x  1 1 1 2 625 25 625 25 5
Khi đó diện tích mỗi nhịp cầu là S  2S với S là phần giới hạn bởi y ; y trong khoảng (0;25) 1 1 1 2 0,2 25 2 4 1 2 S  2( ( x x)dx dx   ) 2  9,9m 625 25 5 0 0,2
Vì bề dày nhịp cầu không đổi nên coi thể tích là tích diện tích và bề dày 85
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 3
V S.0, 2  9,9.0, 2  1,98m  số lượng bê tông cần cho mỗi nhip cầu 3  2m
Vậy 10 nhịp cầu 2 bên cần 3
 40m bê tông. Chọn đáp án C
Câu 23.5: Trong không gian với hệ tọa độ Oxyz cho điểm A(1 ;2 ;2) ; B(-1 ;2 ;-1) ; C(1 ;6 ;-1) ; D(-
1 ;6 ;2). ABCD là tứ diện gì ?
A : Tứ diện đều B : Tứ diện vuông C: Tứ diện gần đều D : Tứ diện thường
Giải : Ta có AB CD  13; AC BD  5; AD BC  13  2 5  ABCD là tứ diện gần đều. Chọn C 4i 2  6i
Câu 23.6 : Cho số phức z
; z  (1 i)(1 2i); z
có điểm biểu diễn trong mặt phẳng phức 1 2 3 i 1 3  i
lần lượt là H;I;V. Tìm tọa độ E sao cho HIVE là hình vuông.
A: Điểm E(-1;-1) B: Điểm E(-1; 1) C: Điểm E(1;-1) D: Điểm E(1;1)
Giải: Dễ dàng có H(2;-2); I(3;1); V(0;2), H
IV vuông cân tại I. Để HIVE là hình vuông thì
VE IH E( 1  ; 1  ) Chọn A
Câu 24.1 (Kshs). Một công ti bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ
với giá 2 000 000 đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê
mỗi căn hộ thêm 100 000 đồng một tháng thì có thêm hai căn hộ bị bỏ trống.
Hỏi muốn có thu nhập cao nhất, công ti đó phải cho thuê mỗi căn hộ với giá trị bao nhiêu một tháng? (đồng/tháng) A. 2 250 000 B. 2 450 000 C. 2 300 000 D. 2 225 000 Hướng dẫn giải:
Gọi x (đồng/tháng) là số tiền tăng thêm của giá cho thuê mỗi căn hộ. ( x 0) 2x
Khi đó số căn hộ bị bỏ trống là: (căn hộ). 100 000
Khi đó, số tiền công ti thu được là: 2x 2 2x T x 2 000 000 x 50 100 000 000 10x (đồng/tháng). 100 000 100 000
Khảo sát hàm số T x trên 0; . 86
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 4x T ' x 10 . 100 000 T ' x 0 1000 000 4x 0 x 250 000 . Bảng biến thiên x 0 250 000 T’ 0 T Do đó maxT x T 250 000 . x 0
Vậy để có thu nhập cao nhất thì số tiền cho thuê một căn hộ mỗi tháng là 2 250 000 đồng. Đáp án A.
Câu 24.2 (Thể tích – mặt cầu – mặt nón – mặt trụ). Cho hình lăng trụ tam giác đều ABC.A’B’C’, có
cạnh đáy bằng a và cạnh bên bằng a 2 . Lấy M, N lần lượt trên cạnh AB’, A’C sao cho AM A'N
1 . Tính thể tích V của khối BMNC’C. AB ' A'C 3 A' C' 3 a 6 3 2a 6 3 3a 6 3 a 6 A. B. C. D. N 108 27 108 27 K B' I Hướng dẫn giải: G M
Gọi G, K lần lượt là tâm các hình chữ nhật ABB’A’ và AA’C’C. A C H B 87
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 AM 1 AM 2 Ta có: (Do G trung điểm AB’). AB ' 3 AG 3 AM 2
Xét tam giác ABA’ có AG là trung tuyến và
. Suy ra M là trọng tâm tam giác ABA’. Do đó AG 3
BM đi qua trung điểm I của AA’. A' N 1 A' N 2 Ta có:
(Do K là trung điểm A’C). A'C 3 A' K 3 A' N 2
Xét tam giác AA’C’ có A’K là trung tuyến và
. Suy ra N là trọng tâm của tam giác AA’C’. A' K 3
Do đó C’N đi qua trung điểm I của AA’.
Từ M là trọng tâm tam giác ABA’ và N là trọng tâm của tam giác AA’C’. Suy ra: IM IN 1 . IB IC ' 3
Gọi V ; V lần lượt là thể tích các khối chóp IMNC; IBCC’. Ta có: 1 2 V IM IN IC 1 1 . . V IB IC ' IC 9 2 8 Mà V V V . Suy ra V V . 1 2 2 9
Hạ AH vuông góc với BC tại H thuộc BC. Ta được AH vuông góc với mặt phẳng (BB’C’C). AA’
song song với mặt phẳng BB 'C 'C nên khoẳng cách từ I đến mặt phẳng (BB’C’C) bằng khoẳng
cách từ A đến (BB’C’C) và bằng AH. a 3 Ta có: AH . 2 88
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2 3 1 1 a 3 a 2 a 6 V
.d I; BB 'C 'C .S . . . 2 BCC ' 3 3 2 2 12 3 8 2a 6 Suy ra V V . 2 9 27 Đáp án B.
Câu 24.3 (Mũ - Logarit). Cho ba số dương a, b, c đôi một khác nhau và khác 1. Xét các khẳng định sau: b c (I) 2 2 log log ; a a c b 1 (II) 2 2 log b log c ; a b 2 log a c c a b (III) Trong ba số 2 2 2 log ; log ; log
luôn có ít nhất một số lớn hơn 1. a b c b c a b c a Khẳng định nào đúng? A. Chỉ (I) và (II) B. Chỉ (I) và (III) C. Chỉ (I) D. Cả (I), (II) và (III) Hướng dẫn giải: b 2 2 c + 2 2 log log b log c log c log b log . Khẳng định (I) đúng. a a a a a a c b 1 + 2 2 log b log c a b 2 log a c 2 2 2
log b log c log a 1 a b c 2
log b log c log a 1 a b c 89
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2 log a
1. Khẳng định (II) đúng. a c b a c b a
+ Theo khẳng định (I) ta có: 2 2 log log ; 2 2 log log ; 2 2 log log . a a b c b b c a c c a b b b c c a a c a b b c a Suy ra 2 2 2 2 2 2 log .log .log log .log .log 1 (theo câu b). a b c a b c b c a c a b b c a b c a a c b a b c c a b
Do a, b, c đôi một khác nhau nên các số ; ; . Suy ra các số log ; log ; log b b c c a a a b b c c a b c a đều khác 1. 2 2 2 Ta cũng có a b a c b c 0 2 2 2 a bc b ac c ab 0.
Suy ra ít nhất một trong ba số 2 2 2 a b ; c b a ; c c
ab khác 0. Do đó ít nhất một trong ba số c a b log ;log ; log khác 1 . a b c b c a b c a c a b Khi đó, trong ba số log ; log ; log
luôn có ít nhất một số khác 1. a b b c c a b c a c a b Mà 2 2 2 log .log .log
1 . Do đó khẳng định (III) đúng. a b c b c a b c a Đáp án D. 2
Câu 24.4 (Tích phân - Ứng dụng). Cho I cosn xdx , n , n
2 . Khẳng định nào sau đây n 0 đúng? n 1 n 2 n 1 A. I I B. I I C. I I D. I 2I n n 1 n n n 2 n n n 2 n n n 2 90
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Hướng dẫn giải: 2 Với I ; I cos xdx 1 . 0 1 2 0 Đặt n 1 n 2 u cos x du n 1 cos x.sinxdx . dv cosxdx chọn v sinx . 2 2 Suy ra n n 1 2 n 2 2 cos xdx cos x.sin x n 1 cos x.sin xdx 0 0 0 2 n 2 2 n 1 cos x. 1 cos x dx . 0 2 2 n 2 1 cos . 1 cosn n x dx n x.dx . 0 0 2 2 n n 1 Do đó n 2 cos x.dx cos x.dx . n 0 0 Đáp án C.
Câu 24.5 (Oxyz). Trong không gian tọa độ Oxyz, cho các phương trình mặt phẳng 2 : 3mx 5 1 m y 4mz 20 0, m 1;1 . m Xét các mệnh đề sau: (I) Với mọi m 1;1 thì các mặt phẳng
luôn tiếp xúc với một mặt cầu không đổi. m 91
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 (II) Với mọi m 0 thì các mặt phẳng
luôn cắt mặt phẳng (Oxz). m (III) d ; O 5, m 1;1 . m
Khẳng định nào sau đây đúng? A. Chỉ (I) và (II) B. Chỉ (I) và (III) C. Chỉ (II) và (III) D. Cả 3 đều đúng. Hướng dẫn giải: 20 20 + Ta có d O; 4 , với mọi m 1;1 . m 2 2 2 9m 25 1 m 16m 25
Do đó với mọi m thay đổi trên 1;1 thì các mặt phẳng
luôn tiếp xúc với mặt cầu tâm O, bán m kính R 4. Khẳng đinh (I) đúng.
+ Vectơ pháp tuyến của mặt phẳng là 2 n 3 ;
m 5 1 m ;4m và vectơ pháp tuyến của mặt m phẳng (Oxz) là j 0;1;0 .
cắt (Oxz) khi và chỉ khi n; j 0 m
0 . Khẳng đinh (II) đúng. m + Khẳng đinh (III) sai. Đáp án A. z z
Câu 24.6 (Số phức). Cho hai số phức phân biệt z ; z thỏa điều kiện 1
2 là số ảo. Khẳng định 1 2 z z 1 2 nào sau đây là đúng? A. z 1; z 1 B. z z C. z z D. z z 1 2 1 2 1 2 1 2 92
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Hướng dẫn giải: z z z z 0. 1 2 1 2 z z z z z z Thì 1 2 là số ảo 1 2 1 2 0 . z z z z z z 1 2 1 2 1 2 z z z z 1 2 1 2 0 z z 1 2 z z 1 2 z z z z z z z z 0 . 1 2 1 2 1 2 1 2 z z z z 0 1 1 2 2 z z z z 0 . 1 1 2 2 z z 0 . 1 2 Đáp án C. 1
Câu 25.1. Cho hàm số 3 2
y = x  x có đồ thị là (C). 2
Tìm tất cả những điểm trên đồ thị (C) sao cho hệ số góc của tiếp tuyến với đồ thị (C) tại 2 4x + 3
những điểm đó là giá trị lớn nhất của hàm số: g(x) = . 4 x +1  1   3   4 40  A. ; 0   B. 1  ;   ; ;    2   2   3 27   2 1 2   2 1   2   1  C.   ;     ;  ;    D. ; 0   ;  2  ; 1  0 2 4   2 4    2  Đáp án: B 93
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Hướng dẫn giải: 2 4x + 3
* Tìm giá trị lớn nhất của hàm số: g(x) = 4 x +1 t 4 + 3
- Đặt t = x2, với t  0 ta có hàm số g(t) = ; 2 t +1 2 4  t  6t + 4 1 - g'(t) = ; g’(t) = 0  t = 2  ;t = ; 2 2 (t +1) 2
- Ta lại có: lim g(t)  0 ; lim g(t)  0 , bảng biến thiên của hàm số: t t t  –2 0 1  2 g’(t) – 0 + + 0 – 4 g(t) 0 3 0 –1 2
- Vậy giá trị lớn nhất của hàm số là g(x) = 4, đạt được khi x   2
* Tìm các điểm thuộc đồ thị (C)
- Ta có: y’ = 3x2 – x , giả sử điểm M0(x0, f(x0))(C), thì hệ số góc tiếp tuyến của (C) tại M0 là f’(x0)= 2 3x  x 0 0 4 3 4 40 - Vậy: 2 3x  x = 4 suy ra x
, tung độ tương ứng f(–1) = – ; f( ) = 0 0 0 = –1; x0 = 3 2 3 27  3   4 40 
+ Có hai điểm thỏa mãn giải thiết 1  ;   ; ;   .  2   3 27 
Câu 25.2. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh
S trên mặt phẳng (ABC) là trung điểm cạnh BC. Góc giữa đường thẳng SA và mặt phẳng (ABC) 94
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
bằng 600. Gọi G là trọng tâm tam giác SAC. Bán kính mặt cầu tâm G và tiếp xúc với mặt phẳng (SAB) là: 13a 13a 3 13a 13a A. B. C. D. 13 39 26 26 Đáp án: A S Hướng dẫn giải: M K G H
+ Gọi H là trung điểm BC C B E + ( , ( ))   60o SA ABC SAH A a 3 3a + 0 AH
, SH AH tan 60  2 2 1 2
+ Bán kính mặt cầu là: R d(G, (SAB))  d(C, (SAB))  d(H , (SAB)) 3 3
+ Gọi E là hình chiếu của H trên AB và K là hình chiếu của H trên SE. Chứng minh: HK  (SAB) a 3 3a
+ Tính được: HE  ; HK  4 2 13 2 a + R HK  3 13 1 1 Câu 25.3. Với  
a  0, a  1 , cho biết : 1 log u 1 log a  ; a t t a v a
. Chọn khẳng định đúng : 1  1 1 1 A. 1log    a v u a B. 1 loga t u a C. 1 loga v u a D. 1 loga v u a Đáp án: D 95
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Hướng dẫn giải: 1 1
Từ giả thiết suy ra: log t  .log a a 1 log a u 1 log u a a 1 1 1 1 log u log v  .log a a    a 1 log a t 1 log t 1 log u a a 1 a  1log u a 1 1 1log
 log vlog u 1 log u  log u(1 log v) 1 log a v u   u a a a a a a a 1 log v a x  5
Câu 25.4. Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số y  , trục 1 3  2x
hoành và hai đường thẳng x  1
 ; x  3 quay quanh trục hoành là: A.  5ln 2   1 B. 5ln 2 1 C.  5ln 2   1 D. 5ln 2 1 Đáp án: C Hướng dẫn giải: 3 x  5
+ Thể tích khối tròn xoay tạo ra là V =  dx  (1) 2    (1 3 2x ) 1
+ Đặt t = 1 + 3  2x  3  2x = t – 1  3 + 2x = (t – 1)2  dx = (t – 1)dt
x = – 1  t = 2 ; x = 3  t = 4 4 2 1 t 2t 8 4 1 10 8 + V = 
  (t 1)dt  =    t  3   dt   2 2 t 2 2  t t  2 2 4 2 1  t 8 
=    3t 10ln t   =  5ln 2   1 2  2 t  2
Chú ý: Học sinh có thể sử dụng máy tính để thử kết quả sau khi xác định được (1). 96
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 25.5. Trong không gian với hệ toạ độ Oxyz, cho 2 đường thẳng: x t x  2 y 1 z 1   :  
,  :  y  2  t và mặt cầu 2 2 2
(S) : x y z  2x  2y  6z  5  0 1 1 2 3  2 z 1 2t
Viết phương trình mặt phẳng ( ) song song với hai đường thẳng  ,  và cắt mặt cầu (S) theo giao 1 2 2 365
tuyến là đường tròn (C) có chu vi bằng . 5
A. x  5y  3z  4  0; x  5y  3z 10  0
B. x  5y  3z 10  0
C. x  5y  3z  3 511  0; x  5y  3z  3 511  0
D. x  5y  3z  4  0 Đáp án: B Hướng dẫn giải: +  qua M (2; 1
 ;1) và có vectơ chỉ phương u  (1;2; 3  ) . 1 1 1
 qua M (0;2;1) và có vectơ chỉ phương u  (1; 1  ;2) . 2 2 2
+ Mặt phẳng () song song với  ,  nên có vectơ pháp tuyến: u  ,u   (1; 5  ; 3  ) 1 2 1 2  
 Phương trình mặt phẳng () có dạng: x  5y  3z D  0
+ Mặt cầu (S) có tâm I(1; 1
 ;3) và bán kính R  4 . 2 365 365
Gọi r là bán kính đường tròn (C), ta có: 2 r   r  5 5 35 D  3 35 D  4 
Khi đó: d I,() 2 2  R r      5 35 5 D 10
+ Phương trình mặt phẳng () : x 5y 3z  4  0 (1) hay x 5y 3z 10  0 (2) .
Vì  / /(),  / /() nên M   loại (1). 1 2 1 và M2 không thuộc ( ) 97
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Vậy phương trình mặt phẳng () cần tìm là: x  5y  3z 10  0 .
Câu 25.6. Cho số phức z thỏa điều kiện z 1  z i . Số phức   z  2i  3 có môđun nhỏ nhất là: 1 3 1 1 1 1 1 3 A.  
i B.     i C.    i D.     i 2 2 2 2 2 2 2 2 Đáp án:B Hướng dẫn giải:
+Đặt :   a bi( , a b  )
R z  (a  3)  (b  2)i
+ Từ z 1  z i b a  1 + 2 2 2
  a b  2a  2a 1 . 1 1
+  nhỏ nhất khi a    b   2 2 1 1
+ Vậy     i . 2 2 Câu 26.1 (Kshs).
Tìm diện tích lớn nhất của hình chữ nhật nội tiếp trong nửa đường tròn bán kính 10cm , biết một
cạnh của hình chữ nhật nằm dọc trên đường kính của đường tròn. A. 2 80cm B. 2 100cm C. 2 160cm D. 2 200cm Hướng dẫn giải:
Gọi x(cm) là độ dài cạnh hình chữ nhật không nằm dọc theo đường kính đường tròn 0 x 10 .
Khi đó độ dài cạnh hình chữ nhật nằm dọc trên đường tròn là: 2 2 2 10 x cm .
Diện tích hình chữ nhật: 2 2 S 2x 10 x 2 2x Ta có 2 2 2 2 S 2 10 x 2.10 4x 2 2 10 x 98
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 10 2 x thoûa 2 S 0 10 2 x khoâng thoûa 2 10 2 10 2 S 8x S 40 2 0 . Suy ra x
là điểm cực đại của hàm S x . 2 2 2 10
Vậy diện tích lớn nhất của hình chữ nhật là: 2 2 S 10 2. 10 100 cm 2
Câu 26.2. (Thể tích – mặt cầu-mặt nón – mặt trụ)
Cho hình chóp S.ABC có chân đường cao nằm trong tam giác ABC ; các mặt phẳng (SAB) , (SAC )
và (SBC ) cùng tạo với mặt phẳng (ABC ) một góc bằng nhau. Biết AB 25, BC 17 , AC 26 ;
đường thẳng SB tạo với mặt đáy một góc bằng 45 . Tính thể tích V của khối chóp S.ABC . A. V 680 B. V 408 C. V 578 D. V 600 Hướng dẫn giải:
Gọi J là chân đường cao của hình chóp S.ABC; H, K và L S
lần lượt là hình chiếu của J trên các cạnh AB, BC và CA.
Suy ra, SHJ , SLJ và SKJ lần lượt là góc tạo bởi
mặt phẳng (ABC ) với các mặt phẳng (S AB) , (SBC ) và (SAC ) . z=17 K y=9 A C z=17 J y=9
Theo giả thiết, ta có SHJ SLJ SKJ , H L x=8 x=8
suy ra các tam giác vuông SJH,SJL và SJK bằng nhau. B Từ đó, JH JL
JK . Mà J nằm trong tam giác ABC nên J là tâm đường tròn nội tiếp tam giác ABC.
Áp dụng công thức Hê-rông, ta tính được diện tích của tam giác ABC là S
204 . Kí hiệu p là S 204
nửa chu vi tam giác ABC, r là bán kính đường tròn nội tiếp của ABC. Ta có r 6 . Đặt p 34 x BH
BL , y CL CK , z AH AK . 99
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 x y 17 z y K C x z 25 A Ta có hệ phương trình . y z 26 y z J L
Giải ra được (x; ; y z) (8;9;17) H x x 2 2 2 2 JB JH BH 6 8 10 . B Ta có SBJ (S , B (ABC))
45 , suy ra SJB là tam giác vuông cân tại J. SJ JB 10 . 1
Thể tích V của khối chóp S.ABC là V SJ .S 680 3 ABC
Câu 26.3. (Mũ – Logarit)
Tìm tất cả các giá trị thực của tham số m để phương trình 2 2 2 log x log x 3 m log x 3 2 1 4 có 2 nghiệm thuộc 32; ? A. m 1; 3 . B. m 1; 3 . C. m 1; 3 . D. m 3;1 . Hướng dẫn giải: Điều kiện: x
0. Khi đó phương trình tương đương: 2 log x 2 log x 3 m log x 3 2 2 2 . Đặt t log x x 32 log x log 32 5 t 2 với 2 2 hay 5. Phương trình có dạng 2 t 2t 3 m t 3 * .
Khi đó bài toán được phát biểu lại là: “Tìm m để phương trình (*) có nghiệm t 5 ” Với t 5 thì (*) t 3 . t 1 m t 3
t 3. t 1 m t 3 0 t 1 t 1 m t 3 0 m t 3 t 1 4 4 4 t 1 t 1 Ta có 1 . Với t 5 1 1 1 3 hay 1 3 1 3 t 3 t 3 t 3 5 3 t 3 t 3 suy ra 1 m
3. Vậy phương trình có nghiệm với 1 m 3.
Câu 26.4. (Tích phân - Ứng dụng ) 1 1 5 Cho hàm số 3 2 y x mx 2x 2m
có đồ thị (C). Tìm m 0;
sao cho hình phẳng giới hạn 3 3 6
bởi đồ thị (C) và các đường thẳng x 0, x 2, y
0 và có diện tích bằng 4. 100
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 1 1 1 A. m B. m C. m D. m 1 4 3 2 Hướng dẫn giải: 1 1 Xét hàm số 3 2 y x mx 2x 2m trên 0;2 . Ta có 2 y x 2mx 2 , 3 3 2 x m m 2 5 y 0 . Do m 0; nên 2 2 m m 2 0, 0 m m 2 2 2 x m m 2 6 1 5 và y 0 2m 0, y 2 2m 0. 3 3
Ta có bảng biến thiên trong 0;2 x 0 2 m m 2 2 y 0 y y 0 y 2
Dựa vào BBT suy ra y 0, x 0;2
Gọi S là diện tích hình phẳng cần tìm. Ta có: 2 1 1 3 2 S 4 x mx 2x 2m dx 4 3 3 0 2 1 1 4m 10 1 3 2 x mx 2x 2m dx 4 4 m 3 3 3 2 0 Câu 26.5. (Oxyz) x t
Trong không gian tọa độ Oxyz cho đường thẳng d : y
1 2t và mp P : 2x y 2z 2 0 . z 2 t
Viết phương trình mặt phẳng R qua d và tạo với P một góc nhỏ nhất . A. x y z 3 0 B. x y z 3 0 C. x y z 3 0 D. x y z 3 0 Hướng dẫn giải: 101
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 x y 1 2x y 1 0 1 2
Đường thẳng d là giao tuyến của hai mặt phẳng : . x z 2 x z 2 0 1 1
Do vậy mặt phẳng R qua d thì R thuộc chùm mặt phẳng: 2x y 1 m x z 2 0 . Hay mp R : 2 m x y mz 1 2m
0 (*). Mp R có n
m 2;1;m ;n 2; 1; 2 1 P . n .n 2 m 2 1 2m 5 5 1 5 Vậy : 1 cos P 2 2 2 2 n n m m m m P 2 1 4 1 4 3 2 4 5 3 3 3 1 2 m 1 3
Do nhỏ nhất cho nên cos lớn nhất khi m 1.
Vậy thay vào (*) ta có mp R : x y z 3 0 .
Câu 26.6. (Số phức) Cho z 1 i; z 1 i z z , z , z 1 2 . Tìm 3
sao cho các điểm biểu diễn của 1 2 3 tạo thành tam giác đều. A. z
2 1 i và z 2 1 i z
3 1 i và z 3 1 i 3 3 B. 3 3 C. z
2 1 i và z 2 1 i z
3 1 i và z 3 1 i 3 3 D. 3 3 Hướng dẫn giải:
Để giải bài toán này ta cần chú ý đến kiến thức sau:
Giả sử M x ; y z x y i 1 1
1 biểu diễn số phức 1 1 1
Giả sử M x ; y z x y i 2 2
2 biểu diễn số phức 2 2 2
Khi đó khoảng cách giữa hai điểm M M z z 1
2 bằng môđun của số phức 1 2 . 2 2 Vậy M M z z x x y y 1 2 1 2 1 2 1 2
Áp dụng vào bài toán: Giả sử z x yi 3 102
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Để các điểm biểu diễn của z , z , z 1 2
3 tạo thành một tam giác đều thì z z z z 2 2 2 2 4 4 x 1 y 1 1 2 1 3  x 1 y 1 8 z z z z 2 2 1 2 2 3 x y 0 4 4 x 1 y 1 2 2y 6 y 3 x 3
Vậy có hai số phức thoả mãn là: z
3 1 i và z 3 1 i 3 3 .
Câu 27.1 (Kshs) Cho hàm số 4 2
y  x  2mx 1 m . Định m để đồ thị hàm số trên có ba điểm cực trị
nhận gốc tọa độ làm trực tâm. A. 1  B. 0 C. 1 D. 2 Hướng dẫn giải : . 3
y '  4x  4mx , với m  0 thì đồ thị hàm số có ba cực trị là: A0,1 m ,  2 B m,1 m  m  ,  2 C  m,1 m  m  . . ycbt     3 2 OB.AC 0 m m  m  m  
1  0  m  0  m  0  m  1
 . Vậy đáp án là C.
Câu 27.2. (Thể tích – mặt cầu-mặt nón – mặt trụ) Có một miếng nhôm hình vuông, cạnh là 3dm,
một người dự tính tạo thành các hình trụ (không đáy ) theo hai cách sau:
Cách 1: gò hai mép hình vuông để thành mặt xung quanh của một hình trụ, gọi thể tích là của khối trụ đó là V1
Cách 2: cắt hình vuông ra làm ba, và gò thành mặt xung quanh của ba hình trụ, gọi tổng thể tích của chúng là V2. 103
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 V Khi đó, tỉ số 1 là: V2 1 1 A. 3 B. 2 C. D. 2 3 Hướng dẫn giải : 3 27 .Gọi R 2
1 là bán kính đáy của khối trụ thứ nhất, có 2 R   3  R   V  R  h  1 1 2 1 1 4 1 9 . Gọi R 2
1 là bán kính đáy của khối trụ thứ nhất, có 2 R  1 R   V  3 R  h  2 1 2 2 1 4
Vậy đáp án là A.
Câu 27.3. (Mũ - Logarit) Một người nọ đem gửi tiết kiệm ở một ngân hàng với lãi suất là 12% năm.
Biết rằng cứ sau mỗi một quý ( 3 tháng ) thì lãi sẽ được cộng dồn vào vốn gốc. Hỏi sau tối thiểu bao
nhiêu năm thì người đó nhận lại được số tiền ( bao gồm cả vốn lẫn lãi ) gấp ba lần số tiền ban đầu. A. 8 B. 9 C. 10 D. 11
Hướng dẫn giải : Gọi số tiền người đó gửi là A, lãi suất mỗi quý là 0,03
.Sau n quý, tiền mà người đó nhận được là:   n A 1 0, 03 .
. ycbt  A1 0,03n  3A  n  log 3  37,16 1,03
Vậy số năm tối thiểu là xấp xỉ 9,29 năm. Vậy đáp án là C.
Câu 27.4. (Tích phân - Ứng dụng ) Có một người cần làm một cái của cổng cố xưa, có hình dạng
một parabol bậc hai như hình vẽ. Giả sử đặt cánh cổng vào một hệ trục tọa độ như hình vẽ ( mặt
đất là trục Ox). Hãy tính diện tích của cánh cửa cổng. 104
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 16 32 28 A. B. C. 16 D. 3 3 3 Hướng dẫn giải :
.Dựa vào đồ thị , ta xây dựng được công thức của hàm số là 2 y  4  x . 2 32 .Diện tích là: S   2 4  x dx  
. Vậy đáp án là B. 3 2 
Câu 27.5. (Oxyz) Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A1, 2,0 , B3, 1  ,2 , C2, 1  ,  1 , D0, 2,  1
 . Có bao nhiêu mặt phẳng cách đều năm điểm O, A, B, C, D. A. 4 B. 5 C. 6 D. 7 Hướng dẫn giải :
.Chứng minh được ABCD là hình bình hành và OABCD là hình chóp tứ giác.
.Vậy có 5 mặt phẳng thỏa bài toán. Đáp án là B.
Câu 27.6. (Số phức) Có bao nhiêu điểm có tọa độ là số nguyên biểu diễn cho số phức z có phần ảo
dương và đông thời thỏa mãn z  z  4 , z  z  6 A. 20 B. 15 C. 6 D. 10 Hướng dẫn giải :
.Gọi z  a  bi , gt  2a  4  2
  a  2 và 2bi  6  3   b  3
. Mà z có phần ảo dương, nên b  0  0  b  3 .
Vậy có 10 điểm thỏa mãn. Nên đáp án là D. Câu 28.1 (Kshs).
Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của
mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng Pn  480  20ngam. Hỏi 105
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất ? A. 10 B. 12 C. 16 D. 24 Hướng dẫn giải:
Gọi n là số con cá trên một đơn vị diện tích hồ (n>0). Khi đó: .
n Pn  n480  20n  gam
Trên một đơn vị diện tích thu được . f n 2
 480n  20n ,n0; Xét hàm số
. Ta tìm được n = 12 thì lượng cá lớn nhất. Đáp án B.
Câu 28.2. (Thể tích – mặt cầu-mặt nón – mặt trụ)
Một hình hộp có 6 mặt đều là các hình thoi có góc bằng 600 và cạnh bằng a. Tính thể tích của hình hộp đó. 3 a 3 2a 3 2a 3 2 2a A. B. C. D. 2 2 3 3
Hướng dẫn giải : D' C'
Ta có: AB = AD = BD = a; AA’ = A’B = A’D = a 600
 A’ABCD là tứ diện đều A' B'
 Chân đường cao A’H trùng với tâm của  ABD  2 2 a 3 a 3 HA = HB = HD = AO =  3 3 2 3 D C 2 2  3a 6a O
A’H2 = AA’2 – AH2 = a2 - = 600 600 9 9 H 3 A a B  a 6 2a A’H =
Từ đó tìm được V  3 2 Đáp án B. 106
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 28.3. (Mũ - Logarit) 2 2    
Có bao nhiêu giá trị của tham số m để phương trình x 5x 6 1 x 6 5 .2  2  2.2 x mm có 3 nghiệm phân biệt. A. 1 B. 2 C. 3 D. 4
Hướng dẫn giải :
 2xx   2 x   2xx 
 2xx   2 5 6 1 5 6 5 6 1  2 1 2 1 2 2 1  2 x Pt m m 0   2 x 2 x 5  x6 2  2  0     x  3 2 1 2 x m  2 1 2 x m  *
TH1: (*) có nghiệm duy nhất ( nghiệm x =0)  m  2. 
TH2: (*) Có 2 nghiệm phân biệt trong đó có một nghiệm là 2 và nghiệm còn lại khác 3 3  m  2 . 
TH3: (*) Có 2 nghiệm phân biệt trong đó có một nghiệm là 3 và nghiệm còn lại khác 2 8  m  2 .
Vậy, có 3 giá trị của m thỏa mãn. Đáp án C.
Câu 28.4. (Tích phân - Ứng dụng )
Trong hệ trục Oxy, cho tam giác OAB vuông ở A, điểm B nằm trong góc phàn tư thứ nhất. A nằm   
trên trục hoành, OB = 2017. Góc AOB  , 0    . 
 Khi quay tam giác đó quanh trục Ox ta được  3 
khối nón tròn xoay. Thể tích của khối nón lớn nhất khi : 6 3 1 2 A. sin  B. cos  C. cos  D. sin  3 2 2 3
Hướng dẫn giải :
Phương trình đường thẳng OB : y  .
x tan; OA  2017cos. 107
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Khi đó thể tích nón tròn xoay là: 2017.cos 3 3   2 2 2017 . 2 2017 . V   x tan .dx  .cos.sin   .cos   2 1  cos  . 3 3 0 1  1  Đặt t cos     t  0; . 
 Xét hàm số f t  t  2
1  t , t  0;   .  2   2  3 3 6
Ta tìm được f t  lớn nhất khi t   cos   sin  . 3 3 3 Đáp án A. Câu 28.5. (Oxyz).
Cho hai điểm M 1;2;3, A
2;4;4 và hai mặt phẳng P: x y  2z 1 0,
Q: x 2y z  4  0. Viết phương trình đường thẳng  qua M cắt P, Q lần lượt tại , B C sao
cho tam giác ABC cân tại A và nhận AM là đường trung tuyến. x 1 y  2 z  3 x 1 y  2 z  3 A.  :   B.  :   1  1  1 2 1  1 x 1 y  2 z  3 x 1 y  2 z  3 C.  :   D.  :   1 1 1 1 1  1
Hướng dẫn giải : Gọi B  ; a ;
b c , từ giả thiết suy ra M là trung điểm của BC , suy ra C 2  ; a 4  ; b 6  c .
B  P, C
Q nên có hai pt: a b  2c 1 0  
1 ;  a  2b c  8  0 2. AM  1  ; 2  ;  1 , BC 2  2 ; a 4  2 ; b 6  2c.
Tam giác ABC cân tại A nên: AM.BC  0  a  2b c 8  0 3.
a b  2c 1  0 a  0   Từ  
1 , 2 và 3 có hệ: a  2b c  8  0  b
  3  B0;3;2, C 2;1;4.  
a  2b c  8  0 c  2   x 1 y  2 z  3
Đường thẳng  qua B và C có pt  :   . 1 1  1 108
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Đáp án D.
Câu 28.6. (Số phức). 2z 1
Cho số phức z thỏa mãn z  1 và số phức w 
. Khi đó mô đun của số phức w là: 2  iz
A. w  2 B. 1  w  2. C. w  1 D. w  2
Hướng dẫn giải :
Giả sử z a bi  , a b  . 2 2
z 1 a b 1. 2 2 2z 1
4a  2b  2 2 1 2z 1
4a  2b   1  . Xét 2 2 1
1 ...  a b 1. (vô lí) 2  iz  2  2  b2 2  a 2 iz 2 b 2  a Nên w  1. Đáp án C.
Câu 29.1 (Kshs). Một Bác nông dân cần xây dựng một hố ga không có nắp dạng hình hộp chữ nhật có thể tích 3
3200cm , tỉ số giữa chiều cao của hố và chiều rộng của đáy bằng 2 . Hãy xác định diện
tích của đáy hố ga để khi xây tiết kiệm nguyên vật liệu nhất? A. 2 1200cm B. 2 160cm C. 2 1600cm D. 2 120cm
Hướng dẫn giải :
Gọi x,y (x,y
0) lần lượt là chiều rộng, chiều dài của đáy hố ga. h
Gọi h là chiều cao của hố ga (h 0). Ta có 2 h 2x 1 x suy ra thể tích của hố ga là : 3200 1600 V xyh 3200 y 2 2 xh x 6400 1600 8000
Diện tích toàn phần của hố ga là: 2 2 S 2xh 2yh xy 4x 4x f (x) x x x 109
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Khảo sát hàm số y f (x), x
0 suy ra diện tích toàn phần của hố ga nhỏ nhất bằng 2 1200cm khi x 10cm y
16cm Suy ra diện tích đáy của hố ga là 2 10.16 160cm
Câu 29.2. (Thể tích – mặt cầu-mặt nón – mặt trụ)..................................................................
Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là V . Điểm P là trung điểm của SC
, một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N .Gọi V là thể tích của khối chóp 1 V
S.AMPN . Tìm giá trị nhỏ nhất của 1 ? V 3 1 2 1 A. B. C. D. 8 3 3 8
Hướng dẫn giải : SM SN V Đặt x ;y ,(0 x,y 1) khi đó ta có : V V V V SD SB SABC SADC SABD SBCD 2 V V V V V V 1 SM SP SN SP 1 Ta có : 1 SAMPN SAMP SANP SAMP SANP . x y 1 V V V 2V 2V 2 SD SC SB SC 4 SADC SABC V V V V 1 1 3 Lại có : 1 SAMPN SAMN SMNP xy xy xy 2 V V 2V 2V 2 2 4 SABD SBCD 110
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 1 3 x x 1 Từ (1) và (2) suy ra : x y xy y do 0 y 1 1 x 4 4 3x 1 3x 1 2 2 V1 3 3 x 3x 3 1 Từ (2) suy ra .xy .x f (x), x 1 V 4 4 3x 1 4 3x 1 4 2 1 2 4 V 1 Khảo sát hàm số 1 y f (x), x 1 min f (x) f 1 2 V x x 3 9 3 1 2
Câu 29.3. (Mũ - Logarit)..................................................................
Một Bác nông dân vừa bán một con trâu được số tiền là 20.000.000 (đồng) .Do chưa cần dùng đến
số tiền nên Bác nông dân mang toàn bộ số tiền đó đi gửi tiết kiệm loại kỳ hạn 6 tháng vào ngân
hàng với lãi suất 8.5% một năm thì sau 5 năm 8 tháng Bác nông dân nhận được bao nhiêu tiền cả
vốn lẫn lãi .Biết rằng Bác nông dân đó không rút cả vốn lẫn lãi tất cả các định kì trước và nếu rút
trước thời hạn thì ngân hàng trả lãi suất theo loại không kì hạn 0.01% một ngày (1 tháng tính 30 ngày)
A. 31802750,09 ®ång B. 30802750,09 ®ång C. 32802750,09 ®ång D. 33802750,09 ®ång
Hướng dẫn giải : 8.5% 4.25
Một kì hạn 6 tháng có lãi suất là .6
. Sau 5 năm 6 tháng (có nghĩa là 66 tháng tức là 11 12 100 11 4 2 . 5
kỳ hạn) , số tiền cả vốn lẫn lãi Bác nôn dân nhận được là : A 20000000. 1 (®ång) .Vì 5 năm 100
8 tháng thì có 11 kỳ hạn và dư 2 tháng hay dư 60 ngày nên số tiền A được tính lãi suất không kỳ hạn trong 60 ngày là : 11 0 01 4 2 . 5 B A . . 6 . 0 120000. 1
(®ång) . Suy ra sau 5 năm 8 tháng số tiền bác nông dân nhận 100 100 được là 11 11 4 2 . 5 4 2 . 5 C A B 20000000. 1 120000. 1 31802750,09 ®ång 100 100 111
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 29.4. (Tích phân - Ứng dụng )..................................................................
Từ một khúc gõ hình trụ có đường kính 30cm , người ta cắt khúc gỗ bởi một mặt phẳng đi qua
đường kính đáy và nghiêng với đáy một góc 0
45 để lấy một hình nêm (xem hình minh họa dưới đây) Hình 1 Hình 2
Kí hiệuV là thể tích của hình nêm (Hình 2). Tính V . 225 A. V  cm3 2250  B. V
cm3 C. V  cm3 1250  D. V  cm3 1350  4
Hướng dẫn giải :
Chọn hệ trục tọa độ như hình vẽ .Khi đó hình nêm có đáy
là nửa hình tròn có phương trình : y   x2 225 ,x   1  5;15  
Một một mặt phẳng cắt vuông góc với trục Ox tại điểm có hoành độ x , x   1  5;15  
cắt hình nêm theo thiết diện có diện tích là S x  (xem hình). 1 1
Dễ thấy NP y và MN  0 NPy   2 tan 45
15 x khi đó S x   MN.NP  .225  2 x  suy ra 2 2 15 15 1
thể tích hình nêm là : V   S x dx  .
 225  x2dx  2250cm3 2 15 15 
Câu 29.5. (Oxyz).................................................................. 112
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 x   2  t   : y   1   t 2 t
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng  hai điểm z   t3 
A2;0;3và B 2; 2  ; 3
 . Biết điểmM x ;y ;z thuộc  thì MA4 MB4  nhỏ nhất .Tìm x 0 0 0  0 A. x  0 B. x  1 C. x  2 D. x  3 0 0 0 0
Hướng dẫn giải : x   2 
Phương trình đường thẳng AB là : y   t
. Dễ thấy đường thẳng  và AB cắt nhau tại 1 t1  z   3  t31  điểm I 2; 1
 ;0 suy ra AB và  đồng phẳng . Lại có IA0;1;3,IB 0; 1  ; 3
   IA I
B IA IB AB . 2 2  2  4 1 1 1 1 1
Ta có : MA4  MB4 
MA2 MB2   MAMB   AB4  IAIB . 2 2 2 8 8   Do đó MA4 MB4 
nhỏ nhất khi M trùng với điểm I 2; 1  ;0
Câu 29.6. (Số phức)..................................................................
Cho các số phức z thỏa mãn z  1  2 . Biết rằng tập hợp các điểm biểu diễn các số phức
w  1  i 3z  2 là một đường tròn . Tính bán kính r của đường tròn đó? A. r  4 B. r  2 C. r  16 D. r  25
Hướng dẫn giải : 2
Giả sử z a bi w x yi a b x y    a    b2 ; ; , , , 1  4 x  a 2 b 3 x    
  3  a  1  b 3
Theo đề w  1  i 3z  2  x yi  1  i 3z  2     y
  b a 3 y   3  b  3   a  1 113
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017  2 2 2 2 2 x  y
 a b  b a   a b2 3 3 1 3 1 3 4 1                 16     2 2
x  3  y  3  16 suy ra bán kính đường tròn là r  16  4 .
Cách 2 : Ta có : w  1  i 3z  2  w  2  1  i 3  1  i 3z  1  i 3
w  1  i 3z  2  w  2 1  i 3  1  i 3z  1
 w  3  i 3  1  i 3z  1  4 .
Câu 30.1: (kshs) Nhà Nam có một chiếc bàn tròn có bán kính bằng 2 m. Nam muốn mắc một
bóng điện ở phía trên và chính giữa chiếc bàn sao cho mép bàn nhận được nhiều ánh sáng nhất. sin
Biết rằng cường độ sáng C của bóng điện được biểu thị bởi công thức C c (  là góc tạo bởi 2 l
tia sáng tới mép bàn và mặt bàn, c - hằng số tỷ lệ chỉ phụ thuộc vào nguồn sáng, l khoảng cách từ
mép bàn tới bóng điện) . Khoảng cách nam cần treo bóng điện tính từ mặt bàn là A. 1m B. 1,2m C. 1.5 m D. 2m
Hướng dẫn giải : Đ l h α N M 2 I 114
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Gọi h là độ cao của bóng điện so với mặt bàn (h > 0); Đ là bóng điện; I là hình chiếu của Đ lên mặt
bàn. MN là đường kính của mặt bàn.( như hình vẽ) h 2 l  2 Ta có sin  và 2 2
h l  2 , suy ra cường độ sáng là: C(l)  c (l  2) . l 3 l   l  2 6 l C '  . c  0 l   2 4 2   l . l  2
C 'l   0  l  6 l  2
Lập bảng biến thiên ta thu được kết quả C lớn nhất khi l  6 , khi đó h  2
Câu 30.2: (Thể tích – mặt cầu-mặt nón – mặt trụ)
Với một miếng tôn hình tròn có bán kính bằng R = 6cm. Người ta muốn làm một cái phễu bằng
cách cắt đi một hình quạt của hình tròn này và gấp phần còn lại thành hình nón ( Như hình vẽ).
Hình nón có thể tích lớn nhất khi người ta cắt cung tròn của hình quạt bằng A.  6 cm B. 6 6 cm C. 2 6 cm D. 8 6 cm
Hướng dẫn giải : 115
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 I r N M R h S
Gọi x (x>0) là chiều dài cung tròn của phần được xếp làm hình nón.
Như vậy, bán kính R của hình tròn sẽ là đường sinh của hình nón và đường tròn đáy của hình nón sẽ có độ dài là x. x
Bán kính r của đáy được xác định bởi đẳng thức 2 r x r  . 2 2 x
Chiều cao của hình nón tính theo Định lý Pitago là: h = 2 2 2 R r R  . 2 4 2 2 1   x x
Thể tích của khối nón: 2 2 V   r .H R    . 2 3 3  2  4
Áp dụng Bất đẳng thức Côsi ta có: 3 2 2 2  x x x  2    2 2 2 2 2 R 2 6   2 2 2 4 x x x 4    4 R 2 2 8 8 4 V  . . (R  )     . 2 2 2 9 8 8 4 9  3  9 27     2 2 x x
Do đó V lớn nhất khi và chỉ khi 2  R  2  x
R 6  x  6 6 2 8 4 3
(Lưu ý bài toán có thể sử dụng đạo hàm để tìm giá trị lớn nhất, tuy nhiên lời giải bài toán sẽ dài hơn)
Câu 30.3. ( mũ logarit) 116
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2 log x
Tập các giá trị của m để baapts phương trình 2
m nghiệm đúng với mọi x > 0 bằng 2 log x 1 2 A. ( ;  1] B. [1; )  C.  5  ;2 D. [0;3)
Hướng dẫn giải : Đặt 2 t  log x t  1 2   t Khi đó ta có  m  * t 1
Bất phương trình ban đầu có nghiệm với mọi x > 0   
* nghiệm đúng với mọi t > 1 t
Xét hàm số f t   trên 1; t 1  f t t 2 '   t 13
f 't   0  t  2
lim f t   
lim f t    t t 1  BBT 1 2 t +∞ 0 f'(t) +∞ +∞ f(t) 1
Từ BBT ta có kết luận bất phương trình có nghiệm với mọi t > 1  m 1
Câu 30.4. ( tích phân)
Cho hình phẳng giới hạn bởi hai đường C 2 2 x y  C  2 2 : 4;
' : x y  2x  0 . Diện tích hình phẳng đó bằng 117
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 A.  B. 2 C. 3 D. 4
Hướng dẫn giải :
Ta có C  có tâm I (0;0) bán kính R = 2; C ' có tâm I' (- 1; 0) bán kính R' = 1.
Sử dụng hệ trục tọa độ vẽ 2 đường tròn (C), (C') ta thấy diện tích hình phẳng cần tìm bằng
S   2    2 2 1   3
Lưu ý: có thể sử dụng tích phân để tính nhưng cách làm sẽ dài dòng phức tạp hơn
Câu30. 5. ( tích phân) Cho parabol (P) 2
y x và hai điểm A, B thuộc (P) sao cho AB = 2. Tìm A, B sao cho diện tích hình
phẳng giới hạn bởi (P) và đường thẳng AB đạt giá trị lớn nhất 4 3 2 3 A. B. C. D. 3 4 3 2
Hướng dẫn giải : y B A 1 x Giả sử A 2 a a B 2 ; , ,
b b Pb a sao cho AB = 2
Phương trình đường thẳng AB: y  b ax ab
Gọi S là diện tích hình phẳng cần tìm, ta có b b
S   b ax ab x dx  b a 1 | | [
x ab x ]dx  b a3 2 2 6 a a
Vì AB = 2 nên | b a | b a  2 118
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 4  S  3
Câu 30.6. (Oxyz) Trong hệ trục tọa độ Oxyz cho 3 điểm A ;
a 0;0, B0; ;
b 0,C 0;0; c với , a , b c  0 .Giả sử a, ,
b c thay đổi nhưng thỏa mãn 2 2 2 2
a b c k không đổi. Diện tích tam giác ABC đạt giá trị lớn nhất bằng 2 k 3 2 k 3 A. B. C. 2 k 3 D. 2 k 2 6
Hướng dẫn giải : x y z Phương trình (ABC):   1 a b c Gọi H  ; x ;
y z  là hình chiếu vuông góc của O lên  ABC 2 2  ab cx  2 2 2   
H  ABC
ab bc cab
cx cay abz abc 2 2    a bc Khi đó O
H AB  ax by  0  y OH AC
ax cz  0   
ab2 bc2 ca2 2 2  a b c z   
ab2 bc2 ca2 abcOH
ab2 bc2 ca2 1 1 Ta có VO . A O . B OC abc OABC 6 6 3V 1 ABCDS   abbc ca ABC   2  2  2 OH 2
Áp dụng bất đẳng thức Cosi ta có 4 4 4 4 4 4 a b b c c a 2 2 2 2 2 2 4 4 4
a b b c c a   
a b c 2 2 2
Dấu “=” xảy ra khi và chỉ khi a b c 119
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 4 2 1 k k 3 Vậy max S   2 3 6 Câu 30.7. ( Oxyz)
Trong không gian với hệ toạ độ Oxyz, phương trình mặt phẳng (P) đi qua điểm M(9;1;1) , cắt các tia
Ox, Oy, Oz tại A, B, C sao cho thể tích tứ diện OABC có giá trị nhỏ nhất là x y z x y z x y z x y z A.    1 1 7 3 3 B.    1 27 3 3 C.    D.    1 27 3 3 27 3 3
Giá sử A(a;0;0)Ox,B(0;b;0)Oy,C(0;0;c)Oz (a,b,c  0) . x y z
Khi đó PT mặt phẳng (P) có dạng:    1 a b c . 9 1 1 1
Ta có: M(9;1;1)(P)    1 V  abc a b c (1); OABC 6 (2) 3 3 2
(1) abc  b
9 c  ac  ab ≥ 3 9(abc 2
) (abc)  27.9(abc)  abc  243 9bc  ac  ab a  27   x y z
Dấu "=" xảy ra 9 1 1  b  3    1    1 (P): .   27 3 3  c a b c  3
Câu 30.8. (số phức) 4i 2  6i
Trong mặt phẳng phức cho 3 điểm A,B,C theo thứ tự biểu diễn các số
,1 i1 2i, . Số i 1 3  i
phức biểu diễn bởi điểm D sao cho tứ giác ABCD là hình vuông là A. 1  i B. 1 5i C. 1 i D. 1 5i
Hướng dẫn giải : 4i Ta có
 2  2i A2; 2   i 1
1i12i  3i B3;  1
2  6i  2i C0;2 3  i 120
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Vẽ hệ trục tọa độ biểu diễn các điểm A, B, C và tọa độ điểm D trong các đáp án, dễ dàng kiểm tra
được tam giác ABC vuông cân tại B và D 1  ;  1 thì ABCD là hình vuông. BA BC
(có thể ktra bằng phép toán 2 2 2
BC  10; BA  10;CA  20   2 2 2 AC AB BC
ABCD là hình vuông  AB DC D 1  ;  1  z  1   i )
Câu 31.1: Cho x và y là hai số thực dương thay đổi sao cho: 2 2
x  2x  4y  0 . Giá trị lớn nhất của
tích xy gần nhất với số nào? A. 0,5 B. 0,6 C. 0,7 D. 0,8 1 1 Giải: Ta có 2 2
x  2x  4y  0  2 y
2x x (do y  0 ), suy ra 2 xy
x 2x x 2 2 1 2 3x  2x 3 Xét hàm số 2 g(x) 
x 2x x xác định trên 0; 2 ; g '(x) 
, g '(x)  0  x  2 2 2x x 2 2 3 1 3 3  3  3 3
Vậy g(x) cũng là xy đạt giá trị lớn nhất khi x
và GTLN của xy là: . 2.    0.64   2 2 2 2  2  8 Chọn đáp án B.
Câu 31.2: Nếu một tứ diện chỉ có đúng một cạnh có độ dài lớn hơn 1 thì thể tích tứ diện đó lớn nhất là bao nhiêu? 1 3 1 5 A. B. C. D. 4 4 8 8
Giải: Giả sử tứ diện ABCD có cạnh lớn nhất là AB, suy ra các tam giác ACD và BCD có tất cả các 2 a
cạnh đều không lớn hơn 1. Các chiều cao AF và BE của chúng không lớn hơn 1 , trong đó 4 CD a  1. 2 a
Chiều cao của hình tứ diện AH AF  1 4 121
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
(do tam giác AHF vuông tại H có AF là cạnh huyền)
Thể tích của khối tứ diện là: 2 1 1 1 1 1  a  1 V S
.AH  . .BE.C . D AH  . . . a 1   aa BC  2 4 D  3 3 2 3 2  4  24
Để tìm giá trị lớn nhất của V ta xét biểu thức a  2 4  a  . 1 1
Vì 0  a 1 nên a  2
4  a   3 và V a  2
4  a   . Chọn đáp án C. 24 8
Câu 31.3: Giả sử p và q là các số thực dương sao cho: log p  log q  log
p q . Tìm giá trị của 9 12 16   p q 4 8 1 1 A. B. C. 1 3 D. 1 5 3 5 2 2
Giải: Đặt: t  log p  log q  log p q thì: 9t p  , 12t q  , 16t
  9t 12t p q (1) 9 12 16   2t tt 4   4   4  q
Chia hai vế của (1) cho 9t ta được: 1     , đặt x    0   đưa về phương trình:  3   3   3  p 1 q 1 2
x x 1  0  x
1 5 do x 0, suy ra  1 5. Chọn đáp án D. 2 p 2 2 2017
Câu 31.4: Cho tích phân K   3 2
x  3x  2
dx . Giá trị của K bằng bao nhiêu? 0 A. 0 B. 1 C. 2 D. 1 3 Giải: Ta có 3 2
x  3x  2   x   1  3 x   1
Đặt t x 1  dt dx . Khi x  0  t  1
 ; Khi x  2  t 1 1 2017
Khi đó K    3t 3t
dt  0 (do hàm số f t  t t2017 3 ( ) 3
là hàm số lẻ trên đoạn  1   ;1 . Chọn đáp 1  án A. 122
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 31.5: Trong không gian Oxyz cho 4 điểm A2;3;2 , B6; 1  ; 2   , C  1  ; 4  ;3 , D1;6; 5  . Gọi M
là một điểm nằm trên đường thẳng CD sao cho tam giác MAB có chu vi bé nhất. Khi đó toạ độ điểm M là:
A. M 0;1;  1 B. M 2;11; 9   C. M 3;16; 1  3 D. M  1  ; 4  ;3
Giải: Tam giác MAB có độ dài cạnh AB  4 3 không đổi, do đó chu vi bé nhất khi và chỉ khi
MA MB bé nhất. AB  4; 4  ; 4
  ; CD  2;10; 8  . Vì A .
B CD  0 nên AB CD , suy ra điểm M cần tìm là hình chiếu
vuông góc của A, cũng là hình chiếu vuông góc của B lên đường thẳng CD. Từ đó tìm ra điểm M 0;1;   1 . Chọn đáp án A. Câu 31.6: Cho 2 i  1
 , có bao nhiêu số nguyên n sao cho   4
n i là một số nguyên? A. 1 B. 2 C. 3 D. 4 Giải: Vì 2 4 i  1
 nên n i 4 2
n n    3 6 1
4n  4ni . Số này là số thực khi và chỉ khi: 3
4n  4n  0  n  0 hoặc n  1  . Chọn đáp án C.
Câu 32.1.(Kshs) Đường cong hình dưới là đồ thị của một trong bốn hàm số được cho trong bốn
phương án A,B,C và D dưới đây. Hỏi hàm số đó là hàm số nào ?
A. y = x3 - 3 x 2 +1. B. y = -x4 - x2 +1.
C. y = x 3 - 3x2 +1.
D. y = x4 - 8x2 +1. Hướng dẫn giải: 123
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
+) Đồ thị đối xứng qua trục tung nên loại A.
+) Đồ thị đi qua điểm (1;-1) loại D.
+) B chỉ có 1 điểm cực trị nên loại. +) Chọn đáp án C.
Câu 32.2.(Hhkg) Cho hình chóp S.ABCD có ABCD là hình vuông cạnh 2a, tam giác SAB đều và nằm
trong mặt phẳng vuông góc với (ABCD). Tính bán kính của mặt cầu ngoại tiếp hình chóp trên. a 7 a 21 a 7 a 21 A. . B. . C. . D. . 2 6 4 3 Hướng dẫn giải: æ ö 2 R = (R )2 +(R
)2 - AB = a 21 . Chọn đáp án D. (S ) ntSAB ntABCD èç 2 ø÷ 3 Trong đó:
+) RntSAB là bán kính đường tròn ngoại tiếp tam giác SAB
+) RntABCD là bán kính đường tròn ngoại tiếp hình vuông ABCD
+) (SAB)Ç(ABCD) = AB 2 2
Câu 32.3. (Mũ-Logarit).Tập nghiệm của bất phương trình: x x 1  1  x x 1 3 3 3 3     . a 7 a 21 a 7 a 21 A. . B. . C. . D. . 2 6 4 3 Hướng dẫn giải:
Điều kiện: x  1. 2 2 2 2
Ta có: x x 1  1  x x 1  x x 1  1  x x 1 3 3 3 3 3 3.3 3.3        9  0 Û 3x2 - 3 ( ) 3 x-1-3 ( )£0
+ Với x  1: thoả mãn;
+ Với x  1: Û 3 x-1 £ 3Û x -1 £1Û1£ x £ 2. 124
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Vậy nghiệm của bất phương trình là: 1 x  2 Chọn đáp án A
Câu 32.4 (Tích Phân) Với giá trị nào của m thì diện tích hình phẳng giới hạn bởi parabol
P: y  x2 2x và d: y mxm 0 bằng 27 đơn vị diện tích. A. m = -1. B. m = -2. C. m = Æ. D. m Î . Hướng dẫn giải:   0
Phương trình hoành độ giao điểm  2  2   2  2   x x x mx x m x  0  
x  2  m   0 2m 2m 2m 3 2   2  2      2 2    x 2 mx S x x mx dx x x mx dx     x   3 2 0 0   0 3 2
 m  6m  12m  8  27
Do đó m  1. Chọn đáp A.
Câu 32.5.(Oxyz) Trong không gian với hệ tọa độ Oxyz cho mặt phẳng P : x y z 1  0 và hai điểm A1; 3  ;0, B5; 1  ; 2
 . Tìm tọa độ điểm M trên mặt phẳng P sao cho MAMB đạt giá trị lớn nhất.
A. M(-2;-3;3).
B. M(-2;-3;2).
C. M(-2;-3;6).
D. M(-2;-3;0). Hướng dẫn giải:
Kiểm tra thấy A và B nằm khác phía so với mặt phẳng  P . Gọi B ' ; x ;
y z  là điểm đối xứng với B5; 1  ; 2   Suy ra B ' 1  ; 3  ;4
Lại có MA MB MA MB '  AB '  const
Vậy MA MB đạt giá trị lớn nhất khi M , ,
A B ' thẳng hàng hay M là giao điểm của đường
thẳng AB ' với mặt phẳng  P 125
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017x  1 t
AB ' có phương trình  y  3  z  2  t  x 1 t t   3    y  3  x  2  Tọa độ M  ; x ;
y z là nghiệm của hệ    z  2  t y  3   
x y z 1 0 z  6 Vậy điểm M  2  ; 3  ;6 Chọn đáp án C
Câu 32.6. (Số Phức) Cho các số phức z ,z ,z ,z ,z có điểm biểu diễn lần lượt là A, B, C, D, E trong 1 2 3 4 5
mặt phẳng phức tạo thành một ngũ giác lồi. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC,
CD, DE. Gọi I, J lần lượt là trung điểm các đoạn MP và NQ. Biết I, J là điểm biểu diễn hai số phức
z  1 i; z  2i và z  4  i
5 là số phức có điểm biểu diễn là E. Tìm số phức z ? I J E 1 A. = 2 - 3i. B. = 4 - 7i. C. = 8- 7i. D. = 8- 2i. z1 z1 z1 z1
Ta có 4IJ  2IQ IN
Mà IM IP  0 do đó IQ IN IM MQ IP PN MQ PN 1 1 1
 AEBD DB AE 2 2 2 40   1  4  x x  8 Suy ra A A 4IJ=AE   . 42     1  5  yy  7 AA Chọn đáp án C Câu 33.1 (Kshs). Cho hàm số: 4 2 2
y x  2(m  2)x m  5m  5 . Với giá trị nào của m thì đồ thị hám số có cực đại và
cực tiểu, đồng thời các điểm này tạo thành một tam giác đều A. 3 m  2  3 B. 2  3 C. 3  2 D. 3 3  2 126
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Hướng dẫn giải: Ta có: 3
y '  4x  4(m  2)x x  0 y '  0   2 x  2  m
Hàm số có CĐ, CT  PT f ' x  0 có 3 nghiệm phân biệt  m  2 (*)
Khi đó toạ độ các điểm cực trị là: A 2
0, m  5m  5 , B 2  m;1 m ,C  2  m;1 m  AB   2
m  m m   AC   2 2 ; 4 4 ;
 2  m; m  4m  4 Do ABC luôn cân tại A, nên bài 1 toán thoả mãn khi 0
A  60  cos A  2 A . B AC 3 
 0  m  2  3 AB AC
Câu 33.2. (Thể tích cầu-nón-trụ)
Cho hình lăng trụ ABC.A' B 'C ' có đáy ABC là tam giác đều cạnh a , hình chiếu vuông góc của
A' lên măt phẳng ABC trùng với tâm G của tam giác ABC . Biết khoảng cách giữa AA' và a 3 BC là
. Tính thể tích V của khối lăng trụ ABC.A' B 'C ' . 4 3 a 3 3 a 3 3 a 3 3 a 3 A. V B. V C. V D. V 3 6 12 36 Hướng dẫn giải: A' C' K H B' A C G M B 127
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Gọi M là trung điểm B BC (A' AM)
Gọi H,K lần lượt là hình chiếu vuông góc của G,M trên AA’ a 3
Vậy KM là đọan vuông góc chung củaAA’và BC, do đó d( A A ',BC) KM . 4 KM 3 2 a 3 AGH AMH GH KH GH 2 3 6 a
AA’G vuông tại G,HG là đường cao, A 'G 3 3 a 3 V S .A'G
ABC .A ' B 'C ' ABC 12
Câu 33.3. (Mũ - Logarit)
Tìm các giá trị của m để phương trình: 3x  3  5  3x m có 2 nghiệm phân biệt:
A. 3  5  m  4 B. 2 2  m  4
C. 2 2  m  3  5 m  2 2 Hướng dẫn giải : ĐK: x  log 5 3 Đặt ( ) 3x 3 5 3x f x     với x  log 5 3
3x ln 3 5 3x  3x x x  3 3 ln 3 3 ln 3  f '(x)    2 3x  3 2 5  3x
2 3x  3 5 3x
'( )  0  5  3x  3x f x  3  x 1
lim f (x)  3  5 x Bảng biến thiên: 128
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 x -∞ 1 log 5 3 f’(x) + 0 − 4 f(x) 3  5 2 2
Dựa vào BBT ta có: Đáp án A
Câu 33.4. (Tích phân - Ứng dụng ) 2  1 2 1  Tính tích phân:   dx 
 ta thu được kết quả là: a bln 2 với , a b  . Chọn khẳng 2
x  3 x x  1
định đúng trong các khẳng định:
A. a b  1 B. a  0 C. 2 2 a b  10
D. b  2a  0 Hướng dẫn giải: Ta có: 2  1 2 1     1  1 dx 
 = ln x  3  2ln x     3ln 2   2
x  3 x x   x  2 1 1
Suy ra: a   ;b  3  chọn đáp án A 2 Câu 33.5. (Oxyz) 129
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1;5;0 , B3;3;6 và đường thẳng  có x  1   2t
phương trình tham số  y  1 t
t  . Một điểm M thay đổi trên đường thẳng  , xác định vị trí z  2t
của điểm M để chu vi tam giác MAB đạt giá trị nhỏ nhất. Khi đó toạ độ của điểm M là: A. M 1;0;2 B. M 2;4;3 C. M  3  ;2; 2   D. M 1;4;3
Hướng dẫn giải:
Gọi P là chu vi của tam giác MAB thì P AB AM BM
Vì AB không đổi nên P nhỏ nhất khi và chỉ khi AM BM nhỏ nhất.
Điểm M  nên M  1
  2t;1 t;2t ; 2 2 2 2
AM BM  (3t)  (2 5)  (3t  6)  (2 5)
Trong mặt phẳng tọa độ Oxy , ta xét hai vectơ u  3t;2 5 và v   3  t  6;2 5.
|u | 3t   2 52 2 Ta có   AM BM |
u |  | v | và u v  6;4 5 |
u v | 2 29
| v | 3t 6   2 52 2 
Mặt khác, ta luôn có | u |  | v | |
u v | Như vậy AM BM  2 29 3t 2 5
Đẳng thức xảy ra khi và chỉ khi u, v cùng hướng    t 1 3  t  6 2 5
M 1;0;2 và min AM BM   2 29 . Vậy khi M 1;0;2 thì min P  2 11  29
Câu 33.6. (Số phức)
Trong mặt phẳng tọa độ, tập hợp điểm biểu diển các số phức z thỏa mãn z i 1 i z là:
A. Đường tròn có phương trình 2 2 x y 4x 2y 1 0
B. Đường tròn có phương trình 2 2 x y 2y 3 0
C. Đường tròn có phương trình 2 2 x y 2x 1 0 130
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
D. Đường tròn có phương trình 2 2 x y 2y 1 0 Hướng dẫn giải: Đặt z x yi , x y và M ;
x y là điểm biểu diễn của z trên mặt phẳng Oxy ta có: z i 1 i z x yi i 1 i x iy x y 1 i x y x y i 2 2 2 2 x y 1 x y x y 2 2 2 2 2 2 x y 2y 1 x 2xy y x 2xy y 2 2 x y 2y 1 0
Tập hợp điểm M biểu diển của số phức z là đường tròn có phương trình 2 2 x y 2y 1 0 Vậy chọn D
Câu 34.1 (Kshs). Cho hàm số y  x3  mx  2 có đồ thị (Cm) . Tìm m để đồ thị (Cm) cắt trục hoành
tại một điểm duy nhất. A. m 3 B. m 3 C. m 3 D. m 3
Hướng dẫn giải : 3
Số giao điểm của đồ thị (Cm) với Ox là số nghiệm của phương trình x  mx  2  0
Với m=0 vô nghiệm nên không có giao điểm Với m  0 ta có m 2  x2   f (x);(*) x 2 2(x3  f x 1) '( )  2x   0  x 1 x2 x2 131
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Ta có bảng biến thiên của f(x) như sau: x
 0 1  f '(x) + + 0 - f (x)  -3 
 
Số nghiệm phương trình (*) là số giao điểm của đồ thị hàm f(x) và đường thẳng y=m.
Dựa vào bảng biến thiên ta thấy m
3 thì phương trình (*) có 1 nghiệm duy nhất. Vậy chọn A.
Câu 34.2. (Thể tích – mặt cầu-mặt nón – mặt trụ)
Cho hình chóp đềuS.ABCD , M là trung điểm SA, N, K lần lượt thuộc SB, SC sao cho SB=3SN,
SC=4SK. Hãy chọn đáp án đúng 1 23 A. V  V V V . S MNK S.ABC B.  MNK.CBA S.ABCD 8 48 1 C. V  V . S MNK S.ABD
D. Cả 3 đáp án A, B, C đều sai 12 Hướng dẫn giải:
Áp dụng định lý tỷ số thể tích ta có S V . SM SN SK 1 S MNK K  . .  V SA SB SC . 24 S ABC N M V NK. 23 ABC M   S V . 24 ABC D C  M V NK.ABC  23 S V . 48 ABCD A Vậy chọn B B 1 1 1 
Câu 34.3. (Mũ - Logarit) Cho A   ... logb logb
logb . Biểu thức rút gọn của A là: 1 2 n a a a 132
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2n(n 1) 2n(2n 1) n(n 1) n(n  2) A. B. C. D. 3.logb logb 2.logb 3logb a a a a
Hướng dẫn giải : 1 1 1 1 A   ...
 (1 2 ... n) logb logb logb b n log 1 2 Ta có a a a a n(n 1)  2.logba Vậy chọn C
Câu 34.4. (Tích phân - Ứng dụng ) a
Nếu hàm số f(x) liên tục và là hàm số chẵn trên [-a; a] thì I f (x)dx  bằng a a a a A. 0
B. 2 f (x)dx  C. 2  f (x)dx
D. 2 f (x)dx  0 0 a
Hướng dẫn giải : a 0 a a Ta có I
f (x)dx
f (x)dx
f (x)dx I f (x)dx     1 aa 0 0 0 0 x t   I
f (x)dx f ( t  )d( t  )   1 Đặt a a 0 a a
  f (t)d(t)  f (t)d(t)  f (x)d(x)    a 0 0 a
I  2 f (x)d(x)  Vậy chọn B. 0
Câu 34.5. (Oxyz) Trong hệ trục tọa độ Oxyz cho A(1;2;3).Tìm cặp vecto chỉ phương của mặt (P) đi
qua A và khoảng cách từ O đến (P) là lớn nhất. u   ( 3  ;0;1) u   ( 3  ;0;1) u   ( 3  ;0;1) u   ( 3  ;0;1) A. 1  B. 1  C. 1  D. 1  u   (1;1; 1  )  u   (0; 1  ; 2  ) u   (1;0; 1  ) u   (2;1;0) 2  2  2  2
Hướng dẫn giải : 133
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Khoảng cách từ O đến mặt phẳng (P) lớn nhất khi OA vuông góc với mp(P). Khi đó OA  (1;2;3) là
vecto pháp tuyến của mp(P). Ta thấy ( 3
 ;0;1),(1;1;1 )  (1;2;3)cùng phương với OA  (1;2;3) nên n  ( 1  ; 2  ; 3  ) cũng là vecto pháp tuyến của mp(P). Vậy chọn A.
Câu 34.6. (Số phức) 4 2017 i 1 i 1
Kết quả rút gọn của biểu thức P   là: 2016 i i A. 0 B. i C.1-i D. -1-i
Hướng dẫn giải : Ta có 2 4 i  1   i 1 2017 4 504  i  .( i i )  i i 1 i(i 1) 2  P    
i i  1
  i . Vậy chọn D 2 i i
Câu 36.1. Nhà của 3 bạn A, B, C nằm ở 3 vị trí tạo thành một tam giác vuông tại B ( như hình vẽ),
AB = 10 km; BC = 25 km và 3 bạn tổ chức họp mặt ở nhà bạn C. Bạn B hẹn chở bạn A tại vị trí M trên
đoạn đường BC. Từ nhà, bạn A đi xe buýt đến điểm hẹn M với tốc độ 30km/h và từ M hai bạn A, B
di chuyển đến nhà bạn C bằng xe máy với tốc độ 50km/h. Hỏi điểm hẹn M cách nhà bạn B bao
nhiêu km để bạn A đến n
A hà bạn C nhanh nhất ? B C M A. 5 km B. 7,5 km C.10 km D. 12,5 km
Hướng dẫn giải : 134
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Đặt BM = x (km), x  0 2 100  x 25  x
Thời gian để bạn A di chuyển từ A đến M rồi đến nhà C là: t(x)   (h) 30 50 23 15
Lập bảng biến thiên, ta tìm được giá trị nhỏ nhất của t(x) là khi x  30 2 Chọn đáp án B Câu 36.2.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a, đường thẳng SA vuông góc
với mặt đáy và SA = 2a. Gọi (P) là mặt phẳng đi qua B và vuông góc với SC.
Khi đó diện tích của thiết diện của hình chóp S.ABC khi cắt bởi mặt phẳng (P) là ? 2 a 15 2 a 15 2 a 15 2 a 15 A. B. C. D. 10 5 15 20
Hướng dẫn giải : S N M A C
Gọi M là trung điểm của AC ; Kẻ BN vuô Bng góc SC tại N
Khi đó: thiết diện cần tìm là tam giác BMN vuông tại M MN CM a 5 Ta có: CMN CSA    MN SA CS 5 2 a 15
Vậy: diện tích tam giác BMN bằng 20 Chọn đáp án D
Câu 36.3. Ông A gửi tiết kiệm 100 triệu đồng gửi vào ngân hàng với lãi suất 5% một năm. Ông B 5
cũng đem 100 triệu đồng gửi vào ngân hàng với lãi suất
% một tháng. Sau 10 năm, hai ông A và 12 135
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
B cùng đến ngân hàng rút tiền ra. Khẳng định nào sau đây là đúng ? ( Lưu ý: tiền lãi được tính theo
công thức lãi kép và được làm tròn đến hàng hàng triệu)
A. Số tiền của hai ông A, B khi rút ra là như nhau.
B. Ông B có số tiền nhiều hơn ông A là 1 triệu.
C. Ông B có số tiền nhiều hơn ông A là 2 triệu.
D. Ông B có số tiền nhiều hơn ông A là 3 triệu.
Hướng dẫn giải : Sau 10 năm:
- Số tiền của ông A có được: 100.000.000(1+5%)10  163.000.000.( làm tròn đến hàng triệu)
- Số tiền của ông B có được: 100.000.000(1+5/12%)120  165.000.000.(làm tròn đến hàng triệu) Chọn đáp án C 2   
Câu 36.4. Hình phẳng (H) giới hạn bởi các đường (P): y x
4x 5 và hai tiếp tuyến của (P) tại
điểm A(1;2); B(4;5). Diện tích của (H) là ? 27 9 15 5 A. B. C. D. 4 4 4 2
Hướng dẫn giải :
Phương trình tiếp tuyến của (P) tại A, B lần lượt là ( ) a : y  2  x  4;( )
b : y  4x 11 5 Ta có: 2
x  4  4x 11 x  2 5 2 4 9
Khi đó diện tích của (H) là: 2 2
S  (x  4x  5  2x  4)dx  (x  4x  5  4x 11)dx    4 1 5 2 Chọn đáp án B
Câu 36.5. Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và đường thẳng d: x  3 y 1   z . 2 1 1  136
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Mặt phằng (P) chứa đường thẳng d và có khoảng cách từ A đến (P) là lớn nhất. Khi đó (P) có một véctơ pháp tuyến là A. n  (4;5;13) B. n  (4;5; 1  3) C. n  (4; 5  ;13) D. n  ( 4  ;5;13)
Hướng dẫn giải :
Gọi H,K lần lươt là hình chiếu vuông góc của A lên d và (P)
Khi đó: d(A,(P)) = AK  AH hay d(A,(P)) lớn nhất khi và chỉ khi H K 4 Ta có: ( H 3   2t; 1   t; t  );a  (2;1; 1
 ) và AH.a  0  t  3 4 5 13
Suy ra: AH  ( ;  ;  ) 3 3 3
Hay một véctơ pháp tuyến của (P) là n  (4;5;13) Chọn đáp án A. Câu 36.6.
Cho hình vuông ABCD có tâm H và A,B,C,D,H lần lượt là điểm biểu diễn cho các số phức
a,b,c,d,h. Biết a  2  ; i h  1 i
3 và số phức b có phần ảo dương. Khi đó môđun của số phức b là A. 26 B. 13 C. 4 2 D. 10
Hướng dẫn giải : Ta có: ( A 2  ;1); H 1 ( ;3)  ( C 4;5)  AB   BC
Tam giác ABC vuông cân tại B nên :  A . B BC  0 Giải hệ tìm được ( B 4  ; 4); ( Loại ( B 0; 2  )) Chọn đáp án C. 1
Câu 37.1.Đường thẳng x  3y  6  0 có hệ số góc k   . 3
Tiếp tuyến tại M và N lần lượt có hệ số góc  ,  , từ giả thiết   =3 2 k y' 2 x  1 k y' 1 x  1 k 2 k 137
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 2      và 2     , trong đó 2 x 2m 2 x 6m  1 x 2m 1 x 6m 1 3 1 3 1 x ; 2
x là nghiệm phương trình 2
x  2mx  6m  9  0 (1)
Phương trình (1) có 2 nghiệm x  2m  3 và x  3
Phương trình (1) có hai nghiệm phân biệt   1 x ; 2 x thỏa mãn 1 x 2 x 2 3  2m  3  3   3 3  2m  3  0
  m  3 . Vậy  m  3 thỏa mãn. Chọn đáp án A  2 2 2m  3  3   2 3 25 Câu 37.2. x 1 2 x 5 5 124 . x 5 5 124 0 x 5 t 25(tm) 25 Đặt x pt 2 t 5 ; t 0 5t 124 0 5t 124t 25 0 1 t t (l) 5 Khi đó x 5 25 x 2 3 a Biến đổi thì thấy log
log ab3 a2 , thật vậy a a b 3 a 2 log log ab3 a2 log 3 a log b log . a a3 log b log a2 2 a a a a a a a b Vậy chọn đáp án B S 4xh x2 32 128 Câu 37.3.Ta có S 4x. x2 x2 2 V 32
, để lượng vàng cần dùng là nhỏ V x h h x2 x x2 x2
nhất thì Diện tích S phải nhỏ nhất ta có 128 128 S x2 f x f ' x 2x 0 x 4 , h 2 x x2 Chọn đáp án B 2 2sin x
Câu 37.4. (Kshs). Giá trị lớn nhất của hàm số f x là x x 4 4 sin cos 2 2 138
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 A. 0 B. 4 C.8 D. 2
Hướng dẫn giải : 2 2 2 2sin x 2sin x 4sin x TXĐ: D , ta có f x . 2 x x 1 4 4 2 2 sin x sin cos 1 sin x 2 2 2 4t 8 Đặt 2 sin x t t
0;1 , hàm số trở thành g t với t
0;1 , ta có g ' t 0 t 0;1 t 2 2 t 2
, suy ra hàm số đồng biến trên 0;1 , vậy max f x a m x g t g 1 4 , xảy ra khi t 1 x k k x t 0;1 2
Câu 37.5. (Thể tích – mặt cầu-mặt nón – mặt trụ)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC
2a . Tam giác SAB có góc 60o ASB , SB
a và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ điểm B đến
mặt phẳng (SAC). 3 3 3 A. a B. 2a C. a D. 2a 19 19 16
Hướng dẫn giải : C K A B H S SA  B  ABC,SA 
B ABC  AB; BC  AB BC  SAB
Trong mp (SAB) kẻ BH  SA. Trong tam giác BCH kẻ BK  CH .Ta có BK  SAC .
Vậy khoảng cách từ B đến (SAC) là BK. 139
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 o a 3 BH  SB.sin60 
; Xét tam giác vuông CBH , ta có 2 1 1 1 3    BK  2a . Vậy d B,SAC 3  2a . 2 2 2 BK BH BC 19 19
Câu 37.6. (Mũ – Logarit) xxx 2
Tập nghiệm của bất phương trình: 2 2 x 1 81.9 3 .3     0 là 3
A. S  1;   0 .
B. S  1;.
C. S  0;.
D. S  2;   0 .
Hướng dẫn giải : ĐKXĐ: x  0. 9x x x 2 BPT đã cho 2 81. 3 .3 .3.3 x     0 2 x x x 2 3 3 .3 2.3 x     0 81 3
3x 3 x3x 2.3 x    0 3x 3 x  
 0 (vì 3x  2.3 x  0, x   0.)  x 1 x 1
 3x  3 x x x       x  0 x 0
Vậy tập nghiệm của BPT đã cho là S  1;   0 .
Câu 37.7. (Tích phân - Ứng dụng )
Tìm tham số m để đồ thị hàm số 4 2
y x  2mx m  2C cắt trục ox tại bốn điểm phân biệt và thỏa
mãn hình phẳng giới hạn bởi đồ thị (C) và trục ox của phần nằm phía trên trục ox có diện tích
bằng diện tích hình phẳng giới hạn bởi đồ thị (C) và trục ox của phần nằm phía dưới trục ox . A. 3 B. -3 C.2 D. 4
Hướng dẫn giải :
Điều kiện để (C) cắt trục ox tại 4 điểm phân biệt là m  2 140
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Do tính đối xứng của đồ thị qua trục tung nên bài toán xảy ra khi x3  x 4 2
x  2mx m  2 4 dx     4 2
x  2mx m  2dx 0 x3 x4    4 2
x  2mx m  2 4 2 dx 0
  3x 10mx 15 m  2  0 4 4   0 4 2
x  2mx m  2  0 3m  6
Suy ra x là nghiệm của hệ 4 4 2   x   m  3 4 3
x 10mx 15  m 2 4 4 2  0 m 4 4 Câu37.8. (Oxyz)
Trong không gian tọa độ Oxyz cho điểm ( A 0;1;1), (1 B ;0; 3)
, (C 1; 2; 3) và mặt cầu (S) có phương trình : 2 2 2
x y z  2x  2z  2  0 .Tìm tọa độ điểm D trên mặt cầu (S) sao cho tứ diện ABCD có thể tích lớn nhất.  7 4 1   1  4 5    7 4 1   7 4 1  A. D ;  ;    B. D ; ;   C. D ; ;   D. D ;  ;    3 3 3   3 3 3   3 3 3   3 3 3 
Hướng dẫn giải : Ta có (S) 2 2 2
: (x 1)  y  (z 1)  4 suy ra (S) có tâm I(1;0;-1), bán kính R  2 Và AB  (1; 1  ; 4  ); AC  ( 1  ; 3  ; 4  )
Mặt phẳng (ABC) có một vectơ pháp tuyến là n   A , B AC  ( 8  ;8; 4  )  
Suy ra mp(ABC) có phương trình: 8
 x 8(y 1)  4(z 1)  0  2x  2y  z 1 0 1 Ta có Vd( ;
D ( ABC)).S nên V
lớn nhất khi và chỉ khi d( ;
D (ABC)) lớn nhất . Gọi D D ABCD 3 ABC ABCD 1 2
là đường kính của mặt cầu (S) vuông góc với mp(ABC). Ta thấy với D là 1 điểm bất kỳ thuộc (S) thì d( ;
D (ABC))  maxd(D ;(ABC)); d(D ;(ABC)) . 1 2 
Dấu “=” xảy ra khi D trùng với D1 hoặc D2
Đường thẳng D D đi qua I(1;0;-1), và có VTCP là n   ABC (2; 2;1) 1 2 141
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017x 1 2t
Do đó (D1D2) có phương trình:  y  2  t . z  1    tx 1 2t  2  t   y  2  t  3
Tọa độ điểm D1 và D2 thỏa mãn hệ:    z  1   t 2   t  2 2 2
(x 1)  y (z 1)  4  3  7 4  1    1  4 5    D ; ; & D ; ; 1   2    3 3 3   3 3 3   7 4 1 
Ta thấy: d(D ;(ABC))  d(D ;(ABC)) . Vậy điểm D ;  ; 
là điểm cần tìm 1 2    3 3 3 
Câu 37.9. (Số phức) 2 2017
Tìm phần ảo của số phức z , biết số phức z thỏa mãn .
i z  2  i  1 i ... 1 i . A. 1 B. 1009 2 C. 1009 2  D. 1009 2 i
Hướng dẫn giải : 2 2017 Ta thấy 1; 1 ;
i 1 i ; ........;1 i
lập thành một cấp số nhân gồm 2018 số hạng với u  1 công bội 1 q  1 i . q 1 1 i2018 2018 1 Suy ra . i z Su
i i 1 i2018 2018 1 q 1 i
z 1 1 i
1 1 i 1009 2018 2  1 2i1009 1009 1 2 i   1009
z 1 2 i
Vậy phần ảo của z là 1009 2 . Câu 38.1 (kshs). Cho hàm số 3 2
y x  6x  9x m có đồ thị (C), với m là tham số. Giả sử đồ thị (C) cắt trục hoành
tại ba điểm phân biệt có hoành độ thỏa mãn x x x . 1 2 3
Khẳng định nào sau đây là đúng?
A. 1  x x  3  x  4
B. 0  x  1  x  3  x  4 1 2 3 1 2 3 142
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
C. x  0  1  x  3  x  4
D. 1  x  3  x  4  x 1 2 3 1 2 3 Hướng dẫn giải:
Khảo sát và vẽ đồ thị hàm số 3 2
y  x  6x  9x . Dựa vào đồ thị ta tìm được 4
  m  0 thì đồ thị hàm số 3 2
y x  6x  9x m cắt Ox tại 3 điểm phân biệt.
Ta có y 0.y   1  0; y  
1 .y 3  0; y 3.y 4  0 do đó 0  x 1 x  3  x  4 1 2 3
Câu 38.2 (Thể tích – mặt cầu – mặt nón – mặt trụ).
Cho tứ diện ABCD có tam giác ABD vuông cân tại D, AD a , tam giác ABC cân tại C, 2 2
AC a x . Biết 2 2
CD  2a x , (x>0) hãy tính góc giữa hai đường thẳng AB, CD bằng bao nhiêu? A. 0 45 B. 0 90 C. 0 60 D. 0 30 Hướng dẫn giải:
Gọi H là hình chiếu của C lên mặt phẳng (ABD)
Đặt CH b . Khi đó ta chứng minh được b x
Khi đó AHBD là hình vuông.
Suy ra AB vuông góc với CD. Vậy góc giữa AB, CD bằng 0 90
Câu 38.3 (Mũ – Lôgarit).
Cho u là cấp số nhân với số hạng tổng quát u  0; u  1. Khi đó khẳng định nào sau đây là n n n đúng? log 2017 log 2017  log 2017 u u u A. k 1  k 1  k  log 2017 log 2017  log 2017 u u u k 1  k k 1  log 2017 log 2017  log 2017 u u u B. k 1  k 1  k  log 2017 log 2017  log 2017 u u u k 1  k k 1  log 2017 log 2017  log 2017 u u u C. k 1  k 1  k  log 2017 log 2017  log 2017 u u u k 1  k k 1  log 2017 log 2017  log 2017 u u u D. k 1  k k 1   log 2017 log 2017  log 2017 u u u k 1  k k 1  Hướng dẫn giải:
Vì u là cấp số nhân nên 2
u u .u n k k 1  k 1   2log u  log u  log u 2017 k 2017 k 1  2017 k 1  143
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 1 1 1 1     log 2017 log 2017 log 2017 log 2017 u u u u k k 1  k 1  k log 2017 log 2017  log 2017 u u u k 1  k 1  k   log 2017 log 2017  log 2017 u u u k 1  k k 1 
Câu 38.4 (Tích phân – Ứng dụng). Cho hàm số 4 2
y x  4x m có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C)
với y<0 và trục hoành, S’ là diện tích hình phẳng giới hạn bởi đồ thị (C) với y>0 và trục hoành. Với
giá trị nào của m thì S S ' ? 2 20 A. m  2 B. m  C. m  D. m  1 9 9 Hướng dẫn giải:
Phương trình hoành độ giao điểm 4 2
x  4x m  0 (*) Đặt 2
x t; t  0 , phương trình trở thành: 2
t  4t m  0 (**)
Để S>0, S’>0 thì 0t ;  t ; t ; t với t ; t , t t 1 2  1 2  2 1 1 2
là hai nghiệm dương phân biệt của (**)
Do ĐTHS hàm bậc 4 nhận Oy làm trục đối xứng nên t t 1
S S '    4 2
x  4x m 1 dx    4 2
x  4x mdx 0 t2 t 2 2    t 4t 4 2
x  4x m 2 2 dx  0    m  0 0 5 3 20
Kết hợp với (**) ta được m  . 9
Câu 38.5 (Hình Oxyz).
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (Q): x  2y  z  5  0 và đường thẳng x  y z d 1 1  3 :   2 1
1 . Phương trình mặt phẳng (P) chứa đường thẳng d và tạo với mặt phẳng (Q) một góc nhỏ nhất là
A. P  : y z 4  0
B. P  : x z 4  0
C. P  : x y z 4  0
D. P  : y z 4  0 Hướng dẫn giải: 2 2 2
PT mặt phẳng (P) có dạng: ax  by  cz  d  0 (a  b  c  0) . Gọi a  ((P), Q ( )) . M(P) c   a  b Chọn hai điểm M( 1  ; 1
 ;3), N(1;0;4) d . Ta có:  N  (P)   d  7a  4b 144
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 3 a  b  (P): ax  by ( 2  a  b)z a 7  b 4  0  cos  . 6 a2 5  4ab  2b2 3 b 3 0
TH1: Nếu a = 0 thì cos  .   a  30 . 6 2b2 2 b 1 3  a b
TH2: Nếu a  0 thì cos  . . Đặt x  và f x 2 ( )  cos  6 b a  b 2 5 4 2    a  a    9 x2  2x 1 Xét hàm số f (x)  . 6 . 5  4x  2x2 Dựa vào BBT, ta thấy f x 0 0
min ( )  0  cos  0  a  90  30
Do đó chỉ có trường hợp 1 thoả mãn, tức a = 0. Khi đó chọn b  1,c  1,d  4 .
Vậy: (P): y  z  4  0 .
Câu 38.6 (Số phức).
Gieo một con súc sắc cân đối đồng chất hai lần. Ký hiệu  ;
a b là kết quả xảy ra sau khi gieo, trong
đó a, b lần lượt là số chấm xuất hiện lần thứ nhất, thứ hai. Gọi A là biến cố số chấm xuất hiện trên
hai lần gieo như nhau. Tập hợp các kết quả thuận lợi cho biến cố A là tập hợp con của tập hợp các
điểm biểu diễn của số phức z thỏa mãn điều kiện nào sau đây?
A. z  2  3i  12
B. z  2  3i  10
C. z  2  3i  13
D. z  2  3i  11 Hướng dẫn giải: Ta có A  
 1; 1,2;2,3;3,4;4,5;5,6;6 2 2
Gọi z x y ; i ,
x y R khi đó z  2  3i   x  2   y  3 2 2
Giả sử z  2  3i R
x  2  y 3  R
 x  2   y  2 2 2 3
R . Khi đó tập hợp các điểm biểu diễn số phức z là những điểm thuộc
miền trong và trên đường tròn tâm I  2  ; 3   và bán kính R.
Để tập hợp các kết quả thuận lợi cho biến cố A là tập hợp con của tập hợp các điểm biểu diễn của số phức z thì IM  ; R M   A Khi đó ta được R=13
Câu 39.1 (Kshs). Một người có một dải ruy băng dài 130cm, người đó cần bọc dải ruy băng đó
quanh một hộp quà hình trụ. Khi bọc quà, người này dùng 10cm của dải ruy băng để thắt nơ ở trên 145
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
nắp hộp (như hình vẽ minh họa). Hỏi dải dây duy băng có thể bọc được hộp quà có thể tích lớn nhất là là nhiêu ? A. 3 4000 cm B. 3 1000 cm C. 3 2000 cm D. 3 1600 cm
Hướng dẫn giải : Gọi x(c ) m ;y(c )
m lần lượt là bán kính đáy và chiều của hình trụ (x,y 0;x 30).
Dải dây duy băng còn lại khi đã thắt nơ là: 120 cm Ta có (2x y).4 120 y 30 2x
Thể tích khối hộp quà là: 2 2 V x .y x (30 2x)
Thể tích V lớn nhất khi hàm số 2 f (x) x (30 2x) với 0 x
30 đạt giá trị lớn nhất. 2 f '(x) 6x 60x , cho 2 f '(x) 6x 60x 0 x 10
Lập bảng biến thiên, ta thấy thể tích đạt giá trị lớn nhất là 3 V 1000 (cm ).
Câu 39.2. (Thể tích – mặt cầu-mặt nón – mặt trụ). Cho hình chóp S.ABCD có đáy ABCD là hình
vuông cạnh a, SA vuông góc với mặt phẳng đáy và góc giữa SC với mặt phẳng (SAB) bằng 0 30 .
Gọi M là điểm di động trên cạnh CD và H là hình chiếu vuông góc của S trên đường thẳng BM.
Khi điểm M di động trên cạnh CD thì thể tích của khối chóp S.ABH đạt giá trị lớn nhất bằng? 3 a 2 3 a 2 3 a 2 3 a 2 A. B. C. D. 3 2 6 12
Hướng dẫn giải :
Ta có góc giữa SC và mặt phẳng (SAB) là 0 CSB 30 Trong tam giác SBC có 0 SB BC.cot30 a 3 146
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Trong tam giác SAB có 2 2 SA SB AB a 2 1 1 1 a 2
Thể tích khối chóp S.ABH là: V S .SA . H . AHB.a 2 H . AHB S.ABH 3 ABH 3 2 6 Ta có 2 2 2 2 HA HB AB
a và theo bất đẳng thức AM-GM ta có 2 a 2 2 2 a HA HB 2.H . AHB H . AHB 2 Đẳng thức xảy ra khi 0 HA HB ABM 45 M D 2 3 a 2 a 2 a a 2 Khi đó V H . AHB . S.ABH 6 6 2 12
Câu 39.3. (Mũ - Logarit). Trong một bản hợp ca, coi mọi ca sĩ đều hát với cường độ âm và coi cùng
tần số. Khi một ca sĩ hát thì cường độ âm là 68dB. Khi cả ban hợp ca cùng hát thì đo được mức
cường độ âm là 80dB. Tính số ca sĩ có trong ban hợp ca đó, biết mức cường độ âm L được tính theo I L 10log I công thức
I trong đó I là cường độ âm và 0 là cường độ âm chuẩn 0 A. 16 người B. 12 người C. 10 người D. 18 người
Hướng dẫn giải :
Gọi I ;I lần lượt là cường độ âm của một người và của n người. 1 n I Ta có n I nI n n 1 I1 I I Ta có 1 L 10log 68 ; L 10 n log 80 1 I n I 0 0 I I I Khi đó n 1 L L 10log 10log 10 n log n 1 I I I 0 0 1 L L n 1 6 In 10 5 n 10 10 15, 89 I1 Vậy có 16 ca sĩ. 147
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 a(m/ s)
Câu 39.4. (Tích phân - Ứng dụng ). Một ô tô đang chạy đều với vận tốc thì người lái đạp ( v t) 5 t ( a m/ s)
phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc , trong
đó t là thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi từ vận tốc ban đầu a của ô tô là bao nhiêu,
biết từ lúc đạp phanh đến khi dừng hẳn ô tô di chuyển được 40 mét. A. a 20 B. a 10 C.a 40 D. a 25
Hướng dẫn giải : a
Khi xe dừng hẳn thì vận tốc bằng 0 nên 5 t a 0 t 5 a a 5 5 1 Ta có 2 S v(t)dt ( 5 t a)dt a 10 0 0 1 2 S 40 a 40 a 20 10
Câu 39.5. (Oxyz). Trong không gian với hệ trục Oxyz, cho đường thẳng d có phương trình x 1 y 2 z d :
và điểm A(1 ;4 ;2). Gọi (P) là mặt phẳng chứa d . Khoảng cách lớn nhất d từ 1 1 2 max A đến (P) là : 210 A. d 5 B. d C. d 6 5 D. d 2 5 max max 3 max max
Hướng dẫn giải :
Từ A kẻ một đường thẳng vuông góc với đường thẳng d và cắt đường thẳng d tại H nên d(A;d) AH
Từ A kẻ một đường thẳng vuông góc với mặt phẳng (P) tại K nên d(A;(P)) AK .
Trong tam giác AKH vuông tại K thì AH AK
Do đó để khoảng cách từ A đến (P) lớn nhất khi d(A;(P)) d(A;d) AH . Ta có M(1; 2;0) d , AM
(0; 6; 2) , vectơ chỉ phương của d là u ( 1;1;2). AM,u 210 d d(A;d) . max 3 u 148
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 z 5 z 2 3i 4
Câu 39.6. (Số phức). Cho số phức z có phần thực dương thỏa mãn và . 13z 1 A Tính z 2 A. A 898 B. A 98 C. A 890 D. A 198
Hướng dẫn giải : Gọi z a
bi với a và b là các số thực vàa 0 . 2 2 a b 5 Theo giả thiết ta có 2 2 (a 2) (b 3) 16
Giải hệ trên ta được a 2;b 1. Với z 2 i A 13 27i 898 . tan x  2
Câu 40.1. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y
đồng biến trên khoảng tan x m    0; .    4 
A. m  0 hoặc 1  m  2. B. m  0.
C. 1  m  2. D. m  2. HƯỚNG DẪN GIẢI 1 1
(tan x m)  (tan x  2) 2 2 2 cos x cos  m ' x y   2 2 2 (tan x m)
cos x(tan x m)         
Hàm số đồng biến trên 0; 
 khi và chỉ khi hàm số xác định trên 0; 
 và y’ ≥ 0 ∀ x ∈ 0;    4   4   4      tan x , x   0;   m  0    4    1    m  2 2  m  0 Chọn A 149
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017
Câu 40.2. Sự tăng trưởng của một loài vi khuẩn được tính theo công thức rx f x
( )  Ae , trong đó A là số
lượng vi khuẩn ban đầu, r là tỷ lệ tăng trưởng r  0 , x (tính theo giờ) là thời gian tăng trưởng. Biết số vi
khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Hỏi sao bao lâu thì số lượng vi khuẩn tăng gấp 10 lần
A. 5 ln 20 (giờ) B. 5 ln10 (giờ) C. 10 log 10 (giờ) D. 10 log 20 (giờ) 5 5 HƯỚNG DẪN GIẢI ln 5
Gọi thời gian cần tìm là t. Ta có: 5000 = 1000. e10r nên r = . 10 Do đó, 10000 = 1000. ert ln10 10 ln10 suy ra t = 
10log 10 giờ nên chọn câu C. 5 r ln 5
Câu 40.3. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số  2( 1) x y x
e , trục tung và trục hoành. Tính
thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A. V  4  2 . e
B. V  (4  2 ) e . C. 2
V e  5. D. 2
V  (e  5). HƯỚNG DẪN GIẢI 1 1 2 Ta có x 2 2   2( 1) 
 4 (  2 1) x V x e dx x x e dx  4 I    1 0 0
du  2x  2 2 2 x 1 u
  x  2x 1  e 1 Đặ x 1 t 2 2 2 x   
I  (x  2x 1)
 (x 1)e dx    I e  2 2 x
dv e dv v  2 0 2  0  2 du dx 1 2 x 1 2 x 2 u   x 1  e 1 1 e e x 1 1 Đặ 3 t 1 2 2 x   
I  (x 1)  e dx e      1 2 x dv e dxv  2 0 2 2 4 0 4 4 1  1 0  2 2 e  5 Do vậy I  suy ra V   2 e  5 1 4 Nên chọn D.
Câu 40.4. Cho các số phức z thỏa mãn z  4 . Biết rằng tập hợp các điểm biểu diễn các số phức
w  (3  4i)z i là một đường tròn. Tính bán kính r của đường tròn đó. A. r  4. B. r  5. C. r  20. D. r  22. 150
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 HƯỚNG DẪN GIẢI
a  (b 1)i
a (b1)i(34i)
Gọi w a bi , ta có w a bi  (3  4i)z i z   2 3  4i 9 16i 2 2 3a  4b  4
(3b  4a  3)
(3a  4b  4)  (3b  4a  3)   .i z  25 25 25 Mà z = 4 nên 2 2 2 2 2
 (3a  4b  4)  (3b  4a 3) 100  a b  2b  399
Theo giả thiết, tập hợp các điểm biểu diễn các số phức w  (3  4i)z i là một đường tròn nên ta có 2 2 2 2
a b  2b  399  a  (b 1)  400  r  400  20 Nên chọn C.
Câu 40.5. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho. 5 15 5 15 4 3 5 A. V = B. V = C. V = D. V = . 18 54 27 3 HƯỚNG DẪN GIẢI
Đặt R là bán kính mặt cầu ngoại tiếp khối chóp
Dựng hình như hình bên với IG là trục đường tròn ngoại tiếp tam giác
ABC và IG’ là trục đường tròn ngoại tiếp tam giác SAB 3 3 6
Ta có: G ' H  ;GH   IH  6 6 6 15 4 5 15 Do vậy 2 2 3 R IH HA
V  R  6 3 54 Nên chọn B
Câu 40.6. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; –2; 0), B(0; –1; 1), C(2; 1; –1) và D(3; 1;
4). Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó ? A. 1 mặt phẳng. B. 4 mặt phẳng. C. 7 mặt phẳng.
D. Có vô số mặt phẳng. HƯỚNG DẪN GIẢI 151
GROUP NHÓM TOÁN - TỔNG HỢP CÁC CÂU HỎI VẬN DỤNG CAO – 2016-2017 Ta có: AB  ( 1
 ;1;1); AC  (1;3; 1  ); AD  (2;3;4) Khi đó: A ; B AC.AD  2  4  0  
do vậy A,B,C,D không đồng phẳng
Do đó có 7 mặt phẳng cách đều 4 điểm đã cho bao gồm.
+) Mặt phẳng qua trung điểm của AD và song song với mặt phẳng (ABC)
+) Mặt phẳng qua trung điểm của AB và song song với mặt phẳng (ACD)
+) Mặt phẳng đi qua trung điểm của AC và song song với mặt phẳng (ABD)
+) Mặt phẳng đi qua trung điểm của AB và song song với mặt phẳng (BCD)
+) Mặt phẳng qua trung điểm của AB và CD đồng thời song song với BC và AD
+) Mặt phẳng qua trung điểm của AD và BC đồng thời song song với AB và CD
+) Mặt phẳng qua trung điểm của AC và BD đồng thời song song với BC và AD Nên chọn C.
Document Outline

phan-1-de-baiphan2-huong-dan-giai