Tổng hợp bài giảng môn Cấu trúc dữ liệu và thuật toán_Thầy Nguyễn Đức Nghĩa| Bài giảng môn Cấu trúc dữ liệu và thuật toán| Trường Đại học Bách Khoa Hà Nội

CẤU TRÚC DỮ LIỆU VÀ THUẬT TOÁN
Data Structures and Algorithms 1 NguyỄN ĐỨC NGHĨA
Bộ môn Khoa học Máy tính
Đại học Bách khoa Hà nội
Tel: 0438696121 (Off), 0903210111 (Mob)
nghiand@soict.hut.edu.vn 2 NỘI DUNG • Mục đích, yêu cầu • Nội dung môn học • Tài liệu tham khảo
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Mục ụ đích đ
• Trình bày khảo sát các tính chất cơ bản của các cấu trúc dữ
liệu và các thuật toán thực hiện các thao tác với chúng
• Cách sử dụng các cấu trúc dữ liệu như là công cụ hỗ trợ phát triển thuật toán
• Trình bày các thuật toán sắp xếp, tìm kiếm, các thuật toán trên đồ thị cơ bản. • Trên cơ sở đó:
– Biết lựa chọn phương pháp lưu trữ dữ liệu thích hợp để cài đặt thuật
toán giải các bài toán trong thực tế ứng dụng.
– Biết cách tiếp cận để phát triển thuật toán giải các bài toán thực tế
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT
Mục tiêu của môn học Mục tiêu cụ thể
• Kiến thức: Cung cấp các kiến thức cơ bản về
– Các cấu trúc dữ liệu: mảng, danh sách móc nối đơn, kép,
vòng; ngăn xếp, cấu trúc (bản ghi), hàng đợi, cây thứ tự bộ phận, cây, đồ thị.
– Các thuật toán: sắp xếp, tìm kiếm, duyệt cây, duyệt đồ thị,
tìm đường đi ngắn nhất, tìm cây khung nhỏ nhất; các kĩ
thuật xây dựng thuật toán.
• Kĩ năng: Cài đặt được thuật toán tìm kiếm, sắp xếp, tìm
đường đi ngắn nhất (Dijkstra), tìm cây khung nhỏ nhất (Prim),
thật toán đệ quy, thuật toán quay lui.
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT NỘI DUNG Mở đầu
Chương 1. Các khái niệm cơ bản 1.1. Ví dụ mở đầu
1.2. Thuật toán và độ phức tạp 1.3. Ký hiệu tiệm cận 1.4. Giả ngôn ngữ
1.5. Một số kĩ thuật phân tích thuật toán
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT
Chương 2. Thuật toán đệ qui 2.1. Khái niệm đệ qui 2.2. Thuật toán đệ qui
2.3. Một số ví dụ minh hoạ
2.4. Phân tích thuật toán đệ qui 2.5. Đệ qui có nhớ
2.6. Chứng minh tính đúng đắn của thuật toán đệ qui 2.7. Thuật toán quay lui
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT
Chương 3. Các cấu trúc dữ liệu cơ bản 3.1. Các khái niệm
Kiểu dữ liệu (Data types),
Kiểu dữ liệu trừu tượng (Abstract Data Types),
Cấu trúc dữ liệu (Data Structure) 3.2. Mảng 3.3. Danh sách 3.4. Ngăn xếp 3.5. Hàng đợi
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Chương 4. Cây
4.1. Định nghĩa và các khái niệm
Các thuật ngữ chính; Cây có thứ tự, Cây có nhãn ADT Cây 4.2. Cây nhị phân
Định nghĩa và tính chất, Biểu diễn cây nhị phân Duyệt cây nhị phân
4.3. Các ví dụ ứng dụng
Cây biểu thức; Cây quyết định; Mã Huffman
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT
Chương 5. Các thuật toán sắp xếp 5.1. Bài toán sắp xếp
5.2. Ba thuật toán sắp xếp cơ bản
5.3. Sắp xếp trộn (Merge Sort)
5.4. Sắp xếp nhanh (Quick Sort)
5.5. Sắp xếp vun đống (Heap Sort)
5.6. Độ phức tạp tính toán của bài toán sắp xếp
5.7. Các phương pháp sắp xếp đặc biệt
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Chương 6. Tìm kiếm
6.1. Tìm kiếm tuần tự và tìm kiếm nhị phân
6.2. Cây nhị phân tìm kiếm
6.3. Cây nhị phân tìm kiếm cân bằng
6.4. Tìm kiếm xâu mẫu (String Searching) 6.5. Bảng băm
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT
Chương 7. Đồ thị và các thuật toán đồ thị 7.1. Đồ thị 7.2. Biểu diễn đồ thị
7.3. Các thuật toán duyệt đồ thị
7.4. Một số ứng dụng của tìm kiếm trên đồ thị
7.5. Bài toán cây khung nhỏ nhất
7.6. Bài toán đường đi ngắn nhất
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Tài liệu tham khảo
1. Đỗ Xuân Lôi. Cấu trúc dữ liệu và giải thuật. NXB ĐH Quốc gia, Hà nội, 2005.
2. Robert Sedgewick. Algorithms in C. Third Edition. Addison- Wesley, 1998.
3. Robert Sedgewick. Algorithms in C++, Parts 1-4: Fundamentals,
Data Structures, Sorting, Searching. 3th Edition, Addison-Wesley, 1999.
4. Robert Sedgewick. Algorithms in C++ Part 5: Graph Algorithms
(3rd Edition). 3th Edition, Addison-Wesley, 2002.
5. Michael T. Goodrich, Roberto Tamassia, David M. Mount, Data
Structures and Algorithms in C++. 704 pages. Wiley, 2003.
6. Robert Kruse, Alexander Ryba . Data Structures and Algorithms in
C++. Prentice Hall, 2000.
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Tài liệu tham khảo Robert Sedgewick William O. Baker Professor Department of Computer Science Princeton University
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT • Michael T. Goodrich
Chancellor's Professor at the Department of Computer Science, University of California, • Roberto Tamassia
Professor, Department of Computer Science, Brown University • David Mount
Professor in the Department of Computer Science and UMIACS.
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT
• Robert Kruse, Alexander Ryba.
Data Structures and Algorithms in C++.
2nd Edition. Prentice Hall, 2000.
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Giáo trình
• Nguyễn Đức Nghĩa. Bài giảng cấu trúc dữ liệu và
giải thuật. NXB Đại học Bách khoa Hà nội, 2008.
• Hồ Sĩ Đàm, Nguyễn Việt Hà, Bùi Thế Duy. Cấu trúc
dữ liệu và giải thuật. NXB Giáo dục, 2007.
• và giáo trình của các đại học: Huế, Cần thơ, Sư phạm Hà nội 1,...
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT
CẤU TRÚC DỮ LIỆU VÀ THUẬT TOÁN
Data Structures and Algorithms NguyỄN ĐỨC NGHĨA
Bộ môn Khoa học Máy tính
Đại học Bách khoa Hà nội
Tel: 0438696121 (Off), 0903210111 (Mob)
nghiand@soict.hut.edu.vn Chương 1
CÁC KIẾN THỨC CƠ BẢN
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT NỘI DUNG
1.1. Ví dụ mở đầu
1.2. Thuật toán và độ phức tạp 1.3. Ký hiệu tiệm cận 1.4. Giả ngôn ngữ
1.5. Một số kĩ thuật phân tích thuật toán
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Ví dụ mở đầu
• Bài toán tìm dãy con lớn nhất: Cho dãy số
a , a , … , a 1 2 n Dãy số a , a , …, a
với 1 ≤ i ≤ j ≤ n được gọi là dãy con của dãy i i+1 j đã cho và ∑j
a được gọi là trọng lượng của dãy con này k=i k
Bài toán đặt ra là: Hãy tìm trọng lượng lớn nhất của các dãy con, tức
là tìm cực đại giá trị ∑j
a . Để đơn giản ta gọi dãy con có trọng k=i k
lượng lớn nhất là dãy con lớn nhất.
• Ví dụ: Nếu dãy đã cho là -2, 11, -4, 13, -5, 2 thì cần đưa ra
câu trả lời là 20 (là trọng lượng của dãy con 11, -4, 13)
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thuật toán trực tiếp
• Thuật toán đơn giản đầu tiên có thể nghĩ để giải bài toán đặt ra
là: Duyệt tất cả các dãy con có thể a , a , …, a
với 1 ≤ i ≤ j ≤ n i i+1 j
và tính tổng của mỗi dãy con để tìm ra trọng lượng lớn nhất.
• Trước hết nhận thấy rằng, tổng số các dãy con có thể của dãy đã cho là
C(n,2) + n = n2/2 + n/2 .
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thuật toán trực tiếp
• Thuật toán này có thể cài đặt trong đoạn chương trình sau: int maxSum = 0; for (int i=0; i for (int j=i; j int sum = 0;
for (int k=i; k<=j; k++) sum += a[k]; if sum > maxSum maxSum = sum; } }
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thuật toán trực tiếp
• Phân tích thuật toán: Ta sẽ tính số lượng phép cộng
mà thuật toán phải thực hiện, tức là đếm xem dòng lệnh Sum += a[k]
phải thực hiện bao nhiêu lần. Số lượng phép cộng sẽ là n 1  n 1  n 1  n 1
 (n  i)(n  i 1)
( j  i 1) 
(1 2  ...  (n  i))     i  j i i  i 2 0 0 0 1 n 1 n n  
1  n(n 1)(2n 1) n(n 1) 2   k(k 1)  k  k      2     k  2  k k   2  6 2 1 1 1  3 2 n n n    6 2 3
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thuật toán nhanh hơn
• Để ý rằng tổng các số hạng từ i đến j có thể thu được
từ tổng của các số hạng từ i đến j-1 bởi 1 phép cộng, cụ thể là ta có: j j 1  [ a k]  [ a j]  [ a k]   k i k i
• Nhận xét này cho phép rút bớt vòng lặp for trong cùng.
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thuật toán nhanh hơn
• Ta có thể cài đặt như sau int maxSum = a[0]; for (int i=0; i int sum = 0; for (int j=i; j sum += a[j]; if sum > maxSum maxSum = sum; } }
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thuật toán nhanh hơn
• Phân tích thuật toán. Ta lại tính số lần thực hiện phép cộng
và thu được kết quả sau: n 1  2 n n
(n  i)  n  (n 1)  ... 1    i  2 2 0
• Để ý rằng số này là đúng bằng số lượng dãy con. Dường như
thuật toán thu được là rất tốt, vì ta phải xét mỗi dãy con đúng 1 lần.
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thuật toán đệ qui
• Ta còn có thể xây dựng thuật toán tốt hơn nữa! Ta sẽ sử
dụng kỹ thuật chia để trị. Kỹ thuật này bao gồm các bước sau:
– Chia bài toán cần giải ra thành các bài toán con cùng dạng
– Giải mỗi bài toán con một cách đệ qui
– Tổ hợp lời giải của các bài toán con để thu được lời giải của bài toán xuất phát.
• Áp dụng kỹ thuật này đối với bài toán tìm trọng lượng
lớn nhất của các dãy con: Ta chia dãy đã cho ra thành 2
dãy sử dụng phần tử ở chính giữa và thu được 2 dãy số
(gọi tắt là dãy bên trái và dãy bên phải) với độ dài giảm đi một nửa.
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thuật toán đệ qui
• Để tổ hợp lời giải, nhận thấy rằng chỉ có thể xảy ra một trong 3 trường hợp:
– Dãy con lớn nhất nằm ở dãy con bên trái (nửa trái)
– Dãy con lớn nhất nằm ở dãy con bên phải (nửa phải)
– Dãy con lớn nhất bắt đầu ở nửa trái và kết thúc ở nửa phải (giữa).
• Do đó, nếu ký hiệu trọng lượng của dãy con lớn nhất ở
nửa trái là w , ở nửa phải là w và ở giữa là w thì L R M
trọng lượng cần tìm sẽ là max(w , w , w ). L R M
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thuật toán đệ qui
• Việc tìm trọng lượng của dãy con lớn nhất ở nửa trái
(w ) và nửa phải (w ) có thể thực hiện một cách đệ qui L R
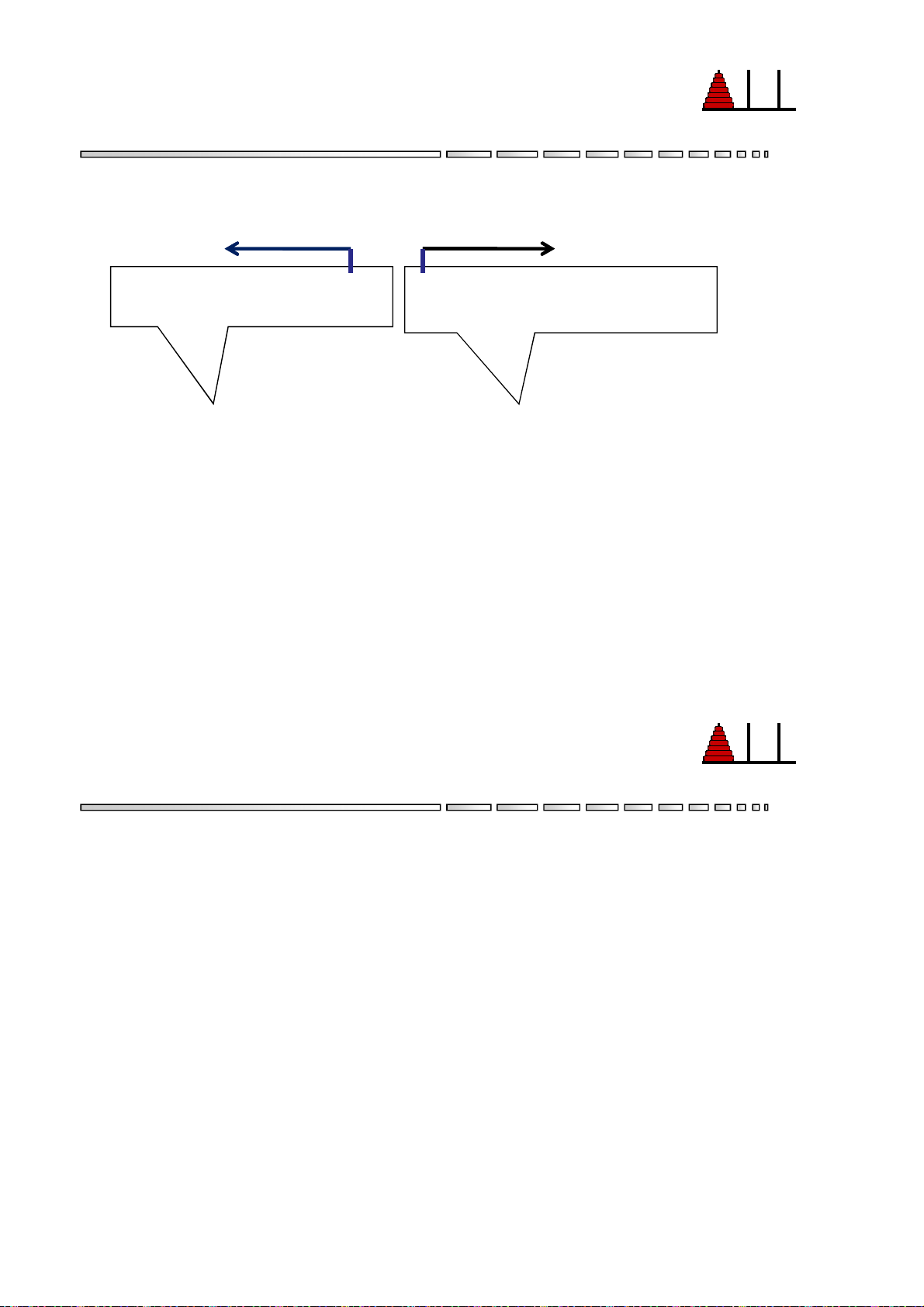
• Để tìm trọng lượng w của dãy con lớn nhất bắt đầu ở M
nửa trái và kết thúc ở nửa phải ta thực hiện như sau:
– Tính trọng lượng của dãy con lớn nhất trong nửa trái kết thúc ở điểm chia (w ) và ML
– Tính trọng lượng của dãy con lớn nhất trong nửa phải bắt đầu ở điểm chia (w ). MR – Khi đó w = w + w . M ML MR
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thuật toán đệ qui
• m – điểm chia của dãy trái, m+1 là điểm chia của dãy phải a , a ,…,a , a , a ,…,a 1 2 m m+1 m+2 n Tính W của dãy con ML Tính W của dãy con MR lớn nhất trong nửa trái
lớn nhất trong nửa phải kết thúc tại am bắt đầu từ am+1
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thuật toán đệ qui •
Để tính trọng lượng của dãy con lớn nhất ở nửa trái (từ
a[i] đến a[j]) kết thúc ở a[j] ta dùng thuật toán sau: MaxLeft(a, i, j); { maxSum = -; sum = 0;
for (int k=j; k>=i; k--) { sum = sum+a[k];
maxSum = max(sum, maxSum); } return maxSum; }
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thuật toán đệ qui
• Để tính trọng lượng của dãy con lớn nhất ở nửa phải (từ
a[i] đến a[j]) bắt đầu từ a[i] ta dùng thuật toán sau: MaxRight(a, i, j); { maxSum = -; sum = 0;
for (int k=i; k<=j; k++){ sum = sum+a[k];
maxSum = max(sum, maxSum); } return maxSum; }
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thuật toán đệ qui
Sơ đồ của thuật toán đệ qui có thể mô tả như sau: MaxSub(a, i, j); { if (i = j) return a[i] else { m = (i+j)/2; wL = MaxSub(a, i, m);
wR = MaxSub(a, m+1, j); wM = MaxLeft(a, i, m)+ MaxRight(a, m+1, j); return max(wL, wR, wM); } }
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thuật toán đệ qui
• Phân tích thuật toán:
Ta cần tính xem lệnh gọi MaxSub(a,1,n) để thực hiện thuật
toán đòi hỏi bao nhiêu phép cộng?
• Truớc hết nhận thấy MaxLeft và MaxRight đòi hỏi
n/2 + n/2 = n phép cộng
• Vì vậy, nếu gọi T(n) là số phép cộng cần tìm, ta có công thức đệ qui sau: 0 n  1  T (n)   n n n
T ( )  T ( )  n  2T ( )  n n  1   2 2 2
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thuật toán đệ qui
• Ta khẳng định rằng T(2k) = k.2k. Ta chứng minh bằng qui nạp
• Cơ sở qui nạp: Nếu k=0 thì T(20) = T(1) = 0 = 0.20.
• Chuyển qui nạp: Nếu k>0, giả sử rằng T(2k-1) = (k-1)2k-1 là đúng. Khi đó
T(2k) = 2T(2k-1)+2k = 2(k-1).2k-1 + 2k = k.2k.
• Quay lại với ký hiệu n, ta có
T(n) = n log n .
• Kết quả thu được là tốt hơn thuật toán thứ hai !
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT So sánh các thuật toán
• Cùng một bài toán ta đã đề xuất 3 thuật toán đòi hỏi số
lượng phép toán khác nhau và vì thế sẽ đòi hỏi thời gian tính khác nhau.
• Các bảng trình bày dưới đây cho thấy thời gian tính với
giả thiết máy tính có thể thực hiện 108 phép cộng trong 1 giây
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT Thời gian tính
Cấu trúc dữ liệu và thuật toán - N.Đ. Nghĩa. Bộ môn KHMT