Tổng hợp bài giảng môn Cấu trúc dữ liệu và thuật toán_Thầy Nguyễn Duy Hiệp| Bài giảng môn Cấu trúc dữ liệu và thuật toán| Trường Đại học Bách Khoa Hà Nội
Tổng hợp bài giảng môn Cấu trúc dữ liệu và thuật toán_Thầy Nguyễn Duy Hiệp| Bài giảng môn Cấu trúc dữ liệu và thuật toán| Trường Đại học Bách Khoa Hà Nội. Tài liệu gồm 269 trang giúp bạn ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem.
Môn: Cấu trúc dữ liệu và thuật toán HUST 35 tài liệu
Trường: Đại học Bách Khoa Hà Nội 3.5 K tài liệu
Tác giả:
Preview text:
Data structures & Algorithms Nguyễn Duy Hiệp nguyenduyhiep@gmail.com tinhocdaicuong.wordpress.com Nội dung
◼ Chương 1 – Các khái niệm cơ bản
◼ Chương 2 – Giải thuật đệ quy
◼ Chương 3 – Các cấu trúc dữ liệu cơ bản
◼ Chương 4 – Cấu trúc cây ◼ Chương 5 – Sắp xếp ◼ Chương 6 – Tìm kiếm ◼ Chương 7 – Đồ thị Tài liệu
◼ [1]. Cấu trúc dữ liệu và giải thuật, Đỗ Xuân Lôi, NXB ĐHQGHN
◼ [2]. Bài giảng cấu trúc dữ liệu và giải thuật, Nguyễn Đức Nghĩa
◼ [3]. Data structures and program design in C++, Robert L. Kruse, Alexander J. Ryba.
◼ [4] Algorithm in C, R. Sedgewick, Addison Wesley
◼ [5]. Data structures and problem solving with C++, Mark Allen Weiss Yêu cầu
◼ Kiến thức cơ bản về toán
◼ Kỹ thuật lập trình cơ bản
◼ Sử dụng được một trong các ngôn ngữ lập trình: PASCAL C/C++ Java .Net Đánh giá ◼ Thi giữa kỳ (30%) ◼ Thi cuối kỳ (70%): Thi viết Sử dụng tài liệu
Nội dung thi : tất cả những gì đã học !
◼ Bài tập cộng điểm (0.5điểm/bài)
Xem thêm trên blog tinhocdaicuong.wordpress.com Bài tập chương 1 Phần 1
Bài 1. Chứng minh rằng
a. a + b có thể nhỏ hơn min(a, b).
b. a × b có thể nhỏ hơn min(a, b).
Bài 2. Bài toán hành trình người du lịch: Cho vị trí n thành phố trong trong không gian. Từ một
thành phố ban đầu, một người du lịch muốn đi thăm tất cả n thành phố đó, sau đó quay trở lại
thành phố ban đầu. Hãy xây dựng hành trình của người du lịch sao cho quãng đường người đó phải đi là ngắn nhất.
Tìm các phản ví dụ cho các thuật toán sau:
Gọi L là danh sách các thành phố
(a) Thuật toán 1. NearestNeighbor(L)
Chọn và thăm thành phố khởi đầu p0 từ L p = p0 i = 0
Trong khi vẫn tồn tại thành phố chưa thăm i = i + 1
Chọn pi là thành phố chưa thăm mà gần nhất với thành phố vừa thăm pi−1 Thăm pi
Trở về p0 từ thành phố pn−1
(b) Thuật toán 2. ClosestPair(P)
Gọi n là số lượng thành phố trong L.
For i = 1 to n − 1 do d = ∞
Với mỗi cặp (s, t) trong tập các cặp thành phố có thể
Nếu dist(s, t) ≤ d thì sm = s, tm = t, và d = dist(s, t)
Kết nối (sm, tm) bởi 1 cạnh
Kết nối hai điểm cuối cùng bằng 1 cạnh
Trong đó dist(s,t) là khoảng cách giữa 2 thành phố s và t.
Bài 3. Cho một tập các số nguyên S = {s1, s2, . . . , sn}, và một giá trị đích T, Tìm một tập con của
S sao cho tổng các số trong tập con đó đúng bằng T. Ví dụ, Tồn tại một tập con trong S = {1, 2,
5, 9, 10} mà tổng là T = 22 nhưng lại không tồn tại với T = 23.
Tìm các phản ví dụ cho các thuật toán sau
(a) Lần lượt chọn các phần tử trong S theo thứ tự từ trái qua phải nếu chúng phù hợp (thuật toán first-fit).
(b) Lần lượt chọn các phần tử trong S theo thứ tự từ nhỏ đến lớn (thuật toán best-fit).
(c) Lần lượt chọn các phần tử trong S theo thứ tự từ lớn nhất đến nhỏ nhất.
Bài 4. Bài toán tập bao trùm (set cover problem) được định nghĩa như sau:
Cho một tập S gồm các tập con S1, ..., Sm của tập vũ trụ U = {1, ..., n}. Tìm số lượng tập con nhỏ
nhất T ⊂ S sao cho ∪ti∈Tti = U. Ví dụ, có các tập con, S1 = {1, 3, 5}, S2 = {2, 4}, S3 = {1, 4}, và S4 =
{2, 5} Tập con bao trùm sẽ là S1 và S2.
Tìm một phản ví dụ của thuật toán tìm các tập bao trùm sau: Lựa chọn tập con có số lương
phần tử lớn nhất (có độ bao phủ lớn nhất), và sau đó loại bỏ các phần tử của tập đó trong tập
vũ trụ U. Lặp lại việc thêm các tập con chứa số lượng các phần tử chưa bị bao phủ phần tử lớn
nhất cho tới khi tất cả các phần tử của tập vũ trụ được bao phủ.
Bài 5. Chứng minh các khẳng định sau bằng phương pháp quy nạp a) n
∑ i = n(n +1) / 2 với mọi n≥0 i 1 = b) n 3 2 2
∑ i = n (n+1) / 4 với mọi n≥0 i 1 = c) n
∑ i(i +1)(i + 2) = n(n +1)(n + 2)(n + 3) / 4 i 1 = d) n 1 n ∑ = với mọi n≥1 i 1
= i(i +1) n +1 e) 3
n + 2n chia hết cho 3 với mọi n≥0
Bài 6. Tốc độ truy cập ổ đĩa cứng thường được tính theo milliseconds (phần ngìn của giây) hay
microseconds (Phần triệu của giây)? Tốc độ truy cập trên RAM là khoảng bao nhiêu? Số lượng
chỉ lệnh - instructions mà một CPU có thể thực hiện trong 1 năm là bao nhiêu nếu máy đó được
chạy liên tục trong suốt thời gian.
Bài 7. Một thuật toán sắp xếp cần 1 giây để sắp xếp 1,000 phần tử trên một máy tính, thời gian
nó cần để sắp xếp 10,000 Phần tử sẽ là bao nhiêu nếu:
(a) thuật toán sắp xếp có thời gian thực hiện tỉ lệ bình phương với kích thước dữ liệu, và
(b) thuật toán sắp xếp có thời gian thực hiện tỉ lệ cỡ n log n với kích thước dữ liệu? (n là kích
thước dữ liệu – số phần tử cần sắp xếp)
Bài 8. Cài đặt 2 thuật toán người du lịch ở trong bài 2. Trong thực tế thì thuật toán nào là tốt
hơn? Bạn có thể đề xuất một thuật toán tốt hơn không ?
Bài 9. Cài đặt thuật toán tối ưu để chọn ra số lượng bộ phim xem được nhiều nhất đã được mô tả trong slide
Bài 10. Viết hàm thực hiện phép chia số nguyên mà không dùng các toán tử / hoặc *. Hãy tìm
các thực hiện nhanh nhất.
Bài 11. Bạn có 25 con ngựa. Tại mỗi lần đua thì chỉ có thể cho tối đa 5 con ngựa tham gia. Bạn
phải xác định 3 con ngựa là nhanh nhất, nhì và ba trong 25 con ngựa. Hãy tìm số lượng vòng
đua tối thiểu để có thể thực hiện việc này. 1/10/2011
Phần I – Giới thiệu về Thuật toán Chương 1.1 KHÁI NIỆM CƠ BẢN Nội dung 1.1 Thuật toán là gì ? • Thuật toán:
• 1.1. Thuật toán là gì?
• thủ tục để thực hiện một nhiệm vụ cụ thể
• 1.2 Tính chất của thuật toán
• ý tưởng nằm sau các chương trình máy tính.
• Thuật toán phải giải quyết bài toán tổng quát, và được định • 1.2 .1 Tính chính xác nghĩa rõ ràng. • 1.2.2 Tính hiệu quả
• Một thuật toán giải bài toán đặt ra là một thủ tục xác định bao
• 1.3 Chứng minh thuật toán đúng
gồm một dãy hữu hạn các bước cần thực hiện để thu được
đầu ra cho một đầu vào cho trước của bài toán.
• 1.4 Biểu diễn thuật toán Đầu vào Đầu ra Các bước thực hiện 1 1/10/2011 1.1 Thuật toán là gì ? 1.2.1 Tính chính xác Bài toán: sắp xếp
• Thuật toán phải cho đầu ra mong muốn ứng với bất cứ đầu
• Đầu vào: một dãy gồm n khóa a , a ,.., a
vào hợp lệ nào của bài toán. 1 2 n
• Đầu ra: một hoán vị có thứ tự của các khóa đầu vào trong đó
• Tính chính xác không phải lúc nào cũng dễ thấy!
a ' a ' .. a ' 1 2 n
VD. Bài toán chọn lịch xem phim
• Đầu vào: Một tập L gồm thời gian chiếu trong ngày của n bộ
Trường hợp cụ thể của bài toán phim • {14, 45, 68, 24, 54, 34}
• Đầu ra: Tập con của L chứa số bộ phim lớn nhất có thể xem
• {Mike, Bob, Sally, Jill, Jan}
(không được chồng nhau về thời gian) Sherlock holmes Up in the air One P1
• Chúng ta chỉ quan tâm đến các thuật toán chính xác và hiệu
quả, và dễ cài đặt Avatar Up Madagasca 2 P2 Angel and demon Alice in the wonderland P3 1.2.1 Tính chính xác 1.2.1 Tính chính xác
• Thuật toán 1. Chọn bộ phim sớm nhất trong L mà không trùng
• Thuật toán 3. Duyệt toàn bộ: duyệt 2n tập con của n bộ phim
với các bộ phim đã chọn trước đó. Lặp lại cho đến khi không
trong L. Chọn ra tập con nào có số lượng phần tử lớn nhất. thể chọn thêm.
Đảm bảo thu được kết quả tối ưu
Thuật toán chạy rất chậm, vd n =20 thì số tập con là 220
• Thuật toán 4. Thuật toán tối ưu: sắp xếp các lịch chiếu phim
theo thứ tự không giảm thời gian kết thúc. Lần lượt xem xét
• Thuật toán 2. Chọn bộ phim có thời gian chiếu ngắn nhất
trong L mà không trùng với các bộ phim đã chọn trước. Lặp lại
các phim trong danh sách đã sắp xếp, bổ sung vào danh sách
cho đến khi không chọn thêm được.
xem bộ phim đang xét nếu nó không chồng lên các bộ phim đã có trong danh sách xem.
• Có những bài toán mà không tồn tại thuật toán chính xác để giải! 2 1/10/2011 1.2.1 Tính chính xác 1.2.2 Tính hiệu quả
• Phân biệt giữa thuật toán chính xác và không chính xác: đưa
“Tại sao không chỉ sử dụng mỗi siêu máy tính? ”
ra một ví dụ thuật toán mà thuật toán cho kết quả sai (phản ví dụ).
• Siêu máy tính chỉ cho người giàu và những người quá
ngốc để có thể thiết kế một thuật toán hiệu quả!
• Chứng minh tính đúng đắn của thuật toán: khó khăn hơn nhiều.
• Thuật toán nhanh hơn chạy trên các máy tính chậm
hơn sẽ thắng trong trường hợp dữ liệu đầu vào đủ lớn.
• Bài tập. Tìm các phản ví dụ cho các thuật toán giải bài toán
hành trình du lịch tối ưu. Bài toán cái túi
Chọn đồ vật có giá trị cao trước
• Đầu vào: n đồ vật, mỗi đồ vật i có một trọng lượng w • i và một
Sắp xếp các đồ vật theo thứ tự giảm về giá trị.
giá trị ci. Một cái túi có thể chứa các đồ vật với trọng lượng tối
• Lần lượt xét các đồ theo thứ tự này, cho đồ vật đang xét vào đa là b
túi nếu nó còn có thể chứa thêm được
• Đầu ra: Cách chất các đồ vật vào túi sao cho trọng lượng tối đa
không vượt quá b, và tổng giá trị các đồ vật trong túi là lớn nhất. ∑ →
• Xây dựng thuật toán chất các đồ vào túi ? 3 1/10/2011
Chọn đồ vật trọng lượng nhỏ trước
Chọn đồ vật theo tỉ lệ ci/wi
• Sắp xếp các đồ vật theo thứ tự tăng trọng lượng
• Sắp xếp các đồ vật theo thứ tự giảm của tỉ lệ giá trị/ trọng
• Lần lượt xét các đồ vật theo thứ tự này, chọn đồ vật đang xét lượng
vào túi nếu nó vẫn có thể chứa thêm …
• Lần lượt xét các đồ vật theo
thứ tự này, chọn đồ vật đang
xét vào túi nếu nó vẫn có thể chứa thêm Tìm phản ví dụ ?
1.3 Chứng minh tính đúng đắn
Chứng minh thuật toán sai bằng
• Thuật toán được định nghĩa đệ quy: Thuật toán được định
cách chỉ ra một phản ví dụ
nghĩa lại bằng chính nó (với kích thước bài toán nhỏ hơn)
• Tìm trong các trường hợp dữ liệu nhỏ ! 1 ế 0 1 ! ế 0
• Các ví dụ mà sát với các tiêu chuẩn
lựa chọn của thuật toán
• Chứng minh tính đúng đắn của thuật toán
đệ quy bằng phương pháp quy nạp
• Các ví dụ của các trường
hợp cực trị (lớn nhất, nhỏ nhất …) 1
Không tìm được phản ví dụ không có nghĩa thuật toán là đúng! 2 4 1/10/2011
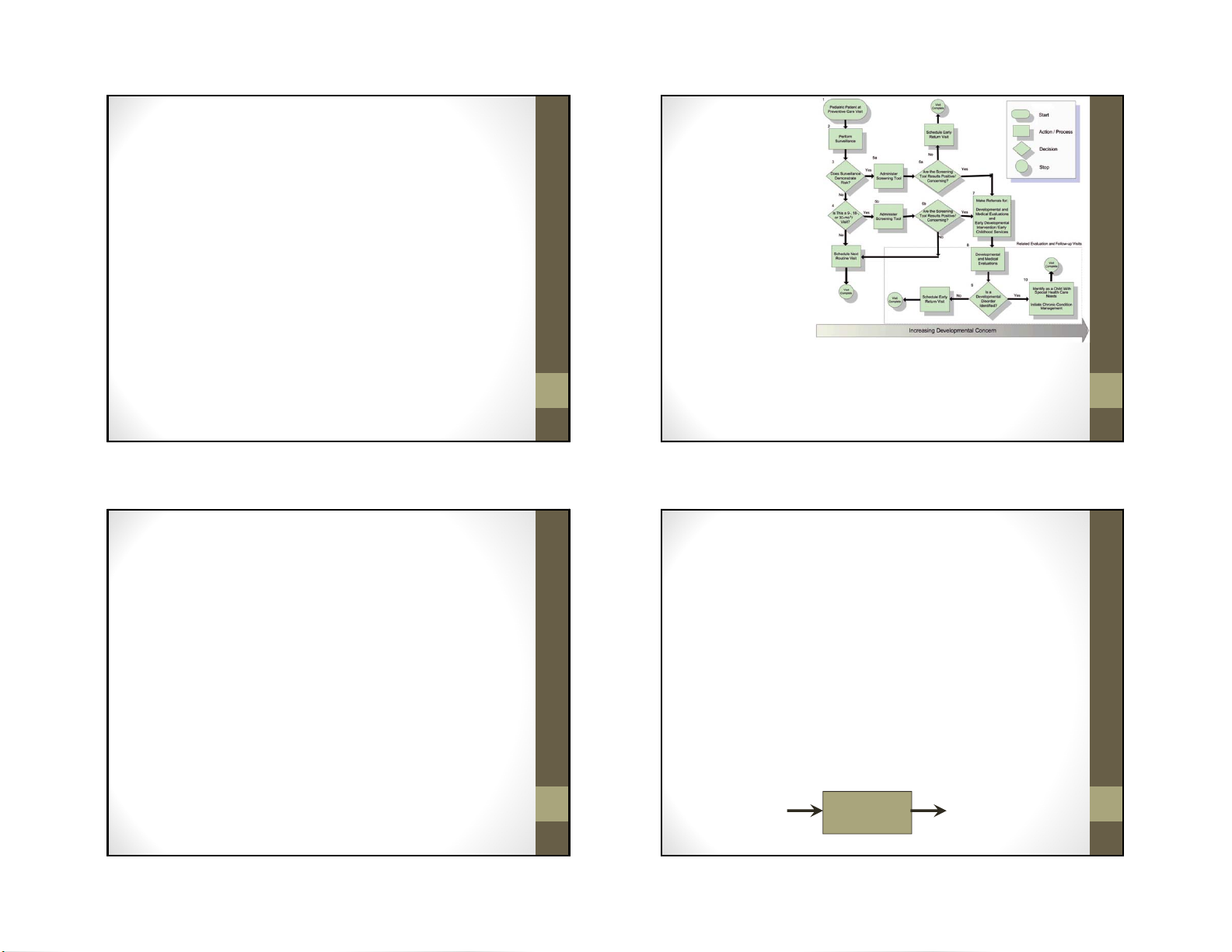
1.4 Biểu diễn thuật toán
• Cần biểu diễn các bước thực hiện tuần tự của thuật toán một cách cụ thể. • Biểu diễn bằng: Tính Tính • Ngôn ngữ tự nhiên chính
• Giả ngôn ngữ (pseudocode) d ễ dàng • Lưu đồ xá c
• Ngôn ngữ lập trình cụ thể (C/C++, java,…) 5 1/10/2011 REVIEW
• Bài toán: Cho một tập các số nguyên S = {s1, s2, . . . , sn}, và
một giá trị đích T. Tìm một tập con của S sao cho tổng các số
trong tập con đó đúng bằng T.
Ví dụ, Tồn tại một tập con trong S = {1, 2, 5, 9, 10} mà tổng là PHÂN TÍCH
T = 22 nhưng lại không tồn tại với T = 23. THUẬT TOÁN
Tìm phản ví dụ cho các thuật toán sau REVIEW NÔI DUNG
• (a) Lần lượt chọn các phần tử trong S theo thứ tự từ trái qua • Phân tích thuật toán
phải nếu chúng phù hợp (thuật toán first‐fit). • Mô hình RAM
• Tốt nhất, tồi nhất, trung bình
• (b) Lần lượt chọn các phần tử trong S theo thứ tự từ nhỏ đến • Ký hiệu O‐lớn
lớn (thuật toán best‐fit). • Phân tích tiệm cận
• Tốc độ tăng và tính thống trị
• (c) Lần lượt chọn các phần tử trong S theo thứ tự từ lớn nhất
• Một số tính chất của phân tích O‐lớn đến nhỏ nhất. 1 1/10/2011 PHÂN TÍCH THUẬT TOÁN? PHÂN TÍCH THUẬT TOÁN?
Bài toán: tìm phần tử lớn nhất thứ k
• Đánh giá hiệu quả của thuật toán mà không cần cài đặt.
• Đầu vào: Dãy số gồm n số nguyên , , . . , , và số nguyên k • 2 mô hình : (0< k ≤ n)
• Mô hình RAM (Random Access Machine)
• Đầu ra: Giá trị phần tử lớn nhất thứ k trong dãy.
• Phân tích tiệm cận độ phức tạp trong trường hợp tồi nhất
Có 2 thuật toán A, B để giải bài toán.
• Đánh giá thuật toán: dự đoán các tài nguyên mà thuật toán Với n = 100,000, k=100 cần.
• A cài đặt bằng C chạy mất 12 s
• Tài nguyên: Thời gian CPU, bộ nhớ, băng thông, phần cứng…
• B cài đặt bằng java chạy mất 19 s
Thuật toán A tốt hơn B ? MÔ HÌNH RAM
TỐT NHẤT, TỒI NHẤT VÀ TRUNG BÌNH
• Thực hiện thuật toán trên một máy tính giả định gọi là Random • Phân tích thuật toán
Access Machine hoặc RAM. trong trường hợp
• Mỗi phép tính đơn giản (+, *, –, =, if, call) thực hiện trong 1 đơn vị tổng quát, với một
thời gian (hoặc 1 bước). đầu vào bất kỳ thỏa
• Vòng lặp, hàm, thủ tục: là kết hợp của nhiều phép tính đơn lẻ mãn
• Mỗi bước truy cập bộ nhớ mất 1 đơn vị thời gian
• Luôn có đủ bộ nhớ cần thiết để thực hiện thuật toán Phân tích trường
hợp: tốt nhất, tồi nhất
• Đánh giá thời gian thực hiện thuật toán bằng cách đếm số đơn và trung bình vị thời gian cần. 2 1/10/2011
TỐT NHẤT, TỒI NHẤT VÀ TRUNG BÌNH KÝ HIÊU O LỚN
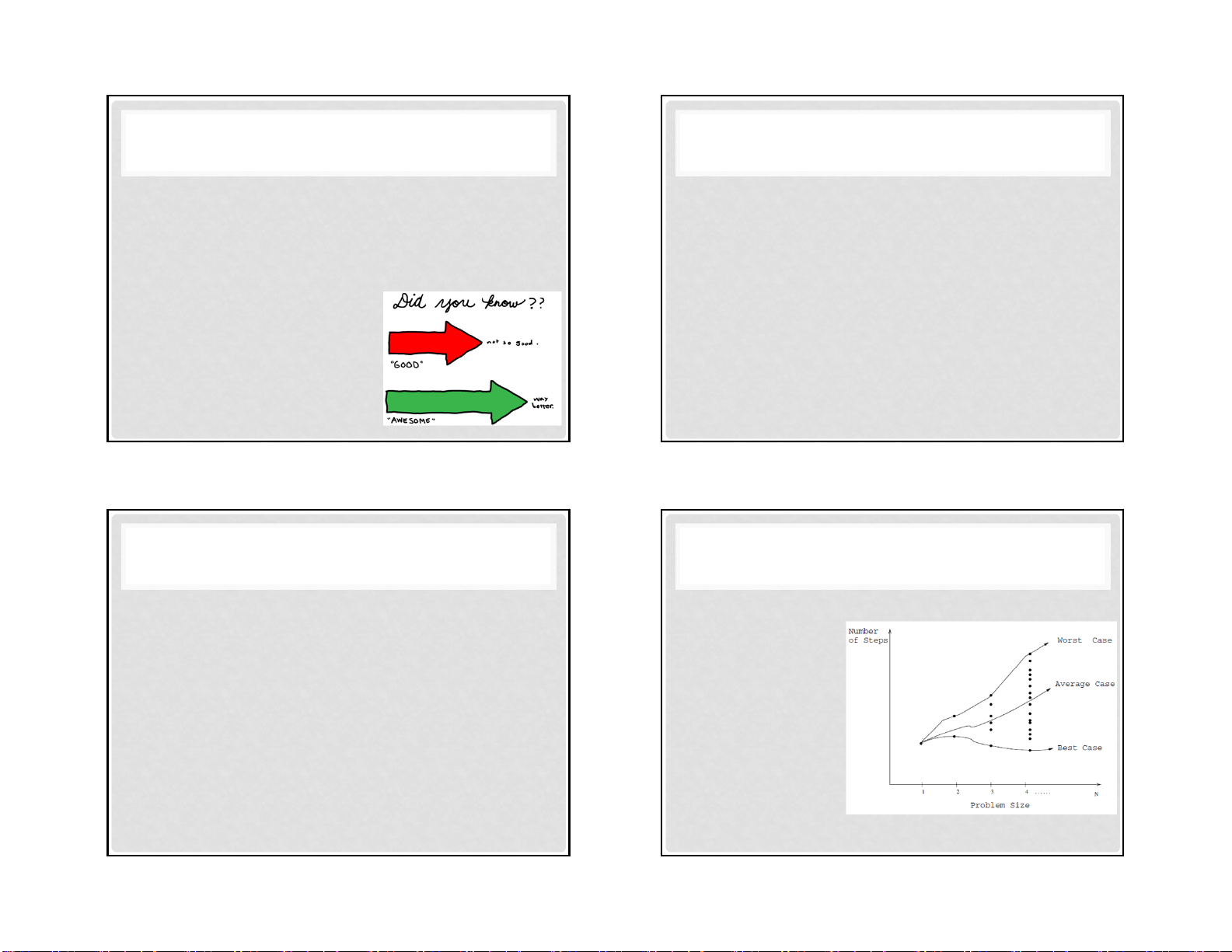
• Độ phức tạp trong trường hợp tồi nhất (worst‐case complexity):
• Khó xác định chính xác các hàm đánh giá độ phức tạp trong
Là số lượng bước lớn nhất thuật toán cần thực hiện với bất cứ
trường hợp tốt nhất, tồi nhất, trung bình
đầu vào kích thước n nào.
• Có rất nhiều điểm lồi: thời gian thực hiện biến đổi trong một số trường
• Độ phức tạp trong trường hợp tốt nhất (best‐case complexity):
hợp đầu vào đặc biệt. VD tìm kiếm nhị phân nếu đầu vào 2 1
Là số lượng bước nhỏ nhất thuật toán cần thực hiện với bất cứ
• Để chính xác thì cần phân tích rất tỉ mỉ.
đầu vào kích thước n nào. 120 12.4 43 9
• Độ phức tạp trong trường hợp trung bình (average‐case
• Ký hiệu O lớn: đơn giản phân tích, bỏ qua những thành phần
complexity): Là số lượng bước trung bình thuật toán cần thực
mà không ảnh hưởng đến khi so sánh các thuật toán
hiện trên tất cả các trường hợp đầu vào kích thước n. Trong phân tích O lớn 2 và 3 5 là tương đương
• Mỗi độ phức tạp là một hàm của thời gian và kích thước đầu vào
• Các ký hiệu tiệm cận , ,
dùng để phân tích độ phức tạp 120 12.4 43 9 trong thực tế PHÂN TÍCH TIÊM CẬN
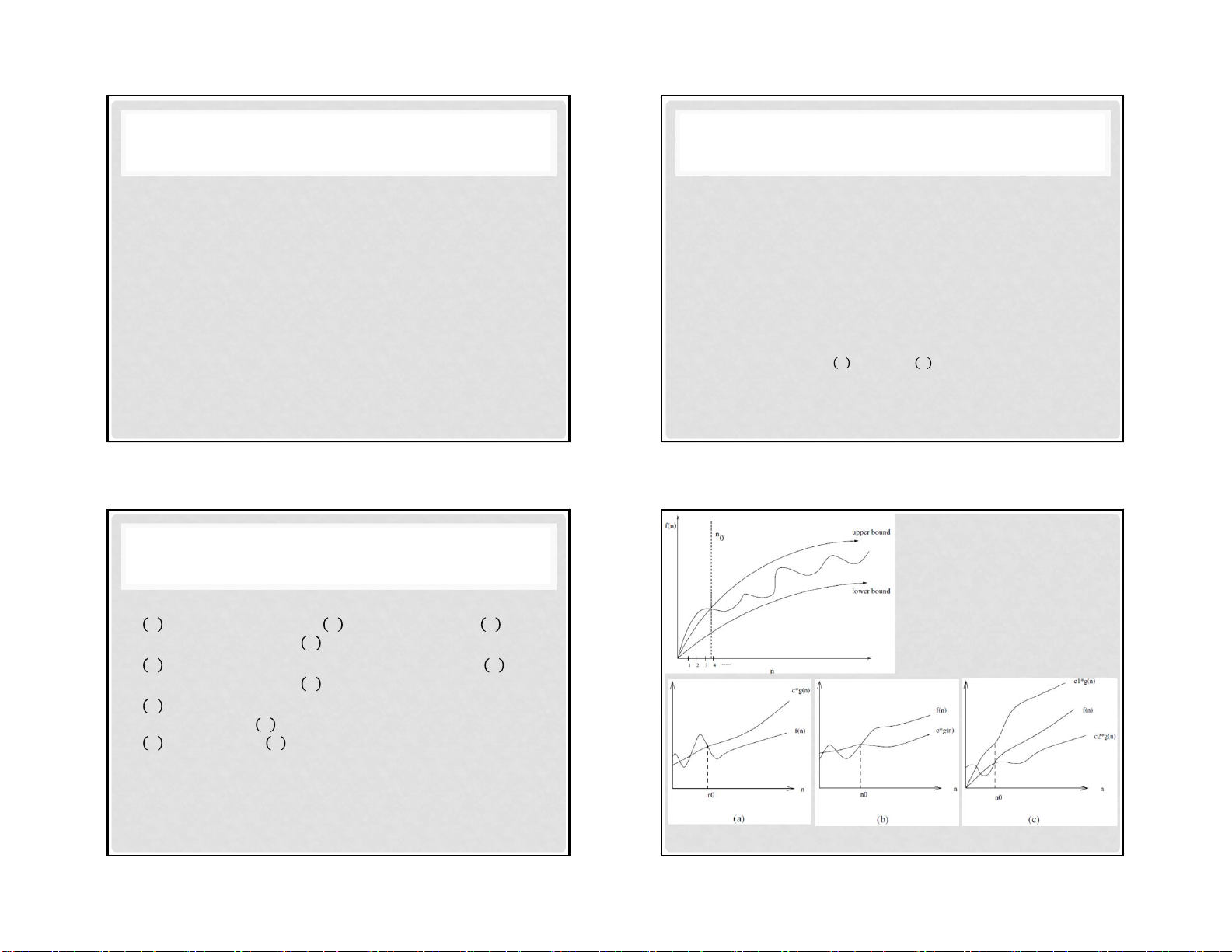
Cận trên, cận dưới để đánh giá
cho độ phức tạp của hàm
Định nghĩa O lớn chính thức: • : nghĩa là . là giới hạn trên của . Do vậy
tồn tại hằng số sao cho . luôn đúng với mọi • Ω : nghĩa là .
là giới hạn dưới của . Do vậy
tồn tại hằng số sao cho . luôn đúng với mọi • Θ : nghĩa là . là giới hạn trên, và . là giới hạn dưới của
. Do vậy tồn tại hằng số và sao cho . và . luôn đúng với mọi . Nói cách khác là giới hạn chặt của Với , ,
là các hằng số dương không phụ thuộc vào , và 0 Ο lớn Ω lớn Θ lớn 3 1/10/2011 KÝ HIÊU O LỚN OMEGA LỚN Ví dụ • vì chọn 1.5 thì 1.5 2 4 5 khi 50 • vì chọn 2 thì 2 2 4 5 •
vì với bất kỳ giá trị thì c 2 4 5 khi đủ lớn ( 100 nếu 1, • vì chọn 1 thì 2 4 5 khi 1 10/ nếu 1) •
vì với bất kỳ hằng số c nào thì •
vì với bất kỳ hằng số c nào thì 2 4 5 2 4 5 khi khi 5 THETA LỚN VÍ DỤ • vì cả Ο, Ω đều đúng
Khẳng định sau đúng hay sai? Tại sao ? • vì chỉ Ο đúng • 2 Θ 2 • vì chỉ Ω đúng • 3 Θ 3 Để chứng minh Θ thì cần chỉ ra • Ο • Ο • Ω 4 1/10/2011 TỐC ĐÔ TĂNG VÀ QUAN
TỐC ĐÔ TĂNG VÀ QUAN HÊ THỐNG TRỊ HÊ THỐNG TRỊ
• O lớn nhóm các hàm thành các lớp hàm. 4 và 100.3 3 là thuộc lớp hàm Θ
• Tốc độ tăng của một số hàm • Hai hàm ,
thuộc hai lớp khác nhau có quan hệ theo các ký hiệu thông dụng tiệm cận Ω, Ο khác nhau
• Các lớp hàm thông dụng: • Hàm hằng
1. Thời gian thực hiện là hằng số VD hàm tính tổng 2 số • Hàm loga . VD tìm kiếm nhị phân • Hàm tuyến tính
. VD Tìm giá trị lớn nhất trong dãy số • Hàm siêu tuyến tính . VD QuickSort, MergeSort • Hàm bậc hai
. VD Sắp xếp nổi bọt (bubble sort ) • Hàm bậc ba . • Hàm mũ , là hằng số >1. • Hàm giai thừa !
TỐC ĐÔ TĂNG VÀ QUAN HÊ THỐNG TRỊ CÁC PHÉP TÍNH VỚI O LỚN • Quan hệ thống trị: • Cộng hai hàm ! ≫ ≫ ≫ ≫ log ≫ ≫ log ≫ 1 • Ο Ο → Ο max ,
• Giới hạn và quan hệ thống trị của các hàm • Ω Ω → Ω max , • thống trị nếu lim 0 → • Θ Θ → Θ max , VD. • Nhân hàm không thống trị 3 5 vì lim 3 → • Ο ⋅ → Ο thống trị . vì lim 0 → • Ω ⋅ → Ω ! ≫ ≫ ≫ ≫ ≫ log ≫ ≫ ≫ log • Θ ⋅ → Θ
≫ log ≫ log /loglog ≫ loglog ≫ 1
là một hằng số dương bất kỳ 5 1/10/2011 CÁC PHÉP TÍNH VỚI O LỚN MỘT SỐ TÍNH CHẤT • Nhân hai hàm
Tính truyền ứng – transitivity • Nếu Ο và Ο thì Ο • Ο ∗ Ο → Ο ∗ • Nếu Ω và Ω thì Ω • Ω ∗ Ω → Ω ∗ • Nếu Θ và Θ thì Θ • Θ ∗ Θ → Θ ∗
Tính đối xứng – symmetry • Θ khi và chỉ khi Θ
Tính đối xứng chuyển vị ‐ transpose symmetry • Ο khi và chỉ khi Ω MỘT SỐ TÍNH CHẤT MỘT SỐ VÍ DỤ Chứng minh
Thuật toán sắp xếp lựa chọn – Selection Sort Nếu Ο và Ο thì Ο selection_sort(int s[], int n) { Ta có int i,j; /* counters */ • Ο tức là với
int min; /* index of minimum */ for (i=0; i• Ο tức là với min=i; Suy ra for (j=i+1; j• với max , if (s[j] < s[min]) min=j; swap(&s[i],&s[min]); Chọn và max , thì khi } Vậy Ο } 6 1/10/2011 MỘT SỐ VÍ DỤ MỘT SỐ VÍ DỤ
• Lệnh được lặp lại nhiều nhất chính là lệnh if
• Phân tích chi tiết hơn • 0 lệnh if lặp 2 lần (từ 1 tới n‐1)
Phân tích trong trường hợp tồi nhất • 1 lệnh if lặp 3 lần (từ 2 tới n‐1)
• Vòng lặp ngoài lặp n lần (từ 0 tới n‐1) … •
2 lệnh if lặp 1 lần (từ n‐1 tới n‐1)
• Vòng lặp trong lặp n lần ứng với mỗi lần lặp của vòng ngoài • 1 lệnh if lặp 0 lần
• Số lần lặp của if sẽ là
• Vậy số lượng bước (thời gian) cần thực hiện trong trường 2 3 ⋯ 1 0 2 1 /2 hợp tồi nhất là → Ο • Vậy Θ MỘT SỐ VÍ DỤ MỘT SỐ VÍ DỤ
• Sắp xếp chèn – Insertion Sort
• Phân tích trong trường hợp tồi nhất for (i=1; i•
1 lệnh cơ sở lặp 1 lần j=i; •
2 lệnh cơ sở lặp 2 lần
while ((j>0) && (s[j] < s[j‐1])) { … swap(&s[j],&s[j‐1]); • 2 lệnh cơ sở lặp 2 lần j = j‐1; • 1 lệnh cơ sở lặp 1 lần }
• Số lần lặp của lệnh cơ sở sẽ là } 1 2 ⋯ 2 1 1 /2 • Vậy Ο
• Lệnh được lặp nhiều nhất là 2 lệnh bên trong while : lệnh cơ sở 7