FUNDAMENTALS OF OPTIMIZATION Introduction CONTENT • Optimization problems
• Optimization problem classification • Applications • Topics Optimization problems
• Maximize or minimize some function relative to some set (range of choices)
• The function represents the quality of the choice, indicating which is the “best” • Example
• A shipper need to find the shortest route to deliver packages to customers 1, 2, …, N 0 3 4 2 5 6 8 7 3 0 3 6 7 2 1 6 0 3 1 6 4 3 0 4 7 1 1 9 3 0 2 4 2 6 4 0 2 8 3 4 1 2 0 5 5 7 7 2 0 6 5 1 6 4 5 0 6 8 1 8 6 0 9 3 8 1 1 3 5 9 0 2 7 6 9 4 1 3 2 0 Notations
• x  Rn : vector of decision variables x for j = 1, 2, …, n j,
• f : Rn → R is the objective function
• g : Rn → R is the constraint function defining restriction on x, i = 1, 2, …, i m
minimize f(x) over x = (x , x ,…, x ) X  Rn satisfying a property P: 1 2 n
g (x) ≤ b , i = 1, 2, …, s i i
g (x) = d , i = s + 1, 2, …, m i i Examples min f(x) = 3x – 5x + 10x 1 2 3 x + x + x ≤ 10 1 2 3
2x + 4x – 5x = 9 (Linear Program) 1 2 3
x , x R+, x  Z 1 2 3 min f(x) = 4𝑥2 2 1 + 3𝑥2 – 7𝑥1 𝑥3 x + 𝑥3 + 4x ≤ 10 1 2 3 2 𝑥2
1 + 4x – 5x = 7 (Nonlinear Program) 2 3
x , x R+, x  Z 1 2 3
Solving optimization problems
• General optimization problems • Very difficult to solve • Some special cases • Linear programming • Least square problem
• Some shortest path problems on networks • Etc. 0 3 4 2 5 6 8 7 • Example TSP 3 0 3 6 7 2 1 6 4 3 0 4 7 1 1 9 0 3 1 6 2 6 4 0 2 8 3 4 3 0 2 4 5 7 7 2 0 6 5 1 1 2 0 5 6 8 1 8 6 0 9 3 6 4 5 0 8 1 1 3 5 9 0 2 7 6 9 4 1 3 2 0 Classification
• Linear Programming (LP): f and g are linear i
• Nonlinear Programming (NLP): some function f, g are nonlinear i
• Continuous optimization: f and g are continuous on an open set i
containing X, X is closed and convex
• Integer Programming (IP): X  {0,1}n or X  Zn
• Constrained optimization: m > 0, X  Rn
• Unconstrained optimization: m = 0, X = Rn Applications • Production Planning • Routing in transportation • Scheduling • Assignment • Packing • Time Tabling • Network designs • Machine learning • . . .
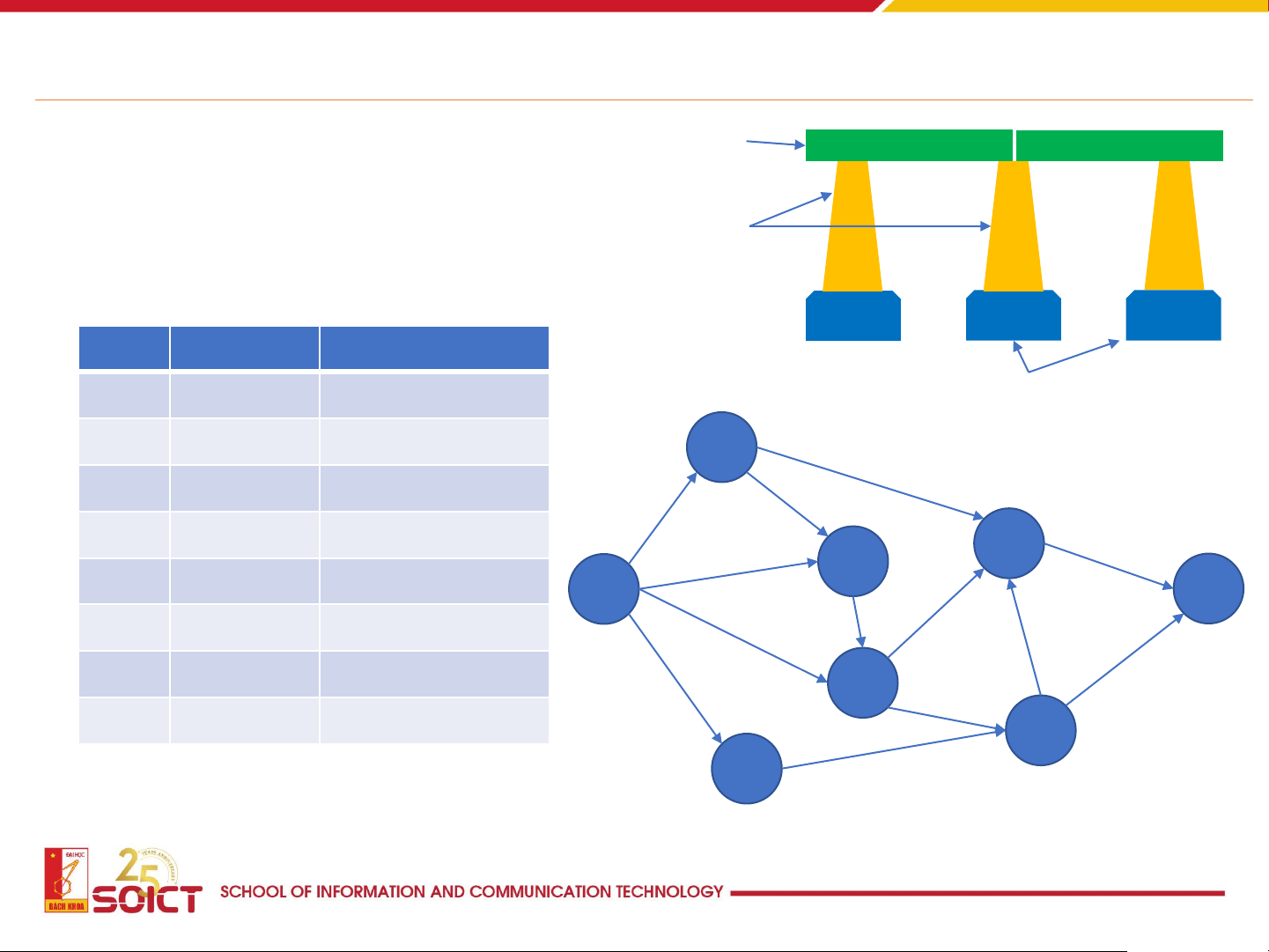
Agriculture Production Planning SKU Chart Demand Fields 10000 25000 32000 42500 Construction Planning Planning beams piles Task Duration Predecessors 1 30 6 bases 2 20 1,4,8 1 3 15 6 4 25 5,6 2 5 5 20 1,6 6 7 6 45 7 40 2,8 4 8 30 3,4 8 3
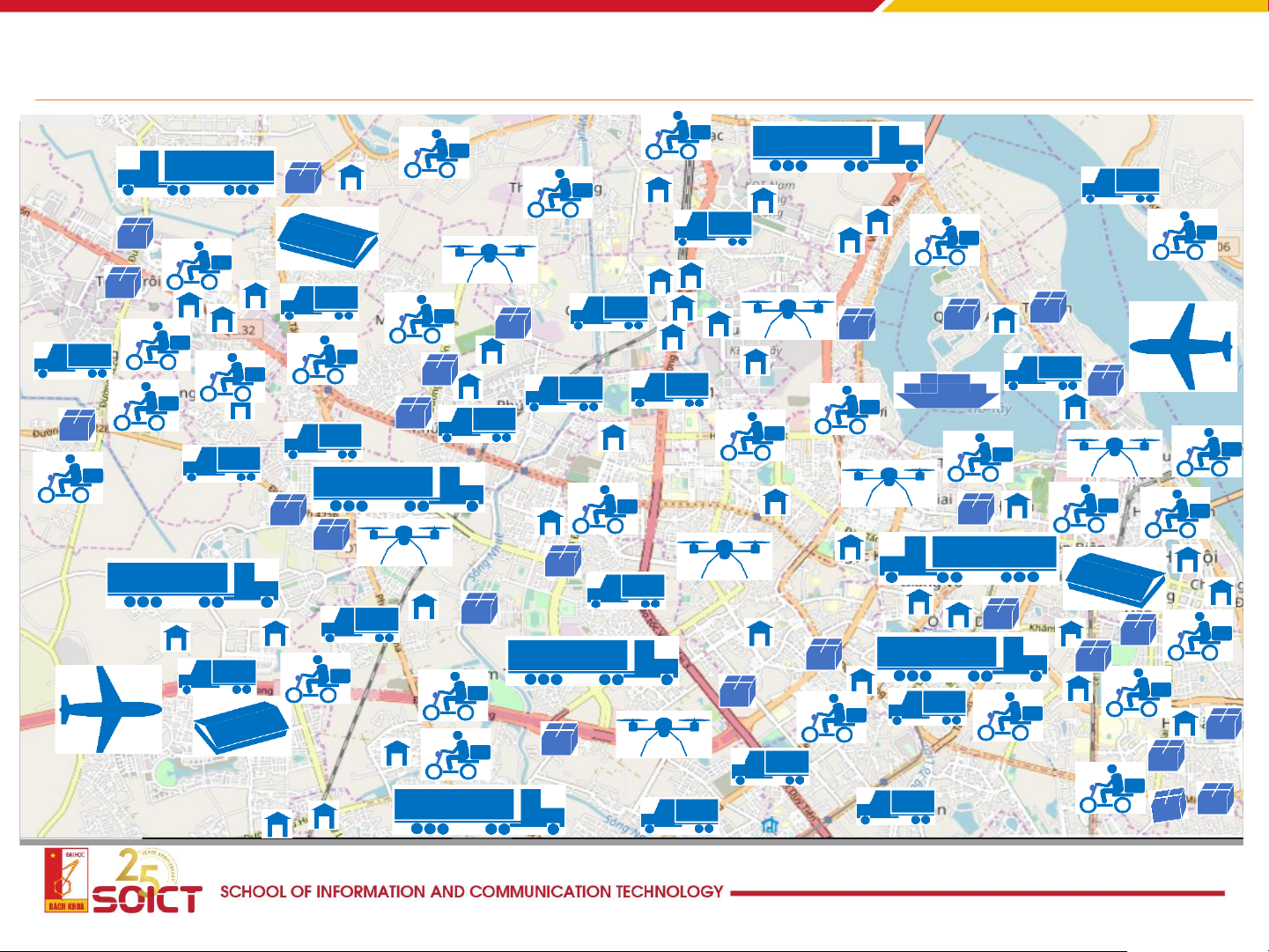
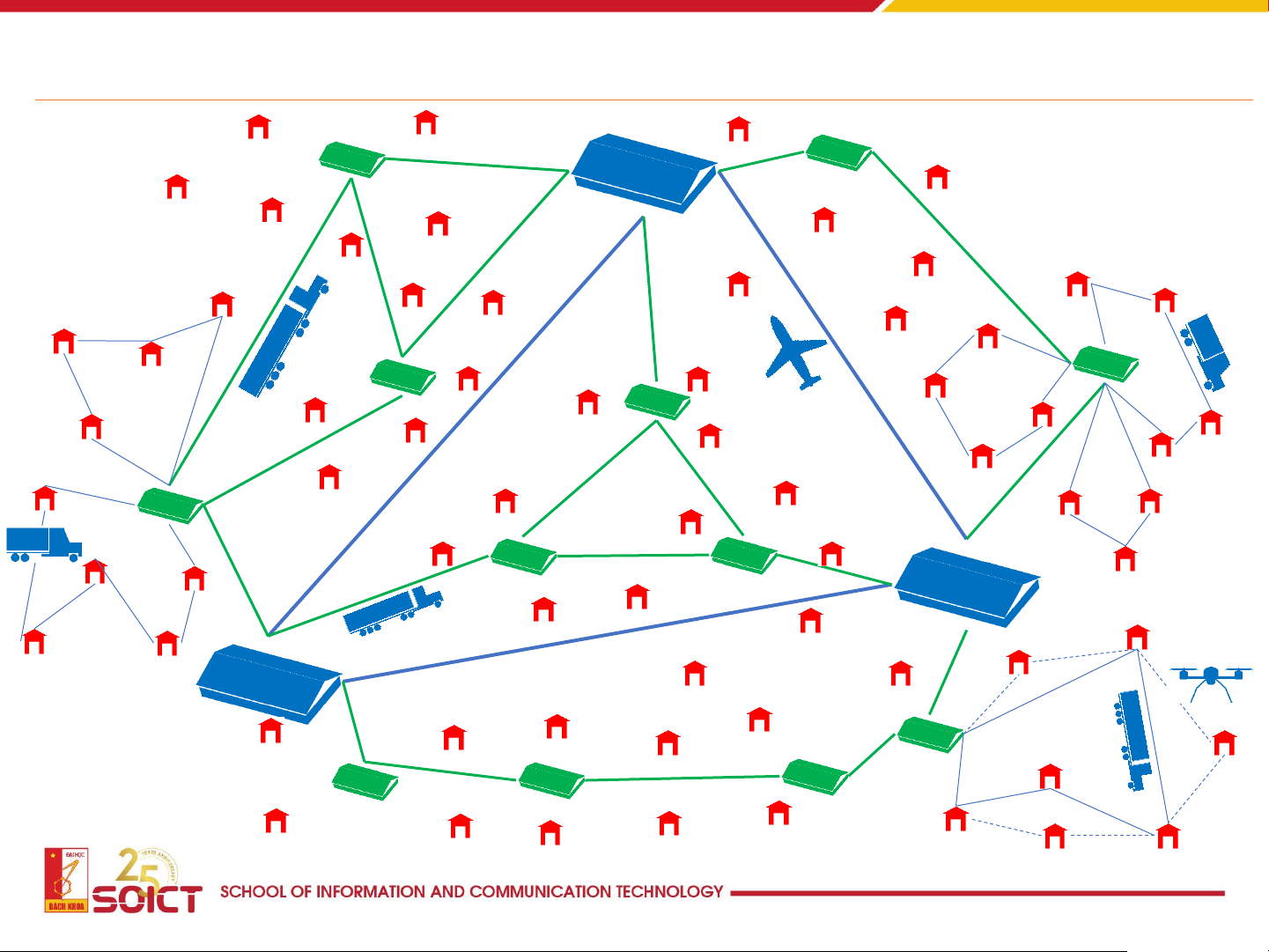
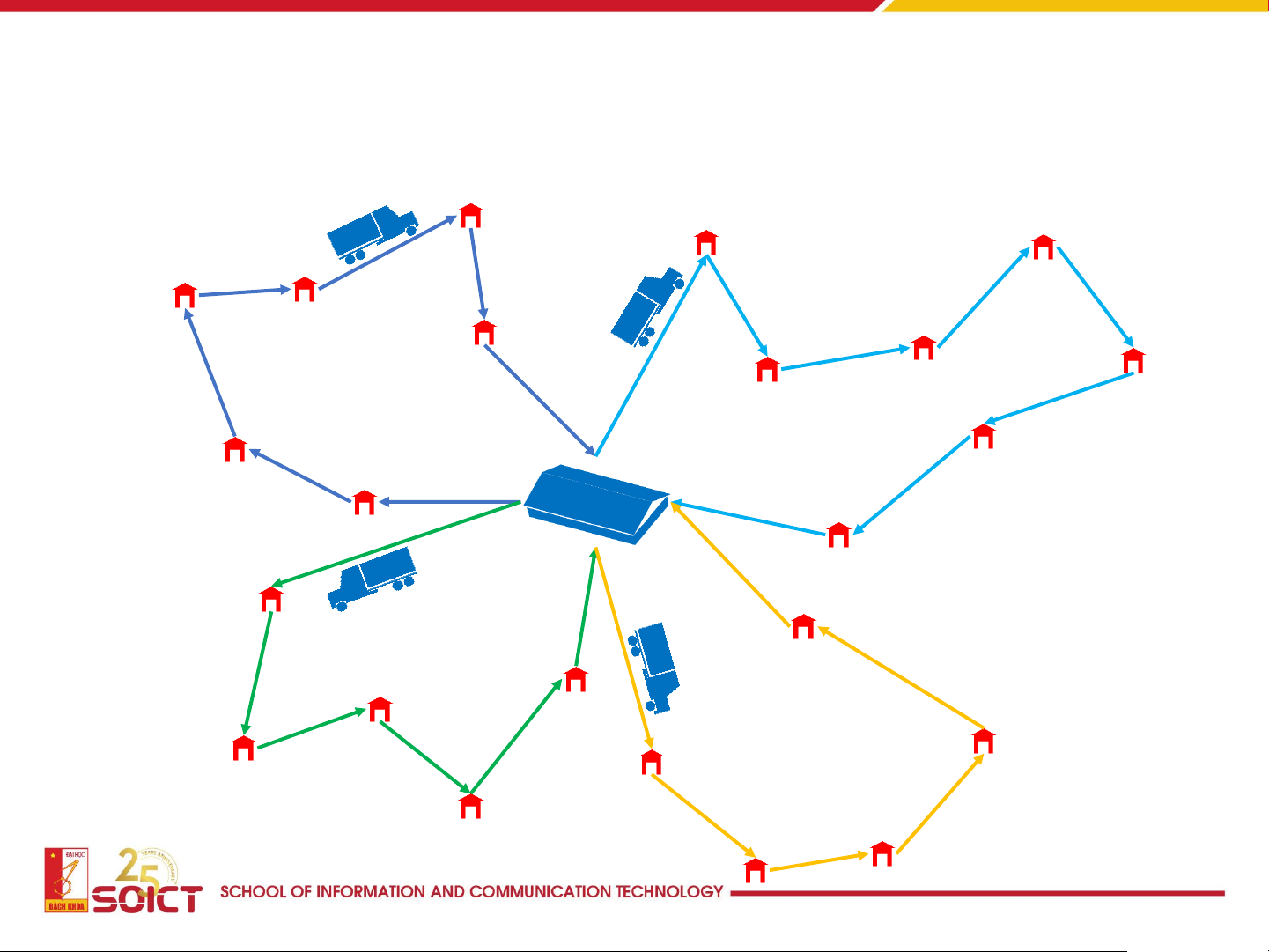
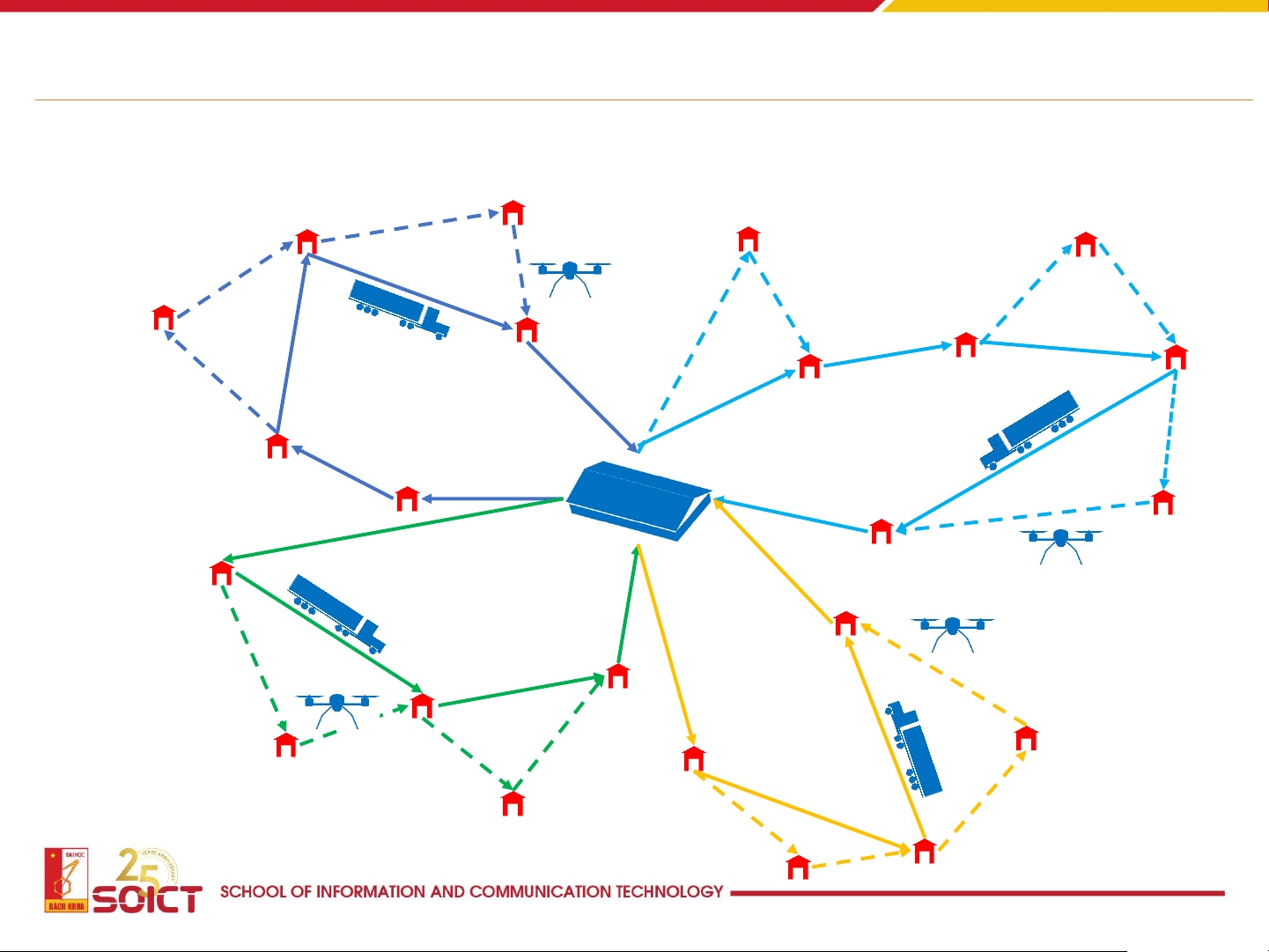
Logistics & Transportation 13
Logistics & Transportation
Logistics & Transportation
 How to make a plan for delivering goods to customers
Logistics & Transportation
 How to make a plan for delivering goods to customers
Logistics & Transportation
 How to pick items in a very large warehouse? Assignment
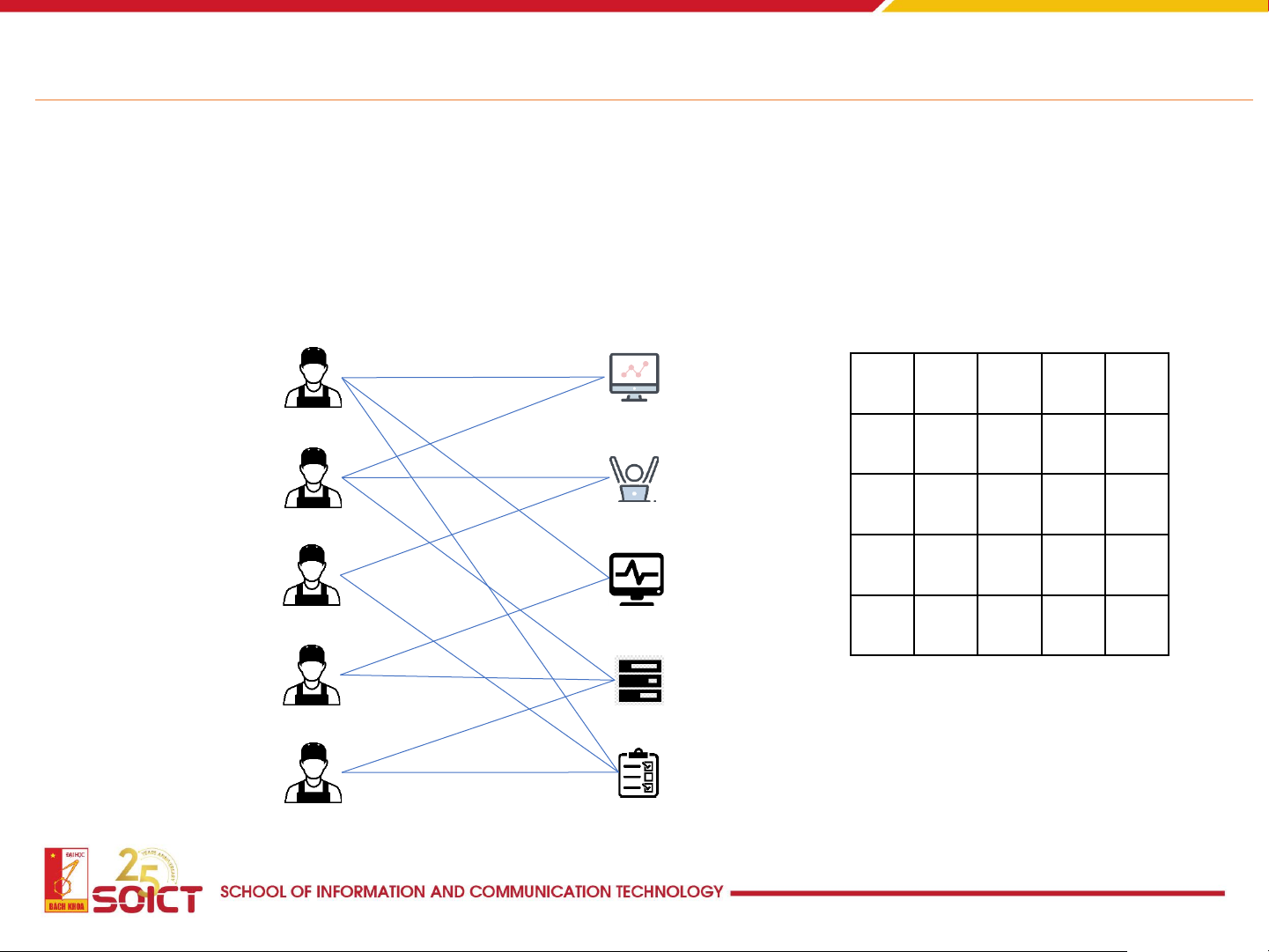
 How to assign tasks to workers in an optimal way workers tasks 4 6 8 2 6 7 5 6 1 4 6 3 Time tabling
 How to assign classes into slots of the timetable Monday Tuesday Wednesday Thursday Friday Data Python Statistics, Technical Networkings structure & Programmin B1-203 writing, B1- , B1-404 Algorithms, g, D9-302 202 TC-305 Fundamenta Java l of advanced, optimization, Machine B1-204 Image B1-402 learning, processing, D6-302 Software Operating D6-303 engineering, systems, D5-102 D9-101 Machine learning  Prediction X Y 43 45 44 46 45 45 46 48 47 47 48 51 49 49 50 ?