


















Preview text:
bé s¸ch to¸n häc cao cÊp - viÖn to¸n häc §inh ThÕ Lôc Ph¹m Huy §iÓn T¹ Duy Ph−îng
Gi¶i tÝch c¸c hµm nhiÒu biÕn
Nh÷ng nguyªn lý c¬ b¶n vµ tÝnh to¸n thùc hµnh
nhµ xuÊt b¶n ®¹i häc quèc gia hµ néi Héi §ång biªn tËp
Hµ Huy Kho¸i (Chñ tÞch) Ng« ViÖt Trung
Ph¹m Huy §iÓn (Th− ký) Gi¶i tÝch c¸c hµm nhiÒu biÕn Nh÷ng nguyªn lý c¬ b¶n vµ tÝnh to¸n thùc hµnh §inh ThÕ Lôc Ph¹m Huy §iÓn T¹ Duy Ph−îng
Bé s¸ch To¸n häc cao cÊp - ViÖn To¸n häc Lời nói đầu
uốn sách này có thể xem là tập tiếp theo của giáo trình giải tích các hàm
số một biến, đã được Nhà xuất bản Giáo dục ấn hành năm 1998, với tựa
C đề "Giải tích Toán học: Những nguyên lý cơ bản và tính toán thực hành".
Trong giáo trình đó chúng ta đã khảo sát dãy số, chuỗi số, hàm số và các
phép tính vi tích phân trong không gian một chiều (trục số thực). Trong tập tiếp
theo này các đối tượng trên sẽ được khảo sát trong không gian nhiều chiều, và đó
chính là sự khác biệt cơ bản giữa hai giáo trình. Để xây dựng các phép tính vi tích
phân trong không gian nhiều chiều, trước hết phải hiểu rõ cấu trúc của những
không gian này. Chương 1 đề cập tới hai cấu trúc quan trọng nhất của không gian
nhiều chiều, cấu trúc tuyến tính và cấu trúc khoảng cách, thông qua một ví dụ điển hình là không gian n
\ . Để giáo trình mang tính độc lập nhất định, không gian này
được xây dựng trực tiếp, mà không dựa vào khái niệm không gian tuyến tính tổng
quát trong giáo trình Đại số tuyến tính. Để tránh cồng kềnh, các khái niệm và kết
quả của chương này được chọn lọc tới mức tối thiểu từ 3 môn Đại số tuyến tính,
Tôpô và Giải tích hàm, vừa đủ sử dụng cho những chương sau, đồng thời dẫn dắt
người học làm quen với những bộ môn quan trọng đó. Các chương từ 2 đến 7
không chỉ thiết lập trong không gian nhiều chiều những gì đã biết trong Giải tích
một biến mà còn đưa ra những khái niệm mới chỉ xuất hiện trong không gian nhiều
chiều. Chương 8 trình bày các kiến thức cơ bản về chuỗi Fourier và phép biến đổi
tích phân Fourier. Chương cuối cùng giới thiệu sơ lược về hệ phương trình vi phân
và phương trình đạo hàm riêng. Hai chương sau này nhằm mục đích củng cố
những kiến thức về vi tích phân đã học trong những chương trước, rèn luyện kỹ
năng tính toán thực hành và trang bị kiến thức để học viên tìm hiểu các môn học
khác như Vật lý, Cơ học, Sinh học,...
Nếu như các khái niệm, kết quả chứng minh trong Giải tích một biến có tính
trực quan cao, dễ hiển thị, thì sang không gian nhiều chiều tính trừu tượng đã tăng
lên rõ rệt. Tuy nhiên, cái đẹp của Toán học nằm trong sự trừu tượng và cái ích của
Toán học nằm trong sự cụ thể. Để hiểu rõ hai mặt ấy của Toán học đồng thời
nhằm rèn luyện phương pháp suy luận toán học cho sinh viên, trong giáo trình này
hai cách tiếp cận thường được sử dụng đan xen nhau: đó là cách đi từ cụ thể tới
trừu tượng và ngược lại, từ trừu tượng tới cụ thể tuỳ theo từng khái niệm, từng
định lý. Mỗi khi các kết quả được phát biểu và chứng minh trong không gian tổng
quát n chiều, thì người đọc có thể hạn chế trong trường hợp n=2 hoặc n=3 để hiểu
dễ dàng và thấu đáo hơn. Trong tài liệu này, chúng tôi cố gắng đưa vào các chứng
minh đầy đủ của những định lý lớn và “hóc búa” thường bị né tránh trong các
giáo trình hiện hành. Những chứng minh này là khó nhưng chứa đựng các phương
pháp suy luận điển hình rất cần cho việc rèn luyện tư duy (nhất là đối với học sinh
cao học và những ai muốn đi sâu hơn vào lĩnh vực Giải tích Toán học). Người đọc i
không cần nhớ chi tiết, mà chỉ cần hiểu được các chứng minh này đã được xem là đạt yêu cầu.
Việc minh hoạ và tính toán trong không gian nhiều chiều vốn là một vấn đề
khó vì không mấy khi có thể thực hiện được bằng thủ công, nhất là về các chủ đề:
Vẽ đồ thị trong không gian, tính tích phân bội, tính vi phân hàm ẩn vectơ nhiều
biến, tính toán các biến đổi tích phân Fourier, giải phương trình đạo hàm riêng,...
Cái khó ở đây bắt đầu ngay từ việc tìm sao cho ra một ví dụ có thể xử lý được.
Chính vì vậy, lĩnh vực này luôn luôn là mơ hồ đối với hầu hết mọi học viên (từ đại
học đến cao học). Nhằm xoá bỏ tình trạng này, chúng tôi mạnh dạn đưa vào giáo
trình phần hướng dẫn tính toán thực hành trên máy, ngay sau mỗi chương lý
thuyết. Qua đây người đọc sẽ thấy rằng ngày nay, với máy tính và phần mềm toán
học thông dụng (có sẵn trên thị trường và trên Internet), chỉ bằng những dòng lệnh
đơn giản tương tự như ngôn ngữ toán học thông thường, người ta có thể "sờ thấy
được" những gì mà trước đây không thể nào hình dung ra nổi. Nếu chưa có sẵn
các chương trình tính toán trên máy cá nhân, người đọc có thể truy cập tới một số
trung tâm cung cấp dịch vụ tính toán qua mạng (thường là miễn phí) để có thể thực
hành tính toán được ngay (bạn đọc có nhu cầu xin liên hệ với các tác giả để biết
thêm thông tin chi tiết). Đối với người học chưa có điều kiện tiếp xúc với máy tính,
việc đọc phần này vẫn rất có tác dụng, vì sẽ biết được cơ chế giao tiếp giữa người
với máy và biết được những gì máy tính có thể thay thế con người trong quá trình
tính toán. Quan trọng hơn, qua các ví dụ minh hoạ về tính toán trên máy trình bày
trong sách, người học sẽ nắm được kiến thức toán học một cách sâu sắc hơn, do
tiếp cận được tới những điều mà trước đây tưởng như là không thể. Khi không còn
bị mặc cảm bởi những bài toán hóc búa, người ta sẽ thấy toán học không còn là
huyền bí và tự tin trong việc đón nhận những bài toán khó nảy sinh từ thực tiễn sản xuất.
Chúng tôi hy vọng rằng cuốn sách này sẽ là một cẩm nang tốt cho những ai
muốn hiểu sâu sắc về Giải tích toán học nói chung, và về giải tích các hàm số
nhiều biến nói riêng. Do đó, nó sẽ là hữu ích đối với các học sinh cao học, cũng
như thầy và trò các trường Tổng hợp, Sư phạm, Kỹ thuật,...
Tập thể tác giả xin chân thành cảm ơn giáo sư Nguyễn Duy Tiến (ĐHQG Hà
Nội) và giáo sư Đoàn Quỳnh (ĐHSP Hà Nội) đã đọc rất kỹ bản thảo và đã cho
những nhận xét quý báu. Việc trình bầy một chủ đề phức tạp sẽ không thể tránh
khỏi những sai sót, cho nên chúng tôi mong tiếp tục nhận được sự phê bình, góp ý
của các đồng nghiệp và học viên gửi về theo địa chỉ: Viện Toán học, Trung tâm
Khoa học Tự nhiên và Công nghệ Quốc gia, 18-Đường Hoàng Quốc Việt, Quận Cầu Giấy, Hà Nội. CÁC TÁC GIẢ ii Chương 1 Không gian Rn & Không gian metric
1.1. Không gian Rn........................................................................................................ 1
1.1.1. Điểm trong không gian n-chiều......................................................................................... 2
1.1.2. Vectơ trong không gian n-chiều........................................................................................ 3
1.1.3. Tích vô hướng ................................................................................................................... 4
1.1.4. Chuẩn của vectơ ................................................................................................................ 5
1.1.5. Ánh xạ tuyến tính .............................................................................................................. 7
1.2. Không gian metric............................................................................................... 10
1.2.1. Định nghĩa và các ví dụ................................................................................................... 10
1.2.2. Tập đóng và tập mở trong không gian metric ................................................................. 12
1.2.3. Hội tụ trong không gian metric ....................................................................................... 15
1.2.4. Tính đầy đủ trong không gian metric .............................................................................. 17
1.2.5. Tính compact trong không gian metric ........................................................................... 19
1.2.6. Ánh xạ trong không gian metric...................................................................................... 24
1.2.7. Không gian siêu metric ................................................................................................... 27
1.1. Không gian Rn
Trong giáo trình này chúng ta sẽ làm việc trên không gian Rn - một ví dụ rất
đặc biệt của không gian n-chiều. Để giáo trình có được tính độc lập nhất định,
chúng tôi sẽ trình bày lại một cách ngắn gọn việc xây dựng không gian Rn. Độc giả
nào quan tâm đến lý thuyết không gian n-chiều nói chung xin xem trong các giáo
trình Đại số tuyến tính. Độc giả nào đã học qua giáo trình Đại số tuyến tính có thể bỏ qua phần này. 2
Giải tích các hàm nhiều biến
1.1.1. Điểm trong không gian n-chiều Ta
đã quen thuộc với cách dùng một số để biểu diễn một điểm trên đường
thẳng (khi trên đường thẳng đó cho sẵn đơn vị dài). Ta cũng đã biết việc dùng một
cặp 2 số (x,y) để biểu diễn một điểm trong mặt phẳng có hệ tọa độ Descartes.
Tương tự như vậy, người ta sử dụng một bộ 3 số (x,y,z) để biểu diễn một điểm trong không gian.
Đường thẳng còn được gọi là không gian 1-chiều, mặt phẳng còn được gọi là
không gian 2-chiều, và không gian vật lý xung quanh ta còn được gọi là không
gian 3-chiều. Như vậy, một số biểu diễn một điểm trong không gian 1-chiều, một
cặp 2 số biểu diễn điểm trong không gian 2-chiều, và một bộ 3 số biểu diễn một
điểm trong không gian 3-chiều. Tuy rằng, ta không thể cho được minh họa hình
học của cách biểu diễn điểm trong không gian có số chiều lớn hơn 3, nhưng bằng
cách khái quát hóa, người ta có thể dùng một bộ n số để biểu diễn một điểm trong
không gian n-chiều. Không gian n-chiều với n ≥ 4 không phải chỉ là sự tưởng
tượng và khái quát hóa của các nhà toán học, mà chúng thật sự tồn tại trong vật lý,
kinh tế, xã hội... Thí dụ để biểu diễn nhiệt độ tại một điểm trong không gian xung
quanh ta thì ngoài 3-chiều thông thường ta phải thêm một chiều thời gian. Hoặc để
biểu diễn tình trạng sức khỏe của một người nào đó ta phải dùng bộ nhiều số: chiều
cao, trọng lượng, vòng ngực, huyết áp, độ thính, tầm nhìn... Chính xác hơn, với số
tự nhiên n cho trước, ta có:
Định nghĩa. Một điểm trong không gian n-chiều là một bộ n số có thứ tự ( 1 x , 2 x ,..., x ) n .
Người ta thường ký hiệu một điểm trong không gian n-chiều bằng một chữ đậm, thí dụ
như x, và viết x = ( 1 x , 2 x ,..., x ) n . Số i
x trong bộ số này được gọi là tọa độ thứ i của điểm x.
Giả sử có 2 điểm trong cùng một không gian n-chiều là a = ( 1 a , 2 a ,...,a )
n và b = ( 1 b , 2 b ,...,b ) n ,
ta định nghĩa tổng của chúng (a+b) là một điểm trong không gian n-chiều với các tọa độ là ( + + + 1 a 1 b , 2 a 2 b ,...,a b ) n n ,
và ta định nghĩa tích của điểm a với một số λ là một điểm với các tọa độ là (λ λ λ 1 a , 2 a ,..., a ) n .
Thí dụ. Trong không gian 3-chiều, với a = (1,3,5), b = (2,0,1), λ = 7, ta có
a+b = (3,3,6) và λa = (7,21,35).
Người ta ký hiệu 0 là điểm (trong không gian n-chiều) có tất cả các tọa độ
bằng 0 (tức là 0 = (0,0,...,0)) và gọi nó là điểm gốc, còn -a là điểm (-1)a (tức là
điểm có các tọa độ ngược dấu với các tọa độ điểm a). Khi ấy dễ dàng kiểm tra rằng
các phép tính trên thỏa mãn các luật sau:
Chương 1. Không gian Rn và không gian metric 3
(1) (a + b) + c = a + (b + c) ;
(2) a + b = b + a ;
(3) λ(a + b) = λa + λb ;
(4) (λ + µ)a = λa + µa và (λµ)a = λ(µa) , với mọi số λ, µ;
(5) 0 + a = a + 0 = a với mọi a ;
(6) 1.a = a và a + (-a) = 0 .
Từ đây người ta cũng quy ước viết a - b thay cho a +(- b) .
Chứng minh các đẳng thức trên là dễ dàng, người đọc có thể tự làm như các
bài tập. Để làm thí dụ, chúng ta chứng minh đẳng thức (3). Theo
định nghĩa a + b = ( + + 1 a 1 b ,...,a b ) n n , nên
λ(a + b) = (λ( + λ + = λ + λ λ + λ = λa + λ 1 a 1 b ),..., (a b )) ( 1 a 1 b ,..., a b ) n n n n b .
1.1.2. Vectơ trong không gian n-chiều
Người ta gọi mỗi cặp điểm a, b trong không gian n-chiều là một vectơ buộc
(hay vectơ định vị) trong không gian n-chiều.
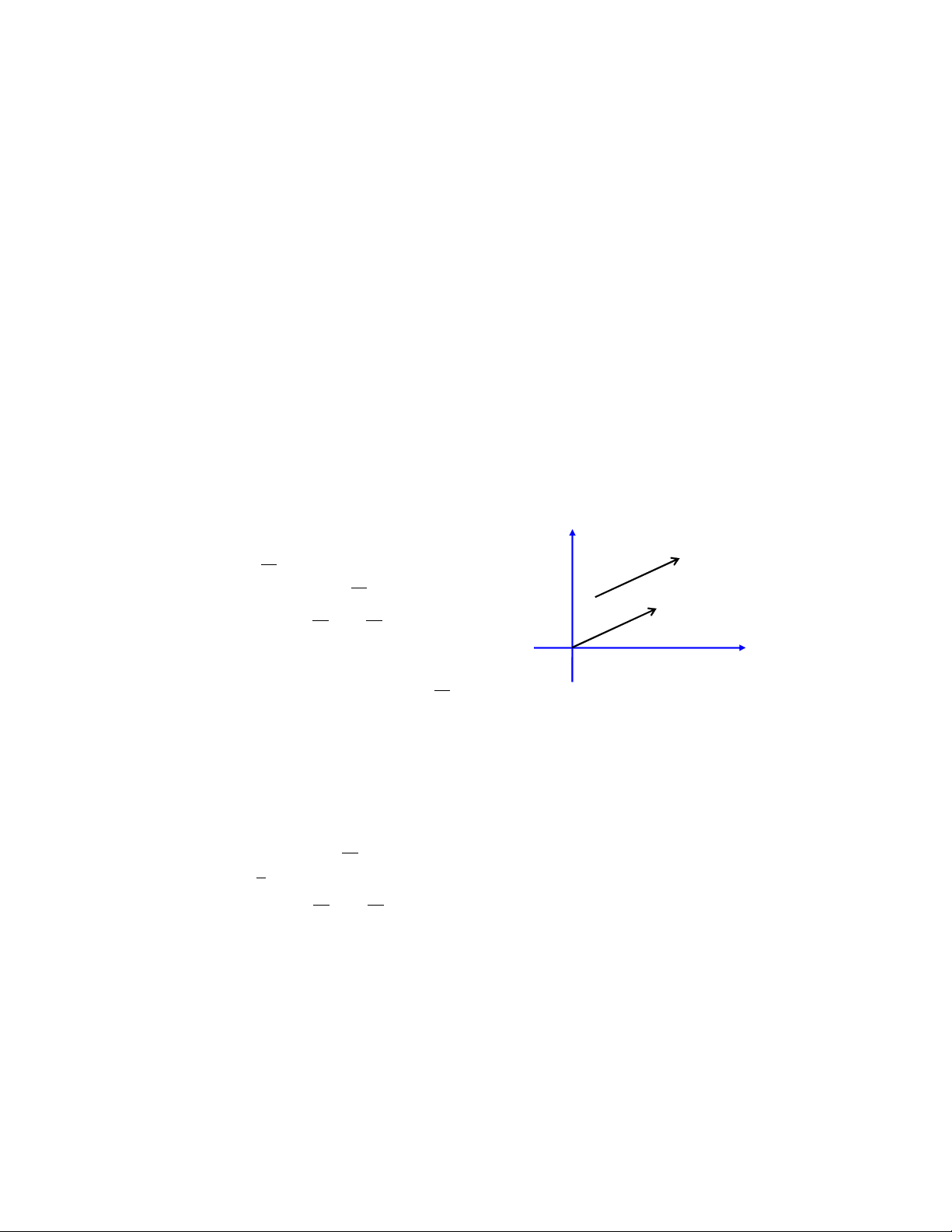
Vectơ xác định bởi cặp điểm a, b được ký b
hiệu là ab . Người ta gọi a là điểm đầu, b là a
điểm cuối, và còn gọi ab là vectơ định vị tại a. b-a Hai
vectơ ab và cd được gọi là tương
đẳng nếu chúng thỏa mãn điều kiện
b − a = d − c . 0 Theo
định nghĩa đó, vectơ ab là tương Hình 1.1
đẳng với vectơ định vị tại gốc 0 và có điểm cuối là b-a. Rõ ràng, chỉ có duy nhất
một vectơ định vị tại gốc tương đẳng với một vectơ cho trước (vì dễ thấy rằng nếu
2 vectơ tương đẳng mà cùng định vị tại gốc thì điểm cuối của chúng cũng trùng
nhau). Điều này được minh họa trong trường hợp 2-chiều như hình vẽ bên.
Vectơ định vị tại gốc được xác định hoàn toàn bởi điểm cuối của nó, cho nên
trong không gian n-chiều ta có mối tương quan 1-1 giữa điểm và vectơ định vị tại
gốc. Như vậy một bộ n số có thể được xem là tọa độ của một điểm a hay của một
vectơ định vị tại gốc 0a , và để cho thuận tiện người ta viết vectơ này một cách đơn
giản là a hay thậm chí là a, trong trường hợp không sợ xảy ra nhầm lẫn. Hai
vectơ ab và cd được gọi là song song nếu tồn tại số λ ≠ 0 sao
cho b − a = λ(d − c) . Khi số λ là dương thì ta nói rằng chúng cùng hướng (hay
cùng chiều), và trong trường hợp ngược lại ta nói rằng chúng ngược hướng (hay
ngược chiều) nhau. 4
Giải tích các hàm nhiều biến
Như vậy, hai vectơ là song song với nhau khi và chỉ khi các vectơ định vị tại
gốc tương đẳng với chúng sai khác nhau một hệ số (khác 0). Nghĩa là, khái niệm
song song ở đây hoàn toàn phù hợp với những gì biết trong trường hợp không gian
2-chiều hoặc 3-chiều (trong giáo trình Hình học giải tích). 1.1.3. Tích vô hướng
Định nghĩa. Tích vô hướng của 2 vectơ a = ( 1 a , 2 a ,...,a )
n và b = ( 1 b , 2 b ,...,b ) n
là một số (ký hiệu là a.b ) xác định như sau:
a.b := + + + 1 a 1 b 2 a 2 b ... n a n b .
(Trong một số giáo trình, để phân biệt tích vô hướng của 2 vectơ với tích thông
thường của 2 số, người ta còn ký hiệu tích vô hướng của 2 vectơ a và b là (a,b)
hay a,b . Tuy nhiên, trong giáo trình này, khi cần phân định rõ sự khác biệt giữa
các vectơ với các số thông thường, chúng ta sẽ dùng phông chữ đậm để biểu diễn
vectơ, cho nên sẽ không xảy ra sự lẫn lộn giữa 2 khái niệm đã nói. Vì vậy, chúng ta
sẽ sử dụng cách ký hiệu đơn giản như đã trình bày trên, như rất nhiều tài liệu nước
ngoài hiện nay, và sẽ chỉ sử dụng ký hiệu <.,.> khi nào thấy cần thiết).
Tính chất. Từ định nghĩa trên ta thấy tích vô hướng của 2 vectơ có những tính chất sau:
1) a.b = . b a ;
2) a.(b + c) = . a b + .
a c = (b + c).a ; 3) ( .
α a).b = .
α (a.b) , với mọi số α ;
4) a.a ≥ 0 , và a.a = 0 khi và chỉ khi a = 0.
Chứng minh. Việc kiểm tra các Tính chất 1 và 3 là dễ dàng và dành lại cho người
đọc. Ta kiểm tra các tính chất còn lại. Đẳng thức đầu trong Tính chất 2 suy ra từ nhận xét sau .(
a b + c) = + + + + + + = 1 a ( 1 b 1 c ) 2 a ( 2 b 2
c ) ... a (b c ) n n n = ( + + + + + + + = a b + 1 a 1 b 2 a 2 b ... a b ) ( n n 1 a 1 c 2 a 2 c ... a c ) n n . a.c
và đẳng thức sau suy ra từ Tính chất 1.
Phần xuôi của Tính chất 4 có ngay từ định nghĩa, còn phần ngược lại thì rút ra
từ nhận xét rằng nếu trong bộ số ( 1 a , 2 a ,...,a )
n có một phần tử nào đó khác 0, thí dụ là i a , thì 2 2 2 2
a.a = + + + ≥ > 1 a 2 a ... a a 0 n i .
Các tính chất đã được kiểm tra xong.
Chương 1. Không gian Rn và không gian metric 5
Để cho thuận tiện người ta hay viết 2 a thay cho .
a a . Lưu ý rằng đây chỉ là quy
ước mang tính hình thức và không có liên quan gì đến phép lũy thừa (hoàn toàn vô nghĩa khi viết 3
a ). Tuy nhiên người đọc có thể dễ dàng kiểm tra các “hằng đẳng
thức” tương tự sau đây: 2 2 2
(a + b) = a + 2 .
a b + b , 2 2 2
(a − b) = a − 2a.b + b . Hai
vectơ a và b được gọi là vuông góc với nhau nếu a.b = 0 . Trong
trường hợp không gian 2-chiều và 3-chiều khái niệm vuông góc ở đây
hoàn toàn trùng hợp với khái niệm vuông góc thông thường. 1.1.4. Chuẩn của vectơ
Bổ đề sau đây có tên là bất đẳng thức Schwarz và sẽ đóng vai trò quan trọng trong lý thuyết vectơ.
Bổ đề (Schwarz). Với 2 vectơ a, b ta luôn có 2
(a.b) ≤ ( . a a).( . b b) .
Chứng minh. Với a = 0 thì bất đẳng thức trên là hiển nhiên. Khi a ≠ 0 từ Tính
chất 4 ta có (ta + b,ta + b) ≥ 0 , với mọi số t. Suy ra 2 2 2
a t + 2a t
b + b ≥ 0 , với mọi t .
Theo định lý về dấu của tam thức bậc 2 (biến t) ta có: 2 2 2
(ab) − a b ≤ 0 .
Đây chính là điều cần chứng minh.
Định nghĩa. Chuẩn (hay độ dài) của vectơ a, ký hiệu là ||a||, là một số xác định như sau: ||a|| = . a a .
Dưới dạng tọa độ thì công thức trên có nghĩa là ||a|| = 2 2 2 + + + 1 a 2 a ... n a ,
và trong trường hợp không gian 2-chiều hoặc 3-chiều thì nó hoàn toàn trùng hợp
với công thức tính độ dài theo định lý Pythagoras.
Rõ ràng vectơ có chuẩn bằng 0 khi và chỉ khi tất cả các tọa độ của nó bằng 0.
Từ bổ đề Schwarz, sau khi lấy căn 2 vế, ta thu được công thức rất hay được sử dụng sau này là
|(a.b)| ≤ ||a||.||b|| . 6
Giải tích các hàm nhiều biến
Ngoài ra độ dài còn có những tính chất quan trọng sau: Định lý
Với số α và các vectơ a, b ta có
||α.a|| = |α|.| a|| ;
||a+b|| ≤ ||a|| + ||b|| .
Chứng minh. Theo định nghĩa ta có 2 2 2 2
|| αa | = (αa).(αa) = α (a.a) = α || a || .
Lấy căn 2 vế ta được đẳng thức cần chứng minh.
Tiếp theo, từ bổ đề Schwarz ta có
2a.b ≤ 2.||a||.||b| .
Theo định nghĩa của chuẩn dễ dàng suy ra bất đẳng thức trên tương đương với 2 2
a.a + 2a.b + . b b
≤ || a || +2 | a | .| b | + || b | . Điều này có nghĩa là
( + ).( + ) ≤ (|| || + | ||)2 a b a b a b .
Sau khi khai căn 2 vế ta thu được điều cần chứng minh.
Bất đẳng thức trong định lý trên thường được gọi là bất đẳng thức tam giác, vì về
mặt hình học nó khẳng định một điều rất quen thuộc là: độ dài của một cạnh trong
tam giác không thể vượt quá tổng độ dài của 2 cạnh còn lại.
Hệ quả (Định lý Pythagoras) Nếu 2 vectơ a và b vuông góc với nhau thì 2 2 2
|| a + b || |
= a || + || b || . Chứng minh. Ta có 2 2 2 2 2 2
|| a + b || = (a + b) = a + 2a.b + b ||
= a || + || b || , do 0 a.b = . Ta
định nghĩa khoảng cách giữa 2 vectơ a và b là chuẩn của hiệu 2 vectơ đó, nghĩa là bằng
|| a − b || =
(a − b).(a − b) .
Các vectơ nói đến ở đây đều là vectơ định vị tại gốc nên hoàn toàn được xác định
bởi điểm cuối. Khoảng cách giữa 2 vectơ cũng có thể được xem như khoảng cách
giữa 2 điểm cuối của chúng, và do đó ta cũng có khái niệm khoảng cách giữa 2
điểm trong không gian n-chiều.
Chương 1. Không gian Rn và không gian metric 7 Với a = ( 1 a , 2 a ,...,a )
n , b = ( 1 b , 2 b ,...,b )
n ta có thể viết lại công thức định nghĩa
khoảng cách dưới dạng: 2 2 2
|| a − b || = ( − + − + + − 1 a 1 b ) ( 2 a 2 b ) ... (a b ) n n .
Rõ ràng, khoảng cách giữa a và b là bằng khoảng cách giữa b và a, và hoàn toàn
trùng hợp với khái niệm khoảng cách mà ta đã biết khi không gian là 2-chiều hoặc
3-chiều. Từ các tính chất của chuẩn, ta dễ dàng suy ra khoảng cách giữa 2 vectơ (2
điểm) có những tính chất đặc trưng sau đây:
(1) || a − b || ≥ 0 ;
(2) || a − b | = 0 khi và chỉ khi a = b ;
(3) || a − b || = || b − a || ;
(4) || a − b || ≤ || a − c || + || c − b || .
Chứng minh. Các Tính chất (1),(2),(3) là hiển nhiên. Tính chất cuối cùng có ngay
từ bất đẳng thức tam giác, bởi vì a - b = (a - c) + (c - b).
Nhận xét. Như vậy ta đã xây dựng được không gian các vectơ (các điểm) trên cơ
sở các bộ n số và trang bị trên đó các phép tính cộng, nhân với số, tích vô hướng và
khái niệm khoảng cách. Không gian này có tên gọi là không gian Euclid n-chiều và
được ký hiệu là Rn. Đây là một không gian có nhiều tính chất thú vị và sẽ đóng vai
trò nền tảng trong suốt giáo trình Giải tích các hàm nhiều biến. Sau này, khi đã làm
việc quen với không gian Rn và không còn sự nhầm lẫn giữa số và bộ n số, chúng
ta có thể dùng chữ thường để biểu thị bộ số hay điểm trong không gian nhiều chiều
(mà không nhất thiết phải dùng chữ đậm như trong mục này).
1.1.5. Ánh xạ tuyến tính Phép
ứng A từ không gian Rn vào không gian Rm được gọi là một ánh xạ
tuyến tính nếu nó có các tính chất sau đây:
(i) A(x + y) = A(x) + A(y) , ∀x, y ∈ Rn ;
(ii) A(λx) = λA(x) , ∀λ∈ R , ∀x∈Rn . Ta
gọi các vectơ e = e = e = 1
(1,0,...,0) , 2 (0,1,...,0) ,..., (0,0,...,1) n trong Rn là
các vectơ trục đơn vị . Dễ dàng thấy rằng một vectơ bất kỳ x = ( 1 x , 2 x ,..., x ) n được
biểu diễn qua các vectơ trục đơn vị bằng công thức sau x = + + +
= e + e + + 1 x (1,0,...,0) 2
x (0,1,...,0) ... x (0,0,..., ) 1 1 x 1 2 x 2 ... n n x n e 8
Giải tích các hàm nhiều biến
và do các tính chất (i)-(ii) ta suy ra ảnh của x qua phép ánh xạ tuyến tính A sẽ
được biểu diễn qua ảnh của các vectơ trục đơn vị theo công thức sau
A(x) = A e + A e + + 1 x ( 1) 2 x
( 2) ... x A(e ) n n . (*) Mỗi ( A ) i
e là một phần tử trong Rm , cho nên nó sẽ là một bộ m số, ký hiệu
là (a 1,a 2,...,a ) i i
im . Ta thiết lập một ma trận chữ nhật A gồm m hàng và n cột, với
các cột là các bộ số A( ) i
e , tức là A := [ A( 1 e ) A( 2
e ) ... A(e ) n ] , hay 11 a 2 a 1 ... a 1 n 12 a 2 a 2 ... n a 2 A := . ... ... ... ... 1 a m 2 a ... m n a m
Ma trận này được gọi là ma trận của ánh xạ tuyến tính A .
Nếu ta coi mỗi vectơ như là một ma trận cột thì ta có thể viết + + 1 x a x ... a x 11 1 1 n n x
a x +...+ a x 2 12 1 n2 n x =
và, do công thức (*), A(x) = . # """"""" n x + + 1 a m 1 x ... n a m n x
Theo phép nhân các ma trận thì công thức (*) có thể được viết lại dưới dạng đơn giản là
A(x) = Ax . (**)
Ngược lại, nếu có một ma trận A (cỡ m×n) thì ta thiết lập được một phép ứng từ
không gian Rn vào không gian Rm theo công thức (**). Với các tính chất của phép
nhân và cộng các ma trận (đã biết trong giáo trình Đại số tuyến tính), ta dễ thấy
rằng phép ứng này thỏa mãn các điều kiện (i)-(ii), cho nên nó là một ánh xạ tuyến
tính. Như vậy, ta có một phép tương ứng giữa tập các ánh xạ tuyến tính (từ không
gian Rn vào không gian Rm ) và tập các ma trận chữ nhật (cỡ m×n). Trong
trường hợp riêng, khi n = m thì A là một ma trận vuông (cấp n) và ánh
xạ tương ứng với nó là một ánh xạ từ không gian Rn vào chính nó (hay còn gọi là
một phép biến đổi trong Rn ). Ta nói ánh xạ tuyến tính là không suy biến nếu như
ma trận tương ứng với nó là không suy biến, tức là có định thức khác 0. Từ giáo
trình Đại số tuyến tính ta biết rằng một ma trận vuông không suy biến có ma trận
nghịch đảo, và dễ dàng kiểm tra rằng ánh xạ tuyến tính tương ứng với ma trận
nghịch đảo này là ánh xạ ngược của ánh xạ ban đầu. Cho nên, mỗi phép biến đổi
không suy biến là một song ánh.
Chương 1. Không gian Rn và không gian metric 9
Người ta định nghĩa chuẩn của ánh xạ tuyến tính A , kí hiệu || A || , là số xác định như sau:
|| A | := sup{ || A(x) ||: x ∈ B(0,1)},
trong đó ta kí hiệu B(0,1) là quả cầu đơn vị trong Rn , tức là tập hợp các vectơ có
độ dài (chuẩn) không vượt quá 1.
Để ý rằng với x = ( ∈ 1
x ,..., x ) B(0,1) n thì | | || x || 1 i x ≤
≤ với mọi i = 1,...,n,
cho nên từ công thức (*) ta suy ra được || A || là một số hữu hạn (không vượt quá
tổng của chuẩn các ảnh của n vectơ trục đơn vị).
Với mọi vectơ x ≠ 0, ta có ( x / || x || ) là vectơ nằm trong quả cầu đơn vị, và do
tính tuyến tính của A ta có: 1 A(x)
|| A(x) || = = x A ≤ | A || , || x || || x || || x | hay là
|| A(x) || ≤ | A || .| x | .
Rõ ràng với x = 0 bất đẳng thức này vẫn đúng, cho nên nó đúng với mọi x. Đây là
một công thức quan trọng, vì nó phản ánh tính liên tục của ánh xạ tuyến tính trong
không gian hữu hạn chiều (như sẽ thấy sau này). Các ánh
xạ tuyến tính là đối tượng được nghiên cứu kỹ trong giáo trình Đại số
tuyến tính, cho nên trong giáo trình này ta sẽ không đi sâu. Tuy nhiên, do vai trò quan
trọng trong rất nhiều lĩnh vực, chúng sẽ được đề cập đến nhiều hơn về khía cạnh thực hành tính toán.
Nhận xét. Không gian Rn là sự mở rộng của các không gian 2-chiều, 3-chiều và
được thừa hưởng nhiều thuộc tính mà ta đã quen biết từ những năm phổ thông. Tuy
nhiên, đối tượng nghiên cứu của Toán học là vô cùng rộng rãi và rất nhiều không
gian mà nó đề cập (với các phần tử không nhất thiết là các bộ số) thường không có
được tất cả các tính chất giống như của Rn . Những không gian chỉ được trang bị
các phép tính cộng, nhân với số (với các tính chất giống như trong Rn) được gọi là
các không gian có cấu trúc tuyến tính và được nghiên cứu kỹ trong giáo trình Đại
số tuyến tính. Những không gian không có được cấu trúc tuyến tính, nhưng lại
được trang bị khái niệm khoảng cách (với các tính chất giống như trong Rn) được
gọi là không gian metric. Không gian này và các dạng tổng quát của nó được
nghiên cứu kỹ trong lý thuyết Tôpô và là một phần rất quan trọng của giáo trình
Giải tích hàm. Tuy nhiên, không gian metric cũng là một công cụ tiện lợi trong 10
Giải tích các hàm nhiều biến
nghiên cứu hàm nhiều biến, cho nên chúng ta cần biết một số khái niệm cơ bản về nó.
1.2. Không gian metric
1.2.1. Định nghĩa và các ví dụ
Định nghĩa. Không gian metric là một tập hợp E≠∅ được trang bị một phép
ứng mỗi cặp điểm p,q∈E với một số thực d(p,q) sao cho
(1) d ( p, q) ≥ 0 ,
∀p,q ∈ E ;
(2) d ( p, q) = 0 ⇔ p = q ;
(3) d ( p, q) = d (q, p) ,
∀p,q ∈ E ;
(4) d ( p, q) ≤ d ( p, r) + d (r, q) ,
∀p,q,r ∈ E (bất đẳng thức tam giác).
Như vậy không gian metric là một cặp (E,d), trong đó E là một tập hợp và d là
một hàm số d : E×E→R thỏa mãn các Tính chất (1)-(4). Thông thường, khi nói về
một không gian metric nào đó với hàm d mà mọi người đều hiểu là gì rồi thì người
ta chỉ dùng tập E để biểu thị thay cho cả cặp (E,d). Điều này tuy không đúng về
mặt logic, nhưng lại thuận tiện cho nên được mọi người chấp nhận.
Số d(p,q) được gọi là khoảng cách giữa 2 điểm p, q, và hàm d được gọi là hàm
khoảng cách hay là metric.
Thí dụ 1. Với E = Rn và hàm d được định nghĩa như sau 2 2 d(a,b) |
= a −b | = ( − + + − 1 b 1 a ) ... (b a ) n n
thì từ các tính chất của khoảng cách trong Rn ta suy ra cặp (Rn,d) là một không
gian metric. Nó sẽ là một không gian metric điển hình trong giáo trình này, và
metric xác định như trên sẽ được coi là metric thông thường trên Rn . Trong
trường hợp đặc biệt, khi n = 1, ta có trục số thực R cũng là một không
gian metric với định nghĩa khoảng cách giữa hai số là giá trị tuyệt đối của hiệu của chúng.
Thí dụ 2. Với E = Rn và hàm d được định nghĩa như sau
d(a,b) = | − + + − 1 b 1 a | ... | b a | n n
Chương 1. Không gian Rn và không gian metric 11
thì cặp (Rn,d) cũng là một không gian metric (người đọc tự kiểm tra như một bài tập).
Thí dụ 3. Với E = Rn ta định nghĩa hàm d như sau
d(a,b) = max{ | b − a | , i =1,2,..., i i n}
thì cũng dễ dàng thấy rằng cặp (Rn,d) là một không gian metric (người đọc tự kiểm tra như một bài tập).
Thí dụ 4. Khi (E,d) là một không gian metric thì mỗi tập con ⊂ 1 E E cùng với thu hẹp của d trên 1 E × 1
E cũng tạo thành một không gian metric, được gọi là không
gian metric con của E và thường được ký hiệu là ( 1 E ,d).
Thí dụ 5. Với E là một tập bất kỳ, ta định nghĩa 0 khi p = q ,
d( p,q) = 1 khi p ≠ q .
Rõ ràng d thỏa mãn mọi điều kiện của một hàm khoảng cách và cặp (E,d) là một
không gian metric. Tuy nhiên không gian này có cấu trúc đơn giản tới mức chẳng
cung cấp cho ta một thông tin đáng kể nào. Cho nên phương pháp xác định hàm
khoảng cách sẽ là yếu tố thực sự đem lại cấu trúc cho một không gian metric.
Mệnh đề. Với các điểm 1 p , 2 p ,..., n
p trong không gian metric E ta luôn có d( ≤ + + + 1
p , p ) d( 1 p , 2 p ) d( 2 p , 3
p ) ... d( p 1, p ) n n− n .
Chứng minh. Suy từ việc áp dụng bất đẳng thức tam giác lặp lại n-1 lần d( ≤ + ≤ + + ≤ 1
p , p ) d ( 1 p , 2 p ) d( 2
p , p ) d( 1 p , 2 p ) d ( 2 p , 3 p ) d ( 3 p , p ) ... n n n
Mệnh đề. Với các điểm 1 p , 2 p , 3
p trong không gian metric E ta luôn có | d ( − ≤ 1 p , 3 p ) d( 2 p , 3 p ) | d( 1 p , 2 p ) .
(Nghĩa là: Hiệu của 2 cạnh trong tam giác luôn nhỏ hơn cạnh còn lại).
Chứng minh. Từ bất đẳng thức tam giác ta có d( ≤ + ≤ + 1 p , 3 p ) d( 1 p , 2 p ) d ( 2 p , 3 p ) và d( 2 p , 3 p ) d ( 2 p , 1 p ) d( 1 p , 3 p ) .
Các bất đẳng thức này có thể viết lại thành d( − ≤ − ≤ 1 p , 3 p ) d( 2 p , 3 p ) d ( 1 p , 2 p ) và d( 2 p , 3 p ) d( 1 p , 3 p ) d ( 1 p , 2 p ) ,
chính là điều cần chứng minh. 12
Giải tích các hàm nhiều biến
1.2.2. Tập đóng và tập mở trong không gian metric Ta
đã biết khái niệm về tập đóng và tập mở trong R. Một cách tương tự, ta có
thể định nghĩa khái niệm này trong không gian metric (nói chung) và trong Rn (nói
riêng). Trước hết ta đưa ra định nghĩa quả cầu trong không gian metric.
Quả cầu mở trong không gian metric (E,d) với tâm tại p ∈ E và bán kính
r > 0 là tập hợp
B( p,r) :={q ∈ E : d ( p,q) < } r .
Quả cầu đóng trong không gian metric (E,d) với tâm tại p ∈ E và bán kính
r > 0 là tập hợp
B( p,r) :={q ∈ E : d( p,q) ≤ r}.
Khi ta không chỉ rõ tâm và bán kính thì ta chỉ cần nói quả cầu thay cho việc nói
quả cầu với tâm là một điểm nào đó và với bán kính là một số dương nào đó.
Thí dụ. Với E = R3 và với metric thông thường thì khái niệm quả cầu như trên
hoàn toàn trùng hợp với quả cầu theo ngôn ngữ đời thường, còn với metric như
trong Thí dụ 3 thì quả cầu sẽ là một hình lập phương (theo ngôn ngữ đời thường).
Quả cầu thông thường không kể phần mặt cầu thì là quả cầu mở, và nếu kể
cả mặt cầu thì là quả cầu đóng.
Với E = R2 và với metric thông thường thì quả cầu là một hình tròn, còn với
metric như trong Thí dụ 3 thì quả cầu là một hình vuông (theo ngôn ngữ thông
thường). Hình tròn không kể vòng tròn bao quanh thì là hình tròn mở, và nếu kể cả
vòng tròn bao quanh thì là hình tròn đóng.
Với E = R thì quả cầu mở chính là một khoảng và quả cầu đóng chính là một
đoạn. Ngược lại, một khoảng (a,b) bất kỳ luôn có thể được xem là một quả cầu mở với tâm tại điểm a b p + = và bán kính b a r − = , vì 2 2 a −b a + b b − a < < ⇔ < − < ⇔ | a + b − | b − a a x b x x < . 2 2 2 2 2
Tương tự như vậy đối với đoạn.
Định nghĩa. Tập con S trong không gian metric E được gọi là mở nếu, với
mỗi p ∈ S , tập này chứa cả một quả cầu tâm p (với bán kính nào đó).
Rõ ràng, khi E = R, khái niệm tập mở ở đây hoàn toàn trùng hợp với khái
niệm tập mở mà ta đã đưa ra trước đây (trong giáo trình Giải tích một biến). Khái
Chương 1. Không gian Rn và không gian metric 13
niệm tập mở (hay không mở) chỉ có nghĩa khi nó là một tập con trong không gian metric.
Mệnh đề. Trong không gian metric E bất kỳ ta luôn có
(1) Tập rỗng ∅ là mở ;
(2) Cả không gian E là mở ;
(3) Hợp của một họ (bất kỳ) tập mở là một tập mở ;
(4) Giao của một họ hữu hạn tập mở là một tập mở .
Chứng minh. Phần (1) là hiển nhiên, vì tập rỗng không chứa điểm nào nên nó
chẳng phải chứa quả cầu nào. Phần (2) cũng là rõ ràng vì mọi quả cầu đều nằm
trong E, nghĩa là E chứa mọi quả cầu với tâm ở bất kỳ điểm nào. Phần (3) dễ dàng
suy ra từ định nghĩa, vì một tập nào đó trong họ mà đã chứa một quả cầu thì hợp
của cả họ ắt phải chứa quả cầu đó. Ta chỉ còn phải chứng minh phần còn lại.
Trường hợp giao của họ các tập mở Si (i=1,2,...,N) là một tập rỗng thì Phần
(1) cho ta điều cần chứng minh.
Trường hợp giao của họ các tập mở Si (i=1,2,...,N) là một tập S khác rỗng thì N
với mỗi điểm p ∈ S := ∩Si ta sẽ chỉ ra rằng tìm được quả cầu tâm p nằm gọn i 1 =
trong S. Thật vậy, do mỗi tập S ∈
i là mở và p
Si , ta tìm được quả cầu tâm p bán kính = i
r nằm gọn trong Si . Lấy r min{ 1r, 2r,...,r } N
, ta dễ dàng thấy rằng quả cầu
tâm p với bán kính r nằm trong quả cầu tâm p bán kính ir (và do đó nằm gọn trong S =
i ), với mọi i
1,2,..., N . Điều này chứng tỏ quả cầu tâm p bán kính r nằm
trong giao của tất cả các tập Si , nghĩa là nó nằm trong S và mệnh đề đã được chứng minh xong.
Nhận xét. Trong giáo trình Giải tích một biến chúng ta đã biết tôpô trên trục số
thực là một họ các tập con thỏa mãn các điều kiện tương tự như họ tập mở nêu
trong mệnh đề trên. Dễ dàng thấy rằng khái niệm tôpô này có thể mở rộng ra cho
tập bất kỳ, và một tập hợp có tôpô được gọi là một không gian tôpô. Như vậy,
mệnh đề trên nói rằng không gian metric là một không gian tôpô (với tôpô là họ các tập mở).
Để giải tỏa mối băn khoăn về sự “xung khắc có thể xảy ra” giữa 2 khái niệm
mở (quả cầu mở và tập mở), ta có mệnh đề sau
Mệnh đề. Quả cầu mở trong không gian metric là một tập mở.
Chứng minh. Cho quả cầu mở bất kỳ B(p,r). Lấy điểm q bất kỳ trong B(p,r), ta chỉ
ra rằng tồn tại quả cầu có tâm tại q (với bán kính nào đó) nằm gọn trong B(p,r).
Thật vậy, do q nằm trong B(p,r) nên d(p,q) < r. Lấy số dương (
s < r − d p,q) ta
có B(q, s) ⊂ B( p,r) , vì rằng 14
Giải tích các hàm nhiều biến
d(q, x) < s ⇒ d ( p, x) ≤ d( p,q) + d(q, x) < d( p,q) + s < r .
Mệnh đề đã được chứng minh xong.
Như vậy đối với quả cầu thì 2 khái niệm mở thực chất chỉ là một.
Nhận xét. Từ 2 mệnh đề trên ta thấy rằng tập mở chính là hợp của các quả cầu mở.
Thật vậy, hợp của các quả cầu mở cho ta một tập mở. Ngược lại, một tập mở có thể
xem là hợp của tất cả các quả cầu nằm trong nó (mỗi điểm của tập mở đều nằm
trong một quả cầu như vậy, nên hợp của tất cả các quả cầu này đương nhiên chứa
tất cả các điểm của tập).
Lưu ý. Giao của một họ vô hạn các tập mở không nhất thiết là một tập mở. Thí dụ,
trong không gian Rn, giao của họ các quả cầu mở 1
B( p, ) với n=1,2,3,.., chỉ là n
một điểm p đơn độc và không phải là tập mở.
Định nghĩa. Một tập con S trong không gian metric E được gọi là đóng nếu
như phần bù của nó là một tập mở.
Nhắc lại rằng phần bù của một tập con S trong không gian E là C(S)=E \ S .
Để tránh nỗi băn khoăn về sự “xung khắc có thể xảy” ra giữa 2 khái niệm đóng đối với
quả cầu (quả cầu đóng và tập đóng) ta có mệnh đề sau đây khẳng định rằng về thực
chất chúng chỉ là một.
Mệnh đề. Quả cầu đóng trong không gian metric là một tập đóng.
Chứng minh. Lấy quả cầu đóng bất kỳ B( p, r) , ta chứng minh rằng phần bù của
nó là một tập mở. Rõ ràng phần bù của nó là
C[B( p,r)] = {x ∈ E : d( p, x) > r}.
Nếu nó rỗng thì đương nhiên nó là mở. Khi nó khác rỗng, ta lấy một điểm q bất kỳ
trong C[B( p,r)] và chỉ ra rằng có quả cầu tâm tại q nằm hoàn toàn
trong C[B( p,r)] . Thật vậy, do q ∈ C[B( p,r)] nên d( p, q) > r và ta tìm được số dương (
s < d p,q) − r . Dễ dàng kiểm tra rằng B(q, s) ⊂ C[B( p,r)] , bởi vì
x ∈ B(q, s) ⇒ d(q, x) < d( p,q) − r ⇒ d( p, x) ≥ d ( p,q) − d(q, x) > r .
Mệnh đề được chứng minh xong.
Tương tự như đối với các tập mở, ta có
Mệnh đề. Trong không gian metric E bất kỳ ta luôn có
(1) Cả không gian E là một tập đóng ;
(2) Tập rỗng ∅ là một tập đóng ;
(3) Giao của một họ (bất kỳ) tập đóng là một tập đóng ;
(4) Hợp của một họ hữu hạn tập đóng là một tập đóng .
Chương 1. Không gian Rn và không gian metric 15
Chứng minh. Các phần (1)-(2) suy ngay từ mệnh đề tương tự đối với tập mở. Các
phần (3)-(4) cũng suy từ mệnh đề ấy kết hợp với một kết quả đã biết trong lý
thuyết tập hợp là: Phần bù của hợp các tập là giao của các phần bù của các tập
này; và phần bù của giao các tập là hợp của các phần bù của các tập này.
Nhận xét. Dễ dàng thấy rằng phần bù của một điểm là một tập mở, cho nên mỗi
điểm là một tập đóng; và từ mệnh đề trên suy ra tập hợp gồm hữu hạn điểm là một
tập đóng. Mặt cầu S( p,r) :={x ∈ E : d ( p, x) = r} có thể xem là giao của quả cầu
đóng với phần bù của quả cầu mở (là một tập đóng) cho nên nó cũng là một tập đóng.
Một tập con trong không gian metric được gọi là giới nội nếu nó nằm trong
một quả cầu nào đó.
Thí dụ.Trong R với metric thông thường, một tập là giới nội nếu tồn tại số r > 0 để
đoạn [-r,r] chứa trọn tập ấy. Dĩ nhiên toàn bộ không gian R không phải là giới nội.
Thế nhưng nếu xét E = R với metric như trong Thí dụ 5 ở mục trước thì R lại là tập giới nội.
1.2.3. Hội tụ trong không gian metric
Sự hội tụ trong không gian metric nói chung cũng tương tự như sự hội tụ trên
trục số thực mà ta đã quen biết, nếu ta coi mỗi khoảng là một quả cầu và khoảng
cách giữa 2 số là trị tuyệt đối của hiệu của chúng. Chính xác hơn ta có định nghĩa sau:
Định nghĩa. Dãy các điểm 1 p , 2 p , 3
p ,... trong không gian metric E được gọi là
hội tụ đến điểm p ∈ E nếu, với mỗi số ε > 0 , tìm được số tự nhiên N sao cho
d( p, p ) < ε > n khi n N . Khi
ấy ta cũng nói rằng p là giới hạn của dãy { } n p , hay dãy { } n
p có giới hạn là p. Và viết lim = n p p . n→∞
Một dãy được gọi là hội tụ nếu nó hội tụ đến một điểm nào đó.
Nếu ta gọi quả cầu tâm p bán kính ε là một ε-lân cận của điểm p thì định
nghĩa trên có thể phát biểu như sau: Dãy các điểm 1 p , 2 p , 3
p ,... trong không gian metric E được gọi là hội tụ đến
điểm p ∈ E nếu, với mỗi số ε > 0 , tìm được số tự nhiên N để mọi p với n > N n
đều nằm trong ε-lân cận của p.



