




Preview text:
Bài tập Cấu trúc dữ liệu và giải thuật
Bài 1. Xét thuật toán tính giá trị của f(x,n)= thể hiện trong hàm F(x,n) sau đây: int F(int x, int n) { if (n= =0) return 1;
else if (n % 2 = = 0) return F(x,n/2)*F(x,n/2);
else return F(x,n/2)*F(x,n/2)*x; }
Gọi T(n) là thời gian tính của thuật toán nói trên.Giả thuyết là các phép toán số học
được thực hiện với thời gian bị chặn là hằng số.
a. Xác định công thức đệ quy cho T(n).
b. Giải công thức đệ quy để đưa ra đánh giá của T(n) trong tình huống tồi nhất.
Bài 2. Đối với mỗi một trong các kiểu cấu trúc dữ liệu sau đây: Danh sách nối đơn,
dánh sách nối kép, hàng đợi dùng mảng.Hãy vẽ cấu trúc dữ liệu có
được sau khi lần lượt
bổ sung các phần tử của dãy các khóa: 4,2,6,7,6,5 Bài 3.
a. Biểu diễn cách sử dụng ngăn xếp để chuyển biểu thức dạng trung tố về dạng hậu tố: a – b * c ^ d – f
b. Hãy trình diễn cách tính giá trị của biểu thức hậu tố sau sử dụng ngăn xếp: 1 2 + 3 1 + * 1 1 + 1 - /
Bài 4. Cho cây nhị phân ở hình bên.Hãy đưa ra thứ tự
các đỉnh xác định bởi duyệt cây theo thứ tự trước, giữa, sau.
Bài 5. Cho mảng A=(0,2,4,3,8,9,6,5,7) biểu diễn 1 Min-heap.
a. Vẽ cây nhị phân tương ứng với Min-heap đã cho.
b. Trình bày các thao tác cần thực hiện trên cây để bổ sung
thêm key=1 vào min-heap nói trên để thu được 1 min-heap mới.
Bài 6. Struct TreeNode { float key; struct TreeNode * LeftPtr; struct TreeNode * RightPtr; };
Typedef struct TreeNode BSTree;
a. Hãy viết hàm C sử dụng cấu trúc dữ liệu trên để thực hiện các thao tác sau đây với cây nhị phân. ● Tạo một nút mới.
BSTree *makeTreeNode(float value);
● Bổ sung một nút mới vào cây nhị phân tìm kiếm.
BSTree *insert(BSTree * nodePtr, float item);
b) Vẽ cây nhị phân tìm kiếm đối với tập các khóa S =(3,2,5,4,7,6,1) thu được nhờ thực
hiện bổ sung lần lượt các khóa theo thứ tự đã cho vào cây nhị
phân.Khởi tạo ban đầu là rỗng Bài tập chương 1 Phần 2
Bài 1. Xác định giá trị trả về của các hàm sau (dưới dạng 1 hàm của n), và phân tích thời gian thực hiện
trong trường hợp tồi nhất sử dụng ký hiệu O-lớn. a) Hàm mystery int mystery(int n) { int r = 0; for (int i = 1; i
for (int j = i + 1; j<=n; j++) for (int k = 1; k<=j; k++) r = r + 1; return r; } b) Hàm pesky int pesky(int n) { int r = 0;
for (int i = 1; i<= n; i++)
for (int j = 1; j<= i; j++)
for (int k = j; k<= i + j; k++) r = r + 1; return r; } c) Hàm prestiferous int prestiferous(int n) { int r = 0;
for (int i = 1; i<= n; i++)
for (int j = 1; j<= i; j++)
for (int k = j; k<= i + j; k++)
for (int l = 1; l<= i + j − k; l++) r = r + 1; return r; } d) Hàm conundrum int conundrum(int n) { int r = 0;
for (int i = 1; i<= n; i++)
for (int j = i + 1; j<= n; j++)
for (int k = i + j − 1; k<= n; k++) r = r + 1; return r; }
Bài 2. Xác định mối quan hệ giữa các cặp hàm 𝑓(𝑛), 𝑔(𝑛). Các mối quan hệ có thể có là
𝑓(𝑛) = Ο(𝑔(𝑛)), 𝑓(𝑛) = Ω(𝑔(𝑛)), 𝑓(𝑛) = Θ(𝑔(𝑛)).
a) 𝑓(𝑛) = log 𝑛2, 𝑔(𝑛) = log 𝑛 + 5.
b) 𝑓(𝑛) = √𝑛, 𝑔(𝑛) = log 𝑛2.
c) 𝑓(𝑛) = log 2 𝑛, 𝑔(𝑛) = log 𝑛.
d) 𝑓(𝑛) = 𝑛, 𝑔(𝑛) = log 2 𝑛.
e) 𝑓(𝑛) = 𝑛 log 𝑛 + 𝑛, 𝑔(𝑛) = log 𝑛.
f) 𝑓(𝑛) = 2𝑛, 𝑔(𝑛) = 10𝑛2
g) 𝑓(𝑛) = 10, 𝑔(𝑛) = log 10
h) 𝑓(𝑛) = 2𝑛, 𝑔(𝑛) = 3𝑛
Bài 3. Với mỗi cặp hàm 𝑓(𝑛), 𝑔(𝑛) sau thì quan hệ nào là đúng trong các quan hệ sau 𝑓(𝑛) = Ο(𝑔(𝑛)),
𝑔(𝑛) = Ο(𝑓(𝑛)), hoặc cả hai.
a) 𝑓(𝑛) = 𝑛(𝑛 − 1)/2, 𝑔(𝑛) = 6𝑛
b) 𝑓(𝑛) = 𝑛 + 2√𝑛, 𝑔(𝑛) = 3𝑛
c) 𝑓(𝑛) = 𝑛 + √𝑛, 𝑔(𝑛) = 𝑛2
d) 𝑓(𝑛) = 𝑛log𝑛, 𝑔(𝑛) = 𝑛√𝑛/3
e) 𝑓(𝑛) = 𝑛 + log𝑛, 𝑔(𝑛) = 3√𝑛 + 10
f) 𝑓(𝑛) = (log𝑛)2, 𝑔(𝑛) = 𝑛log√𝑛
g) 𝑓(𝑛) = 4𝑛 + 3log𝑛, 𝑔(𝑛) = 𝑛2 + √𝑛 Bài 4. Chứng minh
a) 2𝑛2 + 3𝑛 − 6 = Θ(𝑛2)
b) 𝑛2 + 2√𝑛 = Ο(2𝑛)
c) 𝑛3 − 3𝑛 + 3𝑛2 − 1 = Ω(𝑛2)
Bài 5. Xác định mối quan hệ giữa các cặp hàm 𝑓(𝑛) và 𝑔(𝑛) sau đây
a) 𝑓(𝑛) = 𝑛2.5 + 3(𝑛 − 1), 𝑔(𝑛) = 6𝑛
b) 𝑓(𝑛) = 𝑛2 + 3√𝑛 − 1), 𝑔(𝑛) = 𝑛3
c) 𝑓(𝑛) = 2𝑛2.5 + 𝑛, 𝑔(𝑛) = √𝑛5 Bài 6. Chứng minh
a) Nếu 𝑓1(𝑛) = Ο(𝑔1(𝑛)), và 𝑓2(𝑛) = Ο(𝑔2(𝑛)) thì 𝑓1(𝑛) + 𝑓1(𝑛) = Ο(𝑔1(𝑛) + 𝑔2(𝑛))
b) Nếu 𝑓1(𝑛) = Ω(𝑔1(𝑛)), và 𝑓2(𝑛) = Ω(𝑔2(𝑛)) thì 𝑓1(𝑛) + 𝑓1(𝑛) = Ω(𝑔1(𝑛) + 𝑔2(𝑛))
c) Nếu 𝑓1(𝑛) = Ο(𝑔1(𝑛)), và 𝑓2(𝑛) = Ο(𝑔2(𝑛)) thì 𝑓1(𝑛) ∙ 𝑓1(𝑛) = Ο(𝑔1(𝑛) ∙ 𝑔2(𝑛)) Bài 7. Chứng minh
a) 𝑎0 + 𝑎1𝑥 + 𝑎2𝑥2+. . +𝑎𝑛𝑥𝑛 = Ο(𝑥𝑛) với 𝑛 > 1, và các hằng số 𝑎0,𝑎1,. . , 𝑎𝑛là các hằng số bất kỳ
b) (𝑛 + 𝑎)𝑘 = Θ(𝑛𝑘) với 𝑘 ≥ 1, và 𝑎 là hằng số bất kỳ
Bài 8. Sắp xếp các hàm dưới đây theo thứ tự tăng dần độ phức tạp
a) 𝑛, √𝑛, 𝑛 + 3𝑛1/2, lg𝑛, 𝑛log𝑛, 𝑛 + 3ln𝑛, 𝑛2 + 3𝑛1.5, loglog𝑛, 2𝑛3 + loglog𝑛, 𝑛3,
𝑛 − 2𝑛2 + 3𝑛2.5, 𝑛!, (ln𝑛)2, 𝑛 + 2𝑛 log 𝑛5, 2𝑛
b) 6𝑛, (2 + 𝑎)10, (𝑛 + 3)2, 𝑛+2𝑛, 𝑛!, 𝑛loglog𝑛, 𝑛+5𝑛3, (1/3)𝑛 với 𝑎 là hằng số bất kỳ 𝑛 lg𝑛
Bài 9. Những khẳng định sau đây là đúng hay sai, tại sao? a) 3𝑛 = Ο(2𝑛) b) log(5𝑛) = Ο(ln 2𝑛) c) 3𝑛 = Ω(2𝑛) d) log(5𝑛) = Ω(ln 2𝑛)
Bài 10. Tìm dạng hàm 𝑔(𝑛) đơn giản mà 𝑓(𝑛) = Θ(𝑔(𝑛)) cho các hàm 𝑓(𝑛) sau đây a) 𝑓(𝑛) = ∑𝑛 1 𝑖=1 𝑖
b) 𝑓(𝑛) = ∑𝑛𝑖=1 𝑖2
c) 𝑓(𝑛) = ∑𝑛𝑖=1 log 𝑖
d) 𝑓(𝑛) = ∑𝑛𝑖=1 �1� 𝑖
e) 𝑓(𝑛) = ∑𝑛𝑖=1 log(𝑛!)
f) 𝑓(𝑛) = ∑𝑛𝑖=1 √𝑖
g) 𝑓(𝑛) = ∑𝑛𝑖=1 2𝑖
h) 𝑓(𝑛) = ∑𝑛𝑖=1 3𝑖 + 22𝑖
Bài 11. Tìm các hàm 𝑔(𝑛) đơn giản mà 𝑓(𝑛) = Θ(𝑔(𝑛)) cho các hàm 𝑓(𝑛) sau đây a) 𝑓(𝑛) = 2𝑛 + 𝑛2
b) 𝑓(𝑛) = 𝑛2 + 𝑛√𝑛 + log 𝑛
c) 𝑓(𝑛) = log 20𝑛 + 𝑛2
d) 𝑓(𝑛) = (2)𝑛 + 𝑛3 3
Bài 12. Chứng minh rằng
12 − 22 + 32 − 42 + ⋯ + (−1)𝑛−1𝑛2 = (−1)𝑛−1 𝑛(𝑛 − 1) 2 ⁄
Bài 13. Xem xét đoạn chương trình in ra xâu “Hello” sau for (i=1; i<=n; i++) for (j=i; j<=2*i; j++) printf("Hello");
Gọi 𝑇(𝑛) là số lần thực hiện lệnh in ra màn hình. Hãy
a) Xác định hàm 𝑇(𝑛) theo 𝑛.
b) Biểu diễn dạng rút gọn của 𝑇(𝑛) theo ký hiệu O lớn.
Bài 14. Xem xét đoạn chương trình in ra xâu “Hello” sau for (i=1; i<= n/2; i++) for (j=i; j<= n-i; j++) for (k=1; k<= j; k++) printf("Hello");
Gọi 𝑇(𝑛) là số lần thực hiện lệnh in ra màn hình. Hãy
a) Xác định hàm 𝑇(𝑛) theo 𝑛.
b) Biểu diễn dạng rút gọn của 𝑇(𝑛) theo ký hiệu O lớn.
Bài 15. Bài toán khớp xâu:
Đầu vào: Một xâu 𝑡 và một mẫu (xâu con) 𝑝
Đầu ra: 𝑝 có xuất hiện trong 𝑡 hay không, nếu có thì tại vị trí nào.
Ví dụ. 𝑡 = 𝐴𝐵𝐵𝐴𝐴𝐵𝐶𝐷𝐵𝐵𝐴 và 𝑝 = 𝐴𝐵𝐶𝐷 0 1 2 3 4 5 6 7 8 9 0 0 A B C 1 A 2 A 3 A B 4 A B C D A B B A A B C D B B A
int findmatch(char *p, char *t) { int i,j; /* counters */
int m, n; /* string lengths */ m = strlen(p); n = strlen(t);
for (i=0; i<=(n-m); i=i+1) { j=0; while ((j j = j+1; if (j == m) return(i); } return(-1); }
Hãy phân tích thời gian chạy trong trường hợp tồi nhất của thuật toán trên sử dụng ký hiệu O-lớn. ở đây
𝑚, 𝑛 lần lượt là độ dài của xâu 𝑝 và 𝑡.
Bài 16. Nhân hai ma trận
Đầu vào: Ma trận 𝐴 (kích thước 𝑥 × 𝑦) và ma trận 𝐵 (kích thước 𝑦 × 𝑧)
Đầu ra: Ma trân 𝐶 = 𝐴 × 𝐵 (kích thước 𝑥 × 𝑧) for (i=1; i<=x; i++) for (j=1; j<=y; j++) { C[i][j] = 0; for (k=1; k<=z; k++)
C[i][j] += A[i][k] * B[k][j]; }
Hãy phân thuật toán nhân hai ma trận trên theo O-lớn.
Bài 17. Nhân hai số nguyên: Để nhân 2 số nguyên 𝑎, 𝑏 ta thực hiện theo cách nhân lần lượt 𝑎 với các chữ
số trong 𝑏 (có tính trọng số) sau đó tính tổng. VD, 𝑎 = 120, 𝑏 = 142 thì 𝑎 × 𝑏 = 120 × 100 + 120 ×
40 + 120 × 2 = 17,040. Phân tích độ phức tạp của thuật toán trên khi áp dụng để nhân hai số có 𝑛, 𝑚
chữ số. Ở đây ta giả sử phép cộng hoặc nhân từng chữ số có thời gian thực hiện là hằng số( tức là 𝑂(1)) Bài tập chương 1 Phần 3 A. Thuật toán đệ quy
Bài 1. Cho hàm đệ quy sau a) 𝑓(𝑛) = � 2 𝑛ế𝑢 𝑛 ≤ 2
3𝑓(𝑛 − 2) + 𝑓(𝑛 − 1) + 4 𝑛ế𝑢 𝑛 > 2 Hãy tính 𝑓(4), 𝑓(9) b) 𝑓(𝑛) = � 1 𝑛ế𝑢 𝑛 ≤ 0
𝑓(𝑛/2) + 𝑓(𝑛 − 1) 𝑛ế𝑢 𝑛 > 0 Hãy tính 𝑓(3), 𝑓(8) 1 𝑛ế𝑢 𝑛 = 0 c) 𝑓(𝑛) = � 2 𝑛ế𝑢 𝑛 = 1
2𝑓(𝑛%2) + 𝑓(𝑛/2) 𝑛ế𝑢 𝑛 > 1 Hãy tính 𝑓(4), 𝑓(7) 1 𝑛ế𝑢 𝑛 ≤ 0
d) 𝑓(𝑛) = �2𝑓(𝑛/2) + 1 𝑛ế𝑢 𝑛 > 0 𝑣à 𝑐ℎẵ𝑛
2𝑓(𝑛 − 1) 𝑛ế𝑢 0 < 𝑛 𝑣à 𝑙ẻ Hãy tính 𝑓(4), 𝑓(7)
B. Phương pháp thế
Bài 1. Chứng minh rằng
a) 𝑇(𝑛) = 𝑇 ��𝑛�� + 1 là Ο(log 𝑛) 2
b) 𝑇(𝑛) = 2𝑇 ��𝑛�� + 𝑛 là Ο(𝑛 log 𝑛) 2
c) 𝑇(𝑛) = 𝑇 ��𝑛� + 12� + 1 là Ο(log 𝑛) 2
d) 𝑇(𝑛) = 4𝑇 �𝑛� + 𝑛 là 𝑂(𝑛2) 2
e) 𝑇(𝑛) = 2𝑇 �𝑛� + 1 là 𝑂(𝑛) 2
Bài 2. Giải công thức đệ quy
a) 𝑇(𝑛) = 2𝑇�√𝑛� + 1
Bài 3. Giải công thức đệ quy của thuật toán sắp xếp trộn – mergeSort 𝛰(1) 𝑛ế𝑢 𝑛 = 1 𝑇(𝑛) = � 𝑛
2𝑇 �2� + 𝛰(𝑛) 𝑛ế𝑢 𝑛 > 1 C. Cây đệ quy
Bài 1. Xác định một cận trên tốt cho công thức đệ quy 𝑇(𝑛) = 3𝑇 �𝑛� + 𝑛 dùng phương pháp thế để xác 2 nhận lại kết quả.
Bài 2. Vẽ cây đệ quy cho 𝑇(𝑛) = 4𝑇 ��𝑛�� + 𝑐𝑛 với 𝑐 là hằng số. Đưa ra tiệm cận chặt cho công thức đệ 2
quy trên. Xác nhận lại lời giải bằng phương pháp thế. D. Định lý thợ
Bài 1. Dùng định lý thợ để đưa ra các tiệm cận chặt cho các công thức đệ quy sau
a) 𝑇(𝑛) = 4𝑇 �𝑛� + 𝑛 2
b) 𝑇(𝑛) = 4𝑇 �𝑛� + 𝑛2 2
c) 𝑇(𝑛) = 4𝑇 �𝑛� + 𝑛3 2
Bài 2. Dùng định lý thợ để chứng minh thời gian thực hiện của thuật toán tìm kiếm nhị phân 𝑇(𝑛) =
𝑇 �𝑛� + Θ(1) là Θ(log 𝑛) 2
Bài 3. Định lý thợ có thể áp dụng cho công thức đệ quy 𝑇(𝑛) = 4𝑇 �𝑛� + 𝑛2 log 𝑛 được không, Tại sao? 2
Tìm tiệm cận giới hạn trên cho 𝑇(𝑛)
Bài 4. Đánh giá thời gian thực hiện của thuật toán đệ quy sau theo mô hình O-lớn
int findMin(int S[], int start, int end) {
if(start>=end) return S[end]; int div = (end-start)/2; int A,B; A=findMin(S,start,start+div); B=findMin(S,start+div+1,end); return Min(A,B); }
Trong đó hàm Min(A,B) trả về giá trị nhỏ nhất trong 2 số A, B và thời gian thực hiện là Θ(1) E. Viết chương trình
Bài 1. Hãy viết hàm 𝑔𝑐𝑑() để tìm ước số chung lớn nhất của 2 số nguyên dương 𝑎, 𝑏 theo các thuật toán sau:
a) Phương pháp vét cạn: duyệt tất cả các số nguyên dương có thể cho tới khi tìm thấy
b) Dùng thuật toán Euclid: giả sử 𝑏 là số nhở hơn, nếu 𝑏 = 0 thì ước số chung lớn nhất là 𝑎, ngược lại
thì ước số chung lớn nhất của 𝑎 và 𝑏 cũng là ước số chung lớn nhất của 𝑏 và 𝑎%𝑏 (chia module, chia lấy
phần dư). Cài đặt thuật toán Euclid theo 2 cách: lặp và đệ quy
Bài 2. Hãy viết chương trình để in ra màn hình tam giác số Pascal dạng hình vuông như sau 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1
𝐶(𝑛, 0) = 𝐶(𝑛, 𝑛) = 1 với 𝑛 ≥ 0
𝐶(𝑛, 𝑘) = 𝐶(𝑛 − 1, 𝑘) + 𝐶(𝑛 − 1, 𝑘 − 1) với 𝑛 > 𝑘 > 0
a) Vẽ cây đệ quy để tính 𝐶(6,4)
b) Xây dựng hàm đệ quy để tính 𝐶(𝑛, 𝑘)
c) Vẽ tam giác Pascal dạng hình vuông
d) Cải tiến hàm tính 𝐶(𝑛, 𝑘) theo 2 cách: dùng đệ quy có nhớ, và không dùng đệ quy (dùng phương pháp lặp)
e) Đánh giá độ phức tạp của hàm 𝐶(𝑛, 𝑘) trong các trường hợp c,d theo các tiêu chí: bộ nhớ, thời gian
Bài 3. Hàm Ackermann được định nghĩa như sau
𝐴(0, 𝑛) = 𝑛 + 1 với 𝑛 > 0
𝐴(𝑚, 0) = 𝐴(𝑚 − 1,1) với 𝑚 > 0
𝐴(𝑚, 𝑛) = 𝐴(𝑚 − 1, 𝐴(𝑚, 𝑛 − 1)) với 𝑚 > 0 và 𝑛 > 0
a) Tính toán các giá trị hàm Ackermann trong các trường hợp sau
𝐴(0,9) 𝐴(0,9) 𝐴(1,8) 𝐴(2,2) 𝐴(2,0) 𝐴(2,3) 𝐴(3,2) 𝐴(4,2) 𝐴(4,3) 𝐴(4,0)
b) Viết hàm đệ quy để tính giá trị hàm Ackermann
c) Viết hàm không đệ quy để tính giá trị hàm Ackermann F. Thuật toán quay lui
Bài 1. Chiều cao tối đa của cây đệ quy của hàm solve_from trong bài toán 8 hậu ?
Bài 2. Thực hiện tiếp hàm solve_from để giải bài toán 8 hậu với trạng thái hiện tại của bàn cờ là
Chú ý : trong trường hợp này ta xếp các quân hậu lần lượt theo hàng chứ không phải theo cột
Bài 3. Thực hiện thuật toán backtracking bằng tay để tìm ra một lời giải cho bài toán đặt 5 quân hậu trên bàn cờ kích thước 5x5
Bài 4. Cài đặt thuật toán backtracking để in ra lời giải có thể của bài toán 8 hậu
Bài 5. Xây dựng thuật toán backtracking để in ra tất cả các hoán vị của dãy {A,B,C,D,E}
Bài 6. Xây dựng thuật toán backtracking để giải bài toán ma phương (bậc chẵn và bậc lẻ)
Tham khảo : http://mathworld.wolfram.com/MagicSquare.html Bài tập phần II
Phần: Các cấu trúc dữ liệu cơ bản- Mảng, Danh sách
liên kết, danh sách tuyến tính
Bài 1. Kiểu dữ liệu là gì ? cho ví dụ minh họa.
Bài 2. Kiểu dữ liệu trừu tượng là gì? Nó khác gì so với định nghĩa kiểu dữ liệu?
Bài 3. Cấu trúc dữ liệu là gì ?
Bài 4. Phân loại cấu trúc dữ liệu? So sánh đặc điểm của các phân loại đó.
Bài 5. Trình bày ưu nhược điểm của mảng (bao gồm cả mảng cấp phát tĩnh và mảng cấp phát động).
Bài 6. Viết hàm để thực hiện thêm phần tử vào vị trí sau phần tử thứ k trong hai trường hợp :
mảng, và danh sách liên kết đơn.
Bài 7. Viết hàm reverse để in ra các phần tử trong danh sách liên kết đơn theo thứ tự đảo ngược typedef struct Node { int data; struct Node *pNext; } NODE;
//pHead là con trỏ đến đầu danh sách cần đảo ngược void reverse(NODE *pHead) { //Thân hàm }
Ví dụ: với danh sách ban đầu chứa các phần tử {2, 27, 5, 14, 9}, thì kết quả sẽ là 9, 14, 5, 27, 2
Hãy đánh giá thời gian thực hiện thuật toán của bạn theo O-lớn.
Bài 8. Hoàn hiện phần thân hàm reverse để đảo ngược danh sách liên kết đơn typedef struct Node { int data; struct Node *pNext; } NODE;
//pHead là con trỏ đến đầu danh sách cần đảo ngược
void reverse(NODE *&pHead) { //Thân hàm }
Ví dụ với danh sách ban đầu chứa các phần tử {2, 27, 5, 14, 9}, thì kết quả sẽ là danh sách {9, 14, 5, 27, 2} ở dưới
Hãy đánh giá thời gian thực hiện thuật toán của bạn theo O-lớn.
Bài 9. Viết lại các hàm thực hiện các thao tác chèn, tìm kiếm và xóa phần tử trên danh sách liên kết
đơn dùng vòng lặp thay vì dùng đệ quy.
Bài 10. Viết lại hàm xóa phần tử trong danh sách liên kết đơn mà không cần dùng thêm các hàm
search_list, predecessor_list.
Bài 11. Cho một dãy số nguyên bất kỳ có số lượng phần tử lớn hơn 2. Hãy viết hàm find để tìm và
in ra màn hình hai cặp phần tử có độ chênh lệch lớn nhất và nhỏ nhất trong dãy đã cho.
Độ chệnh lệch giữa 2 số 𝑎, 𝑏 được định nghĩa là 𝑑 = |𝑎 − 𝑏|
//A là tên mảng chứa các phần tử
//n là số lượng phần tử trong mảng, n>2 void find(int A[], int n) { //thân hàm }
Ví dụ với dãy {1,5,3,2,7,4} thì cặp phần tử có chêch lệch lớn nhất là (1, 7), cặp phần tử có độ
chêch lệch nhỏ nhất là (2,3). Trong trường hợp có nhiều cặp chỉ cần đưa ra 1 cặp bất kỳ thỏa mãn.
Hãy đưa ra đánh giá thời gian thực hiện của thuật toán của bạn theo O-lớn
Bài 12. Cho một dãy các số nguyên khác nhau đã được sắp theo thứ tự tăng dần. Viết chương trình
kiểm tra xem có tồn tại phần tử nào mà giá trị của nó đúng bằng vị trí của nó.
Ví dụ. trong dãy {−10,−3, 3, 5, 7}, ta tìm được a3 = 3.
Trong dãy {2, 3, 4, 5, 6, 7}, thì không tồn tại phần tử nào như vậy
Chú ý: Vị trí của phần tử được tính bắt đầu từ 1
Bài 13. Để biểu diễn kiểu dữ liệu ADT xâu ký tự trong máy tính người ta có thể làm theo những cách sau
1. Lưu trữ bằng mảng, dùng một ký tự đăc biệt để báo hiệu kết thúc xâu (ký tự ‘\0’). Mảng phải
được khai báo có số phần tử tối đa là lớn hơn bằng số lượng ký tự của xâu.
2. Lưu trữ bằng mảng, phần tử đầu tiên trong mảng ta dùng để chứa số ký tự hiện thời của xâu
ký tự, còn các phần tử tiếp theo sẽ là các ký tự.
3. Dùng danh sách liên kết để chứa các ký tự, kết thúc xâu khi phần tử cuối cùng là NULL.
Hãy nhận xét về hiệu quả của mỗi phương pháp theo các tiêu chí
a) Kích thước bộ nhớ cần dùng để lưu trữ xâu ký tự
b) Các ký tự mà xâu có thể biểu diễn
c) Thời gian để truy cập vào ký tự thứ 𝑖 trong xâu
d) Thời gian thực hiện phép chèn, xóa ký tự trong xâu
Bài 14. Giả sử chúng ta có con trỏ trỏ đến phần tử cần xóa trong danh sách, có cách nào khác để
xóa phần tử đó khỏi danh sách mà không cần phải duyệt danh sách để tìm phần tử đứng trước
nó không ? Nếu có hãy mô tả phương pháp của bạn.
Bài 15. Viết chương trình tìm phần tử có giá trị lớn nhất, nhỏ nhất trong danh sách móc nối đơn.
Bài 16. Xây dựng chương trình biểu diễn đa thức 𝑃𝑛(𝑥) = 𝑎𝑛𝑥𝑛 + 𝑎𝑛−1𝑥𝑛−1+. . +𝑎1𝑥 + 𝑎0 với các
thao tác cơ bản như hiển thị, cộng, trừ, nhân hai đa thức.
Bài 17. So sánh ưu nhược điểm của mảng và cấu trúc liên kết khi dùng để lưu trữ kiểu dữ liệu trừu
tượng danh sách tuyến tính.
Bài 18. Cần phải lưu trữ một danh sách tuyến tính là thông tin về khách hàng trong các ngày trong
tháng ở siêu thị. Ta sẽ chọn cấu trúc dữ liệu nào để lưu trữ sao cho thao tác tìm kiếm là nhanh
nhất và tiết kiệm bộ nhớ nhất nếu chúng ta biết:
a) Không biết trước số lượng khách hàng tối đa
b) Biết trước số lượng khách hàng tối đa nhưng số lượng khách hàng giữa các ngày khác nhau biến động rất lớn
c) Biết trước số lượng khách hàng tối đa, và số lượng khách hàng trong các ngày chênh lệch nhau không nhiều
Các cấu trúc có thể được lựa chọn là : Mảng tĩnh, mảng động, cấu trúc móc nối.
Hãy giải thích lựa chọn của bạn trong từng trường hợp.
Bài 19. Cài đặt chương trình mô phỏng bài toán Josephus trong slide.
Bài 20. Cho một dãy số gồm 𝑛 số, hãy viết chương trình in ra các phần tử trong dãy theo chiều tăng
dần tần số xuất hiện
Ví dụ : dãy 1, 3, 4, 5, 7, 2, 3, 5 thì ta sẽ in ra 1, 2, 4, 7, 3, 5
Bài 21. Cài đặt các hàm thực hiện thao tác thêm, xóa và tìm kiếm đối với danh sách liên kết đôi.
Bài 22. Cài đặt các hàm thực hiện thao tác thêm, xóa và tìm kiếm đối với danh sách liên kết đôi nối
vòng (danh sách nối đôi sử dụng nút đầu giả).
Bài 23. Viết chương trình cài đặt mảng động để lưu trữ danh sách các phần tử theo cách sau:
• Ban đầu ta cấp phát bộ nhớ động là 10 phần tử
• Nếu mà ta phải thêm một phần tử mới khi mảng đã đầy thì ta gấp đôi kích thước mảng
và copy toàn bộ các phần tử của mảng cũ vào nửa đầu mảng mới, sau đó thêm phần tử mới vào mảng mới.
• Nếu mà xóa một phần tử mà sau khi xóa thì số phần tử của mảng nhỏ hơn 1/2 kích
thước của mảng thì ta tiến hành tạo mảng mới với kích thước bằng ½ kích thước mảng
cũ. Sau đó copy toàn bộ các phần tử mảng cũ sang mảng mới.
Hãy đánh giá thời gian thực hiện trong trường hợp tốt nhất, tồi nhất cả các thao tác thêm và xóa phần tử.
Chỉ ra một trường hợp mà cách làm như vậy cho kết quả rất tồi. Bạn có cách nào để cải thiện hiệu quả ?
Bài 24. Cho hai xâu ký tự s1 và s2. Hãy viết hàm stringmatch để kiểm tra xem xâu ký tự s2 có xuất
hiện trong s1 hay không. Nếu có thì trả về vị trí xuất hiện đầu tiên của nó, ngược lại thì trả về giá trị là -1.
Ví dụ: s1=”AbbAbbbabbb”, s2=”ab” thì hàm stringmatch(s1,s2) sẽ trả về giá trị 7
Hãy đánh giá hiệu quả của thuật toán của bạn.
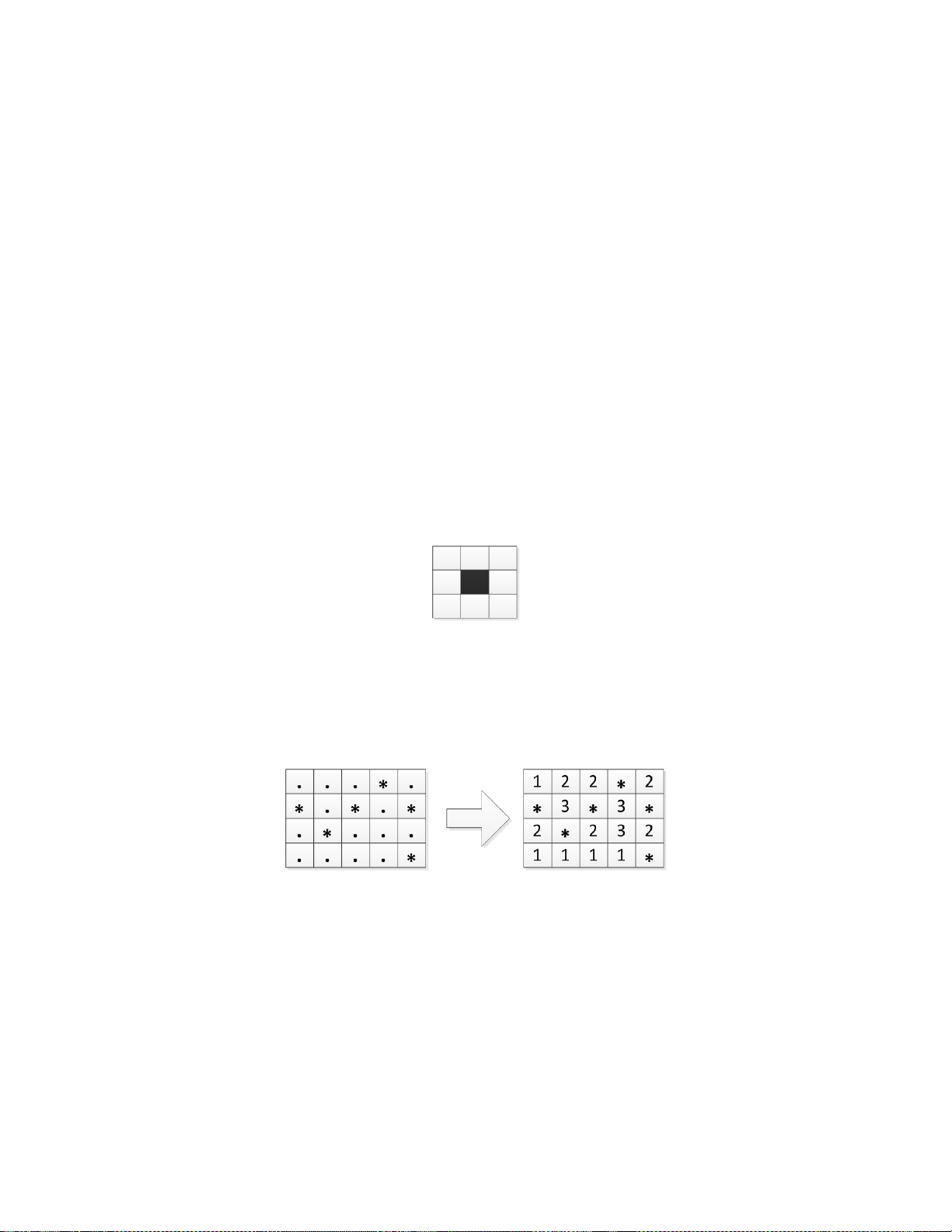
Bài 25. Trò chơi dò mìn
Giả sử chúng ta mô tả bãi mìn bằng một ma trận với kích thước 𝑁 × 𝑀 (𝑁 hàng và 𝑀 cột).
Những vị trí có mìn được đánh dấu bằng ký tự ‘*’, còn những vị trí không có mìn là ký tự ‘.’. Hãy
xây dựng một ma trận tương đương để mô tả các cảnh báo có mìn của các ô xung quanh. Với
mỗi ô có mìn thì ta vẫn biểu diễn bằng ký tự ‘*’, còn những ô xung quanh ta biểu diễn bằng các
chữ số mô tả số ô có mìn mà lân cận với nó.
Ở đây 1 ô sẽ lân cận với 8 ô xung quanh Ví dụ
Bãi mìn kích thước 4 × 5 được biểu diễn lại như sau Hãy xây dựng hàm
Calculate(char MineField[10][10], char Output[10][10], int N, int M)
Để tính toán các giá trị cho mảng Output với đầu vào là mảng mô tả bãi mìn MineField
1 ≤ 𝑁, 𝑀 ≤ 10 là kích thước thực sự của bãi mìn hiện tại
Bài 26. Cho kiểu dữ liệu trừu tượng tập hợp với
• Các phần tử của tập hợp là các số nguyên
• Các phép toán của tập hợp gồm :
o Member(x,S): Kiểm tra xem phần tử x có thuộc tập hợp S hay không
o Union(A,B): Hợp của hai tập hợp A, B, trả về một tập hợp 𝐴 ∪ 𝐵 thông qua tập
hợp A, hoặc B, hoặc hàm
o Intersection(A,B): Giao của hai tập hợp, trả về 𝐴 ∩ 𝐵 thông qua tập hợp A, hoặc B, hoặc hàm
o Substract(A,B): Hiệu của hai tập hơp, trả về 𝐴 − 𝐵 thông qua tập hợp A, hoặc B, hoặc hàm
o Insert(x,S): thêm phần tử x vào tập hợp S
o Delete(x,S) : loại bỏ phần tử x khỏi tập S (nếu x có trong S)
Hãy cài đặt ADT trên sử dụng các phương pháp biểu diễn a) Mảng b) Danh sách liên kết
c) Xâu bit (bit 1 biểu diễn phần tử có trong tập hợp và bit 0 biểu diễn phần tử không có)
Chú ý: Đối với cách biểu diễn thứ 3 các phần tử phải được biểu diễn theo một thứ tự xác định.
Các phần tử trong tập hợp không trùng nhau.
Bài 27. Cho một dãy số nguyên dương gồm n số, khoảng cách giữa hai vị trí chính là độ chênh lệch
về giá trị của hai số tại vị trí đó.
Ví dụ cho dãy gồm 5 số 1, 3, 4, 3, 7. Chêch lệch giữa số thứ 1 và 4 là 3 − 1 = 2.
Chọn một vị trí k bất trong dãy n số, tổng độ chệnh lệch của vị trí k với tất cả 𝑛 − 1 vị trí còn lại
được tính bằng tổng độ chênh lệch của số ở vị trí 𝑘 tới 𝑛 − 1 vị trí còn lại.
Ví dụ với k=2 (số giá trị 3) thì tổng độ chêch lệch ứng với 2 sẽ là 2+1+0+4=7
Hãy viết chương trình tìm vị trí k sao cho có tổng độ chênh lệch là nhỏ nhất.
Bài 28. Viết chương trình đảo ngược thứ tự các từ trong một câu được nhập vào từ bàn phím.
Ví dụ. Câu đầu vào là “ the quick brown fox jumps over the lazy dog”
Thì kết quả hiển thị ra màn hình sẽ là câu “dog lazy the over jumps fox brown quick the”
Bài 29. Nhập vào từ bàn phím một dãy số thực gồm n số (0• In ra màn hình dãy số vừa nhập.
• Tìm và in ra màn hình các số âm trong dãy, nếu không có số nào thì in ra thông báo “Dãy không có số âm”.
• Tìm và in ra màn hình giá trị phần tử dương lớn nhất, nhỏ nhất trong dãy.
• Nhập vào một giá trị k, xóa tất cả các phàn tử có giá trị lớn hơn k trong dãy. In ra màn hình dãy sau khi xóa.
Bài 30. Giáo viên chủ nhiệm muốn quản lý thông tin về tình hình học tập của tất cả các thành viên
trong lớp. Thông tin về mỗi thành viên gồm: • Họ tên • Giới tính
• Ngày sinh (lưu bằng xâu ký tự) • Địa chỉ
• Điểm trung bình cả năm
Hãy xây dựng một cấu trúc dữ liệu phù hợp để lưu thông tin về các thành viên của lớp. Sử dụng
cấu trúc do bạn tự định nghĩa để nhập vào 10 thành viên của lớp. Sau đó thực hiện các công việc sau:
• In ra thông tin về 10 thành viên vừa nhập
• Tìm và in ra thông tin về những thành viên có điểm trung bình cả năm nhỏ hơn 4.0
In ra thông tin về thành viên có điểm trung bình cả năm cao nhất của lớp.
Bài 31. Một cửa hàng cho thuê băng đĩa muốn quản lý thông tin về các băng đĩa mà cửa hàng đó
cho thuê (giả sử với mỗi phim thì của hàng chỉ có một bộ đĩa duy nhất). Mỗi một đĩa có các thông tin sau:
• Mã số : là một xâu ký tự, mỗi đĩa được biểu diễn bởi một xâu duy nhất
• Tiêu đề : thông tin về tên đĩa
• Loại đĩa: là loại CD hay VCD hay DVD (gợi ý: sử dụng số nguyên để biểu diễn 1-CD, 2- VCD, 3-DVD)
Do số lượng đĩa cho thuê trong từng ngày là biến đổi rất nhiều, nên các tối ưu là lưu các đĩa cho
thuê bằng cấu trúc danh sách móc nối. Bạn hãy định nghĩa cấu trúc danh sách móc nối để lưu
thông tin về các đĩa cho thuê. Thêm vào danh sách các thông tin về các đĩa được thuê, ví dụ
1. “D001”, “Kungfu panda”, “VCD”
2. “D003”, “WALL-E”,”DVD”
3. “D005”,”Earth”,”VCD”
Bây giờ khác hàng thuê đĩa có mã “D003” trả, hãy cập nhật lại danh sách cho thuê, xóa nút có
thông tin về đĩa D003 đó đi (gợi ý: thực hiện tìm kiếm trên danh sách móc nối để tìm D003). In
ra màn hình các đĩa đã được thuê trong ngày.
Bài 32. Cho các con trỏ sau int *p, *q, a,b; float *f,x; a=5; b=7; x=9;
Chuyện gì sẽ xảy ra khi ta thực hiện các câu lệnh sau, giải thích 1. p=&a; *p=45; 2. p=&a; q=&b; q=p; *q=5; 3. x=a; f=&x; *f=4.5; 4. f=&a; p=f;
Bài 33. Cho các dữ liệu ban đầu như sau
int a[] = { 3, 8, -4, 6, 2, 6 }; int *p1 = a; int *p3 = &a[5]; int *p2 =a+2;
Thực hiện tuần tự các lệnh sau, hãy cho biết nội dung của mảng a sau khi thực hiện mỗi lệnh 1. *p1=5; 2. *p2=7; 3. *p3 = *p1+*p2; 4. p1=p2-1; 5. *p1=55; 6. *(p1+3)=99; Bài tập chương 2 Phần stack, queue
Bài 1. Thực hiện liên tiếp các lệnh sau đối với một stack rỗng, kết quả thu được sẽ là gì? Vẽ hình minh họa. Push(3); Push(5); Pop() Push(7); Pop(); Push(8); Pop(); Pop();
Bài 2. Cho một danh sách móc nối với cấu trúc mỗi nút như sau: typedef struct node { float data; struct node *pNext; } NODE;
Hãy viết hàm reverse để in ra nội dung danh sách móc nối theo thứ tự ngược void reverse (NODE* pHead) Gợi ý: sử dụng stack
Bài 3. Tính giá trị các biểu thức hậu tố sau, mô tả rõ các bước làm
a) 3 4 + 5 6 7 ∗ 2 − ∗ − b) 3 4 + 2 ^ 6 4 ∗ 2 / − c) 3 4 7 + % 2 3 / −
d) 3 3 5 % ^ 9 5 2 − / 6 ∗ −
Bài 4. Chuyển các biểu thức trung tố sau sang biểu thức hậu tố
a) (𝑎 + 𝑏) ∗ 𝑐^(𝑑 + 4 − 5 ∗ (9/3))
b) 3 + 4/(2 + 𝑎 − 𝑐 ∗ 𝑏) − 7%(5 + 𝑐)
c) 2 + (3 − (4 ∗ (5^𝑎%𝑏)))
d) 3– 𝑎 ∗ (3^2 − 6%(5 + 9))
Bài 5. Định giá các biểu thức hậu tố sau (các toán hạng và toán tử cách nhau 1 dấu cách, các toán
hạng có thể gồm nhiều chữ số) √ là toán tử 1 ngôi căn bậc hai, 𝐴𝑁𝐷, 𝑁𝑂𝑇, 𝑂𝑅 là các toán tử logic,
≥, >, ≤ là các toán tử quan hệ, ! là toán tử 1 ngôi tính giai thừa, 𝑎𝑏𝑠 là toán tử 1 ngôi tính giá trị tuyệt đối
a) 15 2 3 + / 2 ^ 4 12 2 − % +
b) 1 3 5 + + √ 2 ^ 4 12 6 / − +
c) 2 1 27 3 2 ^ / + 3 % − 4 +
d) 3 0 ≥ 45 7 > 5 6 ≤ 𝐴𝑁𝐷 𝑁𝑂𝑇 𝑂𝑅 e) 2 3 1 12 3 4 ∗ / + ^ %
f) 3 4 ! 4 5 + % 12 + 15 − +
g) 1 16 − 𝑎𝑏𝑠 5 + 4 6 + /
Bài 6. Chuyển các biểu thức sau từ dạng trung tố về dạng hậu tố (các toán hạng và toán tử cách nhau
1 dấu cách, các toán hạng có thể gồm nhiều chữ số)
a) 3 + 5 ^ (12 / 6 + 1) – 7 ∗ 15 / 3 + 6
b) 𝑠𝑖𝑛 (5 ∗ 𝑎 + 7) + 2 – 6 ∗ 5 ∗ 𝑏 + 3 ^ 2 ^ 𝑐 / 2
c) 23 + 𝑎 − √ (6 ∗ 𝑏 + 5) / 9 ^ 2 ∗ cos(3 ∗ 𝑐) (chú ý √ (6 ∗ 𝑏 + 5) là tương đương với √6 ∗ 𝑏 + 5)
d) (3 ≥ 𝑎) 𝐴𝑁𝐷 �( 𝑐 ≥ 𝑑) 𝑂𝑅 �𝑁𝑂𝑇 (4 < 𝑑)��
e) 5 ^ 2 ^ 3 ^ (4 ∗ 9 – 5 / 𝑏 + 6) % (7 + 𝑎 + 𝑐)
f) 𝑎𝑏𝑠 (6 − 𝑏 ∗ 2 + 7 ∗ 𝑎) ^ 2 / 𝑐 + 5
Bài 7. Cài đặt thuật toán định giá biểu thức trung tố tổng quát (thực hiện trên tập các toán tử trong slide)
Bài 8. Cài đặt thuật toán chuyển biểu thức ở dạng trung tố sang dạng hậu tố
Bài 9. Bài toán kiểm tra cặp ngoặc trong biểu thức có hợp lệ
Một biểu thức có dấu ngoặc là hợp lệ nếu số dấu ngoặc mở phải bằng số dấu ngoặc đóng cùng loại. Ví dụ: Biểu thức hợp lệ
• {2 + 3 ∗ (5/3^2)}/{7 ∗ 𝑏}
• 2 + {3 ∗ [4 + 6 − (2/3^2)]}
Biểu thức không hợp lệ • {3 + (6 − [5 ∗ 2)} • 4 + (6 ∗ (5 − 𝑎)
Hãy viết chương trình nhận đầu vào là 1 biểu thức, kiểm tra xem biểu thức đó có hợp lệ hay không.
Bài 10. Bài toán đối sánh thẻ HTML
Trong một văn bản HTML thì mỗi thẻ mở phải đi kèm với 1 thẻ đóng Tìm kiếm:
Hãy viết chương trình đọc vào 1 file .html và kiểm tra xem trong file đó có thẻ nào bị lỗi hay không