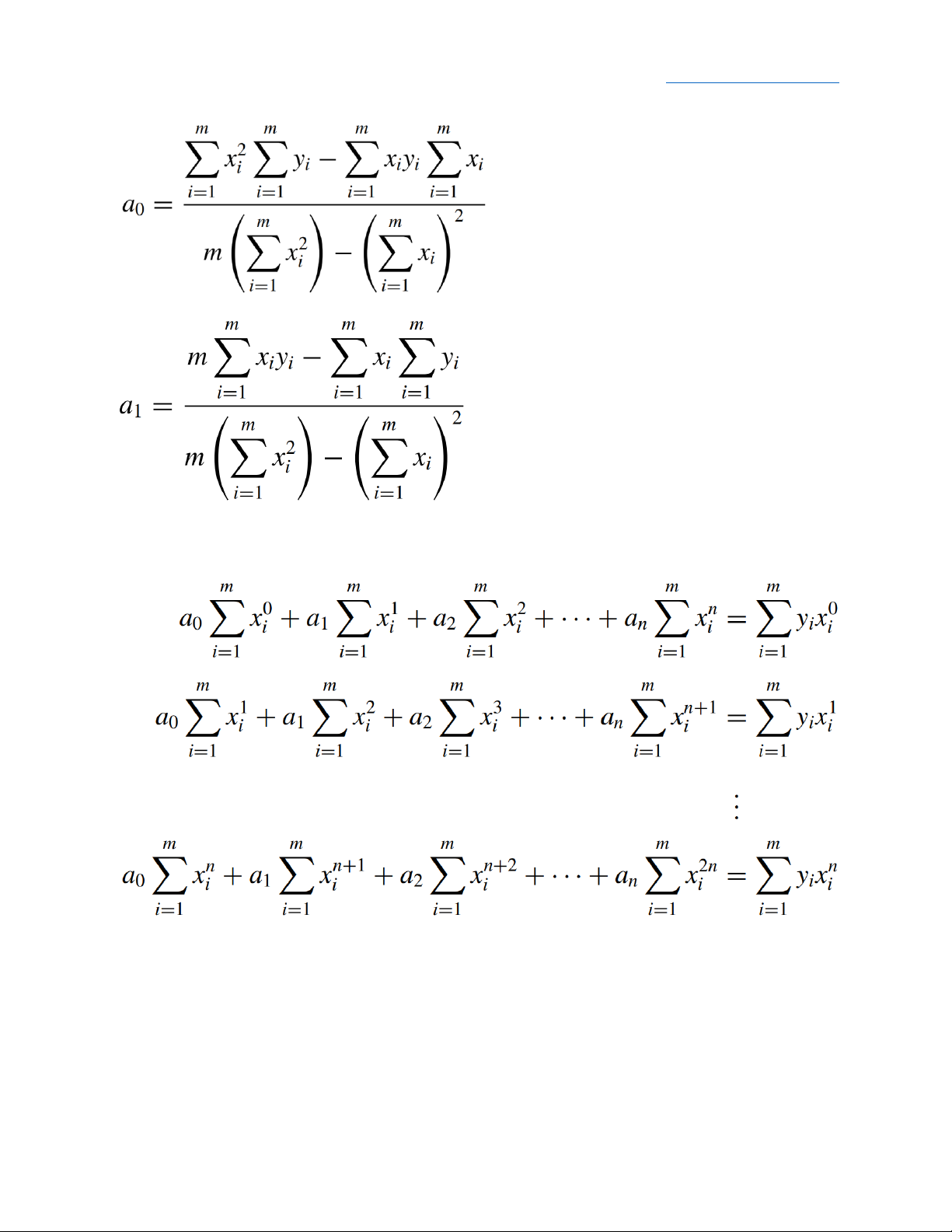




Preview text:
sdsdsd Xét trên 1 đoạn [a. b]
0<𝑚𝑛 ≤ |𝑓(𝑛)(𝑥)| ≤ 𝑀𝑛 < +𝑣ô 𝑐ù𝑛𝑔 Sai số 1. Chương 2: • Chia đôi:
Dừng ở lần thứ n ta có: 1 𝑎𝑛2𝑛
Lấy 𝑎𝑛 là nghiệm, sai số là: | 1
𝑎𝑛 − 𝑛𝑔ℎ𝑖ệ𝑚| ≤ 𝑏𝑛 − 𝑎𝑛= (b-a) 2𝑛
Lấy 𝑏𝑛 là nghiệm, sai số là: | 1
𝑏𝑛 − 𝑛𝑔ℎ𝑖ệ𝑚| ≤ 𝑏𝑛 − 𝑎𝑛= (b-a) 2𝑛 𝑎
Lấy 𝑛+𝑏𝑛 là nghiệm, sai số là: 2 𝑎 𝑏 1
| 𝑛 + 𝑏𝑛 − 𝑛𝑔ℎ𝑖ệ𝑚| ≤ 𝑛 − 𝑎𝑛 = (𝑏 − 𝑎) 2 2 2𝑛+1 • Điểm bất động: 𝑀1 |𝑥𝑛 − ξ|≤ |𝑥 1−𝑀 𝑛−1 − 𝑥𝑛| 1 𝑀 𝑛 |𝑥 1 𝑛 − ξ|≤ |𝑥 1−𝑀 1 − 𝑥0| 1 • Newton: 𝑀 |𝑥 2 𝑛 − ξ| ≤ |𝑥 2 ∗ 𝑚 𝑛−𝑥𝑛−1|2 1 • Dây cung: êfefefefdfdddd v 𝑀 |𝑥 1 − 𝑚1 𝑛 − ξ| ≤ |𝑥 2 ∗ 𝑚 𝑛 − 𝑥𝑛−1| 1 • Điểm sai:
Ko thấy nói, chậm hơn dây cung. 2. Chương 3: • Jacobi: ‖𝑎‖𝑝
‖𝑥(𝑘) − 𝑥∗‖ ≤
. ‖𝑥(𝑘) − 𝑥(𝑘−1)‖ 𝑝 1 − ‖𝑎‖ 𝑝 𝑝 (‖𝑎‖𝑝)𝑘
‖𝑥(𝑘) − 𝑥∗‖ ≤ . ‖𝑥(1) − 𝑥(0)‖ 𝑝 1 − ‖𝑎‖ 𝑝 𝑝 • Gauss-seidel: Chuẩn hàng ∞: p 𝑖−1 i=∑ |𝑎 𝑗=1
𝑖𝑗 |:hàng i ma trận tam giác dưới đường chéo chính q 𝑛 i=∑ |𝑎 𝑗=𝑖
𝑖𝑗 |:hàng I ma trận tam giác trên và bao gồm đường chéo chính 𝑚𝑎𝑥 𝑞 μ = 𝑖 i=1,n 𝑖 1−𝑝𝑖 μ
‖𝑥(𝑘) − 𝑥∗‖ ≤
. ‖𝑥(𝑘) − 𝑥(𝑘−1)‖ ∞ 1 − μ ∞ (μ)𝑘
‖𝑥(𝑘) − 𝑥∗‖ ≤ . ‖𝑥(1) − 𝑥(0)‖ ∞ 1 − μ ∞ Chuẩn cột 1: 𝑚𝑎𝑥 𝑚𝑎𝑥 𝑡 𝑠 = ∑𝑛 |𝑎 ;𝜌 = 𝑗 ,(j=1,n) 𝑗 𝑖=𝑗+1 𝑖𝑗 | 𝑗 1−𝑠𝑗 𝑡 𝑗 𝑛 𝑗 = ∑ |𝑎 1 𝑖𝑗 |,𝑠𝑗 = ∑ |𝑎 𝑖=𝑗+1 𝑖𝑗 |,(j=1,n-1) 𝑠 𝑛 𝑛 = 0,𝑡𝑛 = ∑ |𝑎 1 𝑖𝑛| 𝜌
‖𝑥(𝑘) − 𝑥∗‖ ≤
. ‖𝑥(𝑘) − 𝑥(𝑘−1)‖ 1 (1 − s). (1 − 𝜌) 1 (𝜌)𝑘
‖𝑥(𝑘) − 𝑥∗‖ ≤ . ‖𝑥(1) − 𝑥(0)‖ 1 (1 − s). (1 − 𝜌) 1 3. Chương 4: • Lagrange: 𝑓𝑛+1(𝑐) 𝑅𝑛(𝑥) = 𝜋 (𝑛 + 1)! 𝑛+1(𝑥) 𝑀 |𝑅 𝑛+1 𝑛(𝑥)| ≤ |𝜋 (𝑛 + 1)! 𝑛+1(𝑥)|
𝜋𝑛+1(𝑥) = (𝑥 − 𝑥0)(𝑥 − 𝑥1) … (𝑥 − 𝑥𝑛) • Newton:
Không cách đều sai phân tiến:
𝑅𝑛(𝑥) = (𝑥 − 𝑥0)(𝑥 − 𝑥1) … (𝑥 − 𝑥𝑛−1)(𝑥 − 𝑥𝑛)𝑓[𝑥, 𝑥0, … , 𝑥𝑛]
𝑅𝑛(𝑥) = 𝜋𝑛+1(𝑥)𝑓[𝑥, 𝑥0, … , 𝑥𝑛]
Không cách đều sai phân lùi:
𝑅𝑛(𝑥) = (𝑥 − 𝑥𝑛)(𝑥 − 𝑥𝑛−1) … (𝑥 − 𝑥1)(𝑥 − 𝑥0)𝑓[𝑥, 𝑥𝑛, … , 𝑥0]
𝑅𝑛(𝑥) = 𝜋𝑛+1(𝑥)𝑓[𝑥, 𝑥𝑛, … , 𝑥0]
Cách đều hiệu hữu hạn tiến: x=𝑥0 + ℎ𝑡 ℎ𝑛+1𝑓(𝑛+1)(𝑐)
𝑡(𝑡 − 1) … (𝑡 − 𝑛) 𝑅𝑛(𝑥) =
𝑡(𝑡 − 1). . (𝑡 − 𝑛) ≈ ∆𝑛+1𝑦 (𝑛 + 1)! (𝑛 + 1)! 0
Cách đều hiệu hữu hạn lùi: x=𝑥𝑛 + ℎ𝑡 ℎ𝑛+1𝑓(𝑛+1)(𝑐)
𝑡(𝑡 + 1) … (𝑡 + 𝑛) 𝑅𝑛(𝑥) =
𝑡(𝑡 + 1). . (𝑡 + 𝑛) ≈ ∇𝑛+1𝑦 (𝑛 + 1)! (𝑛 + 1)! 𝑛 • Spline: 5𝑀 𝑚𝑎𝑥
|𝑓(𝑥) − 𝑆(𝑥)| ≤ (𝑥 384 0 ≤ 𝑗 ≤ 𝑛 − 1 𝑗+1 − 𝑥𝑗 )4
𝑚𝑎𝑥𝑎≤𝑥≤𝑏|𝑓(4)(𝑥)| = 𝑀 Chương 5: • Đạo hàm: Đạo hàm lagrange 2 điể ℎ m: 𝑓′′(ξ) 2 Đạo hàm lagrange 3 điể ℎ2 m: 𝑓(3)(ξ) 3 Đạo hàm lagrange 3 điể ℎ4 m: 𝑓(5)(ξ) 5 𝑛 𝑛 𝑓(𝑛+1)(ξ(𝑥𝑗))
𝑓′(𝑥𝑗) = ∑ 𝑓(𝑥𝑘)𝐿′𝑘(𝑥𝑗) + ∏(𝑥 (𝑛 + 1)! 𝑗 − 𝑥𝑘) 𝑘=0 𝑘=0 𝑘≠𝑗 • Tích phân: ℎ2(𝑏−𝑎)
Tích phân hình chữ nhật: . 𝑓′′(ξ) 24 ℎ2(𝑏−𝑎) Tích phân hình thang: . 𝑓′′(ξ) 12
Tích phân simpson 3 điể ℎ4(𝑏−𝑎) m 𝑓(4)(ξ) 180
T217 Numerical analyst- closed Newton-Cotes formulas 4. Chương 6:
Rời rạc: spare error từng điểm.
Đa thức bậc n (hilbert matrix): Tích phân sqare error trên đoạn [a, b]
Tập trực giao: Tương tự 5. Chương 7: • Euler:
Lý thuyết: |𝑦𝑖 − 𝑦(𝑥𝑖)| ≤ 𝑀. ℎ • Euler cải tiến:
Lý thuyết: |𝑦𝑖 − 𝑦(𝑥𝑖)| ≤ 𝑀. ℎ2 Thực tế: ℎ ℎ
|𝑦2𝑛 ( ) − 𝑦(𝑋)| ≈ |𝑦 ) − 𝑦 2 2𝑛 (2 𝑛(ℎ)|
• Runge-Kutta 4 số hạng:
Lý thuyết: |𝑦𝑖 − 𝑦(𝑥𝑖)| ≤ 𝑀. ℎ4
(M=hằng số dương không phụ thuộc vào h) Thực tế: ℎ 1 ℎ
|𝑦2𝑛 ( ) − 𝑦(𝑋)| ≈ |𝑦 ) − 𝑦 2 15 2𝑛 (2 𝑛(ℎ)| Lý thuyết: Chương 4:
𝑔𝑖(𝑥) = 𝑎𝑖(𝑥 − 𝑥𝑖)3 + 𝑏𝑖(𝑥 − 𝑥𝑖)2 + 𝑐𝑖(𝑥 − 𝑥𝑖) + 𝑑𝑖 𝑑𝑖 = 𝑦𝑖
ℎ𝑖 = 𝑥𝑖+1 − 𝑥𝑖
𝑓𝑖 = 𝑦𝑖+1 − 𝑦𝑖 1 𝑎𝑖 = (𝑏 3ℎ 𝑖+1 − 𝑏𝑖 ) 𝑖 𝑓 ℎ 𝑐 𝑖 𝑖 𝑖 = − (𝑏 ℎ 𝑖+1 + 2𝑏𝑖) 𝑖 3 1 2 1 𝑓 𝑓 ℎ (ℎ ℎ 𝑖+1 − 𝑖 3 𝑖𝑏𝑖 + 3
𝑖 + ℎ𝑖+1)𝑏𝑖+1 + 3 𝑖+1𝑏𝑖+2 = ℎ𝑖+1 ℎ𝑖 Clamped Cubin Spline 𝑔′ ′
0(𝑥) = 𝛼, 𝑔𝑛−1(𝑥𝑛) = 𝛽 First mising equation: 2 1 𝑓 ℎ ℎ 0 − 𝛼 3 0𝑏0 + 3 0𝑏1 = ℎ0 Last missing equation: 1 2 𝑓 ℎ ℎ 𝑛−1
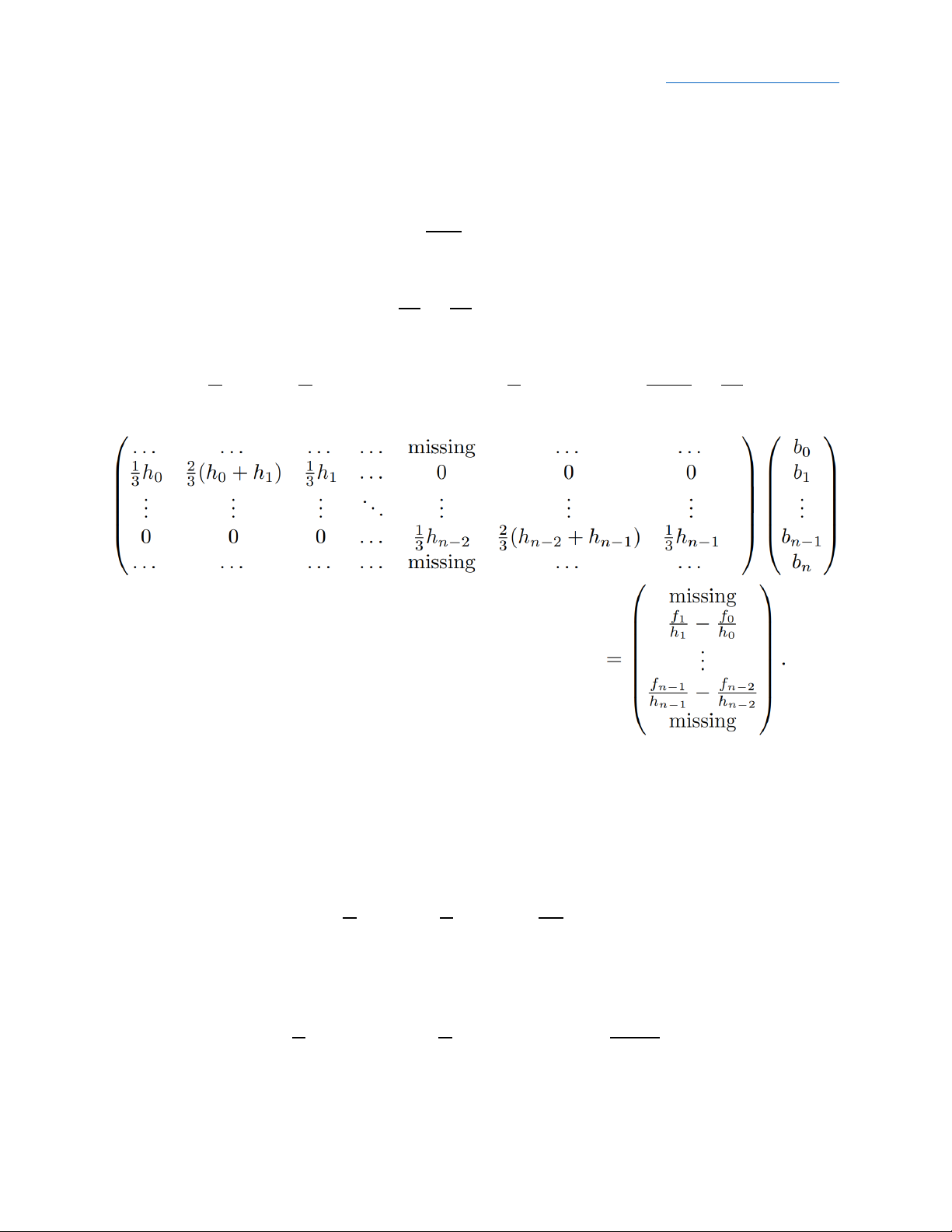
3 𝑛−1𝑏𝑛−1 + 3 𝑛−1𝑏𝑛 = 𝛽 − ℎ𝑛−1 Nature Cubin Spline: 1 ℎ 3 0𝑏0 = 0 1 ℎ 3 𝑛−1𝑏𝑛 = 0 Hoặc:
ℎ1𝑏0 − (ℎ0 + ℎ1)𝑏1 + ℎ0𝑏2 = 0
ℎ𝑛−1𝑏𝑛−2 − (ℎ𝑛−2 + ℎ𝑛−1)𝑏𝑛−1 + ℎ𝑛−2𝑏𝑛 = 0 Chương 5: Five-point Midpoint fomula: Five-point Endpoint fomula:
Second Derivative Midpoint Formula Chương 6: Xấp xỉ dữ liệu: Đường thẳng: Đa thức bậc n:
Hilbert matrix: Dùng tích phân thay vì sigma: Trực giao: 𝑛
𝑃(𝑥) = ∑ 𝑎𝑗𝜑𝑗(𝑥) 𝑗=0 𝑏
∫ 𝑤(𝑥)𝜑𝑗(𝑥)𝑓(𝑥)𝑑𝑥 𝑎 𝑎 𝑗 = 𝑏
∫ 𝑤(𝑥)[𝜑𝑗]2 𝑑𝑥 𝑎
𝜑0 ≡ 1,𝜑1 = 𝑥 − 𝐵1