Tổng hợp công thức Vật lí đại cương - Vật lí đại cương | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh

lOMoARcPSD|45316467 lOMoARcPSD|45316467
TỔNG HỢP CÔNG THỨC VẬT LÝ ĐẠI CƯƠNG
I I.Chương 1: Động lực học chất điểm.
1. Chuyển động thẳng đều: v = const a = 0 s = vt
2. Chuyển động thẳng biến đổi đều: a = const 1 s = 1 (v v = v 0 + 0 + at
v 2− v 2 = 2a.s
s = s 0 + v 0.t + a.t 2 0 2 v).t 2 2h
3. Thời gian rơi từ độ cao h đến khi chạm đất: t = g
4. Chuyển động tròn: v2
- Gia tốc pháp tuyến (gia tốc hướng tâm): a n = = 2r r
- Gia tốc tiếp tuyến: a t = r ( : gia tốc góc)
- Gia tốc toàn phần: a = a 2n + a2t
- Vận tốc dài: v = r 2 2 r
-Chu kỳ: T = = v − = 2 .
-Phương trình động học: Vận tốc góc: 2 2 t = 0 + t 0 1 Góc quay: = 1 ( 0 + ).t 2 t = 0 + 0 t + t 2 2
5. Chuyển động ném xiên:
- Độ cao cực đại (khi vận tốc trục tung bằng 0): vy = 0
- Tầm xa cực đại (khi vật chạm đất): y = 0
Chú ý: Chỉ khi điểm đầu và điểm cuối nằm trên cùng 1 mặt phẳng thì Độ cao cực đại bằng max = v 2 sin 2 tại
v sin . Tầm xa cực đại xmax = v 2sin 2 tại 2v sin h 0 t = 0 0 t = 0 2g g g g
- Vận tốc tại thời điểm t: v = v2 + v2 x y v
- Gia tốc: g 2= a 2n + a 2t tan = x
- Gia tốc tiếp tuyến: a t = g cos vy
- Gia tốc pháp tuyến: a n = g sin
II.Chương 2: Động học.
1. Định luật Newton: Định luật I: F = 0 a = 0 Định luật II: F = ma
Định luật III: A tác dụng lên B 1 lực => B tác dụng lại A 1 lực, 2 lực này là lực trực đối.
2. Lực ma sát: Fms = N
3. Xung lực: p = F. t
4. Mômen động lượng: L = I. L = R p = R mv lOMoARcPSD|45316467
III.Chương 3: Động lực học hệ chất điểm. Động lực học hệ vật rắn. 1. Động lượng: p = m.v
2. Bảo toàn động lượng: p truoc = psau
Va chạm đàn hồi: Bảo toàn đ ộ ng n
ăng và Bảo toàn đ ộng lượ ng
Va chạm không đàn hồi: Bảo toàn động lượng 3. Chuyển động lăn:
- Lăn không trượt: v = r , a = r t
- Công thức Huy-ghen Stenen: I ( ) = I C + M.d2 .
- Động năng: K = K tt + Kq = m.v2 + I C 2 2 2
Chuyển động thẳng hệ chất
Chuyển động quay hệ vật rắn 2
điểm - Khối lượng m
- Mômen quán tính I = R dm VR - Gia tốc a - Gia tốc góc a t
= R hay at = β.R, an = ω2.R - Ngoại lực F
- Mômen ngoại lực M = R F - Vận tốc v - Vận tốc góc ( v = R )
- Động lượng p = m.v
- Mômen động lượng L = I. = R p = R mv - - Quãng đường s Góc quay φ
- Động năng: K = 1m.v2
Động năng quay: K = 1 I. 2 2 2
ĐLBT động lượng: p
ĐLBT mômen động lượng: L = L truoc = psau truoc sau ĐL II Newton: ĐL II Newton: F = ma M=I. F = dp
Định lý động lượng:
Định lý động lượng: M = dL i dt i dt
Phương trình động học:
Phương trình động học: = + t v = v + a.t t 0 t 0 − = 2 .
v2 − v 2 = 2a.s 2 2 0 t 0 s = s = + t + 1t2
0 + v 0.t + 1 a.t2 2 t 0 0 2 s = 1 (v = 1 ( 0 + v).t 0 + ).t 2 2 lOMoARcPSD|45316467
4. Mômen quán tính của một số vật:
- Mômen quán tính của chất điểm có khối lượng m với trục quay: I = m.r2
- Thanh dài l, khối lượng m, trục quay vuông góc và đi qua tâm: I = m.l2 12
- Thanh dài l, trục quay đi qua 1 đầu thanh: I = m.l2 3 m.R 2
- Đĩa tròn hoặc trụ đặc đồng chất: I = 2
- Vành hoặc trụ rỗng: I = m.R 2 2m.R 2
- Khối cầu đặc đồng chất: I = 5
IV.Chương 4: Năng lượng.
1. Thế năng (thế năng trọng trường): Wt = mgh 2. Động năng: m.v 2 K = 2 2 2 t 2 3. Công: 12
A = dA = F.ds = F.v.dt 1 1 t 1
4. Định lý động năng: K
− K truoc = ANgoailuc sau
5. Cơ năng: E = K + Wt
6. Bảo toàn cơ năng: E
= Esau : Hệ kín không có ngoại lực (lực cản, lực ma sát, …). truoc lOMoARcPSD|45316467
1. Một vật chuyển động khối lượng m1 tới va chạm vào vật thứ hai đang đứng yên khối lượng m2
= 1kg. Biết rằng sau va chạm vật thứ nhất đã truyền cho vật thứ hai x = 36% động năng ban đầu
của mình. Coi va chạm là đàn hồi, tính m1.
Gọi v1, v2 = 0 là vận tốc quả cầu thứ nhất và thứ hai tại thời điểm trước khi va chạm, v1’, v2’
là vận tốc quả cầu thứ nhất và thứ hai tại thời điểm sau va chạm.
Định luật bảo toàn động lượng: m v
= m v' + m v' (1)
Định luật bảo toàn cơ năng: 1 1 1 1 1 2 2 K = K'1+ K'2 Trong đó: 1 1 K ' = 0,64K m v ' 2 = 0,64 m v 2 v ' = 0,8v 1 1 1 1 1 1 1 1 2 2 m1
Thế vào (1): v ' 2 = 0, 2v1 m2 1 1 1 m 2 1 m 2 2 1 m 2v' = 0,36 2 1 m v m 2 1 1 0,2v = 0,36 2 1 1 2 1 1 K ' = 0,36K m v = 9 2 2 2 m 2 2 m2
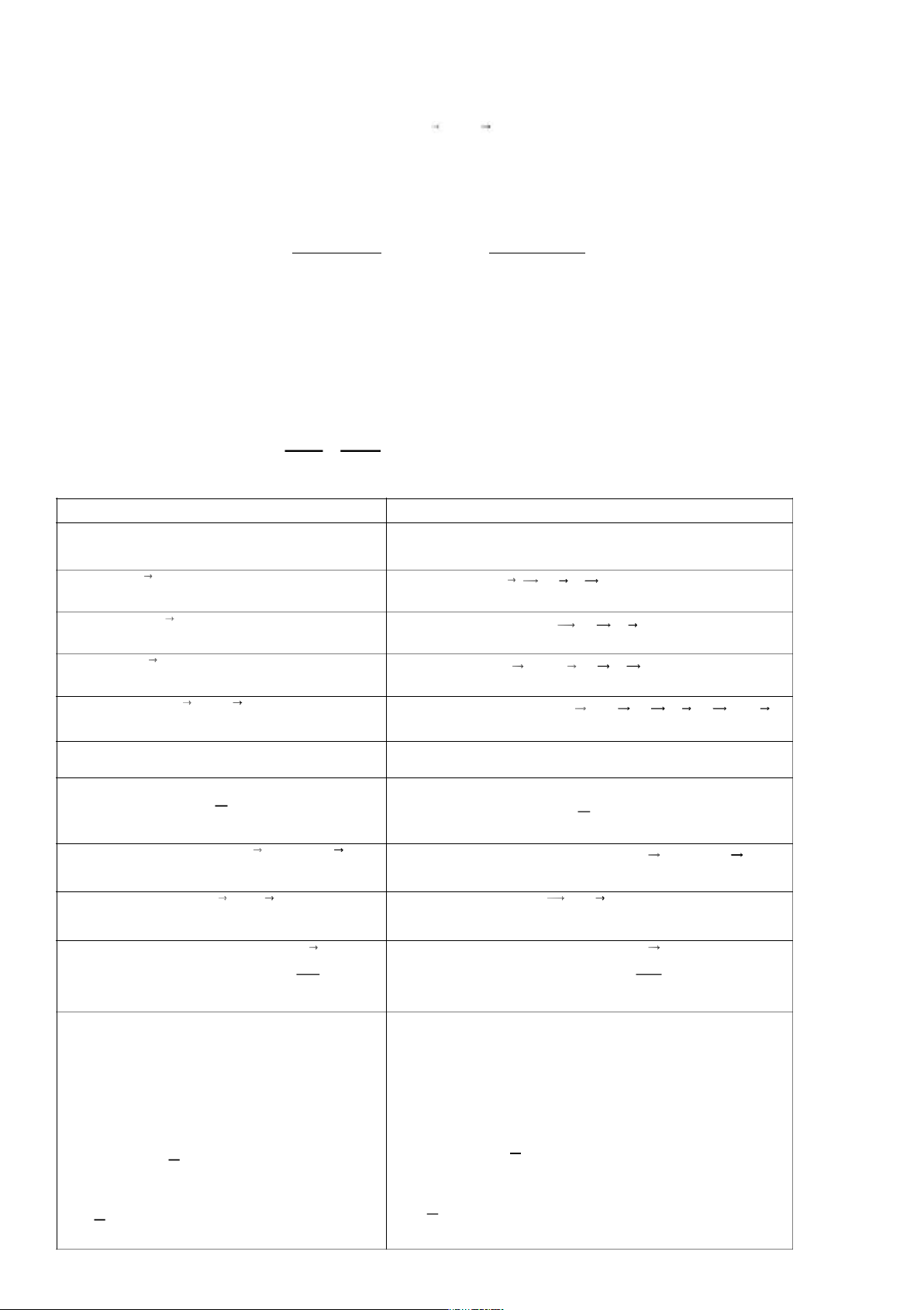
2. Một vật có khối lượng m được ném thẳng đứng từ độ cao h xuống mặt đất với vận tốc ban đầu v0.
Vật lún sâu vào đất một đoạn s. Tính lực cản trung bình của đất lên vật. Bỏ qua ma sát của không khí. 1 1
Định luật bảo toàn cơ năng: 2 mv + mgh = 2 mv v 2 = v 2 + 2gh 0 0 2 2
Định lí động năng: K 2 − K1 = A ( 0 − 1 c )
mv 2 = Fc .s.cos F , s = −Fc .s 2 mv = 1 F = 1 1 2 2 + mgh c 2s mv0 s2
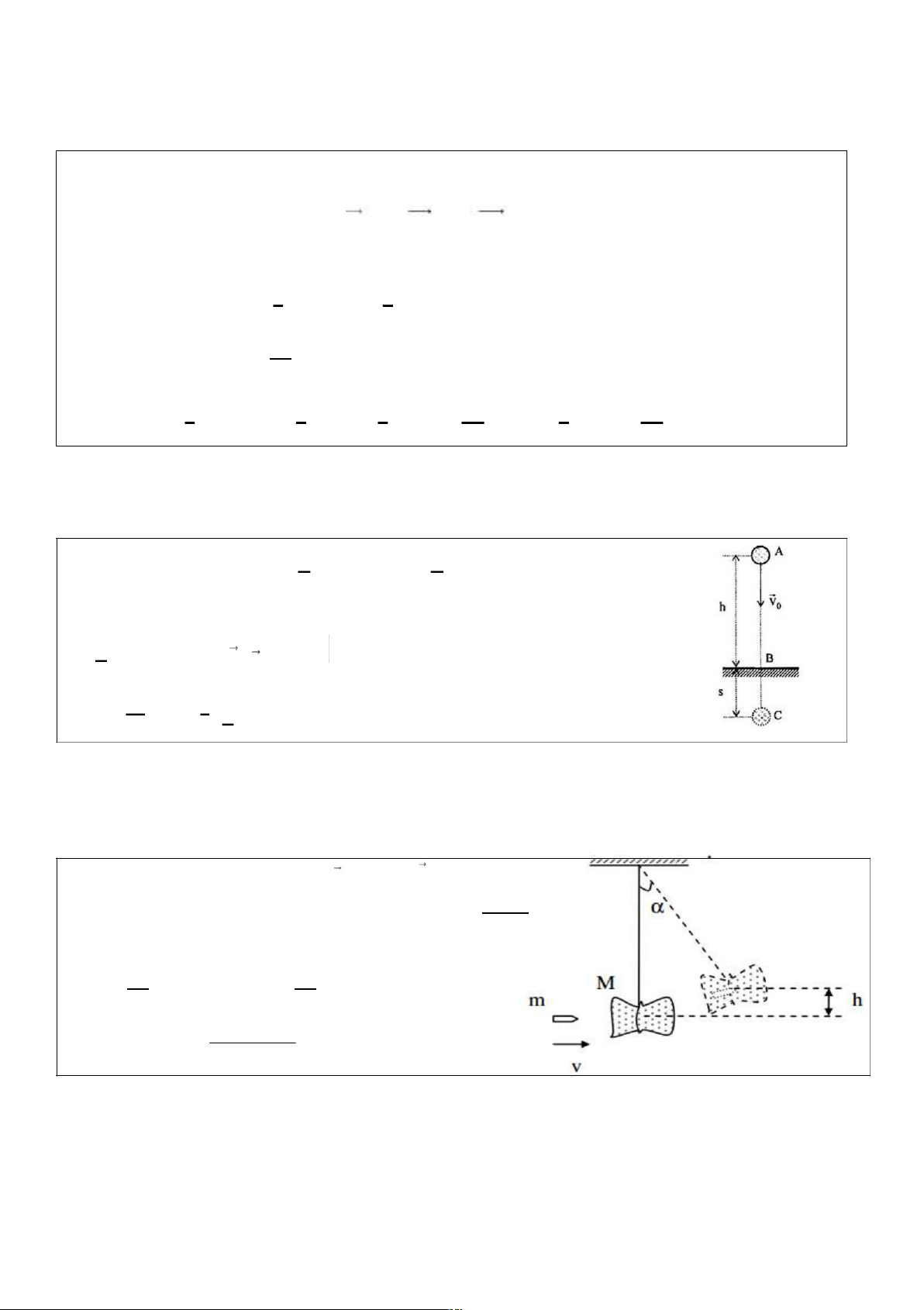
3. Một bao cát treo ở đầu một sợi dây. Một viên đạn chuyển động theo phương ngang xuyên vào
bao cát, bị mắc vào đó còn bao cát được nâng lên độ cao h nào đó. Cho biết vận tốc viên đạn là
v, khối lượng của nó là m và khối lượng bao cát là M. Tính h. mv = (M + m)V
Định luật bảo toàn động lượng: mv = (M + m)V V = m v (1) M + m
Định luật bảo toàn cơ năng:
( m + M ) V 2 = ( m + M )gh h = V2 (2) 2 2g 2v 2
Từ (1) và (2): h = m ( M+ m) 2 2g
4. Hai quả cầu được treo ở đầu hai sợi dây song song dài bằng nhau. Hai đầu kia của các sợi dây được
buộc vào một cái giá sao cho các quả cầu tiếp xúc với nhau và tâm của chúng cùng nằm trên một
đường nằm ngang. Khối lượng của quả cầu lần lượt là 0,2 kg; 0,1kg. Quả cầu thứ nhất được nâng lên
độ cao h = 4,5 cm và thả xuống. Hỏi sau va chạm, các quả cầu được nâng lên độ cao bao nhiêu nếu:
a) Va chạm hoàn toàn đàn hồi.
b) Va chạm là mềm. lOMoARcPSD|45316467
Định luật bảo toàn năng lượng cho quả cầu thứ nhất trước va chạm: m gh = 1m v 2 v = 2gh 1 1 1 2 1 1 1
a) Va chạm đàn hồi:
Gọi v1, v2=0 là vận tốc quả cầu thứ nhất và thứ hai ngay trước khi va chạm, v1’, v2’ là vận tốc lúc sau va chạm.
Định luật bảo toàn động lượng:
m1 v1 = m1 v'1 + m 2 v'2
(m − m )v v ' = 1 2 1 1 1 1 1 m + m 1 2
Định luật bảo toàn cơ năng: m 2 2 2 2 1 v1 = 2 m1 v'1 + 2 m 2 v'2 2m v v ' = 1 1 2 m + m 1 2
Thế số: v'1 = 1 v1; v'2 = 4 v1 3 3
Định luật bảo toàn năng lượng cho hai quả cầu sau va chạm: 1 1 1 1 2 m v' = m gh ' 2 v = gh ' gh = gh ' 2 1 1 1 1 1 2 9 1 1 9 1 1 h ' = 0,5cm 1 1 16 h ' = 8cm 2 m v' 2 = m gh ' 2 9 v 2 = gh ' 16 gh = gh ' 2 9 2 2 2 2 1 2 1 2
a) Va chạm mềm: Sau va chạm hai quả cầu chuyển động cùng vận tốc v’. m v
Định luật bảo toàn động lượng: = 2 v
m1 v1 = ( m1 + m 2 )v' v' = 1 1 m + m 3 1 1 2
Định luật bảo toàn năng lượng cho hai quả cầu sau va chạm:
1 ( m + m ) v' = ( m + m )gh ' 1 4 4 2 2
gh = gh ' h ' = 2cm v = gh ' 2 1 2 1 2 2 9 1 1 9
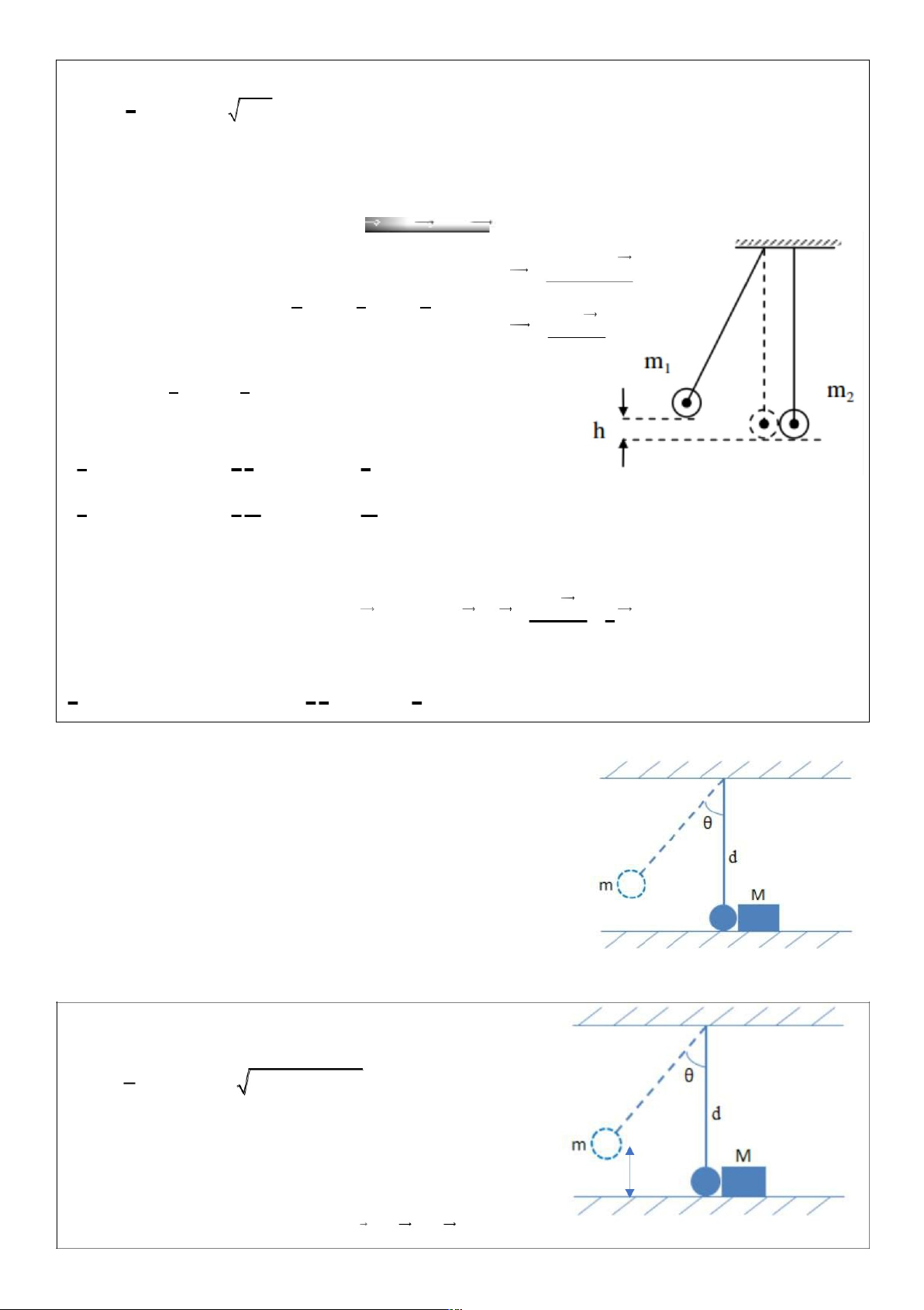
5. Cho quả cầu có khối lượng m được treo vào một sợi dây có chiều
dài d, đầu còn lại của sợi dây được cố định vào một mặt pẳng nằm
ngang. Ban đầu quả cầu được nâng lên để phương sợi dây hợp với
phương thẳng đứng một góc θ, sau đó quả cầu được thả ra và va
chạm đàn hồi với vật có khối lượng M. Hãy xác định: a) Vận tốc
của quả cầu ngay trước lúc va chạm và ngay sau khi va chạm.
b) Giả sử sau va chạm, vật M trượt có ma sát với mặt phẳng ngang
với hệ số ma sát μ. Hãy xác định quãng đường s mà M đi được.
Vận tốc của quả cầu ngay trước lúc va chạm v:
Định luật bảo toàn năng lượng cho quả cầu trước va chạm:
mgh = 1 mv 2 v = 2g(d − d cos ) 2 Va chạm đàn hồi:
Trước khi va chạm, vật khối lượng M đứng yên,
gọi v là vận tốc quả cầu trước khi va chạm, H
v’, V là vận tốc của quả cầu và vật M lúc sau va chạm.
Định luật bảo toàn động lượng: mv = mv' + MV (1) lOMoARcPSD|45316467
Định luật bảo toàn cơ năng: 1 2 = 1 2 mv' + 1 MV 2 mv (2) 2 2 2 v ' = ( m 1 v
( m1 − M) v' = 2g(d − d cos ) Giải (1) và (2): − M ) m + M V + 2m Mm V = 2g(d − d cos ) m + M = 2mv m + M
Quãng đường s mà M đi được: − K = A
Định lý động năng: K = A 1 2 1 Ngoailuc mV 2 Fms 2 A
= F .s = N.s = .M.g.s Fms ms 1 2m 2 4m 2d M 2g(d − d cos ) = .M.g.s s = 2 ( (1 − cos ) m + M) 2 m + M
6. Một khẩu pháo có khối lượng M nhả đạn theo phương nằm ngang. Đạn pháo có khối lượng m,
vận tốc v. Khi bắn hệ pháo giật về phía sau đoạn s. Tính lực cản trung bình tác dụng lên pháo.
V là vận tốc giật lùi của khẩu pháo
Định luật bảo toàn động lượng: m
0 = mv + MV V = − v (1) M
Lực cản tác dụng lên khẩu pháo sinh công làm
giảm động năng khẩu pháo. Định lí động năng: K − K = A 0− 1MV2 ( =
) Fc = 1 MV2 = 1 m 2 v2 Fc .s.cos Fc , s 2 1 c 2 2s2s M
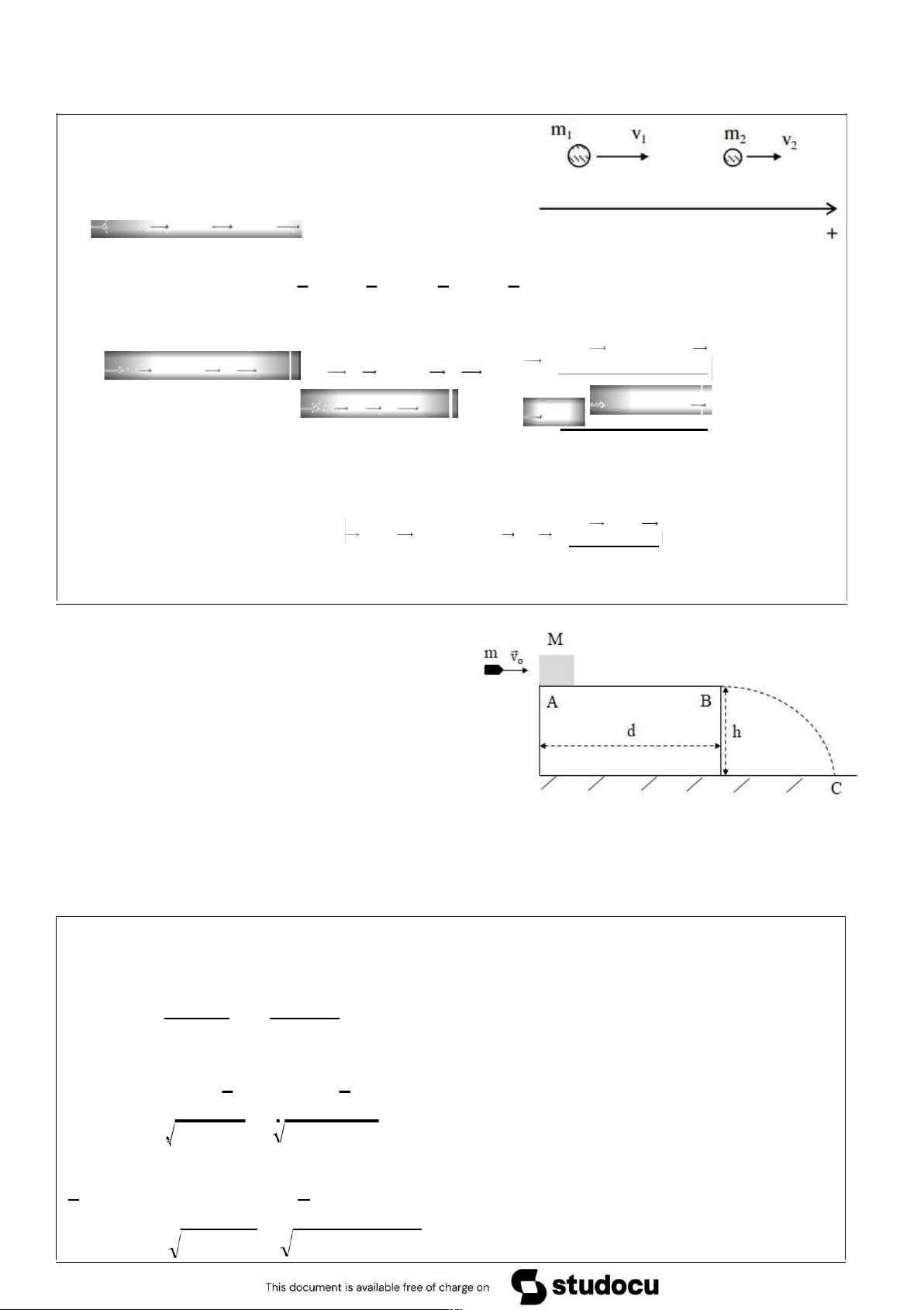
7. Trên đường có một xe khối lượng m1 chuyển động với vận tốc v1. Trên xe có một khẩu pháo
khối lượng m2, nòng pháo nằm ngang và chĩa dọc theo đường. Một viên đạn khối lượng m, khi
bắn có vận tốc so với đất bằng v. Tính vận tốc của xe sau khi bắn trong hai trường hợp:
a) Đạn bắn theo chiều xe chạy.
b) Đạn bắn ngược chiều xe chạy. Cho m1 = 10 tấn, m2 = 0,5 tấn, m = 1kg, v = 500m/s, v1 = 5m/s.
Gọi v2 là vận tốc của xe sau khi bắn. Chiều (+) theo chiều xe chạy.
Định luật bảo toàn động lượng: ( m1 + m 2 + m ) v1 = ( m1 + m)v + mv 2 2
a) Đạn bắn theo chiều xe chạy: ( ( + m )v
m+ m + m ) v = ( m + m ) m1 + m − mv v + mv v 2 1 2 = = 4,95m / s 1 2 1 1 2 2 ( m + m ) 1 2
b) Đạn bắn ngược chiều xe chạy: ( + m )v ( m+ m m + mv + m ) 1 + m v ) v − mv v 2 1 1 = ( m + 1 m = = 5,05m / s 1 2 2 2 2 ( m + m ) 1 2
8. Một quả cầu khối lượng 2 kg, chuyển động với vận tốc 3 m/s, va chạm xuyên tâm với một quả cầu
thứ hai khối lượng 3 kg đang chuyển động cùng chiều quả cầu thứ nhất với vận tốc 1m/s. Tìm vận tốc
các quả cầu sau va chạm nếu:
a) Va chạm hoàn toàn đàn hồi.
b) Va chạm mềm. lOMoARcPSD|45316467
a) Va chạm đàn hồi:
v1, v2 là vận tốc quả cầu thứ nhất và thứ hai trước va chạm,
v1’, v2’ là vận tốc lúc sau quả cầu thứ nhất và thứ hai sau va chạm.
Định luật bảo toàn động lượng: m v + m v = m v' + mv' 1 1 2 2 1 1 2 2 1
Định luật bảo toàn cơ năng: m v 2 + 1 mv 2 = 1 2 m v' + 1 mv' 2 2 2 2 1 1 2 2 2 1 1 2 2
Khai triển toán học: ( 2m + ( m − ) v 1 ( v m 1 1 ) 2 2 ) ) ( ) v' = 2 2 1 2 m ( 1
v' − v = m v − v' m v'1− v = m − v' 1 m + m 2 1 2 v2 1 2 ) ( 1 2 m (v' ) 2 − v 2 = m v 2 − v' 2 v'
2mv + ( m −m ) 2 2
+ v = v + v' = 1 2 1 1 1 1 1 2 2 2 2 1 v2 1 v' m + m 2 1 Thế số:
v' = 0,6m / s;v' = 2,6m / s theo chiều dương (+). 1 2
a) Va chạm mềm: Sau va chạm hai quả cầu chuyển động cùng vận tốc v’.
Định luật bảo toàn động lượng: m1 v1 + m 2 v 2 = ( m1 + m 2 )v' v' = m1 v1 + m 2 v2 m1 + m2
Thế số: v' =1,8m / s theo chiều dương (+).
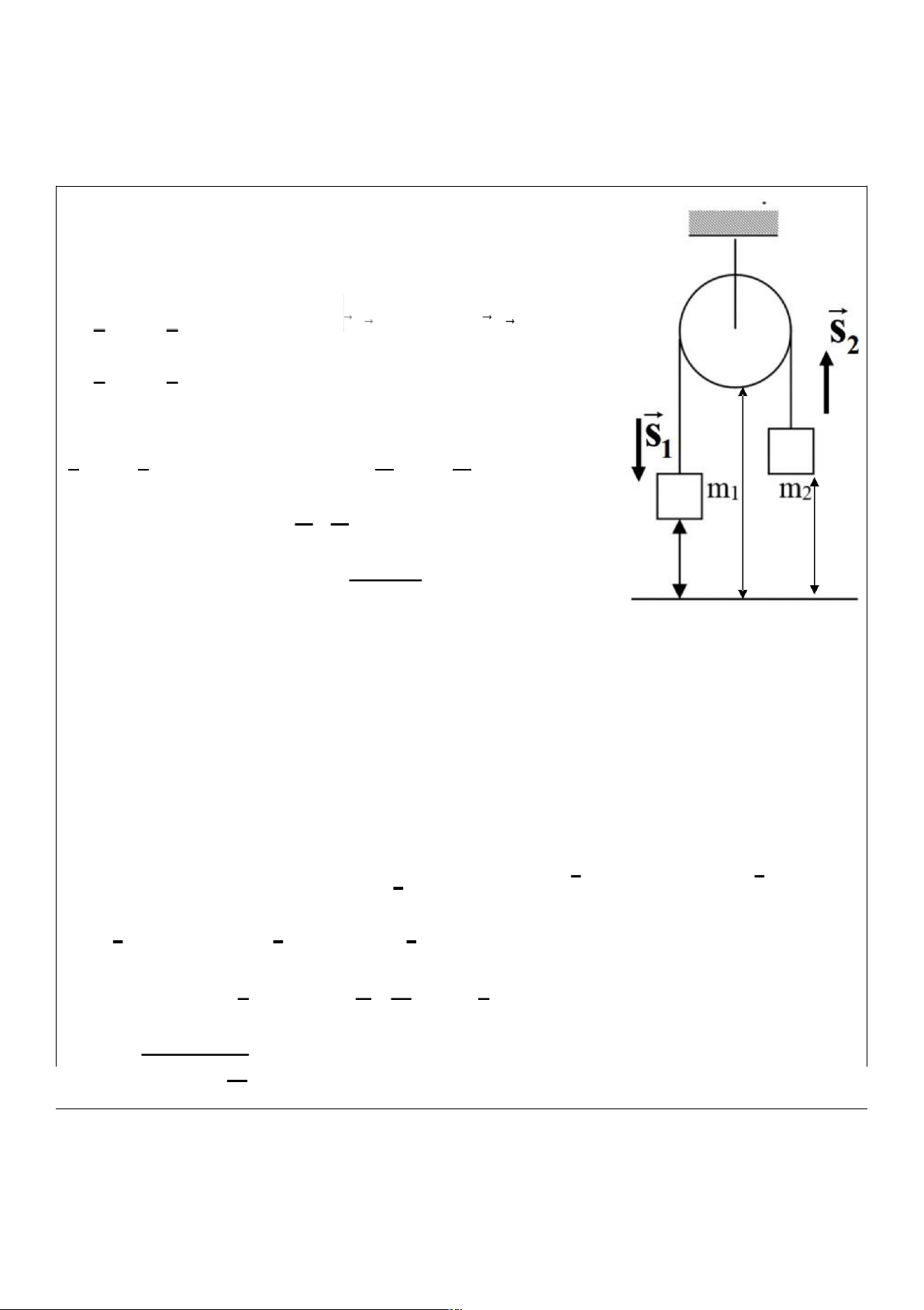
9. Cho một vật có khối lượng M đặt trên một giá đỡ
có chiều dài d và độ cao h so với mặt đất. Một viên
đạn, có khối lượng m chuyển động với vận tốc v0
không đổi theo phương ngang, va chạm mềm với
M. Ngay sau va chạm, hệ vật chuyển động có ma
sát trên mặt phẳng ngang của giá đỡ với hệ số ma
sát μ. Giả sử trước va chạm M đứng yên ở vị trí A.
Cho m = 0,02 kg, M = 1,0 kg, v0 = 700 m/s, g = 10 m/s2, μ = 0,2, d = 1,0 m, h = 0,5
m. a) Tính vận tốc của hệ vật khi chuyển động đến vị trí B.
b) Khi hệ vật chuyển động đến hết giá đỡ (tại B), giả sử hệ vật là một chất điểm, hãy tìm vận
tốc tiếp đất của hệ vật tại C.
a) Theo định luật bảo toàn động lượng giữa đạn-gỗ: mv = (m + M)V 0 A
Vận tốc ban đầu của hệ đạn-gỗ tại A: V = m v = 0,02 700 = 13,7(m / s) A (m + M) 0 (0,02 +1)
Với hệ kín gồm: đạn-gỗ-TĐ. Công mà hệ thực hiện từ A đến B: 1 K (m 2 2
B − KA = −fmsd
+ M)VB = 1 (m + M)VA − (m + M)gd 2 2 V 2
B = VA − 2gd = 13,72 − 2.10.1 = 12,9(m / s)
b) Áp dụng ĐLBTCN tại B và C. Chọn gốc thế năng tại C
1 (m + M)V2+ (m + M)gh = 1 (m + M)V2 2 B 2 C Hay: V =
V2 + 2gh = 12,92 + 2.10.0,5 = 13,3(m / s) C B lOMoARcPSD|45316467
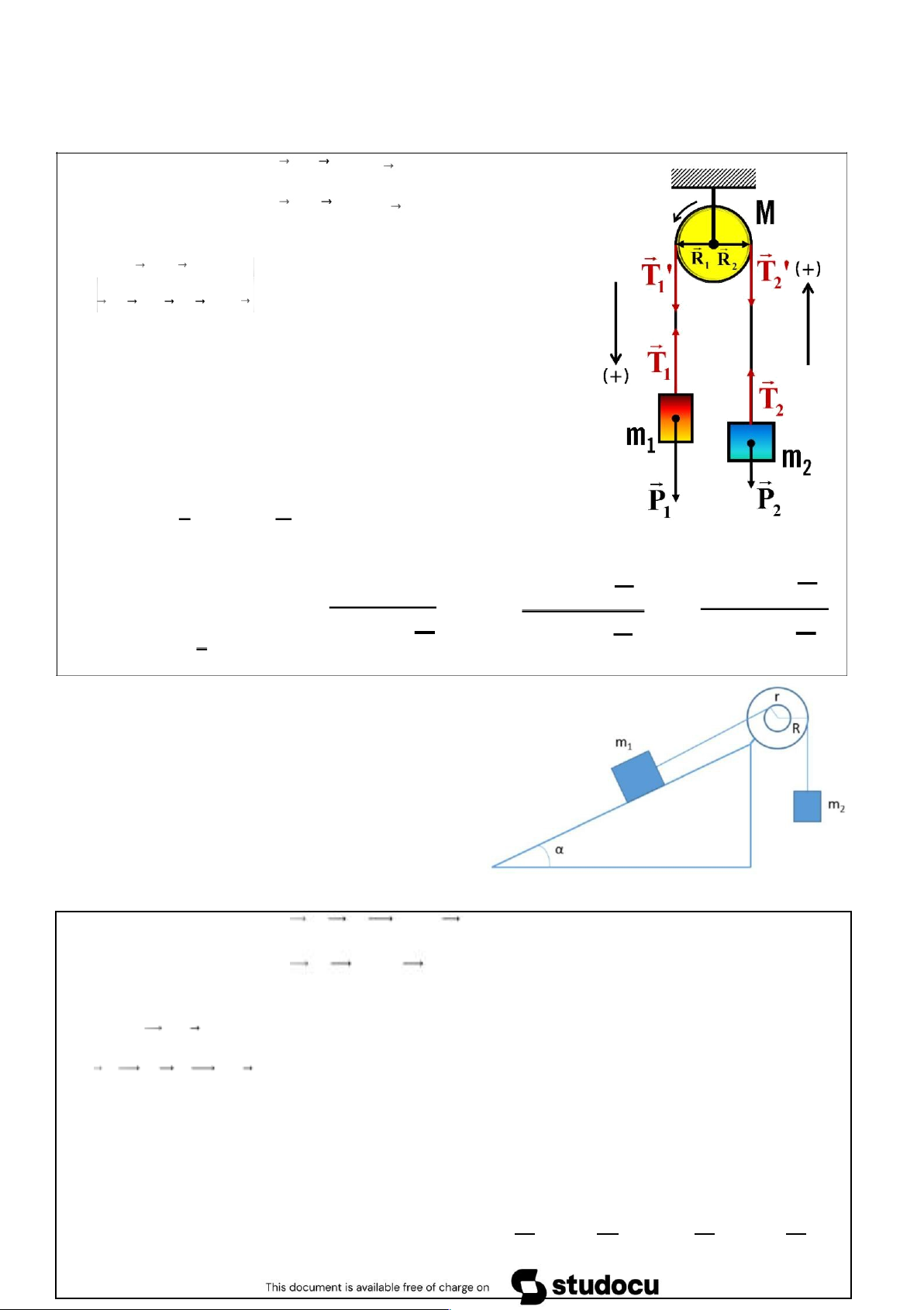
10. Giải bài toán sau bằng phương pháp định luật bảo toàn cơ năng trong trọng trường. Một sợi dây
được vắt qua một ròng rọc bán kính R, hai đầu buộc hai vật khối lượng lần lượt là m1, m2 (m1 > m2).
Tính gia tốc của hệ trong 2 trường hợp: Bỏ qua khối lượng ròng rọc và Ròng rọc có khối lượng M.
a) Bỏ qua khối lượng ròng rọc
Chọn gốc thế năng tại thời điểm ban đầu t0 = 0 hai vật đứng yên ( v 01 = 0)
= v 02 Định lí động năng cho hệ tại t0 và t: M
( K + K ) −( K + K )= A + A 1 2 01 02 P1 P2 1 ( m v 2
2 + 1 m v 2 − 0 = P .s .cos P , s )+ P .s .cos P,s ) 2 2 2 2 1 1 2 2 1 1 ( 1 1 2
1 m v2 + 1 m v 2 = P .s − P .s 2 2 2 1 1 2 2 1 1 2 s = s = s a = a = a Dây không giãn: 1 2 1 2
1 m v 2 + 1 m v 2 = m g.s − m g.s 1 m v 2 + 1m 2
2 v 2 = m1 g − m 2 g 2 1 1 2 2 2 1 2 2s 1 1 2s Trong đó: v2 v2 0 2 − v = 2as 1 = 2 v 2 = a 2s 2s h h2 h
m a + m a = m g − m g a = m − m g 1 1 2 1 2 1 2 m + m 1 2
b) Ròng rọc có khối lượng M
Chọn gốc thế năng tại mặt đất.
Tại thời điểm t0 = 0: v 01 = v 02 = 0
Tại thời điểm t: 1 2 1 2 1 2 s = s = s ; v = v = v ;
a = a = a (Do dây không giãn)
Định luật bảo toàn cơ năng tại thời điểm t0 = 0 và t E 0 = Et
( K 01 + U 01 ) + ( K 02 + U 02 ) + ( K 0RR + U 0RR ) = ( K t1 + U t1 ) + ( K t + U )+(K + U ) 2 t 2 tRR tRR 1 1
( 0 + m .g.h )+(0 + m.g.h ) + ( 0 + M.g.h ) = 1m v s ) + 2 s ) + I. 2 + M.g.h m v 22 .2g. + m ( h 2 +
2 + m .g. ( h 1 − 1 1 2 2 1 1 1 2 2 2 0 = 1 2 m v
+ m .g. ( −s ) +1 2 m + m + 1 2 1 1 2 2 v .g.s I. 2 2 2 1 v a.t 1 Thay: v = a.t ; I = M.R 2 ; = = ; s = a.t 2 2 R R 2 a = m1 − m2 g M m + m + 1 2 2
11. Một hệ gồm một ròng rọc trụ đặc đồng chất khối lượng M, bán kính R, quay quanh trục O nằm
có ngang và hai khối m1, m2 (m1 > m2) treo vàodây vắt qua ròng rọc. Giả sử dây không trượt trên
sợi ròng rọc. Tìm:
a) Gia tốc của vật.
b) Sức căng T1 và T2 của dây treo. lOMoARcPSD|45316467 P + T = m a 1 1 1 1
Định luật II Newton: P + T = ma 2 2 2 2
Phương trình chuyển động quay của ròng rọc: M = I R T1+R T2=I
Chiếu theo chiều (+) của chuyển động: P − T = m a 1 1 1 1 T − P = m a 2 2 2 2
R (T − T ) = I 1 2 Dây không dãn, ròng a = a =
rọc cố định: a 1 2 Trong đó: 1 2 = a I = ; 2 MR R m .g − T = m a M M 1 2 1 1 1 m g 2m 2 + g 1 m 2m + T − m .g = ma a = m − m 2 => 1 2 g 2 T = ; T = 2 2 2 M ; 1 2 ( m + m + m + m + M + m + M m T ) = 1 R − T Ma 1 2 2 1 2 2 1 2 2 1 2 2
12. Cho hai vật có khối lượng m1 và m2 được nối
bằng dây nhẹ, không dãn, vắt qua ròng rọc kép có
bán kính lần lượt là R và r, có momen quán tính I.
Vật m1 đặt trên mặt phẳng nghiêng góc α, bỏ qua
ma sát giữa m1 và mặt phẳng nghiêng. Hãy xác định:
a) Gia tốc chuyển động của m1 và m2.
b) Tính các lực căng dây.
Biết R = 0,1 m, r= 0,05 m, m1 = 3 kg, m2 = 2 kg, g = 9,78 m/s2, α = π/6, I = 2.10-3 kg.m2.
P + T + N = m a 1 1 1 1 1
Định luật II Newton: P + T = m a 2 2 2 2
Phương trình chuyển động quay của ròng rọc: M = I
r T1 ' + R T2 ' = I
T1 − P1 sin = m1a1
Chiếu theo chiều (+) của chuyển động: P2 − T2 = m 2 a2
− r.T '+ R.T ' = I. 1 2 a a a = = ; = 1 ; = 2 a = R a ; = 1 1 2 1 2 2 1
Dây không dãn, ròng rọc cố định: r R r r T =T';T = T ' 1 1 2 2 lOMoARcPSD|45316467
T1 − m1 .g.sin = R.m 2 − r.m1 .g.sin m1a1 − = R a 1 = g m .g T m R 2 I r.m + m + 2 2 2 r a 1 1 r 2 r
R.T − r.T = I a1 2 1 r
Thay số và tính a2, T1 , T2 R
a = 2,1 m/ s 2; a = a = 4, 2 m / s 2 T = m (a + g.sin ) = 21 N
; T = m g − R a =11,2 N 1 2 ; r 1 1 1 1 2 2 1 r
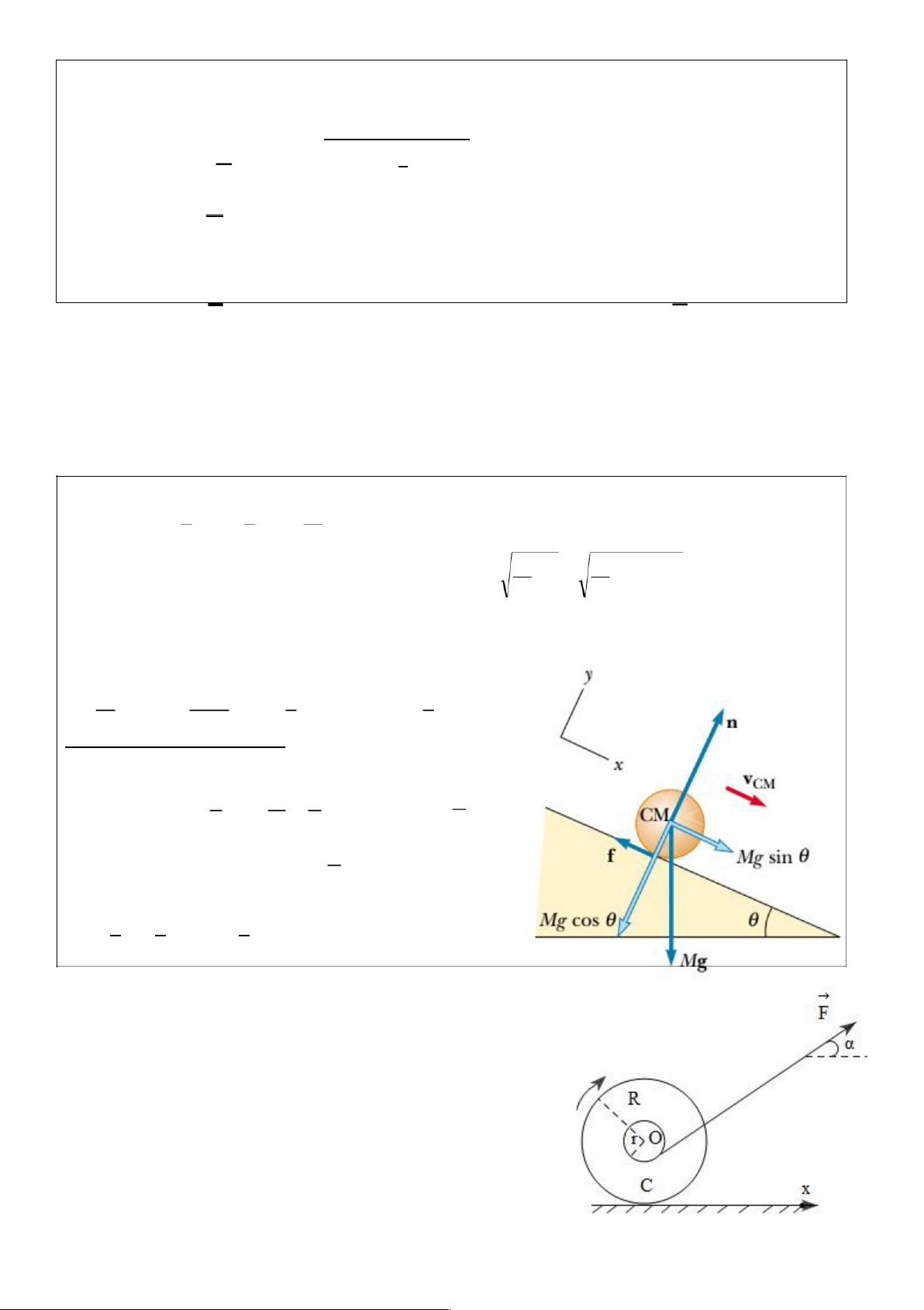
13. Một quả cầu rắn khối lượng m = 10 kg, bán kính R, ban đầu có độ cao H = 1,5 m của một mặt
phẳng nghiêng α = 300. Quả cầu lăn (không trượt) không vận tốc đầu xuống. Lấy g = 9,8 m/s2.
Mômen quán tính của quả cầu I= 2/5mR2.
a) Tính vận tốc của quả cầu tại đáy mặt phẳng nghiêng.
b) Xác định độ lớn của lực ma sát khi nó lăn xuống mặt phẳng.
a) Theo định luật bảo toàn cơ năng cho quả cầu: Eđầu = Esau 1 1 7 2 2 2
mgH = 2mv + 2 I = 10mv
Vận tốc của quả cầu tại đáy mặt phẳng nghiêng: 10 10 v = gH = 9,8 1,5 = 4,6(m/s) 7 7
b) Áp dụng định luật 2 Newton:
mgsin − Fms = ma Fms = mg.sin − m.a
Với v2 = 2a.s = 2a.H/sinα 10 H a = 5g.sinF = 2 g.H = 2a. m.g.sin 7 sin 7 ms 7 C
ó th ể tính theo cách khác:
Phương trình động học của vật rắn quay:
M = F R=I = 2mR a 2 = 2mRa F = 2ma ms => 5 R 5 ms 5 (2)
Từ (1) và (2), ta thu được : 5 a = gsin 7
Thay a và (1), ta thu được:
F =2 m 5 g.sin = 2 m.g.sin = 14N ms 5 7 7
14. Trên mặt phẳng nằm ngang có một cuộn chỉ khối lượng
m, bán kính vành ngoài là R, bán kính phần lõi là r, mômen
quán tính đối với trục của nó bằng I = bmR2, với b là hệ số tỉ
lệ nguyên. Quấn vào lõi cuộn chỉ một sợi dây rồi kéo đầu dây
bằng một lực F không đổi (có cường độ F và hợp với
phương ngang góc α) làm cho nó lăn không trượt. Hãy tìm:
1) Độ lớn của hướng vectơ gia tốc của trục cuộn chỉ.
2) Công của lực F sau thời gian t kể từ lúc nó bắt đầu chuyển
động. Bỏ qua ma sát lăn. lOMoARcPSD|45316467
Kí hiệu a là gia tốc của trục cuộn chỉ theo chiều dương hướng sang phải; Fms là lực ma sát
tác dụng lên cuộn chỉ (hướng sang trái)
F.cosα − Fms = ma (1)
Phương trình theo định luật II Newton:
Phương trình động học của vật rắn quay: M = I
r F' + R Fms ' = I
− r.F + R. Fms = I. (2)
Với β = a.R (vì lăn không trượt) và I = bmR2 (3) F(R.cos − r)
Từ đó suy ra: a = m.R(1 + b) (4)
Từ (4): cosα > r/R thì a > 0 thì chiều của gia tốc phù hợp với chiều dương như đã chọn.
cosα < r/R thì a < 0: chiều dương theo hướng ngược lại, cuộn chỉ chuyển động sang trái.
cosα = r/R thì a = 0 => cuộn chỉ chuyển động thẳng đều; khi đó phương của lực kéo F đi
qua điểm tiếp xúc của cuộn chỉ với mặt phẳng nằm ngang. 1 F 2 2cos (R.cos − r)
Công do lực kéo F thực hiện sau t giây: A = F.s.cos = F. 2 = t a.t 2 2m.R(1 + b)
15. Giải bài toán sau đây bằng phương pháp định luật bảo toàn và chuyển hóa năng lượng. Một
vật m1 được đặt trên một mặt phẳng nghiêng với mặt phẳng nằm ngang một góc α. Dùng một sợi
dây, một đầu buộc m1 vòng qua một ròng rọc trụ đặc, bán kính R, đầu kia treo một vật nặng m2 (m2
> m1). Hệ số ma sát giữa m1 với mặt phẳng nghiêng là k. Giữa m2 và mặt phẳng thẳng đứng không
có ma sát. Tính gia tốc của hệ:
a) Bỏ qua khối lượng ròng rọc.
b) Ròng rọc có khối lượng m.
a) Bỏ qua khối lượng ròng rọc.
Thời điểm ban đầu t0 = 0 hai vật đứng yên (v = v = 0) 01 02
(K + K )− (K + K )= A +A +A
Định lí động năng cho hệ tại t0 và t: 1 2 01 02 P1 Fms1 P2
1 m v 2 +1 m v 2− 0 = P .s .cos(P , s + F .s.cos(F , s + P.s ( ) 2 .cos P2 , s2 2 2 1 1 2 2 1 1 1 1 ) ms1 1 ms1 1 ) 2
1 m v 2 +1 m v 2 = − P sin .s − k.P cos .s + P .s 2 2 2 1 1 2 2 1 1 1 1 2
Dây không giãn: s1 = s 2 = s a1 = a 2 = a
1 m v 2 +1 m v 2 = − m g.sin .s − k.m g.cos .s + m g.s 2 1 1 2 2 2 1 1 2
1 m v 2 + 1 m v 2 = − m g.sin − k.m g.cos + m g 2s 1 1 2s 2 2 112 v 2 v2 Thay v 2 − v 2 0 = 2as 1
= 2 = a vào, ta được: 2s 2s m
m a + m a = −m g.sin − k.m g.cos + m g a =
2 − m1 (sin + k.cos ) g 1 2 1 1 2 m1 + m2 lOMoARcPSD|45316467
b) Ròng rọc có khối lượng M.
Định lí động năng cho hệ tại t ( ) 0 K ) + K = A + A + A và t: + K + K − ( K + K 2 RR 01 02 1 0RR P1 Fms1 P
1m v + 1 m v + 1 I − 0 = ( 2 2 ( 2 ) 2 1 1 2 2 2 2 P .s .cos P , s F , s + P .s .cos P , s 1 1 ms1 1 ms1 1 ) 2 1 1 2 2 2 2 ) + F .s.cos(
1m v + 1 m v + 1 I = − P 2 2 2
sin .s − k.P cos .s + P .s 2 1 1 2 2 2 2 1 1 1 1 2 2 1 v a.t 1 Thay:
= v = v = a.t I = 2 ; = = = s = s = 2 v ; m.R ; s a.t 1 2 2 2 R R 1 2
m a + m a + m a = − m g.sin − k.m g.cos + m g 1 2 2 1 1 2
a = m 2 − m1 (sin + k.cos ) g + m + mm 1 2 2 lOMoARcPSD|45316467
VI.Chương 6: Các công thức cơ bản của nhiệt động học.
1.Phương trình trạng thái của khí lí tưởng: P.V = n.R.T
3.Nhiệt dung riêng (ký hiệu: c)
Nhiệt dung riêng của một chất có thể cho biết nhiệt lượng cần thiết để có thể làm cho 1 kg chất đó
tăng thêm 1 độ C, được đo bằng J/kg.K.
4. Nhiệt dung riêng mol: (ký hiệu: C)
Nhiệ t dung riêng của m ột chất có thể cho biết nhiệt lượng cần thiết để có thể làm cho 1 mol chất
đó tăng thêm 1 độ C, được đo bằng J/mol.K.
5.Mối liên hệ giữa c và C:
µ khối lượng một mol chất. 6. Hệ số Poisson: =CP =1+2 C Vi
Trong đó i là bậc tự do:
Khí đơn nguyên tử (He, Ar, Xe…): i = 3
Khí hai nguyên tử (lưỡng nguyên tử) (H2, O2, N2…): i = 5
Khí ba nguyên tử trở lên (CO2, H2O, NH3…): i = 6 C =C +R; C =i +1 R; C =iR PV P V 2 2
7. Ba trạng thái cơ bản: P
Đẳng tích ( V = const) : P = const hay = P 1 2 T T T 1 2
Đẳng áp ( P = const) : V = const hay V1 =V2 T T1 T2 Đẳ ệ 1 1 2 2
ng nhi t ( T = const): PV = const hay P V = P V lOMoARcPSD|45316467
VII.Chương 7: Nguyên lí I Nhiệt động lực học. 1. Công: V2
dA = −PdV => A = − PdV V1
Đẳng tích ( V = const) : A = 0
Đẳng áp (P = const ) : A = − P (V ) 2 − V1
Đẳng nhiệt (T = const ): A = − m RT ln V2 = − m RT ln P1 V1P2
2. Nội năng của khí lí tưởng: m iR U = T 2
Độ biến thiên nội năng:
U = m iR T = m iR (T − T ) 2 2 2 1
Lưu ý rằng: nội năng chỉ phụ thuộc vào trạng thái đầu và cuối, không phụ thuộc vào quá trình biến đổi. 3.Nguyên lí 1: U=Q+A
Đoạn nhiệt (hệ không trao đổi nhiệt năng với bên ngoài): Q = 0
Đẳng tích (V = const ) : Q = U = m C T = m i R T V2
Đẳng áp (P = const ) : Q = m C T = m i + 1 R T P 2
Đẳng nhiệt ( T = const): Q = − A = m RT ln V = m RT ln P 2 1 V P 1 2
VIII.Chương 8: Nguyên lí II Nhiệt động lực học.
1. Hiệu suất của động cơ nhiệt:
= A' = Q1 −Q2 =1− Q2 Q1Q1Q1
A’: công mà động cơ sinh ra,
Q1: nhiệt lượng động cơ nhận được từ nguồn nóng,
Q2: nhiệt lượng động cơ tỏa ra cho nguồn lạnh.
2. Chu trình Carnot: cho hiệu suất cao nhất, gồm Đẳng nhiệt - Đoạn nhiệt - Đẳng nhiệt - Đoạn nhiệt: max = 1− T2 T1
3. Độ biến thiên entropy: lOMoARcPSD|45316467 (2) Q 2 1
S = S − S = T (1)
- Quá trình thuận nghịch => ΔS = 0
- Tất cả các quá trình tự nhiên đều là quá trình không thuận nghịch nên trong các quá trình đó entropy luôn tăng S 0 .
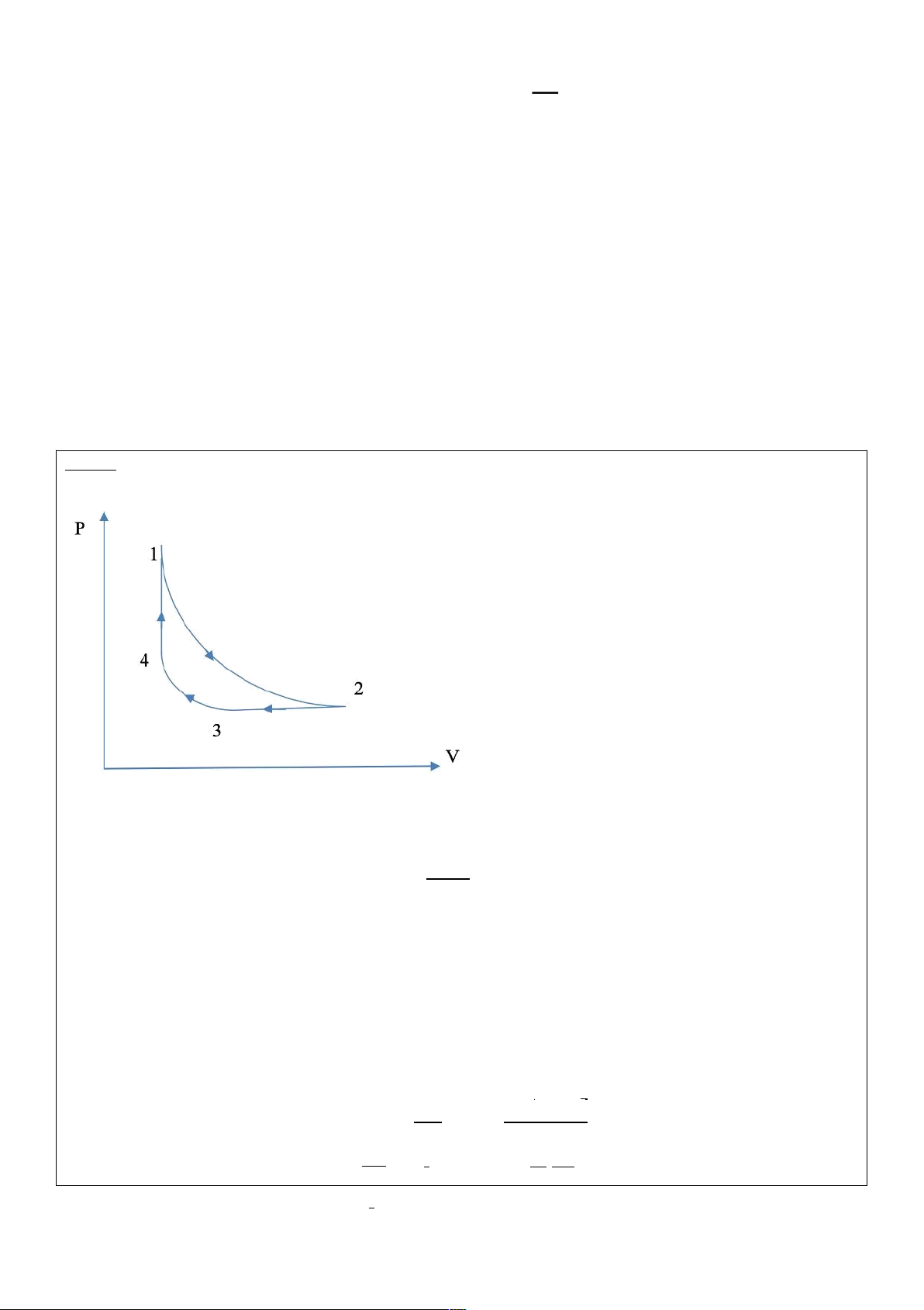
Một mol khí Heli xem như khí lý tưởng thực hiện chu trình biến đổi sau đây: từ trạng thái 1 với áp
suất P1 = 105Pa, nhiệt độ T1 = 600K, dãn nở đẳng nhiệt đến trạng thái 2 có áp suất P2 = 2,5.104Pa,
sau đó bị nén đẳng áp đến trạng thái 3 có nhiệt độ T3 = 300K, tiếp theo bị nén đẳng nhiệt đến
trạng thái 4 và cuối cùng trở về trạng thái 1 bằng quá trình đẳng tích.
a) Vẽ đồ thị biểu diễn chu trình biến đổi này trên giản đồ (P,V)
b) Tìm các nhiệt độ V2, V3, V4 của tác nhân ở các trạng thái (2), (3), (4) tương ứng.
c) Tính hiệu suất của chu trình trên.
Câu 3: (4 điểm) a)
b) Khí Heli có bậc tự do i = 3 1 3 T1=T2=600K 1 = 4 = 1 = 0,0499 2 3 2 = = 0,1994 T3=T4=300K 2 3 2 3 3 ệ ấ ủa chu trình đượ = 2 = 0,0997 ′2 23 + 34 =1− =1+ 1 + 41 12 c) Hi u su t H c
c tính theo công thức: + 2 ( 3 − 2 )+343 = 1 + 2 2 = 0,25 1 1 + (1− 4)