Tổng hợp đề thi giữa kì môn Toán rời rạc| Môn Toán rời rạc| Trường Đại học Bách Khoa Hà Nội

Cấu trúc đề thi giữa kỳ môn Toán Rời Rạc
Mỗi bài 01 điểm. Làm bài luôn vào đề.
Yêu cầu: Viết sáng sủa và ngắn gọn; Không nháp vào bài thi.
Bài 1. Chứng minh một số tính chất đơn giản về đồ thị và cây.
Bài 2. Tìm cặp ghép hoặc tìm đường đi (chu trình) Hamilton.
Bài 3. Thuật toán Dijkstra hoặc Prim.
Bài 4. Thuật toán Kruskal hoặc cấu trúc dữ liệu Disjoint Set.
Bài 5. Tô màu đồ thị.
Bài 6. Tìm thành phần liên thông mạnh.
Bài 7. Tính toán Pr¨ ufer code của cây.
Bài 8. Bài toán Hôn nhân bền vững.
Bài 9. Luồng cực đại và lát cắt cực tiểu.
Bài 10. Bài tập sáng tạo. 1 2
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
Họ và tên:...................................................... MSSV:..................
VIỆN CÔNG NGHỆ THÔNG TIN VÀ TRUYỀN THÔNG
Họ tên SV: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
MSSV: . . . . . . . . . . . . . . . . . . . . . Số thứ tự
Học phần: Toán Rời Rạc . . . . . . . . . . . . . . . . . . . . . . . .
Mã HP: . . . . . . . . . . . . . . . . . . . .
Bài thi [ ] giữa kỳ [X] cuối kỳ . . . . . . . . . . . .
Ngày thi: . . . . . . . . . . . . . . . . . Điểm của bài thi
Chữ ký của (các) cán bộ chấm thi
Chữ ký của cán bộ coi thi
Đề mẫu thi giữa kỳ môn Toán Rời Rạc
Thời gian 90 phút. Không sử dụng tài liệu.
1. Một cây có 2n đỉnh bậc 1, 3n đỉnh bậc 2, n đỉnh bậc 3 và không có đỉnh bậc khác. Hãy xác
định xem n bằng bao nhiêu, từ đó tìm số đỉnh và số cạnh trong cây.
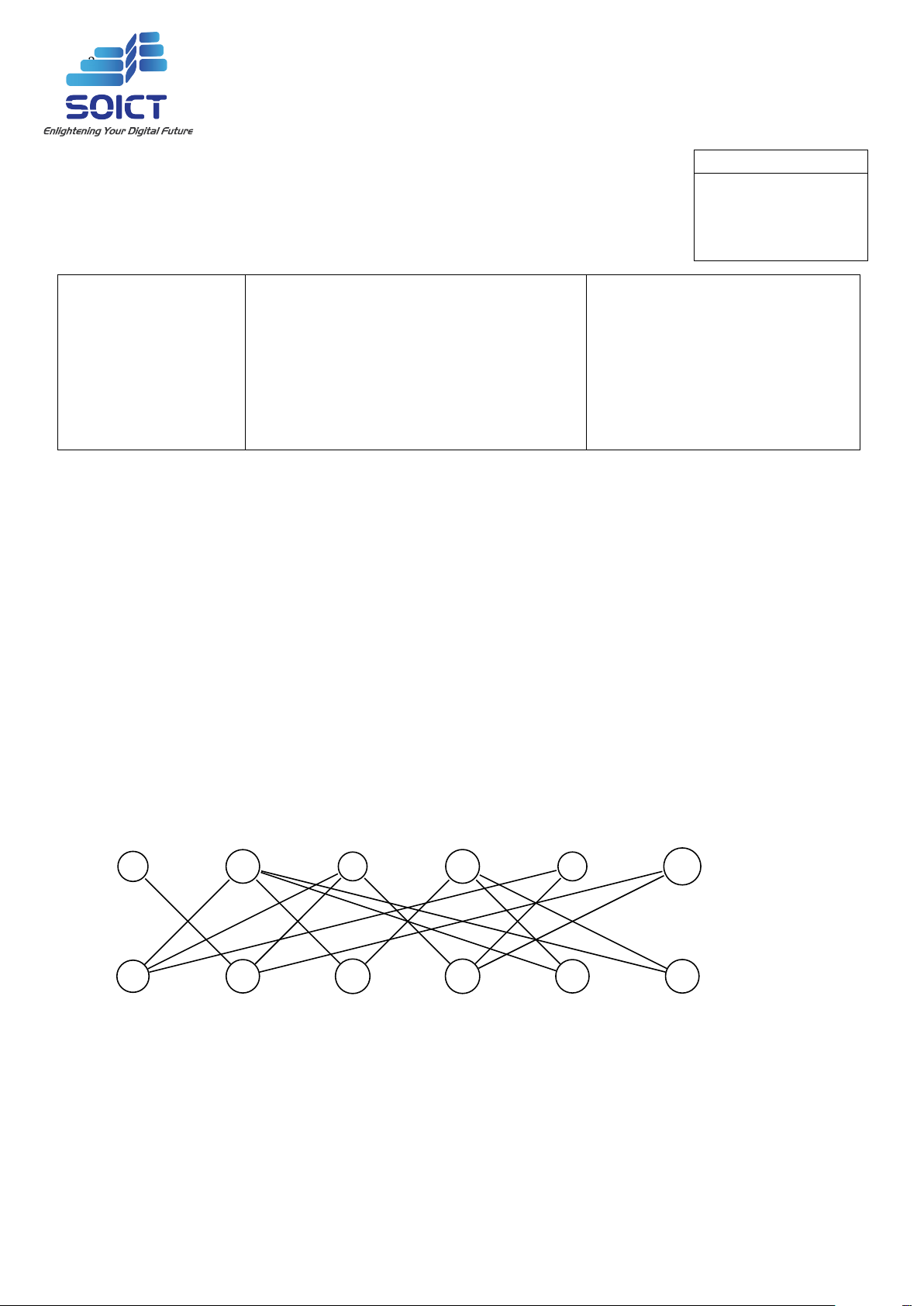
2. Liệu ta có thể ghép cặp đầy đủ cho đồ thị hai phần dưới đây không? Nếu có tô đậm một ghép
cặp như vậy. Nếu không hãy chứng minh. a b c d e f A B C D E F 3
3. Hãy dùng thuật toán Dijkstra để xây dựng cây mô tả đường đi ngắn nhất từ đỉnh A tới tất
cả các đỉnh khác của đồ thị sau: 5 1 1 E F G H 1 4 6 2 1 8 6 A B C D 1 2 1
4. Hãy dùng thuật toán Kruskal để tìm cây bao trùm nhỏ nhất cho đồ thị trong Bài tập 3.
5. Xét đồ thị G thu được từ đồ thị trong Bài 3 sau khi bỏ đi trọng số trên cạnh. Hãy tìm cách tô
màu đồ thị này dùng ít màu nhất có thể. Tại sao số màu bạn dùng lại là ít nhất? 4
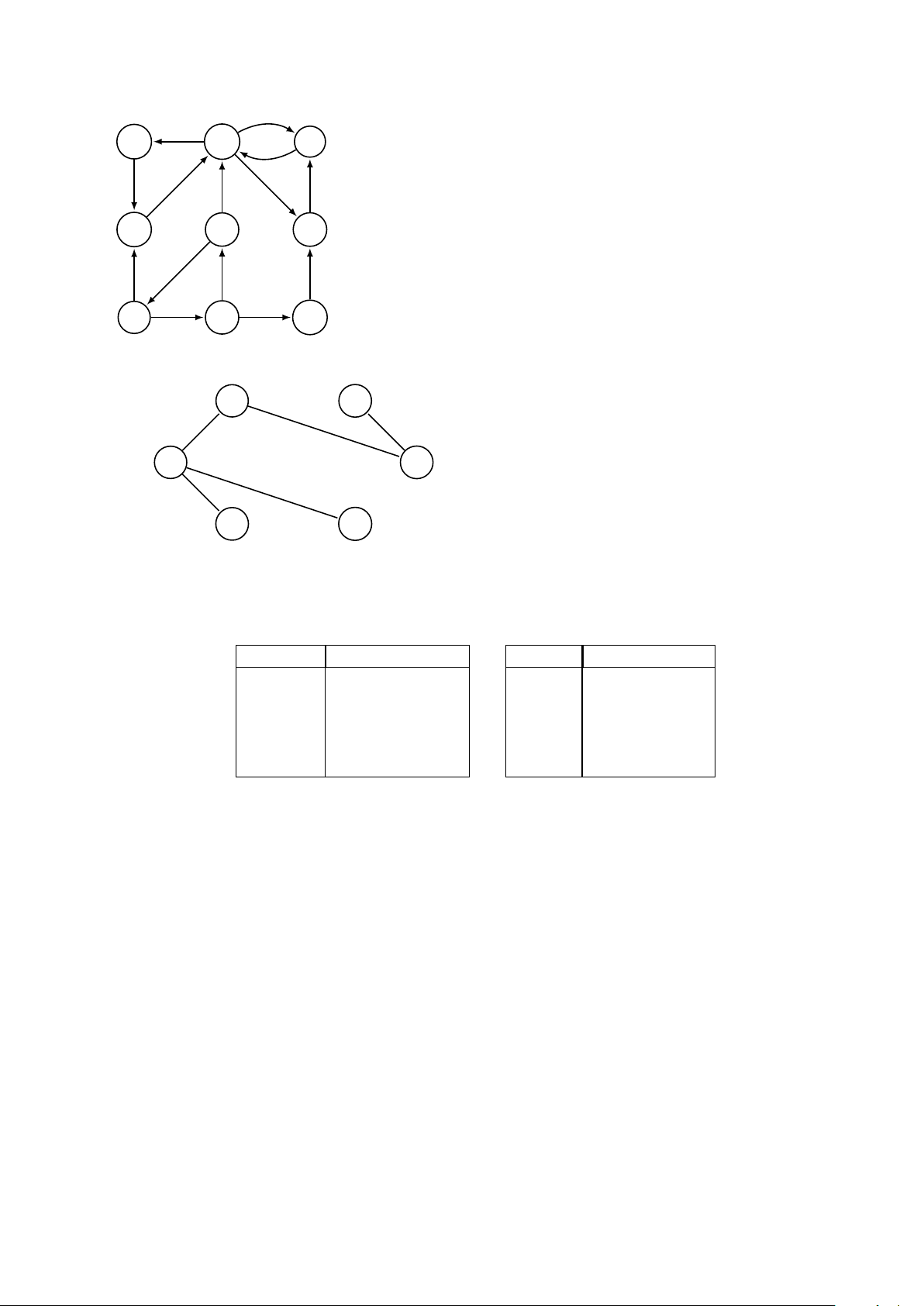
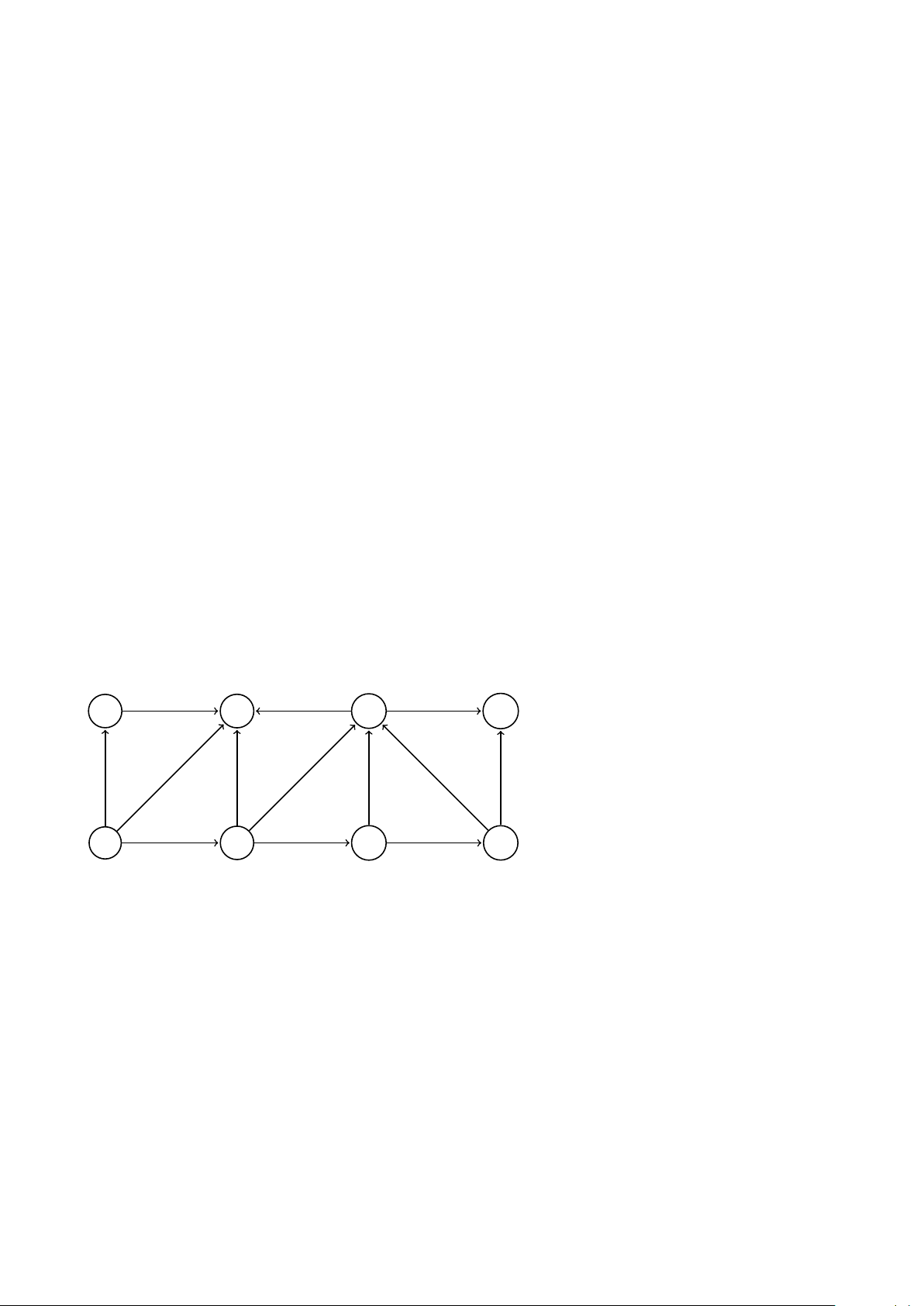
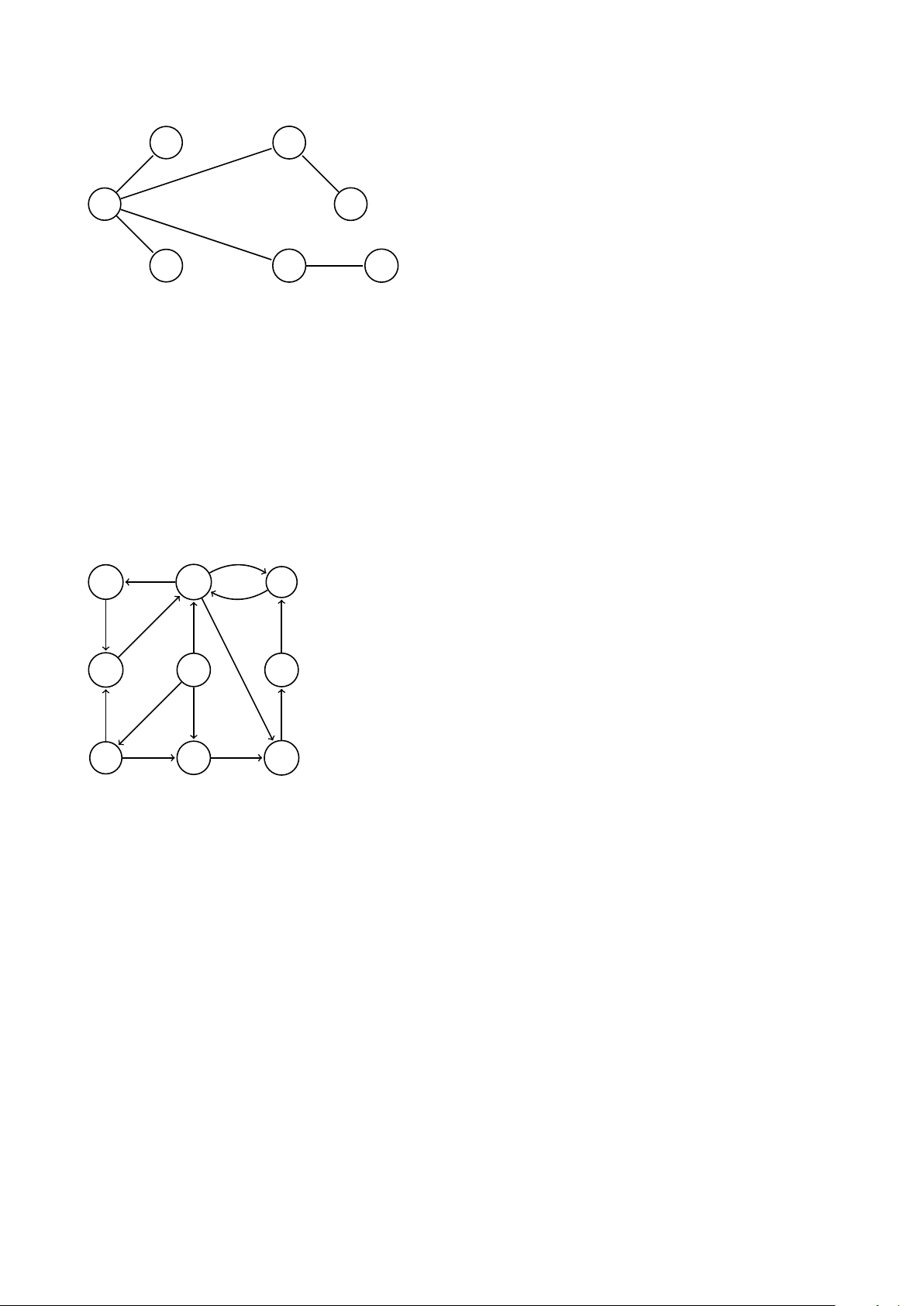
6. Hãy tìm các thành phần liên thông mạnh của đồ thị sau. G H I D E F A B C 7. (a) Xác định Pr¨ ufer code của cây sau: 2 3 1 0 5 4
(b) Xây dựng cây với Pr¨
ufer code là (0, 0, 0, 4, 2, 0, 1, 0).
8. Có năm sinh viên a, b, c, d, e muốn thực tập tại năm công ty A, B, C, D, E. Sau đây là danh sách
xếp hạng mức độ ưa thích của các sinh viên và của các công ty (trái nhất là thích nhất): Sinh viên Công ty Công ty Sinh viên a B A D E C A e a b d c b D B A C E B c b d a e c B E C D A C b c d e a d A D C B E D a e d c b e B D A E C E d b e c a
Hãy dùng thuật toán kén chồng để tìm một cặp ghép ổn định. Cặp ghép ổn định này có phải
là duy nhất không? Tại sao? 5
9. Hãy tìm luồng cực đại và lát cắt cực tiểu của mạng sau đây. 2 a d 3 1 2 10 3 s b 1 t 1 4 5 5 c e
10. Cho một tập các biến x =
1, x2, . . . , x , và một tập các ràng buộc bằng nhau hoặc khác n xi x j nhau x
. Bạn hãy thiết kế thuật toán kiểm tra liệu các biến có thể thỏa mãn mọi ràng i 6= x j buộc.
Ví dụ, các ràng buộc x = = = 1 x2, x2 x3, x3
x4, x1 6= x4 là không thể thỏa mãn.
Đề thi giữa kỳ Toán rời rạc Đề 2 Thời gian 90 phút
Mỗi câu 1 điểm. Không dùng tài liệu. 1. Tính Pr¨ ufer code của cây sau: 2 3 1 0 5 4
2. Xây dựng cây có Pr¨
ufer code là (10, 1, 7, 4, 3, 4, 10, 2, 2, 8).
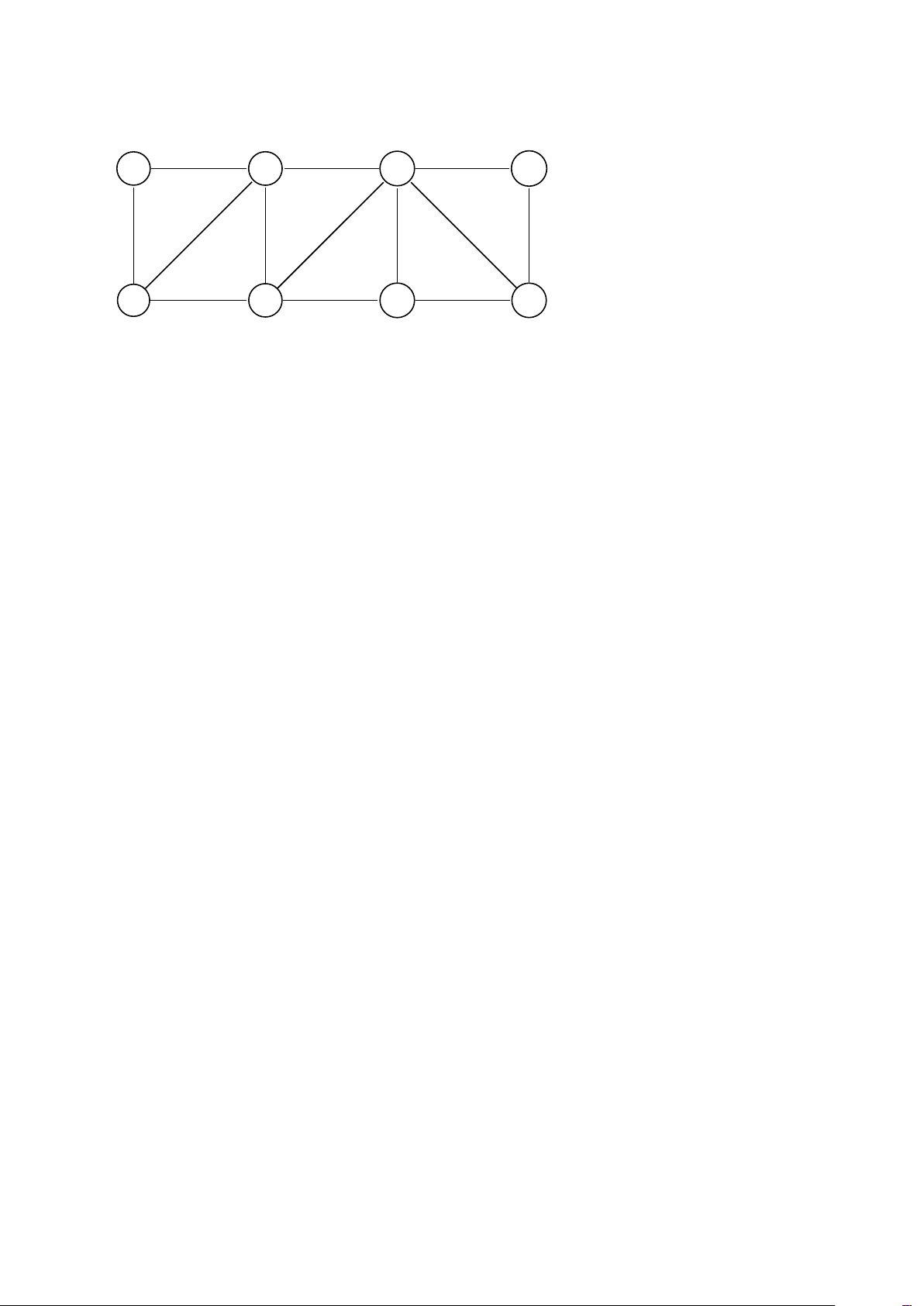
3. Dùng thuật toán Kruskal tìm cây bao trùm lớn nhất của đồ thị sau: 1 2 3 6 1 7 1 7 9 6 5 3 5 4 3
4. Một cây có n2 đỉnh bậc 2, n3 đỉnh bậc 3, · · · , n đỉnh bậc k
k. Các đỉnh còn lại đều có bậc 1.
Hỏi cây đó có bao nhiêu đỉnh bậc 1. Hãy giải thích. 1 2
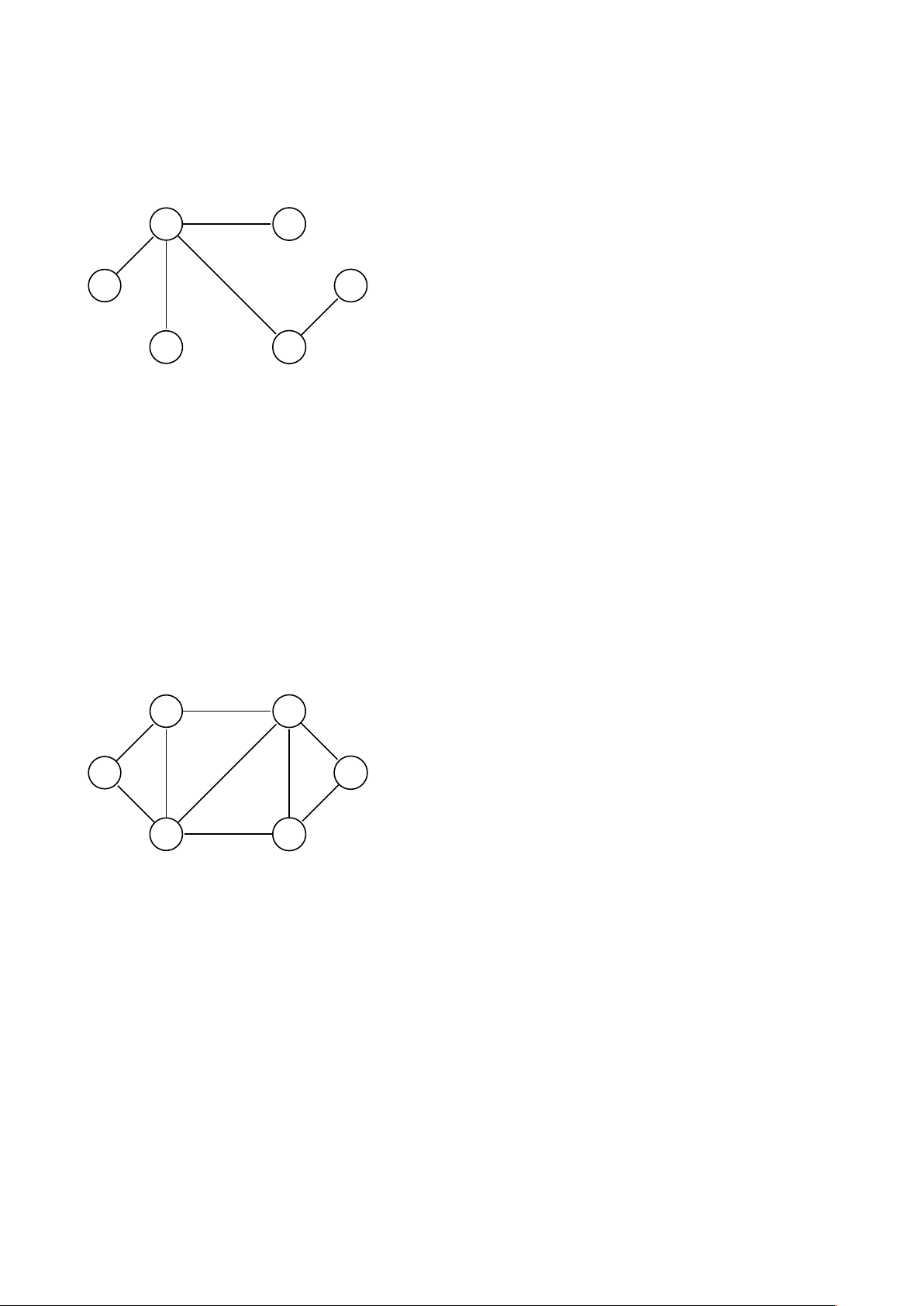
5. Xét đồ thị dưới đây:
(a) Hãy tìm cách gán thứ tự cho các đỉnh của đồ thị để thuật toán tham lam tô màu đồ thị
này dùng ít màu nhất có thể.
(b) Bạn hãy tô màu đồ thị này bằng thuật toán tham lam với thứ tự các đỉnh vừa làm ở
câu (a). Giải thích xem tại sao thuật toán tham lam không thể tô đồ thị này bằng ít màu hơn.
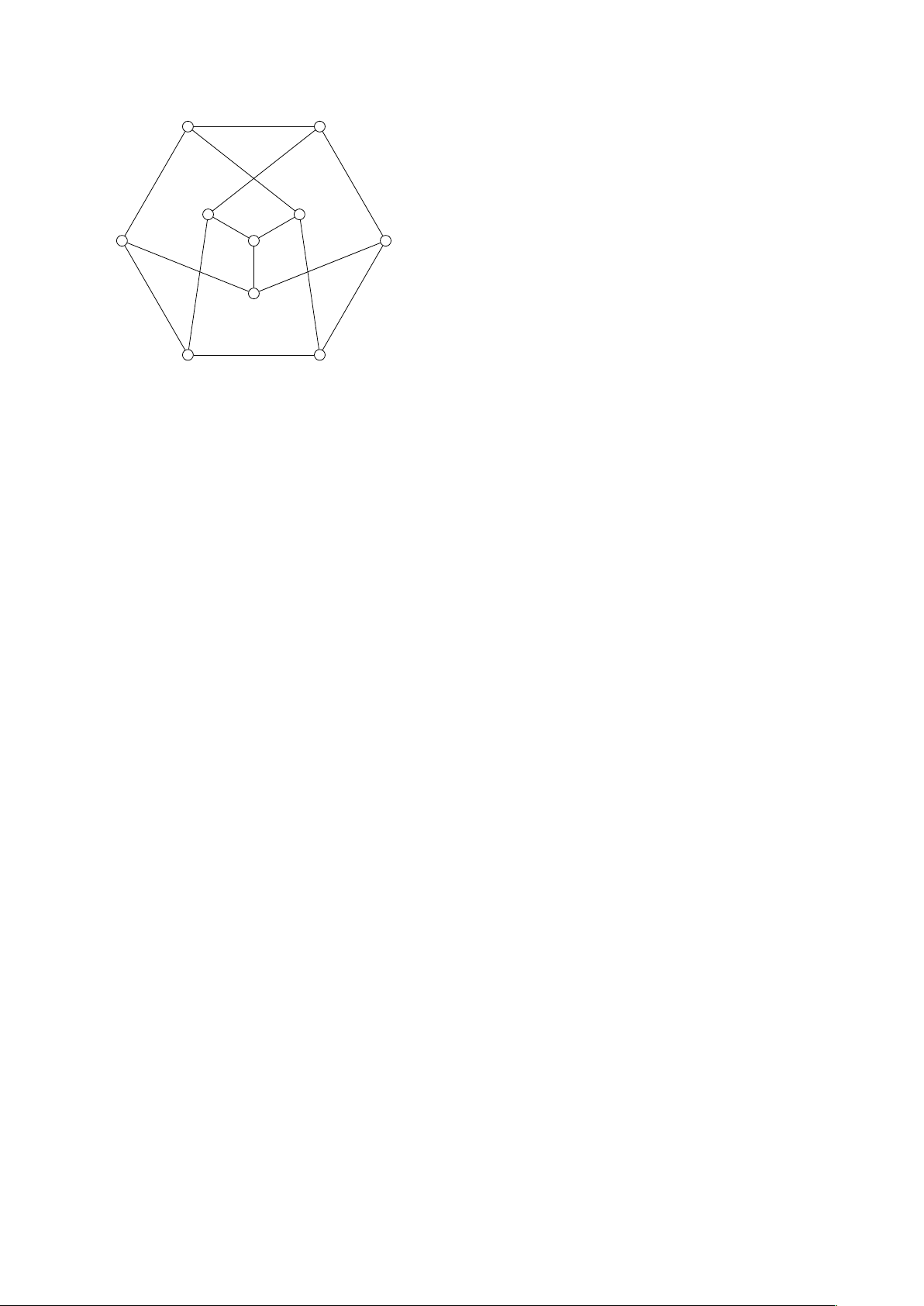
6. Đồ thị Peterson trong bài 5 có phẳng không? Hãy giải thích. 3
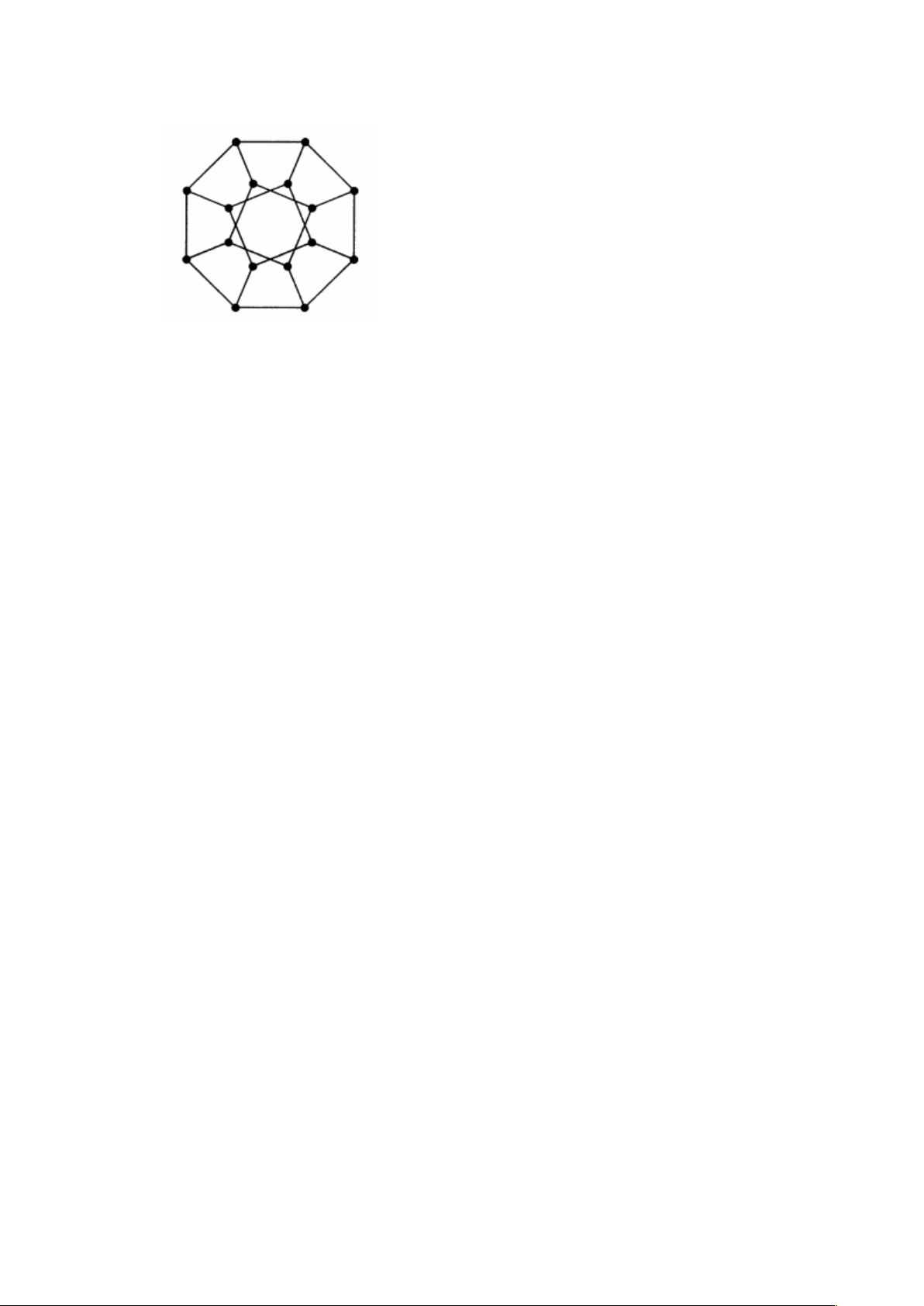
7. Đồ thị sau đây có chu trình Hamilton không? Hãy giải thích.
8. Lấy một bộ bài gồm 52 quân. Mỗi quân bài có một chất và một gía trị. Có bốn chất: Rô, Cơ,
Bích, Nhép; và có 13 giá trị: A, 2, 3, · · · , 10, J, Q, K.
Hãy đề nghị một người bạn xếp bài trên một lưới gồm 4 hàng và 13 cột. Chị ta có thể để các
quân bài theo cách bất kỳ. Trong bài tập này, bạn sẽ chứng minh rằng bạn luôn có thể lấy 13
quân bài, mỗi quân từ một cột trên lưới, sao cho có đủ 13 giá trị.
(a) Hãy mô hình bài toán này bằng cặp ghép trên đồ thị hai phần giữa 13 cột và 13 giá trị.
(b) Chỉ ra rằng mọi nhóm gồm n cột phải chứa ít nhất n giá trị khác nhau và chứng minh
rằng tồn tại cặp ghép. 4
9. Có năm sinh viên V, W, X , Y, Z muốn thực tập tại năm công ty A, B, C, D, E. Sau đây là danh
sách xếp hạng mức độ ưa thích của các sinh viên và của các công ty (trái nhất là thích nhất): Sinh viên Công ty Công ty Sinh viên V A B C D E A W X Y Z V W B C D A E B X Y Z V W X C D A B E C Y Z V W X Y D A B C E D Z V W X Y Z A B C D E E V W X Y Z
Hãy dùng thuật toán kén chồng để tìm một cặp ghép ổn định.
10. Chứng minh rằng trong 14 người luôn có 3 người đôi một quen nhau hoặc 5 người đôi một lạ nhau.
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
Họ và tên:...................................................... MSSV:..................
VIỆN CÔNG NGHỆ THÔNG TIN VÀ TRUYỀN THÔNG
Họ tên SV: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
MSSV: . . . . . . . . . . . . . . . . . . . . . Số thứ tự
Học phần: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Mã HP: . . . . . . . . . . . . . . . . . . . .
Bài thi [X] giữa kỳ [ ] cuối kỳ . . . . . . . . . . . .
Ngày thi: . . . . . . . . . . . . . . . . . Điểm của bài thi
Chữ ký của (các) cán bộ chấm thi
Chữ ký của cán bộ coi thi Tờ .../ ...
Đề thi giữa kỳ môn Toán Rời Rạc
Thời gian: 90 phút. Không sử dụng tài liệu. Làm bài luôn vào đề thi.
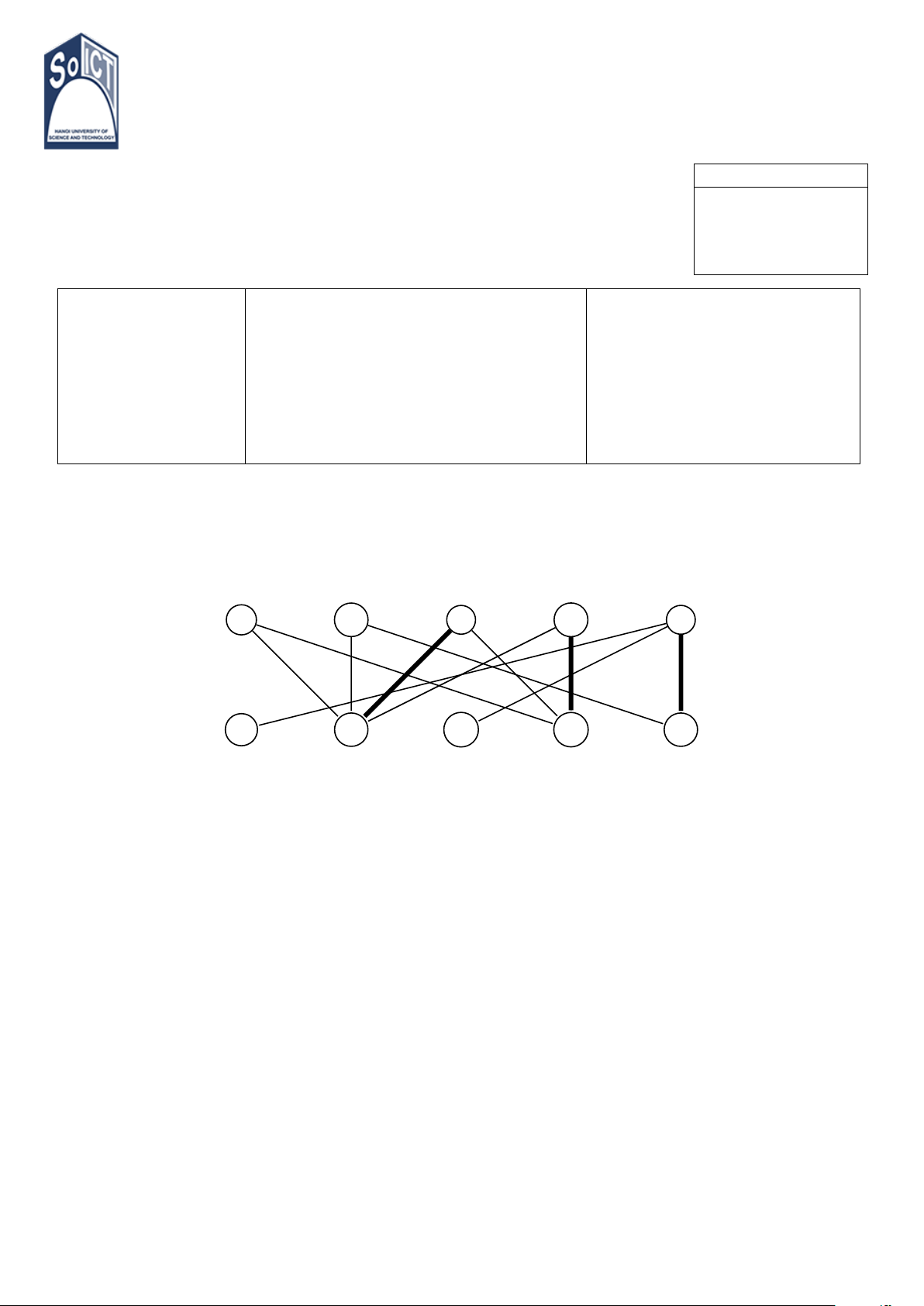
1. Xét M là ghép cặp ký hiệu bởi các đường nét đậm trong đồ thị sau. a b c d e A B C D E
(a) Tìm một đường mở cho M bắt đầu tại đỉnh b.
(b) Dùng đường mở vừa tìm được để xây dựng ghép cặp M 0 kích thước 4.
(c) Kiểm tra xem liệu còn đường mở nào cho M 0 không. Giải thích ngắn gọn.
(d) Liệu M 0 có phải ghép cặp cực đại. 1 2
2. Ngày mai, Viện CNTT&TT sẽ có 10 cuộc họp. Các cuộc họp có thời gian như sau: Cuộc họp 1: 11h – 12h29 6: 9h – 12h29 2: 15h – 16h29 7: 14h – 16h29 3: 9h – 10h29 8: 9h – 10h29 4: 11h – 12h29 9: 13h – 14h29 5: 13h – 14h29 10: 15h – 16h29
Do tính riêng tư, tại một thời điểm, mỗi phòng họp chỉ diễn ra nhiều nhất một cuộc họp. Hãy
xếp lịch họp cho Viện dùng ít phòng nhất. Hãy giải thích ngắn gọn tại sao cách xếp của bạn lại dùng ít phòng nhất.
3. Hãy dùng thuật toán Dijkstra để tìm đường đi ngắn nhất từ đỉnh A tới tất cả các đỉnh khác
của đồ thị sau. Yêu cầu: Vẽ bảng mô tả thuật toán. 5 1 1 E F G H 1 4 6 2 1 8 6 A B C D 1 2 1 3 4. Xác định Pr¨ ufer code của cây sau: 2 3 1 0 5 4 6
5. Xây dựng cây với Pr¨
ufer code là (1, 1, 0, 4, 2, 0, 1, 4).
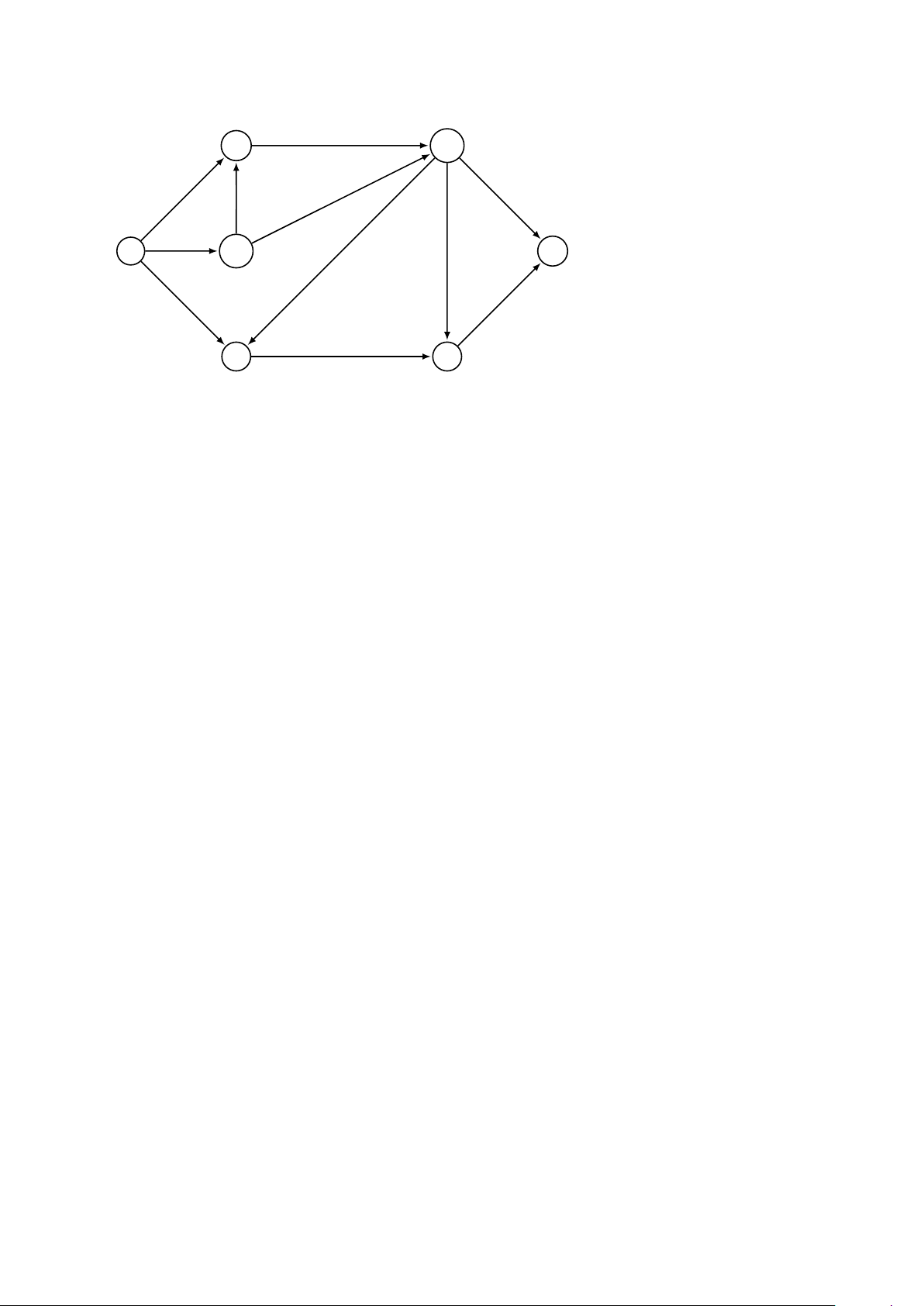
6. Thực hiện thuật toán DFS trên đồ thị G sau. Vẽ rừng DFS với các thông tin post và pre trên
mỗi đỉnh. Nếu cần quyết định thứ tự các đỉnh thăm, bạn hãy sử dụng thứ tự từ điển. Hãy liệt
kê các cạnh ngược (back edge). G H I D E F A B C
7. Hãy tìm các thành phần liên thông mạnh của đồ thị trong bài tập 6. Gợi ý: Tính toán trên đồ
thị GR và sử dụng thông tin post từ bài tập trước. 4
8. Có bốn sinh viên a, b, c, d muốn thực tập tại bốn công ty A, B, C, D. Sau đây là danh sách xếp
hạng mức độ ưa thích của các sinh viên và của các công ty (trái nhất là thích nhất): Sinh viên thích Công ty Công ty thích Sinh viên a A B C D A a b c d b D C B A B b a c d c A B C D C a d c b d C D A B D d c a b
Hãy dùng thuật toán kén chồng để tìm một cặp ghép ổn định. Cặp ghép ổn định này có phải
là duy nhất không? Tại sao?
9. Hãy mô tả một thuật toán nhận đầu vào là đồ thị có hướng G = (V, E), và xác định xem liệu
có hay không một đỉnh s ∈ V thỏa mãn: từ s ta có thể tới được mọi đỉnh của G. Phân tích
thời gian chạy của thuật toán và giải thích tại sao nó chạy đúng.