17 trang 99 lượt tải

Tổng hợp Trọn bộ phương pháp Min Max Số phức | Trọn bộ môn Toán 12

197

Tổng hợp Trọn bộ phương pháp Min Max Số phức | Trọn bộ môn Toán 12. Tài liệu gồm 17 trang giúp bạn tham khảo, củng cố kiến thức và ôn tập đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem!

Chủ đề: Tài liệu chung 297 tài liệu

Môn: Toán 12 3.9 K tài liệu

Tác giả:

Phạm Thị Huyền

11 tháng trước

Danh sách Quiz

TRỌN BỘ PHƯƠNG PHÁP MAX MIN SỐ PHỨC

I. LÝ THUYẾT BỔ TRỢ

Điểm biểu diễn số phức có dạng

... ...

z z

  

=> Là đường thẳng.

...z k 

=> Là đường tròn.

... ...z z k   

=> Có thể là elip, parabol, hypebol, đường thẳng…

Bất đẳng thức tam giác

•

1 2 1 2

z z z z ,  

dấu "=" khi

1 2

z kz

với k ≥ 0. Dùng cho BĐT Mincopxki:

•

1 2 1 2

z - z z + z ,

dấu "=" khi

1 2

z kz

với k ≤ 0. Dùng cho BĐT vecto

•

1 2 1 2

z z z - z , 

dấu "=" khi

1 2

z kz

với k ≤ 0.

•

1 2 1 2

z - z z - z ,

dấu "=" khi

1 2

z kz

với k ≥ 0.

Bất đẳng thức khác

BĐT Cauchy:

 

2 2

A B



 

tìm min

BĐT Bunhia Copski:

 

  

2 2 2 2

Ax By A B x y   

tìm max

BĐT Mincopxki:

   

2 2

2 2 2 2

a x b y a b x y      

tìm min.Dấu = xảy ra khi

a x

b y



BĐT vecto

   

2 2

2 2 2 2

a x b y a b x y      

tìm min. Dấu = xảy ra khi

a x

b y



Chú ý:

1 2

z z z z k   

. Ta tính

1 2

z z

+) Nếu

1 2

z z k 

=> Không tồn tại quỹ tích

+) Nếu

1 2

z z k 

=> Phương trình đường thẳng

Đặt y =ax+b; cho y tìm x và lập hệ tìm a; b

+) Nếu

1 2

z z k 

=> Phương trình elip

Đặt

1 2

z z



 



0 0

1 2 1 2

1 2

1 2 1 2

2 2

z z

z z z z

z z k

z z z z

 

     

 

Sau đó nhân 2 vế với

1 2

z z

đưa về elip.

Bài toán:

Chú ý: +)

...

Bấm Shift hyp +)

: Shift 2 2

MỘT SỐ CÔNG THỨC TÍNH NHANH

Dạng 1: k là số cho trước. Tìm

max/min

Loại 1:

       

2 2

z A k z a bi k x a y b i k x a y b k               

       

2 2

P z B z c di P x c y d i P x c y d              

Đặt

A a bi

B c di

 





 



   

1 2

; ; ;I a b I c d   

           

2 2

1 2

I I a c b d a c b d i a bi c di A B              

Ta có:

max 1 2

P I I k A B k    

min 1 2

P I I k A B k    

Tương tự :

Z A k 

Hỏi

P z B 

(có tâm đối xứng với

qua trục hoành)

max/min

P A B k   

Loại 2 :

Az B k 

B k

A A

  

Hỏi :

P Cz D 

C C

  

hoặc

P C z D 

2 2

P P

D D

z z

c c c c

 

     

 

 

Đặt

;

B D

a bi c di

A C

   

Tương tự trên ta có

1 /

2 /

Max Min

B D k

P c

A C A

B D k

P c

A C A



 

  



 



 



 



 

  

 



 

 



GIẢI MAX MIN SỐ PHỨC

( )z a bi c z a bi c c a bi z c a bi              

Tọa độ z làm cho

max min

;z z

lần lượt là :

max

min

.( )

;

z a bi

a bi a bi



 

Dạng 2:

z a z a k   

;

2 2

k a

Min z Max z



 

Tổng quát :

1 2 1 2

z z z z z z k   

với

1 2

;z a bi z c di   

;

z x yi 

Ta có :

1 1

;

2 2

k z

Min z Max z

z z



 

Dạng 3: Cho a>0 . Tìm Max, min

biết z thỏa mãn

z a

 

2 2

4 4

;

2 2

k k k k

Min z Max z

    

 

PHÂN DẠNG MAX MIN SỐ PHỨC

Dạng 1 :

Cho số phức

thỏa mãn

 

z a bi c  

 

0c 

, tìm giá trị nhỏ nhất,

giá trị lớn nhất của P với

3 3 3 4

; ; .P z z z z z z z   

PHÂN TÍCH

Cách 1:

 

,z a bi c  

 

0c  

Tập hợp các điểm

biểu diễn số phức

là đường tròn có tâm

 

;I a b

và bán kính

.R c

Biểu diễn P là 1 điểm M nào đó, dựa vào hình vẽ xác định max min cho thích hợp.

Ví dụ P =

tức là đường tròn tâm O:

Khi đó :

z OM



max

min

z OM OI R

   





  





Ví dụ P =

z i

tức là đường tròn tâm H (0;-1)

Khi đó :

z HM



max

min

z i HI R

   





  





Cách 2: có thể tham khảo trên link https://www.youtube.com/watch?v=WsN84Q502wE

( )z a bi c z a bi c c a bi z c a bi              

Tọa độ z làm cho

max min

;z z

lần lượt là :

max

min

.( )

;

z a bi

a bi a bi



 

Ví dụ : Cho

4 3 3z i  

, Tìm số phức có module nhỏ nhất, lớn nhất?

Áp dụng công thức:

( )z a bi c z a bi c c a bi z c a bi              

Ta có:

4 3 3 (4 3 ) 3 3 4 3 3 4 3 2 8z i z i i z i z                 

Cách tìm số phức:

C1: Tìm Số phức z có module nhỏ nhất là:

 

2 2 2 2

2 2

10 3

4 3 3

8 6 25 5 4 3 10

4 ( 3) 9

4 4

10 3 6 8

4 25 60 36 0 ;

4 5 5

z i

a b a b

a b

a b a b

a b

b b b b a





   

     



 

   

  

   

    

   



 



 





 





 

          

 

 

C2: Số phức z có module nhỏ nhất là:

min

.( )

2(4 3 ) 8 6

5 5 5

z a bi

z i

a bi





   



Tương tự: Số phức z có module lớn nhất là:

max

.( )

8(4 3 ) 32 24

5 5 5

z a bi

z i

a bi





   



Cách 3: PP lượng giác hóa (Độ chính xác ko tuyệt đối, có sai số nhưng vẫn chấp nhận được)

Vì tọa độ điểm biểu diễn là đường tròn nên đưa về dạng

2 2

1X Y 

(Có thể sử dụng trong trường hợp tọa độ điểm biểu diễn là elip)

Đặt X = cosa; Y=sina

Khi đó P biểu diễn theo cosa và sina

Sử dụng MODE 7 khảo sát với START =0; END=2



; STEP=



(Chú ý dùng lệnh Shift Mode



5 1)

Ví dụ : Cho

4 3 3z i  

, Tìm số phức có module nhỏ nhất, lớn nhất?

   

2 2

4 3

4 3 3 4 3 9 1

3 3

x y

z i x y

 

   

          

   

   

Đặt

4 3cos

4 3

cos ; sin

3 3sin

3 3

x y



 



 



 

  



  



Ta có

   

2 2

4 3cos 3 3sinz x y

 

      

SHIFT MODE 4 -> SHIFT MODE



5 1 ->MODE 7

Nhập

   

 

2 2

4 3cos 3 3sinf x X X    

START =0; END=2



; STEP=



Đọc bảng => Max



8; min



BÀI TẬP:

Bài 1: : Cho

6 8 2z i  

, Tìm số phức có module nhỏ nhất, lớn nhất?

Bài 2

: Cho z thỏa mãn:

2 4 5z i  

Tìm số phức z sao cho

1z 

đạt GTLN; GTNN?

Bài 3: Cho z thỏa mãn:

1 2 5z i  

Bài 4: Cho z thỏa mãn:

2 3 1z i  

Bài 5: Cho z thỏa mãn

2 1



 



; Tìm số phức

min max

;z z

Bài 6: Cho z thỏa mãn

 

1 2 1 1i z i   

. Tìm z để

 

2 1i z i  

đạt GTLN; GTNN

Dạng 2 :

Cho số phức

thỏa mãn

 

z a bi c  

 

0c 

, tìm giá trị nhỏ nhất, giá trị lớn nhất của P với

3 4

P z z z z   

hoặc P chứa

2 3

; ...z z

(sử dụng các hằng đẳng thức đáng nhớ)

Cách 1: PP lượng giác hóa

Vì tọa độ điểm biểu diễn là đường tròn nên đưa về dạng

2 2

1X Y 

(Có thể sử dụng trong trường hợp tọa độ điểm biểu diễn là elip)

Đặt X = cosa; Y=sina

Khi đó P biểu diễn theo cosa và sina

Sử dụng MODE 7 khảo sát với START =0; END=2



; STEP=



(Chú ý dùng lệnh Shift Mode



5 – 1)

Cách 2: Sử dụng pp BĐT

BĐT Bunhia Copski:

 

  

2 2 2 2

Ax By A B x y   

tìm max

BĐT Mincopxki:

   

2 2

2 2 2 2

a x b y a b x y      

tìm min.Dấu = xảy ra khi

a x

b y



BĐT vecto

   

2 2

2 2 2 2

a x b y a b x y      

tìm min. Dấu = xảy ra khi

a x

b y



Ví dụ: Cho số phức

thỏa mãn

1 2z  

. Tìm GTLN của

2T z i z i    

Ta có:

2 2 2 2

1 1 1 1 2z i z i z i uv         

 

(1)

2 2 2 2

2 1 1 1 1 2z i z i z i uv          



(2). Với

,u v

 

biểu diễn

1z 

và

1 i

Cộng (1) với (2) ta được:

2 2 2

2 2 1 4 8z i z i z       

(không đổi).

Áp dụng đẳng thức BNC:

 

2 2

2 2 2 16 4T z i z i z i z i T



            

VD2:

Với 2 số phức

1 2

;z z

thỏa mãn

1 2

8 6z z i  

và

1 2

2z z 

.Tính GTLN của

1 2

P z z 

5 3 5

2 26

4 6

34 3 2

GIẢI:

CÁCH 1: Ta có:

     

2 2 2 2 2 2 2 2

1 2 1 2 1 2 1 2 1 2

2 100 4 2 52z z z z z z z z z z           

Lại có: Áp dụng BĐT Cauchy:

 

   

 

2 2

1 2 1 2

2 2

1 2 1 2 1 2

52 104 2 26

2 2 2

z z z z

A B

A B z z z z z z

 



            

CÁCH 2:

Ta có:

ÁP dụng BĐT Bunhia Copski:

 

  

 

2 2 2 2

1 2 1 2 1 2 1 2 1 2

2 104 2 26Ax By A B x y z z z z z z z z z z               

Bài tập:

Bài 1: Cho số phức z thỏa mãn

1 2 2z i  

. Tìm GTLN của

3 6T z z i   

Bài 2: Cho số phức z thoả mãn

1z 

. Tìm giá trị lớn nhất của biểu thức

1 2 1P z z   

Dạng 3 : Cho

z a z b  

Tìm Max, min P với

3 3 3 4

; ; .P z z z z z z z   

Phân tích :

... ...

z z

  

=> Là đường thẳng

Ví dụ: Cho

2 4 2z i z i   

Tìm z để

min

z 1 i  

z 2 2i  

z 2 2i 

z 3 2i 

Cách 1: Đưa về dạng đường thẳng

2 4 2 4 4z i z i x y y x         

 

2 2 2

4z x y x x     

Đến đây dùng MODE 5-3 giải pt bậc 2 để tìm ra min

=> z=x+yi=2+2i

Cách 2 : PP hình học :

Đưa về dạng đường thẳng

 

2 4 2 4 4z i z i x y y x          

Khi đó

 

min

;z d O 

Cách 3 : Khi có đáp án trắc nghiệm

MODE 2 đưa về số phức

Nhập

2 4 2z i z i   

CALC thử đáp án, ưu tiên đáp án có

min

trước. Nếu kết quả trả về 0 thì nhận

Bài tập

Bài 1 :Cho z thỏa

1 3 4z i z i    

Tìm z có môđun min

Bài 2 : Cho z thỏa

2 3z i z i   

Tìm z có

2 2z i 

min

Bài 3 : Cho z thỏa

  

2 5 1 2 3 1z z z i z i      

Tìm min

2 2z i 

Bài 4 : Trong các số phức z thỏa mãn

2z z

z i 

, tìm số phức có phần thực không âm sao cho



đạt giá trị lớn nhất.

4 2

z  

z 

4 8

z  

8 8

z  

Dạng 4: Cho

z a z b  

Tìm Max, min P với

1 2

P z z z z   

Cách 1:

+) Bước 1: Khai triển

z a z b  

đưa về dạng đường thẳng

+) Bước 2 : Từ P ta tìm tọa độ điểm A ; B và xét vị trí tương đối của A ;B với d

+) Khi đó z là M thỏa mãn P min :

Cách 2:

Áp dụng

BĐT Bunhia Copski:

 

  

2 2 2 2

Ax By A B x y   

nếu tìm max

BĐT Mincopxki:

   

2 2

2 2 2 2

a x b y a b x y      

nếu tìm min.

Cách 3: CASIO MODE 7

Bài tập:

Bài 1: Cho z thỏa

1 1z i z i    

Tìm z để

1 5 2z i z i    

min

Bài 2 : Cho z thỏa

2 3z i z i   

. Tìm z để

2z i z  

min

Bài 3 : : Cho z thỏa

1 3 1z i z i    

. Tìm z để

1 1z i z   

max

Bài 4 : : Cho z thỏa

1z z i  

. Tìm z để

2 3z i z i    

max

Dạng 5: Trong số phức

thỏa mãn

1 2

,z z z z k   

 

0k 

.Tìm giá trị nhỏ nhất, lớn nhất của P

với

3 3 3 4

; ; .P z z z z z z z   

PHÂN TÍCH

Chú ý:

1 2

z z z z k   

Ta tính

1 2

z z

+) Nếu

1 2

z z k 

=> Không tồn tại quỹ tích

+) Nếu

1 2

z z k 

=> Phương trình đường thẳng

Đặt y =ax+b; cho y tìm x và lập hệ tìm a; b

+) Nếu

1 2

z z k 

=> Phương trình elip

Ví dụ:

3 3 6.Cho z i z i    

Tính max min của P=

6 7z i 

Cách 1: PP hình học

Gọi A và B là điểm biểu diễn

1 2

;z z

và M là điểm biểu diễn

; C là điểm biểu diễn

trong P

Khi đó MA + MB = k

Nếu MA+MB=AB thì điểm biểu diễn là đường thẳng

Nếu MA+MB > AB thì điểm biểu diễn là elip

Khi đó ta vẽ hình biểu diễn các điểm A,B,C trên mặt Oxy và xác định M trong các trường hợp là đường

thẳng hoặc elip sao cho MC ngắn nhất hoặc lớn nhất.

Giải:

Gọi A(0;1);B(3;-3);C(6;-7);M(x;y)

Khi đó MA+MB=6; Tìm max min của MC

Ta thấy MA+MB>AB => Elip (Vẽ hơi xấu :v)

Trong đó I là trung điểm AB

Với a=6/2=3;c=IA=5/2

Khi đó

MC min khi MC= B’C=BC-BB’=BC-(a-c)=5-1/2=4,5

MC max khi MC=A’C=AC+AA’=AC+(a-c)=10+1/2=10,5

Cách 2: CASIO

Gán A=

1 2

z z

; B=

1 2

z z

; Ta thấy

B



nên điểm biểu diễn là elip

Nhập

arg

X A



 

 

 

 

(Phép quay đưa về elip chính tắc)

CALC: X=

i

=> c = 5/2; a= 6/2=3

CALC: X= -6+7i => C=



Khi đó MC min = AC=15/2-3=4,5

MC max = CB=15/2+3=10,5

Cách 3: CASIO

( Sử dụng phương pháp lượng giác hóa, tìm pt elip gán vào cosa; sina) sau đó dùng

MODE 7. Tuy nhiên cách này có vẻ dài hơn cách 2 nên thầy không đề cập tới nữa

Bài tập

Bài 1: Cho số phức

thỏa mãn

2 2 6z z   

. Tìm GTLN và GTNN của

1 3P z i  

Bài 2: Cho số phức

thỏa mãn

1 3 2 8z i z i     

. Tìm giá trị lớn nhất, giá trị nhỏ nhất của

2 1 2P z i  

Bài 3: Cho số phức

thỏa mãn

2 4 7 10z i z i     

. Tìm GTLN, GTNN của

1 4P z i  

Bài 4-Trong các số phức

thỏa mãn

3 3 10z i iz   

. Hai số phức

và

có môđun nhỏ

nhất. Hỏi tích

1 2

z z

là bao nhiêu A.

25

16

Bài 5: Trong tất cả các số phức

thỏa mãn

4 4 10z z   

, gọi

,M m

lần lượt là giá trị lớn nhất,

giá trị nhỏ nhất

. Khi đó, giá trị biểu thức

P M m 

bằng?

6P  

13P  

5P  

4P  

Bài 6 : (LẠNG GIANG SỐ 1) Cho số phức

thỏa mãn

3 3 8z z   

. Gọi

lần lượt giá trị

lớn nhất và nhỏ nhất

Khi đó

M m

bằng

4 7.

4 7.

4 5.

Bài 7: Cho số phức z thỏa mãn |z + 3| + |z − 3| = 10. Giá trị nhỏ nhất của |z| là

A. 3

B. 4

C. 5

D. 6

Dạng 6: Trong số phức

thỏa mãn

1 2

,z z z z k   

 

0k 

.Tìm giá trị nhỏ nhất, lớn nhất của P

với

3 4

P z z z z   

hoặc một biểu thức Q chứa

2 3

; ...z z

Cách 1: Sử dụng PP lượng giác hóa

Cách 2: Sử dụng PP BĐT

Bài tập:

Bài 1: Cho 2 số phức

1 2

,z z

thỏa mãn

1 2

5z z 

và

1 2

3z z 

. Tìm GTLN của

1 2

P z z 

Dạng 7: Tập hợp điểm biểu diễn số phức z có dạng

1 2

z z z z k   

hoặc các dạng khác…

+) Khai triển kiểm tra xem có thuộc dạng đường thẳng hay hyperbol không

Áp dụng:

 

2 2

2 4 0A B C A C B C B C B A B C          

 

2 2

2 4A 0A B C A B AB C B A B C          

Nhập

 

4C B A B C  

CALC X =0 => hệ số tự do D

Nhập

 

4C B A B C D   

CALC X=1 => hệ số của

CALC X = i => hệ số

=> pt hyperbol hoặc elip

MỘT SỐ DẠNG BÀI TẬP KHÁC

Câu 1: (TRẦN HƯNG ĐẠO – NB) Cho số phức

thỏa mãn điều kiện

3 4 2.z i  

Trong mặt

phẳng

Oxy

tập hợp điểm biểu diễn số phức

2 1w z i  

là hình tròn có diện tích





. B.

12S





. C.

16S





. D.

25S





Hướng dẫn giải

Chọn C.

2 1

w i

w z i z

 

    

 

3 4 2 3 4 2 1 6 8 4 7 9 4 1

w i

z i i w i i w i

 

                

Giả sử

 

,w x yi x y  

, khi đó

     

2 2

1 7 9 16x y    

Suy ra tập hợp điểm biểu diễn số phức

là hình tròn tâm

 

7; 9I 

, bán kính

4.r 

Vậy diện tích cần tìm là

.4 16 .S

 

 

Câu 2: Cho số phức

thỏa mãn

1z 

. Tìm giá trị lớn nhất của biểu thức

1 .

 

Hướng dẫn giải

Ta có:

5 5 5

1 1 1 6.

i i

z z

      

Khi

6.z i A  



Chọn đáp án C.

Câu 3: Cho số phức

thỏa mãn

1z 

. Tìm giá trị lớn nhất

max

và giá trị nhỏ nhất

min

của

biểu thức

2 3

1 1 .M z z z    

max min

5; 1.M M 

max min

5; 2.M M 

max min

4; 1.M M 

max min

4; 2.M M 

Hướng dẫn giải

Ta có:

2 3

1 1 5M z z z     

, khi

max

1 5 5.z M M    

Mặt khác:

3 3 3 3 3

1 1 1 1 1

1 1,

2 2 2

z z z z z

M z

     

      



khi

min

1 1 1.z M M     



Chọn đáp án A.

Câu 4: Cho số phức

thỏa

2z

. Tìm tích của giá trị lớn nhất và nhỏ nhất của biểu thức

z i





. D.

Hướng dẫn giải

Ta có

1 3

1 1 .

| | 2

z z

    

Mặt khác:

1 1

1 1 .

| | 2

z z

   

Vậy, giá trị nhỏ nhất của

P

là

, xảy ra khi

2 ;z i 

giá trị lớn nhất của

bằng

xảy ra khi

2 .z i



Chọn đáp án A.

Câu 5: Cho số phức

thỏa mãn

1z 

. Tìm giá trị lớn nhất của biểu thức

1 3 1 .P z z   

3 15

6 5

2 20.

Hướng dẫn giải

Gọi

 

; ;z x yi x y    

. Ta có:

2 2 2 2

1 1 1 1;1 .z x y y x x          

 

Ta có:

       

2 2

1 3 1 1 3 1 2 1 3 2 1P z z x y x y x x             

Xét hàm số

     

2 1 3 2 1 ; 1;1 .f x x x x      

 

Hàm số liên tục trên

1;1 

 

và với

 

1;1x  

ta có:

 

1 3 4

0 1;1 .

2 1 2 1

f x x

x x



       

 

Ta có:

   

max

1 2; 1 6; 2 20 2 20.

f f f P

 

      

 

 



Chọn đáp án D.

Câu 6: Cho số phức

thỏa mãn

1.z 

Gọi

và

lần lượt là giá trị lớn nhất và giá trị nhỏ nhất

của biểu thức

1 1 .P z z z    

Tính giá trị của

.M m

13 3

3 3.

Hướng dẫn giải

Gọi

 

; ;z x yi x y    

. Ta có:

1 . 1z z z  

Đặt

1t z 

, ta có

0 1 1 1 2 0; 2 .z z z t          

 

Ta có

  

1 1 1 . 2 2 .

t z z z z z z x x



          

Suy ra

 

2 2 2

1 . 1 2 1 2 1 3z z z z z z z z z x x t             

Xét hàm số

 

3 , 0; 2 .f t t t t     

 

Bằng cách dùng đạo hàm, suy ra

   

13 13 3

max ; min 3 . .

4 4

f t f t M n   



Chọn đáp án A.

Câu 7: Cho số phức

thỏa mãn điều kiện

4 2 .z z 

Khẳng định nào sau đây là đúng?

3 1 3 1

6 6

 

 

5 1 5 1.z   

6 1 6 1.z   

2 1 2 1

3 3

 

 

Hướng dẫn giải

Áp dụng bất đẳng thức

,u v u v  

ta được

2 2

2 4 4 4 2 4 0 5 1.z z z z z z             

2 2

2 4 4 2 4 0 5 1.z z z z z z z            

Vậy,

nhỏ nhất là

5 1,

khi

5z i i  

và

lớn nhất là

5 1,

khi

5.z i i 



Chọn đáp án B.

Câu 8: Cho

1 2

,z z

là hai số phức liên hợp của nhau và thỏa mãn



và

1 2

2 3.z z 

Tính

môđun của số phức

5.z 

3.z 

2.z 

z 

Hướng dẫn giải

Gọi

 

1 2

; ;z a bi z a bi a b       

. Không mất tính tổng quát ta gọi

0.b 

1 2

2 3 2 2 3 3.z z bi b     

1 2

,z z

là hai số phức liên hợp của nhau nên

1 2

.z z  

, mà

 

1 1

2 2

1 2

z z

    

Ta có:

 

   

3 3 2 2 3 2 3 2

2 2

3 3 3 0 1.

z a bi a ab a b b i a b b a

a b





            









Vậy

2 2

2.z a b  



Chọn đáp án C.

Câu 9: Gọi

 

 ,z x yi x y   R

là số phức thỏa mãn hai điều kiện

2 2

2 2 26z z   

và

3 3

2 2

z i 

đạt giá trị lớn nhất. Tính tích

.xy

xy 

Hướng dẫn giải

Đặt

 

 , .z x iy x y   R

Thay vào điều kiện thứ nhất, ta được

2 2

36.x y 

Đặt

3cos , 3sin .x t y t 

Thay vào điều kiện thứ hai, ta có



3 3

18 18 sin 6.

2 2

P z i t



 

      

 

 

Dấu bằng xảy ra khi

3 3 2 3 2

sin 1 .

4 4 2 2

t t z i

 

 

         

 

 



Chọn đáp án D.

Câu 10: Biết số phức

thỏa mãn đồng thời hai điều kiện

3 4 5z i  

và biểu thức

2 2

2M z z i   

đạt giá trị lớn nhất. Tính môđun của số phức

.z i

2 41z i 

3 5.z i 

5 2z i 

41.z i 

Hướng dẫn giải

Gọi

 

; ;z x yi x y    

. Ta có:

     

2 2

3 4 5 : 3 4 5z i C x y       

: tâm

 

3; 4I

và

5.R 

Mặt khác:

 

2 2

2 2 1 4 2 3 : 4 2 3 0.M z z i x y x y x y d x y M

 

                 

 

 

Do số phức

thỏa mãn đồng thời hai điều kiện nên

và

 

có điểm chung

 

; 5 23 10 13 33

2 5

d I d R M M



         

   

2 2

max

4 2 30 0

33 5 4 41.

3 4 5

x y

M z i i z i

x y

   

 



          

 

 

   









Chọn đáp án D.

Câu 11: ( CHUYÊN SƠN LA – L2) Cho số phức

thỏa mãn điều kiện :

1 2 5z i  

và

1w z i  

có môđun lớn nhất. Số phức

có môđun bằng:

2 5

. B.

3 2

. C.

. D.

5 2

Hướng dẫn giải:

Chọn B.

Gọi

     

, 1 2 1 2z x yi x y z i x y i         

Ta có:

       

2 2 2 2

1 2 5 1 2 5 1 2 5z i x y x y            

Suy ra tập hợp điểm

 

;M x y

biểu diễn số phức

thuộc đường tròn

 

tâm

 

1; 2I 

bán kính

5R 

như hình vẽ:

Dễ thấy

 

O C

   

1; 1N C  

Theo đề ta có:

   

;M x y C

là điểm biểu diễn cho số

phức

thỏa mãn:

   

1 1 1 1w z i x yi i x y i          

   

2 2

1 1 1z i x y MN       



Suy ra

1z i 

đạt giá trị lớn nhất

MN

lớn nhất

Mà

 

,M N C

nên

lớn nhất khi

là đường kính đường tròn

 

I

là trung điểm

   

3; 3 3 3 3 3 3 2MN M z i z         

2

1

C. BÀI TẬP TỰ LUYỆN.

BÀI 1 (Sở GD Long An 2017). Cho số phức z thỏa mãn |z − 2 − 3i|

= 1. Tìm giá trị lớn nhất của |z|.

1 3

2 13

13 1

BÀI 2 (THPT Hưng Nhân-Thái Bình 2017 L3). Tìm giá trị lớn nhất của |z| biết

2 3

1 1.

3 2

 

 



B. 2

C. 1

D. 3

BÀI 3 (THPT Nguyễn Huệ-Huế 2017 L2, Hà Huy Tập-Hà Tĩnh 2017 L2). Cho số phức z thỏa mãn

1z i 

. Tìm giá trị lớn nhất của |z|.

A. 2`

2 2

BÀI 4 (Chuyên Nguyễn Trãi-Hải Dương 2017 L3). Xác định số phức z thỏa mãn

2 2 2z i  

mà

|z| đạt giá trị lớn nhất

1 i

3 i

3 3i

1 3i

BÀI 5 (THPT Yên Khánh A-Ninh Bình 2017,THPT Kim Liên-Hà Nội 2017). Cho số phức z thỏa mãn |z

− 2 − 3i| = 1. Giá trị nhỏ nhất của |z + 1 + i| là

13 1

C. 4

13 1

BÀI 6 (THPT Đống Đa-Hà Nội 2017). Cho số phức z thỏa mãn

2 2 1z z z i    

Biểu thức |z| có

giá trị lớn nhất là

2 1

B. 2

2 2

2 1

BÀI 7 (THPT Hùng Vương-Phú Thọ 2017). Cho số phức z thỏa mãn điều kiện |z − 1| = |(1 + i)z|. Đặt m =

|z|, tìm giá trị lớn nhất của m.

2 1

B. 1

2 1

BÀI 8 (THPT Chuyên Lào Cai 2017 L2). Cho số phức z thỏa mãn

 

. Gọi M, m lần lượt là giá

trị lớn nhất và nhỏ nhất của |z|. Tính M + m?

A. 2

2 5

BÀI 9 (THPT Hưng Nhân-Thái Bình 2017 L3). Cho hai số phức z1, z2 thỏa mãn

3 4 1

6 2

z i

  











Tính tổng Giá trị lớn nhất và Giá trị nhỏ nhất của biểu thức

1 2

z z

A. 18

6 2

3 2

BÀI 10 (Sở GD Điện Biên 2017,Gia Lộc-Hải Dương 2017 L2). Cho số phức z thỏa mãn |z| ≤ 1. Đặt

2 1







. Mệnh đề nào dưới đây đúng?

A. |A| < 1

B. |A| ≤ 1

C. |A| ≥ 1

D. |A| > 1

BÀI 11 (Sở GD Hải Dương 2017). Cho số phức z thỏa mãn z.

1z 

. Tìm giá trị nhỏ nhất của biểu thức

3 .P z z z z z   

BÀI 12 (Chuyên Ngoại Ngữ-Hà Nội 2017). Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất của biểu

thức T = |z + 1| + 2|z − 1|

Phương pháp đại số

max 2 5T 

max 2 10T 

max 3 5

max 3 2T 

BÀI 13 (Sở GD Bắc Ninh 2017). Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất của biểu thức T = |z +

1| + 3|z − 1|

max 3 10T 

max 2 10T 

max 6

max 4 2T 

BÀI 14 (Chu Văn An-Hà Nội 2017 L2). Cho số phức z thỏa mãn điều kiện

1 2z  

. Tìm giá trị lớn

nhất của T = |z + i| + |z − 2 − i|

max 8 2T 

max 4T 

max 4 2

max 8T 

BÀI 15 (Sở GD Đà Nẵng 2017). Cho số phức z thỏa mãn |z −

1 + 2i| = 3. Mô đun lớn nhất của số phức z là:

14 6 5

15(14 6 5)



14 6 5

15(14 6 5)



BÀI 16 (THPT Bình Xuyên-Vĩnh Phúc 2017 L3). Cho số phức z thỏa mãn |z−1−2i| = 1. Tìm giá trị nhỏ

nhất của |z|

5 1

BÀI 17 (Chuyên Nguyễn Trãi-Hải Dương 2017 L3). Cho số phức z, w thỏa mãn |z − 1 + 2i| = |z + 5i|, w =

iz + 20. Giá trị nhỏ nhất m của |w| là

3 10

m 

7 10m 

m 

2 10m 

BÀI 18 (THPT Cổ Loa-Hà Nội 2017 L3). Cho số phức z thỏa mãn

z i  

2 .

z i 

Biết biểu

thức Q = |z − 2 − 4i| + |z − 4 − 6i| đạt giá trị nhỏ nhất tại z = a + bi (a, b ∈ R). Tính P = a − 4b

2P  

1333

272

P 

1P  

691

272

P 

BÀI 19 (THPT Cao Nguyên-Dăk Lăk 2017). Cho số phức z thỏa mãn





 



. Gọi M

và m lần lượt là Giá trị lớn nhất và Giá trị nhỏ nhất của |z|. Tính M.m

A. Mm = 2

B. Mm = 1

2 2Mm 

2 3Mm 

BÀI 20 (Lương Đức Trọng 2017). Xét số phức z thỏa mãn 4|z + i| + 3|z − i| = 10. Gọi M, m tương ứng là

giá trị lớn nhất và nhỏ nhất của |z|. Tính M + m

35 2

BÀI 21 (THPT Thăng Long-Hà Nội 2017 L2). Cho z là số phức thay đổi thỏa mãn

2 2 4 2z z   

Trong mặt phẳng tọa độ, gọi M, N là điểm biểu diễn z và z. Tính giá trị lớn nhất của

diện tích tam giác OMN.

4 2

2 2

BÀI 22 (THPT Chuyên Hoàng Văn Thụ-Hòa Bình 2017 L3). Cho

1 2

,z z

là hai nghiệm phương trình |6

− 3i + iz| = |2z − 6 − 9i| thỏa mãn

1 2

z z 

|. Giá trị lớn nhất của

1 2

z z

là

4 2

D. LỜI GIẢI VÀ ĐÁP ÁN

GIẢI BÀI TẬP 1. Ta có

1 2 3 13 1 13z i z z       

Phương pháp hình học

Đáp án là A.

GIẢI BÀI TẬP 2. Ta có

2 3 2 3

1 1 . 1 1 2.

3 2 3 2

i i

z z z z

i i

   

       

 

Đáp án là B.

GIẢI BÀI TẬP 3. Ta có

2 2

1 1 2 2.z i z z z       

Đáp án là D

GIẢI BÀI TẬP 4. Ta có

2 2 2 2 2 3 2z i z z      

Dấu "=" khi z = k(2 + 2i) với

2 2 2 2

k k  

. Vậy k = 3 + 3i.

Đáp án là C

GIẢI BÀI TẬP 5. Ta có

|z + 1 + i| = |z + 1 − i| = |(z − 2 − 3i) + (3 + 2i)| ≥ ||z − 2 − 3i| − |3 + 2i|| =

− 1.

Vậy min

min 1 13 1.z i   

Đáp án là A.

GIẢI BÀI TẬP 6. Ta có

2 2 2

1 0

2 2 ( 1) 1 . 1 1

1 1

z i

z z z i z i z i z i

z i

  



             



  



• Nếu z = i − 1 thì

2z 

• Nếu |z + 1 + i| = 1 thì 1 ≥ |z| − |1 + i| = |z| −

. Do đó |z| ≤ 1 +

Đáp án là A.

GIẢI BÀI TẬP 7. Ta có

|z − 1| = 2|z| ≤ |z| + 1 ⇒ |z| ≤ 1.

Do đó max |z| = 1.

Đáp án là B.

GIẢI BÀI TẬP 8. Ta có

2 2

2 4 2 4 0 1 5z z z z z M         

và

2 2

2 4 2 4 0 1 5z z z z z m          

Vậy M + m = 2

Đáp án là B.

GIẢI BÀI TẬP 9. Ta có

1 2 1 2 1 2

( 3 4 ) ( 6 ) (3 3 ) 2 4 6 3 3 3 3 2 max.z z z i z i i z i z i i                   

và

1 2 1 2 1 2

( 3 4 ) ( 6 ) (3 3 ) 3 3 2 4 6 3 2 3 min.z z z i z i i i z i z i                   

Do đó tổng

Giá trị lớn nhất và Giá trị nhỏ nhất là

6 2

Đáp án là B.

GIẢI BÀI TẬP 10. Ta có

2 2 (2 ) 2 .

A i

A A iz z i A i z A i z

A i



        



Đặt A = a + bi. Suy ra

2 2 2 2 2 2 2 2

4 (2 1) ( 2) 3 3 3 .2 2 11 a b a b a bi A bz aA A i                

Đáp án là B.

GIẢI BÀI TẬP 11. Ta có

2 2

3 3 2 2

3 . 3 . 3 ( ) 1 .z z z z z z z z z z z z          

Suy ra

1 3 3

( ) 1 ( ) .

2 4 4

P z z z z z z

 

         

 

 

Vậy giá trị nhỏ nhất của P là

Đáp án là C.

GIẢI BÀI TẬP 12. Áp dụng công thức trung tuyến ta có

2 2 2

1 1

1 1 2 4

z z z



     

Theo bất đẳng thức Bunhiacopxki thì

2 2

2 2 2

( 1 1 )(1 2 ) 20 2 5T z z T       

Đáp án là A.

GIẢI BÀI TẬP 13. Áp dụng công thức trung tuyến ta có

2 2 2

1 1

1 1 2 4

z z z



     

Theo bất đẳng thức Bunhiacopxki thì

2 2

2 2 2

( 1 1 )(1 3 ) 40 2 10.T z z T       

Đáp án là B.

GIẢI BÀI TẬP 14. Áp dụng công thức trung tuyến ta có

2 2

1 2 2 1 8

z z i z



       

Theo bất đẳng thức Bunhiacopxki thì

2 2

2 2 2

( 1 1 )(1 1 ) 16 4.T z z T       

Đáp án là B.

GIẢI BÀI TẬP 15.

Tập hợp các điểm M biểu diễn số phức z thỏa mãn giả thiết là đường tròn tâm

I(1; −2) bán kính r = 3. Khi đó |z| = OM với O là gốc tọa độ. Do đó

max |z| = OI + r = 3 +

Đáp án là A.

GIẢI BÀI TẬP 16.

Tập hợp các điểm M biểu diễn số phức z thỏa mãn giả thiết là đường tròn tâm I(1;

−2) bán kính r = 1. Khi đó |z| = OM với O là gốc tọa độ. Do đó min |z| = OI − r =

− 1.

Đáp án là D.

GIẢI BÀI TẬP 17.

Gọi A (1; −2), B (0; −5), tập hợp các điểm z thỏa mãn giả thiêt đề bài là đường trung

trực d của AB có phương trình x + 3y + 10 = 0. Ta có

|w| = |iz + 20| = |z − 20i| = OM với M là điểm biểu diễn số phức z và C(0; 20). Do đó

min |w| = d(C.∆) = 7

Đáp án là B.

GIẢI BÀI TẬP 18.

Gọi

5 3

;2 , ; 2 ,

2 2

A B

   

  

   

   

tập hợp các điểm z thỏa mãn giả thiêt đề bài là

đường trung trực d của AB có phương trình x−4y + 2 = 0. Xét hai điểm M(2;

4), N(4; 6) thì Q = IM + IN với I ∈ d. Do đó Q nhỏ nhất khi và chỉ khi I là giao

điểm của M0N với

58 28

' ;

17 17

 



 

 

là điểm đối xứng của M qua d. Vậy

62 24

;

17 17

 

 

 

, ứng với

62 24

17 17

z i 

Đáp án là A.

GIẢI BÀI TẬP 19. Ta có

2 2

4 2 2 2.

1 1

iz iz iz z M

i i

       

 

Theo giả thiết thì số phức z thỏa mãn

2 2

4 1 1 4.

( 1) ( 1)

z z z i z i

i i i i

          

 

Gọi A(−1; 1), B(1; −1) có trung điểm là O(0; 0). Điểm M biểu diễn số phức z. Theo công thức trung tuyến

thì

2 2 2

2 4

MA MB AB

z MO



  

Ta có

2 2

( )

MA MB



  

Do đó

8 8

2 4

m   

Vậy Mn =

2 2

. Đáp án là C.

GIẢI BÀI TẬP 20. Gọi A(0; −1), B(0; 1) có trung điểm là O(0; 0). Điểm M biểu diễn số phức z. Theo công

thức trung tuyến thì

2 2 2

2 4

MA MB AB

z MO



  

Theo giả thiết

4 3 2 2MA MB 

. Đặt

10 4

a MA MB



  

10 7

4 16

2 6 10 7 6 .

3 7 7

MA MB A B a a



           

Ta có

 

2 2 2

5 8 36

10 4 25 80 100

3 9 9

a a a

MA MB a

 

  

 

    

 

 

36 34 11296

5 8 0 (5 8)

7 7 49

a a       

. Suy ra



2 2

4MA MB 

nên

1 1 .z z m   



2 2

1296

340 121

9 49 49

MA MB z M



     

Vậy

M m 

Đáp án là C.

GIẢI BÀI TẬP 21.

Gọi điểm M biểu diễn số phức z = x + iy và N biểu diễn số phức

thì

M, M0 đối xứng nhau qua Ox. Diện tích tam giác OMN là

OMN

S xy

2 2 4 2z z   

nên tập hợp M biểu diễn x là Elip (E):

2 2

8 4

x y

 

. Do đó

2 2 2 2

1 2 . 2 2.

8 4 8 4

2 2

OMN

x y x y

S xy      

Đáp án là D.

Bấm Tải xuống để xem toàn bộ.

Preview text:

TRỌN BỘ PHƯƠNG PHÁP MAX MIN SỐ PHỨC I. LÝ THUYẾT BỔ TRỢ
Điểm biểu diễn số phức có dạng
z . .  z . . => Là đường thẳng.
z . .  z . .
z . .  k => Là đường tròn.
z . .  z . .  k => Có thể là elip, parabol, hypebol, đường thẳng…
Bất đẳng thức tam giác
• z  z  z  z , dấu "=" khi z  kz với k ≥ 0. Dùng cho BĐT Mincopxki: 1 2 1 2 1 2
• z - z  z + z , dấu "=" khi z  kz với k ≤ 0. Dùng cho BĐT vecto 1 2 1 2 1 2
• z  z  z - z , dấu "=" khi z  kz với k ≤ 0. 1 2 1 2 1 2
• z - z  z - z ,dấu "=" khi z  kz với k ≥ 0. 1 2 1 2 1 2
Bất đẳng thức khác A  B 2 2  2
BĐT Cauchy: A  B  tìm min 2
BĐT Bunhia Copski:   2   2 2   2 2 Ax By A B
x  y  tìm max BĐT Mincopxki: 2 2 2 2
a  x  b  y  a  b2   x  y2 tìm min.Dấu = xảy ra khi a x  b y BĐT vecto 2 2 2 2
a  x  b  y  a  b2   x  y2 tìm min. Dấu = xảy ra khi a x  b y
Chú ý: z  z  z  z  k . Ta tính z  z : 1 2 1 2
+) Nếu z  z  k => Không tồn tại quỹ tích 1 2
+) Nếu z  z  k => Phương trình đường thẳng 1 2
Đặt y =ax+b; cho y tìm x và lập hệ tìm a; b
+) Nếu z  z  k => Phương trình elip 1 2  Đặt z z z   0 z z z z 1 2 z   => z z 0 1 2 0 1 2   z    z  k z  z 2 1 2 z  z 2 z  z 2 1 2 1 2 1 2
Sau đó nhân 2 vế với z  z đưa về elip. 1 2 Bài toán:
Chú ý: +) . . Bấm Shift hyp +) z : Shift 2 2
MỘT SỐ CÔNG THỨC TÍNH NHANH
Dạng 1: k là số cho trước. Tìm Pmax/min Loại 1:     
             2    2 2 z A k z a bi k x a y b i k x a y b  k     
         2 P z B z c di P x c
y d i  P  x  c2  y  d 2
A  a  bi
Đặt B cdi I  ; a b  ; I  ; c d 1   2  
 I I  a  c2  b  d 2  a  c  b  d i  a  bi  c  di  A B 1 2         Ta có:
P  I I  k  A B  k max 1 2
P  I I  k  A B  k min 1 2
Tương tự : Z  A  k Hỏi P  z  B (có tâm đối xứng với I qua trục hoành)  P
 A B  k 2 max/min Loại 2 :
Az  B  k B k  z   Hỏi : A A
P  Cz  D P D P D P  D 1    hoặc 2 2        1 z
P  C z  D z z C C 2 c c c  c   
Đặt B   ; D a bi  c  di A C   B D k   P  c    1Max/Min   A C A     Tương tự trên ta có 
 B  D  k  P  c      2Max/Min
 A  C  A      
GIẢI MAX MIN SỐ PHỨC
z  a bi  c  z  (a  bi)  c  c  a  bi  z  c  a  bi z
.(a  bi) z .(a  bi)
Tọa độ z làm cho z ; z lần lượt là : max min ; max min a  bi a  bi Dạng 2: 2 2 k  4 a z k
 a  z  a  k => Min z  ; Max z  2 2
Tổng quát : z z  z  z z  z  k với z  a  bi;z  c  di ; z  x  yi 1 2 1 2 1 2 2 2 k  4 z Ta có : 2  ; k Min z Max z  2 z 2 z 1 1
Dạng 3: Cho a>0 . Tìm Max, min z biết z thỏa mãn 1 z   a z 2 2 k  k  4 k  k  4 Min z  ; Max z  2 2
PHÂN DẠNG MAX MIN SỐ PHỨC Dạng 1 :
Cho số phức z thỏa mãn z  a  bi  c ,c  0 , tìm giá trị nhỏ nhất,
giá trị lớn nhất của P với P  z  z ; z  z ; z .z  z 3 3 3 4 PHÂN TÍCH Cách 1:
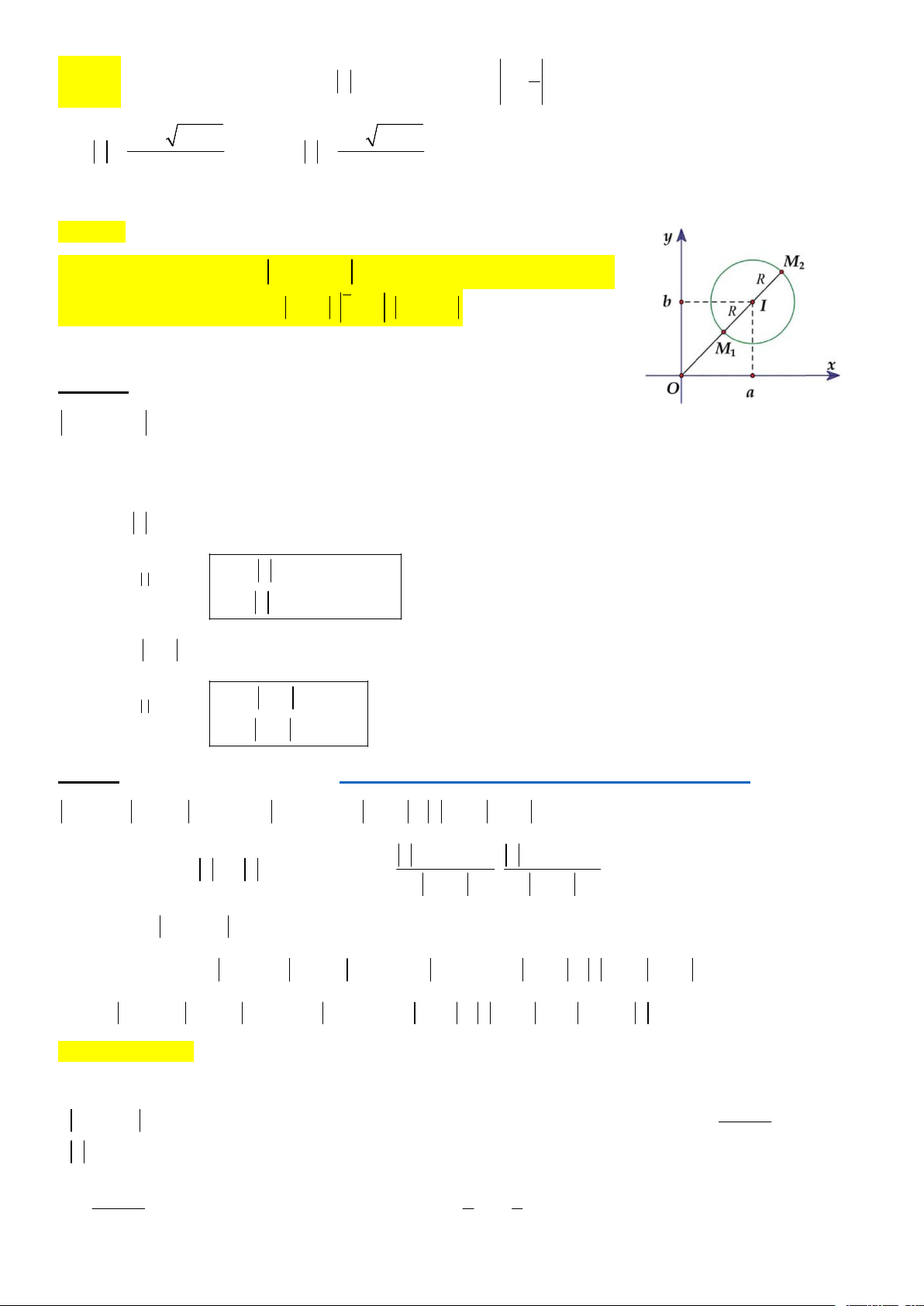
z  a  bi  c, c  0  Tập hợp các điểm M biểu diễn số phức z là đường tròn có tâm I a;b
và bán kính R  .c
Biểu diễn P là 1 điểm M nào đó, dựa vào hình vẽ xác định max min cho thích hợp.
Ví dụ P = z tức là đường tròn tâm O:
max z  OM  OI   R
Khi đó : z OM  2 
min z  OM  OI  R  1
Ví dụ P = z  i tức là đường tròn tâm H (0;-1)
max z  i  HI   R
Khi đó : z HM
 min zi  HI R 
Cách 2: có thể tham khảo trên link https://www.youtube.com/watch?v=WsN84Q502wE
z  a bi  c  z  (a  bi)  c  c  a  bi  z  c  a  bi z
.(a  bi) z .(a  bi)
Tọa độ z làm cho z ; z lần lượt là : max min ; . max min a  bi a  bi
Ví dụ : Cho z  4  3i  3 , Tìm số phức có module nhỏ nhất, lớn nhất?
Áp dụng công thức: z  a  bi  c  z  (a  bi)  c  c  a  bi  z  c  a  bi
Ta có: z  4  3i  3  z  (4  3i)  3  3  4  3i  z  3  4  3i  2  z  8 Cách tìm số phức:
C1: Tìm Số phức z có module nhỏ nhất là:          a  42 2 10 3 4 3 3  (b  3)  9 8  6  25  5 4  3  10 b z i a b a b  a           4 2 2 2 2 2 2  z  2 
a  b  4 a  b  4 a  b  4  2 2 a  b  4 2 10  3b  2 2 6 8   
b  4  25b  60b 36  0  b   ;a    4  5 5
z .(a  bi)
C2: Số phức z có module nhỏ nhất là: 2(4 3i) 8 6 min z     i a  bi 5 5 5 z .(a  bi)
Tương tự: Số phức z có module lớn nhất là: 8(4 3i) 32 24 max z     i a  bi 5 5 5
Cách 3: PP lượng giác hóa (Độ chính xác ko tuyệt đối, có sai số nhưng vẫn chấp nhận được)
Vì tọa độ điểm biểu diễn là đường tròn nên đưa về dạng 2 2 X Y 1
(Có thể sử dụng trong trường hợp tọa độ điểm biểu diễn là elip) Đặt X = cosa; Y=sina
Khi đó P biểu diễn theo cosa và sina 
Sử dụng MODE 7 khảo sát với START =0; END=2 ; STEP=
(Chú ý dùng lệnh Shift Mode  5 1) 12
Ví dụ : Cho z  4  3i  3 , Tìm số phức có module nhỏ nhất, lớn nhất? 2 2      z i
x 2  y 2 x 4 y 3 4 3 3 4 3 9                 1  3   3  x  4 y  3 x  4  3cos Đặt  cos;  sin  3 3 
 y  3 3sin Ta có 2 2
z  x  y  4 3cos 2  3   3sin 2
SHIFT MODE 4 -> SHIFT MODE  5 1 ->MODE 7
Nhập f x   
X 2   X 2 4 3cos 3 3sin  START =0; END=2 ; STEP=12
Đọc bảng => Max  8; min  2 BÀI TẬP:
Bài 1: : Cho z  6  8i  2 , Tìm số phức có module nhỏ nhất, lớn nhất?
Bài 2: Cho z thỏa mãn: z  2  4i  5
Tìm số phức z sao cho z 1 đạt GTLN; GTNN?
Bài 3: Cho z thỏa mãn: z 1 2i  5
Bài 4: Cho z thỏa mãn: z  2 3i 1 
Bài 5: Cho z thỏa mãn 1 i z  2 1 ; Tìm số phức z ; z 1i min max
Bài 6: Cho z thỏa mãn 1 i z  2i 1 1. Tìm z để 2 i z i 1 đạt GTLN; GTNN Dạng 2 :
Cho số phức z thỏa mãn z  a  bi  c ,c  0 , tìm giá trị nhỏ nhất, giá trị lớn nhất của P với
P  z  z  z  z hoặc P chứa 2 3
z ; z ... (sử dụng các hằng đẳng thức đáng nhớ) 3 4
Cách 1: PP lượng giác hóa
Vì tọa độ điểm biểu diễn là đường tròn nên đưa về dạng 2 2 X Y 1
(Có thể sử dụng trong trường hợp tọa độ điểm biểu diễn là elip) Đặt X = cosa; Y=sina
Khi đó P biểu diễn theo cosa và sina 
Sử dụng MODE 7 khảo sát với START =0; END=2 ; STEP=12
(Chú ý dùng lệnh Shift Mode  5 – 1)
Cách 2: Sử dụng pp BĐT
BĐT Bunhia Copski:   2   2 2   2 2 Ax By A B
x  y  tìm max BĐT Mincopxki: 2 2 2 2
a  x  b  y  a  b2   x  y2 tìm min.Dấu = xảy ra khi a x  b y BĐT vecto 2 2 2 2
a  x  b  y  a  b2   x  y2 tìm min. Dấu = xảy ra khi a x  b y
Ví dụ: Cho số phức z thỏa mãn z 1  2 . Tìm GTLN của T  z  i  z  2 i . Ta có: 2 2 2 2 
z  i  z 11 i  z 1  1 i  2uv (1) 2 2 2 2   
z  2  i  z 11 i  z 1  1 i  2uv (2). Với u,v biểu diễn z 1 và 1i .
Cộng (1) với (2) ta được: 2 2 2
z  i  z  2  i  2 z 1  4  8 (không đổi). Áp dụng đẳng thức BNC: 2 T
 z i z 2 i        2 2 2
z  i  z  2  i  16  T  4 VD2:
Với 2 số phức z ;z
z  z  8 6i z  z  2
P  z  z 1 2 thỏa mãn 1 2 và .Tính GTLN của 1 2 1 2 A.53 5 B. 2 26 C. 4 6 D.34  3 2 GIẢI: CÁCH 1: Ta có: 2 2
z  z  z  z  2 2 2
z  z  100 4  2 2 2
z  z   52   2 2 z  z 1 2 1 2 1 2 1 2 1 2 
Lại có: Áp dụng BĐT Cauchy: A  B z  z z  z 2 2   2 2  1 2 2  1 2 2 2 A  B   z  z   52 
 104  z  z
 z  z  2 26 1 2  1 2 2 1 2 2 2 2 CÁCH 2: Ta có:
ÁP dụng BĐT Bunhia Copski:
Ax  By2   2 2 A  B  2 2
x  y    z  z  2 z  z
 z  z  z  z 104  z  z  2 26 1 2 2  2 2 1 2  2 2 1 2 1 2 1 2 Bài tập:
Bài 1: Cho số phức z thỏa mãn z 1 2i  2 . Tìm GTLN của T  z  z 3 6i
Bài 2: Cho số phức z thoả mãn z 1. Tìm giá trị lớn nhất của biểu thức P  z 1  2 z 1
Dạng 3 : Cho z  a  z  b Tìm Max, min P với P  z  z ; z  z ; z .z  z 3 3 3 4
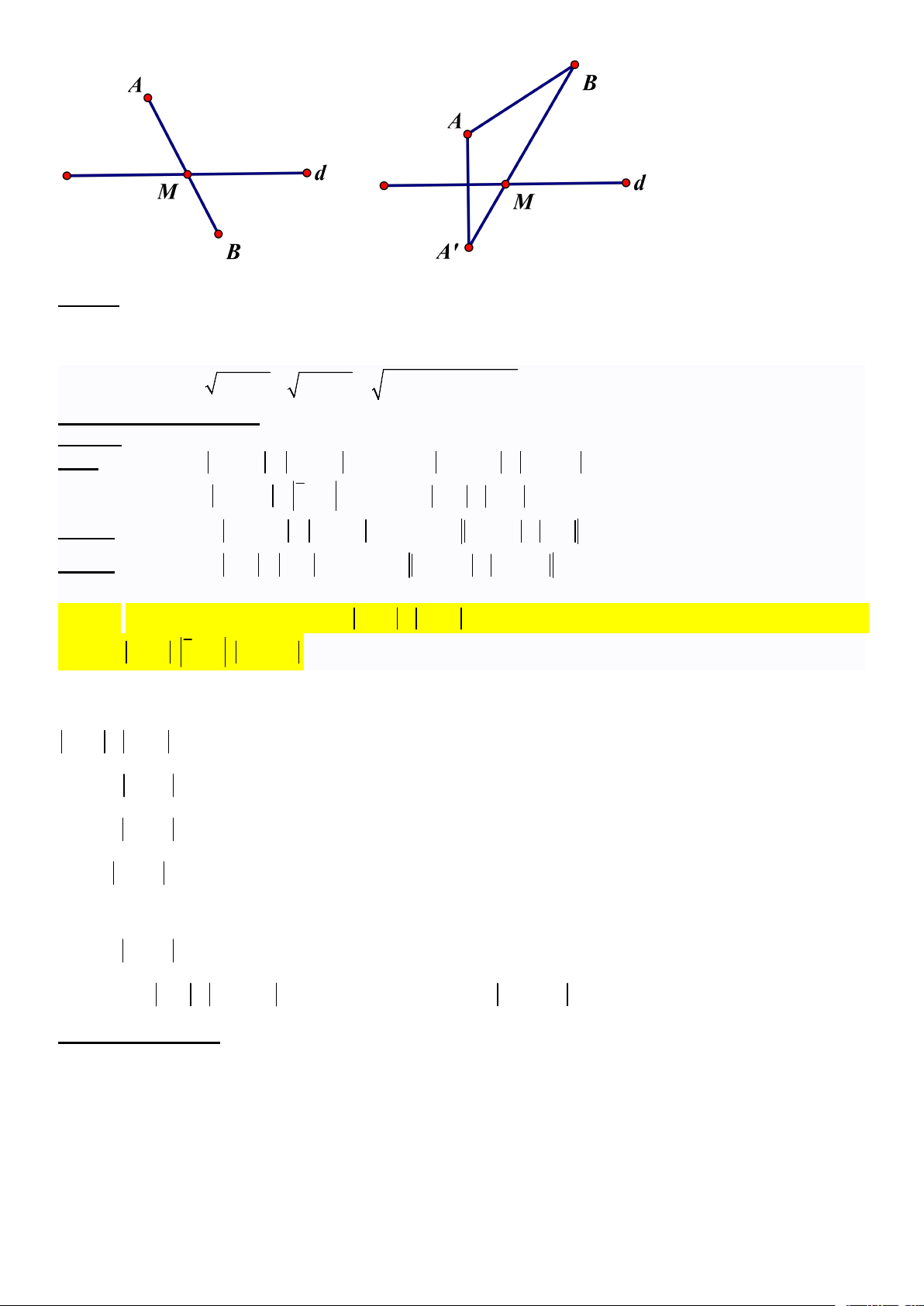
z . .  z . . Phân tích :
=> Là đường thẳng
z . .  z . .
Ví dụ: Cho z  2  4i  z  2i Tìm z để z min A. z  1   i B. z  2   2i
C. z  2  2i D. z  3 2i
Cách 1: Đưa về dạng đường thẳng z  2  4i  z  2i  x  y  4  y  4  x 2 2 2
 z  x  y  x  4  x2
Đến đây dùng MODE 5-3 giải pt bậc 2 để tìm ra min z => z=x+yi=2+2i Cách 2 : PP hình học :
Đưa về dạng đường thẳng z  2  4i  z  2i  x  y  4  y  4  x  Khi đó z
 d O; min
Cách 3 : Khi có đáp án trắc nghiệm MODE 2 đưa về số phức
Nhập z  2  4i  z  2i
CALC thử đáp án, ưu tiên đáp án có z
trước. Nếu kết quả trả về 0 thì nhận min Bài tập
Bài 1 :Cho z thỏa z  i 1  z  3 4i Tìm z có môđun min
Bài 2 : Cho z thỏa z  2 3i  z i Tìm z có z  2  2i min Bài 3 : Cho z thỏa 2
z  2z  5   z 1 2i z  3i  
1 Tìm min z  2  2i
Bài 4 : Trong các số phức z thỏa mãn 2z  z  z  i , tìm số phức có phần thực không âm sao cho 1 z 
đạt giá trị lớn nhất. i A. 6 i i i z   B. z  C. 3 z   D. 6 z   4 2 2 4 8 8 8
Dạng 4: Cho z  a  z  b Tìm Max, min P với P  z  z  z  z 1 2 Cách 1:
+) Bước 1: Khai triển z  a  z  b đưa về dạng đường thẳng
+) Bước 2 : Từ P ta tìm tọa độ điểm A ; B và xét vị trí tương đối của A ;B với d
+) Khi đó z là M thỏa mãn P min : Cách 2: Áp dụng
BĐT Bunhia Copski:   2   2 2   2 2 Ax By A B
x  y  nếu tìm max BĐT Mincopxki: 2 2 2 2
a  x  b  y  a  b2   x  y2 nếu tìm min. Cách 3: CASIO MODE 7 Bài tập:
Bài 1: Cho z thỏa z 1 i  z 1 i Tìm z để z 1 5i  z  2  i min
Bài 2 : Cho z thỏa z  2  i  z  3i . Tìm z để z  i  z  2 min
Bài 3 : : Cho z thỏa z 13i  z 1 i . Tìm z để z 1 i  z 1 max
Bài 4 : : Cho z thỏa z 1  z  i . Tìm z để z  2  i  z  3 i max
Dạng 5: Trong số phức z thỏa mãn z  z  z  z  k, k  0 .Tìm giá trị nhỏ nhất, lớn nhất của P 1 2
với P  z  z ; z  z ; z .z  z 3 3 3 4 PHÂN TÍCH Chú ý:
z  z  z  z  k 1 2
Ta tính z  z : 1 2
+) Nếu z  z  k => Không tồn tại quỹ tích 1 2
+) Nếu z  z  k => Phương trình đường thẳng 1 2
Đặt y =ax+b; cho y tìm x và lập hệ tìm a; b
+) Nếu z  z  k => Phương trình elip 1 2
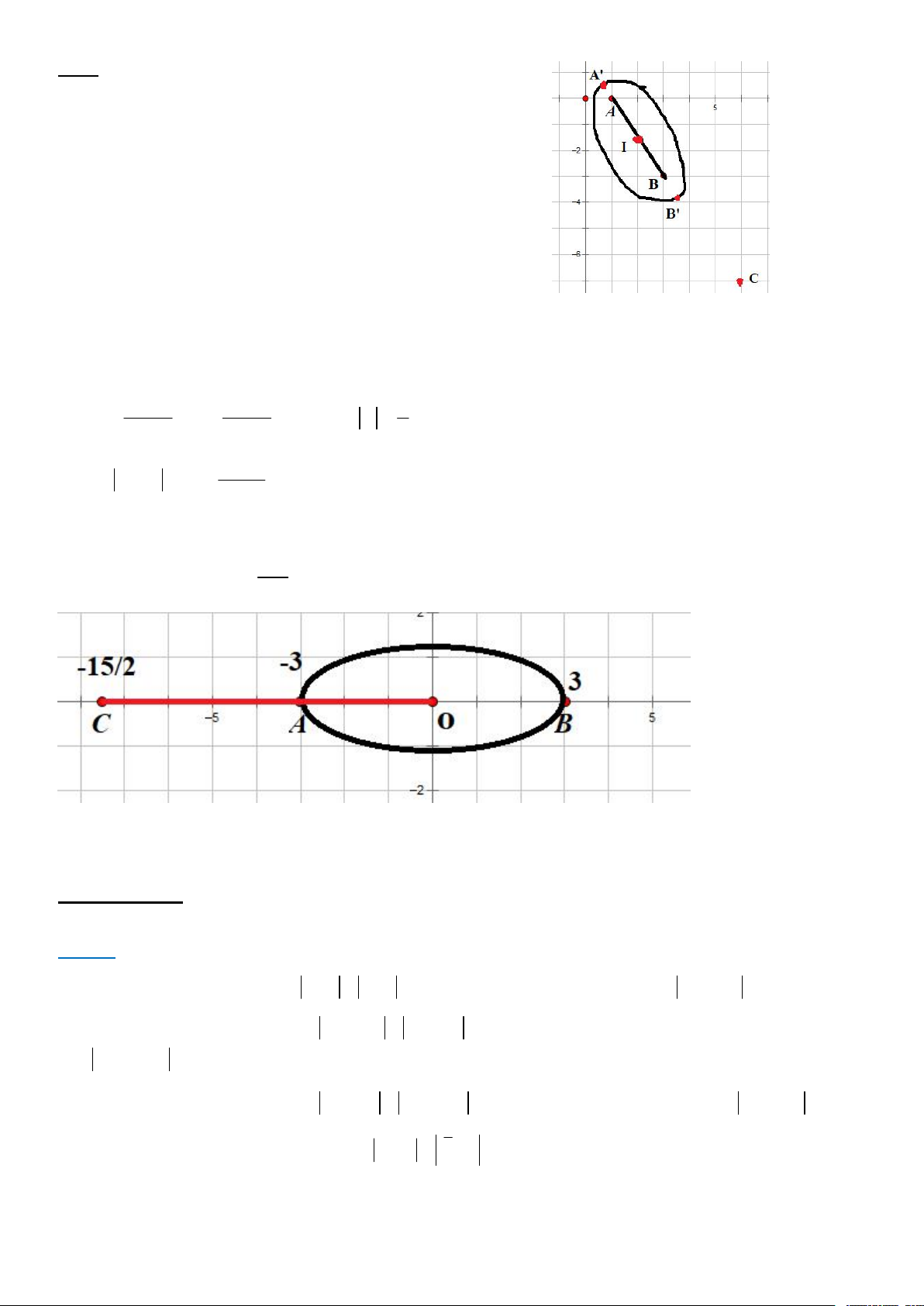
Ví dụ: Cho z i  z 3 3i  6. Tính max min của P= z  6  7i Cách 1: PP hình học
Gọi A và B là điểm biểu diễn z ; z và M là điểm biểu diễn z ; C là điểm biểu diễn z trong P 1 2 3 Khi đó MA + MB = k
Nếu MA+MB=AB thì điểm biểu diễn là đường thẳng
Nếu MA+MB > AB thì điểm biểu diễn là elip
Khi đó ta vẽ hình biểu diễn các điểm A,B,C trên mặt Oxy và xác định M trong các trường hợp là đường
thẳng hoặc elip sao cho MC ngắn nhất hoặc lớn nhất. Giải:
Gọi A(0;1);B(3;-3);C(6;-7);M(x;y)
Khi đó MA+MB=6; Tìm max min của MC
Ta thấy MA+MB>AB => Elip (Vẽ hơi xấu :v)
Trong đó I là trung điểm AB Với a=6/2=3;c=IA=5/2 Khi đó
MC min khi MC= B’C=BC-BB’=BC-(a-c)=5-1/2=4,5
MC max khi MC=A’C=AC+AA’=AC+(a-c)=10+1/2=10,5 Cách 2: CASIO
Gán A= z  z z  z 1 2 ; B= 1 2 ; Ta thấy B 6 
nên điểm biểu diễn là elip 2 2 2 Nhập arg X  A X A    
(Phép quay đưa về elip chính tắc) B   
CALC: X= i => c = 5/2; a= 6/2=3
CALC: X= -6+7i => C= 15 2
Khi đó MC min = AC=15/2-3=4,5 MC max = CB=15/2+3=10,5
Cách 3: CASIO ( Sử dụng phương pháp lượng giác hóa, tìm pt elip gán vào cosa; sina) sau đó dùng
MODE 7. Tuy nhiên cách này có vẻ dài hơn cách 2 nên thầy không đề cập tới nữa Bài tập
Bài 1: Cho số phức z thỏa mãn z  2  z  2  6 . Tìm GTLN và GTNN của P  z 1 3i
Bài 2: Cho số phức z thỏa mãn z 1 3i  z  2 i  8. Tìm giá trị lớn nhất, giá trị nhỏ nhất của
P  2z 1 2i .
Bài 3: Cho số phức z thỏa mãn z  2 i  z  4  7i 10 . Tìm GTLN, GTNN của P  z 1 4i
Bài 4-Trong các số phức z thỏa mãn z 3i  iz  3 10 . Hai số phức z z 1 và 2 có môđun nhỏ
nhất. Hỏi tích z z là bao nhiêu A. C. 1 2 25 B. 25 16 D. 16
Bài 5: Trong tất cả các số phức z thỏa mãn z  4  z  4  10 , gọi M ,m lần lượt là giá trị lớn nhất,
giá trị nhỏ nhất z . Khi đó, giá trị biểu thức 2
P  M  m bằng? A. P  6  B. P  1  3 C. P  5  D. P  4
Bài 6 : (LẠNG GIANG SỐ 1) Cho số phức z thỏa mãn z 3  z 3  8 . Gọi M , m lần lượt giá trị
lớn nhất và nhỏ nhất z . Khi đó M  m bằng A. 4  7. B. 4  7. C. 7. D. 4  5.
Bài 7: Cho số phức z thỏa mãn |z + 3| + |z − 3| = 10. Giá trị nhỏ nhất của |z| là A. 3 B. 4 C. 5 D. 6
Dạng 6: Trong số phức z thỏa mãn z  z  z  z  k, k  0 .Tìm giá trị nhỏ nhất, lớn nhất của P 1 2
với P  z  z  z  z hoặc một biểu thức Q chứa 2 3 z ; z ... 3 4
Cách 1: Sử dụng PP lượng giác hóa
Cách 2: Sử dụng PP BĐT Bài tập:
Bài 1: Cho 2 số phức z , z thỏa mãn z  z  5 và z  z  3 . Tìm GTLN của P  z  z . 1 2 1 2 1 2 1 2
Dạng 7: Tập hợp điểm biểu diễn số phức z có dạng z  z  z  z  k hoặc các dạng khác… 1 2
+) Khai triển kiểm tra xem có thuộc dạng đường thẳng hay hyperbol không Áp dụng: 2 2
A  B  C  A  C  B  2C B  4C B   A  B  C2  0
A  B  C  A  B  AB  C 
B  A B C 2 2 2 2 4A  0 Nhập 2
4C B   A  B  C2
CALC X =0 => hệ số tự do D Nhập 2
4C B   A  B  C2  D
CALC X=1 => hệ số của 2 x CALC X = i => hệ số 2 y
=> pt hyperbol hoặc elip
MỘT SỐ DẠNG BÀI TẬP KHÁC
Câu 1: (TRẦN HƯNG ĐẠO – NB) Cho số phức z thỏa mãn điều kiện z 3 4i  2. Trong mặt
phẳng Oxy tập hợp điểm biểu diễn số phức w  2z 1 i là hình tròn có diện tích A. S  9 . B. S  12 . C. S  16 . D. S  25 . Hướng dẫn giải Chọn C. w 1 2 1 i w z i z        2 w 1  3  4  2  i z i 
 3  4i  2  w 1 i  6  8i  4  w  7  9i  4   1 2
Giả sử w  x  yi  ,
x y, khi đó    x  2   y  2 1 7 9 16
Suy ra tập hợp điểm biểu diễn số phức w là hình tròn tâm I 7;9 , bán kính r  4.
Vậy diện tích cần tìm là 2 S  .4 16. Câu 2: Cho số phức i
z thỏa mãn z  1. Tìm giá trị lớn nhất của biểu thức 5 A  1 . z A. 5. B. 4. C. 6. D. 8. Hướng dẫn giải Ta có: 5i 5i 5 A  1  1   1
 6. Khi z  i  A  6. z z z
 Chọn đáp án C.
Câu 3: Cho số phức z thỏa mãn z  1 . Tìm giá trị lớn nhất M
và giá trị nhỏ nhất M của max min biểu thức 2 3
M  z  z  1  z  1 . A. M  5; M  1. B. M  5; M  2. max min max min C. M  4; M  1. D. M  4; M  2. max min max min Hướng dẫn giải Ta có: 2 3
M  z  z  1  z  1  5 , khi z  1  M  5  M  5. max 3 3 3 3 3 1 z 1 z 1 z 1 z 1 z Mặt khác: 3 M   1 z     1, khi 1 z 2 2 2
z  1  M  1  M  1. min
 Chọn đáp án A. Câu 4: Cho số phức 
z thỏa z  2 . Tìm tích của giá trị lớn nhất và nhỏ nhất của biểu thức z i P  . z A. 3 . B.1. C. 2 . D. 2 . 4 3 Hướng dẫn giải Ta có i 1 3 P i  1  1  . Mặt khác: 1 1 1  1  . z |z| 2 z |z| 2
Vậy, giá trị nhỏ nhất của P là 1 , xảy ra khi z  2i; giá trị lớn nhất của P bằng 3 xảy ra khi 2 2 z  2i.
 Chọn đáp án A.
Câu 5: Cho số phức z thỏa mãn z  1. Tìm giá trị lớn nhất của biểu thức P  1 z  3 1 z . A. 3 15 B. 6 5 C. 20 D. 2 20. Hướng dẫn giải
Gọi z  x  yi; x; y . Ta có: 2 2 2 2
z  1  x  y  1  y  1  x  x  1;1 .  
Ta có: P   z 
 z    x 2  y   x 2 2 2 1 3 1 1 3 1
 y  2 1 x  3 2 1 x  .
Xét hàm số f x  21 x  3 21 x; x 1;1. 
 Hàm số liên tục trên 1;1   và với x 1
 ;1 ta có: f x 1 3 4  
 0  x   1;1. 21 x 21 x 5 Ta có: f    4 1 2;   f  1    6; f   2 20  P    2 20. max  5 
 Chọn đáp án D.
Câu 6: Cho số phức z thỏa mãn z  1. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2
P  z  1  z  z  1 . Tính giá trị của M.m . A. 13 3 . B. 39 . C. 3 3. D. 13 . 4 4 4 Hướng dẫn giải
Gọi z  x  yi; x; y  . Ta có: z  1  .zz  1
Đặt t  z  1 , ta có 0  z 1  z  1  z  1  2  t  0; 2.   Ta có t
 z z  2 2 t 2 1 1
1 z.z z z 2 2x x             . 2
Suy ra z  z   z  z  z z  z z   z   x  2 2 2 2 1 . 1 2
1  2x 1  t  3 .
Xét hàm số f t 2
 t  t  3 ,t  0; 2 . 
 Bằng cách dùng đạo hàm, suy ra f t 13  f t 13 3 max ; min
 3  M.n  . 4 4
 Chọn đáp án A.
Câu 7: Cho số phức z thỏa mãn điều kiện 2
z  4  2 z . Khẳng định nào sau đây là đúng?   A. 3 1 3 1  z  .
B. 5 1  z  5 1. 6 6 C. 6   1  z  6 1. D. 2 1 2 1  z  . 3 3 Hướng dẫn giải
Áp dụng bất đẳng thức u  v  u  v , ta được 2 2 2
2 z  4  z  4  4  z  z  2 z  4  0  z  5  1. 2 2 2 2
2 z  z  z  4  z  4  z  2 z  4  0  z  5 1.
Vậy, z nhỏ nhất là 5  1, khi z  i  i 5 và z lớn nhất là 5  1, khi z  i  i 5.
 Chọn đáp án B. Câu 8: z
Cho z , z là hai số phức liên hợp của nhau và thỏa mãn 1  và z  z  2 3. Tính 1 2 2 z 1 2 2
môđun của số phức z .1 A. z  5. B. z 5  3. C. z  2. D. z  . 1 1 1 1 2 Hướng dẫn giải
Gọi z  a  bi  z  a  bi; a; b . Không mất tính tổng quát ta gọi b  0. 1 2 
Do z  z  2 3  2bi  2 3  b  3. 1 2 3 z z
Do z , z là hai số phức liên hợp của nhau nên z .z  1 1 3     z  . 1 2 1 2  , mà 2 z2 z z12 2 1 b  0
Ta có: z  a  bi3 3   3 2
a  3ab    2 3 3a b  b  2 3 2
i    3a b  b  0    a  1. 1 2 2 3a   b Vậy 2 2
z  a  b  2. 1
 Chọn đáp án C.
Câu 9: Gọi z  x  yi x,yR là số phức thỏa mãn hai điều kiện 2 2
z  2  z  2  26 và 3 3 z  
i đạt giá trị lớn nhất. Tính tích x . y 2 2 A. 9 xy  . B. 13 xy  . C. 16 xy  . D. 9 xy  . 4 2 9 2 Hướng dẫn giải
Đặt z  x  iy x,y R. Thay vào điều kiện thứ nhất, ta được 2 2 x  y  36.
Đặt x  3cost, y  3sin .t Thay vào điều kiện thứ hai, ta có 3 3 P    z  
i  18 18sin t      6. 2 2  4      Dấu bằng xảy ra khi 3 3 2 3 2 sin t   1   t    z      .i  4  4 2 2
 Chọn đáp án D.
Câu 10: Biết số phức z
thỏa mãn đồng thời hai điều kiện z  3  4i  5 và biểu thức 2 2
M  z  2  z  i đạt giá trị lớn nhất. Tính môđun của số phức z  i.
A. z  i  2 41
B. z  i  3 5.
C. z  i  5 2
D. z  i  41. Hướng dẫn giải
Gọi z  x  yi; x; y  . Ta có: z   i 
 C x  2  y  2 3 4 5 : 3
4  5 : tâm I 3; 4 và R  5. Mặt khác: 2 2 M z z i
x 2 y x  y 2 2 2 2 2 1           
 4x  2y  3  d : 4x  2y  3  M  0.  
Do số phức z thỏa mãn đồng thời hai điều kiện nên d và C có điểm chung    d 23 M d I;  R 
 5  23  M  10  13  M  33 2 5
4x  2y  30  0  x  5  M  33    
 z  i  5  4i  z  i  41. max x3 
2 y 42  5 y  5
 Chọn đáp án D.
Câu 11: ( CHUYÊN SƠN LA – L2) Cho số phức z thỏa mãn điều kiện : z 1 2i  5 và
w  z 1 i có môđun lớn nhất. Số phức z có môđun bằng: A. 2 5 . B. 3 2 . C. 6 . D. 5 2 . Hướng dẫn giải: Chọn B.
Gọi z  x  yi  ,
x y   z 1 2i  x  
1   y  2i
Ta có: z   i 
  x  2   y  2 
  x  2   y  2 1 2 5 1 2 5 1 2  5
Suy ra tập hợp điểm M  ;
x y biểu diễn số phức z thuộc đường tròn C tâm I 1; 2   bán kính
R  5 như hình vẽ:
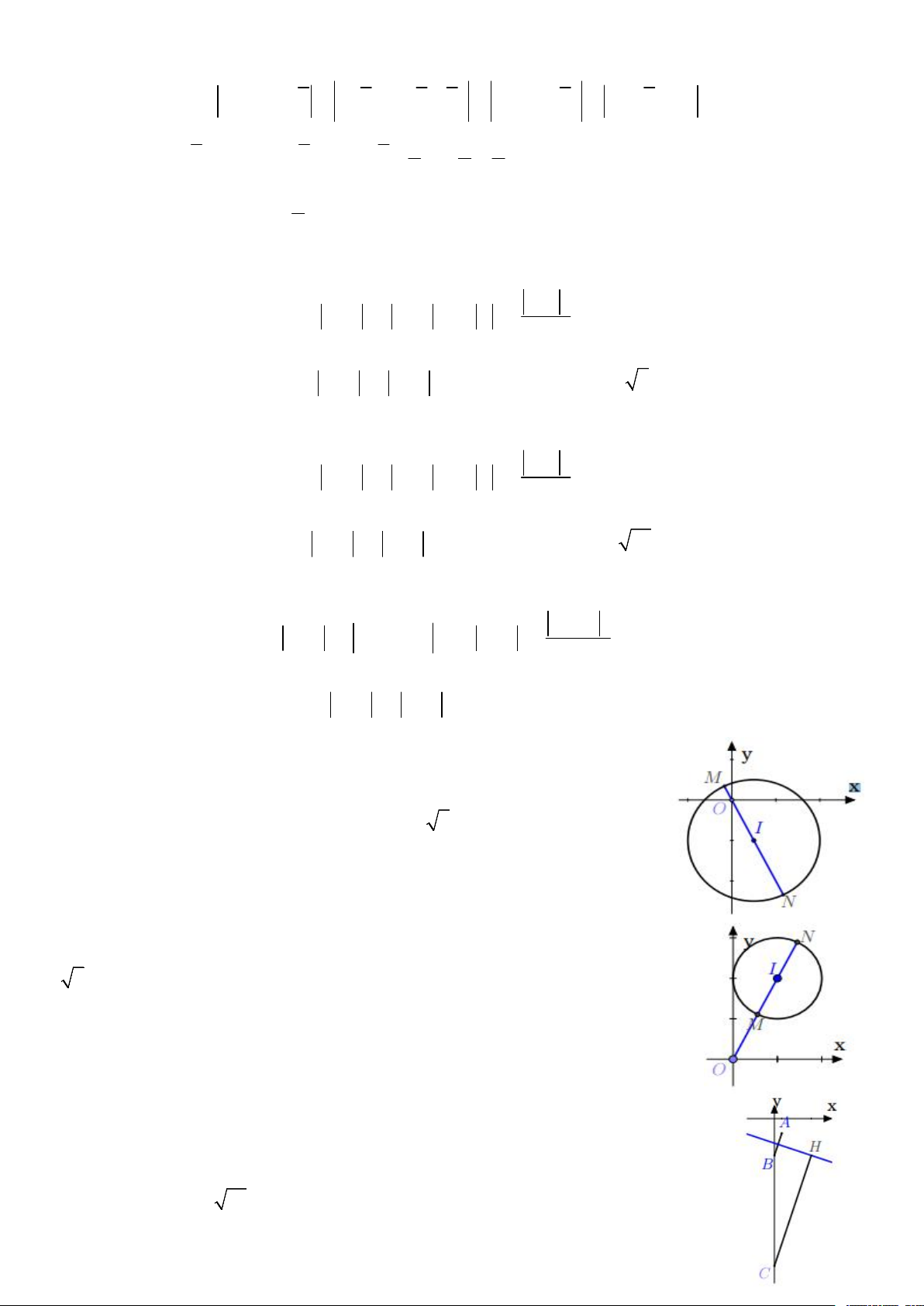
Dễ thấy OC, N  1  ;  1 C y Theo đề ta có: M  ;
x yC là điểm biểu diễn cho số phức z thỏa mãn: 1  x O
w  z 1 i  x  yi 1 i  x   1   y   1 i 1 1   N
 z   i  x  2   y  2 1 1 1  MN 2 I
Suy ra z 1 i đạt giá trị lớn nhất  MN lớn nhất
Mà M, N C nên MN lớn nhất khi MN là đường kính đường tròn C
 I là trung điểm MN  M    2
3; 3  z  3 3i  z  3  32  3 2
C. BÀI TẬP TỰ LUYỆN.
Phương pháp đại số
BÀI 1 (Sở GD Long An 2017). Cho số phức z thỏa mãn |z − 2 − 3i|
= 1. Tìm giá trị lớn nhất của |z|. A. 1 3 B. 13 C. 2  13 D. 13 1
BÀI 2 (THPT Hưng Nhân-Thái Bình 2017 L3). Tìm giá trị lớn nhất của |z| biết 2   3i z 1 1. 3  2i A. 2 B. 2 C. 1 D. 3
BÀI 3 (THPT Nguyễn Huệ-Huế 2017 L2, Hà Huy Tập-Hà Tĩnh 2017 L2). Cho số phức z thỏa mãn 2
z  i  1. Tìm giá trị lớn nhất của |z|. A. 2` B. 5 C. 2 2 D. 2
BÀI 4 (Chuyên Nguyễn Trãi-Hải Dương 2017 L3). Xác định số phức z thỏa mãn z  2  2i  2 mà
|z| đạt giá trị lớn nhất A. 1 i B. 3  i C. 3  3i D. 1 3i
BÀI 5 (THPT Yên Khánh A-Ninh Bình 2017,THPT Kim Liên-Hà Nội 2017). Cho số phức z thỏa mãn |z
− 2 − 3i| = 1. Giá trị nhỏ nhất của |z + 1 + i| là A. 13 1 B. 4 C. 4 D. 13 1
BÀI 6 (THPT Đống Đa-Hà Nội 2017). Cho số phức z thỏa mãn 2
z  2z  2  z 1 i Biểu thức |z| có giá trị lớn nhất là A. 2 1 B. 2 C. 2  2 D. 2 1
BÀI 7 (THPT Hùng Vương-Phú Thọ 2017). Cho số phức z thỏa mãn điều kiện |z − 1| = |(1 + i)z|. Đặt m =
|z|, tìm giá trị lớn nhất của m. A. 2 1 B. 1 C. 2 1 D. 2
BÀI 8 (THPT Chuyên Lào Cai 2017 L2). Cho số phức z thỏa mãn 4i z 
 2 . Gọi M, m lần lượt là giá z
trị lớn nhất và nhỏ nhất của |z|. Tính M + m? A. 2 B. 2 5 C. 13 D. 5
BÀI 9 (THPT Hưng Nhân-Thái Bình 2017 L3). Cho hai số phức z1, z2 thỏa mãn
 z  3  4i  1  1 
 z  6  i  2  2
Tính tổng Giá trị lớn nhất và Giá trị nhỏ nhất của biểu thức z  z . 1 2 A. 18 B. 6 2 C. 6 D. 3 2
BÀI 10 (Sở GD Điện Biên 2017,Gia Lộc-Hải Dương 2017 L2). Cho số phức z thỏa mãn |z| ≤ 1. Đặt 2z 1 A 
. Mệnh đề nào dưới đây đúng? 2  iz A. |A| < 1 B. |A| ≤ 1 C. |A| ≥ 1 D. |A| > 1
BÀI 11 (Sở GD Hải Dương 2017). Cho số phức z thỏa mãn z. z  1 . Tìm giá trị nhỏ nhất của biểu thức 3
P  z  3z  z z  z . A. 15 B. 3 C. 13 D. 3 4 4 4
BÀI 12 (Chuyên Ngoại Ngữ-Hà Nội 2017). Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất của biểu
thức T = |z + 1| + 2|z − 1| A. maxT  2 5 B. maxT  2 10 C. max  3 5 D. maxT  3 2
BÀI 13 (Sở GD Bắc Ninh 2017). Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất của biểu thức T = |z + 1| + 3|z − 1| A. maxT  3 10 B. maxT  2 10 C. max  6 D. maxT  4 2
BÀI 14 (Chu Văn An-Hà Nội 2017 L2). Cho số phức z thỏa mãn điều kiện z 1  2 . Tìm giá trị lớn
nhất của T = |z + i| + |z − 2 − i| A. maxT  8 2 B. maxT  4 C. max  4 2 D. maxT  8
Phương pháp hình học
BÀI 15 (Sở GD Đà Nẵng 2017). Cho số phức z thỏa mãn |z −
1 + 2i| = 3. Mô đun lớn nhất của số phức z là: A. 14  6 5 15(14  6 5) C. 14  6 5  B. D. 15(14 6 5) 5 5
BÀI 16 (THPT Bình Xuyên-Vĩnh Phúc 2017 L3). Cho số phức z thỏa mãn |z−1−2i| = 1. Tìm giá trị nhỏ nhất của |z| A. 2 B. 1 C. 2 D. 5 1
BÀI 17 (Chuyên Nguyễn Trãi-Hải Dương 2017 L3). Cho số phức z, w thỏa mãn |z − 1 + 2i| = |z + 5i|, w =
iz + 20. Giá trị nhỏ nhất m của |w| là B. m  7 10 D. m  2 10 A. 3 10 m  C. 10 m  2 2
BÀI 18 (THPT Cổ Loa-Hà Nội 2017 L3). Cho số phức z thỏa mãn 5 z   i  3
z   2i . Biết biểu 2 2
thức Q = |z − 2 − 4i| + |z − 4 − 6i| đạt giá trị nhỏ nhất tại z = a + bi (a, b ∈ R). Tính P = a − 4b A. P  2 B. 1333 P  C. P  1 D. 691 P  272 272
BÀI 19 (THPT Cao Nguyên-Dăk Lăk 2017). Cho số phức z thỏa mãn 2 iz  + 2 iz   4 . Gọi M 1 i i 1
và m lần lượt là Giá trị lớn nhất và Giá trị nhỏ nhất của |z|. Tính M.m A. Mm = 2 B. Mm = 1 C. Mm  2 2 D. Mm  2 3
BÀI 20 (Lương Đức Trọng 2017). Xét số phức z thỏa mãn 4|z + i| + 3|z − i| = 10. Gọi M, m tương ứng là
giá trị lớn nhất và nhỏ nhất của |z|. Tính M + m A. 35 2 B. 80 C. 50 D. 30 15 7 11 7
BÀI 21 (THPT Thăng Long-Hà Nội 2017 L2). Cho z là số phức thay đổi thỏa mãn
z  2  z  2  4 2 Trong mặt phẳng tọa độ, gọi M, N là điểm biểu diễn z và z. Tính giá trị lớn nhất của diện tích tam giác OMN. A. 1 B. 2 C. 4 2 D. 2 2
BÀI 22 (THPT Chuyên Hoàng Văn Thụ-Hòa Bình 2017 L3). Cho z ,z là hai nghiệm phương trình |6 1 2
− 3i + iz| = |2z − 6 − 9i| thỏa mãn 8
z  z  |. Giá trị lớn nhất của z  z là 1 2 5 1 2 A. 31 B. 56 C. 4 2 D. 5 5 5
D. LỜI GIẢI VÀ ĐÁP ÁN
GIẢI BÀI TẬP 1. Ta có
1  z  2  3i  z  13  z  1 13 . Đáp án là A.
GIẢI BÀI TẬP 2. Ta có 2  3i 2  3i 1  z 1 
. z 1  z 1  z  2. 3  2i 3  2i Đáp án là B.
GIẢI BÀI TẬP 3. Ta có 2 2 2
1  z  i  z 1  z  2  z  2. Đáp án là D
GIẢI BÀI TẬP 4. Ta có
2  z  2  2i  z  2 2  z  3 2 .
Dấu "=" khi z = k(2 + 2i) với 3
2k 2  2 2  k  . Vậy k = 3 + 3i. 2 Đáp án là C
GIẢI BÀI TẬP 5. Ta có
|z + 1 + i| = |z + 1 − i| = |(z − 2 − 3i) + (3 + 2i)| ≥ ||z − 2 − 3i| − |3 + 2i| = 13 − 1.
Vậy min min z 1 i  13 1. Đáp án là A.
GIẢI BÀI TẬP 6. Ta có
z 1 i  0 2 2 2
z  2z  2  (z 1)  i  z 1 i . z 1 i  z 1 i   z 1i 1 
• Nếu z = i − 1 thì z  2
• Nếu |z + 1 + i| = 1 thì 1 ≥ |z| − |1 + i| = |z| − 2 . Do đó |z| ≤ 1 + 2 . Đáp án là A.
GIẢI BÀI TẬP 7. Ta có
|z − 1| = 2|z| ≤ |z| + 1 ⇒ |z| ≤ 1. Do đó max |z| = 1. Đáp án là B. GIẢI BÀI TẬP 8. Ta có 2 2
2 z  z  4  z  2 z  4  0  z  1 5  M . và 2 2
2 z  4  z  z  2 z  4  0  z  1   5  m Vậy M + m = 2 5 . Đáp án là B.
GIẢI BÀI TẬP 9. Ta có
z  z  (z  3  4i ) (z  6  i )  (3  3i )  z  2  4i  z  6  i  3  3i  3  3 2  max. 1 2 1 2 1 2 và
z  z  (z  3  4i) (z  6  i)  (3  3i)  3  3i  z  2  4i  z  6  i  3 2 3  min.Do đó tổng 1 2 1 2 1 2
Giá trị lớn nhất và Giá trị nhỏ nhất là 6 2 . Đáp án là B.
GIẢI BÀI TẬP 10. Ta có 2A  i
2A  Aiz  2z  i  (2  Ai )z  2A  i  z  . 2  Ai Đặt A = a + bi. Suy ra | 2 2 2 2 2 2 2 2
z  1  2A  i  2  A i  4a  (2b  1)  a  (b  2)  3a  3b  3  A  a  b  1. Đáp án là B.
GIẢI BÀI TẬP 11. Ta có 2 2 3 3 2 2
z  3z  z  z .z  3z .z  z  z  3  z  (z  z ) 1 . 2 Suy ra 2  1  3 3
P  (z  z ) 1 (z  z )  z  z    .    2  4 4
Vậy giá trị nhỏ nhất của P là 3 . 4 Đáp án là C.
GIẢI BÀI TẬP 12. Áp dụng công thức trung tuyến ta có 2 2 2 2 1 1
z 1  z 1  2 z   4 2
Theo bất đẳng thức Bunhiacopxki thì 2 2 2 2 2
T  ( z 1  z 1 )(1  2 )  20 T  2 5 . Đáp án là A.
GIẢI BÀI TẬP 13. Áp dụng công thức trung tuyến ta có 2 2 2 2 1 1
z 1  z 1  2 z   4 2
Theo bất đẳng thức Bunhiacopxki thì 2 2 2 2 2
T  ( z 1  z 1 )(1  3 )  40 T  2 10. . Đáp án là B.
GIẢI BÀI TẬP 14. Áp dụng công thức trung tuyến ta có 2 2 2 2 2  2i 2
z 1  z  2  i  2 z 1   8 2
Theo bất đẳng thức Bunhiacopxki thì 2 2 2 2 2
T  ( z 1  z 1 )(1 1 )  16 T  4.. Đáp án là B.
GIẢI BÀI TẬP 15.
Tập hợp các điểm M biểu diễn số phức z thỏa mãn giả thiết là đường tròn tâm
I(1; −2) bán kính r = 3. Khi đó |z| = OM với O là gốc tọa độ. Do đó max |z| = OI + r = 3 + 5 Đáp án là A.
GIẢI BÀI TẬP 16.
Tập hợp các điểm M biểu diễn số phức z thỏa mãn giả thiết là đường tròn tâm I(1;
−2) bán kính r = 1. Khi đó |z| = OM với O là gốc tọa độ. Do đó min |z| = OI − r = 5 − 1. Đáp án là D.
GIẢI BÀI TẬP 17.
Gọi A (1; −2), B (0; −5), tập hợp các điểm z thỏa mãn giả thiêt đề bài là đường trung
trực d của AB có phương trình x + 3y + 10 = 0. Ta có
|w| = |iz + 20| = |z − 20i| = OM với M là điểm biểu diễn số phức z và C(0; 20). Do đó min |w| = d(C.∆) = 7 10 Đáp án là B. GIẢI BÀI TẬP 18. Gọi  5   3 
A  ;2 ,B  ;2 ,   
 tập hợp các điểm z thỏa mãn giả thiêt đề bài là  2   2 
đường trung trực d của AB có phương trình x−4y + 2 = 0. Xét hai điểm M(2;
4), N(4; 6) thì Q = IM + IN với I ∈ d. Do đó Q nhỏ nhất khi và chỉ khi I là giao điểm của M0N với  58 28  M ' ;    17 17 
là điểm đối xứng của M qua d. Vậy  62 24  I ;   , ứng với 62 24 z   i  17 17  17 17 Đáp án là A.
GIẢI BÀI TẬP 19. Ta có 2 2 4  iz   iz 
 2iz  2 z  M  2. 1  i i 1 2 2
Theo giả thiết thì số phức z thỏa mãn z   z 
 4  z 1 i  z 1 i  4. i (i 1) i (i 1)
Gọi A(−1; 1), B(1; −1) có trung điểm là O(0; 0). Điểm M biểu diễn số phức z. Theo công thức trung tuyến 2 2 2 MA  MB AB thì 2 z  MO   . 2 4 2 MA  MB 8 8 Ta có 2 2 ( ) MA  MB   8 Do đó m    2. 2 2 4
Vậy Mn = 2 2 . Đáp án là C.
GIẢI BÀI TẬP 20. Gọi A(0; −1), B(0; 1) có trung điểm là O(0; 0). Điểm M biểu diễn số phức z. Theo công 2 2 2 MA  MB AB thức trung tuyến thì 2 2 z  MO   . 2 4  Theo giả thiết a
4MA  3MB  2 2 . Đặt 10 4
a  MA  MB  . Do 3 10  7a 4 16 MA  MB 
 AB  2  6  10 7a  6   a  . 3 7 7 2 2 10  4a 
25a  80a 100 5a  8  36 2 2 2  2
Ta có MA  MB  a    .    3  9 9 Do 36 34 2 11296   5a  8 
 0  (5a  8)  . Suy ra 7 7 49  2 2
MA  MB  4 nên 2
z  1  z  1  m. 1296  36 340 121  2 2 2 49 MA  MB    z   M . Vậy 60 M  m  . Đáp án là C. 9 49 49 49
GIẢI BÀI TẬP 21.
Gọi điểm M biểu diễn số phức z = x + iy và N biểu diễn số phức z thì
M, M0 đối xứng nhau qua Ox. Diện tích tam giác OMN là S  xy . OMN
Do z  2  z  2  4 2 nên tập hợp M biểu diễn x là Elip (E): 2 2 x y   1. Do đó 8 4 2 2 2 2 x y x y xy 1    2 .   S
 xy  2 2. Đáp án là D. 8 4 8 4 2 2 OMN
Document Outline

BĐT Mincopxki: tìm min.
BĐT vecto tìm min. Dấu
BĐT Mincopxki: tìm min.
BĐT vecto tìm min. Dấu
Ví dụ: Cho số phức thỏa
Bài tập:
Bài 1: Cho số phức z thỏa mãn
Bài 2: Cho số phức z thoả mãn
BĐT Mincopxki: nếu tìm
Cách 3: CASIO MODE 7
Bài tập:
Bài 1: Cho z thỏa Tìm z
Bài 2 : Cho z thỏa . Tìm
Bài 3 : : Cho z thỏa . T
Bài 4 : : Cho z thỏa . T
Dạng 5: Trong số phức t
Dạng 6: Trong số phức t
Cách 1: Sử dụng PP lượng giác hóa
Cách 2: Sử dụng PP BĐT
Bài tập:
Bài 1: Cho 2 số phức thỏ
Dạng 7: Tập hợp điểm biểu diễn số phức z có dạng
+) Khai triển kiểm tra xem có thuộc dạng đường thẳ
Áp dụng:
Nhập
CALC X =0 => hệ số tự do D
Nhập
CALC X=1 => hệ số của
CALC X = i => hệ số

Tổng hợp Trọn bộ phương pháp Min Max Số phức | Trọn bộ môn Toán 12

Tài liệu liên quan:

Vòng tròn lượng giác - Toán 12

Hàm số đồng biến, nghịch biến khi nào? Định nghĩa và cách xác định - Toán 12

Công thức tính nhanh diện tích Parabol | Toán 12

Phương Pháp Ghép Trục Hàm Số | Toán 12

Bài 4 Ôn tập số mũ đúng | Toán 12