
MÔN TOÁN HỌC
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ
Bộ đề theo ma trận đề thi tham khảo của BGD 2023
THAM KHẢO VÀ CẬP NHẬT TỪ NGÂN HÀNG THI THỬ TOÀN QUỐC

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 01_______________
Câu 1: Trên mặt phẳng tọa độ, điểm biểu diễn số phức
32i
có tọa độ là
A.
2;3 .
B.
2;3 .
C.
3;2 .
D.
3; 2 .
Câu 2: Trên khoảng
0; ,
đạo hàm của hàm số
7
logyx
là
A.
1
.y
x
B.
1
.
ln7
y
x
C.
ln7
.y
x
D.
1
.
ln7
y
x
Câu 3: Trên khoảng
0; ,
đạo hàm của hàm số
e
yx
là
A.
1
..
e
y e x
B.
1
.
e
yx
C.
1
.
1
e
x
y
e
D.
..
e
y e x
Câu 4: Tập nghiệm của bất phương trình
24
x
là
A.
;2
B.
0;2
C.
;2
D.
0;2
Câu 5: Cho cấp số nhân
n
u
với
1
5u
và
2
2u
. Công bội của cấp số nhân đó bằng
A.
1
. B.
28
. C.
5
2
. D.
2
5
.
Câu 6: Trong không gian
,Oxyz
cho mặt phẳng
:3 2 0P x z
. Vectơ no dưới đây l một vectơ
php tuyn của
P
?
A.
4
1;0; 1 . n
B.
1
3; 1;2 .n
C.
3
3; 1;0 .n
D.
2
3;0; 1 .n
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị như hình bên dưới :
Tọa độ giao điểm của đồ thị hàm số đã cho với trục tung là
A.
0; 2 .
B.
2;0 .
C.
2;0 .
D.
0;2 .
Câu 8: Cho hàm số
fx
và
gx
liên tục trên đoạn
0;1
và
11
00
d 1, d 3f x x g x x
. Tích phân
1
0
2 3 df x g x x
bằng
A.
9
. B.
5
. C.
10
. D.
11
.
Câu 9: Hàm số no có đồ thị l đường cong trong hình vẽ bên dưới?

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
A.
42
41y x x
. B.
1
2
x
y
x
. C.
32
41y x x
. D.
2
21yx
.
Câu 10: Trong không gian
,Oxyz
cho mặt cầu
2 2 2
: 1 2 1 9S x y z
. Tìm tọa độ tâm
I
và tính bán kính
R
của
.S
A.
1;2;1I
và
3.R
B.
1; 2; 1I
và
3.R
C.
1;2;1I
và
9.R
D.
1; 2; 1I
và
9.R
Câu 11: Trong không gian
,Oxyz
góc giữa hai mặt phẳng
Oxy
và
Oxz
bằng
A.
90 .
B.
60 .
C.
30 .
D.
45 .
Câu 12: Cho số phức
2,zi
phần ảo của số phức
2
z
là
A.
4.
B.
4.i
C.
3.
D.
1.
Câu 13: Cho khối lập phương có cạnh bằng
3.
Thể tích khối lập phương đã cho bằng
A.
9.
B.
27.
C.
18.
D.
3.
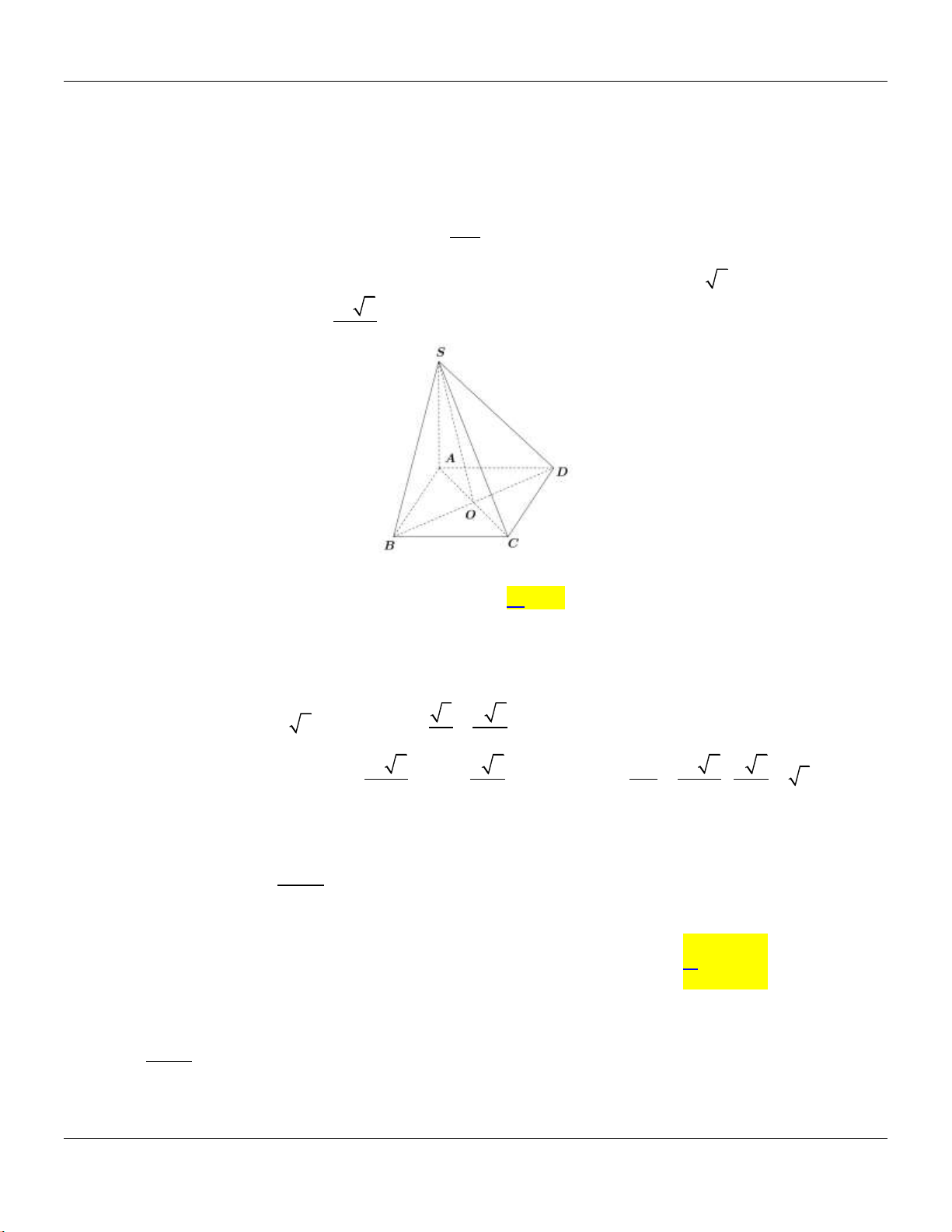
Câu 14: Cho khối chóp
.S ABC
có đy l tam gic vuông tại
, 2, 4,A AB AC SA
vuông góc với đy v
3SA
(tham khảo hình bên).
C
B
A
S
Thể tích khối chóp đã cho bằng
A.
9.
B.
8.
C.
4.
D.
3.
Câu 15: Cho đường thẳng
và mặt cầu
;.S O R
Gọi
d
là khoảng cách từ
O
đn
và
.dR
Số giao
điểm của
và
;S O R
là
A.
1.
B.
2.
C.
0.
D. Vô số.
Câu 16: Phần ảo của số phức
37zi
là
A.
3.
B.
7.
C.
7.
D.
3.
Câu 17: Cho khối nón có đường cao
,h
độ di đường sinh
l
v bn kính đy
.r
Diện tích xung quanh
xq
S
của khối nón được tính theo công thức no dưới đây?
A.
xq
S rl
. B.
1
2
xq
S rl
. C.
2
xq
S rl
. D.
xq
S rh
.
Câu 18: Trong không gian
,Oxyz
đường thẳng
1 2 3
:
3 4 5
x y z
d
đi qua điểm no sau đây?
A.
1; 2;3
. B.
1;2; 3
. C.
3; 4; 5
. D.
3;4;5
.
Câu 19: Cho hàm số
42
y ax bx c
có đồ thị l đường cong như hình bên dưới:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
x
y
-1
-1
-2
O
1
Điểm cực đại của đồ thị hàm số đã cho có tọa độ là
A.
0; 1 .
B.
1;0 .
C.
1; 2 .
D.
1; 2 .
Câu 20: Tiệm cận ngang của đồ thị hàm số
41
2
x
y
x
l đường thẳng có phương trình l
A.
4.y
B.
4.x
C.
2.x
D.
2.y
Câu 21: Tập nghiệm của bất phương trình
2
log 1x
là
A.
;2 .
B.
0;2 .
C.
0;1 .
D.
;1 .
Câu 22: Cho tập
M
có 10 phần tử. Số tập con gồm 3 phần tử của tập hợp
M
là
A.
3!.
B.
10!.
C.
3
10
.A
D.
3
10
.C
Câu 23: Cho
dsin .x x f x C
Khẳng định no dưới đây đúng?
A.
cos .
f x x
B.
cos .
f x x
C.
sin .
f x x
D.
sin .
f x x
Câu 24: Nu
4
2
3 d 12f x x x
thì
4
2
df x x
bằng
A.
6
. B.
0
. C.
2
. D.
10
3
.
Câu 25: Cho hàm số
sin 1f x x x
. Khẳng định no dưới đây đúng?
A.
2
d cos
2
x
f x x x x C
. B.
2
d cos
2
x
f x x x x C
.
C.
d cos 1f x x x C
. D.
2
d cos
2
x
f x x x C
.
Câu 26: Cho hàm số
()y f x
có đồ thị như hình vẽ bên.
Hàm số đã cho đồng bin trên các khoảng no dưới đây?
A.
0; 2
. B.
0;
. C.
0; 4
. D.
1;1
.
Câu 27: Cho hàm số
y f x
có bảng bin thiên như sau:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Đồ thị hàm số
y f x
có điểm cực tiểu là
A.
0;2
. B.
3; 4
. C.
3
CT
x
. D.
4
CT
y
.
Câu 28: Cho
a
,
b
là các số thực dương tùy ý. Khẳng định no sau đây đúng?
A.
ln ln lnab a b
. B.
ln ln lna b a b
.
C.
ln ln .lnab a b
. D.
ln ln .lna b a b
.
Câu 29: Cho hình phẳng
H
giới hạn bởi đồ thị hàm số
2
21y x x
và trục hoành. Thể tích của vật
thể tròn xoay khi quay
H
quanh trục hoành bằng
A.
9
8
. B.
81
80
. C.
81
80
. D.
9
8
.
Câu 30: Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng nhau:
Góc giữa đường thẳng
AB
và mặt phẳng
ABC
bằng
A.
30
. B.
90
. C.
60
. D.
45
.
Câu 31: Cho hàm số
y f x
có bảng bin thiên như sau:
Tập hợp tất cả các giá trị của
m
để phương trình
f x m
có ba nghiệm thực phân biệt
A.
4;2 .
B.
4;2 .
C.
4;2 .
D.
4;2 .
Câu 32: Cho hàm số
fx
có đạo hàm
2
3
1 2 , .
f x x x x x
Khoảng nghịch bin của hàm
số là
A.
2;0
. B.
; 2 ; 0;1
. C.
; 2 ; 0;
. D.
2;0 ; 1;
.
Câu 33: Chọn ngẫu nhiên hai số khác nhau từ
15
số nguyên dương đầu tiên. Xác suất để chọn được
hai số có tổng là một số lẻ bằng
A.
1
7
. B.
8
15
. C.
4
15
. D.
1
14
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 34: Tích các nghiệm của phương trình
1
5
log 6 36 1
xx
bằng
A.
6
log 5.
B.
5
log 6.
C.
5.
D.
0.
Câu 35: Cho số phức
z
thỏa mãn
12z i z
. Trong mặt phẳng phức, quỹ tích điểm biểu diễn
các số phức
z
A. l đường thẳng
3 1 0xy
. B. l đường thẳng
3 1 0xy
.
C. l đường thẳng
3 1 0xy
. D. l đường thẳng
3 1 0xy
.
Câu 36: Trong không gian
Oxyz
, vit phương trình đường thẳng
đi qua
1;1;0M
và vuông góc
với mặt phẳng
: 4 2 0Q x y z
?
A.
1
4
1
xt
yt
z
. B.
1
14
xt
yt
zt
. C.
2
54
1
xt
yt
zt
. D.
1
14
xt
yt
zt
.
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2;3A
. Điểm đối xứng với
A
qua mặt phẳng
Oxy
có
tọa độ là
A.
1; 2;3
. B.
1;2; 3
. C.
1; 2; 3
. D.
1;2;0
.
Câu 38: Cho lăng trụ tam gic đều
.ABC A B C
có tất cả các cạnh bằng
a
. Thể tích khối trụ có hai đy
là hai hình tròn ngoại tip hai đy của lăng trụ đã cho bằng
A.
3
a
. B.
3
12
a
. C.
3
3
a
. D.
3
4
3
a
.
Câu 39: Cắt khối nón
N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đy một góc bằng
0
60
ta được thit diện là một tam giác vuông cân cạnh huyền
2a
. Thể tích khối nón
N
bằng
A.
3
53
24
a
. B.
3
53
72
a
. C.
3
53
8
a
. D.
3
3
72
a
.
Câu 40: Trong không gian
,Oxyz
phương trình mặt phẳng
()P
song song v cch đều hai đường
thẳng
1
:d
2
1 1 1
x y z
và
2
:d
12
2 1 1
x y z
là
A.
2 2 1 0 xz
. B.
2 2 1 0 yz
. C.
2 2 1 0 xy
. D.
2 2 1 0 yz
.
________________________HẾT________________________

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Trên mặt phẳng tọa độ, điểm biểu diễn số phức
32i
có tọa độ là
A.
2;3 .
B.
2;3 .
C.
3;2 .
D.
3; 2 .
Câu 2: Trên khoảng
0; ,
đạo hàm của hàm số
7
logyx
là
A.
1
.y
x
B.
1
.
ln7
y
x
C.
ln7
.y
x
D.
1
.
ln7
y
x
Câu 3: Trên khoảng
0; ,
đạo hàm của hàm số
e
yx
là
A.
1
..
e
y e x
B.
1
.
e
yx
C.
1
.
1
e
x
y
e
D.
..
e
y e x
Câu 4: Tập nghiệm của bất phương trình
24
x
là
A.
;2
B.
0;2
C.
;2
D.
0;2
Lời giải:
Ta có
2 4 2
x
x
Tập nghiệm của bất phương trình l
;2
.
Câu 5: Cho cấp số nhân
n
u
với
1
5u
và
2
2u
. Công bội của cấp số nhân đó bằng
A.
1
. B.
28
. C.
5
2
. D.
2
5
.
Lời giải:
Công bội của cấp số nhân đó bằng
2
1
2
5
u
q
u
.
Câu 6: Trong không gian
,Oxyz
cho mặt phẳng
:3 2 0P x z
. Vectơ no dưới đây l một vectơ
php tuyn của
P
?
A.
4
1;0; 1 . n
B.
1
3; 1;2 .n
C.
3
3; 1;0 .n
D.
2
3;0; 1 .n
Lời giải:
Vectơ php tuyn của mặt phẳng
:3 2 0P x z
l
2
3;0; 1n
.
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị như hình bên dưới :
Tọa độ giao điểm của đồ thị hàm số đã cho với trục tung là
A.
0; 2 .
B.
2;0 .
C.
2;0 .
D.
0;2 .
Câu 8: Cho hàm số
fx
và
gx
liên tục trên đoạn
0;1
và
11
00
d 1, d 3f x x g x x
. Tích phân
1
0
2 3 df x g x x
bằng

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
A.
9
. B.
5
. C.
10
. D.
11
.
Lời giải:
Ta có
1 1 1
0 0 0
2 3 d 2 d 3 d 2.1 3.3 11f x g x x f x x g x x
.
Câu 9: Hàm số no có đồ thị l đường cong trong hình vẽ bên dưới?
A.
42
41y x x
. B.
1
2
x
y
x
. C.
32
41y x x
. D.
2
21yx
.
Lời giải:
Từ đồ thị ta thấy hàm số có 3 điểm cực trị, suy ra hình vẽ l đồ thị hàm số
42
41y x x
.
Câu 10: Trong không gian
,Oxyz
cho mặt cầu
2 2 2
: 1 2 1 9S x y z
. Tìm tọa độ tâm
I
và tính bán kính
R
của
.S
A.
1;2;1I
và
3.R
B.
1; 2; 1I
và
3.R
C.
1;2;1I
và
9.R
D.
1; 2; 1I
và
9.R
Câu 11: Trong không gian
,Oxyz
góc giữa hai mặt phẳng
Oxy
và
Oxz
bằng
A.
90 .
B.
60 .
C.
30 .
D.
45 .
Câu 12: Cho số phức
2,zi
phần ảo của số phức
2
z
là
A.
4.
B.
4.i
C.
3.
D.
1.
Lời giải:
Ta có:
2
2
2 3 4 .z i i
Câu 13: Cho khối lập phương có cạnh bằng
3.
Thể tích khối lập phương đã cho bằng
A.
9.
B.
27.
C.
18.
D.
3.
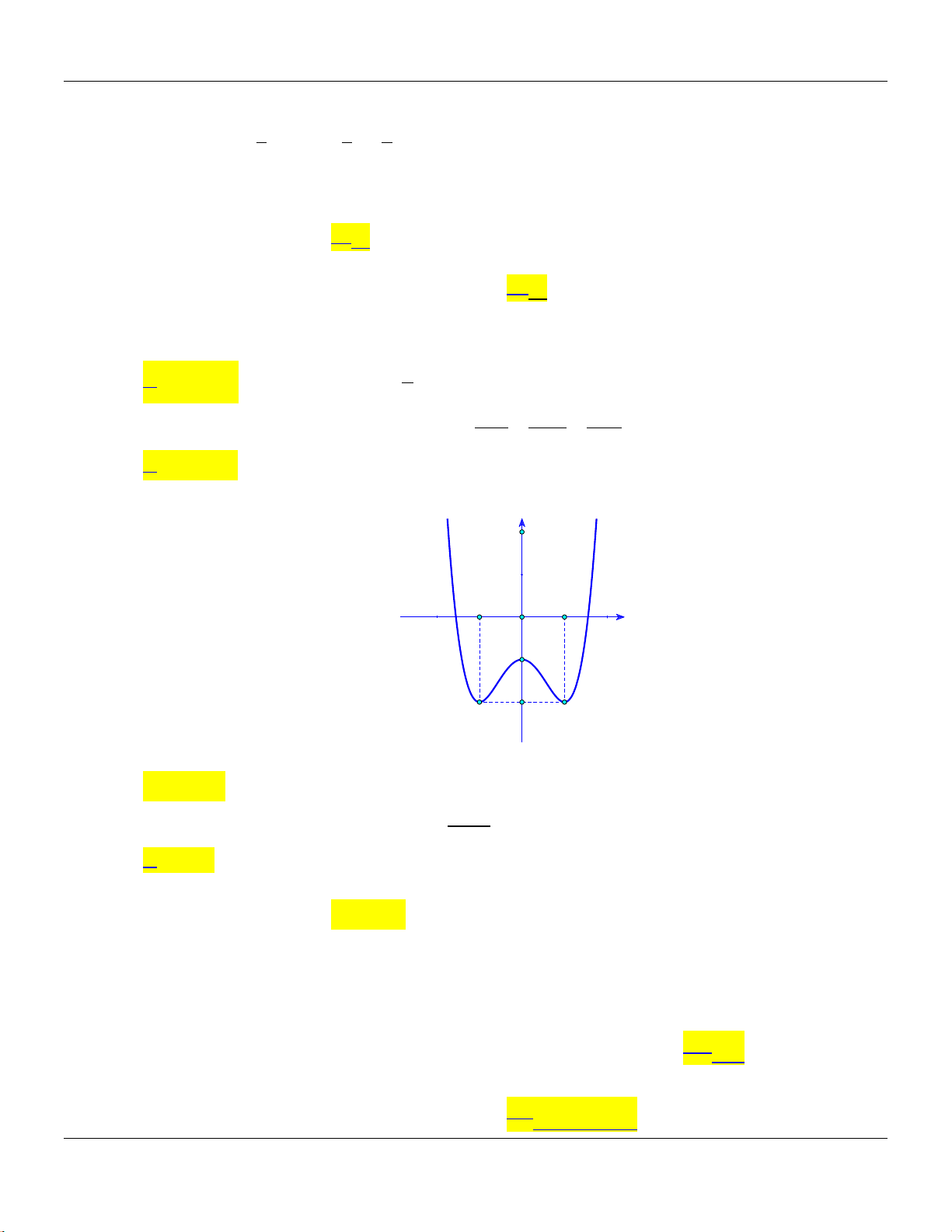
Câu 14: Cho khối chóp
.S ABC
có đy là tam giác vuông tại
, 2, 4,A AB AC SA
vuông góc với đy v
3SA
(tham khảo hình bên).
C
B
A
S
Thể tích khối chóp đã cho bằng
A.
9.
B.
8.
C.
4.
D.
3.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
Lời giải:
Ta có:
.
1 1 1
. . . 4.
3 3 2
S ABC ABC
V SA S SA AB AC
Câu 15: Cho đường thẳng
và mặt cầu
;.S O R
Gọi
d
là khoảng cách từ
O
đn
và
.dR
Số giao
điểm của
và
;S O R
là
A.
1.
B.
2.
C.
0.
D. Vô số.
Câu 16: Phần ảo của số phức
37zi
là
A.
3.
B.
7.
C.
7.
D.
3.
Câu 17: Cho khối nón có đường cao
,h
độ di đường sinh
l
v bn kính đy
.r
Diện tích xung quanh
xq
S
của khối nón được tính theo công thức no dưới đây?
A.
xq
S rl
. B.
1
2
xq
S rl
. C.
2
xq
S rl
. D.
xq
S rh
.
Câu 18: Trong không gian
,Oxyz
đường thẳng
1 2 3
:
3 4 5
x y z
d
đi qua điểm no sau đây?
A.
1; 2;3
. B.
1;2; 3
. C.
3; 4; 5
. D.
3;4;5
.
Câu 19: Cho hàm số
42
y ax bx c
có đồ thị l đường cong như hình bên dưới:
x
y
-1
-1
-2
O
1
Điểm cực đại của đồ thị hàm số đã cho có tọa độ là
A.
0; 1 .
B.
1;0 .
C.
1; 2 .
D.
1; 2 .
Câu 20: Tiệm cận ngang của đồ thị hàm số
41
2
x
y
x
l đường thẳng có phương trình l
A.
4.y
B.
4.x
C.
2.x
D.
2.y
Câu 21: Tập nghiệm của bất phương trình
2
log 1x
là
A.
;2 .
B.
0;2 .
C.
0;1 .
D.
;1 .
Lời giải:
Ta có:
2
0
log 1 0;2 .
2
x
xx
x
Câu 22: Cho tập
M
có 10 phần tử. Số tập con gồm 3 phần tử của tập hợp
M
là
A.
3!.
B.
10!.
C.
3
10
.A
D.
3
10
.C
Câu 23: Cho
dsin .x x f x C
Khẳng định no dưới đây đúng?
A.
cos .
f x x
B.
cos .
f x x
C.
sin .
f x x
D.
sin .
f x x
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Câu 24: Nu
4
2
3 d 12f x x x
thì
4
2
df x x
bằng
A.
6
. B.
0
. C.
2
. D.
10
3
.
Lời giải:
Ta có
4
2
3 d 12f x x x
4 4 4
2
2 2 2
4
1
3 d d 12 3 d 12
2
2
f x x x x f x x x
44
22
3 d 6 12 d 2f x x f x x
.
Câu 25: Cho hàm số
sin 1f x x x
. Khẳng định no dưới đây đúng?
A.
2
d cos
2
x
f x x x x C
. B.
2
d cos
2
x
f x x x x C
.
C.
d cos 1f x x x C
. D.
2
d cos
2
x
f x x x C
.
Câu 26: Cho hàm số
()y f x
có đồ thị như hình vẽ bên.
Hàm số đã cho đồng bin trên các khoảng no dưới đây?
A.
0; 2
. B.
0;
. C.
0; 4
. D.
1;1
.
Câu 27: Cho hàm số
y f x
có bảng bin thiên như sau:
Đồ thị hàm số
y f x
có điểm cực tiểu là
A.
0;2
. B.
3; 4
. C.
3
CT
x
. D.
4
CT
y
.
Lời giải:
Dựa vào bảng bin thiên, ta có đồ thị hàm số
y f x
có điểm cực tiểu là
3; 4
.
Câu 28: Cho
a
,
b
là các số thực dương tùy ý. Khẳng định no sau đây đúng?
A.
ln ln lnab a b
. B.
ln ln lna b a b
.
C.
ln ln .lnab a b
. D.
ln ln .lna b a b
.
Lời giải:
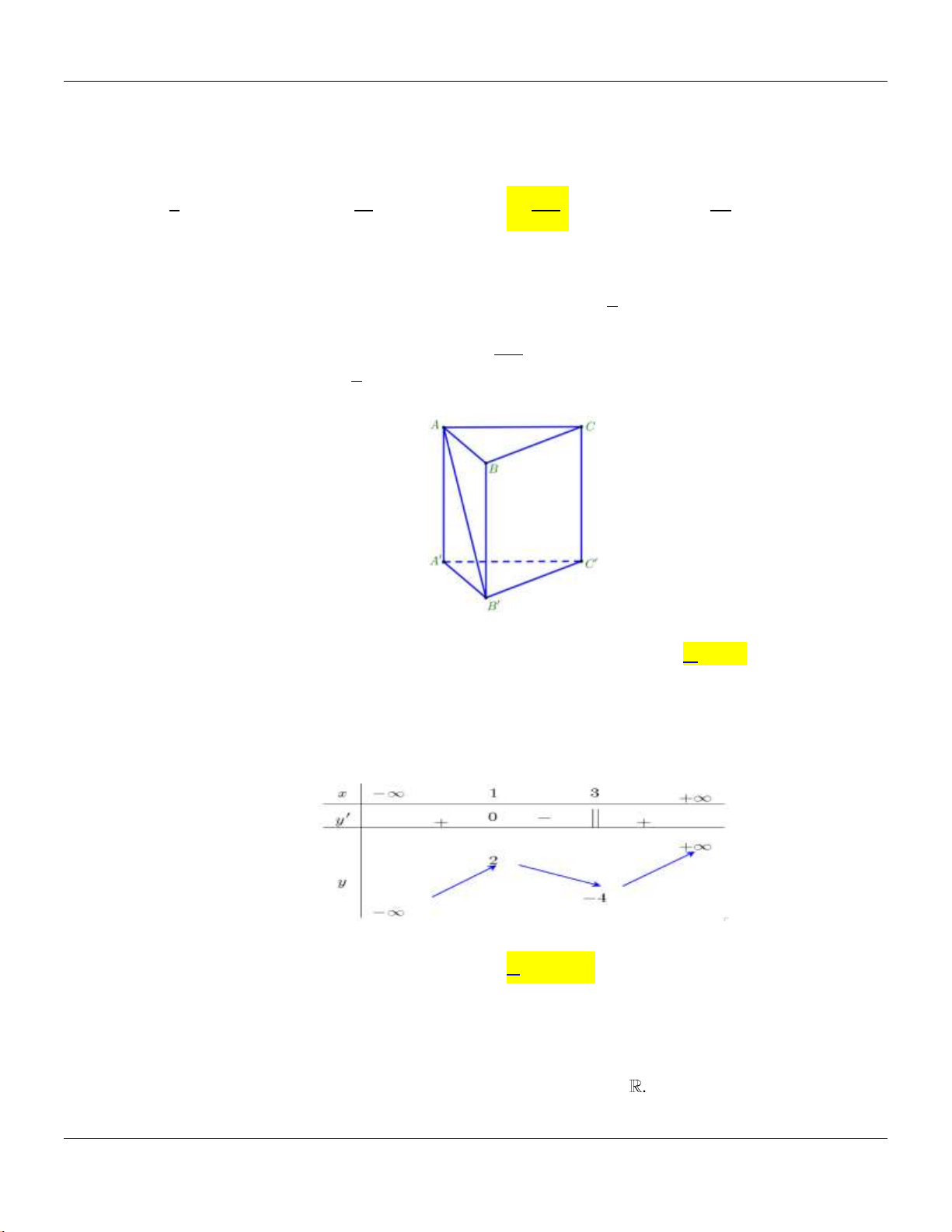
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Theo quy tắc logarit ta có:
ln ln lnab a b
.
Câu 29: Cho hình phẳng
H
giới hạn bởi đồ thị hàm số
2
21y x x
và trục hoành. Thể tích của vật
thể tròn xoay khi quay
H
quanh trục hoành bằng
A.
9
8
. B.
81
80
. C.
81
80
. D.
9
8
.
Lời giải:
+ Phương trình honh độ giao điểm:
2
1
2 1 0
1
2
x
xx
x
.
+ Thể tích cần tìm là
d
1
2
2
1
2
81
21
80
V x x x
.
Câu 30: Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng nhau:
Góc giữa đường thẳng
AB
và mặt phẳng
ABC
bằng
A.
30
. B.
90
. C.
60
. D.
45
.
Lời giải:
Do
AA A B C
nên
;.AB A B C A B A
Do tam giác
AA B
vuông cân nên
45 .A B A
Câu 31: Cho hàm số
y f x
có bảng bin thiên như sau:
Tập hợp tất cả các giá trị của
m
để phương trình
f x m
có ba nghiệm thực phân biệt
A.
4;2 .
B.
4;2 .
C.
4;2 .
D.
4;2 .
Lời giải:
Số nghiệm của phương trình
f x m
là số giao điểm của đồ thị hàm số
y f x
v đường
thẳng
ym
. Dựa vào bảng bin thiên ta thấy
4;2m
.
Câu 32: Cho hàm số
fx
có đạo hàm
2
3
1 2 , .
f x x x x x
Khoảng nghịch bin của hàm
số là

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
A.
2;0
. B.
; 2 ; 0;1
. C.
; 2 ; 0;
. D.
2;0 ; 1;
.
Lời giải:
Ta có:
2
00
1
x
f x x
x
.
Bảng xét dấu:
Vậy hàm số nghịch bin trên khoảng
2;0
.
Câu 33: Chọn ngẫu nhiên hai số khác nhau từ
15
số nguyên dương đầu tiên. Xác suất để chọn được
hai số có tổng là một số lẻ bằng
A.
1
7
. B.
8
15
. C.
4
15
. D.
1
14
.
Lời giải:
Không gian mẫu
2
15
105C
.
Để tổng hai số là một số lẻ ta chọn 1 số lẻ và 1 số chẵn nên ta có
8.7 56
.
Xác suất cần tìm là
56 8
105 15
.
Câu 34: Tích các nghiệm của phương trình
1
5
log 6 36 1
xx
bằng
A.
6
log 5.
B.
5
log 6.
C.
5.
D.
0.
Lời giải:
Điều kiện xc định:
1
6 36 0
xx
Khi đó, phương trình
11
5
log 6 36 1 6 36 5
x x x x
(thoả điều kiện)
6
36 6.6 5 0
6 1 0
6 5 log 5
xx
x
x
x
x
Vậy tích các nghiệm của phương trình đã cho bằng 0.
Câu 35: Cho số phức
z
thỏa mãn
12z i z
. Trong mặt phẳng phức, quỹ tích điểm biểu diễn
các số phức
z
A. l đường thẳng
3 1 0xy
. B. l đường thẳng
3 1 0xy
.
C. l đường thẳng
3 1 0xy
. D. l đường thẳng
3 1 0xy
.
Lời giải:
Gọi
,z x yi x y
.
Ta có
12z i z
2 2 2
2
1 1 2x y x y
3 1 0xy
.
Vậy quỹ tích điểm biểu diễn các số phức
z
l đường thẳng
3 1 0xy
.
Câu 36: Trong không gian
Oxyz
, vit phương trình đường thẳng
đi qua
1;1;0M
và vuông góc
với mặt phẳng
: 4 2 0Q x y z
?

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
A.
1
4
1
xt
yt
z
. B.
1
14
xt
yt
zt
. C.
2
54
1
xt
yt
zt
. D.
1
14
xt
yt
zt
.
Lời giải:
Do đường thẳng
vuông góc với mặt phẳng
: 4 2 0Q x y z
nên đường thẳng
nhận
1; 4; 1u
làm một vectơ chỉ phương.
Kiểm tra phương n C thỏa mãn.
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2;3A
. Điểm đối xứng với
A
qua mặt phẳng
Oxy
có
tọa độ là
A.
1; 2;3
. B.
1;2; 3
. C.
1; 2; 3
. D.
1;2;0
.
Câu 38: Cho lăng trụ tam gic đều
.ABC A B C
có tất cả các cạnh bằng
a
. Thể tích khối trụ có hai đy
là hai hình tròn ngoại tip hai đy của lăng trụ đã cho bằng
A.
3
a
. B.
3
12
a
. C.
3
3
a
. D.
3
4
3
a
.
Lời giải:
Bn kính đường tròn ngoại tip đy của lăng trụ là
3
3
a
R
.
Thể tích khối trụ là
2
3
3
.
33
aa
Va
.
Câu 39: Cắt khối nón
N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đy một góc bằng
0
60
ta được thit diện là một tam giác vuông cân cạnh huyền
2a
. Thể tích khối nón
N
bằng
A.
3
53
24
a
. B.
3
53
72
a
. C.
3
53
8
a
. D.
3
3
72
a
.
Lời giải:
Giả sử khối nón
N
có đỉnh là
S
, tâm đy l
O
và thit diện là giác vuông cân
SAB
.
Gọi
I
l trung điểm của
AB
, khi đó
0
60SIO
,
1
,2
2
SI AB a SB SA a
.
Ta có
2
0 2 2 2
3 3 5
.sin60 , 2
2 4 2
a a a
SO SI OB SB SO a
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Vậy
2
3
2
1 1 5 3 5 3
. . . . .
3 3 2 2 24
a a a
V OB SO
.
Câu 40: Trong không gian
,Oxyz
phương trình mặt phẳng
()P
song song v cch đều hai đường
thẳng
1
:d
2
1 1 1
x y z
và
2
:d
12
2 1 1
x y z
là
A.
2 2 1 0 xz
. B.
2 2 1 0 yz
. C.
2 2 1 0 xy
. D.
2 2 1 0 yz
.
Lời giải:
Đường thẳng
1
d
đi qua điểm
(2;0;0)M
v có véc tơ chỉ phương
1
( 1;1;1)u
.
Đường thẳng
2
d
đi qua điểm
(0;1;2)N
v có véc tơ chỉ phương
2
(2; 1; 1)u
.
Gọi
I
l trung điểm của đoạn thẳng
MN
, suy ra
1
(1; ;1)
2
I
.
Vì mặt phẳng
()P
song song với hai đường thẳng
1
d
và
2
d
nên mặt phẳng
()P
đi qua
I
nhận
véc tơ
12
[ , ] ( 2;0; 1)n u u
lm véc tơ php tuyn. Do đó phương trình mặt phẳng là
11
( ):0.( 1) 1.( ) 1.( 1) 0 0 2 2 1 0.
22
P x y z y z y z
Vậy, phương trình mặt phẳng
()P
:
2 2 1 0.yz
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 02_______________
Câu 1: Cho số phức
23zi
. Trên mặt phẳng tọa độ
Oxy
, điểm biểu diễn số phức
z
là điểm có
tọa độ là
A.
2;3
. B.
3; 2
. C.
3;2
. D.
2; 3
.
Câu 2: Đạo hàm của hàm số
10
x
y
là
A.
10
ln10
x
y
. B.
10 .ln10
x
y
. C.
10
x
y
. D.
10
10 log
x
ye
.
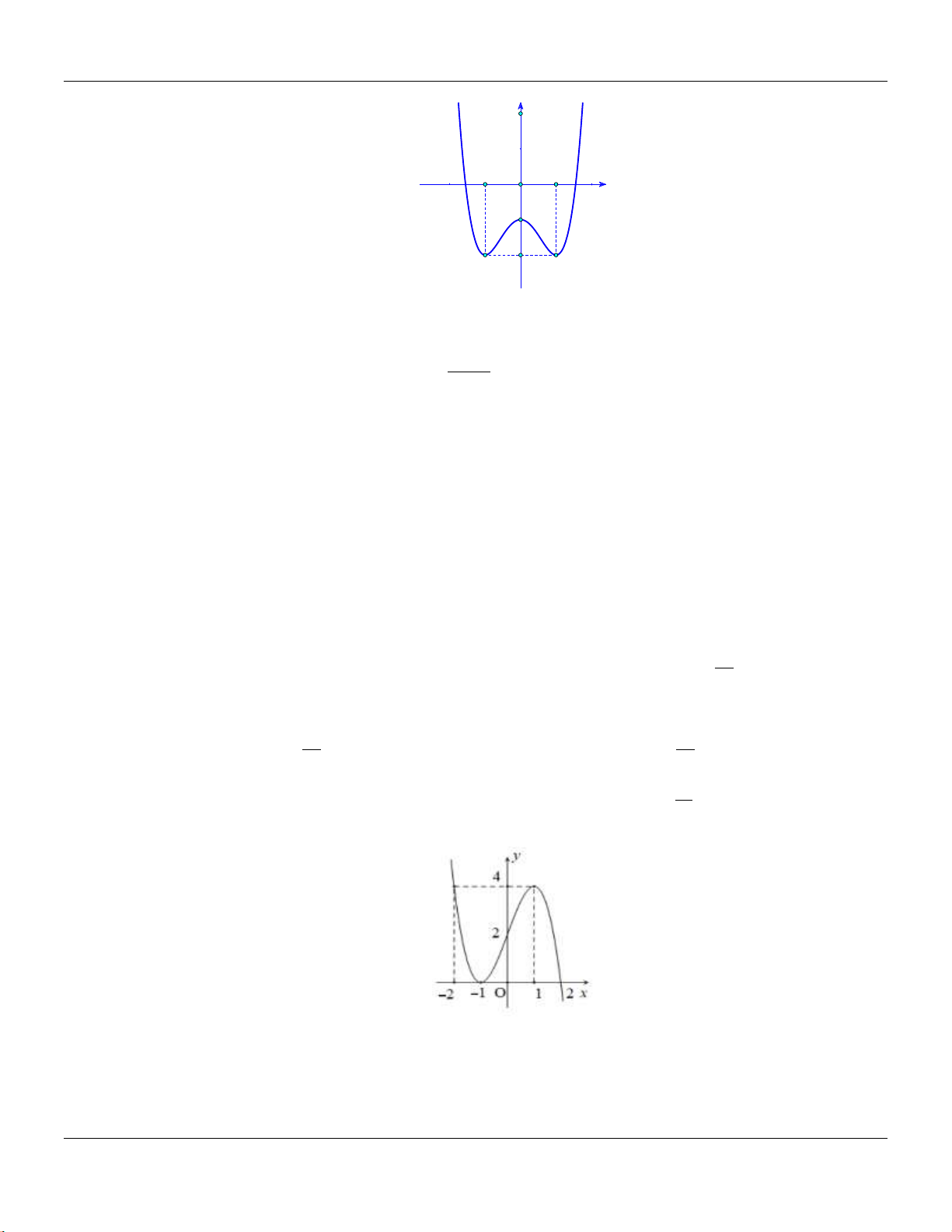
Câu 3: Tập xác định
D
của hàm số
1
3
2yx
là
A.
;2D
. B.
;D
. C.
;2D
. D.
2;D
.
Câu 4: Bất phương trình
3 81 0
x
có tất cả bao nhiêu nghiệm nguyên dương?
A.
3
. B.
4
. C. vô số. D.
5
.
Câu 5: Cho cấp số nhân
()
n
u
với
1
1u
và
4
8u
. Công bội của cấp số nhân đã cho bằng
A.
2.
B.
7.
C.
8.
D.
4.
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
:. P x y z4 3 2 0
Vectơ nào sau đây là vectơ
pháp tuyến của mặt phẳng
P
?
A.
;;n
2
1 4 3
. B.
;; n
3
1 4 3
. C.
4
1; 4;3n
. D.
;;n
1
1 4 3
.
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hình bên dưới:
x
y
O
-2
2
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là
A.
0; 2
. B.
2;0
. C.
2;0
. D.
0;2
.
Câu 8: Cho hàm số
fx
có đạo hàm trên ,
12 f
và
3 2.f
Tính
3
1
d
I f x x
.
A.
4.I
B.
0.I
C.
3.I
D.
4.I
Câu 9: Đồ thị hàm số nào dưới đây có dạng đường cong như hình bên dưới?
A.
42
23y x x
. B.
3
33y x x
. C.
42
23y x x
. D.
42
23y x x
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
:S
2 2 2
2 6 4 2 0. x y z x y z
Xác định tọa độ
tâm
I
và bán kính
R
của mặt cầu
S
.
A.
1; 3;2 , 16IR
. B.
1; 3;2 , 4IR
. C.
1;3; 2 , 16IR
.D.
1;3; 2 , 4IR
.
Câu 11: Trong không gian
Oxyz
, góc giữa hai mặt phẳng
Oyz
và
Oxz
bằng
A.
30 .
B.
90 .
C.
60 .
D.
45 .
Câu 12: Các điểm
, , , M N P Q
trong hình vẽ bên là điểm bểu diễn lần lượt của các số phức
1 2 3 4
, , ,z z z z
. Khi đó
1 2 3 4
3w z z z z
bằng
Q
P
N
M
-1
3
1
-2
2
x
y
O
1
-1
2
-2
-3
A.
64wi
. B.
64wi
. C.
43wi
. D.
34wi
.
Câu 13: Thể tích của khối lăng trụ có diện tích đáy
B
và chiều cao
h
là
A.
1
2
V Bh
. B.
1
3
V Bh
. C.
1
6
V Bh
. D.
V Bh
.
Câu 14: Cho khối hộp chữ nhật
.ABCD A B C D
có
2, 3, 4
AB AD AA
(tham khảo hình vẽ).
D
C
B
A
D'
C'
B'
A'
Thể tích khối hộp đã cho bằng
A.
24
. B.
20
. C.
9
. D.
8
.
Câu 15: Một khối cầu có bán kính bằng
2
, một mặt phẳng
cắt khối cầu đó theo một hình tròn có
diện tích là
2
. Khoảng cách từ tâm khối cầu đến mặt phẳng
bằng
A.
2
. B.
1
. C.
2
2
. D.
2
4
.
Câu 16: Môđun của số phức
34zi
bằng
A.
5
. B.
3
. C.
7
. D.
7
.
Câu 17: Tính chiều cao
h
của hình trụ biết chiều cao
h
bằng bán kính đáy và thể tích khối trụ đó là
8
.
A.
3
32h
. B.
3
4h
. C.
22h
. D.
2h
.
Câu 18: Trong không gian
Oxyz
, điểm nào dưới đây không thuộc đường thẳng
12
:
2 1 1
x y z
d
?
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
A.
1; 2;0Q
. B.
1;2;0M
. C.
1; 3;1N
. D.
3; 1; 1P
.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A.
2x
. B.
2x
. C.
0x
. D.
1x
.
Câu 20: Đường tiệm cận đứng của đồ thị hàm số
32
1
x
y
x
có phương trình là
A.
2x
. B.
1x
. C.
3x
. D.
1x
.
Câu 21: Tập nghiệm của bất phương trình
2
log 1x
là
A.
(0;1]
. B.
( ;2]
. C.
0;2
. D.
(0;2].
Câu 22: Số cách phân công 3 học sinh trong 12 học sinh đi lao động là
A.
12
P
. B. 36. C.
3
12
C
. D.
3
12
A
.
Câu 23: Cho hàm số
y f x
thỏa mãn
2 7cosf x x
,
03f
. Mệnh đề nào dưới đây đúng?
A.
2 7sin 3f x x x
. B.
2 7sin 3f x x
.
C.
2 sin 9f x x x
. D.
2 7sin 3f x x x
.
Câu 24: Nếu
4
0
d5f x x
và
4
2
d1f x x
thì
2
0
df x x
bằng
A.
6
. B.
4
. C.
4
. D.
6
.
Câu 25: Họ tất cả các nguyên hàm của hàm số
24
x
f x x
là
A.
2
2 ln2 2
x
xC
. B.
2
2
2
ln2
x
xC
. C.
2 ln2
x
C
. D.
2
ln2
x
C
.
Câu 26: Cho hàm số
fx
có bảng biến biên dưới đây:
Mệnh đề nào sau đây sai ?
A. Hàm số đã cho nghịch biến trên khoảng
;1
.
B. Hàm số đã cho nghịch biến trên khoảng
0;1
.
C. Hàm số đã cho đồng biến trên khoảng
1;
.
D. Hàm số đã cho nghịch biến trên khoảng
3; 2
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Câu 27: Cho hàm số
fx
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số là
A.
3y
. B.
1y
. C.
4y
. D.
4y
.
Câu 28: Biết
5
2
logyx
. Khi đó
A.
5logyx
. B.
2
5logyx
. C.
2
5 logyx
. D.
2
1
log
5
yx
.
Câu 29: Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
54y x x
và trục
Ox
. Thể tích của
khối tròn xoay sinh ra khi quay hình
H
quanh trục
Ox
là
A.
9
2
V
. B.
81
10
V
. C.
81
10
V
. D.
9
2
V
.
Câu 30: Cho hình chóp
.S ABCD
có đáy là hình thoi tâm
O
,
ABD
đều cạnh
2a
,
SA
vuông góc với
mặt phẳng đáy và
32
2
a
SA
(minh họa như hình bên dưới).
Góc giữa đường thẳng
SO
và mặt phẳng
ABC D
bằng
A.
45
. B.
30
. C.
60
. D.
90
.
Câu 31: Cho hàm số
23
2
x
y
x
có đồ thị
(C)
và đường thẳng
:d y x m
. Với tất cả giá trị nào của
m
thì
d
cắt
(C)
tại hai điểm phân biệt?
A.
2m
. B.
2m
. C.
6m
. D.
2
6
m
m
.
Câu 32: Cho hàm số
y f x
liên tục trên , có đạo hàm
23
2 2 5 ,
f x x x x x
.
Hàm số
y f x
nghịch biến trên khoảng nào sau đây?
A.
;2
. B.
5;
. C.
2;5
. D.
2;
.
Câu 33: Một hộp chứa
10
quả cầu được đánh số theo thứ tự từ
1
đến
10,
lấy ngẫu nhiên
5
quả cầu.
Xác suất để tích các số ghi trên
5
quả cầu đó chia hết cho 3 bằng
A.
11
12
. B.
5
12
. C.
7
12
. D.
1
12
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 34: Biết phương trình
2
22
log 2log 2 1 0xx
có hai nghiệm
12
,xx
. Tính
12
xx
.
A.
12
4xx
. B.
12
1
8
xx
. C.
12
1
2
xx
. D.
12
3xx
.
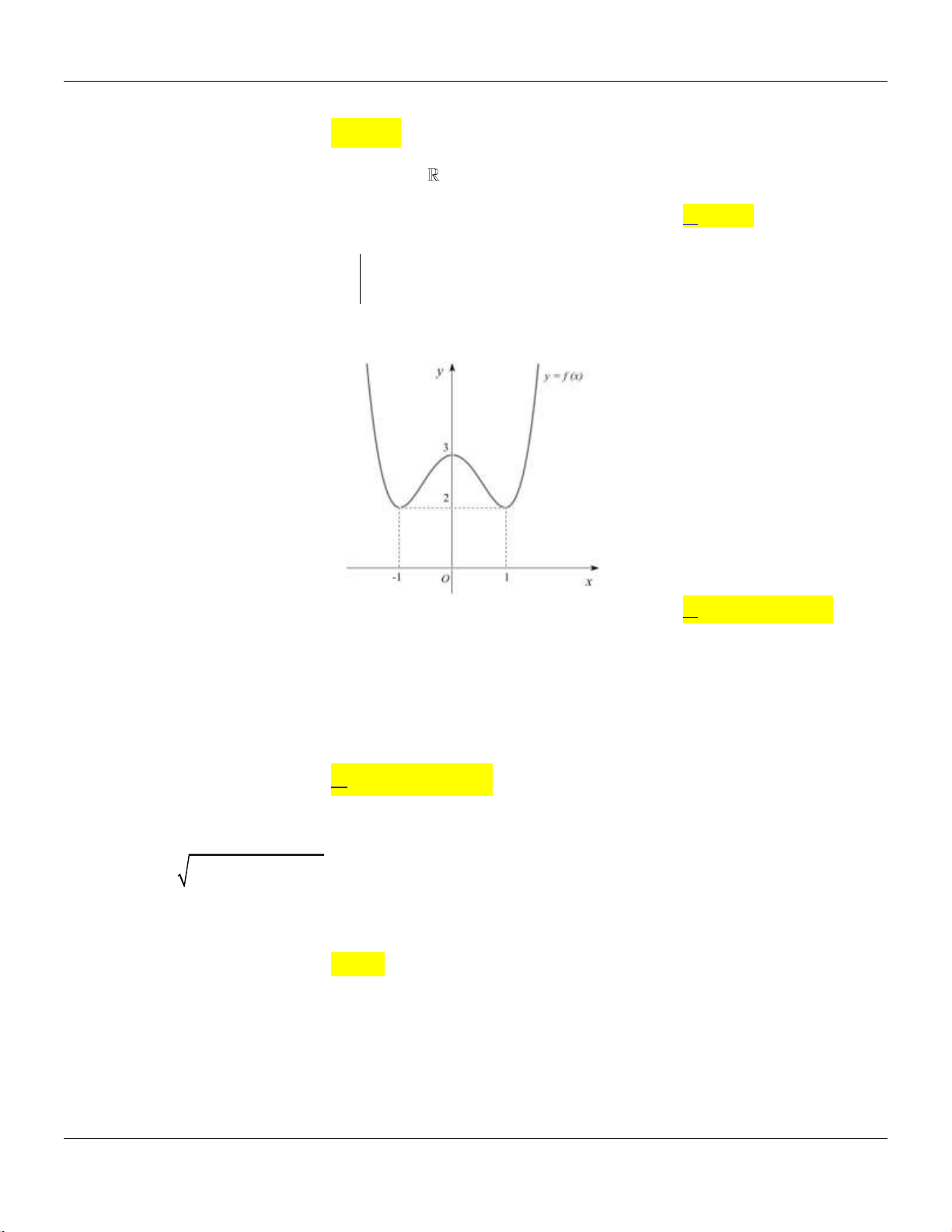
Câu 35: Trên mặt phẳng tọa độ, tập hợp các điểm biểu diễn số phức
,z x yi x y
thỏa mãn
23z i z i
là đường thẳng có phương trình là
A.
1yx
. B.
1yx
. C.
1yx
. D.
1yx
.
Câu 36: Trong không gian
Oxyz
, đường thẳng
d
qua
3;5;6M
và vuông góc với mặt phẳng
:2 3 4 2 0P x y z
thì đường thẳng
d
có phương trình là
A.
3 5 6
2 3 4
xyz
. B.
3 5 6
234
x y z
.
C.
3 5 6
2 3 4
x y z
. D.
1 2 10
2 3 4
x y z
.
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2;3A
. Điểm đối xứng với
A
qua mặt phẳng
Oxz
có
tọa độ là
A.
1;2;3
. B.
1;2; 3
. C.
1;0; 3
. D.
1; 2;3
.
Câu 38: Cắt hình trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng
2
, thiết
diện thu được là hình vuông có diện tích bằng
25
. Thể tích khối trụ bằng
A.
10 2
3
. B.
205
4
. C.
205
12
. D.
10 2
9
.
Câu 39: Cho hình nón có chiều cao bằng
25
. Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón
theo một thiết diện là tam giác đều có diện tích bằng
93
. Thể tích của khối nón được giới
hạn bởi hình nón đã cho bằng
A.
32 5
3
. B.
32
. C.
18 5
3
. D.
32 5
.
Câu 40: Trong không gian
,Oxyz
phương trình đường thẳng đi qua
1;2;4A
song song với
P
:
2 4 0x y z
và cắt đường thẳng
:d
2 2 2
3 1 5
x y z
có phương trình là
A.
1
2
42
xt
y
zt
. B.
12
2
42
xt
y
zt
. C.
12
2
44
xt
y
zt
. D.
1
2
42
xt
y
zt
.
________________________HẾT________________________

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Cho số phức
23zi
. Trên mặt phẳng tọa độ
Oxy
, điểm biểu diễn số phức
z
là điểm có
tọa độ là
A.
2;3
. B.
3; 2
. C.
3;2
. D.
2; 3
.
Lời giải:
Câu 2: Đạo hàm của hàm số
10
x
y
là
A.
10
ln10
x
y
. B.
10 .ln10
x
y
. C.
10
x
y
. D.
10
10 log
x
ye
.
Lời giải:
10 10 .ln10
xx
yy
.
Câu 3: Tập xác định
D
của hàm số
1
3
2yx
là
A.
;2D
. B.
;D
. C.
;2D
. D.
2;D
.
Lời giải:
Tập xác định:
2 0 2xx
Vậy tập xác định của hàm số là
;2D
.
Câu 4: Bất phương trình
3 81 0
x
có tất cả bao nhiêu nghiệm nguyên dương?
A.
3
. B.
4
. C. vô số. D.
5
.
Lời giải:
Ta có:
*
3 81 0 3 81 4 1;2;3;4 .
x
xx
xx
Câu 5: Cho cấp số nhân
()
n
u
với
1
1u
và
4
8u
. Công bội của cấp số nhân đã cho bằng
A.
2.
B.
7.
C.
8.
D.
4.
Lời giải:
Ta có:
33
41
. 8 2.u u q q q
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
:. P x y z4 3 2 0
Vectơ nào sau đây là vectơ
pháp tuyến của mặt phẳng
P
?
A.
;;n
2
1 4 3
. B.
;; n
3
1 4 3
. C.
4
1; 4;3n
. D.
;;n
1
1 4 3
.
Lời giải:
Mặt phẳng
: P x y z4 3 2 0
có một vectơ pháp tuyến là
;;n
2
1 4 3
.
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hình bên dưới:
x
y
O
-2
2
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là
A.
0; 2
. B.
2;0
. C.
2;0
. D.
0;2
.
Câu 8: Cho hàm số
fx
có đạo hàm trên ,
12 f
và
3 2.f
Tính
3
1
d
I f x x
.
A.
4.I
B.
0.I
C.
3.I
D.
4.I
Lời giải:
Ta có
3
1
dI f x x
3
3 1 2 2 4
1
f x f f
.
Vậy
4I
.
Câu 9: Đồ thị hàm số nào dưới đây có dạng đường cong như hình bên dưới?
A.
42
23y x x
. B.
3
33y x x
. C.
42
23y x x
. D.
42
23y x x
.
Lời giải:
Nhìn hình vẽ ta thấy là đồ thị hàm bậc 4 trùng phương
42
0f x ax bx c a
có hệ số
a
dương. Do vậy chọn đáp án D.
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
:S
2 2 2
2 6 4 2 0. x y z x y z
Xác định tọa độ
tâm
I
và bán kính
R
của mặt cầu
S
.
A.
1; 3;2 , 16IR
. B.
1; 3;2 , 4IR
. C.
1;3; 2 , 16IR
.D.
1;3; 2 , 4IR
.
Lời giải:
Ta có mặt cầu
S
:
2 2 2
2 6 4 2 0. x y z x y z
có tâm
1; 3;2I
và bán kính
2
22
1 3 2 2 4R
.
Vậy mặt cầu
S
có tâm
1; 3;2I
và bán kính
4R
.
Câu 11: Trong không gian
Oxyz
, góc giữa hai mặt phẳng
Oyz
và
Oxz
bằng
A.
30 .
B.
90 .
C.
60 .
D.
45 .
Câu 12: Các điểm
, , , M N P Q
trong hình vẽ bên là điểm bểu diễn lần lượt của các số phức
1 2 3 4
, , ,z z z z
. Khi đó
1 2 3 4
3w z z z z
bằng
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
Q
P
N
M
-1
3
1
-2
2
x
y
O
1
-1
2
-2
-3
A.
64wi
. B.
64wi
. C.
43wi
. D.
34wi
.
Lời giải:
Ta có
1 2 3 4
3 2 ; 2 ; 3 ; 2 2z i z i z i z i
.
Suy ra
1 2 3 4
3 3 3 2 2 3 2 2 6 4w z z z z i i i i i
.
Câu 13: Thể tích của khối lăng trụ có diện tích đáy
B
và chiều cao
h
là
A.
1
2
V Bh
. B.
1
3
V Bh
. C.
1
6
V Bh
. D.
V Bh
.
Câu 14: Cho khối hộp chữ nhật
.ABCD A B C D
có
2, 3, 4
AB AD AA
(tham khảo hình vẽ).
D
C
B
A
D'
C'
B'
A'
Thể tích khối hộp đã cho bằng
A.
24
. B.
20
. C.
9
. D.
8
.
Lời giải:
Thể tích khối hộp chữ nhật đã cho bằng:
2.3.4 24V
.
Câu 15: Một khối cầu có bán kính bằng
2
, một mặt phẳng
cắt khối cầu đó theo một hình tròn có
diện tích là
2
. Khoảng cách từ tâm khối cầu đến mặt phẳng
bằng
A.
2
. B.
1
. C.
2
2
. D.
2
4
.
Lời giải:

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Gọi
,OH
lần lượt là tâm khối cầu và tâm hình tròn.
,Rr
lần lượt là bán kính mặt cầu và bán
kính hình tròn.
Diện tích hình tròn
2
2
2
S
s r r
.
Gọi
h
là khoảng cách từ tâm khối cầu đến mặt phẳng
suy ra
22
2.h R r
Câu 16: Môđun của số phức
34zi
bằng
A.
5
. B.
3
. C.
7
. D.
7
.
Lời giải:
Ta có:
32
3 4 5z
.
Câu 17: Tính chiều cao
h
của hình trụ biết chiều cao
h
bằng bán kính đáy và thể tích khối trụ đó là
8
.
A.
3
32h
. B.
3
4h
. C.
22h
. D.
2h
.
Lời giải:
Gọi
R
là bán kính của hình trụ khi đó
Rh
.
Ta có thể tích khối trụ là
23
V R h h
3
8
82
V
hh
.
Vậy chiều cao của khối trụ là
2h
.
Câu 18: Trong không gian
Oxyz
, điểm nào dưới đây không thuộc đường thẳng
12
:
2 1 1
x y z
d
?
A.
1; 2;0Q
. B.
1;2;0M
. C.
1; 3;1N
. D.
3; 1; 1P
.
Lời giải:
Điểm
12
;;
2 1 1
a b c
I a b c d
đúng.
Kiểm tra các điểm
; ; ;Q M N P
trong các phương án A, B, C, D ta thay điểm
1;2;0M
vào
phương trình
d
ta có:
1 1 2 2 0
2 1 1
(vô lý) . Vậy điểm
M
không thuộc đường thẳng
d
.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A.
2x
. B.
2x
. C.
0x
. D.
1x
.
Lời giải:
Vì
y
đổi dấu từ âm sang dương duy nhất tại
2x
nên hàm số đã cho đạt cực tiểu tại
2x
Câu 20: Đường tiệm cận đứng của đồ thị hàm số
32
1
x
y
x
có phương trình là
A.
2x
. B.
1x
. C.
3x
. D.
1x
.
Lời giải:

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Ta có:
( 1) ( 1)
32
lim lim
1
xx
x
y
x
.
Vậy đồ thị hàm số có tiệm cận đứng là đường thẳng
1x
.
Câu 21: Tập nghiệm của bất phương trình
2
log 1x
là
A.
(0;1]
. B.
( ;2]
. C.
0;2
. D.
(0;2].
Lời giải:
Điều kiện:
0.x
Bất phương trình đã cho tương đương
0
02
2
x
x
x
Vậy tập nghiệm của bất phương trình là
(0;2].S
Câu 22: Số cách phân công 3 học sinh trong 12 học sinh đi lao động là
A.
12
P
. B. 36. C.
3
12
C
. D.
3
12
A
.
Lời giải:
Cách chọn 3 học sinh trong 12 học sinh không xếp thứ tự là tổ hợp chập 3 của 12:
3
12
C
Câu 23: Cho hàm số
y f x
thỏa mãn
2 7cosf x x
,
03f
. Mệnh đề nào dưới đây đúng?
A.
2 7sin 3f x x x
. B.
2 7sin 3f x x
.
C.
2 sin 9f x x x
. D.
2 7sin 3f x x x
.
Lời giải:
Ta có:
2 7cos 2 7sinf x x dx x x C
.
Mặt khác:
0 3 3fC
2 7sin 3f x x x
.
Câu 24: Nếu
4
0
d5f x x
và
4
2
d1f x x
thì
2
0
df x x
bằng
A.
6
. B.
4
. C.
4
. D.
6
.
Lời giải:
Ta có
4 2 4 2 4 4
0 0 2 0 0 2
d d d d d d 5 1 6f x x f x x f x x f x x f x x f x x
.
Câu 25: Họ tất cả các nguyên hàm của hàm số
24
x
f x x
là
A.
2
2 ln2 2
x
xC
. B.
2
2
2
ln2
x
xC
. C.
2 ln2
x
C
. D.
2
ln2
x
C
.
Lời giải:
Ta có
2
2
d 2 4 d 2
ln2
x
x
f x x x x x C
.
Câu 26: Cho hàm số
fx
có bảng biến biên dưới đây:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Mệnh đề nào sau đây sai ?
A. Hàm số đã cho nghịch biến trên khoảng
;1
.
B. Hàm số đã cho nghịch biến trên khoảng
0;1
.
C. Hàm số đã cho đồng biến trên khoảng
1;
.
D. Hàm số đã cho nghịch biến trên khoảng
3; 2
.
Lời giải:
Câu A: Sai vì hàm số không liên tục từ
;1
.
Câu B: Đúng vì hàm số nghịch biến trên khoảng
2;1
và khoảng
2;1
chứa khoảng
0;1
Câu C: Đúng quá rõ ràng.
Câu D: Đúng vì hàm số nghịch biến trên khoảng
;2
và khoảng
;2
chứa khoảng
3; 2
Câu 27: Cho hàm số
fx
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số là
A.
3y
. B.
1y
. C.
4y
. D.
4y
.
Lời giải:
Từ bảng biến thiên của hàm số
y f x
, suy ra giá trị cực tiểu của hàm số là
4y
(đạt tại
3)x
.
Câu 28: Biết
5
2
logyx
. Khi đó
A.
5logyx
. B.
2
5logyx
. C.
2
5 logyx
. D.
2
1
log
5
yx
.
Lời giải:
Ta có
5
22
log 5logy x x
.
Câu 29: Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
54y x x
và trục
Ox
. Thể tích của
khối tròn xoay sinh ra khi quay hình
H
quanh trục
Ox
là
A.
9
2
V
. B.
81
10
V
. C.
81
10
V
. D.
9
2
V
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
Phương trình hoành độ giao điểm của đồ thị hàm số
2
54y x x
và trục
Ox
ta có:
2
1
5 4 0
4
x
xx
x
Thể tích của khối tròn xoay sinh ra khi quay hình
H
quanh trục
Ox
44
2
22
11
81
54
10
V f x dx x x dx
.
Câu 30: Cho hình chóp
.S ABCD
có đáy là hình thoi tâm
O
,
ABD
đều cạnh
2a
,
SA
vuông góc với
mặt phẳng đáy và
32
2
a
SA
(minh họa như hình bên dưới).
Góc giữa đường thẳng
SO
và mặt phẳng
ABC D
bằng
A.
45
. B.
30
. C.
60
. D.
90
.
Lời giải:
Do
SA ABCD
nên hình chiếu vuông góc của
SO
lên mặt phẳng
ABC D
là
AO
. Khi đó
góc giữa đường thẳng
SO
và mặt phẳng
ABC D
là
SOA
.
ABD
đều cạnh
2a
nên
36
22
a
AO AB
.
SOA
vuông tại
A
có
32
2
a
SA
,
6
2
a
AO
nên
3 2 6
tan : 3
22
SA a a
SOA
AO
60SOA
.
Vậy góc giữa đường thẳng
SO
và mặt phẳng
ABC D
bằng
60
.
Câu 31: Cho hàm số
23
2
x
y
x
có đồ thị
(C)
và đường thẳng
:d y x m
. Với tất cả giá trị nào của
m
thì
d
cắt
(C)
tại hai điểm phân biệt?
A.
2m
. B.
2m
. C.
6m
. D.
2
6
m
m
.
Lời giải:
Phương trình hoành độ giao điểm là
2
23
( 2) 2 3 ( 2)( ) 2 3 0 (1)
2
x
x m x x x x m x mx m
x

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Để
d
cắt
(C)
tại hai nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân
biệt khác
2
2
0
2
.
6
( 2) 2 2 3 0
m
m
mm
Câu 32: Cho hàm số
y f x
liên tục trên , có đạo hàm
23
2 2 5 ,
f x x x x x
.
Hàm số
y f x
nghịch biến trên khoảng nào sau đây?
A.
;2
. B.
5;
. C.
2;5
. D.
2;
.
Lời giải:
Xét phương trình
0fx
23
2
2 2 5 0 2.
5
x
x x x x
x
Bảng xét dấu:
Suy ra hàm số
()y f x
nghịch biến trên khoảng
2;5
.
Câu 33: Một hộp chứa
10
quả cầu được đánh số theo thứ tự từ
1
đến
10,
lấy ngẫu nhiên
5
quả cầu.
Xác suất để tích các số ghi trên
5
quả cầu đó chia hết cho 3 bằng
A.
11
12
. B.
5
12
. C.
7
12
. D.
1
12
.
Lời giải:
Số phần tử của không gian mẫu
5
10
nC
.
Gọi
A
là biến cố: “Lấy được 5 quả cầu có tích các số trên 5 quả cầu đó chia hết cho 3”
Biến cố
A
: “Lấy được 5 quả cầu có tích các số trên 5 quả cầu đó không chia hết cho 3”
Tính
nA
:
Để tích các số trên 5 quả cầu được chọn không chia hết cho 3 thì trong 5 quả cầu đó không có
các quả cầu mang số 3, 6, 9. Vậy
5
7
n A C
.
5
7
5
10
1
12
nA
C
PA
nC
.
11
1
12
P A P A
.
Câu 34: Biết phương trình
2
22
log 2log 2 1 0xx
có hai nghiệm
12
,xx
. Tính
12
xx
.
A.
12
4xx
. B.
12
1
8
xx
. C.
12
1
2
xx
. D.
12
3xx
.
Lời giải:
ĐKXĐ:
0x
.
Ta có
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
22
2 2 2 2
2
2
log 2log 2 1 0 log 2log 3 0
1
log 1
2
log 3
8
x x x x
x
x
x
x
Vậy
12
4xx
.
Câu 35: Trên mặt phẳng tọa độ, tập hợp các điểm biểu diễn số phức
,z x yi x y
thỏa mãn
23z i z i
là đường thẳng có phương trình là
A.
1yx
. B.
1yx
. C.
1yx
. D.
1yx
.
Lời giải:
2 3 2 1 3z i z i x y i x y i
2 2 2
2 2 2 2 2
2 1 3 4 4 2 1 6 9x y x y x x y y x y y
4 4 4 1y x y x
.
Câu 36: Trong không gian
Oxyz
, đường thẳng
d
qua
3;5;6M
và vuông góc với mặt phẳng
:2 3 4 2 0P x y z
thì đường thẳng
d
có phương trình là
A.
3 5 6
2 3 4
xyz
. B.
3 5 6
234
x y z
.
C.
3 5 6
2 3 4
x y z
. D.
1 2 10
2 3 4
x y z
.
Lời giải:
Ta có
:2 3 4 2 0P x y z
có vectơ pháp tuyến
2; 3;4n
.
dP
d
nhận vectơ pháp tuyến của
P
làm vectơ chỉ phương.
Do đó đường thẳng
d
qua
3;5;6M
và có vectơ chỉ phương
2; 3;4u
.
Kiểm tra phương án D thỏa mãn.
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2;3A
. Điểm đối xứng với
A
qua mặt phẳng
Oxz
có
tọa độ là
A.
1;2;3
. B.
1;2; 3
. C.
1;0; 3
. D.
1; 2;3
.
Câu 38: Cắt hình trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng
2
, thiết
diện thu được là hình vuông có diện tích bằng
25
. Thể tích khối trụ bằng
A.
10 2
3
. B.
205
4
. C.
205
12
. D.
10 2
9
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
Từ đề bài ta có diện tích hình vuông
''ABB A
bằng
25
suy ra
'5AB BB
. Kẻ
OH AB
,
H
là trung điểm của
AB
thì
', ' ' , ' ' 2 d OO ABB A d O ABB A OH
.
Ta có
2
2 2 2
41
22
AB
OA OH AH OH
.
Suy ra khối trụ có
41
' 5;
2
h BB r OA
, vậy
2
205
4
V r h
.
Câu 39: Cho hình nón có chiều cao bằng
25
. Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón
theo một thiết diện là tam giác đều có diện tích bằng
93
. Thể tích của khối nón được giới
hạn bởi hình nón đã cho bằng
A.
32 5
3
. B.
32
. C.
18 5
3
. D.
32 5
.
Lời giải:
Ta có
2
3
93
4
SGF
S SG
2
36SG
6 l SG
* Bán kính đường tròn đáy là
2
2 2 2
6 2 5 4 r l h
* Thể tích khối nón là
22
1 1 32 5
. . .4 .2 5
3 3 3
V r h
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 16
Câu 40: Trong không gian
,Oxyz
phương trình đường thẳng đi qua
1;2;4A
song song với
P
:
2 4 0x y z
và cắt đường thẳng
:d
2 2 2
3 1 5
x y z
có phương trình là
A.
1
2
42
xt
y
zt
. B.
12
2
42
xt
y
zt
. C.
12
2
44
xt
y
zt
. D.
1
2
42
xt
y
zt
.
Lời giải:
Ta có:
2;1;1
P
n
là một vec tơ pháp tuyến của mặt phẳng
P
.
Phương trình tham số của đường thẳng
d
là:
23
2,
25
xt
y t t
zt
.
Gọi
là đường thẳng cần tìm. Gọi
M
là giao điểm của
và
d
2 3 ;2 ;2 5M t t t
1 3 ; ; 2 5AM t t t
Do
// P
nên
. 0 2 1 3 2 5 0 12 0 0
P
AM n t t t t t
1;0; 2AM
.
Phương trình đường thẳng
đi qua
1;2;4A
và nhận
1;0; 2AM
là một vec tơ chỉ
phương là:
1
2,
42
xt
yt
zt
.
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 03_______________
Câu 1: Trong mặt phẳng tọa độ
Oxy
, số phức
23zi
được biểu diễn bởi điểm nào sau đây?
A.
3;2Q
. B.
2;3N
. C.
3;2P
. D.
2; 3M
.
Câu 2: Đạo hàm của hàm số
2
x
y
là
A.
1
.2
x
yx
. B.
2 .ln 2
x
y
. C.
2
x
y
. D.
1
.2 .ln2
x
yx
.
Câu 3: Tập xác định của hàm số
1
2
log 2yx
là
A. . B.
2;
. C.
2;
. D.
0;
.
Câu 4: Tập nghiệm của bất phương trình
1
2
2
x
là
A.
;1
. B.
0;
. C.
1;
. D.
;1
.
Câu 5: Cho cấp số nhân
n
u
với
1
3u
và công bội
2q
. Số hạng thứ
7
của cấp số nhân đó là
A.
384
. B.
192
. C.
192
. D.
384
.
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
( ) :P
1
2 1 3
y
xz
. Vectơ nào dưới đây là một vectơ
pháp tuyến của mặt phẳng
( )?P
A.
2
(2;1;3).n
B.
4
( 3;6; 2).n
C.
1
(3;6;2).n
D.
3
( 3;6;2).n
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hình bên dưới:
x
y
O
-2
2
Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là
A.
0; 2
. B.
2;0
. C.
2;0
. D.
0;2
.
Câu 8: Nếu
35
03
d 3, d 7
f x x f x x
thì
5
0
f x dx
bằng
A.
7
. B.
4
. C.
10
. D.
4
.
Câu 9: Hàm số nào dưới đây có đồ thị dạng như đường cong ở hình vẽ bên dưới ?
A.
32
43 y x x
. B.
3 2
34y x x
. C.
3 2
4y x x
. D.
3
34 y x x
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 1 2 1 4S x y z
. Tọa độ tâm
I
và
bán kính
R
của mặt cầu là
A.
1; 2;1 ; 4IR
. B.
1;2; 1 ; 2IR
.
C.
1; 2;1 ; 2IR
. D.
1;2; 1 ; 4IR
.
Câu 11: Trong không gian
Oxyz
, góc giữa mặt phẳng
Oyz
và trục
Oy
bằng
A.
30 .
B.
90 .
C.
60 .
D.
0.
Câu 12: Biết
1; 2M
và
2;3N
lần lượt là hai điểm biểu diễn cho hai số phức
1
z
và
2
z
trên mặt
phẳng tọa độ
Oxy
. Khi đó, số phức
12
.zz
là
A.
15 i
. B.
8 i
. C.
26 i
. D.
3 i
.
Câu 13: Cho hình hộp có đáy là hình vuông cạnh bằng
a
và chiều cao
3a
. Thể tích của khối hộp đã
cho bằng
A.
3
a
. B.
3
1
3
a
. C.
3
3a
. D.
3
9a
.
Câu 14: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng
ABCD
và
3SA a
(tham khảo hình vẽ).
Thể tích khối chóp
.S ABCD
bằng
A.
3
3a
. B.
3
3a
. C.
3
a
. D.
3
3
3
a
.
Câu 15: Cho khối cầu có bán kính
2R
. Thể tích của khối cầu đã cho bằng
A.
32
3
. B.
16
3
. C.
16
. D.
32
.
Câu 16: Phần ảo của số phức
18 12zi
là
A.
12
. B.
12
. C.
12i
. D.
18
.
Câu 17: Thể tích của khối nón có chiều cao
h
, bán kính đáy
r
bằng
A.
2
1
3
rh
. B.
1
3
rh
. C.
2
1
3
rh
. D.
2
rh
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
1 2 1
:
2 3 1
x y z
d
. Điểm nào dưới đây thuộc
đường thẳng
d
?
A.
2;3;1 .Q
B.
1; 2; 1 .M
C.
1;2;3 .P
D.
1;2; 1 .N
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
Giá trị cực đại của hàm số đã cho bằng
A.
2
. B.
. C.
11
. D.
1
.
Câu 20: Đường tiệm cận ngang của đồ thị hàm số
31
2
x
y
x
là
A.
1
3
y
. B.
3y
. C.
3y
. D.
2y
.
Câu 21: Tập nghiệm của bất phương trình
0,5 1
x
là
A.
;2
. B.
0;
. C.
;0
. D.
2;
.
Câu 22: Có bao nhiêu số tự nhiên có hai chữ số khác nhau mà các chữ số được lấy từ tập hợp
1;2;3;4;5 ?X
A.
2
5
A
. B.
2
5
C
. C.
2
5
. D.
5
2
.
Câu 23: Nếu
d
6
0
18f x x
thì
d
2
0
3f x x
bằng
A.
6
. B.
12
. C.
36
. D.
54
.
Câu 24: Cho
6
2
d5f x x
. Khi đó
6
2
6 3 df x x
bằng
A.
9
. B.
9
. C.
1
. D.
21
.
Câu 25: Xác định
2
sin 2 d .
xx
A.
sin4
8
x
C
. B.
sin4
28
xx
C
. C.
3
cos 2
3
x
C
. D.
sin4
28
xx
C
.
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
2; .
B.
1; .
C.
;3 .
D.
;.
Câu 27: Cho hàm số
y f x
có đạo hàm liên tục trên
và có bảng biến thiên như sau:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Giá trị cực tiểu của hàm số bằng
A.
1
. B.
2
. C.
0
. D.
1
.
Câu 28: Với
,ab
là các số dương tùy ý,
25
3
log ab
bằng
A.
33
2log 5logab
. B.
3
10log ab
. C.
3
7log ab
. D.
33
10 log logab
.
Câu 29: Thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số
2
y x x
và trục
hoành quanh trục hoành là
A.
3
V
. B.
30
V
. C.
15
V
. D.
5
V
.
Câu 30: Cho hình chóp
.S ABCD
có
ABCD
là hình thang vuông tại
A
và
D
, cạnh bên
SD
vuông góc
với đáy,
, 2 , 3AB AD a CD a SA a
.
Góc giữa
SB
và
SAD
bằng
A.
30
. B.
60
. C.
45
. D.
90
.
Câu 31: Có tất cả bao nhiêu giá trị nguyên của tham số
m
để phương trình
42
4 4 2 0x x m
có
4
nghiệm phân biệt?
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 32: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
9
4
mx
y
xm
nghịch biến trên khoảng
0;4
?
A.
6
. B.
7
. C.
5
. D.
11
.
Câu 33: Một hộp chứa 12 tấm thẻ được đánh số bằng các số tự nhiên liên tiếp từ 1 đến 12. Chọn ngẫu
nhiên ra ba tấm thẻ. Xác suất để tích số ghi trên ba tấm thẻ là một số chẵn bằng
A.
11
12
. B.
1
3
. C.
10
11
. D.
1
2
.
Câu 34: Tính tổng các nghiệm của phương trình
11
2 2 5
xx
A.
0
. B.
2
. C.
1
2
. D.
2
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 35: Trong mặt phẳng
Oxy
, tập hợp các điểm biểu diễn số phức
z
thoã điều kiện
3 2 1 2z i i
A. Đường thẳng vuông góc với trục
Ox
. B. Đường tròn tâm
3; 2I
, bán kính
5R
.
C.
Đường tròn tâm
3; 2I
, bán kính
5R
. D. Đường thẳng vuông góc với trục
Oy
.
Câu 36: Trong không gian
Oxyz
, đường thẳng
d
đi qua điểm
1;2;3A
và vuông góc với mặt phẳng
:4 3 7 1 0x y z
có phương trình tham số là
A.
14
23
37
xt
yt
zt
. B.
54
53
47
xt
yt
zt
C.
13
24
37
xt
yt
zt
D.
18
26
3 14
xt
yt
zt
Câu 37: Trong mặt phẳng
Oxyz
, mặt cầu
S
có tâm thuộc trục
Ox
và đi qua hai điểm
1;2;1 , 1;0;3AB
có bán kính bằng
A.
3
. B.
23
. C.
3
. D.
9
.
Câu 38: Cho khối nón
N
có chiều cao bằng
3a
. Cắt hình nón đó bởi một mặt phẳng song song với
mặt đáy, cách mặt đáy một khoảng bằng
a
thu được thiết diện có diện tích bằng
2
64
.
9
a
Khi
đó, thể tích của khối nón
N
bằng
A.
3
16 a
. B.
3
48a
. C.
3
16a
. D.
3
48 a
.
Câu 39: Cho hình trụ có chiều cao bằng
8cm
. Một mặt phẳng
song song với trục của hình trụ
cách trục một khoảng bằng
5cm
và mp
cắt hình trụ theo thiết diện có diện tích bằng
2
32cm
. Khi đó diện tích toàn phần của hình trụ đã cho bằng
A.
2
24 cm
. B.
2
16 cm
. C.
2
66 cm
. D.
2
11 cm
.
Câu 40: Trong không gian
,Oxyz
cho điểm
(1;0;1)M
và đường thẳng
1 2 3
:.
1 2 3
x y z
d
Đường
thẳng đi qua
,M
vuông góc với
d
và cắt
Oz
có phương trình là
A.
13
0
1
xt
y
zt
. B.
13
0
1
xt
y
zt
. C.
13
1
xt
yt
zt
. D.
13
0
1
xt
y
zt
.
________________________HẾT________________________

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Trong mặt phẳng tọa độ
Oxy
, số phức
23zi
được biểu diễn bởi điểm nào sau đây?
A.
3;2Q
. B.
2;3N
. C.
3;2P
. D.
2; 3M
.
Lời giải:
Trong mặt phẳng tọa độ
Oxy
, số phức
23zi
được biểu diễn bởi điểm
2; 3M
.
Câu 2: Đạo hàm của hàm số
2
x
y
là
A.
1
.2
x
yx
. B.
2 .ln 2
x
y
. C.
2
x
y
. D.
1
.2 .ln2
x
yx
.
Lời giải:
Hàm số
2
x
y
có đạo hàm là
' 2 .ln2
x
y
.
Câu 3: Tập xác định của hàm số
1
2
log 2yx
là
A. . B.
2;
. C.
2;
. D.
0;
.
Lời giải:
Điều kiện xác định:
2 0 2 2;x x x
.
Câu 4: Tập nghiệm của bất phương trình
1
2
2
x
là
A.
;1
. B.
0;
. C.
1;
. D.
;1
.
Lời giải:
1
1
2 2 2 1 1
2
x
x
xx
Câu 5: Cho cấp số nhân
n
u
với
1
3u
và công bội
2q
. Số hạng thứ
7
của cấp số nhân đó là
A.
384
. B.
192
. C.
192
. D.
384
.
Lời giải:
Số hạng thứ
7
của cấp số nhân đó là
6
6
71
. 3. 2 192u u q
.
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
( ) :P
1
2 1 3
y
xz
. Vectơ nào dưới đây là một vectơ
pháp tuyến của mặt phẳng
( )?P
A.
2
(2;1;3).n
B.
4
( 3;6; 2).n
C.
1
(3;6;2).n
D.
3
( 3;6;2).n
Lời giải:
Ta có:
1 3 6 2 6 0
2 1 3
y
xz
x y z
. Do đó vectơ pháp tuyến là
1
(3;6;2).n
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hình bên dưới:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
x
y
O
-2
2
Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là
A.
0; 2
. B.
2;0
. C.
2;0
. D.
0;2
.
Câu 8: Nếu
35
03
d 3, d 7
f x x f x x
thì
5
0
f x dx
bằng
A.
7
. B.
4
. C.
10
. D.
4
.
Lời giải:
Ta có:
5 3 5
0 0 3
3 7 10f x dx f x dx f x dx
.
Câu 9: Hàm số nào dưới đây có đồ thị dạng như đường cong ở hình vẽ bên dưới ?
A.
32
43 y x x
. B.
3 2
34y x x
. C.
3 2
4y x x
. D.
3
34 y x x
.
Lời giải:
Nhánh cuối đồ thị đi xuống suy ra hệ số ứng với bậc cao nhất là số âm, nên loại đáp án
B
và
D
Nhận thấy điểm
1;0
thuộc đồ thị, ta thay
1x
và
0y
vào các đáp án còn lại, chọn
được đáp án
A
.
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 1 2 1 4S x y z
. Tọa độ tâm
I
và
bán kính
R
của mặt cầu là
A.
1; 2;1 ; 4IR
. B.
1;2; 1 ; 2IR
.
C.
1; 2;1 ; 2IR
. D.
1;2; 1 ; 4IR
.
Câu 11: Trong không gian
Oxyz
, góc giữa mặt phẳng
Oyz
và trục
Oy
bằng
A.
30 .
B.
90 .
C.
60 .
D.
0.
Câu 12: Biết
1; 2M
và
2;3N
lần lượt là hai điểm biểu diễn cho hai số phức
1
z
và
2
z
trên mặt
phẳng tọa độ
Oxy
. Khi đó, số phức
12
.zz
là
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
A.
15 i
. B.
8 i
. C.
26 i
. D.
3 i
.
Lời giải:
Ta có :
12
1 2 ; 2 3z i z i
. Từ đó suy ra :
12
. 1 2 . 2 3 8z z i i i
.
Câu 13: Cho hình hộp có đáy là hình vuông cạnh bằng
a
và chiều cao
3a
. Thể tích của khối hộp đã
cho bằng
A.
3
a
. B.
3
1
3
a
. C.
3
3a
. D.
3
9a
.
Lời giải:
Thể tích của khối hộp:
23
. .3 3V B h a a a
.
Câu 14: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng
ABCD
và
3SA a
(tham khảo hình vẽ).
Thể tích khối chóp
.S ABCD
bằng
A.
3
3a
. B.
3
3a
. C.
3
a
. D.
3
3
3
a
.
Lời giải:
Ta có
3
2
.
1 1 3
. . 3 .
3 3 3
S ABCD ABCD
a
V SA S a a
.
Câu 15: Cho khối cầu có bán kính
2R
. Thể tích của khối cầu đã cho bằng
A.
32
3
. B.
16
3
. C.
16
. D.
32
.
Lời giải:
Thể tích của khối cầu là
33
4 4 32
. . .2
3 3 3
VR
.
Câu 16: Phần ảo của số phức
18 12zi
là
A.
12
. B.
12
. C.
12i
. D.
18
.
Lời giải:
Phần ảo của số phức
18 12zi
là
12
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Câu 17: Thể tích của khối nón có chiều cao
h
, bán kính đáy
r
bằng
A.
2
1
3
rh
. B.
1
3
rh
. C.
2
1
3
rh
. D.
2
rh
.
Lời giải:
Thể tích của khối nón đã cho là
2
1
3
V r h
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
1 2 1
:
2 3 1
x y z
d
. Điểm nào dưới đây thuộc
đường thẳng
d
?
A.
2;3;1 .Q
B.
1; 2; 1 .M
C.
1;2;3 .P
D.
1;2; 1 .N
Lời giải:
Đường thẳng
d
đi qua
0 0 0
;;M x y z
có một véc tơ chỉ phương là
;;u a b c
thì
d
có phương
trình chính tắc là
0 0 0
:
x x y y z z
d
a b c
.
Vậy
1 2 1
:
2 3 1
x y z
d
đi qua điểm
1; 2; 1M
hay
1; 2; 1M
thuộc đường thẳng
d
.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng
A.
2
. B.
. C.
11
. D.
1
.
Lời giải:
Từ bảng biến thiên của hàm số
y f x
,ta thấy giá trị cực đại của hàm số là
11
.
Câu 20: Đường tiệm cận ngang của đồ thị hàm số
31
2
x
y
x
là
A.
1
3
y
. B.
3y
. C.
3y
. D.
2y
.
Lời giải:
Ta có:
31
lim 3
2
x
x
x
;
31
lim 3
2
x
x
x
nên TCN
3y
.
Câu 21: Tập nghiệm của bất phương trình
0,5 1
x
là
A.
;2
. B.
0;
. C.
;0
. D.
2;
.
Lời giải:
Ta có:
0
0,5 1 0,5 0,5 0
xx
x
.
Câu 22: Có bao nhiêu số tự nhiên có hai chữ số khác nhau mà các chữ số được lấy từ tập hợp
1;2;3;4;5 ?X
A.
2
5
A
. B.
2
5
C
. C.
2
5
. D.
5
2
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Lời giải:
Mỗi số tự nhiên có hai chữ số khác nhau có các chữ số lấy từ tập
X
là một chỉnh hợp chập 2
của 5 phần tử, do đó ta được
2
5
A
số.
Câu 23: Nếu
d
6
0
18f x x
thì
d
2
0
3f x x
bằng
A.
6
. B.
12
. C.
36
. D.
54
.
Lời giải:
Xét tích phân
2
0
3dI f x x
Đặt
3tx
. Khi đó
d
d 3d d
3
t
t x x
.
Với
0 0; 2 6x t x t
.
Khi đó
66
00
d 1 1
. d .18 6
3 3 3
t
I f t f t t
.
Câu 24: Cho
6
2
d5f x x
. Khi đó
6
2
6 3 df x x
bằng
A.
9
. B.
9
. C.
1
. D.
21
.
Lời giải:
Ta có:
6 6 6
2 2 2
6 3 d 6 d 3 df x x x f x x
6
2
6
6 3 d 6. 6 2 3.5 9
2
x f x x
.
Câu 25: Xác định
2
sin 2 d .
xx
A.
sin4
8
x
C
. B.
sin4
28
xx
C
. C.
3
cos 2
3
x
C
. D.
sin4
28
xx
C
.
Lời giải:
Ta có
2
1 cos4
sin 2 d d
2
x
x x x
11
d cos4 d 4
28
x x x
sin4
.
28
xx
C
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
2; .
B.
1; .
C.
;3 .
D.
;.
Lời giải:
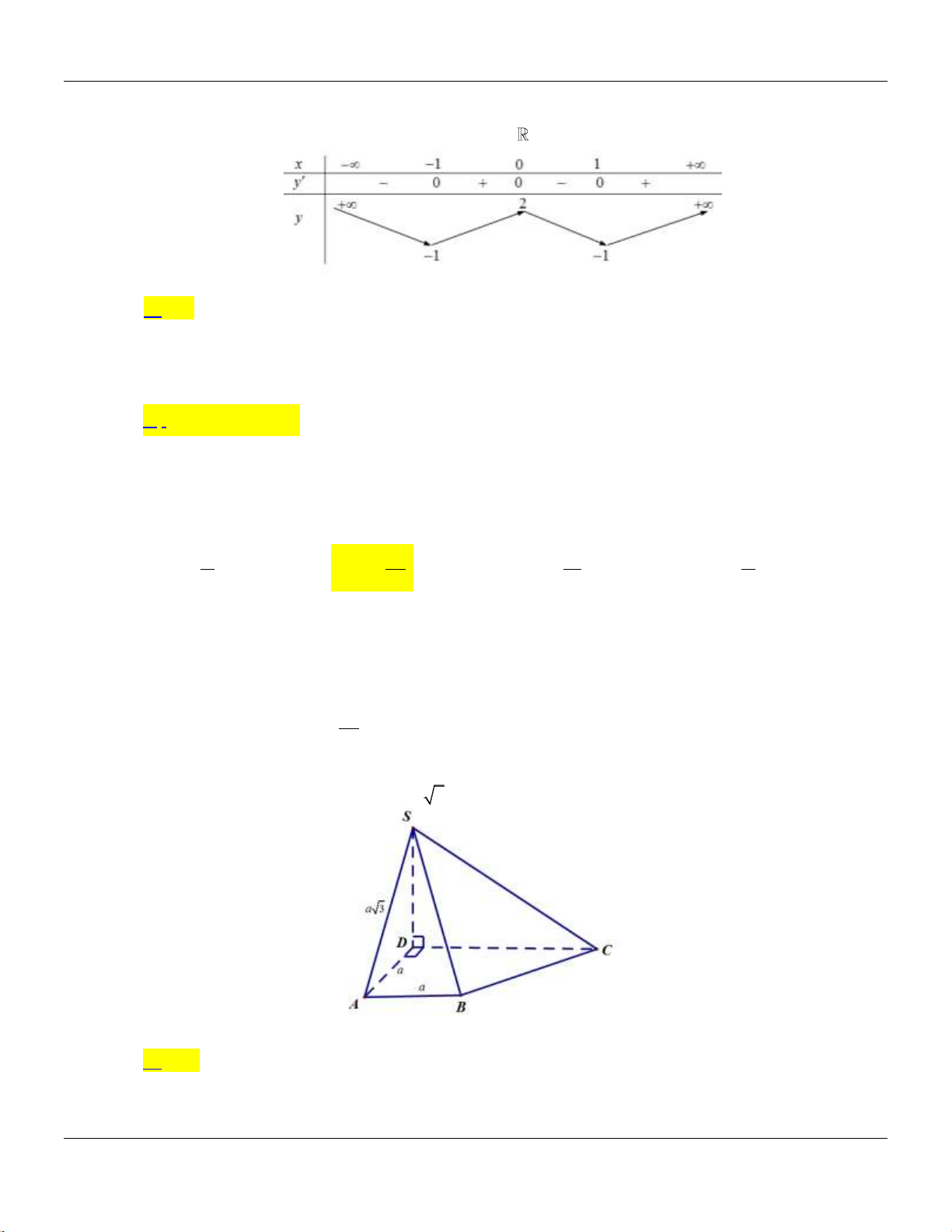
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Từ Bảng biến thiên suy ra hàm số đã cho đồng biến trên
(2; )
.
Câu 27: Cho hàm số
y f x
có đạo hàm liên tục trên
và có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số bằng
A.
1
. B.
2
. C.
0
. D.
1
.
Lời giải:
Từ BBT, ta có giá trị cực tiểu của hàm số là:
CT
1y
.
Câu 28: Với
,ab
là các số dương tùy ý,
25
3
log ab
bằng
A.
33
2log 5logab
. B.
3
10log ab
. C.
3
7log ab
. D.
33
10 log logab
.
Lời giải:
Ta có:
2 5 2 5
3 3 3 3 3
log log log 2log 5loga b a b a b
.
Câu 29: Thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số
2
y x x
và trục
hoành quanh trục hoành là
A.
3
V
. B.
30
V
. C.
15
V
. D.
5
V
.
Lời giải:
Phương trình hoành độ giao điểm của đồ thị hàm số
2
y x x
và trục hoành là
2
0
0
1
x
xx
x
.
Vậy
1
2
2
0
d
30
V x x x
.
Câu 30: Cho hình chóp
.S ABCD
có
ABCD
là hình thang vuông tại
A
và
D
, cạnh bên
SD
vuông góc
với đáy,
, 2 , 3AB AD a CD a SA a
.
Góc giữa
SB
và
SAD
bằng
A.
30
. B.
60
. C.
45
. D.
90
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
Ta có:
AB AD
AB SAD
AB SD
,,SB SAD SB SA BSA
.
Tam giác
SAB
vuông tại
1
tan 30
3
AB
A BSA BSA
SA
.
Câu 31: Có tất cả bao nhiêu giá trị nguyên của tham số
m
để phương trình
42
4 4 2 0x x m
có
4
nghiệm phân biệt?
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải:
Ta có :
42
4 4 2 0x x m
42
4 4 2x x m
1
.
Số nghiệm của phương trình
1
là số giao điểm của đồ thị hàm số
42
44y x x
và đường
thẳng
2ym
.
Xét hàm số
42
44y x x
;
3
48y x x
,
0
0
2
x
y
x
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta có: Phương trình
1
có 4 nghiệm phân biệt khi
8 2 4m
24m
.
Vì
m
nguyên nên
3m
.
Câu 32: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
9
4
mx
y
xm
nghịch biến trên khoảng
0;4
?
A.
6
. B.
7
. C.
5
. D.
11
.
Lời giải:
Tập xác định
\
4
m
D
.
Ta có
2
2
36
4
m
y
xm
.
Hàm số đã cho nghịch biến trên khoảng
0;4
khi và chỉ khi
2
36 0
0;4
4
m
m
66
0
4
4
4
m
m
m
66
06
0
16
m
m
m
m
.
Vì
m
nguyên nên
0;1;2;3;4;5m
.
Vậy có
6
giá trị của
m
thỏa mãn yêu cầu bài toán.
x
y
y
2
0
0
8
4
0
2
0
8

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Câu 33: Một hộp chứa 12 tấm thẻ được đánh số bằng các số tự nhiên liên tiếp từ 1 đến 12. Chọn ngẫu
nhiên ra ba tấm thẻ. Xác suất để tích số ghi trên ba tấm thẻ là một số chẵn bằng
A.
11
12
. B.
1
3
. C.
10
11
. D.
1
2
.
Lời giải:
Chọn 3 trong 12 tấm thẻ có
3
12
220C
cách
220n
.
Gọi biến cố A: “tích số ghi trên ba tấm thẻ là một số lẻ”
Khi đó
3
6
20n A C
.
Nên
20 1
220 11
nA
PA
n
.
Suy ra xác suất để tích số ghi trên ba tấm thẻ là một số chẵn là
1 10
11
11 11
PA
.
Câu 34: Tính tổng các nghiệm của phương trình
11
2 2 5
xx
A.
0
. B.
2
. C.
1
2
. D.
2
.
Lời giải:
Ta có:
11
1
2 2 5 2.2 2. 5
2
x x x
x
.
Đặt
20
x
tt
, phương trình trở thành:
2
2
22
1
2
2 5 2 5 2 0
1
1
1
2
2
2
x
x
t
x
t t t
x
t
t
.
Vậy tổng tất cả các nghiệm của phương trình là 0.
Câu 35: Trong mặt phẳng
Oxy
, tập hợp các điểm biểu diễn số phức
z
thoã điều kiện
3 2 1 2z i i
A. Đường thẳng vuông góc với trục
Ox
. B. Đường tròn tâm
3; 2I
, bán kính
5R
.
C.
Đường tròn tâm
3; 2I
, bán kính
5R
. D. Đường thẳng vuông góc với trục
Oy
.
Lời giải:
Gọi số phức
,z x yi xy
.
Khi đó
22
3 2 1 2 3 2 1 2 3 2 5z i i x y i i x y
Vậy tập hợp các điểm biểu diễn số phức
z
thoã điều kiện đề bài là đường tròn tâm
3; 2I
,
bán kính
5R
.
Câu 36: Trong không gian
Oxyz
, đường thẳng
d
đi qua điểm
1;2;3A
và vuông góc với mặt phẳng
:4 3 7 1 0x y z
có phương trình tham số là
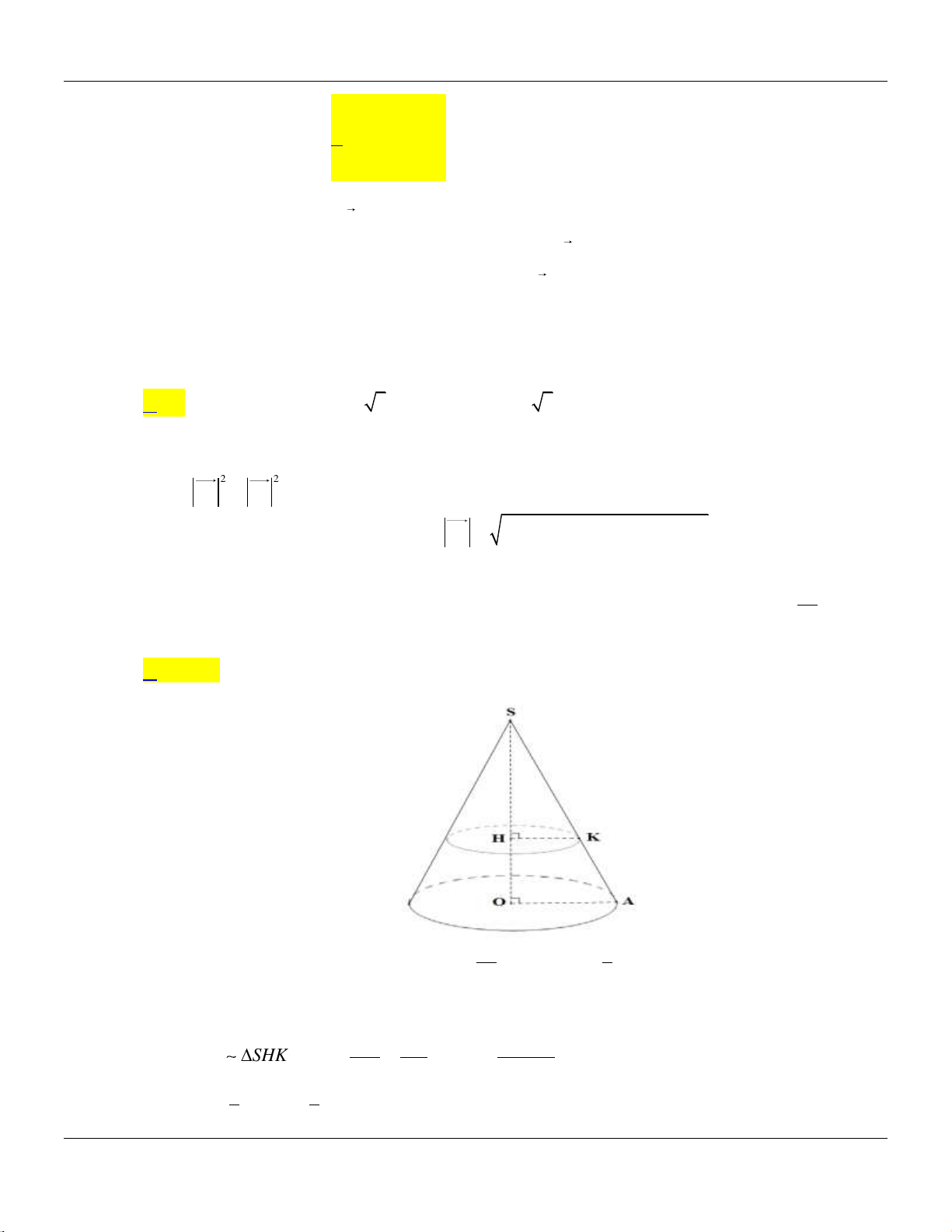
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
A.
14
23
37
xt
yt
zt
. B.
54
53
47
xt
yt
zt
C.
13
24
37
xt
yt
zt
D.
18
26
3 14
xt
yt
zt
Lời giải:
Mặt phẳng
có VTPT
4;3; 7n
.
Đường thẳng
d
vuông góc với mp
nên
d
nhận
4;3; 7n
làm 1 VTCP.
Đường thẳng
d
đi qua điểm
1;2;3A
và có vtcp
4;3; 7 .n
Kiểm tra phương án B thỏa mãn.
Câu 37: Trong mặt phẳng
Oxyz
, mặt cầu
S
có tâm thuộc trục
Ox
và đi qua hai điểm
1;2;1 , 1;0;3AB
có bán kính bằng
A.
3
. B.
23
. C.
3
. D.
9
.
Lời giải:
Giả sử tâm
;0;0I a Ox
.
Ta có
22
22
1 4 1 1 0 9AI BI a a
1 1;0;0aI
2 2 2
1 1 0 2 0 1 3R AI
.
Câu 38: Cho khối nón
N
có chiều cao bằng
3a
. Cắt hình nón đó bởi một mặt phẳng song song với
mặt đáy, cách mặt đáy một khoảng bằng
a
thu được thiết diện có diện tích bằng
2
64
.
9
a
Khi
đó, thể tích của khối nón
N
bằng
A.
3
16 a
. B.
3
48a
. C.
3
16a
. D.
3
48 a
.
Lời giải:
Ta có:
3SO h a
;
2
22
64 8
93
TD
S r HK a HK a
.
Do thiết diện song song và cách mặt đáy một đoạn bằng
a
nên
2.HO a SH SO OH a
Xét
SOA SHK
, ta có:
.
4
OA SO SO HK
OA a
HK SH SH
.
Vậy
2 2 3
11
. . .16 .3 16
33
N
V R h a a a
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
Câu 39: Cho hình trụ có chiều cao bằng
8cm
. Một mặt phẳng
song song với trục của hình trụ
cách trục một khoảng bằng
5cm
và mp
cắt hình trụ theo thiết diện có diện tích bằng
2
32cm
. Khi đó diện tích toàn phần của hình trụ đã cho bằng
A.
2
24 cm
. B.
2
16 cm
. C.
2
66 cm
. D.
2
11 cm
.
Lời giải:
D
O
B
O'
C
A
M
Theo giả thiết, mp
cắt hình trụ theo thiết diện là hình chữ nhật và giả sử là
ABCD
.
Ta có:
2
8
4
. 32
AD OO cm
AB cm
AD AB cm
.
Gọi
M
là trung điểm
AB
Suy ra
2
2 2 2
2 5 2 3MB cm OB OM MB cm
Khi đó hình trụ có bán kính đáy
3r cm
và độ dài đường sinh
8l cm
.
Diện tích toàn phần của hình trụ là
2
2 2 .3. 8 3 66
tp
S r l r cm
.
Câu 40: Trong không gian
,Oxyz
cho điểm
(1;0;1)M
và đường thẳng
1 2 3
:.
1 2 3
x y z
d
Đường
thẳng đi qua
,M
vuông góc với
d
và cắt
Oz
có phương trình là
A.
13
0
1
xt
y
zt
. B.
13
0
1
xt
y
zt
. C.
13
1
xt
yt
zt
. D.
13
0
1
xt
y
zt
.
Lời giải:
Gọi
là đường thẳng cần tìm và
.N Oz
Ta có
(0;0; ).Nc
Vì
qua
,MN
và
M Oz
nên
( 1;0; 1)MN c
là VTCP của
.
d
có 1 VTCP
(1;2;3)u
và
d
nên
41
0 1 3( 1) 0 ( 1;0; ).
33
MN u c c MN
Chọn
( 3;0;1)v
là 1 VTCP của
, phương trình tham số của đường thẳng
là
13
0
1
xt
y
zt
.
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
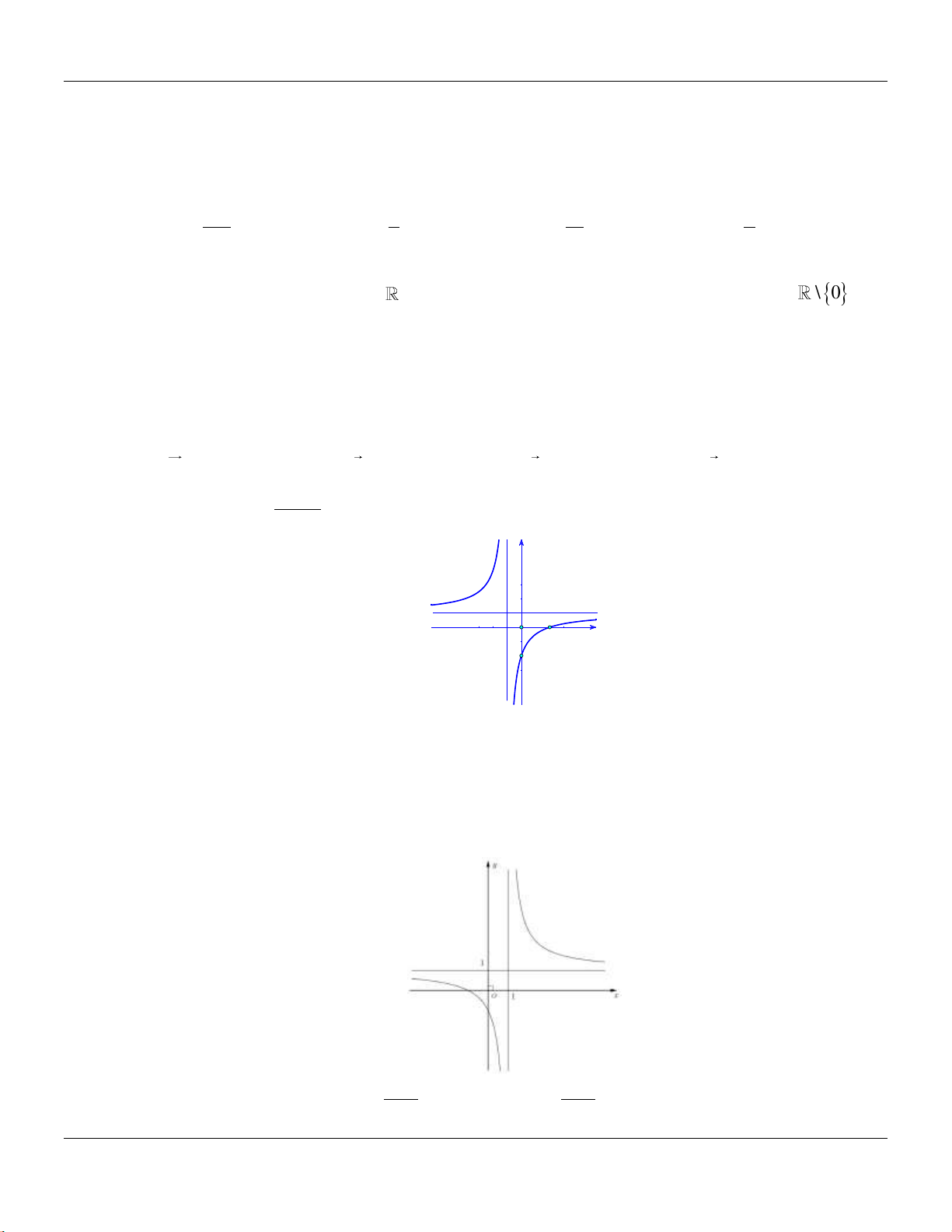
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 04_______________
Câu 1: Số phức nào sau đây có biểu diễn hình học là điểm
3;5M
?
A.
35zi
. B.
35zi
. C.
35zi
. D.
35zi
.
Câu 2: Trên khoảng
0; ,
đạo hàm của hàm số
lnyx
là
A.
1
.
10
y
x
B.
1
.
y
x
C.
1
.
y
ex
D.
.
e
y
x
Câu 3: Tập xác định
D
của hàm số
23
yx
là
A.
0;D
. B.
D
. C.
0;D
. D.
\0D
.
Câu 4: Tập nghim của bt phương trnh
ln 1x
là
A.
;e
. B.
0;e
. C.
;e
. D.
;e
.
Câu 5: Cho cp số nhân
n
u
có
1
2u
và có công bội bằng
3
. Giá trị
2
u
bằng
A.
5
. B.
9
. C.
8
. D.
6
.
Câu 6: Trong không gian
Oxyz
, vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng
Oxy
?
A.
1;1;1m
. B.
1;0;0i
. C.
0;1;0j
. D.
0;0;1k
.
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hnh bên dưới:
x
y
O
-2
2
Số giao điểm của đồ thị hàm số đã cho và trục hoành là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 8: Cho
6
2
d4
f x x
và
6
2
d5
g x x
, khi đó
6
2
3d
f x g x x
bằng
A.
19
. B.
17
. C.
11
. D.
7
.
Câu 9: Đường cong hình vẽ là đồ thị hàm số nào dưới đây?
A.
32
1y x x
. B.
1
1
x
y
x
. C.
1
1
x
y
x
. D.
3
21y x x
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 10: Trong không gian
Oxyz
, mặt cầu có tâm
2; 1;3I
, bán kính
3R
có phương trnh là
A.
2 2 2
2 1 3 3x y z
. B.
2 2 2
2 1 3 3x y z
.
C.
2 2 2
2 1 3 3x y z
. D.
2 2 2
3 1 3 3x y z
.
Câu 11: Trong không gian
Oxyz
, góc giữa mặt phẳng
Oyz
và trục
Ox
bằng
A.
30 .
B.
90 .
C.
60 .
D.
0.
Câu 12: Tìm hai số thực
x
và
y
thỏa mãn
2 3 1 3 6x yi i x i
, với
i
là đơn vị ảo.
A.
1, 3xy
. B.
1, 1xy
. C.
1, 1xy
. D.
1, 3xy
.
Câu 13: Cho khối chóp có din tích đáy
6B
và chiều cao
8h
. Thể tích của khối chóp đã cho bằng
A.
16
. B.
48
. C.
8
. D.
14
.
Câu 14: Thể tích khối lăng trụ tam giác đều có tt cả các cạnh đều bằng
a
bằng
B
C
A
B
C
A
A.
3
3
12
a
. B.
3
a
. C.
3
2a
. D.
3
3
4
a
.
Câu 15: Cho mặt cầu
S
, bán kính
R
và mặt phẳng
. Biết khoảng cách từ tâm của mặt cầu
S
tới
mặt phẳng
bằng
R
. Khẳng định nào sau đây đúng?
A. Mặt phẳng
a
cắt mặt cầu
S
.
B. Thiết din của mặt phẳng
với mặt cầu
S
là một đường tròn.
C. Mặt phẳng
a
tiếp xúc với mặt cầu
S
.
D. Mặt phẳng
a
với mặt cầu
S
không có điểm chung.
Câu 16: Cho số phức
12zi
. Số phức liên hợp của
z
là
A.
12i
. B.
12i
. C.
2 i
. D.
12i
.
Câu 17: Cho hnh nón có độ dài đường sinh bằng
3a
và bán kính đáy bằng
a
. Din tích xung quanh
của hnh nón đã cho bằng
A.
2
12 a
. B.
2
3 a
. C.
2
6 a
. D.
2
a
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
32
:1
23
xt
d y t
zt
. Điểm nào dưới đây thuộc
d
?
A.
3;1;2M
. B.
2;1;3Q
. C.
3; 1; 2P
. D.
2;1;3N
.
Câu 19: Cho hàm số
fx
có bảng xét du
fx
như sau:
Hoành độ điểm cực tiểu của hàm số đã cho bằng
A.
1
. B.
0
. C.
1
. D.
1
và
1
.
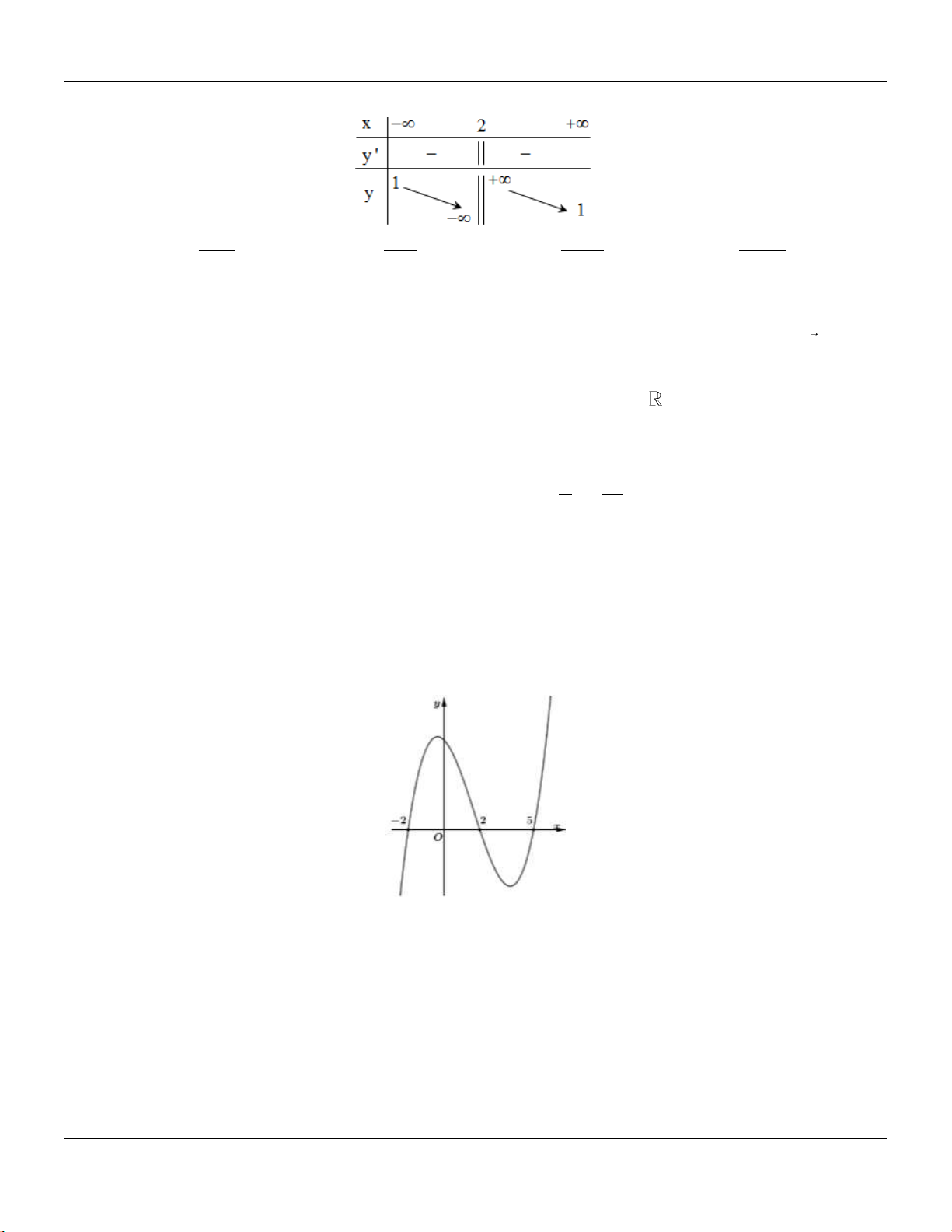
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
Câu 20: Bảng biến thiên sau đây là của hàm số nào ?
A.
1
.
2
x
y
x
B.
1
.
1
x
y
x
C.
21
.
2
x
y
x
D.
3
.
2
x
y
x
Câu 21: Tập nghim của bt phương trnh
1
24
x
là
A.
;3 .
B.
;5 .
C.
1;3 .
D.
1; .
Câu 22: Từ 10 điểm phân bit trong không gian có thể tạo thành bao nhiêu vectơ khác vectơ
0
?
A.
10
2
. B.
10
P
. C.
2
10
A
. D.
2
10
C
.
Câu 23: Cho hàm số
y f x
xác định và liên tục trên
đồng thời thoả mãn:
( ) 3 5sinf x x
,
(0) 14f
. Khẳng định nào sau đây đúng?
A.
( ) 3 5f
. B.
( ) 3 5sin 9f x x x
.
C.
( ) 3 5cos 9f x x x
. D.
3
9
22
f
.
Câu 24: Nếu
d
4
0
( ) 37f x x
thì
d
4
2
0
2 ( ) 3f x x x
bằng
A. 12. B. 18. C.
27
. D. 10.
Câu 25: Họ tt cả các nguyên hàm của hàm số
cos 6f x x x
là
A.
2
sin 3x x C
. B.
sin xC
. C.
2
sin 3x x C
. D.
2
sin 6x x C
.
Câu 26: Cho hàm số
y f x
có đồ thị như hnh bên dưới:
Mnh đề nào sau đây đúng?
A. Hàm số
fx
nghịch biến trên
2;5
. B. Hàm số
fx
nghịch biến trên
0;5
.
C. Hàm số
fx
đồng biến trên
;0
. D. Hàm số
fx
đồng biến trên
5;
.
Câu 27: Cho hàm số
y f x
có bảng biến thiên như sau:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Hàm số đã cho đạt cực tiểu tại
A.
1x
. B.
3.y
C.
3x
. D.
1y
.
Câu 28: Cho khối trụ
T
,
là mặt phẳng đi qua trục và cắt khối trụ
T
theo thiết din là hình
vuông cạnh 2a. Thể tích khối trụ
T
bằng
A.
3
3
a
B.
3
2.a
C.
3
2
3
a
. D.
3
.a
Câu 29: Cho
a
là số thực dương khác
1
. Giá trị của
3
log
a
a
bằng
A.
0.
B.
1
.
3
C.
3.
D.
3.
Câu 30: Thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số
2
43y x x
và
trục hoành quay quanh trục
Ox
là
A.
4
3
V
. B.
16
15
V
. C.
16
15
V
. D.
4
3
V
.
Câu 31: Cho hnh chóp
.S ABC
có đáy
ABC
là tam giác vuông cạnh huyền
BC a
. Hnh chiếu
vuông góc của
S
lên
ABC
trng với trung điểm của
BC
.
H
A
C
B
S
Biết
SB a
. Tính số đo của góc giữa
SA
và
ABC
.
A.
75
. B.
30
. C.
60
. D.
45
.
Câu 32: Cho hàm số bậc ba
y f x
có đồ thị như hnh vẽ bên dưới:
Số giá trị nguyên của tham số
m
để đường thẳng
ym
cắt đồ thị hàm số đã cho tại ba điểm
phân bit là
A. Vô số. B.
3
. C. 0. D.
5
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 33: Có bao nhiêu giá trị nguyên của tham số thực m để hàm số
32
4 9 5y x mx m x
nghịch biến trên khoảng
;
?
A. 5. B. 7. C. 4. D. 6.
Câu 34: Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong
hộp. Xác sut để 5 viên bi được chọn có đủ ba màu và số bi đỏ bằng số bi vàng bằng
A.
11
18
. B.
5
18
. C.
75
408
. D.
95
408
.
Câu 35: Phương trnh
9 4.3 3 0
xx
có tổng các nghim là
A.
1
. B.
4
. C.
1
. D.
4
.
Câu 36: Gọi
12
;zz
là hai nghim phức của phương trnh
2
2 2 0zz
. Tập hợp các điểm bểu diễn
của số phức
w
thỏa mãn
12
w z w z
là đường thẳng có phương trnh
A.
0xy
. B.
0x
. C.
0xy
. D.
0y
.
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2;3A
và đường thẳng
3 1 7
:
2 1 2
x y z
d
. Đường
thẳng
đi qua
A
và song song với
d
có phương trnh là
A.
13
2
37
xt
yt
zt
. B.
3
12
73
xt
yt
zt
. C.
32
3
12
xt
yt
zt
. D.
2
12
23
xt
yt
zt
.
Câu 38: Trong không gian
Oxyz
, cho điểm
1;2;3A
. Điểm đối xứng với
A
qua trục
Oz
có tọa độ là
A.
1;2; 3
. B.
1;2; 3
. C.
1; 2;0
. D.
1; 2;3
.
Câu 39: Cắt hình nón bởi một mặt phẳng đi qua đỉnh và tạo với mặt phẳng đáy một góc
60
được
thiết din là một tam giác vuông cân có cạnh huyền bằng
4.
Tính thể tích của khối nón ban
đầu.
A.
10 3
.
3
V
B.
53
.
3
V
C.
3
.
3
V
D.
53
.
3
V
Câu 40: Trong không gian
Oxyz
, viết phương trnh đường thẳng
d
đi qua điểm
1;2; 1M
, song
song với mặt phẳng
:3P x y z
và vuông góc với đường thẳng
3
: 3 3
2
xt
yt
zt
.
A.
15
23
12
xt
yt
zt
. B.
1
23
12
xt
yt
zt
. C.
1
2
1
xt
yt
zt
. D.
5
32
2
xt
yt
zt
.
________________________HẾT________________________

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Số phức nào sau đây có biểu diễn hình học là điểm
3;5M
?
A.
35zi
. B.
35zi
. C.
35zi
. D.
35zi
.
Lời giải:
3;5M
là điểm biểu diễn hình học của số phức
35zi
.
Câu 2: Trên khoảng
0; ,
đạo hàm của hàm số
lnyx
là
A.
1
.
10
y
x
B.
1
.
y
x
C.
1
.
y
ex
D.
.
e
y
x
Câu 3: Tập xác định
D
của hàm số
23
yx
là
A.
0;D
. B.
D
. C.
0;D
. D.
\0D
.
Lời giải:
Do hàm số
23
yx
là hàm số lũy thừa với số mũ không nguyên nên để hàm số xác định thì
0x
.
Vậy hàm số
23
yx
có tập xác định là
0;D
.
Câu 4: Tập nghim của bt phương trnh
ln 1x
là
A.
;e
. B.
0;e
. C.
;e
. D.
;e
.
Lời giải:
Ta có
1
0
ln 1 0
x
x x e
xe
.
Từ đây ta suy ra tập nghim của bt phương trnh đã cho là
0;e
.
Câu 5: Cho cp số nhân
n
u
có
1
2u
và có công bội bằng
3
. Giá trị
2
u
bằng
A.
5
. B.
9
. C.
8
. D.
6
.
Lời giải:
Ta có:
21
. 2. 3 6u u q
.
Câu 6: Trong không gian
Oxyz
, vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng
Oxy
?
A.
1;1;1m
. B.
1;0;0i
. C.
0;1;0j
. D.
0;0;1k
.
Lời giải:
Vì
Oz
vuông góc với mặt phẳng
Oxy
, nên vectơ pháp tuyến của mặt phẳng
Oxy
là
0;0;1k
.
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hnh bên dưới:

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
x
y
O
-2
2
Số giao điểm của đồ thị hàm số đã cho và trục hoành là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 8: Cho
6
2
d4
f x x
và
6
2
d5
g x x
, khi đó
6
2
3d
f x g x x
bằng
A.
19
. B.
17
. C.
11
. D.
7
.
Lời giải:
Ta có
6 6 6
2 2 2
3 3 3.4 5 7f x g x dx f x dx g x dx
.
Câu 9: Đường cong hình vẽ là đồ thị hàm số nào dưới đây?
A.
32
1y x x
. B.
1
1
x
y
x
. C.
1
1
x
y
x
. D.
3
21y x x
.
Lời giải:
Dựa vào hình vẽ ta có tin cận đứng
1x
và tim cận ngang
1y
.
Câu 10: Trong không gian
Oxyz
, mặt cầu có tâm
2; 1;3I
, bán kính
3R
có phương trnh là
A.
2 2 2
2 1 3 3x y z
. B.
2 2 2
2 1 3 3x y z
.
C.
2 2 2
2 1 3 3x y z
. D.
2 2 2
3 1 3 3x y z
.
Lời giải:
Mặt cầu có tâm
2; 1;3I
, bán kính
3R
có phương trnh là
2 2 2
2 1 3 3x y z
.
Câu 11: Trong không gian
Oxyz
, góc giữa mặt phẳng
Oyz
và trục
Ox
bằng
A.
30 .
B.
90 .
C.
60 .
D.
0.
Câu 12: Tìm hai số thực
x
và
y
thỏa mãn
2 3 1 3 6x yi i x i
, với
i
là đơn vị ảo.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
A.
1, 3xy
. B.
1, 1xy
. C.
1, 1xy
. D.
1, 3xy
.
Lời giải:
Ta có
2 1 1
2 3 1 3 6 2 1 3 3 6
3 3 6 3
x x x
x yi i x i x y i x i
yy
.
Câu 13: Cho khối chóp có din tích đáy
6B
và chiều cao
8h
. Thể tích của khối chóp đã cho bằng
A.
16
. B.
48
. C.
8
. D.
14
.
Lời giải:
Thể tích của khối chóp
11
. .6.8 16
33
V B h
.
Vậy thể tích của khối chóp đã cho bằng
16
.
Câu 14: Thể tích khối lăng trụ tam giác đều có tt cả các cạnh đều bằng
a
bằng
B
C
A
B
C
A
A.
3
3
12
a
. B.
3
a
. C.
3
2a
. D.
3
3
4
a
.
Lời giải:
B
C
A
B
C
A
Thể tích khối lăng trụ là
23
33
..
44
aa
V B h a
.
Câu 15: Cho mặt cầu
S
, bán kính
R
và mặt phẳng
. Biết khoảng cách từ tâm của mặt cầu
S
tới
mặt phẳng
bằng
R
. Khẳng định nào sau đây đúng?
A. Mặt phẳng
a
cắt mặt cầu
S
.
B. Thiết din của mặt phẳng
với mặt cầu
S
là một đường tròn.
C. Mặt phẳng
a
tiếp xúc với mặt cầu
S
.
D. Mặt phẳng
a
với mặt cầu
S
không có điểm chung.
Lời giải:
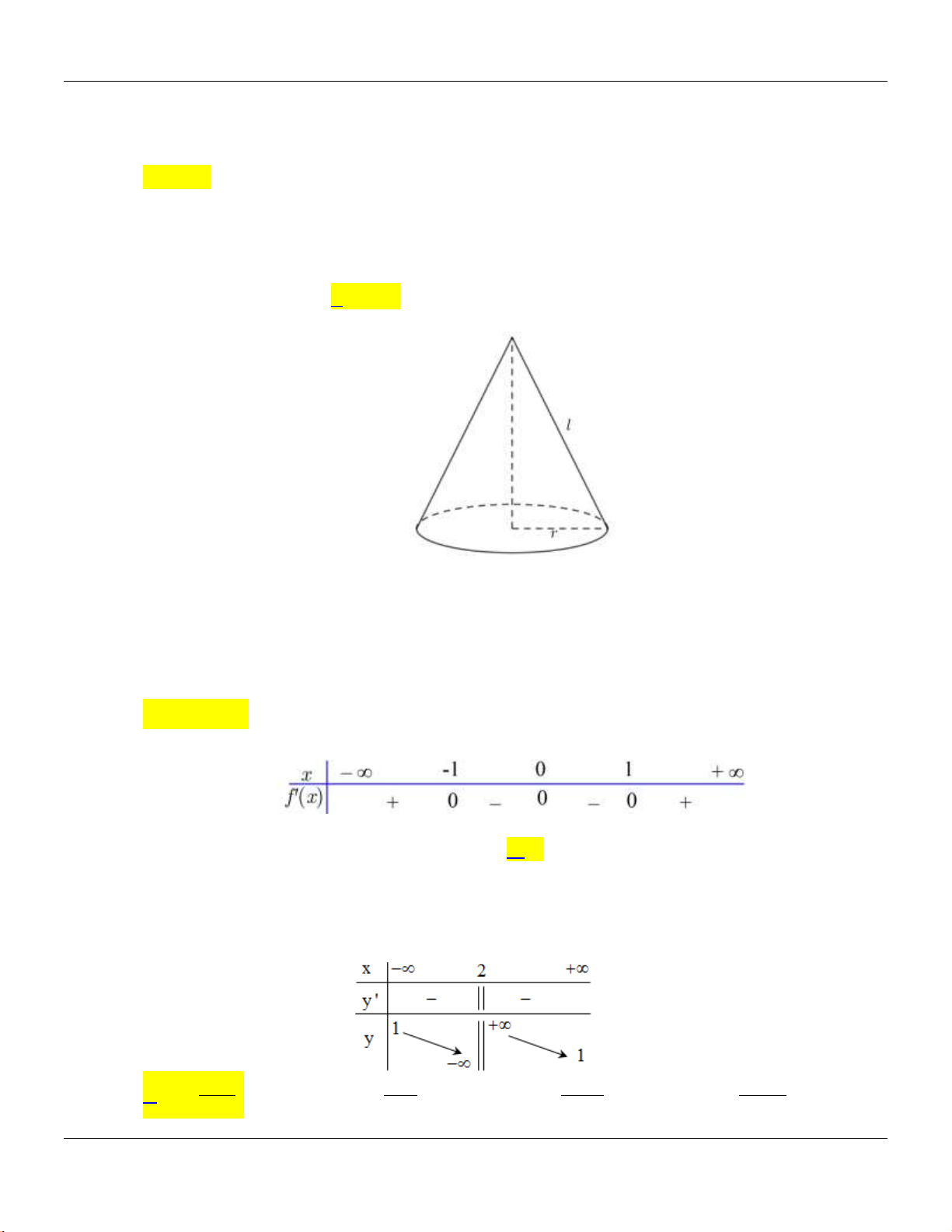
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Khoảng cách từ tâm mặt cầu đến mặt phẳng bằng đúng bán kính nên mặt phẳng tiếp xúc mặt
cầu.
Câu 16: Cho số phức
12zi
. Số phức liên hợp của
z
là
A.
12i
. B.
12i
. C.
2 i
. D.
12i
.
Lời giải:
Theo định nghĩa số phức liên hợp ta có
12i
là số phức liên hợp của
12zi
.
Câu 17: Cho hnh nón có độ dài đường sinh bằng
3a
và bán kính đáy bằng
a
. Din tích xung quanh
của hnh nón đã cho bằng
A.
2
12 a
. B.
2
3 a
. C.
2
6 a
. D.
2
a
.
Lời giải:
Hnh nón có độ dài đường sinh
3la
, bán kính đáy
ra
có din tích xung quanh là
2
. .3 3
xq
S rl a a a
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
32
:1
23
xt
d y t
zt
. Điểm nào dưới đây thuộc
d
?
A.
3;1;2M
. B.
2;1;3Q
. C.
3; 1; 2P
. D.
2;1;3N
.
Câu 19: Cho hàm số
fx
có bảng xét du
fx
như sau:
Hoành độ điểm cực tiểu của hàm số đã cho bằng
A.
1
. B.
0
. C.
1
. D.
1
và
1
.
Lời giải:
Do
fx
xác định và đổi du từ âm sang dương khi đi qua 1, nên hoành độ điểm cực tiểu
của hàm số bằng 1.
Câu 20: Bảng biến thiên sau đây là của hàm số nào ?
A.
1
.
2
x
y
x
B.
1
.
1
x
y
x
C.
21
.
2
x
y
x
D.
3
.
2
x
y
x

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Lời giải:
Từ BBT suy ra:
Tim cận đứng của ĐTHS là:
2x
. Loại B.
Tim cận ngang của ĐTHS là:
1y
. Loại C.
Du của đạo hàm:
'
0y
. Loại D.
Câu 21: Tập nghim của bt phương trnh
1
24
x
là
A.
;3 .
B.
;5 .
C.
1;3 .
D.
1; .
Lời giải:
Ta có:
1
2 4 1 2 3.
x
xx
Câu 22: Từ 10 điểm phân bit trong không gian có thể tạo thành bao nhiêu vectơ khác vectơ
0
?
A.
10
2
. B.
10
P
. C.
2
10
A
. D.
2
10
C
.
Lời giải:
Chọn 2 điểm từ 10 điểm phân bit đã cho rồi xếp vào 2 vị trí điểm đầu - điểm cuối của véc tơ
Số véc tơ tạo thành là
2
10
A
.
Câu 23: Cho hàm số
y f x
xác định và liên tục trên
đồng thời thoả mãn:
( ) 3 5sinf x x
,
(0) 14f
. Khẳng định nào sau đây đúng?
A.
( ) 3 5f
. B.
( ) 3 5sin 9f x x x
.
C.
( ) 3 5cos 9f x x x
. D.
3
9
22
f
.
Lời giải:
Ta có
( )d 3 5s n 3cd 5oi sf x x x Cf x x x x
.
Mà
93.0 5co(0) 14s0f C C
.
Suy ra
3 5cos 9.f x x x
Do đó
93. 5co
3
22
9
2
s
2
f
.
Câu 24: Nếu
d
4
0
( ) 37f x x
thì
d
4
2
0
2 ( ) 3f x x x
bằng
A. 12. B. 18. C.
27
. D. 10.
Lời giải:
Ta có:
4 4 4
4
2 2 3
0
0 0 0
2 ( ) 3 d 2 ( )d 3 d 2.37 74 64 10
f x x x f x x x x x
.
Câu 25: Họ tt cả các nguyên hàm của hàm số
cos 6f x x x
là
A.
2
sin 3x x C
. B.
sin xC
. C.
2
sin 3x x C
. D.
2
sin 6x x C
.
Lời giải:
Ta có
d cos 6 df x x x x x
2
sin 3x x C
. Vậy chọn A.
Câu 26: Cho hàm số
y f x
có đồ thị như hnh bên dưới:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Mnh đề nào sau đây đúng?
A. Hàm số
fx
nghịch biến trên
2;5
. B. Hàm số
fx
nghịch biến trên
0;5
.
C. Hàm số
fx
đồng biến trên
;0
. D. Hàm số
fx
đồng biến trên
5;
.
Lời giải:
Dựa vào đồ thị hàm số
y f x
, hàm số
fx
đồng biến trên
5;
.
Câu 27: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A.
1x
. B.
3.y
C.
3x
. D.
1y
.
Lời giải:
Từ bảng biến thiên ta thy hàm số đã cho đạt cực tiểu tại
3x
.
Câu 28: Cho khối trụ
T
,
là mặt phẳng đi qua trục và cắt khối trụ
T
theo thiết din là hình
vuông cạnh 2a. Thể tích khối trụ
T
bằng
A.
3
3
a
B.
3
2.a
C.
3
2
3
a
. D.
3
.a
Lời giải:
Thiết din của khối trụ
T
được cắt bởi mặt phẳng
là hình vuông cạnh bằng
2a
nên ta
có
2l h a
, bán kính đường tròn đáy bằng
1
.2
2
r a a
. Vậy
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
2 2 3
. .2 2 .V B h r h a a a
Câu 29: Cho
a
là số thực dương khác
1
. Giá trị của
3
log
a
a
bằng
A.
0.
B.
1
.
3
C.
3.
D.
3.
Lời giải:
Ta có
1
3
3
11
log log log .
33
a a a
a a a
Câu 30: Thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số
2
43y x x
và
trục hoành quay quanh trục
Ox
là
A.
4
3
V
. B.
16
15
V
. C.
16
15
V
. D.
4
3
V
.
Lời giải:
Hoành độ giao điểm của đồ thị hàm số
2
43y x x
và trục hoành là nghim phương trnh
2
1
4 3 0
3
x
xx
x
.
Do đó, thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số
2
43y x x
và trục hoành quay quanh trục
Ox
là
3
2
2
1
4 3 dV x x x
3
4 3 2
1
8 22 24 9 dx x x x x
3
53
42
1
22 16
2 12 9
5 3 15
xx
x x x
.
Câu 31: Cho hnh chóp
.S ABC
có đáy
ABC
là tam giác vuông cạnh huyền
BC a
. Hnh chiếu
vuông góc của
S
lên
ABC
trng với trung điểm của
BC
.
H
A
C
B
S
Biết
SB a
. Tính số đo của góc giữa
SA
và
ABC
.
A.
75
. B.
30
. C.
60
. D.
45
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
H
A
C
B
S
Gọi
H
là trung điểm của
BC
.
Theo giả thiết ta có
SH ABC
và góc giữa
SA
và
ABC
là góc
SAH
.
Ta có
2
2 2 2
3
42
aa
SH SB BH a
và
1
22
a
AH BC
.
Ta có
3
2
tan 3 60
2
a
SH
SAH SAH
a
AH
.
Vậy góc giữa
SA
và
ABC
bằng
60
.
Câu 32: Cho hàm số bậc ba
y f x
có đồ thị như hnh vẽ bên dưới:
Số giá trị nguyên của tham số
m
để đường thẳng
ym
cắt đồ thị hàm số đã cho tại ba điểm
phân bit là
A. Vô số. B.
3
. C. 0. D.
5
.
Lời giải:
Từ đồ thị ta thy để đường thẳng
ym
cắt đồ thị hàm số đã cho tại ba điểm phân bit khi
15m
. Vì
m
nguyên nên
2;3;4m
.
Vậy có 3 giá trị nguyên của
m
thoả mãn yêu cầu bài toán
Câu 33: Có bao nhiêu giá trị nguyên của tham số thực m để hàm số
32
4 9 5y x mx m x
nghịch biến trên khoảng
;
?
A. 5. B. 7. C. 4. D. 6.
Lời giải:

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
Ta có
2
' 3 2 4 9y x mx m
.
Hàm số nghịch biến trên
;
' 0,yx
2
' 12 27 0 9 3m m m
(*)
Từ (*) suy ra
9; 8; 7; 6; 5; 4; 3m
là các giá trị nguyên của m thỏa mãn yêu cầu
của bài toán.
Câu 34: Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong
hộp. Xác sut để 5 viên bi được chọn có đủ ba màu và số bi đỏ bằng số bi vàng bằng
A.
11
18
. B.
5
18
. C.
75
408
. D.
95
408
.
Lời giải:
Số phần tử của không gian mẫu là số cách chọn ngẫu nhiên 5 viên bi từ hộp chứa 18 viên bi.
Suy ra
5
18
C
.
Gọi
A
là biến cố 5 viên bi được chọn có đủ ba màu và số bi đỏ bằng số bi vàng. Ta có các
trường hợp thuận lợi cho biến cố
A
là:
TH 1: Chọn 1 viên bi đỏ, 1 viên bi vàng và 3 viên bi xanh. Có
..
1 1 3
6 7 5
CCC
cách chọn.
TH 2: Chọn 2 viên bi đỏ, 2 viên bi vàng và 1 viên bi xanh. Có
..
2 2 1
6 7 5
CCC
cách chọn.
Do đó số phần tử của biến cố
A
là
. . . .
1 1 3 2 2 1
6 7 5 6 7 5
A C C C C C C
.
Vậy xác sut cần tính là
. . . .
1 1 3 2 2 1
6 7 5 6 7 5
5
18
A
C C C C C C 95
PA
C 408
.
Câu 35: Phương trnh
9 4.3 3 0
xx
có tổng các nghim là
A.
1
. B.
4
. C.
1
. D.
4
.
Lời giải:
Ta có:
2
3 1 0
9 4.3 3 0 3 4.3 3 0
1
33
x
x x x x
x
x
x
.
Vậy tổng các nghim của phương trnh là
1
.
Câu 36: Gọi
12
;zz
là hai nghim phức của phương trnh
2
2 2 0zz
. Tập hợp các điểm bểu diễn
của số phức
w
thỏa mãn
12
w z w z
là đường thẳng có phương trnh
A.
0xy
. B.
0x
. C.
0xy
. D.
0y
.
Lời giải:
Phương trnh
2
1
2 2 0
1
zi
zz
zi
.
Gọi
;,w x yi x y
12
2 2 2 2
1 1 1 1
1 1 1 1 0.
w z w z x y i x y i
x y x y y
Do đó tập hợp các điểm bểu diễn của số phức
w
là đường thẳng có phương trnh
0.y
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2;3A
và đường thẳng
3 1 7
:
2 1 2
x y z
d
. Đường
thẳng
đi qua
A
và song song với
d
có phương trnh là
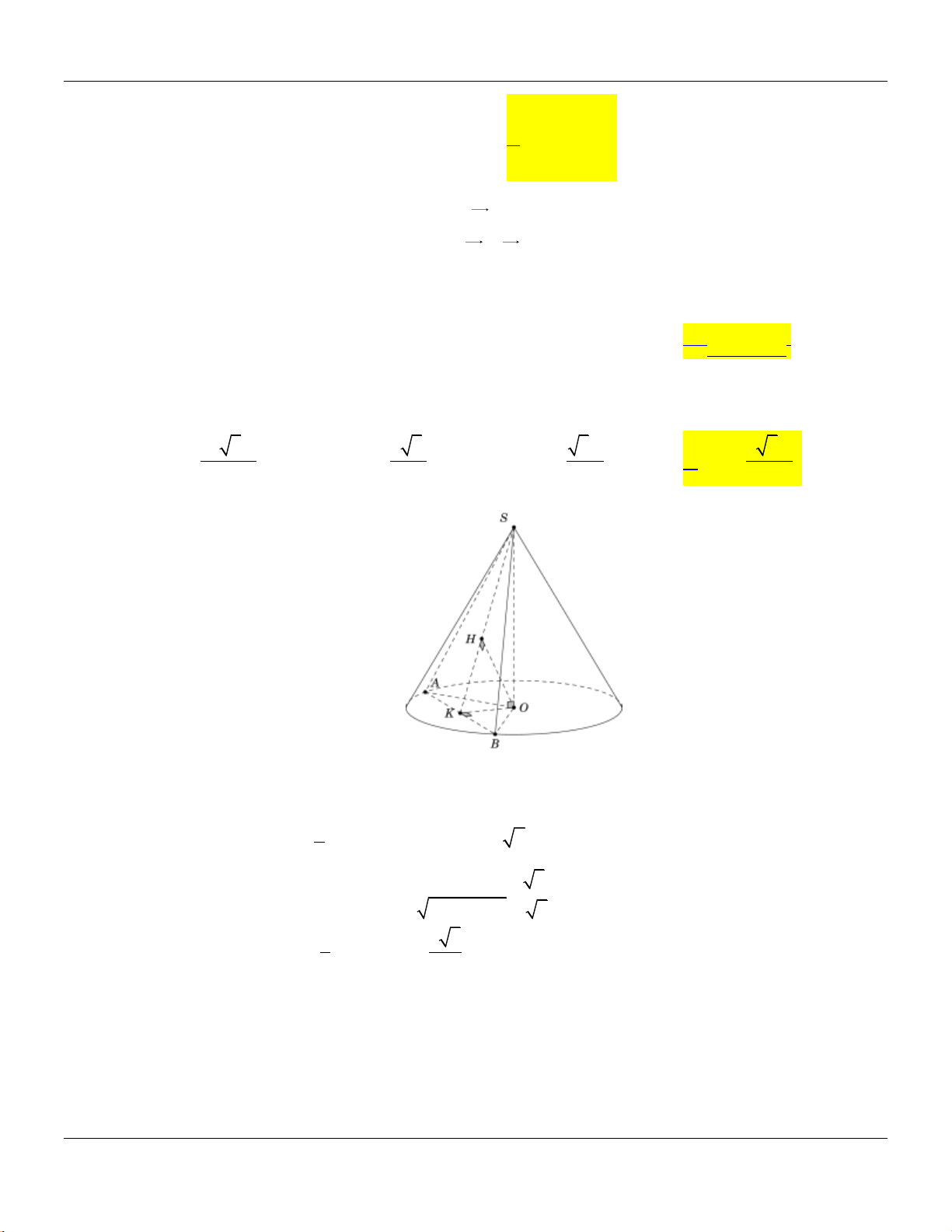
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
A.
13
2
37
xt
yt
zt
. B.
3
12
73
xt
yt
zt
. C.
32
3
12
xt
yt
zt
. D.
2
12
23
xt
yt
zt
.
Lời giải:
Vectơ chỉ phương của đường thẳng
d
là
2;1; 2
d
u
.
Do
//d
nên
có vectơ chỉ phương là
2;1; 2
d
uu
và
đi qua
A
.
Kiểm tra phương án C thỏa mãn.
Câu 38: Trong không gian
Oxyz
, cho điểm
1;2;3A
. Điểm đối xứng với
A
qua trục
Oz
có tọa độ là
A.
1;2; 3
. B.
1;2; 3
. C.
1; 2;0
. D.
1; 2;3
.
Câu 39: Cắt hình nón bởi một mặt phẳng đi qua đỉnh và tạo với mặt phẳng đáy một góc
0
60
được
thiết din là một tam giác vuông cân có cạnh huyền bằng
4.
Tính thể tích của khối nón ban
đầu.
A.
10 3
.
3
V
B.
53
.
3
V
C.
3
.
3
V
D.
53
.
3
V
Lời giải:
Giả sử hnh nón đỉnh
S
tâm
O
, thiết din qua đỉnh ở giả thiết là tam giác vuông cân
SAB
.
Gọi
K
là trung điểm của
AB
, suy ra góc giữa
SAB
và mặt đáy là
60SKO
.
Ta có
1
42
2
AB SK AB
và
22SA SB
.
Tam giác
SKO
vuông tại
: .tan 3O SO SK SKO
.
Tam giác
SAO
vuông tại
22
:5O AO SA SO
.
Thể tích khối nón
2
1 5 3
..
33
V AO SO
.
Câu 40: Trong không gian
Oxyz
, viết phương trnh đường thẳng
d
đi qua điểm
1;2; 1M
, song
song với mặt phẳng
:3P x y z
và vuông góc với đường thẳng
3
: 3 3
2
xt
yt
zt
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 16
A.
15
23
12
xt
yt
zt
. B.
1
23
12
xt
yt
zt
. C.
1
2
1
xt
yt
zt
. D.
5
32
2
xt
yt
zt
.
Lời giải:
VTPT của mặt phẳng
: 1;1; 1
P
Pn
.
VTCP của đường thẳng
: 1;3;2u
.
VTCP của đường thẳng
:;
dP
d u n u
5; 3;2
.
Vậy phương trnh tham số của đường thẳng
15
: 2 3
12
xt
d y t
zt
.
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 05_______________
Câu 1: Điểm
M
trong hình vẽ là điểm biểu diễn số phức nào dưới đây?
A.
2.zi
B.
2.zi
C.
2.zi
D.
2.zi
Câu 2: Đạo hàm của hàm số
2023
x
y
là
A.
1
.2023
x
yx
. B.
2023
ln2023
x
y
. C.
2023 .ln2023
x
y
. D.
2023
x
y
.
Câu 3: Hàm số
ln 2 1yx
có đạo hàm là
A.
2
ln 2 1
y
xx
. B.
1
21
y
x
. C.
2
21
y
x
. D.
1
2 1 ln2
y
x
.
Câu 4: Tập nghiệm của bất phương trình
39
x
là
A.
2;
. B.
0;2
. C.
0;
. D.
2;
.
Câu 5: Cho cấp số cộng
n
u
có
1
3u
và
2
1u
. Công sai của cấp số cộng đó bằng
A.
1
. B.
4
. C.
4
. D.
2
.
Câu 6: Trong không gian
Oxyz
, mặt phẳng nào dưới đây nhận
3;1; 7n
là một vectơ pháp
tuyến?
A.
3 7 0xz
. B.
3 7 1 0x y z
. C.
3 7 0xy
. D.
3 7 3 0x y z
.
Câu 7: Cho hàm số
fx
có bảng biến thiên như sau:
Số nghiệm của phương trình
25fx
là
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 8: Cho
5
2
d 10
f x x
. Khi đó,
5
2
2 3 d
f x x
bằng
A.
32
. B.
36
. C.
42
. D.
46
.
Câu 9: Hàm số nào có đồ thị là hình vẽ sau đây?
A.
32
34y x x
. B.
42
34y x x
. C.
32
34y x x
. D.
21
35
x
y
x
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 10: Trong không gian
,Oxyz
mặt cầu
2 2 2
: 2 1 3 9. S x y z
Tọa độ tâm của mặt cầu
S
là
A.
2;1;3 .
B.
2; 1;3 .
C.
2;1; 3 .
D.
2; 1; 3 .
Câu 11: Trong không gian
,Oxyz
cho điểm
1;0;0 .A
Góc giữa đường thẳng
OA
và mặt phẳng
Oxy
bằng
A.
90 .
B.
60 .
C.
30 .
D.
0.
Câu 12: Cho hai số phức
1
12zi
,
2
26zi
. Tích
12
.zz
bằng
A.
10 2i
. B.
2 12i
. C.
14 10i
. D.
14 2i
.
Câu 13: Cho hình lập phương có cạnh bằng
3
. Tổng diện tích các mặt của hình lập phương đã cho
bằng
A.
54
. B.
12
. C.
36
. D.
24
.
Câu 14: Cho khối tứ diện
ABCD
có
,,AB AC AD
đôi một vuông góc và
2 , 3 AB AC a AD a
. Thể
tích của khối tứ diện đó là
A.
3
4Va
. B.
3
2Va
. C.
3
Va
. D.
3
3Va
.
Câu 15: Diện tích
S
của mặt cầu có bán kính
r
được tính theo công thức nào dưới đây?
A.
2
4Sr
. B.
2
Sr
. C.
2
4
3
Sr
. D.
2
1
3
Sr
.
Câu 16: Trong các số phức sau, số phức nào dưới đây là số thuần ảo?
A.
1 i
. B.
3i
. C.
2
. D.
5
.
Câu 17: Thể tích của khối nón có đường kính đường tròn đáy là
4,
đường cao bằng
6
là
A.
8.
V
B.
32 .
V
C.
24 .
V
D.
96 .
V
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
21
3
3
1
:
zyx
đi qua điểm nào dưới đây?
A.
3; 1;0N
. B.
3; 1;2P
. C.
1;3;0M
. D.
1; 3;0Q
.
Câu 19: Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới:
Giá trị cực đại của hàm số đã cho là
A.
1
. B.
1
. C.
0
. D.
2
.
Câu 20: Cho hàm số
y f x
có
lim 1
x
fx
và
lim 1
x
fx
. Khẳng định nào sau đây đúng?
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là đường thẳng
1y
và đường thẳng
1y
.
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là đường thẳng
1x
và đường thẳng
1x
.
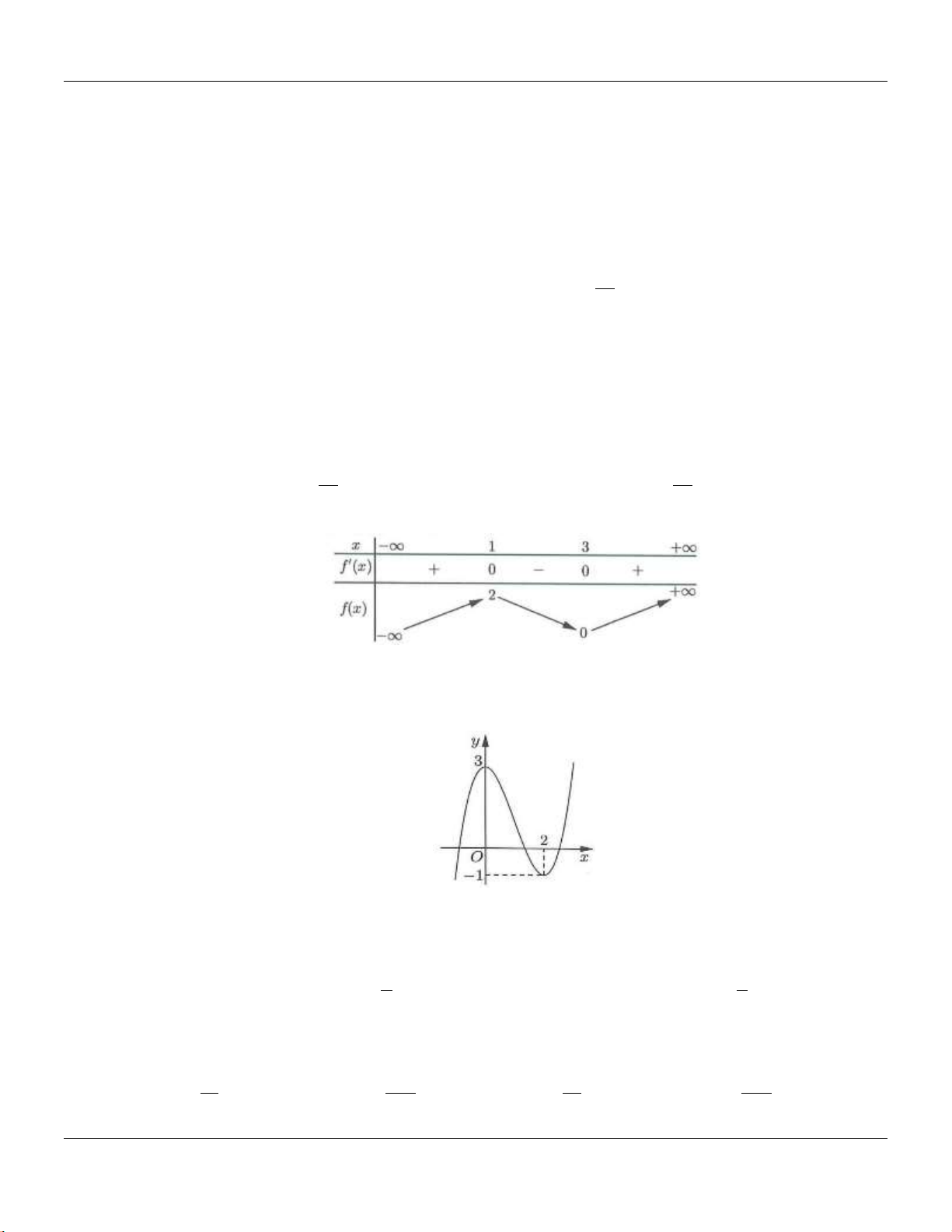
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
Câu 21: Tập nghiệm của bất phương trình
2
log 1 3x
là
A.
;8S
. B.
;7S
. C.
1; 8S
. D.
1; 7S
.
Câu 22: Lớp 10A có 20 học sinh nam và 15 học sinh nữ. Có bao nhiêu cách chọn ra một học sinh của
lớp 10A để làm lớp trưởng?
A.
300
. B.
15
. C.
35
. D.
20
.
Câu 23: Cho
d
x x F x C
. Khẳng định nào dưới đây đúng?
A.
1
Fx
. B.
F x x
. C.
2
2
x
F x C
. D.
F x x
.
Câu 24: Nếu
2
1
d3
f x x
và
2
3
d1
f x x
thì
3
1
d
f x x
bằng
A. 4. B.
2
. C.
2
. D.
4
.
Câu 25: Cho hàm số
cosf x x x
. Khẳng định nào dưới đây đúng?
A.
2
d sin .f x x x x C
B.
2
d sin .f x x x x C
C.
2
d sin .
2
x
f x x x C
D.
2
d sin .
2
x
f x x x C
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
0;2
. B.
3;
. C.
;1
. D.
2;3
.
Câu 27: Cho hàm số bậc ba
y f x
có đồ thị như hình bên dưới:
Giá trị cực tiểu của hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 28: Với
a
là số thực dương tùy ý,
aalog 3 log 2
bằng
A.
loga
. B.
2
log
3
. C.
2
log 6a
. D.
3
log .
2
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường
2
2y x x
và
0y
quanh trục
Ox
là
A.
16
15
V
B.
16
9
V
C.
16
9
V
D.
16
15
V
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Câu 30: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
SA
vuông góc với đáy và
SA a
(tham
khảo hình vẽ).
C
B
A
S
Góc giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
A.
60 .
B.
30
C.
90
D.
45
Câu 31: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để phương trình
f x m
có ba
nghiệm thực phân biệt. Tổng tất cả các phần tử của
S
bằng
A.
3
. B.
5
. C.
3
. D.
4
.
Câu 32: Cho hàm số
()y f x
liên tục trên và có đạo hàm
2
2 1 3 , .
f x x x x x
Hàm
số đồng biến trên khoảng nào dưới đây?
A.
; 1 .
B.
;0 .
C.
3; .
D.
1;3 .
Câu 33: Từ một hộp chứa
11
quả cầu màu đỏ và
4
quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3
quả cầu. Xác suất để lấy được
3
quả cầu màu xanh là
A.
4
.
455
B.
24
.
455
C.
4
.
165
D.
33
.
91
Câu 34: Một khối trụ có thiết diện qua trục là một hình vuông. Biết diện tích xung quanh của khối trụ
bằng
16
. Thể tích của khối trụ đã cho bằng
A.
24
. B.
32
. C.
16
. D.
8
.
Câu 35: Cho phương trình
2
24
log 8log 1 0.xx
Giải phương trình trên bằng cách đặt
2
log ,tx
ta
thu được phương trình nào dưới đây?
A.
2
8 1 0.tt
B.
2
4 1 0.tt
C.
2
16 1 0.tt
D.
2
6 1 0.tt
Câu 36: Cho
A
,
B
,
C
tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức
1
12zi
,
2
25zi
,
3
24zi
. Số phức
z
biểu diễn bởi điểm
D
sao cho tứ giác
ABCD
là hình bình
hành là
A.
17i
. B.
5 i
. C.
15i
. D.
35i
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 37: Trong không gian
Oxyz
, đường thẳng đi qua điểm
3;2;1M
và vuông góc với mặt phẳng
:2 5 4 0P x y
có phương trình là
A.
32
25
1
xt
yt
z
. B.
32
25
1
xt
yt
z
. C.
32
25
xt
yt
zt
. D.
32
2 5 .
1
xt
yt
z
Câu 38: Trong không gian
Oxyz
, cho điểm
3;5;7A
. Hình chiếu vuông góc của điểm
A
lên mặt
phẳng
Oxz
có tọa độ là
A.
3;5;7 .
B.
3;5;0 .
C.
3;0;7 .
D.
0;5;0 .
Câu 39: Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
2,a
cạnh bên bằng
3a
. Khoảng cách từ
A
đến
SCD
bằng
A.
14
3
a
. B.
14
4
a
. C.
14a
. D.
14
2
a
.
Câu 40: Cho hình nón
N
có chiều cao
3.h
Một mặt phẳng đi qua đỉnh của hình nón và cắt hình
nón theo một thiết diện là tam giác vuông có diện tích bằng
8.
Tính thể tích của khối nón giới
hạn bởi hình nón
.N
A.
16 .
B.
21 .
C.
12 .
D.
7.
________________________HẾT________________________

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Điểm
M
trong hình vẽ là điểm biểu diễn số phức nào dưới đây?
A.
2.zi
B.
2.zi
C.
2.zi
D.
2.zi
Lời giải:
Điểm
M
trong hình vẽ là điểm biểu diễn số phức:
2zi
.
Câu 2: Đạo hàm của hàm số
2023
x
y
là
A.
1
.2023
x
yx
. B.
2023
ln2023
x
y
. C.
2023 .ln2023
x
y
. D.
2023
x
y
.
Câu 3: Hàm số
ln 2 1yx
có đạo hàm là
A.
2
ln 2 1
y
xx
. B.
1
21
y
x
. C.
2
21
y
x
. D.
1
2 1 ln2
y
x
.
Lời giải:
Hàm số
ln 2 1yx
có đạo hàm là
2
21
y
x
.
Câu 4: Tập nghiệm của bất phương trình
39
x
là
A.
2;
. B.
0;2
. C.
0;
. D.
2;
.
Lời giải:
Ta có
2
3 9 3 3 2 2;
xx
xx
.
Vậy tập nghiệm của bất phương trình là
2;
.
Câu 5: Cho cấp số cộng
n
u
có
1
3u
và
2
1u
. Công sai của cấp số cộng đó bằng
A.
1
. B.
4
. C.
4
. D.
2
.
Lời giải:
Ta có
2211
1 3 4ddu u u u
.
Câu 6: Trong không gian
Oxyz
, mặt phẳng nào dưới đây nhận
3;1; 7n
là một vectơ pháp
tuyến?
A.
3 7 0xz
. B.
3 7 1 0x y z
. C.
3 7 0xy
. D.
3 7 3 0x y z
.
Lời giải:
Phương trình mặt phẳng
3 7 3 0x y z
có một vectơ pháp tuyến là
3;1; 7n
.
Câu 7: Cho hàm số
fx
có bảng biến thiên như sau:
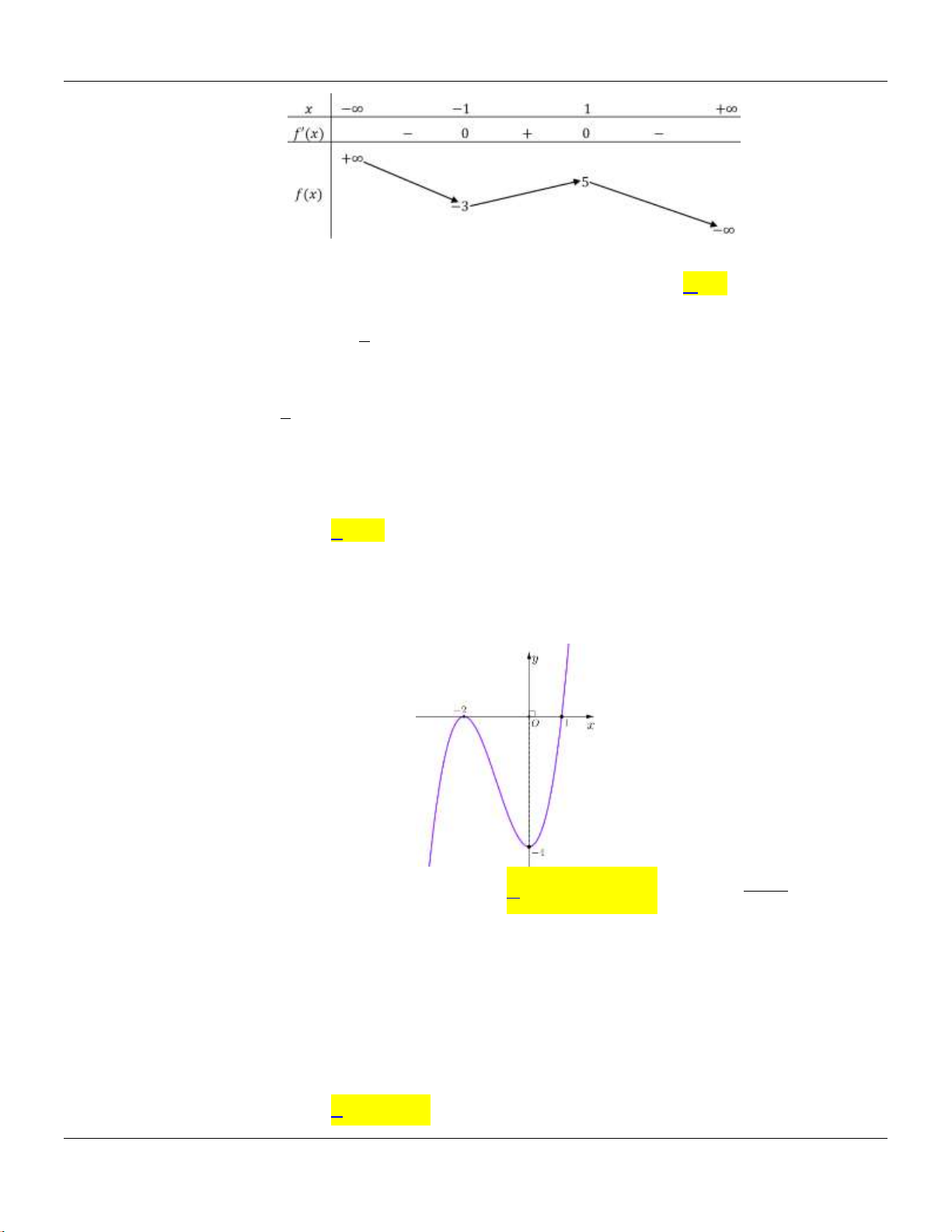
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
Số nghiệm của phương trình
25fx
là
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải:
Ta có:
5
25
2
f x f x
.
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số
y f x
và
đường thẳng
5
2
y
. Từ đồ thị ta thấy có ba giao điểm.
Vậy phương trình đã cho có ba nghiệm.
Câu 8: Cho
5
2
d 10
f x x
. Khi đó
5
2
2 3 d
f x x
bằng
A.
32
. B.
36
. C.
42
. D.
46
.
Lời giải:
Ta có
5 5 5
2 2 2
2 3 d 2d 3 d 36.
f x x x f x x
Câu 9: Hàm số nào có đồ thị là hình vẽ sau đây?
A.
32
34y x x
. B.
42
34y x x
. C.
32
34y x x
. D.
21
35
x
y
x
.
Lời giải:
Dựa vào hình dạng đồ thị, ta thấy đây là đồ thị của hàm số bậc 3, với hệ số
0 lim
x
ay
. Nên loại B và D.
Khi
04xy
.
Câu 10: Trong không gian
,Oxyz
mặt cầu
2 2 2
: 2 1 3 9. S x y z
Tọa độ tâm của mặt cầu
S
là
A.
2;1;3 .
B.
2; 1;3 .
C.
2;1; 3 .
D.
2; 1; 3 .

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
Lời giải:
Phương trình
2 2 2
2; 1;3
2 1 3 9
3
I
x y z
R
Câu 11: Trong không gian
,Oxyz
cho điểm
1;0;0 .A
Góc giữa đường thẳng
OA
và mặt phẳng
Oxy
bằng
A.
90 .
B.
60 .
C.
30 .
D.
0.
Câu 12: Cho hai số phức
1
12zi
,
2
26zi
. Tích
12
.zz
bằng
A.
10 2i
. B.
2 12i
. C.
14 10i
. D.
14 2i
.
Lời giải:
Ta có
12
. 1 2 2 6 14 2z z i i i
.
Câu 13: Cho hình lập phương có cạnh bằng
3
. Tổng diện tích các mặt của hình lập phương đã cho
bằng
A.
54
. B.
12
. C.
36
. D.
24
.
Lời giải:
Tổng diện tích các mặt của hình lập phương là:
2
6.3 54S
.
Câu 14: Cho khối tứ diện
ABCD
có
,,AB AC AD
đôi một vuông góc và
2 , 3 AB AC a AD a
. Thể
tích của khối tứ diện đó là
A.
3
4Va
. B.
3
2Va
. C.
3
Va
. D.
3
3Va
.
Lời giải:
Do khối tứ diện
ABCD
có
,,AB AC AD
đôi một vuông góc nên
3
1
. . 2
6
ABCD
V AB AC AD a
.
Câu 15: Diện tích
S
của mặt cầu có bán kính
r
được tính theo công thức nào dưới đây?
A.
2
4Sr
. B.
2
Sr
. C.
2
4
3
Sr
. D.
2
1
3
Sr
.
Câu 16: Trong các số phức sau, số phức nào dưới đây là số thuần ảo?
A.
1 i
. B.
3i
. C.
2
. D.
5
.
Lời giải:
Số phức
3i
là số phức thuần ảo.
Câu 17: Thể tích của khối nón có đường kính đường tròn đáy là
4,
đường cao bằng
6
là
A.
8.
V
B.
32 .
V
C.
24 .
V
D.
96 .
V
Lời giải:
22
11
.6.2 8
33
V hR
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
21
3
3
1
:
zyx
đi qua điểm nào dưới đây?
A.
3; 1;0N
. B.
3; 1;2P
. C.
1;3;0M
. D.
1; 3;0Q
.
Lời giải:
Ta có:
2
0
1
33
3
11
Suy ra điểm
0;3;1M
thuộc đường thẳng
Câu 19: Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới:

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Giá trị cực đại của hàm số đã cho là
A.
1
. B.
1
. C.
0
. D.
2
.
Lời giải:
Qua đồ thị hàm số
y f x
ta thấy giá trị cực đại của hàm số bằng
1
.
Câu 20: Cho hàm số
y f x
có
lim 1
x
fx
và
lim 1
x
fx
. Khẳng định nào sau đây đúng?
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là đường thẳng
1y
và đường thẳng
1y
.
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là đường thẳng
1x
và đường thẳng
1x
.
Lời giải:
Vì
lim 1
x
fx
và
lim 1
x
fx
nên đồ thị hàm số đã cho có hai tiệm cận ngang là đường
thẳng
1y
và đường thẳng
1y
.
Câu 21: Tập nghiệm của bất phương trình
2
log x 1 3
là
A.
;8S
. B.
;7S
. C.
1; 8S
. D.
1; 7S
.
Lời giải:
Ta có:
2
log 1 3x
3
0 1 2x
17x
Vậy tập nghiệm của bất phương trình
2
13log x
là
1; 7 .S
Câu 22: Lớp 10A có 20 học sinh nam và 15 học sinh nữ. Có bao nhiêu cách chọn ra một học sinh của
lớp 10A để làm lớp trưởng?
A.
300
. B.
15
. C.
35
. D.
20
.
Lời giải:
Lớp có
20 15 35
học sinh.
Suy ra số cách chọn một học sinh của lớp 10A để làm lớp trưởng là
1
35
35C
.
Câu 23: Cho
d
x x F x C
. Khẳng định nào dưới đây đúng?
A.
1
Fx
. B.
F x x
. C.
2
2
x
F x C
. D.
F x x
.
Lời giải:
Ta có
d
F x x x x
.
Câu 24: Nếu
2
1
dx 3fx
và
2
3
dx 1fx
thì
3
1
dxfx
bằng
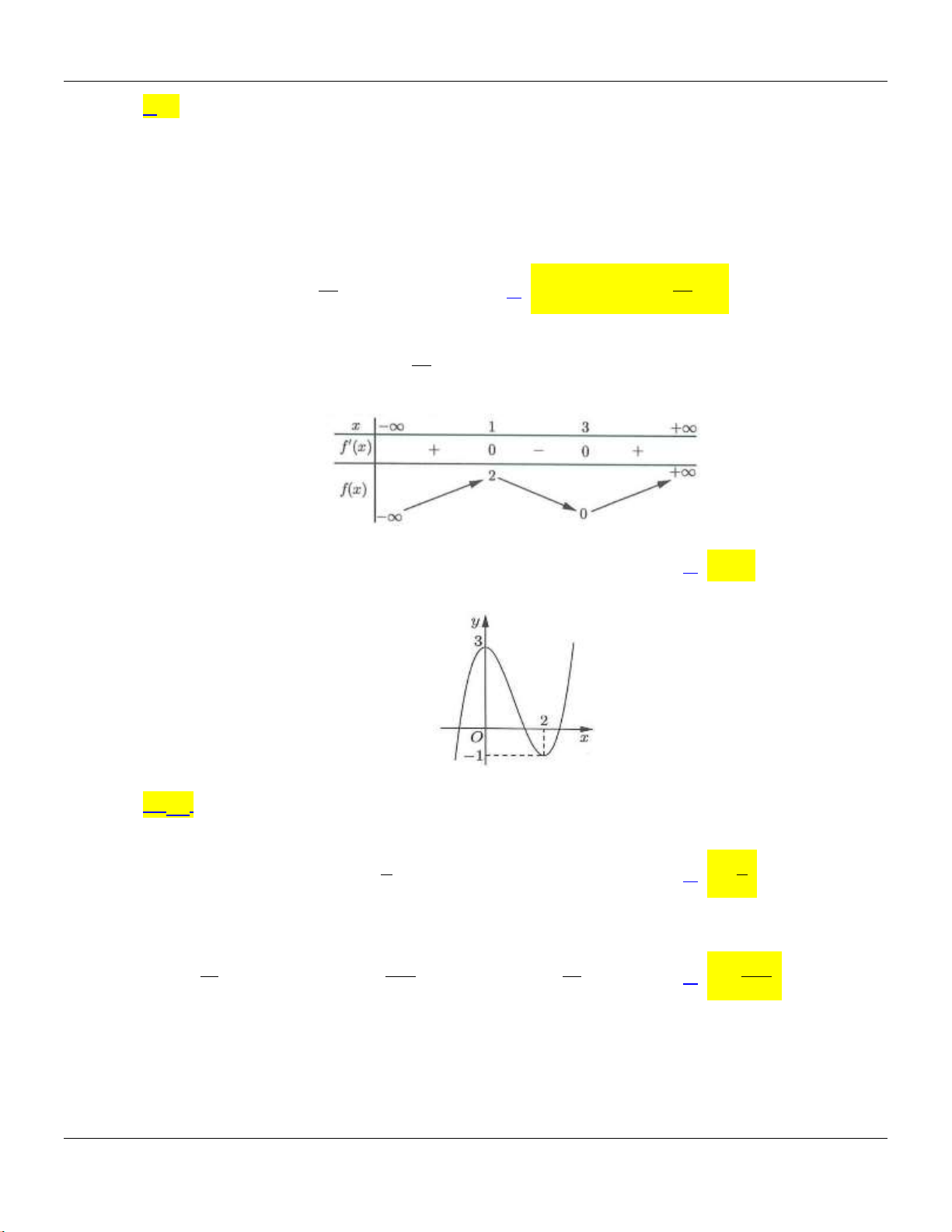
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
A. 4. B.
2
. C.
2
. D.
4
.
Lời giải:
Ta có
23
32
dx 1 dx 1f x f x
khi đó
3 2 3
1 1 2
dx dx dx 3 1 2f x f x f x
.
Câu 25: Cho hàm số
cosf x x x
. Khẳng định nào dưới đây đúng?
A.
2
d sin .f x x x x C
B.
2
d sin .f x x x x C
C.
2
d sin .
2
x
f x x x C
D.
2
d sin .
2
x
f x x x C
Lời giải:
2
d cos d n .
2
si
x
f x x x x x x C
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
0;2
. B.
3;
. C.
;1
. D.
2;3
.
Câu 27: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
Giá trị cực tiểu của hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 28: Với
a
là số thực dương tùy ý,
aalog 3 log 2
bằng
A.
loga
. B.
2
log
3
. C.
2
log 6a
. D.
3
log .
2
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường
2
2y x x
và
0y
quanh trục
Ox
là
A.
16
15
V
B.
16
9
V
C.
16
9
V
D.
16
15
V
Lời giải:
Phương trình hoành độ giao điểm của đường
2
2y x x
và đường
0y
là
2
0
20
2
x
xx
x
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Thể tích là
22
53
2
2 4 3 2 4
00
2
16
2 d 4 4 d 4. .
0
5 3 15
xx
V x x x x x x x x
Câu 30: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
SA
vuông góc với đáy và
SA a
(tham
khảo hình vẽ).
C
B
A
S
Góc giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
A.
60 .
B.
30
C.
90
D.
45
Lời giải:
Ta có:
SA ABC
nên góc giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
SBA
.
Do tam giác
SAB
vuông cân tại
45A SBA
.
Vậy góc giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
45
.
Câu 31: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để phương trình
f x m
có ba
nghiệm thực phân biệt. Tổng tất cả các phần tử của
S
bằng
A.
3
. B.
5
. C.
3
. D.
4
.
Lời giải:
Số nghiệm của phương trình
f x m
bằng số giao điểm của đồ thị hàm số
y f x
và
đường thẳng
:d y m
.
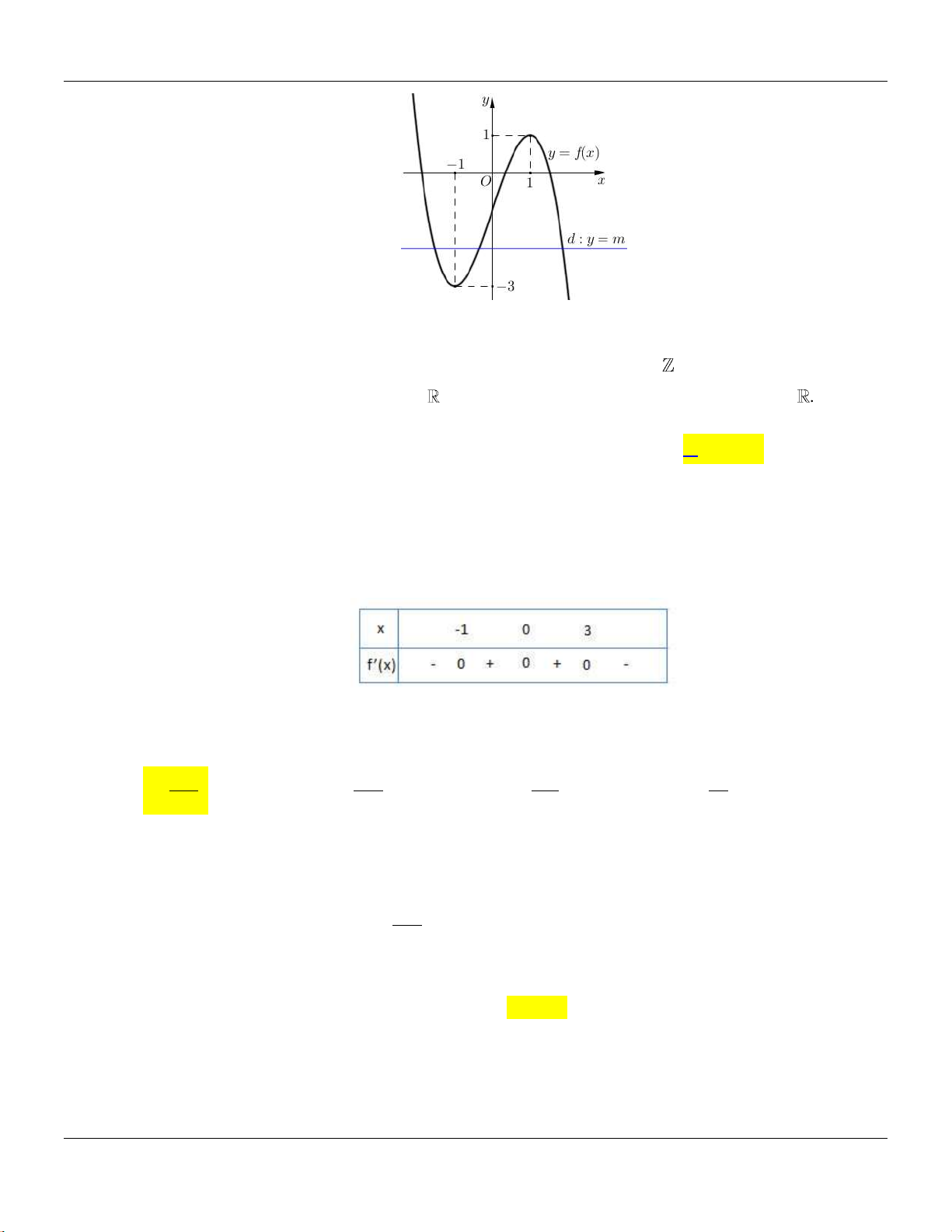
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
Dựa vào hình vẽ, ta có:
Phương trình
f x m
có ba nghiệm thực phân biệt khi đường thẳng
:d y m
cắt đồ thị
hàm số
y f x
tại ba điểm phân biệt, tức là
31m
. Mà
m
nên
2; 1;0m
.
Câu 32: Cho hàm số
()y f x
liên tục trên và có đạo hàm
2
'( ) 2 ( 1)(3 ), . f x x x x x
Hàm số
đồng biến trên khoảng nào dưới đây?
A.
; 1 .
B.
;0 .
C.
3; .
D.
1;3 .
Lời giải:
Ta có:
0
'( ) 0 1
3
x
f x x
x
Bảng xét dấu:
Căn cứ bảng xét dấu ta thấy hàm số đồng biến trên
( 1;3)
.
Câu 33: Từ một hộp chứa
11
quả cầu màu đỏ và
4
quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3
quả cầu. Xác suất để lấy được
3
quả cầu màu xanh là
A.
4
.
455
B.
24
.
455
C.
4
.
165
D.
33
.
91
Lời giải:
Số phần tử của không gian mẫu
3
15
nC
455
.
Gọi
A
là biến cố "
3
quả cầu lấy được đều là màu xanh". Suy ra
3
4
n A C
4
.
Vậy xác suất cần tìm là
4
455
PA
.
Câu 34: Một khối trụ có thiết diện qua trục là một hình vuông. Biết diện tích xung quanh của khối trụ
bằng
16
. Thể tích của khối trụ đã cho bằng
A.
24
. B.
32
. C.
16
. D.
8
.
Lời giải:

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Ta có thiết diện qua trục là hình vuông nên
2hR
Diện tích xung quanh bằng
16
nên
2 16 (*)Rh
Thay
2hR
vào
(*)
ta được
2
2 8 2RR
24hR
Thể tích khối trụ bằng :
2
.4.4 16V R h
.
Câu 35: Cho phương trình
2
24
log 8log 1 0.xx
Giải phương trình trên bằng cách đặt
2
log ,tx
ta
thu được phương trình nào dưới đây?
A.
2
8 1 0.tt
B.
2
4 1 0.tt
C.
2
16 1 0.tt
D.
2
6 1 0.tt
Lời giải:
Ta có:
22
2 4 2 2
log 8log 1 0 log 4log 1 0.x x x x
Đặt
2
log ,tx
phương trình trở thành
2
3 1 0.tt
Câu 36: Cho
A
,
B
,
C
tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức
1
12zi
,
2
25zi
,
3
24zi
. Số phức
z
biểu diễn bởi điểm
D
sao cho tứ giác
ABCD
là hình bình
hành là
A.
17i
. B.
5 i
. C.
15i
. D.
35i
.
Lời giải:
Ta có
1;2A
,
2;5B
,
2;4C
.
Gọi
;D x y
.Ta có
3;3AB
,
2 ;4DC x y
.
Để
ABCD
là hình bình hành thì
AB DC
2 3 5
4 3 1
xx
yy
.
Vậy
5zi
.
Câu 37: Trong không gian
Oxyz
, đường thẳng đi qua điểm
3;2;1M
và vuông góc với mặt phẳng
:2 5 4 0P x y
có phương trình là
A.
32
25
1
xt
yt
z
. B.
32
25
1
xt
yt
z
. C.
32
25
xt
yt
zt
. D.
32
2 5 .
1
xt
yt
z
Lời giải:
Gọi
d
là đường thẳng đi qua điểm
M
và vuông góc với mặt phẳng
P
Ta có
2; 5;0
d
P
d P u n
32
: : 2 5
2; 5;0
1
3;2;1
d
xt
d d y t
Q a M
z
u
u

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
Câu 38: Trong không gian
Oxyz
, cho điểm
3;5;7A
. Hình chiếu vuông góc của điểm
A
lên mặt
phẳng
Oxz
có tọa độ là
A.
3;5;7 .
B.
3;5;0 .
C.
3;0;7 .
D.
0;5;0 .
Câu 39: Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
2,a
cạnh bên bằng
3a
. Khoảng cách từ
A
đến
SCD
bằng
A.
14
3
a
. B.
14
4
a
. C.
14a
. D.
14
2
a
.
Lời giải:
2a
2a
3a
O
D
S
A
B
C
Gọi
.O AC BD
Do
.S ABCD
chóp đều nên đáy
ABCD
là hình vuông và
SO ABCD
.
Ta có:
,
2
,
d A SCD
AC
d O SCD OC
, 2. , 2 d A SCD d O SCD h
.
Xét
ACD
vuông tại
D
có:
22
AC AD CD
2 2 2CD a
2 OC OD a
.
Xét
SOC
vuông tại O có:
22
SO SC OC
2
2
32aa
7 a
.
Do tứ diện
SOCD
có ba cạnh
,OS
,OC
OD
đôi một vuông góc
2 2 2 2
1 1 1 1
h OS OC OD
222
2
1 1 1 8
7
7 2 2
a
aaa
14
4
a
h
.
Vậy khoảng cách từ
A
đến
SCD
bằng
14
2
a
.
Câu 40: Cho hình nón
N
có chiều cao
3.h
Một mặt phẳng đi qua đỉnh của hình nón và cắt hình
nón theo một thiết diện là tam giác vuông có diện tích bằng
8.
Tính thể tích của khối nón giới
hạn bởi hình nón
.N
A.
16 .
B.
21 .
C.
12 .
D.
7.
Lời giải:

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
S
A
B
O
h
r
l
Gọi thiết diện là tam giác
,.SAB SA SB l
Theo giả thiết:
2
8 8 4.
2
SAB
l
Sl
Bán kính của
N
là
22
7.r l h
Vậy thể tích khối nón là
2
1
7.
3
V h r
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
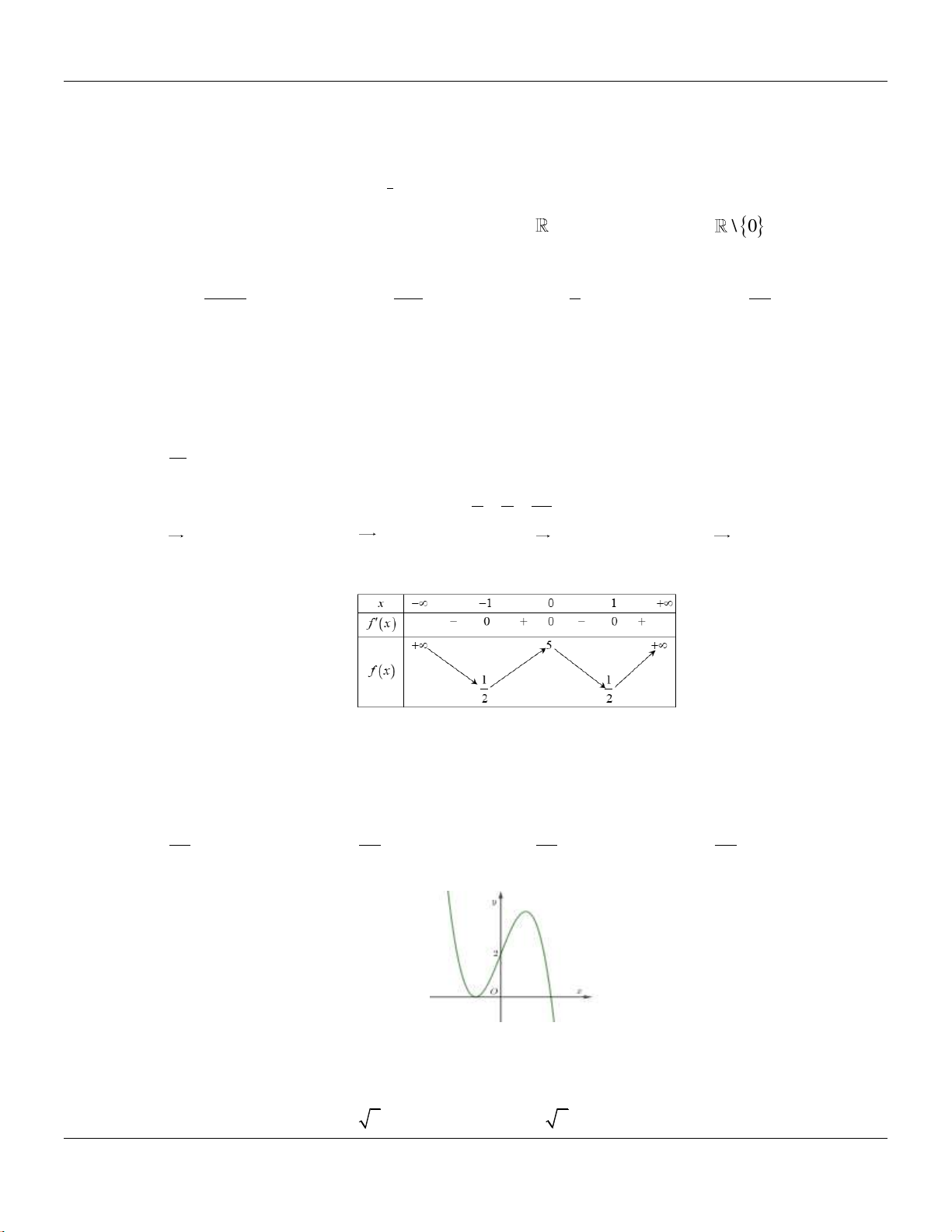
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 06_______________
Câu 1: Trên mặt phẳng tọa độ, cho
4; 3M
là điểm biểu diễn của số phức
z
. Phần ảo của
z
bằng
A.
4
. B.
3i
. C.
4
. D.
3
.
Câu 2: Tập xác định của hàm số
3
2
yx
là
A.
0;
. B.
2;
. C. . D.
\0
.
Câu 3: Trên khoảng
0;
, đạo hàm của hàm số
2
logyx
là
A.
1
ln2
y
x
. B.
ln2
y
x
. C.
1
y
x
. D.
1
2
y
x
.
Câu 4: Tập các nghiệm của bất phương trình
26
x
là
A.
2
log 6;
. B.
;3
. C.
3;
. D.
2
;log 6
.
Câu 5: Cho cấp số cộng
n
u
có số hạng đầu
1
2u
và số hạng thứ tư
4
17u
. Công sai của cấp số
cộng đã cho bằng
A.
15
2
. B.
5
. C.
3
. D.
15
.
Câu 6: Trong không gian
,Oxyz
mặt phẳng
( ): 1
2 2 1
x y z
P
, có một vectơ pháp tuyến là
A.
3
(2;2; 1)n
. B.
4
(1;1; 2)n
. C.
1
(2; 2; 1)n
. D.
2
( 2; 2;1)n
.
Câu 7: Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm của phương trình
60fx
là
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 8: Cho
1
2
0
2 3 d 1
x x f x x
. Tính
1
0
df x x
.
A.
1
3
. B.
5
3
. C.
1
9
. D.
5
9
.
Câu 9: Đường cong trong hình vẽ bên là đồ thị của một hàm số nào?
A.
3
32y x x
. B.
3
32y x x
. C.
42
2y x x
. D.
3
32y x x
.
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 4 2 0S x y z y z
. Bán kính mặt cầu
S
bằng
A.
1
. B.
7
. C.
22
. D.
7
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 11: Trong không gian
,Oxyz
góc giữa trục
Ox
và
Oz
bằng
A.
90 .
B.
60 .
C.
30 .
D.
0.
Câu 12: Cho số phức
z
thỏa mãn
12i z i
. Môđun của số phức
z
bằng
A.
10
2
. B.
3
. C.
2
. D.
10
.
Câu 13: Cho khối lăng trụ đứng
.ABC A B C
có
BB a
, đáy
ABC
là tam giác vuông cân tại
B
và
BA BC a
. Thể tích của khối lăng trụ đã cho là
A.
3
6
a
V
. B.
3
2
a
V
. C.
3
3
a
V
. D.
3
Va
.
Câu 14: Cho khối chóp
.S ABC
có đáy là tam giác đều cạnh
a
,
SA ABC
,
SA a
(tham khảo hình
vẽ).
S
A
B
C
Thể tích của khối chóp đã cho bằng
A.
3
3
4
a
. B.
3
3
6
a
. C.
3
3a
. D.
3
3
12
a
.
Câu 15: Nếu tăng bán kính của một khối cầu gấp
3
lần thì thể tích khối cầu đó thay đổi như thế nào?
A. Thể tích tăng gấp
6
lần. B. Thể tích tăng gấp
9
lần.
C. Thể tích tăng gấp
3
lần. D. Thể tích tăng gấp
27
lần.
Câu 16: Cho số phức bất kì
,z a bi a b
. Khẳng định nào sau đây đúng?
A.
22
z a b
. B.
22
z a b
. C.
33
z a b
. D.
22
z a b
.
Câu 17: Cho tam giác
ABC
vuông tại
A
,
AB a
và
3AC a
. Tính độ dài đường sinh
l
của hình
nón có được khi quay tam giác
ABC
xung quanh trục
AB
.
A.
2la
. B.
2la
. C.
3la
. D.
la
.
Câu 18: Trong không gian
Oxyz
, đường thẳng
12
:
2 1 3
x y z
d
đi qua điểm nào dưới đây?
A.
2; 1;3A
. B.
1;2;0C
. C.
1; 2;0D
. D.
0;2; 1B
.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Tìm giá trị cực đại
CÐ
y
và giá trị cực tiểu
CT
y
của hàm số đã cho.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
A.
3
CÐ
y
và
0
CT
y
. B.
3
CÐ
y
và
2
CT
y
.
C.
2
CÐ
y
và
2
CT
y
. D.
2
CÐ
y
và
0
CT
y
.
Câu 20: Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số
2
2
x
y
x
?
A.
2x
. B.
2x
. C.
1y
. D.
1y
.
Câu 21: Tập nghiệm của bất phương trình
3
log 2 1 2x
là
A.
1
;5
2
S
. B.
1
;5
2
S
. C.
;5S
. D.
5;S
.
Câu 22: Có
3
cây bút đỏ,
4
cây bút xanh trong một hộp bút. Hỏi có bao nhiêu cách lấy ra một cây bút
từ hộp bút đó?
A.
7
. B.
4
. C.
12
. D.
3
.
Câu 23: Cho
dsin .x x G x C
Đạo hàm hàm số
2y G x x
là
A.
2sin 1.yx
B.
2sin 1.yx
C.
2sin .yx
D.
2
2cos .
2
x
y x C
Câu 24: Nếu
d
4
0
( ) 37f x x
thì
d
4
2
0
2 ( ) 3f x x x
bằng
A. 12. B. 18. C.
27
. D. 10.
Câu 25: Cho hàm số
sinf x x x
. Khẳng định nào dưới đây đúng?
A.
2
d cos .
2
x
f x x x C
B.
2
d cos .
2
x
f x x x C
C.
2
d sin .
2
x
f x x x C
D.
2
d cos .
2
x
f x x x C
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
0;2
. B.
2;
. C.
;1
. D.
2;3
.
Câu 27: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
Điểm cực tiểu của hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 28: Với
a
là số thực dương tùy ý,
aa
33
log 5 log 2
bằng
A.
3
log 3 .a
B.
3
2
log .
5
C.
2
3
log 10a
. D.
3
5
log .
2
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường
2
y x x
và
0y
quanh trục
Ox
là
A.
16
15
V
B.
16
15
V
C.
1
30
V
D.
30
V
Câu 30: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
SA
vuông góc với đáy và
2AB SA
(tham khảo hình vẽ).
C
B
A
S
Góc giữa hai mặt phẳng
SBC
và
ABC
bằng
A.
60 .
B.
30
C.
90
D.
45
Câu 31: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
x
y
2
-2
-1
O
1
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
f x m
có ba nghiệm thực
phân biệt?
A.
4
. B.
5
. C.
3
. D.
2
.
Câu 32: Cho hàm số
y f x
có
1 3 , .f x x x x x
Hàm số
y f x
đồng biến trên khoảng
nào dưới đây?
A.
;0 .
B.
0;1 .
C.
1;2 .
D.
2; .
Câu 33: Chọn ngẫu nhiên 2 số tự nhiên khác nhau từ 25 số nguyên dương đầu tiên. Xác suất để chọn
được hai số có tổng là một số chẵn bằng
A.
1
2
. B.
13
25
. C.
12
25
. D.
313
625
.
Câu 34: Số nghiệm của phương trình
22
22
3 10.3 9 0
x x x x
là
A.
4.
B.
1.
C.
0.
D.
2.
Câu 35: Cho số phức
z
thỏa mãn
1 4.zi
Biết tập hợp các điểm biểu diễn số phức
w 3 4 1 2i z i
là đường tròn
.C
Tìm tâm
I
và bán kính
R
của đường tròn
.C
A.
2; 5 , 20.IR
B.
2; 5 , 4.IR
C.
2;5 , 4.IR
D.
2;5 , 20.IR
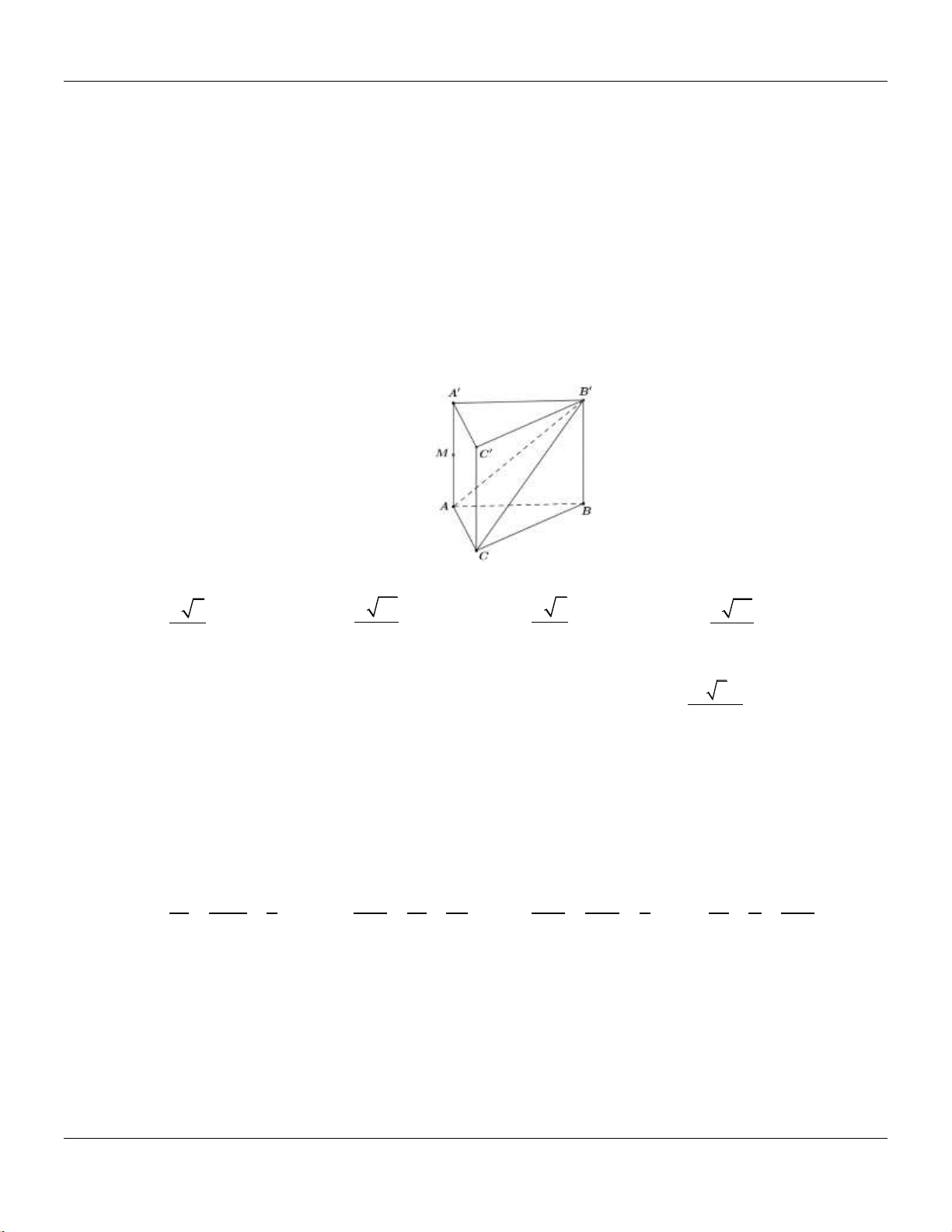
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 36: Trong không gian
Oxyz
, viết phương trình tham số của đường thẳng đi qua hai điểm
1;2; 3 , 2; 3;1AB
.
A.
1
25
32
xt
yt
zt
. B.
2
35
14
xt
yt
zt
. C.
3
85
54
xt
yt
zt
. D.
1
25
34
xt
yt
zt
.
Câu 37: Trong không gian
Oxyz
, cho điểm
3;5;7A
. Hình chiếu vuông góc của điểm
A
lên mặt
phẳng
Oyz
có tọa độ là
A.
3;5;7 .
B.
3;5;0 .
C.
3;0;7 .
D.
0;5;7 .
Câu 38: Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng
a
. Gọi
M
là trung điểm của
AA
.
Khoảng cách từ
M
đến mặt phẳng
AB C
bằng
A.
2
4
a
. B.
21
7
a
. C.
2
2
a
. D.
21
14
a
.
Câu 39: Cho hình nón
N
có chiều cao
2.ha
Một mặt phẳng
P
đi qua đỉnh của hình nón và cắt
hình hình nón theo một thiết diện là tam giác đều có diện tích bằng
2
16 3
.
9
a
Góc giữa
P
và
mặt đáy của
N
bằng
A.
90 .
B.
45 .
C.
60 .
D.
30 .
Câu 40: Trong không gian
,Oxyz
cho điểm
0; 2; 0M
và đường thẳng
43
:2
1
xt
d y t
zt
. Đường thẳng đi
qua
M
, cắt và vuông góc với
d
có phương trình là
A.
2
.
1 1 2
x y z
B.
1
.
1 1 2
x y z
C.
11
.
1 1 2
x y z
D.
1
.
1 1 2
x y z
________________________HẾT________________________

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Trên mặt phẳng tọa độ, cho
4; 3M
là điểm biểu diễn của số phức
z
. Phần ảo của
z
bằng
A.
4
. B.
3i
. C.
4
. D.
3
.
Lời giải:
Ta có:
43zi
nên phần ảo của
z
bằng
3
.
Câu 2: Tập xác định của hàm số
3
2
yx
là
A.
0;
. B.
2;
. C. . D.
\0
.
Lời giải:
Tập xác định của hàm số
3
2
yx
là
0;
.
Câu 3: Trên khoảng
0;
, đạo hàm của hàm số
2
logyx
là
A.
1
ln2
y
x
. B.
ln2
y
x
. C.
1
y
x
. D.
1
2
y
x
.
Lời giải:
Áp dụng công thức
1
log
ln
a
x
xa
. Ta có
1
ln2
y
x
Câu 4: Tập các nghiệm của bất phương trình
26
x
là
A.
2
log 6;
. B.
;3
. C.
3;
. D.
2
;log 6
.
Lời giải:
26
x
2
log 6x
2
log 6;x
.
Câu 5: Cho cấp số cộng
n
u
có số hạng đầu
1
2u
và số hạng thứ tư
4
17u
. Công sai của cấp số
cộng đã cho bằng
A.
15
2
. B.
5
. C.
3
. D.
15
.
Lời giải:
Ta có
41
41
17 2
35
33
uu
u u d d
.
Câu 6: Trong không gian
,Oxyz
mặt phẳng
( ): 1
2 2 1
x y z
P
, có một vectơ pháp tuyến là
A.
3
(2;2; 1)n
. B.
4
(1;1; 2)n
. C.
1
(2; 2; 1)n
. D.
2
( 2; 2;1)n
.
Lời giải:
Ta có
1 2 2 2 2 0
2 2 1
x y z
x y z x y z
Vậy một vectơ pháp tuyến của mặt phẳng
()P
là
4
(1;1; 2)n
.
Câu 7: Cho hàm số
y f x
có bảng biến thiên như sau:
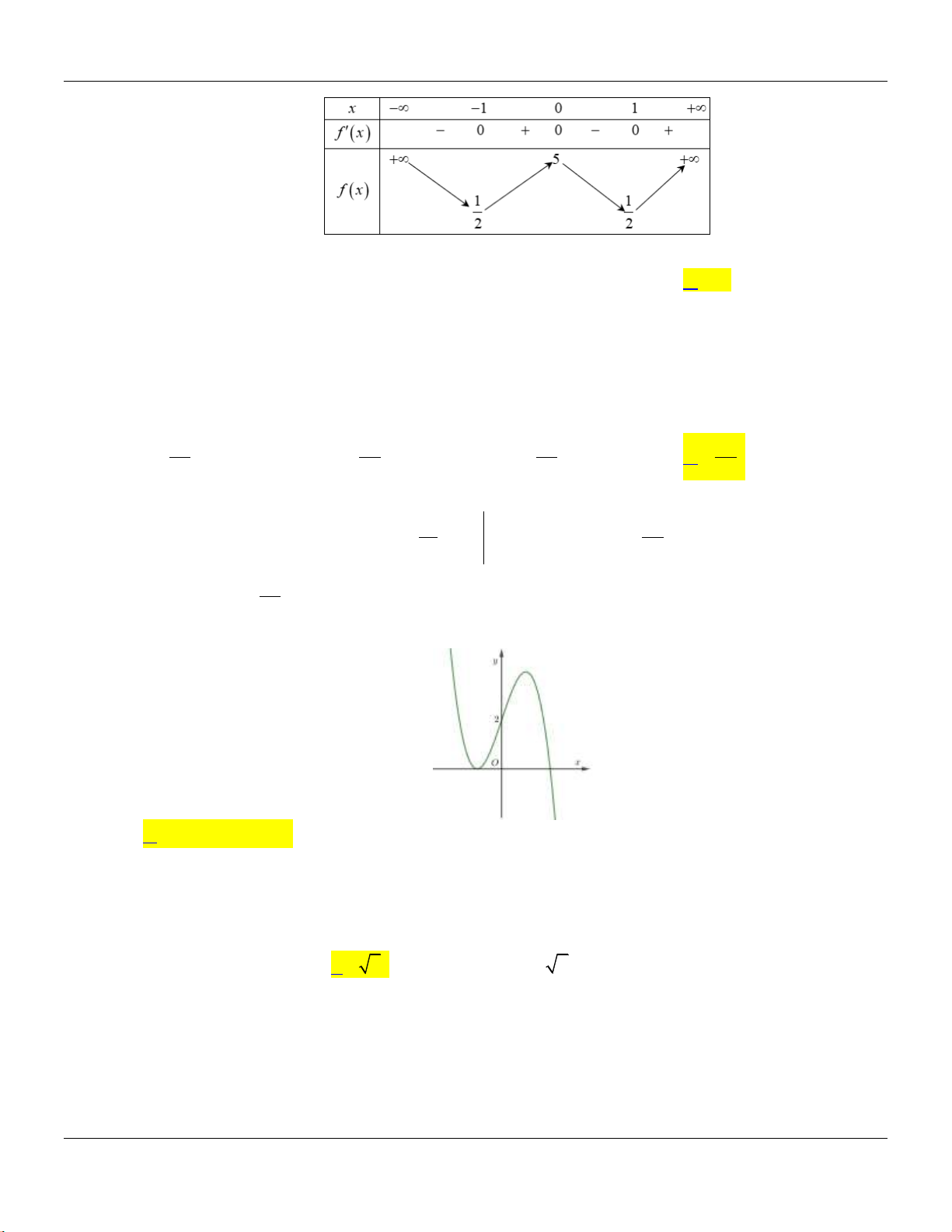
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
Số nghiệm của phương trình
60fx
là
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải:
Ta có
6 0 6f x f x
.
Đường thẳng
6y
cắt đồ thị
y f x
tại 2 điểm phân biệt.
Câu 8: Cho
1
2
0
2 3 d 1
x x f x x
. Tính
1
0
df x x
.
A.
1
3
. B.
5
3
. C.
1
9
. D.
5
9
.
Lời giải:
Ta có
1
1 1 1
3
22
0 0 0
0
2
2 3 d 1 3 d 1 3 d 1
33
x
x x f x x x f x x f x x
1
0
5
d
9
f x x
.
Câu 9: Đường cong trong hình vẽ bên là đồ thị của một hàm số nào?
A.
3
32y x x
. B.
3
32y x x
. C.
42
2y x x
. D.
3
32y x x
.
Lời giải:
Nhánh cuối của đồ thị đi xuống nên
0a
, đồ thị có hai điểm cực trị nên
.0ac
.
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 4 2 0S x y z y z
. Bán kính mặt cầu
S
bằng
A.
1
. B.
7
. C.
22
. D.
7
.
Lời giải:
Ta có
2 2 2
0
1
: 2 4 2 0
2
2
a
b
S x y z y z
c
d
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
Khi đó, bán kính mặt cầu
S
là
2
22
0 1 2 2 7R
.
Câu 11: Trong không gian
,Oxyz
góc giữa trục
Ox
và
Oz
bằng
A.
90 .
B.
60 .
C.
30 .
D.
0.
Câu 12: Cho số phức
z
thỏa mãn
12i z i
. Môđun của số phức
z
bằng
A.
10
2
. B.
3
. C.
2
. D.
10
.
Lời giải:
Ta có
2 1 3 1 3
12
1 2 2 2 2
i
i z i z z i z i
i
.
Vậy
22
1 3 10
2 2 2
z
.
Câu 13: Cho khối lăng trụ đứng
.ABC A B C
có
BB a
, đáy
ABC
là tam giác vuông cân tại
B
và
BA BC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
6
a
V
. B.
3
2
a
V
. C.
3
3
a
V
. D.
3
Va
.
Lời giải:
Ta có:
3
. ' ' '
11
. ' . . ' . . . .
2 2 3
ABC A B C ABC
a
V S BB BA BC BB a a a
Câu 14: Cho khối chóp
.S ABC
có đáy là tam giác đều cạnh
a
,
SA ABC
,
SA a
(tham khảo hình
vẽ).
S
A
B
C
Thể tích của khối chóp đã cho bằng
A.
3
3
4
a
. B.
3
3
6
a
. C.
3
3a
. D.
3
3
12
a
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
S
A
B
C
Vì
SA ABC
nên ta có
SA
là đường cao của hình chóp hay
h SA a
.
Do đáy của hình chóp là tam giác đều cạnh
a
nên ta có:
2
3
4
a
S
.
Khi đó thể tích của khối chóp đã cho là:
1
.
3
V S h
23
1 3 3
..
3 4 12
aa
a
(đvtt).
Câu 15: Nếu tăng bán kính của một khối cầu gấp
3
lần thì thể tích thay đổi như thế nào?
A. Thể tích tăng gấp
6
lần. B. Thể tích tăng gấp
9
lần.
C. Thể tích tăng gấp
3
lần. D. Thể tích tăng gấp
27
lần.
Lời giải:
Gọi
R
là bán kính của khối cầu lúc đầu và
R
là bán kính khối cầu lúc sau.
3RR
.
Khi đó:
3
33
4 4 4
3 .27. 27
3 3 3
V R R R V
.
Vậy thể tích lúc sau tăng gấp
27
lần.
Câu 16: Cho số phức bất kì
,z a bi a b
. Khẳng định nào sau đây đúng?
A.
22
z a b
. B.
22
z a b
. C.
33
z a b
. D.
22
z a b
.
Câu 17: Cho tam giác
ABC
vuông tại
A
,
AB a
và
3AC a
. Tính độ dài đường sinh
l
của hình
nón có được khi quay tam giác
ABC
xung quanh trục
AB
.
A.
2la
. B.
2la
. C.
3la
. D.
la
.
Lời giải:
Quay tam giác
ABC
xung quanh trục
AB
suy ra
h AB a
và
3r AC a
.
Đường sinh
l
của hình nón bằng
22
2l r h a
.
Câu 18: Trong không gian
Oxyz
, đường thẳng
12
:
2 1 3
x y z
d
đi qua điểm nào dưới đây?
A.
2; 1;3A
. B.
1;2;0C
. C.
1; 2;0D
. D.
0;2; 1B
.
Lời giải:
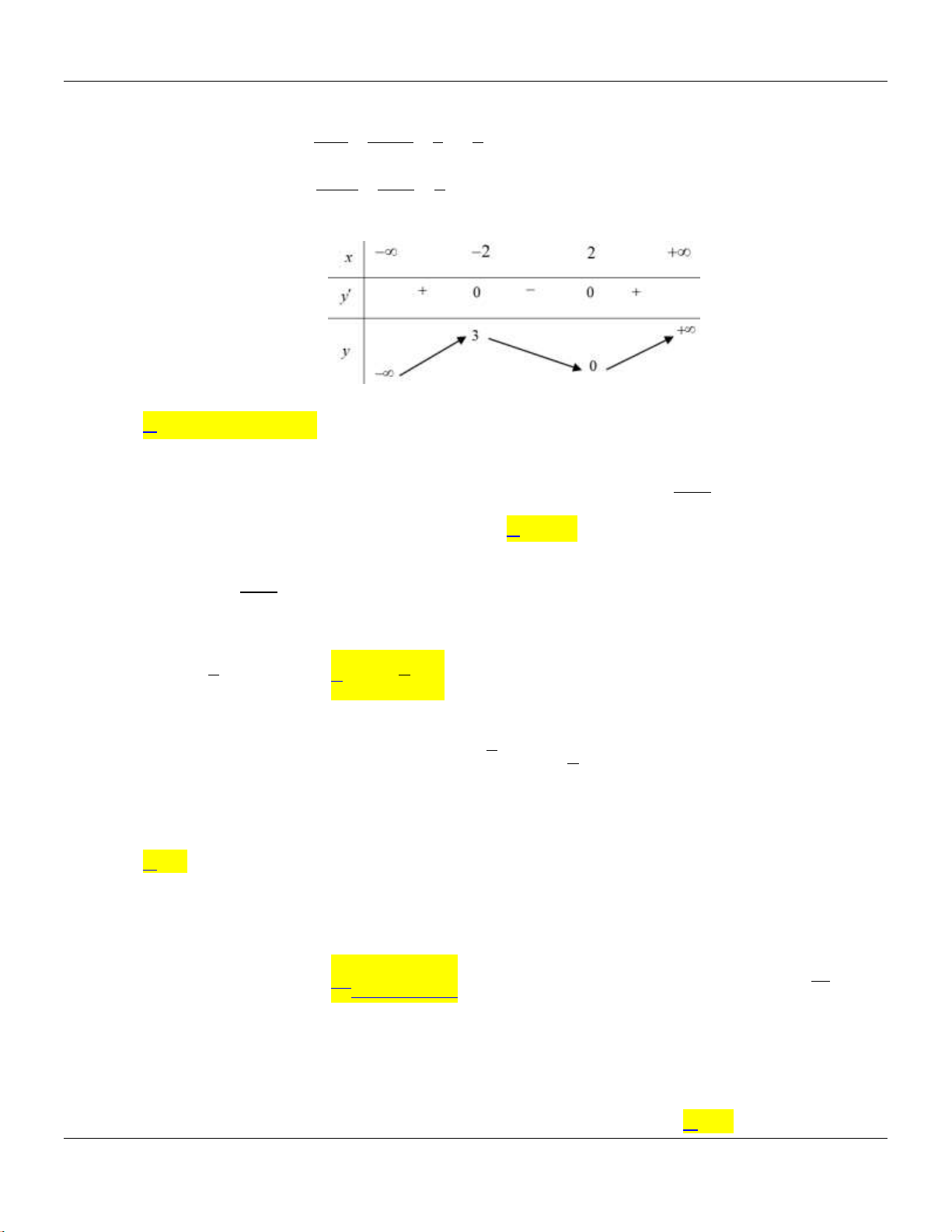
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Lần lượt thay tọa độ các điểm vào phương trình đường thẳng
d
.
Kiểm tra
2; 1;3 :A
2 1 1 2 3 3
1
2 1 3 2
(sai)
Ad
.
Kiểm tra
1;2;0 :C
1 1 2 2 0
00
2 1 3
Cd
.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Tìm giá trị cực đại
CÐ
y
và giá trị cực tiểu
CT
y
của hàm số đã cho.
A.
3
CÐ
y
và
0
CT
y
. B.
3
CÐ
y
và
2
CT
y
.
C.
2
CÐ
y
và
2
CT
y
. D.
2
CÐ
y
và
0
CT
y
.
Câu 20: Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số
2
2
x
y
x
?
A.
2x
. B.
2x
. C.
1y
. D.
1y
.
Lời giải:
Ta có:
2
lim 1 1
2
x
x
y
x
là tiệm cận ngang của đồ thị hàm số.
Câu 21: Tập nghiệm
S
của bất phương trình
3
log 2 1 2x
là
A.
1
;5
2
S
. B.
1
;5
2
S
. C.
;5S
. D.
5;S
.
Lời giải:
Ta có
3
2
1
2 1 0
1
log 2 1 2 ; 5
2
2 1 3
2
5
x
x
xx
x
x
.
Câu 22: Có
3
cây bút đỏ,
4
cây bút xanh trong một hộp bút. Hỏi có bao nhiêu cách lấy ra một cây bút
từ hộp bút đó?
A.
7
. B.
4
. C.
12
. D.
3
.
Lời giải:
Chọn
1
cây bút từ
7
cây bút nên có
7
cách chọn.
Câu 23: Cho
sin d .
x x G x C
Đạo hàm hàm số
2y G x x
là
A.
2sin 1.yx
B.
2sin 1.yx
C.
2sin .yx
D.
2
2cos .
2
x
y x C
Lời giải:
Ta có
2 2sin 1.y G x x x
Câu 24: Nếu
d
4
0
( ) 37f x x
thì
d
4
2
0
2 ( ) 3f x x x
bằng
A. 12. B. 18. C.
27
. D. 10.
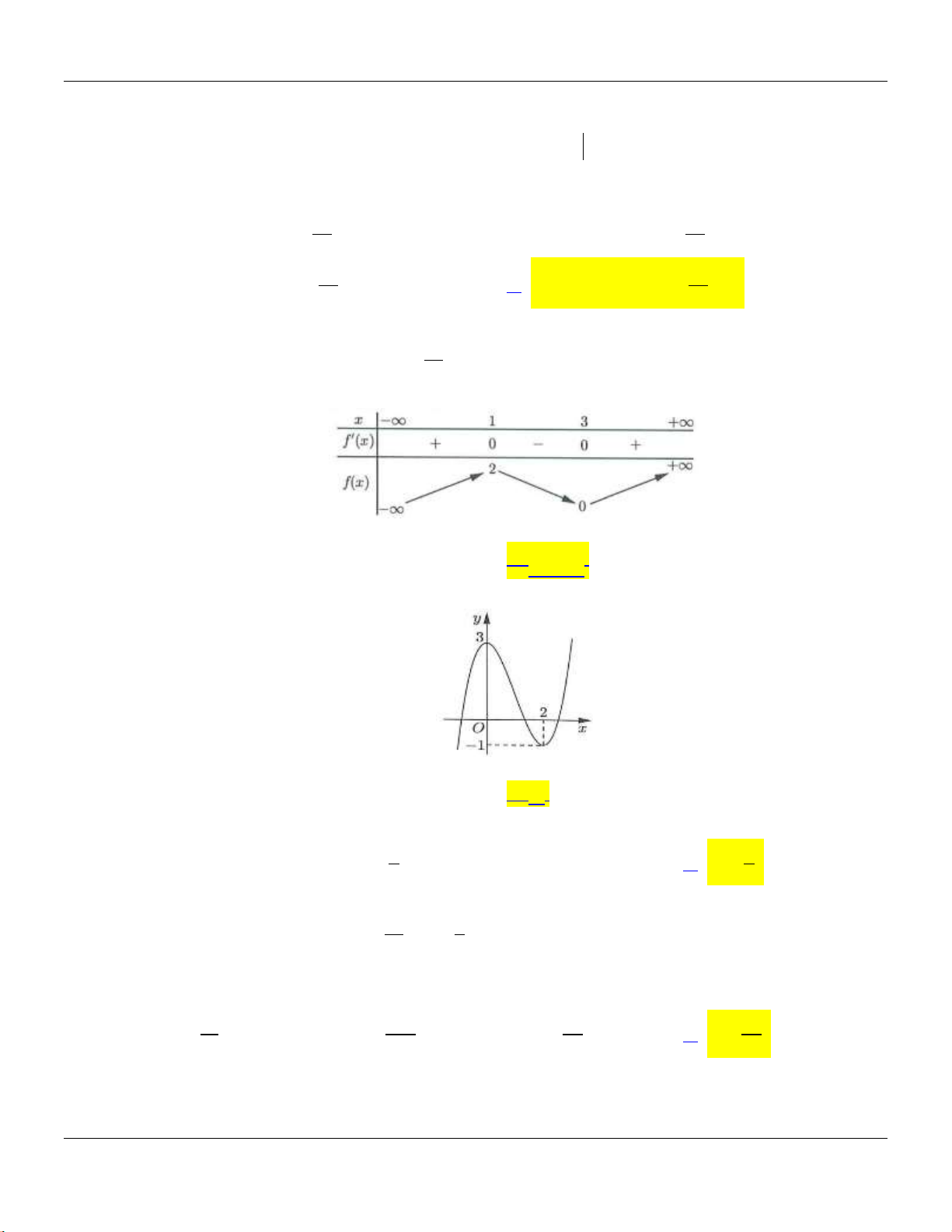
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Lời giải:
Ta có:
4 4 4
4
2 2 3
0
0 0 0
2 ( ) 3 d 2 ( )d 3 d 2.37 74 64 10
f x x x f x x x x x
.
Câu 25: Cho hàm số
sinf x x x
. Khẳng định nào dưới đây đúng?
A.
2
d cos .
2
x
f x x x C
B.
2
d cos .
2
x
f x x x C
C.
2
d sin .
2
x
f x x x C
D.
2
d cos .
2
x
f x x x C
Lời giải:
2
d sin d cos .
2
x
f x x x x x x C
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
0;2
. B.
2;
. C.
;1
. D.
2;3
.
Câu 27: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
Điểm cực tiểu của hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 28: Với
a
là số thực dương tùy ý,
aa
33
log 5 log 2
bằng
A.
3
log 3 .a
B.
3
2
log .
5
C.
2
3
log 10a
. D.
3
5
log .
2
Lời giải:
Ta có
aa
3 3 3 3
55
log 5 log 2 log log .
22
a
a
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường
2
y x x
và
0y
quanh trục
Ox
là
A.
16
15
V
B.
16
15
V
C.
1
30
V
D.
30
V
Lời giải:
Phương trình hoành độ giao điểm của đường
2
y x x
và đường
0y
là
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
2
0
0
1
x
xx
x
.
Thể tích là
11
5 4 3
2
2 4 3 2
00
1
d 2 d .
0
5 2 3 30
x x x
V x x x x x x x
Câu 30: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
SA
vuông góc với đáy và
2AB SA
(tham khảo hình vẽ).
C
B
A
S
Góc giữa hai mặt phẳng
SBC
và
ABC
bằng
A.
60 .
B.
30
C.
90
D.
45
Lời giải:
M
C
B
A
S
Dựng
,AM BC M
là trung điểm
.BC
Ta có:
.
SA BC
BC SAM
AM BC
Suy ra, góc giữa hai mặt phẳng
SBC
và
ABC
bằng
SMA
.
Xét tam giác
SAM
vuông tại
1
: tan 30 .
3
SA
A SMA SMA
AM
Vậy góc giữa hai mặt phẳng
SBC
và
ABC
bằng
30 .
Câu 31: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
x
y
2
-2
-1
O
1
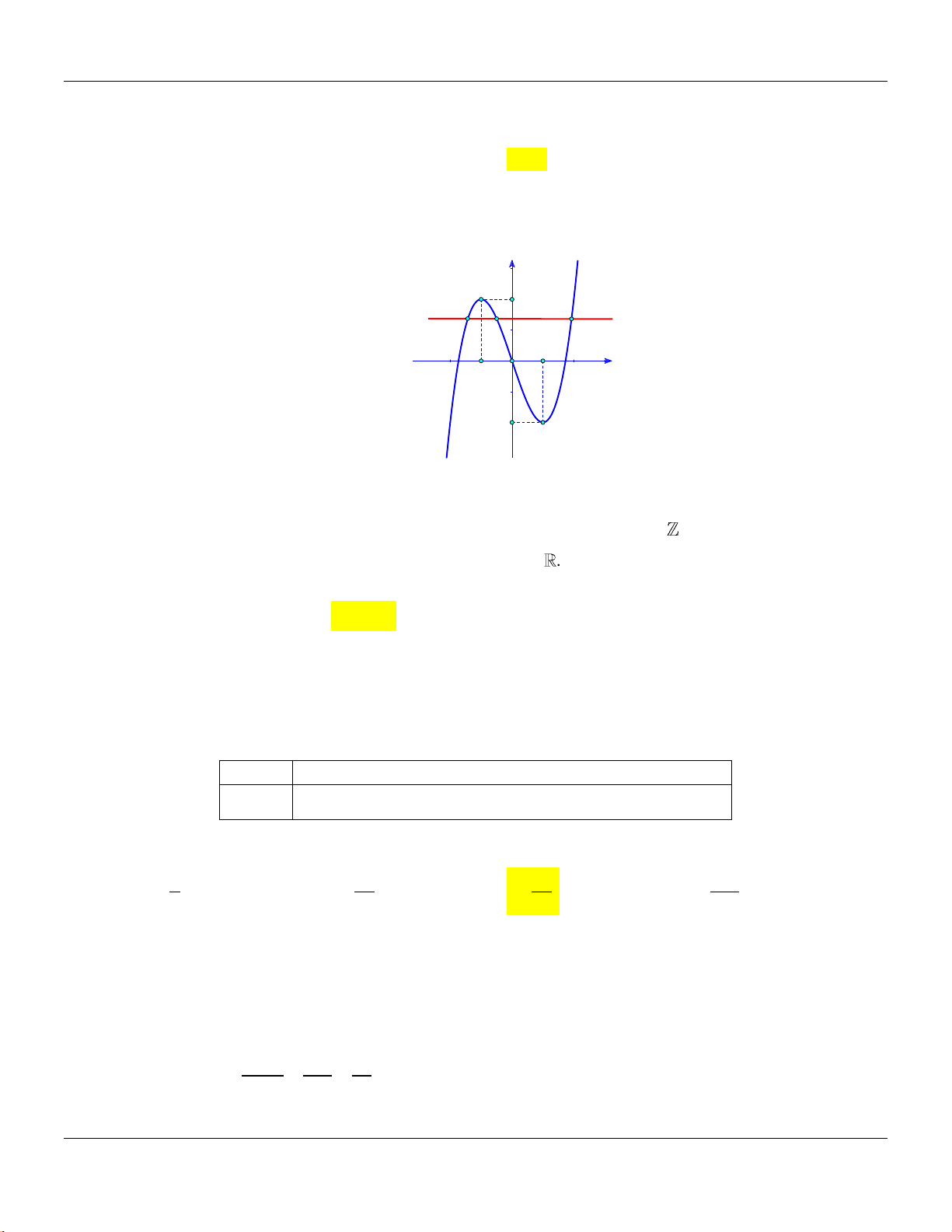
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
f x m
có ba nghiệm thực
phân biệt?
A.
4
. B.
5
. C.
3
. D.
2
.
Lời giải:
Số nghiệm của phương trình
f x m
bằng số giao điểm của đồ thị hàm số
y f x
và
đường thẳng
:d y m
.
x
y
m
2
-2
-1
O
1
Dựa vào hình vẽ, ta có:
Phương trình
f x m
có ba nghiệm thực phân biệt khi đường thẳng
:d y m
cắt đồ thị
hàm số
y f x
tại ba điểm phân biệt, tức là
22 m
. Mà
m
nên
1;0;1m
.
Câu 32: Cho hàm số
y f x
có
1 3 , .f x x x x x
Hàm số
y f x
đồng biến trên khoảng
nào dưới đây?
A.
;0 .
B.
0;1 .
C.
1;2 .
D.
2; .
Lời giải:
Ta có:
0
0 1.
3
x
f x x
x
Bảng xét dấu:
x
0
1
3
fx
0
0
0
Câu 33: Chọn ngẫu nhiên 2 số tự nhiên khác nhau từ 25 số nguyên dương đầu tiên. Xác suất để chọn
được hai số có tổng là một số chẵn bằng
A.
1
2
. B.
13
25
. C.
12
25
. D.
313
625
.
Lời giải:
2
25
300nC
.
Trong 25 số nguyên dương đầu tiên có 13 số lẻ và 12 số chẵn
Gọi
A
là biến cố chọn được hai số có tổng là 1 số chẵn.
Chọn 2 số lẻ trong 13 số lẻ hoặc chọn 2 số chẵn trong 12 số chẵn
22
13 12
144n A C C
.
Vậy
144 12
.
300 25
nA
pA
n
Câu 34: Số nghiệm của phương trình
22
22
3 10.3 9 0
x x x x
là

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
A.
4.
B.
1.
C.
0.
D.
2.
Lời giải:
Điều kiện:
.x
Phương trình
22
2
3 10.3 9 0 *
x x x x
Đặt
2
30
xx
t
, phương trình
*
trở thành:
(tháa m·n)
(tháa m·n)
2
1
10 9 0 .
9
t
tt
t
+) Với
1,t
ta có:
2
2
0
3 1 0 .
1
xx
x
xx
x
+) Với
9,t
ta có:
2
22
1
3 9 2 2 0 .
2
xx
x
x x x x
x
Kết luận: Vậy tập nghiệm của phương trình là
2; 1;0;1 .S
Câu 35: Cho số phức
z
thỏa mãn
1 4.zi
Biết tập hợp các điểm biểu diễn số phức
w 3 4 1 2i z i
là đường tròn
.C
Tìm tâm
I
và bán kính
R
của đường tròn
.C
A.
2; 5 , 20.IR
B.
2; 5 , 4.IR
C.
2;5 , 4.IR
D.
2;5 , 20.IR
Lời giải:
Đặt
w , . x yi x y
Từ giả thiết:
w 3 4 1 2i z i
w+1 2
34
i
z
i
w+1 2
11
34
i
z i i
i
w+2 5
1
34
i
zi
i
w+2 5 1 3 4 w+2 5 20 i z i i i
22
2 5 20xy
22
2 5 400.xy
Vậy tập hợp điểm biểu diễn số phức
w
là đường tròn tâm
2; 5 ,I
bán kính
20.R
Câu 36: Trong không gian
Oxyz
, viết phương trình tham số của đường thẳng đi qua hai điểm
1;2; 3 , 2; 3;1AB
.
A.
1
25
32
xt
yt
zt
. B.
2
35
14
xt
yt
zt
. C.
3
85
54
xt
yt
zt
. D.
1
25
34
xt
yt
zt
.
Lời giải:
Gọi
là đường thẳng đi qua
,AB
thì
nhận
1; 5;4AB
làm VTCP.
Do đó loại đáp án A và. B.
Phương trình chính tắc của
là:
1 2 3
1 5 4
x y z
.
Ta thấy
3; 8;5M
nên
có phương trình tham số là:
3
85
54
xt
yt
zt
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
Câu 37: Trong không gian
Oxyz
, cho điểm
3;5;7A
. Hình chiếu vuông góc của điểm
A
lên mặt
phẳng
Oyz
có tọa độ là
A.
3;5;7 .
B.
3;5;0 .
C.
3;0;7 .
D.
0;5;7 .
Câu 38: Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng
a
. Gọi
M
là trung điểm của
AA
.
Khoảng cách từ
M
đến mặt phẳng
AB C
bằng
A.
2
4
a
. B.
21
7
a
. C.
2
2
a
. D.
21
14
a
.
Lời giải:
Trong
ABB A
, gọi
E
là giao điểm của
BM
và
AB
. Khi đó hai tam giác
EAM
và
EB B
đồng dạng. Do đó
,
11
,,
, 2 2
d M AB C
EM MA
d M AB C d B AB C
d B AB C EB BB
.
Từ
B
kẻ
BN AC
thì
N
là trung điểm của
AC
và
3
2
a
BN
,
BB a
.
Kẻ
BI B N
thì
22
21
,
7
BB BN a
d B AB C BI
BB BN
.
Vậy
1 21
,,
2 14
a
d M AB C d B AB C
.
Câu 39: Cho hình nón
N
có chiều cao
2.ha
Một mặt phẳng
P
đi qua đỉnh của hình nón và cắt
hình hình nón theo một thiết diện là tam giác đều có diện tích bằng
2
16 3
.
9
a
Góc giữa
P
và
mặt đáy của
N
bằng
A.
90 .
B.
45 .
C.
60 .
D.
30 .
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 16
l
r
h
H
O
B
A
S
Gọi thiết diện là tam giác
,.SAB SA SB l
Theo giả thiết:
2 2 2
16 3 3 16 3 8
.
9 4 9 3
SAB
a l a a
Sl
Gọi
H
là trung điểm
®¸y nãn;AB SAB SHO
và
3 4 3
.
23
la
SH
Xét tam giác
SOH
vuông tại
o
3
: sin 60 .
2
SO
O SHO SHO
SH
Câu 40: Trong không gian
,Oxyz
cho điểm
0; 2; 0M
và đường thẳng
43
:2
1
xt
d y t
zt
. Đường thẳng đi
qua
M
, cắt và vuông góc với
d
có phương trình là
A.
2
.
1 1 2
x y z
B.
1
.
1 1 2
x y z
C.
11
.
1 1 2
x y z
D.
1
.
1 1 2
x y z
Lời giải:
Ta có :
4;2; 1
:
3;1;1
d
qua N
d
vtcpu
Gọi
H
là hình chiếu vuông góc của
M
lên
d
MH d
Hd
.0
d
MH u
Hd
43
2
1
3 2 0
xt
yt
zt
x y z
1;1; 2H
.
Đường thẳng
đi qua
M
và vuông góc với
d
có véctơ chỉ phương là
1; 1; 2MH
.
Suy ra, phương trình
2
:
1 1 2
x y z
.
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 07_______________
Câu 1: Trên mặt phẳng toạ độ
Oxy
, biết
1;2M
là điểm biểu diễn số phức
z
, phần thực của
z
bằng
A.
1
. B.
2
. C.
1
. D.
2
.
Câu 2: Tập xác định của hàm số
logyx
là
A.
1;
. B.
0;
. C.
0;
. D.
1;
.
Câu 3: Trên khoảng
0;
, đạo hàm của hàm số
2023
logyx
là
A.
1
ln2023
y
x
. B.
ln2023
y
x
. C.
1
y
x
. D.
1
2023
y
x
.
Câu 4: Tập nghiệm của bất phương trình
52
x
là
A.
5
(log 2; ).
B.
( ; ).
C.
2
;.
5
D.
2
(log 5; )
Câu 5: Cho cấp số nhân
n
u
có
2
2u
và
3
4u
. Công bội của cấp số nhân đã cho bằng
A.
2
. B.
6
. C.
6
. D.
2
.
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
:3 2 2 0P x y z
. Vectơ nào dưới đây là một
vectơ pháp tuyến của
P
?
A.
2
2; 1;2n
. B.
4
3;2;1n
. C.
3
3;2;2n
. D.
1
3;2; 1n
.
Câu 7: Cho hàm số
y f x
có đồ thị là đường cong như hình vẽ bên dưới:
Số nghiệm của phương trình
2fx
bằng
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 8: Biết
2
1
d6f x x
,
5
2
d1f x x
, tính
5
1
dI f x x
.
A.
5I
. B.
5I
. C.
7I
. D.
4I
.
Câu 9: Bảng biến thiên sau đây là của hàm số nào?
A.
3
2
x
fx
x
. B.
3
.
2
x
fx
x
C.
3
2
x
fx
x
. D.
23
.
2
x
fx
x

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 8 2 1 0S x y z x y
. Tìm tọa độ tâm và bán
kính của mặt cầu
S
.
A.
4;1;0I
và
4R
. B.
4; 1;0I
và
2R
.
C.
4;1;0I
và
2R
. D.
4; 1;0I
và
4R
.
Câu 11: Trong không gian
,Oxyz
cho điểm
1;0;0 .A
Góc giữa đường thẳng
OA
và mặt phẳng
Oyz
bằng
A.
90 .
B.
60 .
C.
30 .
D.
0.
Câu 12: Cho số phức
25zi
. Tìm số phức
w iz z
.
A.
73wi
. B.
33wi
. C.
37wi
. D.
77wi
.
Câu 13: Cho khối lăng trụ đứng có chiều cao bằng
5m
, đáy là hình vuông có cạnh bằng
4m
. Thể tích
khối lăng trụ đã cho bằng
A.
3
80m
. B.
3
20m
. C.
3
40m
. D.
3
60m
.
Câu 14: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
,
SA ABCD
,
2SA a
. Tính
thể tích khối chóp
..S ABCD
A.
3
4
3
a
V
. B.
3
4
3
a
V
. C.
3
4Va
. D.
3
4Va
.
Câu 15: Cho mặt cầu
S
có tâm
O
, bán kính
2r
. Một điểm
M
trong không gian thỏa mãn
2OM
. Mệnh đề nào sau đây đúng?
A.
M
là điểm nằm trong mặt cầu
S
. B.
M
là tâm của mặt cầu
S
.
C.
M
là điểm nằm trên mặt cầu
S
. D.
M
là điểm nằm ngoài mặt cầu
S
.
Câu 16: Khẳng định nào sau đây sai?
A. Số
2021i
là số thuần ảo.
B. Số
0
là số phức có mô đun nhỏ nhất.
C. Với số phức
z
bất kì,
z
và
z
là hai số đối nhau.
D. Số phức
z
và số phức
z
có môđun bằng nhau.
Câu 17: Cho hình trụ có bán kính đáy
3r
và chiều cao
4h
. Diện tích xung quanh của hình trụ đã
cho bằng
A.
12
. B.
24
. C.
36
. D.
42
.
Câu 18: Trong không gian
Oxyz
, điểm nào sau đây thuộc đường thẳng
12
:1
xt
yt
zt
?
A.
1; 1; 1M
. B.
2;1; 1N
. C.
1; 1;0P
. D.
2; 1;1Q
.
Câu 19: Cho hàm số
fx
có bảng xét dấu đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
2
. B.
5
. C.
3
. D.
1
.
Câu 20: Cho hàm số
y f x
thỏa mãn
lim 0.
x
fx
Khẳng định nào sau đây đúng?
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
A. Đồ thị hàm số có đường tiệm cận ngang
2y
.
B. Đồ thị hàm số có đường tiệm cận đứng
2x
.
C. Đồ thị hàm số có đường tiệm cận ngang
0y
.
D. Đồ thị hàm số có đường tiệm cận đứng
2x
.
Câu 21: Tập nghiệm của bất phương trình
2
log 1 1x
là
A.
3;
. B.
;3
. C.
1;3
. D.
1;3
.
Câu 22: Có
8
quả ổi và
6
quả xoài. Có bao nhiêu cách chọn ra một quả trong các quả đó?
A.
48
. B.
24
. C.
14
. D.
18
.
Câu 23: Cho
3
d
x x F x C
. Khẳng định nào dưới đây đúng?
A.
21
F
. B.
8.2
F
C.
24
F
. D.
2 16
F
Câu 24: Nếu
1
0
2 d 2f x x x
thì
1
0
df x x
bằng
A. 1. B. 2. C. 0. D. 4.
Câu 25: Cho hàm số
sin cosf x x x
. Khẳng định nào dưới đây đúng?
A.
d sin cos .
f x x x x C
B.
d sin cos .
f x x x x C
C.
d sin cos .
f x x x x C
D.
d sin cos .
f x x x x C
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Khẳng định nào dưới đây đúng?
A.
0 1 .ff
B.
1 2 .ff
C.
4 5 .ff
D.
4 5 .ff
Câu 27: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
Điểm cực đại của hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 28: Với
a
là số thực dương tùy ý,
3
2
log a
bằng
A.
2
log 3 .a
B.
2
3 log .a
C.
2
log .a
D.
2
3log .a
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường
2
4y x x
và
0y
quanh trục
Ox
là
A.
501
15
V
B.
501
15
V
C.
512
15
V
D.
512
15
V
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Câu 30: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
2 2 0.zz
Biết
,AB
lần lượt là
hai điểm biểu diễn
12
,zz
trên mặt phẳng. Tọa độ trung điểm của đoạn thẳng
AB
là
A.
1;0
B.
1;0 .
C.
0;1 .
D.
0; 1 .
Câu 31: Cho hình chóp
.S ABC
có
SA
vuông góc với mặt phẳng
ABC
,
2SA a
, tam giác
ABC
vuông cân tại
B
và
2AB a
.(minh họa như hình vẽ).
A
C
B
S
Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
A.
60
. B.
45
. C.
30
. D.
90
.
Câu 32: Cho hàm số
42
y f x ax bx c
có đồ thị là đường cong trong hình bên dưới:
x
y
-5
-1
O
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
f x m
có bốn nghiệm thực
phân biệt?
A.
4
. B.
5
. C.
3
. D.
2
.
Câu 33: Cho hàm số
y f x
có đạo hàm
22
' 1 ,y f x x x x
. Hàm số
y f x
đồng
biến trên khoảng nào dưới đây?
A.
2;
. B.
0;2
. C.
1;1
. D.
;1
.
Câu 34: Một hộp chứa
11
quả cầu gồm
5
quả màu xanh và
6
quả cầu màu đỏ. Chọn ngẫu nhiên đồng
thời
2
quả cầu từ hộp đó. Xác suất để
2
quả cầu chọn ra cùng màu bằng
A.
5
.
22
B.
6
.
11
C.
5
.
11
D.
8
.
11
Câu 35: Tính tổng
T
tất cả các nghiệm thực của phương trình
4.9 13.6 9.4 0.
x x x
A.
13
4
T
. B.
3T
. C.
1
4
T
. D.
2T
.
Câu 36: Trong không gian
Oxyz
, cho 3 điểm
2;1; 1A
,
1;0;4B
,
0; 2; 1C
. Phương trình mặt
phẳng đi qua
A
và vuông góc với
BC
là
A.
2 5 5 0x y z
. B.
2 5 5 0x y z
. C.
2 5 0xy
. D.
2 5 5 0x y z
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 37: Trong không gian
Oxyz
, cho điểm
3;5;7A
. Hình chiếu vuông góc của điểm
A
lên trục
Oy
có tọa độ là
A.
3;5;7 .
B.
3;5;0 .
C.
3;0;7 .
D.
0;5;0 .
Câu 38: Cho hình nón đỉnh
S
, đáy là đường tròn tâm
O
bán kính
5R
, góc ở đỉnh bằng
60
. Một
mặt phẳng qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm
A
và
B
sao cho
6AB
.
Tính khoảng cách từ
O
đến
SAB
.
A.
20 273
90
. B.
20 270
91
. C.
20 271
91
. D.
20 273
91
.
Câu 39: Trong không gian
,Oxyz
cho mặt phẳng
: 4 2 1 0P x y z
và điểm
(4;2;1)M
. Khi đó
điểm đối xứng với
M
qua mặt phẳng
P
có tọa độ là
A.
( 4;0; 3)
. B.
( 4; 4; 1)
. C.
(4;2;1)
. D.
( 2;0;5)
.
Câu 40: Cho hình trụ
T
có chiều cao bằng
8a
. Một mặt phẳng
song song với trục và cách trục
của hình trụ này một khoảng bằng
3a
, đồng thời
cắt
T
theo thiết diện là một hình
vuông. Diện tích xung quanh của hình trụ đã cho bằng
A.
2
80 a
. B.
2
40 a
. C.
2
30 a
. D.
2
60 a
.
________________________HẾT________________________

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Trên mặt phẳng toạ độ
Oxy
, biết
1;2M
là điểm biểu diễn số phức
z
, phần thực của
z
bằng
A.
1
. B.
2
. C.
1
. D.
2
.
Lời giải:
Vì
1;2M
là điểm biểu diễn số phức
z
nên ta có
12zi
.
Suy ra phần thực của
z
bằng
1
.
Câu 2: Tập xác định của hàm số
logyx
là
A.
1;
. B.
0;
. C.
0;
. D.
1;
.
Lời giải:
Hàm số
logyx
xác định
0x
.
Vậy tập xác định của hàm số là:
0;D
.
Câu 3: Trên khoảng
0;
, đạo hàm của hàm số
2023
logyx
là
A.
1
ln2023
y
x
. B.
ln2023
y
x
. C.
1
y
x
. D.
1
2023
y
x
.
Lời giải:
Áp dụng công thức
1
log
ln
a
x
xa
. Ta có
1
.
ln2023
y
x
Câu 4: Tập nghiệm của bất phương trình
52
x
là
A.
5
(log 2; ).
B.
( ; ).
C.
2
;.
5
D.
2
(log 5; )
Lời giải:
5
5 2 log 2
x
x
.
Câu 5: Cho cấp số nhân
n
u
có
2
2u
và
3
4u
. Công bội của cấp số nhân đã cho bằng
A.
2
. B.
6
. C.
6
. D.
2
.
Lời giải:
Công bội của cấp số nhân là
3
2
4
2
2
u
q
u
.
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
:3 2 2 0P x y z
. Vectơ nào dưới đây là một
vectơ pháp tuyến của
P
?
A.
2
2; 1;2n
. B.
4
3;2;1n
. C.
3
3;2;2n
. D.
1
3;2; 1n
.
Lời giải:
Véc-tơ pháp tuyến của
P
là
1
3;2; 1n
.
Câu 7: Cho hàm số
y f x
có đồ thị là đường cong như hình vẽ bên dưới:
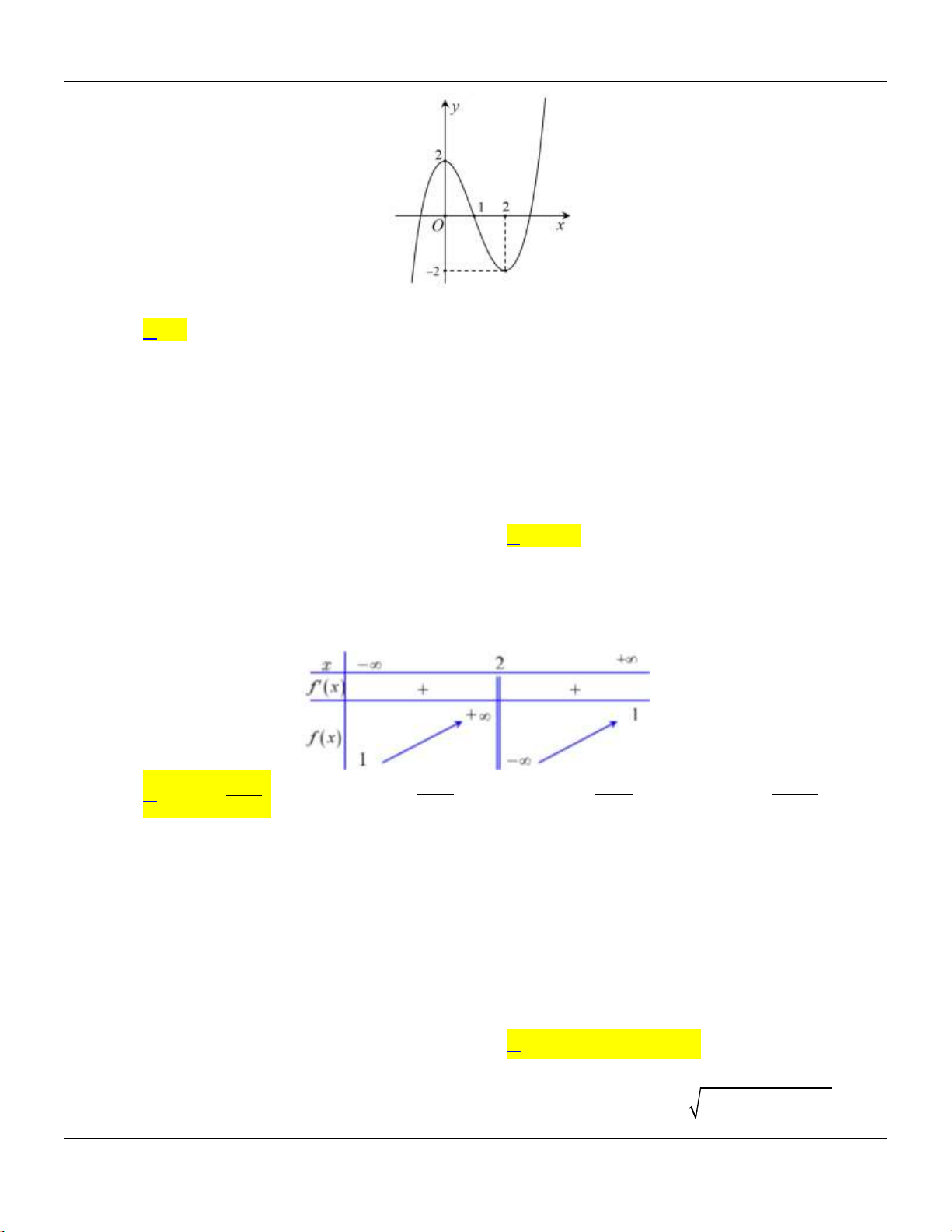
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
Số nghiệm của phương trình
2fx
bằng
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải:
Ta có số nghiệm của phương trình
2fx
là số giao điểm của đồ thị hàm số
()y f x
và
đường thẳng
2y
.
Căn cứ vào đồ thị hàm số ta có số giao điểm bằng 2
Vậy phương trình đã cho có 2 nghiệm.
Câu 8: Biết
2
1
d6f x x
,
5
2
d1f x x
, tính
5
1
dI f x x
.
A.
5I
. B.
5I
. C.
7I
. D.
4I
.
Lời giải:
Ta có:
5 2 5
1 1 2
d d d 6 1 7I f x x f x x f x x
.
Câu 9: Bảng biến thiên sau đây là của hàm số nào?
A.
3
2
x
fx
x
. B.
3
.
2
x
fx
x
C.
3
2
x
fx
x
. D.
23
.
2
x
fx
x
Lời giải:
Ta có
lim 1
x
fx
suy ra đồ thị hàm số có một tiệm cận ngang là
1y
.
2
lim
x
fx
2x
mà một tiệm cận đứng của đồ thị hàm số.
Dựa vào bảng biến thiên, nhận thấy hàm số đồng biến trên từng khoảng xác định.
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 8 2 1 0S x y z x y
. Tìm tọa độ tâm và bán
kính của mặt cầu
S
.
A.
4;1;0I
và
4R
. B.
4; 1;0I
và
2R
.
C.
4;1;0I
và
2R
. D.
4; 1;0I
và
4R
.
Lời giải:
Từ phương trình của mặt cầu suy ra tâm
4; 1;0I
và bán kính
2
22
4 1 0 1 4.R
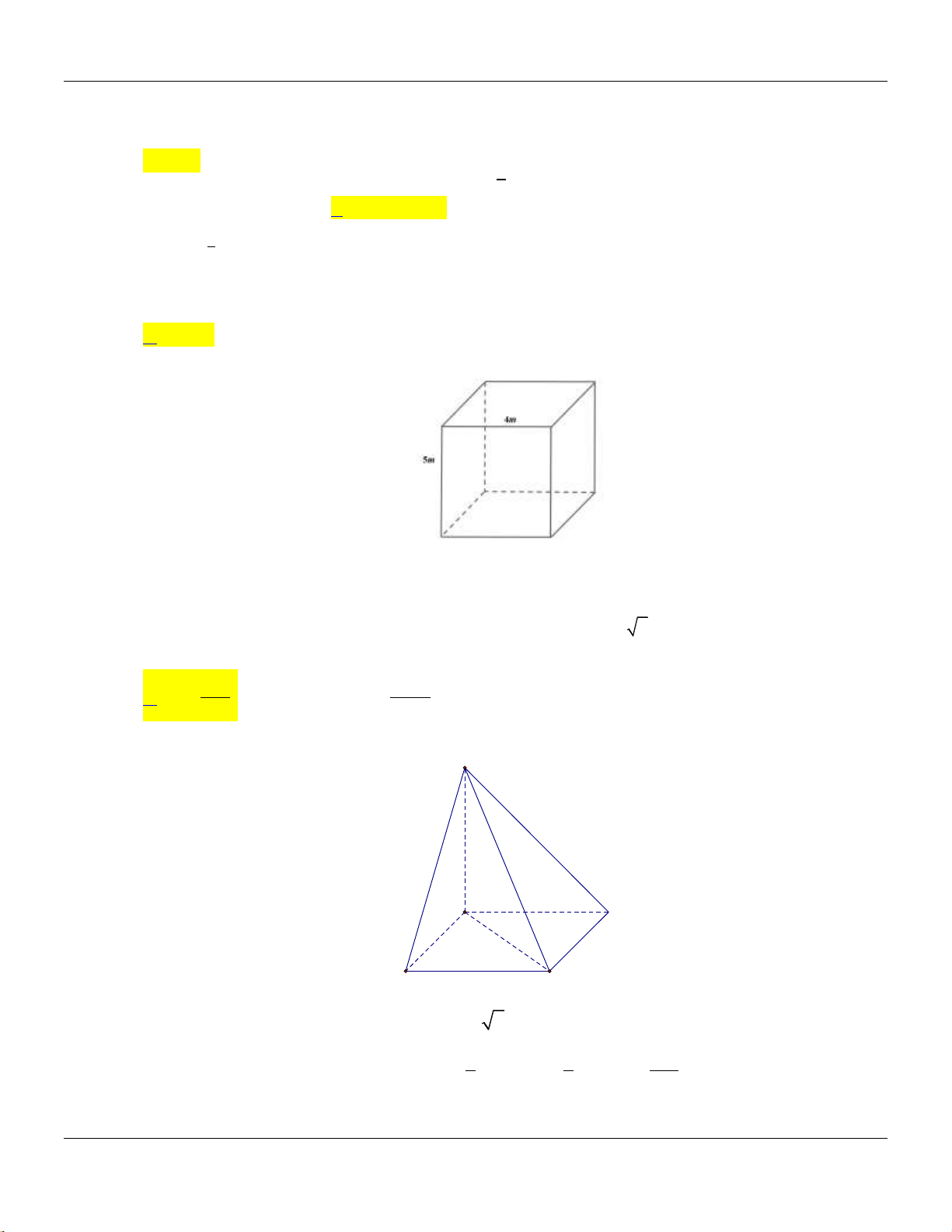
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
Câu 11: Trong không gian
,Oxyz
cho điểm
1;0;0 .A
Góc giữa đường thẳng
OA
và mặt phẳng
Oyz
bằng
A.
90 .
B.
60 .
C.
30 .
D.
0.
Câu 12: Cho số phức
25zi
. Tìm số phức
w iz z
.
A.
73wi
. B.
33wi
. C.
37wi
. D.
77wi
.
Lời giải:
2 5 2 5 5 2 2 5 3 3w iz z i i i i i i
.
Câu 13: Cho khối lăng trụ đứng có chiều cao bằng
5m
, đáy là hình vuông có cạnh bằng
4m
. Thể tích
khối lăng trụ đã cho bằng
A.
3
80m
. B.
3
20m
. C.
3
40m
. D.
3
60m
.
Lời giải:
Ta có diện tích đáy khối lăng trụ đứng là
22
4 16Sm
.
Vậy thể tích khối lăng trụ đã cho
3
16.5 80V Sh m
.
Câu 14: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
,
SA ABCD
,
2SA a
. Tính
thể tích khối chóp
..S ABCD
A.
3
4
3
a
V
. B.
3
4
3
a
V
. C.
3
4Va
. D.
3
4Va
.
Lời giải:
D
C
B
A
S
Diện tích hình vuông
ABCD
là:
2
2
22
ABCD
S a a
Thể tích khối chóp
.S ABCD
là:
3
2
.
1 1 4
. .2 .2
3 3 3
S ABCD ABCD
a
V SAS a a

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Câu 15: Cho mặt cầu
S
có tâm
O
, bán kính
2r
. Một điểm
M
trong không gian thỏa mãn
2OM
. Mệnh đề nào sau đây đúng?
A.
M
là điểm nằm trong mặt cầu
S
. B.
M
là tâm của mặt cầu
S
.
C.
M
là điểm nằm trên mặt cầu
S
. D.
M
là điểm nằm ngoài mặt cầu
S
.
Lời giải:
Vì
2OM r
M
là điểm nằm trên mặt cầu
S
.
Câu 16: Khẳng định nào sau đây sai?
A. Số
2021i
là số thuần ảo.
B. Số
0
là số phức có mô đun nhỏ nhất.
C. Với số phức
z
bất kì,
z
và
z
là hai số đối nhau.
D. Số phức
z
và số phức
z
có môđun bằng nhau.
Lời giải:
Ta có:
z
và
z
được gọi là 2 số phức liên hợp do đó C sai.
Câu 17: Cho hình trụ có bán kính đáy
3r
và chiều cao
4h
. Diện tích xung quanh của hình trụ đã
cho bằng
A.
12
. B.
24
. C.
36
. D.
42
.
Lời giải:
Diện tích xung quanh của hình trụ đã cho là
2 24
xq
S rh
.
Câu 18: Trong không gian
Oxyz
, điểm nào sau đây thuộc đường thẳng
12
:1
xt
yt
zt
?
A.
1; 1; 1M
. B.
2;1; 1N
. C.
1; 1;0P
. D.
2; 1;1Q
.
Lời giải:
Đường thẳng
12
:1
xt
yt
zt
đi qua điểm
1; 1;0P
vì
1 1 2
1 1 0
0
t
tt
t
.
Câu 19: Cho hàm số
fx
có bảng xét dấu đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
2
. B.
5
. C.
3
. D.
1
.
Lời giải:
Từ bảng xét dấu của đạo hàm thì hàm số đã cho có 2 cực trị.
Câu 20: Cho hàm số
y f x
thỏa mãn
lim 0.
x
fx
Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có đường tiệm cận ngang
2y
.
B. Đồ thị hàm số có đường tiệm cận đứng
2x
.
C. Đồ thị hàm số có đường tiệm cận ngang
0y
.
D. Đồ thị hàm số có đường tiệm cận đứng
2x
.
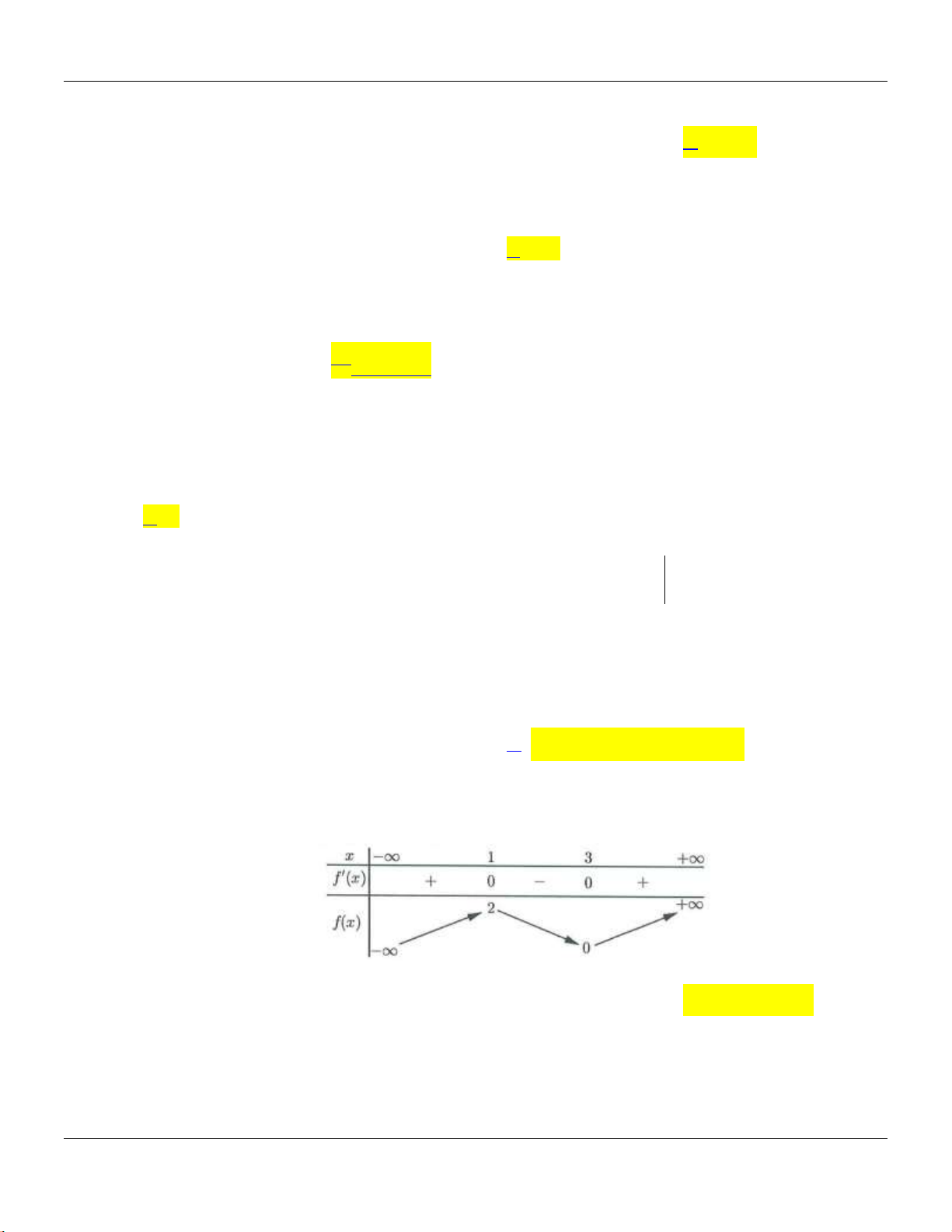
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Câu 21: Tập nghiệm của bất phương trình
2
log 1 1x
là
A.
3;
. B.
;3
. C.
1;3
. D.
1;3
.
Lời giải:
2
log 1 1 0 1 2 1 3.x x x
Câu 22: Có
8
quả ổi và
6
quả xoài. Có bao nhiêu cách chọn ra một quả trong các quả đó?
A.
48
. B.
24
. C.
14
. D.
18
.
Lời giải:
Theo quy tắc cộng có
8 6 14
cách chọn ra một quả trong các quả đã cho.
Câu 23: Cho
3
d
x x F x C
. Khẳng định nào dưới đây đúng?
A.
21
F
. B.
8.2
F
C.
24
F
. D.
2 16
F
Lời giải:
Ta có
33
d 8.2
F x x x x F
Câu 24: Nếu
1
0
2 d 2f x x x
thì
1
0
df x x
bằng
A. 1. B. 2. C. 0. D. 4.
Lời giải:
Ta có:
1 1 1 1
2
0
0 0 0 0
1
2 d 2 d 2 d 2 d 2f x x x f x x x x f x x x
11
00
d 1 0 2 d 1.f x x f x x
Câu 25: Cho hàm số
sin cosf x x x
. Khẳng định nào dưới đây đúng?
A.
d sin cos .
f x x x x C
B.
d sin cos .
f x x x x C
C.
d sin cos .
f x x x x C
D.
d sin cos .
f x x x x C
Lời giải:
d sin cos d cos sin .
f x x x x x x x C
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Khẳng định nào dưới đây đúng?
A.
0 1 .ff
B.
1 2 .ff
C.
4 5 .ff
D.
4 5 .ff
Câu 27: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
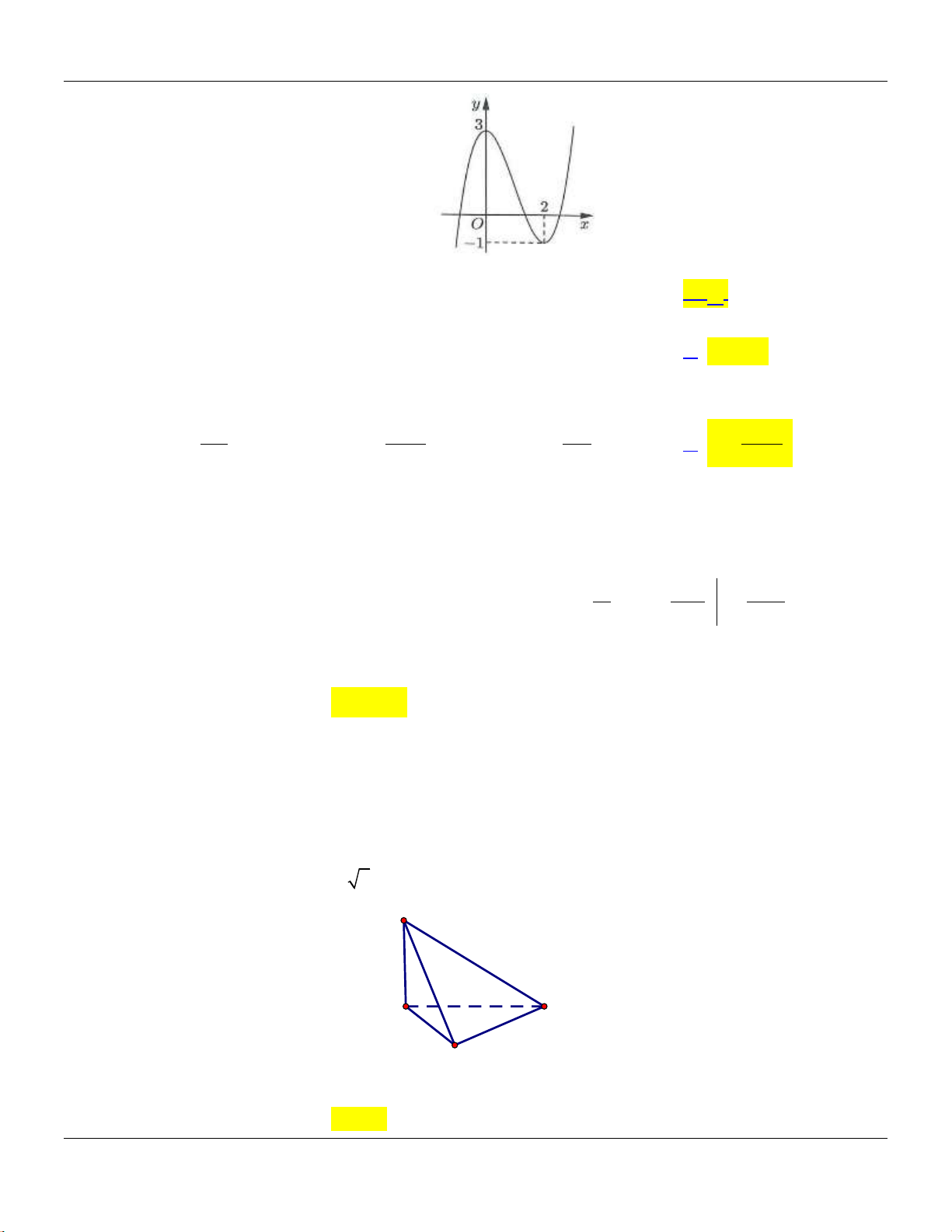
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Điểm cực đại của hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 28: Với
a
là số thực dương tùy ý,
3
2
log a
bằng
A.
2
log 3 .a
B.
2
3 log .a
C.
2
log .a
D.
2
3log .a
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường
2
4y x x
và
0y
quanh trục
Ox
là
A.
501
15
V
B.
501
15
V
C.
512
15
V
D.
512
15
V
Lời giải:
Phương trình hoành độ giao điểm của đường
2
4y x x
và đường
0y
là
2
0
40
4
x
xx
x
.
Thể tích là
44
53
2
2 4 3 2 4
00
4
16 512
4 d 8 16 d 2 .
0
5 3 15
xx
V x x x x x x x x
Câu 30: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
2 2 0.zz
Biết
,AB
lần lượt là
hai điểm biểu diễn
12
,zz
trên mặt phẳng. Tọa độ trung điểm của đoạn thẳng
AB
là
A.
1;0
B.
1;0 .
C.
0;1 .
D.
0; 1 .
Lời giải:
Ta có:
1
2
2
1 1;1
2 2 0 .
1 1; 1
z i A
zz
z i B
I
là trung điểm
1;0 .AB I
Câu 31: Cho hình chóp
.S ABC
có
SA
vuông góc với mặt phẳng
ABC
,
2SA a
, tam giác
ABC
vuông cân tại
B
và
2AB a
.(minh họa như hình vẽ).
A
C
B
S
Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
A.
60
. B.
45
. C.
30
. D.
90
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
Lời giải:
A
C
B
S
Ta có:
SC A BC C
SA ABC
,( ) ( , )SC ABC SC AC SCA
.
Mà:
2 2 2 2
2 2 2AC AB BC a a a SA
.
Vì
SAC
vuông cân tại
A
nên ta có
45SCA
.
Câu 32: Cho hàm số
42
y f x ax bx c
có đồ thị là đường cong trong hình bên dưới:
x
y
-5
-1
O
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
f x m
có bốn nghiệm thực
phân biệt?
A.
4
. B.
5
. C.
3
. D.
2
.
Lời giải:
Số nghiệm của phương trình
f x m
bằng số giao điểm của đồ thị hàm số
y f x
và
đường thẳng
:d y m
.
x
y
m
-5
-1
O
Dựa vào hình vẽ, ta có:

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Phương trình
f x m
có bốn nghiệm thực phân biệt khi đường thẳng
:d y m
cắt đồ thị
hàm số
y f x
tại bốn điểm phân biệt, tức là
51 m
.
Mà
m
nên
4; 3; 2 m
.
Câu 33: Cho hàm số
y f x
có đạo hàm
22
' 1 ,y f x x x x
. Hàm số
y f x
đồng
biến trên khoảng nào dưới đây?
A.
2;
. B.
0;2
. C.
1;1
. D.
;1
.
Lời giải:
Ta có:
0
'0
1
x
fx
x
' '( )y f x y f x
Hàm số
y f x
đồng biến khi và chỉ khi
'( ) 0 ' 0f x f x
1 1 1 1. xx
Câu 34: Một hộp chứa
11
quả cầu gồm
5
quả màu xanh và
6
quả cầu màu đỏ. Chọn ngẫu nhiên đồng
thời
2
quả cầu từ hộp đó. Xác suất để
2
quả cầu chọn ra cùng màu bằng
A.
5
.
22
B.
6
.
11
C.
5
.
11
D.
8
.
11
Lời giải:
Số cách lấy ra 2 quả cầu trong 11 quả là
2
11
C
, Suy ra
2
11
nC
Gọi A là biến cố lấy được 2 quả cùng màu. Suy ra
22
56
n A C C
Xác suất của biến cố A là
22
56
2
11
5
.
11
CC
PA
C
Câu 35: Tính tổng
T
tất cả các nghiệm thực của phương trình
4.9 13.6 9.4 0.
x x x
A.
13
4
T
. B.
3T
. C.
1
4
T
. D.
2T
.
Lời giải:
Phương trình
96
4. 13. 9 0
44
xx
2
33
4. 13. 9 0
22
xx
.
Đặt
3
,0
2
x
tt
.
Phương trình trở thành:
2
1
4 13 9 0
9
4
t
tt
t
( thỏa mãn).
+)
3
1 1 0
2
x
tx
.
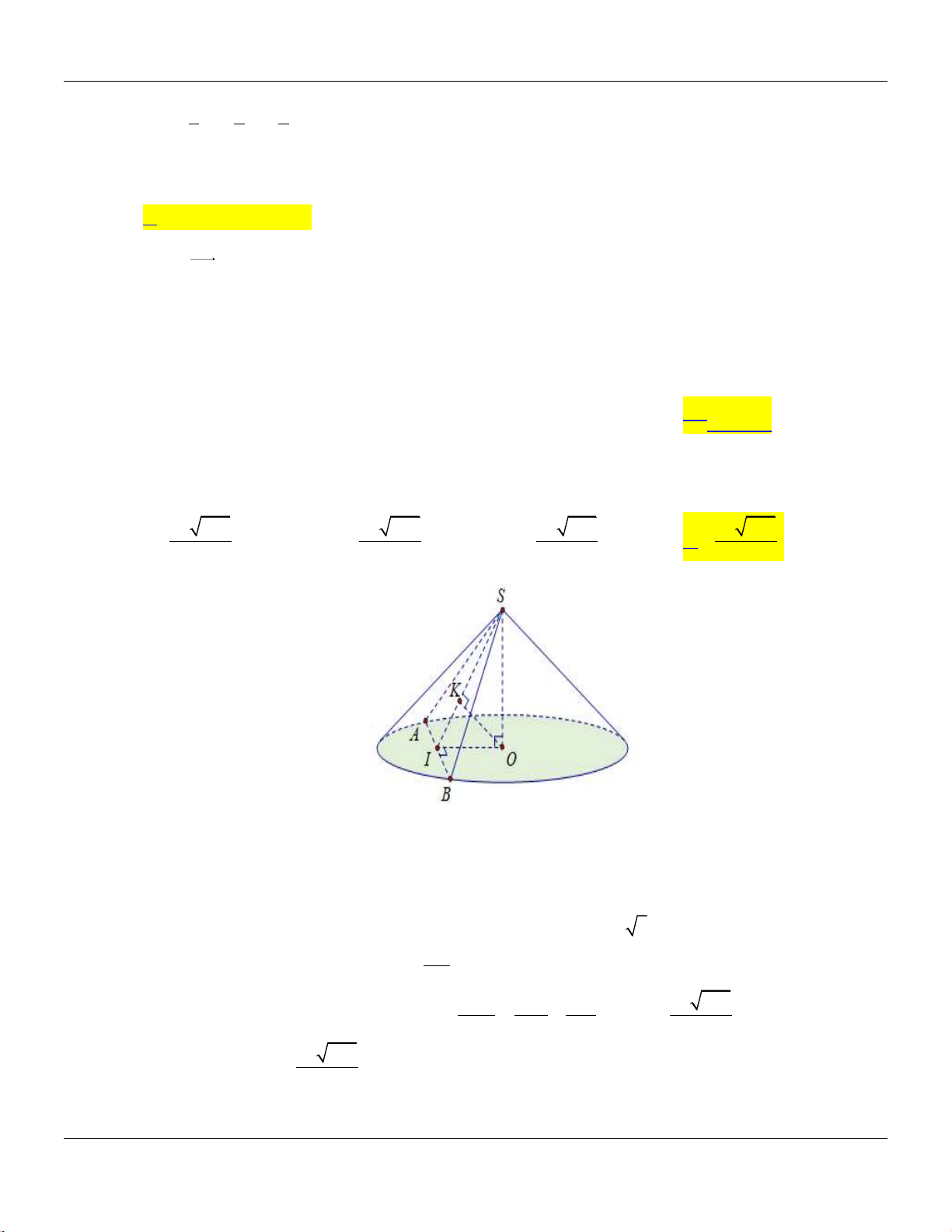
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
+)
9 3 9
2
4 2 4
x
tx
.
Câu 36: Trong không gian
Oxyz
, cho 3 điểm
2;1; 1A
,
1;0;4B
,
0; 2; 1C
. Phương trình mặt
phẳng đi qua
A
và vuông góc với
BC
là
A.
2 5 5 0x y z
. B.
2 5 5 0x y z
. C.
2 5 0xy
. D.
2 5 5 0x y z
.
Lời giải:
Ta có
1; 2; 5BC
.
Vậy phương trình mặt phẳng đi qua
A
và vuông góc với
BC
là:
1 2 2 1 5 1 0 2 5 5 0x y z x y z
.
Câu 37: Trong không gian
Oxyz
, cho điểm
3;5;7A
. Hình chiếu vuông góc của điểm
A
lên trục
Oy
có tọa độ là
A.
3;5;7 .
B.
3;5;0 .
C.
3;0;7 .
D.
0;5;0 .
Câu 38: Cho hình nón đỉnh
S
, đáy là đường tròn tâm
O
bán kính
5R
, góc ở đỉnh bằng
60
. Một
mặt phẳng qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm
A
và
B
sao cho
6AB
.
Tính khoảng cách từ
O
đến
SAB
.
A.
20 273
90
. B.
20 270
91
. C.
20 271
91
. D.
20 273
91
.
Lời giải:
Gọi
I
là trung điểm
AB OI AB
.
Mà
AB SO
(vì
SO
vuông góc với đáy)
AB SIO SAB SIO
Trong
SIO
vẽ
SAB SIOOK SI
OK SAB
,OK d O SAB
.
Góc ở đỉnh bằng
60
30 ASO
, mà
5 5 3OA R SO
IAO
vuông tại
I
có:
5, 3 4
2
AB
OA AI OI
SOI
vuông tại
O
, đường cao
OK
có:
2 2 2
1 1 1 20 273
91
OK
OK SO OI
.
Vậy
20 273
91
,d O SAB
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
Câu 39: Trong không gian
,Oxyz
cho mặt phẳng
: 4 2 1 0P x y z
và điểm
(4;2;1)M
. Khi đó
điểm đối xứng với
M
qua mặt phẳng
P
có tọa độ là
A.
( 4;0; 3)
. B.
( 4; 4; 1)
. C.
(4;2;1)
. D.
( 2;0;5)
.
Lời giải:
Phương trình đường thẳng
d
qua
M
vuông góc với
P
là
44
2
12
xt
yt
zt
Gọi
H d P
0;1; 1H
.
M
đối xứng với
M
qua
P
nên
H
là trung điểm
MM
4;0; 3M
.
Câu 40: Cho hình trụ
T
có chiều cao bằng
8a
. Một mặt phẳng
song song với trục và cách trục
của hình trụ này một khoảng bằng
3a
, đồng thời
cắt
T
theo thiết diện là một hình
vuông. Diện tích xung quanh của hình trụ đã cho bằng
A.
2
80 a
. B.
2
40 a
. C.
2
30 a
. D.
2
60 a
.
Lời giải:
Gọi trục của hình trụ là
OO
8OO a
.
Mặt phẳng
cắt hình trụ theo thiết diện là hình vuông
ABCD
8AB AD a
Theo giả thiết
;3d OO ABCD a
.
Kẻ
OH AB
OH ABCD
; ; 3d OO ABCD d O ABCD OH a
.
Xét tam giác
OAH
vuông tại
H
ta có:
2 2 2
OA OH AH
5OA a
.
Diện tích xung quanh của hình trụ bằng:
2
xq
S rh
2 .5 .8aa
2
80 a
.
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 08_______________
Câu 1: Trong mặt phẳng
,Oxy
điểm
3; 2M
là điểm biểu diễn của số phức nào dưới đây ?
A.
23zi
. B.
32zi
. C.
3 2 .zi
D.
23zi
.
Câu 2: Hệ số góc của tiếp tuyến với đồ thị hàm số
ln 1yx
tại điểm có hoành độ
2x
là
A. 1. B.
ln 2
. C.
1
3
. D.
1
3ln2
.
Câu 3: Đạo hàm của hàm số
2
x
y
là
A.
1
.2
x
yx
. B.
2 .ln 2
x
y
. C.
2
x
y
. D.
1
.2 .ln2
x
yx
.
Câu 4: Tập nghiệm của bất phương trình
21
3 27
x
là
A.
1
;
2
. B.
3;
. C.
2;
. D.
1
;
3
.
Câu 5: Cho cấp số cộng
()
n
u
có
1
2027u
và công sai
3d
. Số hạng
3
u
A.
3
3
2027( 3)u
. B.
3
2021u
. C.
3
2020u
. D.
3
2054u
.
Câu 6: Trong không gian
Oxyz
, mặt phẳng
:3 4 3 0x y z
có một vectơ pháp tuyến là
A.
3;4; 1m
. B.
3;4;1n
. C.
6;8;2a
. D.
3;4; 1 b
.
Câu 7: Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ bên dưới:
Số nghiệm thực của phương trình
3fx
là
A.
1
. B.
2
. C. 0. D. 3.
Câu 8: Cho
d
2
1
( ) 2f x x
và
d
2
1
( ) 1g x x
. Giá trị của
d
2
1
2 ( ) 3 ( )f x g x x
bằng
A. 1. B. 5. C. 7. D.
7
.
Câu 9: Đường cong trong hình vẽ là đồ thị hàm số nào dưới đây?
A.
32
31y x x
. B.
3
31y x x
. C.
42
21y x x
. D.
3
31y x x
.
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
( ):( 2) ( 1) ( 1) 9 S x y z
. Tọa độ tâm
I
và bán
kính
R
của
S
là
A.
( 2;1; 1), 3. IR
B.
( 2;1; 1), 9. IR
C.
(2; 1;1), 3.IR
D.
(2; 1;1), 9.IR
Câu 11: Trong không gian
Oxyz
, cho hai điểm
1;1;2A
và
3; 5;0B
. Tọa độ trung điểm của đoạn
thẳng
AB
là
A.
2; 4;2
B.
4; 6;2
C.
1; 2;1
D.
2; 3; 1
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 12: Cho hai số phức
1
37zi
và
2
23zi
. Tìm số phức
12
z z z
.
A.
1 10zi
. B.
54zi
. C.
3 10zi
. D.
33zi
.
Câu 13: Cho khối lăng trụ đứng có diện tích đáy bằng
2
2a
và cạnh bên bằng
3a
. Thể tích khối lăng
trụ đã cho bằng
A.
3
2a
B.
3
3a
C.
3
18a
D.
3
6a
Câu 14: Cho hình chóp
.S ABC
có đường cao
,SA
tam giác
ABC
vuông tại
A
có
2AB
,
4AC
. Gọi
H
là trung điểm của
BC
(tham khảo hình vẽ).
H
C
B
A
S
Biết diện tích tam giác
SAH
bằng 2, thể tích của khối chóp
.S ABC
bằng
A.
16 5
5
. B.
16 5
15
. C.
45
9
. D.
45
3
.
Câu 15: Cắt một mặt cầu
S
bởi một mặt phẳng qua tâm được thiết diện là hình tròn đường kính
bằng
4.cm
Tính thể tích của khối cầu đã cho.
A.
3
256
.
2
cm
B.
3
16 .
cm
C.
3
32
.
3
cm
D.
3
64 .
cm
Câu 16: Môđun của số phức
1zi
bằng
A.
1
. B.
0
. C.
2
. D.
2
.
Câu 17: Cho hình trụ có bán kính đáy bằng
5
và chiều cao bằng
7
. Diện tích xung quanh của hình trụ
đã cho bằng
A.
175
.
3
B.
175 .
C.
70 .
D.
35 .
Câu 18: Trong không gian
,Oxyz
điểm nào dưới đây thuộc đường thẳng
12
:3
45
xt
d y t
zt
?
A.
3; 2 ; 1P
. B.
2 ;1;5N
. C.
1; 3; 4M
. D.
4;1;3Q
.
Câu 19: Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới:
Hàm số có bao nhiêu điểm cực tiểu trên khoảng
;ab
?
A.
4
. B.
2
. C.
7
. D.
3
.
Câu 20: Tiệm cận đứng của đồ thị hàm số
35
2
x
y
x
là
A.
2x
. B.
2y
. C.
3x
. D.
3y
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
Câu 21: Bất phương trình
22
log (3 2) log (6 5 )xx
có tập nghiệm là
( ; )ab
. Tổng
ab
bằng
A.
8
3
. B.
28
15
. C.
26
5
. D.
11
5
.
Câu 22: Có
10
cái bút khác nhau và
8
quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn
một cái bút và một quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
A.
80
. B.
70
. C.
90
. D.
60
.
Câu 23: Cho hàm số
2
x
f x x e
. Tìm một nguyên hàm
Fx
của hàm số
fx
thỏa mãn
0 2023F
.
A.
2
2022
x
F x x e
. B.
2
2022
x
F x x e
.
C.
2
2021
x
F x x e
. D.
2023
x
F x e
.
Câu 24: Cho
2
2
d1f x x
,
4
2
d4f t t
. Tính
4
2
dI f y y
.
A.
5I
. B.
3I
. C.
3I
. D.
5I
.
Câu 25: Họ nguyên hàm của hàm số
3
2f x x
x
là
A.
2
3
2.C
x
B.
2
2
3
.xC
x
C.
2
ln .x x C
D.
2
3ln .x x C
Câu 26: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trong khoảng nào dưới đây?
A.
2;
. B.
;1
. C.
0;
. D.
0;2
.
Câu 27: Cho hàm số
y f x
xác định, liên tục trên và có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. Hàm số đạt cực đại tại
0x
. B. Hàm số đạt cực tiểu tại
4x
.
C. Hàm số đạt cực đại tại
2x
. D. Hàm số đạt cực đại tại
1x
.
Câu 28: Với
a
và
b
là hai số thực dương tùy ý;
34
2
log ab
bằng
A.
22
11
log log .
34
ab
B.
22
3log 4log .ab
C.
24
2 log log .ab
D.
22
4log 3log .ab
Câu 29: Cho hình phẳng
H
giới hạn bởi các đường
2
2y x x
,
0y
. Quay
H
quanh trục hoành
tạo thành khối tròn xoay có thể tích được tính bởi công thức nào dưới đây?
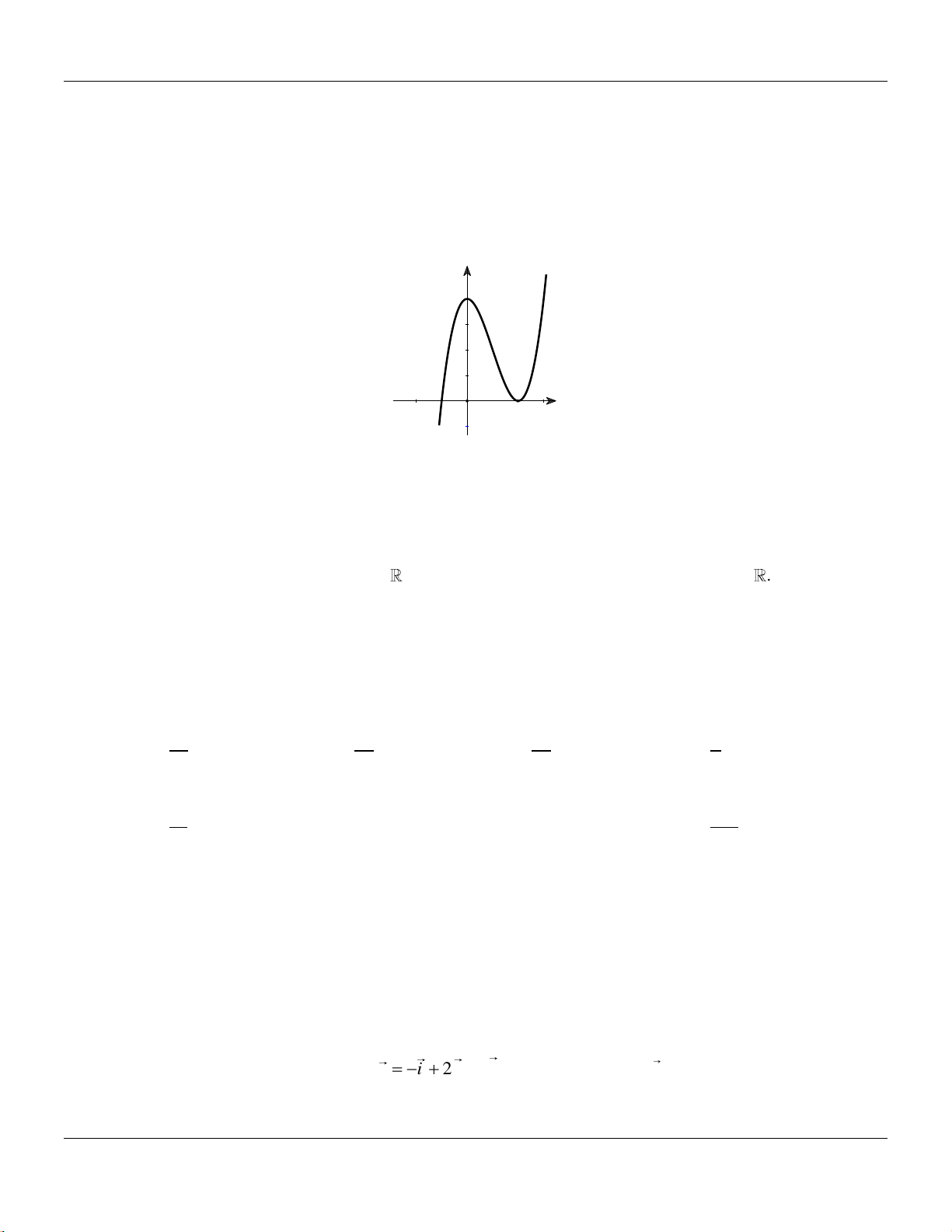
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
A.
2
2
0
2 d .
x x x
B.
2
2
2
0
2 d .
x x x
C.
2
2
2
0
2 d .
x x x
D.
2
2
0
2 d .
x x x
Câu 30: Cho hình lập phương
.
ABCD A B C D
. Góc giữa đường thẳng
AB
và mặt phẳng
ABC D
bằng
A.
60 .
B.
90 .
C.
30 .
D.
45 .
Câu 31: Cho hàm số bậc ba
32
34y x x
có đồ thị như hình vẽ bên dưới:
x
y
-1
2
4
O
Tìm tất cả các giá trị thực của
m
sao cho phương trình
32
3 4 0x x m
có 3 nghiệm thực
phân biệt.
A.
24m
. B.
04m
. C.
4
0
m
m
. D.
04m
.
Câu 32: Hàm số
y f x
liên tục trên và có đạo hàm
2
1 1 , .
f x x x x x
Hàm số
y f x
nghịch biến trên khoảng nào dưới đây?
A.
1;2 .
B.
1;0 .
C.
0;1 .
D.
2; 1 .
Câu 33: Một hộp chứa
15
quả cầu gồm
6
quả màu đỏ được đánh số từ
1
đến
6
và
9
quả màu xanh
được đánh số từ
1
đến
9
. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả
khác màu đồng thời tổng hai số ghi trên chúng là số chẵn bằng
A.
9
.
35
B.
18
.
35
C.
4
.
35
D.
1
.
7
Câu 34: Tích tất cả các nghiệm của phương trình
2
log 2log 3 0 xx
bằng
A.
1
.
10
B.
100.
C.
10.
D.
1
.
100
Câu 35: Trong mặt phẳng
,Oxy
tập hợp các điểm
M
biểu diễn số phức
z
thỏa mãn
| 3 | 2zi
là
A. đường tròn
22
3 1 4xy
. B. đường tròn
22
3 1 4xy
.
C. đường tròn
22
3 1 2xy
. D. đường thẳng
3 2 0.xy
Câu 36: Trong không gian
,Oxyz
phương trình đường thẳng đi qua hai điểm
;;A 1 1 2
và
;;B 3 0 4
là
A.
xt
yt
zt
12
1.
22
B.
xt
yt
zt
12
1.
22
C.
xt
yt
zt
32
.
42
D.
xt
yt
zt
52
1.
62
Câu 37: Trong không gian
,Oxyz
cho
23a i j k
. Tọa độ của vectơ
a
là
A.
1;2; 3
. B.
2; 3; 1
. C.
2; 1; 3
. D.
3;2; 1
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 38: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
,2AB a AD a
SA ABCD
và
SA a
(tham khảo hình vẽ)
Khoảng cách từ
A
đến mặt phẳng
SBD
bằng
A.
3
2
a
. B.
21
7
a
. C.
10
5
a
. D.
2
5
a
.
Câu 39: Trong không gian
,Oxyz
gọi
H
hình chiếu vuông góc của
2;0;1M
lên đường thẳng
12
:
1 2 1
x y z
. Tìm tọa độ điểm
H
.
A.
2;2;3H
. B.
0; 2;1H
. C.
1;0;2H
. D.
1; 4;0H
.
Câu 40: Một hình trụ có bán kính bằng
2a
. Hai điểm
,AB
lần lượt thuộc hai đường tròn đáy sao cho
4A B a
. Biết khoảng cách giữa
AB
và trục bằng
a
. Tính thể tích khối trụ đã cho.
A.
3
2
Va
. B.
3
82
3
a
V
. C.
3
42
Va
. D.
3
8
Va
.
________________________HẾT________________________

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Trong mặt phẳng
,Oxy
điểm
3; 2M
là điểm biểu diễn của số phức nào dưới đây ?
A.
23zi
. B.
32zi
. C.
3 2 .zi
D.
23zi
.
Lời giải:
Số phức thoả mãn yêu cầu đề bài là:
32zi
.
Câu 2: Hệ số góc của tiếp tuyến với đồ thị hàm số
ln 1yx
tại điểm có hoành độ
2x
là
A. 1. B.
ln 2
. C.
1
3
. D.
1
3ln2
.
Lời giải:
Ta có
1
'
1
y
x
. Hệ số góc của tiếp tuyến với đồ thị hàm số
ln 1yx
tại điểm có hoành độ
2x
là:
1
'2
3
y
.
Câu 3: Đạo hàm của hàm số
2
x
y
là
A.
1
.2
x
yx
. B.
2 .ln 2
x
y
. C.
2
x
y
. D.
1
.2 .ln2
x
yx
.
Lời giải:
Hàm số
2
x
y
có đạo hàm là
' 2 .ln2
x
y
.
Câu 4: Tập nghiệm của bất phương trình
21
3 27
x
là
A.
1
;
2
. B.
3;
. C.
2;
. D.
1
;
3
.
Lời giải:
2 1 2 1 3
3 27 3 3 2 1 3 2
xx
xx
.
Vậy bất phương trình có tập nghiệm
2;S
.
Câu 5: Cho cấp số cộng
()
n
u
có
1
2027u
và công sai
3d
. Số hạng
3
u
A.
3
3
2027( 3)u
. B.
3
2021u
. C.
3
2020u
. D.
3
2054u
.
Lời giải:
31
2 2027 2.( 3) 2021u u d
Câu 6: Trong không gian
Oxyz
, mặt phẳng
:3 4 3 0x y z
có một vectơ pháp tuyến là
A.
3;4; 1m
. B.
3;4;1n
. C.
6;8;2a
. D.
3;4; 1 b
.
Lời giải:
Mặt phẳng
:3 4 3 0x y z
có một vectơ pháp tuyến là
3; 4; 1u
nên vectơ
6;8;2a
cũng là một vectơ pháp tuyến của mặt phẳng
.
Câu 7: Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ bên dưới:
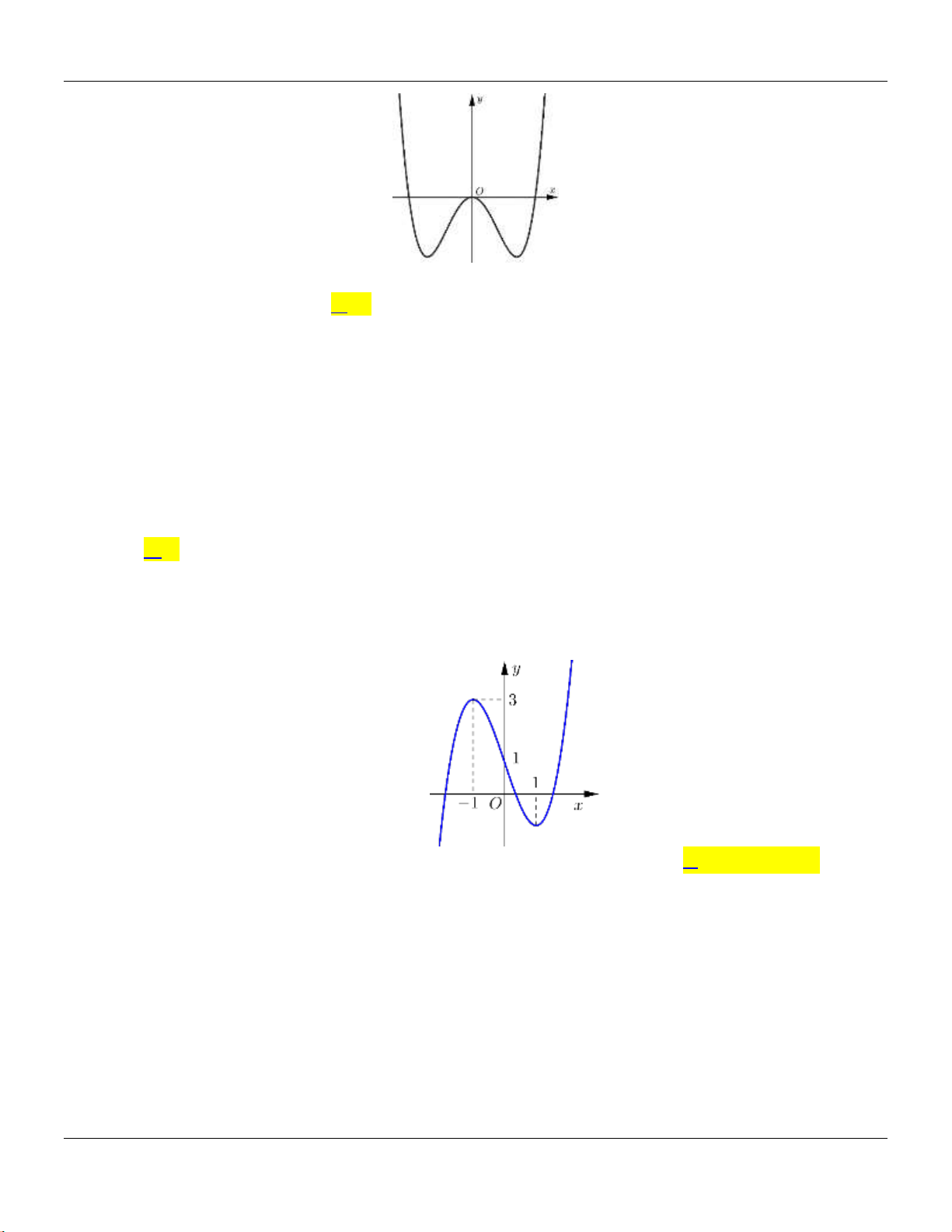
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
Số nghiệm thực của phương trình
3fx
là
A.
1
. B.
2
. C. 0. D. 3.
Lời giải:
Số nghiệm của phương trình
3fx
bằng số giao điểm của đồ thị hàm số
y f x
và
đường thẳng
3y
.
Ta có đường thẳng
3y
song song với trục hoành và cắt trục tung tại điểm có tọa độ
0;3
.
Từ đồ thị ta thấy đường thẳng
3y
cắt đồ thị hàm số
y f x
tại hai điểm phân biệt. Do đó
phương trình
3fx
có 2 nghiệm thực phân biệt.
Câu 8: Cho
d
2
1
( ) 2f x x
và
d
2
1
( ) 1g x x
. Giá trị của
d
2
1
2 ( ) 3 ( )f x g x x
bằng
A. 1. B. 5. C. 7. D.
7
.
Lời giải:
Áp dụng tính chất của tích phân ta có
2 2 2
1 1 1
2 ( ) 3 ( ) 2 ( ) 3 ( ) 4 3 1f x g x dx f x dx g x dx
.
Câu 9: Đường cong trong hình vẽ là đồ thị hàm số nào dưới đây?
A.
32
31y x x
. B.
3
31y x x
. C.
42
21y x x
. D.
3
31y x x
.
Lời giải:
Quan sát hình dạng đồ thị ta loại đáp án hàm số
42
21y x x
do trên hình hàm số có hai
cực trị mà đáp án này hàm số có 3 cực trị.
Do nhánh bên phải của đồ thị đi lên nên loại đáp án
3
31y x x
.
Mặt khác quan sát đồ thị có hai điểm cực trị là
1x
.
Xét đáp án A có
2
0
3 6 0
2
x
y x x
x
nên loại đáp án này.
Vậy hình trên là đồ thị hàm số
3
31y x x
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
( ):( 2) ( 1) ( 1) 9 S x y z
. Tọa độ tâm
I
và bán
kính
R
của
S
là
A.
( 2;1; 1), 3. IR
B.
( 2;1; 1), 9. IR
C.
(2; 1;1), 3.IR
D.
(2; 1;1), 9.IR
Câu 11: Trong không gian
Oxyz
, cho hai điểm
1;1;2A
và
3; 5;0B
. Tọa độ trung điểm của đoạn
thẳng
AB
là
A.
2; 4;2
B.
4; 6;2
C.
1; 2;1
D.
2; 3; 1
Câu 12: Cho hai số phức
1
37zi
và
2
23zi
. Tìm số phức
12
z z z
.
A.
1 10zi
. B.
54zi
. C.
3 10zi
. D.
33zi
.
Lời giải:
Ta có:
12
z z z
3 7 2 3 5 4i i i
.
Câu 13: Cho khối lăng trụ đứng có diện tích đáy bằng
2
2a
và cạnh bên bằng
3a
. Thể tích khối lăng
trụ đã cho bằng
A.
3
2a
B.
3
3a
C.
3
18a
D.
3
6a
Lời giải:
23
. 2 .3 6 V B h a a a
Câu 14: Cho hình chóp
.S ABC
có đường cao
,SA
tam giác
ABC
vuông tại
A
có
2AB
,
4AC
. Gọi
H
là trung điểm của
BC
(tham khảo hình vẽ).
H
C
B
A
S
Biết diện tích tam giác
SAH
bằng 2, thể tích của khối chóp
.S ABC
bằng
A.
16 5
5
. B.
16 5
15
. C.
45
9
. D.
45
3
.
Lời giải:
H
A
C
B
S
Xét tam giác
ABC
vuông tại
A
:
2 2 2 2
2 4 2 5BC AB AC
.
Suy ra
11
.2 5 5
22
AH BC
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Xét tam giác
SAH
vuông tại
A
:
1 1 4 5
. 2 . 5
2 2 5
SAH
S SA AH SA SA
.
Diện tích tam giác
ABC
:
11
. .2.4 4
22
ABC
S AB AC
.
Thể tích khối chóp
.S ABC
:
.
1 1 4 5 16 5
. . .4
3 3 5 15
S ABC ABC
V SA S
.
Câu 15: Cắt một mặt cầu
S
bởi một mặt phẳng qua tâm được thiết diện là hình tròn đường kính
bằng
4.cm
Tính thể tích của khối cầu đã cho.
A.
3
256
.
2
cm
B.
3
16 .
cm
C.
3
32
.
3
cm
D.
3
64 .
cm
Lời giải:
Bán kính
R
của hình tròn thu được bằng bán kính của mặt cầu.
Đường kính hình tròn là:
2 4 2 . R R cm
Thể tích khối cầu là:
3 3 3
4 4 32
.2 .
3 3 3
V R cm
Câu 16: Môđun của số phức
1zi
bằng
A.
1
. B.
0
. C.
2
. D.
2
.
Lời giải:
Ta có
2
2
1 1 2z
.
Câu 17: Cho hình trụ có bán kính đáy bằng
5
và chiều cao bằng
7
. Diện tích xung quanh của hình trụ
đã cho bằng
A.
175
.
3
B.
175 .
C.
70 .
D.
35 .
Lời giải:
Ta có
5; 7 r l h
. Suy ra
2 5 702 . .7
xq
S rl
Câu 18: Trong không gian
,Oxyz
điểm nào dưới đây thuộc đường thẳng
12
:3
45
xt
d y t
zt
?
A.
3; 2 ; 1P
. B.
2 ;1;5N
. C.
1; 3; 4M
. D.
4;1;3Q
.
Câu 19: Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới:
Hàm số có bao nhiêu điểm cực tiểu trên khoảng
;ab
?
A.
4
. B.
2
. C.
7
. D.
3
.
Lời giải:
Từ đồ thị hàm số suy ra hàm số có 3 điểm cực tiểu trên khoảng
;ab
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Câu 20: Tiệm cận đứng của đồ thị hàm số
35
2
x
y
x
là
A.
2x
. B.
2y
. C.
3x
. D.
3y
.
Lời giải:
Ta có
22
35
lim lim
2
xx
x
y
x
;
22
35
lim lim
2
xx
x
y
x
.
Vậy tiệm cận đứng của đồ thị hàm số là
2x
.
Câu 21: Bất phương trình
22
log (3 2) log (6 5 )xx
có tập nghiệm là
( ; )ab
. Tổng
ab
bằng
A.
8
3
. B.
28
15
. C.
26
5
. D.
11
5
.
Lời giải:
22
8 8 1
log (3 2) log (6 5 ) 3 2 6 5 0
66
55
xx
x x x x
xx
Suy ra bất phương trình có tập nghiệm là:
6
1; .
5
Vậy tổng
6 11
1
55
ab
.
Câu 22: Có
10
cái bút khác nhau và
8
quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn
một cái bút và một quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
A.
80
. B.
70
. C.
90
. D.
60
.
Lời giải:
Có
10
cách chọn bút và
8
cách chọn sách.
Số cách chọn một cái bút và một quyển sách là
10.8 80
.
Câu 23: Cho hàm số
2
x
f x x e
. Tìm một nguyên hàm
Fx
của hàm số
fx
thỏa mãn
0 2023F
.
A.
2
2022
x
F x x e
. B.
2
2022
x
F x x e
.
C.
2
2021
x
F x x e
. D.
2023
x
F x e
.
Lời giải:
Ta có
2
2
xx
f x dx x e dx x e C
.
Có
Fx
là một nguyên hàm của
fx
và
0 2023F
.
Suy ra
2
0 2023
x
F x x e C
F
1 2023 2022 CC
.
Vậy
2
2022
x
F x x e
.
Câu 24: Cho
2
2
d1f x x
,
4
2
d4f t t
. Tính
4
2
dI f y y
.
A.
5I
. B.
3I
. C.
3I
. D.
5I
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Do tích phân không phụ thuộc vào biến số nên
44
22
d d 4f t t f x x
.
Ta có
4 4 4 2
2 2 2 2
d d d d 4 1 5I f y y f x x f x x f x x
.
Câu 25: Họ nguyên hàm của hàm số
3
2f x x
x
là
A.
2
3
2.C
x
B.
2
2
3
.xC
x
C.
2
ln .x x C
D.
2
3ln .x x C
Lời giải:
2
3
2 3ln .f x dx x dx x x C
x
Câu 26: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trong khoảng nào dưới đây?
A.
2;
. B.
;1
. C.
0;
. D.
0;2
.
Câu 27: Cho hàm số
y f x
xác định, liên tục trên và có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. Hàm số đạt cực đại tại
0x
. B. Hàm số đạt cực tiểu tại
4x
.
C. Hàm số đạt cực đại tại
2x
. D. Hàm số đạt cực đại tại
1x
.
Lời giải:
Dựa vào bảng biến thiên của hàm số
y f x
ta thấy hàm số đạt cực đại tại
2x
.
Câu 28: Với
a
và
b
là hai số thực dương tùy ý;
34
2
log ab
bằng
A.
22
11
log log .
34
ab
B.
22
3log 4log .ab
C.
24
2 log log .ab
D.
22
4log 3log .ab
Lời giải:
Ta có:
3 4 3 4
2 2 2 2 2
log log log 3log 4loga b a b a b
nên B đúng.
Câu 29: Cho hình phẳng
H
giới hạn bởi các đường
2
2y x x
,
0y
. Quay
H
quanh trục hoành
tạo thành khối tròn xoay có thể tích được tính bởi công thức nào dưới đây?
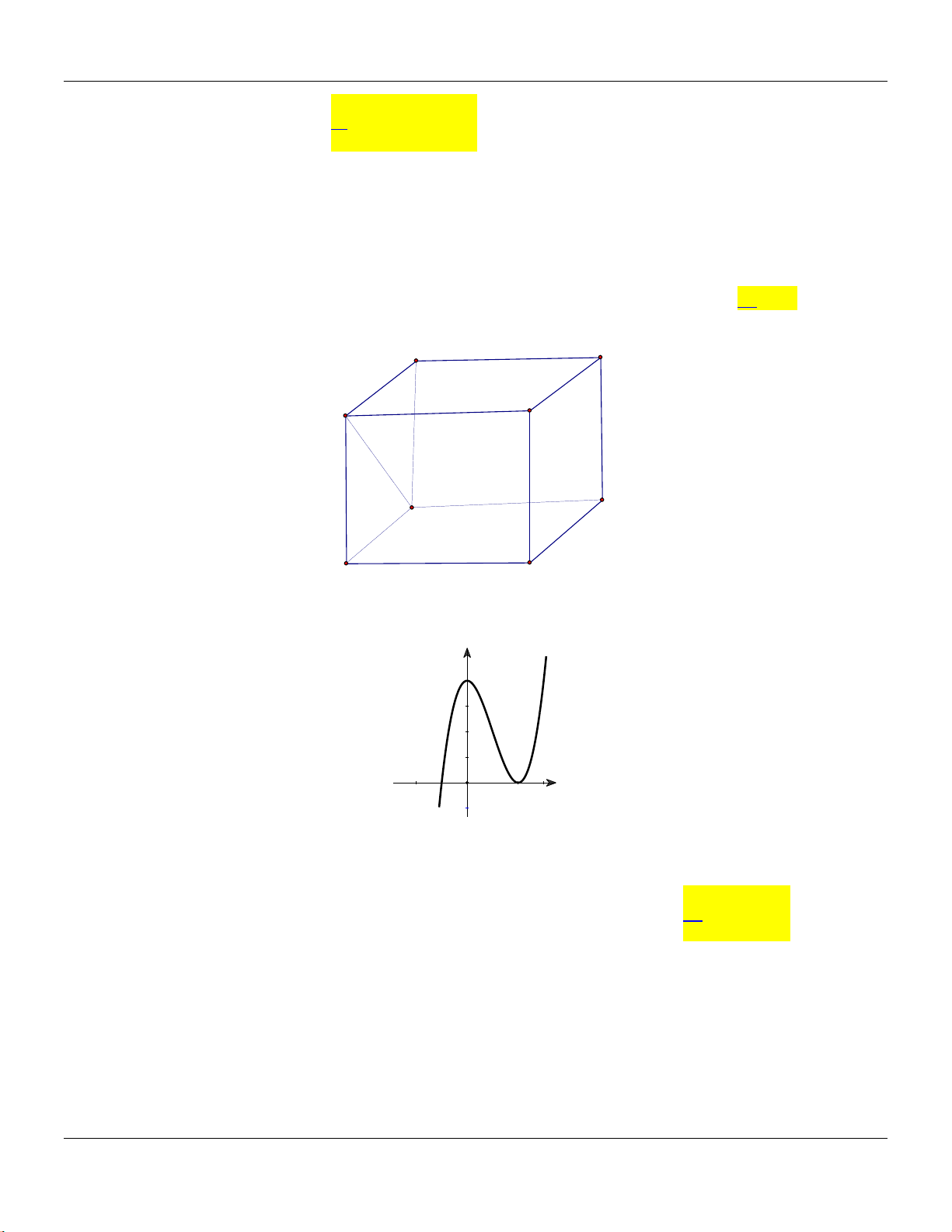
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
A.
2
2
0
2 d .
x x x
B.
2
2
2
0
2 d .
x x x
C.
2
2
2
0
2 d .
x x x
D.
2
2
0
2 d .
x x x
Lời giải:
Theo công thức ta chọn
2
2
2
0
2d
V x x x
.
Câu 30: Cho hình lập phương
.
ABCD A B C D
. Góc giữa đường thẳng
AB
và mặt phẳng
ABC D
bằng
A.
60 .
B.
90 .
C.
30 .
D.
45 .
Lời giải:
A'
D'
B'
C'
B
C
A
D
Góc giữa
AB
và mặt phẳng
ABC D
là góc
0
45
B AB
.
Câu 31: Cho hàm số bậc ba
32
34y x x
có đồ thị như hình vẽ bên dưới:
x
y
-1
2
4
O
Tìm tất cả các giá trị thực của
m
sao cho phương trình
32
3 4 0x x m
có 3 nghiệm thực
phân biệt.
A.
24m
. B.
04m
. C.
4
0
m
m
. D.
04m
.
Lời giải:
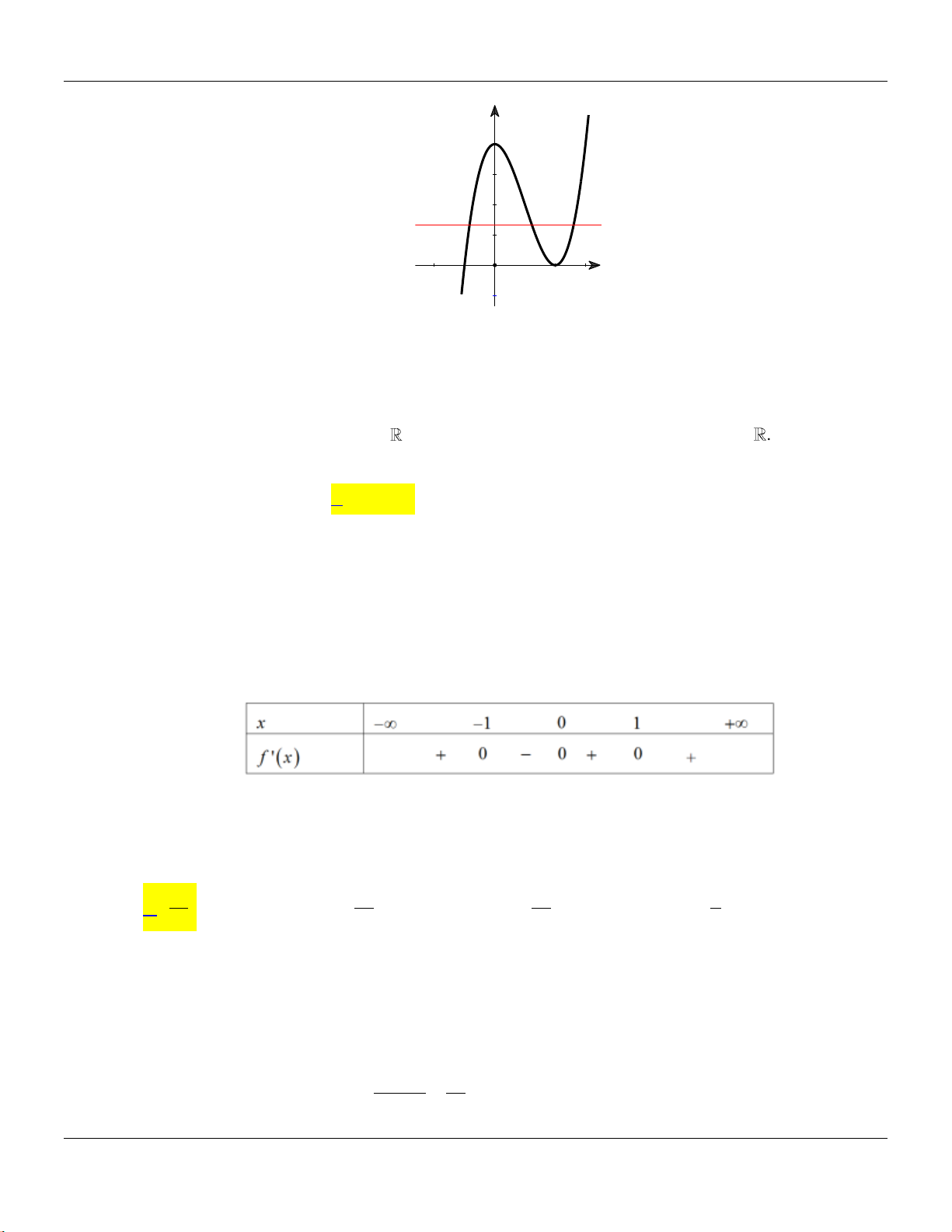
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
x
y
-1
2
4
O
Ta có
3 2 3 2
3 4 0 3 4x x m x x m
. Số nghiệm của phương trình trên là số giao điểm
của đồ thị hàm số
32
34y x x
và đường thẳng
ym
.
Dựa vào đồ thị ta thấy đồ thị hàm số
32
34y x x
và đường thẳng
ym
cắt nhau tại 3
điểm phân biệt khi và chỉ khi
04m
.
Câu 32: Hàm số
y f x
liên tục trên và có đạo hàm
2
1 1 , .
f x x x x x
Hàm số
y f x
nghịch biến trên khoảng nào dưới đây?
A.
1;2 .
B.
1;0 .
C.
0;1 .
D.
2; 1 .
Lời giải:
Xét hàm số
y f x
có
2
2
1 1 1 1f x x x x x x x
.
2
0
0 1 1 0 1
1
x
f x x x x x
x
.
Suy ra bảng xét dấu của hàm
fx
:
Từ bảng xét dấu của hàm
fx
suy ra hàm số
y f x
nghịch biến trên khoảng
1;0
Câu 33: Một hộp chứa
15
quả cầu gồm
6
quả màu đỏ được đánh số từ
1
đến
6
và
9
quả màu xanh
được đánh số từ
1
đến
9
. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả
khác màu đồng thời tổng hai số ghi trên chúng là số chẵn bằng
A.
9
.
35
B.
18
.
35
C.
4
.
35
D.
1
.
7
Lời giải:
Số cách lấy ngẫu nhiên
2
quả cầu từ hộp là:
2
15
105C
cách
Để tổng hai số ghi trên hai quả cầu là số chẵn ta có
2
TH sau:
TH 1: Hai quả cầu khác màu cùng đánh số lẻ:
11
35
. 15CC
cách
TH 2: Hai quả cầu khác màu nhau cùng đánh số chẵn:
11
34
. 12CC
cách
Vậy xác suất cần tính là:
12 15 9
.
105 35
P

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
Câu 34: Tích tất cả các nghiệm của phương trình
2
log 2log 3 0 xx
bằng
A.
1
.
10
B.
100.
C.
10.
D.
1
.
100
Lời giải:
Ta có:
2
3
3
0
10
log 1
10
log 2log 3 0
log 3
10
10
x
x
x
x
xx
x
x
x
Vậy
12
1
..
100
xx
Câu 35: Trong mặt phẳng
,Oxy
tập hợp các điểm
M
biểu diễn số phức
z
thỏa mãn
| 3 | 2zi
là
A. đường tròn
22
3 1 4xy
. B. đường tròn
22
3 1 4xy
.
C. đường tròn
22
3 1 2xy
. D. đường thẳng
3 2 0.xy
Lời giải:
Đặt
,z x yi x y
. Ta có
2 2 2 2
3 2 3 1 2 3 1 4.z i x y x y
Câu 36: Trong không gian
,Oxyz
phương trình đường thẳng đi qua hai điểm
;;A 1 1 2
và
;;B 3 0 4
là
A.
xt
yt
zt
12
1.
22
B.
xt
yt
zt
12
1.
22
C.
xt
yt
zt
32
.
42
D.
xt
yt
zt
52
1.
62
Lời giải:
Kiểm tra sự kiện:
Ad
và vectơ chỉ phương
;;AB 2 1 2
ta thấy phương án D thỏa mãn.
Câu 37: Trong không gian
,Oxyz
cho
23a i j k
. Tọa độ của vectơ
a
là
A.
1;2; 3
. B.
2; 3; 1
. C.
2; 1; 3
. D.
3;2; 1
.
Câu 38: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
,2AB a AD a
SA ABCD
và
SA a
(tham khảo hình vẽ)
Khoảng cách từ
A
đến mặt phẳng
SBD
bằng
A.
3
2
a
. B.
21
7
a
. C.
10
5
a
. D.
2
5
a
.
Lời giải:
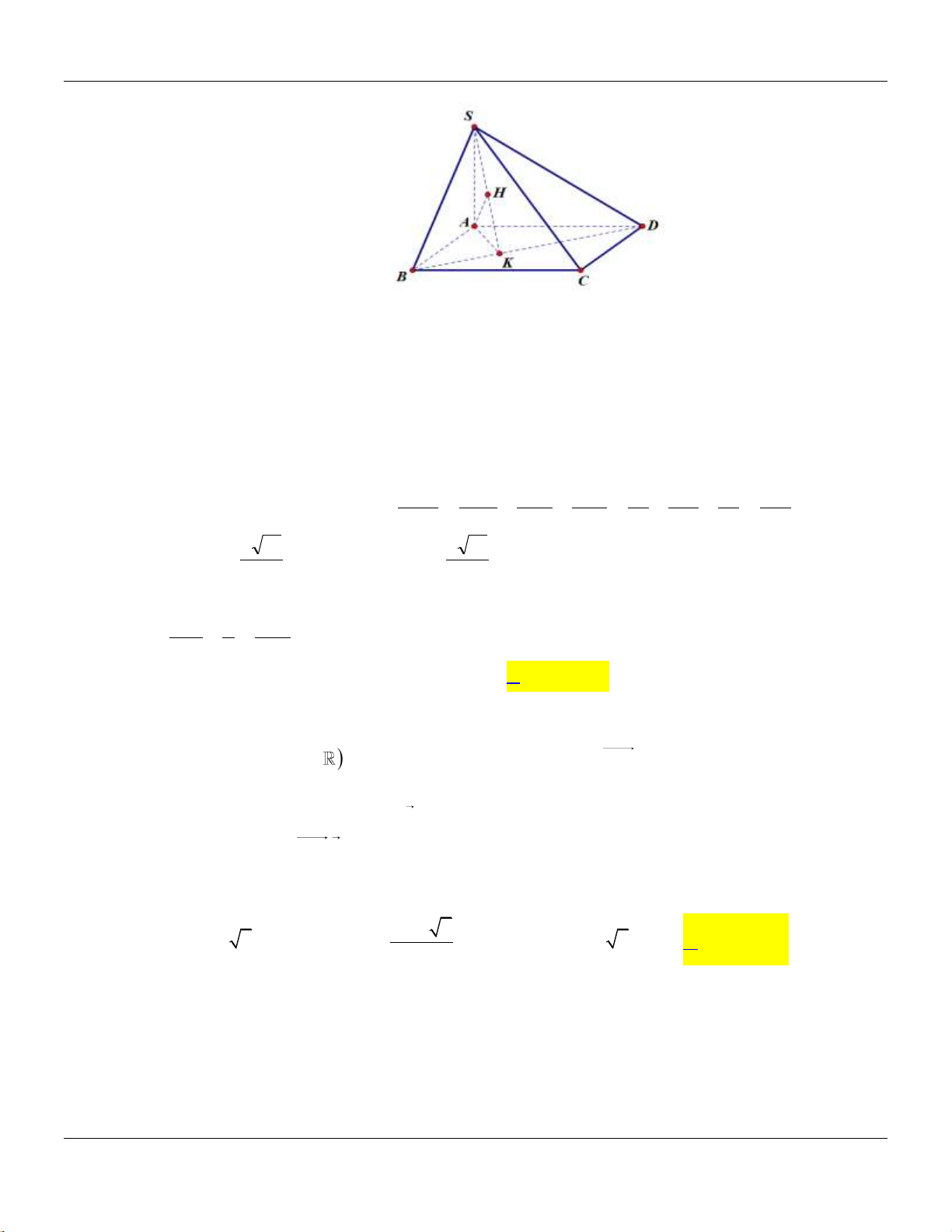
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
Gọi
K
là hình chiếu vuông góc của
A
trên
BD
.
Khi đó:
AK BD
BD SAK
BD SA
.
mà
BD SBD
suy ra
SBD SAK
mà
SBD SAK SK
nên kẻ
AH SK
thì
AH SBD
.
Vậy
,d A SBD AH
Xét tứ diện vuông
AS BD
suy ra
22222222
2
51
2
111111
aaaaASABADAH
.
Suy ra
5
10a
AH
. Vậy
5
10
))(,(
a
SBDAd
.
Câu 39: Trong không gian
,Oxyz
gọi
H
hình chiếu vuông góc của
2;0;1M
lên đường thẳng
12
:
1 2 1
x y z
. Tìm tọa độ điểm
H
.
A.
2;2;3H
. B.
0; 2;1H
. C.
1;0;2H
. D.
1; 4;0H
.
Lời giải:
Ta có
1
:2
2
xt
yt
zt
t
mà
1;2 ; 2 1;2 ; 1H H t t t MH t t t
.
Đường thẳng
có một VTCP là
1;2;1u
.
Khi đó
. 0 1 4 1 0 0 1;0;2MH MH u t t t t H
.
Câu 40: Một hình trụ có bán kính bằng
2a
. Hai điểm
,AB
lần lượt thuộc hai đường tròn đáy sao cho
4A B a
. Biết khoảng cách giữa
AB
và trục bằng
a
. Tính thể tích khối trụ đã cho.
A.
3
2
Va
. B.
3
82
3
a
V
. C.
3
42
Va
. D.
3
8
Va
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 16
a
Dựng các đường sinh
AC
và
BD
.
Ta có
//OO ACBD
, , ,d OO AB d OO ACBD d O ACBD
.
Gọi
H
là trung điểm của
BC
OH ACBD
,.d O ACBD OH a
Tam giác
OHC
vuông tại
H
suy ra
3HC a
nên
23BC a
Tam giác
ABC
vuông tại
C
2AC OO a
.
Vậy khối trụ đã cho có thể tích
2 2 3
.4 .2 8V r h a a a
.
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 09_______________
Câu 1: Cho số phức
21zi
. Điểm nào sau đây là điểm biểu diễn của số phức
z
trên mặt phẳng
tọa độ.
A.
1;2H
. B.
1; 2G
. C.
2; 1T
. D.
2;1K
.
Câu 2: Tập xác định của hàm số
1
2
log 2yx
là
A. . B.
2;
. C.
2;
. D.
0;
.
Câu 3: Đạo hàm của hàm số
2
1
2
x
y
là
A.
2
2
1 .2
x
yx
. B.
2
2
.2 .ln2
x
yx
. C.
2
1
2 .ln 2
x
y
. D.
2
2
x
y
.
Câu 4: Tập nghiệm của bất phương trình
2
23
3 27
xx
là
A.
;0 2;
. B.
0;2
. C.
2;
. D.
;0
.
Câu 5: Cho cấp số cộng
n
u
có
15
2; 14uu
. Công sai của cấp số cộng đã cho là
A.
4d
. B.
12d
. C.
7d
. D.
3d
.
Câu 6: Trong không gian
Oxyz
, mặt phẳng
(P)
:
2 3 5 0xz
có một vectơ pháp tuyến là
A.
1
2; 3;5 .n
B.
2
2; 3;0 .n
C.
3
2;0; 3 .n
D.
1
0;2; 3 .n
Câu 7: Cho hàm số
()y f x
xác định, liên tục trên và có bảng biến thiên như sau:
Số giao điểm giữa đồ thị hàm số
()y f x
và đường thẳng
2023y
là
A.
2
. B.
4
. C.
1
. D.
0
.
Câu 8: Cho
d
1
0
3f x x
và
d
0
1
2g x x
, khi đó
d
1
0
2f x g x x
bằng
A.
1
. B.
1
. C.
7
. D.
5
.
Câu 9: Đồ thị của hàm số sau là đồ thị của hàm số nào dưới đây?
A.
1
21
x
y
x
. B.
1
21
x
y
x
. C.
21
x
y
x
. D.
3
21
x
y
x
.
Câu 10: Trong không gian
Oxyz
, có tất cả bao nhiêu giá nguyên của
m
để
2 2 2 2
2 2 2 1 3 5 0x y z m x m z m
là phương trình một mặt cầu?
A.
4.
B.
6.
C.
5.
D.
7.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 11: Trong không gian
Oxyz
, cho hai điểm
2;1; 3A
và
1;0; 2B
. Độ dài đoạn thẳng
AB
bằng
A.
3 3.
B.
11.
C.
11.
D.
27.
Câu 12: Tìm các số thực
a
và
b
thỏa mãn
4 2 1 6 , ai bi i i
với
i
là đơn vị ảo.
A.
1
,6
4
ab
. B.
1
,6
4
ab
. C.
1, 1ab
. D.
1, 1ab
.
Câu 13: Cho lăng trụ đều
. ' ' 'ABC A B C
có cạnh đáy bằng
2a
, độ dài cạnh bên bằng
3a
. Tính thể
tích
V
của khối lăng trụ.
A.
2
3Va
. B.
3
1
4
a
. C.
3
a
. D.
3
3
4
a
.
Câu 14: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
hai mặt phẳng
SAB
và
SAD
cùng
vuông góc với đáy,
SC
tạo với mặt phẳng
SAB
một góc bằng
30
(tham khảo hình vẽ).
A
B
C
D
S
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
6
.
3
a
V
B.
3
2
.
3
a
V
C.
3
6
.
6
a
V
D.
3
2.Va
Câu 15: Diện tích của mặt cầu có đường kính bằng 6 là
A.
12S
B.
36S
C.
48S
D.
144S
Câu 16: Cho số phức
35zi
. Phần ảo của
z
là
A.
5
. B.
5i
. C.
5
. D.
3
.
Câu 17: Cho hình nón có diện tích xung quanh bằng
2
3 a
, bán kính đáy bằng
a
. Tính độ dài đường
sinh của hình nón đó.
A.
22a
. B.
3
2
a
. C.
2a
. D.
3a
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
2
13
:
2 1 2
y
xz
d
. Điểm nào dưới đây thuộc
d
?
A.
1;2;3P
. B.
1;2; 3Q
. C.
2;1;2N
. D.
2; 1; 2M
.
Câu 19: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đạt cực đại tại điểm nào dưới đây?
A.
4.x
B.
3.x
C.
2.x
D.
1.x
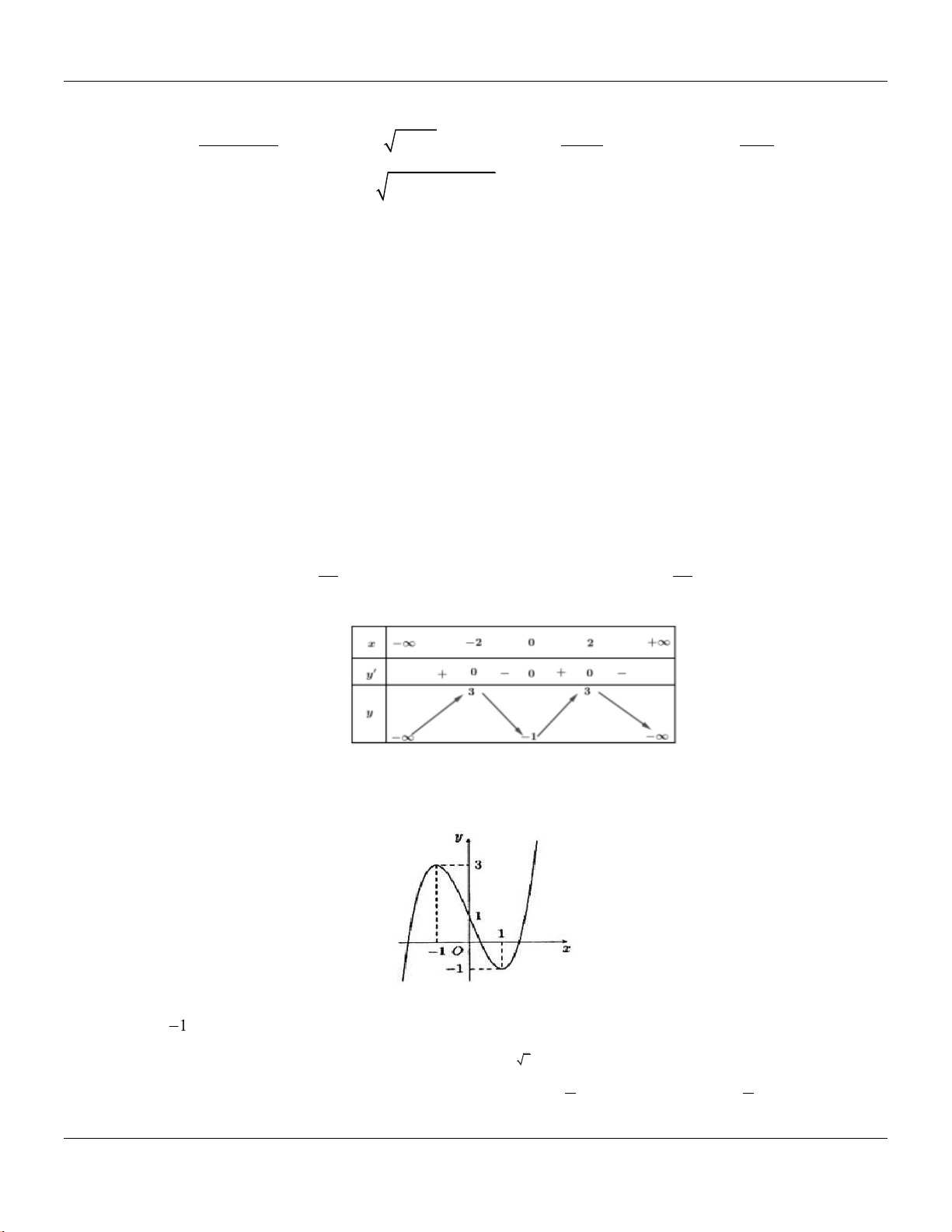
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
Câu 20: Đồ thị của hàm số nào trong các hàm số dưới đây có tiệm cận đứng?
A.
2
32
1
xx
y
x
. B.
2
1yx
. C.
2
2
1
x
y
x
. D.
1
x
y
x
.
Câu 21: Tập xác định của hàm số
2
log 4 1yx
là
A.
;4
. B.
2;4
. C.
;2
. D.
;2
.
Câu 22: Trong tủ quần áo của bạn An có 4 chiếc áo khác nhau và 3 chiếc quần khác nhau. Hỏi bạn An
có bao nhiêu cách chọn 1 bộ quần áo để mặc?
A.
7
. B.
27
. C.
64
. D.
12
.
Câu 23: Hàm số
Fx
nào sau đây là một nguyên hàm của hàm số
.f x g x
, biết
13F
,
1
df x x x C
và
2
2
d?
g x x x C
A.
2
1F x x
. B.
2
3F x x
. C.
2
2F x x
. D.
2
4F x x
.
Câu 24: Nếu các số hữu tỉ
,ab
thỏa mãn
1
0
e d e 2
x
a b x
thì giá trị của biểu thức
ab
bằng
A.
4
. B.
6
. C.
5
. D.
3
.
Câu 25: Cho hàm số
cosf x x x
. Khẳng định nào dưới đây đúng?
A.
2
d sin .f x x x x C
B.
2
d sin .f x x x x C
C.
2
d sin .
2
x
f x x x C
D.
2
d sin .
2
x
f x x x C
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số
()y f x
nghịch biến trên khoảng nào dưới đây?
A.
0;2
B.
2;0
C.
0;
D.
;2
Câu 27: Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới:
Giá trị cực tiểu của hàm số
y f x
bằng
A.
1
. B.
3
. C.
1
. D.
2
.
Câu 28: Cho
a
là số thực dương tùy ý,
1a
và
3
2
log
a
Pa
. Mệnh đề nào sau đây đúng?
A.
6P
. B.
2P
. C.
3
2
P
. D.
2
3
P
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Câu 29: Cắt hình nón
N
bằng một mặt phẳng qua trục của nó, ta thu được thiết diện là tam giác
đều cạnh
2a
. Tính diện tích xung quanh của
N
.
A.
2
2 a
. B.
2
3
2
a
. C.
4 a
. D.
2
2
3
a
.
Câu 30: Cho hình phẳng
H
giới hạn bởi đồ thị hàm số
2
21y x x
và trục hoành. Thể tích của
vật thể tròn xoay khi quay
H
quanh trục hoành bằng
A.
9
8
. B.
81
80
. C.
81
80
. D.
9
8
.
Câu 31: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là một tam giác vuông cân tại
B
,
AB a
,
'3BB a
. Góc giữa đường thẳng
BA'
và mặt phẳng
''BCC B
bằng
A.
30
. B.
90
. C.
60
. D.
45
.
Câu 32: Cho hàm số đa thức bậc ba
y f x
có đồ thị như hình bên dưới:
Số nghiệm của phương trình
0fx
là
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 33: Cho hàm số
fx
có đạo hàm
2
2
1 2 , .f x x x x x
Hàm số
2
22g x f x x
đồng biến trên các khoảng nào trong các khoảng sau?
A.
;0
. B.
2;
. C.
0;2
. D.
;1
.
Câu 34: Một tổ có 10 học sinh trong đó có 2 bạn
A
và
B
hay nói chuyện với nhau. Trong một giờ
ngoại khóa 10 bạn học sinh này được xếp ngẫu nhiên thành 1 hàng ngang. Xác suất để khi
xếp được hàng mà giữa hai bạn
A
và
B
luôn có đúng 3 bạn khác bằng
A.
1
15
. B.
1
5
. C.
2
15
. D.
1
10
.
Câu 35: Cho phương trình
2 10 4
3 6.3 2 0 1
xx
. Nếu đặt
5
30
x
tt
thì
1
trở thành phương
trình nào dưới đây?
A.
2
9 6 2 0.tt
B.
2
18 2 0.tt
C.
2
2 2 0.tt
D.
2
9 2 2 0.tt
Câu 36: Xét các số phức
z
thỏa mãn
22z i z
là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất
cả các điểm biểu diễn các số phức
z
là một đường tròn có tâm là điểm nào dưới đây?
A.
1; 1N
. B.
1;1M
. C.
2; 2P
. D.
2;2Q
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 37: Trong không gian
,Oxyz
phương trình đường thẳng đi qua điểm
;;A 2 1 2
và vuông góc với
mặt phẳng
:P x y z 2 1 0
là
A.
xt
yt
zt
2
1.
22
B.
xt
yt
zt
2
1.
22
C.
xt
yt
zt
2
1.
22
D.
xt
yt
zt
3
2.
42
Câu 38: Trong không gian
,Oxyz
cho các vectơ
1;0;3a
,
2;2;5b
. Tọa độ vectơ
ab
là
A.
1;2;8
. B.
3; 2; 2
. C.
3;2;2
. D.
2;0;15
.
Câu 39: Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
,
SA
vuông góc với
ABCD
và
SA a
(tham khảo hình vẽ)
D
C
B
A
S
Khoảng cách từ
A
đến mặt phẳng
SBD
bằng
A.
2
2
a
. B.
3
2
a
. C.
2
a
. D.
3
4
a
.
Câu 40: Trong không gian
Oxyz
, cho mặt phẳng
: 2 3 0P x y z
và đường thẳng
13
:
22
x y z
d
m
. Giá trị của
m
để
d
vuông góc với
P
là
A.
2
. B.
4
. C.
0
. D.
1
.
________________________HẾT________________________
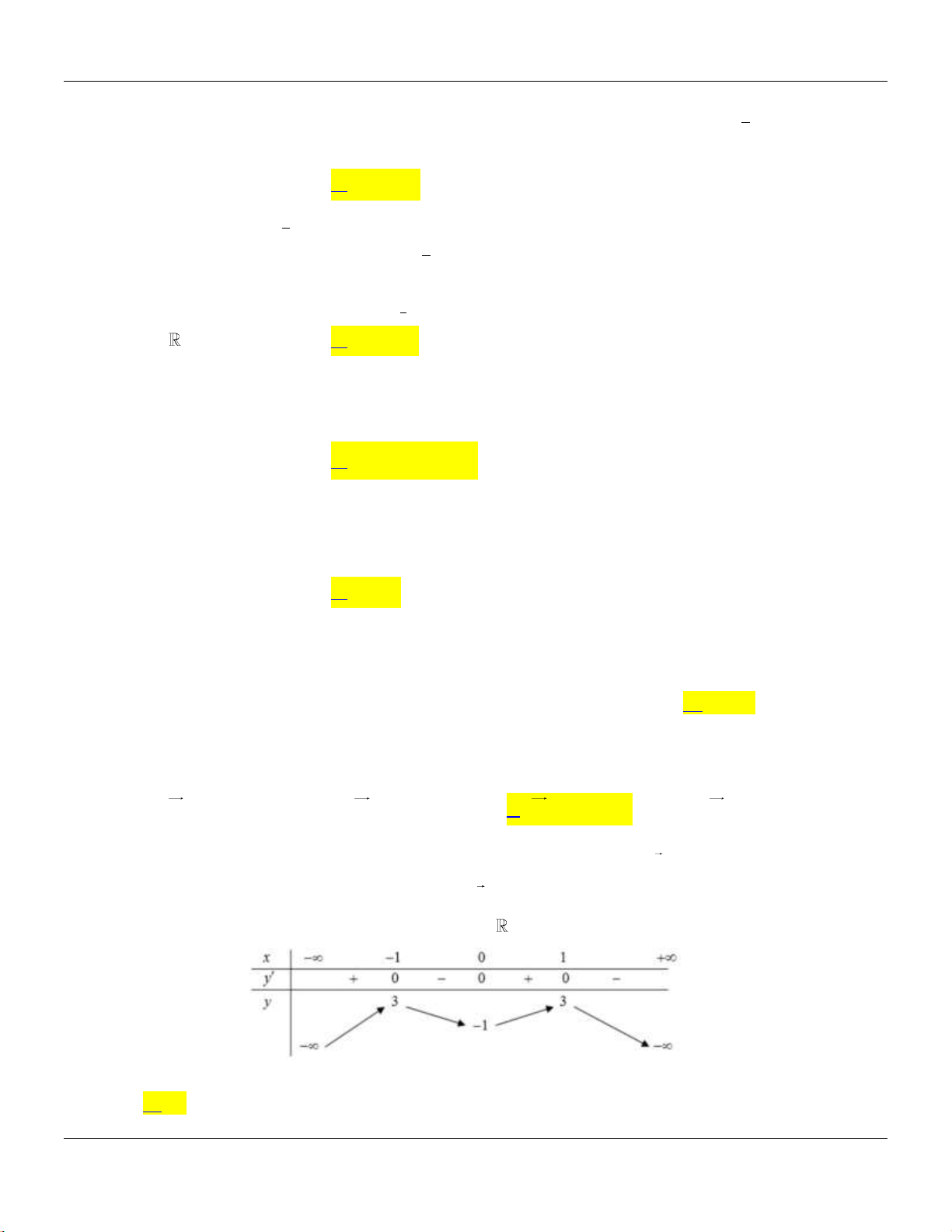
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Cho số phức
21zi
. Điểm nào sau đây là điểm biểu diễn của số phức
z
trên mặt phẳng
tọa độ.
A.
1;2H
. B.
1; 2G
. C.
2; 1T
. D.
2;1K
.
Lời giải:
Ta có
2 1 1 2z i z i
.
Suy ra điểm biểu diễn của số phức
z
trên mặt phẳng tọa độ là điểm
1; 2G
Câu 2: Tập xác định của hàm số
1
2
log 2yx
là
A. . B.
2;
. C.
2;
. D.
0;
.
Lời giải:
Điều kiện xác định:
2 0 2 2;x x x
.
Câu 3: Đạo hàm của hàm số
2
1
2
x
y
là
A.
2
2
1 .2
x
yx
. B.
2
2
.2 .ln2
x
yx
. C.
2
1
2 .ln 2
x
y
. D.
2
2
x
y
.
Lời giải:
Ta có
2
1
2
x
y
2
21
1 .2 .ln2
x
yx
2
1
2 .2 .ln2
x
x
2
2
.2 .ln2
x
x
.
Câu 4: Tập nghiệm của bất phương trình
2
23
3 27
xx
là
A.
;0 2;
. B.
0;2
. C.
2;
. D.
;0
.
Lời giải:
Ta có
2
2 3 2 2
3 27 2 3 3 2 0 0 2
xx
x x x x x
.
Câu 5: Cho cấp số cộng
n
u
có
15
2; 14uu
. Công sai của cấp số cộng đã cho là
A.
4d
. B.
12d
. C.
7d
. D.
3d
.
Lời giải:
Ta có:
51
4 14 2 4 3u u d d d
.
Câu 6: Trong không gian
Oxyz
, mặt phẳng
(P)
:
2 3 5 0xz
có một vectơ pháp tuyến là
A.
1
2; 3;5 .n
B.
2
2; 3;0 .n
C.
3
2;0; 3 .n
D.
1
0;2; 3 .n
Lời giải:
Mặt phẳng
(P)
:
0Ax By Cz D
có một vectơ pháp tuyến là
;;n A B C
nên mặt phẳng
2 3 5 0xz
có một vectơ pháp tuyến là
2;0; 3n
.
Câu 7: Cho hàm số
()y f x
xác định, liên tục trên và có bảng biến thiên như sau:
Số giao điểm giữa đồ thị hàm số
()y f x
và đường thẳng
2023y
là
A.
2
. B.
4
. C.
1
. D.
0
.
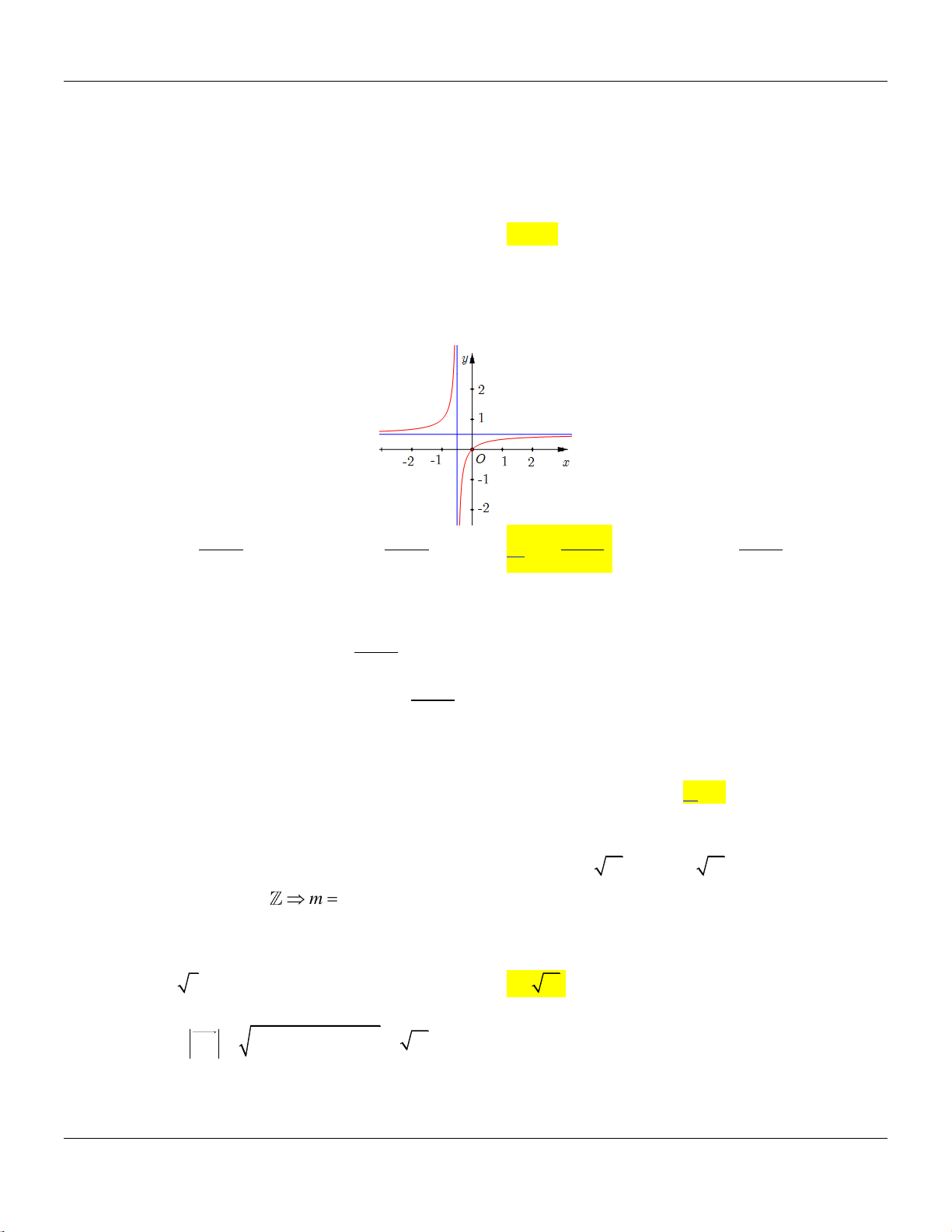
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
Lời giải:
Do:
2023 1
và kết hợp bảng biến thiên ta thấy đường thẳng
2023y
cắt đồ thị hàm số
()y f x
tại 2 điểm phân biệt.
Câu 8: Cho
d
1
0
3f x x
và
d
0
1
2g x x
, khi đó
d
1
0
2f x g x x
bằng
A.
1
. B.
1
. C.
7
. D.
5
.
Lời giải:
Ta có:
1 1 1
0 0 0
2 2 3 2.2 7f x g x dx f x dx g x dx
.
Câu 9: Đồ thị của hàm số sau là đồ thị của hàm số nào dưới đây?
A.
1
21
x
y
x
. B.
1
21
x
y
x
. C.
21
x
y
x
. D.
3
21
x
y
x
.
Lời giải:
Quan sát đò thị ta thầy đồ thị hàm số đi qua điểm
0;0O
.
Mặt khác chỉ có đồ thị
21
x
y
x
đi qua gốc tọa độ.
Vậy đồ thi trên là của hàm số:
21
x
y
x
.
Câu 10: Trong không gian
Oxyz
, có tất cả bao nhiêu giá nguyên của
m
để
2 2 2 2
2 2 2 1 3 5 0x y z m x m z m
là phương trình một mặt cầu?
A.
4.
B.
6.
C.
5.
D.
7.
Lời giải:
Phương trình đã cho là phương trình mặt cầu khi và chỉ khi
22
22
2 1 3 5 0 2 10 0 1 11 1 11 m m m m m m
Theo bài ra
2; 1;0;1;2;3;4 mm
có
7
giá trị của
m
nguyên thỏa mãn bài toán.
Câu 11: Trong không gian
Oxyz
, cho hai điểm
2;1; 3A
và
1;0; 2B
. Độ dài đoạn thẳng
AB
bằng
A.
3 3.
B.
11.
C.
11.
D.
27.
Lời giải:
22
2
3 1 1 11 AB AB
.
Câu 12: Tìm các số thực
a
và
b
thỏa mãn
4 2 1 6 , ai bi i i
với
i
là đơn vị ảo.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
A.
1
,6
4
ab
. B.
1
,6
4
ab
. C.
1, 1ab
. D.
1, 1ab
.
Lời giải:
Ta có:
4 2 1 6ai bi i i
4 2 1 6ai i b i
4 2 1 6b a i i
.
Do đó:
11
4 2 6 1
bb
aa
.
Câu 13: Cho lăng trụ đều
. ' ' 'ABC A B C
có cạnh đáy bằng
2a
, độ dài cạnh bên bằng
3a
. Tính thể
tích
V
của khối lăng trụ.
A.
2
3Va
. B.
3
1
4
a
. C.
3
a
. D.
3
3
4
a
.
Lời giải:
a
3
2
a
C
'
B
'
A
'
C
B
A
Lăng trụ đều
. ' ' 'ABC A B C
là lăng trụ đứng và có đáy
ABC
là tam giác đều.
Chiều cao lăng trụ
'3h AA a
.
Diện tích đáy
ABC
:
2
43
4
ABC
a
S
.
Thể tích khối lăng trụ đã cho là
2
3
43
. 3. 3
4
ABC
a
V h S a a
.
Câu 14: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
hai mặt phẳng
SAB
và
SAD
cùng
vuông góc với đáy,
SC
tạo với mặt phẳng
SAB
một góc bằng
30
(tham khảo hình vẽ).
A
B
C
D
S
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
6
.
3
a
V
B.
3
2
.
3
a
V
C.
3
6
.
6
a
V
D.
3
2.Va
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
a
30
0
A
B
C
D
S
Ta có:
.
SAB ABCD
SA ABCD
SAD ABCD
và
;.
BC AB
BC SAB SC SAB BSC
BC SA
Xét tam giác
SBC
vuông tại
:B
tan
BC
BSC
SB
22
32
tan
BC
SB a SA SB AB a
BSC
và
2
.
ABCD
Sa
Vậy
3
.
12
..
33
S ABCD ABCD
a
V SA S
Câu 15: Diện tích của mặt cầu có đường kính bằng 6 là
A.
12S
B.
36S
C.
48S
D.
144S
Lời giải:
Mặt cầu có đường kính bằng 6, do đó có bán kính
3R
.
Tính diện tích
2
4 36SR
.
Câu 16: Cho số phức
35zi
. Phần ảo của
z
là
A.
5
. B.
5i
. C.
5
. D.
3
.
Lời giải:
Số phức
35zi
có phần ảo là
5
.
Câu 17: Cho hình nón có diện tích xung quanh bằng
2
3 a
, bán kính đáy bằng
a
. Tính độ dài đường
sinh của hình nón đó.
A.
22a
. B.
3
2
a
. C.
2a
. D.
3a
.
Lời giải:
2
3
3
xq
xq
S
a
S Rl l a
Ra
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
2
13
:
2 1 2
y
xz
d
. Điểm nào dưới đây thuộc
d
?
A.
1;2;3P
. B.
1;2; 3Q
. C.
2;1;2N
. D.
2; 1; 2M
.
Lời giải:
Lần lượt thay tọa độ của 4 điểm đã cho vào phương trình đường thẳng
d
, ta thấy tọa độ của
điểm
1;2; 3Q
thỏa mãn. Vậy điểm
1;2; 3Q
thuộc đường thẳng
.d
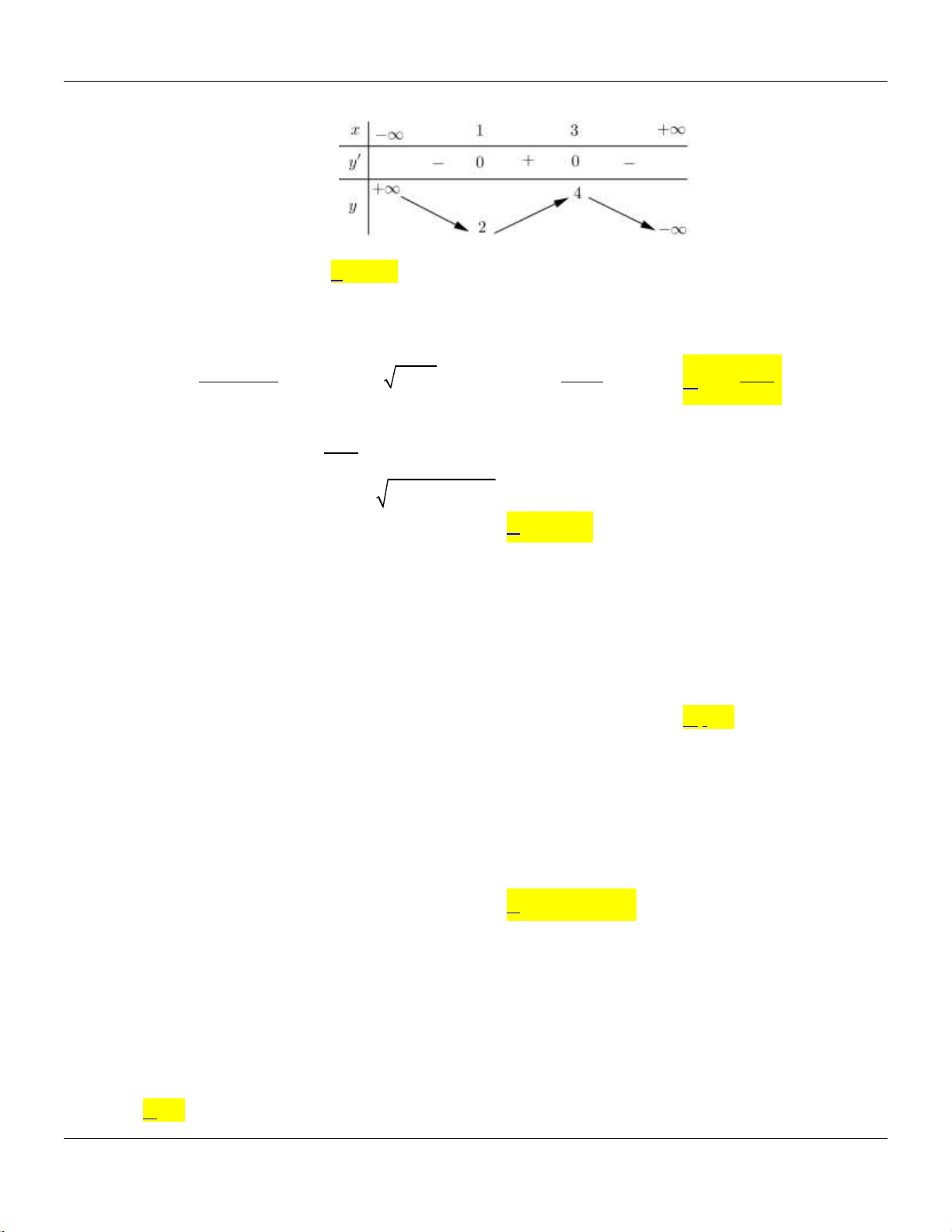
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Câu 19: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đạt cực đại tại điểm nào dưới đây?
A.
4.x
B.
3.x
C.
2.x
D.
1.x
Lời giải:
Từ bảng biến thiên ta thấy hàm số đạt cực đại tại
3x
.
Câu 20: Đồ thị của hàm số nào trong các hàm số dưới đây có tiệm cận đứng?
A.
2
32
1
xx
y
x
. B.
2
1yx
. C.
2
2
1
x
y
x
. D.
1
x
y
x
.
Lời giải:
Đồ thị của hàm số
1
x
y
x
có tiệm cận đứng
1x
.
Câu 21: Tập xác định của hàm số
2
log 4 1yx
là
A.
;4
. B.
2;4
. C.
;2
. D.
;2
.
Lời giải:
Hàm số xác định
2
2
log 4 1
4 2 2
log 4 1 0 2.
4 0 4
40
x
xx
xx
xx
x
Vậy tập xác định của hàm số là:
;2D
.
Câu 22: Trong tủ quần áo của bạn An có 4 chiếc áo khác nhau và 3 chiếc quần khác nhau. Hỏi bạn An
có bao nhiêu cách chọn 1 bộ quần áo để mặc?
A.
7
. B.
27
. C.
64
. D.
12
.
Lời giải:
Chọn 1 chiếc áo trong số 4 chiếc áo khác nhau: có 4 cách chọn.
Chọn 1 chiếc quần trong số 3 chiếc quần khác nhau: có 3 cách chọn.
Theo quy tắc nhân suy ra có
4.3 12
(cách chọn) 1 bộ quần áo để mặc.
Câu 23: Hàm số
Fx
nào sau đây là một nguyên hàm của hàm số
.f x g x
, biết
13F
,
1
df x x x C
và
2
2
d?
g x x x C
A.
2
1F x x
. B.
2
3F x x
. C.
2
2F x x
. D.
2
4F x x
.
Lời giải:
Theo giả thiết ta có:
1fx
và
2g x x
nên
.2f x g x x
.
2
2dF x x x x C
. Vì
1 3 2FC
. Vậy một nguyên hàm
Fx
cần tìm của hàm số
.f x g x
, là
2
2F x x
.
Câu 24: Nếu các số hữu tỉ
,ab
thỏa mãn
1
0
e d e 2
x
a b x
thì giá trị của biểu thức
ab
bằng
A.
4
. B.
6
. C.
5
. D.
3
.
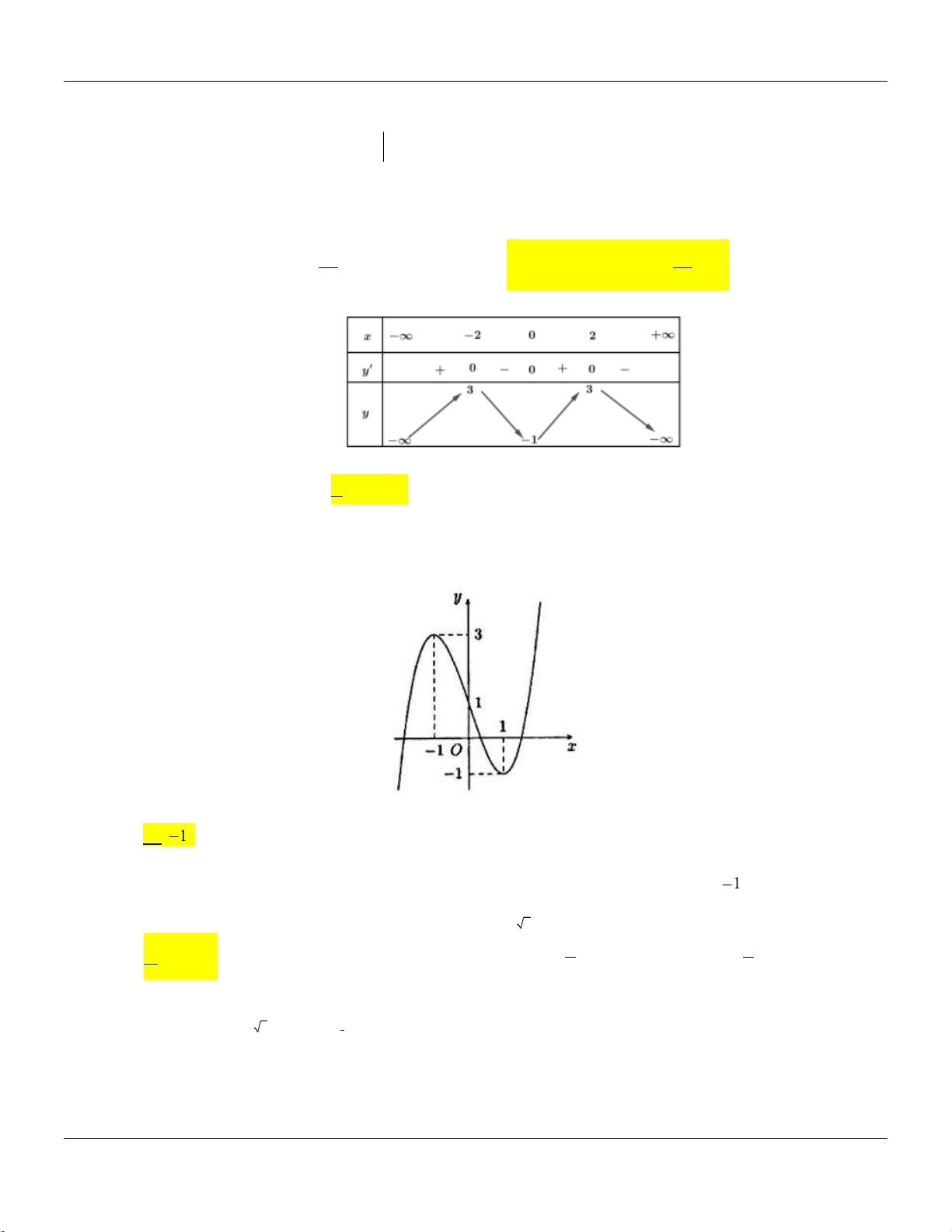
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Lời giải:
Ta có
1
1
0
0
e d e e
xx
a b x a bx a b a
1
2
a
ba
1
4
3
a
ab
b
.
Câu 25: Cho hàm số
cosf x x x
. Khẳng định nào dưới đây đúng?
A.
2
d sin .f x x x x C
B.
2
d sin .f x x x x C
C.
2
d sin .
2
x
f x x x C
D.
2
d sin .
2
x
f x x x C
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số
()y f x
nghịch biến trên khoảng nào dưới đây?
A.
0;2
B.
2;0
C.
0;
D.
;2
Lời giải:
Dựa vào bảng biến thiên ta có hàm số nghịch biến trên các khoảng
2;0
và
2;
.
Câu 27: Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới:
Giá trị cực tiểu của hàm số
y f x
bằng
A.
1
. B.
3
. C.
1
. D.
2
.
Lời giải:
Dựa vào đồ thị hàm số
y f x
ta thấy giá trị cực tiểu của hàm số bằng
1
.
Câu 28: Cho
a
là số thực dương tùy ý,
1a
và
3
2
log
a
Pa
. Mệnh đề nào sau đây đúng?
A.
6P
. B.
2P
. C.
3
2
P
. D.
2
3
P
.
Lời giải:
Ta có:
3
2
log
a
Pa
1
3
2
log
a
a
2.3.log
a
a
6
.
Câu 29: Cắt hình nón
N
bằng một mặt phẳng qua trục của nó, ta thu được thiết diện là tam giác
đều cạnh
2a
. Tính diện tích xung quanh của
N
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
A.
2
2 a
. B.
2
3
2
a
. C.
4 a
. D.
2
2
3
a
.
Lời giải:
Cắt hình nón
N
bằng một mặt phẳng qua trục của nó, ta thu được thiết diện là tam giác
đều cạnh
2a
suy ra
22
2
3
Ra
l h R a
ha
Diện tích xung quanh của
N
là
2
2
xq
S Rl a
.
Câu 30: Cho hình phẳng
H
giới hạn bởi đồ thị hàm số
2
21y x x
và trục hoành. Thể tích của
vật thể tròn xoay khi quay
H
quanh trục hoành bằng
A.
9
8
. B.
81
80
. C.
81
80
. D.
9
8
.
Lời giải:
+ Phương trình hoành độ giao điểm:
2
1
2 1 0
1
2
x
xx
x
.
+ Thể tích cần tìm là
1
2
2
1
2
81
2 1 d
80
V x x x
.
Câu 31: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là một tam giác vuông cân tại
B
,
AB a
,
'3BB a
. Góc giữa đường thẳng
BA'
và mặt phẳng
''BCC B
bằng
A.
30
. B.
90
. C.
60
. D.
45
.
Lời giải:
Ta có:
()
()
A B B C gt
A B BCC B
A B B B gt
suy ra
BB
là hình chiếu vuông góc của
'AB
lên
mặt phẳng
BCC B
. Khi đó
;A B BCC B A BB
.
Xét
A B B
vuông tại
B
, có
3
tan
3
3
A B a
A BB
BB
a
30
A BB
.
Câu 32: Cho hàm số đa thức bậc ba
y f x
có đồ thị như hình bên dưới:
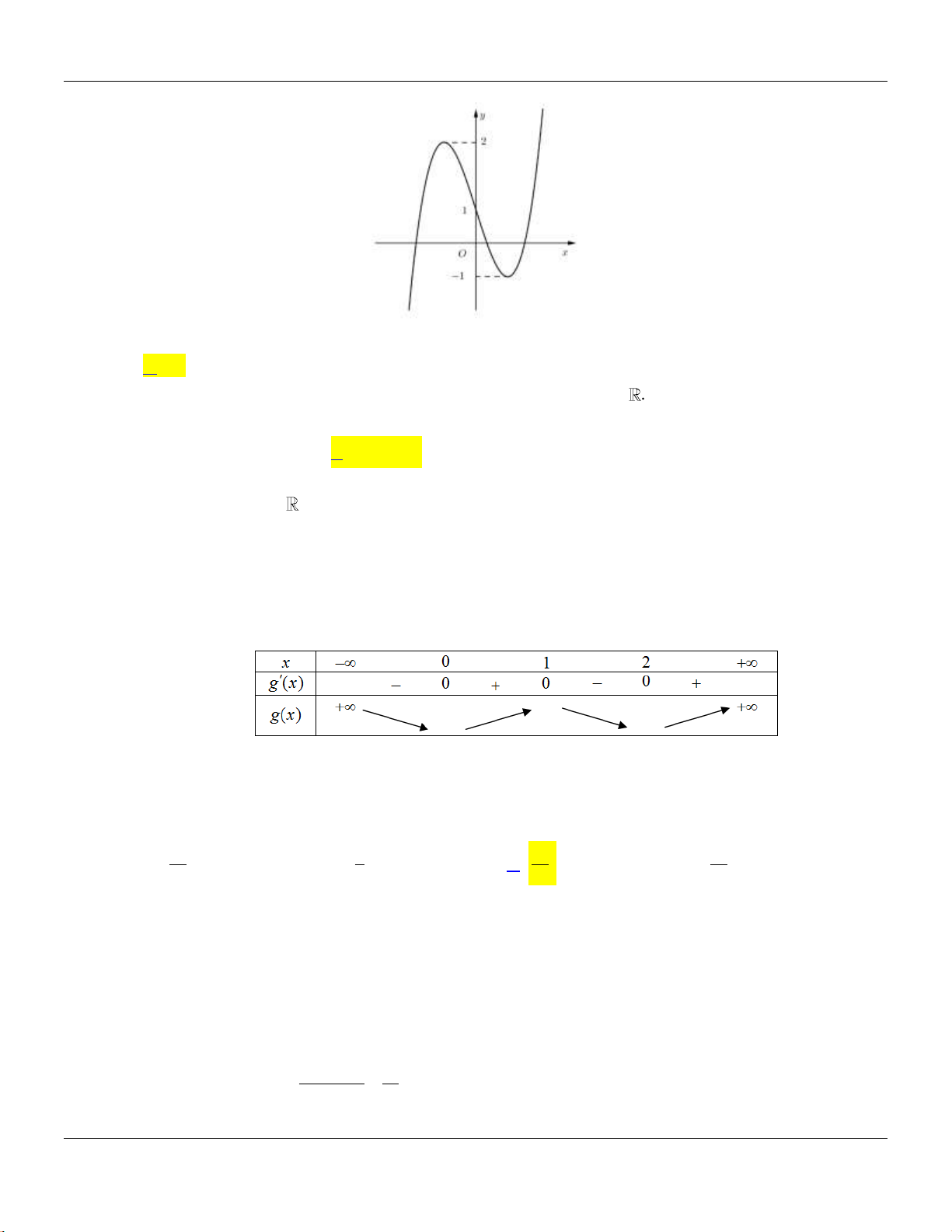
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Số nghiệm của phương trình
0fx
là
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 33: Cho hàm số
fx
có đạo hàm
2
2
1 2 , .f x x x x x
Hàm số
2
22g x f x x
đồng biến trên các khoảng nào trong các khoảng sau?
A.
;0
. B.
2;
. C.
0;2
. D.
;1
.
Lời giải:
Tập xác định
D
.
Ta có
2
2 2 2 2
2 2 2 2 2 2 2 2 1 2 2 2 2 2g x x f x x x x x x x x x
2
22
2 2 2 1 2 2 2x x x x x x x
Phương trình có các nghiệm bội lẻ là:
0;1;2x
Bảng biến thiên:
Vậy hàm số
y g x
đồng biến trên
2;
.
Câu 34: Một tổ có 10 học sinh trong đó có 2 bạn
A
và
B
hay nói chuyện với nhau. Trong một giờ
ngoại khóa 10 bạn học sinh này được xếp ngẫu nhiên thành 1 hàng ngang. Xác suất để khi
xếp được hàng mà giữa hai bạn
A
và
B
luôn có đúng 3 bạn khác bằng
A.
1
15
. B.
1
5
. C.
2
15
. D.
1
10
.
Lời giải:
Xếp 10 bạn tùy ý ta có
10!
cách.
Để xếp được hàng thỏa mãn bài toán ta thực hiện theo các bước sau :
Bước 1: Chọn 3 bạn trong 8 xếp vào giữa hai bạn
A
và
B
có
3
8
C
. Xếp 5 bạn này có
3
8
2. .3!C
cách.
Bước 2: Xếp một nhóm 5 bạn trên cùng với 5 bạn còn lại có
6!
cách.
Số cách xếp thỏa mãn bài toán là
3
8
2. .3!C
6! Cách.
Xác suất cần tìm là
3
8
2. .3!6!
2
10! 15
C
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
Câu 35: Cho phương trình
2 10 4
3 6.3 2 0 1
xx
. Nếu đặt
5
30
x
tt
thì
1
trở thành phương
trình nào dưới đây?
A.
2
9 6 2 0.tt
B.
2
18 2 0.tt
C.
2
2 2 0.tt
D.
2
9 2 2 0.tt
Lời giải:
25
2 10 4 5
3 6.3 2 0 3 2.3 2 0
x
x x x
Vậy khi đặt
5
30
x
tt
thì
1
trở thành phương trình
2
2 2 0.tt
Câu 36: Xét các số phức
z
thỏa mãn
22z i z
là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất
cả các điểm biểu diễn các số phức
z
là một đường tròn có tâm là điểm nào dưới đây?
A.
1; 1N
. B.
1;1M
. C.
2; 2P
. D.
2;2Q
.
Lời giải:
Gọi
,, z x yi x y
.
Ta có:
22
2 2 2 2 2 2 2 2 4z i z x y i x yi x y x y x y i
.
22z i z
là số thuần ảo
22
22
2 2 0 1 1 2x y x y x y
.
Vậy tập hợp tất cả các điểm biểu diễn các số phức
z
là một đường tròn có tâm
1;1M
.
Câu 37: Trong không gian
,Oxyz
phương trình đường thẳng đi qua điểm
;;A 2 1 2
và vuông góc với
mặt phẳng
:P x y z 2 1 0
là
A.
xt
yt
zt
2
1.
22
B.
xt
yt
zt
2
1.
22
C.
xt
yt
zt
2
1.
22
D.
xt
yt
zt
3
2.
42
Lời giải:
Kiểm tra sự kiện:
Ad
và vectơ chỉ phương
;;
P
n 1 1 2
ta thấy phương án D thỏa mãn.
Câu 38: Trong không gian
,Oxyz
cho các vectơ
1;0;3a
,
2;2;5b
. Tọa độ vectơ
ab
là
A.
1;2;8
. B.
3; 2; 2
. C.
3;2;2
. D.
2;0;15
.
Câu 39: Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
,
SA
vuông góc với
ABCD
và
SA a
(tham khảo hình vẽ)
D
C
B
A
S
Khoảng cách từ
A
đến mặt phẳng
SBD
bằng
A.
2
2
a
. B.
3
2
a
. C.
2
a
. D.
3
4
a
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
O
C
A
D
B
S
H
Gọi
O
là tâm hình vuông
ABCD
khi đó
BD AC
(1).
Vì
SA ABCD
nên
SA BD
(2).
Từ (1) và (2), ta có
BD SAC
(3).
Gọi
H
là hình chiếu của
A
lên
SO
, khi đó
AH SO
(4).
Mặt khác, vì
AH SAC
nên theo (3), ta có
BD AH
(5).
Từ (4) và (5) suy ra
AH SBD
, hay
,d A SBD AH
.
Xét tam giác vuông
SAO
, có
AS a
,
11
22
22
AO AC a a
.
Khi đó
SAO
vuông cân tại
A
, suy ra
2
2
a
AH
.
Vậy
2
,
2
a
d A SBD
.
Câu 40: Trong không gian
Oxyz
, cho mặt phẳng
: 2 3 0P x y z
và đường thẳng
13
:
22
x y z
d
m
. Giá trị của
m
để
d
vuông góc với
P
là
A.
2
. B.
4
. C.
0
. D.
1
.
Lời giải:
Mặt phẳng
P
có một vectơ pháp tuyến là
1; 1;2n
, đường thẳng
d
có một vectơ chỉ
phương là
2;2;um
.
Đường thẳng
d
vuông góc với mặt phẳng
P
khi hai vectơ
n
và
u
cùng phương
22
24
1 1 2 2
mm
m
.
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 10_______________
Câu 1: Gi
,AB
ln lưt l đim biu din cho hai s phc
1
1zi
v
2
13zi
. Gi
M
l trung
đim ca
AB
. Khi đ,
M
l đim biu din cho s phc no dưi đây?
A.
1 i
. B.
22i
. C.
i
. D.
1 i
.
Câu 2: Hàm s
1
2
1yx
xác định khi chỉ khi
A.
1x
. B.
x
. C.
1x
. D.
1x
.
Câu 3: Hàm s
21
5
x
y
c đạo hàm là
A.
22
2 1 5
x
yx
. B.
21
5 ln5
x
y
. C.
21
2.5
x
y
. D.
21
2.5 ln5
x
y
.
Câu 4: Tp nghim ca bt phương trnh
ee
2
1xx
l
A.
0;1S
. B.
1;2S
. C.
1;S
. D.
;0S
.
Câu 5: Cho cp s nhân
n
u
có
2
1
4
u
và
3
1u
. Tìm công bội
q
ca cp s nhân đã cho.
A.
1
2
q
. B.
4q
. C.
1
2
q
. D.
4q
.
Câu 6: Trong không gian
Oxyz
, cho hai đim
2; 1; 3A
và
0; 3; 1B
. Gi
là mặt phẳng
trung trực ca đoạn
AB
. Một vectơ pháp tuyến ca
có ta độ là
A.
2;4; 1 .
B.
1;0;1 .
C.
1;1;2 .
D.
1;2; 1 .
Câu 7: Cho hàm s
32
, , ,f x ax bx cx d a b c d
c đồ thị như hnh vẽ bên dưi:
S nghim thực ca phương trnh
4 3 0fx
là
A.
3
B.
2
C.
1
D.
0
Câu 8: Cho
2
0
d3
f x x
,
2
0
d1
g x x
thì
2
0
5d
f x g x x x
bằng
A.
12
. B.
0
. C.
8
. D.
10.
Câu 9: Đường cong trong hình vẽ sau l đồ thị ca hàm s no dưi đây?
x
y
0
A.
42
3 1. y x x
B.
42
3 1. y x x
C.
32
3 1. y x x
D.
32
3 1. y x x
Câu 10: Trong không gian
Oxyz
, cho mặt cu
2 2 2
: 2 4 2 3 0S x y z x y z
. Ta độ tâm
I
ca
mặt cu
S
là
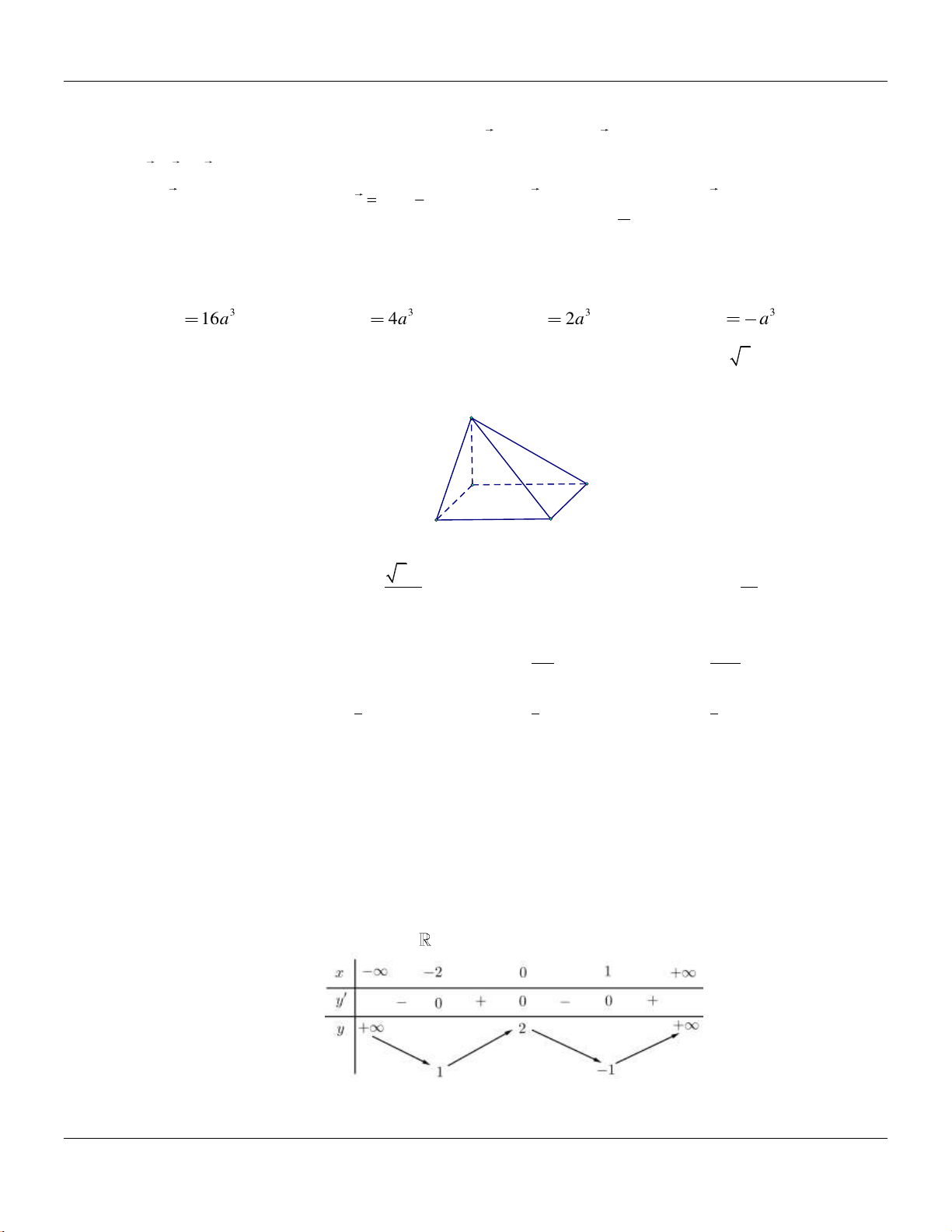
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
A.
1; 2; 1
. B.
2; 4; 2
. C.
1; 2; 1
. D.
2;4;2
.
Câu 11: Trong không gian
Oxyz
, cho hai vectơ
4;5; 3a
,
2; 2;1b
. Tìm ta độ ca vectơ
2x a b
.
A.
2;3; 2x
. B.
0;1; 1x
. C.
0; 1;1x
. D.
8;9;1x
.
Câu 12: Cho hai s phc
1
1zi
và
2
1zi
. Giá trị ca biu thc
12
z iz
bằng
A.
22i
. B.
2i
. C.
2
. D.
22i
.
Câu 13: Tính th tích
V
ca khi lăng trụ có din tích đáy bằng
2
4a
và chiều cao bằng
.a
A.
3
16Va
. B.
3
4Va
. C.
3
2Va
. D.
3
4
3
Va
.
Câu 14: Cho khi chóp
.S ABCD
c đáy
ABCD
là hình chữ nht,
AB a
,
3AD a
,
SA
vuông góc
vi mặt phẳng đáy v mặt phẳng
SBC
tạo vi đáy một góc
60
(tham khảo hình vẽ).
A
B
C
D
S
Tính th tích
V
ca khi chóp
.S ABCD
.
A.
3
3Va
. B.
3
3
3
a
V
. C.
3
Va
. D.
3
3
a
V
.
Câu 15: Cho mặt cu
S
có din tích bằng
4
. Th tích khi cu
S
bằng:
A.
16
. B.
32
. C.
4
3
. D.
16
3
.
Câu 16: S phc liên hp ca s phc
23zi
là
A.
32zi
B.
32zi
C.
23zi
D.
23zi
Câu 17: Cho hnh nn c đường cao v đường kính đáy đều bằng
2a
. Cắt hnh nn đã cho bằng một
mặt phẳng đi qua trục thu đưc din tích thiết din bằng
A.
2
8a
. B.
2
a
. C.
2
2a
. D.
2
4a
.
Câu 18: Trong không gian
Oxyz
, đường thẳng
2
:3
2
xt
d y t
zt
đi qua đim no sau đây?
A.
1;2; 1M
. B.
3;2; 1N
. C.
3; 2; 1P
. D.
3; 2;1Q
.
Câu 19: Cho hàm s
()y f x
liên tục trên và có bảng biến thiên:
Khẳng định no sau đây sai?
A.
0;2M
l đim cực tiu ca đồ thị hàm s.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
B.
( 1)f
là một giá trị cực tiu ca hàm s.
C.
0
o
x
l đim cực đại ca hàm s.
D.
1
o
x
l đim cực tiu ca hàm s.
Câu 20: Đồ thị hàm s
1
41
x
y
x
c đường tim cn ngang l đường thẳng no dưi đây?
A.
1y
. B.
1x
. C.
1
4
y
. D.
1
4
x
.
Câu 21: Bt phương trnh
3
log 1 2x
có nghim nhỏ nht bằng
A. 10. B. 6. C. 9. D. 7.
Câu 22: Cho hai đường thẳng
1
d
và
2
d
song song vi nhau. Trên đường thẳng
1
d
cho 5 đim phân
bit, trên đường thẳng
2
d
cho 7 đim phân bit. S tam giác c đỉnh l các đim trong 12
đim đã cho l
A. 350. B. 210. C. 175. D. 220.
Câu 23: Cho
df x x F x C
. Khi
2 3 df x x
bằng
A.
1
23
2
F x C
. B.
1
23
2
F x C
. C.
23F x C
. D.
23F x C
.
Câu 24: Cho
1
0
d2
f x x
và
4
1
d5
f x x
, khi đ
4
0
d
f x x
bằng
A.
6
. B.
10
. C.
7
. D.
3
.
Câu 25: Tính
sin3 dxx
.
A.
1
cos3
3
xC
. B.
cos3xC
. C.
cos3xC
. D.
1
cos3
3
xC
.
Câu 26: Cho hàm s
()y f x
c đồ thị như sau:
Hàm s đã cho nghịch biến trên khoảng no dưi đây?
A.
0;1
. B.
1;0
. C.
2; 1
. D.
1;1
.
Câu 27: Cho hàm s
y f x
c đạo hàm
3
2
2 1 ,
f x x x x
x
. Hàm s đã cho có bao
nhiêu đim cực trị?
A.
2
. B.
0
. C.
3
. D.
1
.
Câu 28: Cho các s thực dương
,ab
tùy ý,
2
3
log 3 ab
bằng
A.
33
1
log 2log
2
ab
. B.
33
1
1 log 2log
2
ab
.
C.
33
1 log 2logab
. D.
33
1
1 log log
2
ab
.
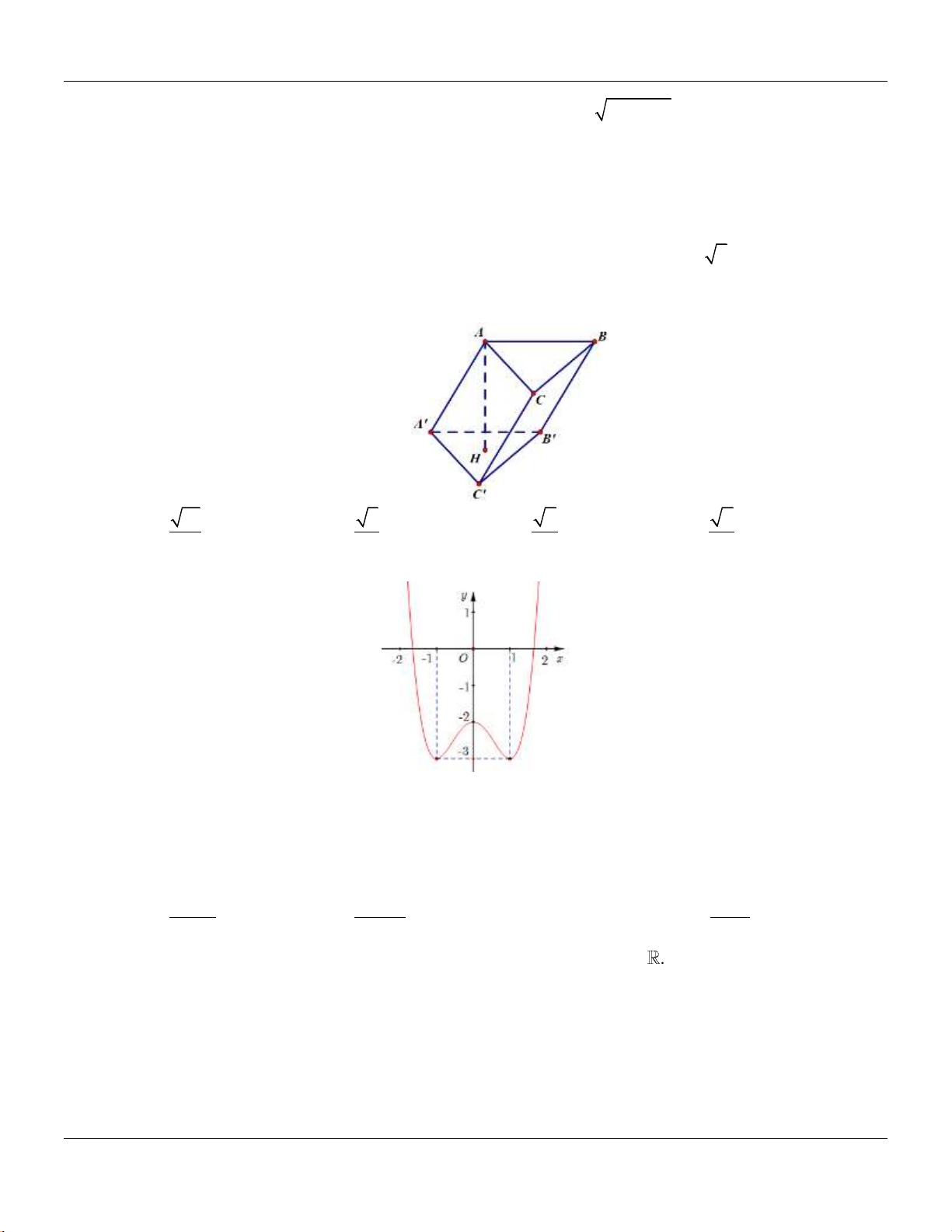
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Câu 29: Cho
H
là hình phẳng gii hạn bởi đồ thị hàm s
4
x
y e x
, trục honh v hai đường
thẳng
1, 2xx
;
V
là th tích ca khi tròn xoay thu đưc khi quay hình
H
quanh trục
hoành. Khẳng định no sau đây đúng?
A.
2
1
4d
x
V e x x
. B.
2
1
4d
x
V x e x
. C.
2
1
4d
x
V e x x
. D.
2
1
4d
x
V x e x
.
Câu 30: Cho hnh lăng trụ
.ABC A B C
c đáy l tam giác đều cạnh
a
,
6BB a
. Hình chiếu vuông
góc
H
ca
A
trên mặt phẳng
ABC
trùng vi trng tâm ca tam giác
ABC
(tham khảo
hình vẽ). Côsin ca góc giữa cạnh bên và mặt đáy bằng
A.
15
15
. B.
3
6
. C.
2
3
. D.
2
6
.
Câu 31: Đường cong trong hình vẽ l đồ thị ca hàm s
42
22y x x
.
Tìm tt cả các giá trị thực ca tham s
m
đ phương trnh
42
2x x m
có 4 nghim phân
bit.
A.
2m
. B.
10m
. C.
3m
. D.
32m
.
Câu 32: Cắt một hình trụ bởi một mặt phẳng qua trục ca n, ta đưc thiết din là một hình vuông có
cạnh bằng
3a
. Tính din tích toàn phn ca hình trụ đã cho.
A.
2
13
6
a
. B.
2
27
2
a
. C.
2
9 a
. D.
2
9
2
a
.
Câu 33: Cho hàm s
y f x
c đạo hàm
2
2 1 , .
f x x x x
Hàm s đã cho đồng biến
trên khoảng no dưi đây?
A.
1;2
. B.
1;
. C.
2;
. D.
;1
.
Câu 34: Có 8 chiếc ghế đưc kê thành một hàng ngang. Xếp ngẫu nhiên 8 hc sinh gồm 3 hc sinh nữ,
5 hc sinh nam ngồi vào hàng ghế đ sao cho mỗi ghế c đúng một hc sinh. Xác xut đ 3
hc sinh nữ ngồi ở 3 ghế cạnh nhau bằng
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
A.
3
56
. B.
1
56
. C.
1
28
. D.
3
28
.
Câu 35: Tích hai nghim ca phương trình
2
33
log 6log 8 0xx
bằng
A.
90
. B.
729
. C.
8
. D.
6
.
Câu 36: Tp hp tt cả các đim trong mặt phẳng ta độ
Oxy
biu din s phc
z
thỏa mãn
1 2 3z i z
l đường thẳng c phương trnh l
A.
2 1 0xy
. B.
2 1 0xy
. C.
2 1 0xy
. D.
2 1 0xy
.
Câu 37: Trong không gian
,Oxyz
phương trnh đường thẳng đi qua đim
;;A 2 1 2
và vuông góc vi
mặt phẳng
:P x y z 10
là
A.
y
xz
1
22
.
1 1 1
B.
y
xz
1
22
.
1 1 1
C.
y
xz
1
22
.
1 1 1
D.
y
xz
2
33
.
1 1 1
Câu 38: Trong không gian
,Oxyz
cho đim
1;2;3 .M
Khoảng cách từ đim
M
đến trục
Ox
bằng
A.
1.
B.
13.
C.
5.
D.
10.
Câu 39: Cho hình chóp
.S A BC
có
SA a
và
SA
vuông góc vi đáy. Biết đáy l tam giác vuông cân tại
A
và
2BC a
.
Tính khoảng cách từ
A
đến mặt phẳng
SBC
.
A.
5
5
a
. B.
3
3
a
. C.
3a
. D.
3
a
Câu 40: Cho hình nón tròn xoay
N
c bán kính đáy v đường cao đều bằng
R
. Một mặt phẳng đi
qua đỉnh ca
N
và tạo vi trục ca
N
một góc
30
. Tính din tích ca thiết din tạo vi
mặt phẳng đ v
N
.
A.
2
22
3
R
. B.
2
2
3
R
. C.
2
3
3
R
. D.
2
32
2
R
.
________________________HẾT________________________

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Gi
,AB
ln lưt l đim biu din cho hai s phc
1
1zi
v
2
13zi
. Gi
M
l trung
đim ca
AB
. Khi đ,
M
l đim biu din cho s phc no dưi đây?
A.
1 i
. B.
22i
. C.
i
. D.
1 i
.
Lời giải:
Do
,AB
ln lưt l đim biu din cho hai s phc
1
1zi
v
2
13zi
nên
1;1 , 1; 3 .AB
Khi đ trung đim
M
ca
AB
c ta độ l
1; 1M
.
Vy đim
M
biu din s phc
1. i
Câu 2: Hàm s
1
2
1yx
xác định khi chỉ khi
A.
1x
. B.
x
. C.
1x
. D.
1x
.
Lời giải:
Hàm s
1
2
1yx
xác định khi
1 0 1xx
.
Câu 3: Hàm s
21
5
x
y
c đạo hàm là
A.
22
2 1 5
x
yx
. B.
21
5 ln5
x
y
. C.
21
2.5
x
y
. D.
21
2.5 ln5
x
y
.
Lời giải:
Ta có:
2 1 2 1
2 1 .5 .ln5 2.5 .ln5
xx
yx
.
Câu 4: Tp nghim ca bt phương trnh
ee
2
1xx
l
A.
0;1S
. B.
1;2S
. C.
1;S
. D.
;0S
.
Lời giải:
Ta c
ee
2
1 2 2
1 1 0 0 1.
xx
x x x x x
Vy tp nghim ca bt phương trnh l
0;1 .S
Câu 5: Cho cp s nhân
n
u
có
2
1
4
u
và
3
1u
. Tìm công bội
q
ca cp s nhân đã cho.
A.
1
2
q
. B.
4q
. C.
1
2
q
. D.
4q
.
Lời giải:
Áp dụng công thc ta có:
3
2
4
u
q
u
.
Câu 6: Trong không gian
Oxyz
, cho hai đim
2; 1; 3A
và
0; 3; 1B
. Gi
là mặt phẳng
trung trực ca đoạn
AB
. Một vectơ pháp tuyến ca
có ta độ là
A.
2;4; 1 .
B.
1;0;1 .
C.
1;1;2 .
D.
1;2; 1 .
Lời giải:
Vì
l mặt phẳng trung trực ca đoạn
AB
nên
nhn
AB
lm vectơ pháp tuyến.
Ta có
2;4; 2AB
. Do đ một vectơ pháp tuyến ca mặt phẳng
là
1; 2; 1 .n
Câu 7: Cho hàm s
32
, , ,f x ax bx cx d a b c d
c đồ thị như hnh vẽ bên dưi:
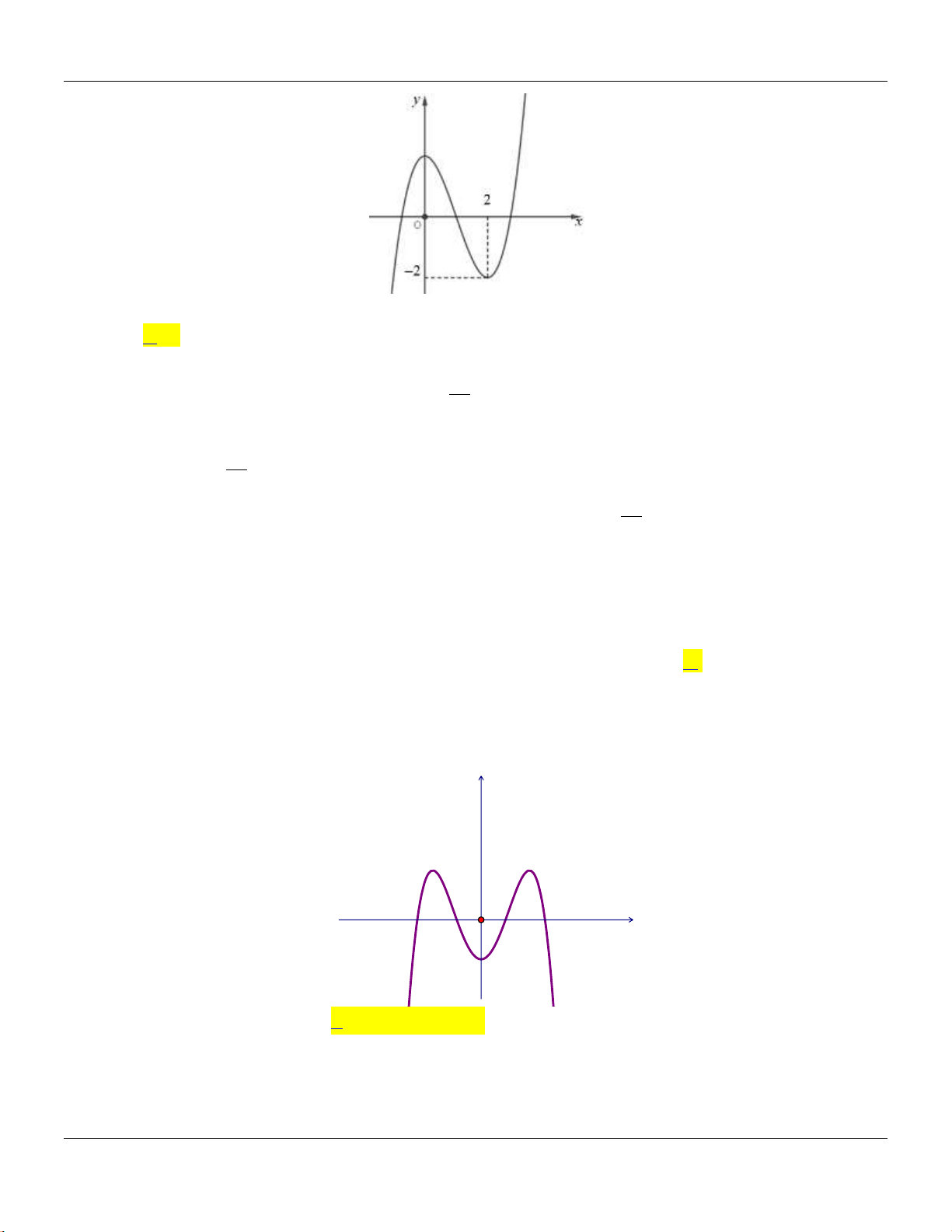
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
S nghim thực ca phương trnh
4 3 0fx
là
A.
3
B.
2
C.
1
D.
0
Lời giải:
Phương trnh
3
4 3 0
4
f x f x
(1).
S nghim ca phương trnh (1) bằng s giao đim ca đồ thị hàm s
y f x
v đường
thẳng
3
4
y
.
Dựa vo đồ thị hàm s
y f x
, ta thy đường thẳng
3
4
y
cắt đồ thị hàm s
y f x
tại
3 đim phân bit.
Vy phương trnh
4 3 0fx
có 3 nghim phân bit.
Câu 8: Cho
2
0
d3
f x x
,
2
0
d1
g x x
thì
2
0
5d
f x g x x x
bằng
A.
12
. B.
0
. C.
8
. D.
10.
Lời giải:
2 2 2 2
0 0 0 0
5 d 5 g d d
f x g x x x f x dx x x x x
3 5 2 10.
Câu 9: Đường cong trong hình vẽ sau l đồ thị ca hàm s no dưi đây?
x
y
0
A.
42
3 1. y x x
B.
42
3 1. y x x
C.
32
3 1. y x x
D.
32
3 1. y x x
Lời giải:
Quan sát đồ thị ta c, đây l đồ thị ca hàm s bc bn trùng phương
42
0y ax bx c a
nên loại phương án C,D
Dựa vào dạng đồ thị suy ra h s
0a
, suy ra chn đáp án B.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
Câu 10: Trong không gian
Oxyz
, cho mặt cu
2 2 2
: 2 4 2 3 0S x y z x y z
. Ta độ tâm
I
ca
mặt cu
S
là
A.
1; 2; 1
. B.
2; 4; 2
. C.
1; 2; 1
. D.
2;4;2
.
Lời giải:
Ta có:
2 2 2
2 2 2
2 4 2 3 0 1 2 1 9x y z x y z x y z
.
Từ đ suy ra mặt cu
S
có tâm là:
1;2;1
.
Câu 11: Trong không gian
Oxyz
, cho hai vectơ
4;5; 3a
,
2; 2;1b
. Tìm ta độ ca vectơ
2x a b
.
A.
2;3; 2x
. B.
0;1; 1x
. C.
0; 1;1x
. D.
8;9;1x
.
Lời giải:
Ta có
2 4 2.2;5 2 2 ; 3 2.1 0;1; 1x a b
.
Câu 12: Cho hai s phc
1
1zi
và
2
1zi
. Giá trị ca biu thc
12
z iz
bằng
A.
22i
. B.
2i
. C.
2
. D.
22i
.
Lời giải:
Ta có
12
1 (1 ) 2.z iz i i i
Câu 13: Tính th tích
V
ca khi lăng trụ có din tích đáy bằng
2
4a
và chiều cao bằng
.a
A.
3
16Va
. B.
3
4Va
. C.
3
2Va
. D.
3
4
3
Va
.
Lời giải:
Ta có th tích khi lăng trụ :
23
. 4 . 4V S h a a a
.
Câu 14: Cho khi chóp
.S ABCD
c đáy
ABCD
là hình chữ nht,
AB a
,
3AD a
,
SA
vuông góc
vi mặt phẳng đáy v mặt phẳng
SBC
tạo vi đáy một góc
60
(tham khảo hình vẽ).
A
B
C
D
S
Tính th tích
V
ca khi chóp
.S ABCD
.
A.
3
3Va
. B.
3
3
3
a
V
. C.
3
Va
. D.
3
3
a
V
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
B
S
D
C
A
60
0
Ta có
2
3
ABCD
Sa
. Vì
SBC ABCD BC
BC SB SBC
BC AB ABCD
,SBC ABCD SBA
. Vy
60 .SBA
Xét tam giác vuông
SAB
có:
tan tan 3
SA
SBA SA AB SBA a
AB
Vy
3
.
1
.
3
S ABCD ABCD
V S SA a
.
Câu 15: Cho mặt cu
S
có din tích bằng
4
. Th tích khi cu
S
bằng:
A.
16
. B.
32
. C.
4
3
. D.
16
3
.
Lời giải:
Din tích mặt cu
S
là:
2
4 . 4 1RR
.
Do đ th tích khi cu
S
là
3
44
. đvtt
33
VR
.
Câu 16: S phc liên hp ca s phc
23zi
là
A.
32zi
B.
32zi
C.
23zi
D.
23zi
Lời giải:
S phc liên hp ca s phc
23zi
là
23zi
.
Câu 17: Cho hnh nn c đường cao v đường kính đáy đều bằng
2a
. Cắt hnh nn đã cho bằng một
mặt phẳng đi qua trục thu đưc din tích thiết din bằng
A.
2
8a
. B.
2
a
. C.
2
2a
. D.
2
4a
.
Lời giải:
Gi
S
l đỉnh hình nón,
O
l tâm đáy hnh nn.
Giả sử thiết din qua trục
SO
là tam giác
SAB
khi đ
O
l trung đim
AB
.
Theo giả thiết ta c đường cao ca hình nón là:
2h SO a
; đường kính đáy
2AB a
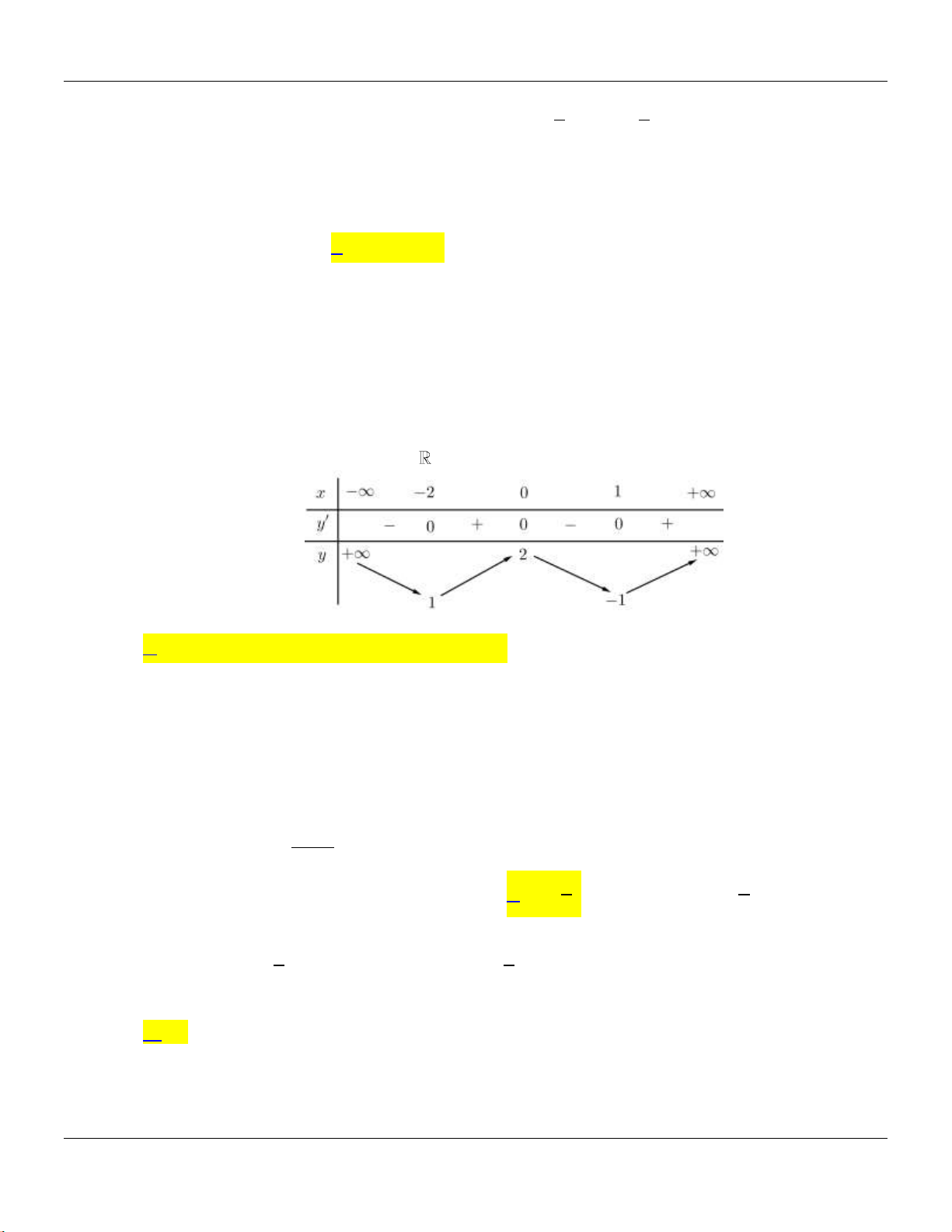
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Tam giác
SAB
cân tại
S
nên din tích bằng:
2
11
. .2 .2 2
22
SAB
S AB SO a a a
.
Câu 18: Trong không gian
Oxyz
, đường thẳng
2
:3
2
xt
d y t
zt
đi qua đim no sau đây?
A.
1;2; 1M
. B.
3;2; 1N
. C.
3; 2; 1P
. D.
3; 2;1Q
.
Lời giải:
Thay ta độ ca đim
A
vo phương trnh đường thẳng
d
.
Vi
3;2; 1P
ta có
32
2 3 1
12
t
tt
t
vy đim
P
nằm trên đường thẳng
d
.
Đi vi các đim khác do không tồn tại giá trị ca
t
nên các đim đ không thuộc đường
thẳng
d
.
Câu 19: Cho hàm s
()y f x
liên tục trên và có bảng biến thiên:
Khẳng định no sau đây sai?
A.
0;2M
l đim cực tiu ca đồ thị hàm s.
B.
( 1)f
là một giá trị cực tiu ca hàm s.
C.
0
o
x
l đim cực đại ca hàm s.
D.
1
o
x
l đim cực tiu ca hàm s.
Lời giải:
Dựa vào bảng biến thiên, ta có
0;2M
l đim cực đại ca đồ thị hàm s. Vy đáp án A l
một khẳng định sai.
Câu 20: Đồ thị hàm s
1
41
x
y
x
c đường tim cn ngang l đường thẳng no dưi đây?
A.
1y
. B.
1x
. C.
1
4
y
. D.
1
4
x
.
Lời giải:
Ta thy
1
lim
4
x
y
suy ra tim cn ngang
1
4
y
.
Câu 21: Bt phương trình
3
log 1 2x
có nghim nhỏ nht bằng
A. 10. B. 6. C. 9. D. 7.
Lời giải:
Ta có
2
3
log 1 2 1 3 10x x x
, từ đ suy ra bt phương trnh đã cho c nghim
nhỏ nht bằng 10.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Câu 22: Cho hai đường thẳng
1
d
và
2
d
song song vi nhau. Trên đường thẳng
1
d
cho 5 đim phân
bit, trên đường thẳng
2
d
cho 7 đim phân bit. S tam giác c đỉnh l các đim trong 12
đim đã cho l
A. 350. B. 210. C. 175. D. 220.
Lời giải:
* S tam giác c 2 đỉnh thuộc
1
d
v 1 đỉnh thuộc
2
d
là:
21
57
. 70CC
.
* S tam giác c 1 đỉnh thuộc
1
d
v 2 đỉnh thuộc
2
d
là:
12
57
. 105CC
.
Vy có
70 105 175
tam giác.
Câu 23: Cho
df x x F x C
. Khi
2 3 df x x
bằng
A.
1
23
2
F x C
. B.
1
23
2
F x C
. C.
23F x C
. D.
23F x C
.
Lời giải:
Ta có
1
d 2 3 d 2 3
2
f x x F x C f x x F x C
.
Câu 24: Cho
1
0
d2
f x x
và
4
1
d5
f x x
, khi đ
4
0
d
f x x
bằng
A.
6
. B.
10
. C.
7
. D.
3
.
Lời giải:
Ta có:
4 1 4
0 0 1
d d d 2 5 7f x x f x x f x x
.
Câu 25: Tính
sin3 dxx
.
A.
1
cos3
3
xC
. B.
cos3xC
. C.
cos3xC
. D.
1
cos3
3
xC
.
Lời giải:
Áp dụng công thc
1
sin d cosax b x ax b C
a
, ta có
1
sin3 d cos3
3
x x x C
.
Câu 26: Cho hàm s
()y f x
c đồ thị như sau:
Hàm s đã cho nghịch biến trên khoảng no dưi đây?
A.
0;1
. B.
1;0
. C.
2; 1
. D.
1;1
.
Lời giải:
Từ đồ thị ta thy hàm s nghịch biến trên khoảng
0;1 .
Câu 27: Cho hàm s
y f x
c đạo hàm
3
2
2 1 ,
f x x x x
x
. Hàm s đã cho c bao
nhiêu đim cực trị?
A.
2
. B.
0
. C.
3
. D.
1
.
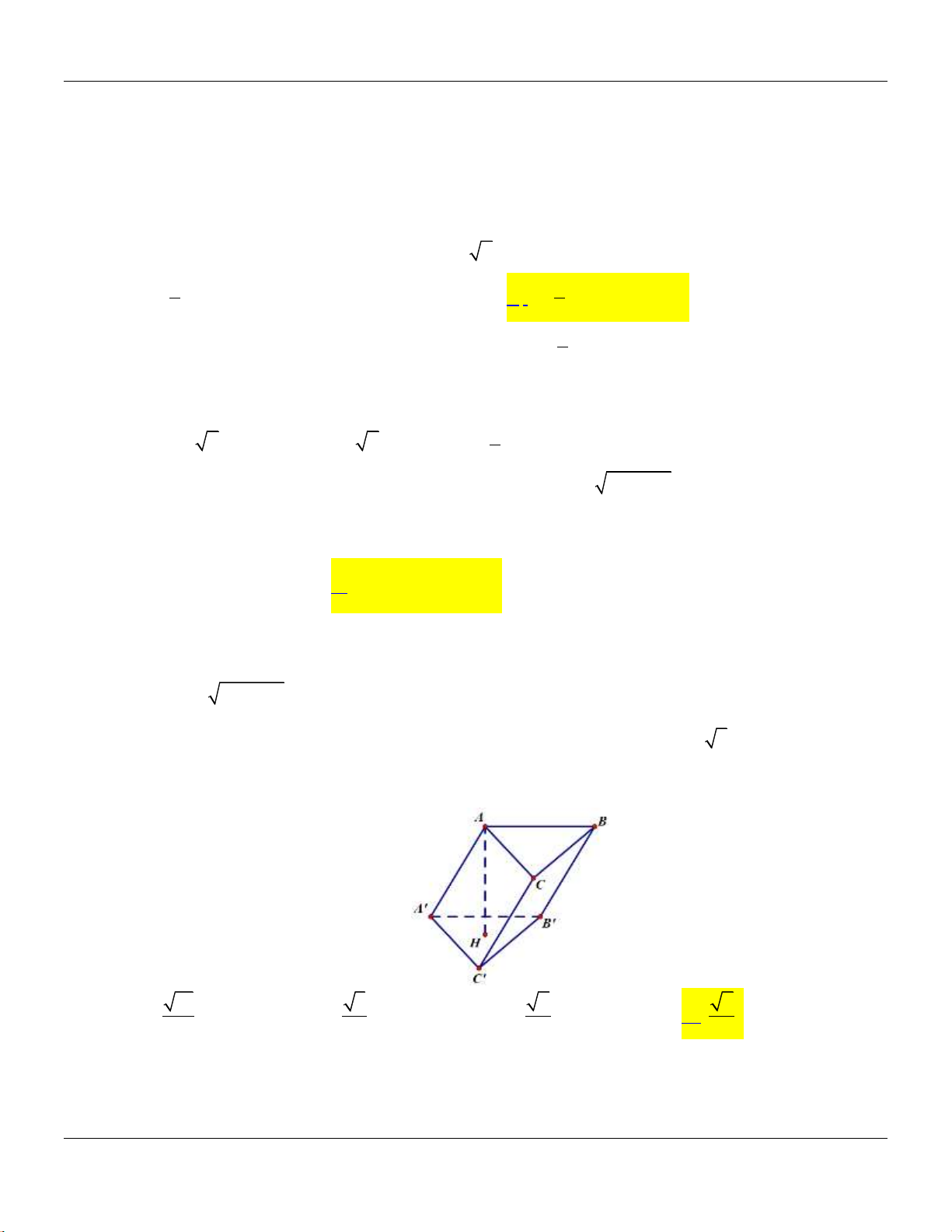
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
Lời giải:
Ta có:
3
2
2
2 1 0 0
1
x
f x x x x x
x
Lp BBT suy ra
fx
c hai đim cực trị.
Câu 28: Cho các s thực dương
,ab
tùy ý,
2
3
log 3 ab
bằng
A.
33
1
log 2log
2
ab
. B.
33
1
1 log 2log
2
ab
.
C.
33
1 log 2logab
. D.
33
1
1 log log
2
ab
.
Lời giải:
Vi
,ab
là các s thực dương, ta c:
22
3 3 3 3
log 3 log 3 log loga b a b
33
1
1 log 2log
2
ab
.
Câu 29: Cho
H
là hình phẳng gii hạn bởi đồ thị hàm s
4
x
y e x
, trục honh v hai đường
thẳng
1, 2xx
;
V
là th tích ca khi tròn xoay thu đưc khi quay hình
H
quanh trục
hoành. Khẳng định no sau đây đúng?
A.
2
1
4d
x
V e x x
. B.
2
1
4d
x
V x e x
. C.
2
1
4d
x
V e x x
. D.
2
1
4d
x
V x e x
.
Lời giải:
Th tích ca khi tròn xoay thu đưc khi quay hình
H
quanh trục hoành là:
22
2
11
44
xx
V e x dx x e dx
.
Câu 30: Cho hnh lăng trụ
.ABC A B C
c đáy l tam giác đều cạnh
a
,
6BB a
. Hình chiếu vuông
góc
H
ca
A
trên mặt phẳng
ABC
trùng vi trng tâm ca tam giác
ABC
(tham khảo
hình vẽ). Côsin ca góc giữa cạnh bên và mặt đáy bằng
A.
15
15
. B.
3
6
. C.
2
3
. D.
2
6
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Gi
M
l trung đim ca
BC
. Ta có:
23
33
a
A H AM
;
6AA BB a
.
AH A B C
AH
là hình chiếu vuông góc ca
AA
lên mặt phẳng
ABC
.
Vy
AA H
là góc giữa
AA
và mặt phẳng
ABC
.
Tam giác
AA H
vuông tại
H
3
3 1 2
3
cos .
36
66
a
AH
AA
a
.
Vy côsin ca góc giữa cạnh bên và mặt đáy bằng
2
6
.
Câu 31: Đường cong trong hình vẽ l đồ thị ca hàm s
42
22y x x
.
Tìm tt cả các giá trị thực ca tham s
m
đ phương trnh
42
2x x m
có 4 nghim phân
bit.
A.
2m
. B.
10m
. C.
3m
. D.
32m
.
Lời giải:
Phương trnh đã cho tương đương
42
2 2 2x x m
1
.
S nghim ca phương trnh
1
chính là s giao đim ca đường thẳng
:2d y m
(song
song hoặc trùng vi trục honh) v đồ thị hàm s
42
( ): 2 2C y x x
.
Do đ
1
có 4 nghim phân bit khi
d
cắt
C
tại 4 đim phân bit.
Dựa vo đồ thị suy ra
3 2 2 1 0mm
.
Câu 32: Cắt một hình trụ bởi một mặt phẳng qua trục ca n, ta đưc thiết din là một hình vuông có
cạnh bằng
3a
. Tính din tích toàn phn ca hình trụ đã cho.
A.
2
13
6
a
. B.
2
27
2
a
. C.
2
9 a
. D.
2
9
2
a
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
Gi thiết din qua trục là hình vuông
ABCD
. Theo đề thì
3AB AD a
.
Bán kính đáy ca hình trụ là
3
22
AB a
R
.
Đường sinh ca hình trụ là
3l AD a
.
Din tích toàn phn ca hình trụ là
2
2
2
3 3 27
2 2 2 . .3 2
2 2 2
tp
a a a
S Rl R a
.
Câu 33: Cho hàm s
y f x
c đạo hàm
2
2 1 , .
f x x x x
Hàm s đã cho đồng biến
trên khoảng no dưi đây?
A.
1;2
. B.
1;
. C.
2;
. D.
;1
.
Lời giải:
Ta có
2
2
10
1
0 2 1 0 1
2
20
x
x
f x x x x
x
x
.
Vy hàm s đồng biến trên khoảng
;1
.
Câu 34: Có 8 chiếc ghế đưc kê thành một hàng ngang. Xếp ngẫu nhiên 8 hc sinh gồm 3 hc sinh nữ,
5 hc sinh nam ngồi vào hàng ghế đ sao cho mỗi ghế c đúng một hc sinh. Xác xut đ 3
hc sinh nữ ngồi ở 3 ghế cạnh nhau bằng
A.
3
56
. B.
1
56
. C.
1
28
. D.
3
28
.
Lời giải:
Xếp tt cả 8 hc sinh vào 8 ghế theo một hàng ngang, ta có s phn tử không gian mẫu
là
8! 40320
(cách).
Gi A là biến c “ 3 hc sinh nữ ngồi ở 3 ghế cạnh nhau”.
Ta có:
Xếp 3 nữ cạnh nhau có
3! 6
cách.
Xếp 5 nam và nhóm nữ có
6!
cách.
Khi đ
6.6! 4320
A
.
Vy xác sut đ xếp 8 hc sinh sao cho 3 hc sinh nữ luôn ngồi cạnh nhau là
3
()
28
A
PA
.
Câu 35: Tích hai nghim ca phương trnh
2
33
log 6log 8 0xx
bằng
A.
90
. B.
729
. C.
8
. D.
6
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
Đk:
0x
.
Ta có:
4
3
2
33
2
3
log 4
3
log 6log 8 0
log 2
3
x
x
xx
x
x
.
Vy tích hai nghim là:
42
3 .3 729
.
Câu 36: Tp hp tt cả các đim trong mặt phẳng ta độ
Oxy
biu din s phc
z
thỏa mãn
1 2 3z i z
l đường thẳng c phương trnh l
A.
2 1 0xy
. B.
2 1 0xy
. C.
2 1 0xy
. D.
2 1 0xy
.
Lời giải:
Gi
,z x yi x y
.
2 2 2
2
1 2 3 1 2 3z i z x y x y
2 2 2 2
2 4 5 6 9 8 4 4 0 2 1 0x y x y x y x x y x y
.
Câu 37: Trong không gian
,Oxyz
phương trnh đường thẳng đi qua đim
;;A 2 1 2
và vuông góc vi
mặt phẳng
:P x y z 10
là
A.
y
xz
1
22
.
1 1 1
B.
y
xz
1
22
.
1 1 1
C.
y
xz
1
22
.
1 1 1
D.
y
xz
2
33
.
1 1 1
Lời giải:
Kim tra sự kin:
Ad
v vectơ chỉ phương
;;
P
n 1 1 2
ta thy phương án D thỏa mãn.
Câu 38: Trong không gian
,Oxyz
cho đim
1;2;3 .M
Khoảng cách từ đim
M
đến trục
Ox
bằng
A.
1.
B.
13.
C.
5.
D.
10.
Câu 39: Cho hình chóp
.S A BC
có
SA a
và
SA
vuông góc vi đáy. Biết đáy l tam giác vuông cân tại
A
và
2BC a
.
Tính khoảng cách từ
A
đến mặt phẳng
SBC
.
A.
5
5
a
. B.
3
3
a
. C.
3a
. D.
3
a
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 16
S
A
C
B
E
H
Gi
E
l trung đim ca
BC
12
22
a
AE BC
Kẻ
AH SE
AH SBC
AH
là khoảng cách từ
A
đến mặt phẳng
SBC
.
Ta có
2 2 2 2 2 2
1 1 1 2 1 3 3
3
a
AH
AH AE SA a a a
.
Câu 40: Cho hình nón tròn xoay
N
c bán kính đáy v đường cao đều bằng
R
. Một mặt phẳng đi
qua đỉnh ca
N
và tạo vi trục ca
N
một góc
30
. Tính din tích ca thiết din tạo vi
mặt phẳng đ v
N
.
A.
2
22
3
R
. B.
2
2
3
R
. C.
2
3
3
R
. D.
2
32
2
R
.
Lời giải:
Gi
J
l trung đim ca
AB
.
Ta có:
AB IJ
AB SJI
AB SI
nên:
.
SAB SIJ
SAB SIJ SJ IH SAB
IH SJ
Suy ra góc hp bởi mặt phẳng đi qua đỉnh ca
N
vi trục ca
N
là góc
30ISH
.
Xét tam giác
SIJ
vuông tại
I
:
23
cos30 .
cos30 3
3
2
SI SI R R
SJ
SJ

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 17
3
tan30 .tan30 .
3
IJ R
IJ SI
SI
Xét tam giác
IJA
vuông tại
J
:
2
2
36
33
RR
AJ R
.
Suy ra
26
2.
3
R
AB AJ
Vy:
2
1 1 2 3 2 6 2 2
. . . .
2 2 3 3 3
SAB
R R R
S SJ AB
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 11_______________
Câu 1: Số phức liên hợp của số phức
25zi
là
A.
25zi
. B.
25zi
. C.
25zi
. D.
25zi
.
Câu 2: Tìm đạo hàm của hàm số
logyx
.
A.
ln10
.
y
x
B.
1
.
ln10
y
x
C.
1
.
10ln
y
x
D.
1
.
y
x
Câu 3: Tìm đạo hàm của hàm số
5
3
yx
.
A.
8
3
3
.
8
yx
B.
2
3
5
.
3
yx
C.
2
3
5
.
3
yx
D.
2
3
3
.
5
yx
Câu 4: Tập nghiệm của bất phương trình
1
11
3 27
x
là
A.
;2
. B.
2;
. C.
2;
. D.
;1
.
Câu 5: Cho cấp số nhân
n
u
có cộng bội
,q
với
1
2u
và
2
4u
. Giá trị của của
q
bằng
A. 3. B.
1
2
. C.
1
4
. D.
2
.
Câu 6: Trong không gian
Oxyz
, cho đường thẳng
2 1 1
:
1 2 3
x y z
d
. Vectơ chỉ phương của
đường thẳng là
A.
1;1;1
d
u
. B.
1; 2;3
d
u
. C.
1;1;1
d
u
. D.
1;2; 3
d
n
.
Câu 7: Toạ độ giao điểm của đồ thị hàm số
3
21y x x
với trục tung là
A.
0; 2
. B.
0; 1
. C.
0;1
. D.
1;0
.
Câu 8: Nếu
3
0
d1f x x
và
5
3
d5f x x
thì
5
0
df x x
bằng
A.
4
. B.
6
. C.
6
. D.
5
.
Câu 9: Đường cong ở hình vẽ bên dưới là đồ thị của hàm số nào dưới đây?
4
2
A.
42
42y x x
. B.
42
32y x x
. C.
42
22y x x
. D.
42
22y x x
.
Câu 10: Trong không gian
,Oxyz
cho mặt cầu
2 2 2
: 1 2 1 9S x y z
. Tìm tọa độ tâm
I
và
tính bán kính
R
của
.S
A.
1;2;1I
và
3.R
B.
1; 2; 1I
và
3.R
C.
1;2;1I
và
9.R
D.
1; 2; 1I
và
9.R
Câu 11: Trong không gian
,Oxyz
góc giữa hai mặt phẳng
Oxy
và
Oxz
bằng
A.
90 .
B.
60 .
C.
30 .
D.
45 .

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 12: Cho số phức
2,zi
phần ảo của số phức
2
z
là
A.
4.
B.
4.i
C.
3.
D.
1.
Câu 13: Cho khối chóp diện tích đáy
2
4Ba
và thể tích
3
8Va
. Chiều cao của khối chóp đã cho
bằng
A.
2a
. B.
6a
. C.
4a
. D.
24a
.
Câu 14: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
, biết
3 , 4AB a AC a
; cạnh bên
SA
vuông góc với đáy và
5SA a
. Tính thể tích V của khối chóp
.S ABC
.
A.
3
30Va
. B.
3
10Va
. C.
3
15Va
. D.
3
60Va
.
Câu 15: Trong không gian
Oxyz
, mặt cầu tâm
2;1; 3I
và tiếp xúc với trục
Oy
có phương trình là
A.
2 2 2
2 1 3 4x y z
. B.
2 2 2
2 1 3 13x y z
.
C.
2 2 2
2 1 3 9x y z
. D.
2 2 2
2 1 3 10x y z
.
Câu 16: Phần thực của số phức
54 zi
là
A.
5
. B.
5
. C.
4
. D.
4
.
Câu 17: Cho hình nón có bán kính đáy
r
và độ dài đường sinh
l
. Khi đó, diện tích toàn phần của
hình nón đã cho bằng
A.
r l r
. B.
2
rl r
. C.
2
rl r
. D.
2
2
rl r
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
21
:
3 2 1
x y z
. Điểm nào sau đây thuộc
?
A.
3;2; 1A
. B.
0;2; 1B
. C.
0;2;1C
. D.
3;2;1D
.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Điểm cực đại của đồ thị hàm số đã cho có tọa độ là:
A.
0;2
. B.
3; 4
. C.
2;0
. D.
4;3
.
Câu 20: Tọa độ giao điểm của hai đường tiệm cận của đồ thị hàm số
21
2
x
y
x
là
A.
2;2
. B.
2; 2
. C.
2; 2
. D.
2;2
.
Câu 21: Tập nghiệm của bất phương trình
2
28
x
là:
A.
1;
. B.
;1
. C.
1;
. D.
;1
.
Câu 22: Cho tập
0;1;2;...;9M
. Số tập con gồm
3
phần tử và không chứa số
1
của
M
bằng
A.
45
. B.
84
. C.
72
. D.
36
.
Câu 23: Cho
2
1
d
x F x C
x
. Khẳng định nào dưới đây đúng?
A.
1
Fx
x
. B.
3
2
Fx
x
. C.
2
1
Fx
x
. D.
2
ln
F x x
.
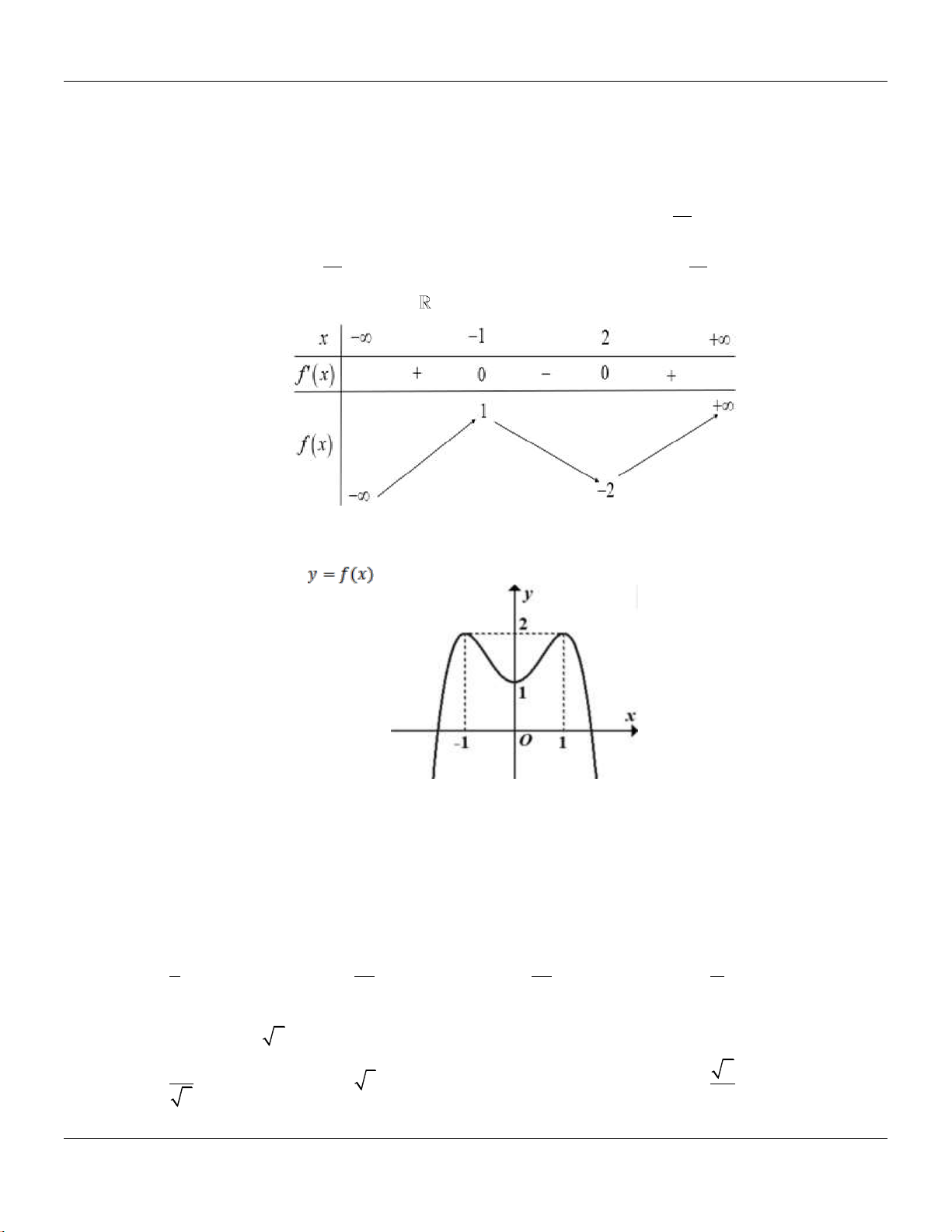
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
Câu 24: Nếu
3
1
d 2023
f x x
thì
3
1
2d
f x x x
bằng
A.
16188
. B.
4050
. C.
16192
. D.
8096
.
Câu 25: Cho hàm số
2
sinf x x x
. Khẳng định nào dưới đây đúng?
A.
d cos 2 .f x x x x C
B.
3
d cos .
3
x
f x x x C
C.
3
d cos .
3
x
f x x x C
D.
3
d cos .
3
x
f x x x C
Câu 26: Cho hàm số
()y f x
liên tục trên và có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
A.
2;1
B.
1;2
. C.
;1
. D.
;2
.
Câu 27: Cho hàm số bậc bốn có đồ thị là đường cong trong hình bên.
Giá trị cực đại của hàm số đã cho là
A.
1
. B.
1
. C.
2
. D.
0
.
Câu 28: Với
a
là số thực dương tùy ý, khi đó
3
4
log 4a
bằng
A.
4
3log 4a
. B.
4
1 3log a
. C.
4
4 3log a
. D.
4
3 log a
.
Câu 29: Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
32y x x
và trục
Ox
. Thể tích của
khối tròn xoay sinh ra khi quay hình
H
quanh trục
Ox
bằng :
A.
1
6
. B.
1
30
. C.
30
. D.
6
.
Câu 30: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
B
có
,2AB a AA a
. Tính tan của góc giữa đường thẳng
AC
với mặt phẳng
AA B B
:
A.
1
3
. B.
3
. C.
1
. D.
2
2
.
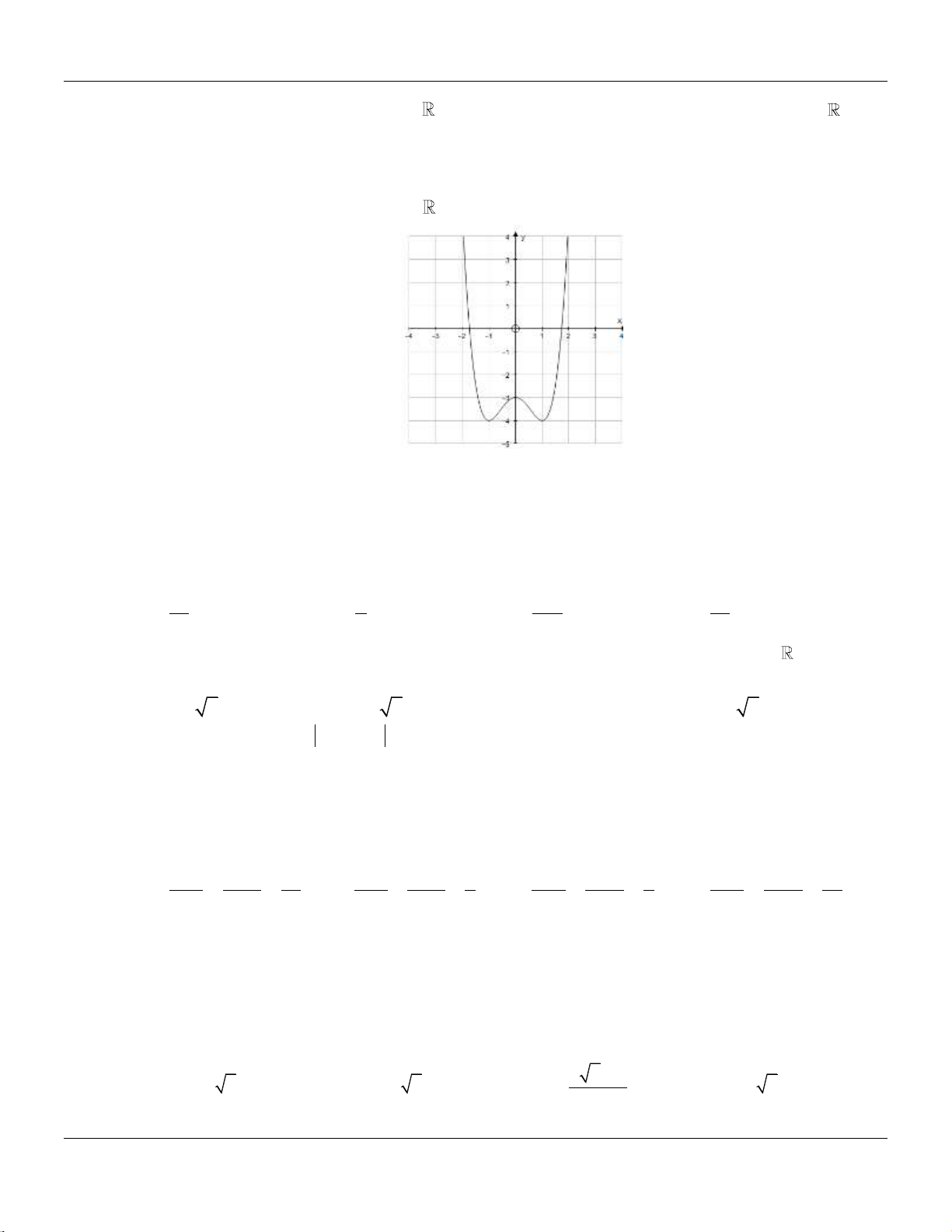
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Câu 31: Cho hàm số
fx
xác định trên và có đạo hàm là
2
3 1 ,
f x x x x x
. Hỏi
hàm số
fx
đồng biến trên khoảng nào dưới đây?
A.
1;
. B.
3;0
. C.
0;1
. D.
;1
.
Câu 32: Cho hàm số
y f x
liên tục trên và có đồ thị như hình vẽ dưới đây:
.
Tìm tất cả các giá trị thực của tham số
m
để phương trình
f x m
có 4 nghiệm thực phân
biệt.
A.
43m
. B.
4; 3m
. C.
43m
. D.
22m
.
Câu 33: Chọn ngẫu nhiên hai số khác nhau từ 23 số nguyên dương đầu tiên. Xác suất để chọn được
hai số có tổng là một số chẵn bằng
A.
11
23
. B.
1
2
. C.
265
529
. D.
12
23
.
Câu 34: Gọi
S
là tập nghiệm của phương trình
2
22
2log 2 2 log 3 2xx
trên . Tổng các
phần tử của
S
bằng
A.
62
. B.
82
. C.
8
. D.
42
.
Câu 35: Cho số phức
z
thỏa
1 2 3iz i
. Biết rằng tập hợp các điểm biểu diễn của số phức
z
trên
mặt phẳng
Oxy
là một đường tròn. Tìm tâm của đường tròn đó.
A.
2; 1I
. B.
1;1I
. C.
0;1I
. D.
1;0I
.
Câu 36: Trong không gian
Oxyz
, cho ba điểm
(1;2;0), (1;1;2)AB
và
(2;3;1)C
. Đường thẳng đi qua
A
và song song với
BC
có phương trình là
A.
12
.
1 2 1
x y z
B.
12
.
3 4 3
x y z
C.
12
.
3 4 3
x y z
D.
12
.
1 2 1
x y z
Câu 37: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
2;3;5A
. Điểm đối xứng với A qua mặt
phẳng
Oxy
có tọa độ là
A.
2;3; 5
. B.
2;3;5
. C.
0;0;5
. D.
0;0; 5
.
Câu 38: Cho hình nón
N
có chiều cao bằng
3.a
Biết thiết diện qua đỉnh của hình nón
N
là tam
giác vuông có diện tích bằng
2
8.a
Diện tích xung quanh của hình nón đã cho là
A.
2
8 7 .
xq
Sa
B.
2
2 7 .
xq
Sa
C.
2
47
.
3
xq
a
S
D.
2
4 7 .
xq
Sa

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 39: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với
,AB a
2,AD a
SA ABCD
và
SA a
. Tính theo
a
khoảng cách từ
D
đến mặt phẳng
SBM
, với
M
là trung điểm của
.CD
A.
2
33
a
. B.
33
a
. C.
4
33
a
. D.
33a
.
Câu 40: Cho hình trụ
T
có bán kính đáy bằng
2.a
Gọi
,AB
lần lượt nằm trên hai đường tròn đáy
của hình trụ
T
sao cho
4.AB a
Biết
AB
cách trục của trụ một khoảng bằng
.a
Thể tích
khối trụ đã cho là
A.
3
6.Va
B.
3
8.Va
C.
3
12 .Va
D.
3
4.Va
________________________HẾT________________________

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Số phức liên hợp của số phức
25zi
là
A.
25zi
. B.
25zi
. C.
25zi
. D.
25zi
.
Lời giải:
Số phức liên hợp của số phức
25zi
là
25zi
.
Câu 2: Tìm đạo hàm của hàm số
logyx
.
A.
ln10
.
y
x
B.
1
.
ln10
y
x
C.
1
.
10ln
y
x
D.
1
.
y
x
Lời giải:
Áp dụng công thức
1
log
ln
a
x
xa
, ta được
1
ln10
y
x
.
Câu 3: Tìm đạo hàm của hàm số
5
3
yx
.
A.
8
3
3
.
8
yx
B.
2
3
5
.
3
yx
C.
2
3
5
.
3
yx
D.
2
3
3
.
5
yx
Lời giải:
Áp dụng công thức
1
.
nn
x n x
, ta được
2
3
5
3
yx
.
Câu 4: Tập nghiệm của bất phương trình
1
11
3 27
x
là
A.
;2
. B.
2;
. C.
2;
. D.
;1
.
Lời giải:
Ta có
1
11
1 3 2.
3 27
x
xx
Vậy
2;S
Câu 5: Cho cấp số nhân
n
u
có cộng bội
,q
với
1
2u
và
2
4u
. Giá trị của của
q
bằng
A. 3. B.
1
2
. C.
1
4
. D.
2
.
Lời giải:
Ta có
2
21
1
.2
u
u q qu
u
Câu 6: Trong không gian
Oxyz
, cho đường thẳng
2 1 1
:
1 2 3
x y z
d
. Vectơ chỉ phương của
đường thẳng là
A.
1;1;1
d
u
. B.
1; 2;3
d
u
. C.
1;1;1
d
u
. D.
1;2; 3
d
n
.
Lời giải:
Ta có
1; 2;3
d
u
Câu 7: Toạ độ giao điểm của đồ thị hàm số
3
21y x x
với trục tung là
A.
0; 2
. B.
0; 1
. C.
0;1
. D.
1;0
.
Lời giải:
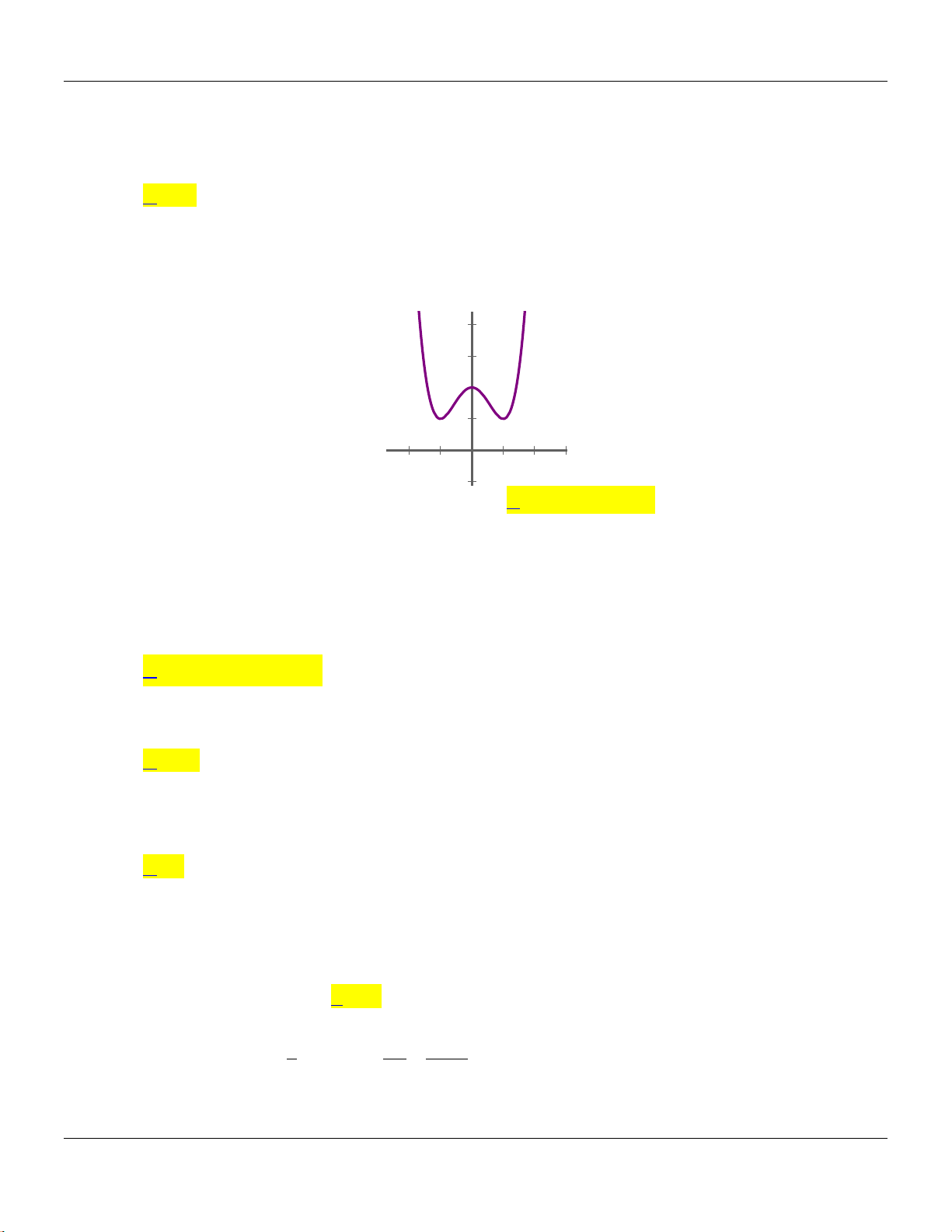
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
Toạ độ giao điểm của đồ thị hàm số
3
21y x x
với trục tung là
0;1
.
Câu 8: Nếu
3
0
d1f x x
và
5
3
d5f x x
thì
5
0
df x x
bằng
A.
4
. B.
6
. C.
6
. D.
5
.
Lời giải:
5
0
df x x
35
03
ddf x x f x x
4
.
Câu 9: Đường cong ở hình vẽ bên dưới là đồ thị của hàm số nào dưới đây?
4
2
A.
42
42y x x
. B.
42
32y x x
. C.
42
22y x x
. D.
42
22y x x
.
Lời giải:
Dựa vào đồ thị hàm số, bề lõm đồ thị hướng lên nên
0a
.
Đồ thị hàm số cắt trục tung tại điểm
0;2
nên chọn
C
.
Câu 10: Trong không gian
,Oxyz
cho mặt cầu
2 2 2
: 1 2 1 9S x y z
. Tìm tọa độ tâm
I
và
tính bán kính
R
của
.S
A.
1;2;1I
và
3.R
B.
1; 2; 1I
và
3.R
C.
1;2;1I
và
9.R
D.
1; 2; 1I
và
9.R
Câu 11: Trong không gian
,Oxyz
góc giữa hai mặt phẳng
Oxy
và
Oxz
bằng
A.
90 .
B.
60 .
C.
30 .
D.
45 .
Lời giải:
Hai mặt phẳng
Oxy
và
Oxz
vuông góc với nhau nên góc giữa chúng bằng
90 .
Câu 12: Cho số phức
2,zi
phần ảo của số phức
2
z
là
A.
4.
B.
4.i
C.
3.
D.
1.
Lời giải:
Ta có
2
2
2 3 4z i i
. Do đó phần ảo của
2
z
là
4
.
Câu 13: Cho khối chóp diện tích đáy
2
4Ba
và thể tích
3
8Va
. Chiều cao của khối chóp đã cho
bằng
A.
2a
. B.
6a
. C.
4a
. D.
24a
.
Lời giải:
Từ công thức
3
2
1 3 3.8
.6
3 4
.
V
V B h h
B
a
a
a
.
Câu 14: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
, biết
3 , 4AB a AC a
; cạnh bên
SA
vuông góc với đáy và
5SA a
. Tính thể tích V của khối chóp
.S ABC
.
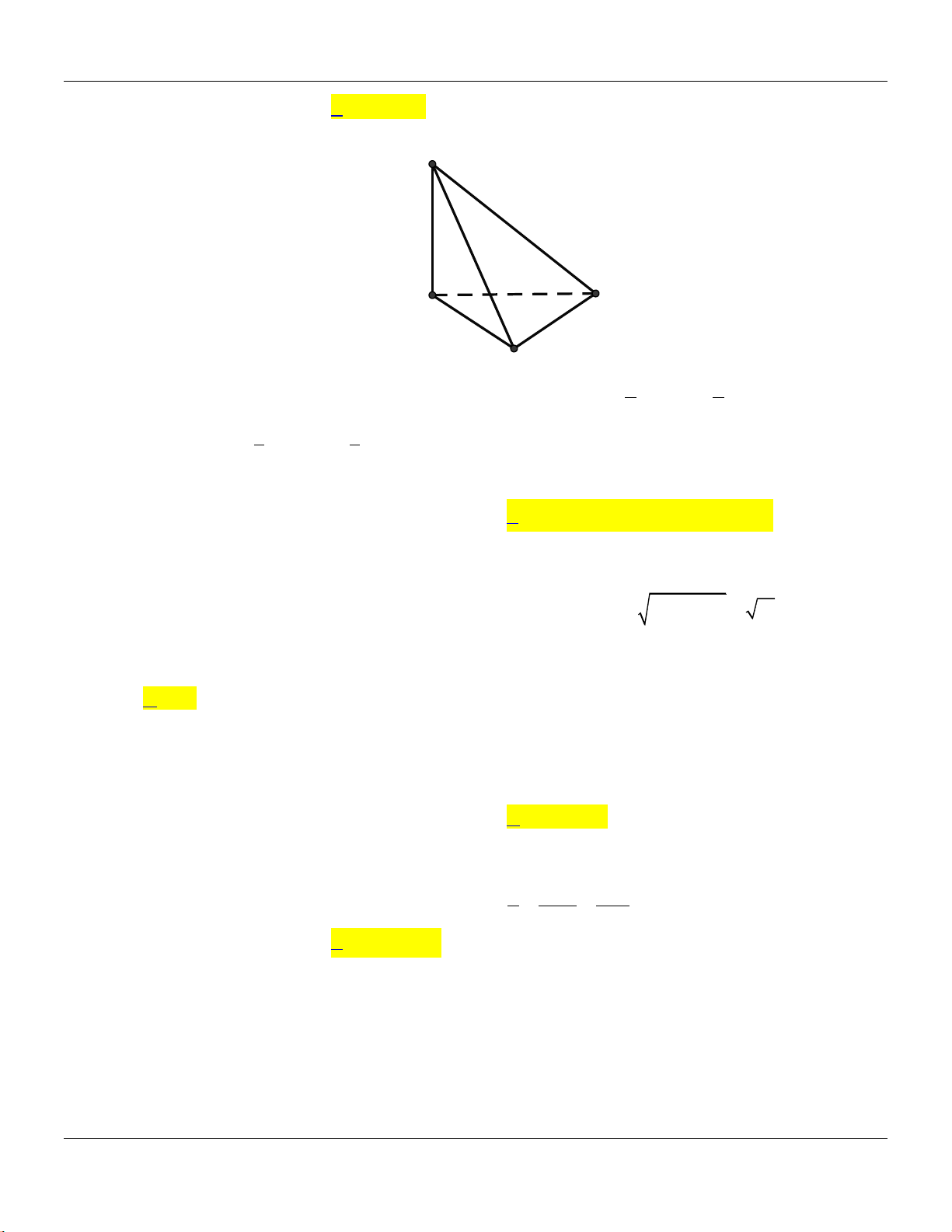
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
A.
3
30Va
. B.
3
10Va
. C.
3
15Va
. D.
3
60Va
.
Lời giải:
S
A
C
B
Đáy
ABC
là tam giác vuông tại
A
nên có diện tích là
2
11
. 3 .4 6
22
ABC
S AB AC a a a
.
Ta có
23
.
11
5 6 10
33
S ABC ABC
V SA S a a a
.
Câu 15: Trong không gian
Oxyz
, mặt cầu tâm
2;1; 3I
và tiếp xúc với trục
Oy
có phương trình là
A.
2 2 2
2 1 3 4x y z
. B.
2 2 2
2 1 3 13x y z
.
C.
2 2 2
2 1 3 9x y z
. D.
2 2 2
2 1 3 10x y z
.
Lời giải:
Mặt cầu tiếp xúc với trục
Oy
nên bán kính của mặt cầu là
2
2
2 3 13R
.
Phương trình mặt cầu là
2 2 2
2 1 3 13x y z
.
Câu 16: Phần thực của số phức
54 zi
là
A.
5
. B.
5
. C.
4
. D.
4
.
Lời giải:
Phần thực của số phức
54 zi
là
5
.
Câu 17: Cho hình nón có bán kính đáy
r
và độ dài đường sinh
l
. Khi đó, diện tích toàn phần của
hình nón đã cho bằng
A.
r l r
. B.
2
rl r
. C.
2
rl r
. D.
2
2
rl r
.
Lời giải:
Diện tích toàn phần của hình nón đã cho bằng
2
tp
S rl r
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
21
:
3 2 1
x y z
. Điểm nào sau đây thuộc
?
A.
3;2; 1A
. B.
0;2; 1B
. C.
0;2;1C
. D.
3;2;1D
.
Lời giải:
Nhận thấy điểm
0;2; 1B
thuộc đường thẳng
.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
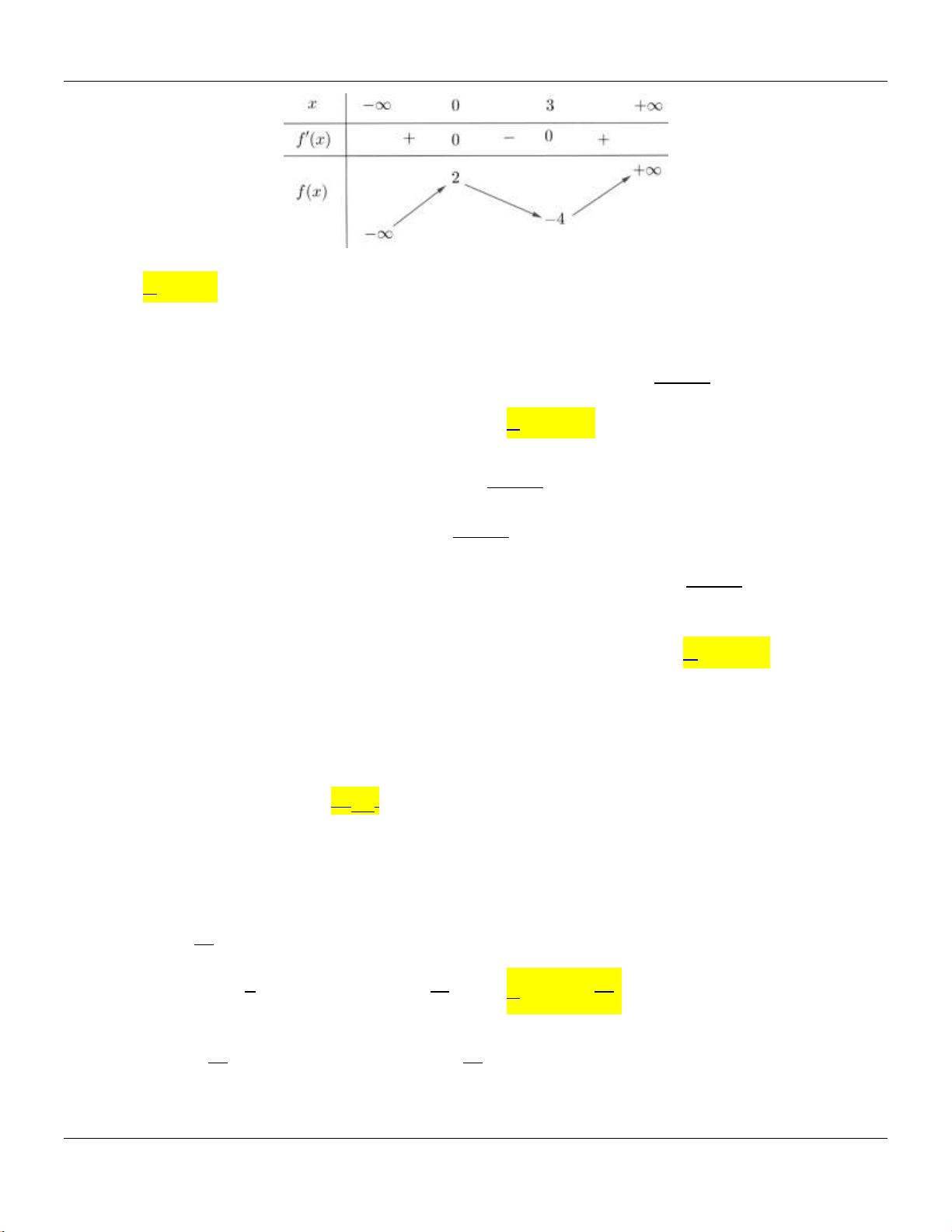
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Điểm cực đại của đồ thị hàm số đã cho có tọa độ là:
A.
0;2
. B.
3; 4
. C.
2;0
. D.
4;3
.
Lời giải:
Ta có điểm cực đại của đồ thị hàm số đã cho có tọa độ là:
0;2
.
Câu 20: Tọa độ giao điểm của hai đường tiệm cận của đồ thị hàm số
21
2
x
y
x
là
A.
2;2
. B.
2; 2
. C.
2; 2
. D.
2;2
.
Lời giải:
Ta có tiệm cận đứng của đồ thị hàm số
21
2
x
y
x
là:
2x
.
Tiệm cận ngang của đồ thị hàm số
21
2
x
y
x
là:
2y
.
Vậy tọa độ giao điểm của hai đường tiệm cận của đồ thị hàm số
21
2
x
y
x
là:
2; 2
.
Câu 21: Tập nghiệm của bất phương trình
2
28
x
là:
A.
1;
. B.
;1
. C.
1;
. D.
;1
.
Lời giải:
Ta có
2
2
2 8 2 log 8 2 3 1
x
x x x
.
Vậy tập nghiệm của bất phương trình là:
;1
.
Câu 22: Cho tập
0;1;2;...;9M
. Số tập con gồm
3
phần tử và không chứa số
1
của
M
bằng
A.
45
. B.
84
. C.
72
. D.
36
.
Lời giải:
Số tập con gồm
3
phần tử là
3
10
120.C
Số tập con gồm
3
phần tử và chứa số
1
của
M
bằng
2
9
36C
.
Vậy số tập con gồm
3
phần tử và không chứa số
1
của
M
bằng
120 36 84.
Câu 23: Cho
2
1
d
x F x C
x
. Khẳng định nào dưới đây đúng?
A.
1
Fx
x
. B.
3
2
Fx
x
. C.
2
1
Fx
x
. D.
2
ln
F x x
.
Lời giải:
Ta có:
2
1
dx F x C
x
suy ra
2
1
Fx
x
.
Câu 24: Nếu
3
1
d 2023
f x x
thì
3
1
2d
f x x x
bằng
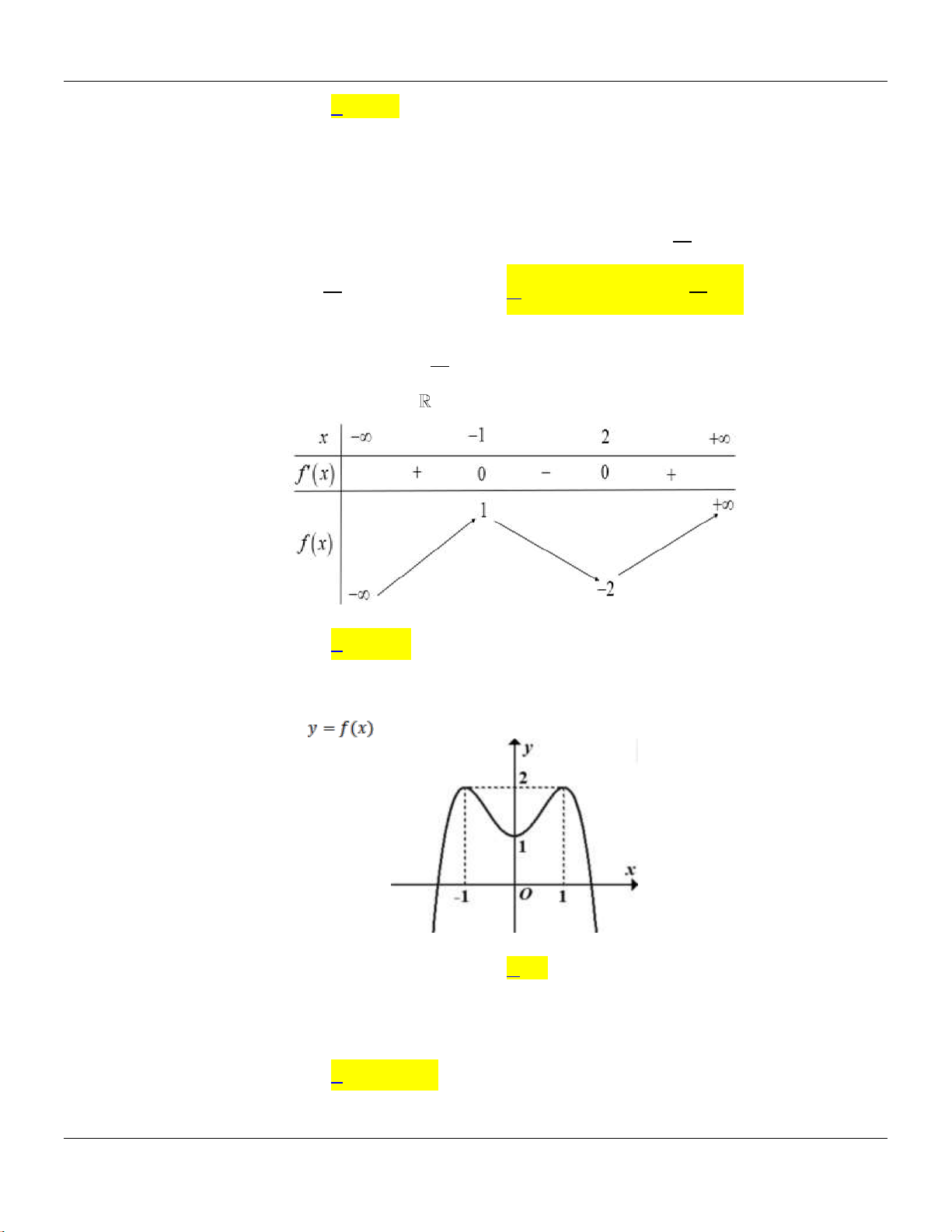
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
A.
16188
. B.
4050
. C.
16192
. D.
8096
.
Lời giải:
Ta có:
3 3 3
1 1 1
2 2 2.2023 4 4050
f x x dx f x dx xdx
.
Câu 25: Cho hàm số
2
sinf x x x
. Khẳng định nào dưới đây đúng?
A.
d cos 2 .f x x x x C
B.
3
d cos .
3
x
f x x x C
C.
3
d cos .
3
x
f x x x C
D.
3
d cos .
3
x
f x x x C
Lời giải:
2
3
d sin cos .
3
x
f x x x x dx x C
Câu 26: Cho hàm số
()y f x
liên tục trên và có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
A.
2;1
B.
1;2
. C.
;1
. D.
;2
.
Lời giải:
Từ Bảng biến thiên ta có hàm số nghịch biến trên
1;2
Câu 27: Cho hàm số bậc bốn có đồ thị là đường cong trong hình bên.
Giá trị cực đại của hàm số đã cho là
A.
1
. B.
1
. C.
2
. D.
0
.
Lời giải:
Từ đồ thị ta có giá trị cực đại hàm số là
2
Câu 28: Với
a
là số thực dương tùy ý, khi đó
3
4
log 4a
bằng
A.
4
3log 4a
. B.
4
1 3log a
. C.
4
4 3log a
. D.
4
3 log a
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
33
4 4 4 4
log 4 log 4 log 1 3loga a a
.
Câu 29: Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
32y x x
và trục
Ox
. Thể tích của
khối tròn xoay sinh ra khi quay hình
H
quanh trục
Ox
bằng :
A.
1
6
. B.
1
30
. C.
30
. D.
6
.
Lời giải:
Hoành độ giao điểm của đồ thị hàm số
2
32y x x
và trục
Ox
là nghiệm phương trình :
2
1
3 2 0
2
x
xx
x
.
Thể tích của khối tròn xoay sinh ra khi quay hình
H
quanh trục
Ox
bằng :
2
2
2
1
3 2 d
30
x x x
.
Câu 30: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
B
có
,2AB a AA a
. Tính tan của góc giữa đường thẳng
AC
với mặt phẳng
AA B B
:
A.
1
3
. B.
3
. C.
1
. D.
2
2
.
Lời giải:
Ta có:
CB AB
CB AA CB ABB A
AA AB A
.
Suy ra
AB
là hình chiếu của
AC
lên mặt phẳng
ABB A
.
C'
B'
A
C
B
A'
Do đó:
,,A C AA B B A C A B BA C
.
Xét
A AB
vuông tại
A
, ta có:
22
3A B A A AB a
.
Xét
A BC
vuông tại
B
, ta có:
1
tan
33
BC a
BA C
AB
a
.
Câu 31: Cho hàm số
fx
xác định trên và có đạo hàm là
2
3 1 ,
f x x x x x
. Hỏi
hàm số
fx
đồng biến trên khoảng nào dưới đây?
A.
1;
. B.
3;0
. C.
0;1
. D.
;1
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
Lời giải:
Ta có:
2
31f x x x x
;
3
00
1
x
f x x
x
.
Dấu của
fx
:
f'(x)
∞
∞
0
+
+
1
3
x
0
0
0
+
Hàm số
fx
đồng biến trên
;3
và
0;1
.
Câu 32: Cho hàm số
y f x
liên tục trên và có đồ thị như hình vẽ dưới đây:
.
Tìm tất cả các giá trị thực của tham số
m
để phương trình
f x m
có 4 nghiệm thực phân
biệt.
A.
43m
. B.
4; 3m
. C.
43m
. D.
22m
.
Lời giải:
Dựa vào đồ thị ta thấy
43m
là giá trị cần tìm.
Câu 33: Chọn ngẫu nhiên hai số khác nhau từ 23 số nguyên dương đầu tiên. Xác suất để chọn được
hai số có tổng là một số chẵn bằng
A.
11
23
. B.
1
2
. C.
265
529
. D.
12
23
.
Lời giải:
Trong 23 số nguyên dương đầu tiên có 12 số lẻ và 11 số chẵn.
Chọn 2 số khác nhau từ 23 số, có
2
23
C
cách chọn nên số phần tử không gian mẫu là
2
23
.nC
Gọi
A
là biến cố: “ Chọn được hai số có tổng là một số chẵn ”.
Để hai số được chọn có tổng là một số chẵn thì hai số đó phải cùng chẵn hoặc cùng lẻ.
+ Trường hợp 1: Chọn hai số chẵn khác nhau từ 11 số chẵn, có
2
11
C
cách chọn.
+ Trường hợp 2: Chọn hai số lẻ khác nhau từ 12 số lẻ, có
2
12
C
cách chọn.
Do đó
22
11 12
n A C C
.
Xác suất cần tính là
22
11 12
2
23
11
23
nA
CC
PA
nC
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Câu 34: Gọi
S
là tập nghiệm của phương trình
2
22
2log 2 2 log 3 2xx
trên . Tổng các
phần tử của
S
bằng
A.
62
. B.
82
. C.
8
. D.
42
.
Lời giải:
Điều kiện:
1
3
x
x
.
2
22
2log 2 2 log 3 2xx
22
22
log 2 2 log 3 2xx
.
2
2
log 2 2 3 2xx
2
22
2 8 6 2xx
.
2
2
2 8 6 2
2 8 6 2
xx
xx
2
2
4 2 0 1
4 4 0 2
xx
xx
.
+)
22
1
2 2 ( )
x
xl
.
+)
22x
.
2;2 2S
.
Vậy tổng các nghiệm của
S
là:
2 2 2 4 2
.
Câu 35: Cho số phức
z
thỏa
1 2 3iz i
. Biết rằng tập hợp các điểm biểu diễn của số phức
z
trên
mặt phẳng
Oxy
là một đường tròn. Tìm tâm của đường tròn đó.
A.
2; 1I
. B.
1;1I
. C.
0;1I
. D.
1;0I
.
Lời giải:
Gọi
M
là điểm biểu diễn số phức
z
.
Do đó
1 2 3iz i
12
3 2 3
i
i z z i
i
3MI
, với
2; 1I
.
Do đó tập hợp điểm
M
là đường tròn tâm
2; 1I
và bán kính
3R
.
Câu 36: Trong không gian
Oxyz
, cho ba điểm
(1;2;0), (1;1;2)AB
và
(2;3;1)C
. Đường thẳng đi qua
A
và song song với
BC
có phương trình là
A.
12
.
1 2 1
x y z
B.
12
.
3 4 3
x y z
C.
12
.
3 4 3
x y z
D.
12
.
1 2 1
x y z
Lời giải:
Gọi
d
là đường thẳng qua
1;2;0A
và song song với
BC
.
Ta có
1;2; 1BC
là véc tơ chỉ phương
12
:
1 2 1
x y z
d
.
Câu 37: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
2;3;5A
. Điểm đối xứng với A qua mặt
phẳng
Oxy
có tọa độ là
A.
2;3; 5
. B.
2;3;5
. C.
0;0;5
. D.
0;0; 5
.
Lời giải:
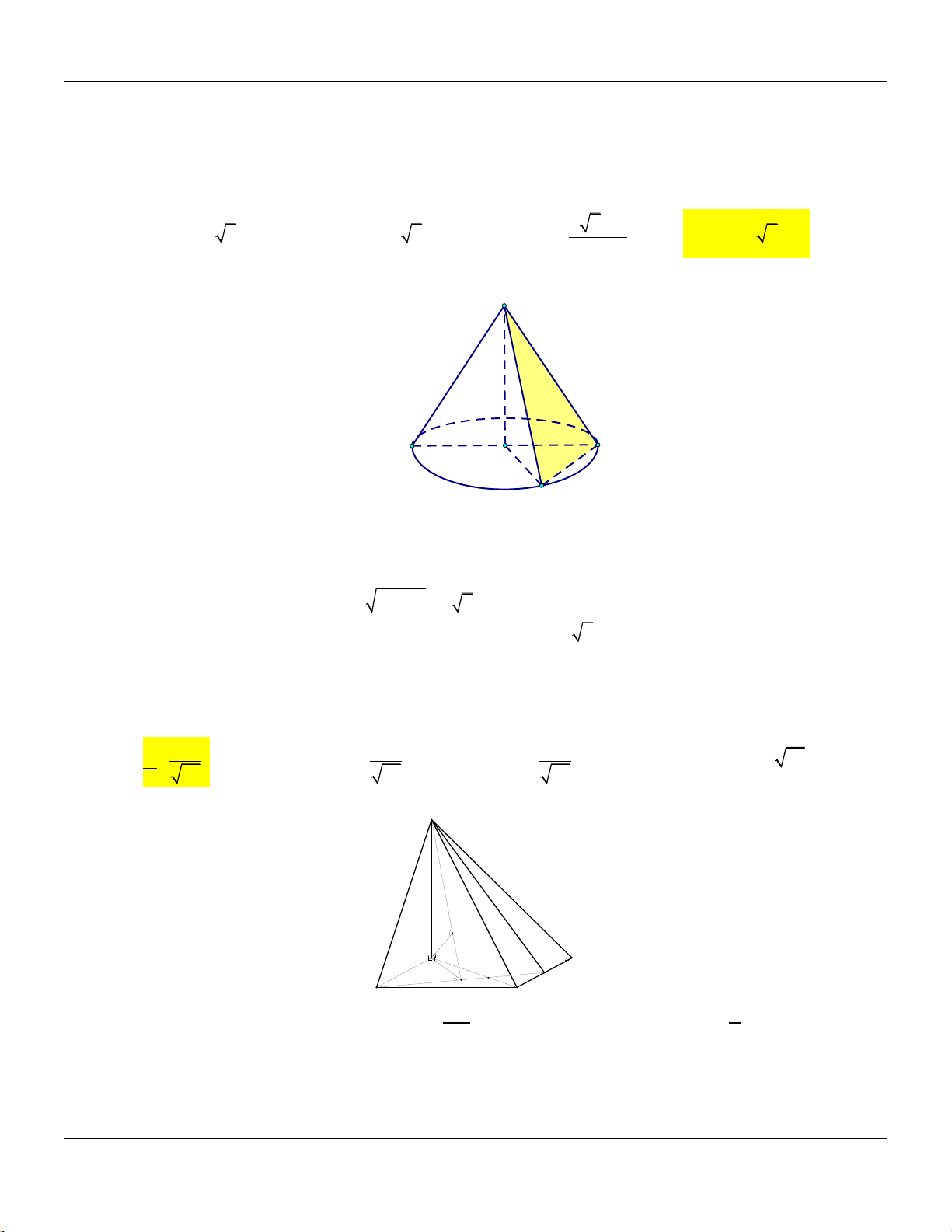
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
Tọa độ hình chiếu của điểm
2;3;5A
trên mặt phẳng
Oxy
là
2;3;0
. Điểm đối xứng
với A qua mặt phẳng
Oxy
có tọa độ là
2;3; 5
.
Câu 38: Cho hình nón
N
có chiều cao bằng
3.a
Biết thiết diện qua đỉnh của hình nón
N
là tam
giác vuông có diện tích bằng
2
8.a
Diện tích xung quanh của hình nón đã cho là
A.
2
8 7 .
xq
Sa
B.
2
2 7 .
xq
Sa
C.
2
47
.
3
xq
a
S
D.
2
4 7 .
xq
Sa
Lời giải:
S
A
B
O
h
r
l
Gọi
O
là tâm đáy hình nón và thiết diện là tam giác
.SAB
Ta có:
2
2
1
. 8 4 .
22
SAB
l
S SA SB a l a
Bán kính đáy của nón là
22
7.r l h a
Vậy diện tích xung quanh của hình nón là
2
4 7 .
xq
S rl a
Câu 39: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với
,AB a
2,AD a
SA ABCD
và
SA a
. Tính theo
a
khoảng cách từ
D
đến mặt phẳng
SBM
, với
M
là trung điểm của
.CD
A.
2
33
a
. B.
33
a
. C.
4
33
a
. D.
33a
.
Lời giải:
2a
a
a
E
M
C
A
D
B
S
N
H
Ta có
1
, , , , ,
2
CE
d D SBM d C SBM d A SBM d D SBM d A SBM
AE
.
Dựng
AN BM
với
N
thuộc
BM
và
AH SN
với
H
thuộc
SN
.
Khi đó,
BM AN
và
BM SA
, suy ra
BM SAN
nên
BM AH
.
Và
AH BM
và
AH SN
, suy ra
AH SBM
nên
,d A SBM AH
.
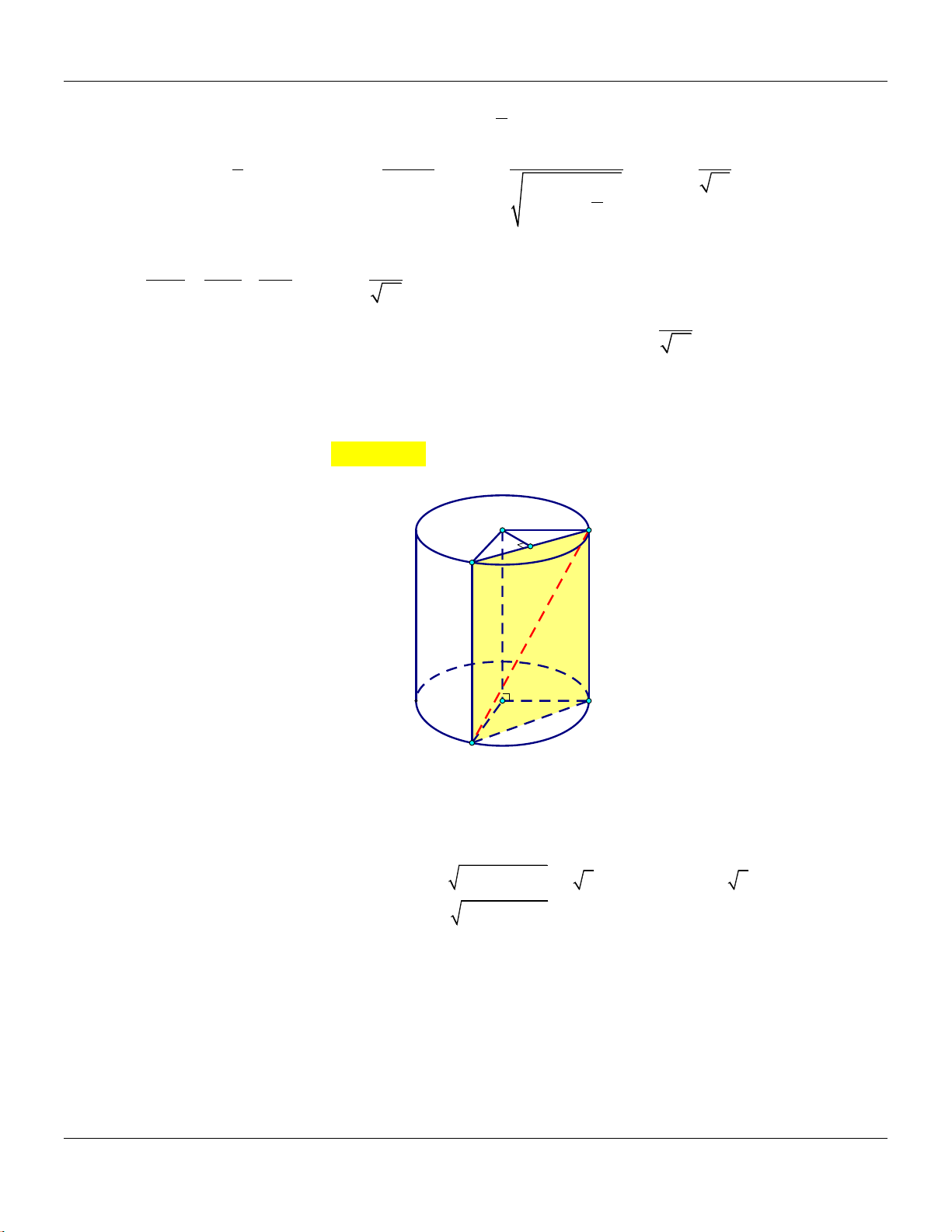
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
Ta có
2 2 2
1
2 2 2.
2
ABM ABCD ADM ABM ABM
S S S S a a S a
.
Mà
2
2
2
2.
1 2 4
.
2
17
2
2
ABM
ABM
S
aa
S AN BM AN AN AN
BM
a
a
.
Trong tam giác vuông
SAN
, vuông tại
,A
với
AH
đường cao, ta có
2 2 2
1 1 1 4
33
a
AH
AH AN AS
.
Vậy khoảng cách từ
D
đến mặt phẳng
SBM
là
2
d D, SBM
33
a
.
Câu 40: Cho hình trụ
T
có bán kính đáy bằng
2.a
Gọi
,AB
lần lượt nằm trên hai đường tròn đáy
của hình trụ
T
sao cho
4.AB a
Biết
AB
cách trục của trụ một khoảng bằng
.a
Thể tích
khối trụ đã cho là
A.
3
6.Va
B.
3
8.Va
C.
3
12 .Va
D.
3
4.Va
Lời giải:
H
B
M
r
l
h
N
O'
O
A
Gọi
,OO
là tâm hai đáy của
.T
Gọi thiết diện tạo bởi mặt phẳng chứa
AB
, song song với
OO
là tứ giác
.AMBN
Dựng
, ; .OH AM H AM OH AMBN d OO AMBN OH a
Xét tam giác
OHA
vuông tại
22
: 3 2 2 3 .H AH OA HO a AM AH a
Xét tam giác
AMB
vuông tại
22
: 2 .M MB AB MB a h
Vậy thể tích khối trụ đã cho là
23
8.V h r a
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 12_______________
Câu 1: Trên mặt phẳng toạ độ, cho số phức
34zi
. Môđun của
z
bằng
A.
16
. B.
5
. C.
25
. D.
7
.
Câu 2: Trên khoảng
0;
, đạo hàm của hàm số
5
x
y
là
A.
5
x
y
. B.
5
ln5
x
y
. C.
5 .ln5
x
y
. D.
1
5
x
y
.
Câu 3: Tập xác định
D
của hàm số
1yx
là
A.
\1D
. B.
D
. C.
1;D
. D.
1;D
.
Câu 4: Tập nghiệm của bất phương trình
1
39
x
là
A.
;2
. B.
;3
. C.
3;
. D.
2;
.
Câu 5: Cho cấp số nhân
n
u
với
1
2023u
và công bội
3q
. Giá trị của
3
u
bằng
A.
2029
. B.
54621
. C.
18207
. D.
6069
.
Câu 6: Trong không gian
xyzO
, mặt phẳng
:2 2023 0P y z
có một vectơ pháp tuyến là
A.
1
0;2; 1n
. B.
2
2; 1;2023n
. C.
3
1;0;2n
. D.
4
2; 1; 2023n
.
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hình bên dưới:
Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là
A.
0; 2
. B.
2;0
. C.
2;0
. D.
0;2
.
Câu 8: Nếu
4
1
d 2023f x x
và
4
1
d 2022g x x
thì
4
1
df x g x x
bằng
A. 5. B. 6. C. 1. D.
1
.
Câu 9: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
42
32y x x
. B.
3
1
x
y
x
. C.
2
41y x x
. D.
3
35y x x
.
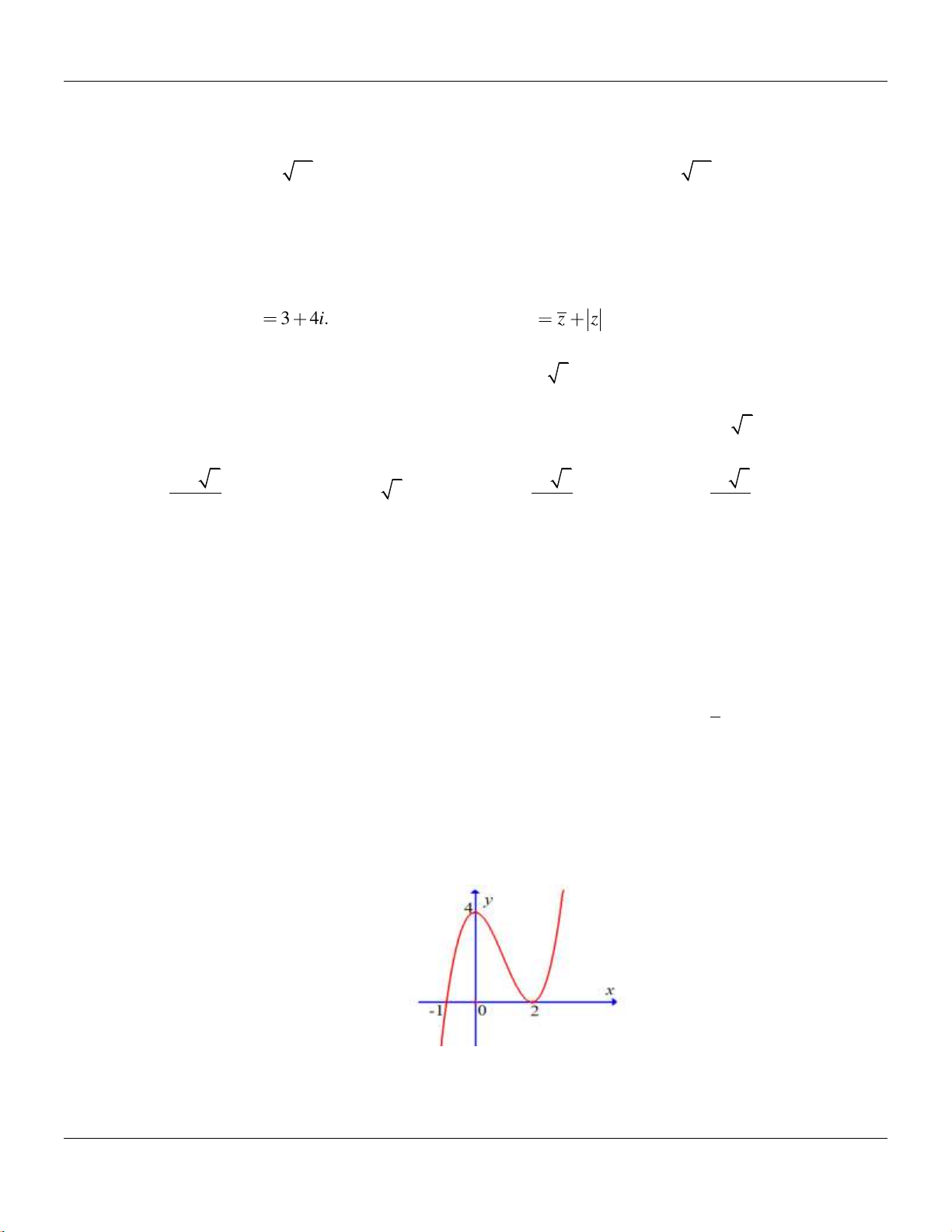
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 10: Trong không gian
,Oxyz
cho mặt cầu
S
có phương trình
2 2 2
2 4 6 0x y z x y z
. Tìm
tọa độ tâm
I
và bán kính
R
của mặt cầu
S
.
A.
1; 2;3 ; 14IR
. B.
1;2; 3 ; 14IR
.
C.
1;2; 3 ; 14IR
. D.
1; 2;3 ; 14IR
.
Câu 11: Trong không gian
Oxyz
, góc giữa hai mặt phẳng
: 11 0P x y z
và
:2 2 2 7 0Q x y z
bằng
A.
0
. B.
90
. C.
180
. D.
45
.
Câu 12: Cho số phức
3 4 .zi
Phần thực của số phức
w z z
là
A.
8
. B.
4
. C.
5
. D.
3
.
Câu 13: Cho khối lập phương có độ dài đường chéo bằng
33
. Thể tích khối lập phương đã cho bằng
A.
9
. B.
12
. C.
27
. D.
18
.
Câu 14: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
,3AB a BC a
,
SA
vuông góc
với đáy và
2SA a
. Thể tích khối chóp đã cho bằng
A.
3
23
3
a
. B.
3
23a
. C.
3
3
3
a
. D.
3
3
6
a
.
Câu 15: Cho mặt phẳng
P
cắt mặt cầu
;S O R
theo thiết diện là một đường tròn. Gọi
d
là khoảng
cách từ
O
đến
P
. Khẳng định nào dưới đây đúng?
A.
dR
. B.
dR
. C.
2dR
. D.
dR
.
Câu 16: Số phức liên hợp của số phức
72zi
là
A.
27zi
. B.
72zi
. C.
72zi
. D.
72zi
.
Câu 17: Cho hình nón có bán kính đáy
r
, độ dài đường sinh
l
và chiều cao
h
. Khi đó, thể tích của
khối nón đã cho bằng
A.
2
r
. B.
rl
. C.
2
rh
. D.
2
1
3
rh
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
3
: 5 2
2
xt
yt
zt
. Điểm nào sau đây thuộc
?
A.
3;5;0M
. B.
3; 5; 2N
. C.
3; 5;0P
. D.
1;2; 2Q
.
Câu 19: Cho hàm số
32
f x ax bx cx d
có đồ thị như hình vẽ bên dưới.
Mệnh đề nào sau đây sai?
A. Hàm số đạt cực tiểu tại
2x
. B. Hàm số đạt cực đại tại
4x
.
C. Hàm số có hai điểm cực trị. D. Hàm số đạt cực đại tại
0x
.
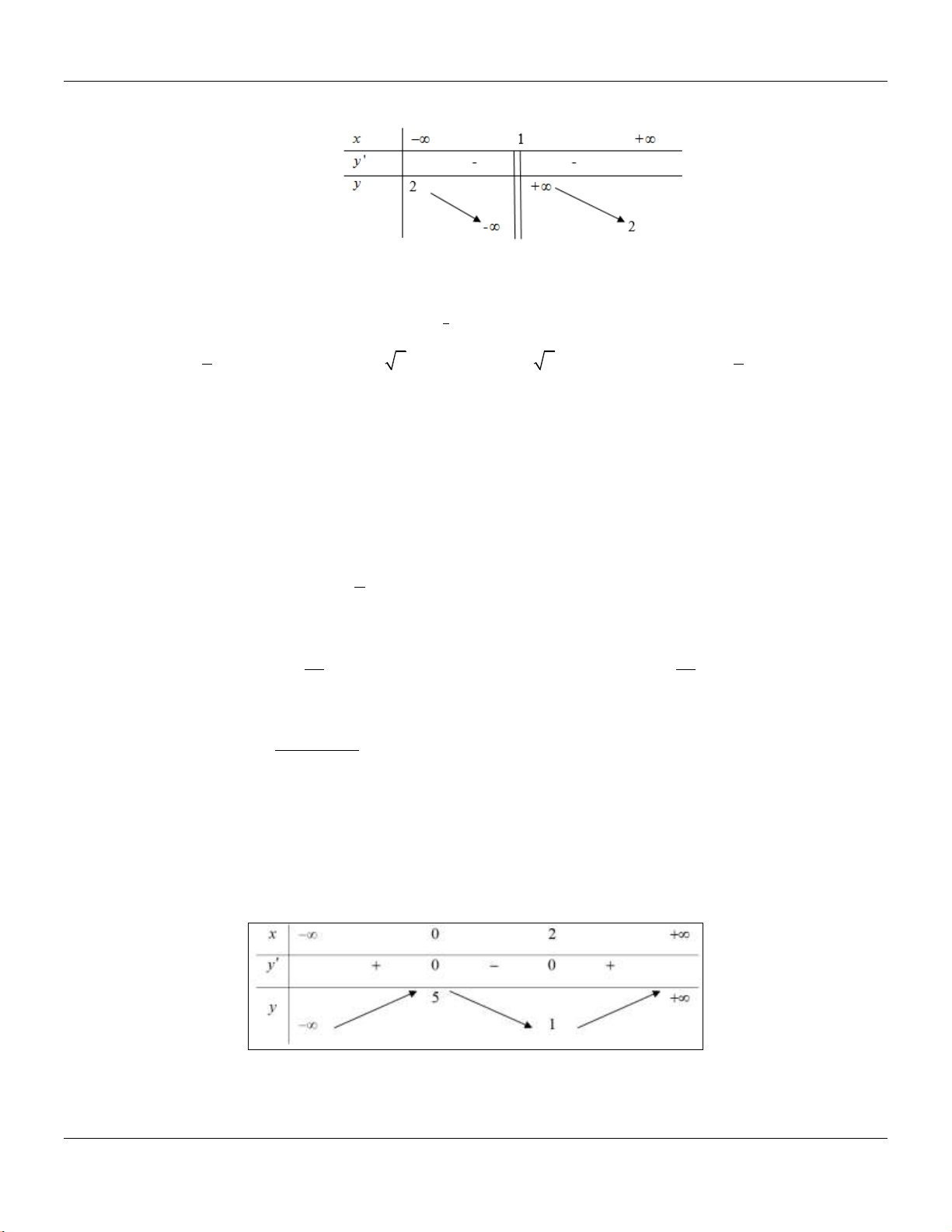
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
Câu 20: Cho hàm số
y f x
có bảng biến thiên như sau:
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho lần lượt là
A.
1, 2xy
. B.
2, 1xy
. C.
2, 2xy
. D.
1, 1xy
.
Câu 21: Tập nghiệm của bất phương trình
2
3
log 2x
là
A.
4
;
9
. B.
3
;4
. C.
3
4;
. D.
4
0;
9
.
Câu 22: Có bao nhiêu số tự nhiên có bốn chữ số khác nhau được lập từ các số
1;3;4;6;7
?
A.
15
. B.
120
. C.
10
. D.
24
.
Câu 23: Cho
2
d 3 sinf x x x x C
. Khẳng định nào sau đây đúng?
A.
6 cosf x x x
. B.
3
cosf x x x
. C.
3
cosf x x x
. D.
6 cosf x x x
.
Câu 24: Cho
ln2
0
2 e d 5
x
f x x
. Tính
ln2
0
df x x
.
A.
3
. B.
5
2
. C.
2
. D.
1
.
Câu 25: Cho hàm số
sin 1f x x x
. Khẳng định nào dưới đây đúng?
A.
2
d cos
2
x
f x x x x C
. B.
2
d cos
2
x
f x x x x C
.
C.
d sin
f x x x x C
. D.
2
d cos
f x x x x x C
.
Câu 26: Cho hàm số
2023 22
1
x
y
x
. Khẳng định nào dưới đây sai?
A.
Hàm số đồng biến trên khoảng
;1
.
B. Hàm số đồng biến trên khoảng
1;2023
.
C. Hàm số đồng biến trên khoảng
;1
.
D. Hàm số đồng biến trên khoảng
1;2023
.
Câu 27: Cho hàm số
y f x
có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại
5x
. B. Hàm số đạt cực tiểu tại
1x
.
C. Hàm số đạt cực tiểu tại
0x
. D. Hàm số đạt cực đại tại
0x
.
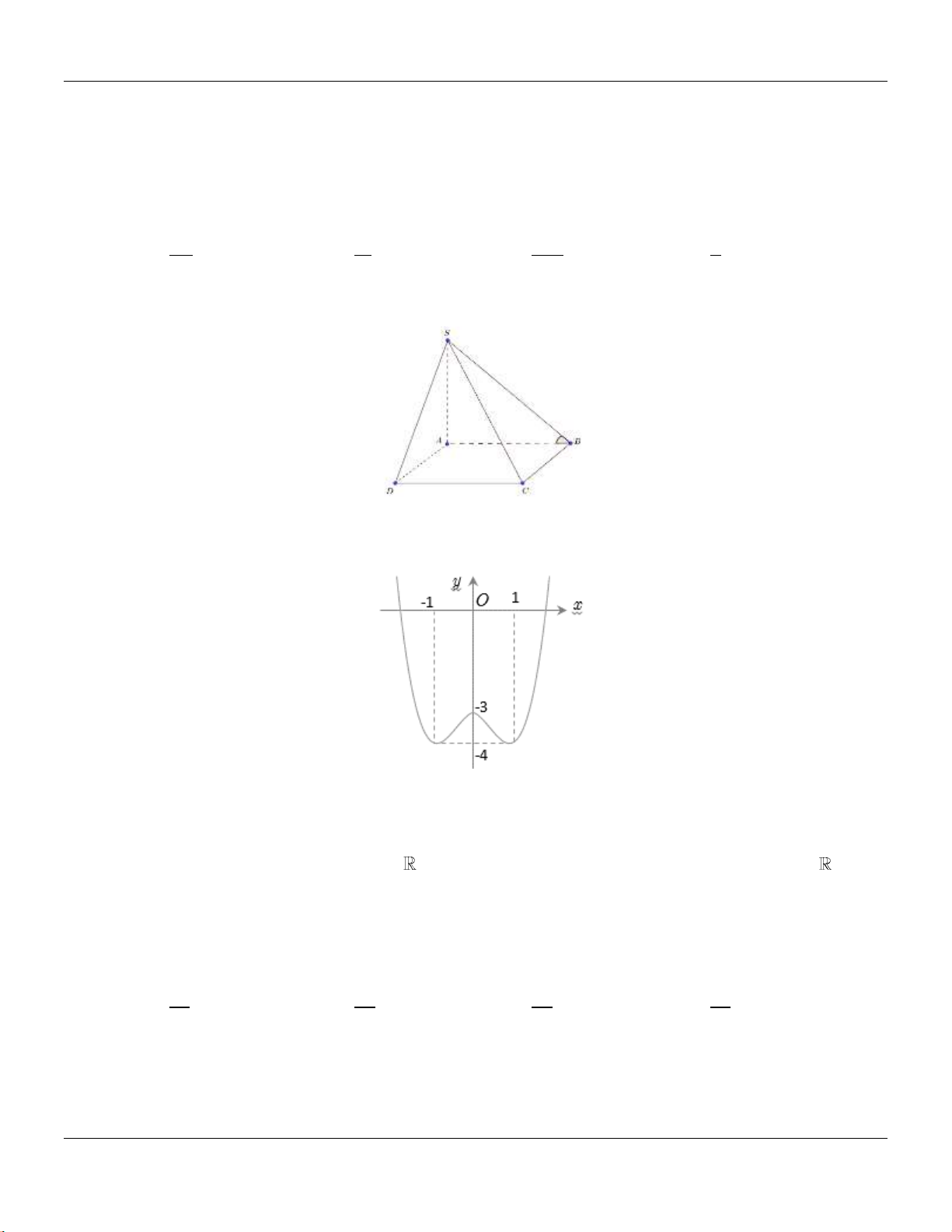
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Câu 28: Cho các số thực dương
;ab
thỏa mãn
2
log ax
,
2
log by
. Giá trị biểu thức
23
2
logP a b
theo
;xy
bằng
A.
23xy
. B.
3xy
. C.
32xy
. D.
23xy
.
Câu 29: Thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số
2
43y x x
và
trục hoành quay quanh trục
Ox
là
A.
4
3
. B.
16
15
. C.
16
15
. D.
4
3
.
Câu 30: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật cạnh
AB a
,
SA
vuông góc với mặt phẳng
đáy và
2SB a
(tham khảo hình bên). Góc giữa mặt phẳng
()SBC
và mặt phẳng đáy bằng
A.
90
. B.
60
. C.
45
. D.
30
.
Câu 31: Cho hàm số
42
f x ax bx c
có đồ thị là đường cong trong hình bên dưới:
Có bao nhiêu giá trị nguyên thuộc đoạn
2;5
của tham số
m
để phương trình
f x m
có
đúng hai nghiệm thực phân biệt?
A.
6
. B. 7. C.
8
. D.
9
Câu 32: Cho hàm số
()fx
xác định trên và có đạo hàm
25
2 1 1 ,
f x x x x x
. Hàm
số đã cho nghịch biến trên khoảng nào dưới đây?
A.
;2 .
B.
2; .
C.
1;2 .
D.
1; .
.
Câu 33: Chọn ngẫu nhiên
2
số khác nhau từ
30
số nguyên dương đầu tiên. Tính xác suất để chọn
được
2
số có tích là một số lẻ.
A.
7
29
. B.
15
29
. C.
22
29
. D.
8
29
.
Câu 34: Biết phương trình
3
2log 2log 3 5
x
x
có hai nghiệm thực
12
xx
. Tính giá trị của biểu thức
2
12
61T x x
.
A.
12T
. B.
10T
. C.
16T
. D.
8T
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 35: Cho số phức
z
thỏa mãn
3 2 3 2 16z i z i
. Biết tập hợp các điểm
M
biểu diễn số
phức
2 2 3w z i
là đường tròn tâm
;I a b
và bán kính
c
. Giá trị của
abc
bằng
A.
11
. B.
10
. C.
17
. D.
18
.
Câu 36: Trong không gian với hệ trục tọa độ
Oxyz
, cho đường thẳng
12
:
2 1 3
x y z
d
và mặt phẳng
: 6 4 27 0P x y z
. Gọi
;;M a b c
là giao điểm của
d
và
P
. Tính
2S a b c
.
A.
10S
. B.
13S
. C.
11S
. D.
12S
.
Câu 37: Cho hình nón
N
có chiều cao bằng
2,a
độ dài đường sinh bằng
3.a
Thiết diện qua đỉnh của
hình nón
N
tạo với mặt đáy hình nón một góc
60 .
Diện tích thiết diện là
A.
2
4 11
.
9
a
S
B.
2
4 11
.
3
a
S
C.
2
2 11
.
9
a
S
D.
2
2 11
.
3
a
S
Câu 38: Trong không gian
Oxyz
, cho điểm
1;2;1M
và mặt phẳng
( ): 6 0P x y z
. Giả sử
;;H a b c
là hình chiếu của
M
trên mặt phẳng
()P
. Khi đó
abc
bằng
A.
4
. B.
2
. C.
1
. D.
1
.
Câu 39: Cho hình chóp
SABCD
có đáy là hình vuông, cạnh
a
. Tam giác
SAB
là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Khoảng cách giữa 2 đường thẳng
AB
và
SC
bằng
A.
3
7
a
. B.
a
. C.
21
7
a
. D.
2
2
a
.
Câu 40: Cho hình trụ
T
có bán kính đáy bằng
2.a
Thiết diện song song và cách trục của hình trụ
T
một khoảng bằng
a
là hình hình chữ nhật có diện tích bằng
2
6.a
Diện tích xung quanh
của hình trụ đã cho là
A.
2
3.
xq
Sa
B.
2
2 3 .
xq
Sa
C.
2
3 3 .
xq
Sa
D.
2
4 3 .
xq
Sa
________________________HẾT________________________

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Trên mặt phẳng toạ độ, cho số phức
34zi
. Môđun của
z
bằng
A.
16
. B.
5
. C.
25
. D.
7
.
Lời giải:
Môđun của
34zi
bằng
2
2
3 4 25
.
Câu 2: Trên khoảng
0;
, đạo hàm của hàm số
5
x
y
là
A.
5
x
y
. B.
5
ln5
x
y
. C.
5 .ln5
x
y
. D.
1
5
x
y
.
Lời giải:
Hàm số
x
ya
có đạo hàm là
.ln
x
y a a
Đạo hàm của hàm số
5
x
y
là
5 .ln5
x
y
.
Câu 3: Tập xác định
D
của hàm số
1yx
là
A.
\1D
. B.
D
. C.
1;D
. D.
1;D
.
Lời giải:
Tập xác định
D
của hàm số
1yx
là
1;D
.
Câu 4: Tập nghiệm của bất phương trình
1
39
x
là
A.
;2
. B.
;3
. C.
3;
. D.
2;
.
Lời giải:
Ta có:
1 1 2
3 9 3 3 1 2
xx
x
3x
.
Câu 5: Cho cấp số nhân
n
u
với
1
2023u
và công bội
3q
. Giá trị của
3
u
bằng
A.
2029
. B.
54621
. C.
18207
. D.
6069
.
Lời giải:
Ta có:
22
31
. 2023.3 18207u u q
.
Câu 6: Trong không gian
xyzO
, mặt phẳng
:2 2023 0P y z
có một vectơ pháp tuyến là
A.
1
0;2; 1n
. B.
2
2; 1;2023n
. C.
3
1;0;2n
. D.
4
2; 1; 2023n
.
Lời giải:
Mặt phẳng
:2 2023 0P y z
có một vectơ pháp tuyến là
1
0;2; 1n
.
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hình bên dưới:
Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là
A.
0; 2
. B.
2;0
. C.
2;0
. D.
0;2
.
Lời giải:

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
Dựa vào đồ thị hàm số: Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là
0; 2
.
Câu 8: Nếu
4
1
d 2023f x x
và
4
1
d 2022g x x
thì
4
1
df x g x x
bằng
A. 5. B. 6. C. 1. D.
1
.
Lời giải:
Ta có:
4 4 4
1 1 1
d d d 2023 2022 1f x g x x f x x g x x
.
Câu 9: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
42
32y x x
. B.
3
1
x
y
x
. C.
2
41y x x
. D.
3
35y x x
.
Lời giải:
Dựa vào đồ thị hàm số, ta có: Đường cong trong hình bên là đồ thị của hàm số
3
35y x x
.
Câu 10: Trong không gian
,Oxyz
cho mặt cầu
S
có phương trình
2 2 2
2 4 6 0x y z x y z
. Tìm
tọa độ tâm
I
và bán kính
R
của mặt cầu
S
.
A.
1; 2;3 ; 14IR
. B.
1;2; 3 ; 14IR
.
C.
1;2; 3 ; 14IR
. D.
1; 2;3 ; 14IR
.
Lời giải:
Phương trình mặt cầu đã cho tương đương với phương trình sau:
2 2 2
1 2 3 14x y z
.
Vậy mặt cầu đã cho có tâm
1; 2;3I
và bán kính
14R
.
Câu 11: Trong không gian
Oxyz
, góc giữa hai mặt phẳng
: 11 0P x y z
và
:2 2 2 7 0Q x y z
bằng
A.
0
. B.
90
. C.
180
. D.
45
.
Lời giải:
1;1; 1
P
n
,
2;2; 2
Q
n
.
Do
P
n
và
Q
n
là hai vectơ cùng phương nên góc giữa
P
và
Q
bằng
0
.
Câu 12: Cho số phức
3 4 .zi
Phần thực của số phức
w z z
là
A.
8
. B.
4
. C.
5
. D.
3
.
Lời giải:

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
Ta có:
22
3 4 ; 3 4 5z i z
.
3 4 5 8 4w z z i i
.
Vậy phần thực của số phức
w
bằng
8
.
Câu 13: Cho khối lập phương có độ dài đường chéo bằng
33
. Thể tích khối lập phương đã cho bằng
A.
9
. B.
12
. C.
27
. D.
18
.
Lời giải:
Độ dài đường chéo hình lập phương bằng
33
nên độ dài cạnh hình lập phương bằng
3
.
Thể tích khối lập phương đã cho là
3
3 27V
.
Câu 14: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
,3AB a BC a
,
SA
vuông góc
với đáy và
2SA a
. Thể tích khối chóp đã cho bằng
A.
3
23
3
a
. B.
3
23a
. C.
3
3
3
a
. D.
3
3
6
a
.
Lời giải:
Diện tích đáy
2
. 3 3
ABCD
B S a a a
.
Thể tích khối chóp đã cho
3
2
1 2 3
3.2
33
ABCD
a
V a a
.
Câu 15: Cho mặt phẳng
P
cắt mặt cầu
;S O R
theo thiết diện là một đường tròn. Gọi
d
là khoảng
cách từ
O
đến
P
. Khẳng định nào dưới đây đúng?
A.
dR
. B.
dR
. C.
2dR
. D.
dR
.
Lời giải:
Mặt phẳng
P
cắt mặt cầu
;S O R
theo thiết diện là một đường tròn suy ra
dR
.
Câu 16: Số phức liên hợp của số phức
72zi
là
A.
27zi
. B.
72zi
. C.
72zi
. D.
72zi
.
Lời giải:
Số phức liên hợp của số phức
72zi
là
72zi
.
Câu 17: Cho hình nón có bán kính đáy
r
, độ dài đường sinh
l
và chiều cao
h
. Khi đó, thể tích của
khối nón đã cho bằng
A.
2
r
. B.
rl
. C.
2
rh
. D.
2
1
3
rh
.
Lời giải:
Thể tích của khối nón đã cho bằng
2
1
3
rh
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
3
: 5 2
2
xt
yt
zt
. Điểm nào sau đây thuộc
?
A.
3;5;0M
. B.
3; 5; 2N
. C.
3; 5;0P
. D.
1;2; 2Q
.
Lời giải:
Nhận thấy điểm
3; 5;0P
thuộc đường thẳng
.
Câu 19: Cho hàm số
32
f x ax bx cx d
có đồ thị như hình vẽ bên dưới.
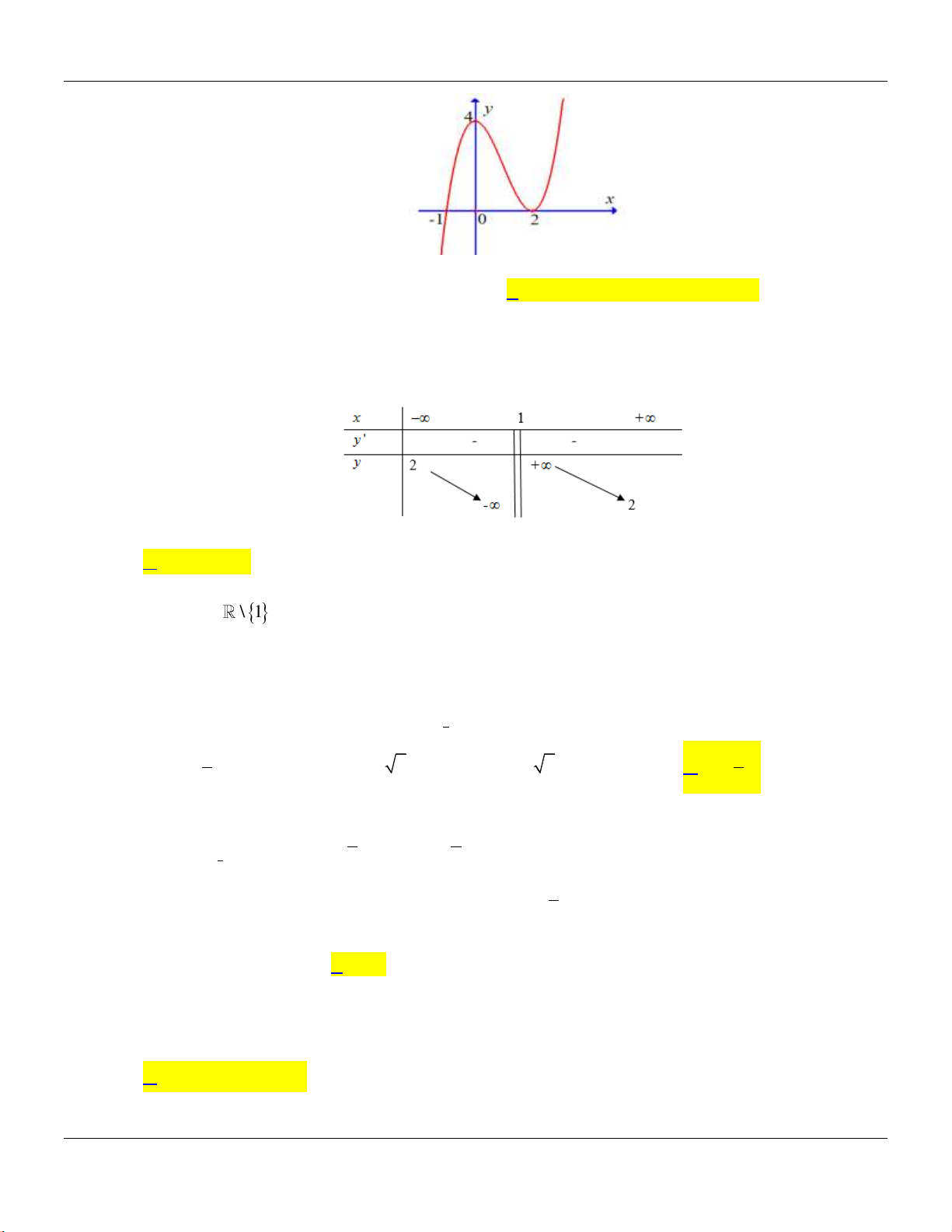
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Mệnh đề nào sau đây sai?
A. Hàm số đạt cực tiểu tại
2x
. B. Hàm số đạt cực đại tại
4x
.
C. Hàm số có hai điểm cực trị. D. Hàm số đạt cực đại tại
0x
.
Lời giải:
Dựa vào đồ thị hàm số ta thấy hàm số đạt cực đại tại
0x
.
Câu 20: Cho hàm số
y f x
có bảng biến thiên như sau:
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho lần lượt là
A.
1, 2xy
. B.
2, 1xy
. C.
2, 2xy
. D.
1, 1xy
.
Lời giải:
TXĐ:
\1D
.
Dựa vào bảng biến thiên ta thấy
1
lim
x
fx
đồ thị hàm số có tiệm cận đứng là
1x
.
Lại có:
lim 2
x
fx
đồ thị hàm số có tiệm cận ngang là
2y
.
Câu 21: Tập nghiệm của bất phương trình
2
3
log 2x
là
A.
4
;
9
. B.
3
;4
. C.
3
4;
. D.
4
0;
9
.
Lời giải:
Ta có
2
2
3
24
log 2 0 0
39
x x x
.
Vậy tập nghiệm của bất phương trình đã cho là
4
0;
9
.
Câu 22: Có bao nhiêu số tự nhiên có bốn chữ số khác nhau được lập từ các số
1;3;4;6;7
?
A.
15
. B.
120
. C.
10
. D.
24
.
Lời giải:
Số các số cần lập là
4
5
120A
.
Câu 23: Cho
2
d 3 sinf x x x x C
. Khẳng định nào sau đây đúng?
A.
6 cosf x x x
. B.
3
cosf x x x
. C.
3
cosf x x x
. D.
6 cosf x x x
.
Lời giải:
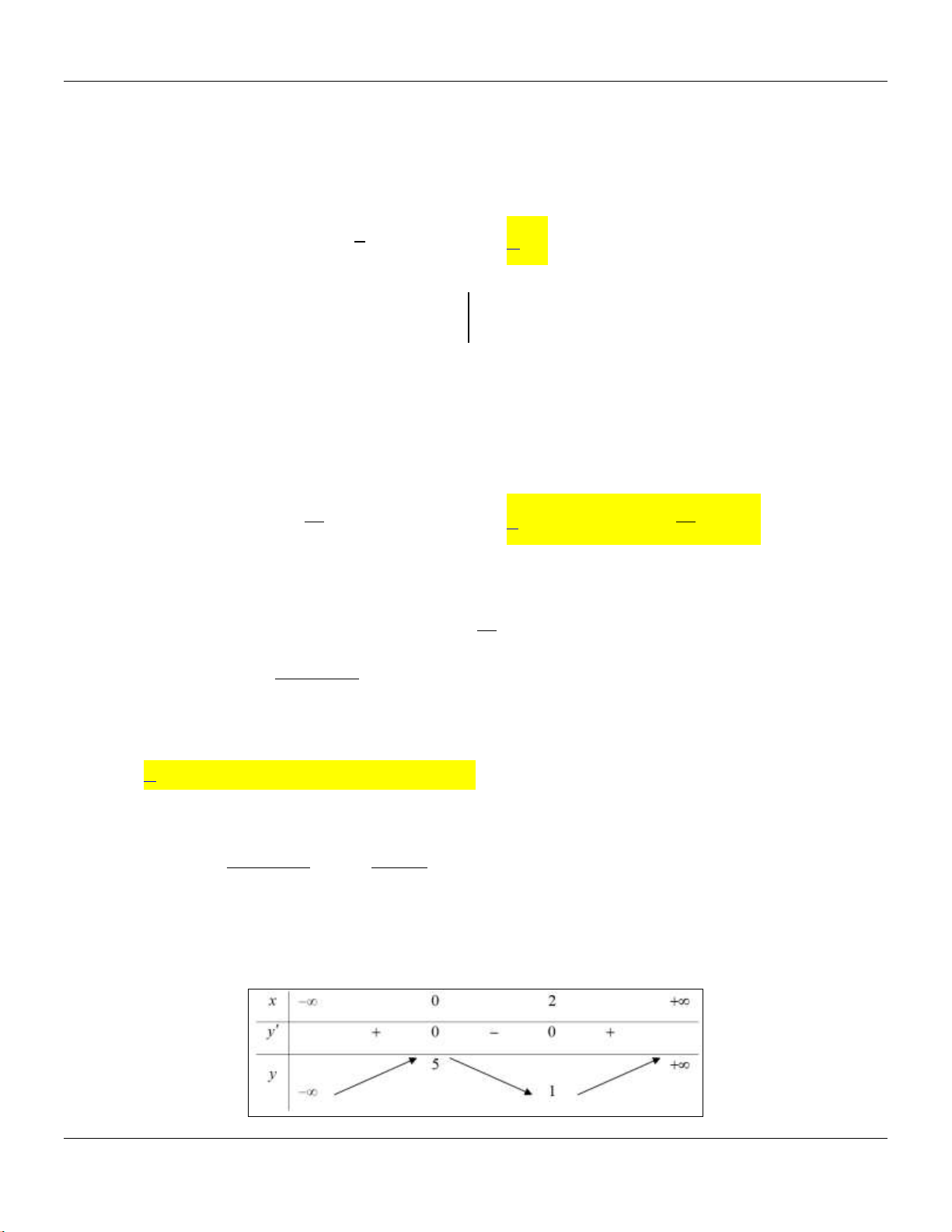
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Ta có :
2
6 cos d 3 sinx x x x x C
.
Do đó:
6 cosf x x x
.
Câu 24: Cho
ln2
0
2 e d 5
x
f x x
. Tính
ln2
0
df x x
.
A.
3
. B.
5
2
. C.
2
. D.
1
.
Lời giải:
Ta có:
ln2 ln2 ln2
ln2 0
0 0 0
ln2
2 e d 2 d e 2 d e e
0
xx
f x x f x x f x x
.
ln2
0
2 d 1f x x
.
Theo bài ra
ln2 ln2
00
2 e d 5 2 d 1 5
x
f x x f x x
ln2
0
d2f x x
.
Câu 25: Cho hàm số
sin 1f x x x
. Khẳng định nào dưới đây đúng?
A.
2
d cos
2
x
f x x x x C
. B.
2
d cos
2
x
f x x x x C
.
C.
d sin
f x x x x C
. D.
2
d cos
f x x x x x C
.
Lời giải:
2
sin cos
2
x
f x dx xdx xdx dx x x C
.
Câu 26: Cho hàm số
2023 22
1
x
y
x
. Khẳng định nào dưới đây sai?
A.
Hàm số đồng biến trên khoảng
;1
.
B. Hàm số đồng biến trên khoảng
1;2023
.
C. Hàm số đồng biến trên khoảng
;1
.
D. Hàm số đồng biến trên khoảng
1;2023
.
Lời giải:
Ta có:
2
2023 22 2045
0; 1
1
1
x
y y x
x
x
.
Vậy hàm số đã cho đồng biến trên các khoảng
;1
và
1;
nên nó cũng đồng biến
trên các khoảng
1;2023
và
1;2023 .
Câu 27: Cho hàm số
y f x
có bảng biến thiên như sau:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại
5x
. B. Hàm số đạt cực tiểu tại
1x
.
C. Hàm số đạt cực tiểu tại
0x
. D. Hàm số đạt cực đại tại
0x
.
Lời giải:
Qua bảng biến thiên ta thấy hàm số có
y
đổi dấu từ dương sang âm qua
0x
nên hàm số
đạt cực đại tại
0x
.
Câu 28: Cho các số thực dương
;ab
thỏa mãn
2
log ax
,
2
log by
. Giá trị biểu thức
23
2
logP a b
theo
;xy
bằng
A.
23xy
. B.
3xy
. C.
32xy
. D.
23xy
.
Lời giải:
Theo tính chất Logarit ta có:
23
2
logP a b
23
22
log logab
22
2log 3logab
23xy
.
Câu 29: Thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số
2
43y x x
và
trục hoành quay quanh trục
Ox
là
A.
4
3
. B.
16
15
. C.
16
15
. D.
4
3
.
Lời giải:
Hoành độ giao điểm của đồ thị hàm số
2
43y x x
và trục hoành là nghiệm phương trình
2
1
4 3 0
3
x
xx
x
.
Do đó, thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số
2
43y x x
và trục hoành quay quanh trục
Ox
là
3
2
2
1
4 3 dV x x x
3
4 3 2
1
8 22 24 9 dx x x x x
3
53
42
1
22 16
2 12 9
5 3 15
xx
x x x
.
Câu 30: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật cạnh
AB a
,
SA
vuông góc với mặt phẳng
đáy và
2SB a
(tham khảo hình bên). Góc giữa mặt phẳng
()SBC
và mặt phẳng đáy bằng
A.
90
. B.
60
. C.
45
. D.
30
.
Lời giải:
Vì
()SA ABCD
nên
SA BC
.
Mặt khác, theo giả thiết
AB BC
. Do đó
()BC SAB
nên
SB BC
.
Góc giữa hai mặt phẳng
()SBC
và
()ABCD
là góc
SBA
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
Ta có
1
cos
22
AB a
SBA
SB a
60SBA
.
Vậy góc giữa hai mặt phẳng
()SBC
và
()ABCD
bằng
60
.
Câu 31: Cho hàm số
42
f x ax bx c
có đồ thị là đường cong trong hình bên dưới:
Có bao nhiêu giá trị nguyên thuộc đoạn
2;5
của tham số
m
để phương trình
f x m
có
đúng hai nghiệm thực phân biệt?
A.
6
. B. 7. C.
8
. D.
9
Lời giải:
Để phương trình
f x m
có đúng hai nghiệm thực phân biệt thì ĐTHS
ym
cắt
ĐTHS
()y f x
tại hai điểm phân biệt .
Dựa vào đồ thị hàm số ta có
3
4
m
m
Do
m
;
2;5m
nên
2; 1;....;5m
. Có
8
giá trị cuả
m
thỏa mãn yêu cầu bài toán.
Câu 32: Cho hàm số
()fx
xác định trên và có đạo hàm
25
2 1 1 ,
f x x x x x
. Hàm
số đã cho nghịch biến trên khoảng nào dưới đây?
A.
;2 .
B.
2; .
C.
1;2 .
D.
1; .
.
Lời giải:
25
2
0 2 1 1 0 1
1
x
f x x x x x
x
Bảng xét dấu
fx

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Từ bảng xét dấu suy ra hàm số nghịch biến trên các khoảng
;1
và
2;
.
Câu 33: Chọn ngẫu nhiên
2
số khác nhau từ
30
số nguyên dương đầu tiên. Tính xác suất để chọn
được
2
số có tích là một số lẻ.
A.
7
29
. B.
15
29
. C.
22
29
. D.
8
29
.
Lời giải:
Không gian mẫu
2
30
435.C
Từ số
1
đến số
30
có
15
số lẻ và
15
số chẵn.
Để chọn được
2
số có tích là một số lẻ thì cả
2
số đó phải đều là số lẻ nên có
2
15
105C
số.
Vậy xác suất cần tìm là:
105 7
435 29
.
Câu 34: Biết phương trình
3
2log 2log 3 5
x
x
có hai nghiệm thực
12
xx
. Tính giá trị của biểu thức
2
12
61T x x
.
A.
12T
. B.
10T
. C.
16T
. D.
8T
.
Lời giải:
Điều kiện:
0
1
x
x
.
Ta có:
3
2log 2log 3 5
x
x
3
3
2
2log 5
log
x
x
2
33
2log 5log 2 0xx
3
3
log 2
1
log
2
x
x
9
3
x
x
(thỏa mãn).
1
3x
;
2
9x
2
12
6 1 6.3 9 1 10T x x
.
Câu 35: Cho số phức
z
thỏa mãn
3 2 3 2 16z i z i
. Biết tập hợp các điểm
M
biểu diễn số
phức
2 2 3w z i
là đường tròn tâm
;I a b
và bán kính
c
. Giá trị của
abc
bằng
A.
11
. B.
10
. C.
17
. D.
18
.
Lời giải:
Gọi:
w x yi
;xy
.
Ta có:
2 3 2 3
2 2 3
22
w i x yi i
w z i z
.
Theo gt:
3 2 3 2 16z i z i
2 3 2 3
3 2 3 2 16
22
x yi i x yi i
ii
2 3 6 4 2 3 6 4
16
22
x yi i i x yi i i
44
16
22
x yi i x yi i
4 1 4 1 64x y i x y i
22
4 1 64xy
.
Suy ra, tập hợp điểm biểu diễn của số phức
w
là đường tròn tâm
4; 1I
và bán kính
8c
.
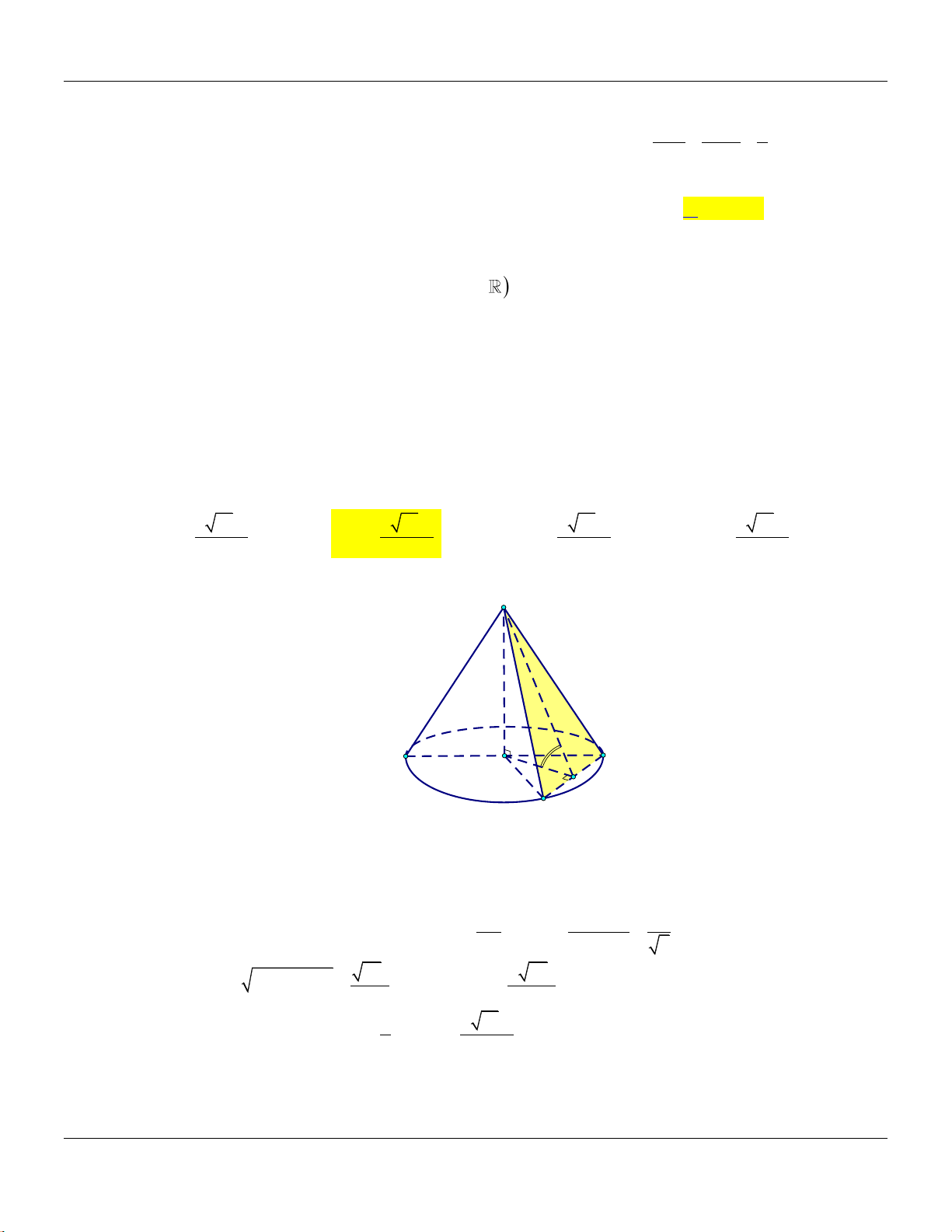
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
Vậy
11abc
.
Câu 36: Trong không gian với hệ trục tọa độ
Oxyz
, cho đường thẳng
12
:
2 1 3
x y z
d
và mặt phẳng
: 6 4 27 0P x y z
. Gọi
;;M a b c
là giao điểm của
d
và
P
. Tính
2S a b c
.
A.
10S
. B.
13S
. C.
11S
. D.
12S
.
Lời giải:
d
có phương trình tham số
12
2,
3
xt
y t t
zt
.
Ta có:
1 2 ; 2 ; 3M t t t d
.
1 2 6 2 4.3 27 0M P t t t
1t
.
Suy ra
3; 3;3M
nên
3, 3, 3a b c
.
Vậy
2 2.3 3 3 12S a b c
.
Câu 37: Cho hình nón
N
có chiều cao bằng
2,a
độ dài đường sinh bằng
3.a
Thiết diện qua đỉnh của
hình nón
N
tạo với mặt đáy hình nón một góc
60 .
Diện tích thiết diện là
A.
2
4 11
.
9
a
S
B.
2
4 11
.
3
a
S
C.
2
2 11
.
9
a
S
D.
2
2 11
.
3
a
S
Lời giải:
l
r
h
H
O
B
A
S
Gọi
O
là tâm đáy hình nón và thiết diện là tam giác
.SAB
Dựng
.OH AB AB SOH AB SH
Suy ra góc giữa thiết diện và đáy nón là
.SHO
Xét tam giác
SHO
vuông tại
4
: sin .
3
sin
SO SO a
O SHO SH
SH
SHO
Ta có:
22
33 2 33
2.
33
aa
AH SA SH AB AH
Vậy diện tích thiết diện là
2
1 4 11
..
23
a
S SH AB
Câu 38: Trong không gian
Oxyz
, cho điểm
1;2;1M
và mặt phẳng
( ): 6 0P x y z
. Giả sử
;;H a b c
là hình chiếu của
M
trên mặt phẳng
()P
. Khi đó
abc
bằng
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
A.
4
. B.
2
. C.
1
. D.
1
.
Lời giải:
Gọi d là đường thẳng qua
M
và vuông góc với
()P
.
Phương trình tham số của
1
: 2 ( )
1
xt
d y t t
zt
Khi đó,
()H d P
1 2 1 6 0 2t t t t
1;4; 1H
.
Câu 39: Cho hình chóp
SABCD
có đáy là hình vuông, cạnh
a
. Tam giác
SAB
là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Khoảng cách giữa 2 đường thẳng
AB
và
SC
bằng
A.
3
7
a
. B.
a
. C.
21
7
a
. D.
2
2
a
.
Lời giải:
M
I
A
B
D
C
S
H
Gọi
I
là trung điểm
AB
.
Ta có
SAB ABCD
SAB ABCD AB
SI ABCD
SI AB
SI SAB
Gọi
M
là trung điểm
CD
. Dựng
IH
là đường cao tam giác
SIM
.
Ta có
CD SI
CD SIM CD IH
CD IM
Do đó
;
IH SM
IH SCD d I SCD IH
IH CD
Suy ra
,,d AB SC d AB SCD
;d I SCD IH
2 2 2
2
3
.
. 21
2
7
3
4
a
a
SI IM a
SI IM a
a
.
Câu 40: Cho hình trụ
T
có bán kính đáy bằng
2.a
Thiết diện song song và cách trục của hình trụ
T
một khoảng bằng
a
là hình hình chữ nhật có diện tích bằng
2
6.a
Diện tích xung quanh
của hình trụ đã cho là
A.
2
3.
xq
Sa
B.
2
2 3 .
xq
Sa
C.
2
3 3 .
xq
Sa
D.
2
4 3 .
xq
Sa
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 16
Lời giải:
H
B'
B
r
l
h
A'
O'
O
A
Gọi
,OO
là tâm hai đáy của
.T
Thiết diện là tứ giác
.ABB A
Dựng
, ; .OH AB H AB OH ABB A d OO ABB A OH a
Xét tam giác
OHB
vuông tại
22
: 3 2 2 3 .H AH OA HA a AB AH a
Theo giả thiết:
22
6 . 6 3 .
ABB A
S a AA AB a AA a
Vậy diện tích xung quanh của hình trụ đã cho là
2
2 4 3 .
xq
S rl a
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 13_______________
Câu 1: Cho số phức
23zi
. Tính
.z
A.
13z
. B.
13z
. C.
7z
. D.
7z
.
Câu 2: Trên khoảng
0;
, đạo hàm của hàm số
ln2yx
là
A.
1
2
y
x
. B.
1
y
x
. C.
2
y
x
. D.
1
y
x
.
Câu 3: Tập xác định của hàm số
2
1yx
là
A.
1;
. B.
;1
. C.
1;
. D.
;1
.
Câu 4: Tập nghim của bt phương trnh
21
3 27
x
l
A.
;2
. B.
2;
. C.
2;
. D.
0;2
.
Câu 5: Cho cp số nhân
n
u
vi
1
3u
công bi
5q
. Tm
3
u
.
A.
15
. B.
45
. C.
75
. D.
75
.
Câu 6: Trong không gian
Oxyz
, mt phng
:2 3 5 0P x y z
c mt vctơ pháp tuyn c tọa đ
l
A.
2;1;3
. B.
2;1;3
. C.
2; 1; 3
. D.
2; 1;3
.
Câu 7: Tung đ giao điểm của đồ thị hàm số
2
1
x
y
x
vi trục tung là
A.
2y
. B.
2y
. C.
1y
. D.
1
2
y
.
Câu 8: Cho
2
1
d3f x x
và
2
1
d5g x x
. Tính
2
1
3d
I f x g x x
.
A.
10I
. B.
4I
. C.
4I
. D.
14I
.
Câu 9: Hàm số no dưi đây c đồ thị như đường cong trong hình vẽ bên dưi?
A.
42
2y x x
. B.
1
2
x
y
x
. C.
42
y x x
. D.
32
21y x x
.
Câu 10: Trong không gian
Oxyz
, cho mt cầu
2 2 2
: 2 4 2 3 0S x y z x y z
. Tính bán kính
R
của mt cầu
S
.
A.
3R
. B.
3R
. C.
9R
. D.
33R
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 11: Trong không gian
Oxyz
, cho hai mt phng
: 5 2 4 0P x y z
và
:2 9 0Q x y z
.
Gọi
là góc tạo bởi hai mt phng
, , cosPQ
là số nào?
A.
5
6
. B.
6
5
. C.
2
3
. D.
3
5
.
Câu 12: Cho số phức
2
1 1 2z i i
. Số phức
z
có phần ảo là
A.
2
. B.
2
. C.
4
. D.
2i
.
Câu 13: Khối hp chữ nhật c ba kích thưc lần lượt là
2 , ,3 .a a a
Thể tích của khối hp chữ nhật bằng
A.
3
6a
. B.
3
3a
. C.
3
5a
. D.
3
a
.
Câu 14: Cho hình chóp tam giác
.S ABC
c đáy
ABC
l tam giác đều cạnh
,a
cạnh bên
SA
vuông
góc vi mt đáy v
.SA a
Tính thể tích
V
của khối chóp
..S ABC
A.
3
2
3
Va
. B.
3
3
12
a
V
. C.
3
3
3
a
V
. D.
3
3
4
a
V
.
Câu 15: Trong không gian
,Oxyz
cho mt phng
: 2 2 24 0P x y z
và mt cầu
2 2 2
: 1 2 3 9.S x y z
Vị trí tương đối của
S
và
P
là
A.
P
đi qua tâm của
S
. B.
P
không cắt
S
.
C.
P
tip xúc vi
S
. D.
P
cắt
S
v không đi qua tâm của
S
.
Câu 16: Số phức có phần thực bằng
1
và phần ảo bằng
3
là
A.
13i
. B.
13i
. C.
13i
. D.
13i
.
Câu 17: Tính din tích xung quanh của hình trụ c bán kính đáy
a
v đường cao
3a
.
A.
2
3a
. B.
2
2 a
. C.
2
23a
. D.
2
a
.
Câu 18: Trong không gian
Oxyz
, điểm no dưi đây thuc đường thng
1
:5
23
xt
d y t
zt
?
A.
1;1;3Q
. B.
1;2;5P
. C.
1;5;2N
. D.
1;1;3M
.
Câu 19: Cho hàm số
32
y ax bx cx d
c đồ thị l đường cong trong hnh bên dưi:
Điểm cực đại của đồ thị hàm số đã cho c toạ đ là
A.
1; 1
. B.
1;1
. C.
1;3
. D.
3; 1
.
Câu 20: Đường tim cận ngang của đồ thị hàm số
21
2
x
y
x
l đường thng c phương trnh l
A.
1y
. B.
1y
. C.
1
2
y
. D.
2y
.
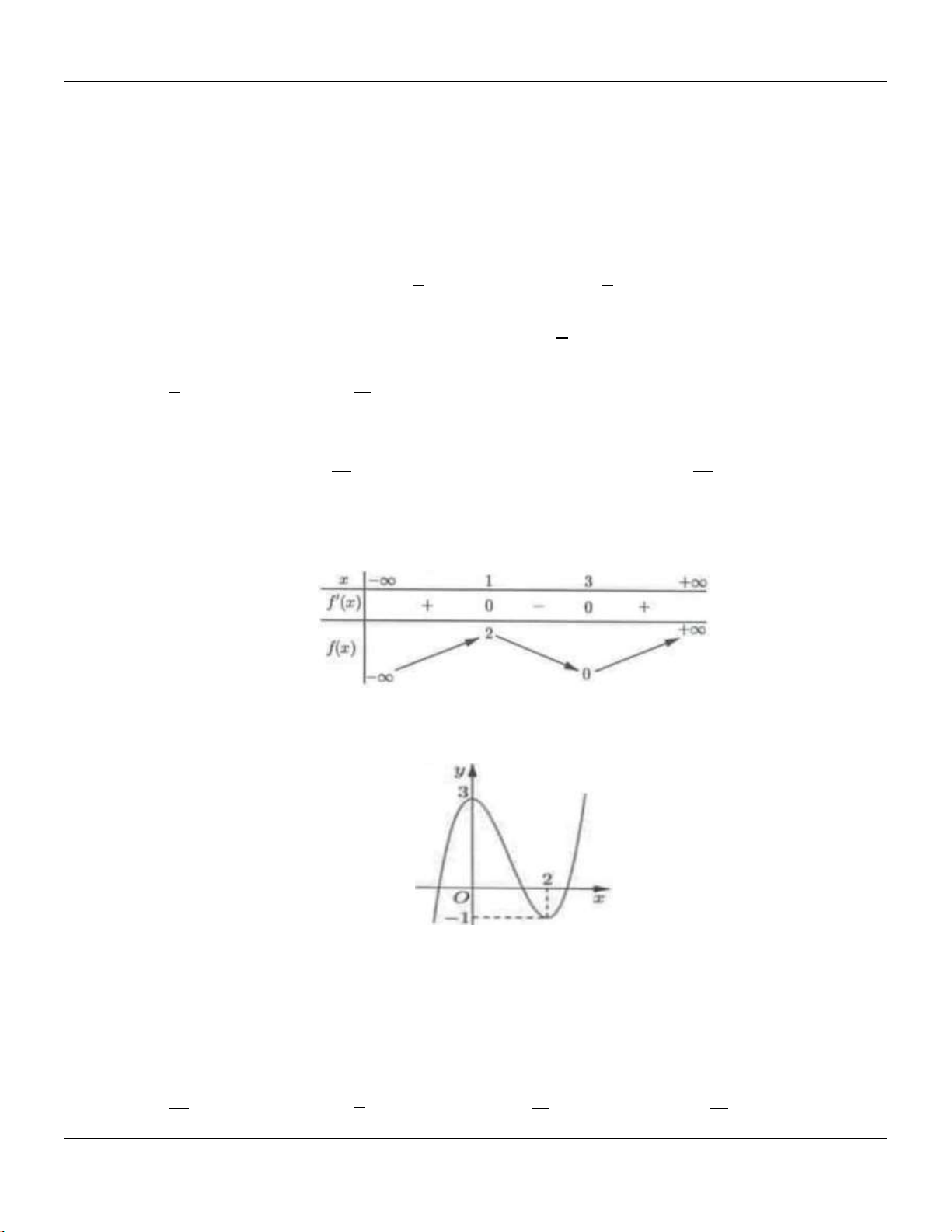
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
Câu 21: Tập nghim của bt phương trnh
2
33
2 2 0
xx
là
A.
1;2
. B.
1;2
. C.
2;1
. D.
1;2
.
Câu 22: Lp 12A1 có
19
học sinh nam và
23
học sinh nữ. Số cách chọn hai học sinh từ lp 12A1 tham
gia trực nhật sao cho có cả nam và nữ là
A.
437
. B.
42
. C.
247
. D.
1722
.
Câu 23: Cho
d 3sin2
Cf x x x
. Khng định no dưi đây đúng
A.
6cos2f x x
. B.
3
cos2
2
f x x
. C.
3
cos2
2
f x x
. D.
6cos2f x x
.
Câu 24: Cho
2
1
d4f x x
và
1
2
d3g x x
thì
1
2
3
2 6x d
2
f x g x x
bằng
A.
7
2
. B.
11
2
. C.
8
. D.
6
.
Câu 25: Cho hàm số
2
( ) tanf x x x
. Khng định no dưi đây đúng?
A.
2
( )d tan
2
x
f x x x x C
. B.
2
( )d tan
2
x
f x x x x C
.
C.
2
( )d tan
2
x
f x x x x C
. D.
2
( )d tan
2
x
f x x x x C
.
Câu 26: Cho hàm số
()y f x
có bảng biên thiên như sau:
Hàm số đã cho đồng bin trên khoảng no dưi đây?
A.
(0;2)
. B.
(6;9)
. C.
( ;3)
. D.
(1;3)
.
Câu 27: Cho hàm số bậc ba
()y f x
c đồ thị l đường cong trong hnh bên dưi:
Hàm số đạt cực tiểu tại điểm no dưi đây?
A. -1. B. 3. C. 2. D. 0.
Câu 28: Vi
b
là số thực dương tùy ý,
2
5
log
25
b
bằng
A.
5
2 log 1b
. B.
5
2 log 1b
. C.
5
2log 1b
. D.
5
log 2b
.
Câu 29: Tính din tích hình phng gii hạn bởi các đồ thị hàm số
2
yx
và
3yx
.
A.
45
2
. B.
9
2
. C.
81
10
. D.
81
10
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Câu 30: Cho hình chóp
.S ABCD
, đáy
ABCD
là hình vuông cạnh
a
và
SA ABCD
(minh họa như
hình vẽ bên).
Bit
6
3
a
SA
. Tính góc giữa
SC
và
ABC D
.
A.
45
. B.
75
. C.
30
. D.
60
.
Câu 31: Cho hàm số bậc ba
y f x
c đồ thị l đường cong trong hnh bên dưi:
Có bao nhiêu giá trị nguyên dương của tham số
m
để phương trnh
21f x m
có ba
nghim thực phân bit?
A.
2
. B.
0
. C.
3
. D.
4
.
Câu 32: Cho hàm số
y f x
c đạo hàm
2
4 2 , f x x x x
. Hàm số đã cho đồng bin trên
khoảng nào dưi đây?
A.
1;3
. B.
2;
. C.
1;
. D.
;2
.
Câu 33: Mt hp có
5
viên bi xanh,
6
viên bi đỏ và
7
viên bi vàng. Chọn ngẫu nhiên
5
viên bi trong
hp, tính xác sut để
5
viên bi được chọn c đủ màu và số bi đỏ bằng số bi vàng.
A.
313
408
. B.
95
408
. C.
5
102
. D.
25
136
.
Câu 34: Tích các nghim của phương trnh
2
lg lg 2 0xx
bằng
A.
100
. B.
2
. C.
2
. D.
10
.
Câu 35: Trên mt phng tọa đ, bit tập hợp điểm biểu diễn các số phức
z
thỏa mãn
2 3 1 2z i z i
l mt đường thng. Vc tơ pháp tuyn của đường thng đ l
A.
3;5n
. B.
1;5n
. C.
3;1n
. D.
1;1n
.
Câu 36: Trong không gian
Oxyz
, vit phương trnh tham số của đường thng
d
đi qua
4;2;1M
và
vuông gc vi mt phng
: 3 2 8 0.P x y z
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
A.
4
23
12
xt
yt
zt
. B.
14
32
2
xt
yt
zt
. C.
4
23
12
xt
yt
zt
. D.
4
23
18
xt
yt
zt
.
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2; 3M
. Gọi
1
M
,
2
M
,
3
M
lần lượt l điểm đối xứng
của M qua các mt phng
Oxy
,
Oxz
,
Oyz
. Vit phương trnh mt phng
1 2 3
M M M
.
A.
6 2 3 6 0x y z
. B.
6 2 3 6 0xyz
.
C.
6 3 2 6 0x y z
. D.
6 3 2 6 0x y z
.
Câu 38: Cho hình trụ
T
c bán kính đáy bằng
3.a
Thit din song song và cách trục của hình trụ
T
mt khoảng bằng
a
là hình vuông. Thể tích khối trụ đã cho l
A.
3
36 2 .Va
B.
3
12 2 .Va
C.
3
18 2 .Va
D.
3
6 2 .Va
Câu 39: Cho hnh chp tam giác đều
.S ABC
có cạnh đáy bằng
2a
và chiều cao bằng
3a
. Gọi
P
là
trung điểm của
SA
. Khoảng cách từ điểm
P
đn mt phng
SBC
bằng
A.
30
10
a
. B.
3 30
10
a
. C.
3 30
20
a
. D.
30
20
a
.
Câu 40: Cho hình nón
N
có chiều cao bằng
.a
Thit din qua đỉnh của hình nón
N
là tam giác
đều có din tích bằng
2
3.a
Khoảng cách từ tâm của đáy hnh nn
N
đn thit din là
A.
6
.
3
a
d
B.
2
.
3
a
d
C.
2
.
6
a
d
D.
2
.
2
a
d
________________________HẾT________________________

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Cho số phức
23zi
. Tính
.z
A.
13z
. B.
13z
. C.
7z
. D.
7z
.
Lời giải:
Ta có:
22
2 3 2 3 13z i z
.
Câu 2: Trên khoảng
0;
, đạo hàm của hàm số
ln2yx
là
A.
1
2
y
x
. B.
1
y
x
. C.
2
y
x
. D.
1
y
x
.
Lời giải:
Ta có:
2
21
ln2
22
x
y x y
x x x
.
Câu 3: Tập xác định của hàm số
2
1yx
là
A.
1;
. B.
;1
. C.
1;
. D.
;1
.
Lời giải:
Điều kin xác định của hàm số là:
1 0 1xx
.
Vậy tập xác định của hàm số là
1;
.
Câu 4: Tập nghim của bt phương trnh
21
3 27
x
l
A.
;2
. B.
2;
. C.
2;
. D.
0;2
.
Lời giải:
Ta có:
21
3 27
x
2 1 3
33
x
2 1 3x
2x
.
Câu 5: Cho cp số nhân
n
u
vi
1
3u
công bi
5q
. Tm
3
u
.
A.
15
. B.
45
. C.
75
. D.
75
.
Lời giải:
Ta có:
22
3 1.
3.5 75u u q
.
Câu 6: Trong không gian
Oxyz
, mt phng
:2 3 5 0P x y z
c mt vctơ pháp tuyn c tọa đ
l
A.
2;1;3
. B.
2;1;3
. C.
2; 1; 3
. D.
2; 1;3
.
Lời giải:
Vc tơ pháp tuyn của mt phng cần tìm là
2; 1;3n
.
Câu 7: Tung đ giao điểm của đồ thị hàm số
2
1
x
y
x
vi trục tung là
A.
2y
. B.
2y
. C.
1y
. D.
1
2
y
.
Lời giải:
Cho
02xy
.
Vậy tung đ giao điểm của đồ thị hàm số
2
1
x
y
x
vi trục tung là
2y
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
Câu 8: Cho
2
1
d3f x x
và
2
1
d5g x x
. Tính
2
1
3d
I f x g x x
.
A.
10I
. B.
4I
. C.
4I
. D.
14I
.
Lời giải:
Ta có
2 2 2
1 1 1
3 - d 3 d d 3.3 5 14I f x g x x f x x g x x
.
Câu 9: Hàm số no dưi đây c đồ thị như đường cong trong hình vẽ bên dưi?
A.
42
2y x x
. B.
1
2
x
y
x
. C.
42
y x x
. D.
32
21y x x
.
Lời giải:
Từ hình dạng đồ thị suy ra đây l đồ thị hàm bậc 4 trùng phương, do đ loại các phương án B
và D
Ta thy
lim
x
y
nên loại phương án C.
Câu 10: Trong không gian
Oxyz
, cho mt cầu
2 2 2
: 2 4 2 3 0S x y z x y z
. Tính bán kính
R
của mt cầu
S
.
A.
3R
. B.
3R
. C.
9R
. D.
33R
.
Lời giải:
2 2 2
: 2 4 2 3 0S x y z x y z
2 2 2
1 2 1 9x y z
.
Vậy bán kính của mt cầu
S
là
3R
.
Câu 11: Trong không gian
Oxyz
, cho hai mt phng
: 5 2 4 0P x y z
và
:2 9 0Q x y z
.
Gọi
là góc tạo bởi hai mt phng
, , cosPQ
là số nào?
A.
5
6
. B.
6
5
. C.
2
3
. D.
3
5
.
Lời giải:
P
Có VTPT là
1
1; 5; 2n
Q
Có VTPT là
2
2;1; 1n
12
1.2 5.1 1.2
5
cos cos ,
6
1 25 4. 4 1 1
nn
.
Câu 12: Cho số phức
2
1 1 2z i i
. Số phức
z
có phần ảo là

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
A.
2
. B.
2
. C.
4
. D.
2i
.
Lời giải:
Ta có:
2
22
1 1 2 1 2 1 2 2 1 2 2 4 4 2z i i i i i i i i i i
.
Suy ra số phức
z
có phần ảo là:
2
.
Câu 13: Khối hp chữ nhật c ba kích thưc lần lượt là
2 , ,3 .a a a
Thể tích của khối hp chữ nhật bằng
A.
3
6a
. B.
3
3a
. C.
3
5a
. D.
3
a
.
Lời giải:
Thể tích của khối hp chữ nhật c kích thưc
,,abc
là
.V abc
Thể tích của khối hp chữ nhật c kích thưc
2 , ,3a a a
là
3
2 . .3 6 .V a a a a
Câu 14: Cho hình chóp tam giác
.S ABC
c đáy
ABC
l tam giác đều cạnh
,a
cạnh bên
SA
vuông
góc vi mt đáy v
.SA a
Tính thể tích
V
của khối chóp
..S ABC
A.
3
2
3
Va
. B.
3
3
12
a
V
. C.
3
3
3
a
V
. D.
3
3
4
a
V
.
Lời giải:
Ta có: Hình chóp
.S ABC
c đáy l tam giác đều cạnh
a
nên
2
3
4
ABC
a
S
.
Thể tích hình chóp là:
23
.
1 1 3 3
.
3 3 4 12
S ABC ABC
aa
V SA S
Câu 15: Trong không gian
,Oxyz
cho mt phng
: 2 2 24 0P x y z
và mt cầu
2 2 2
: 1 2 3 9.S x y z
Vị trí tương đối của
S
và
P
là
A.
P
đi qua tâm của
S
. B.
P
không cắt
S
.
C.
P
tip xúc vi
S
. D.
P
cắt
S
v không đi qua tâm của
S
.
Lời giải:
Mt cầu
S
có tâm
1;2;3I
và bán kính
3.R
Khoảng cách từ tâm
1;2;3I
đn mt phng
P
là
2
22
1 2.2 2.3 24
,9
1 2 2
d I P R
Vậy
P
không cắt
S
.
Câu 16: Số phức có phần thực bằng
1
và phần ảo bằng
3
là
A.
13i
. B.
13i
. C.
13i
. D.
13i
.
Lời giải:
Số phức có phần thực bằng
1
và phần ảo bằng
3
là
13i
.
Câu 17: Tính din tích xung quanh của hình trụ c bán kính đáy
a
v đường cao
3a
.
A.
2
3a
. B.
2
2 a
. C.
2
23a
. D.
2
a
.
Lời giải:
Áp dụng công thức
2
2 2 . . 3 2 3
xq
S rl a a a
.
Câu 18: Trong không gian
Oxyz
, điểm no dưi đây thuc đường thng
1
:5
23
xt
d y t
zt
?

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
A.
1;1;3Q
. B.
1;2;5P
. C.
1;5;2N
. D.
1;1;3M
.
Lời giải:
Xt phương án
1;1;3Q
, vi
12xt
, thay vào
5 3 1y t y
. Do đ
Qd
.
Xt phương án
1;2;5P
, vi
10xt
, thay vào
5 5 2y t y P d
.
Xt phương án
1;5;2N
, vi
10xt
,thay vào
55y t y
, thay vào
2 3 2z t z N d
.
Xt phương án
1;1;3M
, vi
10xt
, thay vào
5 5 1y t y M d
.
Câu 19: Cho hàm số
32
y ax bx cx d
c đồ thị l đường cong trong hnh bên dưi:
Điểm cực đại của đồ thị hàm số đã cho c toạ đ là
A.
1; 1
. B.
1;1
. C.
1;3
. D.
3; 1
.
Lời giải:
Dựa vo đồ thị hàm số ta thy điểm cực đại của đồ thị hàm số là
1;3
.
Câu 20: Đường tim cận ngang của đồ thị hàm số
21
2
x
y
x
l đường thng c phương trnh là
A.
1y
. B.
1y
. C.
1
2
y
. D.
2y
.
Lời giải:
Ta có:
1
2
21
lim lim 2
2
2
1
xx
x
x
x
x
x
x
2y
l đường tim cận ngang của đồ thị hàm số.
Câu 21: Tập nghim của bt phương trnh
2
33
2 2 0
xx
là
A.
1;2
. B.
1;2
. C.
2;1
. D.
1;2
.
Lời giải:
Bt phương trnh tương đương:
2
3 3 1
22
xx
2
3 2 0xx
12x
Vậy tập nghim của bt phương trnh l
1;2S
.
Câu 22: Lp 12A1 có
19
học sinh nam và
23
học sinh nữ. Số cách chọn hai học sinh từ lp 12A1 tham
gia trực nhật sao cho có cả nam và nữ là
A.
437
. B.
42
. C.
247
. D.
1722
.
Lời giải:
Số cách chọn hai học sinh thoả mãn yêu cầu là:
19.23 437
.
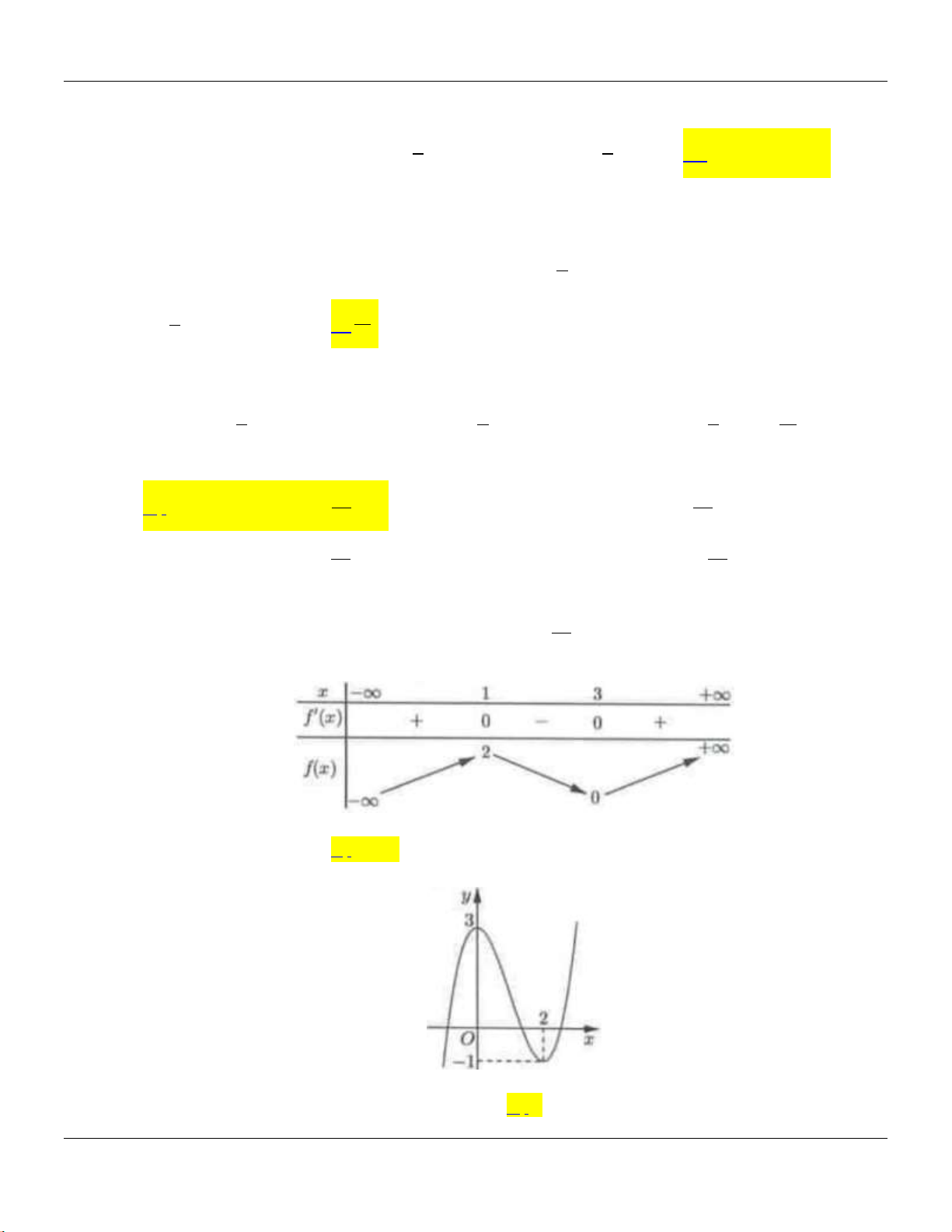
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Câu 23: Cho
d 3sin2
Cf x x x
. Khng định no dưi đây đúng
A.
6cos2f x x
. B.
3
cos2
2
f x x
. C.
3
cos2
2
f x x
. D.
6cos2f x x
.
Lời giải:
Ta có:
2 6cosd3 232 xf x x sin x six nf xC C
.
Câu 24: Cho
2
1
d4f x x
và
1
2
d3g x x
thì
1
2
3
2 6x d
2
f x g x x
bằng
A.
7
2
. B.
11
2
. C.
8
. D.
6
.
Lời giải:
Ta có:
1 1 1 1
2 2 2 2
3 3 3 11
2 6 d 2 d d - 6 d 2. 4 .3 9
2 2 2 2
f x g x x x f x x g x x x x
.
Câu 25: Cho hàm số
2
( ) tanf x x x
. Khng định no dưi đây đúng?
A.
2
( )d tan
2
x
f x x x x C
. B.
2
( )d tan
2
x
f x x x x C
.
C.
2
( )d tan
2
x
f x x x x C
. D.
2
( )d tan
2
x
f x x x x C
.
Lời giải:
Ta có:
2
2
( )d tan 1 1 d tan
2
x
f x x x x x x x C
.
Câu 26: Cho hàm số
()y f x
có bảng biên thiên như sau:
Hàm số đã cho đồng bin trên khoảng no dưi đây?
A.
(0;2)
. B.
(6;9)
. C.
( ;3)
. D.
(1;3)
.
Câu 27: Cho hàm số bậc ba
()y f x
c đồ thị l đường cong trong hnh bên dưi:
Hàm số đạt cực tiểu tại điểm no dưi đây?
A. -1. B. 3. C. 2. D. 0.
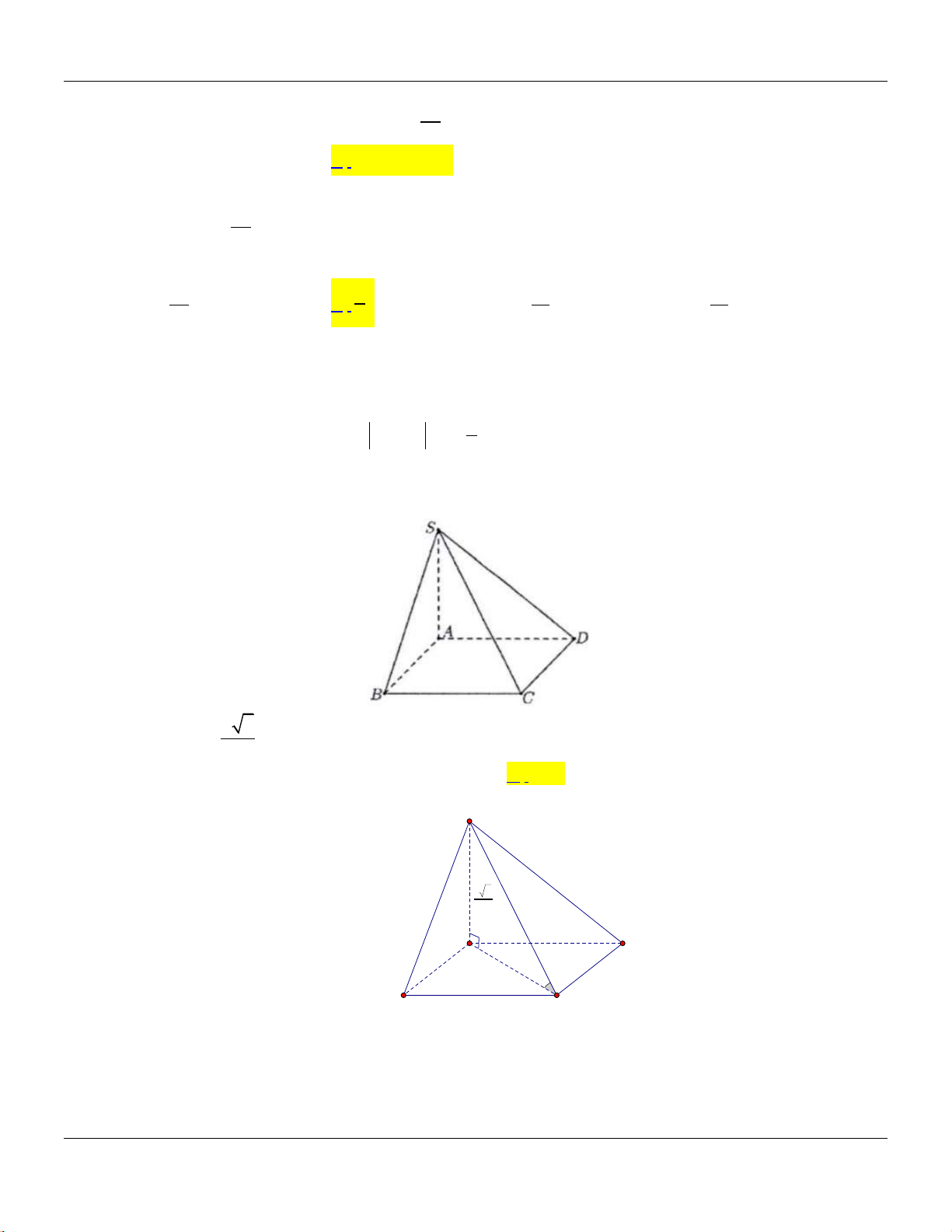
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Câu 28: Vi
b
là số thực dương tùy ý,
2
5
log
25
b
bằng
A.
5
2 log 1b
. B.
5
2 log 1b
. C.
5
2log 1b
. D.
5
log 2b
.
Lời giải:
Ta có:
2
2
5 5 5 5
log log log 25 2 log 1
25
b
bb
.
Câu 29: Tính din tích hình phng gii hạn bởi các đồ thị hàm số
2
yx
và
3yx
.
A.
45
2
. B.
9
2
. C.
81
10
. D.
81
10
.
Lời giải:
Xt phương trnh honh đ giao điểm :
22
0
3 3 0
3
x
x x x x
x
Din tích hình phng :
3
2
0
9
3d
2
S x x x
.
Câu 30: Cho hình chóp
.S ABCD
, đáy
ABCD
là hình vuông cạnh
a
và
SA ABCD
(minh họa như
hình vẽ bên).
Bit
6
3
a
SA
. Tính góc giữa
SC
và
ABC D
.
A.
45
. B.
75
. C.
30
. D.
60
.
Lời giải:
a
6
3
a
a
A
D
B
C
S
Ta có:
SA ABCD
.
Do đ
AC
là hình chiu của
SC
lên
ABC D
.
,SC ABCD
,SC AC
SCA
.
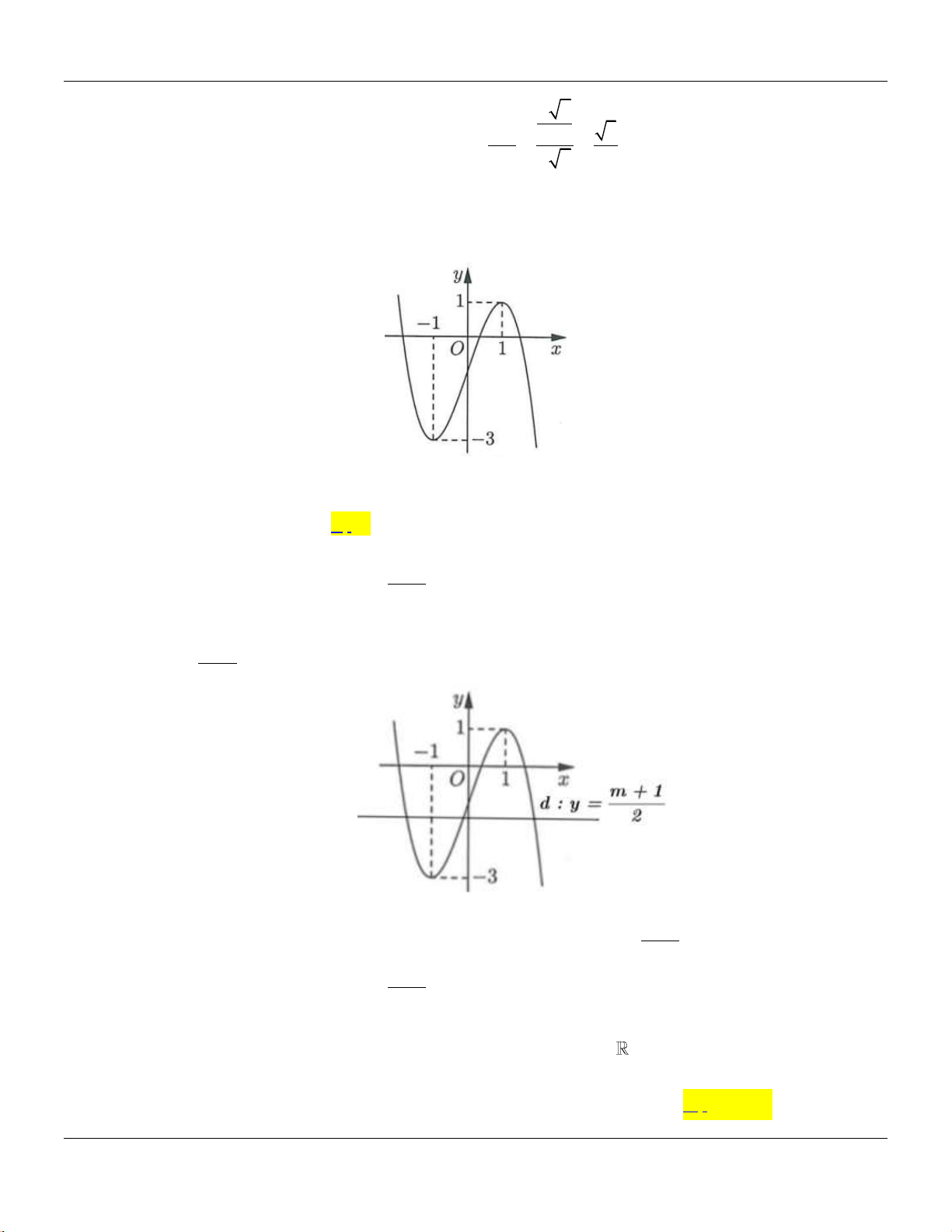
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
Xét tam giác
SAC
vuông tại
A
có
6
3
3
tan
3
2
a
SA
SCA
AC
a
.
30SCA
.
Vậy góc giữa
SC
và
ABC D
bằng
30
.
Câu 31: Cho hàm số bậc ba
y f x
c đồ thị l đường cong trong hnh bên dưi:
Có bao nhiêu giá trị nguyên dương của tham số
m
để phương trnh
21f x m
có ba
nghim thực phân bit?
A.
2
. B.
0
. C.
3
. D.
4
.
Lời giải:
Ta có:
1
21
2
m
f x m f x
1
Số nghim phương trnh
1
bằng số giao điểm của đồ thị
y f x
v đường thng
1
:
2
m
dy
Dựa vào hình vẽ, ta có:
Phương trnh
21f x m
có ba nghim đường thng
1
:
2
m
dy
cắt đồ thị
y f x
tại
ba điểm phân bit, tức là:
1
3 1 7 1
2
m
m
.
Mà
m
nguyên dương nên không c giá trị nào của
m
thỏa mãn.
Câu 32: Cho hàm số
y f x
c đạo hàm
2
4 2 , f x x x x
. Hàm số đã cho đồng bin trên
khoảng no dưi đây?
A.
1;3
. B.
2;
. C.
1;
. D.
;2
.
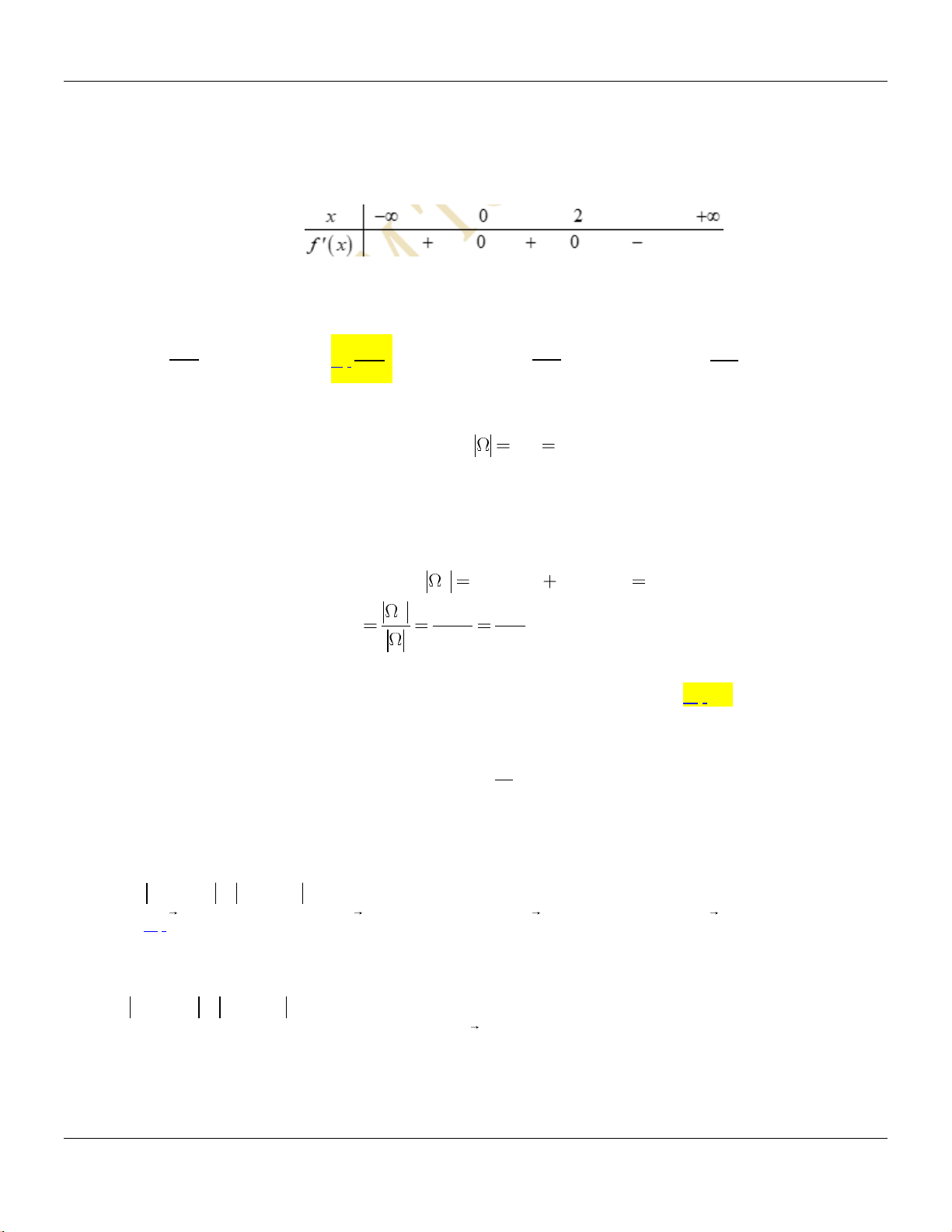
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Lời giải:
Ta có
2
0
0
2
42
0
0
x
x
fx
x
x
.
Bảng xét du
fx
Căn cứ vào bảng xét du của
fx
, hàm số đồng bin trên khoảng
;2
.
Câu 33: Mt hp có
5
viên bi xanh,
6
viên bi đỏ và
7
viên bi vàng. Chọn ngẫu nhiên
5
viên bi trong
hp, tính xác sut để
5
viên bi được chọn c đủ màu và số bi đỏ bằng số bi vàng.
A.
313
408
. B.
95
408
. C.
5
102
. D.
25
136
.
Lời giải:
Không gian mẫu là số cách chọn ngẫu nhiên
5
viên bi từ hp chứa
18
viên bi;
Suy ra số phần tử của không gian mẫu là
5
18
8568C
.
Gọi
A
là bin cố
''
5
viên bi được chọn c đủ màu và số bi đỏ bằng số bi vàng
''
.
Ta c các trường hợp thuận lợi cho bin cố
A
là:
● TH1: Chọn
1
bi đỏ,
1
bi vàng và
3
bi xanh nên có
1 1 3
6 7 5
..C C C
cách.
● TH2: Chọn
2
bi đỏ,
2
bi vàng và
1
bi xanh nên có
2 2 1
6 7 5
..CCC
cách.
Suy ra số phần tử của bin cố
A
là
1 1 3 2 2 1
6 7 5 6 7 5
. . . . 1995
A
C C C C C C
.
Vậy xác sut cần tính
1995 95
8568 408
A
PA
.
Câu 34: Tích các nghim của phương trình
2
lg lg 2 0xx
bằng
A.
100
. B.
2
. C.
2
. D.
10
.
Lời giải:
Điều kin:
0.x
Ta có:
2
1
lg 1
lg lg 2 0
10
lg 2
100
x
x
xx
x
x
Vậy tích các nghim là
10.
Câu 35: Trên mt phng tọa đ, bit tập hợp điểm biểu diễn các số phức
z
thỏa mãn
2 3 1 2z i z i
l mt đường thng. Vc tơ pháp tuyn của đường thng đ l
A.
3;5n
. B.
1;5n
. C.
3;1n
. D.
1;1n
.
Lời giải:
Gọi
z x yi
, khi đ
2 2 2 2
2 3 1 2 2 3 1 2 3 5 4 0z i z i x y x y x y
Vậy vc tơ pháp tuyn của đường thng l
3;5n
Câu 36: Trong không gian
Oxyz
, vit phương trnh tham số của đường thng
d
đi qua
4;2;1M
và
vuông gc vi mt phng
: 3 2 8 0.P x y z
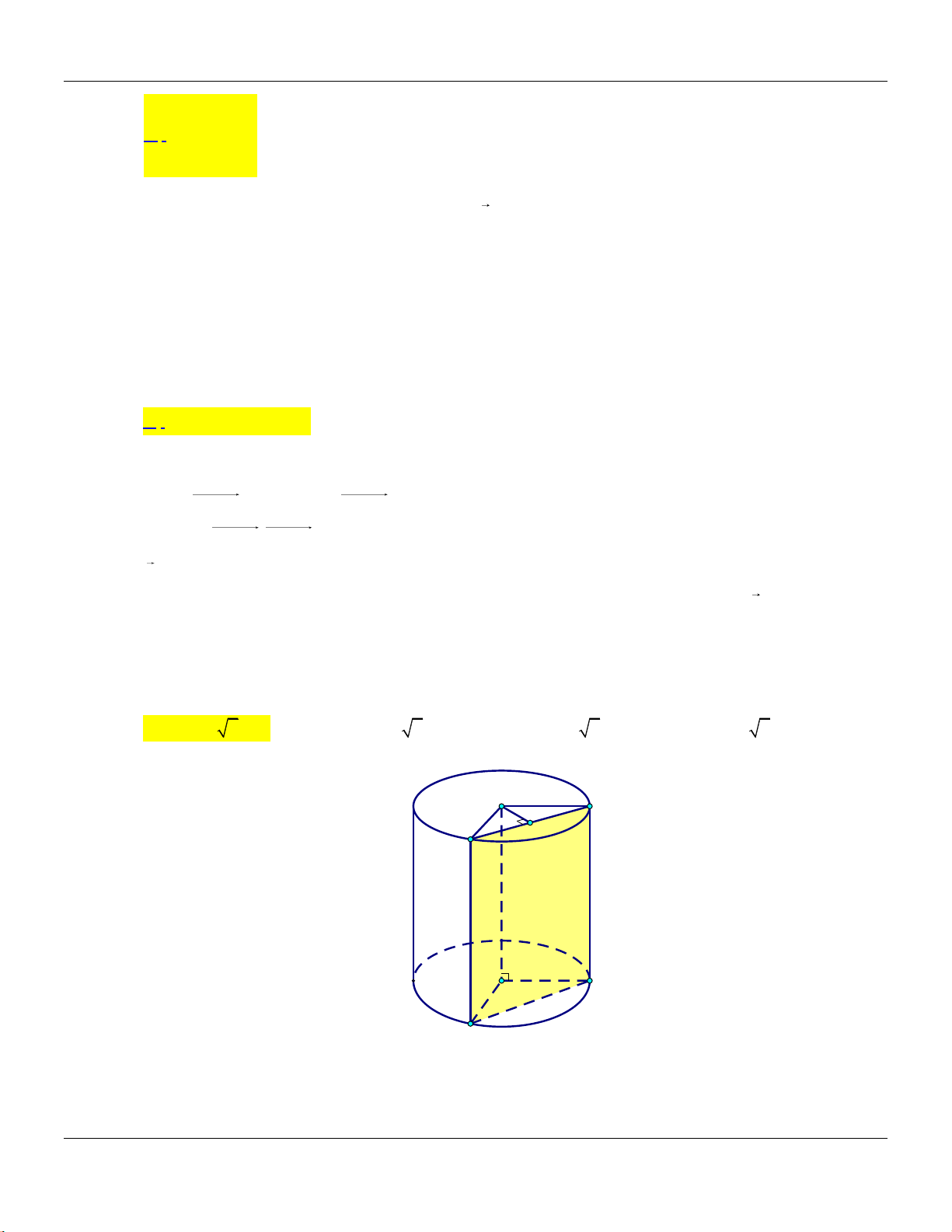
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
A.
4
23
12
xt
yt
zt
. B.
14
32
2
xt
yt
zt
. C.
4
23
12
xt
yt
zt
. D.
4
23
18
xt
yt
zt
.
Lời giải:
Vì
dP
nên
d
c vc tơ chỉ phương l
1;3; 2u
.
Phương trnh tham số của
d
là
4
23
12
xt
yt
zt
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2; 3M
. Gọi
1
M
,
2
M
,
3
M
lần lượt l điểm đối xứng
của M qua các mt phng
Oxy
,
Oxz
,
Oyz
. Vit phương trnh mt phng
1 2 3
M M M
.
A.
6 2 3 6 0x y z
. B.
6 2 3 6 0xyz
.
C.
6 3 2 6 0x y z
. D.
6 3 2 6 0x y z
.
Lời giải:
Tọa đ các điểm
1
M
,
2
M
,
3
M
lần lượt là
1
1;2;3M
,
2
1; 2; 3M
,
3
1;2; 3M
.
Ta có
12
0; 4; 6MM
,
13
2;0; 6MM
.
Khi đ
1 2 1 3
; 24; 12;8M M M M
. Do đ vectơ pháp tuyn của mt phng
1 2 3
M M M
là
6; 3;2n
.
Mt phng
1 2 3
M M M
đi qua điểm
1
1;2;3M
v c vectơ pháp tuyn là
6; 3;2n
có
phương trnh l
6 1 3 2 2 3 0x y z
hay
6 3 2 6 0x y z
.
Câu 38: Cho hình trụ
T
c bán kính đáy bằng
3.a
Thit din song song và cách trục của hình trụ
T
mt khoảng bằng
a
là hình vuông. Thể tích khối trụ đã cho l
A.
3
36 2 .Va
B.
3
12 2 .Va
C.
3
18 2 .Va
D.
3
6 2 .Va
Lời giải:
H
B'
B
r
l
h
A'
O'
O
A
Gọi
,OO
l tâm hai đáy của
.T
Thit din là tứ giác
.ABB A
Dựng
, ; .OH AB H AB OH ABB A d OO ABB A OH a
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
Xét tam giác
OHB
vuông tại
22
: 2 2 2 4 2 .H AH OA HA a AB AH a
Vậy thể tích của khối trụ đã cho l
23
36 2 .V h r a
Câu 39: Cho hnh chp tam giác đều
.S ABC
có cạnh đáy bằng
2a
và chiều cao bằng
3a
. Gọi
P
là
trung điểm của
SA
. Khoảng cách từ điểm
P
đn mt phng
SBC
bằng
A.
30
10
a
. B.
3 30
10
a
. C.
3 30
20
a
. D.
30
20
a
.
Lời giải:
Vì hình chóp
SABC
l chp đều nên
ABC
l tam giác đều cạnh
2a
và
SO ABCD
, vi
O
là trọng tâm tam giác
ABC
.
Gọi
M
l trung điểm cạnh
BC AM BC
,
BC SO BC SMA
,
K
là hình chiu của
O
trên
SM OK SM
và
OK SMA OK BC
. Do đ
OK SBC
tại
K
.
Suy ra
d,O SBC OK
.
Ta có
13
d , d , .3d ,
22 2
1
SBC SBCP A O SBC OK
.
Xét tam giác
ABC
đều cạnh
3
23
3
a
a AM a OM
.
Xét
SOM
vuông tại
O
, ta có
OK
l đường cao nên
2 2 2 2 2 2
1 1 1 9 1 10 30 3 3 30
,
32
d
3 3 10 2 0
aa
OK P SBC OK
OK OM OS a a a
.
Câu 40: Cho hình nón
N
có chiều cao bằng
.a
Thit din qua đỉnh của hình nón
N
là tam giác
đều có din tích bằng
2
3.a
Khoảng cách từ tâm của đáy hnh nn
N
đn thit din là
A.
6
.
3
a
d
B.
2
.
3
a
d
C.
2
.
6
a
d
D.
2
.
2
a
d
Lời giải:
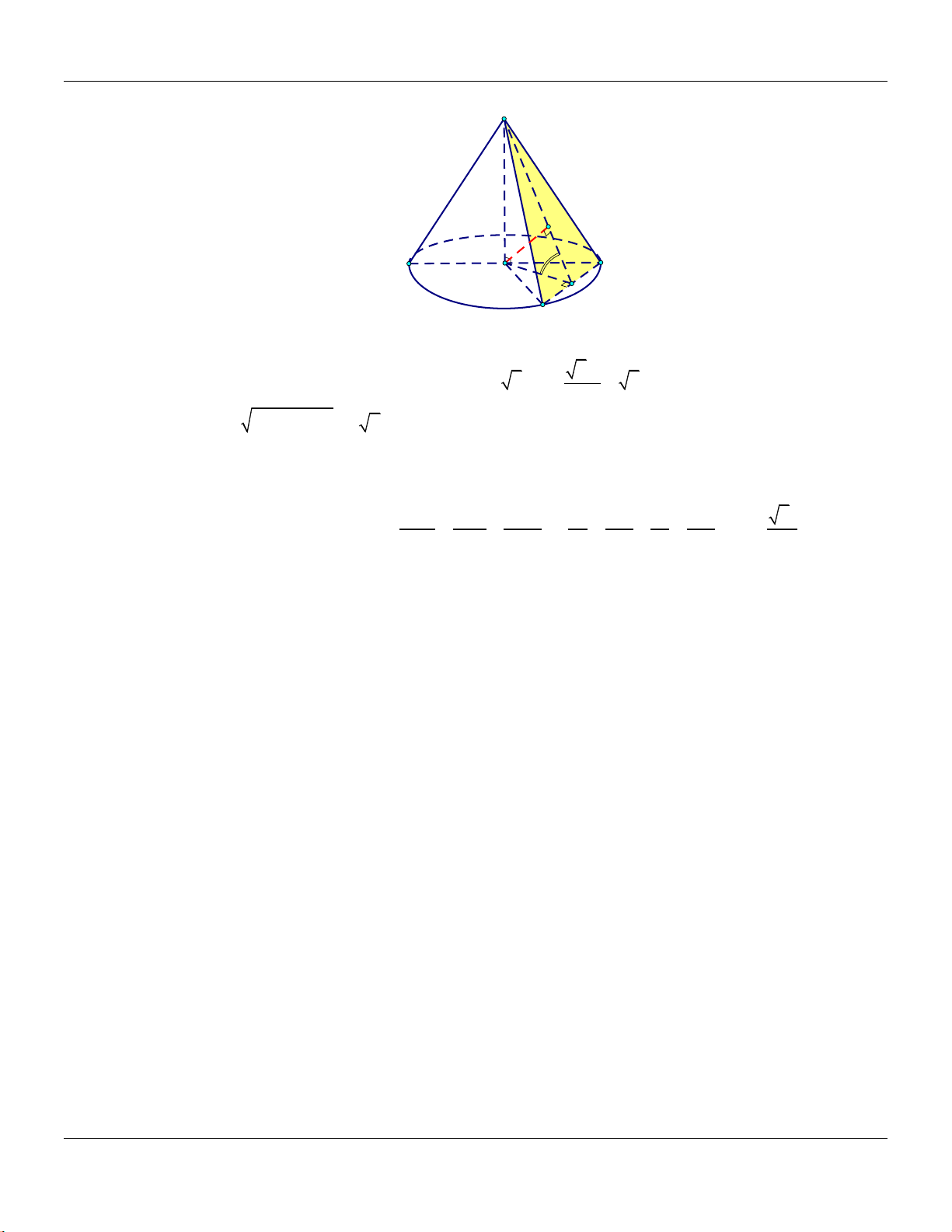
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 16
l
r
h
K
H
O
B
A
S
Gọi
O
l tâm đáy hnh nn v thit din là tam giác
.SAB
Ta có:
.SA SB AB l
Theo giả thit:
2
22
3
3 3 2 .
4
SAB
l
S a a l a
Ta có:
22
2.OH SH SO a
Dựng
.OH AB AB SOH SAB SOH
Dựng
,OK SH K SH OK SAB
hay
;.d O SAB OK d
Xét tam giác
SOH
vuông tại
2 2 2 2 2 2 2
1 1 1 1 1 1 3 6
:.
3
22
a
Od
OK OS OH d a a a
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 14_______________
Câu 1: Trên mt phng to đ
Oxy
, đim biu din ca s phc
23zi
c to đ l
A.
2; 3
. B.
3;2
. C.
3;2
. D.
3; 2
.
Câu 2: Trên khong
1;
, đo hm ca hm s
5
log 1yx
l
A.
ln5
'
1
y
x
. B.
1
'
1 ln5
y
x
. C.
1
'
1
y
x
. D.
' 1 ln5yx
.
Câu 3: Trên khong
0;
, đo hm ca hm s
3
yx
l
A.
31
'3yx
. B.
31
' 3 1yx
. C.
31
1
'
31
yx
. D.
31
1
'
31
yx
.
Câu 4: Tập nghiệm ca bất phương trình
log 1x
là
A.
;10
. B.
10;
. C.
0;10
. D.
0;
.
Câu 5: Cho cấp s nhân
n
u
với
3
9
2
u
và công bi
3q
. Giá trị
1
u
bằng
A.
1
3
2
u
. B.
1
1
2
u
. C.
1
81
2
u
. D.
1
2u
.
Câu 6: Trong không gian
Oxyz
, mt phng
Oxy
có mt vectơ pháp tuyến là
A.
1
1;0;0n
. B.
2
1;1;0n
. C.
3
0;1;0n
. D.
4
0;0;1n
.
Câu 7: Cho hàm s
23
x cx dy ax b
c đồ thị l đường cong trong hình bên dưới:
S nghiệm ca phương trình
1fx
là
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 8: Nếu
2
0
d3f x x
và
2
0
d1g x x
thì
2
0
df x g x x
bằng
A. 4. B. 2. C. 1. D.
2
.
Câu 9: Đồ thị ca hàm s no dưới đây c dng như đường cong trong hình bên?
A.
42
32y x x
. B.
3
1
x
y
x
. C.
2
41y x x
. D.
32
32y x x
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 10: Trong không gian
Oxyz
, cho mt cầu
2 2 2
: 4 2 6 0 S x y z x z
. Tâm ca
S
có to
đ là
A.
4; 2; 6
. B.
2;1; 3
. C.
4;0; 2
. D.
2;0;1
.
Câu 11: Trong không gian
Oxyz
, góc giữa mt phng
Oxy
và trục
Oz
bằng
A.
0
. B.
30
. C.
60
. D.
90
.
Câu 12: Cho s phc
34zi
. Tổng phần thực và phần o ca s phc
2
z
bằng
A.
31
. B.
1
. C.
17
. D.
7
.
Câu 13: Cho khi lăng trụ tam giác đều c đ di tất c các cnh bằng
5
. Th tích khi lăng trụ đã cho
bằng
A.
25 3
2
. B.
75 3
4
. C.
25 3
4
. D.
75 3
2
.
Câu 14: Cho hình chóp
.S ABCD
c đáy l hình vuông cnh
a
, cnh bên
SA
vuông gc với mt
phng đáy v
3SA a
. Th tích ca khi chp đã cho bằng
A.
3
3
6
a
. B.
3
3
4
a
. C.
3
3
3
a
. D.
3
3a
.
Câu 15: Cắt mt cầu
S
bằng mt mt phng cách tâm mt cầu mt khong bằng
6cm
ta được thiết
diện l mt đường tròn c bán kính bằng
8cm
. Bán kính ca mt cầu
S
là
A.
14cm
. B.
8cm
. C.
10cm
. D.
6cm
.
Câu 16: Trên mt phng tọa đ
Oxy
, cho
(3; 2)M
l đim biu din s phc
z
. Phần o ca
z
bằng
A.
2
. B.
3
. C.
3
. D.
2
.
Câu 17: Th tích V ca khi chóp có diện tích đáy l B và chiều cao là h được tính theo công thc nào
dưới đây?
A.
.V B h
. B.
.V B h
. C.
1
.
3
V B h
. D.
1
.
3
V B h
.
Câu 18: Trong không gian
Oxyz
, cho đường thng
d
c phương trình
1
2
3
xt
yt
zt
. Đim no sau đây
không thuc đường thng d ?
A.
(0;3; 4)N
. B.
(2;1; 2)P
. C.
(1;3; 2)M
. D.
(1;2; 3)Q
.
Câu 19: Cho hàm s
32
y ax bx cx d
c đồ thị l đường cong trong hình bên dưới:
Đim cực tiu ca đồ thị hàm s đã cho c tọa đ là
A.
1;2
. B.
1;2
. C.
1; 2
. D.
1; 2
.
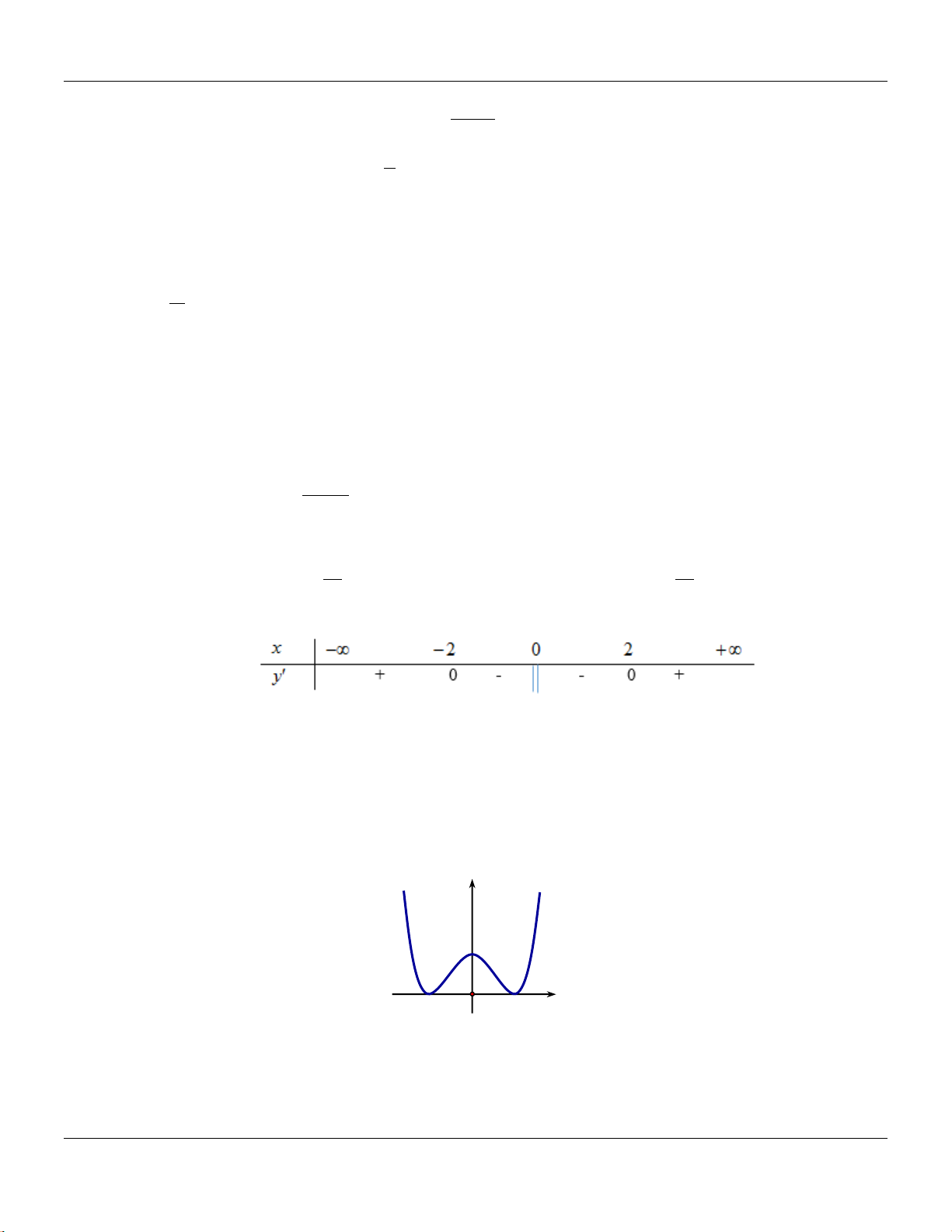
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
Câu 20: Tiệm cận ngang ca đồ thị hàm s
54
21
x
y
x
l đường thng c phương trình
A.
2y
. B.
5
2
y
. C.
2y
. D.
4y
.
Câu 21: Tập nghiệm ca bất phương trình
3
log 1 2x
là
A.
;10
. B.
0;10
. C.
1;9
. D.
1;10
.
Câu 22: S tập con có
3
phần tử ca mt tập hợp có
7
phần tử là
A.
7!
3!
. B.
3
7
C
. C.
3
7
A
. D.
21
.
Câu 23: Cho
cos dx x F x C
. Khng định no dưới đây đúng?
A.
sinF x x
. B.
sinF x x
. C.
cosF x x
. D.
2cosF x x
.
Câu 24: Cho
3
2
d5f x x
. Giá trị ca
3
2
2 3 df x x
bằng
A.
13
. B.
19
. C.
16
. D.
8
.
Câu 25: Cho hàm s
2
2
1
cos
f x x
x
. Khng định no dưới đây đúng?
A.
3
d tan .f x x x x C
B.
3
d tan .f x x x x C
C.
3
d tan .
3
x
f x x x C
D.
3
d tan .
3
x
f x x x C
Câu 26: Cho hàm s
()y f x
có bng xét dấu đo hm như sau:
Mệnh đề no dưới đây đúng?
A. Hàm s đồng biến trên khong
2;0
.
B. Hàm s nghịch biến trên khong
2;0
.
C. Hàm s nghịch biến trên khong
;0
.
D. Hàm s nghịch biến trên khong
;2
.
Câu 27: Cho hàm s
y f x
c đồ thị l đường cong như hình vẽ sau:
Đim cực đi ca hàm s đã cho l
A.
0x
. B.
2x
. C.
1x
. D.
1x
.
Câu 28: Với
a
là s thực dương tùy ý,
5
log 5a
bằng
A.
5
5log .a
B.
5
5 log . a
C.
5
1 log . a
D.
5
1 log . a
O
x
y
1
1
1
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Câu 29: Th tích khi tròn xoay khi quay hình phng
H
xác định bởi các đường
32
1
3
y x x
,
0y
,
0x
và
3x
quanh trục
Ox
là
A.
81
35
. B.
81
35
. C.
71
35
. D.
71
35
.
Câu 30: Cho khi chp đều
.S ABCD
có cnh đáy l
a
, các mt bên to với đáy mt góc
60
. Tính th
tích khi chp đ.
A.
3
3
2
a
. B.
3
3
12
a
. C.
3
3
6
a
. D.
3
3
3
a
.
Câu 31: Cho hàm s
y f x
c đồ thị như hình vẽ bên dưới:
x
y
1
-2
Tìm tất c các giá trị ca tham s
m
đ phương trình
f x m
c bn nghiệm thực phân
biệt.
A.
2m
. B.
21m
. C.
1m
. D.
1m
.
Câu 32: Cho hàm s
fx
có đo hàm
23
1 1 2 , .
f x x x x x
Hàm s
fx
đồng biến
trên khong no dưới đây?
A.
1;1
. B.
1;2
. C.
;1
. D.
2;
.
Câu 33: Mt hp đựng
9
tấm thẻ được đánh s từ
1
đến
9
. Mt bn rút ngẫu nhiên đồng thời
3
tấm
thẻ. Tính xác suất đ tổng
3
s ghi trên
3
thẻ được rút chia hết cho
3
.
A.
5
14
. B.
9
14
. C.
3
14
. D.
1
2
.
Câu 34: Tổng tất c các nghiệm ca phương trình
22
12
9 10.3 1 0
x x x x
bằng
A.
2
. B.
2
. C.
1
. D.
0
.
Câu 35: Trong mt phng tọa đ đim biu din s phc
z
thỏa mãn
1 2 3zi
là
A. đường tròn tâm
1;2I
, bán kính
9.R
B. đường tròn tâm
1;2I
, bán kính
3.R
C. đường tròn tâm
1; 2I
, bán kính
3.R
D. đường thng c phương trình
2 3 0xy
.
Câu 36: Trong không gian
Oxyz
, đường thng đi qua đim
3;1;2A
và vuông góc với mt phng
3 5 0x y z
c phương trình l
A.
3 1 2
.
1 1 3
x y z
B.
1 1 3
.
3 1 2
x y z
C.
1 1 3
.
3 1 2
x y z
D.
3 1 2
.
1 1 3
x y z

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 37: Trong không gian
Oxyz
, cho đim
3; 2; 5A
. Đim đi xng với đim
A
qua trục
Oy
có
tọa đ là:
A.
3;2;5
. B.
3; 2; 5
. C.
3; 2;5
. D.
3; 2;5
.
Câu 38: Cho hình trụ
T
có chiều cao bằng
4.a
Thiết diện song song và cách trục ca hình trụ
T
mt khong bằng
a
là hình vuông. Diện tích xung quanh hình trụ đã cho l
A.
2
4 5 .
xq
Sa
B.
2
8 5 .
xq
Sa
C.
2
6 5 .
xq
Sa
D.
2
6 5 .
xq
Sa
Câu 39: Cho hình chóp
.S ABCD
c đáy
ABCD
là hình chữ nhật,
2,AB a BC a
và
3SB a
. Biết
rằng tam giác
SAB
là tam giác cân ti
S
và nằm trong mt phng vuông góc với mt phng
ABCD
. Khong cách từ đim
A
đến mt phng
SCD
bằng
A.
22
3
a
. B.
6
3
a
. C.
26
3
a
. D.
2
3
a
.
Câu 40: Cho hình nón
N
có chiều cao bằng
,a
đ di đường sinh bằng
2.a
Gọi
O
là tâm hình tròn
đáy
.N
Thiết diện qua đỉnh ca hình nón
N
cắt đường tròn đáy ti hai đim
,AB
thỏa
mãn
60 .AOB
Diện tích thiết diện là
A.
2
3 39
.
4
a
S
B.
2
3 39
.
16
a
S
C.
2
39
.
16
a
S
D.
2
39
.
4
a
S
________________________HẾT________________________

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Trên mt phng to đ
Oxy
, đim biu din ca s phc
23zi
c to đ l
A.
2; 3
. B.
3;2
. C.
3;2
. D.
3; 2
.
Lời giải:
Ta có:
23zi
nên
3; 2ab
đim biu din ca
z
l
3;2M
.
Câu 2: Trên khong
1;
, đo hm ca hm s
5
log 1yx
l
A.
ln5
'
1
y
x
. B.
1
'
1 ln5
y
x
. C.
1
'
1
y
x
. D.
' 1 ln5yx
.
Lời giải:
Theo công thc đo hm ta c :
5
1
' log 1 '
1 ln5
yx
x
Câu 3: Trên khong
0;
, đo hm ca hm s
3
yx
l
A.
31
'3yx
. B.
31
' 3 1yx
. C.
31
1
'
31
yx
. D.
31
1
'
31
yx
.
Lời giải:
Theo công thc đo hm ta c :
3 3 1
' ' 3y x x
Câu 4: Tập nghiệm ca bất phương trình
log 1x
là
A.
;10
. B.
10;
. C.
0;10
. D.
0;
.
Lời giải:
Điều kiện
0x
.
Ta có
1
log 1 10 10x x x
(Thỏa mãn điều kiện)
Tập nghiệm ca bất phương trình l
10;
Câu 5: Cho cấp s nhân
n
u
với
3
9
2
u
và công bi
3q
. Giá trị
1
u
bằng
A.
1
3
2
u
. B.
1
1
2
u
. C.
1
81
2
u
. D.
1
2u
.
Lời giải:
Ta có
2
3
3 1 1
22
9
1
2
.
32
u
u u q u
q
.
Câu 6: Trong không gian
Oxyz
, mt phng
Oxy
có mt vectơ pháp tuyến là
A.
1
1;0;0n
. B.
2
1;1;0n
. C.
3
0;1;0n
. D.
4
0;0;1n
.
Lời giải:
Trong không gian
Oxyz
mt phng
Oxy
c phương trình
0z
. Do đ mt vectơ pháp
tuyến ca mt phng
Oxy
là
4
0;0;1n
.
Câu 7: Cho hàm s
23
x cx dy ax b
c đồ thị là đường cong trong hình bên dưới:
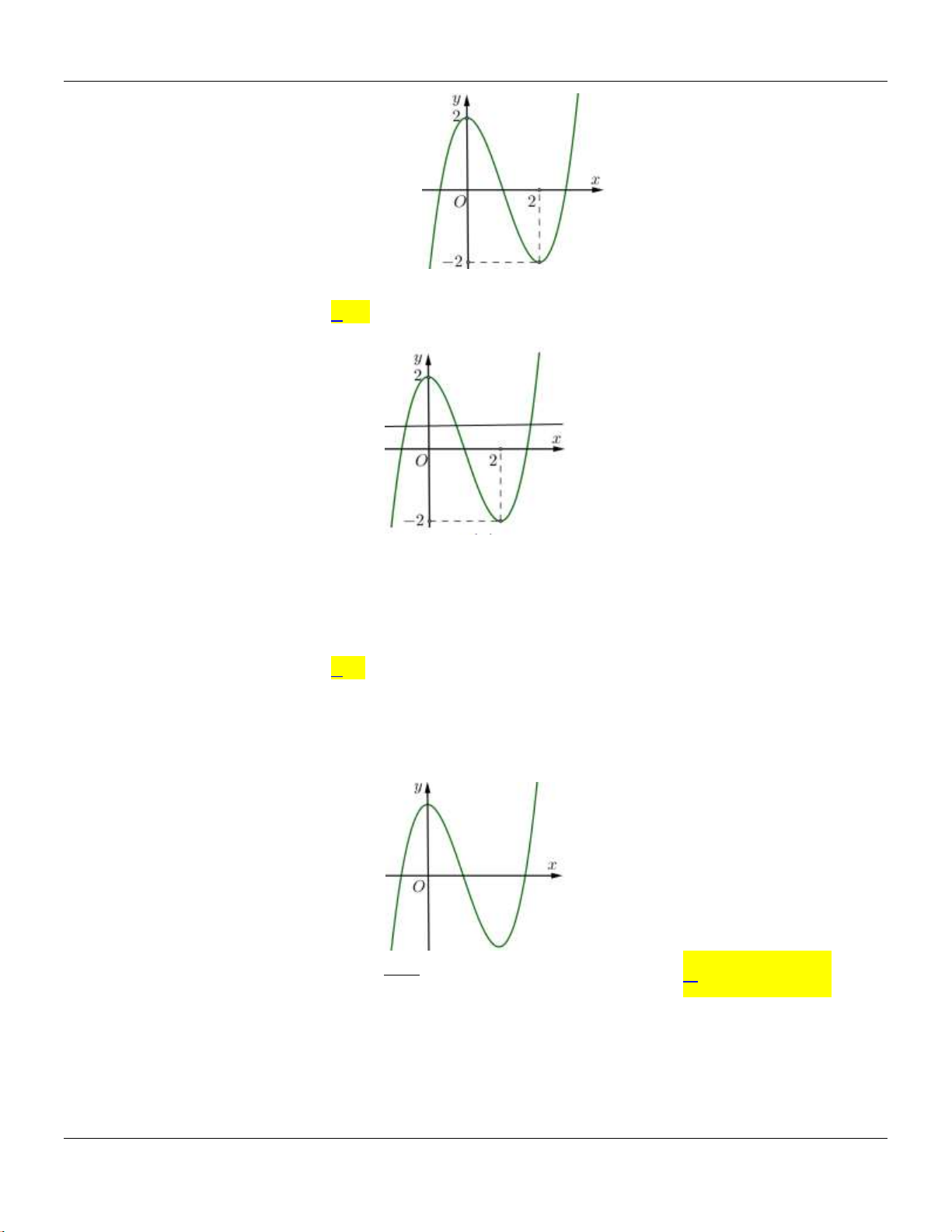
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
S nghiệm ca phương trình
1fx
là
A.
0
. B.
3
. C.
1
. D.
2
.
Lời giải:
Ta thầy đường thng
1y
cắt đồ thị hàm s
y f x
ti
3
đim phân biệt nên phương trình
1fx
có ba nghiệm phân biệt.
Câu 8: Nếu
2
0
d3f x x
và
2
0
d1g x x
thì
2
0
df x g x x
bằng
A. 4. B. 2. C. 1. D.
2
.
Lời giải:
Ta có
2 2 2
0 0 0
d d d 3 1 2f x g x x f x x g x x
.
Câu 9: Đồ thị ca hàm s no dưới đây c dng như đường cong trong hình bên?
A.
42
32y x x
. B.
3
1
x
y
x
. C.
2
41y x x
. D.
32
32y x x
.
Lời giải:
Đường cong có dng ca đồ thị hàm s bậc
3
với hệ s
0a
nên chỉ có hàm s
32
32y x x
thỏa yêu cầu bài toán.
Câu 10: Trong không gian
Oxyz
, cho mt cầu
2 2 2
: 4 2 6 0 S x y z x z
. Tâm ca
S
có to
đ là
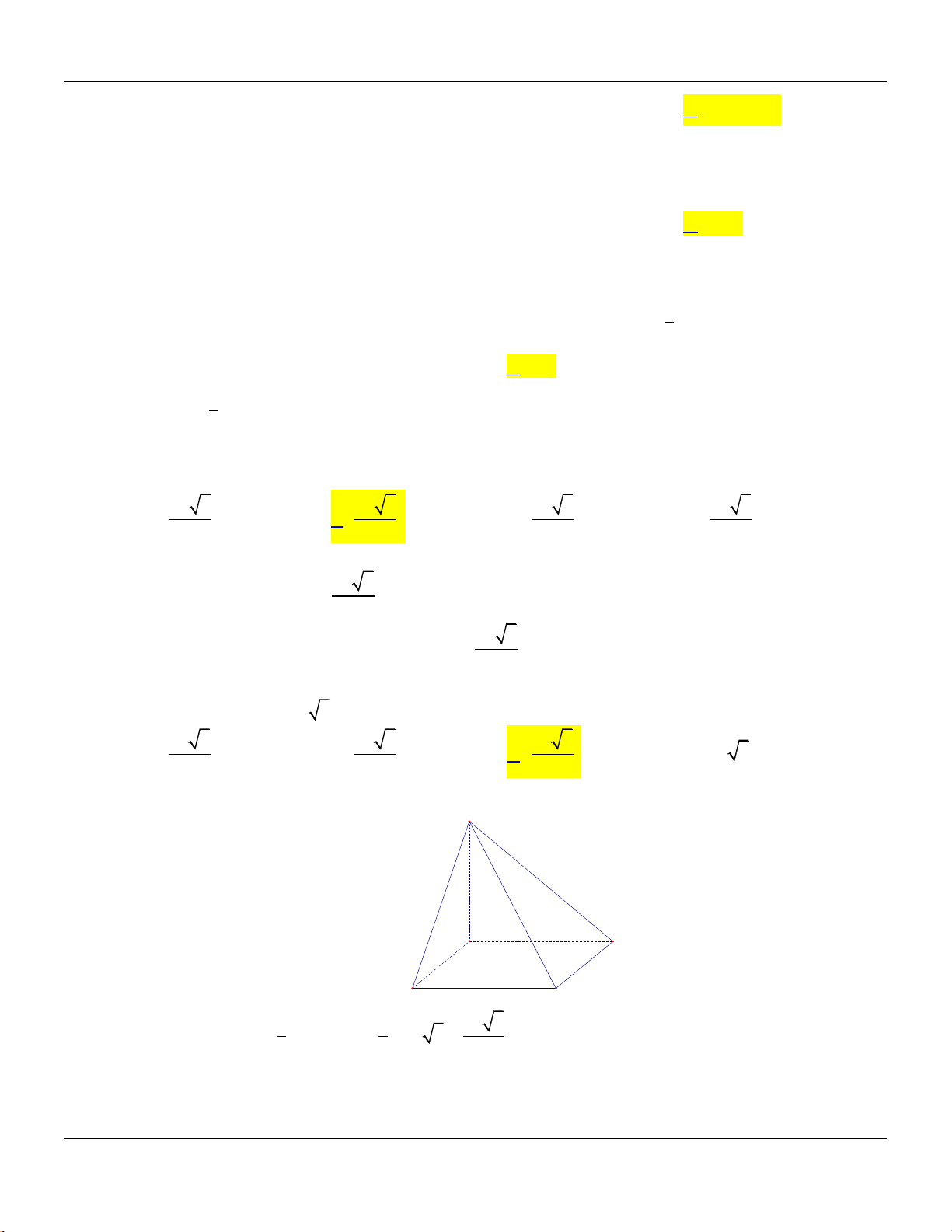
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
A.
4; 2; 6
. B.
2;1; 3
. C.
4;0; 2
. D.
2;0;1
.
Lời giải:
Ta có: Tâm ca
S
có to đ là
2;0;1
Câu 11: Trong không gian
Oxyz
, góc giữa mt phng
Oxy
và trục
Oz
bằng
A.
0
. B.
30
. C.
60
. D.
90
.
Lời giải:
Ta có: trục
Oz
vuông góc với mt phng
Oxy
nên góc giữa mt phng
Oxy
và trục
Oz
bằng
90
.
Câu 12: Cho s phc
34zi
. Tổng phần thực và phần o ca s phc
2
z
bằng
A.
31
. B.
1
. C.
17
. D.
7
.
Lời giải:
Ta có:
2
2
3 4 7 24 z i i
. Do đ,
7 24 17
.
Câu 13: Cho khi lăng trụ tam giác đều c đ di tất c các cnh bằng
5
. Th tích khi lăng trụ đã cho
bằng
A.
25 3
2
. B.
75 3
4
. C.
25 3
4
. D.
75 3
2
.
Lời giải:
Ta c diện tích đáy
25 3
4
B
v chiều cao
5h
.
Vậy th tích ca khi lăng trụ l
75 3
4
V Bh
.
Câu 14: Cho hình chóp
.S ABCD
c đáy l hình vuông cnh
a
, cnh bên
SA
vuông gc với mt
phng đáy v
3SA a
. Th tích ca khi chp đã cho bằng
A.
3
3
6
a
. B.
3
3
4
a
. C.
3
3
3
a
. D.
3
3a
.
Lời giải:
A
B
D
C
S
Ta có
3
2
.
1 1 3
. . 3
333
S ABCD ABCD
a
V S SA a a
.
Câu 15: Cắt mt cầu
S
bằng mt mt phng cách tâm mt cầu mt khong bằng
6cm
ta được thiết
diện l mt đường tròn c bán kính bằng
8cm
. Bán kính ca mt cầu
S
là

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
A.
14cm
. B.
8cm
. C.
10cm
. D.
6cm
.
Lời giải:
P
R
A
I
H
Bán kính mt cầu
2 2 2 2
6 8 10 .R IH AH cm
Câu 16: Trên mt phng tọa đ
Oxy
, cho
(3; 2)M
l đim biu din s phc
z
. Phần o ca
z
bằng
A.
2
. B.
3
. C.
3
. D.
2
.
Lời giải:
Ta có
(3; 2)M
l đim biu din s phc
32zi
. Vậy phần o ca
z
bằng
2
.
Câu 17: Th tích V ca khi chóp có diện tích đáy l B và chiều cao là h được tính theo công thc nào
dưới đây?
A.
.V B h
. B.
.V B h
. C.
1
.
3
V B h
. D.
1
.
3
V B h
.
Lời giải:
Ta có:
1
.
3
V B h
.
Câu 18: Trong không gian
Oxyz
, cho đường thng
d
c phương trình
1
2
3
xt
yt
zt
. Đim no sau đây
không thuc đường thng d ?
A.
(0;3; 4)N
. B.
(2;1; 2)P
. C.
(1;3; 2)M
. D.
(1;2; 3)Q
.
Lời giải:
Thay đim
(1;3; 2)M
đường thng d ta có :
1 1 0
3 2 1
2 3 1
tt
tt
tt
. Vì các giá trị t khác nhau
nên đim
(1;3; 2)M
không thuc đường thng d.
Câu 19: Cho hàm s
32
y ax bx cx d
c đồ thị l đường cong trong hình bên dưới:

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Đim cực tiu ca đồ thị hàm s đã cho c tọa đ là
A.
1;2
. B.
1;2
. C.
1; 2
. D.
1; 2
.
Câu 20: Tiệm cận ngang ca đồ thị hàm s
54
21
x
y
x
l đường thng c phương trình
A.
2y
. B.
5
2
y
. C.
2y
. D.
4y
.
Câu 21: Tập nghiệm ca bất phương trình
3
log 1 2x
là
A.
;10
. B.
0;10
. C.
1;9
. D.
1;10
.
Câu 22: S tập con có
3
phần tử ca mt tập hợp có
7
phần tử là
A.
7!
3!
. B.
3
7
C
. C.
3
7
A
. D.
21
.
Lời giải:
Ta có s tập con có
3
phần tử ca mt tập hợp có
7
phần tử là
3
7
C
.
Câu 23: Cho
cos dx x F x C
. Khng định no dưới đây đúng?
A.
sinF x x
. B.
sinF x x
. C.
cosF x x
. D.
2cosF x x
.
Lời giải:
Theo gi thiết
cos dx x F x C
nên
cosF x C x
cosF x x
.
Câu 24: Cho
3
2
d5f x x
. Giá trị ca
3
2
2 3 df x x
bằng
A.
13
. B.
19
. C.
16
. D.
8
.
Lời giải:
Ta có:
3 3 3
3
2
2 2 2
2 3 2 3 2.5 3 10 9 6 13f x dx f x dx dx x
.
Câu 25: Cho hàm s
2
2
1
cos
f x x
x
. Khng định no dưới đây đúng?
A.
3
d tan .f x x x x C
B.
3
d tan .f x x x x C
C.
3
d tan .
3
x
f x x x C
D.
3
d tan .
3
x
f x x x C
Lời giải:
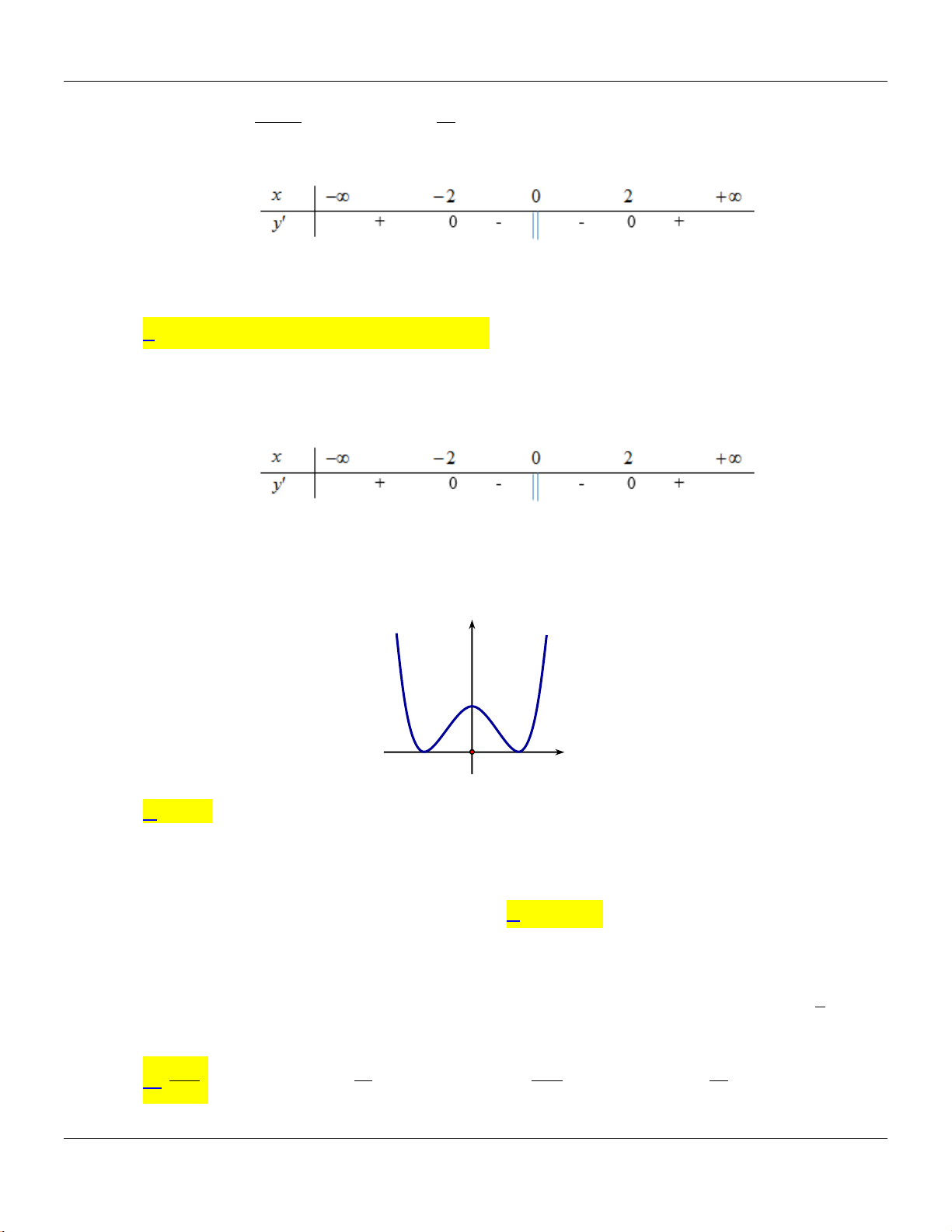
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
2
2
3
1
d d tan .
cos 3
x
f x x x x x C
x
Câu 26: Cho hàm s
()y f x
có bng xét dấu đo hm như sau:
Mệnh đề no dưới đây đúng?
A. Hàm s đồng biến trên khong
2;0
.
B. Hàm s nghịch biến trên khong
2;0
.
C. Hàm s nghịch biến trên khong
;0
.
D. Hàm s nghịch biến trên khong
;2
.
Lời giải:
Nhìn vào bng xét dấu đo hàm ta thấy
0y
trên khong
2;0
, nên hàm s nghịch biến
trên khong
2;0
.
Câu 27: Cho hàm s
y f x
c đồ thị l đường cong như hình vẽ sau:
Đim cực đi ca hàm s đã cho l
A.
0x
. B.
2x
. C.
1x
. D.
1x
.
Lời giải:
Căn c đồ thị ta c đim cực đi ca hàm s là
0x
.
Câu 28: Với
a
là s thực dương tùy ý,
5
log 5a
bằng
A.
5
5log .a
B.
5
5 log . a
C.
5
1 log . a
D.
5
1 log . a
Lời giải:
5 5 5 5
log 5 log 5 log 1 log a a a
Câu 29: Th tích khi tròn xoay khi quay hình phng
H
xác định bởi các đường
32
1
3
y x x
,
0y
,
0x
và
3x
quanh trục
Ox
là
A.
81
35
. B.
81
35
. C.
71
35
. D.
71
35
.
Lời giải:
O
x
y
1
1
1
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
Th tích khi tròn xoay sinh ra khi quay hình phng
H
quanh trục
Ox
là :
2
33
3 2 6 5 4
00
1 1 2 81
dd
3 9 3 35
V x x x x x x x
.
Vậy th tích khi tròn xoay cần tính là :
81
35
V
.
Câu 30: Cho khi chp đều
.S ABCD
có cnh đáy l
a
, các mt bên to với đáy mt góc
60
. Tính th
tích khi chp đ.
A.
3
3
2
a
. B.
3
3
12
a
. C.
3
3
6
a
. D.
3
3
3
a
.
Lời giải:
Gọi
M
l trung đim
BC
, Góc giữa mt bên
SBC
và mt phng
ABC D
là góc
60SMO
.
Xét
SOM
có
2
a
OM
,
60SMO
thì
3
.tan . 3
22
aa
SO OM SMO
Nên
3
.
13
..
36
S ABCD ABCD
a
V SO S
(đvtt). Đáp án được chọn là C.
Câu 31: Cho hàm s
y f x
c đồ thị như hình vẽ bên dưới:
x
y
1
-2
Tìm tất c các giá trị ca tham s
m
đ phương trình
f x m
c bn nghiệm thực phân
biệt.
A.
2m
. B.
21m
. C.
1m
. D.
1m
.
Lời giải:
S nghiệm ca phương trình
f x m
bằng s giao đim ca đồ thị
y f x
v đường
thng
ym
.
Khi đ, phương trình
y f x
c bn nghiệm thực phân biệt
21m
.
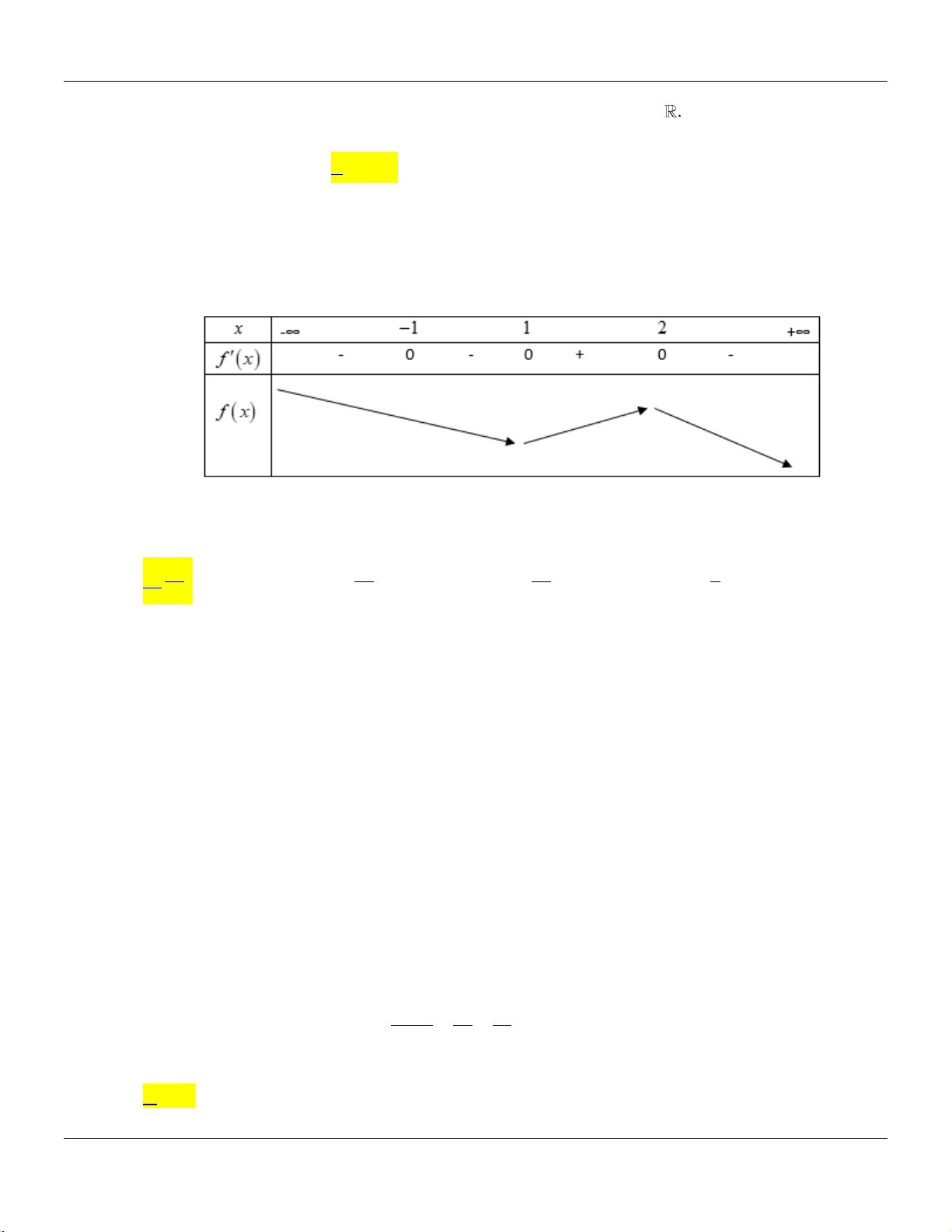
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Câu 32: Cho hàm s
fx
c đo hàm
23
1 1 2 , .
f x x x x x
Hàm s
fx
đồng biến
trên khong no dưới đây?
A.
1;1
. B.
1;2
. C.
;1
. D.
2;
.
Lời giải:
1
01
2
x
f x x
x
.
BBT:
Dựa vào BBT ta thấy: Hàm s
fx
đồng biến trên khong
1;2 .
Câu 33: Mt hp đựng
9
tấm thẻ được đánh s từ
1
đến
9
. Mt bn rút ngẫu nhiên đồng thời
3
tấm
thẻ. Tính xác suất đ tổng
3
s ghi trên
3
thẻ được rút chia hết cho
3
.
A.
5
14
. B.
9
14
. C.
3
14
. D.
1
2
.
Lời giải:
+ Xét phép thử “Rút ngẫu nhiên đồng thời
3
tấm thẻ trong mt hp đựng
9
tấm thẻ”
3
9
84nC
.
+ Gọi
A
là biến c “Rút được
3
tấm thẻ có tổng
3
s ghi trên
3
thẻ là s chia hết cho
3
”.
Trong
9
tấm thẻ được đánh s từ
1
đến
9
có:
3
tấm thẻ ghi s chia cho 3 dư 1 (l 1; 4; 7);
3
tấm thẻ ghi s chia cho 3 dư 2 (l 2; 5; 8);
3
tấm thẻ ghi s chia hết cho 3 (là 3; 6; 9).
Ta c các trường hợp sau đ rút được
3
thẻ có tổng
3
s ghi trên
3
thẻ là s chia hết cho
3
:
TH 1: Lấy được 3 thẻ ghi s chia hết cho 3, có
3
3
1C
cách.
TH 2: Lấy được 3 thẻ ghi s chia cho 3 dư 1, c
3
3
1C
cách.
TH 3: Lấy được 3 thẻ ghi s chia cho 3 dư 2, c
3
3
1C
cách.
TH 4: Lấy được 3 thẻ trong đ c 1 thẻ ghi s chia cho 3 dư 1, 1 thẻ ghi s chia cho 3 dư 2, 1
thẻ ghi s chia hết cho 3, có
111
333
. . 27CCC
cách.
1 1 1 27 30nA
Vậy xác suất cần tìm là
30 5
.
84 14
nA
PA
n
Câu 34: Tổng tất c các nghiệm ca phương trình
22
12
9 10.3 1 0
x x x x
bằng
A.
2
. B.
2
. C.
1
. D.
0
.
Lời giải:

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
Đt
2
1
3 0 ,
xx
tt
khi đ phương trình đã cho tương đương với
2
2
1
2
1
2
3
33
1
3 10 3 0
1
1
0
3
3
3
1
xx
xx
x
t
x
tt
x
t
x
.
Vậy tổng tất c các nghiệm ca phương trình bằng
2
.
Câu 35: Trong mt phng tọa đ đim biu din s phc
z
thỏa mãn
1 2 3zi
là
A. đường tròn tâm
1;2I
, bán kính
9.R
B. đường tròn tâm
1;2I
, bán kính
3.R
C. đường tròn tâm
1; 2I
, bán kính
3.R
D. đường thng c phương trình
2 3 0xy
.
Lời giải:
Gi sử
;M x y
l đim biu din s phc
z
.
Ta có:
22
1 2 3 ( 1) ( 2)i 3 ( 1) ( 2) 9z i x y x y
.
Vậy đim
;M x y
thuc đường tròn
22
( 1) ( 2) 9xy
có tâm
1;2I
và bán kính
3R
.
Câu 36: Trong không gian
Oxyz
, đường thng đi qua đim
3;1;2A
và vuông góc với mt phng
3 5 0x y z
c phương trình l
A.
3 1 2
.
1 1 3
x y z
B.
1 1 3
.
3 1 2
x y z
C.
1 1 3
.
3 1 2
x y z
D.
3 1 2
.
1 1 3
x y z
Lời giải:
Vì đường thng vuông góc với mt phng
3 5 0x y z
nên đường thng sẽ có mt vectơ
chỉ phương l
1;1;3u
.
Vậy phương trình đường thng cần tìm là
3 1 2
.
1 1 3
x y z
Câu 37: Trong không gian
Oxyz
, cho đim
3; 2; 5A
. Đim đi xng với đim
A
qua trục
Oy
có
tọa đ là:
A.
3;2;5
. B.
3; 2; 5
. C.
3; 2;5
. D.
3; 2;5
.
Lời giải:
Tọa đ hình chiếu ca đim
3; 2; 5A
trên trục
Oy
là
0; 2;0
. Đim đi xng với
A
qua trục
Oy
có tọa đ là
3; 2;5
.
Câu 38: Cho hình trụ
T
có chiều cao bằng
4.a
Thiết diện song song và cách trục ca hình trụ
T
mt khong bằng
a
là hình vuông. Diện tích xung quanh hình trụ đã cho l
A.
2
4 5 .
xq
Sa
B.
2
8 5 .
xq
Sa
C.
2
6 5 .
xq
Sa
D.
2
6 5 .
xq
Sa
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
H
B'
B
r
l
h
A'
O'
O
A
Gọi
,OO
l tâm hai đáy ca
.T
Thiết diện là t giác
.ABB A
Dựng
, ; .OH AB H AB OH ABB A d OO ABB A OH a
Theo gi thiết
ABB A
là hình vuông cnh bằng
4 4 .a AB AA a
Xét tam giác
OHB
vuông ti
22
: 5.H OB OH HB a
Vậy diện tích xung quanh ca hình trụ đã cho l
2
2 2 . 8 5 .
xq
S rl OB AA a
Câu 39: Cho hình chóp
.S ABCD
c đáy
ABCD
là hình chữ nhật,
2,AB a BC a
và
3SB a
. Biết
rằng tam giác
SAB
là tam giác cân ti
S
và nằm trong mt phng vuông góc với mt phng
ABCD
. Khong cách từ đim
A
đến mt phng
SCD
bằng
A.
22
3
a
. B.
6
3
a
. C.
26
3
a
. D.
2
3
a
.
Lời giải:
Gọi
H
l trung đim ca
AB
, do
SAB
cân ti
S
nên
SH AB
. Mt khác
DSAB ABC SH ABCD
.
Có
// //AB CD AB SCD
nên
;;d A SCD d H SCD
.
Gọi
I
l trung đim ca
CD
khi đ
HI CD SI CD
và
CD SHI
.

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 16
Dựng
HM SI
. Ta có
HM SI
HM CD
(vì
CD SHI
)
HM SCD
.
Vậy
;;d A SCD d H SCD HM
.
Ta có:
2
2 2 2
32SH SB HB a a a
,
HI BC a
.
Tam giác
SHI
vuông ti
H
có:
2
2 2 2 2 2
1 1 1 1 1 3 6
23
2
a
HM
HM SH HI a a
a
.
Vậy
6
;
3
a
d A SCD
.
Câu 40: Cho hình nón
N
có chiều cao bằng
,a
đ di đường sinh bằng
2.a
Gọi
O
là tâm hình tròn
đáy
.N
Thiết diện qua đỉnh ca hình nón
N
cắt đường tròn đáy ti hai đim
,AB
thỏa
mãn
60 .AOB
Diện tích thiết diện là
A.
2
3 39
.
4
a
S
B.
2
3 39
.
16
a
S
C.
2
39
.
16
a
S
D.
2
39
.
4
a
S
Lời giải:
H
S
A
B
O
h
r
l
Gọi
O
l tâm đáy hình nn v thiết diện là tam giác
.SAB
Từ gi thiết suy ra
OAB
l tam giác đều
22
3.AB OA r l h a
Ta có:
2
2
22
3 13
2.
22
aa
SH SA AH a
Vậy diện tích thiết diện là
2
1 39
..
24
a
S SH AB
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
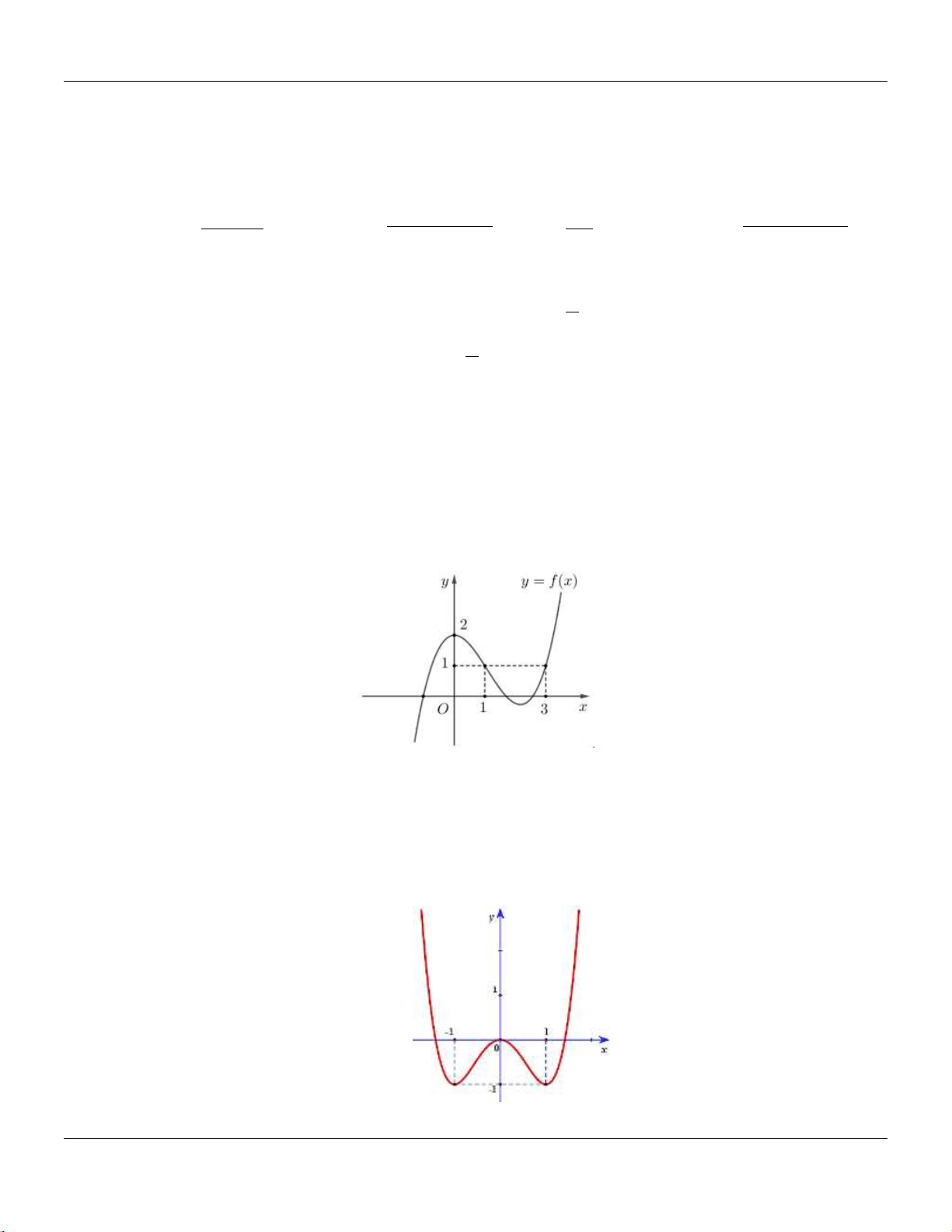
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 15_______________
Câu 1: Trên mặt phẳng tọa độ, điểm biểu diễn số phức liên hợp của số phức
76zi
có tọa độ là
A.
( 6;7)
. B.
(6;7)
. C.
(7;6)
. D.
(7; 6)
.
Câu 2: Trên khoảng
( 2023; )
, đạo hàm của hàm số
ln 2023yx
là
A.
1
2023
y
x
. B.
1
ln 2023
y
xx
. C.
ln3
y
x
. D.
1
2023 ln
y
xx
.
Câu 3: Đạo hàm của hàm số
x
ye
là
A.
x
ye
. B.
x
ye
. C.
1
x
ye
. D.
1x
yx
.
Câu 4: Tập nghiệm của bất phương trình
1
1
x
là
A.
2;
. B.
2;
. C.
2;2
. D.
;2
.
Câu 5: Cho cấp số nhân
n
u
có
2
2u
và
3
4u
, giá trị của công bội
q
là
A.
2q
. B.
4q
. C.
2q
. D.
4q
.
Câu 6: Trong không gian
Oxyz
, điểm nào dưới đây thuộc mặt phẳng
Oxy
?
A.
2;3;1A
. B.
0;0;2B
. C.
0; 2; 1C
. D.
2;1;0D
.
Câu 7: Cho hàm số
32
,0y ax bx cx d a
có đồ thị là đường cong trong hình vẽ bên dưới:
Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là
A.
0; 2
. B.
2;0
. C.
2;0
. D.
0;2
.
Câu 8: Nếu
1
0
d1
f x x
và
1
0
d2
g x x
thì
1
0
2d
f x g x x
bằng
A.
0
. B.
3
. C.
1
. D.
1
.
Câu 9: Đồ thị hàm số nào trong các phương án dưới đây có dạng đường cong như hình bên dưới?
A.
42
31y x x
. B.
42
2y x x
. C.
42
2y x x
. D.
42
2y x x
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 4 2 2 0S x y z x y z
. Bán kính của mặt
cầu
S
là
A.
4
. B.
2
. C.
16
. D.
27
.
Câu 11: Trong không gian
Oxyz
, góc giữa hai mặt phẳng
Oxy
và mặt phẳng
Oxz
bằng
A.
30
. B.
45
. C.
60
. D.
90
.
Câu 12: Cho số phức
23zi
. Số phức liên hợp của số phức
52wz
là
A.
8 15i
. B.
23i
. C.
8 15i
. D.
8 15i
.
Câu 13: Cho hình hộp chữ nhật có ba cạnh lần lượt là 2, 3, 4. Thể tích của khối hộp chữ nhật đã cho
bằng
A. 24. B. 8. C. 12. D. 6.
Câu 14: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Biết
SA ABC
và
3SA a
.
Tính thể tích khối chóp
.S ABC
.
A.
4
a
. B.
3
2
a
. C.
3
4
a
. D.
3
3
4
a
.
Câu 15: Trong không gian cho mặt cầu
;S I R
và đường thẳng
m
. Gọi khoảng cách từ tâm
I
đến
đường thẳng
m
là
d
và
0 dR
. Mệnh đề nào dưới đây đúng?
A.
m
tiếp xúc với
S
. B.
m
cắt
S
tại hai điểm phân biệt.
C.
m
và
S
không có điểm chung. D.
m
đi qua tâm của
S
.
Câu 16: Số phức liên hợp của số phức
26zi
là
A.
26zi
. B.
26zi
. C.
26zi
. D.
26zi
.
Câu 17: Cho hình nón có bán kính đáy
2r
, độ dài đường sinh
4l
. Diện tích xung quanh của hình
nón đã cho bằng
A.
32
. B.
8
. C.
16
. D.
48
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
1 2 1
:
2 3 1
x y z
d
, điểm nào dưới đây thuộc
đường thẳng
?d
A.
2;3;0
. B.
2;3;1
. C.
1; 2; 1
. D.
1;2;1
.
Câu 19: Cho hàm số
()y f x
có đồ thị như hình dưới đây:
Số điểm cực tiểu của đồ thị hàm số
()y f x
là
A.
0
. B.
2
. C.
1
. D.
3
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
Câu 20: Cho hàm số
()fx
có bảng biến thiên như sau :
Số tiệm cận đứng của đồ thị hàm số đã cho là
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 21: Tập nghiệm của bất phương trình
1
1
8
2
x
là
A.
2;
. B.
;2
. C.
; 2 .
. D.
2;
.
Câu 22: Một lớp học có
40
học sinh gồm
25
nam và
15
nữ. Chọn
3
học sinh để tham gia vệ sinh công
cộng toàn trường, hỏi có bao nhiêu cách chọn?
A.
9880.
B.
59280.
C.
2300.
D.
455.
Câu 23: Hàm số
2
x
F x e
là nguyên hàm của hàm số nào trong các hàm số sau?
A.
2
( ) 2
x
f x xe
. B.
2
2
( ) 1
x
f x x e
. C.
2
()
x
f x e
. D.
2
()
2
x
e
fx
x
.
Câu 24: Cho
1
2
d3f x x
. Tính tích phân
1
2
2 1 dI f x x
.
A.
9
. B.
3
. C.
3
. D.
5
.
Câu 25: Cho hàm số
2sin 1f x x x
. Khẳng định nào dưới đây đúng?
A.
2
1
2cos
2
df x x x x Cx
. B.
2
1
2sin
2
df x x x x Cx
.
C.
2
sd cof x x x x Cx
. D.
2
nd sif x x x x Cx
.
Câu 26: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
;3
. B.
;2
. C.
2;4
. D.
4; 1
.
Câu 27: Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ sau:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Giá trị cực tiểu của hàm số đã cho là
A.
1
. B.
2
. C.
0
. D.
3
.
Câu 28: Cho các số thực dương
a
,
b
thỏa mãn
3
log ax
,
3
log by
. Tính
3
log 3P ab
.
A.
3P xy
. B.
3P x y
. C.
P xy
. D.
1P x y
.
Câu 29: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số
3
3y x x
và
yx
là
A.
4S
. B.
8S
. C.
2S
. D.
0S
.
Câu 30: Cho hình chóp
.S ABC
có
,,SA SB SC
đôi một vuông góc với nhau và
.SA SB SC a
Gọi
M
là trung điểm của
AB
. Góc giữa hai đường thẳng
SM
và
BC
bằng
A.
45 .
B.
90 .
C.
60 .
D.
120 .
Câu 31: Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ dưới đây:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2f x m
có bốn nghiệm
thực phân biệt?
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 32: Cho hàm số
y f x
có đồ thị như hình vẽ dưới đây :
Hàm số
y f x
đồng biến trên khoảng nào dưới đây?
A.
1;2
. B.
1;2
. C.
4;2
. D.
1;1
.
Câu 33: Từ bộ 30 câu hỏi khác nhau trong đó có 15 câu hỏi mức độ nhận biết 10 câu hỏi mức độ thông
hiểu và 5 câu hỏi mức độ vận dụng, chọn ra đề kiểm tra. Tính xác suất để chọn được đề kiểm
tra có đúng 5 câu khác nhau, đủ cả ba loại câu hỏi, trong đó số câu hỏi mức độ nhận biết
không ít hơn 2 và luôn lớn hơn số câu hỏi mức độ thông hiểu là 2 câu.
A.
125
783
. B.
235
71253
. C.
50
7917
. D.
125
754
.
Câu 34: Tổng tất cả các nghiệm của phương trình
2
lg 3lg 2 0xx
là
A.
110
. B.
100
. C.
10
. D.
1000
.
Câu 35: Trong mặt phẳng tọa độ, biết tập hợp điểm biểu diễn số phức
z
thỏa mãn
2zi
là một
đường tròn. Bán kính của đường tròn đó bằng
A.
1
. B.
2
. C.
4
. D.
16
.
O
x
y
1
2
4
x
y
O
2
2
1
5
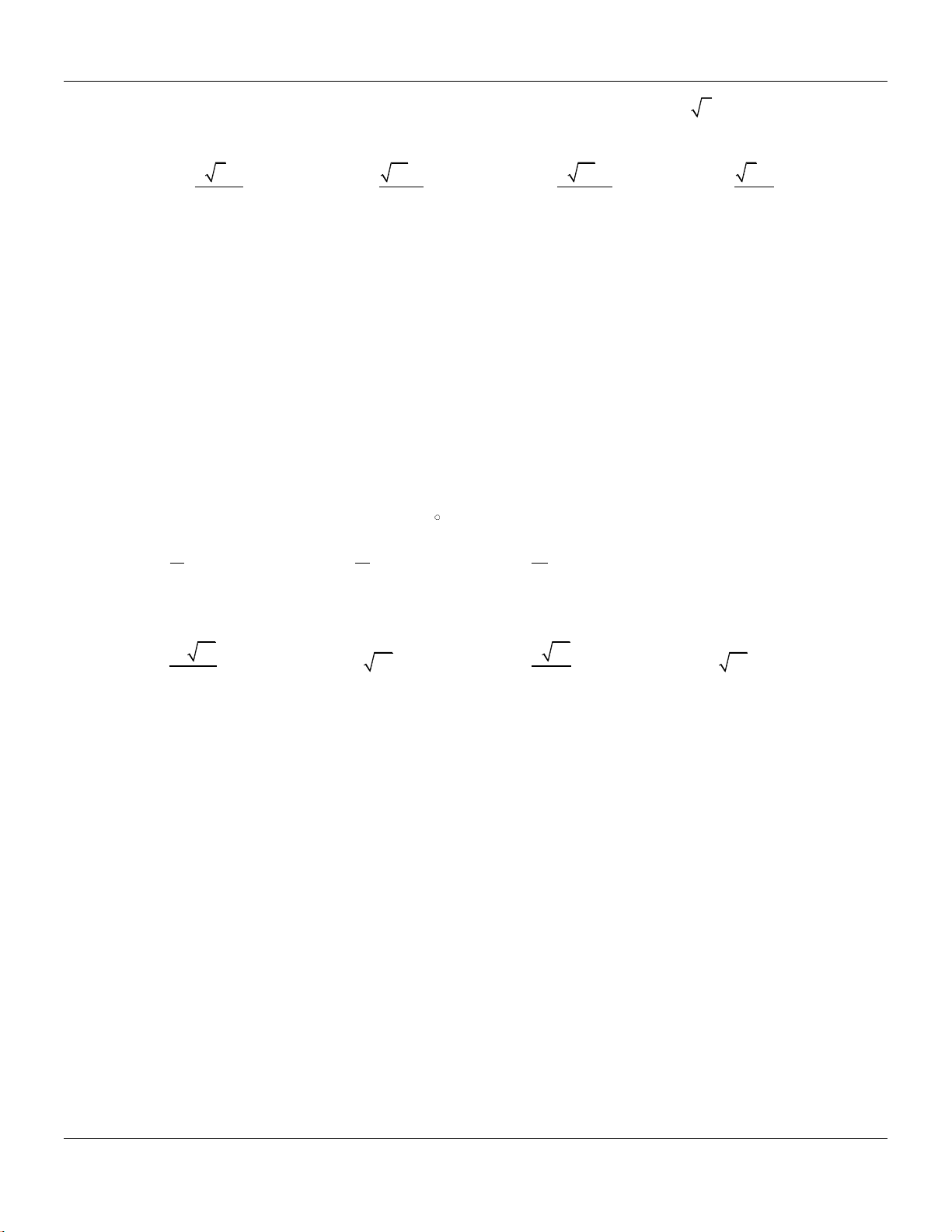
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 36: Cho hình nón
N
có chiều cao bằng
2,a
bán kính đáy nón bằng
2.a
Thiết diện qua đỉnh
của hình nón
N
và cách tâm đáy nón
N
một khoảng bằng
.a
Diện tích thiết diện là
A.
2
42
.
3
a
S
B.
2
11
.
3
a
S
C.
2
2 11
.
3
a
S
D.
2
2
.
3
a
S
Câu 37: Trong không gian
Oxyz
, cho ba điểm
1; 2 ;1A
,
2;0; 1B
,
11;3;5C
. Đường thẳng đi qua
điểm
A
và song song với đường thẳng
BC
có phương trình là
A.
13
2
12
xt
yt
xt
. B.
23
12
xt
yt
xt
. C.
13
26
19
xt
yt
xt
. D.
11 3
3
52
xt
yt
xt
.
Câu 38: Trong không gian
Oxyz
, cho điểm
1;1; 2A
,
5;1; 2B
. Điểm đối xứng với trung điểm
I
của đoạn thẳng
AB
qua mặt phẳng
Oxy
có tọa độ là
A.
3;1;2
. B.
3;1; 2
. C.
3; 1; 2
. D.
3;1;0
.
Câu 39: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Hình chiếu vuông góc của điểm
S
trên mặt phẳng
ABCD
trùng với trọng tâm của tam giác
BCD
. Góc giữa mặt phẳng
SBC
và mặt đáy
ABCD
bằng
30
. Tính khoảng cách giữa hai đường thẳng
AD
và
SC
.
A.
2
a
. B.
6
a
. C.
3
2
a
. D.
a
.
Câu 40: Cắt hình trụ
()T
bởi mặt phẳng song song với trục và cách trục một khoảng bằng
3a
, ta được
thiết diện là một hình vuông có diện tích bằng
2
16a
. Diện tích xung quanh của
()T
bằng
A.
2
16 13
3
a
. B.
2
4 12 a
. C.
2
8 13
3
a
. D.
2
8 13 a
.
________________________HẾT________________________

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Trên mặt phẳng tọa độ, điểm biểu diễn số phức liên hợp của số phức
76zi
có tọa độ là
A.
( 6;7)
. B.
(6;7)
. C.
(7;6)
. D.
(7; 6)
.
Lời giải:
Ta có:
7 6 7 6z i z i
.
Vậy điểm biểu diễn số phức liên hợp của số phức
76zi
có tọa độ là
(7;6)
.
Câu 2: Trên khoảng
( 2023; )
, đạo hàm của hàm số
ln 2023yx
là
A.
1
2023
y
x
. B.
1
ln 2023
y
xx
. C.
ln3
y
x
. D.
1
2023 ln
y
xx
.
Lời giải:
Ta có:
1
ln 2023
2023
yx
x
.
Câu 3: Đạo hàm của hàm số
x
ye
là
A.
x
ye
. B.
x
ye
. C.
1
x
ye
. D.
1x
yx
.
Lời giải:
Ta có:
xx
y e e
.
Câu 4: Tập nghiệm của bất phương trình
1
1
x
là
A.
2;
. B.
2;
. C.
2;2
. D.
;2
.
Lời giải:
Ta có
1 1 1
1
1 1 2 2;
xx
x x S
.
Câu 5: Cho cấp số nhân
n
u
có
2
2u
và
3
4u
, giá trị của công bội
q
là
A.
2q
. B.
4q
. C.
2q
. D.
4q
.
Lời giải:
Ta có
32
4 2 2u u q q q
.
Câu 6: Trong không gian
Oxyz
, điểm nào dưới đây thuộc mặt phẳng
Oxy
?
A.
2;3;1A
. B.
0;0;2B
. C.
0; 2; 1C
. D.
2;1;0D
.
Lời giải:
Mặt phẳng
Oxy
có phương trình là
0z
nên điểm
2;1;0D
thuộc mặt phẳng
Oxy
.
Câu 7: Cho hàm số
32
,0y ax bx cx d a
có đồ thị là đường cong trong hình vẽ bên dưới:
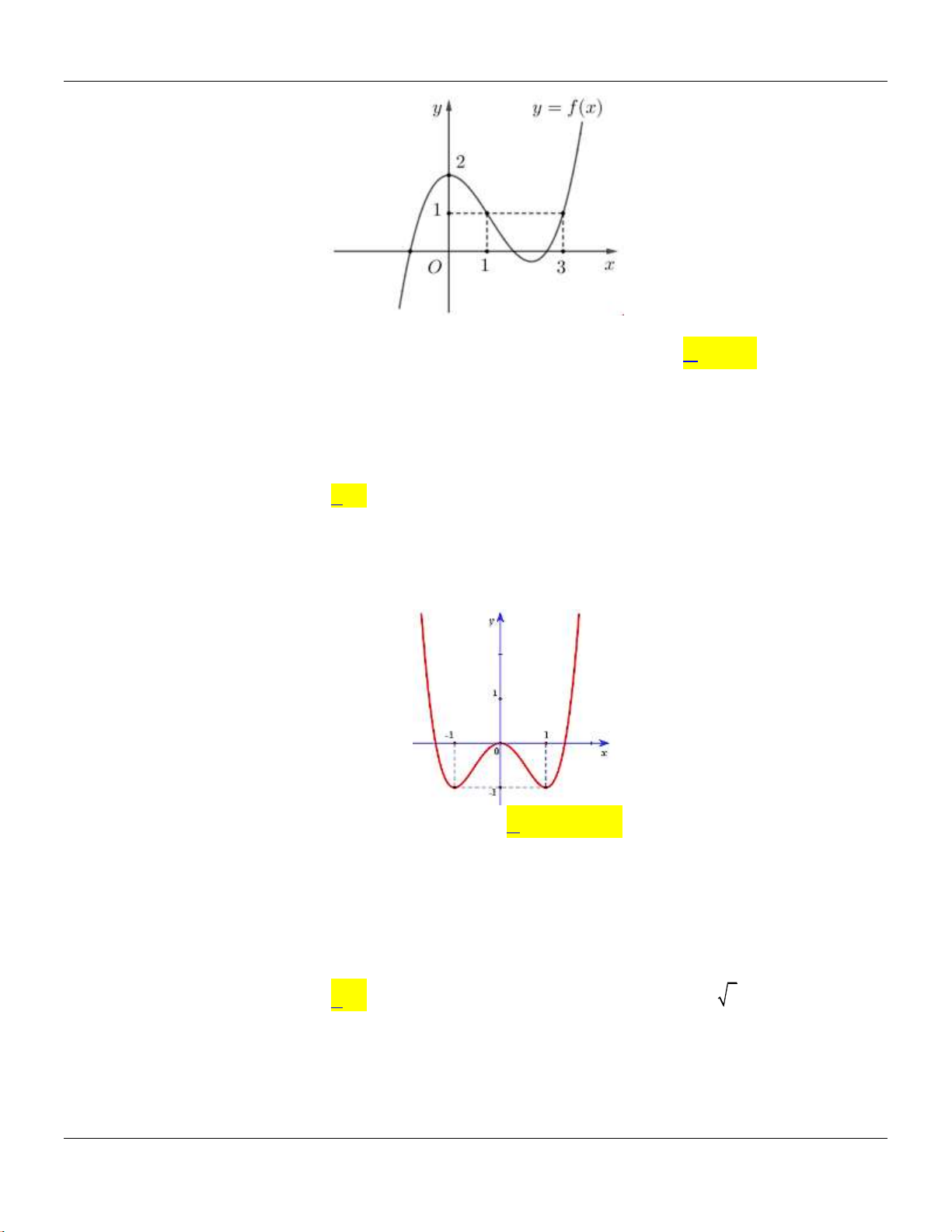
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là
A.
0; 2
. B.
2;0
. C.
2;0
. D.
0;2
.
Lời giải:
Từ đồ thị, ta dễ thấy đồ thị hàm số cắt trục tung tại điểm có tọa độ
0;2
.
Câu 8: Nếu
1
0
d1
f x x
và
1
0
d2
g x x
thì
1
0
2d
f x g x x
bằng
A.
0
. B.
3
. C.
1
. D.
1
.
Lời giải:
Ta có
1 1 1
0 0 0
2 2 1 2.2 3f x g x dx f x dx g x dx
.
Câu 9: Đồ thị hàm số nào trong các phương án dưới đây có dạng đường cong như hình bên dưới?
A.
42
31y x x
. B.
42
2y x x
. C.
42
2y x x
. D.
42
2y x x
.
Lời giải:
Đồ thị đã cho có
3
cực trị nên loại
2
đáp án
,BD
(hàm đa thức).
Đồ thị đã cho đi qua gốc tọa độ nên loại
A
.
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 4 2 2 0S x y z x y z
. Bán kính của mặt
cầu
S
là
A.
4
. B.
2
. C.
16
. D.
27
.
Lời giải:
Ta có:
2 2 2
2 2 2
: 2 4 2 2 0 1 2 1 4S x y z x y z x y z
.
Mặt cầu có bán kính là
2R
.
Câu 11: Trong không gian
Oxyz
, góc giữa hai mặt phẳng
Oxy
và mặt phẳng
Oxz
bằng
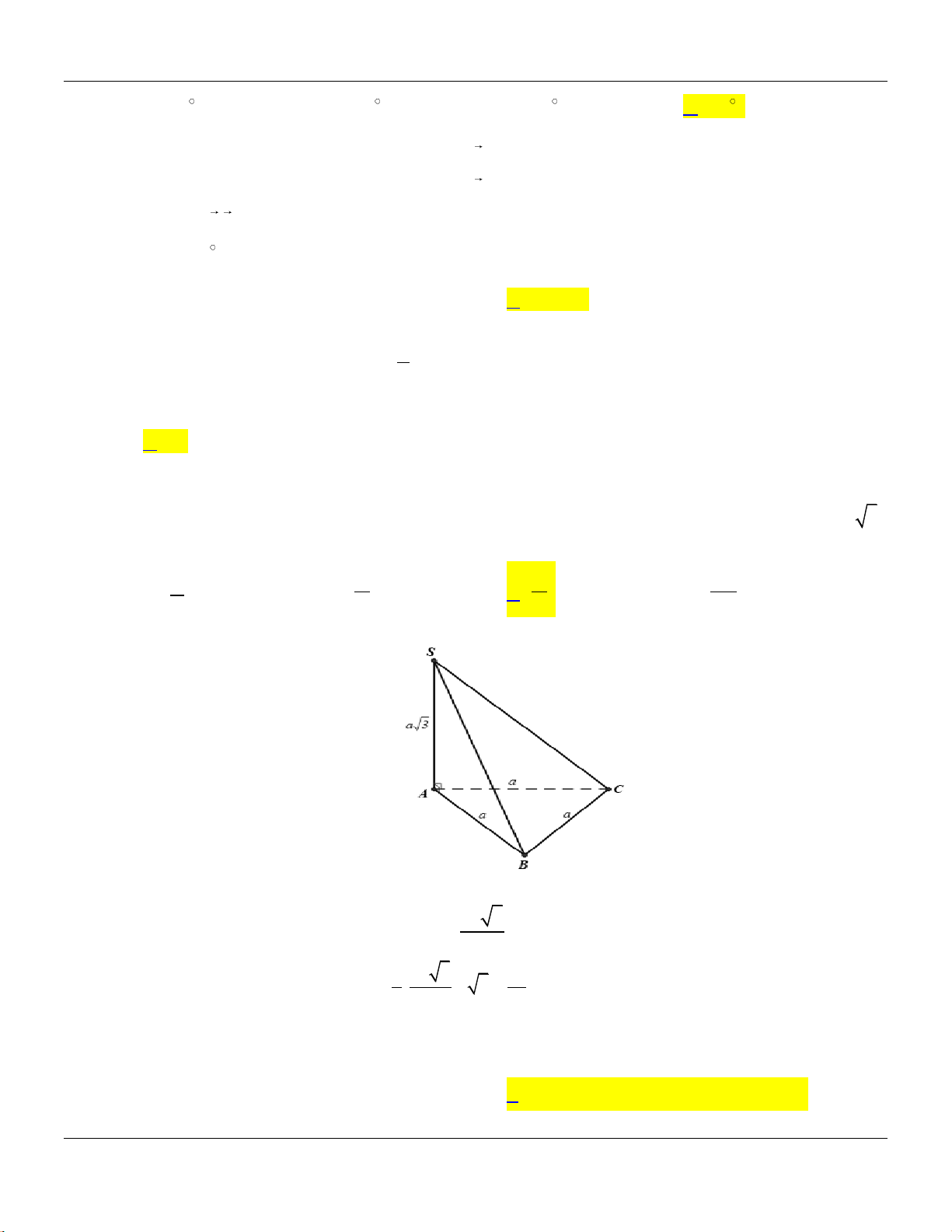
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
A.
30
. B.
45
. C.
60
. D.
90
.
Lời giải:
Mặt phẳng
Oxy
có véc tơ pháp tuyến là
0;0;1k
.
Mặt phẳng
Oxz
có véc tơ pháp tuyến là
0;1;0j
.
Ta thấy
.0k j Oxy Oxz
suy ra góc giữa hai mặt phẳng
Oxy
và mặt phẳng
Oxz
bằng
90
.
Câu 12: Cho số phức
23zi
. Số phức liên hợp của số phức
52wz
là
A.
8 15i
. B.
23i
. C.
8 15i
. D.
8 15i
.
Lời giải:
Ta có
2 3 5 2 8 15z i w z i
.
Vậy số phức liên hợp của
w
là
8 15wi
.
Câu 13: Cho hình hộp chữ nhật có ba cạnh lần lượt là 2, 3, 4. Thể tích của khối hộp chữ nhật đã cho
bằng
A. 24. B. 8. C. 12. D. 6.
Lời giải:
Thể tích khối hộp chữ nhật là
2.3.4 24V
.
Câu 14: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Biết
SA ABC
và
3SA a
.
Tính thể tích khối chóp
.S ABC
.
A.
4
a
. B.
3
2
a
. C.
3
4
a
. D.
3
3
4
a
.
Lời giải:
Ta có
SA
là đường cao hình chóp.
Tam giác
ABC
đều cạnh
a
nên
2
3
4
ABC
a
S
.
Vậy thể tích cần tìm là:
23
.
13
. . 3
3 4 4
S ABC
aa
Va
.
Câu 15: Trong không gian cho mặt cầu
;S I R
và đường thẳng
m
. Gọi khoảng cách từ tâm
I
đến
đường thẳng
m
là
d
và
0 dR
. Mệnh đề nào dưới đây đúng?
A.
m
tiếp xúc với
S
. B.
m
cắt
S
tại hai điểm phân biệt.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
C.
m
và
S
không có điểm chung. D.
m
đi qua tâm của
S
.
Lời giải:
Khoảng cách từ tâm
I
đến đường thẳng
m
là
,d I m d
Vì
0 dR
nên
m
cắt
S
tại hai điểm phân biệt.
Câu 16: Số phức liên hợp của số phức
26zi
là
A.
26zi
. B.
26zi
. C.
26zi
. D.
26zi
.
Lời giải:
Ta có số phức liên hợp của số phức
26zi
là
26zi
.
Câu 17: Cho hình nón có bán kính đáy
2r
, độ dài đường sinh
4l
. Diện tích xung quanh của hình
nón đã cho bằng
A.
32
. B.
8
. C.
16
. D.
48
.
Lời giải:
Ta có diện tích xung quanh hình nón bằng
2.4. 8
xq
S rl
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
1 2 1
:
2 3 1
x y z
d
, điểm nào dưới đây thuộc
đường thẳng
?d
A.
2;3;0
. B.
2;3;1
. C.
1; 2; 1
. D.
1;2;1
.
Lời giải:
Đáp án
A
: thay tọa độ điểm vào phương trình đường thẳng ta có
2 1 3 2 0 1
2 3 1
sai.
Đáp án
B
: thay tọa độ điểm vào phương trình đường thẳng ta có
2 1 3 2 1 1
2 3 1
sai.
Đáp án
C
: thay tọa độ điểm vào phương trình đường thẳng ta có
1 1 2 2 1 1
2 3 1
đúng.
Đáp án
D
: thay tọa độ điểm vào phương trình đường thẳng ta có
1 1 2 2 1 1
2 3 1
sai.
Câu 19: Cho hàm số
()y f x
có đồ thị như hình dưới đây:
Số điểm cực tiểu của đồ thị hàm số
()y f x
là
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải:
Từ đồ thị hàm số thấy hàm số có 1 điểm cực tiểu.
Câu 20: Cho hàm số
()fx
có bảng biến thiên như sau :

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Số tiệm cận đứng của đồ thị hàm số đã cho là
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải:
Quan sát bảng biến thiên ta có
0
lim
x
y
nên đồ thị hàm số có tiệm cận đứng
0x
.
Câu 21: Tập nghiệm của bất phương trình
1
1
8
2
x
là
A.
2;
. B.
;2
. C.
; 2 .
. D.
2;
.
Lời giải:
Ta có
1
1
8
2
x
13
2 2 1 3 2
x
xx
.
Vậy tập nghiệm bất phương trình là
2; .
Câu 22: Một lớp học có
40
học sinh gồm
25
nam và
15
nữ. Chọn
3
học sinh để tham gia vệ sinh công
cộng toàn trường, hỏi có bao nhiêu cách chọn?
A.
9880.
B.
59280.
C.
2300.
D.
455.
Lời giải:
Mỗi nhóm học sinh
3
người được chọn (không phân biệt nam, nữ - công việc) là một tổ hợp
chập
3
của
40
phần tử.
Vì vậy, số cách chọn nhóm học sinh là
3
40
9880C
(cách).
Câu 23: Hàm số
2
x
F x e
là nguyên hàm của hàm số nào trong các hàm số sau?
A.
2
( ) 2
x
f x xe
. B.
2
2
( ) 1
x
f x x e
. C.
2
()
x
f x e
. D.
2
()
2
x
e
fx
x
.
Lời giải:
Ta có
f x F x
22
2
xx
f x e xe
.
Câu 24: Cho
1
2
d3f x x
. Tính tích phân
1
2
2 1 dI f x x
.
A.
9
. B.
3
. C.
3
. D.
5
.
Lời giải:
Ta có
1
2
2 1 dI f x x
11
22
2 d df x x x
1
2
63x
.
Câu 25: Cho hàm số
2sin 1f x x x
. Khẳng định nào dưới đây đúng?
A.
2
1
2cos
2
df x x x x Cx
. B.
2
1
2sin
2
df x x x x Cx
.
C.
2
sd cof x x x x Cx
. D.
2
nd sif x x x x Cx
.
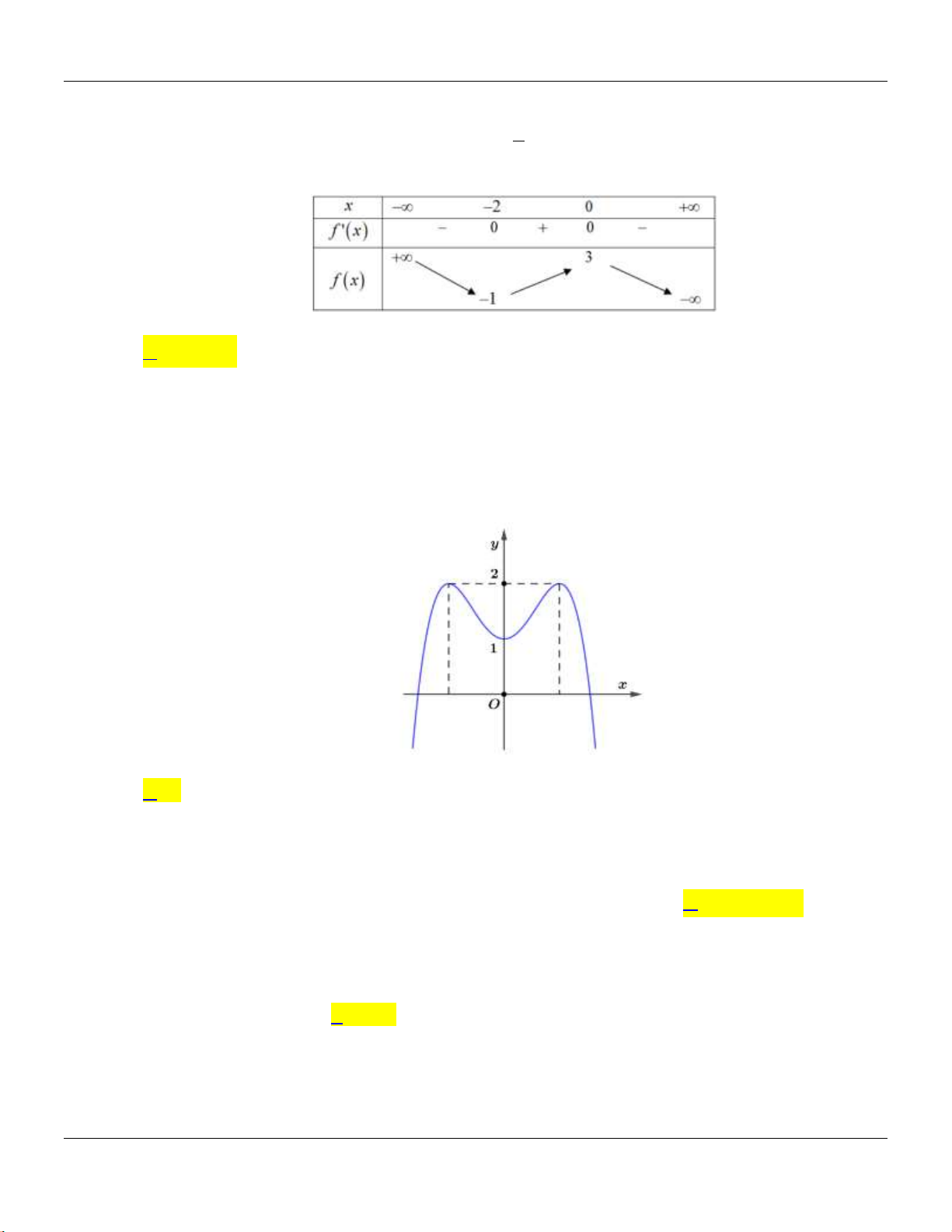
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Lời giải:
Ta có
2
1
2sin 1 2cos
2
ddf x x x x x x Cxx
.
Câu 26: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
;3
. B.
;2
. C.
2;4
. D.
4; 1
.
Lời giải:
Từ bảng biến thiên của hàm số
y f x
ta có hàm số nghịch biến trên các khoảng
;2
và
0;
.
Vì
;2;3
nên hàm số
y f x
nghịch biến trên khoảng
;3
.
Câu 27: Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ sau:
Giá trị cực tiểu của hàm số đã cho là
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải:
Từ đồ thị hàm số bậc bốn
y f x
ta có giá trị cực tiểu của hàm số là
1
.
Câu 28: Cho các số thực dương
a
,
b
thỏa mãn
3
log ax
,
3
log by
. Tính
3
log 3P ab
.
A.
3P xy
. B.
3P x y
. C.
P xy
. D.
1P x y
.
Lời giải:
3 3 3 3
log 3 log 3 log log 1P ab a b x y
.
Câu 29: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số
3
3y x x
và
yx
là
A.
4S
. B.
8S
. C.
2S
. D.
0S
.
Lời giải:
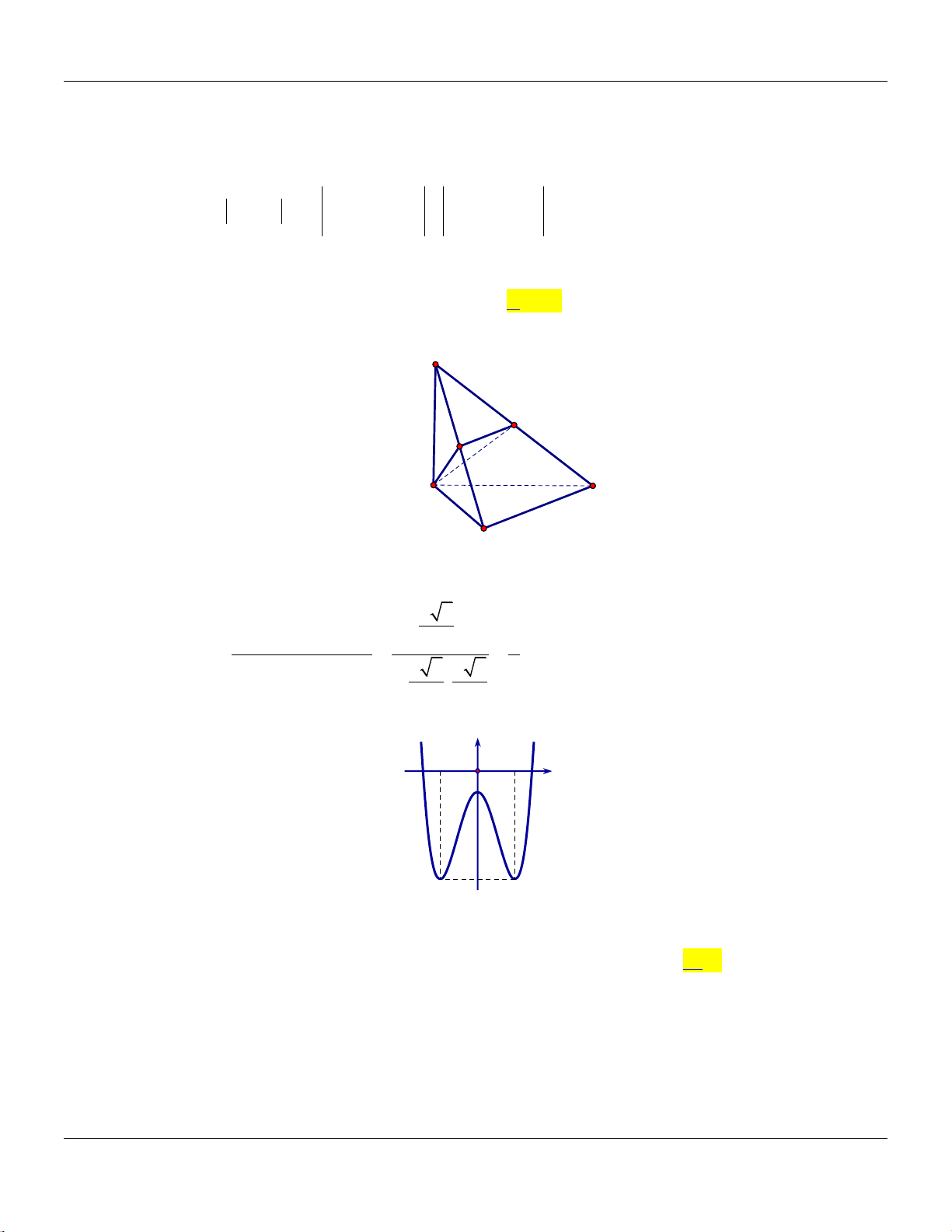
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
Ta có:
3
3x x x
3
40xx
2
0
2
x
x
x
.
Vậy
2 0 2
3 3 3
2 2 0
4 d 4 d 4 dS x x x x x x x x x
4 4 8
.
Câu 30: Cho hình chóp
.S ABC
có
,,SA SB SC
đôi một vuông góc với nhau và
.SA SB SC a
Gọi
M
là trung điểm của
AB
. Góc giữa hai đường thẳng
SM
và
BC
bằng
A.
45 .
B.
90 .
C.
60 .
D.
120 .
Lời giải:
N
M
S
C
B
A
Gọi
N
là trung điểm của
AC
. Ta có
//MN BC
. Suy ra
,,SM BC SM MN SMN
.
2
2 2 2
2
2
1
cos
2. . 2
22
2. .
22
a
SM MN SN
SMN
SM MN
aa
, 60 .SM BC
Câu 31: Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ dưới đây:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2f x m
có bốn nghiệm
thực phân biệt?
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải:
Phương trình
2f x m
có bốn nghiệm thực phân biệt khi và chỉ khi đồ thị hàm số
y f x
cắt đường thẳng có phương trình
2ym
tại
4
điểm phân biệt.
Khi đó
5 2 1 3 1mm
. Vì
m
là số nguyên nên
2; 1;0m
.
Vậy có
3
giá trị nguyên của
m
.
x
y
O
2
2
1
5
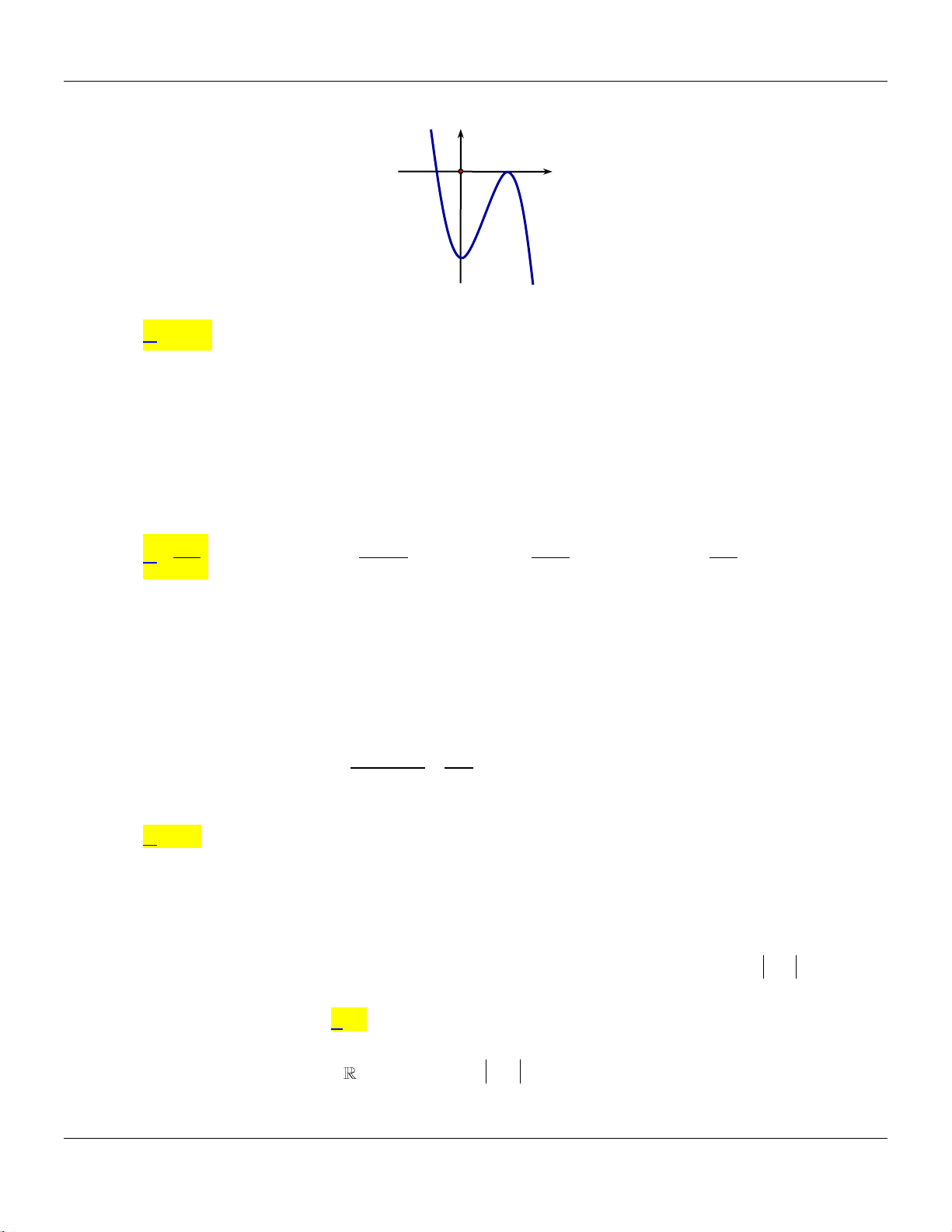
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Câu 32: Cho hàm số
y f x
có đồ thị như hình vẽ dưới đây :
Hàm số
y f x
đồng biến trên khoảng nào dưới đây?
A.
1;2
. B.
1;2
. C.
4;2
. D.
1;1
.
Lời giải:
Dựa vào hình vẽ ta thấy trên khoảng
0;2x
thì đồ thị hàm số đi lên nên hàm số cũng
đồng biến trên khoảng
1;2
.
Câu 33: Từ bộ 30 câu hỏi khác nhau trong đó có 15 câu hỏi mức độ nhận biết 10 câu hỏi mức độ thông
hiểu và 5 câu hỏi mức độ vận dụng, chọn ra đề kiểm tra. Tính xác suất để chọn được đề kiểm
tra có đúng 5 câu khác nhau, đủ cả ba loại câu hỏi, trong đó số câu hỏi mức độ nhận biết
không ít hơn 2 và luôn lớn hơn số câu hỏi mức độ thông hiểu là 2 câu.
A.
125
783
. B.
235
71253
. C.
50
7917
. D.
125
754
.
Lời giải:
Không gian mẫu chọn 5 câu trong 30 câu có số phần tử là
5
30
nC
.
Gọi biến cố
A
: “chọn được 5 câu khác nhau, đủ cả ba loại câu hỏi, trong đó số câu hỏi mức
độ nhận biết không ít hơn 2 và lớn hơn số câu hỏi mức độ thông hiểu là 2 câu”.
Theo yêu cầu biến cố A, ta chọn 5 câu trong đó: 3 câu mức độ nhận biết, 1 câu mức độ thông
hiểu và 1 câu mức độ còn lại (vận dụng) =>
3 1 1
15 10 5
..n A C C C
Xác suất cần tính:
3 1 1
15 10 5
5
30
..
125
783
C C C
pA
C
.
Câu 34: Tổng tất cả các nghiệm của phương trình
2
lg 3lg 2 0xx
là
A.
110
. B.
100
. C.
10
. D.
1000
.
Lời giải:
Phương trình:
2
lg 3lg 2 0xx
lg 1 10
lg 2 100
xx
xx
.
Suy ra tổng các nghiệm của phương trình đã cho là 110.
Câu 35: Trong mặt phẳng tọa độ, biết tập hợp điểm biểu diễn số phức
z
thỏa mãn
2zi
là một
đường tròn. Bán kính của đường tròn đó bằng
A.
1
. B.
2
. C.
4
. D.
16
.
Lời giải:
Đặt
z x yi
, với
,xy
. Theo giả thiết
22
2 ( 1) 4z i x y
.
Do đó tập hợp điểm biểu diễn số phức
z
là đường tròn tâm
0;1I
và bán kính
2R
.
O
x
y
1
2
4
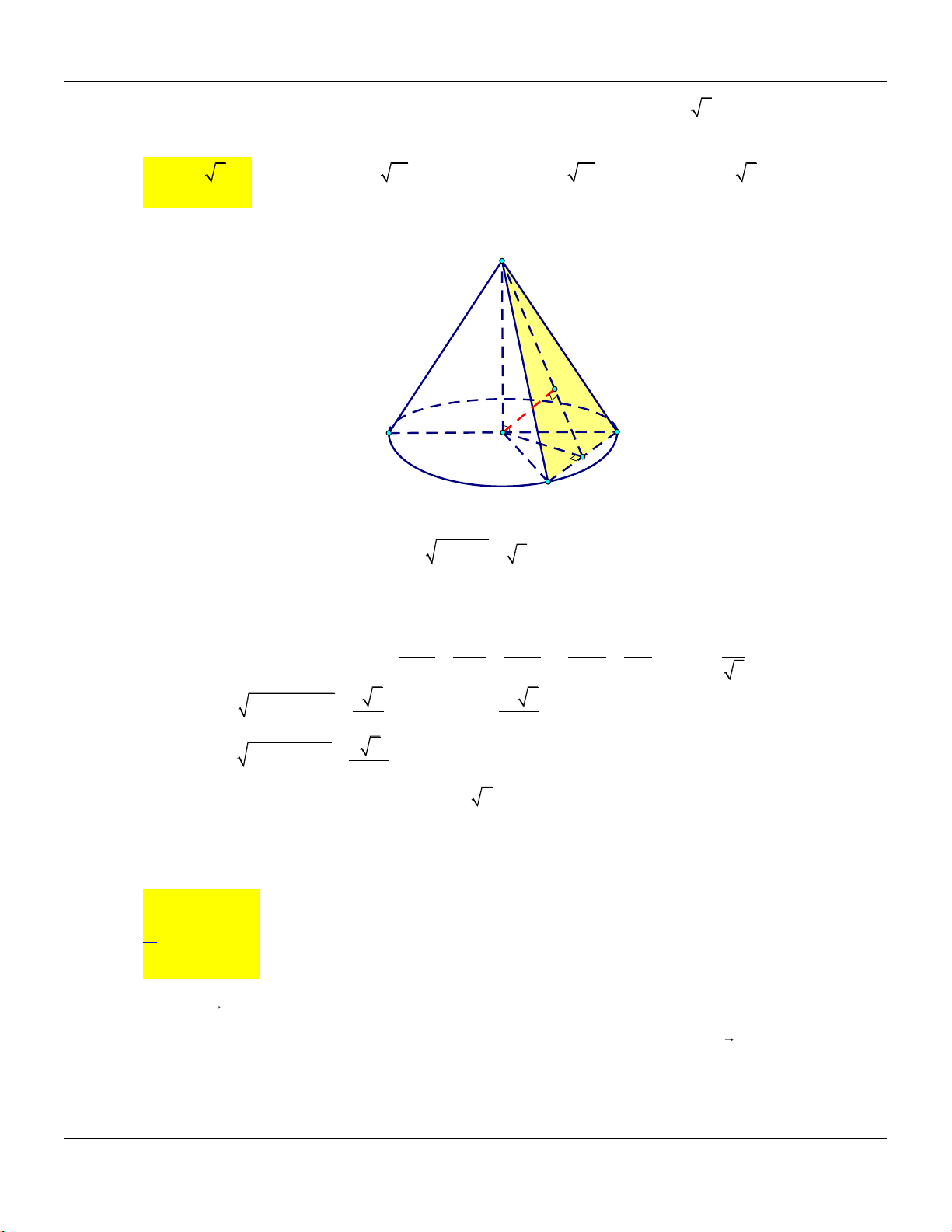
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
Câu 36: Cho hình nón
N
có chiều cao bằng
2,a
bán kính đáy nón bằng
2.a
Thiết diện qua đỉnh
của hình nón
N
và cách tâm đáy nón
N
một khoảng bằng
.a
Diện tích thiết diện là
A.
2
42
.
3
a
S
B.
2
11
.
3
a
S
C.
2
2 11
.
3
a
S
D.
2
2
.
3
a
S
Lời giải:
l
r
h
K
H
O
B
A
S
Gọi
O
là tâm đáy hình nón và thiết diện là tam giác
.SAB
Gọi
H
là trung điểm
.AB
Ta có:
22
6.l r h a
Dựng
.OH AB AB SOH SAB SOH
Dựng
,OK SH K SH OK SAB
hay
;.d O SAB OK d
Xét tam giác
SOH
vuông tại
2 2 2 2 2
1 1 1 1 3 2
:.
3
4
a
O OH
OK OS OH OH a
Ta có:
22
6 2 6
2.
33
aa
HB OB OH AB HB
Ta có:
22
43
.
3
a
SH SA HA
Vậy diện tích thiết diện là
2
1 4 2
..
23
a
S SH AB
Câu 37: Trong không gian
Oxyz
, cho ba điểm
1; 2 ;1A
,
2;0; 1B
,
11;3;5C
. Đường thẳng đi qua
điểm
A
và song song với đường thẳng
BC
có phương trình là
A.
13
2
12
xt
yt
xt
. B.
23
12
xt
yt
xt
. C.
13
26
19
xt
yt
xt
. D.
11 3
3
52
xt
yt
xt
.
Lời giải:
Ta có:
9;3;6 3 3;1;2BC
.
Đường thẳng đi qua điểm A và song song với BC có vectơ chỉ phương là
3;1;2u
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
Suy ra phương trình đường thẳng cần tìm là:
13
21
12
xt
yt
xt
.
Câu 38: Trong không gian
Oxyz
, cho điểm
1;1; 2A
,
5;1; 2B
. Điểm đối xứng với trung điểm
I
của đoạn thẳng
AB
qua mặt phẳng
Oxy
có tọa độ là
A.
3;1;2
. B.
3;1; 2
. C.
3; 1; 2
. D.
3;1;0
.
Lời giải:
Tọa độ trung điểm của
AB
là
3,1, 2I
.
Điểm đối xứng với trung điểm
I
của đoạn thẳng
AB
qua mặt phẳng
Oxy
có tọa độ là
3,1,2 .
Câu 39: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Hình chiếu vuông góc của điểm
S
trên mặt phẳng
ABCD
trùng với trọng tâm của tam giác
BCD
. Góc giữa mặt phẳng
SBC
và mặt đáy
ABCD
bằng
30
. Tính khoảng cách giữa hai đường thẳng
AD
và
SC
.
A.
2
a
. B.
6
a
. C.
3
2
a
. D.
a
.
Lời giải:
O
C
D
A
B
S
G
I
K
Gọi
G
là trọng tâm tam giác
BCD
. Theo giả thiết
SG ABCD
.
Kẻ
GI BC I BC
. Ta có:
BC GI
BC SGI BC SI
BC SG
.
Mặt khác:
SBC ABCD BC
. Suy ra
0
, , 30SBC ABCD SI GI SIG
.
Do
/ / / /AD BC AD SBC
nên ta có:
, , , 3 ,d AD SC d AD SBC d A SBC d G SBC
.
Trong mặt phẳng
SGI
kẻ
1GK SI K SI
.
Vì
2BC SGI BC GK
.
Từ
1
và
2
suy ra
GK SBC
. Nên
,d G SBC GK
.
Ta có:
1
33
GI GC a
GI
AB AC
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 16
Trong tam giác vuông
KGI
có:
.sin
6
a
GK GI KIG
.
Vậy
,
2
a
d AD SC
.
Câu 40: Cắt hình trụ
()T
bởi mặt phẳng song song với trục và cách trục một khoảng bằng
3a
, ta được
thiết diện là một hình vuông có diện tích bằng
2
16a
. Diện tích xung quanh của
()T
bằng
A.
2
16 13
3
a
. B.
2
4 12 a
. C.
2
8 13
3
a
. D.
2
8 13 a
.
Lời giải:
I
C
B
r
l
h
D
O'
O
A
Gọi
()P
là mặt phẳng song song với trục
OO
. Theo đề bài ta có:
()P
cắt
()T
theo thiết diện là
hình vuông
ABCD
.
Ta có:
2
16 4
ABCD
S a AB AD a
.
Gọi
I
là trung điểm của
,AB OI AB OI AD
,
( ) ( ,( )) 3 .OI ABCD d O P OI a
Ta có:
2 2 2 2
9 4 13.r OA OI IA a a a
Diện tích xung quanh của hình trụ
()S
bằng:
2
2 . . 2 . 13 .4 8 13 .
xq
S OA AD a a a
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
Bấm Tải xuống để xem toàn bộ.




