

























































































































































































Preview text:
NGUYỄN THANH TRÀ - THÁI VĨNH HIỂN 250 BÀI TẬP KV THUỘT ĐIỈN TỬ
NHÀ XUẤ T BẢN GIÁO DỤC VIỆT NAM Chưởng 1 ĐIỐT
1.1. TÓM TẮT PHẦN LÝ THUYẾT
Hiệu ứng chỉnh lưu của điốt bán dẫn là tính dẫn điện không đối xứng.
Khi điốt được phân cực thuận, điện trở tiếp giáp thường rất bé. Khi điốt được
phân cực ngược điện trở tiếp giáp thưcmg rất lớn. Khi điện áp ngược đặt vào
đủ lớn điốt bị đánh thủng và mất đi tính chỉnh lưu của nó. Trên thực tế tồn
tại hai phưofng thức đánh thủng đối với điốt bán dẫn. Phưcíng thức thứ nhất
gọi là đánh thủng tạm thời (zener). Phương thức thứ hai gọi là đánh thủng về
nhiệt hay đánh thủng thác lũ. Người ta sử dụng phương thức đánh thủng tạm
thời để làm điốt ổn áp.
Phương trình cơ bản xác định dòng điện Id chảy qua điốt được viết như sau: enu.. ~^DS ( 1- 1) ở đây: -
= — , là thế nhiệt; q
- k = 1,38.10"^^ — , hằng số Boltzman; K
- q = 1,6.10 '’c , điện tích của electron;
- n = 1 đối vói Ge và n = 2 đối với Si;
- T nhiệt độ môi trường tính theo độ K.
Từ phương trình (1-1) người ta xây dựng được đặc tuyến Volt-Ampe
= f(Uj3) cho điốt và dùng nó đé iính toán các thông số có liên quan đối với
các mạch điện dùng điốt.
úhg dụng quan trọng của điốt là: a)
Chỉnh lưu dòng điện xoay chiều thành một chiều nhờ các sơ đồ cơ bản
sử dụng các loại điốt khác nhau (điốt có điều khiển và điốt không điều khiển).
b) Hạn chế biên độ điện áp ờ một giá trị ngưỡng cho trước.
c) Ổn định giá trị điện áp một chiều ở một ngưỡng xác lập Uz nhờ đánh
thủng tạm thời (zener).
Mô hình gần đúng để mô tả điốt trong các mạch điện được xem như:
a) Là một nguồn điện áp lý tưởng có nội trở bằng không khi điốt
chuyển từ trạng thái khoá sang mở tại mức điện áp U^K = Up.
b) Là một nguồn dòng lý tưởng có nội trở rất lớn khi điốt chuyển từ
trạng thái mở sang khoá tại mức điện áp = oV
c) ở chế độ xoay chiều khi tần số tín hiệu còn đủ thấp, điốt sẽ tưcmg đương
như một điện trở xoay chiều được xác định theo biểu thức (1-2) dưới đây : ( 1-2 )
Còn khi' tần số tín hiệu đủ cao, cần chú ý tới giá trị điện dung ký sinh
của điốt Cd, nó được mắc song song với điện trở xoay chiều r^.
1.2. BÀJ TẬP CÓ LỜI GIẢI
Bài tập 1-1. Xác định giá trị thế nhiệt (U-r) của điốt bán dẫn trong điều
kiện nhiệt độ môi trường 20°c. Bài giải
Từ biểu thức cơ bản dùng để xác định thế nhiệt u , = i ĩ q Trong đó:
- k = 1,38.10'^^ — , hằng số Boltzman; K
- q = 1 , 6 . điện tích của electron;
- T nhiệt độ môi trường tính theo độ K.
Tĩiay các đại lượng tưcíng ứng vào biểu thức ta có: U, = ^ = ^ M . 2 5 . 2 7 , n V ^ q 1,6.10"'’
Bài tập 1-2. Xác định điện trở một chiều Rj3 của điốt chỉnh lưu với đặc
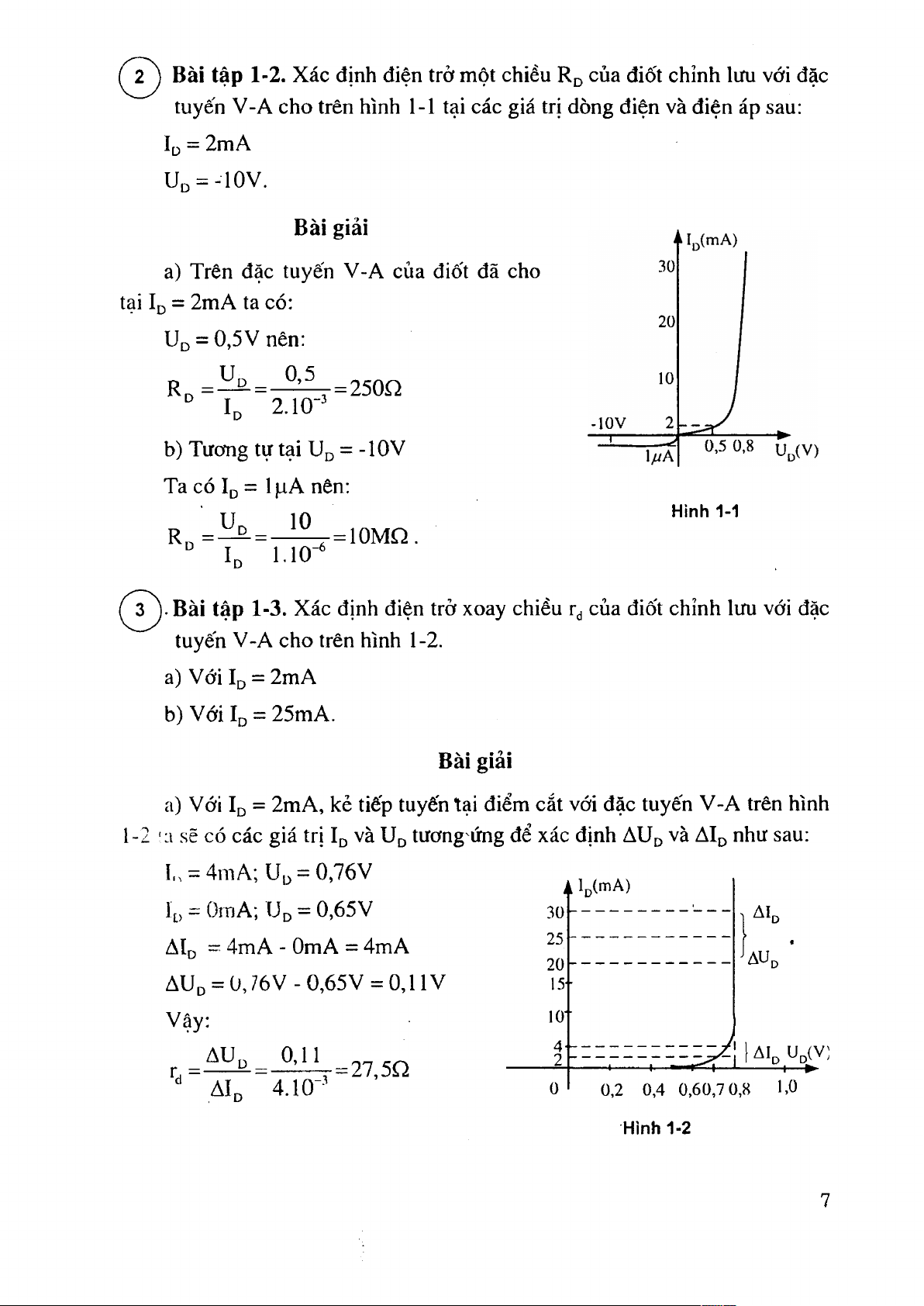
tuyến V-A cho trên hình 1-1 tại các giá trị dòng điện và điện áp sau: = 2mA Uo = -10V. Bài giải a)
Trên đặc tuyến V-A của điốt đã cho tại Iß = 2mA ta có: Ud = 0,5V nên: u .. 0,5 K = — = = 250Q -3 Id 2.10
b) Tương tự tại Uq = -lOV Ta có Id = l|iA nên; Hinh 1-1 10 R„ = 10MQ.
tập 1-3. Xác định điện trở xoay chiều
của điốt chỉnh lưu với đặc
tuyến V-A cho trên hình 1-2. a) Với Id = 2mA b) Với Id = 25mA. Bài giải a)
Với Ij) = 2mA, kẻ tiếp tuyến tại điểm cắt với đặc tuyến V-A trên hình
1-2 'a sẽ có các giá trị Ij3 và Up tương ứng để xác định AUß và AIp như sau:
ỉ„ = 4niA; U^ = 0,76V ẩ In(mA) Ip = OrnA; ưp = 0,65V 30 AI. 25
AIp = 4 m A - OmA = 4m A 20
A U d = 0 , 7 6 V - 0 , 6 5 V = 0 ,1 1 V Vậy: 10 AI, u (v; ---► " AI„ 4.10-’ 0 0,2 0,4 0,60,7 0,8 1,0 Hinh 1-2 b)
Với Id = 25mA. Các bước tương tự như câu a) ta xác định được các
đại lượng tương ứng dưới đây: Id = 30mA; ƯD = 0,8V Id = 20mA; Ud = 0,78V AIjj = 30 - 20 = lOmA
Aưd = 0,8 - 0,78 = 0,02V V â y , = ^ = ^ = 2 « . AI„ 10.10''
04 ) Bài tập 1-4. Cho đặc tuyến V-A của một điốt như trên hình 1-2. Xác
định điện trở một chiều tại hai giá trị dòng điện. a) Ij5 = 2mA.
b) Iq = 25mA và so sánh chúng với giá trị điện trở xoay chiều trong bài tập 1-3. Bài giải
Từ đặc tuyến V-A trên hình 1-2 ta có các giá trị tưoìig ứng sau; a) Id = 2mA; ƯD = 0,7V Nên: R . = ^ = - ^ = 3 5 0 Q AL 2.10 so với = 27,5Q.
b) Id = 25mA; ƯD = 0,79V Nên:
R , = ^ = - ^ ^ = 3 1 , 6 2 Q '* AL 25.10"' so với = 2 Q.
Bài tập 1-5. Cho mạch điện dùng điốí như hình l-3a và đặc tuyến V-A
của điốt như trên hình l-3b.
a) Xác định toạ độ điểm công tác tĩnh Q[Ư£)o; liX)]-
b) Xác định giá ừị điện áp trên tải Ur. Bài giải
a) Theo định luật Kirchoff về điện áp vòng ta có: 8 uD R. u. IkQ a) Hình 1-3
E - u„ - u, = 0 hay E = Uo + ư,
Đây chính là phưcrtig trình đườna tải mội chiều củci mạch diện dùng điỏì trên.
Dựng đường tải một chiều thông qua hai điểm cắl trên trục lung với
U|) = o v và trên trục hoành với Ip = 0.
Tại ưp = 0 ta có E = 0 + IpR, E lOV Nên: ĨD=- = 10mA R 10'o
Tại I|J = 0 la có lì = U|J + (OA).R, Up = E| -lO V Ịíi) ■ <’
Đường tải rnột chiều
(R_) được dựng như trên hình
1-4. Đường tải một chiều
(R_) cắt đặc tuyến (V-A) tại
đicm công tác tĩnh Qflix>
UdoI với toạ độ tưcmg ứng: I[)0 = 9,2 5 m A Upo = 0 ,7 8 V
b) Điện áp rơi trên tải R, sẽ là:
u „ =I„.R, =I„,.R, =9,25.10-M 0’ =9,25V
Hoặc Ur, c ó thể được tính:
Ur, = E - U do= 10-0,78 = 9,22V
Sự khác nhau trong hai kết quả trên do sai số khi xác định theo đồ thi
biểu diễn đặc tuyến V-A đối với điốt trên hình 1-3 và hình 1 -4.
Bài tập 1-6. Tính toán lặp lại như bài tập 1-5 với R, = 2kQ. Bài giải a) Từ biểu thức: E lOV = 5mA R 2kQ U^ = E = 10V
Đường tải một chiều
(R_) được dimg như trên hình
1-5 và ta được toạ độ điểm
Q[Ido; UdoI tưcmg ứng: Ido = 4,6mA Udo = 0,7V
b) Điện áp rơi trên tải R, sẽ là:
=1^ .R, = IdoJR, =4,6.10-' .2.10' =9,2V hoặc
= E - U do= 10V -0,7V = 9,3V
©7 ] Bài tập 1-7. Tính toán lặp lại cho bài tập 1-5 bằng cách tuyến tính hoá
đặc tuyến Volt-Ampe cho trên hình l-3b và điốt loại Si. Bài giải
Với việc tuyến tính hoá đặc tuyến V-A của điốt trên ta vẽ lại đặc tuyến
đó như trên hình 1-6. 10
Dựng đường tải một
chiều (R_) cho mạch
tương tự như trong câu a)
của bài tập 1-5 và được
biểu diễn trên hình 1-6.
Đường tải một chiều đặc
tuyến V-A tại Q với toạ độ tưoíng ứng. Ido = 9,25mA U do = 0,7V. Hình 1-6
( 8 j Bài tập 1-8. Tính toán lặp lại cho bài tập 1-6 bằng cách tuyến tính hoá
đặc tuyến V-A cho trên hình l-3b và điốt loại Si. Bài giải
Với việc tuyến tính
hoá đặc tuyến V-A của điốt
trên ta vẽ lại đặc tuyến đó như trên hình 1-7.
Dựng đưòng tải một
chiều (R_) cho mạch tương
tự như trong câu a) của bài
tập 1-6 và được biểu diễn trên hình 1-7. Hình 1-7
Đường tải một chiều
(R_) cắt đặc tuyến V-A tại
Q. Với toạ độ tương ứng: Ido ~ 4,6rnA = 0,7V.
Bài tập 1-9. Tính toán lặp lại cho bài tập 1-5 bằng cách lý tưởng hoá
đặc tuyến V-A cho trên hình l-3b và điốt loại Si. Bài giải
Với việc lý tưcmg hoá đặc tuyến V-A của điốt, ta có nhánh thuận của
đặc tuyến trùng với trục tung (Ip), còn nhánh ngược trùng với trục hoành
(Ud) như trên hình 1-8. 11
Dựng dưòng lải một chicu
(R_) cho mạch tương tự như
Irong câu a) của bài lập 1-5.
Đường tải một chiều cắt
đặc tuyến V-A tại điểm Q với
toạ độ tưcyng ứng: ỉno = iOmA U,K, = OV.
Đường tải một chiều (R_)
được biểu diễn như trên hình 1-8.
Bài tập 1-10. Cho mạch điện dùng điốt loại Si như hình i -9.
Xác định các giá trị điện áp và dòng điện Uq. U|(, I|y Bài giải
Biết rằng để điốt loại Si làm việc
bình thường ngưỡng thông nằm trong
khoảng lừ 0.5V -r 1,25V. Chọn ngưỡng
ìàm việq cho điốt: U„ = 0,7V; E = 8V.
Điện áp rơi trên điện irở tải R sẽ là:
U, = E - U p = 8 - 0 ,7 = 7,3V Hình 1-9
Dòng điện chảy qua điốt I|) = 1,;, (dòng qua tái R) sẽ ỉà:
Id = Iu = - ' = ^ = - ^ ^ = 3.32mA " ' R 2 ,2 .1 0 '
Bài tập 1-11. Cho mạch điện dùng điốt như hình 1-10. Xác định điện
áp ra trên tải ư„ và dòng điện Id qua các điốt Dị, Dj. Bài giải
Chọn ngưỡng điện áp thông cho hai điốt D| và D, lương ứng.
=0,7V dối vớiđiốtSi 12
= 0,3V đối với điốt Ge. Ip Dj Si D, Ge .
Điện áp ra trên tải sẽ là: L + E 12V u ra = 12-0,7-0,3= liv. 5,6kQ
Dòng điện qua các điốt D|, và E sẽ là: Hình 1-10 11 r r l,96m A . R 5,6.10
(^1^ Bài tập 1-12. Cho mạch điện dùng điốt như hình 1-11
Xác đinh các điên áp và dòng điên u„, Up , Ij3. Bài giải D,Si D.Si
Id Uo,=OV I„= I,,= I,= 0A = I, •— ► — ¿1— ki— —•—• ĩ T u 12V u. 12V D. D R ra rn 2 R- r : 5,6kQ 5,6kfí Hình 1-11 Hình 1-12
Do D| được phân cực thuận, còn Dt được phân cực nghịch, ta vẽ lại sơ đồ
tương đương của mạch với giả thiết cả hai điốt đều lý tưcmg như trên hình 1-12.
Khi đó; u„ = Id.R = Ir.R = OA.R = o v
Vì điốt D, ở trạng thái hở mạch nên điện áp rơi trên nó chính là điện áp nguồn E: U „ ,= E -I 2 V
Nếu theo định luật Kirchoff ta cũng sẽ có kết quả như trên. E - U = 0 D,
u „ = E -U „ ,-U ^ = I 2 - 0 - 0 = 1 2 V . D-, D, ra • 13
(^1^ Bài tập 1-13. Cho mạch điện dùng điốt như hình 1-13
Xác định các dòng điện và điện áp I, U|, Ư2, + u , - D Si ư , . 0’^^ 1—VW^->— I + E ,=10V R 4,7kQ u R, I + L R, u . R, 2,2kQ E ,^ IO V E ,Ậ : 5V E3=-5V Hình 1-13 Hình 1-14
Qiọn điện áp ứiông cho điốt D loại Si 0,7V ta vẽ lại sơ đồ trên như hình 1-14.
Dòng điện I được tính: , ^ E . E - U „ ( 1 0 .5 - 0 ^ ) R,+R2 (4,7+2,2)10^
Điện áp U|, Ư2 tương ứng trên R|, R, sẽ là:
u , =IR, =2,07.10'\4,7.10^ =9,73V
Ư2 =IR2 =2,07.1012,2.10^ =4,55V
Điện áp ra sẽ là:
u„ = Ư2 - E, = 4,55 - 5 = -0,45V
Dấu trừ (-) trong kết quả biểu thị rằng cực tính của điện áp ra (U„) sẽ có Bài giải
Chọn giá trị điện áp thông cho các điốt D ị,
loại Si 0,7V. Sơ đồ 1-15
được vẽ lại như hình 1-16.
Dòng điện I được tính
I = H ^ = ^ = i ^ = 2 8 , 1 8 m A R R 0 ,3 3 .1 0 ' 14 ra Hình 1-15 Hình 1-16
Nếu chọn Dị và D, giống nhau ta có dòng qua chúng sẽ như nhau và tính được; I =I Q g D, D , ^ ọ ’
Điện áp ra chính là điện áp thông rơi trên điốt D| và D, U„ = 0 ,7 V
Bài tập 1-15. Cho mạch điện dùng điốt như hình 1-17. Xác định dòng
điện I chảy qua mạch. Bài giai
Dưới tác động của hai nguồn điện áp E| và Eị. D| được phân cực thuận,
còn Dọ được phân cực nghịch, ta vẽ ỉại sơ đồ tương đưong như hình 1-18 dưới đây: Si — N— 1 I R D. D, ----- ►^ẠA— E|=20V 2,2kQ E,=4V ------ ------- i + R 2.2kn -^E2=4V Si E, -4 :^ 0 V Hình 1-17 Hình 1-18
Dòng điện I được tính: R 2,2.10' 15
Bài tập 1-16. Cho mạch điện dùng điốt như hình 1-19. Xác định điện áp ra trên tải R. E t l 2 V 4rO,3V —• u. R ra 2,2kQ Hình 1-20 Bài giải
Vì D| và D, khác loại (D, - Si; D-, - Ge) nên khi được cấp điện áp phân
cực E điốt D-, (Ge) luôn luôn thông ồ ngưỡng 0,3V, còn điốt D| sẽ luôn luôn
khoá do ngưỡng thông tối thiểu của điốt loại Si là 0,7V.
Sơ đồ tưong đưofng của mạch được vẽ lại như trên hình 1 -20.
Điện áp ra (U„) trên tải R được tính:
U,, = E - u „ = 1 2 - 0 , 3 = 11,7V.
©17 ) Bài tập 1-17. Cho mạch điện dùng điốt,như trên hình 1-21. Xác định dòng điện I„ I,, . Bài giải Si R| 3,3kQ H > h - aXat- i
Chọn ngưỡng điện áp thông cho D. I
hai điốt D„ ¿ 2 loại Si bằng 0,7V. E - i d , ¥ Si
Dòng điện I| được tính: 20V u .D , 0,7 h I,= 3-=0,212mA 4-AAAr R. 3,3.10 5,6kfì
Theo định luật Kirchoff về điện áp Hình 1-21 vòng ta có:
- U « , + E - U „ - U „ , = 0 16 Hay
Ur = E -U c^-Uọ^ = 20-0,7-0,7= 18,6V , _ u 18,6 Do đó: I = — — - ^ = 3 ,3 2 m A R, 5,6.10^
Theo định luật Kirchoff về dòng điện nút ta có;
=1^- I , = 3,32-0,212 = 3,108mA
Bài tập 1-18. Cho mạch điện dùng điốt như hình 1-22 (cổng lôgic OR
dương). Xác định điện áp và dòng điện ra trên tải I„, u„. Bài giải
Vì D ị, Dj đều là điốt loại Si, nếu chọn ngưỡng thông cho chúng bằng
0,7V thì Dị sẽ luôn luôn thông còn Dj luôn luôn bị khoá. Mạch điện được vẽ lại như hình 1-23. Si ưDI (1 ) * - i E.=10V D, t I ' - u 0.7V ( Si 0) u ■S + ra -• *- E, ov D, ra E * :r io v ra R ^ i k n 1 Hình 1-22 Hỉnh 1-23
Điện áp ra sẽ là:
U „ = E - U d,= 1 0 -0 ,7 = 9 ,3 V
I = iÌ2 -= _ Ẽ iL = 9 3mA. R 1.10^
Bài tập 1-19. Cho mạch điện dùng điốt như hình 1-24 (cổng lôgic
AND dương). Xác định dòng điện ra (I„) và điện áp ra (U^) ưên tải R. Bài giải * •
Chọn ngưỡng thông bằng 0,7V cho D| và D2, khi đó sơ đồ 1-24 được vẽ
lại như hình 1-25, tương ứng với thông, còn D, tắt. 2- 250BTKTĐIỆNTỬ.A 17 •« •• 0 , 7 V u I u ra D2 E - i r l O V R ^ Ikn "ị^ElOV Hình 1-25
Điện áp ra chính là điện áp thông cho điốt D2 và bằng Up . Vây ta có: =0,7V .
Dòng điện qua tải R cũng chính là dòng qua D2 và được tính:
E -U ,ì= l£ l^ = 9 ,3 m A . R 1.10'
Bài tập 1-20. Cho mạch chỉnh lưu dùng điốt như hình 1-26.
Vẽ dạng điện áp ra ưên tải R và xác định giá ưị điện áp ra một chiều
sau chỉnh lưu Ujc với điốt D lý tưởng. D uV 2 R 2kQ Hình 1-26 b) Bài giải
Với mạch điện cho trên hình 1-26 điốt D sẽ dẫn điện (thông) trong nửa
chu kỳ dương (+) của tín hiệu vào (từ Ơ4-T/2) còn trong nửa chu kỳ âm (-)
của tín hiệu vào (từ T/2^T) điốt D sẽ bị khoá hoàn toàn. Dạng của điện áp ra
trên tải được biểu diễn như trên hình l-27b, còn sơ đồ tương đưofng được
biểu diễn như hình l-27a. 18 2- 250BTKTĐIỆNTỬ - B + + u R S 2kQ Ude a) Hinh 1-27 b)
Dien áp ra mót chiéu tren tai diídc tính:
Ud, = 0,318U,„ = 0,318.20V = 6,36V
1-21. Cho mach chinh lim düng dió't nhuf trén hinh 1-28.
Ve dang dién áp ra trén tai R va tính giá tri dién áp ra mót chiéu
trén tái R vói dió't D thirc té' loai Si • • D Uv R 2 k Q a) Hinh 1-28 Bái giái
Vói dió't D thuc (khdng 1;^ tucmg)
nói tróf cüa dió't khi phán cuc veri tiimg
nífa chu ky cüa tín hiéu váo sé có giá
trj xác láp. Khi dió't thóng nói trd cüa
D rát bé con khi D khoá sé tuofng úng
rát lón. Vi váy dang dién áp ra diroc
biéu dién nhir trén hinh 1 -29.
Dién áp ra mót chiéu trén tái R Hinh 1-29 duoc tính: = -0,318(U,„ - U^)
= -0 ,3 1 8 (2 0 -0 ,7 ) = -6,14V 19
Như vậy so với trường hợp D lý tưcmg trong bài 1-20 điện áp ra giảm
0,22V tương đưofng 3,5%.
( 2^ Bài tập 1-22. Tính toán lặp lại bài 1-20 và 1-21 với giá trị = 200V
và rút ra kết luận gì? Bài giải
Đối với điốt D lý tưởng ta có:
u.,, = 0,318U^ = 0,318.200V = 63,6V
Đối với điốt D thực (không lý tưởng) ta có: U,, = 0,318(U™,-Uo)
= 0,318 (2 0 0 -0 ,7 ) = 63,38V
Kết luận: Khi điện áp vào có mức lớn = 200V).
Đối với trường hợp điốt thực, điện áp ra một chiều giảm 0,22V tương
đương 0,3459% ít hơn 10 lần so với kết quả trong bài 1-21 khi có mức bé ( u l = 2 0 V ).
(^2^ Bài 1-23. Cho mạch chỉnh lưu hai nửa chu kỳ dừig điốt như trên hình 1-30
a) Vẽ dạng sóng sau chỉnh lưu trên tải R,.
b) Tính giá trị điện áp ra một chiều trên tải Uj,,.
c) Tính giá trị điện áp ngược đặt lên Dị và Dj. Bài giải a)
Đây là mạch chỉnh lưu hai nửa chu kỳ dùng điốt. Để dễ dàng nhận
biết trạng thái làm việc của mạch ta vẽ lại sơ đồ tương đương khi các điốt 20
thông, khoá với từng 1/2 chu kỳ của tín hiệu vào. Ví dụ: với 1/2 chu kỳ
dương của tín hiệu vào (từ O-^T/2) sơ đồ tương đương được biểu diễn trên hình 1-31. + a) b) + + ♦ U.,(V) R. .> ư
2,2k<:ì :> *'•' < ÌRj2.2kO < u.. 5 __ 2.2k ỉìi t(s) 0 T 7 t(s) 2 c) d) Hình 1-31 e)
b) Giá irị điện áp một chiểu trên tải R( sẽ là: =0,63U,„ =0,636^: = 0,636.5 = 3 ,18V
Dạng điện áp ra sau chỉnh lưu đầy đủ cả hai nửa chu kỳ như trên hình 1 -3 le). c)
Điện áp ngược đậl lên D|, D, đúng bằng điện áp ra cực đại u,,„„ trong
từng 1/2 chu kỳ hay bằng 1/2 trị cực đại cũa điện áp vào và bằng 5V.
(^2^ Bài tập 1-24. Cho mạch điện dùng điốt như hình 1-32 (mạch hạn biên nối tiếp)
Vẽ dạng điện áp ra trên tải R: 21 Bài gỉải t Ư,(V) a) Hình 1-32 b)
Giả thiết điốt D lý tưởng, dễ dàng nhận thấy D luôn luôn thông với 1/2
chu kỳ dương (+) của điện áp vào. Mạch điện tương đương lúc này được vẽ như trên hình 1-33.
Điện áp ra sẽ là: = U y + 5V và
điốt D sẽ thông cho đến thời điểm Uy 5V
giảm xuống đến -5V ở nửa chu kỳ âm. Sau U R U
khoảng thời gian đó điốt D sẽ ở trạng thái
phân cực ngược, dòng qua điốt và qua tải
R luôn bằng không, nên điện áp ra cũng sẽ
bằng không (tương ứng với mức điện áp Hinh 1-33
vào U y < -5V. Khi U y > -5V cũng tưcnig
ứng trong khoảng nửa chu kỳ âm của tín hiệu vào, tức khi U v > -5V điốt D
thông trở lại và quá trình sẽ lặp lại như phân tích trên. .
Dạng điện áp ra được biểu diễn như trên hình 1-34: ' U JV ) 25 ^ = 2 0 V + 5 V = 2 5 V 5 / / — 71-------- J -5 2 Hình 1-34 b)
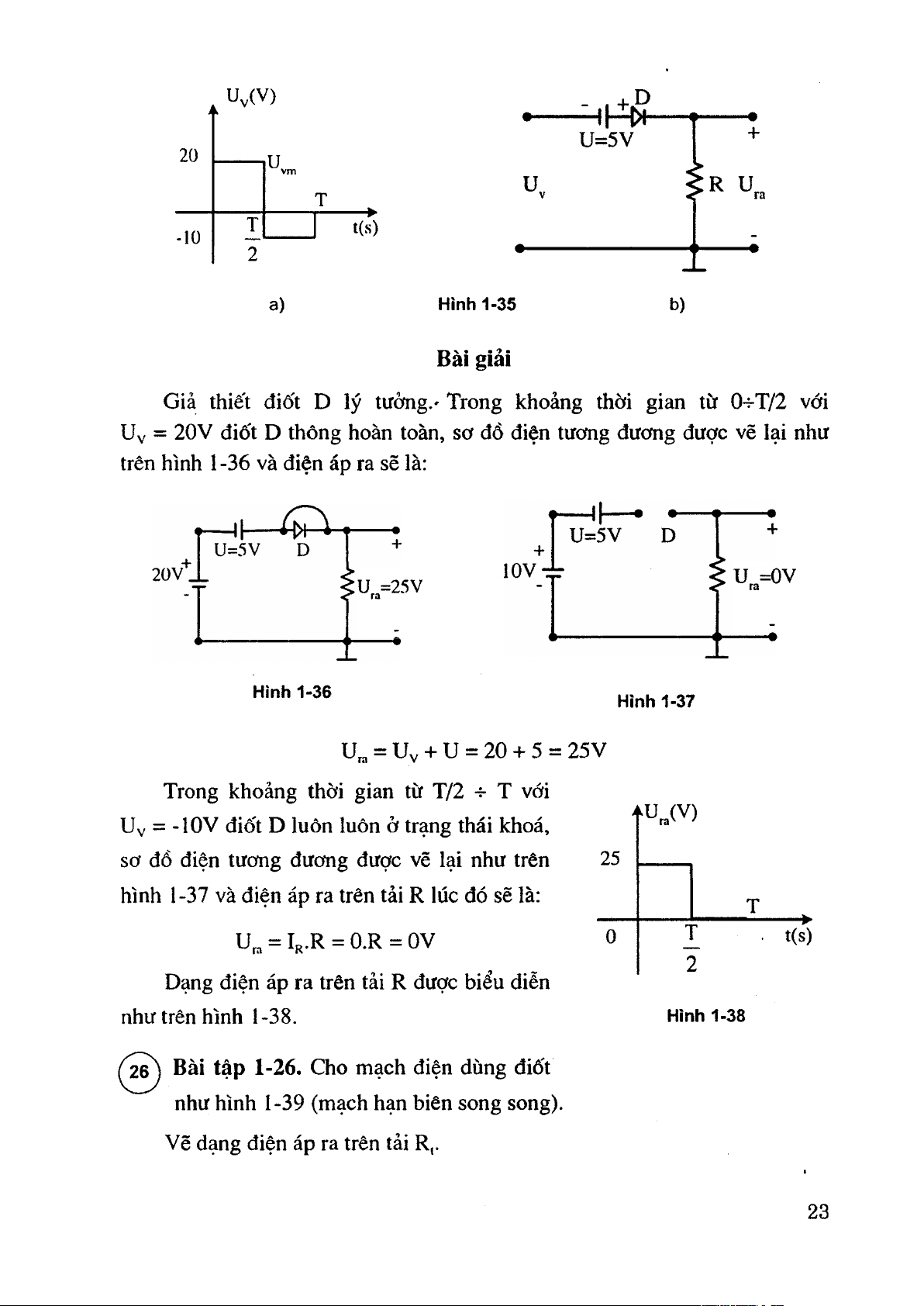
^ 2 ^ Bài tập 1-25. Cho mạch điện dùng điốt như hình 1-35. Vẽ dạng điện áp ra trên tải R. 22 Uv(V) ■ H Ị ^ + U = 5V 20 u. u R u ra -10 t(s) a) Hinh 1-35 b) Bài giải
Giả thiết điốt D lý tưởng.' Trong khoảng thời gian từ O-í-T/2 với
Uv = 20V điốt D thông hoàn toàn, sơ đồ điện tương đương được vẽ lại như
trên hình 1 -36 và điện áp ra sẽ là: ư„=OV U,=25V Hình 1-36 Hình 1-37 = Uv + u = 20 + 5 = 25V
Trong khoảng thời gian từ T/2 T T với 'U„(V)
Uy = -lOV điốt D luôn luôn ở trạng thái khoá,
sơ đồ điện tưcfng đưcmg được vẽ lại như trên 25
hình 1-37 và điện áp ra trên tải R lúc đó sẽ là: T r U^, = Ir.R = O.R = o v 0 ■ t(s) 2
Dạng điện áp ra trên tải R được biểu diễn như trên hình 1-38. Hình 1-38
Bài tập 1-26. Cho mạch điện dùng điốt
như hình 1-39 (mạch hạn biên song song).
Vẽ dạng điện áp ra trên tải R,. 23 Bài giải
Với giả thiết điốt D lý tưỏng, nó sẽ thông khi điện áp vào Uy ^ 4V,
nghĩa là toàn bộ 1/2 chu kỳ âm (-) của điện áp vào và một phần của 1/2 chu
kỳ {+) dương của điện áp vào vói Uv < 4V. Sơ đồ điện tương đương được vẽ
lại như trên hình 1-40 và ữong khoảng thời gian đó điện áp ra luôn luôn bằng nguồn u = = 4V. R R ■vw ' • + ura ỈJ-. ■ v ị t 4V 4V + Hình 1-40 Hình 1-41
Trong khoảng thời gian khi Uy > 4V,
điốt luôn luôn ở trạng thái khoá nên điện
áp ra trên tải sẽ lớn hơn 4V và bằng điện
áp vào. Sơ đồ điện tương đương được vẽ lại như hình 1-41.
Dạng điện áp ra được biểu diễn như
ưên hình 1-42 dưới đây.
( 27^ Bài tập 1-27. Cho mạch điện dùng
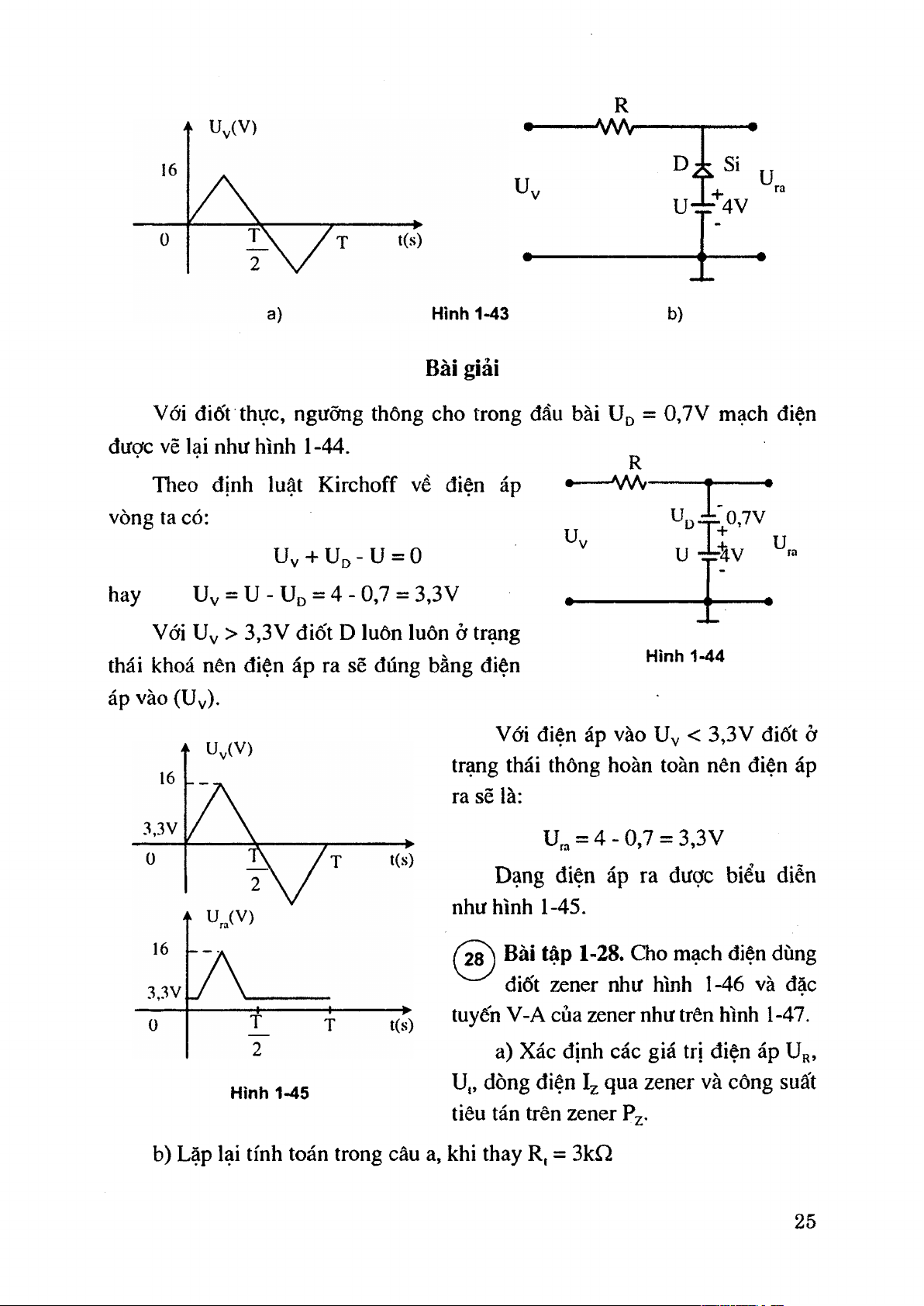
điốt như hình 1-43. Vẽ dạng điện áp
ra khi dùng điốt D loại silic với Ud = 0,7V. Hình 1-42 24 R AÂAr D i : Si U. Ura U -Ì-4V b) Bài giải
Với điốt thực, ngưỡng thông cho trong đầu bài Uo = 0,7V mạch điện
được vẽ lại như hình 1 -44. R
TTieo định luật Kirchoff về điện áp AA/V- vòng ta có: U „ ị'o ,7 V ư. T ĩ U v + U d - U = 0 u -iAv ™ hay
U v = U - U o = 4 - 0 ,7 = 3 ,3 V
Với U v > 3,3V điốt D luôn luôn ở trạng Hình 1-44
thái khoá nên điện áp ra sẽ đúng bằng điện áp vào (U v).
Với điện áp vào Uv < 3 ,3 V điốt ở
trạng thái thông hoàn toàn nên điện áp ra sẽ !à:
U ,, = 4 - 0 ,7 = 3 ,3 V
Dạng điện áp ra được biểu diẻn như hình 1-45. /2^ )
tập 1-28. Cho mạch điện dùng
điốt zener như hình 1-46 và đặc
tuyến V-A của zener như trên hình 1-47. a)
Xác định các giá trị điện áp Ur,
u„ dòng điện Iz qua zener và công suất Hình 1-45
tiêu tán trên zener Pz-
b) Lặp lại tính toán trong câu a, khi thay R, = 3kQ 25 R AA/V- Ikn Ư^=16V U^=10V2 l,2kQ^' Pz„,a.=30mA Hình 1-46 Bài giải a)
Để thuận tiện cho việc R L
tính toán các thông số của IkQ ^ 1
mạch ta vẽ lại sơ đồ tưong
đương như hình 1-48. ^16V u"" l,2kQ^' Từ hình 1-48 ta có: u U = U, = ^ •R ' R+R, Hình 1-48 16V.1,2.10’- = 8,73V 1.10^ + 1,2.10
Điện áp ư = u, đặt lên zener bằng 8,73V luôn luôn nhỏ hơn ư y = lOV
nên zener luôn luôn ở trạng thái khoá và I7 = OA.
Điện áp sụt trên R sẽ là:
Ur = Uv - u, = 16 - 8,73 = 7,27V
Công suất tiêu tán trên zener là:
p^ = U2.Iz = U z .0 = 0W b) Với R, = 3kQ.
Điện áp u trên sơ đồ hình 1-48 sẽ là:
U = - H ^ . R , = 4 5 ^ = , 2 V
R + R, ‘ 1.10’+3.10’ 26
Vì điện áp đặt lên zener u = 12V > Ư2 = lOV nên zener sẽ được mở
thông. Sơ đồ mạch điện được vẽ lại như hình 1-49.
Điện áp trên tải R, chính
bằng điện áp \Jj và bằng lOV I--------------
--------------* ------------------- 1 + = U. = U,. 16-10 = 6V I, = ^ = „ = 3,33mA ' R. 3kQ Hình 1-49 u„ 6V I, 6mA V R IkQ
. I, = 6 - 3,33 = 2,67mA
= Uz.Iz = 10V.2,67mA = 26,7mW
Thấp hơn trị cực đại cho phép = 30mW.
Bài tập 1-29. Cho mạch
ổn áp dùng zener như hình 1-50.
a) Xác định khoảng giá U^=50V
trị điện trở tải R, và dòng điện
qua tải R, sao cho điện áp ra - Iz.ax=32m A
trên nó luôn luôn ổn định U„ = Ư2 = 10V = U,. Hình 1-50
b) Xác định công suất tiêu tán cực đại trên zener. Bài giải a)
Ta biết rằng zener bắt đầu thông khi điện áp ngược đặt lên nó u >U2-
(hình 1-47 hay 1-48). Khi đó điện trở tải cực tiểu R,^i„ được xác định; R = - ^ 250Q u.,-u. 5 0 -1 0
Chú ý: Khi dòng qua zener cực tiểu (lý thuyết thì = 0), dòng qua tải
tương ứng có giá trị cực đại
Với điện áp ổn định trên tải u, = U2 thì 27
trong trường hợp đó giá trị R, được xác định chính là R,„j„ để điện áp ra trên
tải không đổi u, = = const.
Điện áp rơi trên điện trở hạn chế R sẽ là:
U r = U v - U z = 5 0 - 10 = 40V I _ U r _ 4 0 V _ ^
Và L = ^ = - ^ = 4 0 m A " R IkO
Dòng điện cực tiểu trên tải sẽ là:
U = lR-I,n,ax = 4 0 - 3 2 = 8mA
Điện trở tải cực đại sẽ là: u 10 R
T = 1 250 fì= l,25k D I.m ( i i Yn )i n 8-10
Đồ thị biểu diễn vùng ổn áp của mạch vẽ trên hình 1-51. f U,(V) t U,(V) 250n l,25kn R, 0 a) Hinh 1-51 b)
b) Công suất tiêu tán cực đại trên zener sẽ là; Pzmax = u , z .
* *Zmax. = lOV . 32mA = 320mW 0
30 ) Bài tập 1-30. Cho mạch điện dùng điốt ổn áp (zener) như trên hình 1-52.
Xác định khoảng biến đổi của điện áp vào để điện áp ra trên tải luôn
luôn ổn định và bằng lOV = Uz- Bài giải
Ta biết rằng với R, = const (cố định) điện áp thông cho zener bắt đầu từ
ư > Uz đặt lên zener. Từ sơ đồ ta có; ' R + R. ' 28 U,R, + U ,.R = U vR , __ j^a a . . _ Ì r L Nên 220 ũ R. U y= ? ƯJ,=2 0 V í ^ R. < -Jzmax=60rn A Vmin R
Thay các giá trị Uz, R, R, Hình 1-52
ta xác định được được Uvmin là:
U , „ , = 2 0 . í t H 5 l ± ^ = 2 3 , 6 7 V
Dòng qua tải sẽ là fư ,(V ) 20V .
, , = i = i = ^ = , 6 . 6 7 m A ' R, R, 1200
Dòng điện cực đại qua R sẽ là: Ư„(V)
Inmax “ ■^^Zmax ~ 16,67 + 60 23,67 36,87 = 76,67mA Hình 1-53
Điện áp vào cực đại sẽ là: Uvmax ~ “ ^ • Ỉ R m a x Uz
= 220. 76,67.10-^ + 20 = 36,87V
Đồ thị biểu diễn vùng ổn áp của mạch được biểu diễn như trên hình 1-53. 1.3. ĐỀ BÀI TẬP
Bài tập 1-31. Cho mạch điện dùng điốt như trên hình 1-54. Xác định
dòng điện I với điều kiện đặc tuyến V-A của điốt được tuyến tính hoá. p. lỌỌ ÃĂ/V—► Si I R, 12V a) b) c) Hình 1-54 29
(^3^ Bài tập 1-32. Cho mạch điện dùng điốt như trên hình 1-55. Xác định
giá trị dòng điện qua điốt Iu và điện áp ra trên tải R. -5 V Si u ra 2,2kQ a) Hình 1-55 b)
^ 3^ Bài tập 1-33. Cho mạch điện dùng điốt như trên hình 1-56. Xác định
giá trị điện áp ra R, Si E ^ u ■'Wsr-ộị-f 20V Si Ge 2 k n ra lOV l,2kQ u R, 2kQ R2^4,7kQ a) Hình 1-56 b)
( 3^ Bài tập 1-34. Cho mạch điện dùng điốt như trên hình 1-57. Xác định
giá trị điện áp ra u,;, và dòng điện qua điốt Id- D I, iH -» Si ư ra I C ) R R ,< l,2 k n R D 2,2kQ A H a f k . D •w v----- lOmA 20V 6,8kQ a) Hình 1-57 b)
( ^ ) Bài tập 1-35. Cho mạch điện dùng điốt như trên hình 1-58. Xác định
giá trị các điện áp u „ | , u ^ 2 . 30 U., R. E ' .R
• - ---- 1»... v w — lOV Ge Si l,2 k n + 12V Si 4 71^ R, 0 2 $ - Ge :3,3kQ a) Hình 1-58 b)
Bàl tập 1-36. Cho mạch điên dùng điốt như trên hình 1-59. Xác định
giá trị điện áp ra u„ và dòng điện qua điốt Id. 15V Si ± D, D^Ỷ Si Si ư. + 20V D. U. Si R > 2,2kn E2 I -5V a) Hình 1-59 b)
Bài tập 1-37. Cho mạch điện dùng điốt như trên hình 1-60. Xác định
giá trị điện áp ra và dòng điện I. E, T16V E Ịiov D |Ặ Si '' I D, i Si Si D , ị Si I ' U. U. R IkD 12V a) Hinh 1-60 b)
^^3^ Bài tập 1-38. Cho mạch điện dùng điốt như trên hình 1-61. Xác định
các giá trị điện áp và dòng điện I. 31 ura ỉ r - A ^ Ik d Ỷ 0,47kQ E T 20V D2?® ® I Hình 1-61
Bài tập 1-39. Oio mạch điện dùng điốt như trên hình 1-62. Xác định
giá trị điện áp ra và dòng điện qua điốt Iq. 0
4 0 ) Bài tậ p 1-40. Cho mạch điện dùng điốt như trên hình 1-63. (Cổng OR
lôgic âm). Xác định giá trị điện áp ra u,a. Si
041) Bài tập 1-41. Cho mạch điện dùng điốt như trên hình 1-64. (Cổng
AND lôgic âm). Xác định giá trị điện áp ra u„. 32 Si ------ l i - . ov Si Ưra -S- R ^2,2kQ HInh 1-64
(^4^ Bài tập 1-42. Cho mạch điện dùng điốt như trên hình 1-65. Xác định
giá trị điện áp ra Si lOV -KJ- Si Ụ lOV Hình 1-65
( 4^ Bài tập 1-43. Cho mạch điện dùng điốt như trên hình 1-66. Xác định
giá trị điện áp ra u„. Si
044) Bài tập 1-44. Cho mạch điện dùng điốt như trên hình 1-67. Vẽ dạng
điện áp ra trên tải R, và dòng điện Ir. 3- 250BTKTĐIỆNTỬ - A 33 ‘ U^(V) R - A A A 10 Ikn + 0 - -10 2 \ y a) Hình 1-67 b)
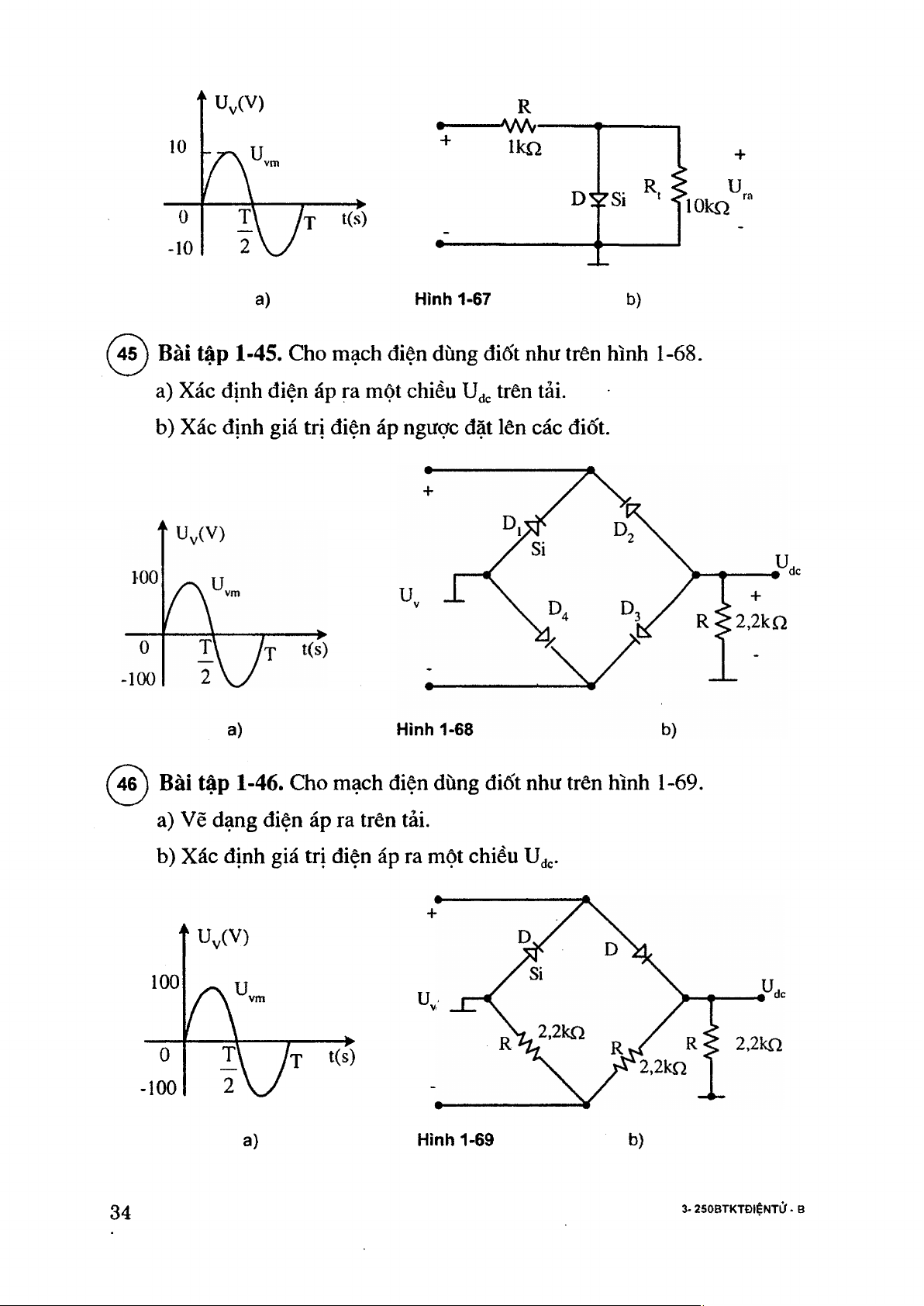
(^4^ Bài tậ p 1-45. Cho mạch điện dùng điốt như trên hình 1-68.
a) Xác định điện áp ra một chiều trên tải.
b) Xác định giá trị điện áp ngược đặt lên các điốt. dc a) 0
46 ) Bài tậ p 1-46. Q io mạch điện dùng điốt như trên hình 1-69.
a) Vẽ dạng điện áp ra trên tải.
b) Xác định giá trị điện áp ra một chiều Ujj.. ‘ U^(V) 100 Uv 0 T \ / t t(s) -100 2 \ y - a) Hinh 1-69 b) 34 3- 250BTKTĐỊỆNTỬ.B
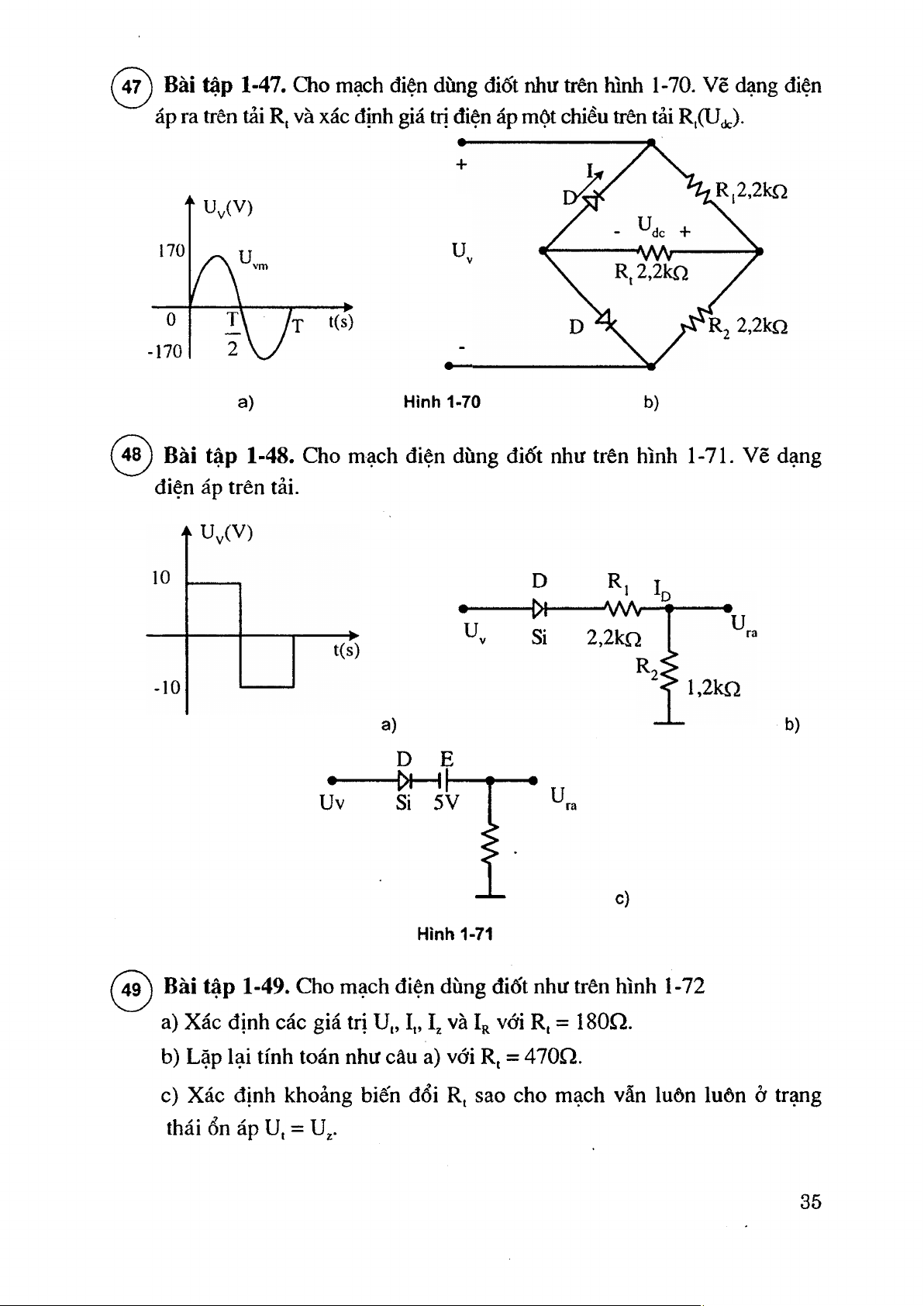
(^4^ Bài tập 1-47. Cho mạch điện dùng điốt như ừên hình 1-70. Vẽ dạng điện
áp ra trên tải Rị và xác định giá trị điện áp một chiều trên tải R,(U R,2,2kn ‘ U^(V) 170 0 t V ỵ-p t(s) 2,2kQ -170 2 v y - a) Hình 1-70 b)
( 4^ Bài tập 1-48. Cho mạch điện dùng điốt như trên hình 1-71. Vẽ dạng
điện áp trên tải. D R1 I — w v Uy Si 2,2kfì a) b) Uv Si 5V ư ra c) Hình 1-71
^^4^ Bài tập 1-49. Cho mạch điện dùng điốt như trên hình 1-72
a) Xác định các giá trị Uị, I„
và Ir với Rị = 180Q.
b) Lặp lại tính toán như câu a) vói R, = 470Q.
c) Xác định khoảng biến đổi R( sao cho mạch vẫn luôn luôn ở trạng thái ổn áp u, = Uj. 35 ' r. + 220 n + 20V U = 1 0 V í í R . | u. Pzrnax=400mW • — Hình 1-72
( 5^ Bài tập 1-50. Cho mạch điện dùng điốt như trên hình 1-73. Xác
định khoảng biến đổi của điện áp vào để điện áp ra trên tải luôn ổn định U, = U, = 8V. R
•--------- ^A ^------------- - 91Q P ^ „ = u , U = 8 V i í ro,22ko Pz.ax=400m W _ Hình 1-73
Bài tập 1-51. Cho mạch điện dùng điốt như trên hình 1-74. Xác định
giá trị điện áp ra một chiều trên tải
với trị hiệu dụng điện áp xoay
chiều trên thứ cấp của biến áp bằng 120V = Ui (rms). Hình 1-74
Bài tập 1-52. Cho mạch điện như hình 1-75. Biết u„ = lOV R„ = 20kQ 36 R, = 2 0 kQ R, = 5 kQ
Giả thiết điốt là lý tưởng,
Khi thông điện trở thuận R,h = OQ
Khi tắt điện trở ngược R„g = ooQ
Hãy xác định điện áp trên R,. D ----- v w - ' J .© R, R. Hình 1-75
Bài tập 1-53. Cho mạch điện chỉnh lưu nửa chu kỳ như hình 1-76. Nếu biết u„ =
sincot; giả thiết điốt D là lý tưởng. Hãy xác định biểu
thức điện áp trên R,. K D AAAr R, u, Hình 1-76
Bài tập 1-54. Cho mạch điện dùng điốt Zener như hình 1-77.
BiếtU, = 8,2V, d ò n g l,= lA R , = lOQ.
Tính điện trở bù R, để đảm bảo u ; = ư , = 8,2V khi điện áp u tha) doi
10% quanh giá trị u = 12V. R. +•- A/W tư ạ R. ị Hình 1-77 37
Bài tập 1-55. Đề và sơ đồ lặp lại bài 1-77.
- Xác định điện áp trên Rj.
- Xác định dòng qua điốt Zener Dj.
- Xác định công suất tiêu tán trên D^.
Bài tập 1-56. Cho mạch điện như hình 1-78.
Nếu biết điện áp một chiều là 12V, điện áp trên LED là 2V, dòng qua LED là 20mA.
a) Hãy xác định điện trở hạn chế Rị.
b) Nếu mắc song song 10 LED thay cho một LED trong sơ đồ. Hãy xác
định điện t r ở c ầ n thiết. +> Ị Îư Hlnh 1-78 38 Chưong 2
TRANSISTOR LƯỠNG cực VÀ TRANSISTOR TRƯỜNG
2.1. TÓM TẮT PHẦN LÝ THUYẾT
Transistor lưftig cực (BJT) gồm ba lớp bán dẫn p và N ghép xen kẽ nhau;
tuỳ thuộc vào các tiếp giáp P-N mà hình thành hai loại transistor: P-N-P
(transistor thuận) và N-P-N (transistor ngược) như ký hiệu trong hình 2-1. + c c I ỉ. B B - t T ransistor riguợc T ransistor thuận a) N-P-N b) P-N-P
Hình 2-1. Ký hiệu hai loại transistor N-P-N và P-N-P
Chiều của dòng điện một chiều chạy qua transistor được chỉ trong hình
vẽ trùng với chiều mũi tên quy ước cực emitơ.
Để làm việc ở chế độ khuếch đại, điện áp nguồn E được cấp cho cực E-
c tuỳ thuộc vào loại transistor được chỉ trong hình 2-1. Điện áp phân cực cho
tiếp giáp B-E phải luôn là phân cực thuận, tức là đối với transistor N-P-N cực
haza phải dương so vói cực emitơ, ngược lại, đối với transistor thuận P-N-P
cực B phải âm hơn so với cực E.
Trong cả hai loại transistor, các dòng điện đều có thể coi như tập trung tại một nút
Ie + Ic + Ib = 0 hay Ie = Ic + Ib và Ig « Ig, ic 39
Có ba cách mắc sơ đồ cơ bản của transistor là emitơ chung (EC) bazơ
chung (BC) và colecto chung (CC) căn cứ vào cực nào được lấy làm điểm
chung cho cả đầu vào và đầu ra.
Trong các sổ tra cứu và thuyết minh thường cho các thông số và đặc
tuyến theo sơ đồ mắc EC hay BC.
Đối với sơ đồ mắc BC dòng điện vào là Ig, dòng điện ra là Ic, hệ số
khuếch đại dòng điện tĩnh a được xác định:
a = Ì £ = _ k _ < i h I c + I b
thực tế hệ số a vào khoảng (0,9 ^ 0,99).
Đối với chế độ xoay chiều, khi điểm làm việc thay đổi trên đặc tuyến
ra, hê số khuếch đai dòng xoay chiều a =
trong đó A I e là biến thiên
dòng điện emitơ còn AIc là biến thiên dòng colectơ. -
Sơ đồ mắc emitơ chung (EC): dòng điện vào là dòng Ig, dòng điện ra
là dông Ic- Hệ số khuếch đại dòng điện tĩnh được xác định;
tuỳ thuộc vào loại transistor p có giá trị từ vài chục đến hàng trăm lần. Ic và
Ib là giá trị dòng điện tại điểm làm việc tĩnh.
ở chế đô xoay chiều hê số p đươc xác đinh p = . AIb
Nếu biết hệ số khuếch đại a có thể xác định được hệ số p và ngược lại: a = ^ v à p = “ p + 1 " 1 - a
Ngoài ra còn các tham số khác như điện trở vào, điện trở ra, hỗ dẫn...
Các tham số của trahsistor cũng có thể xác định gần đúng bằng phương pháp
đồ thị dựa vào đặc tuyến của transistor. 40 AI, Ib,
Điện tri ra R„ = rcB = ^AI,
Để transistor lưỡng cực làm việc bình thường ngoài điện áp cung cấp E cho
cực E và c cần một điện áp phân cực một chiều đặt vào Bazơ-Emitơ gọi là thiên
áp. Điện áp này dùng để thiết lập chế độ một chiều và điểm làm việc tĩnh.
Thiên áp ban đầu UggQ sẽ quyết định dòng điện tĩnh, độ khuếch đại, độ méo.
u B£o « (0,2 4- 0,6) V đối vói transistor Ge
UggQ » (0,5 4-1,0) V đối với transistor Si.
Có ba cách tạo thiên áp cho transistor.
- Tạo thiên áp bằng dòng bazơ (hình 2.2a)
TTiiên áp UggQ được xác định
Suy ra điện trở R| cần thiết E - U - ^BEO BO
Trong đó: E là điện áp nguồn;
Ug£Q là thiên áp cần tạo ra;
IgQ là dòng bazơ xác định theo UggQ trên đặc tuyến vào của transistor. a)
Hình 2-2. Tạo thiên áp dio transistor lưỡng cực b) 41
- Tạo thiên áp bằng phương pháp phân áp (hình 2-2b)
Thiên áp UggQ = Ip.Ra- Suy ra D _ ^BEO
trong đó Ip - dòng phân áp I R| + R 2
Ip được chọn bằng (4 ^ 10)Igo
Nếu cho trước ưggo xác định được Igo trên đặc tuyến vào của transistor.
Điện trở R| xác định từ biểu thức: ^BO
“ E - Ip.R2 = E - UggQ E - U Suy ra R, BEO ĩ p + l B O
Trong trưòmg hợp có điện trở mắc ở emitơ thì trong các công thức trên
phải tính đến sụt áp một chiều trên điện trở đó.
- Chế độ một chiều và đường tải một chiều.
Xác định điểm làm việc tĩnh 0; khi cung cấp cho bazơ thiên áp ban đầu
U beo . thì sẽ thiết lập dòng tĩnh
và điện áp một chiều Ư^EO • Toạ độ của
điểm làm việc tĩnh o (Ico ’UcEo)- Điểm o cũng chính là giao điểm của
đường tải một chiều với đưòng đặc tuyến ứng vói dòng Igo (hình 2-3). a) b)
Hình 2-3. Đặc tuyến vào (a) và đặc tuyến ra (b) 42
- Đường tải một chiều là sự phụ thuộc dòng Ic vào điện áp ứng với
điện trở tải một*chiều
và được xác định theo biểu thức; u „ = E - Ic.R= £ Cách dựng: Cho
= 0 -> I,, = — , xác đinh đươc điểm B. Cho
= 0 ^ u„ = UcE = E, xác định được điểm A.
Nối điểm A với B được đường tải một chiều.
- Đường tải xoay chiều R_, cũng được xây dựng trên đặc tuyến ra nhưng
đối với điện trở tải xoay chiều, tức là khi có tín hiệu vào, đó eũng là đường
thẳng và đi qua điểm làm việc tĩnh o .
Cách dựng: Từ điểm U^gQ trên trục hoành, cộng thêm một điện áp bằng
I(,qR_ , được điểm A'. Kẻ đường thẳng qua hai điểm o và A', được đường tải xoay chiều. E
Cũng có thể xác định dòng !(,
= — được điểm B' trên trục tung, kẻ
đường qua B' và o cũng nhận được đường tải xoay chiều.
Trong các bài tập áp dụng, có thể sử dụng một trong hai cách trên, tuỳ
từng trường hợp cụ thể.
- Transistor trường (FET) là loại transistor được chế tạo dựa vào hiệu
ứng trường, đó là điều khiển độ dẫn điện của bán dẫn loại N hay p, nhờ một
điện trường bên ngoài.
Có hai loại FET - đó là J-FET (điều khiển bằng tiếp xúc P-N) và
MOSPET là loại FET có cực cửa cách ly bằng lớp ôxit. Hình 2-4 là ký hiệu
JFET kênh N và kênh p. D D G a) J-FET kênh N b) J-FET kênh p
Hình 2-4. J-FET kênh N và kênh p 43 s - là cực nguồn D - cực máng G - cực cửa.
Vì phân cực cho cực cửa của J-FET luôn là phân cực ngược nên điện trở
vào rất lớn và dòng điện ly = Iq = 0; Iß = Ij.
Dòng Iịj được điều khiển bằng điện áp đặt vào cực cửa Uqs và được xác
định bằng biểu thức: uOSK
trong đó U gs là điện áp bất kỳ đặt vào G-S;
Ugsk là điện áp khoá ứng với dòng Iq = 0.
Quan hệ giữa Ijj và Uqs được diễn tả bằng đặc tuyến truyền đạt còn quan
hệ Iq = f(ƯDs) với các trị số Uqs khác nhau được gọi là họ đặc tuyến ra. Đây
là hai đặc tuyên đặc trimg cho FET, căn cứ vào đó, có thể xác định gần đúng
các thông số của FET- b)
Hình 2-5. Đặc tuyến truyền đạt (a) và đặc tuyến ra (b) của J-FET kênh N
Hỗ dẫn của FET: g„ =
hay mS (milisimen) chi’ rõ khi điên AUqs V
áp đặt vào cực cửa thay đổi IV thì dòng Iß thay đổi bao nhiêu mA.
MOSFET gồm hai loại: MOSFET kênh đặt sẵn và MOSFET kênh cảm ứng. -
MOSFET kênh đặt sẵn; kênh dẫn điện loại N hay p hình thành ngay từ
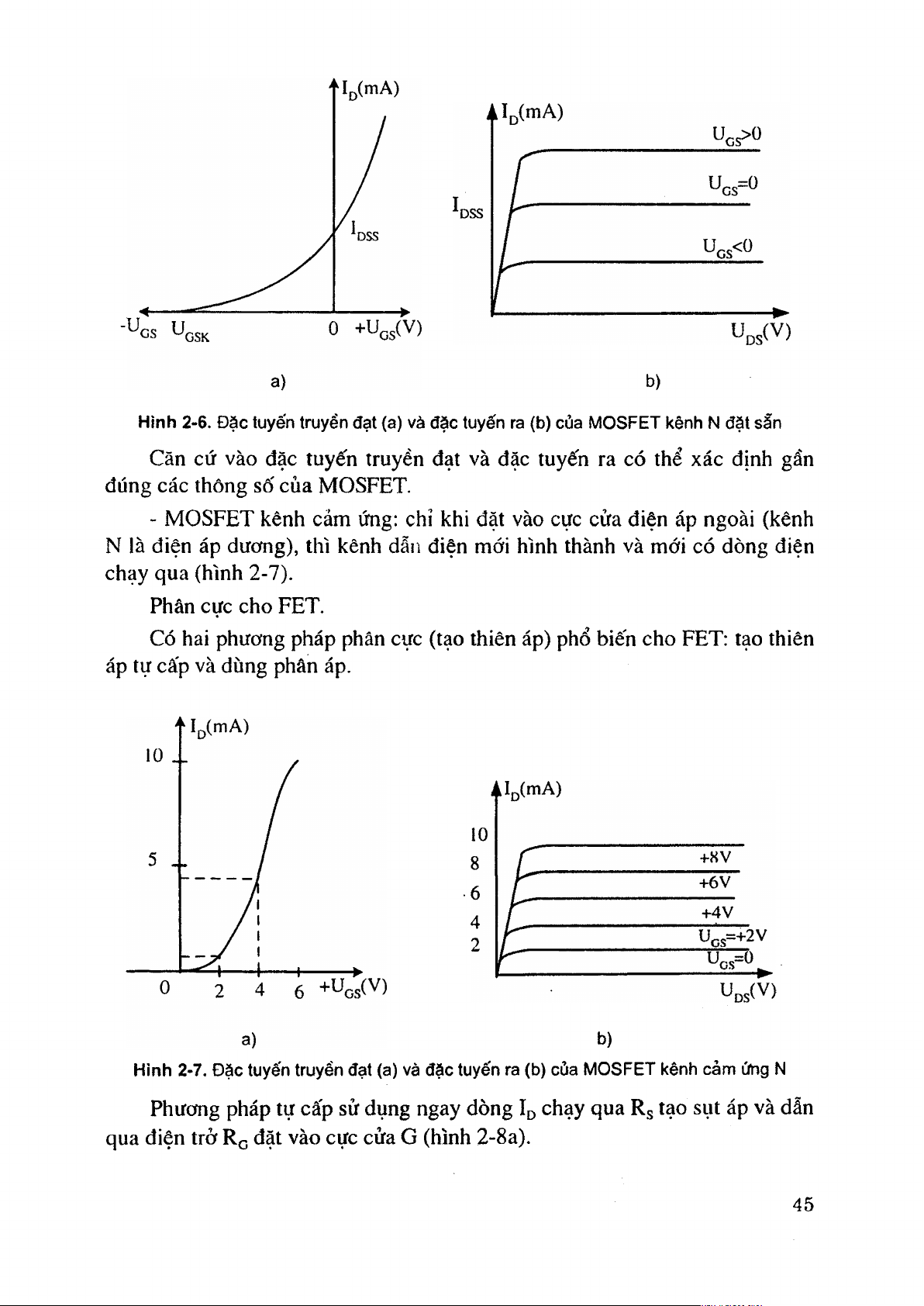
khi chế tạo. Đặc tuyến truyền đạt và đặc tuyện ra chỉ dẫn trong hình 2-6a, b. 44 b)
Hình 2-6. Đặc tuyến truyền đạt (a) và đặc tuyến ra (b) của MOSFET kênh N đặt sẵn
Căn cứ vào đặc tuyến truyền đạt và đặc tuyến ra có thể xác định gần
đúng các thông số của MOSFET. -
MOSFET kênh cảm ứng: chỉ khi đặt vào cực cửa điện áp ngoài (kênh
N là điện áp dương), thì kênh dẫn điện mới hình thành và mói có dòng điện chạy qua (hình 2-7). Phân cực cho FET.
Có hai phương pháp phân cực (tạo thiên áp) phổ biến cho FET: tạo thiên
áp tự cấp và dùng phân áp. b)
Hình 2-7. Đặc tuyến truyền đạt (a) và đặc tuyến ra (b) của MOSFET kênh cảm úhg N
Phưcmg pháp tự cấp sử dụng ngay dòng ĩj) chạy qua Rs tạo sụt áp và dẫn
qua điện trở Rq đặt vào cực cửa G (hình 2-8a). 45
Vì 1(3 = 0; Ip = Ij nên Urs = Id-Rs = Uqs; cực (+) đặt vào cực s và cực (-) đặt vào cực G.
Rị - gọi là điện trở tạo thiên áp.
Rq - là điện trở dẫn thiên áp; Ro có trị số lớn hàng chục hoặc trăm kQ. R , = - ^
Hình 2-8. Tạo thiên áp cho J-FET
Hình 2-8b là sơ đổ tạo thiên áp bằng phương pháp phân áp.
Điện áp trên cực cửa ƯQ được xác định Ư G =— ~ — Ra R.+Ra
Uo là điện áp cực G so với đất.
U gs = U o - U 3 = ư g - I oR s
Mạch phân áp cho MOSFET kênh N đặt sẵn cũng tương tự như hình 2-
8b. Riêng đối với MOSFET kênh cảm ứng, việc tạo thiên áp có khác với J-
FET, nó được tạo thiên áp giống như vói transistor lưỡng cực N-P-N: có thể
dùng phương pháp hồi tiếp từ cực D về cực G hay dùng phưcmg pháp phân áp (hình 2-9a, b).
Trong sơ đồ 2-9a ƯDS = U gs (vì dòng l o = 0, qua Ro không có dòng chạy qua) UdS “ E - Iq-Rq Suy ra Uq5 = E - Iq.R0.
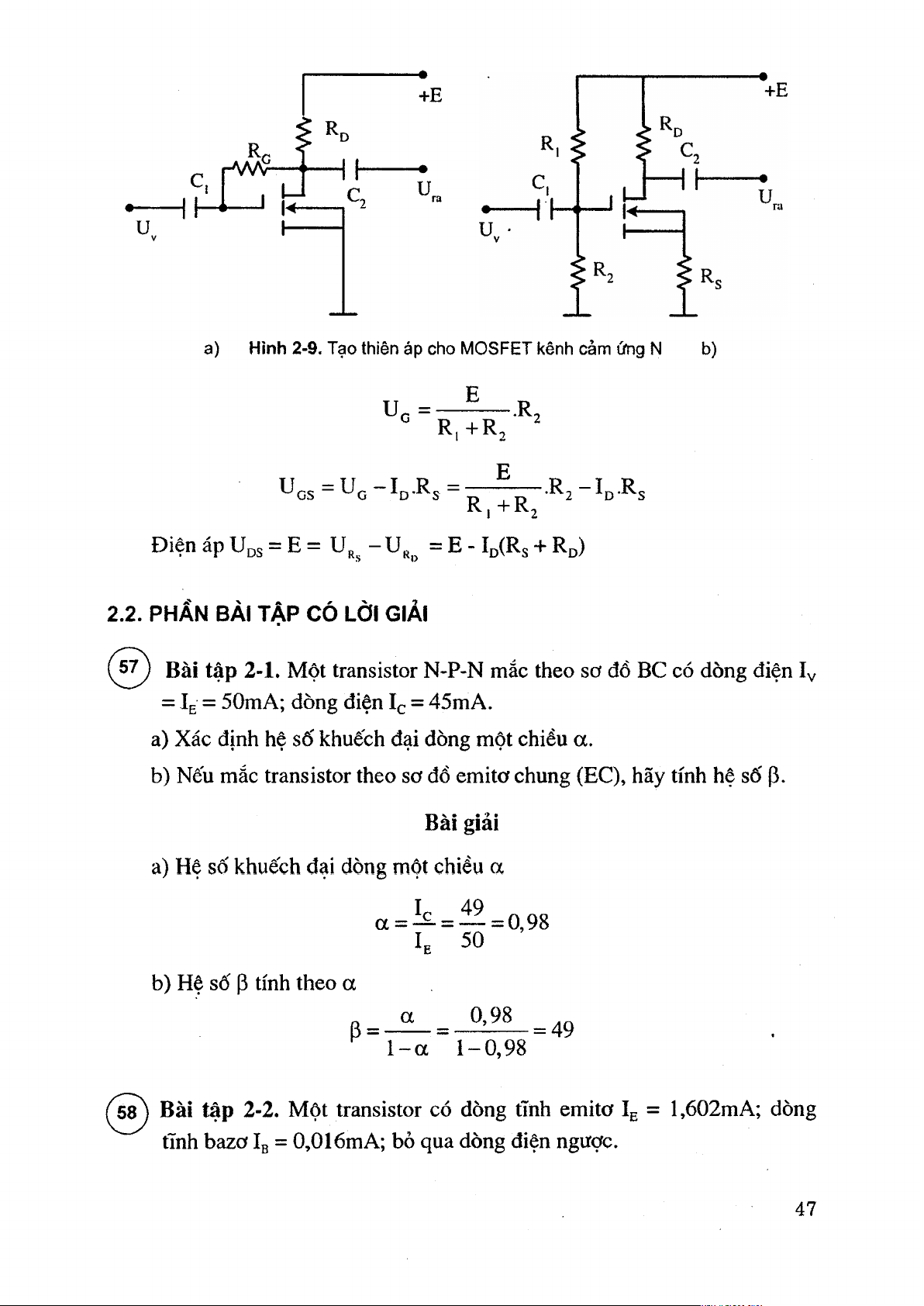
Trong sơ đồ 2-9b, điện áp cực cửa so với đất. 46 +E RD u i- a)
Hình 2-9. Tạo thiên áp cho MOSFET kênh cảm ứng N b) U g = •R R| + R 2 E ^GS ~ ^D'^s ~ R, + R2 Điện áp Uds = E = = E - Id(Rs + Rd)
2.2. PHẦN BÀI TẬP CÓ LỜI GIẢI
( 5^ Bài tập 2-1. Một transistor N-P-N mắc theo sơ đồ BC có dòng điện L
= Ig = 50mA; dòng điện Ic = 45mA.
a) Xác định hệ số khuếch đại dòng một chiều a.
b) Nếu mắc transistor theo sơ đồ emitơ chung (EC), hãy tính hệ số p. Bài giải
a) Hệ số khuếch đại dòng một chiều a I 49 a = -^ = — = 0,98 Ie 50
b) Hệ số p tính theo a
ẹ> = — = ............= 49 1 - a 1-0,98
(^5^ Bàl tập 2-2. Một transistor có dòng tĩnh emitơ Ig = l,602mA; dòng
tĩnh bazơ Ig = 0,016mA; bỏ qua dòng điện ngược. 47
a) Xác định dòng tĩnh colectơ Ic-
b) Tính hệ số khuếch đại p, a. Bài giải
Tính dòng tĩnh colectơ Ic
= Ig - Ig = r,602 - 0,016 = l,586mA
Hê số khuếch đai a = — = ^ = — — = 0,99 Ie Ie 1,602
lẹ _ Iẹ - I b _ 1,6 02 -0 ,0 1 6
Hệ số khuếch đại p 99,125 I,B I 0^016
Cũng có thể xác định p theo công thức: a 0,99 = 99 1 - a 1-0,99
59) Bài tập 2-3. Biết đặc tuyến vào và đặc tuyến ra của transistor mắc theo
sơ đồ emitơ chung EC như hình 2-10.
Bằng phương pháp đồ thị hãy xác định:
a) Hệ số khuếch đại p tại điểm làm việc A. b) Điện trở vào = ĨBE-
c) Hệ số khuếch đại a nếu mắc theo sơ đồ bazơ chung BC.
d) Nếu tín hiệu vào Ig thay đổi, xác định hệ số khuếch đại dòng xoay chiều. -ụ m A ) Ig=0,4iĩiA 40 Ig=03mA l3=0,2mA i . . ĩp=0,lmA 0,2 0,4 0,50,6 0,8 Ugg(V) ưce(V) a) b)
Hình 2-10. Đặc tuyến vào (a) và ra (b) của transistor 48 Bài giải
a) Hệ số khuếch đại tĩnh tại điểm A.
p = Ị ^ = “ : l ° Ị = 100 - 3 0 ,2 .1 0 BO 1..^ 0 ,7 0 -0 ,5 0,65 ^
b) Điên trở vào R v = r,^ = ---- S _ S B - E = _ — — — , = — = 3 ,2 5 k Q AL (0,3-0,1)10-' 0,2.10“' B
c) Nếu mắc theo sơ đồ bazơ chung BC hệ số khuếch đại tĩnh a được xác định a = i = ^ = 0 ,9 8 9 1 + p 1 0 0 + 1
d) Khi dòng điện vào Ig thay đổi từ 0,1 đến 0,3mA, tìm biến thiên dòng
Ic tương ứng trên đặc tuyếh ra, tính được hệ số khuếch đại p xoay chiều. /
6 _ Aĩ c _ ( 2 8 , 5 - 9 , 8 ) 1 0 -^ = 93,5 A L ( 0 ,3 - 0 ,1 ) 1 0 '
(^6^ Bài 2-4. Cho mạch khuếch đại dùng
transistor như hình 2-11 B iết; R c = 5 k Q p = 5 0
điện trở vào Ry = ĩgE = IkO
điện áp vào Uy = UgE = 0,1V
a) Xác định dòng điện vào và dòng điện ra.
b) Tmh hệ số khuếch đại điện áp của transistor. Hình 2-11 Bài giải a) Dòng điện vào 0,1 = 10"" = 0,lm A Dòng điện ra:
I^^ = I^ = pỈ3 = 50.0,1 =5m A 4- 250BTKTĐIỆNTỬ - A 49 Điện áp ra: U , =
= Ic-Rc = 5.10^5.10^ = 25V
b) Hệ số khuếch đại điện áp . 0,1
Bài tập 2-5. Đặc tuyến vào và ra của transistor có dạng như hình 2-12.
a) Hãy xác định hỗ dẫn của transistor tại điểm làm việc o.
b) Nếu biết điện áp ƯBE thay đổi 0,2mV, điện trở Rc = 4kQ. Hãy xác định điện áp ra.
c) Tính hệ sô' khuếch đại điện áp. Ic(mA) 50^iA 1^=4,2 40|J.A U=3,Q. 30^A 20|aA I„=10HA 7 0,8 U„,(V) U c e ( V ) a)
Hình 2-12. Đặc tuyến vào (a) và đặc tuyến ra (b) của transistor b) Bài giải
a) Hỗ dẫn của transistor được xác định bằng phương pháp đồ thị s = _éíc_ AUbb ’ V
s = A 2 Í L - = < iÌ2M )E Ĩ , Í I Ẹ Ĩ = ,2 Í ^ hay 12ms - u „ , 0 ,7 - 0 ,6 0,1 V
b) Nếu AUgg = 0,2V thì dòng Ic biến thiên
AIc = AU Bg.s = 0,2.12 = 2,4mA
Điện áp ra u „ = AIc-Rc = 2,4.10 \ 4 . 10' = 9,6V 50 4- 250BTKTĐ1ỆNTỬ - B
c) Hệ số khuếch đại điện áp K „ = H ^ = M = 48 “ u, 0,2
(^6^ Bài tập 2-6. Transistor lưỡng cực có đặc tuyến vào và ra mắc theo sơ
đồ EC như hình 2-13. Căn cứ vào đặc tuyến hãy xác định gần đúng các thông sô' sau:
a) Điện trở vào tĩnh tại điểm o.
b) Điện trở vào động.
c) Hệ số khuếch đại dòng điện một chiều p.
d) Hệ số khuếch đại dòng xoay chiều. - I b(^ A ) ‘ Ỉ Ặ m A ) 40 250fxA 200n A 250 30 200 25, ISOuA / 15. , L . _ _ iü Q ü A . 50 ỹ f ! ! / I«=50jiA ... ---------► 5 ’ (V) BE lò U^V) a) b)
Hình 2-13. Đặc tuyến vào (a) và ra (b) của transistor luỡng cực Bài giải
a) Điện trở vào tĩnh R = r , = 4 k Q '' Igo 150.10-®
b) Điện trở vào động Rvd o _ - U be, _ 0 ,6 8 - 0 ,5 2 = l,6 k Q ^ V đ “ a t ^ T T AI B Ib, - I b. (200- 100)10
c) Hệ số khuếch đại dòng một chiều p 51 I » I50.10-*
d) Hệ số khuếch đại dòng xoay chiều p_ AI3 ~6
AIb= I3 -Ib_ =(200-100)10-^ = 100.10
Tìm AIc tương ứng trên đặc tuyến ra I„ =30mA; = 15mA AIc = (30-15).10l (200-100)10-"
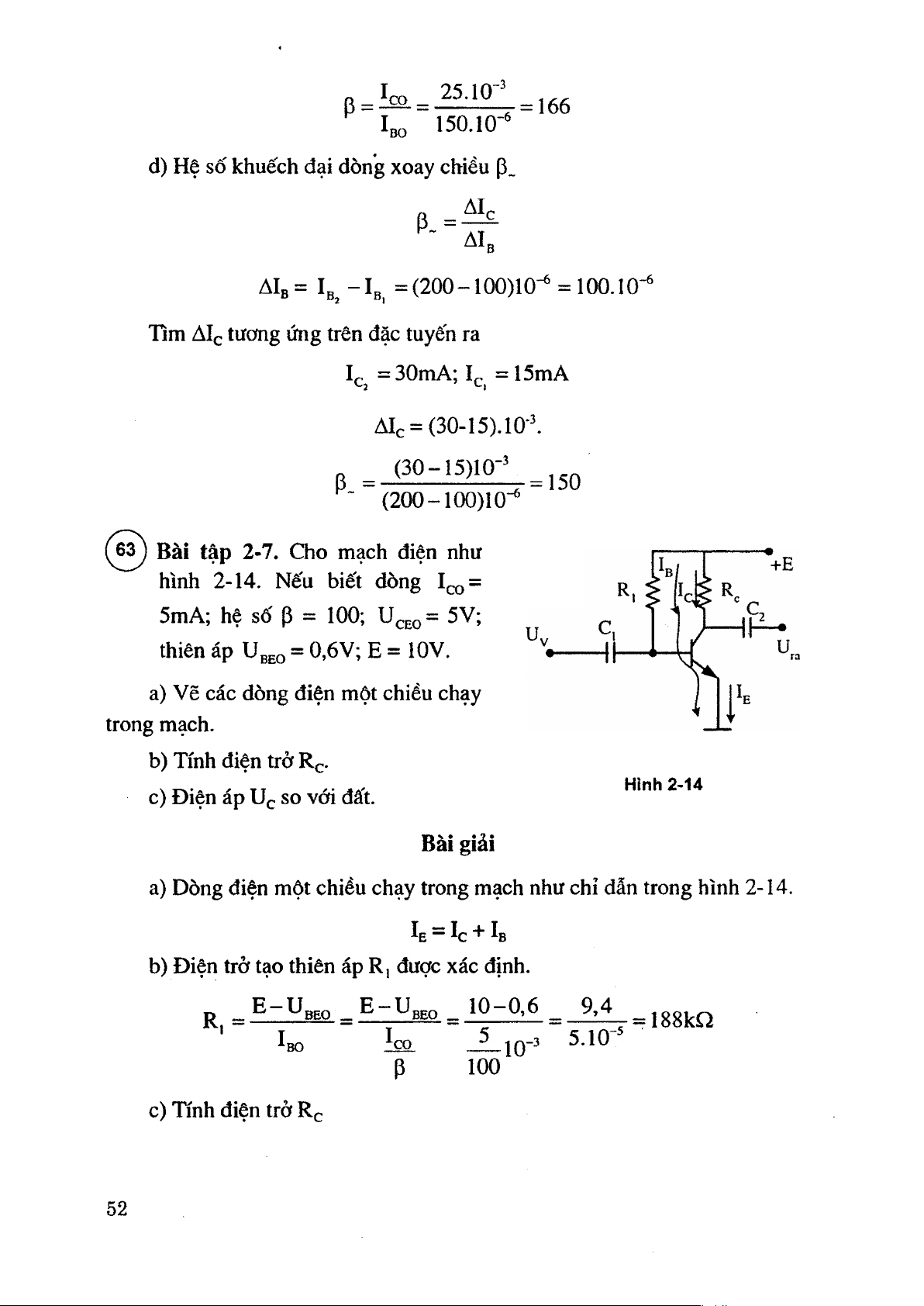
( 6 ^ Bài tập 2-7. Oio mạch điện như
hình 2-14. Nếu biết dòng Ico =
5mA; hệ số p = 100; 5V;
thiên áp U beo = 0,6V; E = lOV.
a) Vẽ các dòng điện một chiều chạy trong mạch.
b) Tính điện trở R e Hình 2-14
c) Điện áp Uc so với đất. Bài giải
a) Dòng điện một chiều chạy trong mạch như chỉ đẫn trong hình 2-14. Ie = Ic + Ib
b) Điện trở tạo thiên áp R| được xác định. E - U ^ E - U ^ o 1 0 -0 ,6 9,4 R, 188ka Ibo ^co ^ ^q-3 5.10 * p 100
c) Tính điện trở R, 52 I „ I „ 5.10-’
d) Điện áp Uc so vái điểm mass chính là điện áp UçgQ U c = U ,,o = 5V @
Bài tập 2-8. Cho mạch điện như hình 2-14. Nếu biết R, = 220k0;
Rc = 2kQ; ß = 50; ưggQ = 0,5V. Hãy xác định các thông số tĩnh:
dòng Ig, Ic, Ie, điện áp Uceo • Bài giải
a) Xác định dòng Igo R, 220.10' 220.10'
b) Dòng Ico = ßlß = 50.34, lụ K = 1,7mA
c) Dòng 1^0 = Ico + I bo = 1 >7 + 0,0342 = 1,7342mA. d) Điện áp U^go
U eEo=E-Ico.Rc=10-l,7.10"'.2.10^=6,6V
Bàl tập 2-9. Mạch điện như bài 2-7 nhưng mắc thêm điện trở Re ở
emitơ và biết sụt áp trên điện trở này là IV.
a) Xác định trị sô' R|, Rc, Re-
b) Xác định điện áp U c Uß so với điểm mass của máy. Bài giải a) Xác định Re U re = I e o - R e = 1 V _ IV IV 1 Suy ra Rb = — = — = ^ ------- = 198Q Iro + — 5 .1 0 '^ + ~ 10-^ “ ß 100 - Điện trở R 53 R _
_ E - ^ beo - U r , _ 1 0 - 0 ,6 - 1 168kQ ' I bo I bo 5.10-^ - Điện trở Rc ^CO‘^ C V. “ ^ ^CE V.V O .V/ ^RI,VJ.- Suyra: R , = = 800Q leo 5 . 10-^ b) Điện áp
Uc = E - Ico R c= 1 0 -5 .1 0 “l8 0 0 = 6V h a y
U c = U , , / + U , ^ = 5 + l = 6V Điện áp
Ub = Uggo + ƯR = 0,6 + 1,0 = 1,6V
( e ^ Bài tập 2-10. Cho mạch điện +E
như hình 2-15. Biết R, = 300kQ; R
Rh = 2,7kQ; p = 100; Ư3,o = 0,5V ;E = 12V.
a) Xác định các tham số tĩnh. ra
b) Nếu mắc R, = 2,7kQ hãy tính R. R.
điện trở tải xoay chiều. Bài giải
a) Trước hết xác 'định dòng tĩnh Hình 2-15 bazơ I„„ ■BO^'1 ' '-'BEO ' ^E O ^'E BEO (ở đ â y
I e o = I co + I b o = I b o + P I b o = 0 + P)Ibo) E - U „ .. 1 2 -0 ,5 Suyra l30 = BEO _ = 20ụA R, +(1 + P)Re
300.10"+(1 + 100).2 ,7.10^
- Dòng tĩnh 1^0 = lOOIgo = 100.20^iA = 2mA
- Dòng tĩnh 1^0 = Ic» + Ibo = 2 + 0,02 = 2,020m A .
- Điện áp trên cực E, cực c và B so với điểm mass: 54
Ue = Ieo-Re = 2,02.10-^2,7.10" = 5,45V Điện áp U c = E = 12 V Điện áp Ub = Ue + = 5.45 + 0,5 = 5,95V
b) Nếu mắc R, = 2,7kQ thì điện trở tải xoay chiều ở mạch emitơ. R = R / / R = A
ì = A Z : ^ = l , 3 5 k Q ^ ' R e+ R , 2,7 + 2 ,7
Bài tập 2-11. Cho mạch khuếch đại dùng ữansistor lưỡng cực như
hình 2-16a. Biết E = lOV; R c = 5kQ; Re = 0,2Rõ R, = 85kO; R , = 15kQ ; = 4 V ; Ico « c ; p = 50-
a) Hãy xác định các tham số tĩnh của transistor.
b) Điểm làm việc tĩnh o và dựng đưòng tải một chiều. a) Hình 2-16 b) Bài giải a) Có thể coi ^EO ~ ^ E - U Suy ra: CEO ■c ' * 'E 1 0 - 4 = 10-^A = lmA Ic o = (5 + l).10- 55
- Dòng tĩnh bazơ IgQ: - Thiên áp Ur£0 BE — O Ip- p R^ 2~ ^RE R E~ ------- ----Rt ~ 2 ^E0 E'^ O EE 10-M0^=0,5V (15+ 85). 10^
b) Toạ độ điểm làm việc tĩnh O:
= lmA;UcE0 = 4 V . t)ể dựng đường
tải một chiều cần xác định một điểm nữa. Từ biểu thức phương trình đưòng tải một chiều. U„ = E -Ic .R c Cho Ic = 0
u„ = E = lOV (điểm A trên trục hoành) nối qua điểm A Bài giải
- Điện trở tải xoay chiều R_. R. = R ^ //R ,= Ì ^ = ^ = 2,5kQ R c+R . 5 + 5 -
Để đựng đường tải xoay chiều R_ cần xác định một điểm trên trục
hoành hay, trên trục tung rồi nối với điểm làm việc tĩnh o. Từ điểm
cộng thêm một đoạn ứng với điện áp bằng IcqR- •
IcoR_= 1012,5.10^ = 2,5V
ta được điểm A' trên trục hoành (hình 2-16b).
Nối điểm A' với điểm o và kéo dài sẽ được đường tải xoay chiểu. Cũng
có thể dựng đường tải xoay chiều bằng cách xác định điểm B' trên trục tung E 10
ứng với dòng I „ = —— = — ——r = 4m A , rồi nối điểm B’ và o . & ^ R_ 2,5.10' 56
( m ) Bài tập 2-13. Cho mạch điện như hình 2-16a. Nếu E = lOV; ƯCEO = 4V ;
Rg = 0,1 Rc‘, Ico=20m A ; Ug£Q=0,7V, từ đặc tuyến vào của
transistor ứng với UggQ = 0 , 7 V , tìm được IgQ = 0 ,2 m A .
a) Xác định trị số các điện trở Rc, Re, Ri, R-> để đảm bảo được các thông số trên.
b) Xây dựng đường tải một chiều. Bài giải
a) Xác định trị số các điện trở Từ biểu thức: E = ^CEO ^EO^E * ^CEO
(ở đây có thể coi I^Q « IgQ để đơn giản cho việc tính toán). Suy ra + R . = - - - ggg = = 300Q ^ lœ 20. 10“^ Re 0,1 Rc = l,lR c ~ 3000 M = 272,70 1,1
Rg = 0 , l R c = 2 7 ,2 Q .
- Điện trở Rj được xác định theo biểu thức: '^BEO ~ Suy ra
(ở đây chọn dòng phân áp Ip = 5 Ißo ) R
0.7 + 2 0.10 -.2 7 ,2 7 ..^ ^ 5.1„ 5.0,2.10-’
- Điện trở R| được xác định từ biểu thức: • I ♦ •
Ri(Ip+ I^q) = E - IpR2 = E - UggQ-^IgQRg " u r a r
E - U „ o - I ^ R , _ 10 - 0 ,7 - 0, 5 4 5 _ , 5 l " + I „ 6.0,2.10- 57
b) Để xây dựng đường tải một chiều, ngoài điểm làm việc tĩnh o đã biết
0(20mA, 4V) cần xác định một điểm nữa.
Từ phương trình UcE = E - Ic(Rc + Re) nếu cho UcE = 0 thì E 10 = 0,0333A = 33,3mA Rị. + Rg 300
ta được điểm B trên trục tung, nối B với o và kéo dài sẽ được đường tải một chiều (hình 2-17). Hình 2-17 0
70) Bài tập 2-14. Biết đặc tuyến truyền đạt và đặc tuyến ra của một J-FET
kênh N như hình 2-18.
a) Xác định trên đồ thị dòng bãơ hoà Ij5ss^ và điện áp khoá U qsk-
b) Tính dòng Iq ứng với các giá trị Uos = OV; Uos = -2 V; Uos = -4V và U g s = -6 V. Bài giải
Từ đặc tuyến truyền đạt Id = f ( Ư G s ) hình 2-18a, dòng bão hoà Ipss ứng
với U q s = ov, Ij5ss = 15mA.
Điện áp khoá U gsk ứng với Iq = 0, trên đồ thị xác định được Uqsk = -8V.
b) Dòng Ij3 phụ thuộc vào điện áp ƯQS và được xác định bởi biểu thức; 58 a) b)
Hình 2-18. Đặc tuyến truyền đạt (a) và đặc tuyến ra (b) của J-FET kênh N Id = Idss(1 - ^ ) ' U GSK
Ugs = 0 ^ Id = Idss = 15mA Uos = -2V-^ = 15 (1 - = 8,437mA. -“0
U gs = -4V ^ l o = 15 = 3,75mA. —o
Ucs = -6V ^ Id = 1 5 (1 -— )' = 0,9375mA.
( 7 1 ^ Bài tập 2-15. Cho mạch điện dùng
J-FET kênh N như hình 2-19. Đặc +E
tuyến của J-FET như bài 2-14.
Biết E = 15V; điểm làm việc tĩnh
được chọn ứng với Rd = IkQ.
a) Xác định trị số Rị. H h -p -H iỊ ra U
b) Xác định thiên áp Uqsq .
c) Điện áp trên cực máng Up. Bài giải Hình 2-19 a)
Điện trở Rs được xác định theo biểu thức: R - - U q d k - 8V = 266Q ^ 21™ 2.15.10-^ 59 b) Thiên áp
= R Jn = 266.7,5.10'" « 2 V GSO S-^D
(ởđây I t , = % = ^ = 7,5mA) • 2 2
c) Điện áp Uq
U d = E - I d. Rd = 15 - 7 ,5 .1 0 ^ 1 0 ^ = 7 ,5 V
Bài tập 2-16. Cho mạch tạo thiên áp
cho J-FET kênh N bằng phương pháp
phân áp như hình 2-20. Biết: E = 15V;
R, = 600kQ; R, = 150kQ; Rß = l,5kQ; Rs = IkQ; 5mA.
a) Xác định Uas-
b) Dòng cực máng Ip.
c) Điện áp trên cực máng Up. Bài giải a)
Hình 2-20. Mạch tạo thiên áp cho J-FET 5.10"\10' = - 2 V GS R| +R j (600 + 150)10 E 15
Điện áp trên cực cửa U f - •_ ,R ,= 150 = 3V R ,+ R , " 600 + 150
Điện áp trên cực nguồn Us = ƯQ - U qs = 3 - (-2 ) = 5V. hay
Us = Is.Rs = Id-Rs = 5.I 0 M 0’ = 5V
b) Xác định lại dòng cực máng Ip
I. = L = ^ = ^ = 5.10-'A = 5mA ^ Rs 10'
c) Điện áp trên cực máng Up
Ud = E -Id.R d= 15-5.10M ,5.10^ = 7,5V
Điện áp U ds = Uo - U s = 7,5 - 5 = 2,5V.
( t ỉ ) Bài tập 2-17. Cho mạch điện dùng MOSFET kênh đặt sẵn như hình
2-21 a và đặc tuyến truyền đạt như hình 2-21b. Biết: E = 12V; Ro = 200kQ; u 3 , 5 V .
a) Hãy xác định trị số điện trở R| để tạo thiên áp yêu cầu U qsq= -2V .
b) Xác định dòng 1,30 • 60 a) b)
Hình 2-21. Mạch điện (a) và đặc tuyến truyền đạt (b) Bài giải a) ư = - U30 = - 2 + 3,5 = 1,5V GSO
Vì dòng lo = 0 nên có thể viết R .= •R. R, + R q Suy ra R. = RG UG 12 200 Thay số: R,
— 200 = 1400k0 = 1,4MQ ' 1,5
b) Dòng 1^0 = 5mA ứng với ƯQ5Q = -2 V (xác định trên đồ thị 2-2 Ib).
( 7^ Bài tập 2-18. Như bài 2-17. Nếu chọn điểm làm việc ứng với
U qsq = - 2 V , dòng IpQ = 5m A ; điện trở Rjj = l,2kQ.
a) Hãy xác định điện áp Uq.
b) Tính điện trở Rs.
c) Khi điện áp vào thay đổi trong khoảng -2V ± 0,5V, hãy xác định biên
độ điện áp ra và hệ số khuếch đại Kụ. Bài giải a) Điện áp
Ud = E - IdqRo = 12 - 5.10M ,2.10^ = 6V. b) Điện trở Rg. 61 3,5 = 7 0 0 0 Ido 5.10-^ c)
Khi điện áp vào U qs thay đổi trong phạm vi -2V ± 0,5V, xác định
trên đồ thị 2-2 Ib dòng Id thay đổi từ 2,5mA đến 6,25mA, như vậy biến thiên
dòng Id từ đỉnh - đỉnh AIó = 6,25 - 2,5 = 3,75mA
Điện áp ra (đỉnh - đỉnh) sẽ biến thiên
u „ = AId-Rd = 3,75.10-M,2.10^ = 4,5V
Hệ số khuếch đại điện áp 1
tập 2-19. Một MC^PETkốih đặt sẵn có đạc tuyái ttuyài đạt như Hình 2-22.
a) Căn cứ vào đặc tuyến xác định hỗ đẫn tại vùng nghèo ƯGS = -2V và
tại vùng giàu ƯQS = +3V. b) Cho nhận xét. iD(mA)' 15 vùng g ià u / ị M 10 7,5 5 vùng nghèo i l í ỉ ' -4 -3 -2 -1 1 2 3 4 Uqs(V) Hình 2-22 Bài giải
a) Tại vùng nghèo, theo đổ thị
U g s = - 2 V - > I d = l,2mA Ugs = -IV Id = 2,5mA A U o s = lV
AIp = 2,5mA - l,2mA = l,3mA 62
Hỗ dẫn g„ = -" -° - = l,3^^^hay l,3mS (milisimen) AUqs V
Tại vùng giàu Uos = +3V -> Id = lOmA Ugs = +4V Id = 15mA Alß 1 5 -1 0 _ mA, _ „ Hỗ dẫn g„ = —
= ——— = 5 —— hay 5mS AU 4 - 3 GS b) Nhận xét:
ở vùng giàu hỗ dẫn của MOSFET lớn hơn vùng nghèo.
Bài tập 2-20. Cho mạch điện dùng
J FET kênh N như hình 2-23. Biết
Ro = 1,5MQ; Rs = 300Q; Rß =
2,2kQ; R, = 15kQ; E = 15V.
a) Xác định điện ttở tải xoay chiầi R_.
b) Hỗ dẫn động tại Uqs = -2V.
c) Tính hệ số khuếch đại Ky.
d) Tính điện áp ra n.ếu Uv = 0,5V. Bàỉ giải
a) Điện trở tải xoay chiều R_
b) Hỗ dẫn tại gốc: ê m o GSK
HỖ dẫn tại điểm Ucs = -2V. U -2 lĩìA 1 GS = 5mS 1 = 3,33 ê m ê mo U -6 GSK .
c) Tính hệ số khuếch đại
K„ = g„R_ = 3,33.10-'. 1,92.10' = 6,393. 63
d) Xác định điện áp ra
Uos = OV; U gs = +2,0V; Uos = -2,0V. Bài giải
- Khi Uq5 = 0 —> Ij) = Idss “ 15mA. -Khi -3
Ucs = +2 V ^ I ^ = I^s3 1 u = 15.10 = 26,66mA -6 GSK -3
- Khi Uqs = -2 V -> In = 15.10 = 6,6mA. -6
Bài tập 2-22. Một MOSFET kênh N cảm ứng có đặc tuyến truyền đạt
và mạch điện như hình 2-24.
a) Hãy xác định bằng phương pháp đồ thị hỗ dẫn g„ tại điểm làm việc 0(8V , 7,5mA). b) Tính trị số Rq.
c) Tính điện áp ra nếu điện áp vào biến thiên IV. .+15V a) Hinh 2-24 b) 64 Bài giải
a) Xác định hỗ dẫn g„. gm = . ?:.^
, 2 , 5 i ^ h a y 2 , 5 m s AUGS 8 V -7 V b) Điện trở Ro
= - — £ p i . = J 5 _ 8 _ ^ chọn Rß =.lkQ -3 I,DO 7,5.10
(ởđâyUos = UGs = 8 V v ìIc = 0).
c) Xác định U,, nếu Uv = 1V.
u„ = Ki^.Uv = g„.Ro.Uv = 2, 5. ỉ ơ^. Ì0M,0 = 2,5V
( t^ Bài tập 2-23. Cho mạch điện
dùng J-FET kênh N như hình 2-25. Biết; E = 12V; Rg = IMQ;
ư c5q = 1,2 V . Điện áp trên Rs,
Urs = 0,2E = 2,4V. HỖ dẫn g„ = 5
. Điện trở cực máng
nguồn r¿^ = 200kQ.
= 0, Ir,^ = 0, 1 ,200kQ = 20kn.
a) Tính điện trở Rị.
b) Tính hệ số khuếch đại Ky. Bài giải a) Tính R, R. R| + R q E.R, E Suy ra R. = - 1 ^RS vU ks- U oso 12 = 10' 1 = 9MQ.
b) Hệ số khuếch đại Ku.
Ku = êm- Rd = 5.10 ^20.10^ = 100. 5- 250BTKTĐÍỆNTỬ-A 65 Chương 3
CÁC MẠCH KHUẾCH ĐẠI TÍN HIỆU BÉ
3.1. TÓM TẮT PHẦN LÝ THUYẾT
Để phân tích và tính toán các thông số kỹ thuật đối với bộ khuếch đại
điện tử dùng transistor làm việc ở chế độ tín hiệu bé thưòng dựa vào các loại
sơ đồ tưcmg đương.
Transistor thường được biểu diễn bằng hai loại sơ đồ tương đương:
- Loại thứ nhất gọi là sơ đồ tương đưcmg vật lý hay sơ đồ tưofng đưcfng
hình T và cũng có tên gọi là sơ đồ tương đương
(The ĩg transistor model).
- Loại thứ hai được gọi là sơ đồ tương đưong tham sô' bao gồm các tham
số trở kháng, điện dẫn hoặc hỗn hợp.
Cả hai loại sơ đồ tương đương của transistor có thể coi là không phụ
thuộc vào tần số đến một phạm vi khá cao:
- Đối với các loại transistor lưỡng cực (BJT) khi tần số tín hiệu
f , < ( 0 , l - f 0,5)f,.
- Đ ối với các loại transistor hiệu ứng trường (FET) khi tần số tín hiệu f,< (1 0 ^ 150)MHz.
ở phạm vi tần số cao hơn những số liệu trên, khi sử dụng các loại sơ đổ
tương đưofng phải được lựa chọn một cách thích hợp và không được bỏ qua
ảnh hưởng của các tụ ký sinh (Cj(;s) bản thân transistor đến sự truyền đạt tín hiệu qua nó.
Với mỗi kiểu mắc đối với transistor có ba họ đặc tuyến Volt-Ampe
quan trọng: họ đặc tuyến vào, họ đặc tuyến ra và họ đặc tuyến truyền đạt.
Có thể xây dựng đường tải một chiều (R.) và đường tải xoay chiều (R_)
trên các họ đặc tuyến cơ bản của transistor và xác định các tham số một
chiều cũng như xoay chiều của tầng khuếch đại điện tử. 6 6 5-250BTKTĐIẸNTỬ.B
Các thông số kỹ thuật cơ bản đối với tầng khuếch đại điện tử dùng
transistor bao gồm; trở kháng vào (Ry), trỏ kháng ra (R^a), các hệ số khuếch
đại điện áp ( K u ) dòng điện ( K ị) , công suất ( K p ) .
Hệ số khuếch đại nhiều tầng ghép liên tiếp bằng tích các hệ số thành phần.
3.2. BÀI TẬP CÓ LỜI GIẢI
( 8^ Bài tập 3-1. Cho tầng khuếch đại dùng BJT như trên hình 3-1. a) Xác định r^.
b) Xác định trở kháng vào của tầng Ry.
c) Xác định trở kháng ra của tầng (với fo = oo)
d) Xác định hệ số khuếch đại điện áp Ku (với ĨQ = oo)
e) Xác định hệ số khuếch đại dòng điện K ¡ (với ĨQ = ũo) E .J 2V CO II— u Cj 10|iF p=100 r„=50kQ Hình 3-1 Bài giải
Chọn transistor T loại Si và thiên áp Uggo =0,7V
a) Dòng tĩnh IgQ sẽ là: 12 V -0 ,7V , Ibo = — = 24,04^iA Rg 470kQ
Dòng tĩnh IgQ sẽ là: 1,0
=(1 + P)l30 = (l + 100)24,04.10-'A = 2,428mA
Điện trở r, được xác định: 67 1^0 2,428.10-'
b) Trở kháng vào được tính:
Ry — Rb // TvT
trong đó Tvt - trở kháng vào của transistor
fy^ = pr,= 100.10,71 = l,071kQ
Ry = 470//1,071 = l,069kQ.
c) Trở kháng ra của tầng được tính:
R „ = Rc / / ĨQ = R c / / °0 = Rc = 3kQ .
d) Hệ số khuếch đại điện áp của tầng: r, 10,71
e) Vì Rg > lOrvT = lOp.r, (470k0 > 10,71k0) nên K ị« p = 10 0
Bài tập 3-2. Tính toán lặp lại cho bài tập trên*hình 3-1 với ĨQ = 50kQ. Bài giải
Ta nhận thấy các thông số trong hai câu a, b sẽ không có gì thay đổi nên; a) r,= 10,710 b) R v= l,0 7 1 k a
c) Trở kháng ra của tầng được tính:
= Re // ro = 3 // 50 = 2,83kũ.
d) Hệ số khuếch đại điện áp của tẩng. -264,24 r. 10,71
e) Hệ số khuếch đại dòng điện Kj Y- _ P-Re-rp : 100.4 7 0 .5 0 ^3 ‘ (ro+R^XRg + r^^) (50+ 3)(470 + 1,071) ’
Có thể tính K: theo biểu thức khác: 68
K , = - K > = 2 H É Í 3 1 ) W 9 =94,16 3
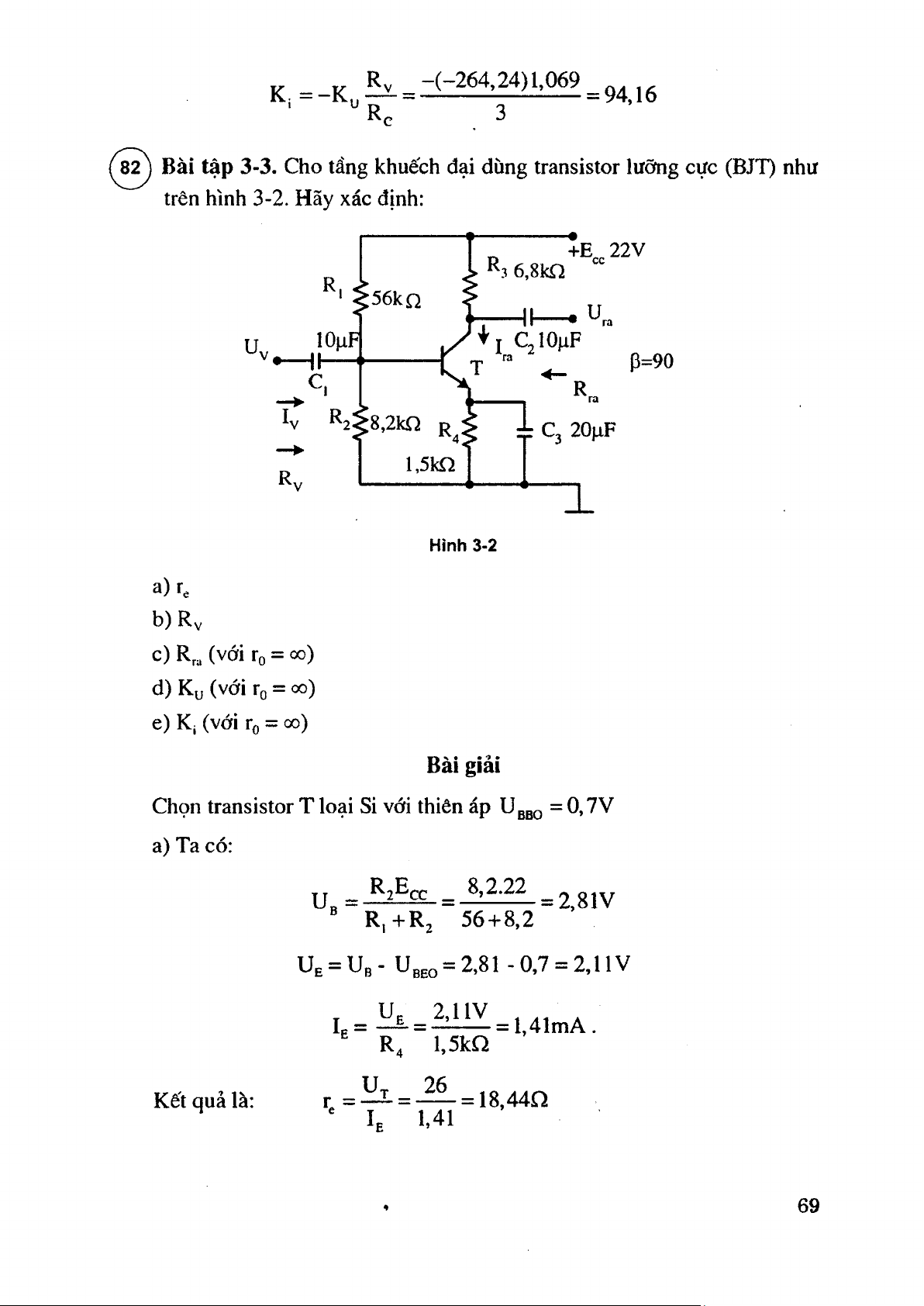
Bài tập 3-3. Cho tầng khuếch đại dùng transistor lưỡng cực (BJT) như
trên hình 3-2. Hãy xác định: +E^22V ^3 6,8kQ R 56kn u n , lO^iF c'lO jiF X - p=90 ^1 Rra ĩ T R
>8,2kfì n < r C3 20|XF l,5kQ R, 1 Hình 3-2 a)r, b) Rv c) R,, (với fo = 00) d) Ku (với To = co) e) Ki (với To = 00) Bài giải
Chọn transistor T loại Si vói thiên áp Uggo = 0,7V a) Ta có: U = -M e e .. ^ 2.22 ^ 2,81V ® R ,+ R 2 56+ 8,2
Ue = Ub- U 3 eo = 2 .8 1 -0 ,7 = 2,11V Ig = - ^ = _ _ = l,41mA . l,5kQ Kết quả là; r, = — = 18,44Q Ĩe 1.41 69
b) Ta có: Rp = R, // Rj = 56kQ // 8,2kQ = 7 ,15kQ Và
Rv = R p// ĨVT = R p// p.r, = 7,15kQ // 9 0 .1 8 ,4 4 n
Rv = 7,15kQ // l,66kQ = l,35kQ.
c) R„ = Rc // fo = Rc // co = Rc = 6,8kO. d)K = - - ^ = - ^ = -368,76 r. 18,44 e ) K ^ = ^ = ^ = 4 | L Ị L = 73,04. R , + r„ R ,+p.r. 7,15+1,66
Bài tập 3-4. Tính toán lặp lại cho bài tập trên hình 3-2. với To = 50kQ. Bài giải
Với hai câu a, b sẽ hoàn toàn tương tự trong bài 3-3 nghĩa là: a )r ,= 18,44Q b) Rv= ỉ,35kQ.
c) R„ = Rc // ro = R, // ro = 6,8kQ // 50kQ = 5,98 kQ. d)K = - ^ = - ^ = -324,3 r, 18,44
_________ P ' ^ p '^0_______ __ P -R p -F p _______ (ĩq+R(,)(Rp H-ry^-) (ĩq+R 3 XRP+Pr^) 90.7,15.50 (50+6,8X7,15 + 1,66)
Bài tập 3-5. Cho tầng khuếch đại dùng transistor như trên hình 3-3 Hãy xác định: a)re b )R v C)R„ d)
e) K ị với mạch không có tụ Q . 70 +E,, 20V 2,2k Q R. 470k U, CIOịìP J— c, 10^F K M 20 r =40ka 0,56kQ lỐụF Hình 3-3 Bài giải
Chọn transistor T loại s¡ với Uggo = 0,7V a) Điện trở
được tính như sau; J ^ 2 0 -0 ,7 = — f -------- - = 35,89|aA R„+(1 + Ị3)R.
470.10’ + 121.0,56.10'
I eo =(P + l)lB0=121.35,89^A = 4,34m A. í _ U j _ 26 và r = = 5 ,9 9 0 . 4,34 EO
b) Rv = R J / rvT mà ĨVT = P(re + Re) = 120(5,99 + 560) = 67,92kQ. Rv = 470kQ//67,92kQ.
c)R„ = R c / / r o - Rc = 2,2kQ. r,„ 67,92 ‘VT R
e) Kị= - K ^ , ^ = -(-3 ,8 9 )^ ? 4 ^ = 104,92. R 2,2
(^8^ Bài tập 3-6. Tính toán lặp lại cho bài tập trên hình 3-3 khi có tụ Q Bài giải
Với câu a việc tính toán hoàn toàn tuofng tự trong bài 3-5, nghĩa là: a) r, = 5,99Q 71
b) Vì điện ứở Re sẽ bị ngắn mạch đối với thành phần xoay chiều của tín hiệu qua tụ Q nên: Ry = Rg / / m à = p.ĩg nên:
Rv = Rb // p.ĩe = 470kQ // 120.599Q
= 4 7 0 k Q / / 7 1 8 ,8 Q = 7 1 7 J 0 Q . c) R„ = Rc = 2,2kQ. d) K„ =
= - ^ 4 4 ^ = -367,28 5,99 PR 120.470.10^ e)K ,= B _ = 119,82. Vr 470.10^+718,8
Bài tập 3-7. Cho tầng khuếch đại dùng transistor như trên hình 3-4
(tầng lặp emitơ). Hãy xác định: a)r, b) Rv c) R . d )K , e) Ki Bài giải
Chọn transistor T loại Si với UggQ = 0,7V
a) Điện tì-ở được tính: 72 Ti,: 2 0 A 2 ^ “ R B + ( l + ß)Rg
2 2 0 k Q + 101.3,3k O
= (1 + ß)ig^ = 101.20,42^A = 2,062mA nên: r = = - — -■ = 12,610 ' Ieo 2 ,0 6 2
b ) R v = R b / / rv T = R b / / ß-re + ( 1 + P ) R e
= 220kQ // 100.12,610 + 101.3,3kü
= 2 2 0 k n / / 3 3 4 ,5 6 k Q = 1 3 2 ,7 2 k fì.
c) R,, = Re // r, = 3,3kQ // 12,61Q = 12,56Q = r,. = = 0,996 Uv r^+Rß 3,3.10^ + 12,61 e ,K ,= - ^
= - - J 5 ^ = - 3 9 , 6 7 .
R^ + Ty j 2 2 0 + 3 3 4 ,5 6
hoặc có thể xác định theo biểu thức khác: Ki = -K „ ^ = -0 ,9 9 6 = -4 0 ,0 6 ' ’ 3,3kQ
( 8^ Bài tập 3-8. Tính toán lặp lại như bài 3-7 với ĨQ = 25kQ, xem hình 3-4. Bài giải
a) Việc tính toán đối với T(. giống như trong bài 3-7 nên: = 12,61Q.
b) Vì To « coQ hay To < lORß nên Tvt được tính như sau: r „ = ß.r. + ^ I0 0 .1 2 .6 in + » 2 9 5 ,7 k fì l + ñ e i + 3,3k£ỉ ĨQ 25kQ v à
R v = R b / / Tvt = 2 2 0 k 0 / / 2 9 5 ,7 k Q = 12 6 ,15 k fì.
c)R „ = RE//re=12,56Q. (1 + ß ) ^ (10 0 + 1) d) ^ = -------- - 1 M I = 0 ,9 9 6 . 1 + —^ l + n i ro 25 73 126,15kQ
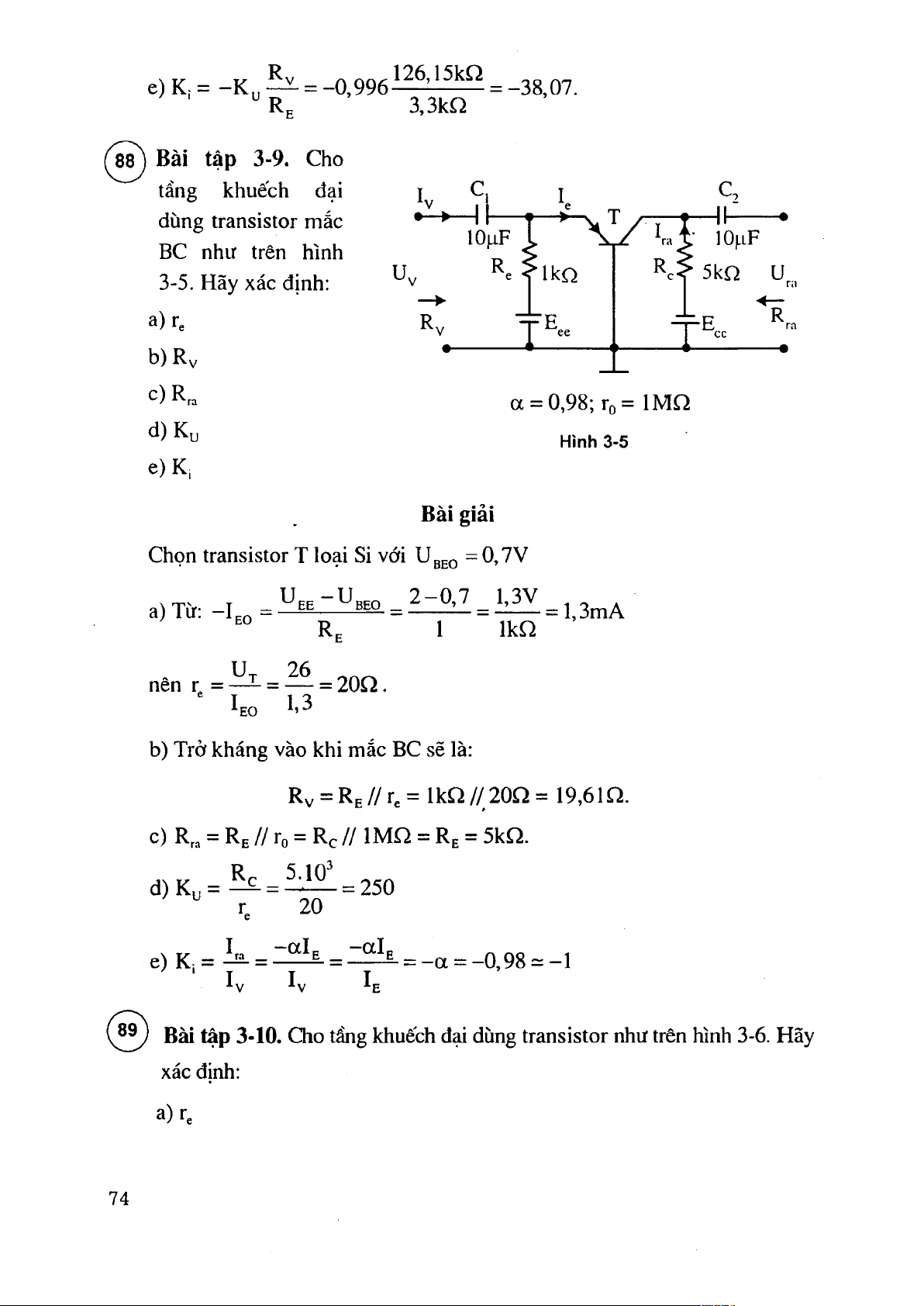
e) K¡= - K ^ ^ = -0,996 = -38,07. 3,3kQ Bài tập 3-9. Cho tầng khuếch đại c, dùng transistor mắc t—1^— •
1 0 ^F 1 ' ^ V l J t,- lO^iF BC như trên hình MkQ ^ 3-5. Hãy xác định: K Ỉ 5 kQ ư a)r, "Eee fEcc b)Rv C)R„ a = 0,98;ro= IMQ d) K, Hình 3-5 e) Ki Bài giải
Chọn transistor T loại Si với UggQ = 0,7V IkQ
nên r , = Ì ỉ i = ^ = 20Q . EO
b) Trở kháng vào khi mắc BC sẽ là:
Rv = Re/ / Te = IkQ / / 20Q = 19,61Q.
c) R,, = Re // ro = Rc // IMQ = Rg = 5kQ. K - _ 5.10^ d) K, = 250 20 e) Ki= i i - = - ^ = - ^
= - a = -0 ,9 8 = - l L, L, L
0 Bài tập 3-10. Qio tầng khuếch đại dùng transistor như trên hình 3-6. Hãy xác định: a)r. 74 b) Rv c) R„ + E „ 9 V 2 ,7 k Q d ) K , R , 1 8 0 k Q U e) K¡ I, QIO^F Bài giải c, lO^iF p=200
Chọn transistor loại Si R., r„=ooQ
v ớ ì U 3 , o = 0 , 7 V . Rra a) Từ: Hình 3-6 9 V -0 ,7 V ^BO ~ — —
= ------ ----- ------------ = 1 l,53|.iA Rg+ịỉR c 180kQ + 200.2,7kQ
Lo = (1 + P)Ibo = (1 + 2 00)11,53|aA = 2,32m A và 2,32 EO 11,21 b) = 560,5Q 1 , 2 , 7 p Rb 2 0 0 1 8 0
c) R,, = Rc // ro // Rb với ĩo > lORc thì
R„ = Rc // Rb và với Rg » Rc ta có; K = Rc-
ở đây ta tính được;
R „ = R c // R b = 2 , 7 k Q // 1 8 0 k Q = 2 , 6 6 k Q . d) Ky = = -240,86 11,21 PR, 200.180 e) K .= = 50. R g+pR c 180 + 200.2,7 0
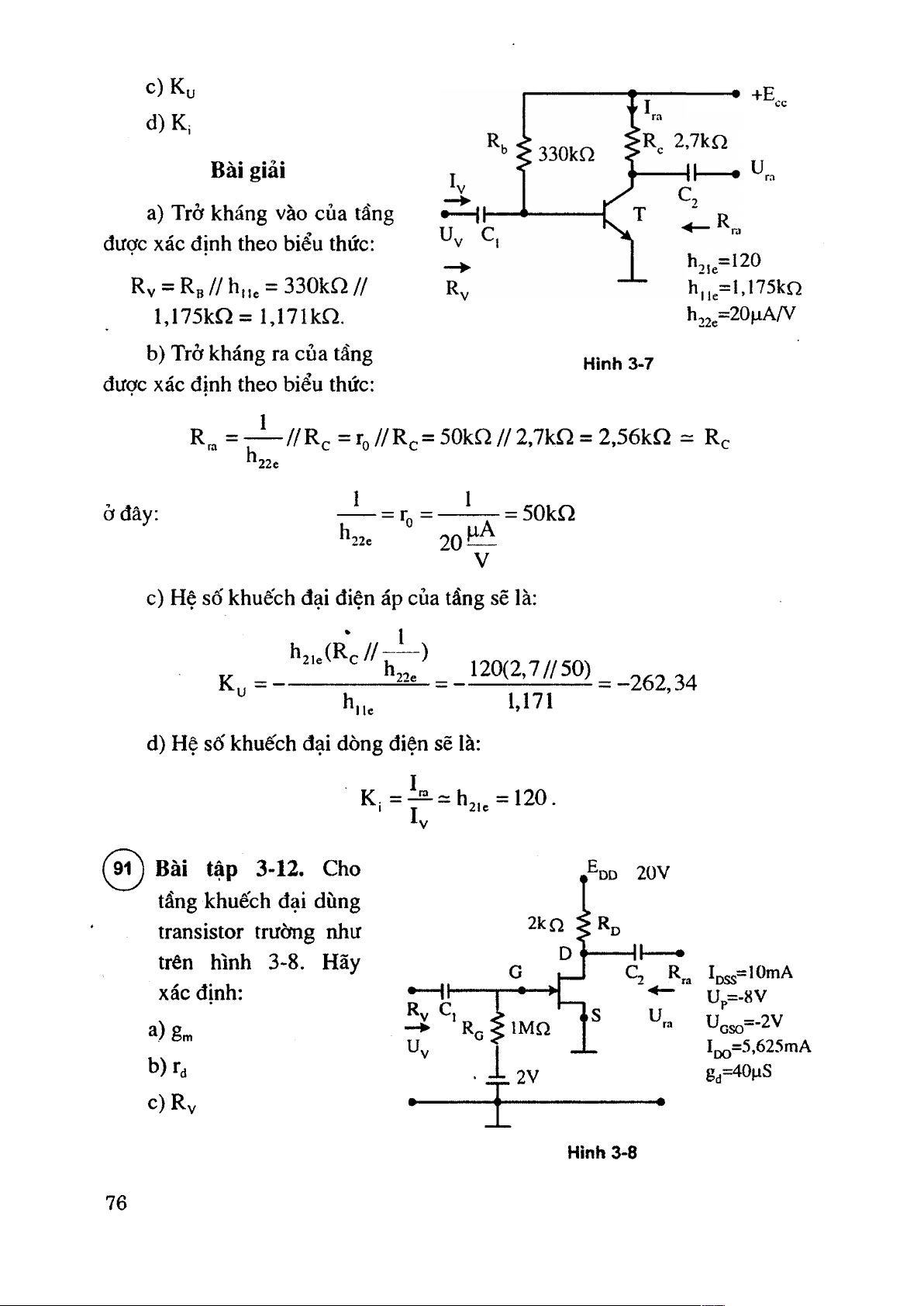
90 ) Bài tập 3-11. Cho tầng khuếch đại dùng transistor như trên hình 3-7. Hãy xác định: a) Rv b) R„ 75 c) • +E d) K; Bài giải u ra
a) Trở kháng vào của tầng được ♦ xác định
• theo biểu thức: h,,= 1 2 0
Rv = R B / / h „ e = 330kQ // h,^=l,!75krì l,175kQ = l,171kQ. h22e=20jiAA^
b) Trở kháng ra của tầng Hình 3-7
được xác định theo biểu thức: 1 R . =
7/R^ = r„ //R ^= 50kQ // 2,7kQ = 2,56kQ =: R, '2 2 e ở đây: = 50kQ '2 2 e 20 V
c) Hệ số khuếch đại điện áp của tầng sẽ là: K „ , . J ! L Z ^ , -2 6 2 ,3 4 1,171 ‘l i e
d) Hệ số khuếch đại dòng điện sẽ là;
K ,= Ị * -= I > j,.= 1 2 0 . Bài tập 3-12. Cho 20V
tầng khuếch đại dùng
transistor trường như 2kn 5R , trên hình 3-8. Hãy D G xác định: Up=-8V Rv c, U. ưgso=-2V a)gm ư. Ij^=5,625mA b)r, Ì 2 V gd=40fiS c) Ry Hình 3-8 76 d) R . e ) K , Bài giải
a) Từ phương trình Shockley đối với transistor trường loại J-FET ta có: 2ĩ_ 2.10mA Sm„ = 2,5mS U 8V UGS„ _ -2
) = 2,5m S(l— ^) = l,88mS ê m B m „ U -8 _Ị^ 1 b) ''d= — = = 25kQ ểd 40.10"*
c) Ry = R(3 / / T yj = Rq / / co — R-G — I M O
d) R„ = Ro // Td = 2 kQ // 25kQ = 1 ,85kO
e) Ku = -gl(Ro // r j = -l,88mS.l,85kO = -3,48.
(^92^ Bài tập 3-13. Cho tầng i
khuếch đại lặp dùng J-FET 'E dd^V 0,05^F
như trên hình 3-9 và biết n ....-..- • i f ----^ thêm: ư o s o = - 2,86V; aOSMF Uv , Up = -4V; =4,56mA; ^ Iivm > R,<> ^2 Idss = 16mA; = 2 5 |^s. 2,2kQ 3 K Hãy xác định: ra a)gm b)r, Hình 3-9 c) Rv d) R™ Bài giải 21 2.16mA a) g = ' = Om« -ỊJ 8mS 4V ểtn êmo^^ = 8mS(l — = 2,28raS U - 4 77 1 b) 1;,= — = = 40kQ gd 25^iS
c) R v = R o / / Tvt = R g / / 00 = R g = I M Q 1
d) R„ = r, // R, // — = 40kQ // 2,2kQ // = 3 6 2 ,5 2 0 g 2,28mS m @
Bài tập 3-14. Cho tầng
khuếch đại dùng D-MOSPET
(MOSPET loại nghèo) như
ừên hình 3-10 và cho biết thêm: Uoso=0,35V;
Iqo = 7,6m A ; Idss = 6mA;
ủp = -3V; g, = ỈOịiS. Hãy xác định; a)gm b)r, Hình 3-10 c)
Vẽ sơ đồ tưcfng đương của tầng d ) R v e) R . f)Ku. Bài giải
a ) g „ „ = ^ = - ^ ^ = 4mS 3V u, 0,35
g . = g . o a - ^ ) = 4(l ) = 4,046mS ư -3
b)fd= — = . - ^ = 100kO. gd c)
Sơ đồ tưofng đương của tầng được vẽ như trên hình 3 -1 1 dưới đây.
d) Rv = R, // R, // rvT = R, // R2 //
= Rj // R, = lOMQ // 1 lOMQ = 9,17MQ. 78
e) R„ = r, // Rd = (100 // l,8)kQ = 1,77kQ
f) Ku = -g„.RD = -4,046mS.l,8 = -7,28. G D »------ m RẬ^ c D D ^ Uv 1 llO M fi lOMQ Sm ^GS lOOkQ l,8 k n " s Hinh 3-11
( 9^ Bài tập 3-15. Qio mạch khu&h đại dùng transistor E-MOSFET như trên hình 3-12. +Edd12 V R 2kQ i; = 6mA R.^IOMO u;=8V Rra Ut=3V U, c, 1 ^F gd = 20ịiS (0,24.10-'AA^') R, k = 0,24.10'’AA^- Ucso = 6,4V Hình 3-12 Itx) = 2,75mA Hãy xác định: a) gm b)r, c) Ry d) R., e) Ku- Bài giải
a) g,„ = 2k(U.so-UT) = 2.0,24.10"^(6,4-3) = l,63mS. 1 b) r,. = — = = 50kQ gd 20|aS 79
R c + r ,//R p _ 10Mfì + 50kQ//2kQ = 2,42MQ
~ 1+ L ( Í . / / R d) ~ l + l,63mS(50kQ//2kQ)
Nếu không tính đến ảnh hưởng của thì: 10 ;g____ __ = 2,53MQ l + g„R^ 1 + 1,63.2
d) R,, = Rc // r, H Rd = lOMQ // 50kQ // 2kQ = 1,92kQ.
Khi r^i > lORp thì trở kháng ra có thể được tính:
R„ = R o //R o = RD = 2kQ
e) Ku = -g^.Ro = -1,63mS.2 = -3,26.
Khi bỏ qua ảnh hưởng của với r lORp.
Khi tính đến r¿ thì:
Ku = -g„,(Rc // ra // Rd) = -1,6ms( 1OMQ // 50kQ // 2kQ) = -3,21.
( 9^ Bài tập 3-16. Qìo tầng UoD 30V
khuếch đại dùng J-FET như R
trên hình 3-13. Hãy xác
định điện trở tải một chiều
Rp của tầng vód hệ số II T
khuếch đại điện áp Ku = 10. Rg > lOMn Ip55 = 1 Olĩl A Up = -4V Bài giải g, = 20tiS
Với Rs = Oíì trên sơ đồ
hình 3-13 của đầu bài ta có Hình 3-13
u Q5 = o v và điều đó có nghĩa là:
Ku = -gn,Rn. = -gm„ Rra = -gmCRo // r
Từ đó ta tính được » : 2I0SS _ 2.10mA -gm„ = = 5mS Up 4V
và ta có; Ky = -10 = -SmSíRp // r^) 10 nên; Rp // = = 2kQ 5mS 80 Mặt khác ta có: 1 1 rd= — = = 50kfì g. 20.10-^
Khi đó: Rd // r, = Rd // 50kQ = 2kQ RoSOkQ R^+SOkQ RoSOkQ = 2(Rd + 50)kQ
Vậy Rj) = 2,08kQ và chọn điện trở Rß theo tiêu chuẩn sẽ là Rjj = 2kQ.
(% ) Bài tập 3-17. Cho mạch khuếch đại dùng J-FET như trên hình 3-14.
Hãy xác định điện trở Rj) và Rs với Ku = 8 và Uqs_ = —Up = - I V . Biết
thêm: Idss = lOmA; Up = -4V; gj = 20|J,S. ^DSS *” ỉômA U p = - 4 V Ga = 20^lS Hình 3-14 Bài giải T- ' _ 2Idss _ 2.10mA Ta có; - = 5mS U,
và g„ = g „ „ ( l - ^ ^ ) = 5 m s ( l - ^ ) = 3,75mS
mặt khác: Ku = -g„(RD // r -8 = -3,75mS(Ro// r,) 6- 250BTKTĐÍỆNTỬ. A 81 nên
Rd // ra = Rd // — = Ri, / / - ^ = Rd //50kQ = 2,13kQ gd 20|aS
Từ đó ta xác định được Ro = 2,2kQ (đúng theo tiêu chuẩn).
Để xác định điện trở Rs có thể xuất phát từ biểu thức; '^GSO “ ~^DO^S uGSO \2 _ ^DO — ^Dss(^ ý = lOmA = 5,625mA Up - 4 Vậy Rs = ^ = 177,80 I 5,625.10 DO
Chọn theo bảng điện trở tiêu chuẩn Rs = 180Q.
{^9^ Bài tập 3-18. Qio tầng khuếch đại dùng J-FET như trên hình 3-14 (xem
số liệu bài tập 3-17). Hãy xác định giá trị R|5, Rs khi không có tụ Q . Bài giải
Khi không có tụ Cs trên mạch, các đại lượng tính toán cho chế độ một
chiều của tầng không có gì thay đổi nghĩa là: ƯQSO = - I V ; Ij3ò = 5,625iĩiA;
Rs = 180fì! (như trong bài 3-17).
Biểu thức tính hệ số khuếch đại điện áp Kjj sẽ là: §m^D — " l + Sn,Rs - 3,75mS.Rj3 _ 3,75mS.Rp 8 = l + 3,75.10"^180 1+0,675
từ đó tính được Rq sẽ là: 13 4
R ^ = - — —- = 3,573kQ ° 3,75mS
Chọn điện trở Rp theo tiêu chuẩn là Rp = 3,6kQ. 82 6- 250BTKTĐIỆNTL
(^98^ Bài tập 3-19. Cho bộ khuếch đại điện tử như trên hình 3-15. Hãy xác định
K^; Ry; Rn.; u^; u ’ với U gso= - 1 ,9 V ; Ioo=2,8m A và R, = lOkQ.
Ipss = lOmA; Up = -4V; Tị và T2 cùng loại và có cùng các tham số. ra Hình 3-15 Bài giải _ _ 2.10mA = 5mS ê m o u 4V U -1>9 ) = 5mS 1 = 2,6mS ê m S m o ^ ^ Up 4 J Ku. = Ku, =
= -ê„Ri = -g„Rs = -2,6mS.2,4kQ = 6,2 -
Hệ số khuếch đại Ku sẽ là:
K ,= K ,,.K ^ ,^ = (-6 ,2 )(-6 ,2 ) = 38,4
Điện áp ra sẽ là:
u „ = Ky.Uv = 38,4. lOmV = 384mV
Trở kháng vào của bộ khuếch đại là: Ry = Rg = R2 3,3MQ
Trở kháng ra của bộ khuếch đại là; 83 R , = R5 = = 2,4kD.
Khi mắc tải R, = lOkQ, điện áp ra trên tải sẽ là:
u, =— —u =—i^384mV = 310mV ‘ R„+R, ” 2,4 + 10
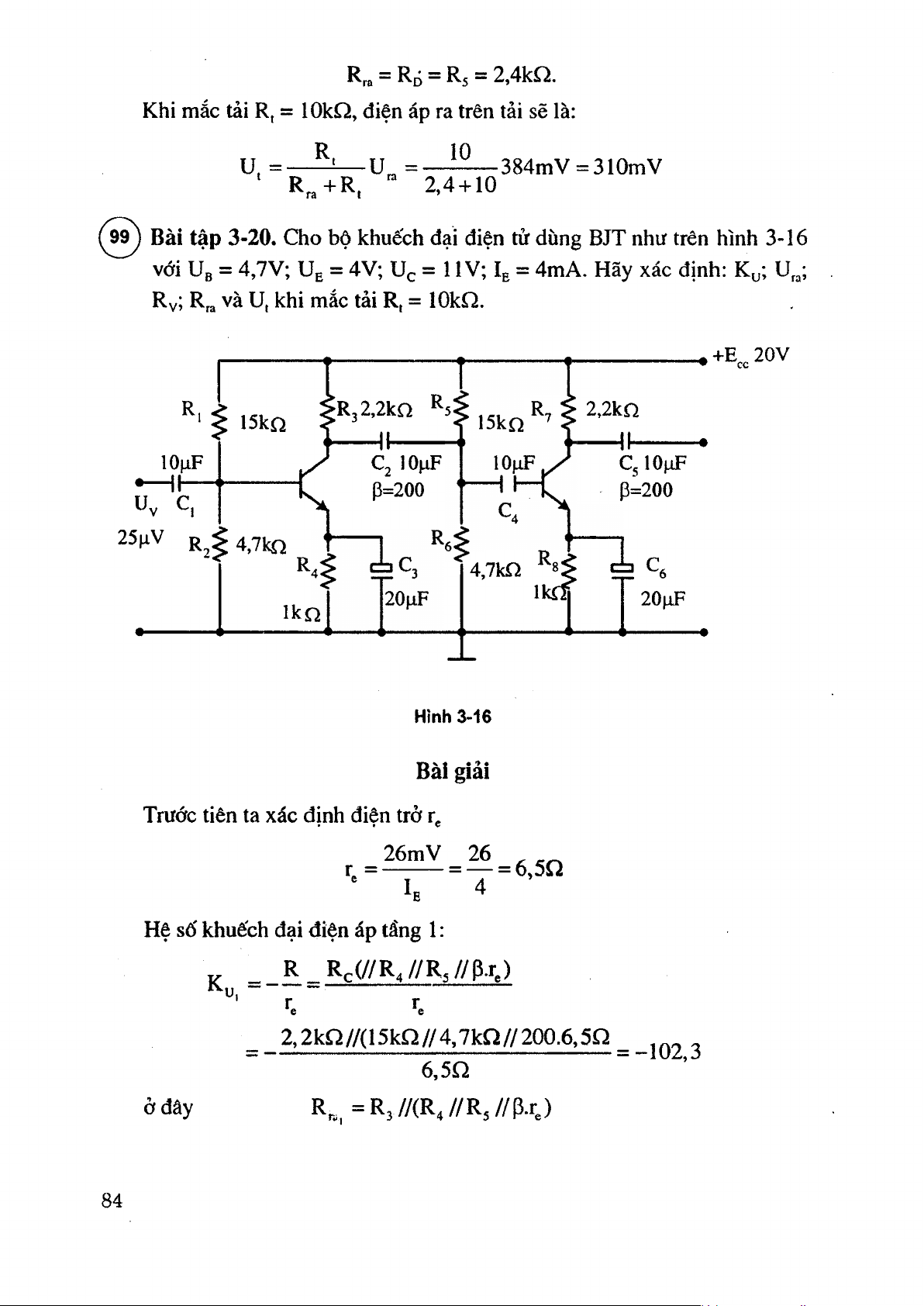
( 9^ Bài tập 3-20. Cho bộ khuếch đại điện tử dùng BJT như trên hình 3-16
với Ub = 4,7V; Ue = 4V; Uc = i 1V; Ie = 4mA. Hãy xác định: K^; u„;
Rv; rI và u, khi mắc tải R, = 1 OkO. • + E ,,20V R :R,2,2ka *^5
R7 > 2,2kO 15kQ 10 )iF q 10nF C , 1 0 |iF h - Uv c, P=20Ó p=200 25^iV R < 4 J Ị ^ 4,7kn ^6 1 20mF Hình 3-16 Bài giải
Trước tiên ta xác định điện trở Tg 26mV 26 = ^ = 6,5Q
Hệ số khuếch đại đỉện áp tầng 1: r.
_ R _ R c(//R 4 //R 5 //P -r.) *^u, ~ “ Te Te
2 ,2kQ //(15kQ//4 ,7kQ//200.6,5Q = -102,3 6,5Q ở đây
R ,, = R 3 //(R ,//R ,//p .r J 84
Hệ số khuếch đại sẽ là: . = _ ^ = _ ^ = _ ^
= _ 2 : ^ . _ 3 3 8 , 4 6 6,5 Ku = Ku,
= (-102,3){-338,46) = 34624
u „ = Kij.Uv = 34624.25^iV = 0,866V
Trở kháng vào của bộ khuếch đại là:
Rv = R, // R, // pr, = 4,7kQ // 15kQ // 200.6,50 = 953.6Q Trở kháng ra: — Rc ” ^6 ~ 2 ,2kQ.
Khi mắc R, = lOkQ điện áp ra trên tải sẽ là:
u = — ^ — U = — 1 ^ 0 .8 6 6 V = 0.71V > 2 , 4 k n ^3 0 ,0 5 ^ F 4,7kQ 4 = . 1 '5 100fxF Hình 3-17 Bài giải
Hệ số khuếch đại của tầng thứ nhất: 85 Ku. =
//R v ,) = -2,6m S(2,4kQ //953,6D ) = -1,77
Hệ số khuếch đại K„ sẽ là:
K^^=K„K„ = (-l,7 7 )(-3 3 8 ,46) = 599,1
Điện áp ra u„ = K^.Uv = 5 9 9 ,l.lm V = 0,6V
Trở kháng vào Rv = Rq = 3,3MQ
Trở kháng ra R,, = Rc = 2,2kQ = R5.
(10^ Bài tập 3-22. Cho tầng khuếch đại cascode như trên hình 3-18. Hãy
xác định Ku của tầng với
= 4 ,9 V ; U 3 = 10,8V ;
!(, = Ic = 3,8mA = 1^ = Ig; P| = p2 = 200; Tị = T2 = T (giống nhau). p, = p, = 200 T, = T, = T (giống nhau) Hình 3-18 Bài giải 26mV 26 = 6,8Q 3,8 86 Vậy
K „= K ., .K„ = -2 6 5 . 'Ü
( 1 ^ Bài tập 3-23. Cho tầng khuếch đại dùng transistor Darlington như ưên
hình 3-19. Hãy xác định hệ số khuếch đại dòng điện K|. Bài giải
Ta có thể vẽ lại sơ đồ tương
đương mạch điện như trên hình 3-20 dưói đây: Pd^b _ 8000.3,3.10® = 4112 3,3.10^+8000.390 Hình 3-20
( 1 ^ Bài tập 3-24. Oio tầng
khuếch đại dùng transistor Darlington như trên hình 3-21. Hãy xác
định Rv; R„; K|; Ku với = 3kQ . 87 Bài giải
Ry = Rg // (r^ + p,p2.Rc) = 2MQ // (3kQ + 140.180.75Q) = 974kQ. R 9 1 a6 K;=p.p2 = 140. 180( - — t) = 3,7.10^ Rg +R v 2.10"+974.10^ R = -!h _ = i i ^ = 0,12Q ™ p,p2 140.180 và K„ = - J M
^ = _ 1 Ị ^ 1 * ^ = 0,9984, p,p2R c+r„ 140.180.75+3000
( í ^ Bài tập 3-25. Cho mạch điện dùng J-FET Edd18V
như trên hình 3-22 (mạch tạo nguồn dòng).
Hãy xác định dòng Id và u„ khi: R, a)R D =l,2kQ . u_ b) Rd = 3,3kQ.
Vód Idss = 4mA và Up = -3,5V. Bài giải Hỉnh 3-22
Từ mạch điện đã cho khi Uqs = ov.
Ij3 = I0SS — 4m A.
a) ư„ = E dd - IdRd = 18V - 4mA.l,2kQ = 13,2V. 88
b) u , , = E do - IdR d = 18- 4 .3 ,3 = 4 ,8 V .
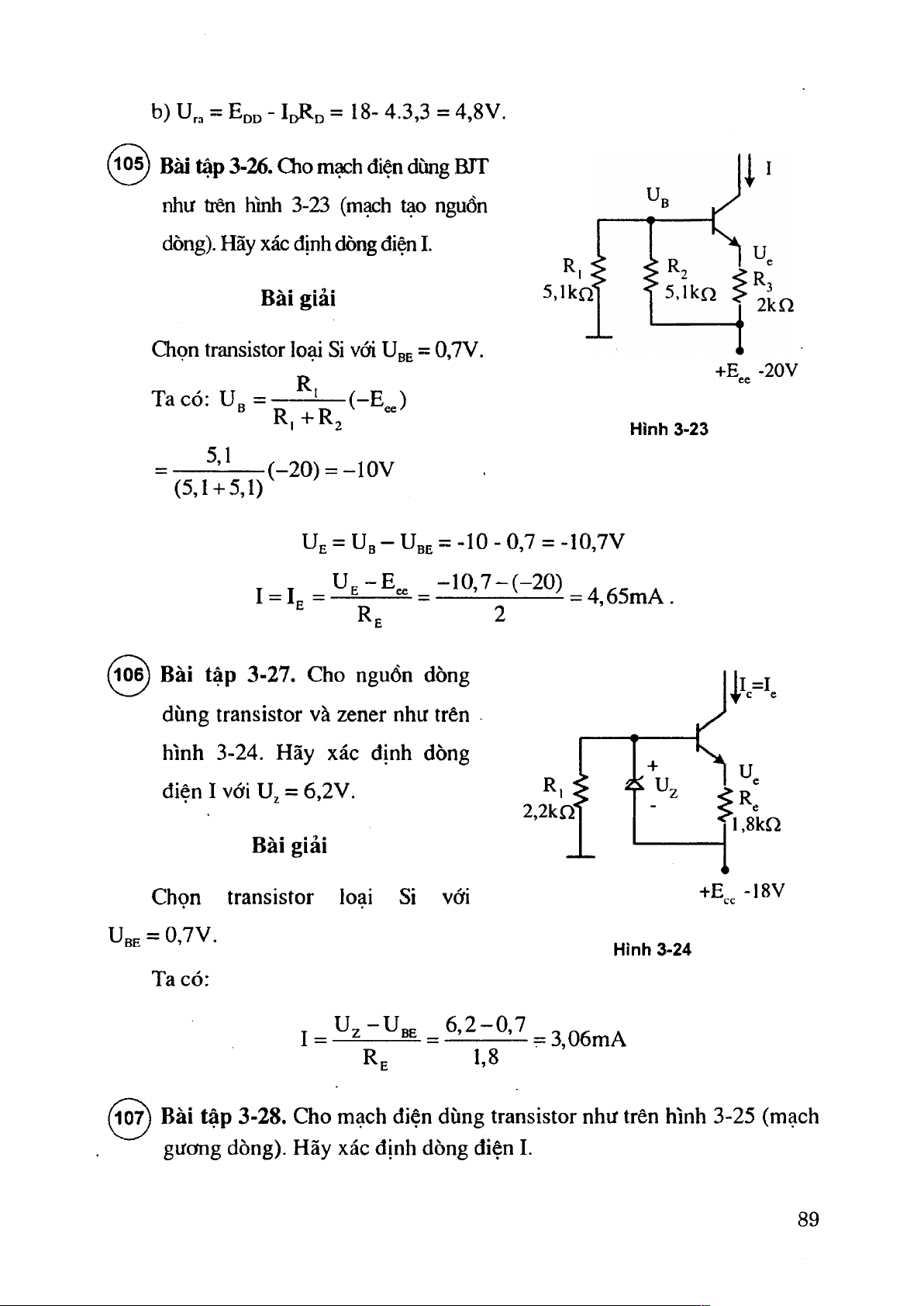
Bài tập 3-26. Cho mạch điện dùng BJT
như trên hình 3-23 (mạch tạo nguồn
dòng). Hãy xác định dòng điện I. Bài giải S.lkQ-
Chọn transistor loại Si với Ugg = 0,7V. +E^ -20V R, cC Ta có: ưg = R, 4-R2 Hình 3-23 5,1 (_20) = -10V (5,1 + 5,1)
Ue = U 3 - U bh = -1 0 -0 ,7 = -10,7V I = I , = l ^
= d Ọ ì Z z m = 4,65mA. ^ R . 2
(1^ Bài tập 3-27. Cho nguồn dòng
dùng transistor và zener như trên
hình 3-24. Hãy xác định dòng
điện I với u , = 6,2V. 2.2kn' l,8kQ Bài giải Chọn transistor loại Si với +E„. -18V Ube = 0,7V. Hinh 3-24 Ta có: R 1,8
(1^ Bài tập 3-28. Cho mạch điện đùng transistor như trên hình 3-25 (mạch
gưomg dòng). Hãy xác định dòng điện I. 89 Bài giải
Chọn transistor T| và T2 cùng loại Si. E - ư Tacó: 1 = 1 R (1 2 -0 ,7 ) = 10,27mA. 1,1
108) Bài tập 3-29. Cho tầng khuếch đại vi
sai dùng BJT như trên hình 3-26. Hãy
xác định điện áp ra u„. Với = 20kQ ; Pi = P2 = ^5. Bài giải
Chọn transistor T| và T, loại Si với Ube = 0,7V. Ta có: E. - U BE h = R 9 - 0 ,7j = 193^iA 43.10 Dòng colectỏ; lẹ 193|aA = 96,5nA. ^ 2 2
Từ đó ta có Uc được tính: Hình 3-26
Uc = Ecc - lẹRc = 9 - 96,5.10 ■^47.10' = 4,5V.
Điện trở được tính; 1-3 96,5.10
Hệ số khuếch đại điện áp Ku sẽ là; K „ = ^ = í ^ = 87,4 2r^ 2.269 90 Vậy u„ sẽ là:
u„ = Ku-Uv = 2.10187,4 = 1,I75V.
(1^ Bài tập 3-30. Hãy xác định hệ số khuếch đại tín hiệu đồng pha của
tầng khuếch đại vi sai dùng transistor trên hình 3-26. Bài giải
Từ biểu thức cơ bản tính toán cho hộ số khuếch đại tín hiệu đồng pha
đối với tầng vi sai ta xác định được Kc như dưới đây: K PRc , 75.47 ^ Uv r^ + 2 (p + l)Rg
20 + (l + 75)2.43 ’
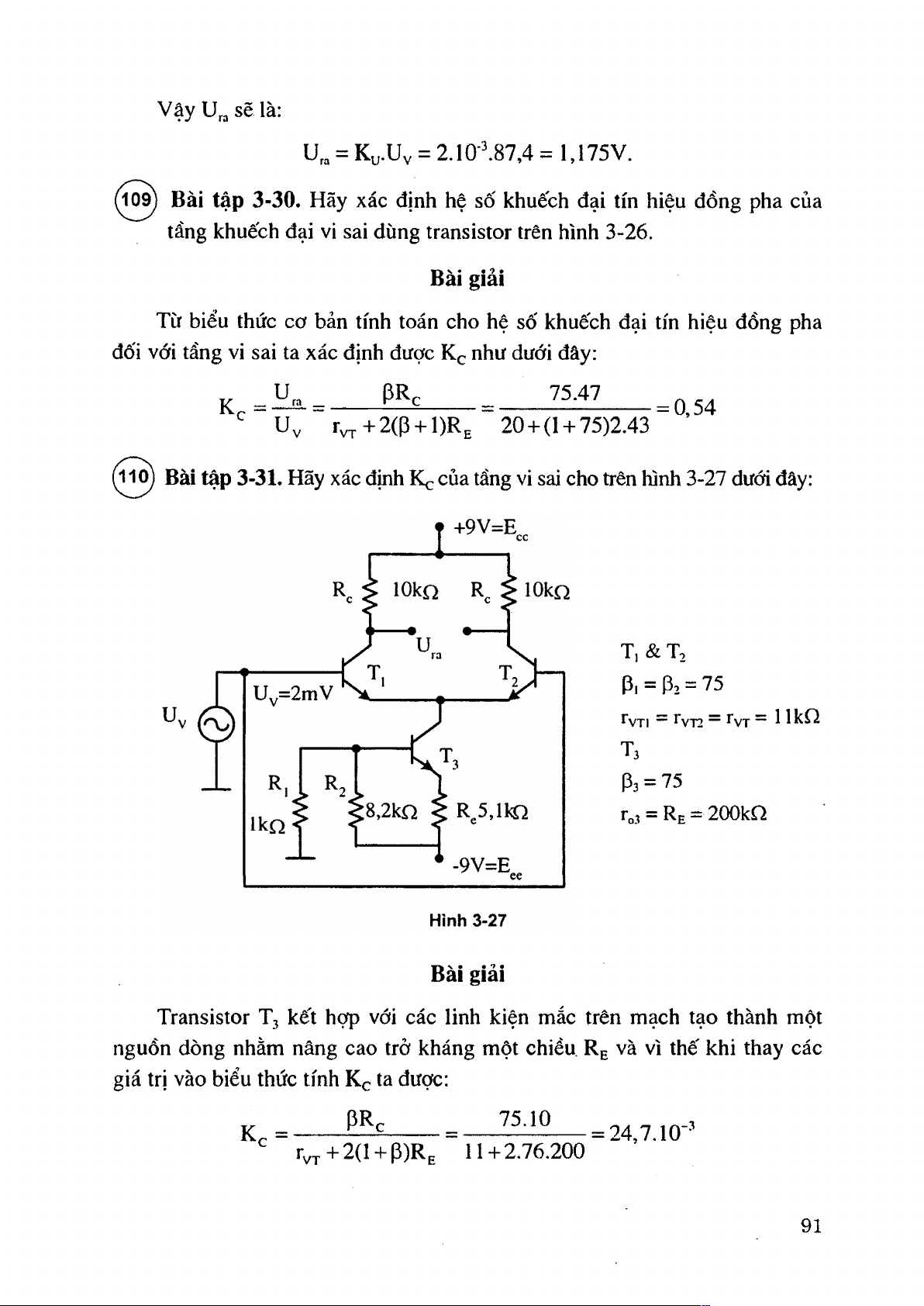
(1^ Bài tập 3-31. Hãy xác định Kc của tầng vi sai cho ừên hình 3-27 dưới đây: T, &Tọ p, = p2 = 75 ^VTl “ “ ^VT IcCầ Ta p3 = 75
r„3 = Re = 2 0 0 k íì Bài giải
Transistor Tj kết hợp với các linh kiện mắc trên mạch tạo thành một
nguồn dòng nhằm nâng cao trở kháng một chiều. Rg và vì thế khi thay các
giá trị vào biểu thức tính Kc ta được:
K , = ------- = 24,7.1 0-' ^ ry^+2(l + p)RE 11 + 2.76.200 91
3.3. ĐỀ BÀI TẬ«P 0
Bài tập 3-32. Cho tầng khuếch đại dùng BJT mắc EC như trên hình 3
28. Hãy xác định Rv; R„; Ku’, Kj a) với ĨQ = 40kQ
b) với Tq = 20kQ. :60 Hinh 3-28
( 1 ^ Bài tập 3-33. Cho mạch điện dùng transistor như trên hình 3-29. Hãy
xác định E c c sao cho Ku = -200.
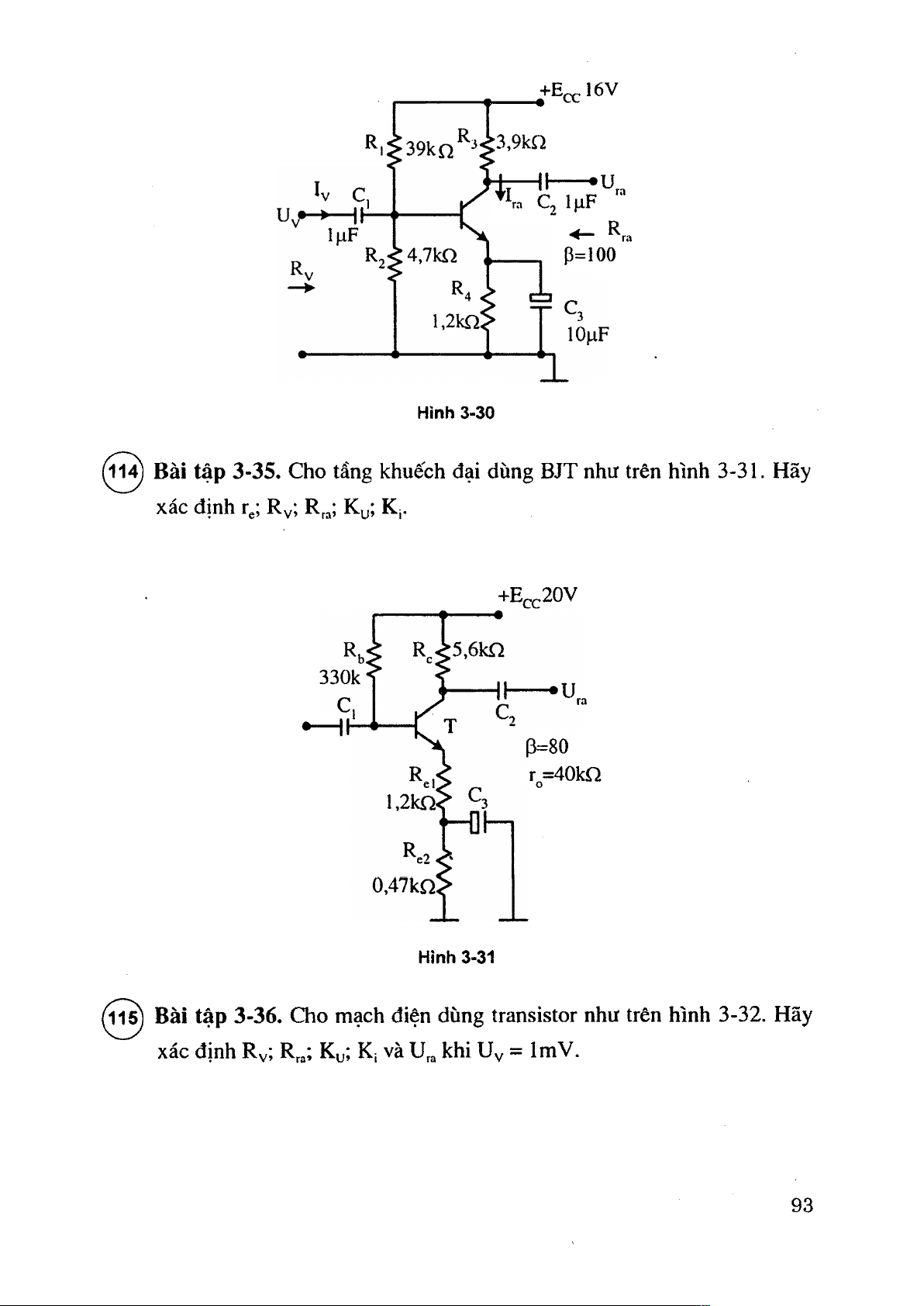
( í ^ Bài tập 3-34. Cho tầng khuếch đại đùng transistor như trên hình 3-30.
Hãy xác định r^; Ry; R„; K^; K| với: a) Tq = 50kQ b) ro = 25kQ. 92 + E ^ 1 6 V R| :3,9kn I , I I - - - *u, q I ^ F ra P=100 Hinh 3-30
( 1 ^ Bài tập 3-35, Cho tầng khuếch đại dùng BJT như trên hình 3-31. Hãy ?CâC cỉĩĩỉỉ) Ku; K, +Ecc20V —H í p=80 r.=40kQ Hình 3-31
Bài tập 3-36. Cho mạch điện dùng transistor như trên hình 3-32. Hãy
xác định R v ; R„; K^; K, và u,, khi Uy = ImV. 93
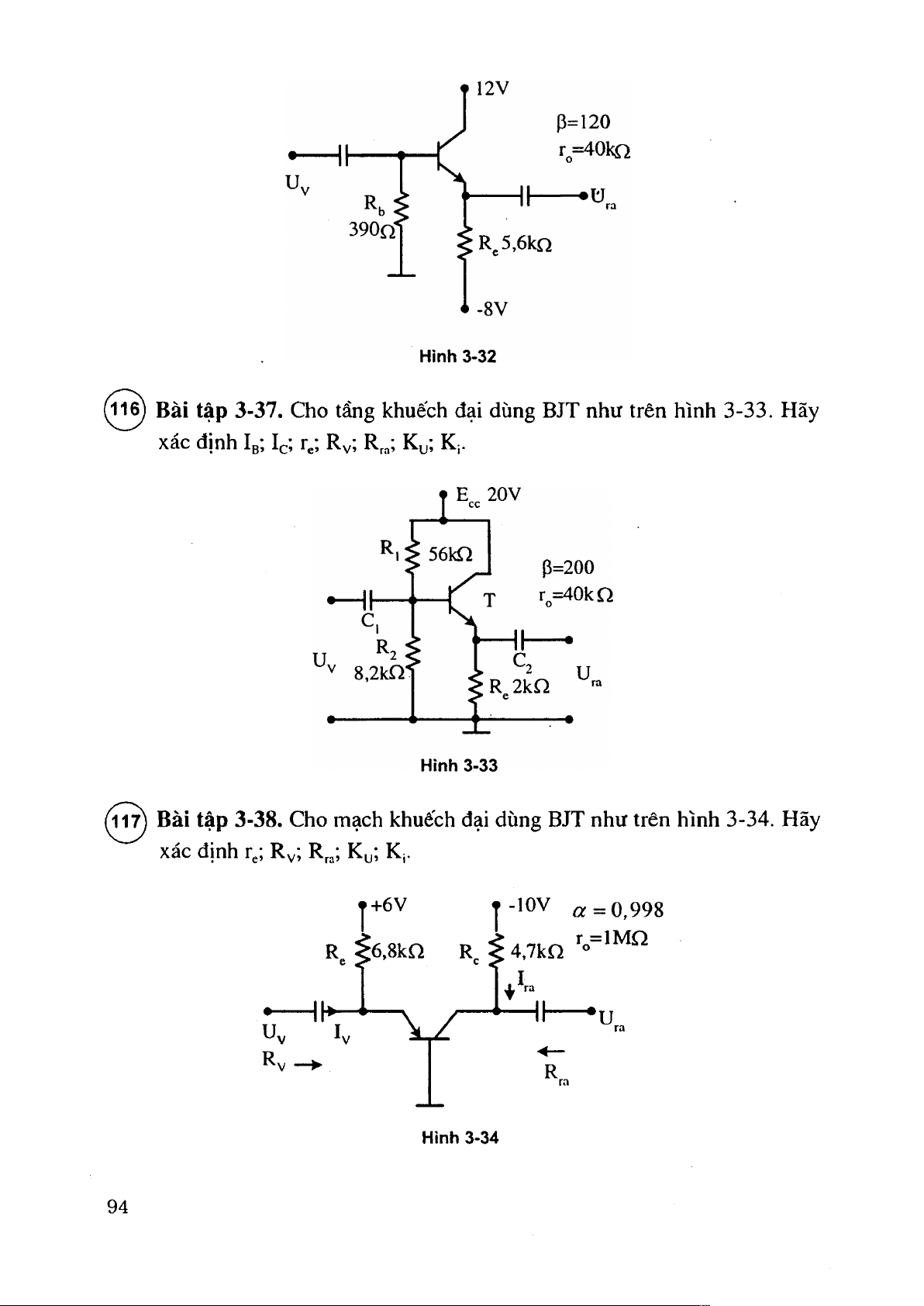
( l ^ Bài tập 3-37. Cho tầng khuếch đại dùng BJT như trên hình 3-33. Hãy
xác định Ib; Ic; r^; R v’, K^; Kị.
(1^ Bài tập 3-38. Cho mạch khuếch đại dùng BJT như trên hình 3-34. Hãy
xác định r^; Rv’, Rraỉ K|. T+6V
Ị-IOV a = 0,998 R ^ 6 ,8 k Q R„ ^ 4 ,7 k n \ ^l---- *ura ư v Iv / R Hình 3-34 94
(ÍĨb) Bài tập 3-39. Cho mạch khuếch đại đùng BJT như trên hình 3-35. Hãy ^
xác đmh Ku; K,. +8V ra -5V Hình 3-35
Bài tập 3-40. Cho tầng khuếch đại dùng BJT như trên.hình 3-36. Hãy
xác định r,; Rv; R,,; K„; K;. t E.. 12V R ,3 .9 kQ R. 220kíí ị l . p=120 -I - ư, r„=40kíì R, Hinh3-36
Bài tập 3-41. Cho tầng khuếch đại dùng BJT như trên hình 3-37. Với r, = loõ; p = 200;
=-160; Kị = 19; To = ã)kn. Hãy xác định Rỏ K Ecc. R. — VSAr u. -lí- u. < Hình 3-37 95
(121^ Bài tập 3-42. Cho tầng khuếch đại dùng BJT như trên hình 3-38 với
h,|^ = 180; hị, = 2 ,75k Q ; h22^ = 25|ẲS. Hãy xác định Rv; Ky; K|; ĩg. ^+Ecc 18V D i 1 ^ 3 i > 68kQ
> 2,2kfì Hình 3-38
Bài tập 3-43. Qio tầng khu&h
đại dùng BJT như tì-ên hình 3-39 H l - vói h2| = -0 ,9 9 2 ; 10ÍiF V / lO^iP y- R ^l,2kQ 2,7kQ ^ R h„ = 9,45Q ; h,, = 1 ^ ^ . • íh ’ ’ 22, Y T 4V 12V R.
Hãy xác định Rv; R„; K^; K^; a; p; r^; Tq. Hình 3-39
Bài tập 3-44. Cho tầng
khuếch đại dùng J-FET như trên hình 3-40. Hãy xác định Rv; R„; Kjj
với Idss - lOmA; Up = -4V; = 40kQ. Edd18V Rol.SkQ Hình 3-40 96
( í ^ Bài tập 3>45. Cho tầng khuếch đại dùng J-FET như trên hình 3-41
Hãy xác định Ry; R„; Ku với
= 3000|iS và gd = 50|aS.
( í ^ Bài tập 3-46. Hãy xác định Rv; R„; Ku của tầng khuech đại dùng J-
FET như trên hình 3-41 (xem bài 3-45) khi ngắt tụ Cj ra khỏi mạch.
( l ^ Bài tập 3-47. Cho tầng khuếch đại dùng J-FET như trên hình 3-42. Hãy
xác định Rv; Rn,; u„ với Uy = 20mV; loss = 12mA; Up = -3V; T¿ = lOOkQ. ra
Bài tập 3-48. Hãy xác định Rv; R„; u „ của tầng khuếch đại dùng J
FET như trên hình 3-42 (xem bài' 3-47) khi ngắt tụ C3 ra khỏi mạch. @
Bài tập 3-49. Tính toán lặp lại cho bài 3-47 khi thay r., = 20kQ.
(1^ Bài tập 3-50. Tính toán lặp lại cho bài 3-48 khi thay = 20kQ. 7. 250BTKTĐIỆNTỬ.A 97
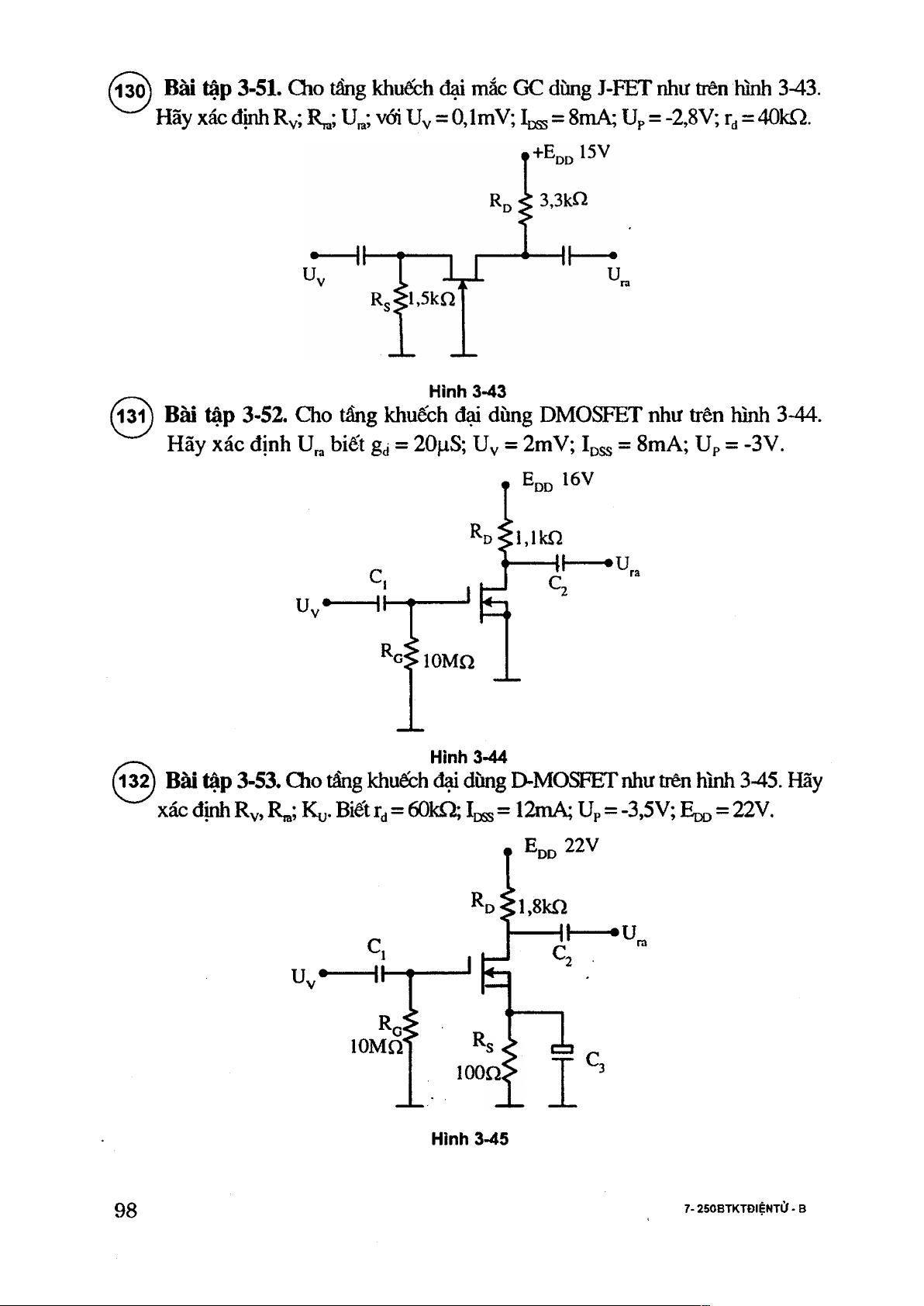
^ 3^ Bài tập 3-51. Cho tầng khuếch đại mắc GC dùng J-FET như trên hình 3-43. ^
Hãy xac định Rv, R„; u^; vói Uv = 0,lmV; Icss= 8mA; Up = -2,8V; = 40ka. ra ® Hinh 3-43
Bài tập 3-52. Cho tầng khuếch đại dùng DMOSPET như ừên hình 3-44. Hãy xác định
biết gj = 20pS; Uy = 2mV; I^ss = 8mA; Up = -3V. 41— *u Hh RG>10Mfì Hỉnh 3-44
(132) Bài tập 3-53. Ơ IO tầng khu&h đại dùng D-MOSFET như trên Kình 3-45. Hãy
xác định Rv, R„; Ky. Biết = 6ỒkQ; Icss = 12mA; ưp= -3,5V; Edd = 22V. Eoo 22V ^ o ịi.s k n 'ưni u. Rq! lOMQ' R Ị. 100 Hình 3-45 98 7-250BTKTĐIỆNTỬ-B
( 1 ^ Bài tập 3-54. Tính toán lặp lại cho bài tập như hình 3-45 với = 25kQ.
( 1 ^ Bài tập 3-55. Cho tầng khuếch đại dùng D-MOSPET như trên hình 3-46. Hãy xác định
với Uv = 4mV; gj = 35|0,S; g„ = 6000|J,S. _________ t E ‘ ' o Do D [ n 91NKÌ > 3 <6,8kn c 1 u."— li------- ' B ’ R2> I 15MQ f Rs > i 3.3kn> T ^ Hình 3-46
Bài tập 3-56. Tính toán lặp lại như bài tập 3-54 trên hình 3-46 với g, = 50ụS; = 3000^8.
( l ^ Bài tập 3-57. Cho tầng khuếch đại dùng E-MOSPET như trên hình 3-47.
Hãy xác định Rv; R„; Ku với k = 0,3.10 ^ Ut = 3V; Td = lOOkQ. Epo 16V Rd L
Rp 10MÍ2 <2,2kíì
r-MAr— í ------- ịị u U v - Hình 3-47
( í ^ Bài tập 3.58. Tính toán lặp lại cho bài 3-57 (xem hình 3-47) với
k = 0,2.10'^ và so sánh các kết quả.
Bài tập 3-59. Hãy xác định
với tầng khuếch đại dùng E-MOSFET
cho trên hình 3-48. Với Uv = 20mV; Uj = 3,5V; k = 0,3.10 ^ gd = 30^iS. 99 . E^d 20V R, R„ 22MD \QkQ r-AAAr- ------- i H ra ¿2 Hinh 3-48
(íã ặ Bài tập 3-60. Hãy xác định u„ của tầng khuếch đại dùng E-MOSPET
cho trên hình 3-48. Biết: Uv = 4mV; Ut = 4V; 1^^^^ = i ; = 4 m A ; -
U , 3 _ = U ; s = 7 V ; g , = 2 0 ^ i s .
Bài tập 3-61. Oio tẩng khuếch đại dùng E-MOSPET như trên hình 3-49.
Hãy xác định u„ với U v = 0,8mV;
= 40kQ; ƯT = 3V; k = 0,4.10 \
Bài tập 3-62. Cho mạch khuếch đại dùng JFET như trên hình 3-50.
Hãy xác định Rjj với: Iqss = 8mA; U p = -2,5V; gd = 25fiS; Ku = 8. 100 ra
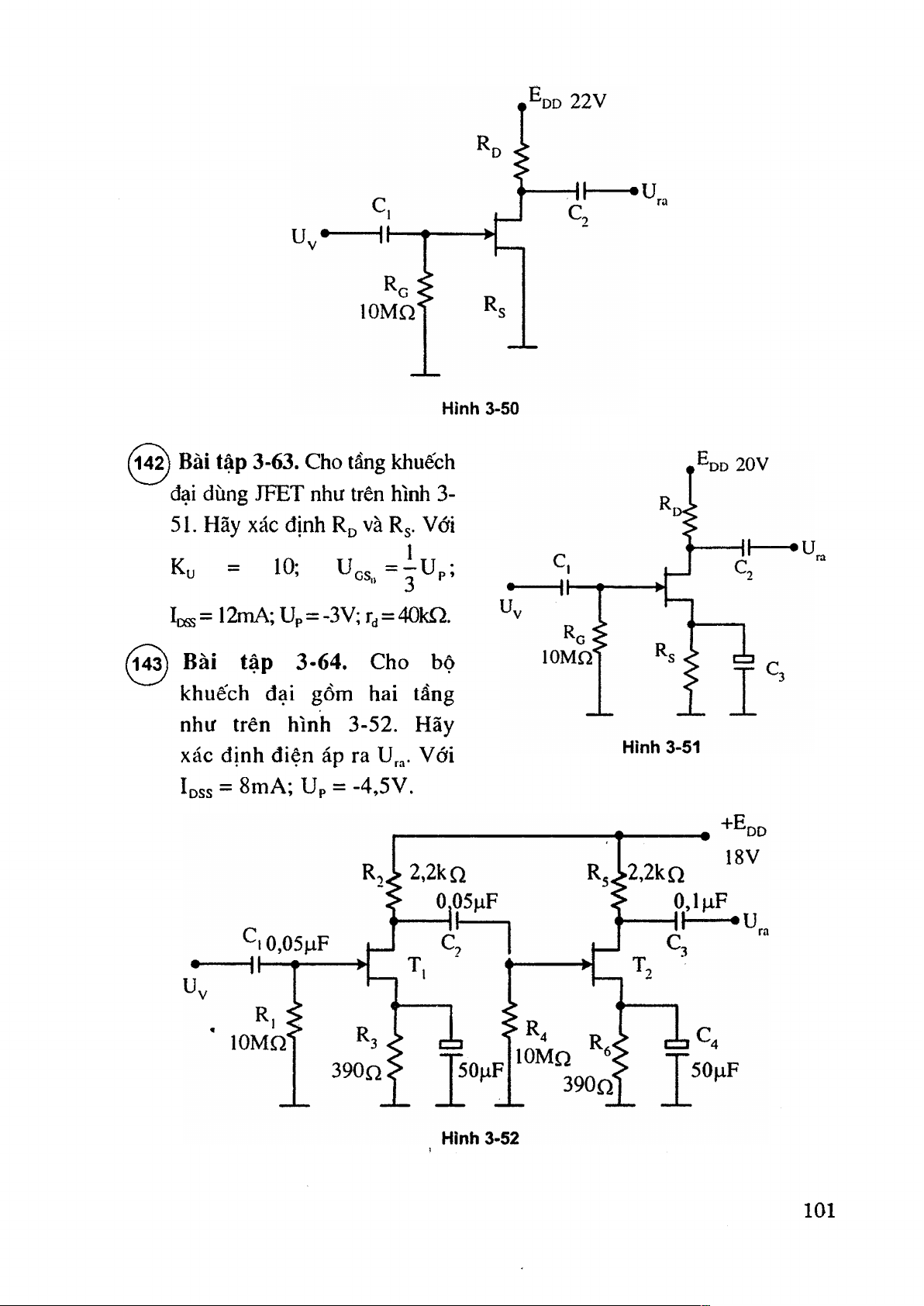
Bài tập 3-63. Cho tầng khuếch
đại dùng JFET như trên hình 3-
51. Hãy xác định Rß và Rs- Với ra Ku = lữ,
Icœ = 12mA; Up= -3V; = 40kQ.
Bài tập 3-64. Cho bộ
khuếch đại gổm hai tầng
như trên hình 3-52. Hãy
xác định điện áp ra u„. Với
I dss = 8mA; ưp = -4,5V. 101
Bài tập 3-65. Cho bộ khuếch đại gồm hai tầng như trên hình 3-53. Hãy
xác định hệ số khuếch đại K„. VỚI Ißss = 6mA, Up = -3V, ß = 150.
( í ^ Bài tập 3-66. Hãy xác định Rv và R„ của bộ khuếch đại cho ứên hình 3-53.
( l ^ Bài tập 3-67. Cho tầng khuếch đại Cascode như trên hình 3-54. Hãy
xác định hệ số khuếch đại K„ và điện áp ra u„. Với Uy = lOmV, ß, = ß, = ß = 200 102
( l ^ Bài tập 3-68. Cho tầng khuếch đại Darlington như trên hình 3-55. Hãy xác định K„.
( í ^ Bài tập 3-69. Cho tầng khuếch đại Darlington như trên hình 3-56. Hãy
xác định điện áp ra ư„. Với Pi = 160; P2 = 200. ra
(1^ Bài tập 3-70. Cho mạch điện đùng JFET như
trên hình 3-57. Hãy xác định dòng điện I với R Ioss = 6mA;Up = -3V. 2 k à i Hình 3-57 103
Bài tập 3-71. Hãy xác định dòng điện I cho mạch điện trên hình 3-58 với p = 100. ị- R, ì 4,3kư l,8kQ +E.. -18V ee Hình 3-58 104 Chương 4 MẠ
m CH KHUẾCH ĐẠ w I CÔNG SUẤT
4.1. TÓM TẮT PHẦN LÝ THUYẾT
Nhiệm vụ của tầng khuếch đại công suất là đưa ra tằi một công suất đủ
lớn theo yêu cầu, có thể từ vài chục mW đến hàng trăm hay hàng ngàn w .
Hệ số khuếch đại công suất đóng vai trò quan trọng, còn hệ số khuếch đại
điện áp chỉ là thứ yếu.
- Tầng công suất có thể làm việc ở các chế độ khác nhau; chế độ A, AB,
B hay chế độ c , nhưng để khuếch đại các tín hiệu điều hòa thường sử dụng
hơn cả là chế độ A và AB (hay còn gọi là chế độ B|).
- Đây là tầng khuếch đại tín hiệu lớn nên buộc phải làm việc ở đoạn
cong của đặc tuyến transistor nên sẽ gây méo phi tuyến.
- Tầng công suất có thể mắc theo sơ đồ đofn hay sơ đồ đẩy kéo, có thể
dùng nguồn cấp điện đơn cực hay nguồn đối xứng có điểm giữa trung hòa.
- Hiệu suất của tầng công suất quyết định hiệu suất của máy khuếch
đại; việc nâng cao hiệu suất ngoài ý nghĩa tiết kiệm năng lượng còn làm
giảm công suất tiêu tán trên vỏ transistor dưới dạng nhiệt.
- Các tầng khuếch đại công
suất được phân ra: tầng đcfn, tầng
đẩy kéo, tầng có biến áp ra, tầng không biến áp ra... *
T ầ n g côìig s u ấ t m ắ c đơn tả i
đ iện tr ỏ (hình 4 -1 )
Hình 4-1. Tầng công suất mắc đơn tải điện trỏ
Để khuếch đại các dao động điều hòa tầng chỉ làm việc ỏ chế độ A,
trong đó transistor làm việc trong cả hai nửa chu kỳ tín hiệu. 105 Công suất ra p = = Is2^ = -Hsm- " 2 2 2R„
Trong đó U,„ = U c B „ = |v à I „ = I„
p_. , = H - k = i Ễ . = i l , E ramax 2 2 2 ^ ° 4 *
Công suất tiêu thụ từ nguồn Po = Ico E
Hiệu suất cực đại khi p„ -> p,ra max n = i ỉ= -|. 100% = 25% 4 I „ E
Thực tế hiệu suất còn thấp hơn.
Điện trở tải xoay chiều tối ưu được xác định: ■^C t.ư h . 2 K
ư u điểm: tín hiệu ít bị méo
Nhược điểm: công suất ra nhỏ, hiệu suất thấp.
* Tầng công suất mắc đơn có biến áp ra (hình 4-2)
Biến áp ra có chức năng ngăn một chiều, dẫn tín hiệu xoay chiều ra tải
Rị đồng thcri phối hợp trở kháng.
Điều kiện phối hợp trở kháng Rra = R( = R( _ w Trong đó n = hệ số biến áp; W2
R„ - điện ừở ra của tầng khuếch đại;
R, - điện trở tải;
R, - điện trở tải quy về sơ cấp biến áp. Từ đó suy ra n = R. i R . 106
Nếu biến áp ra là lý tưỏng thì điện trở tải xoay chiều ở mạch ra u_ U I I ra - co a)
Hinh 4-2. Tầng công suất mắc đớn, có biến áp ra b)
- Công suất ra cực đại ramax 2 2 ■ “
- Công suất tiêu thụ từ nguồn: Po = U ,„.I^ = I,„E - Hiệu • suất cực • đạ•i: 1 E.I = ^100% = 50% Po 2 E.I
Trong thực tế biến áp luôn có tổn hao và tồn tại điện áp dư Udu nên hiệu suất còn nhỏ hơn.
Khi làm việc với tải tối ưu biên độ điện áp cực đại Uca™, bằng 2E YÌ tải
mang tính điện kháng nên xuất hiện sức điện động cảm ứng trong cuộn sơ cấp biến áp.
* T ầ n g cô n g su ấ t m ắ c theo s ơ đ ồ đ ẩ y kéo có biến áp ra (hình 4 -3 )
BAị là biến áp đảo pha;
BAị là biến áp ra.
Tầng có thể làm việc ở chế độ A hay chế độ B nhưng thường là chế độ
AB với dòng tĩnh I,.o« ( 1 0 100) ^A. 107 +E ỉ« . r r" T T ~ V i uy :u - v ị v - ^ ^ L T, BAI Ba2 a)
Hình 4-3. Sơ đồ công suất (a) và đặc tuyến ra (b)
Điện trở tải của mỗi transistor (1/2 cuộn sơ cấp là W| vòng) được xác định, R w,
R’, = n'.R, Suy ra n = n = - ^ R w.
- Công suất ra cực đại một nhánh p
_ il r ; _ I.. UcB. ■_ I.n E ni max 2 2 2
Dòng điện trung bình trong một chu kỳ của một nhánh (1 transistor) 1 I .. I ĩ n
Dòng tiêu thụ từ nguồn E (cả hai nhánh); = 2 .— n
- Công suất tiêu thụ từ nguồn E:
Po = I „ .E = -I,„ E n
Hiệu suất cực đại của tầng p ĩ F. Imax 71 = -100% =78,5% 4 108
Thực tế biến áp có tổn hao và ưcEm < E nên hiệu suất thấp hơn.
Công suất tiêu tán trên colectơ của một transistor dưới dạng nhiệt. P _ p I I 2 Suy ra p = - ^ P wO,4P cmax _2 r;iniax n Kết luận:
- ở chế độ B hay AB khi Uy = 0 tầng không tiêu thụ năng lượng.
- Ngắn mạch tải và hở mạch tải khi có tín hiệu vào đều rất nguy hiểm cho transistor.
* T ầỉìg công su ấ t đ ẩ y kéo m ắc nố i tiếp không hiển á p ra (hình 4 -4 ) 1 R,
R. ịị c, »í • 11 1 • I I ' u. JL R.: ; R, Hình 4-4
Để mắc tải trực tiếp không qua biến áp phải dùng nguồn đối xứng ±E có
điểm giữa trung hoà, các cực + và -E không được nối với vỏ máy. Transistor
T|, Tt là hai nhánh của tầng công suất, dùng hai transistor khác loại dẫn
điện, đều mắc theo sơ đồ tải emitơ nên không khuếch đại được điện áp. Tầng
T, là tầng kích công suất và khuếch đại điện áp, tải xoay chiều là Rj; D| và
D, làm nhiệm vụ tạo thiên áp và ổn định nhiệt cho T| và T,.
Tầng thường làm việc ở chế độ AB. Các tính toán của tầng này giống
như đã xét ở trên.
* T ầ n g công su ấ t m ắ c theo s ơ đ ồ đẩy kéo íỉùng tụ p h á n cách c¡>
Trong trường hợp không có nguồn đối xứng mà chỉ có nguồn đơn cực,
muốn mắc tải trực tiếp, không qua biến áp thì phải dùng tụ phân cách Cp
mắc nối tiếp với tải.
Tụ Cp có hai chức năng: ngàn thành phần dòng một chiều qua R, và làm
nguồn thứ cấp cho T2 khi T| tắt. Tụ Cp sẽ phóng, nạp qua T|, T-, và R,. 109
Tầng Tj và các linh kiện hợp thành giống như sơ đồ dùng nguồn đối xứng.
4.2. PHẨN BÀI TẬP CÓ LỜI GIÀI
(1^ Bài tập 4-1. Cho mạch khuếch đại công suất như hình 4-5 a Biết: E = 1 2 V Rc = 20Q R, = 2kQ
U b e = 0,5V; p = 50
Dòng điện vào có biên độ Iv = I b = 5mA.
a) Xác định điểm làm việc tĩnh 0 và
đường tải một chiều, xoay chiều. Hình 4-5a
b) Xác định dòng Ic ứng với ly = 5mA. Bài giải
a) Dòng tĩnh Ibo được xác định ị I,(m A ) E -U e,o 1 _ 2 _ - _ 0 _ , _ 5 Ạ ^R=R~ = 5,75mA R, 2.10' 1 \ 287,5 ....V Ỵ Dòng tĩnh colectơ V/ /..... x,„ ^ 6,25
Icx) = PIbo = 50.5,75 = 287,5mA U„(V) - Điện ap U (^ = 12-IqqRc =
12 - 287,5. lOMO = 12 - 5,75 = 6,25V Hình 4-5b
Điểm làm việc tĩnh o có toạ độ o (6.25V; 287,5mA).
- Để vẽ đường tải một chiều và xoay G hiều (ở đây = R_ = Rc) cẫn xác
định thêm một điểm nữa ngoài điểm o . Biết phương trình đường tải U,, = E -IcR c Cho Ic = 0
u „ = UcE = E = 12V. Nối điểm o với điểm 12V trên trục
hoành ta được đường tải một chiều.
Trong trường hợp này vì R = R. nên đường tải một chiều và xoay chiều trùng với nhau. 110
b) Khi dòng điện vào Ig biến thiên 5mA thì dòng điện ra sẽ biến thiên
a) Hiệu suất của tầng.
b) Công suất tiêu tán trên colectơ của transistor. Bài giải
a) Để xác định hiệu suất, cần xác định công suất ra tải và công suất tiêu thụ. _ ("250
- Công suất ra p = ^ R = .20 = 0,625W 2 2
- Công suất tiêu thụ từ nguồn
Po = E.I,„ = 12.287,5.10' = 3,45W
Hiệu suất TỊ = ^ ^ 1 0 0 % = 18,1 % ' 3,45
b) Công suất tiêu tán trên colectơ transistor
Pc = Po - Pra = 3,45 - 0,625 = 2,825W
( Q ) Bài tập 4-3. Đề lặp lại bài 4-1.
Nếu giảm biên độ dòng tín hiệu vào còn 3mA Hãy xác định: a) Công suất ra. b) Hiêu suất của tầng.
c) Công suất tiêu tán trên colectơ. d) Cho nhận xét. Bài giải
a) Xác định công suất ra - Dòng điện ra
= Ig .p = 3.50 = 150mA Í15010"^y - Công suất ra = -^ R . = ^ ^ 20 = 0,225W 111
- Công suất tiêu thụ, không đổi
P„= L ,,n = 12. 2 8 7 ,5 .1 0 ' = 3 ,4 5 w
b) líiệu suàì của tầnạ p . . 0 225 n =
100% = - - - 100% - 6,52% K 3,45
c) Công suâì tiêu tán trên colectơ P(. = p„ -
= 3,45 - 0 ,2 2 5 = 3,225W d) Nhận xét:
- Còns suất tiêu thụ từ nguồn là cố định, không phụ thuộc vào mức lín
hiệu vào, vl tầng làm việc ở chế độ A.
- Biên độ tín hiệu vào giảm thì hiệu suất giảm và công suất tiêu tán P(~ tãng lên.
( 1 ^ Bài tập 4-4. Cho mạch khuếch đại công suất có biến áp ra như hình 4-2.
Biết dòng điện tĩnh l|i„ = 3iĩiA; ß = 20; H = 12V; Un|,,) = 0.6V, biên độ
dòntỉ diện vào ỉ|j,„ “ 4mA.
Sụt áp trên R,v : ƯR,.; = 1V; R, = 8Q; n = = 4 .
a) Xác định điện trở R| và R,.
b) Xác định diêm làrn việc tĩnh, đường tải một chiều và xoay chiểu.
c) Xác dinh dòng í^„, và điện áp u^,„. Bài giải
a) Xác định trị số điện trở R| và R,
- u,„ = u,,; + U,„,o = 1.0 + 0,6 = 1 ,6V U,, - I,.R, R, - = % - V - s o n ' l , 4I„„ 4 . 5 . 1 0 '
- U | ^ | = ( I ị, + I ị ịq ) R ị = E - U ị^2 l, + I„, 51., 5.5.10 ‘ 1 2
b) Xác định điểm làm việc tĩnh
Nếu coi biến áp là lý tưởng thì Ư C E O = E = 12V
Ico “ ßlßo — 20.50 = lOOmA
Toạ độ điểm làm việc tĩnh o (12V; lOOmA)
Điện trở tải quy về sơ cấp biến áp
R’, = n-R, = 4 l8 = 1 2 8 n
Từ điểm trên trục hoành có điện áp Uc£0 = 12V công thêm một đoạn điện áp bằng
= 100.10'll28 á = 12,8 V, được điểm B kẻ đường thẳng
qua B và o ta được đường tải xoay chiễu.
Từ đồ thị xác định, ứng với dòng Ißn, biến thiên ±4mA. U c e . « = 22V U c E . i n = U a . = 3 V Icmax= 180 mA Icmin = 2,0 tĩìA. 1 8 0 -2 Biên độ dòng cực đại I = 89mA
Biên độ điện áp ra cực đại I 2 2 - 3 CEmax ^CEmìn U = 9,5V 8- 250BTKTĐIỆNTỪ-A 113
( í ^ Bàì tập 4-5. Đề lặp lại bài 4-4
a) Xác định công suất ra tải.
b) Xác định công suất tiêu thụ.
c) Xác định hiệu suất của tầng.
d) Công suất tiêu tán trên transistor. Bàỉ giải
a) Điện áp hiệu dụng trên cuộn sơ cấp biến áp: TI I — ĩ 79 —'ĩ I = - ĩ ^ = = 6,74 V 7 2 2yÍ2 i S
- Giá trị hiệu đụng điện áp bên thứ cấp biến áp tức là trên tải R,:
U ,= U ™ Ị = Ì A 7 4 = 1.685V
- Công suất ra tải:
p „ = ^ = í l ì ^ = 0 , 3 5 5 W ” R. 8
b) Công suất tiêu thụ từ nguồn:
Po = E.I,„ = 12V.100.10' = 1,2W
c) Hiệu suất của tầng: p ___ 0 355
T1 = -^100% = = 29,58% Po 1,2 ’
d) Công suất tiêu tán ữên vỏ transistor Pc
Pc = Po - Pra = 1,2 - 0,355 = 0,845W
Bài tập 4-6. Đề lặp lại bài 4-4. Nhưng giảm điện trò tải xuống còn
4 0 . Hãy xác định công suất ra, hiệu suất và công suất tiêu tán Pc- Bài giải a)
Nếu Rị = 4Q, thì R’, = n^.R, = 4^.4 = 64Q, toạ độ điểm B trên trục
hoành bây giờ là 12V + 100.10164 = 18,4V. Từ đồ thị (hình 4-6) ứng với
Ib„ = ±4mA so với Igo ta xác định được 8 - 250BTKTOIỆNTỬ - B
U„„., = U ce „ „ = 1 8 V
ư.„ì„ = ư c h „ m = U,„ = 3V Icmin = 2mA Q _ = 1 8 0 m A
Biên độ điện áp ra không méo n - UcB.a.-UcB.n_ 1 8 -3 CEm 2 2
- Điện áp hiệu dụng bên sơ cấp biến áp Ư ™ . = ^ = ^ = 5,32V n/2 >/2
- Điện áp hiệu dụng bên thứ cấp biến áp 1 5 32 U ,= U „ ^ .- = ^ = 1,33V ' ""*4 4 - Công suất ra
P , = ^ = Í!4 ẽ )! = o,442W " R 4
Công suất tiêu thụ
Po = I,„.E = 100.10M 2 = 1,2W p 0 442 b)
Hiệu suất TI = ^ .1 0 0 % = ^ ^ ^ .1 0 0 % = 36,83% Po 1,2
c) Công suất tiêu tán
Pc = Po-p„ = 1,2-0,442 = 0,758 w
Kết luận: Khi điện trở tải giảm công suất ra tăng lên.
( 1 ^ Bài tập 4-7. Cho tầng khuếch đại công suất (KĐCS) mắc đcfn làm việc
ở chế độ A như hình 4-7.
Hãy xác định công suất ra (P„) hiệu suất của tầng (ĩi) với biên độ dòng 20
bazơ Ib„ = lOmA; p = 25; Ic(B) = ^ = — = ÌOOOmA 20 Ecc = ưce(A) = 20V ; Ube = 0,7 V 115 " E 20V 20Q o + Ic T(Si) a) Hình 4-7 Bài giải
Tọa độ điểm Q được xác định theo phưcttig trình đưcmg tải một chiều (R_) R , 1.10'
= ß.Ibo = 25.19,3mA = 0,48 A
Uceo = Ecc - IcoRc = 20 - 0,48. 20 = 10,4V
- Toạ độ hai điểm A và B trên trục hoành và trục tung tưofng ứng sẽ là: 20V và lOOOmA.
- Biên độ dòng ra (dòng colectơ) sẽ là:
Icm = Ibm- ß = lOmA.25 = 250mA p
= Í 2 5 0 ] 0 2 ¿ 20 = 0,625w m 2 ^ 2 P o = E c c - I c o = 2 0 . 0 , 4 8 = 9 , 6 W ^ = ^ 1 0 0 % = ^ ^ 1 0 0 = 6 , 5 % Po 9 ,6
( l ^ Bài tập 4-8. Cho tầng khuếch đại công suất ghép biến áp như hìnầ 4-8. 116
Hãy xác định công suất ra trên tải. E lO V ự ĩ T ĩ A ) l 400ị- ĩ4 m A R. w,5 ^ÍR. 8fì 12m A lOmA l _ = 2 2 5 m A 2oa- 8m A AIc 6 m A u. l^.^ị„=25mA 1001-, 4m A 2mA-ỉj ^ ^ — H-- ^ 5 10 15 p o 25 U J V ) X
Uc.„,„=18.3V a) b) Hình 4-8 w 3
Với các số liệu cho thêm: Ibo = 6mA; I(^ = 4mA; n = — = — = 3 W2 1 Bài giải
Dựng đưòng tải một chiều R_ như trên hình 4-8b, ta có được: = lOV I,,= 140mA
Điện trở tải phản ánh từ thứ cấp về sơ cấp của biến áp là: R’, = n^.R, = 3 \s = 7 2 0
Biên độ dòng colectơ được xác định: I
=Ễí£- = i® =i39m A R ’, 72
Toạ độ điểm B’ trên trục tung sẽ là:
rc..x = Ico + I c . = 140+ 139 = 279mA
Nối điểm Q và B’ ta sẽ được đường tải xoay chiều R. cắt trục hoành tại
điểm có ư ,, = 20V đó là điểm A ’.
Trên hình 4-8b vổi biên độ dòng
= 4mA đường tải R„ cắt các đường
đặc tuyến ra tưomg ứng với
= I|„ + Ibn, = 6 + 4 = lOmA
và Ib„i„ = Ib„ - ĩb„ = 6 - 4 = 2mA r
Khi đó ta có các ‘giá trị điện áp u „ và Ic tương ứng 117 U „„i„=l,7V Ui„ = 25mA u _ = 18,3V u , = 255mA
như trên hình vẽ 4-8b.
Công suất ra sẽ là:
p _ ^^cemax ^cemìn ^^^ciTiax ^cmin^ 8
( 1 8 , 3 - 1 , 7 ) ( 2 5 5 . 1 Q - ^ - 2 5 . 1 0 - ^ ) p 8
(15^ Bài tập 4-9. Cho tầng khuếch đại công suất như hình 4-8 dựa trên kết quả bài tập 4-8.
Hãy xác định Pq; Pc và t|. Bài giải p„ = = 10V.140.10' = 1,4 w
p” = Po - p„= 1,4 - 0,477 = 0,92 w p __ 0 477 11 = - ^ 100% = 100% = 34,1% Po
( í i ặ Bài tập 4-10. Cho bộ KĐCS làm việc ở chế độ B với = 20V, ^ R, = 16Q, E„ = 30V.
Hãy xác định Pq, Pr¡„ "n. Bài giải
Với biên độ điện áp ra 20V và tải 16Q ta túứi được biên độ dòng tải sẽ là: I,m = U = ^ = ^ = U 5 A . lo
Dòng tiêu thụ trung bình là:
I .b = % = - = r ( U 5 ) = 0,796A 71 71
Công suất tiêu thụ từ nguồn cung cấp sẽ là
Po = Ecc.I,b = 30.0,796 = 23,9 w
Công suất ra tải là U i (2 0 f " 2R. 2.16 118
Hiệu suất của tầng là: TI = ^ 100% = — 100% = 52,3% Po 23,9
(l6^ Bài tập 4-11. Cho bộ KĐCS dùng transistor làm việc ở chế độ B mắc đẩy
kéo như hình 4-9 (giả thiết
transistor lý tưởng). Hãy xác định
công suất tiêu tán Pc trên mỗi
ù-ansistor, p„, Po và ĨỊ. Với Uv
hiệu dụng (rms) là 12V = ưvnro- Bài giải
Biên độ điện áp vào là:
u.,„ = >/2.U_ = n/2.12V = 17V vm vrms
Với tầng KĐCS lý tưởng ta coi đúng bằng
(không có tổn hao trên tiếp giáp bazơ-emitơ).
Công suất ra sẽ !à: 17^ p ^ = 36,125W ra 2R. 2.4
Biên độ dòng tải là; U _ 17
I.™ = l.n,= - ^ = J = 4.25A
Dòng trung bình được tính 71
Công suất tiêu thụ từ nguồn cung cấp là: p,b = = 25.2,71 = 67,75W
Công suất tiêu tán trên mỗi transistor là 67,75-36,125 = 15,8W 119 Hiệu suất ĩ] là: ^ 1 0 0 % = 1 0 0 % = 5 3 , 3 % 67,75 tb
162) Bài tập 4-12. Cho tầng KĐCS +E,, 24V
làm việc ở chế độ A như hình
4-10. Hãy xác định dòng tĩnh I(.o
và công suất tiêu thụ từ nguồn cung cấp Po- Bài giải E E Ị — cc ________ cc______ " R _ + R _ R ,+ R ,+ R , E = 2 4 W E 24 =
— = — —— = 1,454A 2R^+R^ 2.8+ 0,5 ~ X r r ^ R , ị t « 'j R ,8 n
( ở đ â y R _ = R ,; R - = R , + R ,) Ĩ I - . í Po = = 24.1,454 = 34,896 w ư
(16^ Bài tập 4-13. Cho tầng KĐCS
nKư hình 4-11. Hãy xác định hệ số
biến áp n với p„ = 9 w? Hình 4-11 Bài giải U:
= 9 W , từ đó ta xác định được biên độ điện áp ra trên tải ư,„ 2R,
U,„.=VP„.2R, = 7 ^ = 12 V
Với giải thiết r, =
(biến áp có cuộn sơ cấp lý tưởng) nên biên độ
điện áp ra phản ánh về sơ cấp u
đúng bằng u „0 và bằng E„.
ư ,„ = U„„ = E,, = 24V u .„ 12 120
( í ^ Bài tập 4-14. Qio tầng KĐCS làm việc ở chế độ A như hình 4-11 (xenn bài
tập 4-13). Hãy xác định công suất tiêu tán trên colectơQỦa transistor T. Bài giải E E 24
Ico = R. + R_ R',+0 n^R, 2\8
Po = E,Ao = 24.0,75 = 18W
Vậy p, = Po - p„ = 18 - 9 = 9 W
( l ^ Bài tập 4-15. Cho mạch khuếch đại công suất như hình 4-12. Biết hai
transistor là lý tưởng
= 0, I^„¡„ = o, E = 20V. Biến áp ra là lý tưởng,
hệ số biến áp n = 2. R, = 8Q; R2= lOOQ.
a) Xác định trị số điện trở R|
để tầng làm việc ở chế độ AB Y T /\ Â \ r VƠI U beo = 0 . 4 V .
b) Tính dòng điện cực đại qua Hinh 4-12 transistor.
c) Tính hiệu suất của tầng.
d) Công suất tiêu tán trên colectơ. Bài giải
a) Thiên áp ƯBEO được xác định theo biểu thức: Suy ra R, = - R, = - ĩ 00 = 4 ,9kfì U ^ 0 4 BEO ^
Biến áp lý tưởng nên UgEo = E = 20V và dòng tĩnh 1^0 = ( )m A
b) Dòng colectơ cực đại E E 20 , ^ = ^T— = , - - = = 1,25A R ’, n".R, 2-.8 121
- Công suất ra cực đại 20.1,25 __ CEm ’ cmax __ = 12,5W
- Công suất tiêu thụ từ nguồn
P„=E.L = E .- .I „ = 2 0 — .1,25 = ]5,92W " 71 3,14
c) Hiệu suất cực đại của tầng:
Tln,.,x = — .100% = - ^ . 1 0 0 % = 78,5% p„ 15,92
d) Công suất tiêu tán: = p„ - = 15,92 - 12,5 = 3,42 w
Bài tập 4-16. Đề lặp lại bài 4-15. Nếu giả thiết tầng làm việc ở chế độ
A với thiên áp U gEo = 1,2V. Hãy xác định điện trở R|. Bài giải
ở chế độ A cả haí transistor T| và T2 làm việc đồng thời, thiên áp đặt vàoT, vàT^là 1,2V R. U b e o = 1 , 2 V = .E R, +Rj Suy ra R, = l,566kQ U beo 1,2
(1^ Bài tập 4-17. Cho tầng
khuếch đại cồng suất như hình
4-13. Hai transistor T| và T2 có
= 0,5V; I„, = ImA. Tầng
làm việc ở chế độ AB. Công
suất , ra p,„ = 25 W; điện trở tải R, = 8Q.
a) Xác định dòng điện cực đại qua transistor.
b) Điện áp nguồn cần thiết. 1 2 2 Bài giải a) Từ biểu thức = — R, (ữong đó
là biên độ dòng điện ra một nháiih) 2P '2.25 Suy ra I,^, - I, = 2,5A b) Từ biểu thức
(U,^ là biên độ điện áp ra cực đại) 2R,
Điện áp U,,, = u,.„ + U,, = ^P„.2R, + ư ,, = V2 5 .2.8 + 0,5 = 20,5V
Điện áp nguồn E = 2(ựP,,„.2R, +
) = 2 (7 2 5 .2.8 + 0,5 ) = 41V E ± 20,5V.
(1^ Bài tập 4-18. Qio mạch khuếch đại công suất như hình 4-14. Biết R, = 8Q;
p„, = 5 w. Hệ số khuếch đại T, và % p = 50
U^I„ = 0,5 V; Tầng làm việc ở chế độ B| có ƯBg()| U = 0,2V BE02
a) Tính dòng cực đại qua transistor. b ) Điện áp U ceo-
c) Điện áp nguồn cung cấp.
d) Công suất ra cực đại. Bài giải
a) Từ biểu thức p,^, = - ^ .R ,
Suy ra dòng cực đại = V R. 8
b) Điện áp Uceo = ^/2P,,,R. +
= ^ /Ĩ 5 I + 0,5 = 9,44V
c) Điện áp nguồn cung cấp
E = 2 ( ^ 2 1 ^ + ) = 2 + 0 ,5 ) = 18,88 V 123
d) Công suất ra cực đại ---- L- = 5W rama* 2 .R^ 2.8
(1^ Bài tập 4-19. Đề lặp lại bài 4-18. Nếu biết dòng colectơ của transistor T,
Icx)3 == 1.5Iboi = l,5Ig02 (Ibom Ibo-> dòng tĩnh bazơ của transistor Tị và Tj)
a) Hãy xác định điện trở Rj và điện trờ nhiệt R,.
b) Xác định công suất tiêu thụ.
c) Xác định hiệu suất của tầng. Bài giải
- Dòng tĩnh qua transistor Tj
leo, = 1,5I„ = 1 , 5 ^ = 1 , 3 - ! ^ = 33,5mA Pmin
a) Điện trở Rj được xác định Ì E = = ^ = = 2 8 1 ,8 « 2 T I O T 'ỉ'ì e i n -3 I*cc o o , I c o . 2 I „ , 2.33,5.10'
- Điện trở nhiệt Rt 2 U 2.0,2 R = .- ...■.EỌ. = = 1 , 9 Q 1 2 f ì ^ Ico3 33,5.10“^
b) Công suất tiêu thụ từ nguồn
p. = - l„ ,..U c B 0 = r ^ l . ' 8 . 9 , 4 4 = 7,095W K J ,1 4
c) Hiệu suất cực đại của tầng p 4 99 X]
= l i ì = -Z1ĨZ_. 100% = 70,33% Po 7,095
( l ^ Bài tập 4-20. Đề bài lặp lại bài 4-18. Nếu thay
bằng hai điốt giống
nhau mắc nối tiếp thuận chiều. Giả sử dòng qua Tj bằng 1,2 Igoi, Ibo->-
Hãy chọn hai điốt; dòng qua điện trở Rj. T 3 , 124 Bài giải
a) Xác định dòng qua Tj
Ia> 5 = 1 . 2 1 « , , = 1 . 2 - ! ^ = 1 . 2 ^ = 2 6 . 8 m A b) Điện trở R.,; U F. Q 44 R
= - 5 - = _ Z lÍ !!_ = 3 5 2 ,2 0 I„, I„, 26,8.10-’
c) Điện trở thuận của hai điốt = ■
f e o i K|£BEỌil. = _ _ M _ = 14,920 IC e03 o3 26,8.10
Chọn hai điốt hoàn toàn giống nhau có điện trở thuận 14 Q2 R d . = R d 2 = - ^ = 7 , 4 6 0 .
( l ^ Bài tập 4-21. Cho mạch khuếch đại công suất như hình 4 - 1 3 . Biết E = ± 2 5 V R, = 4 Q
Giả sử điện áp vào có giá trị hiệu dụng là lOV.
a) Tính công suất ra tải.
b) Tính công suất tiêu thụ từ nguồn.
c) Tính hiệu suất của tầng.
d) Tính công suất tiêu tán trên mỗi transistor. Bài giải
a) Giá trị biên độ của điện áp vào
U .„ = '/2 U .,„ = ^ y 2 .I 0 = 1 4 ,lV
T| và T, mắc theo sơ đồ tải emitơ nên điện áp ra coi như bằng điện áp vào
U . < P ) = 1 4 , 1 V Công suất ra tải 125
Ị C ^ ( H Ị ) 1 , 2 4 , 8 5 W ™ 2R, 2.4
Biên độ dòng điện tải I
= ^ ‘
= = 3 525A
b) Xác định công suất tiêu thụ từ nguồn
- Dòng trung bình I,b trong cả chu kỳ
Công suất tiêu thụ
Po = I,b.E = 2,245.25 = 56,125 w
c) Hiệu suất của tầng p 24 85 ri = ^ 100% = 100% = 44,17% p„ 56,25
d) Công suất tiêu tán trên colectơ của mỗi transistor p _ p.-p„ _ 56.125-24.85 _ 2 2
( l ^ Bài tập 4’22. Một tầng khuếch dại khi chưa cố hồi tiếp âm có hệ số
khuếch đại điện áp k(dB) = 40dB, và điện áp vào Uy = lOOmV. Để tăng
độ ổn định và giảm méo, đưa vào mạch hồi tiếp âm điện áp có hệ số
hồi tiếp k(,t = —^ . ^ 200
a) Tính hệ số khuếch đại khi có hồi tiếp.
b) Điện áp ra khi chưa có hồi tiếp và khi có hổi tiếp.
c) Điện áp hồi tiếp. Bài giải
ạ) Hệ số khuếch đại khi chưa có hồi tiếp kjB = 40 đB. Suy ra K = 100
- Hệ số khuếch đại khi có hồi tiếp âm: 126 = 100 ^ ' + K-K. , + iooJ- 200
b) Điện áp ra khi chưa có hồi tiếp
u „ = K.ưv = 66,6.100.10-' = 6,66V
c) Điện áp hồi tiếp
u» = K^-U„ = ¿ 10 = 0,05V = 50mV
Bài tập 4-23. Một tầng khuếch đại công suất sau khi lắp ráp đo được
tnéo phi tuyến là 6%.
Để giảm méo phi tuyến xuống còn 1 % người ta mắc vào một mạch hồi tiếp âm.
a) Hãy tính độ sâu hồi tiếp.
b) Tính hệ số khuếch đại khi có hồi tiếp. Nếu giả thiết khi chưa có hồi
ũếp ưv = 0,5 V thì u „ = lOV. Bài giải
a) Tính độ sâu hồi tiếp g
Từ biểu tììức y ' = ----------- , frong đó Ỵ. méo phi tuyêh khi chưa có hồi tiếp
y’: méo phi tuyến sau khi có hồi tiếp âm. _____ Y 6
Suy ra đô sâu hồi tiếp g = 1 + KKị,, = -L = — = 6 y' 1 K.Kh, = 6 -l = 5 5 Đã biết K = ^ = — = 20 lần 0,5 K „ = — = 0,25 20
b) Hệ số khuếch đại khi có hồi tiếp 127 K K' = = ^ = 3,33 1 + K.Kht 6
( í ^ Bài tập 4-24. Cho mạch khuếch đại
dùng J-FET có hồi tiếp như hình 4-15. Biết: R, = 120kQ R2 = 30kQ R3 = 20kQ Rd = 20kfì mA
HỖdẫncủaPET g „ = 5
a) Tính hệ số khuếch đại khi chưa có hồi tiếp âm.
b) Tính độ sâu hồi tiếp g và Kị,,.
c) Tính hệ số khuếch đại khi có hồi tiếp K’. , Bài giải
Đây là mạch hồi tiếp âm, khi chưa tính đến hồi tiếp {hở R| và R,)
a) Hệ số khuếch đại
K = g„,.R. trong đó R_ là tải xoay chiều Ri +Rp 20 + 20
K = 5 . l 0 l l 0 " = 50
b) Hệ số hồi tiếp Kh, 30 R| + R j (120+30) 5 1
Độ sâu hồi tiếp g = 1 + K.Kh, = 1+ 50 - = 11
c) Hệ số khuếch đại khi có hổi tiếp âm K K' = . # = 4,545 l + K.Kht 11 128
( l ^ Bài tập 4-25. Để giảm méo phi tuyến cho tầng khuếch đại công suất từ
5% xuống còn 1% người ta đưa vào mạch hồi tiếp âm qua phân áp Rj,
R,. Biết khi chưa có hồi tiếp
K = 20d B .H ãyxácđ ịn h trịsỐ R ,vàR 2. ----- Bài giải
- K(dB) = 20dB. Suy ra K = 10
a) Xác định hệ số hồi tiếp K|,1 Biết y' = Hình 4-16 1 + K.K,, / \ 1 y I _ 4 Kh.= - 1 í - - > ' K I y’ / " 1 0 U ; " 1 0
b) Điện trở phân áp hồi tiếp Rạ - 4 Kh.= R, +R 10 2
giải ra; Rị = 1,5R2 Nếu chọn = 20kQ thì R| = 30kQ.
^ ---------------------- - ---'I ---
( 1 ^ Bài tập 4-26. Mạch khuểch đại thuật toán không đảo như hình 4-17.
Biết hệ số khuếch đại của bản thân bộ
KĐTT Ko = 10“; Rn = IMQ; R, = 20kí2
a)Tính hệ số hồi tiếpKh,. b)
Tinh hệ số khuếch đại khi có hồi tiếp. Bài giải
a) Hệ số hồi tiếp K . = ^ = ^ = 4 = 0.02 ht R 1.10" 50 N
b) Hệ số khuếch đại khi có hồi tiếp âm K’ 1f)4
K' = -----^ — - = ----- --------- = 49,75 1 + K„.K„ l + 10^0,02 9- 250BTKTĐỈỆNTỪ-A 129 Chương 5
BỘ KHUẾCH ĐẠI THUẬT TOÁN m • •
5.1. TÓM TẮT PHẦN LÝ THUYẾT
Bộ khuếch đại thuật toán (KĐTT) là bộ khuếch đại một chiều, có hai
đầu vào một đầu ra, hệ số khuếch đại rất lớn, điện áp ra tỷ lệ với hiệu điện áp
vào, điện trở vào rất lớn và điện trở ra rất nhỏ.
Hiện nay hầu như chỉ sử dụng bộ KĐTT dưới dạng IC. Hình 5 - la là ký hiệu bộ KĐTT. U. N ừra ưp— p -E a) Ký hiệu KĐTT Hình 5-1
Theo định nghĩa u „ = Ko(Up- u,,) = KoU, trong đó:
= Up - Un là sai lệch điện áp đầu vào;
Kq là hệ số khuếch đại của bản thân bộ KĐTT. Nếu ƯN = 0 thì
= Kq Up điện áp ra đồng pha với điện áp vào và cửa p
được gọi là cửa vào thuận, ký hiệu +. Nếu Up = 0 thì
= - KqUn , điện áp ra luồn ngược với điện áp vào và
cửa N được gọi là cửa đảo và ký hiệu là (-). 130 9- 250BTKTOJỆNTỬ-B
Các tham số cơ bản của ICKĐTT Tham số Lý tưởng Thực • - Trở kháng vào Zv 00 Trăm kQ - Trở kháng ra z„ 0 Trăm Q
- Hê số khuếch đại Kq 00 lOUO^
- Dòng điện vào Ip, Ifg 0 Trăm nA
* H ệ s ố nén đ ồ n g p h a Nếu Un = Up =
# 0 (U^.^ gọi là điện áp đồng pha), theo lý thuyết
u„ = 0 , nhưng trong thực tế khác không. u„ = Kc .
- K,. gọi là hệ số khuếch đại đồng pha.
Hệ số nén đồng pha (CMRR) là tỷ số giữa hệ số khuếch đại của IC TT
lý tưỏrng Ko và hệ số khuếch đại đồng pha CMRR = ^ ; CMRR(dB) = 201g ^ , dB. Kp K^,
CMRR vào khoảng (70 ^ 100) dB.
* Đ ặ c tuyển truyền đạt (hình 5-lb) là quan hệ giữa u „ và Uv = Up - Un
u„ và Uv chỉ tuyến tính trong một khoảng hẹp, ngoài phạm vi đó điện áp ra
không thay đổi và gọi là điện áp bão hoà. Khi chưa có mạch hồi tiếp âm bên
ngoài, IC TT làm việc ở chế độ bão hoà » ±E.
* L ệch không và hù ì ệch không
Nếu thông số tĩnh hai cửa vào p và N không hoàn toàn cân bằng Ip và
Z|, ít Zn thì khi Un = Up = 0 vẫn tồn tại điện áp một chiều Uo nào đó Uo = IpZp-lN Zn
Điện áp này được khuếch đại và ở đầu ra tồn tại điện áp u ,0 0 gọi là
điên áp lệch không, bởi vậy phải có biện pháp để u„ luôn bằng 0 khi Uy = 0
gọi là mạch bù lệch không.
Về nguyên lý, mạch bù lệch không được thực hiện bằng cách bù vào
đầu vào một điện áp một chiều có trị số đúng bằng Uq và có cực tính ngược
với ƯQ. Mạch này có thể thực hiện bằng cách đưa điện áp vào cửa p hay N
hoặc IC có sẵn các chân để mắc mạch bù lệch không.
* M a ch khuếch đ a i đảo 131
Điện áp cần khuếch đại được đưa đến cửa đảo N, còn Rn và R| là hai
điện trở hồi tiếp mạch ngoài (hình 5-2).
Đối với IC TT lý tưởng, hệ số khuếch đại khi có hồi tiếp được xác định
K’ = ^ và điên áp ra u , = - ^ .Uv R, " R,
Dấu (-) ở đây có nghĩa là điện áp ra và vào luôn ngược pha. b)
Hình 5-2. Các sd đồ khuếch đại thuật toán cơ bản
* Bộ khuếch đ ại không đảo
Điện áp cần khuếch đại được đưa vào cửa thuận p (hình 5-2b).
Hệ số khuếch đại điện áp được xác định theo biểu thức: U,. = ( l + ^ ) U ,
Nếu giữa Uy và điện áp cửa p có mạch phân áp điện trở thì Up xác định
theo Uy qua mạch phân áp đó.
* M ạ ch cộ n g và tr ừ (hình 5 -3 )
Mạch cộng là mạch thực hiện hàm u„ = A(U|+Ư2+...+U„). Trong đó U|, u ,
là các điện áp vào.
Tuỳ theo sơ đồ có thể là mạch cộng đảo hay cộng không đảo. 132 a) b)
Hinh 5-3. Mạch cộng (a) và trừ (b)
Hình 5-3a là mạch cộng đảo.
Điện áp ra được xác định. K| Kj
Mạch trừ (hình 5-3b)
Có thể giải mạch điện theo nhiều phương pháp khác nhau, nhưng thuận
tiện hon cả là sử dụng phương pháp xếp chồng.
U „ = ( l + ^ ) U p - ^ U , K, K, R R = ( i + ễ ^ ) R| Rj + Rp R,
* Mạch vi phản và tích phân (hình 5-4)
Hình 5-4a là mạch vi phân dùng IC TT R a) b)
Hỉnh 5-4. Mạch vi phân (a) và tích phân (b) 133
Điện áp ra mạch vi phân (hình 5-4a)
U„ = - R C Í ^ = - x ^ dt dt
Hình 5-4b là mạch tích phân dùng IC TT
Điện áp ở đầu ra mạch tích phân (hình 5-4b) u „ = - ^ '|u.(t)dt=-!-|u.dt K U 0 T 0
Trong đó X = RC gọi là hằng số thời gian.
5.2. PHẦN BÀI TẬP CÓ LỜI GIẢI R. @
Bài tập 5-1. Cho mạch KĐTT như hình 5-5 = lOkn R , = 500kQ R N lOkn R p = E = 12V
Viết biểu thức U,,. Tĩnh
nếu Uy = 0,2V và cho nhận xét. Hinh 5-5 Bài giải a)U,. = - ệ ^ U .
b)U„ = . ^ U , = . ^ . 0,2 = - l 0 V. K| lU
Điện áp ra -lOV lớn hcfn E = -12V nên tín hiệu ra nằm trong vùng tuyến
tứih, không bị méo.
( l ^ Bài tập 5-2. Hãy tính toán và thiết kế mạch khuếch đại thuật toán với các yêu cầu sau;
a) Điện áp ra ngược pha với điện áp vào.
b) Nếu U, = 0,5V thì u „ = 15V. Điện trở vào = 20kỉ2. 134 Bài giải
Vì điện áp ra ngược pha với điện áp vào nên đây là mạch khuếch đại
đảo, sơ đồ mạch điện như hình 5-4. • *
Hệ số khuếch đại: • * u . 0,5 Mặt khác
K = - ^ = 30 suy ra Rn = 30R, R,
Vì R, chính là điện trở vào R, = R, = 20kQ
Suy ra Rn = 20k n .30 = 600kQ.
179) Bài tập 5-3. Cho mạch KĐTT như hình 5-6a r R2
^vl»-—-Ạ/S/ỷ^ ^ ra - R 1 a) b) Hinh 5-6 Biết R, = 20kQ Rn = 780kí2 R, = 20ka E = 15V
a) Viết biểu thức xác định Ura-
b) Tính ư,, nếu biết u , = 0,30V. 135 Bài giải
a) Vì điện trở vào cửa p rất lớn nên có thể coi như không có dòng qua / \ / \
R2 nênđiệnápư, = Up,U„= 1 + ^ u U , p = = 1 + ^ p R, / R R ,, J R , J > \ 1 / b)TínhU„:
U„ = ( 1 + ^ ) . 0 , 3 = 1 2 V
u „ = 12V < E = 15V, tín hiệu không bị méo.
Bài tập 5-4. Cho mạch điện như hình 5-6b Biết Rn = 500kí2 R, = 20kQ = 20kn Rj = l o m R4 = 3 0 m = 400mV = SOOmV
a) Xác định biểu thức u„.
b) Tính trị số của u„. Bài giải
*a) Có thể giải mạch điện trên theo các phương pháp khác nhau, nhưng
tiện hơn cả là dùng phương pháp xếp chồng. R
- Nếu chỉ tác động = ì^ + 1 R3//R4 .u R ,+ (R J /R ,)
- Nếu chỉ tác động R, -> u „ = R2//R. u
R1 y R ,+ (R J/R ,) u„ = u„, + u„,= R 3//R , R 3//R , 1 1 + _
ư v , + - ---- *_— .Uv. R. ' R ,+ (R ,//R .) ^2 +CR3//R4)
R3 //R4 = 7,5kfí R3+R , 10 + 30 136 20.30 R2//R4 = = 12kí2 R , + R , 20 + 30
b) Tính trị số u„: Thay số vào U„ = ( l . ^ ) = 9,906V ” 20 20 + 7,5 10 + 12
(18^ Bài tập 5.5. Cho mạch điện như hình 5-7 Đây là mạch gì?
Viết biểu thức tính u^.
Tính u „ nếu biết: ra U, =0,15V Ư2= IV = 500RÍ2, = 20kQ R , = 30kí2, = 20kfì R 2 R p Hình 5-7 Bài giải
a) Đây là mạch trừ, thực hiện thuật toán u„ = AUy2‘
Để thiết lập biểu thức u„, tiện hon cả là giải theo phương pháp xếp‘chồng
- Nếu chỉ tác động nguồn tín hiệu u^ị, đây là mạch khuếch đại đảo VI R
Nếu chỉ tác động tín hiệu u^2 »
là mạch khuếch đại thuận R .UV2 R, R j + R p R R Điện áp ra: = u , , , + 2 = U ìí-.u V2 VI R I Rs +Rp R , b) Thay số vào
. 1,0 - — .0,15 = 6,65 V 20 20 + 30 20
(1^ Bài tập 5-6. Thiết kế và tính toán mạch khuếch đại thuật toán thực
hiện thuật toán sau: • « 137 Y = 2a -4b * Trong đó:
Y là điện áp đầu ra;
a và b là hai điện áp vào; 4 và 2 là hệ số. Bài gỉai
Để thực hiện thuật toán trên phải dùng mạch trừ. Sơ đồ như hình 5-7.
a) Xác định biểu thức điện áp ra R R Y = ( l + : ^ ) R, R, + R_ R, So sánh biểu thức và * suy ra R ( 1 + 4 ^ ) = 2 RỈL = 4 R, RN 4. Suy ra Rn = 4R R T> Thay — = 4 vào: R. R R — ^
= 2 - » ( 1 + 4) ------ ỉ— - = 2 R R, +R^ R . + R .
Như vậy để thực hiện thuật toán trên phải chọn:
Rn = 4R| và Rị = 1,5 Rp.
Nếu R, = 20k n thì Rn = 80ka
Nếu Rp = 20kQ thì R2 = 30kn.
(18^ Bài tập 5-7. Cho mạch khuếch đại thuật toán như hình 5-8
a) Viết biểu thức tính hệ số khuếch đại K„. 138
b) Tính trị số u„ nếu biết:
R, = lOkQ, R2 = 200kí2 R, = 20kQ, R4= 15kí2 R s= 150kO,E= ±15V U, = 0,15V. Cho nhận xét Hình 5-8 Bài giải a)
ở đây có thể coi như hai tầng khuếch đại mắc kế tiếp nhau, tầng IC|
có hệ số khuếch đại là K| tầng IC| có hệ số khuếch đại là Kị.
Hệ số khuếch đại K„ được xác định; U K„ = = K , K , U
Trong đó; K| =(1 + ^ ) R, R R R, =
Suyra:K„ = K,.K3 = ( l + 3 ( - ^ ) R R, R, R, K b) Tính Ura 200^ 1 5 0 1 + .0,15=-16,5V 2 0 j 1 5 139
Nhận xét: Vì điện áp nguồn -E = -15V trong khi = -16,5V, nhu v ậ y
điện áp ra bị xén đỉnh, nên bị méo. Để điện áp ra tuyến tính phải giảm
hay giảm hệ số khuếch đại K„.
(1^ Bài tập 5-8. Xác định phạm vi điều chỉnh điện áp ra trong mạch hình 5-9 Biết: R| = 10k£2 Rn = 250ka = ( 0 - 2 0 ) k a R p = 0,2V U v Bài giải
- Viết biểu thức điện áp ra Hình 5-9 R. u„ = - .U. R,+Rp ■
- Điện áp ra sẽ cực tiểu khi chiết áp Rp = 0Í2 u » = - | ^ u . = — 0 , 2 = - 5 V
- Điện áp ra sẽ cực đại khi Rp = 20kíầ R . 250 u . = -
,u = . _ Ì ^ . 0,2 = - 1 ,66V R.+R.. 10 + 20
Như vậy điện áp ra sẽ biến biến thiên trong khoảng từ -5V đến -1,66V
khi điều chỉnh chiết áp R p .
(1 ^ Bài tập 5-9. Cho mạch KĐTT như hình 5-10. Biết: = 15kO R , Rị = 250kQ R3 = 20kí2 = 470k 0 R 4 E = ± 9 V U, = 25mV ICTTlà lý tưỏng 140
a) Viết biểu thức hệ số khuếch đại K„.
b) Tính trị số u„ và cho nhận xét. Bài giải
Dòng điện tại nút N
I| = I j + I n v ì I n = 0 nên I, = I2 Trong d ó l | = R R U v - U , U^-U^ Suy ra: — - — ^ M R R
Vì N là điểm đất ảo, nên ƯN = Up = 0 và cuối cùng — = . Suy ra = - — Uy * R , R j R ,
Tại nút M: It +I4 - Ij = 0 U m , U . - U m H í R. R. R R, R4 Thay giá trị
từ * vào và giải ra ta được. / \ Í 1 1 1 1 1 U„ = Ì . R , •U. R. ^1^2
Hệ số khuếch đại u I 1 1 K = R u R Tính điện áp ra: 1 1
U„ = - Ỉ ^ . 4 7 0 Í ' + 25.10' « l i v 15 250 20 470
Điện áp ra u,, = 11V > +E = 9V. Tín hiệu ra bị xén đỉnh. 141
( l ^ Bài tập 5-10. Cho mạch cộng đảo như hình 5.11 BiếtR, = 2 0 k í2 R = 25 k a u, .--- V\Ar— +E R, = 30kí2 ; = 500kfì • U. R U U , = 0 , 1 V u ,— -E U, = 0,2V Ư3 = 0,3V
a) Viết biểu thức u„. Hình 5-11 b) Tính u„. Bài giải a)
Đây là mạch cộng với ba điện áp vào U|, u, và u,; giải mạch theo
phưcíng pháp xếp chồng: R
u„=u„,+u„,+u,,,= - ^ . u , + ^ . Ư 3 + ^ . U , R. ' R, ^ R, 5 0 0 , , 5 0 0 , , 5 0 0 , , U, +^— U, +^— U, 2 5 U , + 2 0 U , + — U, 20 ‘ 25 30 ' 30 •’ b) Thay số vào ^500 500 u„ = - .0,1 + 20.0,2 + —
.0,3 = - l l , 5 V 20 30
Bài tập 5-11. Cho mạch điện như hình 5-12
a) Viết biểu thức hệ số khuếch đại K„.
b) Xác định trị số ư„ nếu biết: 142 Uv = 0,5V
R, = 20kQ; R2 = 20kQ; Rj = 30kQ
R4 = 250kQ; R , = lOkQ Hình 5-12 Bài giải
a) Hệ số khuếch đại K„ = Ki-K,
trong đó K| = 1 đây là mạch lặp điện áp u „ = ư, K .= 1 + và K. = 11 I Rs ; .\ R, 5 > y b) Điện áp ra u,. = = (u1 + + ^ — ) --- =T - T U - . U . = = (1 U + + ----- ) ~ .0,5 = 5,2V V _ _ 10 20 + 30 r / r , + R 3 ' 10 2(
(1^ Bài tập 5.12. Cho mạch điện như hình 5-13 Biết Rn = 500kí2 R, =25kí2 ± E = ± 1 2 V
Điện áp bão hoà ± lOV
Xác định điện áp vào cực đại mà điện
áp ra vẫn trong phạm vi tuyến tính.
Xác định u„ với các giá trị u „ = 0 ; u„ = 0,4V.’ Hình 5-13 Bài giải Hê số khuếch đai; 143
K = Ì = . Í 5 5 = . 2 0 . R. 25
Điện áp vào đỉnh - đỉnh Vp.p U
= H ^ = ± ị ^ = ± 0 , 5 V vp-p K 20 u„ = i u = - Ể ^ . U , = -20U R 25 Tính trị số u, ưv ư . ov ov +0,4V -8V -0,4V +8V
Bài tập 5-13. Cho mạch khuếch đại như hình 5-14 U v R . vv\/ w ỉ — Hinh 5-14
a) Viết biểu thức I và u „2
b) Tính trị số u„| và biết: U. = 0,5 V 144
R, = Ra = 2 0 k fì; R3 = 3 0 k a ; R4 = 25kQ
R3 = 500k Q ; Rg = 500kQ ; R7 = 2 5 k Q . Bài giải
a) u„, = K,.K2ư , ; trong đó K, là hệ số khuếch đại của IC,
K2 là hệ số khuếch đại của IC2 R ư ., = - ^ u = + M l . u R.R4 b) Thay số ta có: U«. = .0,5 = lOV R..R 20.25
U „, = . Ì ( u M , . 0 , 5 = . , 0 . 5 V 2 0 ' 25
{1^ Bài tập 5-14. Cho mạch khuếch đại thuật toán như hình 5-15. Hình 5-15
a) Viết biểu thức u„.
b) Xác định trị số nếu biết:
R, = 20kí2 ; R2 = 500ka , R3 = 25kfí
R4 = 2 0 k a ; Rs = 3 0 k a ; = 60k a
ư, = 0 , 2 V ; ư 2 = 0,3V.
10- 250BTKTĐIỆNTỬ.A 145 Bài giải
a) Đây là bộ khuếch đại có hai tầng IC| và IC2 có hai điện áp vào.
Trước hết xác định điện áp Ural ư„,= ư,.
Đây chính là điện áp đưa vào cửa đảo của ICj.
Giải mạch điện ICj: R R i 1 l+Æ Î U,- U. l R3. R R R R (1 + ^ ) U , A + ^ . U
b) Thay số vào để tính u u„ = - = -13,2V 25 20 30
Bài tập 5-15. Cho mạch điện như hình 5-16. Hinh 5-16 Biết: R, = 20kQ
R2 = 20kQ R, = 600kfì 146
10-250BTKTĐỆNTỪ • 8 R4 = 30ka R., = 30kfí = 50k0 R ,= I50kí2; U, = 0,1V
a) Hãy viết biểu thức u„ = f(UJ.
b) Tính trị số u„. Bài giải
a) Thiết íập biểu thức u„
- Điện áp ở đầu ra IC|. u„ I =
vì đây là mạch lặp điện áp. / \ R.
- Điện áp ở đầu ra IC,: = 3 1 + u. ♦ \ R
Cả hai điện áp này đều đưa vào đầu vào đảo của IC, nên đây là mạch cộng đảo.
Giải theo phương pháp xếp chồng: / \ ' R u . = - 3 1 + u. R, R R u„r a= - u.
b) TTiay số vào để tính u„ 150 150 u„ = - 0,1 = - 6,8 V 30 50 (1 . ^ ) 30
(1^ Bài tập 5-16. Cho mạch điện như hình 5-17
a) Xác định biểu thức u„ - f( U|, U-,)
b) Tính trị số u,a nếu biết: U, = 30mV ; U, = 20mV R, = 20kQ , R2 = 40kQ, = 200kQ, R4 = 40ka
R5 = 20k a , Rft = 500kí2. 147 Hinh 5-17 Bài giải
a) - Điện áp đầu ra IC|
Urai = U2 , đây là mạch lặp điện áp vào
- Điện áp đầu ra IC2 u .2 = - \ u . + ^ U
đây là mạch cộng đảo. lR. R
Cả hai điện áp u „ | và u „ 2 đều được đưa vào cửa đảo của IC3 , IC 3 là mạch cộng đảo.
Giải theo phương pháp xếp chồng, ta được: ĩ? R R R
u„r a= - R. ' R / R. ' R, ^ = - + ^ ( ^ u , + ^ u . ) R, R / R . R , '200 ^ . 2 0 .10 ’ • .3010-'+— .2010 = 4,5V 20 40 , 2 0 40
(1^ Bài tập 5-17. Cho mạch điện ICTT lý tưởng như hình 5-18 Biết Rn = 500kí2 R. = 20kQ 148 E = ± 14V
Điện áp bão hoà ± 12V
a) Hãy xác định Uy cực đại mà điện
áp ra vẫn trong phạm vi tuyến tính. b) Xác định với các giá trị
U, = OV; ±0,2V ; ±0,4V Bài giải
a) Hệ số khuếch đại khi có hồi tiếp âm R. 20
Điện áp vào đỉnh - đỉnh cực đại u.,„. = — = ±0,48V vp-p K 25 b) Tính trị số u, = 0 u„ = 0 u , = +0,2V
u „ = -KU, = -25.0,2 = -5V u , = - 0,2V
ư „ = - 25.(-0,2) = 5V u , = + 0,4V
= -K .u, = -25.0,4 = -lOV
u„ = - 0,4V - » ư , = ~ 25.(- 0,4) = +10V ưv 0 -0,2V +0,2V -0,4V + 0,4V 0 5V -5V lOV -lOV
( 0 Bài tập 5-18. Thiết kế mạch R
khuếch đại ửiuật toán thực hiện chức năng sau: dU,(t) u . = - A ra dt
a) Nếu biết Uv = 2Vsinl000t;
R = 2kQ; c = 0,47^iF. Hãy tính ư„.
b) Vẽ dạng điện áp ra. Hình 5-19a 149 Bài giải
a) Chức năng trên là mạch vi phân, sơ đồ như hình 5-19a dU. U „ = - R C dt d(2V.sinl000t) = - 2 . 1 0 ^ 0,4710* dt
= - 2.0,47.10^2.1000 cos lOOOt = - 1,88 coslOOOt.
b) Dạng điện áp ra (hình 5-19b)
( l ^ Bài tập 5-19. Cho mạch điện như hình 5-20. Biết = lOsin lOOt c= 1 ^F R = lOOkQ
a) Đây là mạch gì?
b) Viết biểu thức u„. Bài giải
a) Đây là mạch tích phân, điện áp ra
tỷ lệ với tích phân điện áp vào.
b) Để thiết lập biểu thức u„, viết
phương trình tại nút N.
= 0 (vì ICTT lý tưởng nên = 0) R dt Suy ra; 1 Hình 5-20 u . = - RC TTiay số ta được 1 u„ = lOsinlOOtdt 100. 10M0-" = 1(V) cos lOOt. 150
Bài tập 5-20. Cho mạch điện như hình 5-21
Biết tại thời điểm t = 0, u„ = ov
•R , = R3 = R = lOOkỉí c = 1ịxF
a) Xác định biểu thức u,, = f (U„ + u,^).
b) Tính u „ nếu biết u„ = (IV + lOV sin lOOt). u„, = - IV Bài giải
a) Xác định biểu thức
Phưoíig trình dòng điện tại nút N Hình 5-21 R, R, dt dU^ dt 1 Suy ra u . = - dt vR. b) Tính
ở đây R, = R2 = R = lOOkQ, nên có thể viết: 1 1 ư„ = - ra ( U . , + U 3)dt =
J{l + 1 0 sinl00t - l ) đ t RC ■ ’ lOMO* ư,, = 1(V) cos lOOt. 151 Chương 6 NGUỒN ỔN ÁP
6.1. TÓM TẮT PHẦN LÝ THUYẾT
Mạch ổn áp là mạch điện nhằm bảo đảm cho điện áp nguồn một chiều
Ổn định, không thay đổi khi các tác nhân bất ổn định tác động, ví dụ khi điện
áp lưới điện thay đổi, khi điện trở tải và nhiệt độ thay đổi. Mạch ổn áp được
bố trí sau mạch lọc phẳng của mạch chỉnh lưu. Đồng thời mạch ổn áp cũng
có tác dụng giảm nhiễu, do vậy giảm được trị số phần tử lọc nguồn Ll, Cl
làm cho bộ nguồn đơn giản và gọn nhẹ hơn.
* Mạch ổn áp đơn giản nhất là dùng điốt ổn áp (điốt zener) (hình 6-1 ) Trong sơ đồ
là điốt ổn áp, luôn
được phân cực ngược, mỗi điốt tồn tại một
giá trị điện áp ổn định nhất định là u^.
U, lậ điện áp một chiều sau mạch
chỉnh lưu và lọc chưa ổn định.
Ư2 là điện áp đã ổn định.
Từ sơ đồ có thể viết
Hình 6-1. Mạch ổn áp đơn giản dùng
U , = U r + U, = I,R + U, điốt zener
R ià điện trỏ bù
SuyraU„ = U, = I,.r,= - ^ . r = U , - L R R + r, AU
là điên trở đông của điốt ổn áp r = — - , ữi số
càng nhỏ đô ổn áp AI, càng cao.
Nếu vì lý do nào đó (ví dụ điện áp lưới điện tăng) U ịt -> I^t -» I^.R t . 152
kết quả là u„ được giữ nguyên. Điện trở tĩnh của điốt zener được xác định
bằng tỷ số giữa điện áp đặt vào điốt và dòng điện qua điốt R ,. ,ĩ„h ^
Hệ số ổn áp một chiều chính lả hệ số lọc độ ù _ _ AU, _ R + r, , R R G = — ^
= — _ ỉ - = i + _ « _ V Ì R » r. AU >; Tz hay R 1 — » 1
Mạch ổn áp Crực tiếp dùng điốt zener chỉ dùng cho nguồn công suất nhỏ,
có hiệu suất thấp khoảng 50%, vì tổn hao trên điện trở R và trên khá 1^.
* Mạch ổn úp tham số đơn giản (hình 6-2)
Đây thực chất là mạch lặp emitơ
(tải emitơ). Khi hở tải R, = 00 dòng qua rất nhỏ. ? T vbe L u, L--------u , Ị r^ Dòng tĩnh Iß0 = y . 1_____ J
Điện áp ổn áp ở đầu ra u „ = Uj =
Hình 6-2. Mạch ổn áp tham sô' đơn giản
ở đây UßE rất nhỏ so với nên ư , » = const.
Điện trở trong của bộ ổn áp chính là điện trở ra. của mạch tải emitơ
R. = —^ ; vì Rị < r, nên điện áp ra uđc’ ' 1 + ß
của mạch ổn áp ít phụ thuộc vào R,.
* Mạch ổn áp tham sô (hình 6-3) ư, So sánh uM
Phần tử điều chỉnh có điện trở u I T
thay đổi theo điện áp điều khiển
được mắc nối tiếp với tải R,.
là điện áp chuẩn, thưcmg sử
Hỉnh 6-3. Sđ đồ khối mạch ổn áp ữiam số
dụng điốt ổn áp có = const. 153
Um là điện áp mẫu, tỷ lệ với điện áp ra Uj.
Bộ so sánh: so sánh điện áp mẫu Um và điện áp chuẩn và khuếch đại
lên, tạo ra điện áp điều khiển Uji,.
Điện áp Ut có thể viết:
U, = U , - U , , = U, -I . r, , Trong đó
là điện trở của phần tử điều chỉnh phụ thuộc vào Ud,,. Nếu
vì nguyên nhân hào đó mà u, tăng
u, cũng có xu thế tăng và u^t -> (ƯM - U J f làm cho và kết
quả là Uj^t, cuối cùng U, = U|
— u<ị<. được giữ ổn định.
Hình 6-4 là mạch điện
nguyên lý ổn áp tham số dùng transistor.
Từ sơ đồ mạch điện suy ra Ir3 “ ^B1 U, U m - •^2 — ^BE2 R, + R ,
Điện áp ra được xác định
Hình 6-4. Sơ đồ nguyên lý mạch ồn áp tham sô' theo biểu thức: / \ u , + u „ p , R U 1
2 = ^ - Í ^ ( R 2 + R, ) = (U, + 1 + Ra \ R,
Có thể tính gần đúng u, « u ^ 2 )
Nếu thay đổi tỷ' số R
thì có thể điều chỉnh R. V / R R
được điện áp ra Uj. U, * Mựcỉ ổn áp U,
dùng ỈC thuậĩ toán IC < Thay ch' transistor
T, trong hình 6-4 có thể
dùng IC t' 'lật toán
Hinh 6-5. Mạrh ổn áp dùng IC thuật toán
đồng tbM làm hiệm vụ 154
so sánh và khuếch đại để tạo điện áp điều khiển Udi, như hình 6-5.
Điện áp U2 được xác định theo công thức u , « ụ = u. , v R, R2 J
Tliay đổi trị số R, và R, có thay đổi được điện áp ra u ,.
* M ạ ch IC ổn áp
IC ổn áp có hai loại: Loại không điều chỉnh được điện áp ra và loại có
thể điều chỉnh được điện áp ra. 7805 •+5V
- Loại IC ổn áp không điều chỉnh được
điện áp ra thông thường có 3 chân. Muốn
nguồn ổn áp bao nhiêu vôn thì cần chọn loại
Hình 6-6. IC ổn áp có điện áp
IC ổn áp thích hợp. Hình 6-6 là ví dụ IC ổn áp ra cố định họ 78XX.
- Loại IC ổn áp có thể điều chỉnh được điện áp ra, ví dụ IC LM ! 17
hoặc LM 317 (hình 6-7).
Trường hợp lý tưởng, dòng bổ sung Iadj = 0, điện áp ra được xác định theo biểu thức u . = u .. , v RI J Trong đó: là điện áp chuẩn LM317
bên trong IC và được đặt vào điện trở 'I ADJ ■ u , U-
R|, khi đó tạo ra dòng ị R. ^1
điện áp u,h thường là 1,25V. Tụ c có 1
trị số khoảng lp,F dùng để cải thiện
Hình 6-7. IC ổn áp điều chỉnh được
đặc tuyến ra. Trong trường hợp thực, điện áp ra
tồn tại dòng bổ sung I^DI dù rất nhỏ, 155
khi đó qua Rj có hai dòng điện chạy qua và điện áp ra được xác định. Ua=U,H Rỉ y
Như vậy có thể điều chỉnh điện áp U2 bằng cách thay đổi trị số R,.
Điện áp chưa ổn định ư | phải lớn hơn Ư2 vài vôn.
6.2. PHẦN BÀI TẬP CÓ LỜI GIẢi
(1^ Bài tập 6-1. Một nguồn điện một chiều, khi chưa có tải điện áp là 12V.
Khi có tải điện áp sụt xuống còn lOV. Tĩnh độ mất ổn định điện áp. Bài giải
Độ mất ổn định điện áp
AU = U o - U , = 1 2 - 1 0 = 2V
Trong đó; Uo là điệứ áp khi hở tải
U, là điện áp khi có tải.
Hệ số mất ổn định điện áp ^ 100% = 20% ưt 10
(1^ Bài tập 6-2. Cho mạch ổn áp dùng điốt zener như hình 6-8. Biết U, = 20V U, = U, = 6V Dòng = 30mA R = 400Q
Đặc tuyến điốt ổn áp như hình 6-8b. Xác định phạm vi R, để mạch làm
việc trong dải ổn áp. 156 a) b) Hinh 6-8 Bài giải
- Khi R, có trị số nhỏ nhất, dòng I, lớn nhất và dòng nhỏ nhất.
Iz = ^zmin = omA (căn cứ vào đặc tuyến)
Điện áp trên tải: U| o _ _ r» u R.
u. = u, = — — R, . . Suy ra R, . = ' P j - P u ,- u Thay số R, . = = 171,4Q 2 0 -6 - Khi R, =
Ur = ư , - U , = 2 0 - 6 = 14V Dòng qua R, L = = 35mA " R 400
Dòng qua R, có giá trị nhỏ nhất I.
= I,mi„ = I r - lanax = 35mA - 30mA = 5mA Suy ra R, = ^ = 1,2kO tmin 157
Bài tập 6-^3. Cho mạch ổn áp như
hình 6-9. Biết u, = I2V; Ư2 = 9V Dòng Ij, = 25mA
Xác định điện trờ bù R. Bài giải
Vì điện trở bù R và điốt zerer mắc nối Hinh 6-9
tiếp nên dòng Ir = I;,
Ur = IrR = I,R = u , - U, = u , - u I 25.10-3
(2^ Bài tập 6-4. Cho mạch ổn áp như hình 6-10 Bi ếtu = 12V ‘E
Điện trở động của điốt ổn áp r, = 7Q R i ^M ị l r. V t ị i ị i RE u. R, = 390Q U R. R. D Re= 12kQ I R, = 240Q
U, = 20V khi hở tải R, = co HỊnh 6-10
U, = 18V khi có tải và dòng tải = 5O1Ĩ1A
Hệ số khuếch đại tĩnh của transistor p = 50 Thiên áp Uj,E = 0,6V
a) Vẽ'các dòng điện chạy trong mạch.
b) Tính dòng qua điốt l^hi hở tải và khi có tải. Bài giải
a) Chiều và ký hiệu các dòng điện được thể hiện trong sơ đồ hình 6-10.
b) Tính dòng I, khi hở tải (R, = co, I, = 0)
Ube = IeRe = U. - ưbe = 12V - 0,6V = 11,4V 158 Suy ra L = ^ L H be ^ ^ Q 95mA ^ Rg 12.10^
Dòng I = - i - = - ^ ^ = 18,6.10“^A = 18,6uA ® 1 + ß 1 + 50 ^
Dòng Ic = ßls = 50.18,6. lO'^A = 0,93mA
- Điện áp sụt trên điện trở R|
Ur, = U , - U , = 2 0 - 1 2 = 8V
- Dòng điên qua R, ^ L, = ^ = — = 20,5mA ë V M 1 R' 390
- Dòng điện qua điốt ổn áp = I j ^ , -
1 3 = 2 0 , 5 - 0 , 0 1 8 = 2 0 , 4 8 m A
* K h i có tả i R, = 2 4 0 0 Dòng điện qua R| r U, 12 12 I = 4. 4. _1IL 5 ^ Re R, 12.10' 240
Dòng bazơ L = - i - = .........= ImA ® 1+ß 1+50
Dòng qua điên trở R.; L, = ^ = 15,38mA 6 4 V . R, Dòng qua D,:
I, = Ir, - Iß = 15,38 - 1 = 14,38mA
{2^ Bài tập 6-5. Đề lặp lại bài 6-4.
a) Khi điện áp U| thay đổi 10%, xác định độ mất ổn định đường d ấ f K,, = ^ 100% đđ y
b) Xác định độ mất ổn định tải K, =
100% khi đóng và ngắt tải. Bài giải
a) Độ mất ổn định điện áp Uị khi biến thiên 10% là 159
A U ,= 10%u, = 10%.20 = 2V
AU| sẽ gây ra biến thiên dòng điện trên điện trở Rị là AIRI AL. = ^ = — = 5,128mA ^ R, 390
Dòng điện này coi như đi qua
Độ mất ổn định tuyệt đối của điện áp
ra AƯ2 tỷ lệ với AU,.
AU, = AI,.r, = AIri.ĩ, = 5,128.1017 = 35,89mV « 36mV
Độ mất ổn định đường dây
k „ = 4 Ị = 2 Ị ! Ọ 1 , 0 0 % = 0 , 3 % " u. 12
b) Độ mất ổn định tải K,
Khi I, = 0; I, = 20,48mA
Khi 1, = 50mA; I, = 14,38mA
Sự sai iệch dòng qua
AI, = 20,48 - 14,38 = 6,lmA
AƯ2 = AU, = AI,r, = 6,1.7= 42,7mV
Độ mất ổn định tải 42,7.10 -3 K, = : ^ 1 0 0 % = 100% = 0,356% ' U. 12
Bài tập 6-6. Cho mạch
ổn áp tham số như hình 6-11. Biết: U, = 6V U, = 18V Ư3e = 0,5V
R, = ìOkQ; R2 = lOkQ;
Rp = 5,6kQ; R3 = 5 6 0 a
a) Vẽ dòng điện chạy trong mạch. Hình 6-11 160
b) Xác định phạrri vi điều chỉnh điện áp ra. Bài giải
a) Dòng điện một chiều trong mạch được ký hiệu và chỉ trong sơ đồ
, hình 6-11. Dòng Ie, chính là dòng tải I,.
b) Điện áp ra Ư2 được xác định theo biểu thức ^ R '
u , = ( U , + U , , ) 1+ R
Trorig đó Rị và Rj là điện trở nhánh trên và nhánh dưới củầ phân áp.
- Nếu con chạy cùa chiết áp ở vị ữí a, điện áp ra sẽ nhỏ nhất: Ư2. i n=(U.+Ư3,) 1 + R, = (.6 + 0,5) 1 = 10,66V 10+5, 6;
Nếu con chạy của chiết áp Rp ở vị trí b, điện áp ra sẽ đạt giá trị cực đm: 10 + 5,6^ ị^.R,+Rp = (6+0,5) 1 + = 16,64V R
Bài tập 6-7. Đề lặp lại bài 6-6 .
a) Hãy xác định trị số biến trở Rp để điện áp có thể điều chỉnh nhỏ nhất là 8V.
b) Tính điện áp ra cực đại trong trưòng hợp đó. Bàỉ giải
a) Điện áp ra nhỏ nhất được xác định theo biểu thức. R. =6, 5 1 + = 8V 1 + —^ =
» - ỉ i ------^-5—1=0.2307 Rp4"R2 6,5 Rp+R2 6,5 10 Ra = 10 = 33,346k a 0,2307 0,230T 11-2SOBTKTOlệNTỬ-A 161 b) Khi đó Uramax
U 3. . = ( U , + U „ , ) BE R 10+33,346 = (6 + 0,5) 1 4 = 34,67V 10
Bàl tập 6-8. Cho mạch ổn áp dùng điốt zener như hình 6-12
Yêu cầu điện áp ổn định IrN
cần lấy ra trên R, là Ư2 = 12V. ---- +u. wi -
Điện áp chưa ổn định U, = 18V. Điốt zener có = 6V, và dòng = 25mA. í
a) Xác định ùị số Rị cần ửiiết.
.b) Tính trị số Rn và R|. Bài giải a)
Dòng điện chạy trong Hình 6-12
mạch được chỉ trong sơ đồ 6- 12 .
Nếu IC thuật toán là lý tưởng, thì đòng Ip = 0 Do vậy I 25.10“^
b) Để xác định điện trở Rn và R„ có thể coi đây là bộ KĐTT thuận với yêu cầu:
Nếu Uv = Uo = U , = 6V thì u„ = U , = 12V R, Vậy
Ua = 1 + ■N U R Suy ra — ^ 2
^ = — — l = Ị R. U, 6 và Rn = R|
Nếu Rị chọn bằng 20kQ thì Rn = 20 kQ. 11.250BTKTĐIỆNTỬB 162
Bài tập 6-9. Cho mạch ổn áp tham số dùng IC thuật toán như hình
6-13. Biết: R, = 3 9 0 0 = 5,6kO Rj = 5,6kQ R4 = 4,7kO u, = 20V U, = 6V r, = 7Q
a) Phân tích nguyên lý hoạt
động của mạch ổn áp.
b) Xác định điện áp ra cực
đại và cực tiểu khi điều Hình 6-13 chỉnh R4. Bài giải
a) Bộ phân áp Rj, R 3, R4 tạo điện áp mẫu ƯM tỷ lệ với điện áp ra Ư2 và
được đưa vào cửa N để so sánh vcd điện áp chuẩn do điốt zener tạo
ra, sai lệch điện áp Uj = Up — ƯN được khuếch đại lên và đưa vào điều
khiển transistor T làm cho điện trở TcE của transistor thay đổi theo nguyên
lý, nếu U2 có xu thế tăng lên thì điện trở fcE của T điều chỉnh cũng tăng và
nếu Ư 2 có xu thế giảm thì ĨCE của T cũng giảm, mà Ư2 = Uị — nên Ư2
được giữ ổn định.
b) Điện áp ra cực đại khi con chạy chiết áp ỏ vị trí b R 4 r ^ 5,6 + 4 ,7 ^
u, = u Í ,^ R , + R .ì 2 = 17V max • = 6 R. J 5,6 J
- Điện áp ra cực tiểu khi con chạy của chiết áp ỏ vị trí a R 4 R, 5,6 = 6 1 + = 9,26V R3 + R4 y 5,6 + 4 ,7 j
(2^ Bài tập 6-10. Đề bài lặp lại bài 6r9
Nếu hở tải (R, = 00) thì u, = 21V
Nếu có tải R, = 390Q thì u, = 20V và I, = 50mA Ị.63
a) Xác định độ mất ổn định đường dây
khi U| thay đổi trong phạm vi 10 %.
b) Xác định độ mất ổn định tải khi đóng và ngắt tải. Bài giải
a) Độ mất ổn định đường dây K., = - ^ 100% U,
Khi U, thay đổi 10% -> AU, = 10%u, = 10% 20V = 2V
AU, sẽ làm thay đổi dòng qua AI, = AI„ = = — = 5,128mA R, 390
Biến thiên AU, = AI,.r, = 5,128.10-\7 = 35,89mV
Cuối cùng tính được độ mất ổn định ^ _ AU,
35,89.10-3 100% = 0,598% u. z 6
b) Tính độ mất ổn định tải
Khi hở tải, dòng qua 1 =
— - = —---- = 38,46mA R, 390 Khi có tải:
I . = i i ^ = 2 2 z Ì = 35.89mA ' R, 390 Biến thiên dòng
AI, = 38,46 - 35,89 = 2,57mA
Biến thiên điện áp ra AƯ2 = AU^ = Al^.r^ = 2,57.10'^.7 = 17,99mV AU 17 99 10"^
, K, = ^ 1 0 0 % = i / ’. ^:i .V...ioo% = 0 ,299% ' u ; ' 6 ' 164
( 0 ) Bài tập 6-11. Cho mạch ổn áp song song đơn giản như hình 6-i4. Biết: D — innr^* R, = lOOQ R,= 1200 U, = 9V L D ị Uhe = 0,6V U, R. p = 50
a) Vẽ các dòng điện trong mạch.
Phân tích nguỵên lý ổn áp.
b) Xác định điện áp Uj và các dòng điện I,, I,. Hình 6-14 Bài giải
a) Điện áp một chiều U| chưa ổn áp, còn điện áp Ư2 có thể coi như ổn định
Ư2 = U, + Ube * u , = const (vì u , » ư|5p)
Nếu U| biến thiên thì điện áp trên điện trỏ là
là U rs cũng biến thiên
và Uị được giữ nguyên.
Dòng điện chạy trong mạch như chỉ dẫn trong sơ đồ hình 6-14.
b) Điện áp trên R, được coi là ổn định
U, = ư, + UgE = 9 + 0,6 = 9,6V
- Dòng điện trên R,
I, = ^ = — = 0,08A = 80mA ' R. 120
- Dòng Is qua điện trò Rs U ,, ư , - u 2 0 -9 ,6 = 104mA R, Rs 100
- Dòng (Ic + Ig) — Is I, 50
Ib + Ib = Is- I . - > 5 1 I b = Is -I . 1 0 4 -8 0 SuyraI„ = I , . ^ = 0,47mA 51 51
Ic = PIb = 50.0,47 = 23,53mA 165 ^
Bài tập 6-12, Mậch IC ổn áp LM 317 như hình 6-15. Biết R. R , = 240Q ị LM317 I Ra = 3kQ ------ 1 + U,h = U „ = 1,25V ^ADJ ^Rl 'i
1 <|r , : -\ụ.F u, _1L1] Dòng bổ sung I - adj = 25 ^.A
Hãy xác định điện áp ra Ư2 trong trường hợp: 1 a) Tính đến dòng Hình 6-15
b) Không tính đến dòng I adj- Bài giải
a) Điện áp ra khi tính đến dòng Iadj 3.10^ + 1 ^01-^2 = 1.25 1 + + 25.10-^.3.10^ =16,95V R 240
b) Khi không tính đến dòng Iadj 3.10^ = 1,25 = 16,875V “ 1 R, 1 240 \ I / V /
Sai số giữa IC thực và lý tưởng
AƯ2 = 16,95 - 16,875 = 0,075V = 75mV
(20^ Bài tập 6-13. Đề lặp lại bài 6-12. Nhưng nếu thay điện trở R2 bằng
chiết áp có trị số R2„in = IkQ; R2max = 4,7kO.
a) Hãy xác định phạm vi điều chỉnh điện áp ra U2.
b) Nếu dòng bổ sung cực đại ỈADimax = 100p.A. Hãy xác định sai số điện
áp ra giữa IC thực và lý tưởng. B àỉgỉải
a) Điện áp ra cực tiểu ' R = 125 2m m = 1,25 1 + = 6,458V 240
Điện áp cực đại 166 Ị ^ ^2tnax = 1,25 = 25,73V R 240
Phạm vi điều chỉnh điện áp Ư2 từ 6,458V đến 25,73V
b) Trưcmg hợp tính đến dòng Iadj = lOOịxA 10' Ư2„i„= 1,25 1+ + 100.10-^.10'= 6 ,558V 240 1 J Điện áp ra ư , „ . = 1 . 2 5 ^ADJ ‘^amax 4,7.10 1,25 1 +
+ 100.10-^.4,7.10^ = 2 6 ,2 V 240
a) Hãy xác định trị số điện trở Rj, Rj.
b) Muốn điều chỉnh điện áp Ư2 xuống còn 8 V, xác định điện trở Rj cần thay thế. Bài giải a)
Nếu bỏ qua Iadj (coi IC ổn áp là lý tưởng) thì điện áp ra Ư2 được xác
định qua R| và Rị theo biểu thức. /- _ \ ^ 2 U, = 1,25 1 + - ^ R . 12 = 1,25 V R .y R, 12 12 - 1 -> R 2 = .R R, 1,25 1,25 ) R2 = 8,6R|
Nếu R, = 240Q thì R, = 8,6.240 = 2,064kQ 167
b) Nếu Ư2 = 8V u , = l,25 = 8V RI J / 8 1 ^ R 2 = -1 .R. R, 1,25 u , 2 5
Rj = 5,4 R ,. Nếu R, = 240Q thì Rj = 5,4.240 = 1296Q = l,296kQ
( 0 Bài tập 6-15. Cho mạch IC ổn áp LM 317 như hình 6-16. Biết R, = R j = = 2400Q R4 = 2400Q R5 = 240Q ;U ,h = 1.25V
T„ T2, T3 làm việc ở chế độ
khoá (tắt, mở) bởi xung điều
khiển Xị, X2, X3.
Nếu X = +5V mức 1 thì
ữansistor thồng, r(3 = 0
Nếu X = o v đủ ựansistor tắt,
ĨCE = 00. Bỏ qua dòng Iad,.
Xác định điện áp ra Ư2
trong các trường hợp sau. a ) X ,= X 2 = X3 = 0 Hình 6-16 b) X , = X 2 = 0; X 3 = 1
c) X , = X 2 = X 3= 1 Bài giải
a) Trường hợp X| = X2 = X3 = 0, cả ba transistor đều ở trạng thái khoá *
(fcE = 00) điện trở nhánih dưới phân áp Rp chính là R4 khi đó điện áp ra. Rp 2400 U 2=1,25 1 + = 1,25 1 + = 13,75V R, 240 )
b) Trường hợp X ị =
= 0; X3 = 1; T|, T2 tắt, T3 thông. 168
_ « //n _ R3R4 _ 2400.2400
Khi đó Rp = RJ/Ra = —.^'-r ..= — ——------— = l,2kQ R3 + R , 2400 + 2400 1200 U , = 1,25 1 + ^ = 1,25 1 + = 7,5V R .y 240 j
c) TrưỀmg hợp X| = X2 = Xj = 1 cả ba transistor đều thông.
Khi đóR ^ = R Ự /R :J /R J /R , 2400 R ,//R 2 = = 12000 2 2400 R3//R4 = = 1200Q 1200 R, // R2 // R3 // R4 = = 600Q ư , = l , 2 5 = 1,25 = 4,375V R 240J
Bài tập 6-16. Đề lặp lại bài 6-15, với trị số các điện trở là:
R, = ỉkCl; R2 = 2kO; R3 = 3kQ; R4 = 2,4kQ
Hãy xác định ra cho các trường sau: X, X2 X3 a) 0 0 1 b) 0 1 0 c) 0 1 1 d) l 1 1
a) Trưòng hợp X = 001, Xj = 1 -> T3 thông, khi đó điện trở nhánh dưới Rp
R = R //R , = -M i - = = l,333kQ 3 ” ' R + R , 3 + 2,4 3 1.333^
Điện áp Ư2 = 1,25 = 1,25 = 8,192V R. 240 , 169
b) Trường hợp X = 010. X, = 0; X2 = 1; Xj = o
T, thông, T| và T3 tắt Khi đó R _ M 4 _ = l,09kO ” R2 + R 4 2 + 2,4 R 1090 u , =1,25 1 + = 1,25 1 + = 6,927V 240 J
c) Trường hợp X = 011 -> T| tắt Tj và Tj thông R =
//R j //R , = -------- Ei M
ị -------- = -------- ----------------- ” ' ' ' R jR j+R jR ^+R .R ^ 2.3+ 3 .2 ,4 + 2 ,4 .2 = 0,8kQ = 800Q 800^ u,=l,25 = 1,25 1 + = 5,416V R 240J
d) Trường hợp X =111 -> X, = 1; = 1; X3 = 1 T „ T
2 v à T 3 đ ề u t h ô n g . K h i đ ó R p = R , / / R 2/ / R 3/ / R 4 1 1 1 1 1 1 1 1 1
R “ R, ^ R, ^ R, ^ R “ IkQ ^ 2kQ ^ 3kQ ^ 2,4kQ ■p --I *'2 *'3 1 1
= 2,25 ^ R = - ^ = 0,444kQ R„ 2,25 Rpì 444^
Điện áp u , = 1,25 1 + = 1,25 = 3,56V 2 40j
Cuối cùng cổ thể thiết lập điện áp U2 ứng với tín hiệu số đầu vào điều khiểh transistor. X U2 000 13J5V 001 8,19V 01 0 6,927V 01 1 5,416V 1 1 1 3,56V 170 @
Bài tập 6-17. Cho mạch IC ổn áp LMl 17 như hình 6-17. Biết R, = 240n Rch=l,25V R, = IkQ
Biến trô R3 = 0 -4- 3,3kfìi- Bỏ qua dòng Iad,-
a) Xác định phạm vi điều chỉnh
Ư2 nhờ biến trở Rj.
b) Như câu a nhưng nếu tính đến dòng Ia0j = 50fiA. Bài giải
a) Xác định phạm vi điều chỉnh Ư2 khi bỏ qua Iadj
- Điện áp ra nhỏ nhất ứng với vị trí a của con chạy biến trở R3 . ư 2.i„=1,25 R 1000 = 1,25 1 + = 6,458V
- Điện áp Ư2 lớn nhất ứng ^ới vị trí b của con chạy R; U = ư , _ = l , 2 5 ramax 2max R = 1,25 = 23,64V 0,24 J
Phạm vi điều chỉnh Ư2 từ 6,458V đến 23,64V
b) Trường hc^ tính đến Iadj /* \ 1 + R 1000 = 1,25 1 + + 50.10-^.10^=6,506V 240 J 171 u , . „ = l , 2 5 l + ẵ l l ỉ l R 10^+3.3.10^^ = 1,25
+ 50.10-^ (10^+3,3.100 = 23,855V 240
( 0 ) Băi tập 6-18. Hãy thiết kế mạch ổn áp dùng IC LMl 17 (hình 6-17) với
R3 = 0; để có điện áp ra Ư2 ổn định 24V từ nguồn một chiều không ổn địnhlàSOV.
a) Hãy xác định trị số Rj, R, cần thiết.
b) Nếu dòng Iadj = lOOfxA hãy xác định sai sô'do dòng này gây ra. Bài giải a) Từ biểu thức ^ R 1+ _ .1,25. Suy ra R .. < u . 1,25 1,25 R. TTiay số Rj =
1 .240 = 4368n = 4,368kQ 1.25 )
b) Nếu tính đến dòng I^DJ u, =0,125 + I.rM A DJ- R ‘*'2 R ,. 4368 = 0,125 1 +
= 100.10-^.4,368 = 24,4368V 240
Sai số 24,368 - 24 = 0,368V 0,368 hay 100% = 1,53% 24 172 Chương 7 MẠCH DAO ĐỘNG
7.1. TÓM TẮT PHẦN LÝ THUYẾT
Các mạch dao động hiện nay được chia ra mạch dao động điều hoà hình
sin, mạch tạo xung các dạng khác nhau (xung vuông, chữ nhật, răng cưa,
tam giác...) và các mạch tạo tín hiệu điều chế (AM, FM).
Trong phần này chủ yếu xét mạch dao động điều hoà là loại mạch dao
động được sử dụng rộng rãi trong các hệ thống thông tin, các thiết bị đo
lưồmg kiểm tra và trong các thiết bị điện tử dân dụng, y tế.
Để tạo mạch dao động điều hoà thường sử dụng mạch khuếch đại tự
kích nhờ hồi tiếp dương. Mạch dao động điều hoà có thể làm việc trong
khoảng tần số từ vài Hz đến hàng nghìn MHz.
Hình 7-1 là sơ đổ khối mô tả mạch dao
động điều hoà, đây là mạch khuếch đại đầu ra K ----- ^
nối với đầu vào qua mạch hồi tiếp dương.
Điều kiện dao động của mạch: .... Kne ------ '
K.Kh, = 1 (điều kiện biên độ)
Hình 7-1. Tạo dao động điều
Ọk + 9 ht = 2ri7i (điều kiện pha)
hoà bằng hổi tiếp dương
Trong đó K - hệ số khuếch đại khi chưa có hồi tiếp;
K|,, - hệ số truyền đạt hồi tiếp;
(Pi( - góc lệch pha của bản thân mạch khuếch đại;
(Ph, - góc lệch pha của mạch hồi tiếp.
Nếu đảm bảo cả hai điều kiện trên thì sẽ có dao động điều hoà. 173
* Mạch dao động ha điểm điện dung (hình 7-2a)
Sơ đổ gọi là mạch dao động ba điểm điện dung vì dùng tụ điện C| và c,
để phân áp và lấy một phần điện áp trên C2 hồi tiếp về đầu vào. Điều kiện pha X be = -<0 coC- XcE= - — <0 (ữC XcB = ®L > 0
Lý thuyết đã chứng minh mạch thoả mãn điều kiện cân bằng pha, có hồi tiếp dưofng.
Điều kiện biên độ: KXh, > 1
Trong đó: K là hệ số khuếch đại của tầng mắc theo sơ đồ EC K «--Ễ_ R %E
Kh, là hệ số truyền đạt hồi tiếp. 72. b)
Hình 7-2. Mạch dao động ba điểm điện dung (a) và ba điểm điện cảm (b)
TTioả mãn điều kiện pha và biên độ sẽ có dao động điều hoà hình sin,
tần số dao động được xác định theo biểu thức: 174 f d d = ^ = — ,H z 2„ L _ ^ l ^ V C1 +C2
Trong đó c tính bằng Fara; L tính bằng Henri.
Để thay đổi tần số dao động có thể thay đổi điện cảm L hay điện dung
C|, C2 nhưng trong trường hợp này tiện lợi hofn là thay đổi trị số L.
* Mạch dao động ha điểm điện cẩm (hình 7-2b)
Mạch này chỉ khác mạch dao động ba điểm điện dung ở chỗ mạch phân
áp để tạo điện áp hồi tiếp dùng hai điện cảm L| và L2Ỉ điện áp cuộn L2
được đưa về hồi tiếp.
Điều kiện pha Xị,g = cùL, > 0 “ coỉ-/| ^ 0 X c . = - 4 : < 0 coC
Lý thuyết đã chứng minh thoả mãn điều kiện cân bằng pha vầ có hồi tiếp dưcfng.
Điều kiện biên độ: K.K|,, > 1
Nếu thoả mãn cả hai điều kiện trên, mạch sẽ dao động và tạo ra dao
động điều hoà hình sin.*”
Tần số dao động được xác định theo biểu thức:
L . = ----- _ J = = _ , H z 2nẬLị+L2)C
Để thay đổi tần số dao động ở đây thuận tiện là thay đổi trị số điện dung c.
* Mạch dao động R-C di pha (hình 7-3)
Mạch dao động R-C thích hợp tạo dao động ở tần số thấp; mạch có thể
dùng linh kiện rời rạc transistor hay dùng IC thuật toán.
ở đây các mắt lọc R-C dùng để di pha và chọn lọc tần số, thưcmg dùng
hofn cả là 3 mắt lọc R-C. »
Điều kiện pha; Vì mạch khuếch đại thuật toán là khuếch đại đảo nên để » A • • • •
có hồi tiếp dưcmg thì mạch hồi tiếp gồm ba mắt lọc R-C phải lệch pha thêm 175
một góc (Pht = 180°. Nếu dùng ba mắt lọc R-C giống nhau thì mỗi mắt lọc
R-C phải lệch pha (Pht = 60°.
Lý thuyết đã chứng minh rằng
để thoả mãn điều kiện pha thì 1 0) = S rc và khi đó 2 n S R .C Kh.= 29
Hình 7-3. Mạch dao động R-C di pha -
Để đảm bảo điều kiện biên
đô K.Kị,, > 1 suy ra K > - ^ = 2 9 . Kht
Trong đó K là hệ số khuếch đại của mạch khuếch đại đảo
K = 2 9 = -^ vàRN = 29R ,.
Khi đó tần số dao động. * 1 ,H z
* Mạch dao động cầu Wien
Mạch dao động cầu Wien là
mạch đao động R-C dùng mạch cầu
Wien làm mạch hồi tiếp từ đầu ra về
đầu vào (hình 7-4).
Điều kiện cân bằng pha: vì mạch
hồi tiếp đưa về đầu vào thuận nên đổ
có hồi tiếp dương thì góc lệch pha
(Ph, = 0 và khi đó c o = — . Suy ra tần RC
SỐ chọn lọc f = — và Kh, = - . 2tcRC 3
Điều kiện cân bằng biên độ: 176
K.Kị,, > I. Suy ra K = 3 và Kị,((-).=—
— = - do vậy Rn = 2R|. R ị -f 3
7.2. PHẦN BÀI TẬP CÓ LỜI GIẢí
(2^ Bài tập 7-1. Cho mạch dao động ba điểm điện dung (hình 7-2a). ớiả
thiết mạch đảm bảo điều kiện pha và biên độ.
a) Nếu biết điện cảm L = 0,4mH, điện dung tưcttg đương c = = 0,1
. Hãy xác đinh tần số dao đông. C ị + C 2
b) Nếu giả thiết c = =
o', 47 |iF ■ Hãy xác đinh điên cảm L cần C 1 + C 2 ■ •
thiết để tạo mạch dao động ở tần số 8000 Hz. Bài giải
a) Tần số dao động được xác định theo biểu thức: 1 fdđ -
Thay số vào ta được 2n L. C1C2 'i Cị +C2 ídđ = ---------, ^ = 25,19kHz 2 .3 ,14V0,4.10'^.0,1.10'^
b) Từ biểu thức trên suy ra
L = — Ụ . = ------- ^ -----L _ ------- ^ = 6,74mH (2 7 tf)^ C
( 2 . 3 , 1 4 r ( 8 0 0 0 r . 0 , 4 7 . 1 0 ‘ ‘’
( í ĩ ặ Bài tâp 7-2. Đề lăp lai bài 7-1. Nếu biết c = --?- - ^- = l^iF, điên cảm L V— y Cị + C2
có thể điều chỉnh từ 0,5mH đến l,5mH. Hãy xác định phạm vi thay
đổi tần số dao động. Bài giải
Tần số dao động cực tiểu úììg với trị số L„ax
12- 2S0BTKTĐIỆNTỬ - A 177 ^tnin “
= --------- i .-............ =4111.4 Hz C 2n 1C2 L„. 2.3,14V10'^1,5,10'-'* C| + Ç max
Tần số dao động cực đại ứng với trị số L„j„. 1 _________ Ị________ ^max = 7120Hz 2ti
2.3,14>/l0’^0,5.10'^ rn % c, +c min
Bài tập 7-3. Cho mạch dao động ba điểm điện cảm như hình 7-2b.
Giả sử mạch đảm bảo điều kiện biên độ và pha.
a) Nếu biết L = L| +
= 0,1 mH,, tụ c = 0,47^F. Hãy xác định tần số dao động.
b) Nếu L = Lị + L2 = 0,1 mH. Hãy xác định khoảng biến thiên của tụ c
để mạch dao động từ tần số 12kHz đến 160kHz. Bài giải
a) Tần số dao động được xác định theo biểu thức: f = — ị =
= --------------J---------------- = 23,376 kHz
2WL.C 2.3,14V0,1.10*^0,47.10'^
b) Tần số dao động cực tiểu f„¡„ ứng với trị số cực đại cùa tụ điện n2 ^min 1 1 Thay số ta được ~ = l,76^iF >-3‘ 0, 1.10
tần SỐ dao động cực đại ứng với trị số c„i„. 1 f_ = ^max Suy ra = 2ltyịĩ~c 2% y min Thay số c^:_ = = 9,9.10-^F = 9,9nF.
/21^ Bài tập 7-4. Cho mạch dao động R-C di pha như hình 7-5 dưới đây. Biết R = R, = 10kfì 178 12- 250BTKTĐIẺNTỬ - B C = 0,01^iF Rp= lOkQ
a) Xác định tần sô' dao động của mạch.
b) Tính trị số cần thiết của R^. Bài giải
Hình 7-5. Mạch dao động R-C di pha
a) Xác định tẩn số dao động
f = ---- ^=— = ----------= — ỉ—1----------- ^ = 650,2Hz 27ĩn/6RC
2.3,14.V6.10.10^.0,01.10'^
b) Để mạch dao động phải đảm bảo điều kiện biên độ.
Đã biết để đảm bảo điều kiện pha 9 |,( = 180° thì Kị,ị = — .
Điều kiên biên đô K.Kj,, = 1. Suy ra K = ^ —=29 K:ht Mặt khác K= ^
. Suy ra Rn = 29R, = 29.10 = 290kQ ^1
(2^ Bài tập 7-5. Hãy thiết kế mạch dao động R-C di pha dùng IC thuật
toán để có tần số dao động 2kHz.
Biết trị số tụ điện c trong các mắt lọc R-C là như nhau và được chọn bằng 0,0 l|iF. Bài giải a)
Mạch dao động R-C di pha 3 khâu RC được thiết kế như hình 7-5.
Trước hết xác định trị số R của mắt lọc R-C.
Từ biểu thức tần số dao động f = Suy ra R = 2it>/6R.C 2jtN/6C.f
thay số vào ta được R = = 325 in = 3,25 IkQ
2.3,14.n/6.0,01.10"^2.10^ 179
lấy điện trở chuẩn R = 3,3kQ
Điện trở R, cùng có trị số bằng R. b)TínhRf,
Để đảm bảo điều kiện biên độ đã xác định được hệ số truyền đạt của
mạch hồi tiếp Kh, = ^ • ^ 29
Điều kiên biên đô K.Kị,, = 1. Suy ra K - —^ = 2 9
K là hệ số khuếch đại của mạch IC thuật toán • • • •
= 29 ^ Rn = 29R, = 29.3,25IkQ = 94,279kQ Rn = 94,279kQ
Xác định lại tần số dao động, úng với các trị số điện ữở chọn theo tiêu chuẩn. ---- ^ ^ = 1970Hz
27tV6R.C 2.3,14.V6.3,3.10^0,10.10“^
(2^ Bài tập 7-6. Cho mạch dao động R-C di pha 3 khâu như hình 7-5. Nếu
biết điện trở R = lOkQ.
a) Hãy xác định trị số tụ c của mắt lọc R-C để mạch dao động ở tần số 2500Hz
b) Tính trị số điện trở R^.
c) Nếu thay đổi đồng trục cả ba điện trở R từ 4,7kQ đến 20kQ. Hãy xác
định phạm vi thay đổi tần số. Bài giải
a) Từ biểu thức f = - — ịL_ - Suy ra c = - ^ 27Ta/ 6 R .C 27tN /6R f Thay số ta được
c = --------- = J ----- r------ -2,6.10“^=2,6nF 2.3,14.V6.10.10l2500
b) Để đảm bảo điều kiện biên độ thì hệ số khuếch đại k = 29 180
K = B ỉ i = 29 -> Rn = 29 R, = 29 R = 29.10kQ = 290kQ. c) Khi
= 2 0 k 0 tần số dao động đạt giá trị cực tiểu
fmin = ---- ------------= ------- E— ^
--------- 15- = ỉ250Hz = 1,25kHz
2jt>/6Rn,ax -C 2.3,14.^/6.20.10^.2,6.10"^
Khi R = R„|„ = 4,7kQ tần số dao động đạt giá trị cực đại
fmax = ---- -----------= ----- :..----------------------:;3- = 5320Hz = 5.32kHz
27tN/6R„i„.C 2.3,14.^/6.4,7.10^.2,6.10"^
Bài tập 7-7. Tính toán một mạch dao động R-C di pha ba khâu dùng FET(hinh7-6).
Biết; hỗ dẫn của FET 8mA Sm (8mS); điện trở V cực máng - nguồn
= 50kQ. Điện trỏ mắt lọc R = 20k0.
a) Xác định trị số tụ c để
mạch dao động ở tần số 500Hz.
Hình 7-6. Mạch dao động R-C di pha dùng FET
b) Tính trị số điện trở Ro- Bài giải
a) Từ biểu thức tính tần số dao động
f = — i —— Suy ra c = — Ị=— 2itV6^R.C 2jĩV6Rf
ITiay số vào ta được ’ -6,510’ ^F = 6,5nF 2.3,14.n/6.20.!0^500
b) Để xác định điện ừở Rq, trước hết xét điều kiện biên độ.
Để có dao động điều hoà K > 29; ở đây có thể chọn K = 50. 181 R r
Khi đó K = gm-R., trong đó R_ = — ^
là tải xoay chiều của tầng khuếch đại. ♦
R . , ^ , ^ D ^ S u y r a R „ = J ^ ẽm *ds êm*ds ^
Thay số vào ta được 50.50.10^ R = 7,140kQ d = 8.10"^50.10^-50
(22^ Bài tập 7-8. Cho mạch dao động R-C di pha 3 khâu dùng transistor
như hình 7-7. Biết R = 10kQ,C = 0,01|aF.
Hệ sô' khuếch đại p = 50, điện
trở emitơ-bazơ ĨBE = 2kD, giả
sử mạch đảm bảo điều kiện biên độ và pha.
a) Xác định tẩn số dao động.
b) Tính trị số điện trở Rc- Bài giải
Hình 7-7. Mạch dao động R-C dùng transistor
a) Tần số dao động: ^ = F ^ --------- 3^ = 650Hz 2W6R.C
2.3,14V6.10.10\0,01.10"^
b) Để thoả mãn điều kiện biên độ, thì hệ số khuếch đại K của mạch
khuếch đai transistor mắc EC.
K.Kh, = 1; đã biết Kh, = 29 Vậy K = = 29 Kht
Mặt khác, hệ số khuếch đại của tầng khuếch đại R-C mắc emitơ chung p
K = _ _ Ỉ1 _ R ^ - - S R e I-be 182
Trong đó s = — là hỗ dẫn của transistor; rbe
Dấu - có nghĩa điện áp ra và vào ngược pha. c.. o .Kjbe 29x2.10^ Suy ra = ------------ = l,16kQ ^ ^ p 5 0
Chọn điện trở chuẩn R = l,2kQ.
(2^ Bài tập 7-9. Cho mạch dao
động cầu Wieu như hình 7-8. Biết: R = 33kQ c = lOnF
Giả thiết mạch thoả mãn điều
kiện biên độ và pha.
a) Xác định tần số dao động. b) Tính trị số Rn nếu cho R, =47kQ . Bài giải
a) Tần số dao động
Hình 7-8. Mạch dao động cầu Wien f= ‘ = 482,5kHz 2JtRC 2.3,14.33.10^0,01.10"®
b) Từ điều kiện cân bằng biên độ
Rn = 2R, -> Rn = 2.47.10^ = 94.10^ Q = 94kQ
(2^ Bài tập 7-10. Đề lặp lại bài 7-9. Nếu thay điện trở R bằng chiết áp
đồng trục có điện trở biến đổi từ lOkQ đến lOOkQ. .
Hãy xác định phạm vi tần số dao động. Bài giải
Tần số f^i„ ứng với trị số cực đại của chiết áp = lOOkQ ^min
------!----- = —------ ^ ^ = 159,2.3Hz 27tCR„ax
2.3,14.0,01.Ỉ0""100.10^ 183 Tần số
ứng với trị số cực tiểu của chiết áp R„i„ = lOkQ
fmax = ----- ^— 2------------------------------ r = 1592,3n = l,5921ca 2nCRm¡n
2.3,14.0,01.lO’ ^lO.lO^
Bài tập 7-11. TTiiết kế mạch dao động cầu Wien để tạo dao động hình sm tần số 500Hz. Bài giải
Có thể thiết kế mạch dao động cầu Wien dùng transistor rời rạc hay
dùng IC thuật toán, nhưng thuận tiện hơn là dùng IC thuật toán. Mạch điện
nguyên lý như hình 7-8.
- Muốn có dao động điều hoà hình sin phải đảm bảo điều kiện biên độ và điều kiện pha.
Điều kiện biên độ: Rn = 2Rj; Rị chính là nhánh dưói của phân áp hồi
tiếp, ở đây chọn R = 22kn và khi đó Rn = 2.22kfì = 44kQ.
- Điều kiện pha: Để hồi tiếp về cửa p là hồi tiếp dưoíng thì góc pha «
Ọị, = 0. Suy ra co = —— hay f = RC ^ 2nRC
Muốn dao động ờ tần số 500ĩfe có thể chọn R và c tuỳ ý. Nếu chọn tụ
c có trị số chuẩn là 0,01|iF thì trị số R được xác định: R = — -:;^ = 31,847kQ
• 27ĩfRC 2.3,14.500.0,01.10'^
Như vậy trị số điện trở cần tính toán: R, =22kn,R N = 44kQ
R = 31,847kQ,C = 0,001nF.
Bài tập 7-12. Chơ mạch dao động cầu viên như hình 7-9. Biết R = lÒ k Q R, = 80kQ c = 0,0 22^F
Chiết áp Rp có trị số thay đổi từ 0 đến 30kQ. a)
Hãy xác định phạm vi tần số dao động khi điều chỉnh chiết áp Rp. 184
b) Tính điện trở Rfg. Bài giải a)
Phạm vi tần số dao động phụ ra
thuộc vào trị số chiết áp Rp mắc nối tiếp với R. _ Ị fX J ? v _ v w K R -
Tần số f„|„ ứng với giá trị cực đại của Rp = 30kQ. 1 27t.C ^R + Rpmax) 1
2.3,14.0,022.10"® (10.10^ + 30.10^) 1
Hình 7-9. Mạch dao động cểu Wien có = 180,95Hz
tần số điều chỉnh
2.2,34.0,022.10"^.40.10^
- Tần số cực đại útig với Rp = 0 Q. f , _________ !_________ 723,8Hz 27C.CR
2.3,14.0,022.10’ ^10.10^
b) Xác định trị số Rn
Rn = 2R, = 2.80kQ = 160kQ.
^ 2^ Bài tập 7-13. Cho mạch tạo dao
động cầu Wien như hình 7-10 dưới đây. Biết: R. = 22kQ R = 4,7kQ
a) Xác định trị số Rn cần thiết.
b) Tác dụng của D ịDị.
c) Tĩnh trị số biến đổi của tụ c để
tần sô' dao động từ 100Hz đến 2000Hz. Bài giải a)
Để đảm bảo điều kiện độ, Rn
được tính theo biểu thức 185
Rn = 2R, = 2.22.10' n = 44. lO'n = 44kQ
b) Điốt D| và Dt mắc ngược chiều và song song với điện trở Rn, tức là
song song với nhánh trên của phân áp hồi tiếp, nhằm hạn chế biên độ điện áp
ra. Nếu biên độ điện áp ra tăng quá một ngưỡng nào đó thì hoặc D, hay
dẫn, điện trở của điốt giảm xuống và hệ số khuếch đại của bộ khuếch đại
thuật toán cũng giảm và điện áp ra được hạn chế.
c) Tần số dao động được xác định 2jrRC
Khi tần số cực tiểu
thì trị số tụ c phải đạt giá trị cực đại C— Tna x ------= 0.338^F 2.3,14.4,7.10^100
Khi tần số cực đại
thì trị số của c ià cực tiểu max 1 1 c •
=--- ------=-------------------- = 16,94nF. 2.3,14.4,7.10^2000
(2^ Bài tập 7-14. Cho mạch
dao động cầu Wien như hình 7-11.
Biết: tụ c = 0,05|iF.
Tần số dao động cần thay
đổi được từ 200Hz đến
2000Hz nhờ biến trở R.
a) Phân tích nguyên lý
hoạt động của mạch.
b) Xác định khoảng biến
thiên cần thiết của R. Hinh 7-11 Bài giải
a) Phân tích sơ đồ
Đây là mạch dao động cầu Wien; mạch cầu R-C được mắc giữa đầu ra
và đầu vào p của khuếch đại thuật toán làm thành mạch hồi tiếp dương. Nếũ 186
đảm bảo điều kiện cân bằng pha và biên độ thì sẽ có dao động điều hoà. Trị
số R và c của cầu Wien sẽ quyết định tần số dao động.
Điốt D, R4 và FET nhằm ổn định và hạn chế điện áp ra. Khi ư„ tăng,
điện áp âm qua điốt D đặt vào cực cửa của FET làm cho điện trở máng - nguồn
của FET tăng lên, đây là nhánh dưới của phân áp hồi tiếp nên hệ số
khuếch đại giảm đi và u„ được hạn chế.
b) Từ biểu thức xác định tần số dao động 1 f = suy ra R = 2tcRC ' 2?tCf
Tần số dao động cực đại sẽ ứng với giá trị cực tiểu của R. R _ ^
______________ Ị____________ __ Ị 592Q 27tCf^ax 2.3,14.0,05.10"^2.10^
Tần số dao động cực tiểu f^i„ sẽ ứng với giá trị cực đại của R.
R^... = ---- ỉ---- = — --------- ?----- T— =15,923kfì max 2íiCf^in 2.3,14.0,05.10"®.200
(2^ Bài tập 7-15. Cho mạch điện như hình 7-12.
Biết: R, = 150kQ; R, = 1 OOkQ a) Phân tích mạch.
b) Hãy xác định hằng số thòi gian
X = RC để tạo tm hiệu ra có tần số 1 kHz.
c) Nếu biết c = 0,02 }iF hãy xác
định trị số cần thiết của R.
d) Xác định trị số cực đại của điện
áp U| đặt vào cửa p nếu điện áp bão hoà = ± 12V. Hình 7-12 Bài giải a) Phân tích mạch;
Đây là mạch dao động đa hài (dao động Schmitt, điện áp ra là các xung
chữ nhật có mức +Ư5a, và
R| và R2 là hai điện trở phân áp tạo hồi tiếp
dương, điện áp hồi tiếp đưa về cửa p. 187
Điện áp hồi tiếp về cửa p U , = — H 5ẼL - . R * R j + R 2 ^
Khi trị số trên tụ c nạp bằng ư| thì mạch chuyển trạng thái và = -U
b) Chu kỳ dao động được xác định theo biểu thức T = 2RC In R. T Suy ra X = RC = 21n 1 + R,
Trong đó chu kỳ T = - = -Ịị- = 10 = Ims. 10-3 X = RC = , 2. 100.10- 21n 1 5 0 . 1 0 ^
c) Nếu biết trị số c = 0,02.10'®F, trị số R được xác định T 0 , 5 9 2 . 1 0 " ^ R = —= = 2 9 , 6 k Q c 0,02.10"® 12
d) Điên áp U. = —-^ì2L _r = -------- ^ .3 . 1 0 0 . 1 0 ’ = 4 , 8 V R j+ R 2 100.10^ + 150.10^
Trị số đỉnh đỉnh của điện áp vào U| u,p.p = ± 2.4,8=+ 9,6V
Bài tập 7-16. Cho mạch điện như hình 7-12
Giả sử điện áp bão hoà ±u,„ = ±12V
R, = 30kQ; Ra = 20kQ; R = 12 kQ; c = 0,0 2 ^iF
a) Hãy xác định điện áp hồi tiếp ư | đặt vào cực p.
b) Xác định chu kỳ T và tần số dao động. 188 Bài giải a) Điện áp u ư| 20 = ±4,8V ' R1 +R2 30 + 20
b) Xác định chu kỳ T í, 2.20.10^! T = 2RCln = 2.12.10^0,02.10-^ In = 0,406.10"^s Ri ; 30.10^ J
Tần số dao động f = — = * = 2458,8Hz T 0,406.10'^
(2^ Bài tập 7-17. Cho mạch điện như hình 7-13a. Biết; R, = 10kQ = 20 kQ R = 100 kQ c = 0,01 ịiF.
Giả sử điện áp bão hoà là ±12V
a) Phân tích nguyên lý tạo dao động.
b) Xác định chu kỳ dao động.
c) Xác định tần số dao động.
d) Xác định trị số đỉnh xung chữ nhật và xung tam giác. Hình 7-13a 18Í Hình 7-13b Bài giải a)
Đây là mạch tạo xung vuông U| và xung tam giác U2; IC| là mạch so
(Triger Schmitt) và IC2 là mạch tích phân.
Giả sử tại thời điểm t = 0 điện áp đầu ra IC| là U| = -Uja,.
Điện áp ngưỡng hoặc điện áp lật trạng thái là ±u„g. u„, =
trong đó R, = KR, (hệ số K phải > 1) 2
ở đầu ra của bộ tích phân IC2 u , = -u„,
Ujít) biến thiên theo thời gian t. J t
U2(t) = — — [Uị(t)dt + Ư2(o), ữong đó U-,(t) điên áp Uj tại then điểm t = 0. RC 0 190 ThayU,(t) = -U,„ Ư2(0) = -U„,
Dạng điện áp ở đầu ra IC| — xung vuông và đầu ra IC, — xung tam giác nhưhình7-13b.
b) Chu kỳ dao động T
T = í ^ * đ â y K = | l = ^ = 2 K R| 10 T =
= 2RC = 2.100.10^.0,0 1.10"^ = 0,002s = 2ms 2
c) Tần số dao động
f = ^ = — ỉ— = 500Hz T 2.10“^
d) Trị số đỉnh xung chữ nhật là U|p.p = ±12V
Trị số đỉnh xung tam giác chính là điện áp ngưỡng ±ư„g = = ±6V
(2^ Bài tập 7-18. Thiết kế mạch tạo xung tam giác có tần số 1kHz với
điện áp bão hoà Uja, = ±12V, điện áp đỉnh là 8V. Bài giải
Sơ đồ mạch tạo xung tam giác như hình 7-13a. Điện áp đỉnh - đỉnh là
8V tương ứng với điện áp ngưỡng u„g = 4V, hệ số K = = — = 3 ^ng 4
Điện trở R, và R2 được xác định theo tỷ lệ —
= K . Suy ra Rj = KR| = 3R|.
Chọn R, = 12kQ thì R2 = 36kQ
Hằng số thời gian X = RC được xác định theo biểu thức f = ^ suy ra X = RC = —
— -— = 0,75.10“^s = 75ms 4RC ^ 4f 4.1000
Nếu chọn tụ c = 0,01 |aF thì điện trở R được xác định c 0 ,0 1 .10 "^ 191 Chương 8
CHUYỂN ĐỔI TƯƠNG Tự - s ố VÀ s ố - TƯƠNG Tự
8.1. TÓM TẮT PHẦN LÝ THUYẾT
Trong hệ thống thông tin số bất kỳ bắt buộc phải có bộ chuyển đổi
tưcmg tự - số (AE)C) và sô' - tưcmg tự (DAC). Việc chuyển đổi được thực
hiện ở khâu đầu và khâu cuối của kênh thông tin và dùng mã nhị phân.
Tín hiệu số được biểu diễn dưới dạng mã nhị phân
Ud = b„.,.2"'+b„.2 "-=^+...+b,2 '+b„2°.
Vi dụ: ỉ .2% 0.2^ +1.2V 0.2'+1.2'’ = 45
Tín hiệu ƯD= 101101.
bn.,: là bit có nghĩa lớn nhất (MSB)
b^: là bit có nghĩa nhỏ nhất (LSB).
Số số hạng trong dãy số nhị phân gọi là số bit, ví dụ trên là 6 bit.
Chuyển đổi tương tự - số gồm các khâu chính: lấy mẫu và giữ mức, lượng tử hòá và mã hoá.
Lấy mẫu là rời rạc hoá tín hiệu theo thời gian và phải tuân theo định
luật Shannon. Tần số lấy mẫu được xác định.
hay chu kỳ lấy mẫu T = - ^ ,s *sa Trong đó:
là tần số cực đại của tín hiệu cần chuyển đổi. Nếu số bit
là N bit, điện áp mẫu là Um thì số mức lượng tử là 2"^ và bước lưcmg tử Q
(khoảng cách giữa hai mức lượng tử liển kề) được xác định Q = 2*^-1
Sai số lượng tử lóìi nhất
ứng với — Q , tức là 192 E = - Q = — 2 ^ 2(2 " - 1 )
Như vậy sô' bit N càng lớn thì sai số càng nhỏ.
* Cck' phươììg pháp chuyển đổi AD
Tồn tại một số phưoíng pháp chuyển đổi AD:
- Phương pháp chuyển đổi song song. Điện áp analog cần chuyển đổi
được đồng thời được đưa vào các bộ so sánh để so với điện áp chuẩn đã
được chia áp thành các mức điện áp trùng với các mức lượng tử. Đầu fa
của các mạch so được đưa vào các mạch AND sau đó đưa vào mạch đếm xung và mã hoá.
ư u điểm cùa mạch chuyển đổi A/D song song là tốc độ chuyển đổi rất
cao, vì điện áp chuyển đổi được đưa đồng thời vào các tất cả các bộ so, chỉ
phụ thuộc vào tần số xung nhịp (xung đồng hồ) đưa vào mạch AND.
Nhược điểm: Cấu trúc mạch rất phức tạp, muốn chuyển đổi N bit cần
2'^-1 bộ so sánh và 2^-1 mạch AND.
- Chuyển đổi theo phưcmg pháp tiệm cận gần đúng. Điện áp tương tự
cần chuyển đổi được so sánh với điện áp analog Um- Đây là điện áp được
chuyển đổi ngược từ đầu ra đưa về bộ so (hình 8- 1 ).
Hinh 8-1. Bộ chuyển đổi DA tiệm cận gần đúng Nếu
> Um thì đầu ra bộ so có mức 1 và sau một chu kỳ xung nhịp có
một xung được đưa vào bộ đếm, đồng thời tín hiệu số Uq lại được chuyển
đổi ngược thành điện áp analog u^, rồi lại đưa vào bộ so. Nếu < Um thì
đầu ra bộ so có mức o và không có xung nào được đưa vào bộ đếm và quá
trình chuyển đổi dừng. Số vòng so sánh phụ thuộc vào số bit lưcmg tử N.
ư u điểm: Cấu trúc mạch đơn giản. 13- 250BTKTĐIỆNTỪ - A 193
Nhược điểm: Tốc độ chuyển đổi bị hạn chế, không cao.
- Oiuyển đổi theo phương pháp đếm xung đơn giản (hình 8-2 )
Điện áp cần chuyển đổi
được đưa vào bộ so SS| để so sánh với điện
áp hình răng cưa U c do bộ tạo điện áp răng cưa tạo ra.
Nếu Ua > Uc thì đầu ra SS| có mức 1.
Nếu ƯA < Uc thì đầu ra SS| có mức 0.
Bộ so SS2 so sánh điện áp răng cưa U c với đất. Nếu U c > 0 thì đầu ra SS2 nhận giá ữ ị l .
Hình 8-2. Chuyển đổi theo phương pháp đếm xung đơn giản
Cả hai điện áp ở đầu ra SSj và SS2 là Uss và Uss đều được đưa đến
mạch AND, - Điện áp Uq ờ đẩu ra mạch AND tỷ lệ vái độ lớn của u^.
Tiếp đến xung Uq đưa đến mạch ANDj, đầu vào thứ 2 là xung nhịp.
Từ đầu ra mạch AND2 tín hiệu được đưa đến bộ đếm xung. Số lượng
xung được đếm tỷ lệ với điện áp ƯA-
Điện áp răng cưa Uc = ^ JUch-dt=
Tại thời điểm t = thì U c = ƯA 194 13-250BTKTOlệNTỬ.B
SỐ xung nhịp được đếm ữong khoảng thời gian là
Z = f » . t „ = í * . ^ . R C ch Trong đó
là tần số xung nhịp, Hz. *
Chuyển đổi s ố tương tự (DAC), là quá trình chuyển đổi ngược từ tín
hiệu số ưp sang tín hiệu tương tự ư^. Hai phương pháp được sử dụng rộng
rãi là phương pháp thang điện trở và phương pháp mạng điện ữở.
- Phưcmg pháp thang điện ữở (hình 8-3) 2R u , U 1 A A A r ~ f~“ i ch b 2 N - ' R
Hinh 8-3. Chuyển đổi DAC theo phuơng pháp thang điện trỏ
Điện áp cần chuyển đổi Uj3 đưa đến điều khiển khoá điện tử, hai trạng
thái l và 0 ứng với số hạng bit của Ud và nối qua một thang điện trở, trị số
của chúng được phân bố theo mã nhị phân rồi đưa đến đầu vào bộ khuếch đại thuật toán.
Điện áp đầu ra được xác định theo biểu thức 2R
ƯA = ^ - ư c h í b,. r+h,2-^+.... +b„2^)
Biểu thức b|.2 ‘ + ba .2'^ +...+ b„.2^ là mức chuẩn hoá; b|, ba.. b„ là các
số hạng nhị phân, ứng với giá trị 1 hay 0 ưong dãy số nhị phân Up. 195
Điện áp toàn thang ứng với điều kiện khi tất cả các số hạng \ đều có giá trị 1 . ƯAmax =
( 1 2 - '+ l.2-^+1.2-^+...+ l .2-^) R
Mức lượng tử có giá ưị nhỏ nhất, ứng với b„ = 1 còn tất cả các số hạng
còn lại đều bằng 0 . 2R R
* Chuyển đổi DA theo phương pháp mạng điện trở R-2R (hình 8-4) R., 1
Hlnh 8-4. Chuyển đổi DA theo phương pháp mạng điện trỏ
Điện áp analog ƯA phụ thuộc vào tín hiệu số Up, và được xác định theo biểu thức
= Ua = ^ .U ,, ( b , .2-‘+b2.2 -^+ b32-^+...+b„2 -^)
Trong đó ưch là điện áp chuẩn;
bị, bị, b ,... b„ là các số hạng nhị phân của tín hiệu số Ud ứng với giá trị 1 hay 0 .
Ví dụ: Ud = 1101 thì b, = 1; = 1, ba = 0, = 1.
Điện áp ra cực đại khi tất cả các bit b,, đều có trị số bằng 1. 196 K
Bit có nghĩa nhỏ nhất hay một mức lượng tử ứng với b„ = 1 còn tất cả
các bit bji còn lại đều bằng 0 . I I = ĩ I = N T T 9;N ^ramin “■ ^LSB ”
8.2. PHẦN BÀI TẬP CÓ LỜI GIẢI
Bài tập 8-1. Một hệ xử lý chuyển đổi AD, tín hiệu tưcíng tự Ua có tần
số từ 0 đến 2,5 kHz. Giả sử tốc độ lấy mẫu thực tế lớn hơn tần số lấy
mẫu cực tiểu theo lý thuyết là 50%.
a) Xác định tần số lấy mẫu.
b) Xác định chu kỳ lấy mẫu.
c) Nếu sử dụng chuyển đổi AD với N = 8 bit, hãy xác định độ i-ộng mỗi bit. Bài giải
a) Tần số lấy mẫu nhỏ nhất theo iý thuyết f = = 2 F . ^samm max
ở đây tần số ỉấy mẫu thực tế được chọn lớn hơn lý thuyết là 50%
4 = ỉ ,5 .2 F „ ,,= l,5.2.2,5 = 7,5kHz
b) ƠIU kỳ lấy mẫu T được xác định
T = ^ = —L -= 133,3 Jis L 7500 ^
c) Bộ chuyển đổi AD có khả năng biến đổi mỗi trị số tương tự thành
một từ không vượt quá 133,3M-s. _ 133,3us 133,3ưs
Đ ộ rộng bit X = — — — = — • = 16,66 |IS.
Bài tập 8-2. Tần số lấy mẫu của chuyển AD ưong công nghệ ghi đĩa
compact (CD) là 44,1kHz 197
a) Xác định tần số cao nhất của tín hiệu tưong tự theo lý thuyết khi tạo
lại tín hiệu số đó.
b) Xác định thời gian biến đổi tối đa của bộ chuyển đổi AD (chu kỳ lấy mẫu T). Bài giải
a) Từ biểu thức tần số lấy mẫu fsa=2F„„ = 44,1kHz Suy ra = ^ = 22,05kHz
b) Tĩiời gian biến đổi tối đa của bộ chuyển đổi AD
T= - i - = ---- ỉ— = 22,6us f.. 44,210^ ^
Bài tập 8>3: Một bộ chuyển đổi AD dùng để chuyển đổi tín hiệu tương
tự có tần số 20Hz -i- 10.000Hz. Giả sử tần số lấy mẫu thực tế được
chọn lớn hơn tần số lấy mẫu lý thuyết 25%.
a) Xác định tần số lấy mẫu.
b) Chu kỳ lấy mẫu.
c) Nếu dùng bộ chuyển đổi AD 16 bit, hãy xác định độ rộng bit cục đại? Bài giải
a) Tần số lấy mẫu thực tế
1,25.2F„3, = 1,25.2.10.000Hz = 25.000Hz = 25kHz b) Chu kỳ lấy mẫu
X = - ^ = — L - =40jis f.. . 25.10’
c) Độ rộng bit cực đại _ T _ 4 0 |1 S ,
X = — = ___ĩ_ = 2,5ịas N 16 bit 198
(2^ Bài tập 8-4. Trong một hệ chuyển đổi AD nào đó, cần lượng tử hoá tín
hiệu thành 2048 mức lượng tử.
Hãy xác định số bit cần thiết N cho mỗi mẫu. Bài giải
SỐ mức lượng tử n phụ thuộc vào số bit lượng tử hoá N và được xác định theo biểu thức n = 2'' = 2048
b) Nếu điện áp mẫu Um = 2V, hãy xác định bước lượng từ Q. Bài giải
a) Số mức lượng tử
n = 2"^ = 2'° = 1024 mức
b) Bước lượng tử Q U 2 2 Q = f — = l,955mV. 2"'-l 2'®-l 1024-1
Bài tập 8-6. Một bộ chuyển đổi AD 12 bit dùng để biến đổi tín hiệu
analog có điện áp toàn thang Ua = lOV.
Hãy xác định các đại lượng sau đây:
a) Sô' mức lưcmg tử.
b) Bước lượng tử.
c) Sai số lượng tử cực đại.
d) Sai số lượng tử theo phần trăm. Bài gỉẳỉ
a) Số mức lượng tử
n = 2''= 2'^ = 4096 mức
b) Bước lượng tử 199 Q = - ^ = - 4 ^ = = 0,002442V 2'^-! 2 " - l 4096-1 = 2,442mV
c) Sai số lượng tử cực đại E „,= — = 0,001221 V 2 2 (2 ' -! ) 2(2 " - 1 ) = l,221mV
d) Sai số lượng tử theo phần trãm E%= ^ . 1 0 0 % = .100% = 0,1221 % 10
( 2 ^ Bài tập 8-7. Cho mạch chuyển đổi AD song song (hình 8-5) Biết: N = 3 bit UcH = 7V R = lOkQ
Giải trình chuyển đổi các điện áp sau sang tín hiệu số Up
Ua = IV; 3V; 5 V v à7V . Bài giải R
Mức điện áp U^h được phân áp bởi các điện trỏ R và — rồi đưa vào các
đầu vào và bộ so theo các mức lượng tử
0,5V; 1,5V; 2,5V; 3,5V; 4,5V; 5,5V; 6,5V.
Bước lưọmg tử Q hay IU lsb được xác định
Q = i U i . . = ^ = ỹ ^ = i v
Để giải trình việc chuyển đổi các điện áp trên sang tín hiệu số thiết lập
bảng dưới đây, trong đó diễn tả mối quan hệ giữa điện áp analog u^, các trị
số ở các đầu ra của mạch so và tín hiệu số Ujj ở đầu ra. 200 uD
Hình 8-5. Chuyển đổi AD song song Mức
Đầu ra các mạch so Ud Xo X, X. X3 X4 X5 Xa C B A 0 0 0 0 0 0 0 0 000 i 1 0 0 0 0 0 0 001 2 1 1 0 0 0 0 0 OiO 3 1 1 1 0 0 0 0 0 1 1 4 1 1 1 1 0 0 0 100 5 1 1 1 1 1 0 0 10 1 6 1 1 1 1 1 1 0 110 2 1 1 1 1 1 1 1 1 1 201 U a= 1V -» U d = 001 Ua = 3 V ^ Ud = 0 1 1
Ua = 5 V -> U d = 1 0 1
Ua = 7 V -» U d = 1 1 1
{ ^ ) Bài tập 8-8. Cho mạch chuyển đổi AD theo phương pháp tiệm cận
(xấp xỉ đúng) như hình 8-6. Biết: N = 4bit Ua™x=6V
Xác định U|J cho các điện áp cần chuyển đổi sau:
UA = 0,6V vàƯ A = l,75V .
Hlnh 8*6. Bộ chuyển đổi AD tiệm cận Bài gỉẳi
a) Trước hết xác định bước lượng tử hay bit nhỏ nhất
b) Trường hợp chuyển đổi ƯA = 0,6V
- So sánh lần 1: Um = 0 -> Ua{0,6) > Um(0)
b = 1, một xung được đưa
vào bộ đếm và mã hoá, Up - 0001, chuyển đổi ngược, được Um = 0,4V.
- So sánh lần 2: ƯA = 0,6V; Um = 0,4V Ua >
B = 1, thêm 1 xung vào bộ đếm ƯD = 0010 chuyển đổi
ngược, được Um = 0,8V. 202
- So sánh lần 3. ƯA = 0,6; Um = 0,8
< Um đầu ra B = 0, quá ữình
đếm dừng, như vậy ƯA = 0,6V -» Ud = 0010.
c) Trường hợp ƯA =1.75 V
- Vòng 3: Ua = 1,75; Um = 0,8V -)■ ƯA > Um -> B = 1 và U d = 0011,
chuyển đổi ngược DAC, được Um = 1,2V.
- Vòng 4: Ua = 1,75V; Um = 1,2V
> Um và Up = 0100, chuyển
đổi ngược DAC, được Um = 1 ,6V.
- Vòng 5: Ua = 1,75V; Um = 1,6V > u „ B = 1 và Up = 0101,
chuyển đổi ngược DAC, được Um = 2,0V.
- Vòng 6 ; Ua = 1,75V; Um = 2,0V ƯA < Um B = 0 quá trình chuyển đổi dừng.
Vậy Ua = 1,75V ứng với ƯD = 0101.
Bài tập 8-9. Cho mạch chuyển đổi DAC theo phương pháp thang điện trở như hình 8-7.
Biết: N = 4 bit, Rn = 20kQ; R = 20kQ; u,h = 3 V
a) Hãy xác định bit có nghĩa nhỏ nhất IƯLSB.
b) Tính ƯA nếu Ud = 0110; ƯD = 0011.
c) Tính điện áp toàn thang. 0 . 160kfì '’4
Hình 8-7. Chuyển đổi DAC theo phuong pháp thang điện trở 203 Bài giải
a) Bit có nghĩa nhỏ nhất ứng với 04 = 1 còn tất cả b| = b 2 = = 0 .3.2^ =0,375V LSB R ch 20
b) Theo biểu thức tính u, 2R u *
(b, .2 -' + b ,2 -= + b ,2 -> + 0 , 2 - ) R
Với Ud = 0110 có nghĩa là b, = 64 = 0 b3 = b3 = l
thay trị số của b vào 2.20 2.20
U , = ^ . 3 ( l . 2 - + 1 .2 - ) = ± ^ . 3 = 2,25V ^ 20 > 2 0
v ớ ì U d = 0 0 1 1 - ^ b , = b 2 = 0 ; b j = b 4 = 1 2.20 2.20 J_ = 1,125V 20 ^ ' 20 8 ^ "^16
c) Xác định điện áp toàn thang
Điện áp toàn thang ứng với trường hợp b, = ồ2 = 63 = ồ4 = 1 2R, U R 2.20 1 1 1 1 — = 5,62V 20 2 4 8 16
Bàl tập 8-10. Đê giống như bài 8-9. Nhưng N = 8 bit.
a) Hãy xác định bit có trị số nhỏ nhất IUlsb.
b) Xác định ƯA nếu biết ƯD = 10000000 Ud = 10101010
c) Tính điện áp toàn thang. Bài giải
a) Xác định bit có trị số nhỏ nhất 204
U lsb ứng với trường hợp bg = 1 , còn tất cả các b|j đêu bằng 0 1 2.20 .3 = 0,0234V 2 «j 20 U 5 6 j
b) Nếu Ud = 10000000, có nghĩa là b, = 1 ; bì = Ồ3 = b4 = b , = be = = bg = 0. 2R 2.20
U , = í ^ u 4 i.2 - ) = ^ . 3 i = 3V 20 u
Nếu Ud = 10101010 có nghĩa b, = bj = bj = b, = 1 b-, = = b í = bo = 0 2R
+ 1 .2 -^ + 1 .2 '" + 1 .2 '’ ) R 2.20 1 1 1 ì ) .3 = 3,984V 20 2 8 32 128j c)
Điện áp toàn thang ứng vói trường hợp tất cả các số hạng b|( đều có trị số là 1 .
( 1 .2 -' + 1 .2 '^ + 1 .2 '^ + 1 .2 -^ + 1 .2 *" + 1 .2 -* + 1 .2 '" + 1 .2 '® ) 2.2ồ J ỉ 1 1 1 1 1 1 1 '
= - — .3 — + - + - + — + -----+ ----- = 5,9765V 2Ồ ,2 4 8 16 32 64 128 256,
( 0 ) Bài tập 8-11. Bộ chuyển đổi DAC 4 bit như hình 8-7 Biết u,h = 3V R = lOkQ
a) Hãy xác định trị số Rn để ứng với Uß = 1001 thì Ua = 2,2V.
b) Xác định điện áp toàn thang cho trường hçfp đó. Bài giải a) TTieo biểu thức
u» = ^ u * ( b , r ' + b ,2 -' + b ,2->+ b ,2-') ở đây b| = bị = 1 bj = bj = 0 205 2R
U , = 2 , 2 V = ^ U , , ( l . 2 - ‘ + 1.2-^) 2,2V = ^ U ch R 2,2R 2, 2.10 Suy ra = = 6,518kQ 1 1 2Uch - + 2 .3 ^ 2 16 J 16
b) Xác định điện áp toàn thang 2R U ^ ^
U ,, (1.2-' +1.2-' +1.2-' +1.2-") R 2.6,518 1 1 1 1 .3 = 3,666V 10 ^2 4 8 16;
Bài tập 8-12. Cho mạch chuyển đổi DAC 4 bit như hình 8-7. Biết Rn = 30kQ Uch = 6V
a) Hãy xác định trị số điện trở R để ứng với Ud = 1000 thì ƯA = 9V.
b) Xác định bit có nghĩa nhỏ nhất U lsb và bit có nghĩa lớn nhất U msb
c) Xác định điện áp toàn thang. Bài giải
a) Biểu thức tính ƯA
U a = ^ u ^ ( b , 2 " +b22-“ +b,2-= +b.2-^)
Nếu Ud = 1000 thì b, = 1,02 = 03 = Ồ4 = 0 R|J.U A ch .Suyra R = —ĩL_i:h I 2 j ƯA 30.6 R = = 2 0 k n .
b) Bit có nghĩa nhỏ nhất khi 04 s= 1 còn b| = ồ2 = ba = 0 206 2R _4 2.30 ^ 1
1U lsb= ^ = ^ U . u.1 .2 “^ = ^ = ^ . 6 . — = 1,125V R 2 0 16
Bit có nghĩa lón nhất U m s b ứng vói trường hợp bị = 1, bj = bj = b4 = o TJ tj 1 -i-i 2 .3 0 g 1 q y ' ^ M S B “ "^0" 2
c) Điện áp toàn thang, ứng với trưòng hợp b| = bj = bj =s 64 =s 1 ^
( 1 .2"‘ +1.2-2 +1.2“^ +1.2"^) 2 .3 0 1 1 1 1 .6 ---h------------ = 16,875V 2 0 u 4 8 1 6 j
( ^ ) Bài tập 8-13. Cho mạch chuyển đổi ADC mạng điện trở R-2R, 4 bit như hình 8-8.
Biết: R = lOkD; Rp = lOkQ Uch=10V
Hãy xác định Rn để: a )íu ^ B = 0,5V b)
ứhg vứi Ud = 1000 thì Ua = 6V
c) Điện áp toàn thang = lOV 2R R >-AÃ/V u„=u. ra A uch + 1
Hình 8-8. Chuyển đổi DA tíieo phUdng pháp mạng điện trô R-2R 207 Bài giải
a) Theo biểu thức xác định điện áp ra Ua R u A = ( b , , 2 - ‘ +
, 2 - " + b 3 .2 -= + b , . 2 - ‘ )
Bit có nghĩa nhỏ nhất IU lsb ứng với trường hợp 04 = 1, b| = = bj = 0
Ua = U ,^ = 0 , 5 V = ^ . U , , , 2 Suy ra R .,= N Ue.-2 10.2
b) Uj) = 1000, ikig với bị = 1; b2 = ồ3 =
= 0. Đây chính là bit có nghĩa
lớn nhất U i = U^SB = 6V
U A = - ^ U ,,.2 - '.S u y r a R R,
Ư A = 6 = ^ U , h . 2 - 6R 6R.2 6.10.2 Rịm - = 12kQ -1 U U c h - 2 ch 10
c) Điện áp toàn thang ứng với trường hợp
Ò| — Ò-> — t)3 — — 1 U ^ = 1 0 V 2-*+2"^+2"^+2"'‘ lOR 10.10 R]SJ - - ^ = 10,66kQ 1 '1 1 1
Uch|2‘ ‘ + 2 “' + 2 ‘' + 2 ‘‘ )
10 ------ 1------ ------------Ị_ ------ U 4 8 16;
( 2 ^ Bài tập 8-14. Bộ chuyển đổi DAC mạng điện trở R-2R 8 bit. Biết; Rn = 20kQ UcH = 6V
a) Hãy xác định điện trở R và 2R để bií có trị số nhỏ nhất I U lsb = 0,046875V. 208
b) Xác định bit có trị số lớn nhất U^SB trong ttTíờng hợp đó.
c) Tính điện áp toàn thang. Bài giải
a) Bit có nghĩa nhỏ nhất ứng vód trưòng hợp bg = 1. Các số hạng còn lại đều bằng 0.
U lsb= ^ U . j .2-* =0,046875 Suyra
R = - ^ U ^ . 2 ' * = — — — .6 .4 -= 1 0 k n ’ U lsb ■* 0,046875 2« 2R = 20kfi.
b) Bit có nghĩa lớn nhất Umsb ứng với trường hợp b, = 1, cáq số hạng bịỊ
còn lại đều bằngO.
U msb= % - U ,h.2 -‘ = ^ . 6 . ỉ = 6V R 10 2
c>Điện áp toàn thang ứng với trường hợp b| = Ồ2 = bj = b4 = bs = bg = b7 = b « = l = B u
. (2“^ + 2-2 + 2'^ + 2“^ + 2"^ + 2"^-+ 2“^ + 2"^) f 1 1 1 1 1 1 1 1 1 = ^ . 6 . = 11,953V 10
U 4 8 16 32 64 128 256 j
( ^ ) Bài tập 8-15. C3io mạch chuyển đổi DA như hình 8-8. Biết: N = 4b it R = 1 0 k 0 R N =10k£í
a) Hãy xác định điện áp chuẩn Ud, cần thiết để khi Uđ = 1100 ứừ ƯA = 4,5V. b)TínhU^B. c)
Tính điện áp toàn thang. Bài giải
a) Điện áp ra được xác định ửieo biểu thức
14.250BTKTĐlệNTỪ-A 209
(b ,2- ‘ + h2 2 -2 + b s2 - ’ + b 42 -<) V Ớ i Ư D = 1 1 0 0 t h ì b , = l , b 2 = l , b 3 = b 4 = 0
u , = | i u , , ( r U 2 - ^ ) U aR 10.4,5 Suy ra ưch = r = 6V ( ỉ n R ( ỉ l ì ---- 1------------ N — 1— 1 0 u 4 y u 4 )
b) Xác định bit có nghĩa nhỏ nhất
Ò4= 1; b, =b 2 = b3 = 0
IUlsb = — Uch2"‘ = — .6.2"^ =0,375V LSB R ch V
c) Điện áp Ua toàn thang, ứng vói trường hc^ b| = = bj = 04 = 1 R ,-3 Ụ a =
N u ^ j 2 " ’ +2"2+2-^+2- R = 5,625V 10 u 4 8 16j
(2^ Bài tập 8-16. Oio mạch chuyển đổi DA như hình 9-8 nhung N = 5 bit; U ,h = 10V ;R = 10k Q .
Hãy xáQ định Rn cần thiết để đạt được các điều kiện sau:
a) ứ ig với bit có nghĩa nhỏ nhất thì ƯA = 200mV.
b) Khi điện áp Ud = 10001 thì ƯA = 5V.
c) Điện áp toàn thang ƯA = 12V. Bài giải
a) Bỉt có nghĩa nhố nhất khi bj = 1; bj = 02 = ba = ồ4 = 0
U ^ = 0 ,2 V = .|tU ,,.2 -= Suy ra 10.2-* 210 14-250BTKTĐiệNTỬ.B
b) Khi Ud = 10001 ứng với b, = bs = 1 t>2 = bj = b4 = 0
U ,= 5 V = ^ U ^ ( 2 - ' + 2 - = ) 5.10 Suy ra R = ----- ^ = 9,412kQ U.4 2 - + 2 - ) U . 1 ^ 10 2 32 j
c) Điện áp toàn thang ƯA = 12V ứng vói trưòng hợp ƯQ = 11111
bị = bj = bj = Ò4 = bs = 1 = 12V =
(2-‘ + 2'^ + 2'^ + 2-^ + 2-^ ) U ,R Suy ra = 1 1 1 1 p
------ 1--------- ị---------1------------1---------
ư ch U 4 8 16 32 j 12.10 = 12,387kQ ^ 1 1 1 1 1
— -ị--------- ị---------1------------Ị---------
10 2 4 8 16 32)
Bài tập 8-17. Cho mạch chuyển đổi DA 8 bit dùng IC DA806 (hình 8-9).
Giả sử: R ,4 = R ,5 = r = Rn = lOkQ Ukbf = U,, = 5,12V
a) Hãy xác định bit có nghĩa nhỏ nhất IƯLSB-
b) Xác định điện áp toàn thang. Bàỉ giải
a) Bit có nghĩa nhỏ nhất ứng với bg = 1 còn tất cả các số hạng b|f còn lại đều bằng 0.
U a =U.CB = ^ U . . 2 ‘* = — .5,12.2“® =0,02V A LSB ch *
b) Điện áp toàn thang
ứng với trưỀmg hợp bj = bj = bj = ồ4 = bs = bg ~ ^7 = bg = 1. 211 1_ NC Comp _ 1 6 p 2 - u ref 15. . ' 5 15V GND •— 3 u rcf+ 12V DA806 A,(MSB) (LSB)Ag ^12 6^ Aa A, - 1 ! 8bitU 7_ _10 8_ _ 9 J Rn ■vw u Hình 8-9 ^
(2-* + 2'^ + 2'^ + 2"* + 2'* + 2"* + 2“’ + 2'*) 1 1 1 1 1 1 1 1
= i« .5 ,1 2 — + “ ^ H— H----h
H------h ---- 1--- — = 5,IV 10 2 4 8 16 32 64 128 256;
Bài tập 8-18. Cho mạch chuyển đổi AD 801 8 bit như hình 8-10
Biết U|, U j... Ug là tám mức điện áp ứng với tám trị số 00000001,
00000010, 00000100, 00001000, 00010000, 00100000,
01000000, 10000000.
Hãy tính nhữig điện áp đó. Bài giải
Đối với mỗi trong 8 điện áp được tính ồ đây chỉ có một bit duy nhất ứng
với mức 1, còn các bit khác ứng với mức 0. 212 R=10kíỉ — VVVr- 1 20 I t 3 * 5,12V 12. DBO ^18 LSB> 17 Start DBl i 16 5 - AD 801 DB2 Ư :IN 6 ^15 >u, U iN - -r- 7 U i N . - 1 4 AGND -1 3 u -.12 ch i l O j . DGND DB7 V I MSB
Hinh 8-10. Mạch chuyển đổỉ AD 801 00000001 U, = 5,12V.2* = 20mV 00000010 -> U2 = 5,12V.2-’ = 40mV 00000100 U3 = 5,12V.2« = 80mV 00001000
Ư4 = 5,12 v.2'^= 160 mV 00010000 ->
Us = 5,12 v.a"* = 320 mV 00100000
Us = 5,12 V.2’^ = 640 mV 01000000 -> ư7 = 5,12V.2-2= 1280 mV 10000000 -> Ug = 5,12 v.2'= 2560 mV 213 TÀI LIỆU THAM KHẢO
1. Phạm Minh Hà, 2003. Kỹ thuật mạch điện tử, NXB Khoa học và Kỹ thuật.
2. Đặng Văn Chuyết (Chủ biên), 2004. Giáo trình Kỹ thuật mạch điện tử, NXB Giáo duc. •
3. Nguyễn Viết Nguyên, 2004. Giảo trinh Linh kiện điện tử và ứng dụng, NXB Giáo dục. •
4. Nguyễn Thanh Trà, TTiái Vữih Hiển, 2005. Giáo trình Điện tử dân dụng, NXB Giáo dục.
5. Đỗ Xuân Thụ, Nguyễn Viết Nguyên, 2004. Bài tập Kỹ thuật điện tử, NXB Giáo dục. «
6. William D.Stanley, 1990. Operational dmplifiers with linear integrated
circuits, Macmilan Publishing Company.
7. Lê Văn Doanh, Võ Thạch Sơn, 1994. Kỹ thuật điện tử (Phần Bài tập),
NXB Khoa học và Kỹ thuật. 214 MỤ ■ C LỤ • C Trang Lời nói đầu 3 Chưcmg 1. Điốt
1.1. Tóm tắt phần lý thuyết 5
1.2. Phần bài tập có lời giải 6 1.3. Đề bài tập 29
Chương 2. Transistor lưỡng cực và transistor trường
2.1. Tóm tắt phần lý thuyết 39
2.2. Phần bài tập co lòd giải AI
Qiương 3. Các mạch khuếch đại tín hiệu bé
3.1. Tóm tắt phần lý thuyết 66
3.2. Phần bài tập có lòi giải 67 3.3. Đề bài tập 92
Chưcmg 4. Mạch khuếch đại công suất
4.1. Tóm tắt phần lý thuyết 105
4.2. Phần bài tập co lời giải 110
Chương 5. Bộ khuếch đại thuật toán
5.1. Tóm tắt phần lý thuyết 130
5.2. Phần bài tập có lời giải 134
Chương 6. Nguồn ổn áp
6.1. Tóm tắt phần lý thuyết 152
6.2. Phần bài tập có lòi giải 156
Chương 7. Mạch dao đông
7.1. Tóm tắt phần lý thuyết 173
7.2. Phần bài tập có lèd giải 177
Chương 8. Mạch chuyển đổi tương tự - số và số - tương tự
8.1. Tóm tắt phần lý thuyết 192
8.2. Phần bài tập có lời giải 197 Tài liệu tham khảo 214 215
Document OutlineKV THUỘT ĐIỈN TỬqBài giảiu,=iĩqU, = ^=^M.25.27,nV ^ q 1,6.10"'’Bài giảiBài giảiBài giảiBài giảiBài giảiu, =IR, =2,07.10'\4,7.10^ =9,73VI=——-^=3,32mA R, 5,6.10^R^iknBái giáibé (ul = 20V).Bài giảiU^, = Ir.R = O.R = ovBài giảiup^ = U2.Iz = Uz.0 = 0WBài giảiu.,-u.U,„,=20.ítH5l±^=23,67VI li-.RR, u,+ cỉ.tp+1 " 1-aR, =-^R.+Ra-ụmA)Bài giảip = Ị^=“:l°Ị = 1000,2.10Bài giải0,1.0,1Bài giảis = _éíc_K„=H^ = M = 48 “ u, 0,2I» I50.10-*I„ I„ 5.10-’R =R //R =Aì = AZ:^=l,35kQ(15+ 85). 10^Bài giảiBài giải1,1"ura r E-U„o-I^R,_ 10 -0,7 - 0,545_,5l"+I„ 6.0,2.10-Bài giảiBài giảiBài giảiR.=Bài giảiBài giảiBài giảiR„ = Rc // ĨQ = Rc // °0 = Rc = 3kQ.r, 10,71= Re // ro = 3 // 50 = 2,83kũ.-264,24uU = -Mee.. ^ 2.22 ^ 2,81Vb)Rvd)= —f = 35,89|aAb) Rv = RJ/ rvT mà ĨVT = P(re + Re) = 120(5,99 + 560) = 67,92kQ.2,2Ti,: 20A2^“ RB+(l + ß)Rg 220kQ + 101.3,3kO = (1 + ß)ig^ = 101.20,42^A = 2,062mA' Ieo 2,062b) Rv = Rb // rvT = Rb // ß-re + (1 + P)Re= 220kQ // 100.12,610 + 101.3,3kü = 220kn // 334,56kQ = 132,72kfì.e,K,= -^ = --J5^=-39,67.R^+Tyj 220 + 334,56Ki = -K„ ^ = -0,996 = -40,06Bài giảir„ = ß.r. + ^ I00.12.6in+ »295,7kfìl+ñe i + 3,3k£ỉ(1 + ß)^ (100+1)d) ^ = -1MI = 0,996.K - _ 5.10^K,=Ị*-=I>j,.=120.Bài giảie) R.f)Ku.u,Bài giảid) R,, = Rc // r, H Rd = lOMQ // 50kQ // 2kQ = 1,92kQ.R„ = Ro//Ro = RD = 2kQRoSOkQBài giảivà g„ =g„„(l-^^) = 5ms(l-^) = 3,75mSBài giảiBài giảiBài giải= ^ = 6,5Qr. _ R_Rc(//R4//R5//P-r.)*^u, ~ “Bài giảiBài giải^ R. 21,81,1Bài giảiBài giải-II-41—*uHhxác định Rv, R„; Ky. Biết =6ỒkQ; Icss = 12mA; ưp=-3,5V; Edd = 22V.^oịi.sknu.Ị.[ nc 13.3kn> T ^RdLh. 2KRra = R( = R(_ wu_ U2 2 ■ “Po = U,„.I^ = I,„E12 2Bài giảiIco “ ßlßo — 20.50 = lOOmAUce.« = 22V72 2yÍ2 iSU,=U™Ị = ÌA74 = 1.685V” R. 8Po = E.I,„ = 12V.100.10' = 1,2Wp 0 355Po 1,2 ’Pc = Po - Pra = 1,2 - 0,355 = 0,845WBài giảiR, 1.10'Icm = Ibm- ß = lOmA.25 = 250mA p =Í250]02¿20 = 0,625wPo = Ecc-Ico = 20.0,48 = 9,6W ^ = ^100% = ^^100 = 6,5%Bài giảip ^ = 36,125W2R. 2.4I.™ = l.n,= -^ = J = 4.25A^ 100% = 100% = 53,3%ĨI-.U,„.=VP„.2R, =7^ = 12 Vu.„Bài giảiV R.leo, = 1,5I„ = 1,5^ = 1,3-!^ = 33,5mAR = .-...■.EỌ. = = 1,9Q 12fìp. =-l„,..UcB0 =r^l.'8.9,44 = 7,095W2.0,2ỊC^(HỊ)1,24,85Wp _p.-p„ _ 56.125-24.85 _ 2 2hồi tiếp k(,t = —^.' + K-K. , + iooJ-200Bài giảiBài giảiK. =^ = ^ = 4=0.02U„=(l+^)Up-^U,= (i+ễ^)b)U„ = .^U, = .^.0,2 = -l0V.Bài tập 5-4. Cho mạch điện như hình 5-6b Biết= 20kn Rj = lomR4 = 30m = 400mVBài gỉaiR.+R.R,R, KR,+Rpu»=-|^u.=—0,2 = -5VR.,u =._Ì^.0,2 = -1,66V10 + 20Rị = 250kQ R3 = 20kí2 R4 = 470k0 E=±9V U, = 25mV ICTTlà lý tưỏngR, R4uBài giải^.u, +^.Ư3+^.U, R. ' R, ^ R,500,, 500,, 500,,^500Bài giảiu„ = iu =-Ể^.U, = -20Uu =+Ml.u R.R4ư„,=(1+^)U,A+^.Uu„ = -Bài giảiU, = 30mV ; U, = 20mVu„ = -= - +^(^u, +^u.)R. 20u, = 0 u„ = 0Bài giảiu.= -dtBài giảiR 1 — »1Ua=U,HBài giảiBài giảiu. = u, = ——R, . . Suy ra R, . =RR.1 + —^ = »-ỉi ^-5—1=0.2307U,' u; ' 6 'U,, ư,-u+ 1^01-^2 = 1.25 1 +AƯ2 = 16,95 - 16,875 = 0,075V = 75mV= 125Bài giảiV R.y_« //n _ R3R4 _ 2400.2400R3+R, 2400 + 2400R, // R2 // R3 // R4 = = 600QR = R3 //R, = -Mi- = = l,333kQ” ' R3+R, 3 + 2,4R.Bài giảiBài giải1,25R..240 = 4368n = 4,368kQ4368Chương 7 MẠCH DAO ĐỘNG2„ L _^l^V C1+C2Xc.= -4:<0SrcBài giảiBài giảiBài giảiBài giảiBài giảiBài giải(2^ Bài tập 7-10. Đề lặp lại bài 7-9. Nếu thay điện trở R bằng chiết áp đồng trục có điện trở biến đổi từ lOkQ đến lOOkQ. .Bài giải27t.C^R + Rpmax)f, ! Bài giảiu, = -u„,Ư2(0) = -U„,Bài giảiVi dụ: ỉ .2% 0.2^ +1.2V 0.2'+1.2'’ = 45R.,1T= ^=—L-= 133,3 Jis L 7500 ^Bài giảiBài giảia) Sô' mức lưcmg tử.Bài gỉẳỉBài giảiQ=iUi..= ^=ỹ^=ivBài gỉẳic) Trường hợp ƯA =1.75 V- Vòng 3: Ua = 1,75; Um = 0,8V -)■ ƯA > Um -> B = 1 và Ud = 0011, chuyển đổi ngược DAC, được Um = 1,2V.- Vòng 5: Ua = 1,75V; Um = 1,6V > u„ B = 1 và Up = 0101, chuyển đổi ngược DAC, được Um = 2,0V.Bài tập 8-9. Cho mạch chuyển đổi DAC theo phương pháp thang điện trở như hình 8-7.Biết: N = 4 bit, Rn = 20kQ; R = 20kQ; u,h = 3 Vb) Tính ƯA nếu Ud = 0110; ƯD = 0011.2.20U,=^.3(l.2- + 1.2-) = ±^.3 ^ 20 >20Bài giảiu» =^u*(b,r' +b,2-' + b,2->+b,2-')Nếu Ud = 1000 thì b, = 1,02 = 03 = Ồ4 = 01111= 16,875V20 u 4 8 16ja)íu^B = 0,5V1f 1 1 1 1 1 1 1 1 1 U 4 8 16 32 64 128 256 ju,=|iu,,(rU2-^)10U.42-+2-)10^1111 1u1111111 1TÀI LIỆU THAM KHẢOMỤC LỤC ■ •




