TOP 5 đề phát triển đề minh họa kỳ thi tốt nghiệp THPT 2020 môn Toán

Giới thiệu đến quý thầy, cô giáo và các em học sinh khối 12 tuyển tập 05 đề phát triển đề minh họa kỳ thi tốt nghiệp THPT 2020 môn Toán do thầy Nguyễn Chín Em chia sẻ

43 22 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

95 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Bài thi: MÔN TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao bài
PHÁT TRIỂN ĐỀ MINH HỌA 1
Câu 1. Một hộp chứa 10 quả cầu phân biệt. Số cách lấy ra từ hộp đó cùng lúc 3 quả cầu là
A. 120. B. 10. C. 60. D. 720.
Câu 2. Tính số hạng đầu u
1
và và công sai d của cấp số cộng (u
n
), biết
®
u
1
+ u
5
− u
3
= 10
u
1
+ u
6
= 7.
A. u
1
= −36, d = 13. B. u
1
= 36, d = 13. C. u
1
= 36, d = −13. D. u
1
= −36, d = −13.
Câu 3. Tìm tập nghiệm của phương trình 3
x
2
+2x
= 1.
A. S = {−1; 3}. B. S = {−2; 0}. C. S = {−3; 1}. D. S = {0; 2}.
Câu 4. Cho khối chóp S.ABC có đáy là tam giác đều cạnh a, SA = a
√
3, cạnh bên SA vuông góc với
đáy. Thể tích của khối chóp S.ABC bằng
A.
a
3
√
3
2
. B.
a
3
2
. C.
a
3
√
3
4
. D.
a
3
4
.
Câu 5. Tập xác định của hàm số y = log
2
(4 − x
2
) là tập hợp nào sau đây?
A. D = (−2; 2). B. D = (−∞; −2) ∪ (2; +∞).
C. D = [−2; 2]. D. D = R\{−2; 2}.
Câu 6. Tìm mệnh đề sai trong các mệnh đề sau?
A.
Z
2e
x
dx = 2 (e
x
+ C). B.
Z
x
3
dx =
x
4
+ C
4
.
C.
Z
1
x
dx = ln x + C. D.
Z
sin x dx = −cos x + C.
Câu 7. Hình chóp S.ABC có chiều cao h = a, diện tích tam giác ABC là 3a
2
. Tính thể tích hình chóp
S.ABC.
A.
a
3
3
. B. a
3
. C.
3
2
a
3
. D. 3a
3
.
Câu 8. Cho khối nón có bán kính đáy r =
√
3 và chiều cao h = 4. Tính thể tích V của khối nón đã
cho.
A. V = 12π. B. V = 4π. C. V = 4. D. V = 12.
Câu 9. Một mặt cầu có diện tích xung quanh là π thì có bán kính bằng
A.
√
3
2
. B.
√
3. C.
1
2
. D. 1.
Câu 10.
Cho hàm số y = f(x) có bảng biến thiên như
hình vẽ:
Hàm số đã cho nghịch biến trên khoảng nào dưới
đây?
A. (0; +∞). B. (−1; 1).
C. (−∞; 0). D. (−∞; −2).
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−2−2
33
−2−2
+∞+∞
Câu 11. Với a và b là hai số dương tùy ý, log
2
(a
3
b
4
) bằng
A.
1
3
log
2
a +
1
4
log
2
b. B. 3 log
2
a + 4 log
2
b. C. 2 (log
3
a + log
4
b). D. 4 log
2
a + 3 log
2
b.
Câu 12. Cho khối trụ có thể tích V và bán kính đáy R. Chiều cao của khối trụ đã cho bằng
A.
V
πR
2
. B.
V
3πR
2
. C.
V
R
2
. D.
V
3R
2
.
GeoGebraPro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Câu 13. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số.
A. 3. B. 0. C. 1. D. 2.
x
y
0
y
−∞
−2
0 2
+∞
−
0
+
0
−
0
+
Câu 14.
Đồ thị ở hình bên là của hàm số nào dưới đây?
A. y = −x
3
− 3x
2
− 4. B. y = x
3
− 3x − 4.
C. y = −x
3
+ 3x
2
− 4. D. y = x
3
− 3x − 4.
x
y
O
−1
2
−4
1
−2
1
Câu 15. Tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y =
x + 2
x − 1
là
A. y = 2; x = 1. B. y = 1; x = 1. C. y = −2; x = 1. D. y = 1; x = −2.
Câu 16. Tập nghiệm của bất phương trình log
2
(3 − x) < 2 là
A. (−∞; 1). B. (−1; 3). C. (1; 3). D. (3; +∞).
Câu 17.
Cho hàm số f(x) có đồ thị như hình vẽ. Số nghiệm của phương trình 2f (x)−
3 = 0 là
A. 3. B. 1. C. 2. D. 0.
x
y
−1
3
1
−1
O
Câu 18. Nếu
2
Z
1
f(x) dx = 5,
5
Z
2
f(x) dx = −1 thì
5
Z
1
f(x) dx bằng
A. −2. B. 2. C. 3. D. 4.
Câu 19. Cho số phức z = 2 − 3i. Số phức liên hợp của số phức z là:
A. z = 3 − 2i. B. z = 3 + 2i. C. z = −2 − 3i. D. z = 2 + 3i.
Câu 20. Cho hai số phức z
1
= 1 − i, z
2
= 2 + 3i. Tính mô-đun của số phức z = z
1
+ z
2
.
A. |z| = 1. B. |z| =
√
5. C. |z| = 5. D. |z| =
√
13.
Câu 21. Số phức nào sau đây có điểm biểu diễn là M(1; −2)?
A. −1 − 2i. B. 1 + 2i. C. 1 − 2i. D. −2 + i.
Câu 22. Trong không gian Oxyz, cho M(3; −2; 1), N(1; 0; −3). Gọi M
0
, N
0
lần lượt là hình chiếu của
M và N lên mặt phẳng Oxy. Khi đó độ dài đoạn M
0
N
0
là
GeoGebraPro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
A. M
0
N
0
= 8. B. M
0
N
0
= 4. C. M
0
N
0
= 2
√
6. D. M
0
N
0
= 2
√
2.
Câu 23. Trong không gian Oxyz cho mặt cầy (S): x
2
+ y
2
+ z
2
− 2x + 4z + 1 = 0 có tâm I và bán
kính R là.
A. I(−1; 0; 2), R = 2. B. I(−1; 0; 2), R = 4. C. I(1; 0; −2), R = 2. D. I(1; 0; −2), R = 4.
Câu 24. Trong không gian Oxyz, mặt phẳng (P ): 2x − y + 3 = 0. Một véc tơ pháp tuyến của (P ) có
tọa độ là
A. (2; 1; 0). B. (2; −1; 3). C. (2; −1; 0). D. (2; 1; 3).
Câu 25. Trong không gian Oxyz, đường thẳng d :
x − 1
2
=
y − 2
−1
=
z − 3
2
đi qua điểm nào dưới đây
?
A. Q(2; −1; 2). B. M(−1; −2; −3). C. P (1; 2; 3). D. N(−2; 1; −2).
Câu 26. Cho hình chóp S.ABCD có đáy hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng
a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo góc (MN, SC) bằng
A. 45
◦
. B. 30
◦
. C. 90
◦
. D. 60
◦
.
Câu 27. Cho hàm số y = f (x) liên tục trên [−3; 3] và có bảng xét dấu đạo hàm như hình bên.
x
y
0
−3 −1
0 1 2 3
+
0
−
0
−
0
+
0
−
Mệnh đề nào sau đây sai về hàm số đó?
A. Hàm số đạt cực tiểu tại x = 1. B. Hàm số đạt cực đại tại x = −1.
C. Hàm số đạt cực đại tại x = 2. D. Hàm số đạt cực tiểu tại x = 0.
Câu 28. Cho hàm số y = −x
3
+ 3x
2
+ 2. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số
trên [0; 3]. Tính (M + m).
A. 6. B. 8. C. 10. D. 4.
Câu 29. Với các số a, b > 0 thỏa mãn a
2
+ b
2
= 6ab, biểu thức log
2
(a + b) bằng
A.
1
2
(3 + log
2
a + log
2
b). B.
1
2
(1 + log
2
a + log
2
b).
C. 1 +
1
2
(log
2
a + log
2
b). D. 2 +
1
2
(log
2
a + log
2
b).
Câu 30. Số giao điểm của đường cong y = x
3
− 2x
2
+ 2x + 1 và đường thẳng y = 1 − x là
A. 1. B. 2. C. 3. D. 0.
Câu 31. Tập nghiệm của bất phương trình 3
x
2
−2x
< 27 là
A. (−∞; −1). B. (3; +∞).
C. (−1; 3). D. (−∞; −1) ∪ (3; +∞).
Câu 32. Cho tam giác ABC vuông tại A có AB = a
√
3 và BC = 2a. Tính thể tích khối nón sinh ra
khi quay tam giác ABC quay cạnh AB.
A. V = πa
3
√
3. B. V = 2πa
3
. C. V =
2πa
3
3
. D. V =
πa
3
√
3
3
.
Câu 33. Cho I =
1
Z
0
x
2
√
1 − x
3
dx. Nếu đặt t =
√
1 − x
3
thì ta được
A. I =
3
2
1
Z
0
t
2
dt. B. I = −
3
2
1
Z
0
t
2
dt. C. I = −
2
3
1
Z
0
t
2
dt. D. I =
2
3
1
Z
0
t
2
dt.
Câu 34. Diện tích hình phẳng H được giới hạn bởi hai đồ thị y = x
3
−2x −1 và y = 2x −1 được tính
theo công thức
GeoGebraPro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
A. S =
0
Z
−2
x
3
− 4x
dx. B. S =
2
Z
0
x
3
− 4x
dx.
C. S =
2
Z
−2
x
3
− 4x
dx. D. S =
2
Z
−2
x
3
− 4x
dx.
Câu 35. Cho hai số phức z
1
= 2 + 4i, z
2
= −1 + 3i. Tính môđun của số phức w = z
1
z
2
− 2z
1
.
A. |w| = 2
√
2. B. |w| = 2
√
10. C. |w| = 4
√
2. D. |w| = 2.
Câu 36. Gọi z
1
là nghiệm phức có phần ảo dương của phương trình z
2
+ 6z + 13 = 0. Tìm tọa độ điểm
M biểu diễn số phức w = (i + 1) z
1
.
A. M (−5; −1). B. M (5; 1). C. M (−1; −5). D. M (1; 5).
Câu 37. Trong không gian Oxyz, cho điểm A(2; −1; −3) và mặt phẳng (P ): 3x −2y + 4z −5 = 0. Mặt
phẳng (Q) đi qua A và song song với mặt phẳng (P ) có phương trình là
A. (Q): 3x − 2y + 4z − 4 = 0. B. (Q): 3x − 2y + 4z + 4 = 0.
C. (Q): 3x − 2y + 4z + 5 = 0. D. (Q): 3x + 2y + 4z + 8 = 0.
Câu 38. Trong không gian Oxyz, viết phương trình chính tắc của đường thẳng qua điểm E(1; 2; −3)
và F (3; −1; 1).
A.
x − 1
3
=
y − 2
−1
=
z + 3
1
. B.
x − 3
2
=
y + 1
−3
=
z − 1
4
.
C.
x − 3
1
=
y + 1
2
=
z − 1
−3
. D.
x + 1
2
=
y + 2
−3
=
z − 3
4
.
Câu 39. Có 8 bạn học sinh lớp 11A trong đó có An và Bình được xếp ngẫu nhiên theo một hàng ngang.
Tính xác suất P để An và Bình ngồi cạnh nhau.
A. P =
1
8
. B. P =
1
4
. C. P =
1
64
. D. P =
1
25
.
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SO vuông góc với mặt
phẳng ABCD và SO = a. Khoảng cách giữa SC và AB bằng
A.
2a
√
3
15
. B.
a
√
5
5
. C.
a
√
3
15
. D.
2a
√
5
15
.
Câu 41. Có bao nhiêu giá trị nguyên của tham số m ∈ [−2019; 2019] để hàm số y = (m − 1)x
3
+
3mx
2
+ (4m + 4)x + 1 đồng biến trên khoảng (−∞; +∞)?
A. 4036. B. 2017. C. 2018. D. 4034.
Câu 42. Một người thả một lá bèo vào một chậu nước. Sau 12 giờ, bèo sinh sôi phủ kín mặt nước trong
chậu. Biết rằng sau mỗi giờ lượng bèo tăng gấp 10 lần lượng bèo trước đó và tốc độ tăng không đổi.
Hỏi sau mấy giờ thì bèo phủ kín
1
5
mặt nước trong chậu (kết quả làm tròn đến hàng phần chục).
A. 9,1 giờ. B. 9,7 giờ. C. 10,9 giờ. D. 11,3 giờ.
Câu 43. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
−1
3
+∞
+
0
−
0
+
−∞−∞
55
11
+∞+∞
Đồ thị hàm số y = |f (x)| có bao nhiêu điểm cực trị?
A. 2. B. 3. C. 4. D. 5.
Câu 44. Cho hình trụ có trục OO
0
, chiều cao bằng a. Trên hai đường tròn đáy (O) và (O
0
) lần lượt lấy
hai điểm A và B sao cho khoảng cách giữa hai đường thẳng AB và OO
0
bằng
a
2
. Góc giữa hai đường
thẳng AB và OO
0
bằng 60
◦
. Thể tích của khối trụ đã cho là
GeoGebraPro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
A.
2πa
3
3
. B.
πa
3
3
. C. 2πa
3
. D. πa
3
.
Câu 45. Cho hàm số f (x) liên tục và có đạo hàm trên
0;
π
2
, thỏa mãn f (x) + tan xf
0
(x) =
x
cos
3
x
.
Biết rằng
√
3f
π
3
−f
π
6
= aπ
√
3+b ln 3 trong đó a, b ∈ R. Giá trị của biểu thức P = a+b bằng
A.
14
9
. B. −
2
9
. C.
7
9
. D. −
4
9
.
Câu 46. Cho hàm số y = f (x) có bảng biến thiên như sau:
x
y
0
y
−∞
−2
0 2
+∞
+
0
−
0
+
0
−
−∞−∞
33
−1−1
33
−∞−∞
Hàm số y = f (x
2
− 2) nghịch biến trên khoảng nào dưới đây?
A. (2; +∞). B. (0; 2). C. (−∞; −2). D. (−2; 0).
Câu 47. Xét các số thực dương x, y thoả mãn log
1
2
x + log
1
2
y ≤ log
1
2
(x + y
2
). Tìm giá trị nhỏ nhất
P
min
của biểu thức P = x + 3y
A. P
min
=
17
2
. B. P
min
= 8. C. P
min
= 9. D. P
min
=
25
√
2
4
.
Câu 48. Gọi S là tập hợp các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y =
|x
3
− 3x
2
− 9x + m| trên đoạn [−2; 4] bằng 16. Số phần tử của S là
A. 10. B. 12. C. 14. D. 11.
Câu 49. Cho hình hộp chữ nhật ABCD.A
0
B
0
C
0
D
0
. Khoảng cách giữa AB và B
0
C là
2a
√
5
5
, giữa BC
và AB
0
là
2a
√
5
5
, giữa AC và BD
0
là
a
√
3
3
. Thể tích của khối hộp đó là
A. 8a
3
. B. 4a
3
. C. 2a
3
. D. a
3
.
Câu 50. Xét các số thực dương x, y thỏa mãn log
√
3
x + y
x
2
+ y
2
+ xy + 2
= x(x −3) + y(y −3) + xy. Tìm
giá trị lớn nhất P
max
của P =
3x + 2y + 1
x + y + 6
.
A. 3. B. 2. C. 1. D. 4.
———————–HẾT———————–
GeoGebraPro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
ĐÁP ÁN THAM KHẢO
1. A 2. C 3. D 4. D 5. A 6. C 7. B 8. B 9. C 10. D
11. B 12. A 13. A 14. C 15. B 16. B 17. A 18. D 19. D 20. D
21. C 22. D 23. C 24. C 25. C 26. C 27. D 28. B 29. A 30. A
31. C 32. D 33. D 34. D 35. B 36. A 37. B 38. B 39. B 40. D
41. C 42. D 43. B 44. D 45. D 46. A 47. C 48. D 49. C 50. C
GeoGebraPro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Bài thi: MÔN TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao bài
PHÁT TRIỂN ĐỀ MINH HỌA 1
Câu 1. Một hộp chứa 10 quả cầu phân biệt. Số cách lấy ra từ hộp đó cùng lúc 3 quả cầu là
A. 120. B. 10. C. 60. D. 720.
Lời giải.
Số cách chọn 3 quả cầu từ hộp là C
3
10
= 120.
Chọn phương án A
Câu 2. Tính số hạng đầu u
1
và và công sai d của cấp số cộng (u
n
), biết
®
u
1
+ u
5
− u
3
= 10
u
1
+ u
6
= 7.
A. u
1
= −36, d = 13. B. u
1
= 36, d = 13. C. u
1
= 36, d = −13. D. u
1
= −36, d = −13.
Lời giải.
Theo giả thiết suy ra
®
u
1
+ 2d = 10
2u
1
+ 5d = 7
⇔
®
u
1
= 36
d = −13.
Chọn phương án C
Câu 3. Tìm tập nghiệm của phương trình 3
x
2
+2x
= 1.
A. S = {−1; 3}. B. S = {−2; 0}. C. S = {−3; 1}. D. S = {0; 2}.
Lời giải.
Ta có 3
x
2
+2x
= 1 ⇔ x
2
+ 2x = 0 ⇔
ñ
x = 0
x = −2.
Do đó tập nghiệm của phương trình là S = {0; 2}.
Chọn phương án D
Câu 4. Cho khối chóp S.ABC có đáy là tam giác đều cạnh a, SA = a
√
3, cạnh bên SA vuông góc với
đáy. Thể tích của khối chóp S.ABC bằng
A.
a
3
√
3
2
. B.
a
3
2
. C.
a
3
√
3
4
. D.
a
3
4
.
Lời giải.
Ta có V =
1
3
SA · S
ABC
=
1
3
a
√
3
a
2
√
3
4
=
a
3
4
.
S
B
A C
Chọn phương án D
Câu 5. Tập xác định của hàm số y = log
2
(4 − x
2
) là tập hợp nào sau đây?
A. D = (−2; 2). B. D = (−∞; −2) ∪ (2; +∞).
C. D = [−2; 2]. D. D = R\{−2; 2}.
Lời giải.
Phương pháp:
Điều kiện để hàm số y = log
a
f(x) (0 < a 6= 1) có nghĩa là f(x) > 0.
GeoGebraPro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Cách giải:
Điều kiện xác định 4 − x
2
> 0 ⇔ x ∈ (−2; 2).
Chọn phương án A
Câu 6. Tìm mệnh đề sai trong các mệnh đề sau?
A.
Z
2e
x
dx = 2 (e
x
+ C). B.
Z
x
3
dx =
x
4
+ C
4
.
C.
Z
1
x
dx = ln x + C. D.
Z
sin x dx = −cos x + C.
Lời giải.
Ta có
Z
1
x
dx = ln |x| + C nên mệnh đề ở phương án C sai.
Chọn phương án C
Câu 7. Hình chóp S.ABC có chiều cao h = a, diện tích tam giác ABC là 3a
2
. Tính thể tích hình chóp
S.ABC.
A.
a
3
3
. B. a
3
. C.
3
2
a
3
. D. 3a
3
.
Lời giải.
V
S.ABC
=
1
3
h.S
4ABC
=
1
3
.a.3a
2
= a
3
.
Chọn phương án B
Câu 8. Cho khối nón có bán kính đáy r =
√
3 và chiều cao h = 4. Tính thể tích V của khối nón đã
cho.
A. V = 12π. B. V = 4π. C. V = 4. D. V = 12.
Lời giải.
Thể tích khối nón là
V =
1
3
πr
2
h =
1
3
π(
√
3)
2
· 4 = 4π.
BA O
S
Chọn phương án B
Câu 9. Một mặt cầu có diện tích xung quanh là π thì có bán kính bằng
A.
√
3
2
. B.
√
3. C.
1
2
. D. 1.
Lời giải.
Phương pháp:
Công thức tính diện tích mặt cầu bán kính R là S = 4π · R
2
.
Cách giải:
Ta có: S = π = 4π · R
2
⇔ R
2
=
1
4
⇔ R =
1
2
.
Chọn phương án C
Câu 10.
Cho hàm số y = f(x) có bảng biến thiên như
hình vẽ:
Hàm số đã cho nghịch biến trên khoảng nào dưới
đây?
A. (0; +∞). B. (−1; 1).
C. (−∞; 0). D. (−∞; −2).
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−2−2
33
−2−2
+∞+∞
GeoGebraPro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Lời giải.
Ta có y
0
< 0, ∀x ∈ (−∞; −1) ∪ (0; 1) ⇒ y
0
< 0, ∀x ∈ (−∞; −2).
Chọn phương án D
Câu 11. Với a và b là hai số dương tùy ý, log
2
(a
3
b
4
) bằng
A.
1
3
log
2
a +
1
4
log
2
b. B. 3 log
2
a + 4 log
2
b. C. 2 (log
3
a + log
4
b). D. 4 log
2
a + 3 log
2
b.
Lời giải.
Ta có log
2
(a
3
b
4
) = log
2
a
3
+ log
2
b
4
= 3 log
2
a + 4 log
2
b.
Chọn phương án
B
Câu 12. Cho khối trụ có thể tích V và bán kính đáy R. Chiều cao của khối trụ đã cho bằng
A.
V
πR
2
. B.
V
3πR
2
. C.
V
R
2
. D.
V
3R
2
.
Lời giải.
Ta có V = πR
2
h ⇒ h =
V
πR
2
.
Chọn phương án A
Câu 13. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số.
A. 3. B. 0. C. 1. D. 2.
x
y
0
y
−∞
−2
0 2
+∞
−
0
+
0
−
0
+
Lời giải.
Dựa vào BBT suy ra hàm số có 3 điểm cực trị.
Chọn phương án A
Câu 14.
Đồ thị ở hình bên là của hàm số nào dưới đây?
A. y = −x
3
− 3x
2
− 4. B. y = x
3
− 3x − 4.
C. y = −x
3
+ 3x
2
− 4. D. y = x
3
− 3x − 4.
x
y
O
−1
2
−4
1
−2
1
Lời giải.
Từ đồ thị hàm số ta suy ra hệ số cao nhất a < 0, loại được đáp án B và D.
Đồ thị đi qua điểm (2; 0) nên C là đáp án đúng.
Chọn phương án C
Câu 15. Tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y =
x + 2
x − 1
là
A. y = 2; x = 1. B. y = 1; x = 1. C. y = −2; x = 1. D. y = 1; x = −2.
Lời giải.
Ta có lim
x→+∞
y = lim
x→+∞
x + 2
x − 1
= lim
x→+∞
1 +
2
x
1 −
1
x
= 1 suy ra đường thẳng y = 1 là tiệm cận ngang của đồ thị
hàm số.
GeoGebraPro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
Do lim
x→1
+
(x + 2) = 3 > 0; lim
x→1
+
(x − 1) = 0, x − 1 > 0 ∀x > 1
⇒ lim
x→1
+
y = lim
x→+∞
x + 2
x − 1
= +∞ nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
Chọn phương án B
Câu 16. Tập nghiệm của bất phương trình log
2
(3 − x) < 2 là
A. (−∞; 1). B. (−1; 3). C. (1; 3). D. (3; +∞).
Lời giải.
Điều kiện 3 − x > 0 ⇔ x < 3.
log
2
(3 − x) < 2 ⇔ 3 − x < 4 ⇔ x > −1.
Kết hợp điều kiện ta được tập nghiệm S = (−1; 3) .
Chọn phương án B
Câu 17.
Cho hàm số f(x) có đồ thị như hình vẽ. Số nghiệm của phương trình 2f(x)−
3 = 0 là
A. 3. B. 1. C. 2. D. 0.
x
y
−1
3
1
−1
O
Lời giải.
Ta có 2f (x) − 3 = 0 ⇔ f(x) =
3
2
(∗).
Số nghiệm của phương trình (∗) bằng số giao điểm giữa đồ thị hàm số
y = f(x) và đường thẳng y =
3
2
.
Dựa vào hình vẽ, hai đồ thị cắt nhau tại 3 điểm phân biệt.
Vậy phương trình đã cho có 3 nghiệm.
x
y
−1
3
1
−1
y =
3
2
O
Chọn phương án A
Câu 18. Nếu
2
Z
1
f(x) dx = 5,
5
Z
2
f(x) dx = −1 thì
5
Z
1
f(x) dx bằng
A. −2. B. 2. C. 3. D. 4.
Lời giải.
Ta có
5
Z
1
f(x) dx =
2
Z
1
f(x) dx +
5
Z
2
f(x) dx = 5 + (−1) = 4.
Chọn phương án D
Câu 19. Cho số phức z = 2 − 3i. Số phức liên hợp của số phức z là:
A. z = 3 − 2i. B. z = 3 + 2i. C. z = −2 − 3i. D. z = 2 + 3i.
Lời giải.
Do định nghĩa số phức liên hợp nên số phức liên hợp của z = 2 − 3i là z = 2 + 3i.
Chọn phương án D
GeoGebraPro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 20. Cho hai số phức z
1
= 1 − i, z
2
= 2 + 3i. Tính mô-đun của số phức z = z
1
+ z
2
.
A. |z| = 1. B. |z| =
√
5. C. |z| = 5. D. |z| =
√
13.
Lời giải.
z = z
1
+ z
2
= 3 + 2i ⇒ |z| =
√
3
2
+ 2
2
=
√
13.
Chọn phương án D
Câu 21. Số phức nào sau đây có điểm biểu diễn là M(1; −2)?
A. −1 − 2i. B. 1 + 2i. C. 1 − 2i. D. −2 + i.
Lời giải.
M(1; −2) là điểm biểu diễn cho số phức có phần thực bằng 1 và phần ảo bằng −2, tức là 1 − 2i.
Chọn phương án C
Câu 22. Trong không gian Oxyz, cho M(3; −2; 1), N(1; 0; −3). Gọi M
0
, N
0
lần lượt là hình chiếu của
M và N lên mặt phẳng Oxy. Khi đó độ dài đoạn M
0
N
0
là
A. M
0
N
0
= 8. B. M
0
N
0
= 4. C. M
0
N
0
= 2
√
6. D. M
0
N
0
= 2
√
2.
Lời giải.
Ta có M
0
(3; −2; 0) và N
0
(1; 0; 0) suy ra
# »
M
0
N
0
= (−2; 2; 0) ⇒ M
0
N
0
= 2
√
2.
Chọn phương án D
Câu 23. Trong không gian Oxyz cho mặt cầy (S): x
2
+ y
2
+ z
2
− 2x + 4z + 1 = 0 có tâm I và bán
kính R là.
A. I(−1; 0; 2), R = 2. B. I(−1; 0; 2), R = 4. C. I(1; 0; −2), R = 2. D. I(1; 0; −2), R = 4.
Lời giải.
Dễ thấy mặt cầu (S): x
2
+ y
2
+ z
2
− 2x + 4z + 1 = 0 có:
Tâm I(1; 0; −2) và bán kính R =
p
1
2
+ 0
2
+ (−2)
2
− 1 = 2.
Chọn phương án C
Câu 24. Trong không gian Oxyz, mặt phẳng (P ): 2x − y + 3 = 0. Một véc tơ pháp tuyến của (P ) có
tọa độ là
A. (2; 1; 0). B. (2; −1; 3). C. (2; −1; 0). D. (2; 1; 3).
Lời giải.
Mặt phẳng (P ) có VTPT là
#»
n = (2; −1; 0).
Chọn phương án C
Câu 25. Trong không gian Oxyz, đường thẳng d :
x − 1
2
=
y − 2
−1
=
z − 3
2
đi qua điểm nào dưới đây
?
A. Q(2; −1; 2). B. M(−1; −2; −3). C. P (1; 2; 3). D. N (−2; 1; −2).
Lời giải.
Ta có
1 − 1
2
=
2 − 2
−1
=
3 − 3
2
nên P (1; 2; 3) ∈ d.
Chọn phương án C
Câu 26. Cho hình chóp S.ABCD có đáy hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng
a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo góc (MN, SC) bằng
A. 45
◦
. B. 30
◦
. C. 90
◦
. D. 60
◦
.
Lời giải.
GeoGebraPro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
Ta có MN là đường trung bình của tam giác DAS nên MN ∥ SA.
Suy ra góc của SA với SC bằng góc giữa MN với SC. Gọi O là
tâm của hình vuông ABCD, vì SA = SC = SB = SD nên SO ⊥
(ABCD).
Có AC =
√
2 ⇒ AO =
√
2
2
nên sin
’
ASO =
AO
SA
=
√
2
2
⇒ ∠ASO =
45
◦
nên
’
ASC = 90
◦
.
S
N
OM
A
D
B
C
Chọn phương án C
Câu 27. Cho hàm số y = f (x) liên tục trên [−3; 3] và có bảng xét dấu đạo hàm như hình bên.
x
y
0
−3 −1
0 1 2 3
+
0
−
0
−
0
+
0
−
Mệnh đề nào sau đây sai về hàm số đó?
A. Hàm số đạt cực tiểu tại x = 1. B. Hàm số đạt cực đại tại x = −1.
C. Hàm số đạt cực đại tại x = 2. D. Hàm số đạt cực tiểu tại x = 0.
Lời giải.
Dựa vào bảng xét dấu của đạo hàm ta thấy f
0
(0) = 0 và đạo hàm không đổi dấu khi x qua x
0
= 0 nên
hàm số đã cho không đạt cực tiểu tại x = 0.
Chọn phương án D
Câu 28. Cho hàm số y = −x
3
+ 3x
2
+ 2. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số
trên [0; 3]. Tính (M + m).
A. 6. B. 8. C. 10. D. 4.
Lời giải.
Ta có: y
0
= −3x
2
+ 6x; y
0
= 0 ⇔
ñ
x = 0 /∈ (0; 3)
x = 2 ∈ (0; 3)
y(0) = 2; y(2) = 6; y(3) = 2. Vậy M = 6; m = 2 ⇒ M + m = 8.
Chọn phương án B
Câu 29. Với các số a, b > 0 thỏa mãn a
2
+ b
2
= 6ab, biểu thức log
2
(a + b) bằng
A.
1
2
(3 + log
2
a + log
2
b). B.
1
2
(1 + log
2
a + log
2
b).
C. 1 +
1
2
(log
2
a + log
2
b). D. 2 +
1
2
(log
2
a + log
2
b).
Lời giải.
Ta có: a
2
+ b
2
= 6ab ⇔ (a + b)
2
= 8ab
⇒ log
2
(a + b)
2
= log
2
8ab
⇔ 2log
2
(a + b) = log
2
8 + log
2
a + log
2
b
⇔ log
2
(a + b) =
1
2
(3 + log
2
a + log
2
b).
.
Chọn phương án A
Câu 30. Số giao điểm của đường cong y = x
3
− 2x
2
+ 2x + 1 và đường thẳng y = 1 − x là
A. 1. B. 2. C. 3. D. 0.
Lời giải.
GeoGebraPro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Phương trình hoành độ giao điểm của hai đường trên là
x
3
− 2x
2
+ 2x + 1 = 1 − x ⇔ x
3
− 2x
2
+ 3x = 0 ⇔ x = 0.
Phương trình có một nghiệm nên đường cong và đường thẳng có một giao điểm.
Chọn phương án A
Câu 31. Tập nghiệm của bất phương trình 3
x
2
−2x
< 27 là
A. (−∞; −1). B. (3; +∞).
C. (−1; 3). D. (−∞; −1) ∪ (3; +∞).
Lời giải.
3
x
2
−2x
< 27 ⇔ 3
x
2
−2x
< 3
3
⇔ x
2
− 2x < 3 ⇔ x
2
− 2x − 3 < 0 ⇔ −1 < x < 3.
Chọn phương án C
Câu 32. Cho tam giác ABC vuông tại A có AB = a
√
3 và BC = 2a. Tính thể tích khối nón sinh ra
khi quay tam giác ABC quay cạnh AB.
A. V = πa
3
√
3. B. V = 2πa
3
. C. V =
2πa
3
3
. D. V =
πa
3
√
3
3
.
Lời giải.
Ta có AC =
√
BC
2
− AB
2
= a và thể tích khối nón là
V =
1
3
π · AC
2
· AB =
πa
3
√
3
3
.
B
A
0
A
C
Chọn phương án D
Câu 33. Cho I =
1
Z
0
x
2
√
1 − x
3
dx. Nếu đặt t =
√
1 − x
3
thì ta được
A. I =
3
2
1
Z
0
t
2
dt. B. I = −
3
2
1
Z
0
t
2
dt. C. I = −
2
3
1
Z
0
t
2
dt. D. I =
2
3
1
Z
0
t
2
dt.
Lời giải.
Đặt t =
√
1 − x
3
⇒ t
2
= 1 − x
3
⇒ 2t dt = −3x
2
dx hay x
2
dx = −
2
3
t dt
Đổi cận:
®
x = 0 ⇒ t = 1
x = 1 ⇒ t = 0.
Do đó I = −
2
3
0
Z
1
t
2
dt =
2
3
1
Z
0
t
2
dt.
Chọn phương án D
Câu 34. Diện tích hình phẳng H được giới hạn bởi hai đồ thị y = x
3
−2x −1 và y = 2x −1 được tính
theo công thức
A. S =
0
Z
−2
x
3
− 4x
dx. B. S =
2
Z
0
x
3
− 4x
dx.
C. S =
2
Z
−2
x
3
− 4x
dx. D. S =
2
Z
−2
x
3
− 4x
dx.
Lời giải.
GeoGebraPro Trang 7
https://www.facebook.com/groups/GeoGebraPro/
Phương trình hoành độ giao điểm của y = x
3
− 2x − 1 và y = 2x − 1 là
x
3
− 2x − 1 = 2x − 1 ⇔ x
3
− 4x = 0 ⇔
x = 2
x = 0
x = −2
.
Vậy diện tích hình phẳng H được giới hạn bởi hai đồ thị y = x
3
−2x −1 và y = 2x −1 được tính theo
công thức S =
2
Z
−2
x
3
− 4x
dx.
Chọn phương án D
Câu 35. Cho hai số phức z
1
= 2 + 4i, z
2
= −1 + 3i. Tính môđun của số phức w = z
1
z
2
− 2z
1
.
A. |w| = 2
√
2. B. |w| = 2
√
10. C. |w| = 4
√
2. D. |w| = 2.
Lời giải.
Ta có w = (2+4i)(−1−3i)−2(2−4i) = (10−10i)−(4−8i) = 6−2i. Do đó |w| =
p
6
2
+ (−2)
2
= 2
√
10.
Chọn phương án B
Câu 36. Gọi z
1
là nghiệm phức có phần ảo dương của phương trình z
2
+ 6z + 13 = 0. Tìm tọa độ điểm
M biểu diễn số phức w = (i + 1) z
1
.
A. M (−5; −1). B. M (5; 1). C. M (−1; −5). D. M (1; 5).
Lời giải.
Ta có z
2
+ 6z + 13 = 0 ⇔
ñ
z = −3 + 2i
z = −3 − 2i.
Vì z
1
là nghiệm có phần ảo dương nên z
1
= −3 + 2i.
Ta có w = (i + 1)(−3 + 2i) = −5 − i ⇒ M(−5; −1).
Chọn phương án A
Câu 37. Trong không gian Oxyz, cho điểm A(2; −1; −3) và mặt phẳng (P ): 3x −2y + 4z −5 = 0. Mặt
phẳng (Q) đi qua A và song song với mặt phẳng (P ) có phương trình là
A. (Q): 3x − 2y + 4z − 4 = 0. B. (Q): 3x − 2y + 4z + 4 = 0.
C. (Q): 3x − 2y + 4z + 5 = 0. D. (Q) : 3x + 2y + 4z + 8 = 0.
Lời giải.
Do mặt phẳng (Q) song song với mặt phẳng (P ) nên có vectơ pháp tuyến là
#»
n = (3; −2; 4).
Phương trình mặt phẳng (Q): 3(x − 2) − 2(y + 1) + 4(z + 3) = 0 ⇔ 3x − 2y + 4z + 4 = 0.
Chọn phương án B
Câu 38. Trong không gian Oxyz, viết phương trình chính tắc của đường thẳng qua điểm E(1; 2; −3)
và F (3; −1; 1).
A.
x − 1
3
=
y − 2
−1
=
z + 3
1
. B.
x − 3
2
=
y + 1
−3
=
z − 1
4
.
C.
x − 3
1
=
y + 1
2
=
z − 1
−3
. D.
x + 1
2
=
y + 2
−3
=
z − 3
4
.
Lời giải.
Đường thẳng qua điểm E(1; 2; −3) và F (3; −1; 1) có véc-tơ chỉ phương
#»
u =
# »
EF = (2; −3; 4).
Vậy phương trình chính tắc của đường thẳng EF qua F (3; −1; 1) là
x − 3
2
=
y + 1
−3
=
z − 1
4
.
Chọn phương án B
Câu 39. Có 8 bạn học sinh lớp 11A trong đó có An và Bình được xếp ngẫu nhiên theo một hàng ngang.
Tính xác suất P để An và Bình ngồi cạnh nhau.
GeoGebraPro Trang 8
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
A. P =
1
8
. B. P =
1
4
. C. P =
1
64
. D. P =
1
25
.
Lời giải.
Số cách xếp 8 học sinh thành một hàng ngang là n(Ω) = 8!
Số cách xếp 8 học sinh trong đó An và Bình ngồi cạnh nhau là: 7! · 2!
Vậy xác suất cần tìm là P =
7! · 2!
8!
=
1
4
.
Chọn phương án B
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SO vuông góc với mặt
phẳng ABCD và SO = a. Khoảng cách giữa SC và AB bằng
A.
2a
√
3
15
. B.
a
√
5
5
. C.
a
√
3
15
. D.
2a
√
5
15
.
Lời giải.
Vì AB ∥ (SCD) nên d(AB, SC) = d(AB, (SCD)) =
d(A, (SCD)) = 2d(O, (SCD)).
Gọi K là trung điểm của CD. Khi đó OK ⊥ CD ⇒
CD ⊥ (SOK). Gọi H là hình chiếu vuông góc của O lên
SK ⇒ OH ⊥ (SCD) ⇒ d(O, (SCD)) = OH. Ta có
1
OH
2
=
1
OK
2
+
1
OS
2
=
1
a
2
2
+
1
a
2
=
5
a
2
⇒ OH =
a
√
5
5
.
Vậy d(AB, SC) = 2OH =
2a
√
5
5
.
A
B C
D
K
H
S
O
Chọn phương án D
Câu 41. Có bao nhiêu giá trị nguyên của tham số m ∈ [−2019; 2019] để hàm số y = (m − 1)x
3
+
3mx
2
+ (4m + 4)x + 1 đồng biến trên khoảng (−∞; +∞)?
A. 4036. B. 2017. C. 2018. D. 4034.
Lời giải.
TXĐ: D = R. Đạo hàm: y
0
= 3(m − 1)x
2
+ 6mx + 4m + 4.
Để hàm số đã cho đồng biến trên khoảng (−∞; +∞) thì y
0
≥ 0, ∀x ∈ (−∞; +∞) (y
0
= 0 tại hữu hạn
điểm).
• TH1: m − 1 = 0 ⇔ m = 1 thì y
0
= 6x + 8 ≥ 0 ⇔ x ≥ −
4
3
(không thỏa mãn).
• TH2:
®
a = m − 1 > 0
∆
0
y
0
= (3m)
2
− 3(m − 1)(4m + 4) ≤ 0
⇔
®
m > 1
− 3m
2
+ 12 ≤ 0
⇔
m > 1
ñ
m ≥ 2
m ≤ −2
⇔ m ≥ 2.
Vì m là số nguyên và m ∈ [−2019; 2019] ⇒ m = {2; 3; 4; . . . ; 2019}.
Vậy có 2018 số nguyên m thuộc khoảng m ∈ [−2019; 2019].
Chọn phương án C
Câu 42. Một người thả một lá bèo vào một chậu nước. Sau 12 giờ, bèo sinh sôi phủ kín mặt nước trong
chậu. Biết rằng sau mỗi giờ lượng bèo tăng gấp 10 lần lượng bèo trước đó và tốc độ tăng không đổi.
Hỏi sau mấy giờ thì bèo phủ kín
1
5
mặt nước trong chậu (kết quả làm tròn đến hàng phần chục).
A. 9,1 giờ. B. 9,7 giờ. C. 10,9 giờ. D. 11,3 giờ.
Lời giải.
Giả sử một lá bèo chiếm x (0 < x < 1) phần mặt nước trong chậu.
Sau 12 giờ, bèo sinh sôi phủ kín mặt nước trong chậu nên ta có phương trình
10
12
· x = 1 ⇔ x =
1
10
12
.
GeoGebraPro Trang 9
https://www.facebook.com/groups/GeoGebraPro/
Giả sử t giờ thì bèo phủ kín
1
5
mặt nước, ta có phương trình
1
10
12
· 10
t
=
1
5
⇔ t − 12 = log
1
5
⇔ t ≈ 11,3 giờ.
Chọn phương án D
Câu 43. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
−1
3
+∞
+
0
−
0
+
−∞−∞
55
11
+∞+∞
Đồ thị hàm số y = |f (x)| có bao nhiêu điểm cực trị?
A. 2. B. 3. C. 4. D. 5.
Lời giải.
Cách 1: Số điểm cực trị của đồ thị hàm số y = |f (x)| bằng số điểm cực trị của đồ thị hàm số y = f(x)
cộng với số giao điểm của đồ thị hàm số y = f(x) với trục hoành (không tính điểm cực trị)
Vì đồ thị hàm số y = f(x) có 2 điểm cực trị và cắt trục Ox tại 1 điểm nên đồ thị hàm số y = |f (x)| có
2 + 1 = 3 điểm cực trị.
Cách 2: |f(x)| =
p
f
2
(x) ⇒ (|f(x)|)
0
=
f(x) · f
0
(x)
|f(x)|
⇒ dấu của (|f(x)|)
0
là dấu của f(x) · f
0
(x).
Ta có f (x) · f
0
(x).
f
0
(x) = 0 ⇒ x = −1; x = 3.
Từ bảng biến thiên suy ra f(x) = 0 ⇔ x = x
0
< −1.
Lập bảng xét dấu
x
f
0
(x)
f(x)
f
0
(x) · f(x)
−∞
x
0
−1
3
+∞
+ +
0
−
0
+
−
0
+ + +
−
0
+
0
−
0
+
Từ bảng biến thiên ta thấy f(x) · f
0
(x) đổi dấu 3 lần nên hàm số |f(x)| có 3 cực trị.
Chọn phương án B
Câu 44. Cho hình trụ có trục OO
0
, chiều cao bằng a. Trên hai đường tròn đáy (O) và (O
0
) lần lượt lấy
hai điểm A và B sao cho khoảng cách giữa hai đường thẳng AB và OO
0
bằng
a
2
. Góc giữa hai đường
thẳng AB và OO
0
bằng 60
◦
. Thể tích của khối trụ đã cho là
A.
2πa
3
3
. B.
πa
3
3
. C. 2πa
3
. D. πa
3
.
Lời giải.
GeoGebraPro Trang 10
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Dựng AA
0
vuông góc với mặt phẳng đáy.
AB ⊂ (ABA
0
) nên d(AB, OO
0
) = d(OO
0
, (ABA
0
)) =
d(O
0
, (ABA
0
)).
Gọi I là trung điểm BA
0
. Ta có O
0
I ⊥ BA
0
(vì ∆O
0
BA
0
cân).
Mà O
0
I ⊥ AA
0
nên O
0
I ⊥ (ABA
0
)
hay d(O
0
, (ABA
0
)) = O
0
I =
a
2
.
Mặt khác
ÿ
AB, OO
0
=
ÿ
AB, AA
0
=
’
A
0
AB = 60
◦
.
Xét ∆ABA
0
vuông tại A
0
có tan 60
◦
=
A
0
B
AA
0
⇒ A
0
B = a
√
3 và
BI =
a
√
3
2
.
Xét ∆O
0
BI vuông tại I có O
0
B =
√
O
0
I
2
+ BI
2
= a.
Vậy thể tích của khối trụ đã cho là
V = π · O
0
B
2
· OO
0
= π · a
2
· a = πa
3
.
A
0
O
0
O
B
I
A
Chọn phương án D
Câu 45. Cho hàm số f(x) liên tục và có đạo hàm trên
0;
π
2
, thỏa mãn f(x) + tan xf
0
(x) =
x
cos
3
x
.
Biết rằng
√
3f
π
3
−f
π
6
= aπ
√
3+b ln 3 trong đó a, b ∈ R. Giá trị của biểu thức P = a+b bằng
A.
14
9
. B. −
2
9
. C.
7
9
. D. −
4
9
.
Lời giải.
Ta có f(x) + tan xf
0
(x) =
x
cos
3
x
⇔ cos x · f(x) + sin xf
0
(x) =
x
cos
2
x
⇔ [sin x · f(x)]
0
=
x
cos
2
x
.
Do đó
Z
[sin x · f(x)]
0
dx =
Z
x
cos
2
x
dx ⇒ sin x · f(x) =
Z
x
cos
2
x
dx.
Tính I =
Z
x
cos
2
x
dx.
Đặt
u = x
dv =
dx
cos
2
x
⇒
®
du = dx
v = tan x.
Khi đó I = x · tan x −
Z
tan x dx = x · tan x −
Z
d cos x
cos x
= x · tan x + ln |cos x|.
Suy ra f(x) =
x · tan x + ln |cos x|
sin x
=
x
cos x
+
ln |cos x|
sin x
.
Do
√
3f
π
3
− f
π
6
= aπ
√
3 + b ln 3 =
√
3
Å
2π
3
−
2 ln 2
√
3
ã
−
Ç
π
√
3
9
+ 2 ln
√
3
2
å
=
5π
√
3
9
ln 3.
Khi đó
a =
5
9
b = −1
.
Vậy P = a + b = −
4
9
.
Chọn phương án D
Câu 46. Cho hàm số y = f (x) có bảng biến thiên như sau:
x
y
0
y
−∞
−2
0 2
+∞
+
0
−
0
+
0
−
−∞−∞
33
−1−1
33
−∞−∞
Hàm số y = f (x
2
− 2) nghịch biến trên khoảng nào dưới đây?
A. (2; +∞). B. (0; 2). C. (−∞; −2). D. (−2; 0).
GeoGebraPro Trang 11
https://www.facebook.com/groups/GeoGebraPro/
Lời giải.
Ta có y
0
= 2xf
0
(x
2
− 2).
y
0
= 0 ⇔
ñ
x = 0
f
0
x
2
− 2
= 0
⇔
x = 0
x
2
− 2 = −2
x
2
− 2 = 0
x
2
− 2 = 2
⇔
x = 0
x = ±
√
2
x = ±2
.
Do các nghiệm của phương trình y
0
= 0 đều là nghiệm bội lẻ, mà y
0
(3) = 6f
0
(7) < 0 nên ta có bảng xét
dấu y
0
x
y
0
−∞
−2
−
√
2
0
√
2
2
+∞
+
0
−
0
+
0
−
0
+
0
−
Vậy hàm số y = f (x
2
− 2) nghịch biến trên khoảng (2; +∞).
Chọn phương án A
Câu 47. Xét các số thực dương x, y thoả mãn log
1
2
x + log
1
2
y ≤ log
1
2
(x + y
2
). Tìm giá trị nhỏ nhất
P
min
của biểu thức P = x + 3y
A. P
min
=
17
2
. B. P
min
= 8. C. P
min
= 9. D. P
min
=
25
√
2
4
.
Lời giải.
Phương pháp:
• Sử dụng công thức log
a
x + log
a
y = log
a
(xy) (0 < a 6= 1, x, y > 0), giải bất phương trình lôgarit
cơ bản log
a
f (x) ≤ log
a
g (x) (0 < a < 1) ⇔ f (x) ≥ g (x).
• Rút x theo y thế vào P.
• Đưa P về dạng P = f (y). Lập BBT và tìm GTNN của P = f (y).
Cách giải:
Theo bài ra ta có:
log
1
2
x
+ log
1
2
y
≤ log
1
2
(x + y
2
) ⇔ log
1
2
(xy) ≤ (x + y
2
) ⇔ xy ≥ x + y
2
x (y − 1) ≥ y
2
> 0. Mà x > 0 ⇒ y − 1 > 0 ⇔ y > 1.
x ≥
y
2
y − 1
. Khi đó ta có P = x + 3y ≥
y
2
y − 1
+ 3y với y > 1.
Xét hàm số f (y) =
y
2
y − 1
+ 3y với y > 1 ta có:
f
0
(y) =
2y (y − 1) − y
2
(y − 1)
2
+ 3 =
y
2
− 2y + 3y
2
− 6y + 3
(y − 1)
2
=
4y
2
− 8y + 3
(y − 1)
2
= 0 ⇔
y =
3
2
y =
1
2
.
BBT:
y
f
0
(y)
f(y)
−∞
1
2
1
3
2
+∞
+
0
− −
0
+
−∞−∞
11
−∞
+∞
99
+∞+∞
GeoGebraPro Trang 12
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Từ BBT ta thấy min
y>1
f(y) = f
Å
3
2
ã
= 9.
Vậy P ≥ 9 hay P
min
= 9.
Chọn phương án C
Câu 48. Gọi S là tập hợp các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y =
|x
3
− 3x
2
− 9x + m| trên đoạn [−2; 4] bằng 16. Số phần tử của S là
A. 10. B. 12. C. 14. D. 11.
Lời giải.
Xét hàm số y = f (x) = x
3
− 3x
2
− 9x + m có y
0
= 3x
2
− 6x − 9, y
0
= 0 ⇔
ñ
x = −1
x = 3.
Bảng biến thiên
x
f
0
(x)
f(x)
−2 −1
3 4
+
0
−
0
+
m − 2m − 2
m + 5m + 5
m − 27m − 27
m − 20m − 20
Giá trị lớn nhất của hàm số y = |x
3
− 3x
2
− 9x + m| trên đoạn [−2; 4] bằng 16 khi và chỉ khi
®
m + 5 = 16
27 − m ≤ 16
®
m − 27 = 16
m + 5 ≤ 16
⇔ m = 11.
Vậy m = 11 là giá trị duy nhất thỏa mãn.
Chọn phương án D
Câu 49. Cho hình hộp chữ nhật ABCD.A
0
B
0
C
0
D
0
. Khoảng cách giữa AB và B
0
C là
2a
√
5
5
, giữa BC
và AB
0
là
2a
√
5
5
, giữa AC và BD
0
là
a
√
3
3
. Thể tích của khối hộp đó là
A. 8a
3
. B. 4a
3
. C. 2a
3
. D. a
3
.
Lời giải.
C
C
0
D
0
D
H
A
B
A
0
B
0
K
L
O
GeoGebraPro Trang 13
https://www.facebook.com/groups/GeoGebraPro/
Gọi H, K lần lượt là hình chiếu vuông góc của B lên AB
0
và B
0
C.
Ta có
®
BK ⊥ AB
0
BK ⊥ BC (do BC ⊥ (ABB
0
) ⊃ BK)
⇒ d(AB
0
, BC) = BK =
2a
√
5
5
.
Tương tự ta có d(AB, B
0
C) =
2a
√
5
5
nên AB = BC. Vậy tứ giác ABCD là hình vuông. Suy ra
AC ⊥ BD, mà AC ⊥ AA
0
nên AC ⊥ (BB
0
D
0
D).
Gọi L là hình chiếu vuông góc của O lên BD
0
, suy ra d(AC, BD
0
) = OL =
a
√
3
3
.
Đặt AB = BC = x, BB
0
= y. Ta có
1
x
2
+
1
y
2
=
5
4a
2
. (*)
Mặt khác, do 4BOL v BD
0
D (g - g) nên
OL
DD
0
=
BO
BD
0
⇔
a
√
3
3y
=
x
√
2
2
p
2x
2
+ y
2
⇔
3a
2
9y
2
=
2x
2
8x
2
+ 4y
2
⇔ 2a
2
(8x
2
+ 4y
2
) = 18x
2
y
2
⇔ y
2
=
24a
2
x
2
18x
2
− 12a
2
.
Thay vào (*) ta được
1
x
2
+
18x
2
− 12a
2
24a
2
x
2
=
5
4a
2
⇔
12a
2
+ 18x
2
24a
2
x
2
=
5
4a
2
⇔ x = a ⇒ y = 2a.
Vậy, V
ABCD .A
0
B
0
C
0
D
0
= AB · BC · BB
0
= 2a
3
.
Chọn phương án C
Câu 50. Xét các số thực dương x, y thỏa mãn log
√
3
x + y
x
2
+ y
2
+ xy + 2
= x(x −3) + y(y −3) + xy. Tìm
giá trị lớn nhất P
max
của P =
3x + 2y + 1
x + y + 6
.
A. 3. B. 2. C. 1. D. 4.
Lời giải.
Ta có
log
√
3
x + y
x
2
+ y
2
+ xy + 2
= x(x − 3) + y(y − 3) + xy
⇔ 3(x + y) + log
√
3
(3(x + y)) =
x
2
+ y
2
+ xy + 2
+ log
√
3
x
2
+ y
2
+ xy + 2
.
Hay f(3(x + y)) = f (x
2
+ y
2
+ xy + 2) với f(t) = t + log
√
3
t có f
0
(t) = 1 +
1
t ln
√
3
> 0, ∀t > 0.
Do vậy
3(x + y) = x
2
+ y
2
+ xy + 2
⇔
4x
2
+ 4xy + y
2
+ 3(y
2
− 2y + 1) − 6(2x + y) + 5 = 0
⇒(2x + y)
2
− 6(2x + y) + 5 = −3(y − 1)
2
≤ 0.
Suy ra 1 ≤ 2x + y ≤ 5. Do đó P = 1 +
2x + y − 5
x + y + 6
≤ 1.
Vậy P
max
= 1.
Chọn phương án C
———————–HẾT———————–
GeoGebraPro Trang 14
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
ĐÁP ÁN THAM KHẢO
1. A 2. C 3. D 4. D 5. A 6. C 7. B 8. B 9. C 10. D
11. B 12. A 13. A 14. C 15. B 16. B 17. A 18. D 19. D 20. D
21. C 22. D 23. C 24. C 25. C 26. C 27. D 28. B 29. A 30. A
31. C 32. D 33. D 34. D 35. B 36. A 37. B 38. B 39. B 40. D
41. C 42. D 43. B 44. D 45. D 46. A 47. C 48. D 49. C 50. C
GeoGebraPro Trang 15
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 2
Câu 1. Một chi đoàn có 16 đoàn viên. Cần bầu chọn một Ban Chấp hành ba người gồm Bí thư, Phó
Bí thư và Ủy viên. Số cách chọn ra Ban Chấp hành nói trên là
A. 560. B. 4096. C. 48. D. 3360.
Câu 2. Cho cấp số cộng (u
n
) biết u
3
= 6, u
8
= 16. Tính công sai d và tổng của 10 số hạng đầu tiên.
A. d = 2; S
10
= 100. B. d = 1; S
10
= 80. C. d = 2; S
10
= 120. D. d = 2; S
10
= 110.
Câu 3. Tìm nghiệm của phương trình
Ä
7 + 4
√
3
ä
2x+1
= 2 −
√
3.
A. x =
1
4
. B. x = −
3
4
. C. x = −1. D. x = −
1
4
.
Câu 4. Cho hình lập phương ABCD.A
0
B
0
C
0
D
0
có cạnh bằng a. Tính thể tích V của khối chóp
D
0
.ABCD.
A. V =
a
3
4
. B. V =
a
3
6
. C. V =
a
3
3
. D. V = a
3
.
Câu 5. Tìm tập xác định của hàm số y = log
1
2
(x
2
− 3x + 2).
A. (−∞; 1) ∪ (2; +∞). B. (1; 2). C. (2; +∞). D. (−∞; 1).
Câu 6. Nếu
Z
f(x) dx =
x
3
3
+ e
x
+ C thì f (x) bằng
A. f (x) = 3x
2
+ e
x
. B. f (x) =
x
4
3
+ e
x
. C. f (x) = x
2
+ e
x
. D. f (x) =
x
4
12
+ e
x
.
Câu 7. Cho khối chóp S.ABC có SA ⊥ (ABC) và SA = 2, tam giác ABC vuông cân tại A và AB = 1.
Thể tích khối chóp S.ABC bằng
A.
1
6
. B.
1
3
. C. 1. D.
2
3
.
Câu 8. Cho khối nón có đường cao h và bán kính đáy r. Tính thể tích của khối nón.
A. 2πr
√
h
2
+ r
2
. B.
1
3
πr
2
h. C. πr
√
h
2
+ r
2
. D. πr
2
h.
Câu 9. Một mặt cầu có đường kính bằng a có diện tích S bằng bao nhiêu?
A. S =
4πa
2
3
. B. S =
πa
2
3
. C. S = πa
2
. D. S = 4πa
2
.
Câu 10. Cho hàm số y = x
3
+ 3x
2
− 4 có bảng biến thiên sau, tìm a và b.
x
y
0
y
−∞
−2
0
+∞
+
0
−
0
+
aa
00
bb
+∞+∞
A. a = +∞; b = 2. B. a = −∞; b = −4. C. a = −∞; b = 1. D. a = +∞; b = 3.
Câu 11. Với a, b là các số thực dương tùy ý và a khác 1, đặt P = log
a
b
3
+ log
a
2
b
6
. Mệnh đề nào dưới
đây đúng?
A. P = 27 log
a
b . B. P = 15 log
a
b . C. P = 9 log
a
b . D. P = 6 log
a
b .
Câu 12. Cho hình trụ có bán kính đáy bằng 5 và chiều cao bằng 7 . Diện tích xung quanh của hình
trụ đã cho bằng
A.
175π
3
. B. 175π. C. 70π. D. 35π.
Câu 13. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số.
A. 3. B. 0. C. 1. D. 2.
GeoGebraPro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
x
y
0
y
−∞
−2
0 2
+∞
−
0
+
0
−
0
+
Câu 14.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây ?
A. y =
2x − 1
x − 1
. B. y =
x + 1
x − 1
.
C. y = x
4
+ x
2
+ 1. D. y = x
3
− 3x − 1.
x
y
O
1
1
Câu 15. Tìm đường tiệm cận ngang của đồ thị hàm số y =
2 − 2x
x + 1
.
A. y = −2. B. x = −1. C. x = −2. D. y = 2.
Câu 16. Tìm tập nghiệm của bất phương trình
Å
3
4
ã
x−1
>
Å
3
4
ã
−x+3
.
A. (2; +∞). B. (−∞; 2). C. [2; +∞). D. (−∞; 2].
Câu 17.
Cho hàm số bậc bốn y = f (x) có đồ thị như hình vẽ. Số nghiệm của phương
trình 3f(x) − 8 = 0 bằng
A. 1. B. 2. C. 3. D. 4.
x
y
O
1
−1
1
2
−2
2
−2
Câu 18. Nếu
5
Z
1
dx
2x − 1
= ln c với c ∈ Q thì giá trị của c bằng
A. 9. B. 3. C. 6. D. 81.
Câu 19. Số phức liên hợp của z = 4 + 3i là
A. z = −3 + 4i. B. z = 4 − 3i. C. z = 3 + 4i. D. z = 3 − 4i.
Câu 20. Cho hai số phức z
1
= −1 + 2i, z
2
= −1 − 2i. Giá trị của biểu thức |z
1
|
2
+ |z
2
|
2
bằng
A.
√
10. B. 10. C. −6. D. 4.
Câu 21. Điểm M biểu diễn số phức z = 2 − i trên mặt phẳng tọa độ Oxy là
A. M = (1; −2). B. M = (2; −1). C. M = (−2; 1). D. M = (2; 1).
Câu 22. Trong không gian Oxyz, hình chiếu vuông góc của điểm A(2; 3; 4) lên trục Ox là điểm nào
dưới đây?
A. M(2; 0; 0). B. M(0; 3; 0). C. M (0; 0; 4). D. M (0; 2; 3).
Câu 23. Trong không gian Oxyx, cho mặt cầu (S): (x −2)
2
+ (y + 1)
2
+ (z −1)
2
= 9. Tìm tọa độ tâm
I và bán kính R của mặt cầu (S).
A. I(−2; 1; −1), R = 3. B. I(−2; 1; −1), R = 9. C. I(2; −1; 1), R = 3. D. I(2; −1; 1), R = 9.
Câu 24. Trong không gian Oxyz, cho đường thẳng d :
x + 8
4
=
y − 5
−2
=
z
1
. Khi đó véc-tơ chỉ phương
của đường thẳng d có tọa độ là
A. (4; −2; 1). B. (4; 2; −1). C. (4; −2; −1). D. (4; 2; 1).
GeoGebraPro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P ) : 2x − y + z − 1 = 0. Điểm nào
dưới đây thuộc (P )?
A. M(2; −1; 1). B. N (0; 1; −2). C. P (1; −2; 0). D. Q(1; −3; −4).
Câu 26. Cho hình lập phương ABCD.A
0
B
0
C
0
D
0
. Tính góc giữa AC
0
và BD.
A
B
D
0
C
0
B
0
C D
A
0
A. 90
◦
. B. 45
◦
. C. 60
◦
. D. 120
◦
.
Câu 27. Cho hàm số y = f (x) có bảng xét dấu của hàm đạo hàm như sau:
x
f
0
(x)
−∞
−3
2 3 4
+∞
−
0
+
0
+
0
−
0
+
Số điểm cực trị của hàm số đã cho là
A. 6. B. 4. C. 2. D. 3.
Câu 28. Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x) = x+
4
x
trên đoạn [1; 3] bằng
A.
65
3
. B. 20. C. 6. D.
52
3
.
Câu 29. Cho 0 < a 6= 1 và x, y là các số thực âm. mệnh đề nào dưới đây đúng?
A. log
a
(x
2
y
4
) = 2 (log
a
|x| + log
a
y
2
). B. log
a
(xy) = log
a
x + log
a
y.
C. log
a
(−x
2
y) = 2 log
a
(−x) + log
a
y. D. log
a
Å
x
y
ã
=
log
a
(−x)
log
a
(−y)
.
Câu 30. Số giao điểm của đồ thị hàm số y = x
3
+ x + 2 và đường thẳng y = −2x + 1 là
A. 3. B. 0. C. 2. D. 1.
Câu 31. Tập nghiệm của bất phương trình 4
x+1
≤ 8
x−2
là
A. [8; +∞). B. ∅. C. (0; 8). D. (−∞; 8] .
Câu 32. Cho hình lập phương ABCD.A
0
B
0
C
0
D
0
cạnh a. Tính diện tích toàn phần của vật tròn xoay
thu được khi quay tam giác AA
0
C
0
quanh trục AA
0
.
A. π
Ä
√
6 + 2
ä
a
2
. B. π
Ä
√
3 + 2
ä
a
2
. C. 2π
Ä
√
2 + 1
ä
a
2
. D. 2π
Ä
√
6 + 1
ä
a
2
.
Câu 33. Cho tích phân I =
π
2
Z
0
√
2 + cos x · sin x dx. Nếu đặt t = 2 + cos x thì kết quả nào sau đây
đúng?
A. I =
2
Z
3
√
t dt. B. I =
3
Z
2
√
t dt. C. I = 2
2
Z
3
√
t dt. D. I =
π
2
Z
0
√
t dt.
Câu 34. Cho hàm số y = f (x) liên tục trên đoạn [a; b]. Viết công thức tính diện tích hình thang cong
giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b.
A. S =
b
Z
a
f
2
(x) dx. B. S =
b
Z
a
|f(x)| dx. C. S = π
b
Z
a
|f(x)| dx. D. S =
b
Z
a
f(x) dx.
Câu 35. Cho hai số phức z
1
= 3 − 4i và z
2
= −2 + i. Tìm số phức liên hợp của z
1
+ z
2
.
A. 1 + 3i. B. 1 − 3i. C. −1 + 3i. D. −1 − 3i.
Câu 36. Gọi z
1
là nghiệm phức có phần ảo âm của phương trình z
2
+ 2z + 3 = 0. Trên mặt phẳng tọa
độ, điểm nào sau đây là điểm biểu diễn số phức z
1
?
A. P (−1; −
√
2i). B. Q(−1;
√
2i). C. N (−1;
√
2). D. M (−1; −
√
2).
GeoGebraPro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
Câu 37. Trong không gian Oxyz, cho hai đường thẳng d
1
:
x − 1
2
=
y + 1
3
=
z − 3
−5
và d
2
:
x = −1 + t
y = 4 + 3t
z = 1 + t
.
Tìm phương trình mặt phẳng chứa đường thẳng d
1
và song song với đường thẳng d
2
.
A. 18x + 7y + 3z + 20 = 0. B. 18x − 7y + 3z + 34 = 0.
C. 18x + 7y + 3z − 20 = 0. D. 18x − 7y + 3z − 34 = 0.
Câu 38. Trong không gian với hệ tọa độ Oxyz, viết phương trình chính tắc của đường thẳng d đi qua
điểm A(1; 2; 3) và vuông góc với mặt phẳng (P ): 2 x + 2y + z + 2017 = 0.
A.
x + 1
2
=
y + 2
2
=
z + 3
1
. B.
x − 1
2
=
y − 2
2
=
z − 3
1
.
C.
x − 2
1
=
y − 2
2
=
z − 1
3
. D.
x + 2
1
=
y + 2
2
=
z + 1
3
.
Câu 39. Xếp 5 nam và 2 nữ vào một bàn dài gồm 7 chỗ ngồi. Tính xác suất để 2 nữ không ngồi cạnh
nhau.
A.
6
7
. B.
4
7
. C.
5
7
. D.
2
7
.
Câu 40. Cho lăng trụ tam giác đều ABC.A
0
B
0
C
0
có tất cả các cạnh đều bằng a. Khoảng cách giữa hai
đường thẳng BC và AB
0
bằng
A.
a
√
21
7
. B.
a
√
3
2
. C.
a
√
7
4
. D.
a
√
2
2
.
Câu 41. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (−2019; 2020) để hàm số y =
2x
3
− 3(2m + 1)x
2
+ 6m(m + 1)x + 2019 đồng biến trên khoảng (2; +∞)?
A. 2021. B. 2020. C. 2018. D. 2019.
Câu 42. Cường độ một trận động đất M được cho bởi công thức M = log A − log A
0
, với A là biên
độ rung chấn tối đa và A
0
là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San
Francisco có cường độ 8,3 độ Richter. Trong cùng năm đó, trận động đất khác ở gần đó đo được 7,1 độ
Richter. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu lần trận động đất này?
A. 1,17. B. 2,2. C. 15,8. D. 4.
Câu 43.
Cho hàm số y = f(x). Hàm số y = f
0
(x)
có bảng biến thiên như sau. Bất phương trình
f(x) > sin x+m có nghiệm trên khoảng (−1; 1)
khi và chỉ khi
A. m > f (1) − sin 1.
B. m ≥ f (1) − sin 1.
C. m ≤ f (−1) + sin 1.
D. m < f (−1) + sin 1.
x
y
0
y
−∞
−4
1
+∞
−
0
+
0
−
+∞+∞
−3−3
−1−1
−∞−∞
Câu 44. Cho hình trụ có bán kính đáy bằng a. Cắt hình trụ bởi một mặt phẳng (P ) song song với
trục của hình trụ và cách hình trụ một khoảng bằng
a
2
ta được thiết diện là một hình vuông. Tính thể
tích khối trụ.
A. 3πa
3
. B. πa
3
√
3. C.
πa
3
√
3
4
. D. πa
3
.
Câu 45. Cho hàm số f (x) liên tục trên R và f (2) = 16,
2
R
0
f(x) dx = 4. Tính tích phân I =
1
R
0
x ·
f
0
(2x) dx
A. 13. B. 12. C. 20. D. 7.
Câu 46. Cho hàm số y = f (x) = ax
3
+ bx
2
+ cx + d có bảng biến thiên như sau:
Khi đó |f(x)| = m có bốn nghiệm phân biệt x
1
< x
2
< x
3
<
1
2
< x
4
khi và chỉ khi:
GeoGebraPro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
A. 0 < m < 1.
B. 0 < m ≤ 1.
C.
1
2
< m < 1.
D.
1
2
≤ m < 1.
x
y
0
y
−∞
0 1
+∞
+
0
−
0
+
−∞−∞
11
00
+∞+∞
Câu 47. Cho x, y > 0 thỏa mãn log(x + 2y) = log x + log y. Khi đó, giá trị nhỏ nhất của biểu thức
P =
x
2
1 + 2y
+
4y
2
1 + x
là
A. 6. B.
32
5
. C.
31
5
. D.
29
5
.
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số
y =
x
2
+ mx + m
x + 1
trên [1; 2] bằng 2. Số phần tử của S là
A. 1. B. 4. C. 3. D. 2.
Câu 49. Cho hình hộp chữ nhật ABCD.A
0
B
0
C
0
D
0
có thể tích bằng 1 và G là trọng tâm 4BCD
0
. Thể
tích của khối chóp G.ABC
0
là
A. V =
1
3
. B. V =
1
6
. C. V =
1
12
. D. V =
1
18
.
Câu 50. Có bao nhiêu cặp số nguyên (x; y) thỏa mãn 0 ≤ x ≤ 2020 và log
3
(3x + 3) +x = 2y + 9
y
?
A. 2019. B. 6. C. 2020. D. 4.
———————–HẾT———————–
GeoGebraPro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
ĐÁP ÁN THAM KHẢO
1. D 2. D 3. B 4. C 5. A 6. C 7. B 8. B 9. C 10. B
11. D 12. C 13. A 14. B 15. A 16. B 17. B 18. B 19. B 20. B
21. B 22. A 23. C 24. A 25. D 26. A 27. D 28. B 29. A 30. D
31. A 32. A 33. B 34. B 35. A 36. D 37. D 38. B 39. C 40. A
41. B 42. C 43. D 44. B 45. D 46. C 47. B 48. D 49. D 50. D
GeoGebraPro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 2
Câu 1. Một chi đoàn có 16 đoàn viên. Cần bầu chọn một Ban Chấp hành ba người gồm Bí thư, Phó
Bí thư và Ủy viên. Số cách chọn ra Ban Chấp hành nói trên là
A. 560. B. 4096. C. 48. D. 3360.
Lời giải.
Mỗi cách bầu chọn một Ban Chấp hành ba người gồm Bí thư, Phó Bí thư và Ủy viên là một chỉnh hợp
chập 3 của 16 phần tử. Do đó có A
3
16
=
16!
13!
= 3360 cách.
Chọn phương án D
Câu 2. Cho cấp số cộng (u
n
) biết u
3
= 6, u
8
= 16. Tính công sai d và tổng của 10 số hạng đầu tiên.
A. d = 2; S
10
= 100. B. d = 1; S
10
= 80. C. d = 2; S
10
= 120. D. d = 2; S
10
= 110.
Lời giải.
d =
u
8
− u
3
5
=
16 − 6
5
= 2.
u
1
= u
3
− 2d = 6 − 2 · 2 = 2.
S
10
=
10 · (u
1
+ u
10
)
2
=
10 · (u
1
+ u
1
+ 9 · d)
2
=
10 · (2 + 2 + 9 · 2)
2
= 110.
Chọn phương án D
Câu 3. Tìm nghiệm của phương trình
Ä
7 + 4
√
3
ä
2x+1
= 2 −
√
3.
A. x =
1
4
. B. x = −
3
4
. C. x = −1. D. x = −
1
4
.
Lời giải.
Ta có
Ä
7 + 4
√
3
ä
2x+1
= 2 −
√
3 ⇔ 2x + 1 = log
7+4
√
3
Ä
2 −
√
3
ä
⇔ 2x + 1 = −
1
2
⇔ x = −
3
4
.
Chọn phương án B
Câu 4. Cho hình lập phương ABCD.A
0
B
0
C
0
D
0
có cạnh bằng a. Tính thể tích V của khối chóp
D
0
.ABCD.
A. V =
a
3
4
. B. V =
a
3
6
. C. V =
a
3
3
. D. V = a
3
.
Lời giải.
Diện tích đáy ABCD là S
ABCD
= a
2
, chiều cao D
0
D = a.
Do đó V
D
0
.ABCD
=
1
3
S
ABCD
· D
0
D =
1
3
a
2
· a =
a
3
3
.
Chọn phương án C
Câu 5. Tìm tập xác định của hàm số y = log
1
2
(x
2
− 3x + 2).
A. (−∞; 1) ∪ (2; +∞). B. (1; 2). C. (2; +∞). D. (−∞; 1).
Lời giải.
Điều kiện x
2
− 3x + 2 > 0 ⇔
ï
x < 1
x > 2
nên tập xác định của hàm số (−∞; 1) ∪ (2; +∞).
Chọn phương án A
Câu 6. Nếu
Z
f(x) dx =
x
3
3
+ e
x
+ C thì f (x) bằng
A. f (x) = 3x
2
+ e
x
. B. f (x) =
x
4
3
+ e
x
. C. f (x) = x
2
+ e
x
. D. f (x) =
x
4
12
+ e
x
.
Lời giải.
Ta có
Z
f(x) dx =
x
3
3
+ e
x
+ C ⇒ f (x) = x
2
+ e
x
.
Chọn phương án C
GeoGebraPro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Câu 7. Cho khối chóp S.ABC có SA ⊥ (ABC) và SA = 2, tam giác ABC vuông cân tại A và AB = 1.
Thể tích khối chóp S.ABC bằng
A.
1
6
. B.
1
3
. C. 1. D.
2
3
.
Lời giải.
Ta có S
ABC
=
1
2
AB · AC =
1
2
⇒ V
S.ABC
=
1
3
SA · S
ABC
=
1
3
.
A
S
B
C
Chọn phương án B
Câu 8. Cho khối nón có đường cao h và bán kính đáy r. Tính thể tích của khối nón.
A. 2πr
√
h
2
+ r
2
. B.
1
3
πr
2
h. C. πr
√
h
2
+ r
2
. D. πr
2
h.
Lời giải.
Theo công thức thể tích khối nón V =
1
3
πr
2
h.
Chọn phương án B
Câu 9. Một mặt cầu có đường kính bằng a có diện tích S bằng bao nhiêu?
A. S =
4πa
2
3
. B. S =
πa
2
3
. C. S = πa
2
. D. S = 4πa
2
.
Lời giải.
Vì đường kính mặt cầu bằng a nên bán kính mặt cầu là r =
a
2
.
Diện tích mặt cầu là S = 4π
a
2
2
= πa
2
.
Chọn phương án C
Câu 10. Cho hàm số y = x
3
+ 3x
2
− 4 có bảng biến thiên sau, tìm a và b.
x
y
0
y
−∞
−2
0
+∞
+
0
−
0
+
aa
00
bb
+∞+∞
A. a = +∞; b = 2. B. a = −∞; b = −4. C. a = −∞; b = 1. D. a = +∞; b = 3.
Lời giải.
Phương pháp:
Tính giới hạn của hàm số khi x tiến đến −∞ để tìm a và tính giá trị của hàm số tại x = 0 để tìm b.
Cách giải:
lim
x→−∞
y = −∞, y(0) = −4 ⇒ a = −∞; b = −4.
Chọn phương án B
Câu 11. Với a, b là các số thực dương tùy ý và a khác 1, đặt P = log
a
b
3
+ log
a
2
b
6
. Mệnh đề nào dưới
đây đúng?
A. P = 27 log
a
b . B. P = 15 log
a
b . C. P = 9 log
a
b . D. P = 6 log
a
b .
Lời giải.
Ta có P = log
a
b
3
+ log
a
2
b
6
= 3 log
a
b +
6
2
log
a
b = 3 log
a
b + 3 log
a
b = 6 log
a
b.
Chọn phương án D
Câu 12. Cho hình trụ có bán kính đáy bằng 5 và chiều cao bằng 7 . Diện tích xung quanh của hình
trụ đã cho bằng
GeoGebraPro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
A.
175π
3
. B. 175π. C. 70π. D. 35π.
Lời giải.
Ta có S
xq
= 2πrl = 2π · 5 · 7 = 70π .
Chọn phương án C
Câu 13. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số.
A. 3. B. 0. C. 1. D. 2.
x
y
0
y
−∞
−2
0 2
+∞
−
0
+
0
−
0
+
Lời giải.
Dựa vào BBT suy ra hàm số có 3 điểm cực trị.
Chọn phương án A
Câu 14.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây ?
A. y =
2x − 1
x − 1
. B. y =
x + 1
x − 1
.
C. y = x
4
+ x
2
+ 1. D. y = x
3
− 3x − 1.
x
y
O
1
1
Lời giải.
Đồ thị là của hàm số nhất biến có tiệm cân đứng x = 1 và tiệm cận ngang y = 1
nên là hàm số y =
x + 1
x − 1
Chọn phương án B
Câu 15. Tìm đường tiệm cận ngang của đồ thị hàm số y =
2 − 2x
x + 1
.
A. y = −2. B. x = −1. C. x = −2. D. y = 2.
Lời giải.
Ta có: lim
x→±∞
y = lim
x
→ ±∞
2 − 2x
x + 1
= lim
x→±∞
2
x
− 2
1 +
1
x
= −2 ⇒ y = −2 là đường tiệm cận ngang của hàm
số.
Chọn phương án A
Câu 16. Tìm tập nghiệm của bất phương trình
Å
3
4
ã
x−1
>
Å
3
4
ã
−x+3
.
A. (2; +∞). B. (−∞; 2). C. [2; +∞). D. (−∞; 2].
Lời giải.
Å
3
4
ã
x−1
>
Å
3
4
ã
−x+3
⇔ x − 1 < −x + 3 ⇔ x < 2.
Chọn phương án B
Câu 17.
GeoGebraPro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
Cho hàm số bậc bốn y = f(x) có đồ thị như hình vẽ. Số nghiệm của phương
trình 3f(x) − 8 = 0 bằng
A. 1. B. 2. C. 3. D. 4.
x
y
O
1
−1
1
2
−2
2
−2
Lời giải.
Ta có 3f(x) − 8 = 0 ⇔ f (x) =
8
3
.
Dựa vào đồ thị, đường thẳng y =
8
3
cắt đồ thị y = f(x) tại hai điểm phân
biệt. Vậy phương trình đã cho có hai nghiệm phân biệt.
x
y
O
1
−1
1
2
−2
2
−2
8
3
Chọn phương án B
Câu 18. Nếu
5
Z
1
dx
2x − 1
= ln c với c ∈ Q thì giá trị của c bằng
A. 9. B. 3. C. 6. D. 81.
Lời giải.
5
Z
1
dx
2x − 1
=
1
2
ln |2x − 1|
5
1
= ln 3.
Vậy c = 3.
Chọn phương án B
Câu 19. Số phức liên hợp của z = 4 + 3i là
A. z = −3 + 4i. B. z = 4 − 3i. C. z = 3 + 4i. D. z = 3 − 4i.
Lời giải.
Số phức liên hợp của z = 4 + 3i là z = 4 − 3i.
Chọn phương án B
Câu 20. Cho hai số phức z
1
= −1 + 2i, z
2
= −1 − 2i. Giá trị của biểu thức |z
1
|
2
+ |z
2
|
2
bằng
A.
√
10. B. 10. C. −6. D. 4.
Lời giải.
Ta có |z
1
| =
»
(−1)
2
+ 2
2
=
√
5; |z
2
| =
»
(−1)
2
+ (−2)
2
=
√
5.
|z
1
|
2
+ |z
2
|
2
=
Ä
√
5
ä
2
+
Ä
√
5
ä
2
= 10.
Chọn phương án B
Câu 21. Điểm M biểu diễn số phức z = 2 − i trên mặt phẳng tọa độ Oxy là
A. M = (1; −2). B. M = (2; −1). C. M = (−2; 1). D. M = (2; 1).
Lời giải.
Số phức z = 2 − i có điểm biểu diễn là M = (2; −1).
Chọn phương án B
Câu 22. Trong không gian Oxyz, hình chiếu vuông góc của điểm A(2; 3; 4) lên trục Ox là điểm nào
dưới đây?
A. M(2; 0; 0). B. M(0; 3; 0). C. M(0; 0; 4). D. M(0; 2; 3).
Lời giải.
Hình chiếu vuông góc của điểm A(2; 3; 4) là điểm M(2; 0; 0).
Chọn phương án A
GeoGebraPro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 23. Trong không gian Oxyx, cho mặt cầu (S): (x −2)
2
+ (y + 1)
2
+ (z −1)
2
= 9. Tìm tọa độ tâm
I và bán kính R của mặt cầu (S).
A. I(−2; 1; −1), R = 3. B. I(−2; 1; −1), R = 9. C. I(2; −1; 1), R = 3. D. I(2; −1; 1), R = 9.
Lời giải.
Ta có tọa độ tâm I(2; −1; 1) và bán kính R = 3.
Chọn phương án C
Câu 24. Trong không gian Oxyz, cho đường thẳng d :
x + 8
4
=
y − 5
−2
=
z
1
. Khi đó véc-tơ chỉ phương
của đường thẳng d có tọa độ là
A. (4; −2; 1). B. (4; 2; −1). C. (4; −2; −1). D. (4; 2; 1).
Lời giải.
Tọa độ véc-tơ chỉ phương của đường thẳng d là
#»
u = (4; −2; 1).
Chọn phương án A
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P ) : 2x − y + z − 1 = 0. Điểm nào
dưới đây thuộc (P )?
A. M(2; −1; 1). B. N(0; 1; −2). C. P (1; −2; 0). D. Q(1; −3; −4).
Lời giải.
Ta thấy Q ∈ (P ) vì 2.1 − (−3) − 4 − 1 = 0
Chọn phương án D
Câu 26. Cho hình lập phương ABCD.A
0
B
0
C
0
D
0
. Tính góc giữa AC
0
và BD.
A
B
D
0
C
0
B
0
C D
A
0
A. 90
◦
. B. 45
◦
. C. 60
◦
. D. 120
◦
.
Lời giải.
Gọi O
0
và I lần lượt là tâm hình vuông ABCD và trung điểm CC
0
. Khi đó, ta có IO
0
song song AC
0
.
Suy ra (AC
0
, BD) = (IO
0
, BD).
Ta có
ß
BD ⊥ AC
BD ⊥ AA
0
⇒ BD ⊥ (AA
0
C) ⇒ BD ⊥ IO
0
⇒ (IO
0
, BD) = 90
◦
.
Chọn phương án A
Câu 27. Cho hàm số y = f (x) có bảng xét dấu của hàm đạo hàm như sau:
x
f
0
(x)
−∞
−3
2 3 4
+∞
−
0
+
0
+
0
−
0
+
Số điểm cực trị của hàm số đã cho là
A. 6. B. 4. C. 2. D. 3.
Lời giải.
Do f
0
(x) đổi dấu ba lần nên hàm số có ba điểm cực trị.
Chọn phương án D
Câu 28. Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x+
4
x
trên đoạn [1; 3] bằng
A.
65
3
. B. 20. C. 6. D.
52
3
.
Lời giải.
Ta có: f(x) = x +
4
x
xác định và liên tục trên [1; 3]. Khi đó
f
0
(x) = 1 −
4
x
2
; f
0
(x) = 0 ⇔ 1 −
4
x
2
= 0 ⇔
ï
x = 2
x = −2.
GeoGebraPro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
Nhận thấy: −2 /∈ [1; 3] ⇒ x = −2 (loại).
f(1) = 5; f(2) = 4; f(3) =
13
3
. Khi đó: max
[1;3]
f(x) = 5; m = min
[1;3]
f(x) = 4. Vậy M.m = 20.
Chọn phương án B
Câu 29. Cho 0 < a 6= 1 và x, y là các số thực âm. mệnh đề nào dưới đây đúng?
A. log
a
(x
2
y
4
) = 2 (log
a
|x| + log
a
y
2
). B. log
a
(xy) = log
a
x + log
a
y.
C. log
a
(−x
2
y) = 2 log
a
(−x) + log
a
y. D. log
a
Å
x
y
ã
=
log
a
(−x)
log
a
(−y)
.
Lời giải.
Ta có, log
a
(x
2
y
4
) = log
a
x
2
+ log
a
y
4
= 2 log
a
|x| + 2 log
a
y
2
= 2 (log
a
|x| + log
a
y
2
).
Chọn phương án A
Câu 30. Số giao điểm của đồ thị hàm số y = x
3
+ x + 2 và đường thẳng y = −2x + 1 là
A. 3. B. 0. C. 2. D. 1.
Lời giải.
Xét phương trình hoành độ giao điểm x
3
+ x + 2 = −2x + 1 ⇔ x
3
+ 3x + 1 = 0.
Xét f(x) = x
3
+ 3x + 1, ta có f
0
(x) = 3x
2
+ 3 > 0. Suy ra bảng biến thiên
x
f
0
(x)
f(x)
−∞ +∞
+
−∞−∞
+∞+∞
Do đó phương trình f(x) = 0 có 1 nghiệm.
Chọn phương án D
Câu 31. Tập nghiệm của bất phương trình 4
x+1
≤ 8
x−2
là
A. [8; +∞). B. ∅. C. (0; 8). D. (−∞; 8] .
Lời giải.
Ta có: 4
x+1
≤ 8
x−2
⇔ 2
2x+2
≤ 2
3x−6
⇔ 2x + 2 ≤ 3x − 6 ⇔ 8 ≤ x
Vậy tập nghiệm của bất phương trình là [8; +∞).
Chọn phương án A
Câu 32. Cho hình lập phương ABCD.A
0
B
0
C
0
D
0
cạnh a. Tính diện tích toàn phần của vật tròn xoay
thu được khi quay tam giác AA
0
C
0
quanh trục AA
0
.
A. π
Ä
√
6 + 2
ä
a
2
. B. π
Ä
√
3 + 2
ä
a
2
. C. 2π
Ä
√
2 + 1
ä
a
2
. D. 2π
Ä
√
6 + 1
ä
a
2
.
Lời giải.
Khi quay tam giác AA
0
C
0
quanh trục AA
0
ta được hình nón có bán kính đáy
R = A
0
C
0
= a
√
2, đường sinh l = AC
0
và chiều cao h = AA
0
= a.
Ta có l = AC
0
=
√
A
0
C
02
+ AA
02
=
√
2a
2
+ a
2
= a
√
3.
Ta có
S
tp
= πRl + πR
2
= π(
√
6 + 2)a
2
.
C
0
A
0
A
Chọn phương án A
Câu 33. Cho tích phân I =
π
2
Z
0
√
2 + cos x · sin x dx. Nếu đặt t = 2 + cos x thì kết quả nào sau đây
đúng?
A. I =
2
Z
3
√
t dt. B. I =
3
Z
2
√
t dt. C. I = 2
2
Z
3
√
t dt. D. I =
π
2
Z
0
√
t dt.
GeoGebraPro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Lời giải.
Đặt t = 2 + cos x ⇒ dt = −sin x dx ⇒ sin x dx = −dt.
Đổi cận
x = 0 ⇒ t = 3
x =
π
2
⇒ t = 2.
Vậy tích phân đã cho trở thành
I =
2
Z
3
√
t(−dt) =
3
Z
2
√
t dt.
Chọn phương án B
Câu 34. Cho hàm số y = f (x) liên tục trên đoạn [a; b]. Viết công thức tính diện tích hình thang cong
giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b.
A. S =
b
Z
a
f
2
(x) dx. B. S =
b
Z
a
|f(x)| dx. C. S = π
b
Z
a
|f(x)| dx. D. S =
b
Z
a
f(x) dx.
Lời giải.
Diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a,
x = b là S =
b
Z
a
|f(x)| dx.
Chọn phương án B
Câu 35. Cho hai số phức z
1
= 3 − 4i và z
2
= −2 + i. Tìm số phức liên hợp của z
1
+ z
2
.
A. 1 + 3i. B. 1 − 3i. C. −1 + 3i. D. −1 − 3i.
Lời giải.
Ta có z
1
+ z
2
= (3 − 4i) + (−2 + i) = 1 − 3i ⇒ z
1
+ z
2
= 1 + 3i.
Chọn phương án A
Câu 36. Gọi z
1
là nghiệm phức có phần ảo âm của phương trình z
2
+ 2z + 3 = 0. Trên mặt phẳng tọa
độ, điểm nào sau đây là điểm biểu diễn số phức z
1
?
A. P (−1; −
√
2i). B. Q(−1;
√
2i). C. N(−1;
√
2). D. M(−1; −
√
2).
Lời giải.
Ta có z
2
+ 2z + 3 = 0 ⇔
ñ
z = −1 +
√
2i
z = −1 −
√
2i
. Vì z
1
có phần ảo âm nên z
1
= −1 −
√
2i.
Vậy điểm biểu diễn số phức z
1
là điểm M(−1; −
√
2).
Chọn phương án D
Câu 37. Trong không gian Oxyz, cho hai đường thẳng d
1
:
x − 1
2
=
y + 1
3
=
z − 3
−5
và d
2
:
x = −1 + t
y = 4 + 3t
z = 1 + t
.
Tìm phương trình mặt phẳng chứa đường thẳng d
1
và song song với đường thẳng d
2
.
A. 18x + 7y + 3z + 20 = 0. B. 18x − 7y + 3z + 34 = 0.
C. 18x + 7y + 3z − 20 = 0. D. 18x − 7y + 3z − 34 = 0.
Lời giải.
Đường thẳng d
1
qua M(1; −1; 3) và nhận
#»
u
1
= (2; 3; −5) làm véc-tơ chỉ phương; d
2
có véc-tơ chỉ phương
#»
u
2
= (1; 3; 1).
Mặt phẳng (P ) chứa d
1
và song song d
2
nên nhận véc-tơ
#»
n = [
#»
u
1
,
#»
u
2
] = (18; −7; 3) làm véc-tơ pháp
tuyến.
Vậy phương trình tổng quát của (P ) là
18(x − 1) − 7(y + 1) + 3(z − 3) = 0
⇔ 18x − 7y + 3z − 34 = 0.
Chọn phương án D
GeoGebraPro Trang 7
https://www.facebook.com/groups/GeoGebraPro/
Câu 38. Trong không gian với hệ tọa độ Oxyz, viết phương trình chính tắc của đường thẳng d đi qua
điểm A(1; 2; 3) và vuông góc với mặt phẳng (P ): 2x + 2y + z + 2017 = 0.
A.
x + 1
2
=
y + 2
2
=
z + 3
1
. B.
x − 1
2
=
y − 2
2
=
z − 3
1
.
C.
x − 2
1
=
y − 2
2
=
z − 1
3
. D.
x + 2
1
=
y + 2
2
=
z + 1
3
.
Lời giải.
d vuông góc với (P ) nên d có véc-tơ chỉ phương là
#»
n
P
= (2; 2; 1).
Do đó, phương trình chính tắc đường thẳng d là
x − 1
2
=
y − 2
2
=
z − 3
1
.
Chọn phương án B
Câu 39. Xếp 5 nam và 2 nữ vào một bàn dài gồm 7 chỗ ngồi. Tính xác suất để 2 nữ không ngồi cạnh
nhau.
A.
6
7
. B.
4
7
. C.
5
7
. D.
2
7
.
Lời giải.
Xếp hai nữ cạnh nhau có 2 cách.
Xếp 5 nam và nhóm nữ có 6! cách.
Xếp 5 nam và 2 nữ sao cho 2 nữ cạnh nhau có 2 · 6! cách.
Xác suất để xếp 5 nam và 2 nữ sao cho 2 nữ cạnh nhau là
2 · 6!
7!
=
2
7
.
Vậy xác suất cần tìm là 1 −
2
7
=
5
7
.
Chọn phương án C
Câu 40. Cho lăng trụ tam giác đều ABC.A
0
B
0
C
0
có tất cả các cạnh đều bằng a. Khoảng cách giữa hai
đường thẳng BC và AB
0
bằng
A.
a
√
21
7
. B.
a
√
3
2
. C.
a
√
7
4
. D.
a
√
2
2
.
Lời giải.
Ta có BCkB
0
C
0
⇒ BCk(AB
0
C
0
).
Suy ra:
d(BC, AB
0
) = d(BC, (AB
0
C
0
)) = d(B, (AB
0
C
0
)) =
d(A
0
, (AB
0
C
0
)).
Gọi I và H lần lượt là hình chiếu vuông góc
của A
0
trên B
0
C
0
và AI.
Ta có: B
0
C
0
⊥A
0
I và B
0
C
0
⊥A
0
A
nên B
0
C
0
⊥(A
0
AI) ⇒ B
0
C
0
⊥A
0
H.
Mà AI⊥A
0
H. Do đó (AB
0
C
0
) ⊥A
0
H.
A
B
C
A
0
B
0
C
0
I
H
Khi đó: d (A
0
, (AB
0
C
0
)) = A
0
H =
A
0
A.A
0
I
√
A
0
A
2
+ A
0
I
2
=
a.
a
√
3
2
s
a
2
+
Ç
a
√
3
2
å
2
=
a
√
21
7
.
Vậy khoảng cách cần tìm là
a
√
21
7
.
Chọn phương án A
Câu 41. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (−2019; 2020) để hàm số y =
2x
3
− 3(2m + 1)x
2
+ 6m(m + 1)x + 2019 đồng biến trên khoảng (2; +∞)?
A. 2021. B. 2020. C. 2018. D. 2019.
Lời giải.
Ta có y
0
= 6x
2
− 6(2m + 1)x + 6m
2
+ 6m.
Xét y
0
= 0 ⇔ x
2
−(2m + 1)x + m
2
+ m = 0, có ∆ = (2m + 1)
2
−4 (m
2
+ m) = 1 > 0, ∀m ∈ R. Suy ra
GeoGebraPro Trang 8
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
phương trình y
0
= 0 luôn có hai nghiệm phân biệt: x
1
= m; x
2
= m + 1. Dễ thấy x
1
< x
2
.
Bảng biến thiên
x
y
0
y
−∞
m
m + 1
+∞
+
0
−
0
+
−∞−∞
y(m)y(m)
y(m + 1)y(m + 1)
+∞+∞
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên mỗi khoảng (−∞; m); (m + 1; +∞). Vì thế,
hàm số đồng biến trên (2 : +∞) khi m + 1 ≤ 2 ⇔ m ≤ 1.
Suy ra có 2020 giá trị nguyên của m thỏa mãn yêu cầu đề bài.
Chọn phương án B
Câu 42. Cường độ một trận động đất M được cho bởi công thức M = log A − log A
0
, với A là biên
độ rung chấn tối đa và A
0
là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San
Francisco có cường độ 8,3 độ Richter. Trong cùng năm đó, trận động đất khác ở gần đó đo được 7,1 độ
Richter. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu lần trận động đất này?
A. 1,17. B. 2,2. C. 15,8. D. 4.
Lời giải.
Gọi M
1
, A
1
lần lượt là cường độ, biên độ rung chấn tối đa của trận động đất tại San Francisco.
Gọi M
2
, A
2
lần lượt là cường độ, biên độ rung chấn tối đa của trận động đất tại địa điểm còn lại.
Ta có
M
1
= log A
1
− log A
0
= log
A
1
A
0
⇒
A
1
A
0
= 10
M
1
.
M
2
= log A
2
− log A
0
= log
A
2
A
0
⇒
A
2
A
0
= 10
M
2
.
Khi đó
A
1
A
2
=
10
M
1
10
M
2
= 10
M
1
−M
2
= 10
1,2
≈ 15,8.
Chọn phương án C
Câu 43.
Cho hàm số y = f(x). Hàm số y = f
0
(x)
có bảng biến thiên như sau. Bất phương trình
f(x) > sin x+m có nghiệm trên khoảng (−1; 1)
khi và chỉ khi
A. m > f(1) − sin 1.
B. m ≥ f (1) − sin 1.
C. m ≤ f (−1) + sin 1.
D. m < f (−1) + sin 1.
x
y
0
y
−∞
−4
1
+∞
−
0
+
0
−
+∞+∞
−3−3
−1−1
−∞−∞
Lời giải.
Xét hàm số g(x) = f(x) − sin x.
g
0
(x) = f
0
(x) − cos x.
Với ∀x ∈ (−1; 1), ta có f
0
(x) < −1 ⇒ f
0
(x) − cos x < −1 − cos x < 0 ⇒ g
0
(x) < 0.
Suy ra hàm số g(x) nghịch biến trên khoảng (−1; 1) nên g(x) < g (−1) = f (−1) + sin 1.
Do đó bất phương trình f(x) > sin x + m có nghiệm trên khoảng (−1; 1) khi và chỉ khi bất phương
trình m < f(x) − sin x có nghiệm trên khoảng (−1; 1).
⇔ m < max
[−1;1]
g(x) ⇔ m < f (−1) + sin 1.
Vậy m < f (−1) + sin 1.
Chọn phương án D
Câu 44. Cho hình trụ có bán kính đáy bằng a. Cắt hình trụ bởi một mặt phẳng (P ) song song với
trục của hình trụ và cách hình trụ một khoảng bằng
a
2
ta được thiết diện là một hình vuông. Tính thể
tích khối trụ.
GeoGebraPro Trang 9
https://www.facebook.com/groups/GeoGebraPro/
A. 3πa
3
. B. πa
3
√
3. C.
πa
3
√
3
4
. D. πa
3
.
Lời giải.
Giả sử ABCD là thiết diện hình vuông như hình bên.
Gọi O và O
0
là tâm 2 đáy của hình trụ,
H là hình chiếu của O lên AB.
Ta có AB = 2AH = 2
√
OA
2
− OH
2
= 2
…
a
2
−
a
2
2
= a
√
3.
Vì ABCD là hình vuông nên chiều cao của hình trụ bằng a
√
3.
Vậy V
trụ
= πa
.
a
√
3 = πa
3
√
3.
B
H
D
C
O
0
O
A
Chọn phương án B
Câu 45. Cho hàm số f (x) liên tục trên R và f(2) = 16,
2
R
0
f(x) dx = 4. Tính tích phân I =
1
R
0
x ·
f
0
(2x) dx
A. 13. B. 12. C. 20. D. 7.
Lời giải.
Phương pháp: Sử dụng công thức từng phần:
b
Z
a
u dv = uv|
b
a
−
b
Z
a
v du.
Cách giải:
I =
2
Z
0
x · f
0
(2x) dx =
1
2
1
Z
0
x d (f(2x))
=
1
2
x · f (2x)|
1
0
−
1
2
1
Z
0
f(2x) dx
=
1
2
f(2) −
1
4
1
Z
0
f(2x) d(2x)
đặt t=2x
=
1
2
f(2) −
1
4
2
Z
0
f(t) dt
=
1
2
f(2) −
1
4
2
Z
0
f(x) dx =
1
2
· 16 −
1
4
· 4 = 8 − 1 = 7.
Chọn phương án D
Câu 46. Cho hàm số y = f (x) = ax
3
+ bx
2
+ cx + d có bảng biến thiên như sau:
Khi đó |f(x)| = m có bốn nghiệm phân biệt x
1
< x
2
< x
3
<
1
2
< x
4
khi và chỉ khi:
A. 0 < m < 1.
B. 0 < m ≤ 1.
C.
1
2
< m < 1.
D.
1
2
≤ m < 1.
x
y
0
y
−∞
0 1
+∞
+
0
−
0
+
−∞−∞
11
00
+∞+∞
Lời giải.
GeoGebraPro Trang 10
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Ta có y
0
= 3ax
2
+ 2bx + c, từ bảng biến thiên suy ra:
ß
y
0
(0) = 0
y
0
(1) = 0
⇔
ß
c = 0
3a + 2b = 0
(1)
Ta lại có
ß
y(0) = 1
y(1) = 0
⇔
ß
d = 1
a + b + c + d = 0
(2)
Từ (1), (2) ta có hệ phương trình:
d = 1
c = 0
3a + 2b = 0
a + b + c + d = 0
⇔
d = 1
c = 0
a = 2
b = −3
⇒ y = f(x) = 2x
3
− 3x
2
+ 1
Đồ thị hàm số |f(x)| = |2x
3
− 3x
2
+ 1|
Ta có
f
Å
1
2
ã
=
1
2
Dựa vào đồ thị suy ra phương trình |f(x)| = m có bốn nghiệm phân biệt x
1
< x
2
< x
3
<
1
2
< x
4
khi
và chỉ khi:
1
2
< m < 1
Chọn phương án C
Câu 47. Cho x, y > 0 thỏa mãn log(x + 2y) = log x + log y. Khi đó, giá trị nhỏ nhất của biểu thức
P =
x
2
1 + 2y
+
4y
2
1 + x
là
A. 6. B.
32
5
. C.
31
5
. D.
29
5
.
Lời giải.
Ta có log(x + 2y) = log xy ⇔ x + 2y = xy.
Đặt 2y = z, ta có x, z > 0 thỏa mãn 2(x + z) = xz ≤
x + z
2
2
⇒ x + z ≥ 8. Lại có
P =
x
2
1 + z
+
z
2
1 + x
≥
(x + z)
2
2 + x + z
= x + z − 2 +
4
2 + x + z
.
Xét f(t) = t − 2 +
4
2 + t
, f
0
(t) = 1 −
4
(t + 2)
2
> 0, ∀t ≥ 8 nên min
t≥8
f(t) = f(8) =
32
5
.
Vậy giá trị nhỏ nhất của P là
32
5
khi x = z = 4 hay (x; y) = (4; 2).
Chọn phương án B
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số
y =
x
2
+ mx + m
x + 1
trên [1; 2] bằng 2. Số phần tử của S là
A. 1. B. 4. C. 3. D. 2.
Lời giải.
Xét hàm số f(x) =
x
2
+ mx + m
x + 1
trên [1; 2].
Ta có f(x) liên tục trên [1; 2] và f
0
(x) =
x
2
+ 2x
(x + 1)
2
> 0, ∀x ∈ [1; 2] . Suy ra f(x) đồng biến trên [1; 2]. Do
đó max
[1;2]
f(x) = f(2) =
3m + 4
3
, min
[1;2]
f(x) = f(1) =
2m + 1
2
.
Trường hợp 1:
2m + 1
2
≥ 0 ⇔ m ≥ −
1
2
.
Trong trường hợp này ta có max
[1;2]
|f(x)| =
3m + 4
3
.
Theo yêu cầu bài toán ta có
3m + 4
3
= 2 ⇔ m =
2
3
(thỏa mãn).
Trường hợp 2:
3m + 4
3
≤ 0 ⇔ m ≤ −
4
3
.
Trong trường hợp này ta có max
[1;2]
|f(x)| =
−2m − 1
2
.
GeoGebraPro Trang 11
https://www.facebook.com/groups/GeoGebraPro/
Theo yêu cầu bài toán ta có
−2m − 1
2
= 2 ⇔ m = −
5
2
(thỏa mãn).
Trường hợp 3:
2m + 1
2
< 0 <
3m + 4
3
⇔ −
4
3
< m < −
1
2
.
+) Nếu
−2m − 1
2
≤
3m + 4
3
⇔ −
11
12
≤ m < −
1
2
thì max
[1;2]
|f(x)| =
3m + 4
3
.
Theo yêu cầu bài toán ta có
3m + 4
3
= 2 ⇔ m =
2
3
(không thỏa mãn).
+) Nếu
−2m − 1
2
≥
3m + 4
3
⇔ −
11
12
≥ m > −
4
3
thì max
[1;2]
|f(x)| =
−2m − 1
2
.
Theo yêu cầu bài toán ta có
−2m − 1
2
= 2 ⇔ m = −
5
2
(không thỏa mãn).
Vậy S =
ß
2
3
; −
5
2
™
⇒ |S| = 2.
Chọn phương án D
Câu 49. Cho hình hộp chữ nhật ABCD.A
0
B
0
C
0
D
0
có thể tích bằng 1 và G là trọng tâm 4BCD
0
. Thể
tích của khối chóp G.ABC
0
là
A. V =
1
3
. B. V =
1
6
. C. V =
1
12
. D. V =
1
18
.
Lời giải.
Ta thấy V
ABCD D
0
C
0
= V
G.ABC
0
D
0
+ V
G.ABCD
+
V
G.CC
0
D
0
D
+ V
G.ADD
0
+ V
G.BCC
0
.
Vì G là trọng tâm tam giác BD
0
C nên ta có
IG
ID
=
JG
JB
=
CG
CA
0
=
1
3
.
Do vậy ta được
V
G.ABCD
=
1
3
V
D
0
.ABCD
=
1
9
V
G.CC
0
D
0
D
=
1
3
V
B.CC
0
D
0
D
=
1
9
V
G.ACC
0
=
1
3
V
D
0
.ACC
0
=
1
18
V
G.ADD
0
=
2
3
V
C.ADD
0
=
1
9
.
C
D
C
0
D
0
I
J
A
B
A
0
B
0
G
K
Ta được V
G.ABC
0
D
0
= V
ABCDC
0
D
0
− [V
G.ABCD
+ V
G.CC
0
D
0
D
+ V
G.BCC
0
+ V
G.ADD
0
] =
1
2
−
7
18
=
1
9
.
Ta có V
G.ABC
0
=
1
2
V
G.ABC
0
D
0
=
1
18
.
Chọn phương án D
Câu 50. Có bao nhiêu cặp số nguyên (x; y) thỏa mãn 0 ≤ x ≤ 2020 và log
3
(3x + 3) +x = 2y + 9
y
?
A. 2019. B. 6. C. 2020. D. 4.
Lời giải.
Điều kiện: x > 1.
Ta có log
3
(3x + 3) + x = 2y + 9
y
⇔ log
3
(x + 1) + (x + 1) = 2y + 3
2y
(*)
Xét hàm số f (t) = t + 3
t
, ∀t ∈ R có f
0
(t) = 1 + 3
t
ln 3 > 0, forallt ∈ R tức hàm số luôn đồng biến trên
mathbbR.
Khi đó (∗) ⇔ f (log
3
(x + 1)) = f(2y) ⇔ log
3
(x + 1) = 2y ⇔ x + 1 = 2y ⇔ x = 9
y
− 1.
Vì 0 ≤ x ≤ 2020 nên 0 ≤ 9
y
− 1 ≤ 2020 ⇔ 0 ≤ y ≤ log
9
2021.
Do y nguyên nên y ∈ {{0; 1; 2; 3}}.
⇒ (x; y) ∈ {(0; 0); (8; 1); (80; 2); (728; 3)} nên tổng cộng có 4 cặp (x; y) thỏa đề bài.
Chọn phương án D
———————–HẾT———————–
GeoGebraPro Trang 12
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
ĐÁP ÁN THAM KHẢO
1. D 2. D 3. B 4. C 5. A 6. C 7. B 8. B 9. C 10. B
11. D 12. C 13. A 14. B 15. A 16. B 17. B 18. B 19. B 20. B
21. B 22. A 23. C 24. A 25. D 26. A 27. D 28. B 29. A 30. D
31. A 32. A 33. B 34. B 35. A 36. D 37. D 38. B 39. C 40. A
41. B 42. C 43. D 44. B 45. D 46. C 47. B 48. D 49. D 50. D
GeoGebraPro Trang 13
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 3
Câu 1. Lớp 11A có 25 học sinh nam và 20 học sinh nữ. Hỏi có bao nhiêu cách chọn một học sinh làm
lớp trưởng?
A. 25! + 20! cách. B. 45! cách. C. 45 cách. D. 500 cách.
Câu 2. Cho cấp số cộng có u
1
= 0 và công sai d = 3. Tổng của 26 số hạng đầu tiên của cấp số cộng đó
bằng bao nhiêu?
A. 975. B. 775. C. 875. D. 675.
Câu 3. Tập nghiệm của phương trình 2
x
2
−3x
=
1
4
là
A. S = ∅. B. S = {1; 2}. C. S = {0}. D. S = {1}.
Câu 4. Hình lập phương có đường chéo của mặt bên bằng 4 cm. Tính thể tích khối lập phương đó.
A. 8
√
2 cm
3
. B. 16
√
2 cm
3
. C. 8 cm
3
. D. 2
√
2 cm
3
.
Câu 5. Tập xác định của hàm số y = (x
2
− 3x + 2)
π
là
A. R\{1; 2}. B. (−∞; 1) ∪ (2; +∞). C. (1; 2). D. (−∞; 1] ∪ [2; +∞).
Câu 6. Tìm họ nguyên hàm F (x) của hàm số f(x) =
1
5x + 4
.
A. F (x) =
1
ln 5
ln |5x + 4| + C. B. F (x) = ln |5x + 4| + C.
C. F (x) =
1
5
ln |5x + 4| + C. D. F (x) =
1
5
ln(5x + 4) + C.
Câu 7. Cho khối chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, đường
cao SO. Biết SO =
a
√
2
2
, thể tích khối chóp S.ABCD bằng
A.
a
3
√
2
6
. B.
a
3
√
2
3
. C.
a
3
√
2
2
. D.
a
3
√
3
4
.
Câu 8. Cho khối nón tròn xoay có chiều cao h, đường sinh l và bán kính đường tròn đáy bằng R .
Diện tích toàn phần của khối nón là
A. S
tp
= πR(l + R). B. S
tp
= πR(l + 2R). C. S
tp
= 2πR(l + R). D. S
tp
= πR(2l + R).
Câu 9. Cho hàm số y = f (x) có bảng biến thiên như sau:
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
00
5
2
5
2
00
+∞+∞
Hàm số y = f (x) nghịch biến trên khoảng nào sau đây?
A. (0; +∞). B. (−∞; 0). C. (−1; 0). D. (−∞; −2).
Câu 10. Cho các số thực dương a, b thỏa mãn log a = x, log b = y. Tính P = log (a
2
b
3
)
A. P = 6xy. B. p = x
2
y
3
. C. P = x
2
+ y
3
. D. P = 2x + 3y.
Câu 11. Một hình trụ có diện tích xung quanh bằng S, diện tích đáy bằng diện tích một mặt cầu bán
kính a. Khi đó thể tích của hình trụ bằng
A. Sa. B.
1
2
Sa. C.
1
3
Sa. D.
1
4
Sa.
Biên soạn: Ths Nguyễn Chín Em Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Câu 12.
Cho hàm số y = f (x) có bảng biến thiên
dưới đây. Khẳng định nào sau đây là khẳng
định đúng?
A. Hàm số đạt cực đại tại x = 2.
B. Hàm số đạt cực đại tại x = −2.
C. Hàm số đạt cực đại tại x = 4.
D. Hàm số đạt cực đại tại x = 3.
x
y
0
y
−∞
2 4
+∞
+
0
−
0
+
−∞−∞
33
−2−2
+∞+∞
Câu 13.
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
A. y = −x
4
+ 3x
2
− 2. B. y = −x
4
+ 2x
2
− 1.
C. y = −x
4
+ x
2
− 1. D. y = −x
4
+ 3x
2
− 3.
x
−1
1
−1
y
O
Câu 14. Đồ thị hàm số y =
4x + 4
x
2
+ 2x + 1
có tất cả bao nhiêu đường tiệm cận?
A. 2. B. 0. C. 1. D. 3.
Câu 15. Tập nghiệm của bất phương trình
Å
1
2
ã
x
< 8 là.
A. S = (−∞; −3). B. S =
Å
−∞;
1
3
ã
. C. S = (−3; +∞). D. S =
Å
1
3
; +∞
ã
.
Câu 16. Cho hàm số y = f (x) liên tục trên R và có bảng biến thiên như sau
x
y
0
y
−∞
−1
1
+∞
+
0
−
0
+
−∞−∞
44
00
+∞+∞
Số nghiệm của phương trình 2f(x) + 3 = 0 là
A. 1. B. 2. C. 0. D. 3.
Câu 17. Nếu
5
Z
1
dx
2x − 1
= ln c với c ∈ Q thì giá trị của c bằng
A. 9. B. 3. C. 6. D. 81.
Câu 18. Phần thực và phần ảo của số phức z = 1 + 2i lần lượt là
A. 1 và 2. B. 1 và i. C. 1 và 2i. D. 2 và 1.
Câu 19. Cho hai số phức z
1
= 1 − 2i và z
2
= 3 + 4i. Tìm điểm M biểu diễn số phức z
1
.z
2
trên mặt
phẳng tọa độ.
A. M(−2; 11). B. M(−2; −11). C. M(11; −2). D. M(11; 2).
Câu 20. Cho số phức z = 4 − 3i có điểm biểu diễn trên mặt phẳng tọa độ Oxy là M . Tính độ dài
OM.
A. 5. B. 25. C.
√
7. D. 4.
Câu 21. Trong không gian tọa độ Oxyz, tọa độ điểm G
0
đối xứng với điểm G(5; −3; 7) qua trục Oy là
A. G
0
(−5; 0; −7). B. G
0
(−5; −3; −7). C. G
0
(5; 3; 7). D. G
0
(−5; 3; −7).
Câu 22. Trong không gian Oxyz, cho hai điểm A(−2; 1; 1), B(0; −1; 1). Phương trình mặt cầu đường
kính AB là
A. (x + 1)
2
+ y
2
+ (z − 1)
2
= 8. B. (x + 1)
2
+ y
2
+ (z − 1)
2
= 2.
C. (x + 1)
2
+ y
2
+ (z + 1)
2
= 8. D. (x − 1)
2
+ y
2
+ (z − 1)
2
= 2.
Biên soạn: Ths Nguyễn Chín Em Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 23. Trong không gian Oxyz, cho tam giác đều ABC với A(6; 3; 5) và đường thẳng BC có phương
trình tham số
x = 1 − t
y = 2 + t
z = 2t
. Gọi ∆ là đường thẳng đi qua trọng tâm G của tam giác ABC và vuông góc
với mặt phẳng (ABC). Điểm nào dưới đây thuộc đường thẳng ∆?
A. M(−1; −12; 3). B. N(3; −2; 1). C. P (0; −7; 3). D. Q(1; −2; 5).
Câu 24. Trong không gian Oxyz, cho hai điểm A(1; −1; 0), B(0; 1; 1). Gọi (α) là mặt phẳng chứa đường
thẳng d :
x
2
=
y − 1
−1
=
z − 2
1
và song song với đường thẳng AB. Điểm nào dưới đây thuộc mặt phẳng
(α)?
A. M(6; −4; −1). B. N(6; −4; 2). C. P (6; −4; 3). D. Q = (6; −4; 1).
Câu 25. Cho tứ diện đều cạnh a, M là trunng điểm của BC. Tính cosin của góc giữa hai đường thẳng
AB và DM.
A.
√
3
2
. B.
√
3
6
. C.
√
3
3
. D.
1
2
.
Câu 26. Cho hàm số y = f (x) liên tục trên R và có bảng xét dấu của đạo hàm như sau:
x
f
0
(x)
−∞
−1
0 2 4
+∞
+
0
− +
0
−
0
+
Hàm số đã cho có bao nhiêu cực trị?
A. 3. B. 2. C. 1. D. 4.
Câu 27. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = −x
3
+3x+1 trên đoạn [0; 2] bằng
A. 2. B. 3. C. 1. D. 4.
Câu 28. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y =
√
2 − x
2
− x bằng
A. 2 +
√
2. B. 2. C. 1. D. 2 −
√
2.
Câu 29. Với a là số thực âm bất kỳ, mệnh đề nào dưới đây đúng?
A. log
2
a
2
= 2 log
2
(−a). B. log
2
a
2
= −2 log
2
a. C. log
2
a
2
= 2 log
2
a. D. log
2
a
2
= 2a.
Câu 30. Số giao điểm của đồ thị hàm số y = x
3
+ x + 2 và đường thẳng y = −2x + 1 là
A. 3. B. 0. C. 2. D. 1.
Câu 31. Tập nghiệm của bất phương trình
Å
1
1 + a
2
ã
2x+1
> 1 (với a là tham số, a 6= 0) là
A.
Å
−∞; −
1
2
ã
. B. (−∞; 0). C.
Å
−
1
2
; +∞
ã
. D. (0; +∞).
Câu 32.
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ)
quanh trục DF .
A.
10π
7
a
3
. B.
π
3
a
3
.
C.
5π
2
a
3
. D.
10π
9
a
3
.
B
F
C
D
A
E
a
a
a
30
◦
Câu 33. Cho tích phân I =
e
Z
1
√
1 + ln x
x
dx. Đổi biến t =
√
1 + ln x ta được kết quả nào sau đây?
Biên soạn: Ths Nguyễn Chín Em Trang 3
https://www.facebook.com/groups/GeoGebraPro/
A. I =
√
2
Z
1
t
2
dt. B. I = 2
√
2
Z
1
t
2
dt. C. I = 2
2
Z
1
t
2
dt. D. I = 2
√
2
Z
1
t dt.
Câu 34.
Gọi S là diện tích hình phẳng được tô đậm trong hình vẽ bên. Công
thức tính S là
A. S =
1
Z
−1
f(x) dx +
2
Z
1
f(x) dx. B. S =
1
Z
−1
f(x) dx −
2
Z
1
f(x) dx.
C. S =
2
Z
−1
f(x) dx. D. S = −
2
Z
−1
f(x) dx.
x
y
O
−1 1 2
y = f (x)
Câu 35. Cho hai số phức z
1
= m+3i, z
2
= 2−(m+1)i, với m ∈ R. Tìm các giá trị của m để w = z
1
·z
2
là số thực.
A. m = 1 hoặc m = −2. B. m = 2 hoặc m = −1.
C. m = 2 hoặc m = −3. D. m = −2 hoặc m = −3.
Câu 36. Phương trình bậc hai nào dưới đây nhận hai số phức 2 − 3i và 2 + 3i làm nghiệm ?
A. z
2
+ 4z + 13 = 0. B. z
2
+ 4z + 3 = 0. C. z
2
− 4z + 13 = 0. D. z
2
− 4z + 3 = 0.
Câu 37. Trong không gian Oxyz cho mặt phẳng (P ): 3x −4y + 5z −6 = 0 và đường thẳng d :
x − 1
2
=
y − 2
3
=
z − 3
1
. Gọi ϕ là góc giữa đường thẳng d và mặt phẳng (P ). Tìm khẳng định đúng.
A. sin ϕ =
1
5
√
28
. B. cos ϕ = −
1
5
√
28
. C. cos ϕ =
1
5
√
28
. D. sin ϕ = −
1
5
√
28
.
Câu 38. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1; −2; −3), B(−1; 4; 1) và đường
thẳng d :
x + 2
1
=
y − 2
−1
=
z + 3
2
. Phương trình nào dưới đây là phương trình của đường thẳng đi qua
trung điểm đoạn thẳng AB và song song với d?
A.
x
1
=
y − 1
−1
=
z + 1
2
. B.
x
1
=
y − 2
−1
=
z + 2
2
. C.
x
1
=
y − 1
1
=
z + 1
2
. D.
x
1
=
y + 1
−1
=
z − 1
2
.
Câu 39. Có một dãy ghế gồm 6 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 2 học sinh lớp A, 2 học sinh lớp
B và 2 học sinh lớp C ngồi vào dãy ghế đó sao cho mỗi ghế có đúng 1 học sinh ngồi. Xác suất để không
có học sinh lớp C ngồi cạnh nhau.
A.
2
3
. B.
1
3
. C.
5
6
. D.
1
6
.
Câu 40. Cho hình chóp S.ABC có SA = 3a và SA ⊥ (ABC). Biết AB = BC = 2a và
’
ABC = 120
◦
.
Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng
A.
3a
2
. B.
a
2
. C. a. D. 2a.
Câu 41. Có bao nhiêu giá trị nguyên của tham số m để hàm số y =
mx + 10
2x + m
nghịch biến trên khoảng
(0; 2)?
A. 4. B. 5. C. 6. D. 9.
Câu 42. Dân số thế giới được tính theo công thức S = A · e
ni
trong đó A là dân số của năm lấy làm
mốc tính, S là dân số sau n năm, i là tỉ lệ tăng dân số hàng năm. Cho biết năm 2005 Việt Nam có
khoảng 80.902.400 người và tỉ lệ tăng dân số là 1, 47% một năm. Như vậy, nếu tỉ lệ tăng dân số hàng
năm không đổi thì đến năm 2019 số dân của Việt Nam sẽ gần với số nào nhất sau đây?
A. 99.389.200. B. 99.386.600. C. 100.861.100. D. 99.251.200.
Câu 43. Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Tìm tất cả các giá
trị thực của m để phương trình
1
2
f(x) − m = 0 có đúng hai nghiệm phân biệt.
Biên soạn: Ths Nguyễn Chín Em Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
x
y
0
y
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
00
−3−3
00
+∞+∞
A.
m = 0
m < −
3
2
.
B. m < −3. C. m < −
3
2
. D.
ñ
m = 0
m < −3.
Câu 44. Một hình trụ có bán kính đáy bằng a, mặt phẳng qua trục cắt hình trụ theo một thiết diện
có diện tích bằng 8a
2
. Tính diện tích xung quanh của hình trụ.
A. 4πa
2
. B. 8πa
2
. C. 16πa
2
. D. 2πa
2
.
Câu 45. Cho hàm số f(x) thoả mãn
3
Z
0
[2x ln(x + 1) + xf
0
(x)] dx = 0 và f (3) = 1.
Biết
3
Z
0
f(x) dx =
a + b ln 2
2
với a, b là các số thực dương. Giá trị của a + b bằng
A. 35. B. 29. C. 11. D. 7.
Câu 46. Cho hàm số y = f (x) liên tục trên R và có bảng biến thiên như sau
x
y
0
y
−∞
−1
3
+∞
+
0
−
0
+
−∞−∞
44
−2−2
+∞+∞
Biết f(0) < 0, hỏi phương trình f(|x|) = f (0) có bao nhiêu nghiệm?
A. 4. B. 2. C. 3. D. 5.
Câu 47. Xét các số thực a, b thỏa mãn điều kiện
1
3
< b < a < 1. Tìm giá trị nhỏ nhất của biểu thức
P = log
a
Å
3b − 1
4
ã
+ 12 log
2
b
a
a − 3.
A. min P = 13. B. min P =
1
3
√
2
. C. min P = 9. D. min P =
3
√
2.
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số
y =
x
2
+ mx + m
x + 1
trên [1; 2] bằng 2. Số phần tử của S là
A. 1. B. 4. C. 3. D. 2.
Câu 49. Cho hình hộp ABCD.A
0
B
0
C
0
D
0
có đáy là hình chữ nhật với AB =
√
3, AD =
√
7. Hai mặt
bên (ABB
0
A
0
) và (ADD
0
A
0
) lần lượt tạo với đáy một góc 45
◦
và 60
◦
. Tính thể tích của khối hộp nếu
biết cạnh bên của hình hộp bằng 1.
A. 3. B. 5. C. 4. D. 2.
Câu 50. Cho x, y là các số thực dương thỏa mãn log
3
2x + y + 1
x + y
= x + 2y. Tìm giá trị nhỏ nhất của
biểu thức T =
1
x
+
2
√
y
.
A. 3 +
√
3. B. 4. C. 3 + 2
√
3. D. 6.
———————–HẾT———————–
Biên soạn: Ths Nguyễn Chín Em Trang 5
https://www.facebook.com/groups/GeoGebraPro/
ĐÁP ÁN THAM KHẢO
1. C 2. A 3. B 4. B 5. B 6. C 7. A 8. A 9. D 10. D
11. A 12. A 13. B 14. A 15. C 16. A 17. B 18. A 19. C 20. A
21. B 22. B 23. D 24. C 25. B 26. D 27. A 28. D 29. A 30. D
31. A 32. D 33. B 34. B 35. C 36. C 37. A 38. A 39. A 40. A
41. C 42. A 43. D 44. B 45. A 46. C 47. C 48. D 49. A 50. D
Biên soạn: Ths Nguyễn Chín Em Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 3
Câu 1. Lớp 11A có 25 học sinh nam và 20 học sinh nữ. Hỏi có bao nhiêu cách chọn một học sinh làm
lớp trưởng?
A. 25! + 20! cách. B. 45! cách. C. 45 cách. D. 500 cách.
Lời giải.
Số cách chọn một học sinh làm lớp trưởng: C
1
45
= 45 cách
Chọn phương án C
Câu 2. Cho cấp số cộng có u
1
= 0 và công sai d = 3. Tổng của 26 số hạng đầu tiên của cấp số cộng đó
bằng bao nhiêu?
A. 975. B. 775. C. 875. D. 675.
Lời giải.
Ta có S
n
= nu
1
+
n(n − 1)
2
· d ⇒ S
26
= 26 · 0 +
26.25
2
· 3 = 975.
Chọn phương án A
Câu 3. Tập nghiệm của phương trình 2
x
2
−3x
=
1
4
là
A. S = ∅. B. S = {1; 2}. C. S = {0}. D. S = {1}.
Lời giải.
2
x
2
−3x
=
1
4
⇔ 2
x
2
−3x
= 2
−2
⇔ x
2
− 3x = −2 ⇔ x
2
− 3x + 2 = 0 ⇔ x = 1 ∨ x = 2.
Chọn phương án B
Câu 4. Hình lập phương có đường chéo của mặt bên bằng 4 cm. Tính thể tích khối lập phương đó.
A. 8
√
2 cm
3
. B. 16
√
2 cm
3
. C. 8 cm
3
. D. 2
√
2 cm
3
.
Lời giải.
Độ dài các cạnh hình lập phương là
4
√
2
= 2
√
2 cm.
Thể tích khối lập phương là V = (2
√
2)
3
= 16
√
2 cm
3
.
Chọn phương án B
Câu 5. Tập xác định của hàm số y = (x
2
− 3x + 2)
π
là
A. R\{1; 2}. B. (−∞; 1) ∪ (2; +∞). C. (1; 2). D. (−∞; 1] ∪ [2; +∞).
Lời giải.
Ta có điều kiện: x
2
− 3x + 2 > 0 ⇔
ñ
x < 1
x > 2
.
Chọn phương án B
Câu 6. Tìm họ nguyên hàm F (x) của hàm số f(x) =
1
5x + 4
.
A. F (x) =
1
ln 5
ln |5x + 4| + C. B. F (x) = ln |5x + 4| + C.
C. F (x) =
1
5
ln |5x + 4| + C. D. F (x) =
1
5
ln(5x + 4) + C.
Lời giải.
Ta có
Z
1
5x + 4
dx =
1
5
ln |5x + 4| + C.
Chọn phương án C
Biên soạn: Ths Nguyễn Chín Em Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Câu 7. Cho khối chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, đường
cao SO. Biết SO =
a
√
2
2
, thể tích khối chóp S.ABCD bằng
A.
a
3
√
2
6
. B.
a
3
√
2
3
. C.
a
3
√
2
2
. D.
a
3
√
3
4
.
Lời giải.
Ta có S
ABCD
= a
2
.
Vậy V
S.ABCD
=
1
3
· SO · S
ABCD
=
1
3
·
a
√
2
2
· a
2
=
a
3
√
2
6
.
S
A
C
O
B
D
Chọn phương án A
Câu 8. Cho khối nón tròn xoay có chiều cao h, đường sinh l và bán kính đường tròn đáy bằng R .
Diện tích toàn phần của khối nón là
A. S
tp
= πR(l + R). B. S
tp
= πR(l + 2R). C. S
tp
= 2πR(l + R). D. S
tp
= πR(2l + R).
Lời giải.
S
tp
= S
đ
+ S
xq
= πR
2
+ πRl = πR(l + R).
Chọn phương án A
Câu 9. Cho hàm số y = f (x) có bảng biến thiên như sau:
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
00
5
2
5
2
00
+∞+∞
Hàm số y = f (x) nghịch biến trên khoảng nào sau đây?
A. (0; +∞). B. (−∞; 0). C. (−1; 0). D. (−∞; −2).
Lời giải.
Dựa vào bảng biến thiên ta có hàm số nghịch biến trên (−∞; −1) và (0; 1) nên chọn đáp án D.
Chọn phương án D
Câu 10. Cho các số thực dương a, b thỏa mãn log a = x, log b = y. Tính P = log (a
2
b
3
)
A. P = 6xy. B. p = x
2
y
3
. C. P = x
2
+ y
3
. D. P = 2x + 3y.
Lời giải.
Ta có log (a
2
b
3
) = log (a
2
) + log (b
3
) = 2 log a + 3 log b = 2x + 3y.
Chọn phương án D
Câu 11. Một hình trụ có diện tích xung quanh bằng S, diện tích đáy bằng diện tích một mặt cầu bán
kính a. Khi đó thể tích của hình trụ bằng
A. Sa. B.
1
2
Sa. C.
1
3
Sa. D.
1
4
Sa.
Lời giải.
Gọi r là bán kính đáy của hình trụ, h là chiều cao của hình trụ.
Theo bài ra ta có
®
S = 2πrh
πr
2
= 4πa
2
⇔
r = 2a
h =
S
4πa
.
Thể tích khối trụ là V = πr
2
h = π · 4a
2
·
S
4πa
= Sa.
Biên soạn: Ths Nguyễn Chín Em Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Chọn phương án A
Câu 12.
Cho hàm số y = f(x) có bảng biến thiên
dưới đây. Khẳng định nào sau đây là khẳng
định đúng?
A. Hàm số đạt cực đại tại x = 2.
B. Hàm số đạt cực đại tại x = −2.
C. Hàm số đạt cực đại tại x = 4.
D. Hàm số đạt cực đại tại x = 3.
x
y
0
y
−∞
2 4
+∞
+
0
−
0
+
−∞−∞
33
−2−2
+∞+∞
Lời giải.
Dựa vào bảng biến thiên, ta có hàm số đạt cực đại tại x = 2 và đạt cực tiểu tại x = 4.
Chọn phương án A
Câu 13.
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
A. y = −x
4
+ 3x
2
− 2. B. y = −x
4
+ 2x
2
− 1.
C. y = −x
4
+ x
2
− 1. D. y = −x
4
+ 3x
2
− 3.
x
−1
1
−1
y
O
Lời giải.
Dựa vào dạng đồ thị ta thấy:
• Hàm số đã cho có dạng y = ax
4
+ bx
2
+ c với a < 0.
• Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng −1 nên hàm số có hệ số tự do c = −1. Do
vậy ta loại đáp án A và D.
• Hàm số đạt cực đại tại x = ±1, giá trị cực đại bằng 0.
• Hàm số đạt cực tiểu tại x = 0, gía trị cực tiểu bằng −1 . Do vậy ta chọn đáp án B.
Chọn phương án B
Câu 14. Đồ thị hàm số y =
4x + 4
x
2
+ 2x + 1
có tất cả bao nhiêu đường tiệm cận?
A. 2. B. 0. C. 1. D. 3.
Lời giải.
Ta có: lim
x→±∞
4x + 4
x
2
+ 2x + 1
= 0 nên đồ thị hàm số y =
4x + 4
x
2
+ 2x + 1
có tiệm cận ngang y = 0.
lim
x→−1
+
4x + 4
x
2
+ 2x + 1
= lim
x→−1
+
4 (x + 1)
(x + 1)
2
= lim
x→−1
+
4
x + 1
= +∞ nên đồ thị hàm số y =
4x + 4
x
2
+ 2x + 1
có tiệm
cận đứng x = −1.
Vậy đồ thị hàm số y =
4x + 4
x
2
+ 2x + 1
có tất cả hai đường tiệm cận. Chọn đáp án A.
Chọn phương án A
Câu 15. Tập nghiệm của bất phương trình
Å
1
2
ã
x
< 8 là.
A. S = (−∞; −3). B. S =
Å
−∞;
1
3
ã
. C. S = (−3; +∞). D. S =
Å
1
3
; +∞
ã
.
Lời giải.
Å
1
2
ã
x
< 8 ⇔ x > log
1
2
8 ⇔ x > −3.
Chọn phương án C
Câu 16. Cho hàm số y = f (x) liên tục trên R và có bảng biến thiên như sau
Biên soạn: Ths Nguyễn Chín Em Trang 3
https://www.facebook.com/groups/GeoGebraPro/
x
y
0
y
−∞
−1
1
+∞
+
0
−
0
+
−∞−∞
44
00
+∞+∞
Số nghiệm của phương trình 2f(x) + 3 = 0 là
A. 1. B. 2. C. 0. D. 3.
Lời giải.
Ta có 2f (x) + 3 = 0 ⇔ f(x) = −
3
2
là PTHĐGĐ của đồ thị (C) của hàm số y = f(x) và đường
thẳng d : y = −
3
2
. Dựa vào bảng biến thiên ta thấy (C) và d cắt nhau tại 1 điểm. Vậy Phương trình
2f(x) + 3 = 0 có 1 nghiệm.
Chọn phương án A
Câu 17. Nếu
5
Z
1
dx
2x − 1
= ln c với c ∈ Q thì giá trị của c bằng
A. 9. B. 3. C. 6. D. 81.
Lời giải.
5
Z
1
dx
2x − 1
=
1
2
ln |2x − 1|
5
1
= ln 3.
Vậy c = 3.
Chọn phương án B
Câu 18. Phần thực và phần ảo của số phức z = 1 + 2i lần lượt là
A. 1 và 2. B. 1 và i. C. 1 và 2i. D. 2 và 1.
Lời giải.
Số phức z có phần thực là 1 và phần ảo là 2.
Chọn phương án A
Câu 19. Cho hai số phức z
1
= 1 − 2i và z
2
= 3 + 4i. Tìm điểm M biểu diễn số phức z
1
.z
2
trên mặt
phẳng tọa độ.
A. M(−2; 11). B. M(−2; −11). C. M(11; −2). D. M(11; 2).
Lời giải.
Ta có z
1
.z
2
= (1 − 2i)(3 + 4i) = 11 − 2i.
Vậy M(11; −2).
Chọn phương án C
Câu 20. Cho số phức z = 4 − 3i có điểm biểu diễn trên mặt phẳng tọa độ Oxy là M. Tính độ dài
OM.
A. 5. B. 25. C.
√
7. D. 4.
Lời giải.
Ta có OM = |z| =
p
4
2
+ (−3)
2
= 5.
Chọn phương án A
Câu 21. Trong không gian tọa độ Oxyz, tọa độ điểm G
0
đối xứng với điểm G(5; −3; 7) qua trục Oy là
A. G
0
(−5; 0; −7). B. G
0
(−5; −3; −7). C. G
0
(5; 3; 7). D. G
0
(−5; 3; −7).
Lời giải.
Hình chiếu vuông góc của điểm G(5; −3; 7) lên trục Oy là H(0; −3; 0).
Vì G
0
đối xứng với G qua trục Oy nên H là trung điểm của đoạn GG
0
nên tọa độ của điểm G
0
là
Biên soạn: Ths Nguyễn Chín Em Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
x
G
0
= 2x
H
− x
G
= −5
y
G
0
= 2y
H
− y
G
= −3
z
G
0
= 2z
H
− z
G
= −7.
Vậy tọa độ điểm G
0
(−5; −3; −7).
Chọn phương án B
Câu 22. Trong không gian Oxyz, cho hai điểm A(−2; 1; 1), B(0; −1; 1). Phương trình mặt cầu đường
kính AB là
A. (x + 1)
2
+ y
2
+ (z − 1)
2
= 8. B. (x + 1)
2
+ y
2
+ (z − 1)
2
= 2.
C. (x + 1)
2
+ y
2
+ (z + 1)
2
= 8. D. (x − 1)
2
+ y
2
+ (z − 1)
2
= 2.
Lời giải.
Phương pháp: Phương trình mặt cầu có tâm I(a; b; c), bán kính R là (x−a)2+(y−b)
2
+(z−c)
2
= R
2
.
Cách giải: Tâm mặt cầu là trung điểm của AB, có tọa độ là I(−1; 0; 1).
Bán kính mặt cầu: R = IA =
√
1
2
+ 1
2
+ 0
2
=
√
2.
Phương trình mặt cầu đường kính AB: (x + 1)
2
+ y
2
+ (z − 1)
2
= 2.
Chọn phương án B
Câu 23. Trong không gian Oxyz, cho tam giác đều ABC với A(6; 3; 5) và đường thẳng BC có phương
trình tham số
x = 1 − t
y = 2 + t
z = 2t
. Gọi ∆ là đường thẳng đi qua trọng tâm G của tam giác ABC và vuông góc
với mặt phẳng (ABC). Điểm nào dưới đây thuộc đường thẳng ∆?
A. M(−1; −12; 3). B. N(3; −2; 1). C. P (0; −7; 3). D. Q(1; −2; 5).
Lời giải.
• Gọi M(1 − t; 2 + t; 2t) là hình chiếu của A lên BC.
Ta có
# »
AM = (−5 − t; t − 1; 2t − 5) vuông góc với
#»
u = (−1; 1; 2) là véc-tơ chỉ phương của BC.
Do đó −1(−5 − t) + 1(t − 1) + 2(2t − 5) = 0 ⇔ t = 1. Suy ra M(0; 3; 2).
• Vì ABC là tam giác đều nên M là trung điểm của BC. Suy ra
# »
AG =
2
3
# »
AM ⇒ G(2; 3; 3).
• Đường thẳng ∆ đi qua G, có véc-tơ chỉ phương là
#»
u
∆
=
1
3
î
# »
AM,
#»
u
ó
= (1; 5; −2).
Suy ra ∆:
x = 2 + t
y = 3 + 5t
z = 3 − 2t
. Với t = −1, ta có Q(1; −2; 5) ∈ ∆.
Chọn phương án D
Câu 24. Trong không gian Oxyz, cho hai điểm A(1; −1; 0), B(0; 1; 1). Gọi (α) là mặt phẳng chứa đường
thẳng d :
x
2
=
y − 1
−1
=
z − 2
1
và song song với đường thẳng AB. Điểm nào dưới đây thuộc mặt phẳng
(α)?
A. M(6; −4; −1). B. N(6; −4; 2). C. P (6; −4; 3). D. Q = (6; −4; 1).
Lời giải.
•
# »
AB = (−1; 2; 1).
• Đường thẳng d đi qua M(0; 1; 2) và có véc-tơ chỉ phương
#»
u
d
= (2; −1; 1).
• Mặt phẳng (α) có véc-tơ pháp tuyến là
#»
n =
î
#»
u
d
,
# »
AB
ó
= (−3; −3; 3) và (α) đi qua M.
Phương trình (α) là −3(x − 0) − 3(y − 1) + 3(z − 2) = 0 ⇔ −x − y + z − 1 = 0.
• Ta có −6 + 4 + 3 − 1 = 0 nên P (6; −4; 3) ∈ (α).
Biên soạn: Ths Nguyễn Chín Em Trang 5
https://www.facebook.com/groups/GeoGebraPro/
Chọn phương án C
Câu 25. Cho tứ diện đều cạnh a, M là trunng điểm của BC. Tính cosin của góc giữa hai đường thẳng
AB và DM.
A.
√
3
2
. B.
√
3
6
. C.
√
3
3
. D.
1
2
.
Lời giải.
Kẻ MN ∥ AB, cắt AC tại trung điểm N của AC.
Xét tam giác NMD ta có:
cos
÷
NMD =
MN
2
+ MD
2
− ND
2
2MN · MD
=
a
2
4
+
3a
2
4
−
3a
2
4
2 ·
a
2
·
a
√
3
2
=
√
3
6
.
D
C
B
M
N
A
Chọn phương án B
Câu 26. Cho hàm số y = f (x) liên tục trên R và có bảng xét dấu của đạo hàm như sau:
x
f
0
(x)
−∞
−1
0 2 4
+∞
+
0
− +
0
−
0
+
Hàm số đã cho có bao nhiêu cực trị?
A. 3. B. 2. C. 1. D. 4.
Lời giải.
Dựa vào bảng xét dấu ta thấy đạo hàm của hàm số có 4 lần đổi dấu nên hàm số có 4 điểm cực trị.
Chọn phương án D
Câu 27. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = −x
3
+3x+1 trên đoạn [0; 2] bằng
A. 2. B. 3. C. 1. D. 4.
Lời giải.
Ta có: y
0
= −3x
2
+ 3 = 0 ⇔
ñ
x = 1 ∈ [0; 2]
x = −1 /∈ [0; 2]
.
y(0) = 1; y(1) = 3; y(2) = −1.
Khi đó max
[0;2]
y = 3; min
[0;2]
y = −1. Vậy max
[0;2]
y + min
[0;2]
y = 2.
Chọn phương án
A
Câu 28. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y =
√
2 − x
2
− x bằng
A. 2 +
√
2. B. 2. C. 1. D. 2 −
√
2.
Lời giải.
Biên soạn: Ths Nguyễn Chín Em Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Tập xác định D =
î
−
√
2;
√
2
ó
. Ta có y
0
=
−x
√
2 − x
2
− 1 =
−x −
√
2 − x
2
√
2 − x
2
.
y
0
= 0 ⇔
√
2 − x
2
= −x ⇔
x ≤ 0
ñ
x = 1
x = −1
⇔ x = −1.
Bảng biến thiên
x
y
0
y
−
√
2
−1
√
2
+
0
−
√
2
√
2
22
−
√
2−
√
2
Dựa vào bảng biến thiên, ta có max
[
−
√
2;
√
2
]
y = 2, min
[
−
√
2;
√
2
]
y = −
√
2.
Vậy max
[
−
√
2;
√
2
]
y + min
[
−
√
2;
√
2
]
y = 2 −
√
2.
Chọn phương án D
Câu 29. Với a là số thực âm bất kỳ, mệnh đề nào dưới đây đúng?
A. log
2
a
2
= 2 log
2
(−a). B. log
2
a
2
= −2 log
2
a. C. log
2
a
2
= 2 log
2
a. D. log
2
a
2
= 2a.
Lời giải.
Vì a là số thực âm nên log
2
a
2
= 2 log
2
|a| = 2 log
2
(−a).
Chọn phương án A
Câu 30. Số giao điểm của đồ thị hàm số y = x
3
+ x + 2 và đường thẳng y = −2x + 1 là
A. 3. B. 0. C. 2. D. 1.
Lời giải.
Xét phương trình hoành độ giao điểm x
3
+ x + 2 = −2x + 1 ⇔ x
3
+ 3x + 1 = 0.
Xét f(x) = x
3
+ 3x + 1, ta có f
0
(x) = 3x
2
+ 3 > 0. Suy ra bảng biến thiên
x
f
0
(x)
f(x)
−∞ +∞
+
−∞−∞
+∞+∞
Do đó phương trình f(x) = 0 có 1 nghiệm.
Chọn phương án D
Câu 31. Tập nghiệm của bất phương trình
Å
1
1 + a
2
ã
2x+1
> 1 (với a là tham số, a 6= 0) là
A.
Å
−∞; −
1
2
ã
. B. (−∞; 0). C.
Å
−
1
2
; +∞
ã
. D. (0; +∞).
Lời giải.
Vì 0 <
1
1 + a
2
< 1 nên
Å
1
1 + a
2
ã
2x+1
> 1 ⇔ 2x + 1 < 0 ⇔ x < −
1
2
.
Chọn phương án A
Câu 32.
Biên soạn: Ths Nguyễn Chín Em Trang 7
https://www.facebook.com/groups/GeoGebraPro/
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ)
quanh trục DF.
A.
10π
7
a
3
. B.
π
3
a
3
.
C.
5π
2
a
3
. D.
10π
9
a
3
.
B
F
C
D
A
E
a
a
a
30
◦
Lời giải.
• Khi quay hình vuông ABCD quanh trục DF ta được khối trụ
tròn xoay có chiều cao bằng a và bán kính đáy bằng a. Thể
tích khối trụ này là V
1
= π · a
2
· a = πa
3
.
• Khi quay tam giác vuông AF E quanh trục DF ta được khối
nón tròn xoay có chiều cao bằng a và bán kính đáy bằng
EF = AF · tan 30
◦
=
a
√
3
3
. Thể tích khối nón này là V
2
=
1
3
π ·
Ç
a
√
3
3
å
2
· a =
π
9
a
3
.
B
F
C
D
A
E
Vậy thể tích cần tìm là V = V
1
+ V
2
= πa
3
+
π
9
a
3
=
10π
9
a
3
.
Chọn phương án D
Câu 33. Cho tích phân I =
e
Z
1
√
1 + ln x
x
dx. Đổi biến t =
√
1 + ln x ta được kết quả nào sau đây?
A. I =
√
2
Z
1
t
2
dt. B. I = 2
√
2
Z
1
t
2
dt. C. I = 2
2
Z
1
t
2
dt. D. I = 2
√
2
Z
1
t dt.
Lời giải.
Ta có
t =
√
1 + ln x ⇒ t
2
= 1 + ln x ⇒ 2t dt =
dx
x
.
Với
x = 1 ⇒ t = 1,
x = e ⇒ t =
√
2.
Vậy I =
√
2
Z
1
t · 2t dt = 2
√
2
Z
1
t
2
dt.
Chọn phương án B
Câu 34.
Gọi S là diện tích hình phẳng được tô đậm trong hình vẽ bên. Công
thức tính S là
A. S =
1
Z
−1
f(x) dx +
2
Z
1
f(x) dx. B. S =
1
Z
−1
f(x) dx −
2
Z
1
f(x) dx.
C. S =
2
Z
−1
f(x) dx. D. S = −
2
Z
−1
f(x) dx.
x
y
O
−1 1 2
y = f(x)
Biên soạn: Ths Nguyễn Chín Em Trang 8
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Lời giải.
Dựa vào hình vẽ suy ra S =
1
Z
−1
f(x) dx −
2
Z
1
f(x) dx.
Chọn phương án B
Câu 35. Cho hai số phức z
1
= m+3i, z
2
= 2−(m+1)i, với m ∈ R. Tìm các giá trị của m để w = z
1
·z
2
là số thực.
A. m = 1 hoặc m = −2. B. m = 2 hoặc m = −1.
C. m = 2 hoặc m = −3. D. m = −2 hoặc m = −3.
Lời giải.
Ta có w = z
1
· z
2
= (m + 3i) (2 − (m + 1)i) = 5m + 3 + (6 − m − m
2
) i.
Để w là số thực thì 6 − m − m
2
= 0 ⇔
ñ
m = −3
m = 2.
Chọn phương án C
Câu 36. Phương trình bậc hai nào dưới đây nhận hai số phức 2 − 3i và 2 + 3i làm nghiệm ?
A. z
2
+ 4z + 13 = 0. B. z
2
+ 4z + 3 = 0. C. z
2
− 4z + 13 = 0. D. z
2
− 4z + 3 = 0.
Lời giải.
Đặt z
1
= 2 − 3i; z
2
= 2 + 3i. Khi đó
S = z
1
+ z
2
= 4; P = z
1
· z
2
= (2 − 3i)(2 + 3i) = 4 + 9 = 13.
Do đó z
1
và z
2
là nghiệm của phương trình: z
2
− Sz + P = 0 hay z
2
− 4z + 13 = 0.
Vậy z
2
− 4z + 13 = 0 là phương trình cần tìm.
Chọn phương án C
Câu 37. Trong không gian Oxyz cho mặt phẳng (P ): 3x −4y + 5z −6 = 0 và đường thẳng d:
x − 1
2
=
y − 2
3
=
z − 3
1
. Gọi ϕ là góc giữa đường thẳng d và mặt phẳng (P ). Tìm khẳng định đúng.
A. sin ϕ =
1
5
√
28
. B. cos ϕ = −
1
5
√
28
. C. cos ϕ =
1
5
√
28
. D. sin ϕ = −
1
5
√
28
.
Lời giải.
(P ) có véc-tơ pháp tuyến là
#»
n = (3; −4; 5) và d có véc-tơ chỉ phương
#»
u = (2; 3; 1). Khi đó ta có
sin ϕ = |cos (
#»
n,
#»
u )| =
|
#»
n ·
#»
u |
|
#»
n| · |
#»
u |
=
1
5
√
28
.
Chọn phương án A
Câu 38. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1; −2; −3), B(−1; 4; 1) và đường
thẳng d:
x + 2
1
=
y − 2
−1
=
z + 3
2
. Phương trình nào dưới đây là phương trình của đường thẳng đi qua
trung điểm đoạn thẳng AB và song song với d?
A.
x
1
=
y − 1
−1
=
z + 1
2
. B.
x
1
=
y − 2
−1
=
z + 2
2
. C.
x
1
=
y − 1
1
=
z + 1
2
. D.
x
1
=
y + 1
−1
=
z − 1
2
.
Lời giải.
Gọi M là trung điểm đoạn AB, ta có M(0; 1; −1). Khi đó đường thẳng đi qua M và song song với d có
phương trình
x
1
=
y − 1
−1
=
z + 1
2
.
Chọn phương án A
Câu 39. Có một dãy ghế gồm 6 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 2 học sinh lớp A, 2 học sinh lớp
B và 2 học sinh lớp C ngồi vào dãy ghế đó sao cho mỗi ghế có đúng 1 học sinh ngồi. Xác suất để không
có học sinh lớp C ngồi cạnh nhau.
A.
2
3
. B.
1
3
. C.
5
6
. D.
1
6
.
Lời giải.
Biên soạn: Ths Nguyễn Chín Em Trang 9
https://www.facebook.com/groups/GeoGebraPro/
Cho 2 học sinh lớp C ngồi cạnh nhau thành 1 nhóm D.
2 học sinh lớp C đổi vị trí trong nhóm D: 2! cách.
Nhóm D đổi vị trí với 4 học sinh còn lại: 5! cách.
Không gian mẫu: 6! cách.
Xác suất để 2 học sinh lớp C ngồi cạnh nhau:
2! · 5!
6!
=
1
3
.
Vậy xác suất để 2 học sinh lớp C không ngồi cạnh nhau = 1 −
1
3
=
2
3
.
Chọn phương án A
Câu 40. Cho hình chóp S.ABC có SA = 3a và SA ⊥ (ABC). Biết AB = BC = 2a và
’
ABC = 120
◦
.
Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng
A.
3a
2
. B.
a
2
. C. a. D. 2a.
Lời giải.
Gọi I là hình hình chiếu vuông góc của A trên BC, ta có AI ⊥ BC. (1)
Mặt khác SA ⊥ (ABC) nên SA ⊥ BC. (2)
Từ (1) và (2) suy ra BC ⊥ (SIA). (3)
Gọi H là hình hình chiếu vuông góc của A trên SI, ta có AH ⊥ SI. (4)
Từ (3) và (4) suy ra AH ⊥ (SBC) nên khoảng cách từ A đến mặt phẳng
(SBC) là AH.
Xét tam giác BIA vuông tại I, ta có
AI = AB · sin 120
◦
= 2a ·
√
3
2
= a
√
3.
Xét tam giác SAI vuông tại A, ta có
S
B
A C
I
H
1
AH
2
=
1
AS
2
+
1
AI
2
⇒ AH =
AS
2
· AI
2
AS
2
+ AI
2
=
s
(3a)
2
· (a
√
3)
2
(3a)
2
+ (a
√
3)
2
=
3a
2
.
Vậy khoảng cách từ điểm A đến mặt phẳng (SBC) bằng
3a
2
.
Chọn phương án A
Câu 41. Có bao nhiêu giá trị nguyên của tham số m để hàm số y =
mx + 10
2x + m
nghịch biến trên khoảng
(0; 2)?
A. 4. B. 5. C. 6. D. 9.
Lời giải.
Hàm số y =
mx + 10
2x + m
nghịch biến trên khoảng (0; 2) ⇔
m
2
− 20 < 0
−
m
2
/∈ (0; 2)
⇔
−
√
20 < m <
√
20
−
m
2
≤ 0
−
m
2
≥ 2
⇔
−
√
20 < m <
√
20
ñ
m ≥ 0
m ≤ −4
⇔
"
−
√
20 < m ≤ −4
0 ≤ m <
√
20.
Vậy m ∈ {−4; 0; 1; 2; 3; 4; }.
Chọn phương án C
Câu 42. Dân số thế giới được tính theo công thức S = A · e
ni
trong đó A là dân số của năm lấy làm
mốc tính, S là dân số sau n năm, i là tỉ lệ tăng dân số hàng năm. Cho biết năm 2005 Việt Nam có
khoảng 80.902.400 người và tỉ lệ tăng dân số là 1, 47% một năm. Như vậy, nếu tỉ lệ tăng dân số hàng
năm không đổi thì đến năm 2019 số dân của Việt Nam sẽ gần với số nào nhất sau đây?
Biên soạn: Ths Nguyễn Chín Em Trang 10
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
A. 99.389.200. B. 99.386.600. C. 100.861.100. D. 99.251.200.
Lời giải.
Áp dụng công thức S = A · e
ni
với A = 80.902.400, n = 2019 − 2005 = 14, i = 1, 47% = 0, 0147, ta có
số dân Việt Nam đến năm 2017 là
S = A · e
ni
= 80902400 · e
14·0,0147
≈ 99389203,38.
Như vậy, số dân Việt Nam đến năm 2019 gần với số 99.389.200 nhất.
Chọn phương án A
Câu 43. Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Tìm tất cả các giá
trị thực của m để phương trình
1
2
f(x) − m = 0 có đúng hai nghiệm phân biệt.
x
y
0
y
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
00
−3−3
00
+∞+∞
A.
m = 0
m < −
3
2
.
B. m < −3. C. m < −
3
2
. D.
ñ
m = 0
m < −3.
Lời giải.
Ta có
1
2
f(x) − m = 0 ⇔ f(x) = 2m. (*)
Quan sát bảng biến thiên của hàm số y = f (x), ta thấy, để phương trình (∗) có đúng hai nghiệm phân
biệt thì
ñ
2m = 0
2m < −3
⇔
m = 0
m < −
3
2
.
Chọn phương án D
Câu 44. Một hình trụ có bán kính đáy bằng a, mặt phẳng qua trục cắt hình trụ theo một thiết diện
có diện tích bằng 8a
2
. Tính diện tích xung quanh của hình trụ.
A. 4πa
2
. B. 8πa
2
. C. 16πa
2
. D. 2πa
2
.
Lời giải.
D
C
O
0
A
B
O
Thiết diện qua trục của hình trụ là hình chữ nhật, có độ dài một cạnh là 2a, có diện tích là 8a
2
, suy ra
chiều cao của hình trụ là h =
8a
2
2a
= 4a.
Vậy diện tích xung quanh của hình trụ là: S
xq
= 2πrh = 2 · π · a · 4a = 8πa
2
.
Chọn phương án B
Câu 45. Cho hàm số f(x) thoả mãn
3
Z
0
[2x ln(x + 1) + xf
0
(x)] dx = 0 và f(3) = 1.
Biết
3
Z
0
f(x) dx =
a + b ln 2
2
với a, b là các số thực dương. Giá trị của a + b bằng
Biên soạn: Ths Nguyễn Chín Em Trang 11
https://www.facebook.com/groups/GeoGebraPro/
A. 35. B. 29. C. 11. D. 7.
Lời giải.
Tính I =
3
Z
0
2x ln(x + 1) dx.
Đặt
®
u = ln(x + 1)
dv = 2x dx
⇒
du =
1
x + 1
dx
v = x
2
. Khi đó
I = x
2
ln(x + 1)
3
0
−
3
Z
0
x
2
x + 1
dx = 9 ln 4 −
Å
x
2
2
− x + ln |x + 1|
ã
3
0
= 16 ln 2 −
3
2
.
Tính J =
3
R
0
xf
0
(x) dx.
Đặt
®
u
J
= x
dv
J
= f
0
(x)dx
⇒
®
du
J
= dx
v
J
= f(x)
.
J =
3
Z
0
xf
0
(x) dx = xf (x)|
3
0
−
3
Z
0
f(x) dx = 3 −
3
Z
0
f(x) dx.
Mà
3
Z
0
[2x ln(x + 1) + xf
0
(x)] dx = 0
⇒ I + J = 0 ⇒ 16 ln 2 −
3
2
+ 3 −
3
Z
0
f(x)dx = 0 ⇒
3
Z
0
f(x) dx = 16 ln 2 +
3
2
=
3 + 32 ln 2
2
.
Suy ra
®
a = 3
b = 32
. Vậy a + b = 35.
Chọn phương án A
Câu 46. Cho hàm số y = f (x) liên tục trên R và có bảng biến thiên như sau
x
y
0
y
−∞
−1
3
+∞
+
0
−
0
+
−∞−∞
44
−2−2
+∞+∞
Biết f(0) < 0, hỏi phương trình f(|x|) = f(0) có bao nhiêu nghiệm?
A. 4. B. 2. C. 3. D. 5.
Lời giải.
Đặt f(0) = k < 0. Vì hàm số nghịch biến trên (−1; 3) nên −2 < k < 4.
Ta có hàm số y = f(|x|) là hàm số chẵn nên đồ thị đối xứng qua trục Oy, từ đó ta có bảng biến thiên
sau
x
y
0
y
−∞
−3
0 3
+∞
−
0
+
−
0
+
+∞+∞
−2−2
kk
−2−2
+∞+∞
Từ bảng biến thiên suy ra phương trình f(|x|) = f(0) có 3 nghiệm.
Chọn phương án C
Biên soạn: Ths Nguyễn Chín Em Trang 12
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 47. Xét các số thực a, b thỏa mãn điều kiện
1
3
< b < a < 1. Tìm giá trị nhỏ nhất của biểu thức
P = log
a
Å
3b − 1
4
ã
+ 12 log
2
b
a
a − 3.
A. min P = 13. B. min P =
1
3
√
2
. C. min P = 9. D. min P =
3
√
2.
Lời giải.
Ta có (2b − 1)
2
(b + 1) ≥ 0 ⇒ 3b − 1 ≤ 4b
3
và điều kiện bài toán suy ra log
a
b > 0.
Từ đó suy ra P ≥ 3 log
a
b +
12
(log
a
b − 1)
2
− 3 =
3 log
a
b · (log
a
b − 3)
2
(log
a
b − 1)
2
+ 9 ≥ 9.
Khi b =
1
2
, a =
1
3
√
2
thì P = 9. Vậy, min P = 9.
Chọn phương án C
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số
y =
x
2
+ mx + m
x + 1
trên [1; 2] bằng 2. Số phần tử của S là
A. 1. B. 4. C. 3. D. 2.
Lời giải.
Xét hàm số f(x) =
x
2
+ mx + m
x + 1
trên [1; 2]. Ta có f
0
(x) liên tục trên [1; 2] và
f
0
(x) =
x
2
+ 2x
(x + 1)
2
> 0, ∀x ∈ [1; 2].
Suy ra f(x) đồng biến trên [1; 2]. Do đó max
[1;2]
f(x) = f(2) =
3m + 4
3
, min
[1;2]
f(x) = f(1) =
2m + 1
2
.
Khi đó max
[1;2]
|f(x)| = max
ß
3m + 4
3
,
2m + 1
2
™
. Ta có
3m + 4
3
≥
2m + 1
2
⇔ 4(3m + 4)
2
≥ 9(2m + 1)
2
⇔ m ≥ −
11
12
.
• Với m ≥ −
11
12
, ta có max
[1;2]
|f(x)| =
3m + 4
3
. Theo đề bài, ta có
3m + 4
3
= 2 ⇔
3m + 4
3
= 2
3m + 4
3
= −2
⇔
m =
2
3
(thỏa mãn)
m = −
10
3
loại.
• Với m < −
11
12
, ta có max
[1;2]
|f(x)| =
2m + 1
2
. Theo đề bài, ta có
2m + 1
2
= 2 ⇔
2m + 1
2
= 2
2m + 1
2
= −2
⇔
m = −
5
2
(thỏa mãn)
m =
3
2
loại.
Vậy S =
ß
2
3
; −
5
2
™
⇒ Số phần tử của S là 2.
Chọn phương án D
Câu 49. Cho hình hộp ABCD.A
0
B
0
C
0
D
0
có đáy là hình chữ nhật với AB =
√
3, AD =
√
7. Hai mặt
bên (ABB
0
A
0
) và (ADD
0
A
0
) lần lượt tạo với đáy một góc 45
◦
và 60
◦
. Tính thể tích của khối hộp nếu
biết cạnh bên của hình hộp bằng 1.
A. 3. B. 5. C. 4. D. 2.
Lời giải.
Biên soạn: Ths Nguyễn Chín Em Trang 13
https://www.facebook.com/groups/GeoGebraPro/
Gọi H là hình chiếu vuông góc A
0
lên (ABCD).
Gọi M, N lần lượt là hình chiếu vuông góc H lên
AB, AD ⇒
÷
A
0
NH = 60
◦
và
÷
A
0
MH = 45
◦
.
Đặt A
0
H = x, khi đó A
0
N =
x
sin 60
◦
=
2x
√
3
.
A
0
N =
√
AA
02
− A
0
N
2
=
3 − 4x
2
3
= HM
HM = x. tan 45
◦
= x
⇒
…
3 − 4x
2
3
= x ⇒ x =
…
3
7
.
V
ABCD.A
0
B
0
C
0
D
0
= AB.AD.x =
√
3.
√
7.
…
3
7
= 3.
A
B C
D
A
0
B
0
C
0
D
0
N
HM
x
60
◦
45
◦
Chọn phương án A
Câu 50. Cho x, y là các số thực dương thỏa mãn log
3
2x + y + 1
x + y
= x + 2y. Tìm giá trị nhỏ nhất của
biểu thức T =
1
x
+
2
√
y
.
A. 3 +
√
3. B. 4. C. 3 + 2
√
3. D. 6.
Lời giải.
Ta có:
log
3
2x + y + 1
x + y
= x + 2y
⇔log
3
(2x + y + 1) − log
3
(x + y) = 3(x + y) − (2x + y + 1) + 1
⇔log
3
(2x + y + 1) + (2x + y + 1) = log
3
[3(x + y)] + 3(x + y). (1)
Xét hàm số y = f (a) = log
3
a + a trên (0; +∞).
Dễ thấy hàm số y = f (a) là hàm số đồng biến trên (0; +∞).
Do đó, (1) ⇔ f(2x + y + 1) = f(3(x + y)) ⇔ 2x + y + 1 = 3(x + y) ⇔ x + 2y = 1.
Ta có
1
x
+
2
√
y
=
1
x
+
1
1
2
√
y
≥
1
x
+
1
1
4
+ y
2
=
1
x
+
1
1
4
+ y
+
1
1
4
+ y
≥
(1 + 1 + 1)
2
x +
1
4
+ y +
1
4
+ y
=
9
x + 2y +
1
2
= 6.
Dấu “=” xảy ra khi và chỉ khi x =
1
2
; y =
1
4
.
Chọn phương án D
———————–HẾT———————–
Biên soạn: Ths Nguyễn Chín Em Trang 14
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
ĐÁP ÁN THAM KHẢO
1. C 2. A 3. B 4. B 5. B 6. C 7. A 8. A 9. D 10. D
11. A 12. A 13. B 14. A 15. C 16. A 17. B 18. A 19. C 20. A
21. B 22. B 23. D 24. C 25. B 26. D 27. A 28. D 29. A 30. D
31. A 32. D 33. B 34. B 35. C 36. C 37. A 38. A 39. A 40. A
41. C 42. A 43. D 44. B 45. A 46. C 47. C 48. D 49. A 50. D
Biên soạn: Ths Nguyễn Chín Em Trang 15
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 4
Câu 1. Có bao nhiêu cách xếp một nhóm học sinh gồm 4 bạn nam và 6 bạn nữ thành một hàng
ngang?
A. 10!. B. 4!. C. 6!.4!. D. 6!.
Câu 2. Cho (u
n
) là cấp số cộng với công sai d. Biết u
5
= 16, u
7
= 22. Tính u
1
.
A. u
1
= −5. B. u
1
= −2. C. u
1
= 19. D. u
1
= 4.
Câu 3. Tập nghiệm của phương trình log
0,25
(x
2
− 3x) = −1 là:
A. {4}. B.
®
3 − 2
√
2
2
;
3 + 2
√
2
2
´
.
C. {1; −4}. D. {−1; 4}.
Câu 4. Hình lập phương có đường chéo của mặt bên bằng 4 cm. Tính thể tích khối lập phương đó.
A. 8
√
2 cm
3
. B. 16
√
2 cm
3
. C. 8 cm
3
. D. 2
√
2 cm
3
.
Câu 5. Tìm tập xác định của hàm số y = log
1
2
(x + 1).
A. D = (−∞; −1). B. D = (−1; +∞). C. D = [−1; +∞). D. D = R\{1}.
Câu 6. Hàm số f(x) = cos(4x + 7) có một nguyên hàm là
A. −sin(4x + 7) + x. B.
1
4
sin(4x + 7) − 3. C. sin(4x + 7) − 1. D. −
1
4
sin(4x + 7) + 3.
Câu 7. Cho khối chóp tam giác có đường cao bằng 100 cm và cạnh đáy bằng 20 cm, 21 cm, 29 cm.
Tính thể tích khối chóp này.
A. 7 000
√
2 cm
3
. B. 6 000 cm
3
. C. 6 213 cm
3
. D. 7 000 cm
3
.
Câu 8. Cho khối nón có bán kính đáy r =
√
3 và chiều cao h = 4. Tính thể tích V của khối nón đã
cho.
A. V = 16π
√
3. B. V = 12π. C. V = 4. D. V = 4π.
Câu 9. Tính diện tích của mặt cầu có bán kính r = 2.
A.
32
3
π. B. 8π. C. 32π. D. 16π.
Câu 10. Cho hàm số y = f (x) có đạo hàm liên tục trên R và có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
−1−1
−2−2
−1−1
−∞−∞
Hàm số y = f (x) đồng biến trên khoảng nào sau đây
A. (0; 1). B. (−1; 0). C. (−∞; 1). D. (1; +∞).
Câu 11. Cho a, b > 0, log
3
a = p, log
3
b = p. Đẳng thức nào dưới đây đúng?
A. log
3
Å
3
r
a
m
b
d
ã
= r + pm − qd. B. log
3
Å
3
r
a
m
b
d
ã
= r + pm + qd.
C. log
3
Å
3
r
a
m
b
d
ã
= r − pm − qd. D. log
3
Å
3
r
a
m
b
d
ã
= r − pm + qd.
GeoGebraPro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Câu 12. Một hình trụ có diện tích xung quanh bằng S, diện tích đáy bằng diện tích một mặt cầu bán
kính a. Khi đó thể tích của hình trụ bằng
A. Sa. B.
1
2
Sa. C.
1
3
Sa. D.
1
4
Sa.
Câu 13.
Cho hàm số y = f (x) có bảng biến thiên như sau. Giá
trị cực đại của hàm số bằng
A. 1. B. 2. C. 0. D. 5.
x
y
0
y
−∞
0 2
+∞
−
0
+
0
−
+∞+∞
11
55
−∞−∞
Câu 14.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A. y = x
3
− 3x − 1. B. y = −x
3
− 3x
2
− 1.
C. y = −x
3
+ 3x
2
+ 1. D. y = x
3
− 3x + 1.
x
y
−1
3
1
−1
O
Câu 15. Tiệm cận ngang của đồ thị hàm số y =
5
x − 1
là đường thẳng có phương trình nào dưới
đây?
A. x = 1. B. y = 5. C. x = 0. D. y = 0.
Câu 16. Tập nghiệm của bất phương trình log
2
x > log
2
(8 − x) là
A. (8; +∞). B. (−∞; 4). C. (4; 8). D. (0; 4).
Câu 17. Cho hàm số y = f (x) có bảng biến thiên như hình sau
x
f
0
(x)
f(x)
−∞
−2
0 2
+∞
−
0
+
0
−
0
+
+∞+∞
−2−2
11
−2−2
+∞+∞
Số nghiệm thực của phương trình 2f(x) + 3 = 0 là
A. 4. B. 3. C. 2. D. 1.
Câu 18. Nếu
5
Z
2
f(x)dx = 3 và
7
Z
5
f(x)dx = 9 thì
7
Z
2
f(x)dx bằng bao nhiêu?
A. 3. B. 6. C. 12. D. −6.
Câu 19. Tìm số phức liên hợp của của số z = 5 + i.
A. z = 5 − i. B. z = −5 − i. C. z = 5 + i. D. z = −5 + i.
Câu 20. Cho hai số phức z
1
= 2 − 7i và z
2
= −4 + i. Điểm biểu diễn số phức z
1
+ z
2
trên mặt phẳng
tọa độ là điểm nào dưới đây?
A. Q(−2; −6). B. P (−5; −3). C. N (6; −8). D. M(3; −11).
Câu 21.
GeoGebraPro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Trên mặt phẳng tọa độ Oxy cho điểm M trong hình vẽ bên là điểm biểu diễn của
số phức z. Tìm z.
A. z = −4 + 3i. B. z = −3 + 4i. C. z = 3 − 4i. D. z = 3 + 4i.
x
y
O
M
3
−4
Câu 22. Trong không gian với hệ tọa độ Oxyz, tọa độ hình chiếu vuông góc của điểm A(2; −1; 0) lên
mặt phẳng (P ) : 3x − 2y + z + 6 = 0 là
A. (1; 1; 1). B. (−1; 1; −1). C. (3; −2; 1). D. (5; −3; 1).
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình x
2
+ y
2
+ z
2
−2x + 4y −
6z + 9 = 0. Tọa độ tâm I và bán kính R của mặt cầu là
A. I (1; −2; 3) và R = 5. B. I (1; −2; 3) và R =
√
5.
C. I (−1; 2; −3) và R = 5. D. I (−1; 2; −3) và R =
√
5.
Câu 24. Trong không gian Oxyz, cho mặt phẳng (P ): x −2z + 1 = 0. Vectơ nào dưới đây là một vectơ
pháp tuyến của (P )?
A.
#»
n
1
= (1; 0; −2). B.
#»
n
2
= (1; −2; 1). C.
#»
n
3
= (1; −2; 0). D.
#»
n
4
= (−1; 2; 0).
Câu 25. Trong không gian Oxyz, cho đường thẳng d:
x − 1
2
=
y − 2
1
=
z
−2
. Điểm nào dưới đây thuộc
đường thẳng d?
A. M(−1; −2; 0). B. M(−1; 1; 2). C. M(2; 1; −2). D. M (3; 3; 2).
Câu 26. Cho hình chóp S.ABCD đều có SA = AB = a. Góc giữa SA và CD là
A. 60
◦
. B. 30
◦
. C. 90
◦
. D. 45
◦
.
Câu 27. Gọi M , m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x) =
4
x
+ x + 1 trên đoạn [1; 3].
Tính M − m.
A. 4. B. 9. C. 1. D. 5.
Câu 28. Giá trị nhỏ nhất của hàm số f(x) = x
3
+ 3x + 1 trên đoạn [1; 3] là
A. min
[1;3]
f(x) = 3. B. min
[1;3]
f(x) = 6. C. min
[1;3]
f(x) = 37. D. min
[1;3]
f(x) = 5.
Câu 29. Với a là số thực dương bất kỳ, mệnh đề nào dưới đây đúng?
A. log(3a) = 3 log a. B. log a
3
= 3 log a. C. log(3a) =
1
3
log a. D. log a
3
=
1
3
log a.
Câu 30. Số giao điểm của đồ thị hàm số y =
2x + 1
x − 1
với đường thẳng y = 2x + 3 là
A. 2. B. 3. C. 1. D. 0.
Câu 31. Tập nghiệm của bất phương trình 3
x
2
−2x
< 27 là
A. (−∞; −1). B. (3; +∞).
C. (−1; 3). D. (−∞; −1) ∪ (3; +∞).
Câu 32. Trong không gian, cho tam giác ABC vuông tại A, AB = a và AC = a
√
3. Tính độ dài đường
sinh ` của hình nón có được khi quay tam giác ABC xung quanh trục AB.
A. ` = a. B. ` = 2a. C. ` = a
√
3. D. ` = a
√
2.
Câu 33. Cho tích phân I =
1
Z
0
x
7
(1 + x
2
)
5
dx, giả sử đặt t = 1 + x
2
. Tìm mệnh đề đúng.
A. I =
1
2
2
Z
1
(t − 1)
3
t
5
dt. B. I =
3
Z
1
(t − 1)
3
t
5
dt. C.
1
2
2
Z
1
(t − 1)
3
t
4
dt. D.
3
2
4
Z
1
(t − 1)
3
t
4
dt.
GeoGebraPro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
Câu 34. Thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi parabol (P ): y = x
2
và
đường thẳng d: y = x xoay quanh trục Ox bằng
A. π
1
Z
0
x
2
dx − π
1
Z
0
x
4
dx. B. π
1
Z
0
x
2
dx + π
1
Z
0
x
4
dx.
C. π
1
Z
0
x
2
− x
2
dx. D. π
1
Z
0
x
2
− x
dx.
Câu 35. Cho hai số phức z = 6 + 5i và z
0
= 5 − 4i + z. Tìm mô-đun của số phức w = z · z
0
.
A. |w| = 612. B. |w| = 61. C. |w| = 61
√
2. D. |w| = 6
√
2.
Câu 36. Gọi z
1
và z
2
lần lượt là nghiệm của phươngtrình: z
2
−2z + 5 = 0. Tính P = |z
1
|
2
+ |z
2
|
2
.
A. P = 2
√
5. B. P = 20. C. P = 10. D. P =
√
5.
Câu 37. Trong không gian Oxyz, mặt phẳng chứa trục Ox và đi qua điểm A(1; 1; −1) có phương trình
là
A. z + 1 = 0. B. x − y = 0. C. x + z = 0. D. y + z = 0.
Câu 38. Trong không gian Oxyz, cho hai điểm A(1; 2; 3) và B(2; 4; −1). Phương trình chính tắc của
đường thẳng d đi qua A, B là
A.
x + 2
1
=
y + 4
2
=
z + 1
4
. B.
x + 1
1
=
y + 2
2
=
z + 3
4
.
C.
x − 1
1
=
y − 2
2
=
z − 3
−4
. D.
x + 2
1
=
y + 4
2
=
z − 1
−4
.
Câu 39. Một nhóm có 7 học sinh lớp A và 5 học sinh lớp B. Xếp ngẫu nhiên 12 học sinh trên ngồi vào
một dãy 12 ghế hàng ngang sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất sao cho không
có bất kì 2 học sinh lớp B nào ngồi cạnh nhau.
A.
7
99
. B.
1
132
. C.
7
264
. D.
1
792
.
Câu 40. Cho hình lăng trụ tam giác đều ABC.A
0
B
0
C
0
có tất cả các cạnh đều bằng a. Khoảng cách từ
A đến mặt phẳng (A
0
BC) bằng
A.
a
√
3
4
. B.
a
√
21
7
. C.
a
√
2
2
. D.
a
√
6
4
.
Câu 41. Có bao nhiêu giá trị nguyên của m để hàm số y = x
3
+ 3x
2
− (m
2
− 3m + 2)x + 5 đồng biến
trên (0; 2)?
A. 3. B. 2. C. 4. D. 1.
Câu 42. Các nhà khoa học đã tính toán khi nhiệt độ trung bình của trái đất tăng thêm 2
◦
C thì mực
nước biển sẽ dâng lên 0, 03m. Nếu nhiệt độ tăng lên 5
◦
C thì nước biển sẽ dâng lên 0, 1m và người ta
đưa ra công thức tổng quát như sau: Nếu nhiệt độ trung bình của trái đất tăng lên t
o
C thì nước biển
dâng lên f(t) = ka
t
(m) trong đó k, a là các hằng số dương. Hỏi khi nhiệt độ trung bình của trái đất
tăng thêm bao nhiêu độ C thì mực nước biển dâng lên 0, 2m?
A. 9, 2
◦
C. B. 8, 6
◦
C. C. 7, 6
◦
C. D. 6, 7
◦
C.
Câu 43. Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình bên dưới. Tìm tất cả
các giá trị thực của m để phương trình
1
2
f(x) − m = 0 có đúng hai nghiệm phân biệt.
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
00
−3−3
00
−∞−∞
GeoGebraPro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
A. m = 0 hoặc m < −
3
2
. B. m < −3.
C. m < −
3
2
. D. m = 0 hoặc m < −3.
Câu 44. Cho hình trụ có bán kính đáy bằng a
√
2. Cắt hình trụ bởi một mặt phẳng, song song với trụ
của hình trụ và cách trục của hình trụ một khoảng bằng
a
2
ta được thiết diện là một hình vuông. Tính
thể tích V của khối trụ đã cho.
A. V = πa
3
√
3. B. V =
2πa
3
√
7
3
. C. V = 2πa
3
√
7. D. V = πa
3
.
Câu 45. Cho hàm số y = f(x) liên tục trên R thỏa mãn
1
Z
0
f(x)dx = 3 và
5
Z
0
f(x)dx = 6. Tính tích
phân I =
1
Z
−1
f(|3x − 2|)dx
A. I = 3. B. I = −2. C. I = 4. D. I = 9.
Câu 46. Cho hàm số y = f (x) = ax
3
+ bx
2
+ cx + d có bảng biến thiên như sau
x
y
0
y
−∞
0 1
+∞
+
0
−
0
+
−∞−∞
11
00
+∞+∞
Khi đó |f(x)| = m có bốn nghiệm phân biệt x
1
< x
2
< x
3
<
1
2
< x
4
khi và chỉ khi
A.
1
2
< m < 1. B.
1
2
≤ m < 1. C. 0 < m < 1. D. 0 < m ≤ 1.
Câu 47. Cho x, y là các số dương thỏa mãn xy ≤ 4y−1. Giá trị nhỏ nhất của P =
6 (2x + y)
x
+ln
x + 2y
y
là a + ln b. Tính ab.
A. ab = 45. B. ab = 81. C. ab = 115. D. ab = 108.
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số
y =
x
2
+ mx + m
x + 1
trên [1; 2] bằng 2. Số phần tử của S là
A. 1. B. 4. C. 3. D. 2.
Câu 49. Cho hình hộp ABCD.A
0
B
0
C
0
D
0
có đáy ABCD là hình thoi tâm O, cạnh a, góc
’
ABC = 60
◦
.
Biết rằng A
0
O ⊥ (ABCD) và cạnh bên hợp với đáy một góc bằng 60
◦
. Tính thể tích V của khối đa
diện OABC
0
D
0
.
A. V =
a
3
6
. B. V =
a
3
12
. C. V =
a
3
8
. D. V =
3a
3
4
.
Câu 50 (Thầy: Trương Đức Thịnh). Có bao nhiêu cặp số nguyên dương (x; y) với y ≤ 2020 thỏa
mãn
log
2
x + 2
y + 1
< 4y
4
+ 8y
3
−
x
2
+ 4x
y
2
+ 1
A. 2019.2020. B. 2020.2021. C. 2019
2
. D. 2020
2
.
———————–HẾT———————–
GeoGebraPro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
ĐÁP ÁN THAM KHẢO
1. A 2. D 3. D 4. B 5. B 6. B 7. D 8. D 9. D 10. A
11. C 12. A 13. D 14. D 15. D 16. C 17. A 18. C 19. A 20. A
21. C 22. B 23. C 24. A 25. B 26. A 27. C 28. D 29. B 30. A
31. C 32. B 33. A 34. A 35. C 36. A 37. D 38. C 39. A 40. B
41. B 42. D 43. A 44. C 45. A 46. B 47. B 48. D 49. C 50. D
GeoGebraPro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 4
Câu 1. Có bao nhiêu cách xếp một nhóm học sinh gồm 4 bạn nam và 6 bạn nữ thành một hàng
ngang?
A. 10!. B. 4!. C. 6!.4!. D. 6!.
Lời giải.
Nhóm học sinh đó có tất cả 10 học sinh.
Xếp 10 học sinh thành một hàng ngang có P
10
= 10! cách xếp.
Chọn phương án A
Câu 2. Cho (u
n
) là cấp số cộng với công sai d. Biết u
5
= 16, u
7
= 22. Tính u
1
.
A. u
1
= −5. B. u
1
= −2. C. u
1
= 19. D. u
1
= 4.
Lời giải.
Ta có
®
u
5
= 16
u
7
= 22
⇔
®
u
1
+ 4d = 16
u
1
+ 6d = 22
⇔
®
u
1
= 4
d = 3
.
Vậy u
1
= 4.
Chọn phương án D
Câu 3. Tập nghiệm của phương trình log
0,25
(x
2
− 3x) = −1 là:
A. {4}. B.
®
3 − 2
√
2
2
;
3 + 2
√
2
2
´
.
C. {1; −4}. D. {−1; 4}.
Lời giải.
Điều kiện: x
2
− 3x > 0 ⇔
ñ
x < 0
x > 3
.
Ta có
log
0,25
x
2
− 3x
= −1
⇔ x
2
− 3x = 4
⇔ x
2
− 3x − 4 = 0
⇔
ñ
x = −1 (nhận)
x = 4 (nhận).
Vậy S = {−1; 4}.
Chọn phương án D
Câu 4. Hình lập phương có đường chéo của mặt bên bằng 4 cm. Tính thể tích khối lập phương đó.
A. 8
√
2 cm
3
. B. 16
√
2 cm
3
. C. 8 cm
3
. D. 2
√
2 cm
3
.
Lời giải.
Độ dài các cạnh hình lập phương là
4
√
2
= 2
√
2 cm.
Thể tích khối lập phương là V = (2
√
2)
3
= 16
√
2 cm
3
.
Chọn phương án B
Câu 5. Tìm tập xác định của hàm số y = log
1
2
(x + 1).
A. D = (−∞; −1). B. D = (−1; +∞). C. D = [−1; +∞). D. D = R\{1}.
Lời giải.
GeoGebraPro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Điều kiện x + 1 > 0 ⇔ x > −1. Suy ra tập xác định D = (−1; +∞).
Chọn phương án B
Câu 6. Hàm số f(x) = cos(4x + 7) có một nguyên hàm là
A. −sin(4x + 7) + x. B.
1
4
sin(4x + 7) − 3. C. sin(4x + 7) − 1. D. −
1
4
sin(4x + 7) + 3.
Lời giải.
Hàm số f(x) = cos(4x + 7) có một nguyên hàm là
1
4
sin(4x + 7) − 3.
Chọn phương án B
Câu 7. Cho khối chóp tam giác có đường cao bằng 100 cm và cạnh đáy bằng 20 cm, 21 cm, 29 cm.
Tính thể tích khối chóp này.
A. 7 000
√
2 cm
3
. B. 6 000 cm
3
. C. 6 213 cm
3
. D. 7 000 cm
3
.
Lời giải.
Diện tích đáy
S =
20 + 21 + 29
2
Å
20 + 21 + 29
2
− 20
ãÅ
20 + 21 + 29
2
− 21
ãÅ
20 + 21 + 29
2
− 29
ã
= 210 cm
2
.
Thể tích khối chóp
V =
1
3
· S · h =
1
3
· 210 · 100 = 7 000 cm
3
.
Chọn phương án D
Câu 8. Cho khối nón có bán kính đáy r =
√
3 và chiều cao h = 4. Tính thể tích V của khối nón đã
cho.
A. V = 16π
√
3. B. V = 12π. C. V = 4. D. V = 4π.
Lời giải.
Áp dụng công thức tính thể tích của khối nón ta tính được V =
1
3
πr
2
h =
1
3
.π.(
√
3)
2
.4 = 4π.
Chọn phương án D
Câu 9. Tính diện tích của mặt cầu có bán kính r = 2.
A.
32
3
π. B. 8π. C. 32π. D. 16π.
Lời giải.
Phương pháp
Công thức tính diện tích mặt cầu bán kính R là S = 4πR
2
.
Cách giải
Công thức tính diện tích mặt cầu bán kính r = 2 là S = 4πr
2
= 16π.
Chọn phương án D
Câu 10. Cho hàm số y = f(x) có đạo hàm liên tục trên R và có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
−1−1
−2−2
−1−1
−∞−∞
Hàm số y = f(x) đồng biến trên khoảng nào sau đây
A. (0; 1). B. (−1; 0). C. (−∞; 1). D. (1; +∞).
Lời giải.
Từ bẳng biến thiên suy ra hàm số đã cho đồng biến trên các khoảng (−∞; −1) và (0; 1).
Chọn phương án A
GeoGebraPro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 11. Cho a, b > 0, log
3
a = p, log
3
b = p. Đẳng thức nào dưới đây đúng?
A. log
3
Å
3
r
a
m
b
d
ã
= r + pm − qd. B. log
3
Å
3
r
a
m
b
d
ã
= r + pm + qd.
C. log
3
Å
3
r
a
m
b
d
ã
= r − pm − qd. D. log
3
Å
3
r
a
m
b
d
ã
= r − pm + qd.
Lời giải.
Ta có log
3
Å
3
a
m
b
d
ã
= log
3
3
r
− log
3
a
m
b
d
= r − log
3
a
m
− log
3
b
d
= r − m log
3
a − d log
3
b
Chọn phương án C
Câu 12. Một hình trụ có diện tích xung quanh bằng S, diện tích đáy bằng diện tích một mặt cầu bán
kính a. Khi đó thể tích của hình trụ bằng
A. Sa. B.
1
2
Sa. C.
1
3
Sa. D.
1
4
Sa.
Lời giải.
Gọi r là bán kính đáy của hình trụ, h là chiều cao của hình trụ.
Theo bài ra ta có
®
S = 2πrh
πr
2
= 4πa
2
⇔
r = 2a
h =
S
4πa
.
Thể tích khối trụ là V = πr
2
h = π · 4a
2
·
S
4πa
= Sa.
Chọn phương án A
Câu 13.
Cho hàm số y = f(x) có bảng biến thiên như sau. Giá
trị cực đại của hàm số bằng
A. 1. B. 2. C. 0. D. 5.
x
y
0
y
−∞
0 2
+∞
−
0
+
0
−
+∞+∞
11
55
−∞−∞
Lời giải.
Giá trị cực đại của hàm số bằng 5.
Chọn phương án D
Câu 14.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A. y = x
3
− 3x − 1. B. y = −x
3
− 3x
2
− 1.
C. y = −x
3
+ 3x
2
+ 1. D. y = x
3
− 3x + 1.
x
y
−1
3
1
−1
O
Lời giải.
Đường cong trong hình vẽ có dạng đồ thị của hàm số y = ax
3
+ bx
2
+ cx + d với a 6= 0.
Dựa vào đồ thị, ta có lim
x→+∞
y = +∞. Suy ra a > 0.
Mặt khác, giao điểm của đồ thị với trục tung tại điểm có tung độ dương nên d > 0.
Chỉ có hàm số y = x
3
− 3x + 1 thỏa mãn các đặc điểm trên.
Vậy đường cong trong hình vẽ là đồ thị của hàm số y = x
3
− 3x + 1.
Chọn phương án D
Câu 15. Tiệm cận ngang của đồ thị hàm số y =
5
x − 1
là đường thẳng có phương trình nào dưới
đây?
A. x = 1. B. y = 5. C. x = 0. D. y = 0.
GeoGebraPro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
Lời giải.
Ta có:
lim
x→+∞
5
x − 1
= 0
lim
x→−∞
5
x − 1
= 0
⇒ đồ thị hàm số có tiệm cận ngang là y = 0.
Chọn phương án D
Câu 16. Tập nghiệm của bất phương trình log
2
x > log
2
(8 − x) là
A. (8; +∞). B. (−∞; 4). C. (4; 8). D. (0; 4).
Lời giải.
Điều kiện 0 < x < 8.
Do 2 > 1 nên bất phương trình đã cho tương đương với
x > 8 − x ⇔ 2x > 8 ⇔ x > 4.
Kết hợp với điều kiện 0 < x < 8 ta được tập nghiệm của bất phương trình là (4; 8)
Chọn phương án C
Câu 17. Cho hàm số y = f(x) có bảng biến thiên như hình sau
x
f
0
(x)
f(x)
−∞
−2
0 2
+∞
−
0
+
0
−
0
+
+∞+∞
−2−2
11
−2−2
+∞+∞
Số nghiệm thực của phương trình 2f(x) + 3 = 0 là
A. 4. B. 3. C. 2. D. 1.
Lời giải.
2f(x) + 3 = 0 ⇔ f(x) = −
3
2
.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = −
3
2
.
Mà −2 < −
3
2
< 1 nên số nghiệm thực của phương trình 2f(x) + 3 = 0 là 4.
Chọn phương án A
Câu 18. Nếu
5
Z
2
f(x)dx = 3 và
7
Z
5
f(x)dx = 9 thì
7
Z
2
f(x)dx bằng bao nhiêu?
A. 3. B. 6. C. 12. D. −6.
Lời giải.
Ta có
7
Z
2
f(x)dx =
5
Z
2
f(x)dx +
7
Z
5
f(x)dx = 3 + 9 = 12.
Chọn phương án C
Câu 19. Tìm số phức liên hợp của của số z = 5 + i.
A. z = 5 − i. B. z = −5 − i. C. z = 5 + i. D. z = −5 + i.
Lời giải.
Số phức liên hợp của của số a + bi là a − bi. Do đó z = 5 − i.
Chọn phương án A
Câu 20. Cho hai số phức z
1
= 2 − 7i và z
2
= −4 + i. Điểm biểu diễn số phức z
1
+ z
2
trên mặt phẳng
tọa độ là điểm nào dưới đây?
A. Q(−2; −6). B. P (−5; −3). C. N(6; −8). D. M(3; −11).
Lời giải.
Ta có z
1
+ z
2
= −2 − 6i. Vậy điểm biểu diễn z
1
+ z
2
trên mặt phẳng tọa độ là điểm Q(−2; −6).
Chọn phương án A
GeoGebraPro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 21.
Trên mặt phẳng tọa độ Oxy cho điểm M trong hình vẽ bên là điểm biểu diễn của
số phức z. Tìm z.
A. z = −4 + 3i. B. z = −3 + 4i. C. z = 3 − 4i. D. z = 3 + 4i.
x
y
O
M
3
−4
Lời giải.
Điểm M có tọa độ là M (3; −4) ⇒ điểm M biểu diễn số phức z = 3 − 4i.
Chọn phương án C
Câu 22. Trong không gian với hệ tọa độ Oxyz, tọa độ hình chiếu vuông góc của điểm A(2; −1; 0) lên
mặt phẳng (P ) : 3x − 2y + z + 6 = 0 là
A. (1; 1; 1). B. (−1; 1; −1). C. (3; −2; 1). D. (5; −3; 1).
Lời giải.
Gọi H(x; y; −6−3x +2y) là hình chiếu của A lên mặt phẳng P . Ta có
# »
AH = (x−2; y + 1; −6 −3x+2y).
Do
# »
AH ⊥ (P ) nên hai véc-tơ
# »
AH và
#»
n
P
cùng phương. Suy ra ta có hệ phương trình
x − 2
3
=
y + 1
−2
=
−6 − 3x + 2y
1
. (1)
Giải hệ (1) ta thu được một nghiệm là (−1; 1; −1).
Chọn phương án B
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình x
2
+ y
2
+ z
2
−2x + 4y −
6z + 9 = 0. Tọa độ tâm I và bán kính R của mặt cầu là
A. I (1; −2; 3) và R = 5. B. I (1; −2; 3) và R =
√
5.
C. I (−1; 2; −3) và R = 5. D. I (−1; 2; −3) và R =
√
5.
Lời giải.
Mặt cầu x
2
+ y
2
+ z
2
−2x + 4y −6z + 9 = 0 có tâm I (1; −2; 3) và bán kính R =
√
1 + 4 + 9 − 9 =
√
5.
Chọn phương án C
Câu 24. Trong không gian Oxyz, cho mặt phẳng (P ): x −2z + 1 = 0. Vectơ nào dưới đây là một vectơ
pháp tuyến của (P )?
A.
#»
n
1
= (1; 0; −2). B.
#»
n
2
= (1; −2; 1). C.
#»
n
3
= (1; −2; 0). D.
#»
n
4
= (−1; 2; 0).
Lời giải.
Vectơ pháp tuyến của (P ) là
#»
n = (1; 0; −2).
Chọn phương án A
Câu 25. Trong không gian Oxyz, cho đường thẳng d:
x − 1
2
=
y − 2
1
=
z
−2
. Điểm nào dưới đây thuộc
đường thẳng d?
A. M(−1; −2; 0). B. M(−1; 1; 2). C. M(2; 1; −2). D. M(3; 3; 2).
Lời giải.
Ta có
−1 − 1
2
=
1 − 2
1
=
2
−2
= −1 nên M(−1; 1; 2) thuộc đường thẳng d.
Chọn phương án B
Câu 26. Cho hình chóp S.ABCD đều có SA = AB = a. Góc giữa SA và CD là
A. 60
◦
. B. 30
◦
. C. 90
◦
. D. 45
◦
.
Lời giải.
GeoGebraPro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
Vì AB ∥ CD nên góc giữa SA và CD bằng góc giữa SA và
AB.
Vì SA = AB nên tam giác SAB đều, vậy góc giữa chúng bằng
60
◦
.
S
A
D
B
C
Chọn phương án A
Câu 27. Gọi M, m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) =
4
x
+ x + 1 trên đoạn [1; 3].
Tính M − m.
A. 4. B. 9. C. 1. D. 5.
Lời giải.
Ta có f
0
(x) = −
4
x
2
+ 1 và f
0
(x) = 0 ⇔ −
4
x
2
+ 1 = 0 ⇔
ñ
x = 2 ∈ [1; 3]
x = −2 /∈ [1; 3].
Ta tính được f(1) = 6, f(2) = 5, f(3) =
16
3
.
Kết hợp với f(x) liên tục trên [1; 3] nên M = max
x∈[1;3]
f(x) = 6 = f(1) và m = min
x∈[1;3]
f(x) = 5 = f(2).
Vậy M − m = 1.
Chọn phương án C
Câu 28. Giá trị nhỏ nhất của hàm số f(x) = x
3
+ 3x + 1 trên đoạn [1; 3] là
A. min
[1;3]
f(x) = 3. B. min
[1;3]
f(x) = 6. C. min
[1;3]
f(x) = 37. D. min
[1;3]
f(x) = 5.
Lời giải.
Ta có f
0
(x) = 3x
2
+ 3 > 0 với mọi x. Lại có f(1) = 5, f(3) = 37 nên min
[1;3]
f(x) = 5.
Chọn phương án D
Câu 29. Với a là số thực dương bất kỳ, mệnh đề nào dưới đây đúng?
A. log(3a) = 3 log a. B. log a
3
= 3 log a. C. log(3a) =
1
3
log a. D. log a
3
=
1
3
log a.
Lời giải.
Theo tính chất ta có log a
3
= 3 log a.
Chọn phương án B
Câu 30. Số giao điểm của đồ thị hàm số y =
2x + 1
x − 1
với đường thẳng y = 2x + 3 là
A. 2. B. 3. C. 1. D. 0.
Lời giải.
Xét phương trình hoành độ giao điểm
2x + 1
x − 1
= 2x + 3
⇔2x + 1 = (2x + 3) (x − 1) (do x = 1 không là nghiệm của phương trình)
⇔2x
2
− x − 4 = 0
⇔
x =
1 +
√
33
4
x =
1 −
√
33
4
.
GeoGebraPro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Vậy đường thẳng y = 2x + 3 cắt đồ thị hàm số y =
2x + 1
x − 1
tại hai điểm.
Chọn phương án A
Câu 31. Tập nghiệm của bất phương trình 3
x
2
−2x
< 27 là
A. (−∞; −1). B. (3; +∞).
C. (−1; 3). D. (−∞; −1) ∪ (3; +∞).
Lời giải.
3
x
2
−2x
< 27 ⇔ 3
x
2
−2x
< 3
3
⇔ x
2
− 2x < 3 ⇔ x
2
− 2x − 3 < 0 ⇔ −1 < x < 3.
Chọn phương án C
Câu 32. Trong không gian, cho tam giác ABC vuông tại A, AB = a và AC = a
√
3. Tính độ dài đường
sinh ` của hình nón có được khi quay tam giác ABC xung quanh trục AB.
A. ` = a. B. ` = 2a. C. ` = a
√
3. D. ` = a
√
2.
Lời giải.
Khi quay tam giác ABC vuông tại A xung quanh
trục AB ta được hình nón có đường sinh là BC.
Tam giác ABC vuông tại A nên
BC
2
= AB
2
+ AC
2
= a
2
+ 3a
2
= 4a
2
.
Vậy l = BC = 2a.
C
B
AA C
B
Chọn phương án B
Câu 33. Cho tích phân I =
1
Z
0
x
7
(1 + x
2
)
5
dx, giả sử đặt t = 1 + x
2
. Tìm mệnh đề đúng.
A. I =
1
2
2
Z
1
(t − 1)
3
t
5
dt. B. I =
3
Z
1
(t − 1)
3
t
5
dt. C.
1
2
2
Z
1
(t − 1)
3
t
4
dt. D.
3
2
4
Z
1
(t − 1)
3
t
4
dt.
Lời giải.
Đặt t = 1 + x
2
⇒
1
2
dt = x dx.
Đổi cận x = 0 ⇒ t = 1, x = 1 ⇒ t = 2.
Khi đó
I =
1
Z
0
(x
2
)
3
· x
(1 + x
2
)
5
dx =
1
2
2
Z
1
(t − 1)
3
t
5
dt.
Chọn phương án A
Câu 34. Thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi parabol (P ): y = x
2
và
đường thẳng d: y = x xoay quanh trục Ox bằng
A. π
1
Z
0
x
2
dx − π
1
Z
0
x
4
dx. B. π
1
Z
0
x
2
dx + π
1
Z
0
x
4
dx.
C. π
1
Z
0
x
2
− x
2
dx. D. π
1
Z
0
x
2
− x
dx.
Lời giải.
GeoGebraPro Trang 7
https://www.facebook.com/groups/GeoGebraPro/
Ta có (P ) và d cắt nhau tại hai điểm (0; 0), (1; 1) và x > x
2
, ∀x ∈ (0; 1).
Suy ra thể tích khối tròn xoay đã cho T bằng thể tích khối tròn xoay T
1
trừ
đi thể tích khối tròn xoay T
2
. Trong đó
• T
1
được sinh ra khi quay hình phẳng giới hạn bởi các đường d, trục
Ox, x = 0, x = 1.
• T
2
được sinh ra khi quay hình phẳng giới hạn bởi các đường (P ), trục
Ox, x = 0, x = 1.
Vậy thể tích khối tròn xoay đã cho bằng π
1
Z
0
x
2
dx − π
1
Z
0
x
4
dx.
x
y
O
1
1
Chọn phương án A
Câu 35. Cho hai số phức z = 6 + 5i và z
0
= 5 − 4i + z. Tìm mô-đun của số phức w = z · z
0
.
A. |w| = 612. B. |w| = 61. C. |w| = 61
√
2. D. |w| = 6
√
2.
Lời giải.
Ta có z
0
= 5 − 4i + 6 + 5i = 11 + i ⇒ z · z
0
= 61 + 61i. Do đó |w| = 61
√
2.
Chọn phương án C
Câu 36. Gọi z
1
và z
2
lần lượt là nghiệm của phươngtrình: z
2
−2z + 5 = 0. Tính P = |z
1
|
2
+ |z
2
|
2
.
A. P = 2
√
5. B. P = 20. C. P = 10. D. P =
√
5.
Lời giải.
Ta có z
2
− 2z + 5 = 0 ⇔
ñ
z = 1 − 2i
z = 1 + 2i
. Khi đó, P = |z
1
|
2
+ |z
2
|
2
= 2
√
5.
Chọn phương án A
Câu 37. Trong không gian Oxyz, mặt phẳng chứa trục Ox và đi qua điểm A(1; 1; −1) có phương trình
là
A. z + 1 = 0. B. x − y = 0. C. x + z = 0. D. y + z = 0.
Lời giải.
Mặt phẳng chứa trục Ox có dạng By + Cz = 0, (B
2
+ C
2
6= 0).
Mặt phẳng đi qua điểm A(1; 1; −1) nên B − C = 0 ⇔ B = C. Do đó chọn B = C = 1.
Chọn phương án D
Câu 38. Trong không gian Oxyz, cho hai điểm A(1; 2; 3) và B(2; 4; −1). Phương trình chính tắc của
đường thẳng d đi qua A, B là
A.
x + 2
1
=
y + 4
2
=
z + 1
4
. B.
x + 1
1
=
y + 2
2
=
z + 3
4
.
C.
x − 1
1
=
y − 2
2
=
z − 3
−4
. D.
x + 2
1
=
y + 4
2
=
z − 1
−4
.
Lời giải.
Ta có đường thẳng d đi qua A(1; 2; 3) và có véc-tơ chỉ phương
# »
AB = (1; 2; −4). Vậy phương trình chính
tắc đường thẳng d là
x − 1
1
=
y − 2
2
=
z − 3
−4
·
Chọn phương án C
Câu 39. Một nhóm có 7 học sinh lớp A và 5 học sinh lớp B. Xếp ngẫu nhiên 12 học sinh trên ngồi vào
một dãy 12 ghế hàng ngang sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất sao cho không
có bất kì 2 học sinh lớp B nào ngồi cạnh nhau.
A.
7
99
. B.
1
132
. C.
7
264
. D.
1
792
.
Lời giải.
• Xếp 12 học sinh ngồi vào một dãy 12 ghế hàng ngang sao cho mỗi ghế có đúng một học sinh ngồi
có 12! cách.
GeoGebraPro Trang 8
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
• Xếp 7 học sinh lớp A vào 7 ghế, có 7! cách.
Khi đó 7 ghế đã xếp học sinh lớp A tạo ra 8 khoảng trống, ta xếp 5 học sinh lớp B vào 5 trong 8
khoảng trống đó, có A
5
8
cách.
⇒ có 7! · A
5
8
cách xếp 12 học sinh mà các học sinh lớp B không ngồi cạnh nhau.
Vậy xác suất cần tìm là
7! · A
5
8
12!
=
7
99
.
Chọn phương án A
Câu 40. Cho hình lăng trụ tam giác đều ABC.A
0
B
0
C
0
có tất cả các cạnh đều bằng a. Khoảng cách từ
A đến mặt phẳng (A
0
BC) bằng
A.
a
√
3
4
. B.
a
√
21
7
. C.
a
√
2
2
. D.
a
√
6
4
.
Lời giải.
Gọi H là trung điểm của BC, do giả thiết 4ABC đều nên AH =
a
√
3
2
và AH ⊥ BC (1).
Do AA
0
⊥ (ABC) suy ra AA
0
⊥ BC (2).
Từ (1), (2) ta suy ra BC ⊥ (AA
0
H).
Trong mặt phằng (AA
0
H) kẻ AI ⊥ A
0
H (3).
Theo chứng minh trên BC ⊥ (AA
0
H) nên BC ⊥ AI (4).
Từ (3), (4) suy ra AI ⊥ (AA
0
H) do đó khoảng cách từ A đến mặt
phẳng (A
0
BC) là AI.
Xét 4AA
0
H ta có
1
AI
2
=
1
AA
02
+
1
AH
2
=
1
a
2
+
4
3a
2
suy ra AI
2
=
3a
2
7
⇔ AI =
a
√
21
7
.
Vậy khoảng cách từ A đến mặt phẳng (BA
0
C) bằng
a
√
21
7
.
A
A
0
B
I
C
C
0
H
B
0
Chọn phương án B
Câu 41. Có bao nhiêu giá trị nguyên của m để hàm số y = x
3
+ 3x
2
− (m
2
− 3m + 2)x + 5 đồng biến
trên (0; 2)?
A. 3. B. 2. C. 4. D. 1.
Lời giải.
Ta có y = x
3
+ 3x
2
− (m
2
− 3m + 2)x + 5 ⇒ y
0
= 3x
2
+ 6x − (m
2
− 3m + 2).
Hàm số đồng biến trên khoảng (0; 2) khi y
0
≥ 0, ∀x ∈ (0; 2) và dấu "=" xãy ra tại hữu hạn điểm trên
khoảng đó.
⇔ 3x
2
+ 6x − (m
2
− 3m + 2) ≥ 0, ∀x ∈ (0; 2)
⇔ 3x
2
+ 6x ≥ m
2
− 3m + 2 (∗) với ∀x ∈ (0; 2)
Xét hàm số y = g(x) = 3x
2
+ 6x trên khoảng (0; 2)
Ta có y
0
= g
0
(x) = 6x + 6.
Bảng biến thiên
x
g
0
(x)
g(x)
0 2
+
00
2424
Dựa vào bảng biến thiên suy ra điều kiện để (∗) xảy ra là : m
2
− 3m + 2 ≤ 0 ⇔ 1 ≤ m ≤ 2.
GeoGebraPro Trang 9
https://www.facebook.com/groups/GeoGebraPro/
Do m ∈ Z ⇒ m ∈ {1; 2}.
Vậy có 2 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn phương án B
Câu 42. Các nhà khoa học đã tính toán khi nhiệt độ trung bình của trái đất tăng thêm 2
◦
C thì mực
nước biển sẽ dâng lên 0, 03m. Nếu nhiệt độ tăng lên 5
◦
C thì nước biển sẽ dâng lên 0, 1m và người ta
đưa ra công thức tổng quát như sau: Nếu nhiệt độ trung bình của trái đất tăng lên t
o
C thì nước biển
dâng lên f(t) = ka
t
(m) trong đó k, a là các hằng số dương. Hỏi khi nhiệt độ trung bình của trái đất
tăng thêm bao nhiêu độ C thì mực nước biển dâng lên 0, 2m?
A. 9, 2
◦
C. B. 8, 6
◦
C. C. 7, 6
◦
C. D. 6, 7
◦
C.
Lời giải.
®
0, 03 = ka
2
0, 1 = ka
5
⇒
a =
3
…
10
3
k =
0, 03
a
2
; f(t) = ka
t
⇔ t = log
a
f(t)
k
= log
a
0, 2a
2
0, 03
≈ 6, 7.
Chọn phương án D
Câu 43. Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình bên dưới. Tìm tất cả
các giá trị thực của m để phương trình
1
2
f(x) − m = 0 có đúng hai nghiệm phân biệt.
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
00
−3−3
00
−∞−∞
A. m = 0 hoặc m < −
3
2
. B. m < −3.
C. m < −
3
2
. D. m = 0 hoặc m < −3.
Lời giải.
Ta có
1
2
f(x) = m ⇔ f(x) = 2m.
Số nghiệm của phương trình là số giao điểm của đồ thì hàm số y = f(x) và đường thẳng y = 2m.
Theo yêu cầu bài toán ta có
2m = 0 hoặc 2m < −3 ⇔ m = 0 hoặc m < −
3
2
.
Chọn phương án A
Câu 44. Cho hình trụ có bán kính đáy bằng a
√
2. Cắt hình trụ bởi một mặt phẳng, song song với trụ
của hình trụ và cách trục của hình trụ một khoảng bằng
a
2
ta được thiết diện là một hình vuông. Tính
thể tích V của khối trụ đã cho.
A. V = πa
3
√
3. B. V =
2πa
3
√
7
3
. C. V = 2πa
3
√
7. D. V = πa
3
.
Lời giải.
GeoGebraPro Trang 10
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Gọi O, O
0
lần lượt là tâm các đáy và thiết diện là hình vuông ABCD.
Gọi H là trung điểm AB, ta có
®
OH ⊥ AB
OH ⊥ AA
0
suy ra OH ⊥ (ABB
0
A
0
).
Do đó d (OO
0
, (ABCD)) = OH =
a
2
.
Tam giác OAH vuông tại H nên AH =
√
OA
2
− OH
2
=
…
2a
2
−
a
2
4
=
a
√
7
2
.
Suy ra AB = AA
0
= OO
0
= 2AH = a
√
7 (do ABCD là hình vuông).
Vậy thể tích V = πR
2
h = π ·
Ä
a
√
2
ä
2
· a
√
7 = 2πa
3
√
7.
O
0
B
0
O
B
H
A
A
0
Chọn phương án C
Câu 45. Cho hàm số y = f(x) liên tục trên R thỏa mãn
1
Z
0
f(x)dx = 3 và
5
Z
0
f(x)dx = 6. Tính tích
phân I =
1
Z
−1
f(|3x − 2|)dx
A. I = 3. B. I = −2. C. I = 4. D. I = 9.
Lời giải.
Ta có
1
Z
−1
f(|3x − 2|)dx =
2
3
Z
−1
f(−3x + 2)dx +
1
Z
2
3
f(3x − 2)dx = I
1
+ I
2
.
I
1
=
2
3
Z
−1
f(−3x + 2)dx = −
1
3
2
3
Z
−1
f(−3x + 2)d(−3x + 2).
Đặt t = −3x + 2 suy ra x = −1 ⇒ t = 5; x =
2
3
⇒ x = 0. Do đó I
1
=
1
3
5
Z
0
f(t)dt = 2.
I
2
=
1
Z
2
3
f(3x − 2)dx =
1
3
Z
2
3
1f(3x − 2)d(3x − 2).
Đặt t = 3x − 2 suy ra x = 1 ⇒ t = 1; x =
2
3
⇒ x = 0. Do đó I
2
=
1
3
1
Z
0
f(t)dt = 1.
Vậy I = I
1
+ I
2
= 3.
Chọn phương án A
Câu 46. Cho hàm số y = f(x) = ax
3
+ bx
2
+ cx + d có bảng biến thiên như sau
x
y
0
y
−∞
0 1
+∞
+
0
−
0
+
−∞−∞
11
00
+∞+∞
Khi đó |f(x)| = m có bốn nghiệm phân biệt x
1
< x
2
< x
3
<
1
2
< x
4
khi và chỉ khi
A.
1
2
< m < 1. B.
1
2
≤ m < 1. C. 0 < m < 1. D. 0 < m ≤ 1.
Lời giải.
GeoGebraPro Trang 11
https://www.facebook.com/groups/GeoGebraPro/
Ta có f
0
(x) = 3ax
2
+ 2bx + c. Từ bảng biến thiên của hàm số f(x), ta có
f(0) = 1
f(1) = 0
f
0
(0) = 0
f
0
(1) = 0
⇔
d = 1
a + b + c + d = 0
c = 0
3a + 2b + c = 0
⇔
a = 2
b = −3
c = 0
d = 1.
Như vậy f (x) = 2x
3
− 3x
2
+ 1, f
Å
1
2
ã
=
1
2
.
x
y
0
y
−∞
0 1
+∞
+
0
−
0
+
−∞−∞
11
00
+∞+∞
1
2
1
2
Do đó |f(x)| = m có bốn nghiệm phân biệt x
1
< x
2
< x
3
<
1
2
< x
4
khi và chỉ khi
1
2
≤ m < 1.
Chọn phương án B
Câu 47. Cho x, y là các số dương thỏa mãn xy ≤ 4y−1. Giá trị nhỏ nhất của P =
6 (2x + y)
x
+ln
x + 2y
y
là a + ln b. Tính ab.
A. ab = 45. B. ab = 81. C. ab = 115. D. ab = 108.
Lời giải.
Từ xy ≤ 4y − 1 chia 2 vế cho y
2
ta được
x
y
≤
4
y
−
1
y
2
= 4 −
Å
2 −
1
y
ã
2
≤ 4.
Đặt
x
y
= t thì 0 < t ≤ 4.
Khi đó P = f(t) = 12 +
6
t
+ ln(t + 2) có f
0
(t) =
−6
t
2
+
1
t + 2
=
t
2
− 6t − 12
t
2
(t + 2)
.
Ta có t
2
− 6t − 12 < 0 ⇔ t ∈ (3 −
√
21; 3 +
√
21) ⊃ (0; 4]. Suy ra f
0
(t) < 0, ∀t ∈ (0; 4].
Vậy min
(0;4]
f(t) = f(4) =
27
2
+ ln 6.
Suy ra giá trị nhỏ nhất của P bằng
27
2
+ ln 6 khi y =
1
2
, x = 2.
Khi đó a =
27
2
; b = 6 ⇒ ab = 81.
Chọn phương án B
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số
y =
x
2
+ mx + m
x + 1
trên [1; 2] bằng 2. Số phần tử của S là
A. 1. B. 4. C. 3. D. 2.
Lời giải.
Xét hàm số f(x) =
x
2
+ mx + m
x + 1
trên [1; 2]. Ta có f
0
(x) liên tục trên [1; 2] và
f
0
(x) =
x
2
+ 2x
(x + 1)
2
> 0, ∀x ∈ [1; 2].
Suy ra f(x) đồng biến trên [1; 2]. Do đó max
[1;2]
f(x) = f(2) =
3m + 4
3
, min
[1;2]
f(x) = f(1) =
2m + 1
2
.
Khi đó max
[1;2]
|f(x)| = max
ß
3m + 4
3
,
2m + 1
2
™
. Ta có
3m + 4
3
≥
2m + 1
2
⇔ 4(3m + 4)
2
≥ 9(2m + 1)
2
⇔ m ≥ −
11
12
.
GeoGebraPro Trang 12
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
• Với m ≥ −
11
12
, ta có max
[1;2]
|f(x)| =
3m + 4
3
. Theo đề bài, ta có
3m + 4
3
= 2 ⇔
3m + 4
3
= 2
3m + 4
3
= −2
⇔
m =
2
3
(thỏa mãn)
m = −
10
3
loại.
• Với m < −
11
12
, ta có max
[1;2]
|f(x)| =
2m + 1
2
. Theo đề bài, ta có
2m + 1
2
= 2 ⇔
2m + 1
2
= 2
2m + 1
2
= −2
⇔
m = −
5
2
(thỏa mãn)
m =
3
2
loại.
Vậy S =
ß
2
3
; −
5
2
™
⇒ Số phần tử của S là 2.
Chọn phương án D
Câu 49. Cho hình hộp ABCD.A
0
B
0
C
0
D
0
có đáy ABCD là hình thoi tâm O, cạnh a, góc
’
ABC = 60
◦
.
Biết rằng A
0
O ⊥ (ABCD) và cạnh bên hợp với đáy một góc bằng 60
◦
. Tính thể tích V của khối đa
diện OABC
0
D
0
.
A. V =
a
3
6
. B. V =
a
3
12
. C. V =
a
3
8
. D. V =
3a
3
4
.
Lời giải.
Từ giả thiết, suy ra tam giác ABC đều cạnh a ⇒ OA =
AC
2
=
a
2
.
Vì A
0
O ⊥ (ABCD) nên
60
◦
=
¤
(AA
0
, (ABCD)) =
⁄
(AA
0
, AO) =
’
A
0
AO.
Tam giác vuông A
0
AO có OA
0
= OA. tan
’
A
0
AO =
a
√
3
2
.
Suy ra thể tích khối hộp V = S
ABCD
.OA
0
=
3a
3
4
.
Ta có V = V
O.ABC
0
D
0
+V
AA
0
D
0
.BB
0
C
0
+V
C
0
.BOC
+V
D
0
.AOD
+V
O.CDD
0
C
0
= V
O.ABC
0
D
0
+
1
2
V +
1
12
V +
1
12
V +
1
6
V ⇒ V
O.ABC
0
D
0
=
V
6
=
a
3
8
.
A
B C
D
A
0
B
0
C
0
D
0
O
Chọn phương án C
Câu 50 (Thầy: Trương Đức Thịnh). Có bao nhiêu cặp số nguyên dương (x; y) với y ≤ 2020 thỏa
mãn
log
2
x + 2
y + 1
< 4y
4
+ 8y
3
−
x
2
+ 4x
y
2
+ 1
A. 2019.2020. B. 2020.2021. C. 2019
2
. D. 2020
2
.
Lời giải.
Ta có
log
2
x + 2
y + 1
< 4y
4
+ 8y
3
−
x
2
+ 4x
y
2
+ 1
⇔ log
2
x + 2
y + 1
< 4y
4
+ 8y
3
+ 4y
2
−
x
2
y
2
+ 4xy
2
+ 4y
2
⇔ log
2
xy + 2y
2y + 2
<
2y
2
+ 2y
− (xy + y)
2
⇔ log
2
(xy + 2y) + (xy + 2y)
2
< log
2
2y
2
+ 2y
+
2y
2
+ 2y
2
GeoGebraPro Trang 13
https://www.facebook.com/groups/GeoGebraPro/
Xét hàm số f(t) = log
2
(t) + t
2
đồng biến trên khoảng (0; +∞).
Bất phương trình có dạng: f(xy + 2y) < f (2y
2
+ 2y) ⇔ xy + 2y < 2y
2
+ 2y ⇔ x < 2y.
Do (x; y) và y ≤ 2020 nên
• Với y = 1 ⇒ x < 2 ⇒ x = 1.
• Với y = 2 ⇒ x < 4 ⇒ x ∈ {1; 2; 3}
• Với y = 3 ⇒ x < 6 ⇒ x ∈ {1; 2; 3; 4; 5}
······
• Với y = 2020 ⇒ x < 4040 ⇒ x ∈ {1; 2; 3; ···4039}
Vậy số cặp nguyên dương (x; y) thỏa mãn là 1 + 3 + 4 + ··· + 4039 = 2020
2
.
Chọn phương án D
———————–HẾT———————–
GeoGebraPro Trang 14
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
ĐÁP ÁN THAM KHẢO
1. A 2. D 3. D 4. B 5. B 6. B 7. D 8. D 9. D 10. A
11. C 12. A 13. D 14. D 15. D 16. C 17. A 18. C 19. A 20. A
21. C 22. B 23. C 24. A 25. B 26. A 27. C 28. D 29. B 30. A
31. C 32. B 33. A 34. A 35. C 36. A 37. D 38. C 39. A 40. B
41. B 42. D 43. A 44. C 45. A 46. B 47. B 48. D 49. C 50. D
GeoGebraPro Trang 15
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 5
Câu 1. Có bao nhiêu cách chọn 5 học sinh từ 20 học sinh
lớp 11A?
A. 1860480 cách. B. 120 cách.
C. 15504 cách. D. 100 cách.
Câu 2. Cho dãy (u
n
) là một cấp số cộng có u
1
= 2 và
u
9
= 26. Tìm u
5
.
A. 15. B. 13. C. 12. D. 14.
Câu 3. Gọi x
1
, x
2
là nghiệm của phương trình 7
x
2
−5x+9
=
343. Tính x
1
+ x
2
.
A. x
1
+ x
2
= 4. B. x
1
+ x
2
= 6.
C. x
1
+ x
2
= 5. D. x
1
+ x
2
= 3.
Câu 4. Nếu cạnh của một hình lập phương tăng lên gấp 3
lần thì thể tích của hình lập phương đó tăng lên bao nhiêu
lần?
A. 27. B. 9. C. 6. D. 4.
Câu 5. Trong các hàm số sau, hàm số nào có cùng tập xác
định với hàm số y = x
1
5
?
A. y = x
π
. B. y =
1
5
√
x
.
C. y =
√
x. D. y =
3
√
x.
Câu 6. Họ nguyên hàm của hàm số f (x) = x
2
+cos x là
A. 2x − sin x + C. B.
1
3
x
3
+ sin x + C.
C.
1
3
x
3
− sin x + C. D. x
3
+ sin x + C.
Câu 7. Cho khối chóp S.ABC có đáy là tam giác đều cạnh
bằng a, SA = a
√
3, cạnh bên SA vuông góc với đáy. Thể
tích khối chóp S.ABC bằng
A.
a
3
√
3
2
. B.
a
3
2
. C.
a
3
√
3
4
. D.
a
3
4
.
Câu 8. Cho khối nón có bán kính đáy bằng r, chiều cao h.
Thể tích V của khối nón là
A. V =
1
3
r
2
h. B. V = r
2
h.
C. V = πr
2
h. D. V =
1
3
πr
2
h.
Câu 9. Cho mặt cầu có diện tích bằng
8πa
2
3
. Tính bán
kính r của mặt cầu.
A. r =
a
√
6
3
. B. r =
a
√
3
3
.
C. r =
a
√
6
2
. D. r =
a
√
2
3
.
Câu 10. Cho hàm số y = f (x) có bảng biến thiên như sau
x
y
0
y
−∞
0 2
+∞
+
0
−
0
+
00
11
−3−3
+∞+∞
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. (2; +∞). B. (−∞; 1).
C. (0; +∞). D. (0; 2).
Câu 11. Với a, b là hai số thực dương tùy ý, ln
a
4
e
b
bằng
A. 4 ln a − ln b + 1. B. 4 ln b − ln a + 1.
C. 4 ln a + ln b − 1. D. 4 ln a + ln b + 1.
Câu 12. Khối trụ tròn xoay có đường kính bằng 2a, chiều
cao h = 2a có thể tích là
A. V = 2πa
2
. B. V = 2πa
3
.
C. V = 2πa
2
h. D. V = πa
3
.
Câu 13. Cho hàm số y = f (x) xác định, liên tục trên R và
có bảng biến thiên như sau:
x
y
0
y
−∞
−2
2
+∞
+
0
−
0
+
−∞−∞
33
00
+∞+∞
Tìm giá trị cực đại y
CĐ
và giá trị cực tiểu y
CT
của hàm số
đã cho
A. y
CĐ
= −2 và y
CT
= 2. B. y
CĐ
= 3 và y
CT
= 0.
C. y
CĐ
= 2 và y
CT
= 0. D. y
CĐ
= 3 và y
CT
= −2.
Câu 14. Đường cong trong hình vẽ bên là đồ thị của hàm
số nào dưới đây?
x
y
−1
−1
2
O
A. y =
2x − 1
x + 1
. B. y =
1 − 2x
x + 1
.
C. y =
2x + 1
x − 1
. D. y =
2x + 1
x + 1
.
Câu 15. Đường thẳng nào dưới đây là tiệm cận ngang của
đồ thị hàm số y =
1 − 4x
2x − 1
?
A. y = 2. B. y =
1
2
. C. y = 4. D. y = −2.
Câu 16. Tập nghiệm của bất phương trình log
2
(3x + 1) <
2 là
A.
ï
−
1
3
; 1
ã
. B.
Å
−
1
3
;
1
3
ã
.
C.
Å
−
1
3
; 1
ã
. D. (−∞; 1).
GeoGebraPro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Câu 17.
Cho hàm số f (x) có đồ thị như
hình vẽ. Số nghiệm của phương
trình 2f(x) − 3 = 0 là
x
y
−1
3
1
−1
O
A. 3. B. 1. C. 2. D. 0.
Câu 18. Nếu
5
Z
1
dx
2x − 1
= ln c với c ∈ Q thì giá trị của c
bằng
A. 9. B. 3. C. 6. D. 81.
Câu 19. Tìm phần ảo của số phức z = 8 − 12i.
A. −12. B. 18. C. 12. D. −12i.
Câu 20. Cho hai số phức z
1
= 1 + 2i, z
2
= 3 − i. Tìm số
phức z =
z
2
z
1
.
A. z =
1
10
+
7
10
i. B. z =
1
5
+
7
5
i.
C. z =
1
5
−
7
5
i. D. z = −
1
10
+
7
10
i.
Câu 21. Cho số phức z = 6 + 17i. Điểm biểu diễn cho số
phức z trên mặt phẳng tọa độ Oxy là
A. M (−6; −17). B. M (−17; −6).
C. M (17; 6). D. M (6; 17).
Câu 22. Trong không gian Oxyz, cho điểm M (3; 2; −1).
Hình chiếu vuông góc của điểm M lên trục Oz là điểm
A. M
3
(3; 0; 0). B. M
4
(0; 2; 0).
C. M
1
(0; 0; −1). D. M
2
(3; 2; 0).
Câu 23. Trong không gian với hệ tọa độ Oxyz phương
trình nào sau đây không phải là phương trình của một mặt
cầu?
A. x
2
+ y
2
+ z
2
+ x − 2y + 4z − 3 = 0.
B. 2x
2
+ 2y
2
+ 2z
2
− x − y − z = 0 .
C. x
2
+ y
2
+ z
2
− 2x + 4y − 4z + 10 = 0 .
D. 2x
2
+ 2y
2
+ 2z
2
+ 4x + 8y + 6z + 3 = 0.
Câu 24. Trong không gian Oxyz, mặt phẳng (P ): x+2y−
5 = 0 nhận vec-tơ nào trong các vec-tơ sau làm vec-tơ pháp
tuyến?
A.
#»
n (1; 2; −5). B.
#»
n (0; 1; 2).
C.
#»
n (1; 2; 0). D.
#»
n (1; 2; 5).
Câu 25. Trong không gian (Oxyz), cho đường thẳng
∆:
x = 3 − 3t
y = 1 + 2t
z = 5t
. Điểm nào dưới đây thuộc đường thẳng
∆?
A. N (0; 3; 5). B. M (−3; 2; 5).
C. (P (3; 1; 5). D. Q(6; −1; 5).
Câu 26. Cho hình chóp S.ABCD đều có SA = AB = a.
Góc giữa SA và CD là
A. 60
◦
. B. 30
◦
. C. 90
◦
. D. 45
◦
.
Câu 27. Cho hàm số y = f(x) xác định trên R và có bảng
xét dấu của đạo hàm như sau:
x
y
0
−∞
x
1
x
2
x
3
+∞
−
0
+ −
0
+
Khi đó số điểm cực trị của hàm số y = f(x) là
A. 3. B. 2. C. 4. D. 1.
Câu 28. Giá trị nhỏ nhất của hàm số y = x +
√
18 − x
2
là:
A. 0. B. 6. C. −3
√
2. D. −6.
Câu 29. Cho 0 < b < a < 1, mệnh đề nào dưới đây
đúng?
A. log
b
a < log
a
b. B. log
b
a < 0.
C. log
b
a > log
a
b. D. log
a
b < 1.
Câu 30. Số giao điểm của đồ thị hàm số y = x
2
x
2
− 4
với đường thẳng y = 3 là
A. 8. B. 2 . C. 4. D. 6 .
Câu 31. Tìm tập nghiệm của bất phương trình
log
2
5
(x − 4) + 1 > 0.
A.
ï
13
2
; +∞
ã
. B.
Å
−∞;
13
2
ã
.
C. (4; +∞). D.
Å
4;
13
2
ã
.
Câu 32. Tính thể tích khối tròn xoay sinh ra khi quay tam
giác đều ABC cạnh bằng 1 quanh AB.
A.
3π
4
. B.
π
4
. C.
π
8
. D.
π
√
3
2
.
Câu 33. Cho tích phân I =
3
Z
0
x
1 +
√
x + 1
dx. Nếu đặt
t =
√
x + 1 thì
A. I =
2
Z
1
(t
2
− 2t) dt. B. I =
2
Z
1
(2t
2
− t) dt.
C. I =
2
Z
1
(2t
2
+ 2t) dt. D. I =
2
Z
1
(2t
2
− 2t) dt.
Câu 34. Thể tích của khối tròn xoay do hình phẳng giới
hạn bởi các đường y =
√
x, trục Ox và hai đường thẳng
x = 1; x = 4 khi quay quanh trục hoành được tính bởi công
thức nào?
A. V = π
4
Z
1
x dx. B. V =
4
Z
1
√
x
dx.
C. V = π
2
4
Z
1
x dx. D. V = π
4
Z
1
√
x dx.
Câu 35. Cho hai số phức z
1
= 2 + i, z
2
= 4 − 3i. Khi đó
z
1
· z
2
có phần ảo bằng
A. 11. B. 2. C. −11. D. −2.
Câu 36. Gọi z
1
và z
2
lần lượt là nghiệm của phương trình:
z
2
− 2z + 5 = 0. Tính P = |z
1
| + |z
2
|.
A. 2
√
5. B. 10. C. 3. D. 6.
Câu 37. Trong không gian với hệ trục tọa độ Oxyz, cho
đường thẳng d:
x − 1
1
=
y + 2
−1
=
z
2
. Mặt phẳng (P ) đi qua
điểm M(2; 0; −1) và vuông góc với d có phương trình là
A. x − y + 2z = 0. B. x − 2y − 2 = 0.
C. x + y + 2z = 0. D. x − y −2z = 0.
GeoGebraPro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 38. Trong không gian tọa độ Oxyz, viết phương trình
chính tắc của đường thẳng d đi qua A(1; 2; −1) và vuông
góc với mặt phẳng (P ) : x + 2y − 3z + 1 = 0.
A. d:
x + 1
1
=
y + 2
−2
=
z − 1
−3
.
B. d :
x + 1
1
=
y + 2
2
=
z − 1
−3
.
C. d :
x − 1
1
=
y − 2
2
=
z + 1
3
.
D. d :
x − 1
−1
=
y − 2
−2
=
z + 1
3
.
Câu 39. Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp
12A, 3 học sinh lớp 12B và 5 học sinh lớp 12C trên một bàn
tròn. Tính xác suất P để các học sinh cùng lớp luôn ngồi
cạnh nhau.
A. P =
1
1260
. B. P =
1
126
.
C. P =
1
28
. D. P =
1
252
.
Câu 40. Cho tứ diện OABC có OA, OB, OC đôi một
vuông góc với nhau và OC = 2a, OA = OB = a. Gọi
M là trung điểm của AB. Tính khoảng cách giữa hai đường
thẳng OM và AC.
A.
2a
3
. B.
2
√
5a
5
. C.
√
2a
3
. D.
√
2a
2
.
Câu 41. Cho hàm số y = −x
3
−mx
2
+ (4m + 9)x + 5, với
m là tham số. Có bao nhiêu giá trị nguyên của m để hàm
số nghịch biến R?
A. 6. B. 4. C. 7. D. 5.
Câu 42. Gọi N(t) là số phần trăm cacbon 14 còn lại trong
một bộ phận của một cây sinh trưởng từ t năm trước đây
thì ta có công thức N (t) = 100.(0.5)
t
A
(%) với A là hằng số.
Biết rằng một mẩu gỗ có tuổi khoảng 3754 năm thì lượng
cácbon 14 còn lại là 65%. Phân tích mẩu gỗ từ một công
trình kiến trúc cổ, người ta thấy lượng cácbon 14 còn lại
trong mẩu gỗ là 63%. Hãy xác định tuổi của mẩu gỗ được
lấy từ công trình đó.
A. 3874. B. 3833. C. 3834. D. 3843.
Câu 43.
Cho hàm số y = f (x)
có đạo hàm f
0
(x), biết
rằng đồ thị của hàm
số f
0
(x) như hình vẽ.
Biết f(a) > 0, hỏi đồ
thị hàm số y = f (x)
cắt trục hoành tại nhiều
nhất bao nhiêu điểm?
x
y
O
a
b
c
A. 4. B. 2. C. 3. D. 1.
Câu 44. Cắt khối trụ bởi một mặt phẳng qua trục ta được
thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai
đáy của hình trụ, AB = 4a, AC = 5a. Thể tích V của khối
trụ là
A. V = 16πa
3
. B. V = 4πa
3
.
C. V = 12πa
3
. D. V = 8πa
3
.
Câu 45. Cho hàm số y = f (x) có đạo hàm liên tục trên
đoạn [0; 1] và thỏa mãn f (0) = 0. Biết
1
Z
0
f
2
(x) dx =
9
2
và
1
Z
0
f
0
(x) cos
πx
2
dx =
3π
4
. Tích phân
1
Z
0
f (x) dx bằng.
b
Z
a
f(x) dx.
A.
6
π
. B.
2
π
. C.
4
π
. D.
1
π
.
Câu 46. Cho hàm số y = f(x) có bảng biến thiên như hình
bên.
x
f
0
f
−∞
0 4
+∞
−
0
+
0
−
+∞+∞
−1−1
33
−∞−∞
Phương trình f (4x −x
2
) −2 = 0 có bao nhiêu nghiệm thực
phân biệt?
A. 2. B. 6. C. 4. D. 0.
Câu 47. Cho các số thực a, b thỏa mãn điều kiện 0 <
b < a < 1. Tìm giá trị nhỏ nhất của biểu thức P =
log
a
4(3b − 1)
9
+ 8 log
2
b
a
a − 1.
A. A = 6. B. 3
3
√
2. C. 8. D. 7.
Câu 48. Gọi S là tập hợp tất cả các giá trị của tham
số thực m sao cho trị lớn nhất của hàm số y =
3x
2
− 6x + 2m − 1
trên đoạn [−2; 3] đạt giá trị nhỏ nhất.
Số phần tử của tập S là
A. 0. B. 3. C. 2. D. 1.
Câu 49. Cho hình hộp chữ nhật ABCD.A
0
B
0
C
0
D
0
. Gọi M
là trung điểm của BB
0
. Mặt phẳng (M DC
0
) chia khối hộp
chữ nhật thành hai khối đa diện, một khối chứa đỉnh C và
một khối chứa đỉnh A
0
. Gọi V
1
, V
2
lần lượt là thể tích của
hai khối đa diện chứa C và A
0
. Tính
V
1
V
2
.
A.
V
1
V
2
=
7
24
. B.
V
1
V
2
=
7
17
.
C.
V
1
V
2
=
7
12
. D.
V
1
V
2
=
17
24
.
Câu 50. Xét các số thực dương x, y thỏa mãn
ln
Å
1 − 2x
x + y
ã
= 3x + y − 1. Tìm giá trị nhỏ nhất P
min
của P =
1
x
+
1
√
xy
+ 1
A. P
min
= 8. B. P
min
= 16.
C. P
min
= 9. D. P
min
= 2.
———————–HẾT———————–
GeoGebraPro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
ĐÁP ÁN THAM KHẢO
1. C 2. D 3. C 4. A 5. A 6. B 7. D 8. D 9. A 10. A
11. A 12. B 13. B 14. A 15. D 16. C 17. A 18. B 19. A 20. C
21. D 22. C 23. C 24. C 25. A 26. A 27. A 28. C 29. A 30. D
31. D 32. B 33. D 34. A 35. D 36. A 37. A 38. D 39. B 40. B
41. C 42. B 43. B 44. C 45. A 46. C 47. D 48. D 49. B 50. A
GeoGebraPro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 5
Câu 1. Có bao nhiêu cách chọn 5 học sinh từ 20 học sinh
lớp 11A?
A. 1860480 cách. B. 120 cách.
C. 15504 cách. D. 100 cách.
Lời giải.
Số cách chọn 5 học sinh từ 20 học sinh lớp 11A là C
5
20
=
15504 cách.
Chọn phương án C
Câu 2. Cho dãy (u
n
) là một cấp số cộng có u
1
= 2 và
u
9
= 26. Tìm u
5
.
A. 15. B. 13. C. 12. D. 14.
Lời giải.
Ta có u
1
+u
9
= u
1
+u
1
+8d = 2u
1
+8d = 2(u
1
+4d) = 2u
5
.
Do đó u
5
=
u
1
+ u
9
2
=
2 + 26
2
= 14.
Chọn phương án D
Câu 3. Gọi x
1
, x
2
là nghiệm của phương trình 7
x
2
−5x+9
=
343. Tính x
1
+ x
2
.
A. x
1
+ x
2
= 4. B. x
1
+ x
2
= 6.
C. x
1
+ x
2
= 5. D. x
1
+ x
2
= 3.
Lời giải.
Ta có 7
x
2
−5x+9
= 343 ⇔ 7
x
2
−5x+9
= 7
3
⇔ x
2
− 5x + 9 =
3 ⇔ x
2
− 5x + 6 = 0 ⇔
ñ
x = 2
x = 3.
Do đó tổng hai nghiệm x
1
+ x
2
= 2 + 3 = 5.
Chọn phương án C
Câu 4. Nếu cạnh của một hình lập phương tăng lên gấp 3
lần thì thể tích của hình lập phương đó tăng lên bao nhiêu
lần?
A. 27. B. 9. C. 6. D. 4.
Lời giải.
V
0
= (3a)
3
= 3
3
· a
3
= 27V .
Chọn phương án A
Câu 5. Trong các hàm số sau, hàm số nào có cùng tập xác
định với hàm số y = x
1
5
?
A. y = x
π
. B. y =
1
5
√
x
.
C. y =
√
x. D. y =
3
√
x.
Lời giải.
Ta có tập xác định hàm số y = x
1
5
là (0; +∞).
• Hàm số y = x
π
cũng có tập xác định là (0; +∞).
• Hàm số y =
1
5
√
x
có tập xác định là R \
0
.
• Hàm số y =
√
x có tập xác định là [0; +∞).
• Hàm số y =
3
√
x có tập xác định là R.
Chọn phương án A
Câu 6. Họ nguyên hàm của hàm số f (x) = x
2
+cos x là
A. 2x − sin x + C. B.
1
3
x
3
+ sin x + C.
C.
1
3
x
3
− sin x + C. D. x
3
+ sin x + C.
Lời giải.
Ta có:
Z
(x
2
+ cos x)dx =
1
3
x
3
+ sin x + C.
Chọn phương án B
Câu 7. Cho khối chóp S.ABC có đáy là tam giác đều cạnh
bằng a, SA = a
√
3, cạnh bên SA vuông góc với đáy. Thể
tích khối chóp S.ABC bằng
A.
a
3
√
3
2
. B.
a
3
2
. C.
a
3
√
3
4
. D.
a
3
4
.
Lời giải.
Thể tích khối chóp là
V =
1
3
· SA · S
ABC
=
1
3
· a
√
3 ·
a
2
√
3
4
=
a
3
4
.
C
B
A
S
Chọn phương án D
Câu 8. Cho khối nón có bán kính đáy bằng r, chiều cao h.
Thể tích V của khối nón là
A. V =
1
3
r
2
h. B. V = r
2
h.
C. V = πr
2
h. D. V =
1
3
πr
2
h.
Lời giải.
Ta có V =
1
3
πr
2
h.
Chọn phương án D
Câu 9. Cho mặt cầu có diện tích bằng
8πa
2
3
. Tính bán
kính r của mặt cầu.
A. r =
a
√
6
3
. B. r =
a
√
3
3
.
C. r =
a
√
6
2
. D. r =
a
√
2
3
.
Lời giải.
Diện tích mặt cầu đã cho là 4πr
2
=
8πa
2
3
. Suy ra r =
a
√
6
3
.
Chọn phương án A
Câu 10. Cho hàm số y = f (x) có bảng biến thiên như sau
x
y
0
y
−∞
0 2
+∞
+
0
−
0
+
00
11
−3−3
+∞+∞
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. (2; +∞). B. (−∞; 1).
C. (0; +∞). D. (0; 2).
Lời giải.
GeoGebraPro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Dựa vào bảng biến thiên, hàm số đã cho đồng biến trên các
khoảng (−∞; 0) và (2; +∞).
Chọn phương án A
Câu 11. Với a, b là hai số thực dương tùy ý, ln
a
4
e
b
bằng
A. 4 ln a − ln b + 1. B. 4 ln b − ln a + 1.
C. 4 ln a + ln b − 1. D. 4 ln a + ln b + 1.
Lời giải.
Ta có: ln
a
4
e
b
= ln a
4
+ ln e − ln b = 4 ln a + 1 − ln b =
4 ln a − ln b + 1.
Chọn phương án A
Câu 12. Khối trụ tròn xoay có đường kính bằng 2a, chiều
cao h = 2a có thể tích là
A. V = 2πa
2
. B. V = 2πa
3
.
C. V = 2πa
2
h. D. V = πa
3
.
Lời giải.
Khối trụ tròn xoay có bán kính bằng
2a
2
= a nên có thể
tích là V = πa
2
· 2a = 2πa
3
.
Chọn phương án B
Câu 13. Cho hàm số y = f (x) xác định, liên tục trên R và
có bảng biến thiên như sau:
x
y
0
y
−∞
−2
2
+∞
+
0
−
0
+
−∞−∞
33
00
+∞+∞
Tìm giá trị cực đại y
CĐ
và giá trị cực tiểu y
CT
của hàm số
đã cho
A. y
CĐ
= −2 và y
CT
= 2. B. y
CĐ
= 3 và y
CT
= 0.
C. y
CĐ
= 2 và y
CT
= 0. D. y
CĐ
= 3 và y
CT
= −2.
Lời giải.
Từ bảng biến thiên ta có y
CĐ
= 3 và y
CT
= 0.
Chọn phương án B
Câu 14. Đường cong trong hình vẽ bên là đồ thị của hàm
số nào dưới đây?
x
y
−1
−1
2
O
A. y =
2x − 1
x + 1
. B. y =
1 − 2x
x + 1
.
C. y =
2x + 1
x − 1
. D. y =
2x + 1
x + 1
.
Lời giải.
Đồ thị hàm số có đường tiệm đứng là x = −1. Đồ thị hàm
số đi qua điểm A(0; −1).
Chọn phương án A
Câu 15. Đường thẳng nào dưới đây là tiệm cận ngang của
đồ thị hàm số y =
1 − 4x
2x − 1
?
A. y = 2. B. y =
1
2
. C. y = 4. D. y = −2.
Lời giải.
Ta có: lim
x→+∞
y = −2 và lim
x→−∞
y = −2 nên đường thẳng
y = −2 là đường tiệm cận ngang của đồ thị hàm số.
Chọn phương án D
Câu 16. Tập nghiệm của bất phương trình log
2
(3x + 1) <
2 là
A.
ï
−
1
3
; 1
ã
. B.
Å
−
1
3
;
1
3
ã
.
C.
Å
−
1
3
; 1
ã
. D. (−∞; 1).
Lời giải.
ĐK: x > −
1
3
log
2
(3x + 1) < 2 ⇔ 3x + 1 < 4 ⇔ x < 1.
Kết hợp với điều kiện ta được nghiệm của bất phương trình
là −
1
3
< x < 1.
Vậy tập nghiệm của bất phương trình
Å
−
1
3
; 1
ã
.
Chọn phương án C
Câu 17.
Cho hàm số f (x) có đồ thị như
hình vẽ. Số nghiệm của phương
trình 2f(x) − 3 = 0 là
x
y
−1
3
1
−1
O
A. 3. B. 1. C. 2. D. 0.
Lời giải.
Ta có 2f(x) − 3 = 0 ⇔ f(x) =
3
2
(∗).
Số nghiệm của phương trình (∗)
bằng số giao điểm giữa đồ thị hàm
số y = f(x) và đường thẳng y =
3
2
.
Dựa vào hình vẽ, hai đồ thị cắt
nhau tại 3 điểm phân biệt.
Vậy phương trình đã cho có 3
nghiệm.
x
y
−1
3
1
−1
y =
3
2
O
Chọn phương án A
Câu 18. Nếu
5
Z
1
dx
2x − 1
= ln c với c ∈ Q thì giá trị của c
bằng
A. 9. B. 3. C. 6. D. 81.
Lời giải.
5
Z
1
dx
2x − 1
=
1
2
ln |2x − 1|
5
1
= ln 3.
Vậy c = 3.
Chọn phương án B
GeoGebraPro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 19. Tìm phần ảo của số phức z = 8 − 12i.
A. −12. B. 18. C. 12. D. −12i.
Lời giải.
Phần ảo của số phức z = 8 − 12i là −12.
Chọn phương án A
Câu 20. Cho hai số phức z
1
= 1 + 2i, z
2
= 3 − i. Tìm số
phức z =
z
2
z
1
.
A. z =
1
10
+
7
10
i. B. z =
1
5
+
7
5
i.
C. z =
1
5
−
7
5
i. D. z = −
1
10
+
7
10
i.
Lời giải.
Ta có z =
z
2
z
1
=
z
2
· z
1
z
1
· z
1
=
(3 − i)(1 − 2i)
(1 + 2i)(1 − 2i)
=
1 − 7i
5
=
1
5
−
7
5
i.
Chọn phương án C
Câu 21. Cho số phức z = 6 + 17i. Điểm biểu diễn cho số
phức z trên mặt phẳng tọa độ Oxy là
A. M (−6; −17). B. M (−17; −6).
C. M (17; 6). D. M (6; 17).
Lời giải.
Điểm biểu diễn cho số phức z trên mặt phẳng tọa độ Oxy
là M(6; 17).
Chọn phương án D
Câu 22. Trong không gian Oxyz, cho điểm M (3; 2; −1).
Hình chiếu vuông góc của điểm M lên trục Oz là điểm
A. M
3
(3; 0; 0). B. M
4
(0; 2; 0).
C. M
1
(0; 0; −1). D. M
2
(3; 2; 0).
Lời giải.
Hình chiếu vuông góc của điểm M (3; 2; −1) lên trục Oz là
điểm M
1
(0; 0; −1) .
Chọn phương án C
Câu 23. Trong không gian với hệ tọa độ Oxyz phương
trình nào sau đây không phải là phương trình của một mặt
cầu?
A. x
2
+ y
2
+ z
2
+ x − 2y + 4z − 3 = 0.
B. 2x
2
+ 2y
2
+ 2z
2
− x − y − z = 0 .
C. x
2
+ y
2
+ z
2
− 2x + 4y − 4z + 10 = 0 .
D. 2x
2
+ 2y
2
+ 2z
2
+ 4x + 8y + 6z + 3 = 0.
Lời giải.
Điều kiện để phương trình x
2
+y
2
+z
2
−2ax−2by−2cz+d = 0
là phương trình mặt cầu là R = a
2
+ b
2
+ c
2
− d > 0.
Dựa vào bốn đáp án ta có đáp án C là a = 1, b = −2, c =
2, d = 10 ⇒ R = −1 < 0.
Chọn phương án C
Câu 24. Trong không gian Oxyz, mặt phẳng (P ): x+2y−
5 = 0 nhận vec-tơ nào trong các vec-tơ sau làm vec-tơ pháp
tuyến?
A.
#»
n (1; 2; −5). B.
#»
n (0; 1; 2).
C.
#»
n (1; 2; 0). D.
#»
n (1; 2; 5).
Lời giải.
Mặt phẳng (P ) nhận
#»
n (1; 2; 0) làm vec-tơ pháp tuyến.
Chọn phương án C
Câu 25. Trong không gian (Oxyz), cho đường thẳng
∆:
x = 3 − 3t
y = 1 + 2t
z = 5t
. Điểm nào dưới đây thuộc đường thẳng
∆?
A. N (0; 3; 5). B. M (−3; 2; 5).
C. (P (3; 1; 5). D. Q(6; −1; 5).
Lời giải.
Thế tọa độ của điểm N (0; 3; 5) vào phương trình tham số
của đường thẳng ∆ ta được
0 = 3 − 3t
3 = 1 + 2t
5 = 5t
. Ta thấy t = 1
thỏa mãn hệ phương trình.Vậy điểm N(0; 3; 5) thuộc đường
thẳng ∆.
Chọn phương án A
Câu 26. Cho hình chóp S.ABCD đều có SA = AB = a.
Góc giữa SA và CD là
A. 60
◦
. B. 30
◦
. C. 90
◦
. D. 45
◦
.
Lời giải.
S
A
D
B
C
Vì AB ∥ CD nên góc giữa SA và CD bằng góc giữa SA và
AB.
Vì SA = AB nên tam giác SAB đều, vậy góc giữa chúng
bằng 60
◦
.
Chọn phương án
A
Câu 27. Cho hàm số y = f(x) xác định trên R và có bảng
xét dấu của đạo hàm như sau:
x
y
0
−∞
x
1
x
2
x
3
+∞
−
0
+ −
0
+
Khi đó số điểm cực trị của hàm số y = f(x) là
A. 3. B. 2. C. 4. D. 1.
Lời giải.
Ta thấy f
0
(x) đổi dấu khi x qua x
1
, x
2
, x
3
thuộc tập xác
định của hàm số f(x) nên hàm số f (x) có 3 cực trị.
Chọn phương án A
Câu 28. Giá trị nhỏ nhất của hàm số y = x +
√
18 − x
2
là:
A. 0. B. 6. C. −3
√
2. D. −6.
Lời giải.
TXĐ: D = [−3
√
2; 3
√
2].
Ta có: y
0
= 1 −
x
√
18 − x
2
.
y
0
= 0 ⇔ x = 3.
Ta có: y(3) = 6; y
Ä
3
√
2
ä
= 3
√
2; y
Ä
−3
√
2
ä
= −3
√
2.
⇒ Giá trị nhỏ nhất của hàm số đã cho là −
√
2.
Chọn phương án C
Câu 29. Cho 0 < b < a < 1, mệnh đề nào dưới đây
đúng?
A. log
b
a < log
a
b. B. log
b
a < 0.
C. log
b
a > log
a
b. D. log
a
b < 1.
Lời giải.
GeoGebraPro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
Vì 0 < b < a < 1 nên log
a
b > log
a
a = 1. Do đó
log
b
a =
1
log
a
b
< 1 < log
a
b.
Chọn phương án A
Câu 30. Số giao điểm của đồ thị hàm số y = x
2
x
2
− 4
với đường thẳng y = 3 là
A. 8. B. 2 . C. 4. D. 6 .
Lời giải.
Phương tình hoành độ giao điểm x
2
x
2
− 4
= 3 (1)
nếu x
2
− 4 ≥ 0 ⇔ x ≤ −2 ∪ 2 ≤ x.
Phương trình (1) ⇔ x
2
(x
2
− 4) = 3 ⇔ x
4
− 4x
2
− 3 = 0 ⇔
"
x
2
= 2 +
√
7
x
2
= 2 −
√
7 ( loại )
⇔ x = ±
p
2 +
√
7.
nếu x
2
− 4 < 0 ⇔ −2 < x < 2.
Phương trình (1) ⇔ x
2
(x
2
−4) = −3 ⇔ x
4
−4x
2
+ 3 = 0 ⇔
ñ
x
2
= 3
x
2
= 1
⇔
ñ
x = ±
√
3
x = ±1
.
Vậy phương trình có 6 nghiệm.
Chọn phương án D
Câu 31. Tìm tập nghiệm của bất phương trình
log
2
5
(x − 4) + 1 > 0.
A.
ï
13
2
; +∞
ã
. B.
Å
−∞;
13
2
ã
.
C. (4; +∞). D.
Å
4;
13
2
ã
.
Lời giải.
Ta có log
2
5
(x − 4) + 1 > 0 ⇔ log
2
5
(x − 4) > −1 ⇔ 0 <
x − 4 <
Å
2
5
ã
−1
⇔ 4 < x <
13
2
Vậy tập nghiệm của bất phương trình là
Å
4;
13
2
ã
.
Chọn phương án D
Câu 32. Tính thể tích khối tròn xoay sinh ra khi quay tam
giác đều ABC cạnh bằng 1 quanh AB.
A.
3π
4
. B.
π
4
. C.
π
8
. D.
π
√
3
2
.
Lời giải.
Khi quay tam giác đều ABC quanh cạnh AB ta thu được
hai khối nón bằng nhau.
Do đó, ta có V = 2V
nón
= 2·
1
3
πr
2
h =
2
3
π ·
Ç
1
√
3
2
å
2
·
1
2
=
π
4
(đvtt).
(bán kính r = h
ABC
=
√
3
2
, đường cao h =
1
2
AB =
1
2
).
Chọn phương án B
Câu 33. Cho tích phân I =
3
Z
0
x
1 +
√
x + 1
dx. Nếu đặt
t =
√
x + 1 thì
A. I =
2
Z
1
(t
2
− 2t) dt. B. I =
2
Z
1
(2t
2
− t) dt.
C. I =
2
Z
1
(2t
2
+ 2t) dt. D. I =
2
Z
1
(2t
2
− 2t) dt.
Lời giải.
Đặt t =
√
x + 1 ⇒ t
2
= x + 1 ⇔ x = t
2
− 1, dx = 2t dt.
Đổi cận: Khi x = 0 thì t = 1; khi x = 3 thì t = 2.
I =
3
Z
0
x
1 +
√
x + 1
dx =
2
Z
1
t
2
− 1
1 + t
2t dt =
2
Z
1
2t(t − 1) dt =
2
Z
1
(2t
2
− 2t) dt.
Chọn phương án D
Câu 34. Thể tích của khối tròn xoay do hình phẳng giới
hạn bởi các đường y =
√
x, trục Ox và hai đường thẳng
x = 1; x = 4 khi quay quanh trục hoành được tính bởi công
thức nào?
A. V = π
4
Z
1
x dx. B. V =
4
Z
1
√
x
dx.
C. V = π
2
4
Z
1
x dx. D. V = π
4
Z
1
√
x dx.
Lời giải.
Thể tích là V = π
4
Z
1
x dx.
Chọn phương án A
Câu 35. Cho hai số phức z
1
= 2 + i, z
2
= 4 − 3i. Khi đó
z
1
· z
2
có phần ảo bằng
A. 11. B. 2. C. −11. D. −2.
Lời giải.
z
1
· z
2
= (2 + i)(4 − 3i) = 11 − 2i.
Vậy số phức z
1
· z
2
có phần ảo bằng −2.
Chọn phương án D
Câu 36. Gọi z
1
và z
2
lần lượt là nghiệm của phương trình:
z
2
− 2z + 5 = 0. Tính P = |z
1
| + |z
2
|.
A. 2
√
5. B. 10. C. 3. D. 6.
Lời giải.
Ta có: z
2
− 2z + 5 = 0 ⇔
ñ
z
1
= 1 + 2i
z
2
= 1 − 2i.
Khi đó P = |z
1
| + |z
2
| =
√
5 +
√
5 = 2
√
5.
Chọn phương án A
Câu 37. Trong không gian với hệ trục tọa độ Oxyz, cho
đường thẳng d:
x − 1
1
=
y + 2
−1
=
z
2
. Mặt phẳng (P ) đi qua
điểm M(2; 0; −1) và vuông góc với d có phương trình là
A. x − y + 2z = 0. B. x − 2y − 2 = 0.
C. x + y + 2z = 0. D. x − y −2z = 0.
Lời giải.
Mặt phẳng (P ) có véc-tơ pháp tuyến cùng phương với véc-
tơ chỉ phương của đường thẳng d, suy ra
#»
n
(P )
= (1; −1; 2).
Phương trình mặt phẳng (P ) là
1(x − 2) − 1(y − 0) + 2(z + 1) = 0 ⇔ x − y + 2z = 0.
Chọn phương án A
Câu 38. Trong không gian tọa độ Oxyz, viết phương trình
chính tắc của đường thẳng d đi qua A(1; 2; −1) và vuông
góc với mặt phẳng (P ) : x + 2y − 3z + 1 = 0.
A. d:
x + 1
1
=
y + 2
−2
=
z − 1
−3
.
B. d :
x + 1
1
=
y + 2
2
=
z − 1
−3
.
C. d :
x − 1
1
=
y − 2
2
=
z + 1
3
.
D. d :
x − 1
−1
=
y − 2
−2
=
z + 1
3
.
Lời giải.
d đi qua A(1; 2; −1) và nhận véc-tơ pháp tuyến của (P ) làm
véc-tơ chỉ phương nên có phương trình là
x − 1
−1
=
y −2
−2
=
z + 1
3
.
GeoGebraPro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Chọn phương án D
Câu 39. Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp
12A, 3 học sinh lớp 12B và 5 học sinh lớp 12C trên một bàn
tròn. Tính xác suất P để các học sinh cùng lớp luôn ngồi
cạnh nhau.
A. P =
1
1260
. B. P =
1
126
.
C. P =
1
28
. D. P =
1
252
.
Lời giải.
Số phần tử không gian mẫu là n(Ω) = 9!.
Gọi E là biến cố các học sinh cùng lớp luôn ngồi cạnh nhau.
Ta có các bước sắp xếp như sau:
• Xếp 5 học sinh lớp 12C ngồi vào bàn sao cho các học
sinh này ngồi sát nhau. Số cách sắp xếp là 5!.
• Xếp 3 học sinh lớp 12B vào bàn sao cho các học sinh
này ngồi sát nhau và sát nhóm của học sinh 12C. Số
cách sắp xếp là 3! × 2.
• Xếp 2 học sinh lớp 12A vào hai vị trí còn lại của bàn.
Số cách sắp xếp là 2!.
Số phần tử thuận lợi cho biến cố E là n(E) = 5!×3!×2×2!.
Xác suất của biến cố E là P (E) =
n(E)
n(Ω)
=
1
126
.
Chọn phương án B
Câu 40. Cho tứ diện OABC có OA, OB, OC đôi một
vuông góc với nhau và OC = 2a, OA = OB = a. Gọi
M là trung điểm của AB. Tính khoảng cách giữa hai đường
thẳng OM và AC.
A.
2a
3
. B.
2
√
5a
5
. C.
√
2a
3
. D.
√
2a
2
.
Lời giải.
C
B
O
A
M
D
H
Dựng hình bình hành AMOD, OM ⊥ AM nên hình bình
hành AM OD là hình chữ nhật. Gọi H là hình chiếu vuông
góc của O trên đường thẳng CD. Ta có
®
AD ⊥ DO
AD ⊥ CO
⇒ AD ⊥ OH ⇒ OH ⊥ (ACD). (1)
OM ∥ (ACD) ⇒ d(OM, AC) = d(O, (ACD)). (2)
Từ (1) và (2) suy ra
d(OM, AC) = OH =
OC · OD
√
OC
2
+ OD
2
=
2
√
5a
5
.
Chọn phương án B
Câu 41. Cho hàm số y = −x
3
−mx
2
+ (4m + 9)x + 5, với
m là tham số. Có bao nhiêu giá trị nguyên của m để hàm
số nghịch biến R?
A. 6. B. 4. C. 7. D. 5.
Lời giải.
Tập xác định của hàm số D = R.
Ta có y
0
= −3m
2
− 2mx + 4m + 9.
Do phương trình y
0
= 0 có hữu hạn nghiệm nên hàm số
nghịch biến trên R ⇔ y
0
< 0, ∀x ∈ R.
⇔ −3x
2
− 2mx + 4m + 9 ≤ 0, ∀x ∈ R.
⇔ ∆
0
= m
2
+ 12m + 27 ≤ 0 (do a = −3 < 0)
⇔ −9 ≤ m ≤ −3.
Do m ∈ Z nên m ∈ {−9; −8; −7; −5; −4; −3}.
Vậy có 7 giá trị m thỏa mãn yêu cầu bài toán.
Chọn phương án C
Câu 42. Gọi N(t) là số phần trăm cacbon 14 còn lại trong
một bộ phận của một cây sinh trưởng từ t năm trước đây
thì ta có công thức N (t) = 100.(0.5)
t
A
(%) với A là hằng số.
Biết rằng một mẩu gỗ có tuổi khoảng 3754 năm thì lượng
cácbon 14 còn lại là 65%. Phân tích mẩu gỗ từ một công
trình kiến trúc cổ, người ta thấy lượng cácbon 14 còn lại
trong mẩu gỗ là 63%. Hãy xác định tuổi của mẩu gỗ được
lấy từ công trình đó.
A. 3874. B. 3833. C. 3834. D. 3843.
Lời giải.
Theo bài ta có 65 = 100.(0.5)
3754
A
⇔ 0.65 = (0.5)
3754
A
⇔
3754
A
= log
0.5
0.65 ⇔ A =
3754
log
0.5
0.65
.
Do mẫu gỗ còn 63% lượng Cácbon 14 nên ta có:
63 = 100.(0.5)
t
A
⇔ 0.63 = (0.5)
t
A
⇔
t
A
= log
0.5
0.63 ⇔ t =
A. log
0.5
0.63 =
3754
log
0.5
0.65
. log
0.5
0.63 ≈ 3833.
Chọn phương án B
Câu 43.
Cho hàm số y = f (x)
có đạo hàm f
0
(x), biết
rằng đồ thị của hàm
số f
0
(x) như hình vẽ.
Biết f(a) > 0, hỏi đồ
thị hàm số y = f (x)
cắt trục hoành tại nhiều
nhất bao nhiêu điểm?
x
y
O
a
b
c
A. 4. B. 2. C. 3. D. 1.
Lời giải.
Dựa vào đồ thị của hàm số f
0
(x), ta có bảng biến thiên của
hàm số y = f (x) như sau:
x
f
0
(x)
f(x)
−∞
a
b
c
+∞
−
0
+
0
−
0
+
f(a)f(a)
f(b)f(b)
f(c)f(c)
Vì f(a) > 0 nên ta xét các trường hợp sau:
GeoGebraPro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
• Nếu f(c) > 0 thì toàn bộ đồ thị hàm số nằm ở phía
trên trục hoành, do đó đồ thị hàm số không cắt trục
hoành.
• Nếu f(c) = 0 thì đồ thị hàm số và trục hoành có một
điểm chung duy nhất.
• Nếu f(c) < 0 thì đồ thị hàm số và trục hoành có hai
điểm chung.
Vậy đồ thị hàm số y = f (x) cắt trục hoành nhiều nhất tại
hai điểm.
Chọn phương án B
Câu 44. Cắt khối trụ bởi một mặt phẳng qua trục ta được
thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai
đáy của hình trụ, AB = 4a, AC = 5a. Thể tích V của khối
trụ là
A. V = 16πa
3
. B. V = 4πa
3
.
C. V = 12πa
3
. D. V = 8πa
3
.
Lời giải.
Ta có BC =
√
AC
2
− AB
2
=
√
25a
2
− 16a
2
= 3a.
Bán kính đáy r =
AB
2
= 2a,
chiều cao BC = 3a.
Vậy V = hπr
2
= 3a · 4a
2
=
12πa
3
.
CD
A B4a
5a
Chọn phương án C
Câu 45. Cho hàm số y = f (x) có đạo hàm liên tục trên
đoạn [0; 1] và thỏa mãn f (0) = 0. Biết
1
Z
0
f
2
(x) dx =
9
2
và
1
Z
0
f
0
(x) cos
πx
2
dx =
3π
4
. Tích phân
1
Z
0
f (x) dx bằng.
b
Z
a
f(x) dx.
A.
6
π
. B.
2
π
. C.
4
π
. D.
1
π
.
Lời giải.
• Sử dụng phương pháp từng phần đối với tích phân
1
Z
0
f
0
(x) cos
πx
2
dx =
3π
4
.
• Xét
1
Z
0
h
f (x) + k sin
πx
2
i
2
dx = 0, tìm k, từ đó suy ra
f (x) = −k sin
πx
2
.
•
1
Z
0
f (x) dx =
1
Z
0
−k sin
πx
2
dx.
Đặt
u = cos
πx
2
dv = f
0
(x) dx
⇒
du = −
π
2
sin
πx
2
dx
v = f (x)
.
⇒
1
Z
0
f
0
(x) cos
πx
2
dx = cos
πx
2
f (x)
1
0
+
π
2
1
Z
0
f (x) sin
πx
2
dx =
f (1) · cos
π
2
− f (0) · cos 0 +
π
2
1
Z
0
f (x) sin
πx
2
dx =
π
2
1
Z
0
f (x) sin
πx
2
dx =
3π
4
⇒
1
Z
0
f (x) sin
πx
2
dx =
3
2
.
Xét tích phân
1
Z
0
h
f (x) + k sin
πx
2
i
2
dx = 0
⇔
1
Z
0
h
f
2
(x) + 2kf (x) sin
πx
2
+ k
2
sin
2
πx
2
i
dx = 0
⇔
1
Z
0
f
2
(x) dx + 2k
1
Z
0
f (x) sin
πx
2
+k
2
1
Z
0
sin
2
πx
2
dx = 0 ⇔
9
2
+ 2k
3
2
+
1
2
k
2
= 0 ⇔ k = −3.
Khi đó ta có
1
Z
0
h
f (x) − 3 sin
πx
2
i
2
dx = 0
⇔ f (x) − 3 sin
πx
2
= 0 ⇔ f (x) = 3 sin
πx
2
.
Vậy
1
Z
0
f (x) dx = 3
1
Z
0
sin
πx
2
dx = −3
cos
πx
2
π
2
1
0
=
−6
π
cos
πx
2
1
0
= −
6
π
cos
π
2
− cos 0
=
6
π
.
Chọn phương án A
Câu 46. Cho hàm số y = f(x) có bảng biến thiên như hình
bên.
x
f
0
f
−∞
0 4
+∞
−
0
+
0
−
+∞+∞
−1−1
33
−∞−∞
Phương trình f (4x −x
2
) −2 = 0 có bao nhiêu nghiệm thực
phân biệt?
A. 2. B. 6. C. 4. D. 0.
Lời giải.
Bảng biến thiên của f(x):
x
f
0
f
−∞
0 4
+∞
−
0
+
0
−
+∞+∞
−1−1
33
−∞−∞
Từ bảng biến thiên suy ra phương trình f(x) = 2 có ba
nghiệm thực phân biệt x
1
, x
2
, x
3
với x
1
< 0 < x
2
< 4 < x
3
.
Do đó f(4x − x
2
) − 2 = 0 ⇔ f (4x − x
2
) =
2
4x − x
2
= x
1
(1)
4x − x
2
= x
2
(2)
4x − x
2
= x
3
(3)
với x
1
< 0 < x
2
< 4 < x
3
.
Xét hàm số g(x) = 4x − x
2
. Có g
0
(x) = 4 − 2x, g(x) = 0 ⇔
GeoGebraPro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
x = 2.
Bảng biến thiên của g(x):
x
g
0
g
−∞
2
+∞
+
0
−
−∞−∞
44
−∞−∞
Từ bảng biến thiên của g(x) suy ra phương trình (1) có hai
nghiệm thực phân biệt, phương trình (2) có hai nghiệm thực
phân biệt (không trùng với hai nghiệm của (1) do x
1
< x
2
)
và phương trình (3) vô nghiệm. Vậy phương trình đã cho có
4 nghiệm thực phân biệt.
Chọn phương án C
Câu 47. Cho các số thực a, b thỏa mãn điều kiện 0 <
b < a < 1. Tìm giá trị nhỏ nhất của biểu thức P =
log
a
4(3b − 1)
9
+ 8 log
2
b
a
a − 1.
A. A = 6. B. 3
3
√
2. C. 8. D. 7.
Lời giải.
Ta có: (3b − 2)
2
≥ 2 ⇔
4(3b − 1)
9
≤ b
2
. Khi đó:
P ≥ log
a
b
2
+ 8 log
2
b
a
a − 1 = 2 log
a
b +
8 log
2
b
a
a − 1 = log
a
b + log
a
b + 8 log
2
b
a
a − 1 =
(log
a
b − 1) + (log
a
b − 1) + 8 ·
Å
1
log
a
b − 1
ã
2
+ 1 ≥
3
3
(log
a
b − 1) · (log
a
b − 1) · 8 ·
Å
1
log
a
b − 1
ã
2
+ 1 = 7.
Dấu bằng xảy ra khi a =
3
…
2
3
; b =
2
3
và min(P ) = 7.
Chọn phương án D
Câu 48. Gọi S là tập hợp tất cả các giá trị của tham
số thực m sao cho trị lớn nhất của hàm số y =
3x
2
− 6x + 2m − 1
trên đoạn [−2; 3] đạt giá trị nhỏ nhất.
Số phần tử của tập S là
A. 0. B. 3. C. 2. D. 1.
Lời giải.
Gọi M là giá trị lớn nhất của hàm số y =
3x
2
− 6x + 2m − 1
trên đoạn [−2; 3].
Ta có M ≥ f (−2) = |2m + 23|, M ≥ f (1) = |2m − 4|
⇒ 2M ≥ |2m + 23|+ |2m −4| ≥ |2m + 23 −2m + 4| = 27 ⇒
M ≥
27
2
. Khi M =
27
2
⇒ |2m+23| = |2m−4| ⇔ m = −
19
4
.
Với m = −
19
4
, max
[−2;3]
f(x) = max{f(−2); f(1); f (3)} =
27
2
.
Chọn phương án D
Câu 49. Cho hình hộp chữ nhật ABCD.A
0
B
0
C
0
D
0
. Gọi M
là trung điểm của BB
0
. Mặt phẳng (M DC
0
) chia khối hộp
chữ nhật thành hai khối đa diện, một khối chứa đỉnh C và
một khối chứa đỉnh A
0
. Gọi V
1
, V
2
lần lượt là thể tích của
hai khối đa diện chứa C và A
0
. Tính
V
1
V
2
.
A.
V
1
V
2
=
7
24
. B.
V
1
V
2
=
7
17
.
C.
V
1
V
2
=
7
12
. D.
V
1
V
2
=
17
24
.
Lời giải.
C
0
D
0
D
A
0
B
0
A
K
I
B C
M
Gọi I = BC ∩ C
0
M ⇒ DI ∩ AB = K.
Khi đó ta có V
1
= V
ICDC
0
− V
IBKM
trong đó
V
ICDC
0
=
1
3
IC ·
1
2
CD · CC
0
=
1
3
V ;
Mặt khác
V
IBKM
V
ICDC
0
=
1
8
⇒ V
1
=
1
3
V −
1
8
·
1
3
V =
7
24
V
⇒ V
2
=
17
24
V
⇒
V
1
V
2
=
7
17
.
Chọn phương án B
Câu 50. Xét các số thực dương x, y thỏa mãn
ln
Å
1 − 2x
x + y
ã
= 3x + y − 1. Tìm giá trị nhỏ nhất P
min
của P =
1
x
+
1
√
xy
+ 1
A. P
min
= 8. B. P
min
= 16.
C. P
min
= 9. D. P
min
= 2.
Lời giải.
ln
Å
1 − 2x
x + y
ã
= 3x + y − 1 xác định ⇔
1 − 2x
x + y
> 0.
Do x, y > 0 nên 1 − 2x > 0 ⇔ 0 < x <
1
2
Khi đó: ln
Å
1 − 2x
x + y
ã
= 3x + y − 1
⇔ ln (1 − 2x) − ln(x + y) = (x + y) − (1 − 2x)
⇔ ln (1 − 2x) + (1 − 2x) = ln(x + y) + (x + y)
Xét hàm số f(t) = ln t + t với t > 0
Hàm số f(t) xác định và liên tục trên khoảng (0; +∞)
f
0
(t) =
1
t
+ 1 > 0; ∀t > 0. Suy ra hàm số f (t) đồng biến
trên (0; +∞)
⇒ f (1 − 2x) = f (x + y)
⇔ 1 − 2x = x + y ⇔ y = 1 − 3x > 0
Do đó: P =
1
x
+
1
p
x (1 − 3x)
+ 1 ≥
1
x
+
2
1 − 2x
+ 1 (Dấu
bằng xảy ra khi x = 1 − 3x ⇔ x =
1
4
)
Xét hàm số f(x) =
1
x
+
2
1 − 2x
+ 1; x ∈
Å
0;
1
3
ã
Hàm số f(x) liên tục trên
Å
0;
1
3
ã
f
0
(x) = −
1
x
2
+
4
(1 − 2x)
2
f
0
(x) = 0 ⇔ −
1
x
2
+
4
(1 − 2x)
2
= 0
⇔ 4x
2
= (1 − 2x)
2
⇔ x =
1
4
Bảng biến thiên
GeoGebraPro Trang 7
https://www.facebook.com/groups/GeoGebraPro/
x
y
0
y
0
1
4
1
3
−
0
+
+∞+∞
88
99
Vậy P
min
= 8 tại x =
1
4
Chọn phương án A
———————–HẾT———————–
GeoGebraPro Trang 8
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
ĐÁP ÁN THAM KHẢO
1. C 2. D 3. C 4. A 5. A 6. B 7. D 8. D 9. A 10. A
11. A 12. B 13. B 14. A 15. D 16. C 17. A 18. B 19. A 20. C
21. D 22. C 23. C 24. C 25. A 26. A 27. A 28. C 29. A 30. D
31. D 32. B 33. D 34. A 35. D 36. A 37. A 38. D 39. B 40. B
41. C 42. B 43. B 44. C 45. A 46. C 47. D 48. D 49. B 50. A
GeoGebraPro Trang 9
| 1/95
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÁT TRIỂN ĐỀ MINH HỌA 1
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Bài thi: MÔN TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao bài
Câu 1. Một hộp chứa 10 quả cầu phân biệt. Số cách lấy ra từ hộp đó cùng lúc 3 quả cầu là A. 120. B. 10. C. 60. D. 720. ®u1 + u5 − u3 = 10
Câu 2. Tính số hạng đầu u1 và và công sai d của cấp số cộng (un), biết u1 + u6 = 7. A. u1 = −36, d = 13. B. u1 = 36, d = 13. C. u1 = 36, d = −13. D. u1 = −36, d = −13.
Câu 3. Tìm tập nghiệm của phương trình 3x2+2x = 1. A. S = {−1; 3}. B. S = {−2; 0}. C. S = {−3; 1}. D. S = {0; 2}. √
Câu 4. Cho khối chóp S.ABC có đáy là tam giác đều cạnh a, SA = a 3, cạnh bên SA vuông góc với
đáy. Thể tích của khối chóp S.ABC bằng √ √ a3 3 a3 a3 3 a3 A. . B. . C. . D. . 2 2 4 4
Câu 5. Tập xác định của hàm số y = log (4 − x2) là tập hợp nào sau đây? 2 A. D = (−2; 2).
B. D = (−∞; −2) ∪ (2; +∞). 2019-2020 C. D = [−2; 2]. D. D = R\{−2; 2}.
Câu 6. Tìm mệnh đề sai trong các mệnh đề sau? Z Z x4 + C THPT A. 2ex dx = 2 (ex + C). B. x3 dx = . 4 Z 1 Z C. dx = ln x + C. D. sin x dx = − cos x + C. x GHIỆP
Câu 7. Hình chóp S.ABC có chiều cao h = a, diện tích tam giác ABC là 3a2. Tính thể tích hình chóp N T S.ABC. a3 3 A. . B. a3. C. a3. D. 3a3. TỐ 3 2 √
Câu 8. Cho khối nón có bán kính đáy r =
3 và chiều cao h = 4. Tính thể tích V của khối nón đã THI cho. A. V = 12π. B. V = 4π. C. V = 4. D. V = 12.
Câu 9. Một mặt cầu có diện tích xung quanh là π thì có bán kính bằng LUYỆN √3 √ 1 A. . B. 3. C. . D. 1. 2 2 Câu 10.
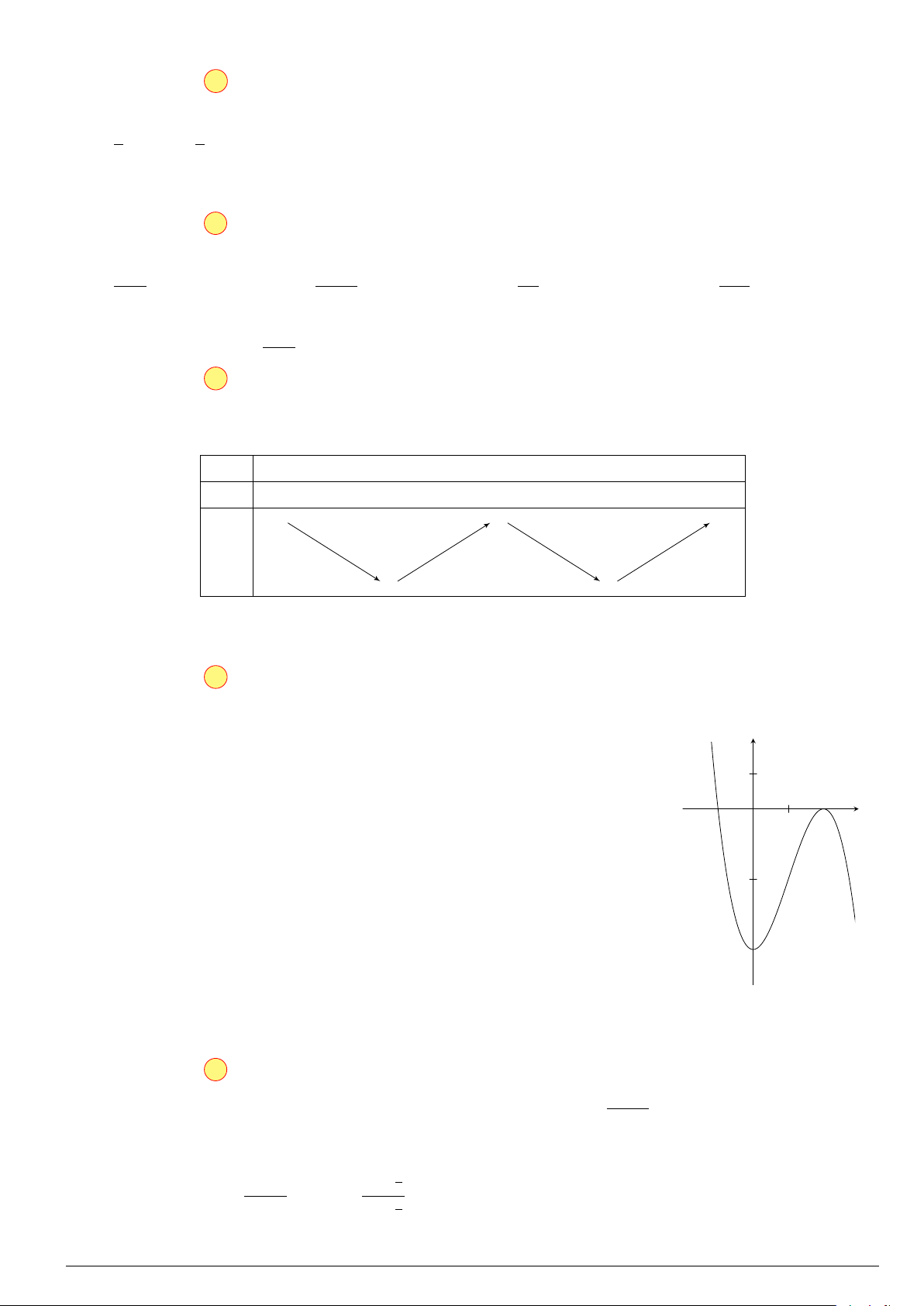
Cho hàm số y = f (x) có bảng biến thiên như x −∞ −1 0 1 +∞ hình vẽ: y0 − 0 + 0 − 0 +
Hàm số đã cho nghịch biến trên khoảng nào dưới +∞ + 3 +∞ + đây? y A. (0; +∞). B. (−1; 1). −2 −2 C. (−∞; 0). D. (−∞; −2).
Câu 11. Với a và b là hai số dương tùy ý, log (a3b4) bằng 2 1 1 A. log a + log b. B. 3 log a + 4 log b. C. 2 (log a + log b). D. 4 log a + 3 log b. 3 2 4 2 2 2 3 4 2 2
Câu 12. Cho khối trụ có thể tích V và bán kính đáy R. Chiều cao của khối trụ đã cho bằng V V V V A. . B. . C. . D. . πR2 3πR2 R2 3R2 GeoGebraPro Trang 1
Câu 13. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số. A. 3. B. 0. C. 1. D. 2. x −∞ −2 0 2 +∞ y0 − 0 + 0 − 0 + y Câu 14.
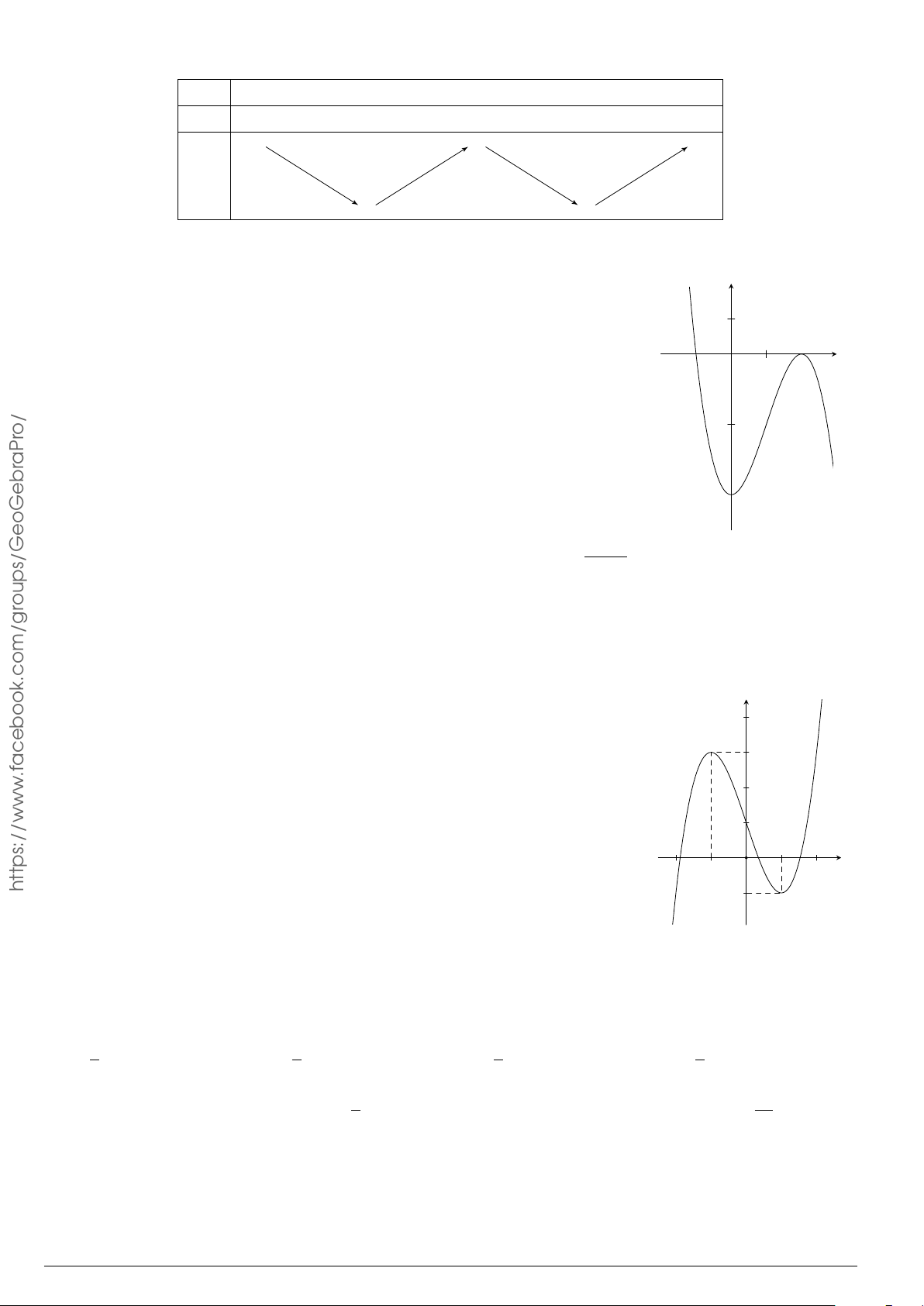
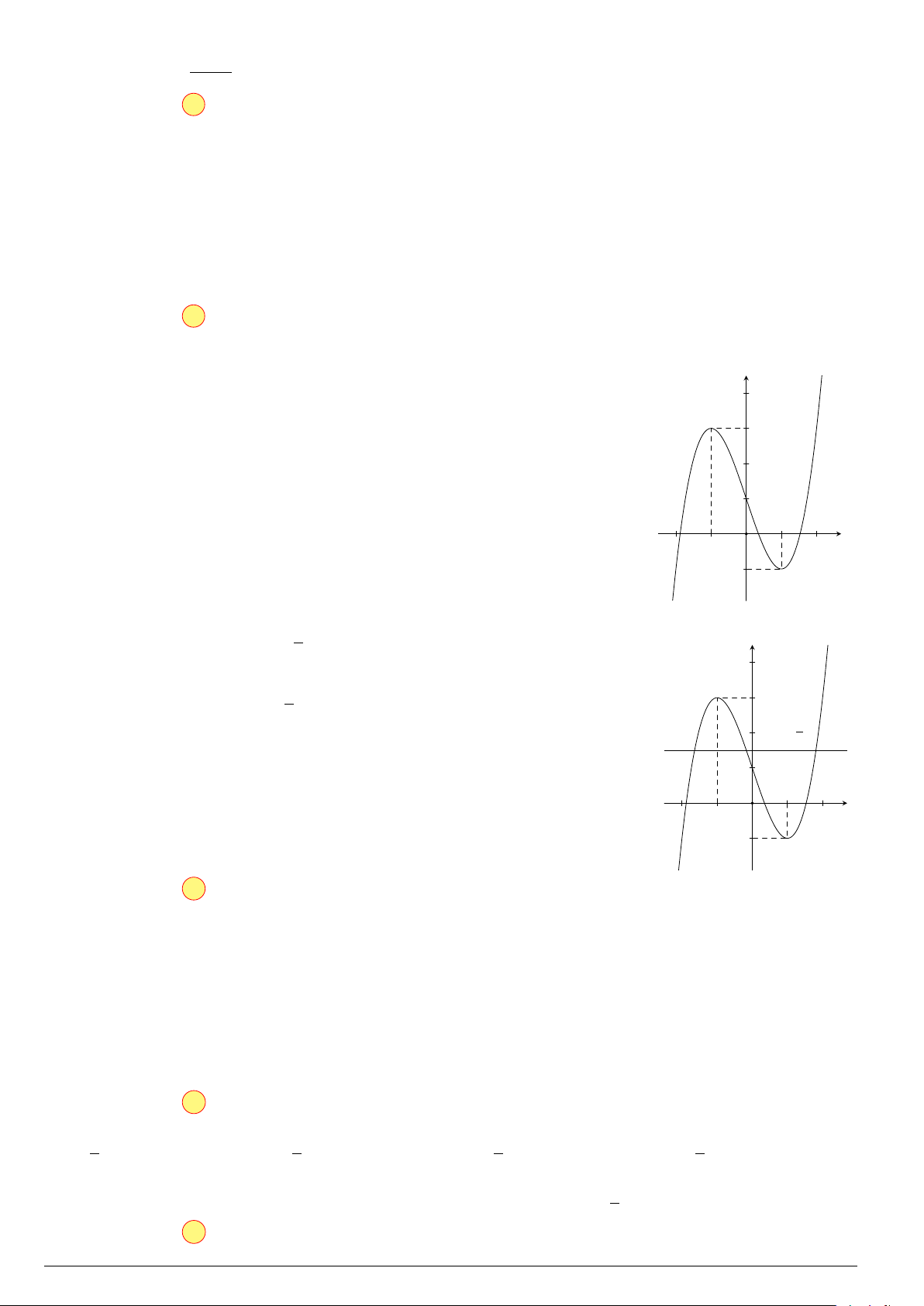
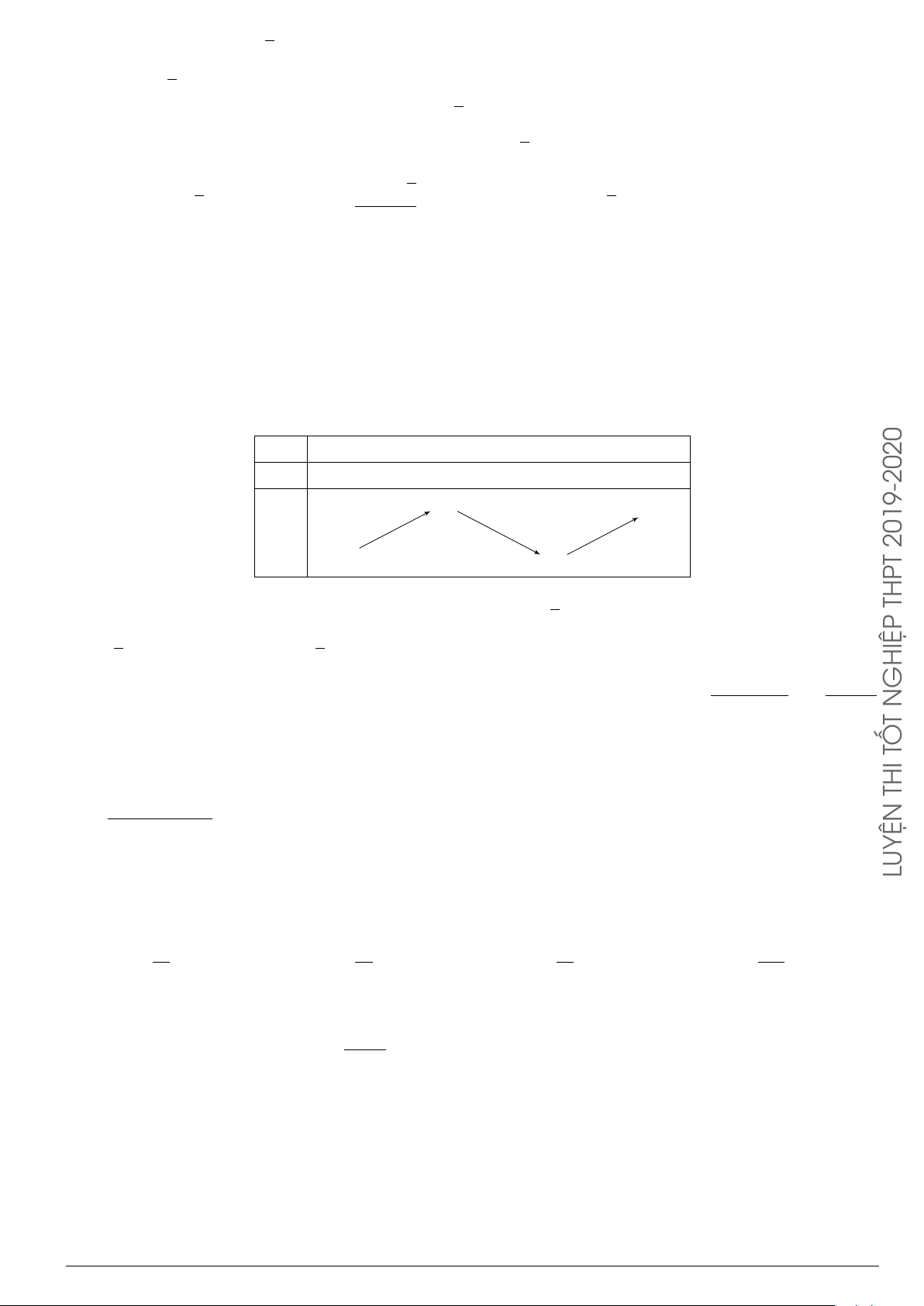
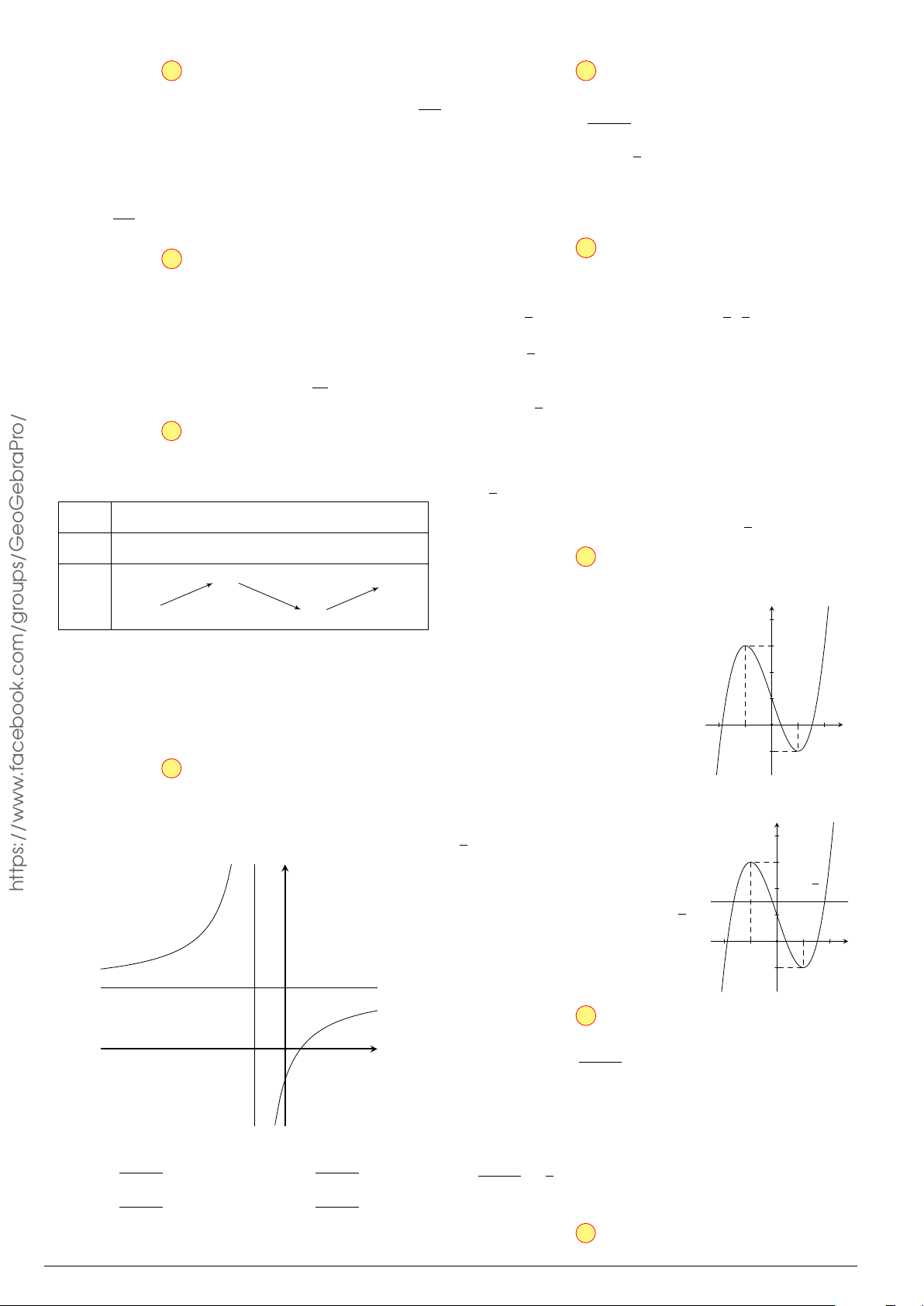
Đồ thị ở hình bên là của hàm số nào dưới đây? y A. y = −x3 − 3x2 − 4. B. y = x3 − 3x − 4. 1 C. y = −x3 + 3x2 − 4. D. y = x3 − 3x − 4. 1 2 x −1 O o/ −2 aPr −4 x + 2
Câu 15. Tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = là x − 1 A. y = 2; x = 1. B. y = 1; x = 1. C. y = −2; x = 1. D. y = 1; x = −2. roups/GeoGebr
Câu 16. Tập nghiệm của bất phương trình log (3 − x) < 2 là 2 A. (−∞; 1). B. (−1; 3). C. (1; 3). D. (3; +∞). Câu 17.
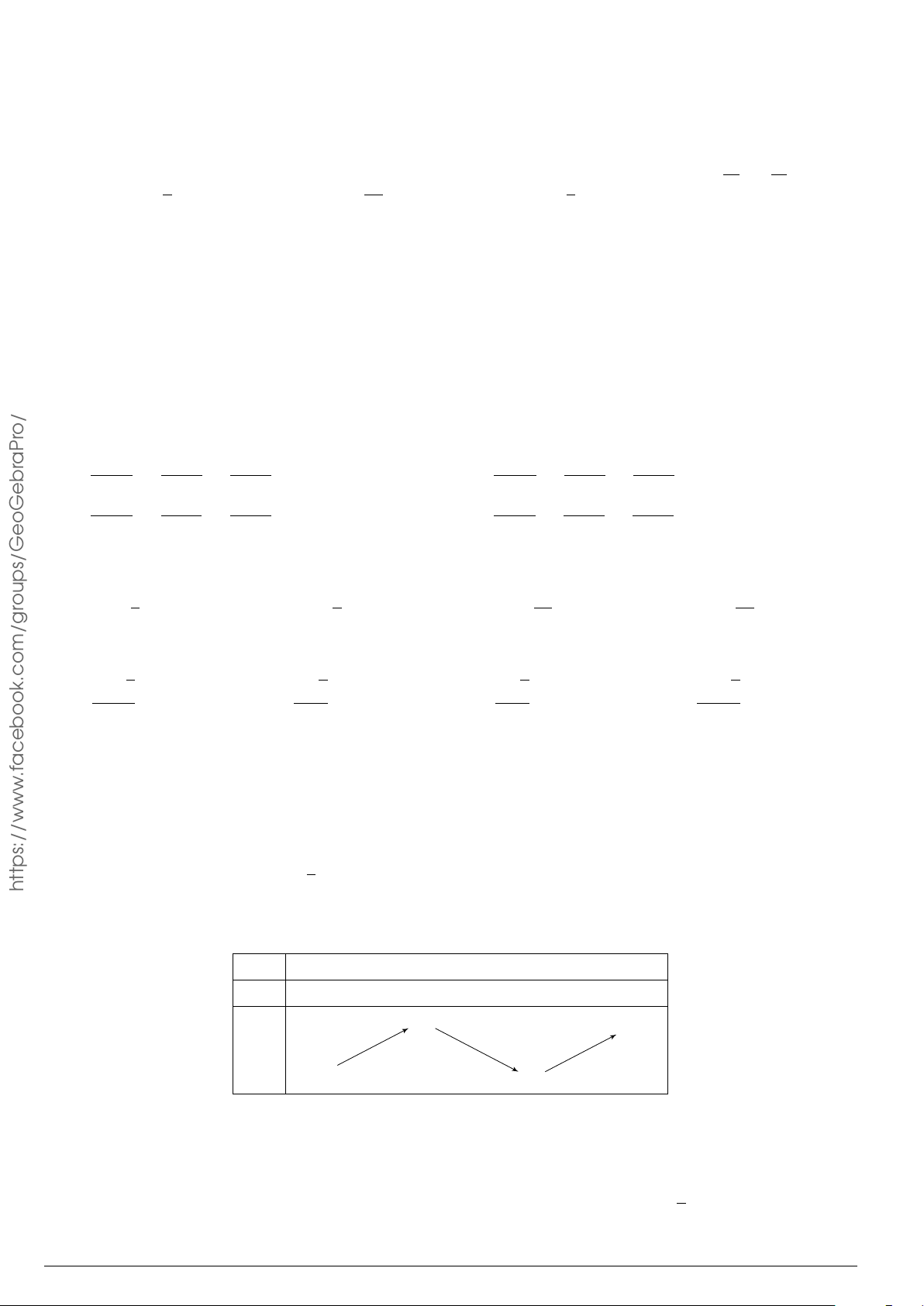
Cho hàm số f (x) có đồ thị như hình vẽ. Số nghiệm của phương trình 2f (x)− y 3 = 0 là A. 3. B. 1. C. 2. D. 0. acebook.com/g 3 .f 1 x −1 O https://www −1 2 5 5 Z Z Z Câu 18. Nếu f (x) dx = 5, f (x) dx = −1 thì f (x) dx bằng 1 2 1 A. −2. B. 2. C. 3. D. 4.
Câu 19. Cho số phức z = 2 − 3i. Số phức liên hợp của số phức z là: A. z = 3 − 2i. B. z = 3 + 2i. C. z = −2 − 3i. D. z = 2 + 3i.
Câu 20. Cho hai số phức z1 = 1 − i, z2 = 2 + 3i. Tính mô-đun của số phức z = z1 + z2. √ √ A. |z| = 1. B. |z| = 5. C. |z| = 5. D. |z| = 13.
Câu 21. Số phức nào sau đây có điểm biểu diễn là M (1; −2)? A. −1 − 2i. B. 1 + 2i. C. 1 − 2i. D. −2 + i.
Câu 22. Trong không gian Oxyz, cho M (3; −2; 1), N (1; 0; −3). Gọi M 0, N 0 lần lượt là hình chiếu của
M và N lên mặt phẳng Oxy. Khi đó độ dài đoạn M 0N 0 là GeoGebraPro Trang 2 √ √ A. M 0N 0 = 8. B. M 0N 0 = 4. C. M 0N 0 = 2 6. D. M 0N 0 = 2 2.
Câu 23. Trong không gian Oxyz cho mặt cầy (S) : x2 + y2 + z2 − 2x + 4z + 1 = 0 có tâm I và bán kính R là. A. I(−1; 0; 2), R = 2. B. I(−1; 0; 2), R = 4. C. I(1; 0; −2), R = 2. D. I(1; 0; −2), R = 4.
Câu 24. Trong không gian Oxyz, mặt phẳng (P ) : 2x − y + 3 = 0. Một véc tơ pháp tuyến của (P ) có tọa độ là A. (2; 1; 0). B. (2; −1; 3). C. (2; −1; 0). D. (2; 1; 3). x − 1 y − 2 z − 3
Câu 25. Trong không gian Oxyz, đường thẳng d : = =
đi qua điểm nào dưới đây 2 −1 2 ? A. Q(2; −1; 2). B. M (−1; −2; −3). C. P (1; 2; 3). D. N (−2; 1; −2).
Câu 26. Cho hình chóp S.ABCD có đáy hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng
a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo góc (M N, SC) bằng A. 45◦. B. 30◦. C. 90◦. D. 60◦.
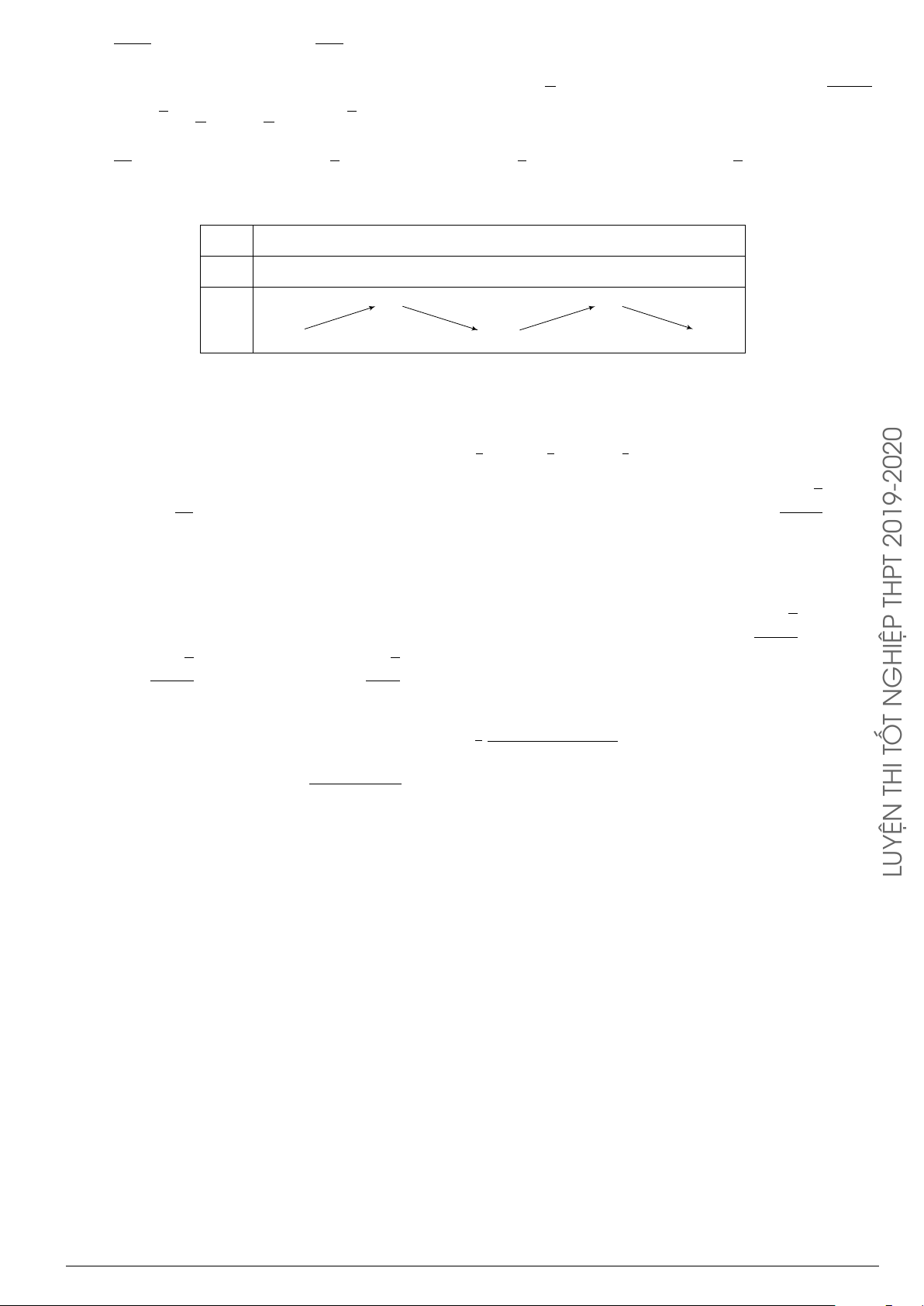
Câu 27. Cho hàm số y = f (x) liên tục trên [−3; 3] và có bảng xét dấu đạo hàm như hình bên. x −3 −1 0 1 2 3 y0 + 0 − 0 − 0 + 0 − 2019-2020
Mệnh đề nào sau đây sai về hàm số đó?
A. Hàm số đạt cực tiểu tại x = 1.
B. Hàm số đạt cực đại tại x = −1.
C. Hàm số đạt cực đại tại x = 2.
D. Hàm số đạt cực tiểu tại x = 0. THPT
Câu 28. Cho hàm số y = −x3 + 3x2 + 2. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số trên [0; 3]. Tính (M + m). A. 6. B. 8. C. 10. D. 4. GHIỆP N
Câu 29. Với các số a, b > 0 thỏa mãn a2 + b2 = 6ab, biểu thức log (a + b) bằng 2 T 1 1 A. (3 + log a + log b). B. (1 + log a + log b). 2 2 2 2 TỐ 2 2 1 1 C. 1 + (log a + log b). D. 2 + (log a + log b). 2 2 2 2 THI 2 2
Câu 30. Số giao điểm của đường cong y = x3 − 2x2 + 2x + 1 và đường thẳng y = 1 − x là A. 1. B. 2. C. 3. D. 0. LUYỆN
Câu 31. Tập nghiệm của bất phương trình 3x2−2x < 27 là A. (−∞; −1). B. (3; +∞). C. (−1; 3).
D. (−∞; −1) ∪ (3; +∞). √
Câu 32. Cho tam giác ABC vuông tại A có AB = a 3 và BC = 2a. Tính thể tích khối nón sinh ra
khi quay tam giác ABC quay cạnh AB. √ √ 2πa3 πa3 3 A. V = πa3 3. B. V = 2πa3. C. V = . D. V = . 3 3 1 Z √ √ Câu 33. Cho I =
x2 1 − x3 dx. Nếu đặt t = 1 − x3 thì ta được 0 1 1 1 1 3 Z 3 Z 2 Z 2 Z A. I = t2 dt. B. I = − t2 dt. C. I = − t2 dt. D. I = t2 dt. 2 2 3 3 0 0 0 0
Câu 34. Diện tích hình phẳng H được giới hạn bởi hai đồ thị y = x3 − 2x − 1 và y = 2x − 1 được tính theo công thức GeoGebraPro Trang 3 0 2 Z Z A. S = x3 − 4x dx. B. S = x3 − 4x dx. −2 0 2 2 Z Z C. S = x3 − 4x dx. D. S = x3 − 4x dx. −2 −2
Câu 35. Cho hai số phức z1 = 2 + 4i, z2 = −1 + 3i. Tính môđun của số phức w = z1z2 − 2z1. √ √ √ A. |w| = 2 2. B. |w| = 2 10. C. |w| = 4 2. D. |w| = 2.
Câu 36. Gọi z1 là nghiệm phức có phần ảo dương của phương trình z2 + 6z + 13 = 0. Tìm tọa độ điểm
M biểu diễn số phức w = (i + 1) z1. A. M (−5; −1). B. M (5; 1). C. M (−1; −5). D. M (1; 5).
Câu 37. Trong không gian Oxyz, cho điểm A(2; −1; −3) và mặt phẳng (P ) : 3x − 2y + 4z − 5 = 0. Mặt
phẳng (Q) đi qua A và song song với mặt phẳng (P ) có phương trình là
A. (Q) : 3x − 2y + 4z − 4 = 0.
B. (Q) : 3x − 2y + 4z + 4 = 0.
C. (Q) : 3x − 2y + 4z + 5 = 0. D. (Q) : 3x + 2y + 4z + 8 = 0.
Câu 38. Trong không gian Oxyz, viết phương trình chính tắc của đường thẳng qua điểm E(1; 2; −3) o/ và F (3; −1; 1). aPr x − 1 y − 2 z + 3 x − 3 y + 1 z − 1 A. = = . B. = = . 3 −1 1 2 −3 4 x − 3 y + 1 z − 1 x + 1 y + 2 z − 3 C. = = . D. = = . 1 2 −3 2 −3 4
Câu 39. Có 8 bạn học sinh lớp 11A trong đó có An và Bình được xếp ngẫu nhiên theo một hàng ngang.
Tính xác suất P để An và Bình ngồi cạnh nhau. 1 1 1 1 roups/GeoGebr A. P = . B. P = . C. P = . D. P = . 8 4 64 25
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SO vuông góc với mặt
phẳng ABCD và SO = a. Khoảng cách giữa SC và AB bằng √ √ √ √ 2a 3 a 5 a 3 2a 5 A. . B. . C. . D. . 15 5 15 15
Câu 41. Có bao nhiêu giá trị nguyên của tham số m ∈ [−2019; 2019] để hàm số y = (m − 1)x3 + acebook.com/g .f
3mx2 + (4m + 4)x + 1 đồng biến trên khoảng (−∞; +∞)? A. 4036. B. 2017. C. 2018. D. 4034.
Câu 42. Một người thả một lá bèo vào một chậu nước. Sau 12 giờ, bèo sinh sôi phủ kín mặt nước trong
chậu. Biết rằng sau mỗi giờ lượng bèo tăng gấp 10 lần lượng bèo trước đó và tốc độ tăng không đổi. 1
Hỏi sau mấy giờ thì bèo phủ kín
mặt nước trong chậu (kết quả làm tròn đến hàng phần chục). https://www 5 A. 9,1 giờ. B. 9,7 giờ. C. 10,9 giờ. D. 11,3 giờ.
Câu 43. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như sau x −∞ −1 3 +∞ f 0(x) + 0 − 0 + 5 +∞ + f (x) −∞ 1
Đồ thị hàm số y = |f (x)| có bao nhiêu điểm cực trị? A. 2. B. 3. C. 4. D. 5.
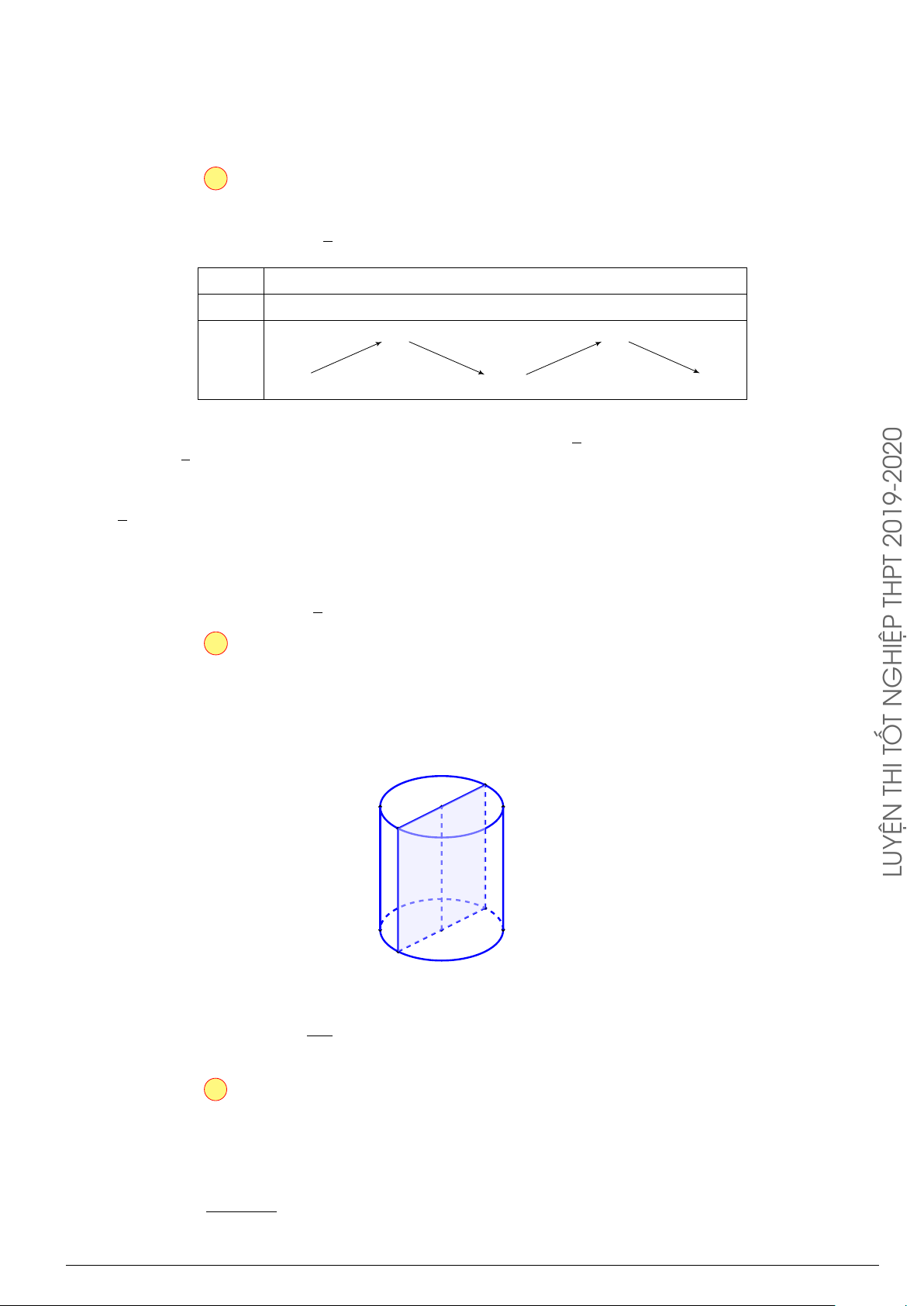
Câu 44. Cho hình trụ có trục OO0, chiều cao bằng a. Trên hai đường tròn đáy (O) và (O0) lần lượt lấy a
hai điểm A và B sao cho khoảng cách giữa hai đường thẳng AB và OO0 bằng . Góc giữa hai đường 2
thẳng AB và OO0 bằng 60◦. Thể tích của khối trụ đã cho là GeoGebraPro Trang 4 2πa3 πa3 A. . B. . C. 2πa3. D. πa3. 3 3 π x
Câu 45. Cho hàm số f (x) liên tục và có đạo hàm trên 0;
, thỏa mãn f (x) + tan xf 0(x) = . 2 cos3 x √ π π √ Biết rằng 3f −f
= aπ 3+b ln 3 trong đó a, b ∈ R. Giá trị của biểu thức P = a+b bằng 3 6 14 2 7 4 A. . B. − . C. . D. − . 9 9 9 9
Câu 46. Cho hàm số y = f (x) có bảng biến thiên như sau: x −∞ −2 0 2 +∞ y0 + 0 − 0 + 0 − 3 3 y −∞ −1 −∞
Hàm số y = f (x2 − 2) nghịch biến trên khoảng nào dưới đây? A. (2; +∞). B. (0; 2). C. (−∞; −2). D. (−2; 0).
Câu 47. Xét các số thực dương x, y thoả mãn log 1 x + log 1 y ≤ log 1 (x + y2). Tìm giá trị nhỏ nhất 2 2 2
Pmin của biểu thức P = x + 3y √ 17 25 2 A. Pmin = . B. Pmin = 8. C. Pmin = 9. D. Pmin = . 2 4 2019-2020
Câu 48. Gọi S là tập hợp các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y =
|x3 − 3x2 − 9x + m| trên đoạn [−2; 4] bằng 16. Số phần tử của S là A. 10. B. 12. C. 14. D. 11. THPT √ 2a 5
Câu 49. Cho hình hộp chữ nhật ABCD.A0B0C0D0. Khoảng cách giữa AB và B0C là , giữa BC √ √ 5 2a 5 a 3 và AB0 là , giữa AC và BD0 là
. Thể tích của khối hộp đó là GHIỆP 5 3 N A. 8a3. B. 4a3. C. 2a3. D. a3. T x + y
Câu 50. Xét các số thực dương x, y thỏa mãn log√
= x(x − 3) + y(y − 3) + xy. Tìm 3 x2 + y2 + xy + 2 TỐ 3x + 2y + 1
giá trị lớn nhất Pmax của P = . THI x + y + 6 A. 3. B. 2. C. 1. D. 4.
———————–HẾT———————– LUYỆN GeoGebraPro Trang 5 ĐÁP ÁN THAM KHẢO 1. A 2. C 3. D 4. D 5. A 6. C 7. B 8. B 9. C 10. D 11. B 12. A 13. A 14. C 15. B 16. B 17. A 18. D 19. D 20. D 21. C 22. D 23. C 24. C 25. C 26. C 27. D 28. B 29. A 30. A 31. C 32. D 33. D 34. D 35. B 36. A 37. B 38. B 39. B 40. D 41. C 42. D 43. B 44. D 45. D 46. A 47. C 48. D 49. C 50. C o/ aPr roups/GeoGebr acebook.com/g .f https://www GeoGebraPro Trang 6 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN
PHÁT TRIỂN ĐỀ MINH HỌA 1
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Bài thi: MÔN TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao bài
Câu 1. Một hộp chứa 10 quả cầu phân biệt. Số cách lấy ra từ hộp đó cùng lúc 3 quả cầu là A. 120. B. 10. C. 60. D. 720. Lời giải.
Số cách chọn 3 quả cầu từ hộp là C3 = 120. 10 Chọn phương án A ®u1 + u5 − u3 = 10
Câu 2. Tính số hạng đầu u1 và và công sai d của cấp số cộng (un), biết u1 + u6 = 7. A. u1 = −36, d = 13. B. u1 = 36, d = 13. C. u1 = 36, d = −13. D. u1 = −36, d = −13. Lời giải. ®u ® 1 + 2d = 10 u1 = 36 Theo giả thiết suy ra ⇔ 2u1 + 5d = 7 d = −13. Chọn phương án C
Câu 3. Tìm tập nghiệm của phương trình 3x2+2x = 1. A. S = {−1; 3}. B. S = {−2; 0}. C. S = {−3; 1}. D. S = {0; 2}. Lời giải. ñx = 0
Ta có 3x2+2x = 1 ⇔ x2 + 2x = 0 ⇔ x = −2.
Do đó tập nghiệm của phương trình là S = {0; 2}. Chọn phương án D √
Câu 4. Cho khối chóp S.ABC có đáy là tam giác đều cạnh a, SA = a 3, cạnh bên SA vuông góc với
đáy. Thể tích của khối chóp S.ABC bằng √ √ a3 3 a3 a3 3 a3 A. . B. . C. . D. . 2 2 4 4 Lời giải. √ 1 1 √ a2 3 a3 Ta có V = SA · SABC = a 3 = . 3 3 4 4 S A C B Chọn phương án D
Câu 5. Tập xác định của hàm số y = log (4 − x2) là tập hợp nào sau đây? 2 A. D = (−2; 2).
B. D = (−∞; −2) ∪ (2; +∞). C. D = [−2; 2]. D. D = R\{−2; 2}. Lời giải. Phương pháp:
Điều kiện để hàm số y = log f (x) (0 < a 6= 1) có nghĩa là f (x) > 0. a GeoGebraPro Trang 1 o/ aPr roups/GeoGebr Cách giải:
Điều kiện xác định 4 − x2 > 0 ⇔ x ∈ (−2; 2). Chọn phương án A
Câu 6. Tìm mệnh đề sai trong các mệnh đề sau? acebook.com/g Z .fZ x4 + C A. 2ex dx = 2 (ex + C). B. x3 dx = . 4 Z 1 Z C. dx = ln x + C. D. sin x dx = − cos x + C. x Lời giải. Z 1 https://www Ta có
dx = ln |x| + C nên mệnh đề ở phương án C sai. x Chọn phương án C
Câu 7. Hình chóp S.ABC có chiều cao h = a, diện tích tam giác ABC là 3a2. Tính thể tích hình chóp S.ABC. a3 3 A. . B. a3. C. a3. D. 3a3. 3 2 Lời giải. 1 1
VS.ABC = h.S4ABC = .a.3a2 = a3. 3 3 Chọn phương án B √
Câu 8. Cho khối nón có bán kính đáy r =
3 và chiều cao h = 4. Tính thể tích V của khối nón đã cho. A. V = 12π. B. V = 4π. C. V = 4. D. V = 12. Lời giải. Thể tích khối nón là 1 1 √ S V = πr2h = π( 3)2 · 4 = 4π. 3 3 A O B Chọn phương án B
Câu 9. Một mặt cầu có diện tích xung quanh là π thì có bán kính bằng √3 √ 1 A. . B. 3. C. . D. 1. 2 2 Lời giải. Phương pháp:
Công thức tính diện tích mặt cầu bán kính R là S = 4π · R2. Cách giải: 1 1
Ta có: S = π = 4π · R2 ⇔ R2 = ⇔ R = . 4 2 Chọn phương án C Câu 10.
Cho hàm số y = f (x) có bảng biến thiên như x −∞ −1 0 1 +∞ hình vẽ: y0 − 0 + 0 − 0 +
Hàm số đã cho nghịch biến trên khoảng nào dưới +∞ + 3 +∞ + đây? y A. (0; +∞). B. (−1; 1). −2 −2 C. (−∞; 0). D. (−∞; −2). GeoGebraPro Trang 2 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN Lời giải.
Ta có y0 < 0, ∀x ∈ (−∞; −1) ∪ (0; 1) ⇒ y0 < 0, ∀x ∈ (−∞; −2). Chọn phương án D
Câu 11. Với a và b là hai số dương tùy ý, log (a3b4) bằng 2 1 1 A. log a + log b. B. 3 log a + 4 log b. C. 2 (log a + log b). D. 4 log a + 3 log b. 3 2 4 2 2 2 3 4 2 2 Lời giải.
Ta có log (a3b4) = log a3 + log b4 = 3 log a + 4 log b. 2 2 2 2 2 Chọn phương án B
Câu 12. Cho khối trụ có thể tích V và bán kính đáy R. Chiều cao của khối trụ đã cho bằng V V V V A. . B. . C. . D. . πR2 3πR2 R2 3R2 Lời giải. V Ta có V = πR2h ⇒ h = . πR2 Chọn phương án A
Câu 13. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số. A. 3. B. 0. C. 1. D. 2. x −∞ −2 0 2 +∞ y0 − 0 + 0 − 0 + y Lời giải.
Dựa vào BBT suy ra hàm số có 3 điểm cực trị. Chọn phương án A Câu 14.
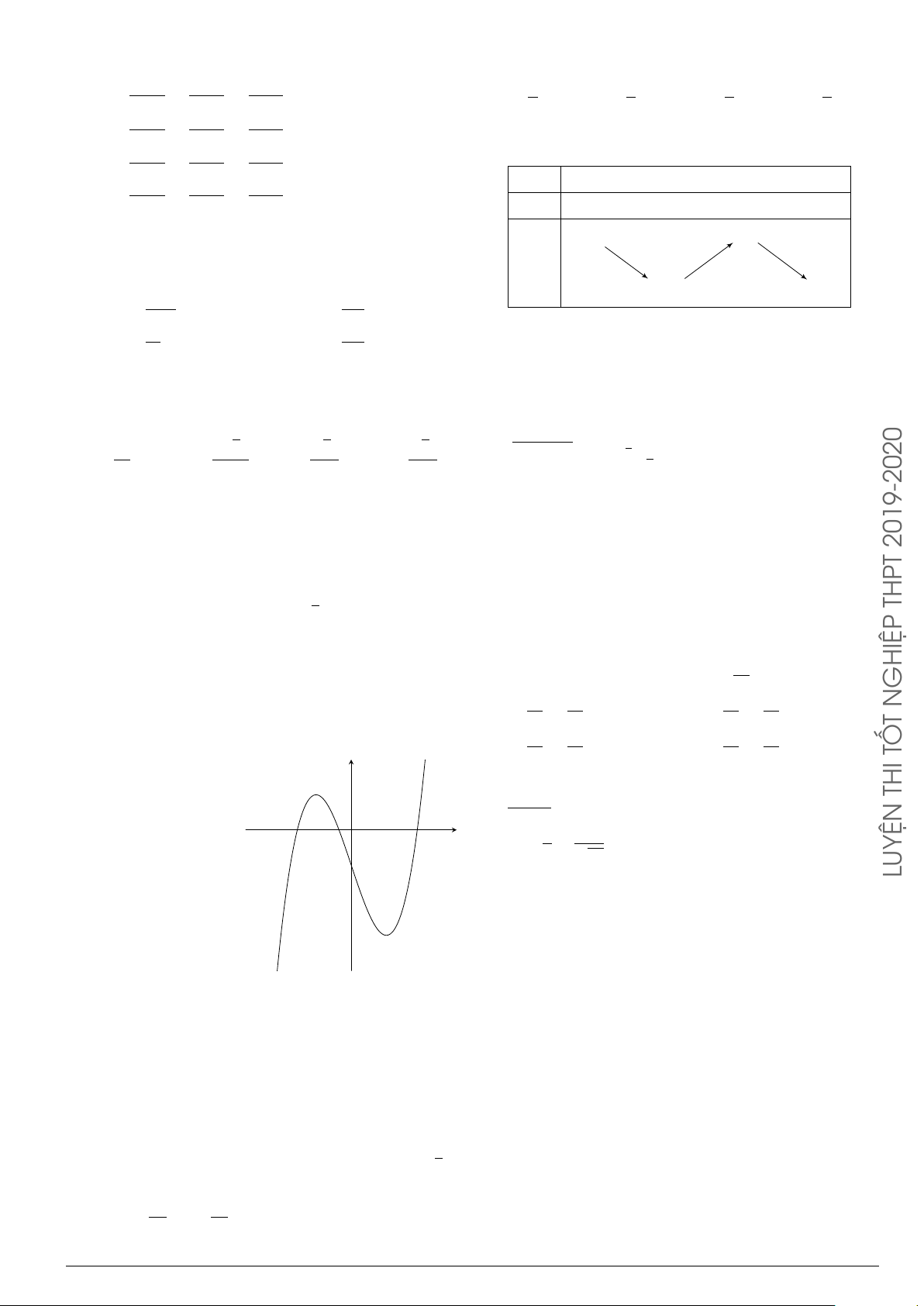
Đồ thị ở hình bên là của hàm số nào dưới đây? y A. y = −x3 − 3x2 − 4. B. y = x3 − 3x − 4. 1 C. y = −x3 + 3x2 − 4. D. y = x3 − 3x − 4. 1 2 x −1 O −2 −4 Lời giải.
Từ đồ thị hàm số ta suy ra hệ số cao nhất a < 0, loại được đáp án B và D.
Đồ thị đi qua điểm (2; 0) nên C là đáp án đúng. Chọn phương án C x + 2
Câu 15. Tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = là x − 1 A. y = 2; x = 1. B. y = 1; x = 1. C. y = −2; x = 1. D. y = 1; x = −2. Lời giải. x + 2 1 + 2 Ta có lim y = lim = lim
x = 1 suy ra đường thẳng y = 1 là tiệm cận ngang của đồ thị x→+∞ x→+∞ x − 1 x→+∞ 1 − 1x hàm số. GeoGebraPro Trang 3 o/ aPr roups/GeoGebr acebook.com/g .f https://www
Do lim (x + 2) = 3 > 0; lim (x − 1) = 0, x − 1 > 0 ∀x > 1 x→1+ x→1+ x + 2 ⇒ lim y = lim
= +∞ nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số. x→1+ x→+∞ x − 1 Chọn phương án B
Câu 16. Tập nghiệm của bất phương trình log (3 − x) < 2 là 2 A. (−∞; 1). B. (−1; 3). C. (1; 3). D. (3; +∞). Lời giải.
Điều kiện 3 − x > 0 ⇔ x < 3.
log (3 − x) < 2 ⇔ 3 − x < 4 ⇔ x > −1. 2
Kết hợp điều kiện ta được tập nghiệm S = (−1; 3) . Chọn phương án B Câu 17.
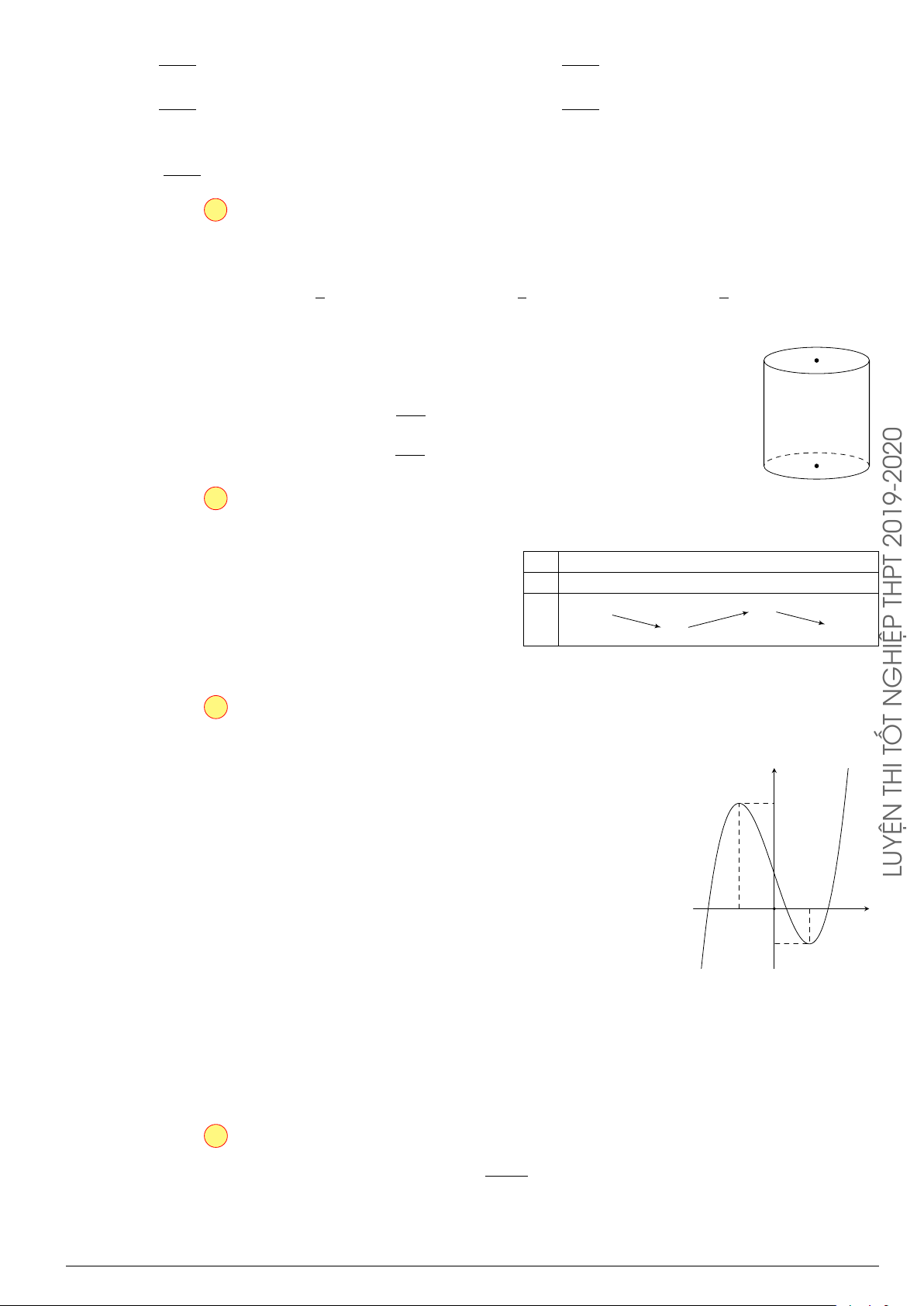
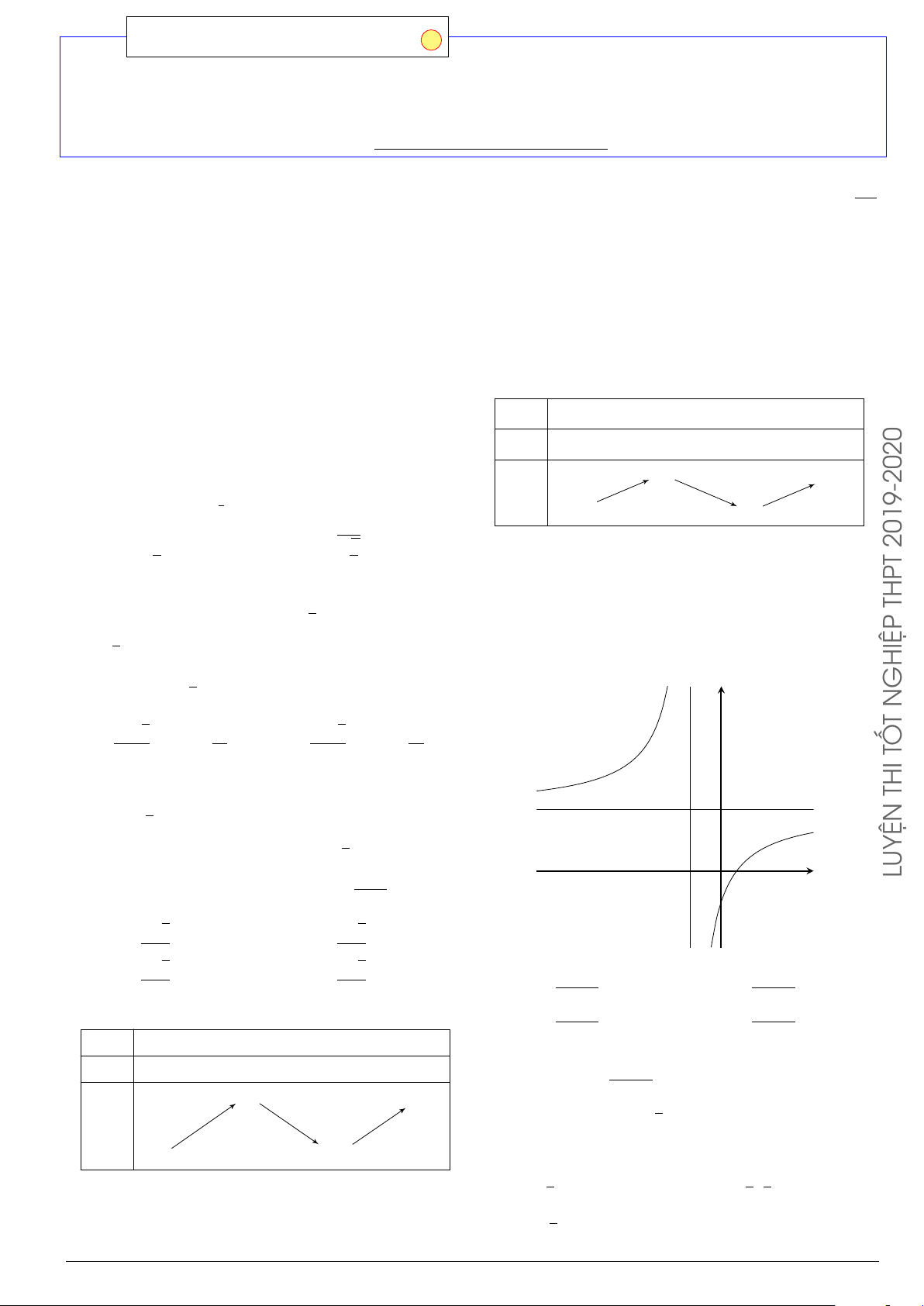
Cho hàm số f (x) có đồ thị như hình vẽ. Số nghiệm của phương trình 2f (x)− y 3 = 0 là A. 3. B. 1. C. 2. D. 0. 3 1 x −1 O −1 Lời giải. 3
Ta có 2f (x) − 3 = 0 ⇔ f (x) = (∗). y 2
Số nghiệm của phương trình (∗) bằng số giao điểm giữa đồ thị hàm số 3
y = f (x) và đường thẳng y = . 3 2 3
Dựa vào hình vẽ, hai đồ thị cắt nhau tại 3 điểm phân biệt. y = 2
Vậy phương trình đã cho có 3 nghiệm. 1 x −1 O −1 Chọn phương án A 2 5 5 Z Z Z Câu 18. Nếu f (x) dx = 5, f (x) dx = −1 thì f (x) dx bằng 1 2 1 A. −2. B. 2. C. 3. D. 4. Lời giải. 5 2 5 Z Z Z Ta có f (x) dx = f (x) dx + f (x) dx = 5 + (−1) = 4. 1 1 2 Chọn phương án D
Câu 19. Cho số phức z = 2 − 3i. Số phức liên hợp của số phức z là: A. z = 3 − 2i. B. z = 3 + 2i. C. z = −2 − 3i. D. z = 2 + 3i. Lời giải.
Do định nghĩa số phức liên hợp nên số phức liên hợp của z = 2 − 3i là z = 2 + 3i. Chọn phương án D GeoGebraPro Trang 4 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN
Câu 20. Cho hai số phức z1 = 1 − i, z2 = 2 + 3i. Tính mô-đun của số phức z = z1 + z2. √ √ A. |z| = 1. B. |z| = 5. C. |z| = 5. D. |z| = 13. Lời giải. √ √ z = z1 + z2 = 3 + 2i ⇒ |z| = 32 + 22 = 13. Chọn phương án D
Câu 21. Số phức nào sau đây có điểm biểu diễn là M (1; −2)? A. −1 − 2i. B. 1 + 2i. C. 1 − 2i. D. −2 + i. Lời giải.
M (1; −2) là điểm biểu diễn cho số phức có phần thực bằng 1 và phần ảo bằng −2, tức là 1 − 2i. Chọn phương án C
Câu 22. Trong không gian Oxyz, cho M (3; −2; 1), N (1; 0; −3). Gọi M 0, N 0 lần lượt là hình chiếu của
M và N lên mặt phẳng Oxy. Khi đó độ dài đoạn M 0N 0 là √ √ A. M 0N 0 = 8. B. M 0N 0 = 4. C. M 0N 0 = 2 6. D. M 0N 0 = 2 2. Lời giải. # » √
Ta có M 0(3; −2; 0) và N 0(1; 0; 0) suy ra M 0N 0 = (−2; 2; 0) ⇒ M 0N 0 = 2 2. Chọn phương án D
Câu 23. Trong không gian Oxyz cho mặt cầy (S) : x2 + y2 + z2 − 2x + 4z + 1 = 0 có tâm I và bán kính R là. A. I(−1; 0; 2), R = 2. B. I(−1; 0; 2), R = 4. C. I(1; 0; −2), R = 2. D. I(1; 0; −2), R = 4. Lời giải.
Dễ thấy mặt cầu (S) : x2 + y2 + z2 − 2x + 4z + 1 = 0 có:
Tâm I(1; 0; −2) và bán kính R = p12 + 02 + (−2)2 − 1 = 2. Chọn phương án C
Câu 24. Trong không gian Oxyz, mặt phẳng (P ) : 2x − y + 3 = 0. Một véc tơ pháp tuyến của (P ) có tọa độ là A. (2; 1; 0). B. (2; −1; 3). C. (2; −1; 0). D. (2; 1; 3). Lời giải. #»
Mặt phẳng (P ) có VTPT là n = (2; −1; 0). Chọn phương án C x − 1 y − 2 z − 3
Câu 25. Trong không gian Oxyz, đường thẳng d : = =
đi qua điểm nào dưới đây 2 −1 2 ? A. Q(2; −1; 2). B. M (−1; −2; −3). C. P (1; 2; 3). D. N (−2; 1; −2). Lời giải. 1 − 1 2 − 2 3 − 3 Ta có = = nên P (1; 2; 3) ∈ d. 2 −1 2 Chọn phương án C
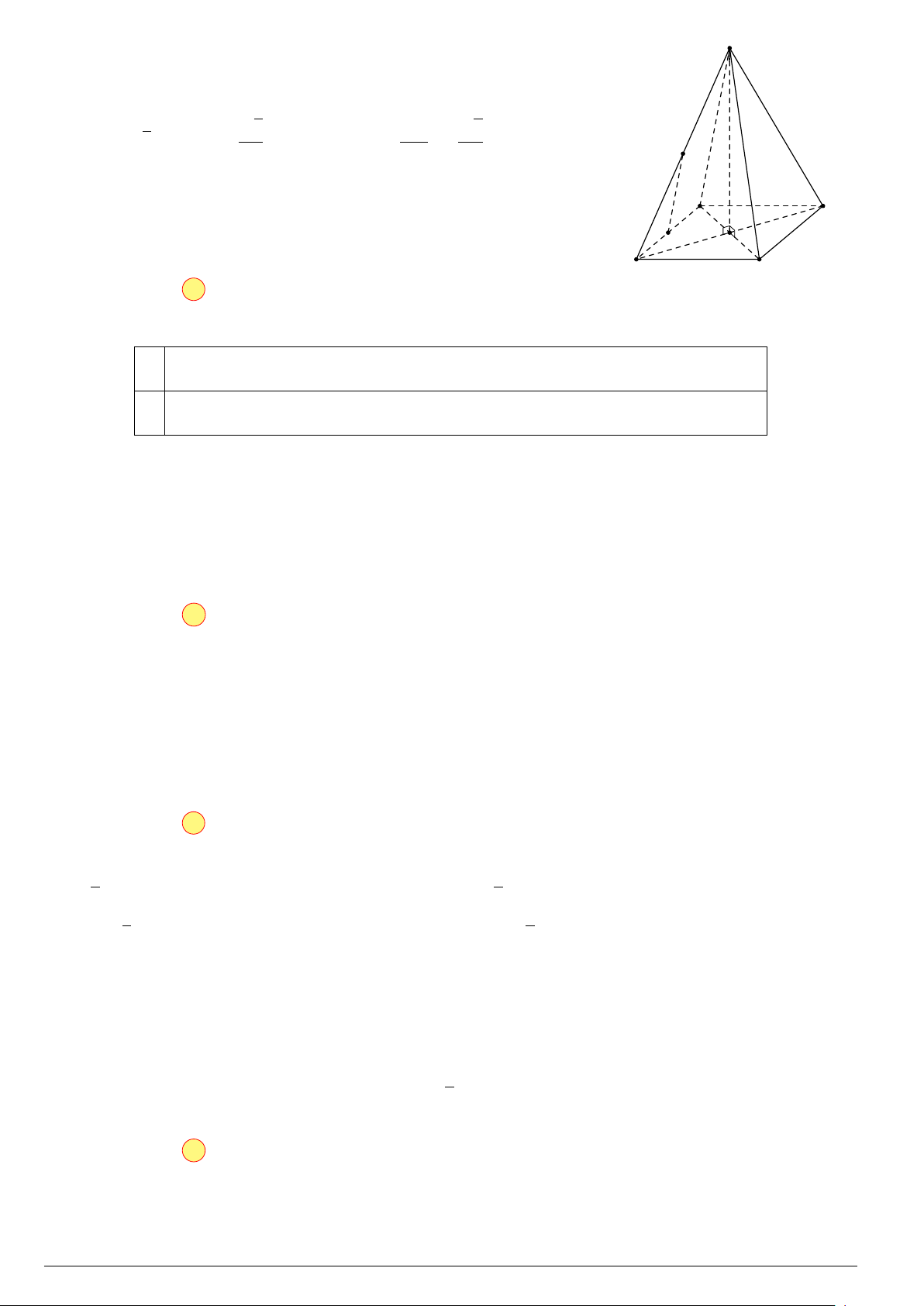
Câu 26. Cho hình chóp S.ABCD có đáy hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng
a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo góc (M N, SC) bằng A. 45◦. B. 30◦. C. 90◦. D. 60◦. Lời giải. GeoGebraPro Trang 5 o/ aPr roups/GeoGebr acebook.com/g .f https://www
Ta có M N là đường trung bình của tam giác DAS nên M N ∥ SA. S
Suy ra góc của SA với SC bằng góc giữa M N với SC. Gọi O là
tâm của hình vuông ABCD, vì SA = SC = SB = SD nên SO ⊥ (ABCD). √ √ √ 2 AO 2 Có AC = 2 ⇒ AO = nên sin ’ ASO = = ⇒ ∠ASO = N 2 SA 2 45◦ nên ’ ASC = 90◦. A B M O D C Chọn phương án C
Câu 27. Cho hàm số y = f (x) liên tục trên [−3; 3] và có bảng xét dấu đạo hàm như hình bên. x −3 −1 0 1 2 3 y0 + 0 − 0 − 0 + 0 −
Mệnh đề nào sau đây sai về hàm số đó?
A. Hàm số đạt cực tiểu tại x = 1.
B. Hàm số đạt cực đại tại x = −1.
C. Hàm số đạt cực đại tại x = 2.
D. Hàm số đạt cực tiểu tại x = 0. Lời giải.
Dựa vào bảng xét dấu của đạo hàm ta thấy f 0(0) = 0 và đạo hàm không đổi dấu khi x qua x0 = 0 nên
hàm số đã cho không đạt cực tiểu tại x = 0. Chọn phương án D
Câu 28. Cho hàm số y = −x3 + 3x2 + 2. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số trên [0; 3]. Tính (M + m). A. 6. B. 8. C. 10. D. 4. Lời giải. ñx = 0 / ∈ (0; 3)
Ta có: y0 = −3x2 + 6x; y0 = 0 ⇔ x = 2 ∈ (0;3)
y(0) = 2; y(2) = 6; y(3) = 2. Vậy M = 6; m = 2 ⇒ M + m = 8. Chọn phương án B
Câu 29. Với các số a, b > 0 thỏa mãn a2 + b2 = 6ab, biểu thức log (a + b) bằng 2 1 1 A. (3 + log a + log b). B. (1 + log a + log b). 2 2 2 2 2 2 1 1 C. 1 + (log a + log b). D. 2 + (log a + log b). 2 2 2 2 2 2 Lời giải.
Ta có: a2 + b2 = 6ab ⇔ (a + b)2 = 8ab ⇒ log (a + b)2 = log 8ab 2 2
⇔ 2log (a + b) = log 8 + log a + log b 2 2 2 2 1 ⇔ log (a + b) = (3 + log a + log b). 2 2 2 2 . Chọn phương án A
Câu 30. Số giao điểm của đường cong y = x3 − 2x2 + 2x + 1 và đường thẳng y = 1 − x là A. 1. B. 2. C. 3. D. 0. Lời giải. GeoGebraPro Trang 6 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN
Phương trình hoành độ giao điểm của hai đường trên là
x3 − 2x2 + 2x + 1 = 1 − x ⇔ x3 − 2x2 + 3x = 0 ⇔ x = 0.
Phương trình có một nghiệm nên đường cong và đường thẳng có một giao điểm. Chọn phương án A
Câu 31. Tập nghiệm của bất phương trình 3x2−2x < 27 là A. (−∞; −1). B. (3; +∞). C. (−1; 3).
D. (−∞; −1) ∪ (3; +∞). Lời giải.
3x2−2x < 27 ⇔ 3x2−2x < 33 ⇔ x2 − 2x < 3 ⇔ x2 − 2x − 3 < 0 ⇔ −1 < x < 3. Chọn phương án C √
Câu 32. Cho tam giác ABC vuông tại A có AB = a 3 và BC = 2a. Tính thể tích khối nón sinh ra
khi quay tam giác ABC quay cạnh AB. √ √ 2πa3 πa3 3 A. V = πa3 3. B. V = 2πa3. C. V = . D. V = . 3 3 Lời giải. √ Ta có AC =
BC2 − AB2 = a và thể tích khối nón là B √ 1 πa3 3 V = π · AC2 · AB = . 3 3 A0 C A Chọn phương án D 1 Z √ √ Câu 33. Cho I =
x2 1 − x3 dx. Nếu đặt t = 1 − x3 thì ta được 0 1 1 1 1 3 Z 3 Z 2 Z 2 Z A. I = t2 dt. B. I = − t2 dt. C. I = − t2 dt. D. I = t2 dt. 2 2 3 3 0 0 0 0 Lời giải.√ 2 Đặt t =
1 − x3 ⇒ t2 = 1 − x3 ⇒ 2t dt = −3x2 dx hay x2 dx = − t dt 3 ®x = 0 ⇒ t = 1 Đổi cận: x = 1 ⇒ t = 0. 0 1 2 Z 2 Z Do đó I = − t2 dt = t2 dt. 3 3 1 0 Chọn phương án D
Câu 34. Diện tích hình phẳng H được giới hạn bởi hai đồ thị y = x3 − 2x − 1 và y = 2x − 1 được tính theo công thức 0 2 Z Z A. S = x3 − 4x dx. B. S = x3 − 4x dx. −2 0 2 2 Z Z C. S = x3 − 4x dx. D. S = x3 − 4x dx. −2 −2 Lời giải. GeoGebraPro Trang 7 o/ aPr roups/GeoGebr acebook.com/g .f https://www
Phương trình hoành độ giao điểm của y = x3 − 2x − 1 và y = 2x − 1 là x = 2
x3 − 2x − 1 = 2x − 1 ⇔ x3 − 4x = 0 ⇔ x = 0 .  x = −2
Vậy diện tích hình phẳng H được giới hạn bởi hai đồ thị y = x3 − 2x − 1 và y = 2x − 1 được tính theo 2 Z công thức S = x3 − 4x dx. −2 Chọn phương án D
Câu 35. Cho hai số phức z1 = 2 + 4i, z2 = −1 + 3i. Tính môđun của số phức w = z1z2 − 2z1. √ √ √ A. |w| = 2 2. B. |w| = 2 10. C. |w| = 4 2. D. |w| = 2. Lời giải. √
Ta có w = (2+4i)(−1−3i)−2(2−4i) = (10−10i)−(4−8i) = 6−2i. Do đó |w| = p62 + (−2)2 = 2 10. Chọn phương án B
Câu 36. Gọi z1 là nghiệm phức có phần ảo dương của phương trình z2 + 6z + 13 = 0. Tìm tọa độ điểm
M biểu diễn số phức w = (i + 1) z1. A. M (−5; −1). B. M (5; 1). C. M (−1; −5). D. M (1; 5). Lời giải. ñz = −3 + 2i
Ta có z2 + 6z + 13 = 0 ⇔ z = −3 − 2i.
Vì z1 là nghiệm có phần ảo dương nên z1 = −3 + 2i.
Ta có w = (i + 1)(−3 + 2i) = −5 − i ⇒ M (−5; −1). Chọn phương án A
Câu 37. Trong không gian Oxyz, cho điểm A(2; −1; −3) và mặt phẳng (P ) : 3x − 2y + 4z − 5 = 0. Mặt
phẳng (Q) đi qua A và song song với mặt phẳng (P ) có phương trình là
A. (Q) : 3x − 2y + 4z − 4 = 0.
B. (Q) : 3x − 2y + 4z + 4 = 0.
C. (Q) : 3x − 2y + 4z + 5 = 0. D. (Q) : 3x + 2y + 4z + 8 = 0. Lời giải. #»
Do mặt phẳng (Q) song song với mặt phẳng (P ) nên có vectơ pháp tuyến là n = (3; −2; 4).
Phương trình mặt phẳng (Q) : 3(x − 2) − 2(y + 1) + 4(z + 3) = 0 ⇔ 3x − 2y + 4z + 4 = 0. Chọn phương án B
Câu 38. Trong không gian Oxyz, viết phương trình chính tắc của đường thẳng qua điểm E(1; 2; −3) và F (3; −1; 1). x − 1 y − 2 z + 3 x − 3 y + 1 z − 1 A. = = . B. = = . 3 −1 1 2 −3 4 x − 3 y + 1 z − 1 x + 1 y + 2 z − 3 C. = = . D. = = . 1 2 −3 2 −3 4 Lời giải.
Đường thẳng qua điểm E(1; 2; −3) và F (3; −1; 1) có véc-tơ chỉ phương #» # » u = EF = (2; −3; 4).
Vậy phương trình chính tắc của đường thẳng EF qua F (3; −1; 1) là x − 3 y + 1 z − 1 = = . 2 −3 4 Chọn phương án B
Câu 39. Có 8 bạn học sinh lớp 11A trong đó có An và Bình được xếp ngẫu nhiên theo một hàng ngang.
Tính xác suất P để An và Bình ngồi cạnh nhau. GeoGebraPro Trang 8 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN 1 1 1 1 A. P = . B. P = . C. P = . D. P = . 8 4 64 25 Lời giải.
Số cách xếp 8 học sinh thành một hàng ngang là n(Ω) = 8!
Số cách xếp 8 học sinh trong đó An và Bình ngồi cạnh nhau là: 7! · 2! 7! · 2! 1
Vậy xác suất cần tìm là P = = . 8! 4 Chọn phương án B
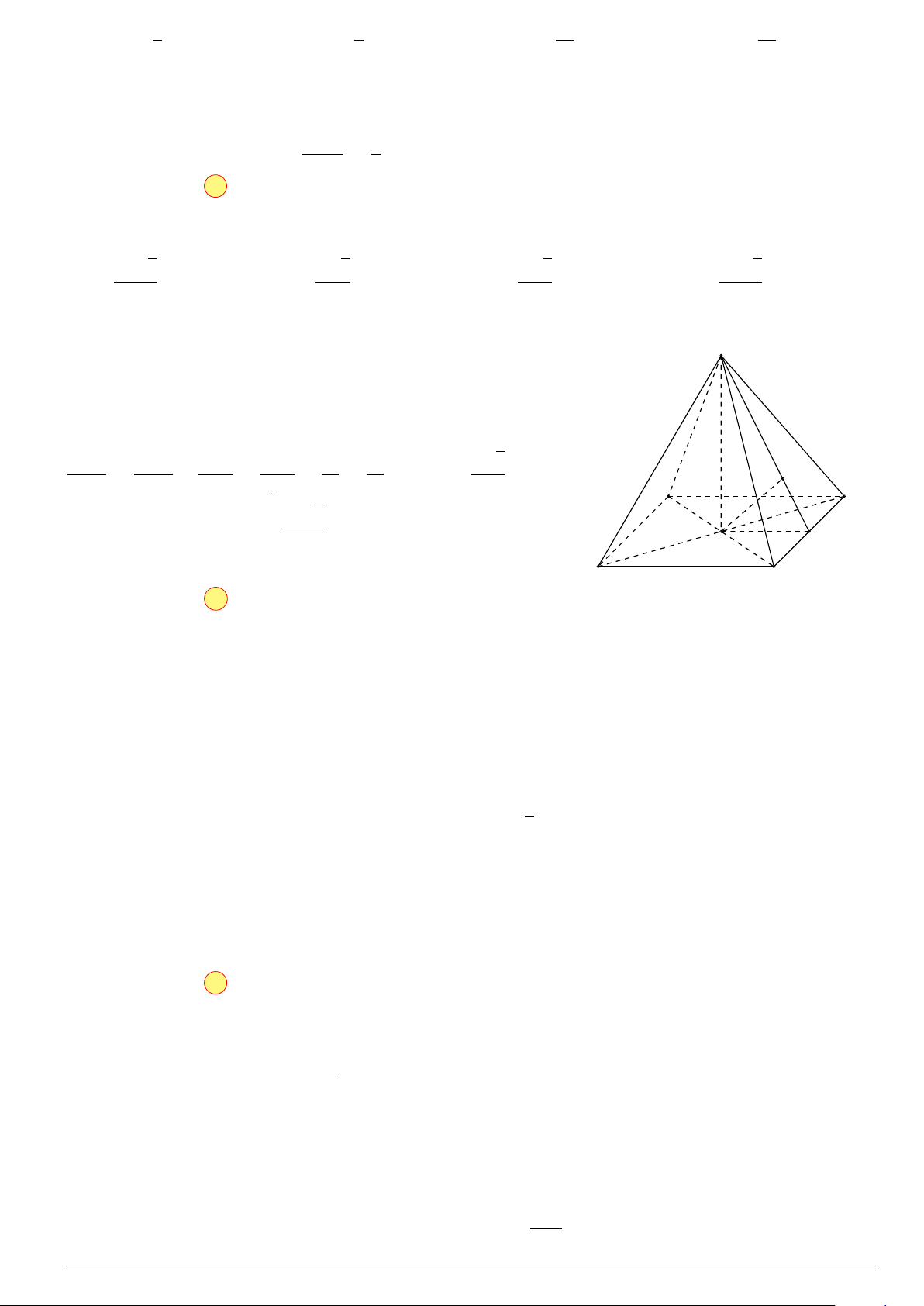
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SO vuông góc với mặt
phẳng ABCD và SO = a. Khoảng cách giữa SC và AB bằng √ √ √ √ 2a 3 a 5 a 3 2a 5 A. . B. . C. . D. . 15 5 15 15 Lời giải.
Vì AB ∥ (SCD) nên d(AB, SC) = d(AB, (SCD)) = S d(A, (SCD)) = 2d(O, (SCD)).
Gọi K là trung điểm của CD. Khi đó OK ⊥ CD ⇒
CD ⊥ (SOK). Gọi H là hình chiếu vuông góc của O lên
SK ⇒ OH ⊥ (SCD) ⇒ d(O, (SCD)) = OH. Ta có √ 1 1 1 1 1 5 a 5 = + = + = ⇒ OH = . OH2 OK2 OS2 a H 2 a2 a2 5 2 √ A D 2a 5 Vậy d(AB, SC) = 2OH = . K 5 O B C Chọn phương án D
Câu 41. Có bao nhiêu giá trị nguyên của tham số m ∈ [−2019; 2019] để hàm số y = (m − 1)x3 +
3mx2 + (4m + 4)x + 1 đồng biến trên khoảng (−∞; +∞)? A. 4036. B. 2017. C. 2018. D. 4034. Lời giải.
TXĐ: D = R. Đạo hàm: y0 = 3(m − 1)x2 + 6mx + 4m + 4.
Để hàm số đã cho đồng biến trên khoảng (−∞; +∞) thì y0 ≥ 0, ∀x ∈ (−∞; +∞) (y0 = 0 tại hữu hạn điểm). 4
• TH1: m − 1 = 0 ⇔ m = 1 thì y0 = 6x + 8 ≥ 0 ⇔ x ≥ − (không thỏa mãn). 3 m > 1 ®a = m − 1 > 0 ®m > 1   • TH2: ⇔ ⇔ ñm ≥ 2 ⇔ m ≥ 2. ∆0 − 3m2 + 12 ≤ 0
y0 = (3m)2 − 3(m − 1)(4m + 4) ≤ 0   m ≤ −2
Vì m là số nguyên và m ∈ [−2019; 2019] ⇒ m = {2; 3; 4; . . . ; 2019}.
Vậy có 2018 số nguyên m thuộc khoảng m ∈ [−2019; 2019]. Chọn phương án C
Câu 42. Một người thả một lá bèo vào một chậu nước. Sau 12 giờ, bèo sinh sôi phủ kín mặt nước trong
chậu. Biết rằng sau mỗi giờ lượng bèo tăng gấp 10 lần lượng bèo trước đó và tốc độ tăng không đổi. 1
Hỏi sau mấy giờ thì bèo phủ kín
mặt nước trong chậu (kết quả làm tròn đến hàng phần chục). 5 A. 9,1 giờ. B. 9,7 giờ. C. 10,9 giờ. D. 11,3 giờ. Lời giải.
Giả sử một lá bèo chiếm x (0 < x < 1) phần mặt nước trong chậu.
Sau 12 giờ, bèo sinh sôi phủ kín mặt nước trong chậu nên ta có phương trình 1 1012 · x = 1 ⇔ x = . 1012 GeoGebraPro Trang 9 o/ aPr roups/GeoGebr acebook.com/g .f https://www 1
Giả sử t giờ thì bèo phủ kín
mặt nước, ta có phương trình 5 1 1 1 · 10t = ⇔ t − 12 = log ⇔ t ≈ 11,3 giờ. 1012 5 5 Chọn phương án D
Câu 43. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như sau x −∞ −1 3 +∞ f 0(x) + 0 − 0 + 5 +∞ + f (x) −∞ 1
Đồ thị hàm số y = |f (x)| có bao nhiêu điểm cực trị? A. 2. B. 3. C. 4. D. 5. Lời giải.
Cách 1: Số điểm cực trị của đồ thị hàm số y = |f (x)| bằng số điểm cực trị của đồ thị hàm số y = f (x)
cộng với số giao điểm của đồ thị hàm số y = f (x) với trục hoành (không tính điểm cực trị)
Vì đồ thị hàm số y = f (x) có 2 điểm cực trị và cắt trục Ox tại 1 điểm nên đồ thị hàm số y = |f (x)| có 2 + 1 = 3 điểm cực trị. f (x) · f 0(x)
Cách 2: |f (x)| = pf 2(x) ⇒ (|f (x)|)0 =
⇒ dấu của (|f (x)|)0 là dấu của f (x) · f 0(x). |f (x)| Ta có f (x) · f 0(x).
f 0(x) = 0 ⇒ x = −1; x = 3.
Từ bảng biến thiên suy ra f (x) = 0 ⇔ x = x0 < −1. Lập bảng xét dấu x −∞ x0 −1 3 +∞ f 0(x) + + 0 − 0 + f (x) − 0 + + + f 0(x) · f (x) − 0 + 0 − 0 +
Từ bảng biến thiên ta thấy f (x) · f 0(x) đổi dấu 3 lần nên hàm số |f (x)| có 3 cực trị. Chọn phương án B
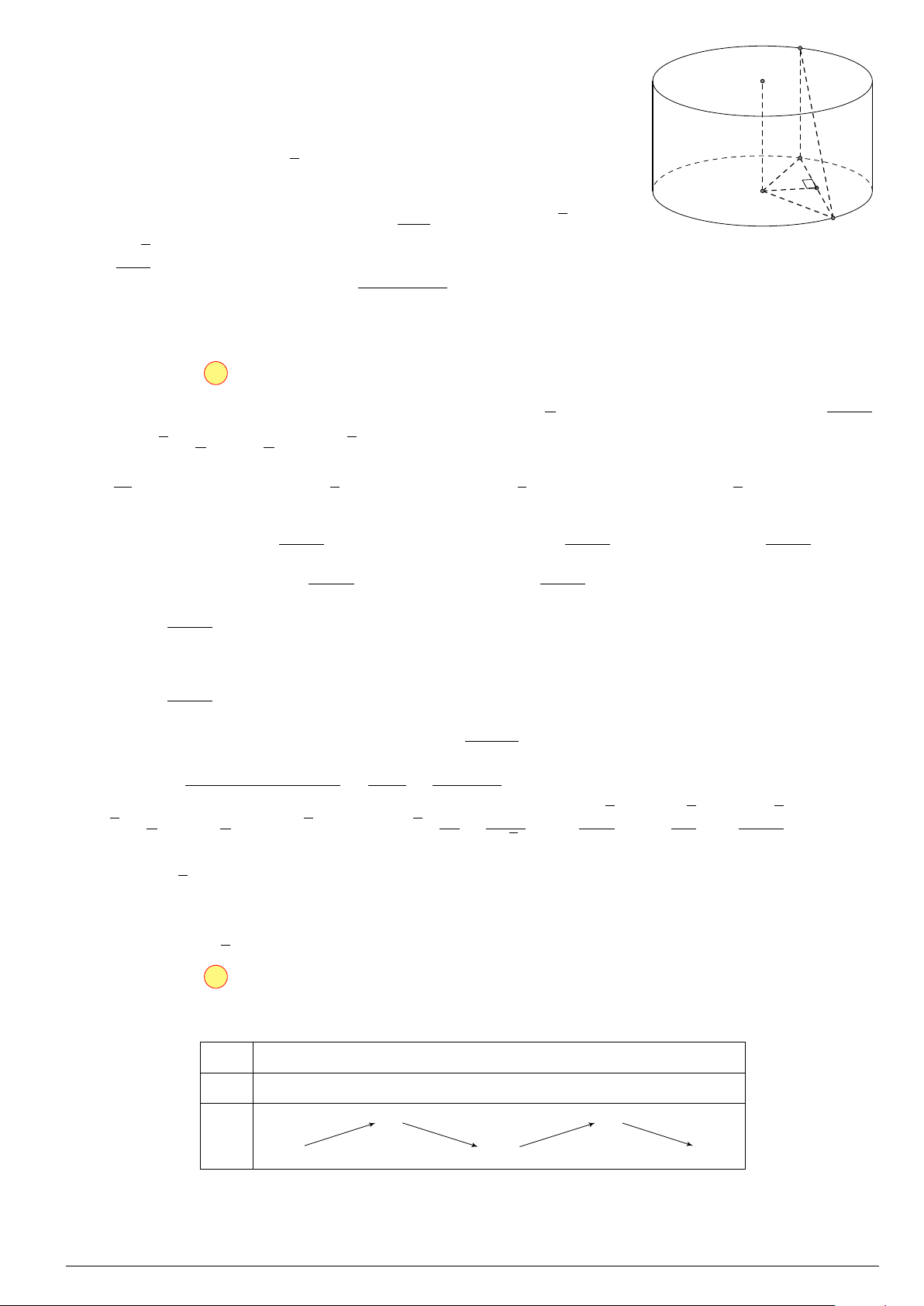
Câu 44. Cho hình trụ có trục OO0, chiều cao bằng a. Trên hai đường tròn đáy (O) và (O0) lần lượt lấy a
hai điểm A và B sao cho khoảng cách giữa hai đường thẳng AB và OO0 bằng . Góc giữa hai đường 2
thẳng AB và OO0 bằng 60◦. Thể tích của khối trụ đã cho là 2πa3 πa3 A. . B. . C. 2πa3. D. πa3. 3 3 Lời giải. GeoGebraPro Trang 10 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN
Dựng AA0 vuông góc với mặt phẳng đáy. A AB ⊂ (ABA0) nên d(AB, OO0) = d(OO0, (ABA0)) = O d(O0, (ABA0)).
Gọi I là trung điểm BA0. Ta có O0I ⊥ BA0 (vì ∆O0BA0 cân).
Mà O0I ⊥ AA0 nên O0I ⊥ (ABA0) a A0 hay d(O0, (ABA0)) = O0I = . 2 O0 Mặt khác ÿ AB, OO0 = ÿ AB, AA0 = ’ A0AB = 60◦. I A0B √
Xét ∆ABA0 vuông tại A0 có tan 60◦ = ⇒ A0B = a 3 và B √ AA0 a 3 BI = . 2 √
Xét ∆O0BI vuông tại I có O0B = O0I2 + BI2 = a.
Vậy thể tích của khối trụ đã cho là
V = π · O0B2 · OO0 = π · a2 · a = πa3. Chọn phương án D π x
Câu 45. Cho hàm số f (x) liên tục và có đạo hàm trên 0;
, thỏa mãn f (x) + tan xf 0(x) = . 2 cos3 x √ π π √ Biết rằng 3f −f
= aπ 3+b ln 3 trong đó a, b ∈ R. Giá trị của biểu thức P = a+b bằng 3 6 14 2 7 4 A. . B. − . C. . D. − . 9 9 9 9 Lời giải. x x x Ta có f (x) + tan xf 0(x) =
⇔ cos x · f (x) + sin xf 0(x) = ⇔ [sin x · f (x)]0 = . cos3 x cos2 x cos2 x Z Z x Z x Do đó [sin x · f (x)]0 dx = dx ⇒ sin x · f (x) = dx. cos2 x cos2 x Z x Tính I = dx. cos2 x u = x ®  du = dx Đặt dx ⇒ v = tan x.  dv = cos2 x Z Z d cos x Khi đó I = x · tan x − tan x dx = x · tan x − = x · tan x + ln | cos x|. cos x x · tan x + ln | cos x| x ln | cos x| Suy ra f (x) = = + . sin x cos x sin x √ √ √ √ Å ã Ç å π π √ √ 2π 2 ln 2 π 3 3 5π 3 Do 3f − f = aπ 3 + b ln 3 = 3 − √ − + 2 ln = ln 3. 3 6 3 3 9 2 9  5 a = Khi đó 9 . b = −1 4 Vậy P = a + b = − . 9 Chọn phương án D
Câu 46. Cho hàm số y = f (x) có bảng biến thiên như sau: x −∞ −2 0 2 +∞ y0 + 0 − 0 + 0 − 3 3 y −∞ −1 −∞
Hàm số y = f (x2 − 2) nghịch biến trên khoảng nào dưới đây? A. (2; +∞). B. (0; 2). C. (−∞; −2). D. (−2; 0). GeoGebraPro Trang 11 o/ aPr roups/GeoGebr acebook.com/g .f https://www Lời giải. Ta có y0 = 2xf 0 (x2 − 2). x = 0 x = 0 ñx = 0 x2 − 2 = −2 √ y0 = 0 ⇔ ⇔    ⇔ x = ± 2 . f 0 x2 − 2 = 0  x2 − 2 = 0  x = ±2 x2 − 2 = 2
Do các nghiệm của phương trình y0 = 0 đều là nghiệm bội lẻ, mà y0(3) = 6f 0(7) < 0 nên ta có bảng xét dấu y0 √ √ x −∞ −2 − 2 0 2 2 +∞ y0 + 0 − 0 + 0 − 0 + 0 −
Vậy hàm số y = f (x2 − 2) nghịch biến trên khoảng (2; +∞). Chọn phương án A
Câu 47. Xét các số thực dương x, y thoả mãn log 1 x + log 1 y ≤ log 1 (x + y2). Tìm giá trị nhỏ nhất 2 2 2
Pmin của biểu thức P = x + 3y √ 17 25 2 A. Pmin = . B. Pmin = 8. C. Pmin = 9. D. Pmin = . 2 4 Lời giải. Phương pháp:
• Sử dụng công thức log x + log y = log (xy) (0 < a 6= 1, x, y > 0), giải bất phương trình lôgarit a a a
cơ bản log f (x) ≤ log g (x) (0 < a < 1) ⇔ f (x) ≥ g (x). a a
• Rút x theo y thế vào P.
• Đưa P về dạng P = f (y). Lập BBT và tìm GTNN của P = f (y). Cách giải: Theo bài ra ta có:
log 1 + log 1 ≤ log 1 (x + y2) ⇔ log 1 (xy) ≤ (x + y2) ⇔ xy ≥ x + y2 x y 2 2 2 2
x (y − 1) ≥ y2 > 0. Mà x > 0 ⇒ y − 1 > 0 ⇔ y > 1. y2 y2 x ≥
. Khi đó ta có P = x + 3y ≥ + 3y với y > 1. y − 1 y − 1 y2 Xét hàm số f (y) = + 3y với y > 1 ta có: y − 1  3 2y (y − 1) − y2 y2 − 2y + 3y2 − 6y + 3 4y2 − 8y + 3 y = f 0 (y) = + 3 = = = 0 ⇔ 2  . (y − 1)2 (y − 1)2 (y − 1)2  1 y = 2 BBT: 1 3 y −∞ 1 +∞ 2 2 f 0(y) + 0 − − 0 + 1 +∞ +∞ + f (y) −∞ −∞ 9 GeoGebraPro Trang 12 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN Å 3 ã
Từ BBT ta thấy min f (y) = f = 9. y>1 2 Vậy P ≥ 9 hay Pmin = 9. Chọn phương án C
Câu 48. Gọi S là tập hợp các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y =
|x3 − 3x2 − 9x + m| trên đoạn [−2; 4] bằng 16. Số phần tử của S là A. 10. B. 12. C. 14. D. 11. Lời giải. ñx = −1
Xét hàm số y = f (x) = x3 − 3x2 − 9x + m có y0 = 3x2 − 6x − 9, y0 = 0 ⇔ x = 3. Bảng biến thiên x −2 −1 3 4 f 0(x) + 0 − 0 + m + 5 m − 20 f (x) m − 2 m − 27
Giá trị lớn nhất của hàm số y = |x3 − 3x2 − 9x + m| trên đoạn [−2; 4] bằng 16 khi và chỉ khi  ®m + 5 = 16  27 − m ≤ 16   ⇔ m = 11. ®  m − 27 = 16  m + 5 ≤ 16
Vậy m = 11 là giá trị duy nhất thỏa mãn. Chọn phương án D √ 2a 5
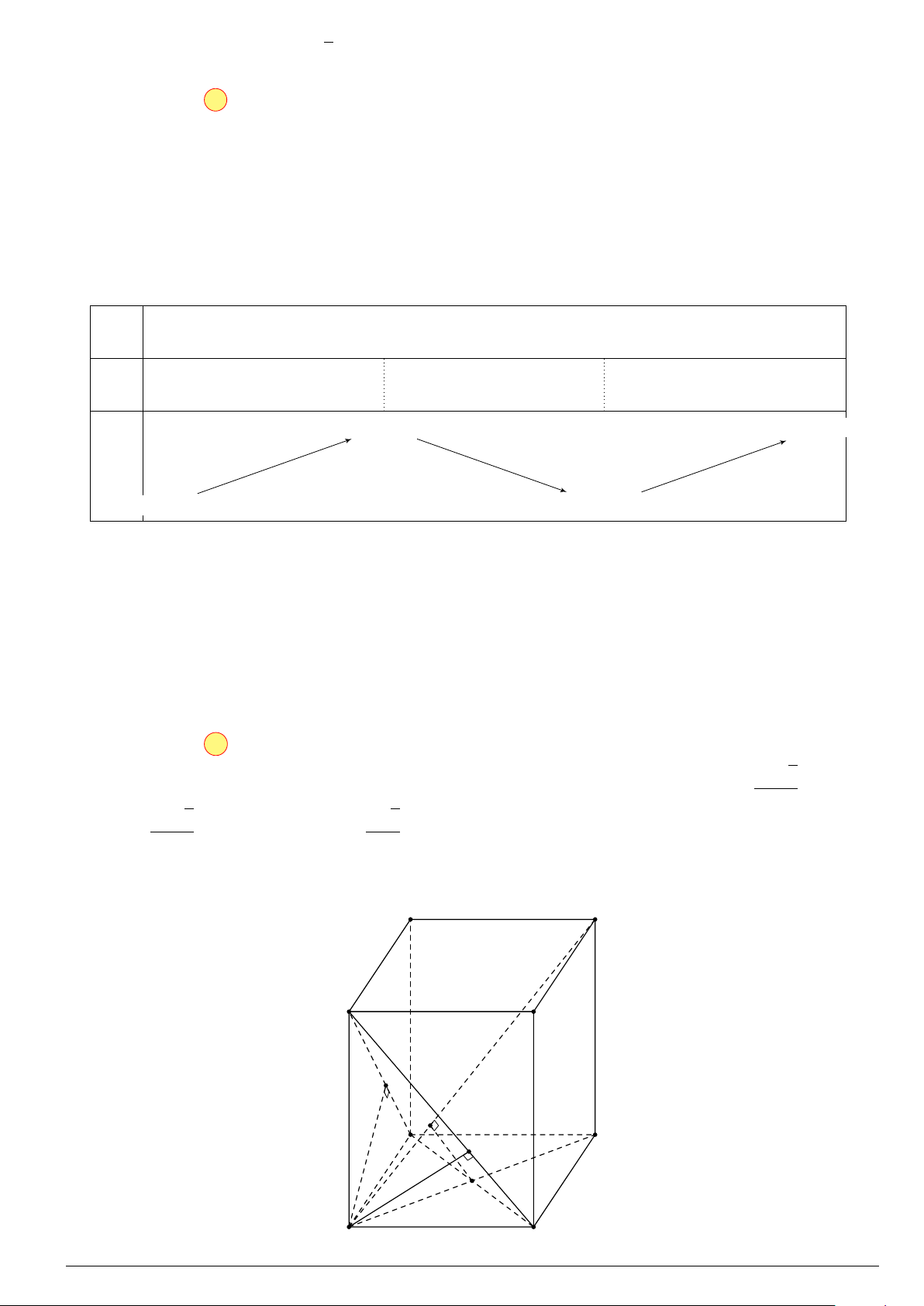
Câu 49. Cho hình hộp chữ nhật ABCD.A0B0C0D0. Khoảng cách giữa AB và B0C là , giữa BC √ √ 5 2a 5 a 3 và AB0 là , giữa AC và BD0 là
. Thể tích của khối hộp đó là 5 3 A. 8a3. B. 4a3. C. 2a3. D. a3. Lời giải. A0 D0 B0 C0 K L A D H O B C GeoGebraPro Trang 13 o/ aPr roups/GeoGebr acebook.com/g .f https://www
Gọi H, K lần lượt là hình chiếu vuông góc của B lên AB0 và B0C. √ ®BK ⊥ AB0 2a 5 Ta có ⇒ d(AB0, BC) = BK = .
BK ⊥ BC (do BC ⊥ (ABB0) ⊃ BK) 5 √ 2a 5
Tương tự ta có d(AB, B0C) =
nên AB = BC. Vậy tứ giác ABCD là hình vuông. Suy ra 5
AC ⊥ BD, mà AC ⊥ AA0 nên AC ⊥ (BB0D0D). √ a 3
Gọi L là hình chiếu vuông góc của O lên BD0, suy ra d(AC, BD0) = OL = . 3 1 1 5
Đặt AB = BC = x, BB0 = y. Ta có + = . (*) x2 y2 4a2
Mặt khác, do 4BOL v BD0D (g - g) nên √ √ OL BO a 3 x 2 = ⇔ = DD0 BD0 3y 2p2x2 + y2 3a2 2x2 ⇔ = 9y2 8x2 + 4y2 ⇔ 2a2(8x2 + 4y2) = 18x2y2 24a2x2 ⇔ y2 = . 18x2 − 12a2 Thay vào (*) ta được 1 18x2 − 12a2 5 12a2 + 18x2 5 + = ⇔ = ⇔ x = a ⇒ y = 2a. x2 24a2x2 4a2 24a2x2 4a2
Vậy, VABCD.A0B0C0D0 = AB · BC · BB0 = 2a3. Chọn phương án C x + y
Câu 50. Xét các số thực dương x, y thỏa mãn log√
= x(x − 3) + y(y − 3) + xy. Tìm 3 x2 + y2 + xy + 2 3x + 2y + 1
giá trị lớn nhất Pmax của P = . x + y + 6 A. 3. B. 2. C. 1. D. 4. Lời giải. Ta có x + y log√ = x(x − 3) + y(y − 3) + xy 3 x2 + y2 + xy + 2
⇔ 3(x + y) + log√ (3(x + y)) = x2 + y2 + xy + 2 + log√ x2 + y2 + xy + 2 . 3 3 1
Hay f (3(x + y)) = f (x2 + y2 + xy + 2) với f (t) = t + log√ t có f 0(t) = 1 + √ > 0, ∀t > 0. 3 t ln 3 Do vậy 3(x + y) = x2 + y2 + xy + 2
⇔ 4x2 + 4xy + y2 + 3(y2 − 2y + 1) − 6(2x + y) + 5 = 0
⇒ (2x + y)2 − 6(2x + y) + 5 = −3(y − 1)2 ≤ 0. 2x + y − 5
Suy ra 1 ≤ 2x + y ≤ 5. Do đó P = 1 + ≤ 1. x + y + 6 Vậy Pmax = 1. Chọn phương án C
———————–HẾT———————– GeoGebraPro Trang 14 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN ĐÁP ÁN THAM KHẢO 1. A 2. C 3. D 4. D 5. A 6. C 7. B 8. B 9. C 10. D 11. B 12. A 13. A 14. C 15. B 16. B 17. A 18. D 19. D 20. D 21. C 22. D 23. C 24. C 25. C 26. C 27. D 28. B 29. A 30. A 31. C 32. D 33. D 34. D 35. B 36. A 37. B 38. B 39. B 40. D 41. C 42. D 43. B 44. D 45. D 46. A 47. C 48. D 49. C 50. C GeoGebraPro Trang 15 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN MỖI NGÀY MỘT ĐỀ THI 2
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Một chi đoàn có 16 đoàn viên. Cần bầu chọn một Ban Chấp hành ba người gồm Bí thư, Phó
Bí thư và Ủy viên. Số cách chọn ra Ban Chấp hành nói trên là A. 560. B. 4096. C. 48. D. 3360.
Câu 2. Cho cấp số cộng (un) biết u3 = 6, u8 = 16. Tính công sai d và tổng của 10 số hạng đầu tiên. A. d = 2; S10 = 100. B. d = 1; S10 = 80. C. d = 2; S10 = 120. D. d = 2; S10 = 110. √ √ Ä ä2x+1
Câu 3. Tìm nghiệm của phương trình 7 + 4 3 = 2 − 3. 1 3 1 A. x = . B. x = − . C. x = −1. D. x = − . 4 4 4
Câu 4. Cho hình lập phương ABCD.A0B0C0D0 có cạnh bằng a. Tính thể tích V của khối chóp D0.ABCD.a3 a3 a3 A. V = . B. V = . C. V = . D. V = a3. 4 6 3
Câu 5. Tìm tập xác định của hàm số y = log 1 (x2 − 3x + 2). 2 A. (−∞; 1) ∪ (2; +∞). B. (1; 2). C. (2; +∞). D. (−∞; 1). Z x3 Câu 6. Nếu f (x) dx = + ex + C thì f (x) bằng 3 x4 x4 A. f (x) = 3x2 + ex. B. f (x) = + ex. C. f (x) = x2 + ex. D. f (x) = + ex. 3 12
Câu 7. Cho khối chóp S.ABC có SA ⊥ (ABC) và SA = 2, tam giác ABC vuông cân tại A và AB = 1.
Thể tích khối chóp S.ABC bằng 1 1 2 A. . B. . C. 1. D. . 6 3 3
Câu 8. Cho khối nón có đường cao h và bán kính đáy r. Tính thể tích của khối nón. √ 1 √ A. 2πr h2 + r2. B. πr2h. C. πr h2 + r2. D. πr2h. 3
Câu 9. Một mặt cầu có đường kính bằng a có diện tích S bằng bao nhiêu? 4πa2 πa2 A. S = . B. S = . C. S = πa2. D. S = 4πa2. 3 3
Câu 10. Cho hàm số y = x3 + 3x2 − 4 có bảng biến thiên sau, tìm a và b. x −∞ −2 0 +∞ y0 + 0 − 0 + 0 +∞ + y a b A. a = +∞; b = 2. B. a = −∞; b = −4. C. a = −∞; b = 1. D. a = +∞; b = 3.
Câu 11. Với a, b là các số thực dương tùy ý và a khác 1, đặt P = log b3 + log a
a2 b6. Mệnh đề nào dưới đây đúng? A. P = 27 log b . B. P = 15 log b . C. P = 9 log b . D. P = 6 log b . a a a a
Câu 12. Cho hình trụ có bán kính đáy bằng 5 và chiều cao bằng 7 . Diện tích xung quanh của hình trụ đã cho bằng 175π A. . B. 175π. C. 70π. D. 35π. 3
Câu 13. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số. A. 3. B. 0. C. 1. D. 2. GeoGebraPro Trang 1 o/ aPr roups/GeoGebr acebook.com/g .f https://www x −∞ −2 0 2 +∞ y0 − 0 + 0 − 0 + y Câu 14.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây ? y 2x − 1 x + 1 A. y = . B. y = . x − 1 x − 1 C. y = x4 + x2 + 1. D. y = x3 − 3x − 1. 1 1 O x 2 − 2x
Câu 15. Tìm đường tiệm cận ngang của đồ thị hàm số y = . x + 1 A. y = −2. B. x = −1. C. x = −2. D. y = 2. Å 3 ãx−1 Å 3 ã−x+3
Câu 16. Tìm tập nghiệm của bất phương trình > . 4 4 A. (2; +∞). B. (−∞; 2). C. [2; +∞). D. (−∞; 2]. Câu 17.
Cho hàm số bậc bốn y = f (x) có đồ thị như hình vẽ. Số nghiệm của phương y trình 3f (x) − 8 = 0 bằng A. 1. B. 2. C. 3. D. 4. 2 1 −2 2 x O 1 −1 −2 5 Z dx Câu 18. Nếu
= ln c với c ∈ Q thì giá trị của c bằng 2x − 1 1 A. 9. B. 3. C. 6. D. 81.
Câu 19. Số phức liên hợp của z = 4 + 3i là A. z = −3 + 4i. B. z = 4 − 3i. C. z = 3 + 4i. D. z = 3 − 4i.
Câu 20. Cho hai số phức z1 = −1 + 2i, z2 = −1 − 2i. Giá trị của biểu thức |z1|2 + |z2|2 bằng √ A. 10. B. 10. C. −6. D. 4.
Câu 21. Điểm M biểu diễn số phức z = 2 − i trên mặt phẳng tọa độ Oxy là A. M = (1; −2). B. M = (2; −1). C. M = (−2; 1). D. M = (2; 1).
Câu 22. Trong không gian Oxyz, hình chiếu vuông góc của điểm A(2; 3; 4) lên trục Ox là điểm nào dưới đây? A. M (2; 0; 0). B. M (0; 3; 0). C. M (0; 0; 4). D. M (0; 2; 3).
Câu 23. Trong không gian Oxyx, cho mặt cầu (S) : (x − 2)2 + (y + 1)2 + (z − 1)2 = 9. Tìm tọa độ tâm
I và bán kính R của mặt cầu (S). A. I(−2; 1; −1), R = 3. B. I(−2; 1; −1), R = 9. C. I(2; −1; 1), R = 3. D. I(2; −1; 1), R = 9. x + 8 y − 5 z
Câu 24. Trong không gian Oxyz, cho đường thẳng d : = =
. Khi đó véc-tơ chỉ phương 4 −2 1
của đường thẳng d có tọa độ là A. (4; −2; 1). B. (4; 2; −1). C. (4; −2; −1). D. (4; 2; 1). GeoGebraPro Trang 2 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P ) : 2x − y + z − 1 = 0. Điểm nào dưới đây thuộc (P )? A. M (2; −1; 1). B. N (0; 1; −2). C. P (1; −2; 0). D. Q(1; −3; −4).
Câu 26. Cho hình lập phương ABCD.A0B0C0D0. Tính góc giữa AC0 và BD. B A C D B0 A0 D0 C0 A. 90◦. B. 45◦. C. 60◦. D. 120◦.
Câu 27. Cho hàm số y = f (x) có bảng xét dấu của hàm đạo hàm như sau: x −∞ −3 2 3 4 +∞ f 0(x) − 0 + 0 + 0 − 0 +
Số điểm cực trị của hàm số đã cho là A. 6. B. 4. C. 2. D. 3. 4
Câu 28. Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x) = x+ trên đoạn [1; 3] bằng x 65 52 A. . B. 20. C. 6. D. . 3 3
Câu 29. Cho 0 < a 6= 1 và x, y là các số thực âm. mệnh đề nào dưới đây đúng?
A. log (x2y4) = 2 (log |x| + log y2). B. log (xy) = log x + log y. a a a a a a Å x ã log (−x)
C. log (−x2y) = 2 log (−x) + log y. D. log = a . a a a a y log (−y) a
Câu 30. Số giao điểm của đồ thị hàm số y = x3 + x + 2 và đường thẳng y = −2x + 1 là A. 3. B. 0. C. 2. D. 1.
Câu 31. Tập nghiệm của bất phương trình 4x+1 ≤ 8x−2 là A. [8; +∞). B. ∅. C. (0; 8). D. (−∞; 8] .
Câu 32. Cho hình lập phương ABCD.A0B0C0D0 cạnh a. Tính diện tích toàn phần của vật tròn xoay
thu được khi quay tam giác AA0C0 quanh trục AA0. √ √ √ √ Ä ä Ä ä Ä ä Ä ä A. π 6 + 2 a2. B. π 3 + 2 a2. C. 2π 2 + 1 a2. D. 2π 6 + 1 a2. π 2 Z √ Câu 33. Cho tích phân I =
2 + cos x · sin x dx. Nếu đặt t = 2 + cos x thì kết quả nào sau đây 0 đúng? π 2 3 2 2 Z √ Z √ Z √ Z √ A. I = t dt. B. I = t dt. C. I = 2 t dt. D. I = t dt. 3 2 3 0
Câu 34. Cho hàm số y = f (x) liên tục trên đoạn [a; b]. Viết công thức tính diện tích hình thang cong
giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = a, x = b. b b b b Z Z Z Z A. S = f 2(x) dx. B. S = |f (x)| dx. C. S = π |f (x)| dx. D. S = f (x) dx. a a a a
Câu 35. Cho hai số phức z1 = 3 − 4i và z2 = −2 + i. Tìm số phức liên hợp của z1 + z2. A. 1 + 3i. B. 1 − 3i. C. −1 + 3i. D. −1 − 3i.
Câu 36. Gọi z1 là nghiệm phức có phần ảo âm của phương trình z2 + 2z + 3 = 0. Trên mặt phẳng tọa
độ, điểm nào sau đây là điểm biểu diễn số phức z1? √ √ √ √ A. P (−1; − 2i). B. Q(−1; 2i). C. N (−1; 2). D. M (−1; − 2). GeoGebraPro Trang 3 o/ aPr roups/GeoGebr acebook.com/g .f https://www x = −1 + t x − 1 y + 1 z − 3 
Câu 37. Trong không gian Oxyz, cho hai đường thẳng d1 : = = và d2 : y = 4 + 3t . 2 3 −5 z = 1 + t
Tìm phương trình mặt phẳng chứa đường thẳng d1 và song song với đường thẳng d2. A. 18x + 7y + 3z + 20 = 0. B. 18x − 7y + 3z + 34 = 0. C. 18x + 7y + 3z − 20 = 0. D. 18x − 7y + 3z − 34 = 0.
Câu 38. Trong không gian với hệ tọa độ Oxyz, viết phương trình chính tắc của đường thẳng d đi qua
điểm A(1; 2; 3) và vuông góc với mặt phẳng (P ) : 2x + 2y + z + 2017 = 0. x + 1 y + 2 z + 3 x − 1 y − 2 z − 3 A. = = . B. = = . 2 2 1 2 2 1 x − 2 y − 2 z − 1 x + 2 y + 2 z + 1 C. = = . D. = = . 1 2 3 1 2 3
Câu 39. Xếp 5 nam và 2 nữ vào một bàn dài gồm 7 chỗ ngồi. Tính xác suất để 2 nữ không ngồi cạnh nhau. 6 4 5 2 A. . B. . C. . D. . 7 7 7 7
Câu 40. Cho lăng trụ tam giác đều ABC.A0B0C0 có tất cả các cạnh đều bằng a. Khoảng cách giữa hai
đường thẳng BC và AB0 bằng √ √ √ √ a 21 a 3 a 7 a 2 A. . B. . C. . D. . 7 2 4 2
Câu 41. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (−2019; 2020) để hàm số y =
2x3 − 3(2m + 1)x2 + 6m(m + 1)x + 2019 đồng biến trên khoảng (2; +∞)? A. 2021. B. 2020. C. 2018. D. 2019.
Câu 42. Cường độ một trận động đất M được cho bởi công thức M = log A − log A0, với A là biên
độ rung chấn tối đa và A0 là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San
Francisco có cường độ 8,3 độ Richter. Trong cùng năm đó, trận động đất khác ở gần đó đo được 7,1 độ
Richter. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu lần trận động đất này? A. 1,17. B. 2,2. C. 15,8. D. 4. Câu 43.
Cho hàm số y = f (x). Hàm số y = f 0(x)
có bảng biến thiên như sau. Bất phương trình x −∞ −4 1 +∞
f (x) > sin x + m có nghiệm trên khoảng (−1; 1) khi và chỉ khi y0 − 0 + 0 − A. m > f (1) − sin 1. B. m ≥ f (1) − sin 1. +∞ + −1 C. m ≤ f (−1) + sin 1. y D. m < f (−1) + sin 1. −3 −∞
Câu 44. Cho hình trụ có bán kính đáy bằng a. Cắt hình trụ bởi một mặt phẳng (P ) song song với a
trục của hình trụ và cách hình trụ một khoảng bằng
ta được thiết diện là một hình vuông. Tính thể 2 tích khối trụ. √ √ πa3 3 A. 3πa3. B. πa3 3. C. . D. πa3. 4 2 1
Câu 45. Cho hàm số f (x) liên tục trên R R R và f (2) = 16,
f (x) dx = 4. Tính tích phân I = x · 0 0 f 0(2x) dx A. 13. B. 12. C. 20. D. 7.
Câu 46. Cho hàm số y = f (x) = ax3 + bx2 + cx + d có bảng biến thiên như sau: 1
Khi đó |f (x)| = m có bốn nghiệm phân biệt x1 < x2 < x3 < < x4 khi và chỉ khi: 2 GeoGebraPro Trang 4 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN A. 0 < m < 1. x −∞ 0 1 +∞ B. 0 < m ≤ 1. 1 y0 + 0 − 0 + C. < m < 1. 2 1 +∞ + 1 D. ≤ m < 1. 2 y −∞ 0
Câu 47. Cho x, y > 0 thỏa mãn log(x + 2y) = log x + log y. Khi đó, giá trị nhỏ nhất của biểu thức x2 4y2 P = + là 1 + 2y 1 + x 32 31 29 A. 6. B. . C. . D. . 5 5 5
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số x2 + mx + m y =
trên [1; 2] bằng 2. Số phần tử của S là x + 1 A. 1. B. 4. C. 3. D. 2.
Câu 49. Cho hình hộp chữ nhật ABCD.A0B0C0D0 có thể tích bằng 1 và G là trọng tâm 4BCD0. Thể
tích của khối chóp G.ABC0 là 1 1 1 1 A. V = . B. V = . C. V = . D. V = . 3 6 12 18
Câu 50. Có bao nhiêu cặp số nguyên (x; y) thỏa mãn 0 ≤ x ≤ 2020 và log (3x + 3) + x = 2y + 9y? 3 A. 2019. B. 6. C. 2020. D. 4.
———————–HẾT———————– GeoGebraPro Trang 5 o/ aPr roups/GeoGebr acebook.com/g .f https://www ĐÁP ÁN THAM KHẢO 1. D 2. D 3. B 4. C 5. A 6. C 7. B 8. B 9. C 10. B 11. D 12. C 13. A 14. B 15. A 16. B 17. B 18. B 19. B 20. B 21. B 22. A 23. C 24. A 25. D 26. A 27. D 28. B 29. A 30. D 31. A 32. A 33. B 34. B 35. A 36. D 37. D 38. B 39. C 40. A 41. B 42. C 43. D 44. B 45. D 46. C 47. B 48. D 49. D 50. D GeoGebraPro Trang 6 MỖI NGÀY MỘT ĐỀ THI 2
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Một chi đoàn có 16 đoàn viên. Cần bầu chọn một Ban Chấp hành ba người gồm Bí thư, Phó
Bí thư và Ủy viên. Số cách chọn ra Ban Chấp hành nói trên là A. 560. B. 4096. C. 48. D. 3360. Lời giải.
Mỗi cách bầu chọn một Ban Chấp hành ba người gồm Bí thư, Phó Bí thư và Ủy viên là một chỉnh hợp 16!
chập 3 của 16 phần tử. Do đó có A3 = = 3360 cách. 16 13! Chọn phương án D
Câu 2. Cho cấp số cộng (un) biết u3 = 6, u8 = 16. Tính công sai d và tổng của 10 số hạng đầu tiên. A. d = 2; S10 = 100. B. d = 1; S10 = 80. C. d = 2; S10 = 120. D. d = 2; S10 = 110. Lời giải. u 16 − 6 d = 8 − u3 = = 2. 5 5
u1 = u3 − 2d = 6 − 2 · 2 = 2. 10 · (u 10 · (u 10 · (2 + 2 + 9 · 2) S 1 + u10) 1 + u1 + 9 · d) 10 = = = = 110. 2 2 2 Chọn phương án D 2019-2020 √ √ Ä ä2x+1
Câu 3. Tìm nghiệm của phương trình 7 + 4 3 = 2 − 3. 1 3 1 THPT A. x = . B. x = − . C. x = −1. D. x = − . 4 4 4 Lời giải. √ √ √ Ä ä2x+1 Ä ä 1 3 Ta có 7 + 4 3 = 2 − 3 ⇔ 2x + 1 = log √ 2 − 3 ⇔ 2x + 1 = − ⇔ x = − . 7+4 3 2 4 GHIỆP Chọn phương án B N T
Câu 4. Cho hình lập phương ABCD.A0B0C0D0 có cạnh bằng a. Tính thể tích V của khối chóp D0.ABCD. TỐ a3 a3 a3 A. V = . B. V = . C. V = . D. V = a3. 4 6 3 THI Lời giải.
Diện tích đáy ABCD là SABCD = a2, chiều cao D0D = a. 1 1 a3
Do đó VD0.ABCD = SABCD · D0D = a2 · a = . LUYỆN 3 3 3 Chọn phương án C
Câu 5. Tìm tập xác định của hàm số y = log 1 (x2 − 3x + 2). 2 A. (−∞; 1) ∪ (2; +∞). B. (1; 2). C. (2; +∞). D. (−∞; 1). Lời giải. ïx < 1
Điều kiện x2 − 3x + 2 > 0 ⇔
nên tập xác định của hàm số (−∞; 1) ∪ (2; +∞). x > 2 Chọn phương án A Z x3 Câu 6. Nếu f (x) dx = + ex + C thì f (x) bằng 3 x4 x4 A. f (x) = 3x2 + ex. B. f (x) = + ex. C. f (x) = x2 + ex. D. f (x) = + ex. 3 12 Lời giải. Z x3 Ta có f (x) dx = + ex + C ⇒ f (x) = x2 + ex. 3 Chọn phương án C GeoGebraPro Trang 1
Câu 7. Cho khối chóp S.ABC có SA ⊥ (ABC) và SA = 2, tam giác ABC vuông cân tại A và AB = 1.
Thể tích khối chóp S.ABC bằng 1 1 2 A. . B. . C. 1. D. . 6 3 3 Lời giải. 1 1 1 1 Ta có SABC = AB · AC = ⇒ VS.ABC = SA · SABC = . 2 2 3 3 S A C B Chọn phương án B
Câu 8. Cho khối nón có đường cao h và bán kính đáy r. Tính thể tích của khối nón. √ 1 √ A. 2πr h2 + r2. B. πr2h. C. πr h2 + r2. D. πr2h. 3 o/ Lời giải. 1 aPr
Theo công thức thể tích khối nón V = πr2h. 3 Chọn phương án B
Câu 9. Một mặt cầu có đường kính bằng a có diện tích S bằng bao nhiêu? 4πa2 πa2 A. S = . B. S = . C. S = πa2. D. S = 4πa2. 3 3 Lời giải. roups/GeoGebr a
Vì đường kính mặt cầu bằng a nên bán kính mặt cầu là r = . 2 a 2
Diện tích mặt cầu là S = 4π = πa2. 2 Chọn phương án C
Câu 10. Cho hàm số y = x3 + 3x2 − 4 có bảng biến thiên sau, tìm a và b. x −∞ −2 acebook.com/g 0 +∞ .f y0 + 0 − 0 + 0 +∞ + y a b https://www A. a = +∞; b = 2. B. a = −∞; b = −4. C. a = −∞; b = 1. D. a = +∞; b = 3. Lời giải. Phương pháp:
Tính giới hạn của hàm số khi x tiến đến −∞ để tìm a và tính giá trị của hàm số tại x = 0 để tìm b. Cách giải:
lim y = −∞, y(0) = −4 ⇒ a = −∞; b = −4. x→−∞ Chọn phương án B
Câu 11. Với a, b là các số thực dương tùy ý và a khác 1, đặt P = log b3 + log a
a2 b6. Mệnh đề nào dưới đây đúng? A. P = 27 log b . B. P = 15 log b . C. P = 9 log b . D. P = 6 log b . a a a a Lời giải. 6 Ta có P = log b3 + log b +
log b = 3 log b + 3 log b = 6 log b. a a2 b6 = 3 loga 2 a a a a Chọn phương án D
Câu 12. Cho hình trụ có bán kính đáy bằng 5 và chiều cao bằng 7 . Diện tích xung quanh của hình trụ đã cho bằng GeoGebraPro Trang 2 175π A. . B. 175π. C. 70π. D. 35π. 3 Lời giải.
Ta có Sxq = 2πrl = 2π · 5 · 7 = 70π . Chọn phương án C
Câu 13. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số. A. 3. B. 0. C. 1. D. 2. x −∞ −2 0 2 +∞ y0 − 0 + 0 − 0 + y Lời giải.
Dựa vào BBT suy ra hàm số có 3 điểm cực trị. Chọn phương án A Câu 14.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây ? y 2x − 1 x + 1 A. y = . B. y = . x − 1 x − 1 2019-2020 C. y = x4 + x2 + 1. D. y = x3 − 3x − 1. 1 THPT 1 O x GHIỆP Lời giải. N T
Đồ thị là của hàm số nhất biến có tiệm cân đứng x = 1 và tiệm cận ngang y = 1 x + 1 TỐ nên là hàm số y = x − 1 Chọn phương án B THI 2 − 2x
Câu 15. Tìm đường tiệm cận ngang của đồ thị hàm số y = . x + 1 A. y = −2. B. x = −1. C. x = −2. D. y = 2. LUYỆN Lời giải. 2 2 − 2x − 2 Ta có: lim y = lim x x → ±∞ = lim
= −2 ⇒ y = −2 là đường tiệm cận ngang của hàm x→±∞ x + 1 x→±∞ 1 1 + x số. Chọn phương án A Å 3 ãx−1 Å 3 ã−x+3
Câu 16. Tìm tập nghiệm của bất phương trình > . 4 4 A. (2; +∞). B. (−∞; 2). C. [2; +∞). D. (−∞; 2]. Lời giải. Å 3 ãx−1 Å 3 ã−x+3 >
⇔ x − 1 < −x + 3 ⇔ x < 2. 4 4 Chọn phương án B Câu 17. GeoGebraPro Trang 3
Cho hàm số bậc bốn y = f (x) có đồ thị như hình vẽ. Số nghiệm của phương y trình 3f (x) − 8 = 0 bằng A. 1. B. 2. C. 3. D. 4. 2 1 −2 2 x O 1 −1 −2 Lời giải. 8
Ta có 3f (x) − 8 = 0 ⇔ f (x) = . 3 y 8 8 3
Dựa vào đồ thị, đường thẳng y =
cắt đồ thị y = f (x) tại hai điểm phân 3 2
biệt. Vậy phương trình đã cho có hai nghiệm phân biệt. 1 −2 2 x O 1 −1 o/ −2 aPr Chọn phương án B 5 Z dx Câu 18. Nếu
= ln c với c ∈ Q thì giá trị của c bằng 2x − 1 1 A. 9. B. 3. C. 6. D. 81. Lời giải. 5 Z 5 roups/GeoGebr dx 1 = ln |2x − 1| = ln 3. 2x − 1 2 1 1 Vậy c = 3. Chọn phương án B
Câu 19. Số phức liên hợp của z = 4 + 3i là A. z = −3 + 4i. B. z = 4 − 3i. C. z = 3 + 4i. D. z = 3 − 4i. acebook.com/g Lời giải. .f
Số phức liên hợp của z = 4 + 3i là z = 4 − 3i. Chọn phương án B
Câu 20. Cho hai số phức z1 = −1 + 2i, z2 = −1 − 2i. Giá trị của biểu thức |z1|2 + |z2|2 bằng √ A. 10. B. 10. C. −6. D. 4. https://www Lời giải. » √ » √ Ta có |z1| = (−1)2 + 22 = 5; |z2| = (−1)2 + (−2)2 = 5. √ √ Ä ä2 Ä ä2 |z1|2 + |z2|2 = 5 + 5 = 10. Chọn phương án B
Câu 21. Điểm M biểu diễn số phức z = 2 − i trên mặt phẳng tọa độ Oxy là A. M = (1; −2). B. M = (2; −1). C. M = (−2; 1). D. M = (2; 1). Lời giải.
Số phức z = 2 − i có điểm biểu diễn là M = (2; −1). Chọn phương án B
Câu 22. Trong không gian Oxyz, hình chiếu vuông góc của điểm A(2; 3; 4) lên trục Ox là điểm nào dưới đây? A. M (2; 0; 0). B. M (0; 3; 0). C. M (0; 0; 4). D. M (0; 2; 3). Lời giải.
Hình chiếu vuông góc của điểm A(2; 3; 4) là điểm M (2; 0; 0). Chọn phương án A GeoGebraPro Trang 4
Câu 23. Trong không gian Oxyx, cho mặt cầu (S) : (x − 2)2 + (y + 1)2 + (z − 1)2 = 9. Tìm tọa độ tâm
I và bán kính R của mặt cầu (S). A. I(−2; 1; −1), R = 3. B. I(−2; 1; −1), R = 9. C. I(2; −1; 1), R = 3. D. I(2; −1; 1), R = 9. Lời giải.
Ta có tọa độ tâm I(2; −1; 1) và bán kính R = 3. Chọn phương án C x + 8 y − 5 z
Câu 24. Trong không gian Oxyz, cho đường thẳng d : = =
. Khi đó véc-tơ chỉ phương 4 −2 1
của đường thẳng d có tọa độ là A. (4; −2; 1). B. (4; 2; −1). C. (4; −2; −1). D. (4; 2; 1). Lời giải. #»
Tọa độ véc-tơ chỉ phương của đường thẳng d là u = (4; −2; 1). Chọn phương án A
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P ) : 2x − y + z − 1 = 0. Điểm nào dưới đây thuộc (P )? A. M (2; −1; 1). B. N (0; 1; −2). C. P (1; −2; 0). D. Q(1; −3; −4). Lời giải.
Ta thấy Q ∈ (P ) vì 2.1 − (−3) − 4 − 1 = 0 Chọn phương án D
Câu 26. Cho hình lập phương ABCD.A0B0C0D0. Tính góc giữa AC0 và BD. B A 2019-2020 C D THPT B0 A0 D0 C0 GHIỆP A. 90◦. B. 45◦. C. 60◦. D. 120◦. N Lời giải. T
Gọi O0 và I lần lượt là tâm hình vuông ABCD và trung điểm CC0. Khi đó, ta có IO0 song song AC0. Suy ra (AC0, BD) = (IO0, BD). TỐ ßBD ⊥ AC Ta có
⇒ BD ⊥ (AA0C) ⇒ BD ⊥ IO0 ⇒ (IO0, BD) = 90◦. THI BD ⊥ AA0 Chọn phương án A
Câu 27. Cho hàm số y = f (x) có bảng xét dấu của hàm đạo hàm như sau: LUYỆN x −∞ −3 2 3 4 +∞ f 0(x) − 0 + 0 + 0 − 0 +
Số điểm cực trị của hàm số đã cho là A. 6. B. 4. C. 2. D. 3. Lời giải.
Do f 0(x) đổi dấu ba lần nên hàm số có ba điểm cực trị. Chọn phương án D 4
Câu 28. Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x) = x+ trên đoạn [1; 3] bằng x 65 52 A. . B. 20. C. 6. D. . 3 3 Lời giải. 4 Ta có: f (x) = x +
xác định và liên tục trên [1; 3]. Khi đó x 4 4 ïx = 2 f 0(x) = 1 − ; f 0(x) = 0 ⇔ 1 − = 0 ⇔ x2 x2 x = −2. GeoGebraPro Trang 5 Nhận thấy: −2 /
∈ [1; 3] ⇒ x = −2 (loại). 13 f (1) = 5; f (2) = 4; f (3) =
. Khi đó: maxf (x) = 5; m = minf (x) = 4. Vậy M.m = 20. 3 [1;3] [1;3] Chọn phương án B
Câu 29. Cho 0 < a 6= 1 và x, y là các số thực âm. mệnh đề nào dưới đây đúng?
A. log (x2y4) = 2 (log |x| + log y2). B. log (xy) = log x + log y. a a a a a a Å x ã log (−x)
C. log (−x2y) = 2 log (−x) + log y. D. log = a . a a a a y log (−y) a Lời giải.
Ta có, log (x2y4) = log x2 + log y4 = 2 log |x| + 2 log y2 = 2 (log |x| + log y2). a a a a a a a Chọn phương án A
Câu 30. Số giao điểm của đồ thị hàm số y = x3 + x + 2 và đường thẳng y = −2x + 1 là A. 3. B. 0. C. 2. D. 1. Lời giải.
Xét phương trình hoành độ giao điểm x3 + x + 2 = −2x + 1 ⇔ x3 + 3x + 1 = 0.
Xét f (x) = x3 + 3x + 1, ta có f 0(x) = 3x2 + 3 > 0. Suy ra bảng biến thiên x −∞ +∞ o/ f 0(x) + aPr +∞ + f (x) −∞
Do đó phương trình f (x) = 0 có 1 nghiệm. Chọn phương án D roups/GeoGebr
Câu 31. Tập nghiệm của bất phương trình 4x+1 ≤ 8x−2 là A. [8; +∞). B. ∅. C. (0; 8). D. (−∞; 8] . Lời giải.
Ta có: 4x+1 ≤ 8x−2 ⇔ 22x+2 ≤ 23x−6 ⇔ 2x + 2 ≤ 3x − 6 ⇔ 8 ≤ x
Vậy tập nghiệm của bất phương trình là [8; +∞). Chọn phương án A acebook.com/g
Câu 32. Cho hình lập phương ABCD.A0B0C0D0 cạnh a. Tính diện tích toàn phần của vật tròn xoay .f
thu được khi quay tam giác AA0C0 quanh trục AA0. √ √ √ √ Ä ä Ä ä Ä ä Ä ä A. π 6 + 2 a2. B. π 3 + 2 a2. C. 2π 2 + 1 a2. D. 2π 6 + 1 a2. Lời giải.
Khi quay tam giác AA0C0 quanh trục AA0 ta được hình nón có bán kính đáy √ A
R = A0C0 = a 2, đường sinh l = AC0 và chiều cao h = AA0 = a. √ √ √ https://www Ta có l = AC0 = A0C02 + AA02 = 2a2 + a2 = a 3. Ta có √
Stp = πRl + πR2 = π( 6 + 2)a2. C0 A0 Chọn phương án A π 2 Z √ Câu 33. Cho tích phân I =
2 + cos x · sin x dx. Nếu đặt t = 2 + cos x thì kết quả nào sau đây 0 đúng? π 2 3 2 2 Z √ Z √ Z √ Z √ A. I = t dt. B. I = t dt. C. I = 2 t dt. D. I = t dt. 3 2 3 0 GeoGebraPro Trang 6 Lời giải.
Đặt t = 2 + cos x ⇒ dt = − sin x dx ⇒ sin x dx = − dt. Đổi cận x = 0 ⇒ t = 3 π x = ⇒ t = 2. 2
Vậy tích phân đã cho trở thành 2 3 Z √ Z √ I = t(− dt) = t dt. 3 2 Chọn phương án B
Câu 34. Cho hàm số y = f (x) liên tục trên đoạn [a; b]. Viết công thức tính diện tích hình thang cong
giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = a, x = b. b b b b Z Z Z Z A. S = f 2(x) dx. B. S = |f (x)| dx. C. S = π |f (x)| dx. D. S = f (x) dx. a a a a Lời giải.
Diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = a, b Z x = b là S = |f (x)| dx. a 2019-2020 Chọn phương án B
Câu 35. Cho hai số phức z1 = 3 − 4i và z2 = −2 + i. Tìm số phức liên hợp của z1 + z2. A. 1 + 3i. B. 1 − 3i. C. −1 + 3i. D. −1 − 3i. THPT Lời giải.
Ta có z1 + z2 = (3 − 4i) + (−2 + i) = 1 − 3i ⇒ z1 + z2 = 1 + 3i. Chọn phương án A GHIỆP
Câu 36. Gọi z1 là nghiệm phức có phần ảo âm của phương trình z2 + 2z + 3 = 0. Trên mặt phẳng tọa N
độ, điểm nào sau đây là điểm biểu diễn số phức z T 1? √ √ √ √ A. P (−1; − 2i). B. Q(−1; 2i). C. N (−1; 2). D. M (−1; − 2). TỐ Lời giải. √ ñz = −1 + 2i √ THI Ta có z2 + 2z + 3 = 0 ⇔
√ . Vì z1 có phần ảo âm nên z1 = −1 − 2i. z = −1 − 2i √
Vậy điểm biểu diễn số phức z1 là điểm M (−1; − 2). Chọn phương án D LUYỆN x = −1 + t x − 1 y + 1 z − 3 
Câu 37. Trong không gian Oxyz, cho hai đường thẳng d1 : = = và d2 : y = 4 + 3t . 2 3 −5 z = 1 + t
Tìm phương trình mặt phẳng chứa đường thẳng d1 và song song với đường thẳng d2. A. 18x + 7y + 3z + 20 = 0. B. 18x − 7y + 3z + 34 = 0. C. 18x + 7y + 3z − 20 = 0. D. 18x − 7y + 3z − 34 = 0. Lời giải. #»
Đường thẳng d1 qua M (1; −1; 3) và nhận u1 = (2; 3; −5) làm véc-tơ chỉ phương; d2 có véc-tơ chỉ phương #» u2 = (1; 3; 1). #» #» #»
Mặt phẳng (P ) chứa d1 và song song d2 nên nhận véc-tơ n = [u1, u2] = (18; −7; 3) làm véc-tơ pháp tuyến.
Vậy phương trình tổng quát của (P ) là
18(x − 1) − 7(y + 1) + 3(z − 3) = 0
⇔ 18x − 7y + 3z − 34 = 0. Chọn phương án D GeoGebraPro Trang 7
Câu 38. Trong không gian với hệ tọa độ Oxyz, viết phương trình chính tắc của đường thẳng d đi qua
điểm A(1; 2; 3) và vuông góc với mặt phẳng (P ) : 2x + 2y + z + 2017 = 0. x + 1 y + 2 z + 3 x − 1 y − 2 z − 3 A. = = . B. = = . 2 2 1 2 2 1 x − 2 y − 2 z − 1 x + 2 y + 2 z + 1 C. = = . D. = = . 1 2 3 1 2 3 Lời giải. #»
d vuông góc với (P ) nên d có véc-tơ chỉ phương là n P = (2; 2; 1). x − 1 y − 2 z − 3
Do đó, phương trình chính tắc đường thẳng d là = = . 2 2 1 Chọn phương án B
Câu 39. Xếp 5 nam và 2 nữ vào một bàn dài gồm 7 chỗ ngồi. Tính xác suất để 2 nữ không ngồi cạnh nhau. 6 4 5 2 A. . B. . C. . D. . 7 7 7 7 Lời giải.
Xếp hai nữ cạnh nhau có 2 cách.
Xếp 5 nam và nhóm nữ có 6! cách.
Xếp 5 nam và 2 nữ sao cho 2 nữ cạnh nhau có 2 · 6! cách. o/ 2 · 6! 2
Xác suất để xếp 5 nam và 2 nữ sao cho 2 nữ cạnh nhau là = . aPr 7! 7 2 5
Vậy xác suất cần tìm là 1 − = . 7 7 Chọn phương án C
Câu 40. Cho lăng trụ tam giác đều ABC.A0B0C0 có tất cả các cạnh đều bằng a. Khoảng cách giữa hai
đường thẳng BC và AB0 bằng √ √ √ √ a 21 a 3 a 7 a 2 roups/GeoGebr A. . B. . C. . D. . 7 2 4 2 Lời giải.
Ta có BCkB0C0 ⇒ BCk (AB0C0). Suy ra: d(BC, AB0) = d(BC, (AB0C0)) = d(B, (AB0C0)) = d(A0, (AB0C0)).
Gọi I và H lần lượt là hình chiếu vuông góc A0 C0 acebook.com/g của A0 trên B0C0 và AI. .f
Ta có: B0C0⊥A0I và B0C0⊥A0A I
nên B0C0⊥ (A0AI) ⇒ B0C0⊥A0H. B0 H
Mà AI⊥A0H. Do đó (AB0C0) ⊥A0H. https://www A C B √ a 3 √ A0A.A0I a. a 21
Khi đó: d (A0, (AB0C0)) = A0H = √ = 2 √ = . A0A2 + A0I2 s Ç å2 7 a 3 a2 + 2 √ a 21
Vậy khoảng cách cần tìm là . 7 Chọn phương án A
Câu 41. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (−2019; 2020) để hàm số y =
2x3 − 3(2m + 1)x2 + 6m(m + 1)x + 2019 đồng biến trên khoảng (2; +∞)? A. 2021. B. 2020. C. 2018. D. 2019. Lời giải.
Ta có y0 = 6x2 − 6(2m + 1)x + 6m2 + 6m.
Xét y0 = 0 ⇔ x2 − (2m + 1)x + m2 + m = 0, có ∆ = (2m + 1)2 − 4 (m2 + m) = 1 > 0, ∀m ∈ R. Suy ra GeoGebraPro Trang 8
phương trình y0 = 0 luôn có hai nghiệm phân biệt: x1 = m; x2 = m + 1. Dễ thấy x1 < x2. Bảng biến thiên x −∞ m m + 1 +∞ y0 + 0 − 0 + y(m) m +∞ + y −∞ y(m ( + 1)
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên mỗi khoảng (−∞; m); (m + 1; +∞). Vì thế,
hàm số đồng biến trên (2 : +∞) khi m + 1 ≤ 2 ⇔ m ≤ 1.
Suy ra có 2020 giá trị nguyên của m thỏa mãn yêu cầu đề bài. Chọn phương án B
Câu 42. Cường độ một trận động đất M được cho bởi công thức M = log A − log A0, với A là biên
độ rung chấn tối đa và A0 là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San
Francisco có cường độ 8,3 độ Richter. Trong cùng năm đó, trận động đất khác ở gần đó đo được 7,1 độ
Richter. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu lần trận động đất này? A. 1,17. B. 2,2. C. 15,8. D. 4. Lời giải.
Gọi M1, A1 lần lượt là cường độ, biên độ rung chấn tối đa của trận động đất tại San Francisco.
Gọi M2, A2 lần lượt là cường độ, biên độ rung chấn tối đa của trận động đất tại địa điểm còn lại. Ta có A1 A1 2019-2020 M1 = log A1 − log A0 = log ⇒ = 10M1. A0 A0 A A M 2 2 2 = log A2 − log A0 = log ⇒ = 10M2. THPT A0 A0 A1 10M1 Khi đó = = 10M1−M2 = 101,2 ≈ 15,8. A2 10M2 GHIỆP Chọn phương án C N T Câu 43.
Cho hàm số y = f (x). Hàm số y = f 0(x) TỐ
có bảng biến thiên như sau. Bất phương trình x −∞ −4 1 +∞
f (x) > sin x + m có nghiệm trên khoảng (−1; 1) THI khi và chỉ khi y0 − 0 + 0 − A. m > f (1) − sin 1. B. m ≥ f (1) − sin 1. +∞ + −1 C. m ≤ f (−1) + sin 1. y LUYỆN D. m < f (−1) + sin 1. −3 −∞ Lời giải.
Xét hàm số g(x) = f (x) − sin x. g0(x) = f 0(x) − cos x.
Với ∀x ∈ (−1; 1), ta có f 0(x) < −1 ⇒ f 0(x) − cos x < −1 − cos x < 0 ⇒ g0(x) < 0.
Suy ra hàm số g(x) nghịch biến trên khoảng (−1; 1) nên g(x) < g (−1) = f (−1) + sin 1.
Do đó bất phương trình f (x) > sin x + m có nghiệm trên khoảng (−1; 1) khi và chỉ khi bất phương
trình m < f (x) − sin x có nghiệm trên khoảng (−1; 1).
⇔ m < max g(x) ⇔ m < f (−1) + sin 1. [−1;1] Vậy m < f (−1) + sin 1. Chọn phương án D
Câu 44. Cho hình trụ có bán kính đáy bằng a. Cắt hình trụ bởi một mặt phẳng (P ) song song với a
trục của hình trụ và cách hình trụ một khoảng bằng
ta được thiết diện là một hình vuông. Tính thể 2 tích khối trụ. GeoGebraPro Trang 9 √ √ πa3 3 A. 3πa3. B. πa3 3. C. . D. πa3. 4 Lời giải.
Giả sử ABCD là thiết diện hình vuông như hình bên. A
Gọi O và O0 là tâm 2 đáy của hình trụ,
H là hình chiếu của O lên AB. O √ H … a 2 √
Ta có AB = 2AH = 2 OA2 − OH2 = 2 a2 − = a 3. 2 √ B
Vì ABCD là hình vuông nên chiều cao của hình trụ bằng a 3. √ √
Vậy Vtrụ = πa.a 3 = πa3 3. D O0 C Chọn phương án B 2 1
Câu 45. Cho hàm số f (x) liên tục trên R R R và f (2) = 16,
f (x) dx = 4. Tính tích phân I = x · 0 0 o/ f 0(2x) dx A. 13. B. 12. C. 20. D. 7. aPr Lời giải. b b Z Z
Phương pháp: Sử dụng công thức từng phần: u dv = uv|b − v du. a a a Cách giải: 2 1 Z Z roups/GeoGebr 1 I = x · f 0(2x) dx = x d (f (2x)) 2 0 0 1 1 1 Z = x · f (2x)|1 − f (2x) dx 2 0 2 0 1 1 1 Z acebook.com/g = f (2) − f (2x) d(2x) .f 2 4 0 2 Z đặt t=2x 1 1 = f (2) − f (t) dt 2 4 0 https://www 2 1 1 Z 1 1 = f (2) − f (x) dx = · 16 − · 4 = 8 − 1 = 7. 2 4 2 4 0 Chọn phương án D
Câu 46. Cho hàm số y = f (x) = ax3 + bx2 + cx + d có bảng biến thiên như sau: 1
Khi đó |f (x)| = m có bốn nghiệm phân biệt x1 < x2 < x3 < < x4 khi và chỉ khi: 2 A. 0 < m < 1. x −∞ 0 1 +∞ B. 0 < m ≤ 1. 1 y0 + 0 − 0 + C. < m < 1. 2 1 +∞ + 1 D. ≤ m < 1. 2 y −∞ 0 Lời giải. GeoGebraPro Trang 10 ßy0(0) = 0 ßc = 0
Ta có y0 = 3ax2 + 2bx + c, từ bảng biến thiên suy ra: ⇔ (1) y0(1) = 0 3a + 2b = 0 ßy(0) = 1 ßd = 1 Ta lại có ⇔ (2) y(1) = 0 a + b + c + d = 0 d = 1 d = 1     c = 0 c = 0
Từ (1), (2) ta có hệ phương trình: ⇔ 3a + 2b = 0 a = 2     a + b + c + d = 0 b = −3
⇒ y = f (x) = 2x3 − 3x2 + 1
Đồ thị hàm số |f (x)| = |2x3 − 3x2 + 1| Å 1 ã 1 Ta có f = 2 2 1
Dựa vào đồ thị suy ra phương trình |f (x)| = m có bốn nghiệm phân biệt x1 < x2 < x3 < < x4 khi 2 1 và chỉ khi: < m < 1 2 Chọn phương án C
Câu 47. Cho x, y > 0 thỏa mãn log(x + 2y) = log x + log y. Khi đó, giá trị nhỏ nhất của biểu thức x2 4y2 P = + là 1 + 2y 1 + x 32 31 29 A. 6. B. . C. . D. . 5 5 5 Lời giải.
Ta có log(x + 2y) = log xy ⇔ x + 2y = xy. 2019-2020 x + z 2
Đặt 2y = z, ta có x, z > 0 thỏa mãn 2(x + z) = xz ≤ ⇒ x + z ≥ 8. Lại có 2 THPT x2 z2 (x + z)2 4 P = + ≥ = x + z − 2 + . 1 + z 1 + x 2 + x + z 2 + x + z 4 4 32 Xét f (t) = t − 2 + , f 0(t) = 1 −
> 0, ∀t ≥ 8 nên min f (t) = f (8) = . GHIỆP 2 + t (t + 2)2 t≥8 5 N 32 T
Vậy giá trị nhỏ nhất của P là
khi x = z = 4 hay (x; y) = (4; 2). 5 TỐ Chọn phương án B
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số THI x2 + mx + m y =
trên [1; 2] bằng 2. Số phần tử của S là x + 1 A. 1. B. 4. C. 3. D. 2. Lời giải. LUYỆN x2 + mx + m Xét hàm số f (x) = trên [1; 2]. x + 1 x2 + 2x
Ta có f (x) liên tục trên [1; 2] và f 0(x) =
> 0, ∀x ∈ [1; 2] . Suy ra f (x) đồng biến trên [1; 2]. Do (x + 1)2 3m + 4 2m + 1 đó maxf (x) = f (2) = , minf (x) = f (1) = . [1;2] 3 [1;2] 2 2m + 1 1 Trường hợp 1: ≥ 0 ⇔ m ≥ − . 2 2 3m + 4
Trong trường hợp này ta có max |f (x)| = . [1;2] 3 3m + 4 2
Theo yêu cầu bài toán ta có = 2 ⇔ m = (thỏa mãn). 3 3 3m + 4 4 Trường hợp 2: ≤ 0 ⇔ m ≤ − . 3 3 −2m − 1
Trong trường hợp này ta có max |f (x)| = . [1;2] 2 GeoGebraPro Trang 11 −2m − 1 5
Theo yêu cầu bài toán ta có = 2 ⇔ m = − (thỏa mãn). 2 2 2m + 1 3m + 4 4 1 Trường hợp 3: < 0 < ⇔ − < m < − . 2 3 3 2 −2m − 1 3m + 4 11 1 3m + 4 +) Nếu ≤ ⇔ − ≤ m < − thì max |f (x)| = . 2 3 12 2 [1;2] 3 3m + 4 2
Theo yêu cầu bài toán ta có = 2 ⇔ m = (không thỏa mãn). 3 3 −2m − 1 3m + 4 11 4 −2m − 1 +) Nếu ≥ ⇔ − ≥ m > − thì max |f (x)| = . 2 3 12 3 [1;2] 2 −2m − 1 5
Theo yêu cầu bài toán ta có = 2 ⇔ m = − (không thỏa mãn). 2 2 ß 2 5 ™ Vậy S = ; − ⇒ |S| = 2. 3 2 Chọn phương án D
Câu 49. Cho hình hộp chữ nhật ABCD.A0B0C0D0 có thể tích bằng 1 và G là trọng tâm 4BCD0. Thể
tích của khối chóp G.ABC0 là o/ 1 1 1 1 A. V = . B. V = . C. V = . D. V = . aPr 3 6 12 18 Lời giải.
Ta thấy VABCDD0C0 = VG.ABC0D0 + VG.ABCD + V A0 G.CC0D0D + VG.ADD0 + VG.BCC0 .
Vì G là trọng tâm tam giác BD0C nên ta có D0 IG J G CG 1 = = = . ID J B CA0 3 roups/GeoGebr Do vậy ta được B0 C0 K  1 1 V V  G.ABCD = D0.ABCD = J  3 9 A     1 1 D  V V  G.CC0D0D = B.CC0D0D = 3 9 G 1 1 acebook.com/g  V V .f  G.ACC0 = D0.ACC0 =  3 18    2 1   B VG.ADD0 = VC.ADD0 = . 3 9 I C 1 7 1
Ta được VG.ABC0D0 = VABCDC0D0 − [VG.ABCD + VG.CC0D0D + VG.BCC0 + VG.ADD0] = − = . 2 18 9 https://www 1 1 Ta có VG.ABC0 = VG.ABC0D0 = . 2 18 Chọn phương án D
Câu 50. Có bao nhiêu cặp số nguyên (x; y) thỏa mãn 0 ≤ x ≤ 2020 và log (3x + 3) + x = 2y + 9y? 3 A. 2019. B. 6. C. 2020. D. 4. Lời giải. Điều kiện: x > 1.
Ta có log (3x + 3) + x = 2y + 9y ⇔ log (x + 1) + (x + 1) = 2y + 32y (*) 3 3
Xét hàm số f (t) = t + 3t, ∀t ∈ R có f 0(t) = 1 + 3t ln 3 > 0, f orallt ∈ R tức hàm số luôn đồng biến trên mathbbR.
Khi đó (∗) ⇔ f (log (x + 1)) = f (2y) ⇔ log (x + 1) = 2y ⇔ x + 1 = 2y ⇔ x = 9y − 1. 3 3
Vì 0 ≤ x ≤ 2020 nên 0 ≤ 9y − 1 ≤ 2020 ⇔ 0 ≤ y ≤ log 2021. 9
Do y nguyên nên y ∈ {{0; 1; 2; 3}}.
⇒ (x; y) ∈ {(0; 0); (8; 1); (80; 2); (728; 3)} nên tổng cộng có 4 cặp (x; y) thỏa đề bài. Chọn phương án D
———————–HẾT———————– GeoGebraPro Trang 12 ĐÁP ÁN THAM KHẢO 1. D 2. D 3. B 4. C 5. A 6. C 7. B 8. B 9. C 10. B 11. D 12. C 13. A 14. B 15. A 16. B 17. B 18. B 19. B 20. B 21. B 22. A 23. C 24. A 25. D 26. A 27. D 28. B 29. A 30. D 31. A 32. A 33. B 34. B 35. A 36. D 37. D 38. B 39. C 40. A 41. B 42. C 43. D 44. B 45. D 46. C 47. B 48. D 49. D 50. D 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN GeoGebraPro Trang 13 MỖI NGÀY MỘT ĐỀ THI 3
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Lớp 11A có 25 học sinh nam và 20 học sinh nữ. Hỏi có bao nhiêu cách chọn một học sinh làm lớp trưởng? A. 25! + 20! cách. B. 45! cách. C. 45 cách. D. 500 cách.
Câu 2. Cho cấp số cộng có u1 = 0 và công sai d = 3. Tổng của 26 số hạng đầu tiên của cấp số cộng đó bằng bao nhiêu? A. 975. B. 775. C. 875. D. 675. 1
Câu 3. Tập nghiệm của phương trình 2x2−3x = là 4 A. S = ∅. B. S = {1; 2}. C. S = {0}. D. S = {1}.
Câu 4. Hình lập phương có đường chéo của mặt bên bằng 4 cm. Tính thể tích khối lập phương đó. √ √ √ A. 8 2 cm3. B. 16 2 cm3. C. 8 cm3. D. 2 2 cm3. π
Câu 5. Tập xác định của hàm số y = (x2 − 3x + 2) là A. R\ {1; 2}. B. (−∞; 1) ∪ (2; +∞). C. (1; 2). D. (−∞; 1] ∪ [2; +∞). 2019-2020 1
Câu 6. Tìm họ nguyên hàm F (x) của hàm số f (x) = . 5x + 4 1 THPT A. F (x) = ln |5x + 4| + C. B. F (x) = ln |5x + 4| + C. ln 5 1 1 C. F (x) = ln |5x + 4| + C. D. F (x) = ln(5x + 4) + C. 5 5
Câu 7. Cho khối chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, đường GHIỆP √ N a 2 cao SO. Biết SO =
, thể tích khối chóp S.ABCD bằng T √ 2 √ √ √ a3 2 a3 2 a3 2 a3 3 TỐ A. . B. . C. . D. . 6 3 2 4 THI
Câu 8. Cho khối nón tròn xoay có chiều cao h, đường sinh l và bán kính đường tròn đáy bằng R .
Diện tích toàn phần của khối nón là A. Stp = πR(l + R). B. Stp = πR(l + 2R). C. Stp = 2πR(l + R). D. Stp = πR(2l + R). LUYỆN
Câu 9. Cho hàm số y = f (x) có bảng biến thiên như sau: x −∞ −1 0 1 +∞ y0 − 0 + 0 − 0 + +∞ + 5 +∞ + y 2 0 0
Hàm số y = f (x) nghịch biến trên khoảng nào sau đây? A. (0; +∞). B. (−∞; 0). C. (−1; 0). D. (−∞; −2).
Câu 10. Cho các số thực dương a, b thỏa mãn log a = x, log b = y. Tính P = log (a2b3) A. P = 6xy. B. p = x2y3. C. P = x2 + y3. D. P = 2x + 3y.
Câu 11. Một hình trụ có diện tích xung quanh bằng S, diện tích đáy bằng diện tích một mặt cầu bán
kính a. Khi đó thể tích của hình trụ bằng 1 1 1 A. Sa. B. Sa. C. Sa. D. Sa. 2 3 4
Biên soạn: Ths Nguyễn Chín Em Trang 1 Câu 12.
Cho hàm số y = f (x) có bảng biến thiên x −∞ 2 4 +∞
dưới đây. Khẳng định nào sau đây là khẳng y0 + 0 − 0 + định đúng? 3 +∞ +
A. Hàm số đạt cực đại tại x = 2. y
B. Hàm số đạt cực đại tại x = −2. −∞ −2
C. Hàm số đạt cực đại tại x = 4.
D. Hàm số đạt cực đại tại x = 3. Câu 13.
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây? y A. y = −x4 + 3x2 − 2. B. y = −x4 + 2x2 − 1. −1 1 x C. y = −x4 + x2 − 1. D. y = −x4 + 3x2 − 3. O −1 4x + 4
Câu 14. Đồ thị hàm số y =
có tất cả bao nhiêu đường tiệm cận? x2 + 2x + 1 o/ A. 2. B. 0. C. 1. D. 3. aPr Å 1 ãx
Câu 15. Tập nghiệm của bất phương trình < 8 là. 2 Å 1 ã Å 1 ã A. S = (−∞; −3). B. S = −∞; . C. S = (−3; +∞). D. S = ; +∞ . 3 3
Câu 16. Cho hàm số y = f (x) liên tục trên R và có bảng biến thiên như sau x −∞ −1 1 +∞ roups/GeoGebr y0 + 0 − 0 + 4 +∞ + y −∞ 0
Số nghiệm của phương trình 2f (x) + 3 = 0 là acebook.com/g .f A. 1. B. 2. C. 0. D. 3. 5 Z dx Câu 17. Nếu
= ln c với c ∈ Q thì giá trị của c bằng 2x − 1 1 A. 9. B. 3. C. 6. D. 81. https://www
Câu 18. Phần thực và phần ảo của số phức z = 1 + 2i lần lượt là A. 1 và 2. B. 1 và i. C. 1 và 2i. D. 2 và 1.
Câu 19. Cho hai số phức z1 = 1 − 2i và z2 = 3 + 4i. Tìm điểm M biểu diễn số phức z1.z2 trên mặt phẳng tọa độ. A. M (−2; 11). B. M (−2; −11). C. M (11; −2). D. M (11; 2).
Câu 20. Cho số phức z = 4 − 3i có điểm biểu diễn trên mặt phẳng tọa độ Oxy là M . Tính độ dài OM . √ A. 5. B. 25. C. 7. D. 4.
Câu 21. Trong không gian tọa độ Oxyz, tọa độ điểm G0 đối xứng với điểm G(5; −3; 7) qua trục Oy là A. G0(−5; 0; −7). B. G0(−5; −3; −7). C. G0(5; 3; 7). D. G0(−5; 3; −7).
Câu 22. Trong không gian Oxyz, cho hai điểm A(−2; 1; 1), B(0; −1; 1). Phương trình mặt cầu đường kính AB là
A. (x + 1)2 + y2 + (z − 1)2 = 8.
B. (x + 1)2 + y2 + (z − 1)2 = 2.
C. (x + 1)2 + y2 + (z + 1)2 = 8.
D. (x − 1)2 + y2 + (z − 1)2 = 2.
Biên soạn: Ths Nguyễn Chín Em Trang 2
Câu 23. Trong không gian Oxyz, cho tam giác đều ABC với A(6; 3; 5) và đường thẳng BC có phương x = 1 − t   trình tham số
y = 2 + t . Gọi ∆ là đường thẳng đi qua trọng tâm G của tam giác ABC và vuông góc  z = 2t
với mặt phẳng (ABC). Điểm nào dưới đây thuộc đường thẳng ∆? A. M (−1; −12; 3). B. N (3; −2; 1). C. P (0; −7; 3). D. Q(1; −2; 5).
Câu 24. Trong không gian Oxyz, cho hai điểm A(1; −1; 0), B(0; 1; 1). Gọi (α) là mặt phẳng chứa đường x y − 1 z − 2 thẳng d : = =
và song song với đường thẳng AB. Điểm nào dưới đây thuộc mặt phẳng 2 −1 1 (α)? A. M (6; −4; −1). B. N (6; −4; 2). C. P (6; −4; 3). D. Q = (6; −4; 1).
Câu 25. Cho tứ diện đều cạnh a, M là trunng điểm của BC. Tính cosin của góc giữa hai đường thẳng AB và D √ M . √ √ 3 3 3 1 A. . B. . C. . D. . 2 6 3 2
Câu 26. Cho hàm số y = f (x) liên tục trên R và có bảng xét dấu của đạo hàm như sau: x −∞ −1 0 2 4 +∞ f 0(x) + 0 − + 0 − 0 + 2019-2020
Hàm số đã cho có bao nhiêu cực trị? A. 3. B. 2. C. 1. D. 4.
Câu 27. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = −x3 +3x+1 trên đoạn [0; 2] bằng THPT A. 2. B. 3. C. 1. D. 4. √
Câu 28. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 − x2 − x bằng √ √ A. 2 + 2. B. 2. C. 1. D. 2 − 2. GHIỆP N
Câu 29. Với a là số thực âm bất kỳ, mệnh đề nào dưới đây đúng? T
A. log a2 = 2 log (−a). B. log a2 = −2 log a. C. log a2 = 2 log a. D. log a2 = 2a. 2 2 2 2 2 2 2 TỐ
Câu 30. Số giao điểm của đồ thị hàm số y = x3 + x + 2 và đường thẳng y = −2x + 1 là A. 3. B. 0. C. 2. D. 1. THI Å 1 ã2x+1
Câu 31. Tập nghiệm của bất phương trình
> 1 (với a là tham số, a 6= 0) là 1 + a2 Å 1 ã Å 1 ã A. −∞; − . B. (−∞; 0). C. − ; +∞ . D. (0; +∞). LUYỆN 2 2 Câu 32.
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) E F quanh trục DF . 10π π A. a3. B. a3. a 7 3 30◦ 5π 10π C. a3. D. a3. 2 9 A B a D C a e √ Z 1 + ln x √ Câu 33. Cho tích phân I = dx. Đổi biến t =
1 + ln x ta được kết quả nào sau đây? x 1
Biên soạn: Ths Nguyễn Chín Em Trang 3 √ √ √ 2 2 2 2 Z Z Z Z A. I = t2 dt. B. I = 2 t2 dt. C. I = 2 t2 dt. D. I = 2 t dt. 1 1 1 1 Câu 34.
Gọi S là diện tích hình phẳng được tô đậm trong hình vẽ bên. Công y thức tính S là y = f (x) 1 2 1 2 Z Z Z Z A. S = f (x) dx + f (x) dx. B. S = f (x) dx − f (x) dx. −1 1 −1 1 x −1 O 1 2 2 2 Z Z C. S = f (x) dx. D. S = − f (x) dx. −1 −1
Câu 35. Cho hai số phức z1 = m + 3i, z2 = 2 − (m + 1)i, với m ∈ R. Tìm các giá trị của m để w = z1 ·z2 là số thực. A. m = 1 hoặc m = −2. B. m = 2 hoặc m = −1. C. m = 2 hoặc m = −3. D. m = −2 hoặc m = −3. o/
Câu 36. Phương trình bậc hai nào dưới đây nhận hai số phức 2 − 3i và 2 + 3i làm nghiệm ? aPr A. z2 + 4z + 13 = 0. B. z2 + 4z + 3 = 0. C. z2 − 4z + 13 = 0. D. z2 − 4z + 3 = 0. x − 1
Câu 37. Trong không gian Oxyz cho mặt phẳng (P ) : 3x − 4y + 5z − 6 = 0 và đường thẳng d : = 2 y − 2 z − 3 =
. Gọi ϕ là góc giữa đường thẳng d và mặt phẳng (P ). Tìm khẳng định đúng. 3 1 1 1 1 1 A. sin ϕ = √ . B. cos ϕ = − √ . C. cos ϕ = √ . D. sin ϕ = − √ . 5 28 5 28 5 28 5 28 roups/GeoGebr
Câu 38. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1; −2; −3), B(−1; 4; 1) và đường x + 2 y − 2 z + 3 thẳng d : = =
. Phương trình nào dưới đây là phương trình của đường thẳng đi qua 1 −1 2
trung điểm đoạn thẳng AB và song song với d? x y − 1 z + 1 x y − 2 z + 2 x y − 1 z + 1 x y + 1 z − 1 A. = = . B. = = . C. = = . D. = = . 1 −1 2 1 −1 2 1 1 2 1 −1 2 acebook.com/g
Câu 39. Có một dãy ghế gồm 6 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 2 học sinh lớp A, 2 học sinh lớp .f
B và 2 học sinh lớp C ngồi vào dãy ghế đó sao cho mỗi ghế có đúng 1 học sinh ngồi. Xác suất để không
có học sinh lớp C ngồi cạnh nhau. 2 1 5 1 A. . B. . C. . D. . 3 3 6 6
Câu 40. Cho hình chóp S.ABC có SA = 3a và SA ⊥ (ABC). Biết AB = BC = 2a và https://www ’ ABC = 120◦.
Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng 3a a A. . B. . C. a. D. 2a. 2 2 mx + 10
Câu 41. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = nghịch biến trên khoảng 2x + m (0; 2)? A. 4. B. 5. C. 6. D. 9.
Câu 42. Dân số thế giới được tính theo công thức S = A · eni trong đó A là dân số của năm lấy làm
mốc tính, S là dân số sau n năm, i là tỉ lệ tăng dân số hàng năm. Cho biết năm 2005 Việt Nam có
khoảng 80.902.400 người và tỉ lệ tăng dân số là 1, 47% một năm. Như vậy, nếu tỉ lệ tăng dân số hàng
năm không đổi thì đến năm 2019 số dân của Việt Nam sẽ gần với số nào nhất sau đây? A. 99.389.200. B. 99.386.600. C. 100.861.100. D. 99.251.200.
Câu 43. Cho hàm số y = f (x) liên tục trên R và có bảng biến thiên như hình vẽ. Tìm tất cả các giá 1
trị thực của m để phương trình
f (x) − m = 0 có đúng hai nghiệm phân biệt. 2
Biên soạn: Ths Nguyễn Chín Em Trang 4 x −∞ −1 0 1 +∞ y0 + 0 − 0 + 0 − 0 0 y −∞ −3 +∞ + m = 0 ñ 3 m = 0 A.  3 B. m < −3. C. m < − . D. m < − . 2 m < −3. 2
Câu 44. Một hình trụ có bán kính đáy bằng a, mặt phẳng qua trục cắt hình trụ theo một thiết diện
có diện tích bằng 8a2. Tính diện tích xung quanh của hình trụ. A. 4πa2. B. 8πa2. C. 16πa2. D. 2πa2. 3 Z
Câu 45. Cho hàm số f (x) thoả mãn
[2x ln(x + 1) + xf 0(x)] dx = 0 và f (3) = 1. 0 3 Z a + b ln 2 Biết f (x) dx =
với a, b là các số thực dương. Giá trị của a + b bằng 2 0 A. 35. B. 29. C. 11. D. 7.
Câu 46. Cho hàm số y = f (x) liên tục trên R và có bảng biến thiên như sau x −∞ −1 3 +∞ 2019-2020 y0 + 0 − 0 + 4 +∞ + THPT y −∞ −2 GHIỆP
Biết f (0) < 0, hỏi phương trình f (|x|) = f (0) có bao nhiêu nghiệm? N A. 4. B. 2. C. 3. D. 5. T 1
Câu 47. Xét các số thực a, b thỏa mãn điều kiện
< b < a < 1. Tìm giá trị nhỏ nhất của biểu thức TỐ 3 Å 3b − 1 ã P = log + 12 log2 a − 3. a b THI 4 a 1 √ A. min P = 13. B. min P = √ . C. min P = 9. D. min P = 3 2. 3 2
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số LUYỆN x2 + mx + m y =
trên [1; 2] bằng 2. Số phần tử của S là x + 1 A. 1. B. 4. C. 3. D. 2. √ √
Câu 49. Cho hình hộp ABCD.A0B0C0D0 có đáy là hình chữ nhật với AB = 3, AD = 7. Hai mặt
bên (ABB0A0) và (ADD0A0) lần lượt tạo với đáy một góc 45◦ và 60◦. Tính thể tích của khối hộp nếu
biết cạnh bên của hình hộp bằng 1. A. 3. B. 5. C. 4. D. 2. 2x + y + 1
Câu 50. Cho x, y là các số thực dương thỏa mãn log
= x + 2y. Tìm giá trị nhỏ nhất của 3 x + y 1 2 biểu thức T = + √ . x y √ √ A. 3 + 3. B. 4. C. 3 + 2 3. D. 6.
———————–HẾT———————–
Biên soạn: Ths Nguyễn Chín Em Trang 5 ĐÁP ÁN THAM KHẢO 1. C 2. A 3. B 4. B 5. B 6. C 7. A 8. A 9. D 10. D 11. A 12. A 13. B 14. A 15. C 16. A 17. B 18. A 19. C 20. A 21. B 22. B 23. D 24. C 25. B 26. D 27. A 28. D 29. A 30. D 31. A 32. D 33. B 34. B 35. C 36. C 37. A 38. A 39. A 40. A 41. C 42. A 43. D 44. B 45. A 46. C 47. C 48. D 49. A 50. D o/ aPr roups/GeoGebr acebook.com/g .f https://www
Biên soạn: Ths Nguyễn Chín Em Trang 6 MỖI NGÀY MỘT ĐỀ THI 3
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Lớp 11A có 25 học sinh nam và 20 học sinh nữ. Hỏi có bao nhiêu cách chọn một học sinh làm lớp trưởng? A. 25! + 20! cách. B. 45! cách. C. 45 cách. D. 500 cách. Lời giải.
Số cách chọn một học sinh làm lớp trưởng: C1 = 45 cách 45 Chọn phương án C
Câu 2. Cho cấp số cộng có u1 = 0 và công sai d = 3. Tổng của 26 số hạng đầu tiên của cấp số cộng đó bằng bao nhiêu? A. 975. B. 775. C. 875. D. 675. Lời giải. n(n − 1) 26.25 Ta có Sn = nu1 + · d ⇒ S26 = 26 · 0 + · 3 = 975. 2 2 Chọn phương án A 2019-2020 1
Câu 3. Tập nghiệm của phương trình 2x2−3x = là 4 A. S = ∅. B. S = {1; 2}. C. S = {0}. D. S = {1}. THPT Lời giải. 1 2x2−3x =
⇔ 2x2−3x = 2−2 ⇔ x2 − 3x = −2 ⇔ x2 − 3x + 2 = 0 ⇔ x = 1 ∨ x = 2. 4 Chọn phương án B GHIỆP N
Câu 4. Hình lập phương có đường chéo của mặt bên bằng 4 cm. Tính thể tích khối lập phương đó. √ √ √ T A. 8 2 cm3. B. 16 2 cm3. C. 8 cm3. D. 2 2 cm3. TỐ Lời giải. 4 √
Độ dài các cạnh hình lập phương là √ = 2 2 cm. THI 2 √ √
Thể tích khối lập phương là V = (2 2)3 = 16 2 cm3. Chọn phương án B π LUYỆN
Câu 5. Tập xác định của hàm số y = (x2 − 3x + 2) là A. R\ {1; 2}. B. (−∞; 1) ∪ (2; +∞). C. (1; 2). D. (−∞; 1] ∪ [2; +∞). Lời giải. ñx < 1
Ta có điều kiện: x2 − 3x + 2 > 0 ⇔ . x > 2 Chọn phương án B 1
Câu 6. Tìm họ nguyên hàm F (x) của hàm số f (x) = . 5x + 4 1 A. F (x) = ln |5x + 4| + C. B. F (x) = ln |5x + 4| + C. ln 5 1 1 C. F (x) = ln |5x + 4| + C. D. F (x) = ln(5x + 4) + C. 5 5 Lời giải. Z 1 1 Ta có dx = ln |5x + 4| + C. 5x + 4 5 Chọn phương án C
Biên soạn: Ths Nguyễn Chín Em Trang 1
Câu 7. Cho khối chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, đường √ a 2 cao SO. Biết SO =
, thể tích khối chóp S.ABCD bằng √ 2 √ √ √ a3 2 a3 2 a3 2 a3 3 A. . B. . C. . D. . 6 3 2 4 Lời giải. Ta có SABCD = a2. √ √ S 1 1 a 2 a3 2 Vậy VS.ABCD = · SO · SABCD = · · a2 = . 3 3 2 6 D A O B C Chọn phương án A o/
Câu 8. Cho khối nón tròn xoay có chiều cao h, đường sinh l và bán kính đường tròn đáy bằng R . aPr
Diện tích toàn phần của khối nón là A. Stp = πR(l + R). B. Stp = πR(l + 2R). C. Stp = 2πR(l + R). D. Stp = πR(2l + R). Lời giải.
Stp = Sđ + Sxq = πR2 + πRl = πR(l + R). Chọn phương án A roups/GeoGebr
Câu 9. Cho hàm số y = f (x) có bảng biến thiên như sau: x −∞ −1 0 1 +∞ y0 − 0 + 0 − 0 + +∞ + 5 +∞ + y 2 0 0 acebook.com/g
Hàm số y = f (x) nghịch biến trên khoảng nào sau đây? .f A. (0; +∞). B. (−∞; 0). C. (−1; 0). D. (−∞; −2). Lời giải.
Dựa vào bảng biến thiên ta có hàm số nghịch biến trên (−∞; −1) và (0; 1) nên chọn đáp án D. Chọn phương án D https://www
Câu 10. Cho các số thực dương a, b thỏa mãn log a = x, log b = y. Tính P = log (a2b3) A. P = 6xy. B. p = x2y3. C. P = x2 + y3. D. P = 2x + 3y. Lời giải.
Ta có log (a2b3) = log (a2) + log (b3) = 2 log a + 3 log b = 2x + 3y. Chọn phương án D
Câu 11. Một hình trụ có diện tích xung quanh bằng S, diện tích đáy bằng diện tích một mặt cầu bán
kính a. Khi đó thể tích của hình trụ bằng 1 1 1 A. Sa. B. Sa. C. Sa. D. Sa. 2 3 4 Lời giải.
Gọi r là bán kính đáy của hình trụ, h là chiều cao của hình trụ.  ®S = 2πrh r = 2a  Theo bài ra ta có ⇔ S πr2 = 4πa2 h = . 4πa S
Thể tích khối trụ là V = πr2h = π · 4a2 · = Sa. 4πa
Biên soạn: Ths Nguyễn Chín Em Trang 2 Chọn phương án A Câu 12.
Cho hàm số y = f (x) có bảng biến thiên x −∞ 2 4 +∞
dưới đây. Khẳng định nào sau đây là khẳng y0 + 0 − 0 + định đúng? 3 +∞ +
A. Hàm số đạt cực đại tại x = 2. y
B. Hàm số đạt cực đại tại x = −2. −∞ −2
C. Hàm số đạt cực đại tại x = 4.
D. Hàm số đạt cực đại tại x = 3. Lời giải.
Dựa vào bảng biến thiên, ta có hàm số đạt cực đại tại x = 2 và đạt cực tiểu tại x = 4. Chọn phương án A Câu 13.
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây? y A. y = −x4 + 3x2 − 2. B. y = −x4 + 2x2 − 1. −1 1 x C. y = −x4 + x2 − 1. D. y = −x4 + 3x2 − 3. O −1 Lời giải. 2019-2020
Dựa vào dạng đồ thị ta thấy:
• Hàm số đã cho có dạng y = ax4 + bx2 + c với a < 0. THPT
• Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng −1 nên hàm số có hệ số tự do c = −1. Do
vậy ta loại đáp án A và D.
• Hàm số đạt cực đại tại x = ±1, giá trị cực đại bằng 0. GHIỆP N
• Hàm số đạt cực tiểu tại x = 0, gía trị cực tiểu bằng −1 . Do vậy ta chọn đáp án B. T Chọn phương án B TỐ 4x + 4
Câu 14. Đồ thị hàm số y =
có tất cả bao nhiêu đường tiệm cận? THI x2 + 2x + 1 A. 2. B. 0. C. 1. D. 3. Lời giải. 4x + 4 4x + 4 Ta có: lim
= 0 nên đồ thị hàm số y = có tiệm cận ngang y = 0. LUYỆN x→±∞ x2 + 2x + 1 x2 + 2x + 1 4x + 4 4 (x + 1) 4 4x + 4 lim = lim = lim
= +∞ nên đồ thị hàm số y = có tiệm x→−1+ x2 + 2x + 1 x→−1+ (x + 1)2 x→−1+ x + 1 x2 + 2x + 1 cận đứng x = −1. 4x + 4
Vậy đồ thị hàm số y =
có tất cả hai đường tiệm cận. Chọn đáp án A. x2 + 2x + 1 Chọn phương án A Å 1 ãx
Câu 15. Tập nghiệm của bất phương trình < 8 là. 2 Å 1 ã Å 1 ã A. S = (−∞; −3). B. S = −∞; . C. S = (−3; +∞). D. S = ; +∞ . 3 3 Lời giải.
Å 1 ãx < 8 ⇔ x > log1 8 ⇔ x > −3. 2 2 Chọn phương án C
Câu 16. Cho hàm số y = f (x) liên tục trên R và có bảng biến thiên như sau
Biên soạn: Ths Nguyễn Chín Em Trang 3 x −∞ −1 1 +∞ y0 + 0 − 0 + 4 +∞ + y −∞ 0
Số nghiệm của phương trình 2f (x) + 3 = 0 là A. 1. B. 2. C. 0. D. 3. Lời giải. 3
Ta có 2f (x) + 3 = 0 ⇔ f (x) = −
là PTHĐGĐ của đồ thị (C) của hàm số y = f (x) và đường 2 3
thẳng d : y = − . Dựa vào bảng biến thiên ta thấy (C) và d cắt nhau tại 1 điểm. Vậy Phương trình 2 2f (x) + 3 = 0 có 1 nghiệm. Chọn phương án A 5 Z dx o/ Câu 17. Nếu
= ln c với c ∈ Q thì giá trị của c bằng 2x − 1 aPr 1 A. 9. B. 3. C. 6. D. 81. Lời giải. 5 Z dx 1 5 = ln |2x − 1| = ln 3. 2x − 1 2 1 1 Vậy c = 3. roups/GeoGebr Chọn phương án B
Câu 18. Phần thực và phần ảo của số phức z = 1 + 2i lần lượt là A. 1 và 2. B. 1 và i. C. 1 và 2i. D. 2 và 1. Lời giải.
Số phức z có phần thực là 1 và phần ảo là 2. acebook.com/g Chọn phương án A .f
Câu 19. Cho hai số phức z1 = 1 − 2i và z2 = 3 + 4i. Tìm điểm M biểu diễn số phức z1.z2 trên mặt phẳng tọa độ. A. M (−2; 11). B. M (−2; −11). C. M (11; −2). D. M (11; 2). Lời giải. https://www
Ta có z1.z2 = (1 − 2i)(3 + 4i) = 11 − 2i. Vậy M (11; −2). Chọn phương án C
Câu 20. Cho số phức z = 4 − 3i có điểm biểu diễn trên mặt phẳng tọa độ Oxy là M . Tính độ dài OM . √ A. 5. B. 25. C. 7. D. 4. Lời giải.
Ta có OM = |z| = p42 + (−3)2 = 5. Chọn phương án A
Câu 21. Trong không gian tọa độ Oxyz, tọa độ điểm G0 đối xứng với điểm G(5; −3; 7) qua trục Oy là A. G0(−5; 0; −7). B. G0(−5; −3; −7). C. G0(5; 3; 7). D. G0(−5; 3; −7). Lời giải.
Hình chiếu vuông góc của điểm G(5; −3; 7) lên trục Oy là H(0; −3; 0).
Vì G0 đối xứng với G qua trục Oy nên H là trung điểm của đoạn GG0 nên tọa độ của điểm G0 là
Biên soạn: Ths Nguyễn Chín Em Trang 4 xG0 = 2xH − xG = −5   yG0 = 2yH − yG = −3  zG0 = 2zH − zG = −7.
Vậy tọa độ điểm G0(−5; −3; −7). Chọn phương án B
Câu 22. Trong không gian Oxyz, cho hai điểm A(−2; 1; 1), B(0; −1; 1). Phương trình mặt cầu đường kính AB là
A. (x + 1)2 + y2 + (z − 1)2 = 8.
B. (x + 1)2 + y2 + (z − 1)2 = 2.
C. (x + 1)2 + y2 + (z + 1)2 = 8.
D. (x − 1)2 + y2 + (z − 1)2 = 2. Lời giải.
Phương pháp: Phương trình mặt cầu có tâm I(a; b; c), bán kính R là (x − a)2 + (y − b)2 + (z − c)2 = R2.
Cách giải: Tâm mặt cầu là trung điểm của AB, có tọa độ là I(−1; 0; 1). √ √
Bán kính mặt cầu: R = IA = 12 + 12 + 02 = 2.
Phương trình mặt cầu đường kính AB: (x + 1)2 + y2 + (z − 1)2 = 2. Chọn phương án B
Câu 23. Trong không gian Oxyz, cho tam giác đều ABC với A(6; 3; 5) và đường thẳng BC có phương x = 1 − t   trình tham số
y = 2 + t . Gọi ∆ là đường thẳng đi qua trọng tâm G của tam giác ABC và vuông góc  z = 2t 2019-2020
với mặt phẳng (ABC). Điểm nào dưới đây thuộc đường thẳng ∆? A. M (−1; −12; 3). B. N (3; −2; 1). C. P (0; −7; 3). D. Q(1; −2; 5). THPT Lời giải.
• Gọi M (1 − t; 2 + t; 2t) là hình chiếu của A lên BC. # » #»
Ta có AM = (−5 − t; t − 1; 2t − 5) vuông góc với u = (−1; 1; 2) là véc-tơ chỉ phương của BC. GHIỆP
Do đó −1(−5 − t) + 1(t − 1) + 2(2t − 5) = 0 ⇔ t = 1. Suy ra M (0; 3; 2). N T # » 2 # »
• Vì ABC là tam giác đều nên M là trung điểm của BC. Suy ra AG = AM ⇒ G(2; 3; 3). 3 TỐ 1 î # » ó • #» #»
Đường thẳng ∆ đi qua G, có véc-tơ chỉ phương là u ∆ = AM , u = (1; 5; −2). THI 3 x = 2 + t   Suy ra ∆ :
y = 3 + 5t . Với t = −1, ta có Q(1; −2; 5) ∈ ∆.   LUYỆN z = 3 − 2t Chọn phương án D
Câu 24. Trong không gian Oxyz, cho hai điểm A(1; −1; 0), B(0; 1; 1). Gọi (α) là mặt phẳng chứa đường x y − 1 z − 2 thẳng d : = =
và song song với đường thẳng AB. Điểm nào dưới đây thuộc mặt phẳng 2 −1 1 (α)? A. M (6; −4; −1). B. N (6; −4; 2). C. P (6; −4; 3). D. Q = (6; −4; 1). Lời giải. # » • AB = (−1; 2; 1). • #»
Đường thẳng d đi qua M (0; 1; 2) và có véc-tơ chỉ phương u d = (2; −1; 1). î # »ó • #» #»
Mặt phẳng (α) có véc-tơ pháp tuyến là n = u d, AB = (−3; −3; 3) và (α) đi qua M .
Phương trình (α) là −3(x − 0) − 3(y − 1) + 3(z − 2) = 0 ⇔ −x − y + z − 1 = 0.
• Ta có −6 + 4 + 3 − 1 = 0 nên P (6; −4; 3) ∈ (α).
Biên soạn: Ths Nguyễn Chín Em Trang 5 Chọn phương án C
Câu 25. Cho tứ diện đều cạnh a, M là trunng điểm của BC. Tính cosin của góc giữa hai đường thẳng AB và DM . √ √ √ 3 3 3 1 A. . B. . C. . D. . 2 6 3 2 Lời giải.
Kẻ M N ∥ AB, cắt AC tại trung điểm N của AC. A Xét tam giác N M D ta có: M N 2 + M D2 − N D2 cos ÷ N M D = 2M N · M D a2 3a2 3a2 √ + − 3 N = 4 4 4 √ = . a a 3 6 D B 2 · · 2 2 M o/ aPr C Chọn phương án B
Câu 26. Cho hàm số y = f (x) liên tục trên R và có bảng xét dấu của đạo hàm như sau: roups/GeoGebr x −∞ −1 0 2 4 +∞ f 0(x) + 0 − + 0 − 0 +
Hàm số đã cho có bao nhiêu cực trị? acebook.com/g .f A. 3. B. 2. C. 1. D. 4. Lời giải.
Dựa vào bảng xét dấu ta thấy đạo hàm của hàm số có 4 lần đổi dấu nên hàm số có 4 điểm cực trị. Chọn phương án D https://www
Câu 27. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = −x3 +3x+1 trên đoạn [0; 2] bằng A. 2. B. 3. C. 1. D. 4. Lời giải. ñx = 1 ∈ [0; 2]
Ta có: y0 = −3x2 + 3 = 0 ⇔ . x = −1 / ∈ [0; 2]
y(0) = 1; y(1) = 3; y(2) = −1.
Khi đó maxy = 3; miny = −1. Vậy maxy + miny = 2. [0;2] [0;2] [0;2] [0;2] Chọn phương án A √
Câu 28. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 − x2 − x bằng √ √ A. 2 + 2. B. 2. C. 1. D. 2 − 2. Lời giải.
Biên soạn: Ths Nguyễn Chín Em Trang 6 √ √ √ î ó −x −x − 2 − x2
Tập xác định D = − 2; 2 . Ta có y0 = √ − 1 = √ . 2 − x2 2 − x2 x ≤ 0 √   y0 = 0 ⇔ 2 − x2 = −x ⇔ ñx = 1 ⇔ x = −1.   x = −1 Bảng biến thiên √ √ x − 2 −1 2 y0 + 0 − 2 y √ √ 2 − 2 √
Dựa vào bảng biến thiên, ta có max y = 2, min y = − 2. √ √ √ √ [− 2; 2] [− 2; 2] √ Vậy max y + min y = 2 − 2. √ √ √ √ [− 2; 2] [− 2; 2] Chọn phương án D
Câu 29. Với a là số thực âm bất kỳ, mệnh đề nào dưới đây đúng?
A. log a2 = 2 log (−a). B. log a2 = −2 log a. C. log a2 = 2 log a. D. log a2 = 2a. 2 2 2 2 2 2 2 Lời giải. 2019-2020
Vì a là số thực âm nên log a2 = 2 log |a| = 2 log (−a). 2 2 2 Chọn phương án A THPT
Câu 30. Số giao điểm của đồ thị hàm số y = x3 + x + 2 và đường thẳng y = −2x + 1 là A. 3. B. 0. C. 2. D. 1. Lời giải. GHIỆP N
Xét phương trình hoành độ giao điểm x3 + x + 2 = −2x + 1 ⇔ x3 + 3x + 1 = 0. T
Xét f (x) = x3 + 3x + 1, ta có f 0(x) = 3x2 + 3 > 0. Suy ra bảng biến thiên TỐ x −∞ +∞ THI f 0(x) + +∞ + f (x) LUYỆN −∞
Do đó phương trình f (x) = 0 có 1 nghiệm. Chọn phương án D Å 1 ã2x+1
Câu 31. Tập nghiệm của bất phương trình
> 1 (với a là tham số, a 6= 0) là 1 + a2 Å 1 ã Å 1 ã A. −∞; − . B. (−∞; 0). C. − ; +∞ . D. (0; +∞). 2 2 Lời giải. 1 Å 1 ã2x+1 1 Vì 0 < < 1 nên
> 1 ⇔ 2x + 1 < 0 ⇔ x < − . 1 + a2 1 + a2 2 Chọn phương án A Câu 32.
Biên soạn: Ths Nguyễn Chín Em Trang 7
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) E F quanh trục DF . 10π π A. a3. B. a3. a 7 3 30◦ 5π 10π C. a3. D. a3. 2 9 A B a D C a Lời giải. E F
• Khi quay hình vuông ABCD quanh trục DF ta được khối trụ
tròn xoay có chiều cao bằng a và bán kính đáy bằng a. Thể
tích khối trụ này là V1 = π · a2 · a = πa3. o/
• Khi quay tam giác vuông AF E quanh trục DF ta được khối A B
nón tròn xoay có chiều cao bằng a và bán kính đáy bằng aPr √ a 3 EF = AF · tan 30◦ =
. Thể tích khối nón này là V2 = 3 √ Ç å2 1 a 3 π π · · a = a3. D C 3 3 9 π 10π
Vậy thể tích cần tìm là V = V1 + V2 = πa3 + a3 = a3. 9 9 roups/GeoGebr Chọn phương án D e √ Z 1 + ln x √ Câu 33. Cho tích phân I = dx. Đổi biến t =
1 + ln x ta được kết quả nào sau đây? x 1 √ √ √ 2 2 2 2 Z Z Z Z A. I = t2 dt. B. I = 2 t2 dt. C. I = 2 t2 dt. D. I = 2 t dt. acebook.com/g 1 1 1 1 .f Lời giải. Ta có √ dx t =
1 + ln x ⇒ t2 = 1 + ln x ⇒ 2t dt = . x Với https://www x = 1 ⇒ t = 1, √ x = e ⇒ t = 2. √ √ 2 2 Z Z Vậy I = t · 2t dt = 2 t2 dt. 1 1 Chọn phương án B Câu 34.
Gọi S là diện tích hình phẳng được tô đậm trong hình vẽ bên. Công y thức tính S là y = f (x) 1 2 1 2 Z Z Z Z A. S = f (x) dx + f (x) dx. B. S = f (x) dx − f (x) dx. −1 1 −1 1 x −1 O 1 2 2 2 Z Z C. S = f (x) dx. D. S = − f (x) dx. −1 −1
Biên soạn: Ths Nguyễn Chín Em Trang 8 Lời giải. 1 2 Z Z
Dựa vào hình vẽ suy ra S = f (x) dx − f (x) dx. −1 1 Chọn phương án B
Câu 35. Cho hai số phức z1 = m + 3i, z2 = 2 − (m + 1)i, với m ∈ R. Tìm các giá trị của m để w = z1 ·z2 là số thực. A. m = 1 hoặc m = −2. B. m = 2 hoặc m = −1. C. m = 2 hoặc m = −3. D. m = −2 hoặc m = −3. Lời giải.
Ta có w = z1 · z2 = (m + 3i) (2 − (m + 1)i) = 5m + 3 + (6 − m − m2) i. ñm = −3
Để w là số thực thì 6 − m − m2 = 0 ⇔ m = 2. Chọn phương án C
Câu 36. Phương trình bậc hai nào dưới đây nhận hai số phức 2 − 3i và 2 + 3i làm nghiệm ? A. z2 + 4z + 13 = 0. B. z2 + 4z + 3 = 0. C. z2 − 4z + 13 = 0. D. z2 − 4z + 3 = 0. Lời giải.
Đặt z1 = 2 − 3i; z2 = 2 + 3i. Khi đó
S = z1 + z2 = 4; P = z1 · z2 = (2 − 3i)(2 + 3i) = 4 + 9 = 13.
Do đó z1 và z2 là nghiệm của phương trình: z2 − Sz + P = 0 hay z2 − 4z + 13 = 0.
Vậy z2 − 4z + 13 = 0 là phương trình cần tìm. 2019-2020 Chọn phương án C x − 1
Câu 37. Trong không gian Oxyz cho mặt phẳng (P ) : 3x − 4y + 5z − 6 = 0 và đường thẳng d : = THPT 2 y − 2 z − 3 =
. Gọi ϕ là góc giữa đường thẳng d và mặt phẳng (P ). Tìm khẳng định đúng. 3 1 1 1 1 1 A. sin ϕ = √ . B. cos ϕ = − √ . C. cos ϕ = √ . D. sin ϕ = − √ . GHIỆP 5 28 5 28 5 28 5 28 N Lời giải. T #» #»
(P ) có véc-tơ pháp tuyến là n = (3; −4; 5) và d có véc-tơ chỉ phương u = (2; 3; 1). Khi đó ta có TỐ #» #» | #» n · #» u | 1 sin ϕ = |cos ( n , u )| = = √ . THI | #» n | · | #» u | 5 28 Chọn phương án A
Câu 38. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1; −2; −3), B(−1; 4; 1) và đường LUYỆN x + 2 y − 2 z + 3 thẳng d : = =
. Phương trình nào dưới đây là phương trình của đường thẳng đi qua 1 −1 2
trung điểm đoạn thẳng AB và song song với d? x y − 1 z + 1 x y − 2 z + 2 x y − 1 z + 1 x y + 1 z − 1 A. = = . B. = = . C. = = . D. = = . 1 −1 2 1 −1 2 1 1 2 1 −1 2 Lời giải.
Gọi M là trung điểm đoạn AB, ta có M (0; 1; −1). Khi đó đường thẳng đi qua M và song song với d có x y − 1 z + 1 phương trình = = . 1 −1 2 Chọn phương án A
Câu 39. Có một dãy ghế gồm 6 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 2 học sinh lớp A, 2 học sinh lớp
B và 2 học sinh lớp C ngồi vào dãy ghế đó sao cho mỗi ghế có đúng 1 học sinh ngồi. Xác suất để không
có học sinh lớp C ngồi cạnh nhau. 2 1 5 1 A. . B. . C. . D. . 3 3 6 6 Lời giải.
Biên soạn: Ths Nguyễn Chín Em Trang 9
Cho 2 học sinh lớp C ngồi cạnh nhau thành 1 nhóm D.
2 học sinh lớp C đổi vị trí trong nhóm D: 2! cách.
Nhóm D đổi vị trí với 4 học sinh còn lại: 5! cách. Không gian mẫu: 6! cách. 2! · 5! 1
Xác suất để 2 học sinh lớp C ngồi cạnh nhau: = . 6! 3 1 2
Vậy xác suất để 2 học sinh lớp C không ngồi cạnh nhau = 1 − = . 3 3 Chọn phương án A
Câu 40. Cho hình chóp S.ABC có SA = 3a và SA ⊥ (ABC). Biết AB = BC = 2a và ’ ABC = 120◦.
Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng 3a a A. . B. . C. a. D. 2a. 2 2 Lời giải.
Gọi I là hình hình chiếu vuông góc của A trên BC, ta có AI ⊥ BC. (1) S
Mặt khác SA ⊥ (ABC) nên SA ⊥ BC. (2)
Từ (1) và (2) suy ra BC ⊥ (SIA). (3) o/
Gọi H là hình hình chiếu vuông góc của A trên SI, ta có AH ⊥ SI. (4) aPr
Từ (3) và (4) suy ra AH ⊥ (SBC) nên khoảng cách từ A đến mặt phẳng (SBC) là AH.
Xét tam giác BIA vuông tại I, ta có √3 √ H AI = AB · sin 120◦ = 2a · = a 3. A C 2 roups/GeoGebr
Xét tam giác SAI vuông tại A, ta có I B s √ 1 1 1 AS2 · AI2 (3a)2 · (a 3)2 3a = + ⇒ AH = = √ = . AH2 AS2 AI2 AS2 + AI2 (3a)2 + (a 3)2 2 3a
Vậy khoảng cách từ điểm A đến mặt phẳng (SBC) bằng . acebook.com/g .f 2 Chọn phương án A mx + 10
Câu 41. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = nghịch biến trên khoảng 2x + m (0; 2)? https://www A. 4. B. 5. C. 6. D. 9. Lời giải.  mx + 10 m2 − 20 < 0  Hàm số y =
nghịch biến trên khoảng (0; 2) ⇔ m 2x + m − / ∈ (0; 2)  2 √ √  − 20 < m < 20 √ √   − 20 < m < 20 √   "  m     − 20 < m ≤ −4 ⇔ − ≤ 0 ⇔ ñ ⇔ √ 2 m ≥ 0    0 ≤ m < 20.  m    m ≤ −4  − ≥ 2 2
Vậy m ∈ {−4; 0; 1; 2; 3; 4; }. Chọn phương án C
Câu 42. Dân số thế giới được tính theo công thức S = A · eni trong đó A là dân số của năm lấy làm
mốc tính, S là dân số sau n năm, i là tỉ lệ tăng dân số hàng năm. Cho biết năm 2005 Việt Nam có
khoảng 80.902.400 người và tỉ lệ tăng dân số là 1, 47% một năm. Như vậy, nếu tỉ lệ tăng dân số hàng
năm không đổi thì đến năm 2019 số dân của Việt Nam sẽ gần với số nào nhất sau đây?
Biên soạn: Ths Nguyễn Chín Em Trang 10 A. 99.389.200. B. 99.386.600. C. 100.861.100. D. 99.251.200. Lời giải.
Áp dụng công thức S = A · eni với A = 80.902.400, n = 2019 − 2005 = 14, i = 1, 47% = 0, 0147, ta có
số dân Việt Nam đến năm 2017 là
S = A · eni = 80902400 · e14·0,0147 ≈ 99389203,38.
Như vậy, số dân Việt Nam đến năm 2019 gần với số 99.389.200 nhất. Chọn phương án A
Câu 43. Cho hàm số y = f (x) liên tục trên R và có bảng biến thiên như hình vẽ. Tìm tất cả các giá 1
trị thực của m để phương trình
f (x) − m = 0 có đúng hai nghiệm phân biệt. 2 x −∞ −1 0 1 +∞ y0 + 0 − 0 + 0 − 0 0 y −∞ −3 +∞ + m = 0 ñ 3 m = 0 A.  3 B. m < −3. C. m < − . D. m < − . 2 m < −3. 2 Lời giải. 1 Ta có
f (x) − m = 0 ⇔ f (x) = 2m. (*) 2 2019-2020
Quan sát bảng biến thiên của hàm số y = f (x), ta thấy, để phương trình (∗) có đúng hai nghiệm phân  ñ2m = 0 m = 0 biệt thì ⇔  3 THPT 2m < −3 m < − . 2 Chọn phương án D
Câu 44. Một hình trụ có bán kính đáy bằng a, mặt phẳng qua trục cắt hình trụ theo một thiết diện GHIỆP
có diện tích bằng 8a2. Tính diện tích xung quanh của hình trụ. N T A. 4πa2. B. 8πa2. C. 16πa2. D. 2πa2. Lời giải. TỐ B O THI A LUYỆN C O0 D
Thiết diện qua trục của hình trụ là hình chữ nhật, có độ dài một cạnh là 2a, có diện tích là 8a2, suy ra 8a2
chiều cao của hình trụ là h = = 4a. 2a
Vậy diện tích xung quanh của hình trụ là: Sxq = 2πrh = 2 · π · a · 4a = 8πa2. Chọn phương án B 3 Z
Câu 45. Cho hàm số f (x) thoả mãn
[2x ln(x + 1) + xf 0(x)] dx = 0 và f (3) = 1. 0 3 Z a + b ln 2 Biết f (x) dx =
với a, b là các số thực dương. Giá trị của a + b bằng 2 0
Biên soạn: Ths Nguyễn Chín Em Trang 11 A. 35. B. 29. C. 11. D. 7. Lời giải. 3 Z Tính I = 2x ln(x + 1) dx. 0  1 ®u = ln(x + 1) du = dx Đặt ⇒ x + 1 . Khi đó dv = 2x dx v = x2 3 3 Z 3 x2 Å x2 ã 3 I = x2 ln(x + 1) − dx = 9 ln 4 −
− x + ln |x + 1| = 16 ln 2 − . x + 1 2 2 0 0 0 3 Tính J = R xf 0(x) dx. 0 ®u ® J = x duJ = dx Đặt ⇒ . dvJ = f 0(x)dx vJ = f (x) 3 3 3 Z Z Z J = xf 0(x) dx = xf (x)|3 − f (x) dx = 3 − f (x) dx. o/ 0 0 0 0 aPr 3 Z Mà
[2x ln(x + 1) + xf 0(x)] dx = 0 0 3 3 3 Z Z 3 3 + 32 ln 2 ⇒ I + J = 0 ⇒ 16 ln 2 − + 3 − f (x)dx = 0 ⇒ f (x) dx = 16 ln 2 + = . 2 2 2 0 0 ® roups/GeoGebr a = 3 Suy ra . Vậy a + b = 35. b = 32 Chọn phương án A
Câu 46. Cho hàm số y = f (x) liên tục trên R và có bảng biến thiên như sau x −∞ −1 3 +∞ acebook.com/g + .f y0 0 − 0 + 4 +∞ + y −∞ −2 https://www
Biết f (0) < 0, hỏi phương trình f (|x|) = f (0) có bao nhiêu nghiệm? A. 4. B. 2. C. 3. D. 5. Lời giải.
Đặt f (0) = k < 0. Vì hàm số nghịch biến trên (−1; 3) nên −2 < k < 4.
Ta có hàm số y = f (|x|) là hàm số chẵn nên đồ thị đối xứng qua trục Oy, từ đó ta có bảng biến thiên sau x −∞ −3 0 3 +∞ y0 − 0 + − 0 + +∞ + k +∞ + y −2 −2 −
Từ bảng biến thiên suy ra phương trình f (|x|) = f (0) có 3 nghiệm. Chọn phương án C
Biên soạn: Ths Nguyễn Chín Em Trang 12 1
Câu 47. Xét các số thực a, b thỏa mãn điều kiện
< b < a < 1. Tìm giá trị nhỏ nhất của biểu thức 3 Å 3b − 1 ã P = log + 12 log2 a − 3. a b 4 a 1 √ A. min P = 13. B. min P = √ . C. min P = 9. D. min P = 3 2. 3 2 Lời giải.
Ta có (2b − 1)2(b + 1) ≥ 0 ⇒ 3b − 1 ≤ 4b3 và điều kiện bài toán suy ra log b > 0. a 12 3 log b · (log b − 3)2
Từ đó suy ra P ≥ 3 log b + − 3 = a a + 9 ≥ 9. a (log b − 1)2 (log b − 1)2 a a 1 1 Khi b = , a = √ thì P = 9. Vậy, min P = 9. 2 3 2 Chọn phương án C
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số x2 + mx + m y =
trên [1; 2] bằng 2. Số phần tử của S là x + 1 A. 1. B. 4. C. 3. D. 2. Lời giải. x2 + mx + m Xét hàm số f (x) =
trên [1; 2]. Ta có f 0(x) liên tục trên [1; 2] và x + 1 x2 + 2x f 0(x) = > 0, ∀ x ∈ [1; 2]. (x + 1)2 2019-2020 3m + 4 2m + 1
Suy ra f (x) đồng biến trên [1; 2]. Do đó max f (x) = f (2) = , min f (x) = f (1) = . [1;2] 3 [1;2] 2 ß 3m + 4 2m + 1 ™ THPT Khi đó max |f (x)| = max , . Ta có [1;2] 3 2 3m + 4 2m + 1 11 ≥
⇔ 4(3m + 4)2 ≥ 9(2m + 1)2 ⇔ m ≥ − . 3 2 12 GHIỆP N 11 3m + 4 T • Với m ≥ − , ta có max |f (x)| = . Theo đề bài, ta có 12 [1;2] 3 TỐ  3m + 4  2 = 2 m = (thỏa mãn) THI 3m + 4 3 3   = 2 ⇔ ⇔   3 3m + 4 10 = −2 m = − loại. 3 3 LUYỆN 11 2m + 1 • Với m < − , ta có max |f (x)| = . Theo đề bài, ta có 12 [1;2] 2  2m + 1  5 2m + 1 = 2 m = − (thỏa mãn) 2 2   = 2 ⇔ ⇔   2 2m + 1 3 = −2 m = loại. 2 2 ß 2 5 ™ Vậy S = ; −
⇒ Số phần tử của S là 2. 3 2 Chọn phương án D √ √
Câu 49. Cho hình hộp ABCD.A0B0C0D0 có đáy là hình chữ nhật với AB = 3, AD = 7. Hai mặt
bên (ABB0A0) và (ADD0A0) lần lượt tạo với đáy một góc 45◦ và 60◦. Tính thể tích của khối hộp nếu
biết cạnh bên của hình hộp bằng 1. A. 3. B. 5. C. 4. D. 2. Lời giải.
Biên soạn: Ths Nguyễn Chín Em Trang 13
Gọi H là hình chiếu vuông góc A0 lên (ABCD). B0 C0
Gọi M, N lần lượt là hình chiếu vuông góc H lên AB, AD ⇒ ÷ A0N H = 60◦ và ÷ A0M H = 45◦. x 2x A0 D0 Đặt A0H = x, khi đó A0N = = √ . sin 60◦ 3  √ 3 − 4x2  A0N = AA02 − A0N 2 = = HM 3 x  HM = x. tan 45◦ = x … 3 − 4x2 … 3 ⇒ = x ⇒ x = . 3 7 B C √ √ 45◦ … 3 M 60◦ H VABCD.A0B0C0D0 = AB.AD.x = 3. 7. = 3. 7 A N D Chọn phương án A 2x + y + 1
Câu 50. Cho x, y là các số thực dương thỏa mãn log
= x + 2y. Tìm giá trị nhỏ nhất của 3 x + y 1 2 biểu thức T = + √ . o/ x y √ √ aPr A. 3 + 3. B. 4. C. 3 + 2 3. D. 6. Lời giải. Ta có: 2x + y + 1 log = x + 2y 3 x + y
⇔ log (2x + y + 1) − log (x + y) = 3(x + y) − (2x + y + 1) + 1 3 3 roups/GeoGebr
⇔ log (2x + y + 1) + (2x + y + 1) = log [3(x + y)] + 3(x + y). (1) 3 3
Xét hàm số y = f (a) = log a + a trên (0; +∞). 3
Dễ thấy hàm số y = f (a) là hàm số đồng biến trên (0; +∞).
Do đó, (1) ⇔ f (2x + y + 1) = f (3(x + y)) ⇔ 2x + y + 1 = 3(x + y) ⇔ x + 2y = 1. 1 2 1 1 Ta có + √ = + x y x 1 √ acebook.com/g y .f 2 1 1 1 1 1 ≥ + = + + x 1 x 1 1 + y + y + y 4 4 4 2 (1 + 1 + 1)2 9 ≥ = = 6. https://www 1 1 1 x + + y + + y x + 2y + 4 4 21 1
Dấu “=” xảy ra khi và chỉ khi x = ; y = . 2 4 Chọn phương án D
———————–HẾT———————–
Biên soạn: Ths Nguyễn Chín Em Trang 14 ĐÁP ÁN THAM KHẢO 1. C 2. A 3. B 4. B 5. B 6. C 7. A 8. A 9. D 10. D 11. A 12. A 13. B 14. A 15. C 16. A 17. B 18. A 19. C 20. A 21. B 22. B 23. D 24. C 25. B 26. D 27. A 28. D 29. A 30. D 31. A 32. D 33. B 34. B 35. C 36. C 37. A 38. A 39. A 40. A 41. C 42. A 43. D 44. B 45. A 46. C 47. C 48. D 49. A 50. D 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN
Biên soạn: Ths Nguyễn Chín Em Trang 15 MỖI NGÀY MỘT ĐỀ THI 4
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Có bao nhiêu cách xếp một nhóm học sinh gồm 4 bạn nam và 6 bạn nữ thành một hàng ngang? A. 10!. B. 4!. C. 6!.4!. D. 6!.
Câu 2. Cho (un) là cấp số cộng với công sai d. Biết u5 = 16, u7 = 22. Tính u1. A. u1 = −5. B. u1 = −2. C. u1 = 19. D. u1 = 4.
Câu 3. Tập nghiệm của phương trình log (x2 − 3x) = −1 là: 0,25 √ √ ® ´ 3 − 2 2 3 + 2 2 A. {4}. B. ; . 2 2 C. {1; −4}. D. {−1; 4}.
Câu 4. Hình lập phương có đường chéo của mặt bên bằng 4 cm. Tính thể tích khối lập phương đó. √ √ √ A. 8 2 cm3. B. 16 2 cm3. C. 8 cm3. D. 2 2 cm3.
Câu 5. Tìm tập xác định của hàm số y = log 1 (x + 1). 2 2019-2020 A. D = (−∞; −1). B. D = (−1; +∞). C. D = [−1; +∞). D. D = R\{1}.
Câu 6. Hàm số f (x) = cos(4x + 7) có một nguyên hàm là 1 1 THPT A. − sin(4x + 7) + x. B. sin(4x + 7) − 3. C. sin(4x + 7) − 1. D. − sin(4x + 7) + 3. 4 4
Câu 7. Cho khối chóp tam giác có đường cao bằng 100 cm và cạnh đáy bằng 20 cm, 21 cm, 29 cm.
Tính thể tích khối chóp này. GHIỆP √ A. 7 000 2 cm3. B. 6 000 cm3. C. 6 213 cm3. D. 7 000 cm3. N √ T
Câu 8. Cho khối nón có bán kính đáy r =
3 và chiều cao h = 4. Tính thể tích V của khối nón đã TỐ cho. √ A. V = 16π 3. B. V = 12π. C. V = 4. D. V = 4π. THI
Câu 9. Tính diện tích của mặt cầu có bán kính r = 2. 32 A. π. B. 8π. C. 32π. D. 16π. 3 LUYỆN
Câu 10. Cho hàm số y = f (x) có đạo hàm liên tục trên R và có bảng biến thiên như sau x −∞ −1 0 1 +∞ f 0(x) + 0 − 0 + 0 − −1 −1 f (x) −∞ −2 −∞
Hàm số y = f (x) đồng biến trên khoảng nào sau đây A. (0; 1). B. (−1; 0). C. (−∞; 1). D. (1; +∞).
Câu 11. Cho a, b > 0, log a = p, log b = p. Đẳng thức nào dưới đây đúng? 3 3 Å 3r ã Å 3r ã A. log = r + pm − qd. B. log = r + pm + qd. 3 ambd 3 ambd Å 3r ã Å 3r ã C. log = r − pm − qd. D. log = r − pm + qd. 3 ambd 3 ambd GeoGebraPro Trang 1
Câu 12. Một hình trụ có diện tích xung quanh bằng S, diện tích đáy bằng diện tích một mặt cầu bán
kính a. Khi đó thể tích của hình trụ bằng 1 1 1 A. Sa. B. Sa. C. Sa. D. Sa. 2 3 4 Câu 13.
Cho hàm số y = f (x) có bảng biến thiên như sau. Giá x −∞ 0 2 +∞
trị cực đại của hàm số bằng y0 − 0 + 0 − A. 1. B. 2. C. 0. D. 5. +∞ + y 5 1 −∞ Câu 14.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? y A. y = x3 − 3x − 1. B. y = −x3 − 3x2 − 1. 3 C. y = −x3 + 3x2 + 1. D. y = x3 − 3x + 1. o/ 1 aPr x −1 O −1 5
Câu 15. Tiệm cận ngang của đồ thị hàm số y =
là đường thẳng có phương trình nào dưới x − 1 đây? roups/GeoGebr A. x = 1. B. y = 5. C. x = 0. D. y = 0.
Câu 16. Tập nghiệm của bất phương trình log x > log (8 − x) là 2 2 A. (8; +∞). B. (−∞; 4). C. (4; 8). D. (0; 4).
Câu 17. Cho hàm số y = f (x) có bảng biến thiên như hình sau acebook.com/g x −∞ −2 0 2 +∞ .f f 0(x) − 0 + 0 − 0 + +∞ + 1 +∞ + f (x) −2 −2 https://www
Số nghiệm thực của phương trình 2f (x) + 3 = 0 là A. 4. B. 3. C. 2. D. 1. 5 7 7 Z Z Z Câu 18. Nếu f (x)dx = 3 và f (x)dx = 9 thì f (x)dx bằng bao nhiêu? 2 5 2 A. 3. B. 6. C. 12. D. −6.
Câu 19. Tìm số phức liên hợp của của số z = 5 + i. A. z = 5 − i. B. z = −5 − i. C. z = 5 + i. D. z = −5 + i.
Câu 20. Cho hai số phức z1 = 2 − 7i và z2 = −4 + i. Điểm biểu diễn số phức z1 + z2 trên mặt phẳng
tọa độ là điểm nào dưới đây? A. Q(−2; −6). B. P (−5; −3). C. N (6; −8). D. M (3; −11). Câu 21. GeoGebraPro Trang 2
Trên mặt phẳng tọa độ Oxy cho điểm M trong hình vẽ bên là điểm biểu diễn của y số phức z. Tìm z. 3 A. z = −4 + 3i. B. z = −3 + 4i. C. z = 3 − 4i. D. z = 3 + 4i. x O −4 M
Câu 22. Trong không gian với hệ tọa độ Oxyz, tọa độ hình chiếu vuông góc của điểm A(2; −1; 0) lên
mặt phẳng (P ) : 3x − 2y + z + 6 = 0 là A. (1; 1; 1). B. (−1; 1; −1). C. (3; −2; 1). D. (5; −3; 1).
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình x2 + y2 + z2 − 2x + 4y −
6z + 9 = 0. Tọa độ tâm I và bán kính R của mặt cầu là √ A. I (1; −2; 3) và R = 5. B. I (1; −2; 3) và R = 5. √
C. I (−1; 2; −3) và R = 5. D. I (−1; 2; −3) và R = 5.
Câu 24. Trong không gian Oxyz, cho mặt phẳng (P ) : x − 2z + 1 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của (P )? #» #» #» #» A. n1 = (1; 0; −2). B. n2 = (1; −2; 1). C. n3 = (1; −2; 0). D. n4 = (−1; 2; 0). x − 1 y − 2 z
Câu 25. Trong không gian Oxyz, cho đường thẳng d : = =
. Điểm nào dưới đây thuộc 2 1 −2 đường thẳng d? 2019-2020 A. M (−1; −2; 0). B. M (−1; 1; 2). C. M (2; 1; −2). D. M (3; 3; 2).
Câu 26. Cho hình chóp S.ABCD đều có SA = AB = a. Góc giữa SA và CD là THPT A. 60◦. B. 30◦. C. 90◦. D. 45◦. 4
Câu 27. Gọi M , m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x) = + x + 1 trên đoạn [1; 3]. x GHIỆP Tính M − m. N A. 4. B. 9. C. 1. D. 5. T
Câu 28. Giá trị nhỏ nhất của hàm số f (x) = x3 + 3x + 1 trên đoạn [1; 3] là TỐ A. min f (x) = 3. B. min f (x) = 6. C. min f (x) = 37. D. min f (x) = 5. [1;3] [1;3] [1;3] [1;3] THI
Câu 29. Với a là số thực dương bất kỳ, mệnh đề nào dưới đây đúng? 1 1 A. log(3a) = 3 log a. B. log a3 = 3 log a. C. log(3a) = log a. D. log a3 = log a. 3 3 LUYỆN 2x + 1
Câu 30. Số giao điểm của đồ thị hàm số y =
với đường thẳng y = 2x + 3 là x − 1 A. 2. B. 3. C. 1. D. 0.
Câu 31. Tập nghiệm của bất phương trình 3x2−2x < 27 là A. (−∞; −1). B. (3; +∞). C. (−1; 3).
D. (−∞; −1) ∪ (3; +∞). √
Câu 32. Trong không gian, cho tam giác ABC vuông tại A, AB = a và AC = a 3. Tính độ dài đường
sinh ` của hình nón có được khi quay tam giác ABC xung quanh trục AB. √ √ A. ` = a. B. ` = 2a. C. ` = a 3. D. ` = a 2. 1 Z x7 Câu 33. Cho tích phân I =
dx, giả sử đặt t = 1 + x2. Tìm mệnh đề đúng. (1 + x2)5 0 2 3 2 4 1 Z (t − 1)3 Z (t − 1)3 1 Z (t − 1)3 3 Z (t − 1)3 A. I = dt. B. I = dt. C. dt. D. dt. 2 t5 t5 2 t4 2 t4 1 1 1 1 GeoGebraPro Trang 3
Câu 34. Thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi parabol (P ) : y = x2 và
đường thẳng d : y = x xoay quanh trục Ox bằng 1 1 1 1 Z Z Z Z A. π x2 dx − π x4 dx. B. π x2 dx + π x4 dx. 0 0 0 0 1 1 Z Z C. π x2 − x2 dx. D. π x2 − x dx. 0 0
Câu 35. Cho hai số phức z = 6 + 5i và z0 = 5 − 4i + z. Tìm mô-đun của số phức w = z · z0. √ √ A. |w| = 612. B. |w| = 61. C. |w| = 61 2. D. |w| = 6 2.
Câu 36. Gọi z1 và z2 lần lượt là nghiệm của phươngtrình: z2 − 2z + 5 = 0. Tính P = |z1|2 + |z2|2. √ √ A. P = 2 5. B. P = 20. C. P = 10. D. P = 5.
Câu 37. Trong không gian Oxyz, mặt phẳng chứa trục Ox và đi qua điểm A(1; 1; −1) có phương trình là A. z + 1 = 0. B. x − y = 0. C. x + z = 0. D. y + z = 0.
Câu 38. Trong không gian Oxyz, cho hai điểm A(1; 2; 3) và B(2; 4; −1). Phương trình chính tắc của o/
đường thẳng d đi qua A, B là aPr x + 2 y + 4 z + 1 x + 1 y + 2 z + 3 A. = = . B. = = . 1 2 4 1 2 4 x − 1 y − 2 z − 3 x + 2 y + 4 z − 1 C. = = . D. = = . 1 2 −4 1 2 −4
Câu 39. Một nhóm có 7 học sinh lớp A và 5 học sinh lớp B. Xếp ngẫu nhiên 12 học sinh trên ngồi vào
một dãy 12 ghế hàng ngang sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất sao cho không roups/GeoGebr
có bất kì 2 học sinh lớp B nào ngồi cạnh nhau. 7 1 7 1 A. . B. . C. . D. . 99 132 264 792
Câu 40. Cho hình lăng trụ tam giác đều ABC.A0B0C0 có tất cả các cạnh đều bằng a. Khoảng cách từ
A đến mặt phẳng (A0BC) bằng √ √ √ √ a 3 a 21 a 2 a 6 A. . B. . C. . D. . 4 7 2 4 acebook.com/g .f
Câu 41. Có bao nhiêu giá trị nguyên của m để hàm số y = x3 + 3x2 − (m2 − 3m + 2)x + 5 đồng biến trên (0; 2)? A. 3. B. 2. C. 4. D. 1.
Câu 42. Các nhà khoa học đã tính toán khi nhiệt độ trung bình của trái đất tăng thêm 2◦C thì mực
nước biển sẽ dâng lên 0, 03m. Nếu nhiệt độ tăng lên 5◦C thì nước biển sẽ dâng lên 0, 1m và người ta https://www
đưa ra công thức tổng quát như sau: Nếu nhiệt độ trung bình của trái đất tăng lên toC thì nước biển
dâng lên f (t) = kat(m) trong đó k, a là các hằng số dương. Hỏi khi nhiệt độ trung bình của trái đất
tăng thêm bao nhiêu độ C thì mực nước biển dâng lên 0, 2m? A. 9, 2◦C. B. 8, 6◦C. C. 7, 6◦C. D. 6, 7◦C.
Câu 43. Cho hàm số y = f (x) liên tục trên R và có bảng biến thiên như hình bên dưới. Tìm tất cả 1
các giá trị thực của m để phương trình
f (x) − m = 0 có đúng hai nghiệm phân biệt. 2 x −∞ −1 0 1 +∞ f 0(x) + 0 − 0 + 0 − 0 0 f (x) −∞ −3 − −∞ GeoGebraPro Trang 4 3 A. m = 0 hoặc m < − . B. m < −3. 2 3 C. m < − . D. m = 0 hoặc m < −3. 2 √
Câu 44. Cho hình trụ có bán kính đáy bằng a 2. Cắt hình trụ bởi một mặt phẳng, song song với trụ a
của hình trụ và cách trục của hình trụ một khoảng bằng
ta được thiết diện là một hình vuông. Tính 2
thể tích V của khối trụ đã cho. √ √ 2πa3 7 √ A. V = πa3 3. B. V = . C. V = 2πa3 7. D. V = πa3. 3 1 5 Z Z
Câu 45. Cho hàm số y = f (x) liên tục trên R thỏa mãn f (x)dx = 3 và f (x)dx = 6. Tính tích 0 0 1 Z phân I = f (|3x − 2|)dx −1 A. I = 3. B. I = −2. C. I = 4. D. I = 9.
Câu 46. Cho hàm số y = f (x) = ax3 + bx2 + cx + d có bảng biến thiên như sau x −∞ 0 1 +∞ y0 + 0 − 0 + 1 +∞ + y 2019-2020 −∞ 0 1 THPT
Khi đó |f (x)| = m có bốn nghiệm phân biệt x1 < x2 < x3 < < x4 khi và chỉ khi 2 1 1 A. < m < 1. B. ≤ m < 1. C. 0 < m < 1. D. 0 < m ≤ 1. 2 2 6 (2x + y) x + 2y GHIỆP
Câu 47. Cho x, y là các số dương thỏa mãn xy ≤ 4y−1. Giá trị nhỏ nhất của P = +ln N x y T là a + ln b. Tính ab. A. ab = 45. B. ab = 81. C. ab = 115. D. ab = 108. TỐ
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số THI x2 + mx + m y =
trên [1; 2] bằng 2. Số phần tử của S là x + 1 A. 1. B. 4. C. 3. D. 2. LUYỆN
Câu 49. Cho hình hộp ABCD.A0B0C0D0 có đáy ABCD là hình thoi tâm O, cạnh a, góc ’ ABC = 60◦.
Biết rằng A0O ⊥ (ABCD) và cạnh bên hợp với đáy một góc bằng 60◦. Tính thể tích V của khối đa diện OABC0D0. a3 a3 a3 3a3 A. V = . B. V = . C. V = . D. V = . 6 12 8 4
Câu 50 (Thầy: Trương Đức Thịnh). Có bao nhiêu cặp số nguyên dương (x; y) với y ≤ 2020 thỏa mãn x + 2 log
< 4y4 + 8y3 − x2 + 4x y2 + 1 2 y + 1 A. 2019.2020. B. 2020.2021. C. 20192. D. 20202.
———————–HẾT———————– GeoGebraPro Trang 5 ĐÁP ÁN THAM KHẢO 1. A 2. D 3. D 4. B 5. B 6. B 7. D 8. D 9. D 10. A 11. C 12. A 13. D 14. D 15. D 16. C 17. A 18. C 19. A 20. A 21. C 22. B 23. C 24. A 25. B 26. A 27. C 28. D 29. B 30. A 31. C 32. B 33. A 34. A 35. C 36. A 37. D 38. C 39. A 40. B 41. B 42. D 43. A 44. C 45. A 46. B 47. B 48. D 49. C 50. D o/ aPr roups/GeoGebr acebook.com/g .f https://www GeoGebraPro Trang 6 MỖI NGÀY MỘT ĐỀ THI 4
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Có bao nhiêu cách xếp một nhóm học sinh gồm 4 bạn nam và 6 bạn nữ thành một hàng ngang? A. 10!. B. 4!. C. 6!.4!. D. 6!. Lời giải.
Nhóm học sinh đó có tất cả 10 học sinh.
Xếp 10 học sinh thành một hàng ngang có P10 = 10! cách xếp. Chọn phương án A
Câu 2. Cho (un) là cấp số cộng với công sai d. Biết u5 = 16, u7 = 22. Tính u1. A. u1 = −5. B. u1 = −2. C. u1 = 19. D. u1 = 4. Lời giải. ®u ® ® 5 = 16 u1 + 4d = 16 u1 = 4 Ta có ⇔ ⇔ . u7 = 22 u1 + 6d = 22 d = 3 Vậy u1 = 4. 2019-2020 Chọn phương án D
Câu 3. Tập nghiệm của phương trình log (x2 − 3x) = −1 là: 0,25 √ √ ® ´ THPT 3 − 2 2 3 + 2 2 A. {4}. B. ; . 2 2 C. {1; −4}. D. {−1; 4}. Lời giải. GHIỆP ñx < 0 N
Điều kiện: x2 − 3x > 0 ⇔ . T x > 3 TỐ Ta có THI log x2 − 3x = −1 0,25 ⇔ x2 − 3x = 4 ⇔ x2 − 3x − 4 = 0 ñ LUYỆN x = −1 (nhận) ⇔ x = 4 (nhận). Vậy S = {−1; 4}. Chọn phương án D
Câu 4. Hình lập phương có đường chéo của mặt bên bằng 4 cm. Tính thể tích khối lập phương đó. √ √ √ A. 8 2 cm3. B. 16 2 cm3. C. 8 cm3. D. 2 2 cm3. Lời giải. 4 √
Độ dài các cạnh hình lập phương là √ = 2 2 cm. 2 √ √
Thể tích khối lập phương là V = (2 2)3 = 16 2 cm3. Chọn phương án B
Câu 5. Tìm tập xác định của hàm số y = log 1 (x + 1). 2 A. D = (−∞; −1). B. D = (−1; +∞). C. D = [−1; +∞). D. D = R\{1}. Lời giải. GeoGebraPro Trang 1
Điều kiện x + 1 > 0 ⇔ x > −1. Suy ra tập xác định D = (−1; +∞). Chọn phương án B
Câu 6. Hàm số f (x) = cos(4x + 7) có một nguyên hàm là 1 1 A. − sin(4x + 7) + x. B. sin(4x + 7) − 3. C. sin(4x + 7) − 1. D. − sin(4x + 7) + 3. 4 4 Lời giải. 1
Hàm số f (x) = cos(4x + 7) có một nguyên hàm là sin(4x + 7) − 3. 4 Chọn phương án B
Câu 7. Cho khối chóp tam giác có đường cao bằng 100 cm và cạnh đáy bằng 20 cm, 21 cm, 29 cm.
Tính thể tích khối chóp này. √ A. 7 000 2 cm3. B. 6 000 cm3. C. 6 213 cm3. D. 7 000 cm3. Lời giải. Diện tích đáy 20 + 21 + 29 Å20 + 21 + 29 ã Å 20 + 21 + 29 ã Å 20 + 21 + 29 ã S = − 20 − 21 − 29 = 210 cm2. 2 2 2 2 o/ Thể tích khối chóp aPr 1 1 V = · S · h = · 210 · 100 = 7 000 cm3. 3 3 Chọn phương án D √
Câu 8. Cho khối nón có bán kính đáy r =
3 và chiều cao h = 4. Tính thể tích V của khối nón đã cho. √ roups/GeoGebr A. V = 16π 3. B. V = 12π. C. V = 4. D. V = 4π. Lời giải. 1 1 √
Áp dụng công thức tính thể tích của khối nón ta tính được V = πr2h = .π.( 3)2.4 = 4π. 3 3 Chọn phương án D
Câu 9. Tính diện tích của mặt cầu có bán kính r = 2. 32 A. π. B. 8π. C. 32π. D. 16π. acebook.com/g 3 .f Lời giải. Phương pháp
Công thức tính diện tích mặt cầu bán kính R là S = 4πR2. Cách giải https://www
Công thức tính diện tích mặt cầu bán kính r = 2 là S = 4πr2 = 16π. Chọn phương án D
Câu 10. Cho hàm số y = f (x) có đạo hàm liên tục trên R và có bảng biến thiên như sau x −∞ −1 0 1 +∞ f 0(x) + 0 − 0 + 0 − −1 −1 f (x) −∞ −2 −∞
Hàm số y = f (x) đồng biến trên khoảng nào sau đây A. (0; 1). B. (−1; 0). C. (−∞; 1). D. (1; +∞). Lời giải.
Từ bẳng biến thiên suy ra hàm số đã cho đồng biến trên các khoảng (−∞; −1) và (0; 1). Chọn phương án A GeoGebraPro Trang 2
Câu 11. Cho a, b > 0, log a = p, log b = p. Đẳng thức nào dưới đây đúng? 3 3 Å 3r ã Å 3r ã A. log = r + pm − qd. B. log = r + pm + qd. 3 ambd 3 ambd Å 3r ã Å 3r ã C. log = r − pm − qd. D. log = r − pm + qd. 3 ambd 3 ambd Lời giải. Å 3 ã Ta có log = log 3r − log
ambd = r − log am − log bd = r − m log a − d log b 3 ambd 3 3 3 3 3 3 Chọn phương án C
Câu 12. Một hình trụ có diện tích xung quanh bằng S, diện tích đáy bằng diện tích một mặt cầu bán
kính a. Khi đó thể tích của hình trụ bằng 1 1 1 A. Sa. B. Sa. C. Sa. D. Sa. 2 3 4 Lời giải.
Gọi r là bán kính đáy của hình trụ, h là chiều cao của hình trụ.  ®S = 2πrh r = 2a  Theo bài ra ta có ⇔ S πr2 = 4πa2 h = . 4πa S
Thể tích khối trụ là V = πr2h = π · 4a2 · = Sa. 4πa Chọn phương án A Câu 13. 2019-2020
Cho hàm số y = f (x) có bảng biến thiên như sau. Giá x −∞ 0 2 +∞
trị cực đại của hàm số bằng y0 − 0 + 0 − A. 1. B. 2. C. 0. D. 5. THPT +∞ + y 5 1 −∞ Lời giải.
Giá trị cực đại của hàm số bằng 5. GHIỆP N Chọn phương án D T Câu 14. TỐ
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? y A. y = x3 − 3x − 1. B. y = −x3 − 3x2 − 1. THI 3 C. y = −x3 + 3x2 + 1. D. y = x3 − 3x + 1. LUYỆN 1 x −1 O −1 Lời giải.
Đường cong trong hình vẽ có dạng đồ thị của hàm số y = ax3 + bx2 + cx + d với a 6= 0.
Dựa vào đồ thị, ta có lim y = +∞. Suy ra a > 0. x→+∞
Mặt khác, giao điểm của đồ thị với trục tung tại điểm có tung độ dương nên d > 0.
Chỉ có hàm số y = x3 − 3x + 1 thỏa mãn các đặc điểm trên.
Vậy đường cong trong hình vẽ là đồ thị của hàm số y = x3 − 3x + 1. Chọn phương án D 5
Câu 15. Tiệm cận ngang của đồ thị hàm số y =
là đường thẳng có phương trình nào dưới x − 1 đây? A. x = 1. B. y = 5. C. x = 0. D. y = 0. GeoGebraPro Trang 3 Lời giải.  5  lim = 0  x→+∞ x − 1 Ta có:
⇒ đồ thị hàm số có tiệm cận ngang là y = 0. 5   lim = 0 x→−∞ x − 1 Chọn phương án D
Câu 16. Tập nghiệm của bất phương trình log x > log (8 − x) là 2 2 A. (8; +∞). B. (−∞; 4). C. (4; 8). D. (0; 4). Lời giải.
Điều kiện 0 < x < 8.
Do 2 > 1 nên bất phương trình đã cho tương đương với
x > 8 − x ⇔ 2x > 8 ⇔ x > 4.
Kết hợp với điều kiện 0 < x < 8 ta được tập nghiệm của bất phương trình là (4; 8) Chọn phương án C
Câu 17. Cho hàm số y = f (x) có bảng biến thiên như hình sau x −∞ −2 0 2 +∞ o/ f 0(x) − 0 + 0 − 0 + aPr +∞ + 1 +∞ + f (x) −2 −2
Số nghiệm thực của phương trình 2f (x) + 3 = 0 là A. 4. B. 3. C. 2. D. 1. Lời giải. roups/GeoGebr 3
2f (x) + 3 = 0 ⇔ f (x) = − . 2 3
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f (x) và đường thẳng y = − . 2 3 Mà −2 < −
< 1 nên số nghiệm thực của phương trình 2f (x) + 3 = 0 là 4. 2 Chọn phương án A acebook.com/g 5 7 7 .f Z Z Z Câu 18. Nếu f (x)dx = 3 và f (x)dx = 9 thì f (x)dx bằng bao nhiêu? 2 5 2 A. 3. B. 6. C. 12. D. −6. Lời giải. 7 5 7 https://www Z Z Z Ta có f (x)dx = f (x)dx + f (x)dx = 3 + 9 = 12. 2 2 5 Chọn phương án C
Câu 19. Tìm số phức liên hợp của của số z = 5 + i. A. z = 5 − i. B. z = −5 − i. C. z = 5 + i. D. z = −5 + i. Lời giải.
Số phức liên hợp của của số a + bi là a − bi. Do đó z = 5 − i. Chọn phương án A
Câu 20. Cho hai số phức z1 = 2 − 7i và z2 = −4 + i. Điểm biểu diễn số phức z1 + z2 trên mặt phẳng
tọa độ là điểm nào dưới đây? A. Q(−2; −6). B. P (−5; −3). C. N (6; −8). D. M (3; −11). Lời giải.
Ta có z1 + z2 = −2 − 6i. Vậy điểm biểu diễn z1 + z2 trên mặt phẳng tọa độ là điểm Q(−2; −6). Chọn phương án A GeoGebraPro Trang 4 Câu 21.
Trên mặt phẳng tọa độ Oxy cho điểm M trong hình vẽ bên là điểm biểu diễn của y số phức z. Tìm z. 3 A. z = −4 + 3i. B. z = −3 + 4i. C. z = 3 − 4i. D. z = 3 + 4i. x O −4 M Lời giải.
Điểm M có tọa độ là M (3; −4) ⇒ điểm M biểu diễn số phức z = 3 − 4i. Chọn phương án C
Câu 22. Trong không gian với hệ tọa độ Oxyz, tọa độ hình chiếu vuông góc của điểm A(2; −1; 0) lên
mặt phẳng (P ) : 3x − 2y + z + 6 = 0 là A. (1; 1; 1). B. (−1; 1; −1). C. (3; −2; 1). D. (5; −3; 1). Lời giải. # »
Gọi H(x; y; −6 − 3x + 2y) là hình chiếu của A lên mặt phẳng P . Ta có AH = (x − 2; y + 1; −6 − 3x + 2y). # » # » #» x − 2 y + 1
Do AH ⊥ (P ) nên hai véc-tơ AH và n P cùng phương. Suy ra ta có hệ phương trình = = 3 −2 −6 − 3x + 2y . (1) 1 2019-2020
Giải hệ (1) ta thu được một nghiệm là (−1; 1; −1). Chọn phương án B THPT
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình x2 + y2 + z2 − 2x + 4y −
6z + 9 = 0. Tọa độ tâm I và bán kính R của mặt cầu là √ A. I (1; −2; 3) và R = 5. B. I (1; −2; 3) và R = 5. √ GHIỆP
C. I (−1; 2; −3) và R = 5. D. I (−1; 2; −3) và R = 5. N Lời giải. T √ √
Mặt cầu x2 + y2 + z2 − 2x + 4y − 6z + 9 = 0 có tâm I (1; −2; 3) và bán kính R = 1 + 4 + 9 − 9 = 5. TỐ Chọn phương án C THI
Câu 24. Trong không gian Oxyz, cho mặt phẳng (P ) : x − 2z + 1 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của (P )? #» #» #» #» A. n1 = (1; 0; −2). B. n2 = (1; −2; 1). C. n3 = (1; −2; 0). D. n4 = (−1; 2; 0). LUYỆN Lời giải. #»
Vectơ pháp tuyến của (P ) là n = (1; 0; −2). Chọn phương án A x − 1 y − 2 z
Câu 25. Trong không gian Oxyz, cho đường thẳng d : = =
. Điểm nào dưới đây thuộc 2 1 −2 đường thẳng d? A. M (−1; −2; 0). B. M (−1; 1; 2). C. M (2; 1; −2). D. M (3; 3; 2). Lời giải. −1 − 1 1 − 2 2 Ta có = =
= −1 nên M (−1; 1; 2) thuộc đường thẳng d. 2 1 −2 Chọn phương án B
Câu 26. Cho hình chóp S.ABCD đều có SA = AB = a. Góc giữa SA và CD là A. 60◦. B. 30◦. C. 90◦. D. 45◦. Lời giải. GeoGebraPro Trang 5
Vì AB ∥ CD nên góc giữa SA và CD bằng góc giữa SA và S AB.
Vì SA = AB nên tam giác SAB đều, vậy góc giữa chúng bằng 60◦. A B D C Chọn phương án A 4
Câu 27. Gọi M , m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x) = + x + 1 trên đoạn [1; 3]. x Tính M − m. A. 4. B. 9. C. 1. D. 5. Lời giải. o/ ñ 4 4 x = 2 ∈ [1; 3] Ta có f 0(x) = − + 1 và f 0(x) = 0 ⇔ − + 1 = 0 ⇔ aPr x2 x2 x = −2 / ∈ [1; 3]. 16
Ta tính được f (1) = 6, f (2) = 5, f (3) = . 3
Kết hợp với f (x) liên tục trên [1; 3] nên M = max f (x) = 6 = f (1) và m = min f (x) = 5 = f (2). x∈[1;3] x∈[1;3] Vậy M − m = 1. Chọn phương án C roups/GeoGebr
Câu 28. Giá trị nhỏ nhất của hàm số f (x) = x3 + 3x + 1 trên đoạn [1; 3] là A. min f (x) = 3. B. min f (x) = 6. C. min f (x) = 37. D. min f (x) = 5. [1;3] [1;3] [1;3] [1;3] Lời giải.
Ta có f 0(x) = 3x2 + 3 > 0 với mọi x. Lại có f (1) = 5, f (3) = 37 nên min f (x) = 5. [1;3] Chọn phương án D acebook.com/g .f
Câu 29. Với a là số thực dương bất kỳ, mệnh đề nào dưới đây đúng? 1 1 A. log(3a) = 3 log a. B. log a3 = 3 log a. C. log(3a) = log a. D. log a3 = log a. 3 3 Lời giải.
Theo tính chất ta có log a3 = 3 log a. https://www Chọn phương án B 2x + 1
Câu 30. Số giao điểm của đồ thị hàm số y =
với đường thẳng y = 2x + 3 là x − 1 A. 2. B. 3. C. 1. D. 0. Lời giải.
Xét phương trình hoành độ giao điểm 2x + 1 = 2x + 3 x − 1
⇔ 2x + 1 = (2x + 3) (x − 1) (do x = 1 không là nghiệm của phương trình) ⇔ 2x2 − x − 4 = 0 √  1 + 33 x = ⇔  4  √  1 − 33 x = . 4 GeoGebraPro Trang 6 2x + 1
Vậy đường thẳng y = 2x + 3 cắt đồ thị hàm số y = tại hai điểm. x − 1 Chọn phương án A
Câu 31. Tập nghiệm của bất phương trình 3x2−2x < 27 là A. (−∞; −1). B. (3; +∞). C. (−1; 3).
D. (−∞; −1) ∪ (3; +∞). Lời giải.
3x2−2x < 27 ⇔ 3x2−2x < 33 ⇔ x2 − 2x < 3 ⇔ x2 − 2x − 3 < 0 ⇔ −1 < x < 3. Chọn phương án C √
Câu 32. Trong không gian, cho tam giác ABC vuông tại A, AB = a và AC = a 3. Tính độ dài đường
sinh ` của hình nón có được khi quay tam giác ABC xung quanh trục AB. √ √ A. ` = a. B. ` = 2a. C. ` = a 3. D. ` = a 2. Lời giải.
Khi quay tam giác ABC vuông tại A xung quanh B B
trục AB ta được hình nón có đường sinh là BC.
Tam giác ABC vuông tại A nên
BC2 = AB2 + AC2 = a2 + 3a2 = 4a2. Vậy l = BC = 2a. C 2019-2020 A C A Chọn phương án B THPT 1 Z x7 Câu 33. Cho tích phân I =
dx, giả sử đặt t = 1 + x2. Tìm mệnh đề đúng. (1 + x2)5 0 GHIỆP 2 3 2 4 Z Z Z Z N 1 (t − 1)3 (t − 1)3 1 (t − 1)3 3 (t − 1)3 T A. I = dt. B. I = dt. C. dt. D. dt. 2 t5 t5 2 t4 2 t4 1 1 1 1 TỐ Lời giải. THI 1 Đặt t = 1 + x2 ⇒ dt = x dx. 2
Đổi cận x = 0 ⇒ t = 1, x = 1 ⇒ t = 2. Khi đó LUYỆN 1 2 Z (x2)3 · x 1 Z (t − 1)3 I = dx = dt. (1 + x2)5 2 t5 0 1 Chọn phương án A
Câu 34. Thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi parabol (P ) : y = x2 và
đường thẳng d : y = x xoay quanh trục Ox bằng 1 1 1 1 Z Z Z Z A. π x2 dx − π x4 dx. B. π x2 dx + π x4 dx. 0 0 0 0 1 1 Z Z C. π x2 − x2 dx. D. π x2 − x dx. 0 0 Lời giải. GeoGebraPro Trang 7
Ta có (P ) và d cắt nhau tại hai điểm (0; 0), (1; 1) và x > x2, ∀x ∈ (0; 1). y
Suy ra thể tích khối tròn xoay đã cho T bằng thể tích khối tròn xoay T1 trừ
đi thể tích khối tròn xoay T2. Trong đó
• T1 được sinh ra khi quay hình phẳng giới hạn bởi các đường d, trục 1 Ox, x = 0, x = 1. x
• T2 được sinh ra khi quay hình phẳng giới hạn bởi các đường (P ), trục O 1 Ox, x = 0, x = 1. 1 1 Z Z
Vậy thể tích khối tròn xoay đã cho bằng π x2 dx − π x4 dx. 0 0 Chọn phương án A
Câu 35. Cho hai số phức z = 6 + 5i và z0 = 5 − 4i + z. Tìm mô-đun của số phức w = z · z0. √ √ A. |w| = 612. B. |w| = 61. C. |w| = 61 2. D. |w| = 6 2. Lời giải. √ o/
Ta có z0 = 5 − 4i + 6 + 5i = 11 + i ⇒ z · z0 = 61 + 61i. Do đó |w| = 61 2. Chọn phương án C aPr
Câu 36. Gọi z1 và z2 lần lượt là nghiệm của phươngtrình: z2 − 2z + 5 = 0. Tính P = |z1|2 + |z2|2. √ √ A. P = 2 5. B. P = 20. C. P = 10. D. P = 5. Lời giải. ñz = 1 − 2i √ Ta có z2 − 2z + 5 = 0 ⇔
. Khi đó, P = |z1|2 + |z2|2 = 2 5. z = 1 + 2i roups/GeoGebr Chọn phương án A
Câu 37. Trong không gian Oxyz, mặt phẳng chứa trục Ox và đi qua điểm A(1; 1; −1) có phương trình là A. z + 1 = 0. B. x − y = 0. C. x + z = 0. D. y + z = 0. Lời giải.
Mặt phẳng chứa trục Ox có dạng By + Cz = 0, (B2 + C2 6= 0). acebook.com/g
Mặt phẳng đi qua điểm A(1; 1; −1) nên B − C = 0 ⇔ B = C. Do đó chọn B = C = 1. .f Chọn phương án D
Câu 38. Trong không gian Oxyz, cho hai điểm A(1; 2; 3) và B(2; 4; −1). Phương trình chính tắc của
đường thẳng d đi qua A, B là x + 2 y + 4 z + 1 x + 1 y + 2 z + 3 A. = = . B. = = . https://www 1 2 4 1 2 4 x − 1 y − 2 z − 3 x + 2 y + 4 z − 1 C. = = . D. = = . 1 2 −4 1 2 −4 Lời giải. # »
Ta có đường thẳng d đi qua A(1; 2; 3) và có véc-tơ chỉ phương AB = (1; 2; −4). Vậy phương trình chính x − 1 y − 2 z − 3 tắc đường thẳng d là = = · 1 2 −4 Chọn phương án C
Câu 39. Một nhóm có 7 học sinh lớp A và 5 học sinh lớp B. Xếp ngẫu nhiên 12 học sinh trên ngồi vào
một dãy 12 ghế hàng ngang sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất sao cho không
có bất kì 2 học sinh lớp B nào ngồi cạnh nhau. 7 1 7 1 A. . B. . C. . D. . 99 132 264 792 Lời giải.
• Xếp 12 học sinh ngồi vào một dãy 12 ghế hàng ngang sao cho mỗi ghế có đúng một học sinh ngồi có 12! cách. GeoGebraPro Trang 8
• Xếp 7 học sinh lớp A vào 7 ghế, có 7! cách.
Khi đó 7 ghế đã xếp học sinh lớp A tạo ra 8 khoảng trống, ta xếp 5 học sinh lớp B vào 5 trong 8
khoảng trống đó, có A5 cách. 8
⇒ có 7! · A5 cách xếp 12 học sinh mà các học sinh lớp B không ngồi cạnh nhau. 8 7! · A5 7
Vậy xác suất cần tìm là 8 = . 12! 99 Chọn phương án A
Câu 40. Cho hình lăng trụ tam giác đều ABC.A0B0C0 có tất cả các cạnh đều bằng a. Khoảng cách từ
A đến mặt phẳng (A0BC) bằng √ √ √ √ a 3 a 21 a 2 a 6 A. . B. . C. . D. . 4 7 2 4 Lời giải.
Gọi H là trung điểm của BC, do giả thiết 4ABC đều nên AH = √ A0 C0 a 3 và AH ⊥ BC (1). 2
Do AA0 ⊥ (ABC) suy ra AA0 ⊥ BC (2).
Từ (1), (2) ta suy ra BC ⊥ (AA0H). B0
Trong mặt phằng (AA0H) kẻ AI ⊥ A0H (3). I
Theo chứng minh trên BC ⊥ (AA0H) nên BC ⊥ AI (4).
Từ (3), (4) suy ra AI ⊥ (AA0H) do đó khoảng cách từ A đến mặt phẳng (A0BC) là AI. A C 1 1 1 1 4 2019-2020 Xét 4AA0H ta có = + = + AI2 AA02 √ AH2 a2 3a2 H 3a2 a 21 suy ra AI2 = ⇔ AI = . 7 7 THPT √ B a 21
Vậy khoảng cách từ A đến mặt phẳng (BA0C) bằng . 7 Chọn phương án B GHIỆP N
Câu 41. Có bao nhiêu giá trị nguyên của m để hàm số y = x3 + 3x2 − (m2 − 3m + 2)x + 5 đồng biến T trên (0; 2)? TỐ A. 3. B. 2. C. 4. D. 1. Lời giải. THI
Ta có y = x3 + 3x2 − (m2 − 3m + 2)x + 5 ⇒ y0 = 3x2 + 6x − (m2 − 3m + 2).
Hàm số đồng biến trên khoảng (0; 2) khi y0 ≥ 0, ∀x ∈ (0; 2) và dấu "=" xãy ra tại hữu hạn điểm trên khoảng đó. LUYỆN
⇔ 3x2 + 6x − (m2 − 3m + 2) ≥ 0, ∀x ∈ (0; 2)
⇔ 3x2 + 6x ≥ m2 − 3m + 2 (∗) với ∀x ∈ (0; 2)
Xét hàm số y = g(x) = 3x2 + 6x trên khoảng (0; 2) Ta có y0 = g0(x) = 6x + 6. Bảng biến thiên x 0 2 g0(x) + 24 g(x) 0
Dựa vào bảng biến thiên suy ra điều kiện để (∗) xảy ra là : m2 − 3m + 2 ≤ 0 ⇔ 1 ≤ m ≤ 2. GeoGebraPro Trang 9 Do m ∈ Z ⇒ m ∈ {1; 2}.
Vậy có 2 giá trị của m thỏa mãn yêu cầu bài toán. Chọn phương án B
Câu 42. Các nhà khoa học đã tính toán khi nhiệt độ trung bình của trái đất tăng thêm 2◦C thì mực
nước biển sẽ dâng lên 0, 03m. Nếu nhiệt độ tăng lên 5◦C thì nước biển sẽ dâng lên 0, 1m và người ta
đưa ra công thức tổng quát như sau: Nếu nhiệt độ trung bình của trái đất tăng lên toC thì nước biển
dâng lên f (t) = kat(m) trong đó k, a là các hằng số dương. Hỏi khi nhiệt độ trung bình của trái đất
tăng thêm bao nhiêu độ C thì mực nước biển dâng lên 0, 2m? A. 9, 2◦C. B. 8, 6◦C. C. 7, 6◦C. D. 6, 7◦C. Lời giải.  … 10 ®  0, 03 = ka2 a = 3  f (t) 0, 2a2 ⇒ 3 ; f(t) = kat ⇔ t = log = log ≈ 6, 7. a a 0, 1 = ka5 0, 03 k 0, 03  k =  o/ a2 aPr Chọn phương án D
Câu 43. Cho hàm số y = f (x) liên tục trên R và có bảng biến thiên như hình bên dưới. Tìm tất cả 1
các giá trị thực của m để phương trình
f (x) − m = 0 có đúng hai nghiệm phân biệt. 2 roups/GeoGebr x −∞ −1 0 1 +∞ f 0(x) + 0 − 0 + 0 − 0 0 f (x) acebook.com/g .f −∞ −3 − −∞ 3 A. m = 0 hoặc m < − . B. m < −3. 2 3 https://www C. m < − . D. m = 0 hoặc m < −3. 2 Lời giải. 1 Ta có f (x) = m ⇔ f (x) = 2m. 2
Số nghiệm của phương trình là số giao điểm của đồ thì hàm số y = f (x) và đường thẳng y = 2m.
Theo yêu cầu bài toán ta có 3
2m = 0 hoặc 2m < −3 ⇔ m = 0 hoặc m < − . 2 Chọn phương án A √
Câu 44. Cho hình trụ có bán kính đáy bằng a 2. Cắt hình trụ bởi một mặt phẳng, song song với trụ a
của hình trụ và cách trục của hình trụ một khoảng bằng
ta được thiết diện là một hình vuông. Tính 2
thể tích V của khối trụ đã cho. √ √ 2πa3 7 √ A. V = πa3 3. B. V = . C. V = 2πa3 7. D. V = πa3. 3 Lời giải. GeoGebraPro Trang 10
Gọi O, O0 lần lượt là tâm các đáy và thiết diện là hình vuông ABCD. ® O0 OH ⊥ AB A0
Gọi H là trung điểm AB, ta có suy ra OH ⊥ (ABB0A0). B0 OH ⊥ AA0 a Do đó d (OO0, (ABCD)) = OH = . 2 √ √ … a2 a 7
Tam giác OAH vuông tại H nên AH = OA2 − OH2 = 2a2 − = . √ 4 2 A
Suy ra AB = AA0 = OO0 = 2AH = a 7 (do ABCD là hình vuông). O √ √ √ Ä ä2 H
Vậy thể tích V = πR2h = π · a 2 · a 7 = 2πa3 7. B Chọn phương án C 1 5 Z Z
Câu 45. Cho hàm số y = f (x) liên tục trên R thỏa mãn f (x)dx = 3 và f (x)dx = 6. Tính tích 0 0 1 Z phân I = f (|3x − 2|)dx −1 A. I = 3. B. I = −2. C. I = 4. D. I = 9. Lời giải. 2 1 3 1 Z Z Z Ta có f (|3x − 2|)dx = f (−3x + 2)dx + f (3x − 2)dx = I1 + I2. −1 −1 2 2019-2020 3 2 2 3 3 Z 1 Z I1 = f (−3x + 2)dx = − f (−3x + 2)d(−3x + 2). THPT 3 −1 −1 5 2 1 Z
Đặt t = −3x + 2 suy ra x = −1 ⇒ t = 5; x = ⇒ x = 0. Do đó I1 = f (t)dt = 2. 3 3 GHIỆP 0 N 1 Z Z T 1 I2 = f (3x − 2)dx = 1f (3x − 2)d(3x − 2). TỐ 3 2 2 3 3 1 THI 2 1 Z
Đặt t = 3x − 2 suy ra x = 1 ⇒ t = 1; x = ⇒ x = 0. Do đó I2 = f (t)dt = 1. 3 3 0 Vậy I = I1 + I2 = 3. LUYỆN Chọn phương án A
Câu 46. Cho hàm số y = f (x) = ax3 + bx2 + cx + d có bảng biến thiên như sau x −∞ 0 1 +∞ y0 + 0 − 0 + 1 +∞ + y −∞ 0 1
Khi đó |f (x)| = m có bốn nghiệm phân biệt x1 < x2 < x3 < < x4 khi và chỉ khi 2 1 1 A. < m < 1. B. ≤ m < 1. C. 0 < m < 1. D. 0 < m ≤ 1. 2 2 Lời giải. GeoGebraPro Trang 11
Ta có f 0(x) = 3ax2 + 2bx + c. Từ bảng biến thiên của hàm số f (x), ta có    f (0) = 1 d = 1 a = 2             f (1) = 0 a + b + c + d = 0 b = −3 ⇔ ⇔ f 0(0) = 0 c = 0 c = 0             f 0(1) = 0 3a + 2b + c = 0 d = 1. Å 1 ã 1
Như vậy f (x) = 2x3 − 3x2 + 1, f = . 2 2 1 x −∞ 0 1 +∞ 2 y0 + 0 − 0 + 1 +∞ + 1 y 2 −∞ 0 1 1
Do đó |f (x)| = m có bốn nghiệm phân biệt x1 < x2 < x3 < < x4 khi và chỉ khi ≤ m < 1. o/ 2 2 Chọn phương án B aPr 6 (2x + y) x + 2y
Câu 47. Cho x, y là các số dương thỏa mãn xy ≤ 4y−1. Giá trị nhỏ nhất của P = +ln x y là a + ln b. Tính ab. A. ab = 45. B. ab = 81. C. ab = 115. D. ab = 108. Lời giải. x 4 1 Å 1 ã2 roups/GeoGebr
Từ xy ≤ 4y − 1 chia 2 vế cho y2 ta được ≤ − = 4 − 2 − ≤ 4. y y y2 y x Đặt = t thì 0 < t ≤ 4. y 6 −6 1 t2 − 6t − 12 Khi đó P = f (t) = 12 + + ln(t + 2) có f 0(t) = + = . t t2 t + 2 t2(t + 2) √ √
Ta có t2 − 6t − 12 < 0 ⇔ t ∈ (3 − 21; 3 +
21) ⊃ (0; 4]. Suy ra f 0(t) < 0, ∀t ∈ (0; 4]. 27 acebook.com/g Vậy minf (t) = f (4) = + ln 6. .f (0;4] 2 27 1
Suy ra giá trị nhỏ nhất của P bằng + ln 6 khi y = , x = 2. 2 2 27 Khi đó a = ; b = 6 ⇒ ab = 81. 2 Chọn phương án B https://www
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số x2 + mx + m y =
trên [1; 2] bằng 2. Số phần tử của S là x + 1 A. 1. B. 4. C. 3. D. 2. Lời giải. x2 + mx + m Xét hàm số f (x) =
trên [1; 2]. Ta có f 0(x) liên tục trên [1; 2] và x + 1 x2 + 2x f 0(x) = > 0, ∀ x ∈ [1; 2]. (x + 1)2 3m + 4 2m + 1
Suy ra f (x) đồng biến trên [1; 2]. Do đó max f (x) = f (2) = , min f (x) = f (1) = . [1;2] 3 [1;2] 2 ß 3m + 4 2m + 1 ™ Khi đó max |f (x)| = max , . Ta có [1;2] 3 2 3m + 4 2m + 1 11 ≥
⇔ 4(3m + 4)2 ≥ 9(2m + 1)2 ⇔ m ≥ − . 3 2 12 GeoGebraPro Trang 12 11 3m + 4 • Với m ≥ − , ta có max |f (x)| = . Theo đề bài, ta có 12 [1;2] 3  3m + 4  2 3m + 4 = 2 m = (thỏa mãn) 3 3   = 2 ⇔ ⇔   3 3m + 4 10 = −2 m = − loại. 3 3 11 2m + 1 • Với m < − , ta có max |f (x)| = . Theo đề bài, ta có 12 [1;2] 2  2m + 1  5 2m + 1 = 2 m = − (thỏa mãn) 2 2   = 2 ⇔ ⇔   2 2m + 1 3 = −2 m = loại. 2 2 ß 2 5 ™ Vậy S = ; −
⇒ Số phần tử của S là 2. 3 2 Chọn phương án D
Câu 49. Cho hình hộp ABCD.A0B0C0D0 có đáy ABCD là hình thoi tâm O, cạnh a, góc ’ ABC = 60◦.
Biết rằng A0O ⊥ (ABCD) và cạnh bên hợp với đáy một góc bằng 60◦. Tính thể tích V của khối đa diện OABC0D0. a3 a3 a3 3a3 A. V = . B. V = . C. V = . D. V = . 6 12 8 4 Lời giải. 2019-2020 AC a
Từ giả thiết, suy ra tam giác ABC đều cạnh a ⇒ OA = = . 2 2 A0 D0 Vì A0O ⊥ (ABCD) nên THPT 60◦ = ( ¤ AA0, (ABCD)) = ⁄ (AA0, AO) = ’ A0AO. √ a 3
Tam giác vuông A0AO có OA0 = OA. tan B0 C0 ’ A0AO = . 2 GHIỆP 3a3 N
Suy ra thể tích khối hộp V = SABCD.OA0 = . 4 T
Ta có V = VO.ABC0D0 +VAA0D0.BB0C0 +VC0.BOC +VD0.AOD+VO.CDD0C0 A D TỐ 1 1 1 1 V a3 = VO.ABC0D0 + V + V + V + V ⇒ VO.ABC0D0 = = . 2 12 12 6 6 8 O THI B C Chọn phương án C LUYỆN
Câu 50 (Thầy: Trương Đức Thịnh). Có bao nhiêu cặp số nguyên dương (x; y) với y ≤ 2020 thỏa mãn x + 2 log
< 4y4 + 8y3 − x2 + 4x y2 + 1 2 y + 1 A. 2019.2020. B. 2020.2021. C. 20192. D. 20202. Lời giải. Ta có x + 2 log
< 4y4 + 8y3 − x2 + 4x y2 + 1 2 y + 1 x + 2 ⇔ log
< 4y4 + 8y3 + 4y2 − x2y2 + 4xy2 + 4y2 2 y + 1 xy + 2y ⇔ log < 2y2 + 2y − (xy + y)2 2 2y + 2
⇔ log (xy + 2y) + (xy + 2y)2 < log 2y2 + 2y + 2y2 + 2y2 2 2 GeoGebraPro Trang 13
Xét hàm số f (t) = log (t) + t2 đồng biến trên khoảng (0; +∞). 2
Bất phương trình có dạng: f (xy + 2y) < f (2y2 + 2y) ⇔ xy + 2y < 2y2 + 2y ⇔ x < 2y. Do (x; y) và y ≤ 2020 nên
• Với y = 1 ⇒ x < 2 ⇒ x = 1.
• Với y = 2 ⇒ x < 4 ⇒ x ∈ {1; 2; 3}
• Với y = 3 ⇒ x < 6 ⇒ x ∈ {1; 2; 3; 4; 5} · · · · · ·
• Với y = 2020 ⇒ x < 4040 ⇒ x ∈ {1; 2; 3; · · · 4039}
Vậy số cặp nguyên dương (x; y) thỏa mãn là 1 + 3 + 4 + · · · + 4039 = 20202. Chọn phương án D
———————–HẾT———————– o/ aPr roups/GeoGebr acebook.com/g .f https://www GeoGebraPro Trang 14 ĐÁP ÁN THAM KHẢO 1. A 2. D 3. D 4. B 5. B 6. B 7. D 8. D 9. D 10. A 11. C 12. A 13. D 14. D 15. D 16. C 17. A 18. C 19. A 20. A 21. C 22. B 23. C 24. A 25. B 26. A 27. C 28. D 29. B 30. A 31. C 32. B 33. A 34. A 35. C 36. A 37. D 38. C 39. A 40. B 41. B 42. D 43. A 44. C 45. A 46. B 47. B 48. D 49. C 50. D 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN GeoGebraPro Trang 15 MỖI NGÀY MỘT ĐỀ THI 5
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Có bao nhiêu cách chọn 5 học sinh từ 20 học sinh a4e
Câu 11. Với a, b là hai số thực dương tùy ý, ln lớp 11A? b A. 1860480 cách. B. 120 cách. bằng C. 15504 cách. D. 100 cách. A. 4 ln a − ln b + 1. B. 4 ln b − ln a + 1. C. 4 ln a + ln b − 1. D. 4 ln a + ln b + 1.
Câu 2. Cho dãy (un) là một cấp số cộng có u1 = 2 và u
Câu 12. Khối trụ tròn xoay có đường kính bằng 2a, chiều 9 = 26. Tìm u5. A. 15. B. 13. C. 12. D. 14. cao h = 2a có thể tích là A. V = 2πa2. B. V = 2πa3.
Câu 3. Gọi x1, x2 là nghiệm của phương trình 7x2−5x+9 = C. V = 2πa2h. D. V = πa3. 343. Tính x1 + x2. A. x
Câu 13. Cho hàm số y = f (x) xác định, liên tục trên 1 + x2 = 4. B. x1 + x2 = 6. R và C. x
có bảng biến thiên như sau: 1 + x2 = 5. D. x1 + x2 = 3.
Câu 4. Nếu cạnh của một hình lập phương tăng lên gấp 3 x −∞ −2 2 +∞
lần thì thể tích của hình lập phương đó tăng lên bao nhiêu lần? y0 + 0 − 0 + A. 27. B. 9. C. 6. D. 4. 3 +∞
Câu 5. Trong các hàm số sau, hàm số nào có cùng tập xác y 1
định với hàm số y = x 5 ? −∞ 0 1 A. y = xπ. B. y = √ . 5 x Tìm giá trị cực đại y 2019-2020 √ √
CĐ và giá trị cực tiểu yCT của hàm số C. y = x. D. y = 3 x. đã cho
Câu 6. Họ nguyên hàm của hàm số f (x) = x2+cos x là A. yCĐ = −2 và yCT = 2. B. yCĐ = 3 và yCT = 0. 1 C. yCĐ = 2 và yCT = 0. D. yCĐ = 3 và yCT = −2. THPT A. 2x − sin x + C. B. x3 + sin x + C. 3
Câu 14. Đường cong trong hình vẽ bên là đồ thị của hàm 1 C. x3 − sin x + C. D. x3 + sin x + C. số nào dưới đây? 3
Câu 7. Cho khối chóp S.ABC có đáy là tam giác đều cạnh √ y GHIỆP
bằng a, SA = a 3, cạnh bên SA vuông góc với đáy. Thể N
tích khối chóp S.ABC bằng √ √ T a3 3 a3 a3 3 a3 A. . B. . C. . D. . 2 2 4 4 TỐ
Câu 8. Cho khối nón có bán kính đáy bằng r, chiều cao h.
Thể tích V của khối nón là THI 1 2 A. V = r2h. B. V = r2h. 3 1 C. V = πr2h. D. V = πr2h. 3 x LUYỆN 8πa2 O
Câu 9. Cho mặt cầu có diện tích bằng . Tính bán −1 3 −1 kính r của mặt cầu. √ √ a 6 a 3 A. r = . B. r = . 3 √ 3 √ a 6 a 2 C. r = . D. r = . 2x − 1 1 − 2x 2 3 A. y = . B. y = . x + 1 x + 1
Câu 10. Cho hàm số y = f (x) có bảng biến thiên như sau 2x + 1 2x + 1 C. y = . D. y = . x − 1 x + 1 x −∞ 0 2 +∞
Câu 15. Đường thẳng nào dưới đây là tiệm cận ngang của y0 + 0 − 0 + 1 − 4x đồ thị hàm số y = ? 2x − 1 1 +∞ 1 A. y = 2. B. y = . C. y = 4. D. y = −2. y 2
Câu 16. Tập nghiệm của bất phương trình log (3x + 1) < 2 0 −3 2 là ï 1 ã Å 1 1 ã
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. − ; 1 . B. − ; . 3 3 3 A. (2; +∞). B. (−∞; 1). Å 1 ã C. (0; +∞). D. (0; 2). C. − ; 1 . D. (−∞; 1). 3 GeoGebraPro Trang 1 Câu 17. x −∞ x1 x2 x3 +∞
Cho hàm số f (x) có đồ thị như y
hình vẽ. Số nghiệm của phương trình 2f (x) − 3 = 0 là y0 − 0 + − 0 + 3
Khi đó số điểm cực trị của hàm số y = f (x) là A. 3. B. 2. C. 4. D. 1. 1 √ x −1 O
Câu 28. Giá trị nhỏ nhất của hàm số y = x + 18 − x2 −1 là: √ A. 0. B. 6. C. −3 2. D. −6. A. 3. B. 1. C. 2. D. 0. 5
Câu 29. Cho 0 < b < a < 1, mệnh đề nào dưới đây Z dx đúng? Câu 18. Nếu
= ln c với c ∈ Q thì giá trị của c 2x − 1 A. log a < log b. B. log a < 0. b a b 1 C. log a > log b. D. log b < 1. bằng b a a A. 9. B. 3. C. 6. D. 81.
Câu 30. Số giao điểm của đồ thị hàm số y = x2 x2 − 4
với đường thẳng y = 3 là
Câu 19. Tìm phần ảo của số phức z = 8 − 12i. A. 8. B. 2 . C. 4. D. 6 . A. −12. B. 18. C. 12. D. −12i. Câu 31. Tìm tập nghiệm của bất phương trình
Câu 20. Cho hai số phức z1 = 1 + 2i, z2 = 3 − i. Tìm số log (x − 4) + 1 > 0. o/ z 2 2 phức z = . 5 ï ã Å ã z 13 13 aPr 1 A. ; +∞ . B. −∞; . 1 7 1 7 2 2 A. z = + i. B. z = + i. Å ã 10 10 5 5 13 1 7 1 7 C. (4; +∞). D. 4; . C. z = − i. D. z = − + i. 2 5 5 10 10
Câu 32. Tính thể tích khối tròn xoay sinh ra khi quay tam
Câu 21. Cho số phức z = 6 + 17i. Điểm biểu diễn cho số
giác đều ABC cạnh bằng 1 quanh AB. √
phức z trên mặt phẳng tọa độ Oxy là 3π π π π 3 A. M (−6; −17). B. M (−17; −6). A. . B. . C. . D. . 4 4 8 2 roups/GeoGebr C. M (17; 6). D. M (6; 17). 3 Z x
Câu 22. Trong không gian Oxyz, cho điểm M (3; 2; −1). Câu 33. Cho tích phân I = √ dx. Nếu đặt
Hình chiếu vuông góc của điểm M lên trục Oz là điểm 1 + x + 1 0 √ A. M3 (3; 0; 0). B. M4 (0; 2; 0). t = x + 1 thì C. M1 (0; 0; −1). D. M2 (3; 2; 0). 2 2 Z Z
Câu 23. Trong không gian với hệ tọa độ Oxyz phương A. I = (t2 − 2t) dt. B. I = (2t2 − t) dt.
trình nào sau đây không phải là phương trình của một mặt 1 1 2 2 cầu? Z Z acebook.com/g .f
A. x2 + y2 + z2 + x − 2y + 4z − 3 = 0. C. I = (2t2 + 2t) dt. D. I = (2t2 − 2t) dt.
B. 2x2 + 2y2 + 2z2 − x − y − z = 0 . 1 1
C. x2 + y2 + z2 − 2x + 4y − 4z + 10 = 0 .
Câu 34. Thể tích của khối tròn xoay do hình phẳng giới
D. 2x2 + 2y2 + 2z2 + 4x + 8y + 6z + 3 = 0. √ hạn bởi các đường y =
x, trục Ox và hai đường thẳng
Câu 24. Trong không gian Oxyz, mặt phẳng (P ) : x + 2y −
x = 1; x = 4 khi quay quanh trục hoành được tính bởi công
5 = 0 nhận vec-tơ nào trong các vec-tơ sau làm vec-tơ pháp thức nào? https://www 4 4 tuyến? Z Z √ #» #» A. V = π x dx. B. V = x A. n (1; 2; −5). B. n (0; 1; 2). dx. #» #» C. n (1; 2; 0). D. n (1; 2; 5). 1 1 4 4 Z Z √
Câu 25. Trong không gian (Oxyz), cho đường thẳng C. V = π2 x dx. D. V = π x dx. x = 3 − 3t   1 1 ∆ :
y = 1 + 2t . Điểm nào dưới đây thuộc đường thẳng Câu 35. Cho hai số phức z 
1 = 2 + i, z2 = 4 − 3i. Khi đó z = 5t
z1 · z2 có phần ảo bằng ∆? A. 11. B. 2. C. −11. D. −2. A. N (0; 3; 5). B. M (−3; 2; 5). C. (P (3; 1; 5). D. Q(6; −1; 5).
Câu 36. Gọi z1 và z2 lần lượt là nghiệm của phương trình:
z2 − 2z + 5 = 0. Tính P = |z1| + |z2|. √
Câu 26. Cho hình chóp S.ABCD đều có SA = AB = a. A. 2 5. B. 10. C. 3. D. 6. Góc giữa SA và CD là A. 60◦. B. 30◦. C. 90◦. D. 45◦.
Câu 37. Trong không gian với hệ trục tọa độ Oxyz, cho x − 1 y + 2 z đường thẳng d: = = . Mặt phẳng (P ) đi qua
Câu 27. Cho hàm số y = f (x) xác định trên R và có bảng 1 −1 2
xét dấu của đạo hàm như sau:
điểm M (2; 0; −1) và vuông góc với d có phương trình là A. x − y + 2z = 0. B. x − 2y − 2 = 0. C. x + y + 2z = 0. D. x − y − 2z = 0. GeoGebraPro Trang 2
Câu 38. Trong không gian tọa độ Oxyz, viết phương trình b Z
chính tắc của đường thẳng d đi qua A(1; 2; −1) và vuông f (x) dx.
góc với mặt phẳng (P ) : x + 2y − 3z + 1 = 0. a x + 1 y + 2 z − 1 6 2 4 1 A. d : = = . A. . B. . C. . D. . 1 −2 −3 π π π π x + 1 y + 2 z − 1 B. d : = = .
Câu 46. Cho hàm số y = f (x) có bảng biến thiên như hình 1 2 −3 x − 1 y − 2 z + 1 bên. C. d : = = . 1 2 3 x − 1 y − 2 z + 1 x −∞ 0 4 +∞ D. d : = = . −1 −2 3 f 0 − 0 + 0 −
Câu 39. Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp +∞ 3
12A, 3 học sinh lớp 12B và 5 học sinh lớp 12C trên một bàn
tròn. Tính xác suất P để các học sinh cùng lớp luôn ngồi f cạnh nhau. − −∞ 1 1 1 A. P = . B. P = . 1260 126 1 1
Phương trình f (4x − x2) − 2 = 0 có bao nhiêu nghiệm thực C. P = . D. P = . 28 252 phân biệt?
Câu 40. Cho tứ diện OABC có OA, OB, OC đôi một A. 2. B. 6. C. 4. D. 0.
vuông góc với nhau và OC = 2a, OA = OB = a. Gọi
Câu 47. Cho các số thực a, b thỏa mãn điều kiện 0 <
M là trung điểm của AB. Tính khoảng cách giữa hai đường
b < a < 1. Tìm giá trị nhỏ nhất của biểu thức P = thẳng OM và AC. √ √ √ 4(3b − 1) log + 8 log2 a − 1. 2a 2 5a 2a 2a a b 9 a A. . B. . C. . D. . √ 3 5 3 2 A. A = 6. B. 3 3 2. C. 8. D. 7.
Câu 41. Cho hàm số y = −x3 − mx2 + (4m + 9)x + 5, với
Câu 48. Gọi S là tập hợp tất cả các giá trị của tham
m là tham số. Có bao nhiêu giá trị nguyên của m để hàm
số thực m sao cho trị lớn nhất của hàm số y = số nghịch biến R? 3x2 − 6x + 2m − 1
trên đoạn [−2; 3] đạt giá trị nhỏ nhất. A. 6. B. 4. C. 7. D. 5. 2019-2020
Số phần tử của tập S là
Câu 42. Gọi N (t) là số phần trăm cacbon 14 còn lại trong A. 0. B. 3. C. 2. D. 1.
một bộ phận của một cây sinh trưởng từ t năm trước đây
Câu 49. Cho hình hộp chữ nhật ABCD.A0B0C0D0. Gọi M t A THPT
thì ta có công thức N (t) = 100.(0.5) (%) với A là hằng số.
là trung điểm của BB0. Mặt phẳng (M DC0) chia khối hộp
Biết rằng một mẩu gỗ có tuổi khoảng 3754 năm thì lượng
chữ nhật thành hai khối đa diện, một khối chứa đỉnh C và
cácbon 14 còn lại là 65%. Phân tích mẩu gỗ từ một công
một khối chứa đỉnh A0. Gọi V1, V2 lần lượt là thể tích của
trình kiến trúc cổ, người ta thấy lượng cácbon 14 còn lại V1
hai khối đa diện chứa C và A0. Tính .
trong mẩu gỗ là 63%. Hãy xác định tuổi của mẩu gỗ được V2 GHIỆP lấy từ công trình đó. V1 7 V1 7 N A. = . B. = . A. 3874. B. 3833. C. 3834. D. 3843. V2 24 V2 17 T V 7 V 17 Câu 43. 1 1 C. = . D. = . TỐ V 12 V 24 Cho hàm số y = f (x) y 2 2 có đạo hàm f 0(x), biết Câu 50. Xét các số thực dương x, y thỏa mãn Å ã THI rằng đồ thị của hàm 1 − 2x ln
= 3x + y − 1. Tìm giá trị nhỏ nhất Pmin số f 0(x) như hình vẽ. a c x x + y
Biết f (a) > 0, hỏi đồ 1 1 b O của P = + √ + 1 thị hàm số y = f (x) x xy
cắt trục hoành tại nhiều A. Pmin = 8. B. Pmin = 16. LUYỆN nhất bao nhiêu điểm? C. Pmin = 9. D. Pmin = 2.
———————–HẾT———————– A. 4. B. 2. C. 3. D. 1.
Câu 44. Cắt khối trụ bởi một mặt phẳng qua trục ta được
thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai
đáy của hình trụ, AB = 4a, AC = 5a. Thể tích V của khối trụ là A. V = 16πa3. B. V = 4πa3. C. V = 12πa3. D. V = 8πa3.
Câu 45. Cho hàm số y = f (x) có đạo hàm liên tục trên 1 Z 9
đoạn [0; 1] và thỏa mãn f (0) = 0. Biết f 2 (x) dx = và 2 0 1 1 Z πx 3π Z f 0 (x) cos dx = . Tích phân f (x) dx bằng. 2 4 0 0 GeoGebraPro Trang 3 ĐÁP ÁN THAM KHẢO 1. C 2. D 3. C 4. A 5. A 6. B 7. D 8. D 9. A 10. A 11. A 12. B 13. B 14. A 15. D 16. C 17. A 18. B 19. A 20. C 21. D 22. C 23. C 24. C 25. A 26. A 27. A 28. C 29. A 30. D 31. D 32. B 33. D 34. A 35. D 36. A 37. A 38. D 39. B 40. B 41. C 42. B 43. B 44. C 45. A 46. C 47. D 48. D 49. B 50. A o/ aPr roups/GeoGebr acebook.com/g .f https://www GeoGebraPro Trang 4 MỖI NGÀY MỘT ĐỀ THI 5
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Có bao nhiêu cách chọn 5 học sinh từ 20 học sinh Lời giải. Z lớp 11A? 1 Ta có: (x2 + cos x)dx = x3 + sin x + C. A. 1860480 cách. B. 120 cách. 3 C. 15504 cách. D. 100 cách. Chọn phương án B Lời giải.
Câu 7. Cho khối chóp S.ABC có đáy là tam giác đều cạnh
Số cách chọn 5 học sinh từ 20 học sinh lớp 11A là C5 = √ 20
bằng a, SA = a 3, cạnh bên SA vuông góc với đáy. Thể 15504 cách.
tích khối chóp S.ABC bằng Chọn phương án C √ √ a3 3 a3 a3 3 a3 A. . B. . C. . D. .
Câu 2. Cho dãy (un) là một cấp số cộng có u1 = 2 và 2 2 4 4 u9 = 26. Tìm u5. Lời giải. A. 15. B. 13. C. 12. D. 14. Thể tích khối chóp là √ S Lời giải. 1 1 V = · SA · SABC = · a 3 · Ta có u √ 3 3
1 + u9 = u1 + u1 + 8d = 2u1 + 8d = 2(u1 + 4d) = 2u5. u a2 3 a3 1 + u9 2 + 26 Do đó u = . 5 = = = 14. 2 2 4 4 Chọn phương án D A C
Câu 3. Gọi x1, x2 là nghiệm của phương trình 7x2−5x+9 = 343. Tính x1 + x2. A. x1 + x2 = 4. B. x1 + x2 = 6. B 2019-2020 C. x1 + x2 = 5. D. x1 + x2 = 3. Chọn phương án D Lời giải.
Ta có 7x2−5x+9 = 343 ⇔ 7x2−5x+9 = 73 ⇔ x2 − 5x + 9 =
Câu 8. Cho khối nón có bán kính đáy bằng r, chiều cao h. ñ THPT x = 2
Thể tích V của khối nón là 3 ⇔ x2 − 5x + 6 = 0 ⇔ 1 x = 3. A. V = r2h. B. V = r2h. 3 Do đó tổng hai nghiệm x 1 1 + x2 = 2 + 3 = 5. C. V = πr2h. D. V = πr2h. Chọn phương án C 3 GHIỆP Lời giải.
Câu 4. Nếu cạnh của một hình lập phương tăng lên gấp 3 N 1
lần thì thể tích của hình lập phương đó tăng lên bao nhiêu Ta có V = πr2h. T 3 lần? Chọn phương án D TỐ A. 27. B. 9. C. 6. D. 4. 8πa2 Lời giải.
Câu 9. Cho mặt cầu có diện tích bằng . Tính bán 3 THI V 0 = (3a)3 = 33 · a3 = 27V . kính r của mặt cầu. √ √ Chọn phương án A a 6 a 3 A. r = . B. r = .
Câu 5. Trong các hàm số sau, hàm số nào có cùng tập xác 3 √ 3 √ 1 định với hàm số y = x a 6 a 2 5 ? C. r = . D. r = . LUYỆN 1 2 3 A. y = xπ. B. y = √ . 5 x Lời giải. √ √ √ C. y = x. D. y = 3 x. 8πa2 a 6
Diện tích mặt cầu đã cho là 4πr2 = . Suy ra r = . Lời giải. 3 3 1
Ta có tập xác định hàm số y = x 5 là (0; +∞). Chọn phương án A
• Hàm số y = xπ cũng có tập xác định là (0; +∞).
Câu 10. Cho hàm số y = f (x) có bảng biến thiên như sau 1 x −∞ 0 2 +∞
• Hàm số y = √ có tập xác định là R \ 0 . 5 x y0 + 0 − 0 + √ • Hàm số y =
x có tập xác định là [0; +∞). 1 +∞ √
• Hàm số y = 3 x có tập xác định là y R. − Chọn phương án A 0 3
Câu 6. Họ nguyên hàm của hàm số f (x) = x2+cos x là
Hàm số đã cho đồng biến trên khoảng nào dưới đây? 1 A. 2x − sin x + C. B. x3 + sin x + C. A. (2; +∞). B. (−∞; 1). 3 1 C. (0; +∞). D. (0; 2). C. x3 − sin x + C. D. x3 + sin x + C. Lời giải. 3 GeoGebraPro Trang 1
Dựa vào bảng biến thiên, hàm số đã cho đồng biến trên các
Đồ thị hàm số có đường tiệm đứng là x = −1. Đồ thị hàm
khoảng (−∞; 0) và (2; +∞).
số đi qua điểm A(0; −1). Chọn phương án A Chọn phương án A a4e
Câu 15. Đường thẳng nào dưới đây là tiệm cận ngang của
Câu 11. Với a, b là hai số thực dương tùy ý, ln 1 − 4x b đồ thị hàm số y = ? bằng 2x − 1 1 A. 4 ln a − ln b + 1. B. 4 ln b − ln a + 1. A. y = 2. B. y = . C. y = 4. D. y = −2. C. 4 ln a + ln b − 1. D. 4 ln a + ln b + 1. 2 Lời giải. Lời giải. a4e Ta có: lim y = −2 và
lim y = −2 nên đường thẳng Ta có: ln
= ln a4 + ln e − ln b = 4 ln a + 1 − ln b = x→+∞ x→−∞ b
y = −2 là đường tiệm cận ngang của đồ thị hàm số. 4 ln a − ln b + 1. Chọn phương án D Chọn phương án A
Câu 16. Tập nghiệm của bất phương trình log (3x + 1) < 2
Câu 12. Khối trụ tròn xoay có đường kính bằng 2a, chiều 2 là cao h = 2a có thể tích là ï 1 ã Å 1 1 ã A. − ; 1 . B. − ; . A. V = 2πa2. B. V = 2πa3. 3 3 3 C. V = 2πa2h. D. V = πa3. Å 1 ã C. − ; 1 . D. (−∞; 1). Lời giải. 3 2a
Khối trụ tròn xoay có bán kính bằng = a nên có thể Lời giải. 2 1
tích là V = πa2 · 2a = 2πa3. ĐK: x > − 3 o/ Chọn phương án B
log (3x + 1) < 2 ⇔ 3x + 1 < 4 ⇔ x < 1. 2 aPr
Câu 13. Cho hàm số y = f (x) xác định, liên tục trên R và Kết hợp với điều kiện ta được nghiệm của bất phương trình
có bảng biến thiên như sau: 1 là − < x < 1. 3 x −∞ −2 2 +∞ Å 1 ã
Vậy tập nghiệm của bất phương trình − ; 1 . 3 y0 + 0 − 0 + Chọn phương án C 3 +∞ + Câu 17. y roups/GeoGebr
Cho hàm số f (x) có đồ thị như y −∞ 0
hình vẽ. Số nghiệm của phương trình 2f (x) − 3 = 0 là 3
Tìm giá trị cực đại yCĐ và giá trị cực tiểu yCT của hàm số đã cho A. yCĐ = −2 và yCT = 2. B. yCĐ = 3 và yCT = 0. C. yCĐ = 2 và yCT = 0. D. yCĐ = 3 và yCT = −2. 1 Lời giải. x −1 O
Từ bảng biến thiên ta có y −1 acebook.com/g CĐ = 3 và yCT = 0. .f Chọn phương án B A. 3. B. 1. C. 2. D. 0.
Câu 14. Đường cong trong hình vẽ bên là đồ thị của hàm Lời giải. số nào dưới đây?
Ta có 2f (x) − 3 = 0 ⇔ f (x) = y 3 (∗). 2 y 3
Số nghiệm của phương trình (∗) 3 https://www
bằng số giao điểm giữa đồ thị hàm y = 2 3
số y = f (x) và đường thẳng y = . 2 1
Dựa vào hình vẽ, hai đồ thị cắt x −
nhau tại 3 điểm phân biệt. 1 O −1 2
Vậy phương trình đã cho có 3 nghiệm. Chọn phương án A x 5 Z dx −1 O Câu 18. Nếu
= ln c với c ∈ Q thì giá trị của c 2x − 1 −1 1 bằng A. 9. B. 3. C. 6. D. 81. Lời giải. 5 2x − 1 1 − 2x Z 5 dx 1 A. y = . B. y = . = ln |2x − 1| = ln 3. x + 1 x + 1 2x − 1 2 2x + 1 2x + 1 1 C. y = . D. y = . 1 x − 1 x + 1 Vậy c = 3. Lời giải. Chọn phương án B GeoGebraPro Trang 2
Câu 19. Tìm phần ảo của số phức z = 8 − 12i. C. (P (3; 1; 5). D. Q(6; −1; 5). A. −12. B. 18. C. 12. D. −12i. Lời giải. Lời giải.
Thế tọa độ của điểm N (0; 3; 5) vào phương trình tham số
Phần ảo của số phức z = 8 − 12i là −12. 0 = 3 − 3t  Chọn phương án A 
của đường thẳng ∆ ta được 3 = 1 + 2t . Ta thấy t = 1 Câu 20. Cho hai số phức z  
1 = 1 + 2i, z2 = 3 − i. Tìm số 5 = 5t z2 phức z = .
thỏa mãn hệ phương trình.Vậy điểm N (0; 3; 5) thuộc đường z11 7 1 7 thẳng ∆. A. z = + i. B. z = + i. Chọn phương án A 10 10 5 5 1 7 1 7 C. z = − i. D. z = − + i.
Câu 26. Cho hình chóp S.ABCD đều có SA = AB = a. 5 5 10 10 Góc giữa SA và CD là Lời giải. A. 60◦. B. 30◦. C. 90◦. D. 45◦. z2 z2 · z1 (3 − i)(1 − 2i) 1 − 7i Ta có z = = = = = Lời giải. z1 z1 · z1 (1 + 2i)(1 − 2i) 5 1 7 − i. S 5 5 Chọn phương án C
Câu 21. Cho số phức z = 6 + 17i. Điểm biểu diễn cho số
phức z trên mặt phẳng tọa độ Oxy là A. M (−6; −17). B. M (−17; −6). C. M (17; 6). D. M (6; 17). Lời giải.
Điểm biểu diễn cho số phức z trên mặt phẳng tọa độ Oxy A B là M (6; 17). Chọn phương án D
Câu 22. Trong không gian Oxyz, cho điểm M (3; 2; −1). D C
Hình chiếu vuông góc của điểm M lên trục Oz là điểm 2019-2020 A. M3 (3; 0; 0). B. M4 (0; 2; 0).
Vì AB ∥ CD nên góc giữa SA và CD bằng góc giữa SA và C. M1 (0; 0; −1). D. M2 (3; 2; 0). AB. Lời giải.
Vì SA = AB nên tam giác SAB đều, vậy góc giữa chúng THPT
Hình chiếu vuông góc của điểm M (3; 2; −1) lên trục Oz là bằng 60◦. điểm M1 (0; 0; −1) . Chọn phương án A Chọn phương án C
Câu 27. Cho hàm số y = f(x) xác định trên R và có bảng
Câu 23. Trong không gian với hệ tọa độ Oxyz phương
xét dấu của đạo hàm như sau: GHIỆP
trình nào sau đây không phải là phương trình của một mặt N cầu? T x −∞ x1 x2 x3 +∞
A. x2 + y2 + z2 + x − 2y + 4z − 3 = 0. TỐ
B. 2x2 + 2y2 + 2z2 − x − y − z = 0 .
C. x2 + y2 + z2 − 2x + 4y − 4z + 10 = 0 . y0 − 0 + − 0 +
D. 2x2 + 2y2 + 2z2 + 4x + 8y + 6z + 3 = 0. THI Lời giải.
Khi đó số điểm cực trị của hàm số y = f (x) là
Điều kiện để phương trình x2+y2+z2−2ax−2by−2cz+d = 0 A. 3. B. 2. C. 4. D. 1.
là phương trình mặt cầu là R = a2 + b2 + c2 − d > 0. Lời giải.
Dựa vào bốn đáp án ta có đáp án C là a = 1, b = −2, c =
Ta thấy f 0(x) đổi dấu khi x qua x LUYỆN 1, x2, x3 thuộc tập xác 2, d = 10 ⇒ R = −1 < 0.
định của hàm số f (x) nên hàm số f (x) có 3 cực trị. Chọn phương án A √ Chọn phương án C
Câu 28. Giá trị nhỏ nhất của hàm số y = x + 18 − x2 là:
Câu 24. Trong không gian Oxyz, mặt phẳng (P ) : x + 2y − √ A. 0. B. 6. C. −3 2. D. −6.
5 = 0 nhận vec-tơ nào trong các vec-tơ sau làm vec-tơ pháp Lời giải. tuyến? √ √ #» #» TXĐ: D = [−3 2; 3 2]. A. n (1; 2; −5). B. n (0; 1; 2). #» #» x C. n (1; 2; 0). D. n (1; 2; 5). Ta có: y0 = 1 − √ . 18 − x2 Lời giải. #» y0 = 0 ⇔ x = 3. √ √ √ √
Mặt phẳng (P ) nhận n (1; 2; 0) làm vec-tơ pháp tuyến. Ä ä Ä ä
Ta có: y(3) = 6; y 3 2 = 3 2; y −3 2 = −3 2. Chọn phương án C √
⇒ Giá trị nhỏ nhất của hàm số đã cho là − 2.
Câu 25. Trong không gian (Oxyz), cho đường thẳng Chọn phương án C x = 3 − 3t 
Câu 29. Cho 0 < b < a < 1, mệnh đề nào dưới đây  ∆ :
y = 1 + 2t . Điểm nào dưới đây thuộc đường thẳng đúng?  z = 5t A. log a < log b. B. log a < 0. b a b ∆? C. log a > log b. D. log b < 1. b a a A. N (0; 3; 5). B. M (−3; 2; 5). Lời giải. GeoGebraPro Trang 3
Vì 0 < b < a < 1 nên log b > log a = 1. Do đó 2 a a Z 1 (2t2 − 2t) dt. log a = < 1 < log b. b log b a a 1 Chọn phương án A Chọn phương án D
Câu 30. Số giao điểm của đồ thị hàm số y = x2 x2 − 4
Câu 34. Thể tích của khối tròn xoay do hình phẳng giới √
với đường thẳng y = 3 là hạn bởi các đường y =
x, trục Ox và hai đường thẳng A. 8. B. 2 . C. 4. D. 6 .
x = 1; x = 4 khi quay quanh trục hoành được tính bởi công Lời giải. thức nào? 4 4
Phương tình hoành độ giao điểm x2 x2 − 4 = 3 (1) Z Z √
nếu x2 − 4 ≥ 0 ⇔ x ≤ −2 ∪ 2 ≤ x. A. V = π x dx. B. V = x dx.
Phương trình (1) ⇔ x2(x2 − 4) = 3 ⇔ x4 − 4x2 − 3 = 0 ⇔ √ 1 1 " 4 4 x2 = 2 + 7 √ p Z Z √ √ ⇔ x = ± 2 + 7. C. V = π2 x dx. D. V = π x dx. x2 = 2 − 7 ( loại ) 1 1
nếu x2 − 4 < 0 ⇔ −2 < x < 2. Lời giải.
Phương trình (1) ⇔ x2(x2 − 4) = −3 ⇔ x4 − 4x2 + 3 = 0 ⇔ √ 4 ñx2 = 3 ñ Z x = ± 3 ⇔ . Thể tích là V = π x dx. x2 = 1 x = ±1 1
Vậy phương trình có 6 nghiệm. Chọn phương án A Chọn phương án D
Câu 35. Cho hai số phức z1 = 2 + i, z2 = 4 − 3i. Khi đó o/ Câu 31. Tìm tập nghiệm của bất phương trình
z1 · z2 có phần ảo bằng log 2 (x − 4) + 1 > 0. A. 11. B. 2. C. −11. D. −2. aPr 5 ï 13 ã Å 13 ã Lời giải. A. ; +∞ . B. −∞; . 2 2
z1 · z2 = (2 + i)(4 − 3i) = 11 − 2i. Å 13 ã Vậy số phức z C. (4; +∞). D. 4; .
1 · z2 có phần ảo bằng −2. 2 Chọn phương án D Lời giải.
Câu 36. Gọi z1 và z2 lần lượt là nghiệm của phương trình:
Ta có log 2 (x − 4) + 1 > 0 ⇔ log 2 (x − 4) > −1 ⇔ 0 < 5 5
z2 − 2z + 5 = 0. Tính P = |z1| + |z2|. √ Å 2 ã−1 13 A. 2 5. B. 10. C. 3. D. 6. x − 4 < ⇔ 4 < x < roups/GeoGebr 5 2 Lời giải. Å 13 ã ñz
Vậy tập nghiệm của bất phương trình là 4; . 1 = 1 + 2i Ta có: z2 − 2z + 5 = 0 ⇔ 2 z2 = 1 − 2i. √ √ √ Chọn phương án D
Khi đó P = |z1| + |z2| = 5 + 5 = 2 5.
Câu 32. Tính thể tích khối tròn xoay sinh ra khi quay tam Chọn phương án A
giác đều ABC cạnh bằng 1 quanh AB. √
Câu 37. Trong không gian với hệ trục tọa độ Oxyz, cho 3π π π π 3 x − 1 y + 2 z A. . B. . C. . D. . đường thẳng d: = = . Mặt phẳng (P ) đi qua 4 4 8 2 1 −1 2 acebook.com/g .f Lời giải.
điểm M (2; 0; −1) và vuông góc với d có phương trình là
Khi quay tam giác đều ABC quanh cạnh AB ta thu được A. x − y + 2z = 0. B. x − 2y − 2 = 0. hai khối nón bằng nhau. √ C. x + y + 2z = 0. D. x − y − 2z = 0. Ç å2 1 2 1 3 1 π Lời giải. Do đó, ta có V = 2V = 2· πr2h = π · · = nón 3 3 2 2 4
Mặt phẳng (P ) có véc-tơ pháp tuyến cùng phương với véc- #» (đvtt).
tơ chỉ phương của đường thẳng d, suy ra n √ (P ) = (1; −1; 2). https://www 3 1 1
Phương trình mặt phẳng (P ) là (bán kính r = hABC = , đường cao h = AB = ). 2 2 2
1(x − 2) − 1(y − 0) + 2(z + 1) = 0 ⇔ x − y + 2z = 0. Chọn phương án B Chọn phương án A 3 Z x Câu 33. Cho tích phân I = √ dx. Nếu đặt
Câu 38. Trong không gian tọa độ Oxyz, viết phương trình 1 + x + 1
chính tắc của đường thẳng d đi qua A(1; 2; −1) và vuông 0 √
góc với mặt phẳng (P ) : x + 2y − 3z + 1 = 0. t = x + 1 thì x + 1 y + 2 z − 1 2 2 A. d : = = . Z Z 1 −2 −3 A. I = (t2 − 2t) dt. B. I = (2t2 − t) dt. x + 1 y + 2 z − 1 B. d : = = . 1 1 1 2 −3 2 2 x − 1 y − 2 z + 1 Z Z C. d : = = . C. I = (2t2 + 2t) dt. D. I = (2t2 − 2t) dt. 1 2 3 x − 1 y − 2 z + 1 1 1 D. d : = = . − − Lời giải. 1 2 3 √ Lời giải. Đặt t =
x + 1 ⇒ t2 = x + 1 ⇔ x = t2 − 1, dx = 2t dt.
d đi qua A(1; 2; −1) và nhận véc-tơ pháp tuyến của (P ) làm
Đổi cận: Khi x = 0 thì t = 1; khi x = 3 thì t = 2. x − 1 y − 2 3 2 2
véc-tơ chỉ phương nên có phương trình là = = Z x Z t2 − 1 Z −1 −2 I = √ dx = 2t dt = 2t(t − 1) dt = z + 1 1 + x + 1 1 + t . 0 1 1 3 GeoGebraPro Trang 4 Chọn phương án D
Câu 41. Cho hàm số y = −x3 − mx2 + (4m + 9)x + 5, với
m là tham số. Có bao nhiêu giá trị nguyên của m để hàm
Câu 39. Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp số nghịch biến R?
12A, 3 học sinh lớp 12B và 5 học sinh lớp 12C trên một bàn A. 6. B. 4. C. 7. D. 5.
tròn. Tính xác suất P để các học sinh cùng lớp luôn ngồi Lời giải. cạnh nhau. 1 1
Tập xác định của hàm số D = R. A. P = . B. P = . 1260 126
Ta có y0 = −3m2 − 2mx + 4m + 9. 1 1
Do phương trình y0 = 0 có hữu hạn nghiệm nên hàm số C. P = . D. P = . 28 252
nghịch biến trên R ⇔ y0 < 0, ∀x ∈ R. Lời giải.
Số phần tử không gian mẫu là n(Ω) = 9!. ⇔
−3x2 − 2mx + 4m + 9 ≤ 0, ∀x ∈ R.
Gọi E là biến cố các học sinh cùng lớp luôn ngồi cạnh nhau. ⇔
∆0 = m2 + 12m + 27 ≤ 0 (do a = −3 < 0)
Ta có các bước sắp xếp như sau: ⇔ −9 ≤ m ≤ −3.
• Xếp 5 học sinh lớp 12C ngồi vào bàn sao cho các học
sinh này ngồi sát nhau. Số cách sắp xếp là 5!.
Do m ∈ Z nên m ∈ {−9; −8; −7; −5; −4; −3}.
Vậy có 7 giá trị m thỏa mãn yêu cầu bài toán.
• Xếp 3 học sinh lớp 12B vào bàn sao cho các học sinh Chọn phương án C
này ngồi sát nhau và sát nhóm của học sinh 12C. Số cách sắp xếp là 3! × 2.
Câu 42. Gọi N (t) là số phần trăm cacbon 14 còn lại trong
một bộ phận của một cây sinh trưởng từ t năm trước đây t
• Xếp 2 học sinh lớp 12A vào hai vị trí còn lại của bàn.
thì ta có công thức N (t) = 100.(0.5) A (%) với A là hằng số. Số cách sắp xếp là 2!.
Biết rằng một mẩu gỗ có tuổi khoảng 3754 năm thì lượng
cácbon 14 còn lại là 65%. Phân tích mẩu gỗ từ một công
Số phần tử thuận lợi cho biến cố E là n(E) = 5! × 3! × 2 × 2!.
trình kiến trúc cổ, người ta thấy lượng cácbon 14 còn lại n(E) 1
Xác suất của biến cố E là P (E) = = .
trong mẩu gỗ là 63%. Hãy xác định tuổi của mẩu gỗ được n(Ω) 126 lấy từ công trình đó. Chọn phương án B A. 3874. B. 3833. C. 3834. D. 3843. Lời giải.
Câu 40. Cho tứ diện OABC có OA, OB, OC đôi một 3754 3754 2019-2020
vuông góc với nhau và OC = 2a, OA = OB = a. Gọi
Theo bài ta có 65 = 100.(0.5) A ⇔ 0.65 = (0.5) A ⇔ 3754 3754
M là trung điểm của AB. Tính khoảng cách giữa hai đường = log 0.65 ⇔ A = . A 0.5 log 0.65 thẳng OM và AC. 0.5 √ √ √ THPT
Do mẫu gỗ còn 63% lượng Cácbon 14 nên ta có: 2a 2 5a 2a 2a A. . B. . C. . D. . t t t 3 5 3 2
63 = 100.(0.5) A ⇔ 0.63 = (0.5) A ⇔ = log 0.63 ⇔ t = A 0.5 Lời giải. 3754 A. log 0.63 = . log 0.63 ≈ 3833. 0.5 log 0.65 0.5 0.5 GHIỆP C Chọn phương án B N T Câu 43. Cho hàm số y = f (x) y TỐ có đạo hàm f 0(x), biết rằng đồ thị của hàm THI số f 0(x) như hình vẽ. a c x
Biết f (a) > 0, hỏi đồ b O H thị hàm số y = f (x) O
cắt trục hoành tại nhiều B LUYỆN nhất bao nhiêu điểm? D M A
Dựng hình bình hành AM OD, OM ⊥ AM nên hình bình A. 4. B. 2. C. 3. D. 1.
hành AM OD là hình chữ nhật. Gọi H là hình chiếu vuông Lời giải.
góc của O trên đường thẳng CD. Ta có
Dựa vào đồ thị của hàm số f 0(x), ta có bảng biến thiên của hàm số y = f (x) như sau:
®AD ⊥ DO ⇒ AD ⊥ OH ⇒ OH ⊥ (ACD). (1) AD ⊥ CO x −∞ a b c +∞ f 0(x) − 0 + 0 − 0 +
OM ∥ (ACD) ⇒ d(OM, AC) = d(O, (ACD)). (2) Từ (1) và (2) suy ra f (b ( ) √ OC · OD 2 5a f (x) d(OM, AC) = OH = √ = . OC2 + OD2 5 f (a) a f (c ( ) c Chọn phương án B
Vì f (a) > 0 nên ta xét các trường hợp sau: GeoGebraPro Trang 5
• Nếu f (c) > 0 thì toàn bộ đồ thị hàm số nằm ở phía 1 π Z πx 3π
trên trục hoành, do đó đồ thị hàm số không cắt trục f (x) sin dx = 2 2 4 hoành. 0 1
• Nếu f (c) = 0 thì đồ thị hàm số và trục hoành có một Z πx 3 ⇒ f (x) sin dx = . điểm chung duy nhất. 2 2 0
• Nếu f (c) < 0 thì đồ thị hàm số và trục hoành có hai Xét tích phân điểm chung. 1 Z h πx i2 f (x) + k sin dx = 0
Vậy đồ thị hàm số y = f (x) cắt trục hoành nhiều nhất tại 2 hai điểm. 0 1 Chọn phương án B Z h πx πx i ⇔ f 2 (x) + 2kf (x) sin + k2sin2 dx = 0 2 2
Câu 44. Cắt khối trụ bởi một mặt phẳng qua trục ta được 0
thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai 1 1 Z Z
đáy của hình trụ, AB = 4a, AC = 5a. Thể tích V của khối πx ⇔ f 2 (x) dx + 2k f (x) sin trụ là 2 0 0 A. V = 16πa3. B. V = 4πa3. 1 C. V = 12πa3. D. V = 8πa3. Z πx 9 3 1 +k2 sin2 dx = 0 ⇔ + 2k + k2 = 0 ⇔ k = −3. Lời giải. 2 2 2 2 Ta có BC = 0 √ A 4a B Khi đó ta có AC2 − AB2 = √ 1 o/ 25a2 − 16a2 = 3a. Z h πx i2 AB 5a f (x) − 3 sin dx = 0 2 aPr Bán kính đáy r = = 2a, 2 0 πx πx chiều cao BC = 3a. ⇔ f (x) − 3 sin = 0 ⇔ f (x) = 3 sin . 2 2 Vậy V = hπr2 = 3a · 4a2 = πx D C 1 1 cos 1 12πa3. Z Z πx Vậy f (x) dx = 3 sin dx = −3 2 = Chọn phương án C 2 π 0 0 0 2
Câu 45. Cho hàm số y = f (x) có đạo hàm liên tục trên − 1 6 πx 6 π 6 1 cos = − cos − cos 0 = . Z 9 π 2 π 2 π 0 roups/GeoGebr
đoạn [0; 1] và thỏa mãn f (0) = 0. Biết f 2 (x) dx = và 2 Chọn phương án A 0 1 1
Câu 46. Cho hàm số y = f (x) có bảng biến thiên như hình Z πx 3π Z f 0 (x) cos dx = . Tích phân f (x) dx bằng. bên. 2 4 0 0 x −∞ 0 4 +∞ b Z f (x) dx. f 0 − 0 + 0 − a +∞ 3 acebook.com/g 6 2 4 1 .f A. . B. . C. . D. . π π π π f Lời giải. −1 −∞
• Sử dụng phương pháp từng phần đối với tích phân 1 Z πx 3π
Phương trình f (4x − x2) − 2 = 0 có bao nhiêu nghiệm thực f 0 (x) cos dx = . phân biệt? 2 4 https://www 0 A. 2. B. 6. C. 4. D. 0. Lời giải. 1 Z h πx i2
Bảng biến thiên của f (x): • Xét f (x) + k sin
dx = 0, tìm k, từ đó suy ra 2 0 x −∞ 0 4 +∞ πx f (x) = −k sin . 2 f 0 − 0 + 0 − 1 1 +∞ 3 Z Z πx • f (x) dx = −k sin dx. 2 f 0 0 −1 − −∞  πx  π πx u = cos du = − sin dx Đặt 2 ⇒ 2 2 .
Từ bảng biến thiên suy ra phương trình f (x) = 2 có ba dv = f 0 (x) dx v = f (x)
nghiệm thực phân biệt x1, x2, x3 với x1 < 0 < x2 < 4 < x3. 1 1 Z 1 πx πx π Z πx Do đó f (4x − x2) − 2 = 0 ⇔ f (4x − x2) = ⇒ f 0 (x) cos dx = cos f (x) + f (x) sin dx =  2 2 4x − x2 = x 2 2 1 (1) 0 0 0 2 4x − x2 = x với x 1 2 (2)
1 < 0 < x2 < 4 < x3.  π π Z πx f (1) · cos − f (0) · cos 0 + f (x) sin dx = 4x − x2 = x3 (3) 2 2 2
Xét hàm số g(x) = 4x − x2. Có g0(x) = 4 − 2x, g(x) = 0 ⇔ 0 GeoGebraPro Trang 6 x = 2. A0 D0
Bảng biến thiên của g(x): B0 C0 x −∞ 2 +∞ g0 + 0 − M D 4 A g K I B C −∞ −∞
Gọi I = BC ∩ C0M ⇒ DI ∩ AB = K. Khi đó ta có V
Từ bảng biến thiên của g(x) suy ra phương trình (1) có hai
1 = VICDC0 − VIBKM trong đó
nghiệm thực phân biệt, phương trình (2) có hai nghiệm thực 1 1 1 VICDC0 = IC · CD · CC0 = V ;
phân biệt (không trùng với hai nghiệm của (1) do x1 < x2) 3 2 3
và phương trình (3) vô nghiệm. Vậy phương trình đã cho có VIBKM 1
4 nghiệm thực phân biệt. Mặt khác = VICDC0 8 Chọn phương án C 1 1 1 7 ⇒ V1 = V − · V = V 3 8 3 24
Câu 47. Cho các số thực a, b thỏa mãn điều kiện 0 < 17 ⇒ V V
b < a < 1. Tìm giá trị nhỏ nhất của biểu thức P = 2 = 24 4(3b − 1) V1 7 log + 8 log2 a − 1. ⇒ = . a b 9 a √ V2 17 A. A = 6. B. 3 3 2. C. 8. D. 7. Chọn phương án B Lời giải. Câu 50. Xét các số thực dương x, y thỏa mãn 4(3b − 1) Ta có: (3b − 2)2 ≥ 2 ⇔ ≤ b2. Khi đó: Å 1 − 2x ã 9 ln
= 3x + y − 1. Tìm giá trị nhỏ nhất Pmin x + y P ≥ log b2 + 8 log2 a − 1 = 2 log b + a b a a 1 1 2019-2020 8 log2 của P = + √ + 1 b a − 1 = log b + log b + 8 log2 a − 1 = a a b x xy a a Å 1 ã2 A. Pmin = 8. B. Pmin = 16.
(log b − 1) + (log b − 1) + 8 · + 1 ≥ a a log b − 1 C. Pmin = 9. D. Pmin = 2. a THPT Lời giải. Å 1 ã2 Å ã
3 3 (log b − 1) · (log b − 1) · 8 · + 1 = 7. 1 − 2x 1 − 2x a a log b − 1 ln
= 3x + y − 1 xác định ⇔ > 0. a x + y x + y … 2 2 1
Dấu bằng xảy ra khi a = 3 ; b = và min(P ) = 7.
Do x, y > 0 nên 1 − 2x > 0 ⇔ 0 < x < GHIỆP 3 3 2 Å 1 − 2x ã N Chọn phương án D Khi đó: ln = 3x + y − 1 x + y T
Câu 48. Gọi S là tập hợp tất cả các giá trị của tham
⇔ ln (1 − 2x) − ln(x + y) = (x + y) − (1 − 2x) TỐ
số thực m sao cho trị lớn nhất của hàm số y =
⇔ ln (1 − 2x) + (1 − 2x) = ln(x + y) + (x + y) 3x2 − 6x + 2m − 1
trên đoạn [−2; 3] đạt giá trị nhỏ nhất. THI
Số phần tử của tập S là
Xét hàm số f (t) = ln t + t với t > 0 A. 0. B. 3. C. 2. D. 1.
Hàm số f (t) xác định và liên tục trên khoảng (0; +∞) 1 Lời giải. f 0(t) =
+ 1 > 0; ∀t > 0. Suy ra hàm số f (t) đồng biến t Gọi M là giá trị lớn nhất của hàm số y = trên (0; +∞) LUYỆN 3x2 − 6x + 2m − 1 trên đoạn [−2; 3].
Ta có M ≥ f (−2) = |2m + 23|, M ≥ f (1) = |2m − 4| ⇒ f (1 − 2x) = f (x + y)
⇒ 2M ≥ |2m + 23| + |2m − 4| ≥ |2m + 23 − 2m + 4| = 27 ⇒
⇔ 1 − 2x = x + y ⇔ y = 1 − 3x > 0 27 27 19 M ≥ . Khi M =
⇒ |2m+23| = |2m−4| ⇔ m = − . 1 1 1 2 2 2 4 Do đó: P = + + 1 ≥ + + 1 (Dấu 19 27 x px (1 − 3x) x 1 − 2x Với m = −
, max f (x) = max{f (−2); f (1); f (3)} = . 4 [−2;3] 2 1
bằng xảy ra khi x = 1 − 3x ⇔ x = ) Chọn phương án D 4 1 2 Å 1 ã Xét hàm số f (x) = + + 1; x ∈ 0;
Câu 49. Cho hình hộp chữ nhật ABCD.A0B0C0D0. Gọi M x 1 − 2x 3 Å ã
là trung điểm của BB0. Mặt phẳng (M DC0) chia khối hộp 1
Hàm số f (x) liên tục trên 0;
chữ nhật thành hai khối đa diện, một khối chứa đỉnh C và 3 1 4
một khối chứa đỉnh A0. Gọi V1, V2 lần lượt là thể tích của f 0(x) = − + V1 x2 (1 − 2x)2
hai khối đa diện chứa C và A0. Tính . V2 1 4 V1 7 V1 7 f 0(x) = 0 ⇔ − + = 0 A. = . B. = . x2 (1 − 2x)2 V2 24 V2 17 V 1 1 7 V1 17 C. = . D. = . ⇔ 4x2 = (1 − 2x)2 ⇔ x = V 4 2 12 V2 24 Lời giải. Bảng biến thiên GeoGebraPro Trang 7 1 1 x 0 4 3 y0 − 0 + +∞ + 9 y 8 1 Vậy Pmin = 8 tại x = 4 Chọn phương án A
———————–HẾT———————– o/ aPr roups/GeoGebr acebook.com/g .f https://www GeoGebraPro Trang 8 ĐÁP ÁN THAM KHẢO 1. C 2. D 3. C 4. A 5. A 6. B 7. D 8. D 9. A 10. A 11. A 12. B 13. B 14. A 15. D 16. C 17. A 18. B 19. A 20. C 21. D 22. C 23. C 24. C 25. A 26. A 27. A 28. C 29. A 30. D 31. D 32. B 33. D 34. A 35. D 36. A 37. A 38. D 39. B 40. B 41. C 42. B 43. B 44. C 45. A 46. C 47. D 48. D 49. B 50. A 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN GeoGebraPro Trang 9
Document Outline

  • PHATTRIEN MINH HOA 01(noLG)
  • PHATTRIEN MINH HOA 01(LG)
  • MOI NGAY MOT DE THI 2
  • MOI NGAY MOT DE THI2(DA)
  • MOI NGAY MOT DE THI 03(No)
  • MOI NGAY MOT DE THI 03(LG)
  • MOI NGAY MOT DE THI 04(noLG)
  • MOI NGAY MOT DE THI 04(LG)
  • MOI NGAY MOT DE THI 05(noLG)
  • MOI NGAY MOT DE THI 05(LG)