TOP 5 đề phát triển đề minh họa kỳ thi tốt nghiệp THPT 2020 môn Toán (phần 2)

Tiếp tục sưu tầm và giới thiệu đến các em học sinh khối 12 tuyển tập 5 đề phát triển đề minh họa kỳ thi tốt nghiệp THPT 2020 môn Toán, phần tiếp theo: từ đề số 06 đến đề số 10.

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

122 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 6
Câu 1. Từ các chữ số 1; 2; 3; 4 có thể lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác
nhau?
A. 42. B. 12. C. 24. D. 4
4
.
Câu 2. Tìm số hạng đầu u
1
và công bội q của cấp số nhân (u
n
) thỏa mãn
(
u
2
− u
4
+ u
5
= 114
u
3
− u
5
+ u
6
= 342
A. u
1
= 2, q = 3. B. u
1
= 3, q = 2. C. u
1
= 1, q = 3. D. u
1
= 1, q = 2.
Câu 3. Tìm nghiệm của phương trình log
2
(3x − 2) = 3.
A. x =
8
3
. B. x =
10
3
. C. x =
16
3
. D. x =
11
3
.
Câu 4. Hình lập phương có đường chéo của mặt bên bằng 4 cm. Tính thể tích khối lập phương đó.
A. 8
√
2 cm
3
. B. 16
√
2 cm
3
. C. 8 cm
3
. D. 2
√
2 cm
3
.
Câu 5. Tập xác định của hàm số y = log
2
3 − x
2x
là
A. D = (3; +∞). B. D = (0; 3].
C. D = (−∞; 0) ∪ (3; +∞). D. D = (0; 3).
Câu 6. Cho hàm số f(x) = 2x + e
x
. Tìm một nguyên hàm F (x) của hàm số f(x) thỏa mãn F (0) =
2019.
A. F (x) = e
x
− 2019. B. F (x) = x
2
+ e
x
− 2018.
C. F (x) = x
2
+ e
x
+ 2017. D. F (x) = x
2
+ e
x
+ 2018.
Câu 7. Cho khối chóp S.ABCD cạnh bên SA vuông góc với đáy, đáy ABCD là hình chữ nhật,
AB = a, AD = 2a, SA = 3a. Thể tích của khối chóp S.ABCD bằng
A. 6a
3
. B.
a
3
3
. C. 2a
3
. D. a
3
.
Câu 8. Cho khối nón (N ) có bán kính r =
√
5, có chiều cao h = 5. Thể tích V của khối nón (N) đã
cho là.
A. V
(N)
=
27π
5
. B. V
(N)
=
16π
5
. C. V
(N)
=
26π
5
. D. V
(N)
=
25π
3
.
Câu 9. Thể tích khối cầu có bán kính bằng
a
2
là
A.
πa
3
2
. B.
πa
2
4
. C.
πa
3
6
. D. πa
2
.
Câu 10.
Cho hàm số y = f (x) có bảng biến thiên như hình
bên. Hàm số đã cho nghịch biến trên khoảng nào
dưới đây?
A. (−∞; −1). B. (−1; 1).
C. (1; +∞). D. (0; 1).
x
y
0
y
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
00
−1−1
00
−∞−∞
Câu 11. Tính giá trị của a
log
√
a
4
với a > 0, a 6= 1.
A. 8. B. 4. C. 16. D. 2.
Câu 12. Một hình trụ có bán kính đáy , r = a độ dài đường sinh l = 2a Diện tích toàn phần của hình
trụ này là
A. 2πa
2
. B. 4πa
2
. C. 6πa
2
. D. 5πa
2
.
GeoGebraPro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Câu 13.
Cho hàm số y = f (x) có bảng biến thiên như hình
vẽ bên. Mệnh đề nào dưới đây đúng?
A. Hàm số có điểm cực tiểu x = 0.
B. Hàm số có điểm cực đại x = 5.
C. Hàm số có điểm cực tiểu x = −1.
D. Hàm số có điểm cực tiểu x = 1.
x
y
0
y
−∞
0 1
+∞
+
0
−
0
+
−∞−∞
55
−1−1
+∞+∞
Câu 14.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A. y = x
4
− 2x
2
− 1. B. y = −x
4
+ 2x
2
− 1.
C. y = x
3
− x
2
− 1. D. y = −x
3
+ x
2
− 1.
x
y
O
Câu 15. Tìm đường tiệm cận ngang của đồ thị hàm số y =
2 − 2x
x + 1
.
A. x = −1. B. x = −2. C. y = 2. D. y = −2.
Câu 16. Tập nghiệm của bất phương trình 3
2x−1
> 27 là
A.
Å
1
2
; +∞
ã
. B. (3; +∞). C.
Å
1
3
; +∞
ã
. D. (2; +∞).
Câu 17.
Cho hàm số y = f (x) có bảng biến thiên như hình vẽ
bên. Số nghiệm của phương trình f (x) = −1 là
A. 1. B. 2. C. 4. D. 3.
x
y
0
y
−∞
−1
1
+∞
−
0
+ +
11
−
√
2−
√
2
+∞
−∞
−1−1
Câu 18. Nếu
2
Z
1
f(x) dx = 3,
5
Z
2
f(x) dx = −1 thì
5
Z
1
f(x) dx bằng
A. 3. B. 4. C. 2. D. −2.
Câu 19. Cho số phức z thỏa mãn z = 3 + 2i. Tìm phần thực và phần ảo của số phức z.
A. Phần thực bằng −3, phần ảo bằng 2. B. Phần thực bằng 3, phần ảo bằng 2.
C. Phần thực bằng 3, phần ảo bằng −2. D. Phần thực bằng −3, phần ảo bằng −2.
Câu 20. Cho hai số phức z
1
= 3 + i, z
2
= 2 − i. Tính giá trị của biểu thức P = |z
1
+ z
1
· z
2
|.
A. P = 85. B. P = 5. C. P = 50. D. P = 10.
Câu 21. Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện |z + 2 −5i| = 6
là đường tròn có tâm I và bán kính R lần lượt là
A. I(−2; 5) và R = 36. B. I(−2; 5) và R = 6. C. I(2; −5) và R = 36. D. I(2; −5) và R = 6.
Câu 22. Trong không gian Oxyz , cho điểm A(−1; 2; 3). Hình chiếu vuông góc của điểm A trên trục
Oz là điểm
A. Q(−1; 0; 3). B. M(0; 0; 3). C. P (0; 2; 3). D. N (−1; 0; 0).
Câu 23. Trong không gian Oxyz, mặt cầu có tâm I (1; 2; −3) và tiếp xúc với trục Oy có bán kính
bằng
A.
√
10. B. 2. C.
√
5. D.
√
13.
Câu 24. Trong không gian Oxyz cho mặt phẳng (P ): x + y − 2z + 4 = 0. Một véc-tơ pháp tuyến của
mặt phẳng (P ) là
A.
#»
n = (1; 1; −2). B.
#»
n = (1; 0; −2). C.
#»
n = (1; −2; 4). D.
#»
n = (1; −1; 2).
GeoGebraPro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 25. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1; −1; 0), B(0; 1; 1). Gọi (α) là
mặt phẳng chứa đường thẳng d :
x
2
=
y − 1
−1
=
z − 2
1
và song song với đường thẳng AB. Điểm nào dưới
đây thuộc mặt phẳng (α)?
A. M(6; −4; −1). B. N(6; −4; 2). C. P (6; −4; 3). D. Q(6; −4; 1).
Câu 26. Cho hình lập phương ABCD.A
0
B
0
C
0
D
0
. Góc giữa hai đường thẳng BA
0
và CD bằng
A. 90
◦
. B. 60
◦
. C. 30
◦
. D. 45
◦
.
Câu 27. Cho hàm số f (x) có đạo hàm f
0
(x) = (x − 1)(x − 2)
2
(x − 3)
3
(x − 4)
4
, ∀x ∈ R. Số điểm cực
trị của hàm số đã cho là
A. 3. B. 5. C. 2. D. 4.
Câu 28. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y =
√
x
2
− 1
x − 2
trên tập
hợp D = (−∞; −1) ∪
ï
1;
3
2
ò
. Tính P = M + m.
A. P = 2. B. P = 0. C. P = −
√
5. D. P =
√
3.
Câu 29. Cho số thực a > 1, b 6= 0. Mệnh đề nào dưới đây đúng?
A. log
a
b
2
= −2 log
a
|b|. B. log
a
b
2
= 2 log
a
b. C. log
a
b
2
= 2 log
a
|b|. D. log
a
b
2
= −2 log
a
b.
Câu 30. Tìm số giao điểm của đồ thị hàm số y = x
3
−3x
2
+3x−1 và đồ thị hàm số y = x
2
−x−1.
A. 1. B. 0. C. 2. D. 3.
Câu 31. Tập nghiệm của bất phương trình log
1
3
(x − 1) + log
3
(11 − 2x) ≥ 0 là
A. (−∞; 4). B. (1; 4]. C. (1; 4). D.
ï
4;
11
2
ã
.
Câu 32. Tính thể tích khối tròn xoay sinh ra khi quay tam giác đều ABC cạnh bằng 1 quanh AB.
A.
3π
4
. B.
π
4
. C.
π
8
. D.
π
√
3
2
.
Câu 33. Cho tích phân I =
1
Z
0
dx
√
4 − x
2
. Nếu đổi biến số x = 2 sin t, t ∈
−
π
2
;
π
2
thì
A. I =
π
6
Z
0
dt. B. I =
π
6
Z
0
t dt. C. I =
π
6
Z
0
dt
t
. D. I =
π
3
Z
0
dt.
Câu 34. Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol
(P ): y = x
2
và đường thẳng d : y = 2x quay quanh trục Ox.
A. π
2
Z
0
x
2
− 2x
2
dx. B. π
2
Z
0
4x
2
dx − π
2
Z
0
x
4
dx.
C. π
2
Z
0
4x
2
dx + π
2
Z
0
x
4
dx. D. π
2
Z
0
2x − x
2
dx.
Câu 35. Cho hai số phức z
1
= 2 + i, z
2
= 1 − 3i. Tính T = |(1 + i)z
1
+ 2z
2
|.
A. T = 18. B. T = 3
√
2. C. T = 0. D. T = 3.
Câu 36. Gọi z
0
là nghiệm phức có phần ảo âm của phương trình 2z
2
− 2z + 13 = 0. Trên mặt phẳng
tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w = iz
0
?
A. M
Å
5
4
;
1
4
ã
. B. N
Å
5
4
; −
1
4
ã
. C. P
Å
5
2
; −
1
2
ã
. D. Q
Å
5
2
;
1
2
ã
.
Câu 37. Trong không gian toạ độ Oxyz, cho đường thẳng (d):
x + 3
1
=
y − 2
−1
=
z − 1
2
. Mặt phẳng
(P ) đi qua điểm M(2; 0; −1) và vuông góc với (d) có phương trình là
A. (P ): x − y − 2z = 0. B. (P ): 2x − z = 0.
GeoGebraPro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
C. (P ): x − y + 2z + 2 = 0. D. (P ): x − y + 2z = 0.
Câu 38. Trong không gian Oxyz, cho hai điểm A(1; 0; 1), B(−1; 2; 1). Viết phương trình đường thẳng
∆ đi qua tâm đường tròn ngoại tiếp tam giác OAB và vuông góc với mặt phẳng (OAB).
A. ∆ :
x = t
y = 1 + t
z = 1 − t
. B. ∆ :
x = t
y = 1 + t
z = 1 + t
. C. ∆ :
x = 3 + t
y = 4 + t
z = 1 − t
. D. ∆ :
x = −1 + t
y = t
z = 3 − t
.
Câu 39. Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp 12A, 3 học sinh lớp 12B và 5 học sinh lớp
12C trên một bàn tròn. Tính xác suất P để các học sinh cùng lớp luôn ngồi cạnh nhau.
A. P =
1
1260
. B. P =
1
126
. C. P =
1
28
. D. P =
1
252
.
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA ⊥ (ABCD) và
SA = a
√
2 . Khoảng cách từ A đến mặt phẳng (SBC) bằng:
A.
2a
√
5
5
. B. a
√
3. C.
a
2
. D.
a
√
3
2
.
Câu 41. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x
3
−(m + 1)x
2
+ 3x + 1 đồng biến
trên khoảng (−∞; +∞)?
A. 6. B. 8. C. 7. D. 5.
Câu 42. Với mức tiêu thụ thức ăn của trang trại A không đổi như dự định thì lượng thức ăn dự trữ
sẽ đủ dùng cho 100 ngày. Nhưng thực tế, mức tiêu thụ thức ăn tăng thêm 4% mỗi ngày (ngày sau tăng
4% so với ngày trước đó). Hỏi thực tế lượng thức ăn dự trữ đó chỉ đủ dùng cho bao nhiêu ngày?
A. 40. B. 41. C. 42. D. 43.
Câu 43. Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau
x
y
0
y
−∞
−1
3
+∞
+
0
−
0
+
−∞−∞
55
11
+∞+∞
Đồ thị hàm số y = |f (x)| có bao nhiêu điểm cực trị?
A. 2. B. 3. C. 4. D. 5.
Câu 44. Cho hình trụ có thiết diện đi qua trục là một hình vuông có cạnh bằng 4a. Diện tích xung
quanh S của hình trụ là
A. S = 4πa
2
. B. S = 8πa
2
. C. S = 24πa
2
. D. S = 16πa
2
.
Câu 45. Cho hàm số f (x) có đạo hàm liên tục trên [−1; 1] và thỏa mãn f(1) = 7,
1
Z
0
xf(x) dx = 1.
Khi đó
1
Z
0
x
2
f
0
(x) dx bằng
A. 6. B. 8. C. 5. D. 9.
Câu 46. Cho hàm số y = f(x) = ax
3
+ bx
2
+ cx + d có bảng biến thiên như sau:
Khi đó |f(x)| = m có bốn nghiệm phân biệt x
1
< x
2
< x
3
<
1
2
< x
4
khi và chỉ khi:
GeoGebraPro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
A. 0 < m < 1.
B. 0 < m ≤ 1.
C.
1
2
< m < 1.
D.
1
2
≤ m < 1.
x
y
0
y
−∞
0 1
+∞
+
0
−
0
+
−∞−∞
11
00
+∞+∞
Câu 47. Cho a, b, c > 1. Biết rằng biểu thức P = log
a
(bc) + log
b
(ac) + 4 log
c
(ab) đạt giá trị nhỏ nhất
bằng m khi log
b
c = n. Tính giá trị m + n.
A. m + n = 14. B. m + n =
25
2
. C. m + n = 12. D. m + n = 10.
Câu 48. Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị nhỏ nhất của hàm số
y = −|x
3
− 3x + m| trên đoạn [0; 2] bằng −3. Tổng tất cả các phần tử của S là
A. 1. B. 2. C. 0. D. 6.
Câu 49. Cho hình hộp chữ nhật ABCD.A
0
B
0
C
0
D
0
. Gọi M là trung điểm của BB
0
. Mặt phẳng (M DC
0
)
chia khối hộp chữ nhật thành hai khối đa diện, một khối chứa đỉnh C và một khối chứa đỉnh A
0
. Gọi
V
1
, V
2
lần lượt là thể tích của hai khối đa diện chứa C và A
0
. Tính
V
1
V
2
.
A.
V
1
V
2
=
7
24
. B.
V
1
V
2
=
7
17
. C.
V
1
V
2
=
7
12
. D.
V
1
V
2
=
17
24
.
Câu 50. Tìm tất cả các giá trị thực của tham số a > 0 thỏa mãn
Å
2
a
+
1
2
a
ã
2020
≤
Å
2
2020
+
1
2
2020
ã
a
.
A. 0 < a < 1. B. 1 < a < 2020. C. 0 < a ≤ 2020. D. a ≥ 2020.
———————–HẾT———————–
GeoGebraPro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
ĐÁP ÁN THAM KHẢO
1. C 2. A 3. B 4. B 5. D 6. D 7. C 8. D 9. C 10. C
11. C 12. C 13. D 14. A 15. D 16. D 17. A 18. C 19. C 20. D
21. B 22. B 23. A 24. A 25. C 26. D 27. C 28. C 29. C 30. C
31. B 32. B 33. A 34. B 35. B 36. D 37. D 38. A 39. B 40. D
41. C 42. B 43. B 44. D 45. C 46. C 47. C 48. C 49. B 50. D
GeoGebraPro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 6
Câu 1. Từ các chữ số 1; 2; 3; 4 có thể lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác
nhau?
A. 42. B. 12. C. 24. D. 4
4
.
Lời giải.
Mỗi số như vậy là một hoán vị của 4 phần tử. Vậy có thể lập được 4! = 24 số thỏa mãn đề bài.
Chọn phương án C
Câu 2. Tìm số hạng đầu u
1
và công bội q của cấp số nhân (u
n
) thỏa mãn
(
u
2
− u
4
+ u
5
= 114
u
3
− u
5
+ u
6
= 342
A. u
1
= 2, q = 3. B. u
1
= 3, q = 2. C. u
1
= 1, q = 3. D. u
1
= 1, q = 2.
Lời giải.
(
u
2
− u
4
+ u
5
= 114
u
3
− u
5
+ u
6
= 342
⇔
(
u
1
q(1 − q
2
+ q
3
) = 114(1)
u
1
q
2
(1 − q
2
+ q
3
) = 342(2)
Lấy phương trình (2) chia cho phương trình (1) ta được q = 3.
Thay vào phương trình (1) ta được u
1
= 2.
Chọn phương án A
Câu 3. Tìm nghiệm của phương trình log
2
(3x − 2) = 3.
A. x =
8
3
. B. x =
10
3
. C. x =
16
3
. D. x =
11
3
.
Lời giải.
Ta có log
2
(3x − 2) = 3 ⇔ 3x − 2 = 2
3
⇔ 3x = 10 ⇔ x =
10
3
.
Chọn phương án B
Câu 4. Hình lập phương có đường chéo của mặt bên bằng 4 cm. Tính thể tích khối lập phương đó.
A. 8
√
2 cm
3
. B. 16
√
2 cm
3
. C. 8 cm
3
. D. 2
√
2 cm
3
.
Lời giải.
Độ dài các cạnh hình lập phương là
4
√
2
= 2
√
2 cm.
Thể tích khối lập phương là V = (2
√
2)
3
= 16
√
2 cm
3
.
Chọn phương án B
Câu 5. Tập xác định của hàm số y = log
2
3 − x
2x
là
A. D = (3; +∞). B. D = (0; 3].
C. D = (−∞; 0) ∪ (3; +∞). D. D = (0; 3).
Lời giải.
Hàm số đã cho xác định khi
3 − x
2x
> 0 ⇔ x ∈ (0; 3).
Chọn phương án D
Câu 6. Cho hàm số f(x) = 2x + e
x
. Tìm một nguyên hàm F (x) của hàm số f(x) thỏa mãn F (0) =
2019.
A. F (x) = e
x
− 2019. B. F (x) = x
2
+ e
x
− 2018.
C. F (x) = x
2
+ e
x
+ 2017. D. F (x) = x
2
+ e
x
+ 2018.
GeoGebraPro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Lời giải.
F (x) =
Z
(2x + e
x
) dx = x
2
+ e
x
+ C.
Do F (0) = 2019 nên 0
2
+ e
0
+ C = 2019 ⇔ C = 2018.
Vậy F (x) = x
2
+ e
x
+ 2018.
Chọn phương án D
Câu 7. Cho khối chóp S.ABCD cạnh bên SA vuông góc với đáy, đáy ABCD là hình chữ nhật,
AB = a, AD = 2a, SA = 3a. Thể tích của khối chóp S.ABCD bằng
A. 6a
3
. B.
a
3
3
. C. 2a
3
. D. a
3
.
Lời giải.
Theo giả thiết ABCD là hình chữ nhật nên thể tích khối chóp S.ABCD là
V =
1
3
SA · AB · AD =
1
3
· 3a · a · 2a = 2a
3
.
S
A
B C
D
Chọn phương án C
Câu 8. Cho khối nón (N) có bán kính r =
√
5, có chiều cao h = 5. Thể tích V của khối nón (N) đã
cho là.
A. V
(N)
=
27π
5
. B. V
(N)
=
16π
5
. C. V
(N)
=
26π
5
. D. V
(N)
=
25π
3
.
Lời giải.
Ta có V
(N)
=
1
3
· 5π
Ä
√
5
ä
2
=
25π
3
.
Chọn phương án D
Câu 9. Thể tích khối cầu có bán kính bằng
a
2
là
A.
πa
3
2
. B.
πa
2
4
. C.
πa
3
6
. D. πa
2
.
Lời giải.
Phương pháp: Công thức tính thể tích khối cầu có bán kính r là: V =
4
3
πr
3
.
Cách giải: Thể tích khối cầu có bán kính bằng
a
2
là: V =
4
3
π
a
2
3
=
πa
3
6
.
Chọn phương án C
Câu 10.
Cho hàm số y = f(x) có bảng biến thiên như hình
bên. Hàm số đã cho nghịch biến trên khoảng nào
dưới đây?
A. (−∞; −1). B. (−1; 1).
C. (1; +∞). D. (0; 1).
x
y
0
y
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
00
−1−1
00
−∞−∞
Lời giải.
Dựa vào bảng biến thiên ta thấy hàm số đã cho nghịch biến trên (−1; 0) và (1; +∞).
Chọn phương án C
Câu 11. Tính giá trị của a
log
√
a
4
với a > 0, a 6= 1.
A. 8. B. 4. C. 16. D. 2.
Lời giải.
Ta có a
log
√
a
4
= a
2 log
a
4
= a
log
a
16
= 16.
GeoGebraPro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Chọn phương án C
Câu 12. Một hình trụ có bán kính đáy , r = a độ dài đường sinh l = 2a Diện tích toàn phần của hình
trụ này là
A. 2πa
2
. B. 4πa
2
. C. 6πa
2
. D. 5πa
2
.
Lời giải.
S
tp
= 2S
d
+ S
xq
= 2πa
2
+ 2πa · 2a = 6πa
2
.
Chọn phương án C
Câu 13.
Cho hàm số y = f (x) có bảng biến thiên như hình
vẽ bên. Mệnh đề nào dưới đây đúng?
A. Hàm số có điểm cực tiểu x = 0.
B. Hàm số có điểm cực đại x = 5.
C. Hàm số có điểm cực tiểu x = −1.
D. Hàm số có điểm cực tiểu x = 1.
x
y
0
y
−∞
0 1
+∞
+
0
−
0
+
−∞−∞
55
−1−1
+∞+∞
Lời giải.
Dựa vào bảng biến thiên ta thấy hàm số có điểm cực tiểu x = 1.
Chọn phương án D
Câu 14.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A. y = x
4
− 2x
2
− 1. B. y = −x
4
+ 2x
2
− 1.
C. y = x
3
− x
2
− 1. D. y = −x
3
+ x
2
− 1.
x
y
O
Lời giải.
Dựa vào hình dáng đồ thị ta suy ra hàm số là hàm trùng phương y = ax
4
+ bx
2
+ c có
• “Đuôi thăng thiên” nên a > 0.
• Cắt trục tung tại điểm nằm phía dưới trục hoành nên c < 0.
• Có 3 cực trị nên a · b < 0 ⇒ b < 0.
Chọn phương án A
Câu 15. Tìm đường tiệm cận ngang của đồ thị hàm số y =
2 − 2x
x + 1
.
A. x = −1. B. x = −2. C. y = 2. D. y = −2.
Lời giải.
Ta có lim
x→+∞
2 − 2x
x + 1
= −2 ⇒ y = −2 là tiệm cận ngang của đồ thị hàm số.
Chọn phương án D
Câu 16. Tập nghiệm của bất phương trình 3
2x−1
> 27 là
A.
Å
1
2
; +∞
ã
. B. (3; +∞). C.
Å
1
3
; +∞
ã
. D. (2; +∞).
Lời giải.
3
2x−1
> 27 ⇔ 2x − 1 > 3 ⇔ x > 2.
Chọn phương án D
Câu 17.
GeoGebraPro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
Cho hàm số y = f (x) có bảng biến thiên như hình vẽ
bên. Số nghiệm của phương trình f (x) = −1 là
A. 1. B. 2. C. 4. D. 3.
x
y
0
y
−∞
−1
1
+∞
−
0
+ +
11
−
√
2−
√
2
+∞
−∞
−1−1
Lời giải.
Số nghiệm của phương trình f (x) = −1 tương ứng với số giao điểm của đồ thị hàm số y = f (x) và
y = −1. Dựa vào bảng biến thiên suy ra số giao điểm hai đồ thị là 2 điểm.
Chọn phương án A
Câu 18. Nếu
2
Z
1
f(x) dx = 3,
5
Z
2
f(x) dx = −1 thì
5
Z
1
f(x) dx bằng
A. 3. B. 4. C. 2. D. −2.
Lời giải.
Theo tính chất tích phân
5
Z
1
f(x) dx =
2
Z
1
f(x) dx +
5
Z
2
f(x) dx = 3 + (−1) = 2.
Chọn phương án C
Câu 19. Cho số phức z thỏa mãn z = 3 + 2i. Tìm phần thực và phần ảo của số phức z.
A. Phần thực bằng −3, phần ảo bằng 2. B. Phần thực bằng 3, phần ảo bằng 2.
C. Phần thực bằng 3, phần ảo bằng −2. D. Phần thực bằng −3, phần ảo bằng −2.
Lời giải.
Vì z = 3 + 2i ⇒ z = 3 − 2i. Do đó số phức z có phần thực bằng 3, phần ảo bằng −2.
Chọn phương án C
Câu 20. Cho hai số phức z
1
= 3 + i, z
2
= 2 − i. Tính giá trị của biểu thức P = |z
1
+ z
1
· z
2
|.
A. P = 85. B. P = 5. C. P = 50. D. P = 10.
Lời giải.
Ta có z
1
· z
2
= (3 + i)(2 − i) = 7 − i ⇒ z
1
+ z
1
· z
2
= 3 + i + 7 − i = 10.
Suy ra P = |z
1
+ z
1
· z
2
| = 10.
Chọn phương án D
Câu 21. Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện |z + 2 −5i| = 6
là đường tròn có tâm I và bán kính R lần lượt là
A. I(−2; 5) và R = 36. B. I(−2; 5) và R = 6. C. I(2; −5) và R = 36. D. I(2; −5) và R = 6.
Lời giải.
Gọi z = x + iy (x, y ∈ R). Ta có |z + 2 − 5i| = 6 ⇔ (x + 2)
2
+ (y − 5)
2
= 36.
Suy ra tập hợp điểm biểu diễn z là đường tròn có tâm I(−2; 5) và bán kính R = 6.
Chọn phương án B
Câu 22. Trong không gian Oxyz , cho điểm A(−1; 2; 3). Hình chiếu vuông góc của điểm A trên trục
Oz là điểm
A. Q(−1; 0; 3). B. M(0; 0; 3). C. P (0; 2; 3). D. N(−1; 0; 0).
Lời giải.
Hình chiếu vuông góc của điểm A(−1; 2; 3) lên trục Oz là điểm M(0; 0; 3).
Chọn phương án B
Câu 23. Trong không gian Oxyz, mặt cầu có tâm I (1; 2; −3) và tiếp xúc với trục Oy có bán kính
bằng
GeoGebraPro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
A.
√
10. B. 2. C.
√
5. D.
√
13.
Lời giải.
Gọi H là hình chiếu vuông góc của tâm I (1; 2; −3) trên trục Oy ⇒ H (0; 2; 0) ⇒ IH =
√
10.
Gọi R là bán kính mặt cầu có tâm I (1; 2; −3) và tiếp xúc với trục Oy ⇒ R = IH =
√
10.
Chọn phương án A
Câu 24. Trong không gian Oxyz cho mặt phẳng (P ): x + y − 2z + 4 = 0. Một véc-tơ pháp tuyến của
mặt phẳng (P ) là
A.
#»
n = (1; 1; −2). B.
#»
n = (1; 0; −2). C.
#»
n = (1; −2; 4). D.
#»
n = (1; −1; 2).
Lời giải.
Phương pháp: Mặt phẳng (P ) : Ax + By + Cz + D = 0 nhận
#»
n = (A; B; C) là 1 vec-tơ pháp tuyến.
Cách giải: Một vec-tơ pháp tuyến của mặt phẳng (P ) là
#»
n = (1; 1; −2).
Chọn phương án A
Câu 25. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1; −1; 0), B(0; 1; 1). Gọi (α) là
mặt phẳng chứa đường thẳng d :
x
2
=
y − 1
−1
=
z − 2
1
và song song với đường thẳng AB. Điểm nào dưới
đây thuộc mặt phẳng (α)?
A. M(6; −4; −1). B. N(6; −4; 2). C. P (6; −4; 3). D. Q(6; −4; 1).
Lời giải.
Ta có
# »
AB = (−1; 2; 1).
Véc-tơ chỉ phương của d là
#»
u
d
= (2; −1; 1).
Suy ra
î
# »
AB,
#»
u
d
ó
= (3; 3; −3) = 3(1; 1 − 1).
Vì (α) chứa d và song song với AB nên véc-tơ
#»
n =
1
3
î
# »
AB,
#»
u
d
ó
= (1; 1 − 1) là một véc-tơ pháp tuyến
của (α).
Lại có, điểm C(0; 1; 2) ∈ d ⇒ C ∈ (α).
Do đó, phương trình của (α) là x + y − z + 1 = 0.
Lần lượt thay tọa độ các điểm trong các phương án ta được điểm P (6; −4; 3) thỏa mãn.
Chọn phương án C
Câu 26. Cho hình lập phương ABCD.A
0
B
0
C
0
D
0
. Góc giữa hai đường thẳng BA
0
và CD bằng
A. 90
◦
. B. 60
◦
. C. 30
◦
. D. 45
◦
.
Lời giải.
Ta có CD ∥ AB, suy ra góc giữa A
0
B với CD bằng góc giữa A
0
B với AB,
góc này bằng 45
◦
.
A B
D
0
C
0
A
0
D C
B
0
Chọn phương án D
Câu 27. Cho hàm số f(x) có đạo hàm f
0
(x) = (x − 1)(x − 2)
2
(x − 3)
3
(x − 4)
4
, ∀x ∈ R. Số điểm cực
trị của hàm số đã cho là
A. 3. B. 5. C. 2. D. 4.
Lời giải.
Ta có f
0
(x) = 0 ⇔
x = 1
x = 2
x = 3
x = 4.
Bảng biến thiên của hàm số f(x) như sau
GeoGebraPro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
x
f
0
(x)
f(x)
−∞
1 2 3 4
+∞
+
0
−
0
−
0
+
0
+
Vậy số điểm cực trị của hàm số đã cho là 2.
Chọn phương án C
Câu 28. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y =
√
x
2
− 1
x − 2
trên tập
hợp D = (−∞; −1) ∪
ï
1;
3
2
ò
. Tính P = M + m.
A. P = 2. B. P = 0. C. P = −
√
5. D. P =
√
3.
Lời giải.
Ta có y
0
=
1 − 2x
(x − 2)
2
√
x
2
− 1
, y
0
= 0 ⇔ 1 − 2x = 0 ⇔ x =
1
2
/∈ D .
Bảng biến thiên
x
y
0
y
−∞
−1
1
3
2
+ −
−1−1
0 00
−
√
5−
√
5
Vậy M = max
D
y = 0 và m = min
D
y = −
√
5.
Do đó P = −
√
5.
Chọn phương án C
Câu 29. Cho số thực a > 1, b 6= 0. Mệnh đề nào dưới đây đúng?
A. log
a
b
2
= −2 log
a
|b|. B. log
a
b
2
= 2 log
a
b. C. log
a
b
2
= 2 log
a
|b|. D. log
a
b
2
= −2 log
a
b.
Lời giải.
Ta có b 6= 0 ⇔ |b| > 0. Khi đó ta có log
a
b
2
= log
a
|b|
2
= 2 log
a
|b|.
Chọn phương án C
Câu 30. Tìm số giao điểm của đồ thị hàm số y = x
3
−3x
2
+3x−1 và đồ thị hàm số y = x
2
−x−1.
A. 1. B. 0. C. 2. D. 3.
Lời giải.
Phương trình hoành độ giao điểm x
3
− 3x
2
+ 3x − 1 = x
2
− x − 1 ⇔ x
3
− 4x
2
+ 4x = 0 ⇔
ñ
x = 0
x = 2
Chọn phương án C
Câu 31. Tập nghiệm của bất phương trình log
1
3
(x − 1) + log
3
(11 − 2x) ≥ 0 là
A. (−∞; 4). B. (1; 4]. C. (1; 4). D.
ï
4;
11
2
ã
.
Lời giải.
Điều kiện: 1 < x <
11
2
.
Bất phương trình tương đương −log
3
(x − 1) + log
3
(11 − 2x) ≥ 0
⇔ log
3
11 − 2x
x − 1
≥ 0 ⇔
11 − 2x
x − 1
≥ 1 ⇔
12 − 3x
x − 1
≥ 0 ⇔ 1 < x ≤ 4.
Chọn phương án B
GeoGebraPro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 32. Tính thể tích khối tròn xoay sinh ra khi quay tam giác đều ABC cạnh bằng 1 quanh AB.
A.
3π
4
. B.
π
4
. C.
π
8
. D.
π
√
3
2
.
Lời giải.
Khi quay tam giác đều ABC quanh cạnh AB ta thu được hai khối nón bằng nhau.
Do đó, ta có V = 2V
nón
= 2 ·
1
3
πr
2
h =
2
3
π ·
Ç
1
√
3
2
å
2
·
1
2
=
π
4
(đvtt).
(bán kính r = h
ABC
=
√
3
2
, đường cao h =
1
2
AB =
1
2
).
Chọn phương án B
Câu 33. Cho tích phân I =
1
Z
0
dx
√
4 − x
2
. Nếu đổi biến số x = 2 sin t, t ∈
−
π
2
;
π
2
thì
A. I =
π
6
Z
0
dt. B. I =
π
6
Z
0
t dt. C. I =
π
6
Z
0
dt
t
. D. I =
π
3
Z
0
dt.
Lời giải.
Ta có x = 2 sin t ⇒ dx = 2 cos t dt.
Với x = 0 ⇒ t = 0, x = 1 ⇒ t =
π
6
.
Do đó I =
π
6
Z
0
2 cos t dt
p
4 − 4 sin
2
t
=
π
6
Z
0
2 cos t dt
2
√
cos
2
t
=
π
6
Z
0
2 cos t dt
2 cos t
=
π
6
Z
0
dt.
Chọn phương án A
Câu 34. Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol
(P ): y = x
2
và đường thẳng d : y = 2x quay quanh trục Ox.
A. π
2
Z
0
x
2
− 2x
2
dx. B. π
2
Z
0
4x
2
dx − π
2
Z
0
x
4
dx.
C. π
2
Z
0
4x
2
dx + π
2
Z
0
x
4
dx. D. π
2
Z
0
2x − x
2
dx.
Lời giải.
Xét phương trình hoành độ giao điểm của (P ) và d, ta có
x
2
= 2x ⇔ x = 0 hoặc x = 2.
Trên đoạn [0; 2] ta thấy 2x ≥ x
2
nên thể tích cần tìm là
V = π
3
Z
0
4x
2
− x
4
dx = π
2
Z
0
4x
2
dx − π
2
Z
0
x
4
dx.
Chọn phương án B
Câu 35. Cho hai số phức z
1
= 2 + i, z
2
= 1 − 3i. Tính T = |(1 + i)z
1
+ 2z
2
|.
A. T = 18. B. T = 3
√
2. C. T = 0. D. T = 3.
Lời giải.
(1 + i)z
1
+ 2z
2
= (1 + i)(2 + i) + 2(1 − 3i) = 3 − 3i ⇒ |(1 + i)z
1
+ 2z
2
| =
√
9 + 9 = 3
√
2.
Chọn phương án B
Câu 36. Gọi z
0
là nghiệm phức có phần ảo âm của phương trình 2z
2
− 2z + 13 = 0. Trên mặt phẳng
tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w = iz
0
?
A. M
Å
5
4
;
1
4
ã
. B. N
Å
5
4
; −
1
4
ã
. C. P
Å
5
2
; −
1
2
ã
. D. Q
Å
5
2
;
1
2
ã
.
GeoGebraPro Trang 7
https://www.facebook.com/groups/GeoGebraPro/
Lời giải.
Phương trình 2z
2
− 2z + 13 = 0 ⇔ z =
1
2
+
5
2
i (loại) hay z =
1
2
−
5
2
i (nhận).
Nên ta có w = iz
0
= i
Å
1
2
−
5
2
i
ã
=
5
2
+
1
2
i. Vậy điểm biểu diễn của w là Q
Å
5
2
;
1
2
ã
.
Chọn phương án D
Câu 37. Trong không gian toạ độ Oxyz, cho đường thẳng (d):
x + 3
1
=
y − 2
−1
=
z − 1
2
. Mặt phẳng
(P ) đi qua điểm M(2; 0; −1) và vuông góc với (d) có phương trình là
A. (P ): x − y − 2z = 0. B. (P ): 2x − z = 0.
C. (P ): x − y + 2z + 2 = 0. D. (P ): x − y + 2z = 0.
Lời giải.
Mặt phẳng (P ) đi qua M(2; 0; −1) có một véc-tơ pháp tuyến
#»
n = (1; −1; 2) có dạng (P ): x−y +2z = 0.
Chọn phương án D
Câu 38. Trong không gian Oxyz, cho hai điểm A(1; 0; 1), B(−1; 2; 1). Viết phương trình đường thẳng
∆ đi qua tâm đường tròn ngoại tiếp tam giác OAB và vuông góc với mặt phẳng (OAB).
A. ∆ :
x = t
y = 1 + t
z = 1 − t
. B. ∆ :
x = t
y = 1 + t
z = 1 + t
. C. ∆ :
x = 3 + t
y = 4 + t
z = 1 − t
. D. ∆ :
x = −1 + t
y = t
z = 3 − t
.
Lời giải.
Tam giác OAB vuông tại O nên tâm đường tròn ngoại tiếp là trung điểm AB có tọa độ I(0; 1; 1).
Mặt phẳng (OAB) có véc-tơ pháp tuyến
#»
n =
î
# »
OA,
# »
OB
ó
= (−2; −2; 2).
Suy ra đường thẳng ∆ có
#»
u = (1; 1; −1) và đi qua I(0; 1; 1). Vậy phương trình đường thẳng ∆ là
∆ :
x = t
y = 1 + t
z = 1 − t
.
Chọn phương án A
Câu 39. Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp 12A, 3 học sinh lớp 12B và 5 học sinh lớp
12C trên một bàn tròn. Tính xác suất P để các học sinh cùng lớp luôn ngồi cạnh nhau.
A. P =
1
1260
. B. P =
1
126
. C. P =
1
28
. D. P =
1
252
.
Lời giải.
Số phần tử không gian mẫu là n(Ω) = 9!.
Gọi E là biến cố các học sinh cùng lớp luôn ngồi cạnh nhau. Ta có các bước sắp xếp như sau:
• Xếp 5 học sinh lớp 12C ngồi vào bàn sao cho các học sinh này ngồi sát nhau. Số cách sắp xếp là
5!.
• Xếp 3 học sinh lớp 12B vào bàn sao cho các học sinh này ngồi sát nhau và sát nhóm của học sinh
12C. Số cách sắp xếp là 3! × 2.
• Xếp 2 học sinh lớp 12A vào hai vị trí còn lại của bàn. Số cách sắp xếp là 2!.
Số phần tử thuận lợi cho biến cố E là n(E) = 5! × 3! × 2 × 2!.
Xác suất của biến cố E là P (E) =
n(E)
n(Ω)
=
1
126
.
Chọn phương án B
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA ⊥ (ABCD) và
SA = a
√
2 . Khoảng cách từ A đến mặt phẳng (SBC) bằng:
A.
2a
√
5
5
. B. a
√
3. C.
a
2
. D.
a
√
3
2
.
Lời giải.
GeoGebraPro Trang 8
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Phương pháp
Chứng minh để tìm khoảng cách sau đó áp dụng hệt thức lượng trong
tam giác vuông để tính toán.
Cách giải:
Kẻ AH ⊥ SB = {H}
Ta có:
®
SA ⊥ AB
BC ⊥ SA
⇒ BC ⊥ (SAB) ⇒ BC ⊥ AH
®
AH ⊥ SB
AH ⊥ BC
⇒ AH ⊥ (SBC) ⇒ d(A; (SBC)) = AH
Áp dụng hệ thức lượng trong 4SAB có đường cao AH ta có:
d(A; (SBC)) = AH =
SA.AB
√
SA
2
+ AB
2
=
a
√
3a
√
3a
2
+ a
2
=
a
√
3
2
.
S
B C
D
H
A
Chọn phương án D
Câu 41. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x
3
−(m + 1)x
2
+ 3x + 1 đồng biến
trên khoảng (−∞; +∞)?
A. 6. B. 8. C. 7. D. 5.
Lời giải.
Ta có y
0
= 3x
2
− 2(m + 1)x + 3.
Hàm số đã cho đồng biến trên (−∞; +∞) khi và chỉ khi ∆
0
= (m + 1)
2
− 9 ≤ 0 ⇔ −4 ≤ m ≤ 2.
Vậy các giá trị nguyên của m thỏa yêu cầu bài toán là −4, −3, −2, −1, 0, 1, 2, tức là có 7 giá trị.
Chọn phương án C
Câu 42. Với mức tiêu thụ thức ăn của trang trại A không đổi như dự định thì lượng thức ăn dự trữ
sẽ đủ dùng cho 100 ngày. Nhưng thực tế, mức tiêu thụ thức ăn tăng thêm 4% mỗi ngày (ngày sau tăng
4% so với ngày trước đó). Hỏi thực tế lượng thức ăn dự trữ đó chỉ đủ dùng cho bao nhiêu ngày?
A. 40. B. 41. C. 42. D. 43.
Lời giải.
Gọi lượng thức ăn tiêu thụ theo dự định hàng ngày là x. Lượng thức ăn dự trữ của trang trại A là 100x.
Ta có x (1 + 1,04 + 1,04
2
+ ... + 1,04
n−1
) = 100x ⇔
1,04
n
− 1
1,04 − 1
= 100 ⇒ n = log
1,04
5 ≈ 41,035.
Do đó lượng thức ăn dự trữ chỉ đủ dùng cho 41 ngày.
Chọn phương án B
Câu 43. Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau
x
y
0
y
−∞
−1
3
+∞
+
0
−
0
+
−∞−∞
55
11
+∞+∞
Đồ thị hàm số y = |f(x)| có bao nhiêu điểm cực trị?
A. 2. B. 3. C. 4. D. 5.
Lời giải.
Số điểm cực trị của đồ thị hàm số y = |f(x)| bằng số điểm cực trị của đồ thị hàm số y = f(x) cộng với
số giao điểm của đồ thị hàm số y = f(x) với trục hoành (không tính điểm cực trị).
Vì đồ thị hàm số y = f(x) có 2 điểm cực trị và cắt trục Ox tại 1 điểm trên đồ thị hàm số y = |f(x)|
có 2 + 1 = 3 điểm cực trị.
Chọn phương án B
GeoGebraPro Trang 9
https://www.facebook.com/groups/GeoGebraPro/
Câu 44. Cho hình trụ có thiết diện đi qua trục là một hình vuông có cạnh bằng 4a. Diện tích xung
quanh S của hình trụ là
A. S = 4πa
2
. B. S = 8πa
2
. C. S = 24πa
2
. D. S = 16πa
2
.
Lời giải.
Phương pháp: Công thức tính diện tích xung quanh hình trụ có bán kính đáy R, chiều cao h là
S
xq
= 2πRh.
Cách giải:
R
h
C
BO
O
0
A
D
Hình trụ có thiết diện đi qua trục là hình vuông ABCD có cạnh bằng 4a.
Do đó h = 2R = 4a ⇒ R = 2a với R, h lần lượt là bán kính đáy và chiều cao của hình trụ.
Vậy S = 2πRh = 16πa
2
Chọn phương án D
Câu 45. Cho hàm số f(x) có đạo hàm liên tục trên [−1; 1] và thỏa mãn f(1) = 7,
1
Z
0
xf(x) dx = 1.
Khi đó
1
Z
0
x
2
f
0
(x) dx bằng
A. 6. B. 8. C. 5. D. 9.
Lời giải.
Xét I =
1
Z
0
x
2
f
0
(x) dx, đặt u = x
2
, dv = f
0
(x) dx ⇒ du = 2x dx, v = f(x), ta được
I = x
2
· f(x)
1
0
−
1
Z
0
2xf(x) dx = f(1) − 2
1
Z
0
xf(x) dx = 5.
Chọn phương án C
Câu 46. Cho hàm số y = f(x) = ax
3
+ bx
2
+ cx + d có bảng biến thiên như sau:
Khi đó |f(x)| = m có bốn nghiệm phân biệt x
1
< x
2
< x
3
<
1
2
< x
4
khi và chỉ khi:
A. 0 < m < 1.
B. 0 < m ≤ 1.
C.
1
2
< m < 1.
D.
1
2
≤ m < 1.
x
y
0
y
−∞
0 1
+∞
+
0
−
0
+
−∞−∞
11
00
+∞+∞
GeoGebraPro Trang 10
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Lời giải.
Ta có y
0
= 3ax
2
+ 2bx + c, từ bảng biến thiên suy ra:
®
y
0
(0) = 0
y
0
(1) = 0
⇔
®
c = 0
3a + 2b = 0
(1)
Ta lại có
®
y(0) = 1
y(1) = 0
⇔
®
d = 1
a + b + c + d = 0
(2)
Từ (1), (2) ta có hệ phương trình:
d = 1
c = 0
3a + 2b = 0
a + b + c + d = 0
⇔
d = 1
c = 0
a = 2
b = −3
⇒ y = f (x) = 2x
3
− 3x
2
+ 1
Đồ thị hàm số |f(x)| = |2x
3
− 3x
2
+ 1|
Ta có
f
Å
1
2
ã
=
1
2
Dựa vào đồ thị suy ra phương trình |f(x)| = m có bốn nghiệm phân biệt x
1
< x
2
< x
3
<
1
2
< x
4
khi
và chỉ khi:
1
2
< m < 1
Chọn phương án C
Câu 47. Cho a, b, c > 1. Biết rằng biểu thức P = log
a
(bc) + log
b
(ac) + 4 log
c
(ab) đạt giá trị nhỏ nhất
bằng m khi log
b
c = n. Tính giá trị m + n.
A. m + n = 14. B. m + n =
25
2
. C. m + n = 12. D. m + n = 10.
Lời giải.
Phương pháp:
log
a
b =
1
log
b
a
, (a, b > 0; a, b 6= 1).
Áp dụng BĐT Cô-si cho 2 số dương: a + b ≥ 2
√
ab.
Cách giải:
Do a, b, c > 1 nên log
a
b, log
c
a, log
b
c > 0.
P = log
a
(bc) + log
b
(ac) + 4 log
c
(ab) = log
a
b + log
a
c + log
b
a + log
b
c + 4 log
c
a + 4 log
a
b
= (log
a
b + log
b
a) + (log
a
c + 4 log
c
a) + (log
b
c + 4 log
c
b)
=
Å
log
a
b +
1
log
a
b
ã
+
Å
1
log
c
a
+ 4 log
c
a
ã
+
Å
log
b
c +
4
log
b
c
ã
≥ 2
log
a
b ·
1
log
a
b
+ 2
1
log
c
· 4 log
c
a + 2
log
b
c ·
4
log
b
c
= 2 + 4 + 4 = 10.
Dấu “ = ” xảy ra khi và chỉ khi
log
a
b =
1
log
a
b
1
log
c
a
= 4 log
c
a
log
b
c =
4
log
c
b
⇔
log
a
b = 1
log
c
a =
1
2
log
b
c = 2.
Vậy, đạt giá trị nhỏ nhất là 10 khi log
b
c = 2 ⇒ m = 10, n = 2 ⇒ m + n = 12.
Chọn phương án C
Câu 48. Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị nhỏ nhất của hàm số
y = −|x
3
− 3x + m| trên đoạn [0; 2] bằng −3. Tổng tất cả các phần tử của S là
A. 1. B. 2. C. 0. D. 6.
Lời giải.
• Nhận xét:
GeoGebraPro Trang 11
https://www.facebook.com/groups/GeoGebraPro/
Tìm m sao cho giá trị nhỏ nhất của hàm số y = −|x
3
− 3x + m| trên đoạn [0; 2] bằng −3
⇔ Tìm m sao cho giá trị lớn nhất của hàm số y = |x
3
− 3x + m| trên đoạn [0; 2] bằng 3.
• Xét hàm số f(x) = x
3
−3x+ m liên tục trên đoạn [0; 2]. Ta có f
0
(x) = 3x
2
−3 = 0 ⇔
ñ
x = 1 (n)
x = −1 (l)
.
• Suy ra GTLN và GTNN của f (x) thuộc {f (0) , f (1) , f (2)} = {m, m − 2, m + 2}.
• Xét hàm số y = |x
3
− 3x + m| trên đoạn [0; 2] ta được giá trị lớn nhất của hàm số y là max
x∈[0;2]
y =
{|m|, |m − 2|, |m + 2|} = 3.
– TH 1: m ≥ 0 ⇒ max
x∈[0;2]
y = m + 2 = 3 ⇔ m = 1.
– TH 2: m < 0 ⇒ max
x∈[0;2]
y = 2 − m = 3 ⇔ m = −1.
• Vậy m ∈ {−1; 1} nên tổng các phần tử của S bằng 0.
Chọn phương án C
Câu 49. Cho hình hộp chữ nhật ABCD.A
0
B
0
C
0
D
0
. Gọi M là trung điểm của BB
0
. Mặt phẳng (MDC
0
)
chia khối hộp chữ nhật thành hai khối đa diện, một khối chứa đỉnh C và một khối chứa đỉnh A
0
. Gọi
V
1
, V
2
lần lượt là thể tích của hai khối đa diện chứa C và A
0
. Tính
V
1
V
2
.
A.
V
1
V
2
=
7
24
. B.
V
1
V
2
=
7
17
. C.
V
1
V
2
=
7
12
. D.
V
1
V
2
=
17
24
.
Lời giải.
Gọi I = BC ∩ C
0
M ⇒ DI ∩ AB = K.
Khi đó ta có V
1
= V
ICDC
0
− V
IBKM
trong đó
V
ICDC
0
=
1
3
IC ·
1
2
CD · CC
0
=
1
3
V ;
Mặt khác
V
IBKM
V
ICDC
0
=
1
8
⇒ V
1
=
1
3
V −
1
8
·
1
3
V =
7
24
V
⇒ V
2
=
17
24
V
⇒
V
1
V
2
=
7
17
.
C
0
D
0
D
A
0
B
0
A
K
I
B C
M
Chọn phương án B
Câu 50. Tìm tất cả các giá trị thực của tham số a > 0 thỏa mãn
Å
2
a
+
1
2
a
ã
2020
≤
Å
2
2020
+
1
2
2020
ã
a
.
A. 0 < a < 1. B. 1 < a < 2020. C. 0 < a ≤ 2020. D. a ≥ 2020.
Lời giải.
Xét hàm f(x) =
ln(2
x
+ 2
−x
)
x
⇒ f
0
(x) =
(2
x
− 2
−x
) ln 2
x
− (2
x
+ 2
−x
) ln(2
x
+ 2
−x
)
x
2
(2
x
+ 2
−x
)
.
Vì ln 2
x
< ln(2
x
+ 2
−x
) và 0 < 2
x
− 2
−x
< 2
x
+ 2
−x
nên f
0
(x) < 0 ⇒ f(x) nghịch biến.
Do vậy
Å
2
a
+
1
2
a
ã
2020
≤
Å
2
2020
+
1
2
2020
ã
a
⇔2020 ln(2
a
+ 2
−a
) ≤ a ln(2
2020
+ 2
−2020
)
⇔
ln(2
a
+ 2
−a
)
a
≤
ln(2
2020
+ 2
−2020
)
2020
⇔a ≥ 2020.
Chọn phương án D
GeoGebraPro Trang 12
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
———————–HẾT———————–
GeoGebraPro Trang 13
https://www.facebook.com/groups/GeoGebraPro/
ĐÁP ÁN THAM KHẢO
1. C 2. A 3. B 4. B 5. D 6. D 7. C 8. D 9. C 10. C
11. C 12. C 13. D 14. A 15. D 16. D 17. A 18. C 19. C 20. D
21. B 22. B 23. A 24. A 25. C 26. D 27. C 28. C 29. C 30. C
31. B 32. B 33. A 34. B 35. B 36. D 37. D 38. A 39. B 40. D
41. C 42. B 43. B 44. D 45. C 46. C 47. C 48. C 49. B 50. D
GeoGebraPro Trang 14
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 7
Câu 1. Một đội xây dựng gồm 3 kỹ sư, 7 công nhân lập một tổ công tác gồm 5 người. Hỏi có bao nhiêu
cách lập tổ công tác gồm 1 kỹ sư làm tổ trưởng, 1 công nhân làm tổ phó và 3 công nhân tổ viên?
A. 420. B. 360. C. 120. D. 240.
Câu 2. Cho cấp số cộng (u
n
) có số hạng đầu u
1
= 2 và công sai d = −3. Tính tổng 10 số hạng đầu
của (u
n
).
A. S
10
= 115. B. S
10
= −155. C. S
10
= −115. D. S
10
= 155.
Câu 3. Tổng tất cả các nghiệm của phương trình log
3
(7 − 3
x
) = 2 − x
A. 2. B. 1. C. 7. D. 3.
Câu 4. Tính thể tích V của khối lập phương ABCD.A
0
B
0
C
0
D
0
biết đường chéo AC
0
= a
√
3.
A.
a
3
3
. B. 3
√
3a
3
. C.
3
√
6a
3
4
. D. a
3
.
Câu 5. Tìm tập xác định D của hàm số y = (x
2
− 3x − 4)
√
2−
√
3
.
A. D = R\(−1; 4). B. D = R.
C. D = (−∞; −1) ∪ (4; +∞). D. D = (−∞; −1] ∪ [4; +∞).
Câu 6. Tìm một nguyên hàm F (x) của hàm số f(x) · g(x) biết F (1) = 3, biết
Z
f(x)dx = x + 2018
và
Z
g(x)dx = x
2
+ 2019.
A. F (x) = x
3
+ 1. B. F (x) = x
3
+ 3. C. F (x) = x
2
+ 2. D. F (x) = x
2
+ 3.
Câu 7. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt (SAB) và (SAC) cùng
vuông góc với đáy. Tính thể tích khối chóp biết SC = a
√
3.
A.
2a
3
√
6
9
. B.
a
3
√
6
12
. C.
a
3
√
3
4
. D.
a
3
√
3
2
.
Câu 8. Cho hình nón có góc ở đỉnh bằng 60
◦
và bán kính đáy bằng a. Diện tích xung quanh của hình
nón bằng bao nhiêu?
A. 2πa
2
. B. 4πa
2
. C. πa
2
. D. πa
2
√
3.
Câu 9. Cho hình lập phương có thể tích bằng 64a
3
. Thể tích của khối cầu nội tiếp hình lập phương đó
bằng
A. V =
8πa
3
3
. B. V =
16πa
3
3
. C. V =
64πa
3
3
. D. V =
32πa
3
3
.
Câu 10.
Cho hàm số y = f(x) có bảng biến thiên
như hình vẽ bên. Hàm số nghịch biến trên
khoảng nào dưới đây?
A. (−1; 5). B. (−∞; 5).
C. (−∞; −1). D. (−1; +∞).
x
f
0
(x)
f(x)
−∞
−1
5
+∞
+
0
−
0
+
−∞−∞
aa
bb
+∞+∞
Câu 11. Cho a, b, c > 0, a, b 6= 1. Tình A = log
a
(b
2
).log
b
(
√
bc) − log
a
(c).
A. log
a
c. B. 1. C. log
a
b. D. log
a
bc.
Câu 12. Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông
có cạnh bằng a. Tính diện tích xung quanh S của khối trụ đó.
GeoGebraPro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
A. S = 2πa
2
. B. S =
πa
2
2
. C. S = πa
2
. D. S = 4πa
2
.
Câu 13. Hàm số nào dưới đây có bảng biến thiên như hình vẽ?
x
y
0
y
−∞
−1
1
+∞
+
0
−
0
+
−∞−∞
22
−2−2
+∞+∞
A. y = x
3
− 3x. B. y = x
3
− 3x − 1. C. y = x
3
+ 3x. D. y = x
4
− 2x
2
.
Câu 14. Đồ thị hàm số y =
x + 1
1 − x
có dạng
A.
x
y
O
−1
−1
. B.
x
y
O
1
1
.
C.
x
y
O
−1
1
. D.
x
y
O
−1
1
.
Câu 15. Biết rằng đồ thị hàm số y =
ax + 1
bx − 2
có đường tiệm cận đứng là x = 2 và đường tiệm cận
ngang là y = 3. Tính giá trị của a + b?
A. 1. B. 5. C. 4. D. 0.
Câu 16. Tìm tập nghiệm S của phương trình (0, 6)
1
x
≤ (0, 6)
1
6
A. S = (−∞; 6]. B. S = (0; 6]. C. [0; 6]. D. (−∞; 0) ∪ [6; +∞).
Câu 17. Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
x
y
O
−1
1
−1
Số nghiệm của phương trình 2019f(x) + 1 = 0 là
A. 1. B. 3. C. 2. D. 4.
Câu 18. Cho
1
Z
0
x dx
(x + 2)
2
= a + b ln 2+ c ln 3 với a, b, c là các số hữu tỷ. Giá trị của 3a + b + c bằng
A. −2. B. −1. C. 2. D. 1.
GeoGebraPro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 19. Tìm hai số thực x và y thỏa mãn (3x + 2yi) + (3 − i) = 4x − 3i với i là đơn vị ảo.
A. x = 3; y = −1. B. x =
2
3
; y = −1. C. x = 3; y = −3. D. x = −3; y = −1.
Câu 20.
Cho các số phức z = −1 + 2i, w = 2 −i. Điểm nào trong hình vẽ bên biểu diễn
số phức z + w?
A. P . B. N. C. Q. D. M.
x
y
O
PN
M
Q
Câu 21. Xét các số phức z thỏa mãn (z + 2i)(z + 2) là số thuần ảo. Biết rằng tập hợp tất cả các điểm
biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là
A. (1; −1). B. (1; 1). C. (−1; 1). D. (−1; −1).
Câu 22. Trong không gian Oxyz, cho
# »
OA =
#»
i −2
#»
j + 3
#»
k , điểm B(3; −4; 1) và C(2; 0; 1). Tọa độ trọng
tâm của tam giác ABC là
A. 1; −2; 3. B. (−2; 2; −1). C. (2; −2; 1). D. (−1; 2; −3).
Câu 23. Trong không gian Oxyz, cho hai điểm I(1; 1; 1) và A(1; 2; 3). Phương trình của mặt cầu có
tâm I và đi qua A là
A. (x + 1)
2
+ (y + 1)
2
+ (z + 1)
2
= 29. B. (x − 1)
2
+ (y − 1)
2
+ (z − 1)
2
= 5.
C. (x − 1)
2
+ (y − 1)
2
+ (z − 1)
2
= 25. D. (x + 1)
2
+ (y + 1)
2
+ (z + 1)
2
= 5.
Câu 24. Trong không gian Oxyz, cho điểm A(2; −1; −3) và mặt phẳng (P ): 3x −2y + 4z −5 = 0. Mặt
phẳng (Q) đi qua A và song song với mặt phẳng (P ) có phương trình là
A. (Q): 3x − 2y + 4z − 4 = 0. B. (Q): 3x − 2y + 4z + 4 = 0.
C. (Q): 3x − 2y + 4z + 5 = 0. D. (Q): 3x + 2y + 4z + 8 = 0.
Câu 25. Trong không gian Oxyz, khoảng cách từ điểm M(2; −4; −1) tới đường thẳng ∆ :
x = t
y = 2 − t
z = 3 + t
bằng
A.
√
14. B.
√
6. C. 2
√
14. D. 2
√
6.
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a ,SA ⊥ (ABCD),SA = a
√
2.
Tìm số đo của góc giữa đường thẳng SC và mặt phẳng (SAD).
A. 45
◦
. B. 30
◦
. C. 90
◦
. D. 60
◦
.
Câu 27. Cho hàm số y = f(x) xác định trên R và có bảng xét dấu của đạo hàm như sau:
x
y
0
−∞
x
1
x
2
x
3
+∞
−
0
+ −
0
+
Khi đó số điểm cực trị của hàm số y = f (x) là
A. 3. B. 2. C. 4. D. 1.
Câu 28. Tìm giá trị lớn nhất M của hàm số y = 2x +
√
8 − 2x
2
trên tập xác định của nó?
A. M = 2
√
5. B. M =
8
√
3
3
. C. M = 2
√
6. D. M = 4.
Câu 29. Cho a > 0, b > 0 thoả mãn log
16
(a+3b) = log
9
a = log
12
b. Giá trị của
a
3
− ab
2
+ b
3
a
3
+ a
2
b + 3b
3
bằng
A.
6 −
√
13
11
. B.
82 − 17
√
13
69
. C.
5 −
√
13
6
. D.
3 −
√
13
11
.
GeoGebraPro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
Câu 30. Có tất cả bao nhiêu giá trị thực của tham số m để đường thẳng d
m
: y = mx + 1 cắt đồ thị
(C) : y = x
3
− x
2
+ 1 tại 3 điểm A, B(0; 1) và C phân biệt sao cho tam giác AOC vuông tại O.
A. 0. B. 1. C. 2. D. 3.
Câu 31. Tập nghiệm S của bất phương trình log
1
3
(x − 1) + log
3
(11 − 2x) ≥ 0 là
A. S =
Å
3;
11
2
ã
. B. S = (−∞; 4]. C. S = (1; 4]. D. S = (1; 4).
Câu 32. Một khối nón có thể tích bằng 9a
3
π
√
2. Tính bán kính R đáy khối nón khi diện tích xung
quanh nhỏ nhất.
A. R = 3a. B. R =
3a
6
√
2
. C. R =
3
√
9a. D. R =
3a
3
√
2
.
Câu 33. Cho hàm số f (x) liên tục và f (3) = 21,
3
Z
0
f(x)dx = 9. Tính tích phân I =
1
Z
0
x·f
0
(3x)dx.
A. I = 6. B. I = 12. C. I = 9. D. I = 15.
Câu 34. Tính thể tích khối tròn xoay sinh bởi Elip (E) :
x
2
4
+
y
2
1
= 1 quay quanh trục Ox.
A.
64π
9
. B.
10π
3
. C.
8π
3
. D.
8π
2
3
.
Câu 35. Xét số phức z thỏa mãn
z + 2
z − 2i
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số
phức z luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng
A. 1. B.
√
2. C. 2
√
2. D. 2.
Câu 36. Cho số phức z thỏa mãn |z| + z + 5i = 25. Khi đó mô-đun z bằng
A. 12. B. 10. C. 11. D. 13.
Câu 37. Trong không gian Oxyz, cho mặt phẳng (P ): x + y + z − 3 = 0 và đường thẳng d :
x
1
=
y + 1
2
=
z − 2
−1
. Hình chiếu vuông góc của d trên (P ) có phương trình là
A.
x + 1
−1
=
y + 1
−4
=
z + 1
5
. B.
x − 1
3
=
y − 1
−2
=
z − 1
−1
.
C.
x − 1
1
=
y − 1
4
=
z − 1
−5
. D.
x − 1
1
=
y − 4
1
=
z + 5
1
.
Câu 38. Trong không gian Oxyz, cho đường thẳng d:
x − 3
2
=
y + 2
1
=
z + 1
−1
và mặt phẳng (P ) : x +
y + z + 2 = 0. Cho đường thẳng ∆ nằm trong mặt phẳng (P ), vuông góc với đường thẳng d đồng thời
khoảng cách từ giao điểm I của d với (P ) đến đường thẳng ∆ bằng
√
42. Gọi M (5; b; c) là hình chiếu
vuông góc của I trên ∆. Giá trị P = bc bằng bao nhiêu?
A. P = −10. B. P = 10. C. P = 12. D. P = −20.
Câu 39. Trong một chiếc hộp có 20 viên bi, trong đó có 9 viên bi màu đỏ, 6 viên bi màu xanh và 5
viên bi màu vàng. Lấy ngẫu nhiên đồng thời 3 viên bi. Tìm xác suất để 3 viên bi lấy ra có không quá
2 màu.
A.
29
38
. B.
9
38
. C.
183
190
. D.
82
95
.
Câu 40. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Hình chiếu vuông góc của S
trên mặt phẳng (ABCD) là điểm H thuộc đoạn BD sao cho HD = 3HB. Biết góc giữa mặt (SCD)
và mặt phẳng đáy bằng 45
◦
. Khoảng cách giữa hai đường thẳng SA và BD là:
A.
2a
√
38
17
. B.
2a
√
13
3
. C.
2a
√
51
13
. D.
3a
√
34
17
.
Câu 41. Cho hàm số y = f(x) liên tục trên R và có đạo hàm f
0
(x) = x
2
(x − 2)(x
2
− 6x + m) với mọi
x ∈ R. Có bao nhiêu số nguyên m thuộc đoạn [−2019; 2019] để hàm số g(x) = f(1 − x) nghịch biến
trên khoảng (−∞; −1)?
A. 2010. B. 2012. C. 2011. D. 2009.
GeoGebraPro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 42. Cường độ một trận động đất M được cho bởi công thức M = log A − log A
0
, với A là biên
độ rung chấn tối đa và A
0
là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San
Francisco có cường độ 8,3 độ Richter. Trong cùng năm đó, trận động đất khác ở gần đó đo được 7,1 độ
Richter. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu lần trận động đất này?
A. 1,17. B. 2,2. C. 15,8. D. 4.
Câu 43. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
0 1
+∞
−
0
+
0
−
+∞+∞
−1−1
33
−∞−∞
Phương trình f(2 − x) − 1 = 0 có bao nhiêu nghiệm?
A. 0. B. 2. C. 1. D. 3.
Câu 44. Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB
và CD thuộc hai đáy của hình trụ, AB = 4a, AC = 5a. Thể tích V của khối trụ là
A. V = 16πa
3
. B. V = 4πa
3
. C. V = 12πa
3
. D. V = 8πa
3
.
Câu 45. Cho hàm số f (x) liên tục trên R thỏa mãn điều kiện: f(0) = 2
√
2, f(x) > 0 với mọi x ∈ R và
f(x).f
0
(x) = (2x + 1)
p
1 + f
2
(x) với mọi x ∈ R. Khi đó giá trị f (1) bằng
A.
√
15. B.
√
23. C.
√
24. D.
√
26.
Câu 46. Tìm tất cả các giá trị của tham số m để phương trình x −m −
√
9 − x
2
= 0 có đúng 1 nghiệm
dương?
A. m ∈ (−3; 3]. B. m ∈ (−3; 3] ∪ {−3
√
2}.
C. m ∈ [0; 3]. D. m = ±3
√
2.
Câu 47. Cho hai số thực a, b > 1. Tìm giá trị nhỏ nhất của biểu thức S =
1
log
(ab)
a
+
1
log
4
√
ab
b
.
A. min S =
4
9
. B. min S =
9
4
. C. min S =
9
2
. D. min S =
1
4
.
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số
y =
x
2
+ mx + m
x + 1
trên [1; 2] bằng 2. Số phần tử của S là
A. 1. B. 4. C. 3. D. 2.
Câu 49. Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng a
√
3. Gọi O
là tâm của đáy ABC, d
1
là khoảng cách từ A đến mặt phẳng (SBC) và d
2
là khoảng cách từ O đến
mặt phẳng (SBC). Tính d = d
1
+ d
2
.
A. d =
2a
√
2
11
. B. d =
2a
√
2
33
. C. d =
8a
√
2
33
. D. d =
8a
√
2
11
.
Câu 50. Cho hàm số y = f(x) có đạo hàm cấp 2, liên tục trên R và thỏa mãn
[f
0
(x)]
2
+ f(x) · f
00
(x) = 15x
4
+ 12x với mọi x ∈ R.
Hàm số g(x) = f (x) · f
0
(x) có bao nhiêu điểm cực trị?
A. 1. B. 2. C. 3. D. 4.
———————–HẾT———————–
GeoGebraPro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
ĐÁP ÁN THAM KHẢO
1. A 2. C 3. A 4. D 5. C 6. C 7. B 8. A 9. D 10. A
11. C 12. C 13. A 14. D 15. C 16. B 17. D 18. B 19. A 20. A
21. D 22. C 23. B 24. B 25. C 26. B 27. A 28. C 29. C 30. B
31. C 32. A 33. A 34. C 35. B 36. D 37. C 38. B 39. A 40. D
41. C 42. C 43. D 44. C 45. C 46. A 47. B 48. D 49. C 50. B
GeoGebraPro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 7
Câu 1. Một đội xây dựng gồm 3 kỹ sư, 7 công nhân lập một tổ công tác gồm 5 người. Hỏi có bao nhiêu
cách lập tổ công tác gồm 1 kỹ sư làm tổ trưởng, 1 công nhân làm tổ phó và 3 công nhân tổ viên?
A. 420. B. 360. C. 120. D. 240.
Lời giải.
Số cách lập tổ công tác gồm 1 kỹ sư làm tổ trưởng, 1 công nhân làm tổ phó và 3 công nhân tổ viên là
3 · 7 · C
3
6
= 420 cách.
Chọn phương án A
Câu 2. Cho cấp số cộng (u
n
) có số hạng đầu u
1
= 2 và công sai d = −3. Tính tổng 10 số hạng đầu
của (u
n
).
A. S
10
= 115. B. S
10
= −155. C. S
10
= −115. D. S
10
= 155.
Lời giải.
Tổng 10 số hạng đầu của (u
n
) là S
10
= u
1
+ u
2
+ ··· + u
10
=
10
2
(2u
1
+ 9d) = 5(4 − 27) = −115.
Chọn phương án C
Câu 3. Tổng tất cả các nghiệm của phương trình log
3
(7 − 3
x
) = 2 − x
A. 2. B. 1. C. 7. D. 3.
Lời giải.
Ta có log
3
(7 − 3
x
) = 2 − x ⇔ 7 − 3
x
= 3
2−x
⇔ 7 − 3
x
=
9
3
x
⇔ (3
x
)
2
− 7 · 3
x
+ 9 = 0. (∗)
Phương trình (∗) có 2 nghiệm phân biệt thỏa 3
x
1
+ 3
x
2
= 7; 3
x
1
· 3
x
2
= 9,
suy ra 3
x
1
+x
2
= 3
2
⇔ x
1
+ x
2
= 2
Chọn phương án A
Câu 4. Tính thể tích V của khối lập phương ABCD.A
0
B
0
C
0
D
0
biết đường chéo AC
0
= a
√
3.
A.
a
3
3
. B. 3
√
3a
3
. C.
3
√
6a
3
4
. D. a
3
.
Lời giải.
Gọi cạnh hình lập phương là x. Ta có AC
02
= 3x
2
= 3a
2
⇒ x = a ⇒ V = a
3
.
Chọn phương án D
Câu 5. Tìm tập xác định D của hàm số y = (x
2
− 3x − 4)
√
2−
√
3
.
A. D = R\(−1; 4). B. D = R.
C. D = (−∞; −1) ∪ (4; +∞). D. D = (−∞; −1] ∪ [4; +∞).
Lời giải.
Điều kiện xác định của hàm số là x
2
− 3x − 4 > 0 ⇔
ñ
x > 4
x < −1.
Vậy D = (−∞; −1) ∪ (4; +∞).
Chọn phương án C
Câu 6. Tìm một nguyên hàm F (x) của hàm số f(x) · g(x) biết F (1) = 3, biết
Z
f(x)dx = x + 2018
và
Z
g(x)dx = x
2
+ 2019.
A. F (x) = x
3
+ 1. B. F (x) = x
3
+ 3. C. F (x) = x
2
+ 2. D. F (x) = x
2
+ 3.
GeoGebraPro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Lời giải.
Ta có
Z
f(x)dx = x + 2018 ⇒ f(x) = (x + 2018)
0
= 1
và
Z
g(x)dx = x
2
+ 2019 ⇒ g(x) = (x
2
+ 2019)
0
= 2x.
⇒ f(x) · g(x) = 2x ⇒ F (x) =
Z
f(x) · g(x)dx = x
2
+ C.
Mặt khác F (1) = 3 ⇒ 1
2
+ C = 3 ⇒ C = 2.
Vậy F (x) = x
2
+ 2.
Chọn phương án C
Câu 7. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt (SAB) và (SAC) cùng
vuông góc với đáy. Tính thể tích khối chóp biết SC = a
√
3.
A.
2a
3
√
6
9
. B.
a
3
√
6
12
. C.
a
3
√
3
4
. D.
a
3
√
3
2
.
Lời giải.
Từ đề bài ta có
(
(SAB) ⊥ (ABC)
(SAC) ⊥ (ABC)
⇒ SA ⊥ (ABC).
Vì tam giác ABC đều cạnh
a ⇒ S
ABC
=
a
2
√
3
4
và AB = AC = BC = a.
Tam giác SAC vuông tại A (do SA ⊥ (ABC) ⇒ SA ⊥ AC) nên theo
định lí Pytago ta có SA =
√
SC
2
− AC
2
=
√
3a
2
− a
2
= a
√
2.
Thể tích khối chóp là
V
S.ABC
=
1
3
S
ABC
· SA =
1
3
·
a
2
√
3
4
· a
√
2 =
a
3
√
6
12
(đvtt).
S
A
B
C
Chọn phương án B
Câu 8. Cho hình nón có góc ở đỉnh bằng 60
◦
và bán kính đáy bằng a. Diện tích xung quanh của hình
nón bằng bao nhiêu?
A. 2πa
2
. B. 4πa
2
. C. πa
2
. D. πa
2
√
3.
Lời giải.
Hình nón đã cho có đỉnh S, đáy là đường tròn tâm O đường kính MN
như hình vẽ.
Ta có bán kính đáy r = OM = a, góc
÷
MSN = 60
◦
suy ra
’
MSO = 30
◦
.
4SOM vuông tại O, ta có
sin
’
MSO =
OM
SM
, suy ra SM =
OM
sin
’
MSO
= 2a, hay đường sinh l = 2a.
Vậy diện tích xung quanh hình nón là
S
xq
= π · r · l = 2πa
2
.
60
◦
S
O
M
N
Chọn phương án A
Câu 9. Cho hình lập phương có thể tích bằng 64a
3
. Thể tích của khối cầu nội tiếp hình lập phương đó
bằng
A. V =
8πa
3
3
. B. V =
16πa
3
3
. C. V =
64πa
3
3
. D. V =
32πa
3
3
.
Lời giải.
GeoGebraPro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Khối lập phương có thể tích 64a
3
nên cạnh bằng 4a.
Khối cầu nội tiếp khối lập phương có bán kính R =
4a
2
= 2a nên thể tích khối cầu
là V =
4
3
πR
3
=
4
3
π(2a)
3
=
32πa
3
3
.
Chọn phương án D
Câu 10.
Cho hàm số y = f(x) có bảng biến thiên
như hình vẽ bên. Hàm số nghịch biến trên
khoảng nào dưới đây?
A. (−1; 5). B. (−∞; 5).
C. (−∞; −1). D. (−1; +∞).
x
f
0
(x)
f(x)
−∞
−1
5
+∞
+
0
−
0
+
−∞−∞
aa
bb
+∞+∞
Lời giải.
Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên miền (−1; 5).
Chọn phương án A
Câu 11. Cho a, b, c > 0, a, b 6= 1. Tình A = log
a
(b
2
).log
b
(
√
bc) − log
a
(c).
A. log
a
c. B. 1. C. log
a
b. D. log
a
bc.
Lời giải.
Có: A = log
a
(b
2
).log
b
(
√
bc) − log
a
(c) = 2log
a
b.
1
2
log
b
(bc) − log
a
(c)
= 2log
a
b.
1
2
(log
b
b + log
b
c) − log
a
(c)
= log
a
b. (1 + log
b
c) − log
a
c = log
a
b + log
a
b. log
b
c − log
a
c = log
a
b + log
a
c − log
a
c = log
a
b.
Chọn phương án C
Câu 12. Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông
có cạnh bằng a. Tính diện tích xung quanh S của khối trụ đó.
A. S = 2πa
2
. B. S =
πa
2
2
. C. S = πa
2
. D. S = 4πa
2
.
Lời giải.
Do thiết diện là hình vuông cạnh a nên bán kính đáy bằng
a
2
và chiều cao h = a.
Diện tích xung quanh: S = 2π ×
a
2
× a = πa
2
.
Chọn phương án C
Câu 13. Hàm số nào dưới đây có bảng biến thiên như hình vẽ?
x
y
0
y
−∞
−1
1
+∞
+
0
−
0
+
−∞−∞
22
−2−2
+∞+∞
A. y = x
3
− 3x. B. y = x
3
− 3x − 1. C. y = x
3
+ 3x. D. y = x
4
− 2x
2
.
Lời giải.
Từ bảng biến thiên ta thấy hàm số có 2 cực trị nên loại C và D.
Đồ thị hàm số đi qua điểm (−1; 2) nên chọn A.
Chọn phương án A
GeoGebraPro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
Câu 14. Đồ thị hàm số y =
x + 1
1 − x
có dạng
A.
x
y
O
−1
−1
. B.
x
y
O
1
1
.
C.
x
y
O
−1
1
. D.
x
y
O
−1
1
.
Lời giải.
Phương pháp:
Đồ thị hàm số y =
ax + b
cx + d
, (ad − bc 6= 0, c 6= 0) có TCĐ: x = −
d
c
và TCN: y =
a
c
.
Nếu ad − bc > 0 thì hàm số đồng biến trên từng khoảng xác định.
Nếu ad − bc < 0 thì hàm số nghịch biến trên từng khoảng xác định.
Cách giải:
Đồ thị hàm số y =
x + 1
1 − x
có TCĐ: x = 1 và TCN y = −1 và đồng biến trên từng khoảng xác định do
1.1 − 1.(−1) = 2 > 0.
Vậy chọn đồ thị ở câu D.
Chọn phương án D
Câu 15. Biết rằng đồ thị hàm số y =
ax + 1
bx − 2
có đường tiệm cận đứng là x = 2 và đường tiệm cận
ngang là y = 3. Tính giá trị của a + b?
A. 1. B. 5. C. 4. D. 0.
Lời giải.
Với b 6= 0 và b 6= −2a, đồ thị hàm số y =
ax + 1
bx − 2
nhận đường thẳng x =
2
b
làm tiệm cận đứng.
Theo đề bài x = 2 là tiệm cận đứng của đồ thị nên 2 =
2
b
⇔ b = 1.
Với b 6= 0 đồ thị hàm số y =
ax + 1
bx − 2
nhận đường thẳng y =
a
b
làm tiệm cận ngang.
Theo đề bài y = 3 là tiệm cận ngang của đồ thị hàm số nên
a
b
= 3 ⇔ a = 3b ⇔ a = 3.
Vậy a + b = 4.
Chọn phương án C
Câu 16. Tìm tập nghiệm S của phương trình (0, 6)
1
x
≤ (0, 6)
1
6
A. S = (−∞; 6]. B. S = (0; 6]. C. [0; 6]. D. (−∞; 0) ∪ [6; +∞).
Lời giải.
Ta có: (0, 6)
1
x
≤ (0, 6)
1
6
⇔
1
x
≥
1
6
⇔
1
x
−
1
6
≥ 0 ⇔
6 − x
x
≥ 0 ⇔ 0 < x ≤ 6.
Tập nghiệm bất phương trình là S = (0; 6].
Chọn phương án B
Câu 17. Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
GeoGebraPro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
x
y
O
−1
1
−1
Số nghiệm của phương trình 2019f(x) + 1 = 0 là
A. 1. B. 3. C. 2. D. 4.
Lời giải.
Ta có 2019f(x) + 1 = 0 ⇔ f (x) = −
1
2019
.
Số nghiệm phương trình 2019f(x) + 1 = 0 chính là số giao điểm của đồ thị hàm số y = f(x) và đường
thẳng d: y = −
1
2019
(cùng phương với trục Ox).
Dựa vào đồ thị như hình vẽ ta có d cắt đồ thị tại 4 điểm phân biệt.
Vậy phương trình có 4 nghiệm phân biệt.
Chọn phương án D
Câu 18. Cho
1
Z
0
x dx
(x + 2)
2
= a + b ln 2+ c ln 3 với a, b, c là các số hữu tỷ. Giá trị của 3a + b + c bằng
A. −2. B. −1. C. 2. D. 1.
Lời giải.
1
Z
0
x dx
(x + 2)
2
=
1
Z
0
x + 2 − 2
(x + 2)
2
dx
=
1
Z
0
x + 2
(x + 2)
2
dx −
1
Z
0
2
(x + 2)
2
dx
=
1
Z
0
1
x + 2
dx −
1
Z
0
2
(x + 2)
2
dx
= ln |x + 2|
1
0
+
2
x + 2
1
0
= ln 3 − ln 2 −
1
3
.
Nên a = −
1
3
, b = −1, c = 1, suy ra 3a + b + c = −1.
Chọn phương án B
Câu 19. Tìm hai số thực x và y thỏa mãn (3x + 2yi) + (3 − i) = 4x − 3i với i là đơn vị ảo.
A. x = 3; y = −1. B. x =
2
3
; y = −1. C. x = 3; y = −3. D. x = −3; y = −1.
Lời giải.
Ta có
(3x + 2yi) + (3 − i) = 4x − 3i ⇔ (3x + 3) + (2y − 1)i = 4x − 3i ⇔
®
3x + 3 = 4x
2y − 1 = −3
⇔
®
x = 3
y = −1.
Chọn phương án A
Câu 20.
GeoGebraPro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
Cho các số phức z = −1 + 2i, w = 2 −i. Điểm nào trong hình vẽ bên biểu diễn
số phức z + w?
A. P . B. N. C. Q. D. M.
x
y
O
PN
M
Q
Lời giải.
Ta có z + w = 1 + i, suy ra điểm biểu diễn số phức z + w là điểm P .
Chọn phương án A
Câu 21. Xét các số phức z thỏa mãn (z + 2i)(z + 2) là số thuần ảo. Biết rằng tập hợp tất cả các điểm
biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là
A. (1; −1). B. (1; 1). C. (−1; 1). D. (−1; −1).
Lời giải.
Giả sử z = a + bi, (a, b ∈ R), ta được
(z + 2i)(z + 2) = [a + (b + 2)i][(a + 2) − bi]
= [a(a + 2) + b(b + 2)] + [(a + 2)(b + 2) − ab]i.
(z + 2i)(z + 2) là số thuần ảo khi và chỉ khi
a(a + 2) + b(b + 2) = 0 ⇔ (a + 1)
2
+ (b + 1)
2
= 2
nên tập hợp tất cả các điểm biểu diễn của z là một đường tròn phương trình
(x + 1)
2
+ (y + 1)
2
= 2
có tâm I(−1; −1).
Chọn phương án D
Câu 22. Trong không gian Oxyz, cho
# »
OA =
#»
i −2
#»
j + 3
#»
k , điểm B(3; −4; 1) và C(2; 0; 1). Tọa độ trọng
tâm của tam giác ABC là
A. 1; −2; 3. B. (−2; 2; −1). C. (2; −2; 1). D. (−1; 2; −3).
Lời giải.
Từ giả thiết
# »
OA =
#»
i − 2
#»
j + 3
#»
k ⇒ A(1; −2; 3).
Gọi G là trọng tâm tam giác ABC, ta có:
x
G
=
x
A
+ x
B
+ x
C
3
=2
y
G
=
y
A
+ y
B
+ y
C
3
= − 2
z
G
=
z
A
+ z
B
+ z
C
3
=1
⇒ G(2; −2; 1).
Chọn phương án C
Câu 23. Trong không gian Oxyz, cho hai điểm I(1; 1; 1) và A(1; 2; 3). Phương trình của mặt cầu có
tâm I và đi qua A là
A. (x + 1)
2
+ (y + 1)
2
+ (z + 1)
2
= 29. B. (x − 1)
2
+ (y − 1)
2
+ (z − 1)
2
= 5.
C. (x − 1)
2
+ (y − 1)
2
+ (z − 1)
2
= 25. D. (x + 1)
2
+ (y + 1)
2
+ (z + 1)
2
= 5.
Lời giải.
Ta có R
2
= IA
2
= (1 − 1)
2
+ (2 − 1)
2
+ (3 − 1)
2
= 5
nên phương trình của mặt cầu là (x − 1)
2
+ (y − 1)
2
+ (z − 1)
2
= 5.
Chọn phương án B
Câu 24. Trong không gian Oxyz, cho điểm A(2; −1; −3) và mặt phẳng (P ): 3x −2y + 4z −5 = 0. Mặt
phẳng (Q) đi qua A và song song với mặt phẳng (P ) có phương trình là
A. (Q): 3x − 2y + 4z − 4 = 0. B. (Q): 3x − 2y + 4z + 4 = 0.
GeoGebraPro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
C. (Q): 3x − 2y + 4z + 5 = 0. D. (Q): 3x + 2y + 4z + 8 = 0.
Lời giải.
Do mặt phẳng (Q) song song với mặt phẳng (P ) nên có vectơ pháp tuyến là
#»
n = (3; −2; 4).
Phương trình mặt phẳng (Q): 3(x − 2) − 2(y + 1) + 4(z + 3) = 0 ⇔ 3x − 2y + 4z + 4 = 0.
Chọn phương án B
Câu 25. Trong không gian Oxyz, khoảng cách từ điểm M(2; −4; −1) tới đường thẳng ∆ :
x = t
y = 2 − t
z = 3 + t
bằng
A.
√
14. B.
√
6. C. 2
√
14. D. 2
√
6.
Lời giải.
Đường thẳng ∆ đi qua N(0; 2; 3), có véc-tơ chỉ phương
#»
u = (1; −1; 2).
Ta có
# »
MN = (−2; 6; 4) và
î
# »
MN,
#»
u
ó
= (16; 8; −4).
Vậy khoảng cách từ M đến đường thẳng ∆ là
d(M, ∆) =
î
# »
MN,
#»
u
ó
|
#»
u |
=
√
336
√
6
= 2
√
14.
Chọn phương án C
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a ,SA ⊥ (ABCD),SA = a
√
2.
Tìm số đo của góc giữa đường thẳng SC và mặt phẳng (SAD).
A. 45
◦
. B. 30
◦
. C. 90
◦
. D. 60
◦
.
Lời giải.
Phương pháp
Góc giữa đường thẳng d với mặt phẳng (P ) là góc giữa đường thẳng d
với hình chiếu của đường thẳng d trên (P ).
Cách giải:
Ta có
®
CD ⊥ SA
CD ⊥ AD
⇒ CD ⊥ (SAD)
¤
(SC; (SAD)) =
’
CSD
’
CSD =
CD
SD
=
a
√
a
2
+ 2a
2
=
a
a
√
3
=
1
√
3
’
CSD = 30
◦
.
S
B C
DA
Chọn phương án B
Câu 27. Cho hàm số y = f(x) xác định trên R và có bảng xét dấu của đạo hàm như sau:
x
y
0
−∞
x
1
x
2
x
3
+∞
−
0
+ −
0
+
Khi đó số điểm cực trị của hàm số y = f (x) là
A. 3. B. 2. C. 4. D. 1.
Lời giải.
Ta thấy f
0
(x) đổi dấu khi x qua x
1
, x
2
, x
3
thuộc tập xác định của hàm số f(x) nên hàm số f(x) có 3
cực trị.
Chọn phương án A
Câu 28. Tìm giá trị lớn nhất M của hàm số y = 2x +
√
8 − 2x
2
trên tập xác định của nó?
A. M = 2
√
5. B. M =
8
√
3
3
. C. M = 2
√
6. D. M = 4.
GeoGebraPro Trang 7
https://www.facebook.com/groups/GeoGebraPro/
Lời giải.
Tập xác định của hàm số: D = [−2; 2].
Ta có y
0
= 2 +
−2x
√
8 − 2x
2
= 0 ⇔
√
8 − 2x
2
= x
⇔
(
x ≥ 0
8 − 2x
2
= x
2
⇔
(
x ≥ 0
8 = 3x
2
⇔ x =
2
√
6
3
∈ [−2; 2].
y(−2) = −4; y(2) = 4; y
Ç
2
√
6
3
å
= 2
√
6.
Vậy giá trị lớn nhất M của hàm số là M = 2
√
6. Chọn C.
Chọn phương án C
Câu 29. Cho a > 0, b > 0 thoả mãn log
16
(a+3b) = log
9
a = log
12
b. Giá trị của
a
3
− ab
2
+ b
3
a
3
+ a
2
b + 3b
3
bằng
A.
6 −
√
13
11
. B.
82 − 17
√
13
69
. C.
5 −
√
13
6
. D.
3 −
√
13
11
.
Lời giải.
Đặt t = log
16
(a + 3b) = log
9
a = log
12
b.
⇒
16
t
= a + 3b
9
t
= a
12
t
= b
⇒ 9
t
+ 3.12
t
= 16
t
⇒
Å
9
16
ã
t
+ 3
Å
3
4
ã
t
= 1 ⇒
Å
3
4
ã
t
=
−3 +
√
13
2
=
a
b
Vậy
a
3
− ab
2
+ b
3
a
3
+ a
2
b + 3b
3
=
a
b
3
−
a
b
+ 1
a
b
3
+
a
b
2
+ 3
=
5 −
√
13
6
.
Chọn phương án C
Câu 30. Có tất cả bao nhiêu giá trị thực của tham số m để đường thẳng d
m
: y = mx + 1 cắt đồ thị
(C) : y = x
3
− x
2
+ 1 tại 3 điểm A, B(0; 1) và C phân biệt sao cho tam giác AOC vuông tại O.
A. 0. B. 1. C. 2. D. 3.
Lời giải.
Phương trình hoành độ giao điểm của d
m
và (C) là:
x
3
− x
2
+ 1 = mx + 1 ⇔ x(x
2
− x − m) = 0 ⇔
ñ
x = 0
x
2
− x − m = 0.
Đường thẳng d
m
cắt đồ thị (C) tại 3 điểm phân biệt A, B(0; 1) và C.
⇔ Phương trình x
2
− x − m = 0 có hai nghiệm phân biệt khác 0.
⇔
®
∆ = 1 + 4m > 0
− m 6= 0
⇔
m > −
1
4
m 6= 0.
Khi đó: A(x
1
; mx
1
+ 1) và C(x
2
; mx
2
+ 1) Theo Vi-et: x
1
và x
2
là nghiệm phương trình x
2
−x −m = 0
nên ta có : x
1
+ x
2
= 1 và x − 1x
2
= −m.
4AOC vuông tại O.
⇔
# »
OA ·
# »
OC = 0
⇔ x
1
x
2
+ (mx
1
+ 1)(mx
2
+ 1) = 0
⇔ (m
2
+ 1)x
1
x
2
+ m(x
1
+ x
2
) + 1 = 0
⇔ (m
2
+ 1)(−m) + m + 1 = 0
⇔ −m
3
+ 1 = 0
⇔ m = 1.(Thỏa mãn điều kiện)
Vậy có 1 giá trị m thỏa mãn bài toán.
Chọn phương án B
GeoGebraPro Trang 8
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 31. Tập nghiệm S của bất phương trình log
1
3
(x − 1) + log
3
(11 − 2x) ≥ 0 là
A. S =
Å
3;
11
2
ã
. B. S = (−∞; 4]. C. S = (1; 4]. D. S = (1; 4).
Lời giải.
Điều kiện
®
x − 1 > 0
11 − 2x > 0
⇔ 1 < x <
11
2
. Ta có
log
1
3
(x − 1) + log
3
(11 − 2x) ≥ 0 ⇔ −log
3
(x − 1) + log
3
(11 − 2x) ≥ 0
⇔ log
3
11 − 2x
x − 1
≥ 0 ⇔
11 − 2x
x − 1
≥ 1 ⇔
11 − 2x
x − 1
− 1 ≥ 0(vì x − 1 > 0)
⇔ 12 − 3x ≥ 0 ⇔ x ≤ 4.
Kết hợp với điều kiện ta có 1 < x ≤ 4.
Vậy S = (1; 4].
Chọn phương án C
Câu 32. Một khối nón có thể tích bằng 9a
3
π
√
2. Tính bán kính R đáy khối nón khi diện tích xung
quanh nhỏ nhất.
A. R = 3a. B. R =
3a
6
√
2
. C. R =
3
√
9a. D. R =
3a
3
√
2
.
Lời giải.
Gọi h, l lần lượt là chiều cao và độ dài đường sinh của khối nón.
V =
1
3
πR
2
h = 9a
3
π
√
2 ⇒ h =
27a
3
√
2
R
2
⇒ l =
√
R
2
+ h
2
=
…
R
2
+ 2 ·
729a
6
R
4
.
S
xq
= πRl = π
…
R
4
+
729a
6
R
2
+
729a
6
R
2
≥ π
3
…
R
4
·
729a
6
R
2
·
729a
6
R
2
.
⇒ S
xq
= 9πa
2
. Nên min S
xq
= 9πa
2
khi R
4
=
729a
6
R
2
⇔ R = 3a.
Chọn phương án A
Câu 33. Cho hàm số f(x) liên tục và f (3) = 21,
3
Z
0
f(x)dx = 9. Tính tích phân I =
1
Z
0
x·f
0
(3x)dx.
A. I = 6. B. I = 12. C. I = 9. D. I = 15.
Lời giải.
Đặt 3x = t ⇒ dx =
dt
3
. Đổi cận
®
x = 0 ⇒ t = 0
x = 1 ⇒ t = 3.
I =
3
Z
0
t
3
f
0
(t)
dt
3
=
1
9
3
Z
0
xf
0
(x)dx.
Đặt
®
u = x
dv = f
0
(x)dx
⇒
®
du = dx
v = f(x)
Suy ra I =
1
9
Ñ
xf(x)
3
0
−
3
Z
0
f(x)dx
é
= 6.
Chọn phương án A
Câu 34. Tính thể tích khối tròn xoay sinh bởi Elip (E) :
x
2
4
+
y
2
1
= 1 quay quanh trục Ox.
A.
64π
9
. B.
10π
3
. C.
8π
3
. D.
8π
2
3
.
Lời giải.
(E) có a
2
= 4 ⇒ a = 2. Do đó hai đỉnh thuộc trục lớn có tọa độ A
0
(−2; 0) và (2; 0).
Vì
x
2
4
+
y
2
1
= 1 ⇒ y
2
= 1 −
x
2
4
.
GeoGebraPro Trang 9
https://www.facebook.com/groups/GeoGebraPro/
Do đó thể tích khối tròn xoay là V
Ox
= π
2
Z
−2
y
2
dx = π
2
Z
−2
Å
1 −
x
2
4
ã
dx =
8π
3
.
Vậy V
Ox
=
8π
3
(đvtt).
Chọn phương án C
Câu 35. Xét số phức z thỏa mãn
z + 2
z − 2i
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số
phức z luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng
A. 1. B.
√
2. C. 2
√
2. D. 2.
Lời giải.
Gọi z = a + bi ta có:
z + 2
z − 2i
=
(a + 2) + bi
a + (b − 2i)i
=
[(a + 2) + bi] [a − (b − 2)i]
[a + (b − 2)i] [a − (b − 2)i]
=
(a + 2)a − (a + 2)(b − 2)i + abi + b(b − 2)
a
2
+ (b − 2)
2
=
a
2
+ 2a + b
2
− 2b
a
2
+ (b − 2)
2
−
(a + 2) (b − 2) − ab
a
2
+ (b − 2)
2
i.
.
Để số trên là số thuần ảo ⇒ có phần thực bằng 0 ⇒ a
2
+ 2a + b
2
− 2b = 0.
Vậy tập hợp các điểm biểu diễn số phức z là đường tròn tâm I(−1; 1), bán kính
R =
»
(−1)
2
+ 1
2
− 0 =
√
2.
Chọn phương án B
Câu 36. Cho số phức z thỏa mãn |z| + z + 5i = 25. Khi đó mô-đun z bằng
A. 12. B. 10. C. 11. D. 13.
Lời giải.
Gọi z = x + yi (x; y ∈ R).
|z| + z + 5i = 25 ⇔
p
x
2
+ y
2
+ x + yi + 5i = 25
⇔
®
p
x
2
+ y
2
+ x = 25
y + 5 = 0
⇔
®
√
x
2
+ 25 = 25 − x
y = −5
⇔
x
2
+ 25 = (25 − x)
2
x ≤ 25
y = −5
⇔
®
x = 12
y = −5
.
Vậy z = 12 − 5i ⇒ |z| =
p
12
2
+ (−5)
2
= 13.
Chọn phương án D
Câu 37. Trong không gian Oxyz, cho mặt phẳng (P ): x + y + z − 3 = 0 và đường thẳng d :
x
1
=
y + 1
2
=
z − 2
−1
. Hình chiếu vuông góc của d trên (P ) có phương trình là
A.
x + 1
−1
=
y + 1
−4
=
z + 1
5
. B.
x − 1
3
=
y − 1
−2
=
z − 1
−1
.
C.
x − 1
1
=
y − 1
4
=
z − 1
−5
. D.
x − 1
1
=
y − 4
1
=
z + 5
1
.
Lời giải.
Gọi A là giao điểm của (P ) và d ta có tọa độ A là nghiệm
x + y + z − 3 = 0
x
1
=
y + 1
2
=
z − 2
−1
⇔ A(1; 1; 1).
d có véctơ chỉ phương
#»
u = (1; 2; −1), (P ) có véctơ pháp tuyến
#»
n = (1; 1; 1) nên mặt phẳng (Q) qua d
vuông góc (P ) có véctơ pháp tuyến là
# »
n
(Q)
= [
#»
u
d
,
# »
n
(P )
] = (3; −2; −1).
Hình chiếu vuông góc của d trên (P ) là giao tuyến ∆ của (P ) và (Q), nên ∆ qua A và có véctơ chỉ
phương là [
# »
n
(P )
,
# »
n
(Q)
] = (1; 4; −5).
Phương trình ∆ là
x − 1
1
=
y − 1
4
=
z − 1
−5
.
Chọn phương án C
GeoGebraPro Trang 10
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 38. Trong không gian Oxyz, cho đường thẳng d:
x − 3
2
=
y + 2
1
=
z + 1
−1
và mặt phẳng (P ) : x +
y + z + 2 = 0. Cho đường thẳng ∆ nằm trong mặt phẳng (P ), vuông góc với đường thẳng d đồng thời
khoảng cách từ giao điểm I của d với (P ) đến đường thẳng ∆ bằng
√
42. Gọi M(5; b; c) là hình chiếu
vuông góc của I trên ∆. Giá trị P = bc bằng bao nhiêu?
A. P = −10. B. P = 10. C. P = 12. D. P = −20.
Lời giải.
Gọi I(3 + 2t; −2 + t; −1 − t) ∈ d, vì I thuộc mặt phẳng (P ) nên
3 + 2t + (−2 + t) + (−1 − t) + 2 = 0
⇔ t = −1
⇒ I(1; −3; 0).
Ta có IM =
√
42 ⇔ (5 − 1)
2
+ (b + 3)
2
+ (c − 0)
2
= 42 ⇔ (b + 3)
2
+ c
2
= 26 (1).
Mà M(5; b; c) ∈ (P ) ⇒ 5 + b + c + 2 = 0 ⇔ c = −7 − b.
Khi đó (1) ⇔ (b + 3)
2
+ (b + 7)
2
= 26 ⇔
ñ
b = −2
b = −8.
Với b = −2 ⇒ c = −5 và b = −8 ⇒ c = 1.
Vậy P = bc = 10 hoặc P = bc = −8.
Chọn phương án B
Câu 39. Trong một chiếc hộp có 20 viên bi, trong đó có 9 viên bi màu đỏ, 6 viên bi màu xanh và 5
viên bi màu vàng. Lấy ngẫu nhiên đồng thời 3 viên bi. Tìm xác suất để 3 viên bi lấy ra có không quá
2 màu.
A.
29
38
. B.
9
38
. C.
183
190
. D.
82
95
.
Lời giải.
Số cách lấy 3 viên bi từ hộp chứa 20 viên bi là C
3
20
= 1140.
Số cách lấy 3 viên bi có đủ 3 màu là 9 · 6 · 5 = 270.
Do đó, số cách lấy được 3 viên bi không quá 2 màu là 1140 − 270 = 870.
Vậy xác suất để 3 viên bi lấy ra có không quá 2 màu là
870
1140
=
29
38
.
Chọn phương án A
Câu 40. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Hình chiếu vuông góc của S
trên mặt phẳng (ABCD) là điểm H thuộc đoạn BD sao cho HD = 3HB. Biết góc giữa mặt (SCD)
và mặt phẳng đáy bằng 45
◦
. Khoảng cách giữa hai đường thẳng SA và BD là:
A.
2a
√
38
17
. B.
2a
√
13
3
. C.
2a
√
51
13
. D.
3a
√
34
17
.
Lời giải.
Kẻ HI ∥ BC(I ∈ CD) ta có:
®
CD ⊥ HI
CD ⊥ SI.
Suy ra góc giữa mặt phẳng (SCD) và mặt phẳng đáy
là góc
‘
SIH = 45
◦
.
Dựng hình bình hành ADBE.
Ta có BD ∥ (SAE) ⇒ d
(SA,BD)
= d
(BD,(SAE))
=
d
(B,(SAE))
= d
(H,(SAE))
.
• Kẻ HJ ⊥ AE(J ∈ AE) ta có AE ⊥ (SHJ) ⇒
(SAE) ⊥ (SHJ) theo giao tuyến SJ.
• Kẻ HK ⊥ SJ(K ∈ SJ)
ta có HK ⊥ (SAE) ⇒ HK = d
(H,(SAE))
.
S
A
C
O
I
B
H
D
E
K
J
2a2a
2a
a
√
2
GeoGebraPro Trang 11
https://www.facebook.com/groups/GeoGebraPro/
Ta có HK =
HJ · HS
SJ
=
HJ · HS
√
HJ
2
+ HS
2
.
Với HJ = AO = a
√
2, HS = HI =
3
4
BC =
3a
2
Vậy HK =
a
√
2 ·
3a
2
…
2a
2
+
9a
2
4
=
3a
√
34
17
.
Chọn phương án D
Câu 41. Cho hàm số y = f(x) liên tục trên R và có đạo hàm f
0
(x) = x
2
(x − 2)(x
2
− 6x + m) với mọi
x ∈ R. Có bao nhiêu số nguyên m thuộc đoạn [−2019; 2019] để hàm số g(x) = f(1 − x) nghịch biến
trên khoảng (−∞; −1)?
A. 2010. B. 2012. C. 2011. D. 2009.
Lời giải.
Ta có
g
0
(x) = −f
0
(1 − x) = −(1 − x)
2
(1 − x − 2)
(1 − x)
2
− 6(1 − x) + m
= −(x − 1)
2
(−1 − x)(x
2
+ 4x + m − 5) = (x − 1)
2
(x + 1)(x
2
+ 4x + m − 5).
Hàm số g(x) nghịch biến trên (−∞; −1)
⇔ g
0
(x) ≤ 0 với mọi x ∈ (−∞; −1)
⇔ (x + 1)(x
2
+ 4x + m − 5) ≤ 0 với mọi x ∈ (−∞; −1)
⇔ x
2
+ 4x + m − 5 ≥ 0 với mọi x ∈ (−∞; −1) (Do x ∈ (−∞; −1) ⇒ x + 1 < 0)
⇔ h(x) = x
2
+ 4x − 5 ≥ −m với mọi x ∈ (−∞; −1)
⇔ −m ≤ min
x∈(−∞;−1]
h(x).
Ta có h
0
(x) = 2x + 4, h
0
(x) = 0 ⇔ x = −2. Bảng biến thiên của hàm số h(x) như sau
x
h
0
(x)
h(x)
−∞
0
+∞
−
0
+
−9−9
Do đó −m ≤ −9 ⇔ m ≥ 9. Mặt khác m ∈ [−2019; 2019] và m nguyên nên m ∈ {9; 10; 11; ··· ; 2019}
hay có 2019 − 9 + 1 = 2011 giá trị của m thỏa mãn.
Chọn phương án C
Câu 42. Cường độ một trận động đất M được cho bởi công thức M = log A − log A
0
, với A là biên
độ rung chấn tối đa và A
0
là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San
Francisco có cường độ 8,3 độ Richter. Trong cùng năm đó, trận động đất khác ở gần đó đo được 7,1 độ
Richter. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu lần trận động đất này?
A. 1,17. B. 2,2. C. 15,8. D. 4.
Lời giải.
Gọi M
1
, A
1
lần lượt là cường độ, biên độ rung chấn tối đa của trận động đất tại San Francisco.
Gọi M
2
, A
2
lần lượt là cường độ, biên độ rung chấn tối đa của trận động đất tại địa điểm còn lại.
Ta có
M
1
= log A
1
− log A
0
= log
A
1
A
0
⇒
A
1
A
0
= 10
M
1
.
M
2
= log A
2
− log A
0
= log
A
2
A
0
⇒
A
2
A
0
= 10
M
2
.
GeoGebraPro Trang 12
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Khi đó
A
1
A
2
=
10
M
1
10
M
2
= 10
M
1
−M
2
= 10
1,2
≈ 15,8.
Chọn phương án C
Câu 43. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
0 1
+∞
−
0
+
0
−
+∞+∞
−1−1
33
−∞−∞
Phương trình f(2 − x) − 1 = 0 có bao nhiêu nghiệm?
A. 0. B. 2. C. 1. D. 3.
Lời giải.
Từ đồ thị hàm số y = f(x), ta thực hiện các bước sau
• Đối xứng đồ thị y = f(x) qua trục Oy ta thu được đồ thị y = f (−x).
• Tịnh tiến đồ thị y = f(−x) sang phải 2 đơn vị ta thu được đồ thị y = f (−x + 2).
Hàm số y = f(−x + 2) có bảng biến thiên sau
x
y
0
y
−∞
1 2
+∞
+
0
−
0
+
−∞−∞
33
−1−1
+∞+∞
Số nghiệm của phương trình f(2 −x) −1 = 0 (1) bằng số giao điểm hai đồ thị y = f (2 −x) và y = 1.
Dựa vào bảng biến thiên suy ra phương trình (1) có 3 nghiệm.
Chọn phương án D
Câu 44. Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB
và CD thuộc hai đáy của hình trụ, AB = 4a, AC = 5a. Thể tích V của khối trụ là
A. V = 16πa
3
. B. V = 4πa
3
. C. V = 12πa
3
. D. V = 8πa
3
.
Lời giải.
Ta có BC =
√
AC
2
− AB
2
=
√
25a
2
− 16a
2
= 3a.
Bán kính đáy r =
AB
2
= 2a, chiều cao BC = 3a.
Vậy V = hπr
2
= 3a · 4a
2
= 12πa
3
.
CD
A B4a
5a
Chọn phương án C
Câu 45. Cho hàm số f(x) liên tục trên R thỏa mãn điều kiện: f(0) = 2
√
2, f(x) > 0 với mọi x ∈ R và
f(x).f
0
(x) = (2x + 1)
p
1 + f
2
(x) với mọi x ∈ R. Khi đó giá trị f(1) bằng
A.
√
15. B.
√
23. C.
√
24. D.
√
26.
Lời giải.
Từ giả thiết ta có 2x + 1 =
f(x) · f
0
(x)
p
1 + f
2
(x)
⇒
Z
f(x) · f
0
(x)
p
1 + f
2
(x)
dx =
Z
(2x + 1) dx.
Bây giờ ta tính I =
Z
f(x) · f
0
(x)
p
1 + f
2
(x)
dx.
Đặt
p
1 + f
2
(x) = t ⇒ 1 + f
2
(x) = t
2
⇒ 2f(x)f
0
(x)dx = 2tdt ⇒ f(x)f
0
(x)dx = tdt.
Do đó I =
Z
t
t
dx =
Z
dt = t + C =
»
1 + f
2
(x) + C.
GeoGebraPro Trang 13
https://www.facebook.com/groups/GeoGebraPro/
Ta nhận được
p
1 + f
2
(x) + C = x
2
+ x. f(0) = 2
√
2 ⇒ C = −3.
Từ đó
p
1 + f
2
(x) − 3 = x
2
+ x. Khi x = 1 ta có
p
1 + f
2
(1) − 3 = 1 + 1 ⇒ 1 + f
2
(1) = 25 ⇒ f (1) =
√
24.
Chọn phương án C
Câu 46. Tìm tất cả các giá trị của tham số m để phương trình x −m −
√
9 − x
2
= 0 có đúng 1 nghiệm
dương?
A. m ∈ (−3; 3]. B. m ∈ (−3; 3] ∪ {−3
√
2}.
C. m ∈ [0; 3]. D. m = ±3
√
2.
Lời giải.
Điều kiện: −3 ≤ x ≤ 3.
Phương trình tương đương với x −
√
9 − x
2
= m.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = x −
√
9 − x
2
và đường thẳng y = m.
Xét hàm số y = x −
√
9 − x
2
với −3 ≤ x ≤ 3
y
0
= 1 +
x
√
9 − x
2
⇒ y
0
= 0 ⇔
√
9 − x
2
= −x ⇔
®
x ≤ 0
9 − x
2
= x
2
⇔ x =
−3
√
2
2
∈ [−3; 3].
BBT:
x
y
0
y
−3
−
3
√
2
2
0 3
−
0
+ +
−3−3
−3
√
2−3
√
2
33
−3
Dựa vào bảng biến thiên suy ra −3 < m ≤ 3.
Chọn phương án A
Câu 47. Cho hai số thực a, b > 1. Tìm giá trị nhỏ nhất của biểu thức S =
1
log
(ab)
a
+
1
log
4
√
ab
b
.
A. min S =
4
9
. B. min S =
9
4
. C. min S =
9
2
. D. min S =
1
4
.
Lời giải.
S = log
a
(ab) +
1
4
log
b
(ab) = 1 + log
a
b +
1
4
(1 + log
b
a) = log
a
b +
1
4 log
a
b
+
5
4
Vì a > 1, b > 1 nên log
a
b > 0. Áp dụng bất đẳng thức Cô - si ta có
S ≥ 2
log
a
b.
1
4 log
a
b
+
5
4
= 1 +
5
4
=
9
4
Dấu “ = ” xảy ra khi log
a
b =
1
4 log
a
b
⇔ (log
a
b)
2
=
1
4
⇔
log
a
b = −
1
2
(l)
log
a
b =
1
2
(T M)
Với log
a
b =
1
2
⇔ b = a
1
2
Chọn phương án B
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số
y =
x
2
+ mx + m
x + 1
trên [1; 2] bằng 2. Số phần tử của S là
A. 1. B. 4. C. 3. D. 2.
Lời giải.
Xét hàm số f(x) =
x
2
+ mx + m
x + 1
trên [1; 2]. Ta có f
0
(x) liên tục trên [1; 2] và
f
0
(x) =
x
2
+ 2x
(x + 1)
2
> 0, ∀x ∈ [1; 2].
GeoGebraPro Trang 14
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Suy ra f(x) đồng biến trên [1; 2]. Do đó max
[1;2]
f(x) = f(2) =
3m + 4
3
, min
[1;2]
f(x) = f(1) =
2m + 1
2
.
Khi đó max
[1;2]
|f(x)| = max
ß
3m + 4
3
,
2m + 1
2
™
. Ta có
3m + 4
3
≥
2m + 1
2
⇔ 4(3m + 4)
2
≥ 9(2m + 1)
2
⇔ m ≥ −
11
12
.
• Với m ≥ −
11
12
, ta có max
[1;2]
|f(x)| =
3m + 4
3
. Theo đề bài, ta có
3m + 4
3
= 2 ⇔
3m + 4
3
= 2
3m + 4
3
= −2
⇔
m =
2
3
(thỏa mãn)
m = −
10
3
loại.
• Với m < −
11
12
, ta có max
[1;2]
|f(x)| =
2m + 1
2
. Theo đề bài, ta có
2m + 1
2
= 2 ⇔
2m + 1
2
= 2
2m + 1
2
= −2
⇔
m = −
5
2
(thỏa mãn)
m =
3
2
loại.
Vậy S =
ß
2
3
; −
5
2
™
⇒ Số phần tử của S là 2.
Chọn phương án D
Câu 49. Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng a
√
3. Gọi O
là tâm của đáy ABC, d
1
là khoảng cách từ A đến mặt phẳng (SBC) và d
2
là khoảng cách từ O đến
mặt phẳng (SBC). Tính d = d
1
+ d
2
.
A. d =
2a
√
2
11
. B. d =
2a
√
2
33
. C. d =
8a
√
2
33
. D. d =
8a
√
2
11
.
Lời giải.
Do tam giác ABC đều tâm O suy ra AO⊥BC tại M là trung điểm của BC.
Ta có: AM =
a
√
3
2
, MO =
1
3
AM =
a
√
3
6
, OA =
2
3
AM =
a
√
3
3
.
Từ giả thiết hình chóp đều suy ra SO⊥(ABC) , SO =
√
SA
2
− OA
2
=
…
3a
2
−
3a
2
9
=
2a
√
6
3
.
Dựng OK⊥SM, AH⊥SM ⇒ AH//OK;
OK
AH
=
OM
AM
=
1
3
.
Có
®
BC⊥SO
BC⊥AM
⇒ BC⊥(SAM) ⇒ BC⊥OK.
Có
®
OK⊥SM
OK⊥BC
⇒ OK⊥(SBC) , AH⊥(SBC) (do AH//OK).
Từ đó có d
1
= d (A, (SBC)) = AH = 3OK; d
2
= d (O, (SBC)) = OK. Trong tam giác vuông OSM có
đường cao OK nên
1
OK
2
=
1
OM
2
+
1
SO
2
=
36
3a
2
+
9
24a
2
=
99
8a
2
⇒ OK =
2a
√
2
33
.
Vậy d = d
1
+ d
2
= 4OK =
8a
√
2
33
.
Chọn phương án C
Câu 50. Cho hàm số y = f(x) có đạo hàm cấp 2, liên tục trên R và thỏa mãn
[f
0
(x)]
2
+ f(x) · f
00
(x) = 15x
4
+ 12x với mọi x ∈ R.
Hàm số g(x) = f(x) · f
0
(x) có bao nhiêu điểm cực trị?
GeoGebraPro Trang 15
https://www.facebook.com/groups/GeoGebraPro/
A. 1. B. 2. C. 3. D. 4.
Lời giải.
Ta có g
0
(x) = [f
0
(x)]
2
+ f(x) · f
00
(x) = 15x
4
+ 12x.
g
0
(x) = 0 ⇔ 15x
4
+ 12x = 0 ⇔
x = 0
x =
3
…
−
4
5
.
Nhận thấy x = 0 và x =
3
…
−
4
5
là các nghiệm đơn nên ta có bảng biến thiên
x
g
0
(x)
g(x)
−∞
3
…
−
4
5
0
+∞
+
0
−
0
+
−∞−∞
+∞+∞
Vậy hàm số g(x) có 2 điểm cực trị.
Chọn phương án B
———————–HẾT———————–
GeoGebraPro Trang 16
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
ĐÁP ÁN THAM KHẢO
1. A 2. C 3. A 4. D 5. C 6. C 7. B 8. A 9. D 10. A
11. C 12. C 13. A 14. D 15. C 16. B 17. D 18. B 19. A 20. A
21. D 22. C 23. B 24. B 25. C 26. B 27. A 28. C 29. C 30. B
31. C 32. A 33. A 34. C 35. B 36. D 37. C 38. B 39. A 40. D
41. C 42. C 43. D 44. C 45. C 46. A 47. B 48. D 49. C 50. B
GeoGebraPro Trang 17
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 8
Câu 1. Một hội đồng gồm 5 nam và 4 nữ được tuyển vào một ban quản trị gồm 4 người. Biết rằng
ban quản trị có ít nhất một nam và một nữ. Hỏi có bao nhiêu cách tuyển chọn?
A 240. B 260. C 126. D 120.
Câu 2. Cho dãy số (u
n
) xác định bởi
u
1
= 1; u
2
= 0
u
n+2
= 2u
n+1
− u
n
; ∀n > 1
. Tính u
5
.
A u
5
= 0. B u
5
= −4. C u
5
= −3. D u
5
= −2.
Câu 3. Số nghiệm của phương trình 9
x
+ 2.3
x+1
− 7 = 0 là
A 0. B 2. C 4. D 1.
Câu 4. Tính thể tích của khối lập phương ABCD.A
0
B
0
C
0
D
0
biết AC = 2a.
A 2
√
2a
3
. B a
3
. C
2
√
2a
3
3
. D
a
3
3
.
Câu 5. Tính đạo hàm của hàm số y = log
8
(6x − 5).
A y
0
=
2
(6x − 5) ln 2
. B y
0
=
1
(6x − 5) ln 8
. C y
0
=
6
6x − 5
. D y
0
=
6
(6x − 5) ln 4
.
Câu 6. Gọi F (x) là một nguyên hàm của hàm số f (x) = e
−x
+ cos x. Tìm khẳng định đúng.
A F (x) = e
−x
+ sin x + 2019. B F (x) = e
−x
+ cos x + 2019.
C F (x) = −e
−x
+ sin x + 2019. D F (x) = −e
−x
− cos x + 2019.
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, SA vuông góc
với mặt phẳng (ABCD), SA = a
√
3. Thể tích của khối chóp S.ABC là
A
a
3
√
3
3
. B a
3
√
3. C
2a
3
√
3
3
. D 2a
3
√
3.
Câu 8. Cho hình nón tròn xoay có chiều cao h = 20 (cm), bán kính đáy r = 25 (cm). Một thiết diện
đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là 12 (cm). Tính
diện tích của thiết diện đó.
A S = 400 (cm
2
). B S = 500 (cm
2
). C S = 406 (cm
2
). D S = 300 (cm
2
).
Câu 9. Cắt mặt cầu (S) bằng một mặt phẳng cách tâm một khoảng bằng 4cm được thiết diện là một
hình tròn có diện tích 9πcm
2
. Tính thể tích khối cầu (S).
A
250π
3
cm
3
. B
2500π
3
cm
3
. C
25π
3
cm
3
. D
500π
3
cm
3
.
Câu 10.
h Geogebra Pro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Cho hàm số f (x) xác định trên R và có đồ thị hàm số y = f
0
(x) là đường
cong trong hình bên.
Mệnh đề nào dưới đây đúng?
A Hàm số f(x) đồng biến trên khoảng (1; 2).
B Hàm số f(x) đồng biến trên khoảng (−2; 1).
C Hàm số f (x) nghịch biến trên khoảng (−1; 1).
D Hàm số f (x) nghịch biến trên khoảng (0; 2).
x
y
2
O
−2
Câu 11. Cho a là số thực dương khác 5. Tính I = log
a
5
Å
a
3
125
ã
.
A I = −
1
3
. B I = −3. C I =
1
3
. D I = 3.
Câu 12. Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng 36πa
2
. Tính
thể tích V của lăng trụ lục giác đều nội tiếp hình trụ.
A V = 27
√
3a
3
. B V = 24
√
3a
3
. C V = 36
√
3a
3
. D V = 81
√
3a
3
.
Câu 13. Cho hàm số y =
x
3
3
− (m + 1)x
2
+ mx − 2. Tìm m để hàm số đạt cực đại tại x = −1.
A m = −1. B m = 1. C không có m. D m = −2.
Câu 14.
Cho hàm số y = f(x) có đồ thị như hình bên. Hàm số đã cho nghịch biến trên
khoảng nào dưới đây?
A (0; 1). B (−1; 0). C (−2; −1). D (−1; 1).
x
y
O
1−2 2
−1
1
2
−2
Câu 15. Cho hàm số y =
x
2
+ x − 2
x
2
− 3x + 2
(C), đồ thị (C) có bao nhiêu đường tiệm cận?
A 0. B 1. C 2. D 3.
Câu 16. Nghiệm của bất phương trình log
2−
√
3
(2x − 5) ≥ log
2−
√
3
(x − 1) là
A
5
2
< x ≤ 4. B 1 < x ≤ 4. C
5
2
≤ x ≤ 4. D x ≥ 4.
Câu 17.
Cho hàm số y = f (x) có đồ thị như hình vẽ. Số nghiệm của phương
trình 2|f(x)| − 5 = 0 là
A 3. B 5 . C 4. D 6.
x
y
O
−1
1
1
−3
Câu 18. Cho
4
Z
3
5x − 8
x
2
− 3x + 2
dx = a ln 3 + b ln 2 + c ln 5 với a, b, c là các số hữu tỉ. Giá trị 2
a−3b+c
bằng
h Geogebra Pro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
A 12. B 6. C 1. D 64.
Câu 19 (2D4B1-2). Cho số phức z = 2 + 5i. Điểm biểu diễn số phức z trong mặt phẳng Oxy có tọa
độ là
A (5; 2). B (2; 5). C (−2; 5). D (2; −5).
Câu 20. Cho a, b là các số thực thỏa mãn a+6i = 2−2bi, với i là đơn vị ảo. Giá trị của a+b bằng
A −1. B 1. C −4. D 5.
Câu 21. Trong hệ tọa độ Oxy, cho điểm M biểu diễn số phức z = −2 + 3i. Gọi N là điểm thuộc
đường thẳng y = 3 sao cho tam giác OMN cân tại O. Điểm N là điểm biểu diễn của số phức nào dưới
đây?
A z = 3 − 2i. B z = −2 − 3i. C z = 2 + 3i. D z = −2 + i.
Câu 22. Trong không gian Oxyz, cho hình bình hành ABCD có A(1; 0; 0), B(0; 0; 1) và C(2; 1; 1). Tìm
tọa độ điểm D.
A D(1; 3; 0) . B D(−3; 1; 0). C D(3; −1; 0). D D(3; 1; 0).
Câu 23. Trong không gian Oxyz, cho hai điểm M (3; −2; 5), N (−1; 6; −3). Mặt cầu đường kính MN
có phương trình là
A (x + 1)
2
+ (y + 2)
2
+ (z + 1)
2
= 6. B (x − 1)
2
+ (y − 2)
2
+ (z − 1)
2
= 6.
C (x + 1)
2
+ (y + 2)
2
+ (z + 1)
2
= 36. D (x − 1)
2
+ (y − 2)
2
+ (z − 1)
2
= 36.
Câu 24. Trong không gian Oxyz khoảng cách giữa hai mặt phẳng (P ): x + 2y + 2z − 10 = 0 và
(Q): x + 2y + 2z − 3 = 0 bằng
A
8
3
. B
7
3
. C 3. D
4
3
.
Câu 25. Trong không gian Oxyz, cho điểm A(2; 0; −1) và mặt phẳng (P ): x + y −1 = 0. Đường thẳng
đi qua A đồng thời song song với (P ) và mặt phẳng (Oxy) có phương trình là
A
x = 3 + t
y = 2t
z = 1 − t
. B
x = 2 + t
y = −t
z = −1
. C
x = 1 + 2t
y = −1
z = −t
. D
x = 3 + t
y = 1 + 2t
z = −t
.
Câu 26. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A cạnh AB = a, SA vuông góc với
mặt đáy và SA = a
√
2. Gọi M là trung điểm của SA, ϕ là góc giữa BM và mặt phẳng (SBC). Tính
sin ϕ.
A sin ϕ =
√
2
2
√
15
. B sin ϕ =
1
√
15
. C sin ϕ =
√
2
√
15
. D sin ϕ =
1
2
√
15
.
Câu 27.
Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Hàm số y = f (x
2
−2) có
bao nhiêu điểm cực trị?
A 4. B 5. C 3. D 2.
x
y
O 3
−4
2
h Geogebra Pro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
Câu 28. Tìm giá trị m để giá trị nhỏ nhất của hàm số y =
x − m
2
− m
x + 1
trên [0; 1] bằng −2.
A m = −2. B m = 1.
C m = −2 và m = −1. D m = −2 và m = 1.
Câu 29. Cho các số thực a, b thỏa mãn 1 < a < b và log
a
b + log
b
a
2
= 3. Tính giá trị của biểu thức
T = log
ab
a
2
+ b
2
.
A
1
6
. B
3
2
. C 6. D
2
3
.
Câu 30.
Đồ thị sau đây là của hàm số y = x
4
− 3x
2
− 3 . Với giá trị nào
của m thì phương trình x
4
−3x
2
−3 = m có 3 nghiệm phân biệt
O
x
y
−3 −2 −1
1 2
−5
−3
−1
1
2
A m = −4 . B m = −3. C m = 0. D m = −5.
Câu 31. Nghiệm nguyên lớn nhất của bất phương trình log
4
2
x − log
2
1
2
Å
x
3
8
ã
+ 9 log
2
32
x
2
< 4 log
2
2
−1
x
là
A x = 7. B x = 8. C x = 4. D x = 1.
Câu 32. Một hình trụ có chiều cao h và bán kính đáy R. Hình nón có đỉnh là tâm đáy trên của hình
trụ và đáy là hình tròn đáy dưới của hình trụ. Gọi V
1
là thể tích của hình trụ, V
2
là thể tích của hình
nón. Tính tỉ số
V
1
V
2
.
A 2. B 2
√
2. C 3. D
1
3
.
Câu 33. Cho hàm số y = f(x) có đạo hàm, liên tục trên R, nhận giá trị dương trên khoảng (0; +∞)
và thỏa mãn f (1) = 1, f
0
(x) = f(x) · (3x
2
+ 2mx + m) với m là tham số. Giá trị của tham số m để
f(3) = e
−4
là
A m = −2. B m =
√
3. C m = −3. D m = 4.
Câu 34. Cho hình phẳng (H) giới hạn bởi đồ thị các hàm số sau y =
√
x, y = 1 đường thẳng x = 4
(tham khảo hình vẽ). Thể tích khối tròn xoay sinh bởi hình (H) khi quay quanh đường thẳng y = 1
bằng
h Geogebra Pro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
x
y
O
1
1
x = 4
4
y = 1
A
9
2
π. B
119
6
π. C
7
6
π. D
21
2
π.
Câu 35. Cho số phức z 6= 0 thỏa mãn
iz − (3i + 1)z
1 + i
= |z|
2
. Số phức w =
26iz
9
có môđun bằng
A 9. B
√
26. C
√
6. D 5.
Câu 36. Cho số phức z thỏa |z − 1 + 2i| = 3. Biết rằng tập hợp các điểm biểu diễn của số phức
w = 2z + i trên mặt phẳng (Oxy) là một đường tròn. Tìm tâm của đường tròn đó.
A I (2; −3). B I(1; 1). C I(0; 1). D I(1; 0).
Câu 37. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α) : x − 2z − 6 = 0 và đường thẳng
d :
x = 1 + t
y = 3 + t
z = −1 − t
. Viết phương trình đường thẳng ∆ nằm trong mặt phẳng (α) cắt đồng thời vuông
góc với d.
A
x − 2
2
=
y − 4
1
=
z + 2
1
. B
x − 2
2
=
y − 4
−1
=
z + 2
1
.
C
x − 2
2
=
y − 3
−1
=
z + 2
1
. D
x − 2
2
=
y − 4
−1
=
z − 2
1
.
Câu 38. Trong không gian Oxyz cho ba đường thẳng d :
x
1
=
y
1
=
z + 1
−2
, ∆
1
:
x − 3
2
=
y
1
=
z − 1
1
,
∆
2
:
x − 1
1
=
y − 2
2
=
z
1
. Đường thẳng ∆ vuông góc với d đồng thời cắt ∆
1
, ∆
2
tương ứng tại H, K sao
cho độ dài HK nhỏ nhất. Biết rằng ∆ có một vectơ chỉ phương
#»
u (h; k; 1). Giá trị h − k bằng
A 0. B 4. C 6. D −2.
Câu 39. Cho hai hộp, hộp thứ nhất chứa 5 viên bi đỏ và 7 viên bi vàng, hộp thứ hai chứa 3 bi đỏ và
n bi vàng (n ∈ N). Khi chọn ngẫu nhiên mỗi hộp một viên bi, xác suất để chọn được hai bi khác màu
là
7
15
. Số bi vàng trong hộp thứ hai là?
A n = 12. B n = 10. C n = 7. D n = 5.
Câu 40.
h Geogebra Pro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
Cho hình hộp chữ nhật ABCD.A
0
B
0
C
0
D
0
có cạnh bằng
AB = 2a, AD = AA
0
= a như hình vẽ. Khoảng cách giữa
hai đường thẳng BD và AD
0
bằng
A a. B
a
2
. C a
√
3. D
2a
3
.
A B
D
C
0
D
0
A
0
C
B
0
Câu 41. Tìm tất cả các giá trị khác nhau của tham số m để hàm số y =
5
−x
+ 2
5
−x
− m
đồng biến trên
(−∞; 0).
A m < −2. B m ≤ −2. C −2 < m ≤ 1. D −2 < m < 1.
Câu 42. Dân số thế giới được tính theo công thức S = A · e
ni
trong đó A là dân số của năm lấy làm
mốc tính, S là dân số sau n năm, i là tỉ lệ tăng dân số hàng năm. Cho biết năm 2005 Việt Nam có
khoảng 80.902.400 người và tỉ lệ tăng dân số là 1, 47% một năm. Như vậy, nếu tỉ lệ tăng dân số hàng
năm không đổi thì đến năm 2019 số dân của Việt Nam sẽ gần với số nào nhất sau đây?
A 99.389.200. B 99.386.600. C 100.861.100. D 99.251.200.
Câu 43.
Cho hàm số y = f (x). Hàm số y = f
0
(x)
có bảng biến thiên như sau. Bất phương trình
f(x) > sin x+m có nghiệm trên khoảng (−1; 1)
khi và chỉ khi
A m > f(1) − sin 1.
B m ≥ f(1) − sin 1.
C m ≤ f (−1) + sin 1.
D
m < f (−1) + sin 1.
x
y
0
y
−∞
−4
1
+∞
−
0
+
0
−
+∞+∞
−3−3
−1−1
−∞−∞
Câu 44. Hình trụ có bán kính đáy bằng a chu vi của thiết diện qua trục bằng 10a Thể tích của khối
trụ đã cho bằng
A 4πa
3
. B πa
3
. C 3πa
3
. D 5πa
3
.
Câu 45. Cho hàm số y = f(x) liên tục và thỏa mãn f (x) + 2f
Å
1
x
ã
= 3x với x ∈
ï
1
2
; 2
ò
. Tính
I =
2
Z
1
2
f(x)
x
dx.
A I =
3
2
. B I = −
3
2
. C I =
9
2
. D I = −
9
2
.
Câu 46. Phương trình |x
3
− 3x| = m
2
+ m có 6 nghiệm phân biệt khi và chỉ khi
A m > 0. B m < −2hoặc m > 1.
C −1 < m < 0. D −2 < m < −1 hoặc 0 < m < 1.
Câu 47. Cho hai số thực a, b > 1 sao cho tồn tại số thực 0 < x 6= 1 thỏa mãn a
log
b
x
= b
log
a
(x
2
)
. Tìm
giá trị nhỏ nhất của P = ln
2
a + ln
2
b − ln(ab).
h Geogebra Pro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
A
1
4
. B −
3 + 2
√
2
12
. C
e
2
. D
1 − 3
√
3
4
.
Câu 48. Có bao nhiêu giá trị nguyên của tham số m để max
[1;3]
|x
3
− 3x
2
+ m| ≤ 4?
A 5. B 4. C 6. D Vô số.
Câu 49. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC), góc giữa đường
thẳng SB và mặt phẳng (ABC) bằng 60
◦
. Khoảng cách giữa hai đường thẳng AC và SB bằng:
A
a
√
2
2
. B 2a. C
a
√
15
5
. D R =
a
√
7
7
.
Câu 50. Cho hàm số y = f (x), biết hàm số y = f
0
(x) có đồ thị như hình bên dưới.
x
y
O
−1−6
2
Hàm số g(x) = f (3 − x
2
) đồng biến trên khoảng?
A (2; 3). B (−1; 0). C (−2; −1). D (0; 1).
———————–HẾT———————–
h Geogebra Pro Trang 7
https://www.facebook.com/groups/GeoGebraPro/
BẢNG ĐÁP ÁN
1. D 2. C 3. D 4. A 5. A 6. C 7. A 8. B 9. D 10. D
11. D 12. D 13. A 14. A 15. C 16. A 17. C 18. D 19. B 20. A
21. C 22. D 23. D 24. B 25. B 26. B 27. B 28. D 29. D 30. B
31. A 32. C 33. C 34. C 35. B 36. A 37. B 38. A 39. C 40. D
41. C 42. A 43. D 44. C 45. A 46. D 47. B 48. A 49. C 50. B
h Geogebra Pro Trang 8
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 8
Câu 1. Một hội đồng gồm 5 nam và 4 nữ được tuyển vào một ban quản trị gồm 4 người. Biết rằng
ban quản trị có ít nhất một nam và một nữ. Hỏi có bao nhiêu cách tuyển chọn?
A 240. B 260. C 126. D 120.
Lời giải.
Số cách chọn 4 người bất kỳ từ 9 người hội đồng là: C
4
9
cách.
Số cách chọn 4 người đều nữ là: C
4
4
cách.
Số cách chọn 4 người đều nam là: C
4
5
cách.
Vậy để có ít nhất một nam và một nữ thì có C
4
9
− (C
4
4
+ C
4
5
) = 120 cách.
Chọn phương án D
Câu 2. Cho dãy số (u
n
) xác định bởi
u
1
= 1; u
2
= 0
u
n+2
= 2u
n+1
− u
n
; ∀n > 1
. Tính u
5
.
A u
5
= 0. B u
5
= −4. C u
5
= −3. D u
5
= −2.
Lời giải.
u
3
= 2u
2
− u
1
= −1; u
4
= 2u
3
− u
2
= −2; u
5
= 2u
4
− u
3
= −3
Chọn phương án C
Câu 3. Số nghiệm của phương trình 9
x
+ 2.3
x+1
− 7 = 0 là
A 0. B 2. C 4. D 1.
Lời giải.
Đặt t = 3
x
, t > 0
Phương trình đã cho trở thành t
2
+ 6t − 7 = 0 ⇔
t = 1 (nhận)
t = −7 (loại)
.
Với t = 1 thì 3
x
= 1 ⇔ x = 0.
Vậy phương trình đã cho có nghiệm duy nhất x = 0.
Chọn phương án D
Câu 4. Tính thể tích của khối lập phương ABCD.A
0
B
0
C
0
D
0
biết AC = 2a.
A 2
√
2a
3
. B a
3
. C
2
√
2a
3
3
. D
a
3
3
.
Lời giải.
h Geogebra Pro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Gọi độ dài cạnh của hình phương là x, x > 0. Khi đó ta có
x
2
+ x
2
= (2a)
2
⇔ x = a
√
2.
Suy ra thể tích khối lập phương V =
Ä
a
√
2
ä
3
= 2
√
2a
3
.
A B
CD
A
0
B
0
C
0
D
0
2a
Chọn phương án A
Câu 5. Tính đạo hàm của hàm số y = log
8
(6x − 5).
A y
0
=
2
(6x − 5) ln 2
. B y
0
=
1
(6x − 5) ln 8
. C y
0
=
6
6x − 5
. D y
0
=
6
(6x − 5) ln 4
.
Lời giải.
Ta có y
0
=
(6x − 5)
0
(6x − 5) · ln 8
=
6
3(6x − 5) · ln 2
=
2
(6x − 5) · ln 2
.
Chọn phương án A
Câu 6. Gọi F (x) là một nguyên hàm của hàm số f (x) = e
−x
+ cos x. Tìm khẳng định đúng.
A F (x) = e
−x
+ sin x + 2019. B F (x) = e
−x
+ cos x + 2019.
C F (x) = −e
−x
+ sin x + 2019. D F (x) = −e
−x
− cos x + 2019.
Lời giải.
Áp dụng công thức
Z
( e
−x
+ cos x) dx = −e
−x
+ sin x + C, với C là hằng số
Cho C = 2019 ta có F (x) = −e
−x
+ sin x + 2019.
Chọn phương án C
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, SA vuông góc
với mặt phẳng (ABCD), SA = a
√
3. Thể tích của khối chóp S.ABC là
A
a
3
√
3
3
. B a
3
√
3. C
2a
3
√
3
3
. D 2a
3
√
3.
Lời giải.
S
B C
A D
a
2a
a
√
3
Ta có: V
S.ABC
=
1
3
· SA ·
1
2
AB · BC =
a
3
√
3
3
.
h Geogebra Pro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Chọn phương án A
Câu 8. Cho hình nón tròn xoay có chiều cao h = 20 (cm), bán kính đáy r = 25 (cm). Một thiết diện
đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là 12 (cm). Tính
diện tích của thiết diện đó.
A S = 400 (cm
2
). B S = 500 (cm
2
). C S = 406 (cm
2
). D S = 300 (cm
2
).
Lời giải.
Thiết diện qua đỉnh là tam giác SAB.
Gọi K là trung điểm AB ⇒ OK⊥AB ⇒ AB⊥(SOK)⇒
(SAB) ⊥(SOK).
Kẻ OH⊥SK (H ∈ SK)⇒ OH⊥(SAB)⇒ OH = 12(cm).
Ta có:
1
OH
2
=
1
OK
2
+
1
OS
2
⇒
1
OK
2
=
1
12
2
−
1
20
2
=
1
225
⇒ OK =
15 (cm).
KB =
√
OB
2
− OK
2
=
√
25
2
− 15
2
= 20 ⇒ AB = 2BK = 40 (cm).
SK =
√
SO
2
+ OK
2
=
√
20
2
+ 15
2
= 25 (cm).
⇒ S
∆SAB
=
1
2
.SK.AB = 500 (cm
2
).
O
S
A
B
K
H
Chọn phương án B
Câu 9. Cắt mặt cầu (S) bằng một mặt phẳng cách tâm một khoảng bằng 4cm được thiết diện là một
hình tròn có diện tích 9πcm
2
. Tính thể tích khối cầu (S).
A
250π
3
cm
3
. B
2500π
3
cm
3
. C
25π
3
cm
3
. D
500π
3
cm
3
.
Lời giải.
Gọi I là tâm mặt cầu (S), H là tâm đường tròn giao tuyến, A là một điểm bất kì trên đường tròn,
R là bán kính của (S).
Ta có d(I, (P )) = 4.
S
(C)
= πAH
2
= 9π ⇒ AH = 3.
Ta có R =
p
AH
2
+ d(I, (P )) =
√
3
2
+ 4
2
= 5.
Thể tích khối cầu (S) là V
(S)
=
4
3
πR
3
=
500π
3
.
(P )
I
HA
Chọn phương án D
Câu 10.
h Geogebra Pro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
Cho hàm số f(x) xác định trên R và có đồ thị hàm số y = f
0
(x) là đường
cong trong hình bên.
Mệnh đề nào dưới đây đúng?
A Hàm số f(x) đồng biến trên khoảng (1; 2).
B Hàm số f(x) đồng biến trên khoảng (−2; 1).
C Hàm số f(x) nghịch biến trên khoảng (−1; 1).
D Hàm số f (x) nghịch biến trên khoảng (0; 2).
x
y
2
O
−2
Lời giải.
Từ đồ thị của y = f
0
(x), ta có với x ∈ (0; 2), f
0
(x) < 0. Suy ra f(x) nghịch biến trên khoảng (0; 2).
Chọn phương án D
Câu 11. Cho a là số thực dương khác 5. Tính I = log
a
5
Å
a
3
125
ã
.
A I = −
1
3
. B I = −3. C I =
1
3
. D I = 3.
Lời giải.
Ta có I = log
a
5
Å
a
3
125
ã
= log
a
5
a
5
3
= 3 log
a
5
a
5
= 3.
Chọn phương án D
Câu 12. Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng 36πa
2
. Tính
thể tích V của lăng trụ lục giác đều nội tiếp hình trụ.
A V = 27
√
3a
3
. B V = 24
√
3a
3
. C V = 36
√
3a
3
. D V = 81
√
3a
3
.
Lời giải.
Thiết diện qua trục hình trụ là hình vuông ADD
0
A
0
. Gọi O, O
0
lần lượt là hai tâm đường tròn đáy (hình vẽ). Suy ra l = 2r.
Theo giả thiết ta có
S
xq
= 2πrl = 36πa
2
⇔ 2πr · 2r = 36πa
2
⇒ r = 3a ⇒ l = 6a.
Lăng trụ lục giác đều ABCDEF.A
0
B
0
C
0
D
0
E
0
F
0
nội tiếp hình trụ
có chiều cao là h = 6a.
S
ABCDEF
= 6S
∆OAB
= 6 ·
(3a)
2
√
3
4
=
27a
2
√
3
2
(vì ∆OAB đều,
cạnh bằng 3a).
Suy ra V =
27a
2
√
3
2
· 6a = 81a
3
√
3.
J
O
A
B
C
D
E
F
C
0
D
0
O
0
I
0
J
0
B
0
A
0
E
0
F
0
I
Chọn phương án D
Câu 13. Cho hàm số y =
x
3
3
− (m + 1)x
2
+ mx − 2. Tìm m để hàm số đạt cực đại tại x = −1.
A m = −1. B m = 1. C không có m. D m = −2.
Lời giải.
Tập xác định: D = R.
y
0
= x
2
− 2(m + 1)x + m; y
00
= 2x − 2(m + 1).
Vì hàm số đã cho là hàm số bậc ba nên
h Geogebra Pro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Hàm số có điểm cực đại là x = −1 khi và chỉ khi
y
0
(−1) = 0
y
00
(−1) < 0
⇔
1 + 2(m + 1) + m = 0
− 2 − 2(m + 1) < 0
⇔
m = −1
m > −2
⇔ m = −1.
Chọn phương án A
Câu 14.
Cho hàm số y = f(x) có đồ thị như hình bên. Hàm số đã cho nghịch biến trên
khoảng nào dưới đây?
A (0; 1). B (−1; 0). C (−2; −1). D (−1; 1).
x
y
O
1−2 2
−1
1
2
−2
Lời giải.
Từ đồ thị ta thấy hàm số nghịch biến trên khoảng (0; 1).
Chọn phương án A
Câu 15. Cho hàm số y =
x
2
+ x − 2
x
2
− 3x + 2
(C), đồ thị (C) có bao nhiêu đường tiệm cận?
A 0. B 1. C 2. D 3.
Lời giải.
Tập xác định D = R\{1; 2}.
Ta có y =
x + 2
x − 2
nên đồ thị hàm số có tiệm cận ngang là y = 1 và tiệm cận đứng là x = 2.
Chọn phương án C
Câu 16. Nghiệm của bất phương trình log
2−
√
3
(2x − 5) ≥ log
2−
√
3
(x − 1) là
A
5
2
< x ≤ 4. B 1 < x ≤ 4. C
5
2
≤ x ≤ 4. D x ≥ 4.
Lời giải.
log
2−
√
3
(2x − 5) ≥ log
2−
√
3
(x − 1) ⇔
2x − 5 ≤ x − 1
2x − 5 > 0
⇔
x ≤ 4
x >
5
2
.
Vậy nghiệm của bất phương trinh là
5
2
< x ≤ 4.
Chọn phương án A
Câu 17.
Cho hàm số y = f(x) có đồ thị như hình vẽ. Số nghiệm của phương
trình 2|f(x)| − 5 = 0 là
A 3. B 5 . C 4. D 6.
x
y
O
−1
1
1
−3
Lời giải.
h Geogebra Pro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
2 |f(x)|− 5 = 0 ⇔ |f(x)| =
5
2
⇔
f(x) =
5
2
(1)
f(x) = −
5
2
(2)
.
Số nghiệm của phương trình đã cho là tổng số nghiệm của phương trình (1) và phương trình (2).
Số nghiệm của phương trình đã cho là số giao điểm của đường thẳng y =
5
2
và đường thẳng y = −
5
2
với đồ thị hàm số y = f (x).
Như vậy, dựa vào đồ thị hàm số ta thấy phương trình đã cho có 4 nghiệm.
Chọn phương án C
Câu 18. Cho
4
Z
3
5x − 8
x
2
− 3x + 2
dx = a ln 3 + b ln 2 + c ln 5 với a, b, c là các số hữu tỉ. Giá trị 2
a−3b+c
bằng
A 12. B 6. C 1. D 64.
Lời giải.
Ta có
4
Z
3
5x − 8
x
2
− 3x + 2
dx =
4
Z
3
Å
3
x − 1
+
2
x − 2
ã
dx = 3 ln |x − 1|
4
3
+ 2 ln |x − 2|
4
3
= 3 ln 3 − 3 ln 2 + 2 ln 2 = −ln 2 + 3 ln 3 ⇒
a = 3
b = −1 ⇒ a − 3b + c = 6
c = 0
.
Chọn phương án D
Câu 19 (2D4B1-2). Cho số phức z = 2 + 5i. Điểm biểu diễn số phức z trong mặt phẳng Oxy có tọa
độ là
A (5; 2). B (2; 5). C (−2; 5). D (2; −5).
Lời giải.
Phương pháp: Số phức z = a + bi, (a; b ∈ R) có điểm biểu diễn số phức trong mặt phẳng Oxy là (a; b).
Cách giải: Điểm biểu diễn số phức z trong mặt phẳng Oxy có tọa độ là (2; 5).
Chọn phương án B
Câu 20. Cho a, b là các số thực thỏa mãn a+6i = 2−2bi, với i là đơn vị ảo. Giá trị của a+b bằng
A −1. B 1. C −4. D 5.
Lời giải.
Ta có a + 6i = 2 − 2bi ⇒
a = 2
6 = −2b
⇒
a = 2
b = −3
⇒ a + b = −1.
Chọn phương án A
Câu 21. Trong hệ tọa độ Oxy, cho điểm M biểu diễn số phức z = −2 + 3i. Gọi N là điểm thuộc
đường thẳng y = 3 sao cho tam giác OMN cân tại O. Điểm N là điểm biểu diễn của số phức nào dưới
đây?
A z = 3 − 2i. B z = −2 − 3i. C z = 2 + 3i. D z = −2 + i.
Lời giải.
Do giả thiết suy ra tọa độ M (−2; 3) nên M thuộc đường thẳng y = 3. Vì tam giác OMN cân tại O
suy ra N đối xứng với M qua Oy nên tọa độ điểm N (2; 3). Khi đó điểm N là biểu diễn của số phức
h Geogebra Pro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
z = 2 + i.
Chọn phương án C
Câu 22. Trong không gian Oxyz, cho hình bình hành ABCD có A(1; 0; 0), B(0; 0; 1) và C(2; 1; 1). Tìm
tọa độ điểm D.
A D(1; 3; 0) . B D(−3; 1; 0). C D(3; −1; 0). D D(3; 1; 0).
Lời giải.
Tứ giác ABCD là hình bình hành khi và chỉ khi
# »
AB =
# »
DC.
Ta có
# »
AB = (−1; 0; 1),
# »
DC = (2 − x
D
; 1 − y
D
; 1 − z
D
).
Suy ra
− 1 = 2 − x
D
0 = 1 − y
D
1 = 1 − z
D
⇔
x
D
= 3
y
D
= 1
z
D
= 0.
Vậy D(3; 1; 0).
Chọn phương án D
Câu 23. Trong không gian Oxyz, cho hai điểm M (3; −2; 5), N (−1; 6; −3). Mặt cầu đường kính MN
có phương trình là
A (x + 1)
2
+ (y + 2)
2
+ (z + 1)
2
= 6. B (x − 1)
2
+ (y − 2)
2
+ (z − 1)
2
= 6.
C (x + 1)
2
+ (y + 2)
2
+ (z + 1)
2
= 36. D (x − 1)
2
+ (y − 2)
2
+ (z − 1)
2
= 36.
Lời giải.
Tâm I của mặt cầu là trung điểm đoạn MN⇒I (1; 2; 1).
Bán kính mặt cầu R =
MN
2
=
»
(−1 − 3)
2
+ (6 + 2)
2
+ (−3 − 5)
2
2
= 6.
Vậy phương trình mặt cầu là (x − 1)
2
+ (y − 2)
2
+ (z − 1)
2
= 36.
Chọn phương án D
Câu 24. Trong không gian Oxyz khoảng cách giữa hai mặt phẳng (P ): x + 2y + 2z − 10 = 0 và
(Q): x + 2y + 2z − 3 = 0 bằng
A
8
3
. B
7
3
. C 3. D
4
3
.
Lời giải.
Dựa vào phương trình (P ), (Q) có véctơ pháp tuyến là
#»
n = (1; 2; 2) nên (P ) k (Q).
Ta có |
#»
n| =
√
1 + 2
2
+ 2
2
= 3; d(O, (P )) =
10
3
; d(O, (Q)) =
3
3
= 1,
suy ra d((P ), (Q)) = d(O, (P )) − d(O, (Q)) =
7
3
.
Chọn phương án B
Câu 25. Trong không gian Oxyz, cho điểm A(2; 0; −1) và mặt phẳng (P ): x + y −1 = 0. Đường thẳng
đi qua A đồng thời song song với (P ) và mặt phẳng (Oxy) có phương trình là
A
x = 3 + t
y = 2t
z = 1 − t
. B
x = 2 + t
y = −t
z = −1
. C
x = 1 + 2t
y = −1
z = −t
. D
x = 3 + t
y = 1 + 2t
z = −t
.
Lời giải.
Ta có:
#»
n
(P )
= (1; 1; 0),
#»
n
(Oxy)
= (0; 0; 1).
Gọi d là đường thẳng đi qua A đồng thời song song với (P ) và mặt phẳng (Oxy).
h Geogebra Pro Trang 7
https://www.facebook.com/groups/GeoGebraPro/
Khi đó
#»
u
d
⊥
#»
n
(P )
#»
u
d
⊥
#»
n
(Oxy)
⇒
#»
u
d
=
#»
n
(P )
,
#»
n
(Oxy)
= (1; −1; 0).
Vậy d:
x = 2 + t
y = −t
z = −1.
Chọn phương án B
Câu 26. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A cạnh AB = a, SA vuông góc với
mặt đáy và SA = a
√
2. Gọi M là trung điểm của SA, ϕ là góc giữa BM và mặt phẳng (SBC). Tính
sin ϕ.
A sin ϕ =
√
2
2
√
15
. B sin ϕ =
1
√
15
. C sin ϕ =
√
2
√
15
. D sin ϕ =
1
2
√
15
.
Lời giải.
Gọi N là trung điểm của BC, ta có AN ⊥ BC, mà SA ⊥ BC nên
suy ra (SAN) ⊥ BC.
Vậy (SAN) vuông góc (SBC) theo giao tuyến SN, kẻ MH ⊥ SN
tại H, khi đó MH ⊥ (SBC).
Vậy góc giữa BM và (SBC) là góc
÷
MBH.
Ta có AN =
1
2
BC =
a
√
2
2
, SN =
√
SA
2
+ AN
2
=
a
√
10
2
.
Mặt khác ta có 4SHM v 4SAN nên
MH
AN
=
SM
SN
⇒ MH =
AN · SM
SN
=
a
√
10
10
.
A C
B
N
S
M
H
Ta lại có MB =
√
AB
2
+ AM
2
=
a
√
6
2
.
Xét 4MBH, có sin
÷
MBH =
MH
MB
=
1
√
15
.
Chọn phương án B
Câu 27.
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Hàm số y = f(x
2
−2) có
bao nhiêu điểm cực trị?
A 4. B 5. C 3. D 2.
x
y
O 3
−4
2
Lời giải.
Ta có y
0
= 2xf
0
(x
2
− 2).
Cho y
0
= 0 ⇔ 2xf
0
(x
2
− 2) = 0 ⇔
x = 0
x
2
− 2 = 0
x
2
− 2 = 2
⇔
x = 0
x = ±
√
2
x = ±2
.
h Geogebra Pro Trang 8
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Dựa vào đồ thị y = f(x), ta có f
0
(x
2
− 2) > 0 ⇔
x
2
− 2 > 2
x
2
− 2 < 0
⇔
x > 2 ∨ x < −2
−
√
2 < x <
√
2
.
f
0
(x
2
− 2) < 0 ⇔ 0 < x
2
− 2 < 2 ⇔ 2 < x
2
< 4 ⇔
− 2 < x < −
√
2
√
2 < x < 2.
Khi đó, ta có bảng xét dấu
x
2x
f
0
(x
2
− 2)
y
0
−∞
−2
−
√
2
0
√
2
2
+∞
− | − | −
0
+ | + | +
+
0
−
0
+ | +
0
−
0
+
−
0
+
0
−
0
+
0
−
0
+
Dựa vào bảng xét dấu suy ra hàm số có 5 điểm cực trị.
Chọn phương án B
Câu 28. Tìm giá trị m để giá trị nhỏ nhất của hàm số y =
x − m
2
− m
x + 1
trên [0; 1] bằng −2.
A m = −2. B m = 1.
C m = −2 và m = −1. D m = −2 và m = 1.
Lời giải.
Ta có y
0
=
m
2
+ m + 1
(x + 1)
2
> 0, ∀x 6= −1.
Suy ra f(x) đồng biến trên [0; 1] ⇒ min
[0;1]
f(x) = f(0) = −m
2
− m = −2 ⇔
m = −2
m = 1.
Chọn phương án D
Câu 29. Cho các số thực a, b thỏa mãn 1 < a < b và log
a
b + log
b
a
2
= 3. Tính giá trị của biểu thức
T = log
ab
a
2
+ b
2
.
A
1
6
. B
3
2
. C 6. D
2
3
.
Lời giải.
Ta có log
a
b + log
b
a
2
= 3 ⇔ log
a
b + 2 log
b
a = 3. (1)
Đặt t = log
a
b. Do 1 < a < b ⇔ t > log
a
b ⇒ t > 1.
Khi đó (1) trở thành: t +
2
t
= 3 ⇔ t
2
− 3t + 2 = 0 ⇔
t = 1 (không thỏa)
t = 2 (thỏa)
.
Với t = 2 ta có log
a
b = 2 ⇔ b = a
2
.
Suy ra T = log
ab
a
2
+ b
2
= log
a
3
a
2
=
2
3
log
a
a =
2
3
.
Chọn phương án D
Câu 30.
h Geogebra Pro Trang 9
https://www.facebook.com/groups/GeoGebraPro/
Đồ thị sau đây là của hàm số y = x
4
− 3x
2
− 3 . Với giá trị nào
của m thì phương trình x
4
−3x
2
−3 = m có 3 nghiệm phân biệt
O
x
y
−3 −2 −1
1 2
−5
−3
−1
1
2
A m = −4 . B m = −3. C m = 0. D m = −5.
Lời giải.
Phương pháp
Số nghiệm của phương trình đã cho là số giao điểm của đồ thị hàm số y = x
4
− 3x
2
− 3 và đường
thẳng y = m. Dựa vào đồ thị hàm số để xác định m thỏa mãn bài toán.
Cách giải:
Số nghiệm của phương trình đã cho là số giao điểm của đồ thị hàm số y = x
4
− 3x
2
− 3 và đường
thẳng y = m. Dựa vào đồ thị hàm số ta thấy đường thẳng y = m cắt đồ thị hàm số y = x
4
− 3x
2
− 3
tại 3 điểm phân biệt ⇔ m = −3 .
Chọn phương án B
Câu 31. Nghiệm nguyên lớn nhất của bất phương trình log
4
2
x − log
2
1
2
Å
x
3
8
ã
+ 9 log
2
32
x
2
< 4 log
2
2
−1
x
là
A x = 7. B x = 8. C x = 4. D x = 1.
Lời giải.
Điều kiện : x > 0.
log
4
2
x − log
2
1
2
Å
x
3
8
ã
+ 9 log
2
32
x
2
< 4 log
2
2
−1
x
⇔ log
4
2
x −
log
2
x
3
− log
2
8
2
+ 9
log
2
32 − log
2
x
2
< 4 log
2
2
x
⇔ log
4
2
x − (3 log
2
x − 3)
2
+ 9 (5 − 2 log
2
x) − 4 log
2
2
x < 0
⇔ log
4
2
x − 13 log
2
2
x + 36 < 0
⇔ (t
2
− 9)(t
2
− 4) < 0( với t = log
2
x)
⇔
− 3 < t < −2
2 < t < 3
⇔
− 3 < log
2
x < −2
2 < log
2
x < 3
⇔
1
8
< x <
1
4
4 < x < 8.
Vậy nghiệm nguyên lớn nhất của bất phương trình đã cho là x = 7.
Chọn phương án A
h Geogebra Pro Trang 10
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 32. Một hình trụ có chiều cao h và bán kính đáy R. Hình nón có đỉnh là tâm đáy trên của hình
trụ và đáy là hình tròn đáy dưới của hình trụ. Gọi V
1
là thể tích của hình trụ, V
2
là thể tích của hình
nón. Tính tỉ số
V
1
V
2
.
A 2. B 2
√
2. C 3. D
1
3
.
Lời giải.
Hai khối nón và khối trụ có cùng chiều cao h và cùng bán kính đáy bằng r.
Do đó ta có
V
1
V
=
πr
2
h
1
3
πr
2
h
= 3.
O
O
0
Chọn phương án C
Câu 33. Cho hàm số y = f(x) có đạo hàm, liên tục trên R, nhận giá trị dương trên khoảng (0; +∞)
và thỏa mãn f (1) = 1, f
0
(x) = f(x) · (3x
2
+ 2mx + m) với m là tham số. Giá trị của tham số m để
f(3) = e
−4
là
A m = −2. B m =
√
3. C
m = −3. D m = 4.
Lời giải.
Theo giả thiết ta có
f
0
(x)
f(x)
= 3x
2
+ 2mx + m ⇒
Z
f
0
(x)
f(x)
dx =
Z
(3x
2
+ 2mx + m) dx.
Nên ln[f(x)] = x
3
+ mx
2
+ mx + C ⇒ f(x) = e
x
3
+mx
2
+mx+C
.
Do f(1) = 1 ⇒ e
1+2m+C
= 1 ⇒ C = −2m − 1.
Vậy f(x) = e
x
3
+mx
2
+mx−2m−1
⇒ f(3) = e
−4
⇔ e
26+10m
= e
−4
⇔ m = −3.
Chọn phương án C
Câu 34. Cho hình phẳng (H) giới hạn bởi đồ thị các hàm số sau y =
√
x, y = 1 đường thẳng x = 4
(tham khảo hình vẽ). Thể tích khối tròn xoay sinh bởi hình (H) khi quay quanh đường thẳng y = 1
bằng
x
y
O
1
1
x = 4
4
y = 1
A
9
2
π. B
119
6
π. C
7
6
π. D
21
2
π.
Lời giải.
h Geogebra Pro Trang 11
https://www.facebook.com/groups/GeoGebraPro/
Phương pháp: Gắn hệ trục tọa độ mới. Cho hai hàm số
y = f (x), y = g(x) liên tục trên [a; b]. Khi đó thể tích vật
thể tròn xoay giới hạn bởi hai đồ thị số y = f(x), y = g(x)
và hai đường thẳng x = a, x = b khi quay quanh trục Ox là:
V = π
b
Z
a
f
2
(x) − g
2
(x)
dx.
Cách giải: Đặt
X = x − 1
Y = y − 1
. Ta được hệ trục tọa độ OXY như
hình vẽ:
x
y
O
1
1
4
3
X
Y
O
0
Ta có: y =
√
x ⇔ Y + 1 =
√
X + 1 ⇔ Y =
√
X + 1 −1.
Thể tích cần tìm là
V = π
3
Z
0
Ä
√
X + 1 −1
ä
2
dX = π
3
Z
0
Ä
X + 2 −2
√
X + 1
ä
dX
= π
Å
1
2
X
2
+ 2X −
4
3
(X + 1)
√
X + 1
ã
3
0
= π
ïÅ
9
2
+ 6 −
32
3
ã
−
Å
−
4
3
ãò
=
7π
6
.
Chọn phương án C
Câu 35. Cho số phức z 6= 0 thỏa mãn
iz − (3i + 1)z
1 + i
= |z|
2
. Số phức w =
26iz
9
có môđun bằng
A 9. B
√
26. C
√
6. D 5.
Lời giải.
Gọi số phức z có dạng : z = a + bi(a, b ∈ R).
Do z 6= 0 nên a
2
+ b
2
> 0. Ta có:
iz − (3i + 1)z
1 + i
= |z|
2
⇔iz − (3i + 1)z = (1 + i) |z|
2
⇔i(a + bi) − (3i + 1)(a − bi) = (1 + i)(a
2
+ b
2
)
⇔ia − b − 3ai − 3b − a + bi = a
2
+ b
2
+ i(a
2
+ b
2
)
⇔(−a − 4b) + (b − 2a)i = a
2
+ b
2
+ i(a
2
+ b
2
)
⇔
− a − 4b = a
2
+ b
2
b − 2a = a
2
+ b
2
⇔
− a − 4b = b − 2a
− a − 4b = a
2
+ b
2
⇔
a = 5b
− 9b = 26b
2
⇔
a = 5b
b = 0
b = −
9
26
⇔
a = b = 0 (loại)
a = −
45
26
, b = −
9
26
Vậy : w =
26
9
i
Å
−
45
26
−
9
26
i
ã
= 1 − 5i ⇒ |w| =
√
26
Chọn phương án B
h Geogebra Pro Trang 12
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 36. Cho số phức z thỏa |z − 1 + 2i| = 3. Biết rằng tập hợp các điểm biểu diễn của số phức
w = 2z + i trên mặt phẳng (Oxy) là một đường tròn. Tìm tâm của đường tròn đó.
A I (2; −3). B I(1; 1). C I(0; 1). D I(1; 0).
Lời giải.
Gọi M là điểm biểu diễn số phức w.
Ta có w = 2z + i ⇔ z =
w − i
2
.
Do đó |z − 1 + 2i| = 3 ⇔
w − i
2
− 1 + 2i
= 3 ⇔ |w − 2 + 3i| = 6 ⇔ MI = 6, với I (2; −3).
Do đó tập hợp điểm M là đường tròn tâm I (2; −3) và bán kính R = 6.
Chọn phương án A
Câu 37. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α) : x − 2z − 6 = 0 và đường thẳng
d :
x = 1 + t
y = 3 + t
z = −1 − t
. Viết phương trình đường thẳng ∆ nằm trong mặt phẳng (α) cắt đồng thời vuông
góc với d.
A
x − 2
2
=
y − 4
1
=
z + 2
1
. B
x − 2
2
=
y − 4
−1
=
z + 2
1
.
C
x − 2
2
=
y − 3
−1
=
z + 2
1
. D
x − 2
2
=
y − 4
−1
=
z − 2
1
.
Lời giải.
Giao điểm I của d và (α) là nghiệm của hệ
x = 1 + t
y = 3 + t
z = −1 − t
x − 2z − 6 = 0
⇒ I (2; 4; −2).
Mặt phẳng (α) có một vectơ pháp tuyến
#»
n = (1; 0; −2) ; đường thẳng d có một vectơ chỉ phương
#»
u = (1; 1; −1).
Khi đó đường thẳng ∆ có một vectơ chỉ phương là [
#»
n,
#»
u ] = (2; −1; 1).
Đường thẳng ∆ qua điểm I (2; 4; −2) và có một vectơ chỉ phương [
#»
n,
#»
u ] = (2; −1; 1) nên có phương
trình chính tắc:
x − 2
2
=
y − 4
−1
=
z + 2
1
.
Chọn phương án B
Câu 38. Trong không gian Oxyz cho ba đường thẳng d :
x
1
=
y
1
=
z + 1
−2
, ∆
1
:
x − 3
2
=
y
1
=
z − 1
1
,
∆
2
:
x − 1
1
=
y − 2
2
=
z
1
. Đường thẳng ∆ vuông góc với d đồng thời cắt ∆
1
, ∆
2
tương ứng tại H, K sao
cho độ dài HK nhỏ nhất. Biết rằng ∆ có một vectơ chỉ phương
#»
u (h; k; 1). Giá trị h − k bằng
A 0. B 4. C 6. D −2.
Lời giải.
Ta có H ∈ ∆
1
⇔ H(3 + 2t; t; 1 + t); K ∈ ∆
2
⇔ K(1 + m; 2 + 2m; m).
Suy ra
# »
HK = (m − 2t − 2; 2m − t + 2; m − t − 1).
Đường thẳng d có một VTCP là
#»
u
d
= (1; 1; −2).
∆ ⊥ d ⇔
#»
u
d
.
# »
HK = 0 ⇔ m − t + 2 = 0 ⇔ m = t − 2 ⇒
# »
HK = (−t − 4; t − 2; −3).
Ta có HK
2
= (−t − 4)
2
+ (t − 2)
2
+ (−3)
2
= 2(t + 1)
2
+ 27 > 27, ∀t ∈ R.
h Geogebra Pro Trang 13
https://www.facebook.com/groups/GeoGebraPro/
⇒ min HK =
√
27, đạt được khi t = −1.
Khi đó ta có
# »
HK = (−3; −3; −3), suy ra
#»
u (1; 1; 1) ⇒ h = k = 1 ⇒ h − k = 0.
Chọn phương án A
Câu 39. Cho hai hộp, hộp thứ nhất chứa 5 viên bi đỏ và 7 viên bi vàng, hộp thứ hai chứa 3 bi đỏ và
n bi vàng (n ∈ N). Khi chọn ngẫu nhiên mỗi hộp một viên bi, xác suất để chọn được hai bi khác màu
là
7
15
. Số bi vàng trong hộp thứ hai là?
A n = 12. B n = 10. C n = 7. D n = 5.
Lời giải.
Không gian mẫu |Ω| = 12 · (n + 3).
Gọi A là biến cố chọn được hai bi khác màu.
Ta có P(A) =
5n + 7 · 3
12(n + 3)
=
7
15
⇒ n = 7.
Chọn phương án C
Câu 40.
Cho hình hộp chữ nhật ABCD.A
0
B
0
C
0
D
0
có cạnh bằng
AB = 2a, AD = AA
0
= a như hình vẽ. Khoảng cách giữa
hai đường thẳng BD và AD
0
bằng
A a. B
a
2
. C a
√
3. D
2a
3
.
A B
D
C
0
D
0
A
0
C
B
0
Lời giải.
Xét hệ trục tọa độ Oxyz sao cho A(0; 0; 0), B(2a; 0; 0), D(0; a; 0), A
0
(0; 0; a). Ta có D
0
(0; a; a).
Khi đó
# »
BD = (−2a; a; 0),
# »
AD
0
= (0; a; a),
# »
AB = (2a; 0; 0).
Ta có
# »
AD
0
∧
# »
BD = (−a
2
; −2a
2
; 2a
2
), (
# »
AD
0
∧
# »
BD)
# »
AB = −2a
3
.
d (AD
0
, BD) =
(
# »
AD
0
∧
# »
BD)
# »
AB
# »
AD
0
∧
# »
BD
=
2a
3
3a
2
=
2a
3
.
Chọn phương án D
Câu 41. Tìm tất cả các giá trị khác nhau của tham số m để hàm số y =
5
−x
+ 2
5
−x
− m
đồng biến trên
(−∞; 0).
A m < −2. B m ≤ −2. C −2 < m ≤ 1. D −2 < m < 1.
Lời giải.
ĐK: 5
−x
6= m. Đặt t = 5
−x
là hàm nghịch biến trên (−∞; 0) (1), suy ra t ∈ (1; +∞).
Xét hàm số y = f(t) =
t + 2
t − m
, f
0
(t) =
−m − 2
(t − m)
2
.
Do (1), để hàm số y =
5
−x
+ 2
5
−x
− m
đồng biến trên (−∞; 0) thì hàm số f (t) =
t + 2
t − m
nghịch biến trên
h Geogebra Pro Trang 14
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
(1; +∞)
⇔ f
0
(t) < 0, ∀t ∈ (1; +∞) ⇔
− m − 2 < 0
m /∈ (1, +∞)
⇔
m > −2
m ≤ 1
⇔ −2 < m ≤ 1.
Chọn phương án C
Câu 42. Dân số thế giới được tính theo công thức S = A · e
ni
trong đó A là dân số của năm lấy làm
mốc tính, S là dân số sau n năm, i là tỉ lệ tăng dân số hàng năm. Cho biết năm 2005 Việt Nam có
khoảng 80.902.400 người và tỉ lệ tăng dân số là 1, 47% một năm. Như vậy, nếu tỉ lệ tăng dân số hàng
năm không đổi thì đến năm 2019 số dân của Việt Nam sẽ gần với số nào nhất sau đây?
A 99.389.200. B 99.386.600. C 100.861.100. D 99.251.200.
Lời giải.
Áp dụng công thức S = A · e
ni
với A = 80.902.400, n = 2019 − 2005 = 14, i = 1, 47% = 0, 0147, ta có
số dân Việt Nam đến năm 2017 là
S = A · e
ni
= 80902400 · e
14·0,0147
≈ 99389203,38.
Như vậy, số dân Việt Nam đến năm 2019 gần với số 99.389.200 nhất.
Chọn phương án A
Câu 43.
Cho hàm số y = f (x). Hàm số y = f
0
(x)
có bảng biến thiên như sau. Bất phương trình
f(x) > sin x+m có nghiệm trên khoảng (−1; 1)
khi và chỉ khi
A m > f(1) − sin 1.
B m ≥ f(1) − sin 1.
C m ≤ f (−1) + sin 1.
D m < f (−1) + sin 1.
x
y
0
y
−∞
−4
1
+∞
−
0
+
0
−
+∞+∞
−3−3
−1−1
−∞−∞
Lời giải.
Xét hàm số g(x) = f(x) − sin x.
g
0
(x) = f
0
(x) − cos x.
Với ∀x ∈ (−1; 1), ta có f
0
(x) < −1 ⇒ f
0
(x) − cos x < −1 − cos x < 0 ⇒ g
0
(x) < 0.
Suy ra hàm số g(x) nghịch biến trên khoảng (−1; 1) nên g(x) < g (−1) = f (−1) + sin 1.
Do đó bất phương trình f(x) > sin x + m có nghiệm trên khoảng (−1; 1) khi và chỉ khi bất phương
trình m < f(x) − sin x có nghiệm trên khoảng (−1; 1).
⇔ m < max
[−1;1]
g(x) ⇔ m < f (−1) + sin 1.
Vậy m < f (−1) + sin 1.
Chọn phương án D
Câu 44. Hình trụ có bán kính đáy bằng a chu vi của thiết diện qua trục bằng 10a Thể tích của khối
trụ đã cho bằng
A 4πa
3
. B πa
3
. C 3πa
3
. D 5πa
3
.
Lời giải.
h Geogebra Pro Trang 15
https://www.facebook.com/groups/GeoGebraPro/
Thiết diện qua trục là 1 hình chữ nhật.
Giả sử chiều cao của khối trụ là b.
Theo đề ta có 2(2a + b) = 10a ⇔ b = 3a.
Thể tích khối trụ là V = S.h = πa
2
.3a = 3πa
3
.
O
0
O
A
A
0
B
B
0
a
b
Chọn phương án C
Câu 45. Cho hàm số y = f(x) liên tục và thỏa mãn f (x) + 2f
Å
1
x
ã
= 3x với x ∈
ï
1
2
; 2
ò
. Tính
I =
2
Z
1
2
f(x)
x
dx.
A I =
3
2
. B I = −
3
2
. C I =
9
2
. D I = −
9
2
.
Lời giải.
Ta có f(x) + 2f
Å
1
x
ã
= 3x và f
Å
1
x
ã
+ 2f(x) = 3 ·
1
x
. Suy ra f(x) =
2
x
− x.
I =
2
Z
1
2
f(x)
x
dx =
2
Z
1
2
Å
2
x
2
− 1
ã
dx =
3
2
.
Chọn phương án A
Câu 46. Phương trình |x
3
− 3x| = m
2
+ m có 6 nghiệm phân biệt khi và chỉ khi
A m > 0. B m < −2hoặc m > 1.
C −1 < m < 0. D −2 < m < −1 hoặc 0 < m < 1.
Lời giải.
Đồ thị của hàm số y = |x
3
− 3x|.
−2 −1 1 2
1
2
x
y
O
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = |x
3
− 3x| và đường thẳng y = m
2
+m.
Suy ra phương trình có 6 nghiệm phân biệt khi và chỉ khi 0 < m
2
+ m < 2 ⇔
0 < m < 1
− 2 < m < −1.
Chọn phương án D
Câu 47. Cho hai số thực a, b > 1 sao cho tồn tại số thực 0 < x 6= 1 thỏa mãn a
log
b
x
= b
log
a
(x
2
)
. Tìm
giá trị nhỏ nhất của P = ln
2
a + ln
2
b − ln(ab).
A
1
4
. B −
3 + 2
√
2
12
. C
e
2
. D
1 − 3
√
3
4
.
Lời giải.
h Geogebra Pro Trang 16
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Ta có
a
log
b
x
= b
log
a
(x
2
)
⇒ x
log
b
a
= (x
2
)
log
a
b
⇒ log
b
a = 2 · log
a
b
⇔
ln a
ln b
= 2 ·
ln b
ln a
⇔ ln
2
a = 2 · ln
2
b
⇒ ln a =
√
2 ln b, (vì a, b > 1).
Ta được
P = ln
2
a + ln
2
b − ln(ab)
= 3 ln
2
b −
Ä
1 +
√
2
ä
ln b
=
Ç
√
2 ln b −
1 +
√
2
2
√
3
å
2
−
Ä
1 +
√
2
ä
2
12
≥ −
3 + 2
√
2
12
.
Chọn phương án B
Câu 48. Có bao nhiêu giá trị nguyên của tham số m để max
[1;3]
|x
3
− 3x
2
+ m| ≤ 4?
A 5. B 4. C 6. D Vô số.
Lời giải.
Xét hàm số f(x) = x
3
− 3x
2
+ m trên [1; 3], f
0
(x) = 0 ⇔ 3x
2
− 6x = 0 ⇔
x = 0 /∈ (1; 3)
x = 2 ∈ (1; 3) .
Bảng biến thiên
x
f
0
(x)
f(x)
1 2 3
−
0
+
m − 2m − 2
m − 4m − 4
mm
Vì m − 4 < m − 2 < m nên max
[1;3]
|f(x)| ≤ 4 ⇔
|m| ≤ 4
|m − 4| ≤ 4
⇔
− 4 ≤ m ≤ 4
0 ≤ m ≤ 8
⇔ 0 ≤ m ≤ 4.
⇒ m ∈ {0; 1; 2; 3; 4}.
Chọn phương án A
Câu 49. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC), góc giữa đường
thẳng SB và mặt phẳng (ABC) bằng 60
◦
. Khoảng cách giữa hai đường thẳng AC và SB bằng:
A
a
√
2
2
. B 2a. C
a
√
15
5
. D R =
a
√
7
7
.
Lời giải.
h Geogebra Pro Trang 17
https://www.facebook.com/groups/GeoGebraPro/
SA ⊥ (ABC) ⇒AB là hình chiếu vuông góc của SB lên
(ABC)
Suy ra
¤
(SB, (ABC)) =
Ÿ
(SB, AB) =
’
SBA = 60
◦
⇒ SA = AB. tan 60
◦
= a
√
3
Lấy điểm D sao cho ACBD là hình bình hành.
Dựng
AK ⊥ BD tại K
AH ⊥ SK tại H
Ta có
BK ⊥ AK
BK ⊥ SA
⇒ BK ⊥ (SAK)⇒ BK ⊥ AH
Từ đó AH ⊥ (SBK)
C
BK
H
S
MA
D
Vì
BK k AC
BK ⊂ (SBK)
AC 6⊂ (SBK)
⇒ AC k (SBK) ⇒ d (AC, SB) = d (A, (SBK)) = AH
Gọi M là trung điểm AC⇒ BM = AK =
a
√
3
2
(với BM đường cao trong 4ABC đều cạnh a).
Xét tam giác SAK vuông tại A ta có:
1
AH
2
=
1
AK
2
+
1
SA
2
=
5
3a
2
⇒ AH =
a
√
15
5
Vậy d (AC, SB) =
a
√
15
5
Chọn phương án C
Câu 50. Cho hàm số y = f(x), biết hàm số y = f
0
(x) có đồ thị như hình bên dưới.
x
y
O
−1−6
2
Hàm số g(x) = f (3 − x
2
) đồng biến trên khoảng?
A (2; 3). B (−1; 0). C (−2; −1). D (0; 1).
Lời giải.
Dựa vào đồ thị, ta có bảng xét dấu
x
y
0
−∞
−6 −1
2
+∞
−
0
+
0
−
0
+
g
0
(x) = −2xf
0
(3 − x
2
).
h Geogebra Pro Trang 18
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
g(x) = 0 ⇔
− 2x = 0
f
3 − x
2
= 0
⇔
x = 0
x = ±3
x = ±2
x = ±1.
f (3 − x
2
) > 0 ⇔
− 6 < 3 − x
2
< −1
2 < 3 − x
2
⇔
− 3 < x < −2
2 < x < 3
− 1 < x < 1.
Bảng biến thiên:
x
f
0
(3 −
x
2
)
−2x
g
0
−∞
−3 −2 −1
0 1 2 3
+∞
−
0
+
0
−
0
+ | +
0
−
0
+
0
−
+ | + | + | +
0
− | − | − | −
−
0
+
0
−
0
+
0
−
0
+
0
−
0
+
Từ BBT suy ra hàm số đồng biến trên (−1; 0).
Chọn phương án B
———————–HẾT———————–
h Geogebra Pro Trang 19
https://www.facebook.com/groups/GeoGebraPro/
BẢNG ĐÁP ÁN
1. D 2. C 3. D 4. A 5. A 6. C 7. A 8. B 9. D 10. D
11. D 12. D 13. A 14. A 15. C 16. A 17. C 18. D 19. B 20. A
21. C 22. D 23. D 24. B 25. B 26. B 27. B 28. D 29. D 30. B
31. A 32. C 33. C 34. C 35. B 36. A 37. B 38. A 39. C 40. D
41. C 42. A 43. D 44. C 45. A 46. D 47. B 48. A 49. C 50. B
h Geogebra Pro Trang 20
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 9
Câu 1. Một trường cấp ba của tỉnh X có 8 giáo viên Toán gồm có 3 nữ và 5 nam, giáo viên Vật lý thì
có 4 giáo viên nam. Hỏi có bao nhiêu cách chọn ra một đoàn thanh tra công tác ôn thi TNTHPT gồm
3 người có đủ 2 môn Toán và Vật lý và phải có giáo viên nam và giáo viên nữ trong đoàn?
A 120 cách. B 60 cách. C 12960 cách. D 90 cách.
Câu 2. Cho cấp số cộng có tổng n số hạng đầu là S
n
= 3n
2
+ 4n, n ∈ N
∗
. Giá trị của số hạng thứ 10
của cấp số cộng là
A u
10
= 55. B u
10
= 67. C u
10
= 61. D u
10
= 59.
Câu 3. Phương trình 7
2x
2
+6x+4
= 49 có tổng tất cả các nghiệm bằng
A 1. B
5
2
. C −1. D −
5
2
.
Câu 4. Hình lập phương có độ dài đường chéo là 6 thì có thể tích là
A 2
√
2. B 54
√
2. C 24
√
3. D 8.
Câu 5. Tìm tập xác định D của hàm số y =
p
log(x + 1) − 1.
A D = (10; +∞). B D = (9; +∞). C D = (−∞; 9). D D = R \ {−1}.
Câu 6. Hàm số F (x) = x
2
ln (sin x − cos x) là nguyên hàm của hàm số nào dưới đây?
A f (x) =
x
2
sin x − cos x
.
B f (x) = 2x ln (sin x − cos x) +
x
2
sin x − cos x
.
C f (x) = 2x ln (sin x − cos x) +
x
2
(cos x + sin x)
sin x − cos x
.
D f (x) =
x
2
(sin x + cosx)
sin x − cos x
.
Câu 7. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, tam giác SAB đều và nằm trong
mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC.
A V =
a
3
8
. B V =
a
3
√
3
3
. C V =
a
3
√
3
4
. D V =
a
3
4
.
Câu 8. Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a. Thể tích của khối nón đã
cho bằng
A
√
3πa
3
3
. B
√
3πa
3
2
. C
2πa
3
3
. D
πa
3
3
.
Câu 9. Cho mặt cầu (S) có diện tích bằng 4a
2
π cm
2
. Tính thể tích khối cầu (S).
A 16a
3
π cm
3
. B 32a
3
π cm
3
. C
4a
3
π
3
cm
3
. D
16a
3
π
3
cm
3
.
Câu 10.
h Geogebra Pro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Cho hàm số y = f(x) có bảng biến thiên
như hình vẽ bên. Hàm số đã cho đồng biến
trên khoảng nào dưới đây?
A (−1; +∞). B (−1; 1).
C (−∞; 1). D (1; +∞).
x
y
0
y
−∞
−1
1
+∞
+
0
−
0
+
−∞−∞
33
−2−2
+∞+∞
Câu 11. Cho a là số thực dương khác 1. Tính T = log
a
a
3
√
a.
A T =
1
3
. B T =
3
4
. C T =
4
3
. D T =
1
4
.
Câu 12. Một hình trụ có bán kính đáy a, có thiết diện qua trục là một hình vuông. Tính diện tích
xung quang của hình trụ.
A 3πa
2
. B 4πa
2
. C 2πa
2
. D πa
2
.
Câu 13. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số
x
y
0
y
−∞
−2
0 2
+∞
−
0
+
0
−
0
+
A 3. B 0. C 1. D 2.
Câu 14. Phương trình tiếp tuyến của đồ thị hàm số y = x
3
− 3x
2
− x + 3 tại điểm M(1; 0) là
A y = −x + 1. B y = −4x − 4. C y = −4x + 4. D y = −4x + 1.
Câu 15.
Cho hàm số y = f(x) có bảng biến thiên như sau.
Tổng số tiệm cận ngang và tiệm cận đứng của đồ
thị hàm số đã cho là
A 4. . B 1.
C 3. D 2.
x
f(x)
−∞
1
+∞
22
+∞
3
55
Câu 16. Tìm tập nghiệm của bất phương trình log
25
(x + 1) >
1
2
.
A S = (−4; +∞). B S = (−∞; 4). C S = (−1; 4). D S = (4; +∞).
Câu 17.
Cho hàm số y = f (x) có đồ thị hàm số như hình bên. Phương trình
f(x) = 1 có bao nhiêu nghiệm thực phân biệt nhỏ hơn 2?
O
x
y
−1 2
−2
2
A 0. B 1. C 2. D 3.
h Geogebra Pro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 18. Nếu
π
2
Z
π
4
sin x − cos x
√
1 + sin 2x
dx =
a
b
ln c, (với a, b, c ∈ Z, a > 0,
a
b
là phân số tối giản) thì a + 2b + 3c
là
A 13. B 14. C 9. D 11.
Câu 19.
Điểm M trong hình vẽ bên là điểm biểu diễn số phức z. Tìm phần
thực và phần ảo của số phức z.
A Phần thực là −2 và phần ảo là i.
B Phần thực là 1 và phần ảo là −2.
C Phần thực là 1 và phần ảo là −2i.
D Phần thực là −2 và phần ảo là 1.
x
y
O
1
−2
M
Câu 20. Trong mặt phẳng tọa độ Oxyz, tập hợp các điểm biểu biễn các số phức z thỏa mãn |z − 1 + 2i| =
|z + 1 + 2i| là đường thẳng có phương trình.
A x − 2y + 1 = 0. B x + 2y = 0. C x − 2y = 0. D x + 2y + 1 = 0.
Câu 21. Cho số phức z thoả mãn z − 4 = (1 + i)|z| − (4 + 3z)i. Môđun của số phức z bằng
A 2. B 1. C 16. D 4.
Câu 22. Trong không gian với hệ trục Oxyz, cho điểm M (3; 2; −1). Gọi A, B lần lượt là hình chiếu
vuông góc của điểm M lên trục Oy, Oz. Tính diện tích tam giác OAB.
A
3
2
. B
1
2
. C 1. D 2.
Câu 23. Trong không gian Oxyz, cho mặt cầu (S) tâm I nằm trên mặt phẳng (Oxy) đi qua ba điểm
A(1; 2; −4), B(1; −3; 1), C(2; 2; 3). Tìm tọa độ điểm I.
A I(2; −1; 0). B I(0; 0; 1). C I(0; 0; −2). D I(−2; 1; 0).
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1; 0; 0), B(0; −1; 0) và C(0; 0; 2). Phương
trình mặt phẳng (ABC) là
A x − 2y + z = 0. B x − y +
z
2
= 1. C x +
y
2
− z = 1. D 2x − y + z = 0.
Câu 25. Trong không gian Oxyz, cho điểm M(3; 2; −1) và mặt phẳng (P ): x +z −2 = 0. Đường thẳng
đi qua M và vuông góc với (P ) có phương trình là
A
x = 3 + t
y = 2
z = −1 + t
. B
x = 3 + t
y = 2 + t
z = −1
. C
x = 3 + t
y = 2t
z = 1 − t
. D
x = 3 + t
y = 1 + 2t
z = −t
.
Câu 26. Cho hình lập phương ABCD.A
0
B
0
C
0
D
0
. Tính góc giữa hai mặt phẳng (A
0
B
0
C) và (C
0
D
0
A).
A 45
◦
. B 30
◦
. C 60
◦
. D 90
◦
.
Câu 27. Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau
x
f
0
(x)
−∞
−2
0 1 3
+∞
+
0
−
0
+
0
−
0
−
h Geogebra Pro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
Hàm số đã cho có bao nhiêu điểm cực trị?
A 3. B 1. C 2. D 4.
Câu 28. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x +
√
4 − x
2
. Hãy
tính P = M + m.
A P = 2
Ä
√
2 − 1
ä
. B P = 2
Ä
√
2 + 1
ä
. C P =
√
2 + 1. D P =
√
2 − 1.
Câu 29. Cho a > 0, b > 0 thỏa mãn a
2
+ 4b
2
= 5ab. Khẳng định nào sau đây đúng?
A 2 log(a + 2b) = 5(log a + log b). B log(a + 1) + log b = 1.
C 2 log
a + 2b
3
=
log a + log b
2
. D log(a + 2b) = log a − log b.
Câu 30. Cho hàm số y = f (x) có đồ thị như hình vẽ bên.
x
y
O
−1 1
4
2
Phương trình |f(x − 2) − 2| = π có bao nhiêu nghiệm thực phân biệt?
A 4. B 2. C 6. D 3.
Câu 31. Tập nghiệm của bất phương trình log
2
Ä
1 + log
1
9
x − log
9
x
ä
< 1 có dạng S =
Å
1
a
; b
ã
với a, b
là những số nguyên. Mệnh đề nào dưới đây đúng?
A a = −b. B a + b = 1. C a = b. D a = 2b.
Câu 32. Cho hình nón tròn xoay có đường cao bằng 20 cm, bán kính đáy bằng 25 cm. Một thiết diện
đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiến diện là 12 cm.
Tính diện tích của thiết diện đó.
A 500 cm
2
. B 1000 cm
2
. C 250 cm
2
. D 250 cm
3
.
Câu 33. Cho hàm số f (x) xác định trên (0; +∞) và thỏa mãn xf
0
(x) = −[f(x)]
2
· ln x; f (1) = 1. Giá
trị f(e) bằng
A
2
3
. B
e
2
. C
2e
3
. D
1
2
.
Câu 34. Cho hình phẳng D được giới hạn bởi hai đường y = 2(x
2
−1); y = 1 − x
2
. Tính thể tích khối
tròn xoay tạo thành do D quay quanh trục Ox.
A
64π
15
. B
32
15
. C
32π
15
. D
64
15
.
Câu 35. Cho số phức z = a + bi (a, b ∈ R) thỏa mãn |z| = 5 và z(2 + i)(1 − 2i) là một số thực. Tính
P = |a| + |b|.
A P = 8. B P = 4. C P = 5. D P = 7.
Câu 36. Tìm mô-đun của số phức z biết z − 4 = (1 + i) |z| − (4 + 3z) i.
h Geogebra Pro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
A |z| =
1
2
. B |z| = 2. C |z| = 4. D |z| = 1.
Câu 37. Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng (d) :
x + 1
2
=
y − 1
1
=
z − 2
3
và
mặt phẳng (P ) : x − y − z − 1 = 0. Viết phương trình đường thẳng (∆) đi qua điểm A(1; 1; −2), biết
(∆) k (P ) và (∆) cắt (d).
A
x − 1
1
=
y − 1
−1
=
z + 2
−1
. B
x − 1
2
=
y − 1
1
=
z + 2
3
.
C
x − 1
8
=
y − 1
3
=
z + 2
5
. D
x − 1
2
=
y − 1
1
=
z + 2
1
.
Câu 38. Trong không gian Oxyz cho hai đường thẳng d
1
:
x
1
=
y + 4
1
=
z − 3
−1
và d
2
:
x − 1
−2
=
y + 3
1
=
z − 4
−5
. Đường thẳng vuông góc với mặt phẳng tọa độ (Oxz) và cắt d
1
và d
2
có phương trình là
A
x = 1
y = −1 + t
z = −1
. B
x =
3
7
y =
−25
7
+ t
z =
18
7
. C
x = 1
y = −3 + t
z = 4
. D
x = t
y = −4 + t
z = 3 + t
.
Câu 39. Cho hai chiếc hộp A và B. Hộp A chứa 6 viên bi trắng, 4 viên bi đen. Hộp B chứa 7 viên
bi trắng, 3 viên bi đen. Người ta lấy ngẫu nhiên một viên bi từ hộp A và bỏ vào hộp B rồi sau đó từ
hộp B lấy ngẫu nhiên ra hai viên bi. Tính xác suất để hai viên bi lấy được từ hộp B là hai viên bi
trắng.
A
126
275
. B
21
55
. C
123
257
. D
37
83
.
Câu 40. Cho hình chóp S.ABC có SA = 3a và SA ⊥ (ABC). Biết AB = BC = 2a và
’
ABC = 120
◦
.
Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng
A
3a
2
. B
a
2
. C a. D 2a.
Câu 41. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (−2019; 2019) để hàm số
y = sin
3
x − 3 cos
2
x − m sin x − 1 đồng biến trên đoạn
h
0;
π
2
i
?
A 2020. B 2019. C 2028. D 2018.
Câu 42. Một người mỗi tháng đều đặn gửi vào một ngân hàng một khoản tiền T theo hình thức lãi
kép với lãi suất 0,6% mỗi tháng. Biết sau 15 tháng người đó có số tiền là 10 triệu đồng. Hỏi số tiền T
gần với số tiền nào nhất sau đây?
A 635.000 đồng. B 645.000 đồng. C 613.000 đồng. D 535.000 đồng.
Câu 43.
Cho hàm số y = f(x) xác định trên R \{0} có bảng biến
thiên như hình vẽ bên. Số nghiệm của phương trình
2 |f (2x − 3)| − 13 = 0 là
A 3. B 2. C 4. D 1.
x
y
0
y
−∞
−2
0
+∞
−
0
+ +
+∞+∞
77
+∞
−∞
+∞+∞
Câu 44. Cho hình trụ có bán kính đáy bằng a và chiều cao h. Tính thể tích V của khối lăng trụ tam
giác đều tam giác đều nội tiếp hình trụ đã cho.
A V =
√
3a
2
h
4
. B V =
3
√
3a
2
h
4
.
h Geogebra Pro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
C V =
π
3
Å
h
2
+
4a
2
3
ã
…
h
2
4
+
a
2
3
. D V =
3
√
3πa
2
h
4
.
Câu 45. Cho hàm số f(x), f(−x) liên tục trên R và thỏa mãn 2f(x) + 3f (−x) =
1
4 + x
2
. Tính
I =
2
Z
−2
f(x) dx.
A
π
20
. B
π
10
. C −
π
20
. D −
π
10
.
Câu 46. Cho hàm số y = f (x) có bảng biến thiên như sau:
x
y
0
y
−∞
−1
3
+∞
+
0
−
0
+
−∞−∞
55
11
+∞+∞
Phương trình f (x) − 2 = 0 có bao nhiêu nghiệm?
A 1. B 3. C 2. D 0 .
Câu 47. Cho x, y là hai số thực dương thỏa mãn ln x + ln y ≥ ln(x
2
+ y). Tìm giá trị nhỏ nhất của
P = x + y.
A P = 2 + 3
√
2. B P = 6. C P = 2
√
2 + 3. D P =
√
17 +
√
3.
Câu 48. Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị nhỏ nhất của hàm số
y =
sin
4
x + cos 2x + m
bằng 2. Số phần tử của S là
A 4. B 3. C 1. D 2.
Câu 49. Cho hình hộp ABCD.A
0
B
0
C
0
D
0
có đáy là hình thoi cạnh a
√
3, BD = 3a, hình chiếu vuông
góc của B trên mặt phẳng (A
0
B
0
C
0
D
0
) trùng với trung điểm của A
0
C
0
. Gọi (α) là góc tạo bởi hai mặt
phẳng (ABCD) và (CDD
0
C
0
), cos α =
√
21
7
. Tính thể tích khối hộp.
A
3a
3
4
. B
9
√
3a
3
4
. C
9a
3
4
. D
3
√
3a
3
4
.
Câu 50. Có bao nhiêu số nguyên m ∈ (−7; 7) để đồ thị hàm số y = |x
4
− 3mx
2
− 4| có đúng 3 điểm
cực trị A, B, C và diện tích tam giác ABC lớn hơn 4.
A 4. B 2. C 1. D 3.
———————–HẾT———————–
h Geogebra Pro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
BẢNG ĐÁP ÁN
1. D 2. C 3. D 4. C 5. B 6. C 7. A 8. A 9. C 10. D
11. C 12. C 13. A 14. C 15. C 16. D 17. C 18. D 19. B 20. C
21. A 22. C 23. D 24. B 25. A 26. D 27. A 28. A 29. C 30. B
31. C 32. A 33. A 34. A 35. D 36. B 37. C 38. B 39. A 40. A
41. B 42. A 43. B 44. B 45. A 46. B 47. C 48. D 49. C 50. C
h Geogebra Pro Trang 7
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 9
Câu 1. Một trường cấp ba của tỉnh X có 8 giáo viên Toán gồm có 3 nữ và 5 nam, giáo viên Vật lý thì
có 4 giáo viên nam. Hỏi có bao nhiêu cách chọn ra một đoàn thanh tra công tác ôn thi TNTHPT gồm
3 người có đủ 2 môn Toán và Vật lý và phải có giáo viên nam và giáo viên nữ trong đoàn?
A 120 cách. B 60 cách. C 12960 cách. D 90 cách.
Lời giải.
TH1: Đoàn công tác gồm 2 giáo viên Toán và 1 giáo viên Vật lý.
Trường hợp này có C
1
4
C
1
3
C
1
5
+ C
1
4
C
2
3
= 72.
TH2: Đoàn công tác gồm 2 giáo viên Vật lý và 1 giáo viên Toán. Trường hợp này có C
2
4
C
1
3
= 18.
Vậy có 72 + 18 = 90 cách chọn một đoàn công tác thỏa mãn yêu cầu.
Chọn phương án D
Câu 2. Cho cấp số cộng có tổng n số hạng đầu là S
n
= 3n
2
+ 4n, n ∈ N
∗
. Giá trị của số hạng thứ 10
của cấp số cộng là
A u
10
= 55. B u
10
= 67. C u
10
= 61. D u
10
= 59.
Lời giải.
Ta có S
1
= 7 ⇒ u
1
= 7.
S
2
= 3(2)
2
+ 4(2) = 20 ⇒ u
1
+ u
2
= 20 ⇒ u
2
= 13.
Do đó công sai d = 6. Khi đó u
10
= u
1
+ 9d = 7 + 9 · 6 = 61.
Chọn phương án C
Câu 3. Phương trình 7
2x
2
+6x+4
= 49 có tổng tất cả các nghiệm bằng
A 1. B
5
2
. C −1. D −
5
2
.
Lời giải.
Phương trình đã cho tương đương với
7
2x
2
+6x+4
= 7
2
⇔ 2x
2
+ 5x + 4 = 2 ⇔
x = −
1
2
x = −2.
Vậy tổng tất cả các nghiệm bằng −
1
2
− 2 = −
5
2
.
Chọn phương án D
Câu 4. Hình lập phương có độ dài đường chéo là 6 thì có thể tích là
A 2
√
2. B 54
√
2. C 24
√
3. D 8.
Lời giải.
Phương pháp:
Sử dụng công thức hình lập phương cạnh a có độ dài đường chéo chính là a
√
3.
Thể tích hình lập phương cạnh a là V = a
3
.
h Geogebra Pro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Cách giải:
Gọi độ dài cạnh hình lập phương là a, (a > 0) thì độ dài đường chéo hình lập phương là a
√
3 = 6 ⇔
a = 2
√
3.
Thể tích hình lập phương là V =
Ä
2
√
3
ä
3
= 24
√
3.
Chọn phương án C
Câu 5. Tìm tập xác định D của hàm số y =
p
log(x + 1) − 1.
A D = (10; +∞). B D = (9; +∞). C D = (−∞; 9). D D = R \ {−1}.
Lời giải.
Điều kiện:
x + 1 > 0
log(x + 1) − 1 ≥ 0
⇔
x + 1 > 0
log(x + 1) ≥ 1
⇔
x + 1 > 0
x + 1 ≥ 10
⇔ x ≥ 9.
Vậy D = (9; +∞).
Chọn phương án B
Câu 6. Hàm số F (x) = x
2
ln (sin x − cos x) là nguyên hàm của hàm số nào dưới đây?
A f (x) =
x
2
sin x − cos x
.
B f (x) = 2x ln (sin x − cos x) +
x
2
sin x − cos x
.
C f (x) = 2x ln (sin x − cos x) +
x
2
(cos x + sin x)
sin x − cos x
.
D f (x) =
x
2
(sin x + cosx)
sin x − cos x
.
Lời giải.
Vì F (x) là một nguyên hàm của f (x) nên
f (x) = F
0
(x) = 2x · ln (sin x − cos x) + x
2
·
(sin x − cos x)
0
sin x − cos x
= 2x · ln (sin x − cos x) + x
2
·
sin x + cos x
sin x − cos x
.
Chọn phương án C
Câu 7. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, tam giác SAB đều và nằm trong
mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC.
A V =
a
3
8
. B V =
a
3
√
3
3
. C V =
a
3
√
3
4
. D V =
a
3
4
.
Lời giải.
Gọi H là trung điểm AB, suy ra SH⊥(ABCD).
Ta có V
S.ABC
=
1
3
× SH × S
∆ABC
=
1
3
×
a
√
3
2
×
a
2
√
3
4
=
a
3
8
.
Chọn phương án A
Câu 8. Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a. Thể tích của khối nón đã
cho bằng
A
√
3πa
3
3
. B
√
3πa
3
2
. C
2πa
3
3
. D
πa
3
3
.
Lời giải.
Chiều cao h =
p
(2a)
2
− a
2
= a
√
3.
Thể tích V =
1
3
Bh =
1
3
πa
2
a
√
3 =
√
3πa
3
3
.
Chọn phương án A
h Geogebra Pro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 9. Cho mặt cầu (S) có diện tích bằng 4a
2
π cm
2
. Tính thể tích khối cầu (S).
A 16a
3
π cm
3
. B 32a
3
π cm
3
. C
4a
3
π
3
cm
3
. D
16a
3
π
3
cm
3
.
Câu 10.
Cho hàm số y = f(x) có bảng biến thiên
như hình vẽ bên. Hàm số đã cho đồng biến
trên khoảng nào dưới đây?
A (−1; +∞). B (−1; 1).
C (−∞; 1). D (1; +∞).
x
y
0
y
−∞
−1
1
+∞
+
0
−
0
+
−∞−∞
33
−2−2
+∞+∞
Lời giải.
Từ bảng biến thiên ta thấy y
0
> 0, ∀x > 1 suy ra hàm số đồng biến trên khoảng (1; +∞).
Chọn phương án D
Câu 11. Cho a là số thực dương khác 1. Tính T = log
a
a
3
√
a.
A T =
1
3
. B T =
3
4
. C T =
4
3
. D T =
1
4
.
Lời giải.
Ta có T = log
a
a
1+
1
3
= log
a
a
4
3
=
4
3
.
Chọn phương án
C
Câu 12. Một hình trụ có bán kính đáy a, có thiết diện qua trục là một hình vuông. Tính diện tích
xung quang của hình trụ.
A 3πa
2
. B 4πa
2
. C 2πa
2
. D πa
2
.
Lời giải.
Ta có r = a và l = h = 2r = 2a.
Khi đó, diện tích xung quanh hình trụ là
S
xq
= 2πrl = 2π · a · 2a = 4πa
2
.
Chọn phương án C
Câu 13. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số
x
y
0
y
−∞
−2
0 2
+∞
−
0
+
0
−
0
+
A 3. B 0. C 1. D 2.
Lời giải.
Từ bảng biến thiên, ta suy ra hàm số có 3 điểm cực trị.
Chọn phương án A
Câu 14. Phương trình tiếp tuyến của đồ thị hàm số y = x
3
− 3x
2
− x + 3 tại điểm M(1; 0) là
A y = −x + 1. B y = −4x − 4. C y = −4x + 4. D y = −4x + 1.
Lời giải.
h Geogebra Pro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
Ta có y
0
= 3x
2
− 6x − 1 ⇒ y
0
(1) = −4.
Phương trình tiếp tuyến của đồ thị hàm số tại điểm M(1; 0) là y = −4(x − 1) ⇔ y = −4x + 4.
Chọn phương án C
Câu 15.
Cho hàm số y = f(x) có bảng biến thiên như sau.
Tổng số tiệm cận ngang và tiệm cận đứng của đồ
thị hàm số đã cho là
A 4. . B 1.
C 3. D 2.
x
f(x)
−∞
1
+∞
22
+∞
3
55
Lời giải.
lim
x→−∞
y = 2 ⇒ y = 2 là tiệm cận ngang
lim
x→+∞
y = 5 ⇒ y = 5 là tiệm cận ngang
lim
x→1
+
y = +∞ ⇒ x = 1 là tiệm cận đứng
Vậy tổng số tiệm cận ngang và tiệm cận đứng là 3.
Chọn phương án C
Câu 16. Tìm tập nghiệm của bất phương trình log
25
(x + 1) >
1
2
.
A S = (−4; +∞). B S = (−∞; 4). C S = (−1; 4). D S = (4; +∞).
Lời giải.
Ta có: log
25
(x + 1) >
1
2
⇔ x + 1 > 25
1
2
⇔ x > 4.
Chọn phương án D
Câu 17.
Cho hàm số y = f (x) có đồ thị hàm số như hình bên. Phương trình
f(x) = 1 có bao nhiêu nghiệm thực phân biệt nhỏ hơn 2?
O
x
y
−1 2
−2
2
A 0. B 1. C 2. D 3.
Lời giải.
Phương pháp
Số nghiệm của phương trình f(x) = 1 là số giao điểm của đồ thị hàm số y = f (x) và đường thẳng
y = 1.
Dựa vào đồ thị hàm số để biện luận số nghiệm của phương trình.
Cách giải:
Số nghiệm của phương trình f(x) = 1 là số giao điểm của đồ thị hàm số y = f (x) và đường thẳng
y = 1.
Dựa vào đồ thị hàm số ta thấy đường thẳng y = 1 cắt đồ thị hàm số y = f (x) tại 3 điểm phân biệt
trong đó có hai điểm có hoành độ nhỏ hơn 2.
h Geogebra Pro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Chọn phương án C
Câu 18. Nếu
π
2
Z
π
4
sin x − cos x
√
1 + sin 2x
dx =
a
b
ln c, (với a, b, c ∈ Z, a > 0,
a
b
là phân số tối giản) thì a + 2b + 3c
là
A 13. B 14. C 9. D 11.
Lời giải.
Có
√
1 + sin 2x =
p
(sin x + cos x)
2
= sin x + cos x, vì x ∈
h
π
4
;
π
2
i
. Suy ra
π
2
Z
π
4
sin x − cos x
√
1 + sin 2x
dx =
π
2
Z
π
4
sin x − cos x
sin x + cos x
dx
= −
π
2
Z
π
4
d(sin x + cos x)
sin x + cos x
= − ln |sin x + cos x||
π
2
π
4
= −
Ä
ln 1 − ln
√
2
ä
=
1
2
ln 2.
Suy ra a = 1, b = 2, c = 2. Vậy a + 2b + 3c = 11.
Chọn phương án D
Câu 19.
Điểm M trong hình vẽ bên là điểm biểu diễn số phức z. Tìm phần
thực và phần ảo của số phức z.
A Phần thực là −2 và phần ảo là i.
B Phần thực là 1 và phần ảo là −2.
C Phần thực là 1 và phần ảo là −2i.
D Phần thực là −2 và phần ảo là 1.
x
y
O
1
−2
M
Lời giải.
Điểm M có tọa độ M (1; −2) nên z = 1 − 2i.
Vậy phần thực là 1 và phần ảo là −2.
Chọn phương án B
Câu 20. Trong mặt phẳng tọa độ Oxyz, tập hợp các điểm biểu biễn các số phức z thỏa mãn |z − 1 + 2i| =
|z + 1 + 2i| là đường thẳng có phương trình.
A x − 2y + 1 = 0. B x + 2y = 0. C x − 2y = 0. D x + 2y + 1 = 0.
Lời giải.
Đặt z = x + yi (x, y ∈ R) ⇒ z = x − yi và M(x; y) là điểm biểu diễn của số phức z.
h Geogebra Pro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
Ta có:
|z − 1 + 2i| = |z + 1 + 2i|
⇔ |x + yi − 1 + 2i| = |x − yi + 1 + 2i|
⇔ |(x − 1) + (y + 2)i| = |(x + 1) + (2 − y)i|
⇔
»
(x − 1)
2
+ (y + 2)
2
=
»
(x + 1)
2
+ (2 − y)
2
⇔ x
2
− 2x + 1 + y
2
+ 4y + 4 = x
2
+ 2x + 1 + y
2
− 4y + 4
⇔ x − 2y = 0.
Vậy tập hợp các điểm biểu biễn các số phức z thỏa mãn yêu cầu bài toán là đường thẳng có phương
trình là x − 2y = 0.
Chọn phương án C
Câu 21. Cho số phức z thoả mãn z − 4 = (1 + i)|z| − (4 + 3z)i. Môđun của số phức z bằng
A 2. B 1. C 16. D 4.
Lời giải.
Đặt z = a + bi. Khi đó ta có
a + bi − 4 = (1 + i)
√
a
2
+ b
2
− (4 + 3a + 3bi)i
⇔ a − 4 + bi =
√
a
2
+ b
2
+ i
√
a
2
+ b
2
− (4 + 3a)i + 3b
⇔ a − 3b −
√
a
2
+ b
2
− 4 + (b −
√
a
2
+ b
2
+ 3a + 4)i = 0
⇔
a − 3b −
√
a
2
+ b
2
− 4 = 0
3a + b −
√
a
2
+ b
2
+ 4 = 0
⇔
a − 3b −
√
a
2
+ b
2
− 4 = 0
2a + 4b + 8 = 0
⇔
− 2b − 4 − 3b −
»
(−2b − 4)
2
+ b
2
− 4 = 0
a = −2b − 4
⇔
»
(−2b − 4)
2
+ b
2
= 5b + 8
a = −2b − 4
⇔
5b
2
+ 16b + 16 = 25b
2
+ 80b + 64
a = −2b − 4
⇔
20b
2
+ 64b + 48 = 0
a = −2b − 4
⇔
b = −
6
5
a = −
8
5
b = −2
a = 0
.
Với cả hai trường hợp ta đều có |z| =
√
a
2
+ b
2
= 2.
h Geogebra Pro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Chọn phương án A
Câu 22. Trong không gian với hệ trục Oxyz, cho điểm M (3; 2; −1). Gọi A, B lần lượt là hình chiếu
vuông góc của điểm M lên trục Oy, Oz. Tính diện tích tam giác OAB.
A
3
2
. B
1
2
. C 1. D 2.
Lời giải.
Hình chiếu vuông góc của điểm M (3; 2; −1) lên trục Oy là điểm A (0; 2; 0) .
Hình chiếu vuông góc của điểm M (3; 2; −1) lên trục Oz là điểm B (0; 0; −1) .
Vậy diện tích tam giác vuông OAB là S =
1
2
· OA · OB =
1
2
· 2 · 1 = 1.
Chọn phương án C
Câu 23. Trong không gian Oxyz, cho mặt cầu (S) tâm I nằm trên mặt phẳng (Oxy) đi qua ba điểm
A(1; 2; −4), B(1; −3; 1), C(2; 2; 3). Tìm tọa độ điểm I.
A I(2; −1; 0). B I(0; 0; 1). C I(0; 0; −2). D I(−2; 1; 0).
Lời giải.
Vì I ∈ (Oxy) ⇒ I(a; b; 0). Ta có
# »
AI = (a −1; b −2; 4);
# »
BI = (a − 1; b + 3; −1);
# »
CI = (a − 2; b − 2; −3).
Do I là tâm cầu nên
IA = IB
IA = IC
⇔
(a − 1)
2
+ (b − 2)
2
+ 4
2
= (a − 1)
2
+ (b + 3)
2
+ 1
(a − 1)
2
+ (b − 2)
2
+ 4
2
= (a − 2)
2
+ (b − 2)
2
+ 9
⇔
− 4b + 20 = 6b + 10
− 2a + 17 = −4a + 13
⇔
b = 1
a = −2
⇒ I(−2; 1; 0).
Chọn phương án D
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1; 0; 0), B(0; −1; 0) và C(0; 0; 2). Phương
trình mặt phẳng (ABC) là
A x − 2y + z = 0. B x − y +
z
2
= 1. C x +
y
2
− z = 1. D 2x − y + z = 0.
Lời giải.
Áp dụng phương trình mặt phẳng đoạn chắn ta có phương trình mặt phẳng (ABC) là x − y +
z
2
= 1.
Chọn phương án B
Câu 25. Trong không gian Oxyz, cho điểm M(3; 2; −1) và mặt phẳng (P ): x +z −2 = 0. Đường thẳng
đi qua M và vuông góc với (P ) có phương trình là
A
x = 3 + t
y = 2
z = −1 + t
. B
x = 3 + t
y = 2 + t
z = −1
. C
x = 3 + t
y = 2t
z = 1 − t
. D
x = 3 + t
y = 1 + 2t
z = −t
.
h Geogebra Pro Trang 7
https://www.facebook.com/groups/GeoGebraPro/
Lời giải.
Mặt phẳng (P ): x + z − 2 = 0 có véc-tơ pháp tuyến là
#»
n
(P )
= (1; 0; 1).
Đường thẳng ∆ đi qua M và vuông góc với (P ) nhận
#»
n
(P )
làm véc-tơ chỉ phương có phương trình là
x = 3 + t
y = 2
z = −1 + t.
Chọn phương án A
Câu 26. Cho hình lập phương ABCD.A
0
B
0
C
0
D
0
. Tính góc giữa hai mặt phẳng (A
0
B
0
C) và (C
0
D
0
A).
A 45
◦
. B 30
◦
. C 60
◦
. D 90
◦
.
Lời giải.
Gọi I = B
0
C ∩ BC
0
, J = A
0
D ∩ AD
0
, ta có
(A
0
B
0
C) ∩ (C
0
D
0
A) = IJ
IJ ⊥ B
0
C ⊂ (A
0
B
0
C)
IJ ⊥ BC
0
⊂ (C
0
D
0
A).
Từ đó, suy ra góc giữa mặt phẳng (A
0
B
0
C) và mặt phẳng (C
0
D
0
A) là
góc giữa đường thẳng B
0
C và BC
0
hay là bằng 90
◦
.
D
A
C
B
A
0
D
0
C
0
B
0
IJ
Chọn phương án D
Câu 27. Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau
x
f
0
(x)
−∞
−2
0 1 3
+∞
+
0
−
0
+
0
−
0
−
Hàm số đã cho có bao nhiêu điểm cực trị?
A 3. B 1. C 2. D 4.
Lời giải.
Dựa vào bảng xét dấu của f
0
(x) ta suy ra:
Hàm số đạt cực đại tại x = −2 và x = 1.
Hàm số đạt cực tiểu tại x = 0.
Hàm số không đạt cực trị tại x = 3 do đạo hàm không đổi dấu khi đi qua điểm x = 3.
Vậy hàm số đã cho có 3 điểm cực trị.
Chọn phương án A
Câu 28. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x +
√
4 − x
2
. Hãy
tính P = M + m.
A P = 2
Ä
√
2 − 1
ä
. B P = 2
Ä
√
2 + 1
ä
. C P =
√
2 + 1. D P =
√
2 − 1.
Lời giải.
h Geogebra Pro Trang 8
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Tập xác định: D = [−2; 2].
y
0
= 1 −
x
√
4 − x
2
.
y
0
= 0 ⇔
√
4 − x
2
= x ⇔
x ≥ 0
x
2
= 2
⇔ x =
√
2.
y(−2) = −2; y(2) = 2; y(
√
2) = 2
√
2.
Suy ra m = −2; M = 2
√
2.
Vậy P = 2
Ä
√
2 − 1
ä
.
Chọn phương án A
Câu 29. Cho a > 0, b > 0 thỏa mãn a
2
+ 4b
2
= 5ab. Khẳng định nào sau đây đúng?
A 2 log(a + 2b) = 5(log a + log b). B log(a + 1) + log b = 1.
C 2 log
a + 2b
3
=
log a + log b
2
. D log(a + 2b) = log a − log b.
Lời giải.
Ta có a
2
+ 4b
2
= 5ab ⇔ (a + 2b)
2
= 9ab.
Logarit cơ số 10 hai vế ta được
log(a + 2b)
2
= log(9ab) ⇔ 2 log(a + 2b) = log 9 + log a + log b
⇔ 2(log(a + 2b) − log 3) = log a + log b
⇔ 2 log
a + 2b
3
=
log a + log b
2
.
Chọn phương án C
Câu 30. Cho hàm số y = f (x) có đồ thị như hình vẽ bên.
x
y
O
−1 1
4
2
Phương trình |f(x − 2) − 2| = π có bao nhiêu nghiệm thực phân biệt?
A 4. B 2. C 6. D 3.
Lời giải.
Số giao điểm của đồ thị hàm số y = f (x) với đường thẳng y = k và số giao điểm của đồ thị hàm số
y = f (x + p) với đường thẳng y = k luôn như nhau. Do đó nghiệm của phương trình |f(x − 2) − 2| = π
cũng chính là nghiệm của phương trình |f(x) − 2| = π.
Phương trình |f(x) − 2| = π ⇔
f(x) − 2 = π
f(x) − 2 = −π
⇔
f(x) = 2 + π
f(x) = 2 − π
.
Xét phương trình f(x) = 2 + π : Vì 2 + π > 4 nên phương trình có 1 nghiệm.
h Geogebra Pro Trang 9
https://www.facebook.com/groups/GeoGebraPro/
Xét phương trình f(x) = 2 − π : Vì 2 − π < 0 nên phương trình có 1 nghiệm.
Vậy phương trình đã cho có 2 nghiệm thực.
Chọn phương án B
Câu 31. Tập nghiệm của bất phương trình log
2
Ä
1 + log
1
9
x − log
9
x
ä
< 1 có dạng S =
Å
1
a
; b
ã
với a, b
là những số nguyên. Mệnh đề nào dưới đây đúng?
A a = −b. B a + b = 1. C a = b. D a = 2b.
Lời giải.
Điều kiện x > 0.
log
2
Ä
1 + log
1
9
x − log
9
x
ä
< 1 ⇔ 0 < 1 + log
1
9
x − log
9
x < 2 ⇔ −
1
2
< log
9
x <
1
2
⇔
1
3
< x < 3.
Do đó tập nghiệm của bất phương trình là S =
Å
1
3
; 3
ã
. Suy ra a = b.
Chọn phương án C
Câu 32. Cho hình nón tròn xoay có đường cao bằng 20 cm, bán kính đáy bằng 25 cm. Một thiết diện
đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiến diện là 12 cm.
Tính diện tích của thiết diện đó.
A 500 cm
2
. B 1000 cm
2
. C 250 cm
2
. D 250 cm
3
.
Lời giải.
Ký hiệu S là đỉnh của hình nón và O là tâm của đường tròn
đáy.
Gọi A, B là hai giao điểm (khác đỉnh S của hình nón) của mặt
phẳng với hình nón. Suy ra thiết diện của mặt phẳng với hình
nón là tam giác SAB.
Gọi M là trung điểm của AB.
Kẻ OH ⊥ SM tại H.
Xét đường thẳng AB và mặt phẳng (SOM) có
AB ⊥ SO
AB ⊥ OM
⇒ AB ⊥ (SOM).
S
A
O
H
B
M
Cho nên (SAB) ⊥ (SOM).
Mà (SAM ) ∩ (SOM ) = SM và OH ⊥ SM nên OH là khoảng cách từ tâm của đáy đến mặt phẳng
chứa thiến diện. Suy ra OH = 12 cm.
Ta có
1
OH
2
=
1
SO
2
+
1
OM
2
⇔
1
OM
2
=
1
OH
2
−
1
SO
2
⇔ OM =
OH
2
· SO
2
SO
2
− OH
2
⇔ OM = 15.
Khi đó SM =
√
SO
2
+ OM
2
= 25 và AB = 2AM = 2
√
25
2
− 15
2
= 40.
Vậy diện tích của thiết diện SAB bằng
1
2
· 40 · 25 = 500 cm
2
.
Chọn phương án A
Câu 33. Cho hàm số f (x) xác định trên (0; +∞) và thỏa mãn xf
0
(x) = −[f(x)]
2
· ln x; f (1) = 1. Giá
trị f(e) bằng
A
2
3
. B
e
2
. C
2e
3
. D
1
2
.
h Geogebra Pro Trang 10
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Lời giải.
Ta có xf
0
(x) = −[f (x)]
2
· ln x; f(1) = 1 ⇒ −
f
0
(x)
[f(x)]
2
=
ln x
x
.
Suy ra
Z
−
f
0
(x)
[f(x)]
2
dx =
Z
ln x
x
dx =
Z
ln x d(ln x) ⇒
1
f(x)
=
ln
2
x
2
+ C
Theo giả thiết f(1) = 0 + C = 1 ⇒ C = 1. Khi x = e ⇒
1
f(e)
=
1
2
+ 1 =
3
2
⇒ f(e) =
2
3
.
Chọn phương án A
Câu 34. Cho hình phẳng D được giới hạn bởi hai đường y = 2(x
2
−1); y = 1 − x
2
. Tính thể tích khối
tròn xoay tạo thành do D quay quanh trục Ox.
A
64π
15
. B
32
15
. C
32π
15
. D
64
15
.
Lời giải.
Phương trình hoành độ giao điểm của 2 đồ thị hàm số y = 2(x
2
− 1)
và y = 1 − x
2
là
2(x
2
− 1) = 1 − x
2
⇔ x = ±1.
Lấy đối xứng đồ thị hàm số y = 2(x
2
−1) qua trục Ox ta được đồ thị
hàm số y = 2(1 − x
2
).
Ta có 2(1 − x
2
) ≥ 1 − x
2
, ∀x ∈ [−1; 1].
Khi đó trên đoạn [−1; 2] phần thể tích của hàm số y = 2(x
2
−1) chứa
cả phần thể tích của hàm số y = 1 − x
2
.
x
y
O
−1 1
1
2
−2
y = 2x
2
− 2
y = 1 − x
2
y = −2x
2
+ 2
Suy ra thể tích khối tròn xoay cần tìm là
V = π
1
Z
−1
2(x
2
− 1)
2
dx =
64π
15
.
Chọn phương án A
Câu 35. Cho số phức z = a + bi (a, b ∈ R) thỏa mãn |z| = 5 và z(2 + i)(1 − 2i) là một số thực. Tính
P = |a| + |b|.
A P = 8. B P = 4. C P = 5. D P = 7.
Lời giải.
Ta có
z(2 + i)(1 − 2i) = (a + bi)(4 − 3i) = 4a + 3b + (−3a + 4b)i. (1)
Do z(2 + i)(1 − 2i) là một số thực nên từ (1) suy ra −3a + 4b = 0 ⇔ b =
3
4
a. (2)
Mặt khác |z| = 5 ⇔ a
2
+ b
2
= 25. (3)
Thế (2) vào (3) ta được phương trình
a
2
+
Å
3
4
a
ã
2
= 25 ⇔ a
2
= 16 ⇔ a = ±4.
Với a = 4 ⇒ b = 3 và a = −4 ⇒ b = −3.
Vậy P = |a| + |b| = 3 + 4 = 7.
Chọn phương án
D
h Geogebra Pro Trang 11
https://www.facebook.com/groups/GeoGebraPro/
Câu 36. Tìm mô-đun của số phức z biết z − 4 = (1 + i) |z| − (4 + 3z) i.
A |z| =
1
2
. B |z| = 2. C |z| = 4. D |z| = 1.
Lời giải.
Ta có
z − 4 = (1 + i) |z| − (4 + 3z) i
⇔z − 4 = |z| + i|z| − 4i − 3iz
⇔z(1 + 3i) = |z| + 4 + (|z| − 4) i
⇒|z(1 + 3i)| = ||z| + 4 + (|z| − 4) i|(lấy mô-đun hai vế)
⇔|z| ·
√
10 =
»
(|z| + 4)
2
+ (|z| − 4)
2
⇔10|z|
2
= 2|z|
2
+ 32
⇔|z|
2
= 4 ⇔ |z| = 2.
Chọn phương án B
Câu 37. Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng (d) :
x + 1
2
=
y − 1
1
=
z − 2
3
và
mặt phẳng (P ) : x − y − z − 1 = 0. Viết phương trình đường thẳng (∆) đi qua điểm A(1; 1; −2), biết
(∆) k (P ) và (∆) cắt (d).
A
x − 1
1
=
y − 1
−1
=
z + 2
−1
. B
x − 1
2
=
y − 1
1
=
z + 2
3
.
C
x − 1
8
=
y − 1
3
=
z + 2
5
. D
x − 1
2
=
y − 1
1
=
z + 2
1
.
Lời giải.
Gọi M = (d) ∩ (∆) ⇒ M (−1 + 2t; 1 + t; 2 + 3t).
Khi đó
# »
AM = (2t − 2; t; 3t + 4) là một véc-tơ chỉ phương của (∆).
(∆) k (P ) ⇔
# »
AM ⊥
#»
n
(P )
với
#»
n
(P )
= (1; −1; −1).
⇔
# »
AM ·
#»
n
(P )
= 0 ⇔ 2t − 2 − t − 3t − 4 = 0 ⇔ t = −3 ⇒
# »
AM = (−8; −3; −5).
Vậy (∆) :
x − 1
8
=
y − 1
3
=
z + 2
5
.
Chọn phương án C
Câu 38. Trong không gian Oxyz cho hai đường thẳng d
1
:
x
1
=
y + 4
1
=
z − 3
−1
và d
2
:
x − 1
−2
=
y + 3
1
=
z − 4
−5
. Đường thẳng vuông góc với mặt phẳng tọa độ (Oxz) và cắt d
1
và d
2
có phương trình là
A
x = 1
y = −1 + t
z = −1
. B
x =
3
7
y =
−25
7
+ t
z =
18
7
. C
x = 1
y = −3 + t
z = 4
. D
x = t
y = −4 + t
z = 3 + t
.
Lời giải.
Gọi d là đường thẳng cần tìm, A = d ∩ d
1
và B = d ∩ d
2
.
Ta có tọa độ A = (u; −4 + u; 3 − u), B = (1 − 2v; −3 + v; 4 − 5v)
⇒
# »
AB = (1 − 2v − u; 1 + v − u; 1 − 5v + u) là véc-tơ chỉ phương của d.
Do d ⊥ (Oxz) nên
# »
AB và
#»
n
Oxz
= (0; 1; 0) cùng phương.
h Geogebra Pro Trang 12
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Từ đó ta có
# »
AB ·
#»
i = 0
# »
AB ·
#»
j = 0
⇔
1 − 2v − u = 0
1 − 5v + u = 0
⇔
u =
3
7
u =
2
7
.
Nên tọa độ A(
3
7
;
−25
7
;
18
7
).
Vậy d đi qua A và có véc-tơ chỉ phương
# »
AB = (0; 1; 0) có phương trình là
x =
3
7
y =
−25
7
+ t
z =
18
7
.
Chọn phương án B
Câu 39. Cho hai chiếc hộp A và B. Hộp A chứa 6 viên bi trắng, 4 viên bi đen. Hộp B chứa 7 viên
bi trắng, 3 viên bi đen. Người ta lấy ngẫu nhiên một viên bi từ hộp A và bỏ vào hộp B rồi sau đó từ
hộp B lấy ngẫu nhiên ra hai viên bi. Tính xác suất để hai viên bi lấy được từ hộp B là hai viên bi
trắng.
A
126
275
. B
21
55
. C
123
257
. D
37
83
.
Lời giải.
Không gian mẫu n(Ω) = 10 · C
2
11
.
Trường hợp 1: Lấy một viên bi đen từ hộp A bỏ vào hộp B ta có 4 cách. Khi đó số cách lấy hai bi
trắng từ hộp B là C
2
7
.
Trường hợp 2: Lấy một viên bi trắng từ hộp A bỏ vào hộp B khi đó ta có 6 cách. Với mỗi cách đó
thì số cách lấy hai bi trắng từ hộp B là C
2
8
.
Vậy số cách lấy hai viên bi trắng từ hộp B là 4 · C
2
7
+ 6 · C
2
8
.
Xác suất cần tìm là P =
4 · C
2
7
+ 6 · C
2
8
10 · C
2
11
=
126
275
.
Chọn phương án A
Câu 40. Cho hình chóp S.ABC có SA = 3a và SA ⊥ (ABC). Biết AB = BC = 2a và
’
ABC = 120
◦
.
Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng
A
3a
2
. B
a
2
. C a. D 2a.
Lời giải.
Gọi I là hình hình chiếu vuông góc của A trên BC, ta có AI ⊥ BC. (1)
Mặt khác SA ⊥ (ABC) nên SA ⊥ BC. (2)
Từ (1) và (2) suy ra BC ⊥ (SIA). (3)
Gọi H là hình hình chiếu vuông góc của A trên SI, ta có AH ⊥ SI. (4)
Từ (3) và (4) suy ra AH ⊥ (SBC) nên khoảng cách từ A đến mặt phẳng
(SBC) là AH.
Xét tam giác BIA vuông tại I, ta có
AI = AB · sin 120
◦
= 2a ·
√
3
2
= a
√
3.
Xét tam giác SAI vuông tại A, ta có
S
B
A C
I
H
h Geogebra Pro Trang 13
https://www.facebook.com/groups/GeoGebraPro/
1
AH
2
=
1
AS
2
+
1
AI
2
⇒ AH =
AS
2
· AI
2
AS
2
+ AI
2
=
s
(3a)
2
· (a
√
3)
2
(3a)
2
+ (a
√
3)
2
=
3a
2
.
Vậy khoảng cách từ điểm A đến mặt phẳng (SBC) bằng
3a
2
.
Chọn phương án A
Câu 41. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (−2019; 2019) để hàm số
y = sin
3
x − 3 cos
2
x − m sin x − 1 đồng biến trên đoạn
h
0;
π
2
i
?
A 2020. B 2019. C 2028. D 2018.
Lời giải.
Phương pháp:
Sử dụng công thức cos
2
x = 1 − sin
2
x, đặt ẩn phụ t = sin x.
Để hàm số y = f (x) đồng biến trên (a; b) ⇒ f
0
(x) ≥ 0 ∀x ∈ (a; b).
Cách giải:
y = sin
3
x − 3 cos
2
x − m sin x − 1 = sin
3
x − 3
1 − sin
2
x
− m sin x − 1.
y = sin
3
x + 3 sin
2
x − m sin x − 4.
Đặt t = sin x, với x ∈
h
0;
π
2
i
⇒ t ∈ [0; 1].
Bài toán trở thành tìm m để hàm số y = t
3
+ 3t
2
− mt − 4 đồng biến trên [0; 1].
TXĐ: D = R. Ta có y
0
= 3t
2
+ 6t − m.
Để hàm số đồng biến trên [0; 1]
⇒ y
0
≥ 0 ∀t ∈ [0; 1] ⇒ 3t
2
+ 6t − m ≥ 0 ∀t ∈ [0; 1] ⇔ m ≤ 3t
2
+ 6t ∀t ∈ [0; 1].
⇒ m ≤ f (t) = 3t
2
+ 6t ∀t ∈ [0; 1] ⇔ m ≤ min
[0;1]
f(t).
Xét hàm số f (t) = 3t
2
+ 6t, ta có f (0) = 0, f (1) = 9 ⇒ min
[0;1]
f(t) = 0 ⇔ m ≤ 0.
Kết hợp điều kiện đề bài ⇒
m ∈ (−2019; 0]
m ∈ Z
⇒ Có 2019 giá trị của m thoả mãn.
Chọn phương án B
Câu 42. Một người mỗi tháng đều đặn gửi vào một ngân hàng một khoản tiền T theo hình thức lãi
kép với lãi suất 0,6% mỗi tháng. Biết sau 15 tháng người đó có số tiền là 10 triệu đồng. Hỏi số tiền T
gần với số tiền nào nhất sau đây?
A 635.000 đồng. B 645.000 đồng. C 613.000 đồng. D 535.000 đồng.
Lời giải.
Gọi r là lãi suất kép hàng tháng.
Gọi T
n
là số tiền người đó có được ở cuối tháng thứ n, ta có:
- Cuối tháng thứ nhất người đó có số tiền là: T
1
= T + T · r = T (1 + r).
- Đầu tháng thứ hai, người đó gửi số tiền là:
T (1 + r) + T = T [(1 + r) + 1] =
T
(1 + r) − 1
· [(1 + r)
2
− 1] =
a
r
[(1 + r)
2
− 1].
- Cuối tháng thứ hai người đó có số tiền là:
T
2
=
T
r
[(1 + r)
2
− 1] +
T
r
[(1 + r)
2
− 1] r =
T
r
[(1 + r)
2
− 1] (1 + r).
h Geogebra Pro Trang 14
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
- Cuối tháng thứ n người đó có số tiền là:
T
n
=
T
r
[(1 + r)
n
− 1] (1 + r).
Suy ra: T =
T
n
r
[(1 + r)
n
− 1] (1 + r)
.
Do đó số tiền ban đàu người đó gửi là:
T =
10000000 · 0,6%
[(1 + 0,6%)
15
− 1] (1 + 0,6%)
≈ 635301 đồng.
Chọn phương án A
Câu 43.
Cho hàm số y = f(x) xác định trên R \{0} có bảng biến
thiên như hình vẽ bên. Số nghiệm của phương trình
2 |f (2x − 3)| − 13 = 0 là
A 3. B 2. C 4. D 1.
x
y
0
y
−∞
−2
0
+∞
−
0
+ +
+∞+∞
77
+∞
−∞
+∞+∞
Lời giải.
Đặt t = 2x − 3. Cứ mỗi một t 6= 0 sẽ cho một x.
Phương trình đã cho trở thành |f(t)| =
13
2
⇔
f(t) =
13
2
f(t) = −
13
2
.
Ta có −
13
2
<
13
2
< 7 nên dựa vào bảng biến thiên đã cho, ta có
Phương trình f(t) =
13
2
có 1 nghiệm t
1
> 0.
Phương trình f(t) = −
13
2
có 1 nghiệm t
2
thỏa mãn 0 < t
2
< t
1
.
Suy ra phương trình đã cho có 2 nghiệm phân biệt.
Chọn phương án B
Câu 44. Cho hình trụ có bán kính đáy bằng a và chiều cao h. Tính thể tích V của khối lăng trụ tam
giác đều tam giác đều nội tiếp hình trụ đã cho.
A V =
√
3a
2
h
4
. B V =
3
√
3a
2
h
4
.
C V =
π
3
Å
h
2
+
4a
2
3
ã
…
h
2
4
+
a
2
3
. D V =
3
√
3πa
2
h
4
.
Lời giải.
Gọi x là cạnh đáy của khối lăng trụ tam giác đều nội tiếp hình trụ, bán
kính đường tròn ngoại tiếp tam giác đều cạnh x là
x
√
3
3
, do đó:
x
√
3
3
= a ⇔ x = a
√
3.
Diện tích mặt đáy của hình lăng trụ: S =
x
2
√
3
4
=
(a
√
3)
2
√
3
4
=
3
√
3a
2
4
.
Thể tích khối lăng trụ tam giác đều tam giác đều nội tiếp hình trụ đã
cho là
V = Bh =
3
√
3a
2
4
· h =
3
√
3a
2
h
4
.
A
0
B
0
C
0
O
0
A
B
C
O
h Geogebra Pro Trang 15
https://www.facebook.com/groups/GeoGebraPro/
Chọn phương án B
Câu 45. Cho hàm số f(x), f(−x) liên tục trên R và thỏa mãn 2f(x) + 3f (−x) =
1
4 + x
2
. Tính
I =
2
Z
−2
f(x) dx.
A
π
20
. B
π
10
. C −
π
20
. D −
π
10
.
Lời giải.
Xét I =
2
Z
−2
f(x) dx.
Đặt x = −u ⇒ dx = −du.
Với x = −2 ⇒ u = 2.
Với x = 2 ⇒ u = −2.
Suy ra I = −
−2
Z
2
f(−u) du =
2
Z
−2
f(−u) du =
2
Z
−2
f(−x) dx.
Từ đó ta có 5I = 2I + 3I = 2
2
Z
−2
f(x) dx + 3
2
Z
−2
f(−x) dx =
2
Z
−2
1
x
2
+ 4
dx.
Tính J =
2
Z
−2
1
x
2
+ 4
dx.
Đặt x = 2 tan v ⇒ dx = 2(1 + tan
2
v) dv.
Đổi cận
Với x = −2 ⇒ v = −
π
4
.
Với x = 2 ⇒ v =
π
4
.
Suy ra J =
π
4
Z
−
π
4
1
4 tan
2
v + 4
· 2(1 + tan
2
v) dv =
π
4
Z
−
π
4
1
2
dv =
π
4
.
Từ đó suy ra I =
π
20
.
Chọn phương án A
Câu 46. Cho hàm số y = f (x) có bảng biến thiên như sau:
x
y
0
y
−∞
−1
3
+∞
+
0
−
0
+
−∞−∞
55
11
+∞+∞
Phương trình f (x) − 2 = 0 có bao nhiêu nghiệm?
h Geogebra Pro Trang 16
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
A 1. B 3. C 2. D 0 .
Lời giải.
Phương trình f (x) − 2 = 0 ⇔ f (x) = 2.
Số giao điểm của đồ thị hàm số y = f (x) và y = 2 là số nghiệm của phương trình f (x) − 2 = 0 (∗)
Dựa vào bảng biến thiên suy ra phương trình (∗) có 3 nghiệm.
Chọn phương án B
Câu 47. Cho x, y là hai số thực dương thỏa mãn ln x + ln y ≥ ln(x
2
+ y). Tìm giá trị nhỏ nhất của
P = x + y.
A P = 2 + 3
√
2. B P = 6. C P = 2
√
2 + 3. D P =
√
17 +
√
3.
Lời giải.
Từ ln x + ln y ≥ ln(x
2
+ y) ⇔ xy ≥ x
2
+ y ⇔ (x − 1)y ≥ x
2
.
Nếu 0 < x ≤ 1 thì y ≥ xy ≥ x
2
+ y ⇔ 0 ≥ x
2
(vô lý).
Nếu x > 1 thì (x − 1) y ≥ x
2
⇔ y ≥
x
2
x − 1
. Vậy P = x + y ≥ x +
x
2
x − 1
.
Xét hàm số f(x) = x +
x
2
x − 1
trên (1; +∞). f
0
(x) =
2x
2
− 4x + 1
x
2
− 2x + 1
= 0 ⇒
x =
2 −
√
2
2
(loại)
x =
2 +
√
2
2
(nhận).
Lập bảng biến thiên suy ra min
(1;+∞)
f(x) = f
Ç
2 +
√
2
2
å
= 2
√
2 + 3.
Chọn phương án
C
Câu 48. Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị nhỏ nhất của hàm số
y =
sin
4
x + cos 2x + m
bằng 2. Số phần tử của S là
A 4. B 3. C 1. D 2.
Lời giải.
Ta có y =
sin
4
x + cos 2x + m
=
sin
4
x − 2 sin
2
x + m + 1
.
Đặt t = sin
2
x, t ∈ [0; 1], hàm số trở thành y = |t
2
− 2t + m + 1|.
Xét hàm f (t) = t
2
− 2t + m + 1, với t ∈ [0; 1]. Ta có f
0
(t) = 2t − 2 ≤ 0, với ∀t ∈ [0; 1], suy ra hàm số
nghịch biến trên [0; 1]. Do đó f(1) ≤ f(t) ≤ f(0) ⇔ m ≤ f(t) ≤ m + 1.
Xét các trường hợp sau
m + 1 ≤ 0 ⇔ m ≤ −1. Khi đó, min y = −m − 1. Theo giả thiết −m − 1 = 2 ⇔ m = −3 (thỏa
mãn).
−1 < m ≤ 0. Khi đó, min y = 0 (loại).
m > 0. Khi đó, min y = m. Theo giả thiết m = 2 (thỏa mãn).
Vậy tập hợp S có 2 phần tử.
Chọn phương án D
Câu 49. Cho hình hộp ABCD.A
0
B
0
C
0
D
0
có đáy là hình thoi cạnh a
√
3, BD = 3a, hình chiếu vuông
góc của B trên mặt phẳng (A
0
B
0
C
0
D
0
) trùng với trung điểm của A
0
C
0
. Gọi (α) là góc tạo bởi hai mặt
phẳng (ABCD) và (CDD
0
C
0
), cos α =
√
21
7
. Tính thể tích khối hộp.
h Geogebra Pro Trang 17
https://www.facebook.com/groups/GeoGebraPro/
A
3a
3
4
. B
9
√
3a
3
4
. C
9a
3
4
. D
3
√
3a
3
4
.
Lời giải.
Gọi O và O
0
lần lượt là tâm của hình thoi ABCD
và A
0
B
0
C
0
D
0
. Vì BO
0
⊥ (A
0
B
0
C
0
D
0
) nên OD
0
⊥
(ABCD).
Ta có AD = a
√
3, DO =
3a
2
nên
AO =
√
AD
2
− DO
2
=
a
√
3
2
.
Suy ra AC = a
√
3, do đó, tam giác ACD đều.
B
0
B
A
0
D
0
C
C
0
A
D
O
H
O
0
Từ O kẻ OH ⊥ CD, kết hợp với OD
0
⊥ CD (do OD
0
⊥ (ABCD)) suy ra HD
0
⊥ CD.
Suy ra góc giữa hai mặt phẳng (ABCD) và (CDD
0
C
0
) là
÷
OHD
0
.
Ta có OH =
1
2
· h
A
=
3a
4
,
÷
OHD
0
= α và tan α =
2
√
3
3
. Suy ra OD
0
= OH · tan α =
a
√
3
2
.
Diện tích đáy hình hộp là S
ABCD
=
1
2
· AC · BD =
3a
2
√
3
2
.
Từ đó, V = S
ABCD
· OD
0
=
9a
3
4
.
Chọn phương án C
Câu 50. Có bao nhiêu số nguyên m ∈ (−7; 7) để đồ thị hàm số y = |x
4
− 3mx
2
− 4| có đúng 3 điểm
cực trị A, B, C và diện tích tam giác ABC lớn hơn 4.
A 4. B 2. C 1. D 3.
Lời giải.
Đặt f(x) = x
4
− 3mx
2
− 4. Ta thấy f (0) = −4.
Do vậy y = |f (x)| có đúng 3 cực trị ⇔ f(x) có 1 cực trị ⇔ m ≤ 0. (1)
Ta thấy S
4ABC
=
1
2
· AO · BC = 4 · |x
C
|.
Theo giả thiết, ta được
3m +
√
9m
2
+ 16
2
> 1
⇔
√
9m
2
+ 16 > 2 − 3m
⇔
m >
2
3
m ≤
2
3
m > −1
(1)
⇒ −1 < m ≤ 0.
Vậy có 1 giá trị m nguyên thuộc (−7; 7) là m = 0 thỏa mãn đề bài.
x
y
O
A
B C
Chọn phương án C
———————–HẾT———————–
h Geogebra Pro Trang 18
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
BẢNG ĐÁP ÁN
1. D 2. C 3. D 4. C 5. B 6. C 7. A 8. A 9. C 10. D
11. C 12. C 13. A 14. C 15. C 16. D 17. C 18. D 19. B 20. C
21. A 22. C 23. D 24. B 25. A 26. D 27. A 28. A 29. C 30. B
31. C 32. A 33. A 34. A 35. D 36. B 37. C 38. B 39. A 40. A
41. B 42. A 43. B 44. B 45. A 46. B 47. C 48. D 49. C 50. C
h Geogebra Pro Trang 19
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 10
Câu 1. Một tổ có 6 học sinh nam và 9 học sinh nữ. Hỏi có bao nhiêu cách chọn 6 học sinh đi lao động
trong đó có 2 học sinh nam?
A C
2
6
+ C
4
9
. B A
2
6
· A
4
9
. C C
2
6
· C
4
9
. D C
4
6
· C
2
9
.
Câu 2. Cho cấp số cộng (u
n
) biết u
n
= 3 − 5n. Tìm công sai d của cấp số cộng (u
n
).
A d = 3. B d = −5. C d = −3. D d = 5.
Câu 3. Tìm tập nghiệm S của phương trình 4
x
− 6 · 2
x
+ 8 = 0.
A S = {1; 2}. B S = (1; 2). C S = {1}. D S = {2}.
Câu 4. Tổng diện tích các mặt của khối lập phương bằng 96. Tìm thể tích của khối lập phương đó.
A 48. B 84. C 64. D 91.
Câu 5. Tập xác định của hàm số y = log
2
x + 3
2 − x
là
A D = R\{−3; 2}. B D = (−∞; −3) ∪ (2; +∞).
C D = [−3; 2]. D D = (−3; 2).
Câu 6. Cho F (x) là nguyên hàm của f (x) =
1
√
x + 2
thỏa mãn F (2) = 4. Giá trị F (−1) bằng
A
√
3. B 1. C 2
√
3. D 2.
Câu 7. Cho hình chóp S.ABC có (SAB) ⊥ (ABC), tam giác ABC đều cạnh 2a, tam giác SAB vuông
cân tại S. Tính thể tích hình chóp S.ABC.
A
a
3
√
3
3
. B
a
3
√
3
6
. C
2a
3
√
3
3
. D
a
3
√
3
12
.
Câu 8. Khối nón tròn xoay có chiều cao bằng 8 cm và độ dài đường sinh bằng 10 cm có thể tích
bằng
A 128π cm
3
. B 96π cm
3
. C 124π cm
3
. D 140π cm
3
.
Câu 9. Tính diện tích mặt cầu (S) khi biết chu vi đường tròn lớn của nó bằng 4π.
A S = 32π. B S = 16π. C S = 64π. D S = 8π.
Câu 10. Cho hàm số y = f (x) có bảng biến thiên như hình dưới. Hàm số nghịch biến trong khoảng
nào?
x
y
0
y
−∞
−1
2
+∞
+
0
−
0
+
A (−∞; 2). B (0; 2). C (−1; 2). D (2; +∞).
h Geogebra Pro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Câu 11. Cho a là số thực dương và a 6= 1. Tính giá trị của biểu thức Q = log
a
a
3
·
3
√
a
2
√
a
.
A Q =
19
5
. B Q =
19
7
. C Q =
19
4
. D Q =
19
6
.
Câu 12. Một hình trụ có bán kính đáy r = 5 cm, chiều cao h = 7 cm. Tính diện tích xung quanh của
hình trụ.
A 85π cm
2
. B 35π cm
2
. C
35
3
π cm
2
. D 70π cm
2
.
Câu 13.
Cho hàm số y = f(x) có bảng biến thiên
như hình vẽ. Hỏi hàm số có bao nhiêu
cực trị?
A 2. B 3. C 1. D
4.
x
y
0
y
−∞
−1
0 2
+∞
+
0
− +
0
−
−∞−∞
22
−1 −1
33
22
Câu 14. Cho hàm số y = f (x) có đồ thị như hình vẽ. Xác định hàm số trên.
A y =
2x + 1
x − 1
. B y =
2x − 1
x − 1
. C y =
2x − 1
x + 1
. D y =
3x + 1
2x + 2
.
x
y
O
2−2−4
2
4
6
−2
Câu 15. Đồ thị hàm số y =
√
9 − x
2
x
2
− 6x + 8
có bao nhiêu đường tiệm cận?
A 1. B 4. C 3. D 2.
Câu 16. Tập nghiệm của bất phương trình log
1
5
4x + 6
x
≥ 0 là
A
Å
−2, −
3
2
ò
. B
ï
−2, −
3
2
ò
. C
Å
−2, −
3
2
ã
. D
ï
−2, −
3
2
ã
.
Câu 17.
h Geogebra Pro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Cho hàm số y = f (x) liên tục trên đoạn [−2; 2] và có đồ thị là đường cong
như hình vẽ bên. Tìm số nghiệm của phương trình |f (x) | = 1 trên đoạn
[−2; 2].
A 4. B 6. C 3. D 5.
x
y
O
x
1
x
2
2
4
−2
−4
−2
2
Câu 18. Cho hàm số f (x) có đạo hàm liên tục trên [1; 2], có f (2) = 14 và
2
Z
1
f(x)
x
dx = 6. Tính
I =
2
Z
1
f
0
(x) ln x dx.
A I = 14 ln 2 − 6. B I = 7 ln 2 − 6. C I = 7 ln 2 − 6. D I = 14 ln 2 + 6.
Câu 19. Cho số phức z thỏa mãn z − 3 + i = 0. Môđun của z bằng bao nhiêu?
A
√
10. B 10. C
√
3. D 4.
Câu 20. Cho số phức z
1
= 3 + 2i, z
2
= 6 + 5i. Tìm số phức liên hợp của z = 6z
1
+ 5z
2
.
A ¯z = 51 + 40i. B ¯z = 51 − 40i. C ¯z = 48 + 37i. D ¯z = 48 − 37i.
Câu 21. Gọi A, B, C là các điểm trong mặt phẳng Oxy theo thứ tự biểu diễn các số phức 2 + 3i, 3 + i,
1 + 2i. Trọng tâm G của tam giác ABC biểu diễn số phức z. Tìm z.
A z = 1 + i. B z = 1 − i. C z = 2 − 2i. D z = 2 + 2i.
Câu 22 (2H3B1-1). Trong không gian với hệ tọa độ Oxyz, tìm tọa độ điểm M trên trục Ox cách
đều hai điểm A (1; 2; −1) và điểm B (2; 1; 2)
A M
Å
1
2
; 0; 0
ã
. B M
Å
3
2
; 0; 0
ã
. C M
Å
2
3
; 0; 0
ã
. D M
Å
1
3
; 0; 0
ã
.
Câu 23. Trong hệ tọa độ Oxyz, cho điểm I(2; −1; −1) và mặt phẳng (P ): x − 2y − 2z + 3 = 0. Viết
phương trình mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng (P ).
A S : x
2
+ y
2
+ z
2
− 4x + 2y + 2z − 3 = 0. B S : x
2
+ y
2
+ z
2
− 2x + y + z − 3 = 0.
C S : x
2
+ y
2
+ z
2
− 4x + 2y + 2z + 1 = 0. D S : x
2
+ y
2
+ z
2
− 2x + y + z + 1 = 0.
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P ): 2x −2y + z + 4 = 0. Tính khoảng
cách d từ điểm M(1; 2; 1) đến (P ).
A d = 3. B d = 4. C d = 1. D d =
1
3
.
Câu 25. Trong hệ tọa độ Oxyz, cho đường thẳng d :
x − 1
2
=
y − 3
−1
=
z − 1
1
cắt mặt phẳng (P ) :
2x − 3y + z − 2 = 0 tại điểm I(a; b; c). Khi đó a + b + c bằng
A 9. B 5. C 3. D 7.
Câu 26. Cho lăng trụ tam giác đều ABC.A
0
B
0
C
0
có diện tích đáy bằng
√
3a
2
(đvdt), diện tích tam
giác A
0
BC bằng 2a
2
(đvdt). Tính góc giữa hai mặt phẳng (A
0
BC) và (ABC)?
h Geogebra Pro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
A 120
◦
. B 60
◦
. C 30
◦
. D 45
◦
.
Câu 27. Cho hàm số y = f (x) liên tục trên [−3; 3] và có bảng xét dấu đạo hàm như hình bên.
x
y
0
−3 −1
0 1 2 3
+
0
−
0
−
0
+
0
−
Mệnh đề nào sau đây sai về hàm số đó?
A Hàm số đạt cực tiểu tại x = 1. B Hàm số đạt cực đại tại x = −1.
C Hàm số đạt cực đại tại x = 2. D Hàm số đạt cực tiểu tại x = 0.
Câu 28. Tìm giá trị nhỏ nhất của hàm số y = 2x +
√
5 − x
2
.
A 5. B 2
√
5. C −3. D −2
√
5.
Câu 29. Cho a, b là các số dương thỏa mãn log
9
a = log
16
b = log
12
5b − a
2
. Tính giá trị T =
a
b
.
A T =
3 +
√
6
4
. B T = 7 − 2
√
6. C T = 7 + 2
√
6. D T =
3 −
√
6
4
.
Câu 30. Phương trình x
3
− 3x + 2m − 2 = 0 có đúng một nghiệm dương khi m thỏa
A m = 2 hoặc m ≤ 1. B m ∈ ∅. C m > 1. D m < 1 hoặc m > 2.
Câu 31. Bất phương trình 6 · 4
x
− 13 · 6
x
+ 6 · 9
x
> 0 có tập nghiệm là?
A S = (−∞; −2) ∪ (1; +∞). B S = (−∞; −1) ∪ (1; +∞).
C S = (−∞; −2] ∪ [2; +∞). D S = (−∞; −1) ∪ (1; +∞).
Câu 32. Cho khối nón có thể tích V =
√
3
4
πa
3
và thiết diện qua trục là tam giác đều. Diện tích xung
quanh của hình nón đó là
A S
xq
= πa
2
3
…
1
16
. B S
xq
= 2πa
2
3
…
9
16
. C S
xq
= 3πa
2
3
…
9
16
. D S
xq
= 3πa
2
3
…
2
16
.
Câu 33. Cho hàm số y = f (x) dương có đạo hàm liên tục trên đoạn
î
0;
√
3
ó
, biết rằng f
0
(x)−
√
x
2
+ 1·
f(x) = 0 và f
Ä
√
3
ä
= e
3
. Tính I =
√
3
Z
0
ln [f(x)] dx.
A 2
√
3. B 3
√
3 −
7
3
. C 3
√
3 +
7
3
. D 3
√
3 − 2.
Câu 34. Cho hình D giới hạn bởi các đường y = x
2
− 2 và y = −|x|. Khi đó diện tích của hình D
là
A
13
3
. B
7
3
. C
7π
3
. D
13π
3
.
Câu 35. Cho hai số phức z
1
, z
2
thỏa mãn |2z −i| = |iz + 2|, biết |z
1
−z
2
| =
√
2. Tính giá trị của biểu
thức A = |z
1
− 2z
2
|.
A A =
√
5. B A =
√
5
2
. C A =
√
3. D A =
√
3
2
.
Câu 36. Cho phương trình z
2
−4z +5 = 0 có hai nghiệm phức là z
1
, z
2
. Tính A = |z
1
|+|z
2
|+z
1
·z
2
.
A A = 25 + 2
√
5. B A = 0. C A = 5 − 2
√
5. D A = 5 + 2
√
5.
Câu 37. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình là x
2
+ y
2
+ z
2
= 9
và điểm A (0; −1; 2). Gọi (P ) là mặt phẳng qua A và cắt mặt cầu (S) theo một đường tròn có chu vi
nhỏ nhất. Phương trình của (P ) là
h Geogebra Pro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
A y − 2z + 5 = 0. B x − y + 2z − 5 = 0. C −y + 2z + 5 = 0. D y − 2z − 5 = 0.
Câu 38. Trong không gian Oxyz, cho hai điểm A(1; 2; 3), B(3; 4; 5) và mặt phẳng (P ) : x+2y+3z−14 =
0. Gọi ∆ là một đường thẳng thay đổi nằm trong mặt phẳng (P ). Gọi H, K lần lượt là hình chiếu vuông
góc của A, B trên ∆. Biết rằng AH = BK thì trung điểm của HK luôn thuộc một đường thẳng d cố
định, phương trình của đường thẳng d là
A
x = t
y = 13 − 2t
z = −4 + t
. B
x = t
y = 13 + 2t
z = −4 + t
. C
x = 1
y = 13 − 2t
z = −4 + t
. D
x = t
y = 13 − 2t
z = −4 − t
.
Câu 39. Từ một hộp chứa 5 viên bi đỏ, 4 viên bi xanh và 3 viên bi vàng lấy ngẫu nhiên 3 viên bi.
Tính xác suất để 3 viên bi lấy ra có đủ 3 màu.
A
3
11
. B
1
22
. C
3
220
. D
11
3
.
Câu 40. Cho lăng trụ tam giác đều ABC.A
0
B
0
C
0
có tất cả các cạnh đều bằng a. Khoảng cách giữa hai
đường thẳng BC và AB
0
bằng
A
a
√
21
7
. B
a
√
3
2
. C
a
√
7
4
. D
a
√
2
2
.
Câu 41. Cho hàm số y =
mx − 4m + 5
x + 3m
với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên
của m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S.
A 2. B 4. C 3. D 5.
Câu 42. Một người gửi tiết kiệm với lãi suất 8,4%/năm và lãi hàng năm được nhập vào vốn. Hỏi sau
bao nhiêu năm người đó có được gấp đôi số tiền ban đầu?
A 9. B 10. C 7. D 8.
Câu 43. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như sau
x
y
0
y
−∞
−1
3
+∞
+
0
−
0
+
−∞−∞
55
11
+∞+∞
Đồ thị hàm số y = |f (x)| có bao nhiêu điểm cực trị?
A 2. B 3. C 4. D 5.
Câu 44. Cho hình trụ có thiết diện qua trục là hình vuông cạnh 2a. Mặt phẳng (P ) song song với trục
và cách trục một khoảng
a
2
. Tính diện tích thiết diện của hình trụ cắt bởi mặt phẳng (P ).
A 2
√
3a
2
. B a
2
. C πa
2
. D
√
3a
2
.
Câu 45. Cho hàm số f(x) có đạo hàm trên [0; 1] thỏa mãn f(1) = 1,
1
Z
0
xf(x) dx =
4
15
,
1
Z
0
[f
0
(x)]
2
dx =
49
45
. Tích phân
1
Z
0
[f(x)]
2
dx bằng
A
2
9
. B
1
6
. C
4
63
. D 1.
h Geogebra Pro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
Câu 46. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ bên.
x
y
0
y
−∞
−2
3
+∞
+
0
−
0
+
−∞−∞
44
−2−2
+∞+∞
Số nghiệm của phương trình |f(x − 1)| = 2 là
A 5. B 4. C 3. D 2.
Câu 47. Cho x, y là các số thực dương, thỏa mãn log
1
3
x + log
1
3
y ≤ log
1
3
(x + y
2
) . Tìm giá trị nhỏ nhất
P
min
của biểu thức P = 2x + 3y.
A P
min
= 7 + 3
√
2. B P
min
=
√
2 +
√
3. C P
min
= 7 − 2
√
10. D P
min
= 7 + 2
√
10.
Câu 48. Gọi S là tập hợp các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y =
|x
3
− 3x
2
− 9x + m| trên đoạn [−2; 4] bằng 16. Số phần tử của S là
A 10. B 12. C 14. D 11.
Câu 49. Cho khối chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SC, N thuộc
cạnh SD sao cho SN = 3N D. Mặt phẳng (AMN) cắt khối chóp thành hai phần, gọi thể tích phần
chứa đỉnh S là V
1
, thể tích khối chóp S.ABCD là V
2
. Tính tỉ số
V
1
V
2
.
A
V
1
V
2
=
27
80
. B
V
1
V
2
=
1
3
. C
V
1
V
2
=
27
53
. D
V
1
V
2
=
29
80
.
Câu 50. Có bao nhiêu giá trị nguyên âm của m để phương trình log
2
(2x+m) = log
√
2
(x−1) có nghiệm
duy nhất:
A 0. B 1. C 2. D 3.
———————–HẾT———————–
h Geogebra Pro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
BẢNG ĐÁP ÁN
1. C 2. B 3. A 4. C 5. D 6. D 7. A 8. B 9. B 10. C
11. D 12. D 13. A 14. C 15. A 16. D 17. B 18. A 19. A 20. D
21. D 22. B 23. A 24. C 25. D 26. C 27. D 28. D 29. B 30. A
31. B 32. B 33. B 34. B 35. A 36. D 37. A 38. A 39. A 40. A
41. C 42. A 43. B 44. A 45. A 46. A 47. D 48. D 49. A 50. D
h Geogebra Pro Trang 7
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
MỖI NGÀY MỘT ĐỀ THI 10
Câu 1. Một tổ có 6 học sinh nam và 9 học sinh nữ. Hỏi có bao nhiêu cách chọn 6 học sinh đi lao động
trong đó có 2 học sinh nam?
A C
2
6
+ C
4
9
. B A
2
6
· A
4
9
. C C
2
6
· C
4
9
. D C
4
6
· C
2
9
.
Lời giải.
Số cách chọn 2 học sinh nam là C
2
6
.
Số cách chọn 4 học sinh nữ là C
4
9
.
Số cách chọn 6 học sinh đi lao động trong đó có 2 học sinh nam là C
2
6
· C
4
9
.
Chọn phương án C
Câu 2. Cho cấp số cộng (u
n
) biết u
n
= 3 − 5n. Tìm công sai d của cấp số cộng (u
n
).
A d = 3. B d = −5. C d = −3. D d = 5.
Lời giải.
Theo giả thiết suy ra u
n+1
= 3 − 5(n + 1) = −2 − 5n ⇒ u
n+1
− u
n
= −5, ∀n ≥ 1.
Suy ra (u
n
) là cấp số cộng, công sai d = −5.
Chọn phương án B
Câu 3. Tìm tập nghiệm S của phương trình 4
x
− 6 · 2
x
+ 8 = 0.
A S = {1; 2}. B S = (1; 2). C S = {1}. D S = {2}.
Lời giải.
Ta có 4
x
− 6 · 2
x
+ 8 = 0 ⇔
2
x
= 4
2
x
= 2
⇔
x = 2,
x = 1.
Chọn phương án A
Câu 4. Tổng diện tích các mặt của khối lập phương bằng 96. Tìm thể tích của khối lập phương đó.
A 48. B 84. C 64. D 91.
Lời giải.
Khối lập phương có 6 mặt và theo đề bài tổng diện tích các mặt của khối lập phương là 96 nên diện
tích một mặt của khối lập phương là 96 ÷ 6 = 16.
Suy ra cạnh của hình lập phương là
√
16 = 4. Do đó, thể tích của khối lập phương là 4
2
= 16.
Chọn phương án C
Câu 5. Tập xác định của hàm số y = log
2
x + 3
2 − x
là
A D = R\{−3; 2}. B D = (−∞; −3) ∪ (2; +∞).
C D = [−3; 2]. D D = (−3; 2).
Lời giải.
Hàm số log
2
x + 3
2 − x
có nghĩa khi
x + 3
2 − x
> 0 ⇔ −3 < x < 2.
h Geogebra Pro Trang 1
https://www.facebook.com/groups/GeoGebraPro/
Chọn phương án D
Câu 6. Cho F (x) là nguyên hàm của f(x) =
1
√
x + 2
thỏa mãn F (2) = 4. Giá trị F (−1) bằng
A
√
3. B 1. C 2
√
3. D 2.
Lời giải.
F (x) =
Z
f(x) dx =
Z
1
√
x + 2
dx = 2
√
x + 2 + C.
Theo đề bài F (2) = 4 nên 2
√
2 + 2 + C = 4 ⇔ C = 0 ⇒ F (−1) = 2
√
−1 + 2 = 2.
Vậy F (−1) = 2.
Chọn phương án D
Câu 7. Cho hình chóp S.ABC có (SAB) ⊥ (ABC), tam giác ABC đều cạnh 2a, tam giác SAB vuông
cân tại S. Tính thể tích hình chóp S.ABC.
A
a
3
√
3
3
. B
a
3
√
3
6
. C
2a
3
√
3
3
. D
a
3
√
3
12
.
Lời giải.
S
H A
C
B
2a
Kẻ SH ⊥ AB ⇒ SH ⊥ (ABC) Vì (ABC) ∩ (ABC) = AB và (ABC) ⊥ (ABC).
Ta có: SH =
AB
2
= a (Do SAB là tam giác vuông cân tại S cạnh huyền AB = 2a).
Diện tích tam giác ABC là S
4ABC
= (2a)
2
√
3
4
=
√
3a
2
.
Vậy thể tích khối chóp SABC là: V
SABC
=
1
3
.SH.S
4ABC
=
1
3
.a.
√
3a
2
=
a
3
√
3
3
.
Chọn phương án A
Câu 8. Khối nón tròn xoay có chiều cao bằng 8 cm và độ dài đường sinh bằng 10 cm có thể tích
bằng
A 128π cm
3
. B 96π cm
3
. C 124π cm
3
. D 140π cm
3
.
Lời giải.
Bán kính đáy r =
√
l
2
− h
2
= 6 cm.
Thể tích khối nón V =
1
3
S
đáy
· h =
1
3
· π · 6
2
· 8 = 96πcm
3
.
h
l
h Geogebra Pro Trang 2
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Chọn phương án B
Câu 9. Tính diện tích mặt cầu (S) khi biết chu vi đường tròn lớn của nó bằng 4π.
A S = 32π. B S = 16π. C S = 64π. D S = 8π.
Lời giải.
Đường tròn lớn có bán kính bằng bán kính R của mặt cầu.
Do đó, chu vi của đường tròn lớn là 2πR = 4π ⇔ R = 2.
Vậy diện tích của mặt cầu (S) là 4πR
2
= 16π.
Chọn phương án B
Câu 10. Cho hàm số y = f(x) có bảng biến thiên như hình dưới. Hàm số nghịch biến trong khoảng
nào?
x
y
0
y
−∞
−1
2
+∞
+
0
−
0
+
A (−∞; 2). B (0; 2). C (−1; 2). D (2; +∞).
Lời giải.
Từ bảng biến thiên ta có f
0
(x) < 0, ∀x ∈ (−1; 2), suy ra hàm số y = f(x) nghịch biến trên khoảng
(−1; 2).
Chọn phương án C
Câu 11. Cho a là số thực dương và a 6= 1. Tính giá trị của biểu thức Q = log
a
a
3
·
3
√
a
2
√
a
.
A Q =
19
5
. B Q =
19
7
. C Q =
19
4
. D Q =
19
6
.
Lời giải.
Q = log
a
a
3
·
3
√
a
2
√
a
= log
a
a
3+
2
3
−
1
2
= log
a
a
19
6
=
19
6
.
Chọn phương án D
Câu 12. Một hình trụ có bán kính đáy r = 5 cm, chiều cao h = 7 cm. Tính diện tích xung quanh của
hình trụ.
A 85π cm
2
. B 35π cm
2
. C
35
3
π cm
2
. D 70π cm
2
.
Lời giải.
Hình trụ có độ dài đường sinh l = h = 7 cm.
Diện tích xung quanh của hình trụ S
xq
= 2πrl = 2π · 5 · 7 =70π cm
2
.
h = 7cm
r = 5cm
l
Chọn phương án D
Câu 13.
h Geogebra Pro Trang 3
https://www.facebook.com/groups/GeoGebraPro/
Cho hàm số y = f(x) có bảng biến thiên
như hình vẽ. Hỏi hàm số có bao nhiêu
cực trị?
A 2. B 3. C 1. D
4.
x
y
0
y
−∞
−1
0 2
+∞
+
0
− +
0
−
−∞−∞
22
−1 −1
33
22
Câu 14. Cho hàm số y = f(x) có đồ thị như hình vẽ. Xác định hàm số trên.
A y =
2x + 1
x − 1
. B y =
2x − 1
x − 1
. C y =
2x − 1
x + 1
. D y =
3x + 1
2x + 2
.
x
y
O
2−2−4
2
4
6
−2
Lời giải.
Đồ thị hàm số nhận đường x = −1 là tiệm cận đứng nên ta loại ngay đáp án A và B vì đồ thị của hai
hàm số này đều nhận đường x = 1 là tiệm cận đứng.
Đồ thị hàm số nhận đường y = 2 là tiệm cận ngang.
Ta có lim
x→+∞
2x − 1
x + 1
= 2 ⇒ y = 2 là tiệm cận ngang của đồ thị hàm số y =
2x − 1
x + 1
.
lim
x→−∞
2x − 1
x + 1
= 2 ⇒ y = 2 là tiệm cận ngang của đồ thị hàm số y =
2x − 1
x + 1
.
Vậy hàm số y =
2x − 1
x + 1
thỏa mãn bài toán.
Chọn phương án C
Câu 15. Đồ thị hàm số y =
√
9 − x
2
x
2
− 6x + 8
có bao nhiêu đường tiệm cận?
A 1. B 4. C 3. D 2.
Lời giải.
Hàm số có nghĩa khi chỉ khi x ∈ [−3; 2) ∪ (2; 3], do đó hàm số không có tiệm cận ngang.
Ta có x
2
− 6x + 8 = 0 ⇔ x = 2 hoặc x = 4 /∈ [−3; 3].
Mà lim
x→2
+
√
9 − x
2
x
2
− 6x + 8
= −∞ nên hàm số có duy nhất một tiệm cận đứng x = 2.
Chọn phương án A
Câu 16. Tập nghiệm của bất phương trình log
1
5
4x + 6
x
≥ 0 là
A
Å
−2, −
3
2
ò
. B
ï
−2, −
3
2
ò
. C
Å
−2, −
3
2
ã
. D
ï
−2, −
3
2
ã
.
h Geogebra Pro Trang 4
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Lời giải.
Điều kiện xác định:
4x + 6
x
> 0
x 6= 0
⇔
x > 0
x < −
3
2
.
Bất phương trình tương đương:
4x + 6
x
≤ 1 ⇔
4x + 6 − x
x
≤ 0 ⇔
3x + 6
x
≤ 0 ⇔ −2 ≤ x < 0.
Kết hợp với điều kiện ta được: −2 ≤ x < −
3
2
.
Vậy tập nghiệm của bất phương trình là
ï
−2, −
3
2
ã
.
Chọn phương án D
Câu 17.
Cho hàm số y = f (x) liên tục trên đoạn [−2; 2] và có đồ thị là đường cong
như hình vẽ bên. Tìm số nghiệm của phương trình |f (x) | = 1 trên đoạn
[−2; 2].
A 4. B 6. C 3. D 5.
x
y
O
x
1
x
2
2
4
−2
−4
−2
2
Lời giải.
Số nghiệm của phương trình |f(x)| = 1 là số giao điểm của hai đồ thị hàm
số y = |f(x)| và đường thẳng y = 1. Theo đồ thị ta được số nghiệm là 6.
x
y
O
x
1
x
2
2
4
−2
2
Chọn phương án B
Câu 18. Cho hàm số f(x) có đạo hàm liên tục trên [1; 2], có f (2) = 14 và
2
Z
1
f(x)
x
dx = 6. Tính
I =
2
Z
1
f
0
(x) ln x dx.
A I = 14 ln 2 − 6. B I = 7 ln 2 − 6. C I = 7 ln 2 − 6. D I = 14 ln 2 + 6.
Lời giải.
Đặt
u = ln x
v
0
= f
0
(x)
⇒
u
0
=
1
x
v = f(x)
. Khi đó I = f(x) ln x|
2
1
−
2
Z
1
f(x)
x
dx = f (2) ln 2 − 0 − 6 = 14 ln 2 − 6.
h Geogebra Pro Trang 5
https://www.facebook.com/groups/GeoGebraPro/
Chọn phương án A
Câu 19. Cho số phức z thỏa mãn z − 3 + i = 0. Môđun của z bằng bao nhiêu?
A
√
10.
B 10. C
√
3. D 4.
Lời giải.
Ta có |z| = |z| = |3 − i| =
√
10.
Chọn phương án A
Câu 20. Cho số phức z
1
= 3 + 2i, z
2
= 6 + 5i. Tìm số phức liên hợp của z = 6z
1
+ 5z
2
.
A ¯z = 51 + 40i. B ¯z = 51 − 40i. C ¯z = 48 + 37i. D ¯z = 48 − 37i.
Lời giải.
Ta có z = 6z
1
+ 5z
2
= 48 + 37i nên ¯z = 48 − 37i.
Chọn phương án D
Câu 21. Gọi A, B, C là các điểm trong mặt phẳng Oxy theo thứ tự biểu diễn các số phức 2 + 3i, 3 + i,
1 + 2i. Trọng tâm G của tam giác ABC biểu diễn số phức z. Tìm z.
A z = 1 + i. B z = 1 − i. C z = 2 − 2i. D z = 2 + 2i.
Lời giải.
Ta có: A (2; 3), B (3; 1), C (1; 2) ⇒ G (2; 2) là điểm biểu diễn số phức z = 2 + 2i.
Chọn phương án D
Câu 22 (2H3B1-1). Trong không gian với hệ tọa độ Oxyz, tìm tọa độ điểm M trên trục Ox cách
đều hai điểm A (1; 2; −1) và điểm B (2; 1; 2)
A M
Å
1
2
; 0; 0
ã
. B M
Å
3
2
; 0; 0
ã
. C M
Å
2
3
; 0; 0
ã
. D M
Å
1
3
; 0; 0
ã
.
Lời giải.
Ta có M ∈ Ox ⇒ M (m; 0; 0).
Theo bài ta có:
MA = MB ⇔ MA
2
= MB
2
⇔ (m − 1)
2
+ 2
2
+ 1
2
= (m − 2)
2
+ 1
2
+ 2
2
⇔ (m − 1)
2
= (m − 2)
2
⇔
m − 1 = m − 2
m − 1 = 2 − m
⇔ m =
3
2
⇒ M
Å
3
2
; 0; 0
ã
.
Chọn phương án B
Câu 23. Trong hệ tọa độ Oxyz, cho điểm I(2; −1; −1) và mặt phẳng (P ): x − 2y − 2z + 3 = 0. Viết
phương trình mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng (P ).
A S : x
2
+ y
2
+ z
2
− 4x + 2y + 2z − 3 = 0. B S : x
2
+ y
2
+ z
2
− 2x + y + z − 3 = 0.
C S : x
2
+ y
2
+ z
2
− 4x + 2y + 2z + 1 = 0. D S : x
2
+ y
2
+ z
2
− 2x + y + z + 1 = 0.
Lời giải.
Gọi R là bán kính mặt cầu.
Do (S) tiếp xúc với (P ) nên R = d(I, (P )) =
|2 − 2(−1) − 2(−1) + 3|
p
1
2
+ (−2)
2
+ (−2)
2
= 3.
Vậy phương trình S : (x − 2)
2
+ (y + 1)
2
+ (z + 1)
2
= 9 ⇔ x
2
+ y
2
+ z
2
− 4x + 2y + 2z − 3 = 0.
h Geogebra Pro Trang 6
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Chọn phương án A
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P ): 2x −2y + z + 4 = 0. Tính khoảng
cách d từ điểm M(1; 2; 1) đến (P ).
A d = 3. B d = 4. C d = 1. D d =
1
3
.
Lời giải.
Khoảng cách d từ điểm M(1; 2; 1) đến (P ) là d(M, (P )) =
|2 · 1 − 2 · 2 + 1 + 4|
p
2
2
+ (−2)
2
+ 1
2
= 1.
Chọn phương án C
Câu 25. Trong hệ tọa độ Oxyz, cho đường thẳng d :
x − 1
2
=
y − 3
−1
=
z − 1
1
cắt mặt phẳng (P ) :
2x − 3y + z − 2 = 0 tại điểm I(a; b; c). Khi đó a + b + c bằng
A 9. B 5. C 3. D 7.
Lời giải.
Ta có {I} = d ∩ (P ) suy ra I ∈ d và I ∈ (P ).
Vì I ∈ d nên tọa độ của I có dạng (1 + 2t; 3 − t; 1 + t) với t ∈ R.
Vì I ∈ (P ) nên ta có phương trình: 2(1 + 2t) − 3(3 − t) + 1 + t − 2 = 0 ⇔ t = 1.
Vậy I(3; 2; 2) suy ra a + b + c = 3 + 2 + 2 = 7.
Chọn phương án D
Câu 26. Cho lăng trụ tam giác đều ABC.A
0
B
0
C
0
có diện tích đáy bằng
√
3a
2
(đvdt), diện tích tam
giác A
0
BC bằng 2a
2
(đvdt). Tính góc giữa hai mặt phẳng (A
0
BC) và (ABC)?
A 120
◦
. B 60
◦
. C 30
◦
. D 45
◦
.
Lời giải.
• Ta có 4ABC là hình chiếu vuông góc của ∆A
0
BC trên mặt phẳng (ABC).
• Gọi ϕ là góc giữa (A
0
BC) và (ABC).
Ta có: cos ϕ =
S
4ABC
S
∆A
0
BC
=
a
2
√
3
2a
2
=
√
3
2
⇒ ϕ = 30
◦
.
B
A
0
A
B
0
C
0
C
Chọn phương án C
Câu 27. Cho hàm số y = f(x) liên tục trên [−3; 3] và có bảng xét dấu đạo hàm như hình bên.
x
y
0
−3 −1
0 1 2 3
+
0
−
0
−
0
+
0
−
Mệnh đề nào sau đây sai về hàm số đó?
A Hàm số đạt cực tiểu tại x = 1. B Hàm số đạt cực đại tại x = −1.
C Hàm số đạt cực đại tại x = 2. D Hàm số đạt cực tiểu tại x = 0.
Lời giải.
Dựa vào bảng xét dấu của đạo hàm ta thấy f
0
(0) = 0 và đạo hàm không đổi dấu khi x qua x
0
= 0 nên
hàm số đã cho không đạt cực tiểu tại x = 0.
h Geogebra Pro Trang 7
https://www.facebook.com/groups/GeoGebraPro/
Chọn phương án D
Câu 28. Tìm giá trị nhỏ nhất của hàm số y = 2x +
√
5 − x
2
.
A 5. B 2
√
5. C −3. D −2
√
5.
Lời giải.
Tập xác định: D = R. Ta có y
0
= 2 −
x
√
5 − x
2
.
y
0
= 0 ⇔ 2 −
x
√
5 − x
2
= 0 ⇔ x = 1.
y(1) = 4; y(
√
5) = 2
√
5; y(−
√
5) = −2
√
5.
Chọn phương án D
Câu 29. Cho a, b là các số dương thỏa mãn log
9
a = log
16
b = log
12
5b − a
2
. Tính giá trị T =
a
b
.
A T =
3 +
√
6
4
. B T = 7 − 2
√
6. C T = 7 + 2
√
6. D T =
3 −
√
6
4
.
Lời giải.
Đặt log
9
a = log
16
b = log
12
5b − a
2
= t, ta được a = 9
t
, b = 16
t
,
5b − a
2
= 12
t
.
Suy ra
5 · 16
t
− 9
t
2
= 12
t
⇔ 5 · 16
t
− 2 · 12
t
− 9
t
= 0 ⇔ 5 − 2 ·
Å
3
4
ã
t
−
Å
3
4
ã
2t
⇔
Å
3
4
ã
t
=
√
6 − 1.
Do đó
a
b
=
9
t
16
t
=
Å
3
4
ã
2t
= (
√
6 − 1)
2
= 7 − 2
√
6.
Chọn phương án B
Câu 30. Phương trình x
3
− 3x + 2m − 2 = 0 có đúng một nghiệm dương khi m thỏa
A m = 2 hoặc m ≤ 1. B m ∈ ∅. C m > 1. D m < 1 hoặc m > 2.
Lời giải.
Phương trình đã cho tương đương: x
3
− 3x = 2 − 2m. Đặt y = x
3
− 3x (C) và y = 2 − 2m (d).
Ta có bảng biến thiên của y = x
3
− 3x là
x
y
0
y
−∞
−1
1
+∞
+
0
−
0
+
−∞−∞
22
−2−2
+∞+∞
Số nghiệm phương trình chính là số giao điểm của (d) và (C). Yêu cầu bài toán là phương trình đã
cho có đúng một nghiệm dương, tức là trong số các giao điểm của (d) và (C) chỉ có đúng một điểm có
hoành độ dương.
Dựa vào bảng biến thiên của (C) ta có các trường hợp thỏa yêu cầu
2 − 2m ≥ 0
2 − 2m = −2
⇔
m ≤ 1
m = 2
Chọn phương án A
Câu 31. Bất phương trình 6 · 4
x
− 13 · 6
x
+ 6 · 9
x
> 0 có tập nghiệm là?
A S = (−∞; −2) ∪ (1; +∞). B S = (−∞; −1) ∪ (1; +∞).
C S = (−∞; −2] ∪ [2; +∞). D S = (−∞; −1) ∪ (1; +∞).
Lời giải.
Chia cả hai vế của bất phương trình cho 9
x
ta được 6 ·
Å
2
3
ã
2x
− 13 ·
Å
2
3
ã
x
+ 6 > 0.
h Geogebra Pro Trang 8
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Đặt
Å
2
3
ã
x
= t (t > 0). Ta được bất phương trình mới 6t
2
− 13t + 6 > 0 ⇔
t <
3
2
t >
3
2
.
Suy ra
Å
2
3
ã
x
<
2
3
Å
2
3
ã
x
>
3
2
⇔
x > 1
x < −1.
Vậy tập nghiệm của bất phương trình là S = (−∞; −1) ∪ (1; +∞).
Chọn phương án B
Câu 32. Cho khối nón có thể tích V =
√
3
4
πa
3
và thiết diện qua trục là tam giác đều. Diện tích xung
quanh của hình nón đó là
A S
xq
= πa
2
3
…
1
16
. B S
xq
= 2πa
2
3
…
9
16
. C S
xq
= 3πa
2
3
…
9
16
. D S
xq
= 3πa
2
3
…
2
16
.
Lời giải.
Do thiết diện qua trục là tam giác đều nên l = 2R và h =
2R
√
3
2
= R
√
3.
Theo đề bài khối nón có thể tích
V =
√
3
4
πa
3
⇔
1
3
h · πR
2
=
π
√
3a
3
4
⇔
1
3
πR
3
√
3 =
π
√
3a
3
4
⇔ R
3
=
3
4
a
3
⇔ R =
3
…
3
4
· a
⇒ đường sinh của hình nón là l = 2
3
…
3
4
· a.
Diện tích xung quanh hình nón là S
xq
= πRl = 2πa
2
3
…
9
16
.
Chọn phương án B
Câu 33. Cho hàm số y = f(x) dương có đạo hàm liên tục trên đoạn
î
0;
√
3
ó
, biết rằng f
0
(x)−
√
x
2
+ 1·
f(x) = 0 và f
Ä
√
3
ä
= e
3
. Tính I =
√
3
Z
0
ln [f(x)] dx.
A 2
√
3. B 3
√
3 −
7
3
. C 3
√
3 +
7
3
. D 3
√
3 − 2.
Lời giải.
Ta có
f
0
(x) −
√
x
2
+ 1 · f(x) = 0 ⇔
f
0
(x)
f(x)
=
√
x
2
+ 1
⇒
Z
f
0
(x)
f(x)
dx =
Z
√
x
2
+ 1 dx
⇒ ln f(x) =
x
2
√
x
2
+ 1 +
1
2
ln
Ä
x +
√
x
2
+ 1
ä
+ C.
Ta có f
Ä
√
3
ä
= e
3
⇒ C = 3 −
√
3 −
1
2
ln
Ä
√
3 + 2
ä
.
Do đó
√
3
Z
0
ln f(x) dx =
√
3
Z
0
ï
x
2
√
x
2
+ 1 +
1
2
ln
Ä
x +
√
x
2
+ 1
ä
+
Å
3 −
√
3 −
1
2
ln
Ä
√
3 + 2
ä
ãò
dx
= 3
√
3 −
7
3
·
Chọn phương án B
h Geogebra Pro Trang 9
https://www.facebook.com/groups/GeoGebraPro/
Câu 34. Cho hình D giới hạn bởi các đường y = x
2
− 2 và y = −|x|. Khi đó diện tích của hình D
là
A
13
3
. B
7
3
. C
7π
3
. D
13π
3
.
Lời giải.
Xét phương trình x
2
− 2 = −|x| ⇔
x
2
− 2 = x nếu x < 0
x
2
− 2 = −x nếu x > 0
⇔ x = −1 và x = 1.
Do đó ta có S =
Z
0
−1
(x + 2 − x
2
)dx +
Z
1
0
(−x − x
2
+ 2)dx =
7
3
.
Chọn phương án B
Câu 35. Cho hai số phức z
1
, z
2
thỏa mãn |2z −i| = |iz + 2|, biết |z
1
−z
2
| =
√
2. Tính giá trị của biểu
thức A = |z
1
− 2z
2
|.
A A =
√
5. B A =
√
5
2
. C A =
√
3. D A =
√
3
2
.
Lời giải.
Gọi z
1
= x
1
+ y
1
i, z
2
= x
2
+ y
2
i với x
1
, y
1
, x
2
, y
2
∈ R. Theo giả thiết ta có
|2x
1
+ (2y
1
− 1)i| = |2 − y
1
+ x
1
i|
|2x
2
+ (2y
2
− 1)i| = |2 − y
2
+ x
2
i|
(x
1
− x
2
)
2
+ (y
1
− y
2
)
2
= 2
⇔
x
2
1
+ y
2
1
= 1
x
2
2
+ y
2
2
= 1
x
1
x
2
+ y
1
y
2
= 0
Do đó, A
2
= |z
1
− 2z
2
|
2
= (x
1
− 2x
2
)
2
+ (y
1
− 2y
2
)
2
= (x
2
1
+ y
2
1
) + 4(x
2
2
+ y
2
2
) − 4(x
1
x
2
+ y
1
y
2
) = 5. Khi
đó A =
√
5.
Chọn phương án A
Câu 36. Cho phương trình z
2
−4z +5 = 0 có hai nghiệm phức là z
1
, z
2
. Tính A = |z
1
|+|z
2
|+z
1
·z
2
.
A A = 25 + 2
√
5. B A = 0. C A = 5 − 2
√
5. D A = 5 + 2
√
5.
Lời giải.
Do z
1
, z
2
là hai số phức liên hợp của nhau nên |z
1
|
2
= |z
2
|
2
= z
1
· z
2
= 5.
Suy ra A = 5 + 2
√
5.
Chọn phương án D
Câu 37. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình là x
2
+ y
2
+ z
2
= 9
và điểm A (0; −1; 2). Gọi (P ) là mặt phẳng qua A và cắt mặt cầu (S) theo một đường tròn có chu vi
nhỏ nhất. Phương trình của (P ) là
A y − 2z + 5 = 0. B x − y + 2z − 5 = 0. C −y + 2z + 5 = 0. D y − 2z − 5 = 0.
Lời giải.
Mặt cầu (S) có tâm O(0; 0; 0) và bán kính R = 3. A(0; −1; 2) là điểm nằm bên trong mặt cầu (S). (P )
là mặt phẳng qua A và cắt mặt cầu (S) theo một đường tròn có bán kính r.
Gọi H là hình chiếu của O lên (P ). Ta có
r
2
= R
2
− OH
2
. r
min
⇔ OH
max
⇔ H ≡ A.
Khi đó (P ) nhận
# »
OA = (0; −1; 2) là véc-tơ pháp tuyến. Vậy phương trình (P ): y − 2z + 5 = 0.
Chọn phương án A
h Geogebra Pro Trang 10
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 38. Trong không gian Oxyz, cho hai điểm A(1; 2; 3), B(3; 4; 5) và mặt phẳng (P ) : x+2y+3z−14 =
0. Gọi ∆ là một đường thẳng thay đổi nằm trong mặt phẳng (P ). Gọi H, K lần lượt là hình chiếu vuông
góc của A, B trên ∆. Biết rằng AH = BK thì trung điểm của HK luôn thuộc một đường thẳng d cố
định, phương trình của đường thẳng d là
A
x = t
y = 13 − 2t
z = −4 + t
. B
x = t
y = 13 + 2t
z = −4 + t
. C
x = 1
y = 13 − 2t
z = −4 + t
. D
x = t
y = 13 − 2t
z = −4 − t
.
Lời giải.
Gọi I là trung điểm của HK.
Xét các tam giác AHI và BKI, ta có các tam giác này vuông tại
H, K, theo giả thiết AH = BK, IH = IK ⇒ 4HIA = 4IKB ⇒
IA = IB ⇒ I thuộc mặt phẳng trung trực của AB.
Theo giả thiết I ∈ (P ) ⇒ I thuộc giao tuyến của mặt phẳng trung
trực (α) của AB với (P ).
Mặt phẳng (α):
Qua I
0
(2; 3; 4)
Có véc-tơ pháp tuyến
# »
AB = (1; 1; 1).
Suy ra (α): x + y + z − 9 = 0.
Tọa độ các điểm M ∈ d thỏa mãn hệ
x + 2y + 3z − 14 = 0
x + y + z − 9 = 0.
I
A
H
K
B
Đặt x = t ⇒
x = t
y = 13 − 2t
z = −4 + t
⇒ phương trình của đường thẳng d là
x = t
y = 13 − 2t
z = −4 + t.
Chọn phương án A
Câu 39. Từ một hộp chứa 5 viên bi đỏ, 4 viên bi xanh và 3 viên bi vàng lấy ngẫu nhiên 3 viên bi.
Tính xác suất để 3 viên bi lấy ra có đủ 3 màu.
A
3
11
. B
1
22
. C
3
220
. D
11
3
.
Lời giải.
Số phần tử của không gian mẫu là n(Ω) = C
3
12
= 220.
Gọi A là biến cố: "3 viên bi lấy ra có đủ 3 màu".
Số phần tử của biến cố A là n(A) = C
1
5
C
1
4
C
1
3
= 60.
Xác suất của biến cố A là P (A) =
n(A)
n(Ω)
=
60
220
=
3
11
.
Chọn phương án A
Câu 40. Cho lăng trụ tam giác đều ABC.A
0
B
0
C
0
có tất cả các cạnh đều bằng a. Khoảng cách giữa hai
đường thẳng BC và AB
0
bằng
A
a
√
21
7
. B
a
√
3
2
. C
a
√
7
4
. D
a
√
2
2
.
Lời giải.
h Geogebra Pro Trang 11
https://www.facebook.com/groups/GeoGebraPro/
Ta có BCkB
0
C
0
⇒ BCk(AB
0
C
0
).
Suy ra:
d(BC, AB
0
) = d(BC, (AB
0
C
0
)) = d(B, (AB
0
C
0
)) =
d(A
0
, (AB
0
C
0
)).
Gọi I và H lần lượt là hình chiếu vuông góc
của A
0
trên B
0
C
0
và AI.
Ta có: B
0
C
0
⊥A
0
I và B
0
C
0
⊥A
0
A
nên B
0
C
0
⊥(A
0
AI) ⇒ B
0
C
0
⊥A
0
H.
Mà AI⊥A
0
H. Do đó (AB
0
C
0
) ⊥A
0
H.
A
B
C
A
0
B
0
C
0
I
H
Khi đó: d (A
0
, (AB
0
C
0
)) = A
0
H =
A
0
A.A
0
I
√
A
0
A
2
+ A
0
I
2
=
a.
a
√
3
2
s
a
2
+
Ç
a
√
3
2
å
2
=
a
√
21
7
.
Vậy khoảng cách cần tìm là
a
√
21
7
.
Chọn phương án
A
Câu 41. Cho hàm số y =
mx − 4m + 5
x + 3m
với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên
của m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S.
A 2. B 4. C 3. D 5.
Lời giải.
y
0
=
3m
2
+ 4m − 5
(x + 3m)
2
.
Để hàm số nghịch biến thì 3m + 4m − 5 < 0 ⇔
2 −
√
19
3
< m <
2 +
√
19
3
.
Vậy các giá trị nguyên của m là 0, 1, 2.
Chọn phương án C
Câu 42. Một người gửi tiết kiệm với lãi suất 8,4%/năm và lãi hàng năm được nhập vào vốn. Hỏi sau
bao nhiêu năm người đó có được gấp đôi số tiền ban đầu?
A 9. B 10. C 7. D 8.
Lời giải.
Gọi số tiền ban đầu người đó gửi vào ngân hàng là A, r = 8,4% là lãi suất hàng năm, P
n
là số tiền
nhận được sau n năm. Vì lãi hàng năm nhập vào vốn nên theo công thức lãi kép ta có
P
n
= A · (1 + r)
n
⇒ 2A = A · (1 + r)
n
⇒ 2 = (1 + r)
n
⇒ n = log
1+r
2 ≈ 9.
Chọn phương án A
Câu 43. Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau
x
y
0
y
−∞
−1
3
+∞
+
0
−
0
+
−∞−∞
55
1
1
+∞+∞
Đồ thị hàm số y = |f(x)| có bao nhiêu điểm cực trị?
h Geogebra Pro Trang 12
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
A 2. B 3. C 4. D 5.
Lời giải.
Số điểm cực trị của đồ thị hàm số y = |f(x)| bằng số điểm cực trị của đồ thị hàm số y = f(x) cộng với
số giao điểm của đồ thị hàm số y = f(x) với trục hoành (không tính điểm cực trị).
Vì đồ thị hàm số y = f(x) có 2 điểm cực trị và cắt trục Ox tại 1 điểm trên đồ thị hàm số y = |f(x)|
có 2 + 1 = 3 điểm cực trị.
Chọn phương án B
Câu 44. Cho hình trụ có thiết diện qua trục là hình vuông cạnh 2a. Mặt phẳng (P ) song song với trục
và cách trục một khoảng
a
2
. Tính diện tích thiết diện của hình trụ cắt bởi mặt phẳng (P ).
A 2
√
3a
2
. B a
2
. C πa
2
. D
√
3a
2
.
Lời giải.
Gọi ABB
0
A
0
là thiết diện qua trục của hình trụ. Từ giả thiết ta
suy ra đường cao hình trụ là AA
0
= 2a, bán kính đường tròn đáy
hình trụ là R =
AB
2
= a.
Mặt phẳng (P ) song song với trục nên cắt hình trụ theo thiết
diện là hình chữ nhật có một cạnh MQ = AA
0
= 2a, và cách trục
một khoảng
a
2
nên O
0
H =
a
2
với H là trung điểm của P Q. Khi
đó P Q = 2
p
O
0
Q
2
− O
0
H
2
= 2
…
a
2
−
a
2
4
= a
√
3.
Do đó diện tích thiết diện cần tìm là MQ · P Q = 2
√
3a
2
.
B
O
M
N
A
P
O
0
A
0
B
0
Q
H
Chọn phương án A
Câu 45. Cho hàm số f(x) có đạo hàm trên [0; 1] thỏa mãn f(1) = 1,
1
Z
0
xf(x) dx =
4
15
,
1
Z
0
[f
0
(x)]
2
dx =
49
45
. Tích phân
1
Z
0
[f(x)]
2
dx bằng
A
2
9
. B
1
6
. C
4
63
. D 1.
Lời giải.
Đặt
u = xf(x)
dv = dx
⇒
du = [f(x) + xf
0
(x)] dx
v = x
. Khi đó
1
Z
0
xf(x) dx = x
2
f(x)
1
0
−
1
Z
0
x[f(x) + xf
0
(x)] dx
= f(1) −
1
Z
0
xf(x) dx −
1
Z
0
x
2
f
0
(x) dx.
h Geogebra Pro Trang 13
https://www.facebook.com/groups/GeoGebraPro/
Suy ra
1
Z
0
x
2
f
0
(x) dx = 1 − 2 ·
4
15
=
7
15
. Khi đó dự đoán dạng f
0
(x) = mx
2
, với m ∈ R. Ta có
1
Z
0
[mx
2
− f
0
(x)]
2
dx =
1
Z
0
m
2
x
4
dx −
1
Z
0
2mx
2
f
0
(x) dx +
1
Z
0
[f
0
(x)]
2
dx
=
m
2
5
−
14m
15
+
49
45
=
(3m − 7)
2
45
.
Ta cần
1
Z
0
[mx
2
− f
0
(x)]
2
dx = 0 ⇔
(3m − 7)
2
45
= 0 ⇔ m =
7
3
. Như vậy ta có
1
Z
0
ï
7
3
x
2
− f
0
(x)
ò
2
dx = 0.
Suy ra f
0
(x) =
7
3
x
2
⇒ f(x) =
7x
3
9
+ C. Từ f (1) = 1 ⇒ C =
2
9
. Khi đó f(x) =
7x
3
9
+
2
9
thỏa mãn
1
Z
0
xf(x) dx =
4
15
. Vậy
1
Z
0
[f(x)]
2
dx =
1
Z
0
Å
7x
3
9
+
2
9
ã
2
dx =
2
9
.
Chọn phương án A
Câu 46. Cho hàm số y = f(x) có bảng biến thiên như hình vẽ bên.
x
y
0
y
−∞
−2
3
+∞
+
0
−
0
+
−∞−∞
44
−2−2
+∞+∞
Số nghiệm của phương trình |f(x − 1)| = 2 là
A
5. B 4. C 3. D 2.
Lời giải.
Từ bảng biến thiên suy ra phương trình f(x) = 0 có 3 nghiệm phân biệt là x
1
, x
2
, x
3
thỏa mãn
x
1
< −2 < x
2
< 3 < x
3
. Khi đó phương trình f(x−1) = 0 có 3 nghiệm phân biệt là x
1
+1, x
2
+1, x
3
+1.
Suy ra bảng biến thiên của hàm số y = |f (x − 1)| như sau
x
y
0
y
−∞
x
1
+ 1
−1
x
2
+ 1
4
x
3
+ 1
+∞
− + − + − +
+∞+∞
00
44
00
22
00
+∞+∞
Dựa vào bảng biến thiên ta suy ra phương trình |f(x − 1)| = 2 có 5 nghiệm.
Chọn phương án A
h Geogebra Pro Trang 14
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Câu 47. Cho x, y là các số thực dương, thỏa mãn log
1
3
x + log
1
3
y ≤ log
1
3
(x + y
2
) . Tìm giá trị nhỏ nhất
P
min
của biểu thức P = 2x + 3y.
A P
min
= 7 + 3
√
2. B P
min
=
√
2 +
√
3. C P
min
= 7 − 2
√
10. D P
min
= 7 + 2
√
10.
Lời giải.
log
1
3
x + log
1
3
y ≤ log
1
3
(x + y
2
) ⇔ xy ≥ x + y
2
⇔ x(y − 1) ≥ y
2
. Từ đây, do x, y dương nên ta suy ra
y > 1 và x ≥
y
2
y − 1
= y + 1 +
1
y − 1
.
Do đó, P ≥ 5y +2+
2
y − 1
= 5(y −1)+
2
y − 1
+7 ≥ 2
√
10+7. Dấu bằng xảy ra khi y = 1+
√
10
5
, x =
2 +
7
√
10
10
.
Chọn phương án D
Câu 48. Gọi S là tập hợp các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y =
|x
3
− 3x
2
− 9x + m| trên đoạn [−2; 4] bằng 16. Số phần tử của S là
A 10. B 12. C 14. D 11.
Lời giải.
Xét hàm số y = f(x) = x
3
− 3x
2
− 9x + m có y
0
= 3x
2
− 6x − 9, y
0
= 0 ⇔
x = −1
x = 3.
Bảng biến thiên
x
f
0
(x)
f(x)
−2 −1
3 4
+
0
−
0
+
m − 2m − 2
m + 5m + 5
m − 27m − 27
m − 20m − 20
Giá trị lớn nhất của hàm số y = |x
3
− 3x
2
− 9x + m| trên đoạn [−2; 4] bằng 16 khi và chỉ khi
m + 5 = 16
27 − m ≤ 16
m − 27 = 16
m + 5 ≤ 16
⇔ m = 11.
Vậy m = 11 là giá trị duy nhất thỏa mãn.
Chọn phương án D
Câu 49. Cho khối chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SC, N thuộc
cạnh SD sao cho SN = 3ND. Mặt phẳng (AMN) cắt khối chóp thành hai phần, gọi thể tích phần
chứa đỉnh S là V
1
, thể tích khối chóp S.ABCD là V
2
. Tính tỉ số
V
1
V
2
.
A
V
1
V
2
=
27
80
. B
V
1
V
2
=
1
3
. C
V
1
V
2
=
27
53
. D
V
1
V
2
=
29
80
.
Lời giải.
h Geogebra Pro Trang 15
https://www.facebook.com/groups/GeoGebraPro/
Gọi O là tâm là hình bình hành ABCD.
Trong mặt phẳng (SAC) gọi I là giao điểm của SO và AM.
Trong mặt phẳng (SBD) gọi E là giao điểm của NI và SB.
Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN)
là tứ giác ANME.
Cách 1. Dùng tỉ số thể tích
Ta có
V
SANE
V
SADB
=
SN
SD
·
SE
SB
=
3
4
·
SE
SB
. (1)
V
SMN E
V
SCDB
=
SM
SC
·
SN
SD
·
SE
SB
=
1
2
·
3
4
·
SE
SB
=
3
8
·
SE
SB
. (2)
Lấy (1) cộng (2) ta được
V
1
1
2
V
2
=
9
8
·
SE
SB
⇔
V
1
V
2
=
9
16
·
SE
SB
. (3)
A
N
B
C
M
E
S
O
D
I
Ta có
V
SNAM
V
SDAC
=
SN
SD
·
SM
SC
=
3
4
·
1
2
=
3
8
. (4)
V
SEAM
V
SBAC
=
SE
SB
·
SM
SC
=
1
2
·
SE
SB
. (5)
Lấy (4) cộng (5) ta được
V
1
1
2
V
2
=
3
8
+
1
2
·
SE
SB
⇔
V
1
V
2
=
3
16
+
1
4
·
SE
SB
. (6)
Từ (3) và (6) ta có phương trình
9
16
·
SE
SB
=
3
16
+
1
4
·
SE
SB
⇔
SE
SB
=
3
5
. (7)
Thế (7) vào (3) ta được
V
1
V
2
=
9
16
·
SE
SB
=
9
16
·
3
5
=
27
80
.
Cách 2. Dùng tính chất thiết diện
Tính chất. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng (P ) cắt các cạnh
SA, SB, SC, SD lần lượt tại A
0
, B
0
, C
0
, D
0
thì ta có đẳng thức
SA
SA
0
+
SC
SC
0
=
SB
SB
0
+
SC
SC
0
.
Ta có
SD
SN
+
SB
SE
=
SC
SM
+
SA
SA
⇔
SB
SE
= 1 + 2 −
4
3
=
5
3
⇔
SE
SB
=
3
5
.
h Geogebra Pro Trang 16
LUYỆN THI TỐT NGHIỆP THPT 2019-2020
Ta có
V
SAMN
V
SACD
=
SN
SD
·
SM
SC
=
3
4
·
1
2
=
3
8
⇒ V
SAMN
=
3
16
V
2
.
V
SAME
V
SACB
=
SM
SC
·
SE
SB
=
1
2
·
3
5
=
3
10
⇒ V
SAME
=
3
20
V
2
.
Suy ra
V
1
= V
SAMN
+ V
SAME
=
3
16
V
2
+
3
20
V
2
=
27
80
V
2
.
Vậy
V
1
V
2
=
27
80
.
Chọn phương án A
Câu 50. Có bao nhiêu giá trị nguyên âm của m để phương trình log
2
(2x+m) = log
√
2
(x−1) có nghiệm
duy nhất:
A 0. B 1. C 2. D 3.
Lời giải.
log
2
(2x + m) = log
√
2
(x − 1) ⇔
2x + m > 0
x − 1 > 0
log
2
(2x + m) = log
2
(x − 1)
2
⇔
x > 1
2x + m = (x − 1)
2
⇔
x > 1
x
2
− 4x + 1 − m = 0 (1).
PT log
2
(2x + m) = log
√
2
(x −1) có nghiệm duy nhất khi phương trình (1) có nghiệm duy nhất lớn hơn
1.
Ta có (1) ⇔ m = x
2
− 4x + 1. Xét hàm số f(x) = x
2
− 4x + 1 trên khoảng (1; +∞) ta được
m = −3
m > −2
⇒ m ∈ {−3; −2; −1}.
Chọn phương án D
———————–HẾT———————–
h Geogebra Pro Trang 17
https://www.facebook.com/groups/GeoGebraPro/
BẢNG ĐÁP ÁN
1. C 2. B 3. A 4. C 5. D 6. D 7. A 8. B 9. B 10. C
11. D 12. D 13. A 14. C 15. A 16. D 17. B 18. A 19. A 20. D
21. D 22. B 23. A 24. C 25. D 26. C 27. D 28. D 29. B 30. A
31. B 32. B 33. B 34. B 35. A 36. D 37. A 38. A 39. A 40. A
41. C 42. A 43. B 44. A 45. A 46. A 47. D 48. D 49. A 50. D
h Geogebra Pro Trang 18
| 1/122
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

MỖI NGÀY MỘT ĐỀ THI 6
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Từ các chữ số 1; 2; 3; 4 có thể lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau? A. 42. B. 12. C. 24. D. 44. (u2 − u4 + u5 = 114
Câu 2. Tìm số hạng đầu u1 và công bội q của cấp số nhân (un) thỏa mãn u3 − u5 + u6 = 342 A. u1 = 2, q = 3. B. u1 = 3, q = 2. C. u1 = 1, q = 3. D. u1 = 1, q = 2.
Câu 3. Tìm nghiệm của phương trình log (3x − 2) = 3. 2 8 10 16 11 A. x = . B. x = . C. x = . D. x = . 3 3 3 3
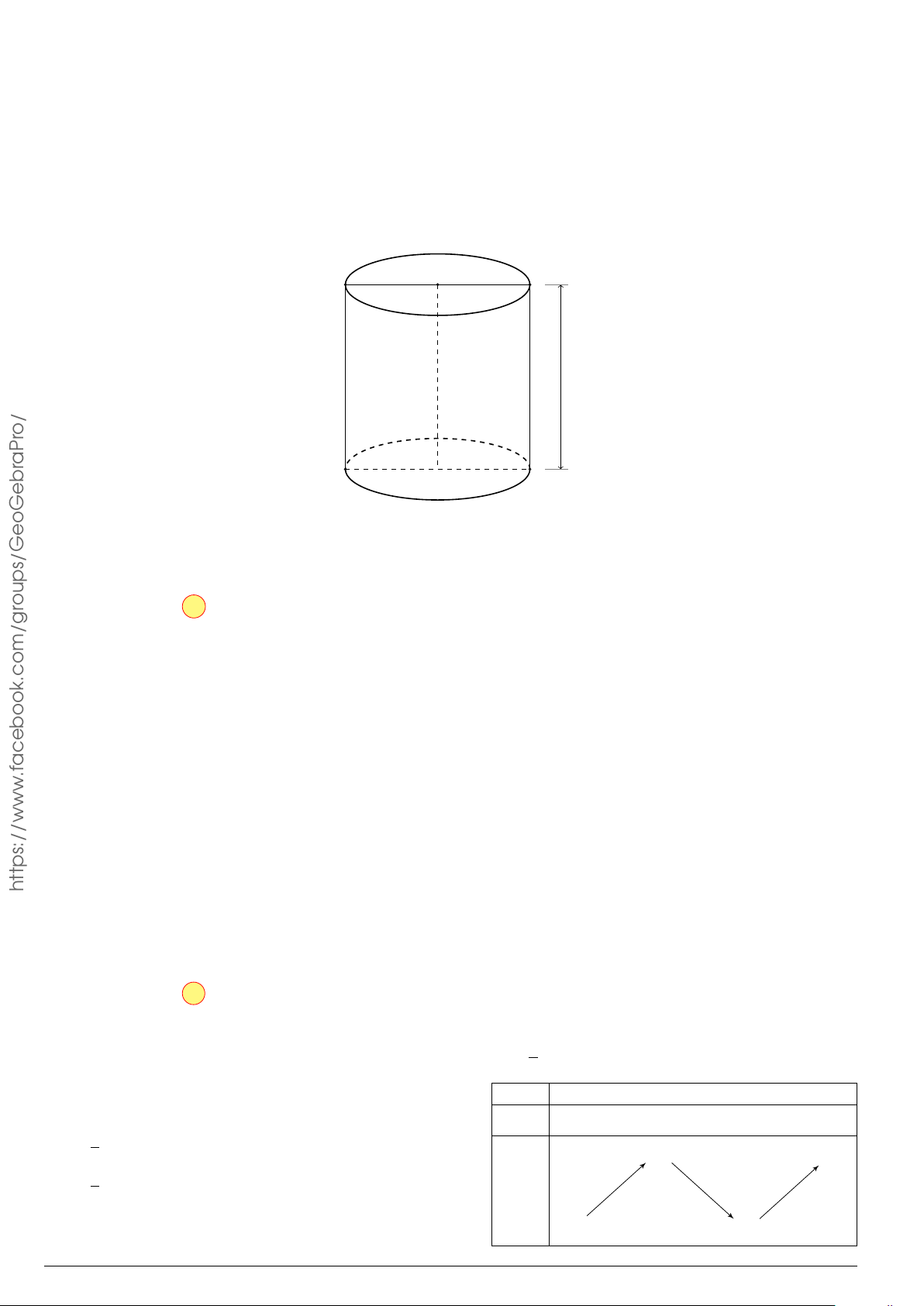
Câu 4. Hình lập phương có đường chéo của mặt bên bằng 4 cm. Tính thể tích khối lập phương đó. √ √ √ A. 8 2 cm3. B. 16 2 cm3. C. 8 cm3. D. 2 2 cm3. 3 − x
Câu 5. Tập xác định của hàm số y = log là 2 2x A. D = (3; +∞). B. D = (0; 3]. 2019-2020
C. D = (−∞; 0) ∪ (3; +∞). D. D = (0; 3).
Câu 6. Cho hàm số f (x) = 2x + ex. Tìm một nguyên hàm F (x) của hàm số f (x) thỏa mãn F (0) = THPT 2019. A. F (x) = ex − 2019. B. F (x) = x2 + ex − 2018. C. F (x) = x2 + ex + 2017. D. F (x) = x2 + ex + 2018. GHIỆP
Câu 7. Cho khối chóp S.ABCD cạnh bên SA vuông góc với đáy, đáy ABCD là hình chữ nhật, N
AB = a, AD = 2a, SA = 3a. Thể tích của khối chóp S.ABCD bằng T a3 A. 6a3. B. . C. 2a3. D. a3. TỐ 3 √
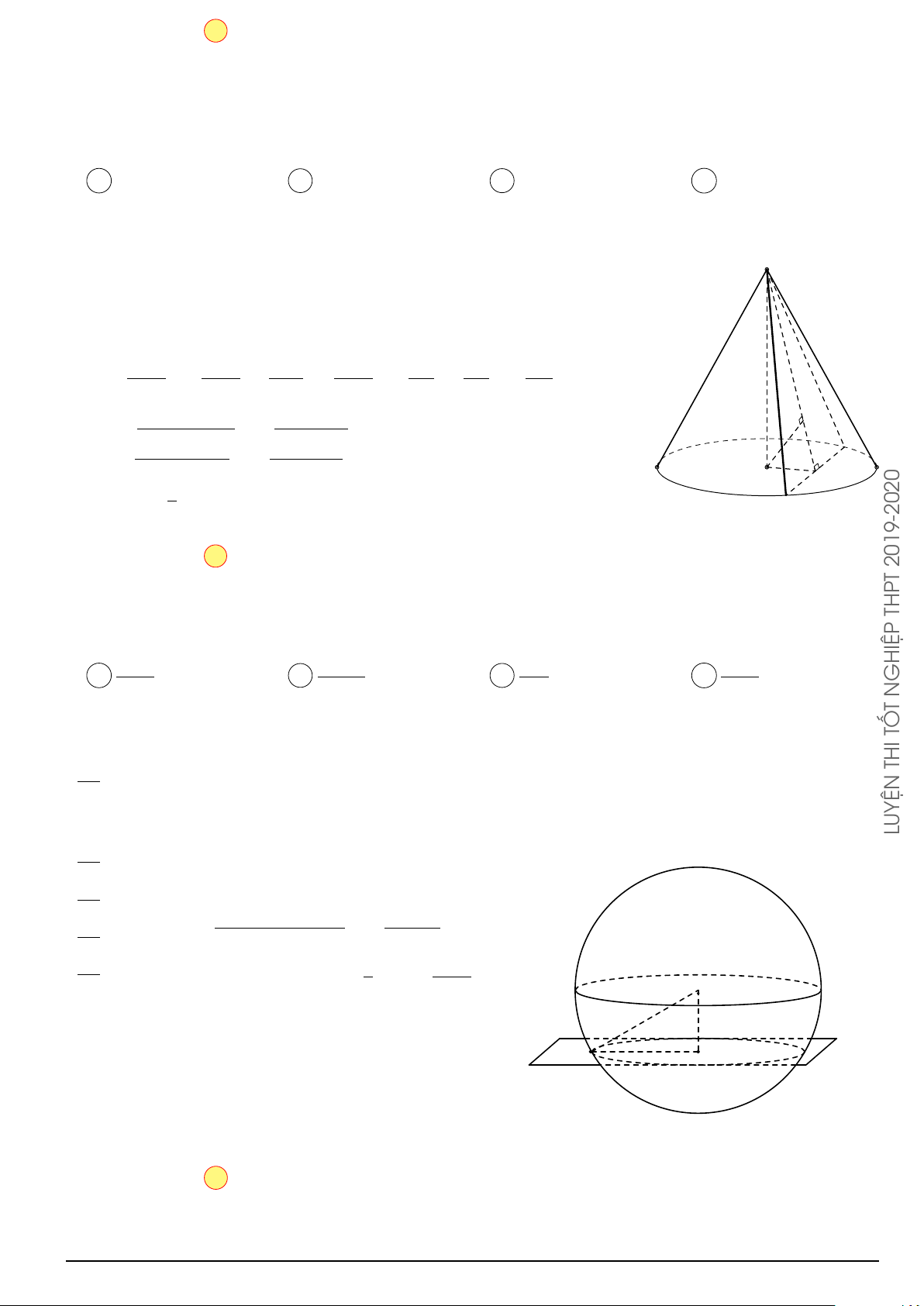
Câu 8. Cho khối nón (N ) có bán kính r =
5, có chiều cao h = 5. Thể tích V của khối nón (N ) đã THI cho là. 27π 16π 26π 25π A. V(N) = . B. V(N) = . C. V(N) = . D. V(N) = . 5 5 5 3 a
Câu 9. Thể tích khối cầu có bán kính bằng là LUYỆN 2 πa3 πa2 πa3 A. . B. . C. . D. πa2. 2 4 6 Câu 10.
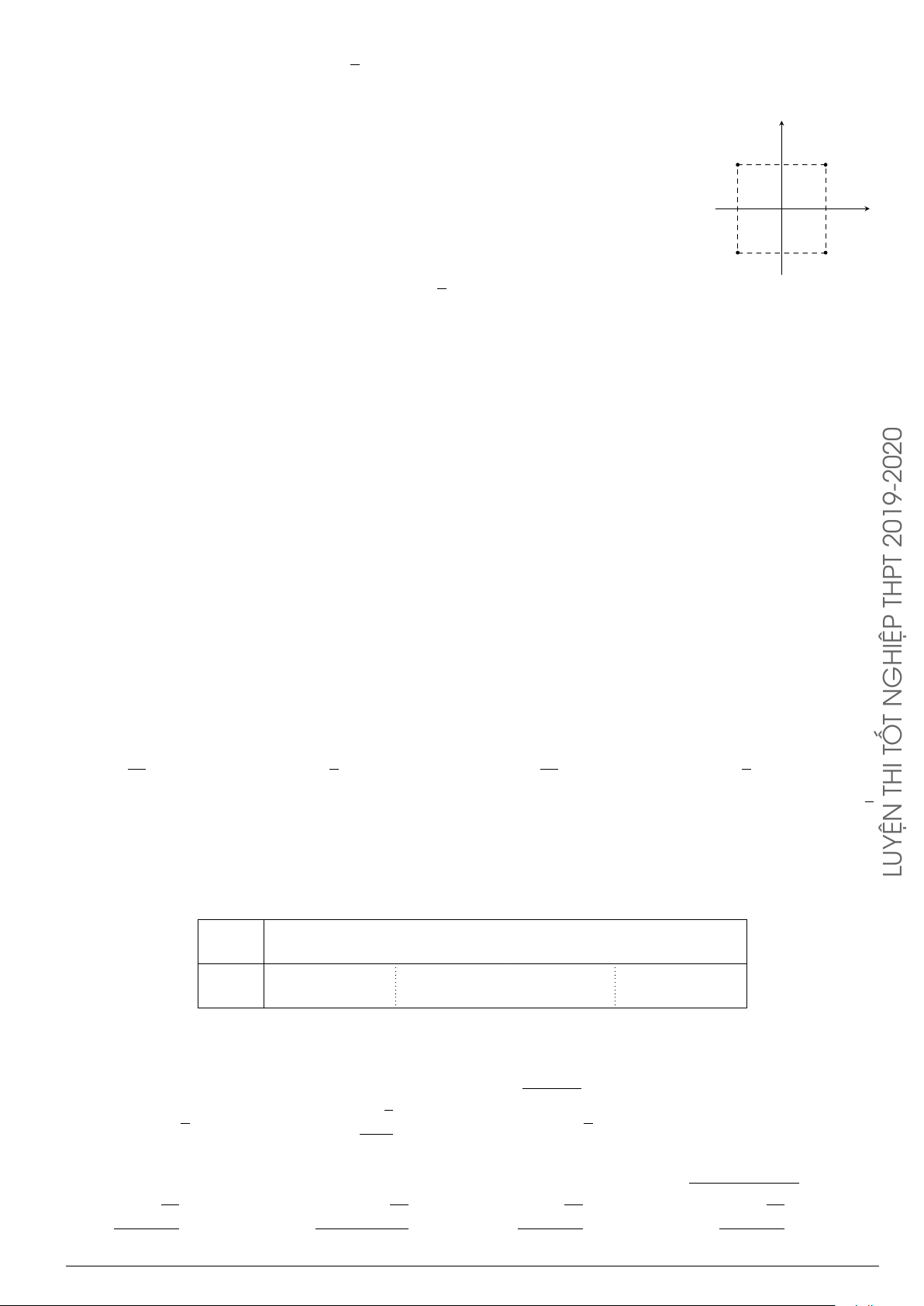
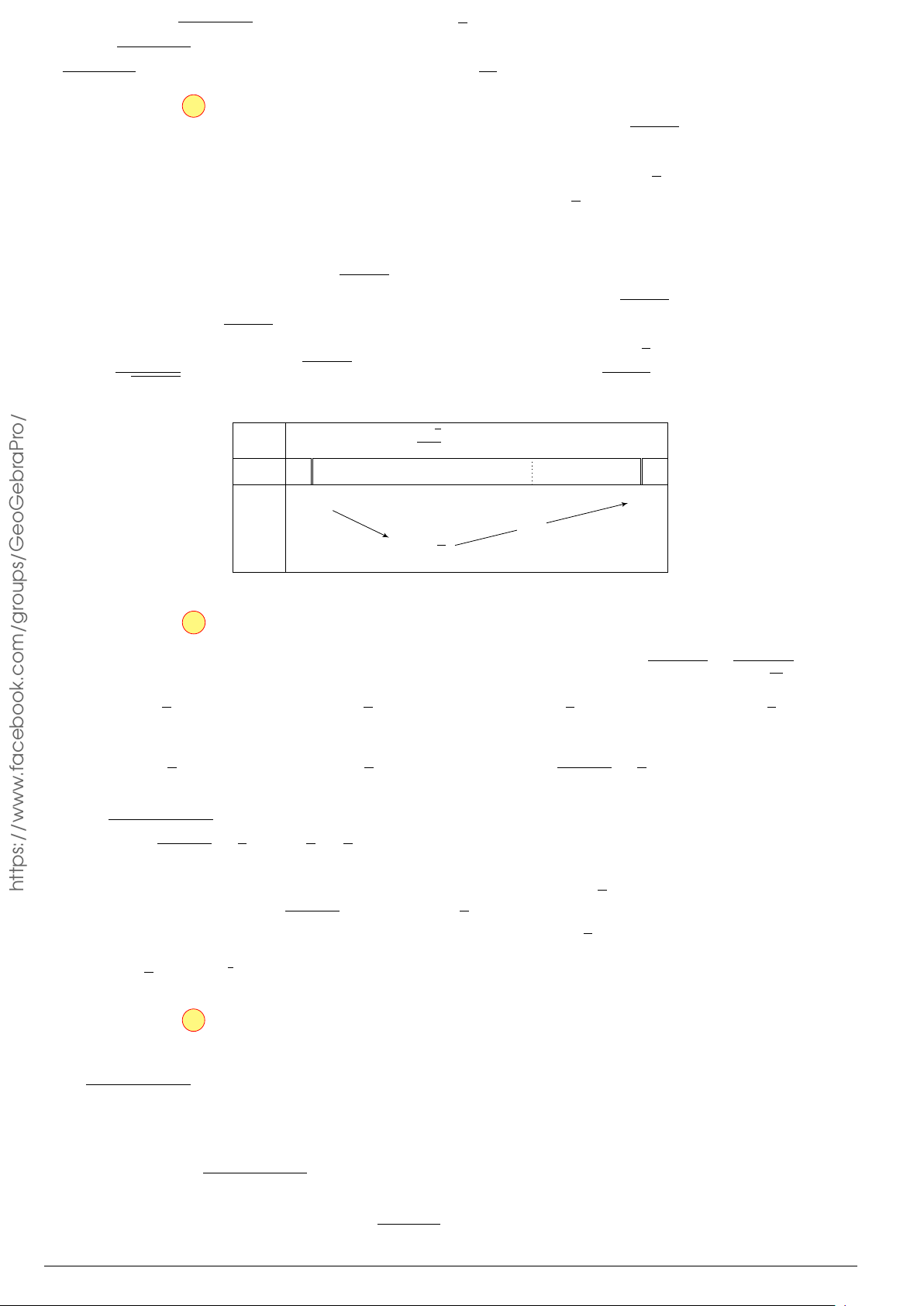
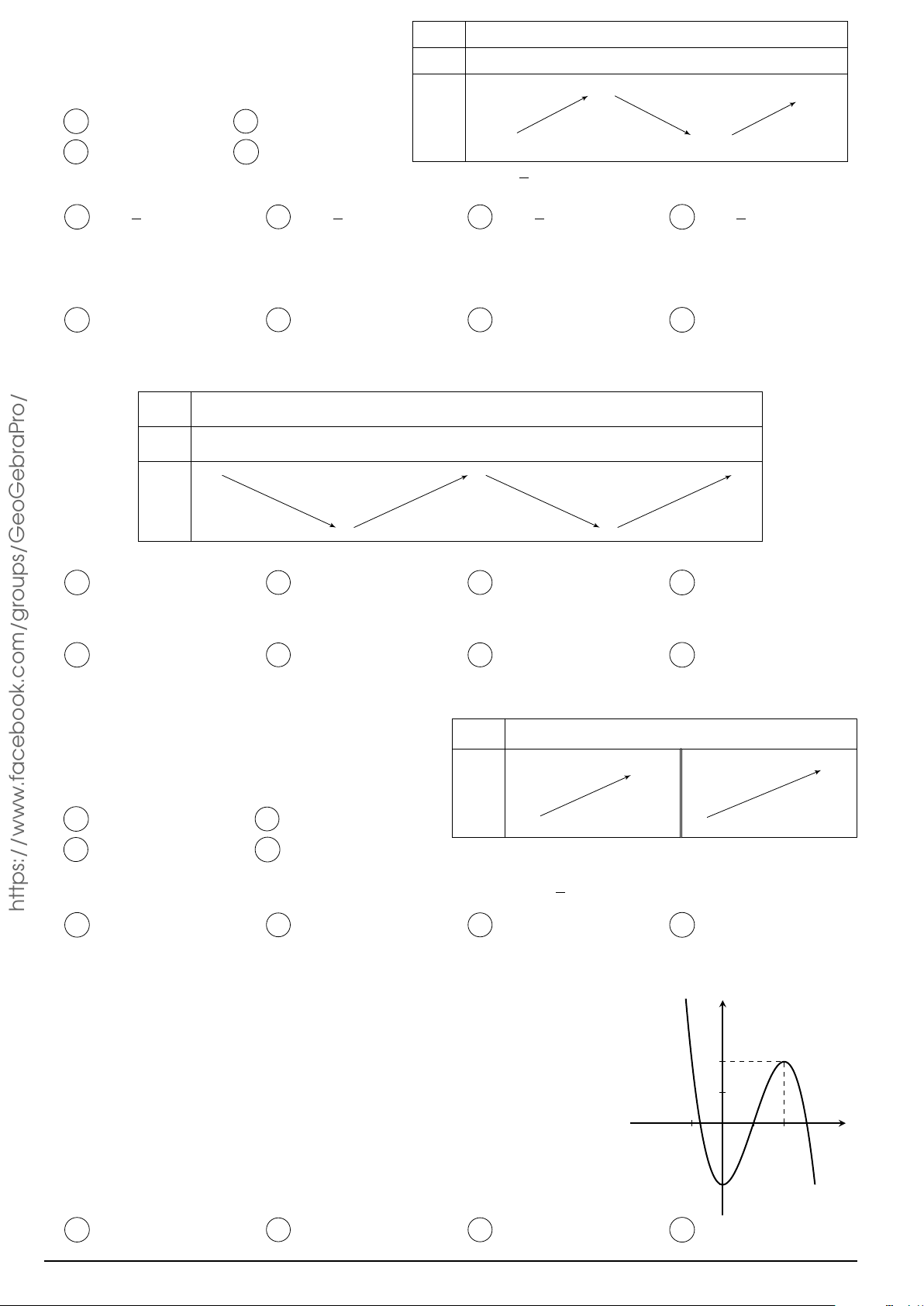
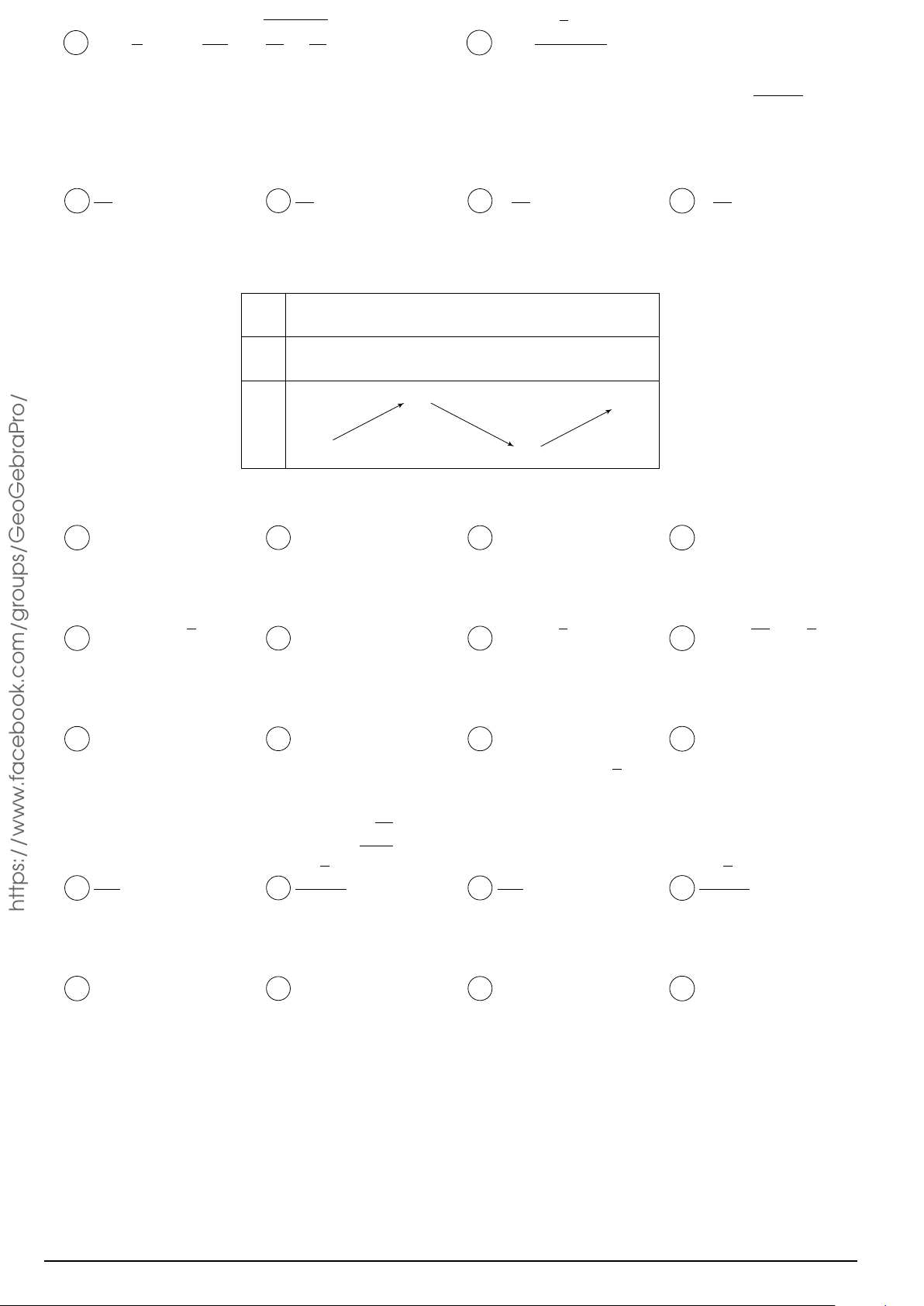
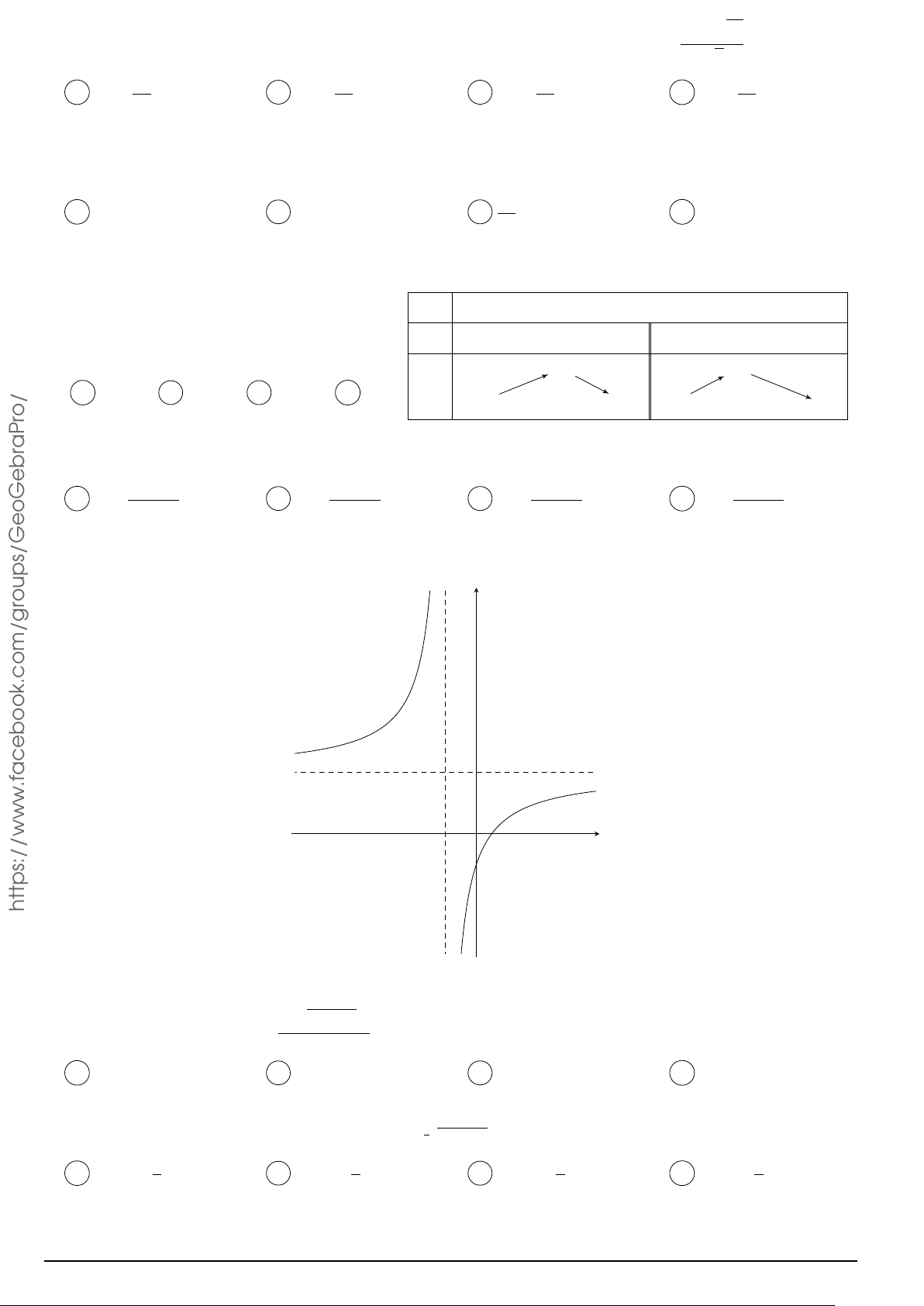
Cho hàm số y = f (x) có bảng biến thiên như hình x −∞ −1 0 1 +∞
bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? y0 + 0 − 0 + 0 − A. (−∞; −1). B. (−1; 1). 0 0 y C. (1; +∞). D. (0; 1). −∞ −1 −∞
Câu 11. Tính giá trị của alog√a 4 với a > 0, a 6= 1. A. 8. B. 4. C. 16. D. 2.
Câu 12. Một hình trụ có bán kính đáy , r = a độ dài đường sinh l = 2a Diện tích toàn phần của hình trụ này là A. 2πa2. B. 4πa2. C. 6πa2. D. 5πa2. GeoGebraPro Trang 1 Câu 13.
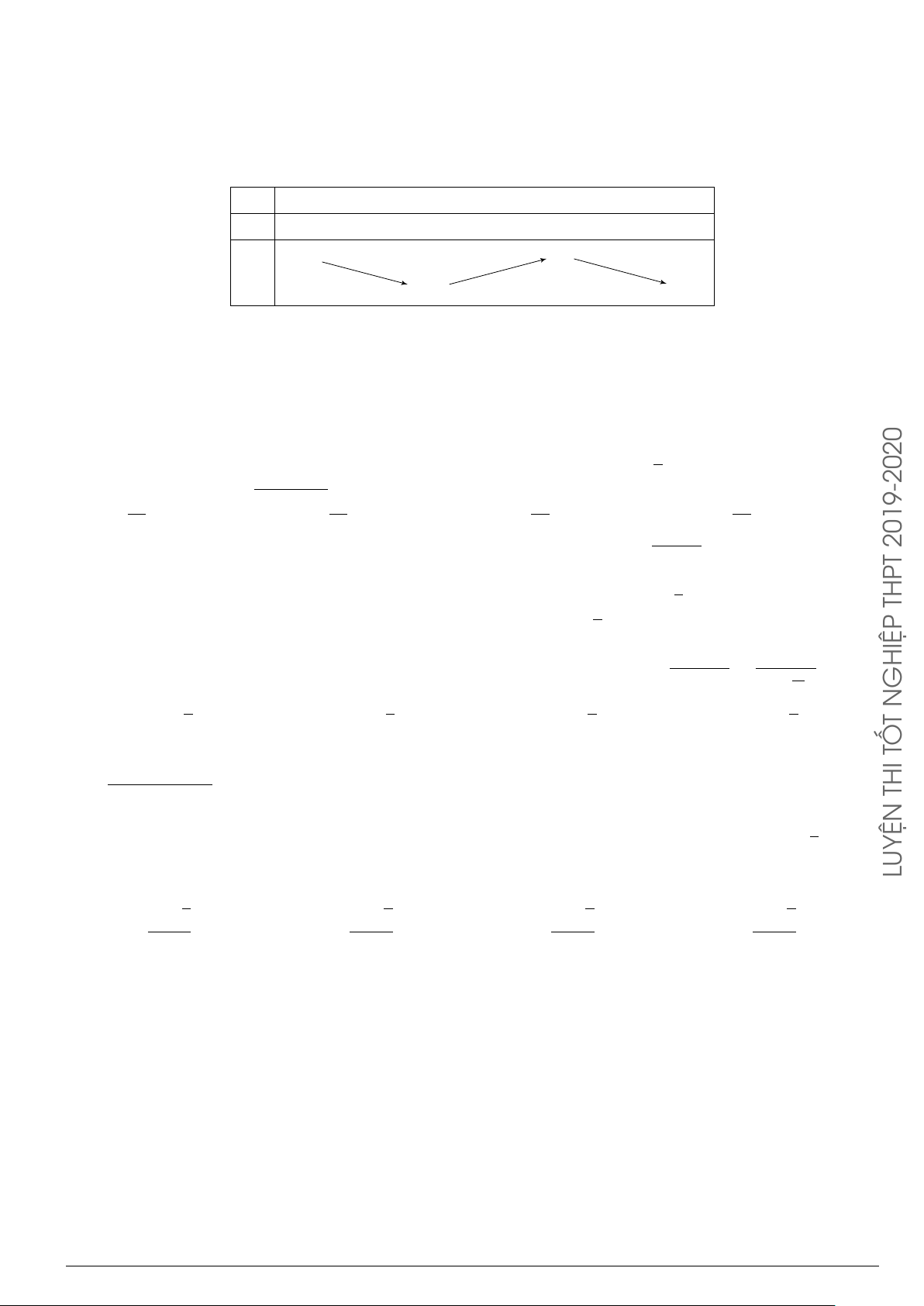
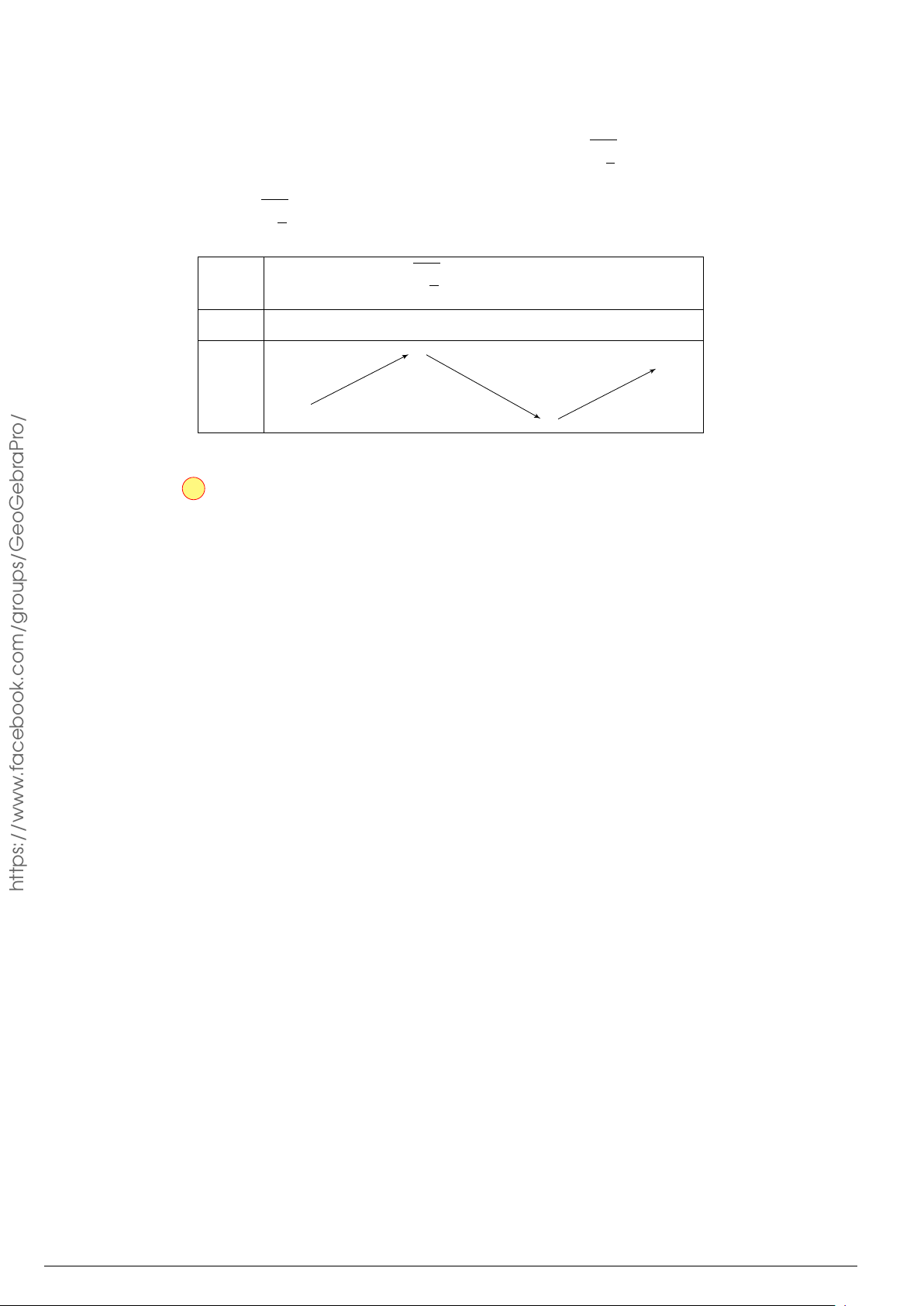
Cho hàm số y = f (x) có bảng biến thiên như hình x −∞ 0 1 +∞
vẽ bên. Mệnh đề nào dưới đây đúng? y0 + 0 − 0 +
A. Hàm số có điểm cực tiểu x = 0. 5 +∞ +
B. Hàm số có điểm cực đại x = 5. y
C. Hàm số có điểm cực tiểu x = −1. −∞ −1
D. Hàm số có điểm cực tiểu x = 1. Câu 14.
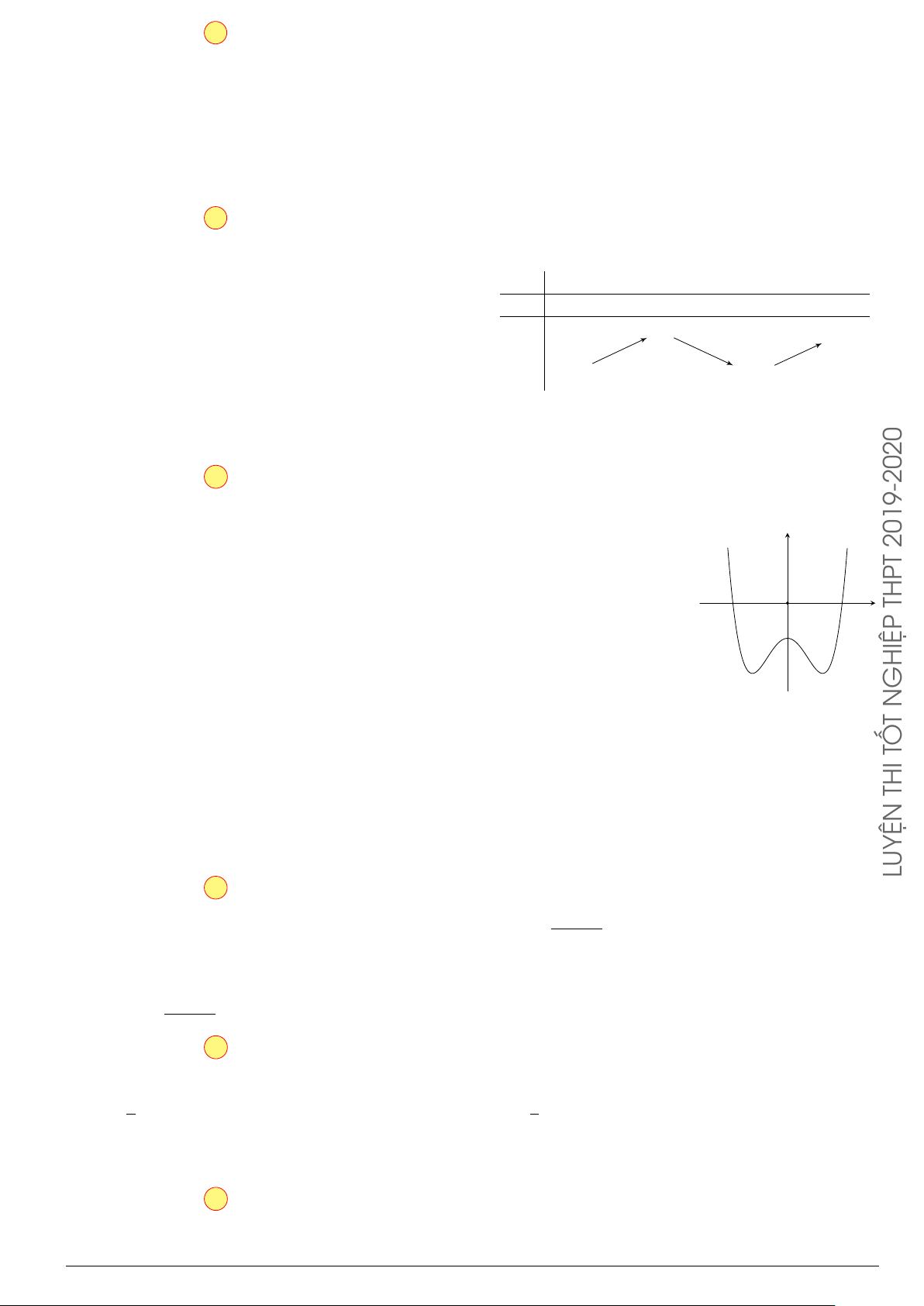
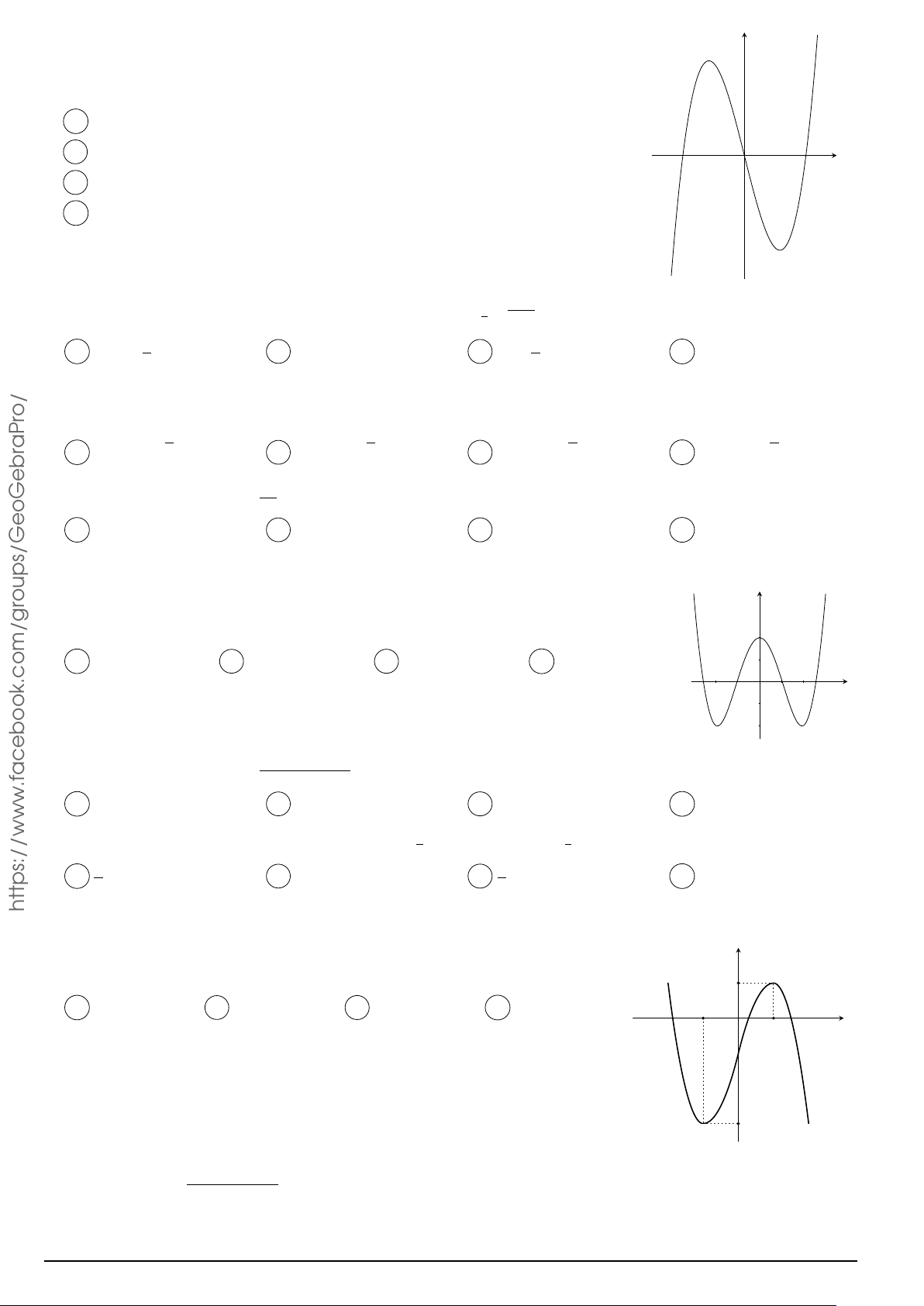
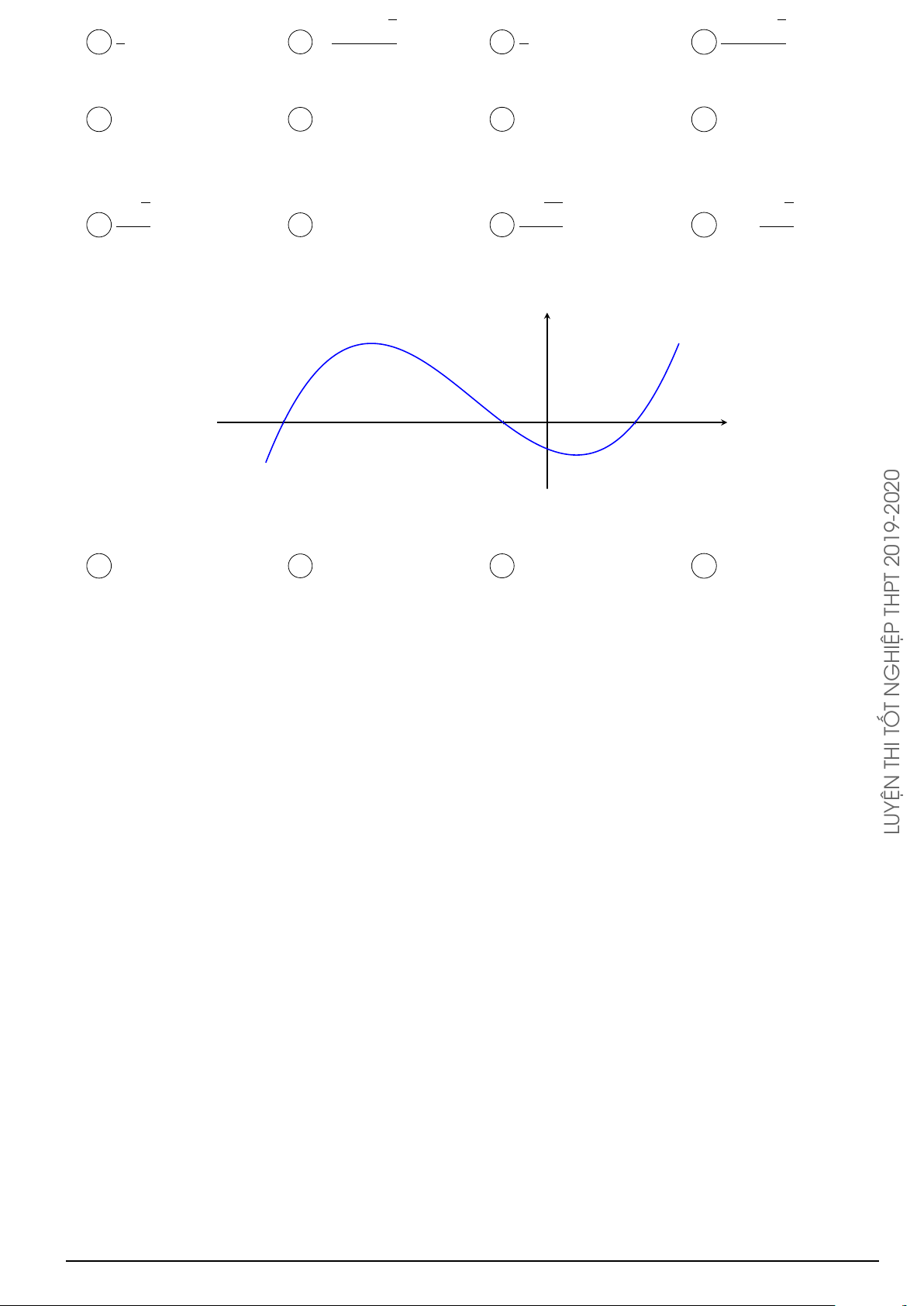
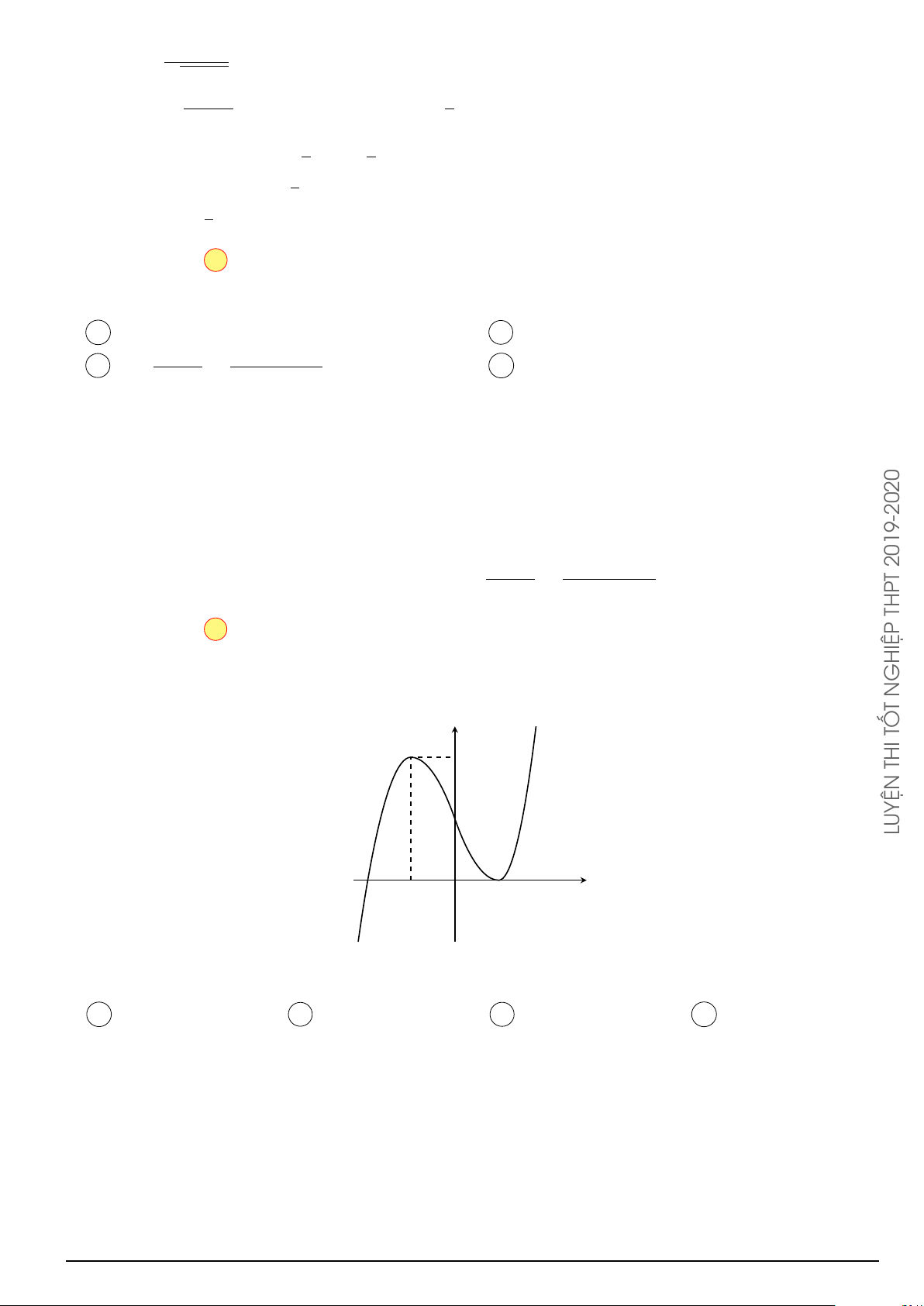
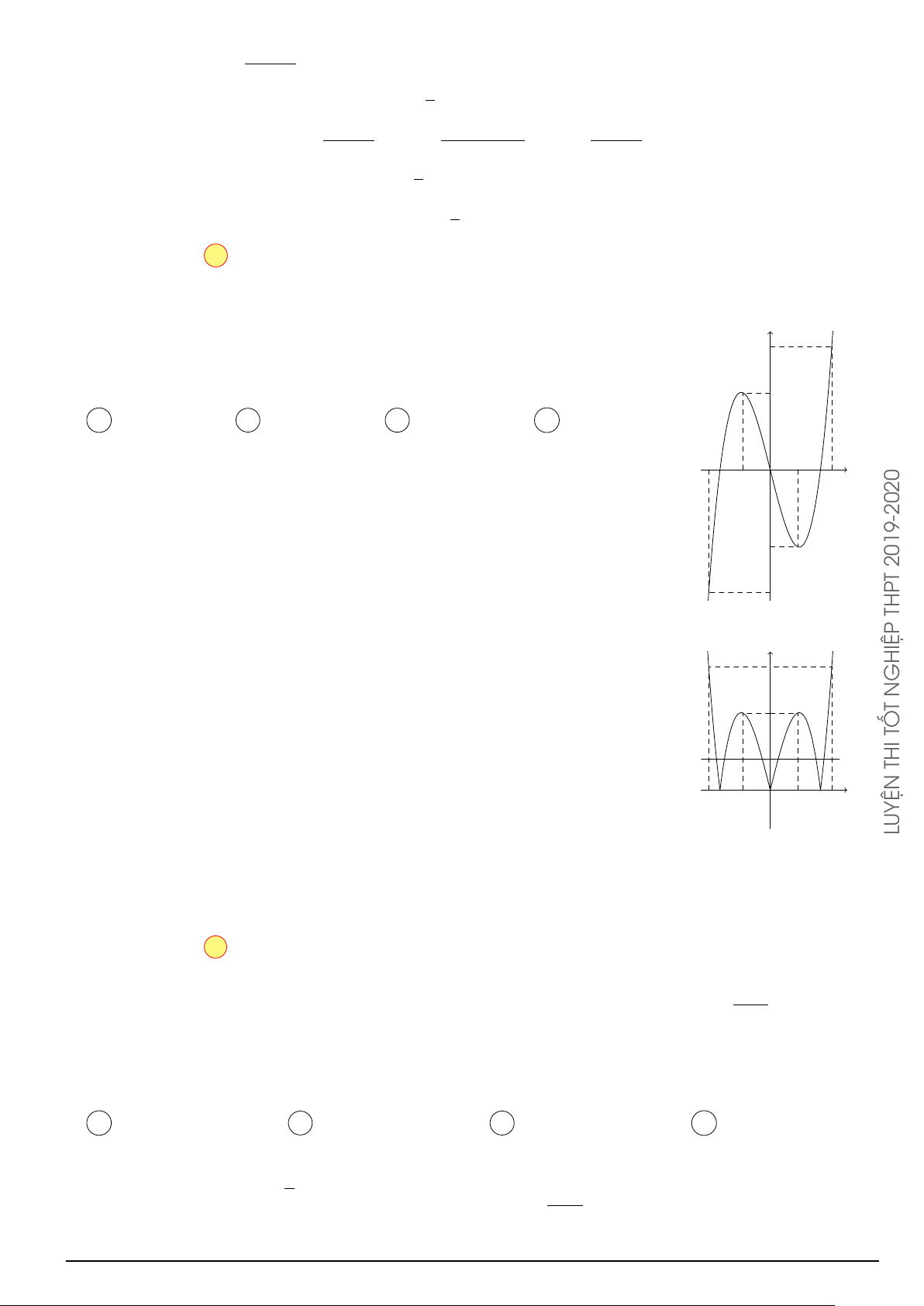
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? y A. y = x4 − 2x2 − 1. B. y = −x4 + 2x2 − 1. C. y = x3 − x2 − 1. D. y = −x3 + x2 − 1. O x 2 − 2x
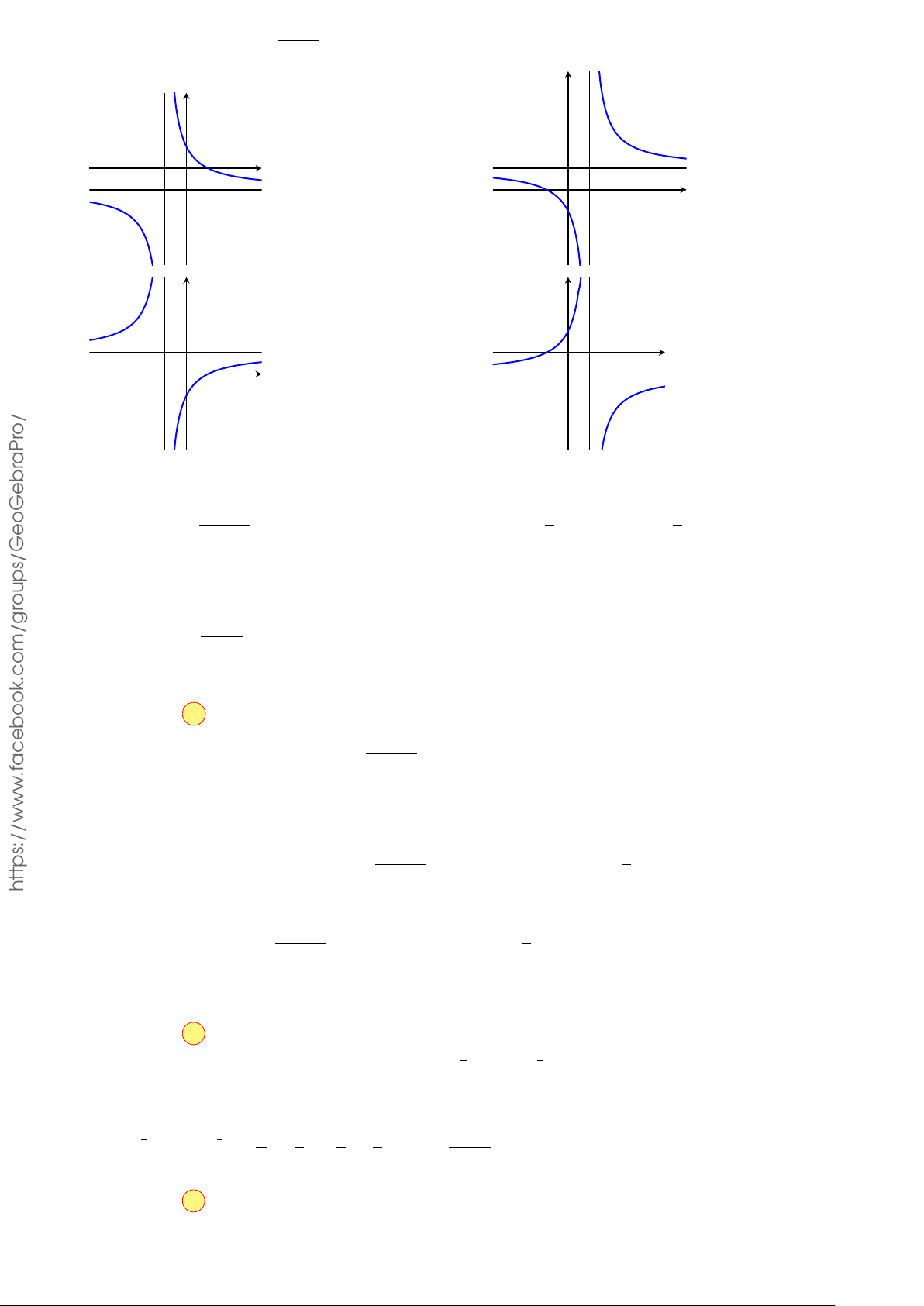
Câu 15. Tìm đường tiệm cận ngang của đồ thị hàm số y = . o/ x + 1 A. x = −1. B. x = −2. C. y = 2. D. y = −2. aPr
Câu 16. Tập nghiệm của bất phương trình 32x−1 > 27 là Å 1 ã Å 1 ã A. ; +∞ . B. (3; +∞). C. ; +∞ . D. (2; +∞). 2 3 Câu 17.
Cho hàm số y = f (x) có bảng biến thiên như hình vẽ x −∞ −1 1 +∞ roups/GeoGebr
bên. Số nghiệm của phương trình f (x) = −1 là y0 − 0 + + A. 1. B. 2. C. 4. D. 3. 1 +∞ −1 y √ − 2 −∞ 2 5 5 Z Z Z Câu 18. Nếu f (x) dx = 3, f (x) dx = −1 thì f (x) dx bằng acebook.com/g 1 2 1 .f A. 3. B. 4. C. 2. D. −2.
Câu 19. Cho số phức z thỏa mãn z = 3 + 2i. Tìm phần thực và phần ảo của số phức z.
A. Phần thực bằng −3, phần ảo bằng 2.
B. Phần thực bằng 3, phần ảo bằng 2.
C. Phần thực bằng 3, phần ảo bằng −2.
D. Phần thực bằng −3, phần ảo bằng −2. https://www
Câu 20. Cho hai số phức z1 = 3 + i, z2 = 2 − i. Tính giá trị của biểu thức P = |z1 + z1 · z2|. A. P = 85. B. P = 5. C. P = 50. D. P = 10.
Câu 21. Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện |z + 2 − 5i| = 6
là đường tròn có tâm I và bán kính R lần lượt là A. I(−2; 5) và R = 36. B. I(−2; 5) và R = 6. C. I(2; −5) và R = 36. D. I(2; −5) và R = 6.
Câu 22. Trong không gian Oxyz , cho điểm A(−1; 2; 3). Hình chiếu vuông góc của điểm A trên trục Oz là điểm A. Q(−1; 0; 3). B. M (0; 0; 3). C. P (0; 2; 3). D. N (−1; 0; 0).
Câu 23. Trong không gian Oxyz, mặt cầu có tâm I (1; 2; −3) và tiếp xúc với trục Oy có bán kính bằng √ √ √ A. 10. B. 2. C. 5. D. 13.
Câu 24. Trong không gian Oxyz cho mặt phẳng (P ) : x + y − 2z + 4 = 0. Một véc-tơ pháp tuyến của mặt phẳng (P ) là #» #» #» #» A. n = (1; 1; −2). B. n = (1; 0; −2). C. n = (1; −2; 4). D. n = (1; −1; 2). GeoGebraPro Trang 2
Câu 25. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1; −1; 0), B(0; 1; 1). Gọi (α) là x y − 1 z − 2
mặt phẳng chứa đường thẳng d : = =
và song song với đường thẳng AB. Điểm nào dưới 2 −1 1
đây thuộc mặt phẳng (α)? A. M (6; −4; −1). B. N (6; −4; 2). C. P (6; −4; 3). D. Q(6; −4; 1).
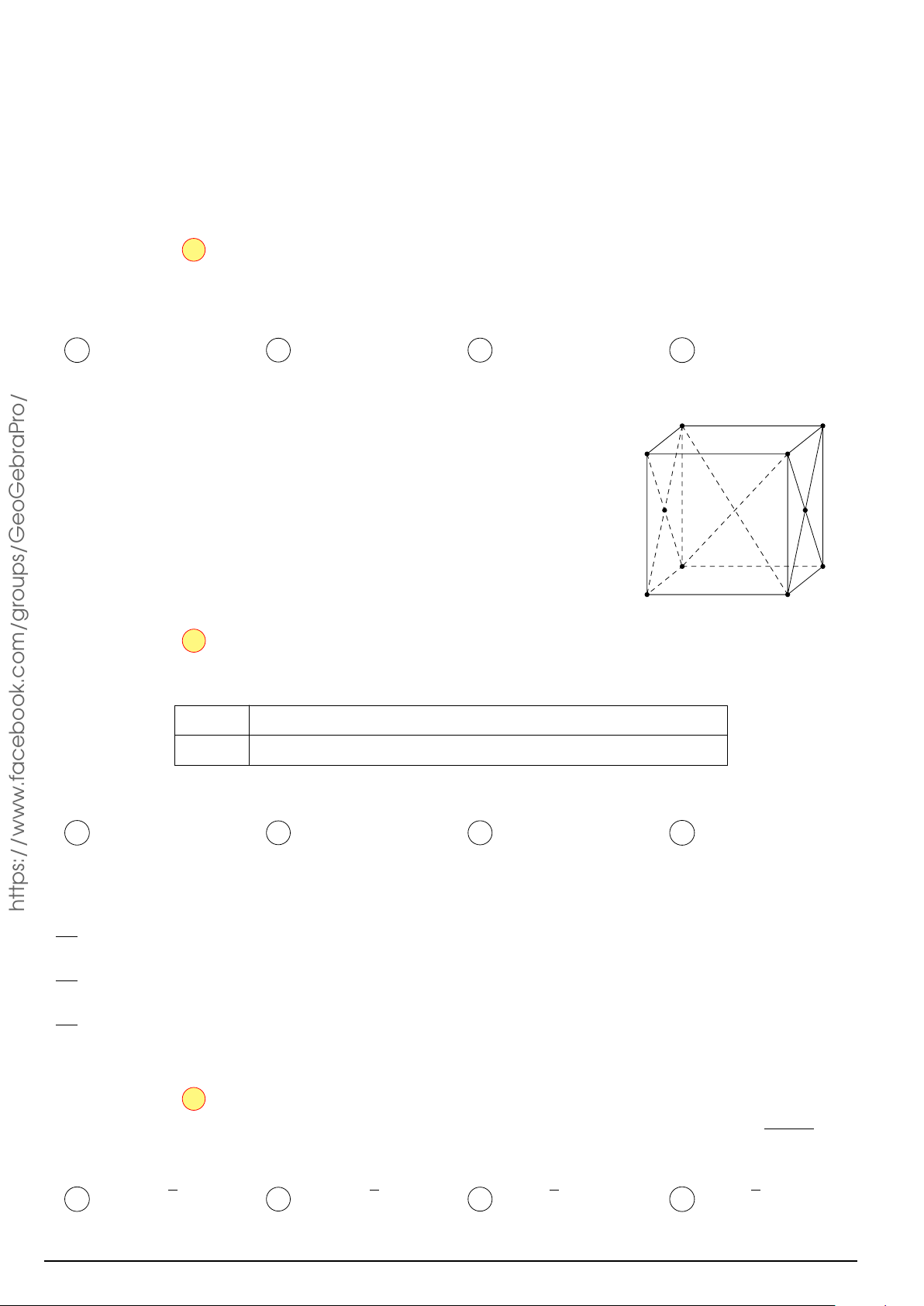
Câu 26. Cho hình lập phương ABCD.A0B0C0D0. Góc giữa hai đường thẳng BA0 và CD bằng A. 90◦. B. 60◦. C. 30◦. D. 45◦.
Câu 27. Cho hàm số f (x) có đạo hàm f 0(x) = (x − 1)(x − 2)2(x − 3)3(x − 4)4, ∀x ∈ R. Số điểm cực
trị của hàm số đã cho là A. 3. B. 5. C. 2. D. 4. √x2 −1
Câu 28. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = trên tập x − 2 ï 3 ò
hợp D = (−∞; −1) ∪ 1; . Tính P = M + m. 2 √ √ A. P = 2. B. P = 0. C. P = − 5. D. P = 3.
Câu 29. Cho số thực a > 1, b 6= 0. Mệnh đề nào dưới đây đúng? A. log b2 = −2 log |b|. B. log b2 = 2 log b. C. log b2 = 2 log |b|. D. log b2 = −2 log b. a a a a a a a a
Câu 30. Tìm số giao điểm của đồ thị hàm số y = x3 − 3x2 + 3x − 1 và đồ thị hàm số y = x2 − x − 1. A. 1. B. 0. C. 2. D. 3.
Câu 31. Tập nghiệm của bất phương trình log 1 (x − 1) + log (11 − 2x) ≥ 0 là 3 3 ï 11 ã 2019-2020 A. (−∞; 4). B. (1; 4]. C. (1; 4). D. 4; . 2
Câu 32. Tính thể tích khối tròn xoay sinh ra khi quay tam giác đều ABC cạnh bằng 1 quanh AB. √ THPT 3π π π π 3 A. . B. . C. . D. . 4 4 8 2 1 Z dx π π GHIỆP Câu 33. Cho tích phân I = √
. Nếu đổi biến số x = 2 sin t, t ∈ − ; thì 2 2 N 4 − x2 0 T π π π π 6 6 6 3 Z Z Z dt Z TỐ A. I = dt. B. I = t dt. C. I = . D. I = dt. t 0 0 0 0 THI
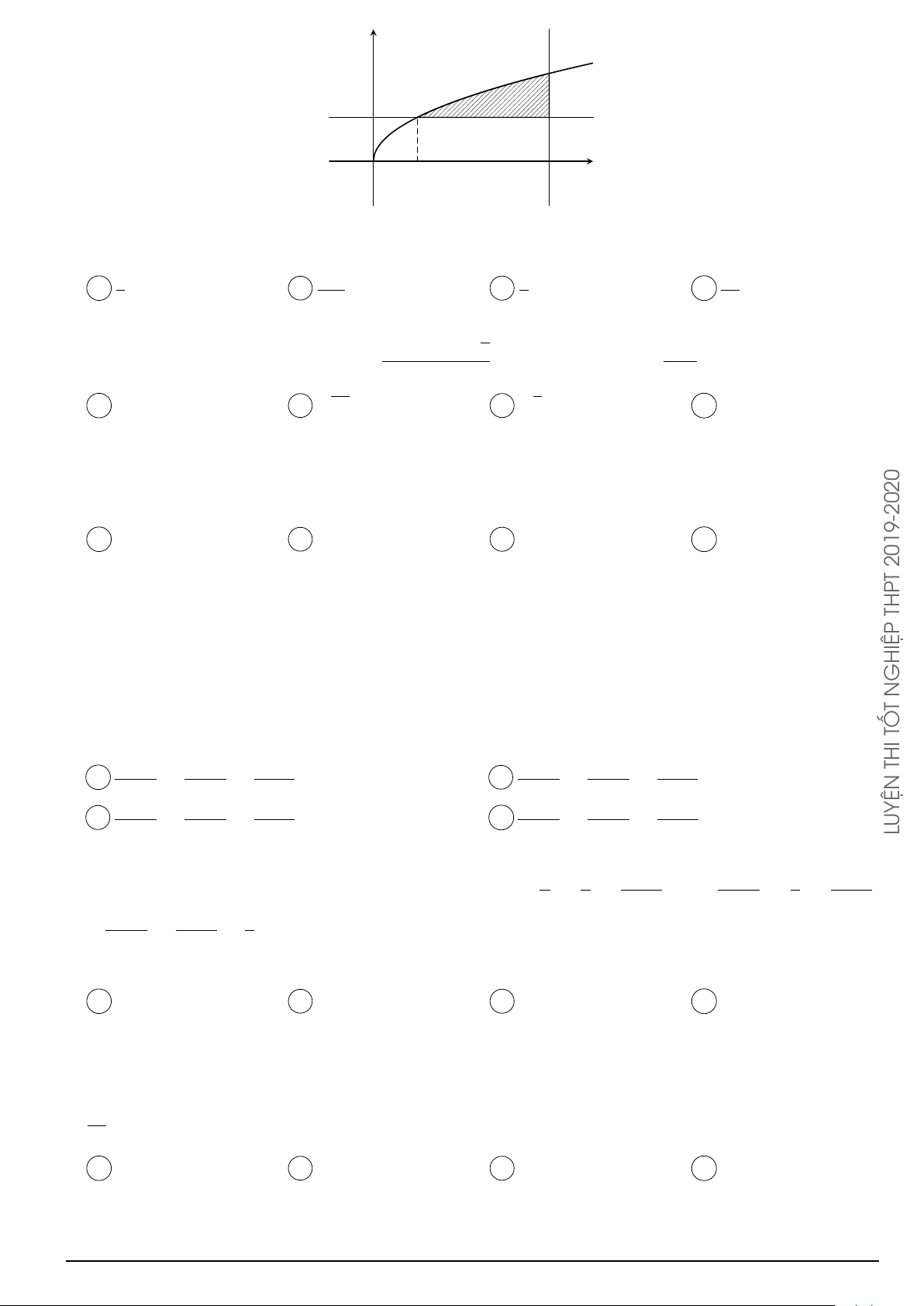
Câu 34. Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol
(P ) : y = x2 và đường thẳng d : y = 2x quay quanh trục Ox. 2 2 2 Z Z Z LUYỆN A. π x2 − 2x2 dx. B. π 4x2 dx − π x4 dx. 0 0 0 2 2 2 Z Z Z C. π 4x2 dx + π x4 dx. D. π 2x − x2 dx. 0 0 0
Câu 35. Cho hai số phức z1 = 2 + i, z2 = 1 − 3i. Tính T = |(1 + i)z1 + 2z2|. √ A. T = 18. B. T = 3 2. C. T = 0. D. T = 3.
Câu 36. Gọi z0 là nghiệm phức có phần ảo âm của phương trình 2z2 − 2z + 13 = 0. Trên mặt phẳng
tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w = iz0? Å 5 1 ã Å 5 1 ã Å 5 1 ã Å 5 1 ã A. M ; . B. N ; − . C. P ; − . D. Q ; . 4 4 4 4 2 2 2 2 x + 3 y − 2 z − 1
Câu 37. Trong không gian toạ độ Oxyz, cho đường thẳng (d) : = = . Mặt phẳng 1 −1 2
(P ) đi qua điểm M (2; 0; −1) và vuông góc với (d) có phương trình là A. (P ) : x − y − 2z = 0. B. (P ) : 2x − z = 0. GeoGebraPro Trang 3
C. (P ) : x − y + 2z + 2 = 0. D. (P ) : x − y + 2z = 0.
Câu 38. Trong không gian Oxyz, cho hai điểm A(1; 0; 1), B(−1; 2; 1). Viết phương trình đường thẳng
∆ đi qua tâm đường tròn ngoại tiếp tam giác OAB và vuông góc với mặt phẳng (OAB). x = t x = t x = 3 + t x = −1 + t         A. ∆ : y = 1 + t . B. ∆ : y = 1 + t . C. ∆ : y = 4 + t . D. ∆ : y = t .     z = 1 − t z = 1 + t z = 1 − t z = 3 − t
Câu 39. Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp 12A, 3 học sinh lớp 12B và 5 học sinh lớp
12C trên một bàn tròn. Tính xác suất P để các học sinh cùng lớp luôn ngồi cạnh nhau. 1 1 1 1 A. P = . B. P = . C. P = . D. P = . 1260 126 28 252
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA ⊥ (ABCD) và √
SA = a 2 . Khoảng cách từ A đến mặt phẳng (SBC) bằng: √ √ 2a 5 √ a a 3 A. . B. a 3. C. . D. . 5 2 2 o/
Câu 41. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x3 − (m + 1)x2 + 3x + 1 đồng biến aPr trên khoảng (−∞; +∞)? A. 6. B. 8. C. 7. D. 5.
Câu 42. Với mức tiêu thụ thức ăn của trang trại A không đổi như dự định thì lượng thức ăn dự trữ
sẽ đủ dùng cho 100 ngày. Nhưng thực tế, mức tiêu thụ thức ăn tăng thêm 4% mỗi ngày (ngày sau tăng
4% so với ngày trước đó). Hỏi thực tế lượng thức ăn dự trữ đó chỉ đủ dùng cho bao nhiêu ngày? roups/GeoGebr A. 40. B. 41. C. 42. D. 43.
Câu 43. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như sau x −∞ −1 3 +∞ y0 + 0 − 0 + 5 +∞ + acebook.com/g .f y −∞ 1
Đồ thị hàm số y = |f (x)| có bao nhiêu điểm cực trị? https://www A. 2. B. 3. C. 4. D. 5.
Câu 44. Cho hình trụ có thiết diện đi qua trục là một hình vuông có cạnh bằng 4a. Diện tích xung quanh S của hình trụ là A. S = 4πa2. B. S = 8πa2. C. S = 24πa2. D. S = 16πa2. 1 Z
Câu 45. Cho hàm số f (x) có đạo hàm liên tục trên [−1; 1] và thỏa mãn f (1) = 7, xf (x) dx = 1. 0 1 Z Khi đó x2f 0(x) dx bằng 0 A. 6. B. 8. C. 5. D. 9.
Câu 46. Cho hàm số y = f (x) = ax3 + bx2 + cx + d có bảng biến thiên như sau: 1
Khi đó |f (x)| = m có bốn nghiệm phân biệt x1 < x2 < x3 < < x4 khi và chỉ khi: 2 GeoGebraPro Trang 4 A. 0 < m < 1. x −∞ 0 1 +∞ B. 0 < m ≤ 1. y0 + 0 − 0 + 1 C. < m < 1. +∞ + 2 1 1 D. ≤ m < 1. y 2 −∞ 0
Câu 47. Cho a, b, c > 1. Biết rằng biểu thức P = log (bc) + log (ac) + 4 log (ab) đạt giá trị nhỏ nhất a b c
bằng m khi log c = n. Tính giá trị m + n. b 25 A. m + n = 14. B. m + n = . C. m + n = 12. D. m + n = 10. 2
Câu 48. Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị nhỏ nhất của hàm số
y = − |x3 − 3x + m| trên đoạn [0; 2] bằng −3. Tổng tất cả các phần tử của S là A. 1. B. 2. C. 0. D. 6.
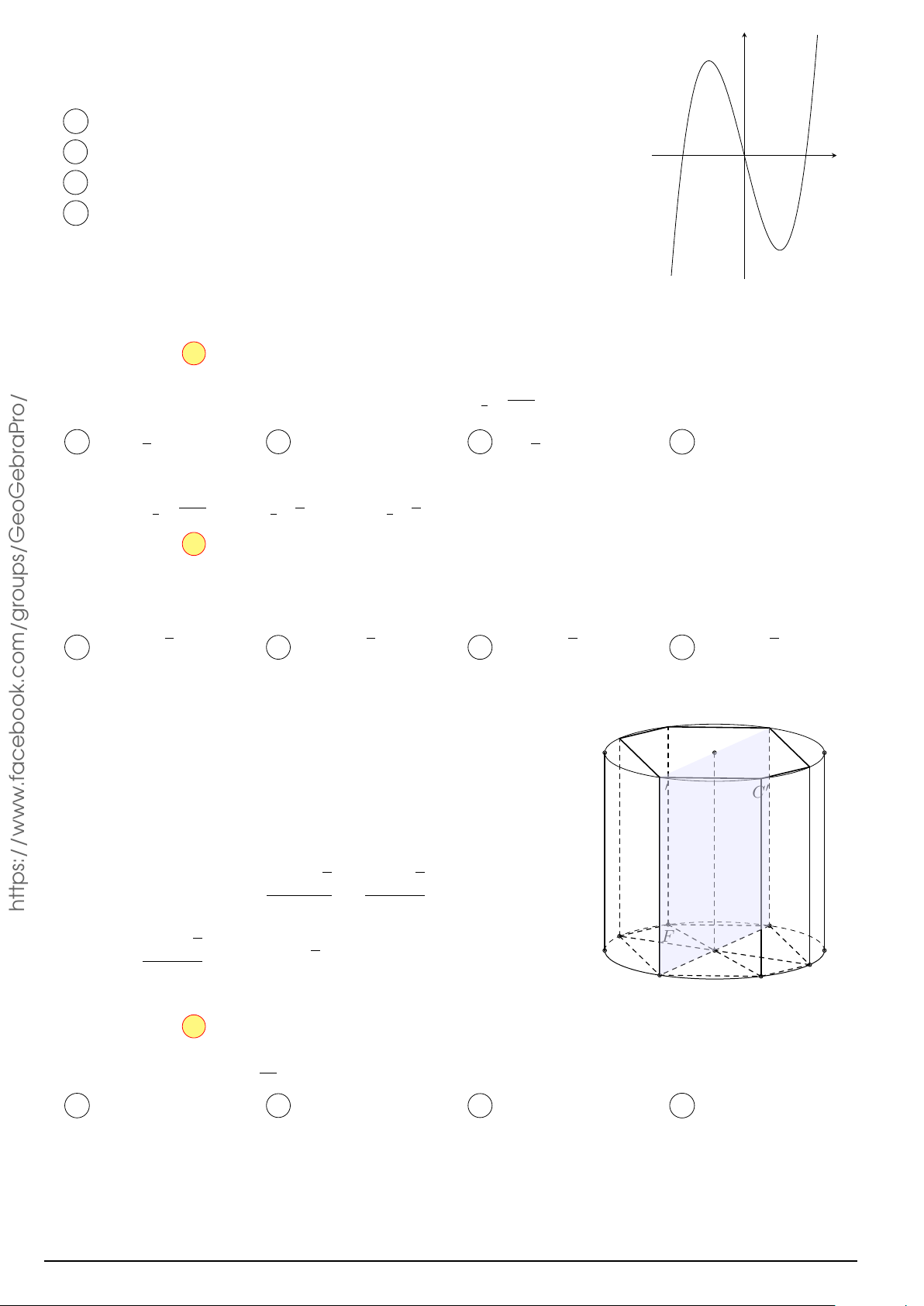
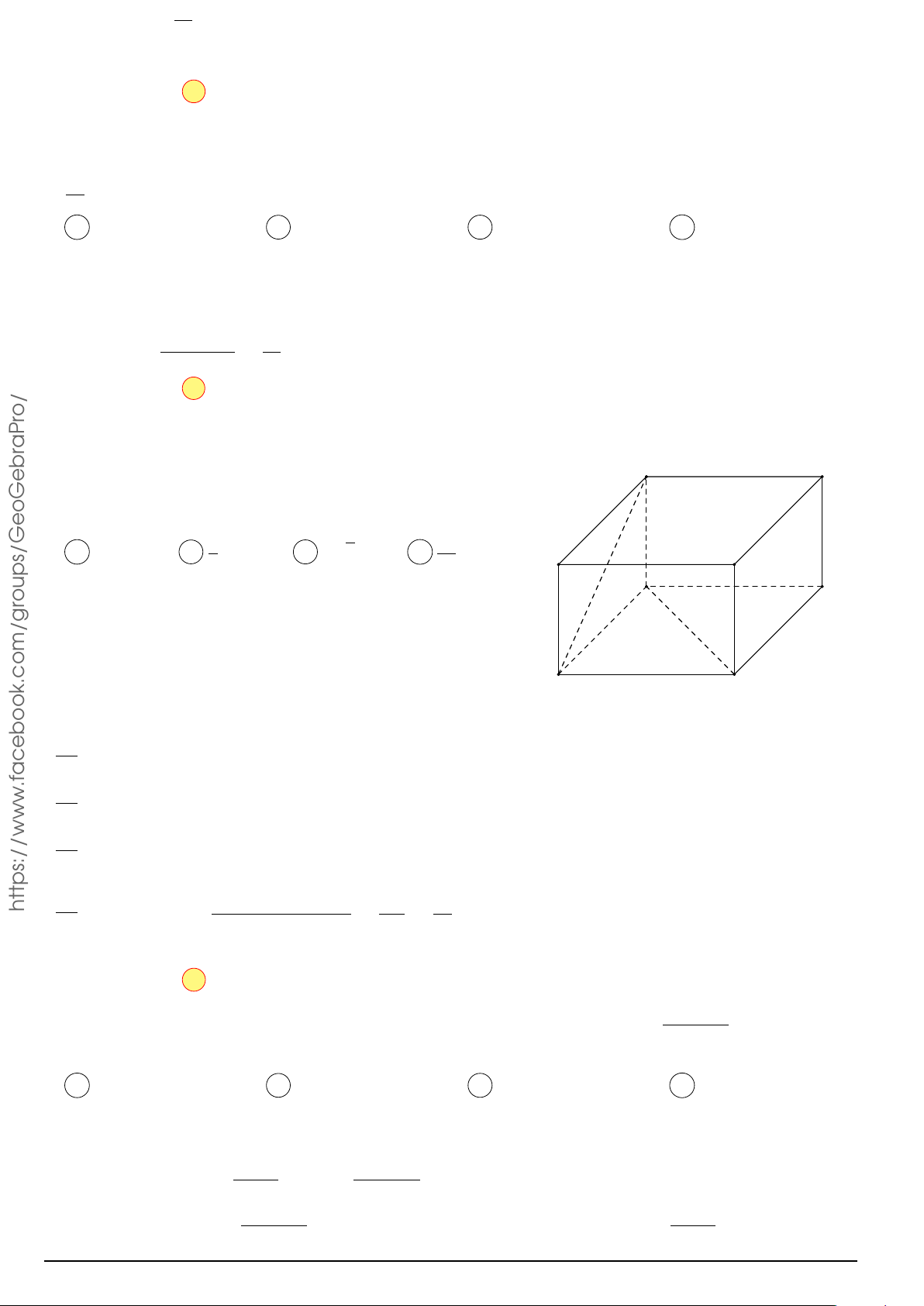
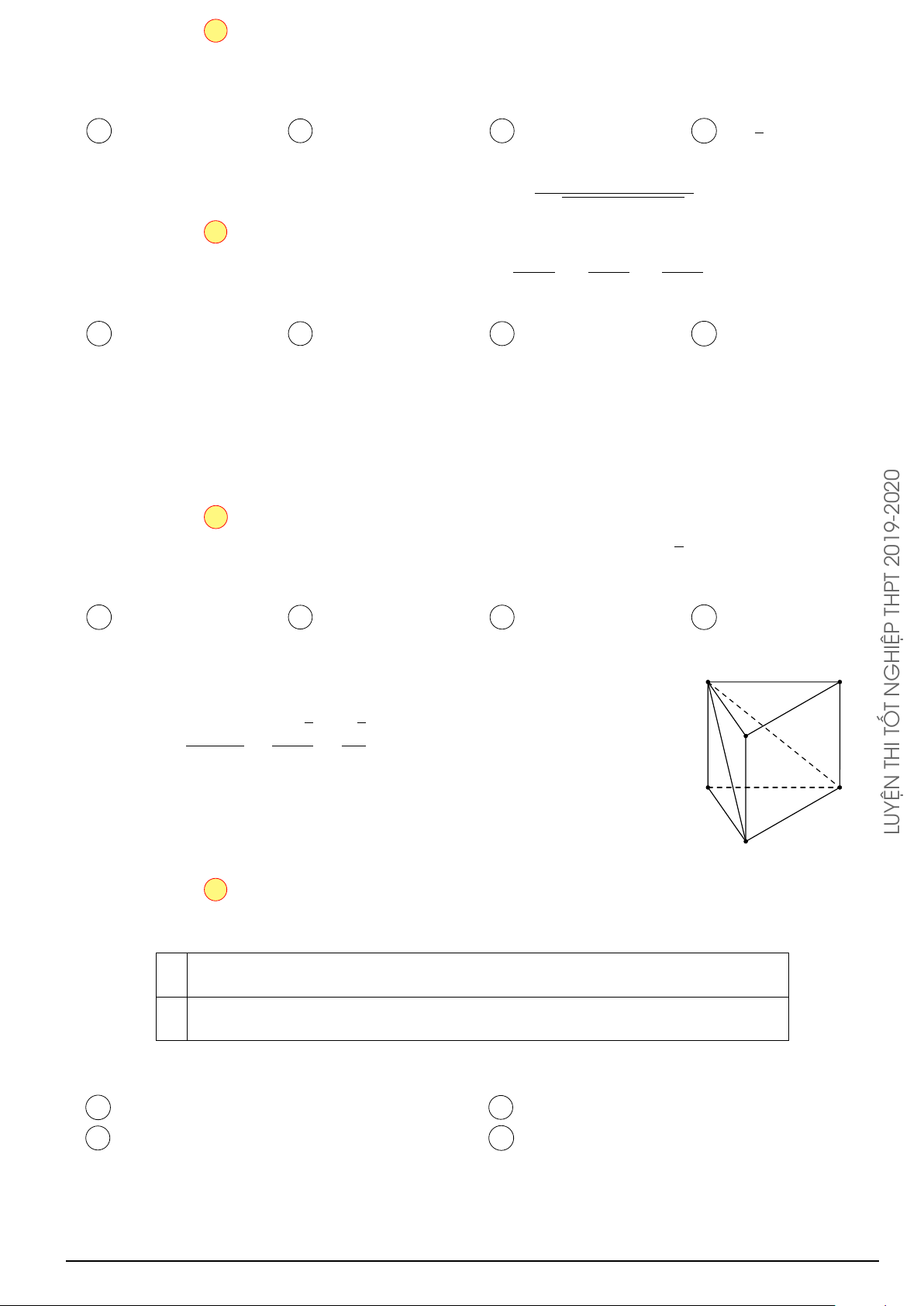
Câu 49. Cho hình hộp chữ nhật ABCD.A0B0C0D0. Gọi M là trung điểm của BB0. Mặt phẳng (M DC0)
chia khối hộp chữ nhật thành hai khối đa diện, một khối chứa đỉnh C và một khối chứa đỉnh A0. Gọi V V 1
1, V2 lần lượt là thể tích của hai khối đa diện chứa C và A0. Tính . V2 V1 7 V1 7 V1 7 V1 17 A. = . B. = . C. = . D. = . V2 24 V2 17 V2 12 V2 24 Å 1 ã2020 Å 1 ãa
Câu 50. Tìm tất cả các giá trị thực của tham số a > 0 thỏa mãn 2a + ≤ 22020 + . 2a 22020 2019-2020 A. 0 < a < 1. B. 1 < a < 2020. C. 0 < a ≤ 2020. D. a ≥ 2020.
———————–HẾT———————– THPT GHIỆP N T TỐ THI LUYỆN GeoGebraPro Trang 5 ĐÁP ÁN THAM KHẢO 1. C 2. A 3. B 4. B 5. D 6. D 7. C 8. D 9. C 10. C 11. C 12. C 13. D 14. A 15. D 16. D 17. A 18. C 19. C 20. D 21. B 22. B 23. A 24. A 25. C 26. D 27. C 28. C 29. C 30. C 31. B 32. B 33. A 34. B 35. B 36. D 37. D 38. A 39. B 40. D 41. C 42. B 43. B 44. D 45. C 46. C 47. C 48. C 49. B 50. D o/ aPr roups/GeoGebr acebook.com/g .f https://www GeoGebraPro Trang 6 MỖI NGÀY MỘT ĐỀ THI 6
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Từ các chữ số 1; 2; 3; 4 có thể lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau? A. 42. B. 12. C. 24. D. 44. Lời giải.
Mỗi số như vậy là một hoán vị của 4 phần tử. Vậy có thể lập được 4! = 24 số thỏa mãn đề bài. Chọn phương án C (u2 − u4 + u5 = 114
Câu 2. Tìm số hạng đầu u1 và công bội q của cấp số nhân (un) thỏa mãn u3 − u5 + u6 = 342 A. u1 = 2, q = 3. B. u1 = 3, q = 2. C. u1 = 1, q = 3. D. u1 = 1, q = 2. Lời giải. ( ( u2 − u4 + u5 = 114 u ⇔ 1q(1 − q2 + q3) = 114(1) u3 − u5 + u6 = 342 u1q2(1 − q2 + q3) = 342(2)
Lấy phương trình (2) chia cho phương trình (1) ta được q = 3. 2019-2020
Thay vào phương trình (1) ta được u1 = 2. THPT Chọn phương án A
Câu 3. Tìm nghiệm của phương trình log (3x − 2) = 3. 2 8 10 16 11 A. x = . B. x = . C. x = . D. x = . 3 3 3 3 GHIỆP Lời giải. N 10 T
Ta có log (3x − 2) = 3 ⇔ 3x − 2 = 23 ⇔ 3x = 10 ⇔ x = . 2 3 TỐ Chọn phương án B THI
Câu 4. Hình lập phương có đường chéo của mặt bên bằng 4 cm. Tính thể tích khối lập phương đó. √ √ √ A. 8 2 cm3. B. 16 2 cm3. C. 8 cm3. D. 2 2 cm3. Lời giải. 4 √ LUYỆN
Độ dài các cạnh hình lập phương là √ = 2 2 cm. 2 √ √
Thể tích khối lập phương là V = (2 2)3 = 16 2 cm3. Chọn phương án B 3 − x
Câu 5. Tập xác định của hàm số y = log là 2 2x A. D = (3; +∞). B. D = (0; 3].
C. D = (−∞; 0) ∪ (3; +∞). D. D = (0; 3). Lời giải. 3 − x
Hàm số đã cho xác định khi > 0 ⇔ x ∈ (0; 3). 2x Chọn phương án D
Câu 6. Cho hàm số f (x) = 2x + ex. Tìm một nguyên hàm F (x) của hàm số f (x) thỏa mãn F (0) = 2019. A. F (x) = ex − 2019. B. F (x) = x2 + ex − 2018. C. F (x) = x2 + ex + 2017. D. F (x) = x2 + ex + 2018. GeoGebraPro Trang 1 Lời giải. Z F (x) = (2x + ex) dx = x2 + ex + C.
Do F (0) = 2019 nên 02 + e0 + C = 2019 ⇔ C = 2018. Vậy F (x) = x2 + ex + 2018. Chọn phương án D
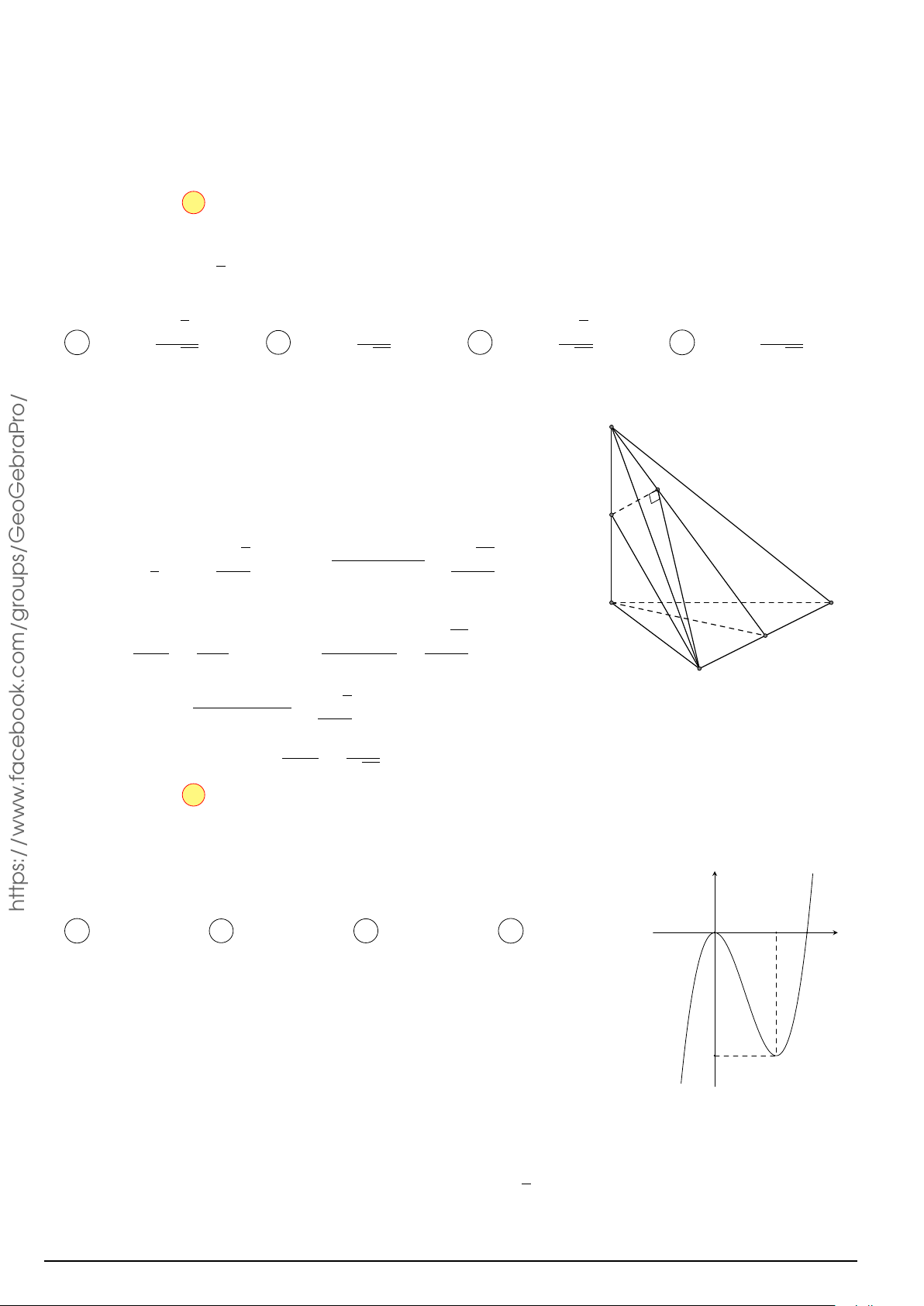
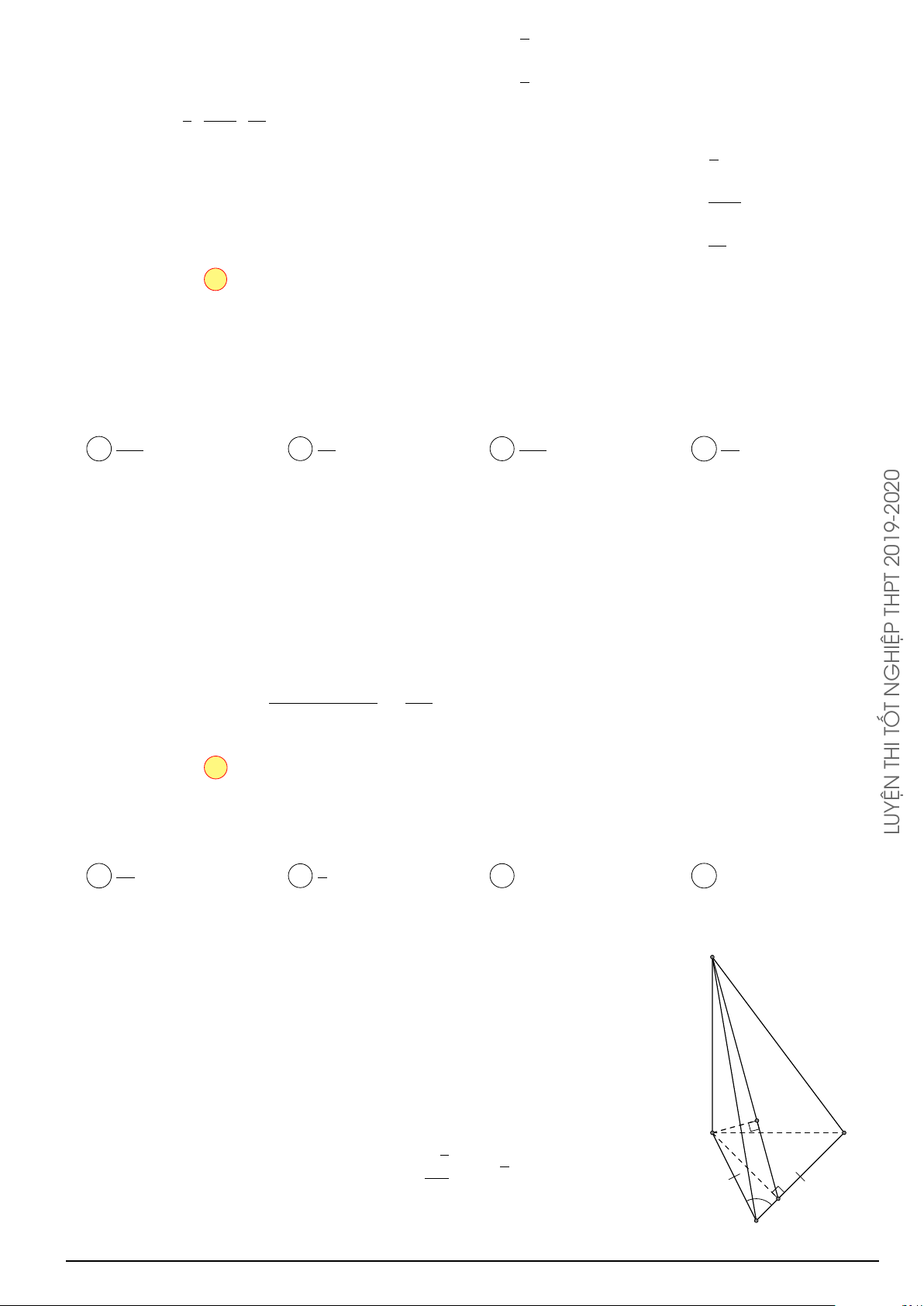
Câu 7. Cho khối chóp S.ABCD cạnh bên SA vuông góc với đáy, đáy ABCD là hình chữ nhật,
AB = a, AD = 2a, SA = 3a. Thể tích của khối chóp S.ABCD bằng a3 A. 6a3. B. . C. 2a3. D. a3. 3 Lời giải.
Theo giả thiết ABCD là hình chữ nhật nên thể tích khối chóp S.ABCD là S 1 1 V = SA · AB · AD = · 3a · a · 2a = 2a3. 3 3 D A o/ aPr B C Chọn phương án C √
Câu 8. Cho khối nón (N ) có bán kính r =
5, có chiều cao h = 5. Thể tích V của khối nón (N ) đã cho là. 27π 16π 26π 25π A. V(N) = . B. V(N) = . C. V(N) = . D. V(N) = . 5 5 5 3 roups/GeoGebr Lời giải. 1 √ Ä ä2 25π Ta có V(N) = · 5π 5 = . 3 3 Chọn phương án D a
Câu 9. Thể tích khối cầu có bán kính bằng là 2 πa3 πa2 πa3 A. . B. . C. . D. πa2. acebook.com/g 2 4 6 .f Lời giải. 4
Phương pháp: Công thức tính thể tích khối cầu có bán kính r là: V = πr3. 3 a 4 a 3 πa3
Cách giải: Thể tích khối cầu có bán kính bằng là: V = π = . 2 3 2 6 https://www Chọn phương án C Câu 10.
Cho hàm số y = f (x) có bảng biến thiên như hình x −∞ −1 0 1 +∞
bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? y0 + 0 − 0 + 0 − A. (−∞; −1). B. (−1; 1). 0 0 y C. (1; +∞). D. (0; 1). −∞ −1 −∞ Lời giải.
Dựa vào bảng biến thiên ta thấy hàm số đã cho nghịch biến trên (−1; 0) và (1; +∞). Chọn phương án C
Câu 11. Tính giá trị của alog√a 4 với a > 0, a 6= 1. A. 8. B. 4. C. 16. D. 2. Lời giải.
Ta có alog√a 4 = a2 loga 4 = aloga 16 = 16. GeoGebraPro Trang 2 Chọn phương án C
Câu 12. Một hình trụ có bán kính đáy , r = a độ dài đường sinh l = 2a Diện tích toàn phần của hình trụ này là A. 2πa2. B. 4πa2. C. 6πa2. D. 5πa2. Lời giải.
Stp = 2Sd + Sxq = 2πa2 + 2πa · 2a = 6πa2. Chọn phương án C Câu 13.
Cho hàm số y = f (x) có bảng biến thiên như hình x −∞ 0 1 +∞
vẽ bên. Mệnh đề nào dưới đây đúng? y0 + 0 − 0 +
A. Hàm số có điểm cực tiểu x = 0. 5 +∞ +
B. Hàm số có điểm cực đại x = 5. y
C. Hàm số có điểm cực tiểu x = −1. −∞ −1 −
D. Hàm số có điểm cực tiểu x = 1. Lời giải.
Dựa vào bảng biến thiên ta thấy hàm số có điểm cực tiểu x = 1. Chọn phương án D Câu 14.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? y 2019-2020 A. y = x4 − 2x2 − 1. B. y = −x4 + 2x2 − 1. C. y = x3 − x2 − 1. D. y = −x3 + x2 − 1. THPT O x GHIỆP Lời giải. N T
Dựa vào hình dáng đồ thị ta suy ra hàm số là hàm trùng phương y = ax4 + bx2 + c có TỐ
• “Đuôi thăng thiên” nên a > 0. THI
• Cắt trục tung tại điểm nằm phía dưới trục hoành nên c < 0.
• Có 3 cực trị nên a · b < 0 ⇒ b < 0. LUYỆN Chọn phương án A 2 − 2x
Câu 15. Tìm đường tiệm cận ngang của đồ thị hàm số y = . x + 1 A. x = −1. B. x = −2. C. y = 2. D. y = −2. Lời giải. 2 − 2x Ta có lim
= −2 ⇒ y = −2 là tiệm cận ngang của đồ thị hàm số. x→+∞ x + 1 Chọn phương án D
Câu 16. Tập nghiệm của bất phương trình 32x−1 > 27 là Å 1 ã Å 1 ã A. ; +∞ . B. (3; +∞). C. ; +∞ . D. (2; +∞). 2 3 Lời giải.
32x−1 > 27 ⇔ 2x − 1 > 3 ⇔ x > 2. Chọn phương án D Câu 17. GeoGebraPro Trang 3
Cho hàm số y = f (x) có bảng biến thiên như hình vẽ x −∞ −1 1 +∞
bên. Số nghiệm của phương trình f (x) = −1 là y0 − 0 + + A. 1. B. 2. C. 4. D. 3. 1 +∞ −1 y √ − 2 −∞ Lời giải.
Số nghiệm của phương trình f (x) = −1 tương ứng với số giao điểm của đồ thị hàm số y = f (x) và
y = −1. Dựa vào bảng biến thiên suy ra số giao điểm hai đồ thị là 2 điểm. Chọn phương án A 2 5 5 Z Z Z Câu 18. Nếu f (x) dx = 3, f (x) dx = −1 thì f (x) dx bằng 1 2 1 A. 3. B. 4. C. 2. D. −2. Lời giải. Theo tính chất tích phân o/ 5 2 5 Z Z Z aPr f (x) dx = f (x) dx + f (x) dx = 3 + (−1) = 2. 1 1 2 Chọn phương án C
Câu 19. Cho số phức z thỏa mãn z = 3 + 2i. Tìm phần thực và phần ảo của số phức z.
A. Phần thực bằng −3, phần ảo bằng 2.
B. Phần thực bằng 3, phần ảo bằng 2. roups/GeoGebr
C. Phần thực bằng 3, phần ảo bằng −2.
D. Phần thực bằng −3, phần ảo bằng −2. Lời giải.
Vì z = 3 + 2i ⇒ z = 3 − 2i. Do đó số phức z có phần thực bằng 3, phần ảo bằng −2. Chọn phương án C
Câu 20. Cho hai số phức z1 = 3 + i, z2 = 2 − i. Tính giá trị của biểu thức P = |z1 + z1 · z2|. A. P = 85. B. P = 5. C. P = 50. D. P = 10. acebook.com/g Lời giải. .f
Ta có z1 · z2 = (3 + i)(2 − i) = 7 − i ⇒ z1 + z1 · z2 = 3 + i + 7 − i = 10.
Suy ra P = |z1 + z1 · z2| = 10. Chọn phương án D
Câu 21. Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện |z + 2 − 5i| = 6 https://www
là đường tròn có tâm I và bán kính R lần lượt là A. I(−2; 5) và R = 36. B. I(−2; 5) và R = 6. C. I(2; −5) và R = 36. D. I(2; −5) và R = 6. Lời giải.
Gọi z = x + iy (x, y ∈ R). Ta có |z + 2 − 5i| = 6 ⇔ (x + 2)2 + (y − 5)2 = 36.
Suy ra tập hợp điểm biểu diễn z là đường tròn có tâm I(−2; 5) và bán kính R = 6. Chọn phương án B
Câu 22. Trong không gian Oxyz , cho điểm A(−1; 2; 3). Hình chiếu vuông góc của điểm A trên trục Oz là điểm A. Q(−1; 0; 3). B. M (0; 0; 3). C. P (0; 2; 3). D. N (−1; 0; 0). Lời giải.
Hình chiếu vuông góc của điểm A(−1; 2; 3) lên trục Oz là điểm M (0; 0; 3). Chọn phương án B
Câu 23. Trong không gian Oxyz, mặt cầu có tâm I (1; 2; −3) và tiếp xúc với trục Oy có bán kính bằng GeoGebraPro Trang 4 √ √ √ A. 10. B. 2. C. 5. D. 13. Lời giải. √
Gọi H là hình chiếu vuông góc của tâm I (1; 2; −3) trên trục Oy ⇒ H (0; 2; 0) ⇒ IH = 10. √
Gọi R là bán kính mặt cầu có tâm I (1; 2; −3) và tiếp xúc với trục Oy ⇒ R = IH = 10. Chọn phương án A
Câu 24. Trong không gian Oxyz cho mặt phẳng (P ) : x + y − 2z + 4 = 0. Một véc-tơ pháp tuyến của mặt phẳng (P ) là #» #» #» #» A. n = (1; 1; −2). B. n = (1; 0; −2). C. n = (1; −2; 4). D. n = (1; −1; 2). Lời giải. #»
Phương pháp: Mặt phẳng (P ) : Ax + By + Cz + D = 0 nhận n = (A; B; C) là 1 vec-tơ pháp tuyến. #»
Cách giải: Một vec-tơ pháp tuyến của mặt phẳng (P ) là n = (1; 1; −2). Chọn phương án A
Câu 25. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1; −1; 0), B(0; 1; 1). Gọi (α) là x y − 1 z − 2
mặt phẳng chứa đường thẳng d : = =
và song song với đường thẳng AB. Điểm nào dưới 2 −1 1
đây thuộc mặt phẳng (α)? A. M (6; −4; −1). B. N (6; −4; 2). C. P (6; −4; 3). D. Q(6; −4; 1). Lời giải. # » Ta có AB = (−1; 2; 1). #»
Véc-tơ chỉ phương của d là u d = (2; −1; 1). î # » #» ó
Suy ra AB, u d = (3; 3; −3) = 3(1; 1 − 1). 2019-2020 #» 1 î # » #» ó
Vì (α) chứa d và song song với AB nên véc-tơ n =
AB, u d = (1; 1 − 1) là một véc-tơ pháp tuyến 3 của (α). THPT
Lại có, điểm C(0; 1; 2) ∈ d ⇒ C ∈ (α).
Do đó, phương trình của (α) là x + y − z + 1 = 0.
Lần lượt thay tọa độ các điểm trong các phương án ta được điểm P (6; −4; 3) thỏa mãn. GHIỆP Chọn phương án C N T
Câu 26. Cho hình lập phương ABCD.A0B0C0D0. Góc giữa hai đường thẳng BA0 và CD bằng A. 90◦. B. 60◦. C. 30◦. D. 45◦. TỐ Lời giải. THI
Ta có CD ∥ AB, suy ra góc giữa A0B với CD bằng góc giữa A0B với AB, A B góc này bằng 45◦. D C LUYỆN A0 B0 D0 C0 Chọn phương án D
Câu 27. Cho hàm số f (x) có đạo hàm f 0(x) = (x − 1)(x − 2)2(x − 3)3(x − 4)4, ∀x ∈ R. Số điểm cực
trị của hàm số đã cho là A. 3. B. 5. C. 2. D. 4. Lời giải. x = 1 x = 2 Ta có f 0(x) = 0 ⇔   x = 3  x = 4.
Bảng biến thiên của hàm số f (x) như sau GeoGebraPro Trang 5 x −∞ 1 2 3 4 +∞ f 0(x) + 0 − 0 − 0 + 0 + f (x)
Vậy số điểm cực trị của hàm số đã cho là 2. Chọn phương án C √x2 − 1
Câu 28. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = trên tập x − 2 ï 3 ò
hợp D = (−∞; −1) ∪ 1; . Tính P = M + m. 2 √ √ A. P = 2. B. P = 0. C. P = − 5. D. P = 3. Lời giải. 1 − 2x 1 Ta có y0 = √
, y0 = 0 ⇔ 1 − 2x = 0 ⇔ x = / ∈ D. (x − 2)2 x2 − 1 2 o/ Bảng biến thiên aPr x −∞ −1 1 3 2 y0 + − 0 0 y √ −1 − − 5 roups/GeoGebr √
Vậy M = max y = 0 và m = min y = − 5. D D √ Do đó P = − 5. Chọn phương án C
Câu 29. Cho số thực a > 1, b 6= 0. Mệnh đề nào dưới đây đúng? | | acebook.com/g A. log b2 = −2 log b|. B. log b2 = 2 log b. C. log b2 = 2 log b|. D. log b2 = −2 log b. a a a a a a a a .f Lời giải.
Ta có b 6= 0 ⇔ |b| > 0. Khi đó ta có log b2 = log |b|2 = 2 log |b|. a a a Chọn phương án C
Câu 30. Tìm số giao điểm của đồ thị hàm số y = x3 − 3x2 + 3x − 1 và đồ thị hàm số y = x2 − x − 1. https://www A. 1. B. 0. C. 2. D. 3. Lời giải. ñx = 0
Phương trình hoành độ giao điểm x3 − 3x2 + 3x − 1 = x2 − x − 1 ⇔ x3 − 4x2 + 4x = 0 ⇔ x = 2 Chọn phương án C
Câu 31. Tập nghiệm của bất phương trình log 1 (x − 1) + log (11 − 2x) ≥ 0 là 3 3 ï 11 ã A. (−∞; 4). B. (1; 4]. C. (1; 4). D. 4; . 2 Lời giải. 11 Điều kiện: 1 < x < . 2
Bất phương trình tương đương − log (x − 1) + log (11 − 2x) ≥ 0 3 3 11 − 2x 11 − 2x 12 − 3x ⇔ log ≥ 0 ⇔ ≥ 1 ⇔ ≥ 0 ⇔ 1 < x ≤ 4. 3 x − 1 x − 1 x − 1 Chọn phương án B GeoGebraPro Trang 6
Câu 32. Tính thể tích khối tròn xoay sinh ra khi quay tam giác đều ABC cạnh bằng 1 quanh AB. √ 3π π π π 3 A. . B. . C. . D. . 4 4 8 2 Lời giải.
Khi quay tam giác đều ABC quanh cạnh AB ta thu được hai khối nón bằng nhau. √ Ç å2 1 2 1 3 1 π Do đó, ta có V = 2V = 2 · πr2h = π · · = (đvtt). nón 3 3 2 2 4 √3 1 1 (bán kính r = hABC = , đường cao h = AB = ). 2 2 2 Chọn phương án B 1 Z dx π π Câu 33. Cho tích phân I = √
. Nếu đổi biến số x = 2 sin t, t ∈ − ; thì 4 − x2 2 2 0 π π π π 6 6 6 3 Z Z Z dt Z A. I = dt. B. I = t dt. C. I = . D. I = dt. t 0 0 0 0 Lời giải.
Ta có x = 2 sin t ⇒ dx = 2 cos t dt. π
Với x = 0 ⇒ t = 0, x = 1 ⇒ t = . 6 π π π π 6 6 6 6 Z 2 cos t dt Z 2 cos t dt Z 2 cos t dt Z Do đó I = = √ = = dt. p4 − 4 sin2 t 2 cos2 t 2 cos t 2019-2020 0 0 0 0 Chọn phương án A
Câu 34. Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol THPT
(P ) : y = x2 và đường thẳng d : y = 2x quay quanh trục Ox. 2 2 2 Z Z Z A. π x2 − 2x2 dx. B. π 4x2 dx − π x4 dx. GHIỆP 0 0 0 N 2 2 2 Z Z Z T C. π 4x2 dx + π x4 dx. D. π 2x − x2 dx. TỐ 0 0 0 Lời giải. THI
Xét phương trình hoành độ giao điểm của (P ) và d, ta có
x2 = 2x ⇔ x = 0 hoặc x = 2. LUYỆN
Trên đoạn [0; 2] ta thấy 2x ≥ x2 nên thể tích cần tìm là 3 2 2 Z Z Z V = π 4x2 − x4 dx = π 4x2 dx − π x4 dx. 0 0 0 Chọn phương án B
Câu 35. Cho hai số phức z1 = 2 + i, z2 = 1 − 3i. Tính T = |(1 + i)z1 + 2z2|. √ A. T = 18. B. T = 3 2. C. T = 0. D. T = 3. Lời giải. √ √
(1 + i)z1 + 2z2 = (1 + i)(2 + i) + 2(1 − 3i) = 3 − 3i ⇒ |(1 + i)z1 + 2z2| = 9 + 9 = 3 2. Chọn phương án B
Câu 36. Gọi z0 là nghiệm phức có phần ảo âm của phương trình 2z2 − 2z + 13 = 0. Trên mặt phẳng
tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w = iz0? Å 5 1 ã Å 5 1 ã Å 5 1 ã Å 5 1 ã A. M ; . B. N ; − . C. P ; − . D. Q ; . 4 4 4 4 2 2 2 2 GeoGebraPro Trang 7 Lời giải. 1 5 1 5
Phương trình 2z2 − 2z + 13 = 0 ⇔ z = + i (loại) hay z = − i (nhận). 2 2 2 2 Å 1 5 ã 5 1 Å 5 1 ã Nên ta có w = iz0 = i − i = +
i. Vậy điểm biểu diễn của w là Q ; . 2 2 2 2 2 2 Chọn phương án D x + 3 y − 2 z − 1
Câu 37. Trong không gian toạ độ Oxyz, cho đường thẳng (d) : = = . Mặt phẳng 1 −1 2
(P ) đi qua điểm M (2; 0; −1) và vuông góc với (d) có phương trình là A. (P ) : x − y − 2z = 0. B. (P ) : 2x − z = 0.
C. (P ) : x − y + 2z + 2 = 0. D. (P ) : x − y + 2z = 0. Lời giải. #»
Mặt phẳng (P ) đi qua M (2; 0; −1) có một véc-tơ pháp tuyến n = (1; −1; 2) có dạng (P ) : x − y + 2z = 0. Chọn phương án D
Câu 38. Trong không gian Oxyz, cho hai điểm A(1; 0; 1), B(−1; 2; 1). Viết phương trình đường thẳng
∆ đi qua tâm đường tròn ngoại tiếp tam giác OAB và vuông góc với mặt phẳng (OAB). x = t x = t x = 3 + t x = −1 + t o/         A. ∆ : y = 1 + t . B. ∆ : y = 1 + t . C. ∆ : y = 4 + t . D. ∆ : y = t . aPr     z = 1 − t z = 1 + t z = 1 − t z = 3 − t Lời giải.
Tam giác OAB vuông tại O nên tâm đường tròn ngoại tiếp là trung điểm AB có tọa độ I(0; 1; 1). #» î # » # »ó
Mặt phẳng (OAB) có véc-tơ pháp tuyến n = OA, OB = (−2; −2; 2). #»
Suy ra đường thẳng ∆ có u = (1; 1; −1) và đi qua I(0; 1; 1). Vậy phương trình đường thẳng ∆ là x = t roups/GeoGebr   ∆ : y = 1 + t .  z = 1 − t Chọn phương án A
Câu 39. Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp 12A, 3 học sinh lớp 12B và 5 học sinh lớp
12C trên một bàn tròn. Tính xác suất P để các học sinh cùng lớp luôn ngồi cạnh nhau. acebook.com/g 1 1 1 1 .f A. P = . B. P = . C. P = . D. P = . 1260 126 28 252 Lời giải.
Số phần tử không gian mẫu là n(Ω) = 9!.
Gọi E là biến cố các học sinh cùng lớp luôn ngồi cạnh nhau. Ta có các bước sắp xếp như sau: https://www
• Xếp 5 học sinh lớp 12C ngồi vào bàn sao cho các học sinh này ngồi sát nhau. Số cách sắp xếp là 5!.
• Xếp 3 học sinh lớp 12B vào bàn sao cho các học sinh này ngồi sát nhau và sát nhóm của học sinh
12C. Số cách sắp xếp là 3! × 2.
• Xếp 2 học sinh lớp 12A vào hai vị trí còn lại của bàn. Số cách sắp xếp là 2!.
Số phần tử thuận lợi cho biến cố E là n(E) = 5! × 3! × 2 × 2!. n(E) 1
Xác suất của biến cố E là P (E) = = . n(Ω) 126 Chọn phương án B
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA ⊥ (ABCD) và √
SA = a 2 . Khoảng cách từ A đến mặt phẳng (SBC) bằng: √ √ 2a 5 √ a a 3 A. . B. a 3. C. . D. . 5 2 2 Lời giải. GeoGebraPro Trang 8 Phương pháp S
Chứng minh để tìm khoảng cách sau đó áp dụng hệt thức lượng trong
tam giác vuông để tính toán. Cách giải: Kẻ AH ⊥ SB = {H} H ®SA ⊥ AB Ta có: ⇒ BC ⊥ (SAB) ⇒ BC ⊥ AH BC ⊥ SA A D
®AH ⊥ SB ⇒ AH ⊥ (SBC) ⇒ d(A;(SBC)) = AH AH ⊥ BC
Áp dụng hệ thức lượng trong 4SAB có đường cao AH ta có: B C √ √ SA.AB a 3a a 3 d(A; (SBC)) = AH = √ = √ = . SA2 + AB2 3a2 + a2 2 Chọn phương án D
Câu 41. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x3 − (m + 1)x2 + 3x + 1 đồng biến trên khoảng (−∞; +∞)? A. 6. B. 8. C. 7. D. 5. Lời giải.
Ta có y0 = 3x2 − 2(m + 1)x + 3.
Hàm số đã cho đồng biến trên (−∞; +∞) khi và chỉ khi ∆0 = (m + 1)2 − 9 ≤ 0 ⇔ −4 ≤ m ≤ 2.
Vậy các giá trị nguyên của m thỏa yêu cầu bài toán là −4, −3, −2, −1, 0, 1, 2, tức là có 7 giá trị. 2019-2020 Chọn phương án C
Câu 42. Với mức tiêu thụ thức ăn của trang trại A không đổi như dự định thì lượng thức ăn dự trữ THPT
sẽ đủ dùng cho 100 ngày. Nhưng thực tế, mức tiêu thụ thức ăn tăng thêm 4% mỗi ngày (ngày sau tăng
4% so với ngày trước đó). Hỏi thực tế lượng thức ăn dự trữ đó chỉ đủ dùng cho bao nhiêu ngày? A. 40. B. 41. C. 42. D. 43. GHIỆP Lời giải. N
Gọi lượng thức ăn tiêu thụ theo dự định hàng ngày là x. Lượng thức ăn dự trữ của trang trại A là 100x. T 1,04n − 1
Ta có x (1 + 1,04 + 1,042 + ... + 1,04n−1) = 100x ⇔ = 100 ⇒ n = log 5 ≈ 41,035. 1,04 TỐ 1,04 − 1
Do đó lượng thức ăn dự trữ chỉ đủ dùng cho 41 ngày. THI Chọn phương án B
Câu 43. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như sau LUYỆN x −∞ −1 3 +∞ y0 + 0 − 0 + 5 +∞ + y −∞ 1
Đồ thị hàm số y = |f (x)| có bao nhiêu điểm cực trị? A. 2. B. 3. C. 4. D. 5. Lời giải.
Số điểm cực trị của đồ thị hàm số y = |f (x)| bằng số điểm cực trị của đồ thị hàm số y = f (x) cộng với
số giao điểm của đồ thị hàm số y = f (x) với trục hoành (không tính điểm cực trị).
Vì đồ thị hàm số y = f (x) có 2 điểm cực trị và cắt trục Ox tại 1 điểm trên đồ thị hàm số y = |f (x)|
có 2 + 1 = 3 điểm cực trị. Chọn phương án B GeoGebraPro Trang 9
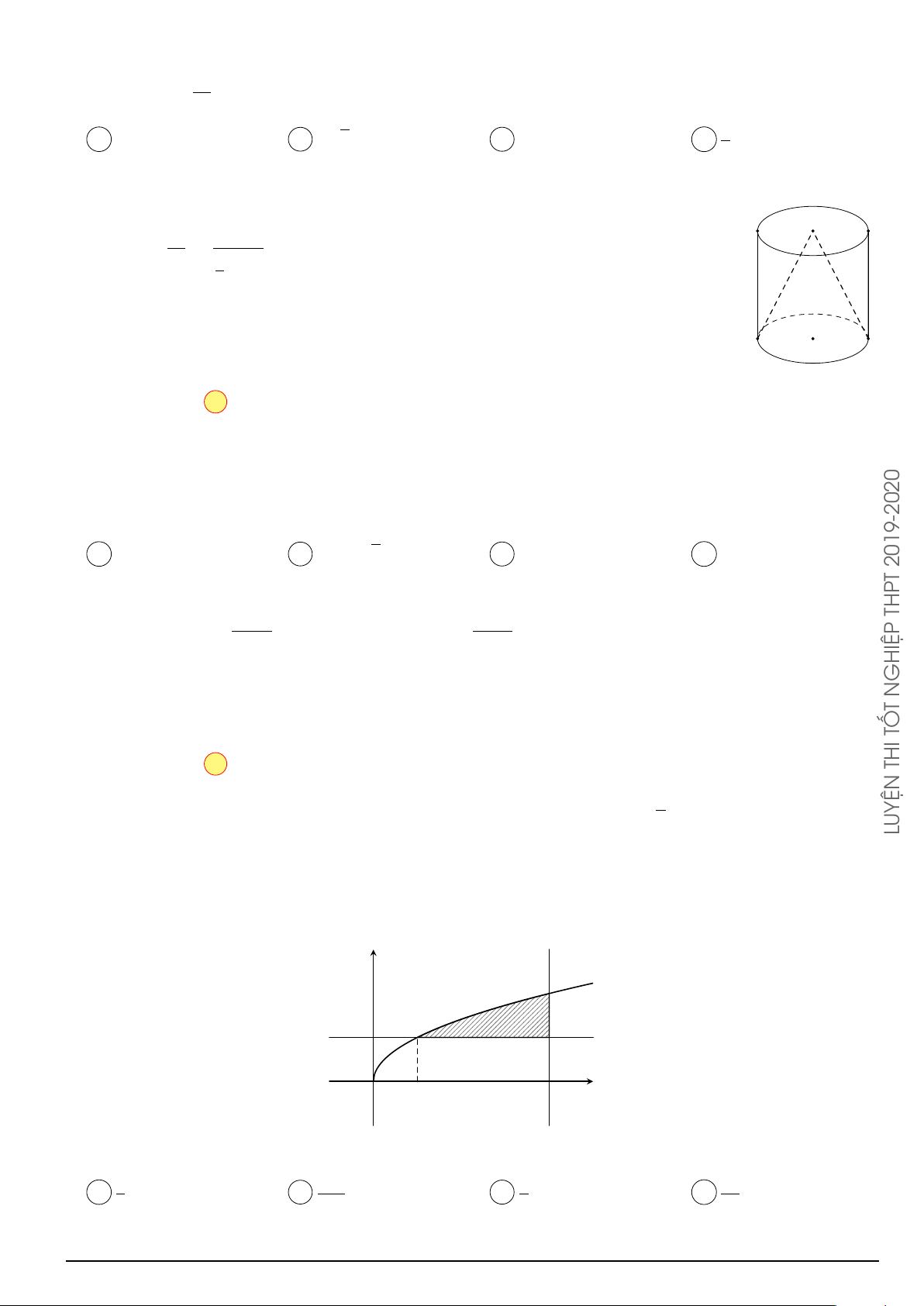
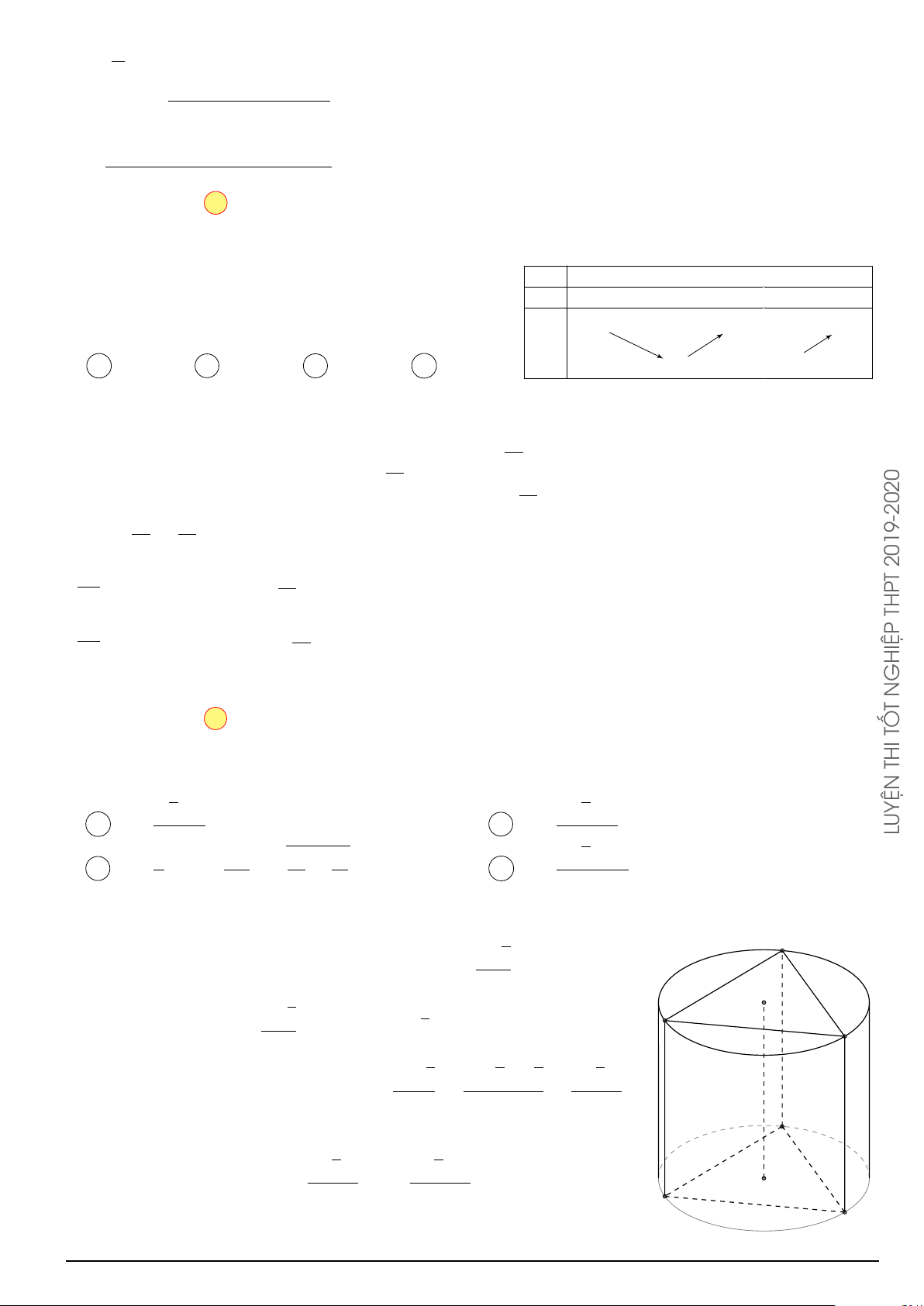
Câu 44. Cho hình trụ có thiết diện đi qua trục là một hình vuông có cạnh bằng 4a. Diện tích xung quanh S của hình trụ là A. S = 4πa2. B. S = 8πa2. C. S = 24πa2. D. S = 16πa2. Lời giải.
Phương pháp: Công thức tính diện tích xung quanh hình trụ có bán kính đáy R, chiều cao h là Sxq = 2πRh. Cách giải: A O R B h o/ aPr D O0 C
Hình trụ có thiết diện đi qua trục là hình vuông ABCD có cạnh bằng 4a.
Do đó h = 2R = 4a ⇒ R = 2a với R, h lần lượt là bán kính đáy và chiều cao của hình trụ. Vậy S = 2πRh = 16πa2 roups/GeoGebr Chọn phương án D 1 Z
Câu 45. Cho hàm số f (x) có đạo hàm liên tục trên [−1; 1] và thỏa mãn f (1) = 7, xf (x) dx = 1. 0 1 Z Khi đó x2f 0(x) dx bằng acebook.com/g 0 .f A. 6. B. 8. C. 5. D. 9. Lời giải. 1 Z Xét I =
x2f 0(x) dx, đặt u = x2, dv = f 0(x) dx ⇒ du = 2x dx, v = f (x), ta được 0 https://www 1 1 Z Z 1 I = x2 · f (x) − 2xf (x) dx = f (1) − 2 xf (x) dx = 5. 0 0 0 Chọn phương án C
Câu 46. Cho hàm số y = f (x) = ax3 + bx2 + cx + d có bảng biến thiên như sau: 1
Khi đó |f (x)| = m có bốn nghiệm phân biệt x1 < x2 < x3 < < x4 khi và chỉ khi: 2 A. 0 < m < 1. x −∞ 0 1 +∞ B. 0 < m ≤ 1. y0 + 0 − 0 + 1 C. < m < 1. +∞ + 2 1 1 D. ≤ m < 1. y 2 −∞ 0 GeoGebraPro Trang 10 Lời giải. ®y0(0) = 0 ®c = 0
Ta có y0 = 3ax2 + 2bx + c, từ bảng biến thiên suy ra: ⇔ (1) y0(1) = 0 3a + 2b = 0 ®y(0) = 1 ®d = 1 Ta lại có ⇔ (2) y(1) = 0 a + b + c + d = 0   d = 1 d = 1         c = 0 c = 0
Từ (1), (2) ta có hệ phương trình: ⇔ 3a + 2b = 0 a = 2         a + b + c + d = 0 b = −3
⇒ y = f (x) = 2x3 − 3x2 + 1
Đồ thị hàm số |f (x)| = |2x3 − 3x2 + 1| Å 1 ã 1 Ta có f = 2 2 1
Dựa vào đồ thị suy ra phương trình |f (x)| = m có bốn nghiệm phân biệt x1 < x2 < x3 < < x4 khi 2 1 và chỉ khi: < m < 1 2 Chọn phương án C
Câu 47. Cho a, b, c > 1. Biết rằng biểu thức P = log (bc) + log (ac) + 4 log (ab) đạt giá trị nhỏ nhất a b c
bằng m khi log c = n. Tính giá trị m + n. b 25 A. m + n = 14. B. m + n = . C. m + n = 12. D. m + n = 10. 2019-2020 2 Lời giải. Phương pháp: THPT 1 log b = , (a, b > 0; a, b 6= 1). a log a b √
Áp dụng BĐT Cô-si cho 2 số dương: a + b ≥ 2 ab. GHIỆP Cách giải: N
Do a, b, c > 1 nên log b, log a, log c > 0. a c b T TỐ
P = log (bc) + log (ac) + 4 log (ab) = log b + log c + log a + log c + 4 log a + 4 log b a b c a a b b c a
= (log b + log a) + (log c + 4 log a) + (log c + 4 log b) a b a c b c THI Å 1 ã Å 1 ã Å 4 ã = log b + + + 4 log a + log c + a log b log a c b log c a c b 1 1 4 LUYỆN ≥ 2 log b · + 2 · 4 log a + 2 log c · = 2 + 4 + 4 = 10. a log b log c b log c a c b  1   log b =  a  log b  log b = 1  a  a    1  1
Dấu “ = ” xảy ra khi và chỉ khi = 4 log a ⇔ log a = log a c c 2  c     4    log c = 2.  log c = b  b log b c
Vậy, đạt giá trị nhỏ nhất là 10 khi log c = 2 ⇒ m = 10, n = 2 ⇒ m + n = 12. b Chọn phương án C
Câu 48. Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị nhỏ nhất của hàm số
y = − |x3 − 3x + m| trên đoạn [0; 2] bằng −3. Tổng tất cả các phần tử của S là A. 1. B. 2. C. 0. D. 6. Lời giải. • Nhận xét : GeoGebraPro Trang 11
Tìm m sao cho giá trị nhỏ nhất của hàm số y = − |x3 − 3x + m| trên đoạn [0; 2] bằng −3
⇔ Tìm m sao cho giá trị lớn nhất của hàm số y = |x3 − 3x + m| trên đoạn [0; 2] bằng 3. ñx = 1 (n)
• Xét hàm số f (x) = x3 − 3x + m liên tục trên đoạn [0; 2]. Ta có f 0(x) = 3x2 − 3 = 0 ⇔ . x = −1 (l)
• Suy ra GTLN và GTNN của f (x) thuộc {f (0) , f (1) , f (2)} = {m, m − 2, m + 2}.
• Xét hàm số y = |x3 − 3x + m| trên đoạn [0; 2] ta được giá trị lớn nhất của hàm số y là max y = x∈[0;2]
{|m|, |m − 2| , |m + 2|} = 3.
– TH 1: m ≥ 0 ⇒ max y = m + 2 = 3 ⇔ m = 1. x∈[0;2]
– TH 2: m < 0 ⇒ max y = 2 − m = 3 ⇔ m = −1. x∈[0;2]
• Vậy m ∈ {−1; 1} nên tổng các phần tử của S bằng 0. Chọn phương án C
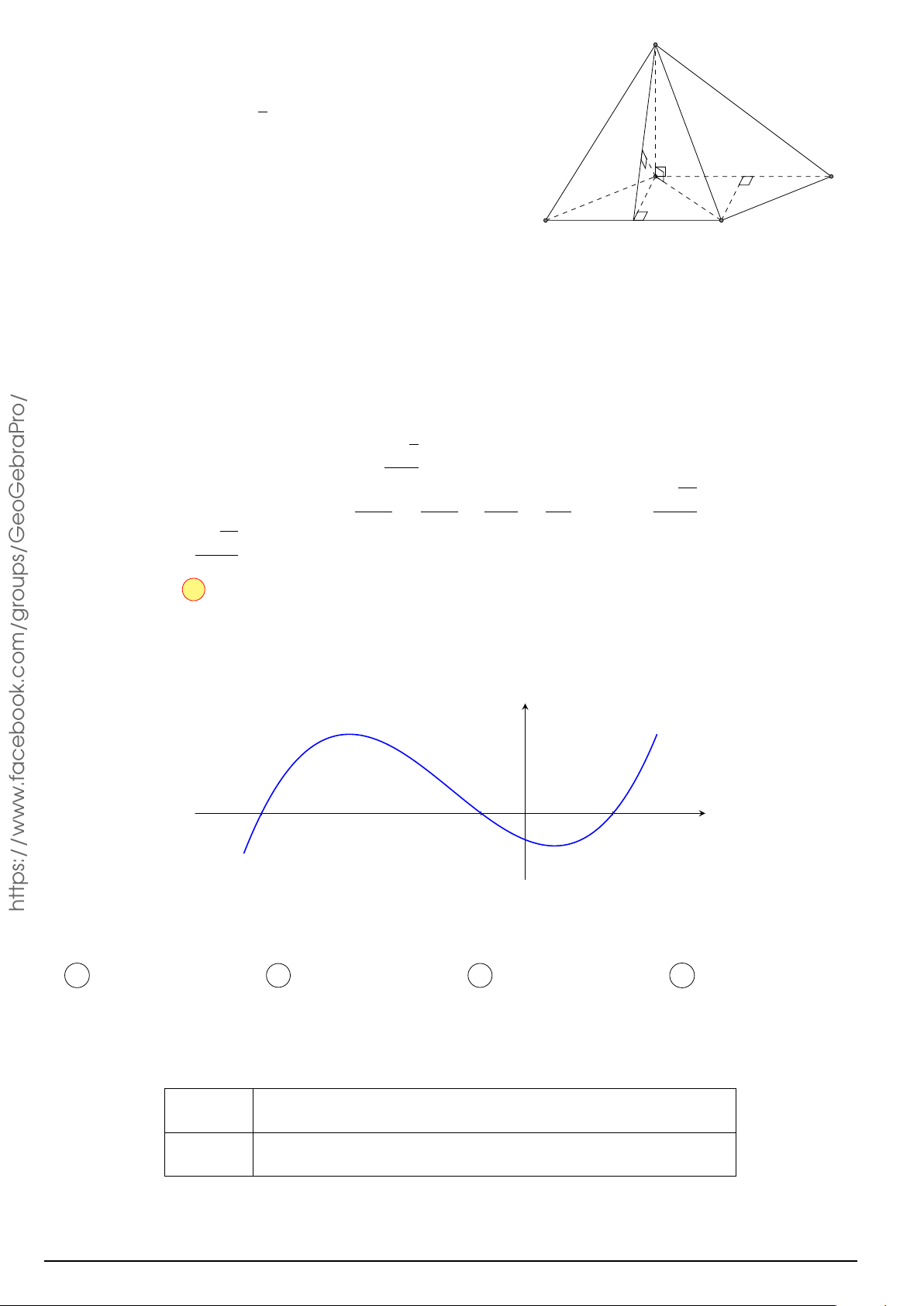
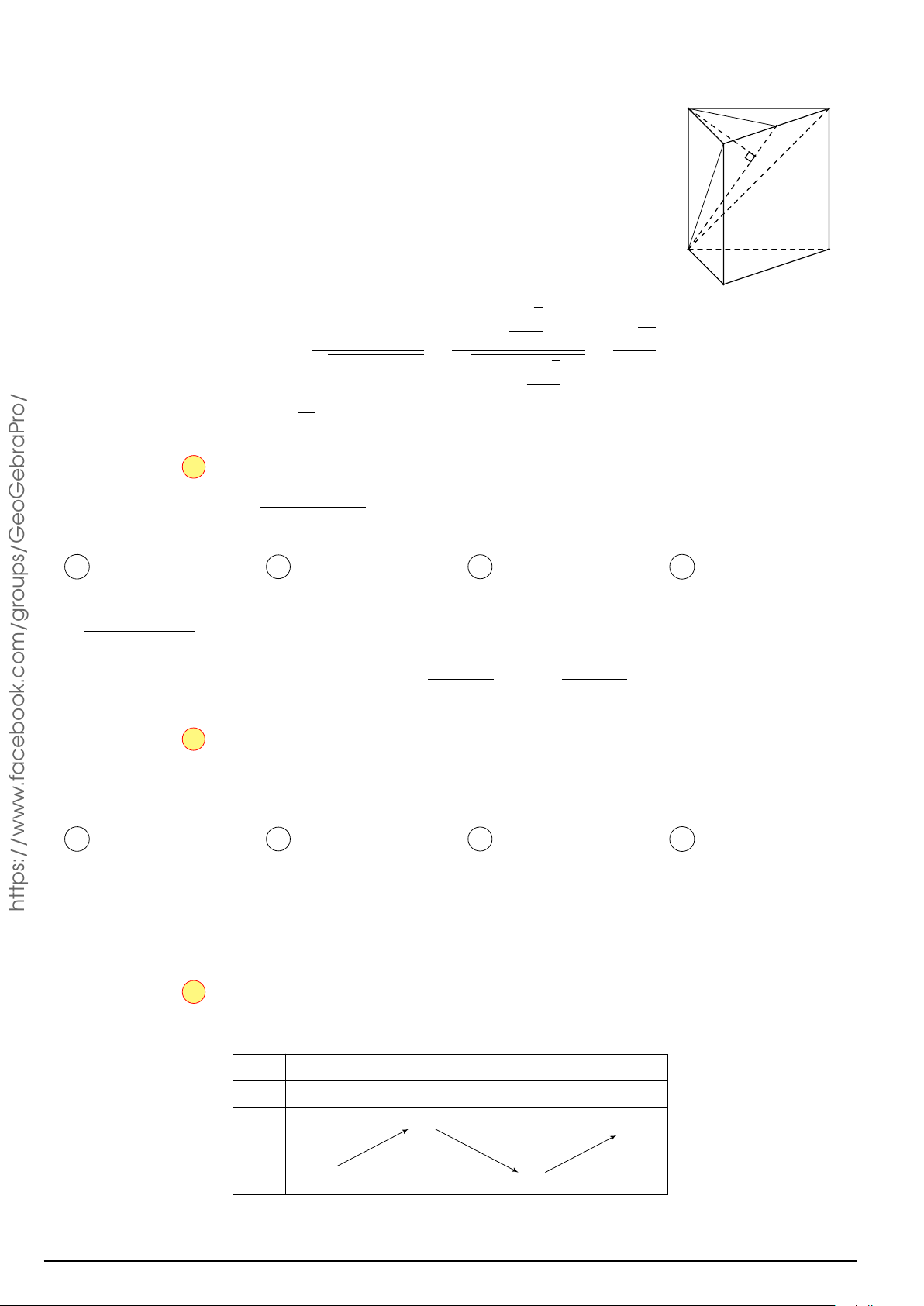
Câu 49. Cho hình hộp chữ nhật ABCD.A0B0C0D0. Gọi M là trung điểm của BB0. Mặt phẳng (M DC0) o/
chia khối hộp chữ nhật thành hai khối đa diện, một khối chứa đỉnh C và một khối chứa đỉnh A0. Gọi V aPr V 1
1, V2 lần lượt là thể tích của hai khối đa diện chứa C và A0. Tính . V2 V1 7 V1 7 V1 7 V1 17 A. = . B. = . C. = . D. = . V2 24 V2 17 V2 12 V2 24 Lời giải.
Gọi I = BC ∩ C0M ⇒ DI ∩ AB = K. A0 D0
Khi đó ta có V1 = VICDC0 − VIBKM trong đó roups/GeoGebr 1 1 1 B0 C0 VICDC0 = IC · CD · CC0 = V ; 3 2 3 M VIBKM 1 D Mặt khác = A VICDC0 8 1 1 1 7 K ⇒ V I 1 = V − · V = V 3 8 3 24 B C acebook.com/g 17 .f ⇒ V2 = V 24 V 7 ⇒ 1 = . V2 17 Chọn phương án B Å 1 ã2020 Å 1 ãa https://www
Câu 50. Tìm tất cả các giá trị thực của tham số a > 0 thỏa mãn 2a + ≤ 22020 + . 2a 22020 A. 0 < a < 1. B. 1 < a < 2020. C. 0 < a ≤ 2020. D. a ≥ 2020. Lời giải. ln(2x + 2−x)
(2x − 2−x) ln 2x − (2x + 2−x) ln(2x + 2−x) Xét hàm f (x) = ⇒ f 0(x) = . x x2(2x + 2−x)
Vì ln 2x < ln(2x + 2−x) và 0 < 2x − 2−x < 2x + 2−x nên f 0(x) < 0 ⇒ f (x) nghịch biến. Do vậy Å 1 ã2020 Å 1 ãa 2a + ≤ 22020 + 2a 22020
⇔2020 ln(2a + 2−a) ≤ a ln(22020 + 2−2020) ln(2a + 2−a) ln(22020 + 2−2020) ⇔ ≤ a 2020 ⇔a ≥ 2020. Chọn phương án D GeoGebraPro Trang 12
———————–HẾT———————– 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN GeoGebraPro Trang 13 ĐÁP ÁN THAM KHẢO 1. C 2. A 3. B 4. B 5. D 6. D 7. C 8. D 9. C 10. C 11. C 12. C 13. D 14. A 15. D 16. D 17. A 18. C 19. C 20. D 21. B 22. B 23. A 24. A 25. C 26. D 27. C 28. C 29. C 30. C 31. B 32. B 33. A 34. B 35. B 36. D 37. D 38. A 39. B 40. D 41. C 42. B 43. B 44. D 45. C 46. C 47. C 48. C 49. B 50. D o/ aPr roups/GeoGebr acebook.com/g .f https://www GeoGebraPro Trang 14 MỖI NGÀY MỘT ĐỀ THI 7
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Một đội xây dựng gồm 3 kỹ sư, 7 công nhân lập một tổ công tác gồm 5 người. Hỏi có bao nhiêu
cách lập tổ công tác gồm 1 kỹ sư làm tổ trưởng, 1 công nhân làm tổ phó và 3 công nhân tổ viên? A. 420. B. 360. C. 120. D. 240.
Câu 2. Cho cấp số cộng (un) có số hạng đầu u1 = 2 và công sai d = −3. Tính tổng 10 số hạng đầu của (un). A. S10 = 115. B. S10 = −155. C. S10 = −115. D. S10 = 155.
Câu 3. Tổng tất cả các nghiệm của phương trình log (7 − 3x) = 2 − x 3 A. 2. B. 1. C. 7. D. 3. √
Câu 4. Tính thể tích V của khối lập phương ABCD.A0B0C0D0 biết đường chéo AC0 = a 3. √ a3 √ 3 6a3 A. . B. 3 3a3. C. . D. a3. 3 4 √ √
Câu 5. Tìm tập xác định D của hàm số y = (x2 − 3x − 4) 2− 3. A. D = R\(−1; 4). B. D = R. 2019-2020
C. D = (−∞; −1) ∪ (4; +∞).
D. D = (−∞; −1] ∪ [4; +∞). Z
Câu 6. Tìm một nguyên hàm F (x) của hàm số f (x) · g(x) biết F (1) = 3, biết f (x)dx = x + 2018 THPT Z và g(x)dx = x2 + 2019. A. F (x) = x3 + 1. B. F (x) = x3 + 3. C. F (x) = x2 + 2. D. F (x) = x2 + 3. GHIỆP
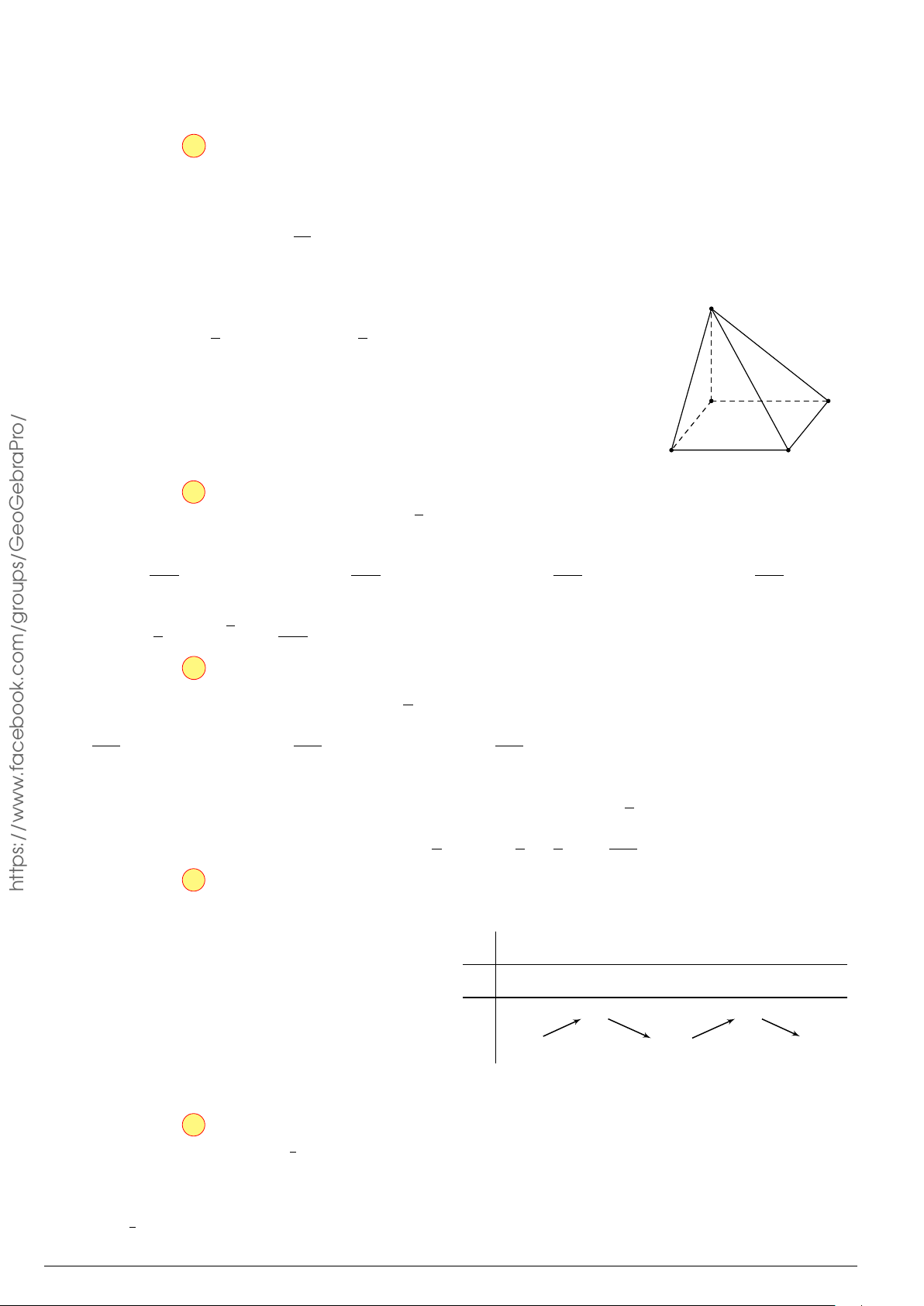
Câu 7. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt (SAB) và (SAC) cùng N √
vuông góc với đáy. Tính thể tích khối chóp biết SC = a 3. T √ √ √ √ 2a3 6 a3 6 a3 3 a3 3 TỐ A. . B. . C. . D. . 9 12 4 2 THI
Câu 8. Cho hình nón có góc ở đỉnh bằng 60◦ và bán kính đáy bằng a. Diện tích xung quanh của hình nón bằng bao nhiêu? √ A. 2πa2. B. 4πa2. C. πa2. D. πa2 3.
Câu 9. Cho hình lập phương có thể tích bằng 64a3. Thể tích của khối cầu nội tiếp hình lập phương đó LUYỆN bằng 8πa3 16πa3 64πa3 32πa3 A. V = . B. V = . C. V = . D. V = . 3 3 3 3 Câu 10.
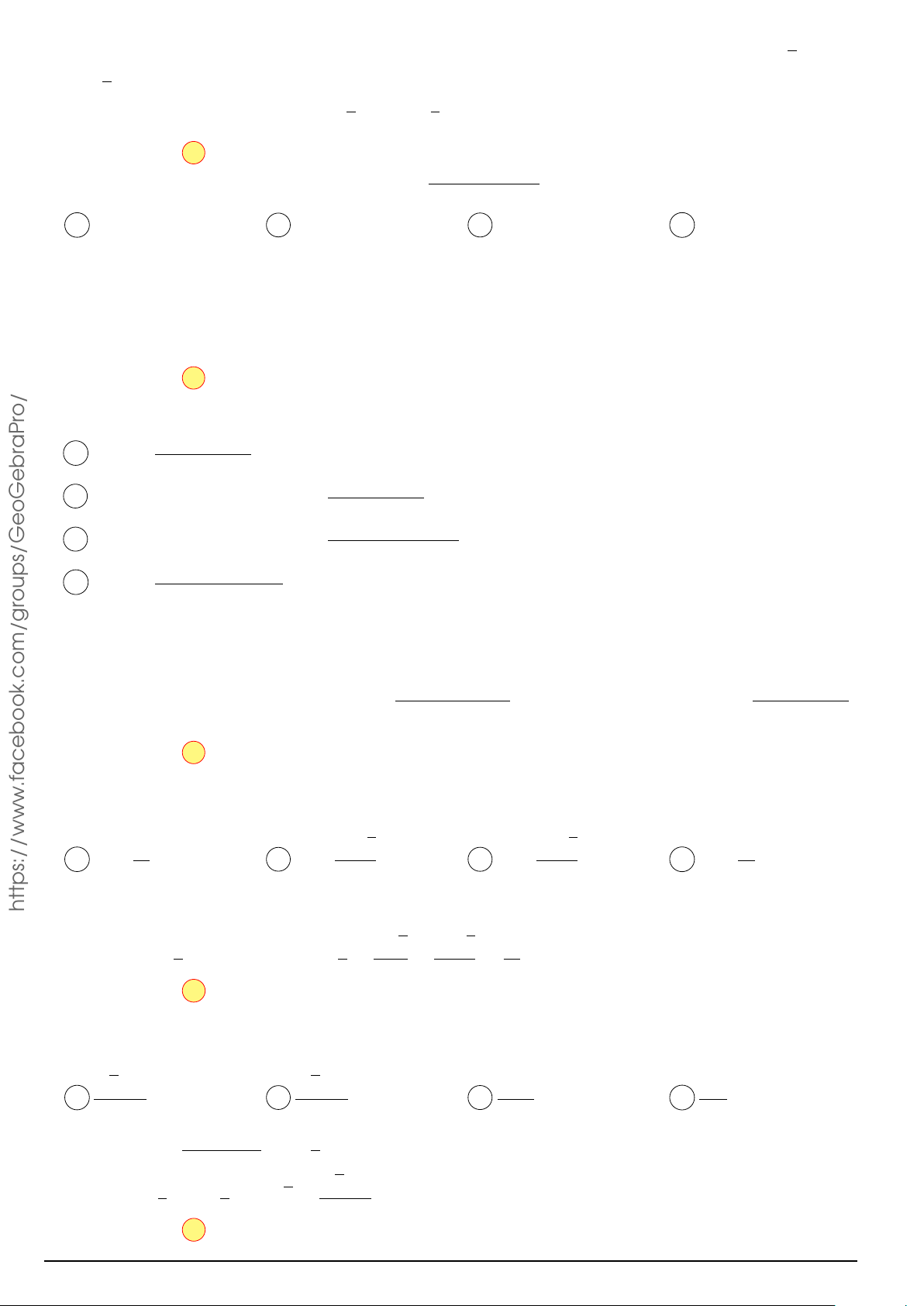
Cho hàm số y = f (x) có bảng biến thiên x −∞ −1 5 +∞
như hình vẽ bên. Hàm số nghịch biến trên f 0(x) + 0 − 0 + khoảng nào dưới đây? a +∞ + A. (−1; 5). B. (−∞; 5). f (x) C. (−∞; −1). D. (−1; +∞). −∞ b √
Câu 11. Cho a, b, c > 0, a, b 6= 1. Tình A = log (b2).log bc) − log (c). a b( a A. log c. B. 1. C. log b. D. log bc. a a a
Câu 12. Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông
có cạnh bằng a. Tính diện tích xung quanh S của khối trụ đó. GeoGebraPro Trang 1 πa2 A. S = 2πa2. B. S = . C. S = πa2. D. S = 4πa2. 2
Câu 13. Hàm số nào dưới đây có bảng biến thiên như hình vẽ? x −∞ −1 1 +∞ y0 + 0 − 0 + 2 +∞ + y −∞ −2 A. y = x3 − 3x. B. y = x3 − 3x − 1. C. y = x3 + 3x. D. y = x4 − 2x2. x + 1
Câu 14. Đồ thị hàm số y = có dạng 1 − x y y o/ −1 1 aPr x O −1 x O 1 A. . B. . y y 1 roups/GeoGebr 1 x O x O −1 −1 C. . D. . ax + 1 acebook.com/g
Câu 15. Biết rằng đồ thị hàm số y =
có đường tiệm cận đứng là x = 2 và đường tiệm cận .f bx − 2
ngang là y = 3. Tính giá trị của a + b? A. 1. B. 5. C. 4. D. 0. 1 1
Câu 16. Tìm tập nghiệm S của phương trình (0, 6) x ≤ (0, 6) 6 A. S = (−∞; 6]. B. S = (0; 6]. C. [0; 6]. D. (−∞; 0) ∪ [6; +∞). https://www
Câu 17. Cho hàm số y = f (x) có đồ thị như hình vẽ bên. y −1 O 1 x −1
Số nghiệm của phương trình 2019f (x) + 1 = 0 là A. 1. B. 3. C. 2. D. 4. 1 Z x dx Câu 18. Cho
= a + b ln 2 + c ln 3 với a, b, c là các số hữu tỷ. Giá trị của 3a + b + c bằng (x + 2)2 0 A. −2. B. −1. C. 2. D. 1. GeoGebraPro Trang 2
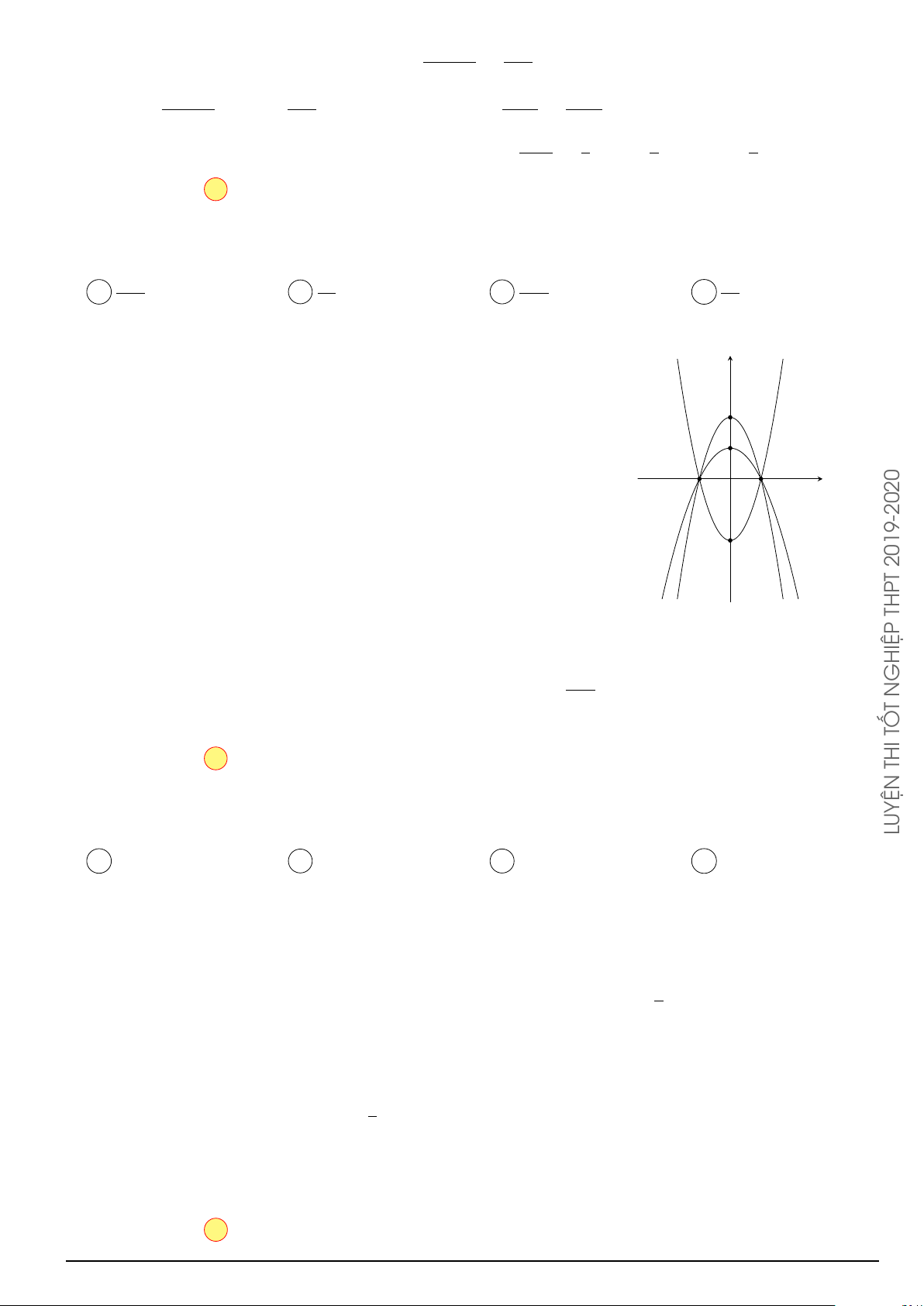
Câu 19. Tìm hai số thực x và y thỏa mãn (3x + 2yi) + (3 − i) = 4x − 3i với i là đơn vị ảo. 2 A. x = 3; y = −1. B. x = ; y = −1. C. x = 3; y = −3. D. x = −3; y = −1. 3 Câu 20.
Cho các số phức z = −1 + 2i, w = 2 − i. Điểm nào trong hình vẽ bên biểu diễn y số phức z + w? N P A. P . B. N . C. Q. D. M . O x M Q
Câu 21. Xét các số phức z thỏa mãn (z + 2i)(z + 2) là số thuần ảo. Biết rằng tập hợp tất cả các điểm
biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là A. (1; −1). B. (1; 1). C. (−1; 1). D. (−1; −1). # » #» #» #»
Câu 22. Trong không gian Oxyz, cho OA = i − 2 j + 3 k , điểm B(3; −4; 1) và C(2; 0; 1). Tọa độ trọng tâm của tam giác ABC là A. 1; −2; 3. B. (−2; 2; −1). C. (2; −2; 1). D. (−1; 2; −3).
Câu 23. Trong không gian Oxyz, cho hai điểm I(1; 1; 1) và A(1; 2; 3). Phương trình của mặt cầu có tâm I và đi qua A là
A. (x + 1)2 + (y + 1)2 + (z + 1)2 = 29.
B. (x − 1)2 + (y − 1)2 + (z − 1)2 = 5.
C. (x − 1)2 + (y − 1)2 + (z − 1)2 = 25.
D. (x + 1)2 + (y + 1)2 + (z + 1)2 = 5. 2019-2020
Câu 24. Trong không gian Oxyz, cho điểm A(2; −1; −3) và mặt phẳng (P ) : 3x − 2y + 4z − 5 = 0. Mặt
phẳng (Q) đi qua A và song song với mặt phẳng (P ) có phương trình là THPT
A. (Q) : 3x − 2y + 4z − 4 = 0.
B. (Q) : 3x − 2y + 4z + 4 = 0.
C. (Q) : 3x − 2y + 4z + 5 = 0. D. (Q) : 3x + 2y + 4z + 8 = 0. x = t   GHIỆP
Câu 25. Trong không gian Oxyz, khoảng cách từ điểm M (2; −4; −1) tới đường thẳng ∆ : y = 2 − t N   T z = 3 + t bằng TỐ √ √ √ √ A. 14. B. 6. C. 2 14. D. 2 6. THI √
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a ,SA ⊥ (ABCD),SA = a 2.
Tìm số đo của góc giữa đường thẳng SC và mặt phẳng (SAD). A. 45◦. B. 30◦. C. 90◦. D. 60◦. LUYỆN
Câu 27. Cho hàm số y = f (x) xác định trên R và có bảng xét dấu của đạo hàm như sau: x −∞ x1 x2 x3 +∞ y0 − 0 + − 0 +
Khi đó số điểm cực trị của hàm số y = f (x) là A. 3. B. 2. C. 4. D. 1. √
Câu 28. Tìm giá trị lớn nhất M của hàm số y = 2x +
8 − 2x2 trên tập xác định của nó? √ √ 8 3 √ A. M = 2 5. B. M = . C. M = 2 6. D. M = 4. 3 a3 − ab2 + b3
Câu 29. Cho a > 0, b > 0 thoả mãn log (a+3b) = log a = log b. Giá trị của bằng 16 9 12 a3 + a2b + 3b3 √ √ √ √ 6 − 13 82 − 17 13 5 − 13 3 − 13 A. . B. . C. . D. . 11 69 6 11 GeoGebraPro Trang 3
Câu 30. Có tất cả bao nhiêu giá trị thực của tham số m để đường thẳng dm : y = mx + 1 cắt đồ thị
(C) : y = x3 − x2 + 1 tại 3 điểm A, B(0; 1) và C phân biệt sao cho tam giác AOC vuông tại O. A. 0. B. 1. C. 2. D. 3.
Câu 31. Tập nghiệm S của bất phương trình log 1 (x − 1) + log (11 − 2x) ≥ 0 là 3 3 Å 11 ã A. S = 3; . B. S = (−∞; 4]. C. S = (1; 4]. D. S = (1; 4). 2 √
Câu 32. Một khối nón có thể tích bằng 9a3π 2. Tính bán kính R đáy khối nón khi diện tích xung quanh nhỏ nhất. 3a √ 3a A. R = 3a. B. R = √ . C. R = 3 9a. D. R = √ . 6 2 3 2 3 1 Z Z
Câu 33. Cho hàm số f (x) liên tục và f (3) = 21,
f (x)dx = 9. Tính tích phân I = x·f 0(3x)dx. 0 0 A. I = 6. B. I = 12. C. I = 9. D. I = 15. x2 y2
Câu 34. Tính thể tích khối tròn xoay sinh bởi Elip (E) : + = 1 quay quanh trục Ox. 4 1 64π 10π 8π 8π2 o/ A. . B. . C. . D. . 9 3 3 3 aPr z + 2
Câu 35. Xét số phức z thỏa mãn
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số z − 2i
phức z luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng √ √ A. 1. B. 2. C. 2 2. D. 2.
Câu 36. Cho số phức z thỏa mãn |z| + z + 5i = 25. Khi đó mô-đun z bằng A. 12. B. 10. C. 11. D. 13. roups/GeoGebr x
Câu 37. Trong không gian Oxyz, cho mặt phẳng (P ) : x + y + z − 3 = 0 và đường thẳng d : = 1 y + 1 z − 2 =
. Hình chiếu vuông góc của d trên (P ) có phương trình là 2 −1 x + 1 y + 1 z + 1 x − 1 y − 1 z − 1 A. = = . B. = = . −1 −4 5 3 −2 −1 x − 1 y − 1 z − 1 x − 1 y − 4 z + 5 C. = = . D. = = . acebook.com/g 1 4 −5 1 1 1 .f x − 3 y + 2 z + 1
Câu 38. Trong không gian Oxyz, cho đường thẳng d : = = và mặt phẳng (P ) : x + 2 1 −1
y + z + 2 = 0. Cho đường thẳng ∆ nằm trong mặt phẳng (P ), vuông góc với đường thẳng d đồng thời √
khoảng cách từ giao điểm I của d với (P ) đến đường thẳng ∆ bằng
42. Gọi M (5; b; c) là hình chiếu
vuông góc của I trên ∆. Giá trị P = bc bằng bao nhiêu? https://www A. P = −10. B. P = 10. C. P = 12. D. P = −20.
Câu 39. Trong một chiếc hộp có 20 viên bi, trong đó có 9 viên bi màu đỏ, 6 viên bi màu xanh và 5
viên bi màu vàng. Lấy ngẫu nhiên đồng thời 3 viên bi. Tìm xác suất để 3 viên bi lấy ra có không quá 2 màu.29 9 183 82 A. . B. . C. . D. . 38 38 190 95
Câu 40. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Hình chiếu vuông góc của S
trên mặt phẳng (ABCD) là điểm H thuộc đoạn BD sao cho HD = 3HB. Biết góc giữa mặt (SCD)
và mặt phẳng đáy bằng 45◦. Khoảng cách giữa hai đường thẳng SA và BD là: √ √ √ √ 2a 38 2a 13 2a 51 3a 34 A. . B. . C. . D. . 17 3 13 17
Câu 41. Cho hàm số y = f (x) liên tục trên R và có đạo hàm f 0(x) = x2(x − 2)(x2 − 6x + m) với mọi
x ∈ R. Có bao nhiêu số nguyên m thuộc đoạn [−2019; 2019] để hàm số g(x) = f (1 − x) nghịch biến trên khoảng (−∞; −1)? A. 2010. B. 2012. C. 2011. D. 2009. GeoGebraPro Trang 4
Câu 42. Cường độ một trận động đất M được cho bởi công thức M = log A − log A0, với A là biên
độ rung chấn tối đa và A0 là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San
Francisco có cường độ 8,3 độ Richter. Trong cùng năm đó, trận động đất khác ở gần đó đo được 7,1 độ
Richter. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu lần trận động đất này? A. 1,17. B. 2,2. C. 15,8. D. 4.
Câu 43. Cho hàm số y = f (x) có bảng biến thiên như sau x −∞ 0 1 +∞ y0 − 0 + 0 − +∞ + 3 y −1 −∞
Phương trình f (2 − x) − 1 = 0 có bao nhiêu nghiệm? A. 0. B. 2. C. 1. D. 3.
Câu 44. Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB
và CD thuộc hai đáy của hình trụ, AB = 4a, AC = 5a. Thể tích V của khối trụ là A. V = 16πa3. B. V = 4πa3. C. V = 12πa3. D. V = 8πa3. √
Câu 45. Cho hàm số f (x) liên tục trên R thỏa mãn điều kiện: f (0) = 2 2, f (x) > 0 với mọi x ∈ R và
f (x).f 0(x) = (2x + 1)p1 + f 2(x) với mọi x ∈ R. Khi đó giá trị f (1) bằng √ √ √ √ A. 15. B. 23. C. 24. D. 26. √ 2019-2020
Câu 46. Tìm tất cả các giá trị của tham số m để phương trình x − m −
9 − x2 = 0 có đúng 1 nghiệm dương? √ A. m ∈ (−3; 3].
B. m ∈ (−3; 3] ∪ {−3 2}. THPT √ C. m ∈ [0; 3]. D. m = ±3 2. 1 1
Câu 47. Cho hai số thực a, b > 1. Tìm giá trị nhỏ nhất của biểu thức S = + . log a log √ b (ab) 4 ab GHIỆP 4 9 9 1 N A. min S = . B. min S = . C. min S = . D. min S = . T 9 4 2 4
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số TỐ x2 + mx + m y =
trên [1; 2] bằng 2. Số phần tử của S là THI x + 1 A. 1. B. 4. C. 3. D. 2. √
Câu 49. Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng a 3. Gọi O
là tâm của đáy ABC, d1 là khoảng cách từ A đến mặt phẳng (SBC) và d2 là khoảng cách từ O đến LUYỆN
mặt phẳng (SBC). Tính d = d1 + d2. √ √ √ √ 2a 2 2a 2 8a 2 8a 2 A. d = . B. d = . C. d = . D. d = . 11 33 33 11
Câu 50. Cho hàm số y = f (x) có đạo hàm cấp 2, liên tục trên R và thỏa mãn
[f 0(x)]2 + f (x) · f 00(x) = 15x4 + 12x với mọi x ∈ R.
Hàm số g(x) = f (x) · f 0(x) có bao nhiêu điểm cực trị? A. 1. B. 2. C. 3. D. 4.
———————–HẾT———————– GeoGebraPro Trang 5 ĐÁP ÁN THAM KHẢO 1. A 2. C 3. A 4. D 5. C 6. C 7. B 8. A 9. D 10. A 11. C 12. C 13. A 14. D 15. C 16. B 17. D 18. B 19. A 20. A 21. D 22. C 23. B 24. B 25. C 26. B 27. A 28. C 29. C 30. B 31. C 32. A 33. A 34. C 35. B 36. D 37. C 38. B 39. A 40. D 41. C 42. C 43. D 44. C 45. C 46. A 47. B 48. D 49. C 50. B o/ aPr roups/GeoGebr acebook.com/g .f https://www GeoGebraPro Trang 6 MỖI NGÀY MỘT ĐỀ THI 7
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Một đội xây dựng gồm 3 kỹ sư, 7 công nhân lập một tổ công tác gồm 5 người. Hỏi có bao nhiêu
cách lập tổ công tác gồm 1 kỹ sư làm tổ trưởng, 1 công nhân làm tổ phó và 3 công nhân tổ viên? A. 420. B. 360. C. 120. D. 240. Lời giải.
Số cách lập tổ công tác gồm 1 kỹ sư làm tổ trưởng, 1 công nhân làm tổ phó và 3 công nhân tổ viên là 3 · 7 · C3 = 420 cách. 6 Chọn phương án A
Câu 2. Cho cấp số cộng (un) có số hạng đầu u1 = 2 và công sai d = −3. Tính tổng 10 số hạng đầu của (un). A. S10 = 115. B. S10 = −155. C. S10 = −115. D. S10 = 155. Lời giải. 10
Tổng 10 số hạng đầu của (un) là S10 = u1 + u2 + · · · + u10 =
(2u1 + 9d) = 5(4 − 27) = −115. 2 2019-2020 Chọn phương án C
Câu 3. Tổng tất cả các nghiệm của phương trình log (7 − 3x) = 2 − x 3 THPT A. 2. B. 1. C. 7. D. 3. Lời giải. 9
Ta có log (7 − 3x) = 2 − x ⇔ 7 − 3x = 32−x ⇔ 7 − 3x = ⇔ (3x)2 − 7 · 3x + 9 = 0. (∗) 3 3x GHIỆP
Phương trình (∗) có 2 nghiệm phân biệt thỏa 3x1 + 3x2 = 7; 3x1 · 3x2 = 9, N suy ra 3x1+x2 = 32 ⇔ x T 1 + x2 = 2 Chọn phương án A TỐ √
Câu 4. Tính thể tích V của khối lập phương ABCD.A0B0C0D0 biết đường chéo AC0 = a 3. √ THI a3 √ 3 6a3 A. . B. 3 3a3. C. . D. a3. 3 4 Lời giải.
Gọi cạnh hình lập phương là x. Ta có AC02 = 3x2 = 3a2 ⇒ x = a ⇒ V = a3. LUYỆN Chọn phương án D √ √
Câu 5. Tìm tập xác định D của hàm số y = (x2 − 3x − 4) 2− 3. A. D = R\(−1; 4). B. D = R.
C. D = (−∞; −1) ∪ (4; +∞).
D. D = (−∞; −1] ∪ [4; +∞). Lời giải. ñx > 4
Điều kiện xác định của hàm số là x2 − 3x − 4 > 0 ⇔ x < −1.
Vậy D = (−∞; −1) ∪ (4; +∞). Chọn phương án C Z
Câu 6. Tìm một nguyên hàm F (x) của hàm số f (x) · g(x) biết F (1) = 3, biết f (x)dx = x + 2018 Z và g(x)dx = x2 + 2019. A. F (x) = x3 + 1. B. F (x) = x3 + 3. C. F (x) = x2 + 2. D. F (x) = x2 + 3. GeoGebraPro Trang 1 Lời giải. Z Ta có
f (x)dx = x + 2018 ⇒ f (x) = (x + 2018)0 = 1 Z và
g(x)dx = x2 + 2019 ⇒ g(x) = (x2 + 2019)0 = 2x. Z
⇒ f (x) · g(x) = 2x ⇒ F (x) = f (x) · g(x)dx = x2 + C.
Mặt khác F (1) = 3 ⇒ 12 + C = 3 ⇒ C = 2. Vậy F (x) = x2 + 2. Chọn phương án C
Câu 7. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt (SAB) và (SAC) cùng √
vuông góc với đáy. Tính thể tích khối chóp biết SC = a 3. √ √ √ √ 2a3 6 a3 6 a3 3 a3 3 A. . B. . C. . D. . 9 12 4 2 Lời giải. Từ đề bài ta có S ( o/ (SAB) ⊥ (ABC) ⇒ SA ⊥ (ABC). aPr (SAC) ⊥ (ABC)
Vì tam giác ABC đều cạnh √ a2 3 a ⇒ SABC = và AB = AC = BC = a. 4
Tam giác SAC vuông tại A (do SA ⊥ (ABC) ⇒ SA ⊥ AC) nên theo √ √ √ định lí Pytago ta có SA = SC2 − AC2 = 3a2 − a2 = a 2. A C Thể tích khối chóp là roups/GeoGebr √ √ 1 1 a2 3 √ a3 6 VS.ABC = SABC · SA = · · a 2 = (đvtt). 3 3 4 12 B Chọn phương án B
Câu 8. Cho hình nón có góc ở đỉnh bằng 60◦ và bán kính đáy bằng a. Diện tích xung quanh của hình acebook.com/g nón bằng bao nhiêu? .f √ A. 2πa2. B. 4πa2. C. πa2. D. πa2 3. Lời giải.
Hình nón đã cho có đỉnh S, đáy là đường tròn tâm O đường kính M N S như hình vẽ. https://www
Ta có bán kính đáy r = OM = a, góc ÷ M SN = 60◦ suy ra ’ M SO = 30◦. 60◦ 4SOM vuông tại O, ta có OM OM sin ’ M SO = , suy ra SM =
= 2a, hay đường sinh l = 2a. SM sin ’ M SO
Vậy diện tích xung quanh hình nón là N S O xq = π · r · l = 2πa2. M Chọn phương án A
Câu 9. Cho hình lập phương có thể tích bằng 64a3. Thể tích của khối cầu nội tiếp hình lập phương đó bằng 8πa3 16πa3 64πa3 32πa3 A. V = . B. V = . C. V = . D. V = . 3 3 3 3 Lời giải. GeoGebraPro Trang 2
Khối lập phương có thể tích 64a3 nên cạnh bằng 4a. 4a
Khối cầu nội tiếp khối lập phương có bán kính R =
= 2a nên thể tích khối cầu 2 4 4 32πa3 là V = πR3 = π(2a)3 = . 3 3 3 Chọn phương án D Câu 10.
Cho hàm số y = f (x) có bảng biến thiên x −∞ −1 5 +∞
như hình vẽ bên. Hàm số nghịch biến trên f 0(x) + 0 − 0 + khoảng nào dưới đây? a +∞ + A. (−1; 5). B. (−∞; 5). f (x) C. (−∞; −1). D. (−1; +∞). −∞ b Lời giải.
Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên miền (−1; 5). Chọn phương án A √
Câu 11. Cho a, b, c > 0, a, b 6= 1. Tình A = log (b2).log bc) − log (c). a b( a A. log c. B. 1. C. log b. D. log bc. a a a Lời giải. 2019-2020 √ 1 Có: A = log (b2).log bc) − log (c) = 2log log (bc) − log (c) a b( a ab. 2 b a 1
= 2logab. (log b + log c) − log (c) THPT 2 b b a
= log b. (1 + log c) − log c = log b + log b. log c − log c = log b + log c − log c = log b. a b a a a b a a a a a Chọn phương án C
Câu 12. Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông GHIỆP N
có cạnh bằng a. Tính diện tích xung quanh S của khối trụ đó. T πa2 A. S = 2πa2. B. S = . C. S = πa2. D. S = 4πa2. TỐ 2 Lời giải. a THI
Do thiết diện là hình vuông cạnh a nên bán kính đáy bằng và chiều cao h = a. 2 a
Diện tích xung quanh: S = 2π × × a = πa2. 2 Chọn phương án C LUYỆN
Câu 13. Hàm số nào dưới đây có bảng biến thiên như hình vẽ? x −∞ −1 1 +∞ y0 + 0 − 0 + 2 +∞ + y −∞ −2 A. y = x3 − 3x. B. y = x3 − 3x − 1. C. y = x3 + 3x. D. y = x4 − 2x2. Lời giải.
Từ bảng biến thiên ta thấy hàm số có 2 cực trị nên loại C và D.
Đồ thị hàm số đi qua điểm (−1; 2) nên chọn A. Chọn phương án A GeoGebraPro Trang 3 x + 1
Câu 14. Đồ thị hàm số y = có dạng 1 − x y y −1 1 x O −1 x O 1 A. . B. . y y 1 1 x O x O −1 o/ −1 C. . D. . aPr Lời giải. Phương pháp: ax + b d a Đồ thị hàm số y =
, (ad − bc 6= 0, c 6= 0) có TCĐ: x = − và TCN: y = . cx + d c c
Nếu ad − bc > 0 thì hàm số đồng biến trên từng khoảng xác định.
Nếu ad − bc < 0 thì hàm số nghịch biến trên từng khoảng xác định. roups/GeoGebr Cách giải: x + 1 Đồ thị hàm số y =
có TCĐ: x = 1 và TCN y = −1 và đồng biến trên từng khoảng xác định do 1 − x 1.1 − 1.(−1) = 2 > 0.
Vậy chọn đồ thị ở câu D. Chọn phương án D ax + 1 acebook.com/g
Câu 15. Biết rằng đồ thị hàm số y =
có đường tiệm cận đứng là x = 2 và đường tiệm cận .f bx − 2
ngang là y = 3. Tính giá trị của a + b? A. 1. B. 5. C. 4. D. 0. Lời giải. ax + 1 2
Với b 6= 0 và b 6= −2a, đồ thị hàm số y = nhận đường thẳng x = làm tiệm cận đứng. bx − 2 b https://www 2
Theo đề bài x = 2 là tiệm cận đứng của đồ thị nên 2 = ⇔ b = 1. b ax + 1 a
Với b 6= 0 đồ thị hàm số y = nhận đường thẳng y = làm tiệm cận ngang. bx − 2 ba
Theo đề bài y = 3 là tiệm cận ngang của đồ thị hàm số nên = 3 ⇔ a = 3b ⇔ a = 3. b Vậy a + b = 4. Chọn phương án C 1 1
Câu 16. Tìm tập nghiệm S của phương trình (0, 6) x ≤ (0, 6) 6 A. S = (−∞; 6]. B. S = (0; 6]. C. [0; 6]. D. (−∞; 0) ∪ [6; +∞). Lời giải. 1 1 1 1 1 1 6 − x
Ta có: (0, 6) x ≤ (0, 6) 6 ⇔ ≥ ⇔ − ≥ 0 ⇔ ≥ 0 ⇔ 0 < x ≤ 6. x 6 x 6 x
Tập nghiệm bất phương trình là S = (0; 6]. Chọn phương án B
Câu 17. Cho hàm số y = f (x) có đồ thị như hình vẽ bên. GeoGebraPro Trang 4 y −1 O 1 x −1
Số nghiệm của phương trình 2019f (x) + 1 = 0 là A. 1. B. 3. C. 2. D. 4. Lời giải. 1
Ta có 2019f (x) + 1 = 0 ⇔ f (x) = − . 2019
Số nghiệm phương trình 2019f (x) + 1 = 0 chính là số giao điểm của đồ thị hàm số y = f (x) và đường 1 thẳng d : y = −
(cùng phương với trục Ox). 2019
Dựa vào đồ thị như hình vẽ ta có d cắt đồ thị tại 4 điểm phân biệt.
Vậy phương trình có 4 nghiệm phân biệt. Chọn phương án D 1 Z x dx Câu 18. Cho
= a + b ln 2 + c ln 3 với a, b, c là các số hữu tỷ. Giá trị của 3a + b + c bằng (x + 2)2 0 2019-2020 A. −2. B. −1. C. 2. D. 1. Lời giải. 1 1 THPT Z x dx Z x + 2 − 2 = dx (x + 2)2 (x + 2)2 0 0 1 1 GHIỆP Z x + 2 Z 2 N = dx − dx (x + 2)2 (x + 2)2 T 0 0 TỐ 1 1 Z 1 Z 2 = dx − dx THI x + 2 (x + 2)2 0 0 1 2 1 = ln |x + 2| + x + 2 0 0 LUYỆN 1 = ln 3 − ln 2 − . 3 1
Nên a = − , b = −1, c = 1, suy ra 3a + b + c = −1. 3 Chọn phương án B
Câu 19. Tìm hai số thực x và y thỏa mãn (3x + 2yi) + (3 − i) = 4x − 3i với i là đơn vị ảo. 2 A. x = 3; y = −1. B. x = ; y = −1. C. x = 3; y = −3. D. x = −3; y = −1. 3 Lời giải. Ta có ®3x + 3 = 4x ®x = 3
(3x + 2yi) + (3 − i) = 4x − 3i ⇔ (3x + 3) + (2y − 1)i = 4x − 3i ⇔ ⇔ 2y − 1 = −3 y = −1. Chọn phương án A Câu 20. GeoGebraPro Trang 5
Cho các số phức z = −1 + 2i, w = 2 − i. Điểm nào trong hình vẽ bên biểu diễn y số phức z + w? N P A. P . B. N . C. Q. D. M . O x M Q Lời giải.
Ta có z + w = 1 + i, suy ra điểm biểu diễn số phức z + w là điểm P . Chọn phương án A
Câu 21. Xét các số phức z thỏa mãn (z + 2i)(z + 2) là số thuần ảo. Biết rằng tập hợp tất cả các điểm
biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là A. (1; −1). B. (1; 1). C. (−1; 1). D. (−1; −1). Lời giải.
Giả sử z = a + bi, (a, b ∈ R), ta được
(z + 2i)(z + 2) = [a + (b + 2)i][(a + 2) − bi] o/
= [a(a + 2) + b(b + 2)] + [(a + 2)(b + 2) − ab]i. aPr
(z + 2i)(z + 2) là số thuần ảo khi và chỉ khi
a(a + 2) + b(b + 2) = 0 ⇔ (a + 1)2 + (b + 1)2 = 2
nên tập hợp tất cả các điểm biểu diễn của z là một đường tròn phương trình roups/GeoGebr (x + 1)2 + (y + 1)2 = 2 có tâm I(−1; −1). Chọn phương án D # » #» #» #»
Câu 22. Trong không gian Oxyz, cho OA = i − 2 j + 3 k , điểm B(3; −4; 1) và C(2; 0; 1). Tọa độ trọng tâm của tam giác ABC là A. 1; −2; 3. B. (−2; 2; −1). C. (2; −2; 1). D. (−1; 2; −3). acebook.com/g .f Lời giải. # » #» #» #»
Từ giả thiết OA = i − 2 j + 3 k ⇒ A(1; −2; 3).  xA + xB + xC x =2  G =  3    y
Gọi G là trọng tâm tam giác ABC, ta có: y A + yB + yC G = = − 2 ⇒ G(2; −2; 1). https://www 3    z  A + zB + zC z =1  G = 3 Chọn phương án C
Câu 23. Trong không gian Oxyz, cho hai điểm I(1; 1; 1) và A(1; 2; 3). Phương trình của mặt cầu có tâm I và đi qua A là
A. (x + 1)2 + (y + 1)2 + (z + 1)2 = 29.
B. (x − 1)2 + (y − 1)2 + (z − 1)2 = 5.
C. (x − 1)2 + (y − 1)2 + (z − 1)2 = 25.
D. (x + 1)2 + (y + 1)2 + (z + 1)2 = 5. Lời giải.
Ta có R2 = IA2 = (1 − 1)2 + (2 − 1)2 + (3 − 1)2 = 5
nên phương trình của mặt cầu là (x − 1)2 + (y − 1)2 + (z − 1)2 = 5. Chọn phương án B
Câu 24. Trong không gian Oxyz, cho điểm A(2; −1; −3) và mặt phẳng (P ) : 3x − 2y + 4z − 5 = 0. Mặt
phẳng (Q) đi qua A và song song với mặt phẳng (P ) có phương trình là
A. (Q) : 3x − 2y + 4z − 4 = 0.
B. (Q) : 3x − 2y + 4z + 4 = 0. GeoGebraPro Trang 6
C. (Q) : 3x − 2y + 4z + 5 = 0. D. (Q) : 3x + 2y + 4z + 8 = 0. Lời giải. #»
Do mặt phẳng (Q) song song với mặt phẳng (P ) nên có vectơ pháp tuyến là n = (3; −2; 4).
Phương trình mặt phẳng (Q) : 3(x − 2) − 2(y + 1) + 4(z + 3) = 0 ⇔ 3x − 2y + 4z + 4 = 0. Chọn phương án B x = t  
Câu 25. Trong không gian Oxyz, khoảng cách từ điểm M (2; −4; −1) tới đường thẳng ∆ : y = 2 − t  z = 3 + t bằng √ √ √ √ A. 14. B. 6. C. 2 14. D. 2 6. Lời giải. #»
Đường thẳng ∆ đi qua N (0; 2; 3), có véc-tơ chỉ phương u = (1; −1; 2). # » î # » #»ó
Ta có M N = (−2; 6; 4) và M N , u = (16; 8; −4).
Vậy khoảng cách từ M đến đường thẳng ∆ là î # » #»ó √ M N , u √ 336 d(M, ∆) = = √ = 2 14. | #» u | 6 Chọn phương án C √
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a ,SA ⊥ (ABCD),SA = a 2.
Tìm số đo của góc giữa đường thẳng SC và mặt phẳng (SAD). 2019-2020 A. 45◦. B. 30◦. C. 90◦. D. 60◦. Lời giải. THPT Phương pháp S
Góc giữa đường thẳng d với mặt phẳng (P ) là góc giữa đường thẳng d
với hình chiếu của đường thẳng d trên (P ). Cách giải: GHIỆP ®CD ⊥ SA N Ta có ⇒ CD ⊥ (SAD) T CD ⊥ AD TỐ A D (¤ SC; (SAD)) = ’ CSD CD a a 1 THI √ √ √ ’ CSD = = = = SD a2 + 2a2 a 3 3 ’ CSD = 30◦. B C Chọn phương án B LUYỆN
Câu 27. Cho hàm số y = f (x) xác định trên R và có bảng xét dấu của đạo hàm như sau: x −∞ x1 x2 x3 +∞ y0 − 0 + − 0 +
Khi đó số điểm cực trị của hàm số y = f (x) là A. 3. B. 2. C. 4. D. 1. Lời giải.
Ta thấy f 0(x) đổi dấu khi x qua x1, x2, x3 thuộc tập xác định của hàm số f (x) nên hàm số f (x) có 3 cực trị. Chọn phương án A √
Câu 28. Tìm giá trị lớn nhất M của hàm số y = 2x +
8 − 2x2 trên tập xác định của nó? √ √ 8 3 √ A. M = 2 5. B. M = . C. M = 2 6. D. M = 4. 3 GeoGebraPro Trang 7 Lời giải.
Tập xác định của hàm số: D = [−2; 2]. −2x √ Ta có y0 = 2 + √ = 0 ⇔ 8 − 2x2 = x 8 − 2x2 √ ( ( x ≥ 0 x ≥ 0 2 6 ⇔ ⇔ ⇔ x = ∈ [−2; 2]. 8 − 2x2 = x2 8 = 3x2 3 √ Ç å 2 6 √ y(−2) = −4; y(2) = 4; y = 2 6. 3 √
Vậy giá trị lớn nhất M của hàm số là M = 2 6. Chọn C. Chọn phương án C a3 − ab2 + b3
Câu 29. Cho a > 0, b > 0 thoả mãn log (a+3b) = log a = log b. Giá trị của bằng 16 9 12 a3 + a2b + 3b3 √ √ √ √ 6 − 13 82 − 17 13 5 − 13 3 − 13 A. . B. . C. . D. . 11 69 6 11 Lời giải.
Đặt t = log (a + 3b) = log a = log b. 16 9 12  o/ 16t = a + 3b √   Å 9 ãt Å 3 ãt Å 3 ãt −3 + 13 a aPr ⇒ 9t = a ⇒ 9t + 3.12t = 16t ⇒ + 3 = 1 ⇒ = = 16 4 4 2 b   12t = b a 3 a √ a3 − ab2 + b3 − + 1 5 − 13 Vậy = b b = . a3 + a2b + 3b3 a 3 a 2 6 + + 3 b b Chọn phương án C roups/GeoGebr
Câu 30. Có tất cả bao nhiêu giá trị thực của tham số m để đường thẳng dm : y = mx + 1 cắt đồ thị
(C) : y = x3 − x2 + 1 tại 3 điểm A, B(0; 1) và C phân biệt sao cho tam giác AOC vuông tại O. A. 0. B. 1. C. 2. D. 3. Lời giải.
Phương trình hoành độ giao điểm của dm và (C) là: acebook.com/g ñx = 0 .f
x3 − x2 + 1 = mx + 1 ⇔ x(x2 − x − m) = 0 ⇔ x2 − x − m = 0.
Đường thẳng dm cắt đồ thị (C) tại 3 điểm phân biệt A, B(0; 1) và C.
⇔ Phương trình x2 − x − m = 0 có hai nghiệm phân biệt khác 0.  1 ®∆ = 1 + 4m > 0 m > − https://www ⇔ ⇔ 4 − m 6= 0 m 6= 0.
Khi đó: A(x1; mx1 + 1) và C(x2; mx2 + 1) Theo Vi-et: x1 và x2 là nghiệm phương trình x2 − x − m = 0
nên ta có : x1 + x2 = 1 và x − 1x2 = −m. 4AOC vuông tại O. # » # » ⇔ OA · OC = 0
⇔ x1x2 + (mx1 + 1)(mx2 + 1) = 0
⇔ (m2 + 1)x1x2 + m(x1 + x2) + 1 = 0 ⇔ (m2 + 1)(−m) + m + 1 = 0 ⇔ −m3 + 1 = 0
⇔ m = 1.(Thỏa mãn điều kiện)
Vậy có 1 giá trị m thỏa mãn bài toán. Chọn phương án B GeoGebraPro Trang 8
Câu 31. Tập nghiệm S của bất phương trình log 1 (x − 1) + log (11 − 2x) ≥ 0 là 3 3 Å 11 ã A. S = 3; . B. S = (−∞; 4]. C. S = (1; 4]. D. S = (1; 4). 2 Lời giải. ®x − 1 > 0 11 Điều kiện ⇔ 1 < x < . Ta có 11 − 2x > 0 2
log 1 (x − 1) + log (11 − 2x) ≥ 0 ⇔ − log (x − 1) + log (11 − 2x) ≥ 0 3 3 3 3 11 − 2x 11 − 2x 11 − 2x ⇔ log ≥ 0 ⇔ ≥ 1 ⇔
− 1 ≥ 0(vì x − 1 > 0) 3 x − 1 x − 1 x − 1
⇔ 12 − 3x ≥ 0 ⇔ x ≤ 4.
Kết hợp với điều kiện ta có 1 < x ≤ 4. Vậy S = (1; 4]. Chọn phương án C √
Câu 32. Một khối nón có thể tích bằng 9a3π 2. Tính bán kính R đáy khối nón khi diện tích xung quanh nhỏ nhất. 3a √ 3a A. R = 3a. B. R = √ . C. R = 3 9a. D. R = √ . 6 2 3 2 Lời giải.
Gọi h, l lần lượt là chiều cao và độ dài đường sinh của khối nón. √ 1 √ 27a3 2 √ … 729a6 V = πR2h = 9a3π 2 ⇒ h = ⇒ l = R2 + h2 = R2 + 2 · . 3 R2 R4 2019-2020 … 729a6 729a6 … 729a6 729a6 S 3 xq = πRl = π R4 + + ≥ π R4 · · . R2 R2 R2 R2 THPT 729a6
⇒ Sxq = 9πa2. Nên min Sxq = 9πa2 khi R4 = ⇔ R = 3a. R2 Chọn phương án A 3 1 GHIỆP Z Z N
Câu 33. Cho hàm số f (x) liên tục và f (3) = 21,
f (x)dx = 9. Tính tích phân I = x·f 0(3x)dx. T 0 0 A. I = 6. B. I = 12. C. I = 9. D. I = 15. TỐ Lời giải. ® THI dt x = 0 ⇒ t = 0 Đặt 3x = t ⇒ dx = . Đổi cận 3 x = 1 ⇒ t = 3. 3 3 Z t dt 1 Z I = f 0(t) = xf 0(x)dx. LUYỆN 3 3 9 0 0 ®u = x ®du = dx Đặt ⇒ dv = f 0(x)dx v = f (x) Ñ 3 é 1 Z 3 Suy ra I = xf (x) − f (x)dx = 6. 9 0 0 Chọn phương án A x2 y2
Câu 34. Tính thể tích khối tròn xoay sinh bởi Elip (E) : + = 1 quay quanh trục Ox. 4 1 64π 10π 8π 8π2 A. . B. . C. . D. . 9 3 3 3 Lời giải.
(E) có a2 = 4 ⇒ a = 2. Do đó hai đỉnh thuộc trục lớn có tọa độ A0 (−2; 0) và (2; 0). x2 y2 x2 Vì + = 1 ⇒ y2 = 1 − . 4 1 4 GeoGebraPro Trang 9 2 2 Z Z Å x2 ã 8π
Do đó thể tích khối tròn xoay là VOx = π y2 dx = π 1 − dx = . 4 3 −2 −2 8π Vậy VOx = (đvtt). 3 Chọn phương án C z + 2
Câu 35. Xét số phức z thỏa mãn
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số z − 2i
phức z luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng √ √ A. 1. B. 2. C. 2 2. D. 2. Lời giải. Gọi z = a + bi ta có: z + 2 (a + 2) + bi
[(a + 2) + bi] [a − (b − 2)i] = = z − 2i a + (b − 2i)i
[a + (b − 2)i] [a − (b − 2)i]
(a + 2)a − (a + 2)(b − 2)i + abi + b(b − 2) = . a2 + (b − 2)2 a2 + 2a + b2 − 2b (a + 2) (b − 2) − ab o/ = − i. a2 + (b − 2)2 a2 + (b − 2)2 aPr
Để số trên là số thuần ảo ⇒ có phần thực bằng 0 ⇒ a2 + 2a + b2 − 2b = 0.
Vậy tập hợp các điểm biểu diễn số phức z là đường tròn tâm I(−1; 1), bán kính » √ R = (−1)2 + 12 − 0 = 2. Chọn phương án B
Câu 36. Cho số phức z thỏa mãn |z| + z + 5i = 25. Khi đó mô-đun z bằng roups/GeoGebr A. 12. B. 10. C. 11. D. 13. Lời giải. Gọi z = x + yi (x; y ∈ R).
|z| + z + 5i = 25 ⇔ px2 + y2 + x + yi + 5i = 25 √ x2 + 25 = (25 − x)2 ®px2 + y2 + x = 25 ® x2 + 25 = 25 − x  ®  x = 12 ⇔ ⇔ ⇔ x ≤ 25 ⇔ . y + 5 = 0 y = −5 y = −5  acebook.com/g y = −5 .f
Vậy z = 12 − 5i ⇒ |z| = p122 + (−5)2 = 13. Chọn phương án D x
Câu 37. Trong không gian Oxyz, cho mặt phẳng (P ) : x + y + z − 3 = 0 và đường thẳng d : = 1 y + 1 z − 2 https://www =
. Hình chiếu vuông góc của d trên (P ) có phương trình là 2 −1 x + 1 y + 1 z + 1 x − 1 y − 1 z − 1 A. = = . B. = = . −1 −4 5 3 −2 −1 x − 1 y − 1 z − 1 x − 1 y − 4 z + 5 C. = = . D. = = . 1 4 −5 1 1 1 Lời giải. x + y + z − 3 = 0 
Gọi A là giao điểm của (P ) và d ta có tọa độ A là nghiệm x y + 1 z − 2 ⇔ A(1; 1; 1).  = = 1 2 −1 #» #»
d có véctơ chỉ phương u = (1; 2; −1), (P ) có véctơ pháp tuyến n = (1; 1; 1) nên mặt phẳng (Q) qua d # » #» # »
vuông góc (P ) có véctơ pháp tuyến là n(Q) = [ud, n(P )] = (3; −2; −1).
Hình chiếu vuông góc của d trên (P ) là giao tuyến ∆ của (P ) và (Q), nên ∆ qua A và có véctơ chỉ # » # »
phương là [n(P ), n(Q)] = (1; 4; −5). x − 1 y − 1 z − 1 Phương trình ∆ là = = . 1 4 −5 Chọn phương án C GeoGebraPro Trang 10 x − 3 y + 2 z + 1
Câu 38. Trong không gian Oxyz, cho đường thẳng d : = = và mặt phẳng (P ) : x + 2 1 −1
y + z + 2 = 0. Cho đường thẳng ∆ nằm trong mặt phẳng (P ), vuông góc với đường thẳng d đồng thời √
khoảng cách từ giao điểm I của d với (P ) đến đường thẳng ∆ bằng
42. Gọi M (5; b; c) là hình chiếu
vuông góc của I trên ∆. Giá trị P = bc bằng bao nhiêu? A. P = −10. B. P = 10. C. P = 12. D. P = −20. Lời giải.
Gọi I(3 + 2t; −2 + t; −1 − t) ∈ d, vì I thuộc mặt phẳng (P ) nên
3 + 2t + (−2 + t) + (−1 − t) + 2 = 0 ⇔ t = −1 ⇒ I(1; −3; 0). √ Ta có IM =
42 ⇔ (5 − 1)2 + (b + 3)2 + (c − 0)2 = 42 ⇔ (b + 3)2 + c2 = 26 (1).
Mà M (5; b; c) ∈ (P ) ⇒ 5 + b + c + 2 = 0 ⇔ c = −7 − b. ñb = −2
Khi đó (1) ⇔ (b + 3)2 + (b + 7)2 = 26 ⇔ b = −8.
Với b = −2 ⇒ c = −5 và b = −8 ⇒ c = 1.
Vậy P = bc = 10 hoặc P = bc = −8. Chọn phương án B
Câu 39. Trong một chiếc hộp có 20 viên bi, trong đó có 9 viên bi màu đỏ, 6 viên bi màu xanh và 5 2019-2020
viên bi màu vàng. Lấy ngẫu nhiên đồng thời 3 viên bi. Tìm xác suất để 3 viên bi lấy ra có không quá 2 màu.29 9 183 82 THPT A. . B. . C. . D. . 38 38 190 95 Lời giải.
Số cách lấy 3 viên bi từ hộp chứa 20 viên bi là C3 = 1140. 20 GHIỆP
Số cách lấy 3 viên bi có đủ 3 màu là 9 · 6 · 5 = 270. N
Do đó, số cách lấy được 3 viên bi không quá 2 màu là 1140 − 270 = 870. T 870 29
Vậy xác suất để 3 viên bi lấy ra có không quá 2 màu là = . TỐ 1140 38 Chọn phương án A THI
Câu 40. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Hình chiếu vuông góc của S
trên mặt phẳng (ABCD) là điểm H thuộc đoạn BD sao cho HD = 3HB. Biết góc giữa mặt (SCD)
và mặt phẳng đáy bằng 45◦. Khoảng cách giữa hai đường thẳng SA và BD là: √ √ √ √ LUYỆN 2a 38 2a 13 2a 51 3a 34 A. . B. . C. . D. . 17 3 13 17 Lời giải. ®CD ⊥ HI
Kẻ HI ∥ BC(I ∈ CD) ta có: S CD ⊥ SI.
Suy ra góc giữa mặt phẳng (SCD) và mặt phẳng đáy là góc ‘ SIH = 45◦. Dựng hình bình hành ADBE.
Ta có BD ∥ (SAE) ⇒ d(SA,BD) = d(BD,(SAE)) = 2a K B 2a E d(B,(SAE)) = d(H,(SAE)). C √ H I
• Kẻ HJ ⊥ AE(J ∈ AE) ta có AE ⊥ (SHJ) ⇒ a 2 O J 2a
(SAE) ⊥ (SHJ ) theo giao tuyến SJ . D A • Kẻ HK ⊥ SJ(K ∈ SJ)
ta có HK ⊥ (SAE) ⇒ HK = d(H,(SAE)). GeoGebraPro Trang 11 HJ · HS HJ · HS Ta có HK = = √ . SJ HJ 2 + HS2 √ 3 3a Với HJ = AO = a 2, HS = HI = BC = 4 2 √ 3a √ a 2 · 3a 34 Vậy HK = 2 = . … 9a2 17 2a2 + 4 Chọn phương án D
Câu 41. Cho hàm số y = f (x) liên tục trên R và có đạo hàm f 0(x) = x2(x − 2)(x2 − 6x + m) với mọi
x ∈ R. Có bao nhiêu số nguyên m thuộc đoạn [−2019; 2019] để hàm số g(x) = f (1 − x) nghịch biến trên khoảng (−∞; −1)? A. 2010. B. 2012. C. 2011. D. 2009. Lời giải. Ta có
g0(x) = −f 0(1 − x) = −(1 − x)2(1 − x − 2) (1 − x)2 − 6(1 − x) + m o/
= −(x − 1)2(−1 − x)(x2 + 4x + m − 5) = (x − 1)2(x + 1)(x2 + 4x + m − 5). aPr
Hàm số g(x) nghịch biến trên (−∞; −1)
⇔ g0(x) ≤ 0 với mọi x ∈ (−∞; −1)
⇔ (x + 1)(x2 + 4x + m − 5) ≤ 0 với mọi x ∈ (−∞; −1)
⇔ x2 + 4x + m − 5 ≥ 0 với mọi x ∈ (−∞; −1) (Do x ∈ (−∞; −1) ⇒ x + 1 < 0)
⇔ h(x) = x2 + 4x − 5 ≥ −m với mọi x ∈ (−∞; −1) roups/GeoGebr ⇔ −m ≤ min h(x). x∈(−∞;−1]
Ta có h0(x) = 2x + 4, h0(x) = 0 ⇔ x = −2. Bảng biến thiên của hàm số h(x) như sau x −∞ 0 +∞ h0(x) − 0 + acebook.com/g .f h(x) −9
Do đó −m ≤ −9 ⇔ m ≥ 9. Mặt khác m ∈ [−2019; 2019] và m nguyên nên m ∈ {9; 10; 11; · · · ; 2019} https://www
hay có 2019 − 9 + 1 = 2011 giá trị của m thỏa mãn. Chọn phương án C
Câu 42. Cường độ một trận động đất M được cho bởi công thức M = log A − log A0, với A là biên
độ rung chấn tối đa và A0 là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San
Francisco có cường độ 8,3 độ Richter. Trong cùng năm đó, trận động đất khác ở gần đó đo được 7,1 độ
Richter. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu lần trận động đất này? A. 1,17. B. 2,2. C. 15,8. D. 4. Lời giải.
Gọi M1, A1 lần lượt là cường độ, biên độ rung chấn tối đa của trận động đất tại San Francisco.
Gọi M2, A2 lần lượt là cường độ, biên độ rung chấn tối đa của trận động đất tại địa điểm còn lại. Ta có A A M 1 1 1 = log A1 − log A0 = log ⇒ = 10M1. A0 A0 A A M 2 2 2 = log A2 − log A0 = log ⇒ = 10M2. A0 A0 GeoGebraPro Trang 12 A1 10M1 Khi đó = = 10M1−M2 = 101,2 ≈ 15,8. A2 10M2 Chọn phương án C
Câu 43. Cho hàm số y = f (x) có bảng biến thiên như sau x −∞ 0 1 +∞ y0 − 0 + 0 − +∞ + 3 y −1 −∞
Phương trình f (2 − x) − 1 = 0 có bao nhiêu nghiệm? A. 0. B. 2. C. 1. D. 3. Lời giải.
Từ đồ thị hàm số y = f (x), ta thực hiện các bước sau
• Đối xứng đồ thị y = f (x) qua trục Oy ta thu được đồ thị y = f (−x).
• Tịnh tiến đồ thị y = f (−x) sang phải 2 đơn vị ta thu được đồ thị y = f (−x + 2).
Hàm số y = f (−x + 2) có bảng biến thiên sau x −∞ 1 2 +∞ y0 + 0 − 0 + 2019-2020 3 +∞ + y −∞ −1 − THPT
Số nghiệm của phương trình f (2 − x) − 1 = 0
(1) bằng số giao điểm hai đồ thị y = f (2 − x) và y = 1.
Dựa vào bảng biến thiên suy ra phương trình (1) có 3 nghiệm. Chọn phương án D GHIỆP N
Câu 44. Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB T
và CD thuộc hai đáy của hình trụ, AB = 4a, AC = 5a. Thể tích V của khối trụ là TỐ A. V = 16πa3. B. V = 4πa3. C. V = 12πa3. D. V = 8πa3. Lời giải. THI √ √ Ta có BC = AC2 − AB2 = 25a2 − 16a2 = 3a. A 4a B AB Bán kính đáy r = = 2a, chiều cao BC = 3a. 2 5a LUYỆN
Vậy V = hπr2 = 3a · 4a2 = 12πa3. D C Chọn phương án C √
Câu 45. Cho hàm số f (x) liên tục trên R thỏa mãn điều kiện: f (0) = 2 2, f (x) > 0 với mọi x ∈ R và
f (x).f 0(x) = (2x + 1)p1 + f 2(x) với mọi x ∈ R. Khi đó giá trị f (1) bằng √ √ √ √ A. 15. B. 23. C. 24. D. 26. Lời giải. f (x) · f 0(x) Z f (x) · f 0(x) Z
Từ giả thiết ta có 2x + 1 = ⇒ dx = (2x + 1) dx. p1 + f2(x) p1 + f2(x) Z f (x) · f 0(x) Bây giờ ta tính I = dx. p1 + f2(x)
Đặt p1 + f 2(x) = t ⇒ 1 + f 2(x) = t2 ⇒ 2f (x)f 0(x)dx = 2tdt ⇒ f (x)f 0(x)dx = tdt. Z t Z » Do đó I = dx = dt = t + C = 1 + f 2(x) + C. t GeoGebraPro Trang 13 √
Ta nhận được p1 + f 2(x) + C = x2 + x. f (0) = 2 2 ⇒ C = −3.
Từ đó p1 + f 2(x) − 3 = x2 + x. Khi x = 1 ta có √
p1 + f2(1) − 3 = 1 + 1 ⇒ 1 + f2(1) = 25 ⇒ f(1) = 24. Chọn phương án C √
Câu 46. Tìm tất cả các giá trị của tham số m để phương trình x − m −
9 − x2 = 0 có đúng 1 nghiệm dương? √ A. m ∈ (−3; 3].
B. m ∈ (−3; 3] ∪ {−3 2}. √ C. m ∈ [0; 3]. D. m = ±3 2. Lời giải.
Điều kiện: −3 ≤ x ≤ 3. √
Phương trình tương đương với x − 9 − x2 = m. √
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = x −
9 − x2 và đường thẳng y = m. √ Xét hàm số y = x −
9 − x2 với −3 ≤ x ≤ 3 √ ® x √ x ≤ 0 −3 2 y0 = 1 + √ ⇒ y0 = 0 ⇔ 9 − x2 = −x ⇔ ⇔ x = ∈ [−3; 3]. 9 − x2 9 − x2 = x2 2 BBT: o/ √ x −3 − 3 2 0 3 2 aPr y0 − 0 + + −3 3 y −3 √ −3 2 roups/GeoGebr
Dựa vào bảng biến thiên suy ra −3 < m ≤ 3. Chọn phương án A 1 1
Câu 47. Cho hai số thực a, b > 1. Tìm giá trị nhỏ nhất của biểu thức S = + . log a log √ b (ab) 4 ab 4 9 9 1 A. min S = . B. min S = . C. min S = . D. min S = . 9 4 2 4 Lời giải. acebook.com/g 1 1 1 5 .f S = log (ab) + log (ab) = 1 + log b + (1 + log a) = log b + + a 4 b a 4 b a 4 log b 4 a
Vì a > 1, b > 1 nên log b > 0. Áp dụng bất đẳng thức Cô - si ta có a 1 5 5 9 S ≥ 2 log b. + = 1 + = a 4 log b 4 4 4 a  1 https://www 1 1 log b = − (l) a
Dấu “ = ” xảy ra khi log b = ⇔ (log b)2 = ⇔ 2  a 4 log b a 4  1 a log b = (T M ) a 2 1 1 Với log b = ⇔ b = a 2 a 2 Chọn phương án B
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số x2 + mx + m y =
trên [1; 2] bằng 2. Số phần tử của S là x + 1 A. 1. B. 4. C. 3. D. 2. Lời giải. x2 + mx + m Xét hàm số f (x) =
trên [1; 2]. Ta có f 0(x) liên tục trên [1; 2] và x + 1 x2 + 2x f 0(x) = > 0, ∀ x ∈ [1; 2]. (x + 1)2 GeoGebraPro Trang 14 3m + 4 2m + 1
Suy ra f (x) đồng biến trên [1; 2]. Do đó max f (x) = f (2) = , min f (x) = f (1) = . [1;2] 3 [1;2] 2 ß 3m + 4 2m + 1 ™ Khi đó max |f (x)| = max , . Ta có [1;2] 3 2 3m + 4 2m + 1 11 ≥
⇔ 4(3m + 4)2 ≥ 9(2m + 1)2 ⇔ m ≥ − . 3 2 12 11 3m + 4 • Với m ≥ − , ta có max |f (x)| = . Theo đề bài, ta có 12 [1;2] 3  3m + 4  2 3m + 4 = 2 m = (thỏa mãn) 3 3   = 2 ⇔ ⇔   3 3m + 4 10 = −2 m = − loại. 3 3 11 2m + 1 • Với m < − , ta có max |f (x)| = . Theo đề bài, ta có 12 [1;2] 2  2m + 1  5 2m + 1 = 2 m = − (thỏa mãn) 2 2   = 2 ⇔ ⇔   2 2m + 1 3 = −2 m = loại. 2 2 ß 2 5 ™ Vậy S = ; −
⇒ Số phần tử của S là 2. 2019-2020 3 2 Chọn phương án D √
Câu 49. Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng a 3. Gọi O THPT
là tâm của đáy ABC, d1 là khoảng cách từ A đến mặt phẳng (SBC) và d2 là khoảng cách từ O đến
mặt phẳng (SBC). Tính d = d1 + d2. √ √ √ √ 2a 2 2a 2 8a 2 8a 2 GHIỆP A. d = . B. d = . C. d = . D. d = . 11 33 33 11 N Lời giải. T
Do tam giác ABC đều tâm O suy ra AO⊥BC tại M là trung điểm của BC. √ √ √ TỐ a 3 1 a 3 2 a 3 Ta có: AM = , M O = AM = , OA = AM = . 2 3 6 3 3 THI √ √ … 3a2 2a 6
Từ giả thiết hình chóp đều suy ra SO⊥ (ABC) , SO = SA2 − OA2 = 3a2 − = . 9 3 OK OM 1
Dựng OK⊥SM, AH⊥SM ⇒ AH//OK; = = . LUYỆN AH AM 3 ® BC⊥SO Có ⇒ BC⊥ (SAM ) ⇒ BC⊥OK. BC⊥AM ®OK⊥SM Có
⇒ OK⊥ (SBC) , AH⊥ (SBC) (do AH//OK). OK⊥BC
Từ đó có d1 = d (A, (SBC)) = AH = 3OK; d2 = d (O, (SBC)) = OK. Trong tam giác vuông OSM có √ 1 1 1 36 9 99 2a 2 đường cao OK nên = + = + = ⇒ OK = . OK2 OM 2 √ SO2 3a2 24a2 8a2 33 8a 2 Vậy d = d1 + d2 = 4OK = . 33 Chọn phương án C
Câu 50. Cho hàm số y = f (x) có đạo hàm cấp 2, liên tục trên R và thỏa mãn
[f 0(x)]2 + f (x) · f 00(x) = 15x4 + 12x với mọi x ∈ R.
Hàm số g(x) = f (x) · f 0(x) có bao nhiêu điểm cực trị? GeoGebraPro Trang 15 A. 1. B. 2. C. 3. D. 4. Lời giải.
Ta có g0(x) = [f 0(x)]2 + f (x) · f 00(x) = 15x4 + 12x. x = 0
g0(x) = 0 ⇔ 15x4 + 12x = 0 ⇔ …  4 . x = 3 − 5 … 4
Nhận thấy x = 0 và x = 3 −
là các nghiệm đơn nên ta có bảng biến thiên 5 … 4 x −∞ 3 − 0 +∞ 5 g0(x) + 0 − 0 + +∞ + g(x) −∞ o/ aPr
Vậy hàm số g(x) có 2 điểm cực trị. Chọn phương án B
———————–HẾT———————– roups/GeoGebr acebook.com/g .f https://www GeoGebraPro Trang 16 ĐÁP ÁN THAM KHẢO 1. A 2. C 3. A 4. D 5. C 6. C 7. B 8. A 9. D 10. A 11. C 12. C 13. A 14. D 15. C 16. B 17. D 18. B 19. A 20. A 21. D 22. C 23. B 24. B 25. C 26. B 27. A 28. C 29. C 30. B 31. C 32. A 33. A 34. C 35. B 36. D 37. C 38. B 39. A 40. D 41. C 42. C 43. D 44. C 45. C 46. A 47. B 48. D 49. C 50. B 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN GeoGebraPro Trang 17 MỖI NGÀY MỘT ĐỀ THI 8
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Một hội đồng gồm 5 nam và 4 nữ được tuyển vào một ban quản trị gồm 4 người. Biết rằng
ban quản trị có ít nhất một nam và một nữ. Hỏi có bao nhiêu cách tuyển chọn? A 240. B 260. C 126. D 120.  u1 = 1; u2 = 0
Câu 2. Cho dãy số (un) xác định bởi . Tính u5.
un+2 = 2un+1 − un; ∀n > 1 A u5 = 0. B u5 = −4. C u5 = −3. D u5 = −2.
Câu 3. Số nghiệm của phương trình 9x + 2.3x+1 − 7 = 0 là A 0. B 2. C 4. D 1.
Câu 4. Tính thể tích của khối lập phương ABCD.A0B0C0D0 biết AC = 2a. √ 2019-2020 √ 2 2a3 a3 A 2 2a3. B a3. C . D . 3 3 THPT
Câu 5. Tính đạo hàm của hàm số y = log (6x − 5). 8 2 1 6 6 A y0 = . B y0 = . C y0 = . D y0 = . GHIỆP (6x − 5) ln 2 (6x − 5) ln 8 6x − 5 (6x − 5) ln 4 N T
Câu 6. Gọi F (x) là một nguyên hàm của hàm số f (x) = e−x + cos x. Tìm khẳng định đúng. TỐ
A F (x) = e−x + sin x + 2019.
B F (x) = e−x + cos x + 2019. THI
C F (x) = − e−x + sin x + 2019.
D F (x) = − e−x − cos x + 2019. LUYỆN
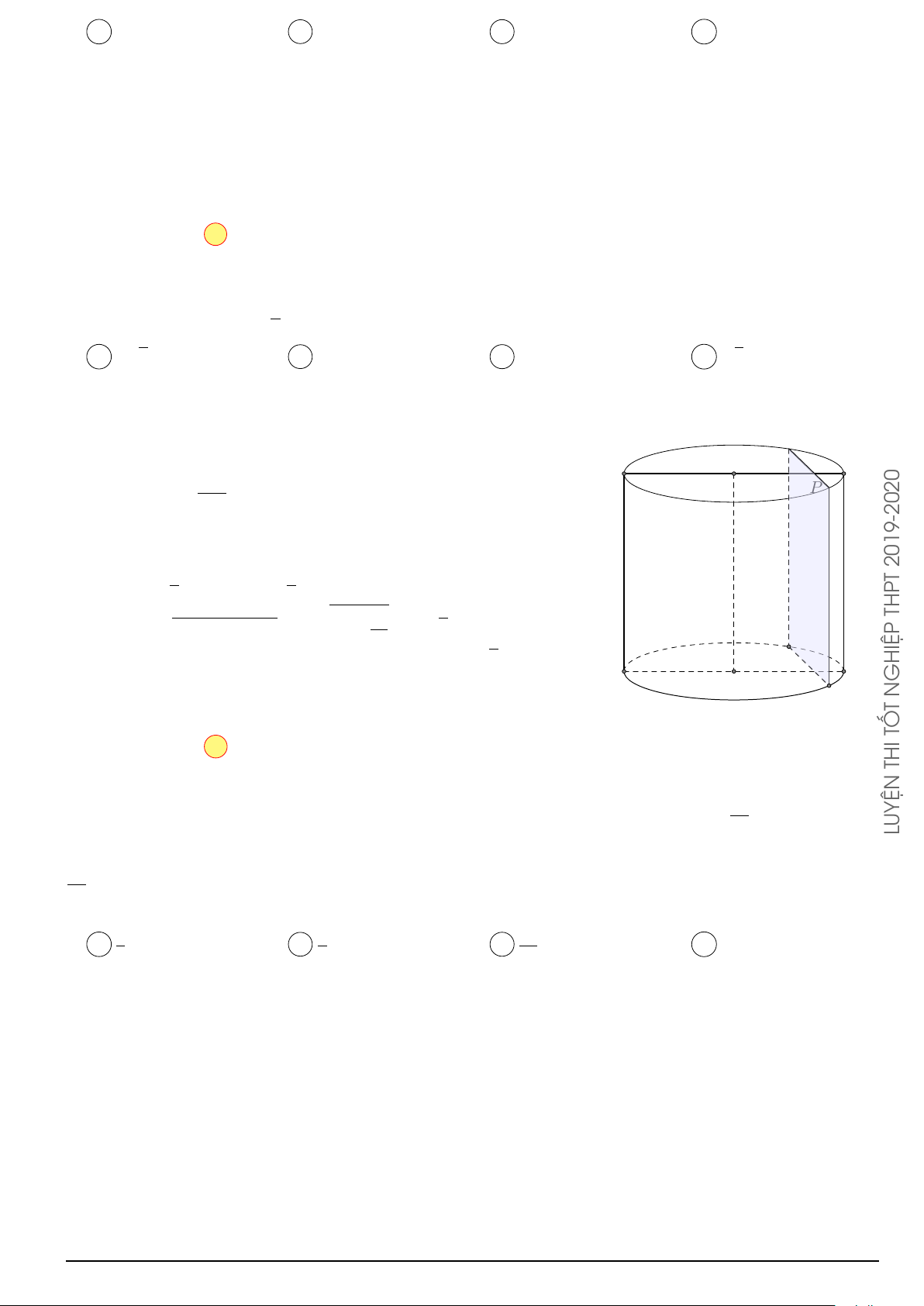
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, SA vuông góc √
với mặt phẳng (ABCD), SA = a 3. Thể tích của khối chóp S.ABC là √ √ a3 3 √ 2a3 3 √ A . B a3 3. C . D 2a3 3. 3 3
Câu 8. Cho hình nón tròn xoay có chiều cao h = 20 (cm), bán kính đáy r = 25 (cm). Một thiết diện
đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là 12 (cm). Tính
diện tích của thiết diện đó. A S = 400 (cm2). B S = 500 (cm2). C S = 406 (cm2). D S = 300 (cm2).
Câu 9. Cắt mặt cầu (S) bằng một mặt phẳng cách tâm một khoảng bằng 4cm được thiết diện là một
hình tròn có diện tích 9πcm2. Tính thể tích khối cầu (S). 250π 2500π 25π 500π A cm3. B cm3. C cm3. D cm3. 3 3 3 3 Câu 10. h Geogebra Pro Trang 1
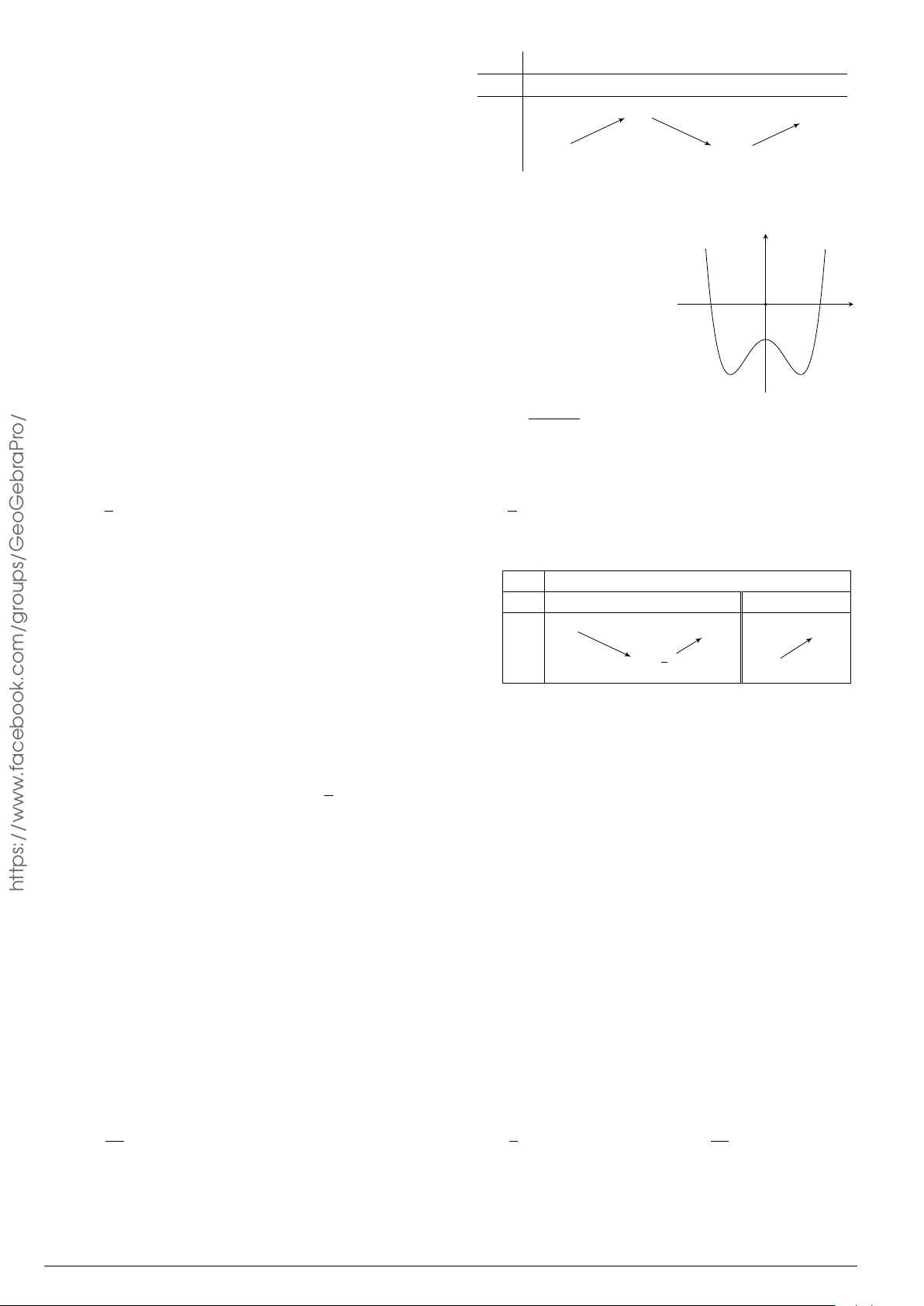
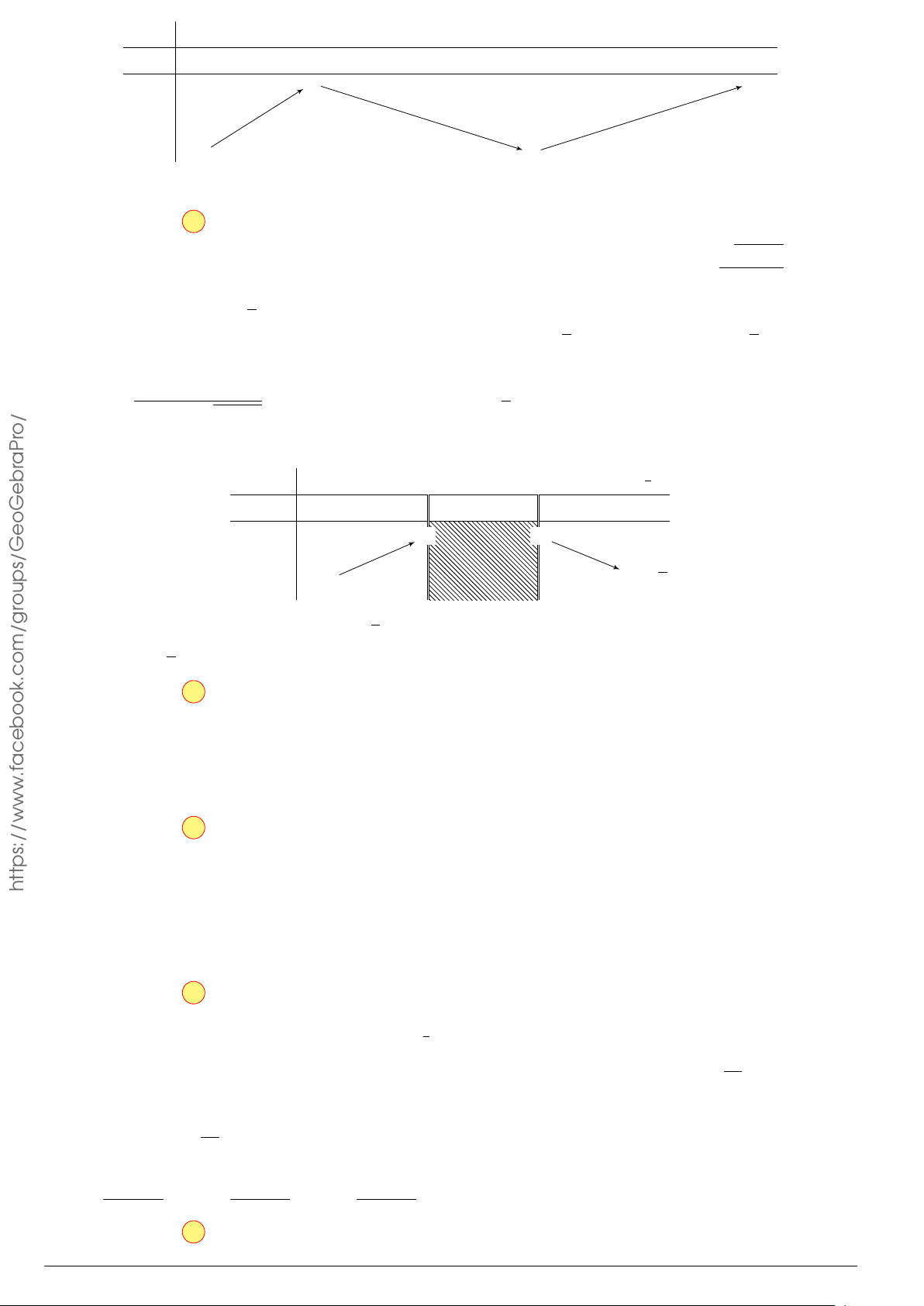
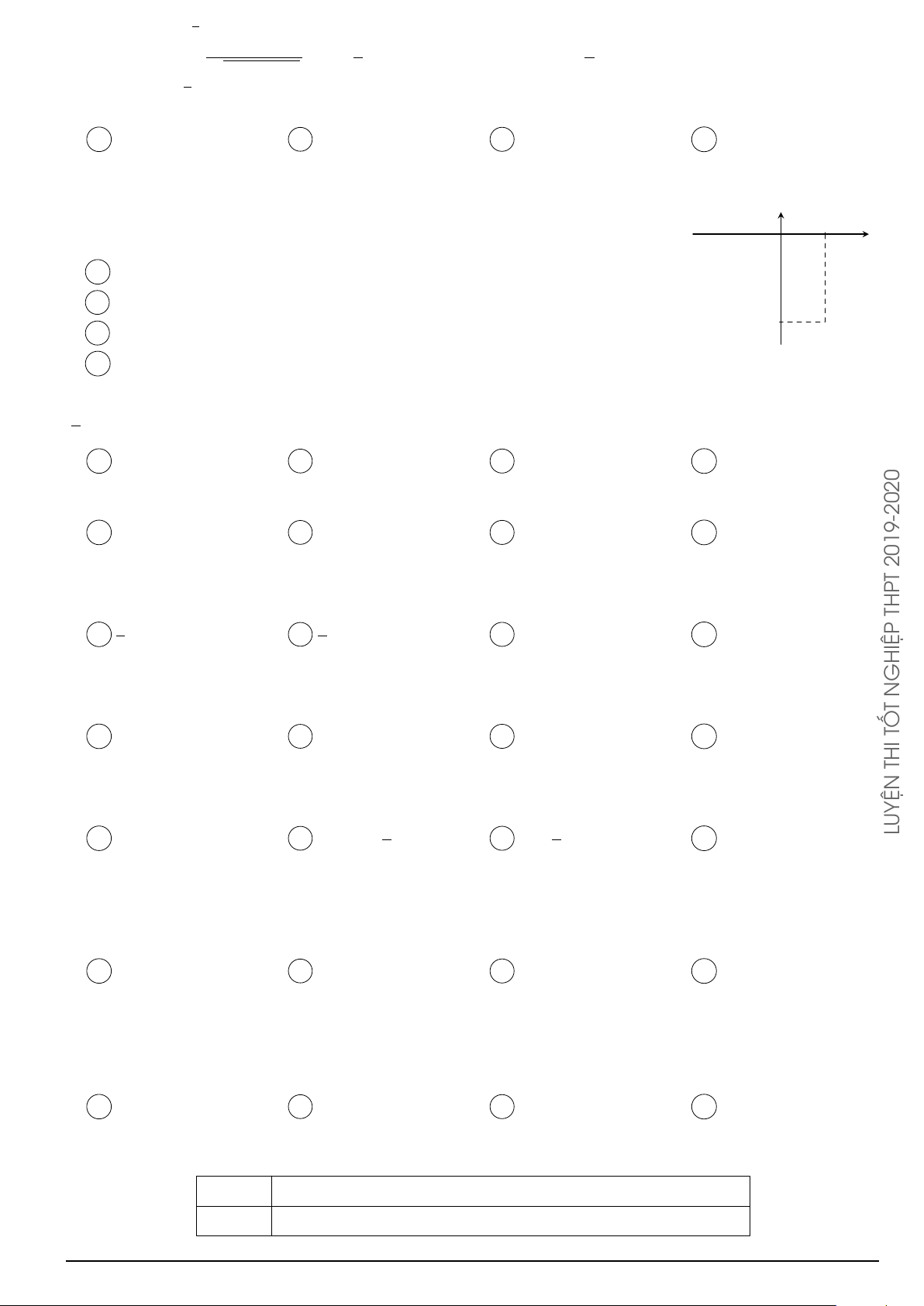
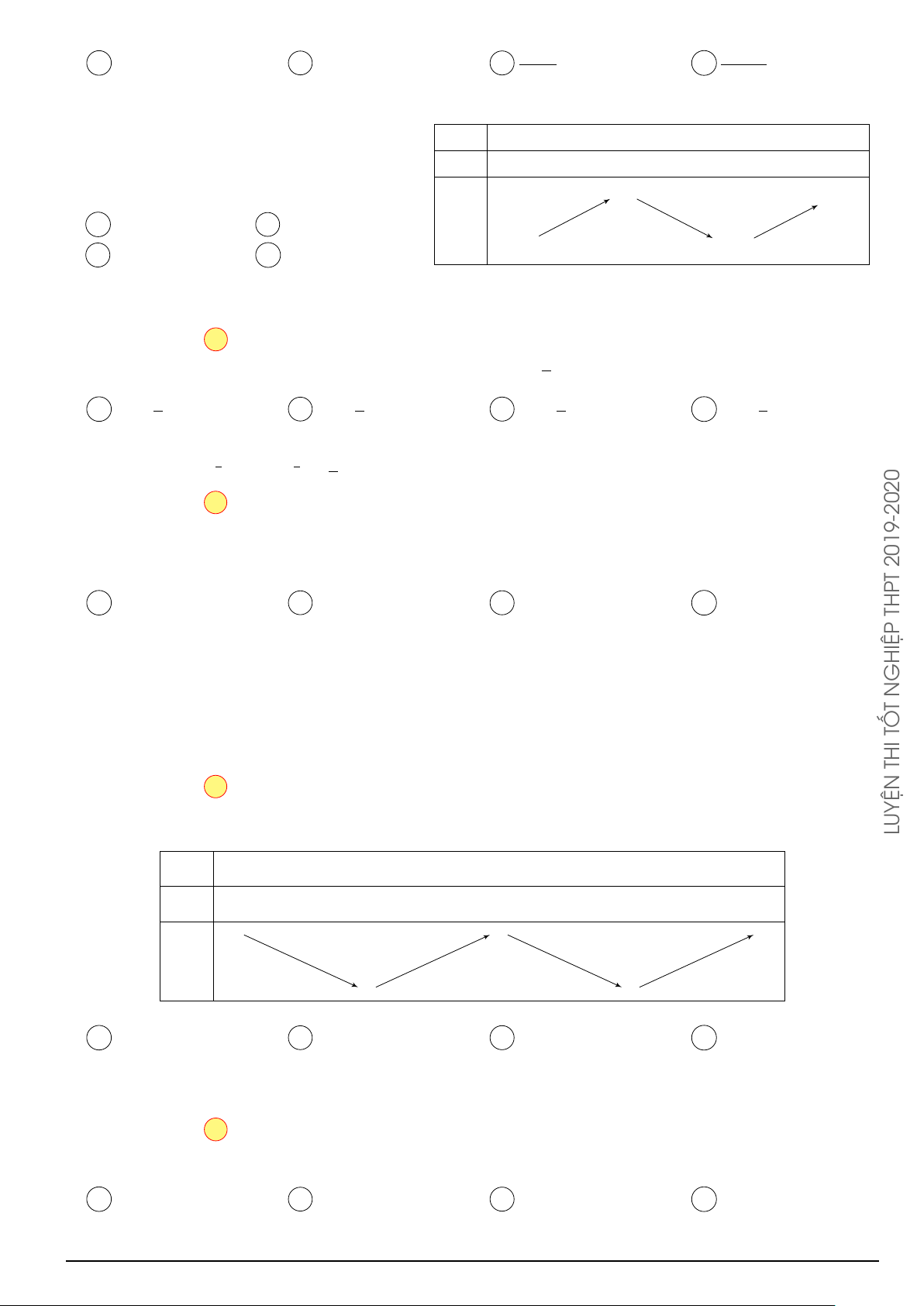
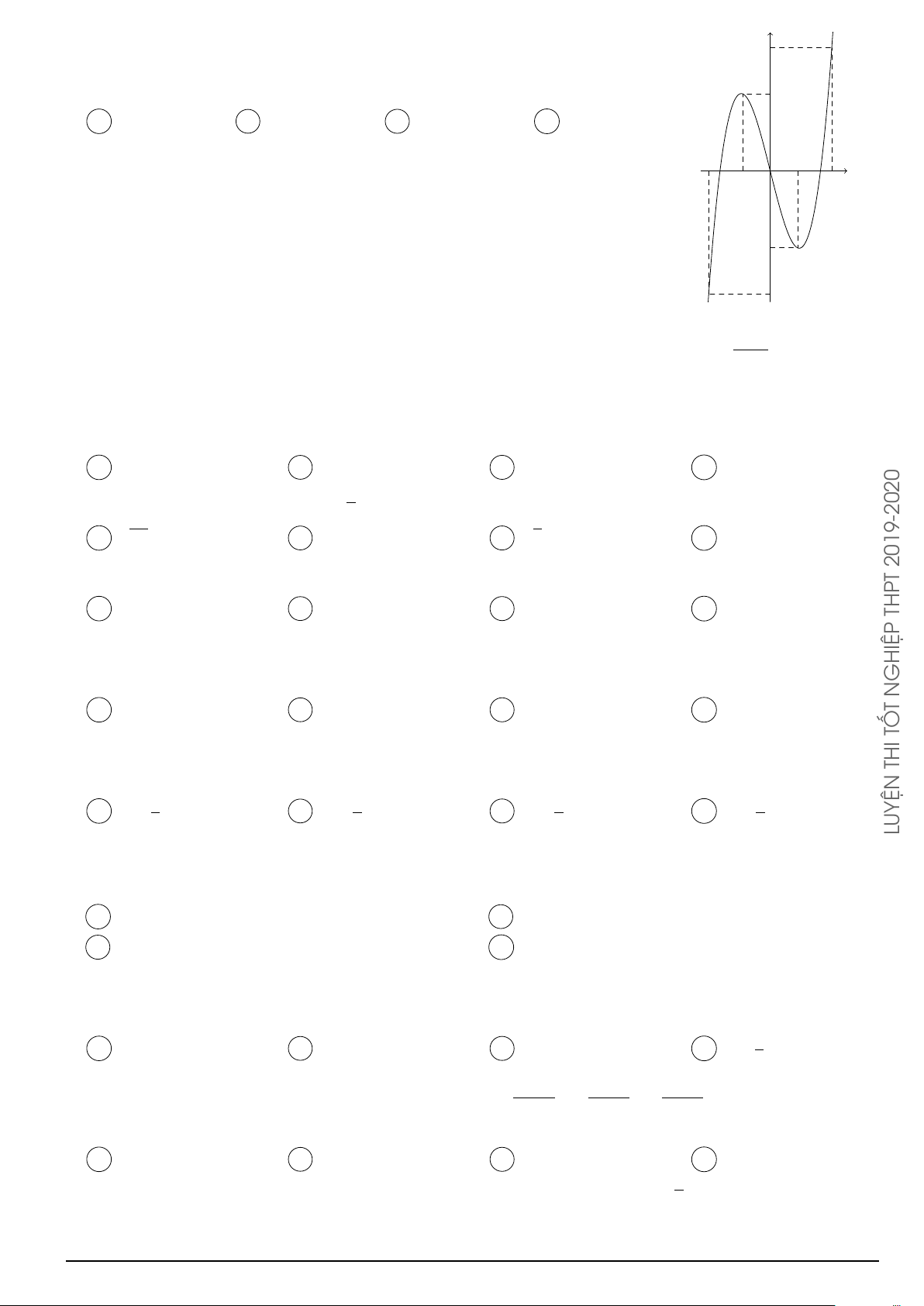
Cho hàm số f (x) xác định trên R và có đồ thị hàm số y = f 0(x) là đường y cong trong hình bên.
Mệnh đề nào dưới đây đúng?
A Hàm số f (x) đồng biến trên khoảng (1; 2).
B Hàm số f (x) đồng biến trên khoảng (−2; 1). x −2 O 2
C Hàm số f (x) nghịch biến trên khoảng (−1; 1).
D Hàm số f (x) nghịch biến trên khoảng (0; 2). Å a3 ã
Câu 11. Cho a là số thực dương khác 5. Tính I = log a . 5 125 1 1 A I = − . B I = −3. C I = . D I = 3. 3 3
Câu 12. Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng 36πa2. Tính o/
thể tích V của lăng trụ lục giác đều nội tiếp hình trụ. aPr √ √ √ √ A V = 27 3a3. B V = 24 3a3. C V = 36 3a3. D V = 81 3a3. x3 Câu 13. Cho hàm số y =
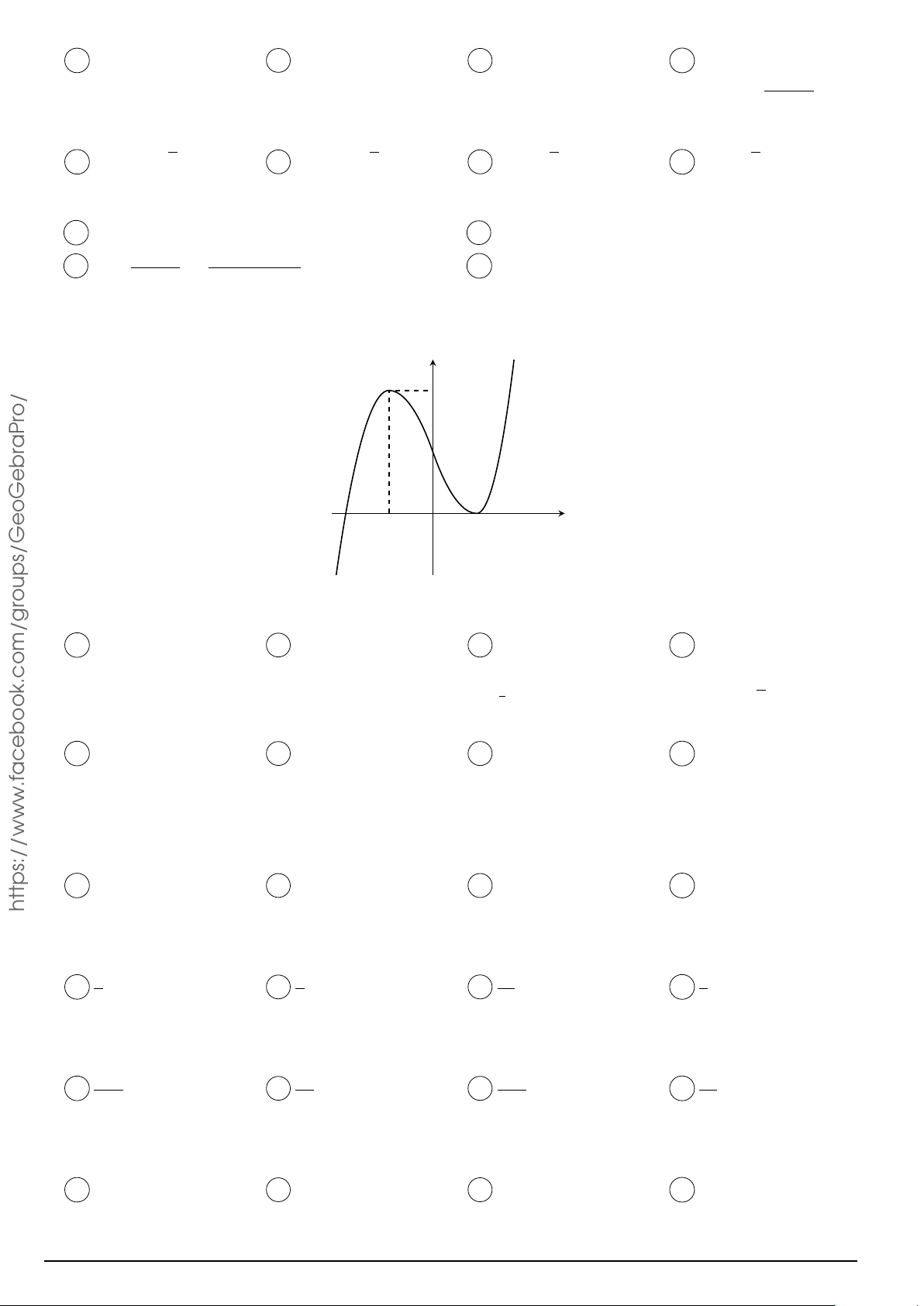
− (m + 1)x2 + mx − 2. Tìm m để hàm số đạt cực đại tại x = −1. 3 A m = −1. B m = 1. C không có m. D m = −2. Câu 14. roups/GeoGebr
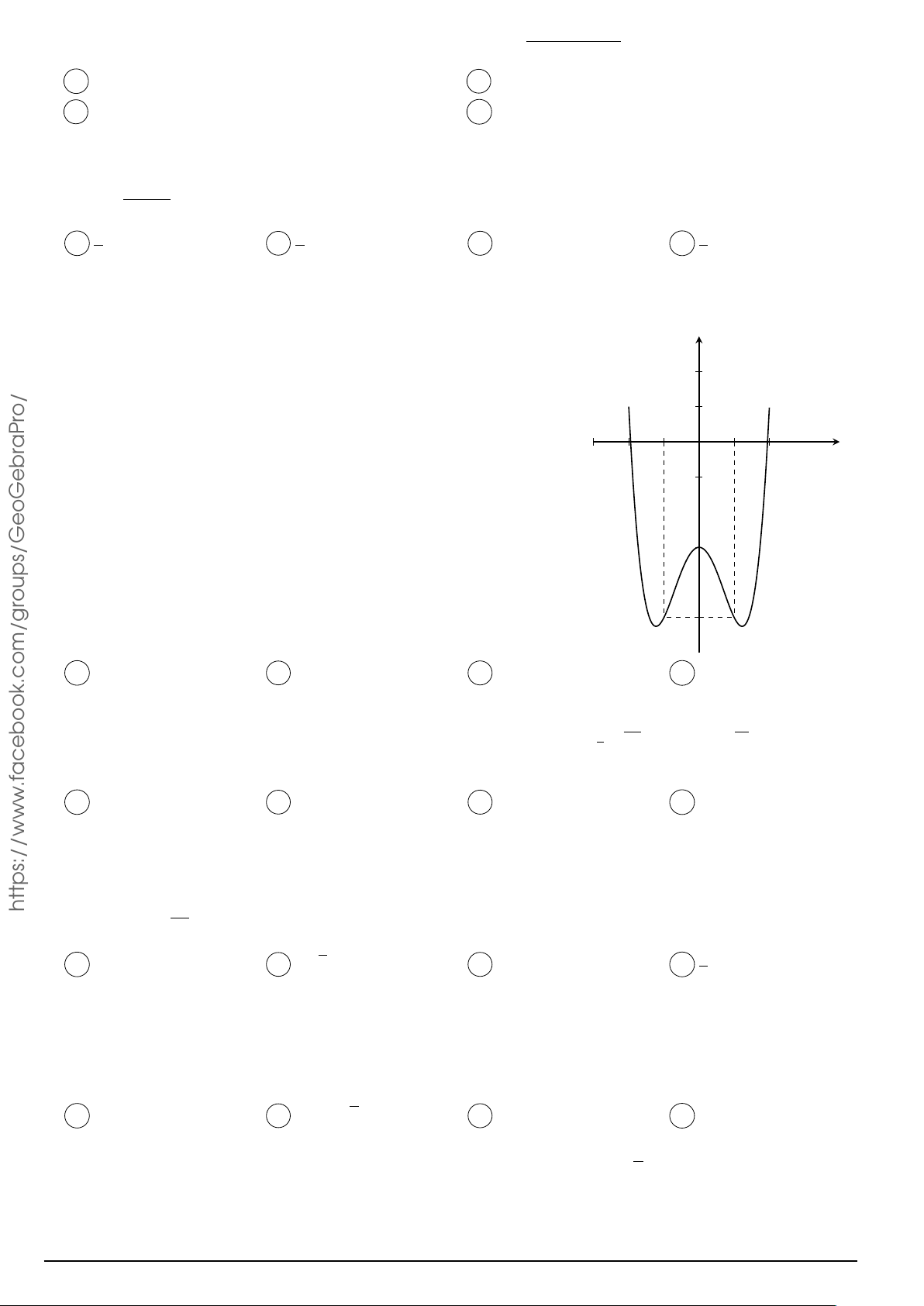
Cho hàm số y = f (x) có đồ thị như hình bên. Hàm số đã cho nghịch biến trên y khoảng nào dưới đây? 2 A (0; 1). B (−1; 0). C (−2; −1). D (−1; 1). 1 x −2 O 1 2 −1 −2 x2 + x − 2 acebook.com/g Câu 15. Cho hàm số y =
(C), đồ thị (C) có bao nhiêu đường tiệm cận? .f x2 − 3x + 2 A 0. B 1. C 2. D 3.
Câu 16. Nghiệm của bất phương trình log
√ (2x − 5) ≥ log √ (x − 1) là 2− 3 2− 3 5 5 A < x ≤ 4. B 1 < x ≤ 4. C ≤ x ≤ 4. D x ≥ 4. 2 2 https://www Câu 17.
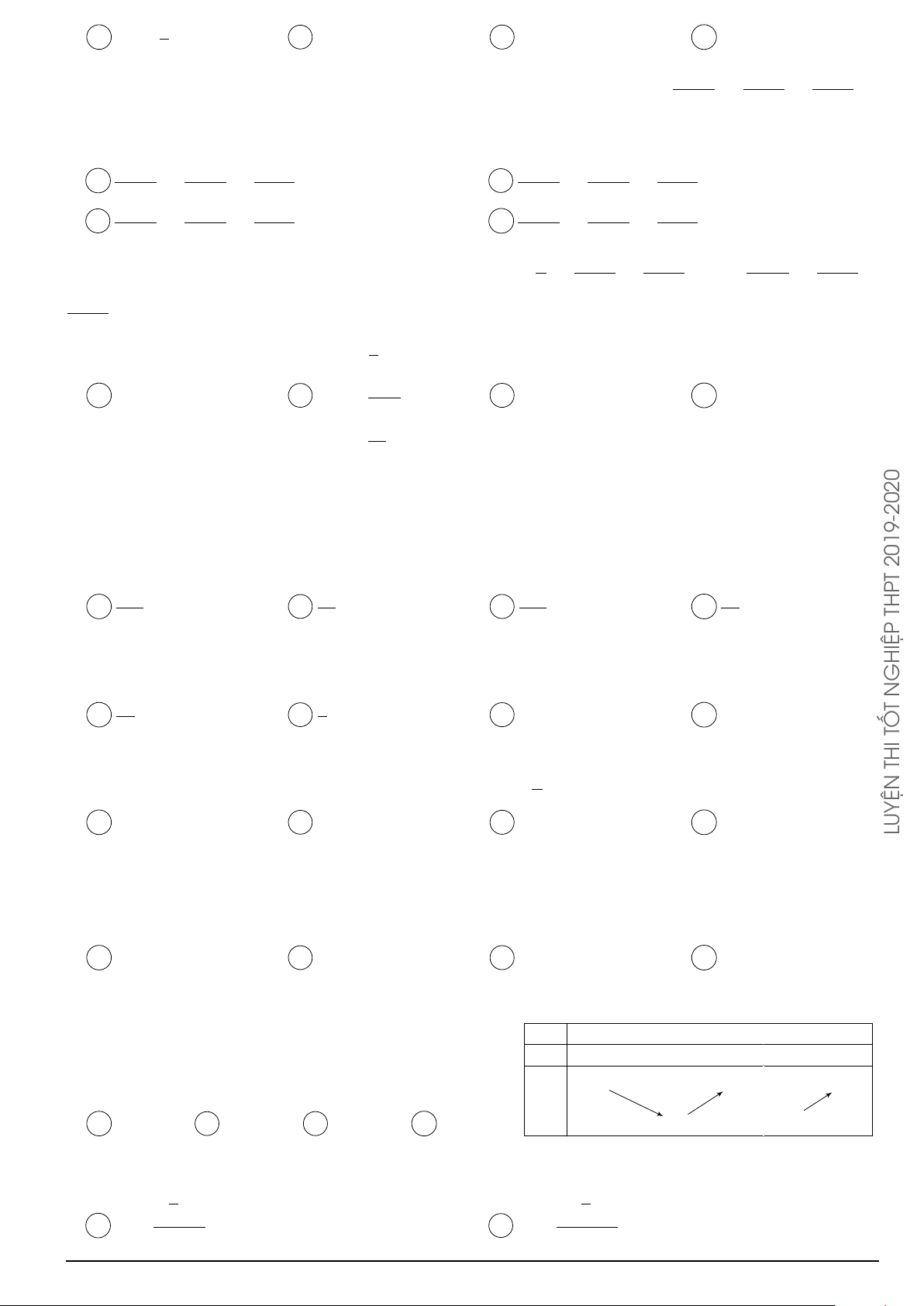
Cho hàm số y = f (x) có đồ thị như hình vẽ. Số nghiệm của phương y trình 2|f (x)| − 5 = 0 là 1 A 3. B 5 . C 4. D 6. −1 O 1 x −3 4 Z 5x − 8 Câu 18. Cho
dx = a ln 3 + b ln 2 + c ln 5 với a, b, c là các số hữu tỉ. Giá trị 2a−3b+c x2 − 3x + 2 3 bằng h Geogebra Pro Trang 2 A 12. B 6. C 1. D 64.
Câu 19 (2D4B1-2). Cho số phức z = 2 + 5i. Điểm biểu diễn số phức z trong mặt phẳng Oxy có tọa độ là A (5; 2). B (2; 5). C (−2; 5). D (2; −5).
Câu 20. Cho a, b là các số thực thỏa mãn a + 6i = 2 − 2bi, với i là đơn vị ảo. Giá trị của a + b bằng A −1. B 1. C −4. D 5.
Câu 21. Trong hệ tọa độ Oxy, cho điểm M biểu diễn số phức z = −2 + 3i. Gọi N là điểm thuộc
đường thẳng y = 3 sao cho tam giác OM N cân tại O. Điểm N là điểm biểu diễn của số phức nào dưới đây? A z = 3 − 2i. B z = −2 − 3i. C z = 2 + 3i. D z = −2 + i.
Câu 22. Trong không gian Oxyz, cho hình bình hành ABCD có A(1; 0; 0), B(0; 0; 1) và C(2; 1; 1). Tìm tọa độ điểm D. A D(1; 3; 0) . B D(−3; 1; 0). C D(3; −1; 0). D D(3; 1; 0).
Câu 23. Trong không gian Oxyz, cho hai điểm M (3; −2; 5), N (−1; 6; −3). Mặt cầu đường kính M N có phương trình là
A (x + 1)2 + (y + 2)2 + (z + 1)2 = 6.
B (x − 1)2 + (y − 2)2 + (z − 1)2 = 6.
C (x + 1)2 + (y + 2)2 + (z + 1)2 = 36.
D (x − 1)2 + (y − 2)2 + (z − 1)2 = 36. 2019-2020
Câu 24. Trong không gian Oxyz khoảng cách giữa hai mặt phẳng (P ) : x + 2y + 2z − 10 = 0 và THPT
(Q) : x + 2y + 2z − 3 = 0 bằng 8 7 4 A . B . C 3. D . 3 3 3 GHIỆP N
Câu 25. Trong không gian Oxyz, cho điểm A(2; 0; −1) và mặt phẳng (P ) : x + y − 1 = 0. Đường thẳng T
đi qua A đồng thời song song với (P ) và mặt phẳng (Oxy) có phương trình là TỐ     x = 3 + t x = 2 + t x = 1 + 2t x = 3 + t         THI     A y = 2t . B y = −t . C y = −1 . D y = 1 + 2t .             z = 1 − t z = −1 z = −t z = −t LUYỆN
Câu 26. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A cạnh AB = a, SA vuông góc với √
mặt đáy và SA = a 2. Gọi M là trung điểm của SA, ϕ là góc giữa BM và mặt phẳng (SBC). Tính sin ϕ. √ √ 2 1 2 1 A sin ϕ = √ . B sin ϕ = √ . C sin ϕ = √ . D sin ϕ = √ . 2 15 15 15 2 15 Câu 27.
Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Hàm số y = f (x2 − 2) có y
bao nhiêu điểm cực trị? O 2 3 A 4. B 5. C 3. D 2. x −4 h Geogebra Pro Trang 3 x − m2 − m
Câu 28. Tìm giá trị m để giá trị nhỏ nhất của hàm số y = trên [0; 1] bằng −2. x + 1 A m = −2. B m = 1. C m = −2 và m = −1. D m = −2 và m = 1.
Câu 29. Cho các số thực a, b thỏa mãn 1 < a < b và log b + log a2 = 3. Tính giá trị của biểu thức a b a2 + b T = log . ab 2 1 3 2 A . B . C 6. D . 6 2 3 Câu 30.
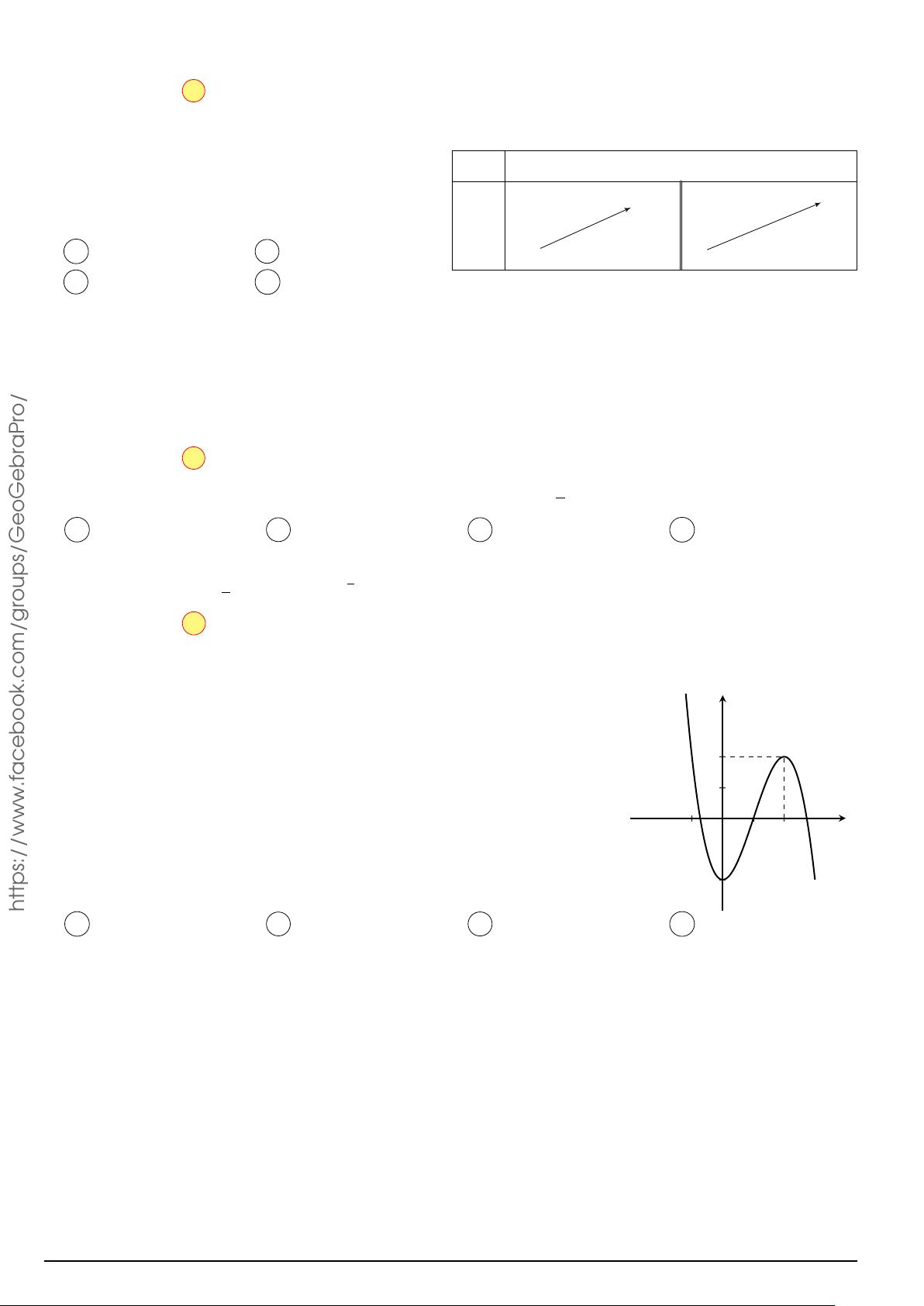
Đồ thị sau đây là của hàm số y = x4 − 3x2 − 3 . Với giá trị nào y
của m thì phương trình x4 − 3x2 − 3 = m có 3 nghiệm phân biệt 2 1 o/ −3 −2 −1 1 2 aPr O x −1 −3 roups/GeoGebr −5 A m = −4 . B m = −3. C m = 0. D m = −5. Å x3 ã
Câu 31. Nghiệm nguyên lớn nhất của bất phương trình log4 x − log2 + 9 log 32 < 4 log2 2 1 2 x2 2−1 x 2 8 acebook.com/g là .f A x = 7. B x = 8. C x = 4. D x = 1.
Câu 32. Một hình trụ có chiều cao h và bán kính đáy R. Hình nón có đỉnh là tâm đáy trên của hình
trụ và đáy là hình tròn đáy dưới của hình trụ. Gọi V1 là thể tích của hình trụ, V2 là thể tích của hình https://www V1 nón. Tính tỉ số . V2 √ 1 A 2. B 2 2. C 3. D . 3
Câu 33. Cho hàm số y = f (x) có đạo hàm, liên tục trên R, nhận giá trị dương trên khoảng (0; +∞)
và thỏa mãn f (1) = 1, f 0(x) = f (x) · (3x2 + 2mx + m) với m là tham số. Giá trị của tham số m để f (3) = e−4 là √ A m = −2. B m = 3. C m = −3. D m = 4. √
Câu 34. Cho hình phẳng (H) giới hạn bởi đồ thị các hàm số sau y =
x, y = 1 đường thẳng x = 4
(tham khảo hình vẽ). Thể tích khối tròn xoay sinh bởi hình (H) khi quay quanh đường thẳng y = 1 bằng h Geogebra Pro Trang 4 y x = 4 1 y = 1 x O 1 4 9 119 7 21 A π. B π. C π. D π. 2 6 6 2 iz − (3i + 1)z 26iz
Câu 35. Cho số phức z 6= 0 thỏa mãn = |z|2. Số phức w = có môđun bằng 1 + i 9 √ √ A 9. B 26. C 6. D 5.
Câu 36. Cho số phức z thỏa |z − 1 + 2i| = 3. Biết rằng tập hợp các điểm biểu diễn của số phức
w = 2z + i trên mặt phẳng (Oxy) là một đường tròn. Tìm tâm của đường tròn đó. A I (2; −3). B I(1; 1). C I(0; 1). D I(1; 0). 2019-2020
Câu 37. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α) : x − 2z − 6 = 0 và đường thẳng  THPT  x = 1 + t     d :
y = 3 + t . Viết phương trình đường thẳng ∆ nằm trong mặt phẳng (α) cắt đồng thời vuông GHIỆP   N    z = −1 − t T TỐ góc với d. x − 2 y − 4 z + 2 x − 2 y − 4 z + 2 THI A = = . B = = . 2 1 1 2 −1 1 x − 2 y − 3 z + 2 x − 2 y − 4 z − 2 C = = . D = = . 2 −1 1 2 −1 1 LUYỆN x y z + 1 x − 3 y z − 1
Câu 38. Trong không gian Oxyz cho ba đường thẳng d : = = , ∆1 : = = , 1 1 −2 2 1 1 x − 1 y − 2 z ∆2 : = =
. Đường thẳng ∆ vuông góc với d đồng thời cắt ∆1, ∆2 tương ứng tại H, K sao 1 2 1 #»
cho độ dài HK nhỏ nhất. Biết rằng ∆ có một vectơ chỉ phương u (h; k; 1). Giá trị h − k bằng A 0. B 4. C 6. D −2.
Câu 39. Cho hai hộp, hộp thứ nhất chứa 5 viên bi đỏ và 7 viên bi vàng, hộp thứ hai chứa 3 bi đỏ và
n bi vàng (n ∈ N). Khi chọn ngẫu nhiên mỗi hộp một viên bi, xác suất để chọn được hai bi khác màu 7 là
. Số bi vàng trong hộp thứ hai là? 15 A n = 12. B n = 10. C n = 7. D n = 5. Câu 40. h Geogebra Pro Trang 5
Cho hình hộp chữ nhật ABCD.A0B0C0D0 có cạnh bằng C0 D0
AB = 2a, AD = AA0 = a như hình vẽ. Khoảng cách giữa
hai đường thẳng BD và AD0 bằng a √ 2a A a. B . C a 3. D . 2 3 A0 B0 C D A B 5−x + 2
Câu 41. Tìm tất cả các giá trị khác nhau của tham số m để hàm số y = đồng biến trên 5−x − m (−∞; 0). A m < −2. B m ≤ −2. C −2 < m ≤ 1. D −2 < m < 1.
Câu 42. Dân số thế giới được tính theo công thức S = A · eni trong đó A là dân số của năm lấy làm o/
mốc tính, S là dân số sau n năm, i là tỉ lệ tăng dân số hàng năm. Cho biết năm 2005 Việt Nam có aPr
khoảng 80.902.400 người và tỉ lệ tăng dân số là 1, 47% một năm. Như vậy, nếu tỉ lệ tăng dân số hàng
năm không đổi thì đến năm 2019 số dân của Việt Nam sẽ gần với số nào nhất sau đây? A 99.389.200. B 99.386.600. C 100.861.100. D 99.251.200. Câu 43.
Cho hàm số y = f (x). Hàm số y = f 0(x) roups/GeoGebr x −∞ −4 1 +∞
có bảng biến thiên như sau. Bất phương trình
f (x) > sin x + m có nghiệm trên khoảng (−1; 1) y0 − 0 + 0 − khi và chỉ khi +∞ + −1 A m > f (1) − sin 1. y B m ≥ f (1) − sin 1. −3 −∞ acebook.com/g C m ≤ f (−1) + sin 1. .f D m < f (−1) + sin 1.
Câu 44. Hình trụ có bán kính đáy bằng a chu vi của thiết diện qua trục bằng 10a Thể tích của khối trụ đã cho bằng A 4πa3. B πa3. C 3πa3. D 5πa3. https://www Å 1 ã ï 1 ò
Câu 45. Cho hàm số y = f (x) liên tục và thỏa mãn f (x) + 2f = 3x với x ∈ ; 2 . Tính x 2 2 Z f (x) I = dx. x 1 2 3 3 9 9 A I = . B I = − . C I = . D I = − . 2 2 2 2
Câu 46. Phương trình |x3 − 3x| = m2 + m có 6 nghiệm phân biệt khi và chỉ khi A m > 0. B m < −2hoặc m > 1. C −1 < m < 0.
D −2 < m < −1 hoặc 0 < m < 1.
Câu 47. Cho hai số thực a, b > 1 sao cho tồn tại số thực 0 < x 6= 1 thỏa mãn alogb x = bloga(x2). Tìm
giá trị nhỏ nhất của P = ln2 a + ln2 b − ln(ab). h Geogebra Pro Trang 6 √ √ 1 3 + 2 2 e 1 − 3 3 A . B − . C . D . 4 12 2 4
Câu 48. Có bao nhiêu giá trị nguyên của tham số m để max |x3 − 3x2 + m| ≤ 4? [1;3] A 5. B 4. C 6. D Vô số.
Câu 49. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC), góc giữa đường
thẳng SB và mặt phẳng (ABC) bằng 60◦. Khoảng cách giữa hai đường thẳng AC và SB bằng: √ √ √ a 2 a 15 a 7 A . B 2a. C . D R = . 2 5 7
Câu 50. Cho hàm số y = f (x), biết hàm số y = f 0(x) có đồ thị như hình bên dưới. y −6 −1 O 2 x
Hàm số g(x) = f (3 − x2) đồng biến trên khoảng? 2019-2020 A (2; 3). B (−1; 0). C (−2; −1). D (0; 1).
———————–HẾT———————– THPT GHIỆP N T TỐ THI LUYỆN h Geogebra Pro Trang 7 BẢNG ĐÁP ÁN 1. D 2. C 3. D 4. A 5. A 6. C 7. A 8. B 9. D 10. D 11. D 12. D 13. A 14. A 15. C 16. A 17. C 18. D 19. B 20. A 21. C 22. D 23. D 24. B 25. B 26. B 27. B 28. D 29. D 30. B 31. A 32. C 33. C 34. C 35. B 36. A 37. B 38. A 39. C 40. D 41. C 42. A 43. D 44. C 45. A 46. D 47. B 48. A 49. C 50. B o/ aPr roups/GeoGebr acebook.com/g .f https://www h Geogebra Pro Trang 8 MỖI NGÀY MỘT ĐỀ THI 8
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Một hội đồng gồm 5 nam và 4 nữ được tuyển vào một ban quản trị gồm 4 người. Biết rằng
ban quản trị có ít nhất một nam và một nữ. Hỏi có bao nhiêu cách tuyển chọn? A 240. B 260. C 126. D 120. Lời giải.
Số cách chọn 4 người bất kỳ từ 9 người hội đồng là: C4 cách. 9
Số cách chọn 4 người đều nữ là: C4 cách. 4
Số cách chọn 4 người đều nam là: C4 cách. 5
Vậy để có ít nhất một nam và một nữ thì có C4 − (C4 + C4) = 120 cách. 9 4 5 Chọn phương án D  2019-2020 u1 = 1; u2 = 0
Câu 2. Cho dãy số (un) xác định bởi . Tính u5.
un+2 = 2un+1 − un; ∀n > 1 THPT A u5 = 0. B u5 = −4. C u5 = −3. D u5 = −2. GHIỆP Lời giải. N T
u3 = 2u2 − u1 = −1; u4 = 2u3 − u2 = −2; u5 = 2u4 − u3 = −3 TỐ Chọn phương án C THI
Câu 3. Số nghiệm của phương trình 9x + 2.3x+1 − 7 = 0 là LUYỆN A 0. B 2. C 4. D 1. Lời giải. Đặt t = 3x, t > 0  t = 1 (nhận)
Phương trình đã cho trở thành t2 + 6t − 7 = 0 ⇔  . t = −7 (loại)
Với t = 1 thì 3x = 1 ⇔ x = 0.
Vậy phương trình đã cho có nghiệm duy nhất x = 0. Chọn phương án D
Câu 4. Tính thể tích của khối lập phương ABCD.A0B0C0D0 biết AC = 2a. √ √ 2 2a3 a3 A 2 2a3. B a3. C . D . 3 3 Lời giải. h Geogebra Pro Trang 1
Gọi độ dài cạnh của hình phương là x, x > 0. Khi đó ta có D C √ x2 + x2 = (2a)2 ⇔ x = a 2. √ √ 2a Ä ä3
Suy ra thể tích khối lập phương V = a 2 = 2 2a3. A B C0 D0 A0 B0 Chọn phương án A
Câu 5. Tính đạo hàm của hàm số y = log (6x − 5). o/ 8 2 1 6 6 A y0 = . B y0 = . C y0 = . D y0 = . aPr (6x − 5) ln 2 (6x − 5) ln 8 6x − 5 (6x − 5) ln 4 Lời giải. (6x − 5)0 6 2 Ta có y0 = = = . (6x − 5) · ln 8 3(6x − 5) · ln 2 (6x − 5) · ln 2 Chọn phương án A
Câu 6. Gọi F (x) là một nguyên hàm của hàm số f (x) = e−x + cos x. Tìm khẳng định đúng. roups/GeoGebr
A F (x) = e−x + sin x + 2019.
B F (x) = e−x + cos x + 2019.
C F (x) = − e−x + sin x + 2019.
D F (x) = − e−x − cos x + 2019. Lời giải. Z Áp dụng công thức
( e−x + cos x) dx = − e−x + sin x + C, với C là hằng số
Cho C = 2019 ta có F (x) = − e−x + sin x + 2019. Chọn phương án C acebook.com/g .f
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, SA vuông góc √
với mặt phẳng (ABCD), SA = a 3. Thể tích của khối chóp S.ABC là √ √ a3 3 √ 2a3 3 √ A . B a3 3. C . D 2a3 3. 3 3 Lời giải. https://www S √ a 3 2a A D a B C √ 1 1 a3 3 Ta có: VS.ABC = · SA · AB · BC = . 3 2 3 h Geogebra Pro Trang 2 Chọn phương án A
Câu 8. Cho hình nón tròn xoay có chiều cao h = 20 (cm), bán kính đáy r = 25 (cm). Một thiết diện
đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là 12 (cm). Tính
diện tích của thiết diện đó. A S = 400 (cm2). B S = 500 (cm2). C S = 406 (cm2). D S = 300 (cm2). Lời giải.
Thiết diện qua đỉnh là tam giác SAB. S Gọi K là trung điểm AB ⇒ OK⊥AB ⇒ AB⊥ (SOK)⇒ (SAB) ⊥ (SOK).
Kẻ OH⊥SK (H ∈ SK)⇒ OH⊥ (SAB)⇒ OH = 12(cm). 1 1 1 1 1 1 1 Ta có: = + ⇒ = − = ⇒ OK = OH2 OK2 OS2 OK2 122 202 225 15 (cm). H √ √ KB = OB2 − OK2 =
252 − 152 = 20 ⇒ AB = 2BK = 40 (cm). √ √ A SK = SO2 + OK2 = 202 + 152 = 25 (cm). 1 O K
⇒ S∆SAB = .SK.AB = 500 (cm2). 2 B Chọn phương án B 2019-2020
Câu 9. Cắt mặt cầu (S) bằng một mặt phẳng cách tâm một khoảng bằng 4cm được thiết diện là một THPT
hình tròn có diện tích 9πcm2. Tính thể tích khối cầu (S). 250π 2500π 25π 500π A cm3. B cm3. C cm3. D cm3. GHIỆP 3 3 3 3 N T Lời giải. TỐ THI
Gọi I là tâm mặt cầu (S), H là tâm đường tròn giao tuyến, A là một điểm bất kì trên đường tròn, R là bán kính của (S). LUYỆN Ta có d(I, (P )) = 4. S(C) = πAH2 = 9π ⇒ AH = 3. √ Ta có R = pAH2 + d(I, (P )) = 32 + 42 = 5. 4 500π
Thể tích khối cầu (S) là V(S) = πR3 = . 3 3 I (P ) A H Chọn phương án D Câu 10. h Geogebra Pro Trang 3
Cho hàm số f (x) xác định trên R và có đồ thị hàm số y = f 0(x) là đường y cong trong hình bên.
Mệnh đề nào dưới đây đúng?
A Hàm số f (x) đồng biến trên khoảng (1; 2).
B Hàm số f (x) đồng biến trên khoảng (−2; 1). x −2 O 2
C Hàm số f (x) nghịch biến trên khoảng (−1; 1).
D Hàm số f (x) nghịch biến trên khoảng (0; 2). Lời giải.
Từ đồ thị của y = f 0(x), ta có với x ∈ (0; 2), f 0(x) < 0. Suy ra f (x) nghịch biến trên khoảng (0; 2). Chọn phương án D Å a3 ã
Câu 11. Cho a là số thực dương khác 5. Tính I = log a . o/ 5 125 1 1 aPr A I = − . B I = −3. C I = . D I = 3. 3 3 Lời giải. Å a3 ã a 3 a Ta có I = log a = log a = 3 log a = 3. 5 125 5 5 5 5 Chọn phương án D
Câu 12. Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng 36πa2. Tính roups/GeoGebr
thể tích V của lăng trụ lục giác đều nội tiếp hình trụ. √ √ √ √ A V = 27 3a3. B V = 24 3a3. C V = 36 3a3. D V = 81 3a3. Lời giải.
Thiết diện qua trục hình trụ là hình vuông ADD0A0. Gọi O, O0 F 0 A0 E0
lần lượt là hai tâm đường tròn đáy (hình vẽ). Suy ra l = 2r. O0 I0 J 0 B0 acebook.com/g .f Theo giả thiết ta có C0 D0
Sxq = 2πrl = 36πa2 ⇔ 2πr · 2r = 36πa2 ⇒ r = 3a ⇒ l = 6a.
Lăng trụ lục giác đều ABCDEF.A0B0C0D0E0F 0 nội tiếp hình trụ có chiều cao là h = 6a. √ √ (3a)2 3 27a2 3 S = (vì ∆OAB đều, https://www ABCDEF = 6S∆OAB = 6 · 4 2 cạnh bằng 3a). √ F A 27a2 3 √ I E J Suy ra V = · 6a = 81a3 3. O 2 B D C Chọn phương án D x3 Câu 13. Cho hàm số y =
− (m + 1)x2 + mx − 2. Tìm m để hàm số đạt cực đại tại x = −1. 3 A m = −1. B m = 1. C không có m. D m = −2. Lời giải. Tập xác định: D = R.
y0 = x2 − 2(m + 1)x + m; y00 = 2x − 2(m + 1).
Vì hàm số đã cho là hàm số bậc ba nên h Geogebra Pro Trang 4   y0(−1) = 0 1 + 2(m + 1) + m = 0
Hàm số có điểm cực đại là x = −1 khi và chỉ khi ⇔ ⇔ y00(−1) < 0  − 2 − 2(m + 1) < 0  m = −1 ⇔ m = −1. m > −2 Chọn phương án A Câu 14.
Cho hàm số y = f (x) có đồ thị như hình bên. Hàm số đã cho nghịch biến trên y khoảng nào dưới đây? 2 A (0; 1). B (−1; 0). C (−2; −1). D (−1; 1). 1 x −2 O 1 2 −1 −2 Lời giải.
Từ đồ thị ta thấy hàm số nghịch biến trên khoảng (0; 1). Chọn phương án A x2 + x − 2 Câu 15. Cho hàm số y =
(C), đồ thị (C) có bao nhiêu đường tiệm cận? x2 − 3x + 2 A 0. B 1. C 2. D 3. 2019-2020 Lời giải. THPT
Tập xác định D = R\ {1; 2}. x + 2 Ta có y =
nên đồ thị hàm số có tiệm cận ngang là y = 1 và tiệm cận đứng là x = 2. x − 2 GHIỆP Chọn phương án C N T
Câu 16. Nghiệm của bất phương trình log
√ (2x − 5) ≥ log √ (x − 1) là TỐ 2− 3 2− 3 5 5 A < x ≤ 4. B 1 < x ≤ 4. C ≤ x ≤ 4. D x ≥ 4. THI 2 2 Lời giải.   2x − 5 ≤ x − 1 x ≤ 4 LUYỆN   log
√ (2x − 5) ≥ log √ (x − 1) ⇔ ⇔ 2− 3 2− 3 5 2x − 5 > 0 x > .  2 5
Vậy nghiệm của bất phương trinh là < x ≤ 4. 2 Chọn phương án A Câu 17.
Cho hàm số y = f (x) có đồ thị như hình vẽ. Số nghiệm của phương y trình 2|f (x)| − 5 = 0 là 1 A 3. B 5 . C 4. D 6. −1 O 1 x −3 Lời giải. h Geogebra Pro Trang 5  5 5 f (x) = (1)
2 |f (x)| − 5 = 0 ⇔ |f (x)| = ⇔ 2  . 2  5 f (x) = − (2) 2
Số nghiệm của phương trình đã cho là tổng số nghiệm của phương trình (1) và phương trình (2). 5 5
Số nghiệm của phương trình đã cho là số giao điểm của đường thẳng y = và đường thẳng y = − 2 2
với đồ thị hàm số y = f (x).
Như vậy, dựa vào đồ thị hàm số ta thấy phương trình đã cho có 4 nghiệm. Chọn phương án C 4 Z 5x − 8 Câu 18. Cho
dx = a ln 3 + b ln 2 + c ln 5 với a, b, c là các số hữu tỉ. Giá trị 2a−3b+c x2 − 3x + 2 3 bằng A 12. B 6. C 1. D 64. Lời giải. o/ 4 4 Z 5x − 8 Z Å 3 2 ã 4 4 aPr Ta có dx = +
dx = 3 ln |x − 1| + 2 ln |x − 2| x2 − 3x + 2 x − 1 x − 2 3 3 3 3  a = 3   
= 3 ln 3 − 3 ln 2 + 2 ln 2 = − ln 2 + 3 ln 3 ⇒
b = −1 ⇒ a − 3b + c = 6 .    c = 0 Chọn phương án D roups/GeoGebr
Câu 19 (2D4B1-2). Cho số phức z = 2 + 5i. Điểm biểu diễn số phức z trong mặt phẳng Oxy có tọa độ là A (5; 2). B (2; 5). C (−2; 5). D (2; −5). Lời giải.
Phương pháp: Số phức z = a + bi, (a; b ∈ R) có điểm biểu diễn số phức trong mặt phẳng Oxy là (a; b). acebook.com/g .f
Cách giải: Điểm biểu diễn số phức z trong mặt phẳng Oxy có tọa độ là (2; 5). Chọn phương án B
Câu 20. Cho a, b là các số thực thỏa mãn a + 6i = 2 − 2bi, với i là đơn vị ảo. Giá trị của a + b bằng A −1. B 1. C −4. D 5. https://www Lời giải.   a = 2 a = 2 Ta có a + 6i = 2 − 2bi ⇒ ⇒ ⇒ a + b = −1. 6 = −2b b = −3 Chọn phương án A
Câu 21. Trong hệ tọa độ Oxy, cho điểm M biểu diễn số phức z = −2 + 3i. Gọi N là điểm thuộc
đường thẳng y = 3 sao cho tam giác OM N cân tại O. Điểm N là điểm biểu diễn của số phức nào dưới đây? A z = 3 − 2i. B z = −2 − 3i. C z = 2 + 3i. D z = −2 + i. Lời giải.
Do giả thiết suy ra tọa độ M (−2; 3) nên M thuộc đường thẳng y = 3. Vì tam giác OM N cân tại O
suy ra N đối xứng với M qua Oy nên tọa độ điểm N (2; 3). Khi đó điểm N là biểu diễn của số phức h Geogebra Pro Trang 6 z = 2 + i. Chọn phương án C
Câu 22. Trong không gian Oxyz, cho hình bình hành ABCD có A(1; 0; 0), B(0; 0; 1) và C(2; 1; 1). Tìm tọa độ điểm D. A D(1; 3; 0) . B D(−3; 1; 0). C D(3; −1; 0). D D(3; 1; 0). Lời giải. # » # »
Tứ giác ABCD là hình bình hành khi và chỉ khi AB = DC. # » # »
Ta có AB = (−1; 0; 1), DC = (2 − xD; 1 − yD; 1 − zD).   −  1 = 2 − xD xD = 3       Suy ra 0 = 1 − y ⇔ Vậy D(3; 1; 0). D yD = 1       1 = 1 − zD zD = 0. Chọn phương án D
Câu 23. Trong không gian Oxyz, cho hai điểm M (3; −2; 5), N (−1; 6; −3). Mặt cầu đường kính M N có phương trình là
A (x + 1)2 + (y + 2)2 + (z + 1)2 = 6.
B (x − 1)2 + (y − 2)2 + (z − 1)2 = 6.
C (x + 1)2 + (y + 2)2 + (z + 1)2 = 36.
D (x − 1)2 + (y − 2)2 + (z − 1)2 = 36. 2019-2020 Lời giải.
Tâm I của mặt cầu là trung điểm đoạn M N ⇒I (1; 2; 1). THPT » M N
(−1 − 3)2 + (6 + 2)2 + (−3 − 5)2 Bán kính mặt cầu R = = = 6. 2 2
Vậy phương trình mặt cầu là (x − 1)2 + (y − 2)2 + (z − 1)2 = 36. GHIỆP N Chọn phương án D T TỐ
Câu 24. Trong không gian Oxyz khoảng cách giữa hai mặt phẳng (P ) : x + 2y + 2z − 10 = 0 và THI
(Q) : x + 2y + 2z − 3 = 0 bằng 8 7 4 A . B . C 3. D . 3 3 3 LUYỆN Lời giải. #»
Dựa vào phương trình (P ), (Q) có véctơ pháp tuyến là n = (1; 2; 2) nên (P ) k (Q). √ 10 3 Ta có | #» n | = 1 + 22 + 22 = 3; d(O, (P )) = ; d(O, (Q)) = = 1, 3 3 7
suy ra d((P ), (Q)) = d(O, (P )) − d(O, (Q)) = . 3 Chọn phương án B
Câu 25. Trong không gian Oxyz, cho điểm A(2; 0; −1) và mặt phẳng (P ) : x + y − 1 = 0. Đường thẳng
đi qua A đồng thời song song với (P ) và mặt phẳng (Oxy) có phương trình là     x = 3 + t x = 2 + t x = 1 + 2t x = 3 + t             A y = 2t . B y = −t . C y = −1 . D y = 1 + 2t .             z = 1 − t z = −1 z = −t z = −t Lời giải. #» #»
Ta có: n (P ) = (1; 1; 0), n (Oxy) = (0; 0; 1).
Gọi d là đường thẳng đi qua A đồng thời song song với (P ) và mặt phẳng (Oxy). h Geogebra Pro Trang 7  #»  u d ⊥ #» n (P ) #» Khi đó #» ⇒ #» u d = #»
n (P ), n (Oxy) = (1; −1; 0).  u d ⊥ #» n (Oxy)  x = 2 + t    Vậy d : y = −t    z = −1. Chọn phương án B
Câu 26. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A cạnh AB = a, SA vuông góc với √
mặt đáy và SA = a 2. Gọi M là trung điểm của SA, ϕ là góc giữa BM và mặt phẳng (SBC). Tính sin ϕ. √ √ 2 1 2 1 A sin ϕ = √ . B sin ϕ = √ . C sin ϕ = √ . D sin ϕ = √ . 2 15 15 15 2 15 Lời giải. o/
Gọi N là trung điểm của BC, ta có AN ⊥ BC, mà SA ⊥ BC nên S aPr suy ra (SAN ) ⊥ BC.
Vậy (SAN ) vuông góc (SBC) theo giao tuyến SN , kẻ M H ⊥ SN H
tại H, khi đó M H ⊥ (SBC). M
Vậy góc giữa BM và (SBC) là góc ÷ M BH. √ √ 1 a 2 √ a 10 Ta có AN = BC = , SN = SA2 + AN 2 = . 2 2 2 A C roups/GeoGebr
Mặt khác ta có 4SHM v 4SAN nên √ M H SM AN · SM a 10 = ⇒ M H = = . N AN SN SN 10 B √ √ a 6 Ta lại có M B = AB2 + AM 2 = . 2 M H 1 Xét 4M BH, có sin = √ . acebook.com/g ÷ M BH = MB .f 15 Chọn phương án B Câu 27.
Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Hàm số y = f (x2 − 2) có y https://www
bao nhiêu điểm cực trị? O 2 3 A 4. B 5. C 3. D 2. x −4 Lời giải. Ta có y0 = 2xf 0(x2 − 2).   x = 0 x = 0   √
Cho y0 = 0 ⇔ 2xf 0(x2 − 2) = 0 ⇔ x2 − 2 = 0 ⇔ x = ± 2 .     x2 − 2 = 2 x = ±2 h Geogebra Pro Trang 8   x2 − 2 > 2 x > 2 ∨ x < −2
Dựa vào đồ thị y = f (x), ta có f 0 (x2 − 2) > 0 ⇔  ⇔  √ √ . x2 − 2 < 0 − 2 < x < 2  √ − 2 < x < − 2
f 0 (x2 − 2) < 0 ⇔ 0 < x2 − 2 < 2 ⇔ 2 < x2 < 4 ⇔ √2 < x < 2.
Khi đó, ta có bảng xét dấu √ √ x −∞ −2 − 2 0 2 2 +∞ 2x − | − | − 0 + | + | + f 0(x2 − 2) + 0 − 0 + | + 0 − 0 + y0 − 0 + 0 − 0 + 0 − 0 +
Dựa vào bảng xét dấu suy ra hàm số có 5 điểm cực trị. Chọn phương án B x − m2 − m
Câu 28. Tìm giá trị m để giá trị nhỏ nhất của hàm số y = trên [0; 1] bằng −2. x + 1 2019-2020 A m = −2. B m = 1. C m = −2 và m = −1. D m = −2 và m = 1. THPT Lời giải. m2 + m + 1 Ta có y0 = > 0, ∀x 6= −1. (x + 1)2 GHIỆP  N m = −2 T
Suy ra f (x) đồng biến trên [0; 1] ⇒ min f (x) = f (0) = −m2 − m = −2 ⇔  [0;1] TỐ m = 1. THI Chọn phương án D
Câu 29. Cho các số thực a, b thỏa mãn 1 < a < b và log b + log a2 = 3. Tính giá trị của biểu thức a b LUYỆN a2 + b T = log . ab 2 1 3 2 A . B . C 6. D . 6 2 3 Lời giải.
Ta có log b + log a2 = 3 ⇔ log b + 2 log a = 3. (1) a b a b
Đặt t = log b. Do 1 < a < b ⇔ t > log b ⇒ t > 1. a a  2 t = 1 (không thỏa) Khi đó (1) trở thành: t +
= 3 ⇔ t2 − 3t + 2 = 0 ⇔  . t t = 2 (thỏa)
Với t = 2 ta có log b = 2 ⇔ b = a2. a a2 + b 2 2 Suy ra T = log = log log a = . ab 2 a3 a2 = 3 a 3 Chọn phương án D Câu 30. h Geogebra Pro Trang 9
Đồ thị sau đây là của hàm số y = x4 − 3x2 − 3 . Với giá trị nào y
của m thì phương trình x4 − 3x2 − 3 = m có 3 nghiệm phân biệt 2 1 −3 −2 −1 1 2 O x −1 −3 −5 A m = −4 . B m = −3. C m = 0. D m = −5. Lời giải. o/ Phương pháp aPr
Số nghiệm của phương trình đã cho là số giao điểm của đồ thị hàm số y = x4 − 3x2 − 3 và đường
thẳng y = m. Dựa vào đồ thị hàm số để xác định m thỏa mãn bài toán. Cách giải:
Số nghiệm của phương trình đã cho là số giao điểm của đồ thị hàm số y = x4 − 3x2 − 3 và đường
thẳng y = m. Dựa vào đồ thị hàm số ta thấy đường thẳng y = m cắt đồ thị hàm số y = x4 − 3x2 − 3 roups/GeoGebr
tại 3 điểm phân biệt ⇔ m = −3 . Chọn phương án B Å x3 ã
Câu 31. Nghiệm nguyên lớn nhất của bất phương trình log4 x − log2 + 9 log 32 < 4 log2 2 1 2 x2 2−1 x 2 8 là acebook.com/g A x = 7. B x = 8. C x = 4. D x = 1. .f Lời giải. Điều kiện : x > 0. Å x3 ã https://www log4 x − log2 + 9 log 32 < 4 log2 2 1 2 x2 2−1 x 2 8
⇔ log4 x − log x3 − log 82 + 9 log 32 − log x2 < 4 log2 x 2 2 2 2 2 2
⇔ log4 x − (3 log x − 3)2 + 9 (5 − 2 log x) − 4 log2 x < 0 2 2 2 2
⇔ log4 x − 13 log2 x + 36 < 0 2 2
⇔ (t2 − 9)(t2 − 4) < 0( với t = log x) 2    1 1 − 3 < t < −2 − 3 < log x < −2 < x < 2 ⇔ 8 4  ⇔  ⇔  2 < t < 3 2 < log x < 3 2 4 < x < 8.
Vậy nghiệm nguyên lớn nhất của bất phương trình đã cho là x = 7. Chọn phương án A h Geogebra Pro Trang 10
Câu 32. Một hình trụ có chiều cao h và bán kính đáy R. Hình nón có đỉnh là tâm đáy trên của hình
trụ và đáy là hình tròn đáy dưới của hình trụ. Gọi V1 là thể tích của hình trụ, V2 là thể tích của hình V1 nón. Tính tỉ số . V2 √ 1 A 2. B 2 2. C 3. D . 3 Lời giải.
Hai khối nón và khối trụ có cùng chiều cao h và cùng bán kính đáy bằng r. O0 V1 πr2h Do đó ta có = = 3. V 1 πr2h 3 O Chọn phương án C
Câu 33. Cho hàm số y = f (x) có đạo hàm, liên tục trên R, nhận giá trị dương trên khoảng (0; +∞)
và thỏa mãn f (1) = 1, f 0(x) = f (x) · (3x2 + 2mx + m) với m là tham số. Giá trị của tham số m để f (3) = e−4 là √ A m = −2. B m = 3. C m = −3. D m = 4. 2019-2020 Lời giải. Z Z THPT f 0(x) f 0(x) Theo giả thiết ta có = 3x2 + 2mx + m ⇒ dx = (3x2 + 2mx + m) dx. f (x) f (x)
Nên ln[f (x)] = x3 + mx2 + mx + C ⇒ f (x) = ex3+mx2+mx+C . GHIỆP N
Do f (1) = 1 ⇒ e1+2m+C = 1 ⇒ C = −2m − 1. T
Vậy f (x) = ex3+mx2+mx−2m−1 ⇒ f (3) = e−4 ⇔ e26+10m = e−4 ⇔ m = −3. TỐ Chọn phương án C THI √
Câu 34. Cho hình phẳng (H) giới hạn bởi đồ thị các hàm số sau y =
x, y = 1 đường thẳng x = 4 LUYỆN
(tham khảo hình vẽ). Thể tích khối tròn xoay sinh bởi hình (H) khi quay quanh đường thẳng y = 1 bằng y x = 4 1 y = 1 x O 1 4 9 119 7 21 A π. B π. C π. D π. 2 6 6 2 Lời giải. h Geogebra Pro Trang 11
Phương pháp: Gắn hệ trục tọa độ mới. Cho hai hàm số y Y
y = f (x), y = g(x) liên tục trên [a; b]. Khi đó thể tích vật
thể tròn xoay giới hạn bởi hai đồ thị số y = f (x), y = g(x)
và hai đường thẳng x = a, x = b khi quay quanh trục Ox là: 1 O0 3 X b Z V = π f 2(x) − g2(x) dx. x O 1 4 a  X = x − 1 Cách giải: Đặt
. Ta được hệ trục tọa độ OXY như  Y = y − 1 hình vẽ: √ √ √ Ta có: y = x ⇔ Y + 1 = X + 1 ⇔ Y = X + 1 − 1. Thể tích cần tìm là 3 3 Z √ Z √ Ä ä2 Ä ä V = π X + 1 − 1 dX = π X + 2 − 2 X + 1 dX o/ 0 0 3 aPr Å 1 4 √ ã ïÅ 9 32 ã Å 4 ãò 7π = π X2 + 2X − (X + 1) X + 1 = π + 6 − − − = . 2 3 2 3 3 6 0 Chọn phương án C iz − (3i + 1)z 26iz
Câu 35. Cho số phức z 6= 0 thỏa mãn = |z|2. Số phức w = có môđun bằng 1 + i 9 √ √ A 9. B 26. C 6. D 5. roups/GeoGebr Lời giải.
Gọi số phức z có dạng : z = a + bi(a, b ∈ R).
Do z 6= 0 nên a2 + b2 > 0. Ta có: iz − (3i + 1)z = |z|2 1 + i acebook.com/g
⇔iz − (3i + 1)z = (1 + i) |z|2 .f
⇔i(a + bi) − (3i + 1)(a − bi) = (1 + i)(a2 + b2)
⇔ia − b − 3ai − 3b − a + bi = a2 + b2 + i(a2 + b2)
⇔(−a − 4b) + (b − 2a)i = a2 + b2 + i(a2 + b2)   https://www  − a − 4b = a2 + b2  − a − 4b = b − 2a ⇔ ⇔ b − 2a = a2 + b2  − a − 4b = a2 + b2  a = 5b     a = 5b   ⇔ ⇔ b = 0  − 9b = 26b2    9    b = − 26 a = b = 0 (loại) ⇔  45 9 a = − , b = − 26 26 26 Å 45 9 ã √ Vậy : w = i − − i = 1 − 5i ⇒ |w| = 26 9 26 26 Chọn phương án B h Geogebra Pro Trang 12
Câu 36. Cho số phức z thỏa |z − 1 + 2i| = 3. Biết rằng tập hợp các điểm biểu diễn của số phức
w = 2z + i trên mặt phẳng (Oxy) là một đường tròn. Tìm tâm của đường tròn đó. A I (2; −3). B I(1; 1). C I(0; 1). D I(1; 0). Lời giải.
Gọi M là điểm biểu diễn số phức w. w − i Ta có w = 2z + i ⇔ z = . 2 w − i
Do đó |z − 1 + 2i| = 3 ⇔
− 1 + 2i = 3 ⇔ |w − 2 + 3i| = 6 ⇔ M I = 6, với I (2; −3). 2
Do đó tập hợp điểm M là đường tròn tâm I (2; −3) và bán kính R = 6. Chọn phương án A
Câu 37. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α) : x − 2z − 6 = 0 và đường thẳng   x = 1 + t     d :
y = 3 + t . Viết phương trình đường thẳng ∆ nằm trong mặt phẳng (α) cắt đồng thời vuông      z = −1 − t góc với d. x − 2 y − 4 z + 2 x − 2 y − 4 z + 2 A = = . B = = . 2 1 1 2 −1 1 x − 2 y − 3 z + 2 x − 2 y − 4 z − 2 C = = . D = = . 2 −1 1 2 −1 1 2019-2020 Lời giải.   x = 1 + t  THPT       y = 3 + t
Giao điểm I của d và (α) là nghiệm của hệ ⇒ I (2; 4; −2).  z = −1 − t GHIỆP    N    T  x − 2z − 6 = 0 TỐ #»
Mặt phẳng (α) có một vectơ pháp tuyến n = (1; 0; −2) ; đường thẳng d có một vectơ chỉ phương THI #» u = (1; 1; −1). #» #»
Khi đó đường thẳng ∆ có một vectơ chỉ phương là [ n , u ] = (2; −1; 1). #» #» LUYỆN
Đường thẳng ∆ qua điểm I (2; 4; −2) và có một vectơ chỉ phương [ n , u ] = (2; −1; 1) nên có phương x − 2 y − 4 z + 2 trình chính tắc: = = . 2 −1 1 Chọn phương án B x y z + 1 x − 3 y z − 1
Câu 38. Trong không gian Oxyz cho ba đường thẳng d : = = , ∆1 : = = , 1 1 −2 2 1 1 x − 1 y − 2 z ∆2 : = =
. Đường thẳng ∆ vuông góc với d đồng thời cắt ∆1, ∆2 tương ứng tại H, K sao 1 2 1 #»
cho độ dài HK nhỏ nhất. Biết rằng ∆ có một vectơ chỉ phương u (h; k; 1). Giá trị h − k bằng A 0. B 4. C 6. D −2. Lời giải.
Ta có H ∈ ∆1 ⇔ H(3 + 2t; t; 1 + t); K ∈ ∆2 ⇔ K(1 + m; 2 + 2m; m). # »
Suy ra HK = (m − 2t − 2; 2m − t + 2; m − t − 1). #»
Đường thẳng d có một VTCP là ud = (1; 1; −2). # » # » ∆ ⊥ d ⇔ #»
ud.HK = 0 ⇔ m − t + 2 = 0 ⇔ m = t − 2 ⇒ HK = (−t − 4; t − 2; −3).
Ta có HK2 = (−t − 4)2 + (t − 2)2 + (−3)2 = 2(t + 1)2 + 27 > 27, ∀t ∈ R. h Geogebra Pro Trang 13 √ ⇒ min HK =
27, đạt được khi t = −1. # » #»
Khi đó ta có HK = (−3; −3; −3), suy ra u (1; 1; 1) ⇒ h = k = 1 ⇒ h − k = 0. Chọn phương án A
Câu 39. Cho hai hộp, hộp thứ nhất chứa 5 viên bi đỏ và 7 viên bi vàng, hộp thứ hai chứa 3 bi đỏ và
n bi vàng (n ∈ N). Khi chọn ngẫu nhiên mỗi hộp một viên bi, xác suất để chọn được hai bi khác màu 7 là
. Số bi vàng trong hộp thứ hai là? 15 A n = 12. B n = 10. C n = 7. D n = 5. Lời giải.
Không gian mẫu |Ω| = 12 · (n + 3).
Gọi A là biến cố chọn được hai bi khác màu. 5n + 7 · 3 7 Ta có P(A) = = ⇒ n = 7. 12(n + 3) 15 Chọn phương án C o/ Câu 40. aPr
Cho hình hộp chữ nhật ABCD.A0B0C0D0 có cạnh bằng C0 D0
AB = 2a, AD = AA0 = a như hình vẽ. Khoảng cách giữa
hai đường thẳng BD và AD0 bằng a √ 2a A a. B . C a 3. D . 2 3 A0 B0 C roups/GeoGebr D A B Lời giải.
Xét hệ trục tọa độ Oxyz sao cho A(0; 0; 0), B(2a; 0; 0), D(0; a; 0), A0(0; 0; a). Ta có D0(0; a; a). acebook.com/g .f # » # » # »
Khi đó BD = (−2a; a; 0), AD0 = (0; a; a), AB = (2a; 0; 0). # » # » # » # » # »
Ta có AD0 ∧ BD = (−a2; −2a2; 2a2), (AD0 ∧ BD)AB = −2a3. # » # » # » (AD0 ∧ BD)AB https://www 2a3 2a d (AD0, BD) = = = . # » # » AD0 ∧ BD 3a2 3 Chọn phương án D 5−x + 2
Câu 41. Tìm tất cả các giá trị khác nhau của tham số m để hàm số y = đồng biến trên 5−x − m (−∞; 0). A m < −2. B m ≤ −2. C −2 < m ≤ 1. D −2 < m < 1. Lời giải.
ĐK: 5−x 6= m. Đặt t = 5−x là hàm nghịch biến trên (−∞; 0) (1), suy ra t ∈ (1; +∞). t + 2 −m − 2 Xét hàm số y = f (t) = , f 0(t) = . t − m (t − m)2 5−x + 2 t + 2 Do (1), để hàm số y =
đồng biến trên (−∞; 0) thì hàm số f (t) = nghịch biến trên 5−x − m t − m h Geogebra Pro Trang 14 (1; +∞)    − m − 2 < 0 m > −2
⇔ f 0(t) < 0, ∀t ∈ (1; +∞) ⇔ ⇔ ⇔ −2 < m ≤ 1. m / ∈ (1, +∞) m ≤ 1 Chọn phương án C
Câu 42. Dân số thế giới được tính theo công thức S = A · eni trong đó A là dân số của năm lấy làm
mốc tính, S là dân số sau n năm, i là tỉ lệ tăng dân số hàng năm. Cho biết năm 2005 Việt Nam có
khoảng 80.902.400 người và tỉ lệ tăng dân số là 1, 47% một năm. Như vậy, nếu tỉ lệ tăng dân số hàng
năm không đổi thì đến năm 2019 số dân của Việt Nam sẽ gần với số nào nhất sau đây? A 99.389.200. B 99.386.600. C 100.861.100. D 99.251.200. Lời giải.
Áp dụng công thức S = A · eni với A = 80.902.400, n = 2019 − 2005 = 14, i = 1, 47% = 0, 0147, ta có
số dân Việt Nam đến năm 2017 là
S = A · eni = 80902400 · e14·0,0147 ≈ 99389203,38.
Như vậy, số dân Việt Nam đến năm 2019 gần với số 99.389.200 nhất. Chọn phương án A Câu 43. 2019-2020
Cho hàm số y = f (x). Hàm số y = f 0(x) x −∞ −4 1 +∞
có bảng biến thiên như sau. Bất phương trình THPT
f (x) > sin x + m có nghiệm trên khoảng (−1; 1) y0 − 0 + 0 − khi và chỉ khi +∞ + −1 GHIỆP A m > f (1) − sin 1. y N T B m ≥ f (1) − sin 1. −3 −∞ TỐ C m ≤ f (−1) + sin 1. THI D m < f (−1) + sin 1. Lời giải. LUYỆN
Xét hàm số g(x) = f (x) − sin x. g0(x) = f 0(x) − cos x.
Với ∀x ∈ (−1; 1), ta có f 0(x) < −1 ⇒ f 0(x) − cos x < −1 − cos x < 0 ⇒ g0(x) < 0.
Suy ra hàm số g(x) nghịch biến trên khoảng (−1; 1) nên g(x) < g (−1) = f (−1) + sin 1.
Do đó bất phương trình f (x) > sin x + m có nghiệm trên khoảng (−1; 1) khi và chỉ khi bất phương
trình m < f (x) − sin x có nghiệm trên khoảng (−1; 1).
⇔ m < max g(x) ⇔ m < f (−1) + sin 1. [−1;1] Vậy m < f (−1) + sin 1. Chọn phương án D
Câu 44. Hình trụ có bán kính đáy bằng a chu vi của thiết diện qua trục bằng 10a Thể tích của khối trụ đã cho bằng A 4πa3. B πa3. C 3πa3. D 5πa3. Lời giải. h Geogebra Pro Trang 15
Thiết diện qua trục là 1 hình chữ nhật. O0 A0 B0
Giả sử chiều cao của khối trụ là b.
Theo đề ta có 2(2a + b) = 10a ⇔ b = 3a. b
Thể tích khối trụ là V = S.h = πa2.3a = 3πa3. A B O a Chọn phương án C Å 1 ã ï 1 ò
Câu 45. Cho hàm số y = f (x) liên tục và thỏa mãn f (x) + 2f = 3x với x ∈ ; 2 . Tính x 2 2 Z f (x) I = dx. x 1 2 3 3 9 9 A I = . B I = − . C I = . D I = − . 2 2 2 2 o/ Lời giải. Å ã Å ã aPr 1 1 1 2 Ta có f (x) + 2f = 3x và f + 2f (x) = 3 · . Suy ra f (x) = − x. x x x x 2 2 Z f (x) Z Å 2 ã 3 I = dx = − 1 dx = . x x2 2 1 1 2 2 Chọn phương án A roups/GeoGebr
Câu 46. Phương trình |x3 − 3x| = m2 + m có 6 nghiệm phân biệt khi và chỉ khi A m > 0. B m < −2hoặc m > 1. C −1 < m < 0.
D −2 < m < −1 hoặc 0 < m < 1. Lời giải.
Đồ thị của hàm số y = |x3 − 3x|. acebook.com/g y .f 2 1 x https://www −2 −1 O 1 2
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = |x3 − 3x| và đường thẳng y = m2 +m.  0 < m < 1
Suy ra phương trình có 6 nghiệm phân biệt khi và chỉ khi 0 < m2 + m < 2 ⇔  − 2 < m < −1. Chọn phương án D
Câu 47. Cho hai số thực a, b > 1 sao cho tồn tại số thực 0 < x 6= 1 thỏa mãn alogb x = bloga(x2). Tìm
giá trị nhỏ nhất của P = ln2 a + ln2 b − ln(ab). √ √ 1 3 + 2 2 e 1 − 3 3 A . B − . C . D . 4 12 2 4 Lời giải. h Geogebra Pro Trang 16 Ta có alogb x = bloga(x2) ⇒ xlogb a = (x2)loga b ⇒ log a = 2 · log b b a ln a ln b ⇔ = 2 · ln b ln a ⇔ ln2 a = 2 · ln2 b √ ⇒ ln a = 2 ln b, (vì a, b > 1). Ta được P = ln2 a + ln2 b − ln(ab) √ Ä ä = 3 ln2 b − 1 + 2 ln b √ √ Ä ä2 Ç√ å2 1 + 2 1 + 2 = 2 ln b − √ − 2 3 12 √ 3 + 2 2 ≥ − . 12 2019-2020 Chọn phương án B THPT
Câu 48. Có bao nhiêu giá trị nguyên của tham số m để max |x3 − 3x2 + m| ≤ 4? [1;3] A 5. B 4. C 6. D Vô số. GHIỆP N Lời giải. T  x = 0 / ∈ (1; 3) TỐ
Xét hàm số f (x) = x3 − 3x2 + m trên [1; 3], f 0(x) = 0 ⇔ 3x2 − 6x = 0 ⇔  THI x = 2 ∈ (1; 3) . Bảng biến thiên LUYỆN x 1 2 3 f 0(x) − 0 + m − 2 m f (x) m − 4    |m| ≤ 4  − 4 ≤ m ≤ 4
Vì m − 4 < m − 2 < m nên max |f (x)| ≤ 4 ⇔ ⇔ ⇔ 0 ≤ m ≤ 4. [1;3]  |m − 4| ≤ 4 0 ≤ m ≤ 8 ⇒ m ∈ {0; 1; 2; 3; 4}. Chọn phương án A
Câu 49. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC), góc giữa đường
thẳng SB và mặt phẳng (ABC) bằng 60◦. Khoảng cách giữa hai đường thẳng AC và SB bằng: √ √ √ a 2 a 15 a 7 A . B 2a. C . D R = . 2 5 7 Lời giải. h Geogebra Pro Trang 17
SA ⊥ (ABC) ⇒AB là hình chiếu vuông góc của SB lên S (ABC) Suy ra ( ¤ SB, (ABC)) = Ÿ (SB, AB) = ’ SBA = 60◦ √ ⇒ SA = AB. tan 60◦ = a 3
Lấy điểm D sao cho ACBD là hình bình hành.  H A M C AK ⊥ BD tại K Dựng AH ⊥ SK tại H D K B  BK ⊥ AK Ta có ⇒ BK ⊥ (SAK)⇒ BK ⊥ AH BK ⊥ SA Từ đó AH ⊥ (SBK)  BK k AC     Vì BK ⊂ (SBK)
⇒ AC k (SBK) ⇒ d (AC, SB) = d (A, (SBK)) = AH o/     AC 6⊂ (S BK ) aPr √ a 3
Gọi M là trung điểm AC⇒ BM = AK =
(với BM đường cao trong 4ABC đều cạnh a). 2 √ 1 1 1 5 a 15
Xét tam giác SAK vuông tại A ta có: = + = ⇒ AH = √ AH2 AK2 SA2 3a2 5 a 15 Vậy d (AC, SB) = 5 Chọn phương án C roups/GeoGebr
Câu 50. Cho hàm số y = f (x), biết hàm số y = f 0(x) có đồ thị như hình bên dưới. y acebook.com/g .f −6 −1 O 2 x https://www
Hàm số g(x) = f (3 − x2) đồng biến trên khoảng? A (2; 3). B (−1; 0). C (−2; −1). D (0; 1). Lời giải.
Dựa vào đồ thị, ta có bảng xét dấu x −∞ −6 −1 2 +∞ y0 − 0 + 0 − 0 + g0(x) = −2xf 0 (3 − x2). h Geogebra Pro Trang 18 x = 0   − 2x = 0 x = ±3 g(x) = 0 ⇔   ⇔  f 3 − x2 = 0 x = ±2   x = ±1.  − 3 < x < −2
 − 6 < 3 − x2 < −1  f (3 − x2) > 0 ⇔   ⇔ 2 < x < 3  2 < 3 − x2  − 1 < x < 1. Bảng biến thiên: x −∞ −3 −2 −1 0 1 2 3 +∞ f 0(3 − − 0 + 0 − 0 + | + 0 − 0 + 0 − x2) −2x + | + | + | + 0 − | − | − | − g0 − 0 + 0 − 0 + 0 − 0 + 0 − 0 +
Từ BBT suy ra hàm số đồng biến trên (−1; 0). Chọn phương án B 2019-2020
———————–HẾT———————– THPT GHIỆP N T TỐ THI LUYỆN h Geogebra Pro Trang 19 BẢNG ĐÁP ÁN 1. D 2. C 3. D 4. A 5. A 6. C 7. A 8. B 9. D 10. D 11. D 12. D 13. A 14. A 15. C 16. A 17. C 18. D 19. B 20. A 21. C 22. D 23. D 24. B 25. B 26. B 27. B 28. D 29. D 30. B 31. A 32. C 33. C 34. C 35. B 36. A 37. B 38. A 39. C 40. D 41. C 42. A 43. D 44. C 45. A 46. D 47. B 48. A 49. C 50. B o/ aPr roups/GeoGebr acebook.com/g .f https://www h Geogebra Pro Trang 20 MỖI NGÀY MỘT ĐỀ THI 9
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Một trường cấp ba của tỉnh X có 8 giáo viên Toán gồm có 3 nữ và 5 nam, giáo viên Vật lý thì
có 4 giáo viên nam. Hỏi có bao nhiêu cách chọn ra một đoàn thanh tra công tác ôn thi TNTHPT gồm
3 người có đủ 2 môn Toán và Vật lý và phải có giáo viên nam và giáo viên nữ trong đoàn? A 120 cách. B 60 cách. C 12960 cách. D 90 cách.
Câu 2. Cho cấp số cộng có tổng n số hạng đầu là S ∗
n = 3n2 + 4n, n ∈ N . Giá trị của số hạng thứ 10 của cấp số cộng là A u10 = 55. B u10 = 67. C u10 = 61. D u10 = 59.
Câu 3. Phương trình 72x2+6x+4 = 49 có tổng tất cả các nghiệm bằng 5 5 A 1. B . C −1. D − . 2 2
Câu 4. Hình lập phương có độ dài đường chéo là 6 thì có thể tích là 2019-2020 √ √ √ A 2 2. B 54 2. C 24 3. D 8. THPT
Câu 5. Tìm tập xác định D của hàm số y = plog(x + 1) − 1. A D = (10; +∞). B D = (9; +∞). C D = (−∞; 9). D D = R \ {−1}. GHIỆP N
Câu 6. Hàm số F (x) = x2 ln (sin x − cos x) là nguyên hàm của hàm số nào dưới đây? T x2 TỐ A f (x) = . sin x − cos x THI x2
B f (x) = 2x ln (sin x − cos x) + . sin x − cos x x2 (cos x + sin x)
C f (x) = 2x ln (sin x − cos x) + . LUYỆN sin x − cos x x2 (sin x + cosx) D f (x) = . sin x − cos x
Câu 7. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, tam giác SAB đều và nằm trong
mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC. √ √ a3 a3 3 a3 3 a3 A V = . B V = . C V = . D V = . 8 3 4 4
Câu 8. Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a. Thể tích của khối nón đã cho bằng √ √ 3πa3 3πa3 2πa3 πa3 A . B . C . D . 3 2 3 3
Câu 9. Cho mặt cầu (S) có diện tích bằng 4a2π cm2. Tính thể tích khối cầu (S). 4a3π 16a3π A 16a3π cm3. B 32a3π cm3. C cm3. D cm3. 3 3 Câu 10. h Geogebra Pro Trang 1
Cho hàm số y = f (x) có bảng biến thiên x −∞ −1 1 +∞
như hình vẽ bên. Hàm số đã cho đồng biến y0 + 0 − 0 +
trên khoảng nào dưới đây? 3 +∞ + A (−1; +∞). B (−1; 1). y C (−∞; 1). D (1; +∞). −∞ −2 √
Câu 11. Cho a là số thực dương khác 1. Tính T = log a 3 a. a 1 3 4 1 A T = . B T = . C T = . D T = . 3 4 3 4
Câu 12. Một hình trụ có bán kính đáy a, có thiết diện qua trục là một hình vuông. Tính diện tích xung quang của hình trụ. A 3πa2. B 4πa2. C 2πa2. D πa2.
Câu 13. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số o/ x −∞ −2 0 2 +∞ aPr y0 − 0 + 0 − 0 + y A 3. B 0. C 1. D 2. roups/GeoGebr
Câu 14. Phương trình tiếp tuyến của đồ thị hàm số y = x3 − 3x2 − x + 3 tại điểm M (1; 0) là A y = −x + 1. B y = −4x − 4. C y = −4x + 4. D y = −4x + 1. Câu 15.
Cho hàm số y = f (x) có bảng biến thiên như sau. x −∞ 1 +∞
Tổng số tiệm cận ngang và tiệm cận đứng của đồ acebook.com/g +∞ 5 .f thị hàm số đã cho là f (x) A 4. . B 1. 2 3 C 3. D 2. 1
Câu 16. Tìm tập nghiệm của bất phương trình log (x + 1) > . https://www 25 2 A S = (−4; +∞). B S = (−∞; 4). C S = (−1; 4). D S = (4; +∞). Câu 17.
Cho hàm số y = f (x) có đồ thị hàm số như hình bên. Phương trình y
f (x) = 1 có bao nhiêu nghiệm thực phân biệt nhỏ hơn 2? 2 −1 O 2 x −2 A 0. B 1. C 2. D 3. h Geogebra Pro Trang 2 π 2 Z sin x − cos x a a Câu 18. Nếu √ dx =
ln c, (với a, b, c ∈ Z, a > 0,
là phân số tối giản) thì a + 2b + 3c 1 + sin 2x b b π 4 là A 13. B 14. C 9. D 11. Câu 19.
Điểm M trong hình vẽ bên là điểm biểu diễn số phức z. Tìm phần y 1
thực và phần ảo của số phức z. x O
A Phần thực là −2 và phần ảo là i.
B Phần thực là 1 và phần ảo là −2. −2 M
C Phần thực là 1 và phần ảo là −2i.
D Phần thực là −2 và phần ảo là 1.
Câu 20. Trong mặt phẳng tọa độ Oxyz, tập hợp các điểm biểu biễn các số phức z thỏa mãn |z − 1 + 2i| =
|z + 1 + 2i| là đường thẳng có phương trình. A x − 2y + 1 = 0. B x + 2y = 0. C x − 2y = 0. D x + 2y + 1 = 0.
Câu 21. Cho số phức z thoả mãn z − 4 = (1 + i)|z| − (4 + 3z)i. Môđun của số phức z bằng A 2. B 1. C 16. D 4. 2019-2020
Câu 22. Trong không gian với hệ trục Oxyz, cho điểm M (3; 2; −1). Gọi A, B lần lượt là hình chiếu
vuông góc của điểm M lên trục Oy, Oz. Tính diện tích tam giác OAB. THPT 3 1 A . B . C 1. D 2. 2 2
Câu 23. Trong không gian Oxyz, cho mặt cầu (S) tâm I nằm trên mặt phẳng (Oxy) đi qua ba điểm GHIỆP N
A(1; 2; −4), B(1; −3; 1), C(2; 2; 3). Tìm tọa độ điểm I. T TỐ A I(2; −1; 0). B I(0; 0; 1). C I(0; 0; −2). D I(−2; 1; 0). THI
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1; 0; 0), B(0; −1; 0) và C(0; 0; 2). Phương trình mặt phẳng (ABC) là z y LUYỆN A x − 2y + z = 0. B x − y + = 1. C x + − z = 1. D 2x − y + z = 0. 2 2
Câu 25. Trong không gian Oxyz, cho điểm M (3; 2; −1) và mặt phẳng (P ) : x + z − 2 = 0. Đường thẳng
đi qua M và vuông góc với (P ) có phương trình là     x = 3 + t x = 3 + t x = 3 + t x = 3 + t             A y = 2 . B y = 2 + t . C y = 2t . D y = 1 + 2t .             z = −1 + t z = −1 z = 1 − t z = −t
Câu 26. Cho hình lập phương ABCD.A0B0C0D0. Tính góc giữa hai mặt phẳng (A0B0C) và (C0D0A). A 45◦. B 30◦. C 60◦. D 90◦.
Câu 27. Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau x −∞ −2 0 1 3 +∞ f 0(x) + 0 − 0 + 0 − 0 − h Geogebra Pro Trang 3
Hàm số đã cho có bao nhiêu điểm cực trị? A 3. B 1. C 2. D 4. √
Câu 28. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x + 4 − x2. Hãy tính P = M + m. √ √ √ √ Ä ä Ä ä A P = 2 2 − 1 . B P = 2 2 + 1 . C P = 2 + 1. D P = 2 − 1.
Câu 29. Cho a > 0, b > 0 thỏa mãn a2 + 4b2 = 5ab. Khẳng định nào sau đây đúng?
A 2 log(a + 2b) = 5(log a + log b). B log(a + 1) + log b = 1. a + 2b log a + log b C 2 log = .
D log(a + 2b) = log a − log b. 3 2
Câu 30. Cho hàm số y = f (x) có đồ thị như hình vẽ bên. y 4 o/ aPr 2 x −1 O 1 roups/GeoGebr
Phương trình |f (x − 2) − 2| = π có bao nhiêu nghiệm thực phân biệt? A 4. B 2. C 6. D 3. Å ã Ä ä 1
Câu 31. Tập nghiệm của bất phương trình log
1 + log x − log x < 1 có dạng S = ; b với a, b 2 1 9 9 a
là những số nguyên. Mệnh đề nào dưới đây đúng? A a = −b. B a + b = 1. C a = b. D a = 2b. acebook.com/g .f
Câu 32. Cho hình nón tròn xoay có đường cao bằng 20 cm, bán kính đáy bằng 25 cm. Một thiết diện
đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiến diện là 12 cm.
Tính diện tích của thiết diện đó. A 500 cm2. B 1000 cm2. C 250 cm2. D 250 cm3. https://www
Câu 33. Cho hàm số f (x) xác định trên (0; +∞) và thỏa mãn xf 0(x) = −[f (x)]2 · ln x; f (1) = 1. Giá trị f (e) bằng 2 e 2e 1 A . B . C . D . 3 2 3 2
Câu 34. Cho hình phẳng D được giới hạn bởi hai đường y = 2(x2 − 1); y = 1 − x2. Tính thể tích khối
tròn xoay tạo thành do D quay quanh trục Ox. 64π 32 32π 64 A . B . C . D . 15 15 15 15
Câu 35. Cho số phức z = a + bi (a, b ∈ R) thỏa mãn |z| = 5 và z(2 + i)(1 − 2i) là một số thực. Tính P = |a| + |b|. A P = 8. B P = 4. C P = 5. D P = 7.
Câu 36. Tìm mô-đun của số phức z biết z − 4 = (1 + i) |z| − (4 + 3z) i. h Geogebra Pro Trang 4 1 A |z| = . B |z| = 2. C |z| = 4. D |z| = 1. 2 x + 1 y − 1 z − 2
Câu 37. Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng (d) : = = và 2 1 3
mặt phẳng (P ) : x − y − z − 1 = 0. Viết phương trình đường thẳng (∆) đi qua điểm A(1; 1; −2), biết
(∆) k (P ) và (∆) cắt (d). x − 1 y − 1 z + 2 x − 1 y − 1 z + 2 A = = . B = = . 1 −1 −1 2 1 3 x − 1 y − 1 z + 2 x − 1 y − 1 z + 2 C = = . D = = . 8 3 5 2 1 1 x y + 4 z − 3 x − 1 y + 3
Câu 38. Trong không gian Oxyz cho hai đường thẳng d1 : = = và d2 : = = 1 1 −1 −2 1
z − 4 . Đường thẳng vuông góc với mặt phẳng tọa độ (Oxz) và cắt d −
1 và d2 có phương trình là 5  3    x =  x = 1  7 x = 1 x = t           −25   A y = −1 + t . B y = + t . C y = −3 + t . D y = −4 + t . 7           18   z = −1  z = 4 z = 3 + t  z = 7
Câu 39. Cho hai chiếc hộp A và B. Hộp A chứa 6 viên bi trắng, 4 viên bi đen. Hộp B chứa 7 viên
bi trắng, 3 viên bi đen. Người ta lấy ngẫu nhiên một viên bi từ hộp A và bỏ vào hộp B rồi sau đó từ
hộp B lấy ngẫu nhiên ra hai viên bi. Tính xác suất để hai viên bi lấy được từ hộp B là hai viên bi 2019-2020 trắng. 126 21 123 37 A . B . C . D . THPT 275 55 257 83
Câu 40. Cho hình chóp S.ABC có SA = 3a và SA ⊥ (ABC). Biết AB = BC = 2a và ’ ABC = 120◦. GHIỆP
Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng N 3a a T A . B . C a. D 2a. 2 2 TỐ
Câu 41. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (−2019; 2019) để hàm số THI h π i
y = sin3 x − 3 cos2 x − m sin x − 1 đồng biến trên đoạn 0; ? 2 A 2020. B 2019. C 2028. D 2018. LUYỆN
Câu 42. Một người mỗi tháng đều đặn gửi vào một ngân hàng một khoản tiền T theo hình thức lãi
kép với lãi suất 0,6% mỗi tháng. Biết sau 15 tháng người đó có số tiền là 10 triệu đồng. Hỏi số tiền T
gần với số tiền nào nhất sau đây? A 635.000 đồng. B 645.000 đồng. C 613.000 đồng. D 535.000 đồng. Câu 43.
Cho hàm số y = f (x) xác định trên R \ {0} có bảng biến x −∞ −2 0 +∞ y0 −
thiên như hình vẽ bên. Số nghiệm của phương trình 0 + + +∞ + +∞ +∞
2 |f (2x − 3)| − 13 = 0 là y A 3. B 2. C 4. D 1. 7 −∞
Câu 44. Cho hình trụ có bán kính đáy bằng a và chiều cao h. Tính thể tích V của khối lăng trụ tam
giác đều tam giác đều nội tiếp hình trụ đã cho. √ √ 3a2h 3 3a2h A V = . B V = . 4 4 h Geogebra Pro Trang 5 √ π Å 4a2 ã … h2 a2 3 3πa2h C V = h2 + + . D V = . 3 3 4 3 4 1
Câu 45. Cho hàm số f (x), f (−x) liên tục trên R và thỏa mãn 2f (x) + 3f (−x) = . Tính 4 + x2 2 Z I = f (x) dx. −2 π π π π A . B . C − . D − . 20 10 20 10
Câu 46. Cho hàm số y = f (x) có bảng biến thiên như sau: x −∞ −1 3 +∞ y0 + 0 − 0 + 5 +∞ + o/ y aPr −∞ 1
Phương trình f (x) − 2 = 0 có bao nhiêu nghiệm? A 1. B 3. C 2. D 0 .
Câu 47. Cho x, y là hai số thực dương thỏa mãn ln x + ln y ≥ ln(x2 + y). Tìm giá trị nhỏ nhất của roups/GeoGebr P = x + y. √ √ √ √ A P = 2 + 3 2. B P = 6. C P = 2 2 + 3. D P = 17 + 3.
Câu 48. Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị nhỏ nhất của hàm số
y = sin4 x + cos 2x + m bằng 2. Số phần tử của S là A 4. B 3. C 1. D 2. acebook.com/g √ .f
Câu 49. Cho hình hộp ABCD.A0B0C0D0 có đáy là hình thoi cạnh a 3, BD = 3a, hình chiếu vuông
góc của B trên mặt phẳng (A0B0C0D0) trùng với trung điểm của A0C0. Gọi (α) là góc tạo bởi hai mặt √21
phẳng (ABCD) và (CDD0C0), cos α =
. Tính thể tích khối hộp. √ 7 √ 3a3 9 3a3 9a3 3 3a3 A . B . C . D . https://www 4 4 4 4
Câu 50. Có bao nhiêu số nguyên m ∈ (−7; 7) để đồ thị hàm số y = |x4 − 3mx2 − 4| có đúng 3 điểm
cực trị A, B, C và diện tích tam giác ABC lớn hơn 4. A 4. B 2. C 1. D 3.
———————–HẾT———————– h Geogebra Pro Trang 6 BẢNG ĐÁP ÁN 1. D 2. C 3. D 4. C 5. B 6. C 7. A 8. A 9. C 10. D 11. C 12. C 13. A 14. C 15. C 16. D 17. C 18. D 19. B 20. C 21. A 22. C 23. D 24. B 25. A 26. D 27. A 28. A 29. C 30. B 31. C 32. A 33. A 34. A 35. D 36. B 37. C 38. B 39. A 40. A 41. B 42. A 43. B 44. B 45. A 46. B 47. C 48. D 49. C 50. C 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN h Geogebra Pro Trang 7 MỖI NGÀY MỘT ĐỀ THI 9
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Một trường cấp ba của tỉnh X có 8 giáo viên Toán gồm có 3 nữ và 5 nam, giáo viên Vật lý thì
có 4 giáo viên nam. Hỏi có bao nhiêu cách chọn ra một đoàn thanh tra công tác ôn thi TNTHPT gồm
3 người có đủ 2 môn Toán và Vật lý và phải có giáo viên nam và giáo viên nữ trong đoàn? A 120 cách. B 60 cách. C 12960 cách. D 90 cách. Lời giải.
TH1: Đoàn công tác gồm 2 giáo viên Toán và 1 giáo viên Vật lý.
Trường hợp này có C1C1C1 + C1C2 = 72. 4 3 5 4 3
TH2: Đoàn công tác gồm 2 giáo viên Vật lý và 1 giáo viên Toán. Trường hợp này có C2C1 = 18. 4 3
Vậy có 72 + 18 = 90 cách chọn một đoàn công tác thỏa mãn yêu cầu. Chọn phương án D
Câu 2. Cho cấp số cộng có tổng n số hạng đầu là S ∗
n = 3n2 + 4n, n ∈ N . Giá trị của số hạng thứ 10 2019-2020 của cấp số cộng là A u THPT 10 = 55. B u10 = 67. C u10 = 61. D u10 = 59. Lời giải. Ta có S1 = 7 ⇒ u1 = 7. GHIỆP N
S2 = 3(2)2 + 4(2) = 20 ⇒ u1 + u2 = 20 ⇒ u2 = 13. T TỐ
Do đó công sai d = 6. Khi đó u10 = u1 + 9d = 7 + 9 · 6 = 61. Chọn phương án C THI
Câu 3. Phương trình 72x2+6x+4 = 49 có tổng tất cả các nghiệm bằng 5 5 LUYỆN A 1. B . C −1. D − . 2 2 Lời giải.
Phương trình đã cho tương đương với  1 x = −
72x2+6x+4 = 72 ⇔ 2x2 + 5x + 4 = 2 ⇔ 2  x = −2. 1 5
Vậy tổng tất cả các nghiệm bằng − − 2 = − . 2 2 Chọn phương án D
Câu 4. Hình lập phương có độ dài đường chéo là 6 thì có thể tích là √ √ √ A 2 2. B 54 2. C 24 3. D 8. Lời giải. Phương pháp: √
Sử dụng công thức hình lập phương cạnh a có độ dài đường chéo chính là a 3.
Thể tích hình lập phương cạnh a là V = a3. h Geogebra Pro Trang 1 Cách giải: √
Gọi độ dài cạnh hình lập phương là a, (a > 0) thì độ dài đường chéo hình lập phương là a 3 = 6 ⇔ √ a = 2 3. √ √ Ä ä3
Thể tích hình lập phương là V = 2 3 = 24 3. Chọn phương án C
Câu 5. Tìm tập xác định D của hàm số y = plog(x + 1) − 1. A D = (10; +∞). B D = (9; +∞). C D = (−∞; 9). D D = R \ {−1}. Lời giải.    x + 1 > 0 x + 1 > 0 x + 1 > 0 Điều kiện : ⇔ ⇔ ⇔ x ≥ 9.  log(x + 1) − 1 ≥ 0  log(x + 1) ≥ 1 x + 1 ≥ 10 Vậy D = (9; +∞). Chọn phương án B o/
Câu 6. Hàm số F (x) = x2 ln (sin x − cos x) là nguyên hàm của hàm số nào dưới đây? aPr x2 A f (x) = . sin x − cos x x2
B f (x) = 2x ln (sin x − cos x) + . sin x − cos x x2 (cos x + sin x)
C f (x) = 2x ln (sin x − cos x) + . sin x − cos x x2 (sin x + cosx) D f (x) = . roups/GeoGebr sin x − cos x Lời giải.
Vì F (x) là một nguyên hàm của f (x) nên (sin x − cos x)0 sin x + cos x
f (x) = F 0 (x) = 2x · ln (sin x − cos x) + x2 ·
= 2x · ln (sin x − cos x) + x2 · . sin x − cos x sin x − cos x Chọn phương án C acebook.com/g .f
Câu 7. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, tam giác SAB đều và nằm trong
mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC. √ √ a3 a3 3 a3 3 a3 A V = . B V = . C V = . D V = . 8 3 4 4 Lời giải. https://www
Gọi H là trung điểm AB, suy ra SH⊥(ABCD). √ √ 1 1 a 3 a2 3 a3 Ta có VS.ABC = × SH × S∆ABC = × × = . 3 3 2 4 8 Chọn phương án A
Câu 8. Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a. Thể tích của khối nón đã cho bằng √ √ 3πa3 3πa3 2πa3 πa3 A . B . C . D . 3 2 3 3 Lời giải. √
Chiều cao h = p(2a)2 − a2 = a 3.√ 1 1 √ 3πa3 Thể tích V = Bh = πa2a 3 = . 3 3 3 Chọn phương án A h Geogebra Pro Trang 2
Câu 9. Cho mặt cầu (S) có diện tích bằng 4a2π cm2. Tính thể tích khối cầu (S). 4a3π 16a3π A 16a3π cm3. B 32a3π cm3. C cm3. D cm3. 3 3 Câu 10.
Cho hàm số y = f (x) có bảng biến thiên x −∞ −1 1 +∞
như hình vẽ bên. Hàm số đã cho đồng biến y0 + 0 − 0 +
trên khoảng nào dưới đây? 3 +∞ + A (−1; +∞). B (−1; 1). y C (−∞; 1). D (1; +∞). −∞ −2 Lời giải.
Từ bảng biến thiên ta thấy y0 > 0, ∀x > 1 suy ra hàm số đồng biến trên khoảng (1; +∞). Chọn phương án D √
Câu 11. Cho a là số thực dương khác 1. Tính T = log a 3 a. a 1 3 4 1 A T = . B T = . C T = . D T = . 3 4 3 4 Lời giải. 4 4
Ta có T = log a1+ 13 = log a 3 = . a a 3 Chọn phương án C
Câu 12. Một hình trụ có bán kính đáy a, có thiết diện qua trục là một hình vuông. Tính diện tích 2019-2020 xung quang của hình trụ. A 3πa2. B 4πa2. C 2πa2. D πa2. THPT Lời giải.
Ta có r = a và l = h = 2r = 2a. GHIỆP N
Khi đó, diện tích xung quanh hình trụ là T TỐ
Sxq = 2πrl = 2π · a · 2a = 4πa2. THI Chọn phương án C
Câu 13. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số LUYỆN x −∞ −2 0 2 +∞ y0 − 0 + 0 − 0 + y A 3. B 0. C 1. D 2. Lời giải.
Từ bảng biến thiên, ta suy ra hàm số có 3 điểm cực trị. Chọn phương án A
Câu 14. Phương trình tiếp tuyến của đồ thị hàm số y = x3 − 3x2 − x + 3 tại điểm M (1; 0) là A y = −x + 1. B y = −4x − 4. C y = −4x + 4. D y = −4x + 1. Lời giải. h Geogebra Pro Trang 3
Ta có y0 = 3x2 − 6x − 1 ⇒ y0(1) = −4.
Phương trình tiếp tuyến của đồ thị hàm số tại điểm M (1; 0) là y = −4(x − 1) ⇔ y = −4x + 4. Chọn phương án C Câu 15.
Cho hàm số y = f (x) có bảng biến thiên như sau. x −∞ 1 +∞
Tổng số tiệm cận ngang và tiệm cận đứng của đồ +∞ 5 thị hàm số đã cho là f (x) A 4. . B 1. 2 3 C 3. D 2. Lời giải.
limx→−∞ y = 2 ⇒ y = 2 là tiệm cận ngang
limx→+∞ y = 5 ⇒ y = 5 là tiệm cận ngang lim o/
x→1+ y = +∞ ⇒ x = 1 là tiệm cận đứng
Vậy tổng số tiệm cận ngang và tiệm cận đứng là 3. aPr Chọn phương án C 1
Câu 16. Tìm tập nghiệm của bất phương trình log (x + 1) > . 25 2 A S = (−4; +∞). B S = (−∞; 4). C S = (−1; 4). D S = (4; +∞). Lời giải. 1 1 Ta có: log (x + 1) >
⇔ x + 1 > 25 2 ⇔ x > 4. roups/GeoGebr 25 2 Chọn phương án D Câu 17.
Cho hàm số y = f (x) có đồ thị hàm số như hình bên. Phương trình y
f (x) = 1 có bao nhiêu nghiệm thực phân biệt nhỏ hơn 2? acebook.com/g 2 .f −1 O 2 x −2 https://www A 0. B 1. C 2. D 3. Lời giải. Phương pháp
Số nghiệm của phương trình f (x) = 1 là số giao điểm của đồ thị hàm số y = f (x) và đường thẳng y = 1.
Dựa vào đồ thị hàm số để biện luận số nghiệm của phương trình. Cách giải:
Số nghiệm của phương trình f (x) = 1 là số giao điểm của đồ thị hàm số y = f (x) và đường thẳng y = 1.
Dựa vào đồ thị hàm số ta thấy đường thẳng y = 1 cắt đồ thị hàm số y = f (x) tại 3 điểm phân biệt
trong đó có hai điểm có hoành độ nhỏ hơn 2. h Geogebra Pro Trang 4 Chọn phương án C π 2 Z sin x − cos x a a Câu 18. Nếu √ dx =
ln c, (với a, b, c ∈ Z, a > 0,
là phân số tối giản) thì a + 2b + 3c 1 + sin 2x b b π 4 là A 13. B 14. C 9. D 11. Lời giải. √ h π π i Có
1 + sin 2x = p(sin x + cos x)2 = sin x + cos x, vì x ∈ ; . Suy ra 4 2 π π 2 2 Z sin x − cos x Z sin x − cos x √ dx = dx 1 + sin 2x sin x + cos x π π 4 4 π 2 Z d(sin x + cos x) π √ Ä ä 1 = −
= − ln | sin x + cos x|| 2π = − ln 1 − ln 2 = ln 2. sin x + cos x 4 2 π 4 2019-2020
Suy ra a = 1, b = 2, c = 2. Vậy a + 2b + 3c = 11. THPT Chọn phương án D GHIỆP Câu 19. N T
Điểm M trong hình vẽ bên là điểm biểu diễn số phức z. Tìm phần y TỐ 1
thực và phần ảo của số phức z. x O THI
A Phần thực là −2 và phần ảo là i.
B Phần thực là 1 và phần ảo là −2. LUYỆN −2 M
C Phần thực là 1 và phần ảo là −2i.
D Phần thực là −2 và phần ảo là 1. Lời giải.
Điểm M có tọa độ M (1; −2) nên z = 1 − 2i.
Vậy phần thực là 1 và phần ảo là −2. Chọn phương án B
Câu 20. Trong mặt phẳng tọa độ Oxyz, tập hợp các điểm biểu biễn các số phức z thỏa mãn |z − 1 + 2i| =
|z + 1 + 2i| là đường thẳng có phương trình. A x − 2y + 1 = 0. B x + 2y = 0. C x − 2y = 0. D x + 2y + 1 = 0. Lời giải.
Đặt z = x + yi (x, y ∈ R) ⇒ z = x − yi và M (x; y) là điểm biểu diễn của số phức z. h Geogebra Pro Trang 5 Ta có: |z − 1 + 2i| = |z + 1 + 2i|
⇔ |x + yi − 1 + 2i| = |x − yi + 1 + 2i|
⇔ |(x − 1) + (y + 2)i| = |(x + 1) + (2 − y)i| » » ⇔ (x − 1)2 + (y + 2)2 = (x + 1)2 + (2 − y)2
⇔ x2 − 2x + 1 + y2 + 4y + 4 = x2 + 2x + 1 + y2 − 4y + 4 ⇔ x − 2y = 0.
Vậy tập hợp các điểm biểu biễn các số phức z thỏa mãn yêu cầu bài toán là đường thẳng có phương trình là x − 2y = 0. Chọn phương án C
Câu 21. Cho số phức z thoả mãn z − 4 = (1 + i)|z| − (4 + 3z)i. Môđun của số phức z bằng o/ A 2. B 1. C 16. D 4. aPr Lời giải.
Đặt z = a + bi. Khi đó ta có √
a + bi − 4 = (1 + i) a2 + b2 − (4 + 3a + 3bi)i √ √ ⇔ a − 4 + bi =
a2 + b2 + i a2 + b2 − (4 + 3a)i + 3b √ √ roups/GeoGebr ⇔ a − 3b − a2 + b2 − 4 + (b − a2 + b2 + 3a + 4)i = 0  √ a − 3b − a2 + b2 − 4 = 0 ⇔ √ 3a + b − a2 + b2 + 4 = 0  √ a − 3b − a2 + b2 − 4 = 0 ⇔ 2a + 4b + 8 = 0 acebook.com/g  » .f  − 2b − 4 − 3b − (−2b − 4)2 + b2 − 4 = 0 ⇔ a = −2b − 4 »  (−2b − 4)2 + b2 = 5b + 8 ⇔ a = −2b − 4 https://www 
5b2 + 16b + 16 = 25b2 + 80b + 64 ⇔ a = −2b − 4  20b2 + 64b + 48 = 0 ⇔ a = −2b − 4   6 b = −  5   8   a = − ⇔   5    b = −2   . a = 0 √
Với cả hai trường hợp ta đều có |z| = a2 + b2 = 2. h Geogebra Pro Trang 6 Chọn phương án A
Câu 22. Trong không gian với hệ trục Oxyz, cho điểm M (3; 2; −1). Gọi A, B lần lượt là hình chiếu
vuông góc của điểm M lên trục Oy, Oz. Tính diện tích tam giác OAB. 3 1 A . B . C 1. D 2. 2 2 Lời giải.
Hình chiếu vuông góc của điểm M (3; 2; −1) lên trục Oy là điểm A (0; 2; 0) .
Hình chiếu vuông góc của điểm M (3; 2; −1) lên trục Oz là điểm B (0; 0; −1) . 1 1
Vậy diện tích tam giác vuông OAB là S = · OA · OB = · 2 · 1 = 1. 2 2 Chọn phương án C
Câu 23. Trong không gian Oxyz, cho mặt cầu (S) tâm I nằm trên mặt phẳng (Oxy) đi qua ba điểm
A(1; 2; −4), B(1; −3; 1), C(2; 2; 3). Tìm tọa độ điểm I. A I(2; −1; 0). B I(0; 0; 1). C I(0; 0; −2). D I(−2; 1; 0). Lời giải. # » # » # »
Vì I ∈ (Oxy) ⇒ I(a; b; 0). Ta có AI = (a − 1; b − 2; 4); BI = (a − 1; b + 3; −1); CI = (a − 2; b − 2; −3). Do I là tâm cầu nên  I A = I B 2019-2020 I A = I C  THPT
(a − 1)2 + (b − 2)2 + 42 = (a − 1)2 + (b + 3)2 + 1 ⇔
(a − 1)2 + (b − 2)2 + 42 = (a − 2)2 + (b − 2)2 + 9  GHIỆP  − 4b + 20 = 6b + 10 N ⇔ T  − 2a + 17 = −4a + 13 TỐ  b = 1 THI ⇔ a = −2 ⇒ I(−2; 1; 0). LUYỆN Chọn phương án D
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1; 0; 0), B(0; −1; 0) và C(0; 0; 2). Phương trình mặt phẳng (ABC) là z y A x − 2y + z = 0. B x − y + = 1. C x + − z = 1. D 2x − y + z = 0. 2 2 Lời giải. z
Áp dụng phương trình mặt phẳng đoạn chắn ta có phương trình mặt phẳng (ABC) là x − y + = 1. 2 Chọn phương án B
Câu 25. Trong không gian Oxyz, cho điểm M (3; 2; −1) và mặt phẳng (P ) : x + z − 2 = 0. Đường thẳng
đi qua M và vuông góc với (P ) có phương trình là     x = 3 + t x = 3 + t x = 3 + t x = 3 + t             A y = 2 . B y = 2 + t . C y = 2t . D y = 1 + 2t .             z = −1 + t z = −1 z = 1 − t z = −t h Geogebra Pro Trang 7 Lời giải. #»
Mặt phẳng (P ) : x + z − 2 = 0 có véc-tơ pháp tuyến là n (P ) = (1; 0; 1). #»
Đường thẳng ∆ đi qua M và vuông góc với (P ) nhận n (P ) làm véc-tơ chỉ phương có phương trình là  x = 3 + t    y = 2    z = −1 + t. Chọn phương án A
Câu 26. Cho hình lập phương ABCD.A0B0C0D0. Tính góc giữa hai mặt phẳng (A0B0C) và (C0D0A). A 45◦. B 30◦. C 60◦. D 90◦. Lời giải. o/
Gọi I = B0C ∩ BC0, J = A0D ∩ AD0, ta có A0 B0 aPr  D0
(A0B 0C ) ∩ (C 0D0A) = I J   C0  IJ ⊥ B0C ⊂ (A0B0C)  J I   I J ⊥ BC 0 ⊂ (C 0D0A). A B
Từ đó, suy ra góc giữa mặt phẳng (A0B0C) và mặt phẳng (C0D0A) là roups/GeoGebr
góc giữa đường thẳng B0C và BC0 hay là bằng 90◦. D C Chọn phương án D
Câu 27. Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau x −∞ −2 0 1 3 +∞ f 0(x) + 0 − 0 + 0 − 0 − acebook.com/g .f
Hàm số đã cho có bao nhiêu điểm cực trị? A 3. B 1. C 2. D 4. Lời giải.
Dựa vào bảng xét dấu của f 0(x) ta suy ra: https://www
Hàm số đạt cực đại tại x = −2 và x = 1.
Hàm số đạt cực tiểu tại x = 0.
Hàm số không đạt cực trị tại x = 3 do đạo hàm không đổi dấu khi đi qua điểm x = 3.
Vậy hàm số đã cho có 3 điểm cực trị. Chọn phương án A √
Câu 28. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x + 4 − x2. Hãy tính P = M + m. √ √ √ √ Ä ä Ä ä A P = 2 2 − 1 . B P = 2 2 + 1 . C P = 2 + 1. D P = 2 − 1. Lời giải. h Geogebra Pro Trang 8
Tập xác định: D = [−2; 2]. x y0 = 1 − √ . 4 − x2  √ x ≥ 0 √ y0 = 0 ⇔ 4 − x2 = x ⇔ ⇔ x = 2. x2 = 2 √ √
y(−2) = −2; y(2) = 2; y( 2) = 2 2. √ Suy ra m = −2; M = 2 2. √ Ä ä Vậy P = 2 2 − 1 . Chọn phương án A
Câu 29. Cho a > 0, b > 0 thỏa mãn a2 + 4b2 = 5ab. Khẳng định nào sau đây đúng?
A 2 log(a + 2b) = 5(log a + log b). B log(a + 1) + log b = 1. a + 2b log a + log b C 2 log = .
D log(a + 2b) = log a − log b. 3 2 Lời giải.
Ta có a2 + 4b2 = 5ab ⇔ (a + 2b)2 = 9ab.
Logarit cơ số 10 hai vế ta được
log(a + 2b)2 = log(9ab) ⇔ 2 log(a + 2b) = log 9 + log a + log b
⇔ 2(log(a + 2b) − log 3) = log a + log b 2019-2020 a + 2b log a + log b ⇔ 2 log = . 3 2 THPT Chọn phương án C
Câu 30. Cho hàm số y = f (x) có đồ thị như hình vẽ bên. GHIỆP N T TỐ y 4 THI 2 LUYỆN x −1 O 1
Phương trình |f (x − 2) − 2| = π có bao nhiêu nghiệm thực phân biệt? A 4. B 2. C 6. D 3. Lời giải.
Số giao điểm của đồ thị hàm số y = f (x) với đường thẳng y = k và số giao điểm của đồ thị hàm số
y = f (x + p) với đường thẳng y = k luôn như nhau. Do đó nghiệm của phương trình |f (x − 2) − 2| = π
cũng chính là nghiệm của phương trình |f (x) − 2| = π.   f (x) − 2 = π f (x) = 2 + π
Phương trình |f (x) − 2| = π ⇔  ⇔  . f (x) − 2 = −π f (x) = 2 − π
Xét phương trình f (x) = 2 + π : Vì 2 + π > 4 nên phương trình có 1 nghiệm. h Geogebra Pro Trang 9
Xét phương trình f (x) = 2 − π : Vì 2 − π < 0 nên phương trình có 1 nghiệm.
Vậy phương trình đã cho có 2 nghiệm thực. Chọn phương án B Å ã Ä ä 1
Câu 31. Tập nghiệm của bất phương trình log
1 + log x − log x < 1 có dạng S = ; b với a, b 2 1 9 9 a
là những số nguyên. Mệnh đề nào dưới đây đúng? A a = −b. B a + b = 1. C a = b. D a = 2b. Lời giải. Điều kiện x > 0. Ä ä 1 1 1 log
1 + log x − log x < 1 ⇔ 0 < 1 + log x − log x < 2 ⇔ − < log x < ⇔ < x < 3. 2 1 9 1 9 9 9 9 2 2 3 Å 1 ã
Do đó tập nghiệm của bất phương trình là S = ; 3 . Suy ra a = b. 3 Chọn phương án C o/
Câu 32. Cho hình nón tròn xoay có đường cao bằng 20 cm, bán kính đáy bằng 25 cm. Một thiết diện aPr
đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiến diện là 12 cm.
Tính diện tích của thiết diện đó. A 500 cm2. B 1000 cm2. C 250 cm2. D 250 cm3. Lời giải.
Ký hiệu S là đỉnh của hình nón và O là tâm của đường tròn S đáy. roups/GeoGebr
Gọi A, B là hai giao điểm (khác đỉnh S của hình nón) của mặt
phẳng với hình nón. Suy ra thiết diện của mặt phẳng với hình nón là tam giác SAB.
Gọi M là trung điểm của AB. H Kẻ OH ⊥ SM tại H. acebook.com/g
Xét đường thẳng AB và mặt phẳng (SOM ) có B .f M O  AB ⊥ S O ⇒ AB ⊥ (SOM ). A AB ⊥ OM Cho nên (SAB) ⊥ (SOM ). https://www
Mà (SAM ) ∩ (SOM ) = SM và OH ⊥ SM nên OH là khoảng cách từ tâm của đáy đến mặt phẳng
chứa thiến diện. Suy ra OH = 12 cm. Ta có 1 1 1 1 1 1 OH2 · SO2 = + ⇔ = − ⇔ OM = ⇔ OM = 15. OH2 SO2 OM 2 OM 2 OH2 SO2 SO2 − OH2 √ √ Khi đó SM =
SO2 + OM 2 = 25 và AB = 2AM = 2 252 − 152 = 40. 1
Vậy diện tích của thiết diện SAB bằng · 40 · 25 = 500 cm2. 2 Chọn phương án A
Câu 33. Cho hàm số f (x) xác định trên (0; +∞) và thỏa mãn xf 0(x) = −[f (x)]2 · ln x; f (1) = 1. Giá trị f (e) bằng 2 e 2e 1 A . B . C . D . 3 2 3 2 h Geogebra Pro Trang 10 Lời giải. f 0(x) ln x
Ta có xf 0(x) = −[f (x)]2 · ln x; f (1) = 1 ⇒ − = . [f (x)]2 x Z f 0(x) Z ln x Z 1 ln2 x Suy ra − dx = dx = ln x d(ln x) ⇒ = + C [f (x)]2 x f (x) 2 1 1 3 2
Theo giả thiết f (1) = 0 + C = 1 ⇒ C = 1. Khi x = e ⇒ = + 1 = ⇒ f (e) = . f (e) 2 2 3 Chọn phương án A
Câu 34. Cho hình phẳng D được giới hạn bởi hai đường y = 2(x2 − 1); y = 1 − x2. Tính thể tích khối
tròn xoay tạo thành do D quay quanh trục Ox. 64π 32 32π 64 A . B . C . D . 15 15 15 15 Lời giải.
Phương trình hoành độ giao điểm của 2 đồ thị hàm số y = 2(x2 − 1) y và y = 1 − x2 là y = 2x2 − 2 2
2(x2 − 1) = 1 − x2 ⇔ x = ±1. 1
Lấy đối xứng đồ thị hàm số y = 2(x2 − 1) qua trục Ox ta được đồ thị x −1 O 1 hàm số y = 2(1 − x2).
Ta có 2(1 − x2) ≥ 1 − x2, ∀x ∈ [−1; 1]. −2 y = 1 − x2 2019-2020
Khi đó trên đoạn [−1; 2] phần thể tích của hàm số y = 2(x2 − 1) chứa
cả phần thể tích của hàm số y = 1 − x2. y = −2x2 + 2 THPT
Suy ra thể tích khối tròn xoay cần tìm là 1 Z 64π GHIỆP V = π 2(x2 − 1)2 dx = . N 15 T −1 TỐ Chọn phương án A THI
Câu 35. Cho số phức z = a + bi (a, b ∈ R) thỏa mãn |z| = 5 và z(2 + i)(1 − 2i) là một số thực. Tính P = |a| + |b|. LUYỆN A P = 8. B P = 4. C P = 5. D P = 7. Lời giải. Ta có
z(2 + i)(1 − 2i) = (a + bi)(4 − 3i) = 4a + 3b + (−3a + 4b)i. (1) 3
Do z(2 + i)(1 − 2i) là một số thực nên từ (1) suy ra −3a + 4b = 0 ⇔ b = a. (2) 4
Mặt khác |z| = 5 ⇔ a2 + b2 = 25. (3)
Thế (2) vào (3) ta được phương trình Å 3 ã2 a2 + a = 25 ⇔ a2 = 16 ⇔ a = ±4. 4
Với a = 4 ⇒ b = 3 và a = −4 ⇒ b = −3.
Vậy P = |a| + |b| = 3 + 4 = 7. Chọn phương án D h Geogebra Pro Trang 11
Câu 36. Tìm mô-đun của số phức z biết z − 4 = (1 + i) |z| − (4 + 3z) i. 1 A |z| = . B |z| = 2. C |z| = 4. D |z| = 1. 2 Lời giải. Ta có
z − 4 = (1 + i) |z| − (4 + 3z) i
⇔z − 4 = |z| + i|z| − 4i − 3iz
⇔z(1 + 3i) = |z| + 4 + (|z| − 4) i
⇒ |z(1 + 3i)| = ||z| + 4 + (|z| − 4) i| (lấy mô-đun hai vế) √ » ⇔|z| · 10 = (|z| + 4)2 + (|z| − 4)2 ⇔10|z|2 = 2|z|2 + 32 ⇔|z|2 = 4 ⇔ |z| = 2. o/ aPr Chọn phương án B x + 1 y − 1 z − 2
Câu 37. Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng (d) : = = và 2 1 3
mặt phẳng (P ) : x − y − z − 1 = 0. Viết phương trình đường thẳng (∆) đi qua điểm A(1; 1; −2), biết
(∆) k (P ) và (∆) cắt (d). x − 1 y − 1 z + 2 x − 1 y − 1 z + 2 roups/GeoGebr A = = . B = = . 1 −1 −1 2 1 3 x − 1 y − 1 z + 2 x − 1 y − 1 z + 2 C = = . D = = . 8 3 5 2 1 1 Lời giải.
Gọi M = (d) ∩ (∆) ⇒ M (−1 + 2t; 1 + t; 2 + 3t). # »
Khi đó AM = (2t − 2; t; 3t + 4) là một véc-tơ chỉ phương của (∆). # » #» acebook.com/g (∆) k (P ) ⇔ AM ⊥ #»
n (P ) với n (P ) = (1; −1; −1). .f # » # » ⇔ AM · #»
n (P ) = 0 ⇔ 2t − 2 − t − 3t − 4 = 0 ⇔ t = −3 ⇒ AM = (−8; −3; −5). x − 1 y − 1 z + 2 Vậy (∆) : = = . 8 3 5 Chọn phương án C x y + 4 z − 3 x − 1 y + 3 https://www
Câu 38. Trong không gian Oxyz cho hai đường thẳng d1 : = = và d2 : = = 1 1 −1 −2 1
z − 4 . Đường thẳng vuông góc với mặt phẳng tọa độ (Oxz) và cắt d −
1 và d2 có phương trình là 5  3    x =  x = 1  7 x = 1 x = t           −25   A y = −1 + t . B y = + t . C y = −3 + t . D y = −4 + t . 7           18   z = −1  z = 4 z = 3 + t  z = 7 Lời giải.
Gọi d là đường thẳng cần tìm, A = d ∩ d1 và B = d ∩ d2.
Ta có tọa độ A = (u; −4 + u; 3 − u), B = (1 − 2v; −3 + v; 4 − 5v) # »
⇒ AB = (1 − 2v − u; 1 + v − u; 1 − 5v + u) là véc-tơ chỉ phương của d. # » #»
Do d ⊥ (Oxz) nên AB và n Oxz = (0; 1; 0) cùng phương. h Geogebra Pro Trang 12   # » #»  3 u = AB · i = 0 1 − 2v − u = 0  Từ đó ta có 7 # » #» ⇔ ⇔ 2 AB · j = 0 1 − 5v + u = 0  u = . 7 3 −25 18 Nên tọa độ A( ; ; ). 7 7 7  3 x =   7 # »    −25
Vậy d đi qua A và có véc-tơ chỉ phương AB = (0; 1; 0) có phương trình là y = + t 7    18   z = . 7 Chọn phương án B
Câu 39. Cho hai chiếc hộp A và B. Hộp A chứa 6 viên bi trắng, 4 viên bi đen. Hộp B chứa 7 viên
bi trắng, 3 viên bi đen. Người ta lấy ngẫu nhiên một viên bi từ hộp A và bỏ vào hộp B rồi sau đó từ
hộp B lấy ngẫu nhiên ra hai viên bi. Tính xác suất để hai viên bi lấy được từ hộp B là hai viên bi trắng. 126 21 123 37 A . B . C . D . 275 55 257 83 Lời giải.
Không gian mẫu n(Ω) = 10 · C2 . 11
Trường hợp 1: Lấy một viên bi đen từ hộp A bỏ vào hộp B ta có 4 cách. Khi đó số cách lấy hai bi 2019-2020 trắng từ hộp B là C2. 7
Trường hợp 2: Lấy một viên bi trắng từ hộp A bỏ vào hộp B khi đó ta có 6 cách. Với mỗi cách đó THPT
thì số cách lấy hai bi trắng từ hộp B là C2. 8
Vậy số cách lấy hai viên bi trắng từ hộp B là 4 · C2 + 6 · C2. 7 8 GHIỆP 4 · C2 + 6 · C2 126 7 8 N Xác suất cần tìm là P = = . T 10 · C2 275 11 TỐ THI Chọn phương án A
Câu 40. Cho hình chóp S.ABC có SA = 3a và SA ⊥ (ABC). Biết AB = BC = 2a và ’ ABC = 120◦. LUYỆN
Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng 3a a A . B . C a. D 2a. 2 2 Lời giải.
Gọi I là hình hình chiếu vuông góc của A trên BC, ta có AI ⊥ BC. (1) S
Mặt khác SA ⊥ (ABC) nên SA ⊥ BC. (2)
Từ (1) và (2) suy ra BC ⊥ (SIA). (3)
Gọi H là hình hình chiếu vuông góc của A trên SI, ta có AH ⊥ SI. (4)
Từ (3) và (4) suy ra AH ⊥ (SBC) nên khoảng cách từ A đến mặt phẳng (SBC) là AH.
Xét tam giác BIA vuông tại I, ta có H A C √3 √ AI = AB · sin 120◦ = 2a · = a 3. 2 I
Xét tam giác SAI vuông tại A, ta có B h Geogebra Pro Trang 13 s √ 1 1 1 AS2 · AI2 (3a)2 · (a 3)2 3a = + ⇒ AH = = √ = . AH2 AS2 AI2 AS2 + AI2 (3a)2 + (a 3)2 2 3a
Vậy khoảng cách từ điểm A đến mặt phẳng (SBC) bằng . 2 Chọn phương án A
Câu 41. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (−2019; 2019) để hàm số h π i
y = sin3 x − 3 cos2 x − m sin x − 1 đồng biến trên đoạn 0; ? 2 A 2020. B 2019. C 2028. D 2018. Lời giải. Phương pháp:
Sử dụng công thức cos2 x = 1 − sin2 x, đặt ẩn phụ t = sin x. o/
Để hàm số y = f (x) đồng biến trên (a; b) ⇒ f 0 (x) ≥ 0 ∀x ∈ (a; b). aPr Cách giải:
y = sin3 x − 3 cos2 x − m sin x − 1 = sin3 x − 3 1 − sin2 x − m sin x − 1.
y = sin3 x + 3 sin2 x − m sin x − 4. h π i
Đặt t = sin x, với x ∈ 0; ⇒ t ∈ [0; 1]. 2
Bài toán trở thành tìm m để hàm số y = t3 + 3t2 − mt − 4 đồng biến trên [0; 1]. roups/GeoGebr
TXĐ: D = R. Ta có y0 = 3t2 + 6t − m.
Để hàm số đồng biến trên [0; 1]
⇒ y0 ≥ 0 ∀t ∈ [0; 1] ⇒ 3t2 + 6t − m ≥ 0 ∀t ∈ [0; 1] ⇔ m ≤ 3t2 + 6t ∀t ∈ [0; 1].
⇒ m ≤ f (t) = 3t2 + 6t ∀t ∈ [0; 1] ⇔ m ≤ min f (t). [0;1]
Xét hàm số f (t) = 3t2 + 6t, ta có f (0) = 0, f (1) = 9 ⇒ min f (t) = 0 ⇔ m ≤ 0. [0;1]  acebook.com/g m ∈ (−2019; 0] .f 
Kết hợp điều kiện đề bài ⇒
⇒ Có 2019 giá trị của m thoả mãn. m ∈ Z Chọn phương án B
Câu 42. Một người mỗi tháng đều đặn gửi vào một ngân hàng một khoản tiền T theo hình thức lãi https://www
kép với lãi suất 0,6% mỗi tháng. Biết sau 15 tháng người đó có số tiền là 10 triệu đồng. Hỏi số tiền T
gần với số tiền nào nhất sau đây? A 635.000 đồng. B 645.000 đồng. C 613.000 đồng. D 535.000 đồng. Lời giải.
Gọi r là lãi suất kép hàng tháng.
Gọi Tn là số tiền người đó có được ở cuối tháng thứ n, ta có:
- Cuối tháng thứ nhất người đó có số tiền là: T1 = T + T · r = T (1 + r).
- Đầu tháng thứ hai, người đó gửi số tiền là: T a
T (1 + r) + T = T [(1 + r) + 1] = · [(1 + r)2 − 1] = [(1 + r)2 − 1]. (1 + r) − 1 r
- Cuối tháng thứ hai người đó có số tiền là: T T T T2 = [(1 + r)2 − 1] + [(1 + r)2 − 1] r = [(1 + r)2 − 1] (1 + r). r r r h Geogebra Pro Trang 14
- Cuối tháng thứ n người đó có số tiền là: T Tn = [(1 + r)n − 1] (1 + r). r Tnr Suy ra: T = . [(1 + r)n − 1] (1 + r)
Do đó số tiền ban đàu người đó gửi là: 10000000 · 0,6% T = ≈ 635301 đồng.
[(1 + 0,6%)15 − 1] (1 + 0,6%) Chọn phương án A Câu 43.
Cho hàm số y = f (x) xác định trên R \ {0} có bảng biến x −∞ −2 0 +∞ y0 −
thiên như hình vẽ bên. Số nghiệm của phương trình 0 + + +∞ + +∞ +∞
2 |f (2x − 3)| − 13 = 0 là y A 3. B 2. C 4. D 1. 7 −∞ Lời giải.
Đặt t = 2x − 3. Cứ mỗi một t 6= 0 sẽ cho một x.  13 13 f (t) =
Phương trình đã cho trở thành |f (t)| = ⇔ 2  2  13 f (t) = − . 2 13 13 Ta có − <
< 7 nên dựa vào bảng biến thiên đã cho, ta có 2 2 2019-2020 13 Phương trình f (t) = có 1 nghiệm t1 > 0. 2 THPT 13 Phương trình f (t) = −
có 1 nghiệm t2 thỏa mãn 0 < t2 < t1. 2 GHIỆP
Suy ra phương trình đã cho có 2 nghiệm phân biệt. N T Chọn phương án B TỐ
Câu 44. Cho hình trụ có bán kính đáy bằng a và chiều cao h. Tính thể tích V của khối lăng trụ tam THI
giác đều tam giác đều nội tiếp hình trụ đã cho. √ √ 3a2h 3 3a2h A V = . B V = . LUYỆN 4 4 √ π Å 4a2 ã … h2 a2 3 3πa2h C V = h2 + + . D V = . 3 3 4 3 4 Lời giải.
Gọi x là cạnh đáy của khối lăng trụ tam giác đều nội tiếp hình trụ, bán √ C0 x 3
kính đường tròn ngoại tiếp tam giác đều cạnh x là , do đó: 3 O0 √ A0 x 3 √ = a ⇔ x = a 3. B0 3 √ √ √ √ x2 3 (a 3)2 3 3 3a2
Diện tích mặt đáy của hình lăng trụ: S = = = . 4 4 4
Thể tích khối lăng trụ tam giác đều tam giác đều nội tiếp hình trụ đã C cho là √ √ 3 3a2 3 3a2h V = Bh = · h = . 4 4 O A B h Geogebra Pro Trang 15 Chọn phương án B 1
Câu 45. Cho hàm số f (x), f (−x) liên tục trên R và thỏa mãn 2f (x) + 3f (−x) = . Tính 4 + x2 2 Z I = f (x) dx. −2 π π π π A . B . C − . D − . 20 10 20 10 Lời giải. 2 Z Xét I = f (x) dx. −2
Đặt x = −u ⇒ dx = −du. Với x = −2 ⇒ u = 2. Với x = 2 ⇒ u = −2. o/ −2 2 2 Z Z Z aPr Suy ra I = − f (−u) du = f (−u) du = f (−x) dx. 2 −2 −2 2 2 2 Z Z Z 1
Từ đó ta có 5I = 2I + 3I = 2 f (x) dx + 3 f (−x) dx = dx. x2 + 4 −2 −2 −2 2 Z 1 Tính J = dx. roups/GeoGebr x2 + 4 −2
Đặt x = 2 tan v ⇒ dx = 2(1 + tan2 v) dv. Đổi cận π Với x = −2 ⇒ v = − . 4 π acebook.com/g Với x = 2 ⇒ v = . .f 4 π π 4 4 Z 1 Z 1 π Suy ra J = · 2(1 + tan2 v) dv = dv = . 4 tan2 v + 4 2 4 − π − π 4 4 π Từ đó suy ra I = . https://www 20 Chọn phương án A
Câu 46. Cho hàm số y = f (x) có bảng biến thiên như sau: x −∞ −1 3 +∞ y0 + 0 − 0 + 5 +∞ + y −∞ 1
Phương trình f (x) − 2 = 0 có bao nhiêu nghiệm? h Geogebra Pro Trang 16 A 1. B 3. C 2. D 0 . Lời giải.
Phương trình f (x) − 2 = 0 ⇔ f (x) = 2.
Số giao điểm của đồ thị hàm số y = f (x) và y = 2 là số nghiệm của phương trình f (x) − 2 = 0 (∗)
Dựa vào bảng biến thiên suy ra phương trình (∗) có 3 nghiệm. Chọn phương án B
Câu 47. Cho x, y là hai số thực dương thỏa mãn ln x + ln y ≥ ln(x2 + y). Tìm giá trị nhỏ nhất của P = x + y. √ √ √ √ A P = 2 + 3 2. B P = 6. C P = 2 2 + 3. D P = 17 + 3. Lời giải.
Từ ln x + ln y ≥ ln(x2 + y) ⇔ xy ≥ x2 + y ⇔ (x − 1)y ≥ x2.
Nếu 0 < x ≤ 1 thì y ≥ xy ≥ x2 + y ⇔ 0 ≥ x2 (vô lý). x2 x2
Nếu x > 1 thì (x − 1) y ≥ x2 ⇔ y ≥ . Vậy P = x + y ≥ x + . x − 1 x − 1 √  2 − 2 x2 2x2 − 4x + 1 x = (loại) Xét hàm số f (x) = x + trên (1; +∞). f 0(x) = = 0 ⇒  2  √ x − 1 x2 − 2x + 1  2 + 2 x = (nhận). √ 2 Ç å 2 + 2 √
Lập bảng biến thiên suy ra min f (x) = f = 2 2 + 3. (1;+∞) 2 2019-2020 Chọn phương án C THPT
Câu 48. Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị nhỏ nhất của hàm số
y = sin4 x + cos 2x + m bằng 2. Số phần tử của S là GHIỆP A 4. B 3. C 1. D 2. N T Lời giải. TỐ
Ta có y = sin4 x + cos 2x + m = sin4 x − 2 sin2 x + m + 1. THI
Đặt t = sin2 x, t ∈ [0; 1], hàm số trở thành y = |t2 − 2t + m + 1|.
Xét hàm f (t) = t2 − 2t + m + 1, với t ∈ [0; 1]. Ta có f 0(t) = 2t − 2 ≤ 0, với ∀t ∈ [0; 1], suy ra hàm số LUYỆN
nghịch biến trên [0; 1]. Do đó f (1) ≤ f (t) ≤ f (0) ⇔ m ≤ f (t) ≤ m + 1. Xét các trường hợp sau
m + 1 ≤ 0 ⇔ m ≤ −1. Khi đó, min y = −m − 1. Theo giả thiết −m − 1 = 2 ⇔ m = −3 (thỏa mãn).
−1 < m ≤ 0. Khi đó, min y = 0 (loại).
m > 0. Khi đó, min y = m. Theo giả thiết m = 2 (thỏa mãn).
Vậy tập hợp S có 2 phần tử. Chọn phương án D √
Câu 49. Cho hình hộp ABCD.A0B0C0D0 có đáy là hình thoi cạnh a 3, BD = 3a, hình chiếu vuông
góc của B trên mặt phẳng (A0B0C0D0) trùng với trung điểm của A0C0. Gọi (α) là góc tạo bởi hai mặt √21
phẳng (ABCD) và (CDD0C0), cos α =
. Tính thể tích khối hộp. 7 h Geogebra Pro Trang 17 √ √ 3a3 9 3a3 9a3 3 3a3 A . B . C . D . 4 4 4 4 Lời giải.
Gọi O và O0 lần lượt là tâm của hình thoi ABCD A D
và A0B0C0D0. Vì BO0 ⊥ (A0B0C0D0) nên OD0 ⊥ O H (ABCD). B C √ 3a Ta có AD = a 3, DO = nên 2 √ √ a 3 AO = AD2 − DO2 = . 2 A0 D0 √
Suy ra AC = a 3, do đó, tam giác ACD đều. O0 B0 C0
Từ O kẻ OH ⊥ CD, kết hợp với OD0 ⊥ CD (do OD0 ⊥ (ABCD)) suy ra HD0 ⊥ CD.
Suy ra góc giữa hai mặt phẳng (ABCD) và (CDD0C0) là ÷ OHD0. √ √ 1 3a 2 3 a 3 o/ Ta có OH = · hA = , ÷ OHD0 = α và tan α = . Suy ra OD0 = OH · tan α = . 2 4 3 √ 2 aPr 1 3a2 3
Diện tích đáy hình hộp là SABCD = · AC · BD = . 2 2 9a3 Từ đó, V = SABCD · OD0 = . 4 Chọn phương án C
Câu 50. Có bao nhiêu số nguyên m ∈ (−7; 7) để đồ thị hàm số y = |x4 − 3mx2 − 4| có đúng 3 điểm roups/GeoGebr
cực trị A, B, C và diện tích tam giác ABC lớn hơn 4. A 4. B 2. C 1. D 3. Lời giải.
Đặt f (x) = x4 − 3mx2 − 4. Ta thấy f (0) = −4. y
Do vậy y = |f (x)| có đúng 3 cực trị ⇔ f (x) có 1 cực trị ⇔ m ≤ 0. (1) A 1 Ta thấy S4ABC = · AO · BC = 4 · |xC|. acebook.com/g 2 .f
Theo giả thiết, ta được √ 3m + 9m2 + 16 > 1 2 √ ⇔ 9m2 + 16 > 2 − 3m x B O C  2 https://www m > 3    ⇔ 2  m ≤    3   m > −1 (1) ⇒ −1 < m ≤ 0.
Vậy có 1 giá trị m nguyên thuộc (−7; 7) là m = 0 thỏa mãn đề bài. Chọn phương án C
———————–HẾT———————– h Geogebra Pro Trang 18 BẢNG ĐÁP ÁN 1. D 2. C 3. D 4. C 5. B 6. C 7. A 8. A 9. C 10. D 11. C 12. C 13. A 14. C 15. C 16. D 17. C 18. D 19. B 20. C 21. A 22. C 23. D 24. B 25. A 26. D 27. A 28. A 29. C 30. B 31. C 32. A 33. A 34. A 35. D 36. B 37. C 38. B 39. A 40. A 41. B 42. A 43. B 44. B 45. A 46. B 47. C 48. D 49. C 50. C 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN h Geogebra Pro Trang 19 MỖI NGÀY MỘT ĐỀ THI 10
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Một tổ có 6 học sinh nam và 9 học sinh nữ. Hỏi có bao nhiêu cách chọn 6 học sinh đi lao động
trong đó có 2 học sinh nam? A C2 + C4. B A2 · A4. C C2 · C4. D C4 · C2. 6 9 6 9 6 9 6 9
Câu 2. Cho cấp số cộng (un) biết un = 3 − 5n. Tìm công sai d của cấp số cộng (un). A d = 3. B d = −5. C d = −3. D d = 5.
Câu 3. Tìm tập nghiệm S của phương trình 4x − 6 · 2x + 8 = 0. A S = {1; 2}. B S = (1; 2). C S = {1}. D S = {2}.
Câu 4. Tổng diện tích các mặt của khối lập phương bằng 96. Tìm thể tích của khối lập phương đó. A 48. B 84. C 64. D 91. x + 3
Câu 5. Tập xác định của hàm số y = log là 2 2 − x 2019-2020 A D = R\ {−3; 2}.
B D = (−∞; −3) ∪ (2; +∞). C D = [−3; 2]. D D = (−3; 2). THPT 1
Câu 6. Cho F (x) là nguyên hàm của f (x) = √
thỏa mãn F (2) = 4. Giá trị F (−1) bằng x + 2 √ √ GHIỆP A 3. B 1. C 2 3. D 2. N T
Câu 7. Cho hình chóp S.ABC có (SAB) ⊥ (ABC), tam giác ABC đều cạnh 2a, tam giác SAB vuông TỐ
cân tại S. Tính thể tích hình chóp S.ABC. √ √ √ √ THI a3 3 a3 3 2a3 3 a3 3 A . B . C . D . 3 6 3 12
Câu 8. Khối nón tròn xoay có chiều cao bằng 8 cm và độ dài đường sinh bằng 10 cm có thể tích LUYỆN bằng A 128π cm3. B 96π cm3. C 124π cm3. D 140π cm3.
Câu 9. Tính diện tích mặt cầu (S) khi biết chu vi đường tròn lớn của nó bằng 4π. A S = 32π. B S = 16π. C S = 64π. D S = 8π.
Câu 10. Cho hàm số y = f (x) có bảng biến thiên như hình dưới. Hàm số nghịch biến trong khoảng nào? x −∞ −1 2 +∞ y0 + 0 − 0 + y A (−∞; 2). B (0; 2). C (−1; 2). D (2; +∞). h Geogebra Pro Trang 1 √ a3 · 3 a2
Câu 11. Cho a là số thực dương và a 6= 1. Tính giá trị của biểu thức Q = log √ . a a 19 19 19 19 A Q = . B Q = . C Q = . D Q = . 5 7 4 6
Câu 12. Một hình trụ có bán kính đáy r = 5 cm, chiều cao h = 7 cm. Tính diện tích xung quanh của hình trụ. 35 A 85π cm2. B 35π cm2. C π cm2. D 70π cm2. 3 Câu 13.
Cho hàm số y = f (x) có bảng biến thiên x −∞ −1 0 2 +∞
như hình vẽ. Hỏi hàm số có bao nhiêu y0 + 0 − + 0 − cực trị? 2 3 y A 2. B 3. C 1. D o/ −∞ −1 −1 2 4. aPr
Câu 14. Cho hàm số y = f (x) có đồ thị như hình vẽ. Xác định hàm số trên. 2x + 1 2x − 1 2x − 1 3x + 1 A y = . B y = . C y = . D y = . x − 1 x − 1 x + 1 2x + 2 y roups/GeoGebr 6 4 acebook.com/g .f 2 x −4 −2 O 2 −2 https://www √9 − x2
Câu 15. Đồ thị hàm số y =
có bao nhiêu đường tiệm cận? x2 − 6x + 8 A 1. B 4. C 3. D 2. 4x + 6
Câu 16. Tập nghiệm của bất phương trình log 1 ≥ 0 là 5 x Å 3 ò ï 3 ò Å 3 ã ï 3 ã A −2, − . B −2, − . C −2, − . D −2, − . 2 2 2 2 Câu 17. h Geogebra Pro Trang 2
Cho hàm số y = f (x) liên tục trên đoạn [−2; 2] và có đồ thị là đường cong y 4
như hình vẽ bên. Tìm số nghiệm của phương trình |f (x) | = 1 trên đoạn [−2; 2]. 2 A 4. B 6. C 3. D 5. −2 x2 x1 x O 2 −2 −4 2 Z f (x)
Câu 18. Cho hàm số f (x) có đạo hàm liên tục trên [1; 2], có f (2) = 14 và dx = 6. Tính x 1 2 Z I = f 0(x) ln x dx. 1 A I = 14 ln 2 − 6. B I = 7 ln 2 − 6. C I = 7 ln 2 − 6. D I = 14 ln 2 + 6.
Câu 19. Cho số phức z thỏa mãn z − 3 + i = 0. Môđun của z bằng bao nhiêu? √ √ A 10. B 10. C 3. D 4. 2019-2020
Câu 20. Cho số phức z1 = 3 + 2i, z2 = 6 + 5i. Tìm số phức liên hợp của z = 6z1 + 5z2. A ¯ z = 51 + 40i. B ¯ z = 51 − 40i. C ¯ z = 48 + 37i. D ¯ z = 48 − 37i. THPT
Câu 21. Gọi A, B, C là các điểm trong mặt phẳng Oxy theo thứ tự biểu diễn các số phức 2 + 3i, 3 + i, GHIỆP
1 + 2i. Trọng tâm G của tam giác ABC biểu diễn số phức z. Tìm z. N T A z = 1 + i. B z = 1 − i. C z = 2 − 2i. D z = 2 + 2i. TỐ
Câu 22 (2H3B1-1). Trong không gian với hệ tọa độ Oxyz, tìm tọa độ điểm M trên trục Ox cách THI
đều hai điểm A (1; 2; −1) và điểm B (2; 1; 2) Å 1 ã Å 3 ã Å 2 ã Å 1 ã A M ; 0; 0 . B M ; 0; 0 . C M ; 0; 0 . D M ; 0; 0 . 2 2 3 3 LUYỆN
Câu 23. Trong hệ tọa độ Oxyz, cho điểm I(2; −1; −1) và mặt phẳng (P ) : x − 2y − 2z + 3 = 0. Viết
phương trình mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng (P ).
A S : x2 + y2 + z2 − 4x + 2y + 2z − 3 = 0.
B S : x2 + y2 + z2 − 2x + y + z − 3 = 0.
C S : x2 + y2 + z2 − 4x + 2y + 2z + 1 = 0.
D S : x2 + y2 + z2 − 2x + y + z + 1 = 0.
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P ) : 2x − 2y + z + 4 = 0. Tính khoảng
cách d từ điểm M (1; 2; 1) đến (P ). 1 A d = 3. B d = 4. C d = 1. D d = . 3 x − 1 y − 3 z − 1
Câu 25. Trong hệ tọa độ Oxyz, cho đường thẳng d : = = cắt mặt phẳng (P ) : 2 −1 1
2x − 3y + z − 2 = 0 tại điểm I(a; b; c). Khi đó a + b + c bằng A 9. B 5. C 3. D 7. √
Câu 26. Cho lăng trụ tam giác đều ABC.A0B0C0 có diện tích đáy bằng 3a2 (đvdt), diện tích tam
giác A0BC bằng 2a2 (đvdt). Tính góc giữa hai mặt phẳng (A0BC) và (ABC)? h Geogebra Pro Trang 3 A 120◦. B 60◦. C 30◦. D 45◦.
Câu 27. Cho hàm số y = f (x) liên tục trên [−3; 3] và có bảng xét dấu đạo hàm như hình bên. x −3 −1 0 1 2 3 y0 + 0 − 0 − 0 + 0 −
Mệnh đề nào sau đây sai về hàm số đó?
A Hàm số đạt cực tiểu tại x = 1.
B Hàm số đạt cực đại tại x = −1.
C Hàm số đạt cực đại tại x = 2.
D Hàm số đạt cực tiểu tại x = 0. √
Câu 28. Tìm giá trị nhỏ nhất của hàm số y = 2x + 5 − x2. √ √ A 5. B 2 5. C −3. D −2 5. 5b − a a
Câu 29. Cho a, b là các số dương thỏa mãn log a = log b = log . Tính giá trị T = . 9 16 12 √ 2 √ b o/ 3 + 6 √ √ 3 − 6 A T = . B T = 7 − 2 6. C T = 7 + 2 6. D T = . aPr 4 4
Câu 30. Phương trình x3 − 3x + 2m − 2 = 0 có đúng một nghiệm dương khi m thỏa A m = 2 hoặc m ≤ 1. B m ∈ ∅. C m > 1. D m < 1 hoặc m > 2.
Câu 31. Bất phương trình 6 · 4x − 13 · 6x + 6 · 9x > 0 có tập nghiệm là?
A S = (−∞; −2) ∪ (1; +∞).
B S = (−∞; −1) ∪ (1; +∞). roups/GeoGebr
C S = (−∞; −2] ∪ [2; +∞).
D S = (−∞; −1) ∪ (1; +∞). √3
Câu 32. Cho khối nón có thể tích V =
πa3 và thiết diện qua trục là tam giác đều. Diện tích xung 4
quanh của hình nón đó là … 1 … 9 … 9 … 2 A Sxq = πa2 3 . B Sxq = 2πa2 3 . C Sxq = 3πa2 3 . D Sxq = 3πa2 3 . 16 16 16 16 √ √ î ó
Câu 33. Cho hàm số y = f (x) dương có đạo hàm liên tục trên đoạn 0; 3 , biết rằng f 0(x) − x2 + 1 · acebook.com/g √ .f 3 √ Z Ä ä f (x) = 0 và f 3 = e3. Tính I = ln [f (x)] dx. 0 √ √ 7 √ 7 √ A 2 3. B 3 3 − . C 3 3 + . D 3 3 − 2. 3 3 https://www
Câu 34. Cho hình D giới hạn bởi các đường y = x2 − 2 và y = −|x|. Khi đó diện tích của hình D là 13 7 7π 13π A . B . C . D . 3 3 3 3 √
Câu 35. Cho hai số phức z1, z2 thỏa mãn |2z − i| = |iz + 2|, biết |z1 − z2| =
2. Tính giá trị của biểu thức A = |z1 − 2z2|. √ √ √ 5 √ 3 A A = 5. B A = . C A = 3. D A = . 2 2
Câu 36. Cho phương trình z2 −4z +5 = 0 có hai nghiệm phức là z1, z2. Tính A = |z1|+|z2|+z1 ·z2. √ √ √ A A = 25 + 2 5. B A = 0. C A = 5 − 2 5. D A = 5 + 2 5.
Câu 37. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình là x2 + y2 + z2 = 9
và điểm A (0; −1; 2). Gọi (P ) là mặt phẳng qua A và cắt mặt cầu (S) theo một đường tròn có chu vi
nhỏ nhất. Phương trình của (P ) là h Geogebra Pro Trang 4 A y − 2z + 5 = 0. B x − y + 2z − 5 = 0. C −y + 2z + 5 = 0. D y − 2z − 5 = 0.
Câu 38. Trong không gian Oxyz, cho hai điểm A(1; 2; 3), B(3; 4; 5) và mặt phẳng (P ) : x+2y+3z−14 =
0. Gọi ∆ là một đường thẳng thay đổi nằm trong mặt phẳng (P ). Gọi H, K lần lượt là hình chiếu vuông
góc của A, B trên ∆. Biết rằng AH = BK thì trung điểm của HK luôn thuộc một đường thẳng d cố
định, phương trình của đường thẳng d là     x = t x = t x = 1 x = t             A y = 13 − 2t . B y = 13 + 2t . C y = 13 − 2t . D y = 13 − 2t .             z = −4 + t z = −4 + t z = −4 + t z = −4 − t
Câu 39. Từ một hộp chứa 5 viên bi đỏ, 4 viên bi xanh và 3 viên bi vàng lấy ngẫu nhiên 3 viên bi.
Tính xác suất để 3 viên bi lấy ra có đủ 3 màu. 3 1 3 11 A . B . C . D . 11 22 220 3
Câu 40. Cho lăng trụ tam giác đều ABC.A0B0C0 có tất cả các cạnh đều bằng a. Khoảng cách giữa hai
đường thẳng BC và AB0 bằng √ √ √ √ a 21 a 3 a 7 a 2 A . B . C . D . 7 2 4 2 mx − 4m + 5 Câu 41. Cho hàm số y =
với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên x + 3m
của m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S. 2019-2020 A 2. B 4. C 3. D 5.
Câu 42. Một người gửi tiết kiệm với lãi suất 8,4%/năm và lãi hàng năm được nhập vào vốn. Hỏi sau THPT
bao nhiêu năm người đó có được gấp đôi số tiền ban đầu? A 9. B 10. C 7. D 8. GHIỆP N T
Câu 43. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như sau TỐ x −∞ −1 3 +∞ THI y0 + 0 − 0 + 5 +∞ + y LUYỆN −∞ 1
Đồ thị hàm số y = |f (x)| có bao nhiêu điểm cực trị? A 2. B 3. C 4. D 5.
Câu 44. Cho hình trụ có thiết diện qua trục là hình vuông cạnh 2a. Mặt phẳng (P ) song song với trục a
và cách trục một khoảng
. Tính diện tích thiết diện của hình trụ cắt bởi mặt phẳng (P ). 2 √ √ A 2 3a2. B a2. C πa2. D 3a2. 1 1 Z 4 Z
Câu 45. Cho hàm số f (x) có đạo hàm trên [0; 1] thỏa mãn f (1) = 1, xf (x) dx = , [f 0(x)]2 dx = 15 0 0 1 49 Z . Tích phân [f (x)]2 dx bằng 45 0 2 1 4 A . B . C . D 1. 9 6 63 h Geogebra Pro Trang 5
Câu 46. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ bên. x −∞ −2 3 +∞ y0 + 0 − 0 + 4 +∞ + y −∞ −2 −
Số nghiệm của phương trình |f (x − 1)| = 2 là A 5. B 4. C 3. D 2.
Câu 47. Cho x, y là các số thực dương, thỏa mãn log 1 x + log 1 y ≤ log 1 (x + y2) . Tìm giá trị nhỏ nhất 3 3 3
Pmin của biểu thức P = 2x + 3y. √ √ √ √ √ A Pmin = 7 + 3 2. B Pmin = 2 + 3. C Pmin = 7 − 2 10. D Pmin = 7 + 2 10.
Câu 48. Gọi S là tập hợp các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y = o/
|x3 − 3x2 − 9x + m| trên đoạn [−2; 4] bằng 16. Số phần tử của S là aPr A 10. B 12. C 14. D 11.
Câu 49. Cho khối chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SC, N thuộc
cạnh SD sao cho SN = 3N D. Mặt phẳng (AM N ) cắt khối chóp thành hai phần, gọi thể tích phần V1
chứa đỉnh S là V1, thể tích khối chóp S.ABCD là V2. Tính tỉ số . V2 V1 27 V1 1 V1 27 V1 29 A = . B = . C = . D = . roups/GeoGebr V2 80 V2 3 V2 53 V2 80
Câu 50. Có bao nhiêu giá trị nguyên âm của m để phương trình log (2x + m) = log√ (x − 1) có nghiệm 2 2 duy nhất: A 0. B 1. C 2. D 3.
———————–HẾT———————– acebook.com/g .f https://www h Geogebra Pro Trang 6 BẢNG ĐÁP ÁN 1. C 2. B 3. A 4. C 5. D 6. D 7. A 8. B 9. B 10. C 11. D 12. D 13. A 14. C 15. A 16. D 17. B 18. A 19. A 20. D 21. D 22. B 23. A 24. C 25. D 26. C 27. D 28. D 29. B 30. A 31. B 32. B 33. B 34. B 35. A 36. D 37. A 38. A 39. A 40. A 41. C 42. A 43. B 44. A 45. A 46. A 47. D 48. D 49. A 50. D 2019-2020 THPT GHIỆP N T TỐ THI LUYỆN h Geogebra Pro Trang 7 MỖI NGÀY MỘT ĐỀ THI 10
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. Một tổ có 6 học sinh nam và 9 học sinh nữ. Hỏi có bao nhiêu cách chọn 6 học sinh đi lao động
trong đó có 2 học sinh nam? A C2 + C4. B A2 · A4. C C2 · C4. D C4 · C2. 6 9 6 9 6 9 6 9 Lời giải.
Số cách chọn 2 học sinh nam là C2. 6
Số cách chọn 4 học sinh nữ là C4. 9
Số cách chọn 6 học sinh đi lao động trong đó có 2 học sinh nam là C2 · C4. 6 9 Chọn phương án C
Câu 2. Cho cấp số cộng (un) biết un = 3 − 5n. Tìm công sai d của cấp số cộng (un). A d = 3. B d = −5. C d = −3. D d = 5. Lời giải. 2019-2020
Theo giả thiết suy ra un+1 = 3 − 5(n + 1) = −2 − 5n ⇒ un+1 − un = −5, ∀n ≥ 1.
Suy ra (un) là cấp số cộng, công sai d = −5. THPT Chọn phương án B
Câu 3. Tìm tập nghiệm S của phương trình 4x − 6 · 2x + 8 = 0. GHIỆP N A S = {1; 2}. B S = (1; 2). C S = {1}. D S = {2}. T Lời giải. TỐ   2x = 4 x = 2, THI
Ta có 4x − 6 · 2x + 8 = 0 ⇔  ⇔  2x = 2 x = 1. LUYỆN Chọn phương án A
Câu 4. Tổng diện tích các mặt của khối lập phương bằng 96. Tìm thể tích của khối lập phương đó. A 48. B 84. C 64. D 91. Lời giải.
Khối lập phương có 6 mặt và theo đề bài tổng diện tích các mặt của khối lập phương là 96 nên diện
tích một mặt của khối lập phương là 96 ÷ 6 = 16. √
Suy ra cạnh của hình lập phương là
16 = 4. Do đó, thể tích của khối lập phương là 42 = 16. Chọn phương án C x + 3
Câu 5. Tập xác định của hàm số y = log là 2 2 − x A D = R\ {−3; 2}.
B D = (−∞; −3) ∪ (2; +∞). C D = [−3; 2]. D D = (−3; 2). Lời giải. x + 3 x + 3 Hàm số log có nghĩa khi > 0 ⇔ −3 < x < 2. 2 2 − x 2 − x h Geogebra Pro Trang 1 Chọn phương án D 1
Câu 6. Cho F (x) là nguyên hàm của f (x) = √
thỏa mãn F (2) = 4. Giá trị F (−1) bằng x + 2 √ √ A 3. B 1. C 2 3. D 2. Lời giải. Z Z 1 √ F (x) = f (x) dx = √ dx = 2 x + 2 + C. x + 2 √ √
Theo đề bài F (2) = 4 nên 2 2 + 2 + C = 4 ⇔ C = 0 ⇒ F (−1) = 2 −1 + 2 = 2. Vậy F (−1) = 2. Chọn phương án D
Câu 7. Cho hình chóp S.ABC có (SAB) ⊥ (ABC), tam giác ABC đều cạnh 2a, tam giác SAB vuông
cân tại S. Tính thể tích hình chóp S.ABC. √ √ √ √ a3 3 a3 3 2a3 3 a3 3 A . B . C . D . 3 6 3 12 Lời giải. o/ S aPr B H A roups/GeoGebr 2a C
Kẻ SH ⊥ AB ⇒ SH ⊥ (ABC) Vì (ABC) ∩ (ABC) = AB và (ABC) ⊥ (ABC). AB Ta có: SH =
= a (Do SAB là tam giác vuông cân tại S cạnh huyền AB = 2a). 2 √ √ acebook.com/g 3 .f
Diện tích tam giác ABC là S4ABC = (2a)2 = 3a2. 4 √ 1 1 √ a3 3
Vậy thể tích khối chóp SABC là: VSABC = .SH.S4ABC = .a. 3a2 = . 3 3 3 Chọn phương án A
Câu 8. Khối nón tròn xoay có chiều cao bằng 8 cm và độ dài đường sinh bằng 10 cm có thể tích https://www bằng A 128π cm3. B 96π cm3. C 124π cm3. D 140π cm3. Lời giải. √ Bán kính đáy r = l2 − h2 = 6 cm. 1 1 Thể tích khối nón V = S · h = · π · 62 · 8 = 96πcm3. 3 đáy 3 l h h Geogebra Pro Trang 2 Chọn phương án B
Câu 9. Tính diện tích mặt cầu (S) khi biết chu vi đường tròn lớn của nó bằng 4π. A S = 32π. B S = 16π. C S = 64π. D S = 8π. Lời giải.
Đường tròn lớn có bán kính bằng bán kính R của mặt cầu.
Do đó, chu vi của đường tròn lớn là 2πR = 4π ⇔ R = 2.
Vậy diện tích của mặt cầu (S) là 4πR2 = 16π. Chọn phương án B
Câu 10. Cho hàm số y = f (x) có bảng biến thiên như hình dưới. Hàm số nghịch biến trong khoảng nào? x −∞ −1 2 +∞ y0 + 0 − 0 + y A (−∞; 2). B (0; 2). C (−1; 2). D (2; +∞). 2019-2020 Lời giải. THPT
Từ bảng biến thiên ta có f 0(x) < 0, ∀x ∈ (−1; 2), suy ra hàm số y = f (x) nghịch biến trên khoảng (−1; 2). GHIỆP Chọn phương án C N √ T a3 · 3 a2
Câu 11. Cho a là số thực dương và a 6= 1. Tính giá trị của biểu thức Q = log √ . TỐ a a 19 19 19 19 THI A Q = . B Q = . C Q = . D Q = . 5 7 4 6 Lời giải. √ a3 · 3 a2 2 1 19 − 19 LUYỆN Q = log √ = log a3+ 3 2 = log a 6 = . a a a a 6 Chọn phương án D
Câu 12. Một hình trụ có bán kính đáy r = 5 cm, chiều cao h = 7 cm. Tính diện tích xung quanh của hình trụ. 35 A 85π cm2. B 35π cm2. C π cm2. D 70π cm2. 3 Lời giải.
Hình trụ có độ dài đường sinh l = h = 7 cm.
Diện tích xung quanh của hình trụ Sxq = 2πrl = 2π · 5 · 7 =70π cm2. h = 7cm l r = 5cm Chọn phương án D Câu 13. h Geogebra Pro Trang 3
Cho hàm số y = f (x) có bảng biến thiên x −∞ −1 0 2 +∞
như hình vẽ. Hỏi hàm số có bao nhiêu y0 + 0 − + 0 − cực trị? 2 3 y A 2. B 3. C 1. D −∞ −1 −1 2 4.
Câu 14. Cho hàm số y = f (x) có đồ thị như hình vẽ. Xác định hàm số trên. 2x + 1 2x − 1 2x − 1 3x + 1 A y = . B y = . C y = . D y = . x − 1 x − 1 x + 1 2x + 2 y 6 4 o/ aPr 2 x −4 −2 O 2 −2 roups/GeoGebr Lời giải.
Đồ thị hàm số nhận đường x = −1 là tiệm cận đứng nên ta loại ngay đáp án A và B vì đồ thị của hai
hàm số này đều nhận đường x = 1 là tiệm cận đứng.
Đồ thị hàm số nhận đường y = 2 là tiệm cận ngang. acebook.com/g .f 2x − 1 2x − 1 Ta có lim
= 2 ⇒ y = 2 là tiệm cận ngang của đồ thị hàm số y = . x→+∞ x + 1 x + 1 2x − 1 2x − 1 lim
= 2 ⇒ y = 2 là tiệm cận ngang của đồ thị hàm số y = . x→−∞ x + 1 x + 1 2x − 1 Vậy hàm số y = thỏa mãn bài toán. x + 1 https://www Chọn phương án C √9 − x2
Câu 15. Đồ thị hàm số y =
có bao nhiêu đường tiệm cận? x2 − 6x + 8 A 1. B 4. C 3. D 2. Lời giải.
Hàm số có nghĩa khi chỉ khi x ∈ [−3; 2) ∪ (2; 3], do đó hàm số không có tiệm cận ngang.
Ta có x2 − 6x + 8 = 0 ⇔ x = 2 hoặc x = 4 / ∈ [−3; 3]. √9 − x2 Mà lim
= −∞ nên hàm số có duy nhất một tiệm cận đứng x = 2. x→2+ x2 − 6x + 8 Chọn phương án A 4x + 6
Câu 16. Tập nghiệm của bất phương trình log 1 ≥ 0 là 5 x Å 3 ò ï 3 ò Å 3 ã ï 3 ã A −2, − . B −2, − . C −2, − . D −2, − . 2 2 2 2 h Geogebra Pro Trang 4 Lời giải.  4x + 6   x > 0  > 0 Điều kiện xác định: x ⇔  3  x < − . x 6= 0 2 4x + 6 4x + 6 − x 3x + 6
Bất phương trình tương đương: ≤ 1 ⇔ ≤ 0 ⇔ ≤ 0 ⇔ −2 ≤ x < 0. x x x 3
Kết hợp với điều kiện ta được: −2 ≤ x < − . 2 ï 3 ã
Vậy tập nghiệm của bất phương trình là −2, − . 2 Chọn phương án D Câu 17.
Cho hàm số y = f (x) liên tục trên đoạn [−2; 2] và có đồ thị là đường cong y 4
như hình vẽ bên. Tìm số nghiệm của phương trình |f (x) | = 1 trên đoạn [−2; 2]. 2 A 4. B 6. C 3. D 5. −2 x2 x1 x O 2 −2 2019-2020 −4 THPT Lời giải.
Số nghiệm của phương trình |f (x)| = 1 là số giao điểm của hai đồ thị hàm y 4 GHIỆP
số y = |f (x)| và đường thẳng y = 1. Theo đồ thị ta được số nghiệm là 6. N 2 T TỐ THI −2 x1 x2 x O 2 LUYỆN Chọn phương án B 2 Z f (x)
Câu 18. Cho hàm số f (x) có đạo hàm liên tục trên [1; 2], có f (2) = 14 và dx = 6. Tính x 1 2 Z I = f 0(x) ln x dx. 1 A I = 14 ln 2 − 6. B I = 7 ln 2 − 6. C I = 7 ln 2 − 6. D I = 14 ln 2 + 6. Lời giải.   1 2  Z u = ln x u0 = f (x) Đặt ⇒ x
. Khi đó I = f (x) ln x|2 −
dx = f (2) ln 2 − 0 − 6 = 14 ln 2 − 6. 1 x v0 = f 0(x)  v = f (x) 1 h Geogebra Pro Trang 5 Chọn phương án A
Câu 19. Cho số phức z thỏa mãn z − 3 + i = 0. Môđun của z bằng bao nhiêu? √ √ A 10. B 10. C 3. D 4. Lời giải. √ Ta có |z| = |z| = |3 − i| = 10. Chọn phương án A
Câu 20. Cho số phức z1 = 3 + 2i, z2 = 6 + 5i. Tìm số phức liên hợp của z = 6z1 + 5z2. A ¯ z = 51 + 40i. B ¯ z = 51 − 40i. C ¯ z = 48 + 37i. D ¯ z = 48 − 37i. Lời giải.
Ta có z = 6z1 + 5z2 = 48 + 37i nên ¯ z = 48 − 37i. Chọn phương án D
Câu 21. Gọi A, B, C là các điểm trong mặt phẳng Oxy theo thứ tự biểu diễn các số phức 2 + 3i, 3 + i, o/
1 + 2i. Trọng tâm G của tam giác ABC biểu diễn số phức z. Tìm z. aPr A z = 1 + i. B z = 1 − i. C z = 2 − 2i. D z = 2 + 2i. Lời giải.
Ta có: A (2; 3), B (3; 1), C (1; 2) ⇒ G (2; 2) là điểm biểu diễn số phức z = 2 + 2i. Chọn phương án D
Câu 22 (2H3B1-1). Trong không gian với hệ tọa độ Oxyz, tìm tọa độ điểm M trên trục Ox cách roups/GeoGebr
đều hai điểm A (1; 2; −1) và điểm B (2; 1; 2) Å 1 ã Å 3 ã Å 2 ã Å 1 ã A M ; 0; 0 . B M ; 0; 0 . C M ; 0; 0 . D M ; 0; 0 . 2 2 3 3 Lời giải.
Ta có M ∈ Ox ⇒ M (m; 0; 0). Theo bài ta có: acebook.com/g .f M A = M B ⇔ M A2 = M B2
⇔ (m − 1)2 + 22 + 12 = (m − 2)2 + 12 + 22  m − 1 = m − 2
⇔ (m − 1)2 = (m − 2)2 ⇔  m − 1 = 2 − m https://www 3 Å 3 ã ⇔ m = ⇒ M ; 0; 0 . 2 2 Chọn phương án B
Câu 23. Trong hệ tọa độ Oxyz, cho điểm I(2; −1; −1) và mặt phẳng (P ) : x − 2y − 2z + 3 = 0. Viết
phương trình mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng (P ).
A S : x2 + y2 + z2 − 4x + 2y + 2z − 3 = 0.
B S : x2 + y2 + z2 − 2x + y + z − 3 = 0.
C S : x2 + y2 + z2 − 4x + 2y + 2z + 1 = 0.
D S : x2 + y2 + z2 − 2x + y + z + 1 = 0. Lời giải.
Gọi R là bán kính mặt cầu.
|2 − 2(−1) − 2(−1) + 3|
Do (S) tiếp xúc với (P ) nên R = d(I, (P )) = = 3. p12 + (−2)2 + (−2)2
Vậy phương trình S : (x − 2)2 + (y + 1)2 + (z + 1)2 = 9 ⇔ x2 + y2 + z2 − 4x + 2y + 2z − 3 = 0. h Geogebra Pro Trang 6 Chọn phương án A
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P ) : 2x − 2y + z + 4 = 0. Tính khoảng
cách d từ điểm M (1; 2; 1) đến (P ). 1 A d = 3. B d = 4. C d = 1. D d = . 3 Lời giải. |2 · 1 − 2 · 2 + 1 + 4|
Khoảng cách d từ điểm M (1; 2; 1) đến (P ) là d(M, (P )) = = 1. p22 + (−2)2 + 12 Chọn phương án C x − 1 y − 3 z − 1
Câu 25. Trong hệ tọa độ Oxyz, cho đường thẳng d : = = cắt mặt phẳng (P ) : 2 −1 1
2x − 3y + z − 2 = 0 tại điểm I(a; b; c). Khi đó a + b + c bằng A 9. B 5. C 3. D 7. Lời giải.
Ta có {I} = d ∩ (P ) suy ra I ∈ d và I ∈ (P ).
Vì I ∈ d nên tọa độ của I có dạng (1 + 2t; 3 − t; 1 + t) với t ∈ R.
Vì I ∈ (P ) nên ta có phương trình: 2(1 + 2t) − 3(3 − t) + 1 + t − 2 = 0 ⇔ t = 1.
Vậy I(3; 2; 2) suy ra a + b + c = 3 + 2 + 2 = 7. Chọn phương án D √
Câu 26. Cho lăng trụ tam giác đều ABC.A0B0C0 có diện tích đáy bằng 3a2 (đvdt), diện tích tam 2019-2020
giác A0BC bằng 2a2 (đvdt). Tính góc giữa hai mặt phẳng (A0BC) và (ABC)? THPT A 120◦. B 60◦. C 30◦. D 45◦. Lời giải.
• Ta có 4ABC là hình chiếu vuông góc của ∆A0BC trên mặt phẳng (ABC). GHIỆP A0 C0 N T
• Gọi ϕ là góc giữa (A0BC) và (ABC). √ √ S a2 3 3 TỐ 4ABC Ta có: cos ϕ = = = ⇒ ϕ = 30◦. B0 S∆A0BC 2a2 2 THI A C LUYỆN B Chọn phương án C
Câu 27. Cho hàm số y = f (x) liên tục trên [−3; 3] và có bảng xét dấu đạo hàm như hình bên. x −3 −1 0 1 2 3 y0 + 0 − 0 − 0 + 0 −
Mệnh đề nào sau đây sai về hàm số đó?
A Hàm số đạt cực tiểu tại x = 1.
B Hàm số đạt cực đại tại x = −1.
C Hàm số đạt cực đại tại x = 2.
D Hàm số đạt cực tiểu tại x = 0. Lời giải.
Dựa vào bảng xét dấu của đạo hàm ta thấy f 0(0) = 0 và đạo hàm không đổi dấu khi x qua x0 = 0 nên
hàm số đã cho không đạt cực tiểu tại x = 0. h Geogebra Pro Trang 7 Chọn phương án D √
Câu 28. Tìm giá trị nhỏ nhất của hàm số y = 2x + 5 − x2. √ √ A 5. B 2 5. C −3. D −2 5. Lời giải. x
Tập xác định: D = R. Ta có y0 = 2 − √ . 5 − x2 x y0 = 0 ⇔ 2 − √ = 0 ⇔ x = 1. 5 − x2 √ √ √ √
y(1) = 4; y( 5) = 2 5; y(− 5) = −2 5. Chọn phương án D 5b − a a
Câu 29. Cho a, b là các số dương thỏa mãn log a = log b = log . Tính giá trị T = . 9 16 12 2 b √ √ 3 + 6 √ √ 3 − 6 A T = . B T = 7 − 2 6. C T = 7 + 2 6. D T = . 4 4 Lời giải. o/ 5b − a 5b − a Đặt log a = log b = log
= t, ta được a = 9t, b = 16t, = 12t. 9 16 12 aPr 2 2 5 · 16t − 9t Å 3 ãt Å 3 ã2t Å 3 ãt √ Suy ra
= 12t ⇔ 5 · 16t − 2 · 12t − 9t = 0 ⇔ 5 − 2 · − ⇔ = 6 − 1. 2 4 4 4 a 9t Å 3 ã2t √ √ Do đó = = = ( 6 − 1)2 = 7 − 2 6. b 16t 4 Chọn phương án B
Câu 30. Phương trình x3 − 3x + 2m − 2 = 0 có đúng một nghiệm dương khi m thỏa roups/GeoGebr A m = 2 hoặc m ≤ 1. B m ∈ ∅. C m > 1. D m < 1 hoặc m > 2. Lời giải.
Phương trình đã cho tương đương: x3 − 3x = 2 − 2m. Đặt y = x3 − 3x (C) và y = 2 − 2m (d).
Ta có bảng biến thiên của y = x3 − 3x là x −∞ −1 1 +∞ acebook.com/g y0 + .f 0 − 0 + 2 +∞ + y −∞ −2 https://www
Số nghiệm phương trình chính là số giao điểm của (d) và (C). Yêu cầu bài toán là phương trình đã
cho có đúng một nghiệm dương, tức là trong số các giao điểm của (d) và (C) chỉ có đúng một điểm có hoành độ dương.   2 − 2m ≥ 0 m ≤ 1
Dựa vào bảng biến thiên của (C) ta có các trường hợp thỏa yêu cầu  ⇔  2 − 2m = −2 m = 2 Chọn phương án A
Câu 31. Bất phương trình 6 · 4x − 13 · 6x + 6 · 9x > 0 có tập nghiệm là?
A S = (−∞; −2) ∪ (1; +∞).
B S = (−∞; −1) ∪ (1; +∞).
C S = (−∞; −2] ∪ [2; +∞).
D S = (−∞; −1) ∪ (1; +∞). Lời giải. Å 2 ã2x Å 2 ãx
Chia cả hai vế của bất phương trình cho 9x ta được 6 · − 13 · + 6 > 0. 3 3 h Geogebra Pro Trang 8  3 Å 2 ãx t < Đặt
= t (t > 0). Ta được bất phương trình mới 6t2 − 13t + 6 > 0 ⇔ 2  3  3 t > . 2 Å 2 ãx 2 <  3 3 x > 1 Suy ra   ⇔ Å ãx   2 3 > x < −1. 3 2
Vậy tập nghiệm của bất phương trình là S = (−∞; −1) ∪ (1; +∞). Chọn phương án B √3
Câu 32. Cho khối nón có thể tích V =
πa3 và thiết diện qua trục là tam giác đều. Diện tích xung 4
quanh của hình nón đó là … 1 … 9 … 9 … 2 A Sxq = πa2 3 . B Sxq = 2πa2 3 . C Sxq = 3πa2 3 . D Sxq = 3πa2 3 . 16 16 16 16 Lời giải. √ 2R 3 √
Do thiết diện qua trục là tam giác đều nên l = 2R và h = = R 3. 2 Theo đề
√ bài khối nón có thể tíc √ h √ 3 1 π 3a3 1 √ π 3a3 3 … 3 V = πa3 ⇔ h · πR2 = ⇔ πR3 3 = ⇔ R3 = a3 ⇔ R = 3 · a 4 3 4 3 4 4 4 … 3
⇒ đường sinh của hình nón là l = 2 3 · a. 4 … 9
Diện tích xung quanh hình nón là S . 2019-2020 xq = πRl = 2πa2 3 16 Chọn phương án B THPT √ √ î ó
Câu 33. Cho hàm số y = f (x) dương có đạo hàm liên tục trên đoạn 0; 3 , biết rằng f 0(x) − x2 + 1 · √3 √ Z Ä ä GHIỆP f (x) = 0 và f 3 = e3. Tính I = ln [f (x)] dx. N T 0 √ √ 7 √ 7 √ TỐ A 2 3. B 3 3 − . C 3 3 + . D 3 3 − 2. 3 3 THI Lời giải. Ta có LUYỆN √ f 0(x) √ f 0(x) − x2 + 1 · f (x) = 0 ⇔ = x2 + 1 f (x) Z f 0(x) Z √ ⇒ dx = x2 + 1 dx f (x) x √ 1 √ Ä ä ⇒ ln f (x) = x2 + 1 + ln x + x2 + 1 + C. 2 2 √ √ √ Ä ä 1 Ä ä Ta có f 3 = e3 ⇒ C = 3 − 3 − ln 3 + 2 . 2 Do đó √ √ 3 3 Z Z ï x √ 1 √ Å √ √ ãò Ä ä 1 Ä ä ln f (x) dx = x2 + 1 + ln x + x2 + 1 + 3 − 3 − ln 3 + 2 dx 2 2 2 0 0√ 7 = 3 3 − · 3 Chọn phương án B h Geogebra Pro Trang 9
Câu 34. Cho hình D giới hạn bởi các đường y = x2 − 2 và y = −|x|. Khi đó diện tích của hình D là 13 7 7π 13π A . B . C . D . 3 3 3 3 Lời giải.  x2 − 2 = x nếu x < 0
Xét phương trình x2 − 2 = −|x| ⇔  ⇔ x = −1 và x = 1. x2 − 2 = −x nếu x > 0 Z 0 Z 1 7 Do đó ta có S = (x + 2 − x2)dx + (−x − x2 + 2)dx = . − 3 1 0 Chọn phương án B √
Câu 35. Cho hai số phức z1, z2 thỏa mãn |2z − i| = |iz + 2|, biết |z1 − z2| =
2. Tính giá trị của biểu thức A = |z1 − 2z2|. √ √ √ 5 √ 3 A A = 5. B A = . C A = 3. D A = . 2 2 Lời giải. o/ Gọi z aPr
1 = x1 + y1i, z2 = x2 + y2i với x1, y1, x2, y2 ∈ R. Theo giả thiết ta có   |2x x2 + y2 = 1 
1 + (2y1 − 1)i| = |2 − y1 + x1i|    1 1     |2x ⇔
2 + (2y2 − 1)i| = |2 − y2 + x2i| x2 + y2 = 1 2 2        
(x1 − x2)2 + (y1 − y2)2 = 2 x1x2 + y1y2 = 0 roups/GeoGebr
Do đó, A2 = |z1 − 2z2|2 = (x1 − 2x2)2 + (y1 − 2y2)2 = (x2 + y2) + 4(x2 + y2) − 4(x 1 1 2 2 1x2 + y1y2) = 5. Khi √ đó A = 5. Chọn phương án A
Câu 36. Cho phương trình z2 −4z +5 = 0 có hai nghiệm phức là z1, z2. Tính A = |z1|+|z2|+z1 ·z2. √ √ √ A A = 25 + 2 5. B A = 0. C A = 5 − 2 5. D A = 5 + 2 5. Lời giải. acebook.com/g .f
Do z1, z2 là hai số phức liên hợp của nhau nên |z1|2 = |z2|2 = z1 · z2 = 5. √ Suy ra A = 5 + 2 5. Chọn phương án D
Câu 37. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình là x2 + y2 + z2 = 9 https://www
và điểm A (0; −1; 2). Gọi (P ) là mặt phẳng qua A và cắt mặt cầu (S) theo một đường tròn có chu vi
nhỏ nhất. Phương trình của (P ) là A y − 2z + 5 = 0. B x − y + 2z − 5 = 0. C −y + 2z + 5 = 0. D y − 2z − 5 = 0. Lời giải.
Mặt cầu (S) có tâm O(0; 0; 0) và bán kính R = 3. A(0; −1; 2) là điểm nằm bên trong mặt cầu (S). (P )
là mặt phẳng qua A và cắt mặt cầu (S) theo một đường tròn có bán kính r.
Gọi H là hình chiếu của O lên (P ). Ta có
r2 = R2 − OH2. rmin ⇔ OHmax ⇔ H ≡ A. # »
Khi đó (P ) nhận OA = (0; −1; 2) là véc-tơ pháp tuyến. Vậy phương trình (P ) : y − 2z + 5 = 0. Chọn phương án A h Geogebra Pro Trang 10
Câu 38. Trong không gian Oxyz, cho hai điểm A(1; 2; 3), B(3; 4; 5) và mặt phẳng (P ) : x+2y+3z−14 =
0. Gọi ∆ là một đường thẳng thay đổi nằm trong mặt phẳng (P ). Gọi H, K lần lượt là hình chiếu vuông
góc của A, B trên ∆. Biết rằng AH = BK thì trung điểm của HK luôn thuộc một đường thẳng d cố
định, phương trình của đường thẳng d là     x = t x = t x = 1 x = t             A y = 13 − 2t . B y = 13 + 2t . C y = 13 − 2t . D y = 13 − 2t .             z = −4 + t z = −4 + t z = −4 + t z = −4 − t Lời giải.
Gọi I là trung điểm của HK. B
Xét các tam giác AHI và BKI, ta có các tam giác này vuông tại
H, K, theo giả thiết AH = BK, IH = IK ⇒ 4HIA = 4IKB ⇒
IA = IB ⇒ I thuộc mặt phẳng trung trực của AB.
Theo giả thiết I ∈ (P ) ⇒ I thuộc giao tuyến của mặt phẳng trung
trực (α) của AB với (P ). A K H I  Qua I0 (2; 3; 4) Mặt phẳng (α) : # »
Có véc-tơ pháp tuyến AB = (1; 1; 1).
Suy ra (α) : x + y + z − 9 = 0.  x + 2y + 3z − 14 = 0 2019-2020
Tọa độ các điểm M ∈ d thỏa mãn hệ x + y + z − 9 = 0. THPT   x = t x = t       Đặt x = t ⇒
y = 13 − 2t ⇒ phương trình của đường thẳng d là y = 13 − 2t GHIỆP     N   z = −4 + t z = −4 + t. T TỐ Chọn phương án A THI
Câu 39. Từ một hộp chứa 5 viên bi đỏ, 4 viên bi xanh và 3 viên bi vàng lấy ngẫu nhiên 3 viên bi.
Tính xác suất để 3 viên bi lấy ra có đủ 3 màu. LUYỆN 3 1 3 11 A . B . C . D . 11 22 220 3 Lời giải.
Số phần tử của không gian mẫu là n(Ω) = C3 = 220. 12
Gọi A là biến cố: "3 viên bi lấy ra có đủ 3 màu".
Số phần tử của biến cố A là n(A) = C1C1C1 = 60. 5 4 3 n(A) 60 3
Xác suất của biến cố A là P (A) = = = . n(Ω) 220 11 Chọn phương án A
Câu 40. Cho lăng trụ tam giác đều ABC.A0B0C0 có tất cả các cạnh đều bằng a. Khoảng cách giữa hai
đường thẳng BC và AB0 bằng √ √ √ √ a 21 a 3 a 7 a 2 A . B . C . D . 7 2 4 2 Lời giải. h Geogebra Pro Trang 11
Ta có BCkB0C0 ⇒ BCk (AB0C0). Suy ra: d(BC, AB0) = d(BC, (AB0C0)) = d(B, (AB0C0)) = A0 C0 d(A0, (AB0C0)). I
Gọi I và H lần lượt là hình chiếu vuông góc B0 H của A0 trên B0C0 và AI.
Ta có: B0C0⊥A0I và B0C0⊥A0A
nên B0C0⊥ (A0AI) ⇒ B0C0⊥A0H. A C
Mà AI⊥A0H. Do đó (AB0C0) ⊥A0H. B √ a 3 √ A0A.A0I a. a 21
Khi đó: d (A0, (AB0C0)) = A0H = √ = 2 √ = . A0A2 + A0I2 s Ç å2 7 a 3 a2 + 2 o/ √ a 21 aPr
Vậy khoảng cách cần tìm là . 7 Chọn phương án A mx − 4m + 5 Câu 41. Cho hàm số y =
với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên x + 3m
của m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S. A 2. B 4. C 3. D 5. roups/GeoGebr Lời giải. 3m2 + 4m − 5 y0 = . (x + 3m)2 √ √ 2 − 19 2 + 19
Để hàm số nghịch biến thì 3m + 4m − 5 < 0 ⇔ < m < . 3 3
Vậy các giá trị nguyên của m là 0, 1, 2. Chọn phương án C acebook.com/g .f
Câu 42. Một người gửi tiết kiệm với lãi suất 8,4%/năm và lãi hàng năm được nhập vào vốn. Hỏi sau
bao nhiêu năm người đó có được gấp đôi số tiền ban đầu? A 9. B 10. C 7. D 8. Lời giải. https://www
Gọi số tiền ban đầu người đó gửi vào ngân hàng là A, r = 8,4% là lãi suất hàng năm, Pn là số tiền
nhận được sau n năm. Vì lãi hàng năm nhập vào vốn nên theo công thức lãi kép ta có
Pn = A · (1 + r)n ⇒ 2A = A · (1 + r)n ⇒ 2 = (1 + r)n ⇒ n = log 2 ≈ 9. 1+r Chọn phương án A
Câu 43. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như sau x −∞ −1 3 +∞ y0 + 0 − 0 + 5 +∞ + y −∞ 1
Đồ thị hàm số y = |f (x)| có bao nhiêu điểm cực trị? h Geogebra Pro Trang 12 A 2. B 3. C 4. D 5. Lời giải.
Số điểm cực trị của đồ thị hàm số y = |f (x)| bằng số điểm cực trị của đồ thị hàm số y = f (x) cộng với
số giao điểm của đồ thị hàm số y = f (x) với trục hoành (không tính điểm cực trị).
Vì đồ thị hàm số y = f (x) có 2 điểm cực trị và cắt trục Ox tại 1 điểm trên đồ thị hàm số y = |f (x)|
có 2 + 1 = 3 điểm cực trị. Chọn phương án B
Câu 44. Cho hình trụ có thiết diện qua trục là hình vuông cạnh 2a. Mặt phẳng (P ) song song với trục a
và cách trục một khoảng
. Tính diện tích thiết diện của hình trụ cắt bởi mặt phẳng (P ). 2 √ √ A 2 3a2. B a2. C πa2. D 3a2. Lời giải.
Gọi ABB0A0 là thiết diện qua trục của hình trụ. Từ giả thiết ta Q
suy ra đường cao hình trụ là AA0 = 2a, bán kính đường tròn đáy O0 A0 H B0 AB hình trụ là R = = a. P 2
Mặt phẳng (P ) song song với trục nên cắt hình trụ theo thiết
diện là hình chữ nhật có một cạnh M Q = AA0 = 2a, và cách trục 2019-2020 a a một khoảng nên O0H =
với H là trung điểm của P Q. Khi 2 2 … √ THPT a2 đó P Q = 2pO0Q2 − O0H2 = 2 a2 − = a 3. 4 √
Do đó diện tích thiết diện cần tìm là M Q · P Q = 2 3a2. M A B GHIỆP O N N T TỐ Chọn phương án A THI 1 1 Z 4 Z
Câu 45. Cho hàm số f (x) có đạo hàm trên [0; 1] thỏa mãn f (1) = 1, xf (x) dx = , [f 0(x)]2 dx = 15 LUYỆN 0 0 1 49 Z . Tích phân [f (x)]2 dx bằng 45 0 2 1 4 A . B . C . D 1. 9 6 63 Lời giải.   u = xf (x)  du = [f (x) + xf 0(x)] dx Đặt ⇒ . Khi đó  dv = dx v = x 1 1 Z Z 1 xf (x) dx = x2f (x) − x[f (x) + xf 0(x)] dx 0 0 0 1 1 Z Z = f (1) − xf (x) dx − x2f 0(x) dx. 0 0 h Geogebra Pro Trang 13 1 Z 4 7 Suy ra x2f 0(x) dx = 1 − 2 · =
. Khi đó dự đoán dạng f 0(x) = mx2, với m ∈ R. Ta có 15 15 0 1 1 1 1 Z Z Z Z [mx2 − f 0(x)]2 dx = m2x4 dx − 2mx2f 0(x) dx + [f 0(x)]2 dx 0 0 0 0 m2 14m 49 (3m − 7)2 = − + = . 5 15 45 45 1 Z (3m − 7)2 7 Ta cần [mx2 − f 0(x)]2 dx = 0 ⇔ = 0 ⇔ m = . Như vậy ta có 45 3 0 1 Z ï 7 ò2 x2 − f 0(x) dx = 0. 3 0 o/ 7 7x3 2 7x3 2 aPr Suy ra f 0(x) = x2 ⇒ f (x) = + C. Từ f (1) = 1 ⇒ C = . Khi đó f (x) = + thỏa mãn 3 9 9 9 9 1 Z 4 xf (x) dx = . Vậy 15 0 1 1 Z Z Å 7x3 2 ã2 2 [f (x)]2 dx = + dx = . 9 9 9 0 0 roups/GeoGebr Chọn phương án A
Câu 46. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ bên. x −∞ −2 3 +∞ y0 + 0 − 0 + 4 +∞ + acebook.com/g .f y −∞ −2 −
Số nghiệm của phương trình |f (x − 1)| = 2 là A 5. B 4. C 3. D 2. https://www Lời giải.
Từ bảng biến thiên suy ra phương trình f (x) = 0 có 3 nghiệm phân biệt là x1, x2, x3 thỏa mãn
x1 < −2 < x2 < 3 < x3. Khi đó phương trình f (x − 1) = 0 có 3 nghiệm phân biệt là x1 + 1, x2 + 1, x3 + 1.
Suy ra bảng biến thiên của hàm số y = |f (x − 1)| như sau x −∞ x1 + 1 −1 x2 + 1 4 x3 + 1 +∞ y0 − + − + − + +∞ + 4 2 +∞ + y 0 0 0
Dựa vào bảng biến thiên ta suy ra phương trình |f (x − 1)| = 2 có 5 nghiệm. Chọn phương án A h Geogebra Pro Trang 14
Câu 47. Cho x, y là các số thực dương, thỏa mãn log 1 x + log 1 y ≤ log 1 (x + y2) . Tìm giá trị nhỏ nhất 3 3 3
Pmin của biểu thức P = 2x + 3y. √ √ √ √ √ A Pmin = 7 + 3 2. B Pmin = 2 + 3. C Pmin = 7 − 2 10. D Pmin = 7 + 2 10. Lời giải.
log 1 x + log 1 y ≤ log 1 (x + y2) ⇔ xy ≥ x + y2 ⇔ x(y − 1) ≥ y2. Từ đây, do x, y dương nên ta suy ra 3 3 3 y2 1 y > 1 và x ≥ = y + 1 + . y − 1 y − 1 √ 2 2 √ 10 Do đó, P ≥ 5y + 2 + = 5(y − 1) +
+ 7 ≥ 2 10 + 7. Dấu bằng xảy ra khi y = 1 + , x = y − 1 y − 1 5 √ 7 10 2 + . 10 Chọn phương án D
Câu 48. Gọi S là tập hợp các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y =
|x3 − 3x2 − 9x + m| trên đoạn [−2; 4] bằng 16. Số phần tử của S là A 10. B 12. C 14. D 11. Lời giải.  x = −1
Xét hàm số y = f (x) = x3 − 3x2 − 9x + m có y0 = 3x2 − 6x − 9, y0 = 0 ⇔  x = 3. Bảng biến thiên 2019-2020 x −2 −1 3 4 THPT f 0(x) + 0 − 0 + GHIỆP m + 5 m − 20 N T f (x) TỐ m − 2 m − 27 THI
Giá trị lớn nhất của hàm số y = |x3 − 3x2 − 9x + m| trên đoạn [−2; 4] bằng 16 khi và chỉ khi LUYỆN   m + 5 = 16   27 − m ≤ 16   ⇔ m = 11.   m − 27 = 16    m + 5 ≤ 16
Vậy m = 11 là giá trị duy nhất thỏa mãn. Chọn phương án D
Câu 49. Cho khối chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SC, N thuộc
cạnh SD sao cho SN = 3N D. Mặt phẳng (AM N ) cắt khối chóp thành hai phần, gọi thể tích phần V1
chứa đỉnh S là V1, thể tích khối chóp S.ABCD là V2. Tính tỉ số . V2 V1 27 V1 1 V1 27 V1 29 A = . B = . C = . D = . V2 80 V2 3 V2 53 V2 80 Lời giải. h Geogebra Pro Trang 15
Gọi O là tâm là hình bình hành ABCD. S
Trong mặt phẳng (SAC) gọi I là giao điểm của SO và AM .
Trong mặt phẳng (SBD) gọi E là giao điểm của N I và SB. M
Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AM N ) N I là tứ giác AN M E. E D
Cách 1. Dùng tỉ số thể tích C Ta có O V A B SAN E SN SE 3 SE = · = · . (1) VSADB SD SB 4 SB VSMNE SM SN SE 1 3 SE 3 SE = · · = · · = · . (2) VSCDB SC SD SB 2 4 SB 8 SB
Lấy (1) cộng (2) ta được V1 9 SE V1 9 SE o/ = · ⇔ = · . (3) 1 8 SB V 16 SB V 2 aPr 2 2 Ta có VSNAM SN SM 3 1 3 = · = · = . (4) VSDAC SD SC 4 2 8 VSEAM SE SM 1 SE = · = · . (5) VSBAC SB SC 2 SB roups/GeoGebr
Lấy (4) cộng (5) ta được V1 3 1 SE V 3 1 SE = + · ⇔ 1 = + · . (6) 1 8 2 SB V 16 4 SB V 2 2 2
Từ (3) và (6) ta có phương trình acebook.com/g .f 9 SE 3 1 SE SE 3 · = + · ⇔ = . (7) 16 SB 16 4 SB SB 5 Thế (7) vào (3) ta được V1 9 SE 9 3 27 = · = · = . V 16 SB 16 5 80 https://www 2
Cách 2. Dùng tính chất thiết diện
Tính chất. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng (P ) cắt các cạnh
SA, SB, SC, SD lần lượt tại A0, B0, C0, D0 thì ta có đẳng thức SA SC SB SC + = + . SA0 SC0 SB0 SC0 Ta có SD SB SC SA + = + SN SE SM SA SB 4 5 ⇔ = 1 + 2 − = SE 3 3 SE 3 ⇔ = . SB 5 h Geogebra Pro Trang 16 Ta có VSAMN SN SM 3 1 3 3 = · = · = ⇒ VSAMN = V2. VSACD SD SC 4 2 8 16 VSAME SM SE 1 3 3 3 = · = · = ⇒ VSAME = V2. VSACB SC SB 2 5 10 20 Suy ra 3 3 27 V1 = VSAMN + VSAME = V2 + V2 = V2. 16 20 80 V1 27 Vậy = . V2 80 Chọn phương án A
Câu 50. Có bao nhiêu giá trị nguyên âm của m để phương trình log (2x + m) = log√ (x − 1) có nghiệm 2 2 duy nhất: A 0. B 1. C 2. D 3. Lời giải.  2x + m > 0   
log (2x + m) = log√ (x − 1) ⇔ 2 2 x − 1 > 0     log (2x + m) = log 2 2(x − 1)2   2019-2020 x > 1 x > 1 ⇔ ⇔ 2x + m = (x − 1)2 x2 − 4x + 1 − m = 0 (1). THPT
PT log (2x + m) = log√ (x − 1) có nghiệm duy nhất khi phương trình (1) có nghiệm duy nhất lớn hơn 2 2 1. GHIỆP N
Ta có (1) ⇔ m = x2 − 4x + 1. Xét hàm số f (x) = x2 − 4x + 1 trên khoảng (1; +∞) ta được T  m = −3 TỐ  ⇒ m ∈ {−3; −2; −1}. m > −2 THI Chọn phương án D
———————–HẾT———————– LUYỆN h Geogebra Pro Trang 17 BẢNG ĐÁP ÁN 1. C 2. B 3. A 4. C 5. D 6. D 7. A 8. B 9. B 10. C 11. D 12. D 13. A 14. C 15. A 16. D 17. B 18. A 19. A 20. D 21. D 22. B 23. A 24. C 25. D 26. C 27. D 28. D 29. B 30. A 31. B 32. B 33. B 34. B 35. A 36. D 37. A 38. A 39. A 40. A 41. C 42. A 43. B 44. A 45. A 46. A 47. D 48. D 49. A 50. D o/ aPr roups/GeoGebr acebook.com/g .f https://www h Geogebra Pro Trang 18
Document Outline

  • MOI NAY 1 DE THI06(noLG)
  • MOI NAY 1 DE THI06(LG)
  • MOI NAY 1 DE THI07(noLG)
  • MOI NAY 1 DE THI07(LG)
  • MOI NAY 1 DE THI08(noLG)
  • MOI NAY 1 DE THI08(LG)
  • MOI NGAY 1 DE THI09(noLG)
  • MOI NGAY 1 DE THI09(LG)
  • MOI NGAY MOT DE THI 10(noLG)
  • MOI NGAY MOT DE THI 10(LG)