TOP 50 câu trắc nghiệm số phức có đáp án và lời giải chi tiết

TOP 50 câu trắc nghiệm số phức có đáp án và lời giải chi tiết giúp các em học sinh nắm chắc các dạng Toán thường gặp trong đề thi, luyện giải đề thật nhuần nhuyễn để ôn thi vào lớp 12 năm 2023 - 2024 đạt kết quả cao. Đề thi được thiết kế dưới dạng PDF bao gồm 9 trang. Mời các em tham khảo.

 

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

9 trang 8 tháng trước

Tác giả:

Profile ha phan
Trang 1
BÀI TẬP SỐ PHỨC CÓ ĐÁP ÁN VÀ LỜI GIẢI
Câu 1. Tính môđun của số phức
34zi
.
A.
3
. B.
5
. C.
7
. D.
7
.
Câu 2. Số phức liên hợp của số phức
12z i i
có điểm biểu diễn là điểm nào dưới đây?
A.
2; 1E
. B.
1;2B
. C.
1;2A
. D.
2;1F
.
Câu 3. Điểm
trong hình vẽ bên dưới biểu diễn cho số phức
z
.
Mệnh đề nào sau đây đúng?
A. Phần thực là
3
, phần ảo là
2
.
B. Phần thực là
3
, phần ảo là
2i
.
C. Phần thực là
3
, phần ảo là
2i
.
D. Phần thực là
3
, phần ảo là
2
.
Câu 4. Cho số phức
12zi
. Điểm nào dưới đây là điểm biểu diễn của số phức
w z iz
trên mặt phẳng
toạ độ?
A.
3;3M
. B.
3;2Q
. C.
2;3N
. D.
3;3P
.
Câu 5. Cho hai số phức
1
23zi
,
2
1zi
. Giá trị của biểu thức
12
3zz
là
A.
55
. B.
5
. C.
6
. D.
61
.
Câu 6. Gọi
0
z
là nghiệm phức có phần ảo dương của phương trình
2
2 10 0zz
. Tính
0
iz
.
A.
0
3iz i
. B.
0
31iz i
. C.
0
3iz i
. D.
0
31iz i
.
Câu 7. Phần thực và phần ảo của số phức liên hợp của số phức
1zi
là:
A. Phần thực là
1
, phần ảo là
1
. B. Phần thực là
1
, phần ảo là
i
.
C. Phần thực là
1
, phần ảo là
i
. D. Phần thực là
1
, phần ảo là
1
.
Câu 8. Xác định phần ảo của số phức
18 12zi
.
A.
12
. B.
18
. C.
12
. D.
12i
.
Câu 9. Điểm biểu diễn của số phức
z
là
1;2M
. Tọa độ của điểm biểu diễn cho số phức
2w z z
là
A.
2; 3
. B.
2;1
. C.
1;6
. D.
2;3
.
Câu 10. Gọi
và
2
z
lần lượt là hai nghiệm của phương trình
2
4 5 0zz
. Giá trị của biểu thức
1 2 2 1
2 . 4P z z z z
bằng:
A.
10
. B.
10
. C.
5
. D.
15
.
Câu 11. Cho số phức
2
1 1 2z i i
. Số phức
z
có phần ảo là:
A.
2
. B.
4
. C.
2
. D.
2i
.
Câu 12. Điểm
M
trong hình bên là điểm biểu diễn cho số phức
A.
2 2 5z i i
.
B.
1 2 4z i i
.
C.
31zi
.
D.
13zi
.
Câu 13. Cho số phức
12zi
. Số phức liên hợp của
z
là
Trang 2
A.
12zi
. B.
12zi
.
C.
2zi
. D.
12zi
.
Câu 14. Tìm tọa độ điểm biểu diễn của số phức
2 3 4
32
ii
z
i

.
A.
1; 4
. B.
1;4
. C.
1; 4
. D.
1;4
.
Câu 15. Cho số phức
z a bi
,ab
. Khẳng định nào sau đây sai?
A.
22
z a b
. B.
z a bi
. C.
2
z
là số thực. D.
.zz
là số thực.
Câu 16. Cho hai số phức
1
3zi
và
2
4zi
. Tính môđun của số phức
2
12
zz
.
A.
12
. B.
10
. C.
13
. D.
15
.
Câu 17. Cho số phức
z
thỏa mãn
1 1 5 0z i i
. Số phức
1wz
bằng
A.
13i
.
B.
13i
. C.
23i
. D.
23i
.
Câu 18. Gọi
,ab
lần lượt là phần thực và phần ảo của số phức
1 3 1 2 3 4 2 3 .z i i i i
Giá trị của
ab
là
A.
7
. B.
7
. C.
31
. D.
31
.
Câu 19. Cho số phức
1
32zi
,
2
65zi
. Tìm số phức liên hợp của số phức
12
65z z z
A.
51 40zi
. B.
51 40zi
. C.
48 37zi
. D.
48 37zi
.
Câu 20. Cho số phức
z
thỏa mãn
1 2 1 2 2i z i i
. Mô đun của
z
bằng
A.
2
. B.
1
. C.
2
. D.
10
.
Câu 21. Số phức
z
nào sau đây thỏa
5z
và
z
là số thuần ảo?
A.
5z
. B.
23zi
. C.
5zi
. D.
5zi
.
Câu 22. Trong mặt phẳng phức gọi
M
là điểm biểu diễn cho số phức
z a bi
(
,ab
,
0ab
),
M
là
điểm biểu diễn cho số phức
z
. Mệnh đề nào sau đây đúng?
A.
M
đối xứng với
M
qua
Oy
. B.
M
đối xứng với
M
qua
Ox
.
C.
M
đối xứng với
M
qua đường thẳng
yx
. D.
M
đối xứng với
M
qua
.
Câu 23. Chohai số phức
1
12zi
,
2
12zi
. Giá trị của biểu thức
22
12
zz
bằng
A.
10
. B.
10
. C.
6
. D.
4
.
Câu 24. Cho số phức
z
thỏa mãn:
2
3 2 2 4i z i i
. Hiệu phần thực và phần ảo của số phức
z
là
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 25. Biết
z a bi
,ab
là số phức thỏa mãn
3 2 2 15 8i z iz i
. Tổng
ab
là
A.
5ab
. B.
1ab
. C.
9ab
. D.
1ab
.
Câu 26. Cho số phức
13
22
zi
. Tìm số phức
2
1w z z
.
A.
23i
. B.
1
. C.
0
. D.
13
22
i
.
Câu 27. Tính môđun của số phức
z
thỏa mãn:
3 . 2024 48 2023 .z z z z i
Trang 3
A.
4z
. B.
2 506z
. C.
17 7z
. D.
3z
.
Câu 28. Cho số phức
z a bi
,ab
thỏa
13
1
12
i
a b i
i
. Giá trị nào dưới đây là môđun của
z
?
A.
5
. B.
1
. C.
10
. D.
5
.
Câu 29. Trong các số phức:
3
1 i
,
4
1 i
,
5
1 i
,
6
1 i
số phức nào là số phức thuần ảo?
A.
3
1 i
. B.
4
1 i
. C.
5
1 i
. D.
6
1 i
.
Câu 30. Cho số phức
,z a bi a b
thỏa mãn
2 5 5zi
và
. 82zz
. Tính giá trị của biểu thức
P a b
.
A.
10
. B.
8
. C.
35
. D.
7
.
Câu 31. Cho số phức
z mi
,
()m
. Tìm phần ảo của số phức
1
z
?
A.
1
m
. B.
1
m
. C.
1
i
m
. D.
1
i
m
.
Câu 32. Tập hợp các điểm biểu diễn cho số phức
z
thỏa mãn
3 4 5zi
là
A.Một đường tròn. B.Một đường thẳng. C.Một đường parabol. D.Một đường Elip.
Câu 33. Trong mặt phẳng phức, gọi
,
,
,
D
lần lượt là các điểm biểu diễn số phức
1
1zi
,
2
12zi
,
3
2zi
,
4
3zi
. Gọi
S
là diện tích tứ giác
ABCD
. Tính
S
.
A.
17
2
S
. B.
19
2
S
. C.
23
2
S
. D.
21
2
S
.
Câu 34. Cho số phức
z
thoả mãn
3 4 5zi
. Biết rằng tập hợp điểm trong mặt phẳng toạ độ biểu diễn các
số phức
z
là một đường tròn. Tìm toạ độ tâm
I
và bán kính
của đường tròn đó.
A.
3; 4I
,
5R
. B.
3;4I
,
5R
. C.
3; 4I
,
5R
. D.
3;4I
,
5R
.
Câu 35. Cho các số phức
z
thỏa mãn
5zi
. Biết rằng tập hợp điểm biểu diễn số phức
1w iz i
là
đường tròn. Tính bán kính của đường tròn đó.
A.
22r
. B.
20r
. C.
4r
. D.
5r
.
Câu 36. Cho số phức thỏa
3z
. Biết rằng tập hợp số phức
w z i
là một đường tròn. Tìm tâm của đường
tròn đó.
A.
0;1I
. B.
0; 1I
. C.
1;0I
. D.
1;0I
.
Câu 37. Có bao nhiêu số phức
z
thỏa mãn
1z z z
?
A.
0
. B.
1
. C.
4
. D.
3
.
Câu 38. Tập hợp các điểm biểu diễn số phức
z
thỏa mãn
2 1 2z z z
trên mặt phẳng tọa độ là một
A. đường thẳng. B. đường tròn. C. parabol. D. hypebol.
Câu 39. Cho số phức
z a bi
,ab
thỏa mãn
2 1 0z i z i
và
1z
. Tính
P a b
.
A.
1P 
. B.
5P 
. C.
3P
. D.
7P
.
Câu 40. Tổng các nghiệm phức của phương trình
32
20zz
là
A.
1
. B.
1
. C.
1 i
. D.
1 i
.
Trang 4
Câu 41. Kí hiệu
là nghiệm phức có phần ảo âm của phương trình
2
4 16 17 0.zz
Trên mặt phẳng tọa
độ điểm nào dưới đây là điểm biểu diễn số phức
1
3
12
2
w i z i
?
A.
2;1 .M
B.
3; 2 .M
C.
3;2 .M
D.
2;1 .M
Câu 42. Trên mặt phẳng phức tập hợp các số phức
z x yi
thỏa mãn
23z i z i
là đường thẳng có
phương trình
A.
1yx
. B.
1yx
. C.
1yx
. D.
1yx
.
Câu 43. Có bao nhiêu số phức
,z a bi a b
thỏa mãn
13
1
z z i
z i z i



?
A.
0
. B.
1
. C.
2
. D.
4
.
Câu 44. Có bao nhiêu số phức
z
thỏa mãn
1 3 3 2zi
và
2
2zi
là số thuần ảo?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 45. Số phức
z a bi
( với
a
,
b
là số nguyên) thỏa mãn
13iz
là số thực và
2 5 1zi
. Khi đó
ab
là
A.
9
. B.
8
. C.
6
. D.
7
.
Câu 46. Trong tất cả các số phức
z
thỏa mãn điều kiện
13
2
zz
z
, gọi số phức
iz x y
là số phức có
mô-đun nhỏ nhất. Tính
2022 2023 2024S x y
.
A.
2024
. B.
2020
. C.
2023
. D.
2022
Câu 47. Cho số phức
z
thõa mãn
12zi
. Tìm giá trị lớn nhất của biểu thức
22
2 2 3P z i z i
.
A.
18
. B.
38 8 10
. C.
18 2 10
. B.
16 2 10
.
Câu 48. Cho hai số phức
z
,
thỏa mãn
23zw
,
2 3 6zw
và
47zw
. Tính giá trị của biểu thức
..P z w z w
.
A.
14Pi
. B.
28Pi
. C.
14P 
. D.
28P 
.
Câu 49. Cho hai số phức
12
,zz
thoả mãn
12
2, 3zz
. Gọi
M
,
N
là các điểm biểu diễn cho
và
2
iz
.
Biết
30MON 
. Tính
22
12
4S z z
.
A.
52
. B.
33
. C.
47
. D.
5
.
Câu 50. Cho số phức
z
thỏa mãn
11
3
2
z
zi
. Tìm giá trị lớn nhất của biểu thức
2 4 7P z i z i
.
A.
8
. B.
20
. C.
25
. D.
45
.
________________HẾT________________
ÑAÙP AÙN
1
2
3
4
5
6
7
8
9
10
B
A
A
A
D
C
A
A
C
D
11
12
13
14
15
16
17
18
19
20
A
B
D
A
C
C
D
B
D
C
Trang 5
21
22
23
24
25
26
27
28
29
30
D
B
B
D
C
C
A
D
D
B
31
32
33
34
35
36
37
38
39
40
A
A
A
D
D
A
C
C
D
B
41
42
43
44
45
46
47
48
49
50
C
D
B
C
B
B
B
D
C
B
Lôøi giaûi caâu hoûi vaän duïng cao
Câu 43. Có bao nhiêu số phức
,z a b i a b
thỏa mãn
13
1
z z i
z i z i



?
A.
0
. B.
1
. C.
2
. D.
4
.
Hướng dẫn giải:
Ta có:
1
3
z z i
z i z i
22
22
22
22
11
31
a b a b
a b a b
2 1 2 1
6 9 2 1
ab
bb
1
1
a
b
.
Suy ra
1zi
. Vậy có một số phức thỏa mãn.
Choïn
B
Câu 44. Có bao nhiêu số phức
z
thỏa mãn
1 3 3 2zi
và
2
2zi
là số thuần ảo?
A.
1
. B.
2
. C.
3
. D.
4
.
Hướng dẫn giải:
Giả sử
z x yi
,xy
. Ta có:
22
1 3 3 2 1 3 18 1z i x y
.
Xét
2
22
2
2 2 2 2 2
ab
w z i x y i x y x y i


.
Theo giả thiết:
thuần ảo
2
2
2
20
2
xy
xy
xy

.
Trường hợp 1:
2xy
, thay vào
1
ta được:
2
2 0 0 2y y x
1
2z
.
Trường hợp 2:
2xy
, thay vào
1
ta được:
2
15
2 4 8 0
15
y
yy
y


23
3 5 1 5 , 3 5 1 5z i z i
.
Vậy có
3
số phức thỏa mãn yêu cầu bài toán.
Choïn
C
Câu 45. Số phức
z a bi
( với
a
,
b
là số nguyên) thỏa mãn
13iz
là số thực và
2 5 1zi
. Khi đó
ab
là
A.
9
. B.
8
. C.
6
. D.
7
.
Hướng dẫn giải:
Xét số phức
13w i z
13i a bi
33a b b a i
.
Theo giả thiết
là số thực nên
30ba
3ba
1
.
Trang 6
Ta lại có:
2 5 1zi
2 5 1a b i
22
2 5 1ab
2
.
Thế
1
vào
2
ta có:
22
2 5 3 1aa
2
10 34 28 0aa
26
7
(
5
ab
a
loaïi)
.
Vậy
2 6 8ab
.
Choïn
B
Câu 46. Trong tất cả các số phức
z
thỏa mãn điều kiện
13
2
zz
z
, gọi số phức
iz x y
là số phức có
mô-đun nhỏ nhất. Tính
2022 2023 2024S x y
.
A.
2024
. B.
2020
. C.
2023
. D.
2022
Hướng dẫn giải:
Gọi
,z x yi x y
. Theo giả thiết:
22
2
1 3 1 3
2
x yi x yi
x yi x y x
22
2 1 6 9 4 8x y x y x
(1).
Mô-đun của z là:
(1)
2
2 2 2
4 8 2 4 4 2z x y x x x
.
Do vậy
min
2z
; khi đó:
2, 0xy
. Do vậy
2022 2023 2024 2020S x y
.
Choïn
B
Câu 47. Cho số phức
z
thõa mãn
12zi
. Tìm giá trị lớn nhất của biểu thức
22
2 2 3P z i z i
.
A.
18
. B.
38 8 10
. C.
18 2 10
. B.
16 2 10
.
Hướng dẫn giải:
Lưu ý:Giả sử
z
có điểm biểu diễn là M, khi đó:
1)
z a bi MN
với
;N a b
.
2)
z a bi c
(với
0c
) là phương trình đường tròn tâm
;,I a b
bán kính
rc
.
3) Xét tam giác MAB với I là trung điểm AB, ta có:
22
22
2 2 2
0
22
2
22
22
2 2 .
2 2 2
MA MB MI IA MI IB
MI MI IA IB IA IB
AB AB AB
MI MI




4) Bất đẳng thức Cauchy-Schwarz:
Với hai cặp số
; , ;a x b y
, ta có:
2 2 2 2
ax by a b x y
.
Dấu bằng xảy ra khi và chỉ khi
a b a x
x y b y
(điều kiện mẫu khác 0).
Cáchgiải1:Gọi
;M x y
là điểm biểu diễn cho số phức
z
. Gọi
1; 1I
,
2;1A
,
2;3B
lần
lượt là điểm biểu diễn cho các số phức
1 i
;
2 i
;
23i
. Khi đó, ta có:
Trang 7
1 2 1 2 2
M
I
z i z i MI
; nghĩa là
M
thuộc đường tròn
C
có tâm
1; 1I
,
2R
.
Ta có
22
22
2 2 3 2 2 3
MM
AB
P z i z i z i z i
22
MA MB
.(Xem mục Lưu ý).
Gọi
0;2E
là trung điểm của
AB
, ta có:
2
2
2
2
AB
P ME
. (Xem mục Lưu ý).
Ta thấy AB không đổi, do đó
có giá trị lớn nhất khi và chỉ khi
ME
có giá trị lớn nhất.
Nhận thấy :
1 9 10 2IE R
nên nên điểm E nằm ngoài đường tròn
C
.
Ta có:
max
2 10ME IE R
.
Vậy
2
2
2
max
max
2 2 2 10 10 38 8 10
2
AB
P ME
.
Choïn
B
Cáchgiải2: Giả sử
z x yi
(
,xy
).
;M x y
là điểm biểu diễn của
z
.
Từ giả thiết:
12zi
, suy ra
1
MC
có tâm
1
1; 1I
và bán kính
1
2R
.
Khi đó:
22
22
1 2 1 1 4 2 2 2z i x y x y x y
1
.
Ta có:
22
2 2 2 2
2 2 3 2 1 2 3P z i z i x y x y
.
Suy ra
1
22
2 2 8 18 2 2 2 2 8 18 4 12 22 4 1 12 1 38P x y y x y y x y x y
.
Theo bất đẳng thức Cauchy-Schwarz :
2 2 2
2
4
4 1 12 1 4 12 1 1 8 10x y x y






.
8 10 4 1 12 1 8 10 8 10 38 8 10 38.x y P
Do đó
max
38 8 10P 
.
Dấu bằng xảy ra khi và chỉ khi
14
1 12
4 12 22 38 8 10
x
y
xy

.
Choïn
B
(Học sinh có thể giải tìm x, y bằng phương pháp thế hoặc dùng máy tính bỏ túi).
Câu 48. Cho hai số phức
z
,
thỏa mãn
23zw
,
2 3 6zw
và
47zw
. Tính giá trị của biểu thức
..P z w z w
.
A.
14Pi
. B.
28Pi
. C.
14P 
. D.
28P 
.
Hướng dẫn giải:
Ta có:
23zw
2
29zw
2 . 2 9z w z w
2 . 2 9z w z w
. 2 . . 4 . 9
P
z z z w z w w w



22
2 4 9z P w
1
;
2 3 6zw
2
2 3 36zw
2 3 . 2 3 36z w z w
22
4 6 9 36z P w
2
;
47zw
4 . 4 49z w z w
22
4 16 49z P w
3
.
Trang 8
Giải hệ phương trình gồm
1
,
2
,
3
ta có:
2
2
33
28
8
z
P
w

. Vậy
28P 
.
Choïn
D
Câu 49. Cho hai số phức
12
,zz
thoả mãn
12
2, 3zz
. Gọi
M
,
N
là các điểm biểu diễn cho
và
2
iz
.
Biết
30MON 
. Tính
22
12
4S z z
.
A.
52
. B.
33
. C.
47
. D.
5
.
Hướng dẫn giải:
Nhận xét: Từ giả thiết, ta có:
1 2 2
2, . 3OM z ON iz i z
.
Ta có
2
2 2 2
1 2 1 2 1 2 1 2
4 2 2 . 2S z z z iz z iz z iz
Gọi
là điểm biểu diễn của số phức
2
2iz
, suy ra
22
2 2 2 2 3OP iz i z ON
hay N là trung
điểm OP.
Ta có:
1 2 1 2
2 . 2 .z iz z iz OM OP OM OP
. 2 2 .PM OI PM OI
với I là trung điểm MP.
Xét tam giác OMP với
30MOP MON
, áp
dụng định lí Cô-sin, ta có
2 2 0
2 . .cos30MP OM OP OM OP
3
4 12 2.2.2 3. 2
2
MP
.
Tam giác OMP có trung tuyến OI nên
2 2 2
2
77
24
OM OP MP
OI OI
.
Vậy
2 . 2.2. 7 4 7S PM O I
.
Choïn
C
Câu 50. Cho số phức
z
thỏa mãn
11
3
2
z
zi
. Tìm giá trị lớn nhất của biểu thức
2 4 7P z i z i
.
A.
8
. B.
20
. C.
25
. D.
45
.
Hướng dẫn giải:
Gọi
z x yi
với
,xy
;
; , ;M x y M x y
lần lượt là các điểm biểu diễn số phức
,zz
.
Ta có:
11
3
2
z
zi
2 1 3z z i
2 1 3x yi x y i
22
2 2 2 2 2 2
2 1 3 2 4 2 2 6 9x y x y x x y x y y
22
22
4 6 7 0 2 3 20x y x y x y
.
Trang 9
Như vậy, tập hợp điểm
M
là đường tròn
C
tâm
2;3I
và
bán kính
25R
.
2 4 7 2P z i z i OM OA OM OB
với
0; 1A
,
4; 7B
. Suy ra
2P AM BM

.
Vì
M
đối xứng với M qua
Ox
nên ta cần gọi điểm
4;7B
đối xứng với B qua
Ox
, khi đó
M B MB

. Do đó:
2P AM MB

.
Ta lại có
0; 1A
,
4;7B
thuộc đường tròn
C
và
4 5 2AB R

, vì vậy
AB
là đường kính của đường tròn
C
2 2 2
80MA MB AB

.
Do đó:
2 2 2 2
80
2 1 2 20
Cauchy Shwart
MA MB MA MB




.
Dấu
""
xảy ra khi
22
2
4
8
80
MB MA
MA
MB
MA MB


.Vậy
max 20P
.
Choïn
B
| 1/9
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BÀI TẬP SỐ PHỨC CÓ ĐÁP ÁN VÀ LỜI GIẢI
Câu 1. Tính môđun của số phức z  3 4i . A. 3 . B. 5 . C. 7 . D. 7 .
Câu 2. Số phức liên hợp của số phức z i 1 2i có điểm biểu diễn là điểm nào dưới đây?
A. E 2;   1 . B. B  1  ;2.
C. A1; 2 . D. F  2   ;1 .
Câu 3. Điểm A trong hình vẽ bên dưới biểu diễn cho số phức z .
Mệnh đề nào sau đây đúng?
A. Phần thực là 3 , phần ảo là 2 .
B. Phần thực là 3 , phần ảo là 2i . C. Phần thực là 3
 , phần ảo là 2i . D. Phần thực là 3  , phần ảo là 2 .
Câu 4. Cho số phức z 1 2i . Điểm nào dưới đây là điểm biểu diễn của số phức w z iz trên mặt phẳng toạ độ?
A. M 3;3 .
B. Q 3; 2 .
C. N 2;3 . D. P  3  ;3.
Câu 5. Cho hai số phức z  2  3i , z  1 i . Giá trị của biểu thức z  3z là 1 2 1 2 A. 55 . B. 5 . C. 6 . D. 61 .
Câu 6. Gọi z là nghiệm phức có phần ảo dương của phương trình 2
z  2z 10  0 . Tính iz . 0 0
A. iz  3  i . B. iz  3  i 1.
C. iz  3  i .
D. iz  3i 1. 0 0 0 0
Câu 7. Phần thực và phần ảo của số phức liên hợp của số phức z  1 i là:
A. Phần thực là 1, phần ảo là 1.
B. Phần thực là 1, phần ảo là i .
C. Phần thực là 1, phần ảo là i .
D. Phần thực là 1, phần ảo là 1.
Câu 8. Xác định phần ảo của số phức z 18 12i . A. 12 . B.18 . C.12 . D. 12  i .
Câu 9. Điểm biểu diễn của số phức z là M 1; 2 . Tọa độ của điểm biểu diễn cho số phức w z  2z là A. 2; 3  . B. 2;  1 . C.  1  ;6 . D. 2;3 .
Câu 10. Gọi z và z lần lượt là hai nghiệm của phương trình 2
z  4z  5  0 . Giá trị của biểu thức 1 2
P   z  2z .z  4z bằng: 1 2  2 1 A. 10  . B.10 . C. 5  . D. 15  . 2
Câu 11. Cho số phức z  1 i 1 2i . Số phức z có phần ảo là: A. 2 . B. 4 . C. 2  . D. 2i .
Câu 12. Điểm M trong hình bên là điểm biểu diễn cho số phức
A. z  2  2i   5   i.
B. z  1 2i  4  i. C. z  3  i 1. D. z  1  3i.
Câu 13. Cho số phức z 1 2i . Số phức liên hợp của z là Trang 1 A. z  1   2i . B. z  1   2i.
C. z  2  i .
D. z 1 2i .
23i4 i
Câu 14. Tìm tọa độ điểm biểu diễn của số phức z  . 3  2i A.  1  ; 4   . B. 1; 4 . C. 1; 4   . D.  1  ;4 .
Câu 15. Cho số phức z a bi a,b    . Khẳng định nào sau đây sai? A. 2 2
z a b .
B. z a bi . C. 2 z là số thực.
D. z.z là số thực.
Câu 16. Cho hai số phức z  3  i và z  4  i . Tính môđun của số phức 2 z z . 1 2 1 2 A.12 . B.10 . C.13 . D.15 .
Câu 17. Cho số phức z thỏa mãn 1 z1 i  5  i  0. Số phức w 1 z bằng A. 1  3i . B.1 3i . C. 2  3i . D. 2  3i .
Câu 18. Gọi a, b lần lượt là phần thực và phần ảo của số phức z  1 3i 1 2i  3 4i 2  3i.
Giá trị của a b là A. 7 . B. 7  . C. 31. D. 31  .
Câu 19. Cho số phức z  3  2i , z  6  5i . Tìm số phức liên hợp của số phức z  6z  5z 1 2 1 2
A. z  51 40i .
B. z  51 40i .
C. z  48  37i .
D. z  48 37i .
Câu 20. Cho số phức z thỏa mãn 1 2iz  1 2i   2
  i . Mô đun của z bằng A. 2 . B.1. C. 2 . D. 10 .
Câu 21. Số phức z nào sau đây thỏa z  5 và z là số thuần ảo? A. z  5 . B. z  2  3i .
C. z  5i .
D. z   5i .
Câu 22. Trong mặt phẳng phức gọi M là điểm biểu diễn cho số phức z a bi ( a, b   , ab  0 ), M  là
điểm biểu diễn cho số phức z . Mệnh đề nào sau đây đúng?
A. M  đối xứng với M qua Oy .
B. M  đối xứng với M qua Ox .
C. M  đối xứng với M qua đường thẳng y x .
D. M  đối xứng với M qua O . 2 2
Câu 23. Chohai số phức z  1
  2i , z  1
  2i . Giá trị của biểu thức z z bằng 1 2 1 2 A. 10 . B.10 . C. 6  . D. 4 .
Câu 24. Cho số phức z thỏa mãn:   iz    i2 3 2 2
 4  i . Hiệu phần thực và phần ảo của số phức z là A. 3 . B. 2 . C.1. D. 0 .
Câu 25. Biết z a bi a,b    là số phức thỏa mãn 3  2iz  2iz  15  8i . Tổng a b là
A. a b  5.
B. a b  1  .
C. a b  9.
D. a b 1. 1 3
Câu 26. Cho số phức z    i . Tìm số phức 2
w  1 z z . 2 2 1 3 A. 2  3i . B.1. C. 0 . D.   i . 2 2
Câu 27. Tính môđun của số phức z thỏa mãn: 3 .
z z  2024 z z   48  2023 .i Trang 2 A. z  4 .
B. z  2 506 . C. z  17 7 . D. z  3 .  i
Câu 28. Cho số phức z a bi a, b    thỏa a  b   1 3 1 i
. Giá trị nào dưới đây là môđun của z ? 1 2i A. 5 . B.1. C. 10 . D. 5 .
Câu 29. Trong các số phức:   3 1 i ,   4 1 i ,   5 1 i ,   6 1 i
số phức nào là số phức thuần ảo? A.   3 1 i . B.   4 1 i . C.   5 1 i . D.   6 1 i .
Câu 30. Cho số phức z a bi a,b    thỏa mãn z  2  5i  5 và .
z z  82 . Tính giá trị của biểu thức
P a b . A.10 . B. 8  . C. 35  . D. 7  . 1
Câu 31. Cho số phức z mi , (m   ) . Tìm phần ảo của số phức ? z 1 1 1 1 A.  . B. . C. i . D. i . m m m m
Câu 32. Tập hợp các điểm biểu diễn cho số phức z thỏa mãn z  3  4i  5 là
A.Một đường tròn.
B.Một đường thẳng.
C.Một đường parabol.
D.Một đường Elip.
Câu 33. Trong mặt phẳng phức, gọi A , B , C , D lần lượt là các điểm biểu diễn số phức z  1   i , 1
z  1 2i , z  2  i , z  3
i . Gọi S là diện tích tứ giác ABCD. Tính S . 2 3 4 17 19 23 21 A. S  . B. S  . C. S  . D. S  . 2 2 2 2
Câu 34. Cho số phức z thoả mãn z  3  4i  5 . Biết rằng tập hợp điểm trong mặt phẳng toạ độ biểu diễn các
số phức z là một đường tròn. Tìm toạ độ tâm I và bán kính R của đường tròn đó. A. I 3; 4  , R  5 . B. I  3  ;4 , R  5 . C. I 3; 4  , R  5. D. I  3  ;4 , R  5.
Câu 35. Cho các số phức z thỏa mãn z i  5 . Biết rằng tập hợp điểm biểu diễn số phức w iz 1i là
đường tròn. Tính bán kính của đường tròn đó. A. r  22 . B. r  20 . C. r  4 . D. r  5 .
Câu 36. Cho số phức thỏa z  3 . Biết rằng tập hợp số phức w z i là một đường tròn. Tìm tâm của đường tròn đó. A. I 0;  1 .
B. I 0;   1 . C. I  1  ;0 .
D. I 1;0 .
Câu 37. Có bao nhiêu số phức z thỏa mãn z z z  1? A. 0 . B.1. C. 4 . D. 3 .
Câu 38. Tập hợp các điểm biểu diễn số phức z thỏa mãn 2 z 1  z z  2 trên mặt phẳng tọa độ là một A. đường thẳng. B. đường tròn. C. parabol. D. hypebol.
Câu 39. Cho số phức z a bi a,b    thỏa mãn z  2  i z 1 i  0 và z  1. Tính P a b . A. P  1  . B. P  5  . C. P  3. D. P  7 .
Câu 40. Tổng các nghiệm phức của phương trình 3 2
z z  2  0 là A.1. B. 1. C.1i . D.1 i . Trang 3
Câu 41. Kí hiệu z là nghiệm phức có phần ảo âm của phương trình 2
4z 16z 17  0. Trên mặt phẳng tọa 1 độ 3
điểm nào dưới đây là điểm biểu diễn số phức w  1 2iz i ? 1 2 A. M  2   ;1 . B. M 3; 2  .
C. M 3; 2. D. M 2  ;1 .
Câu 42. Trên mặt phẳng phức tập hợp các số phức z x yi thỏa mãn z  2  i z  3i là đường thẳng có phương trình
A. y x 1.
B. y  x 1.
C. y  x 1.
D. y x 1. z 1 z  3i
Câu 43. Có bao nhiêu số phức z a bi a, b    thỏa mãn  1 z i z  ? i A. 0 . B.1. C. 2 . D. 4 .
Câu 44. Có bao nhiêu số phức z thỏa mãn z 1 3i  3 2 và  z i2 2 là số thuần ảo? A.1. B. 2 . C. 3 . D. 4 .
Câu 45. Số phức z a bi ( với a , b là số nguyên) thỏa mãn 1 3iz là số thực và z  2  5i 1. Khi đó a b là A. 9 . B. 8 . C. 6 . D. 7 . z z
Câu 46. Trong tất cả các số phức z thỏa mãn điều kiện z 1 
 3 , gọi số phức z x yi là số phức có 2
mô-đun nhỏ nhất. Tính S  2022x  2023y  2024 . A. 2024 . B. 2020  . C. 2023. D. 2022  2 2
Câu 47. Cho số phức z thõa mãn z 1 i  2 . Tìm giá trị lớn nhất của biểu thức P z  2  i z  2  3i . A.18 . B. 38  8 10 . C.18  2 10 . B.16  2 10 .
Câu 48. Cho hai số phức z , w thỏa mãn z  2w  3 , 2z  3w  6 và z  4w  7 . Tính giá trị của biểu thức P  . z w  . z w . A. P  14  i . B. P  28  i . C. P  14  . D. P  28  .
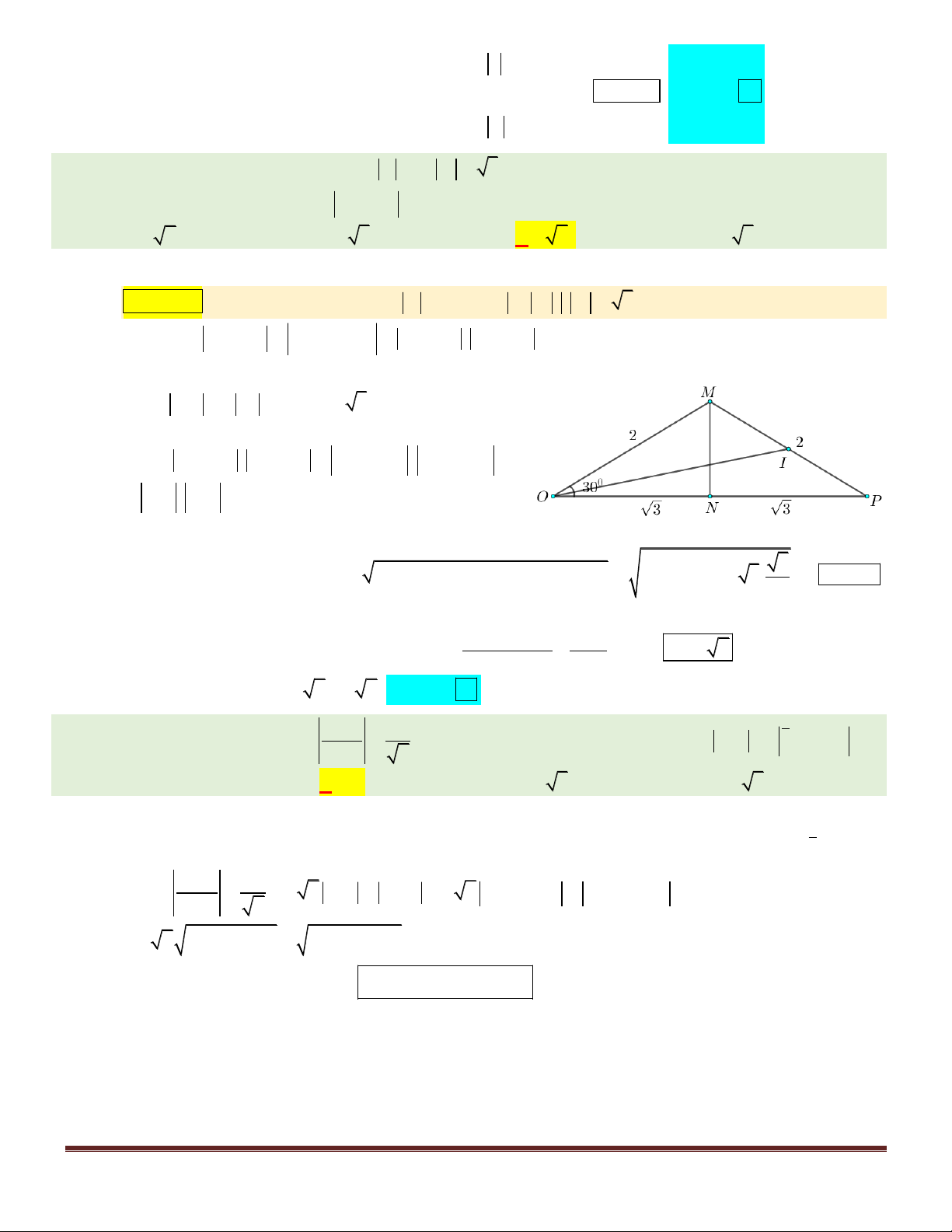
Câu 49. Cho hai số phức z , z thoả mãn z  2, z  3 . Gọi M , N là các điểm biểu diễn cho z và iz . 1 2 1 2 1 2 Biết  MON  30 . Tính 2 2
S z  4z . 1 2 A. 5 2 . B. 3 3 . C. 4 7 . D. 5 . z 1 1
Câu 50. Cho số phức z thỏa mãn 
P z i z   i . z
. Tìm giá trị lớn nhất của biểu thức 2 4 7 3i 2 A. 8 . B. 20 . C. 2 5 . D. 4 5 .
________________HẾT________________ ÑAÙP AÙN 1 2 3 4 5 6 7 8 9 10 B A A A D C A A C D 11 12 13 14 15 16 17 18 19 20 A B D A C C D B D C Trang 4 21 22 23 24 25 26 27 28 29 30 D B B D C C A D D B 31 32 33 34 35 36 37 38 39 40 A A A D D A C C D B 41 42 43 44 45 46 47 48 49 50 C D B C B B B D C B
Lôøi giaûi caâu hoûi vaän duïng cao z 1 z  3i Câu 43.
Có bao nhiêu số phức z a bi a, b    thỏa mãn  1 z i z  ? i A. 0 . B.1. C. 2 . D. 4 . Hướng dẫn giải:  2 2
z 1  z i    a   2 2
1  b a  b   1  2  a 1  2  b 1 a 1 Ta có:        .
z  3i z i  a  
b32  a b 2 2 2 1  6
b  9  2b 1 b  1 Choïn
Suy ra z  1 i . Vậy có một số phức thỏa mãn.   B
Câu 44. Có bao nhiêu số phức z thỏa mãn z 1 3i  3 2 và  z i2 2 là số thuần ảo? A.1. B. 2 . C. 3 . D. 4 . Hướng dẫn giải: 2 2
Giả sử z x yi  ,
x y    . Ta có: z 1 3i  3 2   x  
1   y  3  18   1 . 2 2 2
Xét w   z i  x    y   2 2 2 i  x  
y  2  2xy  2i .      a bx y  2 2
Theo giả thiết: w thuần ảo 2
x   y  2  0   . x     y  2
Trường hợp 1: x y  2 , thay vào   1 ta được: 2
2 y  0  y  0  x  2  z  2 . 1  y 1 5
Trường hợp 2: x   y  2 , thay vào   1 ta được: 2
2 y  4 y  8  0   y 1 5  z  3
  5  1 5 i, z  3
  5  1 5 i . 2   3   Choïn
Vậy có 3 số phức thỏa mãn yêu cầu bài toán.   C
Câu 45. Số phức z a bi ( với a , b là số nguyên) thỏa mãn 1 3iz là số thực và z  2  5i 1. Khi đó a b là A. 9 . B. 8 . C. 6 . D. 7 . Hướng dẫn giải:
Xét số phức w  1 3iz  1 3ia bi  a  3b  b  3ai .
Theo giả thiết w là số thực nên b  3a  0  b  3a   1 . Trang 5 2 2
Ta lại có: z  2  5i  1  a  2  5  bi 1  a  2  5  b  1 2 .
a  2  b  6 2 2 Thế   1 vào 2 ta có:  
a  2  5  3a 1 2
 10a  34a  28  0  7  . a  (loaïi)  5
Vậy a b  2  6  8 . Choïn   B z z
Câu 46. Trong tất cả các số phức z thỏa mãn điều kiện z 1 
 3 , gọi số phức z x yi là số phức có 2
mô-đun nhỏ nhất. Tính S  2022x  2023y  2024 . A. 2024 . B. 2020  . C. 2023. D. 2022  Hướng dẫn giải:
x yi x yi 2 2
Gọi z x yi  ,
x y    . Theo giả thiết: x yi     x   2 1 3
1  y   x  3 2 2 2
2x 1 y  6x  9  y  4x  8 (1). (1) 2 Mô-đun của z là: 2 2 2 z
x y x  4x  8   x  2  4  4  2 . Do vậy z
 2 ; khi đó: x  2
 , y  0 . Do vậy S  2022x  2023 y  2024  2020  . Choïn   B min 2 2
Câu 47. Cho số phức z thõa mãn z 1 i  2 . Tìm giá trị lớn nhất của biểu thức P z  2  i z  2  3i . A.18 . B. 38  8 10 . C.18  2 10 . B.16  2 10 . Hướng dẫn giải:
Lưu ý:Giả sử z có điểm biểu diễn là M, khi đó:
z  a bi  MN 1) với N  ; a b .
2) z  a bi  c (với c  0 ) là phương trình đường tròn tâm I  ;
a b, bán kính r c .
3) Xét tam giác MAB với I là trung điểm AB, ta có:    
MA MB  MI IA2  MI IB2 2 2
     2 2 2
 2MI  2MI IA IB
   IA IB     0  2 2 2  AB   AB AB 2 2  2MI    2MI  .      2   2  2
4) Bất đẳng thức Cauchy-Schwarz: Với hai cặp số  ; a x,  ; b y , ta có:    2 2   2 2 ax by a b x y  .
Dấu bằng xảy ra khi và chỉ khi a b a x
   (điều kiện mẫu khác 0). x y b y
Cáchgiải1:Gọi M  ;
x y là điểm biểu diễn cho số phức z . Gọi I 1;  1 , A 2  ;  1 , B 2;3 lần
lượt là điểm biểu diễn cho các số phức 1i ; 2
 i ; 2  3i . Khi đó, ta có: Trang 6
z 1 i  2  z  1 i  2  MI  2; nghĩa là M thuộc đường tròn C có tâm I 1;  1 , R  2 .  M I 2 2 2 2
Ta có P z  2  i z  2  3i  2 2
z  2  i  z  2  3i  MA MB .(Xem mục Lưu ý).     M M A B 2 AB
Gọi E 0; 2 là trung điểm của AB , ta có: 2 P  2ME
. (Xem mục Lưu ý). 2
Ta thấy AB không đổi, do đó P có giá trị lớn nhất khi và chỉ khi ME có giá trị lớn nhất.
Nhận thấy : IE  1 9  10  2  R nên nên điểm E nằm ngoài đường tròn C . Ta có: ME
IE R  2  10 . max 2 2 2 AB Vậy P  2 ME   2 2  10 1  0 38 8  10 . Choïn   B max  max    2
Cáchgiải2: Giả sử z x yi ( x, y   ). M  ;
x y  là điểm biểu diễn của z .
Từ giả thiết: z 1 i  2 , suy ra M C có tâm I 1; 1 và bán kính R  2 . 1   1  1
Khi đó: z   i   x  2   y  2 2 2 1 2 1 1
 4  x y  2x  2y  2   1 . 2 2 2 2 2 2
Ta có: P z  2  i z  2  3i   x  2   y  
1   x  2   y  3 .   1 Suy ra 2 2
P  2x  2 y  8y 18  22x  2y  2  8y 18  4x 12 y  22  4 x   1 12  y   1  38 .
Theo bất đẳng thức Cauchy-Schwarz :   4 x   1 12  y   1  4   1
 22  x  2 1   y  2 2 1   8 10   .   4   8
 10  4x   1 12  y   1  8 10  8
 10  38  P  8 10  38. Do đó P  38  8 10 . max  x 1 4    Choïn
Dấu bằng xảy ra khi và chỉ khi y 1 12  .   B
4x 12y  22  38 8 10
(Học sinh có thể giải tìm x, y bằng phương pháp thế hoặc dùng máy tính bỏ túi).
Câu 48. Cho hai số phức z , w thỏa mãn z  2w  3 , 2z  3w  6 và z  4w  7 . Tính giá trị của biểu thức P  . z w  . z w . A. P  14  i . B. P  28  i . C. P  14  . D. P  28  . Hướng dẫn giải:
Ta có: z  2w  2
3  z  2w  9   z  2w.z  2w  9  z  2w.z  2w  9    2 2 . z z  2  .
z w z.w      4 .
w w  9  z  2P  4 w  9   1 ;    P 2z  3w  2
6  2z  3w  36  2z  3w.2z  3w  2 2
36  4 z  6P  9 w  36 2 ;
z  4w  7   z  4w.z  4w  2 2
49  z  4P 16 w  49 3 . Trang 7 2  z  33 
Giải hệ phương trình gồm  
1 , 2 , 3 ta có: P  28  . Vậy P  28  . Choïn   D  2  w  8 
Câu 49. Cho hai số phức z , z thoả mãn z  2, z  3 . Gọi M , N là các điểm biểu diễn cho z và iz . 1 2 1 2 1 2 Biết  MON  30 . Tính 2 2
S z  4z . 1 2 A. 5 2 . B. 3 3 . C. 4 7 . D. 5 . Hướng dẫn giải:
Nhận xét: Từ giả thiết, ta có: OM z  2, ON iz i . z  3 . 1 2 2
Ta có S z  4z z  2iz 2 2 2 2
z  2iz . z  2iz 1 2 1 2 1 2 1 2
Gọi P là điểm biểu diễn của số phức 2iz , suy ra 2
OP  2iz  2 iz  2ON  2 3 hay N là trung 2 2 điểm OP.
   
Ta có: z  2iz . z  2iz OM OP . OM OP 1 2 1 2  
PM . 2OI  2PM.OI với I là trung điểm MP.
Xét tam giác OMP với  
MOP MON  30 , áp
dụng định lí Cô-sin, ta có 2 2 0
MP OM OP  3 2OM .O .
P cos 30  4 12  2.2.2 3.  MP  2 2 . 2 2 2 OM OP MP
Tam giác OMP có trung tuyến OI nên 2 OI    7  OI  7 . 2 4 Choïn
Vậy S  2PM .OI  2.2. 7  4 7 .   C z 1 1
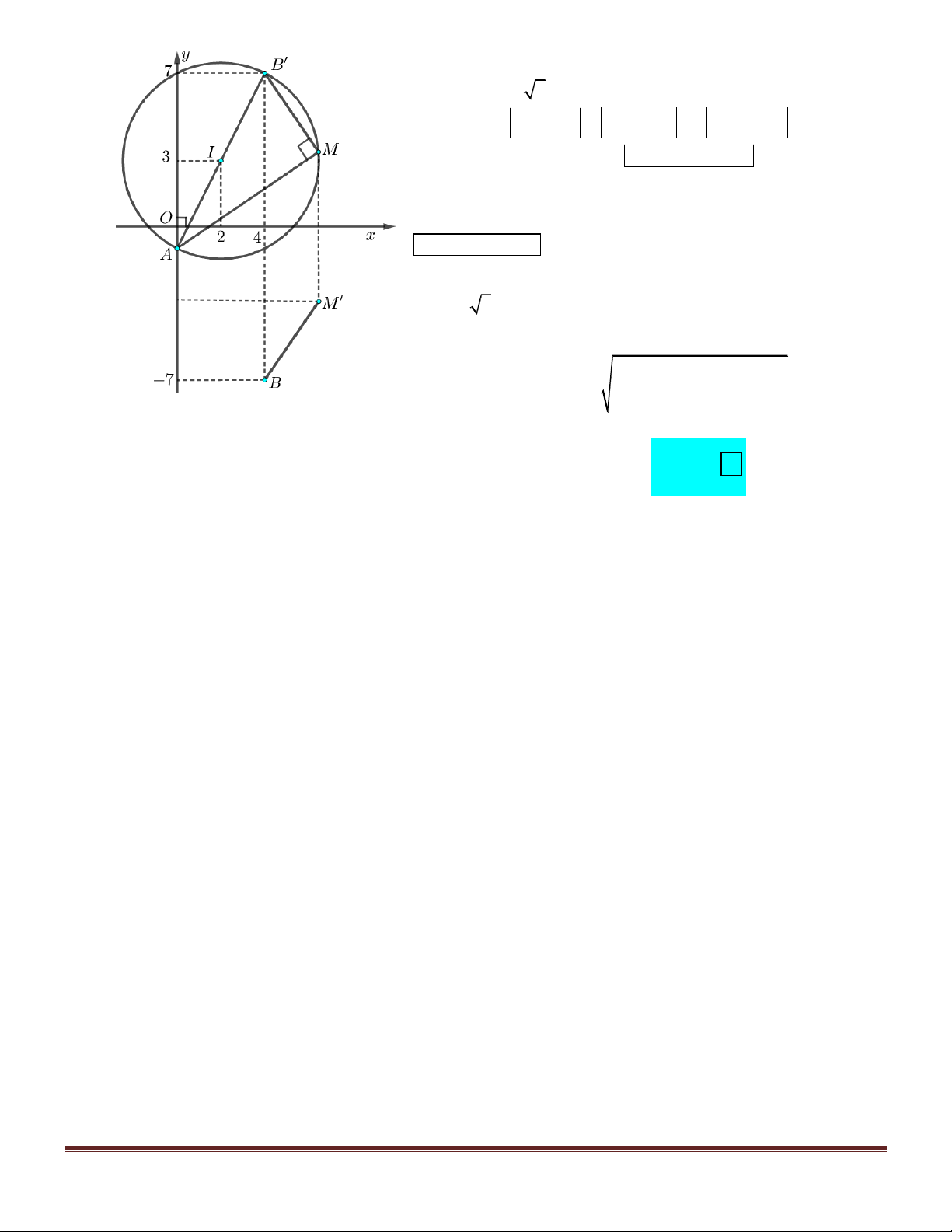
Câu 50. Cho số phức z thỏa mãn 
P z i z   i . z
. Tìm giá trị lớn nhất của biểu thức 2 4 7 3i 2 A. 8 . B. 20 . C. 2 5 . D. 4 5 . Hướng dẫn giải:
Gọi z x yi với x, y   ; M  ;
x y, M  ;
x y lần lượt là các điểm biểu diễn số phức z, z . z 1 1 Ta có: 
 2 z 1  z  3i  2 x  
1  yi x   y  3i z  3i 2 
x  2  y x   y  2 2 2 2 2 2 2 2 1 3
 2x  4x  2  2y x y  6y  9
x y x y    x  2   y  2 2 2 4 6 7 0 2 3  20 . Trang 8
Như vậy, tập hợp điểm M là đường tròn C tâm I 2;3 và bán kính R  2 5 .    
P z i  2 z  4  7i OM OA  2 OM   OB với A0;   1 , B 4; 7
  . Suy ra P AM  2BM .
Vì M  đối xứng với M qua Ox nên ta cần gọi điểm B4;7
đối xứng với B qua Ox , khi đó M B
  MB . Do đó:
P AM  2MB .
Ta lại có A0;  
1 , B4;7 thuộc đường tròn C và
AB  4 5  2R , vì vậy AB là đường kính của đường tròn C 2 2 2
MA MB  AB  80 .  
Do đó: P MA  2MB   2 2 1  2  2 2  MA MB    20 .  80 
  CauchyShwartMB  2MAMA  4 Dấu "  " xảy ra khi    .Vậy max P  20 . Choïn   B 2 2
MA MB  80 MB  8 Trang 9